摘要 传统电场传感器需要标准场或更高准确度等级的传感器进行校准，而基于原子固有能级结构和光谱特征的里德堡原子电场测量可溯源至基本物理常数，量子传感自带校准功能。该文阐述了里德堡原子与外场相互作用的量子相干效应，说明了里德堡原子传感器的电场测量原理，并解析了其自校准性。基于所构建的针对低频电场的里德堡原子传感测量系统，分析了误差来源，定义和计算了各种不确定度分量，得到合成相对标准不确定度为3.885%；保守考虑，在大于或等于95.45%的包含概率下得到扩展不确定度为7.77%。在此过程中，明确了不确定度的主要影响因素并提出了减小其影响的建议。最后给出传感系统实测电磁诱导透明（EIT）光谱频移量与电场强度之间的拟合函数，拟合确定系数达到0.996 9，验证了所构建的低频电场量子测量系统的准确性。
关键词：电场传感器 里德堡原子 自校准性 量值溯源 测量不确定度
电场信号作为电力系统中十分重要的物理量之一，包含了大量智能电网和电气设备的运行信息[1-4]。为了确保电场测量的可靠性，需要对电场传感器进行校准和不确定度评定。传统基于电磁学原理和光学原理的电场传感器校准方法是将其放入一个标定装置产生的数值已知的“标准电场”中[5-6]。目前对于工频及其谐波的标准电场产生方法主要为平行电板法[7]，kHz以上的高频电场则基于IEEE发布的《9 kHz～40 GHz电磁场传感器和探头标定的标准》（IEEE Std 1309—2013）[8]，但要得到标准电场，还需要一个已校准的电场探头。如此循环的结果是电场传感器的校准没有一个绝对标准，电场测量的不确定度来源难以确定，量值传递路径复杂且无法溯源。而基于原子固有能级结构和光谱特征的量子测量，究其电场传感机理就自带校准功能，可以从根本上解决上述问题。
目前大多采用里德堡原子来形成电场量子测量传感器（下文简称“里德堡传感器”）。里德堡原子是一类外层电子具有较大主量子数n、处于高激发态的原子。它具有很大的电偶极矩（～n4）、很高的电极化率（～n7），因此对外场极为敏感[9]。里德堡传感器的核心原子气室如图1所示。将基态碱金属原子蒸气充入真空玻璃气室内，利用激光激发使其跃迁至里德堡态。待测电场作用于里德堡原子时会造成其能级跃迁或移动，从而引起特定的激光光谱变化。提取激光光谱特征量，基于电场特征量与光谱特征量之间内在的数学关系，就可以实现无扰动、无损、精密的电场测量。
图1 原子气室
Fig.1 Vapor cell
基于里德堡传感器能够实现10-8～500 V/cm大范围内的电场强度测量[10-11]，频率可从直流[12-13]、微波MHz[14-15]到GHz[16-18]段，甚至到太赫兹[19]。当施加的电场频率在GHz以上时，易引起里德堡原子共振跃迁，导致原子谱线出现Autler-Townes（AT）分裂现象[20]。AT分裂大小与电场呈线性关系，美国国家标准实验室在利用里德堡原子进行射频电场的测量时发现，若射频电场拉比频率大于两倍的谱线线宽，线性关系的误差可以限制在1%以内[21]。C. L. Holloway等评估了里德堡传感器在1～500 GHz频率范围内电场测量的不确定性[17]，并讨论了这种可溯源至国际单位制（SI）和基本物理常数的里德堡传感器的应用价值[22]。但当电场频率低于GHz时，所具有的能量仅使里德堡原子出现非共振能级移动，体现为激光光谱的Stark频移。现阶段，对基于里德堡传感器的低频电场测量研究偏少，且尚未见对其测量不确定度进行系统和定量分析的报道。文献[23-24]提出了基于里德堡原子测量工频电场的原理和初步方案。文献[25]提出了Stark频移量和电场强度呈一次线性关系，并通过实验数据拟合出对应的函数关系，但该理论模型与文献[26]的实验拟合结果、文献[27-28]理论推导的模型存在差异。
为弥补对于里德堡传感器低频电场测量研究的不足，研究团队构建了对应的传感测量系统并深入探讨了其测量原理，量化分析测量性能参数。本文首先阐述了里德堡原子电场测量原理，通过里德堡原子与外场相互作用的量子相干效应确定了传感系统的自校准性；其次，分析了传感系统的误差来源，针对所构建的系统计算了各种不确定度，进而得到里德堡传感器的合成不确定度和扩展不确定度；最后，基于实验数据采用最小二乘法拟合S态的里德堡原子Stark频移量与外部电场强度的函数关系，并探讨考虑实际测量噪声干扰时二者之间的数学模型。
里德堡原子的低频电场传感的主要原理是电磁诱导透明（Electromagnetically Induced Transparency, EIT）效应和Stark效应。
EIT效应是激光与原子相互作用表现出来的一种非线性量子相干光学效应[29]。具体而言，先通入一束具有特定共振频率的弱探测光，将原子从基态激发到第一激发态，原子吸收光子从而使光谱呈“暗态”；再通入另一频率的强耦合光，将原子进一步激发至里德堡态，同时由于量子干涉相消效应显著地改变了原子的光学吸收特性，在探测光场的共振频率附近形成一个窄的透明窗口。基于EIT效应读取探测光的光谱信号可以直接获得原子内部的变化规律，成为研究里德堡原子与外场相互作用的新方法。与传统的场电离探测方法[30]相比较，EIT光谱可以实现里德堡原子全光学、非破坏性的测量，在量子精密测量方面具有广泛的应用前景[10,20,25,31]。
Stark效应是指里德堡原子与非共振外场发生相干作用时引起原子内部的精细能级分裂，表现为EIT光谱的频率移动。文献[27-28]通过理论推导提出，在出现能级避免交叉之前，电场强度E与Stark频移量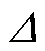
之间的二次关系为
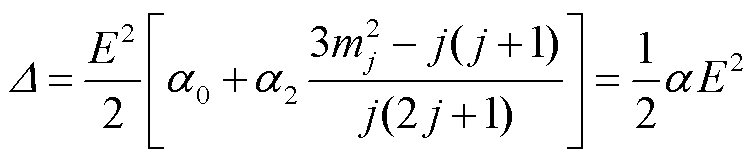（1）
式中，α0和α2分别为里德堡原子的标量和张量极化率；j和mj分别为总角量子数和磁量子数；α为原子极化率。
原子极化率是描述原子能级对外加电场强度响应的物理量，表达式[32]为
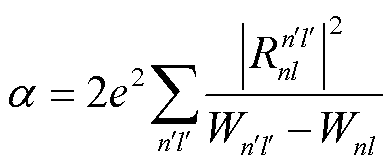（2）
式中，e为元电荷；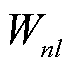
和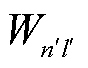
分别为处于|nl〉态和|n'l'〉态的原子能量；
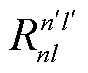=〈nl|r|n'l'〉为偶极跃迁矩阵元。
式（2）中α的误差来源主要为理论计算的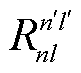
，将在下文关于原子极化率的不确定度研究中具体分析。而分母中原子能态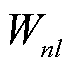、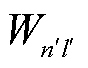在量子力学框架下可通过数值方法精确求解，根据波尔理论，两者之差等于频率为ν的光子吸收或辐射出的能量，即
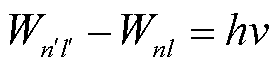（3）
式中，h为普朗克常量，h=6.626070150(69)×10-34 J·s[33]；ν严格等于|nl〉→|n'l'〉的跃迁频率。
结合式（1）～式（3）可以看出，里德堡原子对电场强度进行自校准测量的关键在于电场强度的二次方与原子的极化率直接相关，而原子极化率与e、h等基本物理常数相关，即原子极化率取决于自身固有属性，不随外部环境变化。由此可见，通过测量外场作用下里德堡原子Stark效应引起的EIT光谱频移量，便可将电场强度直接溯源至基本物理常数。
里德堡原子传感测量系统示意图如图2所示，装在玻璃气室内的铯原子是里德堡传感器的核心。利用两台可调谐半导体激光器分别产生的探测光（852 nm，500 μW）和耦合光（509 nm，50 mW），通过二向色镜（Dichroic Mirror, DM）相向射入玻璃气室实现里德堡原子制备并产生EIT光谱，如图2左上插图所示。图2右上插图所示为产生EIT的阶梯型三能级结构，锁定共振频率（对应波长852 nm）的探测光使得铯原子从基态|6S1/2(F=4)〉跃迁至第一激发态|6P3/2(F'=5)〉上，并伴随原子的共振吸收。另以509 nm的波长对应中心频率，扫频输入耦合光使铯原子从|6P3/2(F'=5)〉跃迁到里德堡态|nS1/2〉（n=20～60，对应不同耦合光频率）。
图2 里德堡原子传感测量系统示意图
Fig.2 Schematic diagram of the measurement system based on Rydberg atom
光电探测器接收与里德堡传感器作用后的探测光，将光信号转换成电信号并连接到示波器上。通过调节激光器的压电陶瓷旋钮扫描耦合光可在示波器上观察到无多普勒背景的EIT光谱。
玻璃气室为半径为15 mm、长度为50 mm的圆柱形结构。将信号发生器产生的电压信号施加到两块平行极板上产生外场的作用，其中铜板长100 mm、宽80 mm、厚2 mm，极板间距为30 mm，气室放于极板中心位置。外场作用下里德堡传感器由于Stark效应导致EIT光谱产生频移，测量光谱频移量并将其转换为电场强度。
从式（1）推导出的里德堡传感器的数学模型中可以看出，电场强度取决于原子极化率α和EIT光谱频移量Δ。其中，α既可以通过理论计算得到，也可以通过实验得到，这类涉及理论知识、实验技术手段的非统计方法属于B类不确定度，可根据已有的实验和理论数据，选择合适的概率分布和包含区间进行其不确定度分量的评定；Δ则来自于示波器的测量值，这类受原子自身的量子散粒噪声[34]以及环境的影响引入的不确定度属于A类不确定度，可在一定测量条件下对这类量值统计分析，从而进行不确定度分量的评定。
此外，还需要考虑电场不均匀性引入的不确定度，以及外部光路系统等其他因素带来的不确定度，下面对这几个方面带来的总体不确定度进行详细分析。
按照国家标准GB/T 27418—2017《测量不确定度评定与表示》[35]，计算中所采用的不同概率分布对应的包含因子见表1。
表1 概率分布和包含因子
Tab.1 Probability distribution and coverage factor.
概率分布包含因子kp 均匀分布 正态分布根据包含概率p确定
注：例如，p=68.27%时，kp=1；p=95%时，kp=1.96；p=95.45%时，kp=2；p=99%时，kp=2.576。
还需说明的是，具有不同精细能级结构的里德堡原子会在电场作用下产生不同形态的光谱，采用边带简洁的光谱有利于提升频移量Δ的测量准确性，因此本文算例将里德堡态的角量子数和磁量子数选定为S1/2，根据待测电场强度确定主量子数n。
为了精确得到nS1/2态的铯里德堡原子极化率，采用最新研究得到的量子亏损值[36]计算得到nS1/2态及其邻近态的零场能量。根据文献[28]所述方法数值计算得到50S1/2及其邻近态46F5/2,7/2的Stark结构，并共同绘制在图3中。
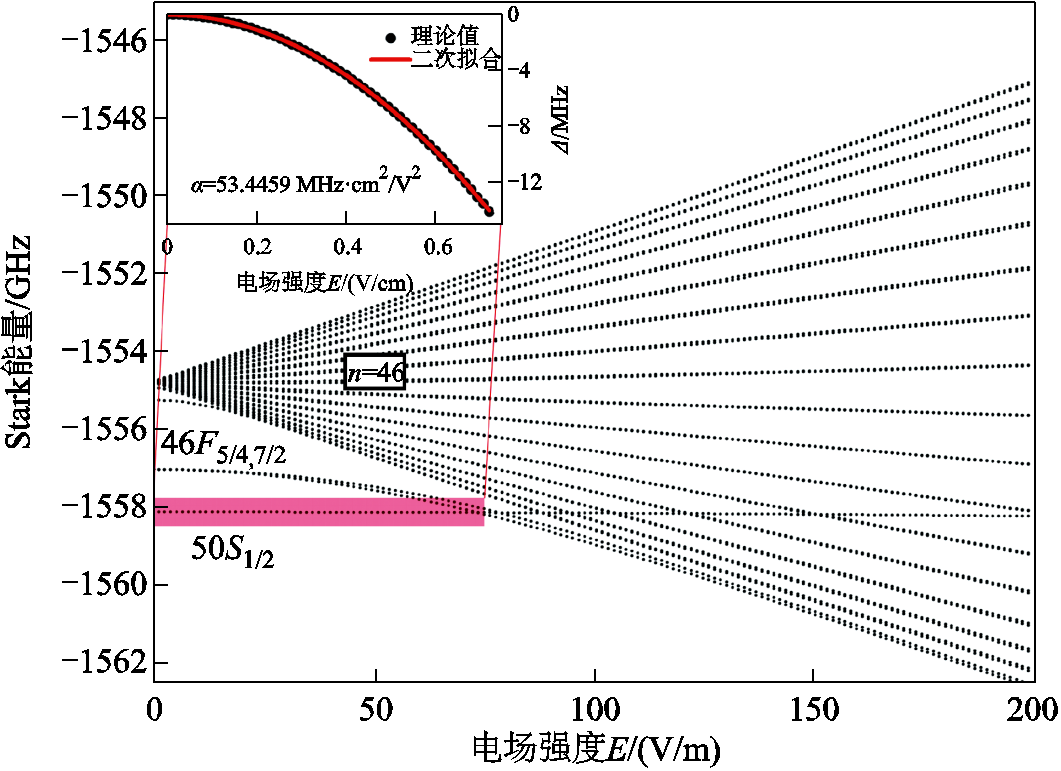
图3 50S1/2态和46F5/2,7/2的Stark结构
Fig.3 The Stark structure diagram of the 50S1/2 state and the 46F5/2,7/2 manifold
从图3中可以看出，50S1/2态在E=75 V/m处与相邻的两个态46F5/2,7/2出现了避免交叉效应。在避免交叉出现之前，即50S1/2态在E=0～75 V/m范围内的Stark能量随电场强度变化趋势如图中红色阴影所示。将这一部分放大，并令E=0时的Stark能量为相对零点，如图3中插图所示，可知频移量Δ与电场强度满足二次方关系。结合式（1），利用最小二乘法拟合理论值得到50S1/2态的极化率α[50S1/2]= 53.445 9 MHz·cm2/V2，拟合确定系数为0.999 9。
对比Dirac-Fock核心极化（Dirac-Fock Core- Polarization, DFCP）方法[37]计算50S1/2态极化率的结果：αDFCP=53.497 2 MHz·cm2/V2，其与本文的计算结果误差为0.096%。美国国家标准局的C. L. Holloway等在对铷原子28S1/2、40S1/2、47S1/2态极化率数值的分析中认为，α的相对标准不确定度能够限制在0.1以内[12]，而在计算α的过程中误差主要来源是偶极跃迁矩阵元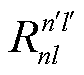
，因此计算值能够控制在1%以内的估计是保守且可靠的。该不确定度服从均匀分布，则里德堡原子极化率α引入的B类标准不确定度为
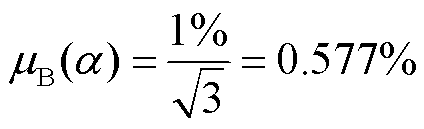（4）
锁定探测光波长为852 nm，耦合光以中心频率（对应波长509 nm）在小范围内扫频输入，产生零场EIT实测光谱如图4a所示。此时EIT光谱包含一个主峰（6S1/2(F=4)→6P3/2(F'=5)→nS1/2形成的EIT光谱）和一个侧峰（6S1/2(F=4)→6P3/2(F'=4)→nS1/2形成的EIT光谱）。主峰脉宽为16 MHz，其与侧峰的间隔等于6P3/2的超精细结构F'=4、F'=5的频率差，理论值为251 MHz[38]。实际上两束激光相向传播引起多普勒频移效应，因此主峰与侧峰的频率间隔应乘以一个多普勒因子λp/λc-1=0.67（λp和λc分别为探测光和耦合光波长），最终主峰与侧峰的频率间隔为168 MHz，对应示波器横轴为16小格，以此可得到频率标尺为10.5 MHz/小格。
图4 有无外场时的EIT光谱
Fig.4 EIT spectra with and without an external field
实验中EIT光谱频移量Δ的不确定度来源主要有两个：一个是环境噪声使EIT光谱的相对位置产生抖动，但由于抖动是随机的，可以通过重复性测量来消除；另一个是外场在导致谱线频移的同时还会伴随着EIT峰值的减小。如图4b所示为实验中外电场强度设置为1.33 V/cm时的EIT光谱，与零场时的EIT峰相比，外场作用下的峰值高度减小了约1/2，这在一定程度上限制了所能测量的最大电场强度。
实验中保持电场强度E=1.33 V/cm不变，对频移量Δ进行10次测量的结果分别为10.5、12.6、10.5、10.5、12.6、10.5、10.5、12.6、10.5、10.5 MHz。测量结果中，12.6 MHz和10.5 MHz的差值2.1 MHz对应示波器0.2小格乘以频率标尺。根据A类评定常用的Bessel公式法估计，此时实验标准偏差（单位为MHz）为
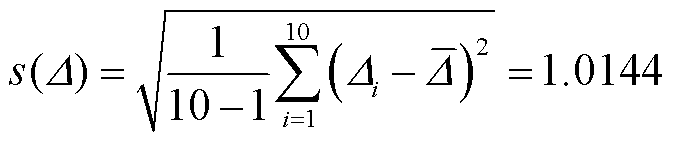（5）
式中，Δi为第i次测量的频移量；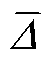
为测量平均值。
因此，Δ测量引入的A类标准不确定度为
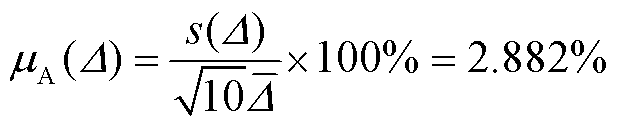（6）
与传统电磁传感器相比，玻璃与铯原子制成的非金属里德堡传感器的优势在于其不会对待测电场造成畸变影响。但由于实验系统中电场加载极板尺寸的限制，极板间的电场强度分布并不均匀。利用COMSOL Multiphysics软件对所加载的电场空间分布进行数值模拟，原子气室与极板的尺寸、材料均与实验装置相同。当模拟电压信号U设置为0.3 V时，空间电场分布仿真结果如图5a所示，其中沿气室中心轴线上的电场分布如图5b所示。原子气室处于图示x=2.5～7.5 cm的范围内。
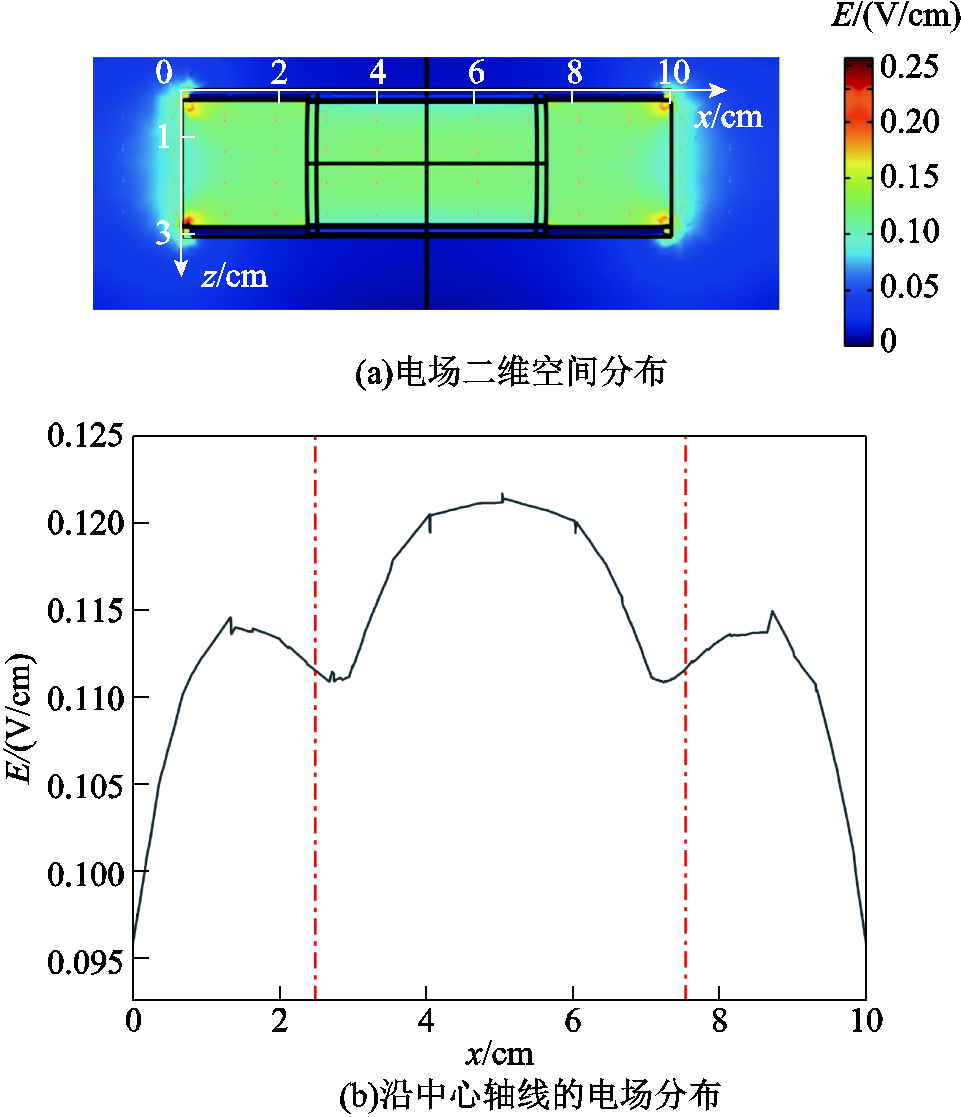
图5 极板间电场分布仿真结果
Fig.5 Simulation results of the electric field distribution between the plates
定义ESimu为仿真所得传感器中心轴线上的平均电场强度；定义ECalc为极板间电压U与间距d的比值；定义电场不均匀度为
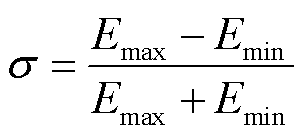（7）
式中，Emax、Emin分别为原子气室内最大、最小电场强度。当U设置范围在0～5 V时，ESimu、ECalc、σ仿真结果见表2。
表2 加载不同电压时各参数仿真结果
Tab.2 Simulation results of various parameters under different voltages loaded
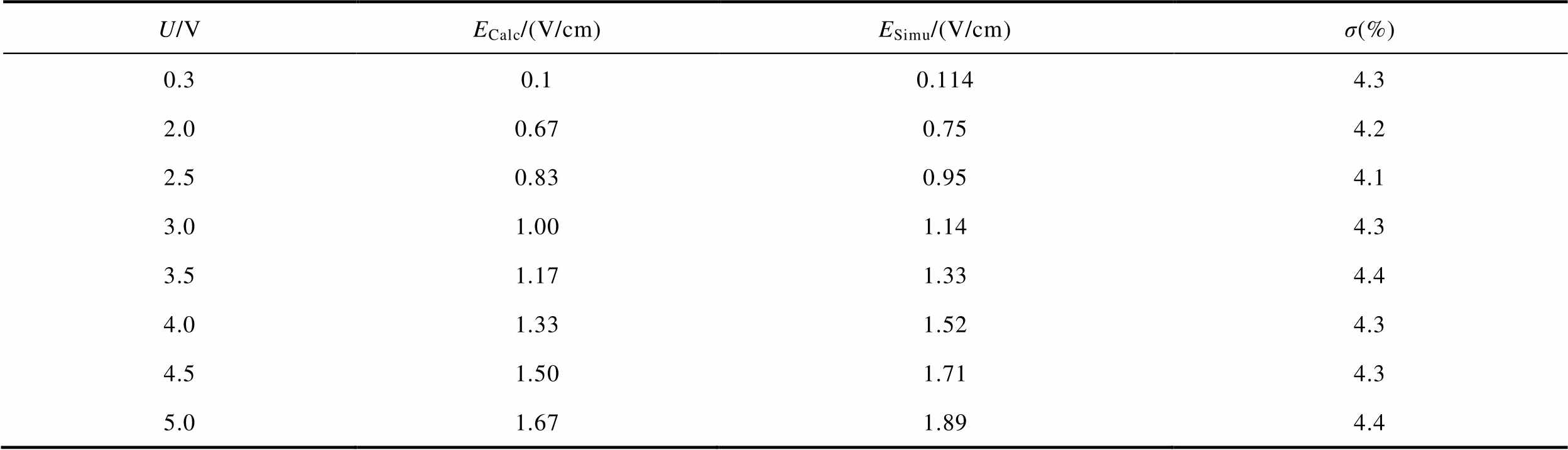
U/VECalc/(V/cm)ESimu/(V/cm)σ(%) 0.30.10.1144.3 2.00.670.754.2 2.50.830.954.1 3.01.001.144.3 3.51.171.334.4 4.01.331.524.3 4.51.501.714.3 5.01.671.894.4
由表2可以看出，在0～5 V的电压范围内，中心轴线上的平均电场强度略高于理论计算电场强度，这是由于玻璃气室具有一定厚度，并不能完全消除对板间电场的干扰。传感器与电场作用区域的电场不均匀度可以控制在4.4%范围内。
此外，考虑玻璃气室厚度对电场不均匀度的影响，首先需考虑玻璃厚度的取值范围。文献[39]提到，为提升气室的透光率将气室玻璃厚度降低至 1 mm；文献[40]提到，考虑抽真空及密封的工艺，气室玻璃不宜过厚。因此，本文取U=0.3 V，气室玻璃厚度τ分别取值1.0、1.2、1.4、1.6、1.8、2.0、2.2、2.4、2.6、2.8、3.0 mm进行电场分布的仿真分析，计算对应的电场不均匀度σ，结果如图6所示。
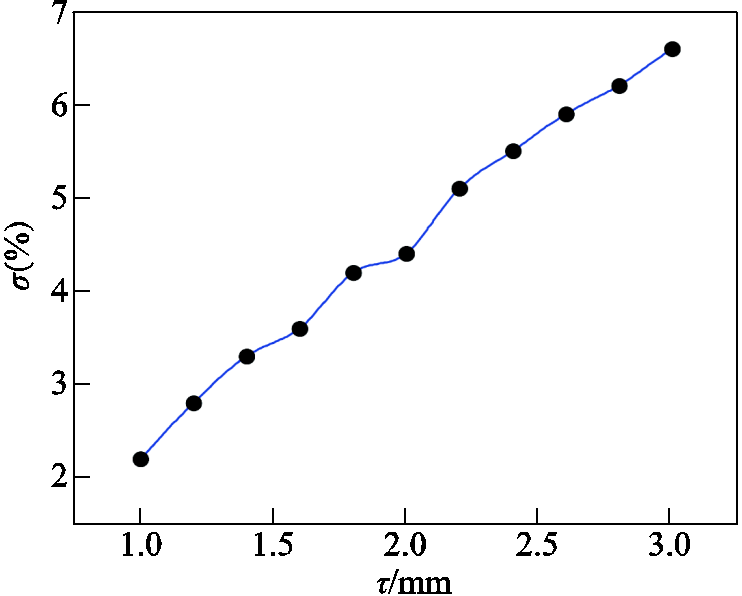
图6 电场不均匀度随玻璃厚度的变化趋势
Fig.6 The variation trend of electric field non-uniformity with glass thickness
由图6可见，σ与τ呈良好的线性关系，又因为τ在1～3 mm内的取值概率是一致的，因此电场不均匀度的分布服从均匀分布，包含因子kp=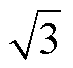
。
综上所述，由电场不均匀性引入的A类标准不确定度为
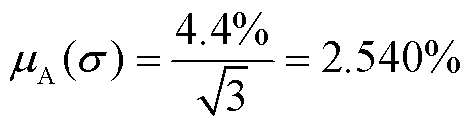（8）
2.4.1 激光器引入的不确定度分量
由于外部环境温度、周围磁场的变化以及机械振动噪声等都会对自由运转的激光器输出波长造成影响，因此外部光路系统中需要搭建合适的稳频系统以提高激光器输出波长的稳定性。
测量系统中使用两台可调谐外腔半导体激光器（External-Cavity Diode Laser, ECDL），其波长分别为852 nm和510 nm，在经过饱和吸收光谱系统稳频后，波长稳定性优于0.01%，输出功率可达1 W，线宽小于1 MHz，其误差服从正态分布。取95%的包含概率，即包含因子取kp=1.96，其B类标准不确定度为
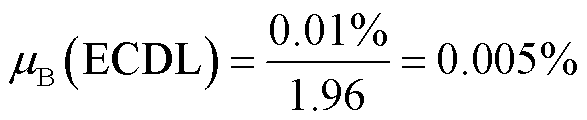（9）
2.4.2 光电探测器引入的不确定度分量
常见的光电探测器包括光电二极管（Photo Diode, PD）、光电倍增管、光电晶体管等多种类型，工作时会受到波长、温度、暗电流、环境光等因素的影响，因此需要结合激光光斑大小、工作波长、实验环境等因素综合考量，选择合适的光电探测器。
测量系统中采用半导体雪崩光电二极管接收852 nm探测光信号，灵敏度波长范围为350～ 1 100 nm，响应时间为0.6 ns，由厂家提供的参数取光谱不确定度为0.1%，按正态分布估计，包含概率p=95%，对应包含因子kp=1.96，其B类标准不确定度为
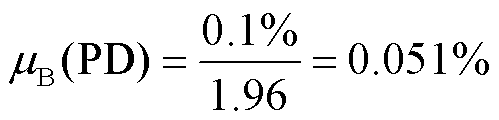（10）
2.4.3 激光光谱标定引入的不确定度分量
采用EIT主峰与侧峰的频率间隔标定坐标时，由于控制激光器扫描频率的压电陶瓷在高速扫频时具有非线性，以及机械振动和热起伏等原因，会导致示波器的时域坐标与光谱频率坐标并非严格的线性关系，从而在标定坐标时引入系统误差。
本实验中频率标尺的间隔为168 MHz，由标尺（ruler）引起的误差一般小于0.01%，按均匀分布估计，包含因子为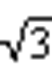
，其B类标准不确定度为
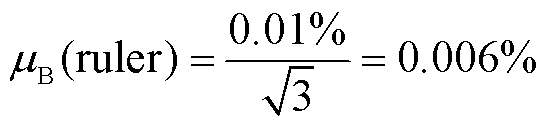（11）
综上所述，由激光器、光电探测器和激光光谱标定引入的不确定度均属于B类不确定度，各分量的合成标准不确定度为
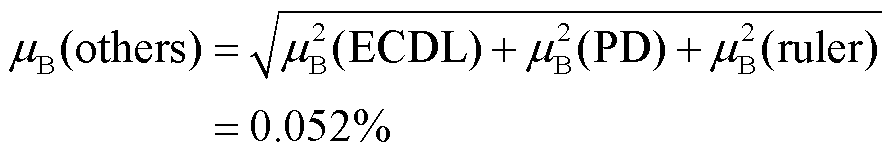（12）
上文详细分析了自校准里德堡传感器不确定度的四个来源：从传感器原理上看，直接影响电场测量精确度的是α和Δ，不确定度分别为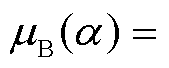
0.577%、
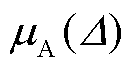=2.882%，可通过更加先进的理论计算方法，以及更精确、灵敏度更高的实验设备来提高校准精度；然后是传感器本身与电场相互作用时带来的误差，仿真结果显示，玻璃制成的传感器对电场强度带来4.4%的电场不均匀度，
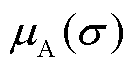=2.540%，后续研究中可进一步优化设计减小对被测电场的扰动；外部光路系统中其他因素的影响对电场测量的影响较小，不确定度仅为
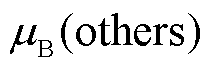=0.052%。假设四个影响因素各不相关，总的合成相对标准不确定度为
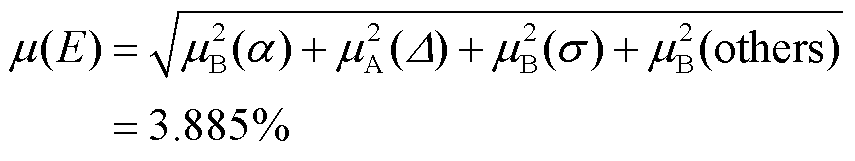（13）
本文对影响里德堡传感器自校准精度的四个不确定度的估值都是保守的，因此，由各分量得到的合成相对标准不确定度也是保守且可靠的。电场测量误差可以按正态分布考虑，当包含概率大于或等于95.45%时，kp=2，得到扩展不确定度εE=kp·μ(E)=7.77%。
为了分析里德堡传感器的线性度，将原子激发至58S1/2态，对应原子极化率为158.64 MHz·cm2/V2。实验中设置了一系列电场强度值，并与2.3节中仿真值相同，尽可能地减小两极板间距，以保证传感器内电场分布均匀。采用重复测试的方式，对每个电场强度下EIT光谱的频移量测量3次取平均值。基于实验所得的频移量Δ-E2数据，利用最小二乘法进行函数拟合，结果如图7所示。
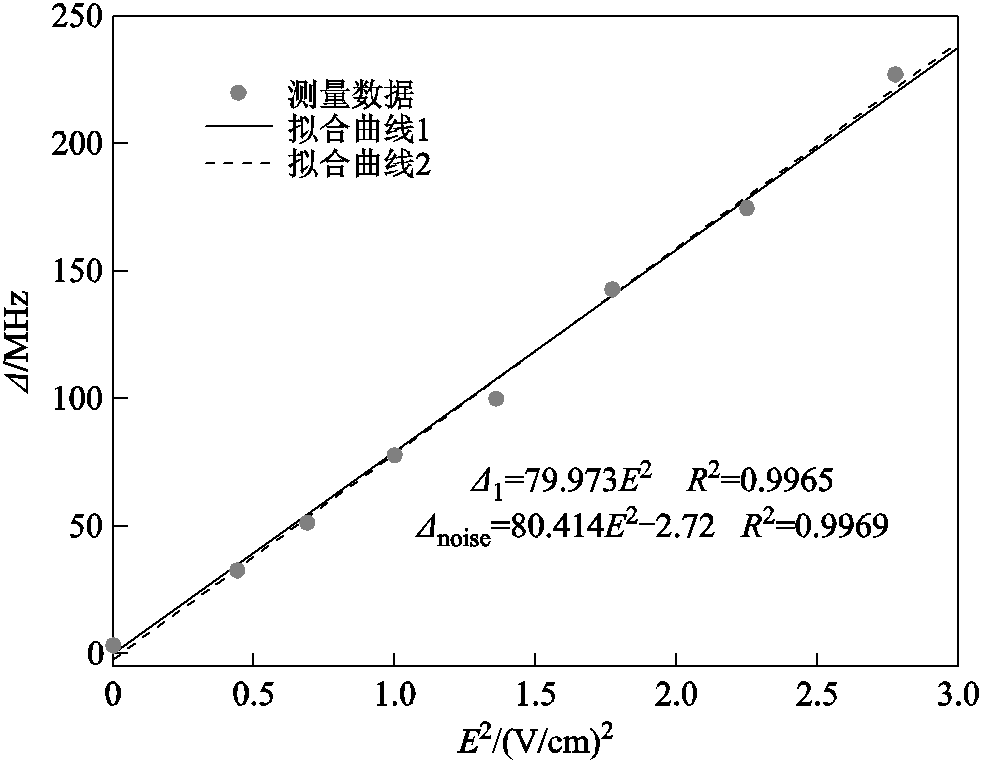
图7 里德堡传感器线性度分析
Fig.7 Analysis of linearity in Rydberg sensors
图7中红色实线是根据式（1）拟合得到，用Δ1表示，拟合函数为
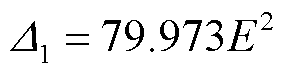（14）
式（14）中对应表征拟合值与测量值相关性的确定系数R2=0.996 5。由此可见，Δ1与E2具有良好的线性关系，与理论分析里德堡传感器自校准原理中所提出的关系（式（1））具有良好的一致性。其中系数79.973的2倍近似等于58S1/2态里德堡原子极化率的理论结果，两者相对误差仅为0.8%。
但由于实验中不可避免地存在外部环境噪声，当E=0时会产生微小的光谱频移量。因此，本文设置含常数项的拟合函数y=ax2+b对测量结果进行拟合，用Δnoise表示，所得结果为
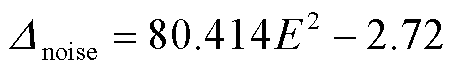（15）
式（15）对应的确定系数R2=0.996 9，其常数项表征Δnoise在零场时含有2.72 MHz的背景噪声光谱。
对比Δ1与Δnoise的确定系数可以发现，考虑实验环境噪声的拟合曲线（图7中虚线）对测量数据的拟合程度更好。对于精密测量来说，这样的模型改进是有必要的。
本文从里德堡原子与外部电场相互作用的原理出发，剖析了里德堡传感器的自校准性，并将电场测量值直接溯源至基本物理常数，突破了传统传感器需要标准场校准才能应用于电场测量的限制，并得到以下结论：
1）从原理上针对影响电场测量精度的两个主要因素α和Δ进行了详细分析，其中α决定了传感器对外部电场的灵敏程度，并取决于原子自身固有属性，50S1/2态下传感器可测电场强度范围为0～75 V/m；Δ与电场强度的二次方线性相关，并通过实验中EIT主峰与侧峰的频率间距标定了Δ。
2）基于本文所设置的传感测量系统，通过理论计算、实验与仿真分析了影响里德堡传感器准确度的因素，得到合成相对标准不确定度为3.885%，在包含概率大于或等于95.45%时，总的扩展不确定度为7.77%。其中传感器自身具有α和Δ的不确定度，可通过更加先进的理论计算方法和更精密的仪器设备来降低。此外还有电场不均匀和其他因素引入的不确定度，可以从电场加载方式和外部光路设计等方面来进行优化，以降低系统总的不确定度。
3）在此基础上，分析了里德堡传感器的线性度，结果表明：传感器拟合曲线与理论分析一致，并在考虑实验环境噪声之后的拟合程度更高，拟合曲线表达式为Δnoise=80.414E2-2.72，拟合确定系数为0.996 9。
参考文献
[1] 王祎凡, 任春光, 张佰富, 等. 基于电压源型PWM整流电路的输电线路测量与感应取电一体化互感器实现方法[J]. 电工技术学报, 2023, 38(1): 15-25.
Wang Yifan, Ren Chunguang, Zhang Baifu, et al. Implementation method of integrated transformer for transmission line measurement and inductive power taking based on voltage source PWM rectifier[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 15-25.
[2] 姜涛, 李雪, 李国庆, 等. 含多端柔性直流的交直流电力系统静态电压稳定域构建方法[J]. 电工技术学报, 2022, 37(7): 1746-1759.
Jiang Tao, Li Xue, Li Guoqing, et al. A predictor-corrector algorithm for forming voltage stability region of hybrid AC/DC power grid with inclusion of VSC-MTDC[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1746-1759.
[3] 高浩予, 任瀚文, 李庆民, 等. 适配光电子学空间电荷测量方法的弹光传感器设计与测试验证[J]. 电工技术学报, 2023, 38(3): 587-598.
Gao Haoyu, Ren Hanwen, Li Qingmin, et al. Design and measurement verification of elasto-optical sensor adapted to space charge measurement method based on optoelectronics[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 587-598.
[4] 雷煜卿, 焦飞, 张树华, 等. MEMS电场传感器测试技术研究及进展[J]. 高压电器, 2022, 58(7): 57-63.
Lei Yuqing, Jiao Fei, Zhang Shuhua, et al. Research and development of MEMS electric field sensor testing technology[J]. High Voltage Apparatus, 2022, 58(7): 57-63.
[5] 吴桂芳, 崔勇, 刘宏, 等. 基于差分进化算法的三维电场传感器解耦标定方法[J]. 电工技术学报, 2021, 36(19): 3993-4001.
Wu Guifang, Cui Yong, Liu Hong, et al. Decoupling calibration method of 3D electric field sensor based on differential evolution algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 3993-4001.
[6] 李振华, 李红斌, 张秋雁, 等. 一种高压电子式电流互感器在线校验系统[J]. 电工技术学报, 2014, 29(7): 229-236.
Li Zhenhua, Li Hongbin, Zhang Qiuyan, et al. An online calibration system for high voltage electronic current transformers[J]. Transactions of China Electrotechnical Society, 2014, 29(7): 229-236.
[7] IEEE Power and Energy Society. Procedures for measurement of power frequency electric and magnetic fields from AC power lines: IEEE 644—2019[S]. IEEE, 2019.
[8] IEEE Electromagnetic Compatibility Society. Calibration of electromagnetic field sensors and probes (excluding antennas) from 9 kHz to 40 GHz: IEEE 1309—2013[S]. IEEE, 2013.
[9] Gallagher T F. Rydberg Atoms[M]. Cambridge: Cambridge University Press, 1994.
[10] Jing Mingyong, Hu Ying, Ma Jie, et al. Atomic superheterodyne receiver based on microwave-dressed Rydberg spectroscopy[J]. Nature Physics, 2020, 16(9): 911-915.
[11] Grimmel J, Mack M, Karlewski F, et al. Measurement and numerical calculation of Rubidium Rydberg Stark spectra[J]. New Journal of Physics, 2015, 17(5): 53005.
[12] Holloway C L, Prajapati N, Sherman J A, et al. Electromagnetically induced transparency based Rydberg-atom sensor for traceable voltage measurements[J]. AVS Quantum Science, 2022, 4(3): 034401.
[13] Ma L, Paradis E, Raithel G. DC electric fields in electrode-free glass vapor cell by photo-illumination [J]. Optics Express, 2020, 28(3): 3676.
[14] 焦月春, 赵建明, 贾锁堂. 基于Rydberg原子的超宽频带射频传感器[J]. 物理学报, 2018, 67(7): 137-145.
Jiao Yuechun, Zhao Jianming, Jia Suotang. Broadband Rydberg atom-based radio-frequency field sensor[J]. Acta Physica Sinica, 2018, 67(7): 137-145.
[15] Liu Bang, Zhang Lihua, Liu Zongkai, et al. Highly sensitive measurement of a megahertz rf electric field with a rydberg-atom sensor[J]. Physical Review Applied, 2022, 18: 014045.
[16] Sedlacek J A, Schwettmann A, Kübler H, et al. Atom-based vector microwave electrometry using rubidium Rydberg atoms in a vapor cell[J]. Physical Review Letters, 2013, 111(6): 063001.
[17] Holloway C L, Gordon J A, Jefferts S, et al. Broadband rydberg atom-based electric-field probe for SI-traceable, self-calibrated measurements[J]. IEEE Transactions on Antennas and Propagation, 2014, 62(12): 6169-6182.
[18] Gordon J A, Holloway C L, Schwarzkopf A, et al. Millimeter wave detection via Autler-Townes splitting in rubidium Rydberg atoms[J]. Applied Physics Letters, 2014, 105(2): 024104
[19] Wade C G, Šibalić N, de Melo N R, et al. Real-time near-field terahertz imaging with atomic optical fluorescence[J]. Nature Photonics, 2017, 11(1): 40-43.
[20] Sedlacek J A, Schwettmann A, Kübler H, et al. Microwave electrometry with Rydberg atoms in a vapour cell using bright atomic resonances[J]. Nature Physics, 2012, 8(11): 819-824.
[21] Holloway C L, Simons M T, Gordon J A, et al. Electric field metrology for SI traceability: systematic measurement uncertainties in electromagnetically induced transparency in atomic vapor[J]. Journal of Applied Physics, 2017, 121(23): 233106.
[22] Holloway C L, Simons M T, Gordon J A, et al. Atom-based RF electric field metrology: from self-calibrated measurements to subwavelength and near-field imaging[J]. IEEE Transactions on Electromagnetic Compatibility, 2017, 59(2): 717-728.
[23] 李伟, 张淳刚, 张好, 等. 基于里德伯原子AC-Stark效应的工频电场测量[J]. 激光与光电子学进展, 2021, 58(17): 144-148.
Li Wei, Zhang Chungang, Zhang Hao, et al. Power-frequency electric field measurement based on AC-stark effect of rydberg atoms[J]. Laser & Optoelectronics Progress, 2021, 58(17): 144-148.
[24] 张淳刚, 李伟, 张好, 等. 基于调制射频场电磁诱导透明光谱的工频电场测量[J]. 光子学报, 2021, 50(6): 162-168.
Zhang Chungang, Li Wei, Zhang Hao, et al. Power frequency electric field measurement based on electromagnetic induced transparent spectrum under radio frequency field[J]. Acta Photonica Sinica, 2021, 50(6): 162-168.
[25] 崔帅威, 彭文鑫, 李松浓, 等. 基于里德堡原子的工频电场测量[J]. 高电压技术, 2023, 49(2): 644-650.
Cui Shuaiwei, Peng Wenxin, Li Songnong, et al. Power frequency electric field measurement based on Rydberg atoms[J]. High Voltage Engineering, 2023, 49(2): 644-650.
[26] Bai Jingxu, Bai Suying, Han Xiaoxuan, et al. Precise measurements of polarizabilities of Cesium nS Rydberg states in an ultra-cold atomic ensemble[J]. New Journal of Physics, 2020, 22(9): 093032.
[27] Khadjavi A, Lurio A, Happer W. Stark effect in the excited states of Rb, Cs, Cd, and Hg[J]. Physical Review, 1968, 167(1): 128-135.
[28] Zimmerman M L, Littman M G, Kash M M, et al. Stark structure of the Rydberg states of alkali-metal atoms [J]. Physical Review A, 1979, 20(6): 2251-2275.
[29] Mohapatra A K, Jackson T R, Adams C S. Coherent optical detection of highly excited Rydberg states using electromagnetically induced transparency[J]. Physical Review Letters, 2007, 98(11): 113003.
[30] Feng Zhigang, Zhang Hao, Che Junling, et al. Collisional loss of cesium Rydberg atoms in a magneto-optical trap[J]. Physical Review A, 2011, 83(4): 042711.
[31] 阎晟, 肖冬萍, 石筑鑫, 等. 原子热运动对电场量子测量的影响及修正方法[J]. 电工技术学报, 2024, 39(10): 2953-2960.
Yan Sheng, Xiao Dongping, Shi Zhuxin, et al. Study on the influence of atomic thermal motion on quantum measurement of electric field and its correction method[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 2953-2960.
[32] Friedrich H. Theoretical Atomic Physics[M]. 4th ed. Cham: Springer, 2017.
[33] Newell D B, Cabiati F, Fischer J, et al. The CODATA 2017 values of h, e, k, and NA for the revision of the SI [J]. Metrologia, 2018, 55(1): L13-L16.
[34] Bussey L W, Burton F A, Bongs K, et al. Quantum shot noise limit in a rydberg RF receiver compared to thermal noise limit in a conventional receiver[J]. IEEE Sensors Letters, 2022, 6(9): 1-4.
[35] 国家质量监督检验检疫总局, 国家标准化管理委员会. 测量不确定度评定与表示: GB/T 27418—2017 [S]. 北京: 中国标准出版社, 2018.
[36] Deiglmayr J, Herburger H, Saßmannshausen H, et al. Precision measurement of the ionization energy of Cs I [J]. Physical Review A, 2016, 93(1): 013424.
[37] Yerokhin V A, Buhmann S Y, Fritzsche S, et al. Electric dipole polarizabilities of Rydberg states of alkali-metal atoms[J]. Physical Review A, 2016, 94(3): 032503.
[38] Steck D A. Cesium D Line Data[DB/OL]. (2019-11-21). http://steck.us/alkalidata.
[39] Mao Ruiqi, Lin Yi, Yang Kai, et al. A high-efficiency fiber-coupled rydberg-atom integrated probe and its imaging applications[J]. IEEE Antennas and Wireless Propagation Letters, 2023, 22(2): 352-356.
[40] 李云超, 党峰, 辛红强, 等. 基于MEMS技术的原子气室封装工艺[J]. 仪表技术与传感器, 2023(2): 22-26.
Li Yunchao, Dang Feng, Xin Hongqiang, et al. Atomic vapor cell packaging technology based on MEMS technology[J]. Instrument Technique and Sensor, 2023(2): 22-26.
Abstract The electric field sensor based on the electromagnetically induced transparency (EIT) effect and the Stark effect of Rydberg atom (Rydberg sensor) has overcome the limitations of traditional sensors that require standard calibration fields and complex traceability chains. It directly traces the electric field value to fundamental physical constants using the inherent energy level structure and spectral features of atoms. Quantum sensing inherently includes calibration capabilities, making it possible to achieve non-invasive, non-destructive, and precise electric field measurements.
Firstly, this article elaborates on the quantum coherent effects of Rydberg atoms interacting with external fields, including the EIT effect and the Stark effect. The EIT effect is a nonlinear quantum coherent optical effect that arises from the interaction of lasers with atoms, resulting in quantum interference between two laser beams and atoms, leading to the formation of a narrow transparent window near the resonant frequency of the detection light field, i.e., the EIT spectral peak. Furthermore, under the influence of low frequency external field, Rydberg atom experience fine-level splitting, causing a frequency shift in the EIT spectrum, known as the Stark frequency shift. By constructing a mathematical model between electric field strength and Stark frequency shift, Rydberg atoms enable all-optical and non-destructive electric field measurements.
Secondly, the Rydberg atom sensing measurement system is constructed in the experiment, using two tunable semiconductor lasers to generate weak probe laser at 852 nm, 500 μW, and strong coupling laser at 509 nm, 50 mW. These lasers propagate in opposite directions into a glass cell to excite atoms to Rydberg states. Based on the EIT effect of Rydberg atoms, the change in the atomic spectra under the influence of the external field is observed. The main peak and sub-peaks form a frequency scale with a strict frequency interval, converting the oscilloscope's horizontal axis into a frequency axis, thus transforming electric field values into optical frequency responses.
Upon establishing the Rydberg sensor measurement system, error sources are analyzed, and various uncertainty components of the sensor are defined and calculated. These mainly include uncertainties introduced by Rydberg atomic polarization, EIT spectral frequency shift, field inhomogeneity, and other factors. By combining the uncertainties of several factors, the combined relative standard uncertainty is 3.885%, and conservatively, the extended uncertainty is 7.77% when the inclusion probability is greater than 95.45%, in this process, the main influencing factors of uncertainty are identified and recommendations for reducing their impact are proposed. In principle, polarizability and EIT spectral frequency shift uncertainties can be reduced through more advanced computational methods and more precise lasers and photodetectors in the future. Additionally, reducing the field inhomogeneity between plates and optimizing the external optical path design can significantly reduce the overall system uncertainty.
Finally, the linearity of the Rydberg sensor is being validated. A series of electric field values is set in the experiment, and a corresponding series of spectral frequency shifts is measured. The least squares method is employed for curve fitting, and the results indicate that the sensor's fitted curve aligns with the theoretical analysis, following a relationship of Δ∝E2. Further consideration of experimental environmental noise yields the fitted relationship: Δnoise=80.414E2-2.72, the constant term represents that Δnoise encompasses a background noise spectrum of 2.72 MHz at zero field, and the coefficient of determination reaches 0.996 9.
keywords：Electric field sensors, Rydberg atoms, self-calibration, traceability of values, measuring uncertainty
中图分类号：TM930
DOI: 10.19595/j.cnki.1000-6753.tces.231167
国家自然科学基金项目（U22B2095）和民用航天技术预先研究项目（D010103）资助。
收稿日期 2023-07-22
改稿日期 2023-09-15
肖冬萍 女，1977年生，副教授，博士生导师，研究方向为电磁测量、量子测量、电磁环境建模与数值计算、电气设备状态监测与故障诊断等。
E-mail：xiaodongping@cqu.edu.cn（通信作者）
石筑鑫 男，1998年生，硕士研究生，研究方向为里德堡原子的量子精密测量。
E-mail：202111131282@cqu.edu.cn
（编辑 李 冰）