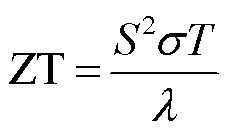 (1)
(1)
摘要 温差发电技术能够实现热能到电能的直接转换,在余热利用、航天器供电和自供电传感器等领域具有广泛应用,其核心之一是用于实现热-电转换的热电材料。热电材料物性参数的表征在热电器件应用、优化设计、故障诊断等研究中有重要意义。目前大多数热电材料物性参数表征方法认为材料的热电参数为常数,忽视了热电参数与温度非线性相关,且没有全面考虑器件中的接触电阻和热阻。该文提出一种基于准稳态法和热电器件测试装置的热电材料变物性参数表征测量方法:首先提出准稳态法对材料物性参数的表征计算方法,通过仿真验证了该方法的正确性;在此基础上,结合热电器件测试装置,采用实验对热电材料进行了变物性参数表征,结果表明,测试结果与厂家参数的最大误差仅为4.3%,能够实现对热电参数的准确表征。该方法实现了在更宽的温度范围内对热电材料物理参数的准确表征,丰富了热电器件测试装置的功能,能够降低材料测试装置的设备投入和测试成本。
关键词:热电材料 变物性参数 稳态法 准稳态法 热电器件测试装置
近年来,随着世界经济和工业生产的发展,能源短缺和环境污染问题日渐突出,加大可再生能源的转化利用及提高现有化石能源综合利用效率成为理想的解决方案,通过前者可逐渐降低未来对传统能源的依赖,而后者成为针对现阶段技术与能源现状更为切实可行的重要举措[1-3]。在化石燃料燃烧过程中,只有不到40%的能量可以得到充分利用,其余的能量以热量的形式流失到环境中,这部分能源的利用将产生巨大的经济和环境效益[4-5]。温差发电技术可以实现热能到电能的直接转换,利用该技术的热电器件具有结构简单、安静、静态运行、免维护和高可靠性的优点[6],为余热利用提供了有力的手段。热电器件中的核心部分是用于实现热-电转换的材料,其性能通过热电优值ZT进行评判。
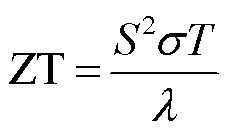 (1)
(1)
式中,T为温度,K;S为塞贝克系数,V/K;σ为电导率,S/m;λ为热导率,W/(m·K)。
表征热电优值的三个参数(S、σ、λ)的值往往是随温度非线性变化的,因此掌握热电材料在不同温度下的热电参数至关重要。一方面,这决定了利用该热电材料的器件的最佳工作温度,有助于常规型、分段型和多层型热电器件的参数与结构设计[7];另一方面,材料非线性参数的引入有助于器件的准确建模和热发电系统设计[8]。以塞贝克系数为例,其随温度变化的非线性引起了热电材料的汤姆逊效应,众多研究表明在高温差和大电流输出情况下汤姆逊效应的影响显著,不可忽略。热导率和电导率的非线性将影响热电器件中温度空间分布及电性能[9-10]。遗憾的是,对于市场上采购的商品化热电器件和材料,很少有厂家直接提供材料的变温度物性参数或提供时需要支付昂贵的测试费,而实验室自制材料也面临着材料的变温度物性参数的测试问题。这给采用大量热电器件进行发电系统设计造成较大的困难,因此对热电材料进行变温区间内物性参数的表征测试具有重要的现实意义。
目前,对于材料变温度物性参数的测量方法,主要有直接测量法和间接测量法两种。直接测量法为直接对材料的S、σ、λ三个值进行测量。对于S和σ的测量,常用的方法为使用日本Quantum Design公司生产的ZEM同时实现测量[11];对于λ的测量,通过λ=DρCp计算得到,其中热扩散系数D需要使用激光导热仪测量,密度ρ需要使用固体密度计测量,定压热容Cp需要使用差示扫描量热仪测量或根据Dulong-Petit定律计算。直接测量法需要多种专业且昂贵的设备,并且对于热导率的测量,若使用Dulong-Petit定律计算恒压热容,需要知道材料的具体成分以计算化合物物质的量和摩尔质量,而商用器件材料配方一般为保密状态,这都造成了直接法表征材料性能的困难。间接测量法为通过将材料组装为热电器件后使用测试装置测试器件的输出性能,根据相关公式,对材料性能进行间接推导计算。近几十年内,研究学者提出了几种不同的表征方法。稳态法[12]是实验操作和理论分析最为简便的方法,通过分别测量不同负载下热电器件冷热端温度稳定时的输出电压、电流以及通过热电器件的热流密度即可获得相应参数,但耗时较长。针对稳态法耗时长的缺陷,S. B. Mahajan 等提出了快速稳态法[13],通过改变外接负载实现开路-短路瞬时切换,因切换时间很短暂,可以认为负载切换前后热状态保持不变,即几乎同时测量了两种负载下热-电信号。快速稳态法大幅提高了实验测量速度,但与稳态法相同,仍不可避免地需要测量难以准确测量的热流。对此,M. G. Revel等提出了一种不需要测热流直接获取热电材料ZT值的方法,但是该方法对不同负载引起的热流波动很敏感。类似地,G. M. Revel在2014年提出“I-V曲线法”[14],以短路电流测量代替温差测量。此外,Harman法利用热电(Thermoelectric, TE)材料的peltier效应,无需测量热流密度,就能对热电器件[15]和薄膜材料[16]进行测量,但其温差受ZT的固有限制而无法在其高低温端产生较大的温度差,温度差一般在5~20 K,不符合实际实验情况。R. Buist对Harman法进行改进,该方法能对塞贝克系数、热导率、电导率进行测量,并且采用双极测试实验消除了焦耳热的影响[17]。然而,上面几种方法均未考虑热电器件中陶瓷基板的热阻以及器件内部的接触阻抗的影响,且认为表征过程中热电参数为常数,均取高低温端温度均值下的物性。实际上,陶瓷基板的热阻和器件内部的接触阻抗的不可逆因素[18-20]及热电参数与温度的非线性[21-24]对热电器件的输出性能影响较大,全面考虑这些因素的影响对热电器件物性参数表征结果的准确性具有重要意义。综上所述,已报道的大多数方法仅可求出温度区间内热电参数的平均值,无法获得变物性参数。热电参数取平均值对于简易电阻模型来说可行,但对于热电器件的准确建模来说是不能满足要求的。此外,多数已报道的方法均忽略了热电臂外界的电热阻影响,其准确性大打折扣。
本文提出了一种基于准稳态法和热电器件测试装置的热电材料变物性参数的表征测量方法,在测量原理的基础上,仿真对比了稳态法和准稳态法的准确性。提出了使用热电器件测试装置对材料参数进行表征的实验方法,并通过实验与厂家测试数据进行了比对。本文方法能够直接使用热电器件测试装置实现对未知材料热电性能变物性参数的表征,丰富了测试装置的功能,减少了热电材料测试的设备投入,降低了测试成本,可推动热电材料应用于器件的设计工作。
热电器件及其工作原理如图1所示,实际应用中热电材料主要为P型半导体和N型半导体材料。将P型和N型热电材料相连形成PN对,即为热电器件的基本组成单元。完整的热电器件由PN对以电串联、热并联的方式组合在一起,以实现足够高的电压和功率输出。对PN对附加陶瓷基板以达到绝缘和导热的目的。工作时,其一端置于高温状态,另外一端处于低温状态,在热激发作用下,高温端载流子浓度比低温端高,在载流子浓度梯度的驱动下,载流子向低温端扩散,从而形成温差电动势,由于P型半导体富集空穴,N型半导体富集电子,载流子极性不同,二者串联时温差电动势叠加,连接负载后能够为负载提供电能[25]。
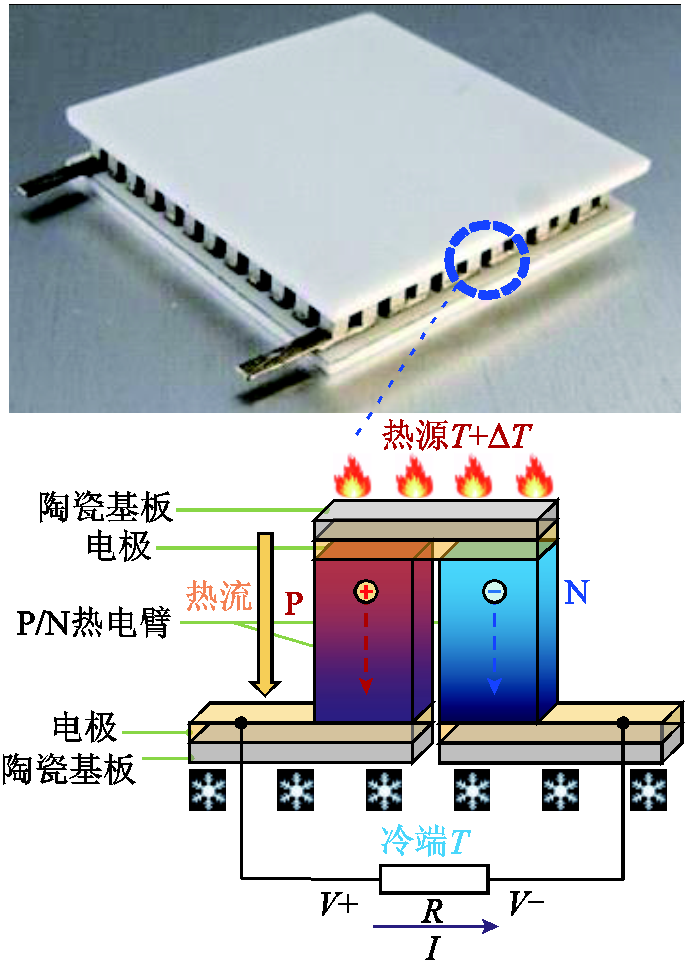
图1 热电器件及其工作原理
Fig.1 Thermoelectric module and working principle
基于以上原理,单一热电臂也能够在给定温差下实现输出,这是使用单臂器件直接表征器件内部单一材料参数的前提。单臂热电器件结构如图2所示。通过引入电极与热电臂之间的接触电阻rcont来代替实际的薄焊层。TH、TL可表示为
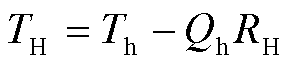 (2)
(2)
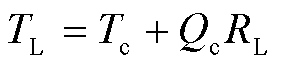 (3)
(3)
式中,下标c、h分别为热电器件冷端、热端;下标L、H分别为热电臂冷端、热端;Th、Tc、Qh和Qc分别为温差发电器件热端温度、冷端温度、热端热流与冷端热流;TH、TL和QH、QL分别为热电臂热端和冷端对应的温度以及热流;RH、RL分别为热电器件的热端热阻和冷端热阻,分别由三部分组成:陶瓷基板的热阻Rs、电极热阻Re和接触热阻Rc,其中Rc为总接触热阻,包括陶瓷基板、电极以及热电臂之间的接触热阻[26]。
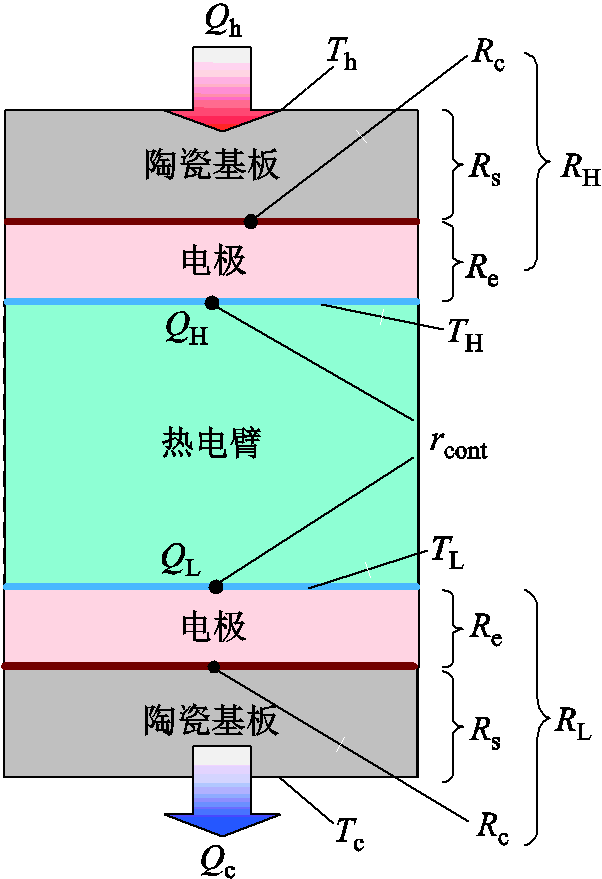
图2 单臂热电器件结构
Fig.2 Structure of single leg thermoelectric module
根据一维传热理论、珀尔贴效应和热电效应,描述热电臂各个量的内部关系如下[27]。
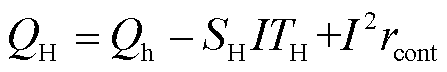 (4)
(4)
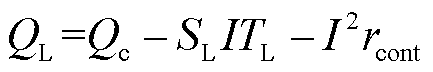 (5)
(5)
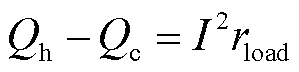 (6)
(6)
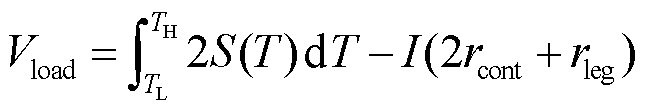 (7)
(7)
式中,rload为外接阻抗,Ω;Vload为输出电压,V;rleg为热电臂的阻抗,Ω;I为热电器件两端的电流,A。
根据上述热电器件的基本原理,其中的材料性能可根据器件在不同温度下的输出和相关公式计算。准稳态法是在稳态法基础上发展而来的,因此本节给出稳态法和准稳态法的原理,并进行材料性能表征的仿真验证和对比。
稳态法[28]是实验操作和理论分析最为简便的方法,根据描述热电器件特性的稳态公式,即式(8)~式(10),可以实现热电材料物性参数的求解。该方法假定在器件冷、热端温度区间内材料常物性,并将平均温度作为所表征材料物性参数对应的温度值。
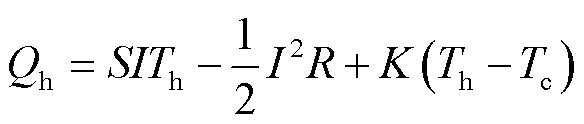 (8)
(8)
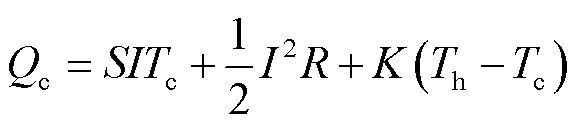 (9)
(9)
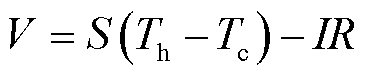 (10)
(10)
式中,K为传热系数,W/K;V为热电器件两端的输出电压,V;R为热电臂内部电阻,Ω。
传统的稳态法未考虑热阻和接触电阻部分,对于单臂热电器件的测试来说,热阻和接触电阻占比可观,可以预见,会造成热电材料参数测试上有较大的误差。为了减小误差,根据测得的热阻和接触电阻参数以及Qh、Th、Qc、Tc值,结合式(2)~(6),可以得到
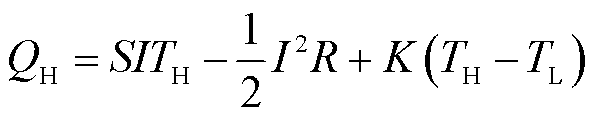 (11)
(11)
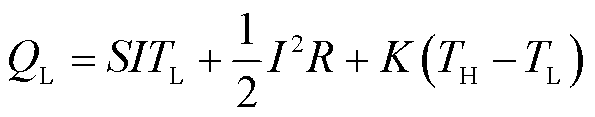 (12)
(12)
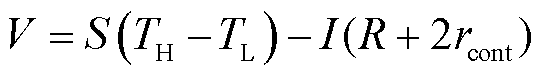 (13)
(13)
在特定的温差条件下,将器件开路进行测试,由式(12)和式(13)可以分别获得塞贝克系数S以及传热系数K,其表达式为
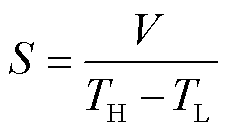 (14)
(14)
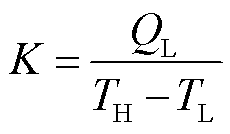 (15)
(15)
随后将器件负载设为短路,重复以上实验过程。在此过程中由于热电器件两端的输出电压为零,此时,由式(13)可以获得给定温差范围情况下热电器件的电阻,其表达式为
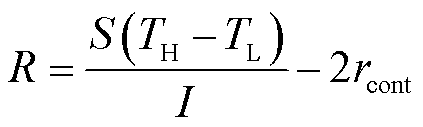 (16)
(16)
为了表征热电材料在不同温度下的性能参数,可根据热电臂的内部温度分布在臂长方向上进行一维离散划分,将热电臂划分为多个等温差连续单元,每个单元所对应的温度区间固定[29]。由于划分的单元较细,温差较小,假设每个单元内的热电性能一致,而不同单元的热电性能随着温度变化,如图3所示。假定单元的总数为N,单元m的长度为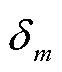 ,其热端与冷端温度分别为Tm和Tm-1,且Tm-Tm-1=ΔT,其对应的热流为
,其热端与冷端温度分别为Tm和Tm-1,且Tm-Tm-1=ΔT,其对应的热流为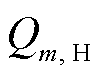 和
和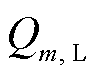 。显然可得,
。显然可得,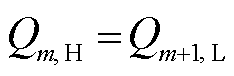 ,
,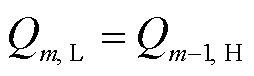 。热电臂内部温度分布微分方程为
。热电臂内部温度分布微分方程为
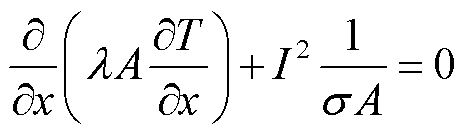 (17)
(17)
式中,A为热电臂的横截面积,m2。
假设单元两端边界条件为x=0,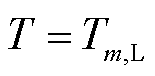 ,
,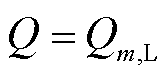 与x=
与x=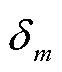 ,
,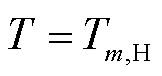 ,
, 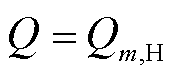 ,通过求解通解公式的二阶微分方程,单元m的热流、温度和长度表达式分别为
,通过求解通解公式的二阶微分方程,单元m的热流、温度和长度表达式分别为
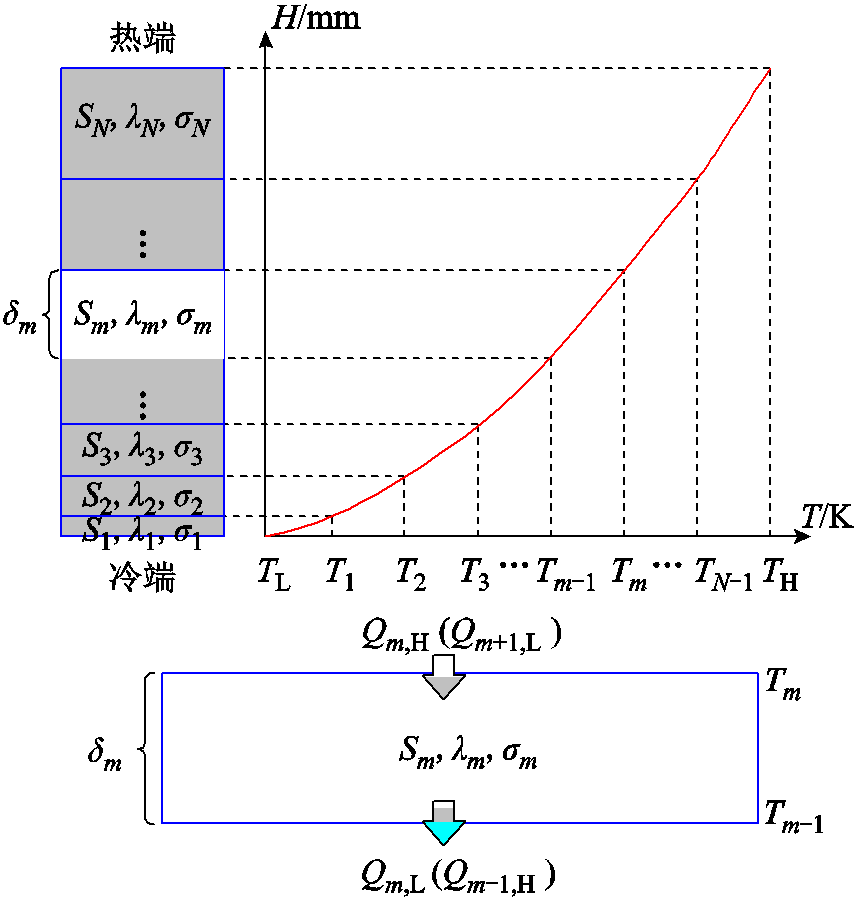
图3 准稳态法热电臂单元划分
Fig.3 Unit division of thermoelectric leg of quasi steady state method
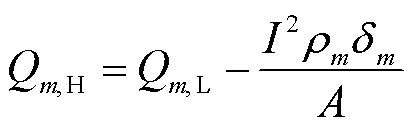 (18)
(18)
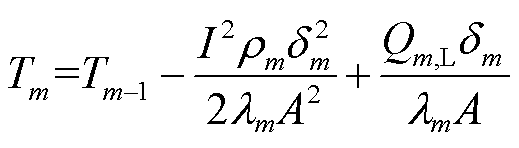 (19)
(19)
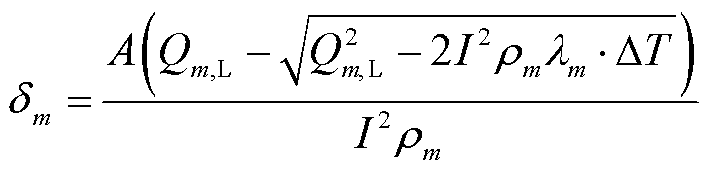 (20)
(20)
由于开路情况下无需考虑焦耳热与珀尔贴热的影响,输入热电器件的热流与输出热电器件的热流相等,因此准稳态法通过开路实验来测量数据以求解单元m的塞贝克系数Sm和热导率λm。由于流过单元m的热流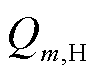 保持不变,两端温度为Tm-1和 Tm的热电臂的塞贝克系数Sm可以根据式(21)确定,热导率可以根据式(22)确定。因此,要获取塞贝克系数Sm和热导率λm首先要求解单元m的电势Vm以及长度
保持不变,两端温度为Tm-1和 Tm的热电臂的塞贝克系数Sm可以根据式(21)确定,热导率可以根据式(22)确定。因此,要获取塞贝克系数Sm和热导率λm首先要求解单元m的电势Vm以及长度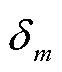 。
。
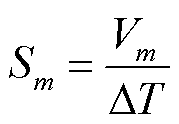 (21)
(21)
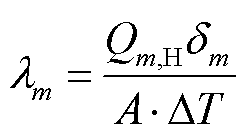 (22)
(22)
同理,基于短路实验测试数据,根据电路与能量理论,电导率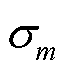 可由式(23)计算。
可由式(23)计算。
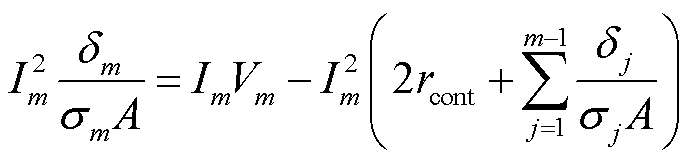 (23)
(23)
式中,Im为热电臂目前的流经电流。
为了验证以上理论的准确性,使用COMSOL Multiphysics软件对单臂热电器件进行仿真,并将根据以上理论的计算结果与厂家参数进行对比。单臂热电器件的物理模型如图4所示,同时给出了温度分布的结果。
采用稳态法、考虑接触电热阻的稳态法、准稳态法仿真计算得到的参数和厂家参数如图5所示。图5a~图5d分别为热导率、塞贝克系数、电导率和ZT值。由于稳态法的计算原理,其对材料性能的表征仅能做到热端温度值的一半,这也是该方法的不足之一;而对于准稳态法来说,由于对材料采用分段表征,能够实现全温度范围的材料性能表征,相较于稳态法具有明显优势。在材料性能表征的准确性方面,由于传统的稳态法未考虑接触参数,结果与厂家参数差异巨大,而考虑接触参数的稳态法和准稳态法与厂家参数接近,但由于稳态法计算的是平均物性参数,相较于准稳态法的变物性参数,与厂家参数的差异较大。以上各参数的误差如图5e所示,相较于热导率和塞贝克系数的误差,电导率的表征误差较大,这也造成了ZT值误差较大。准稳态法在准确性方面相较于其他方法具有较为明显优势。
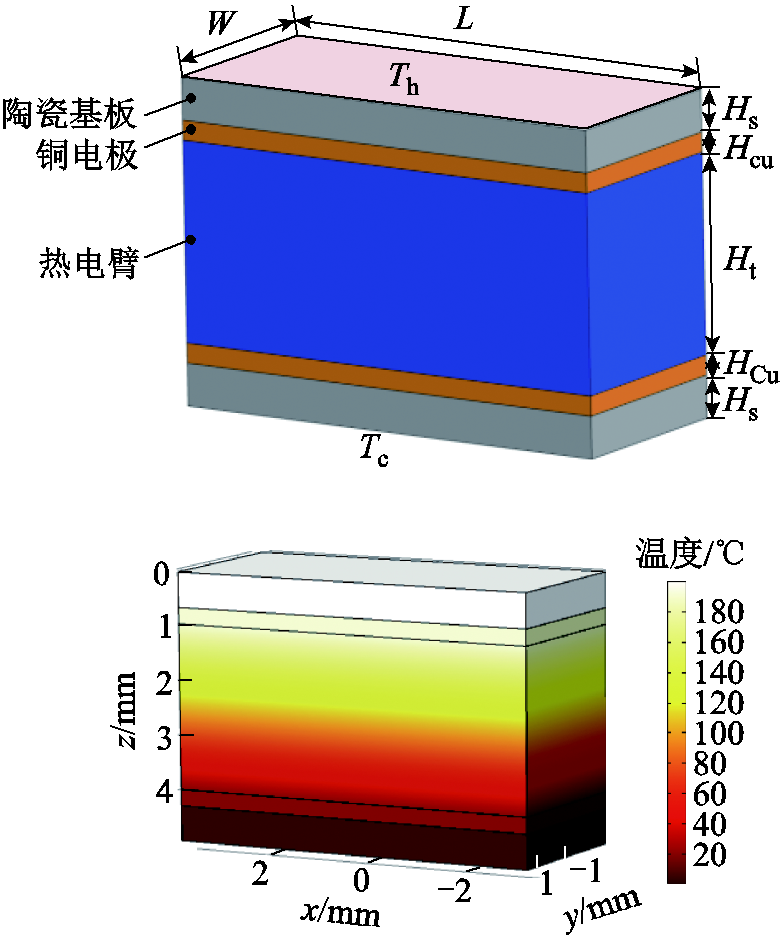
图4 单臂热电器件物理模型
Fig.4 Physical model of single leg thermoelectric module
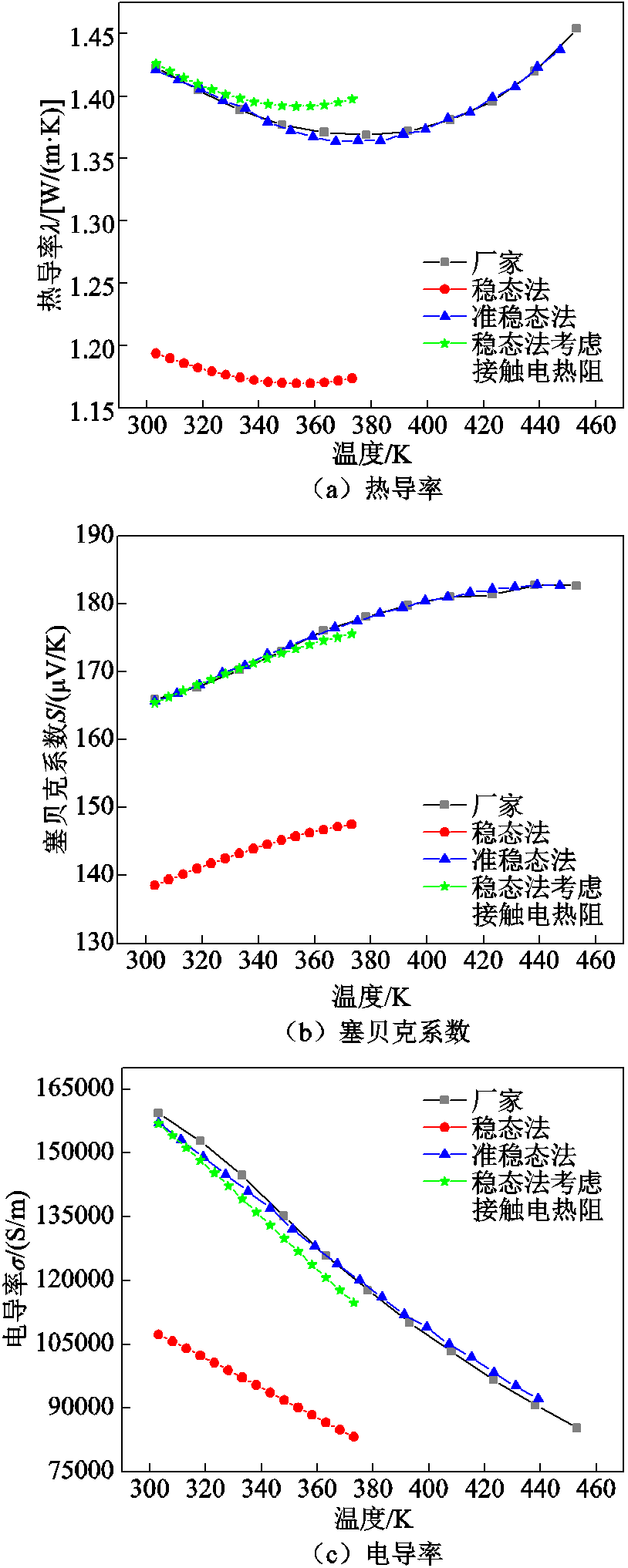
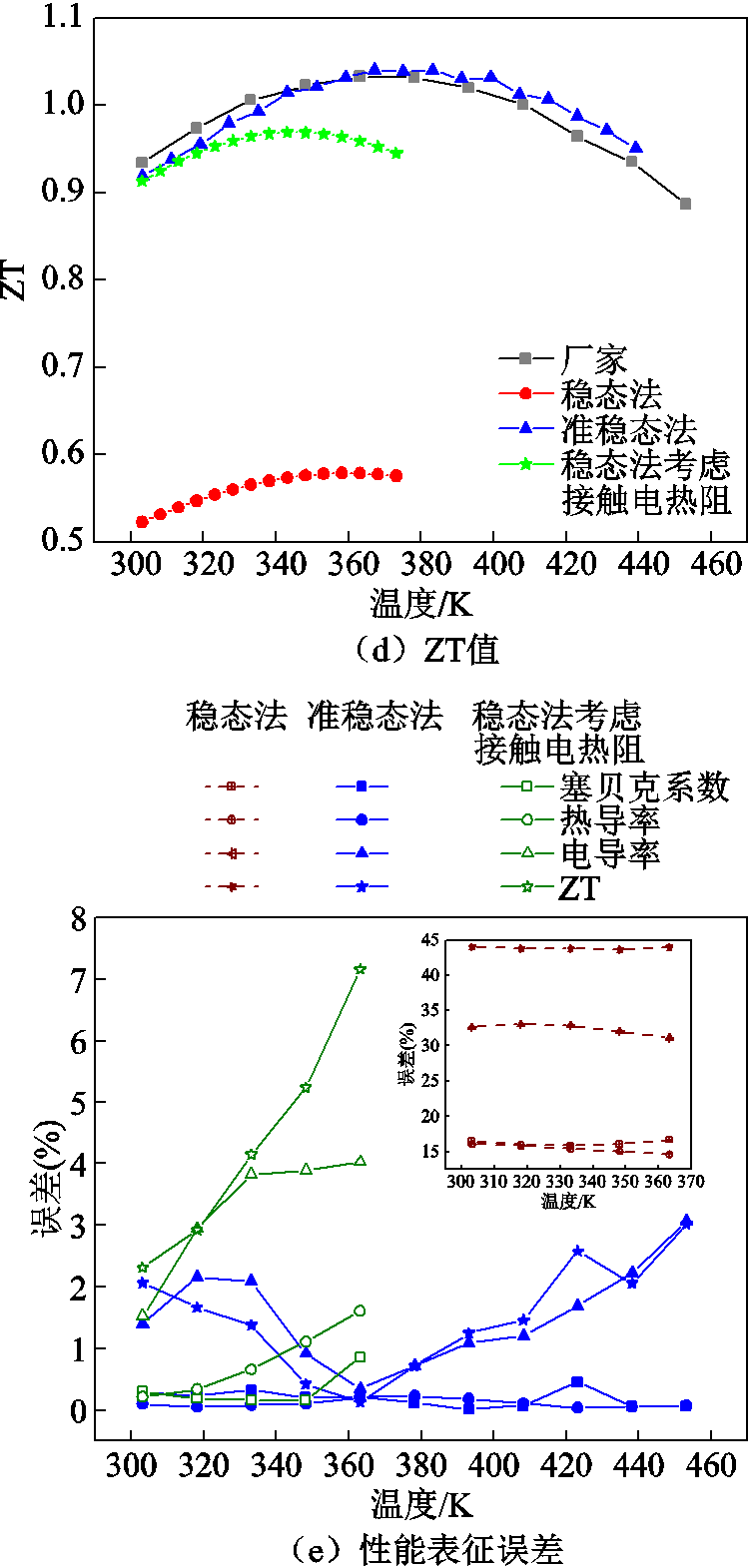
图5 仿真结果
Fig.5 Simulation results
热电材料的性能表征需要结合热电器件测试装置和相关的实验方法获得,由本节具体给出。
热电器件测试装置如图6所示,装置包括真空腔体提供真空环境以消除空气影响;液冷台提供器件冷端低温;热流计测试器件热流,该热流计经过自制的热源进行校准,能够实现对器件冷端热流的准确测量;测试用的单臂热电器件;热源提供热电器件热端温度;压力装置施加器件测试时需要的压力以消除器件外部接触热阻对器件输出性能的影响;电源控制装置提供热源控温供电和测试电流源;信号采集设备采集器件两端的温度信号、热流计温度信号和器件输出的电压电流信号。由于单臂器件内阻极小(mΩ级),目前市售的电子负载设定短路状态仍有几十毫欧的电阻,同时导线及接线端子均有一定的电阻,因此无法做到完全短路状态,将对器件的短路测试准确性产生影响。因此,使用电流源作负载,采用图6中的接线方式,调整电流源输出电流,使器件两端的电压值为0,能够使器件满足短路状态,从而获得短路情况下器件的电流和热流。
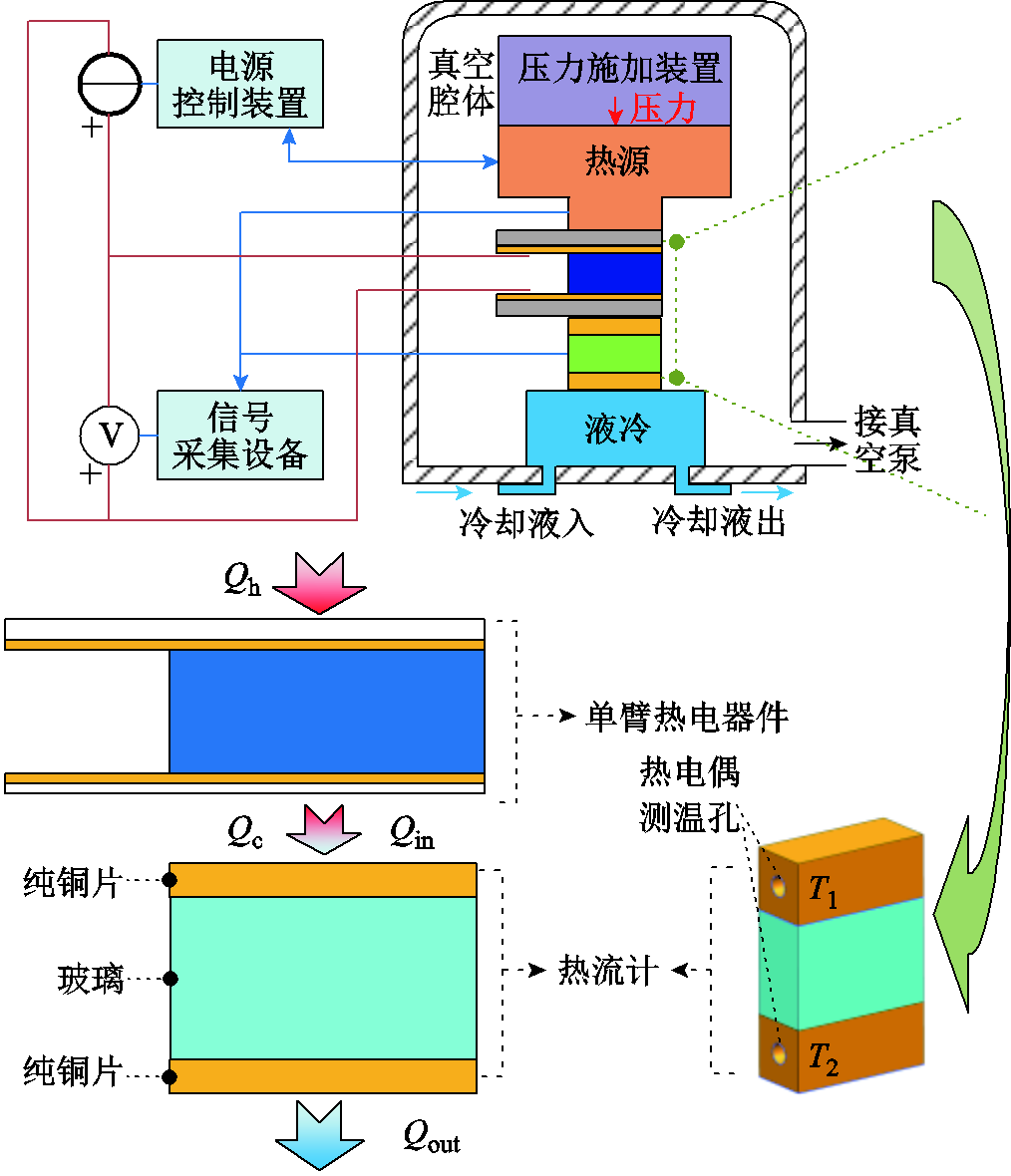
图6 热电器件测试装置
Fig.6 Testing device of thermoelectric module
稳态法测试方法如下:断开直流源,此时为开路情况,保持冷端水冷机温度293.15 K稳定不变,电加热器表面的温度由PID温控仪(LU-962U)控制从303.15 K分段逐渐升温至463.15 K,每段升温10 K。各温差情况下待输出稳定后记录开路电压以及热电器件冷热端的温度,使用热流计测量热电器件冷端的热流密度。在此过程中,通过热电器件的电流I=0,在特定的温差条件下,由式(14)和式(15)可以分别获得塞贝克系数S和传热系数K。随后接通电流源,调整电流值使器件两端电压为0,此时为短路状态,重复以上实验过程,在此过程中由于热电器件两端的输出电压V为0,此时,由式(16)可以获得给定温差范围情况下热电器件的电阻及材料电导率。准稳态法采用与稳态法相同的实验过程,区别之处在于数据处理方式不同,由式(21)~式(23)计算。在物性参数表征计算过程中,温度区间划分的取值ΔT=8 K。
器件的制作过程如图7所示,主要步骤包括在陶瓷覆铜板上均匀涂抹锡膏,将一端覆铜板放入模具,并放置热电臂后压紧,使用回流焊对其进行焊接,焊接完成后得到一侧焊好的器件,如图7e所示,重复上述步骤,焊接热电臂与另一侧陶瓷覆铜板,焊接完成后得到如图7j所示的单臂热电器件。
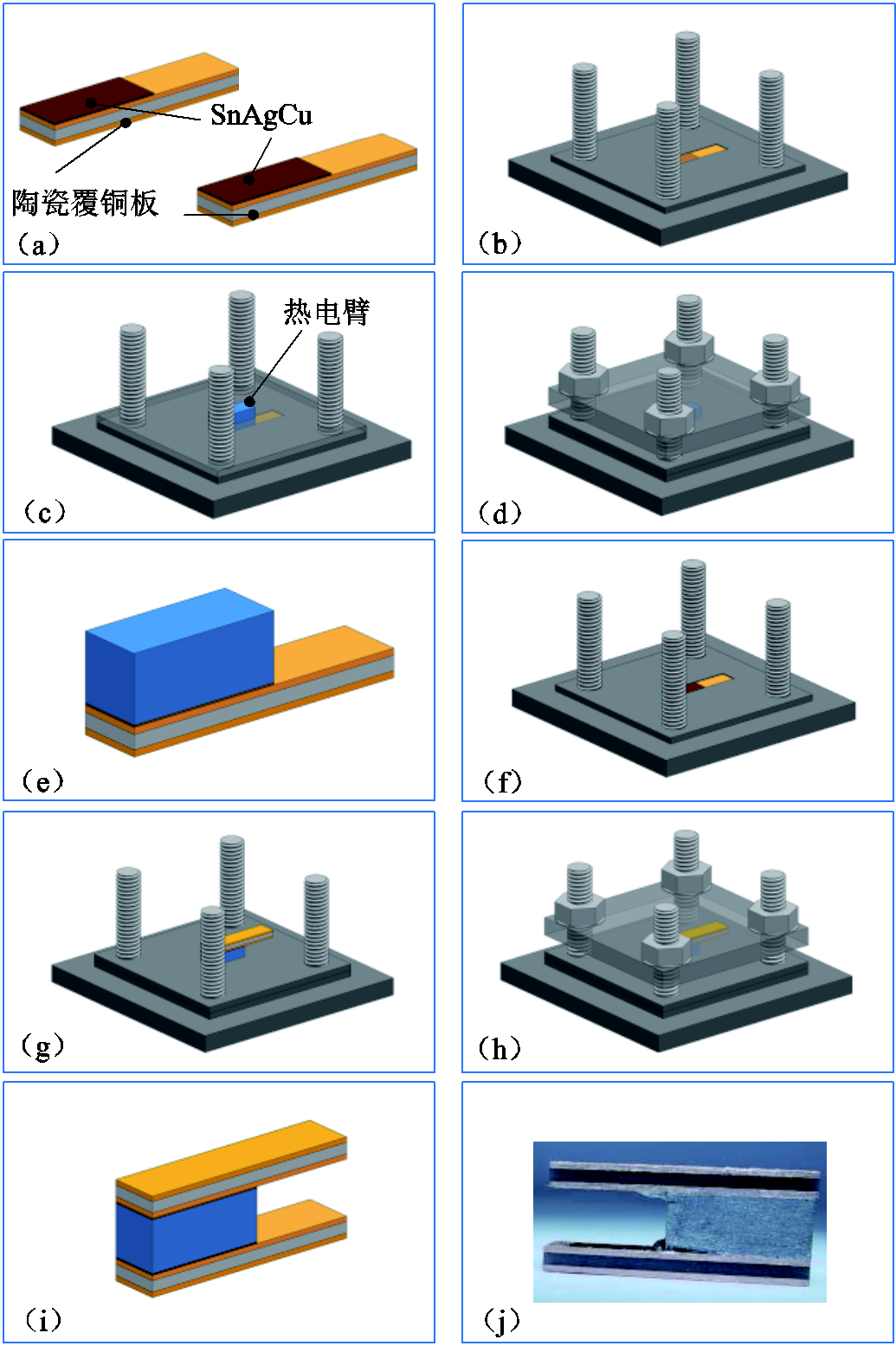
图7 单臂热电器件制作过程
Fig. 7 Manufacturing process of single leg thermoelectric module
基于上述实验装置和热电器件,本节采用实验对准稳态法的理论结果进行验证,并与稳态法进行对比分析。
采用稳态法、考虑接触电热阻的稳态法、准稳态法计算得到的参数和厂家参数如图8所示。图8a~图8d分别为热导率、塞贝克系数、电导率和ZT值。尽管稳态法和准稳态法实验的温度范围一致,根据原理所述,稳态法的表征温度范围不及准稳态法的温度范围大,这与仿真保持了一致性,更宽的温度表征范围也正是准稳态法的优点之一。在材料性能表征的准确性方面,由于传统的稳态法未考虑热阻和接触电阻,结果与厂家参数差异巨大;而考虑接触参数的稳态法和准稳态法与厂家参数接近,但由于稳态法考虑的是平均物性参数,相较于准稳态法的变物性参数,与厂家参数的差异较大。以上各参数的误差如图8e所示。显然,尽管准稳态法在实际应用中较仿真时误差有所增大,最大误差为4.3%,但其相较于其他方法仍具有优势。
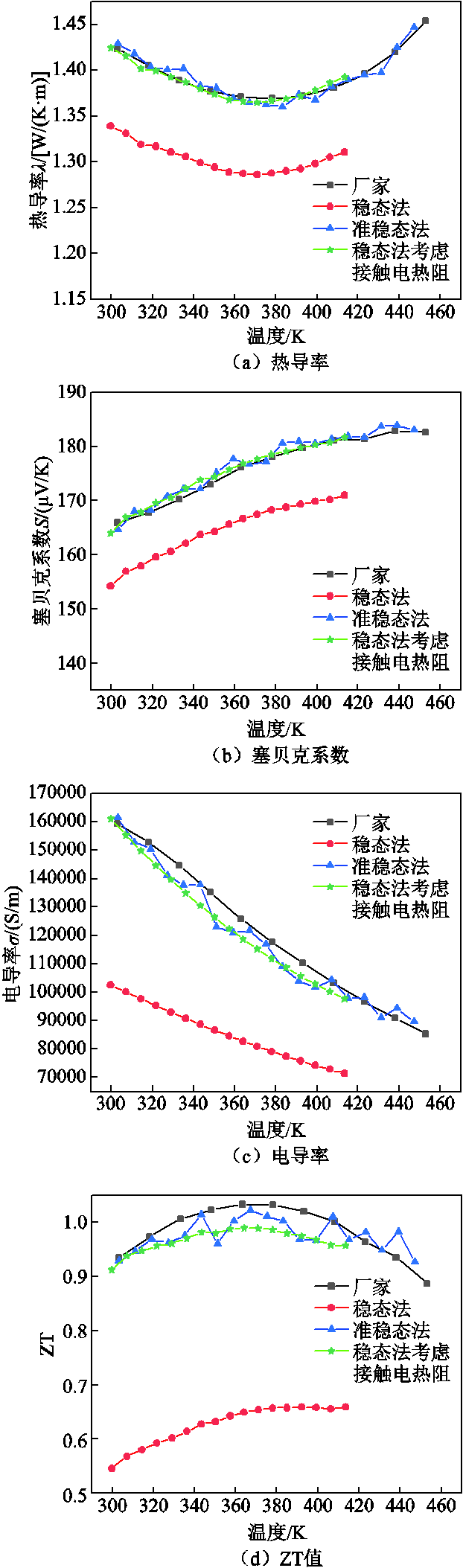
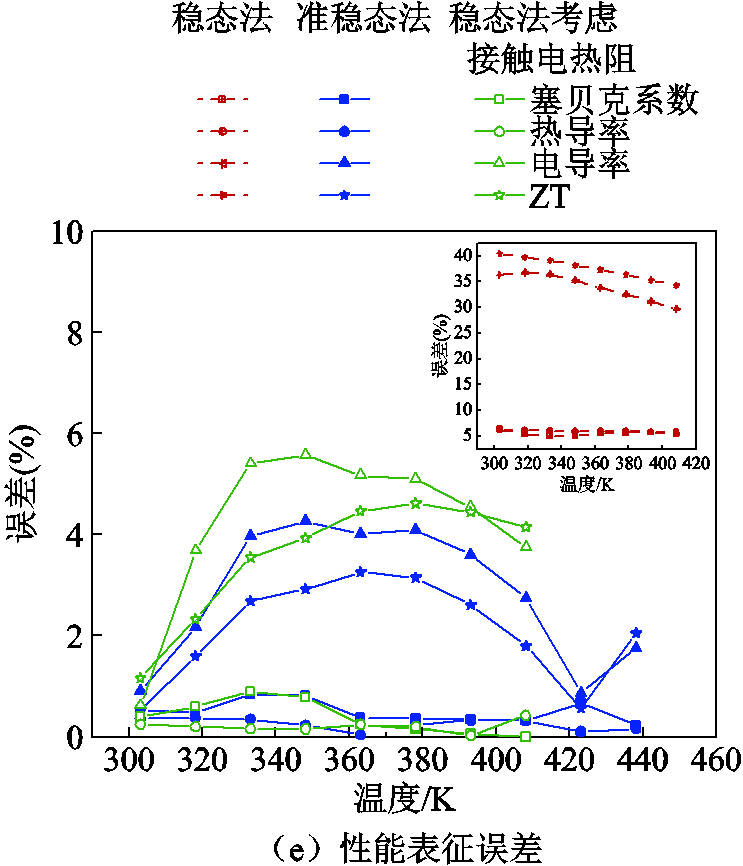
图8 实验结果
Fig.8 Experimental results
本文提出了一种基于准稳态法和热电器件测试装置的热电材料变物性参数的表征测量方法,并与现有的稳态法进行了比较。得到以下结论:
1)器件热阻和接触电阻对物性参数表征结果的准确性影响很大。在不考虑接触电阻和热阻的情况下,稳态法对热电参数的表征误差与实际值有很大差异:不考虑热阻使得材料两端温度与实际值存在差异,造成了塞贝克系数与热导率的测量误差;不考虑接触电阻和不考虑热阻导致的温度偏差共同造成了电导率的测量误差,误差的累积最终使得材料ZT值误差高达40%。而考虑接触电阻和热阻的稳态法和准稳态法对热电参数的表征准确性均有较大提高,误差降低到6%以下。
2)准稳态法具有更好的准确性和更宽的温度表征范围。稳态法获取的结果为材料冷热端平均温度的性能,这使得稳态法在准确性和温度表征范围上存在先天缺陷,特别是当器件冷热端温差较大时,简单地以冷热端温度的平均值来代表这个状态下的参数会导致测量结果误差较大;而准稳态法采用分段计算,能够在对应的小温度区间内获得材料的性能,而不受制于冷端温度,能够更准确地表征材料性能且具有更宽的温度表征范围。
3)基于准稳态法,使用热电器件测试装置能够实现对材料热电性能的表征,而无需采用专用的材料测试装置。相较于传统需要使用多种测试装置才能完成材料性能表征的方法,极大地降低了设备投入,同时使表征更加简单方便。
本文的研究工作丰富了热电材料参数的表征方法和热电器件测试装置的功能,降低了材料测试装置的设备投入和测试成本,且本文方法相较于稳态法结果更为准确并具有更宽的温度表征范围,在一定程度上能够推动温差发电技术的发展。
参考文献
[1] 沈紫嫣, 范武升, 刘方诚, 等. Bi2Te3基可穿戴温差发电器件的制备及性能[J]. 材料科学与工程学报, 2021, 39(2): 181-185.
Shen Ziyan, Fan Wusheng, Liu Fangcheng, et al. Fabrication of Bi2Te3-based wearable thermoelectric generator and its performance[J]. Journal of Materials Science and Engineering, 2021, 39(2): 181-185.
[2] 杨庆新, 张献, 章鹏程. 电动车智慧无线电能传输云网[J]. 电工技术学报, 2023, 38(1): 1-12.
Yang Qingxin, Zhang Xian, Zhang Pengcheng. Intelligent wireless power transmission cloud network for electric vehicles[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 1-12.
[3] 何晨可, 朱继忠, 刘云, 等. 计及碳减排的电动汽车充换储一体站与主动配电网协调规划[J]. 电工技术学报, 2022, 37(1): 92-111.
He Chenke, Zhu Jizhong, Liu Yun, et al. Coordinated planning of electric vehicle charging-swapping- storage integrated station and active distribution network considering carbon reduction[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 92-111.
[4] 崔淑梅, 宋贝贝, 王志远. 电动汽车动态无线供电磁耦合机构研究综述[J]. 电工技术学报, 2022, 37(3): 537-554.
Cui Shumei, Song Beibei, Wang Zhiyuan. Overview of magnetic coupler for electric vehicles dynamic wireless charging[J]. Transactions of China Electro-technical Society, 2022, 37(3): 537-554.
[5] 任志锋, 梁忠鑫, 许聪聪, 等. 热电发电器件能量转换效率测量[J]. 西华大学学报(自然科学版), 2020, 39(5): 1-8.
Ren Zhifeng, Liang Zhongxin, Xu Congcong, et al. Measurement of energy conversion efficiency of thermoelectric devices[J]. Journal of Xihua University (Natural Science Edition), 2020, 39(5): 1-8.
[6] 魏平, 李龙舟, 朱婉婷, 等. 热电转换器件的研究进展与挑战[J]. 中国材料进展, 2022, 41(12): 965-978, 1055.
Wei Ping, Li Longzhou, Zhu Wanting, et al. Development and challenges in thermoelectric conversion devices[J]. Materials China, 2022, 41(12): 965-978, 1055.
[7] He Hailong, Wu Yi, Liu Weiwei, et al. Comprehensive modeling for geometric optimization of a thermoelectricgenerator module[J]. Energy Conversion and Management, 2019, 183: 645-659.
[8] Ma Xiaonan, Shu Gequn, Tian Hua, et al. Performance assessment of engine exhaust-based segmented thermoelectric generators by length ratio optimization [J]. Applied Energy, 2019, 248: 614-625.
[9] Chen Jincan, Yan Zijun, Wu Liqing. The influence of Thomson effect on the maximum power output and maximum efficiency of a thermoelectric generator[J]. Journal of Applied Physics, 1996, 79(11): 8823-8828.
[10] Kaushik S C, Manikandan S. The influence of Thomson effect in the energy and exergy efficiency of an annular thermoelectric generator[J]. Energy Conversion and Management, 2015, 103: 200-207.
[11] QUANTUM量子科学仪器贸易(北京)有限公司. 赛贝克系数/电阻测量系统-ZEM[EB/OL].[2023-05-04]. https:www.qd-china.com/zh/pro/detail/1912041583363.
[12] Rauscher L, Fujimoto S, Kaibe H T, et al. Efficiency determination and general characterization of thermo-electric generators using an absolute measurement of the heat flow[J]. Measurement Science and Technology, 2005, 16(5): 1054-1060.
[13] Mahajan S B, Pierce R D, Stevens R J. Characterizing high temperature thermoelectric modules[C]//ASME 2013 International Mechanical Engineering Congress and Exposition, San Diego, California, USA, 2013: 56284: V06AT07A094.
[14] Revel G M, Arnesano M, Pietroni F. Development and validation of a low-cost infrared measurement system for real-time monitoring of indoor thermal comfort[J]. Measurement Science and Technology, 2014, 25(8): 085101.
[15] Ahiska R, Ahiska G, Ahiska K. Analysis of a new method for measurement of parameters of real thermoelectric module employed in medical cooler for renal hypothermia[J]. Instrumentation Science & Technology, 2009, 37(1): 102-123.
[16] Castillo E E, Borca-Tasciuc T. Development of a scanning transient harman method for thermoelectric properties characterization[C]//Proceedings of ASME 2008 3rd Energy Nanotechnology International Conference Collocated with the Heat Transfer, Fluids Engineering, and Energy Sustainability Conferences, Jacksonville, Florida, USA, 2009: 39-43.
[17] Buist R. Methodology for testing thermoelectric materials and devices[M]//CRC handbook of thermoelectrics. Boca Raton: CRC Press, 1995.
[18] He Hailong, Zhang Yuqian, Niu Chunping, et al. Bonding performance of Ag-Cu brazing solders and half-heusler alloys for high-performance thermoelectric generators[J]. ACS Applied Materials & Interfaces, 2022, 14(36): 41588-41597.
[19] Wang Shixue, Xie Tianxi, Xie Hongxi. Experimental study of the effects of the thermal contact resistance on the performance of thermoelectric generator[J]. Applied Thermal Engineering, 2018, 130: 847-853.
[20] Zhang A B, Wang B L, Pang D D, et al. Influence of leg geometry configuration and contact resistance on the performance of annular thermoelectric generators [J]. Energy Conversion and Management, 2018, 166: 337-342.
[21] Zhang Yuqian, Niu Chunping, He Hailong, et al. First principle study of anisotropic thermoelectric material: Sb2Si2Te6[J]. Journal of Applied Physics, 2021, 130(2): 025102
[22] Ma Baopeng, Ren Hongrui, Zhang Fudong, et al. All cubic-phase δ-TAGS thermoelectrics over the entire mid-temperature range[J]. Small, 2023, 19(17): 2206439.
[23] Yu Ke, Wu Yi, He Hailong, et al. Ultra-low lattice thermal conductivity and enhanced thermoelectric performance in Ag2−xSe1/3S1/3Te1/3 via anion permutation and cation modulation[J]. Journal of Alloys and Compounds, 2021, 885: 161378.
[24] Qing Shaowei, Rezaniakolaei A, Rosendahl L A, et al. An analytical model for performance optimization of thermoelectric generator with temperature dependent materials[J]. IEEE Access, 2018, 6: 60852-60861.
[25] 张维华, 杨逸帆, 赵兵兵, 等. 局部阴影下光热耦合发电系统的温差性能数值分析[J]. 电气技术, 2022, 23(4): 48-54.
Zhang Weihua, Yang Yifan, Zhao Bingbing, et al. Numerical analysis of temperature difference performance of photothermal coupled power generation system under partial shadow[J]. Electrical Engineering, 2022, 23(4): 48-54.
[26] He Hailong, Liu Weiwei, Wu Yi, et al. An approximate and efficient characterization method for temperature-dependent parameters of thermoelectric modules[J]. Energy Conversion and Management, 2019, 180: 584-597.
[27] 喻红涛, 张志丰, 邱清泉, 等. 基于ANSYS的温差发电器性能[J]. 电工技术学报, 2014, 29(7): 253-260.
Yu Hongtao, Zhang Zhifeng, Qiu Qingquan, et al. Performance of thermoelectric generator with ANSYS[J]. Transactions of China Electrotechnical Society, 2014, 29(7): 253-260.
[28] Champier D, Bedecarrats J P, Rivaletto M, et al. Thermoelectric power generation from biomass cook stoves[J]. Energy, 2010, 35(2): 935-942.
[29] He Hailong, Fang Zhenxuan, Niu Chunping, et al. An in-depth study of nonlinear parametric characterization for thermoelectric generator modules[J]. Energy Conversion and Management, 2021, 241: 114314.
Characterization and Measurement Method for Variable Physical Parameters of Thermoelectric Materials Based on Quasi Steady State Method
Abstract The characterization of physical parameters of thermoelectric (TE) materials are of great significance in the application, optimal design, fault diagnosis and other related research of TE modules (TEM). At present, most of the characterization methods of physical parameters of TE materials believe that the TE parameters are constant in the characterization process, ignoring the nonlinear relationship between TE parameters and temperature, and not considering the contact electrical and thermal resistance in the TEM comprehensively. To address these issues, this paper proposes a characterization method of TE material variable physical parameters based on quasi steady state method and TEM testing device, which can realize the accurate characterization of TE parameters.
Firstly, a quasi steady state method is proposed to characterize the physical parameters of material. Based on the temperature distribution of the TE leg, a one-dimensional discrete division can be carried out in the height direction of the leg and the TE leg can be divided into multiple continuous units with equal temperature differences. The temperature, heat flux and height of the unit can be obtained by solving the second-order partial differential equation of the temperature distribution of the TE leg, and further calculation can be carried out to obtain the TE parameters. In order to verify the accuracy of the above theories, a single leg TEM was simulated by using the COMSOL Multiphysics software. The calculation results of the quasi steady state method were closer to the parameters provided by the manufacturer, with a maximum error of only 3.1%. Compared with the steady state method, it has a significant advantage in accuracy.
On this basis, combined with the testing device of TEM, the variable physical properties of TE materials were characterized through experiments. The results showed that although the experiment temperature ranges of the steady state method and the quasi steady state method were consistent, according to the principle, the quasi steady-state method got the wider temperature characterization range of TE material. In terms of the accuracy, due to the fact that the steady-state method considers the average physical parameters, there is a larger difference between the results of the steady-state method and the manufacturer's parameters. While the maximum error of the quasi steady state method in characterizing material prameters is 4.3%, which has more advantages compared to the steady state method.
The following conclusion can be drawn from the results: (1) The thermal and contact resistance of the device have a significant impact on the accuracy of the characterization results of material parameters. Both steady-state and quasi steady-state methods that consider thermal and contact resistance have significantly improved the accuracy of characterizing TE parameters. (2) The quasi steady state method can reduce the error caused by the average temperature taken by the steady state method on both sides of TEM, thus it has better accuracy and a wider range of characterization temperature. (3) Based on the quasi steady state method, the characterization of material prameters can be achieved by using the TEM testuing device, which enriches the functions of TEM testing devices and can reduce material testing equipment investment and testing costs.
keywords:Thermoelectric materials, variable physical parameters, steady state method, quasi steady state method, testing device of thermoelectric module
中图分类号:TM23
DOI: 10.19595/j.cnki.1000-6753.tces.230623
国家电网有限公司科技项目“面向能源互联网自供电传感关键技术研究”资助(52094020006Z)。
收稿日期 2023-04-23
改稿日期 2023-05-14
任鸿睿 男,1998年生,博士研究生,研究方向为热电器件表征与设计。
E-mail:renhongrui@stu.xjtu.edu.cn
何海龙 男,1987年生,博士,副研究员,研究方向为热电转换材料与器件、数字化电力传感器、开关装备智能运维技术。
E-mail:hhlong@xjtu.edu.cn(通信作者)
(编辑 郭丽军)