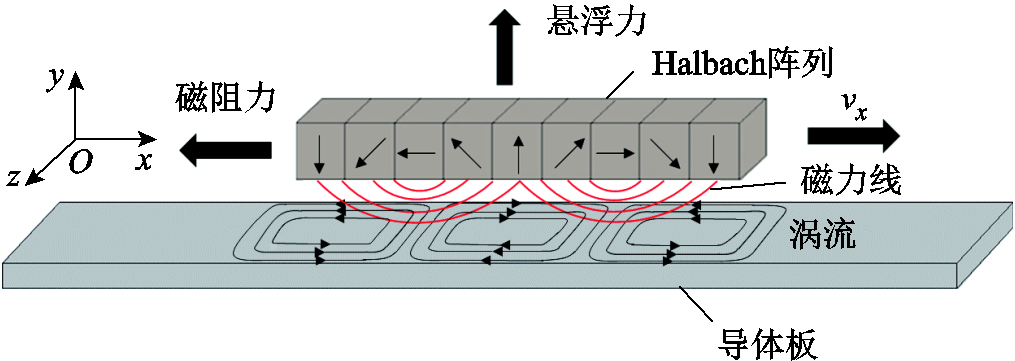
图1 永磁电动悬浮系统三维结构示意图
Fig.1 3-D schematic diagram of the PMEDS
摘要 永磁电动悬浮系统由于自身弱阻尼的特点,运行过程中磁体的姿态易受外界扰动而发生改变,从而影响系统的电磁力特性。该文针对磁体倾斜、横移、偏转等工况,采用解析计算、仿真分析、实验验证相结合的方法来研究系统电磁力特性。首先阐述系统的结构及原理,推导Halbach永磁体阵列在水平、倾斜、偏转状态下的磁场分布函数,建立适用于系统多工况的三维解析模型;其次,搭建三维仿真模型,仿真结果验证了解析模型的正确性,并结合解析模型对比分析系统典型工况下的浮阻特性和悬浮能力;最后,依托组内自研的最高设计时速为600 km/h的动轨实验台,分析了系统在固定参数下的电磁力特性和垂向自稳定能力,并验证解析模型的准确性及磁体在不同横移位置的电磁力特性。
关键词:永磁电动悬浮 多工况 电磁力特性 解析计算 高速实验台 Halbach阵列
作为新兴的无接触式地面高速交通系统,高速磁悬浮列车利用电磁排斥力或吸引力来实现车体非接触式运行,凭借无接触磨损、噪声低、速度高、能耗小等优点,受到众多研究者的青睐。基于悬浮原理,磁悬浮制式可分为电磁悬浮(Electromagnetic Suspension, EMS)、磁通钉扎悬浮(Flux Pining Suspension, FPS)和电动悬浮(Electrodynamic Suspension, EDS)[1-6]。不同磁浮制式特点不同,在应用上各有优势,其中电磁悬浮技术较为成熟已实现商业化。磁通钉扎悬浮能实现悬浮导向一体化的自稳定悬浮,无固有磁阻力。电动悬浮可实现自适应高度悬浮,无需主动控制,悬浮间隙大,在高速和超高速磁悬浮交通领域具有广泛的应用前景[7-8]。
基于轨道形式,永磁电动悬浮可进一步分为线圈式永磁电动悬浮[9-11]和板式永磁电动悬浮[12-14]。板式永磁电动悬浮系统结构简单,载重能力强,造价较低,不需要复杂的控制系统以及冷却系统。此外,随着永磁材料性能的不断提高以及Halbach阵列形式的广泛运用,永磁电动悬浮受到研究者的广泛关注,被用于磁悬浮列车、磁悬浮汽车、管道运输、电磁弹射和磁浮助推等多个领域[12,15-16]。但是,永磁电动悬浮系统存在欠阻尼特性,系统在受到外界扰动时,往往会出现不稳定的响应[17]。为提高系统阻尼,郑杰[18]研究了感应线圈对磁浮系统悬浮稳定性的影响,在磁体与轨道间添加被动感应线圈可以增加系统阻尼,减小因干扰而引起的垂向振动。成玉卫等[19]采用Halbach电磁铁阵列对永磁电动悬浮系统进阻尼补偿,通过控制线圈电流来调节电磁铁产生的悬浮力,改善系统的悬浮稳定性。C. Ham等[20]提出了永磁体与电磁铁组成的混合Halbach阵列,通过调节电磁铁线圈电流控制磁场,对其磁场进行了仿真分析。贺光[21]研究了永磁电动与电磁混合磁悬浮系统,通过在永磁电动悬浮系统中引入EMS主动控制系统,实现系统的动态稳定悬浮。然而,这些研究主要是考虑垂向振动,通过在磁体底部添加无源线圈增强被动阻尼或调节电磁铁电流主动控制悬浮力,以提高系统的垂向稳定性,对磁体在不同姿态下的电磁力特性相关研究较少。此外,电磁力的本质源于车载磁体产生的时变磁场与导体板内的涡流场的电磁反应,当系统受到外界扰动时,其动态性能较差,磁体姿态会发生改变,因此必将影响电磁力,从而影响列车运行品质。
另一方面,永磁电动悬浮的电磁力计算是研究电磁特性的基础。最为通用的电磁力计算方法是有限元分析方法,该方法能考虑几何细节和材料的非线性,实现较高的计算精度,但是较为耗时,也不能反映参数之间的内在关系。因此,研究者针对永磁电动悬浮系统建立了二维和三维解析模型,重点在于准确计算导体板中的涡流分布及产生的磁场。二维解析模型是一种常见的近似方法,假设永磁体阵列横向宽度远大于极距,忽略导体板中的横向电流[13,22],解析结果与实验数据相比存在较大的误差,具有局限性。鉴于此,许多学者建立了三维的解析模型。王厚生[23]对有限宽导体板的三维电磁场进行分析,提出了一种三维涡流分布数学模型。但是其假设磁体的磁场随横向宽度呈正弦变化,这与实际情况并不相符。J. Z. Bird等[24-25]针对轮式永磁电动悬浮系统建立了有限宽导体板的三维解析模型,但磁轮磁场分布与直线型永磁阵列存在较大区别,不适用于直线型悬浮。陈殷等[26-27]采用二阶磁矢势法对电磁场进行三维建模分析,建立了基于双边Halbach阵列的板式永磁电动悬浮三维电磁力解析模型,但是其基于导体板足够大的假设,没有考虑导体板长度和宽度对系统的影响。巫川等[28]建立了包含因有限的导体板宽度导致的横向端部效应的三维解析模型。三维模型相对二维模型的准确性更高,但上述研究也并没有分析磁体倾斜、偏转等状态下的电磁力特性。值得一提的是,为了便于建立和求解,解析模型的建立往往基于诸多假设,将实际物理模型理想化,为验证其实用性和正确性,研究者们搭建了许多实验装置。
由于永磁电动悬浮系统通常由长直导体板轨道和高速移动的永磁体组成,建造实际线路既困难又昂贵。因此,研究者通常“以曲代直”,搭建了不同的旋转型等效装置。陈殷等[27]用一块厚度为3 mm的铝导体板在两个Halbach阵列之间旋转,验证了零磁通永磁电动悬浮模型,速度可达25 m/s。王大志等[29]建立了一个半径为0.115 m的圆盘形实验台,速度可达10 m/s。龙志强等[30]设计了一种圆盘实验装置,铝盘半径为0.35 m,可实现60 m/s的速度。H. W. Cho等[13]使用了一个由直径为1.5 m的转轮制成的实验装置,其轨道铝板宽262 mm、厚35 mm,最大速度可达550 km/h。J. Iniguez等[31]设计了类似的小型实验装置,采用15 mm厚的铜板,速度在10 m/s内。由于采用等效的原理,因此旋转体的半径越大,等效的效果越好,误差越小,但目前提出的等效实验装置的半径较小且设计速度不高。
综上所述,虽然大多研究学者在仿真分析、解析计算和实验测试方面都对永磁电动悬浮系统电磁力特性都开展了实质性的研究,推动了永磁电动悬浮系统的发展,但大都考虑正常运行状态,并未计及磁体姿态改变导致的电磁力特性变化,如磁体横向偏移、左右倾斜、偏转等。鉴于此,本文通过等效面电流法和坐标平移旋转变换求出Halbach永磁体阵列水平、倾斜、偏转状态下空间磁场分布表达式,建立可考虑磁体不同姿态的永磁电动悬浮系统的三维解析模型,得到系统悬浮力和磁阻力的解析表达式。结合三维有限元仿真分析系统正常运行、以及磁体倾斜、偏转、横移工况下的电磁力特性规律。最后利用高速实验台开展等效实验对解析和仿真模型进行验证。
永磁电动悬浮系统主要由永磁体和感应轨道组成,其三维结构如图1所示。永磁体以Halbach阵列形式排布,通过将不同磁化方向的永磁体按照一定顺序排列,产生接近正弦变化的周期磁场,且能够加强磁体阵列一侧磁场,削弱另一侧磁场,从而提高磁场利用率。理想的直线型Halbach磁体,其磁化方向按照正弦函数连续变化。在实际中,通常采用四模块或八模块结构近似等效,所谓模块数指的是单个波长内磁化矢量变化的磁块数,如四模块是指单个波长内有四个磁块且磁化矢量呈90°变化。模块数越多,磁化矢量变化的角度越小,越接近理想型,但磁体的成本和加工难度也越高,综合考虑,认为八模块是较为合适的选择[32]。轨道板为具有弱磁性及良导电性的金属导体(常见的有铝、铜等)。如前所述,当磁体阵列沿导体板移动时,导体板切割永磁体源磁场,在导体板内生成感应涡流。涡流会产生与磁体磁场方向相反的磁场,源场与涡流场相互作用产生电磁力以阻碍相对运动。电磁力在竖直方向上的分量为悬浮力,克服重力实现悬浮,在与运动相反方向上的分量为磁阻力。永磁电动悬浮系统的悬浮力和磁阻力都与速度密切相关。

图1 永磁电动悬浮系统三维结构示意图
Fig.1 3-D schematic diagram of the PMEDS
永磁电动悬浮系统电磁力由源磁场与涡流场相互作用产生,求解电磁力需要得到磁体阵列产生的磁场和导体板中产生的涡流场。本节通过建立关于磁矢势的方程求解不同区域内的磁场分布,利用Maxwell张量法得到电磁力的解析表达式。模型建立过程可分为建立控制方程、求解控制方程通解、建立边界条件、源磁场计算、电磁力求解。由于磁体倾斜、偏转不同工况下的模型只有源磁场形式不同,故本节解析模型建立不涉及源磁场的具体表达式,在下一节中分别计算不同工况下的源磁场。
将永磁电动悬浮系统空间区域分解为三个区域,如图2所示。导电板为区域Ⅱ,长为l,宽为w,厚度为d。导体板的上表面标记为Г1,下表面标记为Г2。区域Ⅰ中Halbach阵列磁源与导体板间的间隙为h。电磁场近似为准静态,忽略位移电流的影响。另外,由于永磁体和导体板的磁导率均与空气接近,因此相对磁导率均取为1。
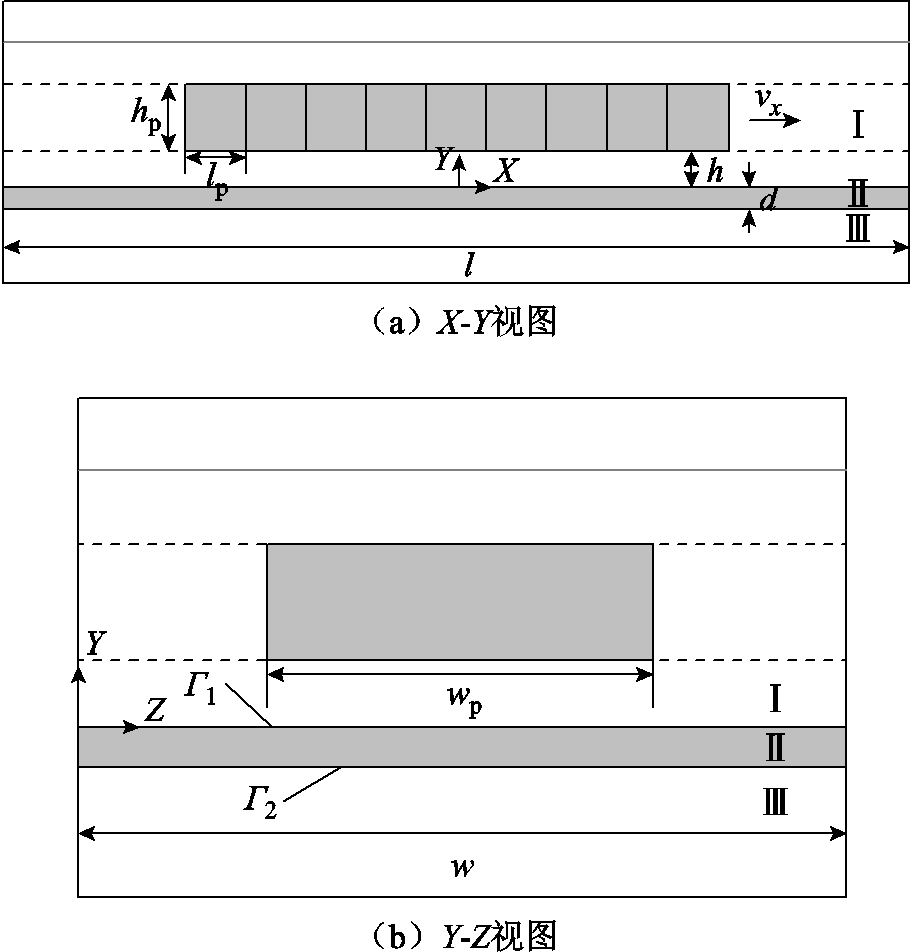
图2 永磁电动悬浮求解区域划分示意图
Fig.2 Schematic diagram of the region division for PMEDS
磁矢势A与磁感应强度B的关系为
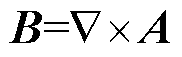 (1)
(1)
通过Maxwell方程组可得各区域控制方程如下。
空气域Ⅰ、Ⅲ,有
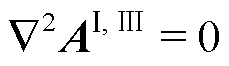 (2)
(2)
导体板区域Ⅱ,有
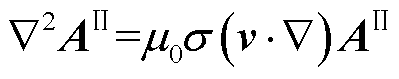 (3)
(3)
式中,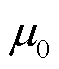 为真空磁导率;
为真空磁导率;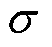 为电导率;v为磁体阵列的运行速度。
为电导率;v为磁体阵列的运行速度。
当永磁体磁源在导板上居中运行时,板内的感应涡流平行于导体板上表面流动,因此忽略磁矢势垂向分量Ay,导体板区域的磁矢势可表示为
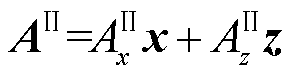 (4)
(4)
导体板长度可视为无穷大,在前后边界上满足Dirichlet边界条件:
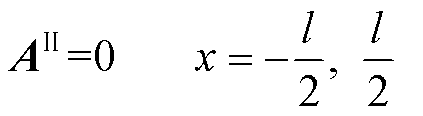 (5)
(5)
根据文献[24],为了确保解的唯一性,在导体板区域的边界面上,有
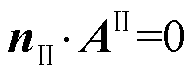 (6)
(6)
式中,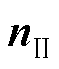 为导体板边界面的法向向量。
为导体板边界面的法向向量。
将式(4)代入式(3)中,通过分离变量法,并结合式(5)和式(6),可得导体板区域控制方程的傅里叶级数解[24]为
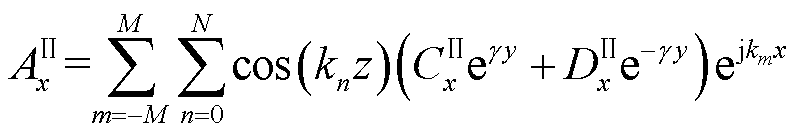 (7)
(7)
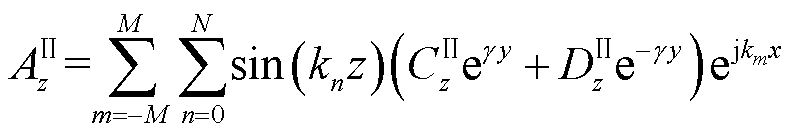 (8)
(8)
其中
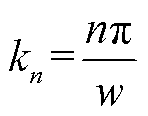 (9)
(9)
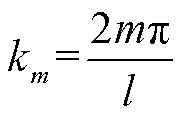 (10)
(10)
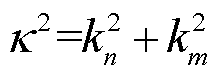 (11)
(11)
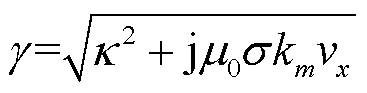 (12)
(12)
式中,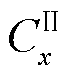 、
、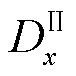 和
和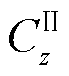 、
、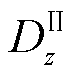 为需要通过边界条件求解的未知系数。
为需要通过边界条件求解的未知系数。
为了确保满足连续性边界条件,区域Ⅰ、Ⅲ的磁矢势表达式应与区域Ⅱ的磁矢势表达式形式一致[24-25],在x和z方向傅里叶级数形式相同。此外,涡流产生的反射场强度随着距导体板距离的增大呈指数衰减。因此,区域Ⅰ、Ⅲ的磁矢势的表达式为
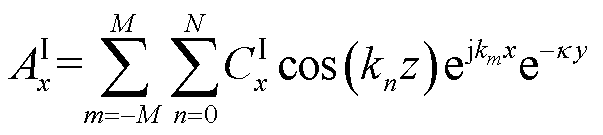 (13)
(13)
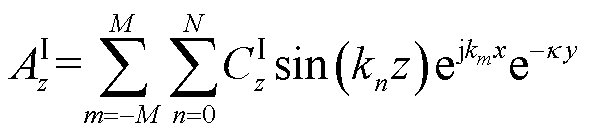 (14)
(14)
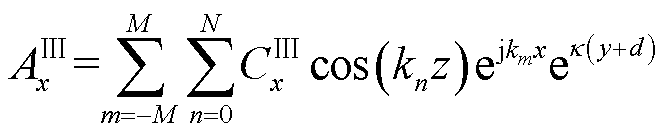 (15)
(15)
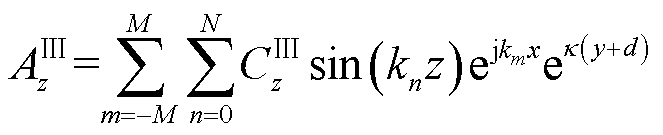 (16)
(16)
空气域内的磁通密度由源场和反射场组成,2.2节已求得反射场对应的磁矢势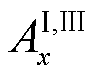 、
、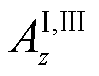 的通解,根据式(1)可计算反射场对应的磁通密度。导体板上、下表面磁场切向分量和磁通密度法向分量连续,又认为导体板和空气域内相对磁导率一致,则在y=0及y=-d处满足
的通解,根据式(1)可计算反射场对应的磁通密度。导体板上、下表面磁场切向分量和磁通密度法向分量连续,又认为导体板和空气域内相对磁导率一致,则在y=0及y=-d处满足
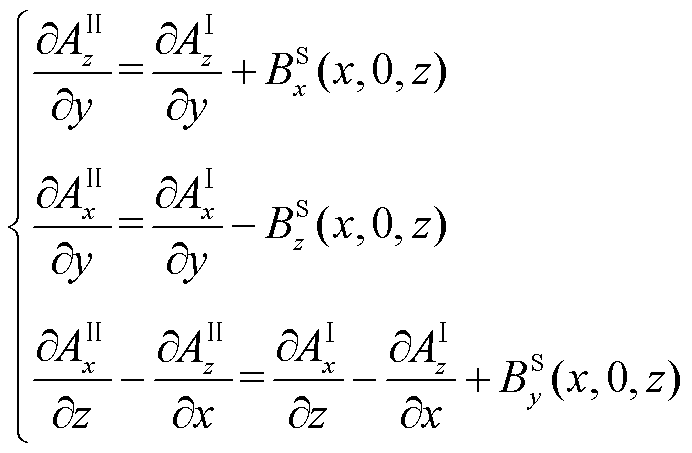 (17)
(17)
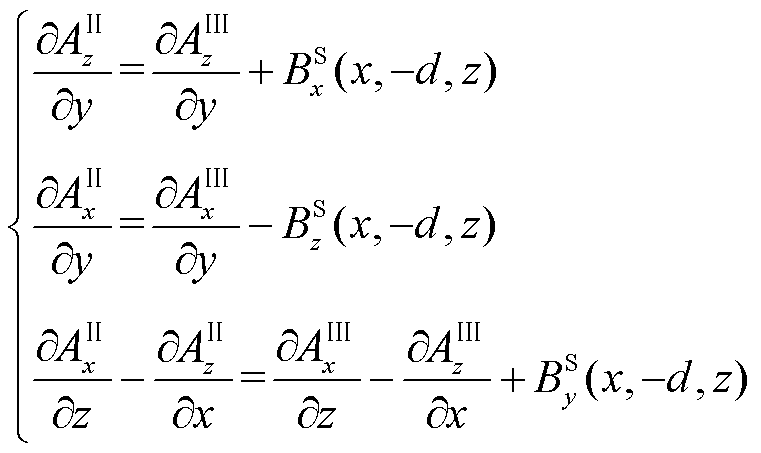 (18)
(18)
式中,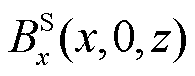 、
、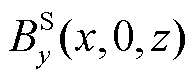 、
、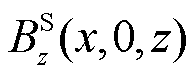 分别为源场磁通密度在y=0处,x、y、z三个方向的分量。
分别为源场磁通密度在y=0处,x、y、z三个方向的分量。
在建立解析模型时,认为源磁场是已知的,将其代入边界条件中即能求得涡流场中未知的系数。由于源磁场分布表达式较为复杂,为能代入边界条件进行求解,将其转换为傅里叶级数的形式。通过式(13)、式(14)和式(1)可以得到反射场的磁通密度表达式。为了匹配涡流场的表达式形式,源磁场采用和反射场相同的本征值[28]。故源磁场在y=0及y= -d处的表达式为
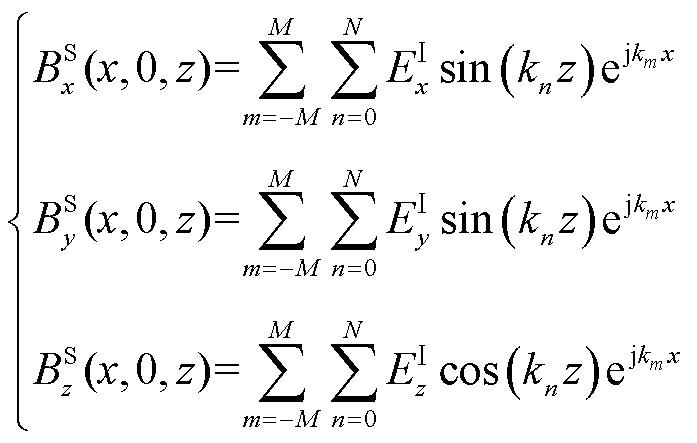 (19)
(19)
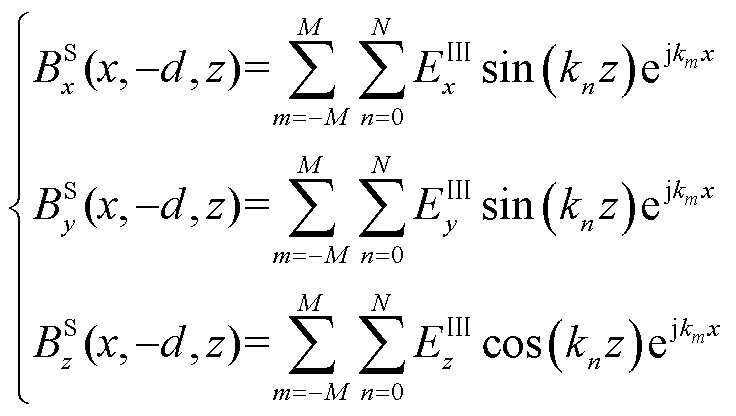 (20)
(20)
式中,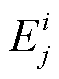 (i=I, III; j=x, y, z)为二维傅里叶系数,由已知的源磁场求得[25-26],源磁场的具体表达式会在下一节进行推导。
(i=I, III; j=x, y, z)为二维傅里叶系数,由已知的源磁场求得[25-26],源磁场的具体表达式会在下一节进行推导。
将式(7)、式(8)、式(13)、式(14)和式(19)代入边界条件式(17),将式(7)、式(8)、式(15)、式(16)和式(20)代入边界条件式(18),结合库伦规范条件,可以求得磁矢势通解中未知的系数。再利用式(1)得到磁通密度表达式,通过Maxwell应力张量法,求得轨道和磁源之间相互作用力为
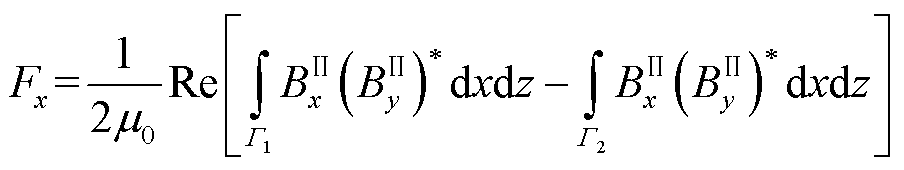 (21)
(21)
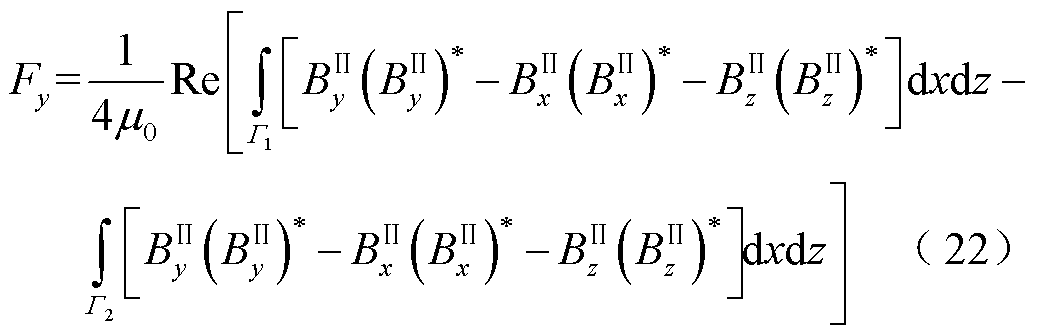
 (23)
(23)
式中,Fx为磁阻力;Fy为悬浮力;Fz为横向力;上标*表示共轭。
在前文建立电磁力解析模型时,源磁场给出的是经过傅里叶变换后的形式。由于磁矢势通解中的未知系数需要源磁场的傅里叶系数作为已知量代入边界条件进行求解,故本节通过等效面电流法和坐标变换求解磁体不同姿态下空间源磁场的具体表达式。
正常工况下,Halbach磁体阵列的位置如图2所示,磁体阵列与导体板间的间隙均匀,居中运行,其磁场可看作N个任意磁化方向的单块永磁体所产生磁场的叠加。模型所用永磁体磁化方向均在XY平面,可以通过求解磁化方向分别为X、Y轴正方向的永磁体磁场,来求解任意磁化方向的单块永磁体的磁场表达式。
Y轴正方向磁化磁体示意图如图3所示。图3中,磁化方向为Y轴正方向,磁化强度为M的单块永磁体,其产生磁通密度可看作电流面1、2、3和4产生的磁通密度的叠加。
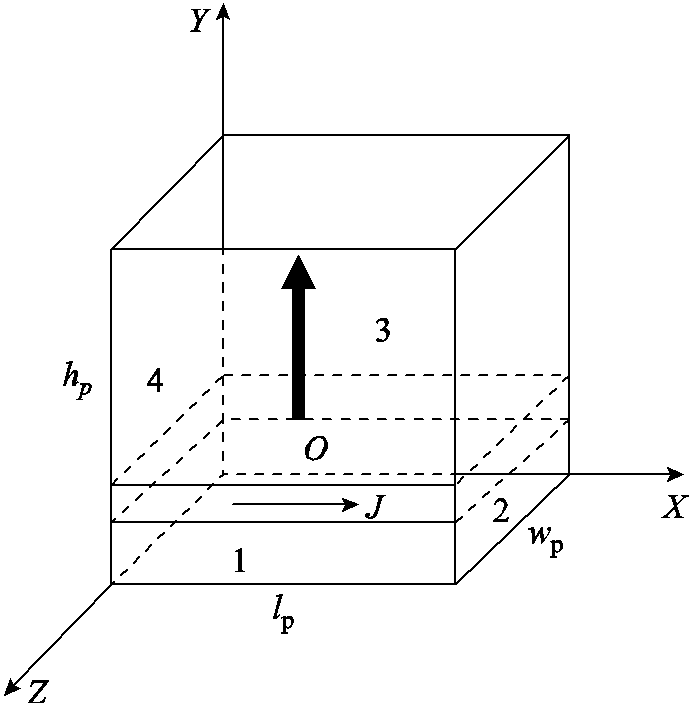
图3 Y轴正方向磁化磁体示意图
Fig.3 Diagram of individual with positive Y-axis magnetization
根据毕奥-萨伐尔定律可得四个电流面产生的磁通密度计算表达式,叠加即为Y轴正向磁化永磁体的磁通密度解析式[33],表示为
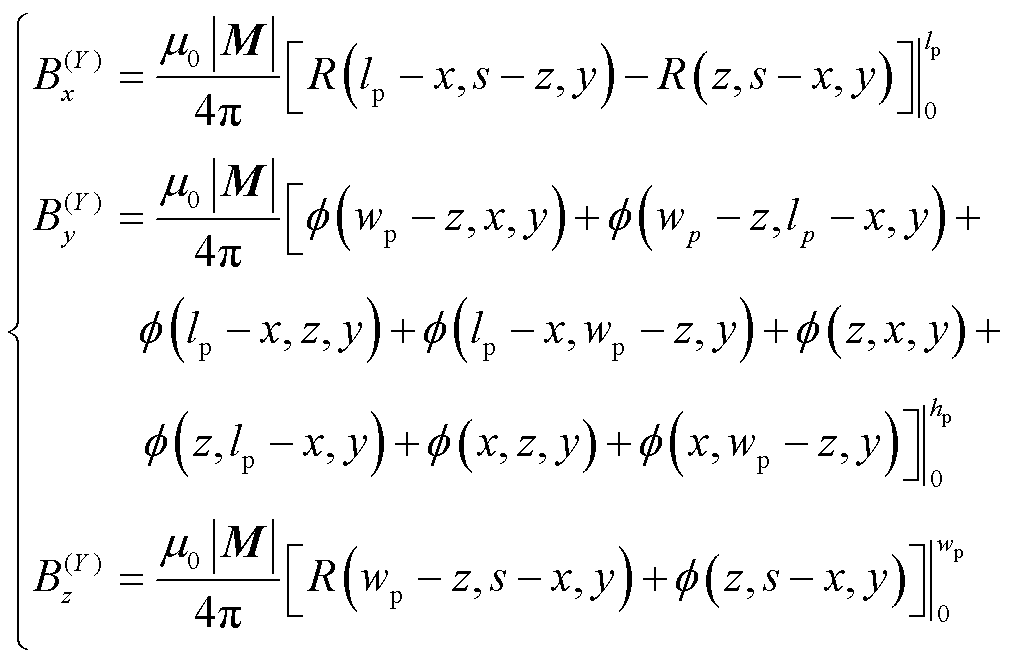 (24)
(24)
其中
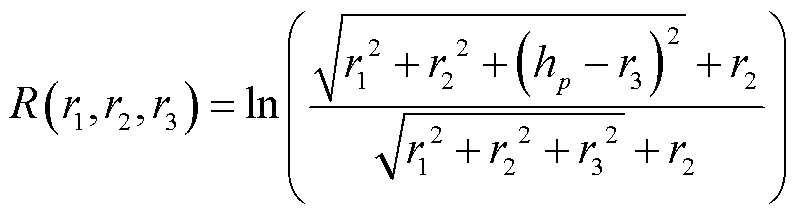 (25)
(25)
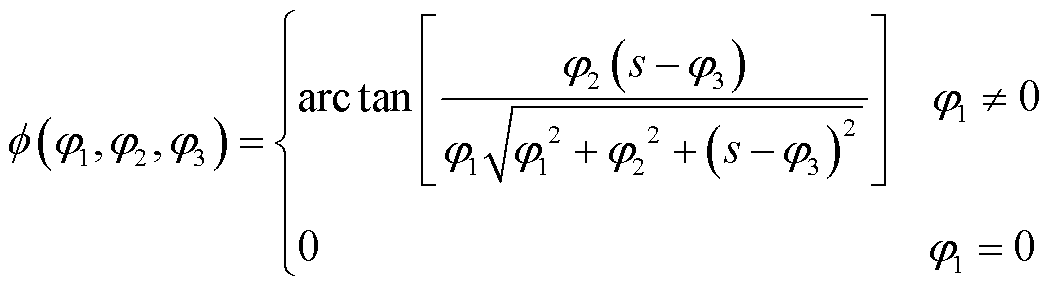 (26)
(26)
式中,“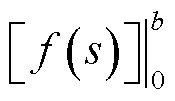 ”表示函数
”表示函数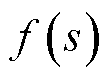 在自变量s分别等于b和0时的差值。
在自变量s分别等于b和0时的差值。
利用坐标变换可以得出当磁化方向为X轴正方向时的磁场表达式为
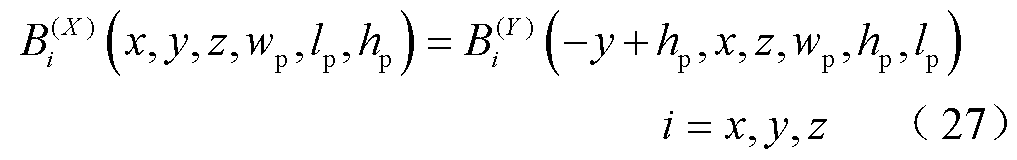
则任意磁化方向的永磁体磁场为
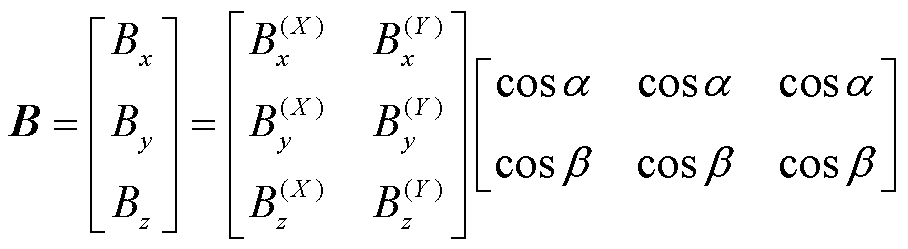 (28)
(28)
式中,α、β分别为磁化强度M与X轴、Y轴正方向的夹角。
正常工况下,磁体阵列位置如图2所示。通过坐标平移变化,在图2所示坐标系中,由N个单块永磁体构成的Halbach阵列在空间中任一点产生的磁通密度可以表示为
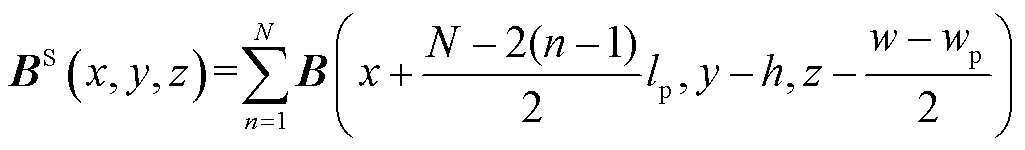 (29)
(29)
磁体倾斜和偏转工况分别如图4和图5所示。磁体倾斜工况相当于是磁体阵列在永磁体局部坐标系下,绕X轴顺时针旋转角度𝜃x,而磁体偏转工况则是绕Y轴逆时针旋转角度𝜃y。
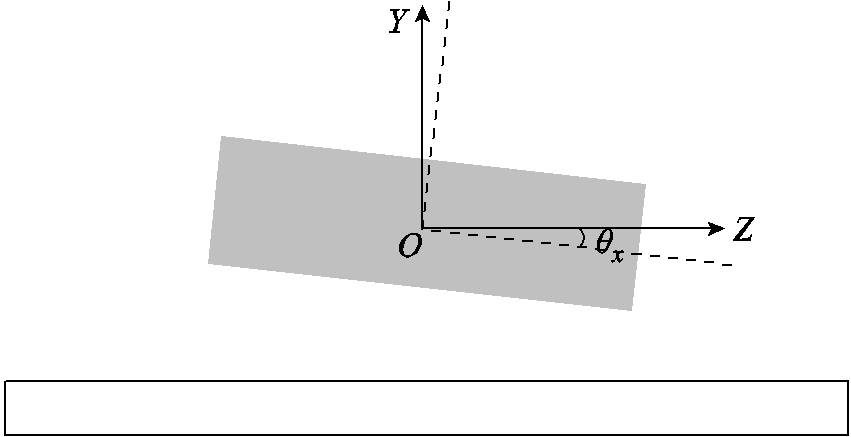
图4 倾斜磁体示意图
Fig.4 Schematic diagram of tilted magnets
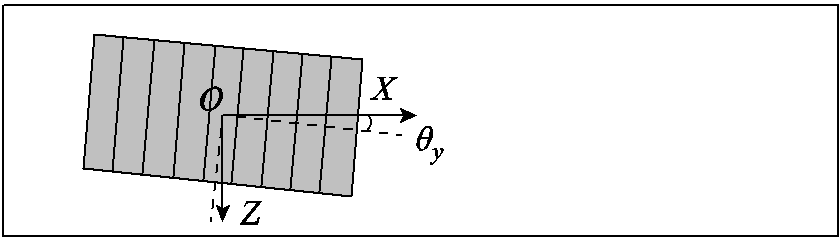
图5 偏转磁体示意图
Fig.5 Schematic diagram of deflecting magnets
若场点Q(x0, y0, z0)的磁通密度为BQ(x0, y0, z0),该点分别绕X轴顺时针旋转𝜃x,Y轴逆时针旋转𝜃y后为点P(x, y, z),磁通密度为BP(x, y, z),则根据坐标旋转公式可得[34]
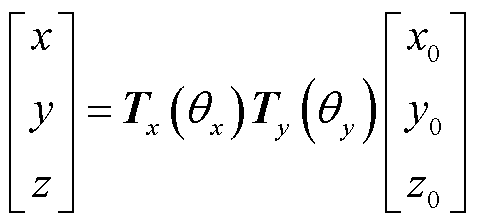
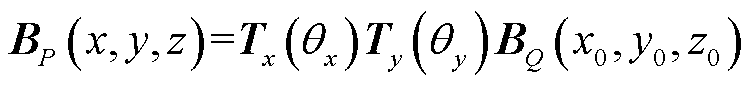 (30)
(30)
其中
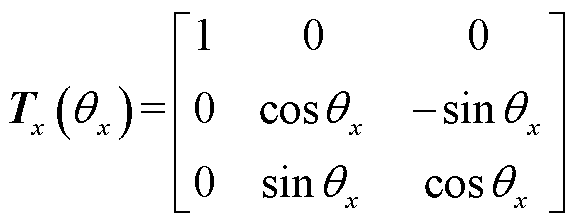 (31)
(31)
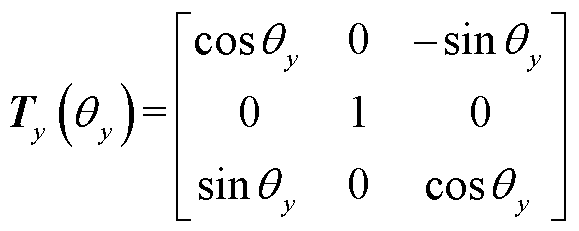 (32)
(32)
故在图1所示全局坐标系,倾斜工况下Halbach阵列的磁场表达式可写为
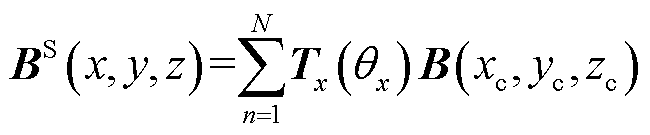 (33)
(33)
其中
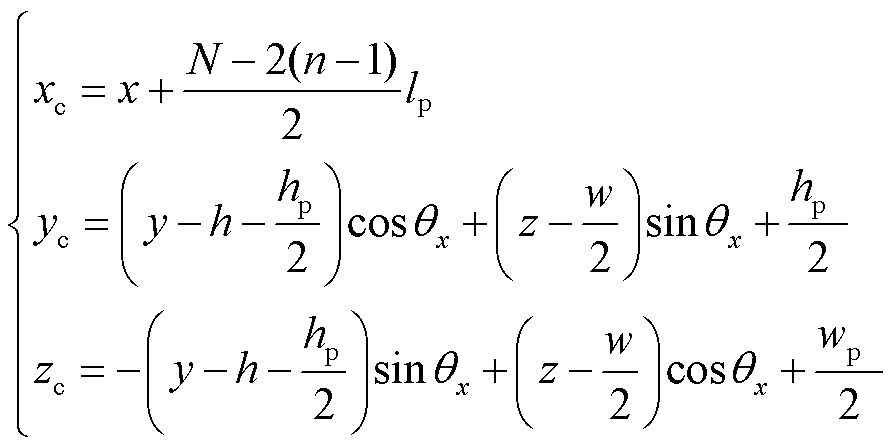 (34)
(34)
偏转工况下Halbach阵列的磁场表达式可写为
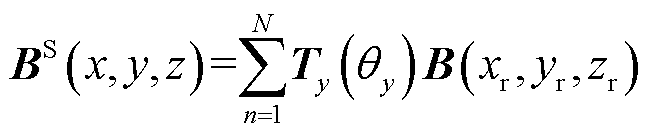 (35)
(35)
其中
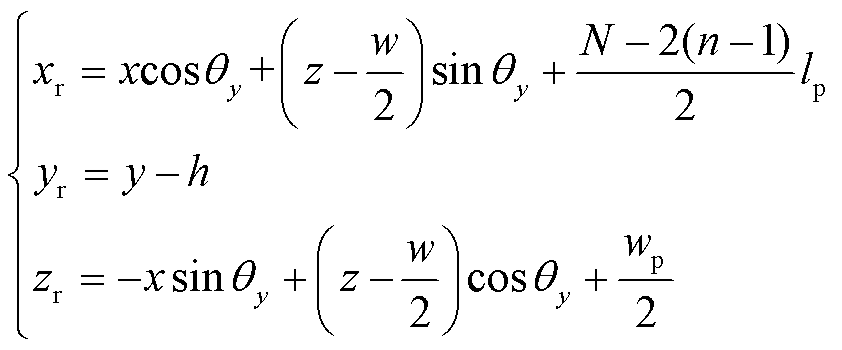 (36)
(36)
求得磁体不同姿态下的磁场具体表达式后,则可通过傅里叶变换得到磁场的傅里叶形式,即式(19)和式(20)。结合边界条件和库伦规范求得导体板区域磁矢势,进而求得磁通密度,根据式(21)~式(23)求出不同工况下的电磁力各分量。
前面针对永磁电动悬浮系统建立了三维电磁力解析模型,本节将建立三维有限元模型对比相同条件下仿真和解析的电磁力计算结果,验证解析模型的准确性。然后分不同工况对永磁电动悬浮系统电磁力特性展开研究,分析磁体水平居中工况,系统不同间隙下悬浮力与磁阻力的速度特性,磁体倾斜、偏转、横移工况对系统电磁力的影响。
利用Ansys Maxwell电磁仿真工具建立如图6所示三维瞬态有限元分析模型,其主要由永磁体阵列、导体板、运动域和求解域组成。表1给出了永磁电动悬浮系统建模参数。磁体和轨道的长度、宽度和高度分别对应图6中的X轴、Z轴、Y轴方向。
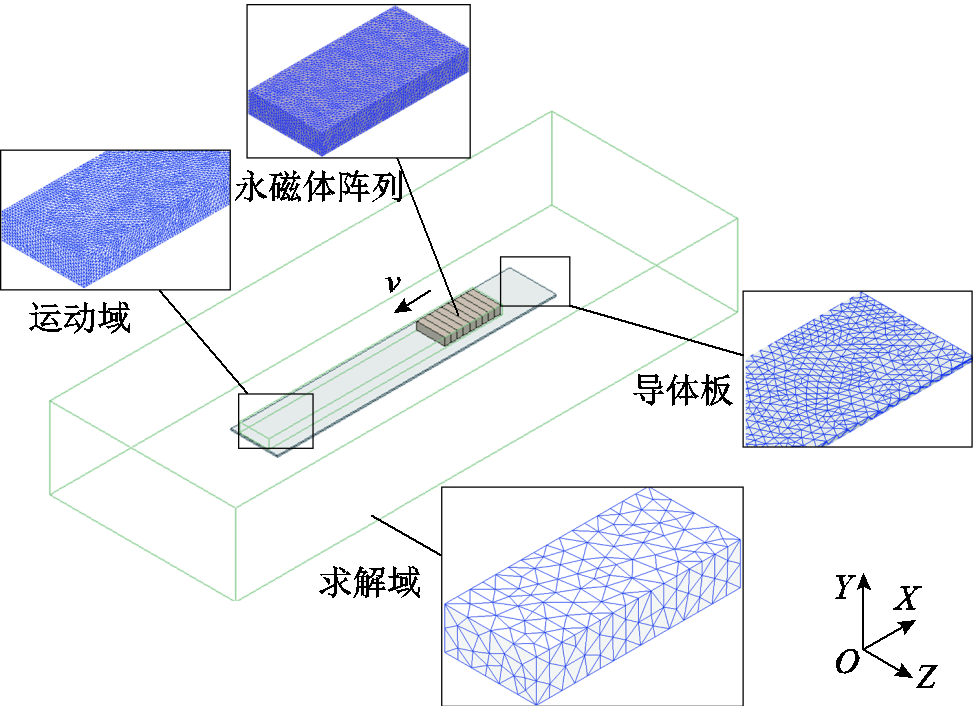
图6 永磁电动悬浮系统三维有限元模型
Fig.6 3-D finite element model of the PMEDS system
表1 永磁电动悬浮系统模型参数
Tab.1 Parameters of the PM-EDS model

参数数值 单块磁体长度lp/mm40 单块永磁体宽度wp/mm180 单块永磁体高度hp/mm50 永磁体数量/块9 磁化角/(°)45 剩磁/T1.48 导体板宽度w/mm300 导体板厚度d/mm10 电导率σ/(S/m)5.8×107 悬浮间隙h/mm30
4.1.1 源磁场对比
源磁场的准确计算是电磁力求解的基础。对正常工况下Halbach阵列下表面30 mm处,XOZ平面上的磁通密度法向分量By进行仿真和解析计算,结果如图7所示。可以看出,解析计算与有限元仿真结果吻合较好,因此验证了磁场解析计算的准确性。

图7 Halbach阵列下表面30 mm处磁通密度垂向分量By
Fig.7 y-component of the flux density at h=30 mm
4.1.2 电磁力对比
为进一步验证解析模型的正确性,对正常工况、悬浮间隙30 mm时,不同速度下的悬浮力和磁阻力进行计算。不同速度下的电磁力解析和仿真结果对比如图8所示。图8中在不同运行速度下解析计算与仿真结果吻合较好,由此表明电磁力解析计算的有效性,故下面将利用解析和仿真模型对不同工况下电磁力特性进行分析。
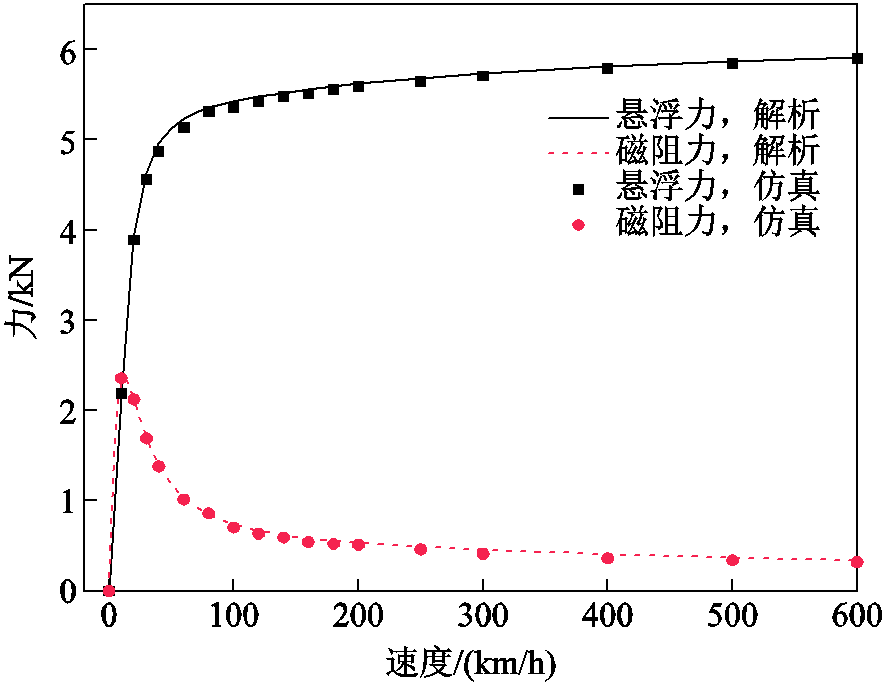
图8 不同速度下的电磁力解析和仿真结果对比
Fig.8 Comparison of electromagnetic forces between analytical and simulation results under different speeds
4.2.1 正常工况
磁体正常居中工况、不同间隙下,采用解析法和三维有限元仿真计算的电磁力随速度变化曲线如图9和图10所示。从图中可以看出,解析解的变化趋势与有限元仿真一致,在不同悬浮间隙下,悬浮力均随速度的增加而单调增大,但逐渐趋于稳定,而磁阻力先快速增大达到峰值,然后单调减小。悬浮力与磁阻力的变化规律可以从电路理论定性分析。随着速度的增加,磁通量变化率增大,由电磁感应定律和欧姆定律可知,感应电流也随之增大。但是,由于电抗也随磁通量变化率的增大而增大,并在高速时在阻抗中占主导地位。因此,在高速下,感应电流增加的速度减缓。悬浮力与涡流幅值成正比,因此表现出与感应涡流类似的变化规律,随速度增大而增大并逐渐趋于稳定。
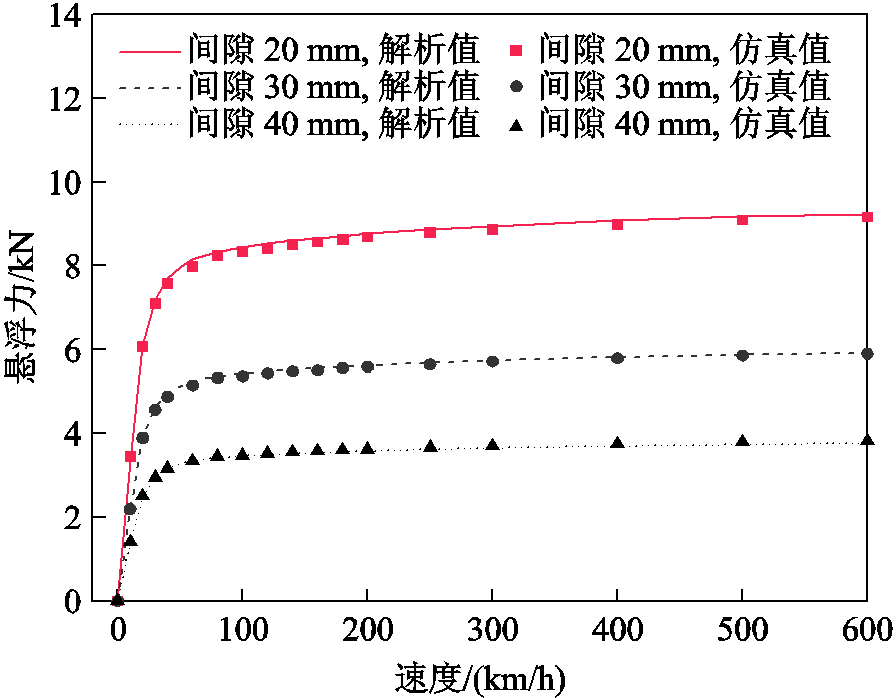
图9 不同气隙下悬浮力随速度的变化
Fig.9 Levitation force with speed at different air gaps
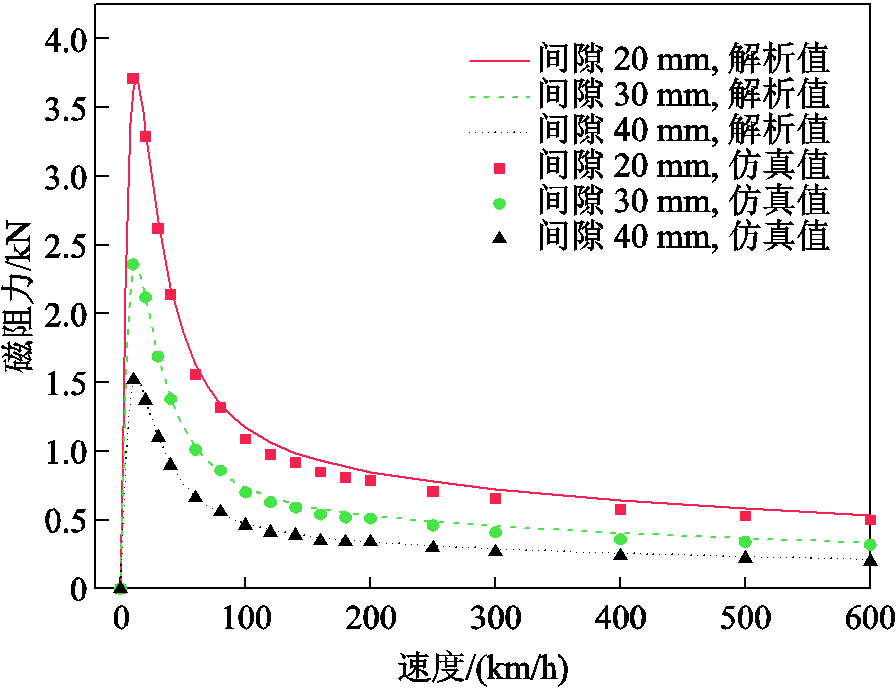
图10 不同气隙下磁阻力随速度的变化
Fig.10 Drag force with speed at different air gaps
磁阻力和速度的乘积反映了系统的欧姆损耗,欧姆损耗与电阻和电流的二次方成正比。在低速时,电流随速度的增加而快速增大,因此磁阻力也随速度增大而增大。在高速时,涡流幅值趋于稳定,欧姆损耗功率几乎保持恒定。因此,磁阻力随速度增大而减小,磁阻力存在峰值。从图10可以看出,峰值速度不随悬浮间隙改变而变化。
浮阻比指的是悬浮力与磁阻力的比值,是电动悬浮系统评估的重要指标[5]。通过解析得到的不同悬浮间隙下浮阻比随速度变化的曲线如图11所示,浮阻比随速度的增加而增大,这也反映了永磁电动悬浮系统适用于高速及超高速应用场景。从图中还可以看出,不同悬浮间隙下,浮阻比大小基本相等,其与间隙无关。
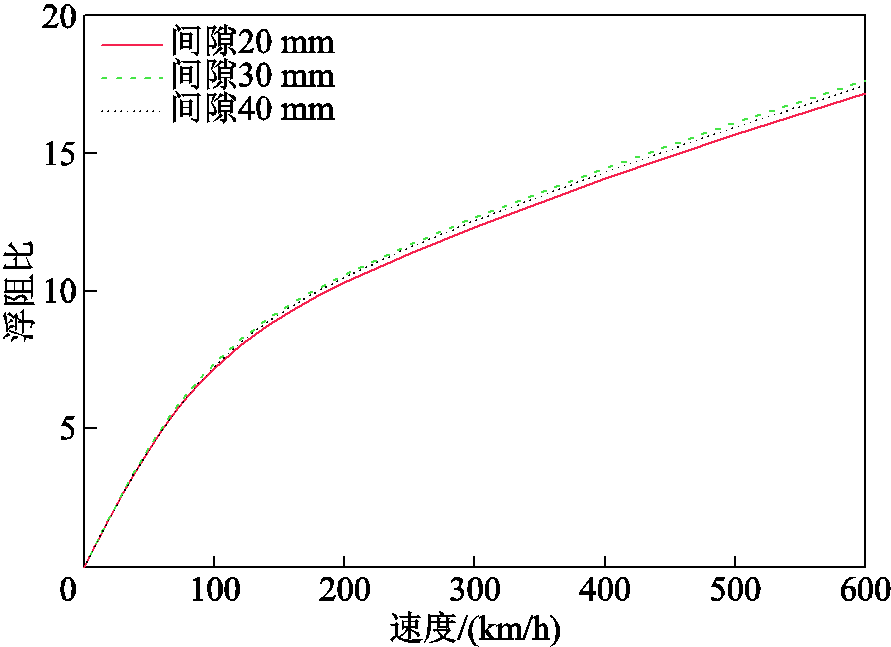
图11 不同悬浮间隙下浮阻比与速度的关系
Fig.11 Levitation-to-drag ratio with speed at different air gaps
悬浮力和磁阻力随悬浮间隙变化曲线如图12所示,当磁体与地面导体板间垂向距离发生改变时,电磁力也会随之变化。由于磁体磁场随气隙的增大呈指数减弱,电磁力也随悬浮间隙的增大呈指数型衰减,同时也反映了系统的自稳定能力。在一定速度下,悬浮力与重力相等,悬浮间隙不变时,悬浮力保持恒定,系统稳定运行;当悬浮间隙变大时,悬浮力减小,小于重力,则磁体下落,使得悬浮间隙减小,悬浮力又增大,与重力平衡时,回到原始位置。
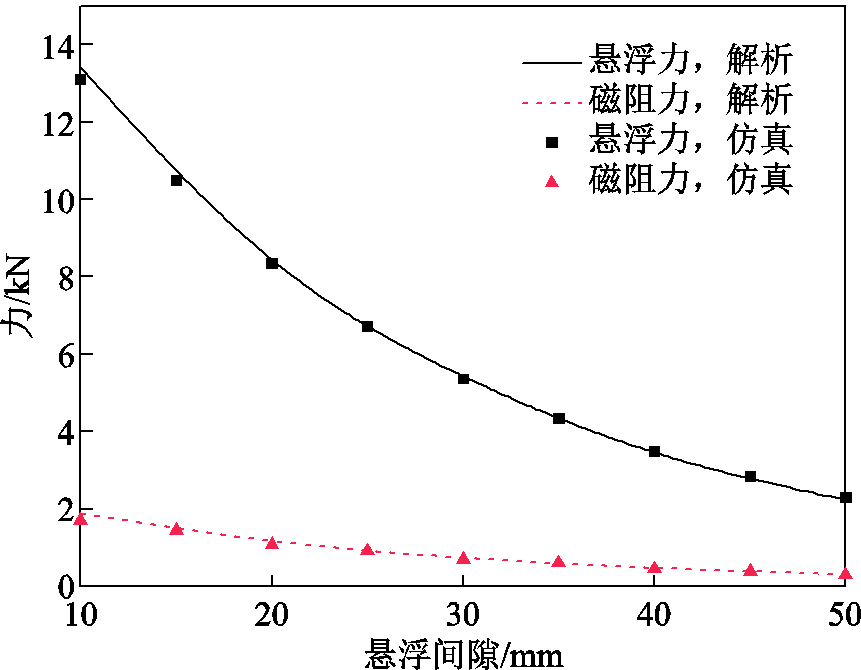
图12 悬浮力和磁阻力随悬浮间隙变化曲线
Fig.12 Curves of levitation and drag force with air gap
在实际应用中,导体板宽度有限,由于横向端部效应的影响,导体板宽度会对电磁力产生影响[35]。图13给出了悬浮力和磁阻力随导体板宽度的变化曲线。随着轨道宽度的增加,感应的有效涡流面积增大,悬浮力和磁阻力增大,当板宽继续增大,涡流趋于饱和,悬浮力趋于稳定,磁阻力因为等效电阻减小而减小。由于设定的磁体速度较高,磁阻力数值较小,变化不明显。
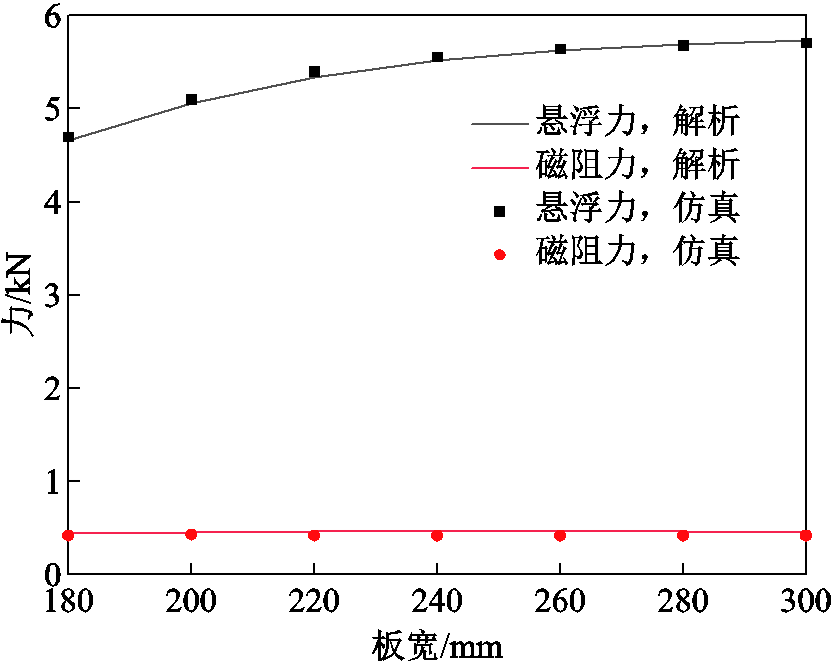
图13 速度300 km/h、间隙30 mm时电磁力随导体板宽度变化曲线
Fig.13 Curves of electromagnetic force with conductive plate width at 300 km/h and gap=30 mm
4.2.2 磁体侧倾
磁体侧倾后,如图4所示,磁体与导体板表面不平行,间隙不均匀,将模型看作左右两部分,左侧间隙增大,右侧间隙减小。由于随间隙增大,电磁力的衰减会逐渐减缓。故相较于未倾斜时,左侧衰减的电磁力小于右侧提升的电磁力,总的电磁力会增大,如图14和图15所示。磁体侧倾后,由于间隙不均匀,还会有横向力产生,其随速度变化曲线如图16所示。其与磁阻力类似,随着速度的增加先增大后减小。当速度为300 km/h,侧倾角对电磁力的影响如图17所示。随着倾斜角度的增大,悬浮力、磁阻力与横向力均有所增大。
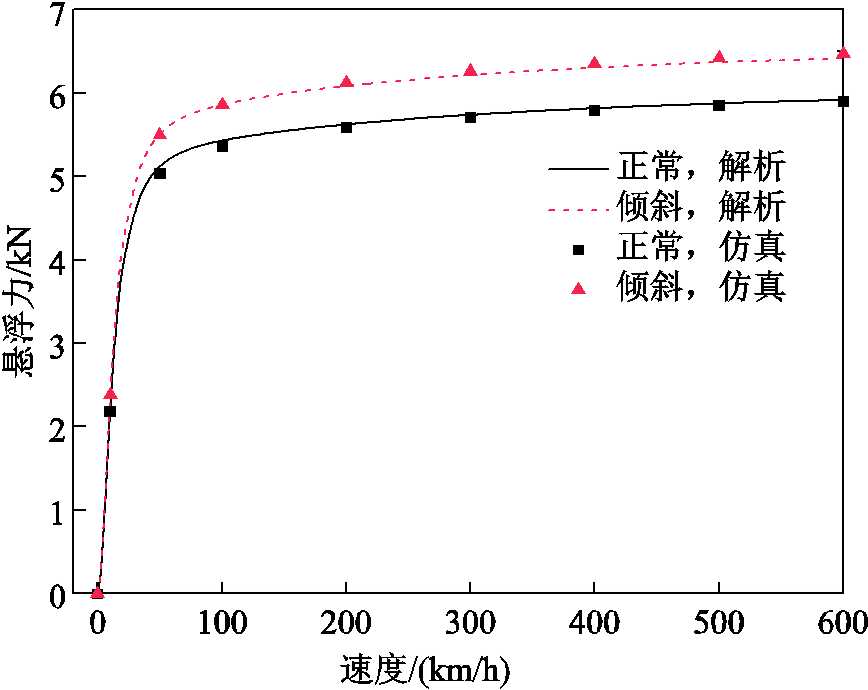
图14 磁体倾斜10°与正常工况悬浮力对比
Fig.14 Comparison of levitation force between normal condition and tilt condition at θ=10°
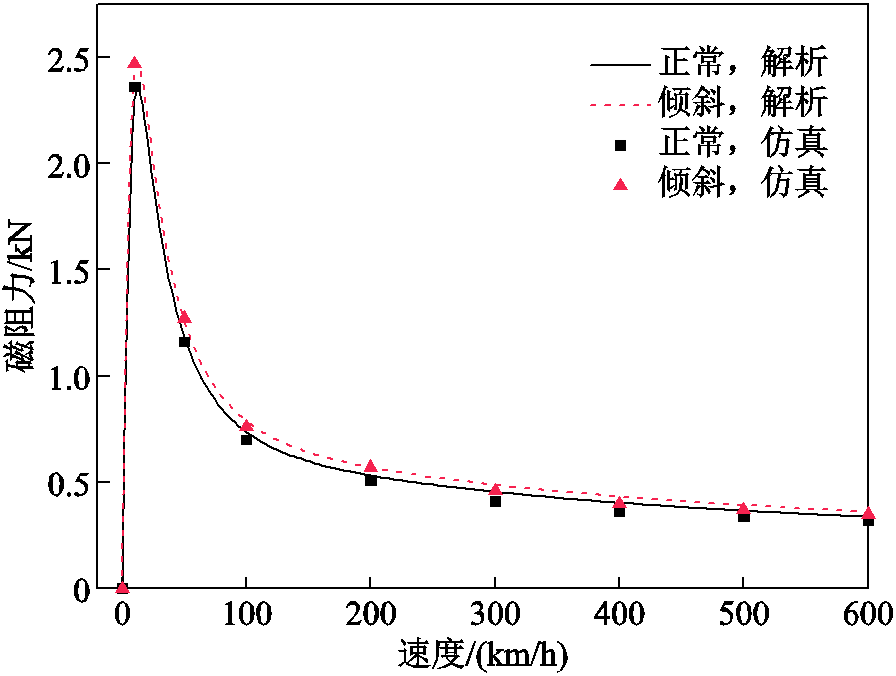
图15 磁体倾斜10°与正常工况磁阻力对比
Fig.15 Comparison of drag force between normal condition and tilt condition at θ=10°
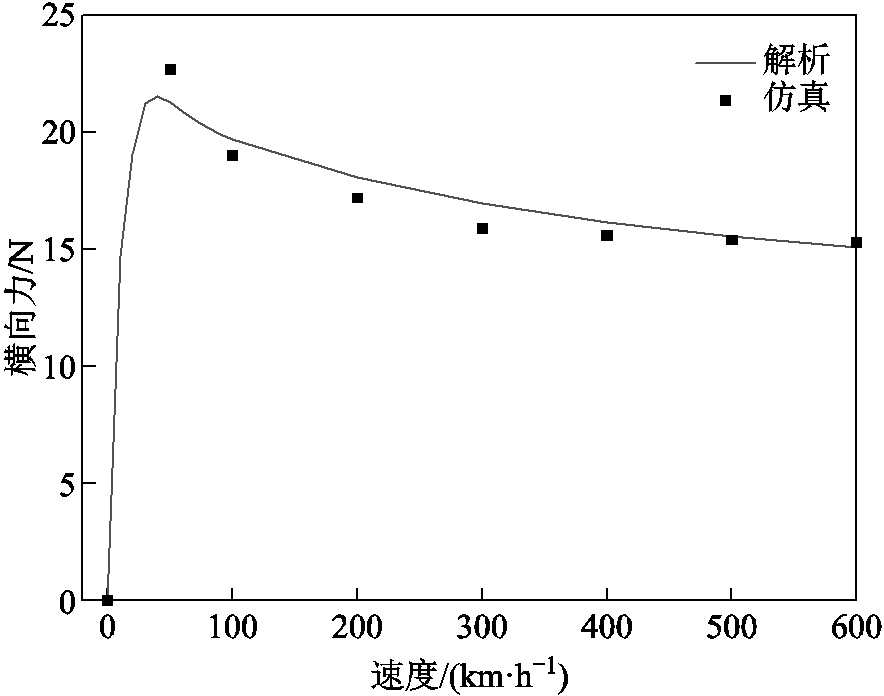
图16 倾斜10°工况横向力随速度变化曲线
Fig.16 Lateral force with speed under tilt condition at θ=10°
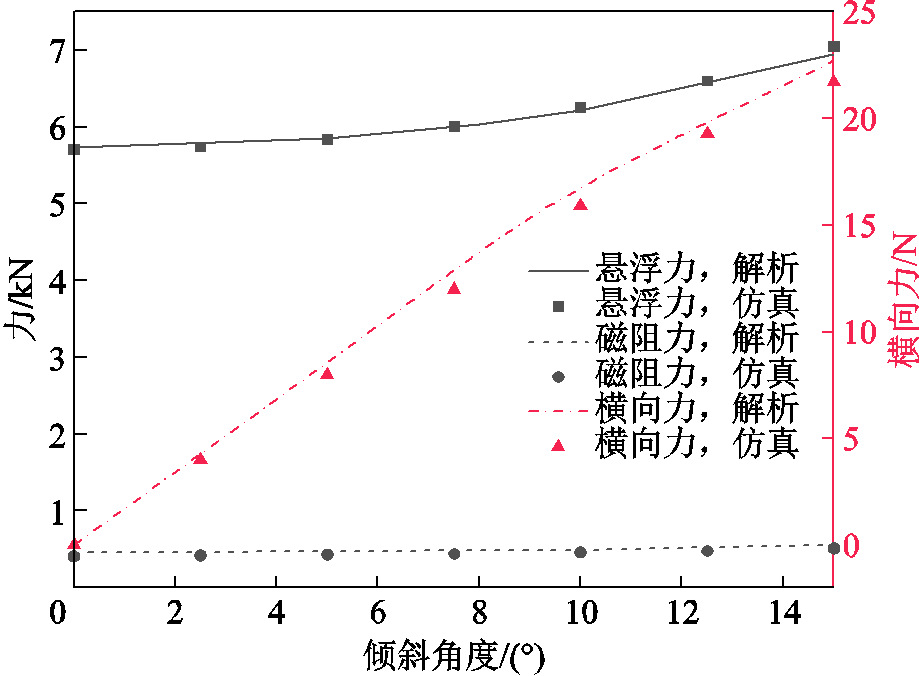
图17 速度300 km/h时电磁力随倾斜角度变化曲线
Fig.17 Curves of electromagnetic force with tilt angle at 300 km/h
4.2.3 磁体偏转
磁体偏转后,磁体中心线与X轴存在夹角。磁体仍沿X轴方向运动,悬浮力与磁阻力的定义与前面相同。图18展示了当v=300 km/h、间隙为30 mm时,磁体偏转角对悬浮力、和磁阻力的影响。随着偏转角的增大,悬浮力和磁阻力均有所减小。在图示偏转角范围,磁体没有偏出导体板区域,悬浮力与磁阻力的变化较小。
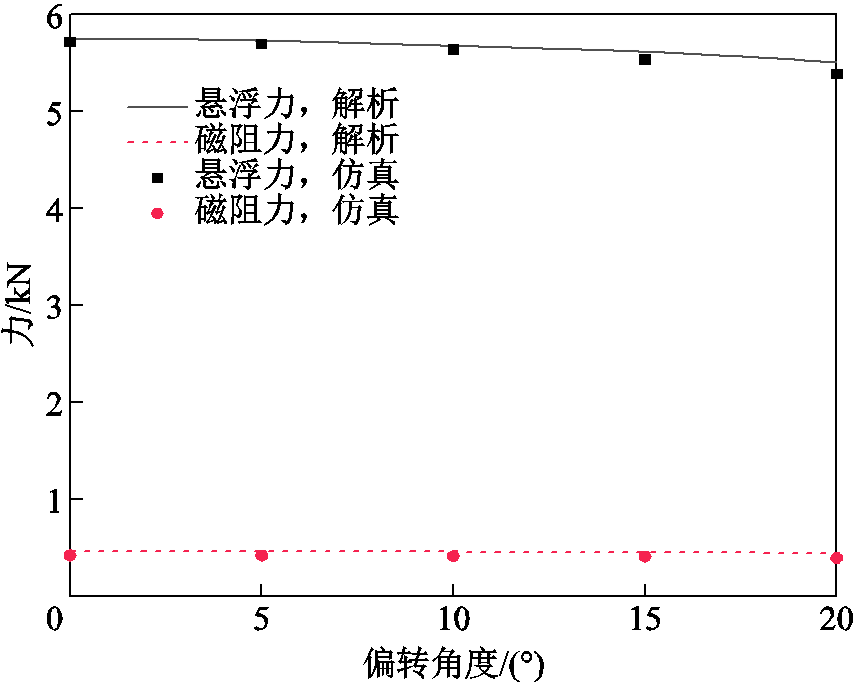
图18 速度300 km/h,间隙30 mm时悬浮力和磁阻力随偏转角度变化曲线
Fig.18 Curves of levitation and drag force with deflection angle at 300 km/h and gap=30 mm
4.2.4 磁体横移
永磁电动悬浮没有横向导向力,当受到外界扰动时磁体可能偏离出轨道边缘,如图19所示。
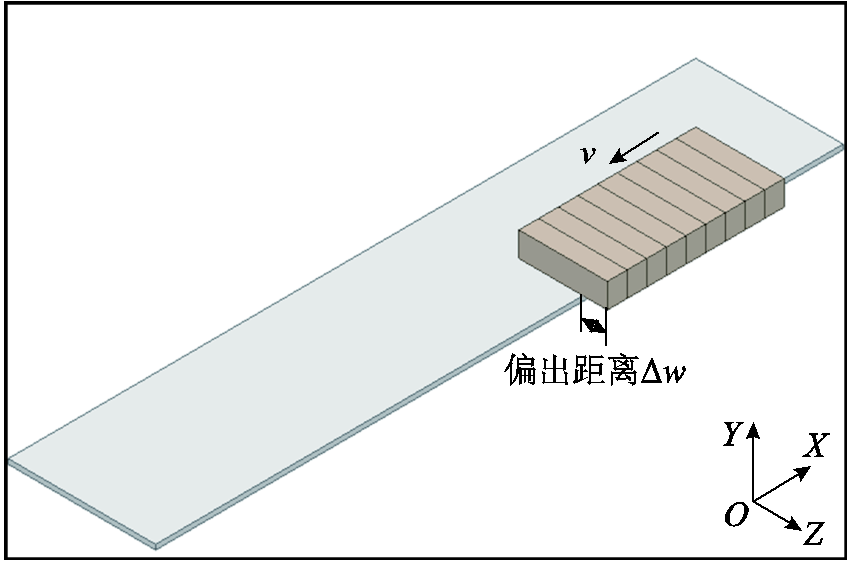
图19 磁体偏离轨道示意图
Fig.19 Schematic diagram of the deviation of magnets
在速度为300 km/h、悬浮间隙为30 mm、磁体偏离出轨道距离Δw为60 mm时,通过仿真得到电磁力随速度的变化如图20所示,对比图9和图10可以看出当磁体偏出轨道边缘,悬浮力与磁阻力相比磁体居中运行状态均会减小,同时还会有横向力产生。图20中给出的是横向力的绝对值,横向力的实际方向与磁体偏出轨道的方向相同,表明横向力会加剧磁体的偏离。悬浮力与磁阻力随速度变化规律不变,横向力与悬浮力类似,随着运行速度的提升而逐渐增大并趋于稳定。图21给出了电磁力随磁体偏出轨道距离变化的曲线。当磁体偏出轨道运行时,随着偏移位移的增加,磁体与轨道相互作用面积减小,悬浮力与磁阻力均随着偏移距离的增加而线性衰减。不同于悬浮力与磁阻力,横向力随着偏离距离的增加会先增大后减小,图21中在偏离距离约为60 mm,即大约为磁体宽度三分之一时,横向力达到最大。从图22可以看出,不同运行速度下,这一位置变化不大。
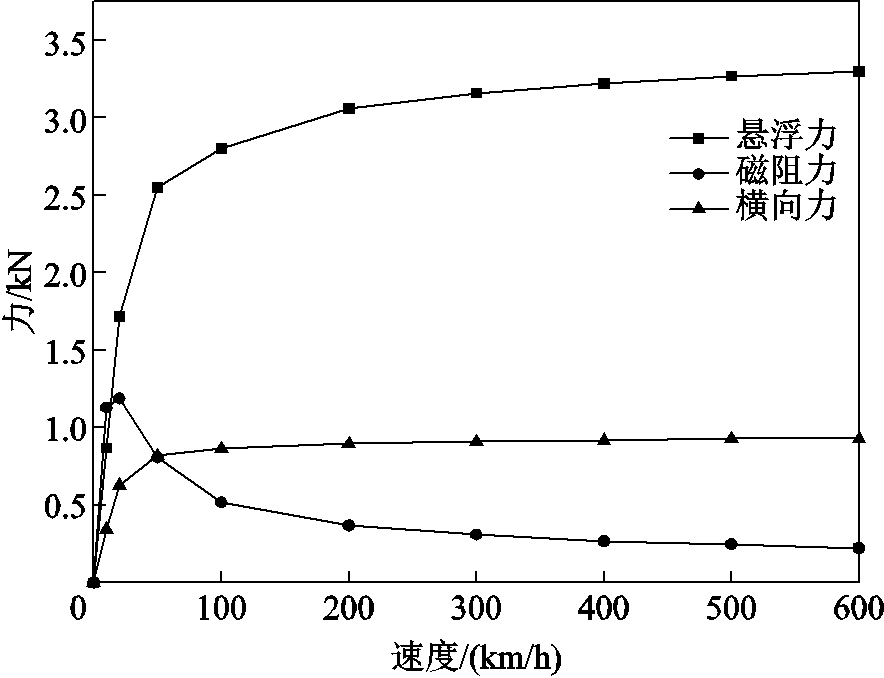
图20 磁体偏出轨道60 mm时电磁力随速度变化
Fig.20 Electromagnetic force with speed atΔw = 60 mm
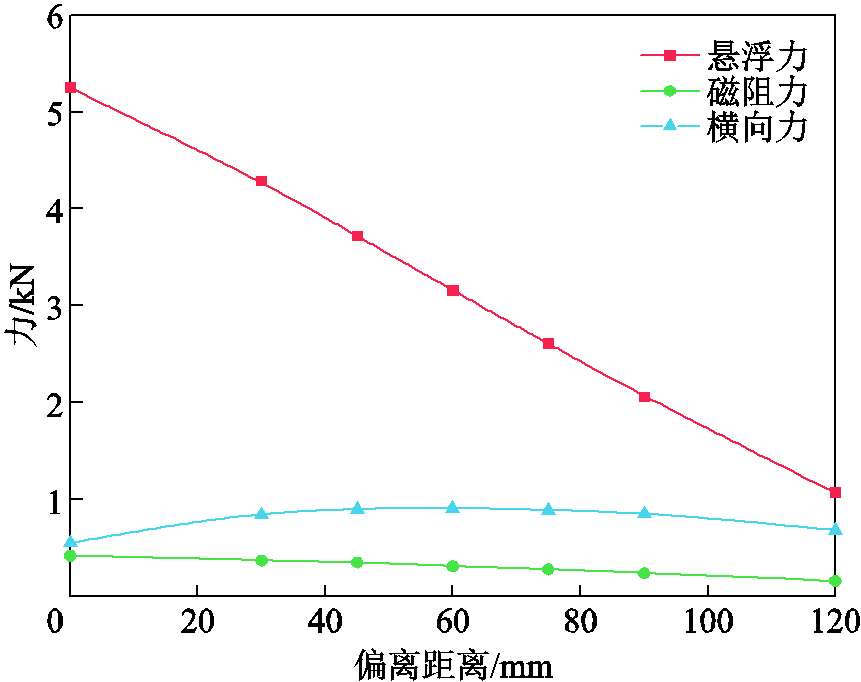
图21 速度300 km/h,间隙30 mm时电磁力随偏离距离变化曲线
Fig.21 Curves of electromagnetic forces with offset Δw when v=300 km/h and gap=30 mm
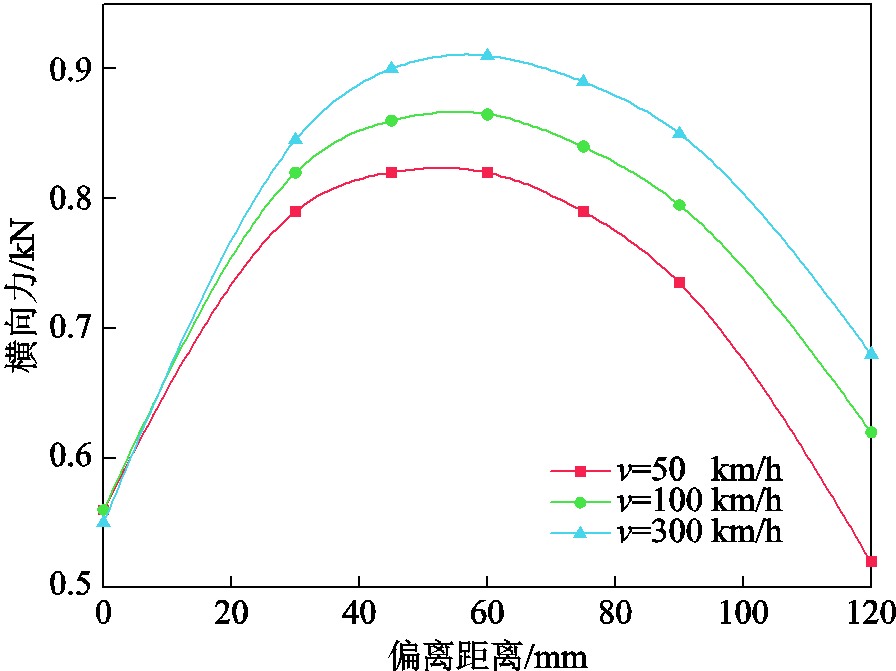
图22 间隙30 mm时不同速度下横向力随偏离距离变化曲线
Fig.22 Curves of lateral force with offset at different speeds when gap=30 mm
前文通过解析及有限元仿真方法对永磁电动悬浮系统不同工况的电磁力特性进行了分析,为了进一步验证解析计算及有限元模型的可靠性,本节利用高速动轨实验台开展相关实验进行验证。首先对实验平台进行介绍;其次测试在固定间隙、不同速度下的电磁力,将其与解析和仿真结果对比,验证解析和仿真模型的准确性;最后针对前文分析的磁体水平居中工况、磁体横移工况进行实验验证。
永磁电动悬浮系统高速实验台实物如图23所示。该实验台主要由交流电机、制动系统、传动机构、弧形永磁体阵列、环形旋转轨道、监测控制平台组成[36]。利用轨道的旋转代替平移运动,铝合金轨道内圆直径为2 210 mm,较大的轨道直径提高了等效的准确性。轨道转子动平衡精度为G2.5,转速控制精度为±1%,定位精度达0.01 mm,最高线速度可达600 km/h。当轨道旋转时,三轴传感器可实时获取作用在永磁体上的电磁力并在检测平台显示。在监测控制平台上可操纵伺服电动机驱动滑台机构使永磁体阵列在横向和垂向移动,调整永磁体阵列的位置。该实验台可开展不同速度、不同悬浮间隙下的电磁力实验测试。表2给出了该实验台的主要参数。

图23 永磁电动悬浮系统高速实验台实物
Fig.23 Physical photo of high-speed test rig for PMEDS system
表2 高速动轨实验台主要参数
Tab.2 Dominating specifications of the high-speed rotary test rig

参数数值 永磁体材料NdFeB-N50 磁化角/(°)90 单块永磁体长度/mm30 单块永磁体宽度/mm100 单块永磁体高度/mm30 剩磁/T1.45 磁体数/块9 铝合金轨道宽度/mm165 铝合金轨道厚度/mm30
首先,利用表2所示的实验台磁体与轨道参数建立解析和仿真模型求解电磁力,与实验结果进行对比,验证正常工况下的解析和仿真模型。图24给出了在悬浮间隙为25 mm时,解析计算、仿真和实验测试电磁力随速度变化的对比曲线。可以看出,解析、仿真与实验得到的电磁力随速度变化趋势一致,数值上存在差异的原因主要有:实验采用旋转等效直线运动产生的误差、实验台电导率与解析和仿真模型电导率的偏差、铝合金轨道的温升影响。总体而言,电磁力结果基本吻合,证明了解析和仿真模型的正确性。
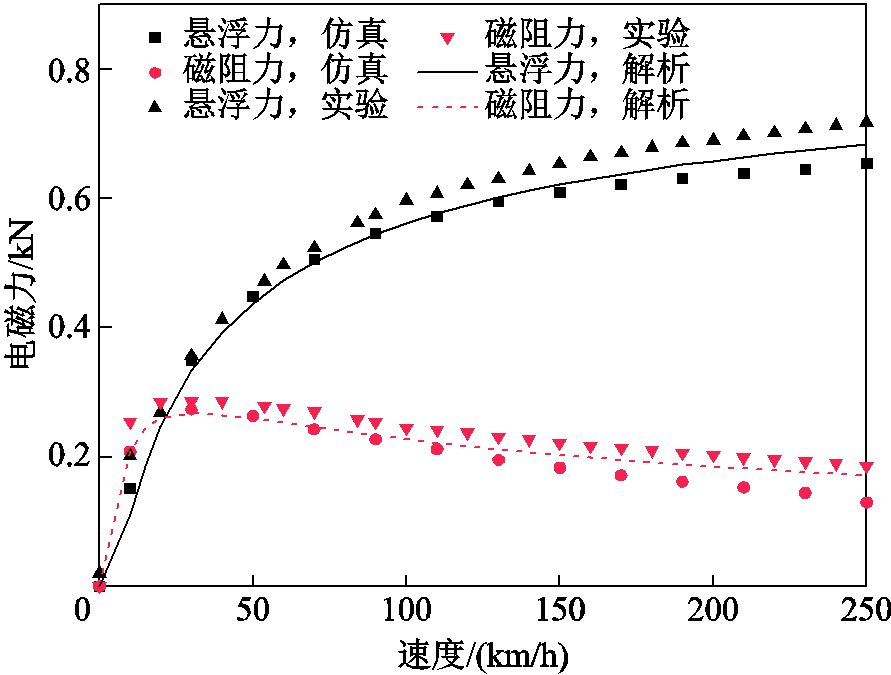
图24 电磁力的仿真,实验与解析结果对比
Fig.24 Comparison of electromagnetic forces between simulation, experiment and analytic results
对于磁体横移工况,也建立了相应的有限元模型与实验对比。图25给出了在悬浮间隙为25 mm、磁体偏离出轨道距离Δw为磁体宽度三分之一时,仿真和实验得到的电磁力随速度变化的曲线。可以看出,仿真和实验测试的电磁力随速度变化趋势一致,有限元模型的有效性得到验证。
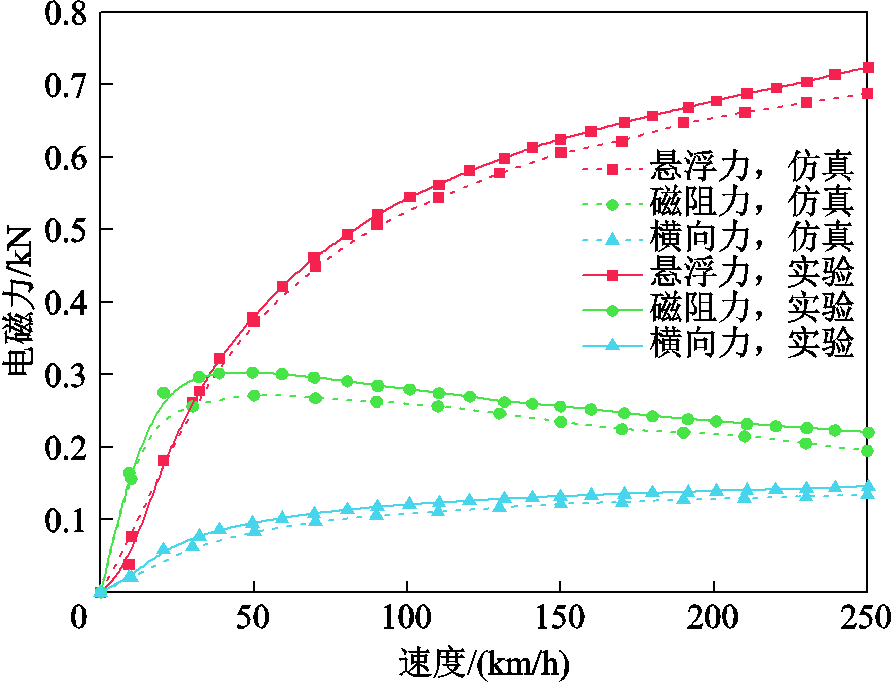
图25 横移工况电磁力仿真与实验结果对比
Fig.25 Comparison of electromagnetic forces between simulation and experiment results under deviated condition
5.2.1 正常工况
图26和图27展示了永磁体阵列正常居中时,悬浮间隙分别为20 mm、25 mm、30 mm,铝合金轨道从0逐渐加速到250 km/h过程中,与永磁体阵列相互作用所产生的悬浮力和磁阻力曲线。由图可知,在不同间隙下,随着速度的增加,悬浮力均逐渐增大,磁阻力均先迅速增加达到峰值然后下降,这与前面的分析一致。
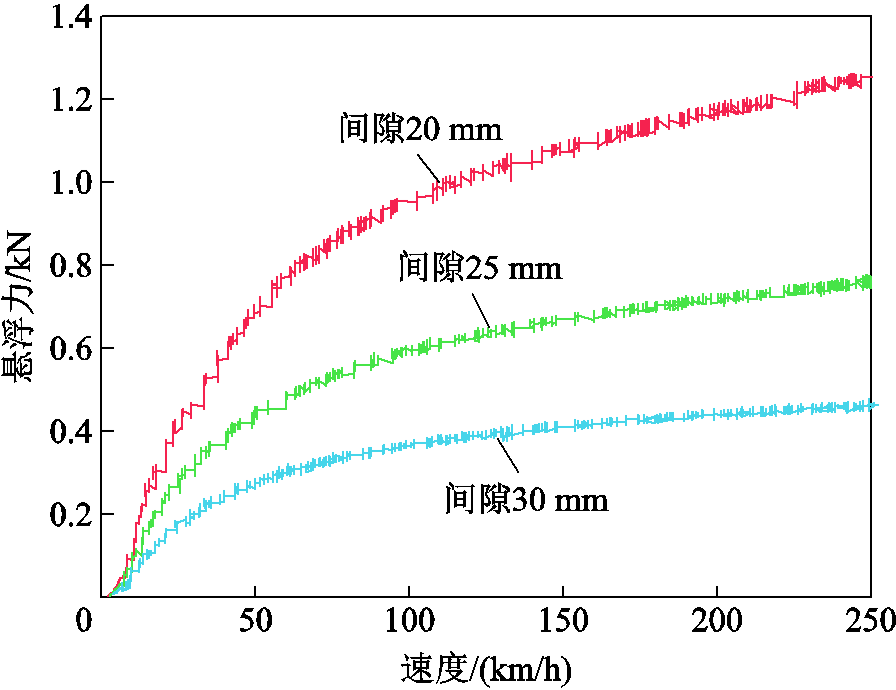
图26 不同间隙下悬浮力的实验结果
Fig.26 Experiment results of levitation forces under different air gaps
图28展示了在铝合金轨道速度为150 km/h、初始间隙为20 mm时,磁体阵列向上移动25 mm再向下移动回到初始位置过程中,悬浮力和磁阻力的变化曲线。同前文分析,悬浮力和磁阻力与悬浮间隙呈指数函数关系,系统垂向有自稳定能力,悬浮力会随悬浮间隙变化而发生相应变化从而使磁体恢复到初始位置。
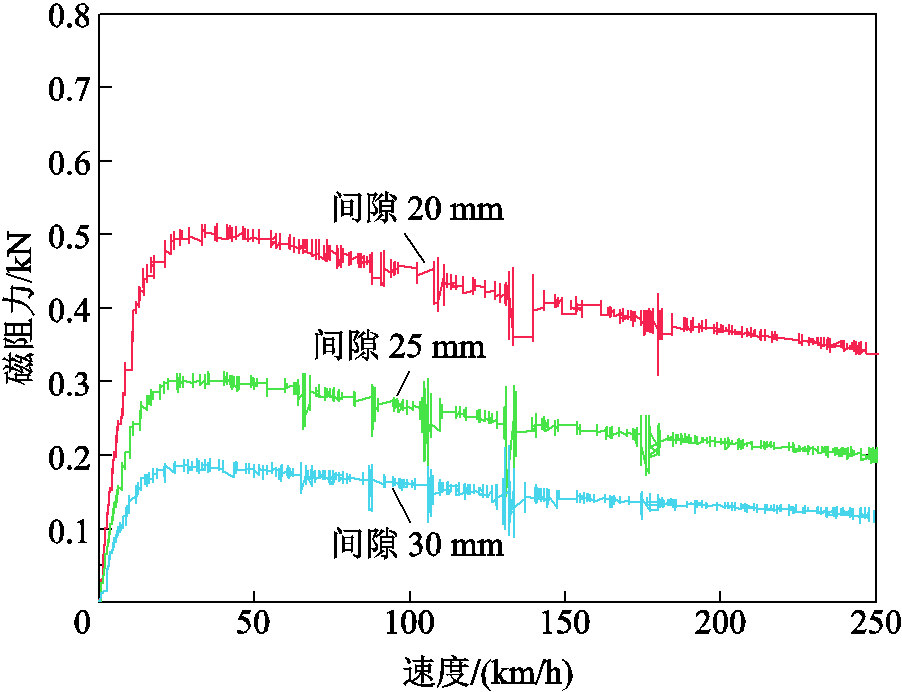
图27 不同间隙下磁阻力的实验结果
Fig.27 Experiment results of drag forces under different air gaps
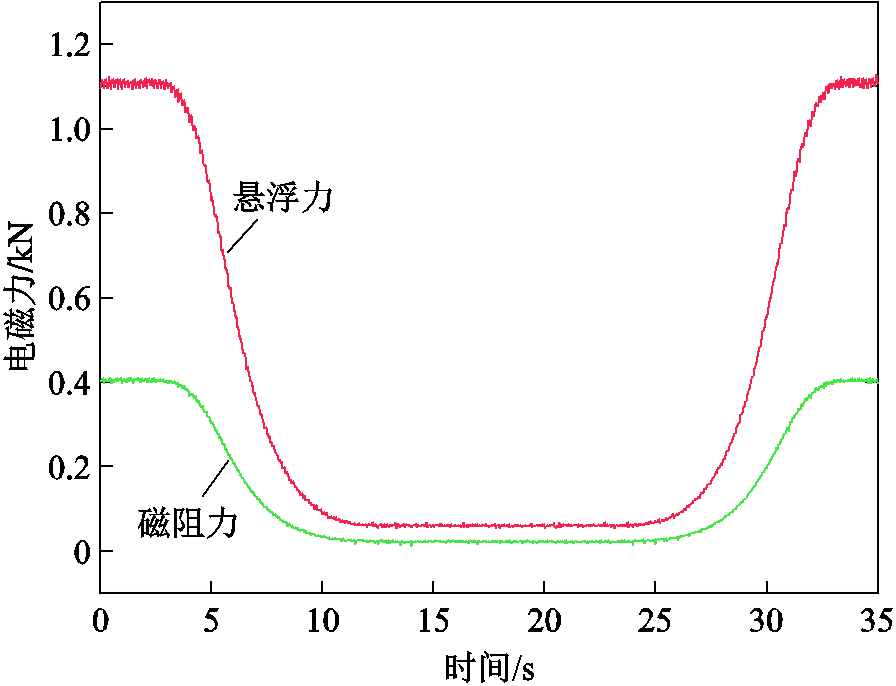
图28 磁体上下运动过程中测试的电磁力变化
Fig.28 Evolution of levitation and drag forces measured under upward and downward movement
5.2.2 磁体横移
图29为铝合金轨道速度为150 km/h、悬浮间隙为20 mm时,磁体阵列从轨道外移进至轨道中央位置再移出轨道过程中,电磁力的变化曲线。在进入和离开轨道过程,悬浮力和磁阻力随横移距离变化线性变化。随磁体横移出现横向力,横向力变化趋势为先增大后减小。磁体进入和离开轨道过程中,横向力均指向轨道外方向,即阻碍了磁体回到轨道中央位置。
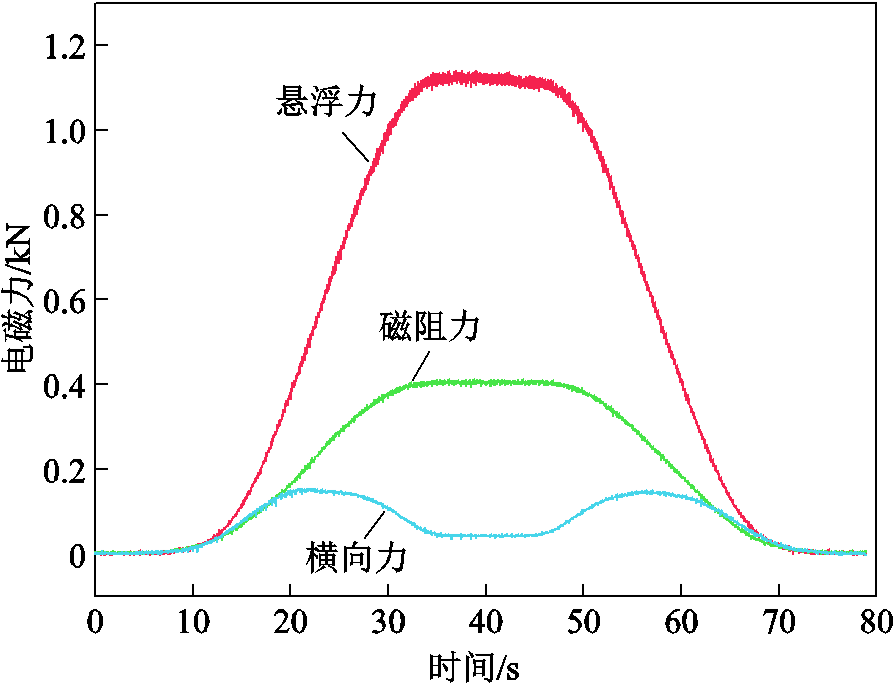
图29 磁体横向移动过程中测试的电磁力变化
Fig.29 Evolution of electromagnetic forces measured under lateral movement
对不同偏离位置,即偏出轨道距离分别为0,磁体宽度的1/5、1/3、1/2、2/3,悬浮间隙为20 mm,不同速度下的悬浮力、磁阻力和横向力进行测试,结果分别如图30、图31和图32所示。不同偏离位置,悬浮力和磁阻力随速度变化的规律均不变,横向力呈现出与悬浮力类似的规律。在不同速度下,当偏出距离为磁体宽度的1/3时,横向力达到最大。
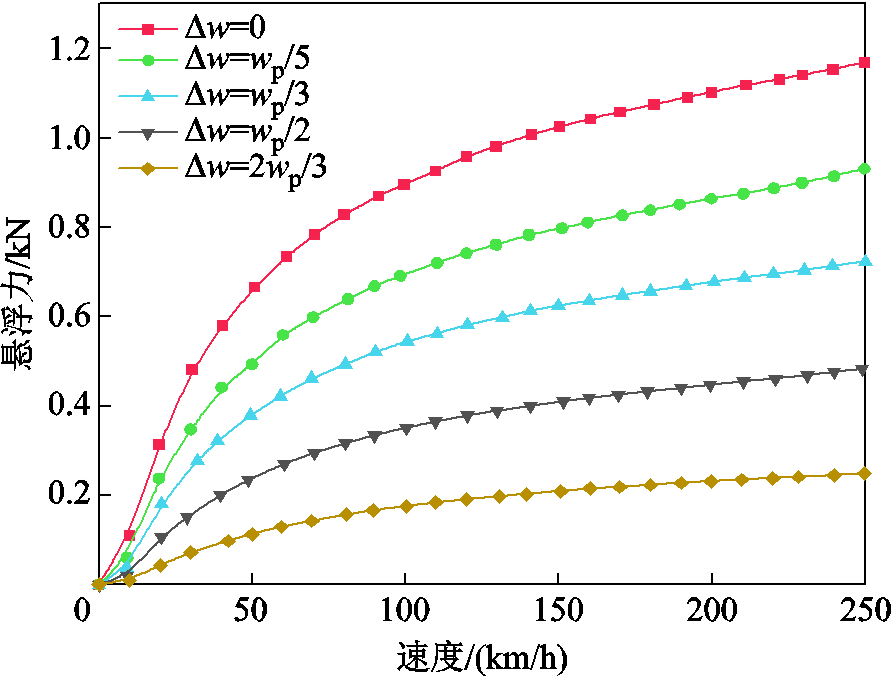
图30 不同偏离位置下悬浮力的实验结果
Fig.30 Experiment results of levitation forces under different offsets
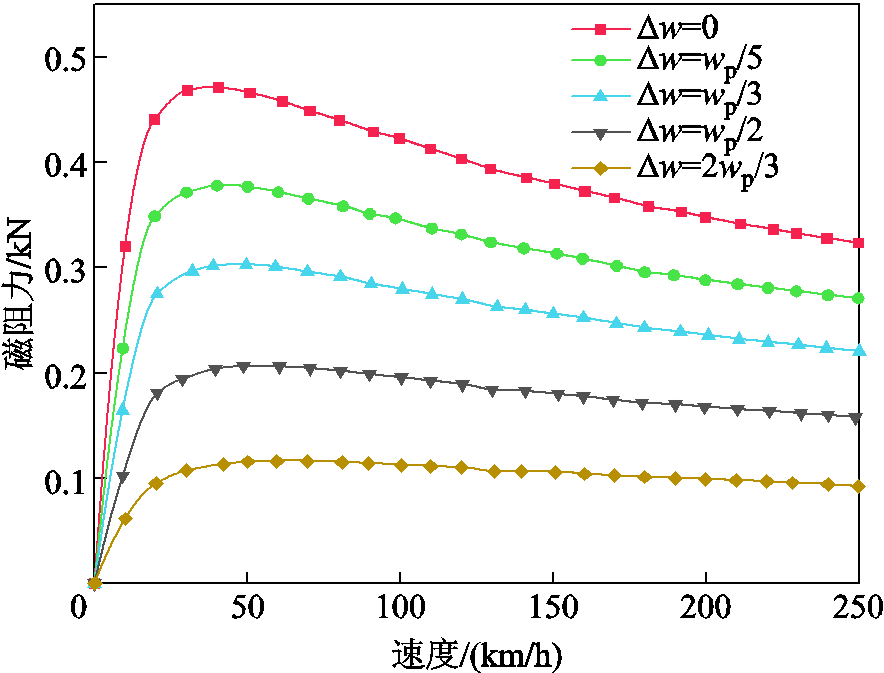
图31 不同偏离距离下磁阻力的实验结果
Fig.31 Experiment results of drag forces under different offsets
本文以板式永磁电动悬浮系统为研究对象,推导了Halbach永磁体阵列在水平、倾斜、偏转状态下的磁场分布函数,建立了适用于系统多工况的电磁力三维解析模型,结合有限元仿真,对系统正常居中、倾斜、偏转、横移工况下的电磁力特性进行了分析。研究结果表明,永磁电动悬浮系统具有垂向自稳定能力,悬浮力与磁阻力随悬浮间隙变化呈指数函数变化。磁体的倾斜使悬浮力和磁阻力略微增大,且电磁力随倾斜角度的增大而增大。磁体偏转后,悬浮力和磁阻力减小,且随偏转角度的增大而减小。当磁体横向偏离轨道板时,会产生磁体偏离方向的横向力,加剧磁体偏离,其随着偏离距离的增加先增大后减小,在偏离距离约为磁体宽度1/3时达到最大,悬浮力和磁阻力则是线性减小。这项工作为永磁电动悬浮的工程应用和设计提供了参考。
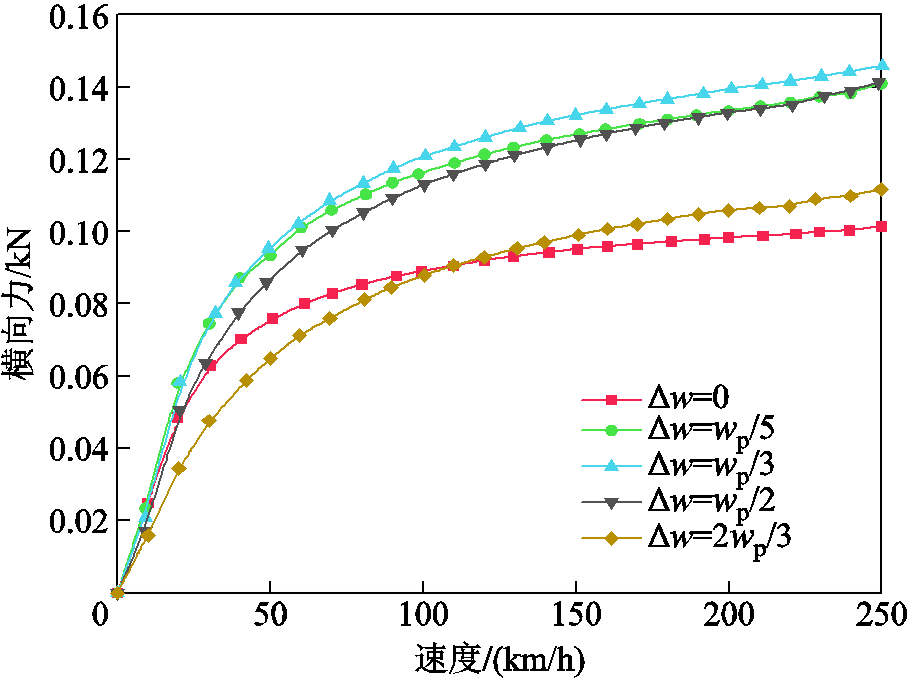
图32 不同偏离距离下横向力的实验结果
Fig.32 Experiment results of lateral forces under different offsets
参考文献
[1] 张瑞华, 严陆光, 徐善纲, 等. 几种典型的高速磁悬浮列车方案比较[J]. 电工电能新技术, 2004, 23(2): 46-50.
Zhang Ruihua, Yan Luguang, XU Shangang, et al. Comparison of several projects of high speed maglev[J]. Advanced Technology of Electrical Engineering and Energy, 2004, 23(2): 46-50.
[2] 邓自刚, 刘宗鑫, 李海涛, 等.磁悬浮列车发展现状与展望[J]. 西南交通大学学报, 2022, 57(3): 455-474.
Deng Zigang, Liu Zongxin, Li Haitao, et al. Development status and prospect of maglev train[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 455-474.
[3] 章九鼎, 卢琴芬. 长定子直线同步电机齿槽效应的计算与影响[J]. 电工技术学报, 2021, 36(5): 964- 972, 1026.
Zhang Jiuding, Lu Qinfen. Calculation and influences of cogging effects in long-stator linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 964-972, 1026.
[4] 赵牧天, 葛琼璇, 朱进权, 等. 中速磁悬浮列车分段式长定子永磁直线同步电机牵引控制策略[J]. 电工技术学报, 2022, 37(10): 2491-2502.
Zhao Mutian, Ge Qiongxuan, Zhu Jinquan, et al. Traction control strategy of segmented long stator permanent magnet linear synchronous motor for medium-speed maglev train[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2491-2502.
[5] 朱进权, 葛琼璇, 张波, 等. 考虑悬浮系统影响的高速磁悬浮列车牵引控制策略[J]. 电工技术学报, 2022, 37(12): 3087-3096.
Zhu Jinquan, Ge Qiongxuan, ZhangBo, et al. Traction control strategy of high-speed maglev considering the influence of suspension system[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3087-3096.
[6] 张明远, 史黎明, 范满义, 等. 长初级双边直线感应电动机分段推力协同控制和测速算法[J]. 电工技术学报, 2023, 38(3): 659-669.
Zhang Mingyuan, Shi Liming, Fan Manyi, et al. Thrust cooperative control and speed measurement algorithm of segmented long primary double-sided linear induction motor[J]. Transactions of China Electro-technical Society, 2023, 38(3): 659-669.
[7] 温旭辉, 徐善纲. 电动式磁悬浮系统分析综述[J]. 电工电能新技术, 1995(3): 7-11.
Wen Xuhui, Xu Shangang. Analysis of electrodynamic levitation systems[J]. Advanced Technology of Electrical Engineering and Energy, 1995, 14(3): 7-11.
[8] 秦伟, 马育华, 吕刚, 等. 一种可用于低真空管道的高温超导无铁心直线感应磁悬浮电机[J]. 电工技术学报, 2022, 37(16): 4038-4046.
Qin Wei, Ma Yuhua, Lü Gang, et al. Analyzing and designing a novel coreless linear induction maglev motor for low vacuum pipeline[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4038-4046.
[9] Storset O F, Paden B E. Discrete track electrodynamic maglev Part I: modelling[J]. IEEE Transactions on Magnetics, 2005: 410-447.
[10] 石洪富, 邓自刚, 黄欢, 等. 零磁通线圈式永磁电动悬浮系统设计及特性研究[J]. 西南交通大学学报, 2023, 58(4): 853-862.
Shi Hongfu, Deng Zigang, Huang Huan, et al. Design and characteristic of null-flux permanent magnet electrodynamic suspension system[J]. Journal of Southwest Jiaotong University, 2023, 58(4): 853-862.
[11] 王一宇, 蔡尧, 宋旭亮, 等. 零磁通式电动悬浮等效模拟系统的特性分析与实验[J]. 电工技术学报, 2021, 36(8): 1628-1635.
Wang Yiyu, Cai Yao, Song Xuliang, et al. Characteristic analysis and experiment of the equivalent simulation system for null-flux electrodynamic suspension[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1628-1635.
[12] Shi Hongfu, Deng Zigang, Zhang Baojian, et al. Thermal-Force Coupling Analysis of Permanent Magnet Electrodynamic Wheel System for Maglev Car[J]. IEEE Transactions on Magnetics, 2023, 59(1): 6300109.
[13] Cho H W, Han H S, Bang J S, et al. Characteristic analysis of electrodynamic suspension device with permanent magnet Halbach array[J]. Journal of Applied Physics, 2009, 105(7): 07A314.
[14] 李春生, 杜玉梅, 夏平畴, 等. 直线型Halbach磁体和导体板构成的电动式磁悬浮系统的分析及实验[J]. 电工技术学报, 2009, 24(1): 18-22.
Li Chunsheng, Du Yumei, Xia Pingchou, et al. analysis and experimental testing of eds maglev with linear halbach and conducting sheet[J]. Transactions of China Electrotechnical Society, 2009, 24(1): 18-22.
[15] Post R F, Ryutov D D. The Inductrack: A simpler approach to magnetic levitation[J]. IEEE Transactions on Applied Superconductivity, 2000, 10(1): 901-904.
[16] Space X. Hyperloop alpha[Z/OL]. http://www.spacex. com/hyperloopalpha, accessed October 2017.
[17] Rote D M, Cai Yigang. Review of dynamic stability of repulsive-force maglev suspension systems[J]. IEEE Transactions on Magnetics, 2002, 38(2): 1383-1390.
[18] 郑杰. 感应线圈对磁浮系统性能影响研究[D]. 长沙: 国防科学技术大学, 2006.
Zheng Jie. Study on effect of induction coil on performance of maglev system[D]. Changsha: National University of Defense Technology, 2006.
[19] Cheng Yuwei, He Guang, Long Zhiqiang. Vertical dynamic stability analysis of EDS levitation systems based on Halbach magnet arrays[C]//2009 Chinese Control and Decision Conference (CCDC 2009). New York: IEEE, 2009: 3726-3730.
[20] Ham C, Ko W, Lin K C, et al. Study of a hybrid magnet array for an electrodynamic maglev control[J]. Journal of Magnetics, 2013, 18(3): 370-374.
[21] 贺光. 基于Halbach结构的永磁电动与电磁混合悬浮技术研究[D]. 长沙: 国防科学技术大学, 2010.
He Guang. Research on permanent-magnet EDS and EMS hybrid suspension system based on Halbach structure[D]. Changsha: National University of Defense Technology, 2010.
[22] Wang Jiangbo, Li Yaohua and Yan Luguang. Study on applying the linear Halbach array to eddy current brake system[J]. International Symposium on Applied Electromagnetics and Mechanics, 2010, 33(1): 111-118.
[23] 王厚生. 永磁电动式导体板磁悬浮列车轨道结构及相关研究[D]. 北京: 中国科学院电工研究所, 2004.
Wang Housheng. Research on PM DMS conducting sheet maglev guideways construction[D]. Beijing: Institute of Electrical Engineering of CAS, 2004.
[24] Paul S, Bird J Z. A 3-D analytic eddy current model for a finite width conductive plate[J]. COMPEL-The International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2014, 33(1-2): 688-706.
[25] Bird J Z, Paul S. Analytic 3-D eddy current model of a finite width conductive plate including edge-effects[J]. International Journal of Applied Electro-magnetics and Mechanics, 2014, 45(1-4): 535-542.
[26] 陈殷. 低速永磁电动悬浮电磁力特性研究[D]. 成都: 西南交通大学, 2015.
Chen Yin. Characteristic analysis of electromagnetic forces created by low-speed PM electrodynamic suspension[D]. Chengdu: Southwest Jiaotong University, 2015.
[27] Chen Yin, Zhang Wenlong, Bird J Z, et al. A 3-D Analytic-based model of a null-flux halbach array electrodynamic suspension device[J]. IEEE Transactions on Magnetics, 2015, 51(11): 8300405.
[28] 巫川, 李冠醇, 王东. 永磁电动悬浮系统三维解析建模与电磁力优化分析[J]. 电工技术学报, 2021, 36(05): 924-934.
Wu Chuan, Li Guanchun, Wang Dong. 3-D analytical modeling and electromagnetic force optimization of permanent magnet electrodynamic suspension system[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 924-934.
[29] Shi Tongyu, Wang Dazhi. 3D Analytical model of drag and lift force for a conductive plate moving above a Halbach magnet array[J]. Transactions of the Institute of Measurement and Control, 2018, 40(12): 3515-3524.
[30] Hu Yongpan, Long Zhiqiang, Zeng Jiewei, et al. Analytical Optimization of Electrodynamic Suspension for Ultrahigh-Speed Ground Transportation[J]. IEEE Transactions on Magnetics, 2021, 57(8): 8000511.
[31] Iniguez J, Raposo V. Numerical simulation of a simple low-speed model for an electrodynamic levitation system based on a Halbach magnet array[J]. Journal of Magnetism and Magnetic Materials, 2010, 322(9-12): 1673-1676.
[32] Han Q, Ham C, Phillips R. Four- and eight-piece Halbach array analysis and geometry optimisation for Maglev[J]. IEE Proceedings-Electric Power Applications, 2005, 152(3): 535-542.
[33] Ma Guangtong, Liu Huifen, Wang Jiasu, et al. 3D modeling permanent magnet guideway for high temperature superconducting maglev vehicle application[J]. Journal of Superconductivity and Novel Magnetism, 2009, 22(8): 841-847.
[34] 秦伟, 马育华, 张洁龙, 等.不均匀气隙工况下轴向磁通永磁电动式磁悬浮电机的磁场与力特性分析[J]. 电工技术学报, 2023, 38(4): 889-902.
Qin Wei, Ma Yuhua, Zhang Jielong, et al. characteristic and magnetic field analysis of an axial flux permanent magnets maglev motor with non-uniform air gap[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 841-847.
[35] 石洪富, 邓自刚, 柯志昊, 等. 平板式永磁电动悬浮系统设计与实验研究[J]. 电工技术学报, 2024, 39(5): 1270-1283.
Shi Hongfu, Deng Zigang, Ke Zhihao, et al. Design and test of the flat-type permanent magnet electromagnetic suspension system[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1270-1283.
[36] Deng Zigang, Zhang Weihua, Wang Li, et al. A high-speed running test platform for high-temperature superconducting maglev[J]. IEEE Transactions on Applied Superconductivity, 2022, 32(4): 3600905.
Investigation of Electromagnetic Force Characteristics of Permanent Magnet Electrodynamic Suspension under Multi-Operation Conditions
Abstract Due to the weak damping properties of permanent magnet electrodynamic suspension (PMEDS) system, the position and orientation of the onboard magnets are easily disturbed under external forces, thereby affecting the electromagnetic force characteristics of the system. Several studies have been carried out on the electromagnetic force characteristics of the PMEDS system under a normal condition in which magnets are in a horizontal state. The influence of the position and orientation of the magnets on the electromagnetic force characteristics is rarely considered. To investigate the electromagnetic force characteristics under various typical operating conditions such as magnets tilt, lateral deviation, and deflection, a comprehensive analysis is performed through analytical calculations, simulation analyses, and experimental verifications.
Firstly, the fundamental structure and principles of the PMEDS system are introduced. Then, the magnetic field distribution functions for Halbach permanent magnet arrays in horizontal, tilted, and deflected states are derived using the Biot-Savart Law, as well as coordinate translation and rotation transformation. Based on the magnetic vector potential, a comprehensive three-dimensional analytical model is developed to accommodate various operating conditions. Secondly, a three-dimensional finite element simulation model is developed. The comparison between the analytical calculations and simulation results for magnetic field and electromagnetic force under identical parameters demonstrates the accuracy and reliability of the analytical model. Combined analytical calculations with simulations, the levitation-drag characteristics of the system are analyzed at different air gaps, as well as the influence of air gap and conductive plate width on levitation and drag forces under the normal condition. The results reveal that the PMEDS system exhibits vertical self-stability ability, and the evolution of levitation and drag forces with air gap follows an exponential function. With the increasing conductive plate width, the levitation force initially increases and then stabilizes, while the drag force first increases and then decreases. Furthermore, the influence of magnet tilt, deflection and lateral deviation on the electromagnetic force are analyzed. Compared with the normal condition, the levitation force and drag force increase slightly under the magnets tilt condition. Additionally, the lateral force is generated. With increasing speed, it increases first and then decreases. As the tilt angle increases, the levitation force, drag force and lateral force all increase. When the magnets are deflected, the levitation force and drag force decrease, with a further decrease as the deflection angle increases. Lateral deviation of the magnets from the conductive plate generates a lateral force, exacerbating the deviation. The lateral force increases with the increase of the speed and tends to be stable. As the deviation distance increases, both the levitation force and drag force linearly decrease, while the lateral force initially increases and then decreases, reaching its maximum at approximately one-third of the magnet width. Finally, using a high-speed rotary test rig with a maximum design speed of 600 km/h, the electromagnetic forces under various speeds at the given air gap are tested under normal and deviated conditions. By comparing the results from analysis, simulation and experiment, the accuracy of the analytical model and simulation is verified. Besides, the electromagnetic forces under vertical and lateral movement of magnets are also tested. The results confirm the vertical self-stability ability of the PM EDS system and the variation of electromagnetic forces with lateral deviation distance.
Keywords:Permanent magnet electrodynamic suspension, multi-operation conditions, electromagnetic force characteristics, analytical calculation, high-speed test rig, Halbach array
中图分类号:TM154.2
DOI: 10.19595/j.cnki.1000-6753.tces.231098
收稿日期 2023-07-10
改稿日期 2023-07-31
曹 婷 女,1999年生,硕士研究生,研究方向为磁悬浮理论及应用。
E-mail:ctsf027@163.com
邓自刚 男,1982年生,研究员,博士生导师,研究方向为超导磁悬浮技术及应用。
E-mail:deng@swjtu.cn(通信作者)
(编辑 郭丽军)