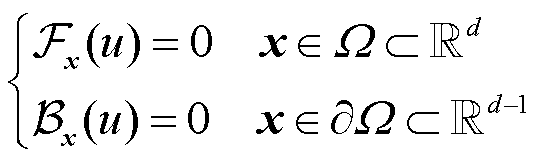 (1)
(1)
摘要 物理信息神经网络(PINNs)将偏微分方程(PDEs)及其定解条件编码进网络中,使PDEs残差最小化的同时逼近定解条件,实现PDEs的求解。由于电磁场计算时存在局部高梯度问题、含源方程引发的训练困难问题和高对比系数界面识别问题等,PINNs在用于电磁场方程求解时训练效率低、计算精度不高,因而目前应用较少。该文对于PINNs在电磁场中的训练困难问题进行理论分析,提出了针对电磁场PDEs形式和神经网络架构的修改方法,实现了基于PINNs的静电场和稳恒磁场求解,计算结果准确性较好。将该方法推广到方程更加复杂的频域涡流场求解中,求解结果表明PINNs可以在复杂的频域方程上保证良好的精度。该研究工作为实现电磁场快速计算提供了新思路。
关键词:物理信息神经网络 电磁场数值计算 深度学习
目前,深度学习已经在自然语言处理、计算机视觉等领域取得显著性成果[1],例如,ChatGPT是一种基于Transformer的语言模型。深度学习由于其对高维参数空间的强大计算能力,目前已经在电磁场逆问题中实现了应用,成为了电磁优化设计的未来趋势,最终服务于电磁场的快速计算[2]。尽管仅依靠标签数据会使得实施过程变得简单,然而这些基于数据驱动的深度学习模型目前仍存在低精度或非物理解问题[3]。
近年来,深度神经网络更是成为偏微分方程(Partial Differential Equations, PDEs)正反问题求解领域的研究热点,M. Raissi等[4]于2019年提出的物理信息神经网络(Physics Informed Neural Networks, PINNs)被广泛用于多个领域的偏微分方程求解,此方法以下称为标准PINNs。此类使用神经网络参数化PDE解的方法还包括鄂维南院士等[5]基于能量泛函提出的深度里兹方法(Deep Ritz Method, DRM),用于求解各种PDE变分问题;文献[6]依据Petrov-Galerkin方法与神经网络的相似性,将分片多项式的基函数空间更换成神经网络空间,提出了深度伽辽金方法(Deep Galerkin Method, DGM)并在高维问题上进行了验证。在这些偏微分方程求解的智能算法中PINNs的应用最为广泛。
PINNs的思想是将控制方程作为神经网络的损失函数的一部分,在确保网络输出逼近边界条件(Boundary Conditions, BCs)或观测数据的同时约束其在求解域内满足控制方程。尽管使用神经网络进行PDE的求解的思想早在20世纪90年代已经出现[7],但是出于硬件、算法和软件的原因并没有得到发展。如今得益于计算机并行计算硬件图形处理单元GPU、非凸优化算法的发展以及自动微分方法的部署[8],目前PINNs已经被应用到包括电磁波[9]、声波[10]、流体[11-12]和力学[13-14]等众多领域,并且涌现出众多PINNs架构,如DeepXDE[15]、Modulus[16]和Mindspore[17]等。PINNs的优势是可以直接使用基于链式求导法则的自动微分方法计算时空导数,是一种典型的无网格算法。区别于基于径向基、移动最小二乘法等形函数对于空间位置进行插值拟合,PINNs使用神经网络可以对除时空变量以外的其他变量进行插值,从而直接求解参数化PDE,因此PINNs在高维问题上具备优势,Nvidia公司于2020年将其应用于DGX-1散热器的设计式仿真[18],大幅节省了计算成本。
虽然PINNs具备直接求解参数化PDE的能力,但是标准PINNs的训练过程困难且精度有限[19]。目前PINNs在低频电磁场领域应用非常少,可查阅的研究仅局限于静电场[20]、静磁场[20-21]。由于文献[20-21]均采用标准PINNs,其注重通过超参数调节获得表现良好的模型。然而相比数据驱动的深度学习,PINNs通过超参调节获取和复现准确结果非常困难,这是出于PINNs特有的梯度病理性原因[22],因此本文不关注超参数,调节过程中的模型而是研究PINNs方法求解电磁场PDE的过程中的模型参数以及对于其精度提升和收敛效率的影响。经过理论分析和实践发现,主要原因在于神经网络本身的光滑性和频率偏好[23],以及PINNs方法与PDEs结合过程中带来的困难。
频率偏好指的是神经网络倾向于优先使用低频或大尺度特征来拟合目标函数,如果目标函数具有低频占优的特性,那么深度学习比较容易取得很好的效果[23]。在电磁场中的高梯度现象属于高频特性的一种,因此考虑数据驱动深度学习中傅里叶特征嵌入神经网络的方法进行解决[24]。
为将PINNs用于频域涡流场的稳定训练,本文主要考虑PINNs方法与电磁场PDE结合中的以下两方面问题:其一为损失函数权重匹配问题,标准PINNs中的第一类BCs并非强制施加,使得损失函数中PDE损失项与BCs损失项之间梯度差异过大导致优化过程失衡,造成结果不准确或者错误。目前损失函数权重匹配问题没有通用解决办法,因此PINNs电磁场中需要合理选择PDE与BCs权重的控制方法以达到高效训练的目的。其二,在数据驱动的深度学习中,神经网络的梯度爆炸是在指训练过程中大的误差梯度不断累积,导致模型权重出现重大更新,造成模型不稳定,无法利用训练数据学习。当PINNs面对实际材料参数时,例如PDE中含高数量级源项(散度源、旋度源和热源等),其在反向传播过程中会产生关于网络权重参数的高梯度(详细解释见2.3.2节),此现象称为PINNs中的梯度爆炸,导致新的网络权重参数过大,根据梯度下降算法新生成的参数并不符合神经网络的学习尺度,导致网络训练持续几步就无法进行。由于PINNs中的损失函数是由PDE构成,这与数据驱动的损失函数有区别,深度学习领域中现有的解决方法,如数据标准化[25]、权重初始化和正则化等效果甚微。本文通过推导在无先验解下的无量纲方程形式解决PINNs中的梯度爆炸问题。
本文重点关注PINNs方法与PDEs结合中出现的困难,针对损失函数权重匹配问题,本文指出对于电磁场中常见的0值边界的高效训练方法并与解析解相对比,证实方法的可靠性;并且指出对于跃变边界权重系数的有效控制方法和神经网络架构,并与目前文献结果对比;第3节以稳恒磁场为例,提出PINNs对于实际高数量级源问题训练困难的原因及稳定的训练方法;第4节综合利用之前章节提出的处理方法,将PINNs推广到频域涡流场中,在导体通入一定电流的情况下,提出PINNs对于此类微分代数方程的解决方案,并将求解结果与有限元方法(Finite Element Method, FEM)进行对比,证实处理手段的有效性。
本文对标准PINNs法在正问题中的原理和实施过程做简要介绍。PDE的一般形式为
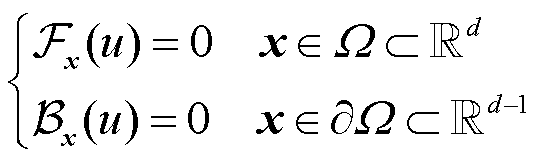 (1)
(1)
式中, 表示实数域;d为空间维度;
表示实数域;d为空间维度; 和
和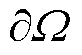 分别为要求解的区域和边界;ℱx(∙), ℬx(∙)为对自变量x的线性或非线性微分算子。文献[4]提出的标准PINNs法求解PDEs的步骤如下:
分别为要求解的区域和边界;ℱx(∙), ℬx(∙)为对自变量x的线性或非线性微分算子。文献[4]提出的标准PINNs法求解PDEs的步骤如下:
首先,建立一个深度神经网络来估计解u(x)。深度神经网络基本架构如图1所示。神经网络的第一部分是线性变换,第ℓ层线性变换可以表达为Τ(ℓ):ℝnℓ-1®ℝnℓ,nℓ为第ℓ隐藏层中神经元个数,隐藏层层数ℓ=1,×××,L,对于每一层的输入z,Τ(ℓ)可以表述为
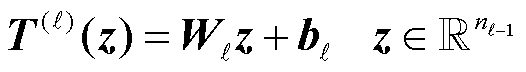 (2)
(2)
式中,WℓÎℝnℓ×nℓ-1和bℓÎℝnℓ分别为神经网络的权重和偏置参数,被称为可学习参数;W1∈ℝN×1, W2∈ℝ1×N为神经网络权重;b1∈ℝN, b2∈ℝ1为神经网络偏置。第二部分是非线性激活函数ψ:ℝ®ℝ,PINNs中常用的激活函数有Tanh和Sigmoid。将ψ运用于向量zÎℝn进行逐元素运算。第ℓ层神经网络被表达为线性变换T(ℓ)和非线性激活函数ψ的复合,即

图1 深度神经网络基本架构
Fig.1 Basic architecture of deep neural networks
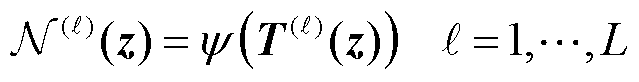 (3)
(3)
记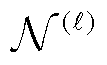 :ℝnℓ-1↦ℝnℓ,L层的神经网络可以被表达为所有
:ℝnℓ-1↦ℝnℓ,L层的神经网络可以被表达为所有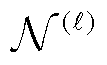 的复合。特别地,对于输入特征xÎℝn0,一般的L层神经网络
的复合。特别地,对于输入特征xÎℝn0,一般的L层神经网络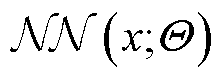 可以被表示为
可以被表示为
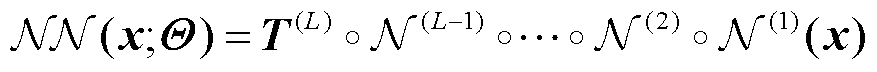 (4)
(4)
式中,“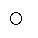 ”表示函数的复合;ΘÎℝN代表L层神经网络中所有的可训练参数,Θ={Wℓ,bℓ| ℓ=1,×××,L},对于全连接神经网络,
”表示函数的复合;ΘÎℝN代表L层神经网络中所有的可训练参数,Θ={Wℓ,bℓ| ℓ=1,×××,L},对于全连接神经网络,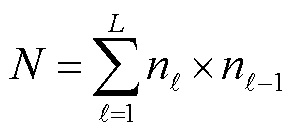 。
。
其次,定义PDE和BCs的残差为
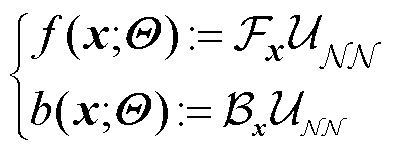 (5)
(5)
式(5)中的导数部分可以通过自动微分方法进行计算[8],该方法可以在深度学习工具如PyTorch[26]和Tensorflow[27]中通过计算图实现。
之后,利用现有的采样策略,如均匀采样、拉丁超立方采样等对空间Ω进行离散化。将采样点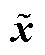 输入神经网络中得到估计解,然后将其代入式(5)得到残差估计值f (
输入神经网络中得到估计解,然后将其代入式(5)得到残差估计值f (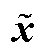 ;Θ)和b(
;Θ)和b(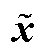 ;Θ)。
;Θ)。
最后,PINNs通过定义与PDEs相关的损失函数,如式(6),并选择合适的非凸优化算法如Adam[28]、L-BFGS[29]等对总损失函数式(7)进行优化,即通过神经网络反向传播寻找最优模型参数Θ*使得损失函数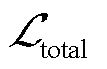 最小,如式(8)所示。
最小,如式(8)所示。
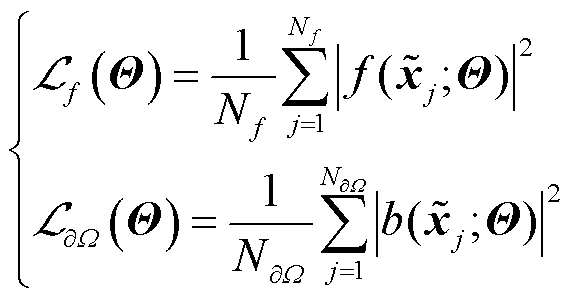 (6)
(6)
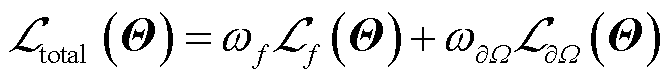 (7)
(7)
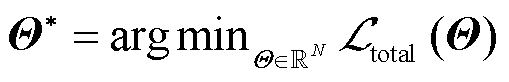 (8)
(8)
式中,Nf、N∂W分别为Ω和∂W上的采样点个数;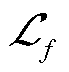 、
、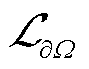 分别为PDE、BCs损失函数;集合
分别为PDE、BCs损失函数;集合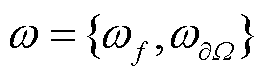 指的是各损失项对应的权重,在标准PINNs中ω均设置为1。
指的是各损失项对应的权重,在标准PINNs中ω均设置为1。
标准PINNs中的模型参数包含两部分,一部分是以全连接神经网络为代表的超参数、一般指的是隐藏层神经元层数和每层神经元的个数、求解器的学习率等;另一部分是由于控制方程和边界条件的引入导致的模型参数,主要是各项损失函数权重系数。超参数的概念来自数据驱动方法,在传统计算机视觉任务中,以卷积神经网络等为例,在此类方法中约束条件是以标签数据为代表的逐点约束方法,其大多可以通过调节超参数实现良好的精度。然而,PINNs中存在特有的梯度病理性问题使边界损失项的梯度消失,导致得到满足控制方程的任意解[22]。因此在PINNs中对于权重参数的处理至关重要。本文从减少或者消除边界条件的角度提升PINNs收敛速度和精度。
静电场的泊松方程定解问题如式(9),参考解为式(10)。设求解域(Ω)的几何区域如图2a所示,边界施加0 V电压,材料的介电常数为1 F/m,并假设内部电荷密度分布函数为r(x,y)=-2p2sin(px)sin(py)。
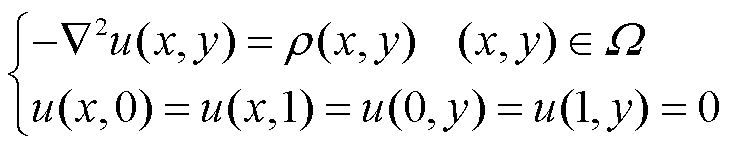 (9)
(9)
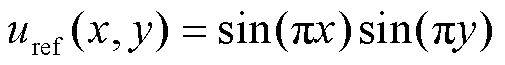 (10)
(10)
式中,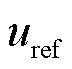 为参考解;u为电压。
为参考解;u为电压。
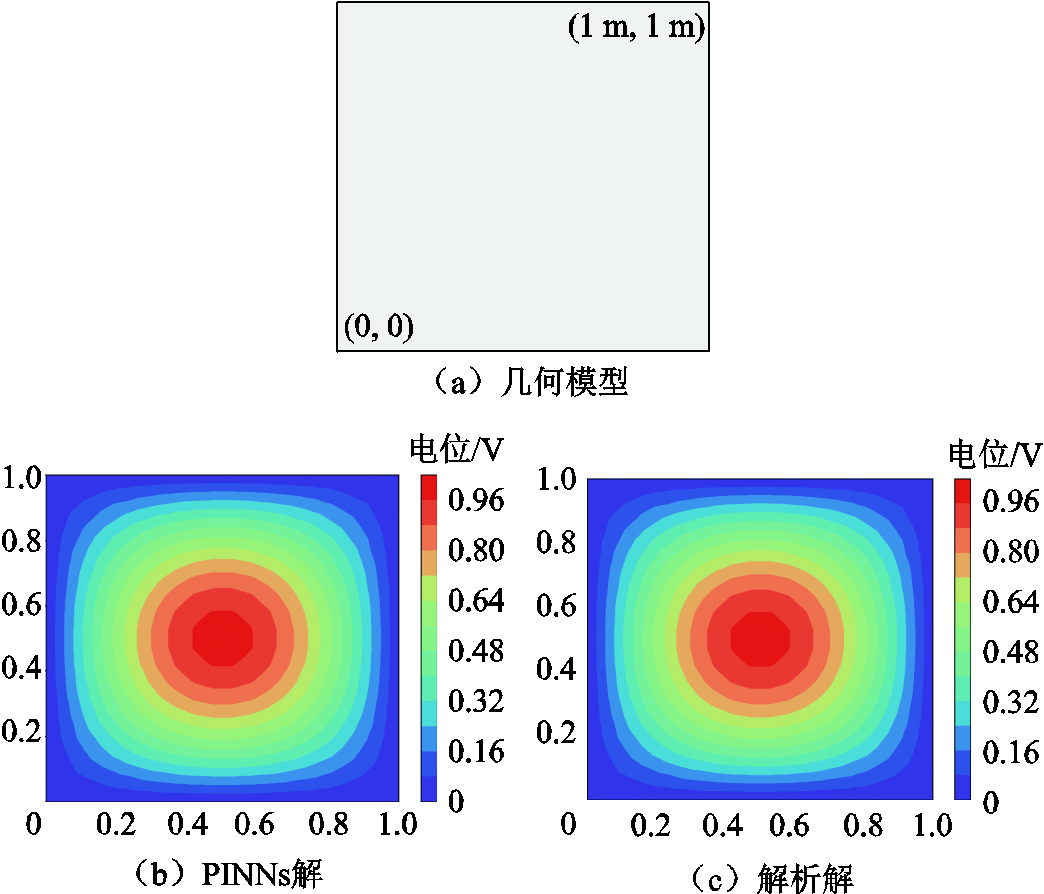
图2 几何模型及标量电位结果对比
Fig.2 Geometry model and comparison of scalar potential results
2.1.1 PINNs中各损失函数梯度不平衡问题
使用标准PINNs求解以上泊松方程定解问题时出现如下困难:损失函数梯度下降的过程中,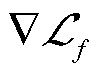 与
与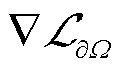 之间往往会存在差异,使得
之间往往会存在差异,使得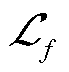 与
与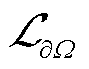 之间的优化不平衡导致边界条件不能很好地满足,因此需要平衡边界条件与PDEs残差之间的权重系数。针对该问题一般性计算方法的研究很多[30-31],但其因PDE、边界条件类型、实施难度和作用范围各不相同,需要进行合理选择。
之间的优化不平衡导致边界条件不能很好地满足,因此需要平衡边界条件与PDEs残差之间的权重系数。针对该问题一般性计算方法的研究很多[30-31],但其因PDE、边界条件类型、实施难度和作用范围各不相同,需要进行合理选择。
2.1.2 电磁场中0值边界条件的处理方法
对于电磁场中常见的空气域外边界条件,由于边界形状规则且为齐次BCs,根据文献[30]提出的硬约束方法将Dirichlet边界条件编码进神经网络中,使得边界强制满足,如图3所示,进而在总损失函数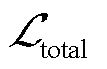 中消除边界损失
中消除边界损失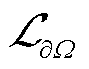 。解的结构如式(11)所示,g(x)为Dirichlet边界条件的右端项,
。解的结构如式(11)所示,g(x)为Dirichlet边界条件的右端项,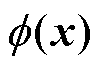 满足式(12),与解析解的结果对比如图3所示,其中
满足式(12),与解析解的结果对比如图3所示,其中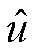 为新的估计值。
为新的估计值。
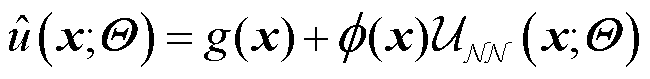 (11)
(11)
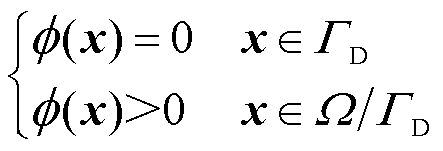 (12)
(12)
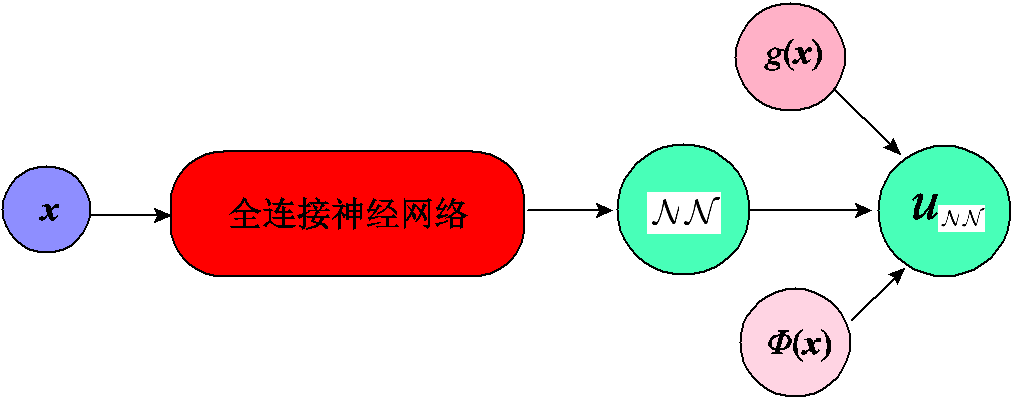
图3 带硬边界的全连接神经网络架构
Fig.3 Fully-connected neural networks with hard constraints
使用Adam求解器进行梯度下降,经过式(13)可以计算得出PINNs与解析解之间L2相对误差ε为9.15×10-6,同时边界条件几乎完全满足。由此可见,在边界损失权重参数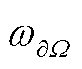 消除后,PINNs模型可以得到较高的求解精度为
消除后,PINNs模型可以得到较高的求解精度为
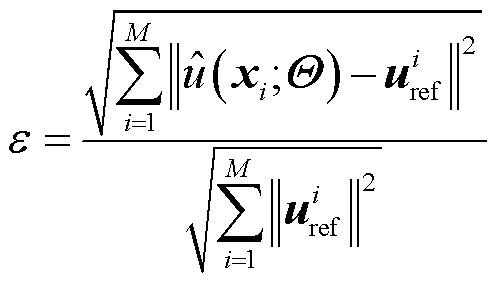 (13)
(13)
式中,uref为u的参考解;M为采样点个数。
本案例选自文献[20],其拉普拉斯方程的定解问题见式(14),几何模型参考图3a。边界条件式(14)表明解在上边界两端存在尖锐梯度,这里标量电位u从0 V跃变至1V,通过文献[20]研究发现标准PINNs不容易训练这类边界条件。
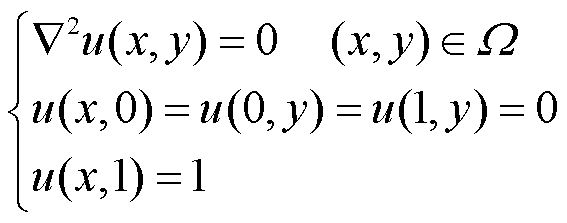 (14)
(14)
2.2.1 PINNs中的跃变边界条件
关于标准PINNs对于高梯度求解困难的原因可以从两方面进行解释:一方面,由于神经网络的学习过程具有谱偏移的特点使其更倾向于学习低频问题[24],这导致神经网络对于高频成分的训练效率和准确性降低,因此需要对标准PINNs的网络架构进行改进以加快学习过程;另一方面,标准PINNs的损失函数权重系数均设置为软边界[4],由于梯度的病理性问题,在反向传播的过程中,损失函数的梯度在上边界和其余边界存在差异,这就会导致由边界与PDEs残差损失组成的多目标优化系统的失衡,使得边界条件不能很好地满足,因此需要对权重系数在每次梯度下降的过程中进行控制。依据以上两方面对神经网络架构进行如下的改进。
2.2.2 对于标准PINNs的相关改进
首先,参考数据驱动深度学习中对于高梯度问题的常用手段,在神经网络中嵌入傅里叶特征对输入进行处理的过程如式(15)所示,由于本文不涉及神经网络基本理论研究,该方法详细原理见文献[24]。
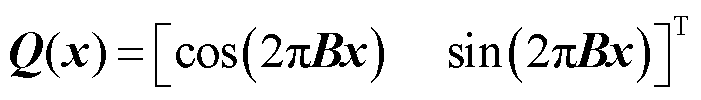 (15)
(15)
式中,B∈ℝm×d,其中元素服从N(0,σ2)分布,σ2为协方差,与几何尺寸有关,考虑到将其作为超参数进行调节是困难的,这里将其经验性地选择为最大几何模型尺寸。事实上在数据驱动中仅凭借式(15)有助于但不能完全解决高梯度问题[24],需要通过平衡BCs项与PDE项的损失函数权重系数来解决梯度病理性问题[22]。为实现权重系数的自适应调整,这里使用式(16)计算当前边界损失权重系数 ,再按照式(17)以移动平均的方法更新下一次迭代的权重系数
,再按照式(17)以移动平均的方法更新下一次迭代的权重系数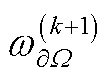 ,使得边界处误差减小[31]。
,使得边界处误差减小[31]。
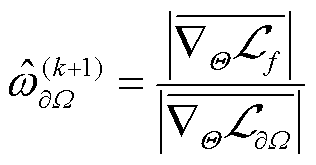 (16)
(16)
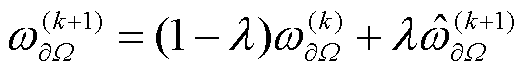 (17)
(17)
式中,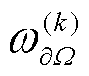 为上次迭代中的权重系数;
为上次迭代中的权重系数;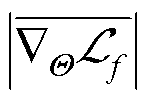 和
和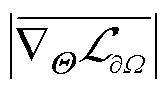 分别为PDE损失
分别为PDE损失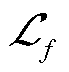 和边界损失
和边界损失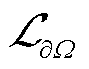 对所有网络参数Θ梯度的平均值。使用λ来控制一个先前动态权重贡献的衰减速度,λ越小表示上次的贡献要比当前动态权重的贡献大,这使得在训练中的调整是稳定的,本案例中选取λ=0.1。
对所有网络参数Θ梯度的平均值。使用λ来控制一个先前动态权重贡献的衰减速度,λ越小表示上次的贡献要比当前动态权重的贡献大,这使得在训练中的调整是稳定的,本案例中选取λ=0.1。
在施加权重系数平衡方法(式(18)和式(19))后导致网络不收敛,为增强神经网络的收敛性,这里使用文献[32]提出的基于全连接神经网络改进网络架构,其考虑了输入层与每一个隐藏层之间的联系进而增强收敛性,前向传播规则如式(18)~式(22)所示。该架构通过两个变换层W1、b1、W2、b2将傅里叶特征映射到高频特征空间中,之后通过哈达玛积⊙将不同的输入相乘,文献[22]指出此结构提高了训练的准确性和收敛性。
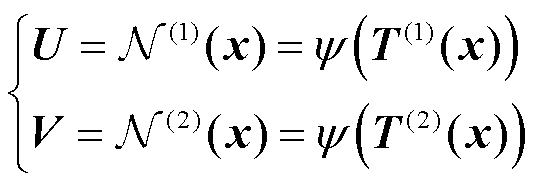 (18)
(18)
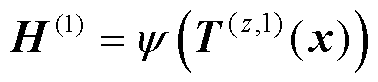 (19)
(19)
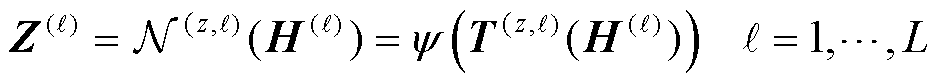 (20)
(20)
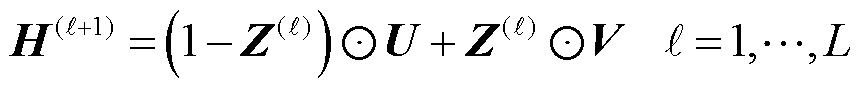 (21)
(21)
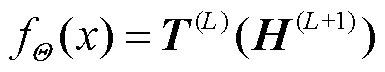 (22)
(22)
式中,x∈ℝn0,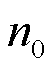 为输入特征个数,这里为空间维数,取
为输入特征个数,这里为空间维数,取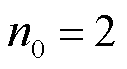 ;T(z,ℓ)可以理解为前向传播的神经网络,该网络的可学习参数集合为{Wz,1, bz,1×××,Wz,L+1, bz,L+1},T(z,ℓ)每次前向传播都会考虑输入层的抽象特征T(1)和T(2),它们的可学习参数维度分别为W1∈ℝn1×n0,b1∈ℝn1×1,W2∈ℝn1×n0,b2∈ℝn1×1,n1为第一隐藏层中神经元的个数;这里式(18)和式(19)中的x为经过式(15)后的结果γ(x),同时注意到傅里叶特征并不会影响网络的可训练参数,当前神经网络的参数集合为Θ={W1, b1, W2, b2, Wz,1, bz,1, ×××,Wz,L+1, bz, L+1,W, b},选用Adam法进行梯度下降更新Θ参数可以得到结果如图4所示。
;T(z,ℓ)可以理解为前向传播的神经网络,该网络的可学习参数集合为{Wz,1, bz,1×××,Wz,L+1, bz,L+1},T(z,ℓ)每次前向传播都会考虑输入层的抽象特征T(1)和T(2),它们的可学习参数维度分别为W1∈ℝn1×n0,b1∈ℝn1×1,W2∈ℝn1×n0,b2∈ℝn1×1,n1为第一隐藏层中神经元的个数;这里式(18)和式(19)中的x为经过式(15)后的结果γ(x),同时注意到傅里叶特征并不会影响网络的可训练参数,当前神经网络的参数集合为Θ={W1, b1, W2, b2, Wz,1, bz,1, ×××,Wz,L+1, bz, L+1,W, b},选用Adam法进行梯度下降更新Θ参数可以得到结果如图4所示。
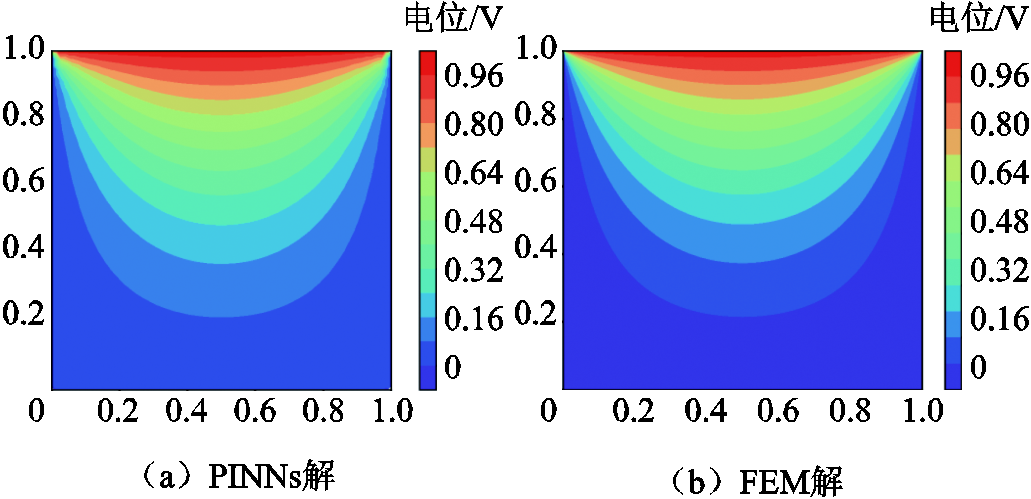
图4 标量电位结果对比
Fig.4 Comparison of scalar potential results
经过式(13)可以计算得出图4a和图4b中PINNs与FEM解之间的L2误差ε为2.4×10-3,同时边界两端高梯度问题得到解决。训练过程中的损失函数以及逐点误差值如图5所示。图5a中标签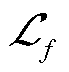 与
与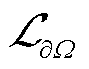 分别指的是PDEs以及BCs的训练损失,由此可见,BCs损失在训练的过程中有效下降至10-7左右,使得跃变BCs合理满足。为与文献[20]相对比,由图5b所示逐点误差可以看出,经过傅里叶特征的嵌入、损失函数权重系数的平衡后,边界附近的误差明显消除,同时区域内部误差几乎为0。
分别指的是PDEs以及BCs的训练损失,由此可见,BCs损失在训练的过程中有效下降至10-7左右,使得跃变BCs合理满足。为与文献[20]相对比,由图5b所示逐点误差可以看出,经过傅里叶特征的嵌入、损失函数权重系数的平衡后,边界附近的误差明显消除,同时区域内部误差几乎为0。
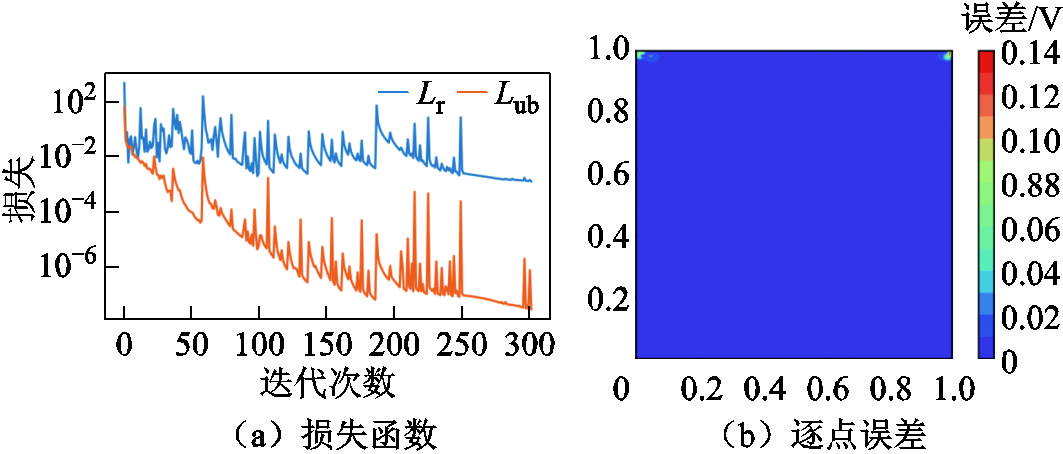
图5 训练过程中的损失函数以及逐点误差值
Fig 5 Loss function and point by point error value during training
设求解域Ω为正方形,代表空气域,内部存在矩形导体,磁导率μ取真空磁导率μ0。通入I=420 A的电流,空气域外边界使用0值边界条件。求解空间中矢量磁位u的分布,其定解问题如式(23)所示。
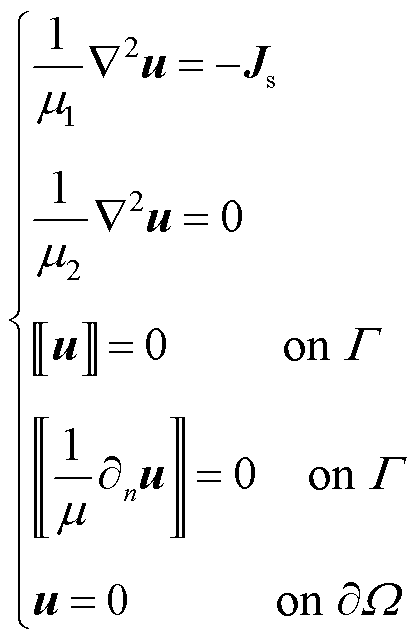 (23)
(23)
式中,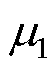 和
和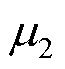 分别为空气和导体区域的磁导率;
分别为空气和导体区域的磁导率;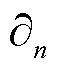 为法向导数;u为矢量磁位;Js为源电流密度;
为法向导数;u为矢量磁位;Js为源电流密度;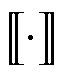 表示在界面Γ上存在跃变,被定义为
表示在界面Γ上存在跃变,被定义为
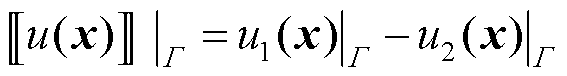 (24)
(24)
式(24)中,u(x)为Ω上的分片连续函数,即
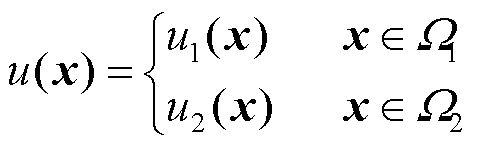 (25)
(25)
式中,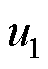 和
和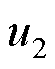 分别为空气和导体区域的矢量磁位。
分别为空气和导体区域的矢量磁位。
在磁导率相同的条件下,式(23)自然满足不予以考虑,本案例中的边界处理方法采用2.1节中的0值边界处理方法。
PINNs在面对电磁场中的含源问题(旋度源或散度源)时,在反向传播中,会发生梯度爆炸问题导致网络难以训练。为方便起见,下面以一维泊松方程和单隐藏层神经网络为例进行解释和推导PDE损失项对于网络参数的梯度,其结果同样可以推广到高维和深层神经网络。
考虑式(26)所示的一维泊松方程,Ω是ℝ上的有界开集。
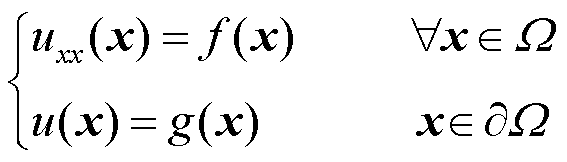 (26)
(26)
单隐藏层全连接神经网络通过前向传播可以得到的估计解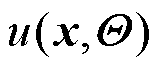 为
为
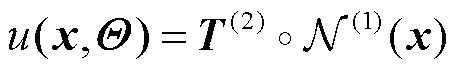 (27)
(27)
对式(27)运用多元函数微分并根据迹的相关性质,可得
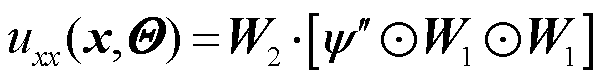 (28)
(28)
式中,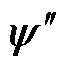 为
为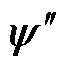 (W1x, b1),同样对标量
(W1x, b1),同样对标量 运用多元微分可得
运用多元微分可得
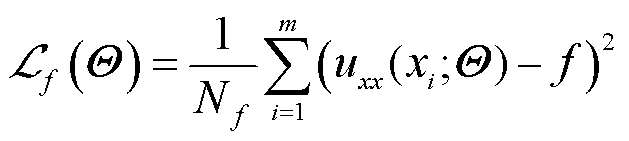 (29)
(29)
式中,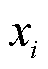 为第i个样本。
为第i个样本。
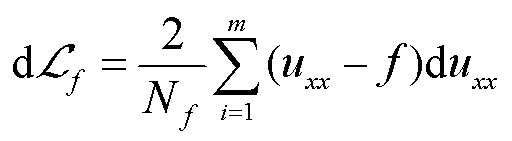 (30)
(30)
因此,由式(30)可以得知,在神经网络初始化和训练过程中,由于源项的作用使得权重参数的初始梯度变得非常大,导致网络无法收敛或者收敛速度非常缓慢。这与深层神经网络中常见的由激活函数引发的梯度爆炸现象原因不同,需要对PDE本身进行处理。
针对PINNs的梯度爆炸问题,采用无量纲方程来解决,由于u的参考值uc很难先验,为实现无先验条件下PINNs对于PDE的高效求解,xc为特征长度这里取区域的最大长度Lc=140 mm,电流尺度Ic取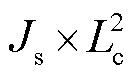 ,时间尺度tc取1 s,质量尺度取μIc2/Lc,因此特征值uc为
,时间尺度tc取1 s,质量尺度取μIc2/Lc,因此特征值uc为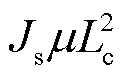 。静磁场的无量纲方程为
。静磁场的无量纲方程为
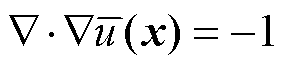 (31)
(31)
式中,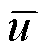 为矢量磁位的无量纲形式;
为矢量磁位的无量纲形式; 指的是对无量纲位置
指的是对无量纲位置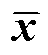 坐标的导数。在无网格点下,使用PINNs求解式(23)PDE后的空间中矢量磁位分布结果如图7a所示,图7b为FEM参考解,这里只要计算出
坐标的导数。在无网格点下,使用PINNs求解式(23)PDE后的空间中矢量磁位分布结果如图7a所示,图7b为FEM参考解,这里只要计算出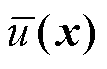 即可通过式(32)得到原解u(x)。
即可通过式(32)得到原解u(x)。
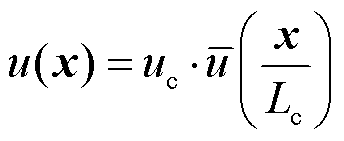 (32)
(32)
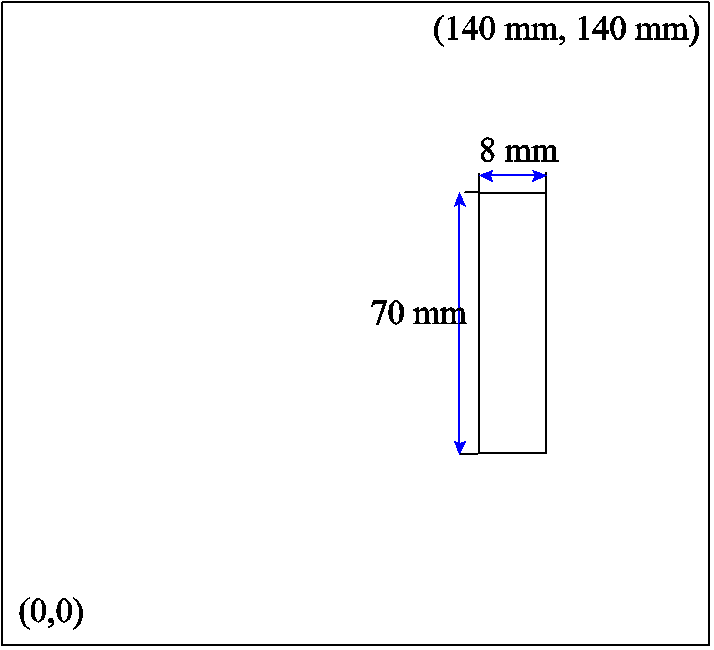
图6 几何模型
Fig.6 Geometry model
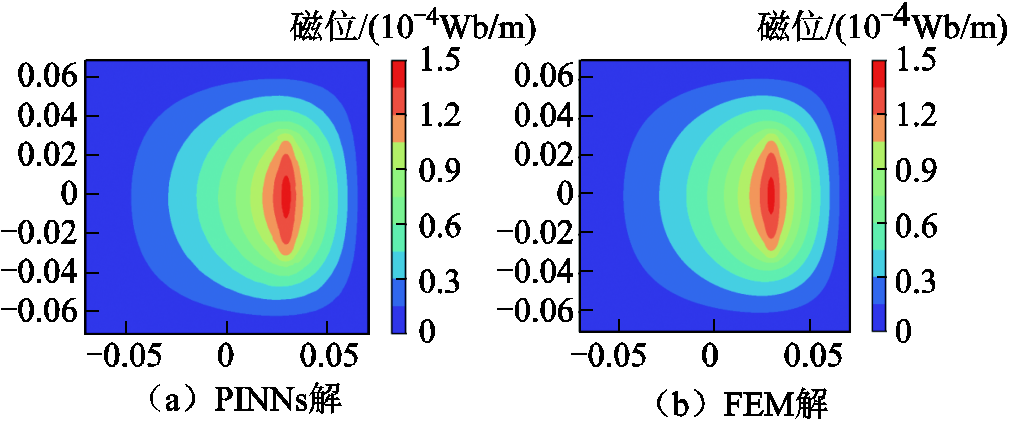
图7 矢量磁位结果对比
Fig.7 Comparison of vector magnetic potential results
由图7a与图7b之间的对比可知,在边界损失权重参数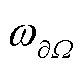 消除后,PINNs模型可以得到较高求解精度。经过式(13)可以从图7中计算得出本案例PINNs与FEM解之间L2相对误差ε为2.24×10-2。
消除后,PINNs模型可以得到较高求解精度。经过式(13)可以从图7中计算得出本案例PINNs与FEM解之间L2相对误差ε为2.24×10-2。
设矩形母线依次为A、B、C三线和N线,三相母线中依次通入频率f为50 Hz、幅值I为420 A的三相正序电流I,其中A相的初始相位为0,其几何模型如图8所示,空气外边界采用磁力线平行边界条件,求解所在空间位置的矢量磁位分布u和涡流损耗密度分布Qe。
该案例中涡流场的控制方程如式(33)所示,界面条件及外边界Dirichlet条件参考式(23)。
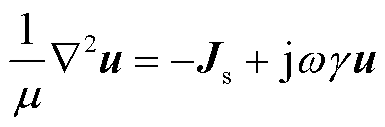 (33)
(33)
式中,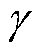 为电导率,其取值为3.225×107 S/m;ω为角频率,其取值为314 rad/s;j为虚数单位。A,B,C和N线矩形导体为金属材料,因此需要对每个导体的标量电位做耦合,其耦合过程如式(34)和式(35)所示。
为电导率,其取值为3.225×107 S/m;ω为角频率,其取值为314 rad/s;j为虚数单位。A,B,C和N线矩形导体为金属材料,因此需要对每个导体的标量电位做耦合,其耦合过程如式(34)和式(35)所示。
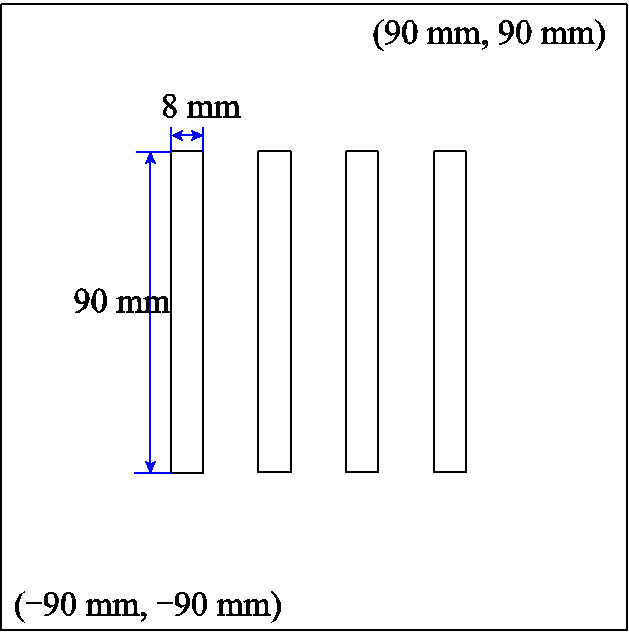
图8 三相涡流场的几何模型
Fig.8 Geometry model of eddy current
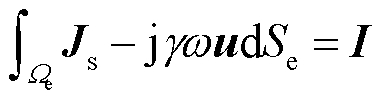 (34)
(34)
式中,Se为每个区域Ωe所对应的面积。由于在每个导体中标量电位相等,因此由式(34)可以得到
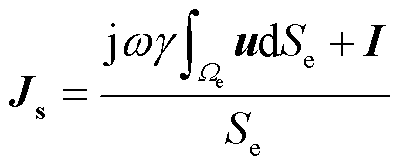 (35)
(35)
频域涡流损耗密度Qe可以通过式(36)进行计算[33]。
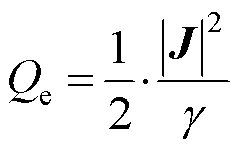 (36)
(36)
式中,|J|为总电流密度的模。PINNs求解以式(23),式(25)组成的微分代数方程。
利用2.1.2节的0值边界处理方法和2.2节的神经网络架构,设置导体材料与空气的相对磁导率相同,于是可以使用同一个神经网络进行表达。在PINNs中将频域量u分解为实部Re(u)和虚部Im(u),这两部分由同一个神经网络经过输出得到。u表示为
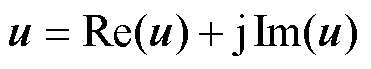 (37)
(37)
由于PINNs是无网格方法,在具体计算时可以通过蒙特卡洛积分法对式(35)中的积分进行离散处理可得
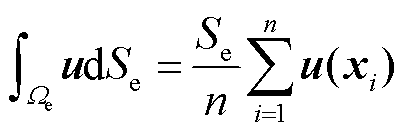 (38)
(38)
式中,n为积分点个数;i为第i个样本;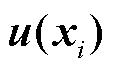 为蒙特卡洛积分点处的矢量磁位值。由于仍然存在高数量级源项问题,因此考虑对式(23)、式(25)无量纲化,同理由于矢量磁位u的特征值无法先验,为维持源项较小的源项量级,xc为特征长度,取值为区域的最大长度Lc(=140 mm),电流尺度Ic取100I,时间尺度tc取γLc2μ,质量尺度mc取γ2Lc3Ic2μ3,因此特征值uc为mcLc/Ictc2。无量纲涡流场方程为
为蒙特卡洛积分点处的矢量磁位值。由于仍然存在高数量级源项问题,因此考虑对式(23)、式(25)无量纲化,同理由于矢量磁位u的特征值无法先验,为维持源项较小的源项量级,xc为特征长度,取值为区域的最大长度Lc(=140 mm),电流尺度Ic取100I,时间尺度tc取γLc2μ,质量尺度mc取γ2Lc3Ic2μ3,因此特征值uc为mcLc/Ictc2。无量纲涡流场方程为
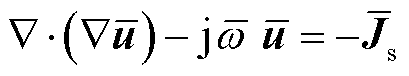 (39)
(39)
式中,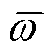 为无量纲角频率,其可以通过以上特征尺度得出。将式(39)的残差作为PDE损失函数,利用TensorFlow提供的自动微分工具对式(39)中的拉普拉斯算子进行计算,使用Adam求解器进行梯度下降得到矢量磁位分布如图9a和图9b所示,可以看到PINNs能够解析涡流场。通过式(36)计算获得电磁损耗密度如图10所示,可以发现N相中存在涡流损耗。
为无量纲角频率,其可以通过以上特征尺度得出。将式(39)的残差作为PDE损失函数,利用TensorFlow提供的自动微分工具对式(39)中的拉普拉斯算子进行计算,使用Adam求解器进行梯度下降得到矢量磁位分布如图9a和图9b所示,可以看到PINNs能够解析涡流场。通过式(36)计算获得电磁损耗密度如图10所示,可以发现N相中存在涡流损耗。
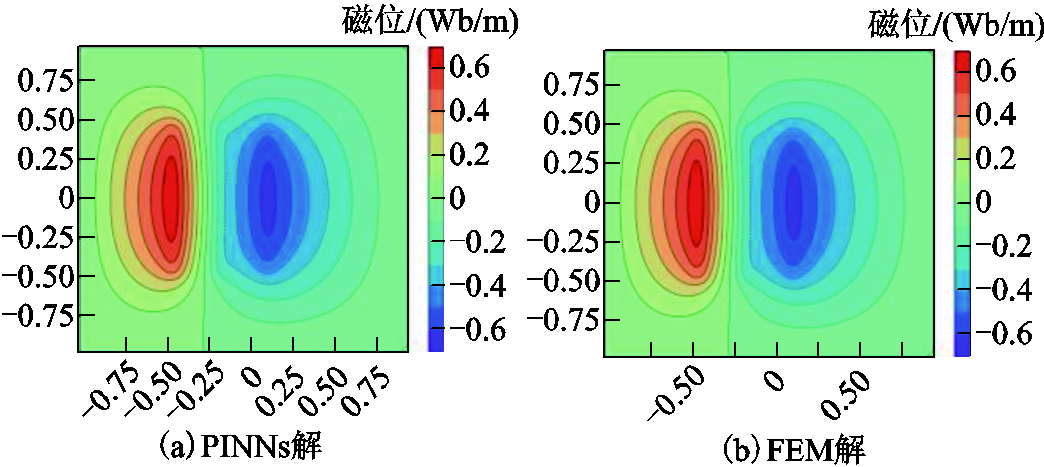
图9 矢量磁位结果对比
Fig.9 Comparison of vector magnetic potential results
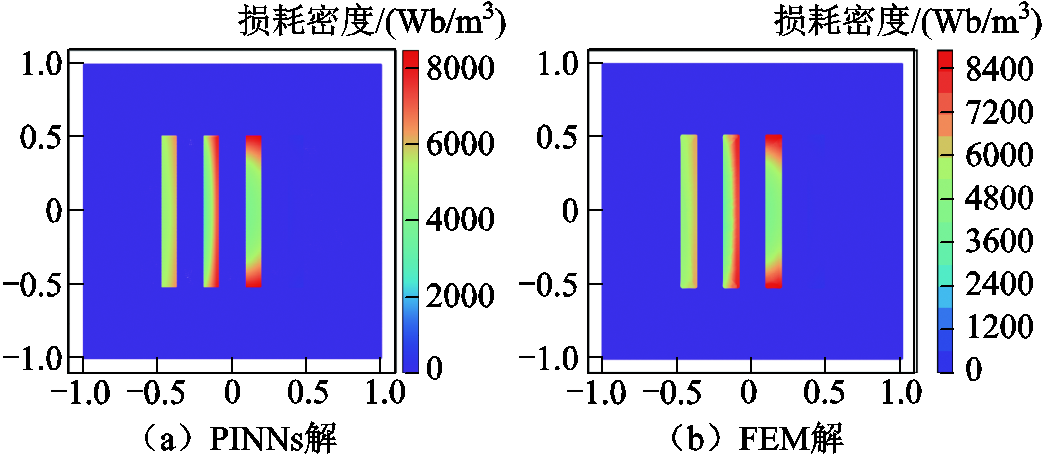
图10 电磁损耗密度
Fig.10 Electromagnetic loss density
由图9a与图9b之间的对比可知,PINNs可以解析受多相交变电流影响而在各自导体中产生涡流的分布情况,经过式(13)运算可得本案例PINNs与FEM解之间矢量磁位的相对L2误差ε为1.3×10-2。由图10a和图10b可知,PINNs解析出的电磁损耗分布情况与FEM法的结果几乎一致,经过式(13)可计算出PINNs的电磁损耗密度与FEM解之间的误差ε为3.3×10-2。
尽管PINNs具备无需网格划分、易于融合观测数据等优势,但目前仍存在训练成本较高、求解精度较低、超参数调节困难等局限性,本文初步将PINNs方法应用于在电磁场分析中,并针对电磁场在PINNs中应用中的典型问题给出相应的解决方法,得到了以下结论:
1)针对边界条件损失项梯度差异引发的训练困难问题,本文分别使用硬边界条件方法和权重自适应方法,通过简单算例与解析解对比证实了消除损失函数中的边界条件损失项可以实现较高的求解精度。
2)对于电磁场中的高数量级源引发的训练困难问题,提出无先验解下无量纲方程的方法进行解决,通过静磁场算例可得矢量磁位的误差量级在10-2左右,证实了无量纲方法处理控制方程可以提高PINNs的求解效率。
3)本文进一步使用PINNs求解频域涡流问题,在导体标量电位耦合与保持区域电流恒定的约束下,通过频域三相涡流场算例可得矢量磁位和电磁损耗密度的误差量级均在10-2左右,证实PINNs方法可以求解较为复杂的频域涡流问题。
参考文献
[1] 金亮, 尹振豪, 刘璐, 等. 基于残差U-Net和自注意力Transformer编码器的磁场预测方法[J]. 电工技术学报, 2024, 39(10): 2937-2952.
Jin Liang, Yi Zhenhao, Liulu, et al. Magnetic field prediction method based on residual U-net and self-attention transformer encoder[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 2937-2952.
[2] 张宇娇, 赵志涛, 徐斌, 等. 基于U-net卷积神经网络的电磁场快速计算方法研究[J]. 电工技术学报, 2024, 39(9): 2730-2742.
Zhang Yujiao, Zhao Zhitao, Xubin, et al. Fast calculation method of electromagnetic field based on U-net convolution neural network[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2730-2742.
[3] ZuoKuijun, Ye Zhengyin, Zhang Weiwei, et al. Fast aerodynamics prediction of laminar airfoils based on deep attention network[J]. Physics of Fluids, 2023, 35(3): 037127.
[4] Raissi M, Perdikaris P, Karniadakis G E. Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations[J]. Journal of Computational Physics, 2019, 378: 686-707.
[5] E Weinan, Yu Bing. The deep ritz method: a deep learning-based numerical algorithm for solving variational problems[J]. Communications in Mathematics and Statistics, 2018, 6(1): 1-12.
[6] Sirignano J, Spiliopoulos K. DGM: a deep learning algorithm for solving partial differential equations[J]. Journal of Computational Physics, 2018, 375: 1339-1364.
[7] Lagaris I E, Likas A, Fotiadis D I. Artificial neural networks for solving ordinary and partial differential equations[J]. IEEE Transactions on Neural Networks, 1998, 9(5): 987-1000.
[8] Baydin A G, Pearlmutter B A, Radul A A, et al. Automatic differentiation in machine learning: a survey[EB/OL]. arXiv, 2015: 1502.05767. http://arxiv. org/ abs/1502.05767v4.
[9] Fujita K. Physics-informed neural networks with data and equation scaling for time domain electromagnetic fields[C]//2022 Asia-Pacific Microwave Conference (APMC), Yokohama, Japan, 2022: 623-625.
[10] Shukla K, Di Leoni P C, Blackshire J, et al. Physics-informed neural network for ultrasound nondestructive quantification of surface breaking cracks[J]. Journal of Nondestructive Evaluation, 2020, 39(3): 61.
[11] Mao Zhiping, Jagtap A D, Karniadakis G E. Physics-informed neural networks for high-speed flows[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 360: 112789.
[12] Chen Donglin, Gao Xiang, Xu Chuanfu, et al. FlowDNN: a physics-informed deep neural network for fast and accurate flow prediction[J]. Frontiers of Information Technology & Electronic Engineering, 2022, 23(2): 207-219.
[13] 唐和生, 何展朋, 廖洋洋, 等. 基于物理驱动深度迁移学习的薄板力学正反问题[J]. 工程力学: 1-10.
Tang Hesheng, He Zhanpeng, Liao Yangyan, et al. Forward and inverse problems of thin plate mechanicsbased on physics-informed deep transfer learning for[J]. Engineering Mechanics: 1-10.
[14] 唐明健, 唐和生. 基于物理信息的深度学习求解矩形薄板力学正反问题[J]. 计算力学学报, 2022, 39(1): 120-128.
Tang Mingjian, Tang Hesheng. A physics-informed deep learning method for solving forward and inverse mechanics problems of thin rectangular plates[J]. Chinese Journal of Computational Mechanics, 2022, 39(1): 120-128.
[15] Lu Lu, Meng Xuhui, Mao Zhiping, et al. DeepXDE: a deep learning library for solving differential equations[J]. SIAM Review, 2021, 63(1): 208-228.
[16] Hennigh O, Narasimhan S, Nabian M A, et al. NVIDIA SimNet™: an AI-accelerated multi-physics simulation framework[C]//International Conference on Computational Science, Cham, Springer, 2021: 447-461.
[17] Huawei MindSpore AI development framework[M]// Artificial intelligence technology. Singapore: Springer, 2023: 137-162.
[18] 阮江军, 张宇, 张宇娇, 等. 电气设备电磁多物理场数值仿真研究与应用[J]. 高电压技术, 2020, 46(3): 739-756.
Ruan Jiangjun, Zhang Yu, Zhang Yujiao, et al. Numerical simulation research and applications of electromagnetic multiphysical field for electrical equipment[J]. High Voltage Engineering, 2020, 46(3): 739-756.
[19] 仲林林, 吴冰钰, 吴奇. 基于元学习的气体放电等离子体电子Boltzmann方程数值求解[J]. 电工技术学报, 2024, 39(11): 3457-3466.
Zhong Linlin, Wu Bingyu, Wu Qi. Numerical solution of electron Boltzmann equation in gas discharge plasmas based on meta learning[J]. Transactions of China Electrotechnical Society, 2024, 39(11): 3457-3466.
[20] Khan A, Lowther D A. Physics informed neural networks for electromagnetic analysis[J]. IEEE Transactions on Magnetics, 2022, 58(9): 7500404.
[21] Beltrán-Pulido A, Bilionis I, Aliprantis D. Physics-informed neural networks for solving parametric magnetostatic problems[J]. IEEE Transactions on Energy Conversion, 2022, 37(4): 2678-2689.
[22] Wang Sifan, TengYujun, Perdikaris P. Understanding and mitigating gradient flow pathologies in physics-informed neural networks[J]. SIAM Journal on Scientific Computing, 2021, 43(5): A3055-A3081.
[23] Xu Z Q J, Zhang Yaoyu, Luo Tao, et al. Frequency principle: Fourier analysis sheds light on deep neural networks[EB/OL]. 2019: 1901.06523.http://arxiv.org /abs/1901.06523v5
[24] Tancik M, Srinivasan P P, Mildenhall B, et al. Fourier features let networks learn high frequency functions in low dimensional domains[C]//Proceedings of the 34th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 2020: 7537-7547.
[25] Machine learning mastery, How to use data scaling improve deep learning model stability and performance [EB/OL]. 2023. https://machinelearningmastery.com.
[26] Paszke A, Gross S, Massa F, et al. PyTorch: an imperative style, high-performance deep learning library[EB/OL]. 2019: 1912.01703. http://arxiv.org /abs/1912.01703v1.
[27] Abadi M, Barham P, Chen J, et al. {TensorFlow}: a system for {Large-Scale} machine learning[C]//12th USENIX symposium on operating systems design and implementation (OSDI 16). 2016: 265-283.
[28] 赵洪山, 孙京杰, 彭轶灏, 等. 基于多尺度窗口和区域注意力残差网络的无线电力终端身份识别方法[J]. 电工技术学报, 2023, 38(1): 107-116.
Zhao Hongshan, Sun Jingjie, Peng Yihao, et al. Wireless power terminal identification method based on multiscale windowed deep residual network[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 107-116.
[29] Fei Yun, Rong Guodong, Wang Bin, et al. Parallel L-BFGS-B algorithm on GPU[J]. Computers & Graphics, 2014, 40: 1-9.
[30] Lu Lu, Pestourie R, Yao Wenjie, et al. Physics-informed neural networks with hard constraints for inverse design[J]. SIAM Journal on Scientific Computing, 2021, 43(6): B1105-B1132.
[31] Jin Xiaowei, Cai Shengze, Li Hui, et al. NSFnets (Navier-Stokes flow nets): physics-informed neural networks for the incompressible Navier-Stokes equations[J]. Journal of Computational Physics, 2021, 426: 109951.
[32] Kingma D P, Ba J. Adam: a method for stochastic optimization[EB/OL]. arXiv, 2014: 1412.6980. http:// arxiv.org/abs/1412.6980v9.
[33] 曾非同, 关向雨, 黄以政, 等. 基于多尺度多物理场的油浸式变压器流动-传热数值研究[J]. 电工技术学报, 2020, 35(16): 3436-3444.
Zeng Feitong, Guan Xiangyu, Huang Yizheng, et al. Numerical study on flow-heat transfer of oil-immersed transformer based on multiple-scale and multiple-physical fields[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3436-3444.
Abstract In recent years, the advent of language models such as GPT and Sora has underscored the computational prowess of data-driven models within high-dimensional parameter spaces. This has positioned them as the forefront of electromagnetic optimization design, and serves the fast computation of electromagnetic fields. However, the efficacy of these data-driven models hinges significantly on labeled data, and they grapple with challenges such as overfitting and a lack of physical understanding. Diverging from natural language processing (NLP), physical fields are usually described by a set of partial differential equations, the emergence of physics informed neural networks (PINNs) addresses this gap.
The core concept of PINNs involves incorporating control equations into the neural network's loss function. This integration ensures that the network output approximates boundary conditions while adhering to the control equations within the solution domain. Nevertheless, PINNs encounter hurdles such as local high gradient issues, training complexities arising from source equations, and difficulties in identifying interfaces with high-contrast coefficients in electromagnetic field computations. Consequently, the training efficiency and computational accuracy of PINNs in solving electromagnetic field equations remain suboptimal, limiting their current applications.
In order to use PINNs for the stabilization training of electromagnetic fields, this paper firstly explores a method for handling zero-value boundary conditions in electromagnetic fields by employing a fully connected neural network architecture with hard boundaries. This approach effectively eliminates boundary loss in the total loss function. Taking electrostatic field equations with sources as an illustration, the L2 error using this method against the analytical solution is 9.15×10-6, with almost complete satisfaction of boundary conditions.
Recognizing the neural network's inclination to prioritize low-frequency or large-scale features, the paper introduces embedded Fourier features to process network inputs. Additionally, an adaptive adjustment strategy for weight coefficients is proposed. To enhance convergence, an improved fully connected neural network framework is utilized, considering connections between the input layer and each hidden layer. This framework is exemplified with boundary conditions involving leapfrog, resulting in a substantially reduced loss of about 10-7 during training, with nearly zero internal error.
To mitigate the gradient explosion issue in PINNs caused by high-order source terms during electromagnetic field training, this study formulates dimensionless equations for the electromagnetic field without prior conditions. These equations are incorporated into the neural network as a novel loss function. The relative L2 error ϵ between the PINNs and the FEM solution is measured at 2.24×10-2 for the static magnetic problem.
Expanding this training methodology to the frequency-domain eddy current field, the study tackles eddy current scenarios. Solving the corresponding differential-algebraic equations with PINNs reveals the distribution of vector magnetic potentials and electromagnetic loss density in the frequency-domain eddy current field. The proposed relative L2 error ε for vector magnetic potentials between PINNs and FEM solution is 1.3×10-2. The resolved electromagnetic losses by PINNs closely match the FEM method, with an error of 3.3×10-2.
In conclusion, this paper presents tailored solutions for typical challenges in applying electromagnetic fields with PINNs, significantly enhancing training efficiency, reducing costs, and introducing innovative approaches for swift electromagnetic field calculations.
keywords:Physical informed neural networks, numerical computing of electromagnetic fields, deep learning
中图分类号:TM15
DOI: 10.19595/j.cnki.1000-6753.tces.231063
国家自然科学基金资助项目(523770058)。
收稿日期 2023-07-04
改稿日期 2023-09-04
张宇娇 女,1978年生,教授,博士生导师,研究方向为电气设备多物理场建模与仿真、电磁多物理场快速计算方法、基于数字孪生技术的电气设备故障诊断与健康寿命管理。
E-mail:zhangyujiao@hfut.edu.cn
孙宏达 男,1998年生,硕士研究生,研究方向为电气设备多物理场建模与仿真、电磁多物理场快速计算方法。
E-mail:2021110379@mail.hfut.edu.cn
(编辑 郭丽军)