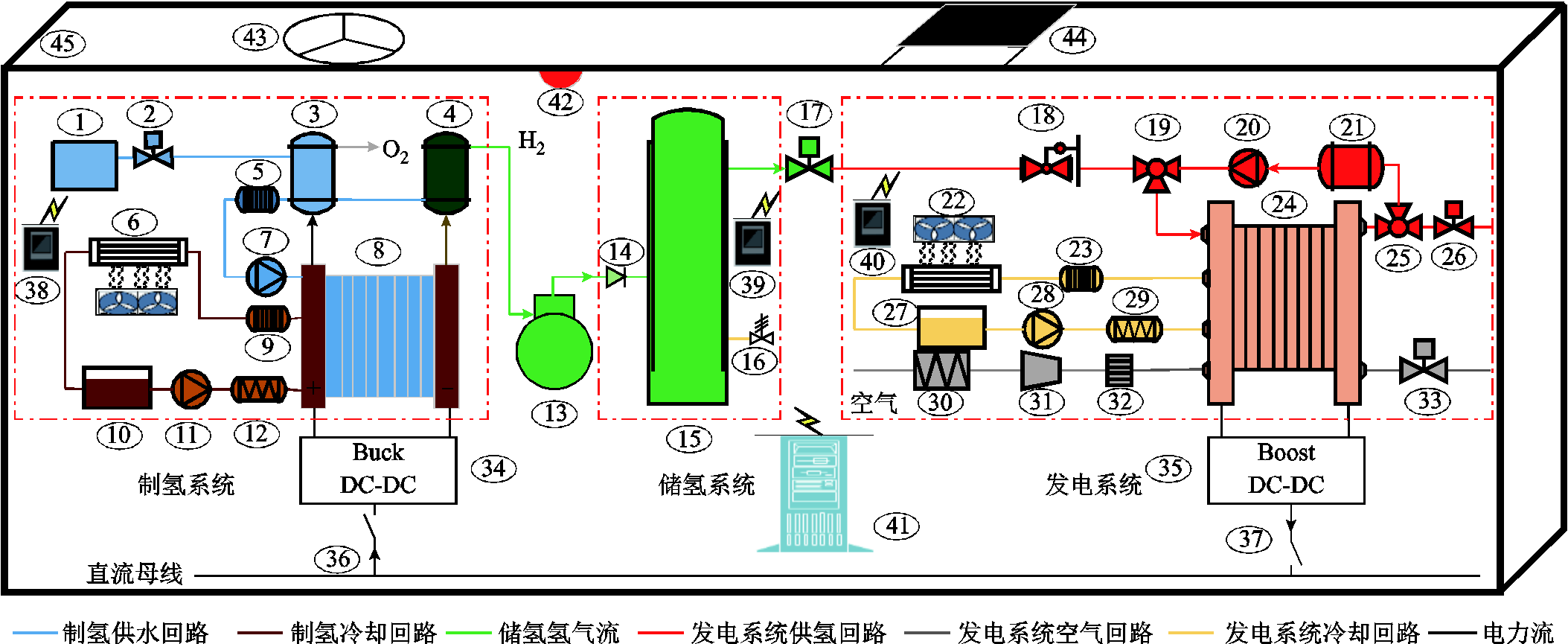
图1 箱式氢能一体化电站结构及控制系统配置
摘要 为解决大规模的“间歇性电源”接入造成的电能供需不平衡的问题，该文提出氢能一体化电站及其运行过程中电-氢-电能量流控制策略。首先，根据一体化电站电-氢-电能量转换特点，基于因果序图（COG）建立了面向控制的制储氢发电一体化电站运行动态模型，该模型能够清晰地反映一体化电站不同物理量之间的关系，实现一体化电站运行过程的表征；其次，在所建模型基础上基于自然因果关系原理设计了一体化电站运行过程的功率流和氢气流控制策略，该策略对于刚性关系过程采用反转模型控制，减少了误差反馈耗时，增强了控制器性能；最后，在基于RT-Lab的硬件在环仿真平台上进行了测试，分析了一体化电站不同物理量之间的变化关系。与比例-积分-微分（PID）控制和自抗扰控制（ADRC）方法的对比结果表明，所提控制策略在响应速度、收敛精度和运行效率上优于传统方法，可以更有效地实现氢能一体化电站运行过程的能量流管理。
关键词：氢能一体化电站 能量流控制 因果序图 硬件在环测试
氢储能技术具有清洁、无自放电、能量密度高的特点，是一种极具潜力的能源存储技术[1]。本文将电解水制氢、储氢和燃料电池发电技术集成在一起，提出氢能一体化电站（Integrated Hydrogen Energy Power Station, IHEPS）的概念。在电网功率富裕的时候利用氢能一体化电站制氢储能；当电网功率不足时，氢能一体化电站将存储的能量转换为电能为用户供电。
质子交换膜燃料电池（Proton Exchange Membrane Fuel Cell, PEMFC）作为氢能一体化电站的燃料电池发电子系统[2]。然而，由于PEMFC是一种非线性多变量系统，很难用常规方法建模[3-5]。文献[6-8]采用基于数据驱动的方法对PEMFC进行建模，该类方法虽然避免了复杂的非线性建模，但是不适用于研究燃料电池内部的动态过程。张雪霞等将极化曲线、等效电路模型方法和弛豫时间分布相结合，建立了可以研究燃料电池动态老化的模型[9]。文献[10-11]设计并构建了用于燃料电池反应物温度和湿度控制的气体加湿电站，并利用实验数据确定了加湿系统热动力学模型参数的低阶模型。但是这种模型是为特定领域设计的，在实际中需根据不同的操作条件或应用工况进行不断修正。为了得到更加通用的模型，美国密歇根大学的J. T. Pukrushpan等[12]基于空气动力学和电化学用微分方程描述了PEMFC进气系统的完整动态过程，该模型可以为研究提升燃料电池性能的控制工作提供仿真理论基础。
另外，由于利用可再生能源制氢极具发展潜力[13-14]，研究人员为了提高电解池性能也建立了许多简化模型。文献[15-16]建立了电解池的等效电路模型，该模型可以考虑功率转换损耗，并根据输入电流和功率计算电解池生成氢气的速率，但是等效电路模型一般会忽略电解池的动态过程。文献[17-18]利用机器学习建立了可以研究电力电子电流纹波对质子交换膜电解池（Proton Exchange Membrane Electrolysis Cell, PEMEC）性能影响的静态-动态模型。文献[19]基于多项式模型，采用数据驱动的方式建立了一个可以反映电解池动态特性的黑盒模型。另外，研究者通过实验测量得到更多的电解池电流-电压特性，发现压力和温度两个参数对电解池运行特性有显著的影响[20-23]。因此，也有一些研究者将实验数据与电化学分析初步结合，建立了包括质子交换膜、阳极流道、阴极流道以及堆电压的电化学半经验模型[24-28]。
在独立的制氢或发电系统上，文献[29-30]分析了新型电力系统背景下一体化氢能电站的发展商业模式和发展前景。由于氢能电站无现成规范和可以借鉴的消防设计案例，文献[31]将氢能火灾特点和现有规范结合设计了氢能综合利用站消防水系统。徐圆圆等建立氢能电站多米诺效应定量风险分析模型，对发生火灾爆炸事故后的风险进行了量化评估[32]。中国人民解放军理工大学的王金全等分析了氢能发电一体化系统的优缺点，并初步提出其组成框架为氢源、燃料电池、电力变换器及其控制系统，但缺乏进一步的详细建模分析与控制研究[33]。因此，目前对于制氢、储氢和发电一体化的氢能电站研究大多仍处于商业模式和经济性可行性研究阶段，对其运行原理和建模的研究还较少。本文提出了集成制氢、储氢和燃料电池发电三个部分的箱式氢能一体化电站，其能量转换过程涉及电-氢-电耦合。为保证其安全稳定运行需要研究制氢、储氢和燃料电池发电系统一体化建模以及能量转换过程中电-氢-电能量流的协调运行控制方法。
因果序图（Causal Ordering Graph, COG）由一种图形语言组成，其能够以明确的物理意义描述动态系统，并且可以基于自然因果关系原理直接为建模对象设计控制方程，实现对象的综合控制[34-36]。因此，本文首先基于COG由部分到整体建立面向控制的氢能一体化电站运行过程模型。该模型能够清晰地反映氢能一体化电站不同物理量之间的关系，实现氢能一体化电站的电-氢-电运行过程表征。其次在建立的模型基础上，基于COG控制原理设计了氢能一体化电站运行过程功率流和氢气流管理策略。最后在基于RT-Lab的硬件在环仿真平台上进行测试，分析了氢能一体化电站不同物理量之间的变化关系，并且与比例-积分-微分（Proportional-Integral-Derivative, PID）控制和自抗扰控制（Active Disturbance Rejection Control, ADRC）方法进行对比，结果表明，所提策略在响应速度、收敛精度和运行效率上优于传统方法，可以更有效地实现氢能一体化电站运行过程的能量流管理。
本文提出了一种制储氢发电一体的箱式氢能一体化电站，其结构及控制系统配置如图1所示，由预制舱、制氢系统、储氢系统、燃料电池发电系统以及辅助控制系统构成。氢能一体化电站的基本工作原理分为储能和发电两种运行模式：①电-氢储能运行模式，电能驱动制氢系统运行电解水制取氢气，然后通过压缩机将制出的氢气压缩进储氢系统，从而实现电能的存储；②氢-电发电运行模式，储氢设备开始释放氢气，并通过燃料电池发电系统将氢能转换为电能供给用户。
图1 箱式氢能一体化电站结构及控制系统配置
1—水箱 2, 17, 26, 33—电动阀 3, 4, 21—汽水分离器 5, 9, 23—去离子器 6, 22—散热器 7, 11, 20, 28—循环泵 8—燃料电池堆 10, 27—膨胀水箱 12, 29—加热管道 13—氢气压缩机 14—止回阀 15—储氢罐 16—安全阀 18—调压阀 19, 25—三通阀 24—电解池堆 30—滤清器 31—空气压缩机 32—加湿器 34, 35—变流器 36, 37—保护开关 38, 39, 40—子系统控制器 41—系统控制器 42—环境温湿度氢浓度监测 43—排风机 44—电动通风窗 45—预制舱
Fig.1 Structure and control system configuration of the box-type IHEPS
为保证氢能一体化电站稳定运行，需要将一体化电站温度、压力等指标控制在合理水平。一体化电站采用分层控制方案配置了一个系统级控制器（41）以及制氢、储氢和发电三个子系统级控制器（38, 39, 40）。系统级控制主要包括一体化电站舱内环境温/湿度以及氢浓度的监测与控制（42, 43, 44）、运行安全保护控制（36, 37）以及系统运行过程能量流控制（13,17, 34, 35）等，用以实现一体化电站系统安全运行。子系统运行控制主要包括三个子系统的自身控制器，用以保证子系统设备安全、高效、长寿命运行。其中制氢子系统控制器实现制氢系统供水回路控制（2, 7）、冷却回路控制（6, 11, 12）等；储氢子系统控制器实现储氢罐储氢量限值控制（16）等；发电子系统控制器实现发电系统供氢回路控制（19, 20, 26）、空气回路控制（31, 33）、冷却回路控制（22, 28, 29）等。
本文主要工作为建立氢能一体化电站运行过程模型并研究一体化电站设备运行过程中电-氢-电能量流控制策略。控制的执行器是Buck DC-DC变换器、Boost DC-DC变换器、氢气压缩机以及氢流量调节阀。
因果序图（COG）是数学方程的图形表示，可用于对系统建模，并且可以基于自然因果关系原理直接为建模对象设计控制方程，以实现对象的综合控制[34-36]。由于氢能一体化电站包含制氢、储氢与发电三部分且涉及复杂的电-氢-电能量转换，对一体化电站采用基于COG的图形建模与传统数学模型相比，可以更加清晰地阐述一体化电站运行过程中电-氢-电的转换关系。并且当被控系统为静态刚性关系时，COG直接采用模型翻转获取控制输入，避免了传统数据驱动控制方法不区分模型特性、完全基于误差反馈求取控制输入所带来的误差反馈延时，增强了控制器性能。因此，本文采用COG方法对一体化电站进行建模与控制。
基于COG的刚性和时间依赖对象建模及控制示意图如图2所示。在COG中，带有方程标号的气球被用来表示建模关系。对于没有时间依赖性的静态刚性关系被描绘成一个带双向箭头的气球，如图2a所示。从物理层面来说，元素具有外在的因果性，系统的输出直接由系统输入决定；在数学层面，其输出与输入关系可以直接由代数方程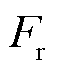
描述。如果输入变量x(t)是外部设定，可得到输出y(t)为
（1）
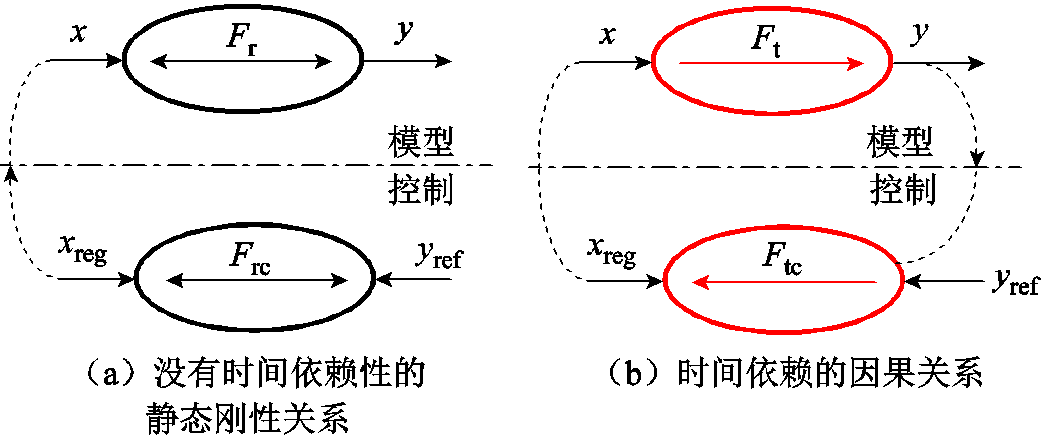
图2 基于COG的刚性和时间依赖对象建模及控制示意图
Fig.2 COG of rigid and time relations with their control schemes
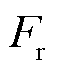的控制方程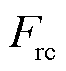
可以通过对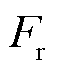反求解得到。因此，输入变量xreg(t)可以由参考输出yref(t)计算得到，表达式为
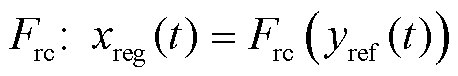（2）
与PID控制需要等到误差发生后才能通过补偿获取控制输入相比，COG直接采用模型翻转获取控制输入，避免了传统数据驱动控制方法基于误差反馈求取控制输入所带来的误差反馈延时，增强了刚性系统的响应速度。当参考信号分别为yref(t)=10和yref(t)=10t时，典型刚性系统y=100x(t)采用PID和COG方法响应的对比分别如图3a和图3b所示。
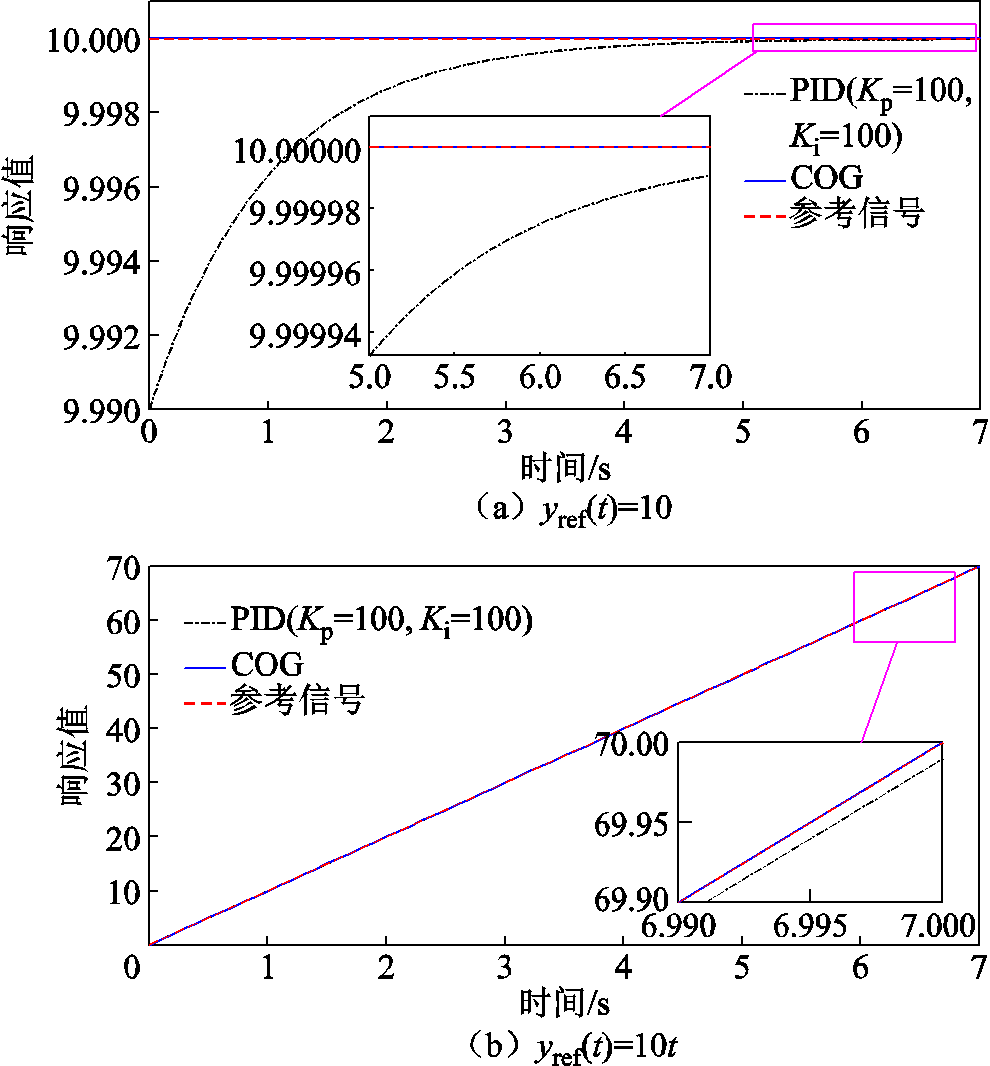
图3 不同控制策略下刚性系统的响应
Fig.3 Responses of rigid systems under different control strategies
时间依赖的因果系统输出不仅由系统输入决定，同时还取决于系统状态，因此，其输入输出具有方向性。从物理层面来说，系统内具有能量积累或者耗散，即元素具有内在的因果性；在数学层面，这类系统的输入输出关系可用具有方向的微分方程描述。系统输出在已知外部输入x(t)和系统状态时通过积分得到（求解微分方程）。
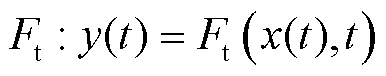（3）
因此，用带一个单向箭头的气球来表示时间依赖性的因果关系，如图2b所示。由于因果系统的输入输出具有方向性，即变量x(t)必须是输入，y(t)必须是输出，无法通过y(t)求取x(t)[35-36]。这样一来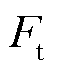，方程
的控制方程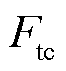
将无法直接通过求解原方程的逆来获取。因此在控制方程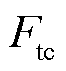中，用一个带校正器Cm的闭环控制来代替直接反转方程，表示为
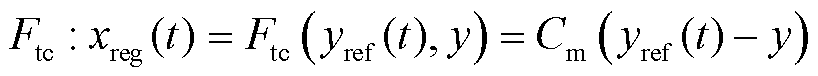（4）
为了简化建模，作如下假设：①氢气干燥纯净，并且在生产、储存和使用过程中不存在泄漏；②一体化电站除氢气压缩机和燃料电池空气压缩机消耗的功率以外，其他辅机系统的消耗忽略不计。
直流母线所提供的电压高于施加在电解池上的电压，因此需要一个降压DC-DC变换器，通过降低直流母线电压为电解池供电，这样传输到电解池的功率可以通过控制降压变换器的占空比dec来调节。Buck DC-DC变换器模型[37]可表示为
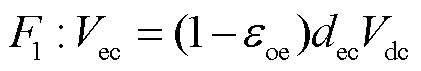（5）
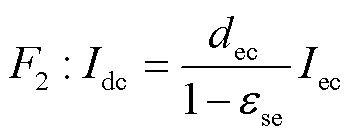（6）
式中，Vdc, Idc和Vec, Iec分别为降压变换器的直流母线和电解池的电压和电流；εoe和εse分别为变换器导通损耗和开关损耗。Buck DC-DC变换器模型的COG及其功率控制如图4所示。
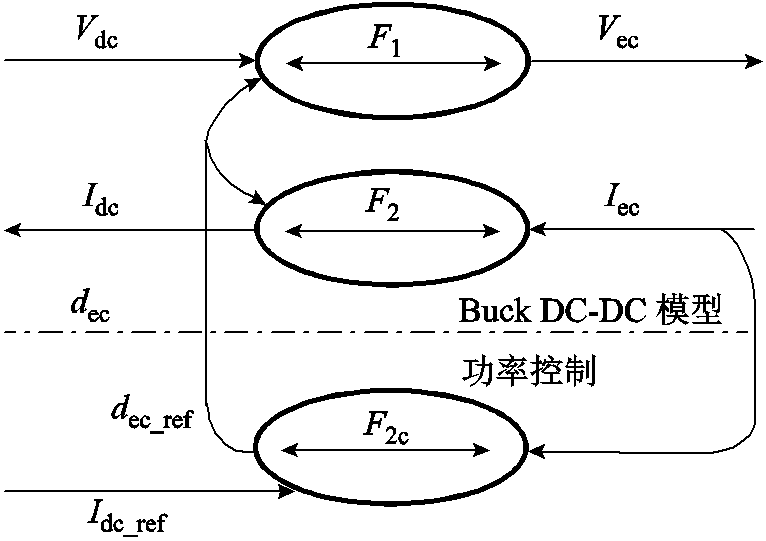
图4 Buck DC-DC变换器模型的COG及其功率控制
Fig.4 COG of Buck DC-DC model and its power control
3.2.1 电压部分
大容量的电解池一般由多片电池串联而成，因此根据欧姆定律以及单电池电压公式[38]，电解池的电压可表示为
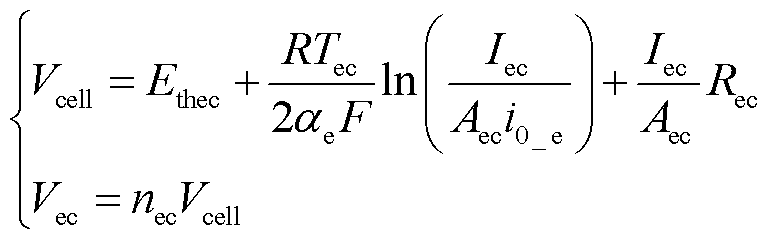（7）
式中，Vcell为单片电池的电压；nec为电解池电池数量；Aec为电解池活化面积；Ethec和Tec分别为电解池热力学电压和电解池温度；αe为电解池活度传递系数；R为通用气体常数；F为法拉第常数；i0_e为电解池交换电流密度；Rec为膜电阻，可由与膜厚度和湿度相关的经验函数获得，具体见附录式（A1）。
根据式（7），在给定温度下由25块活化面积为1 000 cm2电池串联构成的100 kW PEMEC的电流-电压特性曲线如图5所示。
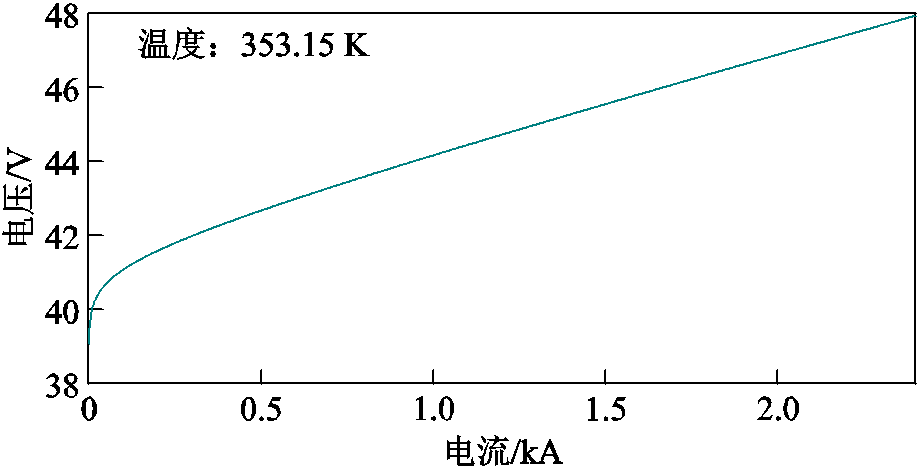
图5 PEMEC的电流-电压特性曲线
Fig.5 The current-voltage curve of the PEMEC
如图5所示，在给定温度参数下，Iec-Vec特性曲线为单调递增。因此，电解池给定电压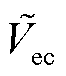
对应的电流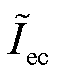
可由直接求解优化式（8）得到。
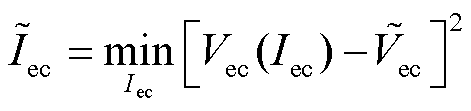（8）
式中，
，
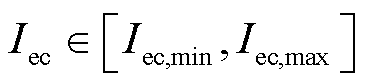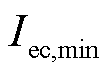和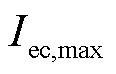
分别为电解电流的最小值和最大值。
根据式（8），扫描电压Vec即可获得符合精度要求的电解池电压-电流表。因此，电解池电压Vec与电流Iec的关系可以通过对电压-电流表中数据进行线性插值获得。
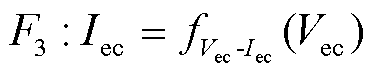（9）
3.2.2 电化学部分
根据法拉第定律，制氢流量fec_pro取决于电解池电流和电解效率，表达式为
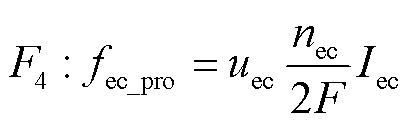（10）
其中
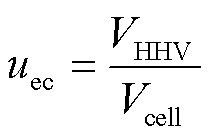
式中，uec为根据较高的热值电压VHHV计算的电解效率，VHHV= 1.48 V[39]。
3.2.3 热部分
电解池的温度对电解池电流-电压曲线和法拉第效率均有影响。但是，由于热域的时间常数（102 s）比电学（10−19 s）、力学（101 s）等其他物理域的时间常数大得多，因此，本文研究电和氢气流时假设电解池温度恒定为Tec。
3.2.4 压力部分
电解池的氢积累流量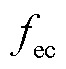
取决于制氢流量fec_pro和氢气出口流量fec_out，表示为
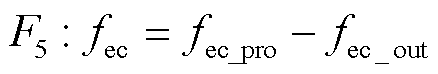（11）
因此，电解池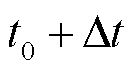
时刻储存的氢气量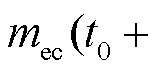
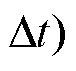为
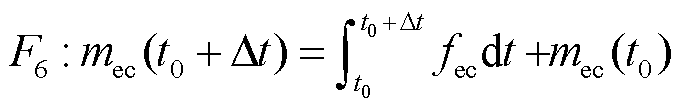（12）
电解池内氢气压力可以用理想气体定律求解为
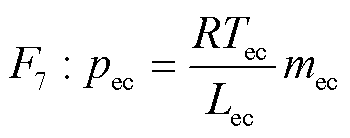（13）
式中，pec为电解池内氢气压力；Lec为阴极的体积。稳态运行时，应调节出氢流量fec_out等于制氢流量fec_pro，保持阴极内储氢量和压力恒定。PEMEC模型的COG及其压力控制如图6所示。
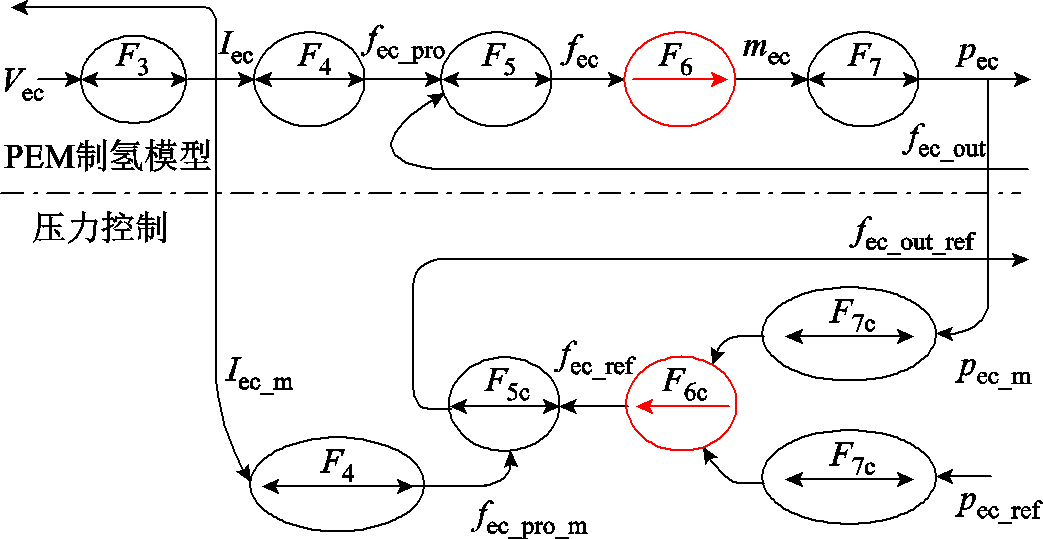
图6 PEMEC模型的COG及其压力控制
Fig.6 COG model of PEMEC and its pressure control
将电解池产生的氢气采用多变氢气压缩机进行增压存储。根据多变压缩机功率计算公式[40]，压缩机消耗功率Pcp与被压缩的氢流量fec_out关系为
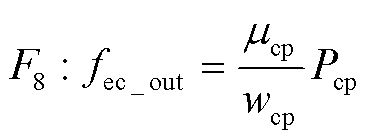（14）
式中，μcp为压缩机效率；wcp为多变功，与进出歧管压比相关，表示为
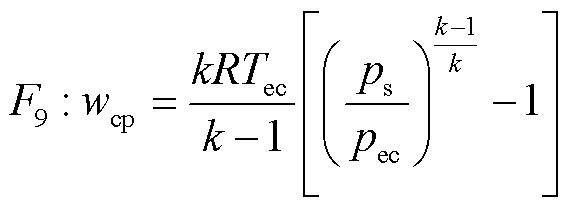（15）
式中，k为多变系数；pec为压缩机进口气体压力，对应电解池内氢气压力；ps为压缩机出口气体压力，对应储氢罐内氢气压力。压缩机模型的COG及其氢气流控制如图7所示。
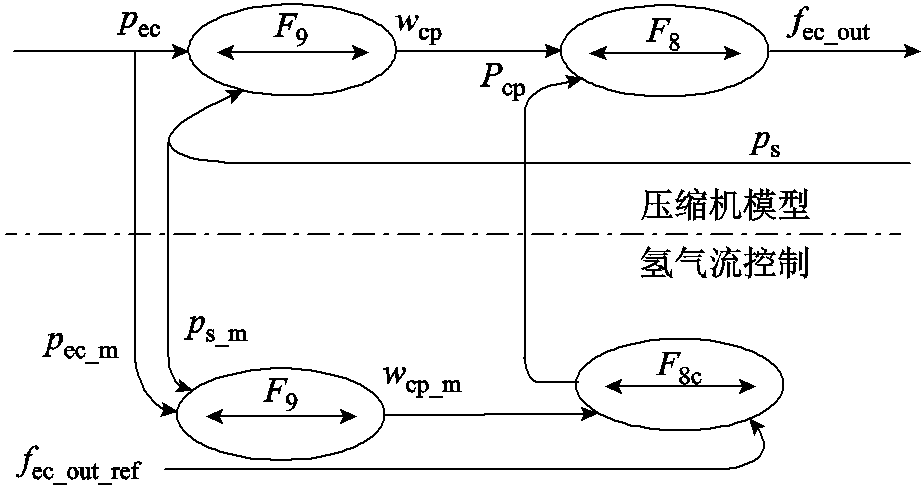
图7 压缩机模型的COG及其氢气流控制
Fig.7 COG of compressor and its hydrogen flow control
正常运行情况下氢气不会发生泄漏，因此设置氢气泄漏流量fleak=0。储氢罐的储氢流量fs取决于储氢罐的进出口流量，即电解池出口流量fec_out和流出储氢罐供给燃料电池的流量ffc，表示为
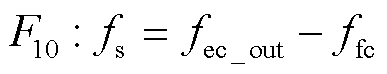（16）
需要注意的是，实际运行时由于效率原因，储能和发电两种模式不会同时运行，因此电解池和燃料电池从不同时工作，即fec_out和ffc至少有一个为零。
储氢罐内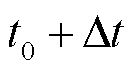时刻的氢气量
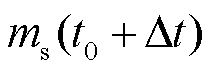为
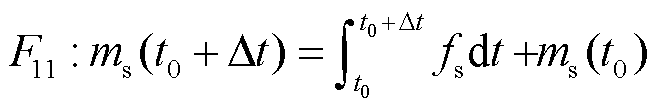（17）
根据理想气体定律，储氢罐压力ps动态方程为
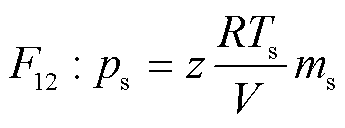（18）
式中，V为氢气罐的容积；z为氢气的压缩常数；Ts为储氢温度。储氢罐模型的COG如图8所示。
图8 储氢罐模型的COG
Fig.8 COG of the hydrogen storage model
采用氢流量调节阀来管理储氢罐流出氢气流。考虑储氢罐压力一般远高于燃料电池进氢气子系统压力，根据非线性喷嘴方程[41]，氢流量调节阀开度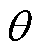
与供给燃料电池发电的氢气流量ffc关系为
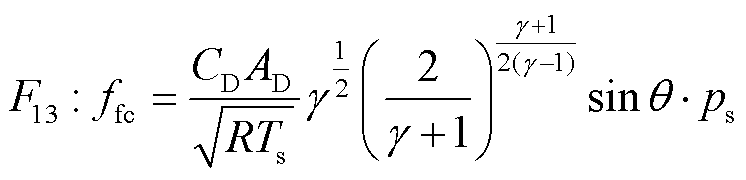（19）
式中，γ为氢气比热比；CD和AD分别为调节阀的开度系数和截面积；ps为调节阀气体入口压力，取储氢罐压力；θ为阀门开度。氢流量调节阀模型的COG及其氢供应控制如图9所示。
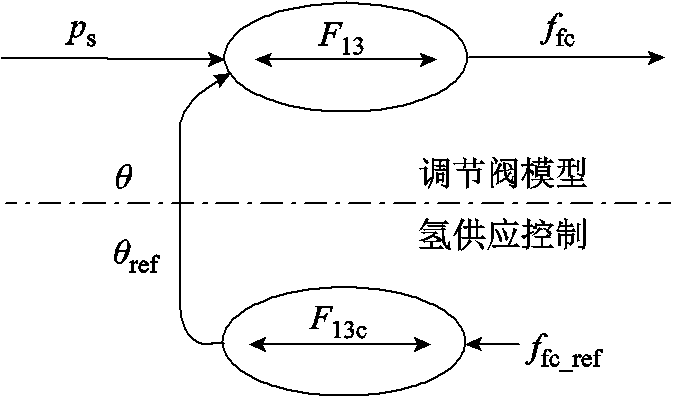
图9 氢流量调节阀模型的COG及其氢供应控制
Fig.9 COG of flow valve and its hydrogen supply control
3.6.1 电化学部分
燃料电池将氢流量调节阀供给的氢气转换为电能。假设燃料电池堆由nfc片单电池串联构成，根据法拉第定律，燃料电池电流Ifc与氢气供给流量ffc的关系为
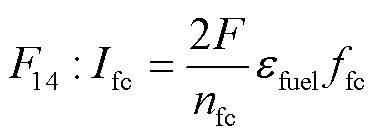（20）
式中，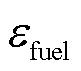
为燃料利用效率，表示为
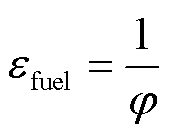（21）
式中，φ为氢气供应化学计量比，本文取1.1[42]。
3.6.2 电学部分
根据燃料电池单电池电压Ucell公式[42]，燃料电池堆的电压Ufc为
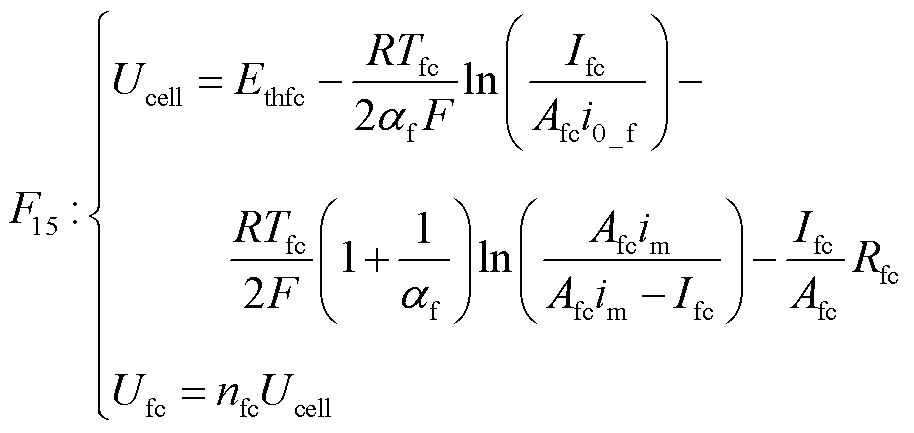（22）
式中，Ethfc为燃料电池热力学电压；Tfc、Afc和αf分别为燃料电池的温度、活化面积和活度传递系数；i0_f和im分别为燃料电池交换电流密度和最大交换电流密度；Rfc为燃料电池的欧姆阻抗。参数取值见附表1。
另外，在实际中，燃料电池发电系统在运行时需要提供额外的附加功率Pa驱动空气压缩机来提供足量的氧气[43-44]。因此，燃料电池的实际输出净功率Pfc与电流的关系为
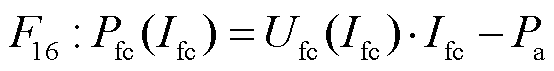（23）
根据式（22）和式（23），在给定温度下由100块活化面积为280 cm2电池串联构成的25 kW PEM燃料电池的电流-功率特性曲线如图10所示。
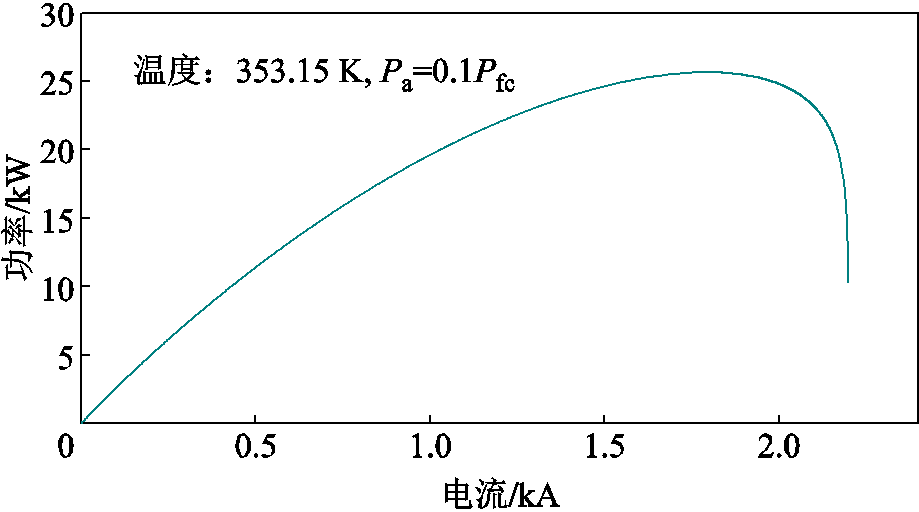
图10 PEMFC的电流-功率特性曲线
Fig.10 The current-power curve of the PEMFC
如图10所示，在给定温度下燃料电池Ifc-Pfc特性曲线为先单调增加后单调减小。在实际中燃料电池为保证运行效率，一般运行在功率单调递增部分。因此，在求解优化式（23）的逆时令电流初值从0开始即可，即
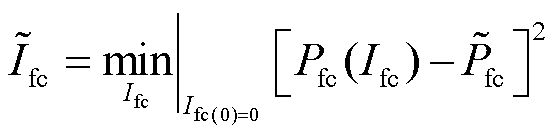（24）
式中，
，
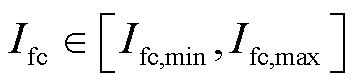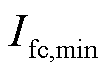和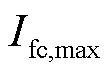
分别为燃料电池电流的最小值和最大值；
、
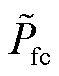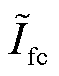分别为燃料电池给定功率及其对应的电流。
扫描给定功率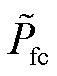
，即可获得符合精度要求的燃料电池功率-电流表。因此，通过线性插值可获得式（23）燃料电池电流Ifc与功率Pfc的反转关系。
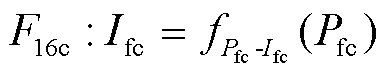（25）
3.6.3 热部分
同电解池模型类似，本文假设燃料电池温度为恒定值Tfc。
综上所述，燃料电池模型的COG及其功率控制如图11所示。
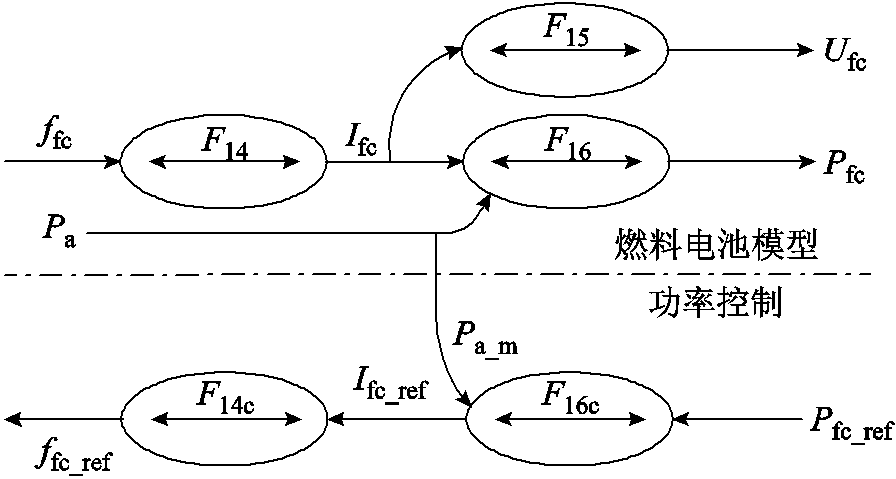
图11 PEMFC燃料电池模型的COG及其功率控制
Fig.11 COG model of PEMEC and its power control
由于燃料电池是一种大电流、低电压的发电电站，其出口电压受电流、温度和压力影响，且一般低于直流母线电压，因此需要一个升压DC-DC变换器来满足燃料电池与直流母线之间的接口电压需要。Boost DC-DC变换器模型[35]可表示为
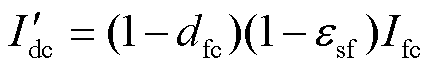（26）
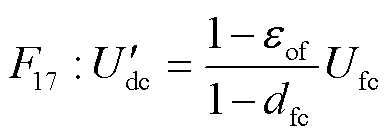（27）
式中，dfc为Boost DC-DC变换器占空比；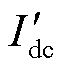
和
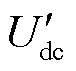分别为燃料电池被调制电流和电压；
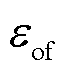和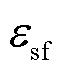
分别为Boost DC-DC变换器导通损耗与开关损耗。
因此，发电时一体化电站最终输出功率为
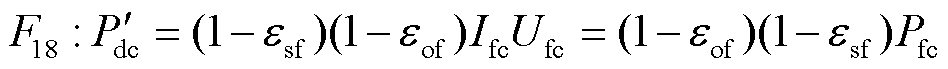（28）
Boost DC-DC变换器模型的COG及其电压控制如图12所示。
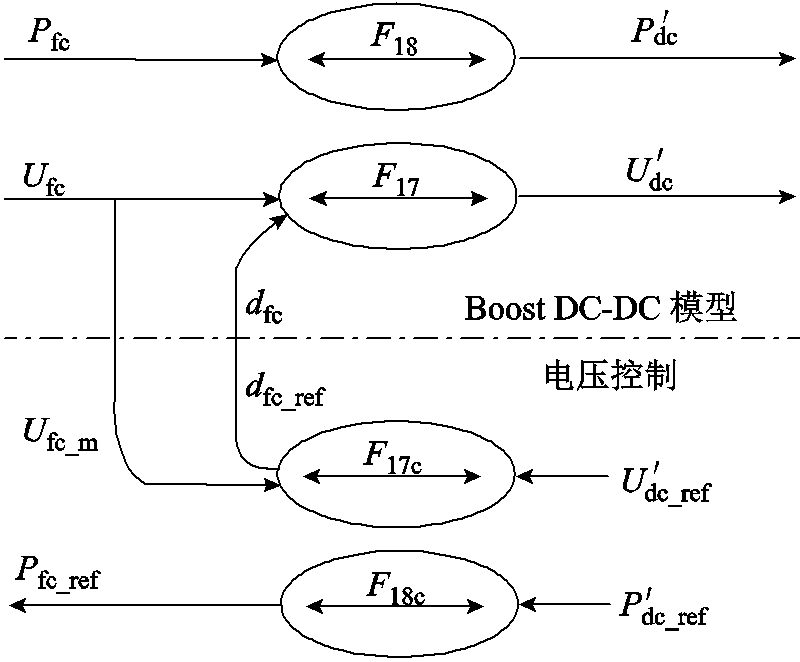
图12 Boost DC-DC变换器模型的COG及其电压控制
Fig.12 COG of Boost DC-DC and its voltage control
储氢系统作为氢能一体化电站中间环节将制氢系统及发电系统连接起来，使得氢能一体化电站运行时可以将电能转换为氢气再转换为电能。因此，先将每个系统模型的COG简化为具有多个输入和输出的块。在此基础上，将各子模型的输入和输出连接在一起即可获得氢能一体化电站运行过程的整体模型，如图13a所示。图13a中，带虚线的块表示具有能量积累可以找到时间依赖关系的部分。从图13a中可以看到，在储能的电-氢阶段，电解池Buck变换器占空比dec以及压缩机功率Pcp为控制输入。直流母线可以看作理想电压源，电解池所消耗电功率的变化则可以用电流的变化来表示。因此，储能时通过调节变换器占空比来调节电解池所消耗的功率适应新能源的波动性，并且通过调节压缩机功率以改变储能氢流量调控储能氢气流，从而维持电解池压力稳定。
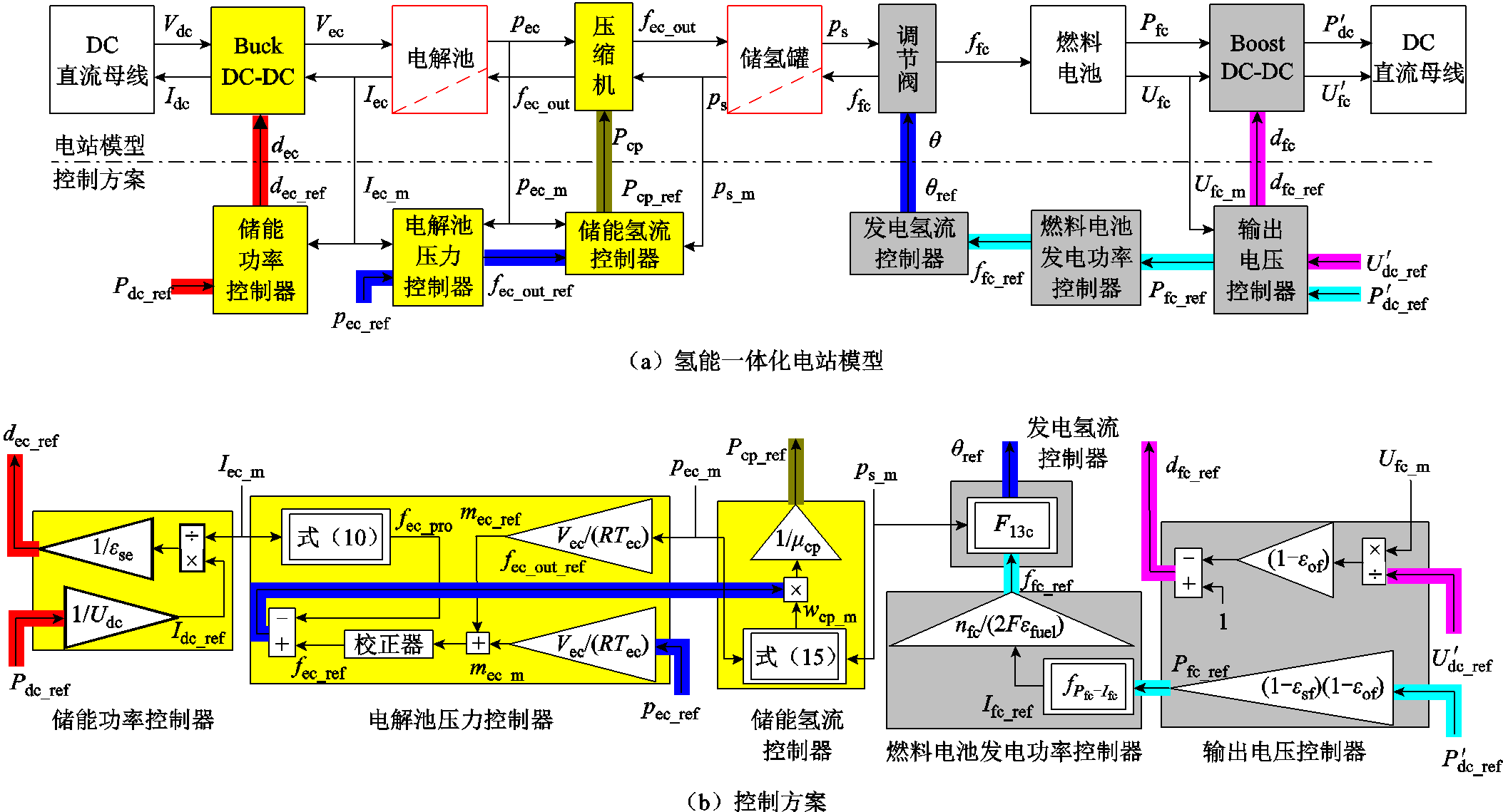
图13 氢能一体化电站模型的COG及其控制方案
Fig.13 COG of the IHEPS model and its control scheme
在发电的氢-电阶段，供氢流量调节阀开度θ和燃料电池Boost变换器占空比dfc为控制输入。供氢流量调节阀通过调节发电氢气流的供应量来调节燃料电池的发电功率，以实现发电功率与负荷需求的适配。并且通过调节燃料电池变换器占空比使供电电压满足接口电压需求，保证电功率送出。
控制系统的设计是基于COG建模的反转。控制系统的目的是对氢能一体化电站运行过程中的电-氢和氢-电能量流进行控制，保证系统安全稳定运行。整体控制方案如图13b所示。
在电能富裕时，通过变换器控制电解池功率消纳电能制氢，并通过压缩机将氢气输送到储氢罐进行存储；电能短缺时，氢能一体化电站控制流量阀释放储氢罐中的氢气，并利用燃料电池进行供电。
4.1.1 电制氢储能过程能量流控制
1）储能功率控制器：通过控制电解池Buck变换器期望占空比dec_ref调节电解池消耗的功率，来匹配需要被消纳的电功率。
2）电解池压力控制器：通过确定电解池的氢气出口流量fec_out_ref，来保证电解槽中氢气压力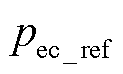
恒定。
3）储能氢流控制器：通过调节氢气压缩机的压缩功率Pcp_ref及时地将电解池流出的氢气驱动至储氢罐。
4.1.2 氢发电过程能量流控制
1）燃料电池发电功率控制器：通过确定燃料电池发电系统所需的氢流量ffc_ref，来保证燃料电池可以供给负荷所需的电功率。
2）发电氢流控制器：通过控制流量阀开度θref，来保证燃料电池所需的期望氢气流量ffc_ref，及时地从储氢罐中释放氢气。
3）输出电压控制器：通过控制燃料电池Boost变换器占空比dfc_ref来调节燃料电池端电压匹配直流总线接口电压，以保证所需发电功率的送出。
4.2.1 储能功率控制器
一体化电站制氢储能时，变换器的控制目标是使电解池功率跟随电源输入功率变化。直流母线一般可以被认为是具有恒定电压Udc的理想直流源。由直流母线传输的电功率变化量DPdc_ec可以通过电流的变化量DIdc表示为
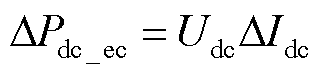（29）
因此，通过电流控制调节可实现电解池的功率调节。由于式（6）所示Buck DC-DC变换器的母线调制电流Idc与电解电流Iec之间为刚性关系，根据COG控制原理，基于COG的电解池功率控制算法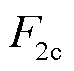
可以通过反转变换器电流方程
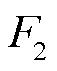（式（6））来给出，即
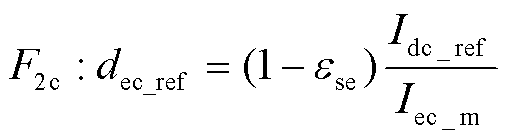（30）
其中
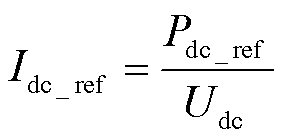
式中，Idc_ref为变换器的直流母线调制电流；Iec_m为测量的电解池电流。储能功率控制模型的COG见图4。
4.2.2 电解池压力控制器
在正常稳定运行时，电解池氢气压力应该被控制在所需的压力水平pec_ref。由式（11）和式（12）可知，若保证电解池压力恒定，需要控制电解池内氢气量恒定，即电解池出氢流量等于制氢流量。但是在实际中氢气流量不容易测量，因此，可通过反转式（13）中刚性的压力与氢量关系
，从参考压力pec_ref和电解池测量压力pec_m推导出期望的氢量mec_ref和实际氢量mec_m。
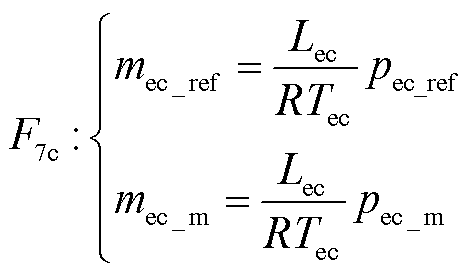（31）
根据式（12），储氢量和储氢流量之间关系
是时间依赖的能量积累过程。因此，根据COG控制原理，通过带校正器Cec的闭环控制，得到电解池内阴极氢气积累流量的参考值fec_ref为
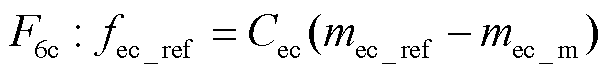（32）
式中，Cec为闭环增益系数。
因此，通过式（11）电解池流量关系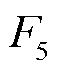
反求电解池氢气出口流量的参考值fec_out_ref为
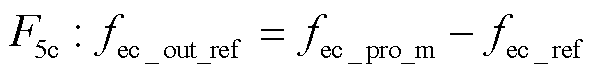（33）
式中，氢气生成流量fec_pro_m可以根据电解池运行电流Iec_m利用式（10）法拉第定律方程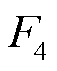
来估计。因此，电解池压力控制模型的COG如图6所示。
4.2.3 储能氢流控制器
氢气压缩机的作用是将PEM电解池生成的氢气以参考出口流量fec_out_ref驱动到储氢罐内。压缩机期望的压缩机功率Pcp_ref可通过反转式（14）压缩机功率与电解池流量方程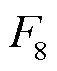
计算，表示为
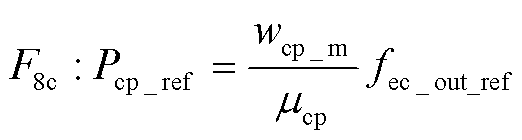（34）
式中，压缩机多变功wcp_m根据测量的储氢压力ps_m和电解池压力pec_m利用式（15）多变功与进出歧管压比关系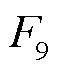
估计得到。因此，储能氢气流控制模型的COG如图7所示。
4.3.1 燃料电池发电功率控制器
在需求功率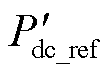
下，燃料电池的实际输出参考功率Pfc_ref可通过反转式（28）Boost DC-DC变换器功率关系
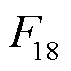（见图12）得到，表示为
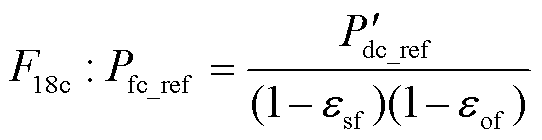（35）
由于燃料电池功率与电流之间没有能量累积过程，为刚性关系，因此燃料电池的参考电流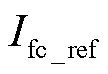
可通过直接将参考功率
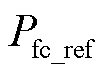代入式（23）的反转式（25）获得，表示为
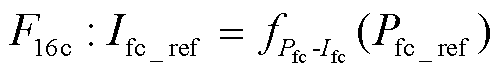（36）
为防止氢气供应不及时导致燃料电池“氢气饥饿”现象发生，需要保证储氢系统供应的流量满足燃料电池系统消耗的氢气量。负荷需求下燃料电池期望的氢气流量ffc_ref可通过反转式（20）计算得到。
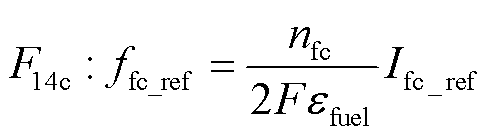（37）
因此，发电功率控制器模型的COG如图11所示。
4.3.2 发电氢流控制器
氢流量调节阀的作用是控制储氢罐中存储的氢气以期望氢气流量ffc_ref进行释放。氢流量调节阀期望的开度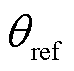
可以通过反转式（19）获得。
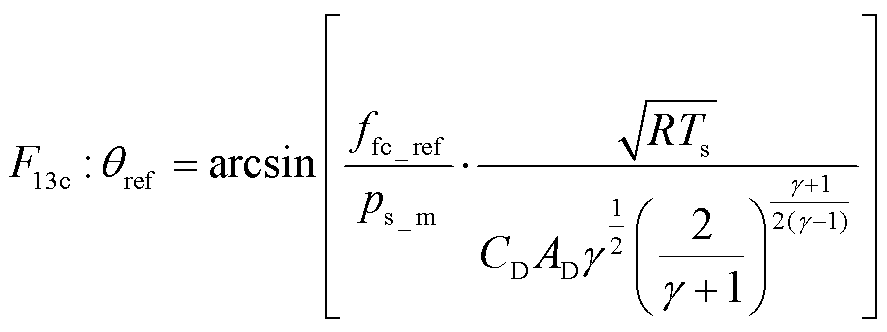（38）
因此，发电氢流控制器模型的COG如图9所示。
4.3.3 输出电压控制器
燃料电池的输出电压低于直流母线的接口电压，因此需要Boost DC-DC变换器调节燃料电池端口的低电压达到直流母线期待的高接口电压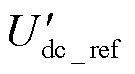
来保证电功率的稳定送出。根据式（27）可知，燃料电池变换器的调制电压Ufc和燃料电池被调制的母线电压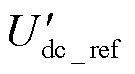之间为刚性关系，因此，燃料电池母线电压控制算法可以通过反转式（27）给出。
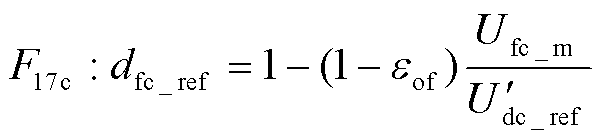（39）
式中，Ufc_m为燃料电池出口测量电压。因此，一体化电站输出电压控制模型的COG如图12所示。
将每一部分控制方案也等效为具有多个输入和输出的块，收集所有的因果序图就可以得到整个一体化电站模型及其控制方案的宏观表示，如图13所示。
氢能一体化电站包括100 kW的PEM制氢系统和25 kW的燃料电池系统。储氢系统的初始压力和容量分别为3.5 MPa和3.2 L。另外，假设两个变换器导通损耗εoe和εof均为3%，开关损耗εse和εsf均为2%；燃料电池的附加功率损耗为输出功率的10%，一体化电站的具体的模型参数见附录。并且，本文在电解池电流-电压特性建模时，Vec采样间隔为0.01 V，扫描范围为37～50 V；燃料电池电流-功率特性建模时，采样间隔为0.001 kW，功率扫描范围为0～25 kW。
在半实物仿真平台上进行硬件在环（Hardware in Loop, HIL）仿真测试，其实验平台、运行原理及模型框架如图14所示。
图14 硬件在环实验平台、运行原理及模型框架
Fig.14 HIL experiment platform, operating principle and model frame
如图14a所示，实验平台由RT-Lab（OP5600）实时仿真机、负荷信号模拟器、DSP控制器（YXSPACE-SP1000）、录波仪和上位机（PC）组成。实验具体运行原理如图14b所示。在实验开始前首先利用上位机将一体化电站的数学模型（图14c）内嵌在RT-Lab中，将控制算法（图14d）嵌入DSP控制器中。实验测试时RT-Lab结合RT-Lab I/O板卡上所提供的负荷信号以及控制器输入求解出一体化电站的状态量，包括功率、电流、电压、氢气流量、温度和压力等；然后将这些状态量通过I/O板卡以模拟电压信号的形式输出并传输给控制器；最后控制器在接收到状态量后，根据内嵌的控制算法输出控制信号并送给RT-Lab的I/O板卡作为RT-Lab的输入，从而实现硬件在环实时仿真。其中，负荷信号由信号模拟器模拟生成。
设置直流母线电压为300 V，负荷曲线如图15所示。一体化电站在0～6 000 s进行储能，6 000～11 000 s进行发电。整个储能过程和发电过程均包括了功率斜坡上升启机、功率斜坡下降停机、恒功率运行、功率阶跃上升和阶跃下降五种工况。在完整的0～12 000 s范围内，一体化电站详细的电-氢储能运行中的制氢功率、储氢流控制，以及氢-电发电过程中的氢供应流量和输出电压控制分析如下。
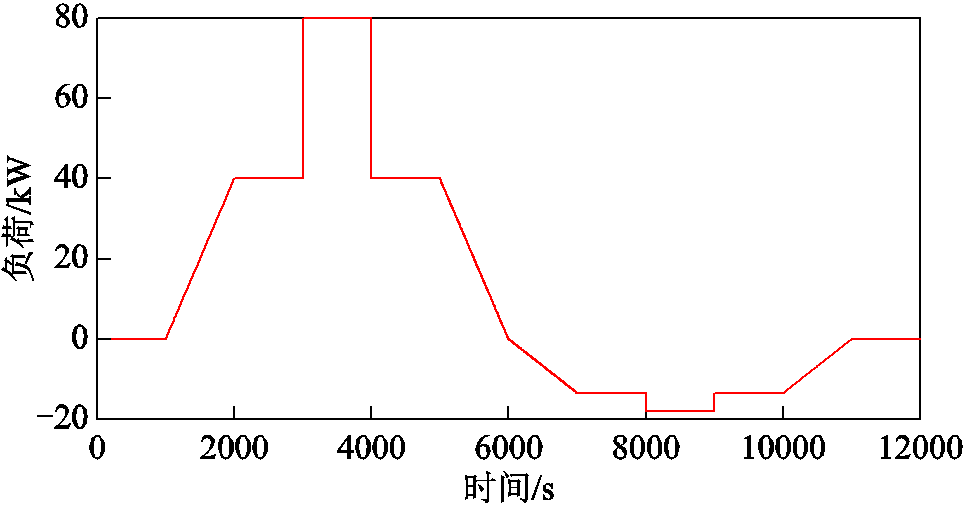
图15 负荷曲线
Fig.15 Load condition curve
5.2.1 电-氢储能运行过程控制分析
1）制氢功率控制分析
在不同工况下，一体化电站的Buck变换器控制信号以及电解池的电压、电流和功率响应情况如图16所示。
首先，分析各变量的依存关系。由图16a可以看到，一体化电站运行期间Buck变换器的占空比跟随着负荷工况（见图15）的变化发生变化。这是因为电解池此时可以看作一个非线性电阻，当电解电压（图16b）改变时，电解电流（图16c）与功率（图16d）也随之变化。因此通过调节Buck DC-DC变换器占空比来改变加载在电解池两端的电压就可以实现电解功率的调节。
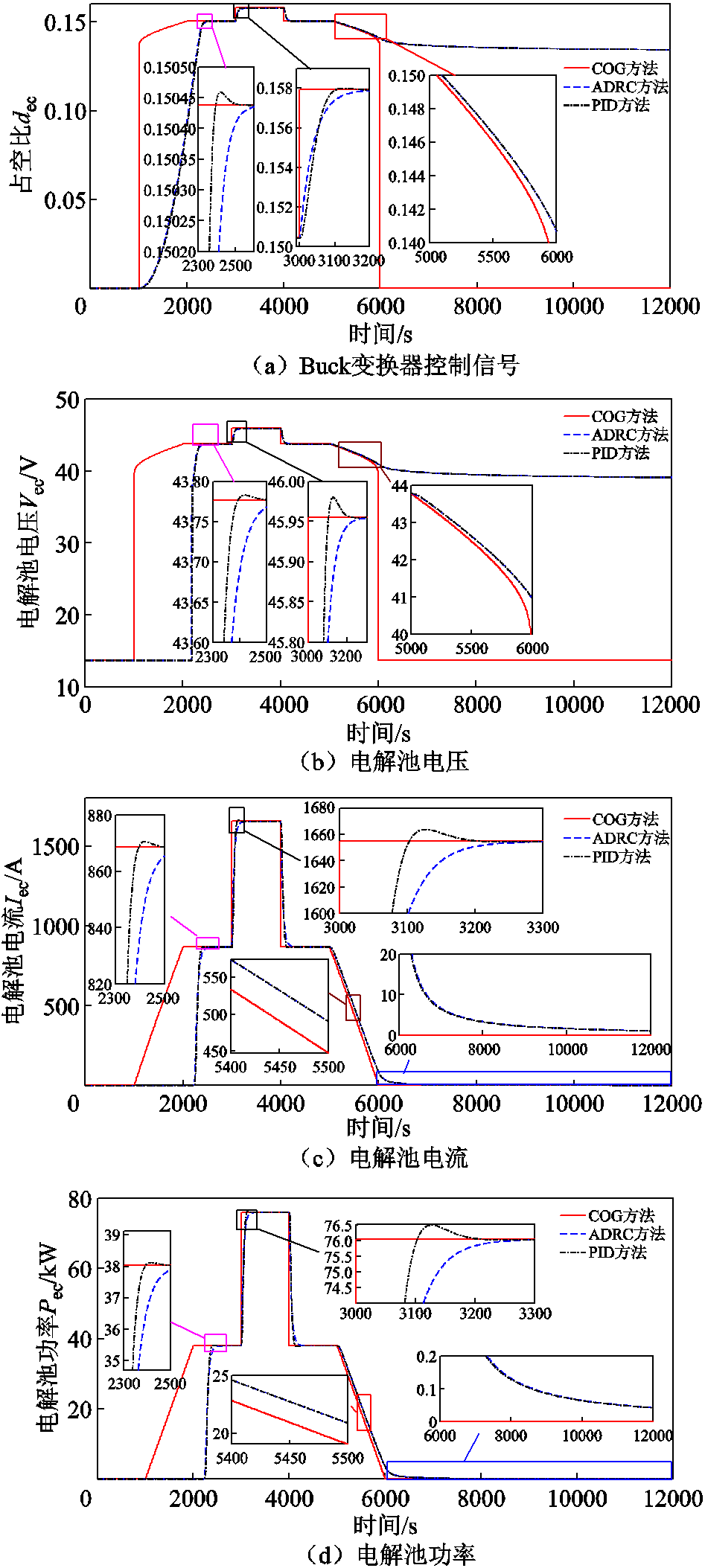
图16 制氢功率控制过程中的状态量
Fig.16 State in hydrogen production power control
然后，从图16d电解池功率控制的效果来看。对于1 000～3 000 s的斜坡上升启动工况，基于PID控制（点画线）和ADRC（虚线）方法的电解池输出功率在1 000～2 200 s为零，在2 200 s以后电解池才开始逐步跟随负荷需求运行，因此基于PID控制和ADRC的储能电功率控制存在启动死区。同样，观察到在6 000 s储能结束停机后，基于PID控制和ADRC的方法始终存在电解功率而无法完全停机，存在停机死区。相比较而言，本文所提基于COG的方法无论是在启动阶段还是停机阶段均可以快速跟随负荷变化，并不存在启动和停机死区。
进一步观察在3 000 s和4 000 s功率阶跃变化时不同方法的性能。以3 000 s时功率阶跃上升为例，基于PID控制和ADRC的方法收敛大约耗时300 s，并且在收敛过程中PID方法出现了超调现象，而本文方法可以直接前馈实现快速无超调收敛。因此，在功率阶跃时，相比其他两种方法，本文所提方法具有更好的性能。同样观察5 000 s功率时变下降的细节，PID和ADRC方法曲线基本重合即性能相近，并且本文所提方法曲线（红色实线）一直处于PID和ADRC方法曲线的下方，因此在负荷时变下降时，本文所提方法也有着更好的响应性能。这是因为电解池电功率调节并不存在大量的能量积累，其并非时间依赖的而是刚性的。本文所提控制方法可以直接基于COG控制原理设计前馈控制律，相比基于误差反馈的PID和ADRC控制，可以节省误差反馈所需耗时，加快响应速度，增强控制性能。
因此，本文设计的一体化电站控制方案可以有效地实现电功率的调节，与PID和ADRC方法相比具有无启停死区、响应性能好的特点。
2）储氢流控制分析
一体化电站的电解池制氢流量、氢气压缩机功率、电解池氢气压力响应情况如图17所示。
同样先分析各变量的依存关系。根据法拉第定律可知，图17a电解池制氢流量随着电解电流变化而变化。对比图17a和图17b可以看到，压缩机输出功率跟随制取氢气的流量变化，压缩机可以及时地将生成的氢气输送至储氢罐，从而保证电解池腔内氢气压力（图17c）一直保持在3 MPa。因此，通过调控压缩机输出功率控制储氢流可以有效地实现电解池的压力调控。
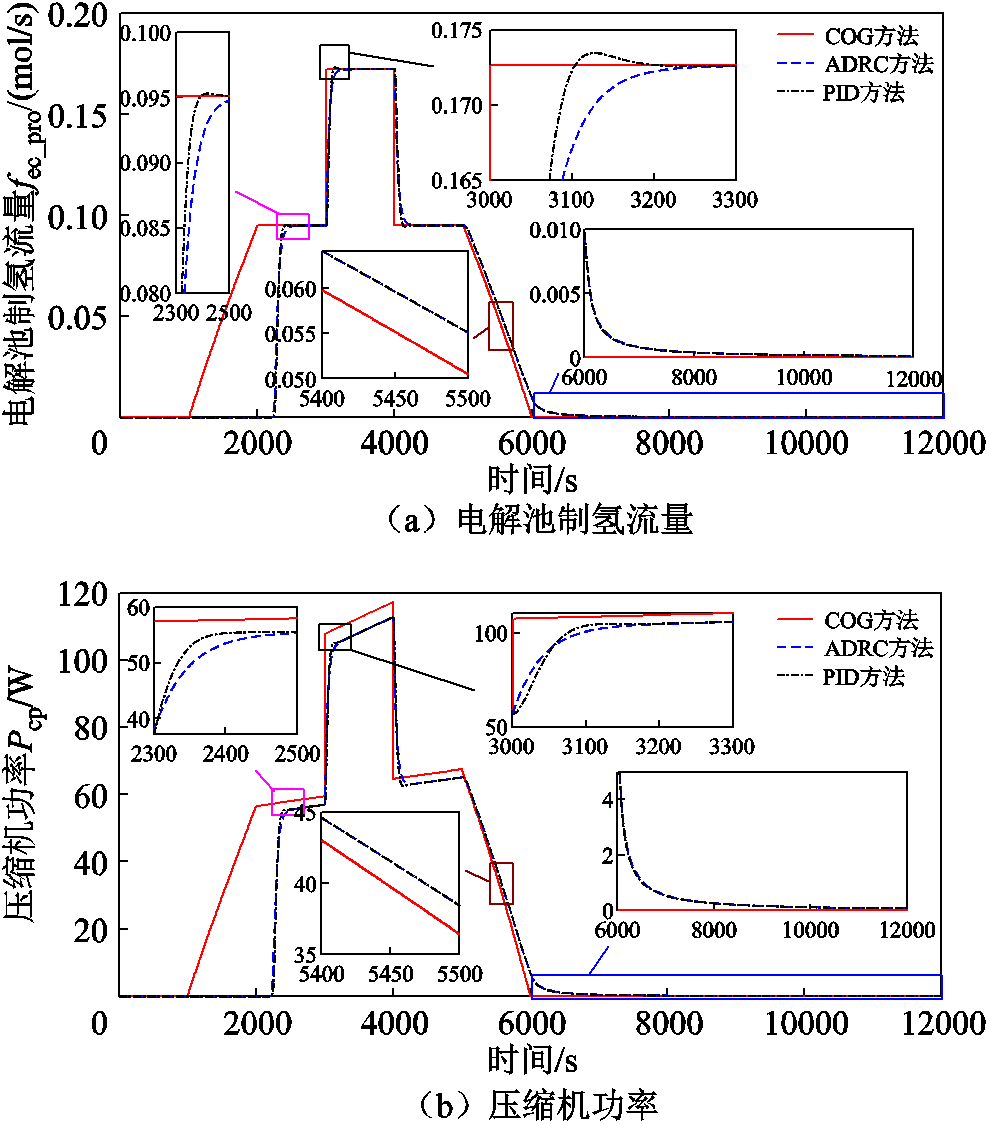
图17 储氢流控制中的状态量
Fig.17 State quantity in hydrogen storage flow control
从图17c中的压力控制效果来看，基于COG、PID和ADRC三种控制方法对电解池压力的控制效果基本一致，都可以及时地将电解池生成的氢气进行压缩存储，并保证电解池压力稳定在3 MPa。这是因为电解池内部腔体压力变化是腔体氢气累积量变化造成的，即电解池的腔体压力是时间依赖的动态能量累积关系而非刚性关系。根据COG控制原理，其腔内压力控制不可以直接通过求逆获取前馈控制率，而是间接地通过误差闭环反馈代替。因此，在压力控制上基于COG方法与基于PID控制或者ADRC方法同属于基于误差反馈的控制，其控制效果类似。
综上所述，本文所设计的控制方案以及所提的基于COG的控制方法与其他方法相比，无死区且收敛更快，可以在所述各类工况下有效地对电-氢储能过程中的制氢功率与储氢流进行调控，保证一体化电站电-氢储能过程的顺利进行。
5.2.2 氢-电发电运行过程分析
1）氢流量供应控制
氢流量调节阀的开度、氢气供应流量以及燃料电池电流和一体化电站输出功率如图18所示。
从图18可以看出，在6 000 s以后一体化电站运行在发电模式，燃料电池将储氢罐中的氢能转换为电能为负荷供电。令氢流量调节阀的开度（图18a）跟随负荷变化而变化，控制储氢罐输送至燃料电池的氢气流量跟随负荷需求的氢气供应参考流量（图18b），燃料电池在供给的氢气流量下得到相应的输出电流（图18c）和输出功率（图18d）。因此可以通过调节流量阀的开度控制供应给燃料电池的氢气量来保证燃料电池输出功率跟随负荷需求。
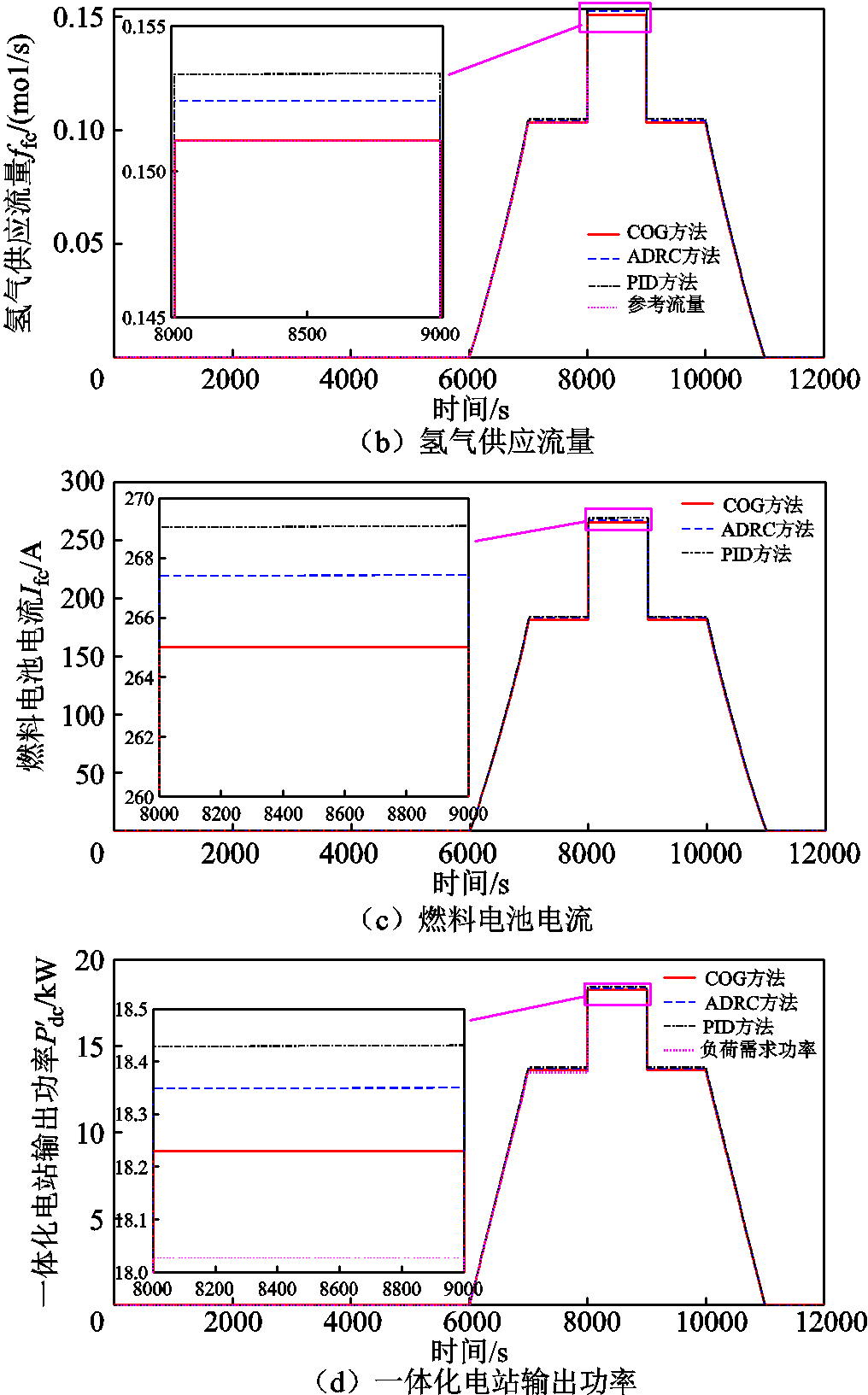
图18 氢供应控制中的状态量
Fig.18 State in hydrogen supply control
从图18b中的氢气流量供应控制效果来看，本文所提方法和基于PID控制、ADRC的方法在各种工况下的氢气供应控制均可以稳定收敛。但是，值得注意的是，在实验过程中尽管对PID控制和ADRC参数进行了多次精调，PID控制和ADRC下始终存在稳态超调，无法做到满足跟踪性能下的无偏差收敛。与PID控制、ADRC方法不同的是，本文所提基于COG的控制方法可以做到无偏差收敛控制。这也是因为在氢气供应以及氢气转换为电能的过程中并不涉及能量积累，调节阀开度与供应的氢气流量是刚性的。基于COG的控制原理可以通过直接设计流量调节阀的前馈控制律来实现快速、无偏差氢气流量供应控制。此外，观察图18d中三种控制方法下一体化电站最终的输出功率可以发现，三种方法输出的功率都可以做到稳态收敛。PID、ADRC和COG方法的超调量分别为0.24%、0.194%和0.128%，COG方法的超调量与PID控制、ADRC相比分别减小了46.7%和34%。因此，在适配输出功率的氢流量供应上，所提基于COG的控制效果也优于基于误差的PID和ADRC的控制效果。
综上所述，本文设计的控制方案可以有效地实现氢气供应量控制，并且本文所提的控制方法优于PID控制和ADRC方法。
2）送出电压控制
燃料电池输出电压、Boost变换器控制信号以及一体化电站送出电压如图19所示。
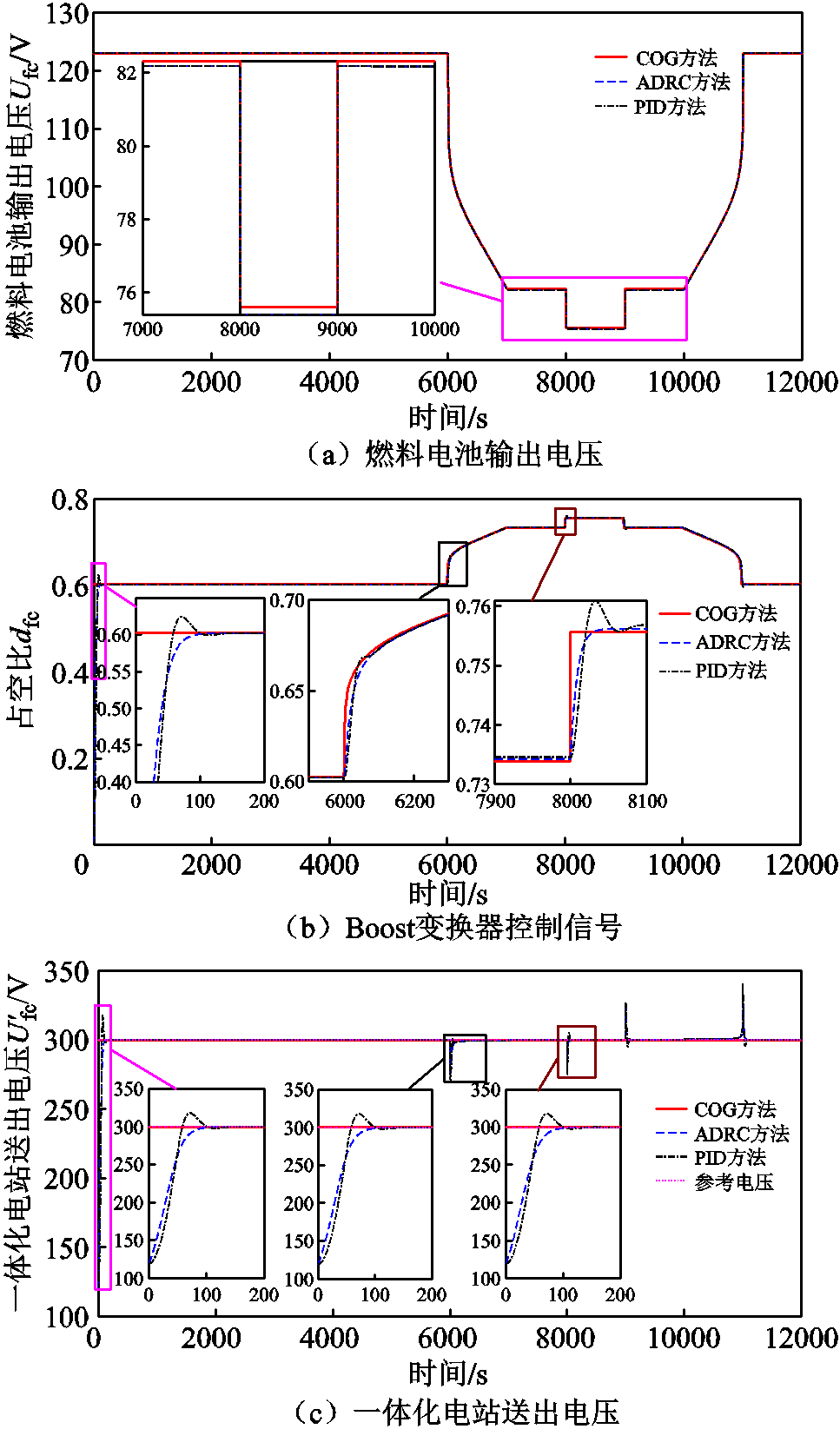
图19 送出电压控制中的状态量
Fig.19 The state quantity in the output voltage control
从图19a可以看到，燃料电池跟随负荷出力需求时，其端电压低于直流送出母线电压的300 V且不断地变化。因此，通过控制Boost变换器的占空比（图19b）跟随燃料电池端电压的变化而变化，使一体化电站的输出电压稳定至母线接口电压300 V（图19c）。
从图19c中一体化电站的输出电压控制效果来看，本文提出的基于COG的控制方法可以快速无差收敛。而PID和ADRC方法大约需要130 s才可以做到无差收敛，并且在收敛过程中PID出现了超调。出现这种现象的原因是变换器电压控制关系是刚性的并不存在能量积累，可以基于COG的控制原理直接设计快速、无偏的前馈电压控制律。因此基于COG的一体化电站的输出电压控制效果也优于基于误差的PID和ADRC方法。此外，在三种控制方法下，整个运行过程中储氢罐的压力曲线如图20所示。
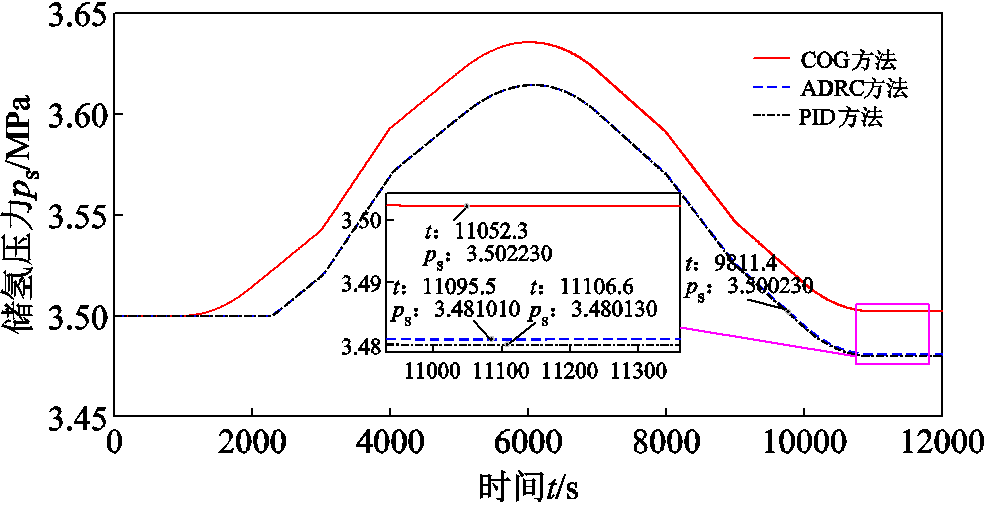
图20 储氢罐的压力
Fig.20 The pressure of the hydrogen storage tank
从图20可以看出，在运行工况相同且起始储氢压力也相同的情况下，基于COG、ADRC和PID方法的最终储氢压力分别为3.502 230、3.481 010、3.480 130 MPa。ADRC和PID控制下的氢气压力只相差880 Pa，基本相同，均低于所提COG方法的氢气压力，即储氢罐中ADRC和PID控制下的氢气剩余量基本相同但低于本文所提的COG方法。因此，PID和ADRC方法的能源利用效率也基本相同且低于本文所提的COG方法。出现该现象的一个原因是PID控制和ADRC在制氢系统存在启动死区，而COG方法不存在；另外一个原因是PID和ADRC在氢气供应时存在更大的稳态超调偏差，使得需在同样负荷功率需求下供给更多燃料，产生燃料浪费。
另外，从图20中可以看到，在本案例中采用COG控制方法时，整个运行过程结束时的氢气压力（3.502 230 MPa）与起始压力（3.5 MPa）相比，增长了约万分之六，可以认为电解产生的氢气全部被利用。根据一体化电站负荷工况（见图15）可知，0～6 000 s内储能过程消耗2×108 W·s电能，6 000～12 000 s内发电过程供应电能5.2×107 W·s，则COG控制下氢能一体化电站的运行效率约为26%。采用PID和ADRC控制方法时，在9 811 s时剩余的氢气量与采用COG在12 000 s时剩余的氢气量相同，此时一体化电站共供应电能4.24×107 W·s，减少电能供应约9.6×106 W·s，则PID控制和ADRC方法下一体化电站运行效率约为21.2%。因此一体化电站采用COG控制比采用PID控制和ADRC时的运行效率提升了22.6%。
综上所述，本文提出的基于COG的一体化电站运行控制方案可以有效地实现一体化电站能量流管理，且其控制效果在响应速度、收敛精度和运行效率上均优于传统方法。
本文首先提出了一种可以和可再生能源结合的箱式氢能一体化电站，并介绍了其构成及工作原理；其次，基于COG建立了面向控制的氢能一体化运行过程动态模型，该模型能够清晰地反映一体化电站不同物理量之间的关系，实现一体化电站的电-氢-电运行过程表征；然后，提出了基于COG的一体化电站运行功率流与氢流控制策略，实现了一体化电站能量流管理；最后，测试结果表明，与传统方法相比，所提控制策略在响应速度、收敛精度和运行效率上均较优，可以更有效地实现氢能一体化电站运行过程的能量流管理。
尽管本文已经建立了面向控制的氢能一体化电站运行过程模型并提出了其运行过程的能量管理策略，然而还有许多需要解决的关键问题，如各子系统的运行控制策略、氢能一体化电站制氢-储氢-发电三部分的经济容量匹配以及氢能一体化电站紧凑式结构设计等。
附 录
附表1 IHEPS模型参数值
App.Tab.1 Model parameter values of IHEPS
参数数值 电解池电池数量25 电解池温度/K353.15 电解池活化面积/cm21 000 法拉第常数F/(C/mol)9.648 5×104 电解池阴极体积/L0.1 气体常数R/[J/(K·mol)]8.314 电解池面积/cm250 热力学电压()/V1.23 电解池活度传递系数0.5 电解池交换电流密度/(A/cm2)1×10-12
（续）
参数数值 电解池膜电阻式（A1） 氢压缩机效率0.8 多变系数k1.4 储氢罐容积V/L10 氢的压缩常数z1.0 氢的比热比γ1.41 储氢温度/K303 调节阀开度系数6.2×10-4 调节阀的截面积/cm236.939 燃料电池数量100 燃料电池活化面积/cm2280 燃料电池交换电流密度/(A/cm2)4.54×10-5 燃料电池最大交换电流密度2.2 燃料电池活度传递系数0.5 燃料电池温度/K353.15 燃料电池膜电阻/Ω式（A3）
电解池膜电阻表达式为
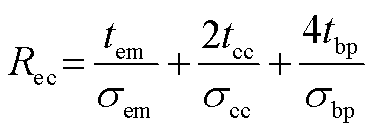（A1）
式中，tem为膜厚度，tem=1.25×10-6 cm；tcc和tbp分别为集流器和双极板厚度，且tcc=0.1 cm，tbp=0.2 cm；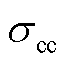
为集流器电导率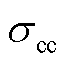，=145 S/cm；
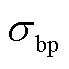为双极板电导率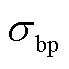， =23 800 S/cm；
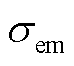为膜电导率（S/cm），表达式为
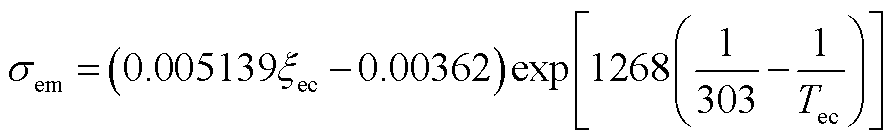（A2）
式中，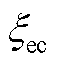
为电解池膜水含量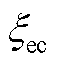，=14。
燃料电池膜电阻表达式为
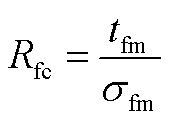（A3）
式中，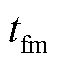
为膜厚度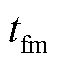，=1.25×10-6 cm；
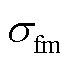为膜电导率（S/cm），表达式为
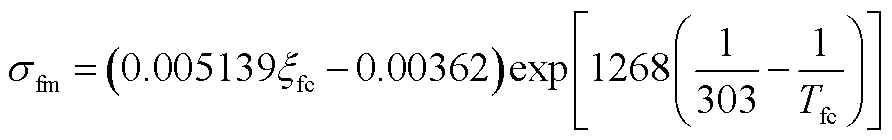（A4）
式中，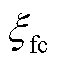
为燃料电池膜水含量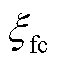，=14。
参考文献
[1] 郜捷, 宋洁, 王剑晓, 等. 支撑中国能源安全的电氢耦合系统形态与关键技术[J]. 电力系统自动化, 2023, 47(19): 1-15.
Gao Jie, Song Jie, Wang Jianxiao, et al. Form and key technologies of integrated electricity-hydrogen system supporting energy security in China[J]. Automation of Electric Power Systems, 2023, 47(19): 1-15.
[2] Jiao Kui, Xuan Jin, Du Qing, et al. Designing the next generation of proton-exchange membrane fuel cells[J]. Nature, 2021, 595(7867): 361-369.
[3] 郑先娜, 林瑞全. 质子交换膜燃料电池控制策略综述[J]. 电气技术, 2017, 18(11): 1-5, 24.
Zheng Xianna, Lin Ruiquan. Summarization of control strategy for proton exchange membrane fuel cell[J]. Electrical Engineering, 2017, 18(11): 1-5, 24.
[4] 马睿, 任子俊, 谢任友, 等. 基于模型特征分析的质子交换膜燃料电池建模研究综述[J]. 中国电机工程学报, 2021, 41(22): 7712-7730.
Ma Rui, Ren Zijun, Xie Renyou, et al. A comprehensive review for proton exchange membrane fuel cell modeling based on model feature analysis[J]. Proceedings of the CSEE, 2021, 41(22): 7712-7730.
[5] 敖文杰, 陈家伟, 陈杰, 等. 燃料电池-锂电池混合供电系统的无源控制策略及参数设计方法[J]. 电工技术学报, 2024, 39(2): 580-594.
Ao Wenjie, Chen Jiawei, Chen Jie, et al. Passivity-based control strategy and parameter design method for fuel cell-lithium battery hybrid power supply system[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 580-594.
[6] Hu Peng, Cao Guangyi, Zhu Xinjian, et al. Modeling of a proton exchange membrane fuel cell based on the hybrid particle swarm optimization with Levenberg-Marquardt neural network[J]. Simulation Modelling Practice and Theory, 2010, 18(5): 574-588.
[7] Zhong Zhidan, Zhu Xinjian, Cao Guangyi. Modeling a PEMFC by a support vector machine[J]. Journal of Power Sources, 2006, 160(1): 293-298.
[8] 杨德友, 崔冬晓, 蔡国伟. 基于云智能控制器的燃料电池最大功率跟踪策略[J]. 电工技术学报, 2018, 33(14): 3362-3370.
Yang Deyou, Cui Dongxiao, Cai Guowei. A maximum power point tracking technology for fuel cells using cloud model based intelligent controller[J]. Tran-sactions of China Electrotechnical Society, 2018, 33(14): 3362-3370.
[9] 张雪霞, 黄平, 蒋宇, 等. 动态机车工况下质子交换膜燃料电池电堆衰退性能分析[J]. 电工技术学报, 2022, 37(18): 4798-4806.
Zhang Xuexia, Huang Ping, Jiang Yu, et al. Degradation performance analysis of proton exchange membrane fuel cell stack under dynamic locomotive conditions[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4798-4806.
[10] 罗悦齐, 张嵩, 高丽萍, 等. 质子交换膜燃料电池低温启动水热管理特性及优化[J]. 电工技术学报, 2018, 33(11): 2626-2635.
Luo Yueqi, Zhang Song, Gao Liping, et al. Optimization of water and thermal management in proton exchange membrane fuel cell during low temperature startup[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2626-2635.
[11] McKay D A, Stefanopoulou A G, Cook J. Model and experimental validation of a controllable membrane-type humidifier for fuel cell applications[C]//2008 American Control Conference, Seattle, WA, USA, 2008: 312-317.
[12] Pukrushpan J T, Peng Huei, Stefanopoulou A G. Control-oriented modeling and analysis for automotive fuel cell systems[J]. Journal of Dynamic Systems, Measurement, and Control, 2004, 126(1): 14-25.
[13] 孙鹤旭, 李争, 陈爱兵, 等. 风电制氢技术现状及发展趋势[J]. 电工技术学报, 2019, 34(19): 4071-4083.
Sun Hexu, Li Zheng, Chen Aibing, et al. Current status and development trend of hydrogen production technology by wind power[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 4071-4083.
[14] 胡俊杰, 童宇轩, 刘雪涛, 等. 计及精细化氢能利用的综合能源系统多时间尺度鲁棒优化策略[J]. 电工技术学报, 2024, 39(5): 1419-1435.
Hu Junjie, Tong Yuxuan, Liu Xuetao, et al. Multi-time-scale robust optimization strategy for integrated energy system considering the refinement of hydrogen energy use[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1419-1435.
[15] Atlam O, Kolhe M. Equivalent electrical model for a proton exchange membrane (PEM) electrolyser[J]. Energy Conversion and Management, 2011, 52(8/9): 2952-2957.
[16] Guilbert D, Vitale G. Variable parameters model of a PEM electrolyzer based model reference adaptive system approach[C]//2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 2020: 1-6.
[17] Hernández-Gómez Á, Ramirez V, Guilbert D, et al. Cell voltage static-dynamic modeling of a PEM electrolyzer based on adaptive parameters: development and experimental validation[J]. Renewable Energy, 2021, 163: 1508-1522.
[18] Mohamed A, Ibrahem H, Yang Rui, et al. Optimization of proton exchange membrane electrolyzer cell design using machine learning[J]. Energies, 2022, 15(18): 6657.
[19] Guilbert D, Zasadzinski M, Rafaralahy H, et al. Modeling of the dynamic behavior of a PEM electrolyzer[C]//2022 10th International Conference on Systems and Control (ICSC), Marseille, France, 2022: 78-84.
[20] 任和, 刘宏伟, 顾亚京, 等. 基于Hammerstein模型的PEM电解槽动态模型[J]. 工程热物理学报, 2022, 43(9): 2324-2332.
Ren He, Liu Hongwei, Gu Yajing, et al. Dynamic modeling of PEM electrolyzer based on Hammerstein model[J]. Journal of Engineering Thermophysics, 2022, 43(9): 2324-2332.
[21] 江悦, 沈小军, 吕洪, 等. 碱性电解槽运行特性数字孪生模型构建及仿真[J]. 电工技术学报, 2022, 37(11): 2897-2908.
Jiang Yue, Shen Xiaojun, Lü Hong, et al. Construction and simulation of operation digital twin model for alkaline water electrolyzer[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2897-2908.
[22] Selamet Ö F, Acar M C, Mat M D, et al. Effects of operating parameters on the performance of a high-pressure proton exchange membrane electrolyzer[J]. International Journal of Energy Research, 2013, 37(5): 457-467.
[23] Espinosa-López M, Darras C, Poggi P, et al. Modelling and experimental validation of a 46 kW PEM high pressure water electrolyzer[J]. Renewable Energy, 2018, 119: 160-173.
[24] 陈锦洲, 林飞, 何洪文, 等. 质子交换膜燃料电池/电解槽系统建模及负荷追踪策略[J]. 电工技术学报, 2020, 35(增刊2): 636-643.
Chen Jinzhou, Lin Fei, He Hongwen, et al. Proton exchange membrane fuel cell/electrolyzer hybrid power system modeling and load tracking strategy[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 636-643.
[25] 李建林, 梁忠豪, 李光辉, 等. 质子交换膜电解槽控制策略研究[J]. 电工技术学报, 2023, 38(17): 4787-4799.
Li Jianlin, Liang Zhonghao, Li Guanghui, et al. Research on control strategy of proton exchange membrane electrolyzer[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4787-4799.
[26] Dale N V, Mann M D, Salehfar H. Semiempirical model based on thermodynamic principles for determining 6kW proton exchange membrane electrolyzer stack characteristics[J]. Journal of Power Sources, 2008, 185(2): 1348-1353.
[27] De Lorenzo G, Agostino R, Fragiacomo P. Dynamic electric simulation model of a proton exchange membrane electrolyzer system for hydrogen production [J]. Energies, 2022, 15: 6437.
[28] Abdin Z, Webb C J, Gray E M. Modelling and simulation of a proton exchange membrane (PEM) electrolyser cell[J]. International Journal of Hydrogen Energy, 2015, 40(39): 13243-13257.
[29] 马若冉, 赵晓丽, 张荣达. 新型电力系统背景下氢能综合利用站发展的商业模式分析[J]. 科技管理研究, 2024, 44(1): 183-191.
Ma Ruoran, Zhao Xiaoli, Zhang Rongda. Research on the business model for the development of hydrogen energy comprehensive utilization station under the background of the new power system[J]. Science and Technology Management Research, 2024, 44(1): 183-191.
[30] 滕越, 王缔, 赵骞, 等. 氢综合能源电站应用前景[J]. 科技与创新, 2022(23): 131-133, 139.
[31] 毕丽敏. 某兆瓦级氢能综合利用站消防水系统设计[J]. 工业用水与废水, 2022, 53(3): 77-80.
Bi Limin. Design of fire water system for a MW hydrogen energy comprehensive utilization station[J]. Industrial Water & Wastewater, 2022, 53(3): 77-80.
[32] 徐圆圆, 滕越, 赵骞, 等. 质子交换膜燃料电池电站多米诺事故概率和风险研究[J]. 中国安全生产科学技术, 2022, 18(7): 187-192.
Xu Yuanyuan, Teng Yue, Zhao Qian, et al. Probability and risk analysis of domino accidents in proton exchange membrane fuel cell power plants[J]. Journal of Safety Science and Technology, 2022, 18(7): 187-192.
[33] 王金全, 王春明, 张永, 等. 氢能发电及其应用前景[J]. 解放军理工大学学报(自然科学版), 2002, 3(6): 50-56.
Wang Jinquan, Wang Chunming, Zhang Yong, et al. Hydrogen-power and its prospects for applications[J]. Journal of PLA University of Science and Technology (Natural Science), 2002, 3(6): 50-56.
[34] Zeng Jia, Barre P J, Degobert P. Modeling and thrust control of PMLSM Using principle of local energy[C]//ICEMS 2003-Proceedings of the 6th International Conference on Electrical Machines and Systems, Beijing, China, 2003, 1: 26-30.
[35] Li P, Degobert P, Francois B, et al. Modeling and control of a gas micro turbine generator by using a causal ordering graph[C]//The Proceedings of the Multiconference on Computational Engineering in Systems Applications, Beijing, China, 2006: 271-277.
[36] Hautier J P, Barre P J. The causal ordering graph a tool for system modelling and control law synthesis[J]. Studies in Informatics and Control, 2004, 13(4): 265-283.
[37] 林渭勋. 现代电力电子技术[M]. 北京: 机械工业出版社, 2006.
[38] Tiktak J. Heat management of PEM electrolysis[D]. Delft: Delft University of Technology, 2019.
[39] Roy A, Watson S, Infield D. Comparison of electrical energy efficiency of atmospheric and high-pressure electrolysers[J]. International Journal of Hydrogen Energy, 2006, 31(14): 1964-1979.
[40] 张瑜, 张桥. 考虑压缩比和进口温度的多级压缩总能耗分析[J]. 计算机与应用化学, 2018, 35(9): 711-718.
Zhang Yu, Zhang Qiao. Analysis of energy consumption for multi-stage compression considering the compression ratio and inlet temperature[J]. Computers and Applied Chemistry, 2018, 35(9): 711-718.
[41] Heywood J. Internal Combustion Engine Fundamentals [M]. 2nd ed. New York: McGraw-Hill Education, 2019.
[42] O’Hayre R, Cha S W, Colella W, et al. Fuel Cell Fundamentals[M]. Hoboken: John Wiley & Sons, 2016.
[43] Liu Zhixiang, Yang Lizhai, Mao Zongqiang, et al. Behavior of PEMFC in starvation[J]. Journal of Power Sources, 2006, 157(1): 166-176.
[44] Ma Libo, Zhao Hongshan, Qu Yuehan, et al. Reduced-order active disturbance rejection control method for PEMFC air intake system based on the estimation of oxygen excess ratio[J]. IET Renewable Power Generation, 2023, 17(4): 951-963.
Operation Process Modeling and Energy Flow Control Strategy of Integrated Hydrogen Energy Power Station Based on Causal Ordering Graph
Abstract Hydrogen energy storage technology is characterized by cleanliness, no self-discharge, and high energy density, making it a highly promising energy storage technology. When the grid has surplus power, hydrogen energy storage absorbs the excess power; when the grid power is insufficient, hydrogen energy is converted into electricity to supply power to users. However, currently, most research on hydrogen energy storage is still in the stage of business model and economic feasibility studies, lacking operation principles and modeling research. To solve these problems, we propose an integrated hydrogen energy power station (IHEPS) that integrates three parts: hydrogen production, hydrogen storage, and fuel cell power generation. Based on causal ordering graph (COG), we establish the operation process model and energy flow control strategy of IHEPS. The proposed model and control strategy not only clearly represent the operation process of the IHEPS but also, by using model inversion control for rigid relationships, reduce error feedback time and enhance controller performance, thus better realizing the energy flow management of the IHEPS.
Firstly, the composition structure, working principles, and control system configuration of the box-type IHEPS are proposed. Then, according to the characteristics of IHEPS electricity-hydrogen-electricity energy conversion, a control-oriented operating dynamic model of hydrogen production, storage and power generation integrated power station is established based on the COG. This model can clearly reflect the relationships between different physical quantities of the IHEPS. Next, based on the established model and the principle of natural causality, a power and hydrogen flow control strategy for the operation process of the IHEPS is designed. This strategy adopts model inversion control for processes with rigid relationships to reduce error feedback time and enhance controller performance. Finally, tests are conducted on the RT-Lab hardware-in-the-loop simulation platform to analyze the relationships between different physical quantities of the integrated station. Comparison results with PID and ADRC methods indicate that the proposed strategy outperforms traditional methods in terms of response speed, convergence accuracy, and operational efficiency, and can realize the energy flow management of IHEPS more effectively.
According to the results of the RT-Lab semi-physical simulation test, the proposed COG method for electro-hydrogen storage operation control does not have start-up and shut-down dead zones, and can achieve fast and accurate convergence across all operating conditions, reducing the convergence time by about 300 seconds compared to PID and ADRC methods; In the hydrogen-to-electricity generation control process, the steady-state overshoot of the COG method is only 0.128%, which is a reduction of 46.7% and 34% compared to PID and ADRC respectively; throughout the operating process, the operating efficiency of the IHEPS controlled by the proposed COG method increased from 21.2% under PID control or ADRC to 26%, an increase of approximately 22.6%. Therefore, the proposed strategy is superior to traditional methods in response speed, convergence accuracy, and operational efficiency, and can more effectively manage the energy flow in the operation of IHEPS.
The conclusions are as follows: (1) This paper proposes a type-box IHEPS that can be combined with renewable energy sources for large-scale consumption of new energy. (2) Based on COG, a control-oriented dynamic model for the IHEPS operation process is established. This model can clearly reflect the relationships between different physical quantities in the integrated power station and characterize the electro-hydrogen-electric operation process of the integrated station. (3) A COG-based control strategy for power and hydrogen flow in the integrated power station has been proposed, realizing the energy flow management of the integrated power station. (4) The results of semi-physical simulation show that compared with the traditional control methods, the proposed control strategy has the advantages of no start-stop dead zone, fast response speed, high convergence accuracy and high operating efficiency.
keywords：Integrated hydrogen energy power station, energy flow control, causal ordering graph, hardware in loop test
中图分类号：TM615
DOI: 10.19595/j.cnki.1000-6753.tces.240015
国家重点研发计划（2018YFE0122200）和国家自然科学基金面上项目（52077078）资助。
收稿日期 2024-01-04
改稿日期 2024-04-10
马利波 男，1994年生，博士研究生，研究方向为氢能一体化电站运行与控制技术。
E-mail：malbo_ncepu@163.com
赵洪山 男，1965年生，博士，教授，博士生导师，研究方向为电力系统动态分析与控制、氢能一体化电站技术、主动配电网以及故障预测等。
E-mail：zhaohshcn@126.com（通信作者）
（编辑 李 冰）