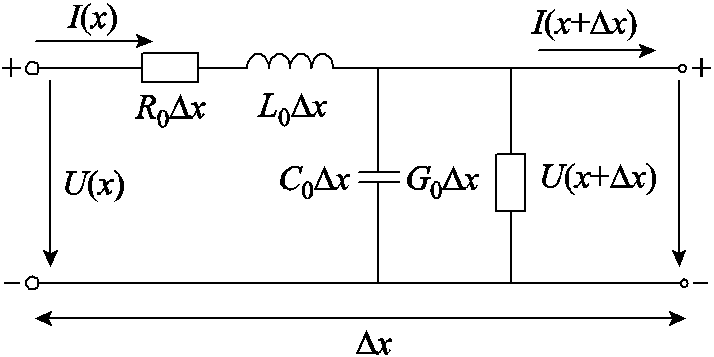
图1 电缆分布参数等效模型
Fig.1 Equivalent model of cable distribution parameters
摘要 针对目前频域反射（FDR）法通过人为主观经验判断缺陷，存在误判率高的问题，提出了一种基于单元平均恒虚警率（CA-CFAR）的电缆缺陷识别方法。首先对FDR测试信号在电缆中存在传播衰减，导致缺陷及末端在定位谱中归一化幅值过小而测不准的问题，先使用实测数据求出衰减因子与测试频率的线性关系，再使用在频域解卷的衰减补偿方法，有效削弱了信号在电缆传播过程中衰减过大带来的负面影响；其次通过恒虚警率（CFAR）的动态阈值来提取电缆中缺陷的位置及归一化幅值信息，其中动态阈值根据测试信号幅值的变化动态地选取缺陷判断的阈值，避免了人为主观经验判别容易误判的问题；最后分别在30 m、105 m和500 m实验室电缆以及1 500 m在运电缆上对该方法进行测试，测试结果表明采用该方法可以准确地识别电缆全部缺陷，证实了该方法的有效性。
关键词：频域反射 衰减补偿 恒虚警率 缺陷识别
随着城市化进程的发展，电力电缆因供电可靠性高、输送容量大、电能损耗较小、节约城市空间资源、视觉美观等优点，被广泛应用于城市电网中[1]。由于电缆运行环境较为恶劣，在长期运行及人为敷设安装不规范等因素影响下，极易产生缺陷。若不及时对缺陷进行排查处理，这些缺陷极有可能会造成大规模停电等事故，带来较大的生命财产损失。因此，对电缆缺陷进行高效的无损探测，有效地排查电缆潜在的缺陷尤为重要。
目前针对电缆系统的状态监测，常用的方法有直流电桥法、局部放电（Partial Discharge, PD）法、时域反射（Time Domain Reflectometry, TDR）法和频域反射（Frequency Domain Reflectometry, FDR）法[1-4]。直流电桥法虽然可以快速定位电缆故障，但其仅适用于测寻电缆低阻或短路故障，并且电阻越大，定位误差越大，而对于高阻、开路故障或早期绝缘下降引起的局部缺陷，无法利用该方法进行定位[4]。PD法包括振荡波、谐振下的PD法等，该方法属于无损检测且具有较好的检测效果，近年来被广泛应用于电缆诊断测试中[5-7]，其检测对象大多为电缆附件，主要检测电缆安装缺陷（如杂质、刀痕等）[6]，难以检测本体/中间接头处的受潮老化、铜屏蔽层腐蚀等缺陷[7]。TDR法是在电缆首端位置注入脉冲信号，然后直接在时域中识别反射波形，该方法可以直观地得到反射波的传播距离和极性[8]，但由于所注入信号中所含高频信号成分较少，并且在信号传播过程中容易受衰减和色散效应、现场电磁干扰的影响，测试精度低，很难实现对电缆本体局部微弱缺陷的定位识别[9-10]。采用扫频信号的FDR法因其入射波所含高频成分较多[11]，且能够快速检测微弱缺陷而被广泛应用于电缆缺陷监测中。基于FDR法发展起来的宽频阻抗谱（Broadband Impedance Spectroscopy, BIS）法[12]、反射系数谱（Reflection Coefficient Spectrum, RCS）法[13]通过扫频信号测量获取电缆特征参数，能高灵敏度地定位电缆局部缺陷。
然而，使用FDR法对缺陷定位进行傅里叶变换时，由于频谱泄漏等原因，会在最终的定位谱上产生许多“伪峰”，这些“伪峰”的存在会导致不容易在定位谱中将缺陷峰位置准确识别出来，且加上人为主观因素的影响，极有可能会发生误判。同时在进行现场检测时，信号的衰减会随着电缆长度的增加而增大，造成许多中长电缆缺陷的漏检，对后续的修复造成很大的经济损失。因此，可引入恒虚警率（Constant False Alarm Rate, CFAR）方法对电缆缺陷进行自动识别，它能自动地在定位图谱中提取缺陷的位置及峰值，可大大减少由频谱泄漏和人为主观因素导致的误判，提高故障的检出率。恒虚警率是雷达目标检测领域常使用的方法。雷达在探测目标的过程中会受到杂波的干扰，恒虚警率检测器随着参考单元的变化自适应地改变检测阈值，实现对目标的CFAR检测[14]。恒虚警率技术经过了近几十年的发展，已经成为一个重要的研究方向，获得了广泛的雷达目标检测结果[15]，其最终目的是判断雷达所检测到的物体是否为目标物体，这与电缆缺陷识别的目的不谋而合。电缆缺陷识别所需要的也是判断定位谱中的异常峰值是否为缺陷，因此CFAR方法也就有了应用的基础。恒虚警率的最基本形式是单元平均恒虚警率（Cell Average CFAR, CA-CFAR）[16]，其算法结构简单、计算速度快，可有效应用于电缆缺陷识别中。
将CFAR应用于电缆缺陷识别时，依据其特性，可直接将已有的定位图谱中的数据点代入算法中进行一维计算，根据定位图谱中每个数据点变化的幅值来动态地选取阈值。若数据点处幅值大于所选取的阈值，则判断为缺陷点；反之，则不为缺陷点。将所有缺陷点处幅值保留，小于阈值的点取0，这样即可提取出定位图谱中所有的缺陷点位置及幅值。同时，由于电缆长度和高频信号本身的特性等原因，还需要考虑信号的衰减等问题。因此，本文提出一种考虑衰减补偿的FDR单元平均恒虚警率电缆缺陷识别方法。首先，为了减少信号衰减效应带来的缺陷测不准问题，使用实测数据求出衰减因子与测试频率的线性关系；其次，采用频域解卷的衰减补偿方法，有效削弱了信号在电缆传播过程中衰减过大带来的负面影响；再次，为了减少人为主观经验判断容易误判的问题，通过CFAR的动态阈值提取电缆中缺陷的位置及归一化幅值信息，根据测试信号幅值的变化动态地选取缺陷判断的阈值，避免了人为主观经验判断的不足；最后，为了测试本方法的有效性，分别在30 m、105 m和500 m实验室电缆以及1 500 m在运电缆上进行测试，测试结果证明了该方法不仅能够准确地提取出缺陷位置，还能有效地解决CFAR检测过程中的缺陷遮蔽问题。
由传输线理论[17-19]可知，在高频条件下，可将电缆等效为无数个如图1所示的微分段分布参数等效电路的级联，图中R0、G0、C0、L0分别为电缆单位长度Dx的电阻、电导、电容、电感。
图1 电缆分布参数等效模型
Fig.1 Equivalent model of cable distribution parameters
因趋肤效应和邻近效应的影响[20]，电缆单位长度的电阻R0（Ω/m）、电感L0（H/m）、电导G0（S/m）和电容C0（F/m）可分别近似表示[19]为
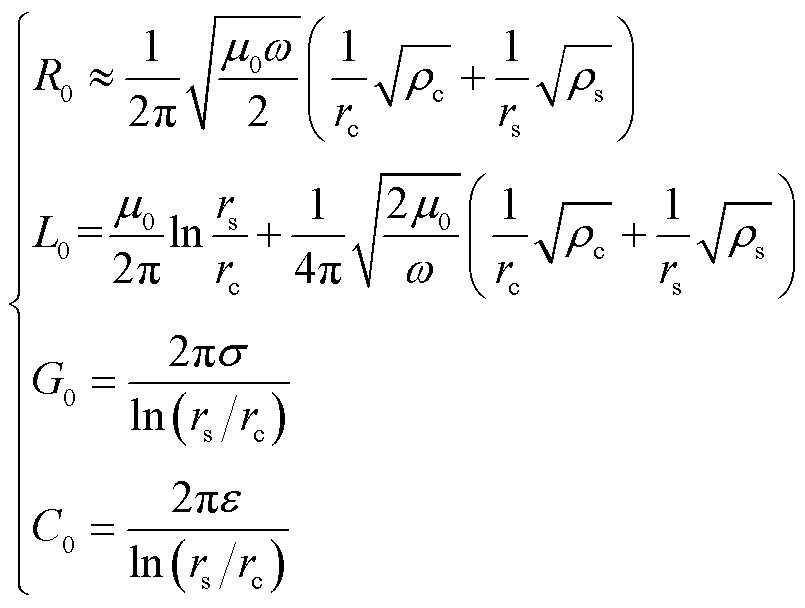（1）
式中，ω为角频率，ω=2πf，其中f为频率；rc、rs分别为电缆缆芯半径和屏蔽层内半径；ρc、ρs分别为缆芯电阻率和屏蔽层电阻率；μ0为真空磁导率；σ、ε分别为电介质的电导率和介电常数。
由传输线理论，长度为l的电缆的首端反射系数Gl可表示为[13]
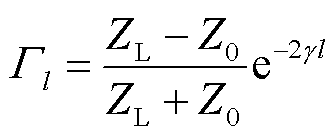（2）
式中，ZL为负载阻抗；g为电缆传播常数；Z0为电缆特性阻抗。g和Z0可分别表示为
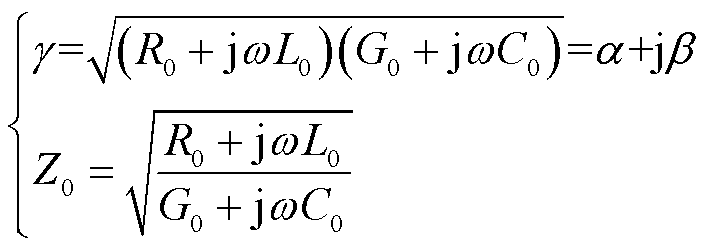（3）
其中
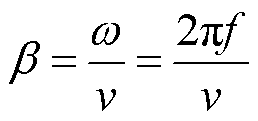
式中，α为衰减因子，表征电缆单位长度的信号幅值衰减特性；β为相位常数，表征电缆单位长度的信号相位滞后特性[21]；v为电缆中电磁波的速度，在高频下为定值。
高频下的特性阻抗可表示为
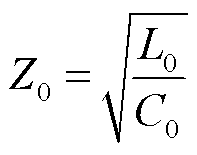（4）
电缆末端开路时（ZL=∞），Gl可表示为
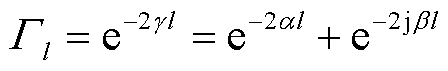（5）
将式（5）进行欧拉公式展开取实部即可得到电缆的首端反射系数谱为
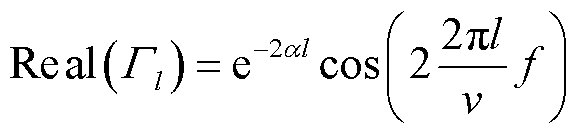（6）
式中，Real(Gl)为首端反射系数Gl的实部。由式（6）可知，Real(Gl)呈指数衰减振荡形式，且频率分量fl=2l/v，其等效为输入信号从电缆首端到距离首端l处阻抗不连续点的往返传播时间，因此可由fl求出电缆的缺陷位置。
由式（6）可发现，在测试过程中，测得的定位谱会在衰减因子α和长度l的双重影响下，造成长电缆中的数据衰减很大，若直接对其进行CFAR检测将会影响缺陷识别的准确率，因此在检测前需对信号进行衰减补偿。
在实际测试中通常将得到的反射系数实部进行快速傅里叶变换后再进行缺陷的定位，其定位谱d为
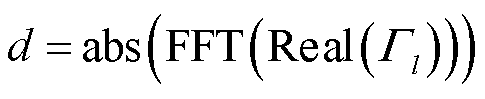（7）
式中，FFT(·)为快速傅里叶变换；abs(·)为取模值。从式（7）可以发现，在整个过程中衰减项e-2αl也进行了快速傅里叶变换和取模值的运算，因此只需消除衰减项的影响即可对最终的定位图谱进行衰减补偿。
衰减项中α是变化的，其值的大小受到频率变化的影响。实际测试的某国产YJLV22-8.7/15-1×95 10 kV的XLPE电力电缆在频段0～100 MHz内的衰减因子如图2所示。从图2中可以看出，对于10 kV电力电缆而言，随着高频电磁波信号频率的增加，衰减因子明显增加。
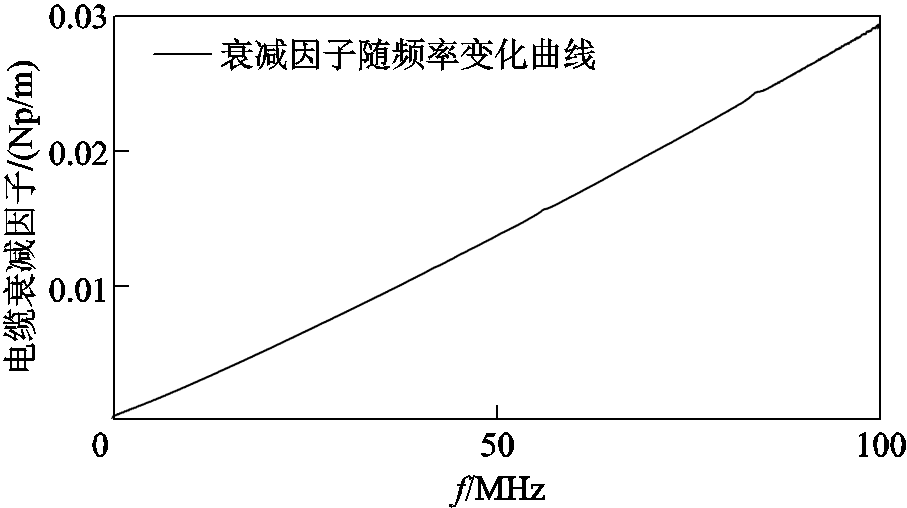
图2 实测电缆中衰减因子随频率变化曲线
Fig.2 Curve of attenuation factor with frequency variation in measured cables
根据图2，在0～100 MHz频段下衰减因子α与频率呈近似的线性关系。而在实际测试中，对于长电缆的测试使用的频段都小于100 MHz，因此α与频率f的关系可近似为
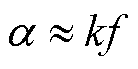（8）
式中，k为系数，由图2的实测数据可知k≈0.000 3。设l为缺陷处距首端的距离，将式（8）代入衰减项中即可得到l处的衰减项为
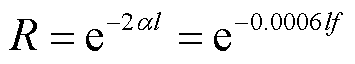（9）
将其进行快速傅里叶变换得到
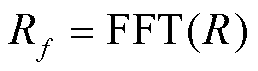（10）
最后将式（7）与式（10）进行反卷积再取模值即可得到衰减补偿后的反射系数谱为
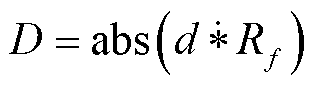（11）
式中，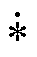
为反卷积运算。为了对此方法进行验证，设置一条总长为500 m的电缆，电缆具体参数见表1。
表1 电缆仿真模型的参数设置
Tab.1 Parameter setting of cable simulation model
参数数值 缆芯半径rc/mm4 屏蔽层内半径rs/mm9.5 缆芯电阻率ρc/(μΩ·mm)17.5 屏蔽层电阻率ρs/(μΩ·mm)17.5 XLPE电导率σ/(S·m)1×10-16 XLPE相对介电常数2.3
在距离首端200 m处和350 m处设置两个中间接头，接头长度都为0.8 m，电容变化倍数都为0.848[22]。定位时首先使用Kaiser窗函数提升对缺陷的辨识能力[23]，再使用衰减补偿方法对得到的定位曲线进行补偿，得到定位曲线如图3所示。
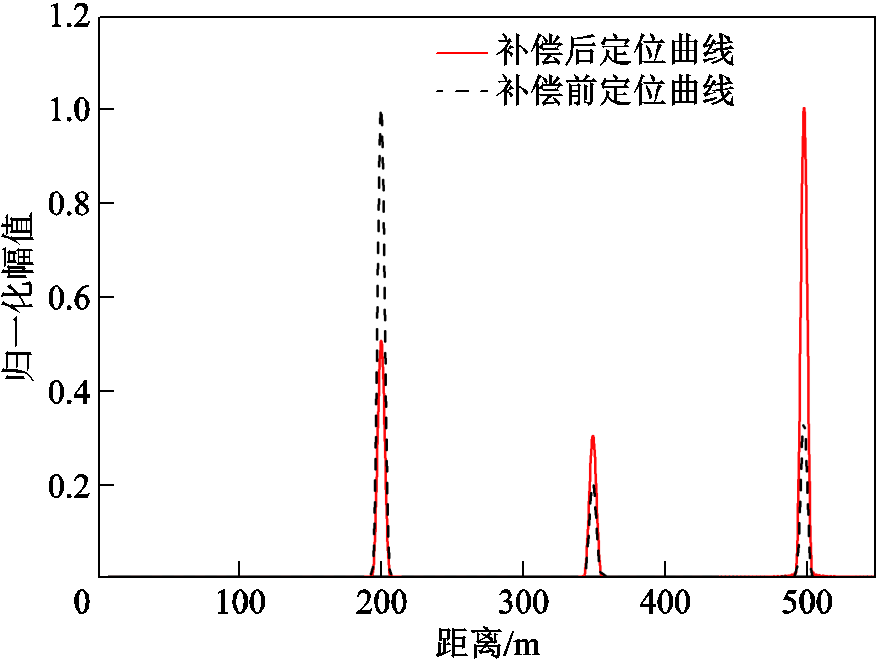
图3 补偿前后定位曲线
Fig.3 Positioning curve before and after compensation
由图3可知，补偿前末端幅值远小于第一个缺陷点，这在实际测试中极有可能造成对末端位置的误判；补偿后可看出，末端的幅值远大于缺陷位置对应的峰值，更易分辨出缺陷点和末端的位置。由此可得出所提衰减补偿方法是有效的。
在现有的FDR缺陷检测中，缺陷在定位图谱中主要体现为其峰值的大小。目前的缺陷识别主要依靠人为的辨识，而由于傅里叶变换中的频谱泄漏会导致定位谱中出现许多“伪峰”，单靠人为识别缺陷比较困难，容易造成误判。CFAR是雷达目标检测领域判断所检测到的物体是否为目标物体的常用方法，这与电缆缺陷识别的目的相一致。因此可将CFAR方法引入缺陷辨识中，根据CFAR变化的阈值来提取定位图谱中缺陷的位置和峰值，可大大减少由于人为主观判断所造成的误判。
CFAR检测信号的基本原理为：对输入的信号进行处理后得到一个自适应变化的门限，将此门限与输入端信号幅值相比，如果输入端信号幅值超过此门限，则判别为有目标；否则，判别为无目标。若检测过程中使用固定的门限，可能会导致目标漏检或者将非目标判断为目标。自适应门限会根据被检测目标点的背景噪声、杂波及干扰信号的强度大小自适应地调整，以保证漏检率为一恒定值[15]。
恒虚警率中最常使用的是单元平均恒虚警率（CA-CFAR），其通过对待检测单元周围相邻单元的信号幅值进行平均得到相应的检测阈值，具有算法结构简单的优点。检测滑动窗口包括待检测单元、保护单元和参考单元[24-25]，其算法原理如图4所示。
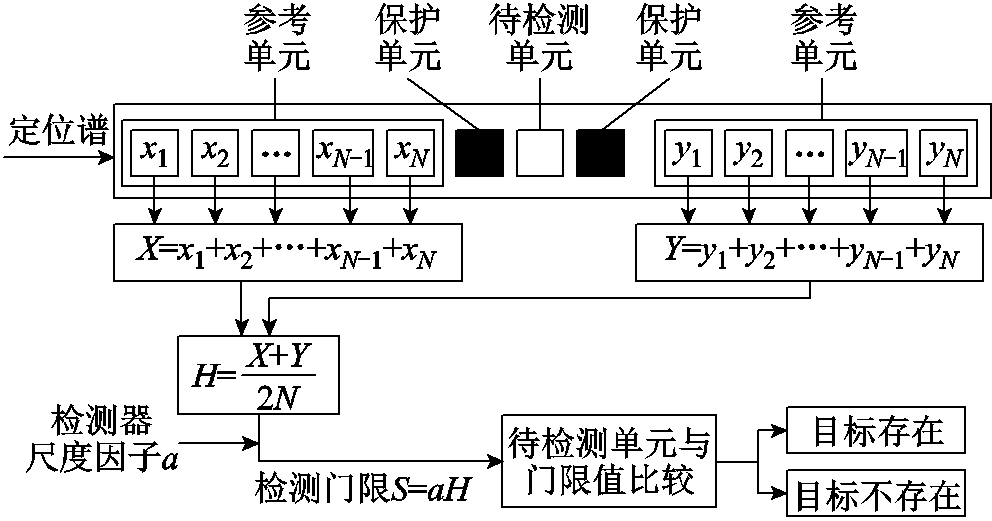
图4 CA-CFAR算法原理
Fig.4 Schematic diagram of CA-CFAR algorithm
如图4所示，白框为待检测单元，参考单元位于待检测单元两侧，前后各有N个。保护单元主要用在单目标情况下，防止目标能量泄漏到参考单元，影响检测效果。若待检测单元幅值大于门限值S则发生虚警；反之不发生虚警。在使用CA-CFAR方法进行电缆缺陷识别时，将预先得到的定位谱数值输入算法中即可对数据进行一维计算，再依据门限值在定位图谱中提取出缺陷位置及归一化幅值即可进行缺陷识别。对于CA-CFAR检测，参考单元的功率幅值符合高斯分布[26-27]，则其概率密度服从指数分布，表示为
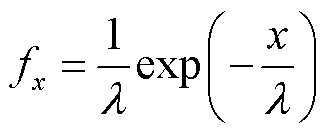（12）
式中，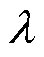
为常数，表示单位时间内发生事件的平均次数。
由图4可以得出，待检测单元左右2N个参考单元的算术平均为
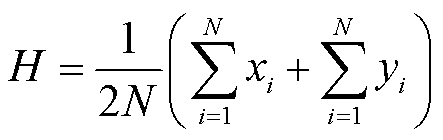（13）
式中，
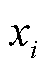和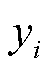
分别为待测单元左边和右边第i个参考单元的值。
则待检测单元处的检测门限值为门限系数a与参考单元算术平均H的乘积，即
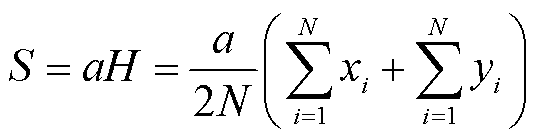（14）
结合式（12）即可得到门限值S的概率密度分布为
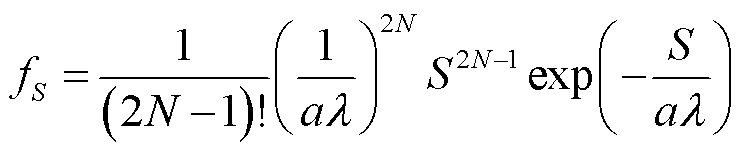（15）
由奈曼-皮尔逊准则[28]，可得到对应的虚警概率的概率密度分布函数为
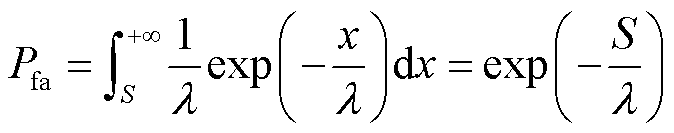（16）
再对S积分可得
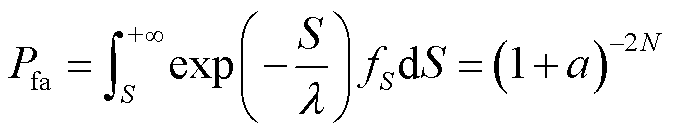（17）
由式（17）可以发现，虚警概率Pfa仅受门限系数和参考单元个数的影响，与杂波和噪声参数无关。因此在确定门限系数a与参考单元个数N之后，虚警概率保持不变。确定虚警概率之后，可得到对应的门限系数为[25]
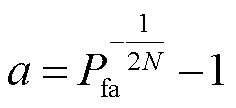（18）
检测过程中Pfa可取10-2、10-3、10-4、10-5、10-6[21-22]。由式（18）可得，在缺陷识别中参考单元N一定时，则门限系数a也一定。为了选取门限系数a的最优值，设置N=5～20的仿真实验来选取Pfa与N，再由式（18）可分别计算出对应的门限系数a。将Pfa=10-2、10-3、10-4、10-5、10-6与N=5～20代入式（18）后结果如图5所示。
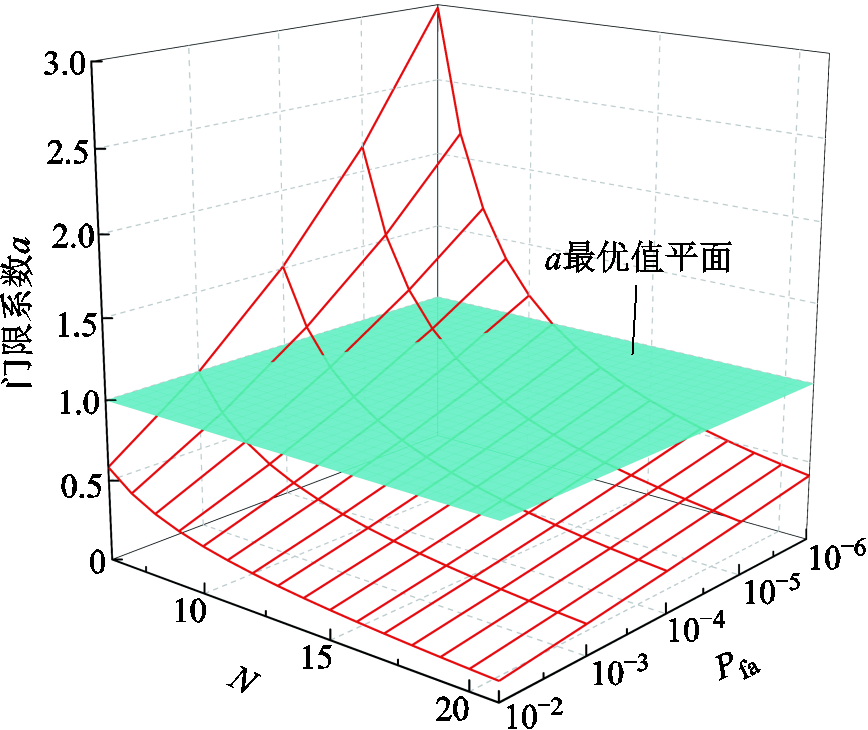
图5 N和Pfa值不同时的CA-CFAR检测结果
Fig.5 CA-CFAR detection results with different N and Pfavalues
由图5可知，随着N和Pfa的增大，门限系数减小。在电缆缺陷识别中为了检测出全部的缺陷，门限系数a应取接近1的值，这样才能使缺陷处幅值刚好大于检测的门限S。此时设置大于S时幅值不变，小于S时幅值置零，这样缺陷处的幅值和位置信息就能被提取出来。从图5可以得到使a值最接近1的取值有两点，分别为(5, 10-3, 0.995)和(10, 10-6, 0.995)。第一个点N=5时参考单元一共只有10个，检测阈值受缺陷处峰值影响较大，可能会导致相邻的缺陷漏检率增大。因此选取第二个点，即N=10时，此时参考单元共有20个，可降低漏检概率。
将N=10，Pfa=10-6，a=0.995代入仿真电缆补偿后的定位谱，得到的检测结果如图6所示。
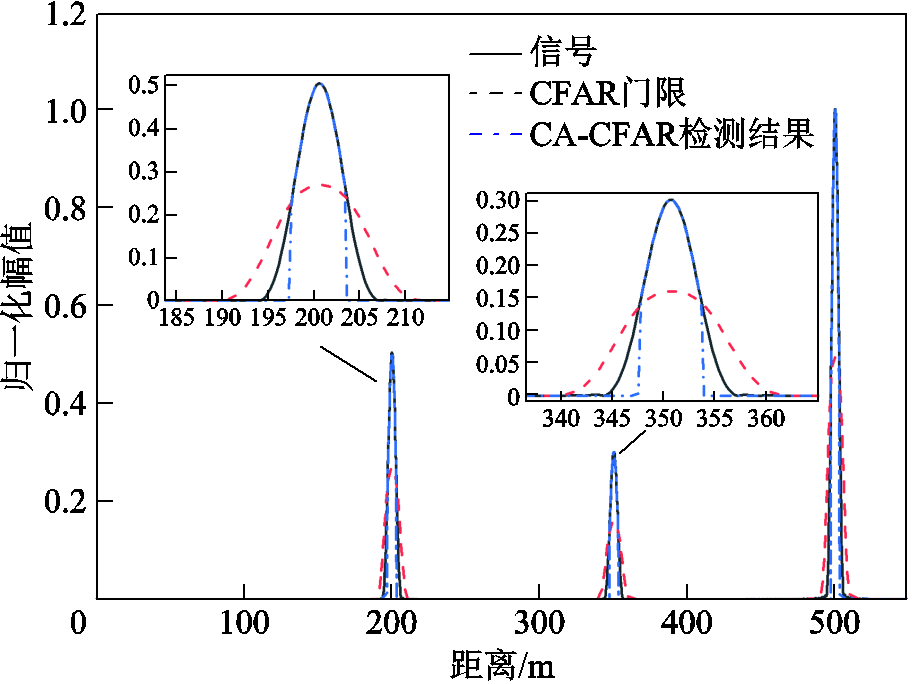
图6 仿真500 m电缆CA-CFAR检测结果
Fig.6 Simulated 500 m cable CA-CFAR detection results
从图6中可发现，使用CA-CFAR方法成功地检测出了200 m处和350 m处的中间接头，表明该方法可以应用到电缆缺陷识别中。
将图6中检测结果缺陷峰值两边放大可得到缺陷峰值两边的伪峰如图7所示。
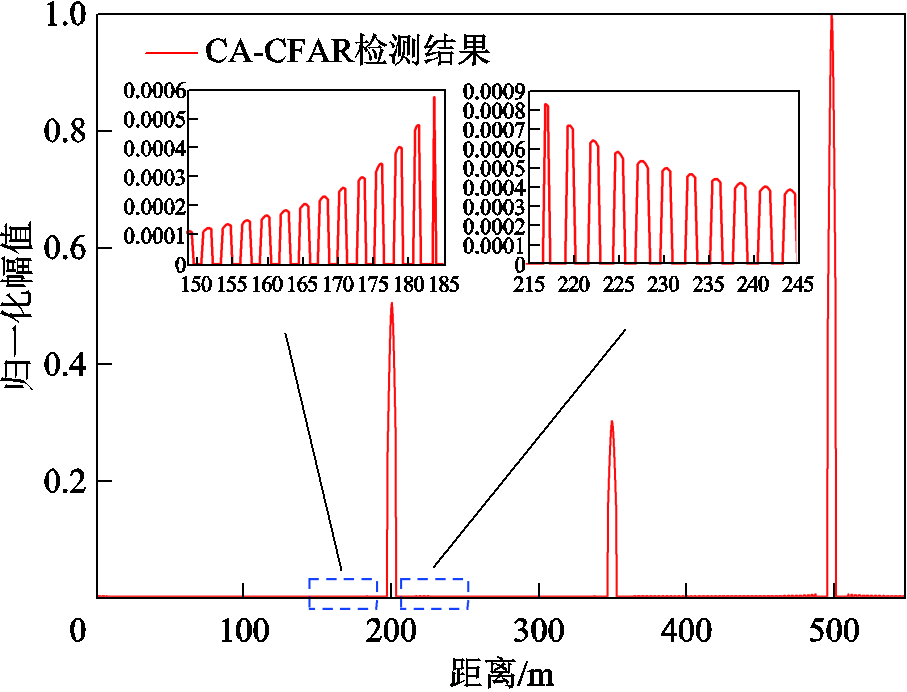
图7 缺陷峰值两边的伪峰
Fig.7 False peaks on both sides of defect peaks
由图7可以发现，由于傅里叶变换中的频谱泄漏，导致在缺陷峰值两边产生了许多“伪峰”。在仿真中这些伪峰的值较小，当缺陷处幅值较大时不易在检测结果中看出来，但是在实测时伪峰的值相对较大，将影响对接头或缺陷的判断，因此需要一固定的阈值区分伪峰与缺陷峰。
缺陷（此处缺陷为接头）处的反射系数为
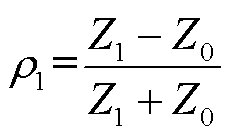（19）
式中，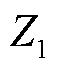
为缺陷段阻抗。
由式（7）可得缺陷处的幅值为
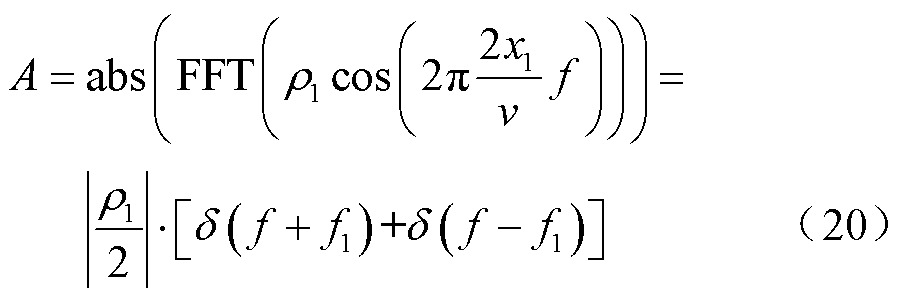
式中，x1为缺陷处到首端的距离；f1为缺陷处频率分量；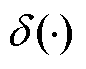
为单位脉冲函数。则缺陷处幅值进行归一化后在定位谱中的幅值为
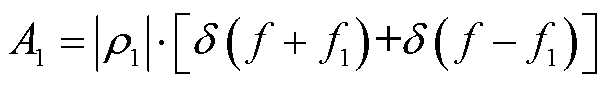（21）
由式（21）可以发现，缺陷处归一化幅值由接头处的反射系数决定。由文献[22]可得缺陷处的电容为本体的0.848，将电容参数代入表1中的电缆模型后由式（19）计算得到r1=0.041 2，因此可将此值设为一固定的阈值。若峰值大于或等于0.041 2则视为接头或缺陷点；反之，则视为伪峰。
综上所述，可得到方法流程如图8所示。
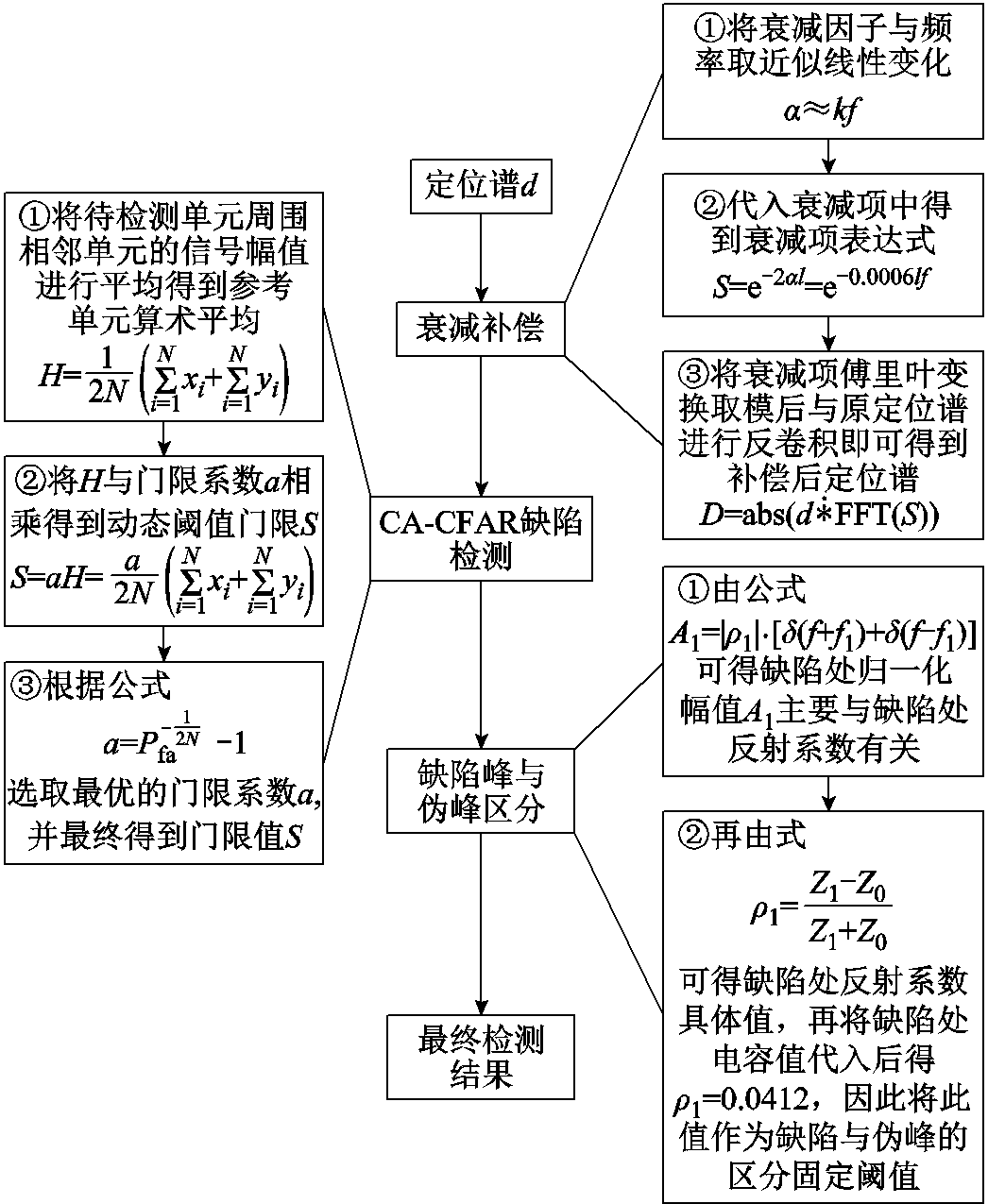
图8 方法流程
Fig.8 Method flow chart
接下来对电缆实测数据进行处理，在实验室中测试一根总长为500 m的YJLV22-8.7/15-1×95 10 kV的XLPE电力电缆，在250 m处制作中间接头。测试频段为150 kHz～10 MHz，采样点数为3 001个。得到的FDR测试结果及衰减补偿后的定位曲线如图9所示。
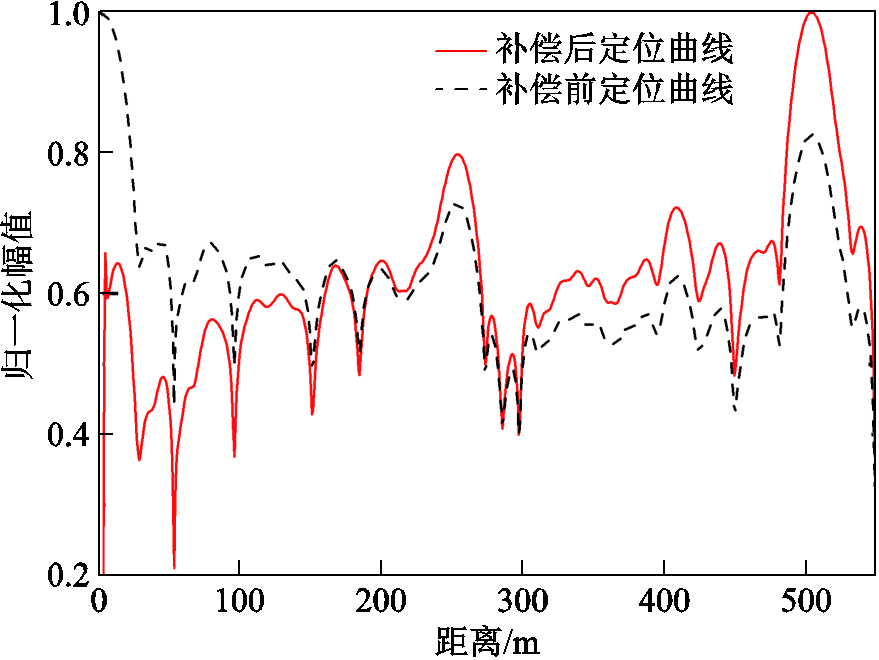
图9 500 m电缆补偿前后定位曲线
Fig.9 Positioning curves of 500 m cable before and after compensation
从图9定位曲线中首端的峰值到末端的峰值可以看出，补偿前信号幅值有一定的衰减，导致末端的峰值小于首端的峰值，因此，使用所提的信号衰减补偿方法可对该定位曲线进行有效的补偿。再使用CA-CFAR对补偿前和补偿后的定位曲线进行缺陷识别，保护单元设置为2，得到的结果如图10所示。
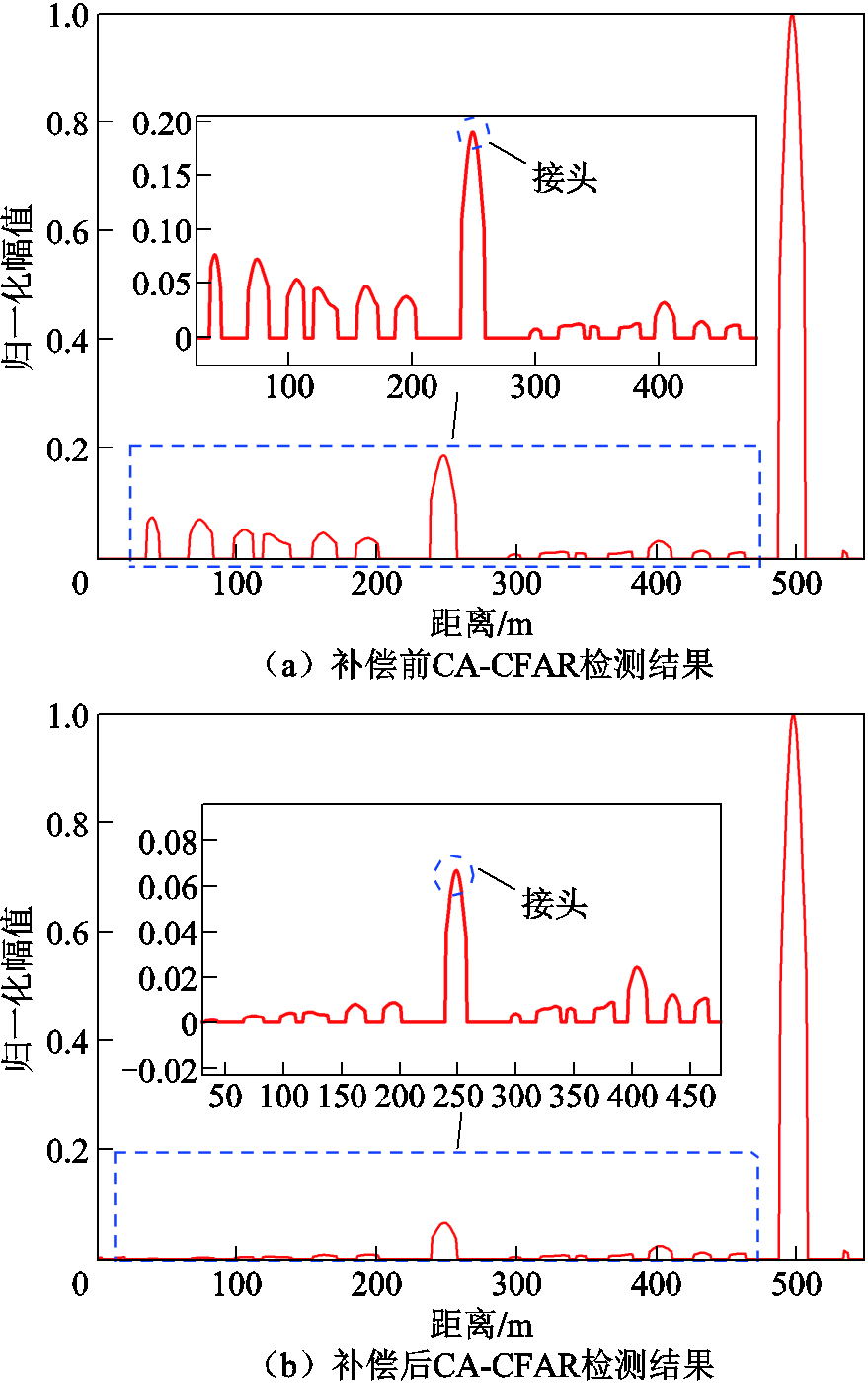
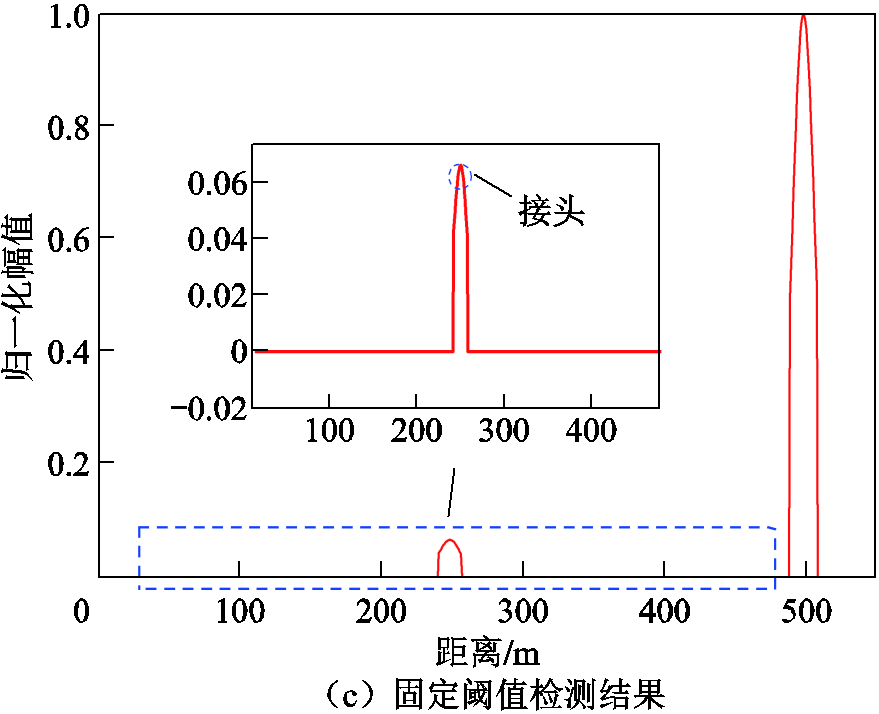
图10 500 m电缆补偿前后CA-CFAR及固定阈值检测结果
Fig.10 CA-CFAR and fixed threshold detection results of 500 m cable before and after compensation
由图10可得，补偿前缺陷处的幅值虽然比补偿后的幅值大，但是其余伪峰处的幅值也相对较大。可以发现补偿前缺陷处的伪峰幅值几乎可以到达0.1，因此补偿前不能使用所提固定阈值检测方法。补偿后的伪峰的幅值都很小，几乎处于同一水平线上，相较于补偿前更不易造成误判，且在补偿后的CA-CFAR检测结果中引入固定阈值后可将伪峰去除。实测结果表明，所提方法可以对电缆中的中间接头或一些缺陷造成的电缆阻抗不连续点进行提取。
为了验证该方法的工程实用性，对一根在运电缆进行测试，该电缆总长为1 500 m，是型号为YJLV22-8.7/15-1×95 10 kV的XLPE电力电缆。根据施工方所提供的信息，该电缆有4个中间接头。FDR测试频段为150 kHz～2.5 MHz，采样点数为3 001个。将测试数据进行衰减补偿后与原始数据进行对比，得到补偿前后的定位曲线如图11所示。
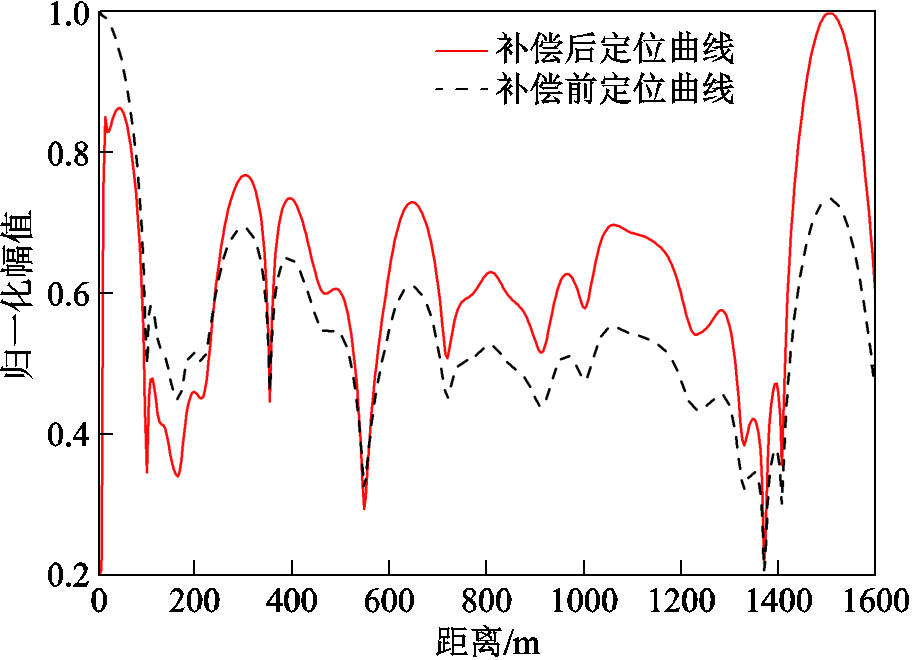
图11 1 500 m补偿前后定位曲线
Fig.11 Positioning curves of 1 500 m cable before and after compensation
由结果可以发现，由于信号在该电缆中的衰减比较大，该电缆上的补偿效果比较明显。然后对衰减补偿前后的定位曲线进行CFAR缺陷提取，保护单元设置为2，得到的检测结果如图12所示。
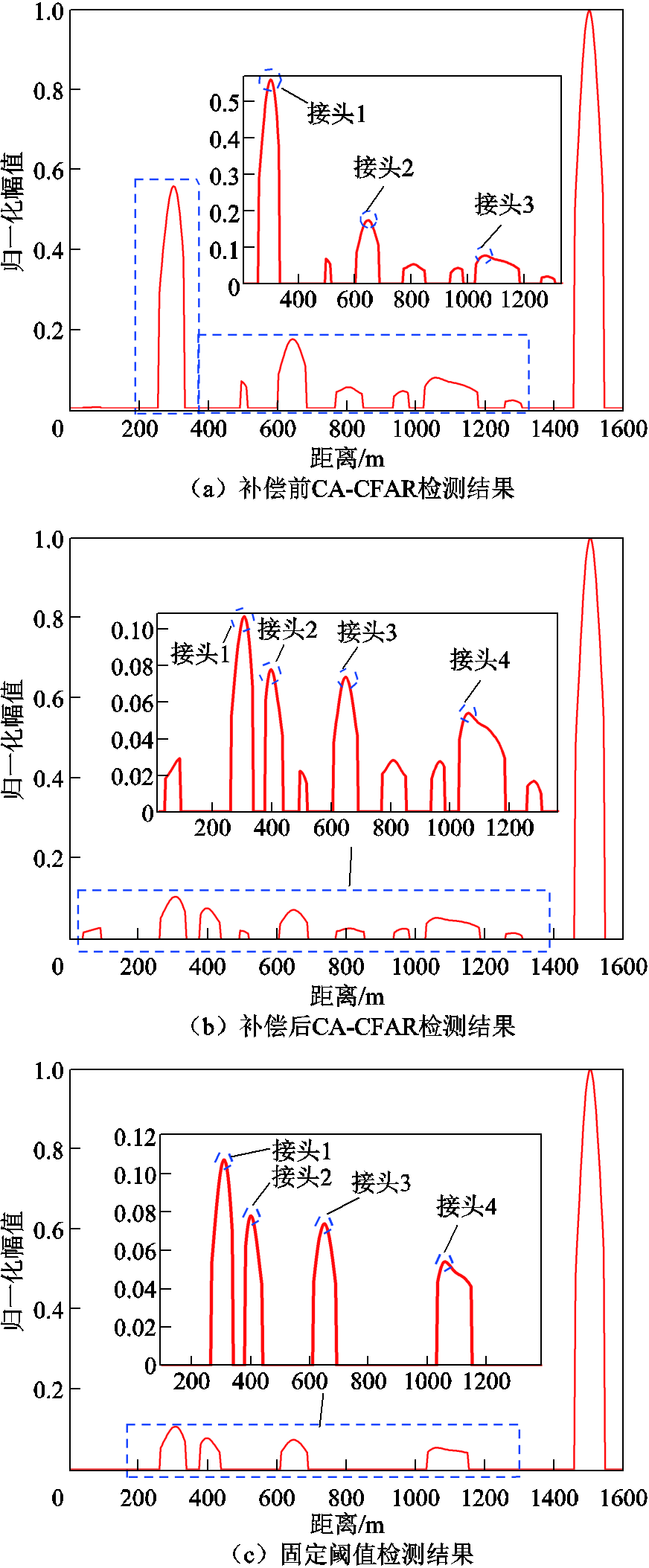
图12 1 500 m补偿前后CA-CFAR及固定阈值检测结果
Fig.12 CA-CFAR and fixed threshold detection results of 1 500 m cable before and after compensation
由图12分析可以发现，补偿前的检测中位于该电缆中前段的缺陷处幅值偏大，且补偿前只检测出了3个接头，分别为300 m、660 m和1 100 m处（800 m和980 m处均为非缺陷），这和已知信息明显不符。由补偿后的结果可以发现，在400 m处有一漏判的缺陷，这是由于补偿前300 m处的缺陷幅值过大，导致CA-CFAR检测过程中将400 m处的缺陷遮蔽，因此对于信号衰减过大时的补偿非常有必要。引入固定阈值后可将伪峰全部去除，只留下接头所在的位置，因此所提方法对接头或缺陷的提取是有效的。
为了验证所提方法对其余缺陷检出的有效性，对实验室105 m的YJLV22-8.7/15-1×95 10 kV XLPE电力电缆进行测试。该电缆在45 m处剖离外护套并将其浸泡在饱和食盐水中，由于饱和食盐水的作用，电缆中铜屏蔽层上产生了铜绿，形成了腐蚀，如图13所示。除此之外，该电缆在90 m左右还有一弯折缺陷。FDR测试频段为150 kHz～25 MHz，采样点数为1 001个。将测试数据进行衰减补偿后与原始测得的数据进行对比，得到补偿前后的定位曲线如图14所示。
图13 铜屏蔽腐蚀缺陷
Fig.13 Copper shielding corrosion defects
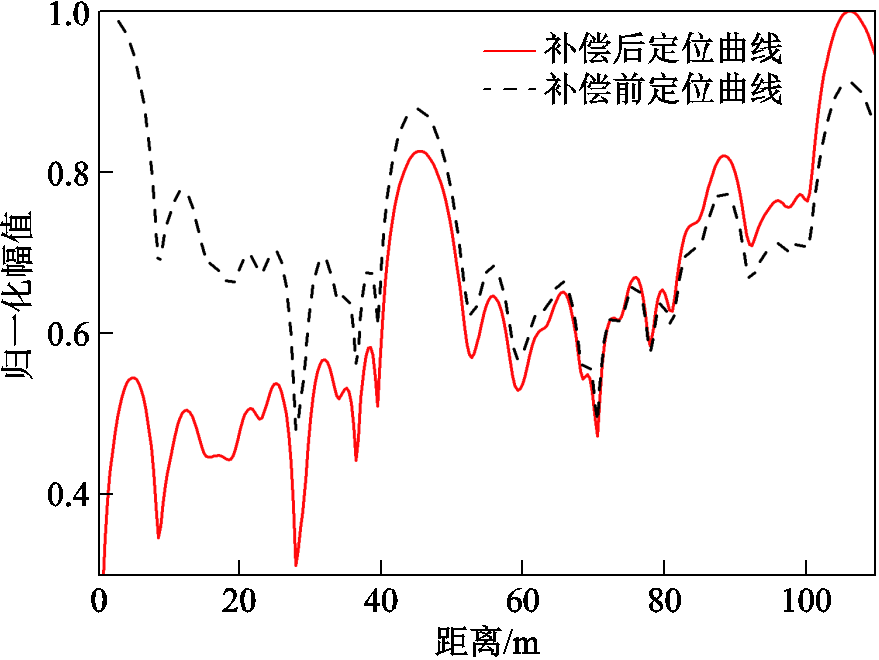
图14 105 m电缆补偿前后定位曲线
Fig.14 Positioning curves of 105 m cable before and after compensation
由图14可知，补偿前末端峰值小于首端峰值，补偿后定位曲线在末端和90 m缺陷处的幅值都明显增大，补偿效果良好。然后对衰减补偿前后的定位曲线进行CFAR缺陷提取，保护单元设置为2，得到的检测结果如图15所示。
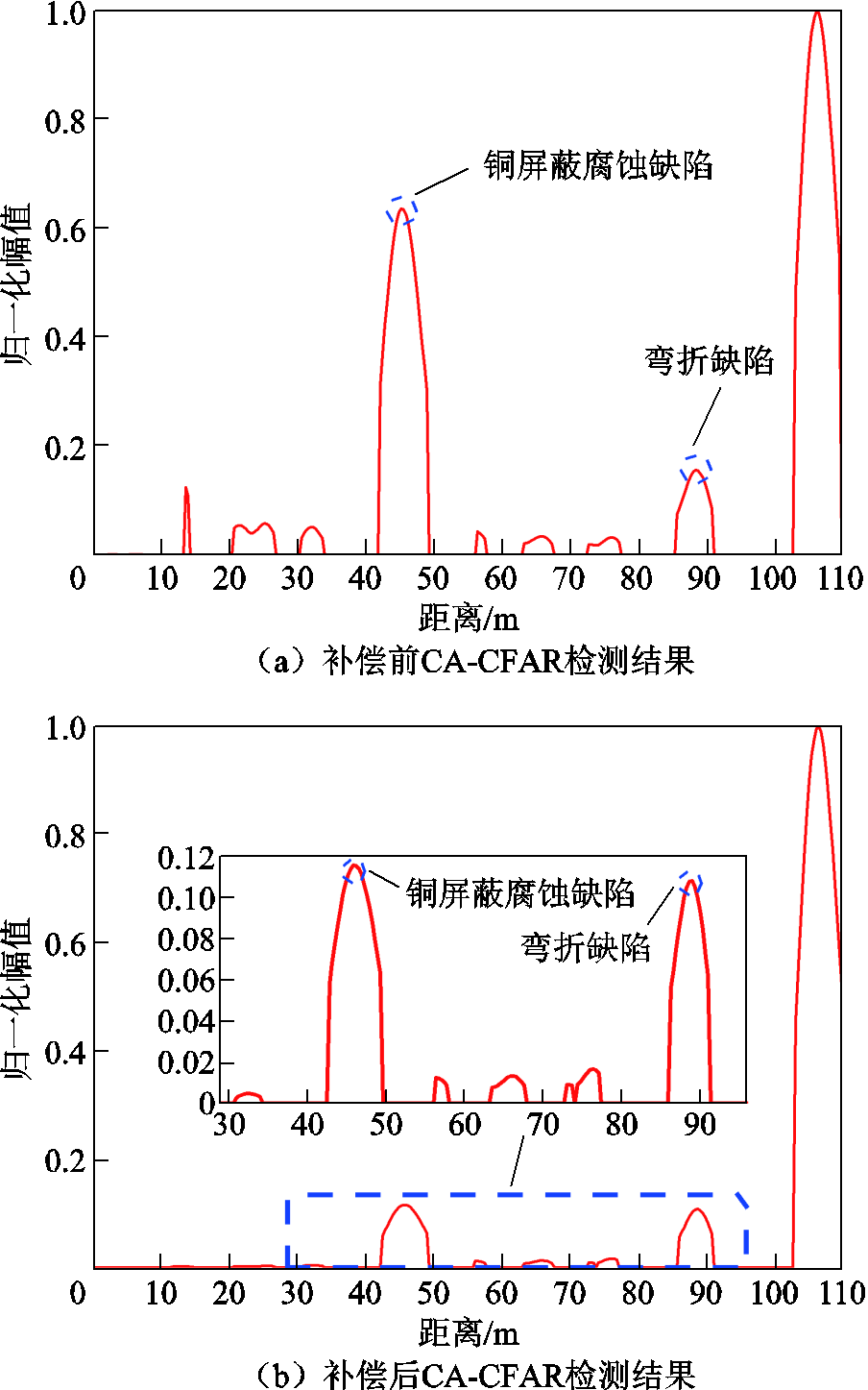
图15 105 m电缆补偿前后CA-CFAR检测结果
Fig.15 CA-CFAR threshold detection results of 105 m cable before and after compensation
由图15可知，补偿前的铜屏蔽腐蚀处幅值偏大，约为弯折处缺陷的3倍，这是由于测试频率过高导致衰减增大，使得第二个缺陷处幅值偏小。进行衰减补偿后可发现，两缺陷处幅值几乎处于同一幅度，且远远大于其余伪峰，因此无需进行伪峰去除即可准确地判断出两缺陷的具体位置，进一步证明了所提方法对其余缺陷识别的有效性。
最后为了验证所提方法对受潮中间接头检测的有效性，在型号为YJLV22-8.7/15-1×95的10 kV XLPE电力电缆上展开实验。测试电缆总长为30 m，分别在距离首端10 m、20 m左右制作了中间接头，并对两处中间接头进行注水处理，模拟中间接头受潮缺陷，如图16所示。测试频段为150 kHz～100 MHz，采样点数为3 001个。将测试数据进行衰减补偿后与原始测得的数据进行对比得到补偿前后的定位曲线如图17所示。
图16 中间接头受潮缺陷
Fig.16 Damping defect of intermediate joint
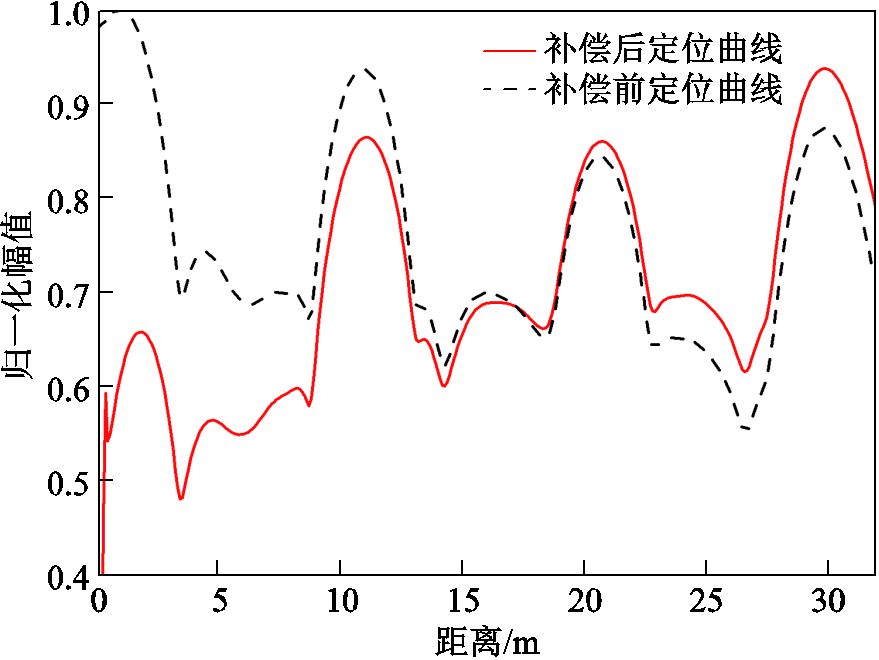
图17 30 m电缆补偿前后定位曲线
Fig.17 Positioning curves of 30 m cable before and after compensation
由图17可知，补偿前后都可以较容易地辨别出两个缺陷位置。但是补偿前首端幅值依旧大于末端幅值，且可以看出第一个缺陷幅值明显大于第二个缺陷幅值。补偿后首端幅值大大减小，且第一与第二个缺陷幅值基本处于同一水平线上，证明衰减方法对于短电缆依旧有效。对衰减补偿前后的定位曲线进行CFAR缺陷提取，保护单元设置为2，得到的检测结果如图18所示。
由图18可知，补偿前第一个接头受潮处幅值偏大，补偿后两缺陷幅值基本一致。缺陷处的峰值远大于其余伪峰，因此无需进行伪峰去除即可将其辨识出来。该实验证明了所提方法对于较短电缆的缺陷识别也是有效的。
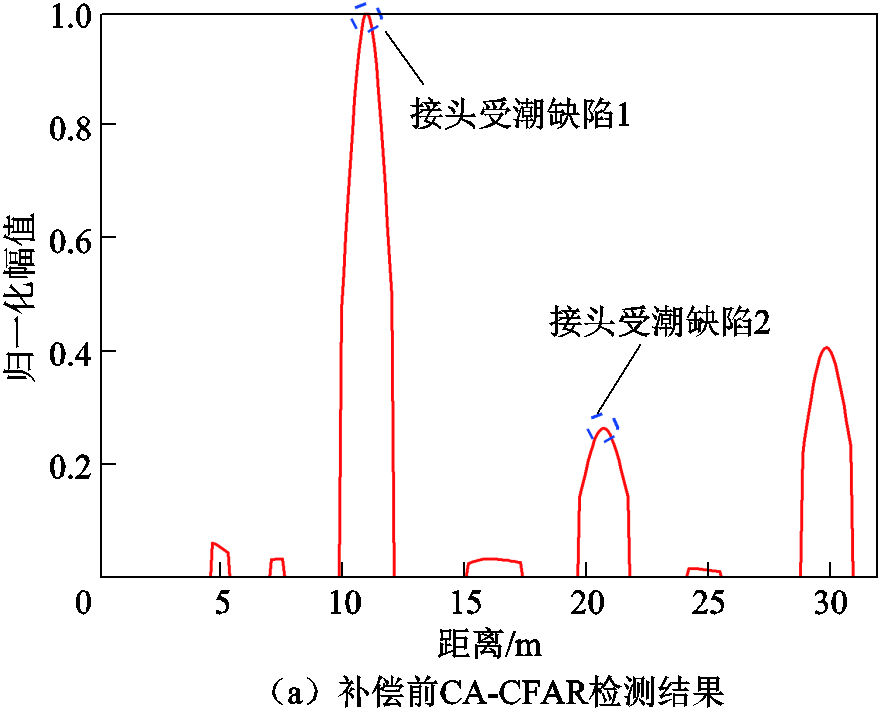
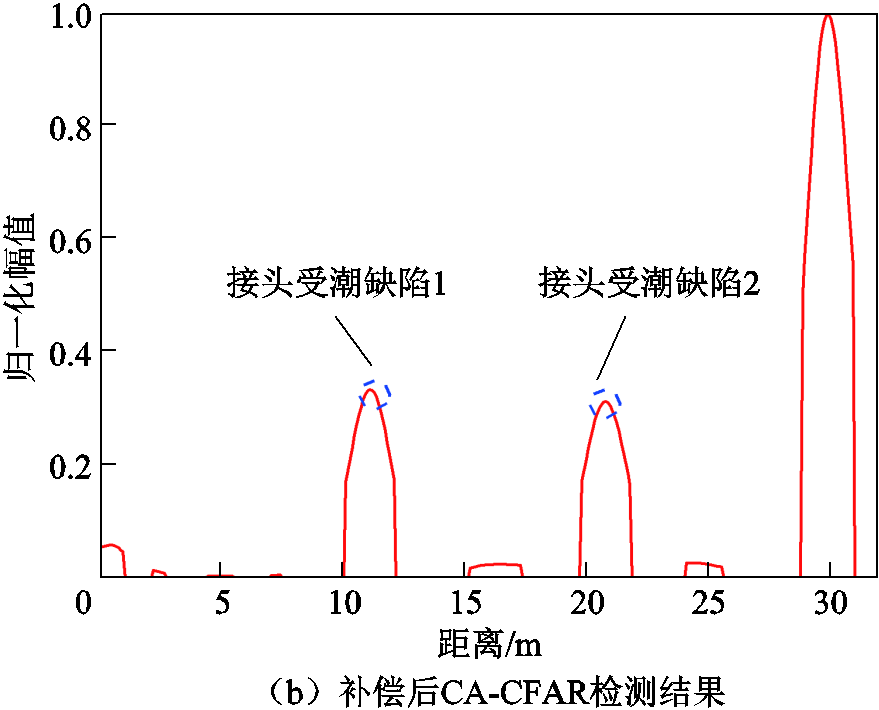
图18 30 m电缆补偿前后CA-CFAR检测结果
Fig.18 CA-CFAR threshold detection results of 30 m cable before and after compensation
针对FDR电缆检测中存在的人为主观经验判断缺陷位置易造成误判的问题，引入了CA-CFAR检测方法，并对信号衰减过大问题提出了信号的衰减补偿方法，解决了以下几个问题：
1）对于FDR检测中长电缆时信号衰减较大问题，首先将衰减系数近似为与频率f呈线性关系的一条曲线，再在频域上使用衰减系数与原首端反射系数谱反卷积的方法，对电缆的信号衰减进行补偿。无论是实验室中的30 m、105 m和500 m的电缆，还是1 500 m的在运电缆，测试结果都表明该方法对电缆测试信号的补偿效果良好。
2）对于实际测试中人为主观经验判断缺陷所造成的易误判问题，引入了雷达目标检测领域所使用的CA-CFAR方法。对实验室500 m电缆测试后，证明了该方法可以对电缆的中间接头或缺陷造成的电缆阻抗不连续点进行提取；对1 500 m在运电缆进行测试后，表明该方法可以在一些复杂情况下对实际电缆的缺陷进行提取，且提取的准确率较高；对实验室30 m和105 m电缆测试后，进一步证明了该方法对电缆其他缺陷识别的有效性。
3）由式（21）发现接头处归一化幅值由反射系数决定，将中间接头电容参数代入仿真模型后可得反射系数为0.041 2，因此可以将此值设置为缺陷判定的阈值，若大于此阈值判定为缺陷；反之则判定为伪峰。在实验室500 m电缆和在运1 500 m电缆的检测结果中发现，该方法可有效地去除伪峰。
参考文献
[1] 汪先进, 周凯, 谢敏, 等. 基于时间反演相位法的电力电缆局部放电定位[J]. 电网技术, 2020, 44(2): 783-790.
Wang Xianjin, Zhou Kai, Xie Min, et al. Research on partial discharge source location for power cables based on time reversal phase method[J]. Power System Technology, 2020, 44(2): 783-790.
[2] 刘凤莲, 夏荣, 李文杰, 等. 高压交联电缆缓冲层烧蚀缺陷检测方法研究[J]. 高压电器, 2022, 58(8): 259-266, 274.
Liu Fenglian, Xia Rong, Li Wenjie, et al. Research on detection method of buffer layer ablation defect in high voltage XLPE cable[J]. High Voltage Apparatus, 2022, 58(8): 259-266, 274.
[3] 赵书静, 詹博博, 龚梁涛, 等. 基于调频连续波相位敏感特性的电缆局部缺陷检测方法[J]. 电工技术学报, 2023, 38(11): 3009-3021.
Zhao Shujing, Zhan Bobo, Gong Liangtao, et al. Research on cable local defect detection method based on phase-sensitive characteristics of frequency modulated continuous wave[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 3009-3021.
[4] 高晓欣. 电力电缆故障分析与探测[D]. 济南: 山东大学, 2012.
Gao Xiaoxin. Power cables fault analyse and detect[D]. Jinan: Shandong University, 2012.
[5] 李泽, 王辉, 钱勇, 等. 基于加速鲁棒特征的含噪局部放电模式识别[J]. 电工技术学报, 2022, 37(3): 775-785.
Li Ze, Wang Hui, Qian Yong, et al. Pattern recognition of partial discharge in the presence of noise based on speeded up robust features[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 775-785.
[6] 周凯, 赵世林, 何珉, 等. 考虑短距离电缆中行波特性的振荡波局部放电定位方法[J]. 电网技术, 2017, 41(6): 2047-2054.
Zhou Kai, Zhao Shilin, He Min, et al. An oscillating wave test method based on traveling wave characteristics of partial discharges for defect location in short cables[J]. Power System Technology, 2017, 41(6): 2047-2054.
[7] 谢敏, 周凯, 赵世林, 等. 考虑相速度频变特性的改进互相关算法局部放电定位[J]. 电网技术, 2018, 42(5): 1661-1667.
Xie Min, Zhou Kai, Zhao Shilin, et al. Research on partial discharge location using modified cross-correlation method considering frequency characteristic of phase velocity[J]. Power System Technology, 2018, 42(5): 1661-1667.
[8] 李保生. 基于时域脉冲反射原理的电线电缆精确测长技术研究[D]. 西安: 西安电子科技大学, 2010.
Li Baosheng. Study on wire-cable length precision measurement technology base on TDPR[D]. Xi’an: Xi’an University of Science and Technology, 2010.
[9] Song E, Shin Y J, Stone P E, et al. Detection and location of multiple wiring faults via time–frequency-domain reflectometry[J]. IEEE Transactions on Electromagnetic Compatibility, 2009, 51(1): 131-138.
[10] Ohki Y, Yamada T, Hirai N. Diagnosis of cable aging by broadband impedance spectroscopy[C]//2011 Annual Report Conference on Electrical Insulation and Dielectric Phenomena, Cancun, Mexico, 2012: 24-27.
[11] 饶显杰, 周凯, 黄永禄, 等. 频域反射法中阻抗变化类型判断技术[J]. 电工技术学报, 2021, 36(16): 3457-3466.
Rao Xianjie, Zhou Kai, Huang Yonglu, et al. Type judgement technology of impedance variation in frequency domain reflection method[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3457-3466.
[12] Zhou Zhiqiang, Zhang Dandan, He Junjia, et al. Local degradation diagnosis for cable insulation based on broadband impedance spectroscopy[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2015, 22(4): 2097-2107.
[13] 饶显杰, 徐忠林, 刘翔宇, 等. 基于反射系数与核函数构建的新型电缆缺陷诊断方法[J]. 电工技术学报, 2024, 39(7): 2184-2192.
Rao Xianjie, Xu Zhonglin, Liu Xiangyu, et al. A new cable defect diagnosis method based on reflection coefficient and kernel function construction[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 2184-2192.
[14] 陈禹. FMCW激光雷达测距测速信号处理算法研究[D]. 哈尔滨: 哈尔滨工业大学, 2021.
Chen Yu. Research on FMCW lidar ranging and velocity signal processing algorithm[D]. Harbin: Harbin Institute of Technology, 2021.
[15] 王蓓. 基于杂波图的恒虚警处理技术研究[D]. 西安: 西安电子科技大学, 2018.
Wang Bei. Research on constant false alarm processing technology based on clutter map[D]. Xi’an: Xi’an University of Science and Technology, 2018.
[16] Yan He, Chen Chao, Jin Guodong, et al. Implementation of a modified faster R-CNN for target detection technology of coastal defense radar[J]. Remote Sensing, 2021, 13(9): 1703.
[17] Paul C R. Analysis of Multiconductor Transmission Lines[M]. Wiley-IEEE Press, 2007.
[18] 谢志远, 孙艳, 郭以贺. 基于传输线理论的中压电力线信道建模和分析[J]. 电力科学与工程, 2010, 26(7): 5-8.
Xie Zhiyuan, Sun Yan, Guo Yihe. Modeling and analysis of medium voltage power line channel base on transmission line theory[J]. Electric Power Science and Engineering, 2010, 26(7): 5-8.
[19] 操雅婷, 周凯, 孟鹏飞, 等. 基于正交匹配-伪魏格纳分布的电缆缺陷定位[J]. 电工技术学报, 2023, 38(16): 4489-4498.
Cao Yating, Zhou Kai, Meng Pengfei, et al. Cable defect location based on orthogonal matching pursuit and pseudo wigner-ville distribution[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4489-4498.
[20] 旷建军, 阮新波, 任小永. 集肤和邻近效应对平面磁性元件绕组损耗影响的分析[J]. 中国电机工程学报, 2006, 26(5): 170-175.
Kuang Jianjun, Ruan Xinbo, Ren Xiaoyong. Analysis of skin and proximity effects on winding losses in planar magnetic components[J]. Proceedings of the CSEE, 2006, 26(5): 170-175.
[21] 宋建辉. 基于时域反射原理的电缆测长若干关键技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2010.
Song Jianhui. Some key techniques of cable length measurement based on time domain reflectometry[D]. Harbin: Harbin Institute of Technology, 2010.
[22] 李蓉, 周凯, 万航, 等. 基于频域反射法的10 kV配电电缆中间接头受潮定位[J]. 电网技术, 2021, 45(2): 825-832.
Li Rong, Zhou Kai, Wan Hang, et al. Moisture location of 10 kV cable joints in medium voltage distribution grid based on frequency domain reflection[J]. Power System Technology, 2021, 45(2): 825-832.
[23] 高云鹏, 滕召胜, 曾博, 等. 基于Kaiser窗频谱校正的介质损耗因数测量[J]. 电工技术学报, 2009, 24(5): 203-208.
Gao Yunpeng, Teng Zhaosheng, Zeng Bo, et al. Dielectric loss factor measurement based on Kaiser window spectral correction[J]. Transactions of China Electrotechnical Society, 2009, 24(5): 203-208.
[24] 邹成晓, 张海霞, 程玉堃. 雷达恒虚警率检测算法综述[J]. 雷达与对抗, 2021, 41(2): 29-35.
Zou Chengxiao, Zhang Haixia, Cheng Yukun. Radar CFAR detection algorithms review[J]. Radar & ECM, 2021, 41(2): 29-35.
[25] Barkat M. Signal Detection and Estimation[M]. 2nd ed. Boston: Artech House, 2005.
[26] Mahafza B R. Radar Systems Analysis and Design Using Matlab[M]. 2nd ed. Boca Raton, FL: Chapman & Hall/CRC, 2005.
[27] 刘宇. 毫米波LFMCW雷达对地探测杂波抑制及恒虚警技术研究[D]. 南京: 南京理工大学, 2018.
[28] 郝迎春. 雷达CFAR检测算法及门限判决系数的优化研究[D]. 成都: 电子科技大学, 2012.
Frequency Domain Reflectometry Cell Average Constant False Alarm Rate Cable Defect Identification Method Considering Attenuation Compensation
Abstract The frequency domain reflectometry(FDR) method using sweep frequency signals is widely used in cable defect monitoring due to its high frequency components in the incident wave and its ability to quickly monitor weak defects. The broadband impedance spectroscopy (BIS) method and reflection coefficient spectrum (RCS) method, developed based on the FDR method, obtain cable characteristic parameters through scanning signal measurement, and can locate local defects in cables with high sensitivity. However, when using FDR to locate defects, spectrum leakage during Fourier transform can result in many "pseudo peaks" on the final localization spectrum. Due to the influence of these "pseudo peaks", it is difficult to accurately identify the position of defect peaks in the localization spectrum, and due to subjective human factors, it is highly likely to lead to misjudgment. At the same time, during on-site testing, the attenuation of the signal will increase with the increase of cable length, resulting in very inconspicuous cable defects during defect detection for some medium and long cables, causing significant economic losses for subsequent repairs. Therefore, the constant false alarm rate (CFAR) method can be introduced for automatic identification of cable defects. It can automatically extract the position and peak value of defects in the positioning spectrum, greatly reducing misjudgments caused by spectrum leakage and subjective human factors, and improving the fault detection rate.
Constant False Alarm Rate is a commonly used method in the field of radar target detection. During the process of detecting targets, radar is subject to interference from clutter. The constant false alarm rate detector adaptively changes the detection threshold with changes in the reference unit to achieve CFAR detection of the target. The ultimate goal is to determine whether the object detected by the radar is a target object, which is consistent with our goal of cable defect recognition. What we need is to determine whether the abnormal peak in the positioning spectrum is a defect. Therefore, the CFAR method has a foundation for application. The most basic form of constant false alarm rate is the cell average constant false alarm rate (CA-CFAR), which has a simple algorithm structure and fast calculation speed, and can be effectively applied in cable defect identification.
Firstly, in order to reduce the uncertainty of defect measurement caused by signal attenuation effect, a attenuation compensation method is adopted by approximating the attenuation factor with the test frequency and then deconvoluting it in the frequency domain. This effectively weakens the negative impact of excessive signal attenuation during cable propagation. Secondly, in order to reduce the problem of human subjective experience judgment being prone to misjudgment, the dynamic threshold of CFAR is used to extract the location and normalized amplitude information of defects in cables. The dynamic threshold dynamically selects the threshold for defect judgment based on the changes in test signal amplitude, avoiding the shortcomings of human subjective experience judgment. In order to test the effectiveness of this method, tests were conducted on 30 m, 105 m, and 500 m cables in the laboratory, as well as on 1500 m running cables. The test results showed that this method can not only accurately extract defect locations, but also effectively solve the problem of defect masking during CFAR detection.
keywords：Frequency domain reflectometry, attenuation compensation, constant false alarm rate, defect identification
中图分类号：TM75
DOI: 10.19595/j.cnki.1000-6753.tces.230882
国家自然科学基金资助项目（52277156）。
收稿日期 2023-06-09
改稿日期 2023-07-20
唐作鑫 男，1998年生，硕士研究生，研究方向为电力设备状态检测。E-mail：tangzx94@qq.com
徐叶飞 男，1991年生，博士，研究方向为无线电力传输及其在电力系统中的应用。
E-mail：xuyefei1991@126.com（通信作者）
（编辑 李 冰）