 (1)
(1)
摘要 特快速暂态过电压(VFTO)仿真研究中,传统电弧黑盒模型因电弧时间常数和散热功率常取经验值会引起VFTO计算结果出现较大误差。对此,该文提出了一种基于双温度磁流体电弧仿真的改进Mayr电弧模型建立方法。首先,建立了双温度磁流体电弧模型,并通过该仿真研究了上述关键参数与电弧电导的关系,建立了改进Mayr电弧模型;其次,搭建了VFTO仿真模型,采用改进Mayr电弧模型和多种传统电弧数学模型计算了特高压GIS隔离开关切合空载短母线过程的VFTO波形;最后,对比分析了各电弧模型的仿真结果与实测结果波形特征的相对误差。结果表明,改进Mayr电弧模型的VFTO仿真结果与实测结果的相对误差较小,计算准确度较高。
关键词:气体绝缘组合电器 隔离开关 特快速暂态过电压 磁流体动力学 电弧黑盒模型
气体绝缘组合电器(Gas Insulated Switchgear, GIS)隔离开关切合空载短母线的过程中会产生特快速暂态过电压(Very Fast Transient Overvoltage, VFTO),对GIS及其相连设备的绝缘造成威胁,污染二次设备的电磁环境,严重影响电力系统的安全稳定运行[1-3]。VFTO仿真计算的准确性与隔离开关的等效电弧模型紧密相关。因此,建立一种能更准确地表征暂态电弧特性的电弧模型,对于VFTO的仿真研究具有重要意义。
在VFTO的仿真计算中,常通过修正隔离开关的电弧数学模型来获得更准确的VFTO计算结果。常用的电弧模型包括时变电弧模型、电弧黑盒模型等。文献[4]总结了VFTO仿真研究中常用的各类时变函数形式的电弧模型,并基于这些电弧模型计算了隔离开关操作回路的VFTO和特快速暂态电流(Very Fast Transient Current, VFTC)。文献[5]基于标准Mayr模型和Cassie模型,通过以电流为变量的过渡函数将二者相结合,建立了Mayr-Cassie组合模型,并通过实验和仿真验证了该模型的准确性。文献[6]基于传统电弧模型建立了动态电弧模型,并结合特高压GIS分析了关键设备处的VFTO波形特征。文献[7]将Cassie和Mayr模型相结合,燃弧阶段使用Cassie模型,熄弧阶段使用Mayr模型,通过设置阈值实现两阶段的电弧模型切换,有效地计算了GIS内部的VFTO波形。文献[8]通过大量实验获得了Mayr-Schwarz电弧模型的参数,建立串联型故障电弧数学模型并对故障电弧进行了仿真分析。然而,传统电弧数学模型在很大程度上只考虑了电弧电阻的变化趋势,其中的一些关键参数,如时变电弧模型中的弧阻系数、电弧时间常数和Mayr模型中的电弧时间常数、散热功率等,均根据经验设置,难以准确计算VFTO。
随着磁流体动力学(Magnetohydrodynamics, MHD)的发展,电弧的磁流体模型能够实现多物理场耦合,其仿真能更为准确地描述电弧发展过程,计算电弧内部能量变化。以双温度磁流体电弧模型为例,该模型假设电弧等离子体中的重粒子和电子分别处于不同的平衡态(即重粒子和电子分别拥有各自的温度),并在此基础上建立了双温度下的磁流体模型,进而可以描述电弧发展过程中的一些非平衡态过程。文献[9]建立了高压SF6断路器的三维能量源动态电弧模型和气流场模型,并通过仿真计算验证了该模型能够反映出电弧从燃弧至熄灭过程的形态变化和能量逸散过程。文献[10-11]建立了电弧的MHD模型,分析了电磁耦合作用下灭弧室内的温度分布和燃弧时间等,研究了不同条件下电弧的运动特性。文献[12]从微观粒子角度出发,建立了cm级间隙的暂态电弧流体数学模型,研究了击穿过程中的电弧电阻变化规律。此外,文献[13]基于电弧的磁流体动力学理论对Cassie和Mayr混合模型进行了改进,得到了改进型交流电弧模型,并通过与实验数据的对比验证了该模型的准确性。尽管文献[13]证明了可以通过平衡态磁流体仿真来建立较为准确的电弧黑盒模型,但依据文献[14]的研究成果说明,在SF6等离子体中,当重粒子温度高于4 000 K时,电子间达到温度平衡所用时间约为2.49×10-13~7.46×10-12 s;重粒子间约为1.04×10-11~1.21×10-8 s;电子与重粒子之间约为1.12×10-8~4.47×10-7 s。当重粒子温度在3 000~4 000 K时,电子与重粒子间达到温度平衡所用时间约为0.69~15.96 μs,因此在GIS隔离开关的特快速暂态过程中,暂态电弧等离子体应当是处于热力学非平衡态[14-18],需要以双温度磁流体仿真来建立更加准确的电弧黑盒模型。
综上所述,传统隔离开关电弧数学模型中的时变电阻模型缺乏准确性,黑盒模型中关键参数的确定过分依赖实验数据,都存在各自的缺陷。磁流体模型能够计算电弧能量进而得到电弧时间常数和散热功率两个关键参数,在一定程度上弥补了黑盒模型的不足之处。本文以特高压单断口GIS隔离开关切合空载短母线为例,考虑了时变电磁场的影响,建立了电弧的双温度磁流体模型,通过双温度磁流体仿真计算了该过程的电弧时间常数、散热功率和电弧电导,并通过参数拟合得到了关键参数和电弧电导的函数关系,最终建立了改进Mayr电弧模型。通过VFTO仿真,计算了特高压GIS隔离开关切合空载短母线过程的VFTO波形,并与实测波形进行对比,验证了本文所提方法的可行性以及通过该方法建立改进Mayr电弧模型的准确性。
传统电弧黑盒模型基于能量守恒定律推导出电弧电导的计算公式,主要有Mayr模型、Cassie模型、Mayr-Schwarz模型、Mayr-Cassie组合模型。
1)Mayr模型
Mayr模型的表达式为
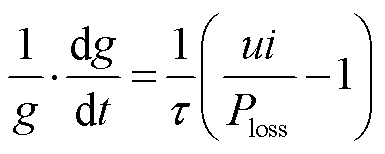 (1)
(1)
式中,g为电弧电导,S;t为时间,s;Ploss为电弧的耗散功率,W;τ为电弧时间常数,s;u为电弧电压,V;i为电弧电流,A。该模型将τ和Ploss视为常数,由此得到的电弧模型适用于大电阻、小电流条件下的电弧特性模拟,即熄弧阶段。
2)Cassie模型
Cassie模型的表达式为
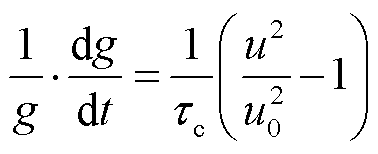 (2)
(2)
式中,τc为Cassie模型电弧时间常数,s;u0为电弧电压常数,V。该模型将τc和u0视为常数,适用于小电阻、大电流条件下的电弧特性模拟,即稳态燃弧阶段。
3)Mayr-Schwarz模型
Mayr-Schwarz模型是在Mayr模型的基础上加以改进,将电弧时间常数和散热功率视为电弧电导的幂函数,电弧模型表示为
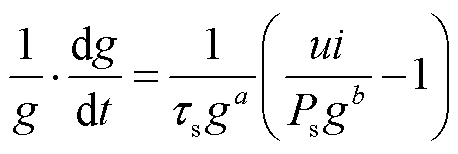 (3)
(3)
式中,系数τs、Ps和指数a、b可以使用实验数据的拟合值或经验参数。
4)Mayr-Cassie组合模型
Mayr-Cassie组合模型综合考虑了二者的适用范围,通过一个以电流为变量的过渡函数将二者进行结合,电弧模型为
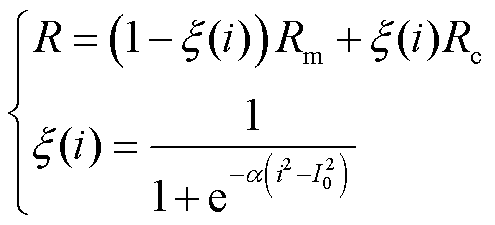 (4)
(4)
式中,R为电弧电阻;Rm为Mayr模型下的电弧电阻;Rc为Cassie模型下的电弧电阻;ξ(i)为过渡函数;I0为过渡电流;α为调节参数[5]。
在上述四种传统电弧黑盒模型中,Mayr模型和Cassie模型受假设条件的限制,电弧时间常数、散热功率、电弧电压常数等都是常量,不能单独运用至GIS的VFTO仿真研究中;Mayr-Schwarz模型中的系数和指数的具体取值依赖大量实验数据或经验值;Mayr-Cassie组合模型虽综合了两种模型的优势,但其中的具体参数取值依然依赖大量实验数据,会给不同条件下的GIS中的VFTO仿真计算带来误差。
因此,本文参考了式(1)的Mayr电弧模型,提出一种改进Mayr电弧模型,表示为
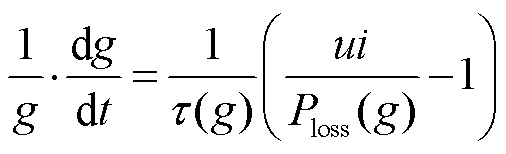 (5)
(5)
式中,τ(g)和Ploss(g)分别为当前电弧时间常数和散热功率。此处参数与Mayr模型中的定义不同,τ(g)和Ploss(g)不是常量,而是随电弧状态(电导)的变化而发生改变。
改进Mayr电弧模型的建立流程如图1所示。首先需要建立双温度磁流体电弧模型,通过电弧仿真计算出每一时间步长的电弧时间常数、散热功率以及电弧电导;然后通过参数拟合得到电弧时间常数、散热功率与电导的具体函数表达式;最后,将其代入式(5)中,获得改进Mayr电弧模型。
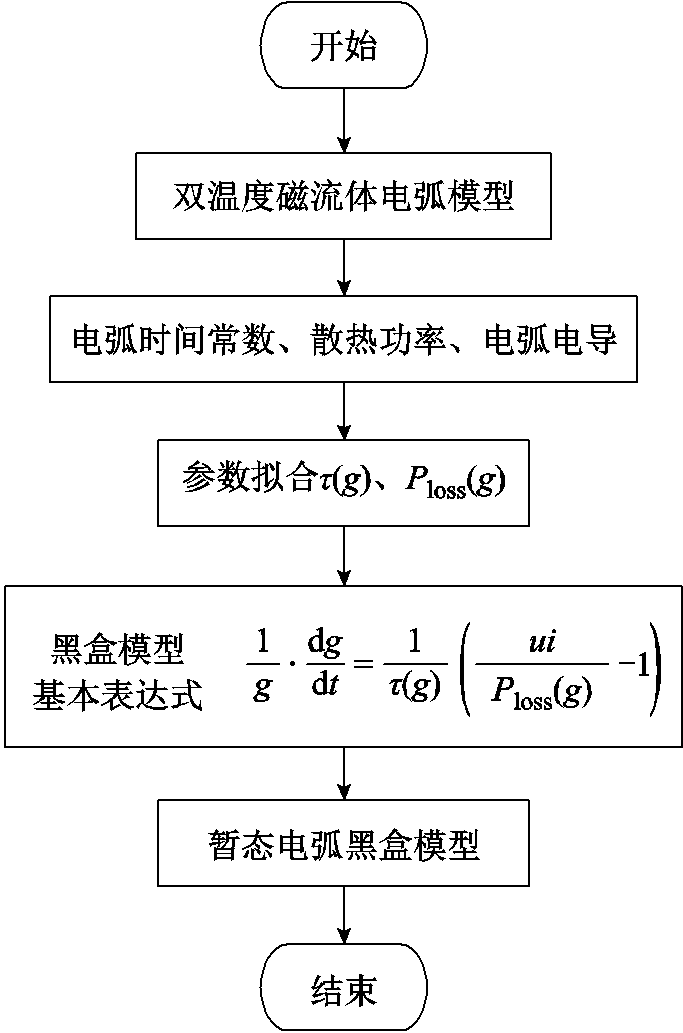
图1 改进Mayr电弧模型建立流程
Fig.1 Improved Mayr arc model establishment process
2.1.1 假设条件
隔离开关电弧发展过程中,电子与重粒子因碰撞能量交换不足而具有不同的温度。此外,在暂态高频电流的影响下,电磁感应现象无法忽略。因此,在建立双温度磁流体模型时,作出如下假设:
1)电弧等离子体处于局部化学平衡态(Local Chemical Equilibrium, LCE),其中微观粒子的运动状态与宏观电弧一致,忽略粒子扩散的影响。
2)将电子和重粒子视为温度不同的两种流体,各自遵循Maxwell-Boltzmann分布。
3)忽略鞘层对电弧的影响以及电弧和电极之间的相互作用。
4)忽略电弧起弧过程。
2.1.2 控制方程
电弧燃烧是一个伴随着气流场、热力场、电磁场互相作用的多物理场耦合过程,为了描述这种复杂的变化过程,本文将整个电弧等离子体视作均匀介质,以Navier-Stokes方程形式为基础,分别以流体速度、能量、电位和矢量磁位为待求场量,建立电弧的二维双温度磁流体模型的控制方程。
1)质量守恒方程
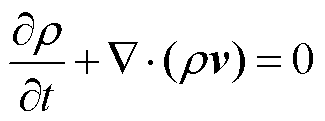 (6)
(6)
式中,ρ为SF6电弧等离子体质量密度,kg/m3;v为SF6电弧等离子体速度,m/s。
2)动量守恒方程
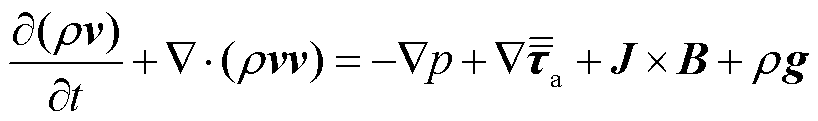 (7)
(7)
式中,p为SF6电弧等离子体气压,Pa;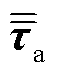 为SF6电弧等离子体黏滞应力张量;J为电流密度,A/m2;B为磁感应强度,T;g为重力加速度,m/s2。其中,洛伦兹力项
为SF6电弧等离子体黏滞应力张量;J为电流密度,A/m2;B为磁感应强度,T;g为重力加速度,m/s2。其中,洛伦兹力项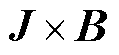 通过求解磁场方程获取。
通过求解磁场方程获取。
3)电子能量守恒方程
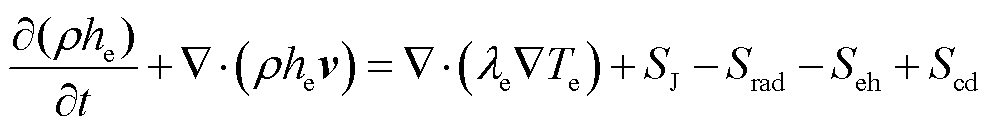 (8)
(8)
式中,he为电子比焓,J/kg;λe为电子热导率,W/(m·K);Te为电子温度,K;SJ、Srad、Seh、Scd为源项,分别代表电流产生的焦耳热项、辐射能量项、电子与重粒子碰撞交换的能量项、电子传导热传递项,计算公式为
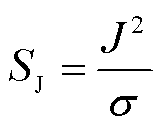 (9)
(9)
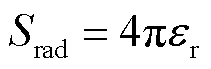 (10)
(10)
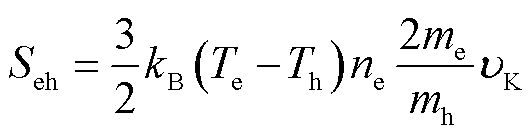 (11)
(11)
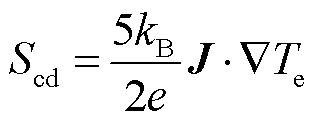 (12)
(12)
式中,σ为SF6电弧等离子体电导率,S/m;εr为净辐射系数,W/(m3·sr);kB为玻耳兹曼常数,J/K;ne为SF6电弧等离子体的电子数密度,m-3;me为电子质量,kg;Th为重粒子温度,K;mh为重粒子质量,kg;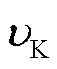 为SF6电弧等离子体中电子与重粒子的能量交换频率,s-1;e为电子电荷量,C。
为SF6电弧等离子体中电子与重粒子的能量交换频率,s-1;e为电子电荷量,C。
仅考虑粒子的平动贡献,可得电子比焓he与电子温度Te的关系为
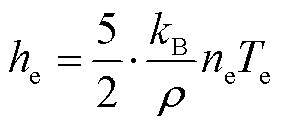 (13)
(13)
4)重粒子能量守恒方程
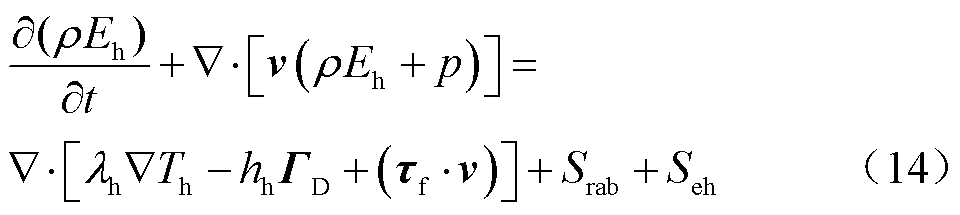
式中,Eh为单位质量重粒子能量,J/kg;λh为重粒子热导率,W/(m·K);hh为重粒子比焓,J/kg;ΓD为扩散通量,kg/(m2·s);τf为重粒子应力张量。
重粒子能量与重粒子比焓之间的关系为
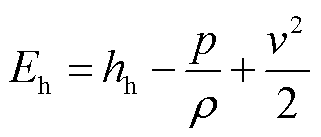 (15)
(15)
5)时变电磁场控制方程
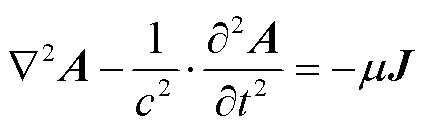 (16)
(16)
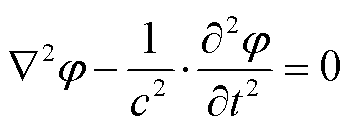 (17)
(17)
式中,A为动态矢量磁位,Wb/m;φ为动态电位,V;μ为磁导率,H/m;c为光速,m/s。
2.1.3 电弧初始形态及边界条件
根据电弧照片可建立双温度磁流体电弧仿真的初始电弧形态,如图2所示。电弧位于动静触头之间,动触头侧和静触头侧弧根分别位于动触头顶部和静触头铝环处,触头开距约为196 mm[19]。根据SF6在非平衡度为1时的电导率曲线[15],如图3所示,SF6气体在约3 000 K温度时开始出现电导率的上升,因此,本文以3 000 K为SF6电弧温度边界。同时,弧心温度按常用值设为10 000 K,并依据图2中的电弧形态确定磁流体仿真电弧的初始形态。

图2 电弧初始形态
Fig.2 The initial shape of the arc
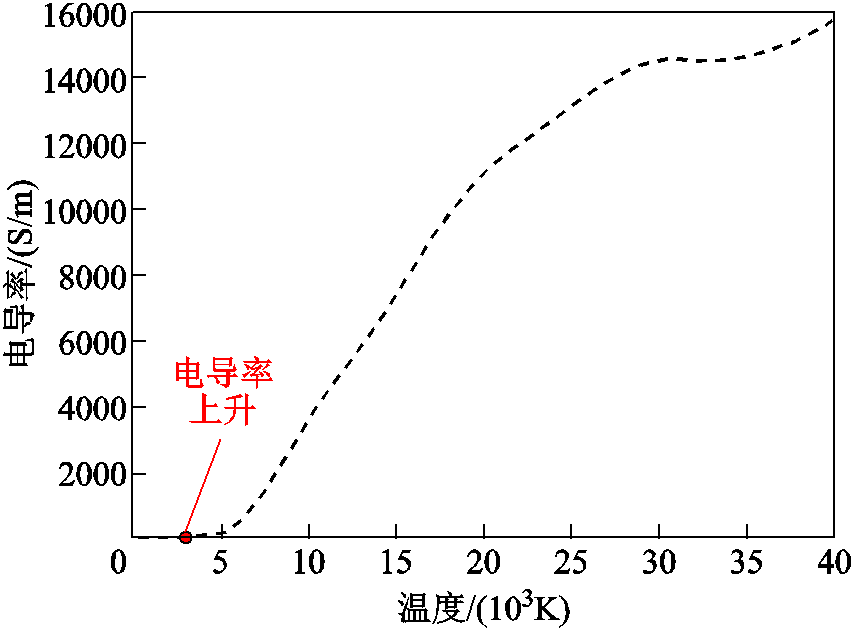
图3 SF6电导率曲线
Fig.3 Electrical conductivity curve of SF6
双温度磁流体电弧仿真简化几何模型及各边界条件类型如图4所示。主要边界条件设置如下。
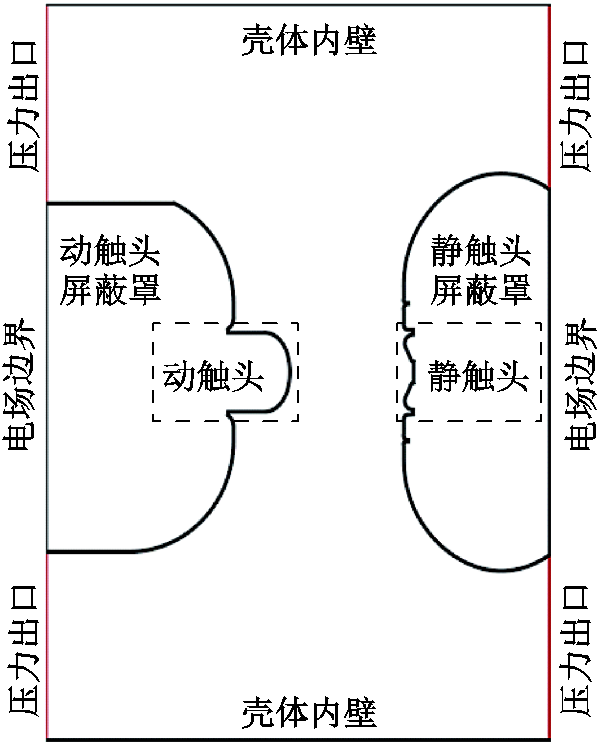
图4 简化几何模型示意图
Fig.4 Simplified geometry schematic
1)压力边界条件
实际SF6充气压力为0.4 MPa,因此设置压力出口边界的压力值为0.4 MPa。
2)温度边界条件
由于电极表面存在厚度为德拜长度的由空间电荷主导的鞘层区域,其温度边界条件未知;电极表面的温度边界条件对SF6电弧等离子体参数求解的影响仅限制在触头附近较小的区域,对电弧电压影响较小,且在假设条件中已经忽略了鞘层影响,因此在动、静触头与电弧等离子体交界面处设置电子和重粒子的热传导为0;计算域外围边界上设置为恒定温度300 K。
3)电场边界条件
动、静触头间隙击穿后,阴极向外发射电子。本文设置动触头为阴极,电位为0;静触头为阳极,其与电弧等离子体界面处的电场边界为耦合边界,即该界面上流入和流出的电流值相同,结合外加电流来计算界面处的电流密度。
根据特高压GIS隔离开关分合闸空载短母线过程中VFTC的相关实验和仿真数据可知,电弧电流呈振荡衰减,其幅值范围为数kA,主频率范围为数MHz[20]。因此,为充分考虑不同电流对改进Mayr电弧模型参数的影响,本文设置幅值为6 kA、主频率为8 MHz的半个周期正弦电流波形作为输入条件,如图5所示,在此半个周期内能计算出电流在0~6 kA范围内的改进Mayr电弧模型参数。
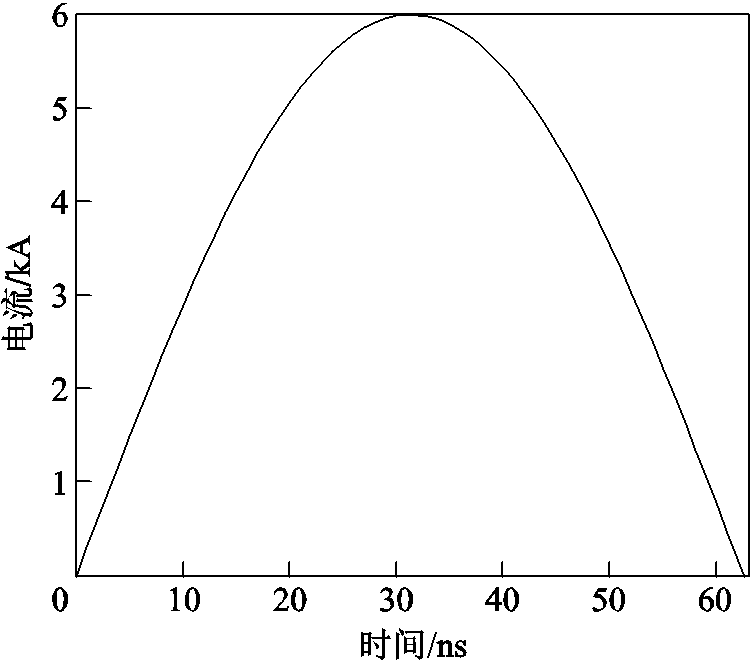
图5 边界条件电流波形
Fig.5 Current waveform for boundary conditions
由于本文仿真结果中重粒子温度和电子温度分布具有相似的规律,因此本文仅展示与电导率密切相关的电子温度分布。通过双温度磁流体电弧仿真可得动、静触头间隙击穿后的电子温度分布如图6所示。由于当电子温度低于3 000 K时,电导率降低至一个很小的值,此时基本可以认为SF6等离子体为绝缘状态,故定义电子温度高于3 000 K的区域为电弧区域;以电弧区域轴线为中心,沿径向若干层网格区域为弧心区域。
由图6可知,t=5 ns时,由于电弧放电通道刚建立,弧柱电子温度由弧心沿径向向外逐渐降低,弧心区域电子温度约为8 000 K。t=10 ns时,电弧电流逐渐增大,外电路输送给电弧的能量也不断增大,弧心电子温度逐渐升高,最高约为9 000 K。 t=20 ns时,电流继续增大,弧心电子温度上升至11 000 K,电弧的整体电子温度呈现出上升趋势,相较20 ns之前略有升高。t=33 ns时,电流上升至峰值,注入电弧的能量随之增大,弧心电子温度进一步上升至12 000 K,此外,从图中还可以看出,弧心附近的电子温度有明显上升,弧心区域得到扩大。t=36 ns时,电流开始下降,注入电弧的能量也开始减少,弧心区域略有收缩,且最高电子温度有所降低,约为10 000 K。t=42 ns时,电流继续减小,弧心区域进一步收缩,电子温度降低,弧心区域整体电子温度约为8 500 K。t=48 ns时,电流继续下降,随着注入能量的减少,电弧弧心区域在收缩的同时,还出现了断裂现象,即整个弧心区域的高温介质并未直接连通,而是在中间出现部分温度较低的区域,使得整个电弧呈现段状,弧心区域电子温度降低至7 500 K左右。t=48~62 ns期间,电流逐渐减小至接近0,由于电流值很小,弧心温度进一步下降,至62 ns时,弧心电子温度已经基本降低至6 000 K左右。
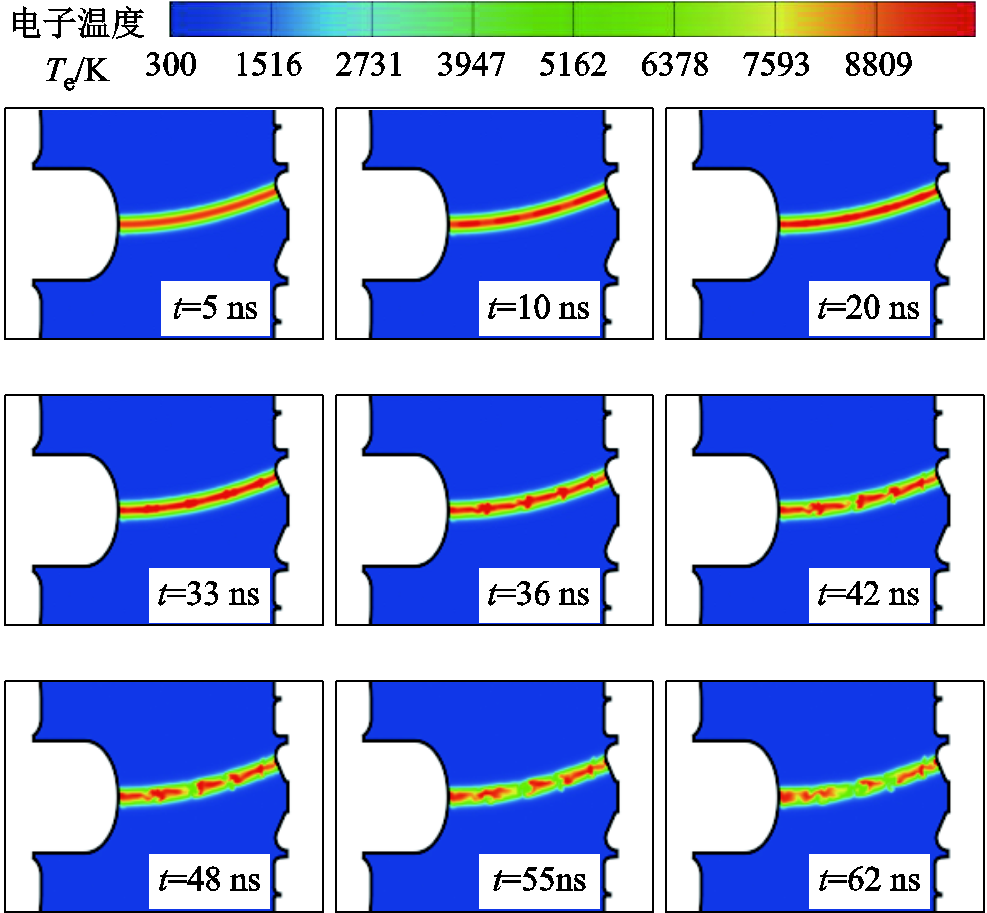
图6 电子温度分布
Fig.6 Distribution of electron temperature
在双温度磁流体电弧仿真中,通过电子能量和重粒子能量方程可计算出每个流体微团内的能量,并根据式(18)和式(19)计算得到传统电弧黑盒模型中的电弧时间常数和散热功率。
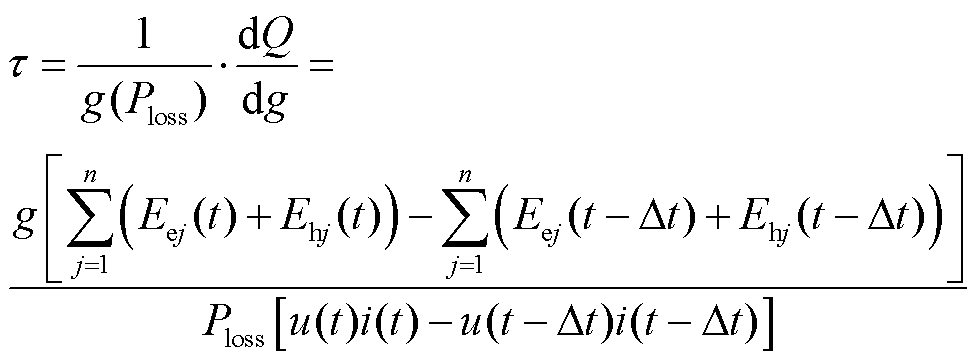 (18)
(18)
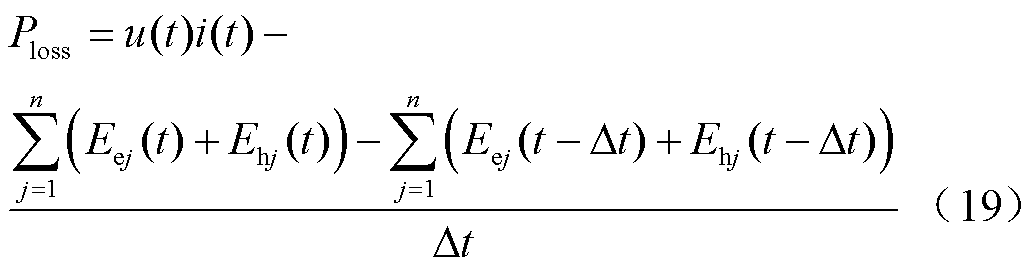
式中,Q为弧柱微团能量,J;Eej为第j个流体微团内的电子能量,J;Ehj为第j个流体微团内的重粒子能量,J;∆t为持续时间,s。
通过仿真计算得到上述参数随电弧电导变化的关系,并通过最小二乘近似进行参数拟合,分别如图7、图8所示。
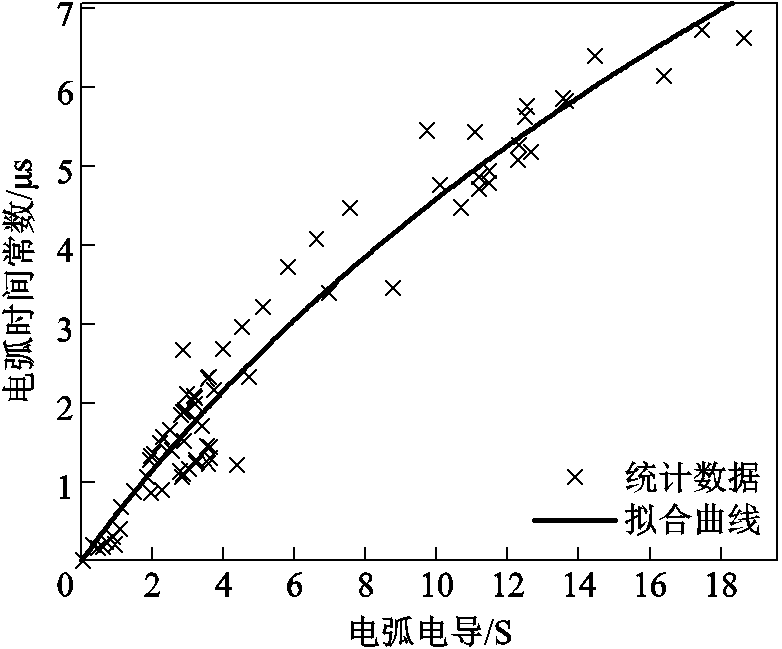
图7 电弧时间常数与电弧电导的关系
Fig.7 The relationship between arc time constant and arc conductance
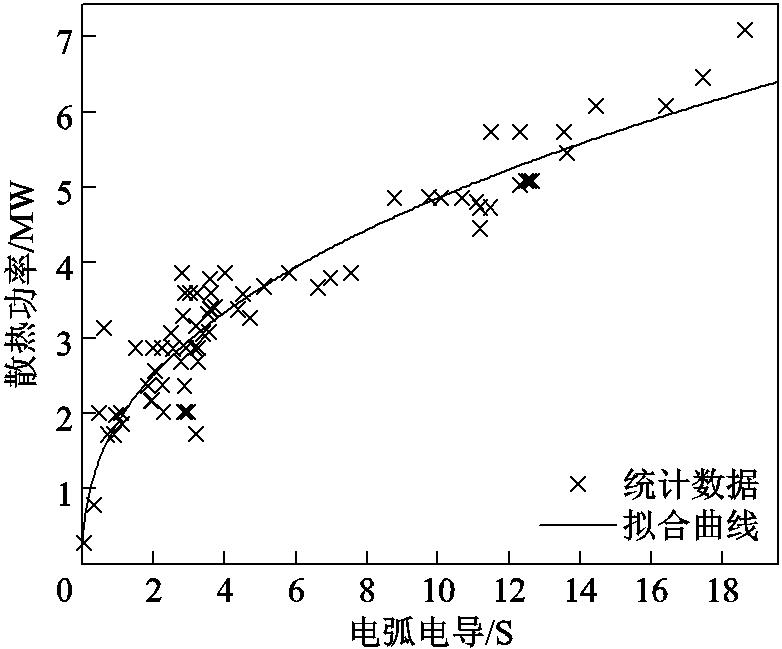
图8 散热功率与电弧电导的关系
Fig.8 The relationship between heat dissipation power and arc conductance
图中,电弧时间常数和散热功率拟合曲线的具体函数表达式分别为
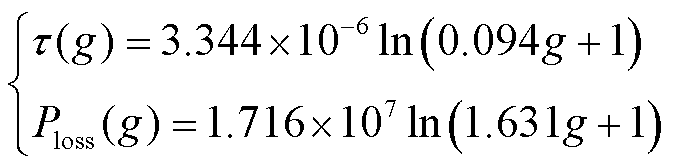 (20)
(20)
将式(20)代入式(5)即可得到基于双温度磁流体电弧仿真的改进Mayr电弧模型。
值得说明的是,由于仿真中电弧的弧柱形态基本没有变化,单位长度上的电弧特性也基本相似,因此,尽管不同开距下电弧的长度不同,但相应的电弧特性却是相似的,即电弧时间常数和电弧散热功率的表达式是相似的。因此,本节建立的改进Mayr电弧模型既可以用于合闸过程的VFTO仿真,也可以用于分闸过程的VFTO仿真。
由于本文在进行MHD仿真时采用的是二维平面模型,该简化方式与一般的二维轴对称简化所反映的实际模型有所不同,因此有必要对二维平面简化与二维轴对称简化方式在本文案例中的差异进行分析。
本节采用二维平面模型和轴对称模型计算了 图2所示电弧的电子温度分布,计算结果如图9所示。为了更合理地对比模型的差异,将图2中电弧的分布简化为位于对称轴上的圆柱体,同时简化了触头结构,其余边界条件与图4模型一致。从图9中可以看出,两种简化模型下,电弧的电子温度变化规律仍然具有较高的相似性。温度分布的相似性即说明了两种简化模型计算出的电弧燃弧特性的相似性。进一步地,两种简化模型计算出的改进的电弧模型参数也较为相似,对比结果如图10和图11所示。
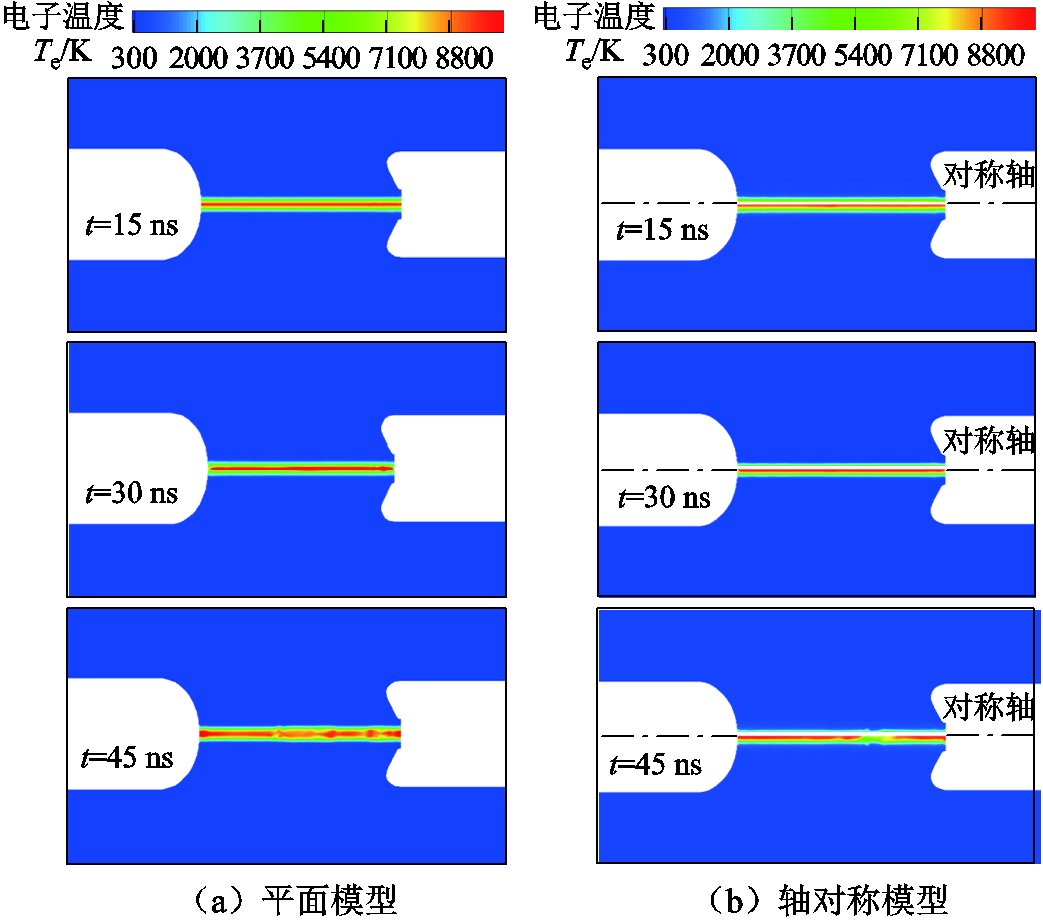
图9 电子温度分布对比
Fig.9 Comparison of electron temperature distribution
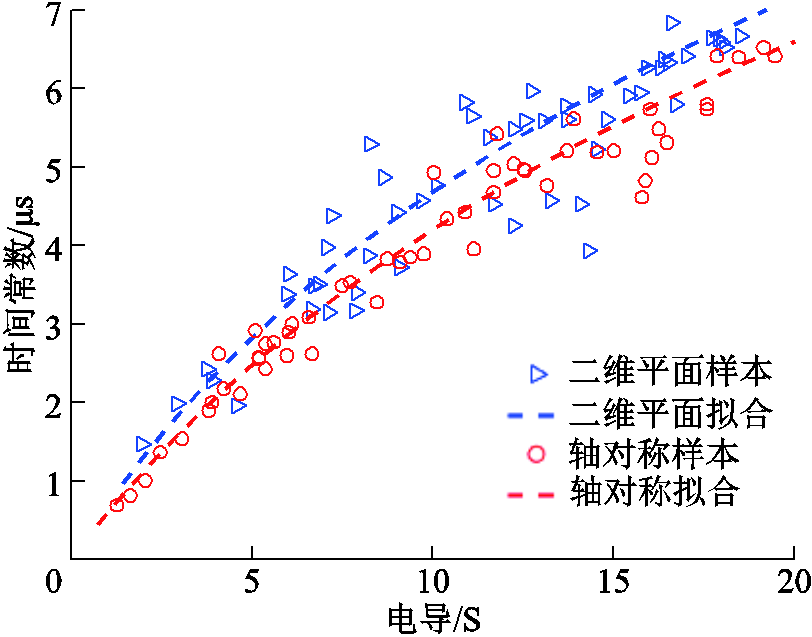
图10 电弧时间常数对比
Fig.10 Comparison of arc time constant
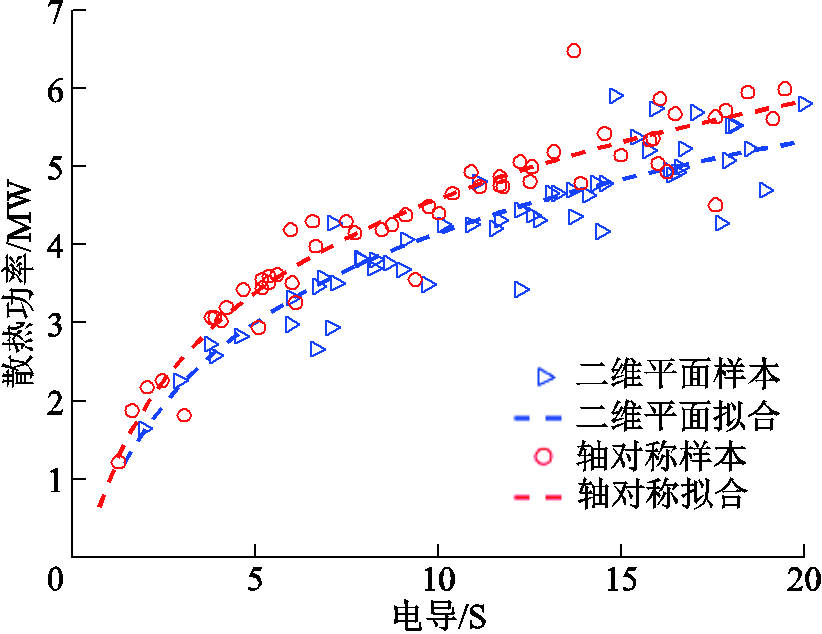
图11 电弧散热功率对比
Fig.11 Comparison of arc heat dissipation power
传统的电弧数学模型广泛应用于VFTO的仿真计算中,具有一定的准确性,通过其获得的VFTO仿真结果具有一定的参考价值。基于此,本文将改进Mayr电弧模型与传统电弧数学模型分别用于特高压GIS隔离开关切合空载短母线的VFTO仿真中,并将仿真结果与实测结果进行对比,主要分析幅值、频率和波前上升时间等波形特征的仿真值与实测值的相对误差,以此确定改进Mayr电弧模型的准确性。具体验证流程如图12所示。
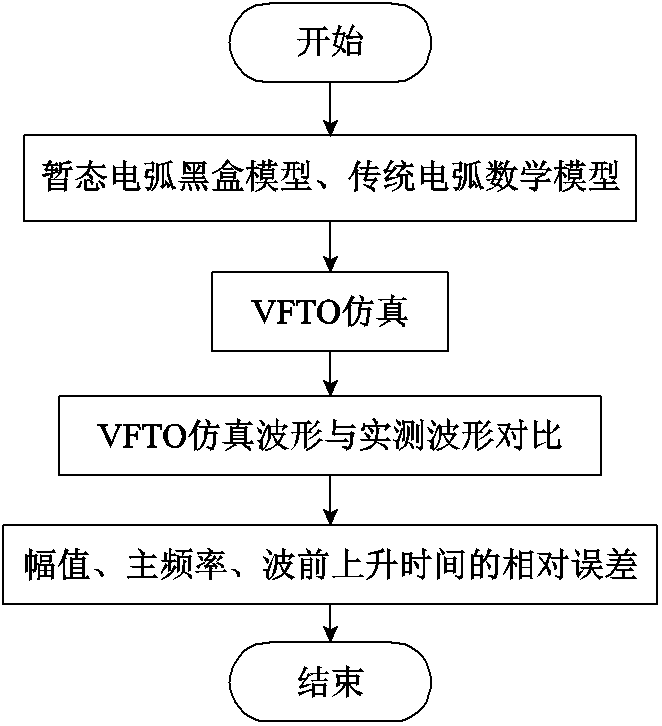
图12 改进Mayr电弧模型验证流程
Fig.12 Improved Mayr arc model validation process
特高压GIS隔离开关切合空载短母线的简化试验回路示意图如图13所示,主要包括变压器、套管、母线、支撑电容、隔离开关等。图中d1和d2分别为试验隔离开关电源侧和负载侧的母线长度[21]。
根据元件等效模型的一般选取规则和参数计算规则,可将上述设备等效为集中参数模型或分布参数模型,具体等效模型及其参数见表1。根据上述等效模型及参数搭建VFTO仿真模型如图14所示,仿真步长为1 ns
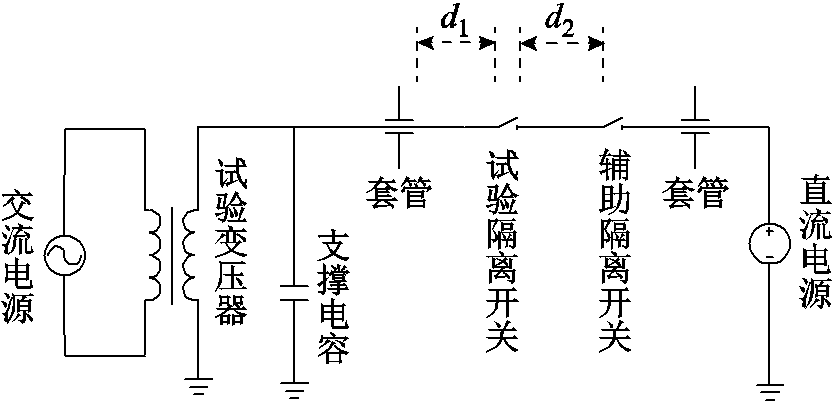
图13 简化试验回路示意图
Fig.13 Simplified test loop schematic
表1 元件等效模型及参数
Tab.1 Equivalent models and parameters of components

元件等效模型模型参数 试验变压器C=10 000 pFL=10 mH 接地开关C=240 pF 隔离开关(燃弧状态)RB由电弧模型确定C=300 pF 套管C=450 pF 母线Z=70 Ωv=277 m/μs
。
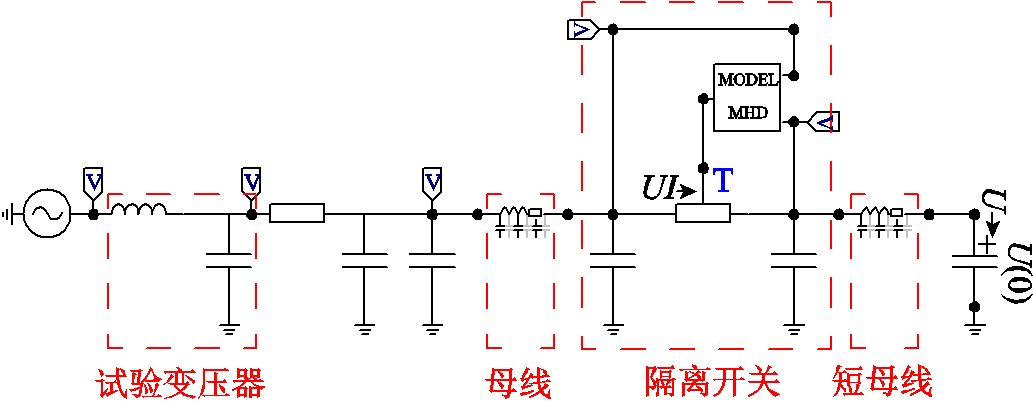
图14 VFTO仿真模型
Fig.14 VFTO simulation model
3.3.1 传统电弧数学模型
为不失一般性,本文选取三种VFTO仿真研究中常用的电弧数学模型。
1)指数函数电弧模型
电弧在燃烧过程中,其电阻值会经历先从无穷大降低至较小值,随后再增大至无穷大的过程。指数函数形式的电弧模型能够较好地反映该过程的电阻变化趋势,且形式简单,如式(21)所示,在VFTO仿真中运用广泛。
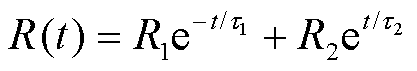 (21)
(21)
式中,R1为隔离开关动静触头间隙击穿之前的SF6绝缘介质等效电阻,取值1012 Ω;R2为电弧稳态燃烧时的等效电阻,取值0.5 Ω;τ1为预击穿阶段电弧时间常数,取1 ns;τ2为熄弧阶段电弧时间常数,取1 μs[22]。
2)分段电弧模型
根据电阻的变化情况,可以将电弧燃烧过程分为三段,其中预击穿阶段使用双曲函数电弧模型、稳态燃弧阶段使用定值电阻模型、熄弧阶段使用Mayr-Schwarz模型,如式(22)所示,其中的相关参数均取经验值。
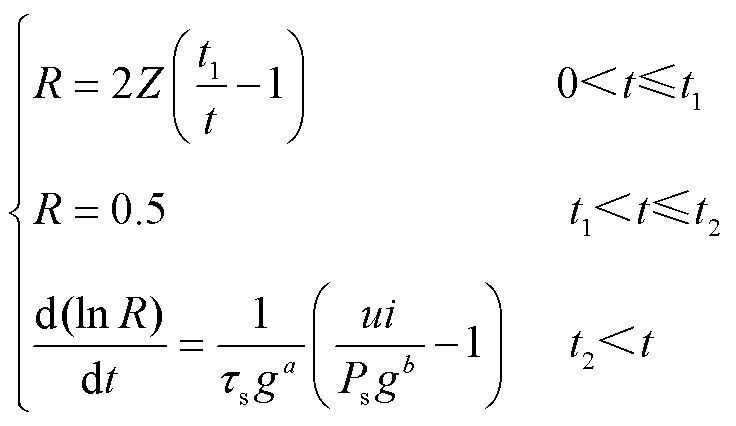 (22)
(22)
式中,Z为母线波阻抗,Ω;t1为击穿延时,取10 ns;t2为稳态燃弧时间,取40 ns;τs为电弧时间常数系数,取1.5 μs;a为电弧时间常数指数,取0.17;Ps为散热功率系数,取4×106 W;b为散热功率指数,取0.68[6]。
3)Mayr-Cassie组合模型
Mayr-Cassie组合模型在VFTO仿真中需与预击穿阶段的时变电阻模型相结合,表示为
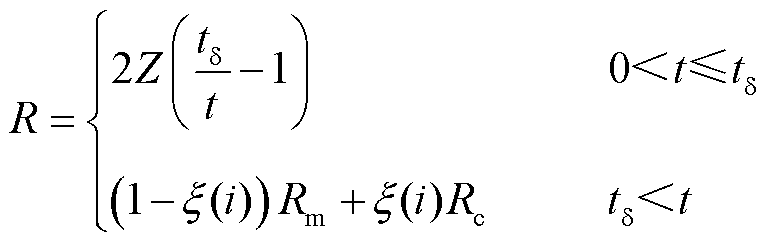 (23)
(23)
式中,tδ为击穿延时,取10 ns。Mayr-Cassie组合模型中的关键参数均为常量[5]。
3.3.2 合闸过程首次击穿VFTO仿真结果及分析
根据改进Mayr电弧模型、指数函数电弧模型、分段电弧模型和Mayr-Cassie组合模型计算合闸过程首次击穿VFTO仿真结果分别如图15a~图15d所示,其中,实测数据来源于文献[19, 21]。值得说明的是,由于试验测量动触头(直流侧)电压时采用的是分压电容,无法测量出其本身的直流分量,因此在击穿前电位显示为0,而随着合闸过程中的预击穿发生,该电位会逐渐趋近于静触头(交流电源侧)电位,在图15a~图15d中,实测波形中对应合闸击穿瞬间的静触头电位约为600 kV。为了避免这种静触头电位随机相位对本文方法准确性探究的干扰,本节在VFTO仿真中设置隔离开关动作瞬间静触头侧电位也为600 kV。
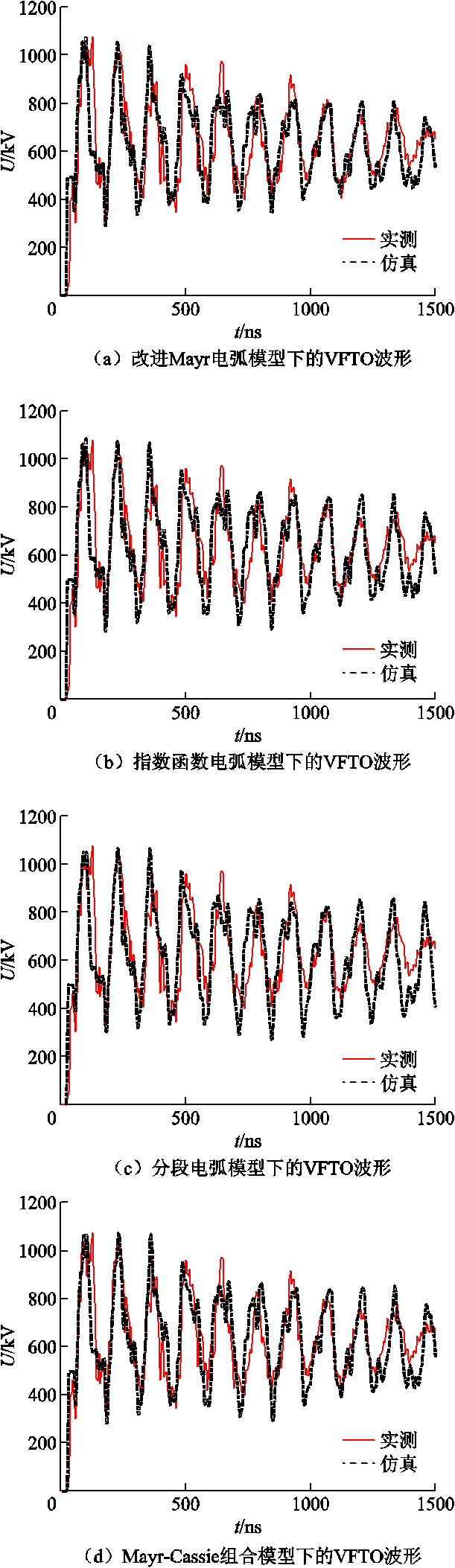
图15 合闸过程首次击穿VFTO仿真结果
Fig.15 Simulation results of the first breakdown VFTO during the closing process
由仿真波形可知,各电弧模型下的VFTO仿真结果与实测结果均有一定吻合度,但在具体波形特征上仍存在差异。为进一步确定改进Mayr电弧模型的准确性,计算每种模型下VFTO波形特征仿真值与实测值的相对误差,具体数值见表2。
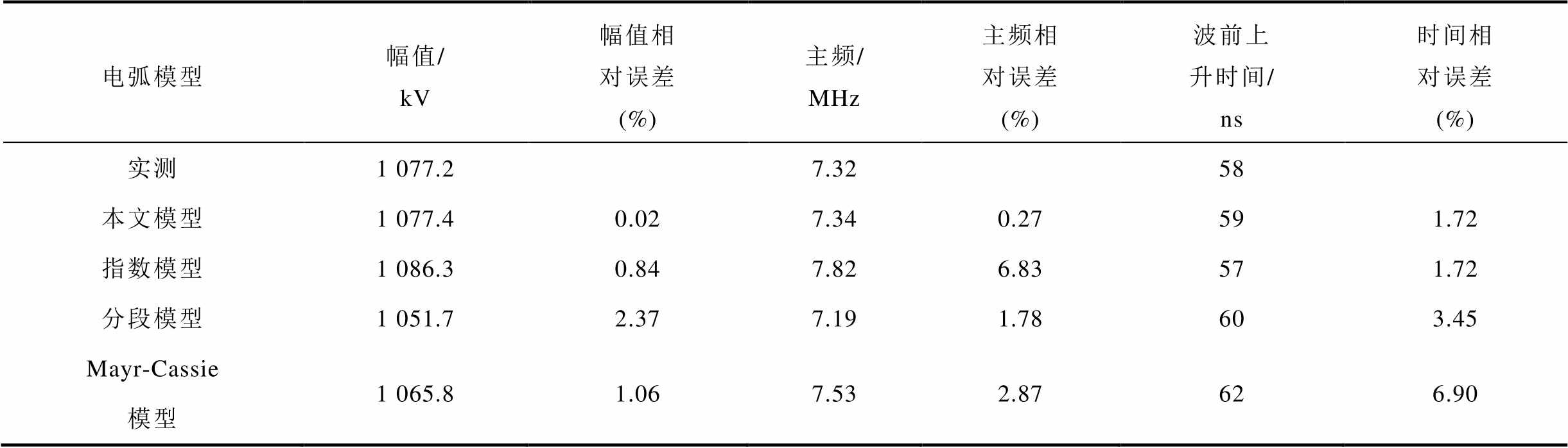
表2 合闸过程首次击穿VFTO仿真结果对比
Tab.2 Comparison of the simulation results of the first breakdown VFTO in the closing process
电弧模型幅值/ kV幅值相对误差 (%)主频/ MHz主频相对误差 (%)波前上升时间/ ns时间相对误差 (%) 实测1 077.27.3258 本文模型1 077.40.027.340.27591.72 指数模型1 086.30.847.826.83571.72 分段模型1 051.72.377.191.78603.45 Mayr-Cassie模型1 065.81.067.532.87626.90
由表2中数据可知,合闸过程首次击穿的VFTO仿真中,改进Mayr电弧模型下的VFTO仿真结果与实测结果最为接近,其幅值、主频率和波前上升时间的相对误差均为几种电弧模型中的最小值。初步证明,改进Mayr电弧模型对电弧电阻的描述更为准确,进而验证了通过双温度磁流体电弧仿真建立改进Mayr电弧模型这一方法的可行性。
3.3.3 分闸过程末次击穿VFTO仿真结果及分析
根据上述四种电弧模型计算得到该回路中分闸过程末次击穿的VFTO仿真结果分别如图16a~图16d所示。值得说明的是,在分闸过程的末次击穿中,动触头(直流侧)的电位一开始与静触头(交流电源侧)的电位(-600 kV)一致,随着电弧逐渐熄灭,动触头电位逐渐趋于0。动触头电位从-600 kV开始的原因是:静触头(交流电源侧)的相位在击穿瞬间是随机的;动触头电位逐渐趋于0的原因是:电弧熄灭后动触头残余电荷贡献的电位属于直流分量,无法被分压式电容测量。为了避免这种静触头电位随机相位对本文方法准确性探究的干扰,本节在VFTO仿真中设置隔离开关动作瞬间静触头侧电位也为-600 kV。
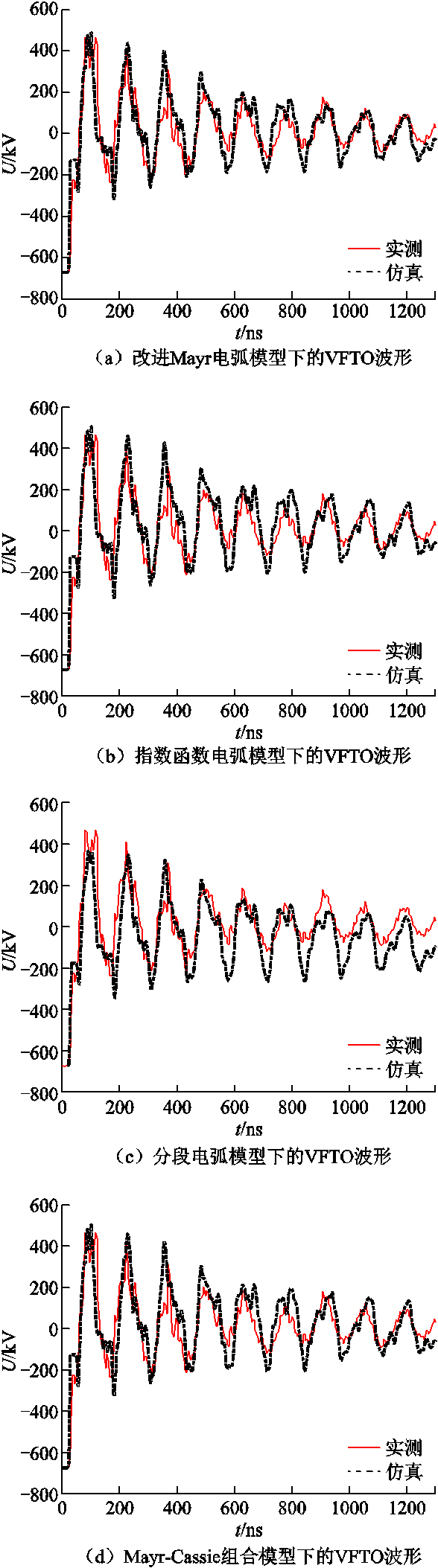
图16 分闸过程末次击穿VFTO仿真结果
Fig.16 Simulation results of the last breakdown VFTO in the opening process
与合闸过程首次击穿过程VFTO仿真结果类似,四种电弧模型下的仿真波形与实测波形均有较高的吻合度,具体波形特征对比见表3。由表3中数据可知,分闸过程末次击穿的VFTO仿真中,改进Mayr电弧模型下的VFTO仿真结果与实测结果最为接近。进一步验证了通过双温度磁流体电弧仿真建立改进Mayr电弧模型这一方法的可行性,以及通过该方法建立改进Mayr电弧模型的准确性。
表3 分闸过程末次击穿VFTO仿真结果对比
Tab.3 Comparison of the simulation results of the last breakdown VFTO in the opening process
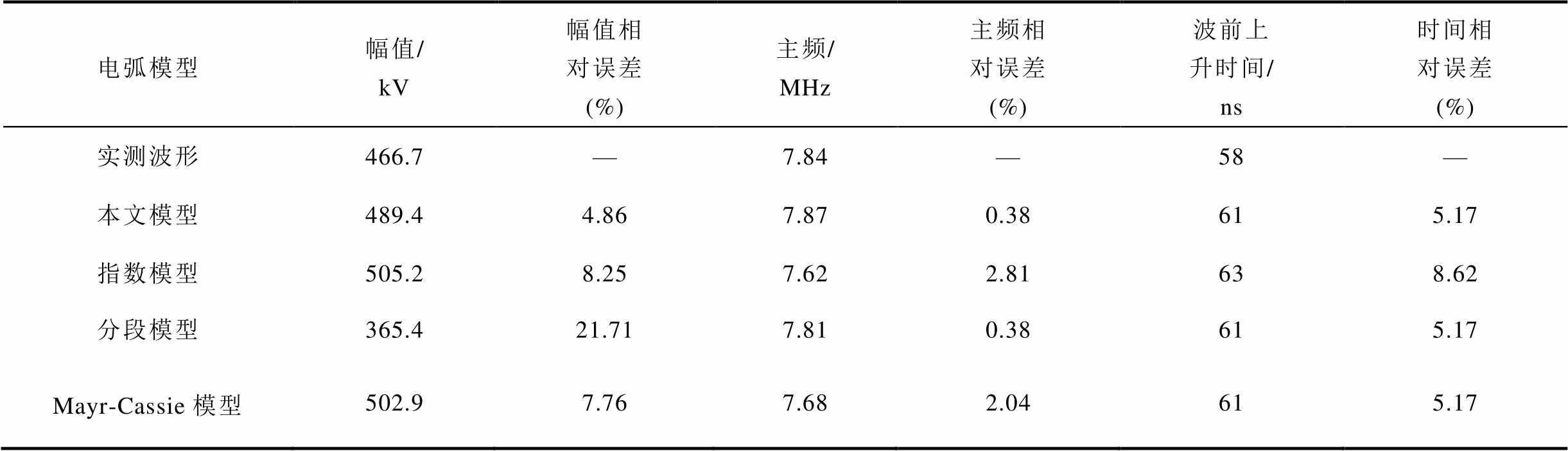
电弧模型幅值/ kV幅值相对误差 (%)主频/MHz主频相对误差 (%)波前上升时间/ ns时间相对误差 (%) 实测波形466.7—7.84—58— 本文模型489.44.867.870.38615.17 指数模型505.28.257.622.81638.62 分段模型365.421.717.810.38615.17 Mayr-Cassie模型502.97.767.682.04615.17
在VFTO仿真研究中,传统电弧数学模型中的时变电阻模型不够准确,经典电弧黑盒模型中的关键参数依赖大量实验数据或经验参数,极大地影响了VFTO的计算准确度。基于此,本文提出了一种基于双温度磁流体电弧仿真的改进Mayr电弧模型建立方法,以特高压GIS隔离开关切合空载短母线为例,建立双温度磁流体电弧模型,进行仿真分析并据此建立改进Mayr电弧模型,计算了多种电弧模型下的VFTO波形。通过对比实测波形和仿真波形,验证了该方法的有效性,得到以下结论:
1)特高压GIS隔离开关切合空载短母线产生的高频暂态电弧实际是SF6气体介质击穿及之后的燃弧过程,该过程频率高、持续时间短,电子与重粒子碰撞能量交换不足,可以采取双温度磁流体电弧仿真研究其电弧演变过程。
2)双温度磁流体电弧仿真能够计算每一个时间步长下的电弧时间常数、散热功率和电弧电导,通过仿真计算拟合得到的关键参数与电弧电导的函数关系在一定程度上代替了大量实验,为特高压领域的VFTO仿真研究提供了一种新途径。
3)基于双温度磁流体电弧仿真的改进Mayr电弧模型能够更准确地表征特高压GIS隔离开关切合空载短母线过程中的电弧暂态特性,该模型下VFTO仿真波形特征中的幅值、主频率和波前上升时间与实测值的相对误差,在合闸过程中分别为0.02%、0.27%、1.72%;在分闸过程中分别为4.86%、0.38%、5.17%。相比传统电弧模型,该模型提高了VFTO计算准确度。
参考文献
[1] 李红斌, 韩林汕, 叶国雄, 等. 基于频敏高-低阻层叠母线结构的特快速暂态过电压高频成分抑制方法[J]. 电工技术学报, 2022, 37(19): 4969-4977.
Li Hongbin, Han Linshan, Ye Guoxiong, et al. A suppressing method for very fast transient overvoltage based on a frequency-sensitive busbar with a laminated-material structure[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4969-4977.
[2] 张文斌, 胡洋. GIS中快速暂态过电压VFTO的抑制研究进展[J]. 高电压技术, 2023, 49(1): 418-431.
Zhang Wenbin, Hu Yang. Research progress in suppression of fast transient overvoltage VFTO in GIS[J]. High Voltage Engineering, 2023, 49(1): 418-431.
[3] 刘鹏, 郭伊宇, 吴泽华, 等. 特高压换流站大尺寸典型电极起晕特性的仿真与试验[J]. 电工技术学报, 2022, 37(13): 3431-3440.
Liu Peng, Guo Yiyu, Wu Zehua, et al. Simulation and experimental study on corona characteristics of large size typical electrodes used in UHV converter station[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3431-3440.
[4] 李振华, 廖星锐, 童悦, 等. 基于动态重燃弧模型的VFTO与VFTC仿真及特性分析[J]. 电力系统保护与控制, 2023, 51(3): 79-88.
Li Zhenhua, Liao Xingrui, Tong Yue, et al. Simulation and characteristic analysis of VFTO and VFTC based on a dynamic reignition arc model[J]. Power System Protection and Control, 2023, 51(3): 79-88.
[5] 杨明波, 龙毅, 樊三军, 等. 基于组合Mayr和Cassie电弧模型的弧光接地故障仿真及分析[J]. 电测与仪表, 2019, 56(10): 8-13.
Yang Mingbo, Long Yi, Fan Sanjun, et al. Simulation and analysis of arc grounding fault based on combined Mayr and Cassie arc models[J]. Electrical Measurement & Instrumentation, 2019, 56(10): 8-13.
[6] 林莘, 王娜, 徐建源. 动态电弧模型下特快速瞬态过电压特性的计算与分析[J]. 中国电机工程学报, 2012, 32(16): 157-164.
Lin Xin, Wang Na, Xu Jianyuan. Calculation and analysis of very fast transient over-voltage characteristic on the condition of dynamic arcing model[J]. Proceedings of the CSEE, 2012, 32(16): 157-164.
[7] 滕辉. 精确电弧模型下GIS中VFTO的计算与分析[D]. 南宁: 广西大学, 2013.
Teng Hui. Calculation and analysis of vesy fast transient overvoltage in GIS based on accurate arc model[D]. Nanning: Guangxi University, 2013.
[8] 刘艳丽, 郭凤仪, 李磊, 等. 一种串联型故障电弧数学模型[J]. 电工技术学报, 2019, 34(14): 2901-2912.
Liu Yanli, Guo Fengyi, Li Lei, et al. A kind of series fault arc mathematical model[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 2901-2912.
[9] 曹云东, 纪腾飞, 刘晓明, 等. 高压SF6断路器三维动态电弧仿真[J]. 沈阳工业大学学报, 2012, 34(2): 125-130.
Cao Yundong, Ji Tengfei, Liu Xiaoming, et al. Three-dimensional dynamic arc simulation for high-voltage SF6 circuit breaker[J]. Journal of Shenyang University of Technology, 2012, 34(2): 125-130.
[10] 李静, 刘凯, 曹云东, 等. 直流接触器分断过程中弧根演变及对重燃的影响分析[J]. 中国电机工程学报, 2019, 39(4): 1241-1251.
Li Jing, Liu Kai, Cao Yundong, et al. Arc root development and its influence on arc reigniting during the breaking process of the DC contactor[J]. Proceedings of the CSEE, 2019, 39(4): 1241-1251.
[11] 彭世东, 李静, 曹云东, 等. 耦合磁场直流空气断路器栅片特性对灭弧性能的影响研究[J]. 电工技术学报, 2022, 37(21): 5587-5597.
Peng Shidong, Li Jing, Cao Yundong, et al. Research on the effect of splitter plate material and structure on arc extinguishing performance with coupling magnetic field[J]. Transactions of China Electro-technical Society, 2022, 37(21): 5587-5597.
[12] 郝莎, 徐建源, 林莘. 隔离开关电弧流体数学模型研究与应用[J]. 电工技术学报, 2021, 36(13): 2710-2718.
Hao Sha, Xu Jianyuan, Lin Xin. Study on the application of fluid arc model in disconnector[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2710-2718.
[13] Yang Fan, Tang Zhaohui, Shen Yu, et al. Parameter determination method of cassie-mayr hybrid arc model based on magnetohydrodynamics plasma theory[J]. Frontiers in Energy Research, 2022, 10: 808289.
[14] 夏亚龙, 林莘, 徐建源, 等. 非平衡态SF6等离子体弛豫特性研究[J]. 电工技术学报, 2018, 33(5): 1125-1132.
Xia Yalong, Lin Xin, Xu Jianyuan, et al. Study on the relaxation characteristics of non-equilibrium SF6 plasma[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 1125-1132.
[15] 郝莎. 隔离开关多次重复击穿电弧及其高频暂态过电压特性研究[D]. 沈阳: 沈阳工业大学, 2020.
Hao Sha. Study on disconnector repeated arc and high frequency transient characteristics of the generated overvoltage[D]. Shenyang: Shenyang University of Technology, 2020.
[16] 荣命哲, 吴翊, 杨飞, 等. 开关电弧电流零区非平衡态等离子体仿真研究现状[J]. 电工技术学报, 2017, 32(2): 1-12, 23.
Rong Mingzhe, Wu Yi, Yang Fei, et al. Review on the simulation method of non-equilibrium arc plasma during current zero period in the circuit breaker[J]. Transactions of China Electrotechnical Society, 2017, 32(2): 1-12, 23.
[17] 林莘, 王亮, 徐建源, 等. 非平衡态双温度SF6等离子体电弧数学模型研究[J]. 高压电器, 2015, 51(3): 1-7, 14.
Lin Xin, Wang Liang, Xu Jianyuan, et al. Non-equilibrium dual temperature SF6 plasma arc mathematical model research[J]. High Voltage Apparatus, 2015, 51(3): 1-7, 14.
[18] 荣命哲, 仲林林, 王小华, 等. 平衡态与非平衡态电弧等离子体微观特性计算研究综述[J]. 电工技术学报, 2016, 31(19): 54-65.
Rong Mingzhe, Zhong Linlin, Wang Xiaohua, et al. Review of microscopic property calculation of equilibrium and non-equilibrium arc plasma[J]. Transactions of China Electrotechnical Society, 2016, 31(19): 54-65.
[19] 申萌, 丁登伟, 李强, 等. GIS隔离开关开合短母线型式试验方式1中VFTO测量系统构建及波形解析[J]. 高压电器, 2022, 58(7): 207-213.
Shen Meng, Ding Dengwei, Li Qiang, et al. Construction of VFTO measurement system and waveform analysis for switching test duty 1 of short busbar by GIS disconnector[J]. High Voltage Apparatus, 2022, 58(7): 207-213.
[20] 魏梅芳, 吴细秀, 田芸, 等. 1100kV GIS中特快速暂态电流VFTC的暂态特性研究[C]//中国电机工程学会高电压专业委员会2015年学术年会论文集, 西安, 中国, 2015: 1-9.
Wei Meifang, Wu Xixiu, Tian Yun, et al. Studying on the transient characteristics of VFTC in a 1100kV GIS[C]//2015 Annual Conference of High Voltage Professional Committee of CSEE, Xi’an, China, 2015: 1-9.
[21] 苏春强, 丁登伟, 李强, 等. GIS隔离开关方式1试验中断口对地击穿时光电暂态过程监测与分析[J]. 高压电器, 2022, 58(5): 56-62.
Su Chunqiang, Ding Dengwei, Li Qiang, et al. Monitoring and analysis of optical and electric transient process induced by breakdown-to-ground during type test duty 1 of GIS disconnector[J]. High Voltage Apparatus, 2022, 58(5): 56-62.
[22] 李博通, 刘涛, 杨昕陆, 等. 故障自清除型直流配电网新型双极短路故障元件识别方法[J]. 电工技术学报, 2022, 37(17): 4423-4434.
Li Botong, Liu Tao, Yang Xinlu, et al. New fault element identification method of bipolar short-circuit fault in DC distribution network with fault self-clearing[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4423-4434.
The Very Fast Transient Overvoltage Simulation Method Based on Two-Temperature MHD Arc Simulation to Improve Mayr Arc Model
Abstract Gas insulated switchgear (GIS) is the core equipment in ultra-high voltage (UHV) transmission engineering.During the process of closing short busbar in the UHV GIS disconnector, the very fast transient overvoltage (VFTO) will inevitably occur, causing insulation threats to the GIS and connected equipment, polluting the electromagnetic environment of secondary equipment, and seriously affecting the safe and stable operation of the power system. Since the accuracy of VFTO simulation is closely related to the equivalent arc model of the disconnertor, it is of great significance for VFTO simulation to establish an arc model that can more accurately characterize transient arc characteristics. In VFTO simulation studies, the traditional time-varying resistance arc model lacks accuracy and the classic arc black-box models rely too heavily on experimental data. To address the problems, an improved Mayr arc model based on two-temperature magnetohydrodynamics (MHD) simulation is established and applied to VFTO simulation to realize the simulation calculation of VFTO during the process of closing short busbar in the UHV GIS disconnector and verified in accuracy.
Firstly, the arc-burning phenomenon during the process of closing short busbar in the UHV GIS disconnector are analyzed, combined with plasma thermodynamic equilibrium conditions and the high frequency characteristics of VFTO. The analysis results show that the arc plasmas in the arc-burning process are in the thermodynamic nonequilibrium state, thus the electromagnetic induction phenomenon cannot be ignored. According to the analysis, the time-varying electromagnetic field control equation is obtained through the Maxwell equation system and Lorentz specification. Subsequently, a two-temperature MHD arc model under multiphysics coupling is established by combining the time-varying electromagnetic field control equation and the airflow field control equation. Through the two-temperature MHD simulation, the arc time constant and heat dissipation power are obtained, the function relationship between the above key parameters and arc conductance is established through parameter fitting, and then the improved Mayr arc model is obtained. Finally, the equivalent model of the electric equipment in the test circuit was selected, and a VFTO simulation model was established, according to the structure of the test circuit, and then the VFTO simulation during the process of closing short busbar in the UHV GIS disconnector is carried out by using the improved Mayr arc model and several traditional arc models as equivalent disconnector module. In addition, the results of VFTO amplitude, main frequency and wavefront rise time of the improved Mayr arc model and several traditional arc models are simulated and compared.
The compared results reveal that the VFTO simulation results obtained by the improved Mayr arc model reach great agreement with the measured results, and the VFTO simulation results under the improved Mayr arc model are more accurate than other traditional arc models. Furthermore, the above work shows that the improved Mayr arc model established by two-temperature MHD simulation can more accurately characterize the transient arc characteristics during the process of closing short busbar in the UHV GIS disconnector, improve the VFTO calculation accuracy compared with the traditional arc models, and reducing the dependence of VFTO simulation on experimental data.
keywords: Gas insulated switchgear, disconnector, very fast transient overvoltage, magnetohydrodynamics, arc black-box model
中图分类号:TM501+.2
DOI: 10.19595/j.cnki.1000-6753.tces.230934
国家电网有限公司科技项目资助(5500-202255135A-1-1-ZN)。
收稿日期 2023-06-23
改稿日期 2023-10-10
崔 建 男,1992年生,博士研究生,研究方向为电弧等离子体及其输运现象。
E-mail:cuijian_bachelor@stu.xjtu.edu.cn
张国钢 男,1976年生,教授,博士生导师,研究方向为智能电器理论与工程、储能与新能源电力系统以及电弧等离子体与电接触等。
E-mail:ggzhang@mail.xjtu.edu.cn(通信作者)
(编辑 李 冰)