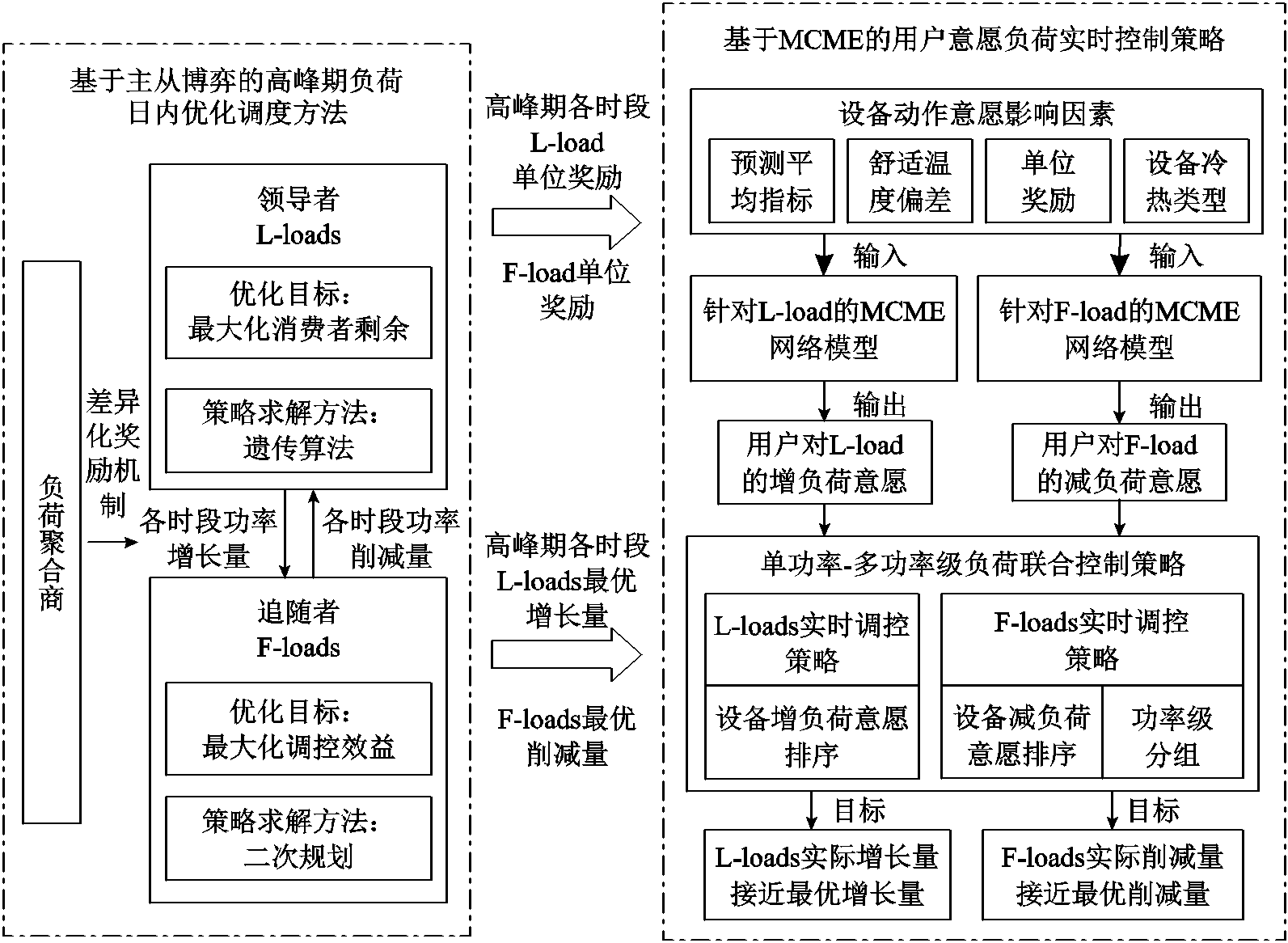
图1 奖励机制与用户意愿结合的高峰期负荷博弈调度框架
Fig.1 Peak load game scheduling framework that combines reward mechanism and user willingness
摘要 在高峰时段,居民冷/热设备占尖峰负荷的比重不断攀升,影响了低压配电网的安全稳定优化运行。为补充供给侧调节能力,提升调控灵活性,亟须引导用户侧可调资源参与电网供需互动。该文提出一种奖励机制与用户意愿相结合的高峰期负荷博弈调度策略。依据用户用能意愿对高峰时段用电负荷进行动态划分,制定基于负载率-奖励函数的差异化补贴机制。将高峰时段需要提升功率的负荷群视为领导者,将具有灵活削减能力的负荷群视为追随者,建立Stackelberg博弈模型,证明博弈均衡的唯一性。进而该文提出了Stackelberg博弈下的用电高峰期负荷日内优化调度方法,优化博弈双方在追求效益最大时的策略。该文构建多通路混合专家网络求解设备动作意愿,提出基于用户意愿的单功率-多功率级负荷联合控制策略,实现负荷的实时精细化调控。最后,算例表明所提策略能够在实现聚合商与用户侧双赢、遵从用户调控意愿的同时,有效地平抑用电高峰期的负荷波动,减小峰谷差。
关键词:主从博弈 高峰期负荷 用户意愿 负载率-奖励函数 混合专家网络
随着经济发展,制冷/制热负荷数量大幅增长,使得居民集中用电时段极易造成负荷尖峰,特别是负载率高的老旧小区,会影响配电网的安全稳定运行,并产生额外的发电成本。由于传统电力系统仅依靠供给侧资源的调节方式已无法满足现阶段的灵活调控需求[1],因此引导居民侧可调节资源规模化地参与削峰服务,已成为用电高峰期平抑负荷波动、减小负荷峰值的有效手段[2]。
目前利用用户侧灵活性资源进行电网削峰的方法主要包括基于电价和基于激励两大类。基于电价的削峰策略即运营商或负荷聚合商(Load Aggregator, LA)通过优化售电价格,引导用户调整负荷的用电时段与功率[3]。文献[4-5]提出最优分时电价策略减小峰谷差。文献[6]提出基于闭环反向主从博弈的定价方法。基于电价的优化方案易造成大量负荷运行在低电价时段,形成新的负荷高峰,且用户对于电价的敏感度具有显著差异,在执行时可控性较差,对用户的吸引力有限[7]。
基于激励的优化策略使用户更积极地参与响应,具有更好的稳定性和可操作性[8],因此被广泛应用。在补贴机制方面,各省发布的电力需求侧管理办法中,同一响应类型大多按照固定补贴单价,响应效果有限。文献[9-10]研究了补贴价格与用户响应量的关系。文献[11]将负荷削减量转换为用户积分以实现储蓄增值功能。文献[12]结合拉格朗日乘子法与分布式次梯度算法求解各时段激励。上述研究在设计补贴机制时,通常根据响应时段、响应程度给予负荷不同的补贴或积分,从而间接地平抑负荷曲线,其平抑效果可能与预期存在差距。
日内负荷用电优化方面,现有研究在进行日前/ 日内用户侧负荷优化时,普遍将用户侧视为一个主体,以用户侧收益最大/成本最小为目标函数,求解各时段最优用能策略[13-14]。主从博弈模型常用于解决多主体间的决策问题,已在日前/日内负荷优化调度领域被广泛应用。文献[15]将配备暖通空调的住户作为Stackelberg博弈模型的追随者,通过LA提供的奖金促使其调整负荷。文献[16]中热水器集群利用区域电网发布的基准激励价格计算其最优能量轨迹。文献[17]提出考虑用户消费偏好的分散式电采暖系统主从博弈优化策略。上述研究的主从博弈模型中,将运营商/LA作为领导者发布电价/激励,将负荷侧作为追随者优化响应量。
负荷调控方面,国内外学者做了大量研究。文献[18-19]考虑运行特性,对居民侧多元异构负荷协同调控。文献[20]对负荷进行基于辨识参数的马尔科夫链控制,在抑制反弹效应的同时削峰效果显著。文献[21]分析大规模空调物理过程与控制过程的耦合关系,实现负荷自治控制。部分文献在负荷调控时考虑了用户意愿,文献[22]考虑价格、温度的影响,计算空调集群的响应意愿。文献[23]利用温度归一化指标衡量冷/热模式下温控负荷的响应意愿。文献[24]除了分析温度舒适度与电价信息,还考虑了用户家庭收入、受教育程度和年龄分布等因素对用户响应意愿的影响。上述研究中用户意愿均由数学表达式计算得到,然而,多重影响因素与用户意愿的关系复杂且非线性,通过数学表达式难以表述,且公式的制定缺乏相关依据。相比之下,神经网络能够从大量数据中学习复杂规律,更适用于实际场景中考虑多影响因素的用户意愿建模。
针对上述问题,本文提出了一种奖励机制与用户意愿结合的高峰期负荷博弈调度策略,在保证用户与LA效益、遵从用户调控意愿的同时,取得理想的负荷波动平抑与削峰效果,为高峰期用户侧负荷优化调度问题提供新的解决思路。本文框架如图1所示,主要创新点如下:
1)依据用户对设备的调控意愿,动态划分高峰时段负荷,制定基于变压器负载率-奖励函数的差异化补贴机制,充分激发负荷响应积极性,使负载率稳定在合理区间。
2)引入主从博弈理论解决负荷群之间的用能决策问题,提出Stackelberg博弈下的高峰期负荷日内优化调度方法,在保证博弈双方效益的同时求解其最优用电策略,有效地平抑了高峰期的负荷波动。
3)构建多通路混合专家(Multi-Channel Mixture-of-Experts, MCME)网络模型,提出基于MCME的用户意愿负荷实时控制策略,实现单功率级与多功率级负荷的联合精细化调控。

图1 奖励机制与用户意愿结合的高峰期负荷博弈调度框架
Fig.1 Peak load game scheduling framework that combines reward mechanism and user willingness
因极端天气、恢复供电等原因,大规模制冷/制热设备短时间内同时开启易造成负荷尖峰,影响老旧小区的用电安全。由于变压器负载率能够直观地反映当前小区的用电水平,本文通过设计基于负载率-奖励函数的补贴机制,使变压器负载率稳定在合理区间,高效地平抑高峰期负荷波动。
依据用户对设备的调控意愿,将高峰时段每时刻的用电负荷划分为三类:①需要提升功率的制冷/制热负荷,记为L-load,将多个L-load构成的负荷群记为L-loads,在尚未满足基本用能需求时,用户对该类负荷有较强的开启意愿;②具有灵活削减能力的制冷/制热负荷,记为F-load,将多个F-load构成的负荷群记为F-loads;③基础负荷。需要注意的是,不同时刻的同一制冷/制热负荷可在L-load与 F-load间动态转换,某设备作为L-load提高功率并持续一段时间后,有条件再度作为F-load削减功率;反之亦然。
由于用户对L-loads与F-loads的用能需求各异,为了使基于负载率的补贴机制充分调动用户参与积极性,本文对L-loads与F-loads制定差异化奖励机制,设计分段奖惩方案,根据各时段的变压器负载率,给予L-load和F-load不同的单位奖励。对于L-loads,需利用与高峰电价叠加后的补贴电价引导负荷在负载率较低时用电;对于F-loads,需利用奖励激发用户对设备的减负荷意愿,避免高峰期负载率过高。变压器负载率为
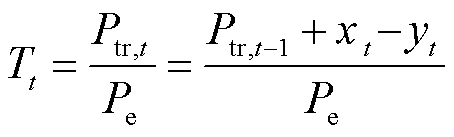 (1)
(1)
式中,Tt为t时段的变压器负载率;Ptr,t为t时段的负荷总功率,由于本文为分时段优化,t-1时段的负荷总功率Ptr,t-1在t时段视为定值;Ptr,0为用电高峰前一时段的负荷总功率;Pe为变压器额定功率;xt为t时段L-loads的功率增长量;yt为t时段F-loads的功率削减量。
对于L-load,高峰时段用户通常倾向于使用电能以满足自身需求。若将L-load的奖励函数设置为分段常数,则在某个负载率区间内,由于L-load获得的奖励/惩罚为定值,在较强的用电意愿下,变压器负载率易趋近区间上限,不利于削峰。若将L-load的奖励设置为单调递减的线性函数,每个负载率对应不同奖惩,使得L-load为追求更高的奖励而减少在高负载率时的用能,达到较好的削峰效果。
此外,GB/T 36040—2018[25]规定,居民住宅小区配电变压器的负载率不宜超过65%。为保证变压器利用率,实际负载率在40%~60%之间最为理想。因此,对于L-load,随着变压器负载率的增加,LA发放的单位奖励应减少,当负载率超过55%时,设备开启需支付罚金;当负载率超过65%时,惩罚力度进一步增大,从而降低用户在高负载率时对L-load的增负荷意愿。L-load的单位奖励Cl为
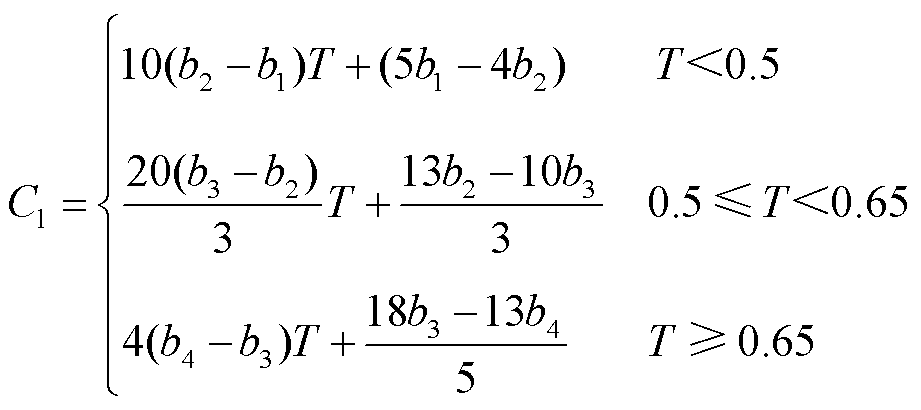 (2)
(2)
式中,b1~b4分别为负载率为0、50%、65%、90%时LA给予L-load的单位奖励。
对于F-load,在高峰时段,即使达到了基本的用能需求,用户的负荷削减意愿仍不足以F-loads提供充足的响应容量,LA需要以较高的补贴激励F-load下调功率从而快速降低峰值,随着负载率增加,对F-load的奖励应不断增大。考虑到F-loads响应积极性的提升效果以及后续章节Stackelberg均衡解唯一性的证明,本文将F-load的奖励设置为分段常数函数。F-load的单位奖励Cf为
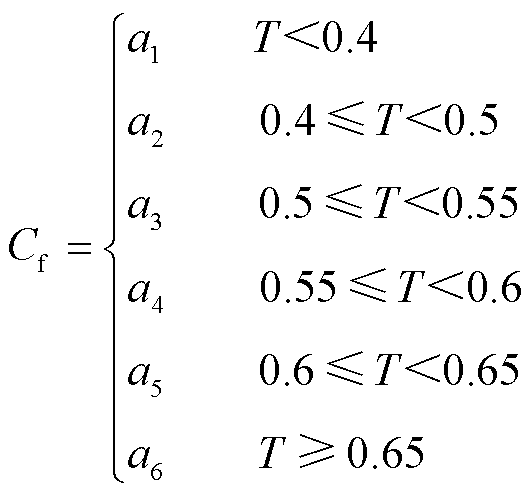 (3)
(3)
式中,a1~a6分别为负载率为0~40%,40%~50%、50%~55%、55%~60%、60%~65%、60%~100%时,LA给予F-load的单位奖励。当本文奖励机制实际应用时,需根据不同场景以及削峰需求,对参数a1~a6、b1~b4进行适当修正,其修正方法具有普适性。
L-load与F-load的负载率-奖励曲线如图2所示。
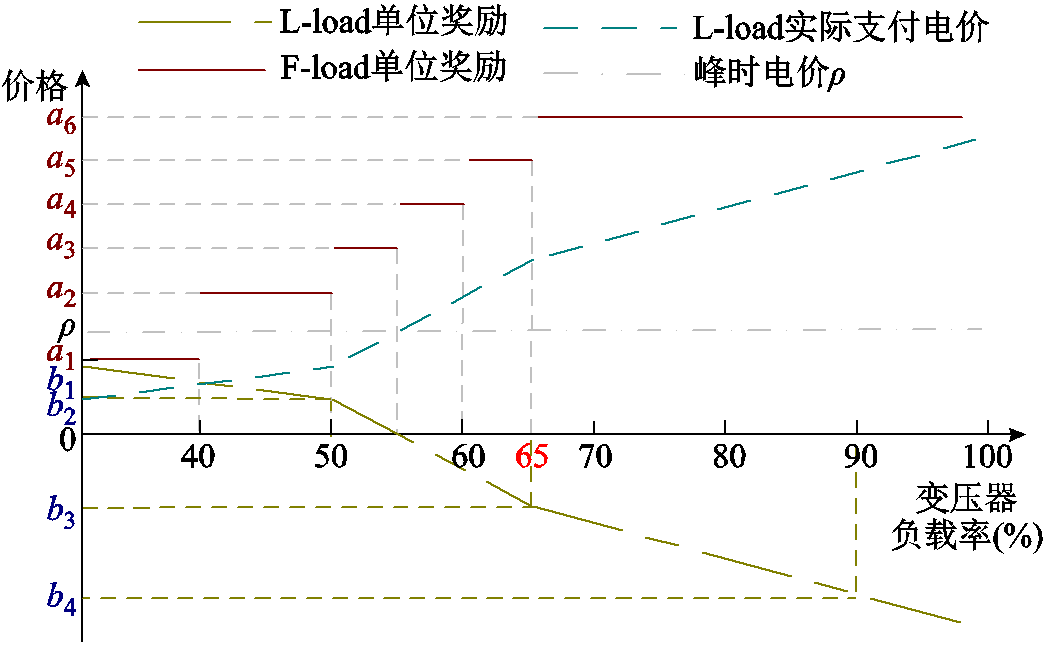
图2 负载率-奖励曲线
Fig.2 Load rate-reward curves
为了使配电网安全稳定运行,应确保高峰期各时段的负载率均处于理想区间。若仅在负荷预测曲线的变压器负载率超过理想区间后进行调控,达到相同削峰效果的情况下,LA需要给用户更多补贴。此外,负荷预测具有不确定性,真实场景下负载率超过60%的时刻可能提前,导致调控效果欠佳。本文方法中,LA预先以较低的补贴对一部分负荷调控,能够取得更好的削峰效果,使变压器负载率始终处于理想区间内,并提高LA的收益,在一定程度上规避了负荷预测误差对调控效果的影响。
需要强调的是,本文的奖励机制与高峰期负荷博弈调度策略由LA制定。LA在设计调度策略时,需考虑激励相容,让自身与用户侧实现双赢。本文策略下用户侧效益的增加,不是牺牲LA的收益导致的,而是因为削峰效果的提升使LA从电力市场获利增多,该收益由LA与用户侧按合同分摊,用户侧的效益也相应增多。
在用电高峰时段,基于LA发布的负载率-奖励机制,L-loads通过调整功率增长量使自身消费者剩余最大化,F-loads基于L-loads提供的功率增长信号,决策使其效益最大化的功率削减量,双方优化结果使变压器负载率改变,进一步作用于L-loads的决策,二者的用能策略具有先后顺序,此过程符合主从递阶结构的动态博弈情况[26]。因此,本文将L-loads和F-loads分别视为领导者和追随者,构建一主一从的Stackelberg博弈模型G为
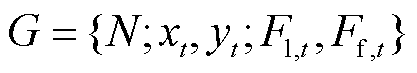 (4)
(4)
式(4)中所包含的博弈必备要素如下:
1)参与者:参与者包括L-loads与F-loads,可表示为N={L-loads, F-loads}。
2)策略:领导者L-loads的策略为t时段的功率增长量xt;追随者F-loads的策略为t时段的功率削减量yt。
3)收益(payoff):L-loads的优化目标为最大化消费者剩余[27],payoff函数为Fl,t(·);F-loads的优化目标为最大化调控效益,payoff函数为Ff,t(·),具体模型见下文。
4)均衡:当L-loads和F-loads均不能通过单方面改变自身策略以获得更大效益时,博弈达到均衡[28]。若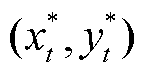 为均衡解,则需满足
为均衡解,则需满足
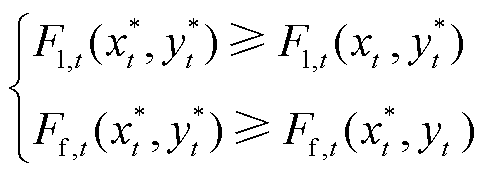 (5)
(5)
L-loads的优化目标为消费者剩余Fl,t最大,即L-loads的用电效用与L-loads的用电成本之差。可表示为
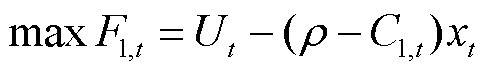 (6)
(6)
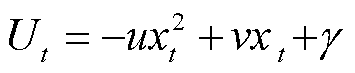 (7)
(7)
式中,Ut为第t时段L-loads的用电效用,反映L-loads消耗电能xt所获得的满意程度;(ρ-Cl,t) xt表示L-loads消耗电能xt所产生的用电成本,ρ为峰时电价;Cl,t为第t时段L-load获得的单位奖励;u、v、γ为用电效用系数,在日内优化时可根据当前情况调整。领导者策略需满足的约束条件为
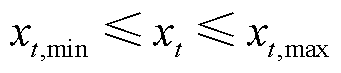 (8)
(8)
式中,xt,max和xt,min分别为L-loads的用能上、下限。
F-loads在L-loads用能决策的基础上,优化自身削减量,实现调控效益Ff,t最大化,可表示为
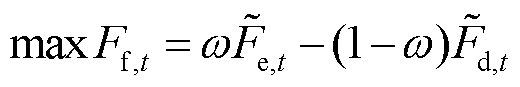 (9)
(9)
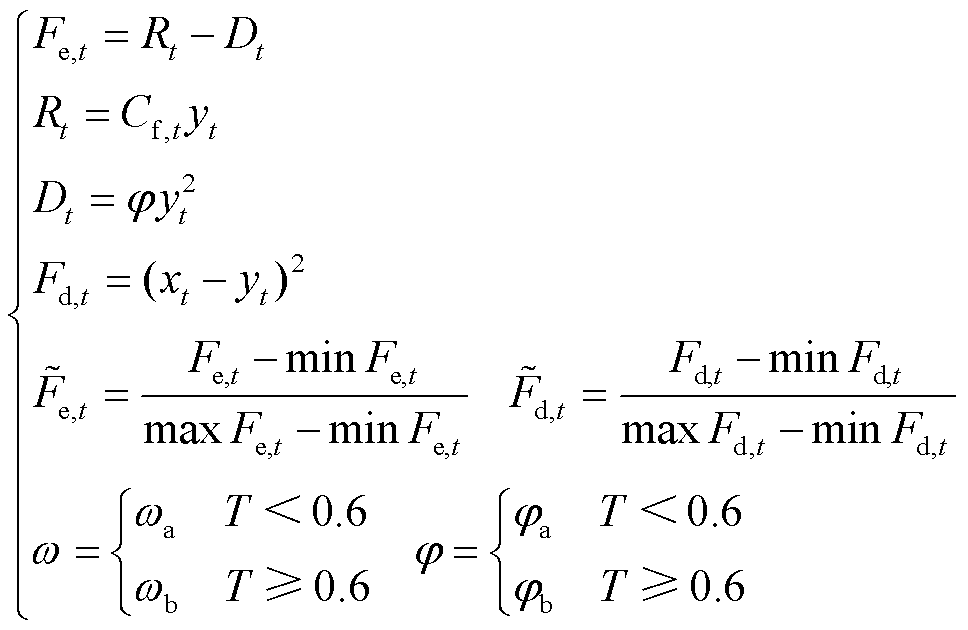 (10)
(10)
式中, 与
与 分别为Fe,t与Fd,t归一化后的值;Fe,t为需要优化的经济目标;Rt为t时段F-loads因削减功率yt而获得的奖励;Dt为F-loads因削减功率yt而造成的不便利损失;φ为阶梯型不便利损失系数,当变压器负载率较大时(T≥0.6)时,用户侧整体用电需求较强,F-loads因削减功率造成的不便利损失变大,因此φa<φb;Fd,t反映了t时段L-loads功率增长量与F-loads功率削减量的偏差,该值应尽可能小,以达到更好的平抑效果;ω为阶梯型权重,当变压器负载率处于理想区间(T<0.6)时,F-loads侧重于追求经济收益
分别为Fe,t与Fd,t归一化后的值;Fe,t为需要优化的经济目标;Rt为t时段F-loads因削减功率yt而获得的奖励;Dt为F-loads因削减功率yt而造成的不便利损失;φ为阶梯型不便利损失系数,当变压器负载率较大时(T≥0.6)时,用户侧整体用电需求较强,F-loads因削减功率造成的不便利损失变大,因此φa<φb;Fd,t反映了t时段L-loads功率增长量与F-loads功率削减量的偏差,该值应尽可能小,以达到更好的平抑效果;ω为阶梯型权重,当变压器负载率处于理想区间(T<0.6)时,F-loads侧重于追求经济收益 ,当T≥0.6时,削峰需求迫切,
,当T≥0.6时,削峰需求迫切, 在目标函数Ff,t中所占比重提升,因此ωa>ωb;ωa、ωb、φa、φb的取值视当前优化需求和用电情况而定;max Fe,t与min Fe,t分别为Fe,t的上、下限;max Fd,t与min Fd,t分别为Fd,t的上、下限。
在目标函数Ff,t中所占比重提升,因此ωa>ωb;ωa、ωb、φa、φb的取值视当前优化需求和用电情况而定;max Fe,t与min Fe,t分别为Fe,t的上、下限;max Fd,t与min Fd,t分别为Fd,t的上、下限。
追随者在某时段的削减量不得超过其调节能力,约束条件为
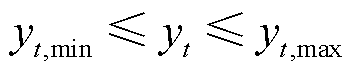 (11)
(11)
式中,yt,max和yt,min分别为F-loads的调节能力上、下限。
本节首先证明了Stackelberg均衡解的存在性及唯一性,并提出Stackelberg博弈下的负荷日内优化方法,用电高峰期前的若干小时,在保证博弈双方效益的同时求解其最优用电策略。
当模型满足以下条件时,则存在唯一的Stackelberg均衡[29]:①参与者的策略集是非空紧凸集[30];②领导者策略给定,追随者存在唯一最优策略;③追随者策略给定,领导者存在唯一最优策略。
存在唯一博弈均衡解的证明如下:
1)根据主从博弈模型可知,领导者策略集满足式(8),追随者策略集满足式(11),因此博弈参与者的策略集都是非空紧凸的。
对于条件②和条件③的证明,由于篇幅限制,本文仅讨论当T<0.4时的情况,其他情况证明过程与之类似。
2)求F-loads的payoff函数式(9)关于yt的一阶导数可得
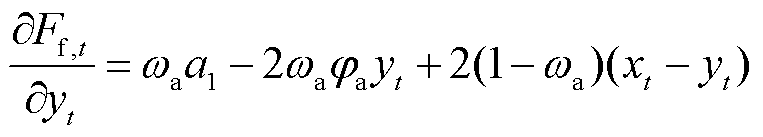 (12)
(12)
令一阶导数等于0可得
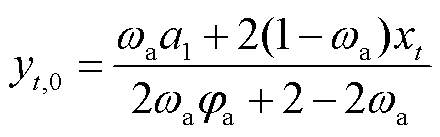 (13)
(13)
对式(9)求关于yt的二阶导数,得到
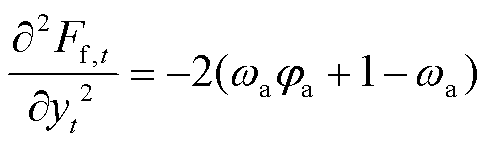 (14)
(14)
由于0≤ωa≤1、φa>0,故二阶导数恒小于0,yt,0为式(9)的极大值点,考虑策略区间约束, F-loads最优策略的取值为
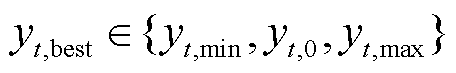 (15)
(15)
因此,当领导者的功率增长量给定,追随者的削减量存在唯一最优解。
3)对于条件③,本文只证明追随者最优策略取值为yt,0或yt,max的情况,当取yt,min时,同理可证领导者的最优策略存在且唯一,过程与之类似。
(1)将追随者的一个优化策略yt,0代入领导者的目标函数式(6),得到
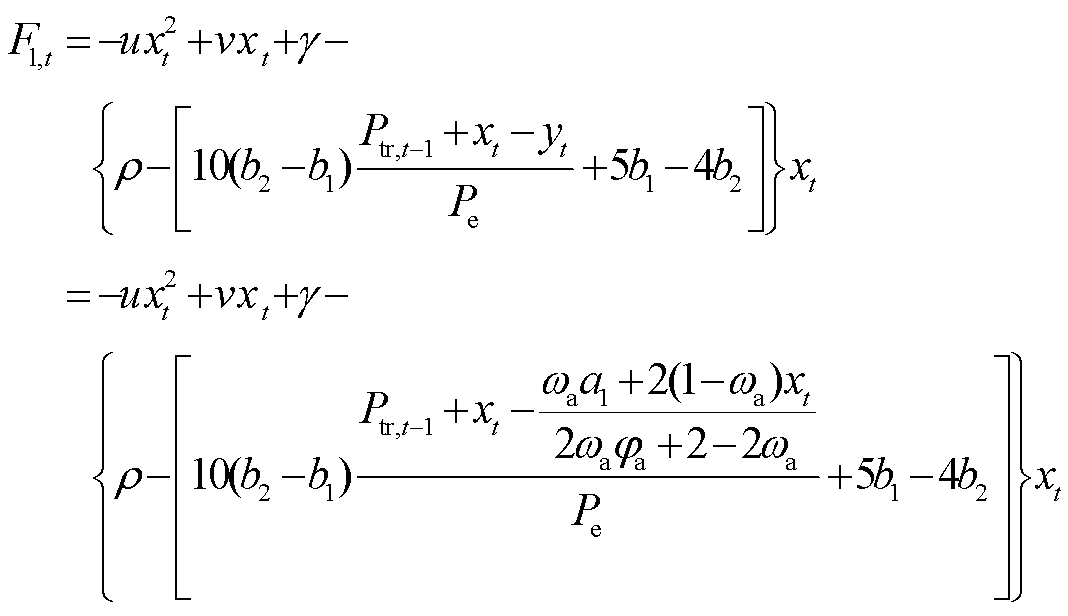 (16)
(16)
对式(16)求关于xt的一阶导数,得到
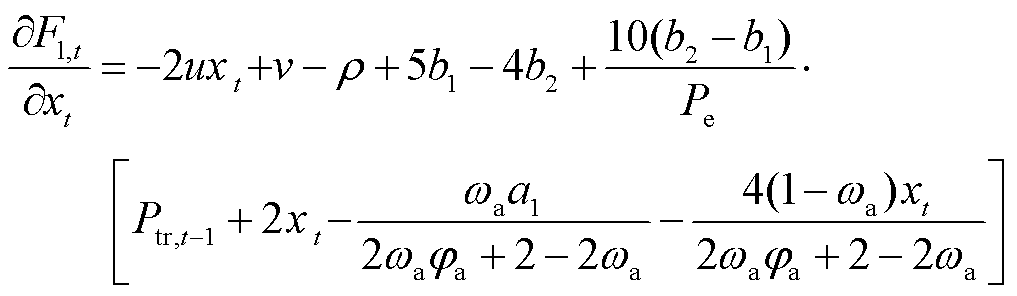 (17)
(17)
对式(16)求关于xt的二阶导数,得到
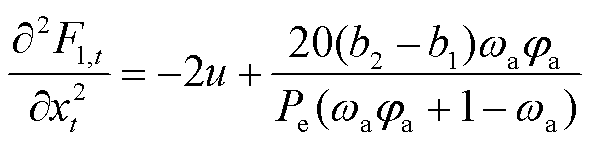 (18)
(18)
因为u>0、b2-b1<0、0≤1-ωa≤1、ωaφa>0,故二阶导数恒小于0,存在极大值点。
(2)将追随者的一个优化策略yt,max代入领导者的目标函数式(6),得到
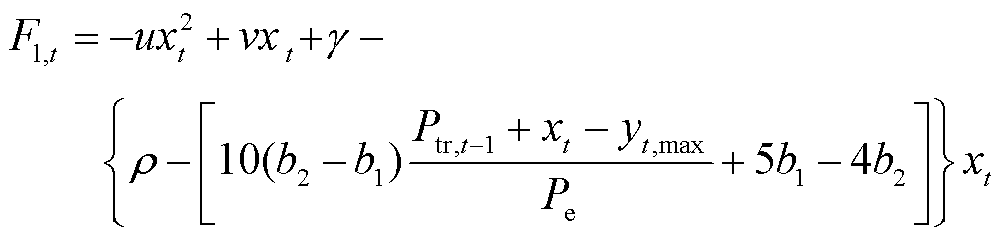 (19)
(19)
对式(19)求关于xt的一阶导数,得到
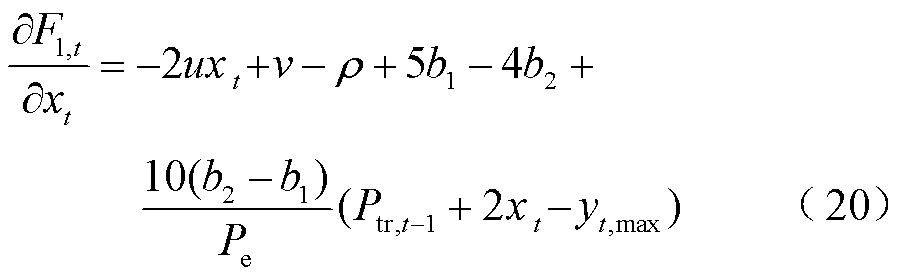
对式(19)求关于xt的二阶导数,得到
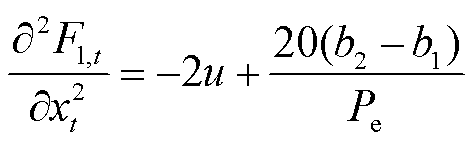 (21)
(21)
因为u>0、b2-b1<0,故二阶导数恒小于0,存在极大值点。
综上所述,模型Stackelberg均衡解存在且唯一。
领导者L-loads的决策是非线性优化问题,采用遗传算法可增强鲁棒性,提升寻优能力[31]。追随者F-loads的优化目标为二次函数,可利用求解速度和精度较高的CPLEX优化[32]。在博弈过程中将二次规划内嵌至遗传算法的迭代过程中,上层通过遗传算法求解L-loads的用能策略,下层用二次规划求解F-loads的削减量,算法流程如图3所示。
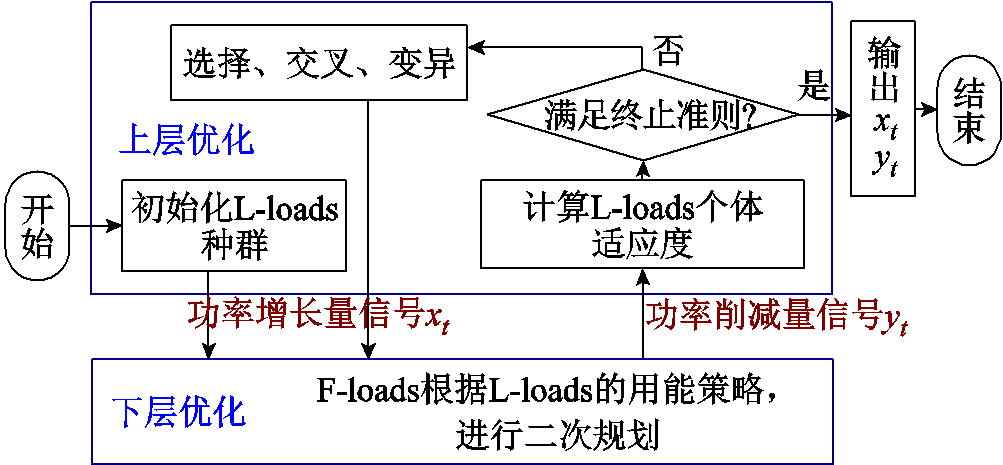
图3 博弈求解流程
Fig.3 Process of solving stackelberg game
本文分别针对L-load和F-load构建MCME网络模型,在负荷实时控制阶段,结合用户舒适度和当前奖励,利用MCME模型求解设备的动作意愿,并提出基于动作意愿的负荷实时控制策略。
4.1.1 特征变量选取
本文通过查阅文献、用户调查的方式确定模型的特征变量。现有文献的用户意愿影响因素主要包括温度舒适度指标、设备冷/热类型、电价/补贴[22-23]。因此,本文选取当前时段的预测平均指标(Predicted Mean Vote, PMV)、舒适温度偏差、LA发放的奖励、设备冷热类型作为MCME模型的特征向量。由于各因素对L-load与F-load的影响程度不同,需分别训练网络,从而精准表征用户对设备的动作意愿。
采用PMV和舒适温度偏差ΔTd量化用户的温度舒适程度。当PMV=0时,用户整体冷热舒适度最高;PMV越偏离0,人体冷热舒适度越低。PMV的简化计算公式[33]为
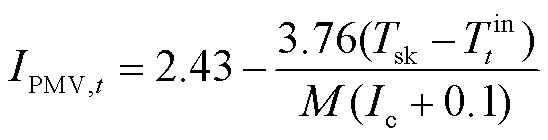 (22)
(22)
式中,IPMV,t为t时段用户的PMV值;Tsk为人体舒适时的皮肤平均温度;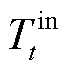 为t时段室温;M为人体代谢率;Ic为服装热阻。
为t时段室温;M为人体代谢率;Ic为服装热阻。
ΔTd为室温与用户设置温度Tset之差,即
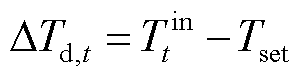 (23)
(23)
由式(22)和式(23)可知,采集用电高峰各时段的室内温度,即可求解PMV与ΔTd。
对于L-load,用户对制热设备的增负荷意愿与IPMV,t和ΔTd,t呈负相关,与日内优化阶段求解的奖励Cl,t呈正相关;用户对制冷设备的增负荷意愿与IPMV,t、ΔTd,t、Cl,t均呈正相关。L-load的特征变量为
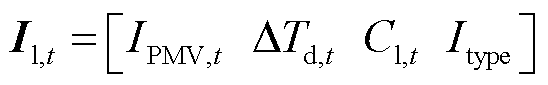 (24)
(24)
式中,Il,t为L-load网络模型的输入特征;Itype为设备冷热类型,1表示制冷设备,2表示制热设备。
对于F-load,用户对制热设备的减负荷意愿与IPMV,t、ΔTd,t、Cf,t均呈正相关;用户对制冷设备的减负荷意愿与IPMV,t和ΔTd,t呈负相关,与Cf,t呈正相关,F-load网络模型的输入特征变量为
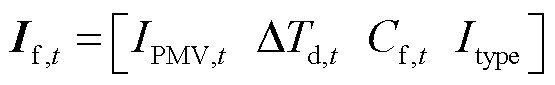 (25)
(25)
4.1.2 考虑多重影响因素的MCME模型
由4.1.1可知,制热和制冷设备的IPMV,t、ΔTd,t、获得奖励与设备动作意愿的对应关系不同,若构建统一的网络,则两类设备的特有规律无法被充分利用;若分别针对制热/制冷设备构建独立网络,则导致单个网络的可学习样本数量下降、网络总优化参数增加、不同类型设备间的共性规律无法被学习。因此本文采用独立-共享-独立的网络结构,引入混合专家(Mixture-of-Experts, MoE)系统[34],提出MCME网络。该网络既包含同类设备的独立结构与参数,又包含不同类型设备之间的共享参数与结构,通过学习冷/热模式下影响因子与设备动作意愿关联的特性规律与共性规律,有效提升模型性能。
MCME模型的网络结构如图4所示,根据设备类型,样本特征向量输入至相应的输入层和门控单元。随后通过混合专家层交换参数,发掘各类设备的共性规律;门控单元通过softmax层得到各专家的权重,与混合专家层的输出加权求和后,通过各类型设备的输出层即可求出[0,1]之间的设备动作意愿Irw。其中,输入层、混合专家层、门控单元和输出层均由具有激活函数的多层感知器组成。
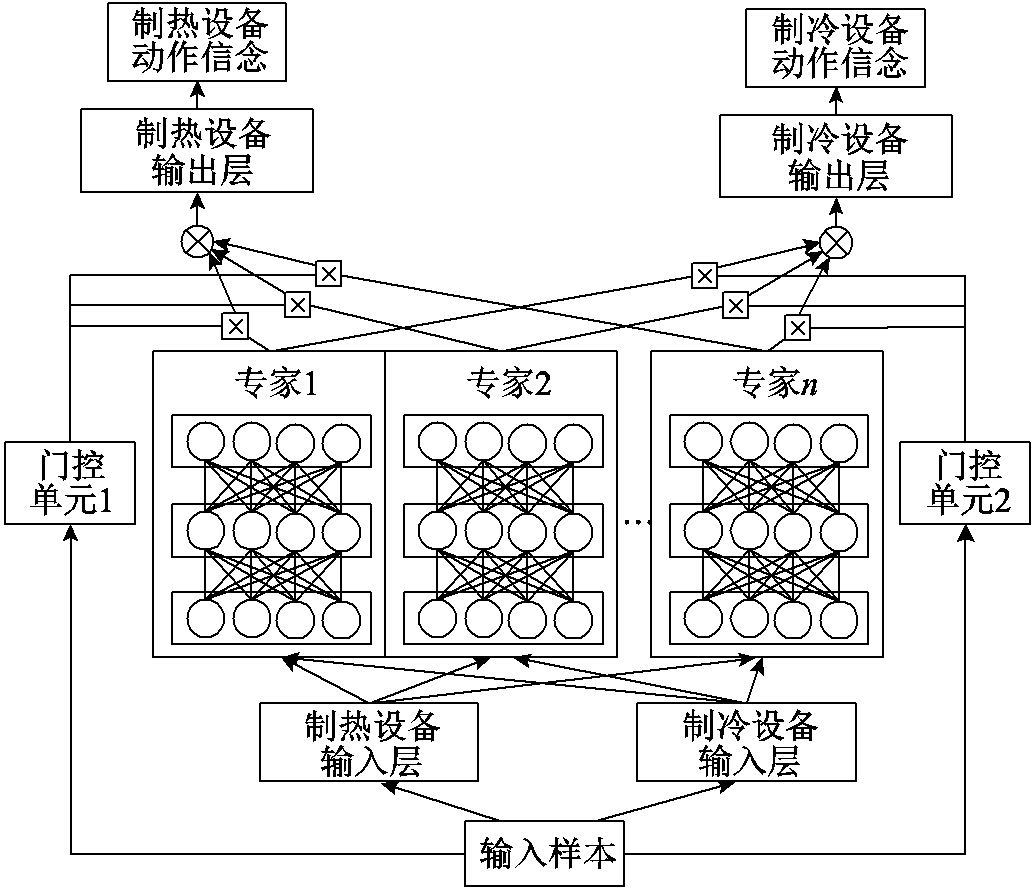
图4 MCME网络结构
Fig.4 MCME network structure
当与用户签订协议时,LA需要绑定所有经用户授权并通过响应能力认证的设备,对其进行接口、电工、环境参数测量等方面的改造,从而确保LA能够实时获取设备所处房间的温度信息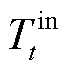 和设备运行状态数据,并实时控制设备。同时,LA还需记录用户的Tsk、M、Ic、Tset、绑定设备的ID、设备类型、功率挡位数量、不同功率挡位下设备额定功率等信息,用于通过本文控制策略确定设备的调控顺序。
和设备运行状态数据,并实时控制设备。同时,LA还需记录用户的Tsk、M、Ic、Tset、绑定设备的ID、设备类型、功率挡位数量、不同功率挡位下设备额定功率等信息,用于通过本文控制策略确定设备的调控顺序。
单功率级设备指除了起停外,无其他功率挡位的设备,例如定频空调;多功率级设备指含有多个功率挡位的设备,各功率挡位之间可相互切换,例如能够调节挡位的电暖器。单功率级与多功率级设备在居民用电负荷中占比较大,其调控需求与调节潜力不可忽视。因此,本文基于设备动作意愿,对L-loads与F-loads分别提出单功率-多功率级负荷联合控制策略,从而实现负荷的精细化调控。
对于L-loads,需完全遵循用户对设备的增负荷意愿,不论单功率级还是多功率级设备,增负荷意愿由大到小排序,依次动作,直至最优功率增长量与当前功率增长量之差小于阈值,即
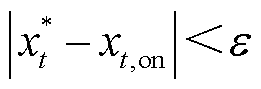 (26)
(26)
式中,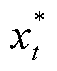 为第3节日内优化阶段求出的t时段L-loads的最优功率增长量;xt,on为t时段L-loads的实际功率增长量;ε为功率阈值。
为第3节日内优化阶段求出的t时段L-loads的最优功率增长量;xt,on为t时段L-loads的实际功率增长量;ε为功率阈值。
对于F-loads,在考虑用户调控意愿的同时,还需要在尽可能短的时间内达到削减需求,基于设备动作意愿的F-loads控制顺序如图5所示。
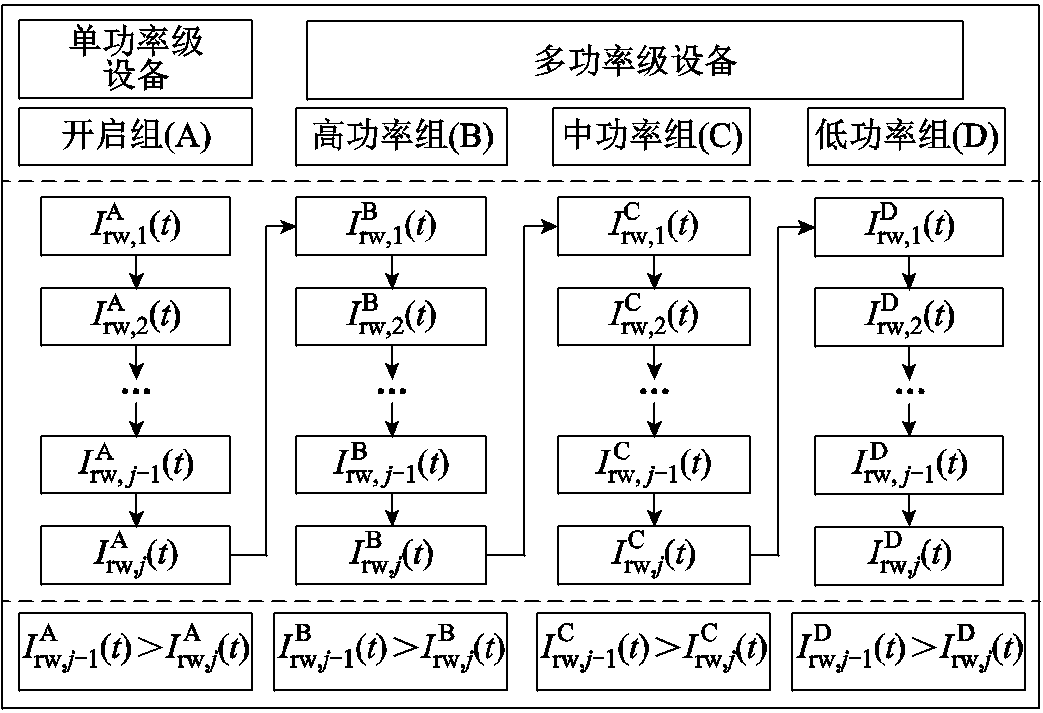
图5 基于设备动作意愿的F-loads控制顺序
Fig.5 F-loads control sequence based on the willingness of the device to act
由于单功率级设备能够快速响应,且调控功率普遍高于多功率级设备相邻挡位功率之差,因此优先控制当前时刻处于开启状态的单功率级设备(A组),接着从当前时刻处于高功率组(B组)的设备开始,以中功率组(C组)、低功率组(D组)的顺序逐级向下调控,每次调控时设备仅在相邻挡位间转换,以便在舒适度影响较小的同时降低能耗。组内各设备按动作意愿从大到小排序,动作意愿在0.5以上时具有调控资格。当F-loads的最优削减量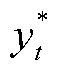 与当前功率组已削减总量之差小于单体设备的额定功率,或者当前功率组满足条件的设备完全遍历后削减总量仍小于
与当前功率组已削减总量之差小于单体设备的额定功率,或者当前功率组满足条件的设备完全遍历后削减总量仍小于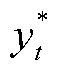 时,需终止当前功率组的设备调控,转至下一功率组,直至精准达到削减目标。
时,需终止当前功率组的设备调控,转至下一功率组,直至精准达到削减目标。
需要注意的是,若一个用户拥有多台制热/制冷设备,本文调控策略同样适用。这是因为一般情况下,用户的多台设备会安装在不同房间。由于空间面积、设施分布、建筑构造、隔热材料等因素,设备所在房间的室温通常存在差异,用户对不同设备的动作意愿也有所不同,因此依旧能够通过动作意愿的大小确定负荷的调控顺序。
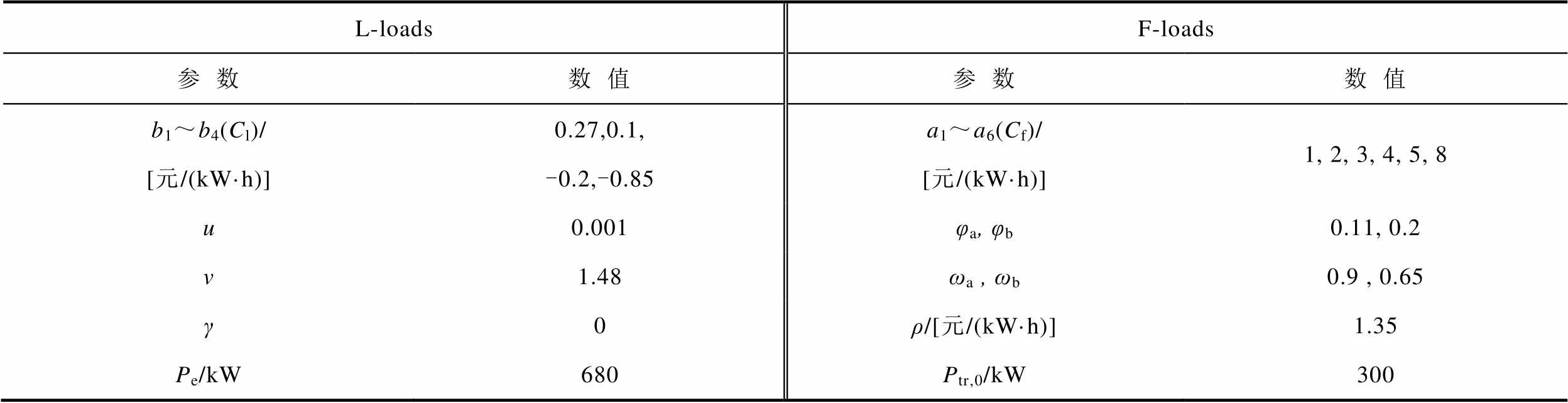
以冬季典型日11:00—12:00,北京某小型居民社区为例,对本文提出的奖励机制与用户意愿结合的高峰期负荷博弈调度策略进行仿真验证。该社区共有900户居民,每户均拥有1台制热设备,其中,额定功率为2 kW的单功率级设备共300个,1.2 kW的单功率级设备共400个,多功率级设备共200个,低功率组为0.5 kW、中功率组为1 kW、高功率组为1.5 kW。社区内采用800 kV·A的箱式变压器,功率因数为0.85。a1~a6、b1~b4通过参考各省份日前削峰响应补贴标准以及尖峰电价波动标准,结合实验效果进行制定。在基于主从博弈的日内优化阶段,L-loads和F-loads的参数设置见表1。
表1 博弈主体参数设置
Tab.1 Parameter settings of the game subject
L-loadsF-loads 参数数值参数数值 b1~b4(Cl)/ [元/(kW·h)]0.27,0.1,-0.2,-0.85a1~a6(Cf)/ [元/(kW·h)]1, 2, 3, 4, 5, 8 u0.001φa, φb0.11, 0.2 v1.48ωa , ωb0.9 , 0.65 γ0ρ/[元/(kW·h)]1.35 Pe/kW680Ptr,0/kW300
在实时控制阶段,需要提前训练针对L-load的MCME模型和针对F-load的MCME模型。本文以发放电子调查问卷的方式获取训练数据集,每个用户的调查问卷分为两部分内容:①用户对L-load(包括制热、制冷设备)的增负荷意愿;②用户对F-load(包括制热、制冷设备)的减负荷意愿。用户需根据问卷的提示与生成的信息,填写对设备的动作意愿,作为样本标签,与问卷程序生成的屋内温度、奖励/惩罚、设备冷热类型共同组成样本。调查共收集到2 700份有效问卷,分别获得5 400个增负荷意愿样本和5 400个减负荷意愿样本,将其按照6:2:2分为训练集、验证集和测试集。MCME模型的超参数设置见表2。功率阈值ε为0.4 kW。
表2 MCME模型超参数设置
Tab.2 MCME model hyperparameter settings

参数数值参数数值 学习率10-4batch_size1 损失函数MSE激活函数GELU dropout0.05epoch30 专家数量/个4中间层神经元数量/个50
为验证高峰期负荷日内博弈调度方法的优势,选取两种对比算法。①选取文献[9]中反映用户调峰贡献度的激励机制进行对比(下文中“策略2”),以验证本文差异化补贴机制在削峰效果与参与方收益方面的优越性。②选取以LA作为领导者优化各时段激励,用户侧作为追随者优化各时段调控量的主从博弈调度策略进行对比(下文中“策略3”),以验证本文负荷群之间主从博弈优化调度的优越性。
用电高峰期负荷日内优化结果如图6所示,可知本文策略能够大幅平抑负荷波动,减少高峰时段用电,策略2与策略3的削峰效果不及本文策略。这是因为本文策略通过差异化奖励机制引导L-loads转移到变压器负载率较低时用电,同时引导F-loads在负载率升高后依然有较高的削减意愿。因此,11:00—11:40的平均负载率较优化前曲线略有提高,11:45—12:00的平均负载率较优化前显著下降,各时段的变压器负载率均处于理想区间。
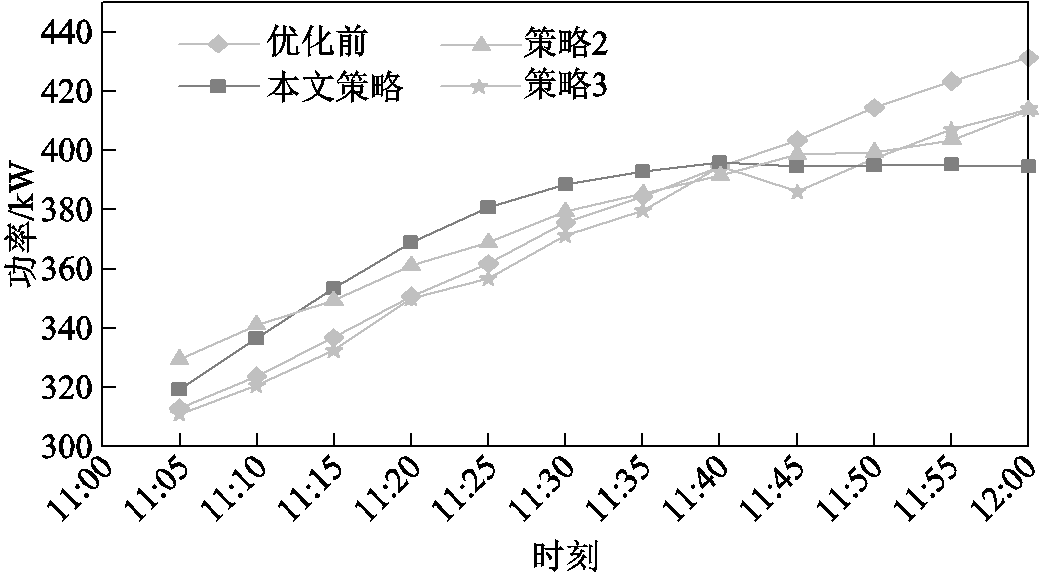
图6 用电高峰期负荷优化结果
Fig.6 Load optimization results during peak hours of power consumption
表3量化了本文策略与两种对比策略的负荷优化效果。可知本文策略的标准差、峰谷差、负荷峰值最小,上述指标较优化前冬季典型日预测曲线分别下降了33.13%、35.31%、8.25%,较策略2分别下降了5.10%、9.03%、4.24%,较策略3分别下降了23.21%、25.57%、4.38%,表明本文策略下负荷波动大幅降低,削峰效果显著。此外,本文策略下,用户侧效益与LA净收益均最高,用户侧效益较策略2与策略3分别提高了11.22%与18.26%,LA净收益较策略2与策略3分别提高了7.30%与9.68%,表明本文策略能够使LA与用户侧实现双赢。
表3 高峰期负荷优化效果对比
Tab.3 Comparison of load optimization effects during peak periods

策略标准差/kW峰谷差/kW负荷峰值/kW用户侧效益/元LA净收益/元 优化前39.54119.02431.65518.877— 本文策略26.4476.99396.03758.093410.62 策略227.8684.63413.57681.614382.70 策略334.43103.44414.17641.021374.37
图7为L-loads与F-loads的用能策略优化结果。L-loads的功率增长量逐渐减低,原因在于随着时段推移,用户侧负荷总功率增加,变压器负载率提高,L-loads获得的单位奖励Cl减小,如图8所示。这使得L-loads在制定策略时,不能一味地提高用能以获得更大的用电满意度,还要充分考虑用电成本,将部分用能转移至较低负载率时段,以降低成本,最终实现L-loads消费者剩余最大化。
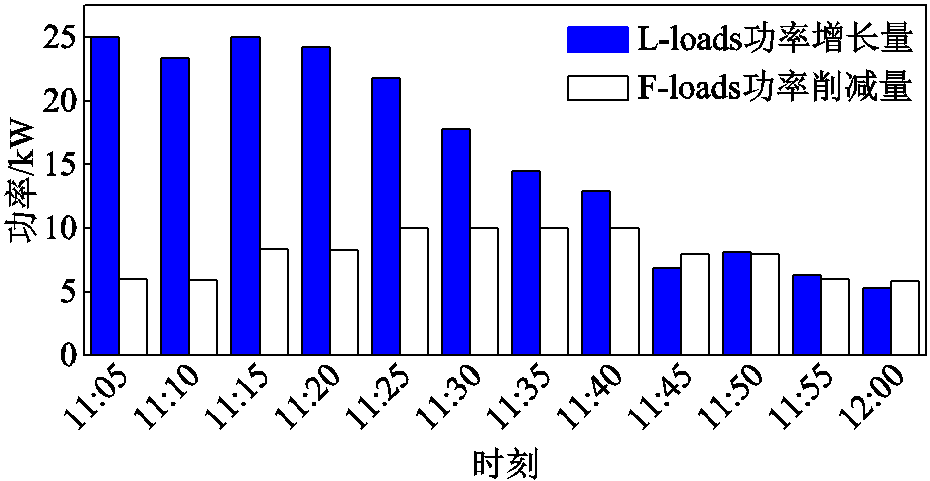
图7 博弈双方用能策略优化结果
Fig.7 Optimal results of energy consumption strategies for both parties in the game
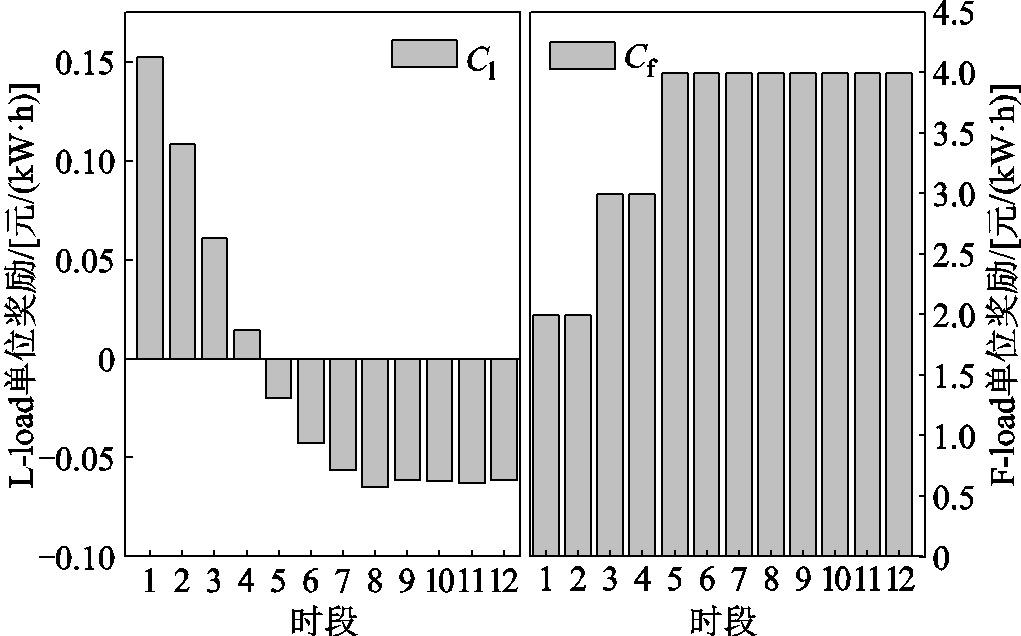
图8 博弈双方单位奖励优化结果
Fig.8 Optimization results of unit rewards for both sides of the game
由图7和图8可知,F-loads的功率削减量呈现先上升后下降的趋势,原因在于当变压器负载率小于60%时(11:40之前),F-loads侧重于追求经济收益,故11:05—11:40的削减量与单位奖励Cf呈正相关;当11:40之后,削峰需求迫切,F-loads的削减量需尽可能地接近L-loads对应时段的功率增长量,以达到更好的负荷平抑效果。
图9为博弈双方各时段的payoff,可知二者payoff的变化趋势分别与其用能策略的趋势接近。
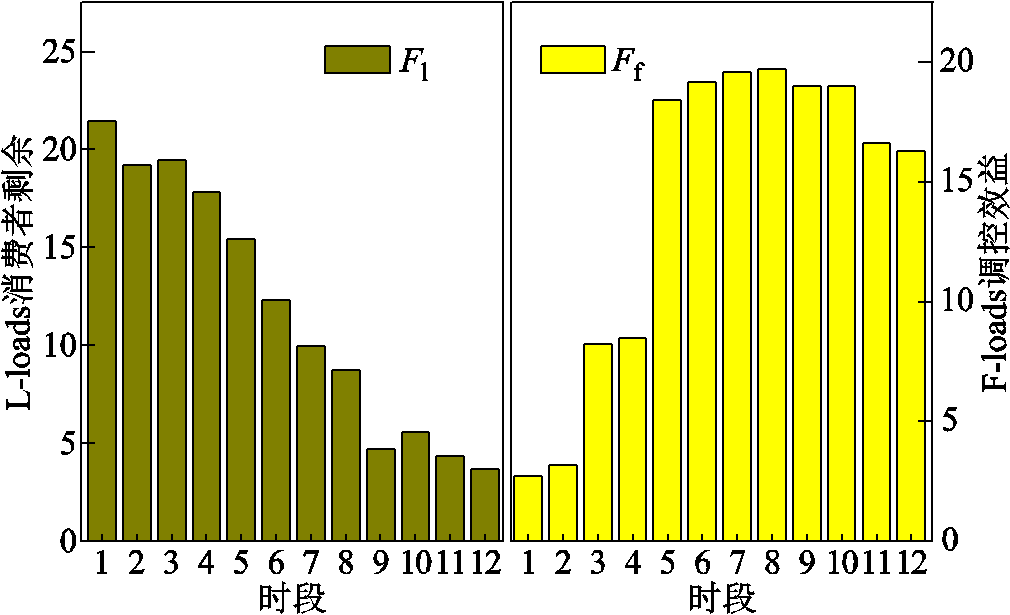
图9 博弈双方payoff优化结果
Fig.9 Payoff optimization results for both sides of game
5.3.1 基于MCME的设备动作意愿求解
为检验MCME模型求解设备动作意愿的效果,本文选取平均绝对误差(Mean Absolute Error, MAE)、均方误差(Mean Square Error, MSE)、方均根误差(Root Mean Square Error, RMSE)、R2为评价指标,对比提升回归树(Boosted Regression Tree, BRT)、精细高斯支持向量机(Support Vector Machines, SVM)、高斯过程回归(Gaussian Process Regression,GPR)、MCME共四种模型在求解用户对L-load的增负荷意愿和对F-load的减负荷意愿时的准确性。不同模型下设备动作意愿求解准确性对比见表4。
表4 不同模型下设备动作意愿求解准确性对比
Tab.4 Comparison of the accuracy of device action willingness solution under different models
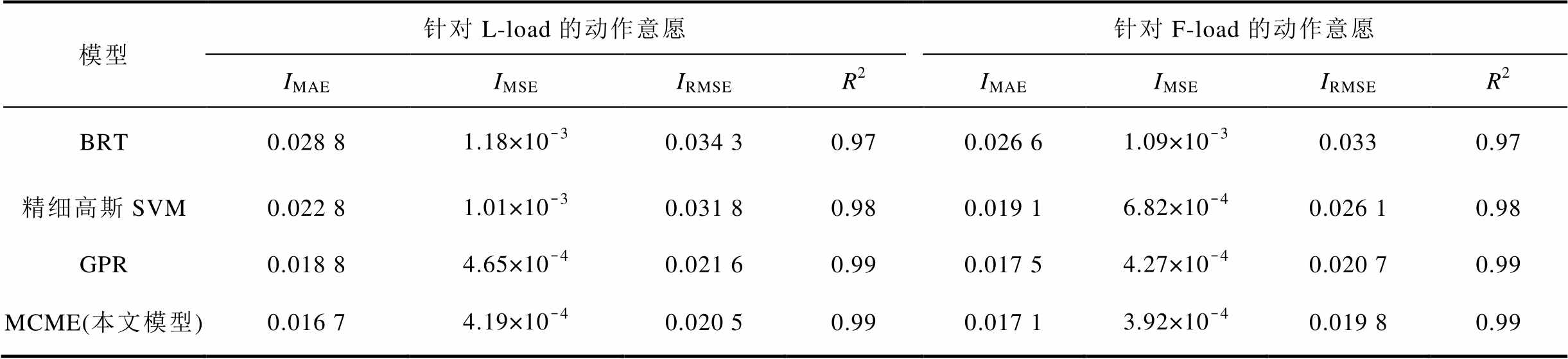
模型针对L-load的动作意愿针对F-load的动作意愿 IMAEIMSEIRMSER2IMAEIMSEIRMSER2 BRT0.028 81.18×10-30.034 30.970.026 61.09×10-30.0330.97 精细高斯SVM0.022 81.01×10-30.031 80.980.019 16.82×10-40.026 10.98 GPR0.018 84.65×10-40.021 60.990.017 54.27×10-40.020 70.99 MCME(本文模型)0.016 74.19×10-40.020 50.990.017 13.92×10-40.019 80.99
由表4可得,BRT模型的求解准确度最低,精细高斯SVM次之,GPR的效果仅次于MCME,MCME模型的IMAE、IMSE、IRMSE最小,R2达到0.99,说明该模型能够最为准确地求解出用户对L-load的增负荷意愿与对F-load的减负荷意愿,具有非常高的模型拟合度。
由于超参数设置对模型学习效果影响较大,因此,本文对MCME模型的超参数进行灵敏度分析,求解不同专家数量、中间层神经元个数下模型的求解精度。设备动作意愿的IMAE与中间层神经元个数及专家数量的关系如图10所示。
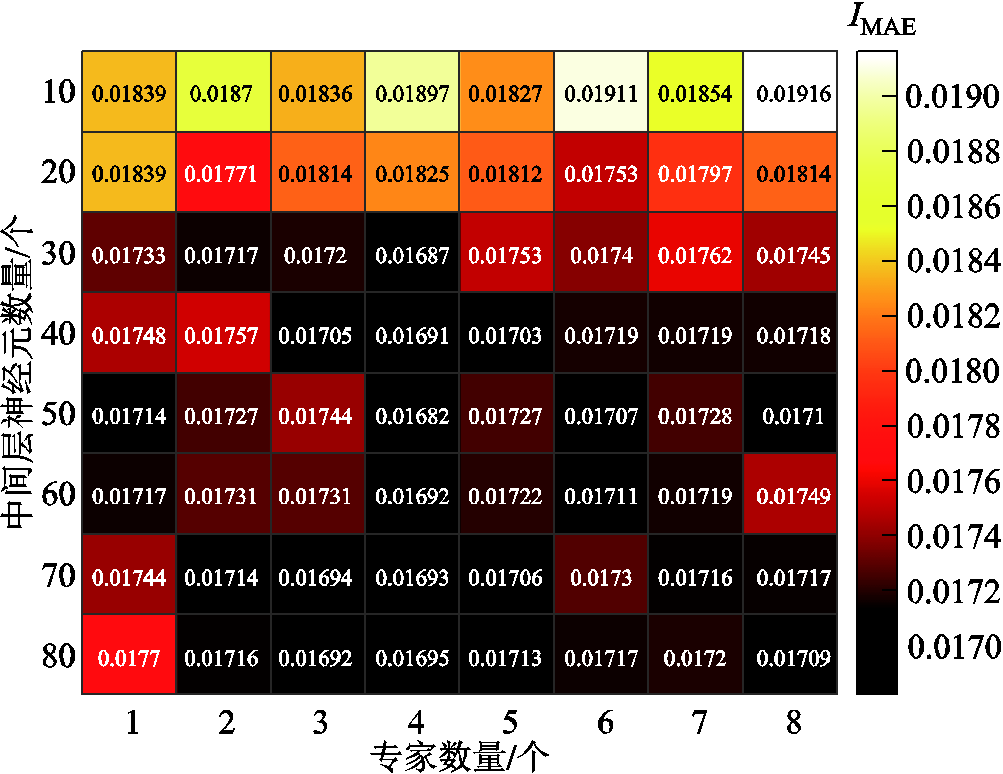
图10 模型超参数灵敏度分析
Fig.10 Model hyperparameter sensitivity analysis
由图10可知,随着中间层神经元个数的增多,IMAE基本呈现了先减小后趋于平稳的趋势,尤其当神经元个数由20变为30时,模型的IMAE呈现了较为明显的下降,这是由于较少的神经元个数使模型在训练集上无法充分学习设备动作意愿的求解规律,而当神经元个数超过一定数量后,其对模型效果的影响不再处于主导作用。随着专家数量的增多,IMAE基本呈现先减小后增大的趋势。当中间层神经元个数为50,专家个数为4时,IMAE最小,此时模型对设备动作意愿的求解精度最高,故将其确定为MCME模型的最终参数。
5.3.2 考虑用户意愿的单功率-多功率级负荷联合调控
在实时控制阶段,LA采集各时段每台设备所在房间室温、设置温度等信息,计算用户在该房间的IPMV和ΔTd,将其与单位奖励、设备冷热类型一同输入训练完成的MCME模型,得到用户对设备的动作意愿,以此为基础对L-load和F-load进行实时控制,选取动作设备,博弈双方各类设备的用能情况如图11所示。
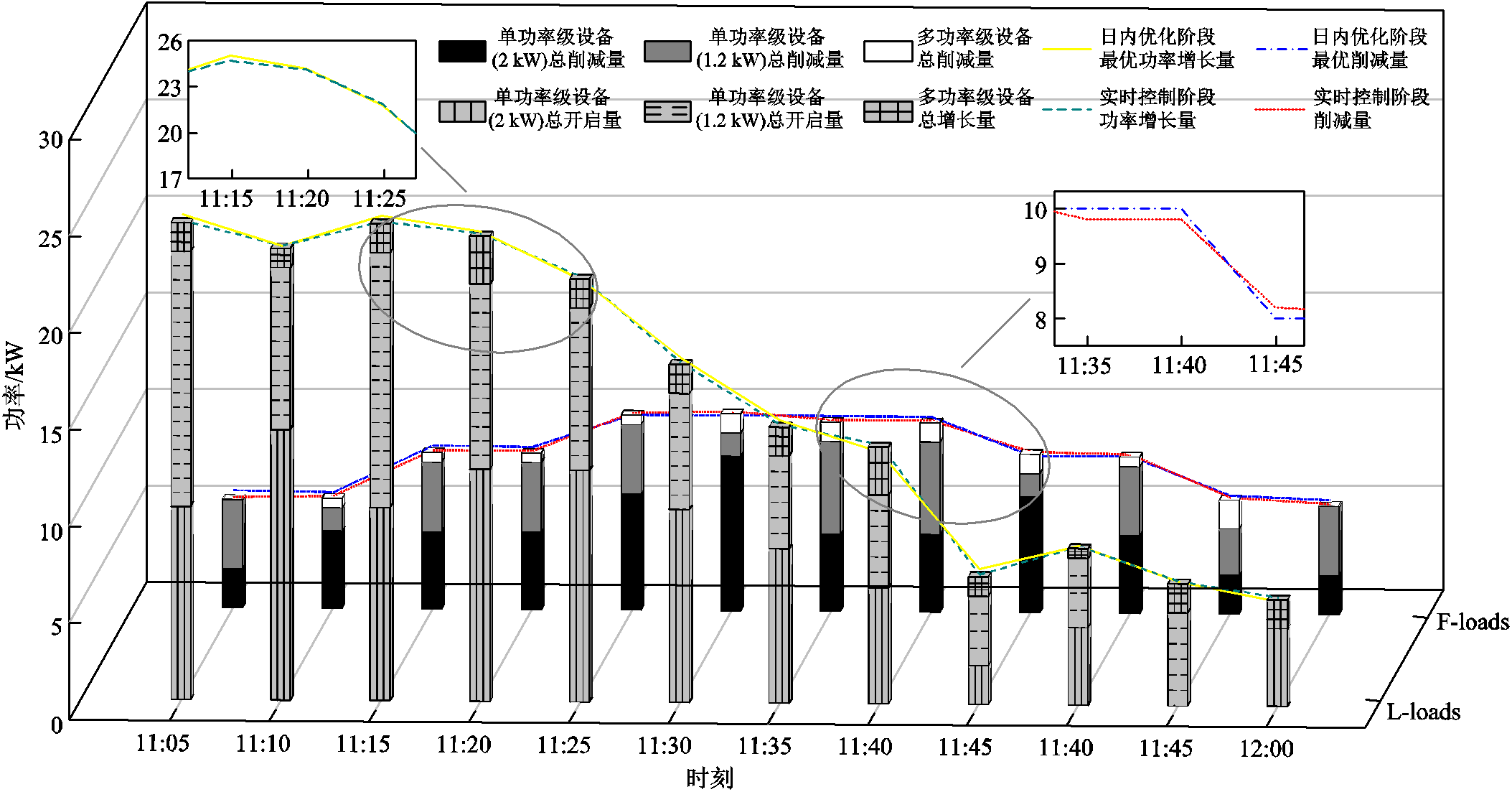
图11 博弈双方各类设备用能情况
Fig.11 Energy consumption of various types of equipment on both sides of the game
对于L-loads,不论是单功率级还是多功率级设备,LA按照用户对设备的增负荷意愿从大到小的顺序依次控制,直至达到日内优化阶段求解的最优功率增长量,L-loads在高峰时段各类设备的用能如图11中位于前方的状图所示,上方实线为日内优化方法求解的最优功率增长量,虚线为实时控制策略下的实际功率增长量,二者的最大偏差仅为0.396 kW,平均绝对偏差为0.183 kW。可知在基于动作意愿的负荷控制策略下,实际功率增长量与最优功率增长量非常接近。
对于F-loads,设备的动作顺序取决于减负荷意愿和设备功率类型,由于在单功率级设备数量充裕的情况下,单功率级负荷优先于多功率级设备参与调控,因此部分时段多功率级设备削减量远小于单功率级设备。F-loads在高峰时段各类设备的用能情况如图11中位于后方的柱状图所示,上方点画线为日内优化方法求解的最优功率削减量,点线为实时控制策略下的实际功率削减量,二者最大偏差为0.362 kW,平均绝对偏差为0.191 kW,可知本文提出的实时调控策略能够准确地匹配日内优化阶段求解的最优调控量。
图12对比了调控前后博弈双方负荷群的平均PMV变化,用以表征调控策略对L-loads与F-loads的冷热舒适度的影响。由图12可得,在利用本文策略调控后,L-loads与F-loads各时段的负荷平均PMV更接近0,表明负荷群的整体冷热舒适度提高。这是由于策略在对L-loads调控时,优先调高室温较低设备的功率,在对F-loads调控时,优先削减室温较高设备的功率,从而使负荷群的平均室温更接近舒适温度。
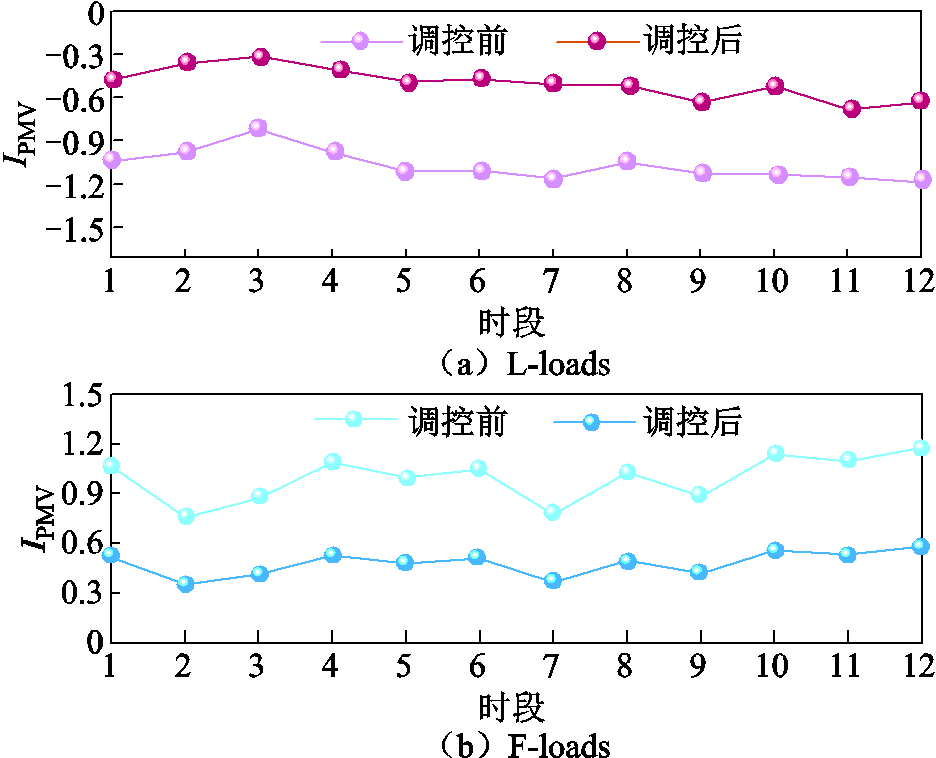
图12 调控前后博弈双方PMV变化对比
Fig.12 Comparison of PMV changes on both sides of the game before and after regulation
多功率级设备各功率组的运行数量如图13所示,可知随着调控的进行,处于高功率组的设备数量逐渐下降,处于中功率组与低功率组的设备数量逐步上升。这是由于处于关闭状态的多功率级设备的室温普遍较低,其用户对设备的增负荷意愿较为强烈,故更容易在L-loads增负荷调控时被选为动作设备,由关闭转变为低功率组;在F-loads减负荷调控时,策略优先将处于高功率组的设备下调至相邻挡位,使中功率组的设备数量增加。
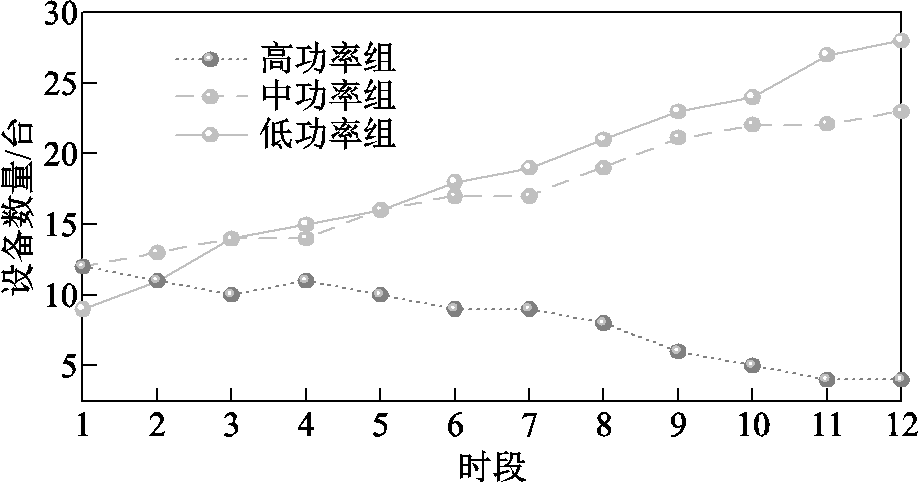
图13 多功率级设备各功率组运行数量
Fig.13 Number of each power group operation of multi-power stage equipment
本文提出的奖励机制与用户意愿结合的高峰期负荷博弈调度策略,有效地减轻了高峰时段电网的供电压力,实现LA与用户侧的双赢,主要结论如下:
1)理论分析证明了本文主从博弈模型存在唯一的均衡策略。仿真结果表明,基于奖励机制的负荷日内优化方法在保证博弈主体效益的同时,取得了显著的削峰与负荷波动平抑效果。
2)仿真结果表明,本文提出的MCME模型能够有效学习数据中的共性规律和特性规律,并准确地求解用户对设备的动作意愿。
3)在实时控制阶段,本文提出的考虑用户意愿的单功率-多功率级负荷联合控制策略,在遵从用户对设备调控意愿的同时,实现了负荷的精细化调控。
下一阶段将深入分析用户意愿的多重影响因素,对其进行全面考量,进一步提升MCME模型的求解精度与效率。
参考文献
[1] 王彩霞, 时智勇, 梁志峰, 等. 新能源为主体电力系统的需求侧资源利用关键技术及展望[J]. 电力系统自动化, 2021, 45(16): 37-48.
Wang Caixia, Shi Zhiyong, Liang Zhifeng, et al. Key technologies and prospects of demand-side resource utilization for power systems dominated by renewable energy[J]. Automation of Electric Power Systems, 2021, 45(16): 37-48.
[2] 吴珊, 边晓燕, 张菁娴, 等. 面向新型电力系统灵活性提升的国内外辅助服务市场研究综述[J]. 电工技术学报, 2023, 38(6): 1662-1677.
Wu Shan, Bian Xiaoyan, Zhang Jingxian, et al. A review of domestic and foreign ancillary services market for improving flexibility of new power system[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1662-1677.
[3] 杨镜司, 秦文萍, 史文龙, 等. 基于电动汽车参与调峰定价策略的区域电网两阶段优化调度[J]. 电工技术学报, 2022, 37(1): 58-71.
Yang Jingsi, Qin Wenping, Shi Wenlong, et al. Two-stage optimal dispatching of regional power grid based on electric vehicles' participation in peak-shaving pricing strategy[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 58-71.
[4] 胡鹏, 艾欣, 张朔, 等. 基于需求响应的分时电价主从博弈建模与仿真研究[J]. 电网技术, 2020, 44(2): 585-592.
Hu Peng, Ai Xin, Zhang Shuo, et al. Modelling and simulation study of TOU stackelberg game based on demand response[J]. Power System Technology, 2020, 44(2): 585-592.
[5] 王海洋, 李珂, 张承慧, 等. 基于主从博弈的社区综合能源系统分布式协同优化运行策略[J]. 中国电机工程学报, 2020, 40(17): 5435-5445.
Wang Haiyang, Li Ke, Zhang Chenghui, et al. Distributed coordinative optimal operation of community integrated energy system based on stackelberg game[J]. Proceedings of the CSEE, 2020, 40(17): 5435-5445.
[6] Sun Xiaotian, Xie Haipeng, Xiao Yunpeng, et al. Incentive compatible pricing for enhancing the controllability of price-based demand response[J]. IEEE Transactions on Smart Grid, 2024, 15(1): 418-430.
[7] Ali Fotouhi Ghazvini M, Faria P, Ramos S, et al. Incentive-based demand response programs designed by asset-light retail electricity providers for the day-ahead market[J]. Energy, 2015, 82: 786-799.
[8] Li Yichang, Hong S H. Real-time demand bidding for energy management in discrete manufacturing facilities[J]. IEEE Transactions on Industrial Electronics, 2017, 64(1): 739-749.
[9] 涂京, 周明, 宋旭帆, 等. 居民用户参与电网调峰激励机制及优化用电策略研究[J]. 电网技术, 2019, 43(2): 443-453.
Tu Jing, Zhou Ming, Song Xufan, et al. Research on incentive mechanism and optimal power consumption strategy for residential users' participation in peak shaving of power grid[J]. Power System Technology, 2019, 43(2): 443-453.
[10] 刘文霞, 姚齐, 王月汉, 等. 基于阶梯型需求响应机制的供需主从博弈电源规划模型[J]. 电力系统自动化, 2022, 46(20): 54-63.
Liu Wenxia, Yao Qi, Wang Yuehan, et al. Generation planning model of stackelberg game between supply and demand based on stepped demand response mechanism[J]. Automation of Electric Power Systems, 2022, 46(20): 54-63.
[11] 徐青山, 刘梦佳, 戴蔚莺, 等. 计及用户响应不确定性的可中断负荷储蓄机制[J]. 电工技术学报, 2019, 34(15): 3198-3208.
Xu Qingshan, Liu Mengjia, Dai Weiying, et al. Interruptible load based on deposit mechanism considering uncertainty of customer behavior[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3198-3208.
[12] 张全明, 崔晓昱, 张笑弟, 等. 计及用户不确定性的多时段耦合需求响应激励优化策略[J]. 中国电机工程学报, 2022, 42(24): 8844-8854.
Zhang Quanming, Cui Xiaoyu, Zhang Xiaodi, et al. Incentive optimization strategy of multi period coupling demand response considering user uncertainty[J]. Proceedings of the CSEE, 2022, 42(24): 8844-8854.
[13] Jia Qiangang, Chen Sijie, Yan Zheng, et al. Optimal incentive strategy in cloud-edge integrated demand response framework for residential air conditioning loads[J]. IEEE Transactions on Cloud Computing, 2022, 10(1): 31-42.
[14] 帅轩越, 马志程, 王秀丽, 等. 基于主从博弈理论的共享储能与综合能源微网优化运行研究[J]. 电网技术, 2023, 47(2): 679-690.
Shuai Xuanyue, Ma Zhicheng, Wang Xiuli, et al. Optimal operation of shared energy storage and integrated energy microgrid based on leader-follower game theory[J]. Power System Technology, 2023, 47(2): 679-690.
[15] Tavakkoli M, Fattaheian-Dehkordi S, Pourakbari-Kasmaei M, et al. Bonus-based demand response using stackelberg game approach for residential end-users equipped with HVAC system[J]. IEEE Transactions on Sustainable Energy, 2021, 12(1): 234-249.
[16] 徐博强, 张沛超, 何光宇, 等. 基于主从博弈的热水器集群的负荷准线控制方法[J]. 中国电机工程学报, 2022, 42(21): 7785-7797.
Xu Boqiang, Zhang Peichao, He Guangyu, et al. Stackelberg game based control method for water heater cluster using customer directrix line[J]. Proceedings of the CSEE, 2022, 42(21): 7785-7797.
[17] 张虹, 王明晨, 尹世诚, 等. 考虑用户消费偏好的分散式电采暖系统主从博弈优化方法[J]. 电网技术, 2023, 47(6): 2262-2273.
Zhang Hong, Wang Mingchen, Yin Shicheng, et al. Master-slave game optimization of decentralized electric-heating system considering user’s consumption preference[J]. Power System Technology, 2023, 47(6): 2262-2273.
[18] 孙毅, 黄绍模, 李泽坤, 等. 考虑时域特性的异构温控负荷联合调控策略[J]. 电网技术, 2020, 44(12): 4722-4734.
Sun Yi, Huang Shaomo, Li Zekun, et al. Joint control strategy of heterogeneous temperature control load considering time domain characteristics[J]. Power System Technology, 2020, 44(12): 4722-4734.
[19] 宁剑, 吴继平, 江长明, 等. 考虑资源运行特性的可调节负荷调峰调频优化控制策略[J]. 电力系统自动化, 2022, 46(15): 11-19.
Ning Jian, Wu Jiping, Jiang Changming, et al. Optimal control strategy of peak and frequency regulation for adjustable loads considering operation characteristics of resources[J]. Automation of Electric Power Systems, 2022, 46(15): 11-19.
[20] 刘凤鸣, 杨秀媛, 陈麒宇. 一种平抑反弹效应的集群空调负荷控制方法[J]. 电网技术, 2021, 45(12): 4759-4767.
Liu Fengming, Yang Xiuyuan, Chen Qiyu. Control method for suppressing rebound effect of air conditioning loads[J]. Power System Technology, 2021, 45(12): 4759-4767.
[21] 王永权, 张沛超, 姚垚. 聚合大规模空调负荷的信息物理建模与控制方法[J]. 中国电机工程学报, 2019, 39(22): 6509-6521.
Wang Yongquan, Zhang Peichao, Yao Yao. Cyber-physical modeling and control method for aggregating large-scale ACLs[J]. Proceedings of the CSEE, 2019, 39(22): 6509-6521.
[22] 胡志勇, 郭雪丽, 王爽, 等. 考虑响应意愿的电动汽车群-空调集群需求响应策略研究[J]. 电力系统保护与控制, 2023, 51(15): 109-119.
Hu Zhiyong, Guo Xueli, Wang Shuang, et al. Demand response strategy for electric vehicles and air conditioners considering response willingness[J]. Power System Protection and Control, 2023, 51(15): 109-119.
[23] 崔屹峰, 李珍国, 魏思雨, 等. 面向需求响应的温控负荷单元随机选择模型[J]. 电力系统自动化, 2021, 45(19): 126-132.
Cui Yifeng, Li Zhenguo, Wei Siyu, et al. Random selection model of thermostatically controlled load units for demand response[J]. Automation of Electric Power Systems, 2021, 45(19): 126-132.
[24] 杨秀, 傅广努, 刘方, 等. 考虑多重因素的空调负荷聚合响应潜力评估及控制策略研究[J]. 电网技术, 2022, 46(2): 699-714.
Yang Xiu, Fu Guangnu, Liu Fang, et al. Potential evaluation and control strategy of air conditioning load aggregation response considering multiple factors[J]. Power System Technology, 2022, 46(2): 699-714.
[25] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. 居民住宅小区电力配置规范: GB/T 36040—2018[S]. 北京: 中国标准出版社, 2018.
[26] 张衡, 张沈习, 程浩忠, 等. Stackelberg博弈在电力市场中的应用研究综述[J]. 电工技术学报, 2022, 37(13): 3250-3262.
Zhang Heng, Zhang Shenxi, Cheng Haozhong, et al. A state-of-the-art review on stackelberg game and its applications in power market[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3250-3262.
[27] 王辉, 王宝全, 李旭阳, 等. 基于主从博弈的楼宇微网优化运行[J]. 电力系统及其自动化学报, 2023, 35(2): 10-18, 26. .
Wang Hui, Wang Baoquan, Li Xuyang, et al. Optimal operation of building microgrid based on stackelberg game[J]. Proceedings of the CSU-EPSA, 2023, 35(2): 10-18, 26.
[28] Yu Mengmeng, Jiang Junhui, Ye Xun, et al. Demand response flexibility potential trading in smart grids: a multileader multifollower Stackelberg game approach[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2023, 53(5): 2664-2675.
[29] Li Yang, Wang Bin, Yang Zhen, et al. Hierarchical stochastic scheduling of multi-community integrated energy systems in uncertain environments via Stackelberg game[J]. Applied Energy, 2022, 308: 118392.
[30] 任洲洋, 程欢, 周桂平, 等. 考虑外部博弈和内部协同的耦合系统时序随机生产模拟[J]. 电工技术学报, 2023, 38(22): 6204-6217.
Ren Zhouyang, Cheng Huan, Zhou Guiping, et al. A sequential probabilistic production simulation method for coupled systems considering external game and internal coordination[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 6204-6217.
[31] 熊宇峰, 司杨, 郑天文, 等. 基于主从博弈的工业园区综合能源系统氢储能优化配置[J]. 电工技术学报, 2021, 36(3): 507-516.
Xiong Yufeng, Si Yang, Zheng Tianwen, et al. Optimal configuration of hydrogen storage in industrial park integrated energy system based on Stackelberg game[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 507-516.
[32] 陈岑, 武传涛, 林湘宁, 等. 计及上下游市场的园区综合能源商购售能策略[J]. 电工技术学报, 2022, 37(1): 220-231.
Chen Cen, Wu Chuantao, Lin Xiangning, et al. Purchase and sale strategies of park integrated energy suppliers in wholesale and retail markets[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 220-231.
[33] 孙毅, 张辰, 李泽坤, 等. 计及多区域用户差异化PMV的柔性负荷多功率级调控策略[J]. 中国电机工程学报, 2021, 41(22): 7574-7586.
Sun Yi, Zhang Chen, Li Zekun, et al. Flexible load multi-power level control strategy taking into account the differentiated PMV of multi-region users[J]. Proceedings of the CSEE, 2021, 41(22): 7574-7586.
[34] Ma Jiaqi, Zhao Zhe, Yi Xinyang, et al. Modeling task relationships in multi-task learning with multi-gate mixture-of-experts[C]//Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, United Kingdom, 2018: 1930-1939.
Peak Load Game Scheduling Strategy Combining Reward Mechanism and User Willingness
Abstract With the substantial growth in the number of cooling/heating loads, load spikes are easily to occure during the concentrated residential power consumption hours, especially in old neighborhoods with high load rate, which affects the safe and stable operation of low-voltage distribution networks. To supplement the supply-side regulation capability and enhance the flexibility of regulation, there is an urgent need to guide the user-side adjustable resources to participate in the interaction between grid supply and demand. This paper proposes a peak load game scheduling strategy, which combines the reward mechanism with the users' willingness to ensure the benefits of users and load aggregators, and complies with the users' regulatory willingness to achieve the ideal load fluctuation smoothing and peak shaving effect at the same time.
Firstly, based on the users' willingness of equipment regulation, the peak-hour loads are divided dynamically, and a differentiated subsidy mechanism based on the transformer load rate-reward function is formulated. The proposed mechanism fully stimulates the users' response motivation and stabilizes the load rate within a reasonable interval. Secondly, the Stackelberg game theory is introduced to solve the energy-use decision-making problem between load groups, where the load group that needs to boost power during peak hours is regarded as the leader, and the load group with flexible cutting ability is regarded as the follower. The Stackelberg game model is established along with the uniqueness of the game equilibrium proved. Then, the intraday optimal scheduling method of peak loads under the Stackelberg game is proposed, which searches for the optimal energy-use strategies for the main subjects of the game while guaranteeing their benefits. Finally, the multi-channel mixture-of-experts (MCME) network is constructed to solve the regulatory willingness at the equipment level, and a joint control strategy of single/multi-power-stage loads based on the users' willingness is proposed.
Simulation results show that by using the proposed load intraday optimization method, the standard deviation, peak-to-valley difference, and load peak all reach their minimum values, which are 33.13%, 35.31% and 8.25% lower than the pre-optimization curves. Both the user-side benefit and the net gain of the load aggregator reach their highest values, which verifies the advantages of the proposed strategy in peak shaving, load fluctuation smoothing and participants' gain guaranteeing. When applying the MCME model to solve the equipment regulatory willingness, both the mean absolute error and root mean square error reach their minimum values, indicating that the MCME model has a high solving accuracy. The optimal power change obtained by the intraday optimization method is very close to that obtained by the real-time control strategy, which verifies the effectiveness of the joint control strategy of single/multi-power-stage loads.
The simulation analysis draws the following conclusions: (1) The load intraday optimization method based on the reward mechanism can achieve a win-win situation for load aggregators and users, and achieve significant peak shaving and load fluctuation smoothing effects. (2) The MCME model can effectively learn the common and characteristic laws from operation data, and accurately solve the users' willingness to regulate the equipment. (3) The joint control strategy of single/multi-power-stage loads, which considers the users' willingness, can realize fine load regulation.
keywords:Stackelberg game, peak load, user willingness, load rate-reward function, mixture-of-experts network
中图分类号:TM73
DOI: 10.19595/j.cnki.1000-6753.tces.230874
国家电网有限公司科技项目资助(5108-202218280A-2-379-XG)。
收稿日期 2023-06-08
改稿日期 2024-01-05
杨雪莹 女,1998年生,博士研究生,研究方向为用户侧灵活性资源调控、需求响应、人工智能技术。
E-mail:18801336632@163.com
祁 琪 女,1992年生,博士,硕士生导师,研究方向为电力系统分析与控制、主动配电网规划与优化运行、智能用电等。
E-mail:qigx0521@163.com(通信作者)
(编辑 赫 蕾)