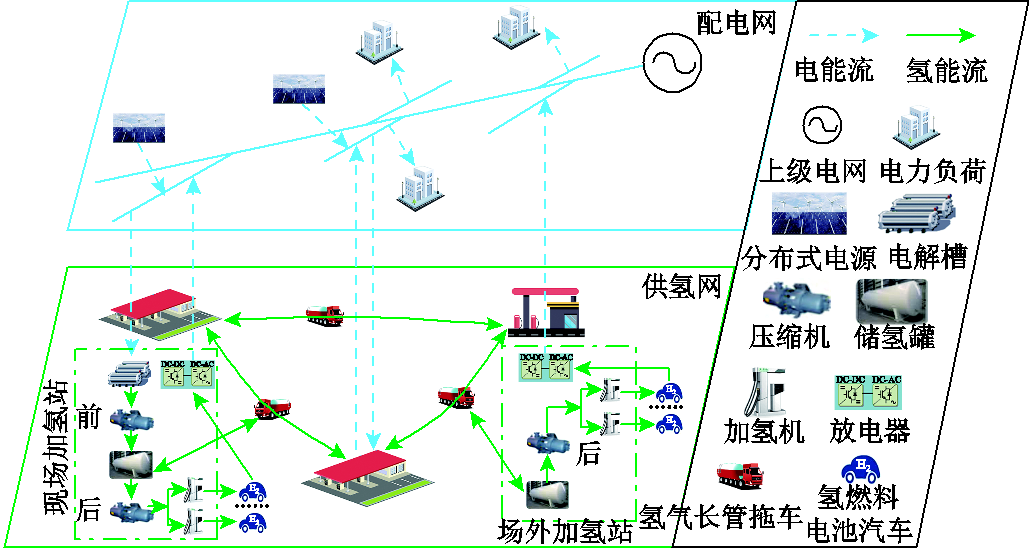
图1 R-EH-IESs结构示意图
Fig.1 The structural diagram of R-EH-IESs
摘要 针对现有研究未考虑区域供氢网间能量交互的灵活运行特征,难以有效评估并提升多区域电氢综合能源系统可靠供能水平的问题,该文提出考虑氢能交互的多区域电氢综合能源系统可靠性评估方法。首先,剖析区域间氢能交互通道与区域内供氢网灵活资源的协调配合规律,提出多区域电氢综合能源系统协同运行机制及其运行模型;其次,以系统总运行成本最小为目标,建立计及氢能交互的多区域电氢综合能源系统最优负荷削减模型,从区域间能量交互水平及其对系统可靠性水平的提升作用等角度出发,建立多区域电氢综合能源系统可靠性评估指标,并基于马尔科夫链蒙特卡洛模拟提出氢能交互下的多区域电氢综合能源系统可靠性评估方法;最后,通过仿真算例分析验证了所提方法的正确性和有效性。该策略能充分挖掘、利用区域间的氢能交互,从而有效提升多区域电氢综合能源系统供能可靠性水平。
关键词:多区域电氢综合能源系统 氢能交互 马尔科夫链蒙特卡洛 供能可靠性
电氢综合能源系统(Electricity-Hydrogen Integrated Energy Systems, EH-IESs)能够充分发挥供氢网低碳和灵活运行等优势,被认为是实现能源系统绿色低碳转型的关键路径之一[1-2]。EH-IESs可靠性评估方法作为电力能源系统规划理论的关键组成部分,可为规划建设和安全运行等提供科学的理论支撑与决策依据,有效指导氢能有序、健康发展,具有重要的理论研究价值和工程应用前景。
EH-IESs可靠性评估属于当前的研究热点,虽吸引了大量学者关注,但总体来看已发表的文献相对较少。文献[3]制定了光伏-热-燃料电池集成系统的评价标准,以评估各组件的风险等级,但无法计算供电、供氢可靠性等指标,难以反映系统的可靠供能水平。文献[4]针对含电动汽车和氢能汽车的新能源充电站,建立了可靠供能的统计评估方法,但忽略了电、氢设备故障失效的情况。文献[5]基于序贯蒙特卡洛模拟建立了含氢能孤岛交直流微电网的供电可靠性评估方法,论证了氢储能系统对提高微电网可靠性水平的积极作用。文献[6]建立了氢能设备的多状态模型,构建了电氢可靠性评估指标体系,并提出了EH-IESs可靠性评估方法,准确量化了系统的可靠供能水平。然而,上述研究均未探讨供氢网内氢燃料电池汽车[7-10]和氢气长管拖车(Hydrogen Tube Trailer, HTT)[11-12]等灵活资源对EH-IESs可靠供能水平的影响,并且均针对单区域电氢综合能源系统(Region Electricity-Hydrogen Integrated Energy Systems, R-EH-IESs),忽略了区域间能量交互对可靠性水平的影响。
现有研究仅有少量文献研究EH-IESs的最优负荷削减计算方法。文献[13]以系统总运行成本最低、新能源弃电量和负荷削减最小为目标,计算系统负荷最优削减量。但该文献仅考虑能源设备容量配置不足造成的负荷削减,并未计及设备非正常运行状态导致的系统供需能量失衡。文献[14]以计及电负荷削减惩罚成本的系统运营成本最小为目标,提出考虑紧急状况下氢储能系统参与恢复供电的配电网滚动调度策略。然而,考虑氢燃料电池汽车和HTT这两类灵活调度资源的最优负荷削减模型构建机理尚未明晰,无法有效分析故障场景下EH-IESs的运行状态。
目前,充分利用区域EH-IESs间的电、氢能量交互潜力,被认为是促进新能源消纳、降低供能风险的有效途径[15-17]。文献[18]以总投资成本、运维成本和碳排放成本最小为目标,提出了多阶段、多区域电氢综合能源系统(Multi-Region Electricity-Hydrogen Integrated Energy Systems, MR-EH-IESs)的扩展规划模型。文献[19]面向可再生能源资源与负荷需求迥异的两个R-EH-IESs,利用氢燃料电池汽车进行区域间能量传输,改善了不同区域的能源平衡情况,降低了系统的能源利用成本。上述文献论证了区域间能量交互对提高系统运行和规划安全性及经济性的积极作用,但目前尚缺少MR-EH-IESs的可靠性评估方法。
HTT不仅能够在单一区域供氢网内的不同加氢站间进行氢气运输,而且可以实现不同区域供氢网间的氢能交互,为促进MR-EH-IESs间能源的互补互济提供了新的通道。充分挖掘利用HTT的灵活运行特性,提高区域间电、氢能量的互补互济能力,对提高MR-EH-IESs可靠供能水平具有重要意义。针对上述问题,本文提出了计及氢能交互的MR-EH-IESs可靠性提升策略,主要贡献如下:
1)考虑区域间氢能交互通道与区域内供氢网灵活调度资源的协调配合,提出MR-EH-IESs的协同运行机制和模型,并基于此建立了计及氢能交互的MR-EH-IESs最优负荷削减模型,有效保障故障场景下MR-EH-IESs的供能可靠性。
2)从区域间能量交互水平及其对系统供能可靠性的提升作用角度出发,建立了计及氢能交互的MR-EH-IESs可靠性评估指标体系。基于马尔科夫链蒙特卡洛模拟法,建立了计及氢能交互的MR-EH-IESs可靠性评估方法,有效评估系统的供能可靠性水平及其提升作用,为系统的规划建设等提供科学合理的决策依据。
R-EH-IESs和MR-EH-IESs的典型结构分别如图1、图2所示。在R-EH-IESs内,现场加氢站的制氢设备通过电解水制氢,满足自身及场外加氢站的氢气需求。在各R-EH-IESs的配电网间,通过电力联络线路进行互联,保障电负荷的可靠供电。相对于现有研究电氢可靠性的文献[6],本文提出了MR-EH-IESs协同运行机制,即考虑区域内供氢网灵活运行及区域间氢能交互特征。

图1 R-EH-IESs结构示意图
Fig.1 The structural diagram of R-EH-IESs
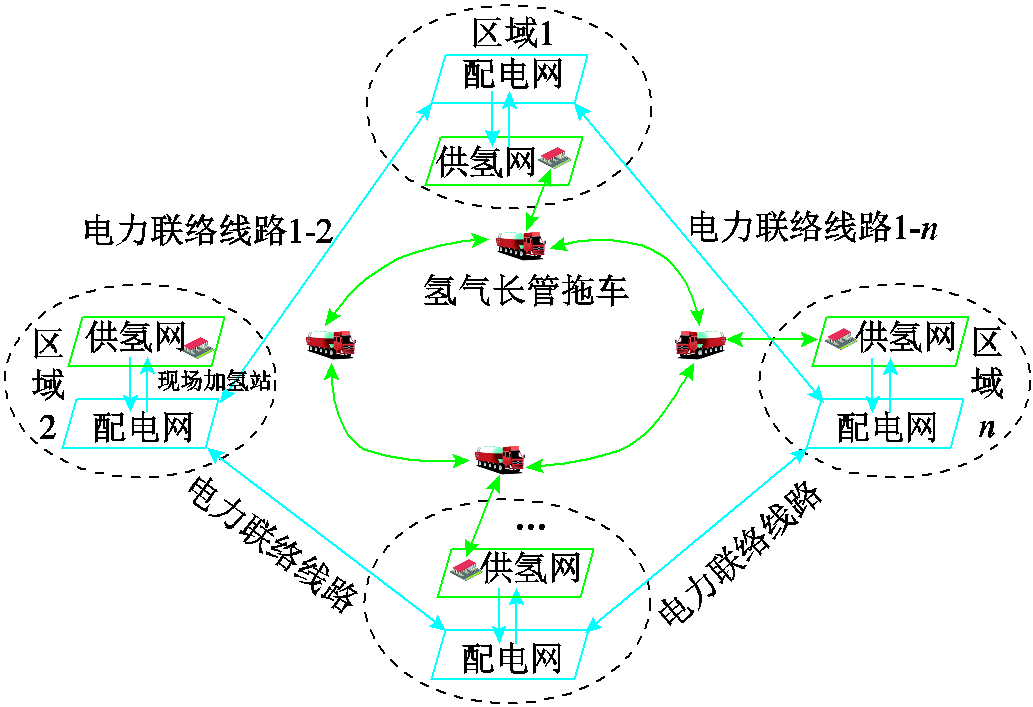
图2 MR-EH-IESs结构示意图
Fig.2 The structural diagram of MR-EH-IESs
在区域内,对于氢燃料电池汽车:一方面,可以通过需求响应策略改变部分氢燃料电池汽车的加氢时间,实现氢负荷的时序转移,以降低储氢罐、加氢机等设备发生故障情况下造成的氢负荷削减;另一方面,当配电网中的电力线路发生故障时,系统通过给予一定的补偿费用吸引氢燃料电池汽车用户利用车载燃料电池发电,并通过放电器反馈至配电网,即(Hydrogen fuel cell vehicle to grid, H2G)模式,以降低系统电负荷削减。对于HTT,在加氢站内电解槽等设备发生故障的场景下,可以通过HTT从氢气富余的加氢站运输氢气,以满足故障加氢站的氢气需求。若某一加氢站所在节点上游的电力线路发生故障,且该加氢站中储存的氢气不足以支撑H2G模式时,其他加氢站可以通过HTT向该加氢站输送氢气,在保障氢燃料电池汽车用户出行需求的基础上通过H2G模式向配电网反馈电能,进一步保障系统的可靠供电。
在区域间,各区域的供氢网间通过HTT进行互联:当某一区域供氢网内加氢站发生设备故障,但其他加氢站因氢负荷需求高等原因无法提供氢气支撑时,可通过区域间HTT从氢气富余的区域运输氢气至发生故障的区域,并通过该区域内HTT灵活运氢提升其供氢可靠性水平;当某一区域的配电网发生线路故障,在无法通过电力联络线路进行负荷转供,且因区域内氢负荷需求较高等原因无法利用氢燃料电池汽车参与H2G模式向配电网提供电能支撑时,则可通过区域间HTT从其他氢气富余的区域供氢网内运输氢气至发生故障的区域供氢网,为该区域内氢燃料电池汽车参与H2G模式提供充足的氢气支撑,从而提升该区域的供电可靠性水平。
基于1.1节所提协同运行机制,本节建立了区域内供氢网灵活调度模型与区域间氢能交互模型。
1.2.1 区域内供氢网灵活调度模型
区域内供氢网灵活调度模型包括氢燃料电池汽车的需求响应模型、H2G模型和HTT运行模型。
1)需求响应模型
氢燃料电池汽车通过参与需求响应策略改变自身的加氢时间,实现氢负荷的时序转移[7-8],如式(1)、式(2)所示。其中,式(1)表示一定比例的氢燃料电池汽车可以参与需求响应策略;式(2)约束了需求响应前后的氢负荷总量不变,以满足氢燃料电池汽车的加氢需求。
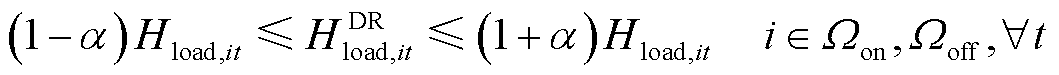 (1)
(1)
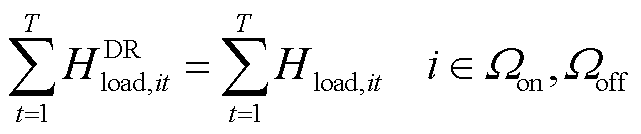 (2)
(2)
式中,Hload,it、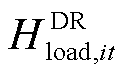 分别为t时刻节点i处加氢站内氢燃料电池汽车参与需求响应策略前、后的氢负荷;α为氢负荷转移比例;Ωon、Ωoff分别为现场加氢站与场外加氢站所在的节点集合;T为调度周期,取24 h。
分别为t时刻节点i处加氢站内氢燃料电池汽车参与需求响应策略前、后的氢负荷;α为氢负荷转移比例;Ωon、Ωoff分别为现场加氢站与场外加氢站所在的节点集合;T为调度周期,取24 h。
2)H2G模型
在H2G模式中,氢燃料电池汽车使用车载燃料电池发电,并通过放电器将电能反馈至配电网[9-10],如式(3)所示;式(4)约束了反馈至配电网的电功率应小于放电器的额定容量。为了满足氢燃料电池汽车用户的出行需求,需要在所处加氢站中补充氢燃料电池汽车因参与H2G模式消耗的氢气,如式(5)所示。
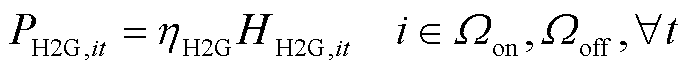 (3)
(3)
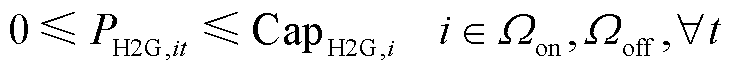 (4)
(4)
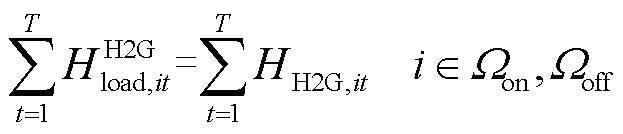 (5)
(5)
式中,HH2G,it、PH2G,it分别为t时刻节点i处加氢站的氢燃料电池汽车参与H2G模式消耗的氢气和反馈至配电网的有功功率;ηH2G为H2G模式的氢-电转换效率;CapH2G,i为节点i处加氢站内放电器的额定容量;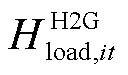 为t时刻节点i处加氢站的氢燃料电池汽车因参与H2G模式所补充的加氢需求。
为t时刻节点i处加氢站的氢燃料电池汽车因参与H2G模式所补充的加氢需求。
在氢燃料电池汽车参与需求响应策略和H2G模式后,各加氢站的氢负荷需求将发生变化。新的氢负荷需求计算式为
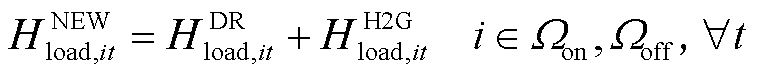 (6)
(6)
式中, 为t时刻节点i处加氢站因氢燃料电池汽车参与需求响应策略和H2G模式产生的新的氢负荷需求。
为t时刻节点i处加氢站因氢燃料电池汽车参与需求响应策略和H2G模式产生的新的氢负荷需求。
3)区域内HTT运行模型
各加氢站间通过HTT运输氢气,当一辆HTT到达某一加氢站时即可进行充氢或放氢操作。考虑HTT的交通转移约束及车载储氢罐的运行约束,建立其运行模型,如式(7)~式(14)所示。式(7)表示同一时刻一辆HTT只能位于某一个加氢站,在下一时刻可选择留在站内或前往其他加氢站;式(8)确保HTT在调度周期初始时刻与末尾时刻所处的加氢站位置一致,便于在下一个周期中进行调度。
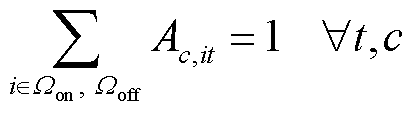 (7)
(7)
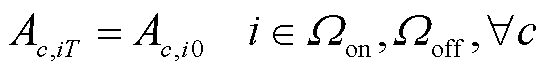 (8)
(8)
式中,Ac,it为第c辆HTT在t时刻是否位于节点i处加氢站的位置状态变量,若为1则表示第c辆HTT在t时刻位于节点i处加氢站,否则为0。
式(9)~式(14)为HTT内车载储氢罐的运行约束[12]。
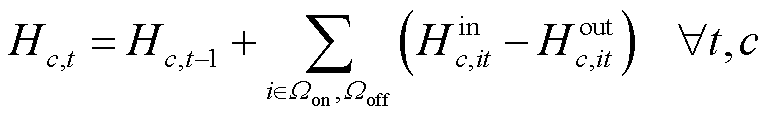 (9)
(9)
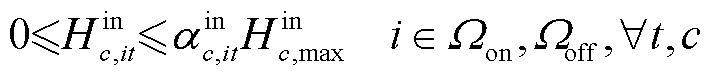 (10)
(10)
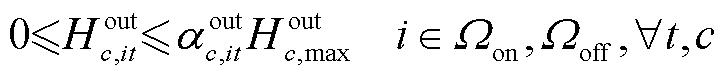 (11)
(11)
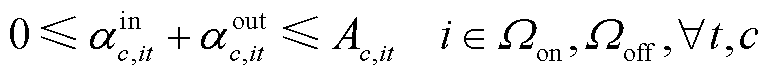 (12)
(12)
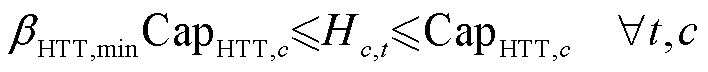 (13)
(13)
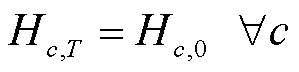 (14)
(14)
式中,Hc,t、Hc,t-1分别t时刻和t-1时刻第c辆HTT的储氢量;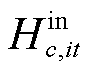 、
、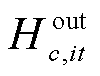 分别为t时刻第c辆HTT在节点i处加氢站的充氢量和放氢量;
分别为t时刻第c辆HTT在节点i处加氢站的充氢量和放氢量;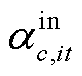 、
、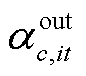 分别为t时刻第c辆HTT在节点i处加氢站的充氢状态变量和放氢状态变量,若为1则表示t时刻第c辆HTT在节点i处加氢站进行充氢或放氢,否则为0;
分别为t时刻第c辆HTT在节点i处加氢站的充氢状态变量和放氢状态变量,若为1则表示t时刻第c辆HTT在节点i处加氢站进行充氢或放氢,否则为0;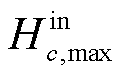 、
、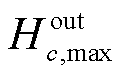 分别为第c辆HTT的最大充氢量和最大放氢量;βHTT,min为HTT的最小容量系数;CapHTT,c为第c辆HTT的额定容量;Hc,T、Hc,0分别为第c辆HTT在调度周期末尾时刻与初始时刻的储氢量。式(9)描述了t时刻第c辆HTT的氢气平衡约束;式(10)限制了t时刻第c辆HTT在节点i处加氢站的充氢量;式(11)限制了t时刻第c辆HTT在节点i处加氢站的放氢量;式(12)确保HTT不能同时充氢和放氢;式(13)限制了t时刻第c辆HTT的储氢量;式(14)确保第c辆HTT在调度周期初始时刻与末尾时刻的储氢量相同,便于在下一个周期中进行调度。
分别为第c辆HTT的最大充氢量和最大放氢量;βHTT,min为HTT的最小容量系数;CapHTT,c为第c辆HTT的额定容量;Hc,T、Hc,0分别为第c辆HTT在调度周期末尾时刻与初始时刻的储氢量。式(9)描述了t时刻第c辆HTT的氢气平衡约束;式(10)限制了t时刻第c辆HTT在节点i处加氢站的充氢量;式(11)限制了t时刻第c辆HTT在节点i处加氢站的放氢量;式(12)确保HTT不能同时充氢和放氢;式(13)限制了t时刻第c辆HTT的储氢量;式(14)确保第c辆HTT在调度周期初始时刻与末尾时刻的储氢量相同,便于在下一个周期中进行调度。
1.2.2 区域间氢能交互模型
考虑到现场加氢站具备制氢能力,其可利用的氢气量相比场外加氢站更多,本文将各区域供氢网内的现场加氢站作为区域间HTT的运输站点,通过这些站点的位置距离建立交通路网模型,并根据HTT的平均行驶速度,将交通路网的距离模型转换为交通耗时模型,对HTT的转移耗时建模[20]。其中,式(15)表示同一时刻一辆HTT只能位于某个现场加氢站或在道路(节点0)上,在下一时刻可选择留在站内或前往其他现场加氢站;式(16)确保HTT在调度周期末尾时刻与初始时刻所处的现场加氢站位置一致,便于在下一个周期中进行调度。式(17)表示HTT在时刻t到达或离开位置r时,对应的位置变化状态hk,rt =1或-1,否则,ht,rt=0;式(18)表示所有加氢站节点的一个HTT位置变化状态的绝对值之和应等于该HTT在道路的位置变化状态的绝对值;式(19)表示HTT在道路上的交通耗时应大于两个加氢站之间所需的行驶时间。
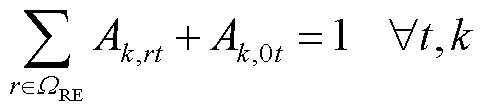 (15)
(15)
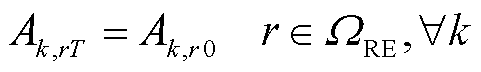 (16)
(16)
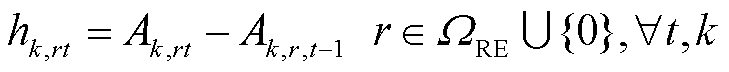 (17)
(17)
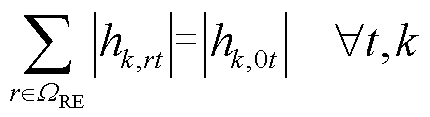 (18)
(18)
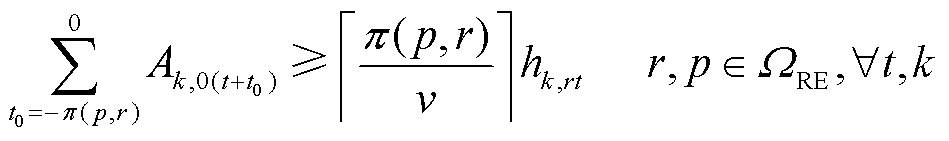 (19)
(19)
式中,Ak,rt为第k辆HTT在t时刻是否位于第r个现场加氢站或道路(r=0)的位置状态变量,若为1则表示第k辆HTT在t时刻位于第r个现场加氢站,否则为0;ΩRE为所有区域供氢网内的现场加氢站集合;hk,rt为第k辆HTT在t时刻位置变化状态;π(p, r)为HTT在两加氢站间转移的交通距离;v为HTT的平均行驶速度;⌈·⌉表示向上取整。
式(20)~式(25)建立了区域间第k辆HTT的车载储氢罐运行约束。
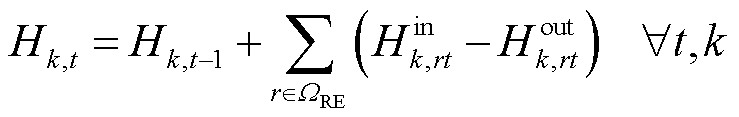 (20)
(20)
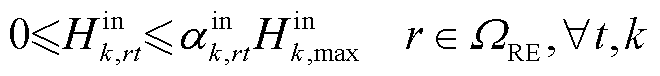 (21)
(21)
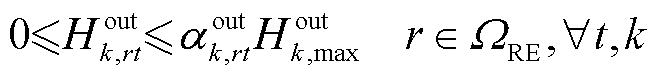 (22)
(22)
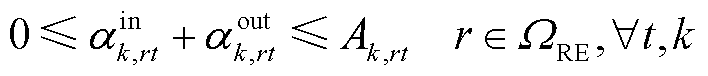 (23)
(23)
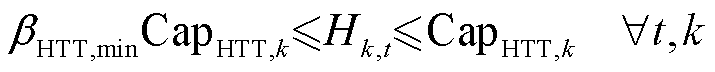 (24)
(24)
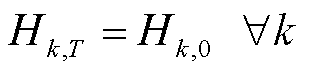 (25)
(25)
式中,Hk,t、Hk,t-1分别t时刻和t-1时刻区域间第k辆HTT的储氢量;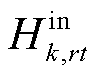 、
、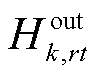 分别为t时刻区域间第k辆HTT在第r个现场加氢站的充氢量和放氢量;
分别为t时刻区域间第k辆HTT在第r个现场加氢站的充氢量和放氢量;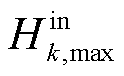 、
、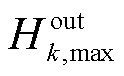 分别为区域间第k辆HTT的最大充氢量和最大放氢量;
分别为区域间第k辆HTT的最大充氢量和最大放氢量;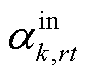 、
、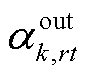 分别为t时刻区域间第k辆HTT在第r个现场加氢站的充氢状态和放氢状态,若为1则表示t时刻区域间第k辆HTT在第r个现场加氢站进行充、放氢,否则为0;CapHTT,k为区域间第k辆HTT的额定容量;Hk,T、Hk,0分别为区域间第k辆HTT在调度周期末尾时刻与初始时刻的储氢量。
分别为t时刻区域间第k辆HTT在第r个现场加氢站的充氢状态和放氢状态,若为1则表示t时刻区域间第k辆HTT在第r个现场加氢站进行充、放氢,否则为0;CapHTT,k为区域间第k辆HTT的额定容量;Hk,T、Hk,0分别为区域间第k辆HTT在调度周期末尾时刻与初始时刻的储氢量。
本节建立了计及氢能交互的MR-EH-IESs最优负荷削减模型。相对于文献[6],本文所提最优负荷削减模型考虑了氢燃料电池汽车与HTT等灵活调度资源对系统负荷削减的影响机理,以MR-EH-IESs总运行成本最小为目标,并综合考虑区域内的供氢网灵活运行约束、异质能量流约束和设备运行约束,以及区域间的氢能交互约束和电能交互约束。
以计及负荷削减惩罚成本的系统总运行成本最小作为目标函数,有
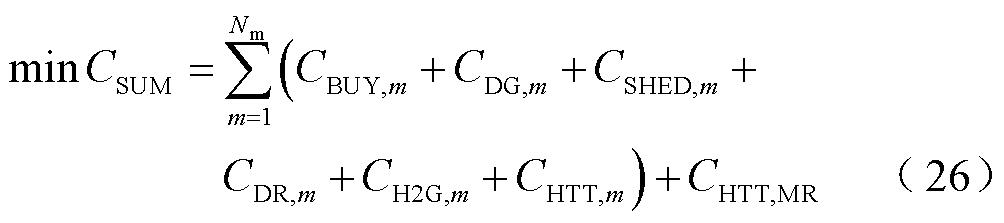
式中,CBUY,m、CDG,m、CSHED,m、CDR,m、CH2G,m和CHTT,m分别为区域m的EH-IESs的购电成本、弃风光惩罚成本、电氢负荷削减惩罚成本、需求响应成本、H2G成本和区域内HTT运行成本;CHTT,MR为区域间HTT的运行成本;Nm为区域数量。
各项成本计算式为
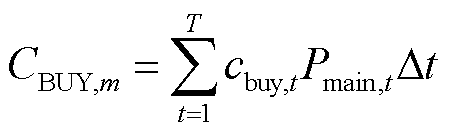 (27)
(27)
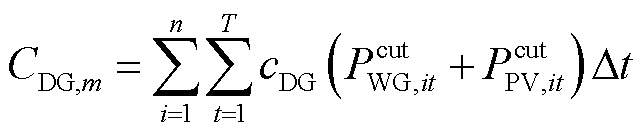 (28)
(28)
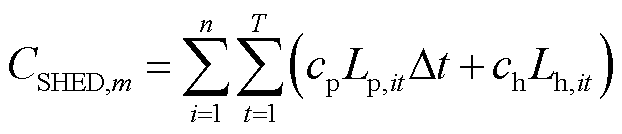 (29)
(29)
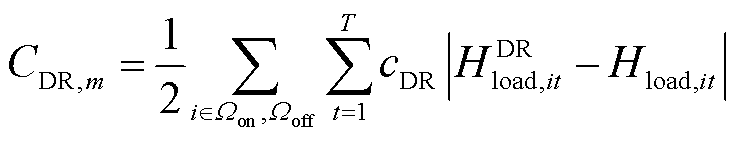 (30)
(30)
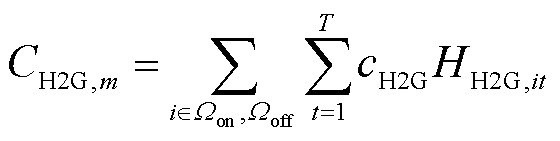 (31)
(31)
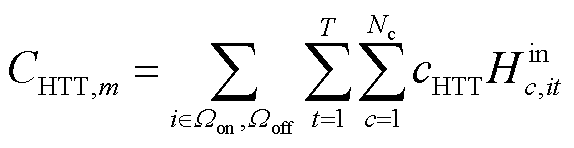 (32)
(32)
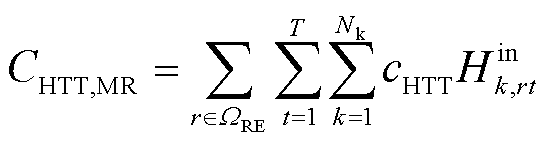 (33)
(33)
式中,cbuy,t为t时刻向上级电网的购电价格;Pmain,t为t时刻配电网向上级电网的购电功率;Dt为单位时间间隔,取1 h;cDG为弃风光电量的单位惩罚成本;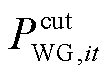 、
、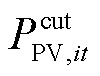 分别为t时刻节点i的弃风、弃光功率;cp、ch分别为电负荷和氢负荷削减的单位惩罚成本;Lp,it、Lh,it分别为t时刻节点i处电负荷有功功率的削减量和加氢站内氢负荷的削减量;cDR为氢燃料电池汽车参与需求响应的单位补偿成本;cH2G为氢燃料电池汽车参与H2G模式的单位补偿成本;cHTT为HTT的单位储运氢气成本;Nc为电氢能源系统内HTT的数量;Nk为区域间HTT的数量。
分别为t时刻节点i的弃风、弃光功率;cp、ch分别为电负荷和氢负荷削减的单位惩罚成本;Lp,it、Lh,it分别为t时刻节点i处电负荷有功功率的削减量和加氢站内氢负荷的削减量;cDR为氢燃料电池汽车参与需求响应的单位补偿成本;cH2G为氢燃料电池汽车参与H2G模式的单位补偿成本;cHTT为HTT的单位储运氢气成本;Nc为电氢能源系统内HTT的数量;Nk为区域间HTT的数量。
区域内供氢网灵活运行约束见式(1)~式(14),区域间氢能交互约束见式(15)~式(25),其余约束如下。
2.2.1 区域内异质能量流约束
本文采用线性化的DistFlow公式[21]模拟配电网潮流约束。其余异质能量流约束包括电功率平衡约束、氢气平衡约束、负荷削减约束和交互功率约束。具体建模如下。
1)电功率平衡约束
对于现场加氢站所在节点,配电网、分布式电源和H2G模式产生的电力将共同满足电负荷与电解槽的用电需求,如式(34)所示;对于场外加氢站所在节点,配电网和H2G模式产生的电力将满足其电负荷需求,如式(35)所示。
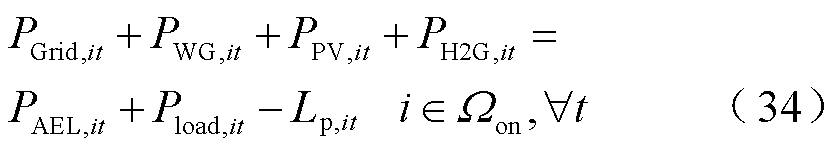
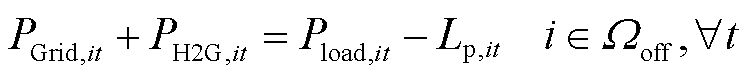 (35)
(35)
式中,PWG,it、PPV,it分别为t时刻节点i处风光机组实际输出的有功功率;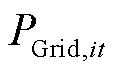 、
、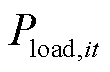 分别为t时刻节点i与配电网交互的有功功率、电负荷的有功功率;
分别为t时刻节点i与配电网交互的有功功率、电负荷的有功功率;
PAEL,it为t时刻节点i处加氢站内电解槽消耗的有功功率。
2)风光机组出力约束
风光机组考虑弃风弃光约束项运行约束为式(36)~式(39),风光机组的无功功率约束与有功功率约束类似,此处不再赘述[22]。
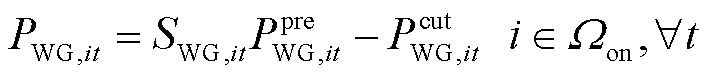 (36)
(36)
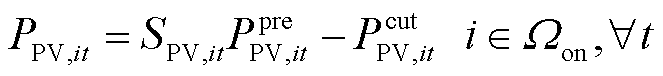 (37)
(37)
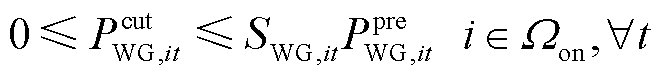 (38)
(38)
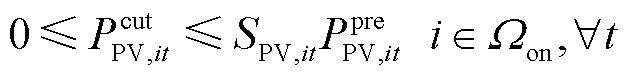 (39)
(39)
式中,SWG,it、SPV,it分别为t时刻节点i处风电机组和光伏机组的运行状态,若为1则表示正常运行状态,若为0则表示故障停运状态;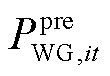 、
、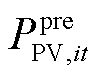 分别为t时刻节点i处风电机组和光伏机组的预测有功功率。
分别为t时刻节点i处风电机组和光伏机组的预测有功功率。
3)氢气平衡约束
在现场加氢站中,储氢罐可以从电解槽、区域内HTT和区域间HTT中获取氢气,如式(40)所示;并且储氢罐可向加氢机组、区域内HTT和区域间HTT供给氢气,如式(41)所示;在场外加氢站中,储氢罐仅从HTT中获取氢气,如式(42)所示。此外,各加氢站中储氢罐可向HTT和加氢机组供给氢气,如式(43)所示;加氢机组输出的氢气则满足氢燃料电池汽车的加氢需求,如式(44)所示。
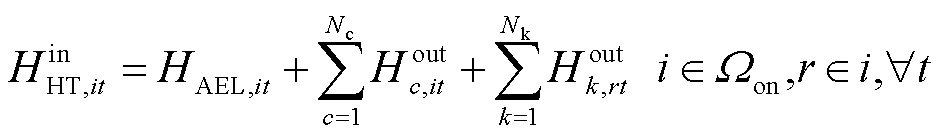 (40)
(40)
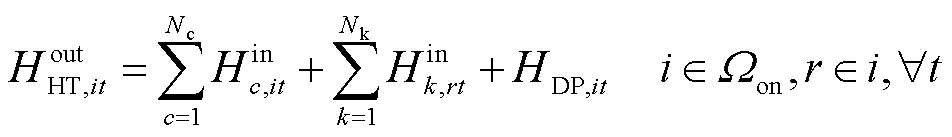 (41)
(41)
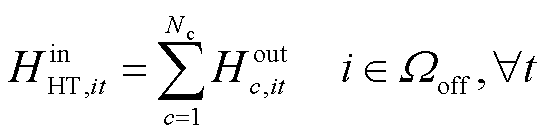 (42)
(42)
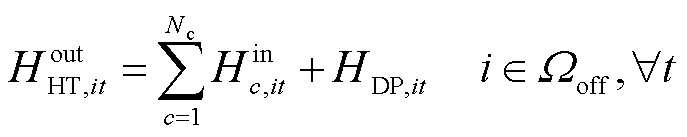 (43)
(43)
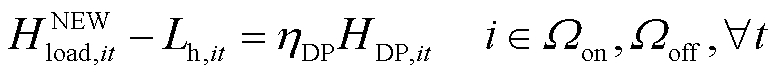 (44)
(44)
式中,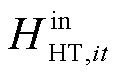 、
、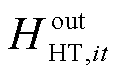 分别为t时刻节点i处加氢站内储氢罐的充氢量和放氢量;HAEL,it为t时刻节点i处加氢站内电解槽产氢量;HDP,it为t时刻节点i处加氢站内加氢机组消耗氢气量;ηDP为加氢机效率;r∈i表示区域间第r个现场加氢站即为某区域配电网节点i处的现场加氢站。
分别为t时刻节点i处加氢站内储氢罐的充氢量和放氢量;HAEL,it为t时刻节点i处加氢站内电解槽产氢量;HDP,it为t时刻节点i处加氢站内加氢机组消耗氢气量;ηDP为加氢机效率;r∈i表示区域间第r个现场加氢站即为某区域配电网节点i处的现场加氢站。
4)负荷削减约束
电负荷有功、无功功率削减约束和氢负荷削减约束分别如式(45)~式(47)所示。
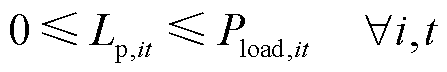 (45)
(45)
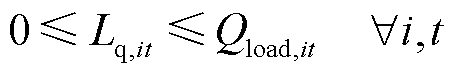 (46)
(46)
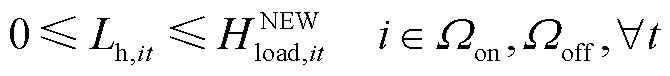 (47)
(47)
式中,Lq,it为t时刻节点i处电负荷无功功率的削减量。
5)交互功率约束
加氢站所在节点与配电网交互功率受变压器等设备容量限制,约束为
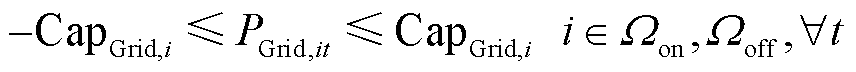 (48)
(48)
式中,CapGrid,i为节点i与配电网的额定交互功率。
2.2.2 区域内设备运行约束
电力线路、风光机组均基于经典的两状态可靠性评估模型建立其运行约束模型[22-23],此处不再赘述。
1)碱性电解槽运行约束
本文采用文献[6]中碱性电解槽的多状态马尔科夫模型,建立其运行约束如式(49)~式(51)所示。其中,式(49)表示碱性电解槽的产氢量与其运行状态相关;式(50)限制了碱性电解槽的耗电功率;式(51)表示碱性电解槽处于正常运行或降额运行状态时可选择是否启停,而处于故障停运状态时则必须停机。
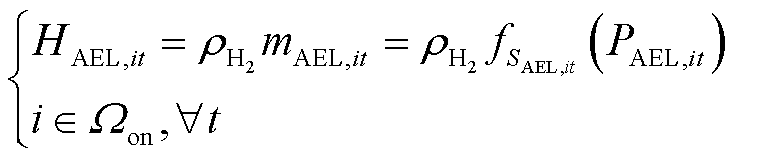 (49)
(49)
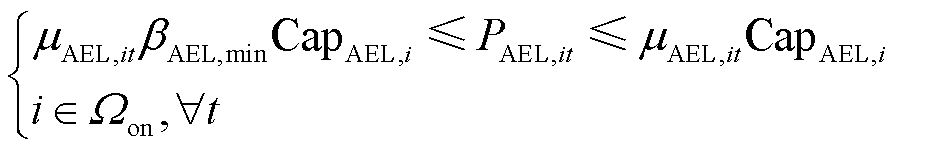 (50)
(50)
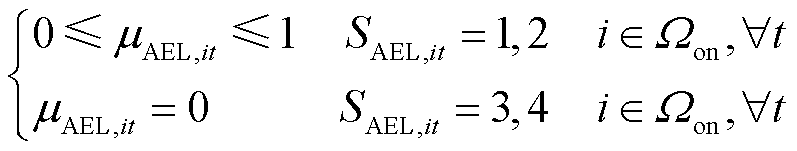 (51)
(51)
式中,ρH2为氢气的标准密度(kg/Nm3);SAEL,it为t时刻节点i处加氢站内碱性电解槽的运行状态; (PAEL,it)表示t时刻节点i处加氢站内碱性电解槽处于状态SAEL,it下产氢量mAEL,it与耗电功率PAEL,it之间的函数关系;βAEL,min为碱性电解槽的最小容量系数;CapAEL,i为节点i处加氢站内碱性电解槽的额定容量;
(PAEL,it)表示t时刻节点i处加氢站内碱性电解槽处于状态SAEL,it下产氢量mAEL,it与耗电功率PAEL,it之间的函数关系;βAEL,min为碱性电解槽的最小容量系数;CapAEL,i为节点i处加氢站内碱性电解槽的额定容量;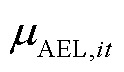 为t时刻节点i处加氢站内碱性电解槽的启停状态变量,若为1则表示启动状态,若为0则表示停机状态。
为t时刻节点i处加氢站内碱性电解槽的启停状态变量,若为1则表示启动状态,若为0则表示停机状态。
2)储氢罐运行约束
加氢站内储氢罐的运行约束如式(52)~式(56)所示[24]。其中,式(52)描述了储氢罐在t时刻的氢气平衡;式(53)、式(54)分别限制了储氢罐的充氢量和放氢量;式(55)限制了储氢罐的储氢量;式(56)确保储氢罐在调度周期末尾时刻与初始时刻的储氢量相同,便于在下一个周期中进行调度。
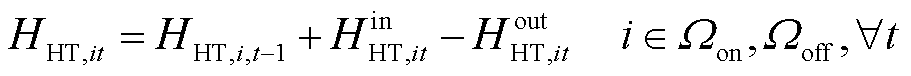 (52)
(52)
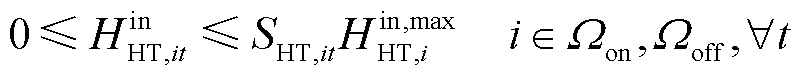 (53)
(53)
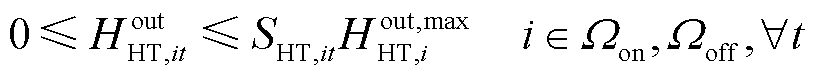 (54)
(54)
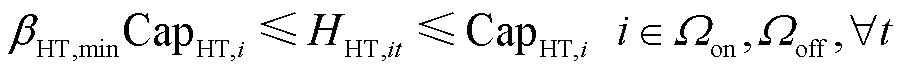 (55)
(55)
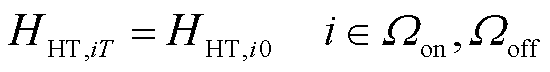 (56)
(56)
式中,HHT,it、HHT,i,t-1分别为t时刻与t-1时刻节点i处加氢站内储氢罐的储氢量;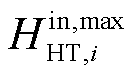 、
、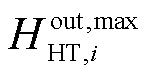 分别为节点i处加氢站内储氢罐的最大充氢量和最大放氢量;SHT,it为t时刻节点i处加氢站内储氢罐的运行状态,若为1则表示正常运行状态,若为0则表示故障停运状态;βHT,min为储氢罐的最小容量系数;CapHT,i为节点i处加氢站内储氢罐的额定容量;HHT,iT、HHT,i0分别为节点i处加氢站内储氢罐在调度周期末尾时刻与初始时刻的储氢量。
分别为节点i处加氢站内储氢罐的最大充氢量和最大放氢量;SHT,it为t时刻节点i处加氢站内储氢罐的运行状态,若为1则表示正常运行状态,若为0则表示故障停运状态;βHT,min为储氢罐的最小容量系数;CapHT,i为节点i处加氢站内储氢罐的额定容量;HHT,iT、HHT,i0分别为节点i处加氢站内储氢罐在调度周期末尾时刻与初始时刻的储氢量。
3)压缩机运行约束
碱性电解槽制取的氢气将由前压缩机进行压缩,并受到前压缩机的容量限制,如式(57)所示;储氢罐输送至加氢机组的氢气将由后压缩机进行压缩,并受到后压缩机的容量限制,如式(58)所示。
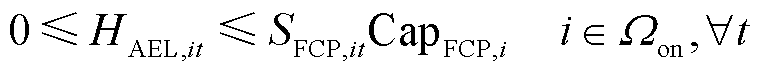 (57)
(57)
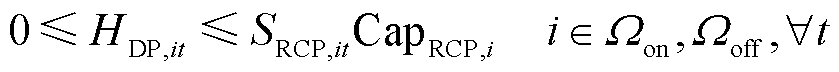 (58)
(58)
式中,SFCP,it、SRCP,it分别为t时刻节点i处加氢站内前压缩机和后压缩机的运行状态,若为1则表示正常运行状态,若为0则表示故障停运状态;CapFCP,i、CapRCP,i分别为节点i处加氢站内前压缩机和后压缩机的额定容量。
4)加氢机组运行约束
本文采用文献[6]中加氢机组的多状态马尔可夫模型,建立其运行约束如式(59)所示,即加氢机组向氢燃料电池汽车供应的氢气应不超过其总可用容量(即所有未故障加氢机的额定容量之和)。
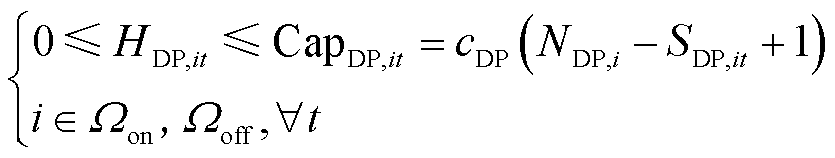 (59)
(59)
式中,CapDP,it为t时刻节点i处加氢站内加氢机组的总可用容量;cDP为单台加氢机的可用容量;NDP,i为节点i处加氢站内加氢机的数量;SDP,it为t时刻节点i处加氢站内加氢机组的运行状态。
2.2.3 区域间电能交互约束
为避免产生较大的短路电流,配电网通常为辐射运行方式。因此,在进行负荷转供时,配电网拓扑应满足辐射运行要求[22,24-25],如式(60)~式(62)所示。其中,式(60)表示线路功率流动的双向性;式(61)表示除变压器低压母线节点外,其余节点均只有一个父节点;式(62)表示变压器低压母线没有父节点。
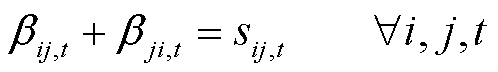 (60)
(60)
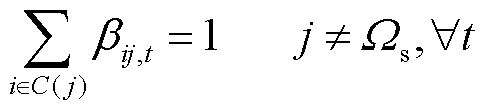 (61)
(61)
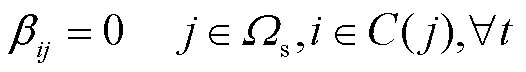 (62)
(62)
式中,sij,t为t时刻线路ij上开关的工作状态,若为1表示开关闭合,若为0则表示开关断开;βij,t为t时刻线路ij功率流动方向的二进制识别变量,若为1表示功率从节点i流向节点j,若为0则表示功率从节点j流向节点i;Ωs为变压器低压母线的节点集合;C(j)为与节点j相连的节点集合。
由于式(30)中存在绝对值项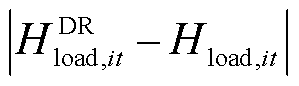 和式(49)中存在非线性函数f(PAEL,it),所提最优负荷削减模型是一个混合整数非线性规划模型。因此本文基于Big-M法[26]和分段线性化方法[27],将所提最优负荷削减模型转换为一个混合整数线性规划模型,由GUROBI或其他商业求解器进行求解。具体线性化方法见附录。
和式(49)中存在非线性函数f(PAEL,it),所提最优负荷削减模型是一个混合整数非线性规划模型。因此本文基于Big-M法[26]和分段线性化方法[27],将所提最优负荷削减模型转换为一个混合整数线性规划模型,由GUROBI或其他商业求解器进行求解。具体线性化方法见附录。
本节从区域间能量交互水平及其对系统供能可靠性水平的提升作用角度出发,建立了MR-EH-IESs可靠性评估指标体系,相对于文献[6],该体系量化了氢能交互对系统供能可靠性水平的提升作用。并结合第2节计及氢能交互的MR-EH-IESs最优负荷削减模型,提出了基于马尔科夫链蒙特卡洛模拟的MR-EH-IESs可靠性评估方法。
针对本文的研究对象,本节在文献[6]提出的电氢可靠性评估指标的基础上,增加了区域交互电量期望、区域交互氢量期望、供电可靠性提升率和供氢可靠性提升率评估指标,以量化MR-EH-IESs中区域间能量交互水平及其对系统供能可靠性水平的提升作用,并构建MR-EH-IESs可靠性评估指标体系。
1)氢负荷削减概率(Loss of Hydrogen Load Probability, LOHLP),即模拟周期内氢负荷削减状态之和与模拟状态总量之比。
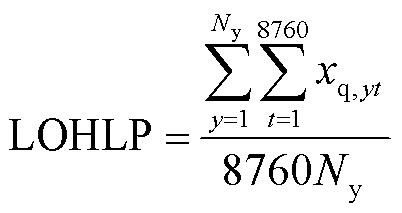 (63)
(63)
式中,xq,yt为第y年t时刻系统氢负荷的削减状态变量,若为1则表示有氢负荷削减,若为0则表示无氢负荷削减;Ny为模拟年限。
2)氢负荷削减时间期望(Loss of Hydrogen Load Expectation, LOHLE),即氢负荷削减概率LOHLP与一年8 760 h的乘积。
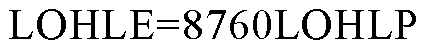 (64)
(64)
3)氢负荷缺供能量期望(Expected Hydrogen Not Supply, EHNS),即模拟周期内氢负荷削减量总和与模拟年限之比。
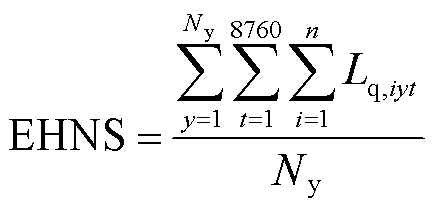 (65)
(65)
式中,Lq,iyt为第y年t时刻节点i处加氢站的氢负荷削减量;n为加氢站节点数量。
4)缺供能量综合损失(Comprehensive Loss of Energy Not Supply, CLENS),即年电负荷和氢负荷缺供能量期望的惩罚成本之和。
 (66)
(66)
式中,EENS为电负荷缺供能量期望。
5)区域交互电量期望(Inter-Regional Expected Electricity Interaction, IREEI),即模拟周期内区域间所有电力联络线路传输的电量总量与模拟年限之比。
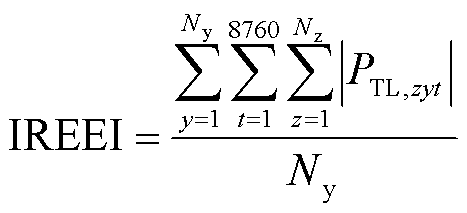 (67)
(67)
式中,PTL,zyt为第y年t时刻第z条联络线路流过的有功功率;Nz为联络线路数量。
6)区域交互氢量期望(Inter-Regional Expected Hydrogen Interaction, IREHI),即模拟周期内所有区域间HTT存储和运输的氢气总量与模拟年限之比。
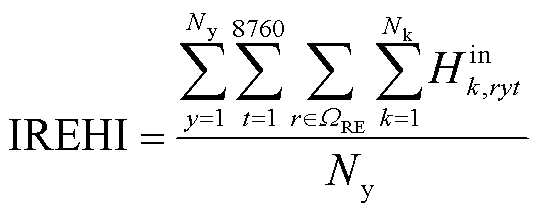 (68)
(68)
式中,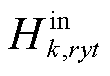 为第y年t时刻区域间第k辆HTT在第r个现场加氢站的充氢量。
为第y年t时刻区域间第k辆HTT在第r个现场加氢站的充氢量。
7)供电可靠性提升率(Improvement Rate of Electricity Supply Reliability, IRESR),即考虑能量交互前后MR-EH-IESs电负荷缺供能量期望EENS的变化率。
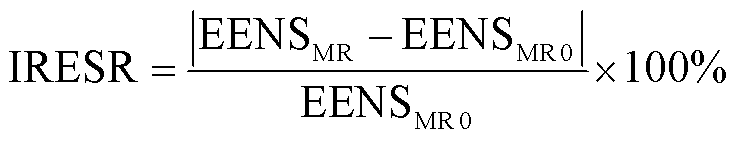 (69)
(69)
式中,EENSMR0、EENSMR分别为考虑能量交互前后MR-EH-IESs的电负荷缺供能量期望。
8)供氢可靠性提升率(Improvement Rate of Hydrogen Supply Reliability, IRHSR),即考虑能量交互前后MR-EH-IESs氢负荷缺供能量期望EHES的变化率。
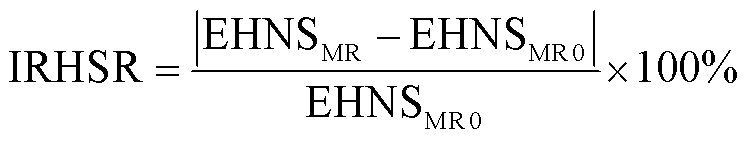 (70)
(70)
式中,EHNSMR0、EHNSMR分别为考虑能量交互前后MR-EH-IESs的氢负荷缺供能量期望。
本节基于文献[6]建立的氢能设备可靠性模型与第2节计及氢能交互的MR-EH-IESs最优负荷削减模型,提出了基于马尔科夫链蒙特卡洛模拟[28]的MR-EH-IESs可靠性评估方法,具体步骤如下:
1)输入MR-EH-IESs的运行参数及设备参数等,设定一年的模拟天数Nd、最大模拟年限Ny,max和缺供能量期望方差系数的收敛阈值Kmin。
2)基于多状态氢能设备可靠性模型和两状态电力设备可靠性模型,通过马尔科夫链蒙特卡洛法抽样模拟系统运行周期内每小时的设备运行状态。
3)令模拟天数d =1、模拟年数y =1和运行时刻t =1。
4)获取第y年第d天第t时的系统运行状态,求解第2节所提计及氢能交互的MR-EH-IESs最优负荷削减模型,得到第d天每个时段的最优负荷削减状态与削减量以及系统运行结果。
5)令t=t+1。若t>24,转向步骤6;否则返回步骤4。
6)令d=d+1。若d>Nd,转向步骤7;否则返回步骤4。
7)令y=y+1。若y>Ny,max或缺供能量期望方差系数K<Kmin,转向步骤8;否则令d =1,返回步骤4。
8)计算并输出MR-EH-IESs可靠性评估指标。
本节基于我国某城市的三个区域配电网构建了MR-EH-IESs进行仿真分析,以验证所提计及氢能交互的MR-EH-IESs可靠性评估方法的有效性及所提策略对系统可靠性的提升作用。该MR-EH-IESs的拓扑结构如附图1所示,各R-EH-IESs的加氢站设备配置方案和分布式电源配置方案见附表1、附表2,现场加氢站交通距离见附表3。三个区域内各配置了2、1、1辆HTT,区域间配置1辆HTT,容量均为250 kg。
碱性电解槽运行模型的参数详见文献[29-30],其与储氢罐的安全运行范围为20%~100%的额定容量。单台加氢机的额定容量为60 kg,工作效率ηDP为96%。在需求响应策略下,氢燃料电池汽车负荷转移比例α设为50%。在H2G模式下,计及车载燃料电池发电效率与放电器的工作效率,其氢-电转换效率ηH2G约为氢气高热值(39 kW·h/kg)的60%,即23.4 kW·h/kg。所提最优负荷削减模型中各项成本参数见附表4[23, 31-33]。MR-EH-IES中各类型设备的可靠性参数见附表5[5,31,34-37]。马尔科夫链蒙特卡洛模拟抽样方法中的最大模拟年限Ny,max和缺供能量期望方差系数的收敛阈值Kmin分别设置为20 000年和0.05。
为了说明本文所提MR-EH-IESs协同运行机制的优势,设置了如下三种仿真方案进行对比分析。
Case 1:各R-EH-IESs仅考虑区域内供氢网灵活运行,区域间不进行能量交互。
Case 2:各R-EH-IESs考虑区域内供氢网灵活运行,区域间仅通过电力联络线进行电能交互[38]。
Case 3:本文方法,考虑所提协同运行机制,即各R-EH-IESs不仅考虑区域内供氢网灵活运行,区域间还通过电力联络线路和HTT进行电氢能量交互。
基于上述三种仿真方案对4.1节构建的算例进行可靠性评估,该MR-EH-IESs的可靠性评估指标计算结果见表1。
表1 不同仿真方案下MR-EH-IESs的可靠性评估指标
Tab.1 Reliability evaluation indexes of the MR-EH-IESs under Cases 1~3

评估指标Case 1Case 2Case 3 LOELP0.003 40.003 10.003 0 LOELE/(h/年)29.3927.0926.15
(续)
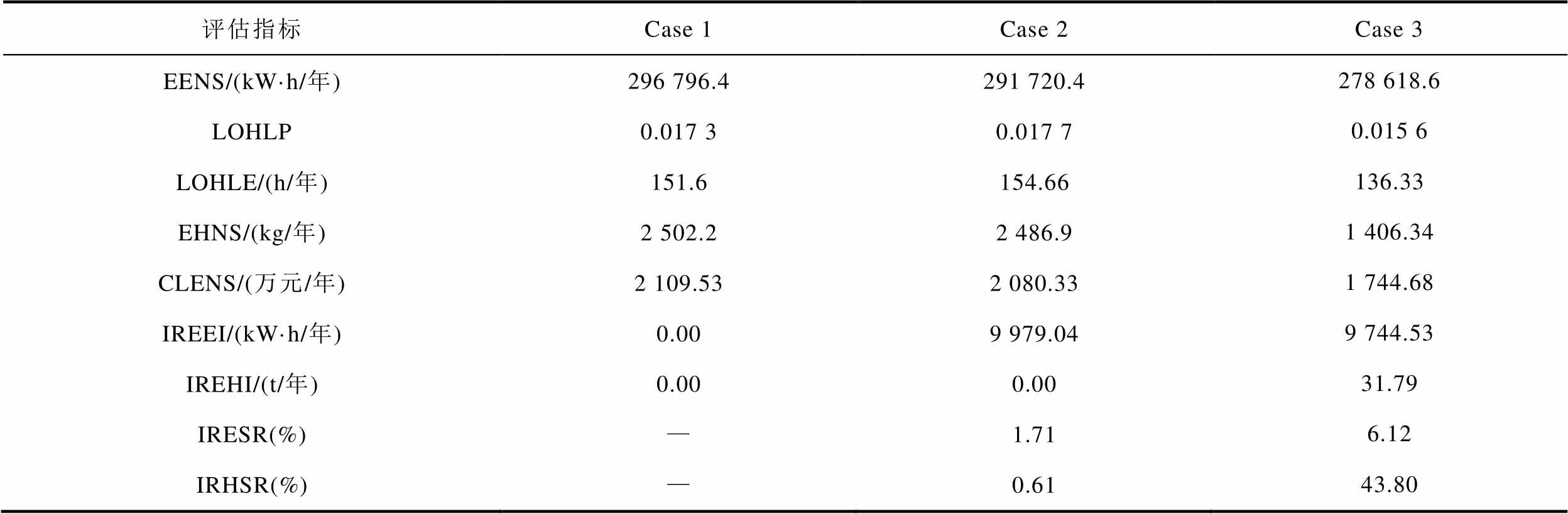
评估指标Case 1Case 2Case 3 EENS/(kW·h/年)296 796.4291 720.4278 618.6 LOHLP0.017 30.017 70.015 6 LOHLE/(h/年)151.6154.66136.33 EHNS/(kg/年)2 502.22 486.91 406.34 CLENS/(万元/年)2 109.532 080.331 744.68 IREEI/(kW·h/年)0.009 979.049 744.53 IREHI/(t/年)0.000.0031.79 IRESR(%)—1.716.12 IRHSR(%)—0.6143.80
从表1可见,由于Case 2考虑了不同区域配电网间通过电力联络线互联以提供电能支撑,整个MR-EH-IESs的区域交互电量期望IREEI达到 9 979.04 kW·h/年,其电负荷缺供能量期望EENSMR相比Case 1降低了1.71%(5 076.00 kW·h/年),即供电可靠性提升率IRESR为1.71%。在供氢可靠性方面,Case 2中整个MR-EH-IESs的氢负荷缺供能量期望EHNSMR相比Case 1仅降低了0.61%(15.3 kg/年),即供氢可靠性提升率IRHSR仅为0.61%。这是因为现场加氢站所在节点均配置有分布式电源,即使所在节点上游线路发生故障,系统将通过分布式电源优先为电解槽提供电能制氢以保障该区域的氢负荷需求。仅在部分负荷高峰时期发生线路故障时,才会通过联络线路由其他区域配电网和所在节点的分布式电源共同向该现场加氢站提供电能支撑,以保障供氢可靠性。
从表1还可以看出,在Case 3中,MR-EH-IESs的区域交互氢量期望IREHI和区域交互电量期望IREEI分别为31.79 t/年和9 744.53 kW·h/年,其供氢可靠性提升率IRHSR和供电可靠性提升率IRESR分别达到了43.80%和6.12%。相比于Case 2,Case 3中MR-EH-IESs的氢负荷缺供能量期望EHNSMR和电负荷缺供能量期望EENSMR也分别降低了43.45% (1 080.56 kg/年)和4.49%(13 101.8 kW·h/年),系统的供能可靠性水平大幅提高。主要原因分析如下:
一方面,相比于Case 2,Case 3在不同区域间通过电力联络线路进行电能交互且通过HTT进行氢能交互。在某区域供氢网内加氢站的电解槽、压缩机等设备发生故障造成供氢不足时,可通过HTT从其余供氢网内运输氢气以满足发生故障供氢网的用氢需求。以秋季典型日区域2供氢网内现场加氢站1的电解槽发生故障(00:00—24:00)为例,图3展示了Case 3中区域间HTT的运行情况,图4展示了Cases 2、3中区域2氢负荷削减情况。从图3、图4可见,在该区域仅有的电解槽发生故障的情况下,在Case 2中无法通过电力联络线路支撑电解槽进行制氢,导致区域2的EH-IESs氢负荷被大量削减;而在Case 3中,区域间HTT从其他区域的现场加氢站中将其富余氢气运输至区域2的现场加氢站内,并将部分氢气通过区域2内的HTT运往其余场外加氢站,从而大幅降低了区域2的EH-IESs氢负荷削减。
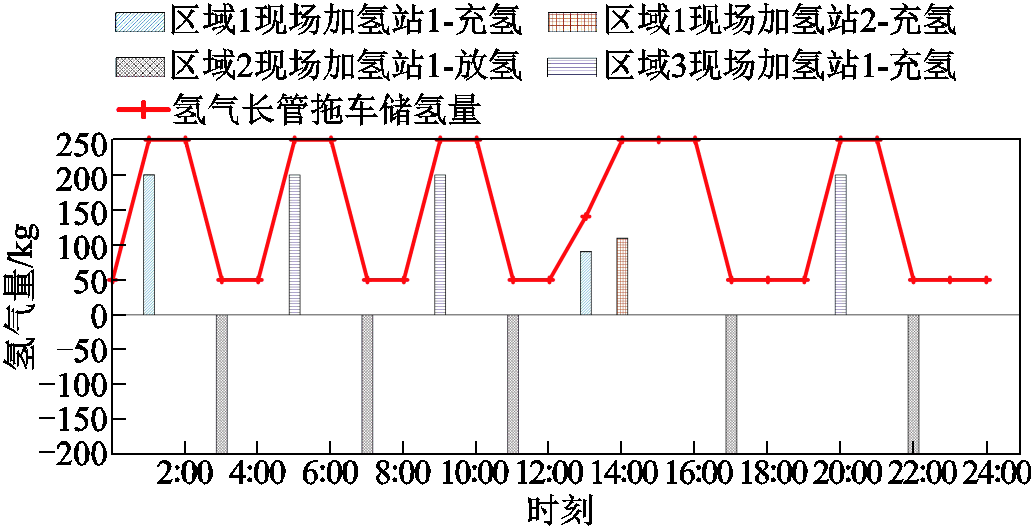
图3 电解槽故障下Case 3中区域间HTT的运行情况
Fig.3 The operation situation of the inter-regional HTT of Case 3 under the fault of electrolyzer
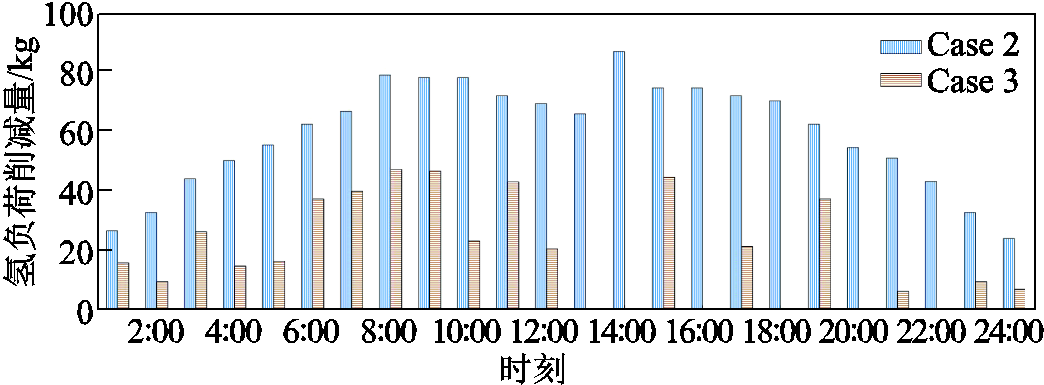
图4 电解槽故障下Cases 2、3中区域2的EH-IESs氢负荷削减量
Fig.4 The hydrogen load shedding of the EH-IES in region 2 of Cases 2, 3 under the fault of electrolyzer
另一方面,由于Case 3计及了区域间的氢能交互作用,还可以在某区域的配电网线路发生故障时,通过HTT从其他区域供氢网内运输氢气,为氢燃料电池汽车参与H2G模式提供充足的氢气支撑,进一步保障系统的可靠供电。以秋季典型日区域2配电网电力线路L61-63发生故障(12:00—17:00)为例,图5展示了Case 3下区域间HTT的运行情况,图6展示了Cases 2、3下区域2电负荷削减情况。由于故障线路下游区域没有通过电力联络线路与其余配电网进行互联,无法通过负荷转供保障供电可靠性,区域2的EH-IESs仅能通过调度聚集在场外加氢站1(节点63处)的H2G模式以保障部分负荷的供电。从图5、图6可见,相比Case 2,在Case 3中,区域间HTT从氢负荷需求较低的区域3中将富余氢气运输至区域2内,为H2G模式提供了充足的氢气支撑,有效地降低了故障时段内区域2的EH-IESs电负荷削减。
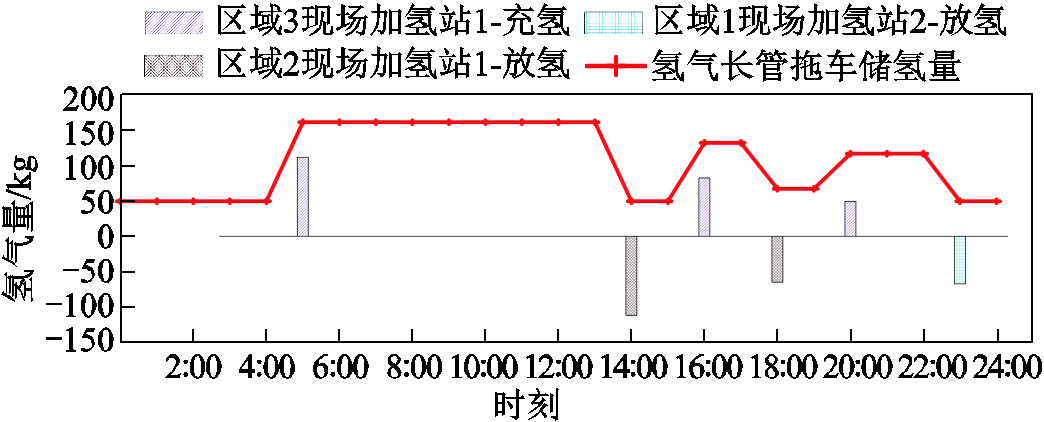
图5 线路L61-63故障下Case 3中区域间HTT的运行情况
Fig.5 The operation situation of the inter-regional HTT of Case 3 under the fault of line L61-63
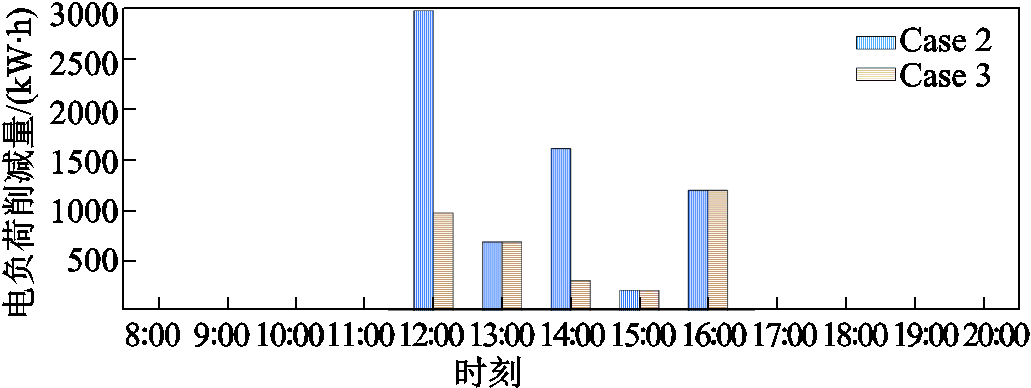
图6 线路L61-63故障下Cases 2、3中区域2的EH-IESs电负荷削减量
Fig.6 The power load shedding of the EH-IES in region 2 of Cases 2, 3 under the fault of line L61-63
综上所述,本文所提协同运行机制能够利用不同区域供能资源和用能需求的差异特性,通过区域间氢能交互通道与区域内供氢网灵活运行机制协调配合,有效提升MR-EH-IESs的供能可靠性水平。
不同仿真方案下MR-EH-IESs的年经济成本期望见表2。
表2 不同仿真方案下MR-EH-IESs的年经济成本期望
Tab.2 Annual economic cost expectations of the MR-EH-IES under Cases 1~3 (单位:万元/年)

经济成本项Case 1Case 2Case 3 年购电成本期望51 774.0251 774.3951 741.10 年弃风光惩罚成本期望0.000.000.00 年电负荷削减惩罚成本期望1 483.981 458.601 393.09 年氢负荷削减惩罚成本期望625.55621.72351.58 年需求响应成本期望0.870.901.71 年H2G成本期望4.674.5110.41 年HTT运行成本期望(区域内)339.82339.81340.17 年HTT运行成本期望(区域间)0.000.0014.94 年总运行成本期望54 228.9154 199.9453 853.01
从表2可见,虽然Case 2通过电力联络线路提升了系统的供电可靠性水平,导致其年购电成本期望相比Case 1有所增加,但其年电负荷、氢负荷削减惩罚成本期望均略有降低,其年总运行成本期望相比Case 1降低了0.05%(28.97万元/年)。由于灵活资源得到了充分利用,Case 3的年需求响应成本期望、年H2G成本期望以及区域内、区域间HTT的年运行成本期望相比Case 2均有所增加。但Case 3的年电负荷、氢负荷削减惩罚成本期望相比Case 2分别降低了4.49%(65.51万元/年)和43.45%(270.14万元/年)。同时,在峰谷电价的背景下, Case 3能够利用不同区域供能资源和用能需求的差异特性,合理安排不同区域现场加氢站的购电制氢时段以及区域间氢气的运输方案,使其年购电成本期望相比Case 2也降低了0.06%(33.29万元/年)。最终,Case 3的年总运行成本期望相比Case 2降低了0.64%(346.93万元/年)。
综上所述,本文所提协同运行机制能够充分利用不同区域供能资源和用能需求的差异特性,通过区域间的氢能交互通道有效降低系统的总运行成本,保障MR-EH-IESs的经济运行水平,对促进MR-EH-IESs间能源的互补互济,实现能源系统的低碳安全转型等具有重要意义。
为了进一步探究氢能交互对MR-EH-IESs可靠性的影响,本节设置了不同的单位氢负荷削减惩罚成本和不同的区域间HTT容量,并基于4.2节设置的仿真方案Case 3对算例进行可靠性评估。
4.4.1 单位氢负荷削减惩罚成本对系统可靠性的影响分析
从2.1节建立的最优负荷削减模型的目标函数可见,系统运行总成本取决于负荷削减惩罚成本和维持系统运行的购能成本。因此,为了分析单位氢负荷削减惩罚成本对系统运行影响,本节以2 500元/kg为单位氢负荷削减惩罚成本的基值,计算不同单位氢负荷削减惩罚成本下仿真方案Case 3的电、氢负荷削减量及系统总运行成本,如图7所示。
从图7可以看出,随着单位氢负荷削减惩罚成本的不断增加,系统运行总成本也不断提高;当单位氢负荷削减惩罚成本小于基值时,通过增大单位氢负荷削减惩罚成本可以明显降低负荷削减量,提升系统供能可靠性水平;当单位氢负荷削减惩罚成本大于等于基值时,增大单位氢负荷削减惩罚成本并不能大幅减小负荷削减量。可见,在本文设置的单位氢负荷削减惩罚成本基值附近,系统供能可靠性及经济性达到相对平衡,此时继续增加单位氢负荷削减惩罚成本并不能明显提升系统供能可靠性。

图7 不同单位氢负荷削减惩罚成本下系统的缺供能量期望和运行总成本
Fig.7 The expected energy not supply and total operating cost of the system under different unit penalty cost of hydrogen load shedding
此外,在单位氢负荷削减惩罚成本小于基值时,随着单位氢负荷削减惩罚成本的逐步降低,系统将尽可能选择削减氢负荷以减少电负荷的削减。由此可知,合理设定单位氢负荷削减惩罚成本,将对平衡系统的异质能源供给可靠性水平及系统运行经济性水平至关重要。
4.4.2 区域间HTT容量对系统可靠性的影响分析
为分析区域间氢能交互通道对MR-EH-IESs可靠性的影响,设置不同的区域间HTT容量,并以系统可靠性指标的变化率作为效益,计算仿真方案Case 3的成本效益。不同区域间HTT容量的年经济成本期望见表3,不同区域间HTT容量下MR-EH-IESs的可靠性水平如图8所示。
表3 不同区域间HTT容量的年经济成本期望
Tab.3 Annual economic cost expectations for different inter-regional HTT capacity
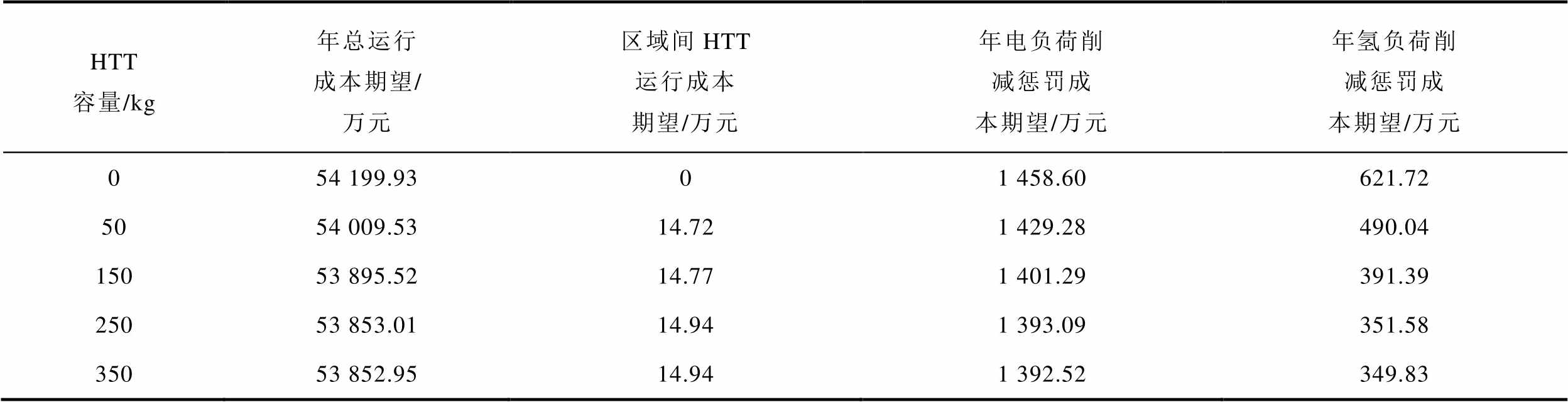
HTT容量/kg年总运行成本期望/万元区域间HTT运行成本期望/万元年电负荷削减惩罚成本期望/万元年氢负荷削减惩罚成本期望/万元 054 199.9301 458.60621.72 5054 009.5314.721 429.28490.04 15053 895.5214.771 401.29391.39 25053 853.0114.941 393.09351.58 35053 852.9514.941 392.52349.83
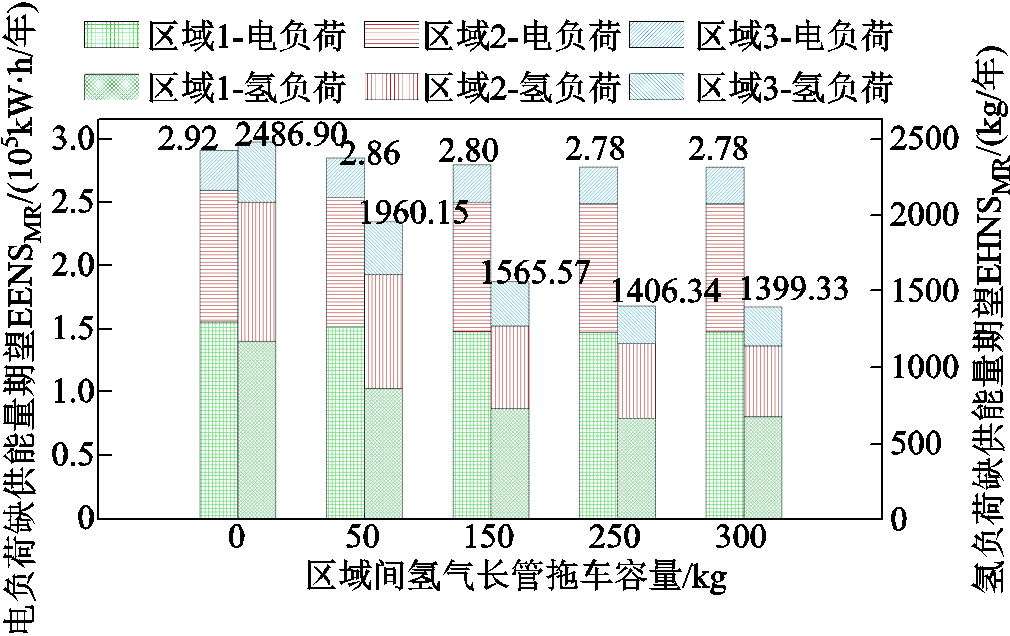
图8 不同区域间HTT容量下MR-EH-IESs的可靠性水平
Fig.8 Reliability levels of theMR-EH-IES under different capacity of the inter-regional HTT
从表3可见,当区域间HTT容量不超过250 kg时,随着容量的不断增加,MR-EH-IESs的年总运行成本期望和年电、氢负荷削减惩罚成本期望均有一定下降,而区域间HTT运行成本期望增加。相比 50 kg和150 kg的容量,当区域间HTT容量为 250 kg时,MR-EH-IESs的年总运行成本期望分别降低了0.29%(156.52万元/年)和0.08%(42.50万元/年),区域间HTT运行成本期望分别增加了1.55%(0.23万元/年)和1.17%(0.17万元/年)。当区域间HTT容量达到350 kg时,系统运行成本已基本不再发生变化。
从图8可见,当区域间HTT容量不超过250 kg时,随着容量的不断增加,不同区域间互相提供氢能支撑的作用也在不断增加,各R-EH-IESs的供电、供氢可靠性水平均有一定提升,但提升幅度也在逐渐变小。相比50 kg和150 kg的容量,当区域间HTT容量为250 kg时,MR-EH-IESs的电负荷缺供能量期望EENSMR分别降低了2.53%(7 237.47 kW·h/年)和0.59%(1 639.74 kW·h/年),氢负荷缺供能量期望EHNSMR分别降低了28.25%(553.81 kg/年)和10.17%(159.23 kg/年),即效益提升。当区域间HTT容量达到350 kg时,系统供电、供氢可靠性水平已基本不再发生变化。
由此可见,增加区域间HTT的容量对MR-EH-IESs的成本效益具有一定的积极影响,即系统总运行成本下降、供能可靠性水平提高,效益提升。但当区域间HTT容量增加到一定容量时,受限于各区域内的供用能情况,不同区域间互相提供氢能支撑的作用将达到上限,即不再对系统效益起到提升作用。
本文提出MR-EH-IESs的协同运行机制及其运行模型,建立计及氢能交互的MR-EH-IESs最优负荷削减模型,提出MR-EH-IESs可靠性评估指标和可靠性评估方法。基于测试系统验证了所提方法的有效性和对系统供能可靠性的提升作用,并得到如下结论:
1)所提方法能够充分利用不同区域供能资源和用能需求的差异特性,通过区域间氢能交互通道与区域内供氢网灵活运行机制的协调配合,有效提升MR-EH-IESs的供能可靠性水平。
2)所提方法能够有效降低系统总运行成本,并且合理设置单位氢负荷削减惩罚成本有利于保障MR-EH-IESs的可靠性水平和经济运行水平。
3)增加区域间HTT的容量对提升MR-EH-IESs可靠性具有一定的积极作用,但受限于各区域的供用能情况。
附 录
1. 模型线性化的相关说明
基于Big-M法[26],引入辅助变量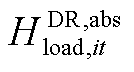 以及二进制变量
以及二进制变量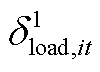 和
和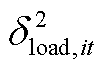 来代替
来代替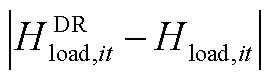 ,即将式(30)转换为式(A1),式(A1)是一个不含绝对值项的线性模型。
,即将式(30)转换为式(A1),式(A1)是一个不含绝对值项的线性模型。
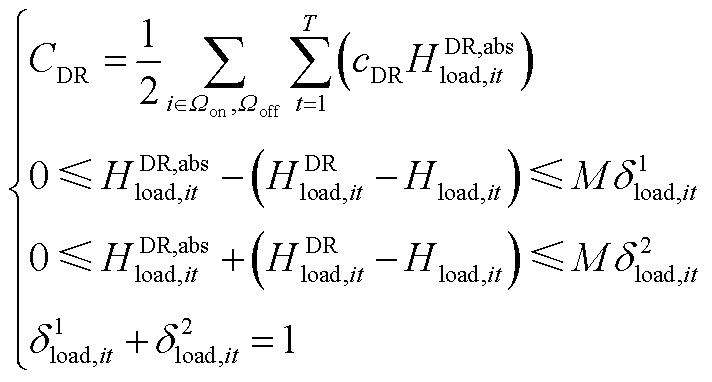 (A1)
(A1)
式中,M为一个较大的常数。
基于分段线性化方法[27],本文将式(49)中的非线性函数f(PAEL,it)转换为式(A2),式(A2)为一个由Np个线性段组合而成的线性模型。
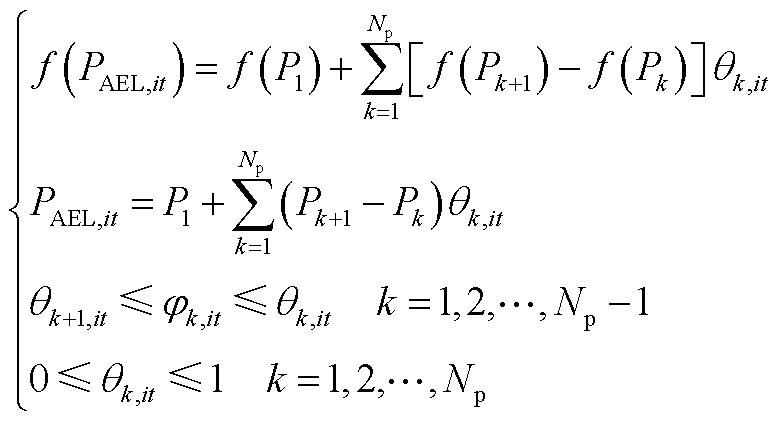 (A2)
(A2)
式中,Pk为第k个分段点;θk,it、φk,it均为辅助变量。
2. MR-EH-IESs的拓扑结构
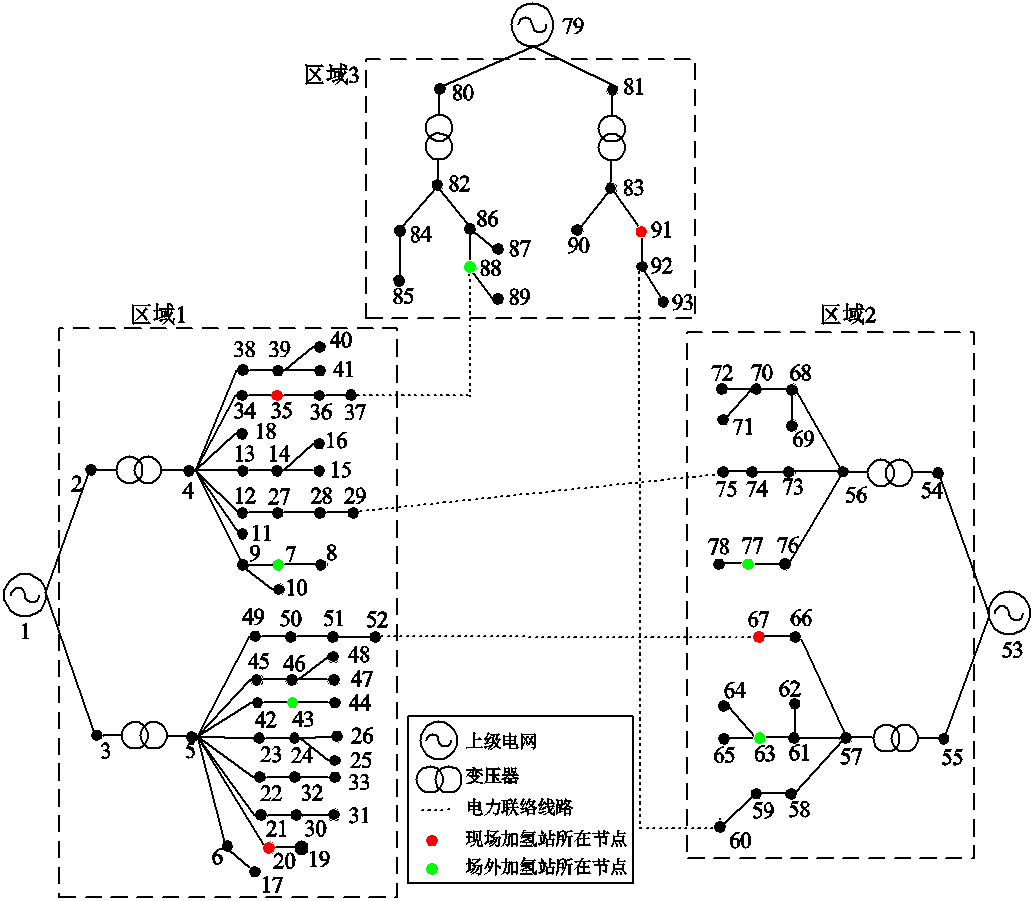
附图1 MR-EH-IESs的拓扑结构
App.Fig.1 The topology network of the MR-EH-IES
3. 仿真算例的相关数据
附表1 各R-EH-IESs的加氢站设备配置方案
App.Tab.1 Equipment configuration schemes of hydrogen refueling stations of R-EH-IESs
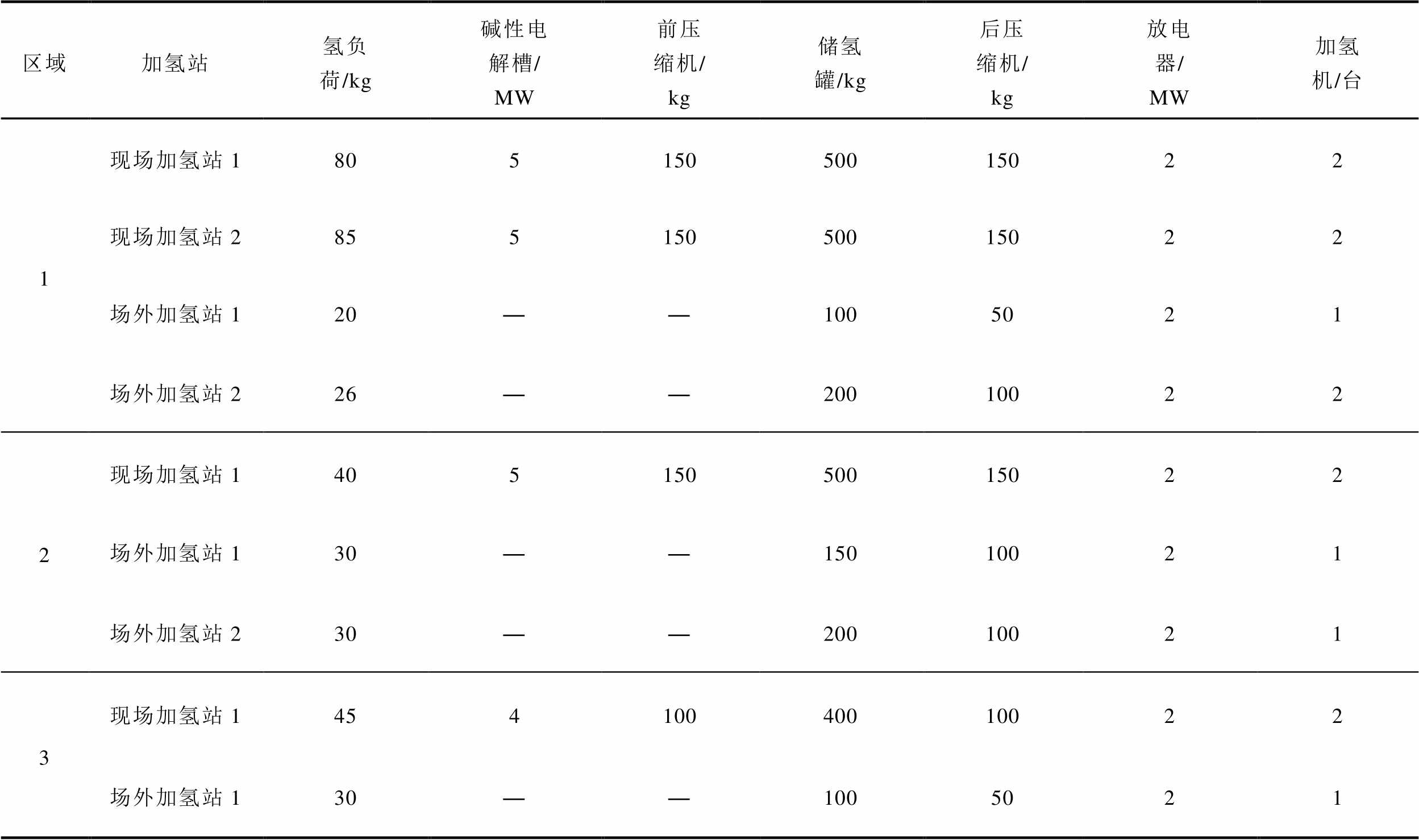
区域加氢站氢负荷/kg碱性电解槽/ MW前压缩机/ kg储氢罐/kg后压缩机/ kg放电器/ MW加氢机/台 1现场加氢站180515050015022 现场加氢站285515050015022 场外加氢站120——1005021 场外加氢站226——20010022 2现场加氢站140515050015022 场外加氢站130——15010021 场外加氢站230——20010021 3现场加氢站145410040010022 场外加氢站130——1005021
附表2 各R-EH-IESs的分布式电源配置方案
App.Tab.2 Configuration schemes of distribution generators of R-EH-IESs

区域节点编号风电机组/kW光伏机组/kg 1201 5002 000
(续)

区域节点编号风电机组/kW光伏机组/kg 2351 5002 000 3671 0001 000 4911 5002 000
附表3 现场加氢站的交通距离
App.Tab.3 Distance to on-site hydrogen refueling stations (单位:km)

距离节点20节点35节点67节点91 节点20155050 节点35157550 节点67507550 节点91505050
附表4 所提模型的成本参数[22,31-33]
App.Tab.4 Cost parameters of the proposed model[22,31-33]

参数数值 cDG /(元/(kW·h)]0.35 cp/(元/(kW·h)]50 ch/(元/kg)2 500 cDR/(元/kg)6.2 cH2G/(元/kg)85.2 cHTT/(元/kg)4.7
附表5 设备的可靠性参数[5,31,34-37]
App.Tab.5 Reliability parameters of equipment[5,31,34-37]
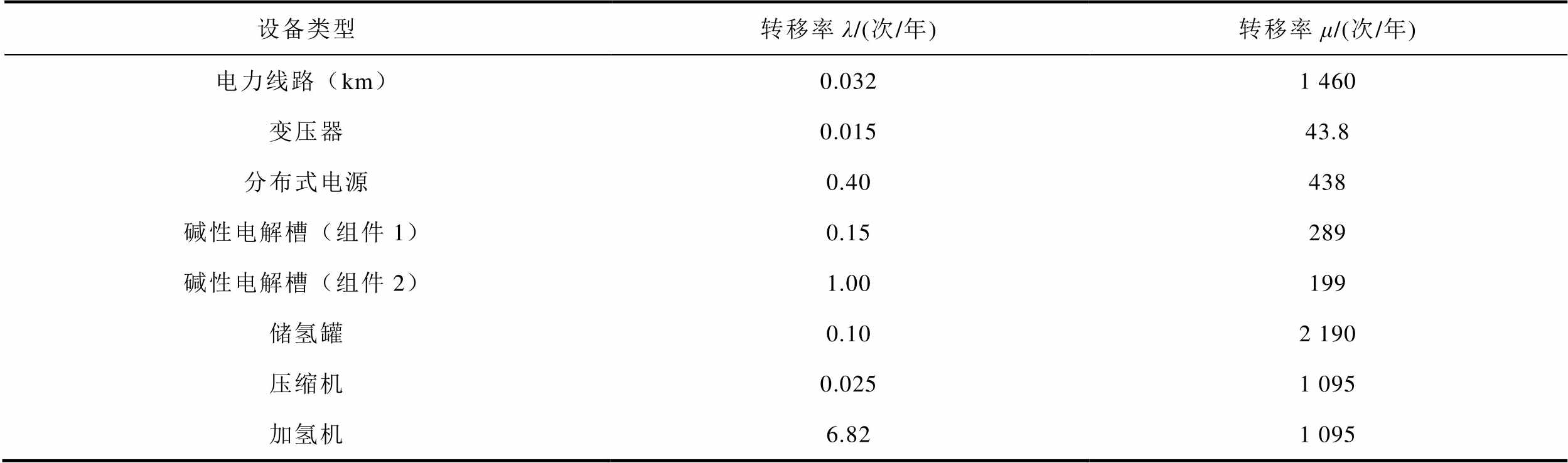
设备类型转移率λ/(次/年)转移率μ/(次/年) 电力线路(km)0.0321 460 变压器0.01543.8 分布式电源0.40438 碱性电解槽(组件1)0.15289 碱性电解槽(组件2)1.00199 储氢罐0.102 190 压缩机0.0251 095 加氢机6.821 095
参考文献
[1] 黄文涛, 邓明辉, 葛磊蛟, 等. 考虑配电网与氢燃料汽车耦合影响的制氢加氢站布点优化策略[J]. 高电压技术, 2023, 49(1): 105-117.
Huang Wentao, Deng Minghui, Ge Leijiao, et al. Layout optimization strategy of hydrogen production and refueling stations considering the coupling effect of distribution network and hydrogen fuel vehicles[J]. High Voltage Engineering, 2023, 49(1): 105-117.
[2] Sun Guangzeng, Li Gengyin, Li Panpan, et al. Coordinated operation of hydrogen-integrated urban transportation and power distribution networks considering fuel cell electric vehicles[J]. IEEE Transactions on Industry Applications, 2022, 58(2): 2652-2665.
[3] Ogbonnaya C, Abeykoon C, Nasser A, et al. Engineering risk assessment of photovoltaic-thermal-fuel cell system using classical failure modes, effects and criticality analyses[J]. Cleaner Environmental Systems, 2021, 2: 100021.
[4] Zheng Wendi, Li Yixin, Zhang Min, et al. Reliability evaluation and analysis for NEV charging station considering the impact of charging experience[J]. International Journal of Hydrogen Energy, 2022, 47(6): 3980-3993.
[5] 岳大为, 袁行行, 赵文体, 等. 含电-氢系统的孤岛型交直流混合微电网可靠性评估[J]. 高电压技术, 2021, 47(11): 4002-4012.
Yue Dawei, Yuan Hanghang, Zhao Wenti, et al. Reliability evaluation of islanded AC/DC hybrid microgrid with electricity-hydrogen system[J]. High Voltage Engineering, 2021, 47(11): 4002-4012.
[6] 任洲洋, 王皓, 李文沅, 等. 基于氢能设备多状态模型的电氢区域综合能源系统可靠性评估[J]. 电工技术学报, 2023, 38(24): 6744-6759.
Ren Zhouyang, Wang Hao, Li Wenyuan, et al. Reliability evaluation of electricity-hydrogen regional integrated energy systems based on the multi-state models of hydrogen energy equipment[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6744-6759.
[7] 袁铁江, 孙传帅, 谭捷, 等. 考虑氢负荷的新型电力系统电源规划[J]. 中国电机工程学报, 2022, 42(17): 6316-6326.
Yuan Tiejiang, Sun Chuanshuai, Tan Jie, et al. Generation planning of new power system considering hydrogen load[J]. Proceedings of the CSEE, 2022, 42(17): 6316-6326.
[8] Nasir M, Rezaee Jordehi A, Matin S A A, et al. Optimal operation of energy hubs including parking lots for hydrogen vehicles and responsive demands[J]. Journal of Energy Storage, 2022, 50: 104630.
[9] Oldenbroek V, Wijtzes S, Blok K, et al. Fuel cell electric vehicles and hydrogen balancing 100 percent renewable and integrated national transportation and energy systems[J]. Energy Conversion and Management: X, 2021, 9: 100077.
[10] Robledo C B, Oldenbroek V, Abbruzzese F, et al. Integrating a hydrogen fuel cell electric vehicle with vehicle-to-grid technology, photovoltaic power and a residential building[J]. Applied Energy, 2018, 215: 615-629.
[11] Dou Xun, Wang Jun, Fan Donglou, et al. Interaction mechanism and pricing strategy of hydrogen fueling station for hydrogen-integrated transportation and power systems[J]. IEEE Transactions on Industry Applications, 2022, 58(2): 2941-2949.
[12] Ban Mingfei, Bai Wenchao, Song Wenlong, et al. Optimal scheduling for integrated energy-mobility systems based on renewable-to-hydrogen stations and tank truck fleets[J]. IEEE Transactions on Industry Applications, 2022, 58(2): 2666-2676.
[13] 刁涵彬, 李培强, 王继飞, 等. 考虑电/热储能互补协调的综合能源系统优化调度[J]. 电工技术学报, 2020, 35(21): 4532-4543.
Diao Hanbin, Li Peiqiang, Wang Jifei, et al. Optimal dispatch of integrated energy system considering complementary coordination of electric/thermal energy storage[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4532-4543..
[14] Haggi H, Sun Wei, Fenton J M, et al. Proactive rolling-horizon-based scheduling of hydrogen systems for resilient power grids[J]. IEEE Transactions on Industry Applications, 2022, 58(2): 1737-1746.
[15] 张亚超, 谢仕炜, 朱蜀. 多区域互联电-气耦合系统分散协调分布鲁棒优化调度[J]. 电力系统自动化, 2022, 46(19): 31-42.
Zhang Yachao, Xie Shiwei, Zhu Shu. Decentralized coordinated distributionally robust optimal scheduling of multi-area interconnected electricity-gas coupling system[J]. Automation of Electric Power Systems, 2022, 46(19): 31-42.
[16] 李晓露, 单福州, 宋燕敏, 等. 考虑热网约束和碳交易的多区域综合能源系统优化调度[J]. 电力系统自动化, 2019, 43(19): 52-59, 131. Li Xiaolu, Shan Fuzhou, Song Yanmin, et al. Optimal dispatch of multi-region integrated energy systems considering heating network constraints and carbon trading[J]. Automation of Electric Power Systems, 2019, 43(19): 52-59, 131.
[17] Zhang Xiaping, Shahidehpour M, Alabdulwahab A, et al. Optimal expansion planning of energy hub with multiple energy infrastructures[J]. IEEE Transactions on Smart Grid, 2015, 6(5): 2302-2311.
[18] Tabandeh A, Hossain M J, Li Li. Integrated multi-stage and multi-zone distribution network expansion planning with renewable energy sources and hydrogen refuelling stations for fuel cell vehicles[J]. Applied Energy, 2022, 319: 119242.
[19] He Yingdong, Zhou Yuekuan, Liu Jia, et al. An inter-city energy migration framework for regional energy balance through daily commuting fuel-cell vehicles[J]. Applied Energy, 2022, 324: 119714.
[20] Zhao Yuxuan, Lin Jin, Song Yonghua, et al. A hierarchical strategy for restorative self-healing of hydrogen-penetrated distribution systems considering energy sharing via mobile resources[J]. IEEE Transactions on Power Systems, 2023, 38(2): 1388-1404.
[21] Baran M E, Wu F F. Network reconfiguration in distribution systems for loss reduction and load balancing[J]. IEEE Transactions on Power Delivery, 1989, 4(2): 1401-1407.
[22] Wang Hao, Ren Zhouyang, Gao Liping, et al. A four-terminal interconnected topology and its application in distribution network expansion planning[J]. International Journal of Electrical Power & Energy Systems, 2022, 141: 108177.
[23] Kou Yu, Bie Zhaohong, Li Gengfeng, et al. Reliability evaluation of multi-agent integrated energy systems with fully distributed communication[J]. Energy, 2021, 224: 120123.
[24] 李健强, 余光正, 汤波, 等. 考虑风光利用率和含氢能流的多能流综合能源系统规划[J]. 电力系统保护与控制, 2021, 49(14): 11-20.
Li Jianqiang, Yu Guangzheng, Tang Bo, et al. Multi-energy flow integrated energy system planning considering wind and solar utilization and containing hydrogen energy flow[J]. Power System Protection and Control, 2021, 49(14): 11-20.
[25] Wang Yifei, Huang Zhiheng, Shahidehpour M, et al. Reconfigurable distribution network for managing transactive energy in a multi-microgrid system[J]. IEEE Transactions on Smart Grid, 2020, 11(2): 1286-1295.
[26] 姜云鹏, 任洲洋, 李秋燕, 等. 考虑多灵活性资源协调调度的配电网新能源消纳策略[J]. 电工技术学报, 2022, 37(7): 1820-1835.
Jiang Yunpeng, Ren Zhouyang, Li Qiuyan, et al. An accommodation strategy for renewable energy in distribution network considering coordinated dispatching of multi-flexible resources[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1820-1835.
[27] Cheng Yaohua, Zhang Ning, Zhang Baosen, et al. Low-carbon operation of multiple energy systems based on energy-carbon integrated prices[J]. IEEE Transactions on Smart Grid, 2020, 11(2): 1307-1318.
[28] Chao Huawei, Hu Bo, Xie Kaigui, et al. A sequential MCMC model for reliability evaluation of offshore wind farms considering severe weather conditions[J]. IEEE Access, 1009, 7: 132552-132562.
[29] Abdelkafi A, Krichen L. Energy management optimization of a hybrid power production unit based renewable energies[J]. International Journal of Electrical Power & Energy Systems, 2014, 62: 1-9.
[30] 余娟, 时权妍, 杨知方, 等. 考虑电解水与甲烷化运行特性的电转气系统日前调度方法[J]. 电力系统自动化, 2019, 43(18): 18-25.
Yu Juan, Shi Quanyan, Yang Zhifang, et al. Day-ahead scheduling method of power-to-gas system considering operation characteristics of water electrolysis and methanation[J]. Automation of Electric Power Systems, 2019, 43(18): 18-25.
[31] 路红池, 谢开贵, 王学斌, 等. 计及多能存储和综合需求响应的多能源系统可靠性评估[J]. 电力自动化设备, 2019, 39(8): 72-78.
Lu Hongchi, Xie Kaigui, Wang Xuebin, et al. Reliability assessment of multi-energy system considering multi-storage and integrated demand response[J]. Electric Power Automation Equipment, 2019, 39(8): 72-78.
[32] 孙传帅. 计及氢负荷的电源规划研究[D]. 大连: 大连理工大学, 2021.
Sun Chuanshuai. Research on generation expansion planning considering hydrogen load[D]. Dalian: Dalian University of Technology, 2021.
[33] 光大证券. 加氢网络是普及氢能应用的基础——燃料电池行业深度报告(二)[EB/OL]. [2019-05-16]. https://pdf.dfcfw.com/pdf/H3_AP201905171330754548_1.pdf?1559747268000. pdf.
[34] 张雪寒, 余涛. 计及风速与负荷相关性的电-气互联系统概率可靠性评估方法[J]. 高电压技术, 2019, 45(10): 3263-3272.
Zhang Xuehan, Yu Tao. Probabilistic reliability evaluation method of electricity-gas integrated energy system considering correlation of wind speeds and loads[J]. High Voltage Engineering, 2019, 45(10): 3263-3272.
[35] Kurtz J, Sprik S, Peters M, et al. Retail hydrogen station reliability status and advances[J]. Reliability Engineering & System Safety, 2020: 106823.
[36] 李崇阳. 配电网-天然气互联系统可靠性评估模型研究[D]. 重庆: 重庆大学, 2018.
Li Chongyang. Research on reliability evalution model of electrical distribution and natural gas interconnected system[D]. Chongqing: Chongqing University, 2018.
[37] 王澜灵, 刘俊勇, 许立雄, 等. 计及实时需求响应的综合能源信息物理系统可靠性分析[J]. 电力建设, 2020, 41(12): 23-38. Wang Lanling, Liu Junyong, Xu Lixiong, et al. Reliability analysis of integrated energy cyber physical system considering real-time demand response[J]. Electric Power Construction, 2020, 41(12): 23-38.
[38] 侯恺, 林主成, 贾宏杰, 等. 可靠性与经济性协调的城市配电网联络线优化规划方法[J]. 天津大学学报(自然科学与工程技术版), 2019, 52(12): 1293-1302.
Hou Kai, Rim J, Jia Hongjie, Jia Hongjie, et al. Optimal planning of urban distribution network tie-line with coordination of reliability and economics[J]. Journal of Tianjin University (Science and Technology), 2019, 52(12): 1293-1302.
Reliability Improvement Strategies of Multi-Region Electricity-Hydrogen Integrated Energy Systems Considering Hydrogen Interaction between Different Regions
Abstract The multi-regional electric-hydrogen integrated energy systems (MR-EH-IESs) formed by the regional interconnection of distribution grids and hydrogen supply networks (HSNs) can give full play to the advantages of low-carbon and flexible operation of HSNs, which is of great significance to the construction of a low-carbon and safe modern energy system.However, the existing research have not analyzed the flexibility mechanism of multi-regional HSNs and the interaction characteristics of inter-regional hydrogen on the reliable supply of electric and hydrogen loads to the system under multiple fault scenarios. And the optimal load shedding model in the existing reliability assessment cannot consider inter-regional energy interactions and multi-regional energy synergistic mechanisms. Moreover, there is a lack of effective reliability assessment indexes for MR-EH-IESs to quantify the level of reliable energy supply of the system.It means that it is not possible to provide a rational decision-making basis for the planning and construction of MR-EH-IESs. A reliability assessment method for MR-EH-IESs under hydrogen interaction is proposed, which effectively quantifies the reliability level of HSNs flexible resources for MR-EH-IESs under different fault scenarios.
Firstly, the cooperative operation mechanism and operation models of MR-EH-IESs are proposed considering the coordination between the inter-regional hydrogen interaction channels and the flexible resources of regional HSNs. Secondly, an optimal load shedding model of MR-EH-IESs considering the hydrogen interaction is established to minimize the total operation cost. Finally, the reliability evaluation indexes of MR-EH-IESs are constructed from the aspects of inter-regional energy interaction levels and their role in improving the reliability levels. A reliability evaluation method of MR-EH-IESs considering the hydrogen interaction is proposed based on Markov Chain Monte Carlo method.
The effectiveness of the proposed method is verified by simulation example analysis. The results of the simulations demonstrate that, when considering the synergistic operation mechanism, the expected inter-regional hydrogen interaction and inter-regional electricity interaction of MR-EH-IESs are 31.79 t/year and 9 744.53 kW·h/year, respectively. This leads to improvement in hydrogen supply reliability (43.80%) and electricity supply reliability (6.12%). And its total system operating cost is reduced by 3.759 million yuan/year. In essence, fully exploiting and utilizing the inter-regional hydrogen interaction can effectively improve the system energy supply reliability and operational economics.Additionally, reasonable configuring the parameters, such as the unit penalty cost of hydrogen load shedding and the capacity of inter-regional hydrogen tube trailer, can maximize the cost-effectiveness of MR-EH-IESs. And this achieving a relative balance between energy supply reliability and operational economics in MR-EH-IESs.
From the simulation results, the following conclusions can be drawn. (1) Considering the cooperative operation mechanism can make full use of the different characteristics of energy supply resources and energy demand in different regions, and effectively improve the reliability level of MR-EH-IESs through the coordination of inter-region hydrogen interaction channels and the flexible operation mechanism of intra-region HSNs. (2) Considering the cooperative operation mechanism can effectively reduce the total operation cost of the system, and the reasonable setting the unit penalty cost of hydrogen load shedding is conducive to guaranteeing the reliability level and economy level of MR-EH-IESs. (3) Increasing the capacity of inter-regional hydrogen tube trailer has a positive impact on enhancing the reliability of MR-EH-IESs, but this effect is limited by the availability and consumption of energy in each region.
keywords:Multi-region electricity-hydrogen integrated energy systems, hydrogen interaction, Markov Chain Monte Carlo, energy supply reliability
中图分类号:TM732
DOI: 10.19595/j.cnki.1000-6753.tces.230976
国家自然科学基金资助项目(52277080)。
收稿日期 2023-06-24
改稿日期 2023-12-28
蒙 军 男,1999年生,硕士研究生,研究方向为电氢综合能源系统运行、规划与可靠性评估等。
E-mail:mengjun0626@stu.cqu.edu.cn
任洲洋 男,1986年生,副教授,博士生导师,研究方向为低碳电力能源系统与人工智能等。
E-mail:rzhouyang1108@163.com(通信作者)
(编辑 赫 蕾)