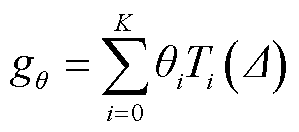（1）
式中，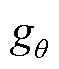
为滤波器；K为切比雪夫阶数；θi为输入特征的可学习参数之一。在T0(
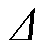)=1，T1(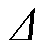)=Δ时，Δ=2Δ/λmax–Ie，Ti(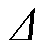)=2ΔTi-1(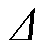)–ΔTi-2(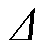)，λmax为最大特征值，Ie为单位矩阵，e=1,…,K。
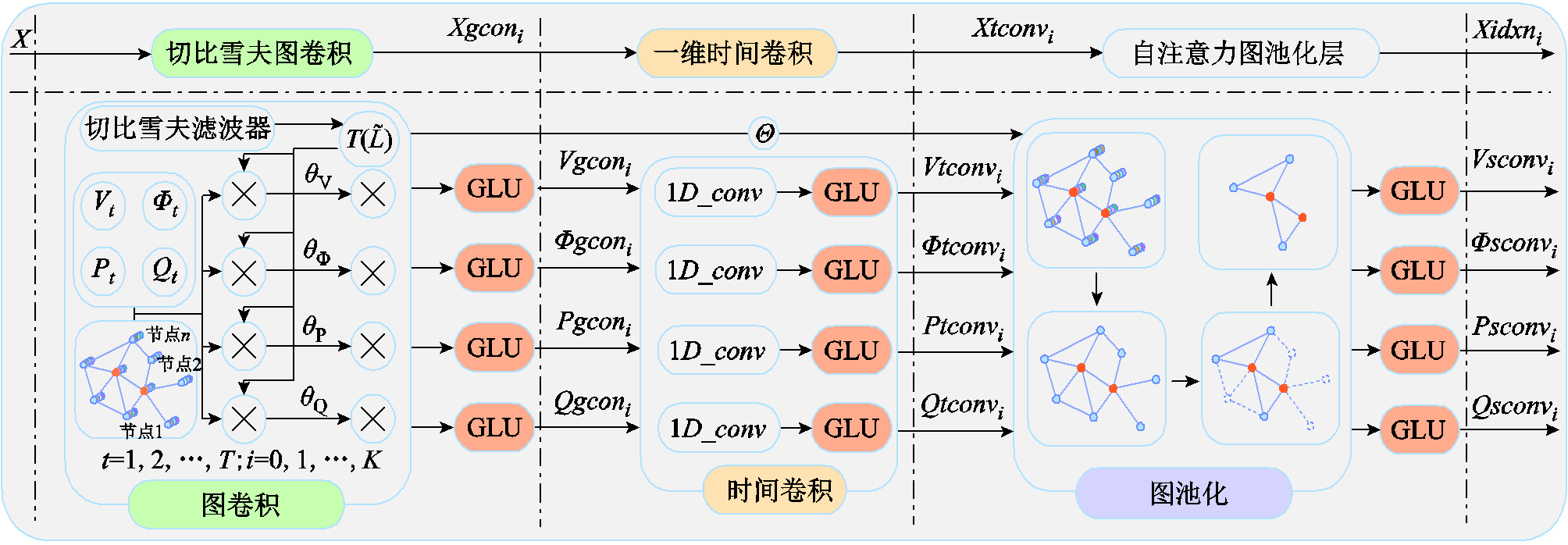
图1 STGCN模型结构
Fig.1 Improved structure of STGCN model
在一个时间步中，输入信号X与滤波器的卷积可以表示为
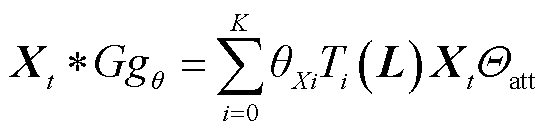（2）
式中，X为具有N个节点和F个维度的输入图， X∈RN×F；Xt为输入图的时间序列；θX为图卷积参数；
为自注意力算子；Ti(L)为切比雪夫滤波器矩阵；L为图拉普拉斯矩阵。在T0(L)=1，T1(L)=L，L=2L/λmax-Ie，L=Ie-D-1/2AD-1/2时，Ti(L)=2LTi-1(L)- Ti-2(L)，A为邻接矩阵，A∈RN×N（A = A + IN），D为图的顶点元素度矩阵，是对角矩阵，D∈RN×N。
Xt经图卷积处理后生成新数据Xgconi。随后，Xgconi中的时间信息被一维时间卷积层进一步处理。在此过程中采用收敛速度更快、精度更高的门控线性单元（Gated Linear Unit, GLU）作为激活函数[21]。因此，输入信号被进一步建模为
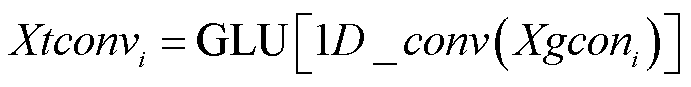（3）
式中，Xtconvi为由一维时间卷积层处理过的新数据；1D_conv为一维时间卷积层；i为时间卷积层的层数。
随后，借由引入的SAM机制，数据由基于SAM机制的SAGPooling[22]处理，该层允许模型缩小特征向量的尺寸以降低参数量来避免模型过拟合。该分层池化策略允许模型尽可能保留有价值的节点特征，并根据保留特征和变化的拓扑有效分配节点以提高模型的泛化能力与鲁棒性。同时，各节点注意力均分可被提取以进行模型的可解释性工作。对于自注意力池化层，其输出信号可以定义为
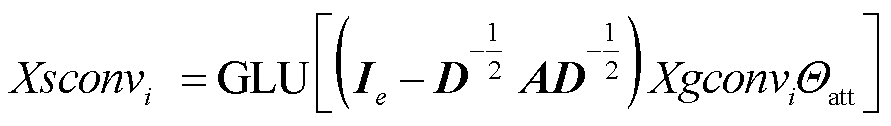（4）
式中，Xsconvi为由自注意力池化层处理过的新数据；Θatt∈RF×1。而各母线注意力得分的平均值Z由M个自注意力池化层中获得[22]，有
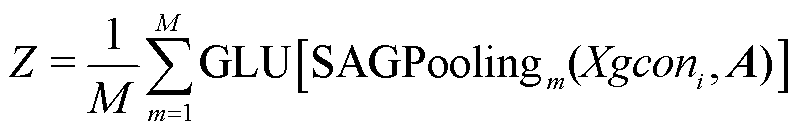（5）
式中，m为自注意力池化层的层数；M为自注意力池化层的最大层数。最后，通过系统读出层聚合各节点特征，并形成固定大小的图形表示，再由全连接层进行处理以生成预测结果。系统读出层的定义为
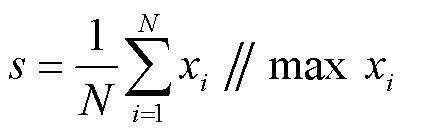（6）
式中，N为节点数；xi为第i个节点的特征向量；//表示串联。
2 基于自注意力机制时空图神经网络的频率稳定评估框架
2.1 输入数据构建
频率稳定预测是一个典型的多输入时序回归任务，并表现出一定的空间分布特征。因此，网络输入包含两部分：故障后时间特征序列和电网拓扑。电网拓扑以邻接矩阵A表征，节点导纳矩阵是A的唯一组成部分。故障后时序数据包含电压幅值（Vt）、相角（Φt）、有功功率注入（Pt）和无功功率注入（Qt）的时间序列数据[22]，定义为
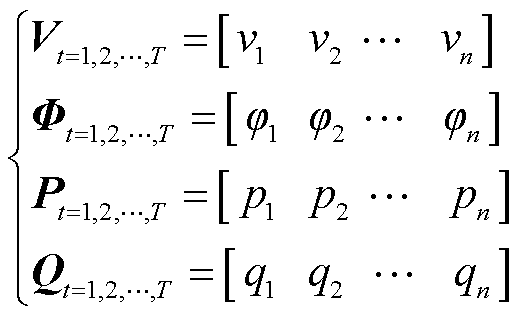（7）
式中，t = 1, 2,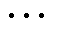
, T，T为采样点序号；n为系统节点编号。在仿真采样率为100 Hz，采样步长ft为0.01 s时，从扰动发生t0时采样，32ft时采样结束。相邻两点选取时序数据，具体输入特征说明见表1。
表1 输入特征说明
Tab.1 Description of input features
序号输入特征 1每个发电机的有功功率与无功功率 2每个发电机的电压幅值 3每条母线的电压幅值与相角 4每条母线的有功功率与无功功率 5每条线路流过的有功功率与无功功率
而系统拓扑邻接矩阵A为
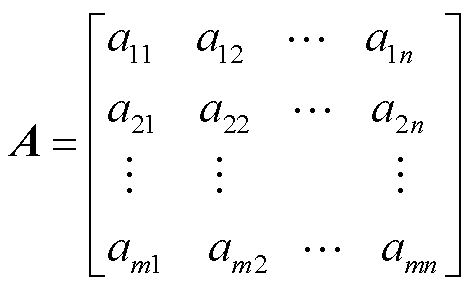（8）
式中，A为反映系统拓扑的邻接矩阵。当m与n节点之间有传输线时，a为这条线的导纳；反之a为无穷大。
2.2 样本生成
采用STGCN模型在修改后的新英格兰39节点系统和修改后的ACTIVSg500节点系统上进行了测试。两系统分别包含13台发电机与90台发电机，余下正文将其分别称为A、B系统。修改后的A、B系统如图2所示。A系统新增3个等效风电场40、41和42，并分别将其连接至母线2、29和39；B系统中在母线9、144、197、17、167和224新增一部分光伏电厂和风电场以替代部分同步发电机。借由调整新能源发电量实现不同渗透率。而在实际电力生产中，电力数据的采集通常会受到各种干扰，即测试所提模型的鲁棒性和适应性是必要的，因此，额外考虑两种情况：①在基本实验数据集中分别加入10、20和30 dB信噪比白高斯噪声；②在100%负荷水平且故障点不变情况下设置随机断线以生成拓扑变化样本。仿真持续60 s，有功扰动在0 s时，仿真采样率为100 Hz[22]，样本生成情况说明见表2。
图2 修改后的A、B系统
Fig.2 The modified A and B system wiring diagram
表2 样本生成情况说明
Tab.2 Description of samples generation
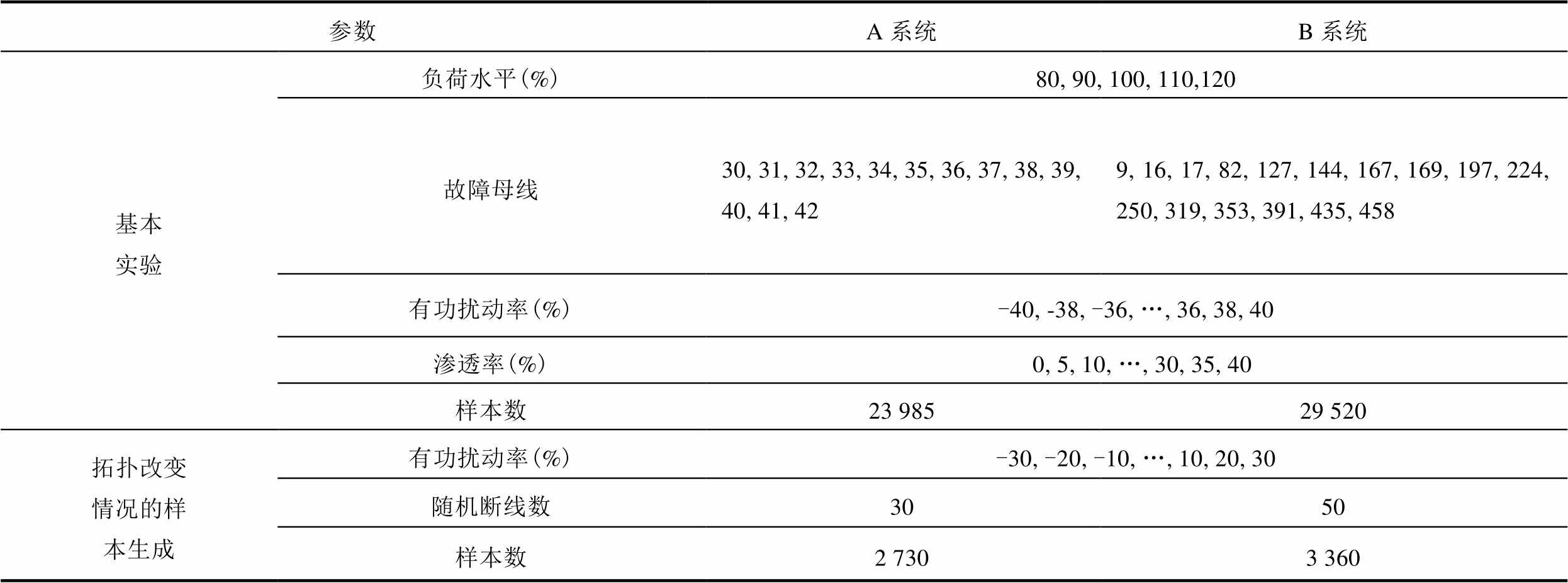
参数A系统B系统 基本实验负荷水平(%)80, 90, 100, 110,120 故障母线30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 429, 16, 17, 82, 127, 144, 167, 169, 197, 224, 250, 319, 353, 391, 435, 458 有功扰动率(%)-40, -38, -36, …, 36, 38, 40 渗透率(%) 0, 5, 10, …, 30, 35, 40 样本数23 98529 520 拓扑改变情况的样本生成有功扰动率(%)-30, -20, -10, …, 10, 20, 30 随机断线数3050 样本数2 7303 360
2.3 频率稳定指标
本文只考虑电力系统突然遭受有功功率扰动后的惯性响应和一次频率调节。采用极值频率fnadir、最大频率变化率RoCoFmax和准稳态频率f ss偏差来衡量频率稳定状态[22-23]。在扰动后的频率变化过程中，各母线频率会围绕fCOI上下波动，一般使用fCOI来表征系统频率，其定义为
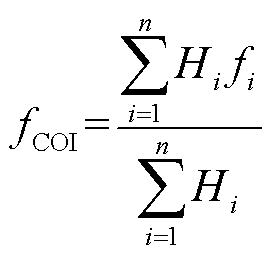（9）
式中，n为电力系统中并网发电机组数量；Hi为第i台发电机组的惯性时间常数；fi为第i台发电机组所在母线频率。
2.4 模型评价指标
为了比较测试模型的性能，本文选取平均绝对百分比误差（Mean Absolute Percentage Error, MAPE）和方均根误差（Root-Mean Squared Error, RMSE）来评价各模型的性能[24]，定义为
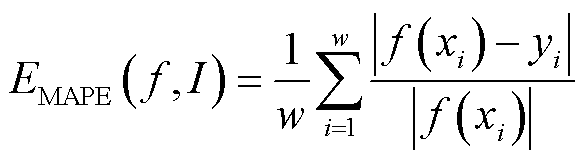（10）
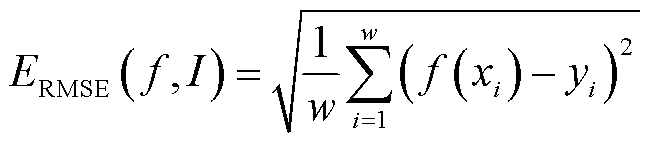（11）
式中，w为样本数量；x和y分别为样本的真实值与预测值。
模型损失函数（L2损失函数）计算公式为
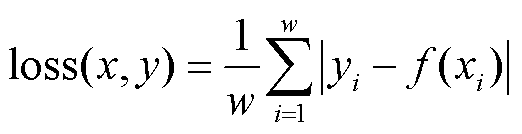（12）
2.5 模型评估流程
所提出的FSP框架包括离线训练阶段和在线预测阶段，流程如图3所示。离线训练阶段，从大量仿真样本中提取时序特征与拓扑作为输入以训练模型。当训练好的STGCN满足精度要求时，将其保存用于在线预测。在线预测阶段则保留故障后的相量测量装置或广域测量系统的测量值和对应电力系统拓扑作为输入数据。最后得到预测结果和模型可解释性分析结果。
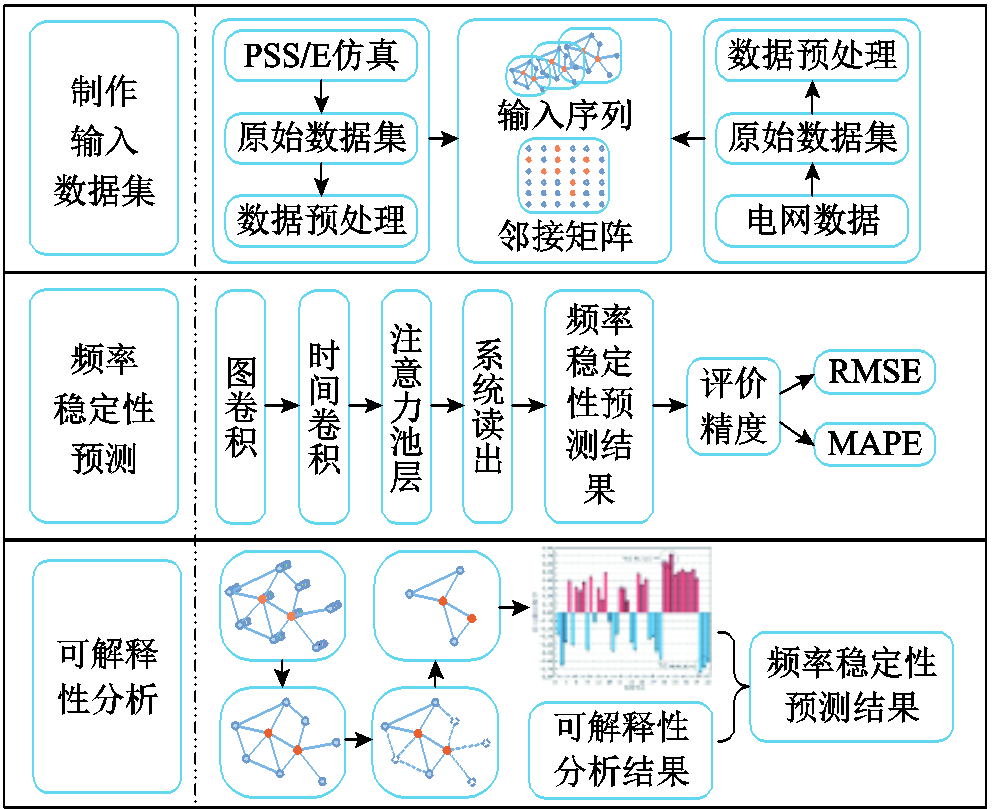
图3 模型评估流程
Fig.3 Flow chart of model evaluation
3 算例分析
仿真平台：Intel(R) Core(TM)i7-12700KF 3.61 GHzCPU、32 GB RAM和NVIDIA GeForce RTX 3070 GPU。对比算法涉及SVM、RVFL、LSTM、深度神经网络（Deep Neural Networks, DNN）、CNN、GCN、原始STGCN和自注意STGCN，所有涉及的算法都在Pytorch-v1.10.1和Scikit-earn-v1.0.2中实现。时域仿真软件为PSS/E 34。
3.1 不同环境下模型的性能比较
3.1.1 各模型有效性比较
本节对各模型的FSP有效性进行了比较，性能指标如图4所示，图中39和500分别代表对应节点系统。对于A系统，自注意STGCN的RMSE和MAPE分别为0.004 07和0.004 26，其误差指标在测试模型中最低。与STGCN相比，由于自注意力机制可以有效关注重要特征对模型的影响，因而其性能优于STGCN。GCN的性能并不理想，因其提取了系统拓扑信息，但不包含任何形式的时间信息用于模型学习。CNN和DNN的表现略差于STGCN和GCN，二者提取了系统的局部位置信息取代系统拓扑，无法准确表征电力系统空间特征。而LSTM、RVFL和SVM表现最差，因为这些模型并没有将拓扑信息纳入模型学习中。综上所述，得益于基于切比雪夫图卷积，STGCN能充分挖掘FSP的时空特征，并使该模型的整体精度优于其他方法。在B系统中的测试也有类似结论。但值得注意的是，在系统特征维度更高时，所有模型的预测误差都在增大。B系统中自注意STGCN的RMSE为0.004 38，与A系统相比增加了0.000 31，尽管如此，其误差指标仍处于各模型的最低点。因此，在复杂系统的FSP任务中，自注意STGCN具有更优越的性能。
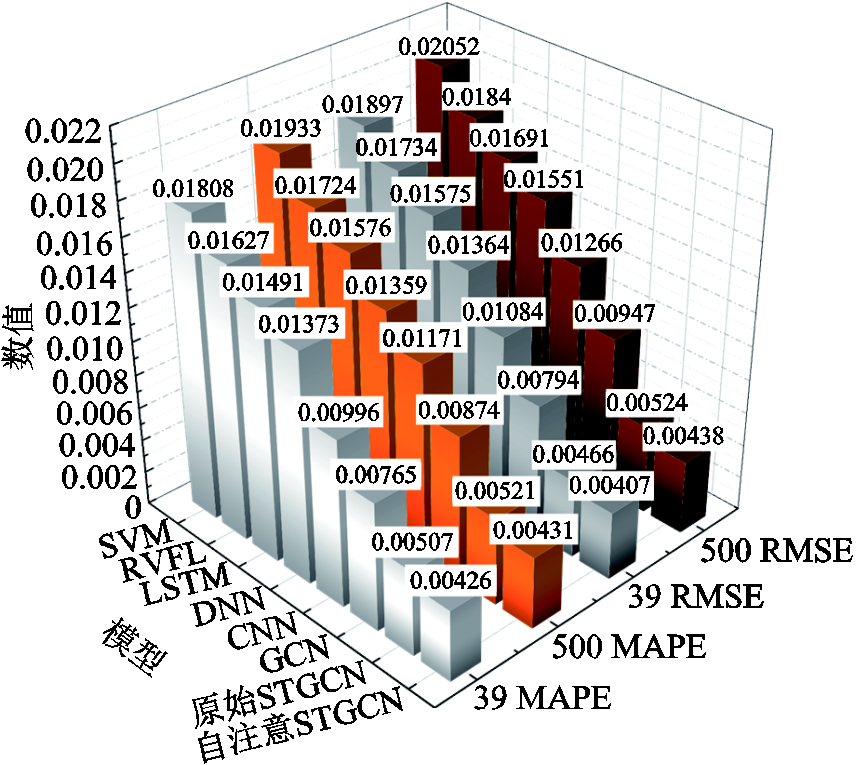
图4 模型有效性比较
Fig.4 Validity comparison of models for FSP
3.1.2 噪声环境下模型的鲁棒性比较
图5显示了测试模型在噪声环境下的表现。对于A系统而言，在30、20和10 dB噪声环境下，STGCN的RMSE分别为0.004 67、0.006 61和0.007 87，其测试误差随噪声水平的提高而增加。其余模型也有类似趋势，但在不同信噪比下，自注意STGCN精度均优于其他模型，其受噪声数据影响相对较小是因为切比雪夫滤波器能有效过滤噪声，自注意力机制能正确过滤注意力较低的特征以提高模型鲁棒性。STGCN与GCN的滤波器和所提模型相同，但其没有引入自注意力机制，噪声过滤能力略逊于自注意STGCN。类似地，CNN和DNN包含滤波结构，但均没有引入自注意力机制与切比雪夫滤波器，这是其噪声过滤能力逊色于前三者的原因。LSTM、RVFL和SVM的性能最不理想，这是因为其浅层结构无法有效提取FSP高维时空特征，也不具备任何形式的滤波器。因此，它们更容易受到噪声的影响。B系统中的测试也有类似结论。尽管自注意STGCN的性能会随着系统规模扩大、噪声水平的增大而受到负面影响，但其RMSE分别为0.008 34、0.007 26和0.004 93，仍处于各模型误差最低点。这是由于基于图卷积的切比雪夫滤波器和自注意力机制具有优越的噪声过滤性能。
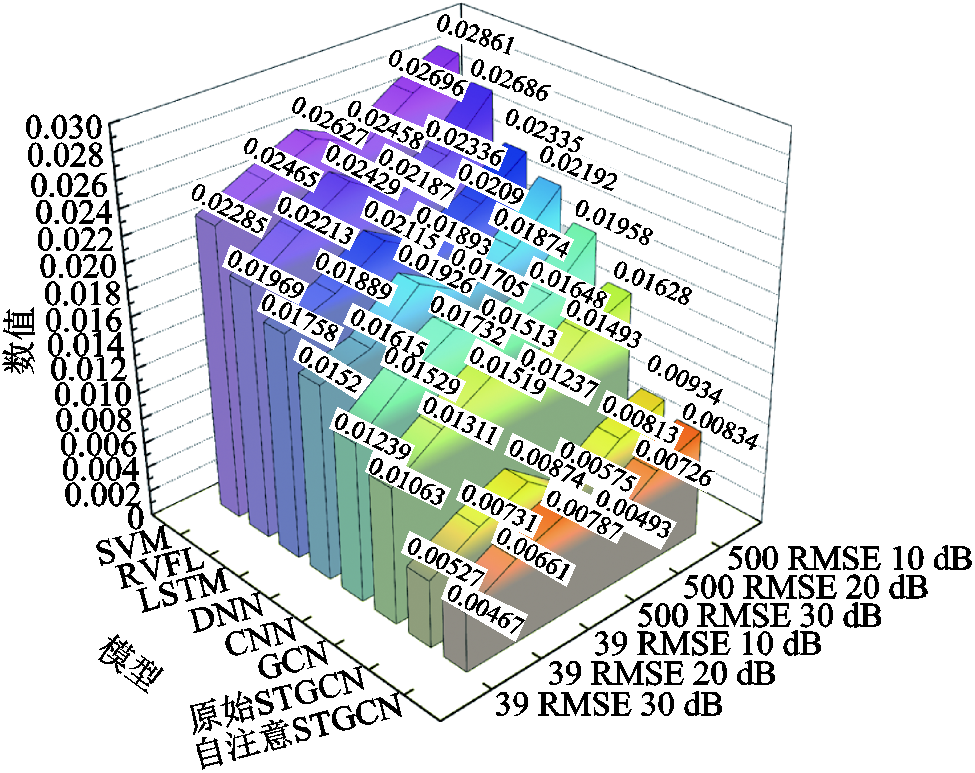
图5 噪声环境下模型鲁棒性比较
Fig.5 Robustness of models under noisy environment
3.1.3 拓扑结构变化下模型的适应性比较
图6描述了当两个系统的拓扑结构发生变化时各种模型的性能。对于A系统，随着拓扑发生变化，尽管自注意STGCN的性能受到了负面影响，其误差指标（RMSE为0.006 27）仍然是测试模型中最低的。系统拓扑结构的变化反映在邻接矩阵和自注意力机制中，这使得自注意STGCN能将FSP完整时空纳入模型训练中以获得更好的性能，因而其性能强于原始STGCN。然而，GCN没有引入自注意力机制，因此其性能差于STGCN。此外，CNN和DNN模型的RMSE分别为0.012 69和0.015 5，由于CNN和DNN提取的矢量位置数据不能有效地反映拓扑结构变化，性能欠佳。LSTM、RVFL和SVM模型不具有时空特性与自注意力机制，它们性能最差。
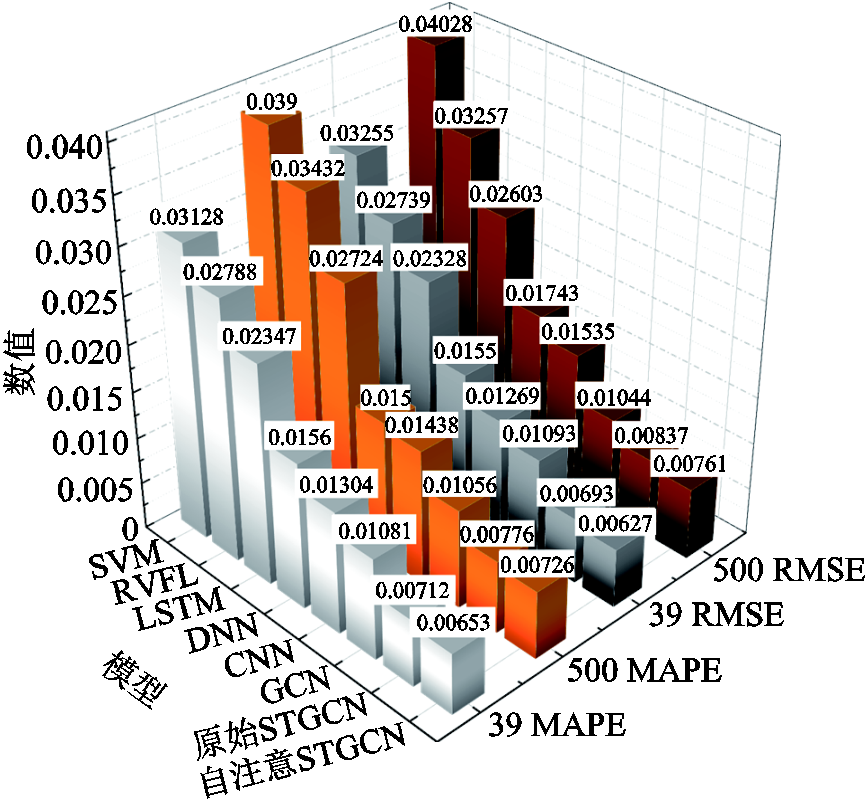
图6 拓扑改变时模型适应性比较
Fig.6 Adaptability of models under topology changes
另外，B系统的测试中亦得类似结论。特别地，随着观测系统规模扩大，所有模型的测试误差均有不同程度的上升，但自注意STGCN精度仍然最高。以自注意STGCN为例，其RMSE值增加了0.001 34。类似地，系统拓扑变化频繁时，各模型的测试误差亦有所上升。总体而言，本研究提出的STGCN测试误差仍优于其他测试模型，这得益于图卷积和自注意力机制对拓扑结构变化的敏感性。
3.2 各模型时效性比较
本节对各模型时效性进行了对比，如图7所示，自注意力STGCN的训练收敛耗时较长，但测试时长最短。模型通过调整注意力权重以更加关注重要特征，忽略非重要特征，这使模型离线训练耗时较长，训练完成后，此机制使其测试时间均低于其余模型。在线应用中，拓扑结构可由调度自动化系统实时反馈，数据生成耗时可忽略，扰动后时序数据采集耗时0.32 s，样本预测耗时0.032 s，总耗时0.352 s，10-1 s耗时级别能满足快速FSP要求。
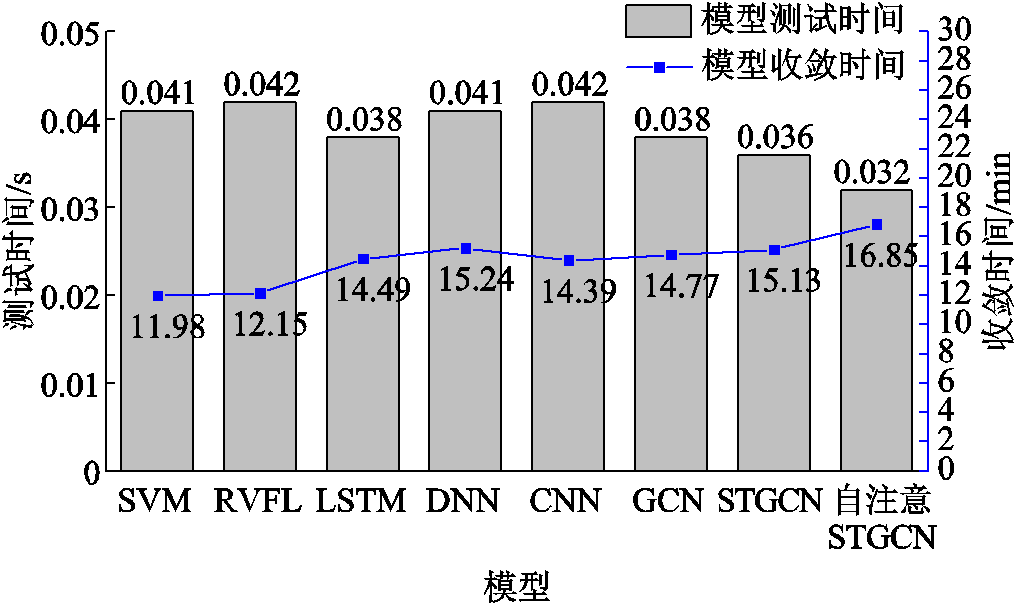
图7 各模型时效性比较
Fig.7 Comparison of model timeliness
3.3 模型决策的可解释性分析
训练有素的STGCN模型可以获取各母线注意力分数，分数反映各母线对FSP的影响。本节对所提模型的决策过程进行了一定程度的可解释性分析。
3.3.1 修改后的新英格兰39母线系统
图8a展示了各母线的平均自注意力得分，图8b展示了10条注意力得分最高母线，即对模型决策产生最大影响的10条母线的样本分布。图中每个点代表一个样本，横坐标表示样本注意力分数，图中点颜色越浅，表示该点特征绝对值越大，而颜色越深则相反；样本的注意力分数越相近，点越聚集；正/负值表示有利/不利影响。
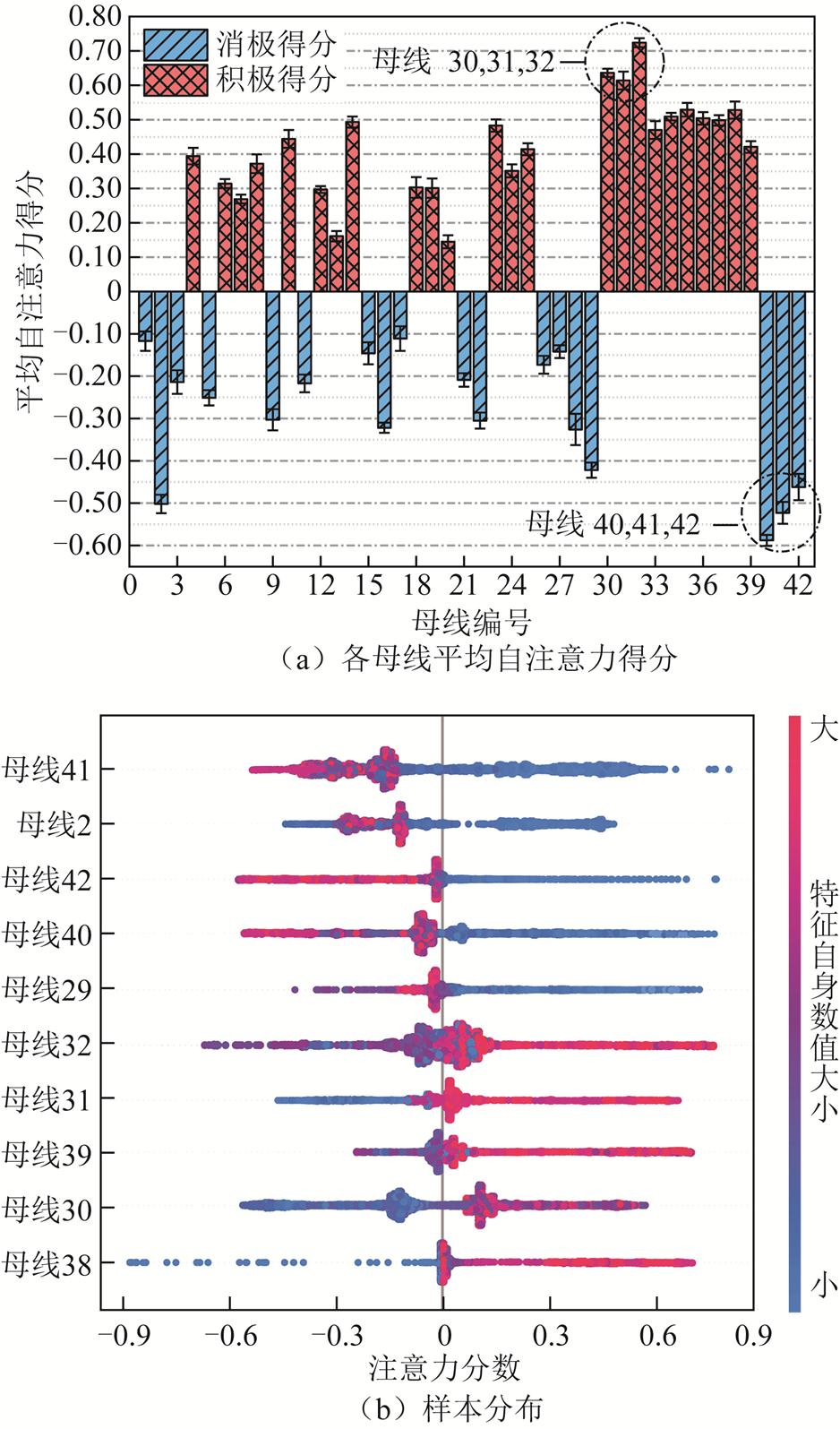
图8 各母线自注意力分数与样本分布
Fig.8 Attention scores and sample distribution
由图8a可知，相较其他母线，母线30、31与32对模型决策具有最大积极影响，母线40、41与42对模型决策具有最大消极影响。将图8b中41与32节点铺开到二维平面如图9所示。如图9a所示，当发生切机扰动时，母线41的注意力得分越接近-0.6，其有功功率越接近最大值140%PN；当其越接近0.87时，其有功功率越接近最小值60%PN；当有功输出在额定值PN的90%～110%时，其样本聚集在注意力均分为[-0.5, -0.15]区间内，表现为样本聚集在图8b中深色区域。这表明母线41与同类母线在系统存在扰动时，模型给出此类节点较高负向关注度，随着出力越接近140%PN，模型给出的负向注意力得分越接近-0.6，模型更容易做出失稳判断。从物理层面解释，母线41是风力发电厂，有功功率越高，其风电装机容量越大，系统总惯性越低，在高渗透率且系统存在扰动的情况下，对系统提供的惯性有限，系统频率失稳可能性较高。
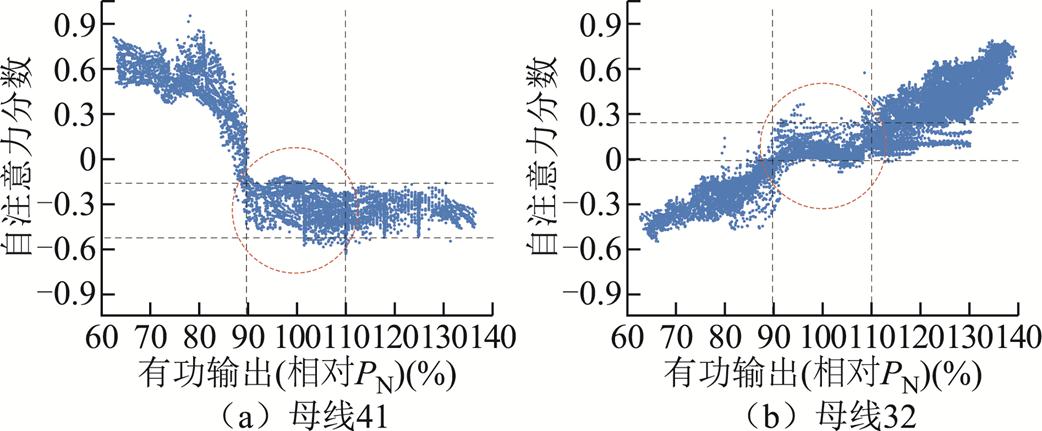
图9 母线41与32的样本注意力分布
Fig.9 Sample distribution of bus 41 and 32
此外，如图9b所示，当发生切机扰动时，对于母线32，其有功功率越接近最大值140%PN，其注意力分数越接近0.9；而有功功率越接近最小值60%PN时，其注意力均分越接近最小值-0.6附近；当有功功率在额定值PN的90%～110%附近时，其样本聚集在注意力均分为[0, 0.23]的区间内，具体表现为图8b中的红色点集，这表明母线32对模型决策产生积极影响。同理，母线30、31和39等也有类似结论。具体体现为母线32与同类母线30、31、39在系统中存在扰动时，模型给出此类节点较高的正向关注度。此外，随着有功输出越来越接近140%PN，模型给予这些节点越高的正向注意力得分0.9。从物理意义上看，同步发电机在系统发生扰动时，具有较大惯性，其有功功率越高，系统惯量越大，能有效抑制系统频率失稳，对频率稳定性有积极贡献。
3.3.2 修改后的ACTIVSg500系统
图10a展示了B系统中50条最具关注度母线的自注意力均分。其中，模型给予母线16、82、169、225和250最大正向关注度，其注意力均分在0.7附近，对模型预测具有积极影响；模型给予母线9、144、197、17和224最大负向关注度，其注意力均分在-0.5附近，对模型决策有消极影响。图10b展示了这10条关注度最高母线的样本分布。
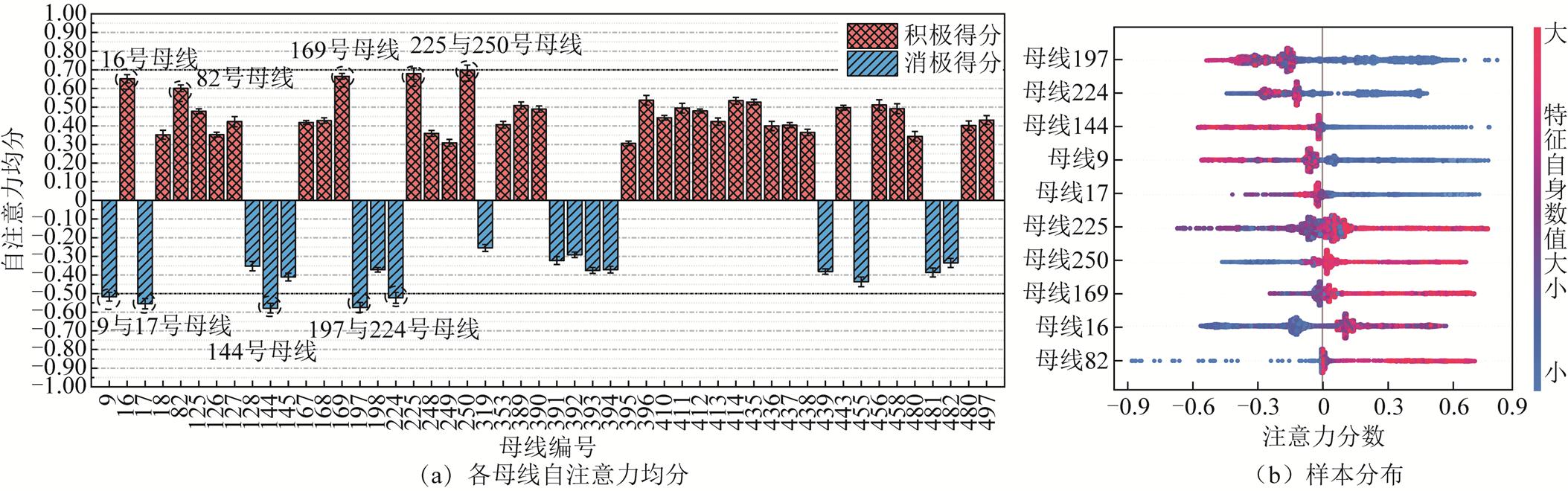
图10 各母线自注意力均分与样本分布
Fig.10 Attention scores and sample distribution
以母线224和225为例，将图10b中224与225节点铺开到二维平面如图11所示。如图11a所示，当发生切机扰动时，母线224的有功功率越接近最大值140%PN，其注意力分数越接近-0.7附近；当有功功率越接近最小值60%PN，其注意力分数越接近0.9附近；当有功功率保持在额定值PN的90%～110%时，其样本聚集在注意力分数为[0, -0.30]的区间内，具体表现为图10b中的深色点集。这表明母线224与同类母线197、144等在系统存在扰动时，模型给出此类节点较高负向关注度，随着有功出力越接近140%PN，模型给予此类节点的负向注意力得分越来越接近-0.7，模型更容易做出失稳判断。从物理层面解释，母线224是等效风力发电厂，其发出有功功率越高，风电装机容量越大，系统总惯量越低，在高渗透率且系统存在扰动情况下，系统频率失稳的可能性较高；反之，失稳可能性较低。
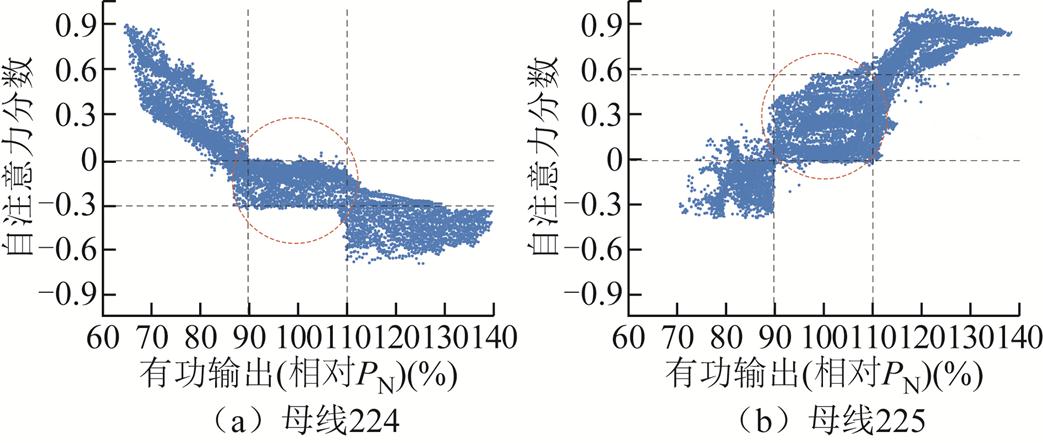
图11 母线224与225的样本注意力分布
Fig.11 Sample distribution of bus 224 and 225
此外，图11b显示了母线225的样本注意力分布。当发生切机扰动时，母线225的有功功率越接近最小值60%PN，其注意力分数越接近-0.5附近；当有功功率越接近最大值140%PN，其注意力分数越接近0.9附近；当有功功率保持在额定值PN的90%～110%时，其样本聚集在注意力分数为[0, 0.57]的区间内，具体表现为图10b中的红色点集，这意味着模型给予母线225、250和169等同类母线对模型决策产生积极影响。具体表现为母线225与同类母线250、169在系统存在扰动时，模型给出此类节点较高的正向关注度。此外，随着有功输出越接近140%PN，模型给予这些节点越高的正向注意力得分0.9，使模型更倾向于给出稳定结果。从物理上看，同步发电机装机容量越大，系统总惯性越高，在系统发生扰动时，抑制频率失稳的能力越强，反之系统失稳风险增大。在两个修改系统的测试中，本文所提STGCN均得出类似结论，其模型决策的可解释性分析与频率稳定一般观点一致[24-25]，说明其符合客观物理规律。
4 结论
为了系统地将FSP的时空动态合理地纳入学习模型，并对模型的预测过程进行具体描述，本文提出了一个基于STGCN与SAM的FSP新框架。通过修改后的新英格兰39节点系统和ACTIVSg500系统验证了该方法的有效性。现有结论如下：
1）与主流模型（GCN、CNN、LSTM等）相比，提出的STGCN在一般环境下具有更高的准确度，在输入数据含有大量噪声时具有更好的鲁棒性，在电力系统拓扑结构变化时具有更好的适应性。
2）在提出的STGCN中引入了基于SAM的SAGPooling层，可以在一定程度上解决STGCN进行模型决策时的可解释性问题。训练有素的STGCN可以根据节点特征及拓扑为电力系统提供每条母线的自我关注得分，这有助于模型决策的分析和解释。
3）采用图时空卷积层提取了FSP的时空特征。随后通过SAM持续关注每个母线的权重并通过时空图卷积层级联以聚合不同感受野的时空特征。最后由模型生成输入特征的高级图表示并提供最终的预测结果。在这个过程中，两个测试系统证明了所提出的STGCN具有更突出的性能和一定程度的可解释性。
但值得注意的是，电力系统具有多变的运行工况，无论样本生成阶段考虑多少种情形，都无法遍历实际中所有可能的系统状态，复杂的工况会使训练数据量大大增加。因此，可通过样本增强、迁移学习等技术快速更新模型以适应系统变化，增加模型新场景下的准确度，这也是论文后续的研究内容。
参考文献
[1] 李兆伟, 方勇杰, 吴雪莲, 等. 频率紧急控制中动作时延和措施量对低惯量系统控制有效性的影响分析[J/OL]. 电工技术学报, 2023: 1-13[2023-10-24]. https://doi.org/10.19595/j.cnki.1000-6753.tces.231175.
Li Zhaowei, Fang Yongjie, Wu Xuelian, et al. Influence of action delay and amount on the control effectiveness of low inertia systems in frequency emergency control[J/OL]. Transactions of China Electrotechnical Society, 2023: 1-13[2023-10-24]. https://doi.org/10.19595/j.cnki.1000-6753.tces.231175.
[2] 柯德平, 冯帅帅, 刘福锁, 等. 新能源发电调控参与的送端电网直流闭锁紧急频率控制策略快速优化[J]. 电工技术学报, 2022, 37(5): 1204-1218.
Ke Deping, Feng Shuaishuai, Liu Fusuo, et al. Rapid optimization for emergent frequency control strategy with the power regulation of renewable energy during the loss of DC connection[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1204-1218.
[3] 李锡林, 查晓明, 田震, 等. 频率突变影响下基于Lyapunov法的孤岛微电网暂态稳定性分析[J]. 电工技术学报, 2023, 38(增刊1): 18-31.
Li Xilin, Zha Xiaoming, Tian Zhen, et al. Lyapunov based transient stability analysis of islanded microgrid under the influence of frequency abrupt change[J]. Transactions of China Electrotechnical Society, 2023, 38(S1): 18-31.
[4] 关中杰, 鲁效平, 李钢强, 等. 基于风速模型的风电机组动态转矩前馈控制技术[J]. 电工技术学报, 2018, 33(22): 5338-5345.
Guan Zhongjie, Lu Xiaoping, Li Gangqiang, et al. Dynamic torque feed forward control technology of wind turbine based on wind speed model[J]. Transactions of China Electrotechnical Society, 2018, 33(22): 5338-5345.
[5] Azizi S, Sun Mingyu, Liu Gaoyuan, et al. Local frequency-based estimation of the rate of change of frequency of the center of inertia[J]. IEEE Transactions on Power Systems, 2020, 35(6): 4948-4951.
[6] 陈宗遥, 卜旭辉, 郭金丽. 基于神经网络的数据驱动互联电力系统负荷频率控制[J]. 电工技术学报, 2022, 37(21): 5451-5461.
Chen Zongyao, Bu Xuhui, Guo Jinli. Neural network based data-driven load frequency control for interconnected power systems[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5451-5461.
[7] 苏玉刚, 颜志琼, 胡宏晟, 等. 基于频率切换实现恒流/恒压输出的电场耦合无线电能传输系统[J]. 中国电机工程学报, 2024, 44(4): 1553-1565.
Su Yugang, Yan Zhiqiong, Hu Hongsheng, et al. Electric-field coupled power transfer system with constant current/constant voltage output characteristics based on frequency switching[J]. Proceedings of the CSEE, 2024, 44(4): 1553-1565.
[8] Cao Yongji, Zhang Hengxu, Zhang Yi, et al. Extending SFR model to incorporate the influence of thermal states on primary frequency response[J]. IET Generation, Transmission & Distribution, 2020, 14(19): 4069-4078.
[9] 石访, 张林林, 胡熊伟, 等. 基于多属性决策树的电网暂态稳定规则提取方法[J]. 电工技术学报, 2019, 34(11): 2364-2374.
Shi Fang, Zhang Linlin, Hu Xiongwei, et al. Power system transient stability rules extraction based on multi-attribute decision tree[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2364-2374.
[10] 马良玉, 程善珍. 基于支持向量数据描述和XGBoost的风电机组异常工况预警研究[J]. 电工技术学报, 2022, 37(13): 3241-3249.
Ma Liangyu, Cheng Shanzhen. Abnormal state early warning of wind turbine generator based on support vector data description and XGBoost[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3241-3249.
[11] 叶瑞丽, 郭志忠, 刘瑞叶, 等. 基于小波包分解和改进Elman神经网络的风电场风速和风电功率预测[J]. 电工技术学报, 2017, 32(21): 103-111.
Ye Ruili, Guo Zhizhong, Liu Ruiye, et al. Wind speed and wind power forecasting method based on wavelet packet decomposition and improved Elman neural network[J]. Transactions of China Electrotechnical Society, 2017, 32(21): 103-111.
[12] 崔昊, 冯双, 陈佳宁, 等. 基于自编码器与长短期记忆网络的宽频振荡广域定位方法[J]. 电力系统自动化, 2022, 46(12): 194-201.
Cui Hao, Feng Shuang, Chen Jianing, et al. Wide-area location method of wide-band oscillations based on autoencoder and long short-term memory network[J]. Automation of Electric Power Systems, 2022, 46(12): 194-201.
[13] 王彦博, 吴俊勇, 季佳伸, 等. 基于深度残差收缩网络的电力系统暂态频率安全集成评估[J]. 电网技术, 2023, 47(2): 482-494. Wang Yanbo, Wu Junyong, Ji Jiashen, et al. Integrated assessment of power system transient frequency security based on deep residual shrinkage network[J]. Power System Technology, 2023, 47(2): 482-494.
[14] 时纯, 刘君, 梁卓航, 等. 基于GAN和多通道CNN的电力系统暂态稳定评估[J]. 电网技术, 2022, 46(8): 3191-3202.
Shi Chun, Liu Jun, Liang Zhuohang, et al. Transient stability assessment of power system based on GAN and multi-channel CNN[J]. Power System Technology, 2022, 46(8): 3191-3202.
[15] 王铮澄, 周艳真, 郭庆来, 等. 考虑电力系统拓扑变化的消息传递图神经网络暂态稳定评估[J]. 中国电机工程学报, 2021, 41(7): 2341-2350.
Wang Zhengcheng, Zhou Yanzhen, Guo Qinglai, et al. Transient stability assessment of power system considering topological change: a message passing neural network-based approach[J]. Proceedings of the CSEE, 2021, 41(7): 2341-2350.
[16] Xie Jian, Sun Wei. A transfer and deep learning-based method for online frequency stability assessment and control[J]. IEEE Access, 2021, 9: 75712-75721.
[17] Zhan Xianwen, Han Song, Rong Na, et al. A two-stage transient stability prediction method using convolutional residual memory network and gated recurrent unit[J]. International Journal of Electrical Power & Energy Systems, 2022, 138: 107973.
[18] 韩天森, 陈金富, 李银红, 等. 电力系统稳定评估机器学习可解释代理模型研究[J]. 中国电机工程学报, 2020, 40(13): 4122-4131.
Han Tiansen, Chen Jinfu, Li Yinhong, et al. Study on interpretable surrogate model for power system stability evaluation machine learning[J]. Proceedings of the CSEE, 2020, 40(13): 4122-4131.
[19] 陈明华, 刘群英, 张家枢, 等. 基于XGBoost的电力系统暂态稳定预测方法[J]. 电网技术, 2020, 44(3): 1026-1034.
Chen Minghua, Liu Qunying, Zhang Jiashu, et al. XGBoost-based algorithm for post-fault transient stability status prediction[J]. Power System Technology, 2020, 44(3): 1026-1034.
[20] Yu Bing, Yin Haoteng, Zhu Zhanxing. Spatio-temporal graph convolutional networks: a deep learning framework for traffic forecasting[J/OL]. ArXiv, 2017: 1709.04875. https://arxiv.org/abs/1709. 04875.pdf.
[21] Zhao Junbo, Tang Yi, Terzija V. Robust online estimation of power system center of inertia frequency[J]. IEEE Transactions on Power Systems, 2019, 34(1): 821-825.
[22] Lee J, Lee I, Kang J. Self-attention graph pooling[C]// Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 2019: 3734-3743.
[23] 赵荣臻, 文云峰, 叶希, 等. 基于改进堆栈降噪自动编码器的预想事故频率指标评估方法研究[J]. 中国电机工程学报, 2019, 39(14): 4081-4093.
Zhao Rongzhen, Wen Yunfeng, Ye Xi, et al. Research on frequency indicators evaluation of disturbance events based on improved stacked denoising autoencoders[J]. Proceedings of the CSEE, 2019, 39(14): 4081-4093.
[24] 赵冬梅, 郑亚锐, 谢家康, 等. 基于轻量级梯度提升机和生成对抗网络的含风电电力系统频率稳定评估[J]. 电网技术, 2022, 46(8): 3181-3193.
Zhao Dongmei, Zheng Yarui, Xie Jiakang, et al. Frequency stability evaluation of power system containing wind power based on light gradient boosting machine and generative adversarial network[J]. Power System Technology, 2022, 46(8): 3181-3193.
[25] 周挺, 杨军, 詹祥澎, 等. 一种数据驱动的暂态电压稳定评估方法及其可解释性研究[J]. 电网技术, 2021, 45(11): 4416-4425.
Zhou Ting, Yang Jun, Zhan Xiangpeng, et al. Data-driven method and interpretability analysis for transient voltage stability assessment[J]. Power System Technology, 2021, 45(11): 4416-4425.
Frequency Stability Prediction Method Based on Modified Spatial Temporal Graph Convolutional Networks and Self-Attention
Abstract Power system frequency dynamic characteristics serve for system stability evaluation and reflects the specific change of frequency when there is a power imbalance between generation and load. On the one hand, the distribution of topology is closely connected with the stability of the power grid in the frequency stability prediction (FSP) problem and the topology of the power grid is typically altered by the random events. On the other hand, the frequency stability characteristics are mirrored in the post-fault response trajectory, so that the time-varying features and dynamic topologies may contribute to the nonlinear spatial-temporal dynamics of FSP. However, the traditional data-driven methods fail to effectively incorporate the system spatial-temporal characteristics into the model training, and suffers from insufficient utilization of system information, poor generalization ability in the face of new topology and interpretability. In addition, the machine learning (ML) model employed for prediction resembles a "black box" internally, and lack of interpretability is one of the primary challenges to ML application in the FSP field. To give a highly accurate FSP reference and denote the potential security hazards of the system, the model is required to identify the major factors that influence the FSP and clarify the decision-making process of model learning.
To address these issues, this paper proposes a FSP prediction method that combines the self-attention mechanism (SAM) and the spatial-temporal graph convolutional network (STGCN). Firstly, the proposed STGCN prediction method utilizes a one-dimensional temporal convolutional layer to extract system temporal information. In addition, it employs Chebyshev graph convolution to approximate the Laplacian matrix through polynomial functions, enabling graph convolution operations to capture the topological structure information of each bus and its neighbors. After that, a differentiable self-attention graph pooling (SAGPooling) layer based on SAM is employed to enhance the generalization ability and robustness of the STGCN model. The layer allows the model to reduce the dimensionality of the feature vectors in order to decrease the number of parameters and avoid overfitting. The hierarchical pooling strategy enables the model to preserve valuable node features as much as possible and effectively allocate nodes based on the preserved features and changing topology to enhance the generalization ability and robustness of the STGCN. Meanwhile, the attention scores of each node can be uniformly extracted. Finally, through the SAM, the attention scores of nodes are obtained according to the active power to perform the interpretability analysis of the STGCN model. In summary, this model converts input data into high-level representations of graphics through graph convolution, time convolution, and SAGPooling to integrate the complete spatiotemporal dynamics of FSP. Therefore, the accuracy, generalization ability, and robustness of the proposed STGCN have been improved, and the interpretable analysis of the model decision-making process can be carried out. The testing results on the modified New England 39-bus system and the modified ACTIVSg500 system, which incorporate renewable energy sources, validate the effectiveness of the proposed STGCN. Among all the tested methods, the STGCN has higher prediction accuracy, better robustness, and generalization capability. In addition, the STGCN can provide critical influence factors of different buses on the prediction results in this work.
keywords：Frequency stability prediction, deep learning, spatial-temporal graph neural networks, self-attention mechanism, interpretability analysis
中图分类号：TM712
DOI: 10.19595/j.cnki.1000-6753.tces.230858
贵州省优秀青年科技人才项目（[2021]5645）、贵州省科技支撑计划项目（[2023]290, [2023]329）和贵州省科学技术基金项目（[2021]277）资助。
收稿日期 2023-06-06
改稿日期 2023-10-25
杜东来 男，1998年生，硕士研究生，研究方向为人工智能技术在电力系统频率稳定性中的应用。
E-mail：1640371942@qq.com
韩 松 男，1978年生，教授，研究方向为交直流电力系统分析、新型电力电子装备以及配网规划。
E-mail：shan@gzu.edu.cn（通信作者）
（编辑 赫 蕾）