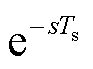和零阶保持器（Zero Order Holder, ZOH）环节。图中虚线框（蓝色）部分为加入的电网电压比例前馈，相应的前馈函数Gff(s)为摘要 在并网逆变器中，锁相环和电网电压前馈是提高并网电流质量和输出性能的环节。然而在弱电网下，这两个环节均有可能对并网系统的稳定性产生影响，同时两者的影响范围存在重叠，导致稳定性问题变得更为复杂。该文针对这一复杂稳定性问题展开研究，分析弱电网下两个环节导致系统不稳定的原因，并进一步提出优化方案。首先考虑加入加权系数，讨论其对于电网电压前馈以及锁相环的影响，兼顾这两种因素，需要对加权系数进行权衡取值；然后考虑在更弱电网下，只加入加权系数对于系统稳定性提升效果是有限的，因此需要增加一条用于改善输出导纳相位的电压前馈通路；最后通过实验证明，加入改进方案后的并网逆变器，在阻抗变化较大的弱电网下依然保持良好的鲁棒性。
关键词：并网逆变器 弱电网 鲁棒性 锁相环 电网电压前馈
在分布式发电系统中，并网逆变器的正常工作对于整个系统的安全稳定运行具有重要作用[1-2]。随着可再生能源的快速发展，分布式发电系统的规模也在逐渐增大。高渗透率成为可再生能源发电的一大趋势[3-4]。由于新能源发电的间歇性、随机性和波动性等特征会导致电网阻抗波动明显。电网阻抗的大小通常用短路比（Short Circuit Ratio, SCR）表示，随着SCR的减小，呈现出弱电网特性，因此并网逆变器要求能够在SCR＞20下稳定运行[5]。在弱电网下，电网阻抗波动通过影响并网逆变器的控制环路增益，使系统失稳。当阻抗更大时，系统中的低频谐波影响更为显著[6]，这会给并网系统的安全高效运行带来更为严峻的挑战。
当电网阻抗的变化范围较宽时，其对于并网逆变器的影响频段也较宽。在这部分频率范围内，导致并网逆变器发生谐振、甚至失稳的影响因素也较多。同时，不同因素的影响频段可能存在交叠，使得稳定性问题变得复杂。文献[7]以弱电网下的直驱风电场为研究对象，分析锁相环、电压环、电流环、延时以及滤波器等环节对于控制性能的影响。根据机组的阻抗特性进行频带划分后，对上述环节作用的频带范围进行总结。进一步地，文献研究了各频带的主导因素以及多个因素重叠时的效应。针对各频带的振荡因素，文献[8]进一步提出抑制策略，通过参数优化设计和控制结构改进的方式对机组的阻抗特性进行重塑，有效地改善了宽频带下的振荡问题。
并网逆变器通过锁相环实现并网电流与电网电压同步[9-10]。在强电网下，锁相环带宽远小于电流环带宽，并且认为两者是独立的。然而随着电网阻抗的增大，电流环带宽迅速降低，就有可能导致锁相环和电流环发生耦合。文献[11-12]指出，锁相环对于两倍锁相环带宽（通常为几十到几百赫兹）范围内的系统性能存在较大影响。此外，电网中存在大量背景谐波，电网电压前馈通过提高低频段的环路增益来改善并网逆变器的谐波抑制能力，同时减小稳态误差[13-15]。电网电压前馈相当于在输出端增加了一个并联阻抗，提高了等效输出阻抗的模值[16-17]。但是受到延时的影响，电网电压前馈会导致等效输出阻抗的相位减小。文献[18-19]中提到，电网电压前馈发生谐振的频率通常在几十到几千赫兹。
锁相环和电网电压前馈是常用的提高并网电流质量的环节，而在弱电网下，两者均有可能对系统的稳定性产生不利影响，且影响频段存在重叠。针对这部分内容，文献[20]指出两者会导致q轴的输出阻抗在低频段呈现负阻特性，文献中提出将q轴电压前馈，并通过调整前馈函数来抵消锁相环和电网电压前馈的影响。文中所提方案适用于三相并网逆变器的应用场合。文献[21]针对锁相环和电网电压前馈展开研究，通过调整前馈环节的比例微分系数提高系统稳定性，但该方法需要电网阻抗测量环节。
在现有文献中，针对这两者同时存在时的稳定性问题展开的研究仍较少，也少有简单有效的改进方案。本文通过分析锁相环和电网电压前馈造成并网逆变器系统不稳定的原因，进一步地，考虑加入加权系数以权衡系统的性能。为了应对宽范围变化的电网阻抗，本文提出一种改进的电压前馈通路，以确保并网系统在较弱的电网下仍保有一定的相位裕度。最后，实验结果对比验证了所提改进方案的有效性。
LCL型并网逆变器的控制结构如图1所示，vg为电网电压，vPCC为公共耦合点（Point of Common Coupling, PCC）电压，Zg为电网阻抗（电网阻抗视为纯感性，即Zg=sLg）；L1、L2和C构成LCL滤波器；Gi(s)为电流调节器，采用比例-积分（PI）调节器；Hil和Hi2分别为滤波电容电流iC和并网电流ig的采样系数。考虑到数字控制延时，加入一拍滞后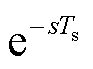和零阶保持器（Zero Order Holder, ZOH）环节。图中虚线框（蓝色）部分为加入的电网电压比例前馈，相应的前馈函数Gff(s)为
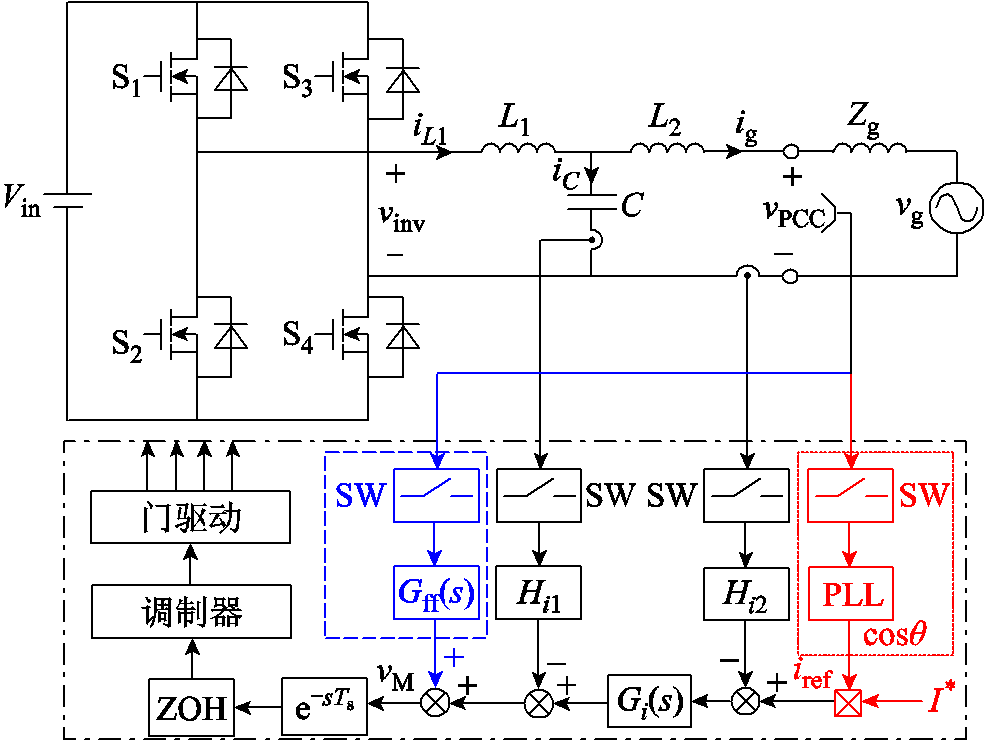
图1 LCL型并网逆变器控制结构
Fig.1 Grid-connected inverter with LCL-filter
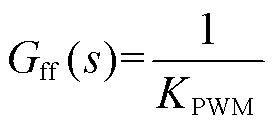（1）
式中，KPWM为调制波到逆变桥输出电压的增益，KPWM=Vin/Vtri，Vtri为三角载波幅值。
此外，图1中的点线框（红色）部分为锁相环环节，PLL检测PCC电压相位后，生成的cosθ与幅值给定值I*相乘，得到并网电流基准iref。图2为所采用的基于延迟的锁相环控制框图，当φ=0时，锁相环传函GPLL(s)为[22-23]
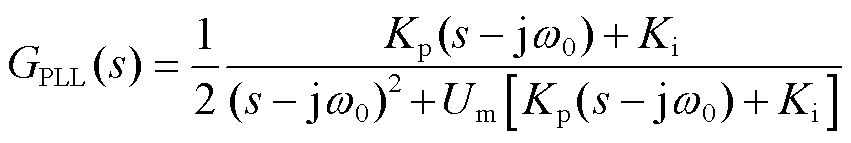（2）
式中，Um、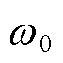
分别为电网电压的峰值和角频率；
、
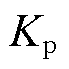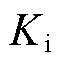为锁相环的比例、积分系数。因此，并网电流基准可以表示为iref(s)= I*GPLL(s)vPCC(s)。
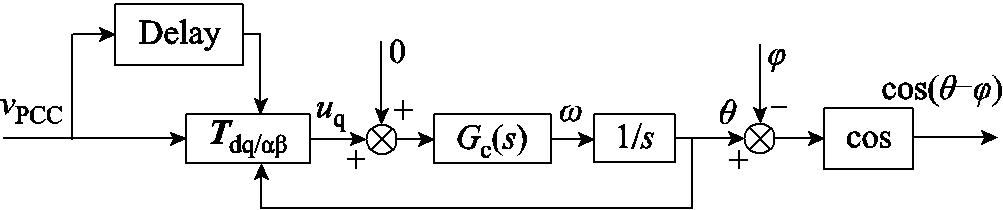
图2 基于延时的锁相环
Fig.2 Delay-based PLL
根据图1所示的控制结构，可以得到考虑锁相环和电网电压前馈后的等效控制框图，如图3所示。其中，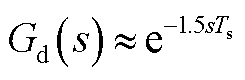
为1.5拍的数字控制延时。进一步地，为了便于分析，上述框图可以简化为如图4所示的简化框图。其中
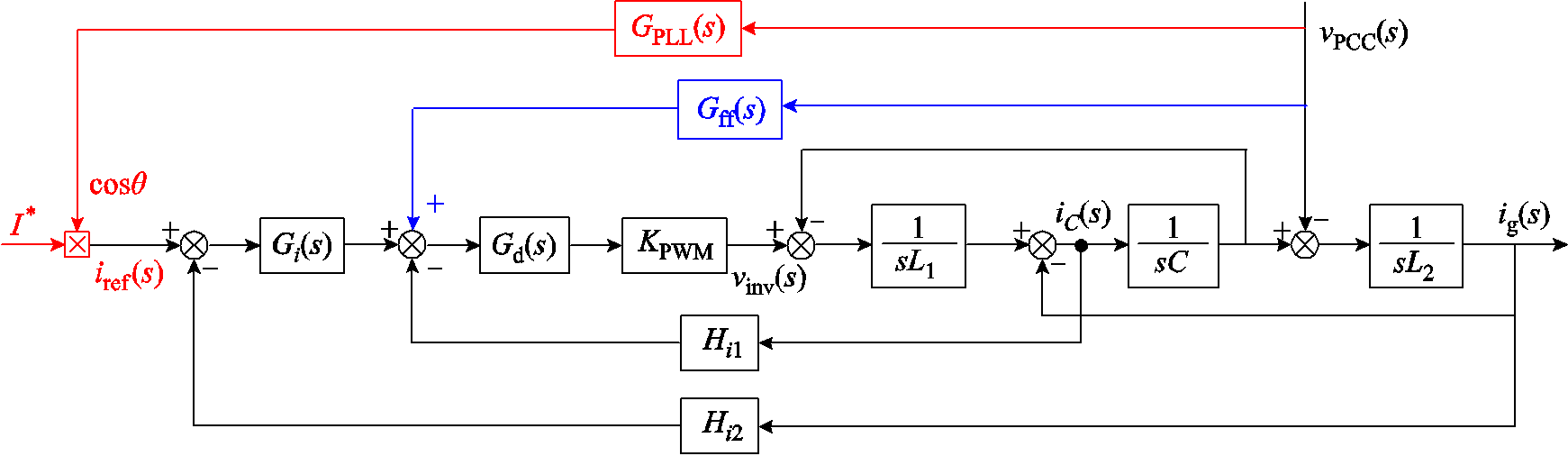
图3 并网逆变器等效控制框图
Fig.3 Equivalent control block diagram of grid-connected inverter
图4 简化的控制框图
Fig.4 Simplified control block diagram
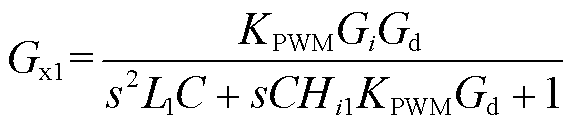（3）
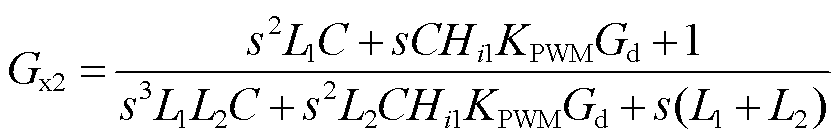（4）
由图4可得ig和vPCC之间的关系式为
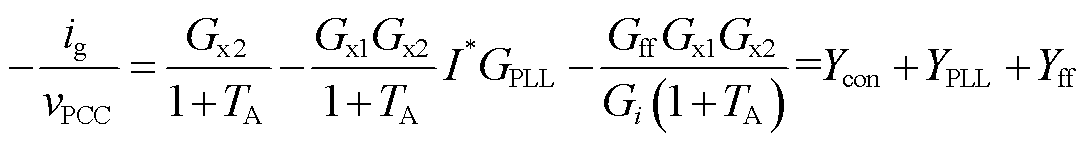（5）
式中，TA为环路增益，TA=Gx1Gx2Hi2。
这表明，逆变器输出导纳Yo(s)分别由电流环Ycon(s)、锁相环YPLL(s)和电网电压前馈Yff(s)组成。当不考虑锁相环和电网电压前馈时，原有并网逆变器的输出导纳为电流环引入导纳Ycon(s)。考虑这两种稳定性影响因素后，其等效输出导纳如图5所示。
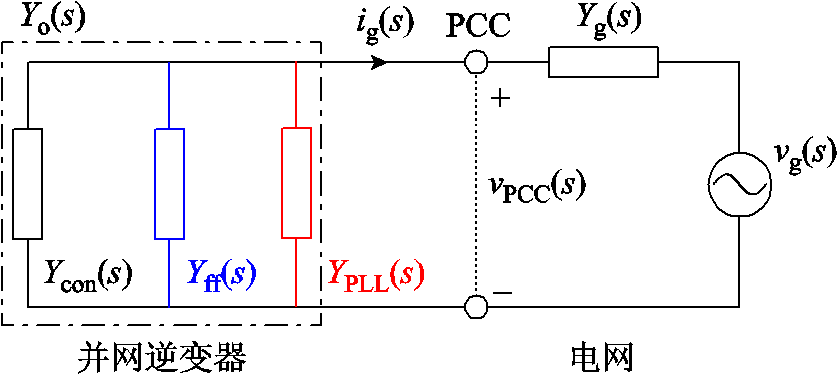
图5 并网逆变器的等效输出导纳
Fig.5 Equivalent output admittance model of inverter
根据图5，逆变器与电网可采用级联系统稳定判据判稳[24]，应符合下列条件：①强电网下逆变器能稳定运行；②Yo(s)/Yg(s)满足奈奎斯特稳定性判据。对于并网逆变器来说，在参数设计时需满足其在理想电网条件下的稳定运行，即保证满足条件①。对于条件②而言，要求Yo(s)与Yg(s)的幅频特性曲线没有交截，或交截频率fz处的相位裕度（Phase Margin, PM）大于0，约束条件为
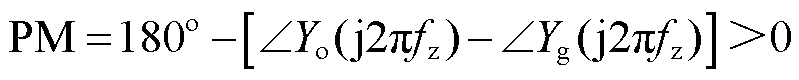（6）
考虑电网阻抗为纯感性，那么Yg(s)的相位为 -90°。要保证系统在弱电网下的稳定性，式（6）转化为要求输出导纳在交截频率处的相位小于90°。
绘制考虑锁相环和电网电压前馈前后的导纳Ycon(s)和Yo(s)的伯德图，如图6a所示。当f＜fd时，Yo(s)的相位大于90°，由式（6）可得，系统不能满足奈奎斯特稳定性判据而无法正常运行。不考虑上述两种影响因素时，如图中的虚线（蓝色）所示，原有并网逆变器的输出导纳Ycon(s)始终满足相位小于90°，并网逆变器能够稳定工作。
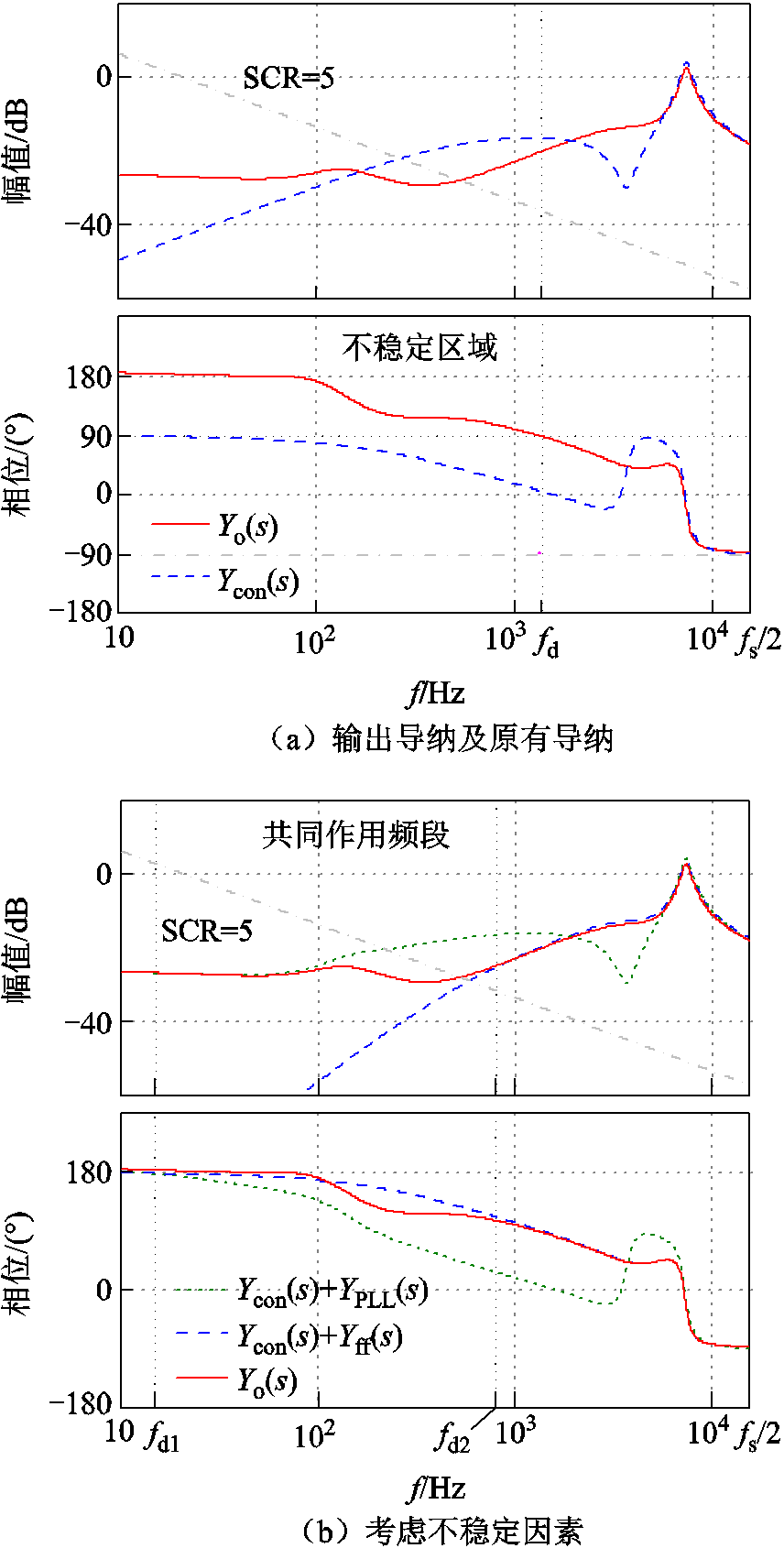
图6 不同情况下的输出导纳伯德图
Fig.6 Bode plots of output admittance of inverter
针对上述不稳定区域，为了分清各因素的作用机理，绘制只考虑锁相环时的输出导纳Ycon(s)+YPLL(s)、只考虑电网电压前馈时的输出导纳Ycon(s)+Yff(s)以及两者共同考虑时的输出导纳Yo(s)的伯德图，如图6b所示。当f＜fd1时，输出导纳Yo(s)的幅频和相频特性曲线基本与只考虑锁相环时的曲线基本重合，说明在该频率段中，锁相环为主导影响因素。同样的，当f＞fd2时，（红色）实线所示的输出导纳曲线与只考虑电网电压前馈时的（蓝色）虚线基本重合，说明该频率段中电网电压前馈为主导影响因素。当fd1＜f＜fd2时，两种因素均不可忽略，此时处于两者共同作用频段。相应的频段划分如图7所示。
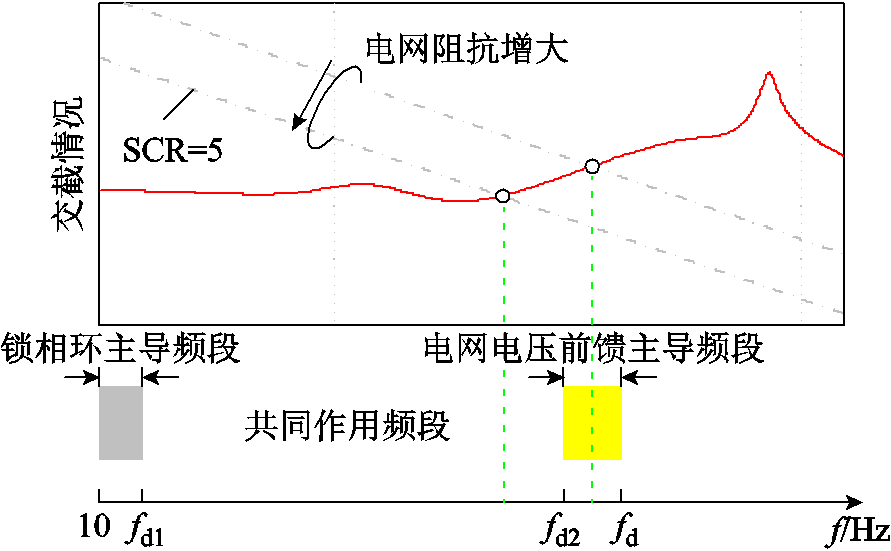
图7 不稳定影响因素的频段划分
Fig.7 Frequency band division of unstable factors
由图7可知，当电网阻抗增大时，率先进入电网电压前馈主导频段，因此首先考虑对电网电压前馈作出改进。考虑到不引入电网电压前馈时，并网逆变器在弱电网下的稳定性较好，但其谐波抑制能力较差，且电流调节器使用PI调节器时，并网电流存在稳态误差。加入电网电压前馈的并网逆变器可以消除稳态误差，同时抑制谐波的影响，但它在输出导纳较大频段内引入相移，使得并网系统对电网阻抗的适应能力变差。因此，考虑加入加权系数，对这两种情况进行折中，以此来保证逆变器的稳定性，并使系统仍保有一定的谐波抑制能力[25-26]。
加权系数记为Kf，前馈函数可以表示为
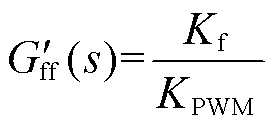（7）
图8绘制了不同加权系数Kf下的输出导纳伯德图。在中低频段，当加权系数减小时，输出导纳的相位减小，有利于系统相位裕度的提高。另一方面，随着加权系数的减小，输出导纳的幅值越大，系统抑制谐波的能力就越弱。同时，由放大图可以看出，基频f0处的输出导纳相频特性曲线与180°的相位差随着加权系数的减小而增大。考虑到输出导纳满足Yo(s)= -ig(s)/vPCC(s)，将ig(s)与vPCC(s)转化为相量信息，当两者同相位时，输出导纳相位呈现-1的相位特性，即相位呈现180°。当加权系数越小时，基频处的输出导纳相位与180°的相位差越大，那么并网电流与PCC处电压的稳态误差增大。因此，加入加权系数后，有必要对基频处的相位进行补偿。
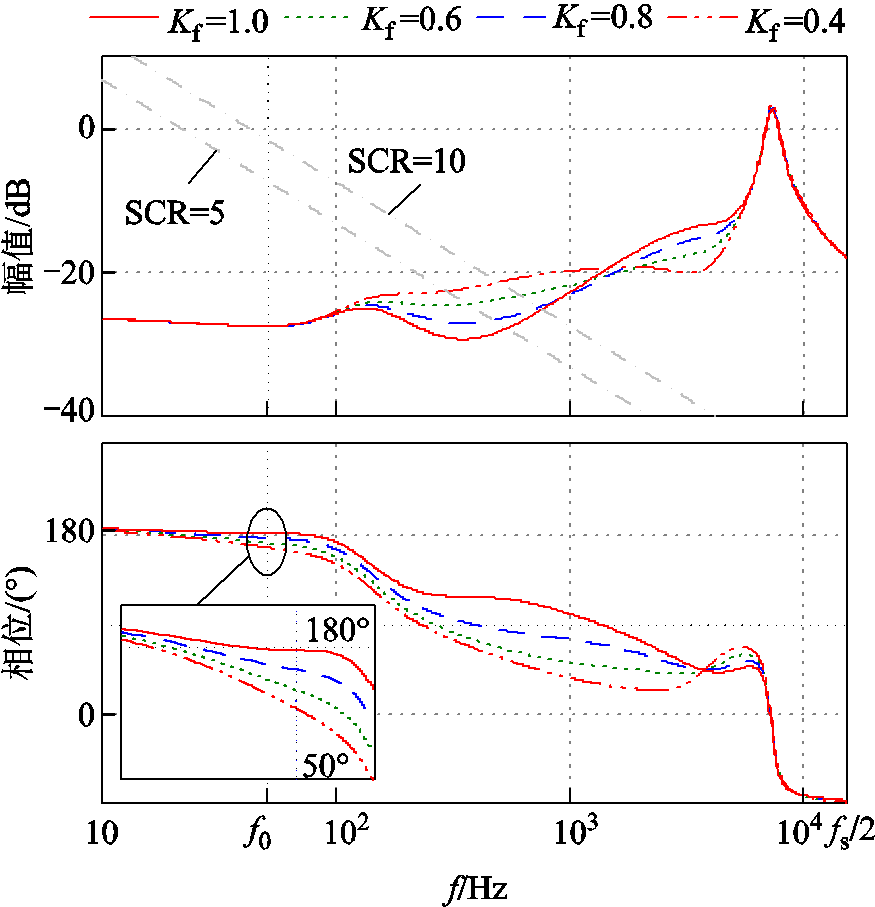
图8 不同加权系数下的输出导纳伯德图
Fig.8 Bode plots of output admittance with different weighted coefficients
当电网阻抗增大时，交截频率进入电网电压前馈和锁相环共同作用频段。下文将分析加权系数对于共同作用情况下的稳定性改善效果。
将PCC电压进行拆分，可以得到如图9a所示的控制框图，图中虚线（蓝色）部分为拆分后的两条前馈通路。从电流环角度来看，PCC电压前馈代替电网电压前馈时，增加了一条额外的并网电流反馈支路，会影响电流环的环路增益。
为了便于求解电流环的环路增益，可以将电网阻抗与网侧电感合并，得到如图9b所示的控制框图，图中灰色阴影区域为变换前后的框图部分。
根据图9中所示框图，可以得到原有电流环的开环环路增益TA(s)及增加并网电流支路后电流环的环路增益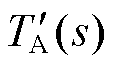
，表达式如式（8）和式（9）所示。式中红色方框部分为额外增加的并网电流正反馈通路部分。
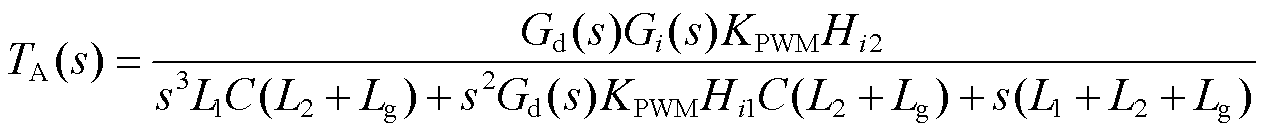（8）
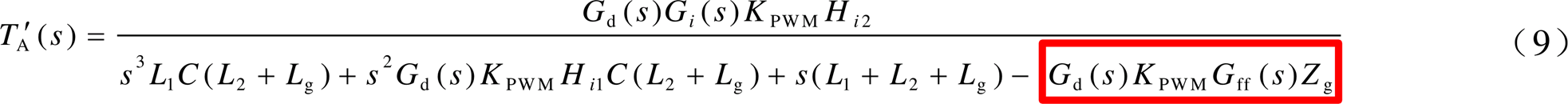
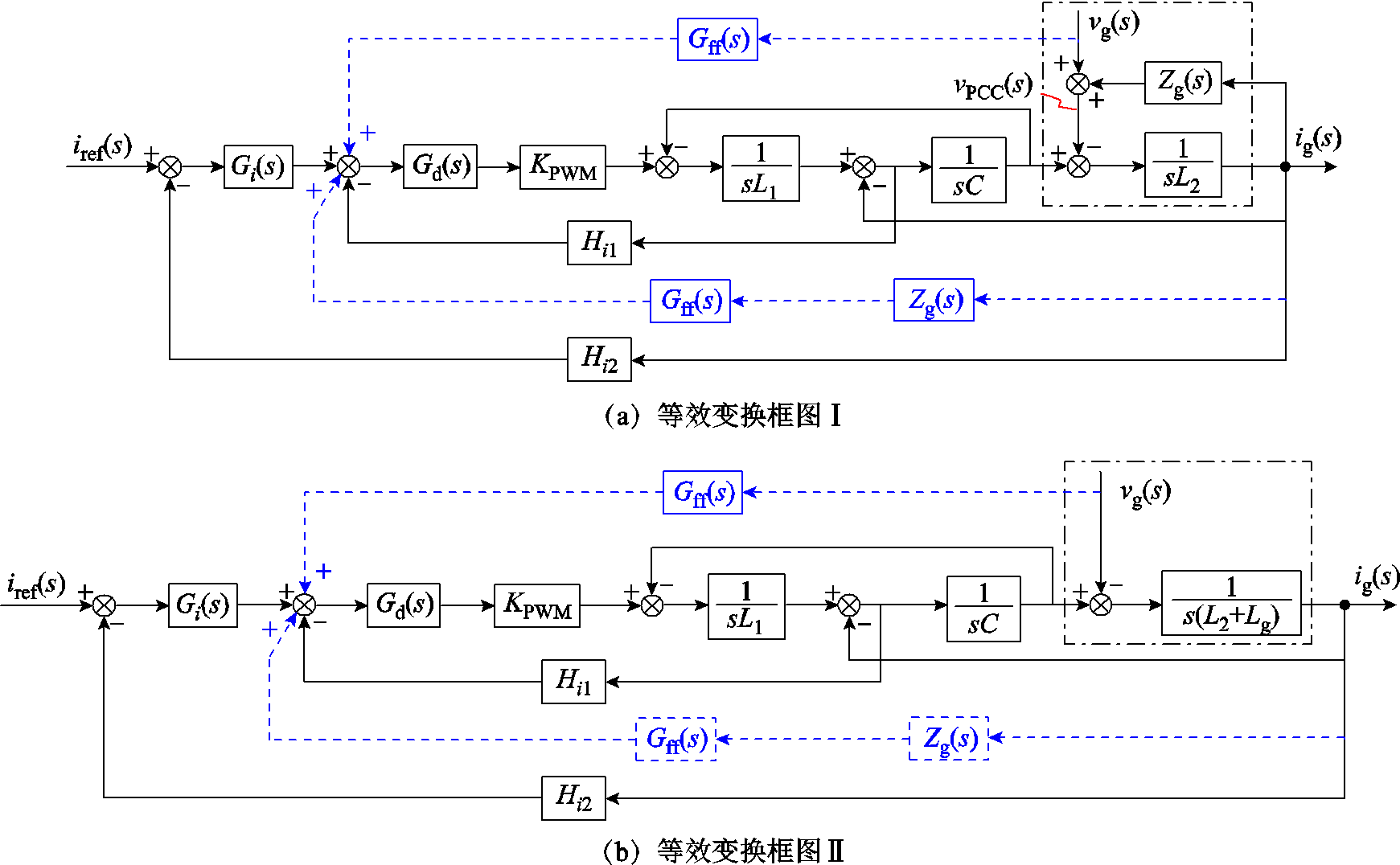
图9 拆分PCC点电压前馈后的控制框图
Fig.9 Control diagram after splitting PCC point voltage feedforward
加入上述带加权系数的电网电压前馈后，由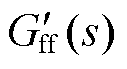
替代式（9）中的Gff(s)，并根据环路增益表达式，绘制电流环带宽变化曲线，如图10所示。当 Kf = 0时，表示未加入电网电压前馈的情况，如图中实线（红色）所示。随着电网阻抗的增大，电流环带宽低至锁相环带宽频段，导致两者发生耦合，影响逆变器的输出电流性能。当Kf =1.0时，表示加入电网电压前馈后的情况，电流环带宽有所提高，有利于降低电流环与锁相环的耦合程度，从而改善锁相环带来的不稳定影响。从这个角度来看，电网电压前馈的加入有利于改善锁相环带来的稳定性问题。此外，由图10可以看出，加权系数越大，对电流环带宽的提高效果越好。因此这里希望加权系数大一些以提高对锁相环稳定性的改善效果。
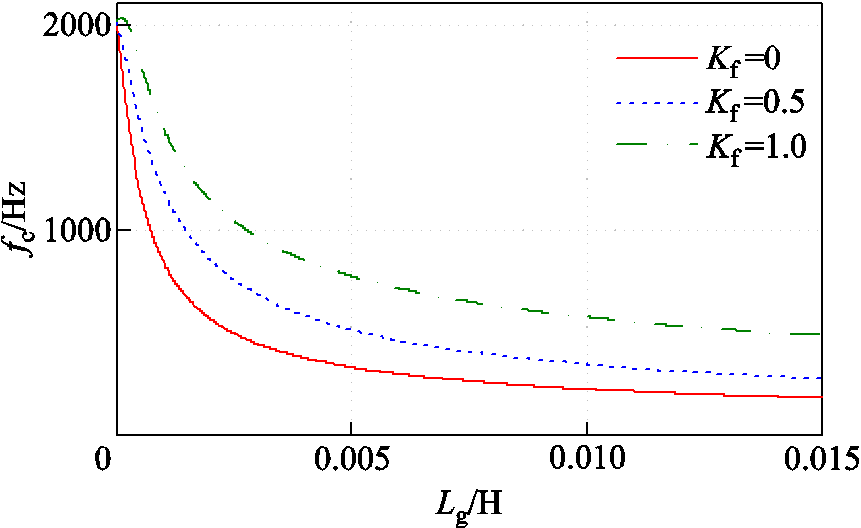
图10 加入加权系数前后的电流环带宽变化曲线
Fig.10 Current loop bandwidth curves before and after adding weighted coefficient
兼顾加权系数对于锁相环和电网电压前馈的影响效果，取图7中两个因素共同作用频段对应的电网情况进行取值。这里取短路比SCR=5的情况，绘制相位裕度PM关于加权系数的变化曲线，如图11所示。当加权系数取Kf=0.54时，对应有相位裕度的最大值PM = 13.2°。因此，取加权系数为0.54，并代入后续分析。此外，图中的N点代表电网电压前馈系数为0，即只考虑锁相环时的情况，此时并网逆变器的相位裕度为7.6°。通过N点与M点情况相比可以看出，电网电压加权前馈除了对于自身电压前馈带来的谐振具有较好的抑制效果之外，其对于锁相环带来的不稳定也具有一定的改善效果。
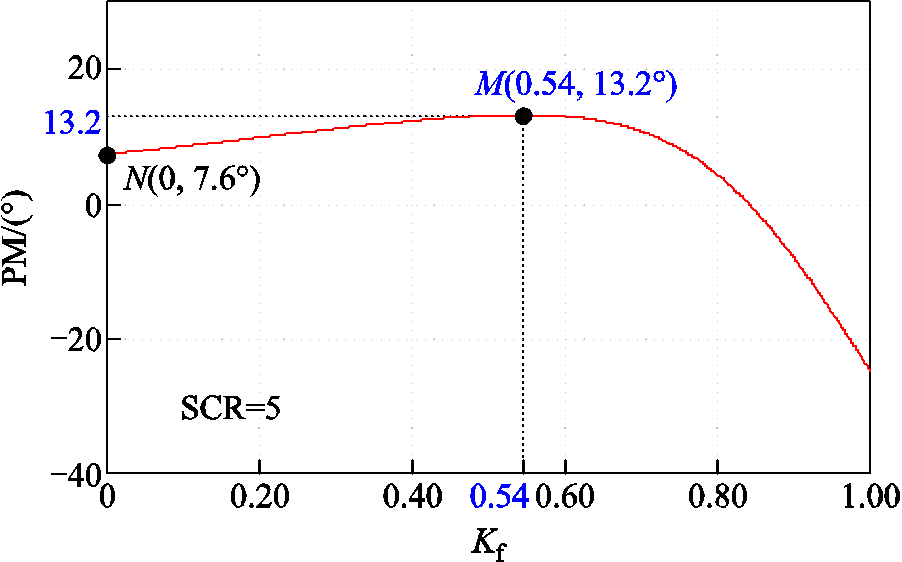
图11 相位裕度关于加权系数的变化曲线
Fig.11 Variation curve of phase margin with respect to weighted coefficient
基于加权系数的电网电压前馈可以改进锁相环带来的稳定性问题，但是改善效果有限。当短路比更小时，相位裕度较小甚至为负，系统仍然不稳定。因此，考虑增加一条电压前馈通路，用以改善锁相环引入导纳的相位，使得系统能够适应更大范围变化的电网阻抗。想要通过电网电压前馈的方式来实现这一效果，相当于在原来电压前馈的基础上，叠加一条支路。额外加入前馈通路后的控制框图如图12所示，前馈函数记为GA(s)。
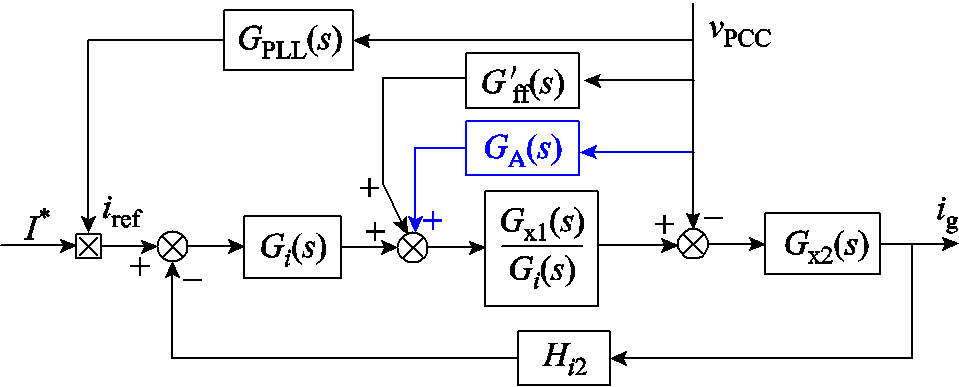
图12 加入改进前馈通路的控制框图
Fig.12 Control block diagram with an improved feedforward path
叠加一条前馈通路，相当于增加了一个并联阻抗，其表达式为
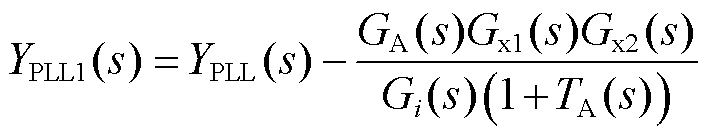（10）
为改善锁相环引入导纳YPLL(s)的相位，这里考虑加入全通滤波器（All-Pass Filter, APF）与其级联。
APF与其他滤波器相比，在相同阶数下引入的相位更大，这里采用一阶全通滤波器，记为GAPF(s)。改进后的导纳相当于
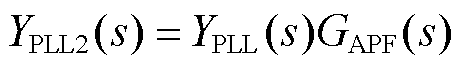（11）
联立式（10）和式（11），得到前馈函数的表达式为
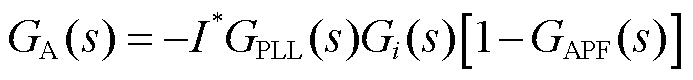（12）
为了方便实现，式（12）中的GPLL(s)省略jω0部分，即锁相环传递函数频谱整体左移ω0。考虑到全通滤波器对全频段幅值无衰减，当其与锁相环引入导纳YPLL(s)级联时，不会在基频处产生幅值误差。而其引入的相位会对基频处的输出导纳相位产生影响。因此，这里需要对全通滤波器进行相位补偿。高通滤波器（High-Pass Filter, HPF）在基频处引入正相移，且在较高频段不改变幅值。考虑将其与全通滤波器级联，作为全通滤波器的相位补偿环节。由此，可以得到整体滤波器GAPF_add(s)的表达式为
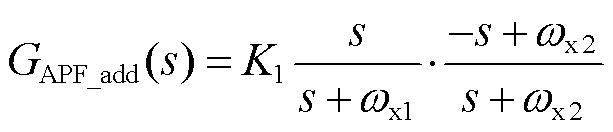（13）
式中，K1为幅值校正环节，用来保证改进后的滤波器不会在基频处产生幅值误差，可以通过|GAPF_add(jω0)|=1求解出K1的取值；ωx1为高通滤波器的截止角频率；ωx2为全通滤波器的角频率。
考虑到GAPF_add(s)中存在两个变量ωx1和ωx2，接下来对其进行设计。考虑到加入的加权系数会令基频处的输出导纳相位偏离180°，使得并网电流与PCC电压存在相位误差，希望利用滤波器GAPF_add(s)实现对输出导纳的相位校正。因此，可以得到一个关于基频处相位的约束关系，可以表示为
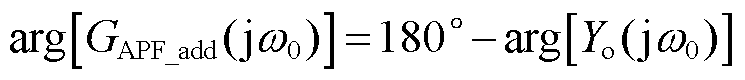（14）
根据式（14），可以求解出变量ωx1和ωx2之间的关系，那么ωx1可以看作是一个关于变量ωx2的函数。因此，GAPF_add(s)只包含一个变量ωx2。图13描绘了一组GAPF_add(s)相对于不同ωx2的频率特性曲线。可以看出，改进的滤波器GAPF_add(s)可以实现基频下的相位校正，满足∆φ0=180°-arg[Yo (jω0)]。同时，还可以看到ωx2越小，GAPF_add(s)在超过基频部分的幅值越大，会放大谐波干扰。因此，希望ωx2的值应该更大，以降低谐波的影响。
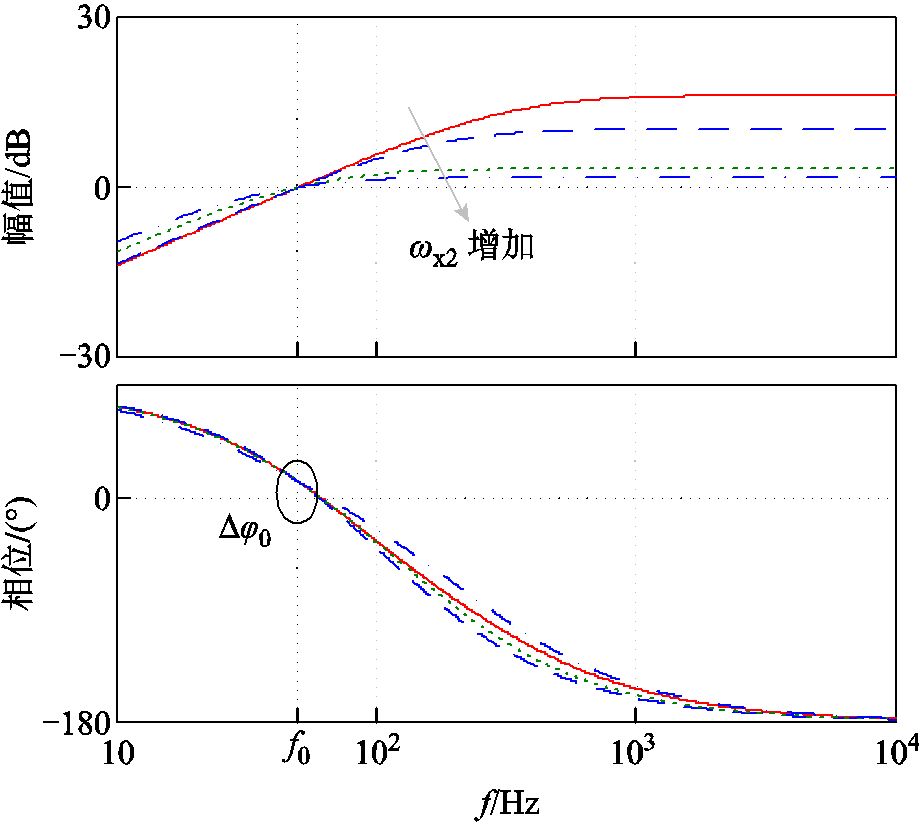
图13 不同ωx2的GAPF_add(s)的频率特性曲线
Fig.13 Frequency characteristic curves for GAPF_add(s) with regard to different ωx2
当SCR=5时，根据伯德图求得加入加权系数后Yo与Yg在322.6 Hz交截，相位裕度为13.2°，此时系统的相位裕度较小。考虑在该交截频率下，对锁相环引入导纳的相位进行补偿。绘制滤波器GAPF_add(s)相位在该频率下关于变量ωx2的变化曲线，如图14a所示。这里考虑引入-100°的相位补偿，此时曲线存在两个交点。由于全通滤波器角频率ωx2增大时，高通滤波器的角频率ωx1越小，那么幅值校正环节K1随之减小，有利于减小谐波干扰。因此选择右侧交点，并得到相应的ωx2 = 1 536 rad/s，进而求出ωx1=221.3 rad/s，K1=1.22。进一步绘制系统相位裕度PM的变化曲线，为了获得良好的动态响应和鲁棒性，将PM取值在(30°, 60°)范围内，对应图中的阴影区域。所取的点对应的PM=46°，此时系统的稳定性较好。
图14 滤波器GAPF_add(s)相位以及系统相位裕度关于ωx2的变化曲线
Fig.14 Curves of GAPF_add(s) phase and phase margin with respect to ωx2
考虑上述改进锁相环相位的前馈通路后，最终的PCC电压前馈函数可以表示为
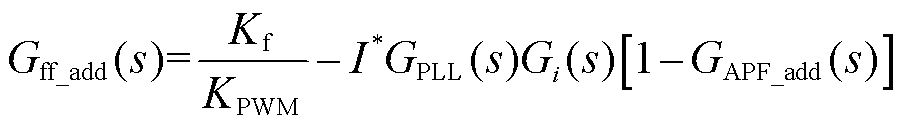（15）
为了比较不同前馈函数对于输出性能的影响，图15分别绘制了加入基于加权系数的电压前馈函数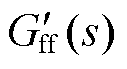和基于改进前馈通路的电压前馈函数Gff_add(s)对应的输出导纳伯德图。当电网阻抗为 1.4 mH时，原有系统相位裕度为PM1=-0.9°，系统处于临界稳定，对应的交截频率fz1 =1 257.2 Hz。加入加权系数后，交截频率
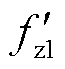=1 257.4 Hz，相位裕度变为
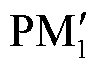=48.1°，系统的稳定性得到提升。但此时会引入并网电流与PCC电压之间的相位误差∆φ=10.7°。
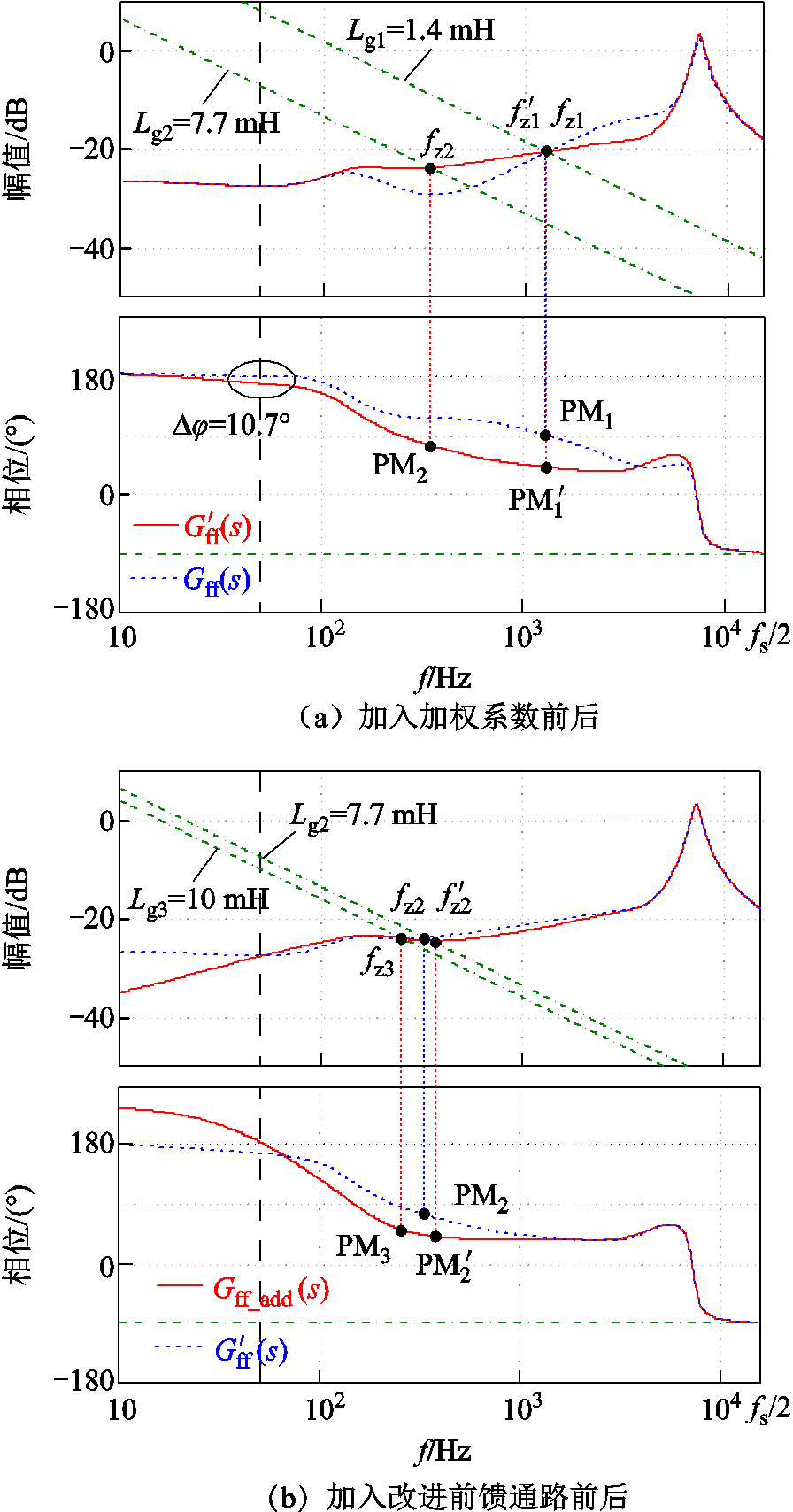
图15 加入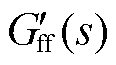
和Gff_add(s)后输出导纳伯德图
Fig.15 Bode plots of output admittance with 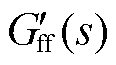and Gff_add(s)
当电网阻抗增大到7.7 mH时，对应短路比等于SCR=5的情况。加入加权系数后的系统相位裕度为PM2 =13.2°，对应的交截频率为fz2 = 322.6 Hz。
当电网电压前馈函数由改进前馈通路Gff_add(s)替代时，在该短路比下，输出导纳与电网导纳的交截频率为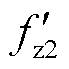
=342.1 Hz，对应的相位裕度变为 
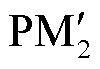=45.8°。此时系统的稳定性得到提升，同时并网电流的稳态误差得到补偿。当电网阻抗进一步增大到10 mH时，交截频率为fz3 = 257.1 Hz，对应的相位裕度PM3 =37.6°。可以看出，加入改进前馈通路后，并网逆变器系统的稳定频段扩大很多。
为验证上述理论，研制了一台额定功率为1 kW的原理样机如图16所示，其主要参数见表1。控制芯片采用TI的TMS320F28035，可编程交流源（Chroma 6460）模拟电网。
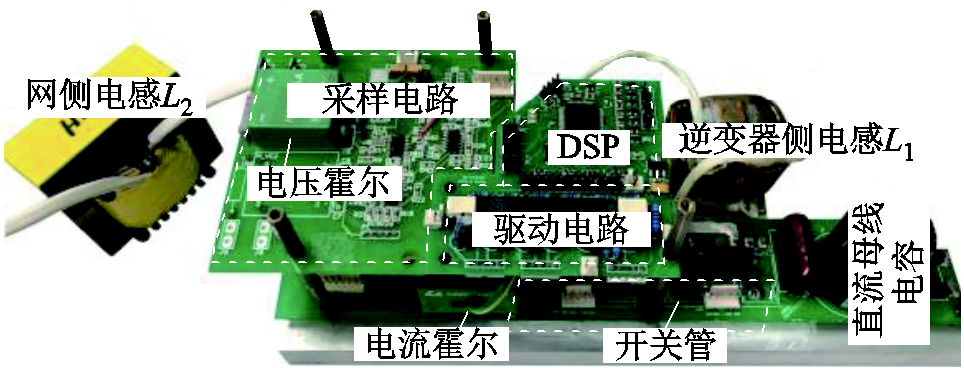
图16 原理样机
Fig.16 Prototype photo
表1 主要参数
Tab.1 Main parameters
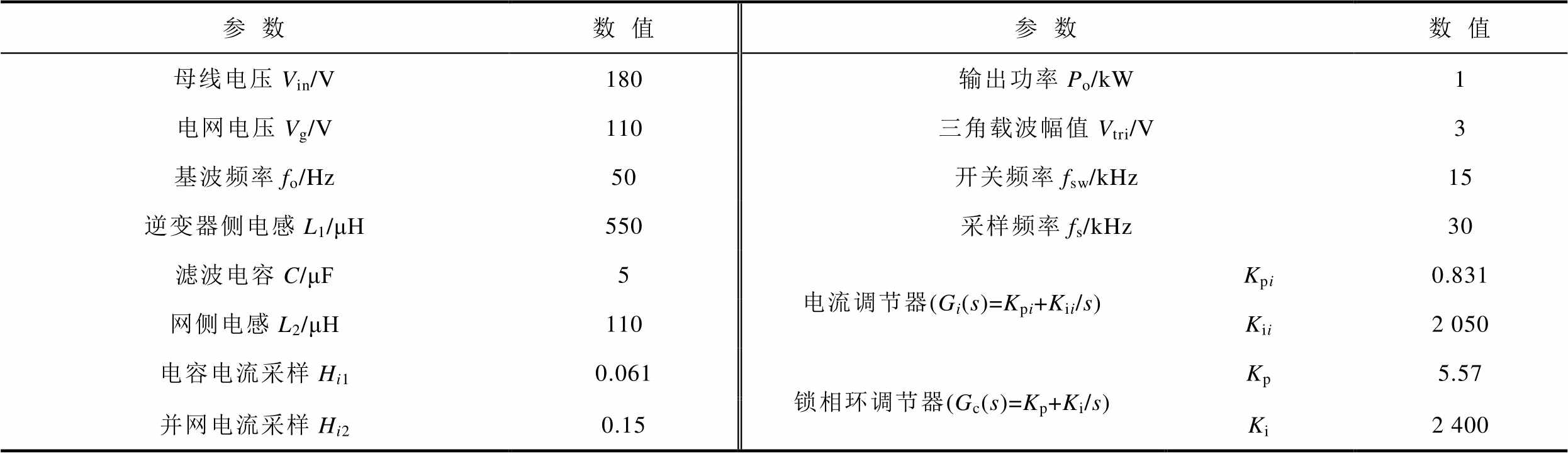
参数数值参数数值 母线电压Vin/V180输出功率Po/kW1 电网电压Vg/V110三角载波幅值Vtri/V3 基波频率fo/Hz50开关频率fsw/kHz15 逆变器侧电感L1/μH550采样频率fs/kHz30 滤波电容C/μF5电流调节器(Gi(s)=Kpi+Kii/s)Kpi0.831 网侧电感L2/μH110Kii2 050 电容电流采样Hi10.061锁相环调节器(Gc(s)=Kp+Ki/s)Kp5.57 并网电流采样Hi20.15Ki2 400
强电网下，加入改进前馈通路前后的系统均可以稳定运行，分别如图17a、图17b所示。
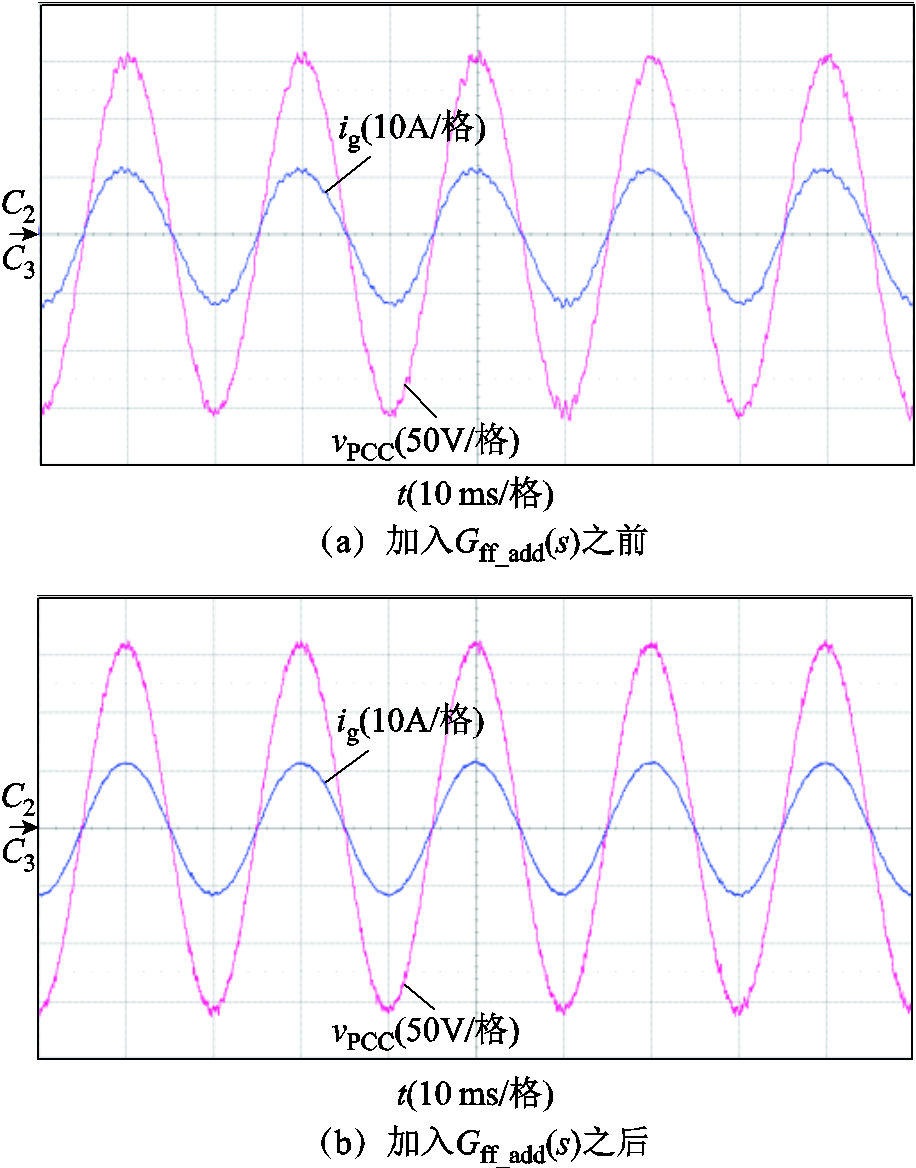
图17 强电网下，加入改进前馈通路前后的实验波形
Fig.17 Experimental waveforms in stiff grid
当电网阻抗增大到Lg=1.4 mH条件下，对应图14a中fz1频率点，采用原有Gff(s)时稳定性较差，并网电压电流发生振荡，如图18a所示；加入基于加权系数的电网电压前馈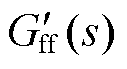后，并网逆变器能够恢复稳定运行，如图18b所示。但此时ig与vPCC之间存在相位差，从波形中读得相位差为10.8°。此外，图18c给出了添加加权系数Kf前后的动态结果，可发现振荡会迅速回退，系统具有良好的动态性能。
图18 Lg=1.4 mH的实验波形
Fig.18 Experimental waveforms when Lg=1.4 mH
当电网阻抗为Lg = 7.8 mH（SCR ≈ 5）的情况，对应图15中fz2频率点附近，此时并网逆变器的相位裕度不足，波形质量较差，如图19a所示。当改进的电压前馈通路Gff_add(s)加入后，对应图中的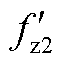
频率点，输出导纳的相位得到补偿，ig与vPCC的波形得以改善，如图19b所示。图19c给出了Gff_add(s)切入前后的动态结果。由图19可知，该系统可以迅速稳定，具有良好的动态性能。
进一步地，图20给出了电网阻抗增大到Lg = 10 mH时的并网逆变器实验波形，对应图15中的fz3频率点，此时系统仍留有一定的相位裕度，并网系统能够稳定运行。
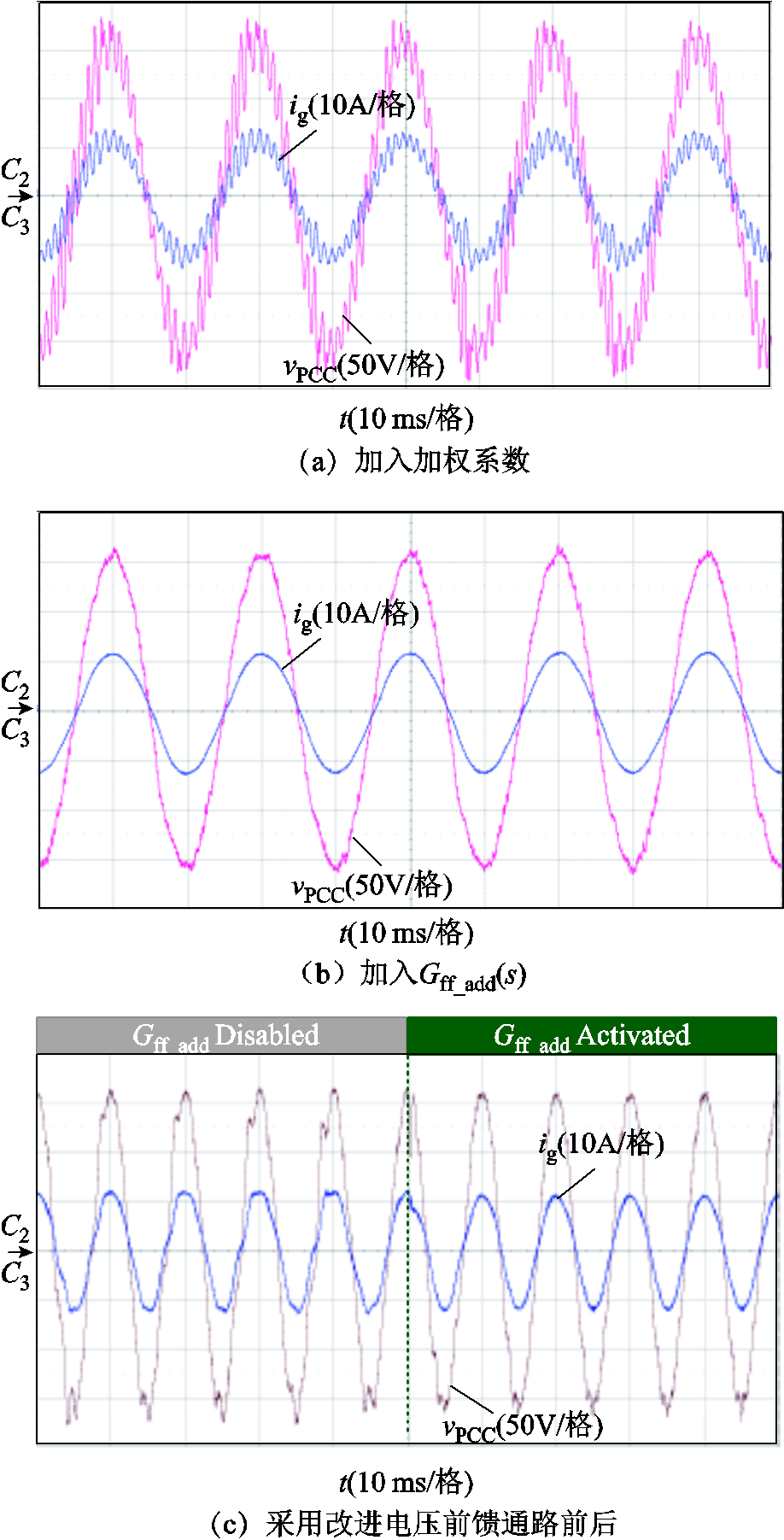
图19 Lg=7.8 mH的实验波形
Fig.19 Experimental waveforms when Lg=7.8 mH
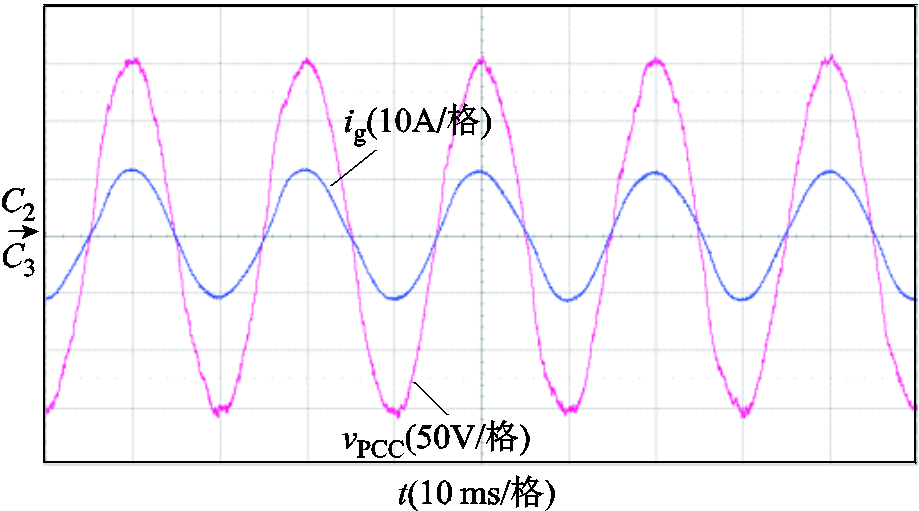
图20 Lg=10 mH的实验波形
Fig.20 Experimental waveforms when Lg=10 mH
同时为了证明本文采用控制策略的优越性，下面加入了仿真波形。图21为不同电网阻抗下的电网电流波形，在电网阻抗较大时，电网电流中含有较高的低次谐波含量，傅里叶变换（Fast Fourier Transform, FFT）结果表明，加入改进前馈通路下的逆变器在弱电网环境下并网后，电能质量仍能得到保障。图22为强电网下加入改进前馈通路前后的动态仿真波形，由仿真结果可以看出，加入改进前馈通路后的并网逆变器在提高弱电网下系统鲁棒性的同时，仍能保有较好的动态性能。
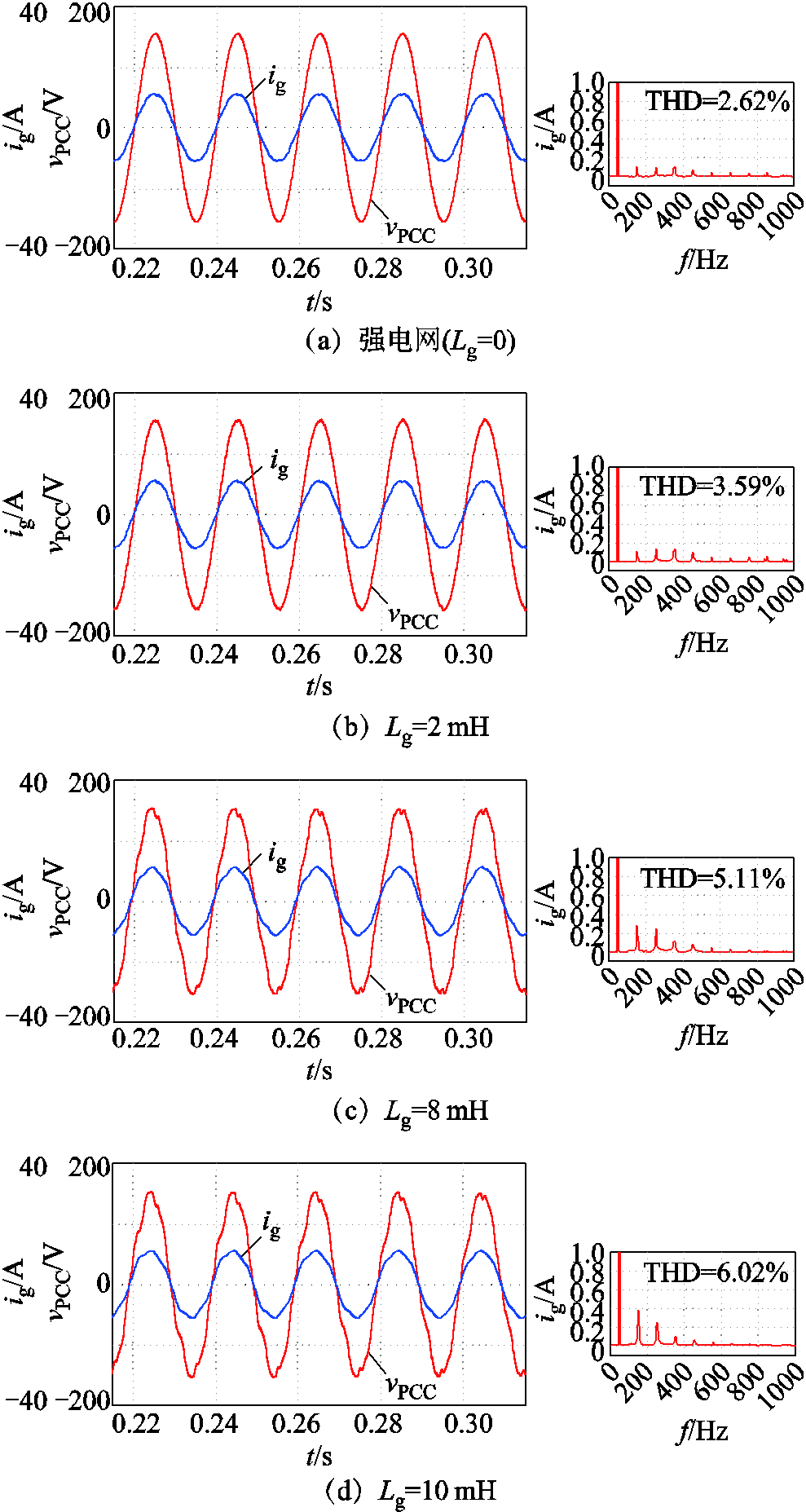
图21 不同电网阻抗下的电网电流波形及其FFT结果
Fig.21 Grid current and FFT results under different grid impedances
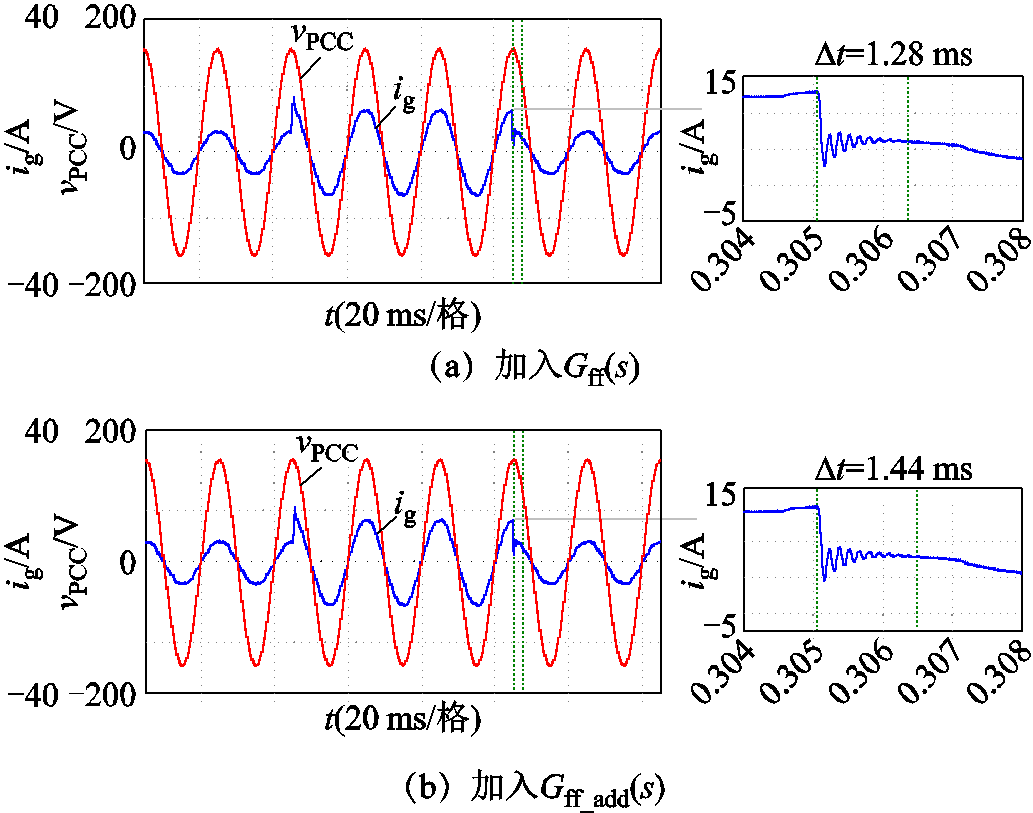
图22 强电网下加入改进前馈通路前后的动态仿真波形
Fig.22 Dynamic simulation waveforms before and after adding improved Gff in strong current network
并网逆变器作为分布式发电系统中不可或缺的环节，其安全稳定运行对于整个系统具有重要作用。在弱电网下，常用的锁相环和电网电压前馈都会对系统稳定产生影响。对于电网电压前馈引入的不稳定，考虑加入加权系数来兼顾系统的稳定性和谐波抑制能力。同时，电网电压前馈额外引入的并网电流支路会影响电流环环路增益，使得电流环带宽提高，从而降低电流环与锁相环的耦合程度，一定程度上改善锁相环的稳定性问题。因此加权系数同样会对锁相环问题产生影响。为了适应更弱电网，本文进一步引入虚拟并联导纳用以改善输出导纳相位，并给出了改进后的电压前馈函数以及设计过程。最后通过实验表明，加入改进方案后的并网逆变器在电网阻抗大范围波动时仍能保持较好的鲁棒性。
参考文献
[1] Lin Zhiheng, Ruan Xinbo, Wu Liguo, et al. Multi resonant component-based grid-voltage-weighted feedforward scheme for grid-connected inverter to suppress the injected grid current harmonics under weak grid[J]. IEEE Transactions on Power Electronics, 2020, 35(9): 9784-9793.
[2] 涂春鸣, 高家元, 赵晋斌, 等. 弱电网下具有定稳定裕度的并网逆变器阻抗重塑分析与设计[J]. 电工技术学报, 2020, 35(6): 1327-1335.
Tu Chunming, Gao Jiayuan, Zhao Jinbin, et al. Analysis and design of grid-connected inverter impedance remodeling with fixed stability margin in weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1327-1335.
[3] 李佳琪, 陈健, 张文, 等. 高渗透率光伏配电网中电池储能系统综合运行控制策略[J]. 电工技术学报, 2019, 34(2): 437-446.
Li Jiaqi, Chen Jian, Zhang Wen, et al. Integrated control strategy for battery energy storage systems in distribution networks with high photovoltaic penetration[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 437-446.
[4] 许津铭, 卞申一阳, 钱浩, 等. 弱电网下单相并网逆变器延时锁相环的鲁棒控制及优化方法[J]. 中国电机工程学报, 2020, 40(7): 2062-2070, 2386.
Xu Jinming, Bian Shenyiyang, Qian Hao, et al. Robust control and optimization of delay-based phase-locked loop of single-phase grid-connected inverters under weak grid conditions[J]. Proceedings of the CSEE, 2020, 40(7): 2062-2070, 2386.
[5] Li Ming, Zhang Xing, Guo Zixuan, et al. The control strategy for the grid-connected inverter through impedance reshaping in q-axis and its stability analysis under a weak grid[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(3): 3229-3242.
[6] Wen Bo, Dong Dong, Boroyevich D, et al. Impedance-based analysis of grid-synchronization stability for three-phase paralleled converters[J]. IEEE Transactions on Power Electronics, 2016, 31(1): 26-38.
[7] 李光辉, 王伟胜, 刘纯, 等. 直驱风电场接入弱电网宽频带振荡机理与抑制方法(一)：宽频带阻抗特性与振荡机理分析[J]. 中国电机工程学报, 2019, 39(22): 6547-6562.
Li Guanghui, Wang Weisheng, Liu Chun, et al. Mechanism analysis and suppression method of wideband oscillation of PMSG wind farms connected to weak grid (partⅠ): analysis of wideband impedancecharacteristics and oscillation mechanism[J]. Proceedings of the CSEE, 2019, 39(22): 6547-6562.
[8] 李光辉, 王伟胜, 刘纯, 等. 直驱风电场接入弱电网宽频带振荡机理与抑制方法(二)：基于阻抗重塑的宽频带振荡抑制方法[J]. 中国电机工程学报, 2019, 39(23): 6908-6920, 7104.
Li Guanghui, Wang Weisheng, Liu Chun, et al. Mechanism analysis and suppression method of wideband oscillation of PMSG wind farms connected to weak grid (part Ⅱ): suppression method of wideband oscillation based on impedance reshaping[J]. Proceedings of the CSEE, 2019, 39(23): 6908-6920, 7104.
[9] 涂春鸣, 高家元, 李庆, 等. 具有复数滤波器结构锁相环的并网逆变器对弱电网的适应性研究[J]. 电工技术学报, 2020, 35(12): 2632-2642.
Tu Chunming, Gao Jiayuan, Li Qing, et al. Research on adaptability of grid-connected inverter with complex coefficient-filter structure phase locked loop to weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2632-2642.
[10] 郭磊, 王丹, 刁亮, 等. 针对电网不平衡与谐波的锁相环改进设计[J]. 电工技术学报, 2018, 33(6): 1390-1399.
Guo Lei, Wang Dan, Diao Liang, et al. A modified design of phase-locked loop for unbalanced and distorted grid voltage conditions[J]. Transactions of China Electrotechnical Society, 2018, 33(6): 1390-1399.
[11] Xu Jinming, Qian Qiang, Zhang Binfeng, et al. Harmonics and stability analysis of single-phase grid-connected inverters in distributed power generation systems considering phase-locked loop impact[J]. IEEE Transactions on Sustainable Energy, 2019, 10(3): 1470-1480.
[12] 许津铭, 卞申一阳, 钱强, 等. 弱电网下基于电网电流前馈的单相逆变器锁相环[J]. 中国电机工程学报, 2020, 40(8): 2647-2657.
Xu Jinming, Bian Shenyiyang, Qian Qiang, et al. Grid current feedforward based phase-locked loop for single-phase-inverters in weak grid case[J]. Proceedings of the CSEE, 2020, 40(8): 2647-2657.
[13] 冯伟, 孙凯, 关雅娟, 等. 孤立微电网中基于输出电压复合控制的电压源型并网逆变器谐波电流抑制策略[J]. 电工技术学报, 2016, 31(7): 72-80.
Feng Wei, Sun Kai, Guan Yajuan, et al. A harmonic current suppression strategy for voltage source grid-connected inverters based on output voltage hybrid control in islanded microgrids[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 72-80.
[14] Timbus A, Liserre M, Teodorescu R, et al. Evaluation of current controllers for distributed power generation systems[J]. IEEE Transactions on Power Electronics, 2009, 24(3): 654-664.
[15] Li Weiwei, Ruan Xinbo, Pan Donghua, et al. Full-feedforward schemes of grid voltages for a three-phase LCL-type grid-connected inverter[J]. IEEE Transactions on Industrial Electronics, 2013, 60(6): 2237-2250.
[16] Yang Dongsheng, Ruan Xinbo, Wu Heng. Impedance shaping of the grid-connected inverter with LCL filter to improve its adaptability to the weak grid condition[J]. IEEE Transactions on Power Electronics, 2014, 29(11): 5795-5805.
[17] Wang Jiangfeng, Yao Jianhui, Hu Haibing, et al. Impedance-based stability analysis of single-phase inverter connected to weak grid with voltage feed-forward control[C]//2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 2016: 2182-2186.
[18] 钱强, 谢少军, 季林, 等. 一种提升逆变器对电网适应能力的电流控制策略[J]. 中国电机工程学报, 2016, 36(22): 6193-6201.
Qian Qiang, Xie Shaojun, Ji Lin, et al. A current control strategy to improve the adaptability to utility for inverters[J]. Proceedings of the CSEE, 2016, 36(22): 6193-6201.
[19] 苗丽芳, 王乐媛, 曹斌, 等. 电网下电网电压前馈控制分布式逆变系统的谐振阻尼特性分析[J]. 高电压技术, 2020, 46(10): 3521-3532.
Miao Lifang, Wang Yueyuan, Cao Bin, et al. Resonance damping characteristic analysis of distributed inverter-based system with grid voltage feed-forward control in weak grid[J]. High Voltage Engineering, 2020, 46(10): 3521-3532.
[20] Li Ming, Zhang Xing, Guo Zixuan, et al. The control strategy for the grid-connected inverter through impedance reshaping in q-axis and its stability analysis under a weak grid[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(3): 3229-3242.
[21] 杜燕, 张梦梦, 杨向真, 等. 基于自适应复合导纳校正的并网逆变器稳定方法[J]. 高电压技术, 2022, 48(6): 2088-2097.
Du Yan, Zhang Mengmeng, Yang Xiangzhen, et al. Grid-connected inverter stabilization method based on adaptive composite admittance correction[J]. High Voltage Engineering, 2022, 48(6): 2088-2097.
[22] Xu Jinming, Hu Yuan, Qian Hao, et al. Delay-based phase-locked loop parameters design based on stability region of grid-connected single-phase inverter under grid voltage sags[J]. IEEE Transactions on Industrial Electronics, 2022, 69(11): 11324-11334.
[23] Xu Jinming, Bian S, Qian Qiang, et al. Robustness improvement of single-phase inverters under weak grid cases by adding grid current feedforward in delay-based phase-locked loop[J]. IEEE Access, 2020, 8: 124275-124287.
[24] Sun Jian. Impedance-based stability criterion for grid-connected inverters[J]. IEEE Transactions on Power Electronics, 2011, 26(11): 3075-3078.
[25] Qin Kuang, Wang Wentao, Wang Xuehua, et al. An adaptive proportional feedforward scheme for LCL-type grid-connected inverter[C]//2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 2020: 3287-3292.
[26] 周青峰. 适用于弱电网下LCL型并网逆变器的电网电压前馈策略研究[D]. 武汉: 华中科技大学, 2018.
Zhou Qingfeng. Feedforward scheme of grid voltage for LCL-type grid-connected inverters under weak grid conditions[D]. Wuhan: Huazhong University of Science and Technology, 2018.
Research on an Improved Voltage Feedforward Path of Grid-Connected Inverter Coping with Complex Stability Issues in Weak Grid
Abstract Phase-locked loop (PLL) and the grid voltage feedforward (GVF) are commonly adopted in grid-connected inverters. However, both of these two links may have impact on the stability of the system in weak grid. From the perspective of impedance, considering PLL and the GVF is equivalent to two additional admittancesYPLL(s) and Yff(s) in parallel on top of the original output admittance. The output admittance Bode plots considering the PLL and grid voltage feed-forward are given in Fig.A1, which shows that the output characteristics in the middle and low frequency bands are influenced by the two factors, resulting in a joint-action frequency band.
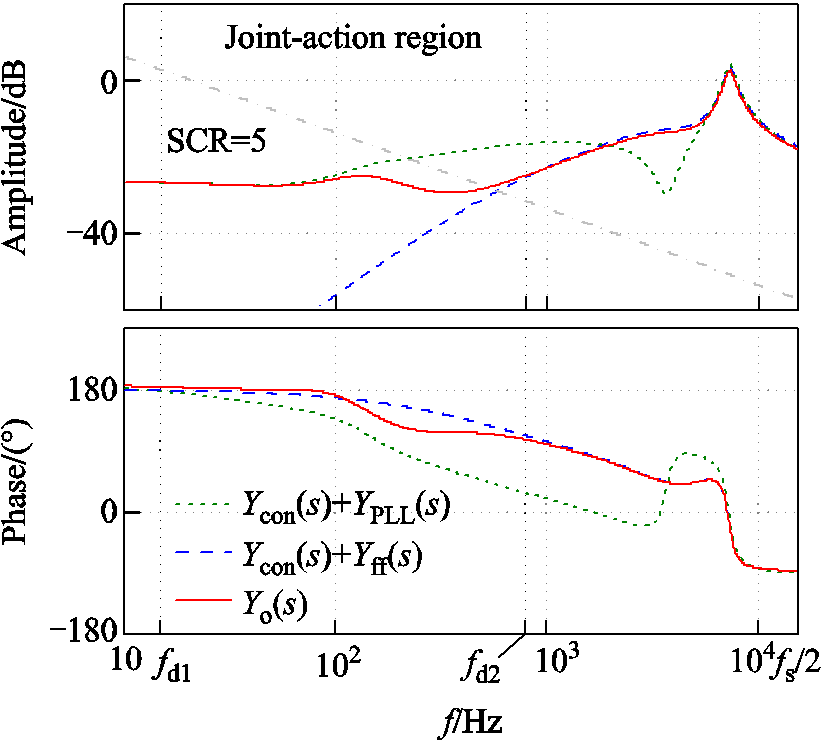
Fig.A1 Bode plots of output admittance of inverter considering dual factors
As the grid impedance increases, the admittance intersection frequency point enters the GVF-dominant frequency range of firstly. Accordingly, the primary consideration is to improve the GVF by introducing weighting coefficient to ensure the stability of the inverter as well as maintain a certain level of harmonic suppression capability of the system.With the increasing of the grid impedance, the bandwidth of the current loop decreases rapidly, approaching the frequency range influenced by the PLL bandwidth. This results in coupling between the current loop and the PLL. The introduction of the weighting coefficient into the GVF can enhance the bandwidth of the current loop, thereby improving the poor robustness induced by PLL.
However, for weaker grids with smaller SCR, the presence of the PLL would bring about a less or even negative phase margin, leading to the system unstable. Consequently, the improving effect of the weighting-coefficient-based GVF is limited in this case.Therefore, as shown in Fig.A2, a voltage feedforward path is added to improve the phase introduced by the phase-locked loop, allowing the system to adapt to a wider range of varying grid impedance. Specifically, an all-pass filter (APF) is added in this path, and then phase compensation is applied to it, which is followed by the design of its parameters at last.
Fig.A2 Control block diagram with an improved feedforward path
Finally, a prototype was constructed, and experimental waveforms verified the theoretical analysis mentioned above. The results indicate that, with the addition of the improved voltage feedforward path to the grid-connected inverter, the system can maintain a certain level of robustness even when the grid impedance varies significantly.The contribution of this article lies in following aspects: (1) The frequency-band division considering dual unstable factors is carried out. Then, the three regions including the PLL-dominant region, joint-action region and GVF-dominant region are acquired. (2) It is found that, the GVF with weighted coefficient has the merit of enhancing the robustness issue caused by the PLL to a certain extent. While, the role of improvement is somewhat limited since the phase margin is not big enough. (3) In joint-action frequency region, on the basis of the weighted coefficient, the improved feedforward path is ultimately introduced to ensure a good stability of the system in weak grid.
keywords：Grid-connected inverter, weak grid, robustness, phase-locked loop, grid voltage feedforward
中图分类号：TM464
DOI: 10.19595/j.cnki.1000-6753.tces.230986
国家自然科学基金（52077102）和江苏省自然科学基金（BK20201299）资助项目。
收稿日期 2023-06-25
改稿日期 2023-08-04
刘 昊 男，2000年生，硕士研究生，研究方向为逆变器等。
E-mail：lh2018@nuaa.edu.cn
方天治 男，1977年生，教授，博士生导师，研究方向为逆变器及电力电子系统集成等。
E-mail：fangtianzhi@126.com（通信作者）
（编辑 郭丽军）