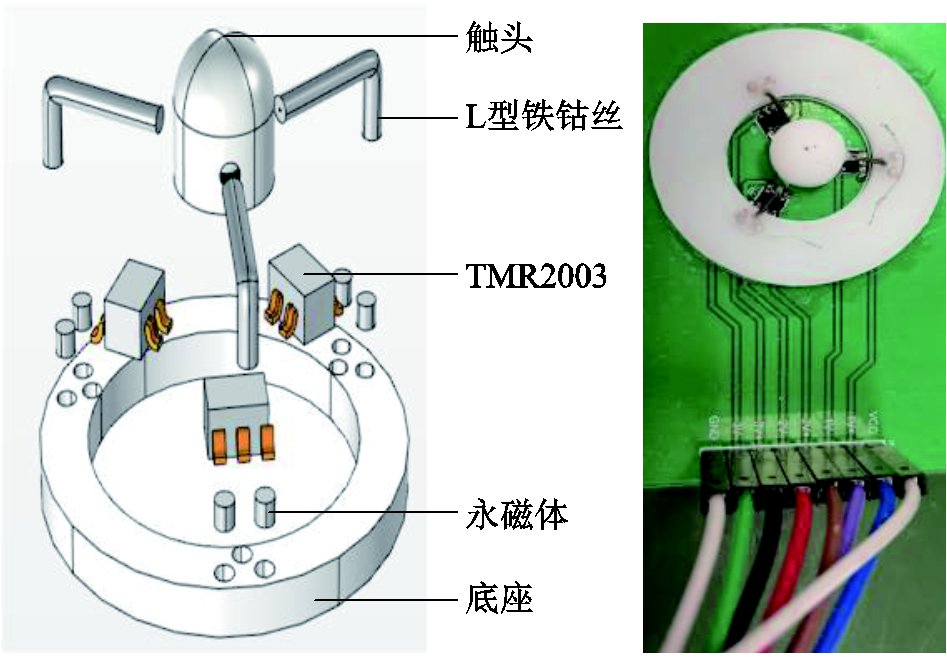
图1 三维力传感器结构示意图
Fig.1 Schematic diagram of the structure of the three-dimensional force sensor
摘要 该文提出了一种基于L型铁钴丝的三维力触觉传感器,利用磁致伸缩材料铁钴合金设计制作了三维力触觉传感单元,并测试了该结构的输出特性。基于电磁原理、逆磁致伸缩效应和欧拉伯努利动力学原理,推导了输出电压方程。搭建触觉传感单元实验平台,对传感器进行法向和切向标定,设计的传感器法向测力范围为0~13 N,切向测力范围为0~6 N,输出特性具有良好的线性关系。其中,0~8 N法向力范围内灵敏度约为23.997 mV/N,9~13 N法向力范围内灵敏度约为17.537 mV/N;0~4 N切向力范围内灵敏度约为11.599 mV/N,5~6 N切向力范围内灵敏度约为6.281 mV/N。在4 Hz频率、2 N法向力条件下,该传感器动态响应的输出电压幅值变化范围为46.5~49.8 mV,与静态力输出电压幅值的相对误差低于5%,响应时间和恢复时间分别为 25 ms和29 ms,表明该传感器具有良好的动态特性。分别采用广义逆矩阵和BP神经网络对传感器测得的三维力进行解耦,其中,BP神经网络解耦方法平均误差仅有2.90%,可有效提高测量精度。该传感器体积小、输出线性度好,可同时实现静态力和动态力的测量,在智能机器人等领域具有良好的应用前景。
关键词:逆磁致伸缩效应 BP神经网络 L型铁钴丝 动态力测量 静态力测量
当今时代,机械手作为人手的替代和功能扩展,已经被广泛应用于各种工业领域。为了满足更加复杂的感知需求,越来越多的三维力触觉传感器应运而生[1]。依据传感机理的不同,三维力触觉传感器可以分为压电式、压阻式、电容式、电磁式、光电式等类型[2]。刘玉露等开发了一种具有十字型电容板和多层复合结构的电容式三维力传感器[3],使用微柱阵列作为介电层,量程分别为0~0.15 N、0~0.15 N和0~0.1 N,差距很小。李静等利用微型电子机械系统(Micro-Electro Mechanical System, MEMS)技术设计了一种十字型压阻式三维力触觉传感器[4],输出最大线性度为0.98,串扰低于7%。王鸿博等设计了一种电磁式三维力触觉传感器[5],由霍尔传感器、弹性体和磁铁构成,通过霍尔元件测量磁场的变化,得到磁铁的位移,再通过推导的数学公式得到施加在弹性体上的三维力。
然而压阻式三维力触觉传感器是通过电阻的阻值变化进行测量的,有一定的滞后,不能很好地测量动态场景下的物理量[6];电容式三维力触觉传感器的测量中,不能忽略寄生电容的影响,并且其测量电路复杂[7];电磁式三维力触觉传感器的测量易受到外部环境的干扰[8]。而磁致伸缩材料作为一种压磁材料,具有材料磁化状态随应力的施加而变化的特性,可以瞬时响应,并且输出信号稳定。这使得磁致伸缩材料在触觉传感方面具有较大优势,可以对动静态力实现快速测量[9-10]。
在众多磁性材料中,以铁镓为代表的新型敏感磁致伸缩材料因其灵敏度高、线性度好的优势,被广泛应用在位移、纹理和触觉等测量微小受力的传感器上[11]。赵智忠等利用铁镓片设计了一种悬臂梁式的三维力传感器,结构整体采用十字型,四个独立的传感单元共用同一个触头以实现对三维力的测量[12]。但是铁镓合金在单一固定取向上才有优良的电磁性能,在多维力测量上具有一定的局限性[13]。为实现多维力的精确测量,人们进行了广泛研究。常见的磁致伸缩材料除了铁镓,还有铁钴、铁镍等。相较于铁镍,铁钴输出的信号更强,且该材料的磁晶各向异性与取向关系不大,性能稳定,可以实现对多维力的精确测量[14]。
本文利用L型铁钴丝作为敏感材料,设计了一种三维力触觉传感器。底座作为固定单元,半球形触头作为受力单元,隧道磁阻(Tunneling Magneto Resistive, TMR)传感器作为磁场检测元件,圆柱形永磁体放置在L型铁钴丝的两侧,三根铁钴丝相差120°排列。较于之前的十字结构,在相同条件下,该结构形变更明显,且减少了一个传感单元,使得结构体积更小,便于集成化,降低了成本。
传感部分由三根相差120°的L型铁钴丝组成,这些丝在受到大压力后需要退火恢复原来的初始状态。在确定了水平梁和垂直梁的尺寸后,需要用压力夹将铁钴丝弯曲成L型,使水平梁和垂直梁之间的角度为90°,然后将丝放入高温电阻炉中,加热到800℃后持续保温40 min。待装置冷却后,取出L型铁钴丝,此时铁钴丝已经基本成形,水平梁和垂直梁在承受高压力时会产生一定的变形,在外力消除后可以迅速恢复到初始位置。三根金属丝插入圆柱体中,为了可以更好地感受力的变化,圆柱体的顶部采用半球形设计,圆柱体的高为2 mm,半球形和圆柱体截面半径为2.5 mm,结构如图1所示。

图1 三维力传感器结构示意图
Fig.1 Schematic diagram of the structure of the three-dimensional force sensor
当外力施加在触头上时,触头向下移动,铁钴丝的水平梁会向下弯曲并使得垂直梁发生弯曲,这会导致垂直梁内部磁感应强度发生变化。具有竖直磁化方向的钕铁硼永磁体放置在L型铁钴丝的两侧,用于提供均匀的偏置磁场。磁场测量元件为位于丝正下方的TMR2003,它的各个端口含义及灵敏度方向如图2所示。
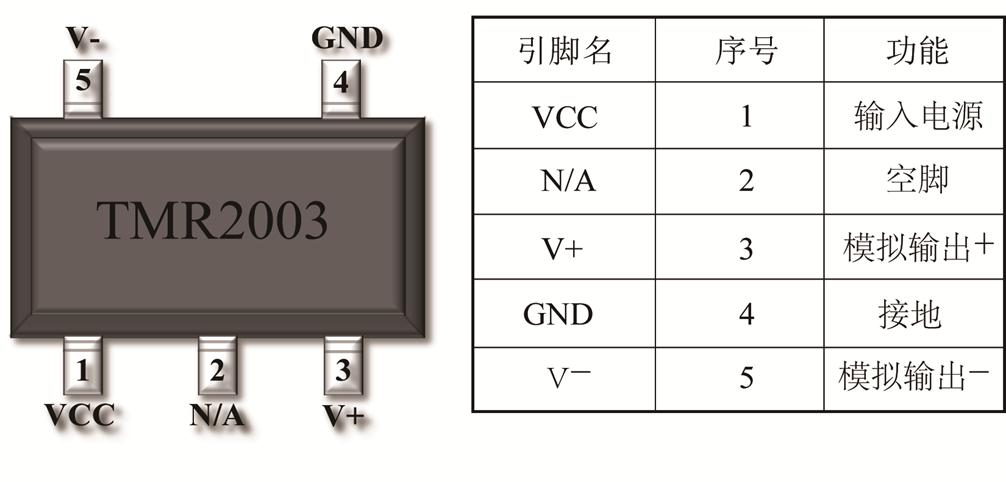
图2 TMR2003磁传感器各个端口及其含义
Fig.2 TMR2003 magnetic sensor ports and their meanings
当铁钴丝垂直梁内部磁感应强度发生变化时,TMR会检测周围磁场的变化,输出电压信号,从而实现力信号、磁信号和电信号的转换。之后再根据推导的电压和受力之间的数学表达式,进行施加力的求解,从而完成力-磁-电-力的整个转换过程,传感流程如图3所示。
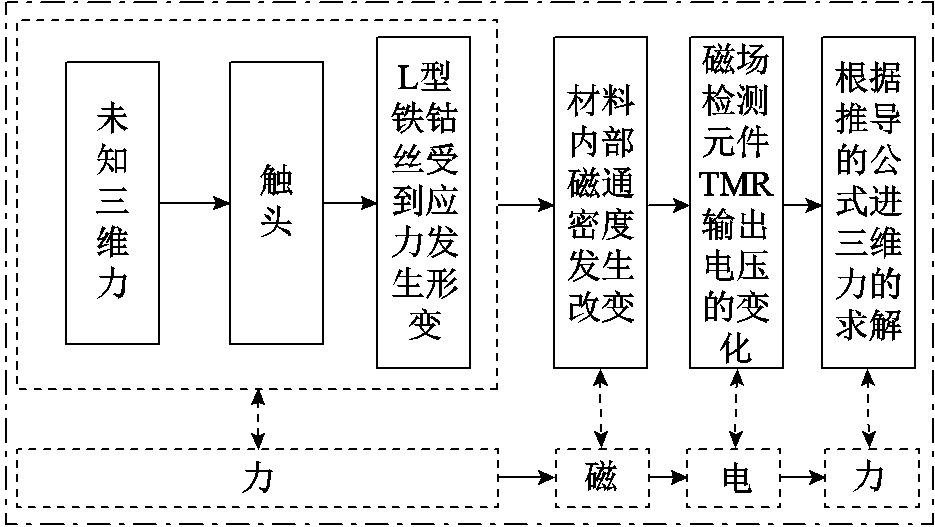
图3 传感流程
Fig.3 Sensing flow chart
通过有限元仿真软件对结构的可行性进行了验证,结果如图4所示。施加法向力时,三根丝的形变是相同的,当施加沿x轴和y轴的切向力时,处于对称位置的丝有相同的形变,而另外一根丝则有区别较大的形变。根据上述仿真,证明了该结构可以对不同方向上的力实现测量。
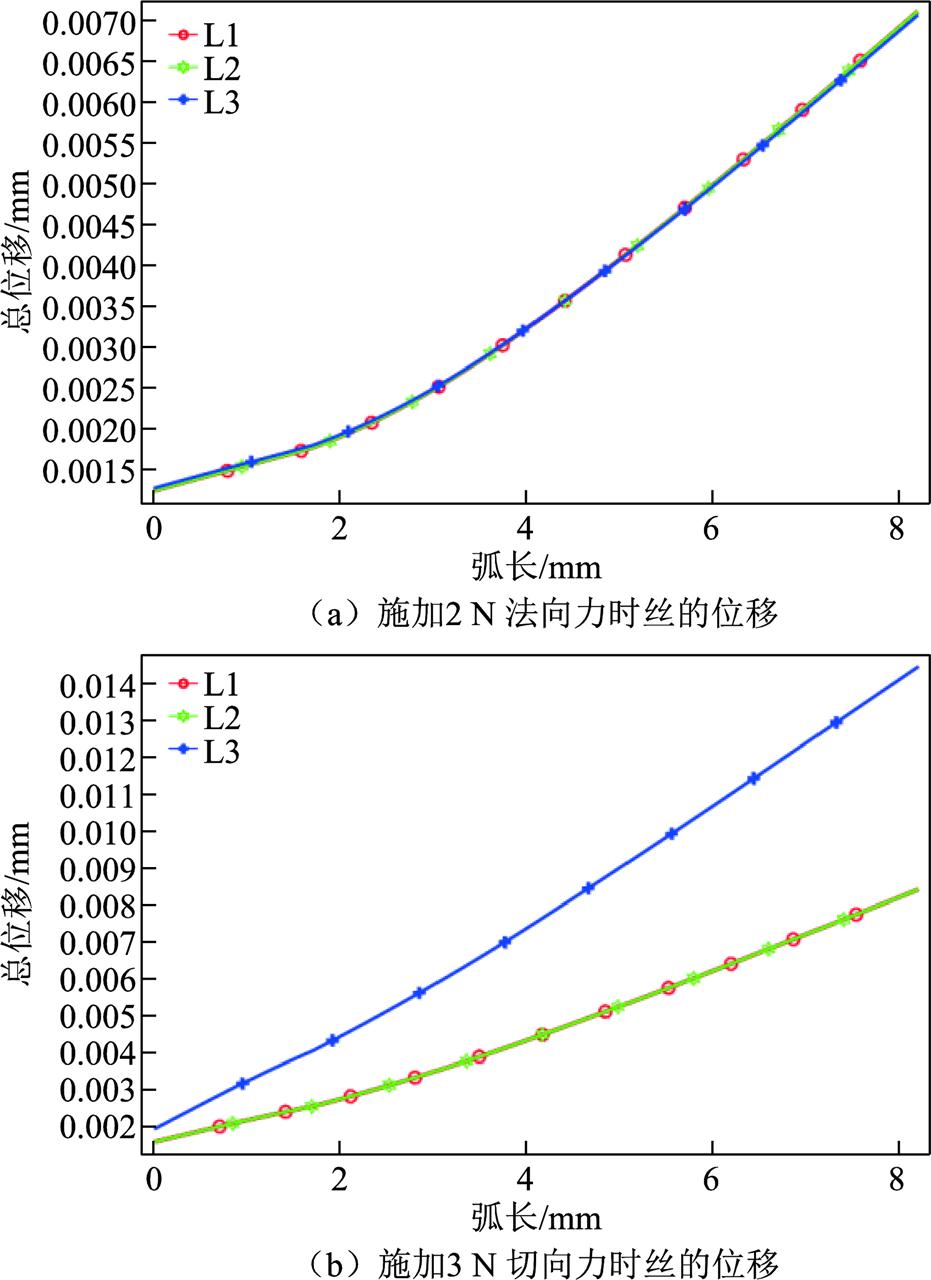
图4 施加不同方向力时三根丝对应的形变
Fig.4 The deformation of the three wires when different directional forces are applied
为实现最优的力磁响应,本文使用永磁体为三根丝提供合适的偏置磁场。使用COMSOL有限元仿真软件对触觉传感阵列进行建模。L型铁钴的参数见表1。
表1 L型铁钴各项参数
Tab.1 L-type iron and cobalt parameters

参数数值 饱和磁化强度/(kA/m)1 609.163 密度/(kg/m3)8 572.42 饱和磁致伸缩(%)97.6´10-4 杨氏模量/GPa188.1 泊松比0.33 初始磁化率13.519 02
在固体力学中,线弹性材料的固体模型设置为各向同性,铁钴丝的位移场和结构速度场的初始值均为0。在磁场-安培定律中永磁体的磁化模型选择为剩余磁感应强度,磁感应强度的大小由用户定义。由图5可以看出,L型铁钴丝内部的磁畴沿着铁钴丝的弯曲方向规则排列,并且以竖的中轴线为分界线,内部磁畴会比外部磁畴更明显地偏转。
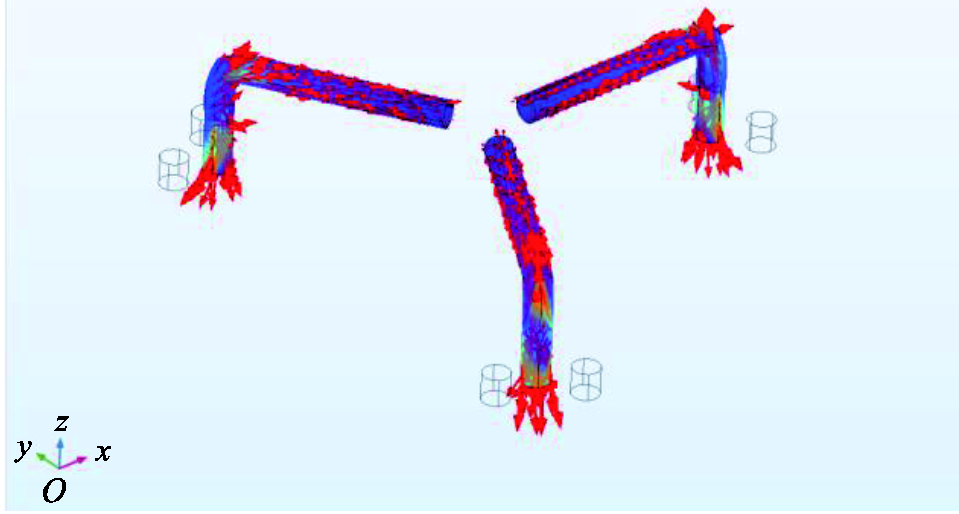
图5 铁钴丝内部磁畴分布
Fig.5 Distribution of magnetic domains inside iron cobalt wires
为了使传感器单元具有更大的输出电压,同时尽可能地增加受力范围,L型铁钴丝水平梁和垂直梁的长度应在放置永磁体后确定。通过使用COMSOL有限元分析软件调整水平梁和垂直梁的长度,获得了垂直梁内弯处的平均磁感应强度,如图6所示,可以看出垂直梁长度在2~4 mm范围内丝的磁感应强度具有较大值。为了确保传感器阵列的输出更大,同时减小尺寸,传感器单元的垂直梁的长度最终确定为3 mm,其中插入底座的长度为1 mm。
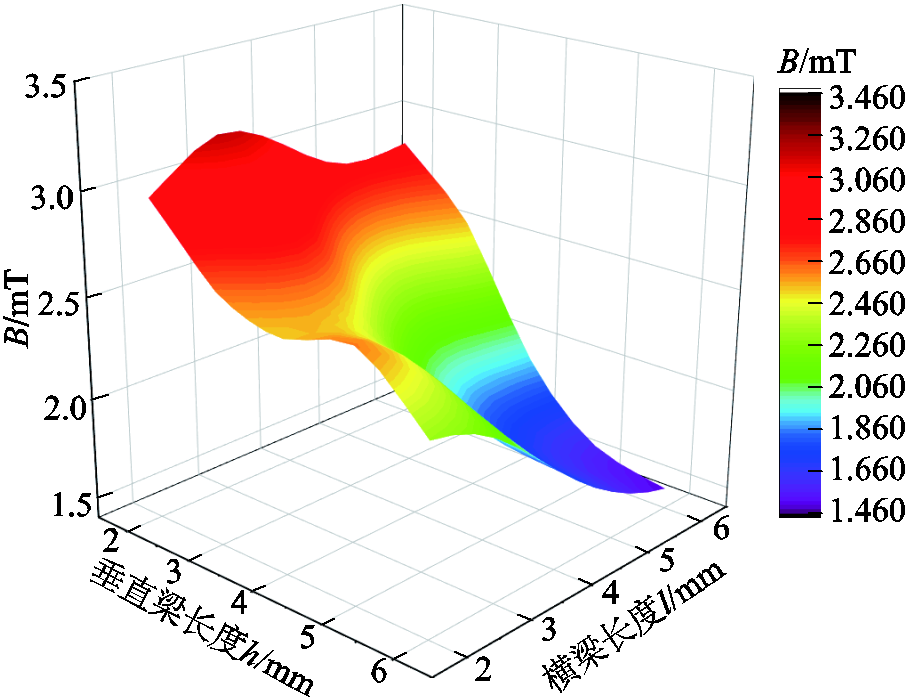
图6 L型三维力传感器磁感应强度随铁钴丝长度的变化
Fig.6 The magnetic induction intensity of the L-type 3D force sensor varies with the length of the iron cobalt wire
同时优化了丝距离中心点的长度,由COMSOL软件仿真可以得到,当三根丝距离中心点1.5 mm时,垂直梁均具有最大的磁感应强度,因此插入圆柱体的长度为1 mm。为确保三根L型铁钴丝都处于线性磁化间隔内,减少反向磁致伸缩效应的滞后,优化了圆柱形永磁体的磁场大小。在L型铁钴丝的水平梁端施加从0 N到8 N的压力,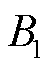 为圆柱形永磁体的磁感应强度,
为圆柱形永磁体的磁感应强度,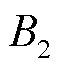 为L型铁钴丝垂直梁内侧的平均磁感应强度,仿真结果如图7所示。由图7可以看出,当
为L型铁钴丝垂直梁内侧的平均磁感应强度,仿真结果如图7所示。由图7可以看出,当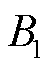 增加到50 mT时,磁感应强度增加变缓,且在50 mT时有较大的磁感应强度,可以满足磁场的需求,故最终选择两个磁感应强度为50 mT的圆柱形永磁体,其半径为 1 mm,高度为1 mm。
增加到50 mT时,磁感应强度增加变缓,且在50 mT时有较大的磁感应强度,可以满足磁场的需求,故最终选择两个磁感应强度为50 mT的圆柱形永磁体,其半径为 1 mm,高度为1 mm。
根据优化的结果,确定内环半径为7 mm,外环半径为8 mm,最后整个触觉传感单元的尺寸为 16 mm×16 mm×6 mm。
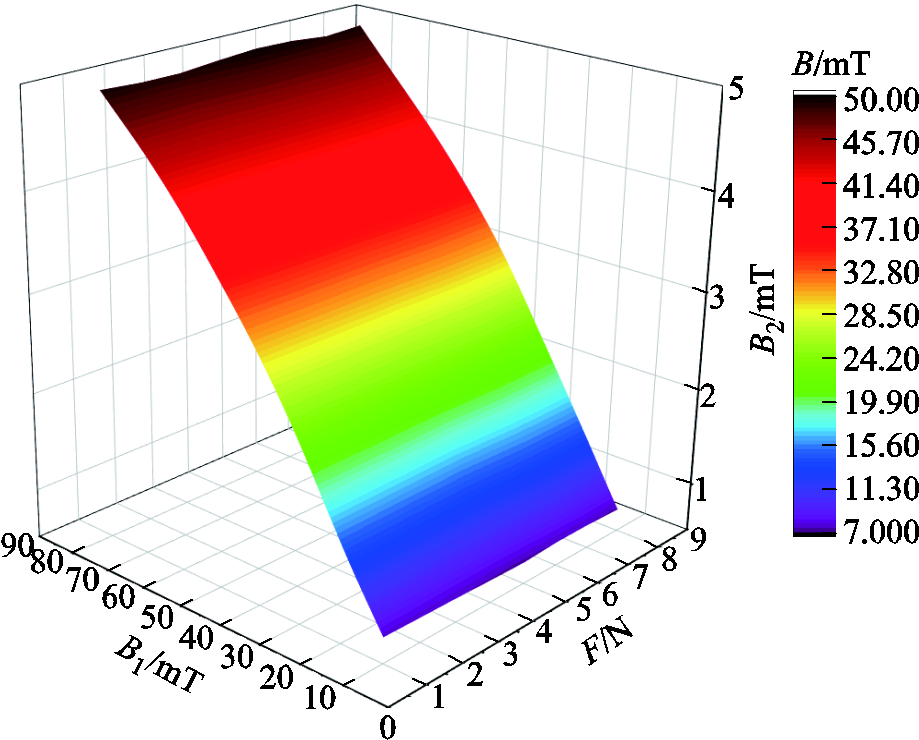
图7 铁钴丝在不同偏置磁场下垂直梁内部的磁感应强度模
Fig.7 The magnetic flux density mode inside the vertical beam under different biased magnetic fields
相比于传统的霍尔元件,TMR检测元件内部包含一个独特的惠斯通电桥,其输出采用双端差分输出模式,能够有效地消除来自零点漂移的影响,并且灵敏度也有所提高。TMR元件内部由推挽式惠斯通电桥结构中的四个磁阻组成,输出处于双端差分输出模式,并且将UA和UB设为差分输出的正电压和负电压,RH和RL分别为TMR传感器在正向和反向磁饱和中显示的电阻值,RM为等效磁阻,则元件TMR的输出电压可以表示为[15]
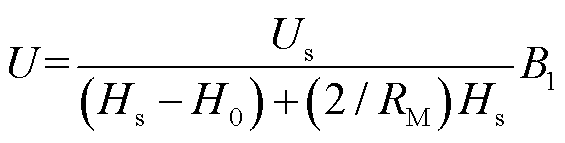 (1)
(1)
式中, 为电源电压;
为电源电压;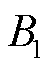 为感应外部的磁感应强度;Hs为传感器饱和下的磁场强度;
为感应外部的磁感应强度;Hs为传感器饱和下的磁场强度;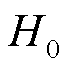 为初始的磁场强度。由于选择了固定的TMR型号,
为初始的磁场强度。由于选择了固定的TMR型号,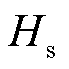 和
和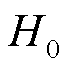 均为确定的数值。根据式(1)可以看出,当
均为确定的数值。根据式(1)可以看出,当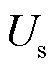 相同时,TMR的灵敏度与等效磁阻成正比。输出电压进而可表示为[16]
相同时,TMR的灵敏度与等效磁阻成正比。输出电压进而可表示为[16]
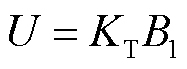 (2)
(2)
式中,KT为TMR磁电转换因子。根据文献[17],铁钴中的磁感应强度可以表示为
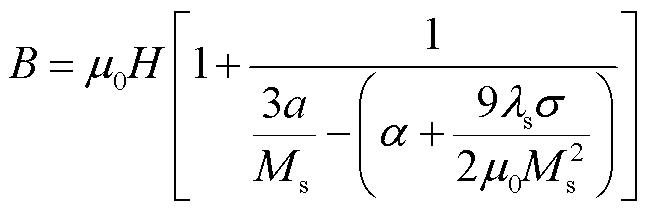 (3)
(3)
式中,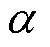 为畴壁相互作用系数;
为畴壁相互作用系数;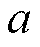 为磁滞磁化的形状因子;
为磁滞磁化的形状因子;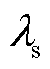 为饱和磁致伸缩系数;
为饱和磁致伸缩系数;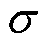 为铁钴材料上受到的应力;
为铁钴材料上受到的应力;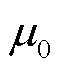 为真空磁导率;Ms为饱和磁化强度。L型铁钴的整体形变状态可以看作是一个小状态的情况,当水平梁受力时,它和垂直梁之间的角度不会发生变化,TMR检测元件检测到的是垂直梁底端的磁感应强度变化,如图8所示。
为真空磁导率;Ms为饱和磁化强度。L型铁钴的整体形变状态可以看作是一个小状态的情况,当水平梁受力时,它和垂直梁之间的角度不会发生变化,TMR检测元件检测到的是垂直梁底端的磁感应强度变化,如图8所示。
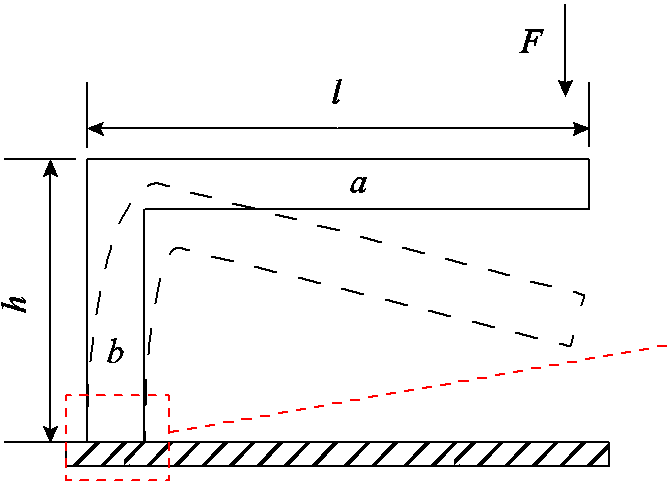
图8 L型铁钴丝受力示意图
Fig.8 L-type iron cobalt wire force diagram
垂直梁受到竖直向下的力和沿顺时针方向的力矩MA,则此处的应力可以表示为
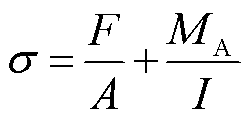 (4)
(4)
式中,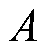 为L型铁钴丝的横截面积;
为L型铁钴丝的横截面积;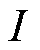 为垂直梁的惯性力矩,
为垂直梁的惯性力矩,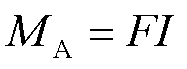 ,
,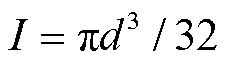 ,
,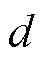 为丝的直径。在校验完成后,可得应力为
为丝的直径。在校验完成后,可得应力为
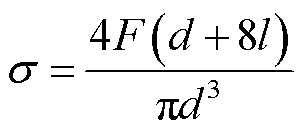 (5)
(5)
整合式(1)~式(5)可得
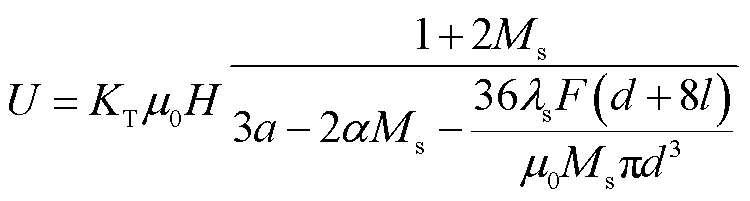 (6)
(6)
由式(6)可以看出,当材料确定以后,输出电压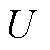 与施加的力
与施加的力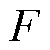 成正比,施加的力越大,输出电压就越大。输出电压模型的各项参数见表2。
成正比,施加的力越大,输出电压就越大。输出电压模型的各项参数见表2。
表2 触觉传感器输出电压模型的参数
Tab.2 Parameters of the haptic sensor output voltage model

参数数值 畴壁相互作用系数7 012 磁滞磁化形状因子0.001 真空磁导率 饱和磁化强度 磁感应传递系数0.003 TMR等效电阻70 TMR饱和磁场强度3 990 TMR初始磁场强度-1 596
为了检测三维方向上的力,建立空间坐标系,其中,y轴沿丝L1方向,z轴竖直向下。当力作用在触头最高点时,力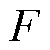 与水平面呈一定的夹角,需要进行力的分解,分解为一个垂直于触头的法向力Fv和一个与触头相比的切向力Fh,而切向力
与水平面呈一定的夹角,需要进行力的分解,分解为一个垂直于触头的法向力Fv和一个与触头相比的切向力Fh,而切向力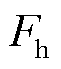 可以继续在水平面xOy上进行分解[18]。其中
可以继续在水平面xOy上进行分解[18]。其中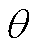 为力
为力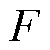 与水平面的夹角,
与水平面的夹角,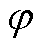 为切向力
为切向力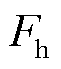 在xOy平面上分解与
在xOy平面上分解与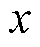 轴正半轴所形成的夹角。通过上述分解,一组
轴正半轴所形成的夹角。通过上述分解,一组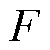 的大小、夹角
的大小、夹角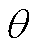 、夹角j就可以准确地表示一个外界未知力的信息,如图9a和图9b所示[19]。
、夹角j就可以准确地表示一个外界未知力的信息,如图9a和图9b所示[19]。
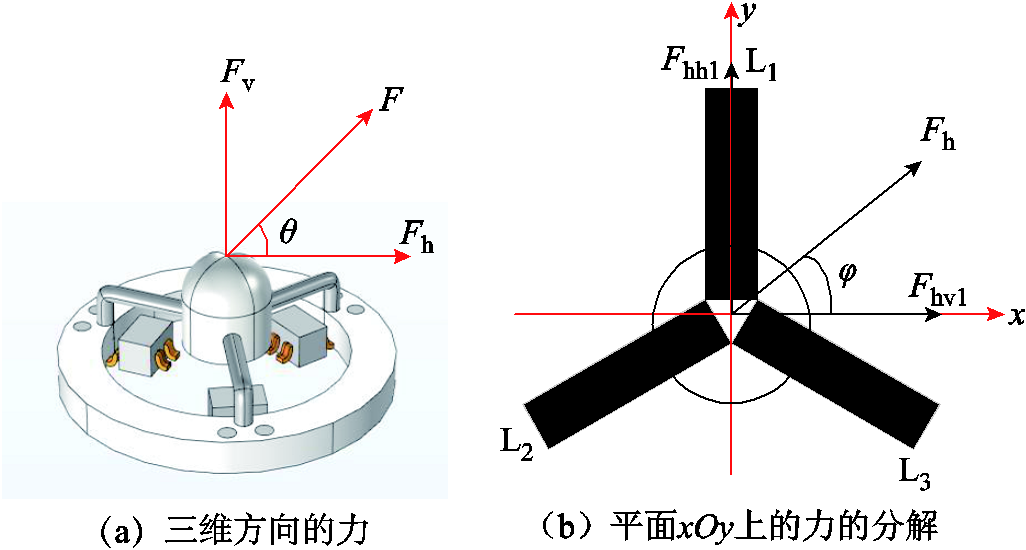
Fig.9 传感器受力时对力进行分解
Fig.9 The force is broken down when the sensor is stressed
由图7可得
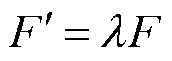 (7)
(7)
式中,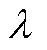 为传递系数,表示接触力
为传递系数,表示接触力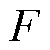 经过触头传输至铁钴丝上作用力的传递性能。通过对力的正交分解,沿
经过触头传输至铁钴丝上作用力的传递性能。通过对力的正交分解,沿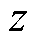 轴方向的力可以表示为
轴方向的力可以表示为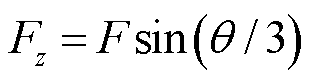 。切向力在水平面上分解,Fhh1与铁钴丝L1平行,由于触头会发生偏转,会对丝产生一个上下方向的形变,力的大小为
。切向力在水平面上分解,Fhh1与铁钴丝L1平行,由于触头会发生偏转,会对丝产生一个上下方向的形变,力的大小为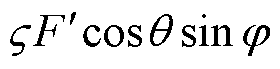 ,
,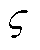 为触头纵向扭转导致L1垂直梁受力的传递系数[20];Fhv1与丝L1垂直,会导致丝有一个左右摆动的效果,力的大小为
为触头纵向扭转导致L1垂直梁受力的传递系数[20];Fhv1与丝L1垂直,会导致丝有一个左右摆动的效果,力的大小为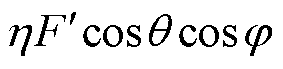 ,h为触头横向扭转导致L1垂直梁受力的传递系数。故作用在每根丝上的力可表示为
,h为触头横向扭转导致L1垂直梁受力的传递系数。故作用在每根丝上的力可表示为
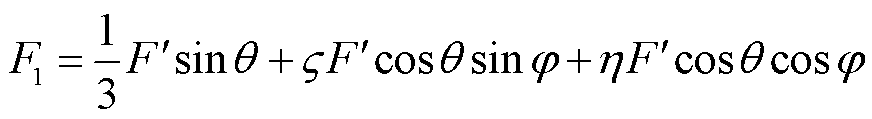 (8)
(8)
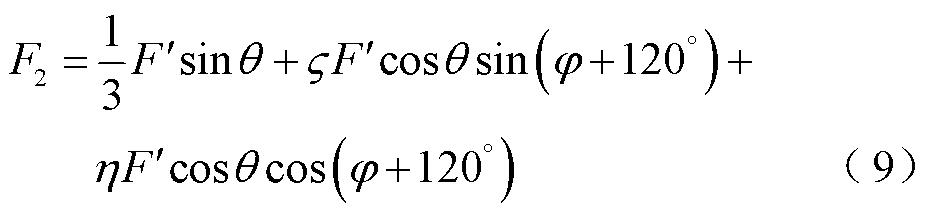
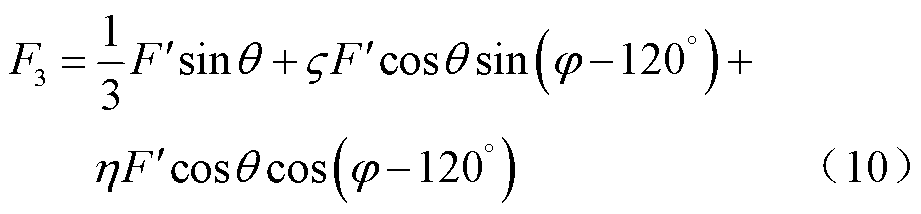
L型铁钴丝在受到磁化方向的外力时,会使材料内部磁感应强度发生变化,且在确定丝的长度和半径时,它的变化是线性的,用公式可以表示为
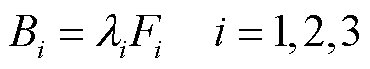 (11)
(11)
式中,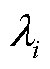 为3个L型铁钴丝对应的压磁系数;
为3个L型铁钴丝对应的压磁系数;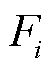 为丝感受到的应力。为了采集3个铁钴传感单元传输的电压信号,需要把磁信号转换为电压信号,电压转换的公式可以表示为[21]
为丝感受到的应力。为了采集3个铁钴传感单元传输的电压信号,需要把磁信号转换为电压信号,电压转换的公式可以表示为[21]
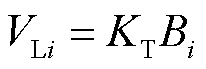 (12)
(12)
在计算三维力前,需要对传感器进行标定。设L型铁钴传感单元Li的切向标定参数值为dhi,法向标定参数值dvi,可表示为[22]
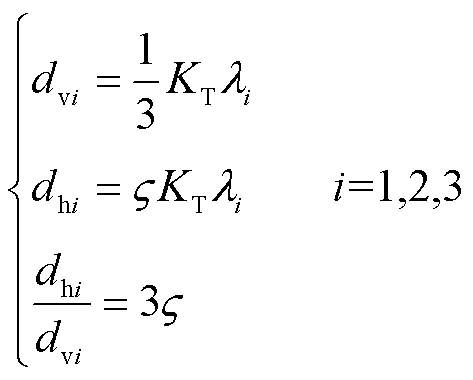 (13)
(13)
通过上述公式,可求得
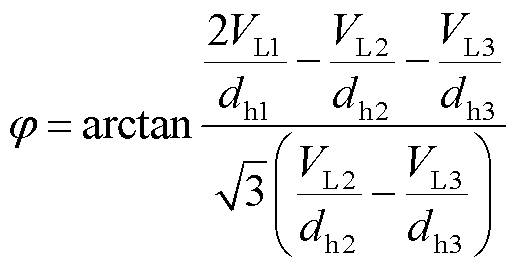 (14)
(14)
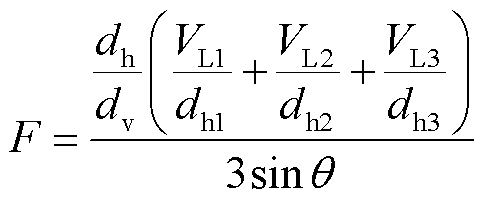 (15)
(15)
根据推导的公式可以看出,在进行三维力测量前,需要标定公式中的一些参数dh1、dh2、dh3、dh/dv。在参数确定时,使用压力机对传感器施加一定数值的力,通过磁场检测元件TMR输出的电压信号即可得到3个L型铁钴丝上感知到的外力大小[23]。
为了得出输出电压与加载力间的关系曲线,法向方向上外力从0起,每次增加1 N,一直增加至8 N,每个测试点重复10次,切向方向上外力从0 N起,每次增加1 N,一直增加至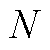 。记录3个传感单元输出信号的电压峰值,取10次测试的平均值作为最终输出结果,从而拟合出式中参数值,按图10所示进行标定,静态特性测试平台如图11所示。
。记录3个传感单元输出信号的电压峰值,取10次测试的平均值作为最终输出结果,从而拟合出式中参数值,按图10所示进行标定,静态特性测试平台如图11所示。
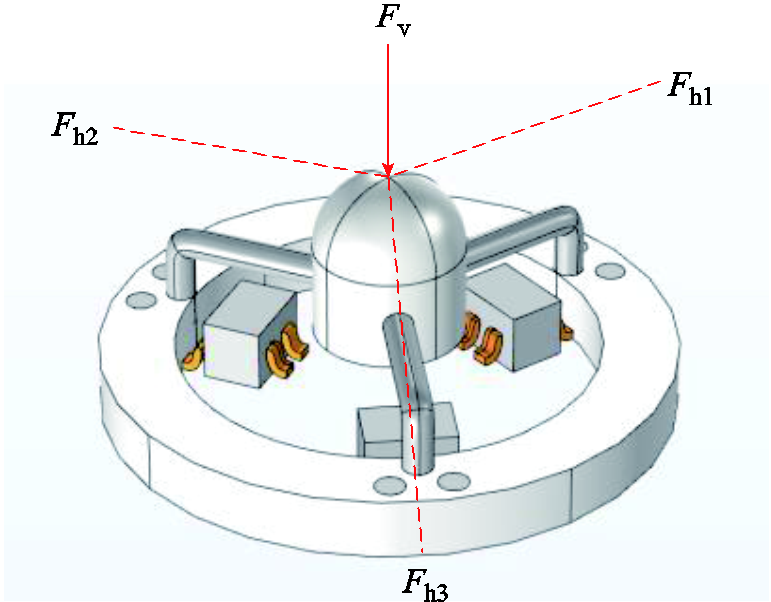
图10 标定示意图
Fig.10 Calibration diagram

图11 静态特性测试平台
Fig.11 Static characterization test platform
法向力标定:由式(11)和式(12)可知,线性拟合表达式为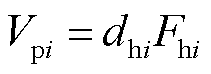 。由于L型铁钴丝为人工制作而成,在弯折时,可能有角度之差,为了保证三根铁钴丝同时受力,在触头半球顶部先施加0.5 N静态的法向力,再继续施加法向力
。由于L型铁钴丝为人工制作而成,在弯折时,可能有角度之差,为了保证三根铁钴丝同时受力,在触头半球顶部先施加0.5 N静态的法向力,再继续施加法向力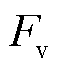 ,每次增加1 N,增加到8 N,观察电压的变化量。在法向力
,每次增加1 N,增加到8 N,观察电压的变化量。在法向力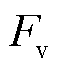 作用下,3个传感单元上输出电压信号峰值与外力之间的关系曲线如图12a~图12c所示,通过线性拟合可得,三维力触觉传感器法向标定参数
作用下,3个传感单元上输出电压信号峰值与外力之间的关系曲线如图12a~图12c所示,通过线性拟合可得,三维力触觉传感器法向标定参数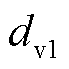 = 24.020 1 mV/N,
= 24.020 1 mV/N,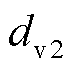 =23.979 1 mV/N,
=23.979 1 mV/N,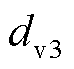 =23.991 5 mV/N。
=23.991 5 mV/N。
切向力标定:外力从0 N起,每次增加1 N,一直增加到4 N。3个传感单元上输出电压信号峰值与外力之间的关系曲线如图12d~图12f所示,通过线性拟合可得,三维力触觉传感器切向标定参数dh1= 11.591 7 mV/N,dh2=11.783 4 mV/N,dh3=11.422 3 mV/N。
根据对传感器灵敏度的定义可知,用输出值除以输入值就可以计算出该类传感器的灵敏性,对于三维力传感器来说,输入为外界的压力,输出值为电压大小,所以将电压除以力就可以得到灵敏的大小,0~8 N法向力范围内灵敏度约为23.997 mV/N,0~4 N切向力范围内灵敏度约为11.599 mV/N。
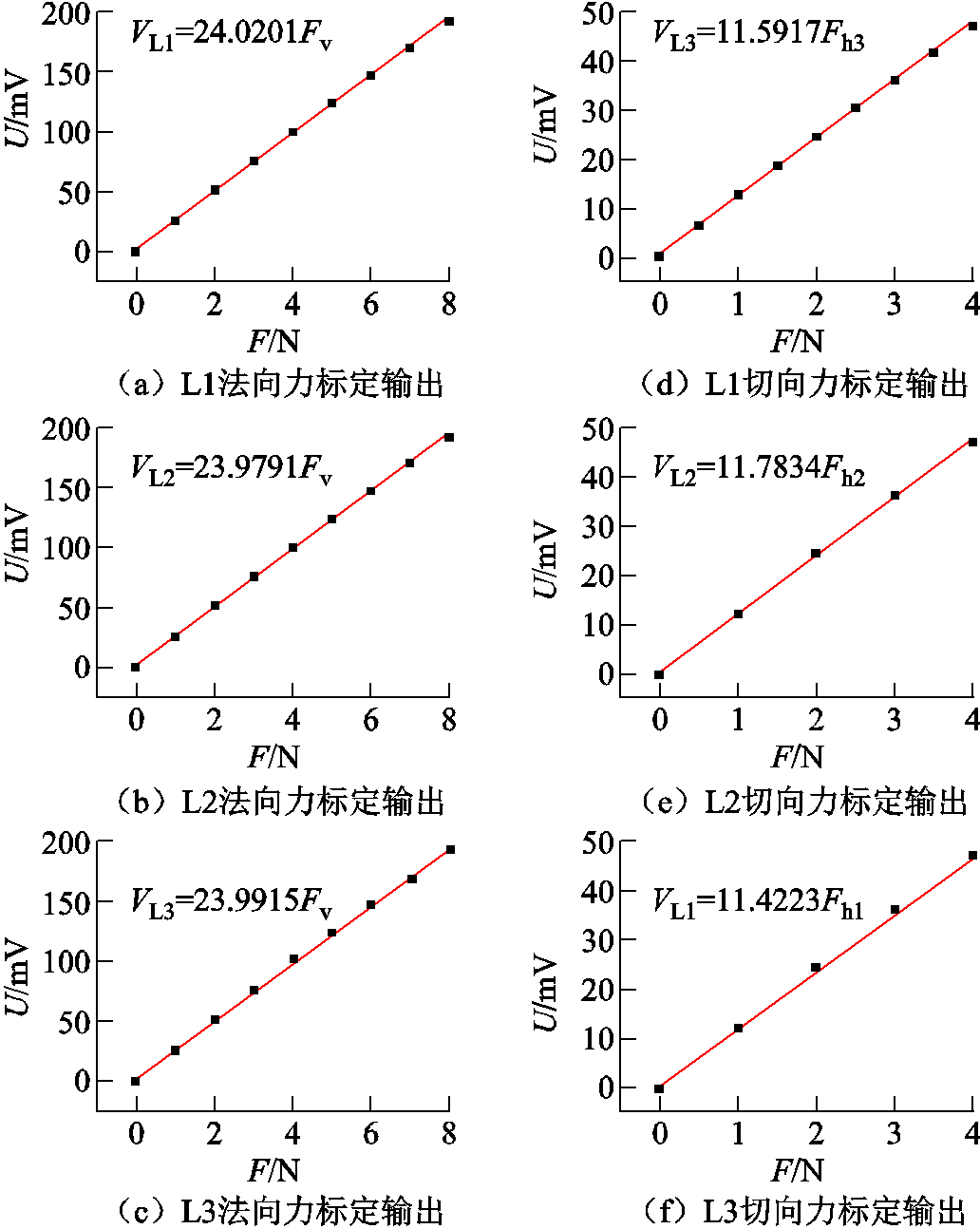
图12 切向力和法向力的标定数据
Fig.12 Calibration data for tangential and normal forces
根据求得的标定参数,得到力和输出电压之间的数学表达式,进而求得传感器三个方向上的测量误差。其中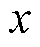 方向上的误差为6.551%,
方向上的误差为6.551%, 方向上的误差为4.692%,
方向上的误差为4.692%, 方向上的误差为7.824%。
方向上的误差为7.824%。
由于机械手在日常抓取物体时通常不超过4 Hz的频率移动。因此,为了测试磁致伸缩触觉传感阵列在不同抓握环境下的动态性能,将信号发生器设置为输出频率为4 Hz的正弦波,并通过功率放大器放大信号。触觉传感阵列的动态特性测试平台如图13所示,振动器的驱动杆跟随信号发生器产生的信号输出振幅为2 N的法向正弦力。传感器的输出连接到数据采集卡,传感器单元的输出波形经接收和处理后由计算机显示,如图14所示,在60个周期激励信号下,传感器的输出电压波形呈近似正弦波的形式变化,传感器输出电压最大幅值的波动范围46.5~49.8 mV,幅值波动在4 mV以内,与静态实验中相同压力下传感器所测的输出电压值基本一致,具有良好的动态稳定性,可用于检测动态力。对传感器进行响应速度的测试,实验结果如图15所示。其中触觉传感器的响应时间和恢复时间分别为25 ms和29 ms。可以看出,传感器在1 N力下的加载和卸载时间较快,输出滞后较小,并且传感器的响应时间比人类皮肤的响应时间快(30~50 ms)。

图13 动态特性测试平台
Fig.13 Dynamic characterization test platform
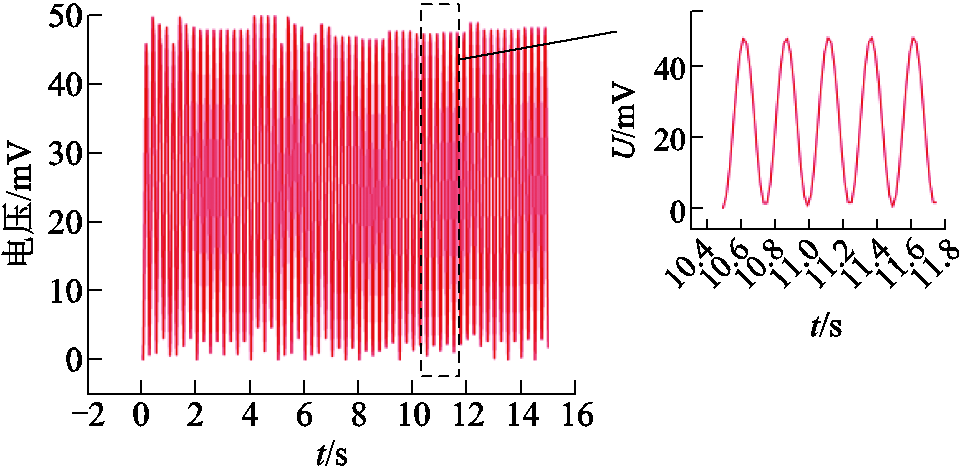
图14 动态力测试
Fig.14 Dynamic force test
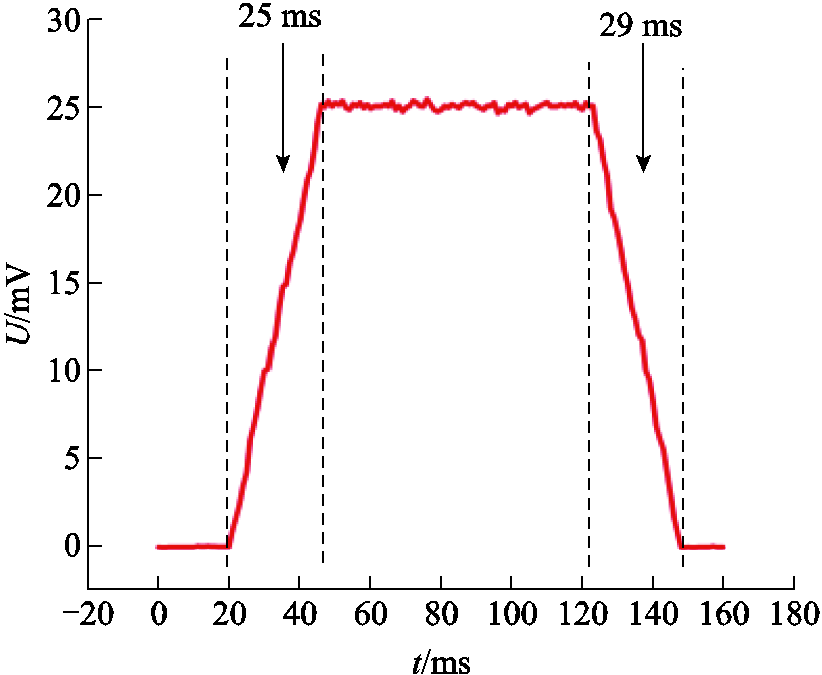
图15 传感器在4 Hz的频率和1 N的力振幅下的响应时间和恢复时间
Fig.15 Response time and recovery time of the sensor at a frequency of 4 Hz and a force amplitude of 1 N
多维力传感器的输出存在一定的耦合,所以需要对传感器进行解耦。首先通过广义逆矩阵对传感器进行线性解耦,得到力和输出电压之间的数学表达式[24]。根据传感器的标定数据和结构进行假设:
1)传感器测量的三维力和输出电压之间为线性关系。
2)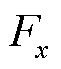 的方向沿
的方向沿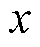 轴正方向,
轴正方向,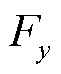 的方向沿
的方向沿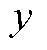 轴正方向,
轴正方向,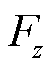 沿
沿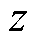 轴竖直向下为正方向。用向量
轴竖直向下为正方向。用向量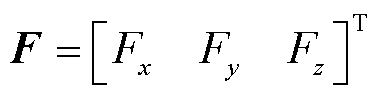 表示任意的三维力,单位为N;向量
表示任意的三维力,单位为N;向量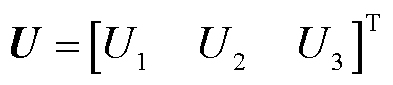 表示三个TMR的输出电压,单位为mV,那么电压与力的关系可以表示为[25]
表示三个TMR的输出电压,单位为mV,那么电压与力的关系可以表示为[25]
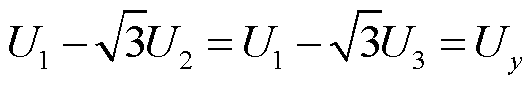 (17)
(17)
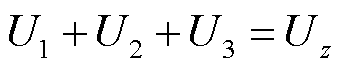 (18)
(18)
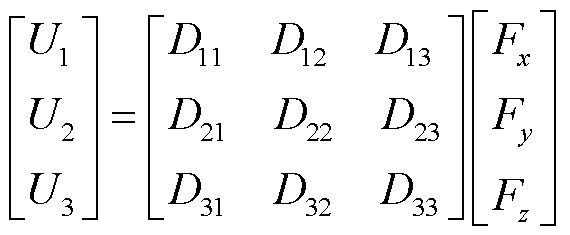 (19)
(19)
即
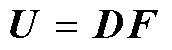 (20)
(20)
通过对式(20)进行变换可以得到解耦矩阵D为
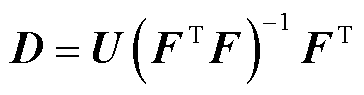 (21)
(21)
建立三维力传感器得到的输出信号和加载力信号的关系式为
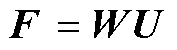 (22)
(22)
通过求解式(22)可得
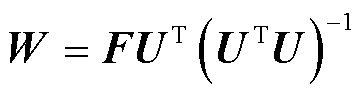 (23)
(23)
通过Matlab计算出矩阵D为
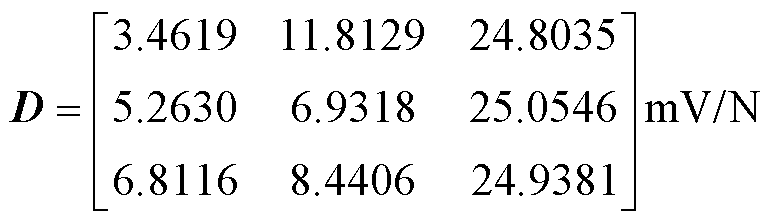 (24)
(24)
通过应用 对D矩阵求逆即得到系数矩阵,这样就求出计算三维力传感器标定的数学模型[26],即
对D矩阵求逆即得到系数矩阵,这样就求出计算三维力传感器标定的数学模型[26],即
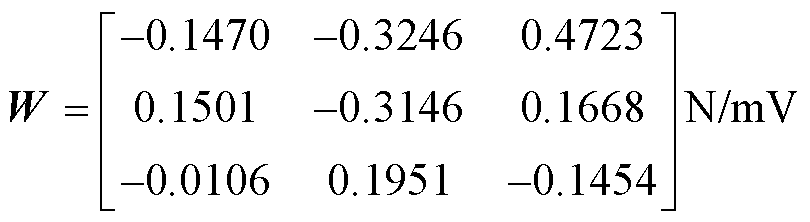 (25)
(25)
用数学式表示为
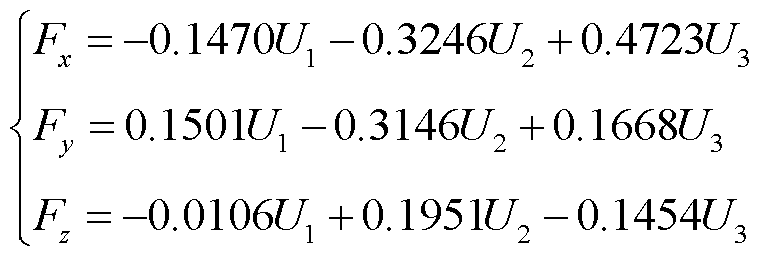 (26)
(26)
根据推导的数学表达式可以求得与实际施加力之间的误差,由测试结果误差计算公式[27]
求得x方向的平均误差为5.70%,y方向的平均误差为6.52%,z方向的平均误差为3.40%,三个方向的平均误差为5.20%。
误差来源分析如下:L型铁钴丝为手动弯折,三根丝水平粱和垂直梁间的角度会存在误差。该传感器三个方向的平均相对误差均小于8%,比基于聚偏二氟乙烯(Polyvinylidene Difuoride, PVDF)的三维力传感器测量误差小,可以在强线性的同时实现精确的测量。
使用BP神经网络对传感器的标定数据进行解耦运算,计算出传感器的误差,方均根误差(Root-Mean-Square Error, RMSE)如图16a~图16c所示,其中横坐标表示样本数量,纵坐标表示预测力的大小和实际施加力的大小的结果对比,y方向的误差为3.642 6%,x方向的误差为3.745 8%,z方向的误差为1.507 4%,三个方向的平均误差为2.90%。可以看出基于BP神经网络的非线性解耦方法能够对三维力传感器进行精确解耦,可以提高传感器的精度[28]。
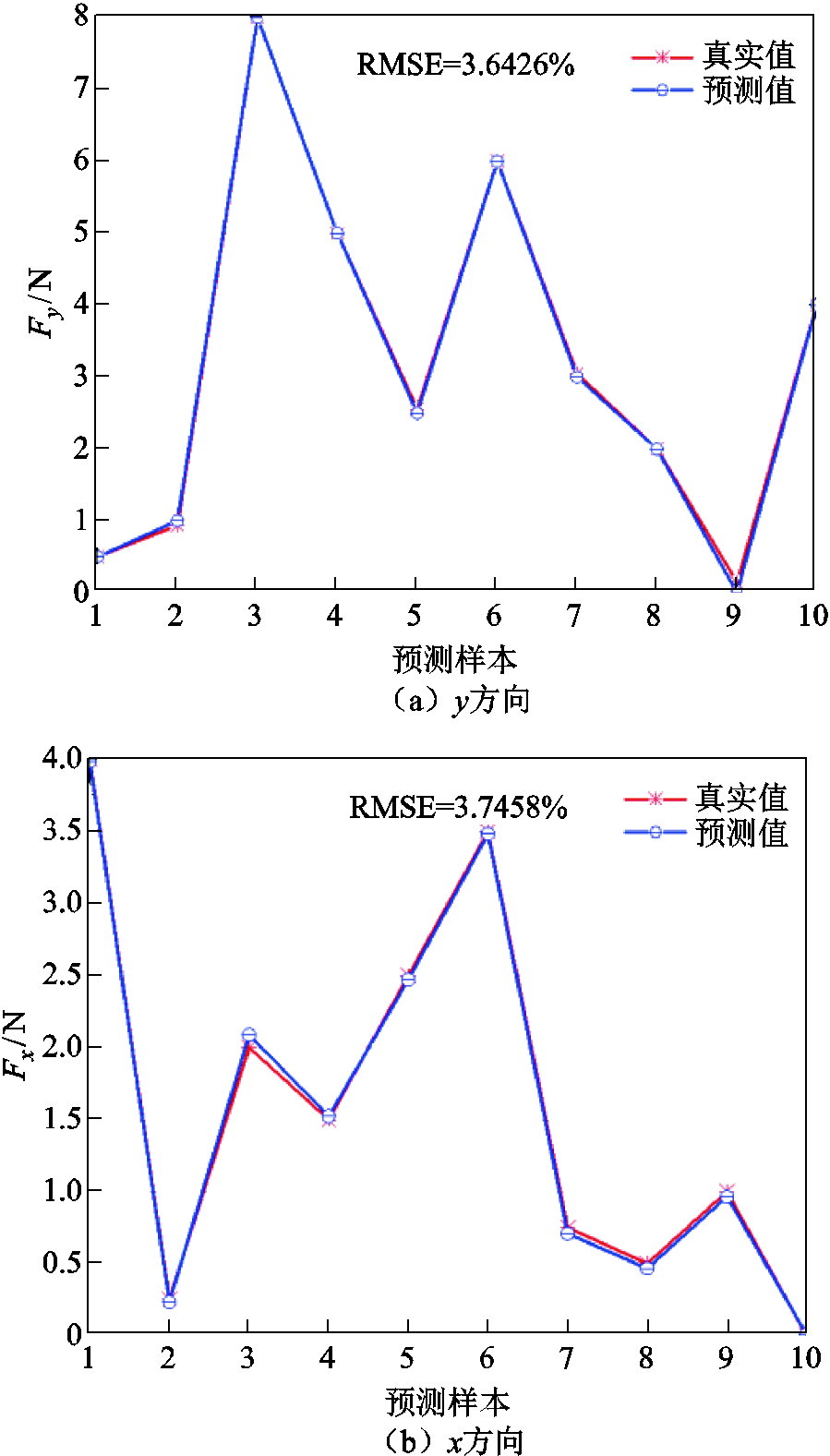
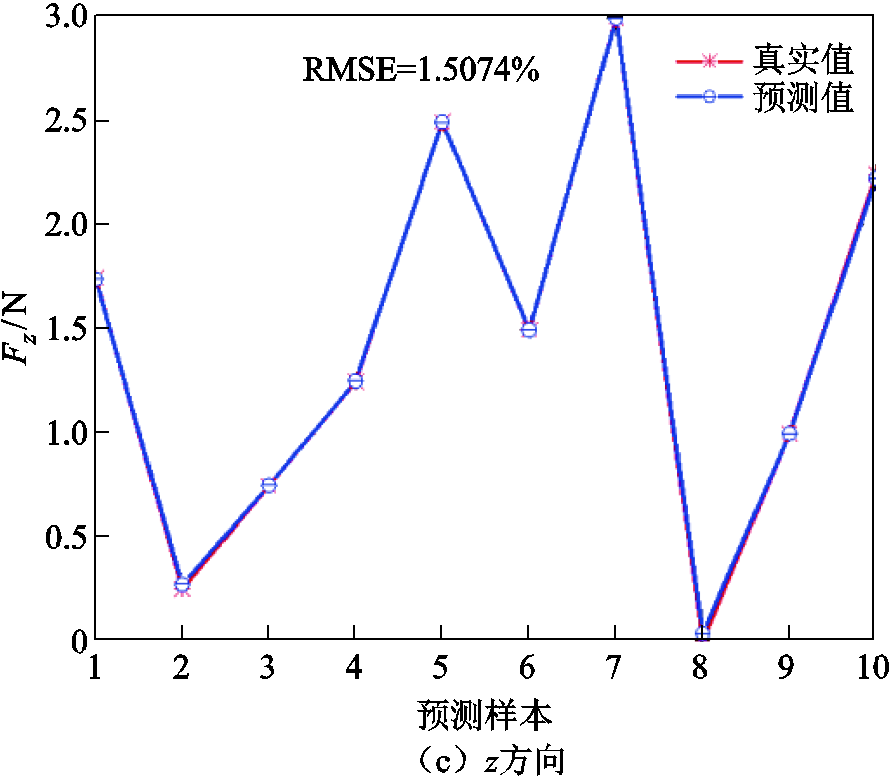
图16 使用BP神经网络对传感器进行三个方向上的解耦
Fig.16 The BP neural network is used to decouple the sensor in three directions
使用角度台使传感器分别处于不同的角度进行测量,模拟爬壁机器人不同的站姿即与地面呈现不同的夹角。对传感器施加1 N的法向力,由表3可以发现,通过对比三个输出电压幅值,可以准确地判断传感器所处的角度,对爬壁机器人脚部传感器的设计具有指导性意义。
表3 不同角度下三个TMR输出电压幅值
Tab.3 Three TMR output voltage amplitudes at different angles
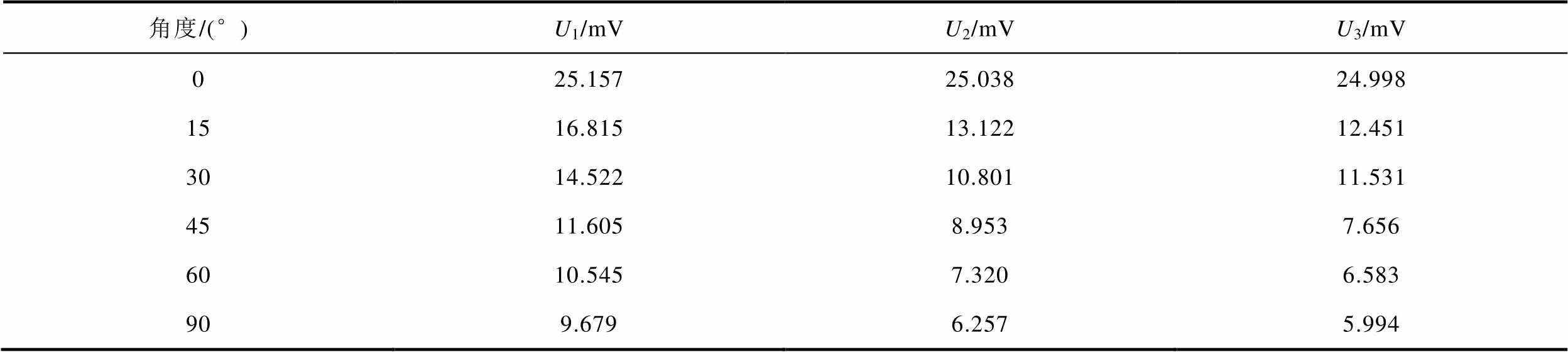
角度/(°)U1/mVU2/mVU3/mV 025.15725.03824.998 1516.81513.12212.451 3014.52210.80111.531 4511.6058.9537.656 6010.5457.3206.583 909.6796.2575.994
本文设计制作了一种基于L型铁钴丝的三维力触觉传感器,传感器由3个夹角为120°的L型铁钴传感单元构成。推导了输出电压方程,同时搭建了触觉传感单元实验平台,对传感器进行法向和切向的标定。测量了0~13 N的法向力和0~6 N的切向力,输出特性具有良好的线性关系,0~8 N范围内法向灵敏度约为23.997 mV/N,0~4 N范围内切向灵敏度约为11.599 mV/N。使用线性广义逆矩阵和BP神经网络两种方式对传感器进行解耦。结果表明,两种方法三个方向上的平均误差分别为5.20%和2.90%。该三维力触觉传感器在穿戴式电子产品、游戏手柄和人机交互等领域拥有良好的应用前景。
参考文献
[1] Weng Ling, Xie Guanran, Zhang Bing, et al. Magnetostrictive tactile sensor array for force and stiffness detection[J]. Journal of Magnetism and Magnetic Materials, 2020, 513: 167068.
[2] Norman M D A, Ferreira S A, Jowett G M, et al. Measuring the elastic modulus of soft culture surfaces and three-dimensional hydrogels using atomic force microscopy[J]. Nature Protocols, 2021, 16(5): 2418-2449.
[3] Liu Yulu, Wo Hualei, Huang Shuyi, et al. A flexible capacitive 3D tactile sensor with cross-shaped capacitor plate pair and composite structure dielectric [J]. IEEE Sensors Journal, 2021, 21(2): 1378-1385.
[4] Li Jing, Zhang Ze, Duan Biao, et al. Design and characterization of a miniature three-axial mems force sensor[J]. Journal of Mechanics in Medicine and Biology, 2020, 20(10): 2040038.
[5] Wang Hongbo, de Boer G, Kow J, et al. Design methodology for magnetic field-based soft tri-axis tactile sensors[J]. Sensors, 2016, 16(9): 1356.
[6] 胡瑞明. 基于复眼微结构的柔性压力传感器制备及测试[J]. 固体电子学研究与进展, 2022, 42(5): 400-404.
Hu Ruiming. Fabrication and test of flexible pressure sensor based on compound eye microstructure[J]. Research & Progress of SSE, 2022, 42(5): 400-404.
[7] 吴佳贝, 刘仪琳, 卢佳飞, 等. 电容式三维力触觉传感器的设计与解耦研究[J]. 科学技术创新, 2023(9): 13-16.
Wu Jiabei, Liu Yilin, Lu Jiafei, et al. Design and decoupling of capacitive three-axis force tactile sensors[J]. Scientific and Technological Innovation, 2023(9): 13-16.
[8] 李志鹏, 王博男, 孟旭, 等. 电磁式扭矩传感器原理、研究现状及发展趋势[J]. 仪器仪表学报, 2021, 42(1): 1-14.
Li Zhipeng, Wang Bonan, Meng Xu, et al. Principle, study status and development trend of the electromagnetic torque sensor[J]. Chinese Journal of Scientific Instrument, 2021, 42(1): 1-14.
[9] 黄文美, 夏志玉, 郭萍萍, 等. 变温条件下TbDyFe合金高频磁特性和损耗特性分析[J]. 电工技术学报, 2022, 37(1): 133-140.
Huang Wenmei, Xia Zhiyu, Guo Pingping, et al. Analysis of high frequency magnetic properties and loss characteristics of TbDyFe alloy under variable temperature[J]. Transactions of China ElectrotechnicalSociety, 2022, 37(1): 133-140.
[10] 黄珊, 王博文, 赵智忠, 等. 应用于机械手的磁致伸缩触觉传感器阵列与物体识别[J]. 电工技术学报, 2021, 36(7): 1416-1424.
Huang Shan, Wang Bowen, Zhao Zhizhong, et al. Object recognition of magnetostrictive tactile sensor array applied to manipulator[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1416-1424.
[11] 赵智忠, 索峰, 万丽丽, 等. 用于纹理辨识的磁致伸缩触觉传感器研究[J]. 仪表技术与传感器, 2021(5): 16-21.
Zhao Zhizhong, Suo Feng, Wan Lili, et al. Research on magnetostrictive tactile sensor for texture identificaition[J]. Instrument Technique and Sensor, 2021(5): 16-21.
[12] 赵智忠, 王春雷, 王博文. 适用于智能机械手的Galfenol悬臂梁式力传感器设计[J]. 仪表技术与传感器, 2020(9): 1-5, 30.
Zhao Zhizhong, Wang Chunlei, Wang Bowen. Galfenol cantilever beam force sensor design suitable for intelligent manipulator[J]. Instrument Technique and Sensor, 2020(9): 1-5, 30.
[13] Steinwachs J, Metzner C, Skodzek K, et al. Three-dimensional force microscopy of cells in biopolymer networks[J]. Nature Methods, 2016, 13: 171-176.
[14] Zhang Bing, Wang Bowen, Li Yunkai, et al. Magnetostrictive tactile sensor array for object recognition[J]. IEEE Transactions on Magnetics, 2019, 55(7): 4002207.
[15] Gao Shaoyang, Weng Ling, Deng Zhangxian, et al. Biomimetic tactile sensor array based on magneto-strictive materials[J]. IEEE Sensors Journal, 2021, 21(12): 13116-13124.
[16] Zhang Bing, Wang Bowen, Weng Ling, et al. A magnetostrictive tactile sensing unit and the integration of sensor array for intelligent manipulator [J]. IEEE Access, 2020, 8: 187848-187857.
[17] Yang Huiwen, Weng Ling, Wang Bowen, et al. Design and characterization of high-sensitivity magneto-strictive tactile sensor array[J]. IEEE Sensors Journal, 2022, 22(5): 4004-4013.
[18] Yang Huiwen, Weng Ling, Wang Bowen, et al. Design and characterization of high-sensitivity magnetostrictive tactile sensor array[J]. IEEE Sensors Journal, 2022, 22(5): 4004-4013.
[19] 黄文美, 刘泽群, 郭万里, 等. 磁致伸缩振动能量收集器的全耦合非线性等效电路模型[J]. 电工技术学报: 1-12.
Huang Wenmei, Liu Zequn, Guo Wanli, et al. Fully coupled nonlinear equivalent circuit model of magneto-strictive vibration energy harvester[J]. Transactions of China Electrotechnical Society:1-12.
[20] 刘莎莎, 王博文, 黄文美, 等. 仿生磁致伸缩触觉传感阵列设计与输出特性[J]. 电工技术学报, 2021, 36(12): 2576-2584.
Liu Shasha, Wang Bowen, Huang Wenmei, et al. Design and output characteristics of bionic magnetostrictive tactile sensor array[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2576-2584.
[21] 黄文美, 陶铮, 郭萍萍, 等. 棒状铁镓合金磁特性测试装置的设计与实验[J]. 电工技术学报, 2023, 38(4): 841-851.
Huang Wenmei, Tao Zheng, Guo Pingping, et al. Design and experiment of high frequency magnetic properties testing device for rod iron-gallium alloy[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 841-851.
[22] 张艳芳, 刘玉荣, 许章铖. 基于PVDF三维力传感器设计[J]. 仪器仪表学报, 2021, 42(7): 66-72.
Zhang Yanfang, Liu Yurong, Xu Zhangcheng. Design of three-dimensional force sensor based on PVDF[J]. Chinese Journal of Scientific Instrument, 2021, 42(7): 66-72.
[23] 李波, 杨家斌, 舒亮, 等. 考虑应力耦合的三维磁致伸缩力传感模型研究[J]. 系统仿真学报, 2018, 30(10): 3671-3680.
Li Bo, Yang Jiabin, Shu Liang, et al. Three-dimensional model of magnetostrictive force sensor considering stress coupling and experimental research [J]. Journal of System Simulation, 2018, 30(10): 3671-3680.
[24] 梁桥康, 成乐凯, 龙建勇, 等. 机器人多维力传感器[J]. 测控技术, 2023, 42(4): 1-8, 21.
Liang Qiaokang, Cheng Lekai, Long Jianyong, et al. Robotic multi-component force/torque sensors: a review[J]. Measurement & Control Technology, 2023, 42(4): 1-8, 21.
[25] Li Junfei, Crivoi A, Peng Xiuyuan, et al. Three dimensional acoustic tweezers with vortex streaming[J]. Communications Physics, 2021, 4: 113.
[26] Shen Lu, Tai Junfei, Crivoi A, et al. Self-stabilizing three-dimensional particle manipulation via a single-transducer acoustic tweezer[J]. Applied Physics Letters, 2023, 122(9): 094106.
[27] 彭浩, 李昕, 周立, 等. 基于三维力传感器的工业机器人力控应用[J]. 科技与创新, 2022(18): 169-172, 175.
Peng Hao, Li Xin, Zhou Li, et al. Application ofindustrial robot force control based on three-dimensional force sensor[J]. Science and Technology & Innovation, 2022(18): 169-172, 175.
[28] 彭小武, 马国鹭, 赵涌, 等. 三维力传感器的设计和静态解耦算法研究[J]. 传感技术学报, 2021, 34(11): 1518-1522.
Peng Xiaowu, Ma Guolu, Zhao Yong, et al. Design of three-dimensional force sensor and research on the static decoupling algorithm[J]. Chinese Journal of Sensors and Actuators, 2021, 34(11): 1518-1522.
Design and Output Characteristics of Three-Dimensional Force Tactile Sensor Based on L-Type Iron and Cobalt
Abstract In today's era, manipulators, as a replacement and function extension for human hands, have been widely used in various industrial fields. In order to meet more complex perception needs, more and more three-dimensional force tactile sensors have emerged. According to the different sensing mechanisms, three-dimensional force sensors can be divided into piezoelectric, piezoresistive, capacitive, electromagnetic, photoelectric and other types. Piezoresistive sensors are measured by the change in resistance of resistance, which has a certain hysteresis and cannot measure the physical quantity in dynamic scenarios well; In the measurement of capacitive sensors, the influence of parasitic capacitance cannot be ignored, and its measurement circuit is complex; Electromagnetic sensors are susceptible to interference from the external environment. As a piezomagnetic material, magnetostrictive material has the characteristics of changing with the magnetization state of the applied material under stress, can respond instantaneously, and the output signal is stable. This gives magnetostrictive materials a great advantage in tactile sensing, enabling fast measurement of dynamic and static forces. Among many magnetic materials, new sensitive magnetostrictive materials represented by iron gallium are widely used in sensors that measure small forces such as displacement, texture and touch due to their high sensitivity and strong linearity.
However, iron-gallium alloy has excellent electromagnetic properties in a single fixed orientation, and has certain limitations in multi-dimensional force measurement. In this paper, a three-dimensional force tactile sensor based on L-type iron-cobalt wire is proposed, and a three-dimensional force tactile sensing unit is designed and fabricated by using magnetostrictive material iron-cobalt alloy, and the output characteristics of the structure are tested. Based on the electromagnetic principle, the inverse magnetostrictive effect and the Euler Bernoulli kinetic principle, the output voltage equation is derived.
The experimental platform of the tactile sensing unit was built, the normal and tangential calibration of the sensor was carried out, and the normal force measurement range of the designed sensor was 0~13 N, the tangential force measurement range was 0~6 N, and the output characteristics had a good linear relationship. Among them, the sensitivity in the range of 0~8 N normal force is about 23.997 mV/N, and the sensitivity in the range of 9~13 N normal force is about 17.537 mV/N; The sensitivity in the range of 0~4 N tangential force is about 11.599 mV/N, and the sensitivity in the range of 5~6 N tangential force is about 6.281 mV/N. Under the condition of 4 Hz frequency and 2 N normal force, the output voltage amplitude change range of the dynamic response of the sensor is 46.5~49.8 mV, the relative error with the amplitude of the static force output voltage is less than 5%, and the response time and recovery time are 25 ms and 29 ms, respectively, indicating that the sensor has good dynamic characteristics. The generalized inverse matrix and BP neural network are used to decouple the three-dimensional force sensed by the sensor, and the average error of the BP neural network decoupling method is only 2.90%, which can effectively improve the measurement accuracy. The sensor has small size and good output linearity, which can realize the measurement of static force and dynamic force at the same time, and has a good application prospect in intelligent robots and other fields.
keywords:Inverse magnetostrictive effect, BP neural networks, L-type iron cobalt wire, dynamic force measurement, static force measurement
中图分类号:TM 274
DOI: 10.19595/j.cnki.1000-6753.tces.231082
国家自然科学基金(51801053, 52077052)、河北省自然科学基金(E2022202067)和中央引导地方科技发展资金(226Z1704G)资助项目。
收稿日期 2023-07-07
改稿日期 2023-08-01
崔 淼 男,1998年生,硕士研究生,研究方向为新型磁性材料与器件。
E-mail:17861857517@163.com
李明明 男,1986年生,副教授,博士生导师,研究方向新型磁性材料与器件。
E-mail:Limm@hebut.edu.cn(通信作者)
(编辑 郭丽军)