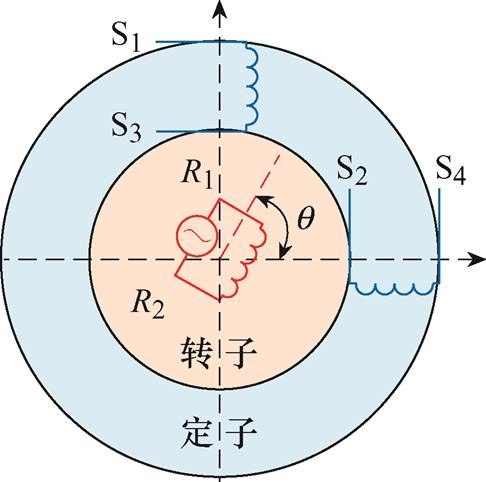
图1 旋转变压器结构示意图
Fig.1 Schematic diagram of the resolvers
摘要 针对旋转变压器解码芯片价格高及常规软件解码方法精度不足等问题,提出一种旋转变压器双采样差分位置解码方法。该方法通过主控芯片产生一路方波信号,并对方波信号进行滤波、放大后产生同频率正弦信号作为旋转变压器激励信号。同时,主控芯片在一个激励周期内触发两次模数转换器(ADC)采样,即对旋转变压器输出的正、余弦信号实施双采样。并计算两次采样值的差分,得到与位置相关的正、余弦包络线信号。最后通过锁相环估计转子位置和速度。所提双采样差分位置解码方法可消除正、余弦信号偏置波动对位置估计的影响,且解调信号幅值增大一倍,可提高位置解码精度。实验结果表明,所提双采样差分位置解码方法,相比常规软件解码方法,位置估计精度更高,电机稳态和动态性能更好。
关键词:旋转变压器 软件解码 双采样 差分计算
随着电动汽车、航空航天、工业机器人等行业的快速发展,高品质、高效率、高可靠性的永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)驱动系统得到越来越广泛的应用[1-3]。为了实现永磁同步电机矢量控制,需要实时准确获得转子磁极位置[4]。常用的位置传感器有光电编码器、磁编码器、旋转变压器等[5]。其中,旋转变压器因其抗振动能力强、检测精度高等优点被广泛应用于电动汽车、航空航天等高可靠性电机系统中[6-8]。
通常,向旋转变压器初级励磁绕组施加一组高频正弦电压激励信号,旋转变压器次级感应绕组受转子磁阻变化的影响感生出一对包络线幅值与转子磁极位置相关的高频正、余弦电压信号。然后,对这两个高频正、余弦信号进行调理、采样、锁相等处理,获得转子位置和转速。目前,常用旋转变压器解码方式是使用专用解码芯片,如日本多摩川公司的AU68x系列、美国ADI公司的AD2S系列等解码芯片。这些解码芯片性能优异,集激励生成、信号调理和信号解码于一体,集成度高,解码效果好,应用广泛[9]。
然而,使用旋转变压器专用解码芯片带来了一些问题。首先,专用解码芯片价格一般较高,增加了系统成本[10-11];其次,应用专用解码芯片需设计解码芯片和主控芯片的通信接口、信号调理电路等,增加了硬件电路复杂性。文献[12]介绍了基于AD2S1210芯片的旋转变压器解码电路设计,但是存在硬件设计复杂、连线多、故障源多等问题,降低了系统整体的可靠性。
针对解码芯片成本高、外围电路复杂等问题,许多学者和公司对旋转变压器软件位置解码(以下简称软解)进行了研究,即不使用专用解码芯片,仅使用主控芯片的外设,如定时器、模数转换器(Analog to Digital Converter, ADC)等外设资源,通过软件方式对旋转变压器位置进行解码[13-14]。旋转变压器软解主要包括四个步骤:①产生高频激励信号;②对旋转变压器次级绕组感生出的正、余弦信号进行差分调理;③通过ADC采集次级绕组输出的正、余弦信号包络线;④对采样后的正、余弦信号使用锁相环(Phase Locked Loop, PLL)、反正切函数等方法对旋转变压器转子位置进行跟踪。
对于步骤①,一般采用高频正弦信号作为旋转变压器激励,正弦激励源常通过控制器的定时器输出方波信号经二阶低通滤波产生。但是,低通滤波器会产生相位滞后,不利于ADC采样旋转变压器输出的正、余弦信号的最高点[15]。此问题可通过调
整ADC采样时刻来解决。对于步骤③、步骤④,还可以引入硬件乘法器和加法电路获得位置误差信号,实现一种硬件PLL[16]。但是该方案需增加外围电路,同时还需引入滤波器,因此会造成有效信号幅值衰减和相位滞后。美国TI公司设计的旋转变压器解码模拟前端TIDA-01527,增加了两路模拟多路选择器芯片,采用交叉差分放大的方式,避免步骤②中差分调理电路增益不一致对位置解调的影响[17]。但是,该方法受模拟选择器通道切换限制,一般无法做到高激励频率,推荐激励信号频率为5 kHz,因此无法满足高动态响应需求。同时,模拟选择器也增加了系统成本。另外,上述软解方法通常都是在一个高频激励周期内进行单次采样,然后减去上电前测好的偏置,获得正、余弦包络线。文献[18]总结了旋转变压器解码中存在的各种误差,包括偏置漂移、幅值差异以及谐波干扰等。虽然单次采样软解方案实现简单,但是若不对非理想旋转变压器信号做特殊处理,会降低位置解调精度[19-21]。幅值差异可以通过调节幅值放大倍数,衰减两个信号中较大的信号进行校正[22]。文献[23]通过积分方式计算误差系数,并分析了闭环相位延时对积分的影响,通过补偿延时,使积分更加准确,消除旋转变压器信号幅值误差带来的影响。谐波干扰的误差包括正交误差、函数误差等[24],文献[24]提出了一种基于改进式二阶广义积分器和锁频环的校正策略,设计两个广义积分器作为频率自适应带通滤波器,以估计频率为中心频率对旋转变压器正、余弦输出信号进行滤波。文献[25]提出了基于模型参考自适应和锁相环在线补偿旋转变压器谐波误差的方法。然而,针对偏置漂移问题,虽然运行前的偏置检测可以解决部分问题,但是对于运行过程中由于正、余弦信号受共模干扰等原因导致的偏置漂移问题,使用常规软解方法无法解决。
为解决旋转变压器位置软件解码中存在的ADC单次采样无法抑制正、余弦信号偏置漂移,精度低,以及增加额外元器件等问题,本文提出一种旋转变压器双采样差分位置解码方法,该算法主要优点如下:
(1)可有效抑制旋转变压器正、余弦信号偏置漂移对位置解码精度的影响。本文所提方法在一个激励周期内进行两次ADC采样,分别采集信号的波峰和波谷,然后求两次采样信号差分值,可直接消除偏置,因而无需上电采集正、余弦信号偏置即可实现位置解码,提高系统运行效率。
(2)位置检测精度更高。常规旋转变压器解码采样方法在一个高频激励周期内只进行一次采样和解算,而利用本文提出的双采样方法,在一个激励周期内进行两次采样和两次位置解算,可提高信噪比和位置更新率,从而提高位置解码精度,减小了解码延迟。
(3)成本低且易于实现。所提方法对硬件要求低,所设计激励信号产生、放大等电路都采用常规元器件和电路拓扑,方案成本低、易于实现。
旋转变压器结构示意图如图1所示。旋转变压器初级绕组R1、R2安装在电机转子上,对初级绕组施加高频信号后,转子旋转时,旋转变压器受转子磁阻变化的影响,次级感应绕组S1、S3与S2、S4正交分布,并感生出一对包含转子磁极位置信息的高频正、余弦电压信号。

图1 旋转变压器结构示意图
Fig.1 Schematic diagram of the resolvers
定义初级绕组高频激励电压为uexct(wt),则次级绕组的理想输出电压可表示为
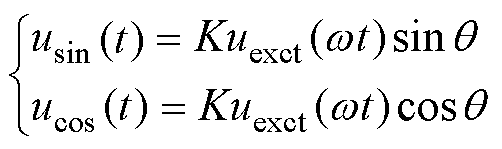 (1)
(1)
式中,K为旋转变压器电压比;w 为高频激励信号角频率;q 为旋转变压器转子角度;usin和ucos分别为旋转变压器次级输出正弦和余弦信号。
旋转变压器原始激励信号一般需经调理电路放大才能施加至旋转变压器初级绕组中。同样,旋转变压器输出正、余弦信号也需要调理电路进行滤波、放大和增加偏置电压等处理才能送入控制器ADC模块被采集。控制器、信号调理电路和旋转变压器之间的关系如图2所示。
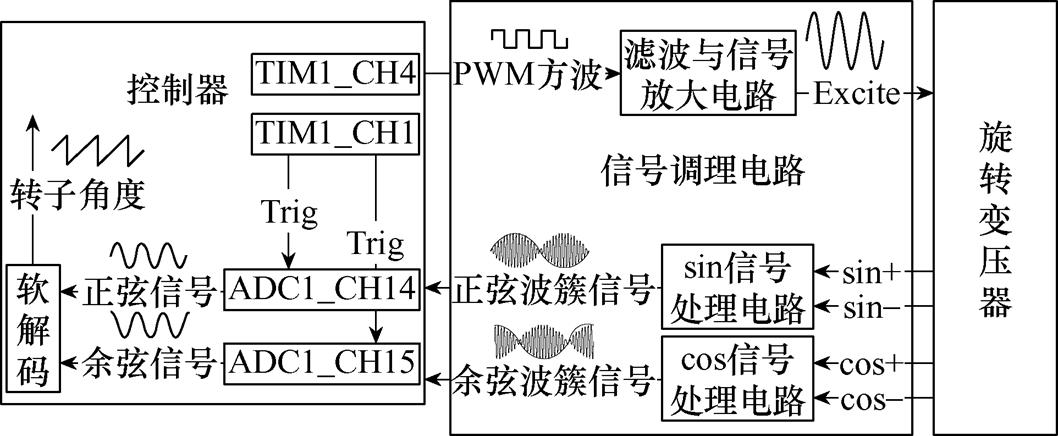
图2 控制器、调理电路和旋转变压器关系
Fig.2 Diagram of relationship of the controller, the processing circuits and the resolver
利用主控微控制器芯片的定时器产生一路PWM方波信号。在本文中,PWM信号频率设定为8 kHz,经过低通滤波电路产生同频的正弦信号。初始PWM方波信号输出幅值和主控芯片有关,通常为3.3 V且输出电流能力一般为mA级别。经滤波电路后,初始高频正弦信号幅值会进一步衰减,在2~3 V之间。然而,旋转变压器激励信号所需电压幅值至少在6 V以上,因而需要对高频正弦信号的幅值进行放大,增加输出驱动能力。利用放大后的高频正弦信号激励旋转变压器初级绕组,而后对旋转变压器次级绕组输出的正、余弦信号进行信号调理、ADC采样便可得到软解码所需的正、余弦包络线信号。
根据式(1),旋转变压器输出的正、余弦信号为高频激励信号与转子位置正、余弦函数值的乘积,具体为差分形式的正、余弦信号,电压范围有正有负。因而,需要调理电路对信号滤波、放大和增加偏置电压等处理才能输出至ADC模块。如图2所示,将旋转变压器输出的正、余弦差分信号送至信号调理电路中,经过信号调理,得到正、余弦单端信号,其表达式为
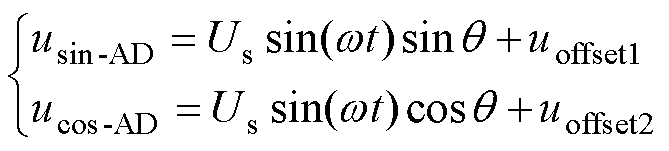 (2)
(2)
式中,usin-AD、ucos-AD分别为包含转子位置信息的正、余弦信号,其频率和激励信号频率一致,幅值与转子位置呈正、余弦关系;Us为调理电路处理后的信号幅值;uoffset1、uoffset2分别为正、余弦信号的偏置总和。旋转变压器信号偏置主要分为由于传感器自身安装、加工等原因存在的自身偏置,调理电路电平抬升和器件不一致导致的电路偏置,以及板级输入正、余弦信号引入的共模干扰,即
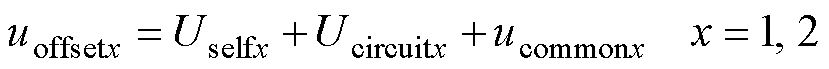 (3)
(3)
式中,Uselfx为自身偏置;Ucircuitx为电路偏置;ucommonx为板级共模干扰信号。
正弦信号调理电路如图3所示。信号调理电路由共模电感、RC滤波电路、差分比例运算电路和电阻分压组成。共模电感为L1,共模电感可有效抑制共模干扰;RC滤波电路包括由R1、C2和R2、C1组成的共模干扰滤波,以及R1、R2和C3组成的差模干扰滤波,通过RC滤波电路可滤除高频共、差模干扰信号。后一级差分及滤波电路由R3、R4、R5、R6、C4、C5和运算放大器组成,通过差分比例运算电路将正弦差分信号转化为正弦单端信号。同时,运放正端由R5与R4并联后与C4组成RC一阶低通滤波电路对输入信号再做一次低通滤波,进一步降低输出信号噪声。差分比例运算电路参考电平由Vref_1.65V(抬升电压)、C4、R5决定,通过设置合适的参考电平能够将输出的正弦信号偏置电压设置为1.65 V左右。运算放大器输出端连接由R7、R8、C6三者构成的电阻分压电路及滤波电路,其作用是将正弦信号控制在0~3.3 V的ADC采样量程范围内,并在进入ADC前做最后一次低通滤波,削弱长线传输干扰,保证ADC能采集到较纯净的正弦信号。余弦信号调理电路与正弦信号调理电路结构一致。
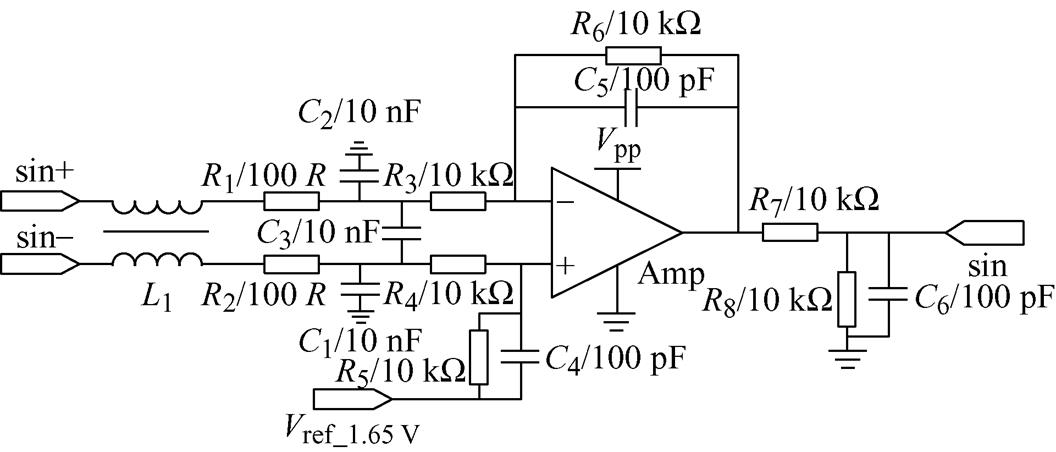
图3 正弦信号调理电路
Fig.3 Sinusoidal signal processing circuit
转子旋转频率一般远低于高频激励信号频率,因而可认为在一个高频激励周期内转子角度q不变。在高频激励信号的每个周期,固定ADC采样时刻,即将式(2)中t固定,则可得到ADC采样后的离散正、余弦信号,表示为
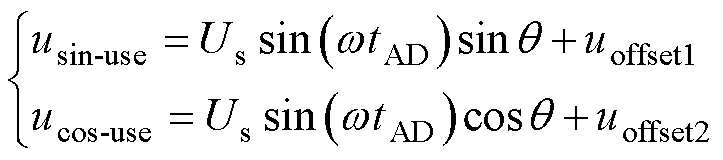 (4)
(4)
式中,tAD为每个周期内固定的采样时刻,得到的离散正、余弦信号为原来信号的包络线。tAD决定了有效信号幅值的大小,为提高软件解码精度,有效信号幅值越大越好。定义正、余弦信号采样系数KAD为
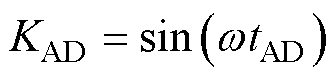 (5)
(5)
因此,KAD越大,信噪比越高,越利于提高软件解码精度。式(4)可表示为
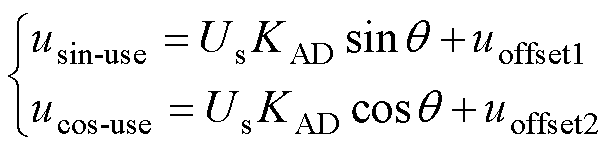 (6)
(6)
为了保证采样时刻在每个激励信号周期内是固定的,ADC采样需要由定时器进行单独触发,这样可保证正、余弦信号采样时刻相对于激励信号的相位不发生偏移,准确地获得正、余弦信号的包络线。
常规旋转变压器软件解码方案只在激励信号波峰处对旋转变压器输出正、余弦信号进行单次采样,以下简称单采样方法。单采样方法在ADC采样获取正、余弦包络线信号后,还需减去正、余弦信号的偏置电压方可进行位置解码,单采样方法无法抑制偏置电压波动对位置解码的影响。为了提高正、余弦信号采样信噪比和位置更新率,同时抑制旋转变压器输出正、余弦信号偏置波动对位置解码的影响,提出一种在正、余弦信号波峰和波谷均进行采样和解算的双采样差分解码方法,以下简称双采样方法。单采样与双采样方法示意图如图4所示。
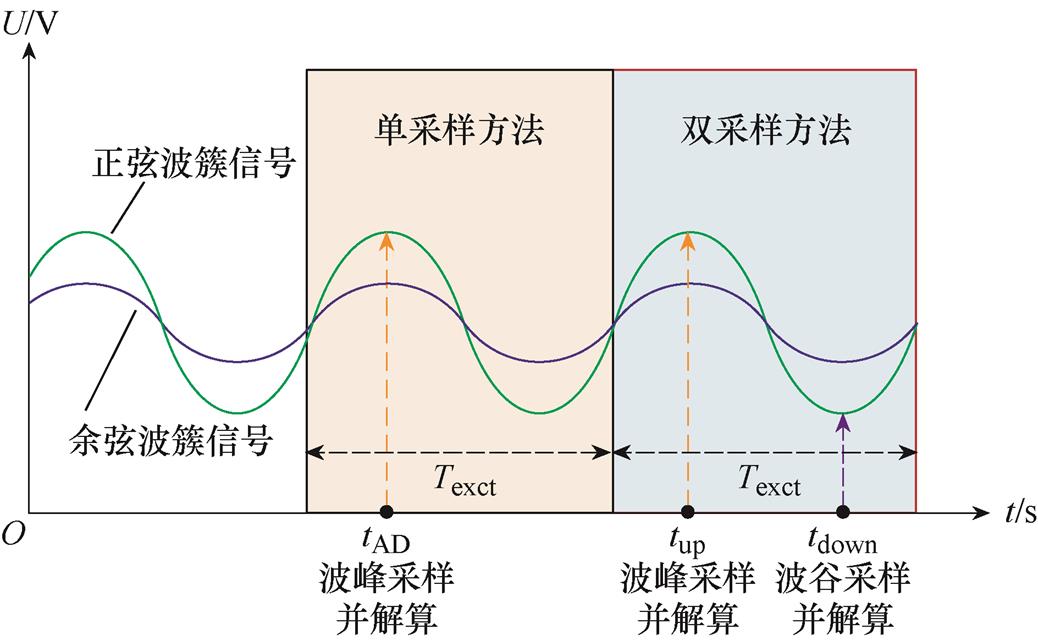
图4 单采样与双采样方法示意图
Fig.4 Single sampling and double sampling methods
图4中,Texct为激励周期;tAD为单采样方法采样时刻;tup、tdown分别为双采样方法的波峰、波谷采样时刻。双采样方法在波峰处采样正、余弦信号为
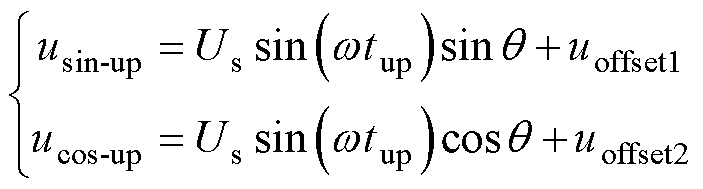 (7)
(7)
在波谷处采样正、余弦信号为
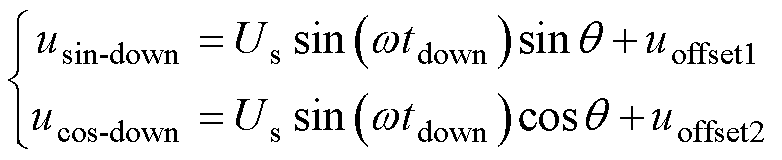 (8)
(8)
波峰波谷相差半个采样周期,有
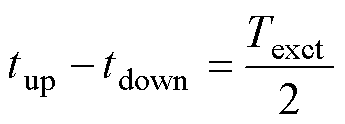 (9)
(9)
根据三角函数有
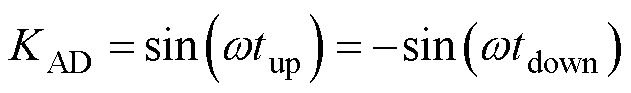 (10)
(10)
将两次采集正、余弦信号波峰和波谷信号差分处理后可得
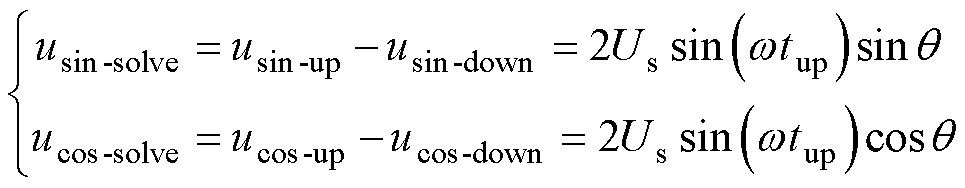 (11)
(11)
式中,usin-solve和ucos-solve分别为进入软件解码的正、余弦信号。将式(10)代入式(11),则有
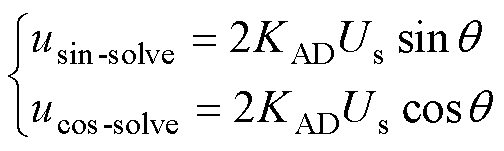 (12)
(12)
旋转变压器正、余弦信号差分采样过程如图5所示。对比式(6)和式(12),双采样方法相对于单采样方法,有效信号幅值提高一倍,且通过差分处理可自动消除正、余弦信号偏置电压uoffset1、uoffset2。另外,双采样方法可以将每次采集信号与上一次信号进行差分,在半激励周期内实现一次位置信号更新,因此能提高位置更新率,减小解码延迟,提升位置估计精度。
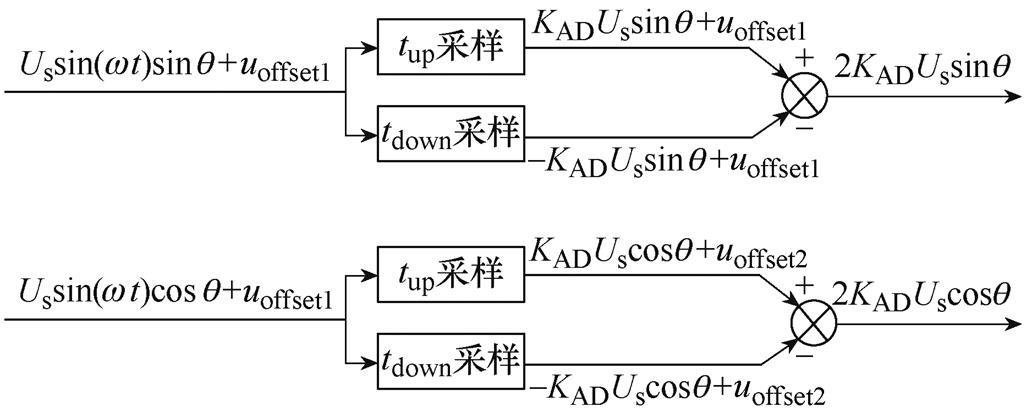
图5 正、余弦信号差分处理过程
Fig.5 Differential processes of sin and cosine signals
在获得上述正、余弦信号后,需要对位置进行跟踪,通常有反正切法[26]和不同阶次的PLL方法[27-29]。本文将分别对三种位置跟踪器性能进行对比。
方法1:采用反正切函数获得位置,即
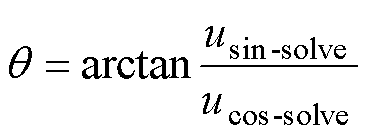 (13)
(13)
方法2:PLL方法根据相位跟踪器可分为二阶PLL[28]与三阶PLL[29]。其中,二阶PLL闭环传递函数为
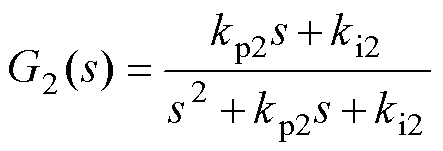 (14)
(14)
式中,kp2和ki2分别为PI的比例和积分系数。按照典型Ⅱ型系统对锁相环PI参数进行近似可得
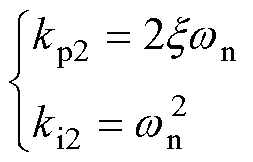 (15)
(15)
式中,x为阻尼比,在工程中常取0.707;wn为无阻尼自然振荡频率,通常选取速度环实际带宽的5~10倍。
方法3:三阶PLL的闭环传递函数为
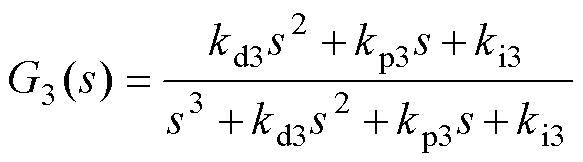 (16)
(16)
式中,kp3、ki3和kd3分别为PID的比例、积分和微分系数。根据劳斯-赫尔维茨稳定判据可将式(16)改写为
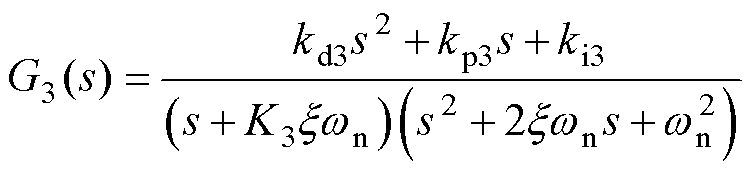 (17)
(17)
式中,K3为实极点位置调节系数,利用参数K3可调节负实数极点到虚轴的距离。一般负实数极点与虚轴的距离应远大于共轭极点对到虚轴的距离,通常取K3≥10。通过合理配置极点位置,可获得最佳的跟踪性能。因此,三阶锁相环PID参数可整定为
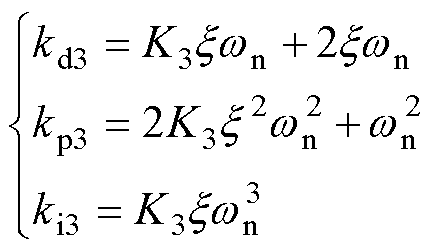 (18)
(18)
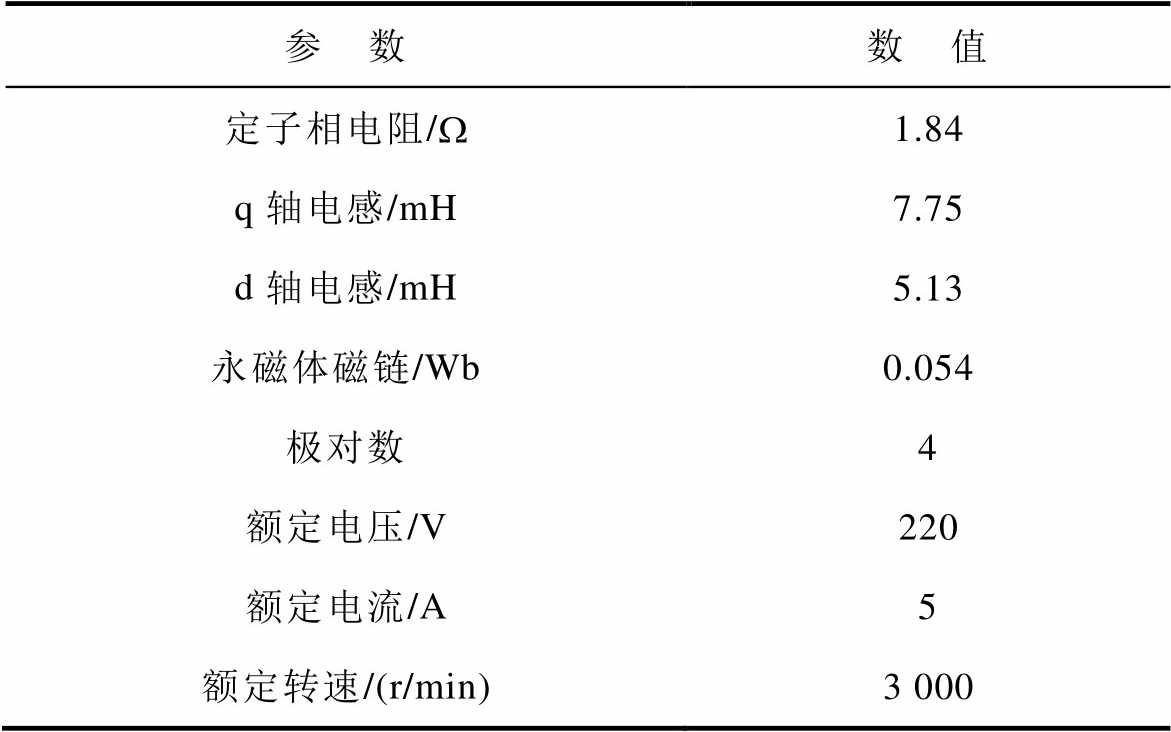
为验证所提位置解码方法的有效性,搭建永磁同步电机驱动实验平台,如图6所示。该驱动器采用STM32H723ZG芯片作为主控芯片,一台750 W永磁同步电机作为驱动电机,其电机参数见表1。旋转变压器激励信号为控制器产生的8 kHz的PWM方波信号经滤波放大后的高频正弦激励信号。旋转变压器输出正、余弦信号经过AD8620运算放大器芯片进行调理后送入主控芯片的ADC。旋转变压器是1对极,被测电机极对数为4,因此旋转变压器解码位置需要乘以电机极对数4,用于伺服电机矢量控制。同时,考虑位置传感器的精度和动态性能,采用同轴安装的2 500线光电编码器实时检测转子位置进行对比。

图6 实验用永磁同步电机驱动系统
Fig.6 The test PMSM drive
表1 实验用永磁同步电机参数
Tab.1 Parameters of the test PMSM
参 数数 值 定子相电阻/W1.84 q轴电感/mH7.75 d轴电感/mH5.13 永磁体磁链/Wb0.054 极对数4 额定电压/V220 额定电流/A5 额定转速/(r/min)3 000
旋转变压器输出正、余弦信号如图7所示,该信号表达式见式(2)。由图7可知,旋转变压器输出信号存在对地偏置电压,实验中发现该偏置电压对地浮动,并非固定值。常规单采样方法在电机运转前先采集旋转变压器偏置。在电机运行时,ADC所采集包络线信号需要减去固定偏置才能进行位置解码。因而,正、余弦信号的偏置浮动会降低位置解码精度。考虑算法通用性和计算量,4.1节和4.2节均采用位置跟踪器中方法2的二阶PLL,x=0.707;wn=300×2p rad/s。
实际旋转变压器输出信号如图8所示。图8实验图与图4示意图一致,单采样方法是在一个激励周期内于正、余弦信号波峰或波谷进行采样和解算,而所提双采样方法是在一个激励周期内于正、余弦信号波峰和波谷均进行采样和解算。
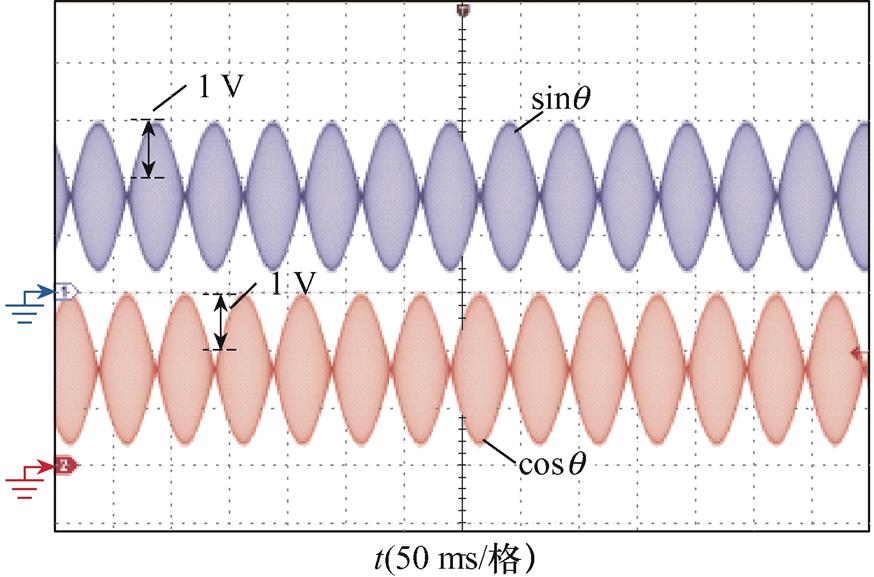
图7 旋转变压器输出正、余弦信号
Fig.7 Sine and cosine signal outputs of the resolver
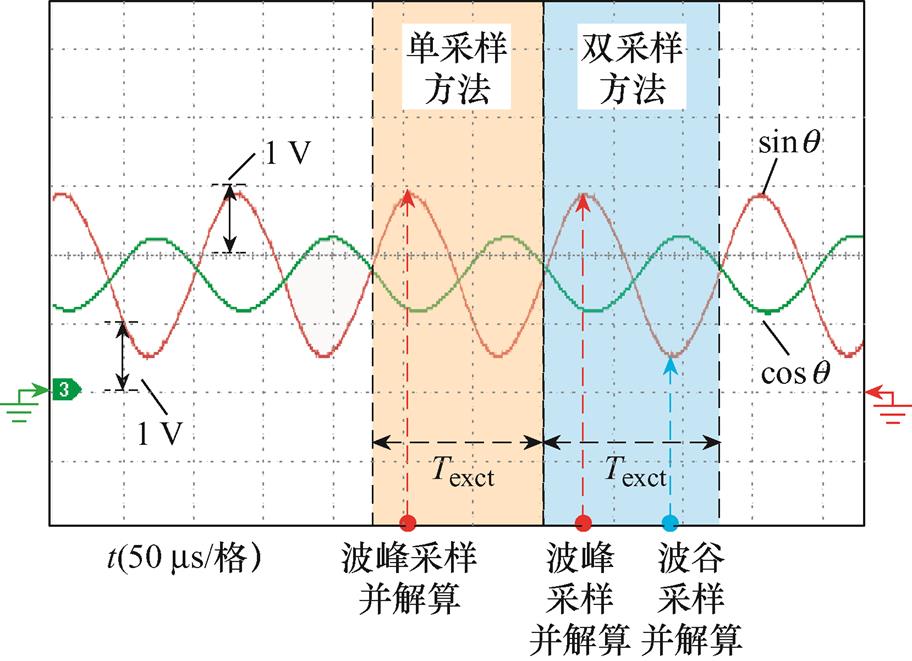
图8 旋转变压器输出正、余弦信号与采样点
Fig.8 Sine and cosine signal outputs and corresponding sampling points
使用双采样解码位置进行速度闭环控制,保持实验电机运行在600 r/min,采用单采样、所提双采样方法进行位置解码的效果分别如图9、图10所示。实验中,通过控制芯片ADC采样模块采集正、余弦信号包络线,再利用二阶PLL解算转子位置。解算出的位置为转子机械角度,将机械角度乘以极对数再减去电机零位偏差后即可得到电机转子电角度qe。
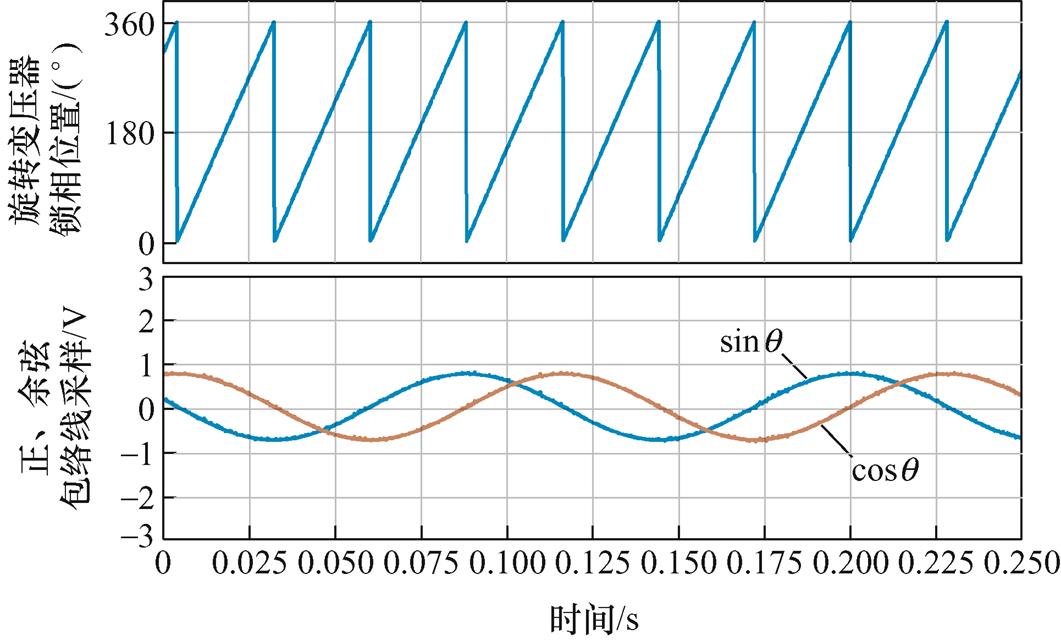
图9 单采样位置解码结果
Fig.9 Single sampling position decoding results
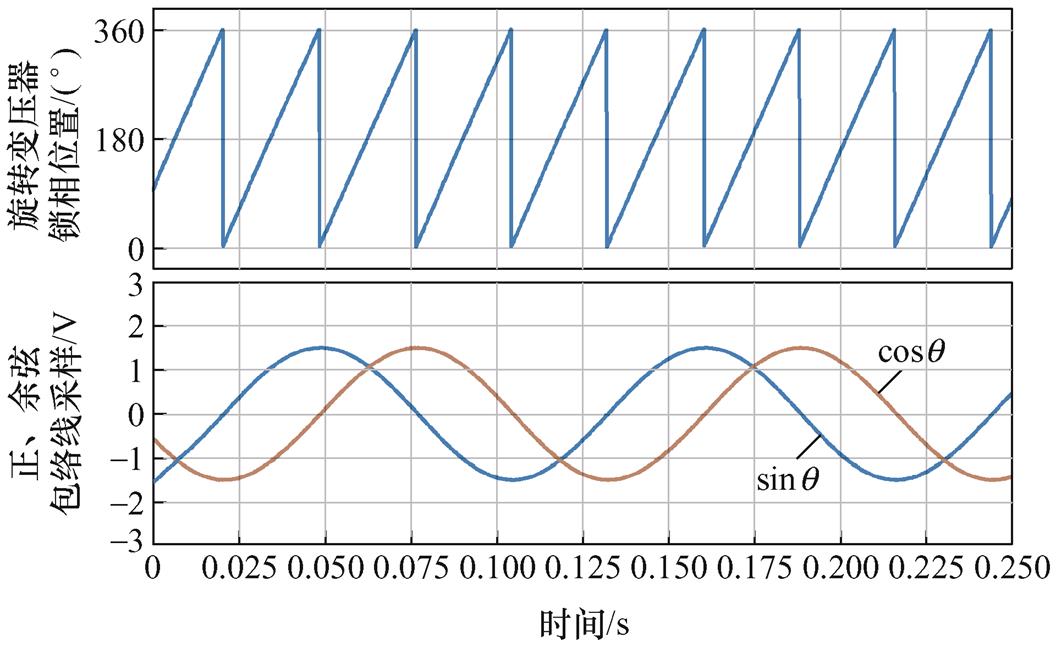
图10 双采样位置解码结果
Fig.10 Double sampling position decoding results
对比图9和图10,单采样和双采样方法均能解码出转子位置,实现永磁同步电机矢量控制。由于在一个电周期采用两次采样和差分解码,双采样采集到的旋转变压器输出正、余弦信号幅值为3 V左右,是单采样幅值1.5 V的两倍左右。因此,所提双采样方法解调信号幅值更高,提高了采样信噪比。
为了进一步分析两种位置解码方法的精度,将两种方法的位置与光编测量位置进行比较。实验中,解码数据通过Jscope仿真器的同步传输模式导出,在Matlab中绘图,计算旋转变压器解码位置与光编位置误差。图11和图12分别给出600 r/min速度闭环控制下两种方法解码位置、光编位置及位置解码误差。此处解码误差定义为旋转变压器解码得到的电机转子电角度qe减去光编解码得到的电机转子电角度。
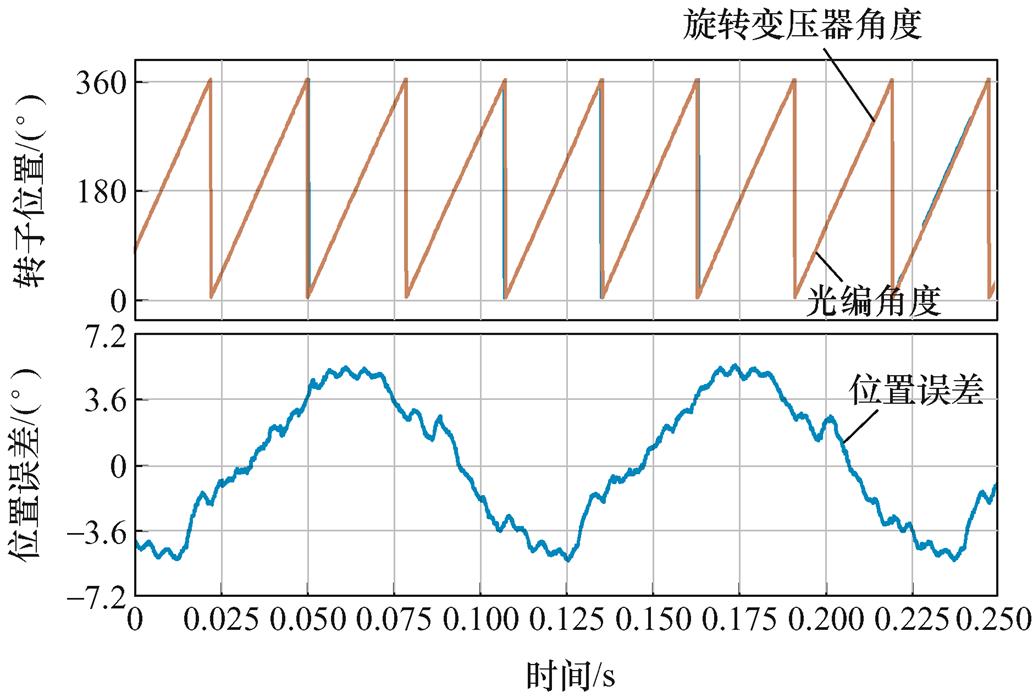
图11 单采样旋转变压器解码位置、光编位置与误差
Fig.11 Single sampling decoding position, optical encoder position and position tracking error
从图11和图12可以看到,单采样方法角度误差在±5.4°以内,而所提双采样方法角度误差在 ±1.5°以内。由此可见,所提双采样方法位置解码精度明显高于单采样方法。
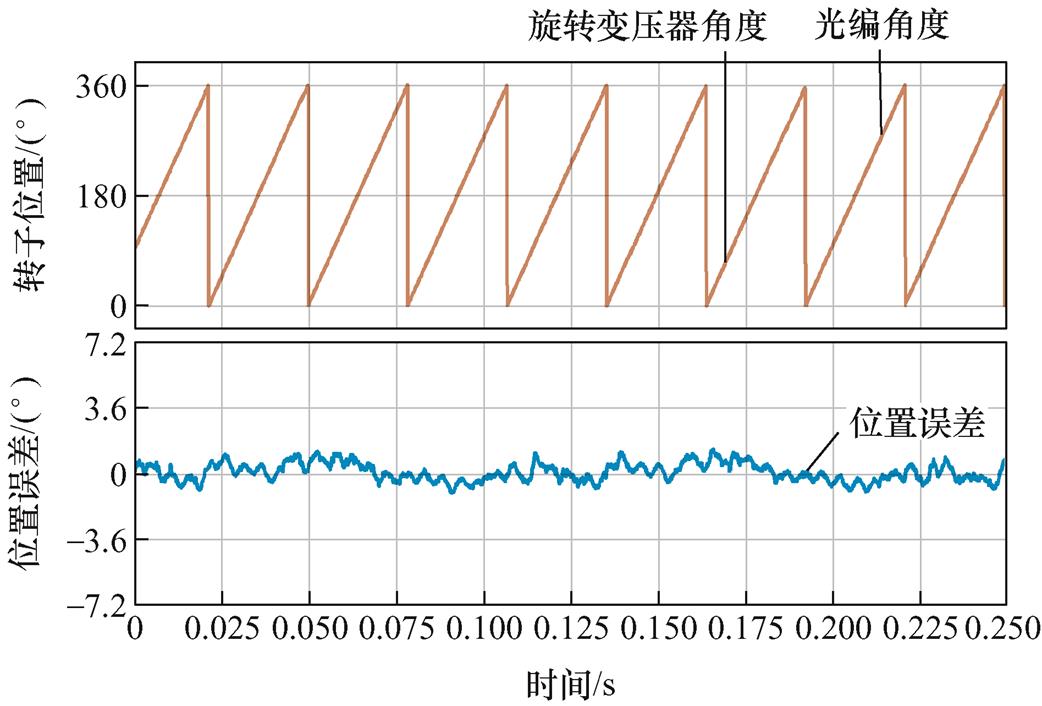
图12 双采样旋转变压器解码位置、光编位置与误差
Fig.12 Double sampling decoding position, optical encoder position and position tracking error
为进一步分析两种位置解码方法的性能,图13给出了图11和图12中两种位置解码方法角度误差的期望与方差对比。单、双采样角度误差的期望分别为3.031 246度和0.416 511度,方差分别为11.643 31度2和0.240 11度2。双采样方法期望和方差明显低于单采样方法,表明双采样方法位置解码精度更高。
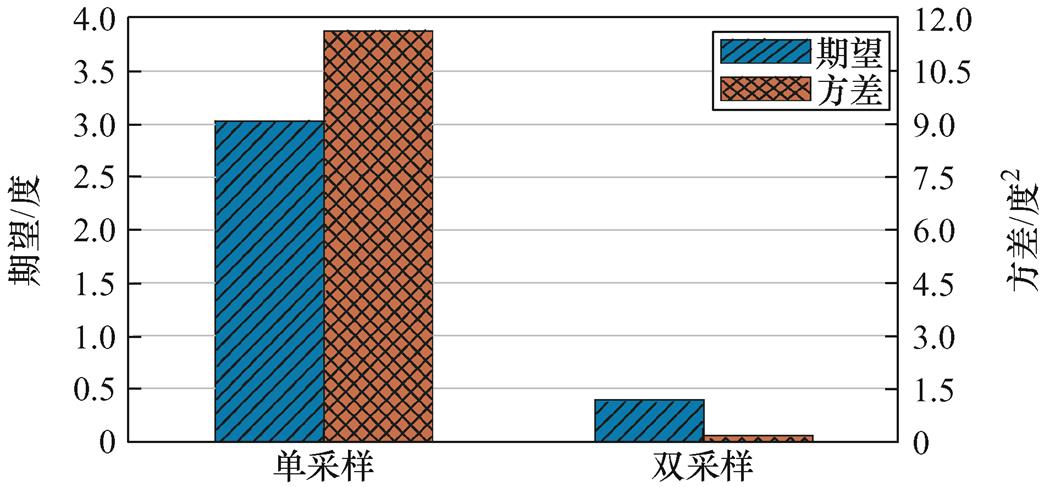
图13 单采样与双采样方法位置稳态误差期望与方差对比
Fig.13 Comparison of the expectation and variance of the steady-state tracking error of the single and double sampling methods
下面进一步探究双采样方法位置解码精度优于单采样方法的原因。从图11可以发现,单采样旋转变压器解码位置与光编位置之间的误差呈规律性,周期与电机极对数相关。由于单采样方式需要分别采样正、余弦包络线偏置,偏置的波动会导致正、余弦偏置不一致,单采样正、余弦采样值标幺化结果如图14所示,致使解码出的旋转变压器位置存在周期性波动。由于旋转变压器位置需要乘以电机极对数获得电气位置,因此电气位置存在4倍频波动。
图15为相同条件下双采样方法获得正、余弦包络线信号标幺值,实验结果显示,双采样的偏置波动微小,这是由于双采样通过波峰、波谷两次采样并做差分,抵消了偏置浮动对包络线的影响。因此,理论上就表明了双采样解码出来的位置相对于单采样方法波动更小,位置检测精度更高。
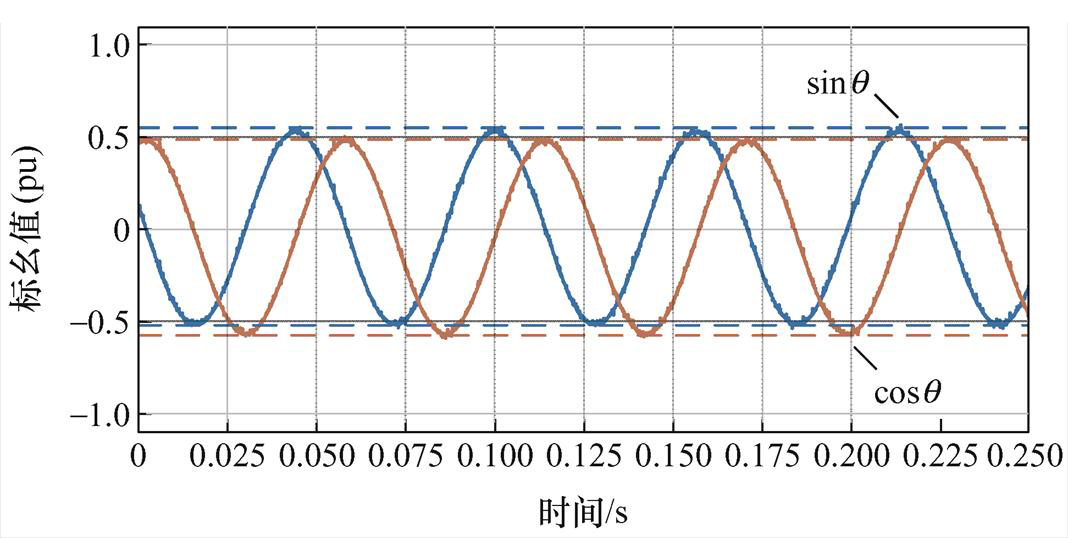
图14 单采样正、余弦采样值标幺化结果
Fig.14 Results of the normalization of sine and cosine envelopes of the single sampling method
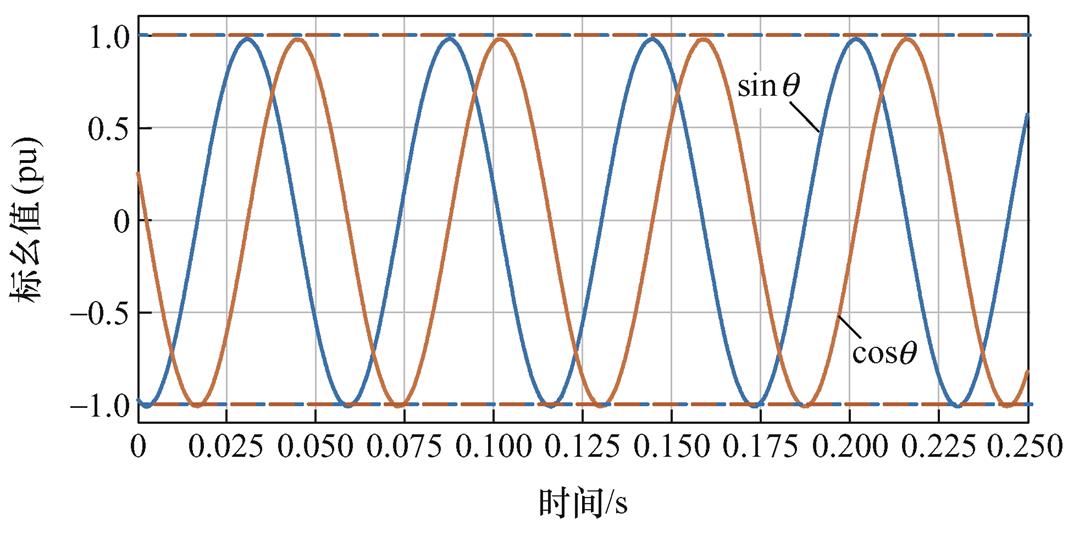
图15 双采样正、余弦采样值标幺化结果
Fig.15 Results of the normalization of sine and cosine envelopes of the double sampling method
为更进一步分析两种解码方法的动态性能,图16和图17分别给出了利用单采样和双采样方法解码出的位置进行电机速度闭环控制的实验结果。
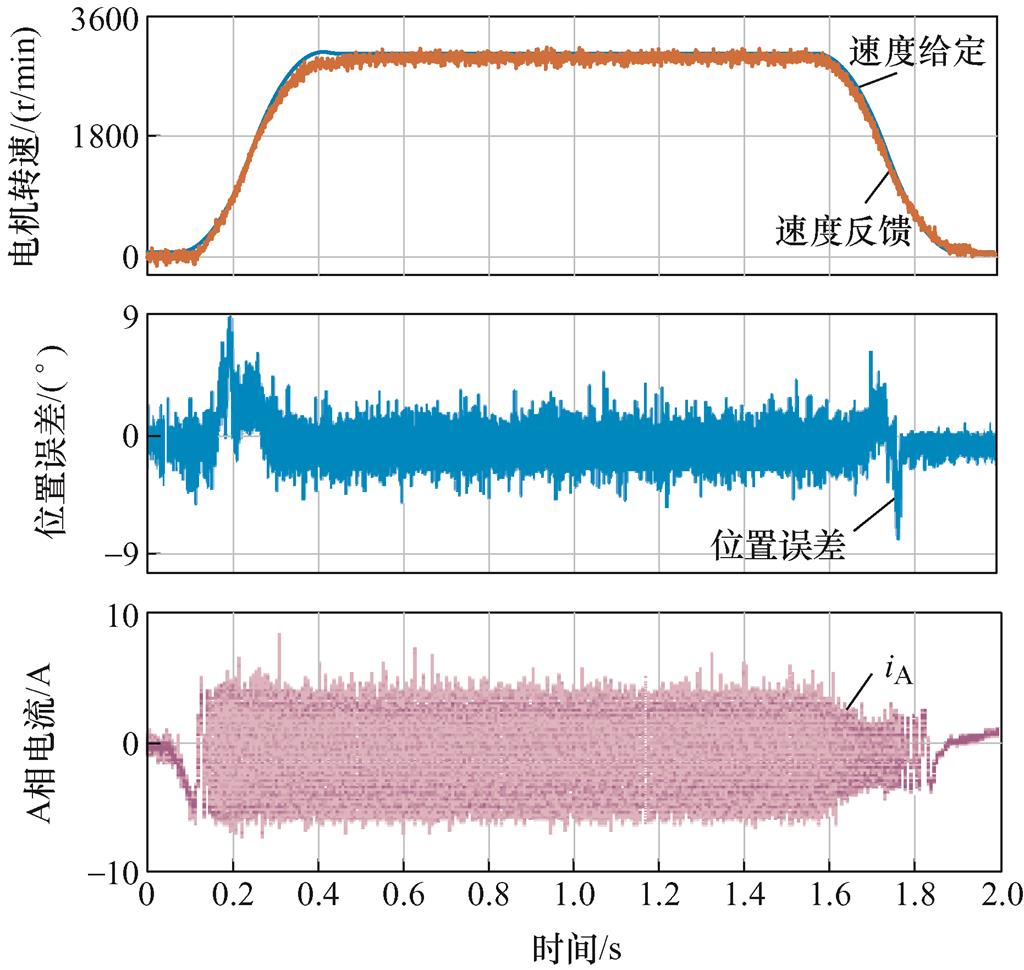
图16 单采样方法电机加减速波形
Fig.16 Tracking performance during the acceleration and deceleration using the single sampling method
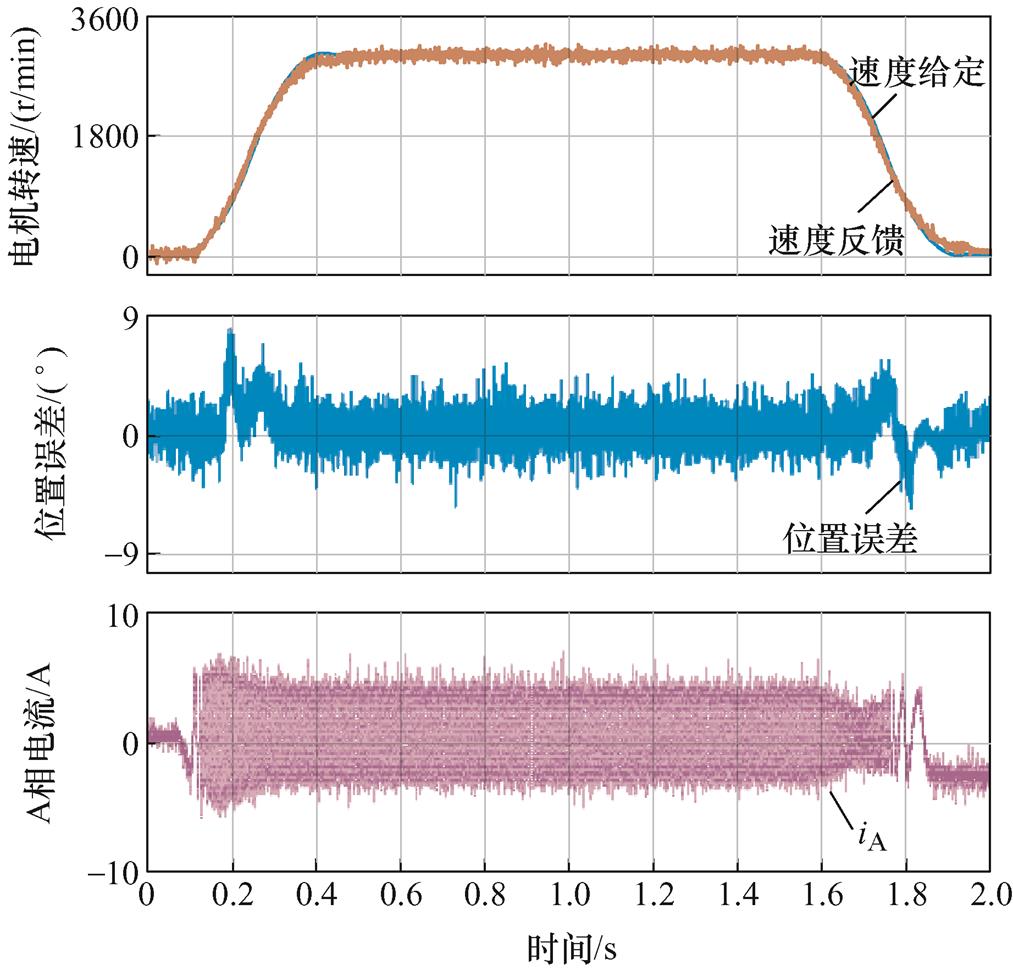
图17 双采样解码电机加减速波形
Fig.17 Tracking performance during the acceleration and deceleration using the double sampling method
图16给出了采用单采样方法的电机设定转速与反馈转速、旋转变压器解码角度与光编角度误差以及相电流的波形。实验中,将电机从零加速至额定转速3 000 r/min,而后又减速至零,加减速过程采用S曲线。从该实验结果可知,利用单采样位置解码方法的电机加减速动态过程位置解码误差较大,电机控制不够平稳。稳态时,单采样方法相电流波动较大,且电流峰峰值达到14 A。同时在加速过程中位置动态误差达到9°,减速过程动态误差达到-8°,误差较大。
图17为相同工况下采用双采样速度闭环控制的实验结果。相比图16实验结果,采用双采样旋转变压器位置解码方法其速度波动明显小于单采样方法。且稳态时,相电流峰峰值为12 A,明显低于单采样方法,电流正负基本对称。同时加速过程中位置动态误差为7.5°,与单采样方式相比动态误差减小16.67%;减速过程中位置动态误差为-7°,与单采样方式相比动态误差减小12.5%,具有更快的动态跟踪性能。
接着,又对比两种位置解码方法在全速域运行的稳态控制精度,分别在低速与高速情况下对单采样与双采样解码位置误差进行分析。图18和图19给出了电机低转速情况下的两种解码方式误差。为提高电机控制稳定性,在低速测试时使用光编角度进行电机控制(由于本驱动器电流量程为100 A,若用旋转变压器直接闭环,低速控制稳定性较差),并与两种方法解调位置进行比较。将电机转速控制在20 r/min(额定转速的0.667%)。由图18可知,单采样方法的低速位置解码误差在±10.8°之间,受到正、余弦包络线偏置波动影响较为明显。
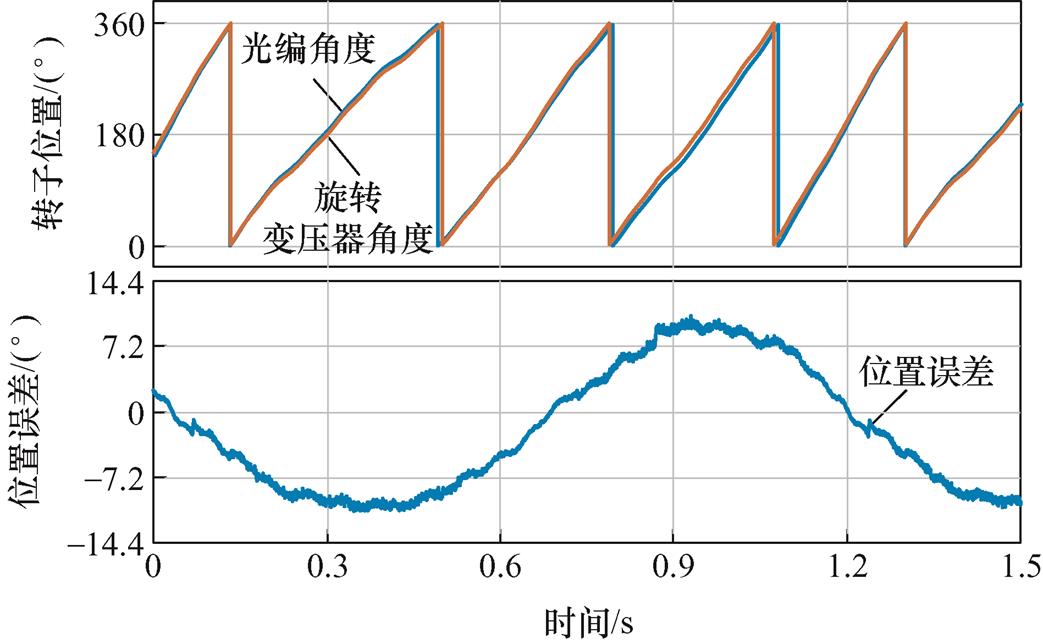
图18 单采样解码低速位置误差
Fig.18 Low-speed position tracking error in single sampling method
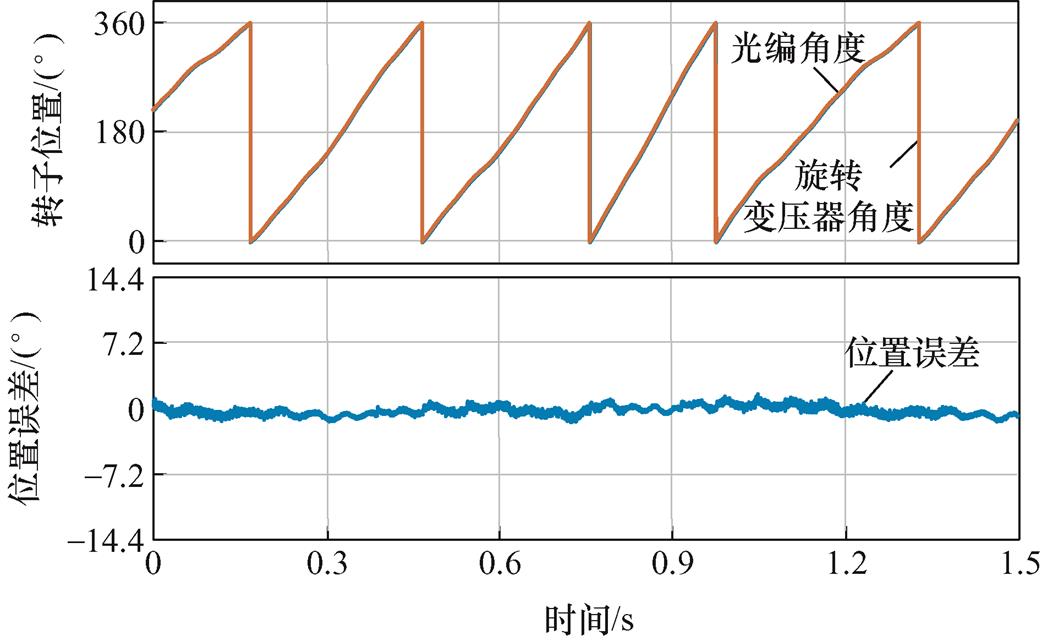
图19 双采样解码低速位置误差
Fig.19 Low-speed position tracking error of the double sampling method
图19为相同条件下测试对比结果,相比图18测试结果,所提双采样方法位置误差范围仅为±2°,约为单采样方法位置误差的18.5%,展现出更高的位置解码精度。
在高速情况下使用旋转变压器解码位置进行电机速度闭环控制测试。将电机转速控制在5 100 r/min(额定转速的170%)。图20为采用单采样方式的实验结果,位置解码误差在-5°~8°之间。
图21为相同条件下采用双采样方法的测试结果,双采样方法位置误差范围为-0.8°~3.4°,位置误差约为单采样误差的37.4%。
由上述实验结果可知,采用双采样方法进行位置解码的稳态精度、加减速过程中的动态误差等均明显优于单采样方法,且全速范围转速控制精度更高、相电流幅值更小。这与双采样方法原理上可抑制旋转变压器输出正、余弦信号偏置浮动,增大采样信噪比,提高位置更新率等所能展现出的效果相符合。
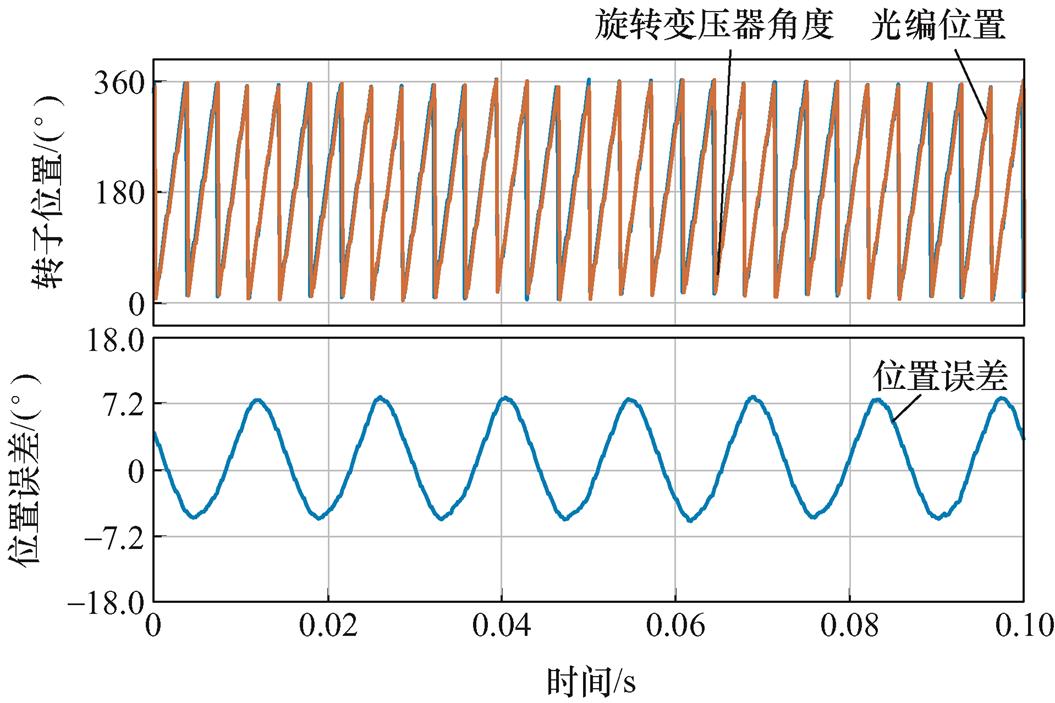
图20 单采样解码高速位置误差
Fig.20 High-speed position tracking error of the single sampling method
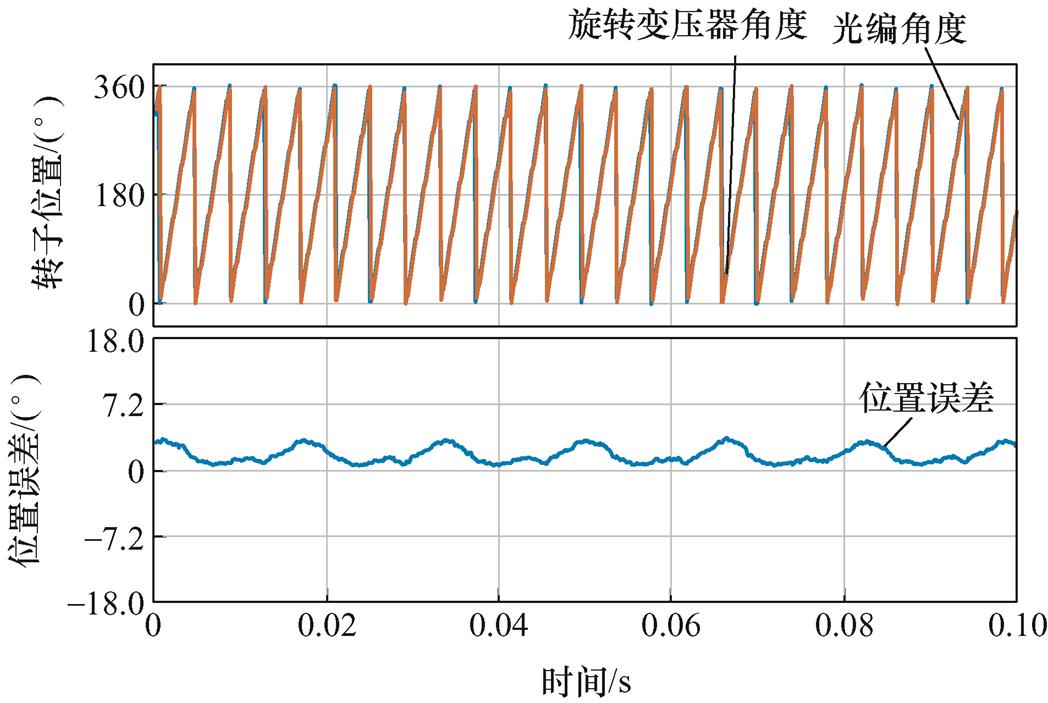
图21 双采样解码高速位置误差
Fig.21 High-speed position tracking error of the double sampling method
本节对反正切法、二阶PLL与三阶PLL三种方法的位置跟踪稳态、动态性能进行实验对比。实验工况是都采用双差分解码方法获得正、余弦信号,空载情况下将电机从静止加速到额定转速3 000 r/min,然后再减速至静止,如图22所示。实验中,二阶与三阶PLL参数选取x =0.707,wn=300× 2p rad/s,K3=10。在加减速过程中,反正切法、二阶PLL和三阶PLL方法位置解码动态误差分别在-2°~3.5°、-1.8°~3.3°和-0.9°~1.1°之间。由此可见,加减速过程中位置跟踪动态误差三阶PLL最优,二阶PLL次之,反正切方法动态误差较大。三阶PLL在速度线性加减速情况下,其理论位置跟踪动态误差为零[29]。这点优于二阶PLL,因为二阶PLL只能保证速度恒定情况的无静差跟踪。另外,二阶PLL与三阶PLL相比,在本例相同阻尼系数和无阻尼自然振荡频率下,带宽更小,因此动态跟踪性能略差。但是,反正切方法虽然没有滤波环节,受噪声影响大,动态误差依然偏大。
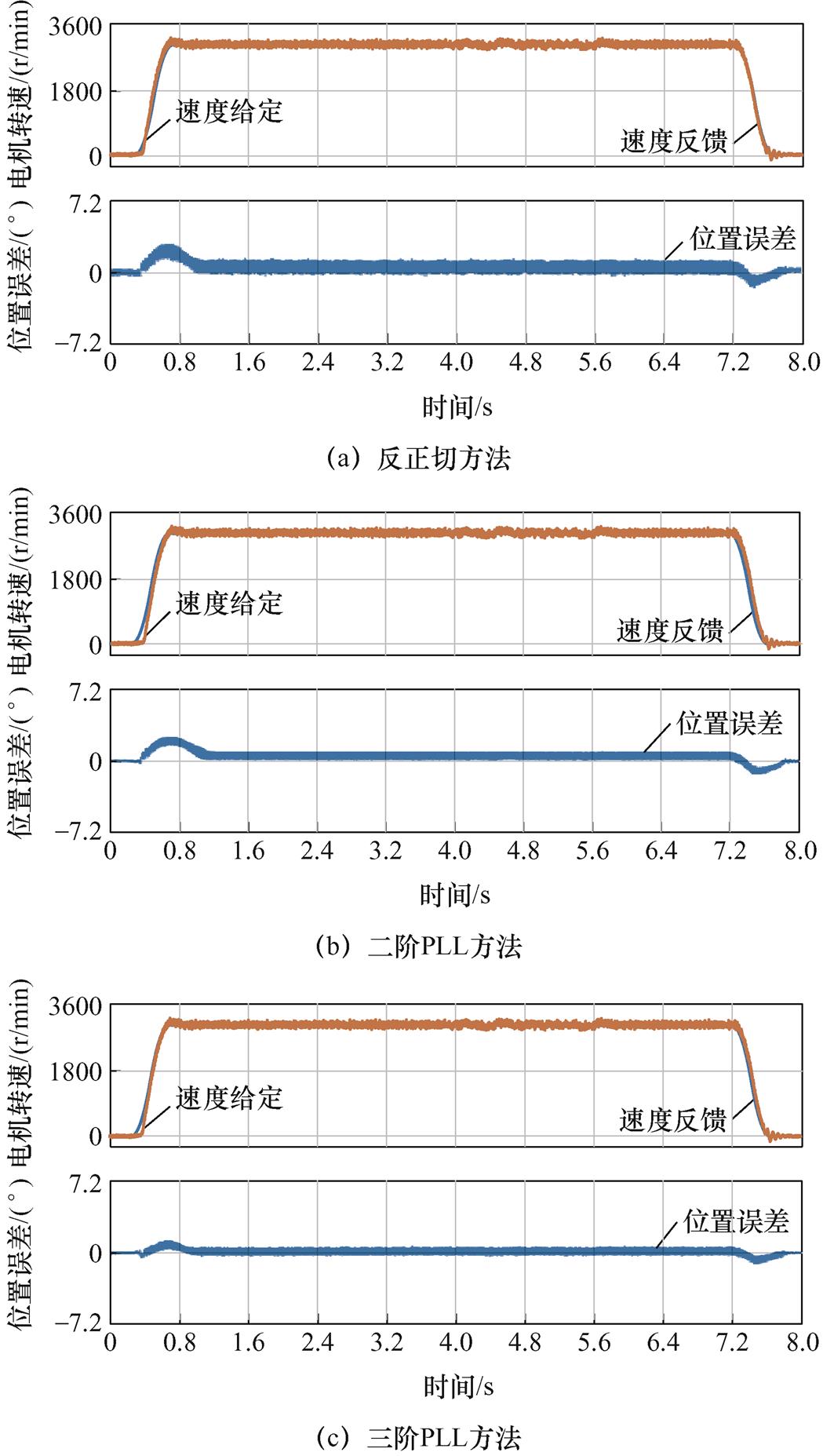
图22 三种位置跟踪器的加减速跟踪性能
Fig.22 Comparison of the tracking performance during the acceleration and deceleration using three methods
进一步比较三种方法的稳态性能,在3~5 s之间分别计算位置跟踪误差的方差与期望,如图23所示。由实验结果可知,二阶PLL与三阶PLL在稳态下位置跟踪的方差和期望都较为接近。然而,反正切法的期望和方差均高于PLL方法,说明该方法的精度较差。这是由于反正切法直接利用输入信号进行计算,受采样噪声影响大;而PLL方法则由于其自身为高阶低通滤波器,有一定的滤波作用,因此跟踪精度有所提高。
综合考虑稳态、动态性能,以及计算复杂性和参数易整定性,二阶PLL方法各方面较均衡,更符合工程应用。
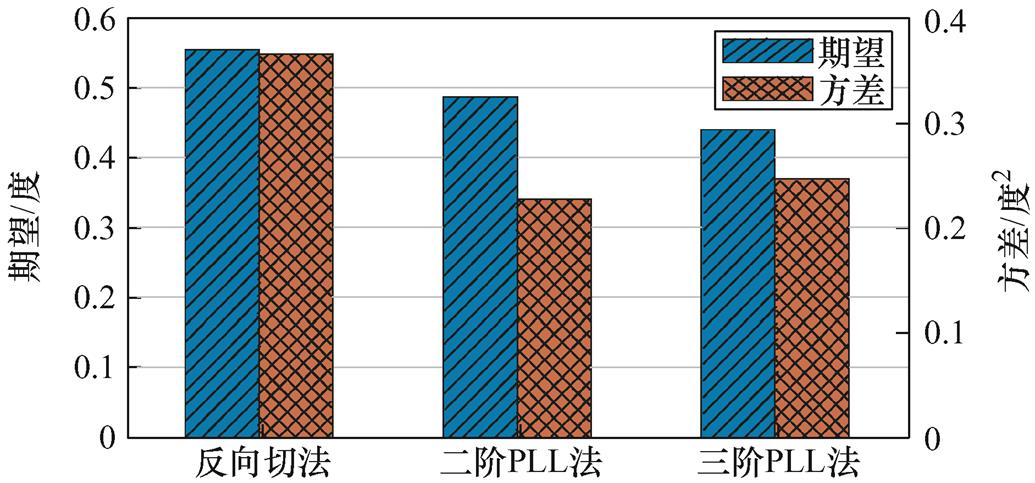
图23 三种位置跟踪器的稳态误差期望与方差对比
Fig.23 Comparison of the expectation and variance of position tracking steady-state error using three trackers
为进一步分析无阻尼自然振荡频率对二阶PLL跟踪效果的影响,分别设计三种不同wn来进行分析,实验位置跟踪数据统计结果如图24所示。实验中,电机稳定运行在600 r/min,分别设置无阻尼自然振荡频率fn=100、300和500 Hz,其中wn=2pfn。当fn较小时,PLL响应较慢,导致稳态误差方差增大;当fn增大后,PLL跟踪速度过快,导致系统抗噪声能力变弱,方差增大。因此,本文二阶PLL中设定fn=300 Hz。
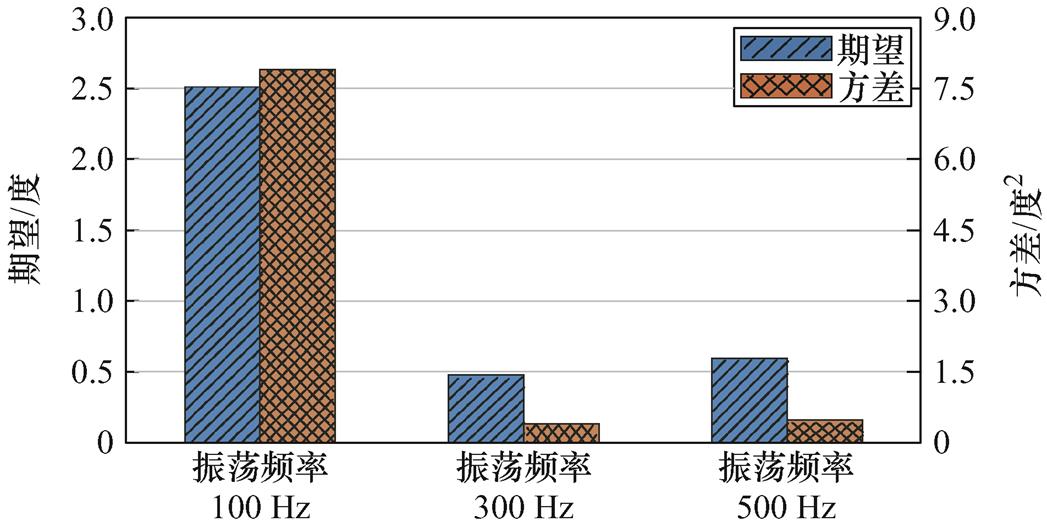
图24 不同wn条件下位置解码误差期望与方差对比
Fig.24 Comparison of the expectation and variance of position tracking error at different wn
本文提出了一种新颖的旋转变压器双采样差分位置软件解码方法,结合所设计硬件电路及软件解码算法可准确解析出电机转子位置和转速。采用本文所提的双采样差分位置解码方法,可有效抑制旋转变压器输出正、余弦信号偏置浮动,降低偏置浮动对位置解码的影响。同时提高解码信号信噪比和位置解码更新率,进而提升位置解码精度,减小解码延迟。另外,给出三种常用的位置跟踪器及设计参数,并实验对比了跟踪性能差异。实验结果表明,本文所提方法相比常规单采样位置解码方法,无需更改硬件,通用性强,位置解码精度高,精度提高了80%以上,可在全速域提升电机控制性能,是一种很好的代替专用解码芯片的低成本、高性能位置软件解码方案。
参考文献
[1] 于安博, 刘利, 阚志忠, 等. 高频脉振信号注入永磁同步电机无滤波器初始位置辨识方法[J]. 电工技术学报, 2021, 36(4): 801-809. Yu Anbo, Liu Li, Kan Zhizhong, et al. Initial position identification of PMSM with filterless high frequency pulse signal injection method[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 801-809.
[2] 李昱, 郭宏, 平朝春, 等. 基于电流源变流器的永磁同步电机驱动系统全状态变量预测转矩控制[J]. 电工技术学报, 2021, 36(1): 15-26. Li Yu, Guo Hong, Ping Zhaochun, et al. A full-state variable predictive torque control of current source converter fed permanent magnet synchronous motor drives[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 15-26.
[3] 章回炫, 范涛, 边元均, 等. 永磁同步电机高性能电流预测控制[J]. 电工技术学报, 2022, 37(17): 4335-4345. Zhang Huixuan, Fan Tao, Bian Yuanjun, et al. Predictive current control strategy of permanent magnet synchronous motors with high performance[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4335-4345.
[4] 王晓琳, 刘思豪, 顾聪. 基于自适应基准锁相环的高速永磁电机转子位置误差全补偿方法[J]. 电工技术学报, 2021, 36(20): 4308-4317. Wang Xiaolin, Liu Sihao, Gu Cong. A rotor position error compensation algorithm for high-speed permanent magnet motor based on phase-locked loop with adaptive reference[J]. Transactions of China Electrotechnical Society, 2021, 36(20): 4308-4317.
[5] 李垣江, 苗奎星, 魏海峰, 等. 基于带通频率跟踪滤波器的永磁同步电机转子位置与速度估算[J]. 电工技术学报, 2022, 37(21): 5402-5413.Li Yuanjiang, Miao Kuixing, Wei Haifeng, et al. Permanent magnet synchronous motor rotor position and speed estimation methodology based on band-pass frequency tracking filter[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5402-5413.
[6] 冉晓贺, 杨玉磊, 尚静, 等. 半波结构轴向磁阻式旋转变压器电磁模型与参数计算[J]. 中国电机工程学报, 2022, 42(9): 3443-3451. Ran Xiaohe, Yang Yulei, Shang Jing, et al. Electromagnetic modeling and parameter computation of half-wave axial reluctance resolver[J]. Proceedings of the CSEE, 2022, 42(9): 3443-3451.
[7] Saneie H, Nasiri-Gheidari Z, Tootoonchian F. Accuracy improvement in variable reluctance resolvers[J]. IEEE Transactions on Energy Conversion, 2019, 34(3): 1563-1571.
[8] Chen Shaohua, Zhao Yunlong, Qiu Haitao, et al. High-precision rotor position correction strategy for high-speed permanent magnet synchronous motor based on resolver[J]. IEEE Transactions on Power Electronics, 2020, 35(9): 9716-9726.
[9] Wang Kan, Wu Zhong. Hardware-based synchronous envelope detection strategy for resolver supplied with external excitation generator[J]. IEEE Access, 2019, 7: 20801-20810.
[10] 文建平, 李红梅, 姚宏洋. 集成故障在线诊断及容错控制的全数字旋转变压器数字转换器[J]. 电工技术学报, 2013, 28(增刊2): 445-450. Wen Jianping, Li Hongmei, Yao Hongyang. All- digital resolver-to-digital converter integrated with online fault diagnosis and fault-tolerant control[J]. Transactions of China Electrotechnical Society, 2013, 28(S2): 445-450.
[11] Bergas-Jané J, Ferrater-Simón C, Gross G, et al. High- accuracy all-digital resolver-to-digital conversion[J]. IEEE Transactions on Industrial Electronics, 2012, 59(1): 326-333.
[12] 汪剑鸣, 袁臣虎, 刘瑞, 等. 基于四线旋转变压器及AD2S1200的叉车线控转向永磁同步电机角度解码研究[J]. 电工技术学报, 2015, 30(增刊2): 95- 100. Wang Jianming, Yuan Chenhu, Liu Rui, et al. Research on PMSM rotor position decoding of the forklift steer-by-wire system based on the four-line resolver and AD2S1200[J]. Transactions of China Electrotechnical Society, 2015, 30(S2): 95-100.
[13] 马泽涛, 崔淑梅, 韩守亮, 等. 全数字转差轴角变换器[J]. 电机与控制学报, 2016, 20(5): 1-6. Ma Zetao, Cui Shumei, Han Shouliang, et al. Research on all digital R2D converter for angular position difference[J]. Electric Machines and Control, 2016, 20(5): 1-6.
[14] Caruso M, Di Tommaso A O, Genduso F, et al. A DSP-based resolver-to-digital converter for high- performance electrical drive applications[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4042-4051.
[15] Shi Tingna, Hao Yajing, Jiang Guokai, et al. A method of resolver-to-digital conversion based on square wave excitation[J]. IEEE Transactions on Industrial Electronics, 2018, 65(9): 7211-7219.
[16] 郝亚静. 基于旋转变压器的永磁同步电机转子位置估计[D]. 天津: 天津大学, 2018.
Hao Yajing. Rotor position estimation of permanent magnet synchronous motor based on the resolver[D]. Tianjin: Tianjin University, 2018.
[17] Texas Instruments. Discrete resolver front-end reference design with C2000™ microcontroller and ±0.1°accuracy[R]. Dallas, TX, USA: TIDA-01527, 2018.
[18] Hanselman D C. Resolver signal requirements for high accuracy resolver-to-digital conversion[J]. IEEE Transactions on Industrial Electronics, 1990, 37(6): 556-561.
[19] Wang Kan, Wu Zhong. Oversampling synchronous envelope detection for resolver-to-digital conversion[J]. IEEE Transactions on Industrial Electronics, 2020, 67(6): 4867-4876.
[20] 艾胜, 程思为, 肖飞, 等. 永磁同步电机转子位置检测滤波方法研究[J]. 电机与控制学报, 2018, 22(3): 66-73. Ai Sheng, Cheng Siwei, Xiao Fei, et al. A study on position signal filtering method for permanent magnet synchronous machines[J]. Electric Machines and Control, 2018, 22(3): 66-73.
[21] 李红梅, 姚宏洋, 王萍. PMSM驱动系统位置传感器故障在线诊断与自适应容错控制[J]. 电工技术学报, 2016, 31(增刊2): 228-235. Li Hongmei, Yao Hongyang, Wang Ping. Position sensor online fault diagnosis and adaptive fault- tolerant control of PMSM drive system[J]. Transa- ctions of China Electrotechnical Society, 2016, 31(S2): 228-235.
[22] Hanselman D C. Techniques for improving resolver- to-digital conversion accuracy[J]. IEEE Transactions on Industrial Electronics, 1991, 38(6): 501-504.
[23] Hwang S H, Kim H J, Kim J M, et al. Compensation of amplitude imbalance and imperfect quadrature in resolver signals for PMSM drives[J]. IEEE Transactions on Industry Applications, 2011, 47(1): 134-143.
[24] Guo Meishan, Wu Zhong, Qin Haoye. Harmonics reduction for resolver-to-digital conversion via second-order generalized integrator with frequency- locked loop[J]. IEEE Sensors Journal, 2021, 21(6): 8209-8217.
[25] Chen Dongdong, Li Jian, Chen Junhua, et al. On-line compensation of resolver periodic error for PMSM drives[J]. IEEE Transactions on Industry Applications, 2019, 55(6): 5990-6000.
[26] Sarma S, Agrawal V K, Udupa S. Software-based resolver-to-digital conversion using a DSP[J]. IEEE Transactions on Industrial Electronics, 2008, 55(1): 371-379.
[27] Benammar M, Gonzales A S P. A novel PLL resolver angle position indicator[J]. IEEE Transactions on Instrumentation and Measurement, 2016, 65(1): 123- 131.
[28] Yim C H, HaI J, KoM S. A resolver-to-digital conversion method for fast tracking[J]. IEEE Transactions on Industrial Electronics, 1992, 39(5): 369-378.
[29] 吴忠, 吕绪明. 基于磁编码器的伺服电机速度及位置观测器设计[J]. 中国电机工程学报, 2011, 31(9): 82-87.Wu Zhong, Lü Xuming. Design of angular velocity and position observer for servo motors with magnetic encoders[J]. Proceedings of the CSEE, 2011, 31(9): 82-87.
Abstract Resolver decoding chips are usually used to obtain the rotor position in high-reliable applications, such as electric vehicles, robots, aerospace, etc. Nevertheless, there are some defects of high cost and complex peripheral circuits, which restrict wide applications in compact and low-cost driver systems. In recent years, some software decoding methods of resolvers have been proposed, but most of them suffered from extra components and low precision due to bias drift of sineand cosine signals. To address these issues, this paper proposes a dual-sampling differential position decoding method for resolvers. By sampling peaks and bottoms of the output signals of resolvers twice in one excitation period, the influence of bias drift of sine and cosine signals on the sampling accuracy is eliminated and the position decoding accuracy canbe improved.
Firstly, the main control chip generates a fixed PWM signals, such as 8 kHz in the paper, which are amplified to excite the primary windings of resolvers. Secondly, after processing the sine and cosine signals generated by the secondary windings of resolvers through the signal processing circuits, the sine and cosine envelope signals required by the software decoding are prepared. Thirdly, a differential dual sampling of the peaks and bottoms of the signal envelopes can increase the amplitude of the signals by onetime and eliminate the influence of the bias voltage of sineand cosine signals. Finally, a second-order PLL is adopted to track the rotor position of the resolvers in comparison with a third-order PLL and arctan function.
The results of dual-sampling position decoding and single-sampling position decoding methods are compared with the actual position measured by a 2 500-line photoelectric encoder. It is found that under the condition of 600 r/min, the position error of the dual-sampling method is within ±1.5° and that of the single-sampling method is within ±5.4°, which proves that the dual-sampling differential position decoding method has better steady-state performance. In the acceleration and deceleration experiments from standstill to 3 000 r/min, the maximum position errors during the acceleration and deceleration processes of the dual-sampling method are 7.5° and -7°, respectively. Meanwhile the errors of the single-sampling method are 9° and -8°, respectively. Moreover, the dual-sampling method has smaller phase current, which proves that the proposed dual-sampling differential position decoding method has better dynamic characteristics. Furthermore, in the low-speed and high-speed experiments of 20 r/min and 5 100 r/min respectively, the position errors of the dual-sampling method are within ±2° at low-speed, and those in the high-speed are -0.6° to 1.3°. In comparison, at the same conditions, the position errors of the single-sampling method are between ±10.8° and -5° to 8°, respectively. This proves that the dual-sampling differential position decoding method has better position tracking accuracy in full-speed range. In addition, the tracking performances of the second-order PLL, a third-order PLL and arctan function are compared in terms of steady-state accuracy and dynamic accuracy.
The experimental results show that: (1) The proposed dual-sampling differential position decoding method can reduce the influence of bias voltage on the output signals of resolvers, improve the signal-to-noise ratio of sine and cosine signals, and increase the update frequency of position decoding. (2) Compared with the conventional single-sampling method, the proposed method is robustness to the environment changing, and has better steady-state and dynamic performances with higher position tracking accuracy in full-speed range.
To sum up, the proposed decoding method is a high-performance software position decoding strategy and can replace the resolver decoding chips in main applications.
keywords:Resolver, software decoding, dual sampling, differential calculation
DOI: 10.19595/j.cnki.1000-6753.tces.230991
中图分类号:TM35
国家自然科学基金(52007169)和浙江省自然科学基金(LY23E070004)资助项目。
收稿日期 2023-06-26
改稿日期 2023-10-09
吴 春 男,1987年生,博士,副教授,研究方向为电机控制。E-mail: wuchun@zjut.edu.cn(通信作者)
应王瑞 男,2000年生,硕士研究生,研究方向为电机控制。E-mail: 201806060130@zjut.edu.cn
(编辑 崔文静)