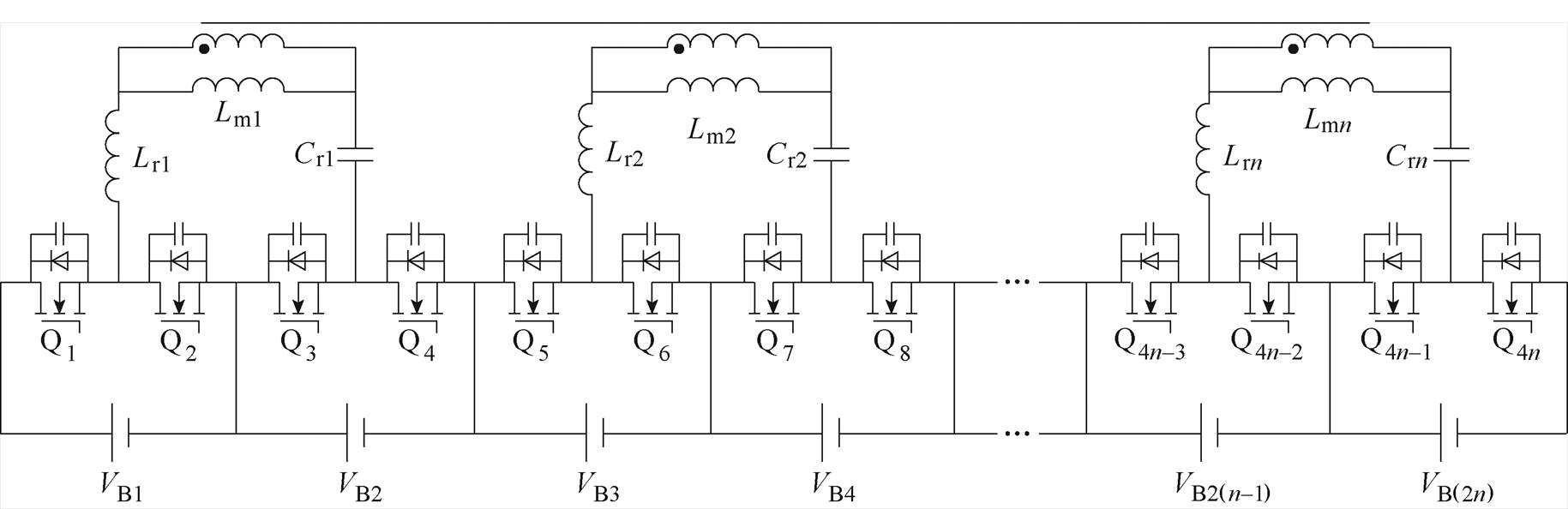
图1 基于双向半桥CLLLC谐振变换器的锂电池均衡电路
Fig.1 Li-ion battery equalization circuit based on a bidirectional half-bridge CLLLC resonant converter
摘要 锂电池因其能量密度高、自放电率低等优点被广泛应用于新能源领域。由于每个电池单体容量不尽相同，在使用时往往伴随着电池过充、过放等问题，电池使用寿命将受到极大影响，严重时甚至会出现自燃、爆炸等安全问题。该文提出基于双向半桥CLLLC谐振变换器的锂电池均衡电路，通过其在不同工作状态下的四种工作路径，可实现任意电池单体间的容量均衡。搭建一套6个电池单体的均衡电路，根据实验结果验证了所提基于双向半桥CLLLC谐振变换器的锂电池均衡电路具有均衡路径灵活、均衡速度快、均衡效率高和绕组数量减半等优点。
关键词：电池均衡 双向半桥CLLLC谐振变换器 模糊控制 多绕组变压器
锂电池因其能量密度高、自放电率低等优点被广泛应用于新能源领域。由于每个电池单体容量不尽相同，在使用时往往伴随着电池过充、过放等问题，电池使用寿命将受到极大影响，严重时甚至会出现自燃、爆炸等安全问题。
电池管理系统（Battery Management System, BMS）是锂电池应用中必不可少的一部分。为提高电池的能量利用率、降低电池系统风险，根据不同的应用场合，BMS可提供电池状态监测、保护电路、故障检测等功能，而其中的电池均衡电路就是用来解决锂电池不均衡现象的主要构成部分。
文献[1]提出了一种分布式开关电容系统（Switched Capacitor System, SCS）型电池均衡电路，该电路控制简单、可靠性高，但是只有一条能量通路，随着电池数量的增加，电路均衡速度会大幅下降。同时，能量只能在相邻电池单体间传递，若要完成电池组的均衡，中间级的电池单体会频繁在充电状态和放电状态之间切换，对电池的使用寿命有较大的影响。文献[2]提出了一种基于升降压变换器（Buck-Boost Converter, BBC）电池均衡电路，与分布式开关电容型电池均衡电路相似，该电路也存在电池数量较多时均衡速度较慢、电池反复充放电的问题。文献[3]提出了一种零电流软开关（Zero Current Switching, ZCS）谐振型电池均衡电路，可实现所有开关的零电流开通和关断。电路均衡效率较高，同时高频化后增加的谐振电感体积也不会过大，但其仍具有分布式开关电容型电池均衡电路的缺点，即均衡速度慢、电池频繁充放电。以上所提三种类型的均衡电路均具有结构上的限制性，因能量通路较少，当电池单体数量增多时，均衡速度很慢。若想提高均衡速度则需要增加额外的能量通路，但又会使得电路所需元器件增加。若想实现能量在任意电池间传递，多绕组变压器则更能兼顾均衡速度和成本。文献[4]提出了基于反激变换器（Flyback Converter, FC）的分布式变压器型均衡电路。该电路可实现任意电池单体与电池组之间的能量传递，通过控制对应开关管的导通，可实现多个电池同时均衡，均衡速度大大提升，但电池组处于充电状态时，高电量电池单体也会充电，使得电池在充放电状态间频繁切换，并且随着电池数量的增加，多绕组变压器的制作难度会大大增加。文献[5]提出了推挽变换器（Push- Pull Converter, PPC）均衡电路，均衡速度大大增加，但随着电池数量的增加，变压器的绕组数量会大大增加。文献[6]提出了基于正反激变换器（Forward and Flyback Converter, FFC）的多绕组变压器型均衡电路，可实现任意电池单体间的能量传递，均衡速度快、灵活度高、控制简单，但其多绕组的制作较为复杂。文献[7-8]提出了基于谐振变换器（Resonant Converter, RC）的锂电池均衡电路，均衡损耗大大降低，但因谐振电路较为复杂，通常采用混合结构来实现不同电池间的均衡。
针对串联锂电池工作时出现的能量不均衡问题，本文分析现有均衡方案中的不足，结合半桥LLC谐振变换器和多绕组变压器两种电池均衡电路的优势，提出了一种基于双向半桥CLLLC谐振变换器的锂离子电池均衡电路。该拓扑既保留了多绕组变压器均衡路径灵活、均衡速度快的优点，同时所有开关实现了软开关，在相同数量电池单体情况下，变压器绕组减少了一半，极大地增加了多绕组变压器的拓展性。最后采用不同均衡控制策略，分别进行静态均衡和动态均衡，并对均衡过程中的电池电压进行记录与统计，对均衡速度和均衡效率进行了分析，验证了所提均衡电路的快速性和高效性，进而证明了本文所提出的基于双向半桥CLLLC谐振变换器的锂电池均衡电路对比现有的均衡电路具有均衡路径灵活、均衡速度快、均衡效率高和绕组数量减半等优点。
基于双向半桥CLLLC谐振变换器的锂电池均衡电路如图1所示，图中，Q1～Q4n分别为均衡电路的开关阵列，每4个开关管对应一个均衡模块；Lr1～Lrn、Cr1～Crn和Lm1～Lmn分别为模块M1～Mn所对应的谐振电感、谐振电容和励磁电感。
图1 基于双向半桥CLLLC谐振变换器的锂电池均衡电路
Fig.1 Li-ion battery equalization circuit based on a bidirectional half-bridge CLLLC resonant converter
模块间通过多绕组变压器T型连接，每一个模块内包含2个电池单体，通过不同开关阵列的导通，可以实现能量在任意电池单体间传递。
在介绍均衡电路拓扑前，首先对双向半桥CLLLC谐振变换器的工作原理进行分析。双向半桥CLLLC谐振变换器拓扑结构如图2所示。
虽然双向半桥CLLLC谐振变换器存在两个不同的谐振网络，但是为了变换器在正反向工作时均可实现软开关，在设计参数时，通常使二次侧谐振电感Lr2和谐振电容Cr2等效至一次侧后与谐振电感Lr1和谐振电容Cr1保持一致，因此双向半桥CLLLC谐振变换器与半桥LLC谐振变换器一样，有两个谐振频率。第一谐振频率为Lr1、Cr1与Lr2、Cr2的谐振频率fn，第二谐振频率为加入励磁电感Lm以后。
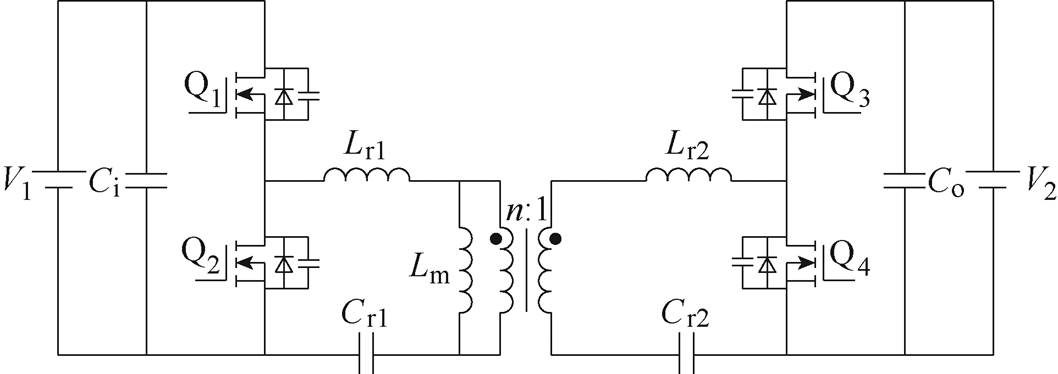
图2 双向半桥CLLLC谐振变换器拓扑结构
Fig.2 Bidirectional half-bridge CLLLC resonant converter topology
根据开关频率fs与fn和fm之间的大小关系，电路可以工作在三种模式：当fm＜fs＜fn时，称半桥CLLLC谐振变换器工作在模式1；当fs=fn时，称半桥CLLLC谐振变换器工作在模式2；当fs＞fn时，称半桥CLLLC谐振变换器工作在模式3。
本文所提均衡电路采用二次侧同步整流的双向半桥CLLLC谐振变换器工作在模式3，因此对该工作模式进行详细分析。图3为电路在二次侧同步整流模式3下的各阶段等效电路，其关键波形如图4所示。
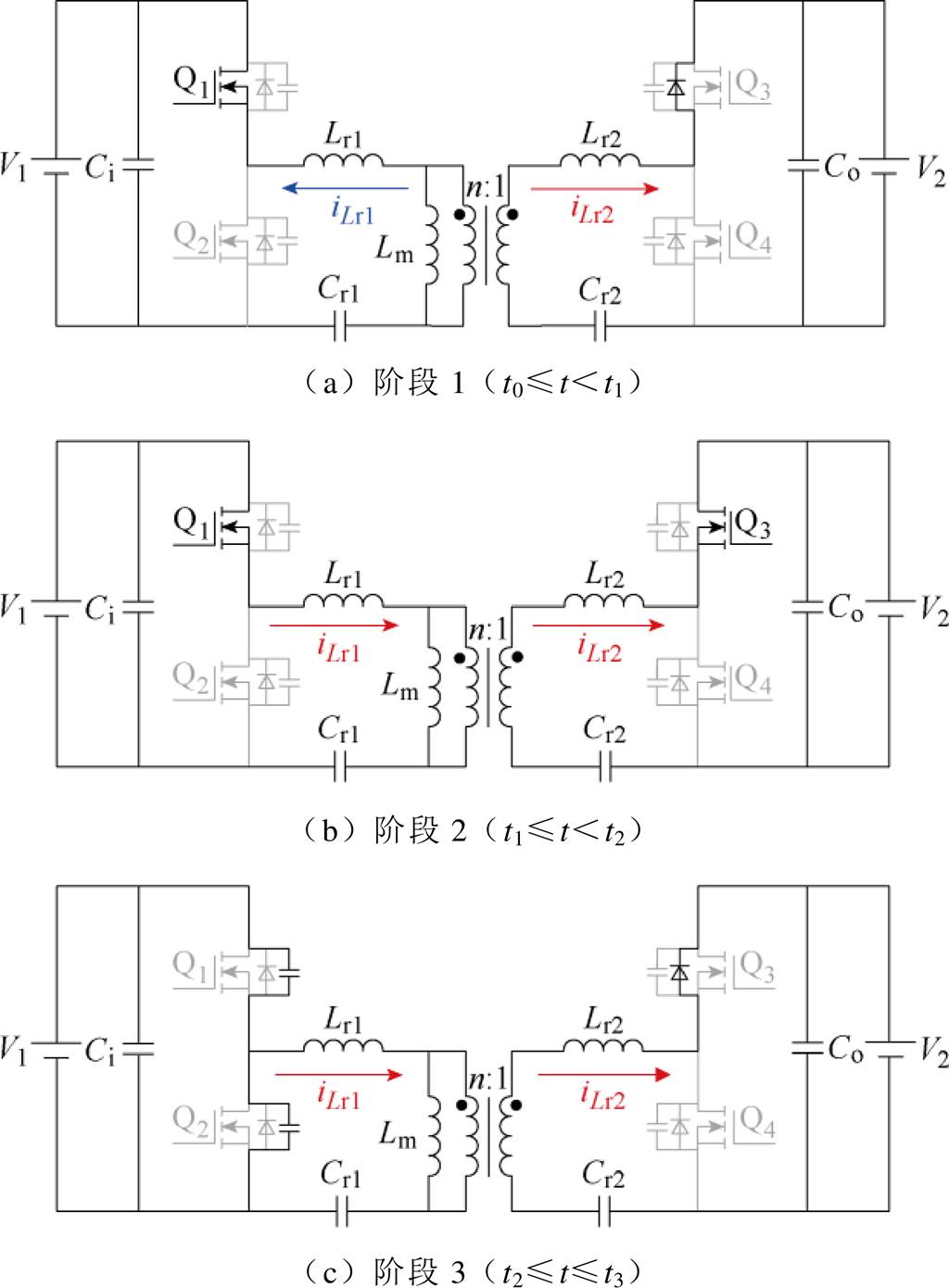
图3 半桥CLLLC谐振变换器二次侧同步整流时工作在模式3下的各阶段等效电路
Fig.3 Equivalent circuit for each phase of a half-bridge CLLLC resonant converter operating in mode 3 during synchronous rectification of the secondary side
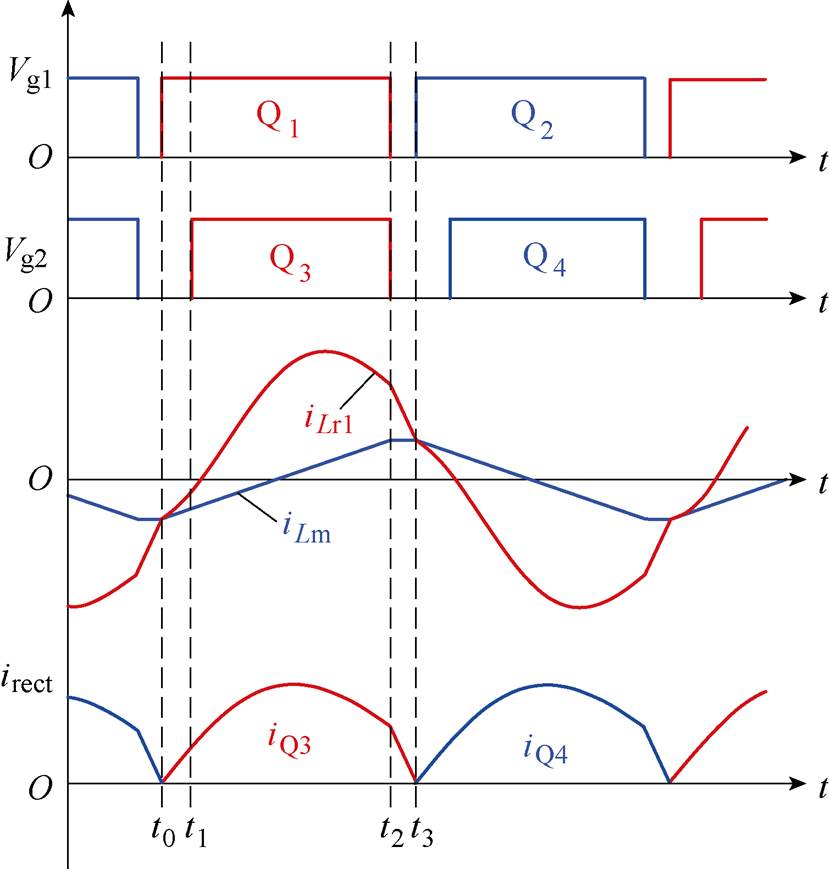
图4 双向半桥CLLLC谐振变换器二次侧同步整流时工作在模式3下的主要波形
Fig.4 Main waveforms of a bidirectional half-bridge CLLLC resonant converter operating in mode 3 with synchronous rectification on the secondary side
阶段1（t0≤t＜t1
：如图3a所示，t0时刻，开关管Q1导通，在此之前二次侧谐振电流iLr1通过Q1的反并联二极管VD1续流，此时Q1为零电压开通（Zero Voltage Switching, ZVS）。当Q1导通后，A点电压为输入电压V1，此时只有谐振电感Lr1、Lr2和谐振电容Cr1、Cr2参与谐振，谐振电流iLr1开始呈正弦规律变化，励磁电感电流iLm呈线性增加，此时二次电流给Q3的寄生电容CQ3放电，给Q4的寄生电容CQ4充电。充放电完成后，开关管Q4的Vds将被充电至输出电压V2，开关管Q3的Vds将被放电至0，使开关管Q3处于零电压开关状态，此时阶段1结束。
阶段2（t1≤t＜t2：如图3b所示，t1时刻，开关管Q3零电压开通，二次电流通过开关管Q3续流，谐振电流iLr1继续呈正弦规律变化，励磁电感电流iLm呈线性增加。当开关管Q1、Q3关断时，阶段2结束，此时谐振电流iLr1仍大于励磁电流iLm。
阶段3（t2≤t≤t3：如图3c所示，t2时刻，开关管Q1、Q3关断，谐振电流iLr1开始给Q1的寄生电容CQ1充电，给Q2的寄生电容CQ2放电。此时二次电流大小为谐振电流iLr1与励磁电流iLm的差值，二次电流通过Q3反并联二极管VD3续流。充放电完成后，开关管Q1的Vds将被充电至输入电压V1，开关管Q2的Vds将被放电至0，此时阶段3结束，前半个开关周期结束。只要驱动信号的死区时间大于此阶段时间，开关管Q2就可以在下一阶段实现零电压开通。
双向半桥CLLLC谐振变换器与其他谐振变换器类似，在谐振点附近工作时，谐振电流接近正弦，可采用基波分析法对CLLLC谐振变换器建立数学模型，将CLLLC谐振变换器等效为一个二端口网络，分析其输入输出特性。
CLLLC谐振变换器基波等效电路如图5所示。图中，Lr1、Cr1为CLLLC谐振变换器一次侧谐振电感和谐振电容，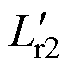
、
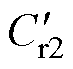为二次侧谐振电感和谐振电容折算至一次侧的等效值。由于电池均衡电路的特殊性，为确保电路无论工作在正、反向状态均能够实现电池间的完全均衡，设计电路时将变压器电压比n设为1，同时，一次侧、二次侧的谐振参数应完全一致。因此在等效电路中，
，
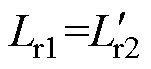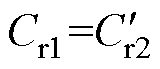，Lm为变压器励磁电感，uAB、uCD分别为一次侧的桥口电压和二次侧折算至一次侧的桥口电压，Req为二次侧折算到一次侧的等效负载。
与单向半桥LLC谐振变换器相比，双向半桥CLLLC谐振变换器二次侧增加了两个谐振元件，其谐振特性更为复杂，有必要对其谐振特性进行分析。
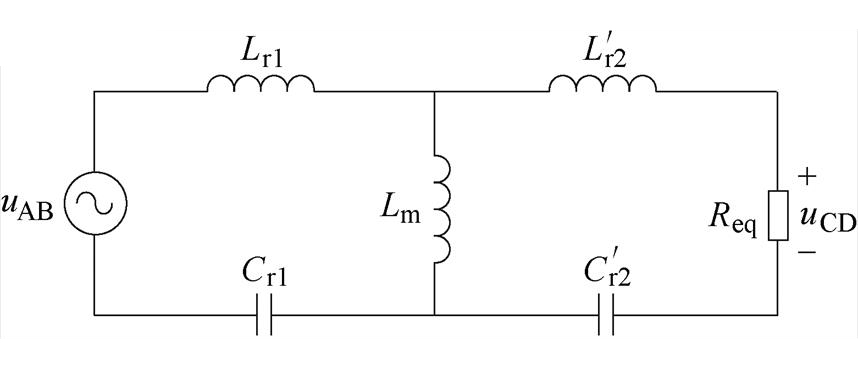
图5 CLLLC谐振变换器基波等效电路
Fig.5 Base wave equivalent circuit diagram for CLLLC resonant converter
为了方便分析，根据图5，先进行如下定义
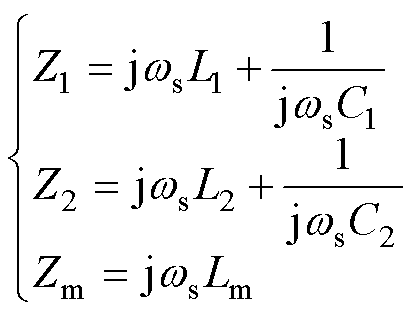（1）
式中，ws为开关角频率；L1、C1分别为一次侧谐振电感和谐振电容；L2、C2分别为二次侧等效谐振电感和等效谐振电容。
结合图5，可求得CLLLC谐振变换器等效电路的传递函数为
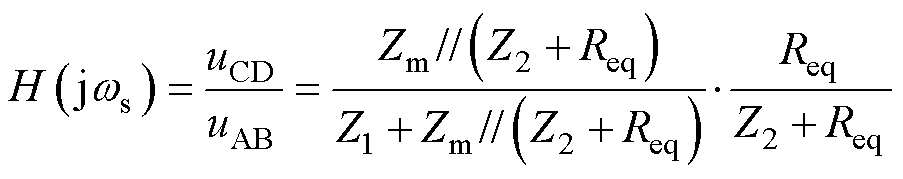（2）
将式（1）代入式（2）可得式（3），在此定义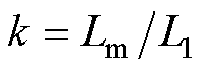
，
，
，
，
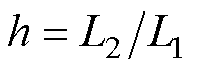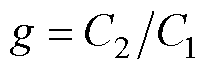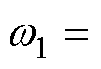
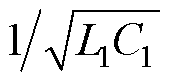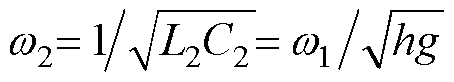，则式（3）可化简为式（4）。
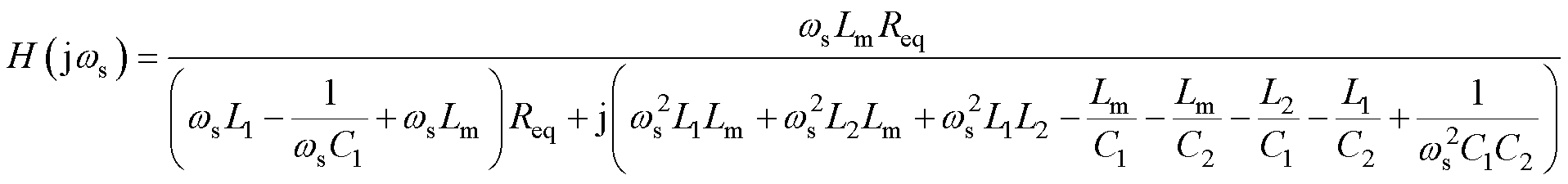（3）
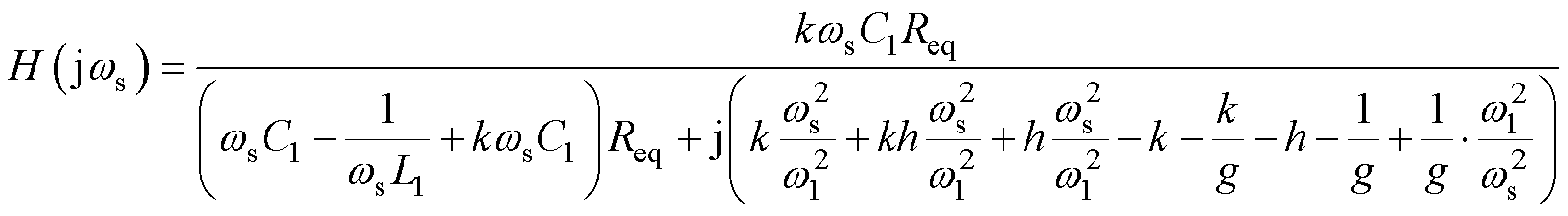（4）
设wn为归一化角频率、Zc为特征阻抗、Q为品质因数，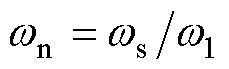
，
，
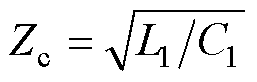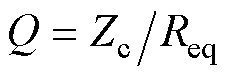，将其代入式（4），得其归一化传递函数为
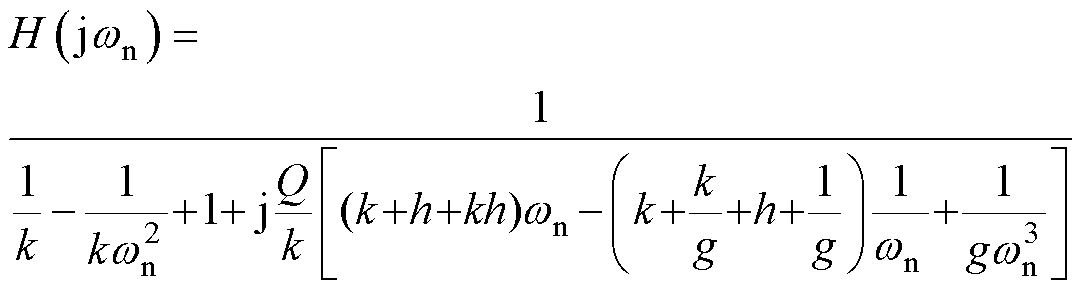（5）
则其电压增益M可表示为
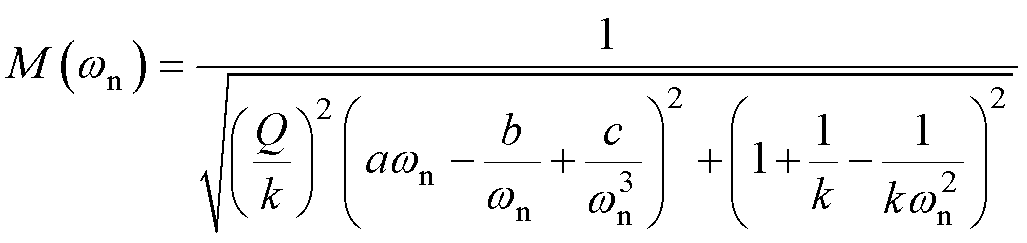（6）
由于电池均衡电路的特殊性，为确保电路无论工作在正、反向状态均能够实现电池间的完全均衡，设计电路时将变压器电压比n设为1，同时一次、二次侧的谐振参数应完全一致。因此在等效电路中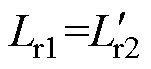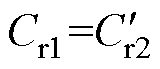，，即h=g=1，那么变换器电压增益M的表达式可化简为
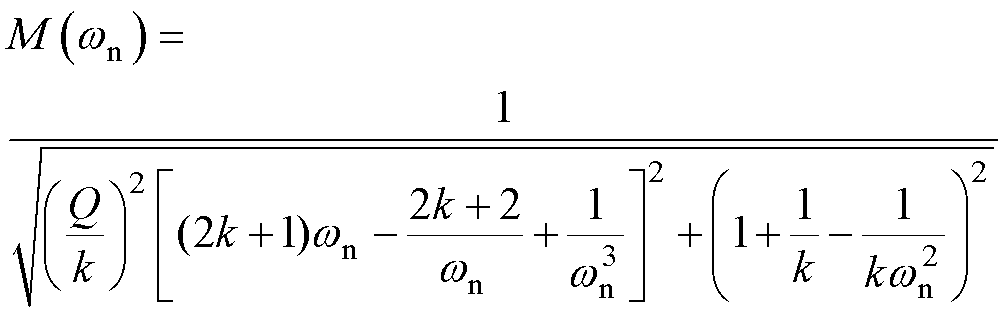（7）
图6为不同Q值、不同k值下电压增益M与wn的关系曲线。可以看出，当Q值一定，wn=1时，CLLLC谐振变换器的电压增益恒为1，随着k值的增加，电压增益曲线在谐振频率点附近的变化越趋于平缓，当k值增大到一定值后，电压增益将不超过1，与此同时，电压增益的最大值点会向归一化频率减小的方向移动。
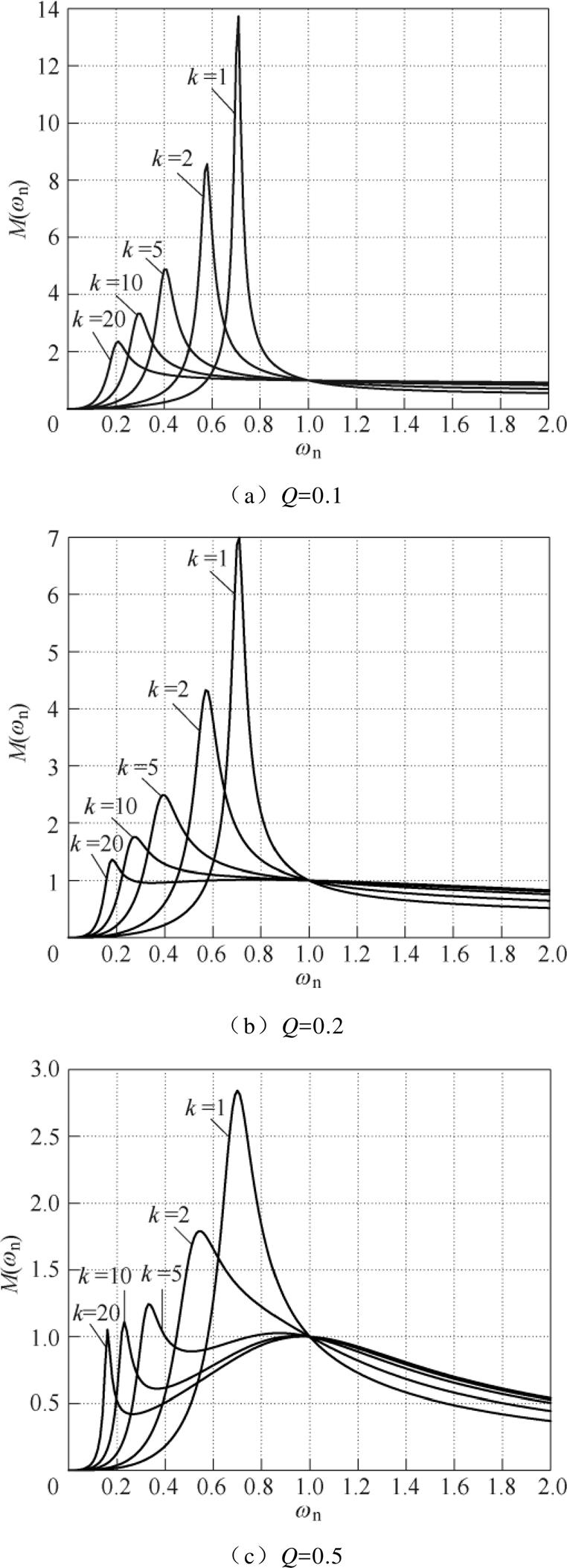
图6 不同Q值、不同k值下的电压增益曲线
Fig.6 Voltage gain curves at different Q values and different k values
当k值一定时，随着Q值的增加，在一定范围内，电压增益的变化趋势保持不变，增益最大值将逐渐减小；超出一定范围后，电压增益曲线将在最大值点与谐振频率点之间产生畸变，这会导致谐振频率点附近的电压增益曲线变化加剧。
从上述分析中可以看出，CLLLC谐振变换器在轻载时，其电压增益特性与LLC谐振变换器基本一致，在重载时，其电压增益特性变化较大，不利于变换器设计和控制。由于电压增益决定了均衡电路的均衡精度和均衡速度，因此在设计电路参数时要着重考虑。
均衡路径的选择对于电池均衡电路的均衡速度、均衡效率和均衡灵活性有着很大的影响，更多的均衡路径意味着更灵活的均衡策略。通过合理地选择均衡路径，可以加快均衡速度，减少均衡过程中的反复充放电过程进而提高均衡效率。本文所提出的基于双向半桥CLLLC谐振变换器的锂电池均衡电路在实现变压器绕组数减半的情况下，根据开关管导通模态不同，共分为四种均衡路径：模块间均衡、模块与任意电池单体间的均衡、任意不同模块的电池单体间均衡和模块内均衡，前三种均衡路径电路均工作在二次侧同步整流状态模式3下，第四种均衡路径的开关频率等于谐振频率。本文将对这四种均衡路径进行介绍，为方便分析，以两绕组变压器为例，将半桥CLLLC谐振变换器的一次侧作为输入侧，二次侧作为输出侧。
1.4.1 均衡路径1：模块与模块间
当开关管Q1～Q4作为输入侧开关管，且Q1、Q4为同一驱动信号，Q2、Q3为另一互补的驱动信号时，模块M1（即电池单体B1和电池单体B2）作为变换器的输入直流源，此时二次侧若Q5、Q8与Q1、Q4驱动信号频率相同，则模块M2（即电池单体B3和电池单体B4）作为变换器的输出侧负载。此时能量可以在任意电池模块之间传递。
图7为模块M1与模块M2间均衡路径的前半周期工作模态，其主要波形可参考图4。可以看出，其本质上是一个双向半桥CLLLC谐振变换器，在阶段2时，能量从一次侧流向二次侧，即从B1、B2流向B3、B4，同时由于该双向半桥CLLLC谐振变换器工作在模式3，因此所有开关管均可实现ZVS。
1.4.2 均衡路径2：模块与任意电池单体间
当开关管Q1～Q4作为输入侧开关管，且Q1、Q4为同一驱动信号，Q2、Q3为另一互补的驱动信号时，模块M1（即电池单体B1和电池单体B2）作为变换器的输入直流源，此时二次侧若Q7保持导通，Q5与Q1、Q4驱动信号频率相同，Q6与Q2、Q3驱动信号频率相同，电池单体B3作为变换器的输出侧负载；若Q6保持导通，Q7与Q1、Q4驱动信号频率相同，Q8与Q2、Q3驱动信号频率相同，则电池单体B4作为变换器的输出侧负载。通过合理地选择开关阵列的导通，可以实现任意模块与任意非同组电池单体间的能量均衡。
图8为模块M1与电池单体B3之间均衡路径的前半周期工作模态，其主要波形可参考图4。在阶段2时，能量从一次侧流向二次侧，即从B1、B2流向B3。若二次侧开关管Q6保持导通，Q7、Q8交替导通，则能量从B1、B2流向B4。
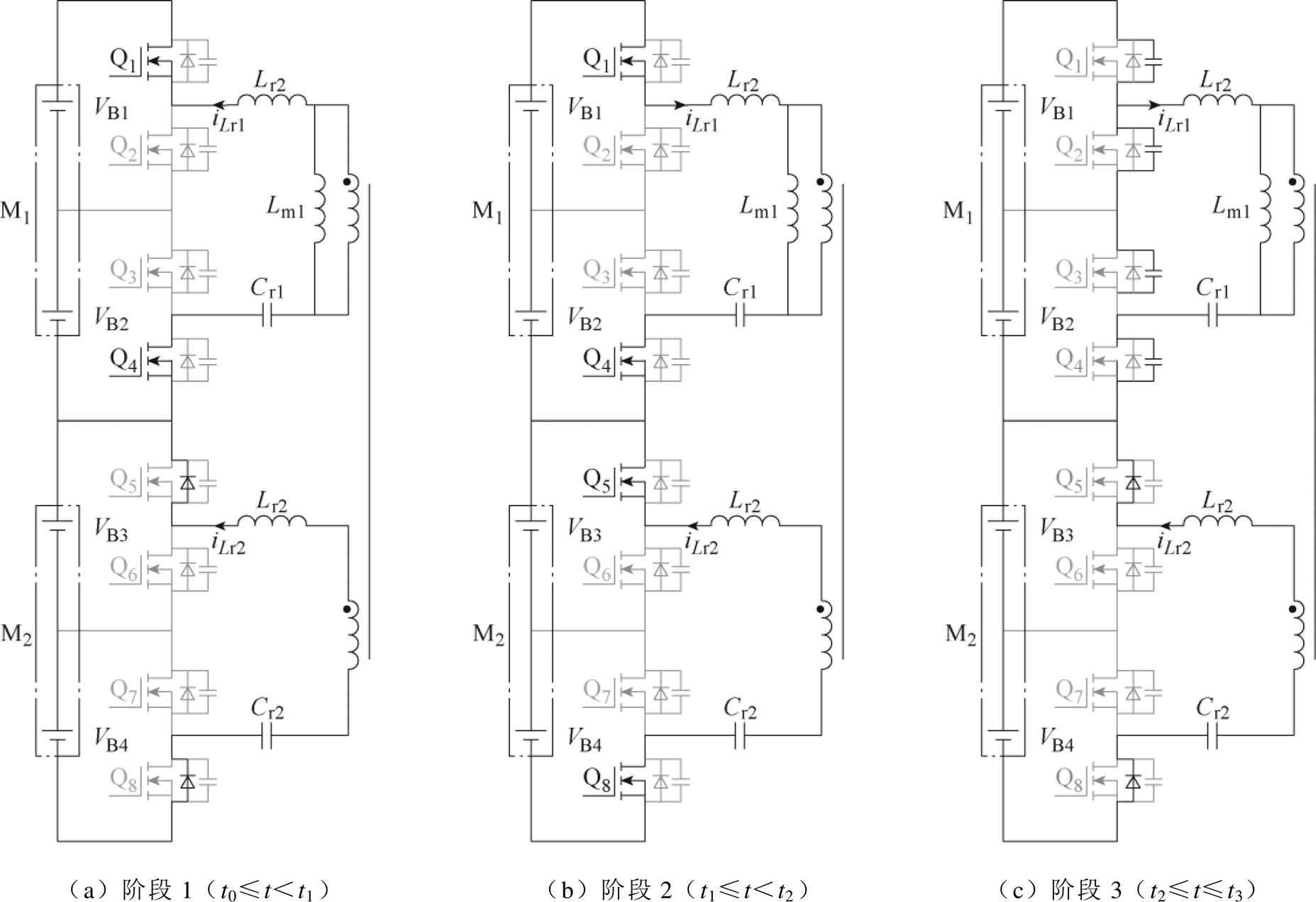
图7 模块与模块间均衡路径前半周期工作模态
Fig.7 First half-cycle operating mode of module-to-module balanced path
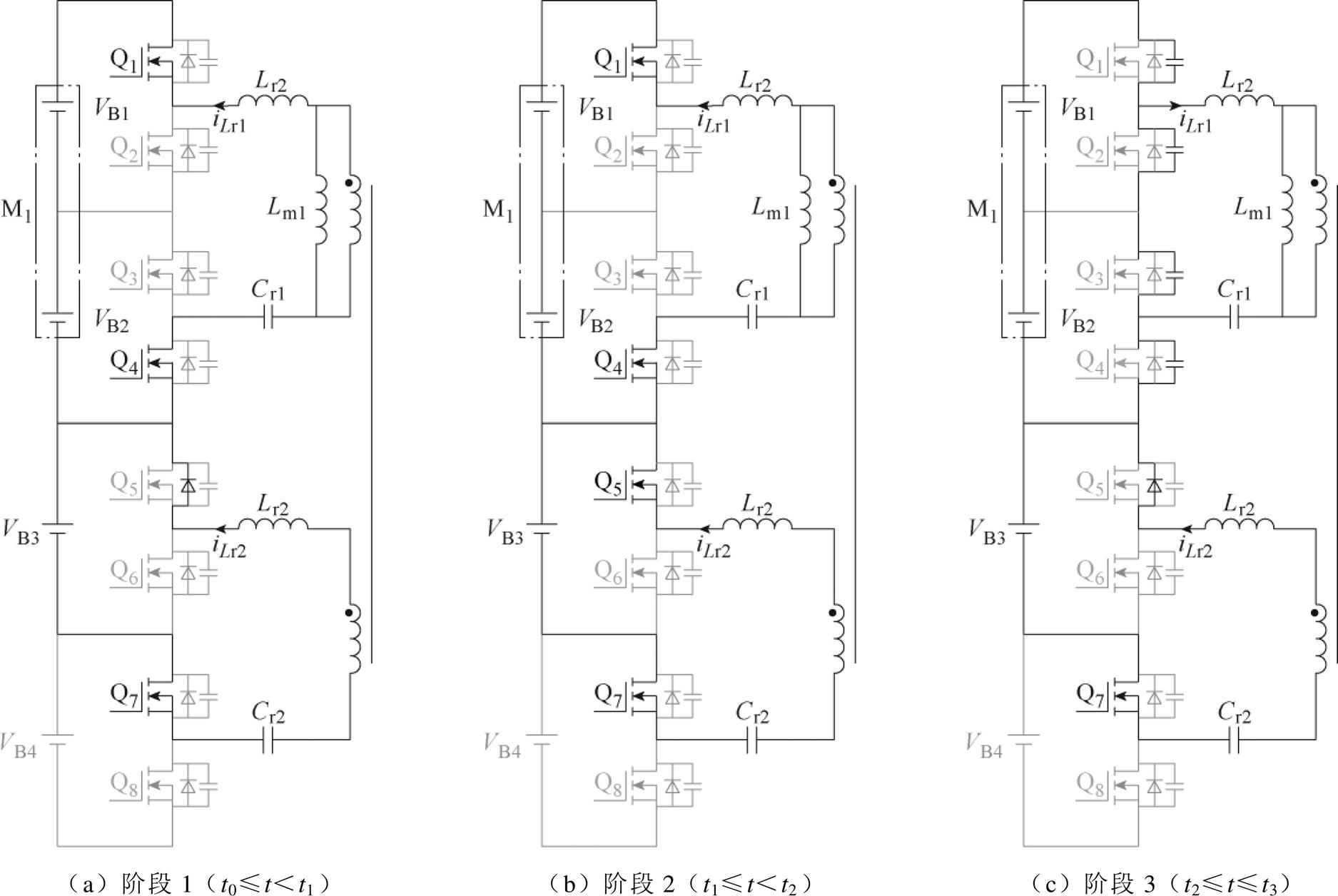
图8 模块与电池单体间均衡路径前半周期工作模态
Fig.8 First half-cycle operating mode of module-to- battery balanced path
1.4.3 均衡路径3：任意不同模块的电池单体间
当开关管Q1、Q2作为输入侧开关管，Q3保持导通，电池单体B1作为变换器的输入直流源，此时二次侧若Q7保持导通，Q5与Q1驱动信号频率相同，Q6与Q2驱动信号频率相同，电池单体B3作为变换器的输出侧负载；若Q6保持导通，Q7与Q1驱动信号频率相同，Q8与Q2驱动信号频率相同，则电池单体B4作为变换器的输出侧负载。同理，若开关管Q3、Q4作为输入侧开关管，Q2保持导通，电池单体B2将作为变换器的输入直流源。通过合理地选择开关阵列的导通，可以实现任意电池到任意非同组电池单体间的能量均衡。
图9为电池单体B1与电池单体B3之间均衡路径的前半周期工作模态，其主要波形可参考图4。在阶段2时，能量从一次侧流向二次侧，即从B1流向B3。
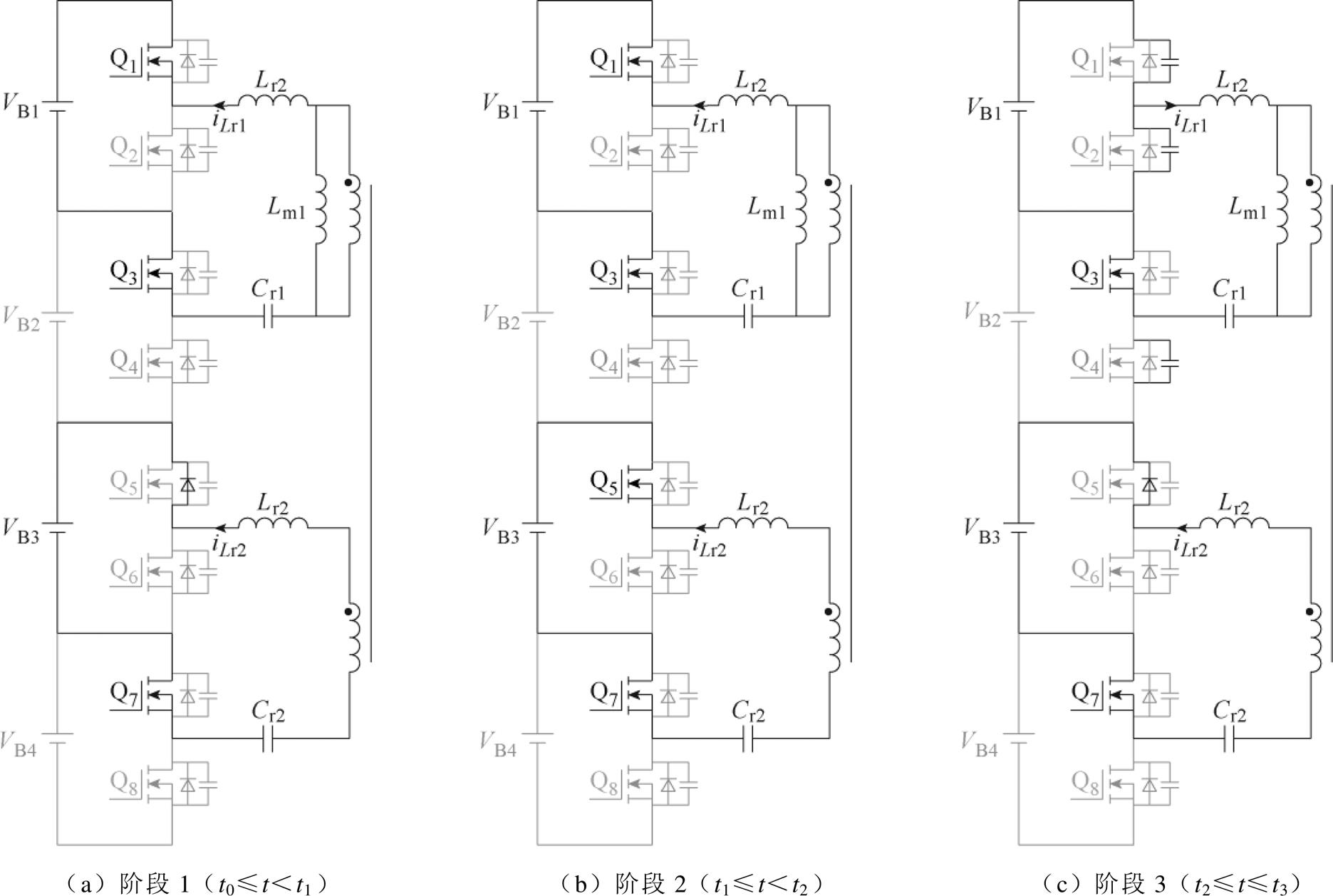
图9 任意不同模块电池单体间均衡路径前半周期工作模态
Fig.9 First half-cycle operating mode of cells of any different modules balanced path
1.4.4 均衡路径4：模块内部两个电池单体间
当开关管Q1、Q3为同一导通信号，开关管Q2、Q4为另一导通信号，两信号为一对频率为谐振频率、占空比为0.5的互补脉冲宽度调制（Pulse Width Modulation, PWM）波时，此时电路输入侧等效为LC谐振型均衡电路，电路工作模态如图10所示。图10a中，当Q1、Q3导通时，VB1与谐振腔并联，VB1向谐振腔放电，此时可得
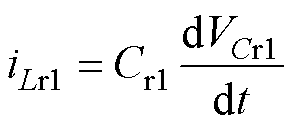（8）
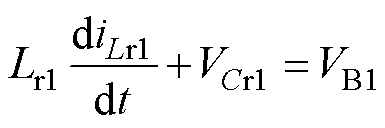（9）
通过式（8）和式（9）可解得此时谐振电流表达式为
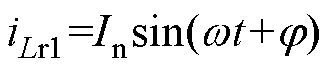（10）
当Q2、Q4导通时，VB2与谐振腔并联，谐振腔向VB2充电，此时可得
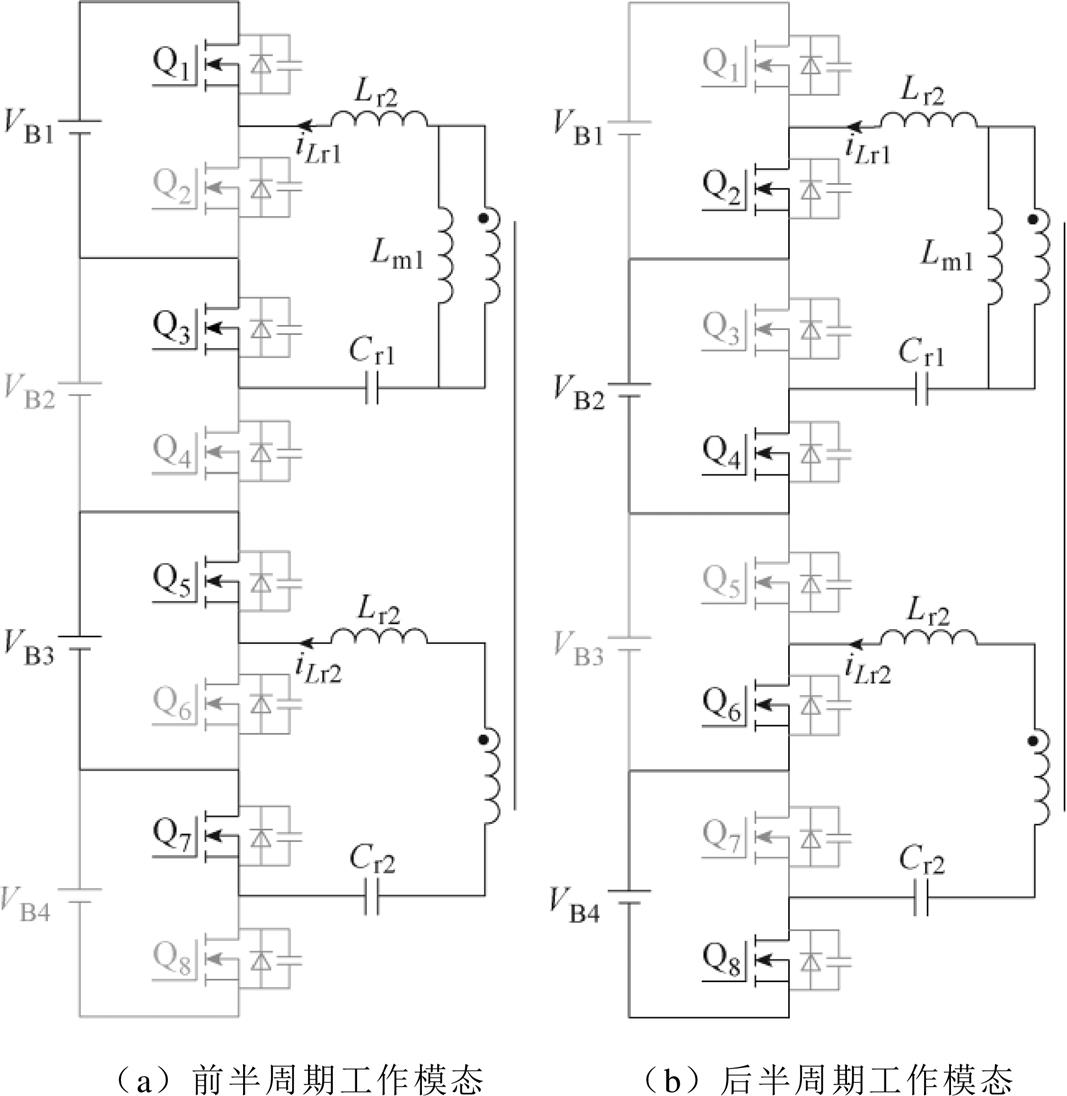
图10 单个模块内部电池单体间均衡路径工作模态
Fig.10 Balanced path operating mode between battery cells within a single module
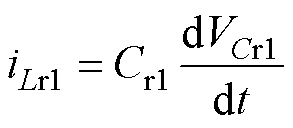（11）
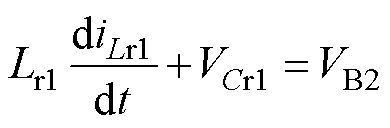（12）
通过式（11）和式（12）可解此时谐振电流表达式为
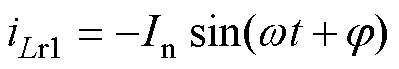（13）
将一次侧的开关信号也给予二次侧开关管，则二次侧模块内的两电池单体间也可实现均衡，电流大小与一次侧谐振电流一致，图10b所示即为B1向B2放电、B4向B3放电。若开关频率与Lr1和Cr1的谐振频率一致时，励磁电感上的励磁电流远远小于谐振电流，则其可以忽略不计。此时开关管每当电流到零时开通和关断，实现了全部开关的零电流软开关。
从1.4节可知，前三种均衡路径除了输入电压大小和负载不同以外，电路本质上均为半桥CLLLC谐振变换器。在二次侧采用同步整流方案的工作模态中，若忽略反并联二极管的导通压降，则工作阶段1和工作阶段2的等效电路相同，工作阶段3仅为过渡阶段，不作为正常功率传输过程，因此不对其进行电流推导。为了简化分析，对均衡电流的推导将忽略一次侧和二次侧的寄生电阻Rpeq、Rseq，并将变压器漏感算入谐振电感中。
能量传输过程中，半桥CLLLC谐振变换器时域等效电路如图11所示，图中，Lr和Cr分别为该电池侧的谐振电感和谐振电容，iLr和VCr分别为它们的状态变量，Vi为该侧电压，VT为变压器励磁电感上的电压，即变压器的端电压，根据均衡路径的不同，电池侧可以是电池组也可以是电池单体。相较于谐振电流，励磁电流对其影响很小，为了简化分析，以下忽略励磁电流对谐振电流的影响。根据基尔霍夫定律，对于n绕组变压器，易知VT为
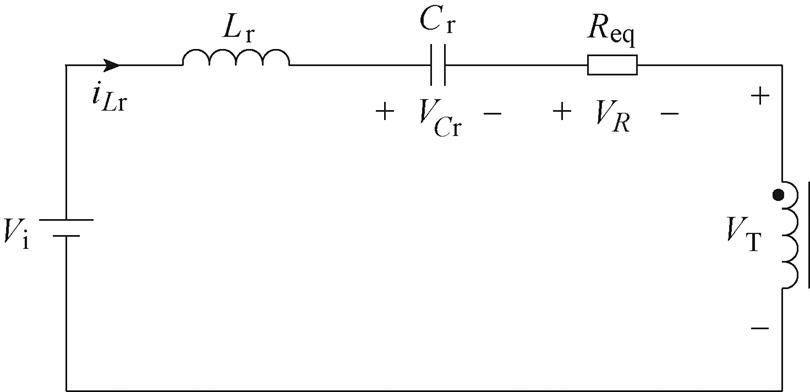
图11 半桥CLLLC谐振变换器时域等效电路
Fig.11 Time domain equivalent circuit diagram of a half bridge CLLLC resonant converter
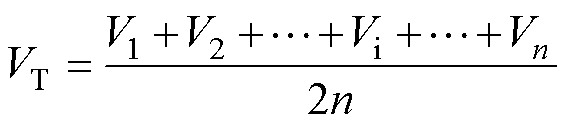（14）
若Vi＞VT，则Vi为半桥CLLLC谐振变换器的输入侧，该侧电池组或电池单体为放电电池；若 Vi＜VT，则Vi为半桥CLLLC谐振变换器的输出侧，该侧电池组或电池单体为充电电池。现以Vi＞VT时的情况来分析，那么可以得到输入侧等效电路的时域微分方程为
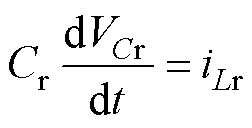（15）
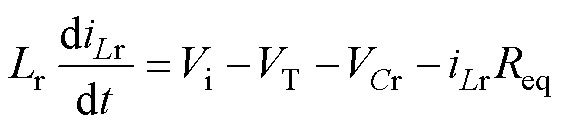（16）
将式（15）代入式（16）可得关于VCr的二阶微分方程为
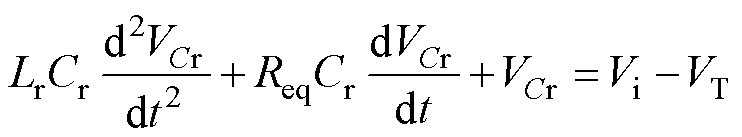（17）
可解得电容电压与电感电流分别为
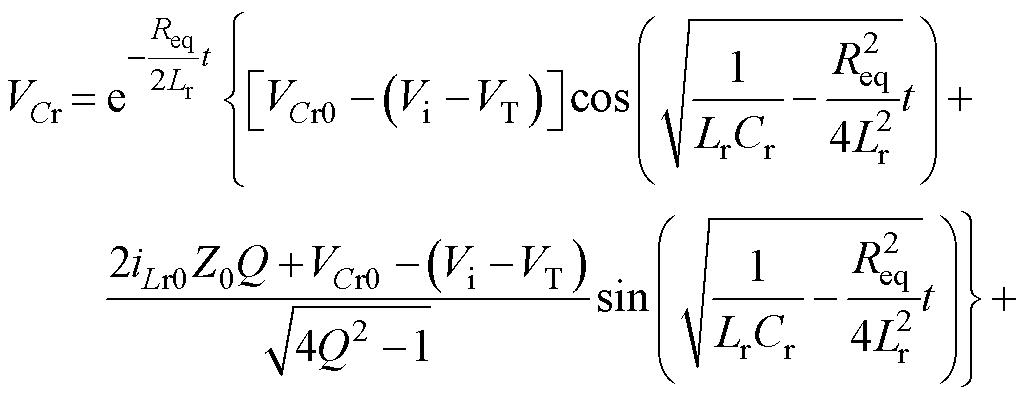
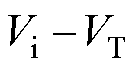（18）
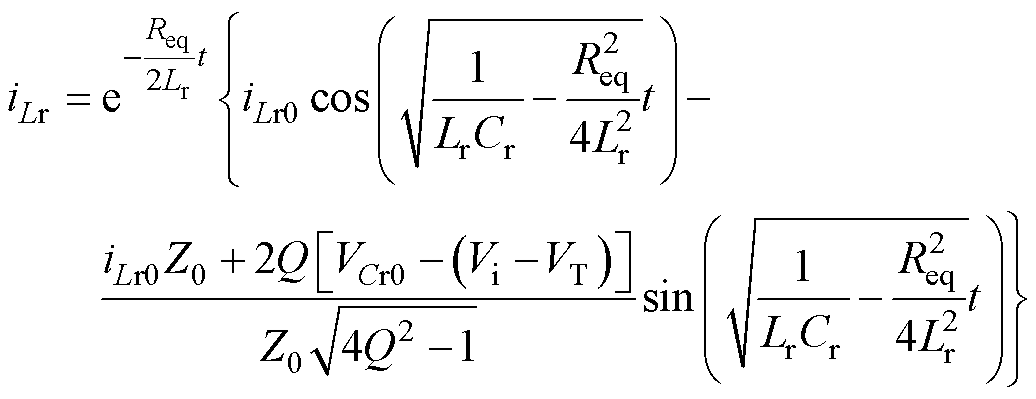（19）
式中，VCr0为电容电压初值。
半桥CLLLC谐振变换器工作在准谐振状态时，二次侧谐振电流相位与励磁电流相同，一次侧谐振电流为二次侧谐振电流与励磁电流之和，因此一次侧谐振电流与二次侧谐振电流间存在一定的相位差。在此次分析中，已经假设励磁电流足够小，忽略其对谐振电流的影响，因此可以令谐振电流初值iLr0=0，代入式（19）后可得
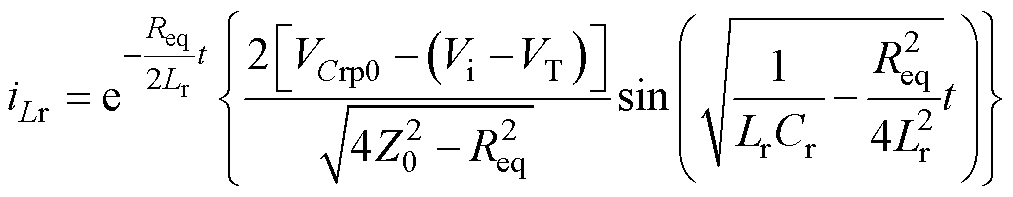（20）
若Vi＜VT时，除了谐振腔两端电压为VT-Vi，其余分析与上述完全一致，在此不再进行推导，只给出此时谐振电流为
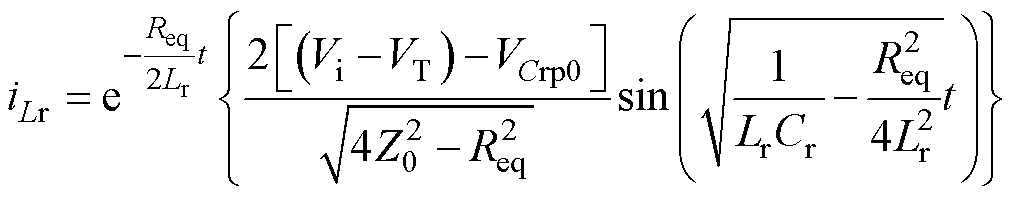（21）
现有控制策略[9-17]可以分为以下几种：
（1）极值均衡法。该均衡方法是根据最高电压和最低电压电池单体所在的位置控制均衡路径的，这种均衡方法可以有效地防止电池的过充和过放，但与此同时只有电池单体最高的与最低的电池在进行均衡，造成了均衡速度的低下。
（2）平均值均衡法。该均衡方法是以所有电池单体的平均值为基准，电池向该平均值均衡，因此该方法的均衡精度很高，但是该均衡方法会出现电池单体的重复充放电问题，对电池寿命有不利影响。
（3）模糊控制均衡法。该均衡方法是针对特定的均衡电路，根据不同电路特性设计最有利于均衡效果的控制方法，但是由于每一种均衡电路的特性不尽相同，因此此种均衡方法不适合广泛运用。
静态均衡和动态均衡中，均衡目的不完全一样。动态均衡时，电池组所有电池均在大电流充放电状态，此时均衡电路的主要目的是防止电压过高或过低的电池单体过充或过放；静态均衡时，只有均衡电流对电池电压有影响，因此电池过充、过放问题在静态均衡时并不突出，此时均衡电路的主要目的应是提高均衡精度和均衡效率。
根据本文所提均衡电路，在静态均衡和动态均衡时采用不同的控制策略，下面对两种控制策略进行介绍。
不同电压阶段锂电池恢复稳态时所需时间如图12所示，在结束充放电后的一段时间内，电池电压会出现一定程度的下降，由于电池均衡往往需要多个均衡周期才能实现更高的均衡精度，这种非线性特性会导致大部分电路难以实现完全均衡。
与此同时，如果不对本文所提出的均衡电路的均衡路径进行合理控制，会造成均衡速度过慢、电池过均衡等情况出现。因此，在静置均衡时，为方便控制以保证均衡精度，只让电路工作在模块与模
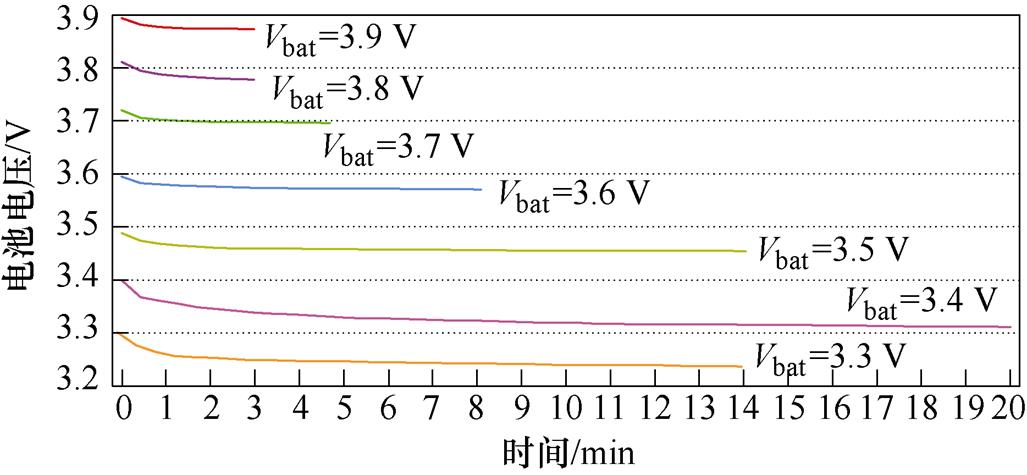
图12 不同电压阶段锂电池恢复稳态时所需时间
Fig.12 Time required for the recovery of a lithium battery to steady state at different voltage stages
块间均衡和模块内均衡模式。在单次周期内，为减轻过均衡现象，两种均衡状态的工作时间占比将由模糊算法得出。
根据1.5节的分析可知，均衡电流的大小与输入电压与输出电压差值有关，在均衡末期由于电池间压差较小，均衡电流很小，此时只有极个别电池单体还未完成均衡，若仍采用模块与模块间均衡和模块内均衡会极大地延长均衡时间，因此当均衡电路进入末期时需要采用均衡电流更大的模块与电池单体间的均衡模式。
为保证均衡精度，在均衡过程进入末期时，需要缩短单次均衡周期时间并给予电池一定的静置时间，以减小电池电压跌落所带来的均衡误差，此时均衡时间与静置时间的占比将由第二套模糊算法得出。
对于第一套均衡时间模糊控制器，同一模块内单体压差最大值DVB_max和模块电压最大差值DVM_max作为其输入量，模块内均衡模式工作时间的占比作为其输出量。如图13所示为均衡时间模糊控制器的输出结果。
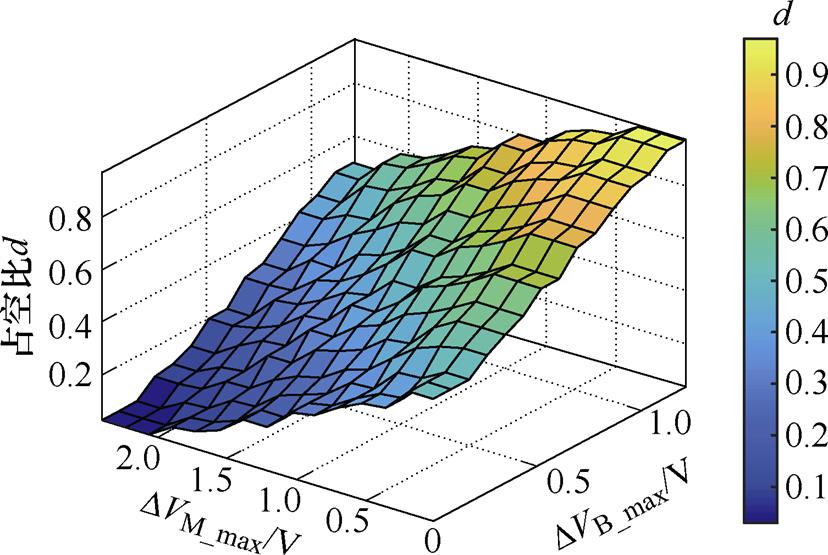
图13 均衡时间模糊控制器输出结果
Fig.13 Graph of the output of the equilibrium time fuzzy controller
均衡时间模糊控制器主要工作在均衡主要过程中，因此其目的是保持均衡电流在最大值，以实现快速均衡和降低均衡损耗。由第3节中对谐振电流的推导可知，均衡电流主要跟谐振腔两端的压差有关，也可认为跟半桥CLLLC谐振变换器的输入输出差值有关，因此为加快均衡速度，应尽量保证半桥CLLLC谐振变换器的输入输出差值最大。对于第二套均衡时间模糊控制器，平均电压Vavg和极差R作为其输入量，电路均衡时间和静置时间的比例作为其输出控制量。图14为均衡状态模糊控制器的控制规则。末期调节模糊控制器主要工作在均衡末期，此时模糊控制器工作主要有两个目的：第一是保证均衡速度不会过慢；第二是根据不同电压阶段调整静置时间，以保证较高的均衡精度。根据图12可知，锂电池电压在3.3 V附近时，所需恢复到稳态的时间最长，越远离此值，所需时间越短。
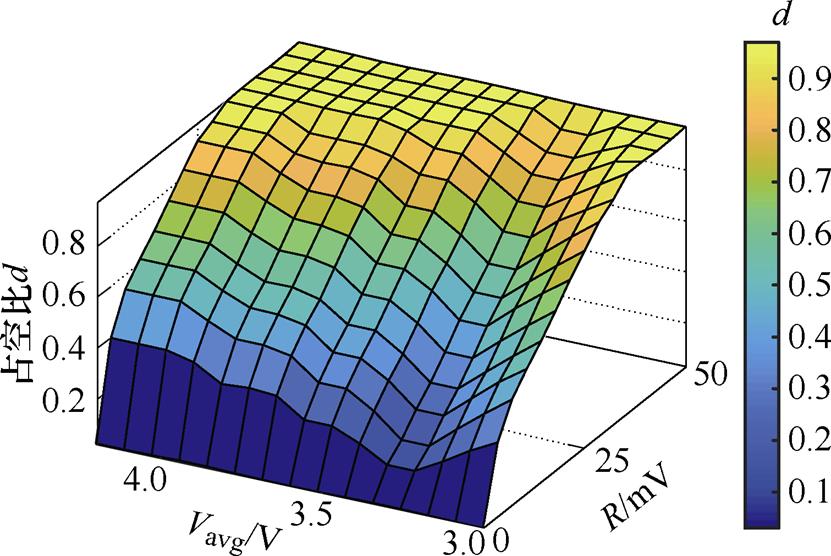
图14 末期调节模糊控制器输出结果
Fig.14 Graph of the output of the end-regulation fuzzy controller
动态均衡的主要目的是防止电压过高或过低的电池单体过充或过放，因此极值均衡法的均衡方式更适合作为此时的主导控制策略，但是极值均衡法因无法精确均衡且同时均衡电池单体较少导致均衡速度较慢，因此结合本文所提出的均衡电路，对极值均衡法进行了一定的优化。
优化后的极值均衡法根据最大电池单体电压与最小电池单体电压及其同组电池单体电压情况，合理选择均衡路径。当最大电压电池单体与最小电压电池单体在同一模块时，均衡电路工作在模块内均衡状态；当最大电压电池单体与最小电压电池单体在不同模块时，均衡电路工作在模块间均衡状态。与此同时，为防止均衡末期均衡电流过小导致均衡时间过长，当DVB_max＜50 mV或DVM_max＜100 mV时，采用静置均衡末期时同样的控制策略以加快均衡末期速度。
本文搭建了如图15所示的6个电池单体均衡电路实验平台，其具体参数见表1。
图15 6个锂电池均衡电路实验平台
Fig.15 6 batteries equalization circuit experimental platform
表1 均衡电路主要参数
Tab.1 Key parameters of the equalization circuit
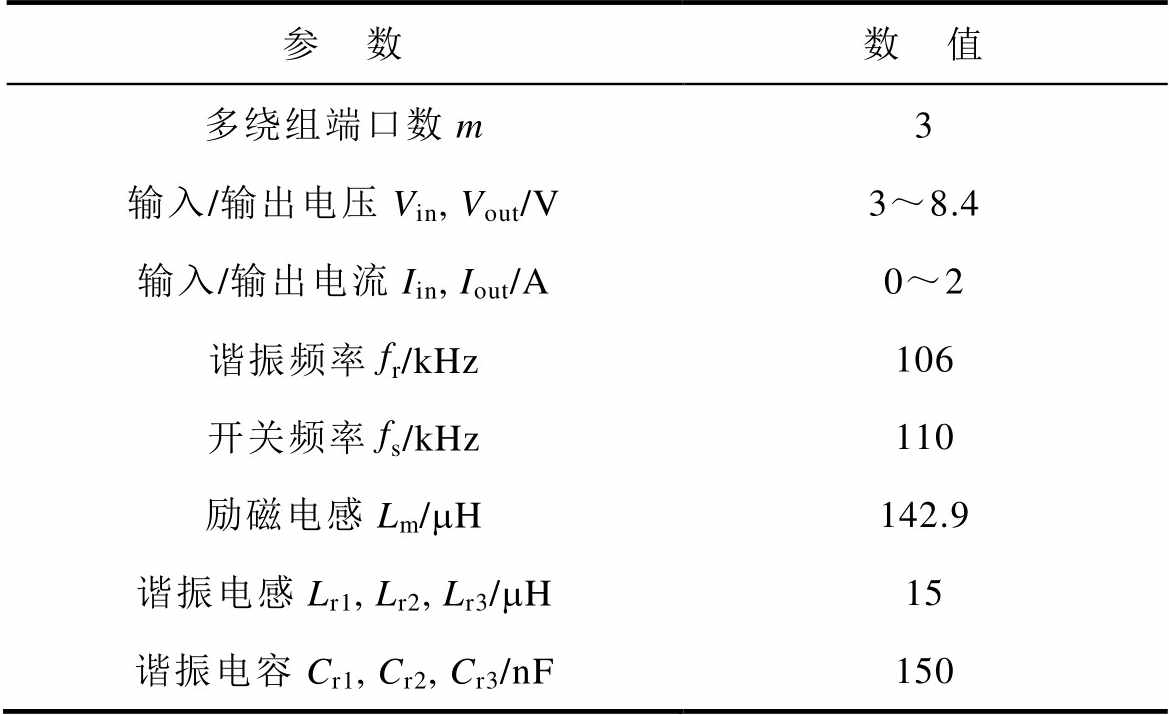
参 数数 值 多绕组端口数m3 输入/输出电压Vin, Vout/V3～8.4 输入/输出电流Iin, Iout/A0～2 谐振频率fr/kHz106 开关频率fs/kHz110 励磁电感Lm/mH142.9 谐振电感Lr1, Lr2, Lr3/mH15 谐振电容Cr1, Cr2, Cr3/nF150
图16为均衡路径1工作在110 kHz频率下的主要波形。均衡电路工作在二次侧同步整流状态下，从波形中可以看出，所有开关管均实现了ZVS。此时模块M1作为放电模块，向模块M2和模块M3 均衡。
图17为均衡路径2工作在110 kHz频率下的主要波形。此时模块M1、电池单体B3和电池单体B5接入电路，模块M1以较大电流向电池单体B3和电池单体B5放电。此时可以看出在较大电流情况下，所有开关管仍能够实现ZVS。
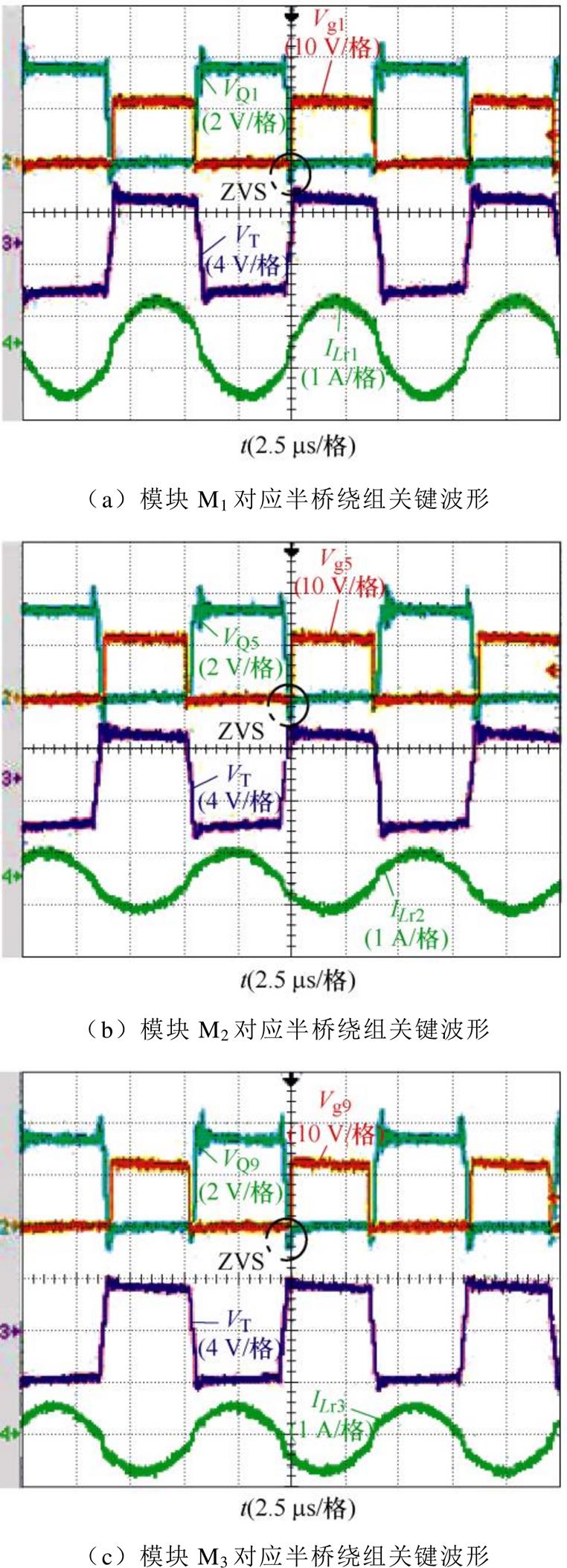
图16 均衡路径1工作波形
Fig.16 Equalisation path 1 operating waveforms
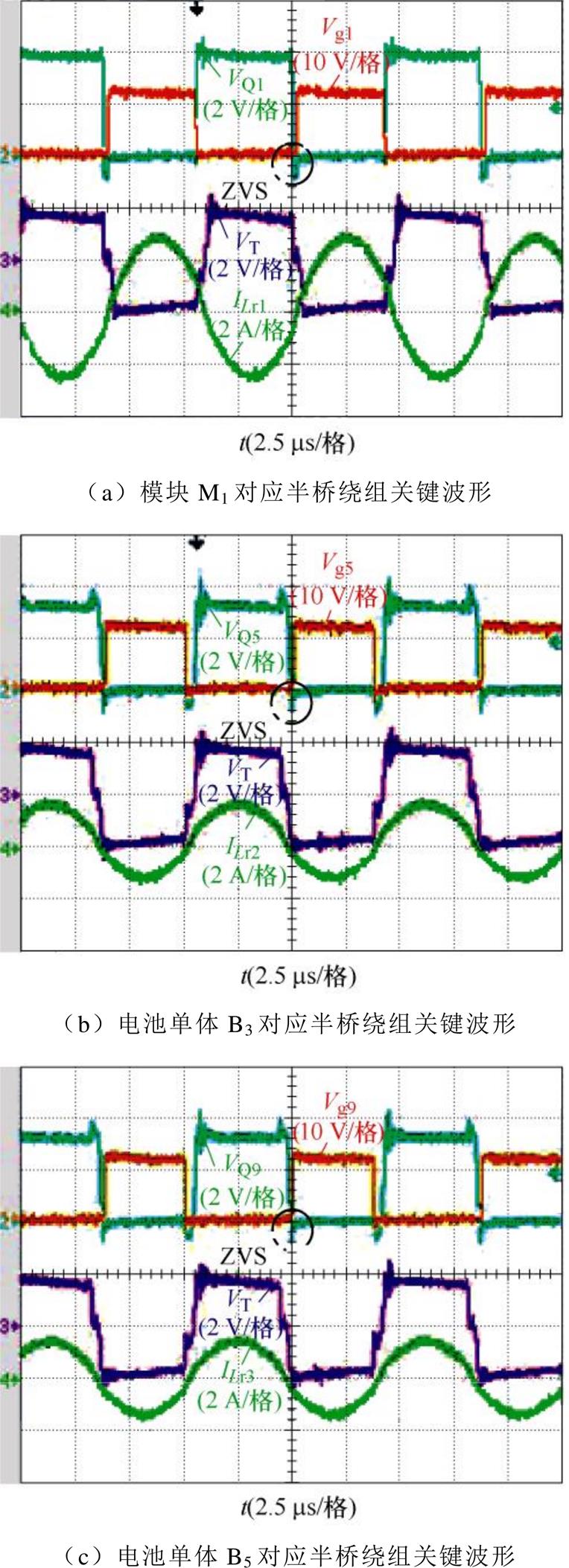
图17 均衡路径2工作波形
Fig.17 Equalisation path 2 operating waveforms
图18为均衡路径4工作在106 kHz频率下的主要波形。此时模块内部两个电池单体在一个开关周期内实现能量的传递。在此工作频率下，所有开关管导通关断近似ZCS关断，同时可以看出变压器两端电压很小，励磁电感不参与谐振，电路近似为一个LC串联谐振（LC Series Resonance, LCSR）均衡电路。
本文利用所提均衡策略，在6个锂电池均衡电路实验平台上分别进行了静态均衡与动态均衡实验。在分析实验结果前，先讨论均衡电路好坏的评判标准。
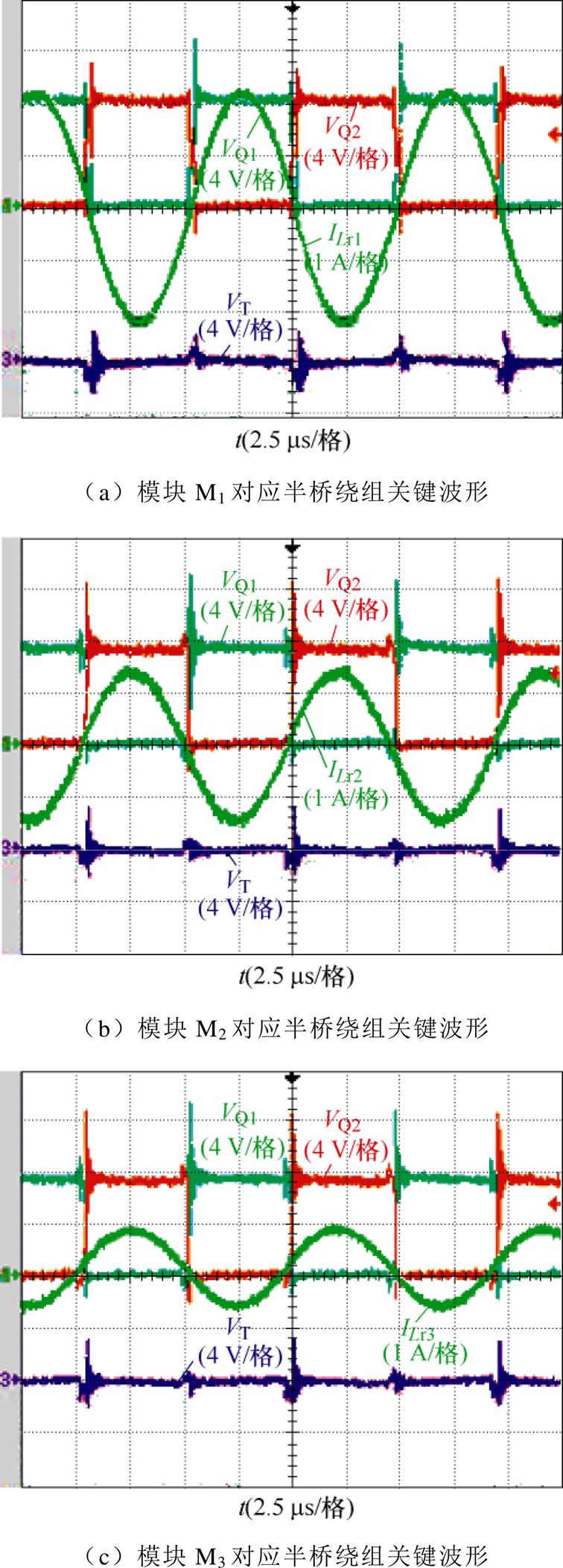
图18 均衡路径4工作波形
Fig.18 Equalisation path 4 operating waveforms
均衡电路的首要目标是具有较强的均衡能力。将均衡电流与电池组容量结合，以此来评判均衡电路的好坏更具合理性。在此定义均衡电流与电池容量之比为均衡电路的电流均衡比，电流均衡比越小，说明均衡电路均衡能力越强。
本文所提均衡电路，最大工作电流为2 A，可均衡6节标称容量为3.3 A·h的锂电池，经计算，电流均衡比约为0.101 A/(A·h)。表2为本文所提均衡电路的电流均衡比与其他文献所提方案的电流均衡比的对比，可以看出相较于其他方案[18-23]，本文所提方案性能提升了10.6%～79.8%。
表2 电流均衡比对比
Tab.2 Comparison of current balance ratios （单位: A/(A·h)）
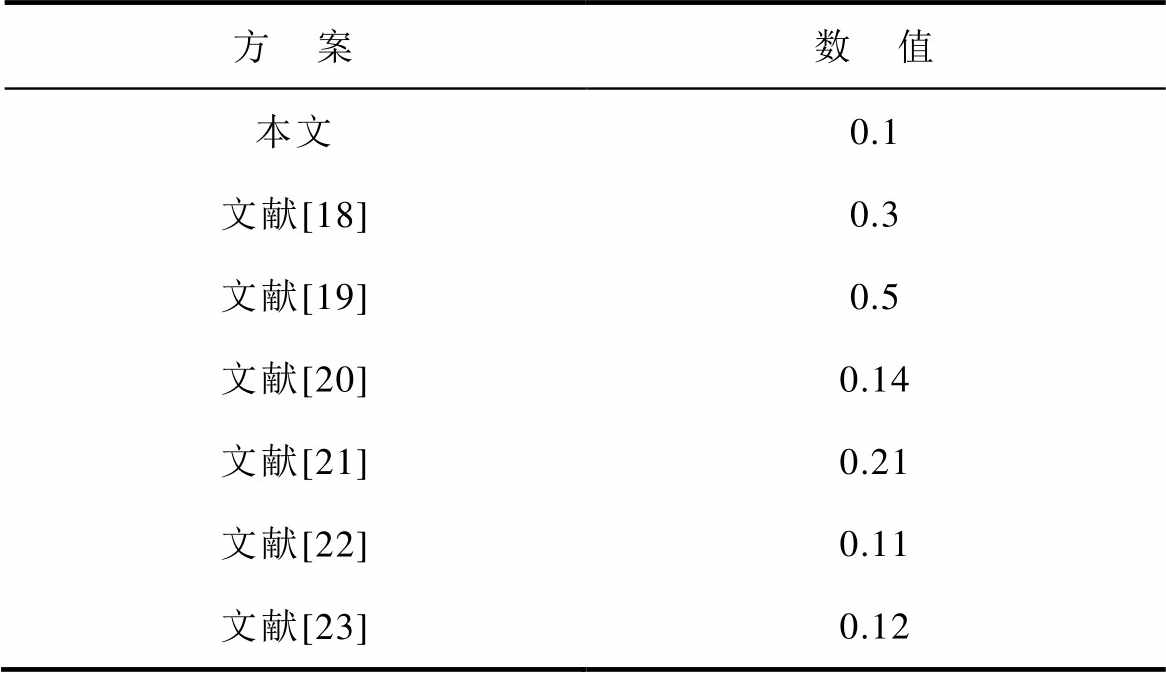
方 案数 值 本文0.1 文献[18]0.3 文献[19]0.5 文献[20]0.14 文献[21]0.21 文献[22]0.11 文献[23]0.12
3.2.1 静态均衡实验
针对所提基于模糊控制均衡法的静态均衡策略，对6个锂电池单体进行了静态均衡实验。静态均衡是指电池单体间均衡，只有均衡电路在工作。在不考虑实验设备对采集数据的影响的前提下。表3展示了6个锂电池的初始电压，其均衡过程电压曲线如图19所示。
表3 静态均衡电池初始电压
Tab.3 Static equalization of the initial battery voltage （单位: V）
VB1VB2VB3VB4VB5VB6 3.6423.7703.5333.3153.4243.595
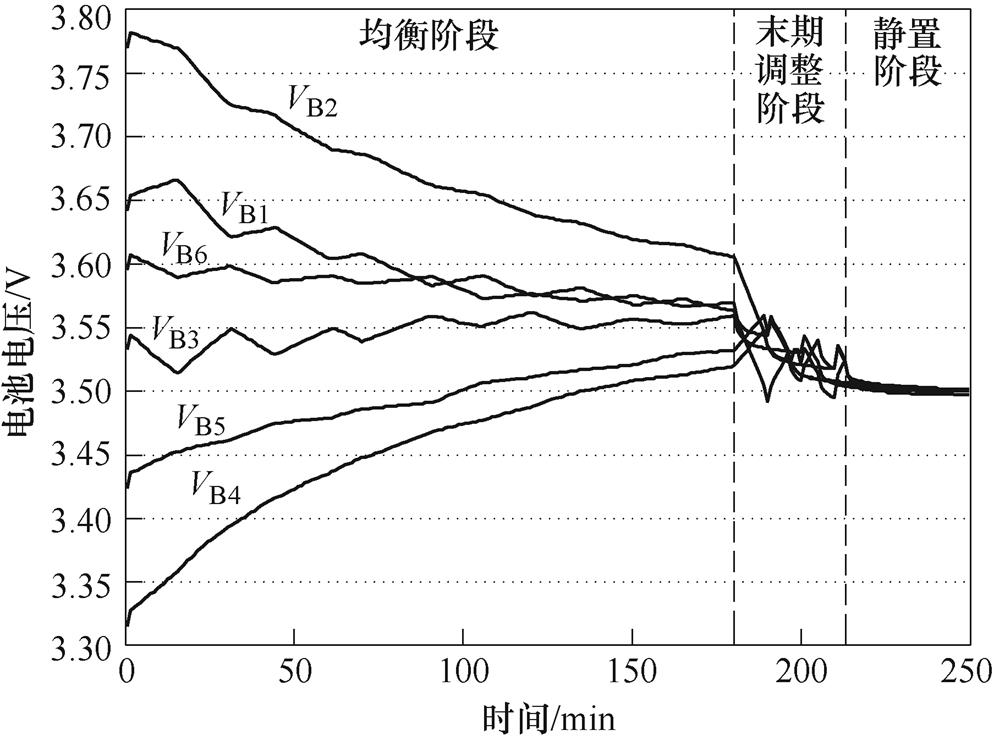
图19 静态均衡电压曲线
Fig.19 Static equalisation voltage curves
从均衡曲线中可以看出，整个均衡一共分为三个阶段：第一阶段为主要均衡阶段，此阶段电路工作在均衡路径1和4，周期内各路径工作时间占比由所设计的均衡时间模糊算法控制，均衡至180 min时，DVB_max＜50 mV，开始进入第二阶段；第二阶段为末期均衡阶段，此时主要通过均衡路径2均衡，均衡电流较大，同时还伴随着适当的静置时间，因此，此阶段电池电压波动较大，会存在一定的过均衡现象，均衡至214 min时，均衡阶段结束，电池开始进入第三阶段，静置阶段。本次实验均衡时间共214 min，均衡效率为97.24%，最后均衡最大压差为5 mV。
3.2.2 动态均衡实验
针对所提基于极值均衡法的动态均衡策略，对6个锂电池单体进行了动态均衡实验。动态均衡指电池单体工作在充电或放电状态，均衡电路也在工作。表4展示了6个锂电池的初始电压，其均衡过程电压曲线如图20所示。
从图20中可以看出，在此次均衡中共有四个阶段：第一阶段检测到最大压差出现在模块M2内部，因此电路工作在均衡路径4，均衡至50 min时，电路检测到DVM_max＜100 mV，开始采用均衡路径2进行均衡；第二阶段均衡至70 min时，DVM_max又开始大于100 mV，因此电路恢复到正常均衡状态；第三阶段此时最大压差出现在模块间，因此电路工作在均衡路径1，均衡至90 min时，DVM_max＜100 mV，电路又进入了调整阶段；第四阶段电路工作在均衡路径2，均衡至101 min时均衡结束。
表4 动态均衡电池初始电压
Tab.4 Dynamic equalization of the initial battery voltage （单位: V）
VB1VB2VB3VB4VB5VB6 3.6823.5903.7133.4793.6843.625
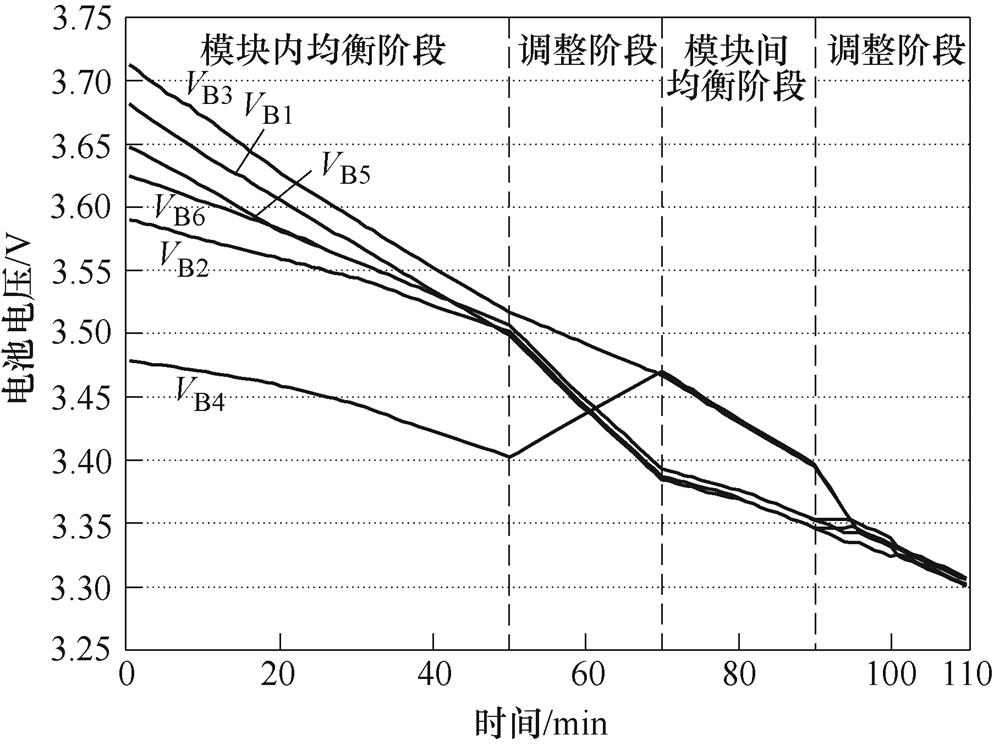
图20 动态均衡电压曲线
Fig.20 Dynamic equalization voltage curves
通过对6个锂电池的静态均衡和动态均衡，验证了本文所提均衡电路在静态均衡时具有良好的准确度与均衡效率，在动态均衡时具有快速的均衡速度。与文献[24]所提的混合架构相比，在使用绕组数量减半的情况下，均衡效率相较于其最高均衡效率提高了6.84%，静态均衡误差减小了91.25%，动态均衡时间加快了29.86%。
本文针对电池能量管理系统中的均衡电路进行了研究，分析了现有均衡电路的优缺点；结合对双向半桥CLLLC谐振变换器的分析，提出了基于双向半桥CLLLC谐振变换器的锂电池均衡电路；针对该均衡电路，提出了两种均衡控制策略；通过实验验证了所提电路具有均衡路径灵活、均衡速度快、均衡效率高和绕组数量减半等优点。
参考文献
[1] Pascual C, Krein P T. Switched capacitor system for automatic series battery equalization[C]//Proceedings of APEC 97-Applied Power Electronics Conference, Atlanta, GA, USA, 2002: 848-854.
[2] 刘红锐, 张昭怀. 锂离子电池组充放电均衡器及均衡策略[J]. 电工技术学报, 2015, 30(8): 186-192.
Liu Hongrui, Zhang Zhaohuai. The equalizer of charging and discharging and the balancing strategies for lithium-ion battery pack[J]. Transactions of China Electrotechnical Society, 2015, 30(8): 186-192.
[3] 李泉, 周云山, 王建德, 等. 基于双层准谐振开关电容的锂电池组均衡方法[J]. 电工技术学报, 2017, 32(21): 9-15.
Li Quan, Zhou Yunshan, Wang Jiande, et al. Equalization method of lithium battery pack based on double-tiered quasi-resonant switched capacitor[J]. Transactions of China Electrotechnical Society, 2017, 32(21): 9-15.
[4] Lim C, Lee K, Ku N, et al. A modularized equalization method based on magnetizing energy for a series-connected lithium-ion battery string[J]. IEEE Transactions on Power Electronics, 2014: 1791-1799.
[5] 刘倩怡, 徐顺刚, 许建平, 等. 一种基于推挽变换器的模块化电池均衡电路[J]. 电工技术学报, 2018, 33(14): 3213-3221.
Liu Qianyi, Xu Shungang, Xu Jianping, et al. A modularized equalizer for series-connected batteries based on push-pull converter[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3213- 3221.
[6] Shang Yunlong, Xia Bing, Zhang Chenghui, et al. An automatic battery equalizer based on forward and flyback conversion for series-connected battery strings[C]//2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 2017: 3218-3222.
[7] Peng Faxiang, Wang Haoyu, Wei Zhengqi. An LLC-based highly efficient S2M and C2C hybrid hierarchical battery equalizer[J]. IEEE Transactions on Power Electronics, 2020, 35(6): 5928-5937.
[8] Park H S, Kim C E, Kim C H, et al. A modularized charge equalizer for an HEV lithium-ion battery string[J]. IEEE Transactions on Industrial Electronics, 2009, 56(5): 1464-1476.
[9] 赵靖英, 胡劲, 张雪辉, 等. 基于锂电池模型和分数阶理论的SOC-SOH联合估计[J]. 电工技术学报, 2023, 38(17): 4551-4563.
Zhao Jingying, Hu Jin, Zhang Xuehui, et al. Joint estimation of the SOC-SOH based on lithium battery model and fractional order theory[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4551- 4563.
[10] 高凯. 基于Buck-Boost变换器的电池均衡电路研究[D]. 成都: 西南交通大学, 2021.
[11] 魏业文, 李应智, 曹斌, 等. 含Buck电路的锂电池低功耗电量均衡技术研究[J]. 电工技术学报, 2018, 33(11): 2575-2583.
Wei Yewen, Li Yingzhi, Cao Bin, et al. Research on power equalization of lithium-ion batteries with less-loss Buck chopper[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2575-2583.
[12] Wei Zhengqi, Wang Haoyu, Lu Yiqing, et al. Bidire- ctional constant current S2C battery equalizer based on fixed-frequency L2C3 resonant converter[C]//2022 IEEE Applied Power Electronics Conference and Exposition (APEC), Houston, TX, USA, 2022: 52-57.
[13] 廖嘉睿, 杭丽君, 但志敏, 等. 宽范围CLLLC双向同步整流数字控制方法[J]. 电工技术学报, 2022, 37(14): 3632-3642.
Liao Jiarui, Hang Lijun, Dan Zhimin, et al. Digital control method of wide-range CLLLC bidirectional synchronous rectification[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3632-3642.
[14] Zhang Zhiliang, Gui Handong, Gu Dongjie, et al. A hierarchical active balancing architecture for lithium- ion batteries[J]. IEEE Transactions on Power Elec- tronics, 2017, 32(4): 2757-2768.
[15] 周国华, 王淇, 邓伦博. 宽增益高效率CLLLC变换器的变频双移相调制策略[J]. 电工技术学报, 2024, 39(8): 2511-2522.
Zhou Guohua, Wang Qi, Deng Lunbo. Variable- frequency dual-phase-shift modulation strategy for CLLLC converter with wide voltage gain and high efficiency[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2511-2522.
[16] Lee Y S, Cheng Mingwang. Intelligent control battery equalization for series connected lithium-ion battery strings[J]. IEEE Transactions on Industrial Elec- tronics, 2005, 52(5): 1297-1307.
[17] Zhang Chenghui, Shang Yunlong, Li Zeyuan, et al. An interleaved equalization architecture with self- learning fuzzy logic control for series-connected battery strings[J]. IEEE Transactions on Vehicular Technology, 2017, 66(12): 10923-10934.
[18] Mestrallet F, Kerachev L, Crebier J C, et al. Multi- phase interleaved converter for lithium battery active balancing[J]. IEEE Transactions on Power Electronics, 2014, 29(6): 2874-2881.
[19] Lim C S, Lee Kuijun, Ku N J, et al. A modularized equalization method based on magnetizing energy for a series-connected lithium-ion battery string[J]. IEEE Transactions on Power Electronics, 2014, 29(4): 1791-1799.
[20] Imtiaz A M, Khan F H. Time shared flyback converter based regenerative cell balancing technique for series connected Li-ion battery strings[J]. IEEE Transa- ctions on Power Electronics, 2013, 28(12): 5960- 5975.
[21] Ugle R, Li Yaoyu, Dhingra A. Equalization integrated online monitoring of health map and worthiness of replacement for battery pack of electric vehicles[J]. Journal of Power Sources, 2013, 223: 293-305.
[22] Costinett D, Nguyen H, Zane Regan, et al. GaN-FET based dual active bridge DC-DC converter[C]//2011 Twenty-Sixth Annual IEEE Applied Power Elec- tronics Conference and Exposition (APEC), Fort Worth, TX, USA, 2011: 1425-1432.
[23] Huang H. Designing an LLC resonant half-bridge power converter[Z]. TI Literature, 2010.
[24] 桂涵东. 锂电池主动均衡管理与效率优化[D]. 南京: 南京航空航天大学, 2016.
Abstract Lithium batteries are widely used in the new energy sector due to their high energy density and low self-discharge rate. As the capacity of each battery unit is different, overcharging and over-discharging greatly affect the battery life. This paper focuses on the safety of series lithium batteries.
Firstly, the existing series of lithium battery equalization circuits are summarized, and the advantages and disadvantages of different circuits are analyzed. Regarding the disadvantages of multi-winding transformer-type equalization circuits, this paper proposes a Lithium-ion battery equalization circuit based on a bidirectional half-bridge CLLLC resonant converter.
FSecondly, the working principle and mode of the bidirectional half-bridge CLLLC resonant converter are explained, and its resonance and gain characteristics are analyzed using fundamental analysis. In addition, a control method for synchronous rectification of the secondary side of the half-bridge CLLLC resonant converter is proposed.
FThen, for the proposed Lithium-ion battery equalization circuit, the operating principles of its four equalization paths are analyzed, and the equalization current expressions for each path are derived. The parameter design method of the equalization circuit is given according to the analysis of the bidirectional half-bridge CLLLC resonant converter. Based on the four equalization paths of the equalization circuit and the different purposes of dynamic and static equalization, two equalization strategies are proposed.
FFinally, the relevant hardware parameters of the equalization circuit are designed, and the device selection is carried out. The fabrication method of the magnetic components is also given. A set of equalization circuits for six battery cells is built. The equalization path and the soft circuit switching are verified by simulation and experiment. According to the proposed control strategy, static equalization and dynamic equalization are carried out for six battery cells. The experimental results show that the proposed equalization circuit has the advantages of a flexible equalization path, fast equalization speed, high equalization efficiency, and a half number of windings.
keywords：Battery equalization, bidirectional half-bridge CLLLC resonant converter, fuzzy control, multi-winding transformer
DOI: 10.19595/j.cnki.1000-6753.tces.230903
中图分类号：TM912
收稿日期 2023-06-03
改稿日期 2023-11-03
蔡瑞佳 男，1997年生，硕士研究生，研究方向为锂电池均衡电路。E-mail: 245362390@qq.com
马运东 男，1969年生，副教授，硕士生导师，研究方向为电力电子技术：三电平技术、软开关技术、UPS及其并联技术和风力发电系统控制技术。E-mail: kyleo@nuaa.edu.cn（通信作者）
（编辑 陈 诚）