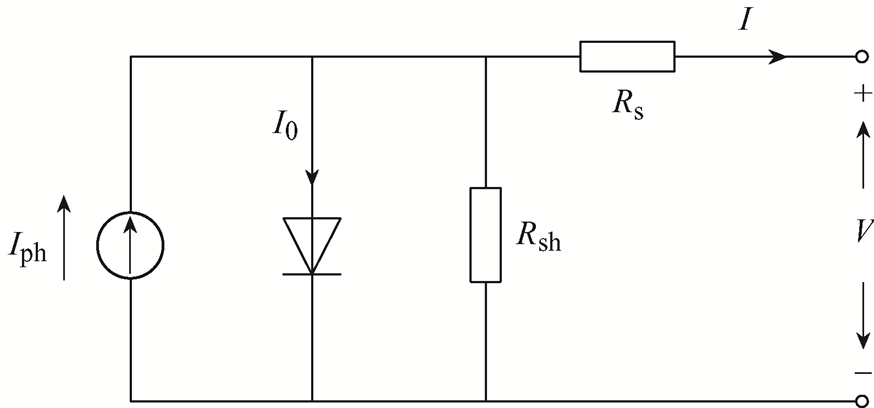
图1 光伏组件电池等效电路模型
Fig.1 Equivalent circuit model of PV module
摘要 光伏系统的健康程度检测对预防故障及保障系统安全运行至关重要。选取光伏组件的光生电流、串联电阻和并联电阻为其健康参数,该文提出了一种考虑健康参数权重与辐照度分层映射的光伏组件健康程度检测方法,来提高健康程度检测的精度与适用范围。首先依据光伏组件I-V曲线,通过蝠鲼觅食优化(MRFO)算法进行参数辨识;其次根据辐照度高低将辨识结果分层映射至两种辐照度参考状态,提高低辐照状态下的映射精度;然后根据组件预期寿命内允许的功率衰减情况建立光伏组件自然衰减模型,估算参数预期值作为参考,再结合实际的参数提取结果计算参数劣化度;最后使用熵权法确定参数权重,计算表征光伏组件健康程度的健康指数。仿真与实验结果表明,该方法可对任何环境参数下的光伏组件健康程度进行有效检测。
关键词:光伏组件 健康参数辨识 分层映射 自然衰减模型 健康参数权重
近年来,光伏产业进入快速发展期,光伏装机容量激增[1-2]。随着时间的推移,安装在户外的光伏组件的电气性能会不断退化,恶劣的运行环境还会加剧光伏组件衰减程度,导致组件光电转换效率下降甚至故障失效,影响整个光伏系统的输出效率[3]。为了保障光伏系统的高效稳定运行,有必要建立光伏组件的健康程度检测系统,及时对光伏系统进行预测性和纠正性维护。
目前,基于光伏组件输出特性的健康状态检测研究较为普遍。文献[4]利用灰色关联分析量化光伏阵列仿真模型输出的理论I-V特性曲线和实测I-V特性曲线之间的差异,差异越小,健康程度越高;文献[5]提出一种基于筛选的健康检测方法,通过逐个遮挡组串中的光伏电池,检测和比较组串的输出特性曲线,筛选出退化最严重的光伏组件;文献[6]基于深度置信网络提取I-V特性曲线的特征参数,通过计算健康样本和实测样本间的特征参数的豪斯多夫距离确定组件健康状态。基于现场测量技术的健康状态评估是另一个主要研究方向,主要包括红外图像分析法和电致发光测试法。文献[7]建立了基于深度卷积神经网络的光伏组件故障检测与分类模型,通过热成像图像数据集对模型进行训练,并使用迁移学习模型对检测模型进行微调,进一步提高了模型诊断的准确率;文献[8]对光伏电池采用主动式电磁激励获取热成像序列,能对光伏电池的缺陷进行快速、高分辨率的检测。此外,部分学者将智能算法用于光伏系统健康状态检测方向。文献[9-11]将开路电压、短路电流、最大功率点电压、最大功率点电流等特征向量作为神经网络的输入,光伏组件的健康状态作为网络的输出,神经网络经过学习便能对组件健康状态进行诊断识别。
以上几种主要的健康状态检测方法都存在不足之处。基于现场测量技术的检测方法成本过高,难以广泛应用。基于智能算法的检测方法需要大量的训练数据,模型的准确性依赖数据的数量级。基于输出特性曲线的检测方法对于特征参数的获取较为方便,但目前的研究基本只针对光伏组件的某几种健康状态进行检测,无法精确完整地展示组件的健康程度,并且缺少对组件自然衰减的考虑,对工作于低辐照下的组件健康状态检测也存在困难。
为此,本文提出一种光伏组件健康程度检测的新方法。分析选取了影响组件健康程度的主要参数,利用蝠鲼觅食优化(Manta Ray Foraging Opti- mization, MRFO)算法对组件输出的I-V特性曲线进行参数辨识,为提高低辐照环境下的检测精度,辨识结果依据运行环境的辐照度高低进行分层映射。建立光伏组件自然衰减模型,根据组件运行年份估算参数预期值并计算参数劣化度。使用熵权法计量参数对健康程度的影响权重,结合劣化度计算出可以量化光伏组件健康程度的健康指数(Health Index, HI)。通过仿真和实验,验证了该方法的可行性和有效性。
光伏组件电池等效电路模型如图1所示。

图1 光伏组件电池等效电路模型
Fig.1 Equivalent circuit model of PV module
根据基尔霍夫定律,光伏电池的I-V特性曲线在数学上可以表示[12-13]为
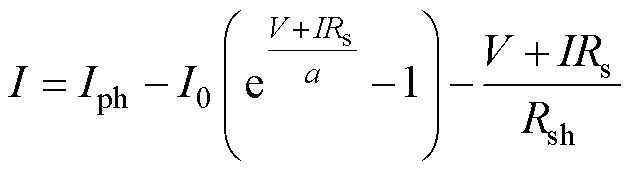 (1)
(1)
式中,I为组件输出电流实际值;V为组件输出电压;Iph为光生电流;I0为二极管反向饱和电流;Rs为等效串联电阻;Rsh为等效并联电阻;a为理想因子,a=nkT/q,n为二极管品质因子,k为玻耳兹曼常数,k=1.380´10-23 J/K,T为温度,q为电子电荷常数,q=1.602´10-19 C。
由式(1)可知,参数Iph、I0、Rsh、Rs、a共同决定了光伏组件的输出特性。
光伏组件由多块部件封装而成,常见的组件内部结构如图2所示。由于湿度和高温等环境因素的影响,组件的工作性能和参数会随时间发生退化。
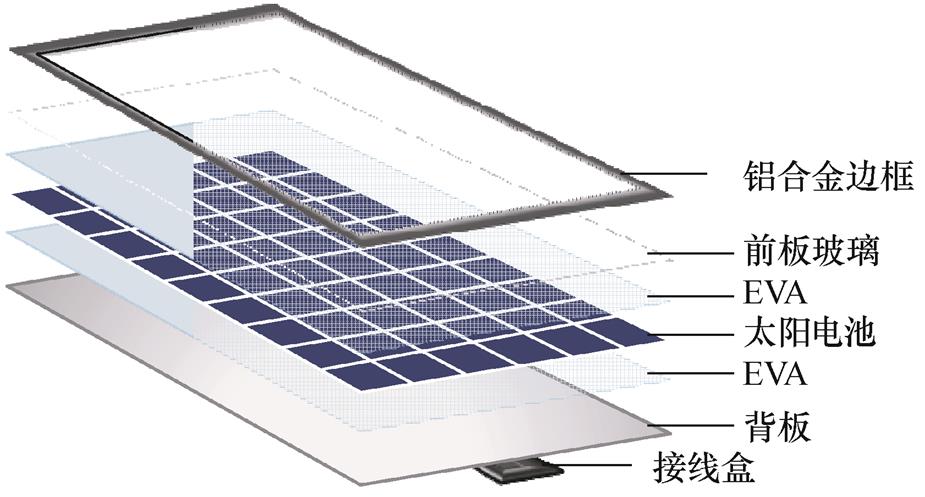
图2 光伏组件结构示意图
Fig.2 Structural diagram of PV module
常见的光伏组件退化包括光学损失和电气老化,具体表现为灰尘污物的遮挡;前板玻璃层的腐蚀或破裂、抗反射涂层氧化;乙烯-醋酸乙烯酯(EVA)褐变;部件间的粘合剂失效造成气泡、分层;电池片破损、焊带偏移或断裂;电势诱导衰减(Potential Induced Degradation, PID);接线盒、旁路二极管老化失效;背板老化等[14-16]。
这些退化模式主要以三种方式影响组件的输出特性:①降低透光率t 导致光生电流Iph下降;②增加串联电阻Rs;③降低并联电阻Rsh[16]。
研究发现,光伏组件的各种退化现象会互相影响,造成组件输出特性下降的参数衰减是同步发生的。如水汽侵入电池会导致粘合剂失效、分层,引发EVA黄变,造成透光率下降;分层又会促进水汽进入组件内部,造成串联电阻的增加;潮湿环境还会腐蚀接线盒中的金属连接器、诱发PID效应,造成串联电阻增加、并联电阻下降;连接器腐蚀会伴随发热问题,加速其他部件的老化。
综上所述,可以选取光生电流Iph、串联电阻Rs、并联电阻Rsh作为特征参数,评估光伏组件健康程度。组件自然退化时,3个参数会随时间同步衰减,当组件发生异常退化时,部分参数的衰减情况会加剧。因此,可以通过参数的衰减异常程度判断组件的健康程度。
光伏组件模型的内部参数难以通过测量获取,也无法利用基本初等函数计算求取。采用元启发式算法进行光伏组件参数辨识是目前的主流方法,参数辨识步骤如下:
(1)测量光伏组件I-V特性曲线。
(2)参数辨识。基于测量得到的电流序列和电压序列,通过元启发式算法拟合式(1)中的5个参数P={Iph, I0, a, Rsh, Rs}。
(3)计算输出电流。
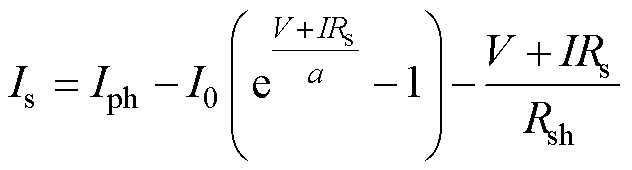 (2)
(2)
式中,Is为输出电流计算值。
(4)判断辨识精度。精度指标用计算电流与测量电流的方均根误差(Root Mean Square Error, RMSE)表示,误差越小,代表参数辨识精度越高。
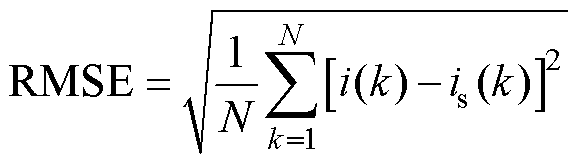 (3)
(3)
式中,i(k)为电流I的第k个取值。
重复步骤(2)~(4),算法对参数进一步寻优,直到精度达标或达到最大迭代次数。
本文采用的元启发式算法为蝠鲼觅食优化算法。蝠鲼觅食优化算法源于蝠鲼的觅食行为,模仿了蝠鲼的三种觅食策略,包括链条觅食、旋风觅食和翻滚觅食。独特多样的搜素策略能够广泛且密集地搜索全局最优值,具有收敛性强、参数少、可以有效避免陷入局部最优等优点[17]。
链条觅食时蝠鲼排成一列进行捕食,数学模型描述为
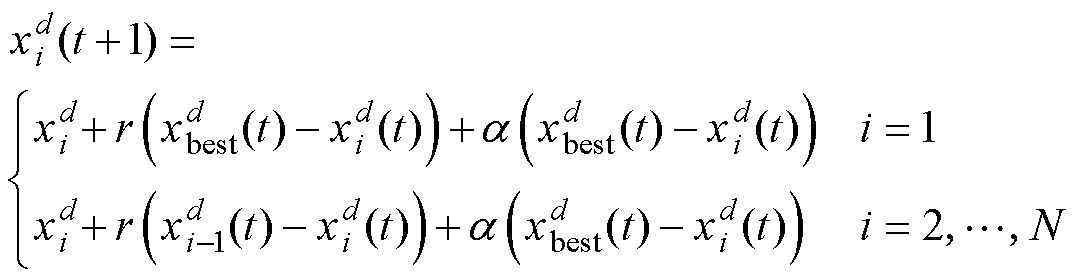 (4)
(4)
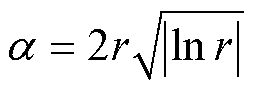 (5)
(5)
式中,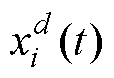 为t时刻第i个个体在d维空间的位置;
为t时刻第i个个体在d维空间的位置;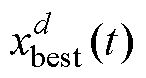 为t时刻种群在d维空间找到的最优位置;a 为权重系数;r为[0, 1]上的随机数;t为目前迭代次数。
为t时刻种群在d维空间找到的最优位置;a 为权重系数;r为[0, 1]上的随机数;t为目前迭代次数。
旋风觅食时蝠鲼形成觅食链螺旋向食物移动,数学模型描述为
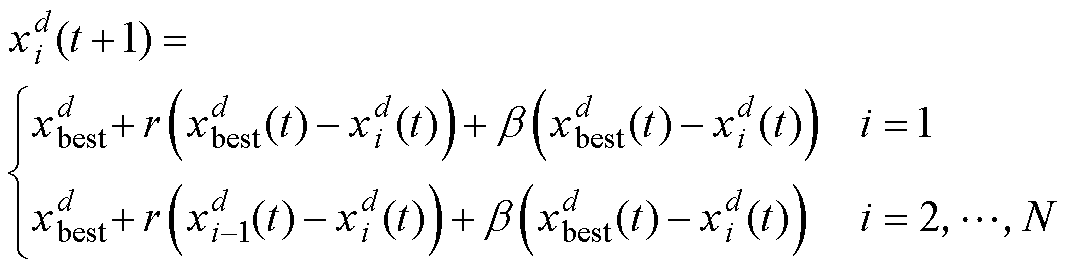 (6)
(6)
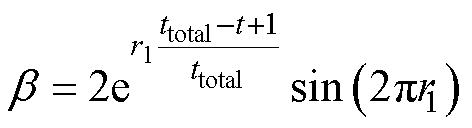 (7)
(7)
式中,b 为权重系数;ttotal为总迭代数;r1为[0, 1]上的随机数。
通过在空间分配随机的参考位置,可以使MRFO实现广泛的全局搜索,数学方程为
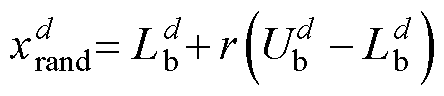 (8)
(8)
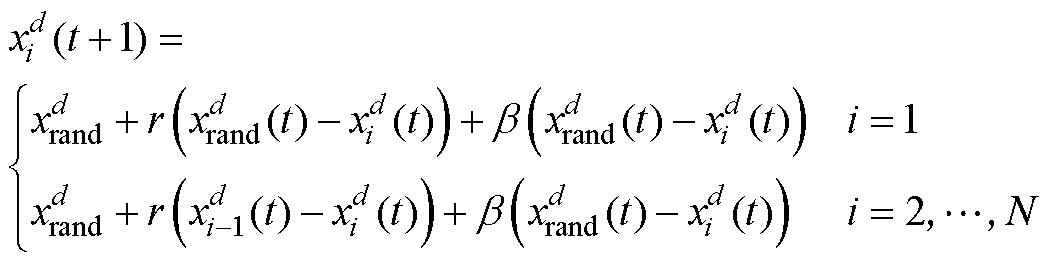 (9)
(9)
式中,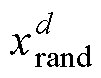 为随机生成的参考位置;
为随机生成的参考位置;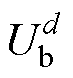 、
、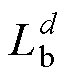 分别为d维空间的上、下界。
分别为d维空间的上、下界。
翻滚觅食时每个蝠鲼个体都以食物为枢轴,围绕枢轴来回翻滚捕食,数学模型描述为
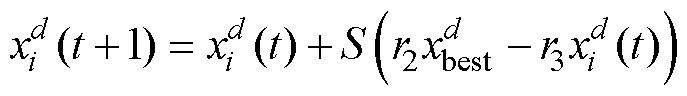 (10)
(10)
式中,S为翻滚因子,决定个体的翻滚范围,S=2;r2和r3为[0, 1]上的随机数。
环境温度、辐照度的变化,均会引起光伏组件的输出特性变化,因此不同运行环境下辨识的组件参数无法直接进行比较。为消除环境因素的影响,需要将参数辨识结果统一映射至合适的参考状态[18]。
光生电流由光生伏打效应产生,几乎是辐照度的线性函数,也会受温度影响,公式可写为
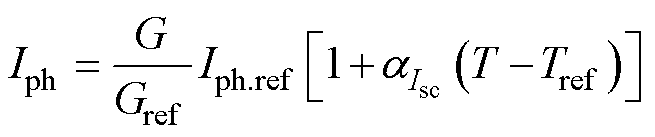 (11)
(11)
式中,G、T分别为辐照度、温度;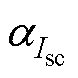 为短路电流温度系数;下标ref代表参考状态值。
为短路电流温度系数;下标ref代表参考状态值。
Messenger和Ventre推导出二极管反向饱和电流与环境温度和半导体的带隙能量有关[19],有
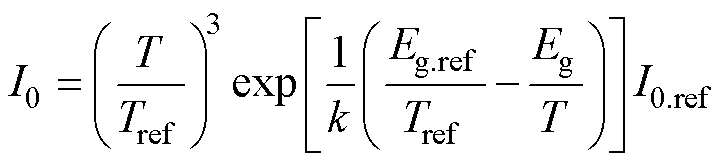 (12)
(12)
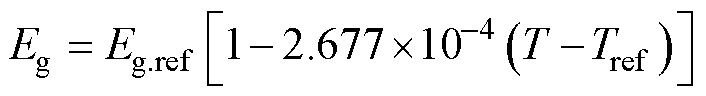 (13)
(13)
式中,Eg为材料带隙能量,硅电池为1.12 eV。
根据理想因子a的表达式a=nkT/q可知,它是温度的线性函数,因此有
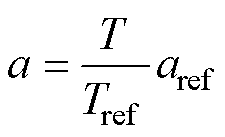 (14)
(14)
大量实验发现并联电阻与辐照度成反比,经验公式[20]为
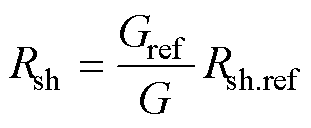 (15)
(15)
部分学者认为串联电阻与温度有关[21],其关系式可表示为
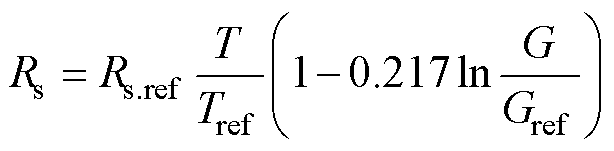 (16)
(16)
将式(11)、式(12)、式(14)~式(16)取反运算,获得5个参数映射方程,即
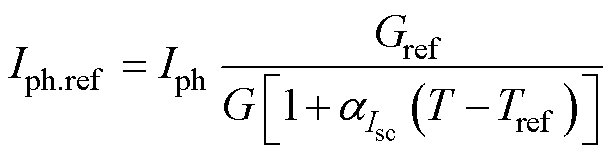 (17)
(17)
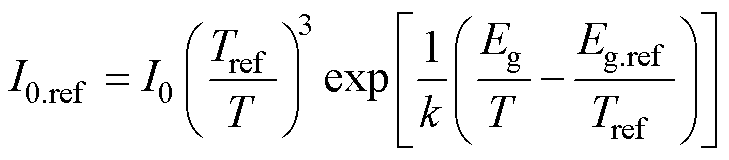 (18)
(18)
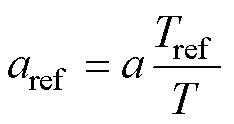 (19)
(19)
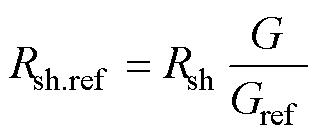 (20)
(20)
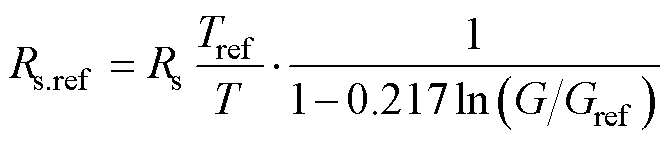 (21)
(21)
目前的研究一般将参数映射至标准工作状态(Standard Test Conditions, STC),即参考状态[Gref, Tref]=[1 000 W/m2, 25℃]。研究发现,工作环境离STC越远,映射精度越低[21],意味着在早、晚以及阴天等辐照度低的情况下光伏组件的参数提取结果较差。因此,低辐照下的光伏组件健康程度通常难以检测。
为了解决这一问题,本文考虑设置两种参考状态,根据测量I-V曲线时的辐照度对参数进行分层映射。当辐照度高于500 W/m2时,将参数映射至标准参考状态[Gref.H, Tref.H]=[1 000 W/m2, 25℃];当辐照度低于500 W/m2时,将参数映射至低辐照参考状态[Gref.L, Tref.L]=[500 W/m2, 12.5℃]。通过对高低辐照度的划分提高参数提取精度。
影响光伏组件健康程度的特征参数随着使用年份的增长而自然衰减,造成组件输出功率逐年降低,此过程称为组件的自然老化。仅发生自然老化的组件可以被认定是健康的;当参数发生异常衰减时被认定组件偏离了健康状态。为了判断参数是否发生异常衰减,需要建立光伏组件自然衰减模型作为参考标准。
组件退化因子可用组件的功率衰减表示为
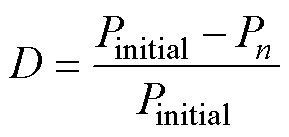 (22)
(22)
式中,Pinitial为组件出厂时的输出功率;Pn为组件运行n年时的输出功率。
《光伏制造行业规范条件》规定,晶硅组件衰减率首年不高于2.5%,后续每年不高于0.6%,25年内不高于17%[22]。将此作为组件自然衰减的阈值,组件退化因子小于这一界限时认为组件健康。
大量研究表明,光伏组件的功率衰减基本等于输出电流(最大功率点电流Im和短路电流Isc)的衰减,而输出电压(最大功率点电压Vm和开路电压Voc)的衰减较小,约为功率衰减的1/7[23-24]。输出电流与电压的衰减因子可分别表示为
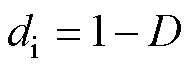 (23)
(23)
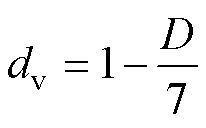 (24)
(24)
通过构建组件参数与输出电压、电流间的函数关系式,可以推导出组件参数的自然衰减过程。
光伏组件短路时,短路电流为
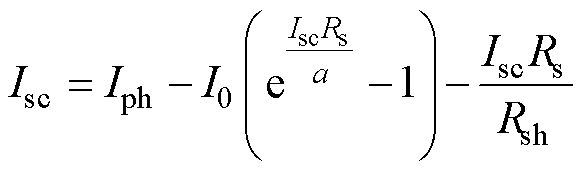 (25)
(25)
忽略二极管电流,光生电流可表示为
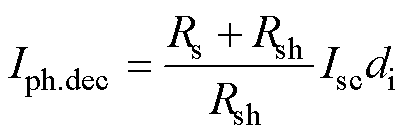 (26)
(26)
式中,下标dec代表经历过自然衰减后的参数值,其余皆为参数初始值。
光伏组件开路时,有
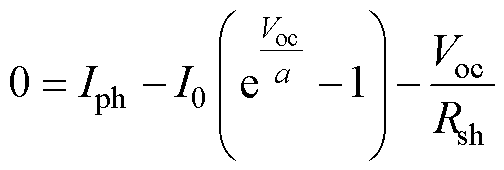 (27)
(27)
推导出I0衰减的表达式为
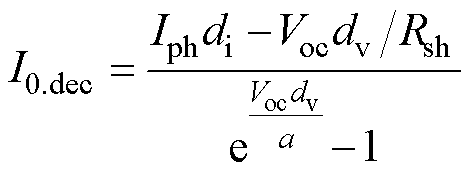 (28)
(28)
光伏组件工作在最大功率点时,电流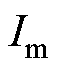 为
为
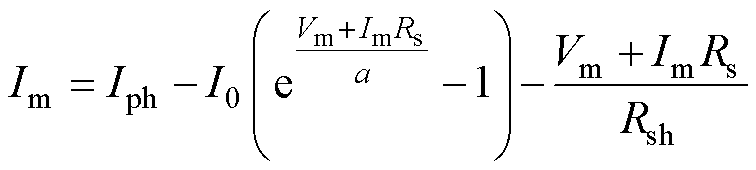 (29)
(29)
并联电阻Rsh经换算后可表示为
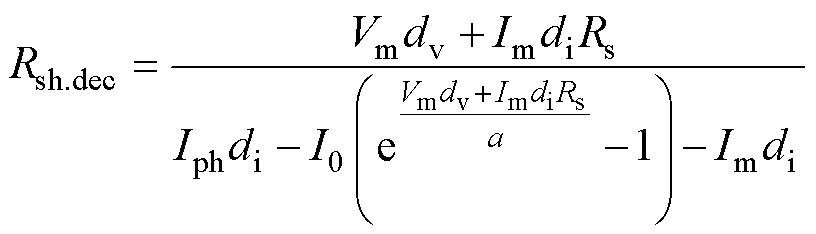 (30)
(30)
文献[25]推导了a和Rs经历自然衰减后的表达式分别为
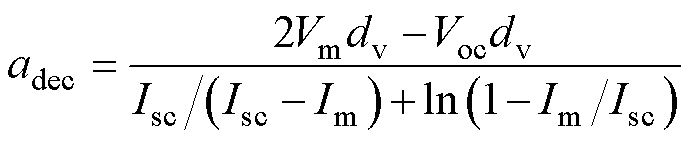 (31)
(31)
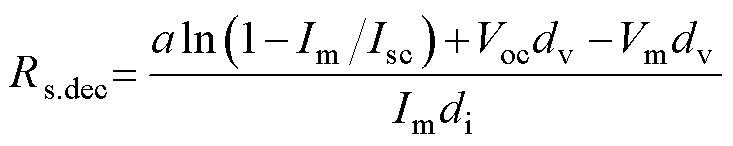 (32)
(32)
本文基于组件输出电压与输出电流的衰减因子推算出组件参数的衰减值,建立光伏组件的自然衰减模型,为光伏组件健康程度检测提供参考标准。
根据光伏组件自然衰减模型可以推算出特征参数25年内预期值的变化情况。对于运行n年的光伏组件,通过参数提取获得组件的实际参数值,再通过劣化度函数L(x)计算参数的异常衰减程度。
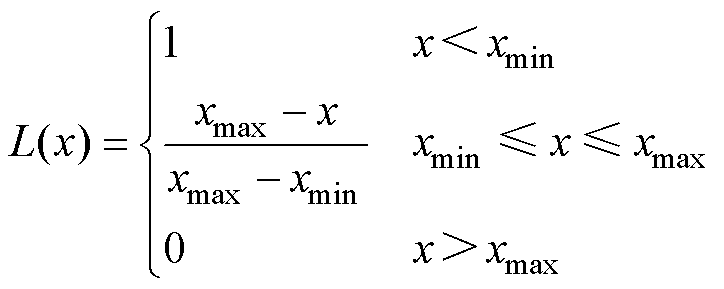 (33)
(33)
式中,xmin为组件运行25年时的参数预期值;xmax为组件运行n年时的参数预期值;x为组件运行n年时的参数提取结果。
式(33)适用于正向指标,如参数值随着组件退化不断降低的光生电流、并联电阻。参数值随退化不断增加的串联电阻属于负向指标,计算方式为
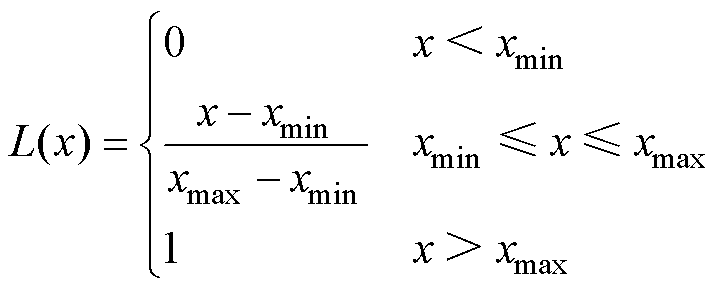 (34)
(34)
劣化度越接近1代表参数异常衰减程度越深。
参数的异常衰减会导致组件健康程度下降。不同参数对组件整体的影响程度存在区别,因此需要分析健康参数权重。为了得到更客观的光生电流、串联电阻和并联电阻对于光伏组件健康程度的影响权重,本文采用熵权法来确定特征参数的权重系数。
1)构建样本数据矩阵。假设有m个样本,g个参评指标,构建的原始数据样本矩阵为X=(xij)m×g,其中xij为第i个样本的第j个指标的数值。本文选取的样本为不同健康程度的光伏组件特征参数值。
2)对指标进行标准化处理
正向指标
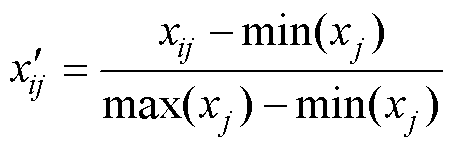 (35)
(35)
负向指标
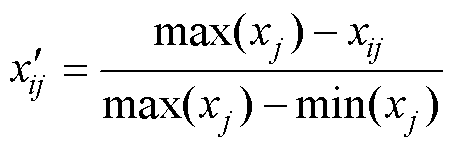 (36)
(36)
式中,max(xj)和min(xj)分别为j项指标的最大值与最小值。
3)计算指标的信息熵ej
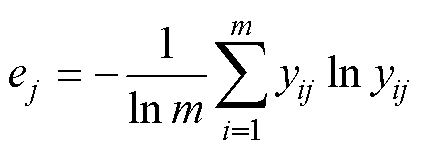 (37)
(37)
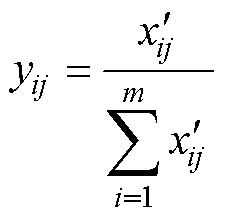 (38)
(38)
式中,yij为第i个样本的第j个指标比重。
4)计算指标权重
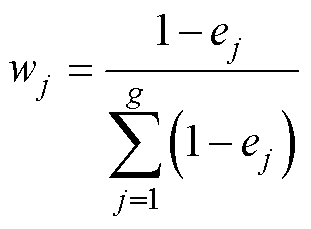 (39)
(39)
权重wj体现了指标的信息量,熵权值越大,该指标对健康程度的决策作用越大。
为了更直观地表征光伏组件的整体健康程度,将3个参数的劣化度赋以权重计算健康指数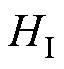 ,有
,有
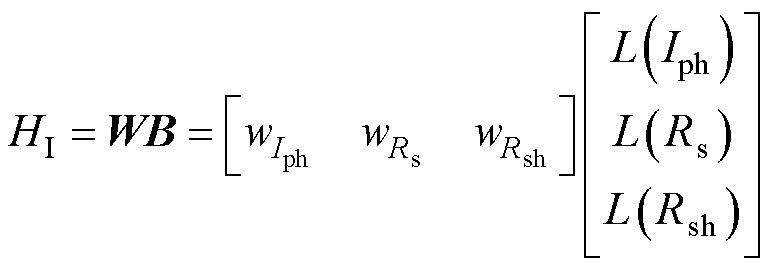 (40)
(40)
式中,W为熵权法计算的权重向量;B为劣化度向量;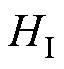 是一个[0,1]的数,数学上表示光伏组件的综合劣化度,组件的健康程度越高,
是一个[0,1]的数,数学上表示光伏组件的综合劣化度,组件的健康程度越高,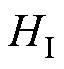 越小。
越小。
图3为光伏组件健康程度检测的基本流程。
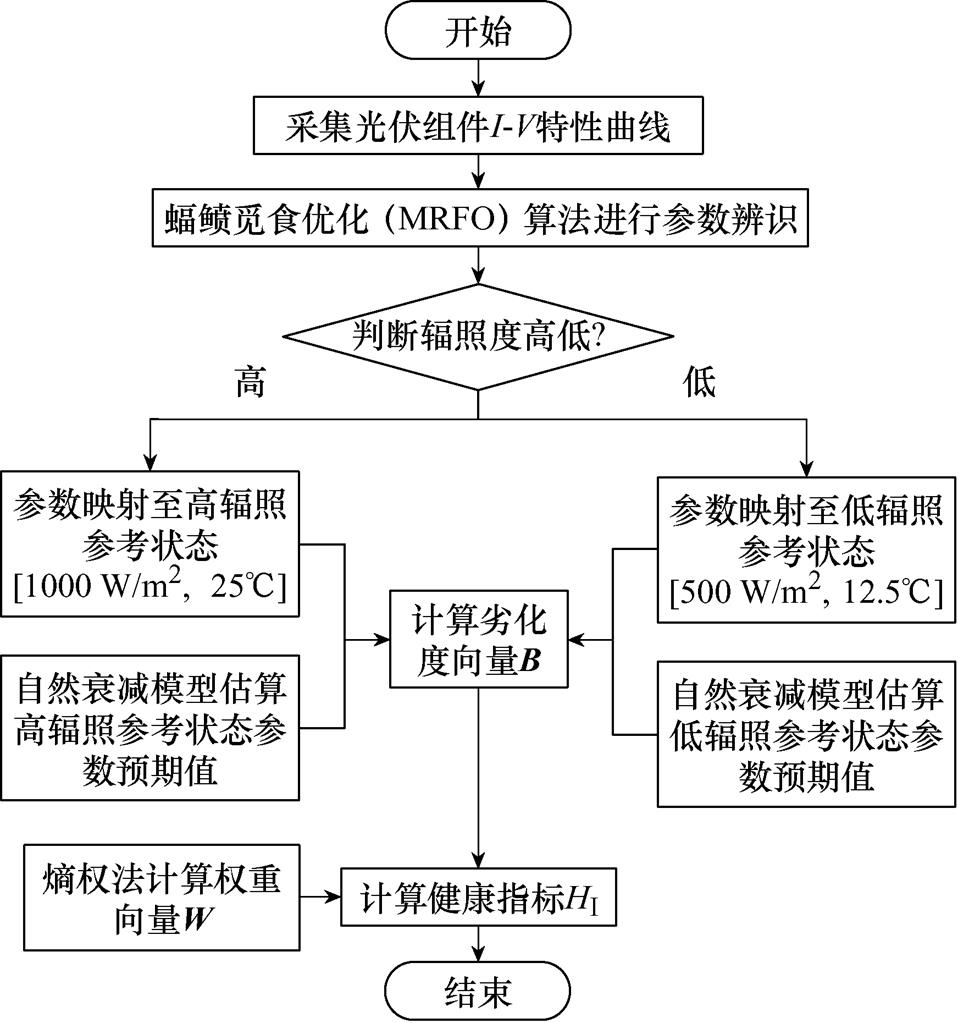
图3 光伏组件健康程度检测流程
Fig.3 Health detection process of PV module
在Matlab/Simulink中搭建光伏组件模型进行仿真验证,所使用的组件型号为Anji Technology AJP-M660-250,组件参数见表1。将仿真获得的光伏组件I-V特性曲线作为参数辨识的数据源,分别用粒子群优化(Particle Swarm Optimization, PSO)算法、鲸鱼算法(Whale Optimization Algorithm, WOA)、蝠鲼觅食优化(MRFO)算法进行参数辨识,运行50次后取平均得到表2的结果。图4为上述算法迭代500次后RMSE的对比,结果表明MRFO的收敛速度与寻优能力均优于一般的元启发式算法。
表1 光伏组件仿真模型电气参数(STC)
Tab.1 Electrical parameters of PV module simulation model (STC)

参 数数 值参 数数 值 最大功率点电压Vm/V31.14等效并联电阻Rsh/W275.5 最大功率点电流Im/A8.03等效串联电阻Rs/W0.189 开路电压Voc/V37.32电流温度系数ui/(%/℃)-0.359 短路电流Isc/A8.5二极管品质因子1.005 5
表2 不同算法的参数辨识结果
Tab.2 Parameter identification results of different algorithms
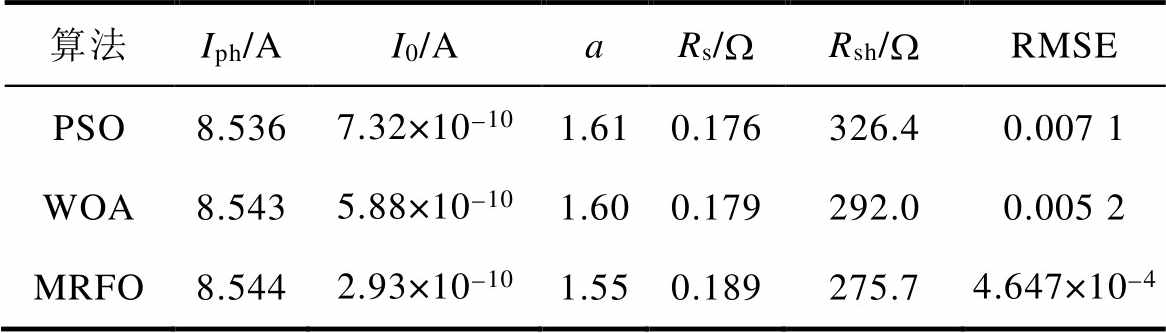
算法Iph/AI0/AaRs/WRsh/WRMSE PSO8.5367.32×10-101.610.176326.40.007 1 WOA8.5435.88×10-101.600.179292.00.005 2 MRFO8.5442.93×10-101.550.189275.74.647×10-4
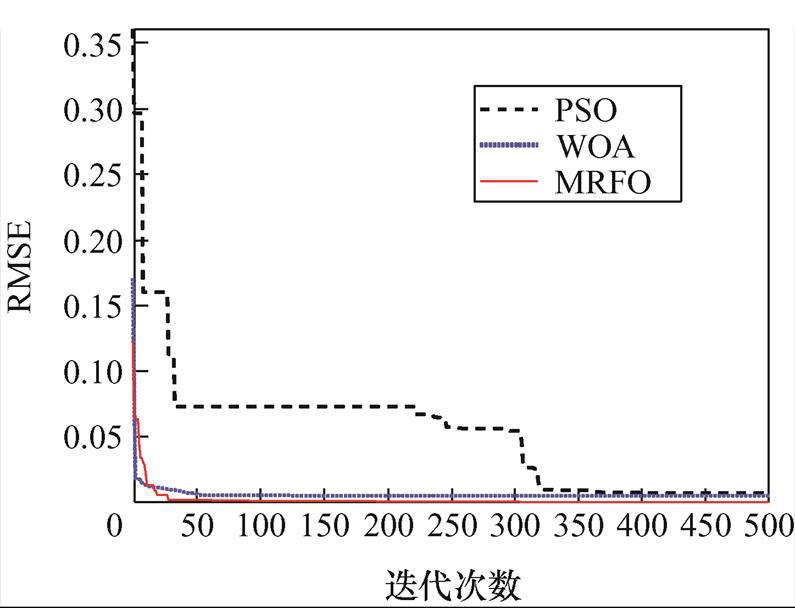
图4 不同算法的RMSE结果对比
Fig.4 RMSE results of different algorithms
参数辨识后,依据组件仿真时设定的环境参数(温度和辐照度),通过式(17)~式(21)进行分层映射。为了观察映射效果,将映射后的参数代入式(1)获得映射后的I-V曲线,计算映射曲线与参考状态下的I-V曲线之间的RMSE,参数映射结果见表3。
表3 不同环境下的参数映射结果
Tab.3 Parameter mapping results in different environments
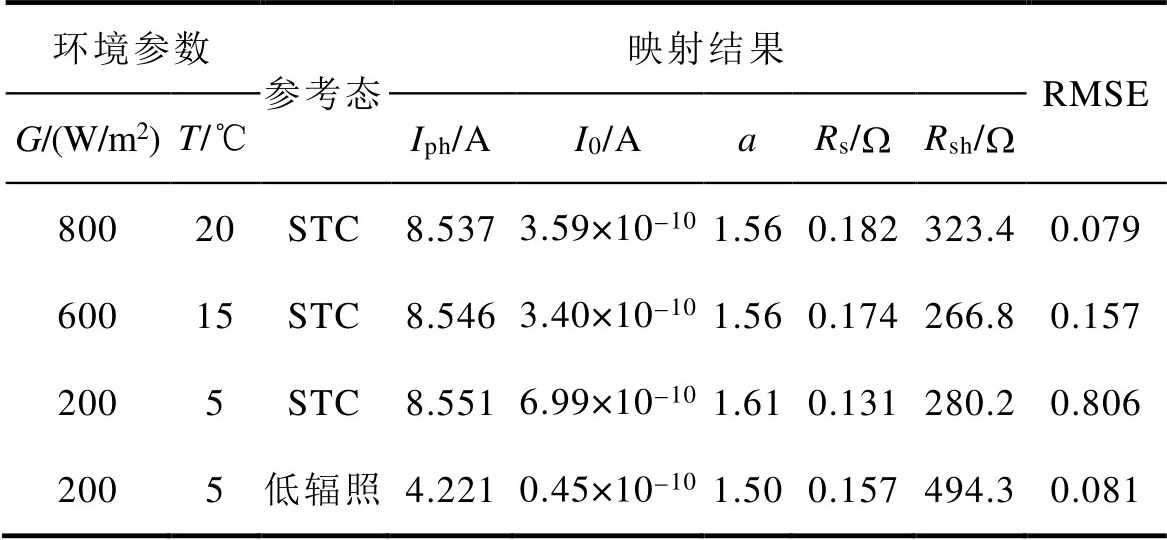
环境参数参考态映射结果RMSE G/(W/m2)T/℃Iph/AI0/AaRs/WRsh/W 80020STC8.5373.59×10-101.560.182323.40.079 60015STC8.5463.40×10-101.560.174266.80.157 2005STC8.5516.99×10-101.610.131280.20.806 2005低辐照4.2210.45×10-101.500.157494.30.081
映射曲线与参考曲线的对比情况如图5所示。
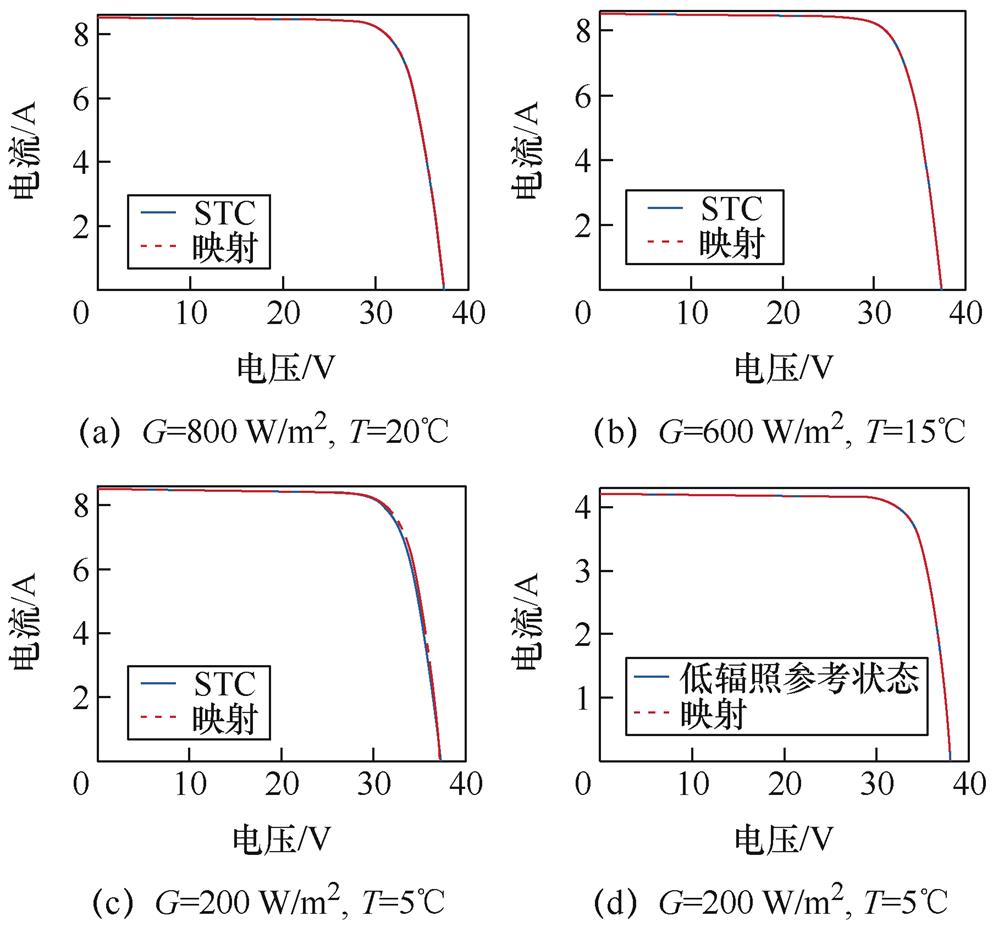
图5 映射结果
Fig.5 Mapping results
由图5和表3中可以发现,当辐照和温度条件较低时,若仍然按照常规方式将参数映射至标准测试条件(Standard Test Condition, STC),映射结果的误差较大,如G=200 W/m2的仿真组,映射至(STC)时误差为0.806,将该仿真组映射至低辐照参考状态,映射误差可降为0.081。分层映射为参数设置两个比较基准,确保任意工作环境下的组件都能有较高的映射精度,消除环境因素的影响,有利于提高光伏组件健康程度检测的精度和适用性。
分层映射将参数归为两类,每类参数都需要一个比较基准来判断参数的劣化度,因此,需要通过自然衰减模型分别估算工作在STC、低辐照参考状态下的光伏组件参数预期值。
光伏组件的初始电气参数可通过商家或仿真获取。以STC为例,组件自然衰减时,特征参数Iph、Rs、Rsh的变化情况见表4。
表4 组件自然衰减时的特征参数变化
Tab. 4 Changes in characteristic parameters as module naturally attenuate

运行时间/年Iph/ARs/WRsh/W 08.5060.188275.6 58.0970.222164.0 107.8470.243134.5 157.5970.264115.7 207.3470.286102.7 257.0970.30993.3
从表4中可以发现,随着运行年份的增加,光生电流Iph与并联电阻Rsh呈下降趋势,串联电阻Rs呈上升趋势,与1.2节分析相符。将自然衰减后的参数代入式(1),获得组件自然衰减时输出特性曲线随运行年份的变化情况,如图6所示。
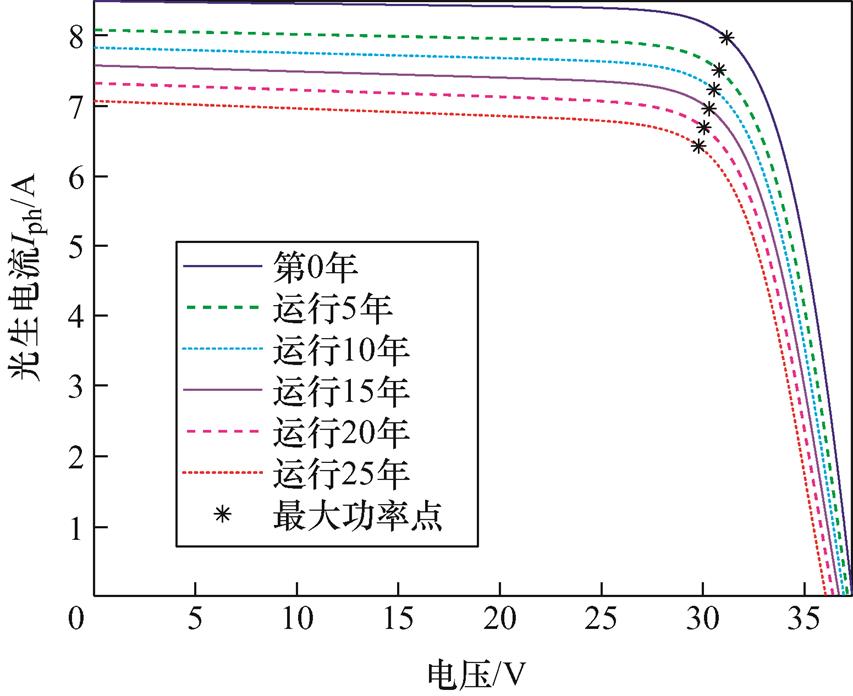
图6 光伏组件自然衰减情况
Fig.6 Natural attenuation of PV module
从图6发现,参数的衰减主要导致输出电流的下降,输出电压的下降幅度较小。观察到最大功率点电压、电流的下降幅度略大于短路电流和开路电压,该现象源于参数Rsh、Rs的衰减,符合实际情况,进一步验证了模型的有效性。
通过降低组件透光率、外加并联电阻、外加串联电阻可以改变参数Iph、Rsh、Rs模拟组件衰减。根据自然衰减模型第25年的参数预期值可知,当组件设置的透光率范围为[1, 0.83]、外加并联电阻范围为[1 000 W, 100 W]、外加串联电阻范围为[0 W, 0.15 W],可以模拟仿真组件各参数从健康到完全劣化的衰减过程。
仿真模拟了正常、单参数衰减、双参数衰减、三参数衰减等八种工作模式。除正常模式外,每种模式的参数变化范围均分为100份,共计701份数据表征组件的各种健康状态。
采集各种健康状态下的光伏组件输出特性曲线,对其进行参数辨识,辨识结果作为样本,通过熵权法计算3个参数的权重,计算结果见表5。
表5 参数权重计算结果
Tab.5 Calculation results of the parameter weights

参数IphRsRsh 权重w(%)71.02421.7907.187
仿真组件内部参数为初始值,视为第0年运行,计算劣化度时选择第0年与第25年的参数预期值为阈值,结合参数劣化度与权重系数计算健康指数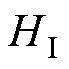 。计算结果如图7所示。
。计算结果如图7所示。
图7展示了光伏组件八种工作模式下的健康指数计算结果。除正常和三参数衰减模式外,每种工作模式展示三组参数衰减由小到大的健康程度检测结果。同时选取四种不同环境参数和映射方式下的检测结果进行对比。
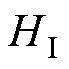 越接近0代表组件越健康。从图7中可以发现,任意工作模式下的组件健康程度都能进行有效辨识,遮光率对健康程度的影响最大,串联电阻次之,并联电阻影响最小。以1 000 W/m2辐照强度下的检测结果为参照值,当参数进行分层映射(800 W/m2进行高辐照映射、400 W/m2进行低辐照映射)时,健康程度检测结果与参照值基本一致,当参数只进行STC映射(400 W/m2进行高辐照映射)时,检测结果与参照值存在明显差异,证明分层映射能有效提高低辐射状态下光伏组件健康程度检测的准确性。
越接近0代表组件越健康。从图7中可以发现,任意工作模式下的组件健康程度都能进行有效辨识,遮光率对健康程度的影响最大,串联电阻次之,并联电阻影响最小。以1 000 W/m2辐照强度下的检测结果为参照值,当参数进行分层映射(800 W/m2进行高辐照映射、400 W/m2进行低辐照映射)时,健康程度检测结果与参照值基本一致,当参数只进行STC映射(400 W/m2进行高辐照映射)时,检测结果与参照值存在明显差异,证明分层映射能有效提高低辐射状态下光伏组件健康程度检测的准确性。
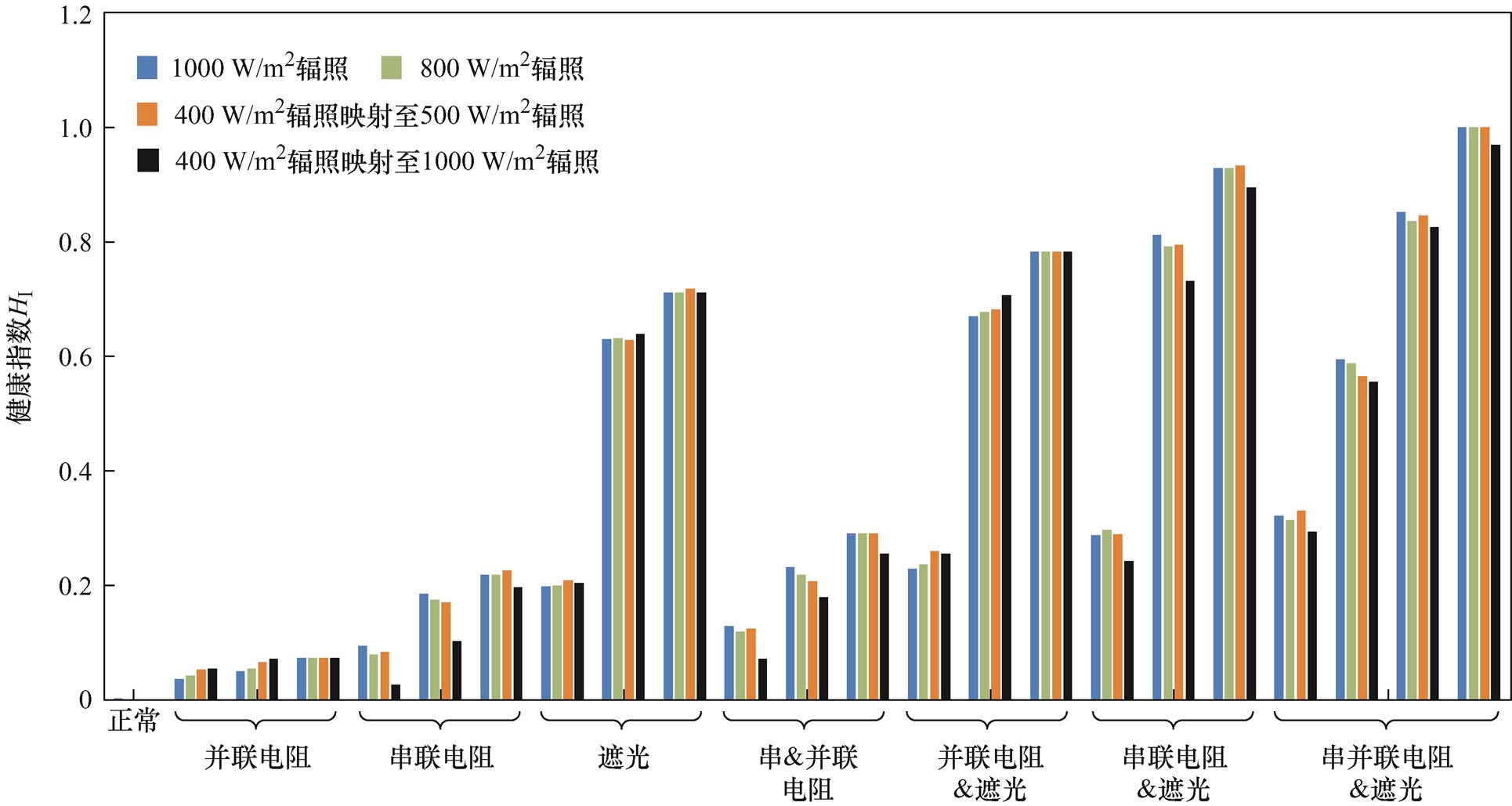
图7 仿真组件健康程度检测结果
Fig.7 Health detection results of simulation module
实验在室外条件下进行,所使用的实验平台如图8所示,实验中采用的光伏组件型号为TSM- 300DD05A(II),其主要参数见表6。
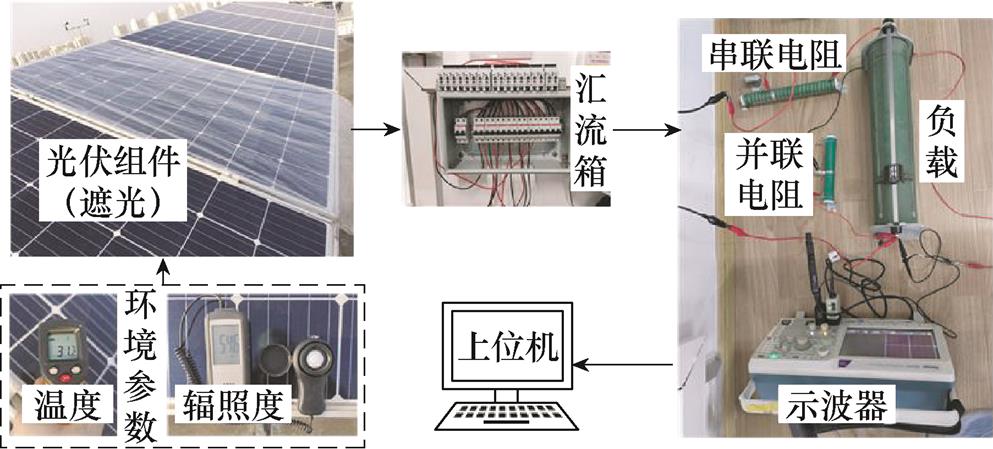
图8 实验平台
Fig.8 Experimental platform
表6 光伏组件电气参数(STC)
Tab.6 Electrical parameters of PV module (STC)
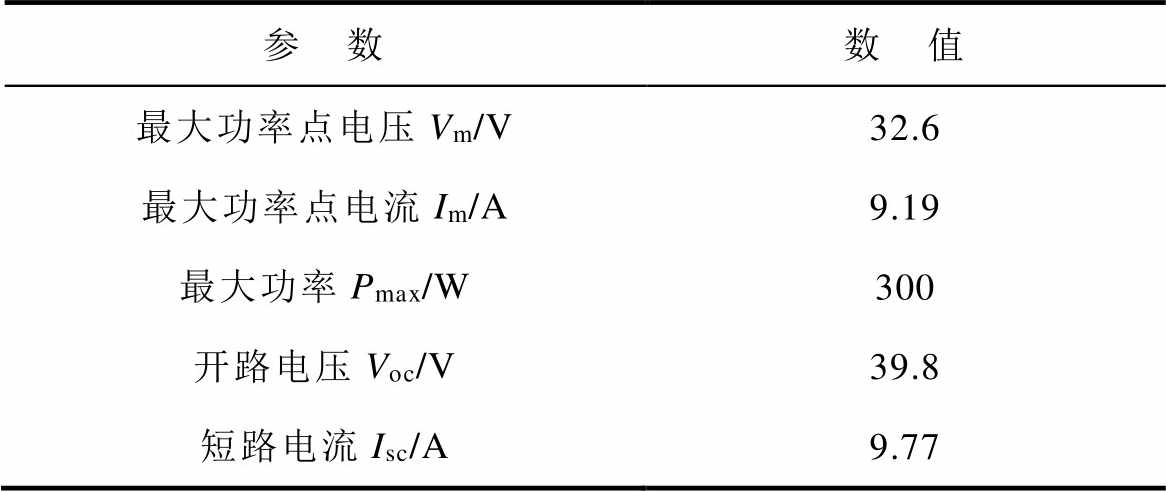
参 数数 值 最大功率点电压Vm/V32.6 最大功率点电流Im/A9.19 最大功率Pmax/W300 开路电压Voc/V39.8 短路电流Isc/A9.77
实验使用辐照仪与测温仪测量光伏组件运行时的环境参数。参数Iph的衰减通过在组件表面覆盖塑料薄膜进行模拟,一层塑料膜可降低4.5%~5.5%的透光率。光伏组件输出端口串联一台0.5 W 的滑动变阻器模拟参数Rs的衰减,并联一台500 W 的滑动变阻器模拟参数Rsh的衰减,外接一台1 000 W 的滑动变阻器作为电路负载,示波器间隔性扫描I-V特性曲线,传输至上位机进行参数辨识与健康程度检测。
实验通过降低透光率、外加串联电阻、外加并联电阻模拟了不同衰减类型、不同衰减程度的光伏组件。实验时间为2023年3月10日至3月14日的9 00—17
00—17 00,辐照度范围为[300 W/m2, 900 W/m2],共计300组实验样本。实验组件已投入使用5年,通过自然老化模型计算组件第5年的参数预期值,结合实验组件参数测量值计算参数劣化度和健康指数
00,辐照度范围为[300 W/m2, 900 W/m2],共计300组实验样本。实验组件已投入使用5年,通过自然老化模型计算组件第5年的参数预期值,结合实验组件参数测量值计算参数劣化度和健康指数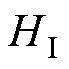 ,健康程度检测结果见表7。
,健康程度检测结果见表7。
表7 实验组件健康程度检测结果
Tab.7 Health test results of experimental PV module
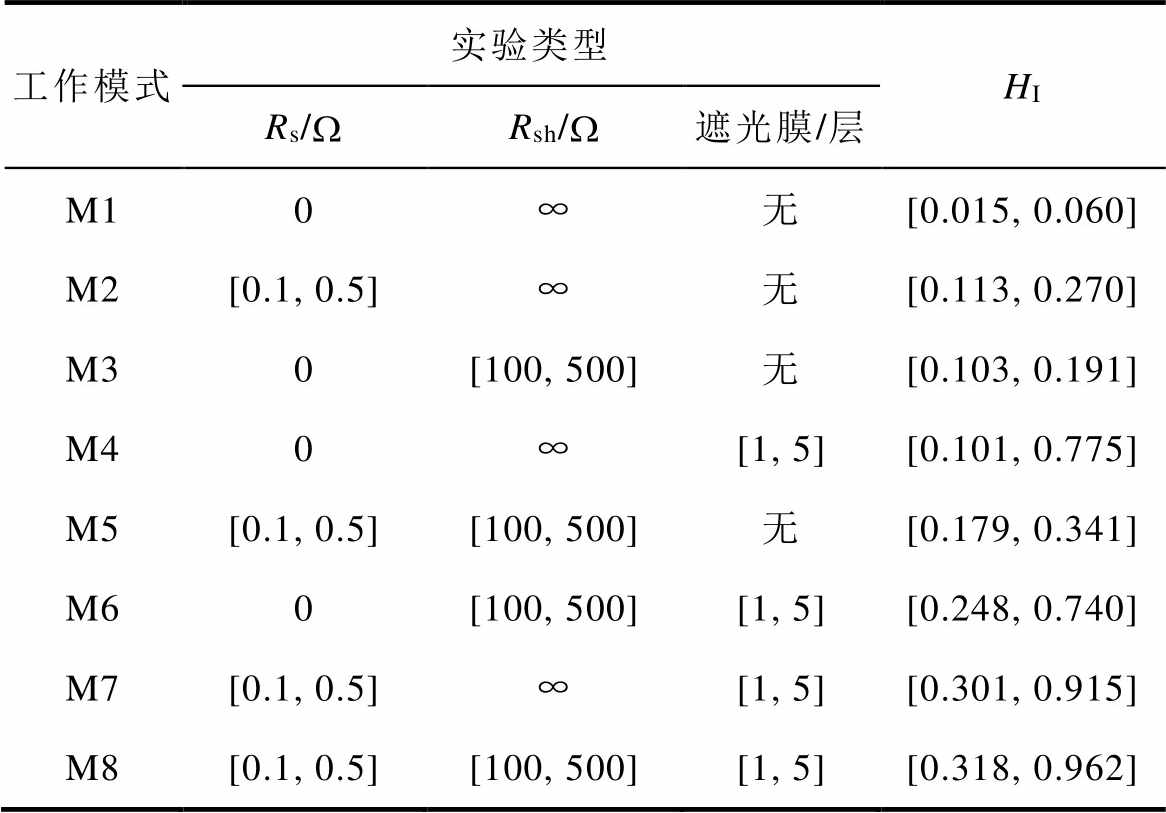
工作模式实验类型HI Rs/WRsh/W遮光膜/层 M10∞无[0.015,0.060] M2[0.1,0.5]∞无[0.113,0.270] M30[100,500]无[0.103,0.191] M40∞[1,5][0.101,0.775] M5[0.1,0.5][100,500]无[0.179,0.341] M60[100,500][1,5][0.248,0.740] M7[0.1,0.5]∞[1,5][0.301,0.915] M8[0.1,0.5][100,500][1,5][0.318,0.962]
实验设置的工作模式与仿真一致,M1没有设置参数衰减条件,检测结果为健康,表明实验使用的光伏组件未发生异常退化。M2~M4模拟单参数异常衰减,以M3为例,由于Rsh对组件输出特性的影响较小,所以当并联电阻完全劣化时组件的健康指数仍然低至0.191,代表组件接近健康状态,检测结果证明考虑参数权重能有效提高光伏组件健康程度检测的可靠性和准确性。M5~M7模拟双参数异常衰减,M8模拟三参数异常衰减,检测结果表明,随着组件异常退化的部位增多,发生异常衰减的参数数目增加,组件健康程度将进一步降低。
观察M2~M4发现,单参数衰减程度较小时, 均为0.1左右,检测结果为相对健康,对组件的健康程度诊断基本符合预期,但检测结果没有体现出三个参数对健康程度影响权重的不同。对检测结果进行进一步分析,每种工作模式选取一组实验样本,由表8提供参数劣化度计算结果。
均为0.1左右,检测结果为相对健康,对组件的健康程度诊断基本符合预期,但检测结果没有体现出三个参数对健康程度影响权重的不同。对检测结果进行进一步分析,每种工作模式选取一组实验样本,由表8提供参数劣化度计算结果。
表8 参数劣化度计算结果
Tab.8 Calculation results of parameter deterioration
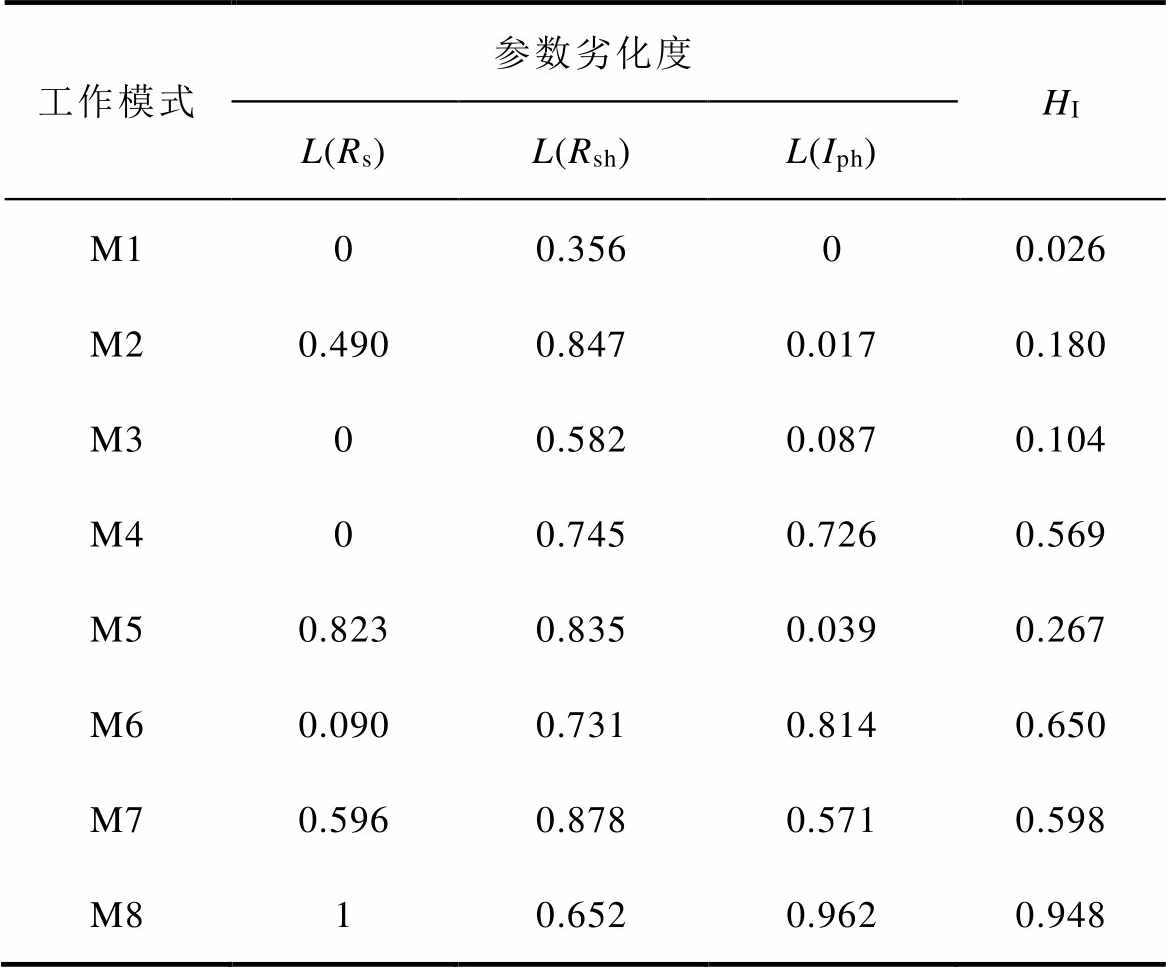
工作模式参数劣化度HI L(Rs)L(Rsh)L(Iph) M100.35600.026 M20.4900.8470.0170.180 M300.5820.0870.104 M400.7450.7260.569 M50.8230.8350.0390.267 M60.0900.7310.8140.650 M70.5960.8780.5710.598 M810.6520.9620.948
将参数劣化度乘以权重系数表达参数的损耗占比d,即d=Lw,并将三参数的损耗占比计算结果绘制为图9所示的雷达图。
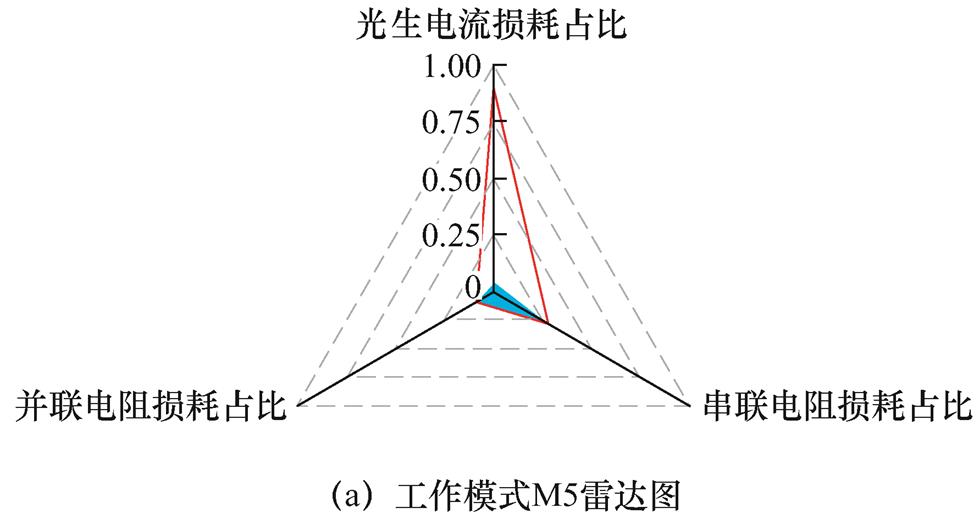
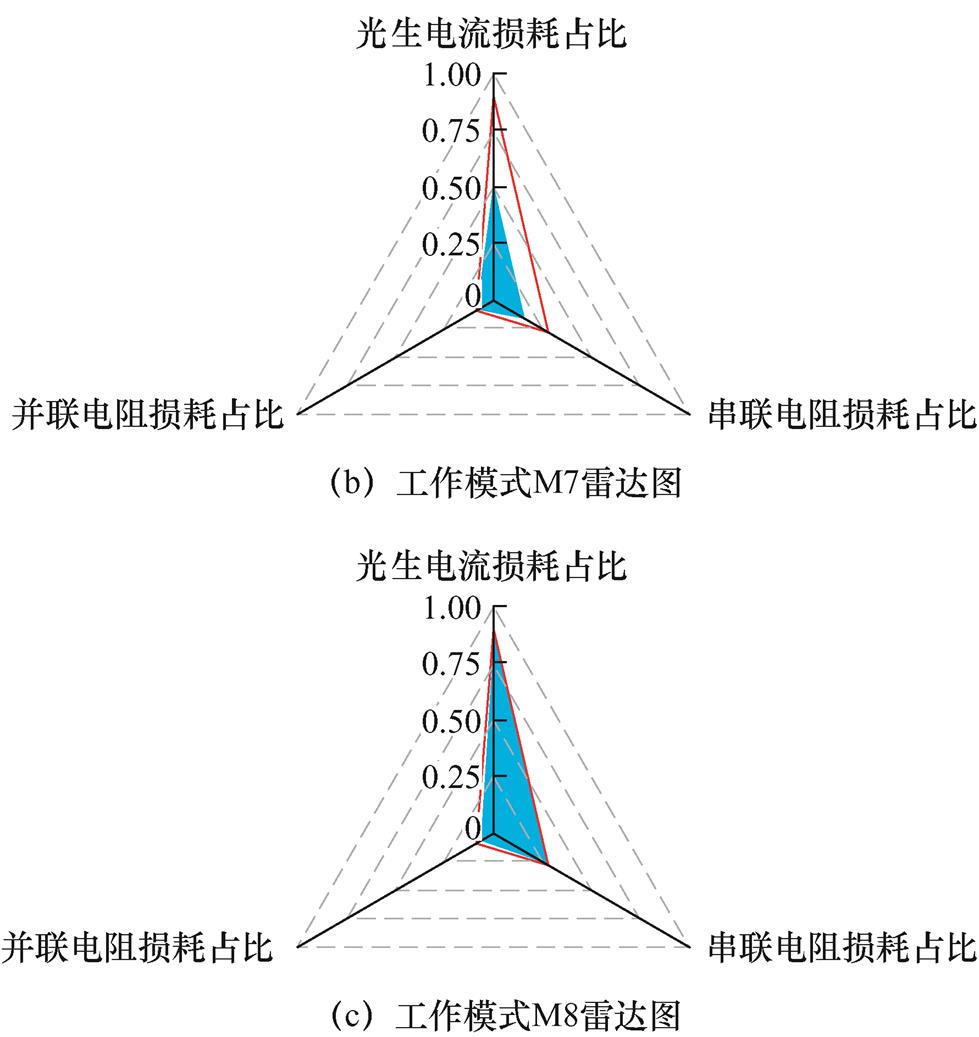
图9 部分实验数据雷达图
Fig.9 Radar charts of partial experimental data
根据表7的设定,工作模式M2、M4只设定串联电阻、透光率发生衰减,表8中的检测结果却显示并联电阻具有较高的劣化度。分析认为并联电阻Rsh的衰减对组件输出特性曲线的影响较小,而实验扫描I-V曲线时辐照度存在随机波动,最终测得的I-V曲线与选取的环境参数都会存在少许误差,导致并联电阻的辨识结果存在较大误差。通过考虑参数权重,可以有效地避免Rsh的辨识误差对光伏组件健康程度诊断结果的影响。
对光伏组件进行健康程度检测时,可以借助雷达图观察组件发生异常衰减的参数以及衰减程度。图9选取了三组实验样本进行展示,图中坐标轴为参数损耗值,代表单个参数对组件健康程度的影响,(红)实线代表光伏组件健康程度的下限,即组件完全劣化,(蓝色)阴影部分代表被测组件的劣化程度,通过雷达图的填充面积可以直观地观测出光伏组件的健康程度。
实验结果证明,本文方法能对各种辐照环境下的光伏组件健康程度进行有效检测,帮助运营商实时掌握设备的具体运行状态,为光伏组件的检修维护与故障预测提供重要参考。
本文选取光生电流、串联电阻、并联电阻为特征参数,通过参数辨识与分层映射进行参数提取,考虑参数权重建立了光伏组件健康程度指标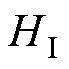 。该方法只需获取光伏组件的I-V特性曲线和环境参数,即可计算健康指数
。该方法只需获取光伏组件的I-V特性曲线和环境参数,即可计算健康指数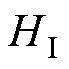 表征光伏组件的健康程度,为后续进行光伏阵列的健康程度检测研究奠定了基础。论文主要贡献如下:
表征光伏组件的健康程度,为后续进行光伏阵列的健康程度检测研究奠定了基础。论文主要贡献如下:
1)采用MRFO算法对I-V曲线进行参数辨识,该算法比常用的元启发式算法收敛速度更快,不易陷入局部最优。
2)根据辐照度高低对特征参数进行分层映射,有效提高了低辐照环境下光伏组件的参数提取和健康程度检测精度。
3)建立光伏组件自然衰减模型,根据组件运行年份估算特征参数预期值,避免组件自然衰减对计算参数劣化度的影响。
4)采用熵权法计算参数权重,结合参数劣化度建立健康指数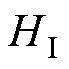 ,考虑了参数对组件健康状态的影响程度的差异性,提高了光伏组件健康程度检测的可靠性和准确性。
,考虑了参数对组件健康状态的影响程度的差异性,提高了光伏组件健康程度检测的可靠性和准确性。
参考文献
[1] 王尧, 马桐桐, 赵宇初, 等. 基于电磁辐射时延估计的串联光伏直流电弧故障定位方法[J]. 电工技术学报, 2023, 38(8): 2233-2243. Wang Yao, Ma Tongtong, Zhao Yuchu, et al. Series DC arc-fault location method based on electro- magnetic radiation delay estimation for photovoltaic systems[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2233-2243.
[2] 刘晓艳, 王珏, 姚铁锤, 等. 基于卫星遥感的超短期分布式光伏功率预测[J]. 电工技术学报, 2022, 37(7): 1800-1809. Liu Xiaoyan, Wang Jue, Yao Tiechui, et al. Ultra short-term distributed photovoltaic power prediction based on satellite remote sensing[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1800-1809.
[3] 顾崇寅, 徐潇源, 王梦圆, 等. 基于CatBoost算法的光伏阵列故障诊断方法[J]. 电力系统自动化, 2023, 47(2): 105-114. Gu Chongyin, Xu Xiaoyuan, Wang Mengyuan, et al. CatBoost algorithm based fault diagnosis method for photovoltaic arrays[J]. Automation of Electric Power Systems, 2023, 47(2): 105-114.
[4] 丁坤, 陈富东, 翁帅, 等. 基于Ⅰ-Ⅴ特性灰色关联分析的光伏阵列健康状态评估[J]. 电网技术, 2021, 45(8): 3087-3095. Ding Kun, Chen Fudong, Weng Shuai, et al. Health state evaluation of photovoltaic array based on Ⅰ-Ⅴ characteristics and grey relational analysis[J]. Power System Technology, 2021, 45(8): 3087-3095.
[5] Han C, Lee H. A field-applicable health monitoring method for photovoltaic system[J]. Reliability Engineering & System Safety, 2019, 184: 219-227.
[6] Ding Kun, Chen Xiang, Weng Shuai, et al. Health status evaluation of photovoltaic array based on deep belief network and Hausdorff distance[J]. Energy, 2023, 262: 125539.
[7] Kellil N, Aissat A, Mellit A. Fault diagnosis of photovoltaic modules using deep neural networks and infrared images under Algerian climatic conditions[J]. Energy, 2023, 263: 125902.
[8] 杨瑞珍, 杜博伦, 何赟泽, 等. 晶体硅光伏电池电磁感应激励红外热辐射缺陷检测与成像技术[J]. 电工技术学报, 2018, 33(增刊2): 321-330. Yang Ruizhen, Du Bolun, He Yunze, et al. Infrared radiation defect detection and imaging technique under active electromagnetic induction excitation for crystalline silicon photovoltaic cells[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 321-330.
[9] 赵靖英, 吴晶晶, 张雪辉, 等. 基于萤火虫扰动麻雀搜索算法-极限学习机的光伏阵列故障诊断方法研究[J]. 电网技术, 2023, 47(4): 1612-1625. Zhao Jingying, Wu Jingjing, Zhang Xuehui, et al. Fault diagnosis of photovoltaic arrays based on sparrow search algorithm with firefly perturbation- extreme learning machine[J]. Power System Technology, 2023, 47(4): 1612-1625.
[10] He Zengxiang, Chu Pengpeng, Li Chenxi, et al. Compound fault diagnosis for photovoltaic arrays based on multi-label learning considering multiple faults coupling[J]. Energy Conversion and Management, 2023, 279: 116742.
[11] 陈凌, 韩伟, 张经炜. 基于数据融合的光伏组件故障诊断[J]. 电网技术, 2017, 41(6): 1864-1872. Chen Ling, Han Wei, Zhang Jingwei. PV module fault diagnosis based on data fusion[J]. Power System Technology, 2017, 41(6): 1864-1872.
[12] 周亮, 武美娜, 胡安. 局部遮挡下光伏阵列的快速建模及极值点分布特征研究[J]. 电工技术学报, 2021, 36(增刊2): 572-581. Zhou Liang, Wu Meina, Hu An. Fast modeling and analysis of power peaks characteristics of PV arrays under partial shading conditions[J]. Transactions of ChinaElectrotechnical Society, 2021, 36(S2): 572-581.
[13] 李畸勇, 张伟斌, 赵新哲, 等. 改进鲸鱼算法优化支持向量回归的光伏最大功率点跟踪[J]. 电工技术学报, 2021, 36(9): 1771-1781. Li Jiyong, Zhang Weibin, Zhao Xinzhe, et al. Global maximum power point tracking for PV array based on support vector regression optimized by improved whale algorithm[J]. Transactions of China ElectrotechnicalSociety, 2021, 36(9): 1771-1781.
[14] 吴春华, 俞薛颖, 李智华, 等. 基于FCM与高斯隶属度的光伏组件健康状态诊断[J]. 电网技术, 2022, 46(5): 1887-1896. Wu Chunhua, Yu Xueying, Li Zhihua, et al. Health state diagnosis of photovoltaic modules based on FCM and Gaussian membership[J]. Power System Technology, 2022, 46(5): 1887-1896.
[15] Huang Chao, Wang Long. Simulation study on the degradation process of photovoltaic modules[J]. Energy Conversion and Management, 2018, 165: 236-243.
[16] 程泽, 巩力, 刘艳莉. 光学损失故障对单晶硅光伏电池参数的影响[J]. 电工技术学报, 2016, 31(17): 217-223. Cheng Ze, Gong Li, Liu Yanli. The influence of optical losses on monocrystalline silicon solar cells parameters[J]. Transactions of China Electrotechnical Society, 2016, 31(17): 217-223.
[17] Houssein E H, Zaki G N, Diab A A Z, et al. An efficient Manta Ray Foraging optimization algorithm for parameter extraction of three-diode photovoltaic model[J]. Computers & Electrical Engineering, 2021, 94: 107304.
[18] 邱纯. 任意辐照度与温度条件下光伏系统输出特性建模[D]. 武汉: 华中科技大学, 2011.
[19] Messenger R A, Ventre J. Photovoltaic Systems Engineering Second Edi. Taylor&Francis, 2004.
[20] De Soto W, Klein S A, Beckman W A. Improvement and validation of a model for photovoltaic array performance[J]. Solar Energy, 2006, 80(1): 78-88.
[21] 李智华, 马浩强, 吴春华, 等. 基于三参数的光伏组件老化程度诊断[J]. 中国电机工程学报, 2022, 42(9): 3327-3338. Li Zhihua, Ma Haoqiang, Wu Chunhua, et al. Diagnosing the aging degree of photovoltaic modules based on three parameters[J]. Proceedings of the CSEE, 2022, 42(9): 3327-3338.
[22] 中华人民共和国工业和信息化部公告—光伏制造行业规范条件[J]. Solar Energy, 2013(20): 6-8.
[23] Lillo-Sánchez L, López-Lara G, Vera-Medina J, et al. Degradation analysis of photovoltaic modules after operating for 22 years. A case study ith comparisons[J]. Solar Energy, 2021, 222: 84-94.
[24] da Fonseca J E F, de Oliveira F S, Massen Prieb C W, et al. Degradation analysis of a photovoltaic generator after operating for 15 years in southern Brazil[J]. Solar Energy, 2020, 196: 196-206.
[25] Townsend T U. A method for estimating the long- term performance of direct-coupled photovoltaic systems[D]. Madison: University of Wisconsin, 1989.
Abstract Traditional health status detection of photovoltaic (PV) modules generally includes only two states: health or fault, which is not conducive to fault prediction and system maintenance. Recently, some methods have been presented to detect the health degree of PV modules. However, it is difficult to detect the health status of PV modules in a low-irradiation environment, and the effect of the parameter weights and natural attenuation is ignored. This paper proposes a detection method to characterize the health of PV modules by calculating the health index through parameter deterioration degree and parameter weights.
Firstly, according to the I-V curve of the PV modules, the health parameters are identified by the manta ray foraging optimization (MRFO) algorithm, including the photo generated current Iph, series resistance Rs, and parallel resistance Rsh. Secondly, setting the high/low irradiation reference state, according to the irradiance measured when the I-V curve was acquired, the parameters identification results are hierarchically mapped, which improves the accuracy of parameter extraction in a low irradiation environment. Thirdly, the expected value of parameters after n years of natural attenuation is obtained by establishing the natural attenuation model of PV modules and used as a reference for calculating the parameter deterioration degree. Finally, taking the health parameters of PV modules in various health states as samples, the parameter weights are calculated by the entropy weight method, and the health index of the range [0, 1] is calculated by combining the parameter deterioration degree. The smaller the index, the healthier the PV module. Different parameters influence the health status of PV modules, and the reliability of detection results can be increased by considering the parameter weights.
Simulation and experimental results show that the convergence speed of parameter identification using MRFO is fast, and the identification error is as low as 4.647×10-4. The parameter identification results are mapped in different ways. When the irradiance is 200 W/m2, the hierarchical mapping reduces the root mean square error by 89.95% compared with the traditional mapping method. The health detection results of PV modules under a low irradiation state are consistent with the reference value using hierarchical mapping. The natural attenuation model provides the natural attenuation parameters as the expected value of parameters, combined with the parameter extraction value to calculate the parameter deterioration. The calculation results show that Rsh is prone to large detection errors. However, the parameter weight of Rsh is only 7.187%, which has little impact on the health status. The health index with parameter weights is in line with expectations. With the increase of abnormal attenuation degree of experimental modules’ characteristic parameters, the health index gradually increases from 0.015 to 0.962, indicating that the health of the PV modules is decreasing.
The following conclusions can be drawn. (1) MRFO has a fast convergence speed and strong optimization ability, which is appropriate for parameter identification. (2) Hierarchical mapping can effectively improve the accuracy of parameter extraction and health detection of PV modules in low-radiation environments. (3) The natural attenuation model of PV modules calculates the parameters’ expected value according to the operation year of modules, which avoids natural attenuation affecting the accuracy of parameter deterioration degree. (4) The parameter weights consider the influence of parameters on the health status, which effectively improves the reliability and accuracy of the health detection of PV modules.
keywords:Photovoltaic modules, identification of health parameters, hierarchical mapping, natural attenuation model, health parameter weights
DOI: 10.19595/j.cnki.1000-6753.tces.230896
中图分类号:TM 615
国家自然科学基金资助项目(51677112)。
收稿日期 2023-06-09
改稿日期 2023-09-23
吴春华 男,1978年生,副教授,研究方向为光伏发电、电力变换等。E-mail: wuchunhua@shu.edu.cn(通信作者)
易 苑 女,1999年生,硕士研究生,研究方向为光伏发电。E-mail: yiyuan2024@163.com
(编辑 郭丽军)