基于PWM+移相的双有源半桥DC-DC变换器分析及其控制
任 强 康 薇 姜亚鹏 秦 祝
(电磁能技术全国重点实验室(海军工程大学) 武汉 430033)
摘要 该文针对双有源半桥(DAHB)DC-DC变换器宽电压范围运行下电容电压计算不准确、单移相控制粗放等不足,提出一种基于PWM+移相的三自由度优化控制(TFC)策略。首先,基于DAHB的数学模型,推导桥臂串联电容稳态电压表达式。在此基础上,从最小化回流功率角度得到三自由度控制的最优开关模式,推导了电流、功率等关键电气量的解析表达式,并获得以电流应力最小化为目标的包含等式和不等式约束的局部最优解方程组。其次,针对最优方程组难以解析求解的问题,采用模型简化+线性近似的方法求取其局部最优解,得到DAHB全工况PWM+移相的三自由度优化控制策略。然后,分析所提出的三自由度优化控制下DAHB变换器的软开关特性。最后,通过仿真及实验验证了桥臂串联电容稳态电压表达式的正确性和三自由度优化控制策略的有效性。
关键词:直流变换器 双有源半桥 三自由度 优化控制 软开关
0 引言
在动力电池充放电应用中,双有源全桥(Dual- Active Bridge, DAB)DC-DC变换器以电气隔离、功率密度高、效率高等优势,在充电桩、电动汽车、储能电站等中大功率直流电能变换场合得到了广泛的应用[1-3]。对于小功率双向直流电能变换应用,双有源半桥(Dual-Active Half-Bridge, DAHB)DC-DC变换器,继承了DAB的电气优势,以更少的开关器件、更简单的系统控制,成为有效的技术路线[4-6]。
典型DAHB变换器拓扑如图1所示,包含变压器一次、二次侧半桥、电感L和高频变压器(匝比为n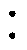 1)。变换器输入输出端直流电压分别为U1、U2,电流分别为i1、i2;变压器两端电压分别为up、us,电流为ip、is;半桥结构由开关器件(开关管S1~S4、反并联二极管VD1~VD4)和串联电容(C1~C4)组成,电容稳态电压分别为u1~u4。通过高频交流链路实现电气隔离,高频化有助于减小无源器件的体积,进而实现高功率密度。为实现双向功率变换,半桥开关器件占空比通常为50%,通过调节两侧半桥输出电压间的相位,实现功率流向和功率大小的控制。此种单移相控制(Single Phase Shift, SPS)调制策略,仅利用了DAHB的一个控制自由度,在电压不匹配工况下,特别是中轻负载范围内,控制策略粗放,存在电流应力大、软开关范围小、效率低等问题[7-8]。
1)。变换器输入输出端直流电压分别为U1、U2,电流分别为i1、i2;变压器两端电压分别为up、us,电流为ip、is;半桥结构由开关器件(开关管S1~S4、反并联二极管VD1~VD4)和串联电容(C1~C4)组成,电容稳态电压分别为u1~u4。通过高频交流链路实现电气隔离,高频化有助于减小无源器件的体积,进而实现高功率密度。为实现双向功率变换,半桥开关器件占空比通常为50%,通过调节两侧半桥输出电压间的相位,实现功率流向和功率大小的控制。此种单移相控制(Single Phase Shift, SPS)调制策略,仅利用了DAHB的一个控制自由度,在电压不匹配工况下,特别是中轻负载范围内,控制策略粗放,存在电流应力大、软开关范围小、效率低等问题[7-8]。
为有效提升DAHB全工况运行效率,部分文献基于其多自由度控制和谐振控制等展开研究。文献[9]研究了DAHB“平顶”调制、零电压软开关(Zero Voltage Switching, ZVS)范围以及电流最小值优化控制。然而,一、二次电压匹配的限制条件,对具有宽范围电压的电池类负载应用受限。文献[10]半定量分析了一种类似扩展移相的两自由度调制方式。文献[11]采用强化学习算法得到两自由度调制的优化方案,但二者均未得到控制算法的解析表达。文献[12]针对一种两自由度控制方法,计算了各开关模式的电流和功率,并得出电流应力最小的开关模式;基于电流有效值最小的目标,采用拉格朗日乘子法求解,得到了两自由度优化控制策略。文献[13]以电流波形正负对称为目标,基于仿真软件得出优化运行的条件,以此确定电流有效值最小的三自由度优化控制策略。然而,采用3个PI调节器实现优化控制,使得反馈量多、控制器参数选择难度大。文献[14]以开关切换时刻的绕组电流近似为零作为占空比选择的依据,得到三自由度优化控制策略,并采用多输入多输出(Multi-Input Multi-Output, MIMO)实现不同控制环路间的解耦控制。整个优化策略不依赖于直流电压,但控制器计算量大,应用于高频场合时受限。
在DAHB的结构和参数优化等方面,文献[15]结合光伏储能,分析了DAHB零电压开关范围和变压器漏感参数间的数学关系,通过优化电感参数降低无功功率。文献[16]基于谐振电路结构,分析了谐振型全桥结构和谐振型半桥结构的双向DC-DC变换器,利用电路谐振降低开关时刻的电流,从而减少关断损耗。文献[17]针对DAHB非对称运行,建立了三自由度控制的全阶动态模型和降阶动态模型,并分析了各自的应用局限,为DAHB控制器设计提供参考。为提高DAHB宽范围工况运行下的稳态特性和动态响应,文献[18]提出一种数字几何序列控制方法,并能在DSP或FPGA中简单实现。文献[19-21]从引入附加电路的角度出发,改善DAHB的软开关性能和运行范围等,但容易造成拓扑和调控策略复杂化。
在现有针对DAHB桥臂串联电容电压的研究中,大多认为单侧半桥电容电压仅与该半桥的占空比以及直流电压有关,文献[4-6, 9-14]中串联电容平均电压计算公式见表1,其正确性有待论证。
表1 文献[4-6, 9-14]中串联电容平均电压计算公式
Tab.1 Average voltage of series capacitor

电 压表达式 u1(1-d1)U1 u2d1U1 u3(1-d2)U2 u4d2U2
然而,在DAHB多自由度工作模式下,其半桥串联电容电压与电容取值、开关器件占空比、输入输出直流电压密切相关。将单侧半桥独立等效为Buck电路而得到电容平均电压和开关占空比成比例的结论,忽视了变压器一、二次侧耦合关系,容易导致电容电压计算模型不准确。
综上所述,当前DAHB的理论研究多集中于控制策略和电路拓扑的优化方面,针对DAHB多自由度运行场景,大多数控制算法计算量大、模型复杂,相关模型和调制策略有待进一步完善。为进一步厘清DAHB运行机理并制定简洁有效的优化控制策略,本文首先基于DAHB的等效模型,推导了半桥串联电容的稳态电压表达式。在此基础上,从最小化电流应力的角度选取最优开关模式。采用模型简化+线性近似的方法,求出PWM+移相的三自由度优化控制策略的解析形式,得到了DAHB全工况多自由度运行策略,并对优化策略的软开关范围进行分析。最后通过实验对DAHB的模型分析和优化控制进行验证。
1 DAHB串联电容电压精确求解
定义DAHB变换器的电压比为R=nU2/U1,一次、二次侧电容取值分别为Cp和Cs;两侧半桥在一个开关周期内的占空比分别为d1和d2,取值范围为[0, 1];半桥输出电压相位差在整个开关周期内占比为df,称为DAHB的移相比,取值范围为[-0.25, 0.25],所对应的移相角为-90°~90°。
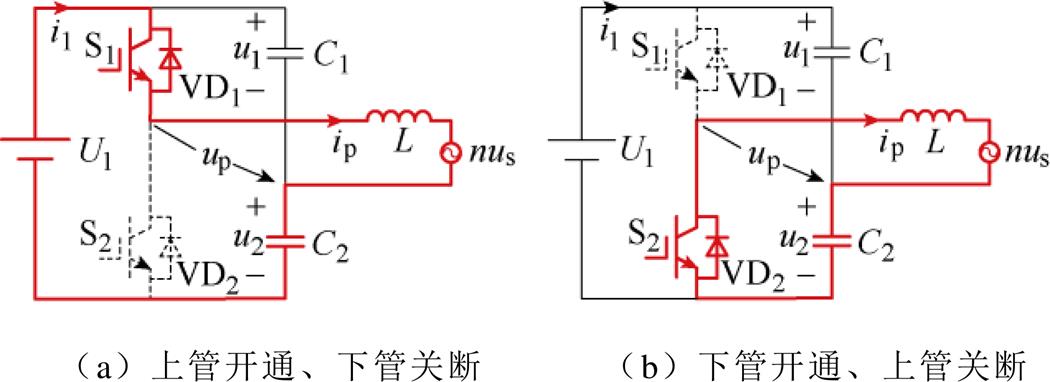
考虑变压器两侧电路的耦合关系,将二次侧参数等效到一次侧,根据一次侧的开关状态可将DAHB分解为两个对称、双向Buck-Boost电路,如图2所示。电感L等效为Buck-Boost电路的滤波电感,电容C1、C2等效为输出滤波电容。每个开关周期,通过控制半桥开关斩波直流电压,实现电容稳态电压的调整。
稳态条件下,根据一个开关周期中电感L的伏秒平衡可得
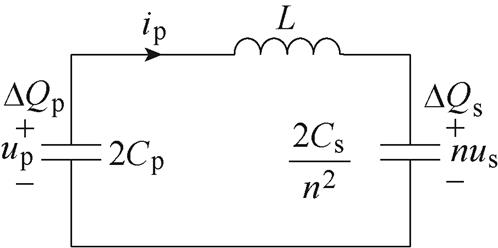
绕组电流对电容的充放电导致电容电荷变化,即
进而得到
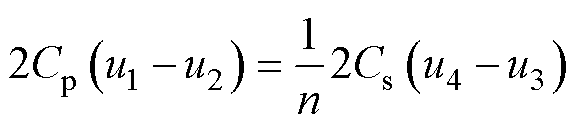 (2)
(2)
根据串联电容满足的电压关系为
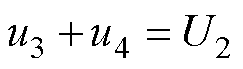 (4)
(4)
联立(1)~式(4)可得电容电压稳态平均值为
可知,电容C1~C4的稳态平均电压与变压器匝比n、占空比d1和d2、直流电压U1和U2以及电容值Cp、Cs相关,与移相占空比df(也即传输功率)无关。df仅影响电容电压的波动幅值,df越大(传输功率越大),电容电压波动越大。通常,设二次侧电容折算到一次侧,与一次侧电容相等,即Cs=n2Cp,则式(5)可化简为
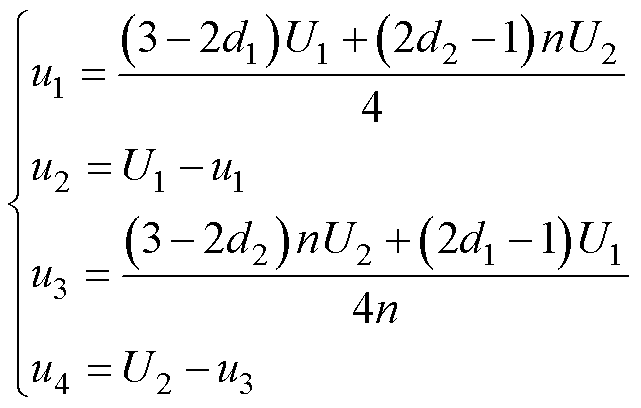 (6)
(6)
2 基于PWM+移相的三自由度优化控制
针对电池电压宽范围波动的应用场景,为降低系统回流功率、提升软开关范围,对DAHB变换器采用PWM+移相的三自由度控制(Three-degree of Freedom Control, TFC)策略,根据一、二次电压实时调节三个控制自由度,从而实现优化控制。根据电压比R的大小,对R<1、R>1和R=1三种工况进行分析。
2.1 最优开关模式
对于R<1工况,变压器二次侧等效直流电压低于一次侧直流电压。根据d1、d2与0.5间的大小关系和df的取值范围,可得R<1工况下的18种开关模式,见表2。根据DAHB简化模型及式(5)可知,当d1<0.5时,u1>u2;当d1>0.5时,u1<u2。同样地,d2、u3和u4也有类似的关系。
参考DAB功率传输特性,为减小系统回流功率,变压器直接传输功率的比重应尽量大,通过漏感转移的功率比重应尽量小[3],一、二次电压的正(负)脉冲应重叠且伏秒积尽量相等。可知,R<1工况下的最优开关模式应满足df∈[|d1-d2|/2, (d1+d2)/2],即模式2、5、8、11、14、17六种开关模式具有相同的电气描述。由DAB的多移相控制理论可知,同一输出功率下,占空比D>0.5时回流功率相比D<0.5时更大[22]。从最小化无功功率的角度出发,选取开关模式11为R<1工况的最优开关模式。
表2 R<1工况的开关模式
Tab.2 Switching modes of R<1 situation
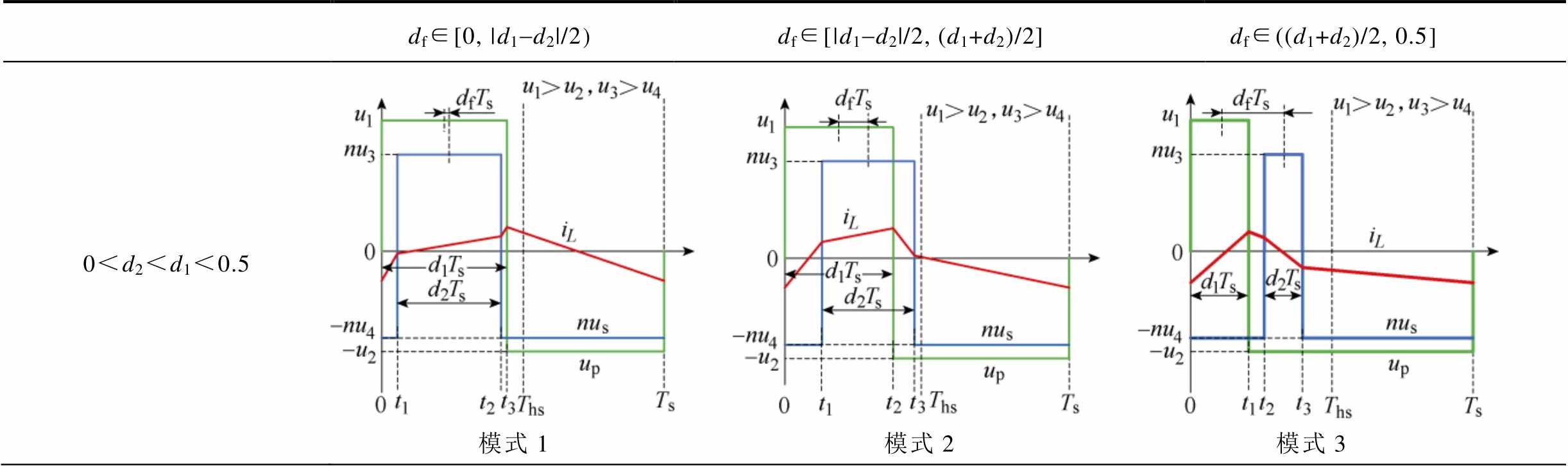
df∈[0, |d1-d2|/2df∈[|d1-d2|/2, (d1+d2)/2]df∈((d1+d2)/2, 0.5 0<d2<d1<0.5模式1 模式2 模式3
(续)

df∈[0, |d1-d2|/2df∈[|d1-d2|/2, (d1+d2)/2]df∈((d1+d2)/2, 0.5 0<d2<0.5<d1模式4 模式5 模式6 0.5<d2<d1模式7 模式8 模式9 0<d1<d2<0.5模式10 模式11 模式12 0<d1<0.5<d2模式13 模式14 模式15 0.5<d1<d2模式16 模式17 模式18
对于R>1工况,根据对称性,可得最优开关模式如图4所示。
对比R<1和R>1工况最优开关模式的波形可知,两者具有相同的电气描述关系,在理论推导时,二者的表达形式统一。而对于R=1工况,一、二次电压匹配,采用SPS控制即可获得最佳效果。
2.2 电流应力最小的优化策略
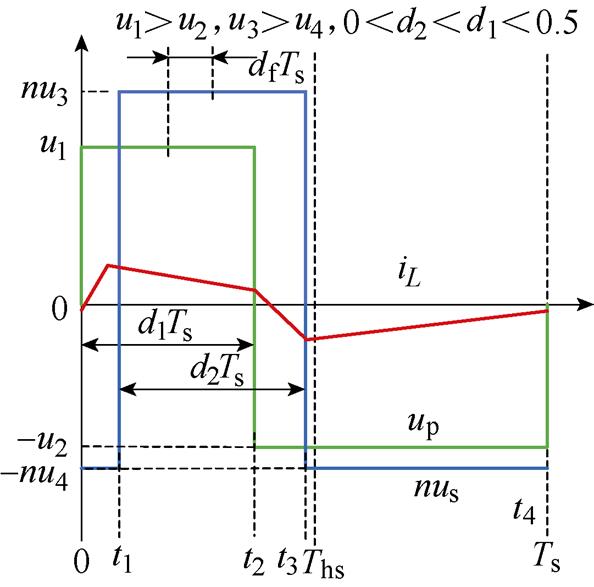
对于R<1工况开关模式11,其移相角和占空比取值范围:df∈[(d2-d1)/2, (d1+d2)/2],0<d1< d2<0.5,由波形可得一个开关周期内漏感电流表达式为
为简化表达,本文中电流及功率表达式分别对IN和PN进行标幺化得
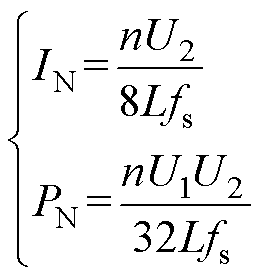
DAHB开关周期内漏感电流波形不具有对称性,但稳态下其平均值为零。将电容电压表达式(6)代入漏感电流表达式(7)并化简,由此可得各开关时刻的电流值为
由此可得每个开关周期传输的有功功率为
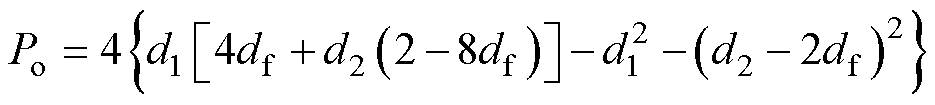 (9)
(9)
漏感电流最大值为
综上所述,三自由度控制下DAHB各开关时刻电流与输入输出电压,一、二次侧半桥占空比,移相角有关,传输功率可由三个控制自由度计算得到。
基于卡鲁什库恩塔克(Karush-Kuhn-Tucker, KKT)法[3],可建立等式和不等式约束下的多项式方程组,有
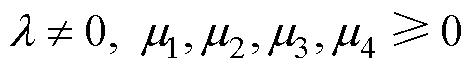 (11)
(11)
式中,L(x)为构建的拉格朗日多项式;l 和m1~m4为等式约束和不等式约束的乘子因子。由此求解满足移相角取值范围和输出功率约束条件下的漏感电流最大值的极小值,即可得到DAHB电流应力最小时的TFC局部最优解。
然而,通过求解式(11)可知,由于目标函数表达式较为复杂,无法直接求取满足约束条件的条件极值解析解,更难以在数字控制器中实时计算应用。因此,不能通过解析方法获取以电流应力最小化为目标的TFC策略。
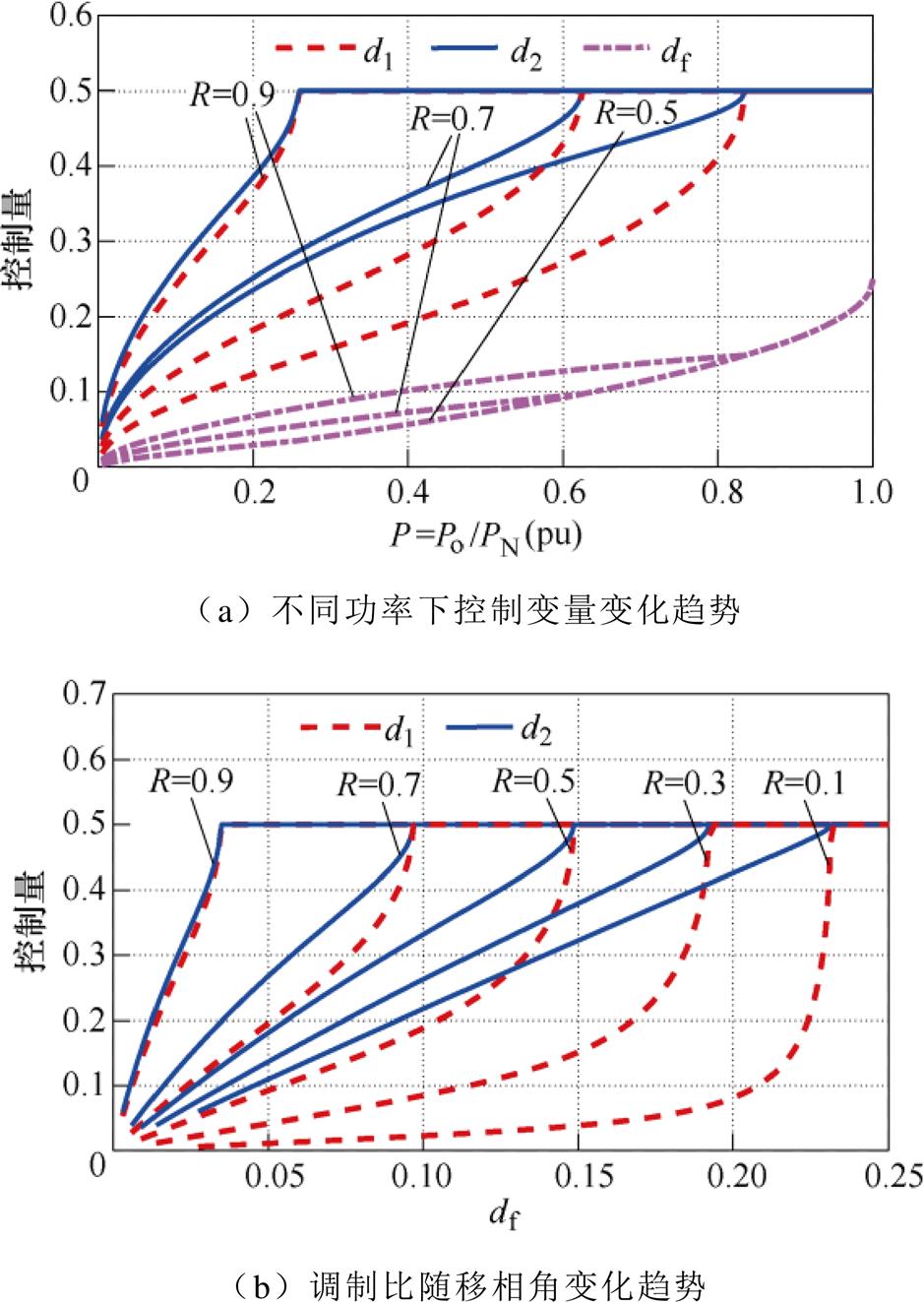
为分析TFC的可行性,以降压变换为例,采用数值分析方法。利用Matlab的Fmincon寻优函数求解式(11)目标函数,得到不同电压比R和不同输出功率P下控制量d1、d2、df取值如图5所示。
由图5可知,对于不同输出功率,调制比、移相角呈现出强非线性特性,且随着电压比的变化,最优控制参数曲线发生变化。DAHB全工况范围包含两种工作模式:TFC模式和SPS模式。对于TFC模式,考察图5b最优控制时的d1、d2与df的对应关系可知,对于同一R值,d2与df近似呈线性关系,而d1与df呈强非线性关系。因此,在TFC模式区间内,可将d2近似看作df的线性函数。
由此,根据R<1离散工况下的寻优结果,搜索出d2随df变化时DAHB由TFC模式向SPS模式转换的拐点,进而拟合得到TFC模式下d2随df变化的函数。式(12)为采用二次函数拟合得到的d2与df间的关系。
式中,k为误差校正系数,调节k取值可减小拟合误差,本文取k=0.95。
另外,采用TFC以获取最小电流应力时,结合DAHB波形特性,参考文献[13]指出,对于降压变换(R<1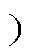 ,电流iL(t1)和iL(t3)应近似对称;对于升压变换(R>1),电流iL(t0)和iL(t2)应近似对称。由此得到
,电流iL(t1)和iL(t3)应近似对称;对于升压变换(R>1),电流iL(t0)和iL(t2)应近似对称。由此得到
联立式(12)和式(13),得到R<1工况下TFC模式区间的电流有效值最小的控制策略为
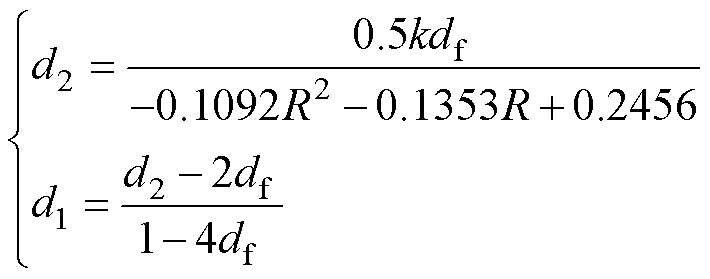 (14)
(14)
由此可得R<1时全功率范围内包含TFC模式和SPS模式的全局优化控制策略,如式(15)所示。根据对称性可得R>1工况下的全局优化控制策略如式(16)所示。
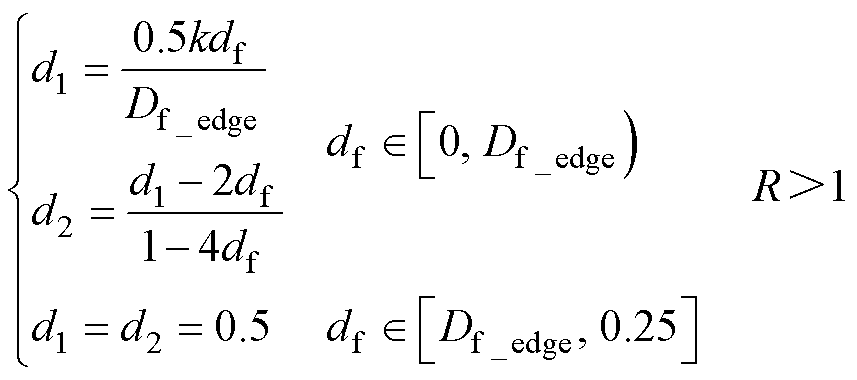 (16)
(16)
式中,Df_edge为拟合所得的全工况内SPS模式与TFC模式的分界点,即
对于R=1工况,SPS控制即能达到电流应力最小,相应的控制策略为
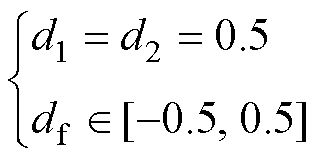 (17)
(17)
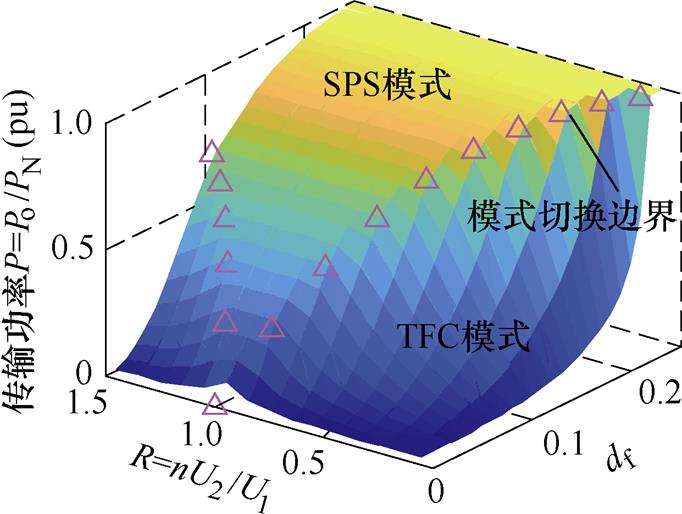
由此可得,随着R变化,全工况的优化控制策略如图6所示,其中三角形为TFC与SPS调制的功率边界。以R=0.5为例,模式切换边界处功率为P= 0.84(pu),即在输出功率低于84%PN时采用TFC调制;高于84%PN时采用SPS调制。
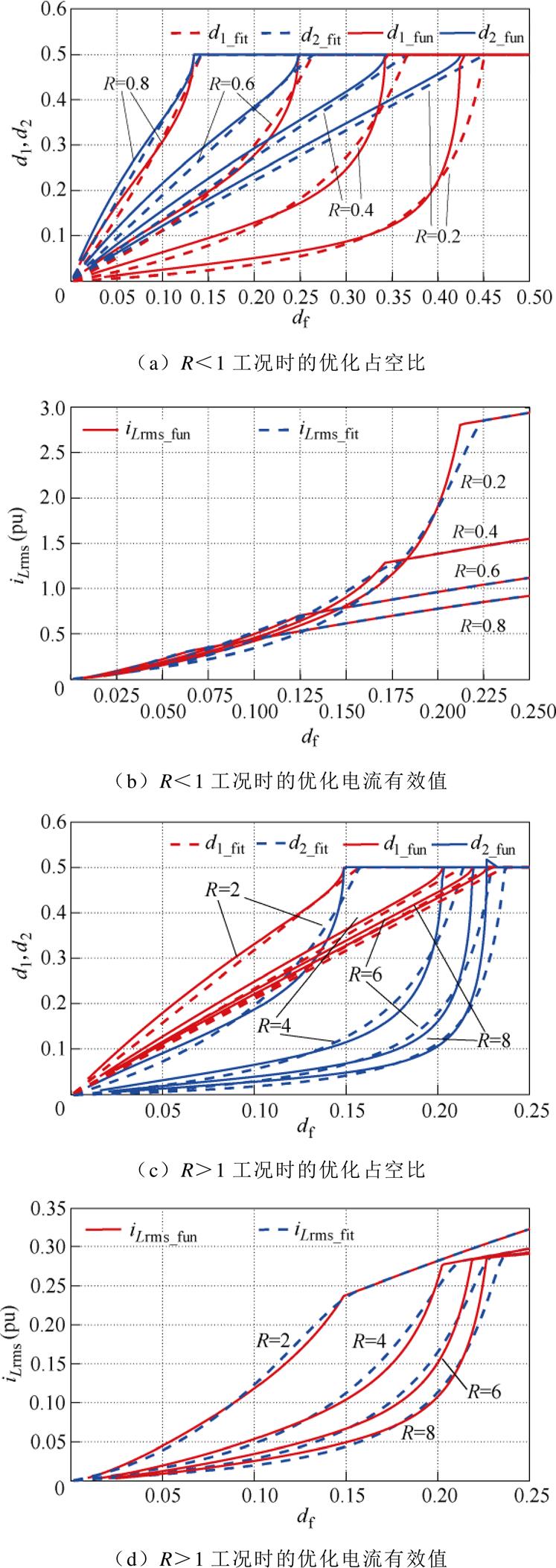
为分析TFC优化策略的有效性,对于不同的R,基于Fmincon函数的最优控制和基于模型分析和数值拟合的最优控制结果如图7所示。图中,d1_fit、d2_fit和iLrms_fit为本文TFC的优化结果;d1_fun、d2_fun和iLrms_fun为Fmincon函数的优化结果。
由图7可知,随着电压匹配程度的降低(R偏离1的程度增大),相比Fmincon寻优函数得到的最优控制指令,采用同时结合模型分析和数值拟合所得到的TFC优化控制指令d1和d2的拟合误差逐渐增大,但总体电流有效值误差较小,基本达到目标优化的效果。另外,为进一步减小拟合误差,可采用3次或更高阶次拟合函数对d2和df间的关系进行曲线拟合。
综上所述,对DAHB变换器采用三自由度控制,为规避常规解析求解不可行的问题,本文采用模型分析和数值拟合的方法对局部最优解进行求解,所得到的TFC优化策略具有统一的表达形式,且在全工况范围内连续可调,表达形式简单,计算量较小,具有较好的工程适应性。
3 DAHB优化控制开关特性
根据图6的优化策略可知,全工况内DAHB同时涉及TFC和SPS工作模式,TFC模式工作于中小功率区间,SPS模式工作于中大功率区间,两种模式平滑切换。由于TFC和SPS模式仅控制量取值范围不同,因此可采用统一模型求取各开关切换时刻的电流。
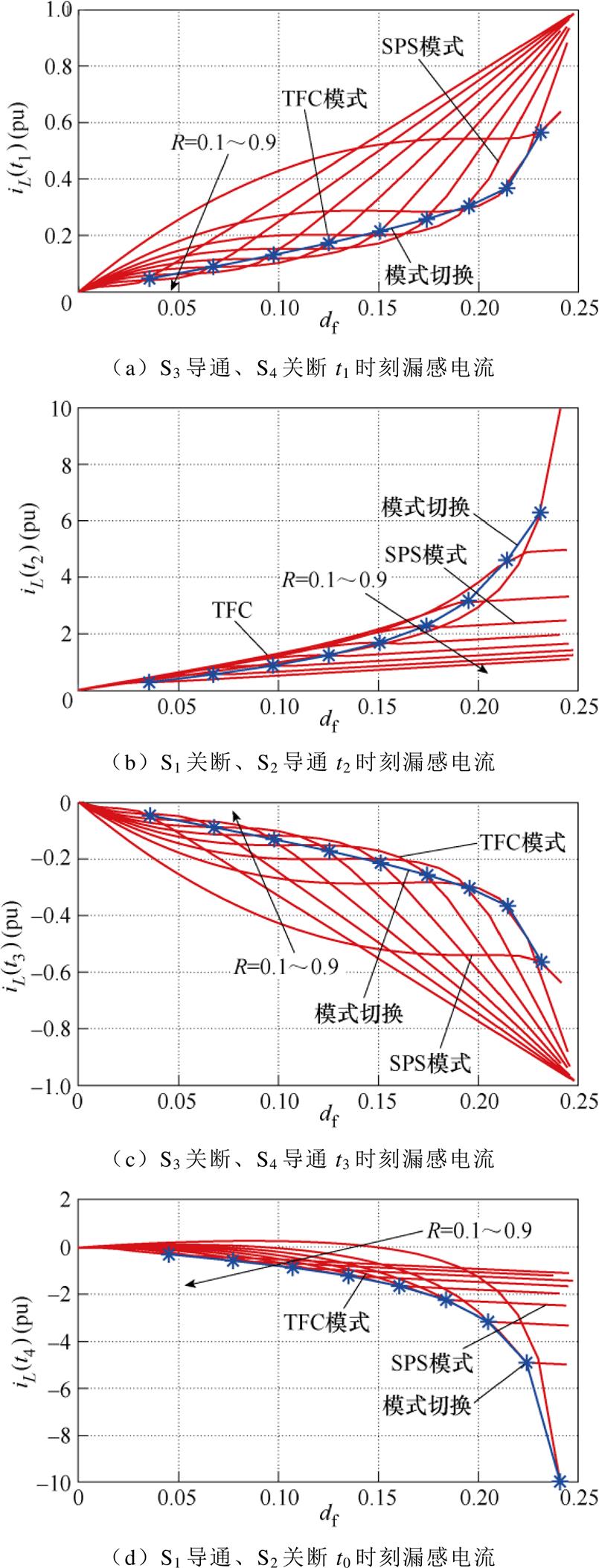
对于表2中R<1工况的最优开关模式11,不考虑死区影响,将式(15)、式(16)代入式(8),得到各开关时刻漏感上的电流如图8所示。
由图8可知,全工况内,t1时刻S3导通、S4关断,iL(t1)始终为正;t2时刻S1关断、S2导通,iL(t2)始终为正;t3时刻S3关断、S4导通,iL(t3)始终为负;t4时刻S1导通、S2关断,同时存在iL(t4)>0和iL(t4)<0的情况。
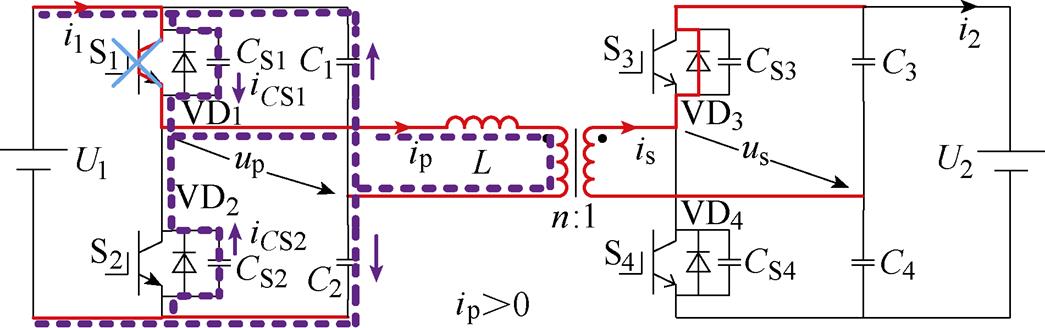
为得到各器件的开关特性,以图9所示的S1关断、S2导通过程(t2时刻)为例进行分析。在t2时刻前,S1和S3导通,漏感电流iL>0,电流流经S1、C2、VD3和C3。t2时刻S1关断,电感L和开关管寄生电容CS1和CS2谐振,使得CS1充电、CS2放电,电流从S1换流至VD2。根据图8b可知,S2开通时iL>0,VD2续流,S2实现零电压开通。因此,在t2时刻S1实现硬关断,S2实现零电压开通。
同理可得降压变换下采用优化控制策略时DAHB全功率范围内其他器件的开关特性:图8a中,S3为ZVS开通,S4为硬关断。图8c中,S3为硬关断,S4为ZVS开通。图8d中,iL>0时,S1小电流开通、S2零电流关断;iL<0时,S1为ZVS开通、S2硬关断。
综上所述,对于R<1降压变换,采用TFC策略,DAHB所有开关器件均可实现软开关。根据DAHB对称性,可得R>1升压变换时,采用TFC策略,各开关器件也能实现全工况的软开关,从而降低开关损耗。
4 仿真、实验与分析
为验证所提出的TFC优化控制策略的有效性,搭建DAHB仿真模型和400 W样机平台,如图10所示。
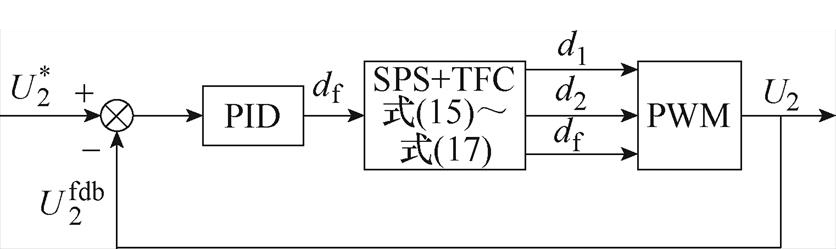
DAHB实验参数见表3。采用图11所示的单电压闭环控制框图,PID调节器生成的移相角经优化调制关系换算占空比和移相比,最后生成PWM脉冲。
表3 DAHB实验参数
Tab.3 Experimental parameters of DAHB

参 数数 值 输入电压U1/V200 变压器匝比n1 漏感L/mH80 输出电压U2/V100~300 开关频率fs/kHz20 额定功率Prate/W400
4.1 桥臂串联电容平均电压计算
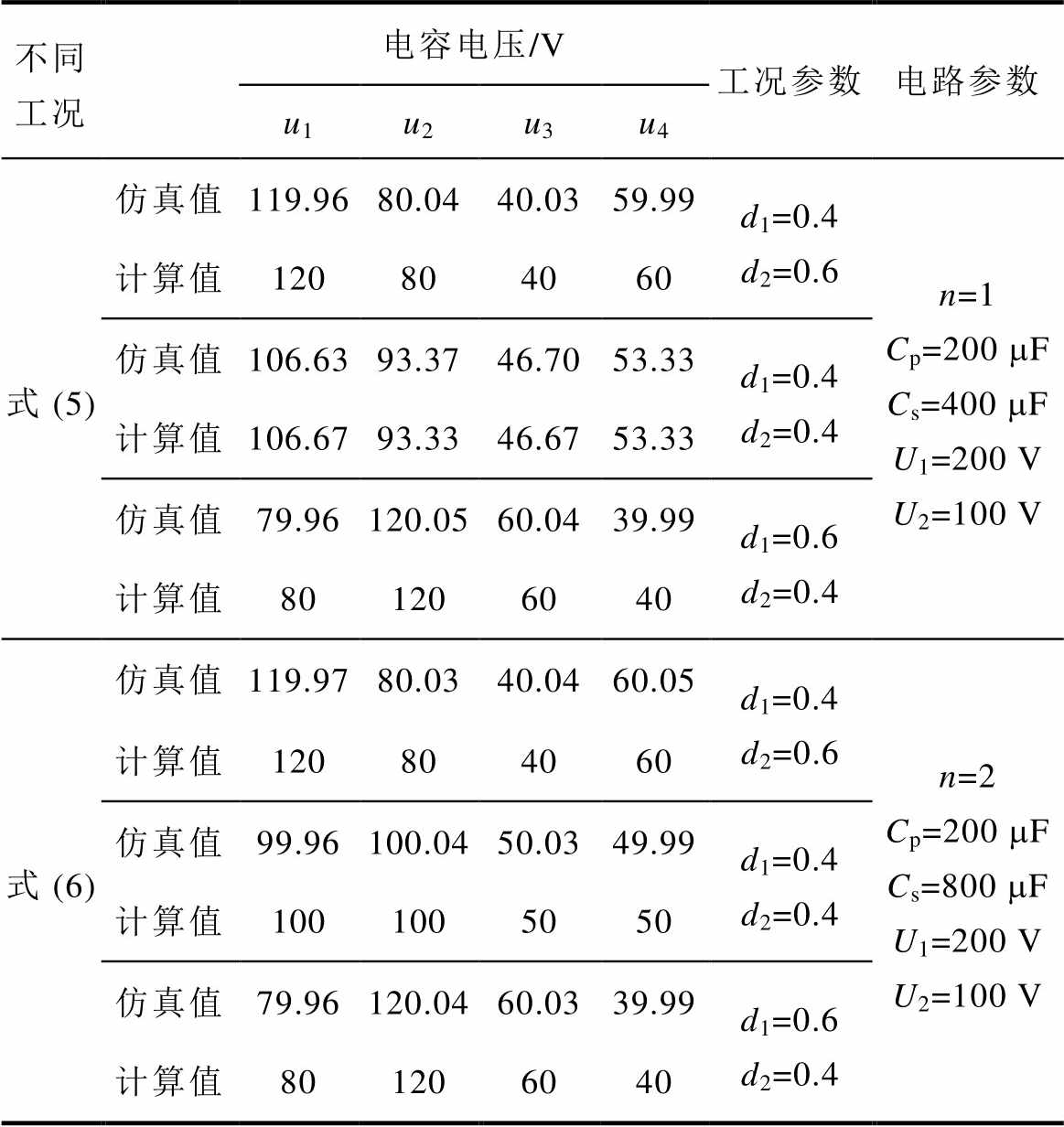
根据DAHB数学模型推导,桥臂串联电容稳态平均电压不仅和占空比d1、d2相关,还和变压器匝比n、直流电压U1和U2、电容Cp和Cs取值相关。表4为R=0.5时,不同工况下一、二次侧桥臂串联电容稳态平均电压的仿真值和计算值。
表4 R=0.5时不同工况下电容电压仿真值和计算值对比
Tab.4 Simulation and calculation value of capacitor voltage when R=0.5
不同工况电容电压/V工况参数电路参数 u1u2u3u4 式 (5)仿真值119.9680.0440.0359.99d1=0.4 d2=0.6n=1Cp=200 mFCs=400 mFU1=200 VU2=100 V 计算值120804060 仿真值106.6393.3746.7053.33d1=0.4 d2=0.4 计算值106.6793.3346.6753.33 仿真值79.96120.0560.0439.99d1=0.6 d2=0.4 计算值801206040 式 (6)仿真值119.9780.0340.0460.05d1=0.4 d2=0.6n=2Cp=200 mFCs=800 mFU1=200 VU2=100 V 计算值120804060 仿真值99.96100.0450.0349.99d1=0.4 d2=0.4 计算值1001005050 仿真值79.96120.0460.0339.99d1=0.6 d2=0.4 计算值801206040
结果显示,在U1=200 V、U2=100 V时,不同的电压比、占空比和电容取值下,桥臂串联电容稳态电压的仿真值和式(5)、式(6)计算值高度吻合,误差在0.1%以内,从而验证了电容电压理论计算的正确性。
4.2 TFC优化控制验证
为减小DAHB电压不匹配时的电流应力、提升效率,采用TFC策略。以R=0.5工况为例,不同输出功率下的交流链路时域波形如图12所示。
由图12可知,电压不匹配以及负载差异(即占空比差异),导致同一桥臂串联电容稳态电压存在偏差,一、二次侧输出不对称的矩形波电压,绕组电流为不对称波形。随着工况变化,占空比和移相角实时调整,进而优化开关器件电流应力,提升变换器效率。
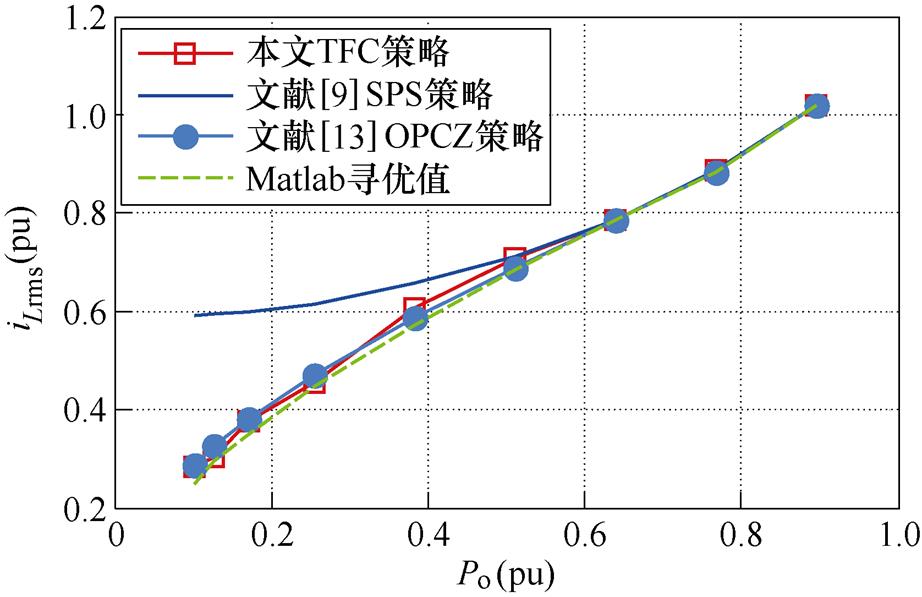
当DAHB以恒压模式运行时,随着输出功率变化,不同控制策略下的交流链路电流应力如图13所示。
由图13可知,对于R=0.5工况,在中小功率区间,采用SPS控制的电流应力比采用多自由度控制策略的电流应力大很多;本文的TFC优化效果和Matlab寻优结果、文献[13]优化效果相当。然而,Matlab所采用的理论优化策略无法获得解析解,且文献中的优化策略需要3个PI调节器,而本文只需1个PI调节器,解析解连续、简洁。
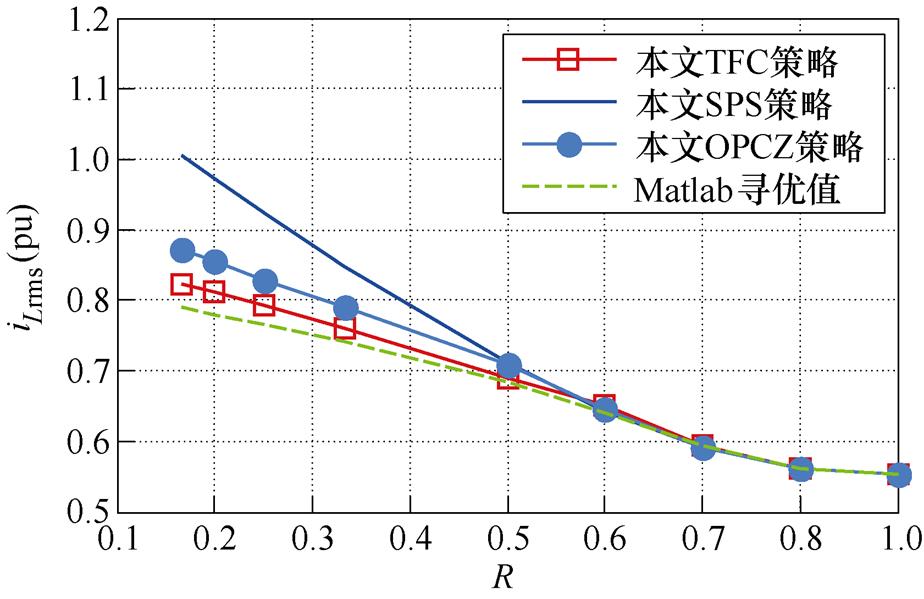
当DAHB输出电流恒定时,随着R(等效于输出功率)变化,Io=2 A时不同控制策略的交流链路电流应力如图14所示。
由图14可知,随着R接近1,一、二次电压匹配程度增大,各策略下电流应力减小。本文TFC策略所获得的电流应力比文献[13]中的OPC策略小,略大于Matlab解析计算的结果,可能的原因是线性拟合和近似等效方法造成的误差。
4.3 功率器件开关特性
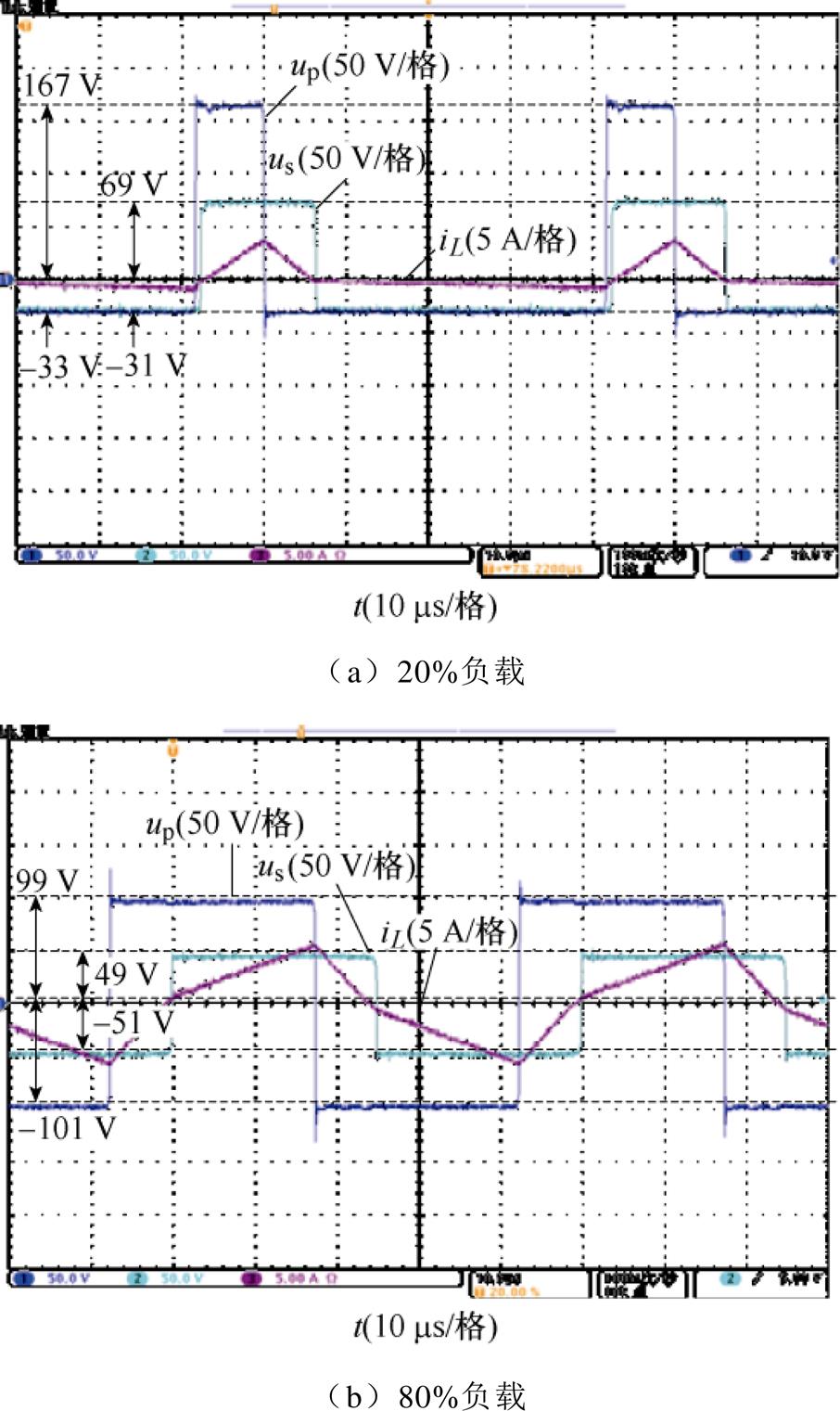
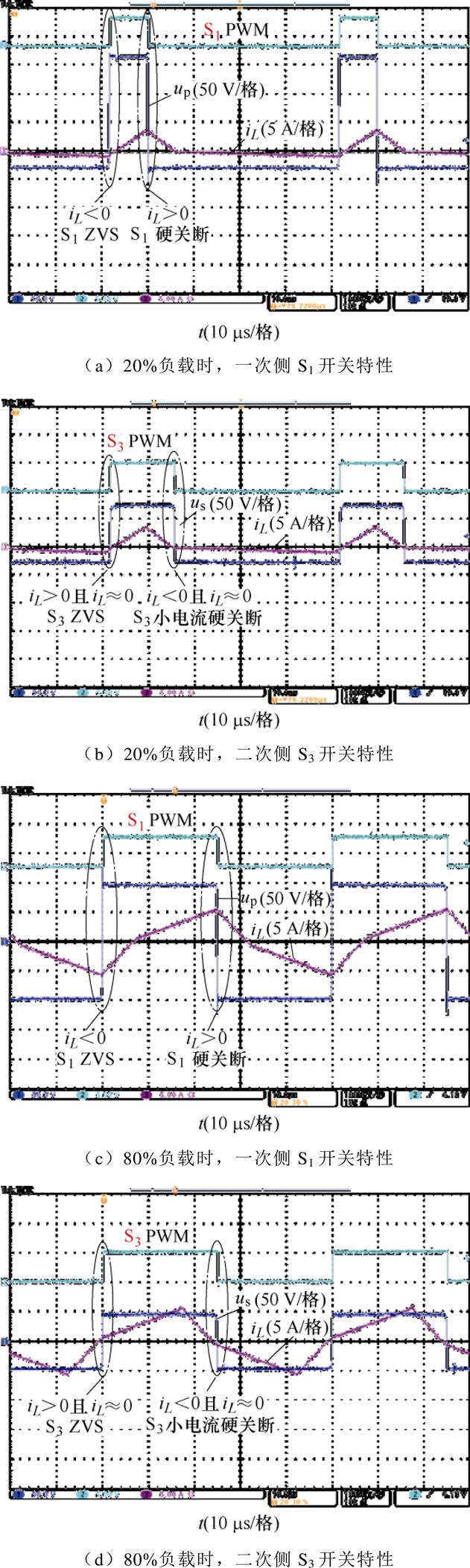
对于不匹配电压工况,采用TFC策略,不仅可以减小开关器件的电流应力,同时也能获得几乎全工况的软开关特性。当DAHB输出R=0.5时,在20%负载和80%负载工况下,一、二次侧开关器件的开关波形如图15所示。
半桥上、下管互补导通,从图15可知,在轻载和重载工况下,一次侧开关管S1、S2均能实现零电压开通和硬关断;二次侧开关管S3、S4均能实现零电压开通和小电流硬关断;滞后桥臂的开关电流近似为零。另外,结合DAHB结构的对称性以及TFC控制策略在R>1和R<1工况的对称性可知,将 R<1工况下的开关特性推广到R>1工况,可知在采用TFC后,DAHB可实现全工况的软开关。
5 结论
本文针对DAHB变换器电压不匹配运行时存在的回流功率大、电流应力高等问题,从DAHB等效数学模型出发,推导了三自由度控制下的桥臂串联电容稳态电压的解析表达式;在此基础上,得到三自由度控制下的最优开关模式;采用模型分析加数值拟合的方法,得到基于PWM+移相的三自由度全工况优化控制策略,并分析了各开关器件的全工况软开关特性;最后,通过仿真及实验验证了桥臂串联电容电压计算的正确性以及优化控制策略的有效性。实验表明,相对现有的SPS和双自由度控制策略,所提出的三自由度优化控制可在电压不匹配工况中、特别是轻载条件下,提高DAHB变换器的效率,减少其电流应力及损耗;与现有的三自由度控制策略相比,本文提出的控制策略更加简洁,减少了PI调节器数量,更易于工程实现。
参考文献
[1] 刘计龙, 陈鹏, 肖飞, 等. 面向舰船综合电力系统的10 kV/2 MW模块化多电平双向直流变换器控制策略[J]. 电工技术学报, 2023, 38(4): 983-997.
Liu Jilong, Chen Peng, Xiao Fei, et al. Control strategy of 10 kV/2 MW modular multilevel bidire- ctional DC-DC converter for vessel integrated power system[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 983-997.
[2] 杨向真, 王锦秀, 孔令浩, 等. 电压不匹配运行条件下双有源桥变换器的效率优化方法[J]. 电工技术学报, 2022, 37(24): 6239-6251.
Yang Xiangzhen, Wang Jinxiu, Kong Linghao, et al. Efficiency optimization method of DAB converters under wide-voltage operating conditions[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(24): 6239-6251.
[3] 任强, 艾胜. 全工况范围的DAB三自由度优化控制策略[J]. 中国电机工程学报, 2020, 40(11): 3613- 3622.
Ren Qiang, Ai Sheng. A three degree freedom optimal control strategy of dual-active-bridge converters for full range operations[J]. Proceedings of the CSEE, 2020, 40(11): 3613-3622.
[4] 熊飞, 吴俊勇, 郝亮亮, 等. 隔离型双半桥DC-DC变换器的软开关特性[J]. 电工技术学报, 2017, 32(10): 196-205, 221.
Xiong Fei, Wu Junyong, Hao Liangliang, et al. Soft switching characteristics of the dual-half-bridge DC- DC converter[J]. Transactions of China Electrotech- nical Society, 2017, 32(10): 196-205, 221.
[5] Kang Xiangli, Li Shouxiang, Smedley K M. Decoupled PWM plus phase-shift control for a dual- half-bridge bidirectional DC-DC converter[J]. IEEE Transactions on Power Electronics, 2018, 33(8): 7203-7213.
[6] Gao Fei, Mugwisi N, Rogers D J. Average modeling of a dual-half-bridge converter modulated with three degrees of freedom[J]. IEEE Transactions on Transpo- rtation Electrification, 2021, 7(3): 1016-1030.
[7] Zhao Biao, Song Qiang, Liu Wenhua, et al. Overview of dual-active-bridge isolated bidirectional DC-DC converter for high-frequency-link power-conversion system[J]. IEEE Transactions on Power Electronics, 2014, 29(8): 4091-4106.
[8] 吴俊娟, 孟德越, 申彦峰, 等. 双重移相控制与传统移相控制相结合的双有源桥式DC-DC变换器优化控制策略[J]. 电工技术学报, 2016, 31(19): 97- 105.
Wu Junjuan, Meng Deyue, Shen Yanfeng, et al. Optimal control strategy of dual active bridge DC-DC converter with combined dual-phase-shift and traditional-phase-shift controls[J]. Transactions of China Electrotechnical Society, 2016, 31(19): 97- 105
[9] Chakraborty S, Chattopadhyay S. Analysis and com- parison of voltage-source and current-source asymme- tric dual-active half-bridge converters[C]//2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 2014: 2072-2079.
[10] Gao Fei, Rogers D. Duty-cycle plus phase-shift control for a dual active half bridge based bipolar DC microgrid[C]//2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 2018: 1479-1485.
[11] 胡广, 胡维昊, 唐远鸿, 等. 基于强化学习的双主动半桥直流变换器的效率优化方案[J]. 电工技术学报, 2022, 37(增刊1): 225-234.
Hu Guang, Hu Weihao, Tang Yuanhong, et al. Efficiency optimization scheme of dual-active-half- bridge DC-DC converter based on reinforcement learning[J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 225-234.
[12] Chakraborty S, Chattopadhyay S. Minimum-RMS- current operation of asymmetric dual active half- bridge converters with and without ZVS[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5132-5145.
[13] Chakraborty S, Tripathy S, Chattopadhyay S. Mini- mum RMS current operation of the dual-active half- bridge converter using three degree of freedom control[C]//2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 2017: 1-8.
[14] Chakraborty S, Chattopadhyay S. Fully ZVS, mini- mum RMS current operation of the dual-active half-bridge converter using closed-loop three-degree- of-freedom control[J]. IEEE Transactions on Power Electronics, 2018, 33(12): 10188-10199.
[15] Zhao Shuang, Umuhoza J, Zhang Yuzhi, et al. Analysis and optimization of a high-efficiency resi- dential energy harvesting system with dual half- bridge converter[C]//2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 2017: 2838-2844.
[16] He Peiwen, Khaligh A. Comprehensive analyses and comparison of 1 kW isolated DC-DC converters for bidirectional EV charging systems[J]. IEEE Transa- ctions on Transportation Electrification, 2017, 3(1): 147-156.
[17] Chakraborty S, Palmal M, Chattopadhyay S. Appro- aches for continuous-time dynamic modeling of the asymmetric dual-active half-bridge converter[C]// 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 2018: 952-958.
[18] Tissières M, Askarian I, Pahlevani M, et al. A digital robust control scheme for dual half-bridge DC-DC converters[C]//2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 2018: 311-315.
[19] 侯旭, 曾正, 冉立, 等. 基于扩展移相控制的双向有源桥变换器回流功率优化[J]. 中国电机工程学报, 2018, 38(23): 7004-7014, 7134.
Hou Xu, Zeng Zheng, Ran Li, et al. Backflow power optimization of dual active bridge converter based on extended-phase-shift control[J]. Proceedings of the CSEE, 2018, 38(23): 7004-7014, 7134.
[20] Lin Nan, Zhao Zhe, Diao Fei, et al. A current-fed dual-half-bridge-based composite converter with improved light-load efficiency through a multi- variable optimization[J]. IEEE Transactions on Trans- portation Electrification, 2022, 8(2): 3008-3020.
[21] Li Haoyu, Zhao Lei, Xu Chuanyu, et al. A dual half-bridge phase-shifted converter with wide ZVZCS switching range[J]. IEEE Transactions on Power Electronics, 2018, 33(4): 2976-2985.
[22] 侯旭, 曾正, 冉立, 等. 基于扩展移相控制的双向有源桥变换器回流功率优化[J]. 中国电机工程学报, 2018, 38(23): 7004-7014, 7134.
Hou Xu, Zeng Zheng, Ran Li, et al. Backflow power optimization of dual active bridge converter based on extended-phase-shift control[J]. Proceedings of the CSEE, 2018, 38(23): 7004-7014, 7134.
Analysis and Control of Dual-Active Half-Bridge DC-DC Converter with PWM Plus Phase Shift
Ren Qiang Kang Wei Jiang Yapeng Qin Zhu
(National key Laboratory of Electromagnetic Energy Naval University of Engineering Wuhan 430033 China)
Abstract The dual-active half-bridge (DAHB) converter has the advantages of high-frequency galvanic isolation, symmetric topology, and soft-switching. It has few power devices, low count, and no dc offset current, suitable for low-power dc–dc power conversion applications. In the case of renewable energy and energy storage equipment access, the DAHB converter operates in a broad input and output voltage range, where the rough traditional single-phase shift control (SPC) strategy usually leads to high current stress and power loss. Existing DAHB multi-phase shift control has problems like inaccurate capacitor voltage calculation, complicated control algorithm, and large computational quantity. Therefore, this paper presents a three-degree freedom control (TFC) strategy based on PWM plus phase-shift concepts.
Firstly, according to the operation mechanism of the DAHB converter, the equivalent circuit is established considering the coupling relationship between the primary and secondary sides of the transformer. The accurate expression of the series capacitor voltage is derived from the voltage-second balance of inductance L and the charge balance of capacitors in the charge and discharge process. The capacitor voltage of each bridge arm is related to the transformer turn ratio n, duty cycle d1d2, input and output voltage U1U2, and capacitance value CpCs. Secondly, based on the principle of PWM and phase-shift control, 18 possible switching modes of DAHB in a wide voltage range are listed, with three control degrees of freedom (phase shift df, primary- and secondary-side duty cycles d1d2) as variables. The optimal switching mode is chosen for minimum reactive power, and the analytical expressions of key electrical parameters are derived. Thirdly, according to the Karush-Kuhn-Tucker (KKT) method, the local optimal equation containing equality and inequality constraints is established to solve the optimal control strategy. This paper adopts model simplification and linear approximation methods to solve complicated optimal equations. Using MATLAB’s ‘fmincon’ function, the optimal combination of duty cycles and phase shifts in different working conditions is obtained. Then, drawing duty cycle change curves with phase shifts under different powers, the linear fitting between d2 and df is carried out. According to the current waveform characteristics, the constraint relationship between d1 and d2 df is analyzed. Thus, the analytical expression of the TFC strategy under boost and buck conditions is obtained. The optimal control strategy of the DAHB converter in the full power range consists of SPS and TFC strategies. Finally, the optimization effect and soft switching characteristics of the TFC are analyzed by PLECS simulation and a 400 W DAHB converter experiment platform.
The following conclusions can be drawn from simulation and experimental results: (1) The capacitor voltage calculation formula can accurately calculate the capacitor voltage of the DAHB bridge arm in various working conditions. The error is verified by simulation within 0.1%. (2) Compared with existing SPC and other dual-degree freedom control strategies, the proposed TFC strategy reduces the current stress and power loss of the DAHB under voltage mismatch, especially in light load. (3) The proposed strategy reduces the number of PI regulators, which is easy to implement in engineering.
keywords:DC-DC converter, dual-active half-bridge (DAHB), three-degree of freedom, optimal control, soft switching
DOI: 10.19595/j.cnki.1000-6753.tces.230917
中图分类号:TM46
国家自然科学基金资助项目(52107063)。
收稿日期 2023-06-14
改稿日期 2023-07-25
作者简介
任 强 男,1989年生,助理研究员,研究方向为电力电子电能变换。E-mail: im_qiangren@126.com
康 薇 女,1998年生,博士研究生,研究方向为DC-DC变换器调制控制策略与优化设计。E-mail: kangxiaodouxjtu@163.com(通信作者)
(编辑 陈 诚)
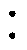 1)。变换器输入输出端直流电压分别为U1、U2,电流分别为i1、i2;变压器两端电压分别为up、us,电流为ip、is;半桥结构由开关器件(开关管S1~S4、反并联二极管VD1~VD4)和串联电容(C1~C4)组成,电容稳态电压分别为u1~u4。通过高频交流链路实现电气隔离,高频化有助于减小无源器件的体积,进而实现高功率密度。为实现双向功率变换,半桥开关器件占空比通常为50%,通过调节两侧半桥输出电压间的相位,实现功率流向和功率大小的控制。此种单移相控制(Single Phase Shift, SPS)调制策略,仅利用了DAHB的一个控制自由度,在电压不匹配工况下,特别是中轻负载范围内,控制策略粗放,存在电流应力大、软开关范围小、效率低等问题[7-8]。
1)。变换器输入输出端直流电压分别为U1、U2,电流分别为i1、i2;变压器两端电压分别为up、us,电流为ip、is;半桥结构由开关器件(开关管S1~S4、反并联二极管VD1~VD4)和串联电容(C1~C4)组成,电容稳态电压分别为u1~u4。通过高频交流链路实现电气隔离,高频化有助于减小无源器件的体积,进而实现高功率密度。为实现双向功率变换,半桥开关器件占空比通常为50%,通过调节两侧半桥输出电压间的相位,实现功率流向和功率大小的控制。此种单移相控制(Single Phase Shift, SPS)调制策略,仅利用了DAHB的一个控制自由度,在电压不匹配工况下,特别是中轻负载范围内,控制策略粗放,存在电流应力大、软开关范围小、效率低等问题[7-8]。

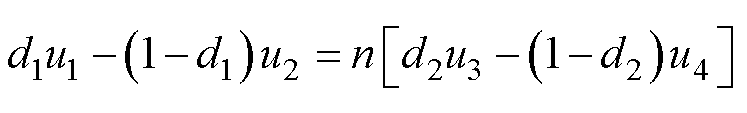 (1)
(1)
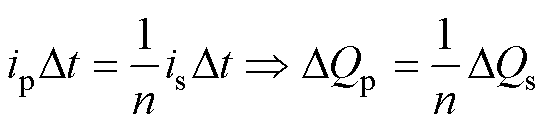
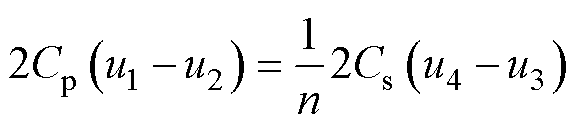 (2)
(2)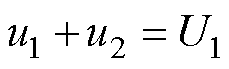 (3)
(3)
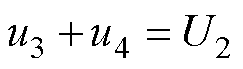 (4)
(4)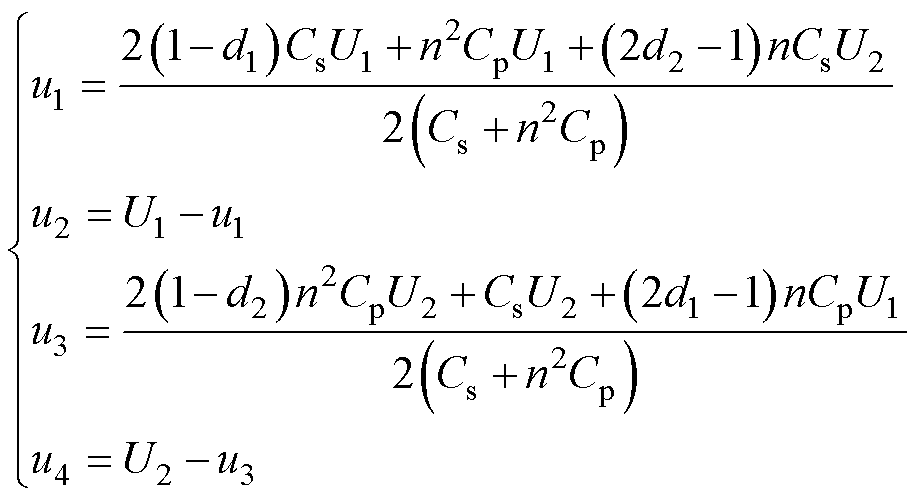 (5)
(5)
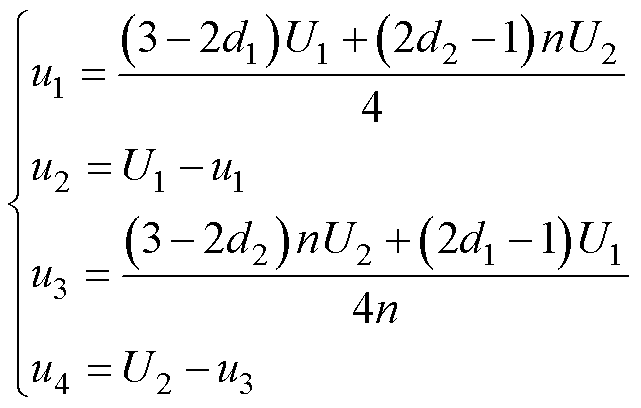 (6)
(6)

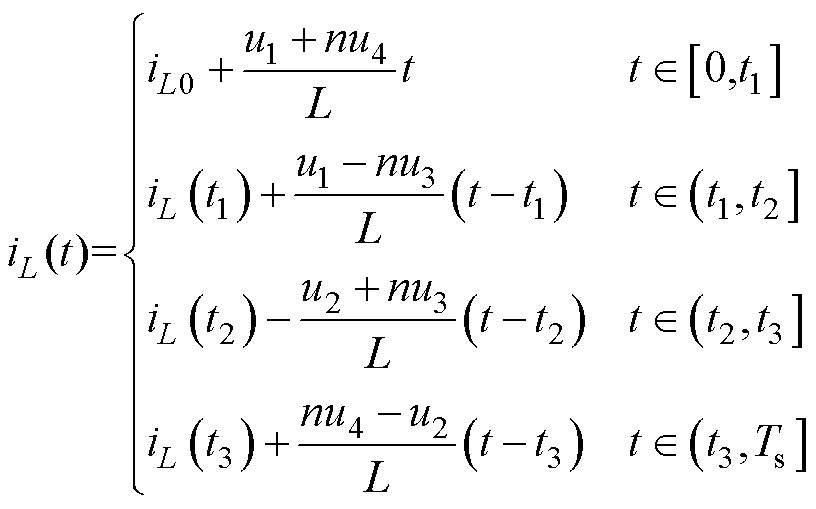 (7)
(7)
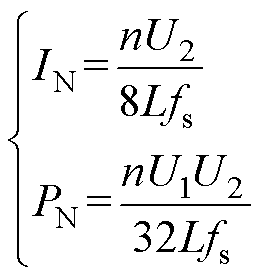
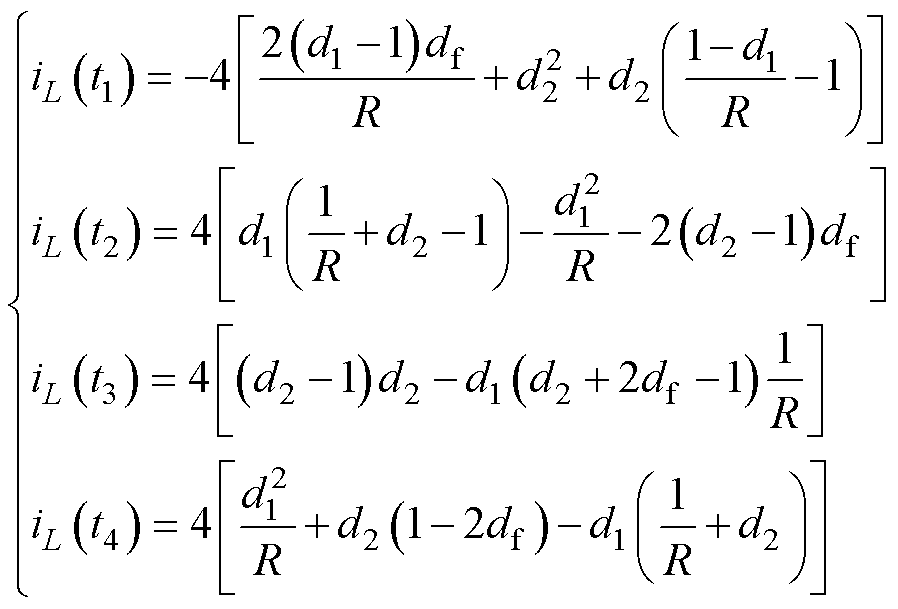 (8)
(8)
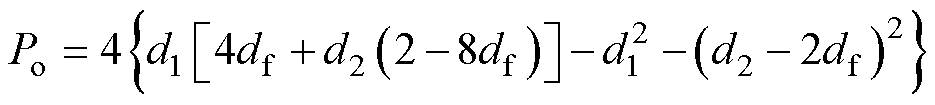 (9)
(9)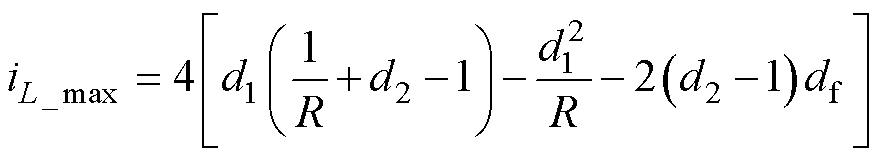 (10)
(10)
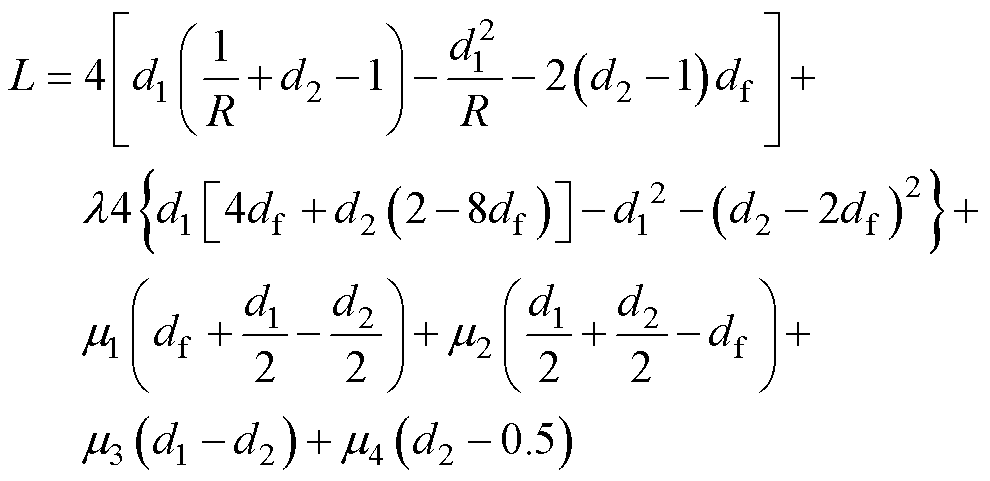
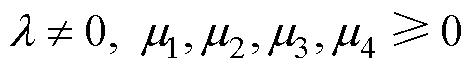 (11)
(11)
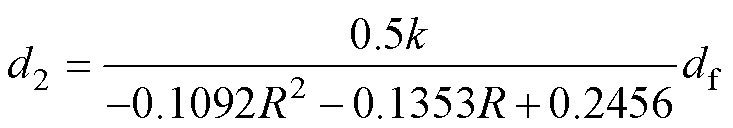 (12)
(12)
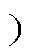 ,电流i
,电流i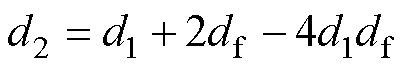 (13)
(13)
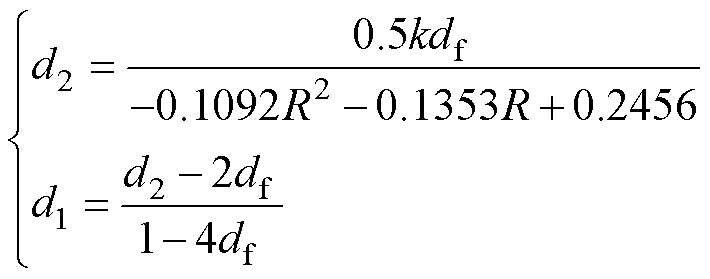 (14)
(14)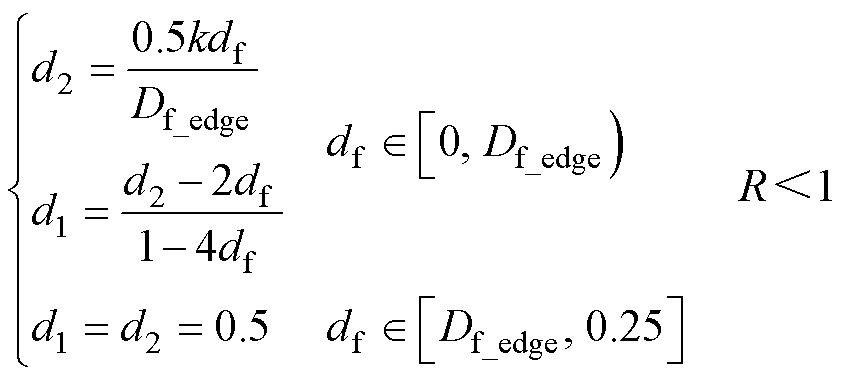 (15)
(15)
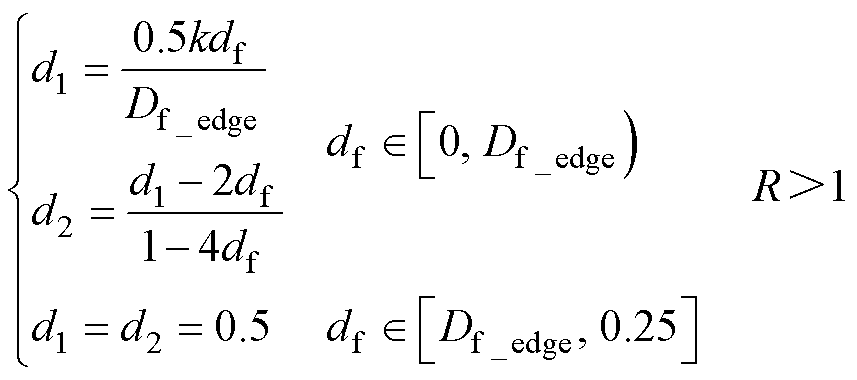 (16)
(16)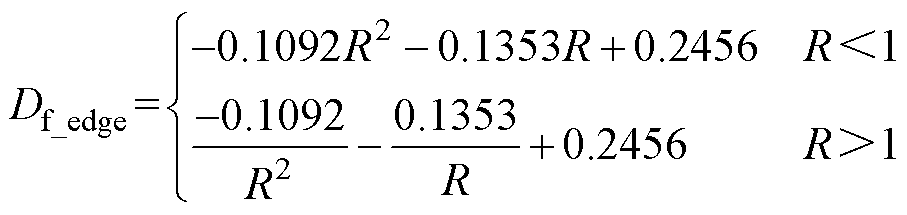
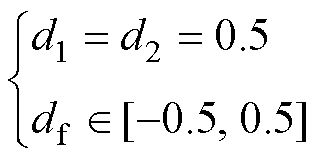 (17)
(17)