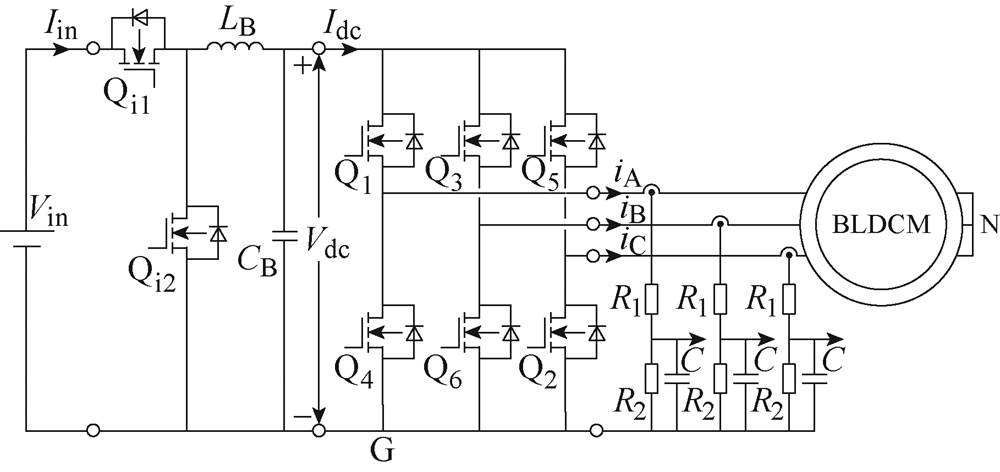
图1 无刷直流电机驱动及采样电路
Fig.1 BLDCM drive and sampling circuit
摘要 超高速无刷直流电机广泛应用于超高速空压机、晶圆切割、飞轮储能等系统。针对超高速无刷直流电机控制中的三相绕组不完全对称和参考零点不确定偏移导致的失步问题,该文以脉幅调制控制器为基础,通过对非理想电机的研究,建立过零点抗扰动的模型,提出一种综合考虑不平衡过零点和不对称过零点补偿的改进控制策略,建立适用于三种非理想过零点模型的基础延迟时间择优策略的数学模型和换向时间补偿函数。同时,在不平衡不对称过零点扰动存在的前提下,考虑负载变化等因素引起的换相误差并提出相应的变速误差补偿策略。实验结果表明,改进控制策略可以有效减小无刷直流电机的换相误差,显著地提高电机换相的精度进而提高其运行速度上限,为无速度传感器超高速无刷直流电机稳定运行提供了一定的理论基础。
关键词:脉幅调制 反电动势过零点 三相绕组不完全对称 参考零点偏移 超高速控制
超高速电机广泛应用于高速空压机[1]、晶圆切割、飞轮储能等系统,在无刷直流电机控制领域,采用无位置传感器技术来替代霍尔传感器具有诸多优势[2]。在众多无传感器技术中,基于反电动势过零点(Zero-Crossing Point, ZCP)的换相技术凭借其配置简单和控制容易而在高速电机控制领域广泛应用。然而,在超高速运行时,如果无刷直流电机(Brushless DC Motor, BLDCM)的过零点检测出现严重的非理想误差,电机将会发生失步故障。当转子处于超高速旋转且失去控制时,会释放出巨大的不可控能量,从而导致灾难性后果。
目前,基于反电动势ZCP的无刷直流电机换相检测技术的研究主要集中在转速为60 000 r/min以下的中高速电机控制领域。文献[3]提出了一种考虑反电动势不对称问题的高精度无传感器最优换相偏差校正策略,但未考虑不平衡ZCP对换相造成的影响,且实验转速较低,在超高速条件下算法的可靠性有待验证。文献[4]提出一种基于Buck变换器的无刷直流电机无位置传感器控制方法,有效地削弱了PWM过程中高频谐波信号对前后级电路的冲击,母线电流及相电流波形更加平稳,并提出了一种结构简单、学习能力强的基于模糊神经网络(Fuzzy Neural Network, FNN)的相位调节器,但未考虑检测获得ZCP存在非理想因素的问题,且实验转速等级较低,超高速条件下算法的可靠性和可行性有待验证。文献[5]深入分析了非对称电机参数,即相电阻和电感对无传感器换相的影响,并提出了响应的解决办法,但提出方法仅适用于3次谐波反电动势的换相策略。文献[6]提出了利用不平衡ZCP相互抵消的方式解决了参考零点存在不确定的偏移问题,并给出了相应的电角度到时间的导出函数,但未给出参考零点偏移的判定方法,也未考虑电机三相绕组不完全对称的问题。文献[7-9]引入了闭环校正的方式进行换相延时的校正,对于制造精度较高的电机,此类方法效果显著,但是对于制造工艺一般的电机,由于三相绕组本身就是不对称的,六步换相的每一步延时并不是完全相同的,这是此类闭环校正方法存在的问题。文献[10-12]采用高频注入结合自适应位置观测器的方法对转子位置进行观测。文献[13]在高频电压注入基础上采用位置反馈的电流解调方法,但上述控制算法的复杂度过高且均会提高控制器的成本。
上述利用反电动势和反电动势ZCP的换相检测技术,都未完全解决电机三相绕组不完全对称和参考零点存在不确定偏移的问题,这些问题使得反电动势ZCP的换相检测技术,在电机的转速达100 000 r/min以上的超高速控制领域的应用遇到瓶颈。如果引入复杂的补偿方法来解决这一问题,将会给控制器带来相对较大的工作量增加控制器的负担,从而丧失反电动势ZCP的换相检测技术配置和控制十分简单的优势。因此,必须要寻找到一种相对简单高效的方式来解决这一问题。
本文采用Buck变换器来替代传统的PWM斩波方式,实现无位置传感器控制的无刷直流电机。旨在突破传统电压源逆变器[14-15]调制方式对电机转速的限制。通过对非理想电机可能存在的三相绕组不对称和参考零点不确定偏移问题进行详细分析,探索反电动势ZCP间隔之间的内在规律。本文提出了一种综合考虑不平衡ZCP和不对称ZCP的新型补偿方法,并推导出三种非理想ZCP情况下的基础延迟时间设定方法。同时,给出了相对应的电角度到时间的导出函数的设定方法,该函数可广泛应用于各种电角度延迟时间的计算。所提出的补偿算法简单方便、易于实现,有效地解决了超高速条件下电机三相绕组不完全对称和参考零点不确定偏移的问题,使得电机在转速达到230 000 r/min时能够稳定运行。
基于Buck的无刷直流电机驱动系统及采样电路如图1所示。前端Buck斩波电路进行的脉幅调制(Pulse Amplitude Modulation, PAM),三相逆变桥只参与换相,不进行调制。图中,Vin和Iin分别为供电电源的电压和电流,Vdc和Idc分别为Buck电路输出的电压和电流,iA、iB、iC分别为电机三相电流,R1和R2分别为端电压采样电阻。
电机定子在六步换相的任何一步,只有两个相位处于活动状态,其中电流流入一相并流出另一 相[16]。例如,在0~60°范围内,A相和B相都导通,而C相是悬空的。此阶段,Idc=-iA=iB,iC=0。只考虑反电动势暴露出来的情况,电机的端电压与反电动势之间的关系[17-18]为:

图1 无刷直流电机驱动及采样电路
Fig.1 BLDCM drive and sampling circuit
当AB相导通、C相悬空时,有
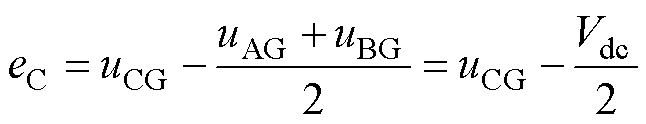 (1)
(1)
当AC相导通、B相悬空时,有
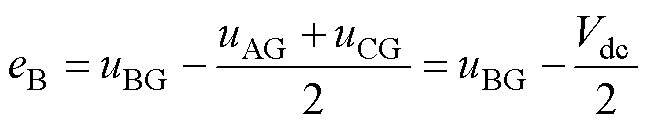 (2)
(2)
当BC相导通、A相悬空时,有
 (3)
(3)
式中,eA、eB、eC分别为A、B、C相反电动势;uAG、uBG、uCG分别为A、B、C相的端电压;Vdc为Buck变换器的输出母线电压。
分析式(1)~式(3)可知,当其中一相处于悬空状态时,该相的反电动势将通过其端电压得以显示。在实际应用中,还需考虑到换相过程中二极管的续流现象。二极管的续流完成后,该相的反电动势将完全暴露在端电压的检测中。
ZCP的检测方法主要分为两种:一种是采用端电压中暴露出来的反电动势与直流链路[19]电压比较来检测ZCP;另一种是利用三相端电压合成虚拟中心点[20]电压,并将端电压中暴露出来的反电动势与虚拟中心点电压进行比较来检测ZCP。这两种方法本质上都是通过端电压中暴露出来的反电动势电压与Vdc/2进行比较来检测ZCP,在理论上这两种方法是等效的。
实际上,反电动势法在检测过零点时,是检测采集端电压上升部分和下降部分,波形上、下平顶部分对过零点检测没有影响。理想情况为如图2所示的Vdc/2电压参考线与反电动势通过比较检测出平衡的ZCP,再通过30°电角度的延时便可以得到平衡的换相时刻。然而,高速电机在运行的过程中,会产生不确定的电压降和直流链路电压偏移,这使得实际测得的等效Vdc电压出现偏移的情况,实测端电压变成Vdc_offset,进而检测出不平衡的ZCP并产生不平衡换相时刻,设Vdc_offset造成的不平衡ZCP偏移电角度为q1,q1的分布情况如图2所示,图中ZCP和CMTN分别表示过零点和换相点。

图2 不平衡ZCP分析
Fig.2 Unbalanced ZCP analysis
图2的不平衡ZCP分析不考虑三相绕组不对称的影响。对不平衡ZCP间隔的电角度进行定量分析见表1。
表1 不平衡ZCP间隔的电角度分布
Tab.1 Electrical angle distribution at unbalanced ZCP intervals (单位: rad)
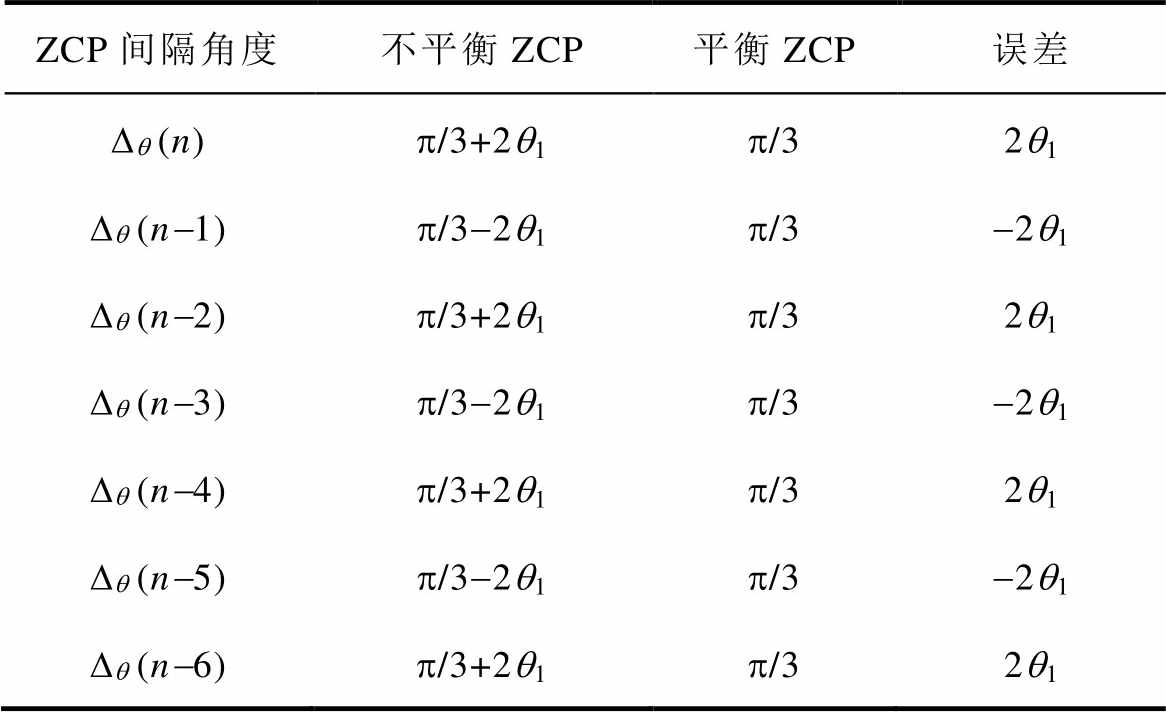
ZCP间隔角度不平衡ZCP平衡ZCP误差 Dq (n)p/3+2q1p/32q1 Dq (n-1)p/3-2q1p/3-2q1 Dq (n-2)p/3+2q1p/32q1 Dq (n-3)p/3-2q1p/3-2q1 Dq (n-4)p/3+2q1p/32q1 Dq (n-5)p/3-2q1p/3-2q1 Dq (n-6)p/3+2q1p/32q1
分析图2和表1,给出参考零点是否存在偏移而引起的ZCP不平衡由式(4)和式(5)判别。
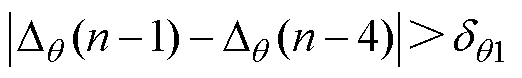 (4)
(4)
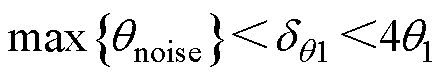 (5)
(5)
式中,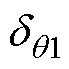 为q1存在的判定门限;Dq (n-1)、Dq (n-4)均为ZCP间隔角度;qnoise为噪声对应的电角度。
为q1存在的判定门限;Dq (n-1)、Dq (n-4)均为ZCP间隔角度;qnoise为噪声对应的电角度。
若式(4)满足,则表示参考零点存在明显偏移,此时的延迟电角度的公式为
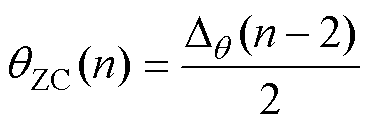 (6)
(6)
延迟时间的公式为
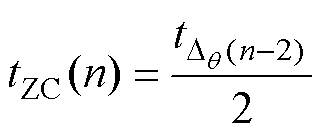 (7)
(7)
式中,qZC(n)、tZC(n)分别为第n个ZCP到下一换相点的延迟电角度和对应的时间;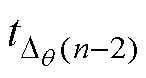 为Dq (n-2)对应的时间间隔。
为Dq (n-2)对应的时间间隔。
转速稳定时,电角度到达时间的导出函数为
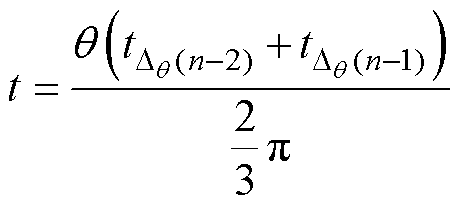 (8)
(8)
理想情况下,电机三相绕组的空间位置是对称的,然而实际电机存在诸多非理想因素[20]。这主要受电机制造工艺和安装精度等方面的影响,实际的无刷直流电机普遍存在三相绕组空间位置不完全对称的问题,中低速条件下这种不对称性对系统性能影响不明显,但是高速和超高速条件下会导致过零点的淹没,进而造成电机失步[21]。具体来说,三相绕组空间位置不对称会使得三相反电动势之间存在差异,造成相邻过零点的间隔时间不完全相等或零点分布并不对称。
取A相绕组为参考绕组,假设B相和C相绕组均存在空间位置不对称,且相对于三相对称绕组位置的偏离角度分别为qsB和qsC(正角度表示逆时针偏移,负角度表示顺时针偏移),具体如图3所示。图3b中的浅色绕组位置对应图3a对称绕组位置。
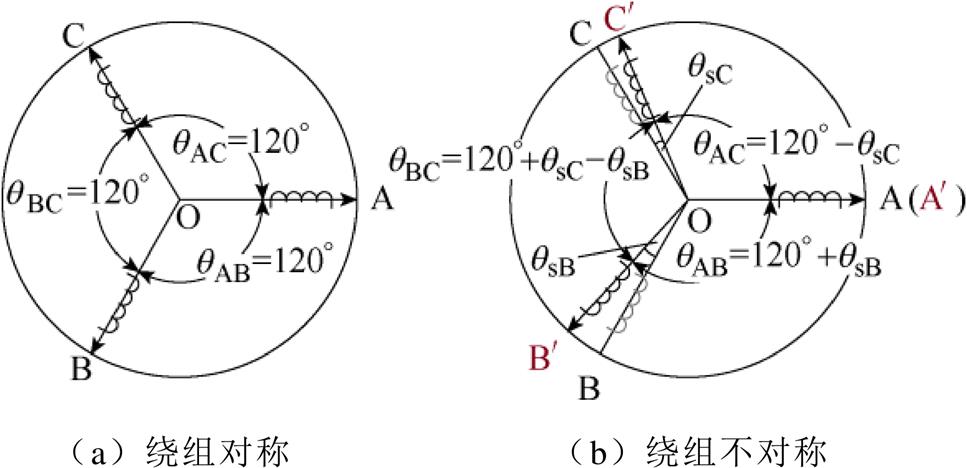
图3 三相对称绕组和三相不对称绕组图示
Fig.3 Three phase symmetrical winding and three phase asymmetric winding diagram
为了定量分析三相绕组的空间位置不对称程度,引入不对称标准偏差为
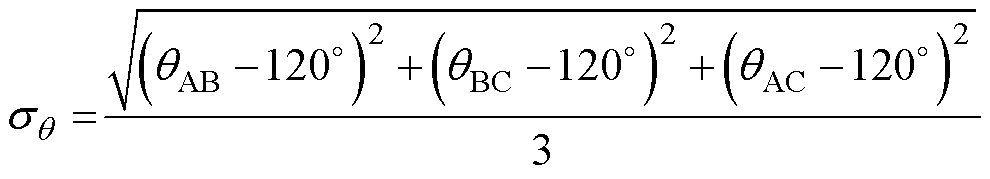 (9)
(9)
式中,qAB、qBC和qAC为绕组间的空间电角度。
绕组空间位置的偏移会直接影响一个周期内过零点的分布,以A相为参考相,B相和C相绕组偏移qsB和qsC引起的过零点偏移角分别为qB和qC,不考虑不平衡ZCP的影响,单独对绕组不对称引起的不对称过零点分布进行分析,如图4所示。

图4 不对称ZCP分析
Fig.4 Asymmetric ZCP analysis
图4的不对称ZCP分析不考虑参考零点偏移的影响。将ZCP间隔进行定量分析见表2。
表2 不对称ZCP间隔的电角度分布
Tab.2 Electrical angle distribution at asymmetric ZCP intervals (单位: rad)
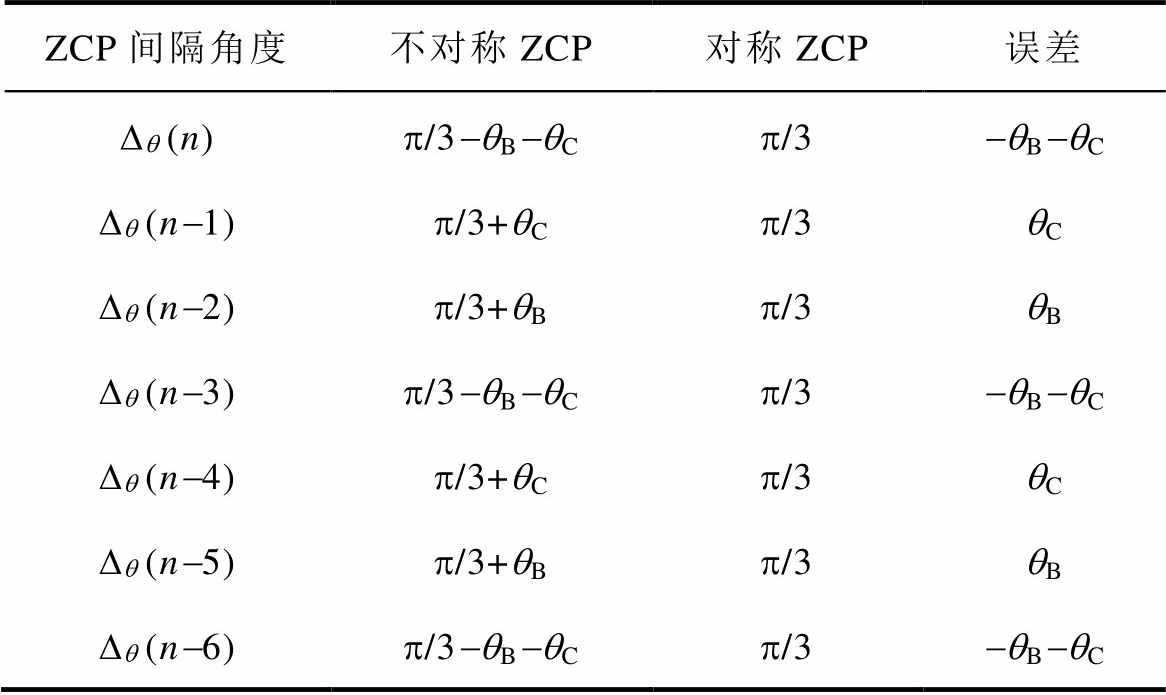
ZCP间隔角度不对称ZCP对称ZCP误差 Dq (n)p/3-qB-qCp/3-qB-qC Dq (n-1)p/3+qCp/3qC Dq (n-2)p/3+qBp/3qB Dq (n-3)p/3-qB-qCp/3-qB-qC Dq (n-4)p/3+qCp/3qC Dq (n-5)p/3+qBp/3qB Dq (n-6)p/3-qB-qCp/3-qB-qC
定义q2为Dq (n-1)和Dq (n-3)差值的绝对值,q2最小值q2min确定方法为
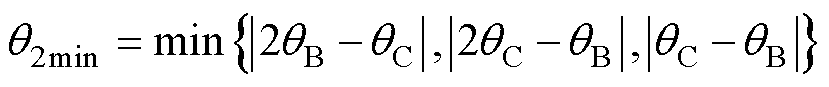 (10)
(10)
分析图4和表2,给出三相绕组是否存在不对称情况的判别方法为
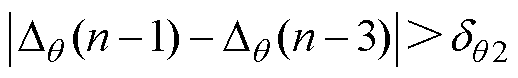 (11)
(11)
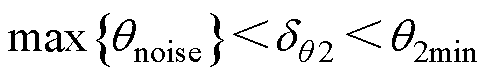 (12)
(12)
式中,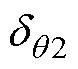 为q2存在的判定门限。
为q2存在的判定门限。
若式(11)满足,则说明三相绕组存在明显不对称,此时的延迟电角度公式为
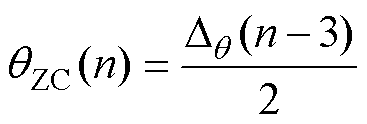 (13)
(13)
延迟时间公式为
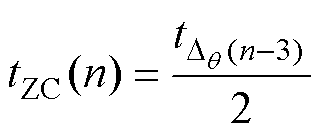 (14)
(14)
式中,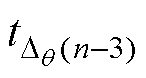 为Dq (n-3)对应的时间间隔。
为Dq (n-3)对应的时间间隔。
转速稳定时,电角度到时间的导出函数为
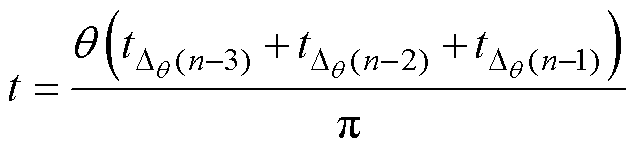 (15)
(15)
在1.1~1.4节的研究中,对ZCP不平衡现象和ZCP不对称现象进行了详细分析,并提出了相应的解决方法。然而,在实际的电机控制过程中,ZCP的不平衡和不对称现象往往同时存在,并共同影响着电机的换相。因此,下面将综合考虑这两种因素对ZCP分布的影响并给出两种因素同时存在时的分析,不平衡不对称ZCP分析如图5所示。
图5考虑了参考零点偏移和三相绕组不对称的问题,对一个周期的电角度分布情况做出图解分析。接下来对不平衡不对称ZCP间隔的电角度进行定量分析见表3。
分析图5和表3可知,当不平衡和不对称现象同时存在时,必须先对参考零点是否存在偏移进行判定,因为参考零点的偏移是不稳定的也是不确定的,而三相绕组的不对称是稳定的且确定的,利用三相绕组不对称ZCP间隔Dq (n-1)和Dq (n-4)相互抵消的特点排除三绕组不对称对参考零点是否存在偏移的判定的影响。
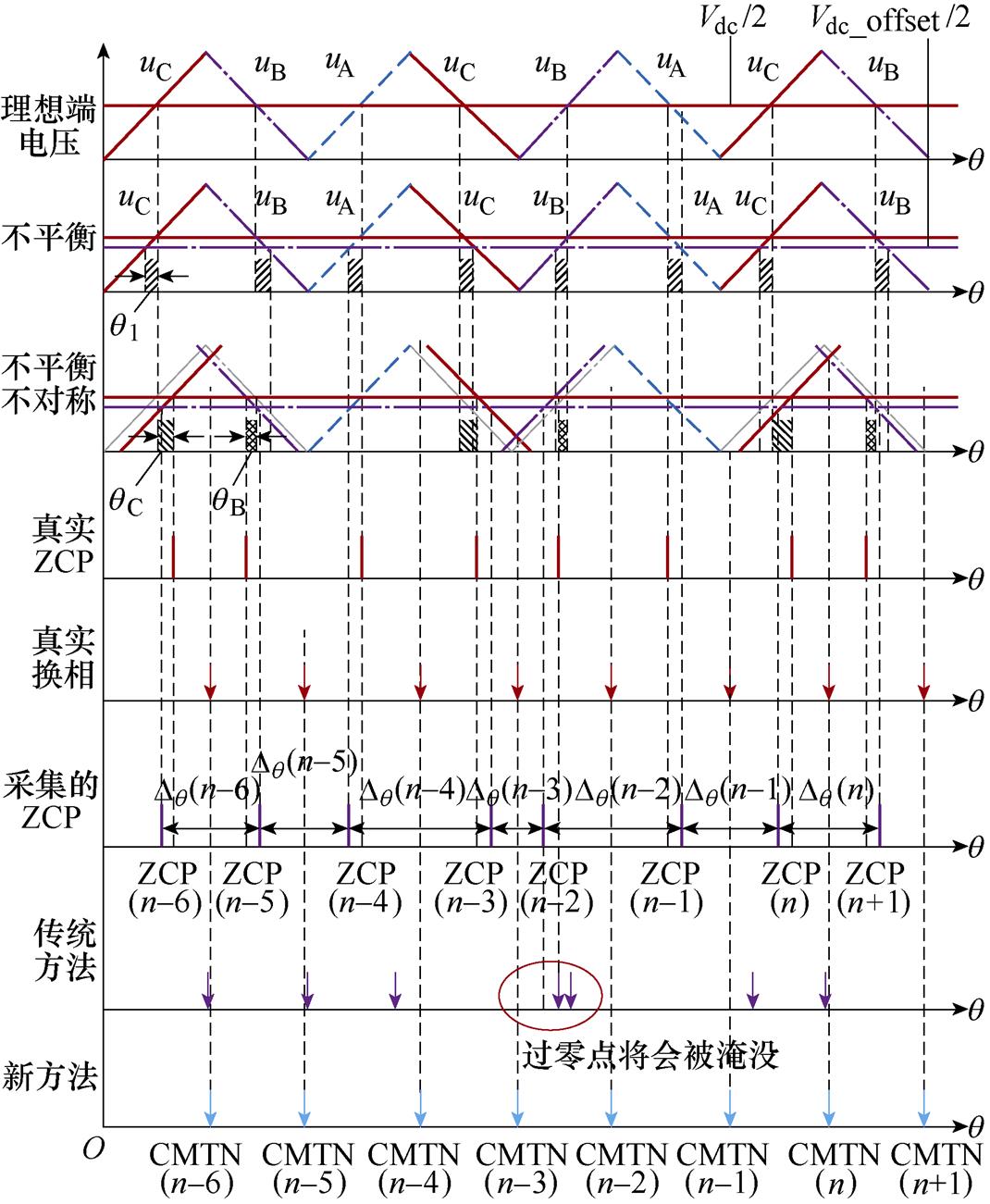
图5 不平衡不对称ZCP分析
Fig.5 Unbalanced and asymmetric ZCP analysis
表3 不平衡不对称ZCP间隔的电角度分布
Tab.3 Electrical angle distribution of unbalanced and asymmetrical ZCP intervals (单位: rad)
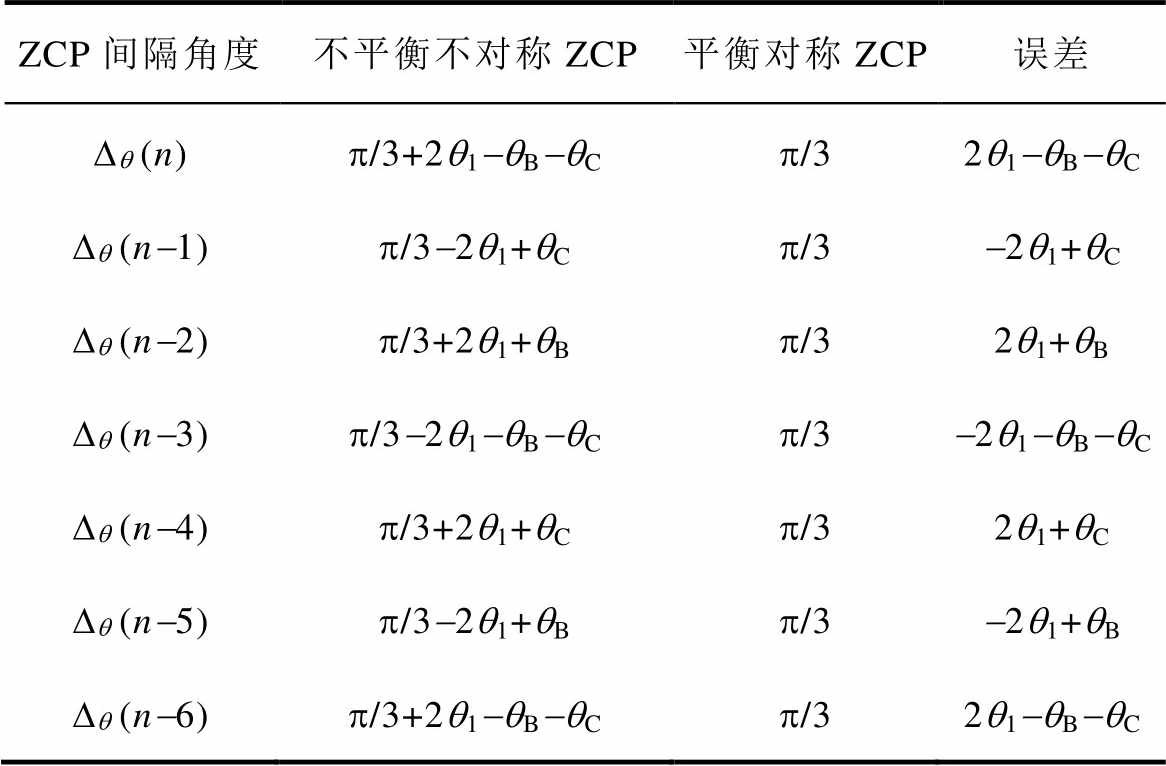
ZCP间隔角度不平衡不对称ZCP平衡对称ZCP误差 Dq (n)p/3+2q1-qB-qCp/32q1-qB-qC Dq (n-1)p/3-2q1+qCp/3-2q1+qC Dq (n-2)p/3+2q1+qBp/32q1+qB Dq (n-3)p/3-2q1-qB-qCp/3-2q1-qB-qC Dq (n-4)p/3+2q1+qCp/32q1+qC Dq (n-5)p/3-2q1+qBp/3-2q1+qB Dq (n-6)p/3+2q1-qB-qCp/32q1-qB-qC
首先利用式(4)判定参考零点是否存在偏移,若式(4)满足,再利用不平衡ZCP间隔Dq (n-1)和Dq (n-3)相互抵消的特点排除参考零点偏移对三相绕组是否不对称的影响,也就是利用式(11)进行判定。
若式(4)和式(11)的顺序判定同时满足,则说明同时存在着严重的ZCP不平衡和不对称现象,分析表3可知,Dq (n-1)~Dq (n-5)已经不存在可以准确获得延迟角度的ZCP间隔,因此需要降低延迟时间获得的实效性,向前推一个周期采用上一周期的等效ZCP间隔,也就是选取Dq (n-6)来获得延迟角度,延迟电角度公式为
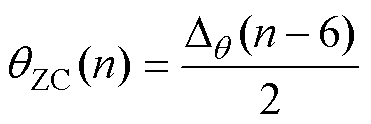 (16)
(16)
延迟时间公式为
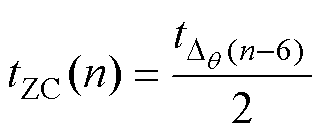 (17)
(17)
式中,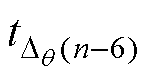 为Dq (n-6)对应的时间间隔。
为Dq (n-6)对应的时间间隔。
转速稳定时,电角度到时间的导出函数为
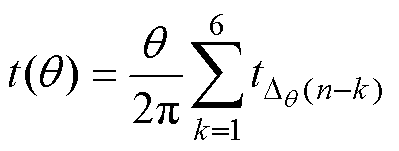 (18)
(18)
综上所述,给出完整的ZCP间隔选用规则和电角度到时间的导出函数。
当稳态运行的电机ZCP是完全对称时,即式(4)不成立且式(11)不成立,有
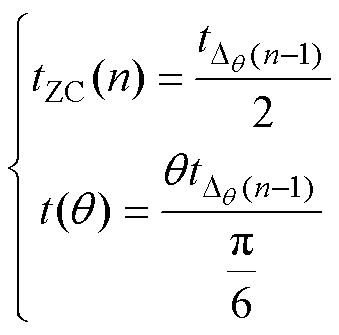 (19)
(19)
由于没有非理想因素的干扰,为了削弱噪声的干扰,同样可以使用
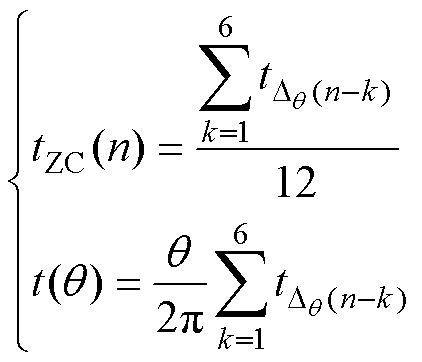 (20)
(20)
当稳态运行的电机ZCP仅存在不平衡现象时,即式(4)成立且式(11)不成立,有
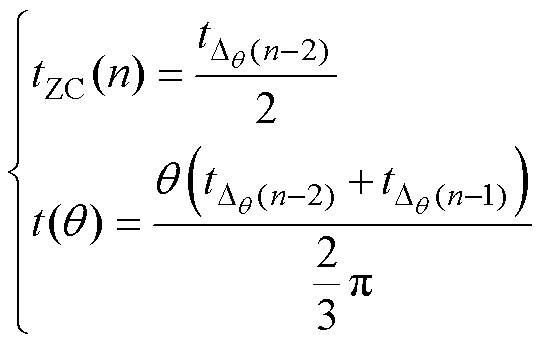 (21)
(21)
当稳态运行的电机ZCP仅存在不对称现象时,即式(4)不成立且式(11)成立,有
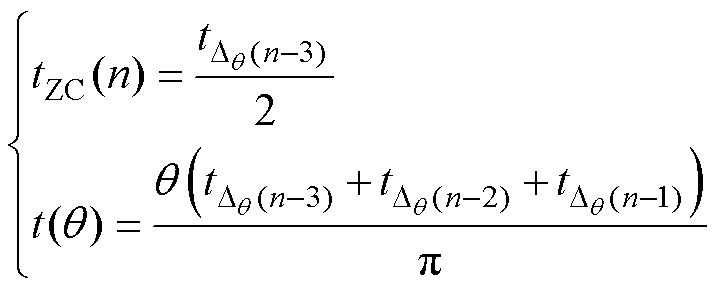 (22)
(22)
当稳态运行的电机ZCP同时存在不平衡和不对称现象时,即式(4)成立且式(11)成立,有
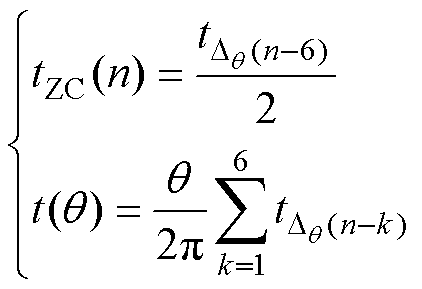 (23)
(23)
使用本文提出的基础换相延时设定方法可以有效地解决过零点淹没问题。具体来说,错误设置基础换相时间会导致换相时刻落后于下一过零点时刻,进而造成过零点淹没。观察图5,传统方法在两种非理想因素同时存在且叠加影响时,导致估测的换向时刻已经滞后于下一个过零点时刻,出现过零点被淹没的问题,本文提出的算法可以合理地设置基础换相延时,避免因设定过长的基础换相时间而出现过零点淹没问题。
以上分析是在电机转速基本不变的前提下进行的,但是实际工业应用电机的转速是不断变化的,如实际工作中需要电机主动升速或降速、风机或空压机的负载不断变化而导致电机转速被动变化等情形,这些情形下的转速变动都会带来一定的换相误差。
根据文献[22]提出的基于速度变化率转子位置误差补偿策略的基本原理和设计方法,并结合本文考虑的电机非理想因素,提出基于转速变化和不对称不平衡的ZCP换相误差补偿方法。
首先,由于电机非理想因素的存在,相邻ZCP间隔时间本身就不相同,因此,采用连续的两个ZCP间隔来计算变速度引起的换相误差补偿时间并不合适,电机的非理想因素只会影响一个周期内的ZCP分布,一个完整的六步换相周期内不平衡和不对称抵消。因此,计算当前ZCP对应的前一个周期的平均ZCP间隔时间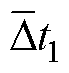 和前一个ZCP对应的前一个周期的平均ZCP间隔时间
和前一个ZCP对应的前一个周期的平均ZCP间隔时间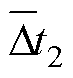 分别为
分别为
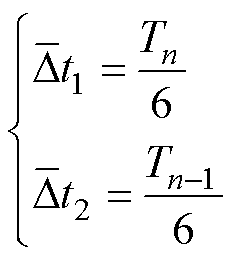 (24)
(24)
其中
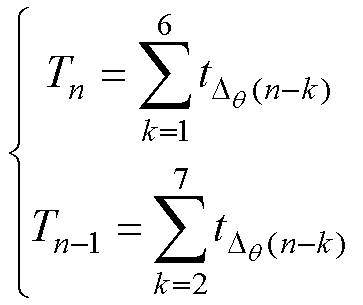 (25)
(25)
当电机转速变化时,电机相邻的两个60°电角度所用的平均时间不同,设两次时间差为Dtx,结合文献[22]的推导方法可得
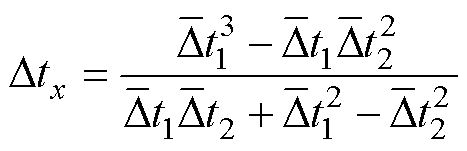 (26)
(26)
理论上当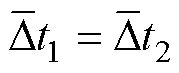 时,电机的转速为匀速。考虑到噪声等实际因素的影响,在实际控制中即使电机匀速转动
时,电机的转速为匀速。考虑到噪声等实际因素的影响,在实际控制中即使电机匀速转动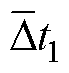 和
和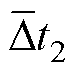 ,也不会严格相等,因此与式(4)和式(11)方法类似仍然使用门限的方法进行判定
,也不会严格相等,因此与式(4)和式(11)方法类似仍然使用门限的方法进行判定
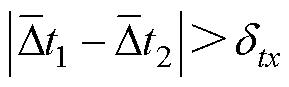 (27)
(27)
当式(27)不成立,即电机的转速为匀速时,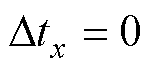 ,此时本文提出的检测方法不会产生换相误差;当式(27)成立时,
,此时本文提出的检测方法不会产生换相误差;当式(27)成立时,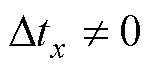 ,电机换相时间就需要补偿
,电机换相时间就需要补偿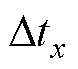 ,从而达到准确换相的目的。
,从而达到准确换相的目的。
综合式(19)~式(27),对择优算法导出的基础延迟换向时间进行进一步的补偿,最终得到更加准确的换相时刻。
图6展示了所提算法的框图结构,算法框图主要分为两个部分,即判定不对称不平衡情形并生成基础换相延迟时间模块(以下简称择优模块)和速度变化引起的换相误差补偿模块(以下简称变速补偿模块)。择优模块负责消除电机非理想因素造成的ZCP扰动并生成基础换相延时,变速度补偿模块在择优模块的基础上消除由于速度变化引起的换相误差,从而达到准确换相的目的。
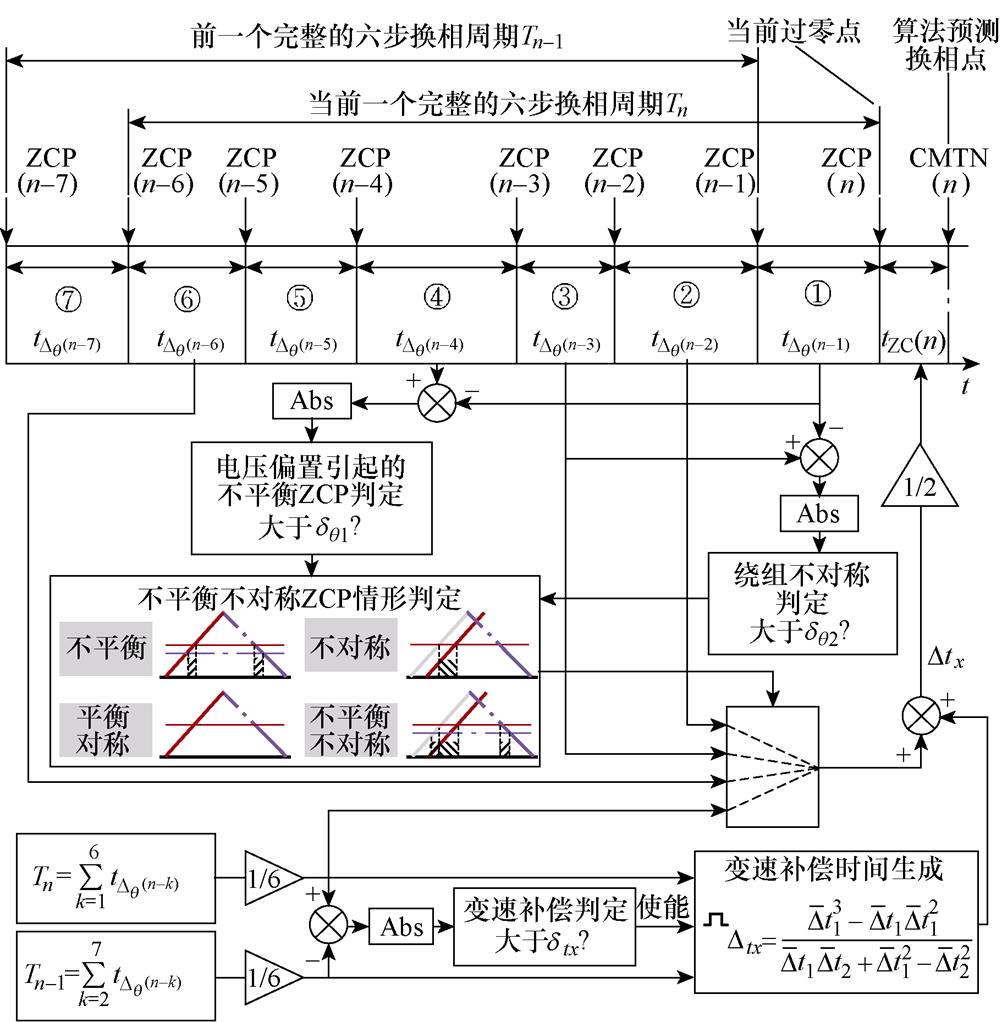
图6 提出算法框架
Fig.6 Proposed algorithm framework
分析目前基于过零点延迟换相的五种主流算法的基本原理,对比本文提出算法与这五种传统算法之间的性能优劣。详细对比见表4。
表4 本文算法与传统算法的对比
Tab.4 The comparison between the proposed algorithm and the traditional algorithm
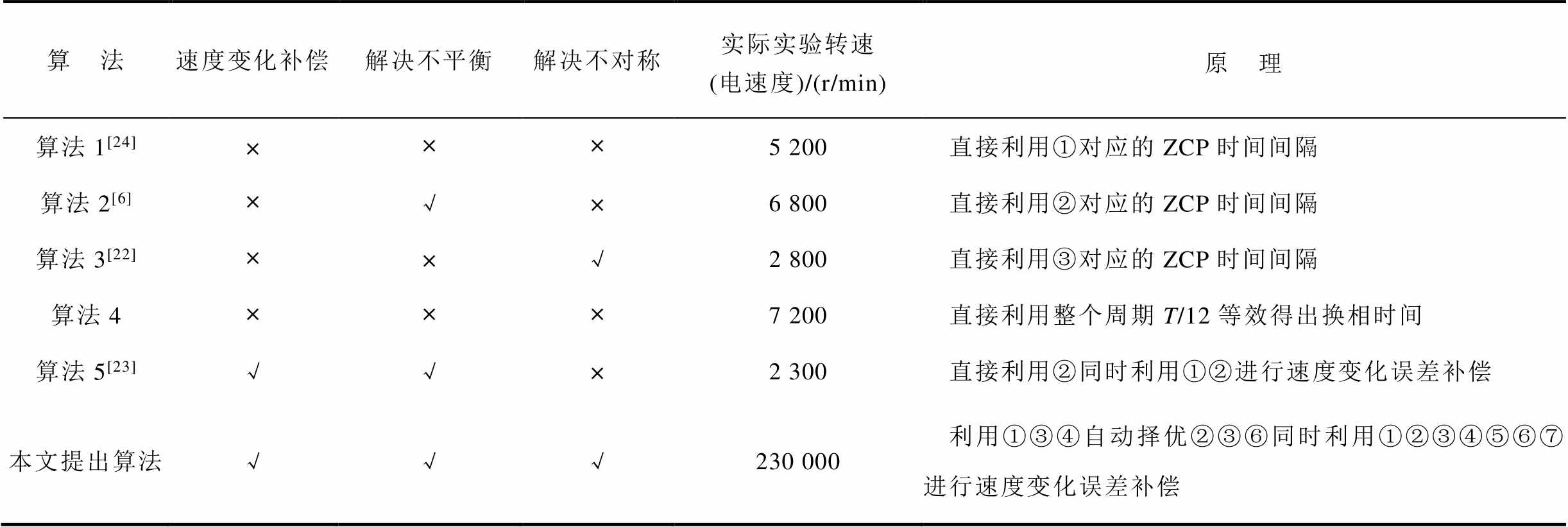
算 法速度变化补偿解决不平衡解决不对称实际实验转速 (电速度)/(r/min)原 理 算法1[24]×××5 200直接利用①对应的ZCP时间间隔 算法2[6]×√×6 800直接利用②对应的ZCP时间间隔 算法3[22]××√2 800直接利用③对应的ZCP时间间隔 算法4×××7 200直接利用整个周期T/12等效得出换相时间 算法5[23]√√×2 300直接利用②同时利用①②进行速度变化误差补偿 本文提出算法√√√230 000利用①③④自动择优②③⑥同时利用①②③④⑤⑥⑦进行速度变化误差补偿
注:√代表可以解决该问题;×代表不可以解决该问题;①②③④⑤⑥⑦分别代表图4中对应的ZCP时间间隔,算法4为TI公司官方电机控制例程提供的算法。
相较于传统算法,本文提出算法综合考虑各种引起换相误差的因素,充分利用①~⑦ZCP间隔时间的内在规律来解决问题。前述公式和算法结构并不依赖于电机参数(后文解决二极管续流等问题需要依赖电机参数),因此,可以适用不同参数的无刷直流电机。所提算法可以很好地解决不平衡不对称ZCP扰动问题,同时,在实际实验转速方面,本文算法在230 000 r/min的转速下得到验证,其他传统算法都只在10 000 r/min以下的转速下进行实验。
对于运行速度高达100 000 r/min以上的超高速电机控制系统,在补偿了不平衡不对称ZCP对换相产生的影响之后,各种延迟成为了影响电机换相准确性的主要因素,换相误差的大小应在(-90°, +90°)范围之内;否则,电机失步,将无法稳定运行[24]。因此对超高速电机的各种延迟做出准确的延迟补偿是十分有必要的,超高速情形下,主要的相移来源于低通滤波器(Low-Pass Filter, LPF),当然,除此之外整个硬件系统的线路还会有其他的相移因素,但是其造成的影响很小。同时,重负载时二极管的续流时间也会影响ZCP的获取,这些影响均可以从软件层面上加以补偿。
LPF的影响会叠加在采集的端电压上,二极管的续流时间会叠加到最终确定的ZCP上,两种主要延迟因素对ZCP获取的影响如图7所示。
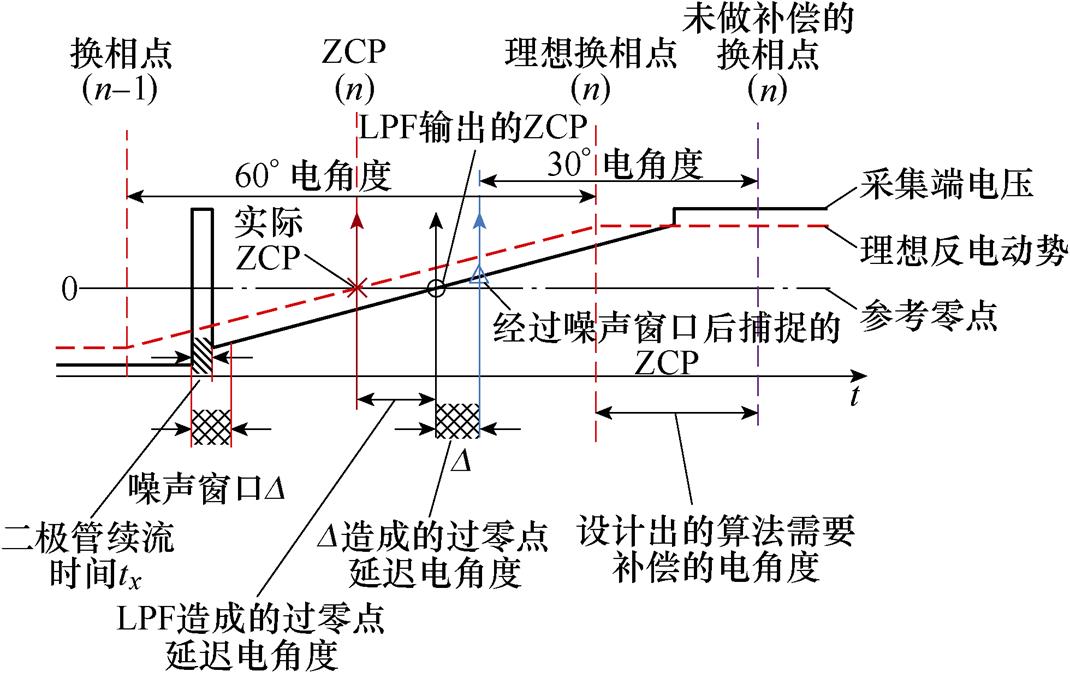
图7 超高速延迟分析
Fig.7 Ultra-high speed delay analysis
为了减弱前置PAM的PWM谐波对ZCP检测的影响,必须要根据转子的频率计算并选取合适的LPF参数[25]。在本文中,利用式(19)~式(23)可以得到准确的电角度到时间的导出函数,将此与LPF的相移公式相结合,便可得到LPF的准确延迟时间。具体来说,先求出LPF的延迟电角度qLPF为
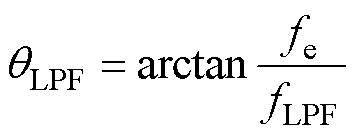 (28)
(28)
式中,fe、fLPF分别为转子的旋转频率和滤波器的截止频率。
再将求解出的LPF的延迟电角度qLPF代入式(19)~式(23),得到LPF的延迟时间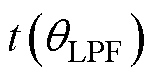 为
为
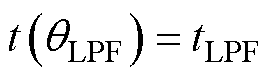 (29)
(29)
在实际电机控制过程中,二极管续流现象是一个不可忽视的因素,其产生的尖峰电压会对反电动势过零点(ZCP)的检测准确性造成严重影响。为了解决这一问题,本研究引入了噪声窗口的概念,用于判断采集得到的反电动势是否达到真正过零点。
通过设置一个合适的噪声窗口,可以解决由二极管续流引起的尖峰电压干扰。在该窗口内,对端电压进行连续采样。如果在窗口内的连续采样符号发生变化,即从正变为负或从负变为正,那么可以确定该点是一个真正的过零点。二极管的续流时间为(以A相反电动为例)
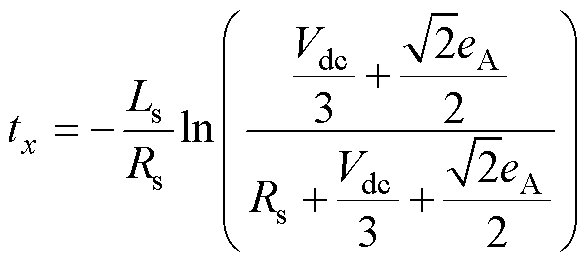 (30)
(30)
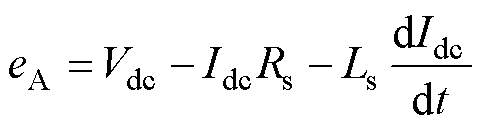 (31)
(31)
为了消除二极管续流时间的影响,同时也要兼顾对控制器性能的利用,噪声窗口延迟时间D 是根据tx动态设定的,D 范围为
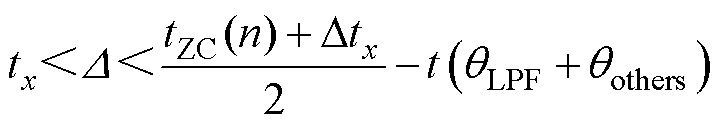 (32)
(32)
式中,tx为二极管的续流时间;qothers为本文未考虑的其他相移角。
基于以上分析,设计超高速无刷直流电机的整体控制框架,其由换相部分和控制部分组成。
换相部分,首先,采集ZCP检测得到的前8个ZCP的时间信息,通过计算得到前7个ZCP间隔的时间,进入择优算法和变速补偿算法得到基础换相延迟时间。然后,在基础换相延迟时间上对LPF所产生的相移进行补偿。最后,再对噪声窗口时间进行补偿即可得到最终的换相延迟时间。
控制部分采用转速环+电流环+电压环的三闭环结构,三闭环同时兼顾超高速电机的转速性能、转矩性能和Buck变换器电压输出性能(三闭环不属于本文研究范畴,因此不做详细分析)。
控制部分和换相部分共同组成超高速电机的总体控制框架,如图8所示。
为了全面验证所提算法的有效性,首先,在dSPACE虚拟控制器平台上进行了快速实验。此部分实验主要用来快速验证算法的正确性。然后,为了更好地适应实际工业应用场景,采用了由TI公司提供的TMS320F28335芯片作为主控DSP并进行算法验证,此部分实验主要用于验证算法在超高速条件下的极限性能,基于dSPACE虚拟控制器实验平台的硬件组成如图9所示,基于DSP控制器实验平台的硬件组成如图10所示。
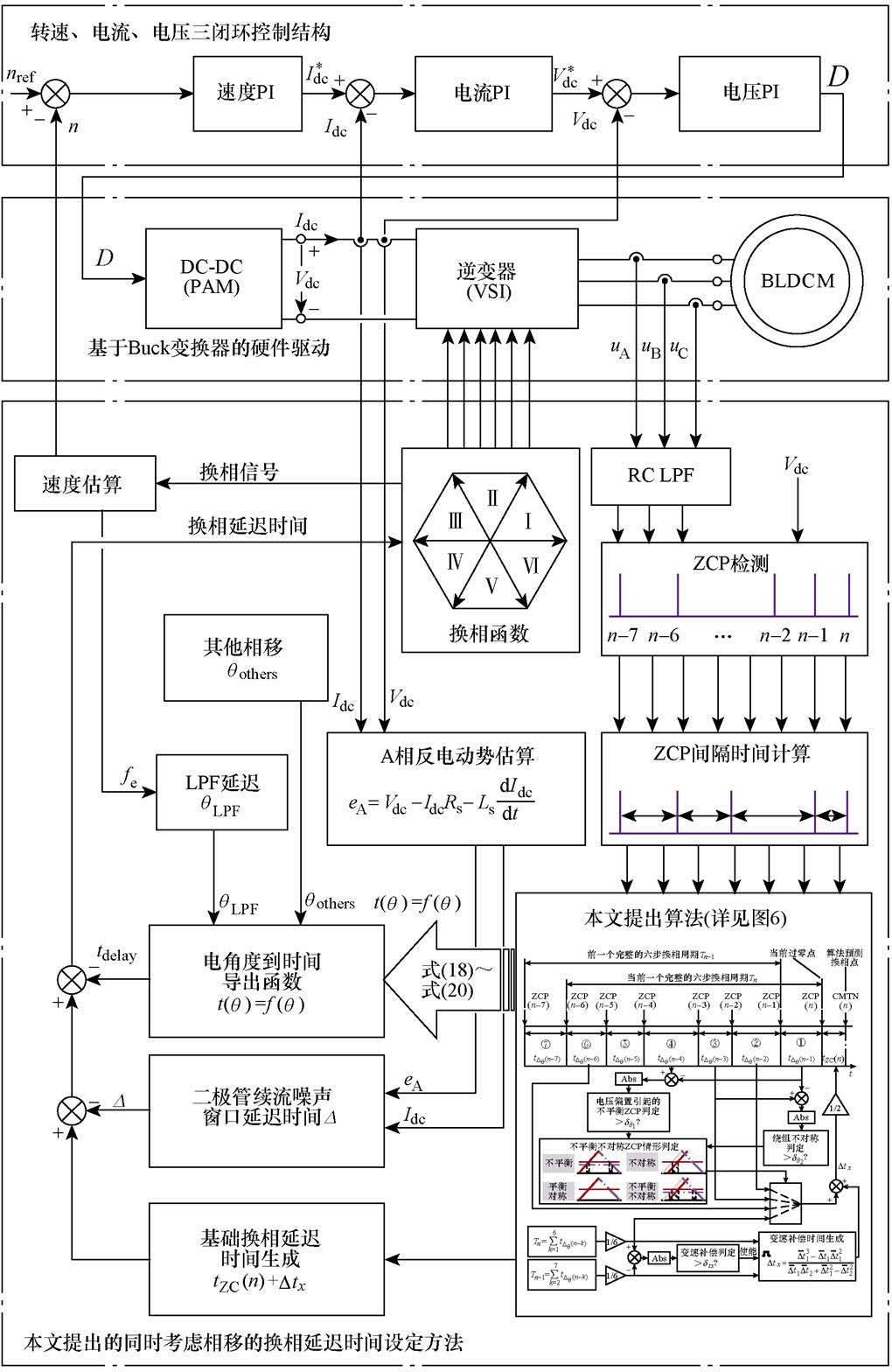
图8 提出的总体控制框图
Fig.8 Proposed overall control block diagram

图9 基于dSPACE的快速实验平台
Fig.9 Experimental platform of RCP based on dSPACE

图10 基于DSP的实验平台
Fig.10 Experimental platform based on DSP
实验分别在高速和超高速条件下进行。在高速情况下,采用高速对拖电机进行实验,通过控制电机在高速范围内运行,同时监测和记录电机的换相信号、相电流和端电压等信息。在该过程中,应用本文提出的择优算法和变速补偿算法对不平衡不对称ZCP造成的换相误差进行补偿,并根据所推导的延迟电角度到延迟时间的导出函数来补偿相关的相移延迟时间。
超高速实验场景中,将验证所提算法在极限转速下的可行性。具体来说,超高速阶段采用与高速阶段同样算法和延迟补偿措施,将电机推至超高速运行状态。下面是实验用到的变换器和电机的详细参数,见表5。
表5 变换器和电机参数
Tab.5 Converter and motor parameters
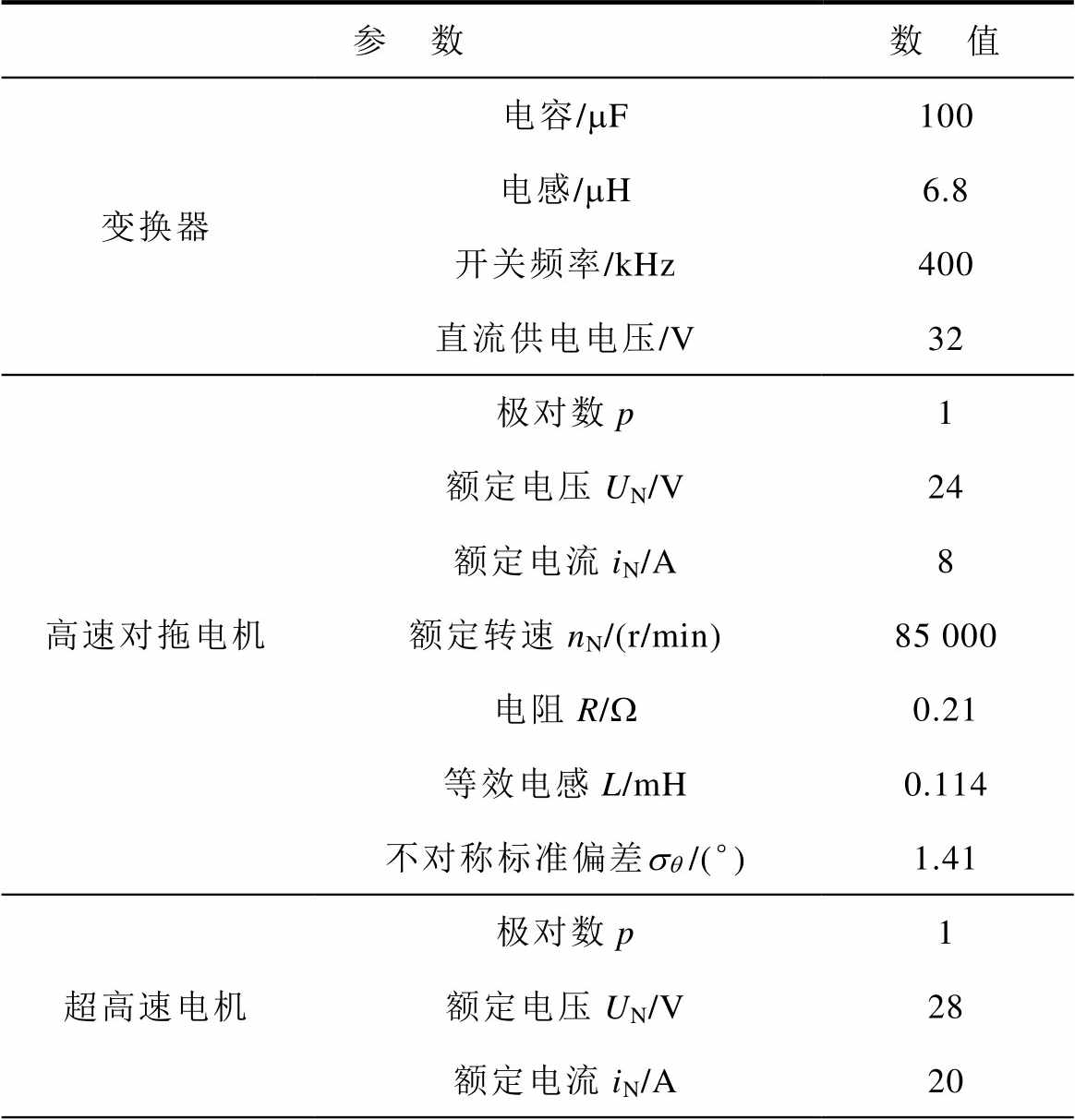
参 数数 值 变换器电容/mF100 电感/mH6.8 开关频率/kHz400 直流供电电压/V32 高速对拖电机极对数p1 额定电压UN/V24 额定电流iN/A8 额定转速nN/(r/min)85 000 电阻R/W0.21 等效电感L/mH0.114 不对称标准偏差sq /(°)1.41 超高速电机极对数p1 额定电压UN/V28 额定电流iN/A20
(续)
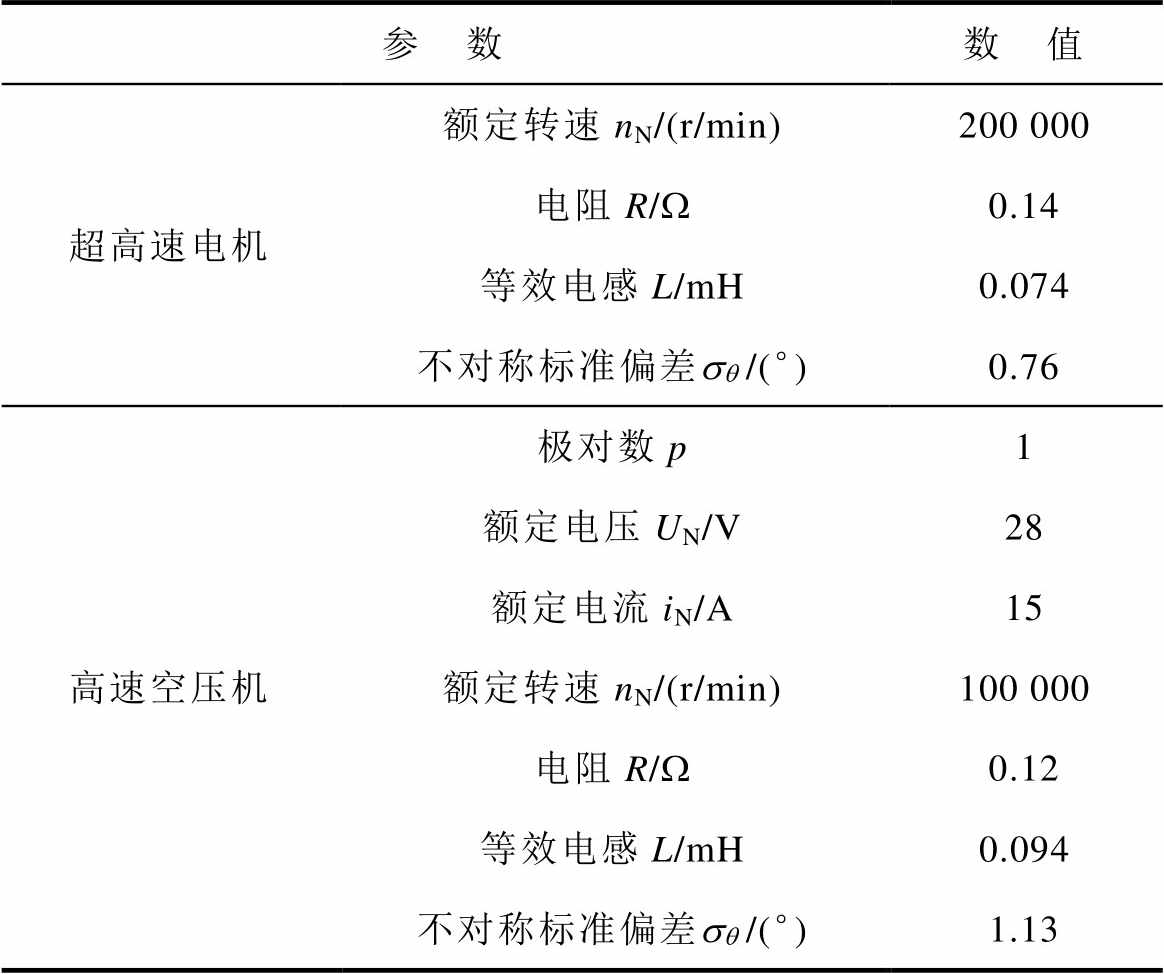
参 数数 值 超高速电机额定转速nN/(r/min)200 000 电阻R/W0.14 等效电感L/mH0.074 不对称标准偏差sq /(°)0.76 高速空压机极对数p1 额定电压UN/V28 额定电流iN/A15 额定转速nN/(r/min)100 000 电阻R/W0.12 等效电感L/mH0.094 不对称标准偏差sq /(°)1.13
在高速情形下,采用高速对拖电机进行实验。为使实验结果更加直观。先设定电机转速为87 000 r/min,待电机转速稳定后,开始计时,第2.5 s前使用算法1进行换相;在第2.5 s时切入算法3换相;在第6.5 s切入本文算法换相。全程连续实验,连续实验结果和触发如图11和图12所示。
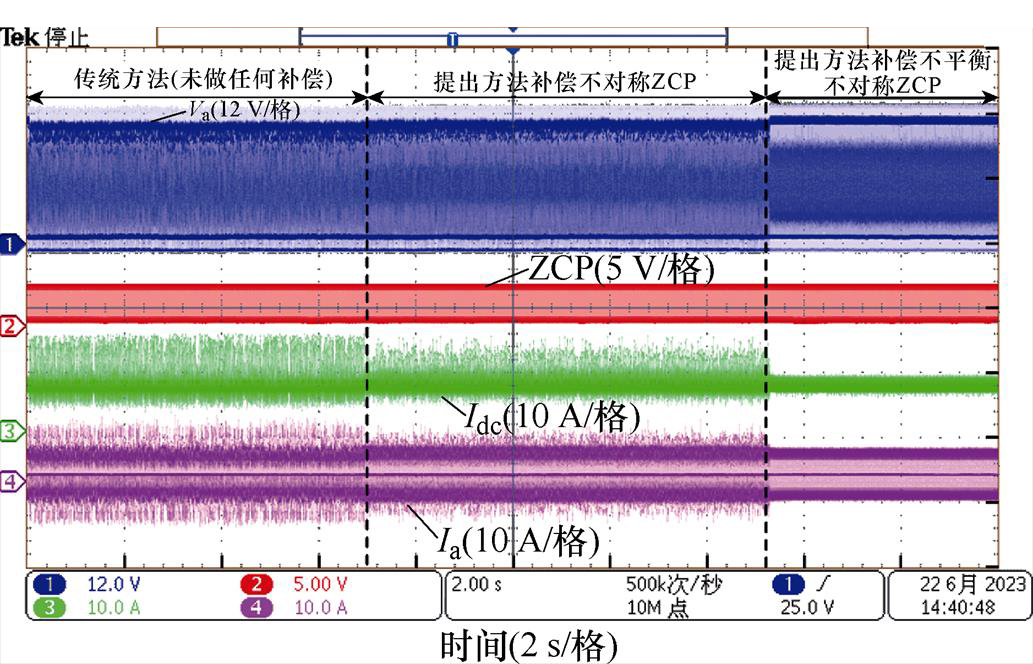
图11 不同算法的波形对比
Fig.11 Comparison diagram of different algorithms
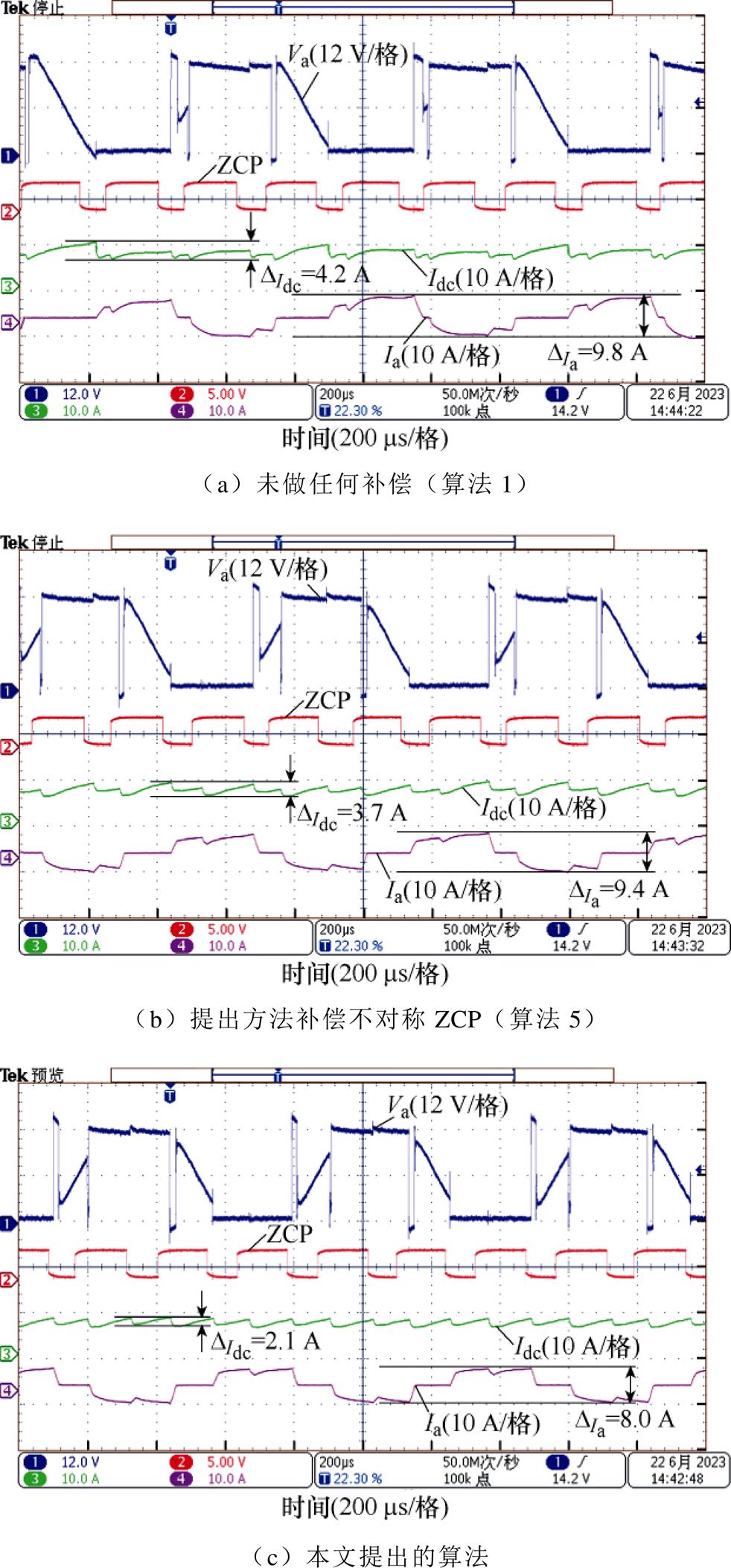
图12 本文算法与其他算法详细对比
Fig.12 The proposed algorithm is compared with other algorithms in detail
图11中,Va为A相端电压,ZCP是软件检测到的过零点(由于噪声窗口的设定实际检测得到的ZCP相较于真实的ZCP均存在相同的延时),Idc为Buck变换器输出的电流,Ia为A相的相电流。
从图11中可以看出,传统方法换相不稳定,母线电流和相电流的纹波最大;对不对称ZCP做补偿后可以减弱部分母线电流和相电流的纹波;使用本文提出的算法后能消除绝大部分的纹波。
从图12中可以看出,本文提出算法相比于算法1和算法3,可以在不平衡和不对称ZCP干扰的情况下准确换相,进而大幅降低电流纹波,本文提出算法相较于其他算法在减少母线电流和相电流纹波上的提升率,实验结果见表6。
表6 实验结果
Tab.6 Experimental results

项目母线电流纹波/AA相电流纹波/A 算法14.29.8 算法33.79.4 本文提出算法2.18.0 提升率(%)5022.5
通过以上实验可以充分验证所提出的算法在高速情况下的可靠性和准确性。
为了更贴合实际应用,实验采用高速空压机作为测试机,实验时,在转速上升阶段测取空压机A相相电流波形和转子位置波形,通过对比换相误差补偿前后无刷直流电机波形与转子位置信号,以此验证变速补偿策略是否正确。
设定电机转速为100 000 r/min,采用斜坡升速的方式控制电机加速,在电机转速为60 000 r/min时,截取空压机A相相电流波形和转子位置波形。算法仅启用择优模块和相移补偿模块,未启用变速补偿模块,电机相电流波形和转子位置信号如图13所示。
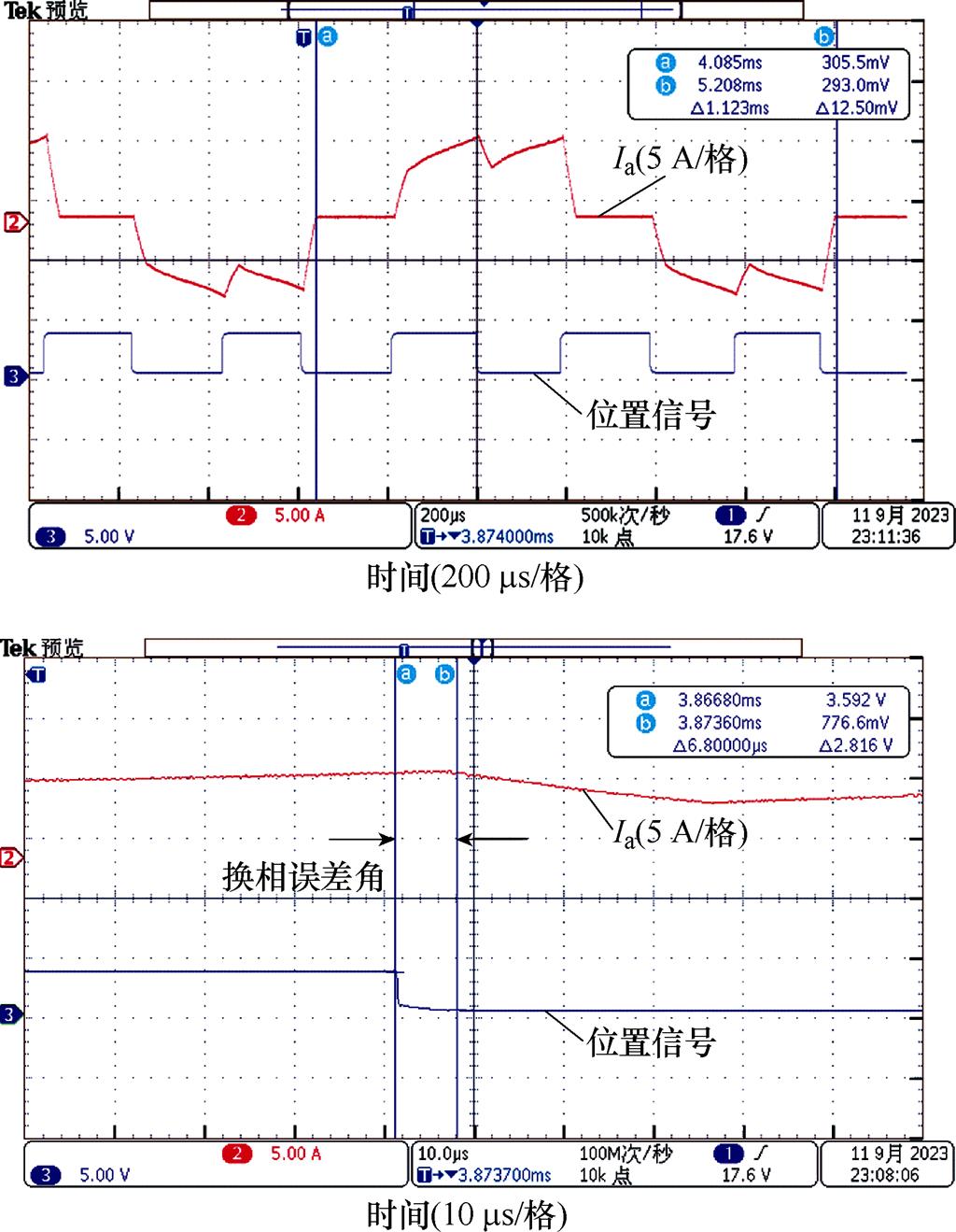
图13 未进行变速补偿时电机相电流波形和转子位置信号
Fig.13 Phase current waveform and position signal diagram without variable speed compensation
一个周期360°电角度大约为1.123 ms,换相误差时间约为6.8 ms,由角度与周期及电机极对数的关系可以计算出换相误差角约为2.18°;未进行变速补偿时,由于无位置检测系统换相时间与根据电机非导通相反电动势过零点时间所计算的换相时间误差较大,使得电机在需要换相时未能及时换相,导致电机换相期间有较大的续流,如图13中相电流波形所示。根据式(26)计算经过30°延时后补偿了约1.81°。在相同机械转矩下,当无位置传感器无刷直流电机系统采用变速补偿后,电机相电流实验波形和转子位置信号如图14所示。
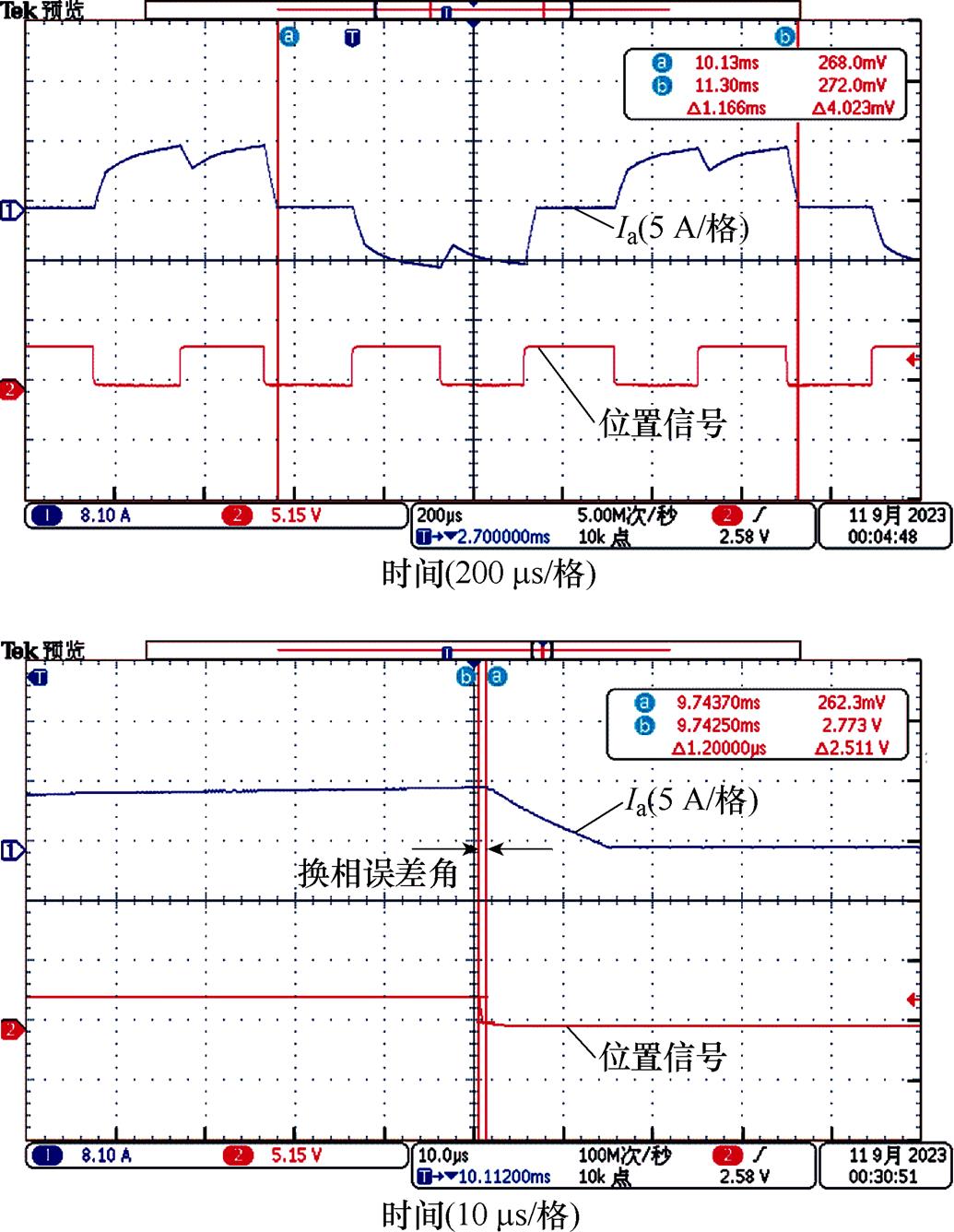
图14 进行变速补偿时电机相电流波形和转子位置信号
Fig.14 Phase current waveform and position signal diagram with variable speed compensation
与图14中未进行变速补偿的无刷直流电机相电流波形和位置信号相比,补偿后的非导通相绕组内的续流明显减小。
在超高速条件下,使用传统的换相方法换相,由于过零点的剧烈扰动,控制系统无法正常换相,电机在未达到额定转速前就已经出现失步现象。为了验证所提算法在超高速条件下的可行性,直接使用本文提出的换相算法将额定转速为200 000 r/min的超高速电机推至电机的极限转速230 000 r/min,端电压如图15所示。
观察图15,一个完整的端电压周期为261.1 ms换算成电机转速约为230 000 r/min。由此可见,使用本文提出的算法可以顺利地将超高速电机推至极限转速并稳定运行。
本文以反电动势过零点为前提,针对无刷直流电机在超高速情形下影响其换相准确性的不平衡不对称ZCP问题,详细分析了造成不平衡ZCP和不对称ZCP原因,将具体情形划分成四种。并提出相应的存在性判别方法、补偿措施和电角度到时间的导出方式。此外,在不平衡不对称ZCP扰动存在的前提下,考虑负载变化等因素引起的换相误差提出相应的变速误差补偿策略。最后,结合超高速时主要的相移因素,如低通滤波器(LPF),提出了相应的补偿方法:
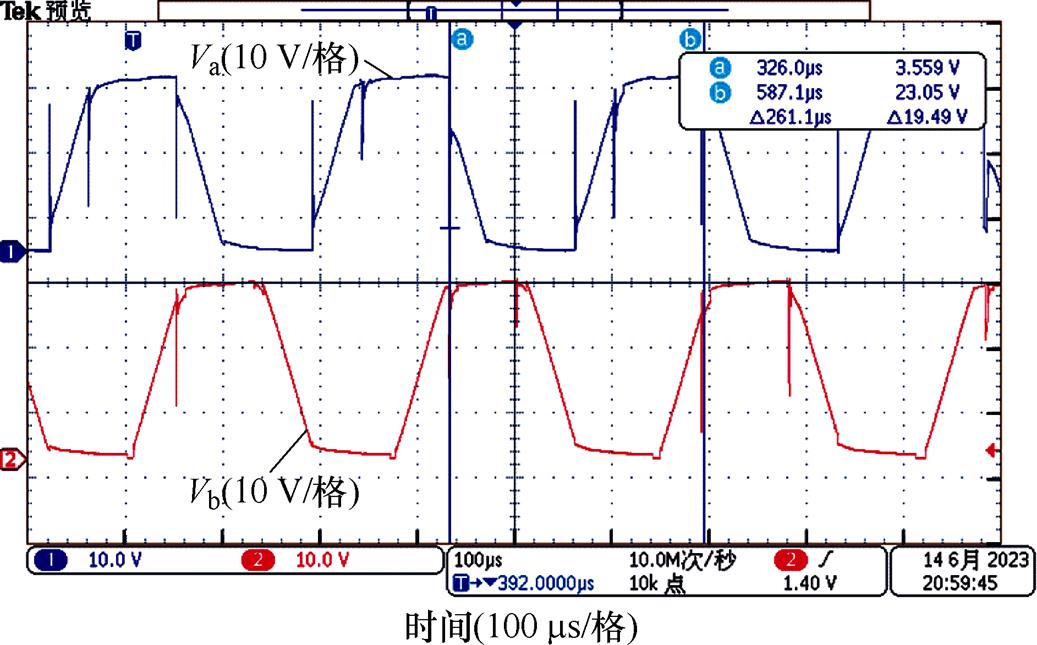
图15 算法补偿后的达到230 000 r/min的极限转速
Fig.15 After the algorithm compensation, the limit speed of 230 000 r/min is reached
1)从无刷直流电机存在的参考零点偏移问题和三相绕组不对称问题出发,分析了不平衡不对称ZCP的规律,并将具体情形划分成四类,给出每一类的判定依据和参数选取。
2)推导并给出每一类情况的换相基础时间的导出方式,并结合各种电角度延迟给出对应的延迟电角度到延迟时间的导出函数。
3)考虑负载变化引起的换相误差,给出相应的变速补偿策略。
4)经过实验验证,本文提出的新算法可以很好地解决超高速电机运行时出现的不平衡不对称ZCP问题,而且算法简单有效、工程适用性强。
参考文献
[1] Zhang Hongjie, Yu Wenfei, Hua Wei. Design and key technology of oil-free centrifugal air compressor for hydrogen fuel cell[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(1): 11-19.
[2] Xu Dianguo, Wang Bo, Zhang Guoqiang, et al. A review of sensorless control methods for AC motor drives[J]. CES Transactions on Electrical Machines and Systems, 2018, 2(1): 104-115.
[3] Zhang Haifeng, Liu Gang, Zhou Xinxiu, et al. High- precision sensorless optimal commutation deviation correction strategy of BLDC motor with asymmetric back EMF[J]. IEEE Transactions on Industrial Informatics, 2021, 17(8): 5250-5259.
[4] Zhou Xinxiu, Zhou Yongping, Peng Cong, et al. Sensorless BLDC motor commutation point detection and phase deviation correction method[J]. IEEE Transactions on Power Electronics, 2019, 34(6): 5880-5892.
[5] Yang Lei, Zhu Z Q, Bin Hong, et al. Virtual third harmonic back EMF-based sensorless drive for high-speed BLDC motors considering machine parameter asymmetries[J]. IEEE Transactions on Industry Applications, 2021, 57(1): 306-315.
[6] Park J S, Lee K D, Lee S G, et al. Unbalanced ZCP compensation method for position sensorless BLDC motor[J]. IEEE Transactions on Power Electronics, 2019, 34(4): 3020-3024.
[7] Jin Hao, Liu Gang, Zhang Haifeng, et al. Error sign detection-based compensation of commutation error for use in sensorless position control of BLDCM[J]. IEEE Transactions on Industrial Electronics, 2022, 69(9): 9279-9287.
[8] Jin Hao, Liu Gang, Li Haitao, et al. A fast commutation error correction method for sensorless BLDC motor considering rapidly varying rotor speed[J]. IEEE Transactions on Industrial Electronics, 2022, 69(4): 3938-3947.
[9] Li Yang, Song Xinda, Zhou Xinxiu, et al. A sensorless commutation error correction method for high-speed BLDC motors based on phase current integration[J]. IEEE Transactions on Industrial Informatics, 2020, 16(1): 328-338.
[10] 阙鸿杰, 全力, 张丽, 等. 基于自适应滤波器在线解耦的磁场增强型永磁电机无位置传感器控制[J]. 电工技术学报, 2022, 37(2): 344-354.
Que Hongjie, Quan Li, Zhang Li, et al. Sensorless control of flux-intensifying permanent magnet synchronous motor based on adaptive Notch filter online decoupling[J]. Transactions of China Electro- technical Society, 2022, 37(2): 344-354.
[11] 王菁, 颜建虎, 季国东, 等. 一种基于双位置观测器的永磁同步电机低速无位置传感器控制方法[J]. 电工技术学报, 2023, 38(2): 375-386.
Wang Jing, Yan Jianhu, Ji Guodong, et al. A sensorless control method for permanent magnet synchronous machine based on dual position observers at low speed[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 375-386.
[12] 刘伟, 刘浩民. 改进的脉振高频注入永磁同步电动机无传感器控制[J]. 电气技术, 2023, 24(6): 6-12, 20.
Liu Wei, Liu Haomin. Improved sensorless control for pulsating high frequency signal injection of permanent magnet synchronous motor[J]. Electrical Engineering, 2023, 24(6): 6-12, 20.
[13] 麦志勤, 刘计龙, 肖飞, 等. 基于估计位置反馈电流解调算法的改进型高频旋转电压注入无位置传感器控制策略[J]. 电工技术学报, 2022, 37(4): 870-881, 891.
Mai Zhiqin, Liu Jilong, Xiao Fei, et al. Sensorless control strategy of improved HF rotating voltage injection based on estimated position feedback current demodulation algorithm[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 870-881, 891.
[14] 姚钢, 杨浩猛, 周荔丹, 等. 大容量海上风电机组发展现状及关键技术[J]. 电力系统自动化, 2021, 45(21): 33-47.
Yao Gang, Yang Haomeng, Zhou Lidan, et al. Development status and key technologies of large- capacity offshore wind turbines[J]. Automation of Electric Power Systems, 2021, 45(21): 33-47.
[15] 申永鹏, 刘迪, 梁伟华, 等. 三相桥式逆变电路电流检测方法综述[J]. 电工技术学报, 2023, 38(2): 465-484.
Shen Yongpeng, Liu Di, Liang Weihua, et al. Review of current detection methods for three-phase bridge inverter circuits[J]. Transactions of China Electro- technical Society, 2023, 38(2): 465-484.
[16] Zhao Dongdong, Wang Xipo, Tan Bo, et al. Fast commutation error compensation for BLDC motors based on virtual neutral voltage[J]. IEEE Transactions on Power Electronics, 2021, 36(2): 1259-1263.
[17] 李珍国, 孙启航, 王鹏磊, 等. 无刷直流电机无直轴电枢反应的非正弦转子磁场定向矢量控制技术[J]. 电工技术学报, 2022, 37(16): 4094-4103.
Li Zhenguo, Sun Qihang, Wang Penglei, et al. Non- sinusoidal rotor field oriented vector control technology without d-axis armature reaction in brushless DC motor[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4094-4103.
[18] Zhang Haifeng, Wu Haoting, Jin Hao, et al. High-dynamic and low-cost sensorless control method of high-speed brushless DC motor[J]. IEEE Transa- ctions on Industrial Informatics, 2023, 19(4): 5576- 5584.
[19] Chen Shaohua, Liu Gang, Zhu Lianqing. Sensorless control strategy of a 315 kW high-speed BLDC motor based on a speed-independent flux linkage function[J]. IEEE Transactions on Industrial Electronics, 2017, 64(11): 8607-8617.
[20] Bian Chunyuan, Li Xiaoxia, Zhao Guannan. The peak current control of permanent magnet brushless DC machine with asymmetric dual-three phases[J]. CES Transactions on Electrical Machines and Systems, 2018, 2(1): 129-135.
[21] 林明耀, 周谷庆, 刘文勇. 基于直接反电动势法的无刷直流电机准确换相新方法[J]. 东南大学学报(自然科学版), 2010, 40(1): 89-94.
Lin Mingyao, Zhou Guqing, Liu Wenyong. New accurate commutation method based on direct back- EMF method for brushless DC motor[J]. Journal of Southeast University (Natural Science Edition), 2010, 40(1): 89-94.
[22] 边春元, 邢海洋, 李晓霞, 等. 基于速度变化率的无位置传感器无刷直流电机风力发电系统换相误差补偿策略[J]. 电工技术学报, 2021, 36(11): 2374- 2382.
Bian Chunyuan, Xing Haiyang, Li Xiaoxia, et al. Compensation strategy for commutation error of sensorless brushless DC motor wind power generation system based on speed change rate[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2374- 2382.
[23] 夏长亮. 无刷直流电机控制系统[M]. 北京: 科学出版社, 2009.
[24] 施晓青, 王晓琳, 徐同兴, 等. 高速无刷直流电机自寻优换相校正策略[J]. 电工技术学报, 2019, 34(19): 3997-4005.
Shi Xiaoqing, Wang Xiaolin, Xu Tongxing, et al. Self-optimization commutation correction strategy for high-speed brushless DC motor[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 3997- 4005.
[25] Huang C L, Wu Chijun, Yang S C. Full-region sensorless BLDC drive for permanent magnet motor using pulse amplitude modulation with DC current sensing[J]. IEEE Transactions on Industrial Elec- tronics, 2021, 68(11): 11234-11244.
Abstract The ultra-high-speed brushless DC motor (BLDCM) finds extensive application in various systems, including ultra-high-speed air compressors, silicon wafer cutting, and flywheel energy storage. However, controlling ultra-high-speed BLDCM presents several challenges stemming from the incomplete symmetry of the three-phase windings and the uncertainty associated with reference zero-offset, often leading to stalling issues. Therefore, it is necessary to design different commutation delay setting methods and put forward a comprehensive solution.
First, based on pulse amplitude modulation control, a fundamental disturbance model for zero-crossing point (ZCP) resilience is established by investigating non-ideal motors. The influence of the reference zero offsets of ZCP and the incomplete spatial position symmetry of the stator windings on the ZCP position distribution in one cycle is analyzed. Then, the influence of their coexistence on the ZCP position distribution in one cycle is analyzed. An improved control strategy is proposed to address the compensation for unbalanced and asymmetric ZCPs. The proposed method mainly uses the ZCP interval law in the previous cycle to offset the interference of non-ideal factors. It selects the optimal setting of the base delay time through the proposed non-ideal situation judgment method. At the same time, the derived function of electrical angle to time is derived for each non-ideal case to accurately compensate for the phase shift error in the motor control process.
Furthermore, the commutation errors caused by speed changes under varying loads are considered under unbalanced and asymmetric ZCP disturbances. Different from the traditional use of the first two ZCP intervals, the first seven ZCP intervals are used for compensation, and the internal cancellation of ZCP disturbance within one cycle is used to eliminate the influence of ZCP disturbance on variable speed commutation error compensation. A compensation method for variable velocity commutation error is proposed based on unbalanced and asymmetric ZCP disturbance. Finally, the phase shift caused by the low-pass filter under ultra-high-speed and the diode continuous current under heavy loads are considered. The corresponding solutions and parameter selection rules are given.
The experimental results describe the performance of the new commutation delay setting method. Compared with the traditional method, the bus current ripple is reduced by 50%, and the phase current ripple is reduced by 22.5%. By compensating the phase shift factor of the low-pass filter and applying the proposed variable speed compensation strategy, the commutation error can be controlled to 1.81 electrical angle, and the ultra-high speed of 230 kr/min can be achieved.
keywords:Pulse amplitude modulation, back electromotive force ZCP, incomplete symmetry of the three-phase winding, reference zero-offset, ultra-high speed control
DOI: 10.19595/j.cnki.1000-6753.tces.230985
中图分类号:TM351
湖南省自然科学基金项目(2022JJ50082)和教育部产学合作协同育人项目(202102264003)资助。
收稿日期 2023-06-26
改稿日期 2023-12-02
余 岳 男,1978年生,博士,副教授,研究方向为电力电子及电力传动。E-mail: yuyue@hut.edu.cn
刘建华 男,1981年生,博士,副教授,研究方向为电力牵引、传动与控制方面的理论及应用技术。E-mail: 35450965@qq.com(通信作者)
(编辑 陈 诚)