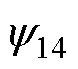 表达式为
表达式为摘要 由于人工无轴承心脏泵要求微型化,所以心脏泵系统不能采用大体积的电涡流传感器来采集径向位移信息。基于霍尔测径向位移的无轴承永磁薄片电机采用霍尔同时辨识转角和径向位移,大幅降低系统体积。霍尔输出信号直接影响无轴承电机悬浮性能,当单个霍尔传感器故障时,由于缺失一相磁链导致电机失浮。为了提高基于霍尔测径向位移的无轴承永磁薄片电机容错能力,该文针对单霍尔传感器故障时角度和径向位移信息会重新耦合,难以高精度分离的问题,提出基于谐波补偿的霍尔磁链重构算法。首先,采用磁链重构思想,利用剩余非故障霍尔重构解算径向位移的一相磁链;然后,对上述重构磁链中不偏心3次谐波进行补偿,并构建霍尔矫正表求解径向位移;最后,搭建实验平台,通过仿真和实验验证了所提算法的准确性。
关键词:无轴承永磁薄片电机 径向位移 霍尔传感器 容错控制 谐波补偿
无轴承永磁薄片电机具有定转子完全分离、集成度高、体积小等优点,作为超洁净运输设备在医疗器械、半导体产业、化工产业等领域具有很好的应用前景[1-3]。近年来新冠疫情爆发,以无轴承永磁薄片电机为主体的人工心脏泵能为心肺衰竭患者提供体外血液循环,因而受到社会广泛关注[4]。无轴承永磁薄片电机作为人工心脏泵的驱动核心,除了满足最基本的稳定悬浮旋转运输血液需求外,其系统可靠性及容错能力越来越受到人们重视[5]。
基于霍尔测径向位移的无轴承永磁薄片电机,采用霍尔同时辨识转角和径向位移。转角和径向位移信息都来自霍尔信号,霍尔健康状况直接影响薄片电机系统悬浮可靠性。由于温度、电磁等干扰,霍尔容易发生故障损坏,系统转角和径向位移无法辨识。由于其应用场合的特殊性,即使霍尔发生故障,也必须保证系统在性能波动允许范围内稳定运行,一旦失去悬浮能力关机维修,或者更换备用薄片电机,暂停运输血液会给患者造成无法挽回的损伤,酿成重大安全事故[6]。所以,要求薄片电机系统具有高可靠性和强容错能力。
为了提高无轴承永磁薄片电机系统容错能力,国内外学者进行了许多研究。目前,无轴承电机容错研究主要集中在电机绕组、功率开关管故障时实现系统容错运行。
文献[7]对单绕组无轴承永磁薄片电机绕组开路情况进行了研究,保证了电机在单相和相对两相绕组开路情况下正常运行。文献[8]对电流控制多相片式无轴承电机绕组开路故障进行分析,实现了电机在单相、相邻或相对两相绕组开路故障下的稳定运行。文献[9]对单绕组无轴承永磁薄片电机绕组短路情况进行研究,实现了电机绕组单相短路容错运行。文献[10]针对绕组断路情况提出了通用型绕组断路故障容错技术,实现了电机绕组发生短路、断路和两相短路故障情况下的容错运行。文献[11]对H桥驱动下的单绕组无轴承永磁薄片电机功率开关管短路和开路故障进行研究,实现了一相功率开关管开路和短路情况下容错运行。
霍尔传感器研究主要集中在以下几个方面:
(1)霍尔安装误差信号校正。在电机实际应用中,由于人工安装霍尔无法避免会存在位置偏差,导致霍尔输出信号幅值和初相位有误差。如何在安装偏差情况下对霍尔输出信号进行校正是一个重要的研究方向。常用的霍尔输出信号校正方法有平均值修正法[12]、离线标定法[13]。
(2)霍尔位置估算误差补偿。霍尔自身精度存在差异,本身输出信号不对称和相位偏差会影响控制算法转角计算精度,不准确的转角信息会使电机出现明显的转速和输出转矩波动。所以对霍尔转角误差进行补偿是提高系统稳态精度的一种重要方法。常用的位置补偿方法有磁通观测法[14]、基于坐标变化误差补偿法[15]和外插估计法[16]。
(3)霍尔故障系统容错控制。长时间工作、电机振动和霍尔接线松动都会导致霍尔输出信号丢失,系统转角无法辨识,致使电机三相电流畸变和剧烈机械振动,降低系统可靠性,所以,在霍尔故障下重新辨识位置对提高系统可靠性具有重大意义。常用的容错控制方法有离散傅里叶法[17]、改进矢量控制器法[18]和电流滑模观测器法[19]。
综上所述,目前无轴承永磁薄片电机容错主要是绕组开路、断路状态和逆变器功率开关管故障下系统容错运行。对于霍尔容错控制,采用上述误差补偿和容错控制方法可以减少转角辨识误差。但上述方法都不能用于霍尔故障情况下解算系统径向位移,目前也没有学者在霍尔故障下对无轴承永磁薄片电机径向位移进行研究。
无轴承永磁薄片电机常在电机定子齿槽放置霍尔,通过锁相环解算转子角度。根据霍尔一体两用思想,可以采样霍尔信号解算出径向位移信息。考虑到单霍尔故障时角度和径向位移信息会重新耦合,难以高精度分离,输出霍尔信号不对称使得相对霍尔无法求和消除3次谐波,并且3次谐波系数未知导致3次谐波难以补偿,本文对无轴承永磁薄片电机单霍尔容错进行研究,采用霍尔磁链重构思想,以Hall1故障为例,重构Hall1输出信号,再对不偏心基础磁链3次谐波系数进行详细推导从而补偿霍尔磁链中缺失3次谐波,再构造故障下的霍尔信号矫正表并用负序解耦法解算出径向位移信息;最后分析整个控制系统框图并进行实验验证,实验结果证明了单霍尔容错算法的准确性。
霍尔根据霍尔效应检测电机气隙磁场强度并转化为电压输出信号,转角影响霍尔输出信号相位,径向位移影响霍尔输出信号幅值。
系统的转角和径向位移信息都来自霍尔传感器。霍尔传感器当角度传感器使用时,可以忽略微弱的径向位移信息带来的输出幅值信号变化,当位移传感器使用时面临转角和径向位移耦合问题。单霍尔传感器故障时,采用谐波补偿的霍尔磁链重构法,利用其余非故障霍尔信号重构故障霍尔信号,并对3次谐波进行补偿,补全缺失的一相径向位移磁链。
图1为系统控制框图。转矩控制部分内环为电流环,单霍尔传感器故障时,确定故障霍尔编号,在剩余非故障霍尔中选取机械位置对称分布的三个霍尔经过锁相环求解转角,对重构霍尔磁链进行3次谐波补偿,实现外环速度环闭环。悬浮控制部分外环为位移环,通过霍尔磁链重构法解算的径向位移与给定径向位移作差,用于内环电流环闭环[20]。
图2为无轴承永磁薄片电机结构示意图,本文电机采用六齿一对极结构,电机转矩绕组为一对极,悬浮绕组为两对极,两套绕组相差一对极,实现电机径向悬浮的同时维持稳定旋转。此外,在电机定子齿槽口间均匀安置6个可编程线性霍尔传感器,按照逆时针方向编号为Hall1~Hall6。其中,Hall1和Hall4正对一对极转子充磁方向,Hall1安置在水平位置,定义其初始机械角度q0=0。
由文献[21-23]可知,把相对霍尔当成空间分布的绕组,在永磁体激励、悬浮电流和转矩电流共同作用下的相对霍尔磁链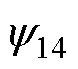 表达式为
表达式为
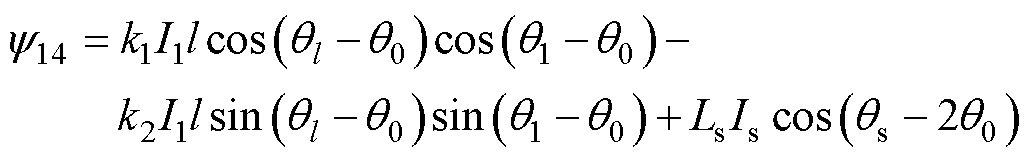 (1)
(1)
式中,k1、k2为偏心径向位移系数,k1=k2=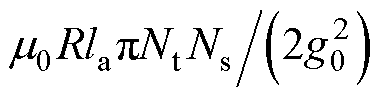 ,μ0为真空磁导率,R为转子外半径,la为轴向长度,g0为不偏心时气隙长度,Ns为相对霍尔等效绕组匝数,Nt为永磁体等效绕组匝数;I1为一对极合成磁场幅值;l为偏心径向位移;q1为一对极合成磁场电角度;qs为悬浮电流合成角度;ql为偏心角度;Ls、Is分别为悬浮绕组自感和电流幅值。
,μ0为真空磁导率,R为转子外半径,la为轴向长度,g0为不偏心时气隙长度,Ns为相对霍尔等效绕组匝数,Nt为永磁体等效绕组匝数;I1为一对极合成磁场幅值;l为偏心径向位移;q1为一对极合成磁场电角度;qs为悬浮电流合成角度;ql为偏心角度;Ls、Is分别为悬浮绕组自感和电流幅值。
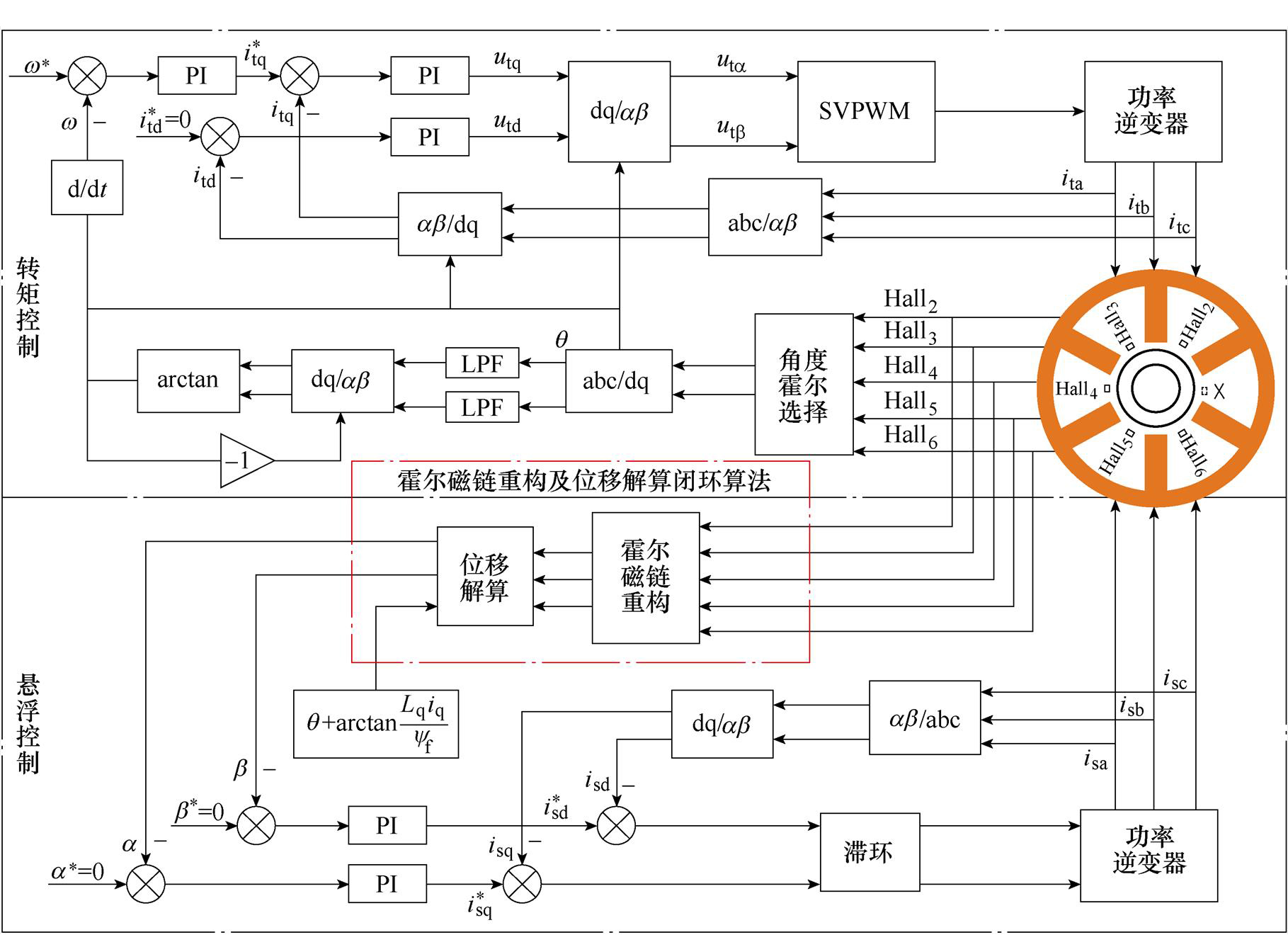
图1 系统控制框图
Fig.1 System control block diagram
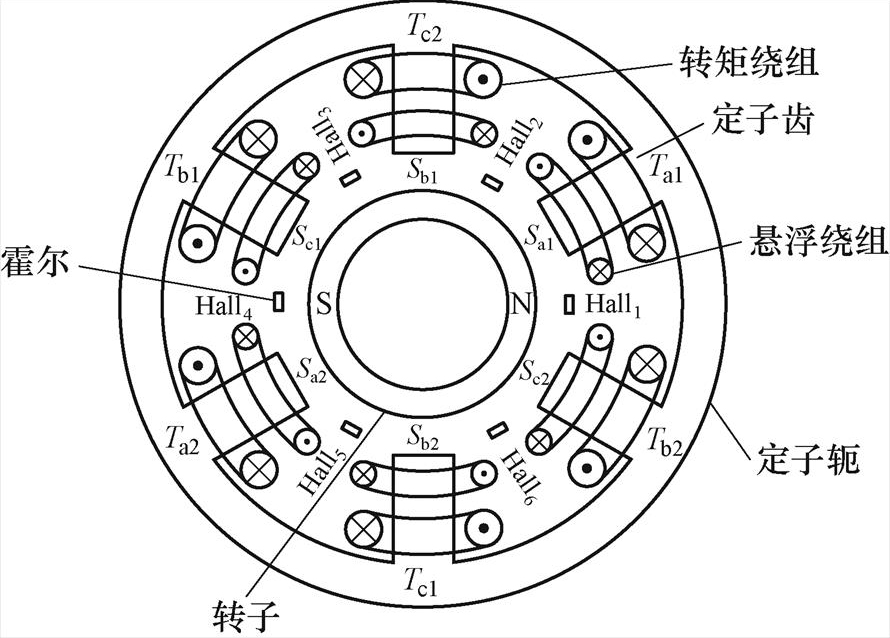
图2 无轴承永磁薄片电机结构示意图
Fig.2 Structure schematic diagram of permanent bearingless slice motor
同理可得其余相对霍尔磁链表达式为
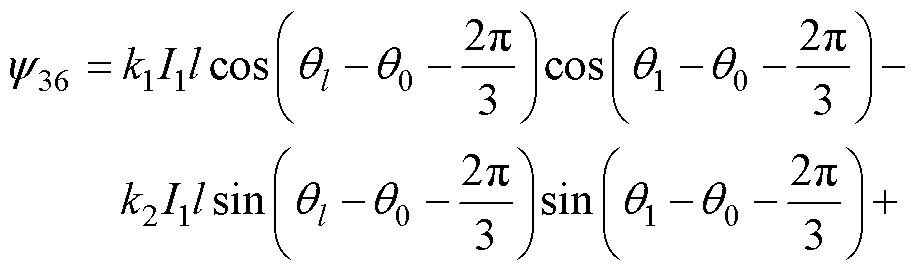
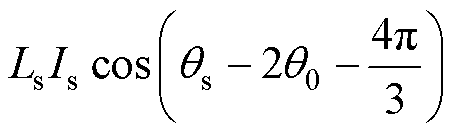 (2)
(2)
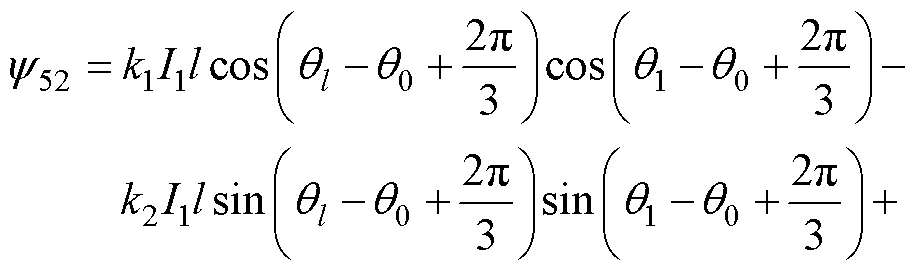
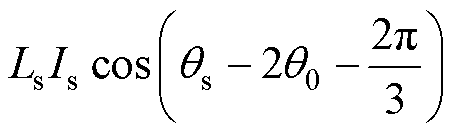 (3)
(3)
当转子不偏心时单位角度的磁导[24]为
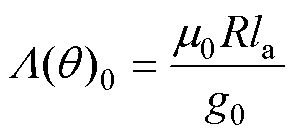 (4)
(4)
机械位置上单个霍尔(Hall1)可以当作一对极分布的绕组,其空间分布函数表达式为Nscosq 及谐波Nscos(2q)、Nscos(3q) 等。转子平行充磁,空间磁动势为如NtIf cos(q-w t) 形式的一对极行波,其中,If为不偏心时永磁体等效励磁幅值。
由于永磁体磁钢充磁不均匀,存在少量3次谐波[25]。根据电机空间磁通连续原理,有
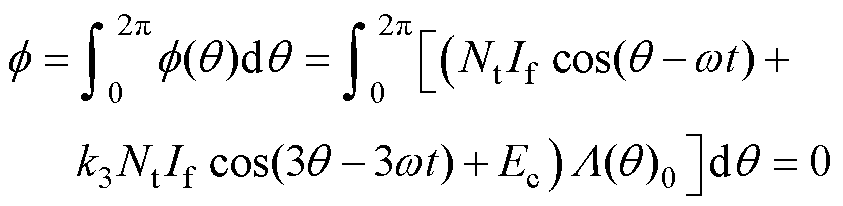 (5)
(5)
式中,f为转子磁通;q 为转子角度;w 为转子磁场机械角速度;k3为永磁体中3次谐波与基波比例。可得此时转子磁动势补偿Ec=0,故转子磁动势Er为
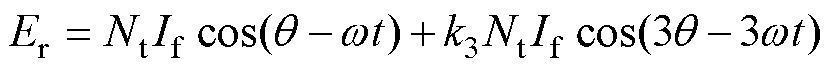 (6)
(6)
绕组空间分布函数与磁通的乘积在圆上积分得到空间磁链,并且定义Hall1的初始角度为q0,有
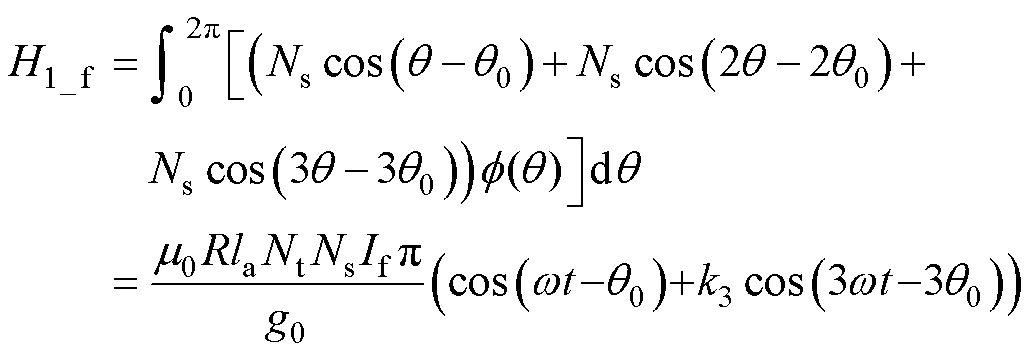
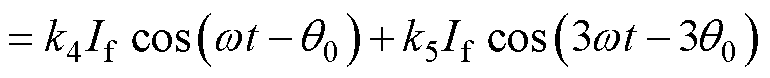 (7)
(7)
式中,H1_f为转子空间磁链;k4为基波径向位移系数,其值为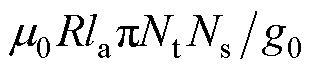 ;k5为3次谐波径向位移系数。
;k5为3次谐波径向位移系数。
由于转矩绕组也为一对极绕组,故不偏心状态下单霍尔磁链表达式中的转矩分量可以表示为
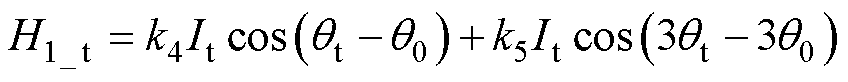 (8)
(8)
式中,It为转矩电流幅值;qt为转矩电流合成角度。
故结合式(7)、式(8),可得永磁体和转矩电流共同作用下的不偏心基础磁链为
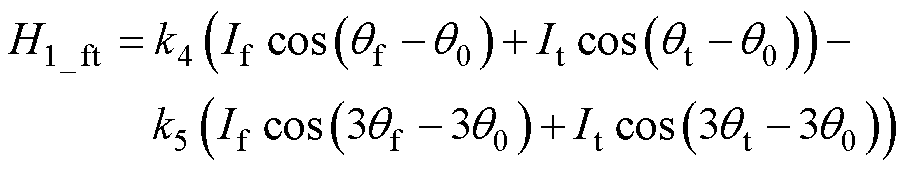 (9)
(9)
式中,qf为永磁体激励角度。
在霍尔非故障情况下,采用6个霍尔实现转子不偏心稳定悬浮,消除转子偏心对霍尔输出信号的影响,用示波器采样此时Hall1的输出信号,并用Matlab进行傅里叶分解,得到转子中3次谐波与基波的比例,谐波阶数含量如图3所示。由于悬浮电流的干扰,霍尔输出信号中含有少量的偶次谐波。由图3可知,3次谐波与基波的比例为0.024 6。
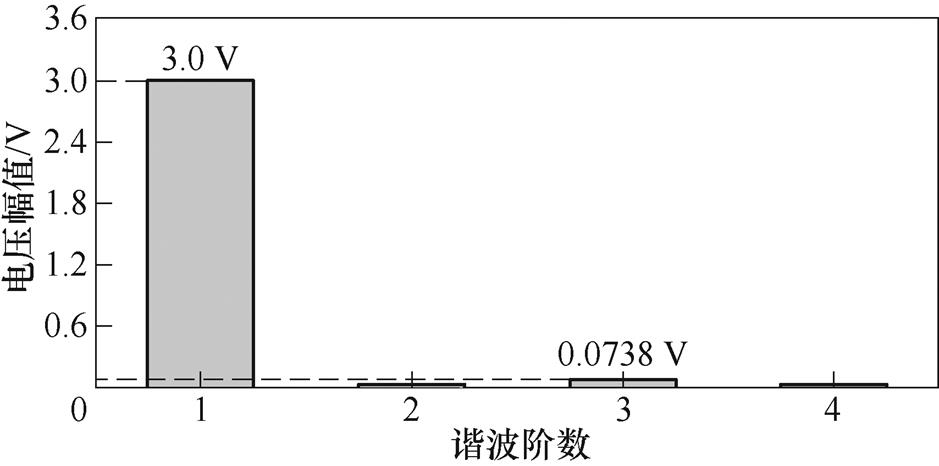
图3 谐波阶数含量
Fig.3 Diagram of Harmonic order content
综上所述,考虑3次谐波的Hall1的输出表达式为
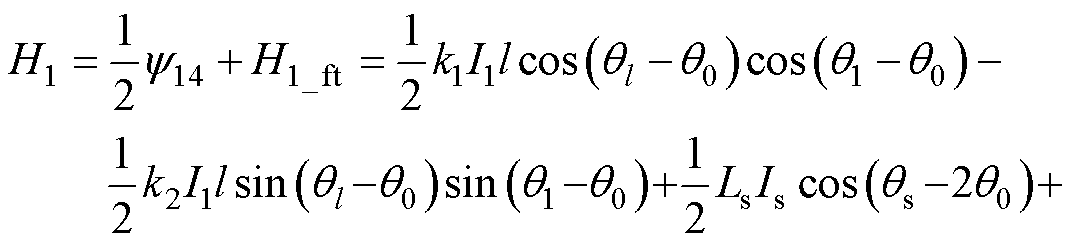
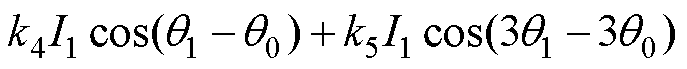 (10)
(10)
当不考虑3次谐波时,Hall1输出信号表达式为
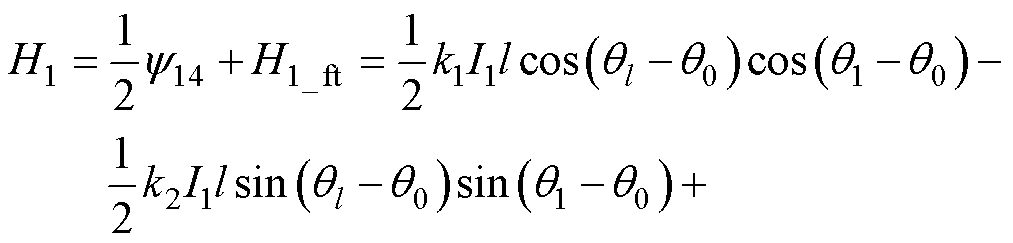
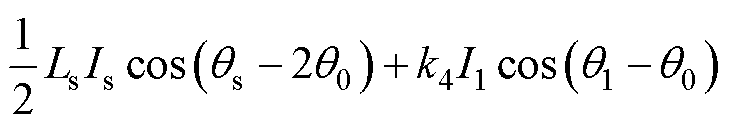 (11)
(11)
仿真中不考虑3次谐波,只保留转矩激励,基波径向位移系数k4=0.005 Wb/A,由于系数k5与系数k4比例为0.024 6,3次谐波径向位移系数k5= 0.000 123 Wb/A。
悬浮控制系统外环采用位移环,其中外部A-D检测6个霍尔输出信号,经过逆序解耦法作为位移环的反馈量,外部A-D检测的霍尔信号反映了当前霍尔工作状态,可以根据检测信号是否恒为静态偏置电压来判断当前霍尔是否处于故障状态。图4为霍尔故障编号检测流程,程序中为了提高算法的抗干扰性和准确性,采用滑动求和的方法,对霍尔输出信号与偏置电压差值在k个周期内求和,当其小于给定的阈值时,便判定该霍尔处于故障状态,其霍尔故障检测信号由高电平变为低电平。
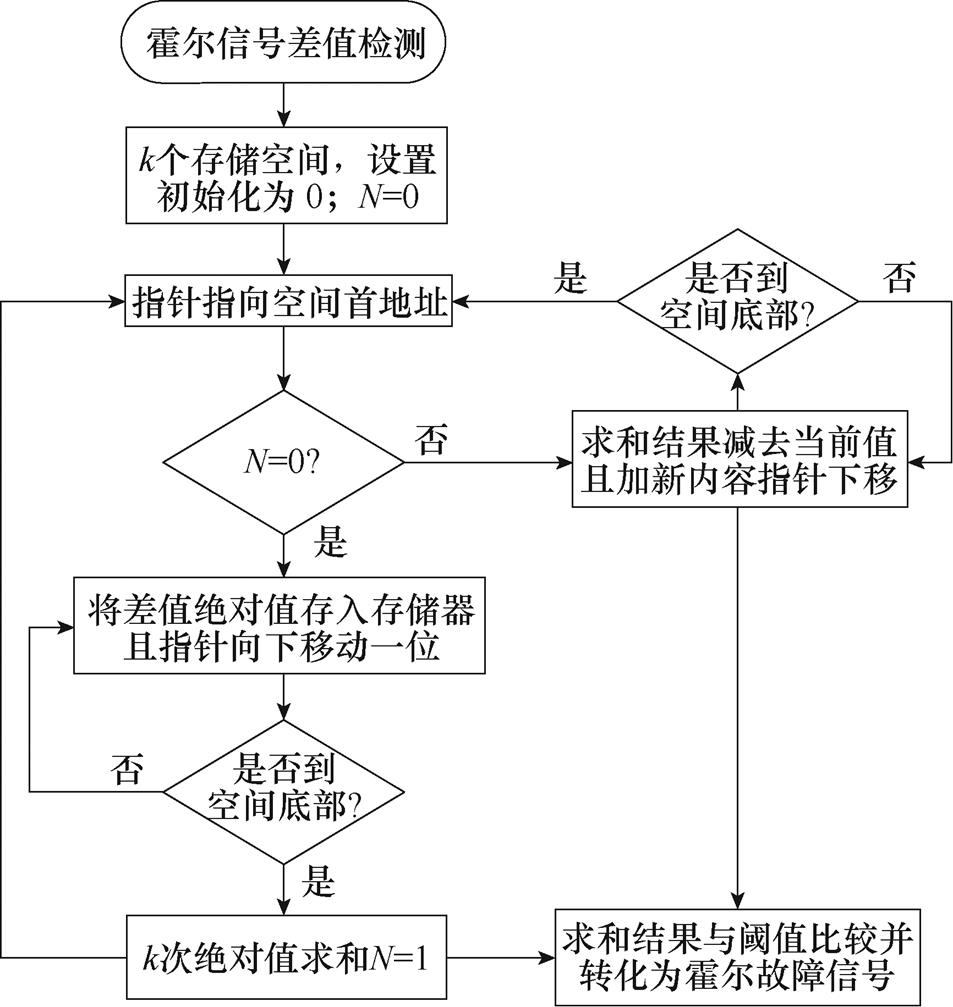
图4 霍尔故障编号检测流程
Fig.4 Hall fault number detection flow diagram
根据式(10)得到其余5个霍尔输出信号表达式H2~H6。以Hall1故障为例,用非故障相对的两个霍尔输出信号作差并求和得到不偏心基础磁链为
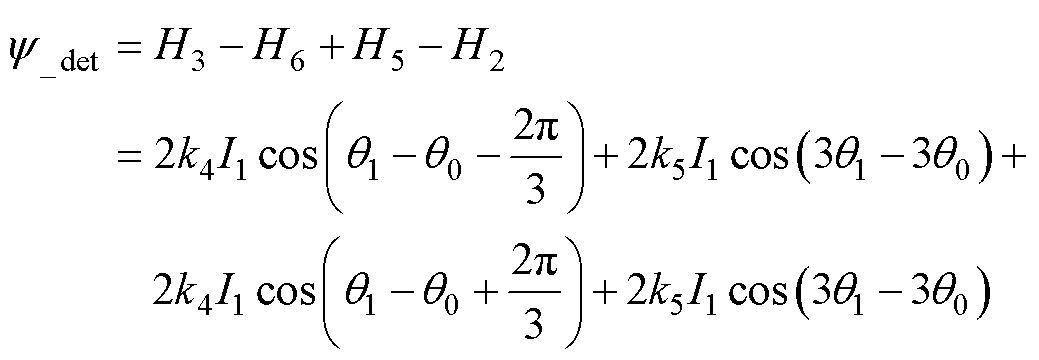 (12)
(12)
用与故障霍尔机械位置相对的霍尔输出信号的两倍减去上述不偏心基础磁链得到重构后的磁链表达式为
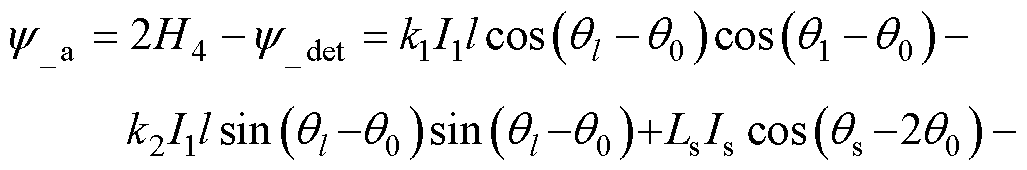
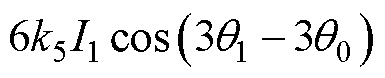 (13)
(13)
对上述重构后的磁链y_a补偿3次谐波6k5I1cos(3q1-3q0),得到重构后的霍尔空间分布磁链表达式为
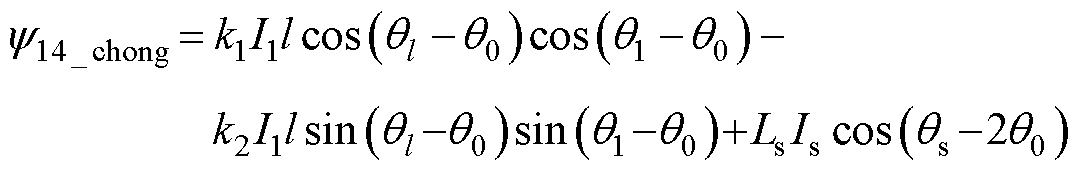 (14)
(14)
在Matlab中将a 和b 两方向位移作为横纵坐标,y14-chong磁链幅值作为竖坐标构建如图5所示的三维霍尔矫正表。该霍尔矫正表作为重构霍尔信号的参考输入,来减少霍尔磁链重构算法重构的霍尔磁链误差。
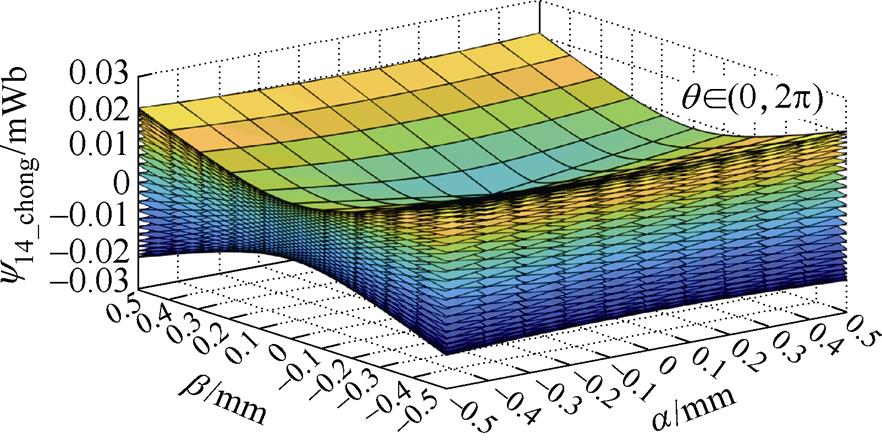
图5 霍尔矫正表
Fig.5 Hall correction table
在Ansys仿真软件中设置Hall1初相位q0=0;转子平行向右正对Hall1进行充磁;三相转矩电流幅值20 A,合成电角度45°;三相悬浮电流幅值4 A,合成电角度45°;转子a、b 方向径向位移都为0.3 mm;转子转速6 000 r/min。
图6为按照上述霍尔磁链重构算法得到的y14-chong和实际仿真得到的y14的对比,可见两者偏差较小,证明上述霍尔磁链重构算法的正确性。
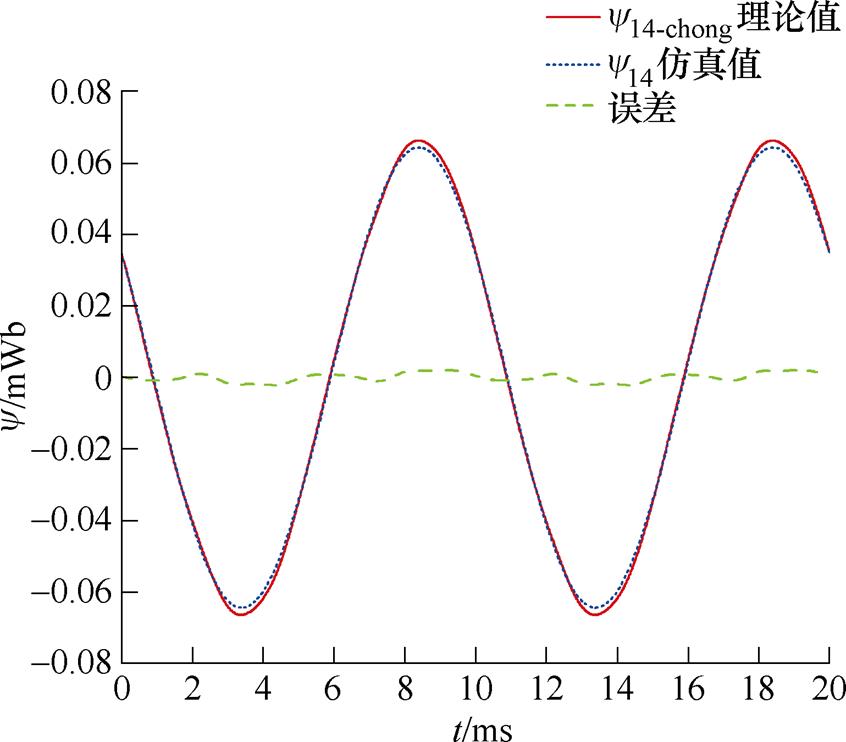
图6 y14仿真值和y14-chong理论值
Fig.6 y14 simulation value and y14-chong theoretical value
在最后的径向位移解算中如果不对重构的霍尔磁链补偿3次谐波,会造成最终解算的径向位移叠加关于转角的二倍频和四倍频信号,由于径向位移信息较小,该叠加信号会淹没径向位移信息,造成较大的径向位移辨识误差。
三相径向位移磁链表达式中前两项是关于径向位移信息的函数,第三项是与径向位移无关的悬浮漏磁,且其对径向位移解算干扰较大,通过仿真得到的悬浮绕组自感Ls消除对径向位移解算的影 响[26],得到前面两项关于径向位移信息的表达式用于解算径向位移,记作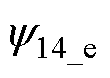 、
、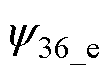 、
、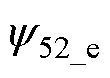 。
。
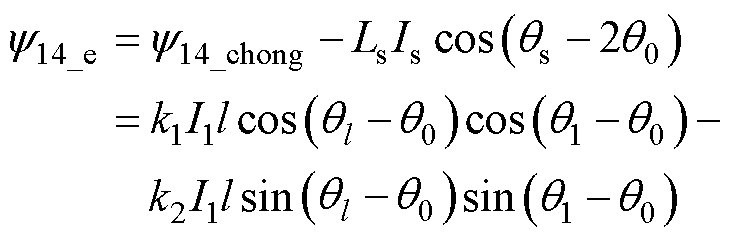 (15)
(15)
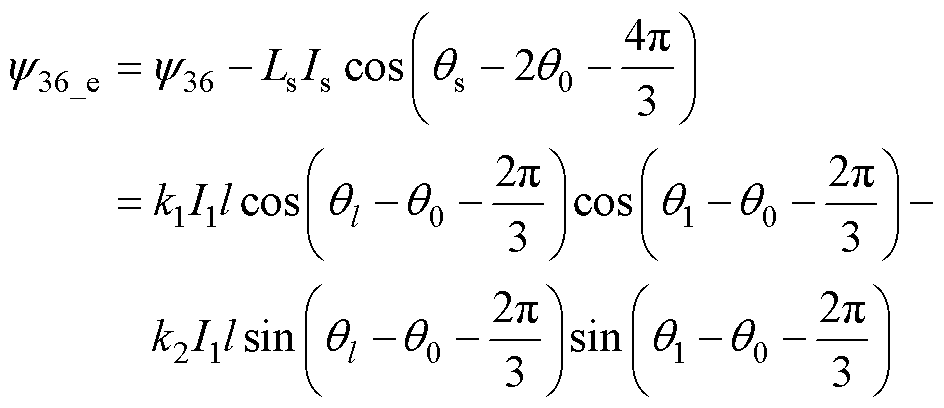 (16)
(16)
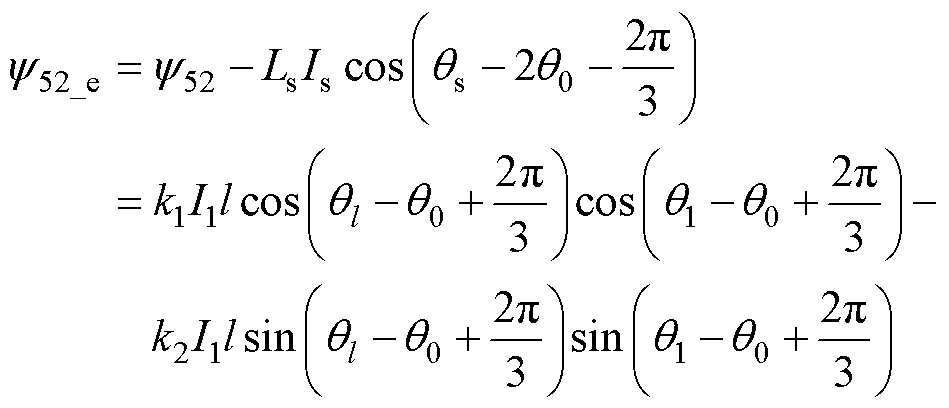 (17)
(17)
式中,y36、y52为另外两项相对霍尔磁链表达式。
径向位移解算采用负序解耦法,即把上述三相径向位移磁链表达式往逆频率一对极磁场投影,实现转角和径向位移解耦,进而得到径向位移。式(18)、式(19)为负序解耦法计算表达式,按照最终的计算结果可以得到径向位移ab,两者径向位移系数为K=3(k1+k2)I1/4。
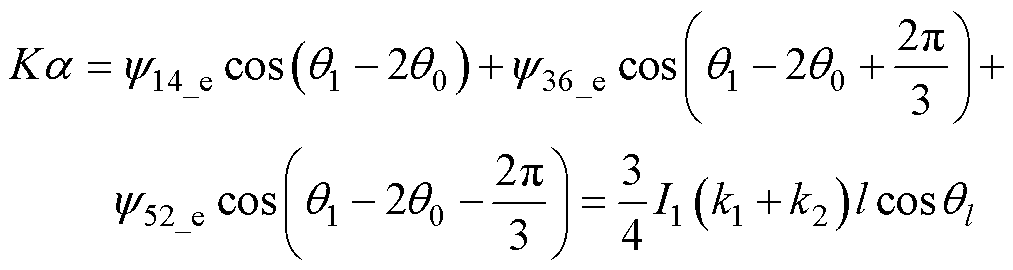 (18)
(18)
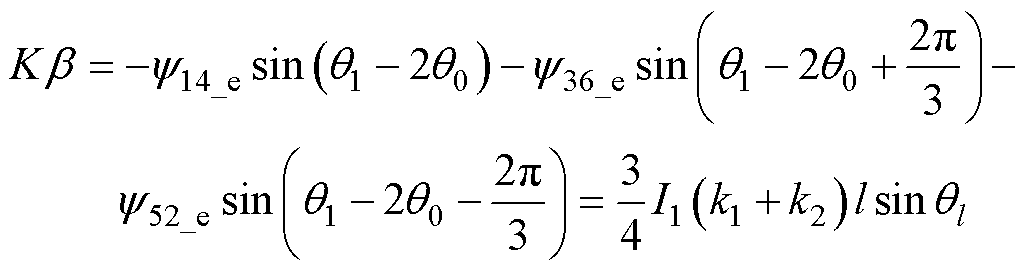 (19)
(19)
式中,Ka 为K倍a 方向径向位移;Kb为K倍b 方向径向位移。
图7为霍尔磁链重构及径向位移解算框图,当Hall1故障时,通过基于谐波补偿的霍尔磁链重构算法补偿缺失的一相径向位移磁链,得到霍尔故障下的三相径向位移磁链。径向位移进行反馈得到霍尔磁链矫正信号,与上述三相径向位移磁链作差,经过单比例调节器对三相霍尔磁链误差进行调节。当单比例调节器kp为零时,最终的重构霍尔信号与实际霍尔信号完全重合,消除累积误差。再通过负序解耦法实现转角和径向位移解耦,得到两个方向径向位移,最后径向位移反馈回霍尔故障下的霍尔信号矫正表,实现整体控制算法闭环。
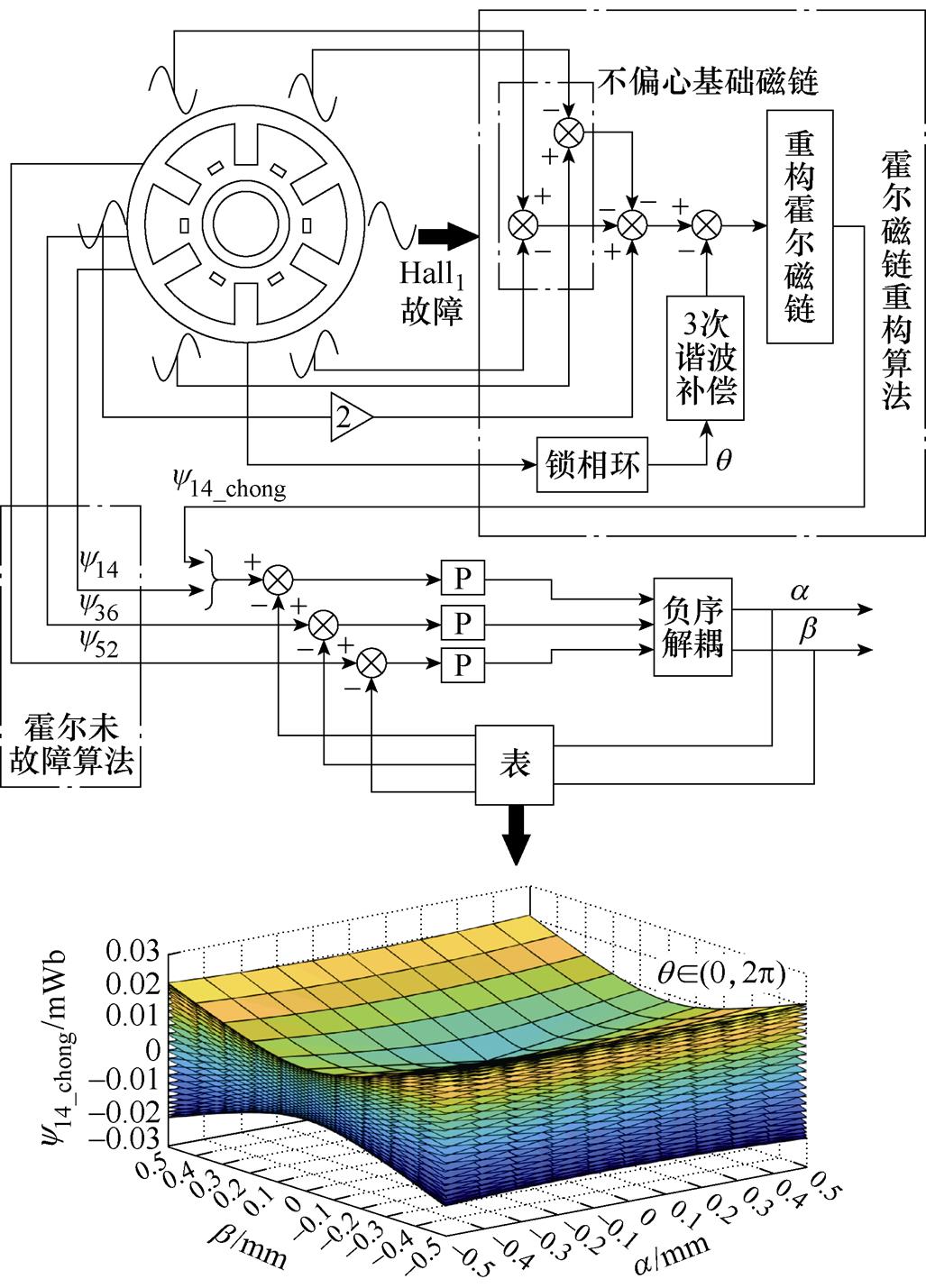
图7 霍尔磁链重构及径向位移解算框图
Fig.7 Hall flux linkage reconstruction and radial displacement calculation block diagram
本文在Matlab/Simulink中模拟单霍尔故障,搭建了上述的霍尔磁链重构算法和径向位移解算模块。在单霍尔故障的情况下,确定故障霍尔编号,随机给定转子偏心径向位移,查看经过重构算法和径向位移解算模块的径向位移。给定径向位移与解算径向位移对比如图8所示,可以看出,在随机给定转子径向位移下,给定径向位移与解算径向位移重合度很高,表明霍尔磁链重构算法和负序解耦法的正确性。
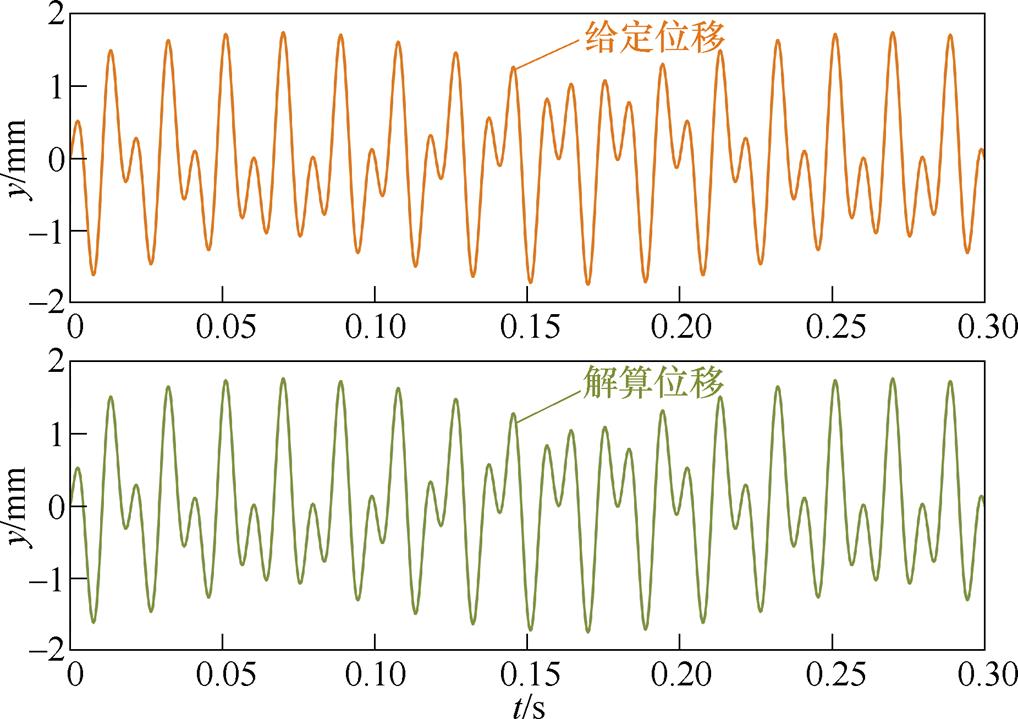
图8 给定径向位移与解算径向位移的对比
Fig.8 Diagram of the given and calculated radial displacement
本文搭建了如图9所示的无轴承永磁薄片电机实验平台来验证上述提出的霍尔磁链重构算法的正确性,电机实验平台由无轴承永磁薄片电机本体、DSP28335数字控制器、转矩和悬浮两套逆变器构成。其中,无轴承永磁薄片电机具体参数见表1。平台采用的可编程线性霍尔型号为A1363LKTTN-1-T,输出电压范围为0~5 V,灵敏度设置为1 mV/G,设置静态偏置电压为2.15 V,电机转子最大最小磁场下,磁场波动为±2 000 G,故霍尔传感器输出电压范围为0.15~4.15V,满足检测范围。

图9 无轴承永磁薄片电机实验平台
Fig.9 Experimental platform of bearingless permanent magnet slice motor
表1 电机参数
Tab.1 Motor parameters
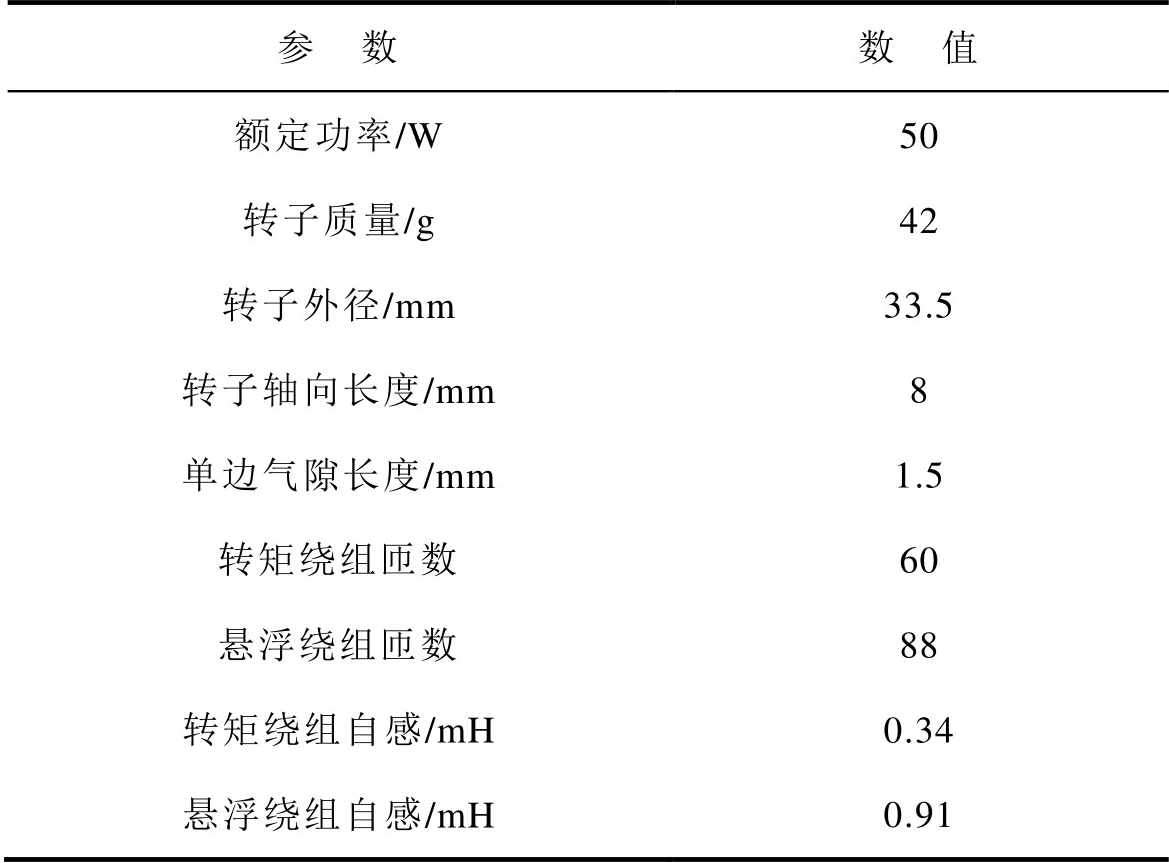
参 数数 值 额定功率/W50 转子质量/g42 转子外径/mm33.5 转子轴向长度/mm8 单边气隙长度/mm1.5 转矩绕组匝数60 悬浮绕组匝数88 转矩绕组自感/mH0.34 悬浮绕组自感/mH0.91
图10为霍尔故障检测,在电机运行中,随机任意霍尔故障(如Hall3故障),可见当Hall3故障时其输出电压变为偏置电压保持不变,此时Hall3的故障检测信号立即由高电平转化为低电平,证明图4中的霍尔故障检测方法准确,通过该算法可以辨识任意霍尔故障。
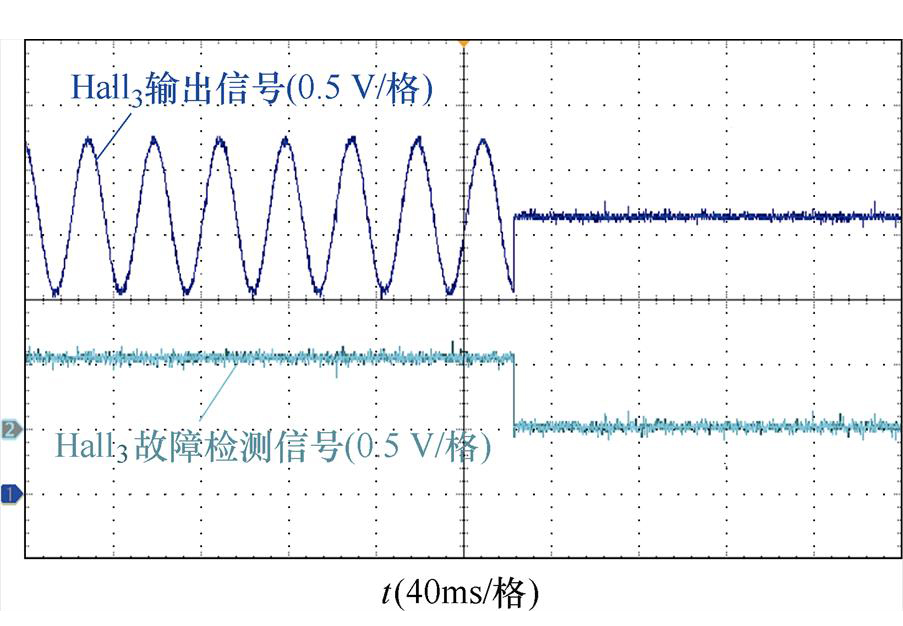
图10 霍尔故障检测
Fig.10 Hall fault detection diagram
图11为静止悬浮开启和关闭径向位移。由图可知,静止悬浮未开启前,转子只受到定子齿的磁拉力,没有悬浮电流控制力,转子a 和b 分别处于0.32 mm和-0.24 mm位置处。当静止悬浮开启后,转子受到悬浮电流控制力实现径向位移闭环,在40 ms内由随机贴边状态到电机机械位置中心并保持静止稳定悬浮,悬浮波动不超过80 mm,表明控制算法的准确性。当静止悬浮关闭后,转子失去悬浮电流控制力,又回到一开始的贴边状态。
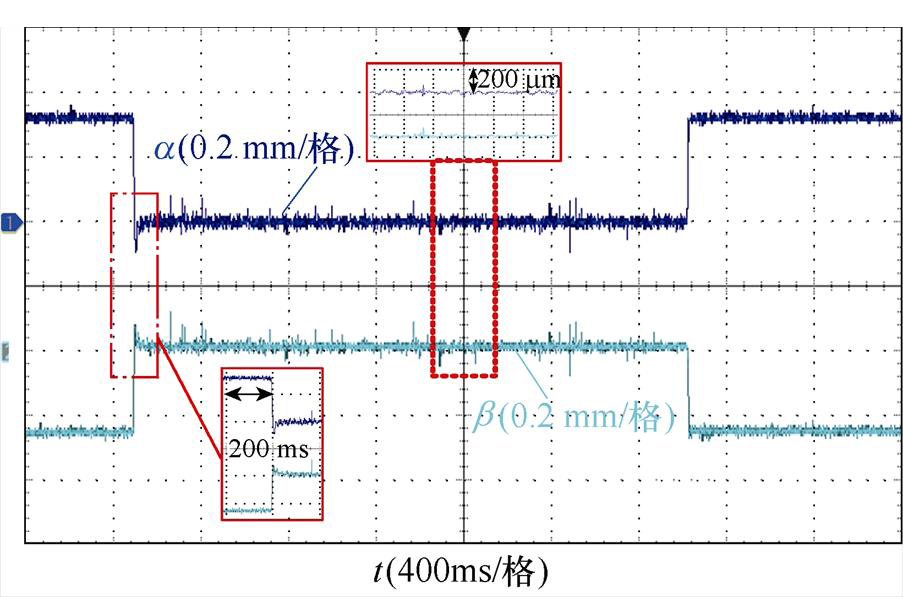
图11 静止悬浮开启和关闭径向位移
Fig.11 Radial displacement when static suspension control is started and closed
转速和转角变化如图12所示,经过1 s时间转子从静止状态达到给定转速5 000 r/min,且转速稳定时波动不超过30 r/min,说明算法动态性良好。且转速稳定在5 000 r/min时,转角波形规律平滑。
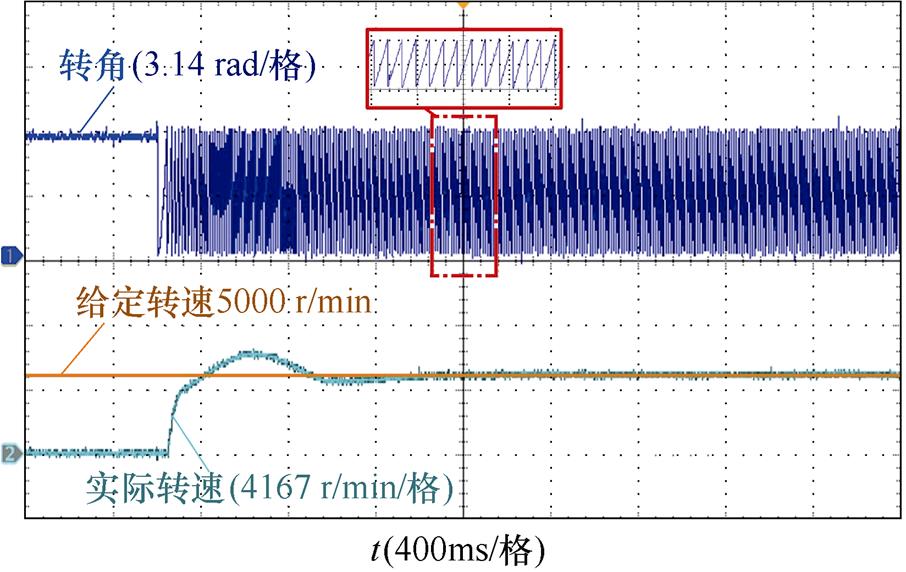
图12 5 000 r/min转速和转角波形
Fig.12 Speed and angle waveforms at 5 000 r/min
图13为霍尔非故障情况和单霍尔故障情况下的转子辨识角度对比。单霍尔故障下转子角度辨识误差不超过9°,说明选取非故障3个对称霍尔经过锁相环辨识角度方法准确度高。
图14为实际Hall1输出信号和重构Hall1输出信号对比。重构Hall1输出信号误差不超过8%,说明重构算法准确。
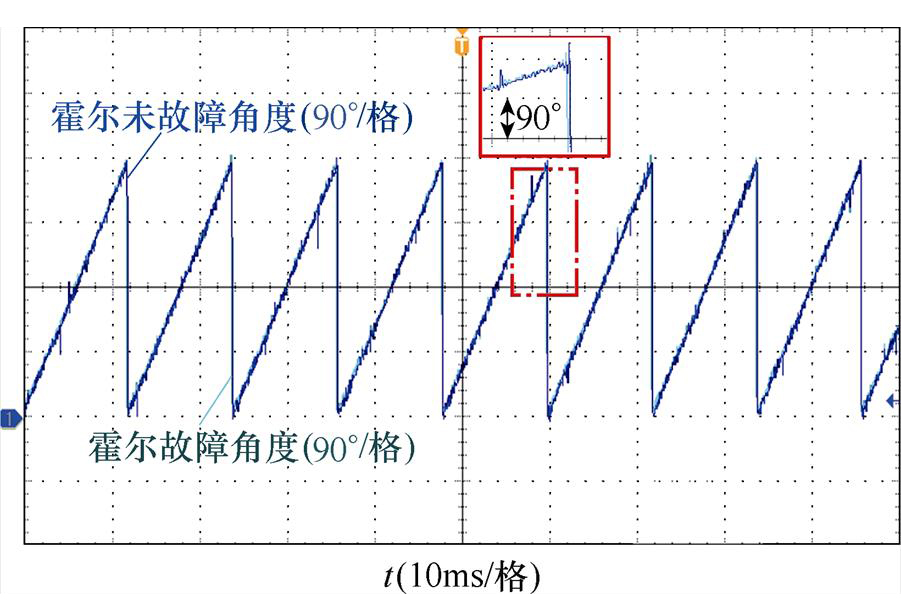
图13 霍尔非故障和单霍尔故障转角
Fig.13 The angle of Hall non-fault and single Hall fault
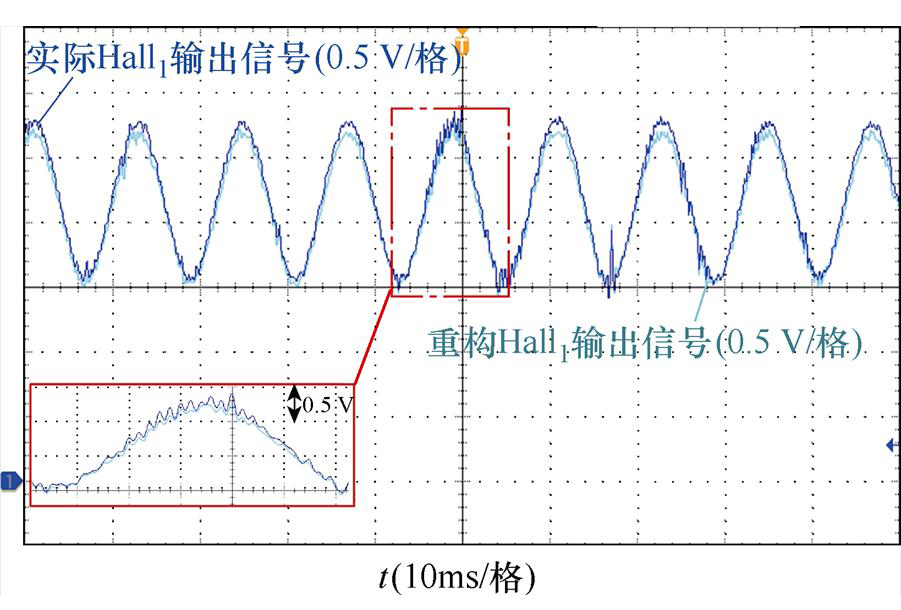
图14 实际Hall1和重构Hall1输出信号
Fig.14 Actual Hall1 and reconstructed Hall1 output signals
图15为霍尔非故障和霍尔故障两方向径向位移对比。采用霍尔磁链重构算法实现径向位移闭环,其中a 方向径向位移误差不超过0.06 mm,b 方向径向位移误差不超过0.08 mm,证明容错算法径向位移辨识精确。
图16为容错算法切入时两方向径向位移变化,可见在16 ms内容错算法成功切入,切入后两方向径向位移并没有发生严重抖动。由于薄片霍尔竖立放置,故a 和b 两方向径向位移精度稍有区别,稳定时a 方向径向位移不超过0.2 mm,b 方向径向位移不超过0.3 mm,可见稳态时径向位移精度较高。b 方向径向位移精度稍低,这与图15中b 方向径向位移误差较大是对应的。
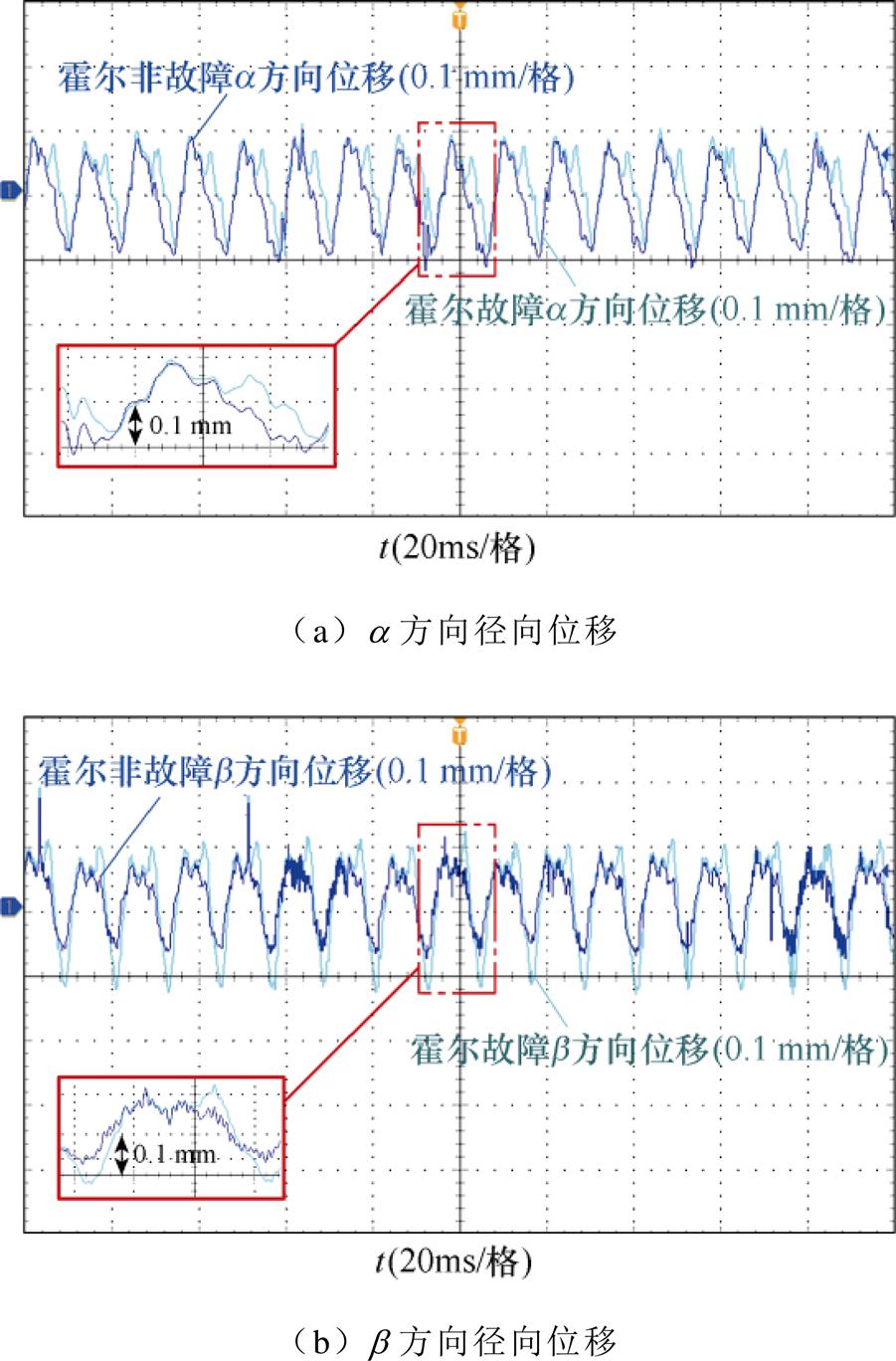
图15 霍尔非故障和霍尔故障两方向径向位移
Fig.15 Radial displacement in two directions of Hall non-fault and Hall fault
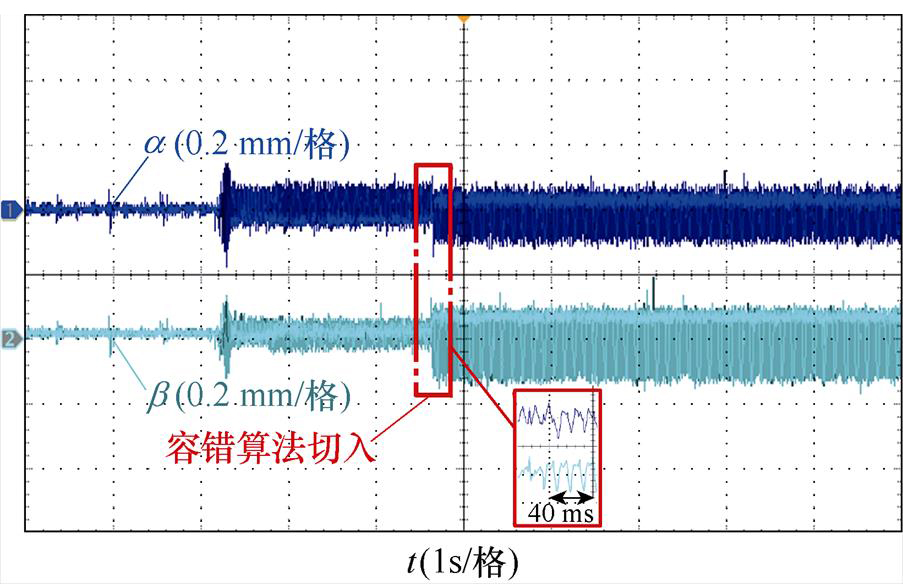
图16 容错算法切入两方向径向位移波形
Fig.16 Fault tolerant algorithm cuts into the two direction radial displacement waveforms
图17为电机转速从0到3 000 r/min,3 000 r/min到6 000 r/min切换时实际转速与给定转速对比。可见电机转速切换时动态响应快,两次转速切换动态时间均在1 s以内,且转速并未发生明显抖动,说明转速切换性能良好。
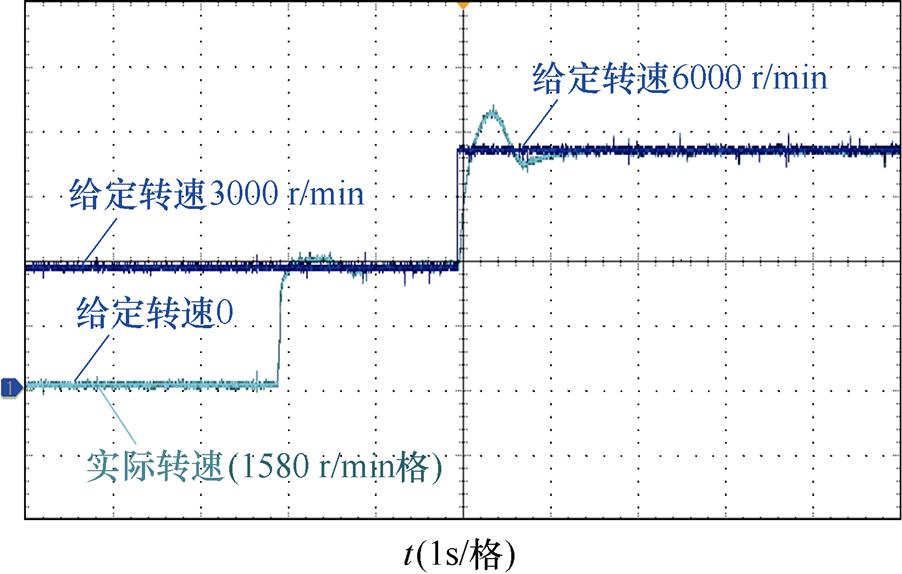
图17 0-3 000 r/min-6 000 r/min切换时的给定转速与实际转速
Fig.17 Given speed and actual speed when switching from 0 to 3 000 r/min, 3 000 to 6 000 r/min
图18为电机转速从0到3 000 r/min,3 000 r/min到6 000 r/min切换时径向位移波形。由于缺失一个霍尔信号,转子轴向抖动对霍尔磁链重构影响无法量化消除,当转速突变时轻微的轴向抖动会影响两方向悬浮精度。两次转速突变时,a 方向径向位移波动不超过0.3 mm,b 方向径向位移波动不超过0.4 mm,且转速越高径向位移越稳定,说明径向位移动态切换性能优越。
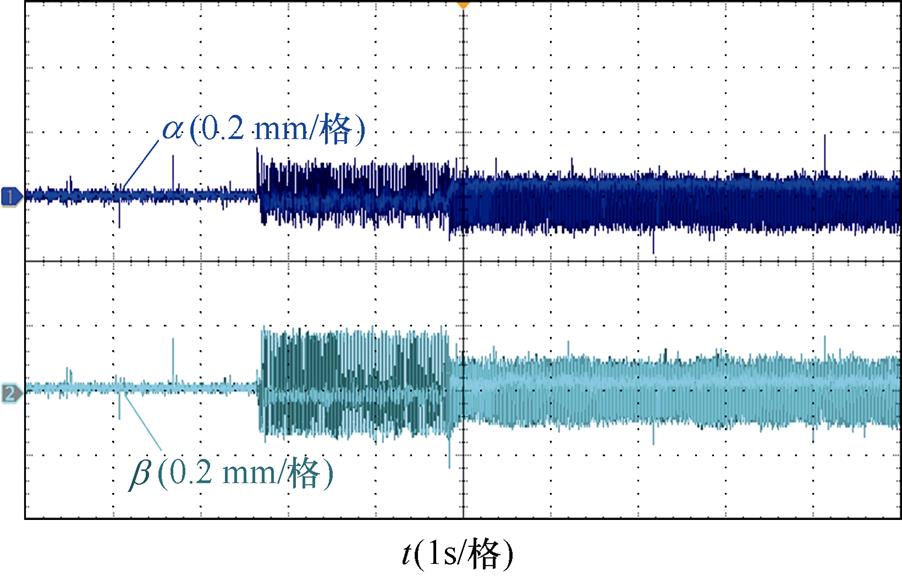
图18 0-3 000 r/min-6 000 r/min切换时的径向位移波形
Fig.18 Radial displacement waveforms when switching from 0 to 3 000 r/min, 3 000 to 6 000 r/min
本文针对无轴承永磁薄片电机单霍尔传感器故障进行研究,可以得到如下结论:
1)单霍尔故障情况下,霍尔输出信号减少和剩余信号不对称使得径向位移解算缺失一相磁链,导致系统转角和径向位移信息重新耦合。
2)本文提出的霍尔磁链重构方法,在单霍尔故障情况下,对霍尔磁链进行重构并补偿3次谐波,得到相对两霍尔空间分布的磁链表达式,保证在缺失霍尔信号时重新对转子径向位移和转角实现解耦,提高无轴承系统的可靠性和容错能力。可作为人工心脏泵的容错方案,提高体外血液循环稳定性,避免重大安全事故发生。
3)本文针对单霍尔故障进行研究,对双霍尔和多霍尔故障情况没有考虑,需要后续进一步研究。
参考文献
[1] 禹春敏, 邓智泉, 梅磊, 等. 基于精确磁路的新型混合型轴向-径向磁悬浮轴承研究[J]. 电工技术学报, 2021, 36(6): 1219-1228.
Yu Chunmin, Deng Zhiquan, Mei Lei, et al. Research of new hybrid axial-radial magnetic bearing based on accurate magnetic circuit[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1219-1228.
[2] 李志, 苏振中, 胡靖华, 等. 磁轴承复合位移传感设计与实验研究[J]. 电工技术学报, 2021, 36(7): 1425-1433.
Li Zhi, Su Zhenzhong, Hu Jinghua, et al. Design and experimental research of magnetic bearing compound displacement sensor[J]. Transactions of China Elec- trotechnical Society, 2021, 36(7): 1425-1433.
[3] 周天豪, 陈磊, 祝长生, 等. 基于自适应变步长最小均方算法的磁悬浮高速电机不平衡补偿[J]. 电工技术学报, 2020, 35(9): 1900-1911.
Zhou Tianhao, Chen Lei, Zhu Changsheng, et al. Unbalance compensation for magnetically levitated high-speed motors based on adaptive variable step size least mean square algorithm[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1900- 1911.
[4] Ronco C, Navalesi P, Vincent J L. Coronavirus epidemic: preparing for extracorporeal organ support in intensive care[J]. The Lancet Respiratory Medicine, 2020, 8(3): 240-241.
[5] 刘鑫, 曲洪一, 王聪, 等. 第3代人工心脏泵研究进展及应用[J]. 中国生物医学工程学报, 2022, 41(3): 339-350.
Liu Xin, Qu Hongyi, Wang Cong, et al. Research progress and application of the third generation of artificial heart pump[J]. Chinese Journal of Biomedical Engineering, 2022, 41(3): 339-350.
[6] 岳盛奏, 王晓琳, 邓智泉, 等. 单绕组无轴承永磁薄片电机缺相运行特性分析[J]. 中国电机工程学报, 2010, 30(12): 69-75.
Yue Shengzou, Wang Xiaolin, Deng Zhiquan, et al. Operation characteristics analysis of the single winding bearingless PM slice motor at lacking- phase[J]. Proceedings of the CSEE, 2010, 30(12): 69-75.
[7] Wang Xiaolin, Zhong Qingchang, Deng Zhiquan, et al. Fault-tolerant control of multi-phase permanent magnetic bearing-less motors[C]//The XIX Inter- national Conference on Electrical Machines-ICEM, Rome, Italy, 2010: 1-6.
[8] Wang Xiaolin, Zhong Qingchang, Deng Zhiquan, et al. Current-controlled multiphase slice permanent mag- netic bearingless motors with open-circuited phases: fault-tolerant controllability and its verification[J]. IEEE Transactions on Industrial Electronics, 2012, 59(5): 2059-2072.
[9] 盛旺, 王晓琳, 邓智泉, 等. 单绕组无轴承永磁薄片电机短路容错运行[J]. 中国电机工程学报, 2011, 31(6): 66-72.
Sheng Wang, Wang Xiaolin, Deng Zhiquan, et al. Operation of single winding bearingless PM slice motor at short-circuit in fault-tolerance[J]. Pro- ceedings of the CSEE, 2011, 31(6): 66-72.
[10] 王晓琳, 盛旺, 邓智泉, 等. 多相无轴承永磁薄片电机故障运行特性分析[J]. 中国电机工程学报, 2011, 31(18): 73-78.
Wang Xiaolin, Sheng Wang, Deng Zhiquan, et al. Operating characteristics analysis of multi-phase bearingless permanent magnet slice motors with faulty phases[J]. Proceedings of the CSEE, 2011, 31(18): 73-78.
[11] 任新宇, 王晓琳. H桥驱动下的单绕组无轴承薄片电机功率系统故障分析及容错控制[J]. 中国电机工程学报, 2012, 32(15): 74-83, 12.
Ren Xinyu, Wang Xiaolin. Power inverter fault analysis and fault-tolerant control of a single winding bearingless slice motor driven by H-bridge[J]. Pro- ceedings of the CSEE, 2012, 32(15): 74-83, 12.
[12] Samoylenko N, Han Qiang, Jatskevich J. Dynamic performance of brushless DC motors with unbalanced Hall sensors[J]. IEEE Transactions on Energy Con- version, 2008, 23(3): 752-763.
[13] 严乐阳, 叶佩青, 张勇, 等. 圆筒型永磁直线同步电机用线性霍尔位置检测的误差补偿[J]. 电工技术学报, 2017, 32(5): 26-32.
Yan Leyang, Ye Peiqing, Zhang Yong, et al. Error compensation of linear Hall based position detection for tubular permanent magnetic linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2017, 32(5): 26-32.
[14] Beccue P B, Pekarek S D, Deken B J, et al. Compensation for asymmetries and misalignment in a Hall-effect position observer used in PMSM torque- ripple control[J]. IEEE Transactions on Industry Applications, 2007, 43(2): 560-570.
[15] 王晓琳, 刘思豪, 顾聪. 基于线性霍尔误差补偿的高速永磁同步电机转子位置检测技术[J]. 电机与控制学报, 2021, 25(7): 11-19.
Wang Xiaolin, Liu Sihao, Gu Cong. Rotor position detection for permanent magnetic synchronous motor based on error compensation of linear Hall sensors[J]. Electric Machines and Control, 2021, 25(7): 11-19.
[16] 董亮辉, 刘景林. 霍尔传感器故障下的永磁无刷电机容错控制及其动态性能研究[J]. 中国电机工程学报, 2017, 37(12): 3602-3611, 3689.
Dong Lianghui, Liu Jinglin. Research on the fault tolerant control and its dynamic performance of brushless permanent magnet motor with faults in Hall sensor[J]. Proceedings of the CSEE, 2017, 37(12): 3602-3611, 3689.
[17] Tashakori A, Ektesabi M. A simple fault tolerant control system for Hall effect sensors failure of BLDC motor[C]//2013 IEEE 8th Conference on Industrial Electronics and Applications (ICIEA), Melbourne, VIC, Australia, 2013: 1011-1016.
[18] Dong Lianghui, Huang Yingwei, Jatskevich J, et al. Improved fault-tolerant control for brushless per- manent magnet motor drives with defective Hall sensors[J]. IEEE Transactions on Energy Conversion, 2016, 31(2): 789-799.
[19] 阎鹏宇, 朱志宇, 张明明, 等. 霍尔传感器故障下的永磁同步电机容错控制[J]. 电力电子技术, 2020, 54(7): 45-49.
Yan Pengyu, Zhu Zhiyu, Zhang Mingming, et al. Fault-tolerant control of permanent magnet syn- chronous motors with Hall sensor failure[J]. Power Electronics, 2020, 54(7): 45-49.
[20] 胡烽, 孙宏博, 蒋栋, 等. 基于四相全桥的磁悬浮轴承开关器件开路故障容错控制策略[J]. 电工技术学报, 2022, 37(9): 2295-2305, 2340.
Hu Feng, Sun Hongbo, Jiang Dong, et al. Fault- tolerant strategy of four-phase full-leg for active magnetic bearing in case of open circuit fault of switching device[J]. Transactions of China Elec- trotechnical Society, 2022, 37(9): 2295-2305, 2340.
[21] 杨帆, 袁野, 祝贵, 等. 12/14磁悬浮开关磁阻电机悬浮力全周期模型构建[J]. 电工技术学报, 2023, 38(2): 330-339.
Yang Fan, Yuan Ye, Zhu Gui, et al. Suspension force modeling for 12/14 bearingless switched reluctance motor considering flux multi teeth hinge[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(2): 330-339.
[22] Chiba A, Fukao T, Ichikawa O, et al. Magnetic bearings and bearingless drives[M]. New York: Elsevier, 2005.
[23] 张艺, 王宇, 张成糕. 基于霍尔负序解调法的无轴承永磁薄片电机径向位移检测方法[J]. 中国电机工程学报, 2023, 43(19): 7659-7669.
Zhang Yi, Wang Yu, Zhang Chenggao. Radical dis- placement detection method based on negative sequence demodulation method on Hall signals of bearingless permanent magnet slice motor[J]. Pro- ceedings of the CSEE, 2023, 43(19): 7659-7669.
[24] 王晓琳, 石滕瑞, 鲍旭聪. 基于频域拟合的无轴承永磁薄片电机径向悬浮力建模分析[J]. 电工技术学报, 2023, 38(2): 317-329.
Wang Xiaolin, Shi Tengrui, Bao Xucong. Accurate mathematical modeling of radial suspension force on bearingless permanent magnet slice motors based on frequency domain fitting[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 317-329.
[25] 刘刚, 肖烨然, 宋欣达. 永磁同步电机用线性霍尔位置检测的误差补偿[J]. 电机与控制学报, 2014, 18(8): 36-42, 54.
Liu Gang, Xiao Yeran, Song Xinda. Error com- pensation of rotor position detection for permanent magnetic synchronous motor based on linear Hall sensors[J]. Electric Machines and Control, 2014, 18(8): 36-42, 54.
[26] Chen Yao, Zhou Yangzhong. Radial displacement sensorless control of bearingless flux-switching permanent magnet machines based on difference of symmetric-winding flux linkages[J]. IEEE Transa- ctions on Industrial Electronics, 2021, 68(9): 7793- 7803.
Abstract High-precision displacement sensors are required to implement the displacement closed-loop control in the traditional bearingless permanent magnet slice motor system. Currently, bearingless permanent magnet slice motors are controlled by eddy current sensors. However, the increasing volume of the sensor probe can expand the bearingless motor's axial and radial dimensions. Due to their large volume, eddy current sensors cannot meet the accuracy and integration requirements of artificial heart pumps. According to the idea of Hall integrated dual-use, the angle and radial displacement can be identified simultaneously, reducing the volume of the artificial heart pump significantly.
As the Hall signal provides angle and radial displacement information, the health status of Hall directly influences the bearingless motor's suspension reliability. In the case of a single Hall fault, taking Hall1 as an example, considering the third harmonic caused by the permanent magnet processing, the third harmonic coefficient is calculated. The expression of a single Hall output signal considering permanent magnet excitation, torque current excitation, and suspension current excitation is derived.
The Hall flux linkage reconstruction algorithm is proposed using the remaining five non-faulty Hall output signals. The reconstructed flux linkage expression is obtained by subtracting the non-eccentric basic flux linkage from twice the Hall output signal opposite to the mechanical position of the faulty Hall. The reconstructed flux linkage is compensated for the third harmonic, and the Hall signal correction table under Hall faults is constructed. The radial displacement is calculated using the negative sequence demodulation method. The three-phase radial displacement flux linkage is projected onto a pair of poles to synthesize the magnetic field, which decouples the angle and radial displacement. Accordingly, the radial displacement information is obtained.
The platform of the bearingless permanent magnet slice motor is built, and the stable suspension of the bearingless motor under Hall1 faults is realized in static, steady state, and transient states. The radial displacement fluctuation of the static suspension is no more than 80 mm. The angle identification error of the steady state suspension is no more than 9° at 5 000 r/min, the a radial displacement error does not exceed 0.06 mm, and the b radial displacement error does not exceed 0.08 mm. When the speed changes from 0 to 3 000 r/min to 6 000 r/min, the switching dynamic time of the transient suspension speed is less than 1 s, and the speed has no apparent jitter.
The following conclusions can be drawn. (1) The reduction of Hall output signals leads to the lack of one-phase radial displacement flux linkage in displacement calculation under single Hall faults, resulting in system angle and radial displacement information recoupling. (2) The Hall flux linkage reconstruction algorithm reconstructs and compensates the third harmonic for the Hall flux linkage under single Hall faults, improving the reliability and fault tolerance of the bearingless motor. It can be used as a fault-tolerant scheme of artificial heart pumps to improve extracorporeal blood circulation stability.
keywords:Bearingless permanent magnet slice motor, radial displacement, Hall sensor, fault tolerant control, harmonic compensation
DOI: 10.19595/j.cnki.1000-6753.tces.230961
中图分类号:TM351
国家自然科学基金项目(51977107)、航空科学基金项目(2020HKZ0001)、江苏省重点研发项目(PCA21001)和南京航空航天大学科研与实践创新计划项目(xcxjh20220345)资助。
收稿日期 2023-06-23
改稿日期 2023-08-22
赵 攀 男,1998年生,硕士研究生,研究方向为无轴承电机控制。E-mail: 983663916@qq.com
王 宇 男,1982年生,副教授,硕士生导师,研究方向为交流电机本体及其控制。E-mail: wanghaohao@nuaa.edu.cn(通信作者)
(编辑 崔文静)