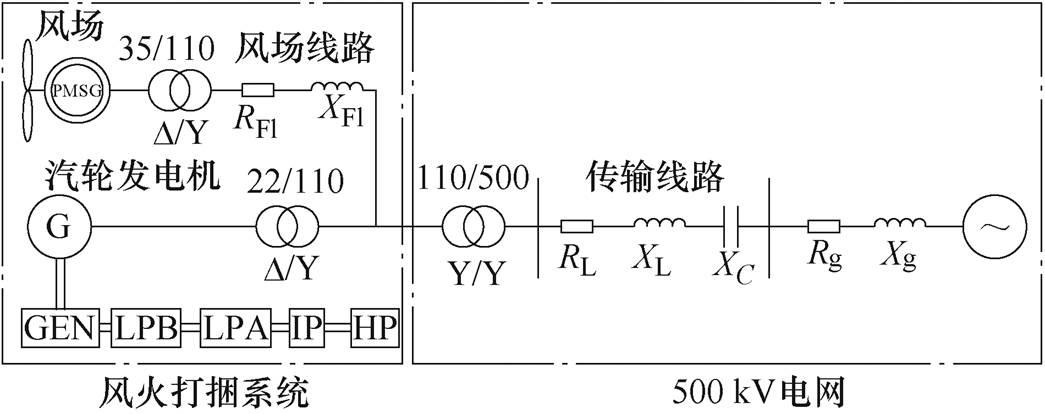
图1 风火打捆外送系统结构示意图
Fig.1 Schematic diagram of wind-thermal bundled delivery system
摘要 与状态空间法和复转矩系数法相比,基于阻抗的分析方法更便于拓扑扩展和黑盒系统建模。然而,现有的汽轮发电机阻抗模型,如RL串联阻抗模型或同步发电机等效电路阻抗模型,仅关注汽轮发电机的电气特性。上述简化的阻抗模型无法考虑汽轮发电机轴系特性的影响,甚至导致错误的分析结果。针对这一问题,该文建立了考虑轴系特性的汽轮发电机阻抗模型,并以风火打捆外送系统为研究对象,对比了基于RL等效阻抗模型和所建立阻抗模型的振荡分析结果。验证了所建立模型在含有新能源以及电力电子设备的电力系统中进行稳定性分析的适用性与准确性。研究结果可为含汽轮发电机的复杂结构电力系统的稳定性分析提供模型。
关键词:阻抗模型 汽轮发电机 轴系扭振 风火打捆
阻抗分析法由于其易扩展性强、有利于黑匣子系统建模的优点,被应用于各种结构的电力系统振荡分析当中[1-2]。尤其是随着大规模新能源发电与高压直流输电的快速发展,电力系统电力电子化的程度逐年提高,同时为了保证电能输出系统的稳定与经济效益,新能源发电系统电源侧呈现风、火多电源并存的格局,电力系统结构面临着更为复杂的局面[3-4]。在这种情况下,阻抗分析法模块化、易扩展性强的优势使其成为分析这些复杂系统的一个有效方法[5]。
目前,随着新能源通过大量电力电子装置接入电网、高压直流输电的广泛应用、大规模的电力电子装置的渗透,使得电网的动态特征发生改变,不仅会引起电力系统的低频振荡,而且可能诱发汽轮发电机轴系扭振从而导致电力系统次/超同步振荡[6-7]。例如,2015年,新疆哈密某个风场产生了次/超同步振荡[8],并传递到距离300 km的某电厂汽轮机组,激发了汽轮机组轴系的固有扭振模式,导致该机组切机,严重影响电力系统稳定可靠运行。
针对汽轮发电机的建模,学术界已经开展了大量的研究,常用的方法有状态空间法、复转矩系数法与阻抗分析法[9]。状态空间法在电力系统稳定性研究中得到了充分的应用,该方法可以根据矩阵的特征根对系统进行判稳[10-11],但是当系统结构更为复杂时,必须重新建立所有状态空间模型,并且会增加空间模型的阶数,这限制了该方法在大型系统中的应用[12]。复转矩系数法主要应用于机电系统的研究[13],该模型将系统分为机械系统与电气系统,分别建立转子角度扰动在各部分的转矩响应方程,通过研究自然谐振点处的系统阻尼,分析系统的稳定性。该方法能够表征系统在不同频段的电气阻尼,因此具备明确的物理意义。然而,通常采用复转矩系数法研究轴系特性,对于未来研究多个电力电子器件的电力系统振荡,可能难以识别所有机电振荡状态或给出精确的振荡模态阻尼[14]。阻抗分析法的优势在于其每一部分都是独立的[1],当系统结构发生变化时无需重新建立模型,可扩展性强。并且该方法在实际工程应用中通过端口激励/响应关系即可得到模块化的阻抗模型,对装置参数依赖性不强,更有利于黑匣子系统的建模。然而,面对电力电子装置渗透率逐渐增大、电力系统结构日益复杂的局面,目前针对汽轮发电机的阻抗模型研究较少,研究时通常将汽轮发电机阻抗用RL串联阻抗或者同步发电机等效电路阻抗代替[15-16],但是该简化模型不能表征汽轮发电机的轴系特性,无法分析汽轮发电机轴系对系统次/超同步振荡的影响,可能导致在轴系自然扭振频率附近的分析结果不准确。因此,随着电力系统中的电力电子设备投入数量增多,电力系统的结构日益复杂,迫切需要一种能够准确表征全频段特性的汽轮发电机阻抗模型。
本文首先建立了考虑轴系扭振特性的汽轮发电机阻抗模型,弥补了目前汽轮发电机阻抗只能反映电气部分特性而不能反映机械部分特性的空白。然后采用频率扫描法对本文建立的阻抗模型进行验证,并与传统汽轮发电机阻抗模型进行了对比。最后建立了风火打捆外送系统次/超同步振荡实例。分别基于阻抗分析法与复转矩系数法对系统进行了 次/超同步振荡分析。
本文的研究对象为图1所示的风火打捆外送系统,其中汽轮发电机系统结构及参数参照IEEE次同步谐振第一标准模型[17]。图1中,HP为高压缸,IP为中压缸,LPA与LPB分别为两个低压缸;GEN为同步发电机;汽轮发电机与风场的变压器电压比分别为22 kV/110 kV与35 kV/110 kV,再经110 kV/ 500 kV变压器并入500 kV电网;RL、XL、XC为500 kV侧线路电阻、感抗以及串补电容电抗;Rg、Xg为电网的电阻和感抗;RFl、XFl为风场输出线路的电阻与感抗。

图1 风火打捆外送系统结构示意图
Fig.1 Schematic diagram of wind-thermal bundled delivery system
本文将针对图1所示点画线框中的汽轮发电机建立阻抗模型,从而建立风火打捆系统的阻抗模型,并进行次/超同步振荡分析,风火打捆外送系统阻抗模型示意图如图2所示。图中,左侧点画线框内代表风火打捆系统的阻抗模型,其包含了图1点画线框中的汽轮发电机与风力发电机两部分;右侧点画线框内代表电网侧阻抗模型,包含变压器阻抗、线路阻抗及电网内阻抗。
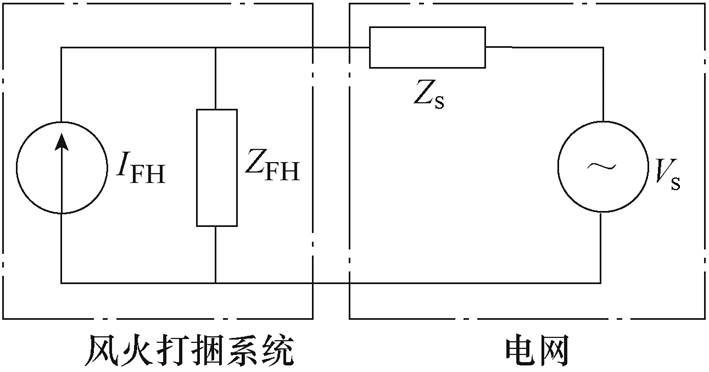
图2 风火打捆外送系统阻抗模型示意图
Fig.2 Impedance model diagram of wind-thermal bundled delivery system
风火打捆系统阻抗计算的关键在于如何计算风机阻抗ZWF以及汽轮发电机阻抗ZTG,对于风机的阻抗模型研究已经较为完备[18],在此不做赘述。而对于考虑轴系特性的汽轮发电机阻抗模型ZTG,在dq坐标系下,其表达式为
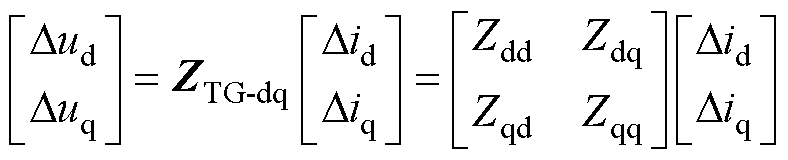 (1)
(1)
式中,Dud、Duq与Did、Did分别为dq坐标系下汽轮机发电机端口的电压和电流;ZTG-dq为dq坐标系下的汽轮发电机阻抗。该阻抗模型为二维矩阵形式,共包含四个元素,对角线元素Zdd与Zqq分别为d轴与q轴之间的自阻抗,非对角元素Zdq与Zqd分别为d轴与q轴之间的耦合阻抗。汽轮发电机阻抗公式ZTG-dq将在第2节进行详细推导。
汽轮发电机电气部分为同步发电机的定、转子电气部分。机械部分主要包括调速器、汽轮机及轴系质量弹簧模型。为简化分析,在本研究中汽轮发电机采用恒励磁控制。汽轮发电机各部分参数传递关系如图3所示[19]。
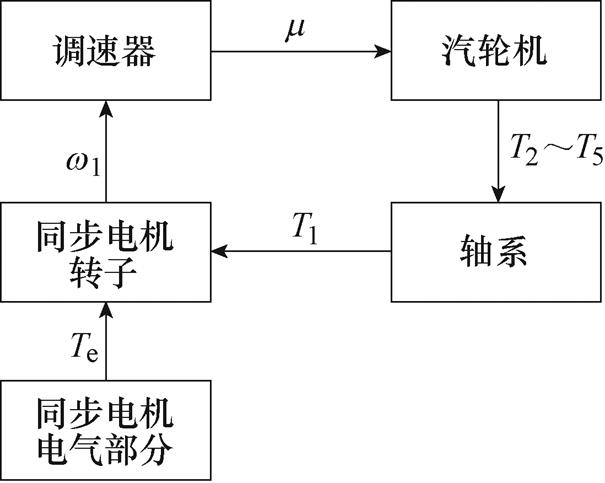
图3 汽轮发电机参数传递关系
Fig.3 Transfer relationship of turbo-generator parameter
图3中,m 为汽轮机的汽门开度,T1~T5为轴系各质量块的力矩,同时T1也被称为同步发电机输入机械转矩,Te为同步发电机转子受到的电磁转矩,w1为同步发电机转子转速。
本文将汽轮发电机分为同步发电机、低压缸A、低压缸B、中压缸及高压缸5个质量块,并定义质量块1为同步发电机质量块。其具体轴系质量弹簧模型示意图如图4所示[20]。
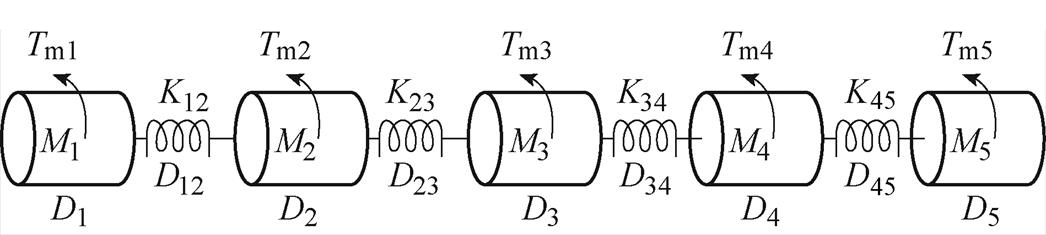
图4 汽轮发电机轴系质量弹簧模型示意图
Fig.4 Schematic diagram of the turbo-generator shafting mass-spring model
图4中,Di为汽轮机质量块的自阻尼系数;Tmi为第i个质量块上的机械(原动)转矩,需要注意的是,发电机转子质量块和励磁机质量块上的机械转矩通常为0;Kij为质量块之间的弹性系数,弹性系数矩阵为
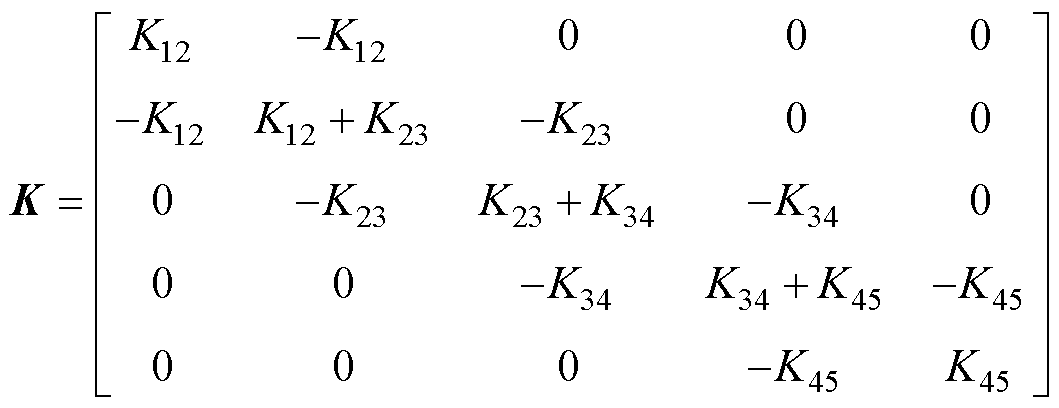 (2)
(2)
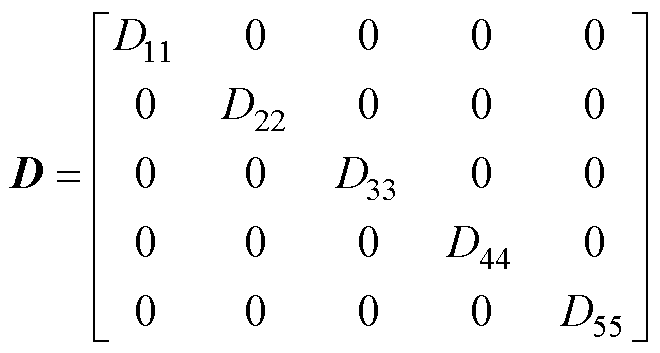 (3)
(3)
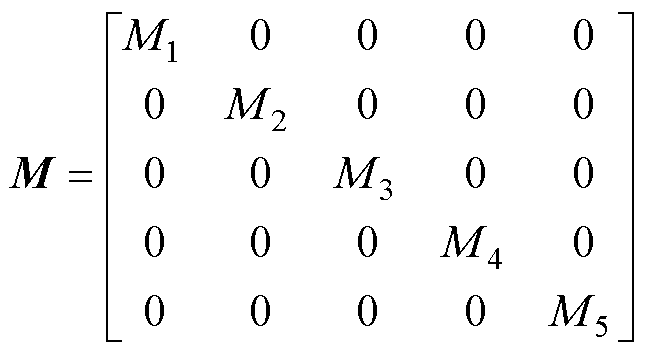 (4)
(4)
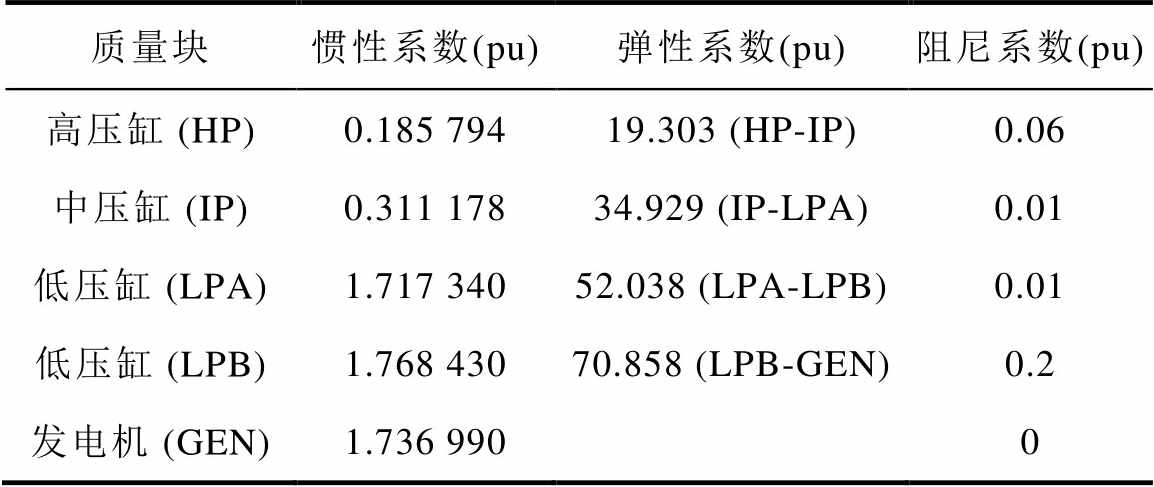
式中,Dij为质量块之间的互阻尼系数,本文不考虑互阻尼系数的影响;D为阻尼系数矩阵;Mi为第i个质量块的惯性时间常数;M为惯性时间常数矩阵。汽轮发电机轴系参数来自次同步谐振第一标准模型[17],见表1。
表1 汽轮发电机轴系参数
Tab.1 Turbo-generator shafting parameters
质量块惯性系数(pu)弹性系数(pu)阻尼系数(pu) 高压缸 (HP)0.185 79419.303 (HP-IP)0.06 中压缸 (IP)0.311 17834.929 (IP-LPA)0.01 低压缸 (LPA)1.717 34052.038 (LPA-LPB)0.01 低压缸 (LPB)1.768 43070.858 (LPB-GEN)0.2 发电机 (GEN)1.736 9900
在引言所述的电力系统次/同步振荡事件已经表明,机组的固有扭振模式会导致机组切机,进而引发较为严重的影响。因此,计算汽轮机组轴系固有扭振频率十分必要。参考文献[20-21]可以计算该机组的固有扭振频率,得到轴系的4个扭振频率为43.32、29.40、23.23和14.61 Hz,将汽轮发电机轴系扭振模式被激发时对应的电气振荡频率定义为电气扭振频率,该频率和固有扭振频率关于工频互补,分别为6.68、20.60、26.77以及35.39 Hz。
阻抗建模的基本原理是对线性化后的汽轮发电机端口注入小扰动电压,得到扰动电流响应,建立如式(1)所示的激励/响应关系,从而得到能够表征汽轮发电机端口特性的阻抗模型。
由式(1)可以推断,若要建立dq坐标系下的汽轮发电机阻抗模型,需要得到Dud、Duq与Did、Diq的关系式,因此首先对汽轮发电机电气部分进行小信号线性化处理。
在本研究中,假设发电机在理想状态下运行,即认为铁心导磁系数为常数、电机结构完全对称并且定子和转子表面光滑,并对其进行标幺化。另外,为了反映感应涡流对发电机的影响,考虑发电机的转子轴d和q分别有两个绕组。d轴有励磁绕组f和阻尼绕组D, q轴有另外两个阻尼绕组g和Q,dq坐标系下的同步发电机方程为
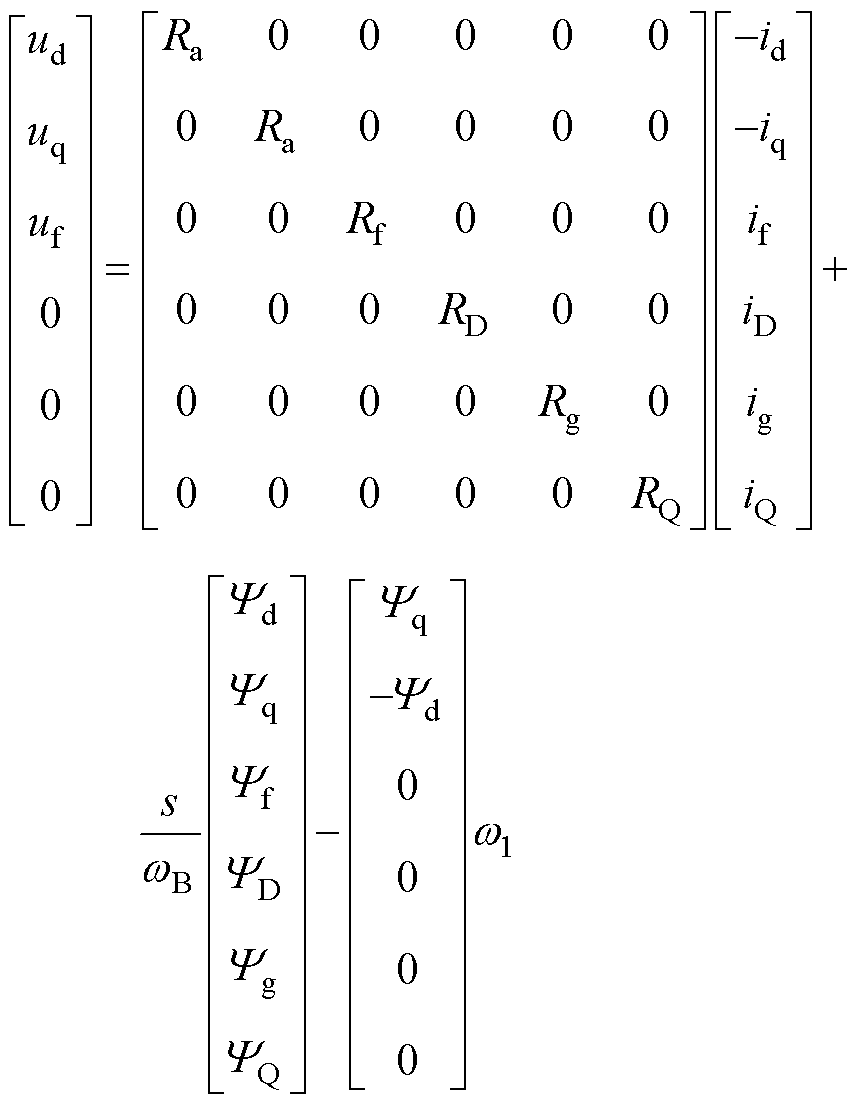 (5)
(5)
其中,磁链与电流的关系为
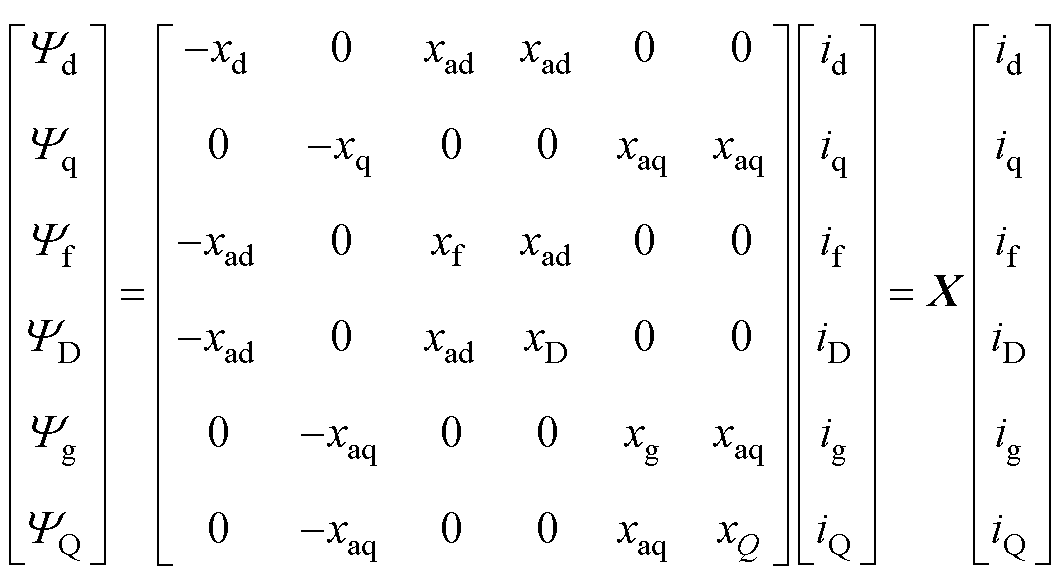 (6)
(6)
式中,Ra与Rf分别为定子绕阻和励磁绕组的阻值;RD、Rg与RQ分别为d轴和q轴的阻尼绕组阻值;uf与if分别为励磁电压、电流;iD、ig与iQ分别为d轴和q轴阻尼绕组的电流;Yd、Yq、Yf、YD、Yg与YQ分别为d轴、q轴、励磁以及阻尼绕组的磁链;ud、uq和id、iq分别为机端d轴与q轴的电压和电流;uf、if分别为励磁电压和电流,本文采用恒定励磁;iD、ig、iQ为3个阻尼绕组的电流;Ra为定子电阻;Rf为励磁绕组电阻;RD、Rg、RQ为3个阻尼绕组电阻;xd与xq分别为直轴与交轴同步电抗;xad与xaq分别为直轴与交轴电枢反应电抗;xf为励磁绕组电抗;xD、xg、xQ为3个阻尼绕组电抗;Yd与Yq分别为d轴和q轴定子绕组的磁链;Yf为励磁磁链;YD、Yg、YQ为3个阻尼绕组的磁链;w1为同步发电机转子转速。对式(6)进行小信号线性化处理,得到
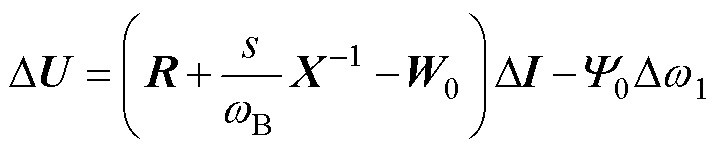 (7)
(7)
式中,DU与DI分别为d轴、q轴的定子绕组、励磁绕组、阻尼绕组的电压、电流向量;R、X分别为式(5)、式(6)中的电阻、电抗矩阵;W0DI与Y0Dw1为dq轴磁链耦合项小信号线性化后的两个部分。
观察式(7)发现,只需要消去Dw1即可得到DU与DI的关系式。而Dw1将电气部分与轴系机械部分联系到了一起,接下来将针对轴系各部分机械结构进行建模。
汽轮发电机机械部分包含轴系、汽轮机和速度调节器三方面。
2.2.1 轴系部分
轴系分为高压缸、中压缸、低压缸A、低压缸B和同步发电机5个轴段,定义同步发电机为第一个质量块,随后依次为低压缸B、低压缸A、中压缸和高压缸,轴系质量弹簧模型示意图如图4所示。轴系小信号线性化方程为
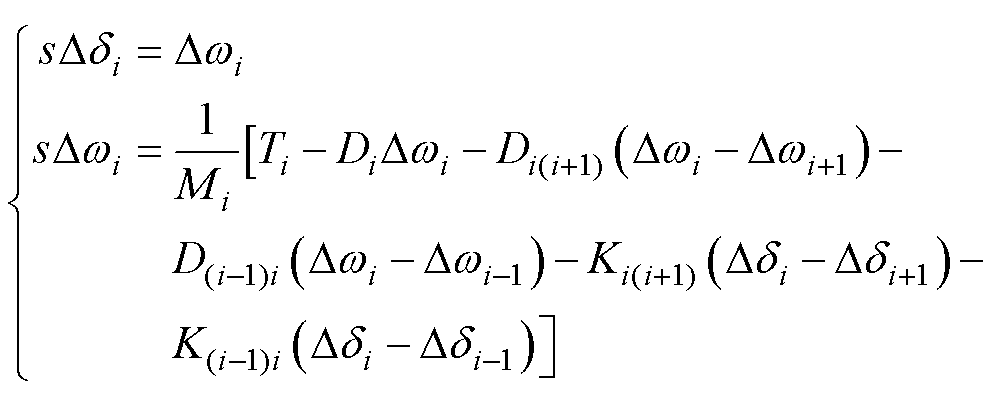
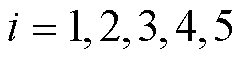 (8)
(8)
式中,di为轴系第i个质量块相对于同步旋转参考轴的电气扭角;wi为第i个质量块的转速;Mi为第i个质量块的惯性时间常数;Ti为第i个质量块的机械力矩,由于质量块1对应同步发电机转子轴段,因此T1=-Te;D为阻尼系数,分为自阻尼系数Di和互阻尼系数Dij,其中互阻尼系数为0。
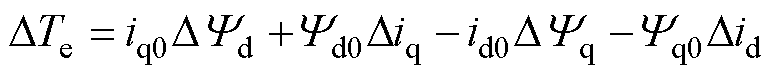 (9)
(9)
式中,iq0、id0、Yq0、Yd0分别为d轴和q轴电流和磁链的初始值(pu);DTe、Diq、Diq、DYd、DYq分别为电磁转矩、dq轴电流和磁链的小扰动信号。基于Matlab/Simulink平台将同步机设置为电源电压节点,改变输出功率并使用Powergui对其进行初始化即可得到电流和磁链的标幺化初始值。
2.2.2 汽轮机
汽轮机方程用于描述汽门开度和各汽室输出机械功率之间的数学关系,为简化分析,在电力系统分析中常用的汽轮机动态数学模型只考虑蒸汽容积效应,根据汽缸不同通常分为一阶、二阶和三阶汽轮机数学模型。本文研究的汽轮发电机有高压缸、中压缸以及两个低压缸,因此采用三阶汽轮机数学模型,其传递函数框图如图5所示。
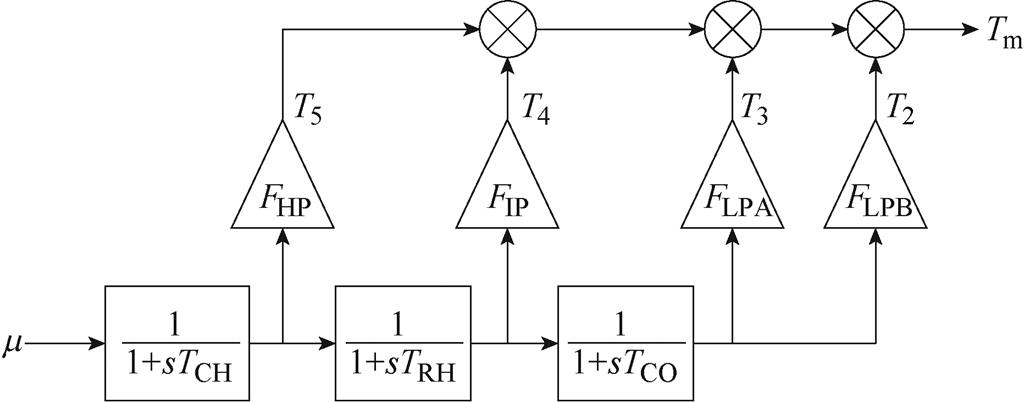
图5 汽轮机传递函数框图
Fig.5 Transfer function block diagram of turbo-generator
图5中,Ti为第i个质量块的机械转矩输出,汽轮机输入为调速器输出的汽门开度m,TCH和TRH分别为高压室和中间再热管的时间常数,TCO为跨接管的时间常数,FHP、FIP、FLPA、FLPB分别为高、中、低压缸A、低压缸B的机械功率比例且四者之和为1,本文以FHP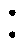 FIP
FIP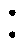 FLPA
FLPA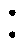 FLPB=0.3
FLPB=0.3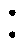 0.26
0.26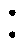 0.22
0.22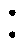 0.22的配比方式进行功率分配。根据传递框图可以得到频域下汽轮机线性化方程为
0.22的配比方式进行功率分配。根据传递框图可以得到频域下汽轮机线性化方程为
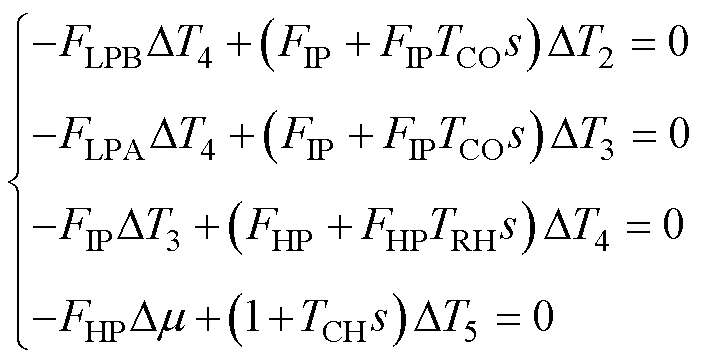 (10)
(10)
2.2.3 速度调节器
汽轮发电机常用速度调节器分为液压调节器和功频电液调速器两种,本文采用液压调节器进行控制,该调节器由转速测量和液压随动系统组成,忽略限幅环节,控制框图如图6所示。

图6 汽轮发电机速度调节器框图
Fig.6 Block diagram of turbo-generator speed regulator
图6中,wref为同步发电机转子转速参考值,Kg为转速调节器放大系数,TSM为油动机积分时间常数,TSR代表继动器的一阶惯性环节。则频域下速度调节器线性化方程表示为
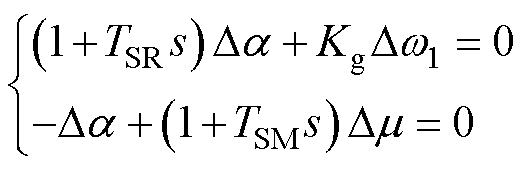 (11)
(11)
式中, a 为继动器传递函数输出端的中间变量,以辅助计算。
至此,联立式(7)~式(11)即可得到汽轮发电机小信号线性化方程式为
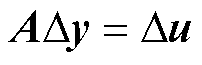 (12)
(12)
其中
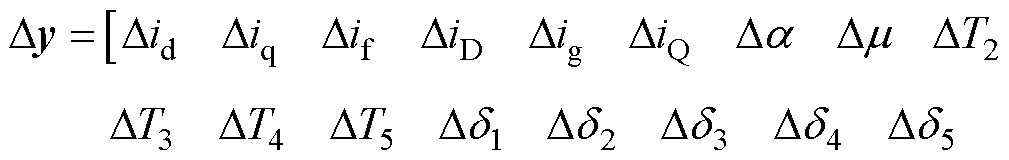
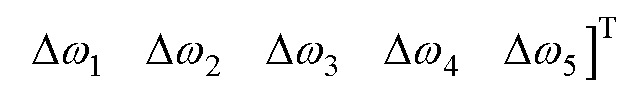 (13)
(13)
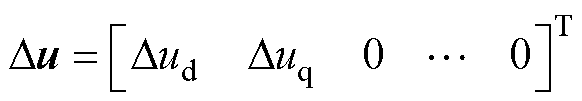 (14)
(14)
式中,A为整合了式(7)~式(11)后包含汽轮发电机机械和电气部分的整体系统矩阵; Dy和Du为小扰动信号。
进而得到Dud、Duq与Did、Diq的关系式为
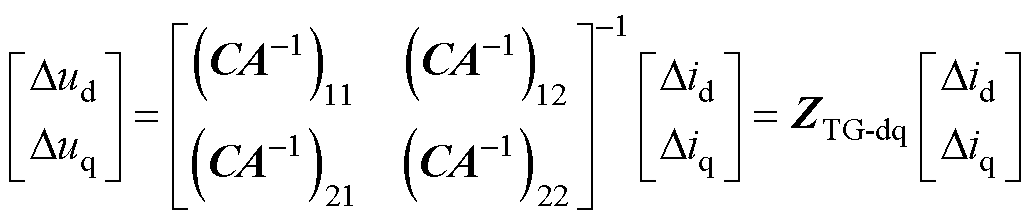 (15)
(15)
其中
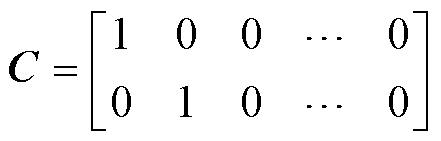 (16)
(16)
至此,dq坐标系下同时包含了电气与机械部分的汽轮发电机阻抗模型已经建立完毕。同时,根据参考文献[22]中提出的不同坐标系阻抗矩阵的转换关系可以得到汽轮发电机的序阻抗模型,以供需要的学者使用,其表达式为
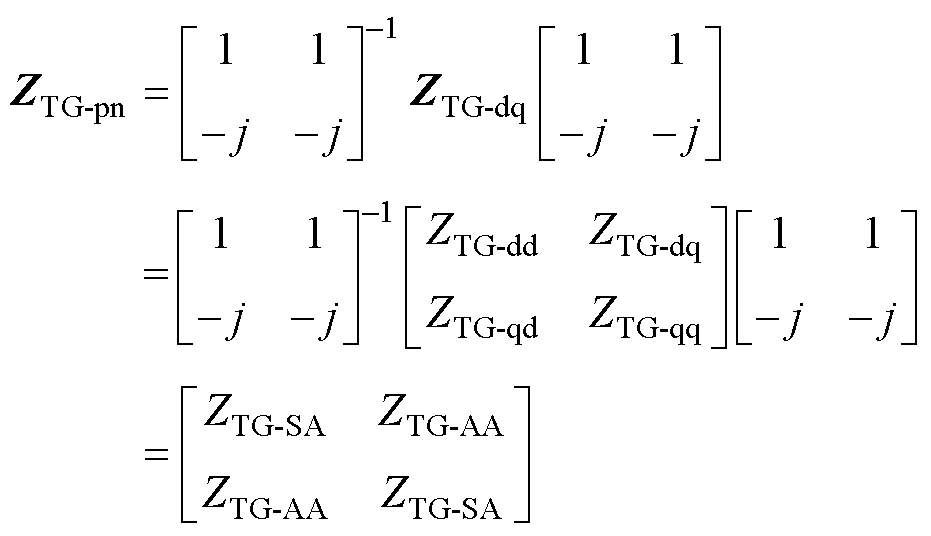 (17)
(17)
式中,ZTG-pn为汽轮发电机的序阻抗模型。定义矩阵对角元素ZTG-SA为自阻抗,非对角元素ZTG-AA为伴随阻抗。
为验证本文所建立的汽轮发电机阻抗模型,在Matlab/Simulink中搭建了汽轮发电机的仿真模型,结构如图7所示。将仿真频率扫描的结果与解析数学模型进行对比验证。
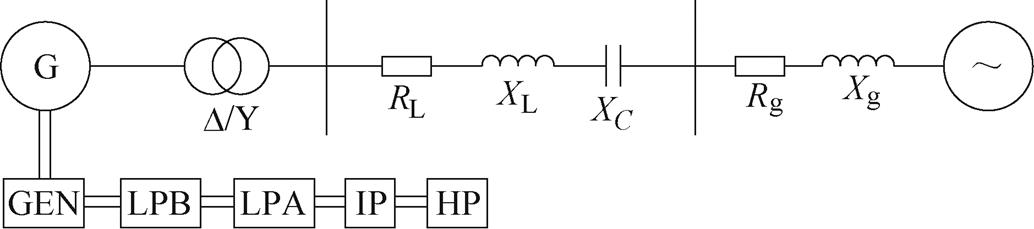
图7 汽轮发电机并网系统结构
Fig.7 Structure of turbo-generator grid-connected system
在进行验证前,考虑到网侧阻抗与汽轮发电机阻抗会产生耦合效应,其响应关系如图8所示[23-24]。因此本节进行验证与应用的模型是考虑了频率耦合效应之后的等效阻抗模型,其表达式为
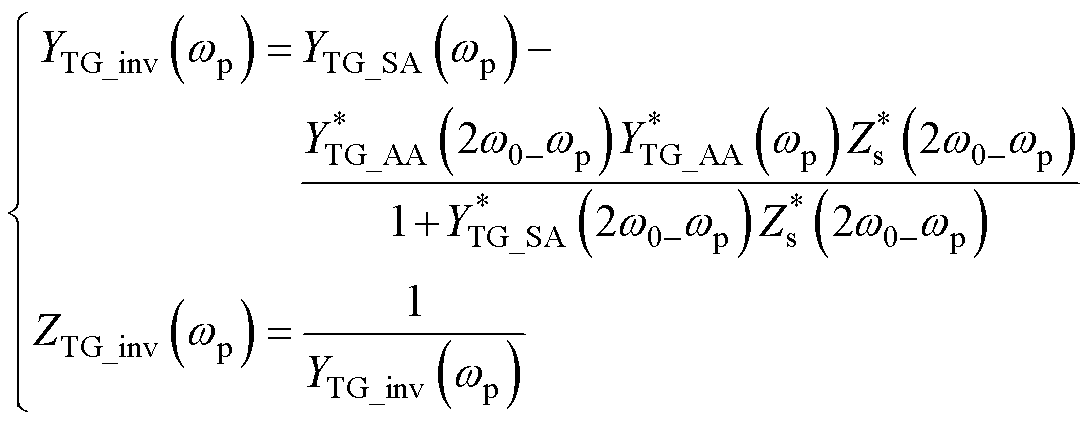 (18)
(18)
式中,YTG_inv与ZTG_inv分别为考虑的频率耦合效应的汽轮发电机导纳和阻抗模型;YTG_SA与YTG_AA分别为汽轮发电机的自导纳和伴随导纳;Zs为汽轮发电机端口向外看的电网阻抗,其表达式为
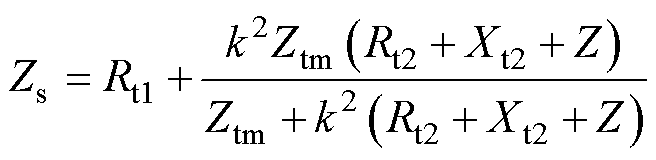 (19)
(19)
式中,k为汽轮发电机并网变压器电压比;Rt1为变压器一次侧电阻;Rt2和Xt2分别为变压器二次侧电阻和电抗;Z为电网内阻抗;Ztm为变压器的励磁 阻抗。
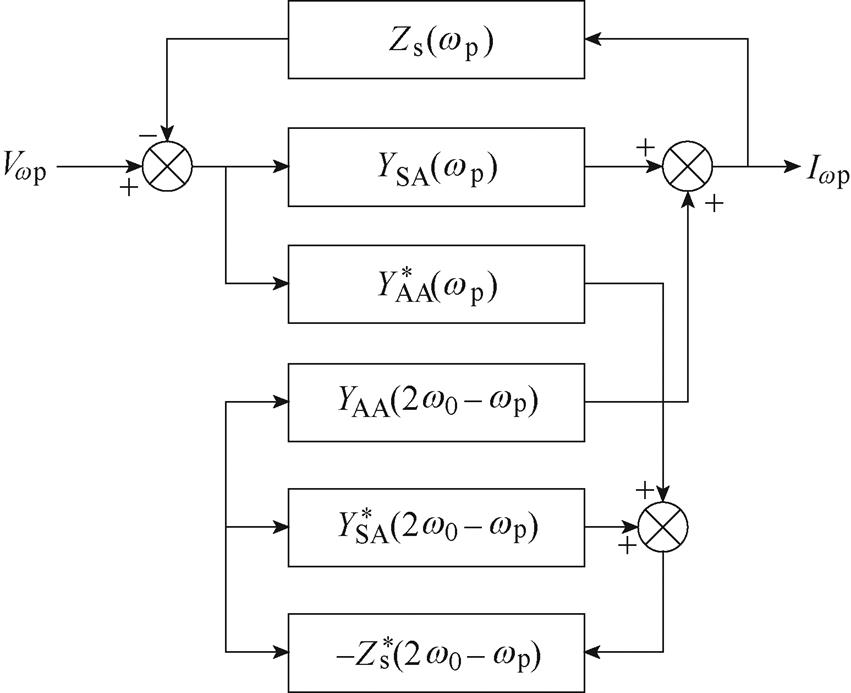
图8 汽轮发电机并网系统中电压激励与电流响应关系
Fig.8 Relationship between voltage exitation and current response in turbo-generator grid-connected system
汽轮发电机参数以及网侧系统参数见表2和表3。
表2 汽轮发电机参数
Tab.2 Parameters of turbo-generator
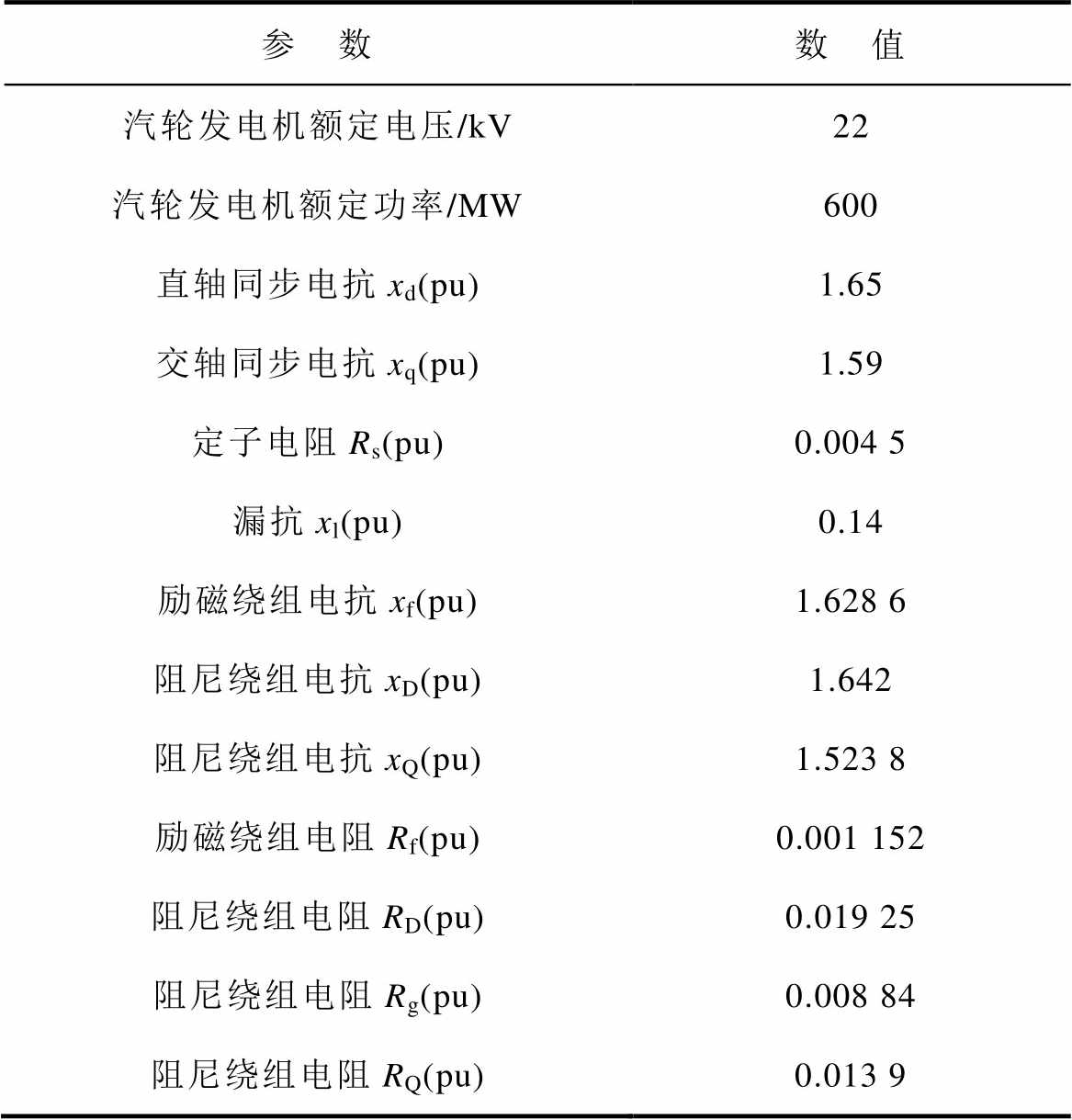
参 数数 值 汽轮发电机额定电压/kV22 汽轮发电机额定功率/MW600 直轴同步电抗xd(pu)1.65 交轴同步电抗xq(pu)1.59 定子电阻Rs(pu)0.004 5 漏抗xl(pu)0.14 励磁绕组电抗xf(pu)1.628 6 阻尼绕组电抗xD(pu)1.642 阻尼绕组电抗xQ(pu)1.523 8 励磁绕组电阻Rf(pu)0.001 152 阻尼绕组电阻RD(pu)0.019 25 阻尼绕组电阻Rg(pu)0.008 84 阻尼绕组电阻RQ(pu)0.013 9
表3 网侧系统参数
Tab.3 Parameters of grid-side system
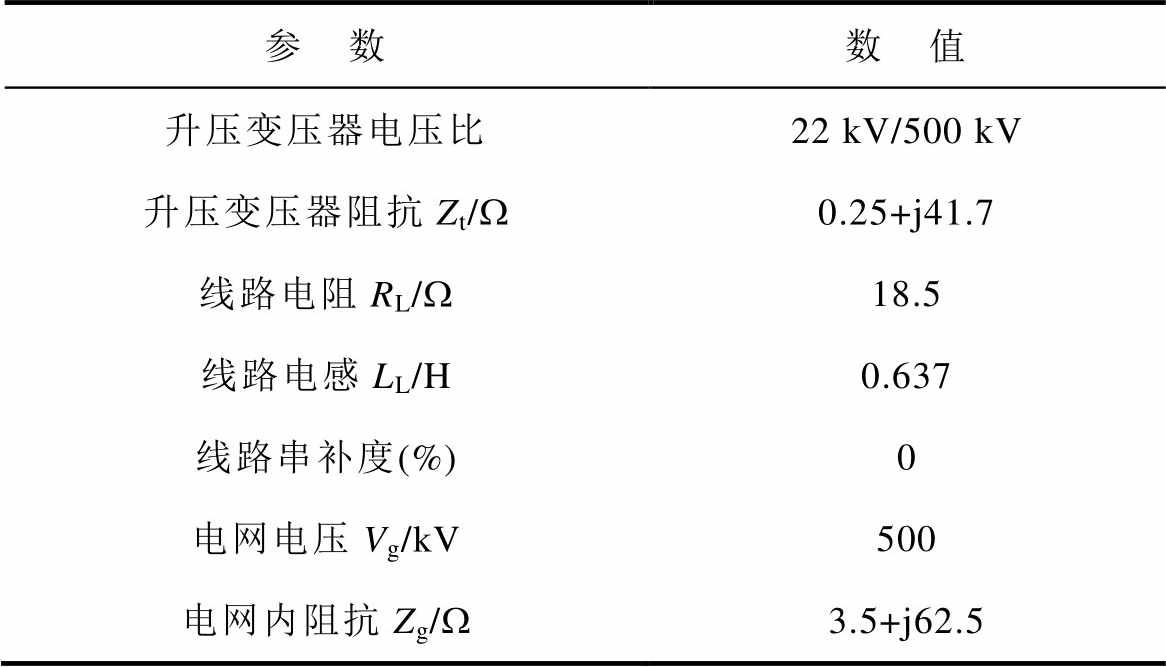
参 数数 值 升压变压器电压比22 kV/500 kV 升压变压器阻抗Zt/W0.25+j41.7 线路电阻RL/W18.5 线路电感LL/H0.637 线路串补度(%)0 电网电压Vg/kV500 电网内阻抗Zg/W3.5+j62.5
为了保证扫描结果的正确性和准确度,需要注意以下两点:
(1)建议将注入的电压扰动幅值设置为5%左右,若注入电压扰动幅值过高可能会导致系统失稳,若注入的电压扰动幅值过低则会导致测量误差较大。
(2)在汽轮发电机电气扭振频率点具有谐振峰,因此为了进一步增加准确性,在电气扭振频率点6.68、20.60、26.77以及35.39 Hz附近适当缩短步长进行扫描。
理论计算与扫描结果对比如图9所示。图中,圆圈为基于Matlab/Simulink仿真模型扫描计算得到的扫描阻抗,实线是依据式(18)计算得到的汽轮发电机等效阻抗。由图9可知,等效阻抗的数学模型和频率扫描结果一致,即仿真测量数据验证了建立的等效阻抗模型的正确性。
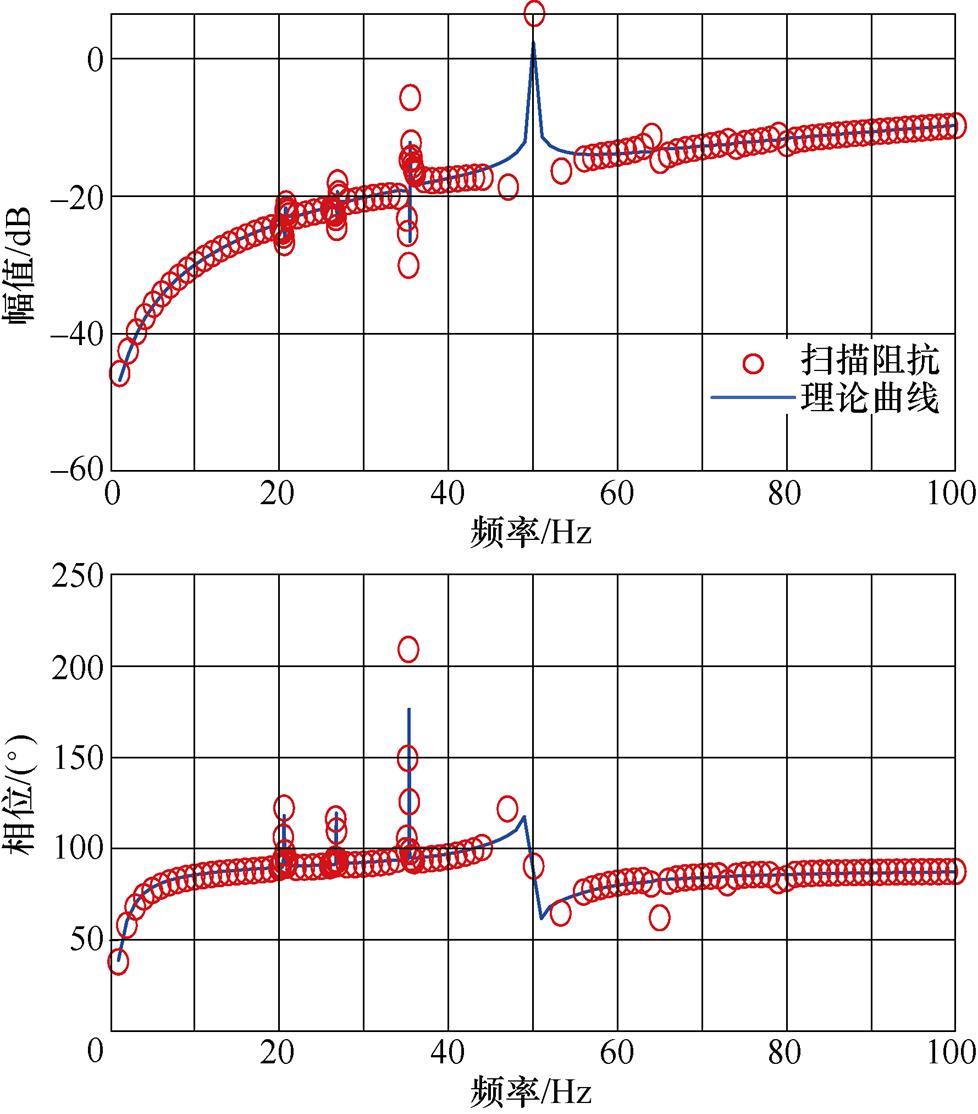
图9 考虑了频率耦合的汽轮发电机等效阻抗模型仿真扫描验证
Fig.9 Simulation and scanning verification of turbo-generator equivalent impedance model considering frequency coupling
此外,由图9可知,所建立的汽轮发电机阻抗模型能够准确描述汽轮发电机轴系特性:阻抗曲线的谐振点为6.68、20.60、26.77及35.39 Hz,分别对应轴系扭振的互补频率,即电气扭振频率。这说明序阻抗表征的是汽轮发电机对外部呈现的电气特性。观察图9的汽轮发电机阻抗曲线,比较明显的谐振点有20.60、26.77及35.39 Hz,而6.68 Hz的谐振点只有局部放大后能观察到。基于电力系统小干扰稳定的特征结构分析中参与因子的思想[25],主要原因是43.32 Hz对应的扭振模型下电气系统的参与因子几乎为零,发电机的模态分量小,因此反映到电气端口的分量较小。
目前,针对汽轮发电机的阻抗模型,大多是将汽轮发电机阻抗用同步发电机等效电路阻抗代替,相应的等效电路如图10所示[15-16],对应的阻抗模型表示为
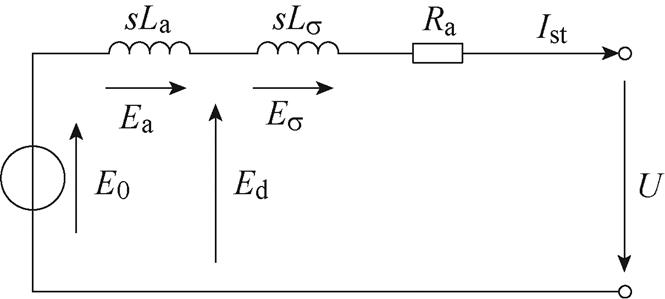
图10 汽轮发电机等效电路
Fig.10 Turbo-generator equivalent circuit
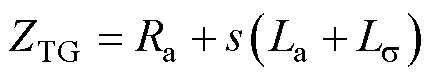 (20)
(20)
将本文建立的阻抗与同步发电机等效电路阻抗对比,如图11所示。图11中,实线为本文建立的汽轮发电机等效阻抗,虚线为同步发电机等效电路阻抗,由图可知,两条阻抗曲线在电气扭振频率附近存在明显差异,等效电路阻抗曲线在电气扭振频率处没有畸变,而汽轮发电机阻抗曲线在电气扭振频率附近存在谐振峰,这表明轴系特征会明显影响汽轮发电机的阻抗特性。在相对同一外部系统时,采用同步发电机等效电路阻抗分析出的系统相位裕度远大于采用本文建立的等效阻抗分析出的相位裕度,因此使用同步发电机等效电路阻抗进行振荡分析时会存在较大误差。
而在低频段和高频段,本文建立的汽轮发电机阻抗模型与传统的同步发电机等效电路阻抗模型保持一致。因此,本文建立的汽轮发电机阻抗模型适用于包括低频段、次超同步频段以及高频段的理论分析。
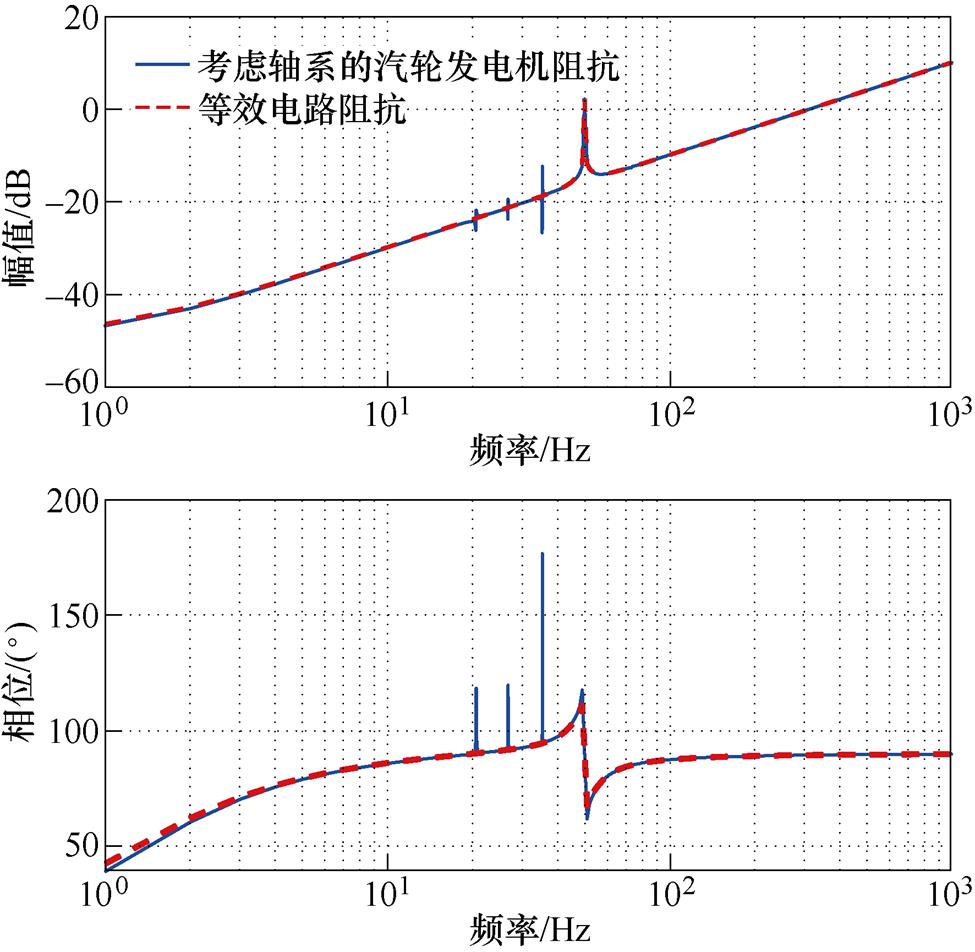
图11 同步发电机等效电路阻抗与汽轮发电机阻抗的比较
Fig.11 Comparison of synchronous generator circuit impedance and turbo-generator impedance
为验证本文建立的汽轮发电机阻抗模型在含有新能源以及电力电子设备的复杂系统中的实用性。在本实例中,将火力与风力发电系统打捆向外输送功率。其中,风力发电机的阻抗模型研究已经较为完备[18],在此不做赘述。本节内容将本文建立的汽轮发电机阻抗模型与同步发电机等效电路阻抗模型分别代入计算风火打捆系统总阻抗,并分别对不同串补度时的并网系统进行振荡分析。系统结构如图1所示,系统参数见表2~表4。
本节研究对象为风火打捆外送系统,系统结构如图1所示。将系统从110 kV汇流处分为两部分,电网侧小信号等效电路如图12所示。
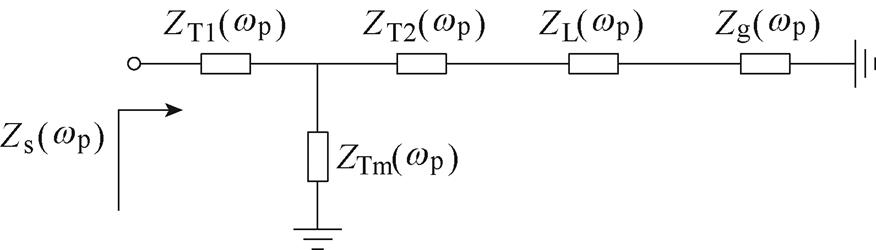
图12 电网侧小信号等效电路
Fig.12 Small-signal equivalent circuit of grid side
由图12所示的小信号等效电路可以求出折算到110 kV侧的网侧阻抗为
表4 风机参数
Tab.4 Parameters of wind turbine

参 数数 值 风速/(m/s)10 风机额定容量/(MV·A)2 风机额定电压/V 发电机磁链/(Vs)9.3 发电机极对数30 定子电阻/mW7.89 定子d轴电感/mH0.835 定子q轴电感/mH1.445 直流母线电容/mF20 输出滤波电感/mH0.139 机侧变流器d轴电流控制器(1.11+1 407.97)/s 机侧变流器q轴电流控制器(1.93+2 428.84)/s 直流电压参考值/V1500 网侧变流器直流电压控制器(0.89+147.98)/s 网侧变流器电流控制器(0.22+217.82)/s 锁相环[(0.39+96.62)/s]/s
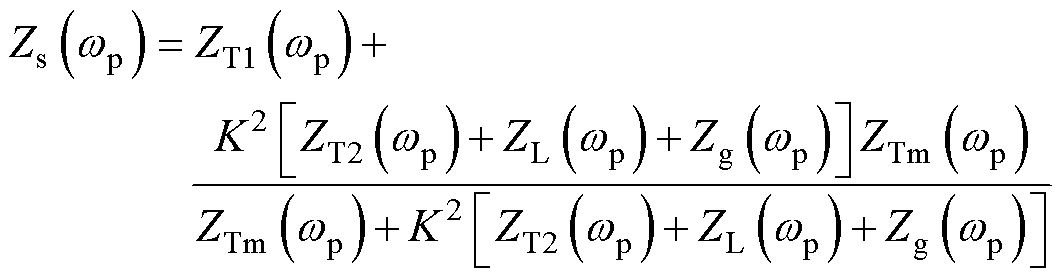 (21)
(21)
式中,ZT1(wp)、ZT2(wp)和ZTm(wp)分别为变压器低压侧、高压侧和励磁阻抗;ZL(wp)为线路阻抗;Zg(wp)为电网内阻抗;K为变压器电压比,K=110 kV/500 kV。
基于本文建立的汽轮发电机阻抗模型和直驱风场阻抗模型[18]可以得到风火打捆系统的自导纳和伴随导纳,表达式分别为
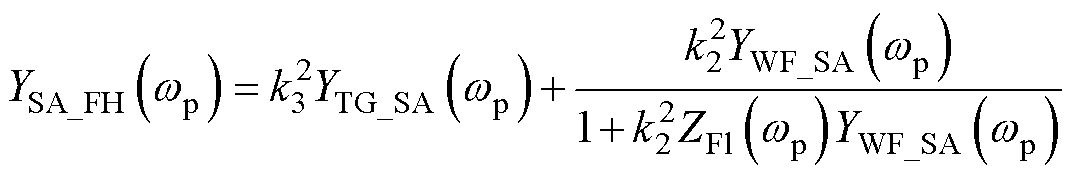 (22)
(22)
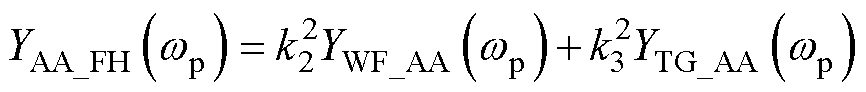 (23)
(23)
式中,k2为风电场到并网点的变压器电压比,k2= 35 kV/110 kV;k3为汽轮发电机到并网点的变压器电压比,k3=22 kV/110 kV;YTG_SA与YTG_AA分别为汽轮发电机的自导纳和互导纳;YWF_SA和YWF_AA分别为风场的自导纳和互导纳;ZFl为风场输出线路阻抗。同样建立考虑频率耦合效应影响的风火打捆系统等效阻抗,参照式(18)可得
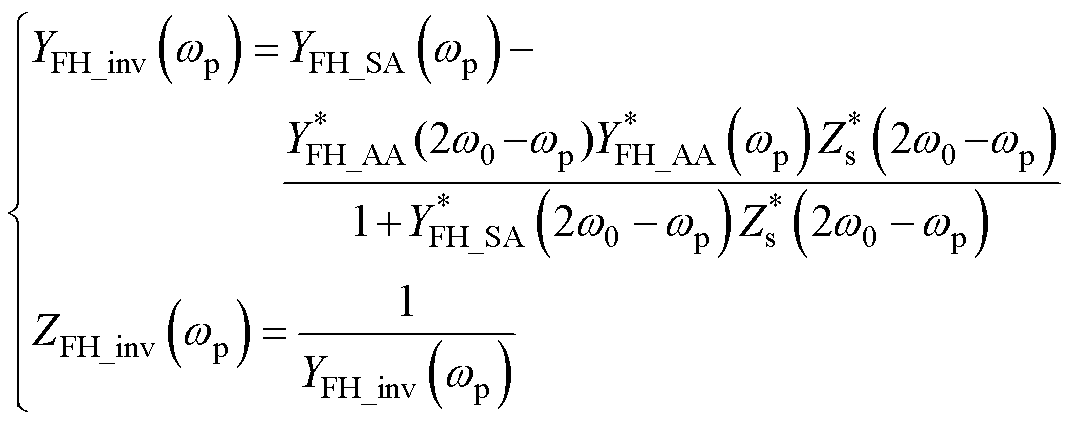 (24)
(24)
式中,YFH_SA与YFH_AA分别为风火打捆系统的自导纳和互导纳。
由于阻抗模型是线性化模型,仅能分析平衡点附近的情况。装备工况变化如输出功率改变均会导致平衡点偏移,因此为了表征不同工况下的阻抗模型,通常考虑不同工况如不同输出功率下系统的稳态工作点,进而建立不同平衡点下的阻抗模型。进一步地,为了分析汽轮发电机在不同工况,如轻载、半载、满载等运行情况的阻抗特性。根据2.2.1节所述过程,分别按照0.2、0.5、0.8、1.0(pu)输出功率设置d轴和q轴的电流与磁链的初始标幺值,如式(25)~式(28)所示。其他参数见表1、表2以及2.2节。
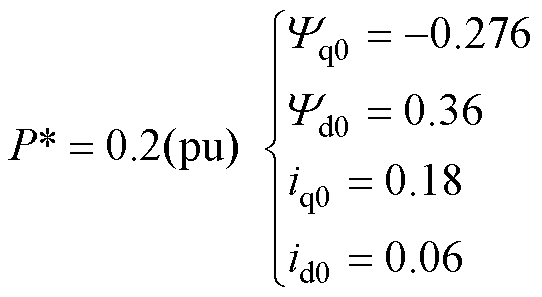 (25)
(25)
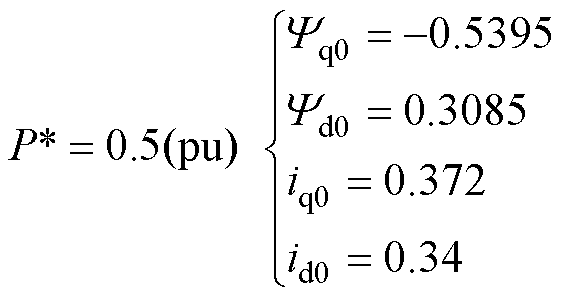 (26)
(26)
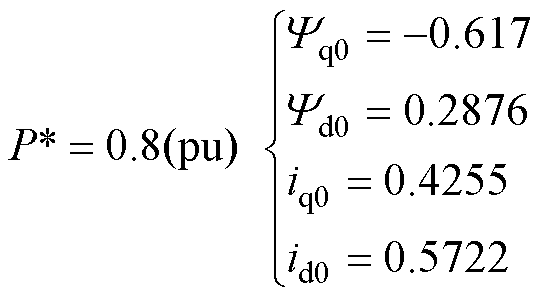 (27)
(27)
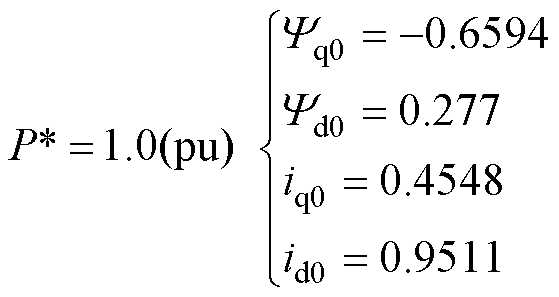 (28)
(28)
可得到工况分别为0.2、0.5、0.8、1.0(pu)时的风火打捆系统阻抗曲线,如图13所示。
观察不同工况时的风火打捆系统阻抗曲线可以发现,当汽轮发电机输出功率增大时,系统整体的阻抗特性保持不变,但在自然扭振点附近变化较大。通过局部缩放图可以看出,输出功率增大时风火打捆系统的相位也随之不断增大,系统稳定裕度则不断减小,增加了次/超同步振荡的风险。本节将代入输出功率为0.5(pu)工况时的模型进行振荡分析。
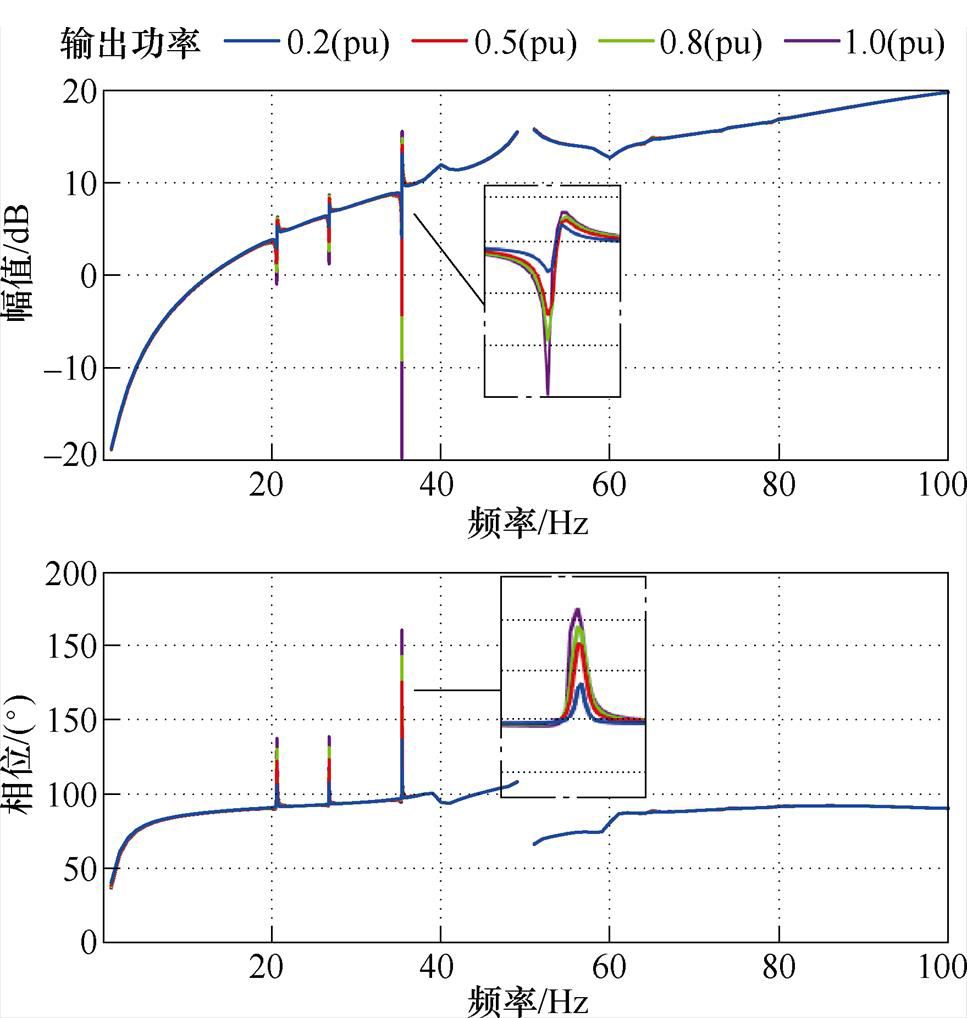
图13 汽轮发电机不同输出功率时风火打捆系统的阻抗曲线
Fig.13 Impedance curves of wind-thermal bundled system with different output power of turbo-generator
基于本文建立阻抗模型的风火打捆系统阻抗以及不同串补度时的网侧阻抗伯德图如图14所示。
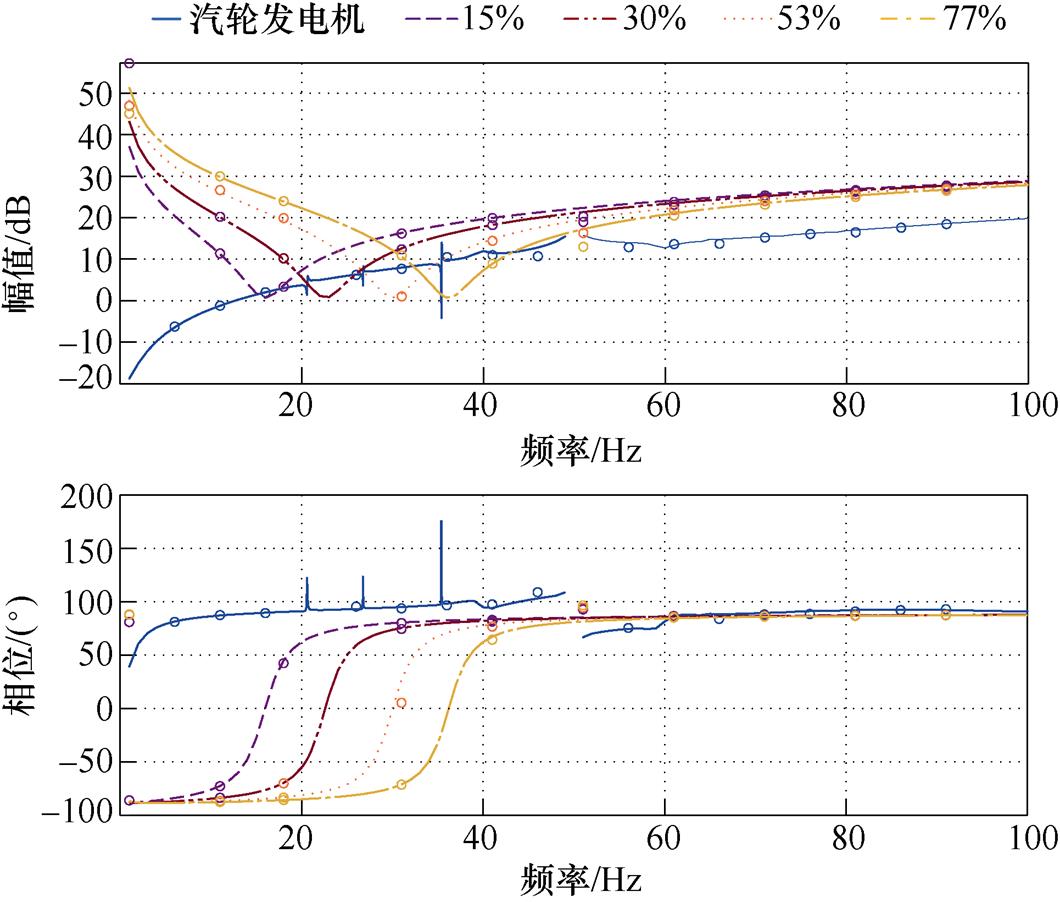
图14 不同串补度时的阻抗曲线交点
Fig.14 Intersection point of impedance curves of different series complements
图14中,蓝色实线为本文建立的风火打捆系统阻抗曲线,其余为不同串补度下的线路阻抗,其中线条表征理论模型,圆圈则表征对应各个模型的频率扫描结果,可以看出,扫描结果与理论曲线能够很好地吻合,表明了本文建立阻抗模型的正确性。由图14可知,不同串补度的网侧阻抗均和风火打捆系统阻抗有多个交点,将四种串补度时的最大相位差的交点信息以表5形式直接列出。
表5 阻抗曲线交点信息汇总(基于本文建立的汽轮发电机阻抗模型)
Tab.5 Impedance curve intersection information summary (based on the turbo-generator impedance model established in this paper)
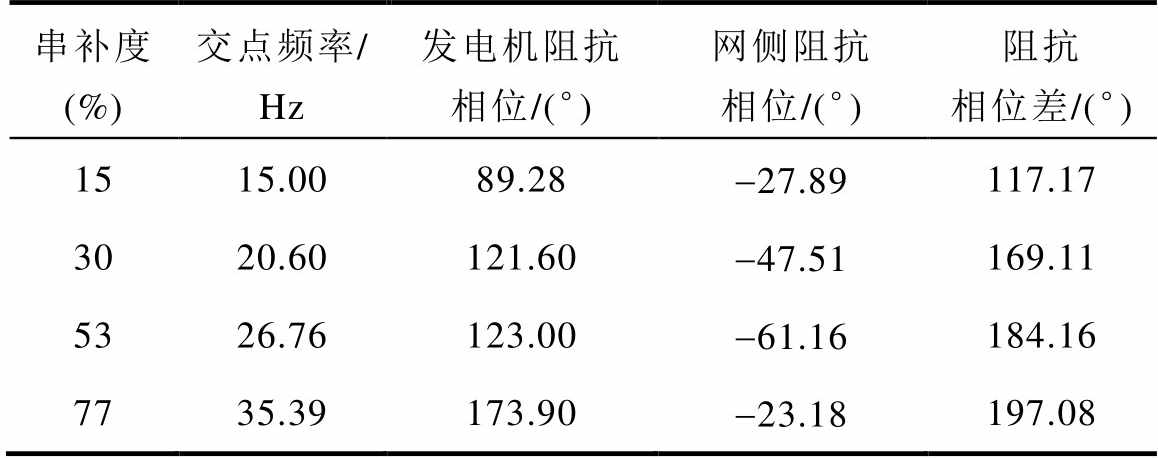
串补度(%)交点频率/ Hz发电机阻抗相位/(°)网侧阻抗相位/(°)阻抗相位差/(°) 1515.0089.28-27.89117.17 3020.60121.60-47.51169.11 5326.76123.00-61.16184.16 7735.39173.90-23.18197.08
由表5可知,串补度为15%和30%时阻抗相位差均小于180°,稳定裕度大于0,因此系统处于稳定运行状态;串补度为53%和77%时阻抗相位差均已大于180°,稳定裕度小于0,说明此时系统已经处于失稳状态,存在振荡现象。当串补度为53%时,系统振荡电流频率为27 Hz与73 Hz;当串补度为77%时,系统振荡电流频率为35.5 Hz与64.5 Hz。
为验证上述分析结果,分别对四种串补度时的系统进行仿真分析,风火打捆送出系统公共点处电流以及振荡情况下的电流频谱分析结果分别如图15和图16所示。
由电流波形和频谱分析结果可知:串补度为15%和30%时风火打捆系统电流均为标准正弦波,不含有谐波分量,系统处于稳定运行状态。在串补度为53%时,风火打捆系统电流含有27 Hz和73 Hz的谐波分量,在串补度为77%时,风火打捆系统电流含有35.5 Hz和64.5 Hz的谐波分量,经过一段时间后,两者的电流均振荡发散,系统不能维持稳定运行,该结论与基于本文建立的阻抗模型理论分析结果一致。
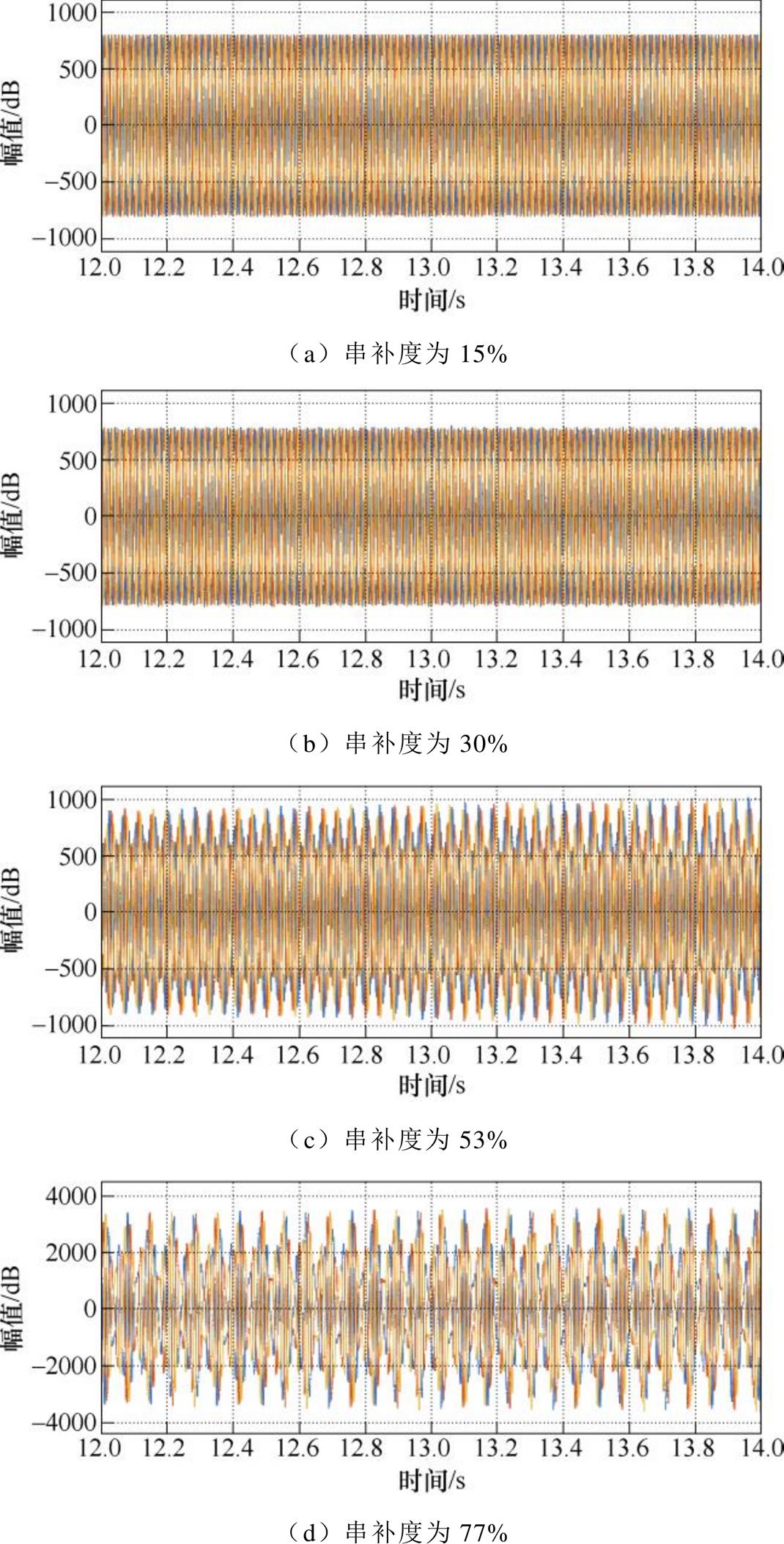
图15 风火打捆系统送出电流波形
Fig.15 The current waveforms deliveried by the wind-thermal bundled system
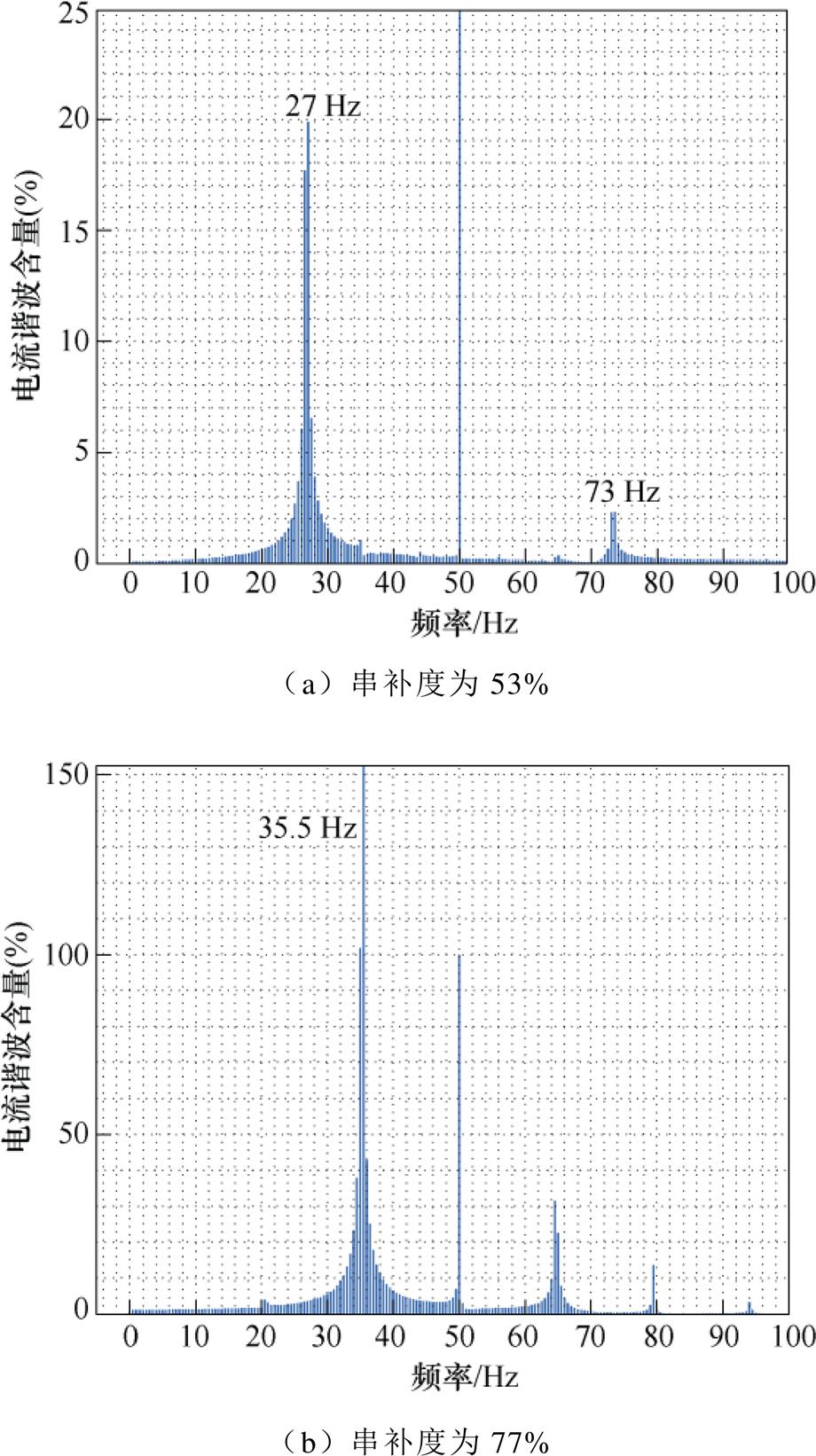
图16 风火打捆系统电流频谱分析
Fig.16 Current spectrum analysis of wind-thermal bundled system
根据3.2节所述内容,同步发电机等效电路阻抗如式(21)所示,因此该等效电路仅包含自导纳,而没有互导纳。因此,将式(29)代入式(23)~式(25)即可得到基于同步发电机等效电路阻抗的风火打捆系统总阻抗模型。
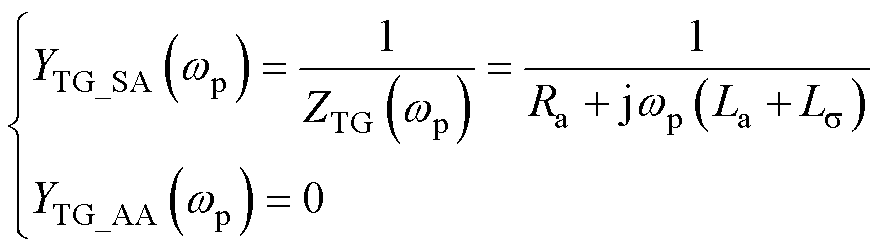 (29)
(29)
基于同步发电机等效电路阻抗的汽轮发电机阻抗模型的风火打捆系统阻抗以及不同串补度时的网侧阻抗伯德图如图17所示。
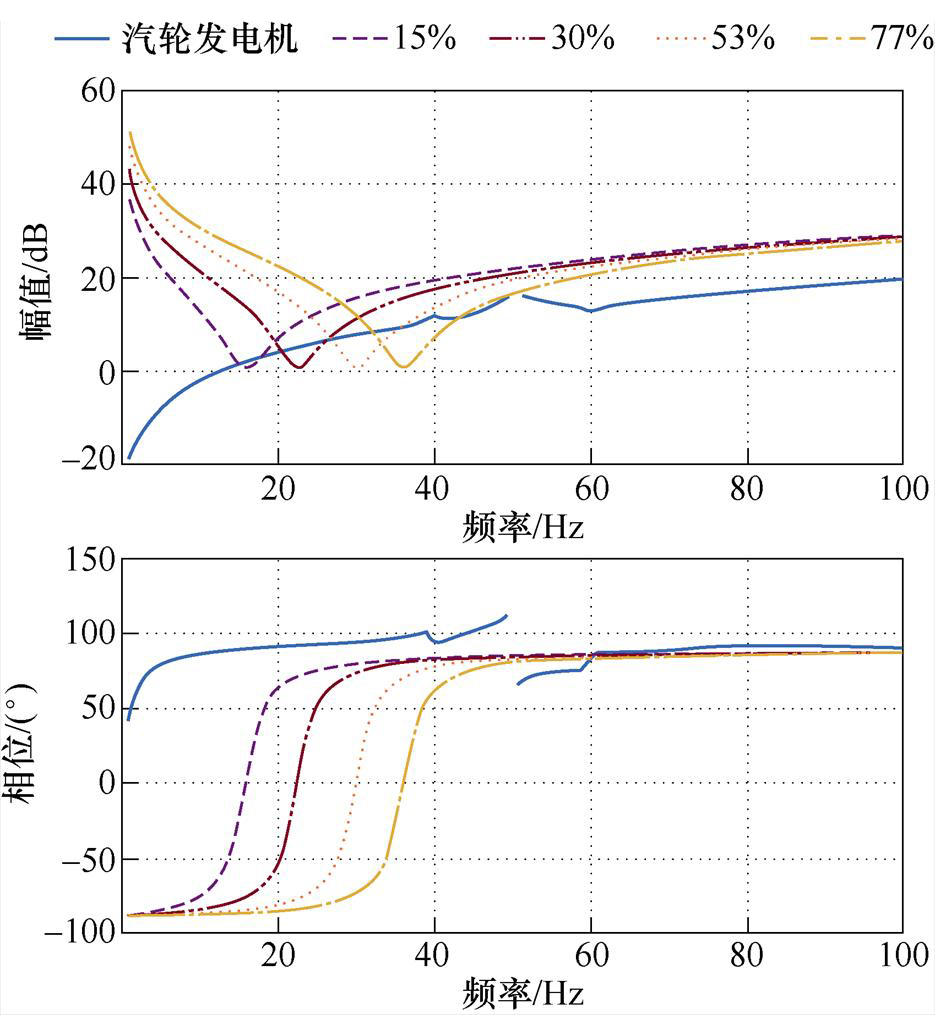
图17 不同串补度时的阻抗曲线交点(基于同步发电机等效电路阻抗模型)
Fig.17 Intersection point of impedance curves of different series complements (based on the synchronous generator equivalent circuit impedance model)
图17中,实线为基于同步发电机等效电路阻抗的风火打捆系统阻抗曲线,其他曲线均为不同串补度时的网侧阻抗,同样列出四种串补度时的最大相位差的交点信息,见表6。
表6 阻抗曲线交点信息汇总(基于同步发电机等效电路阻抗模型)
Tab.6 Impedance curve intersection information summary (based on the synchronous generator equivalent circuit impedance model)
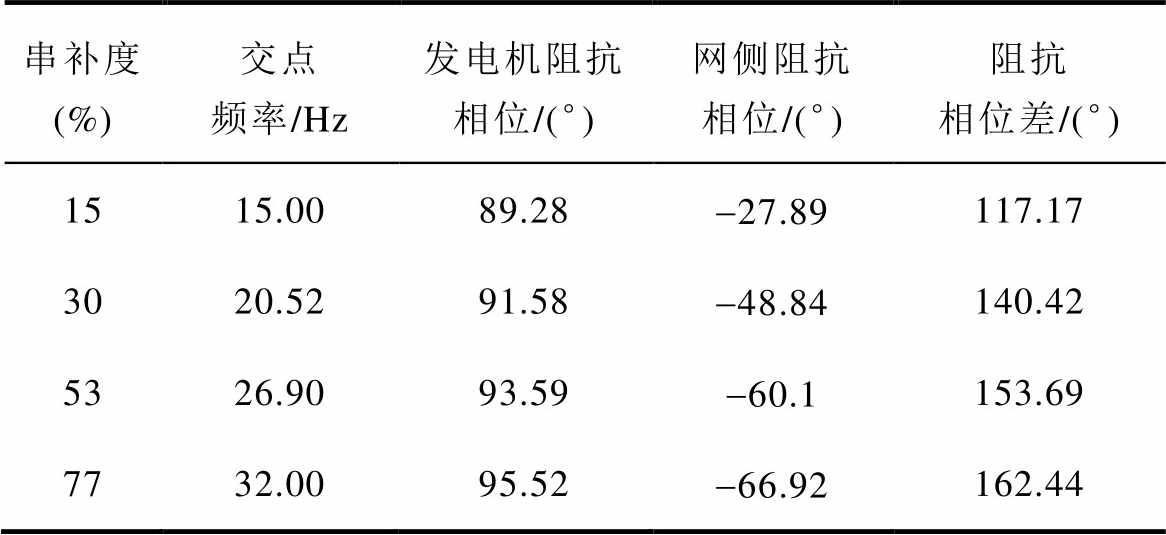
串补度(%)交点频率/Hz发电机阻抗相位/(°)网侧阻抗相位/(°)阻抗相位差/(°) 1515.0089.28-27.89117.17 3020.5291.58-48.84140.42 5326.9093.59-60.1153.69 7732.0095.52-66.92162.44
由图17和表6的结果可以看出,风火打捆系统代入等效电路阻抗进行分析时,四种串补度的阻抗曲线交点处相位差均小于180°,因此理论分析结果为:四种串补度下的系统均处于稳定运行状态,不会发生次同步振荡,这与仿真分析结果不一致。
综上所述,在针对风火打捆外送系统次/超同步振荡分析时,基于同步发电机等效电路阻抗的理论分析结果在串补度为53%或77%时系统稳定无振荡,与仿真结果不一致。这是因为基于同步发电机等效电路的阻抗模型主要考虑汽轮发电机的电气特性,而忽略了轴系对阻抗特性的影响,在轴系系统固有频率附近无法成功分析振荡风险。因此,若系统未考虑轴系特性所建立的模型,可能会导致错误的分析结果。产生的振荡频率分别为27 Hz与35.5 Hz,与汽轮发电机的轴系电气扭振频率26.77 Hz以及35.39 Hz相近,在工程上可能会导致汽轮发电机的轴系产生扭振,甚至对大轴造成永久损坏。
基于本文建立的汽轮发电机阻抗模型分析结果与仿真结果一致,即当串联互补度为53%时,振荡频率为27 Hz和73 Hz,当串联互补度为77%时,振荡频率为35.5 Hz与64.5 Hz,在这两种情况下,系统不稳定并发生振荡。这表明,所建立的阻抗模型能够准确分析含有新能源和电力电子设备的复杂电力系统的稳定性,并计算出系统的次/超同步振荡频率,可以为实际工程提供建议,避免该工况的产生,进而避免系统产生振荡现象。
根据I. M. Canay和K. Mortensen推导的复转矩系数法所用的关系式[26-27],可计算机械阻尼转矩系数,另外采用测试信号法可以单独计算电气部分的阻尼转矩系数[28]。根据文献[29]的稳定性判据即可判断该发电机在自然扭振频率处是否会产生扭振不稳定。
根据理论计算的机械转矩阻尼系数与测试信号法计算的电气转矩阻尼系数,可以得到阻尼转矩系数曲线如图18所示。
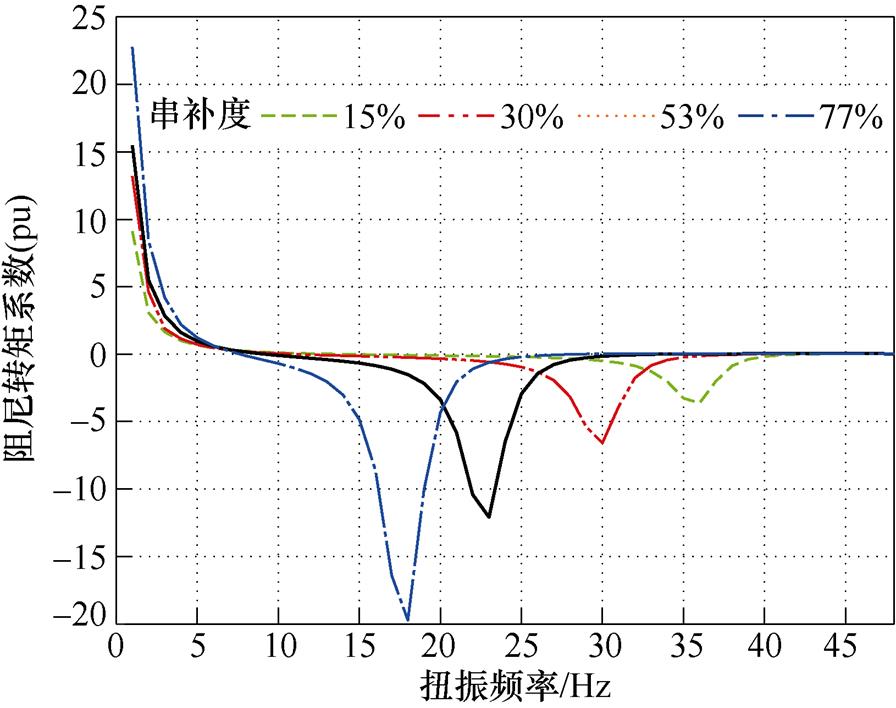
图18 不同串补度下的阻尼转矩系数曲线
Fig.18 Curves of damping torque coefficient under different series compensation
可以看出,随着串补度不断增加,阻尼系数最低点的频率不断左移。本文研究的汽轮发电机的扭振频率为43.32、29.40、23.23和14.61 Hz,接下来根据复转矩系数法稳定性判据对结果进行分析。
观察图18可以发现,当串补度为53%和77%时,对应扭振频率23.23 Hz和14.61 Hz处汽轮发电机的阻尼转矩系数为负,此时系统存在次同步振荡风险,且振荡频率应为对应的电气扭振频率,即26.76 Hz与35.31 Hz附近。当串补度为15%时,对应扭振频率43.32 Hz处汽轮发电机的阻尼转矩系数不为负,此时系统无振荡风险。而当串补度为30%时,对应扭振频率29.40 Hz处的阻尼转矩系数为负,且数值较大。根据复转矩系数理论分析结果表明,系统应该也处于不稳定的运行状态,且振荡频率应当为对应的电气扭振频率,即20.60 Hz附近,这与电磁暂态模型仿真结果不符。
综上所述,复转矩系数法能够分析含串补的风火打捆外送系统的部分振荡风险,但在串补度为30%时分析结果不准确。这是由于复转矩系数在多机系统情况下失去了复转矩系数法的基本前提,仅适用于单机对固定频率电源系统,不适用于多机系统[28]。因此,在含有大量电力电子装置的新型电力系统中,基于复转矩系数的稳定性分析方法还需要开展进一步的研究,而阻抗分析法在这种情况下在准确性上具有一定的优势。
本研究建立了考虑调速器模块、汽轮机模块与轴系模块等机械部分的汽轮发电机阻抗模型,通过仿真频率扫描验证了阻抗模型的正确性,并与传统汽轮发电机建模方法进行了比对。另外,建立了风火打捆外送系统振荡分析实例,分别将本文建立的汽轮发电机阻抗与同步发电机等效电路阻抗代入计算风火打捆系统总阻抗,并对不同串补度时的并网系统进行了振荡分析。同时对比了基于复转矩系数法的分析结果。本研究得出以下结论:
1)与同步电机等效电路阻抗相比,本研究建立的阻抗模型在汽轮发电机的轴系自然扭振频率附近更加准确,提升了模型的精度。
2)本文提出的汽轮发电机阻抗模型在含有新能源以及电力电子设备的复杂电力系统中能够很好地进行稳定性分析,相较于传统汽轮发电机阻抗模型在次/超同步频段具有更好的准确性。
3)相较于复转矩系数法,在含有电力电子装置的多机系统中,阻抗分析法在准确性上具有一定的优势。
最后,本研究结果可以为包含汽轮发电机与电力电子装置的电力系统稳定性分析提供模型基础。
参考文献
[1] 刘欣, 郭志博, 贾焦心, 等. 基于序阻抗的虚拟同步发电机并网稳定性分析及虚拟阻抗设计[J]. 电工技术学报, 2023, 38(15): 4130-4146.
Liu Xin, Guo Zhibo, Jia Jiaoxin, et al. Stability analysis and virtual impedance design of virtual synchronous machine based on sequence impe- dance[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4130-4146.
[2] 于彦雪, 关万琳, 陈晓光, 等. 基于序阻抗的虚拟同步机同步频率谐振现象[J]. 电工技术学报, 2022, 37(10): 2584-2595.
Yu Yanxue, Guan Wanlin, Chen Xiaoguang, et al. Synchronous frequency resonance in virtual syn- chronous generator based on sequence-impedance[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2584-2595.
[3] 刘朋印, 谢小荣, 马宁宁, 等. 风电次/超同步振荡激发汽轮机组轴系扭振风险的在线评估与预警技术[J]. 中国电机工程学报, 2021, 41(增刊1): 52-58.
Liu Pengyin, Xie Xiaorong, Ma Ningning, et al. Online assessment and early warning of torsional vibration risk for turbine generators stimulated by sub-/super-synchronous oscillations associated with wind power[J]. Proceedings of the CSEE, 2021, 41(S1): 52-58.
[4] 李宽, 王军, 赵斌超, 等. 风火捆绑经HVDC送电引起轴系扭振研究[J]. 电工技术学报, 2017, 32(6): 115-122.
Li Kuan, Wang Jun, Zhao Binchao, et al. Shafting vibration research of wind power and thermal power bundle supply through HVDC[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 115- 122.
[5] 刘其辉, 洪晨威, 逄思敏, 等. 基于弹性系数的双馈风电机组控制参数对次同步振荡作用分析及调整方法[J]. 电工技术学报, 2022, 37(14): 3528- 3541.
Liu Qihui, Hong Chenwei, Pang Simin, et al. Analysis and adjustment method of doubly-fed fan control parameters on subsynchronous oscillation based on impedance elastic sensitivity[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3528- 3541.
[6] Chi Yongning, Tang Bingjie, Hu Jiabing, et al. Overview of mechanism and mitigation measures on multi-frequency oscillation caused by large-scale integration of wind power[J]. CSEE Journal of Power and Energy Systems, 2019, 5(4): 433-443.
[7] Liu Huakun, Xie Xiaorong, He Jingbo, et al. Subsynchronous interaction between direct-drive PMSG based wind farms and weak AC networks[J]. IEEE Transactions on Power Systems, 2017, 32(6): 4708-4720.
[8] 孙东阳, 孟繁易, 王南, 等. 基于反步自适应准谐振控制的双馈风机次同步振荡抑制策略[J]. 电工技术学报, 2023, 38(9): 2375-2390, 2434.
Sun Dongyang, Meng Fanyi, Wang Nan, et al. DFIG sub-synchronous oscillation suppression strategy based on backstepping adaptive quasi-resonant control[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2375-2390, 2434.
[9] 付强, 杜文娟, 王海风. 柔性直流输电控制与交流系统次同步交互机理研究[J]. 中国电机工程学报, 2018, 38(13): 3717-3726, 4013.
Fu Qiang, Du Wenjuan, Wang Haifeng. The mechanism of sub-synchronous interactions between converter control of VSC HVDC and power systems[J]. Proceedings of the CSEE, 2018, 38(13): 3717-3726, 4013.
[10] 王晖, 吴命利. 电气化铁路低频振荡研究综述[J]. 电工技术学报, 2015, 30(17): 70-78.
Wang Hui, Wu Mingli. Review of low-frequency oscillation in electric railways[J]. Transactions of China Electrotechnical Society, 2015, 30(17): 70-78.
[11] 郭春义, 吕乃航, 张加卿. 提高LCC-HVDC在弱交流系统下的稳定性和动态性能的控制参数优化方法[J]. 电工技术学报, 2023, 38(7): 1751-1764, 1779.
Guo Chunyi, Lü Naihang, Zhang Jiaqing. Optimi- zation of control parameters to enhance stability and dynamic performance of LCC-HVDC under weak AC condition[J]. Transactions of China Electrotechnical Society, 2023, 38(7): 1751-1764, 1779.
[12] 朱晓娟, 胡海涛, 陶海东, 等. 光伏并网系统的谐波不稳定产生机理及影响规律[J]. 电工技术学报, 2017, 32(10): 33-41.
Zhu Xiaojuan, Hu Haitao, Tao Haidong, et al. The mechanism and influence of harmonic instability for photovoltaic grid-connected system[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 33-41.
[13] Canay I M. A novel approach to the torsional interaction and electrical damping of the synchronous machine part Ⅱ: application to an arbitrary net- work[J]. IEEE Transactions on Power Apparatus and Systems, 1982, 101(10): 3639-3647.
[14] Tabesh A, Iravani R. On the application of the complex torque coefficients method to the analysis of torsional dynamics[J]. IEEE Transactions on Energy Conversion, 2005, 20(2): 268-275.
[15] Zhao Wei, Wang Shihao, Sun Xiaofeng, et al. Impedance modeling and stability research of hybrid parallel system with synchronous generator and inverters[C]//2018 IEEE International Power Elec- tronics and Application Conference and Exposition (PEAC), Shenzhen, China, 2018: 1-6.
[16] Gu Yunjie, Li Yitong, Zhu Yue, et al. Impedance- based whole-system modeling for a composite grid via embedding of frame dynamics[J]. IEEE Transa- ctions on Power Systems, 2021, 36(1): 336-345.
[17] IEEE Subsynchronous Resonance Working Group. First benchmark model for computer simulation of subsynchronous resonance[J]. IEEE Transactions on Power Apparatus and Systems, 1977, 96(5): 1565- 1572.
[18] Zou Xiaoming, Du Xiong, Tai Hengming. Two- variable admittance model for D-PMSG-based wind turbine and stability criterion based on magnitude and phase contour plot[J]. IEEE Transactions on Power Electronics, 2020, 35(2): 1484-1498.
[19] IEEE Committee Report. Dynamic models for steam and hydro turbines in power system studies[J]. IEEE Transa- ctions on Power Apparatus and Systems, 1973, 92(6): 1904-1915.
[20] 谢小荣, 韩英铎, 郭锡玖. 电力系统次同步谐振的分析与控制[M]. 北京: 科学出版社, 2015.
[21] IEEE Subsynchronous Resonance Working Group. Terms, definitions and symbols for subsynchronous oscillations[J]. IEEE Transactions on Power Apparatus and Systems, 1985, 104(6): 1326-1334.
[22] Rygg A, Molinas M, Zhang Chen, et al. A modified sequence-domain impedance definition and its equivalence to the dq-domain impedance definition for the stability analysis of AC power electronic systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(4): 1383- 1396.
[23] 杜程茂, 杜雄, 邹小明, 等. 考虑频率耦合效应的并网模块化多电平变流器阻抗建模及稳定性分析[J]. 中国电机工程学报, 2020, 40(9): 2866-2877.
Du Chengmao, Du Xiong, Zou Xiaoming, et al. Impedance modeling and stability analysis of grid-connected modular multilevel converter con- sidering frequency coupling effect[J]. Proceedings of the CSEE, 2020, 40(9): 2866-2877.
[24] 邹小明, 杜雄, 王国宁, 等. 三相并网逆变器频率耦合机理分析及稳定性判定[J]. 电力系统自动化, 2018, 42(18): 57-63.
Zou Xiaoming, Du Xiong, Wang Guoning, et al. Frequency coupling mechanism analysis and stability judgement for three-phase grid-connected inverter[J]. Automation of Electric Power Systems, 2018, 42(18): 57-63.
[25] 程时杰, 曹一家, 江全元. 电力系统次同步振荡的理论与方法[M]. 北京: 科学出版社, 2009.
[26] 王一珺, 杜文娟, 陈晨, 等. 基于改进复转矩系数法的风电场并网引发电力系统次同步振荡研究[J]. 电工技术学报, 2020, 35(15): 3258-3269.
Wang Yijun, Du Wenjuan, Chen Chen, et al. Study on sub-synchronous oscillations of power systems caused by grid-connected wind farms based on the improved complex torque coefficients method[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3258-3269.
[27] Mortensen K, Larsen E V, Piwko R J. Field tests and analysis of torsional interaction between the coal creek turbine-generators and the CU HVDC system[J]. IEEE Transactions on Power Apparatus and Systems, 1981, 100(1): 336-344.
[28] 徐政. 复转矩系数法的适用性分析及其时域仿真实现[J]. 中国电机工程学报, 2000, 20(6): 1-4.
Xu Zheng. The complex torque coefficient approach’s applicability analysis and its realization by time domain simulation[J]. Proceedings of the CSEE, 2000, 20(6): 1-4.
[29] Bosetti H, Khan S. Transient stability in oscillating multi-machine systems using Lyapunov vectors[J]. IEEE Transactions on Power Systems, 2018, 33(2): 2078-2086.
Abstract Due to the increasing number of electronic power devices in power systems, power system structures have become complicated, and analyzing power system stability containing power electronic devices and turbo-generators is difficult. The impedance-based analysis method is a good choice because extending the system topology and establishing the black box system model is easy. However, the impedance of the turbo-generator only reflects electrical characteristics. This paper establishes an impedance model of the turbo-generator considering the mechanical part of the turbine, governor, and shafting mass-spring.
The turbo-generator is divided into electrical and mechanical parts. For the electrical part modeling, an ideal state is assumed, and the small signal equation of the synchronous motor is standardized. For the mechanical part modeling, a small signal model is established for the shafting part, steam turbine, and speed regulator. Calculation results show that the impedance model of the turbo-generator in the d-q coordinate system is a 2nd-order matrix. Finally, the impedance model of the turbo-generator considering the shafting part is obtained by converting it into a sequence impedance model and considering the frequency coupling effect.
The theoretical model is verified by the frequency scanning method. The experimental results of frequency scanning points agree with the theoretical model, which verifies the correctness of the impedance model. Taking the wind-thermal bundling delivery system as the research object, compared with the oscillation analysis based on the RL equivalent impedance model, the proposed impedance model can identify the sub-/super-synchronous oscillation risk. The proposed model for stability analysis in power systems containing new energy and power electronic equipment is verified. Finally, the classical turbo-generator stability analysis, i.e., the complex torque coefficient method, is used to analyze the oscillation of the wind-thermal bundled system.
This study draws the following conclusions. (1) Compared with the equivalent circuit impedance of the synchronous motor, the proposed impedance model is more accurate near the natural torsional vibration frequency of the turbo-generator shafting, improving the model’s accuracy. (2) The turbo-generator impedance model can perform stability analysis well in complex power systems containing new energy systems and power electronic equipment. It is more accurate than the traditional turbo-generator impedance model in the sub-/super-synchronous frequency band. (3) Compared with the complex torque coefficient method, the impedance-based analysis has advantages in accuracy in multi-machine systems containing electronic power devices.
keywords:Impedance model, turbo-generator, torsional vibration of shaft system, wind-thermal bundled system
DOI: 10.19595/j.cnki.1000-6753.tces.230773
中图分类号:TM311; TM712
国家自然科学基金重点资助项目(51937001)。
收稿日期 2023-05-26
改稿日期 2023-09-12
李佳龙 男,1999年生,硕士研究生,研究方向为电力电子系统稳定性。E-mail: 20173549@cqu.edu.cn
杜 雄 男,1979年生,教授,博士生导师,研究方向新能源并网系统稳定性、电力电子装备可靠性和直流输电系统稳定性。E-mail: duxiong@cqu.edu.cn(通信作者)
(编辑 崔文静)