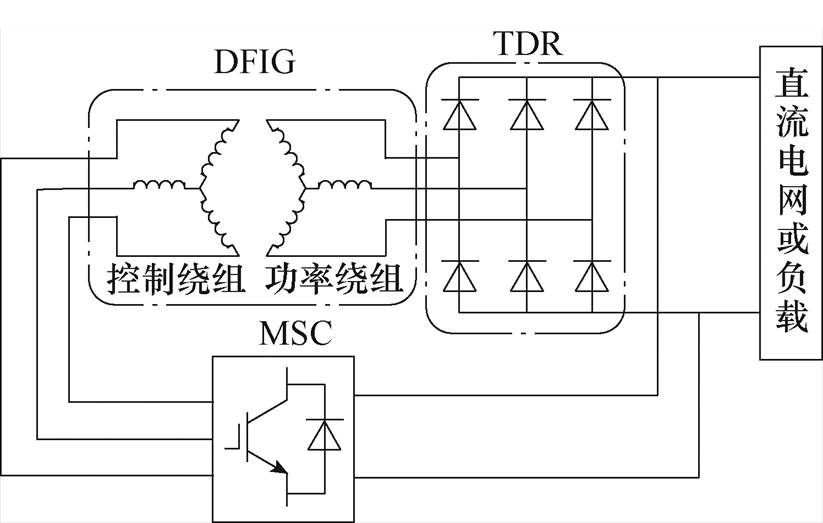
图1 DFIG-DC系统基本结构
Fig.1 Basic structure of the DFIG-DC system
摘要 在非正弦和不平衡运行条件下，双馈感应发电机会面临显著的转矩脉动问题，严重威胁系统的安全稳定运行，因此有必要采取转矩脉动抑制措施。近些年，诸多学者针对该问题进行了广泛研究，并取得了一系列的科研成果，但鲜有对其进行总结归纳的文献。为此，该文首先介绍了双馈感应发电机系统结构，分析了非正弦和不平衡运行条件下转矩脉动成因，并明确了转矩脉动抑制的主要目标。其次，从硬件结构改进法和控制策略改进法两方面对现有技术方案进行归类总结，并从七个维度进行综合对比分析。最后，从软硬件协同抑制、参数鲁棒性提升、谐波损耗抑制和故障穿越四个方面对双馈感应发电机转矩脉动抑制方法的未来发展趋势进行了展望。
关键词：非正弦运行 不平衡运行 双馈感应发电机 转矩脉动抑制
随着社会经济的不断发展，人们对于能源的需求日益增长，而传统化石能源正面临枯竭的风险，急需开发替代能源来缓解能源困境[1-3]。二十大报告中也提出积极稳妥推进“碳达峰、碳中和”，加快规划建设新型能源体系。在这样的时代背景下，风电行业迎来了历史性发展机遇，风电将发挥主力军的作用，在未来能源系统中扮演至关重要的角色[4-6]。据国家能源局统计，截至2023年12月底，全国累计风电装机容量约4.4亿kW，同比增长20.7%。据中电联推算，2024年，我国新增风电装机容量预计约89 GW，总装机容量可达5.3亿kW。
发电机及其控制系统作为风电系统的核心部分，影响着整个发电系统的运行性能。在各类风力发电机中，有刷双馈感应发电机因其造价低廉、变流器容量小、控制灵活等优势，长期占据主流地 位[7-8]。无刷双馈感应发电机是近些年来发展起来的一种由两套不同极对数的定子绕组和一套转子绕组构成的新型双馈感应发电机，两套定子绕组之间没有直接的电磁耦合，需要经过特殊设计的转子绕组实现能量传递[9-10]。无刷双馈感应发电机不仅继承了有刷双馈感应发电机结构简单、坚固耐用的优势，还取消了电刷和集电环，运行安全可靠[11]，但因其功率密度和转矩密度较低[12]，目前尚未得到大规模应用。尽管如此，在对可靠性要求较高的场合，如海上风力发电系统[13-14]，无刷双馈感应发电机依然具有较大优势，未来有望在风电市场占有一席之地。为了描述方便，现将有刷双馈感应发电机和无刷双馈感应发电机统称为双馈感应发电机（Doubly-Fed Induction Generator, DFIG），将主功率输出绕组和变流器供电绕组分别称为功率绕组和控制绕组。
随着碳化硅、氮化镓等宽禁带半导体材料的发展[15-16]，大量电力电子设备高密度应用于风力发电系统。特别是不可控电力电子器件对系统造成了严重的谐波污染，导致电压和电流等物理量出现谐波畸变，使得系统处于非正弦运行状态[17-18]。除此以外，电网远端故障或三相负载不平衡时有发生，由此产生的负序分量会导致发电系统三相电压和电流不平衡[19-21]。非正弦和不平衡等非理想运行条件不仅会降低系统发电质量[22]和效率[23]，还会使得电机产生转矩脉动[24]，对齿轮箱和传动轴产生极大的危害。根据有关数据统计[25]，轴系故障约占感应电动机总故障的41%左右。每年使用的轴承中，约45%需要停车检验，约34%因故障无法使用要进行更换。因此，研究非理想运行条件下的转矩脉动抑制方法对于降低风力发电系统故障发生率，保证系统安全可靠运行至关重要。
近年来，国内外许多学者针对非理想运行条件下的DFIG转矩脉动问题，提出了若干解决方案。这些方案基本可分为两大类：硬件结构改进法和控制策略改进法。硬件结构改进法可以有效抑制转矩脉动，但需要改变电机结构或增加额外硬件，导致系统成本增加。控制策略改进法无需增加额外硬件，但可能会加剧控制器的运算负担，导致控制周期延长，从而使得电机的控制精度下降。这些方法的出发点和手段各不相同，需要进行归类总结，以便相关领域学者快速了解此类技术研究现状和发展态势，推动DFIG转矩脉动抑制技术的进一步发展。
本文首先介绍了DFIG直流、交流发电系统结构，并构建了非理想运行条件下的DFIG转矩谐波数学模型，明确了转矩脉动抑制的主要目标。然后，总结已有的DFIG转矩脉动抑制方法，并从多个维度进行综合对比分析。最后，对DFIG转矩脉动抑制方法未来的发展态势进行了展望，并讨论了相关技术的潜在研究热点。
目前，DFIG已广泛应用于直流和交流发电系统中，其基本结构分别如图1和图2所示。
在图1所示的双馈感应发电机直流（Doubly Fed Induction Generator DC, DFIG-DC）系统中，功率绕组与三相不控整流器（Three-phase Diode Rectifier, TDR）相连，控制绕组连接机侧变流器（Machine Side Converter, MSC），TDR和MSC均与直流电网或负载相连。尽管TDR可以节约系统成本，但其不可控的导通性会导致功率绕组电压和电流等物理量出现谐波畸变，进而引发转矩脉动。
图1 DFIG-DC系统基本结构
Fig.1 Basic structure of the DFIG-DC system
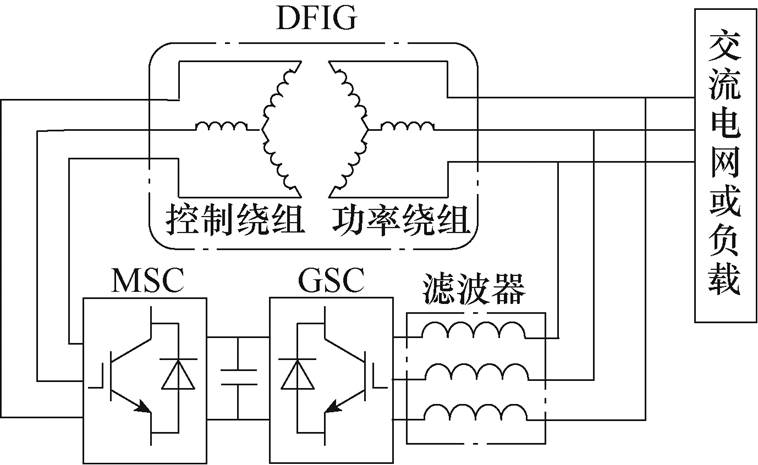
图2 DFIG-AC系统基本结构
Fig.2 Basic structure of the DFIG-AC system
在图2所示的双馈感应发电机交流（Doubly Fed Induction Generator AC, DFIG-AC）系统中，功率绕组连接交流电网或负载，控制绕组经四象限变流器和滤波器连接到功率绕组，其中的四象限变流器由MSC、直流母线电容和网侧变流器（Grid Side Converter, GSC）构成。当负载为TDR或电网电压发生谐波畸变时，交流发电系统会呈现出与直流发电系统相似的特征。此外，电网三相不对称故障或三相负载不平衡在交流发电系统中时有发生，这会导致功率绕组电压和电流等物理量产生负序分量，同样会引发转矩脉动。
由上述分析可知，无论是DFIG-DC系统还是DFIG-AC系统，在非理想运行条件下都存在转矩脉动问题，这会严重威胁系统的安全稳定运行。因此，有必要构建非理想运行条件下的转矩谐波数学模型，从而有针对性地制定转矩谐波抑制策略，缓解转矩脉动。
方便起见，现忽略转子电阻项对无刷DFIG转矩的影响，认为功率绕组和控制绕组直接耦合，转子仅起到极对数转换器的作用[26]。基于上述假设，无刷DFIG转矩表达式可以写为
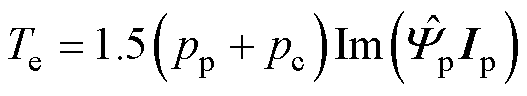（1）
式中，Te为电磁转矩；p为极对数；Y 为磁链矢量，其值可用dq旋转坐标系下的磁链分量表示为yd+ jyq，也可用ab 坐标下的磁链分量表示为ya+jyb；I为电流矢量，其表示方法与磁链矢量一致；上标“
”为共轭；下标“p”代表功率绕组变量；下标“c”代表控制绕组变量。另外，后文的电压矢量U也与磁链矢量的表示方法一致。
利用功率绕组磁链和电流表示的有刷DFIG转矩表达式[27]通常可以写为
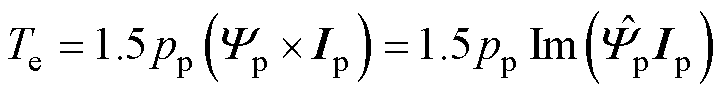（2）
对比式（1）和式（2）不难发现，有刷DFIG和无刷DFIG的转矩表达式形式相似，不同之处仅在于极对数。方便起见，定义变量pe，将DFIG的转矩表达式统一为
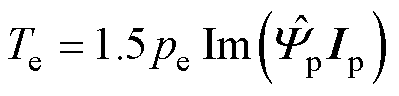（3）
式中，pe为等效极对数，在无刷DFIG中的值等于功率绕组和控制绕组极对数之和，在有刷DFIG中的值等于绕组极对数。
当系统处于非正弦和不平衡运行条件时，功率绕组磁链和电流中会含有6k±1次谐波和负序分 量[28]。因此，式（3）可进一步写为
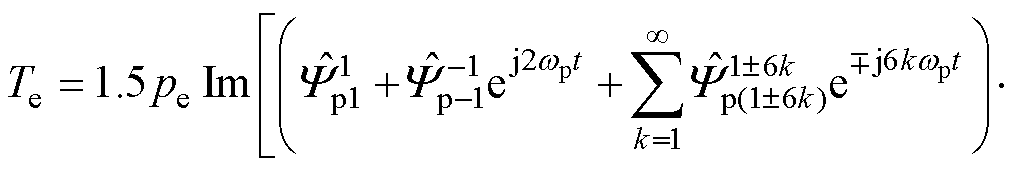
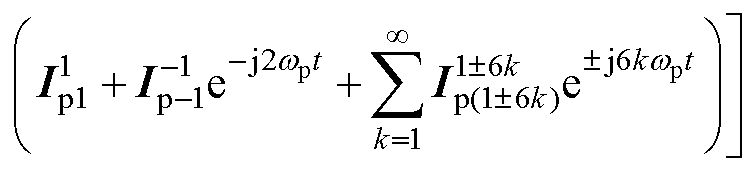（4）
式中，wp为功率绕组角频率；磁链和电流下标的数字表示变量的频率阶次，上标的数字表示变量所在旋转坐标系的频率阶次，本文中的所有变量均遵循这一原则。另外，为了后文描述方便，现将谐波和负序分量统称为非理想分量，用下标h表示；将以谐波和负序分量的角频率为旋转角速度的坐标系称为非理想旋转坐标系，用上标h表示。
非理想分量之间的耦合作用对转矩脉动的影响相对较小，因此可仅考虑基波与基波之间、基波与非理想分量之间的耦合作用。将式（4）展开可得
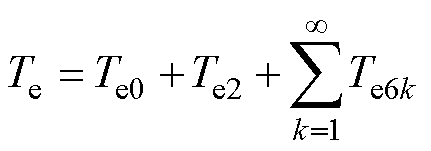（5）
其中
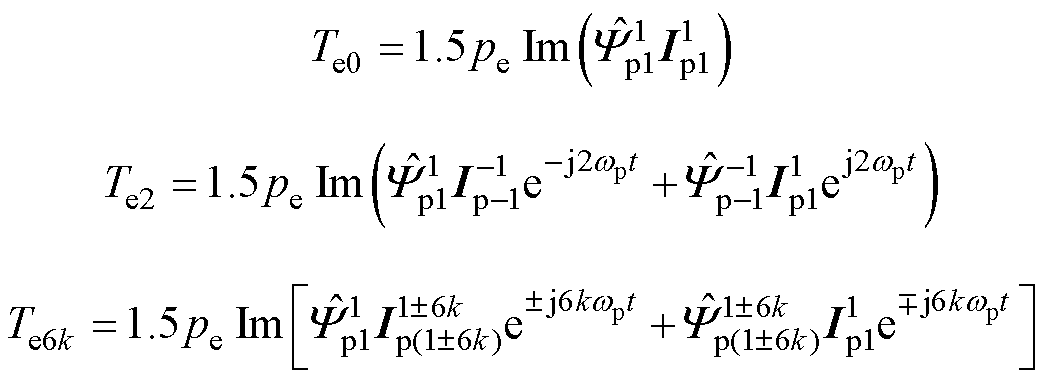
式中，Te0、Te2和Te6k分别为平均转矩、2次谐波转矩和6k次谐波转矩。由式（5）可知，在非理想运行条件下，转矩脉动主要是由2次和6k次谐波转矩引起的，这些特征谐波也是制定转矩脉动抑制策略时需要考虑的主要控制目标。接下来，对目前已有的转矩脉动抑制方法进行详细介绍。
根据所增加硬件装置的不同，现有的硬件结构改进法可分为三类：采用多脉冲整流器、增加无源滤波器和采用电压源变流器。下面对上述三类硬件结构改进法进行详细介绍。
为了抑制图1所示DFIG-DC系统中较为显著的转矩6次谐波，文献[29]提出了一种基于三绕组变压器的十二脉冲DFIG-DC系统，结构如图3所示。三绕组变压器的一次绕组采用星形联结与功率绕组相连，二次侧两套绕组分别采用星形联结和三角形联结与TDR相连，形成了十二脉冲整流器。此外，为了消除星形联结和三角形联结法导致的相电流幅值差异，需要设置二次侧两绕组的匝数比为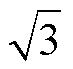
。文献[30]提出了一种基于六相电机的十二脉冲DFIG- DC发电系统，如图4所示。六相DFIG的两套功率绕组相差30°电角度，且分别连接一组TDR，以实现系统的十二脉冲整流输出。
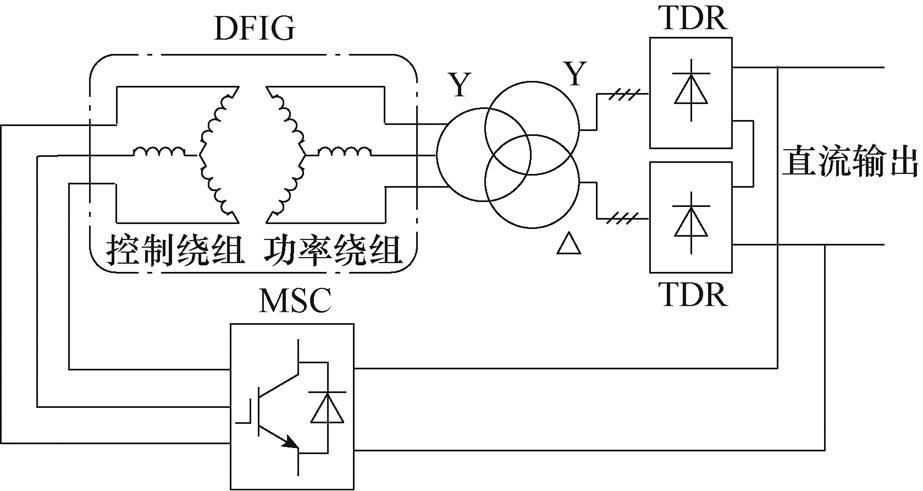
图3 基于三绕组变压器的十二脉冲DFIG-DC系统结构
Fig.3 Structure of the twelve-pulse DFIG-DC system based on the three-winding transformer
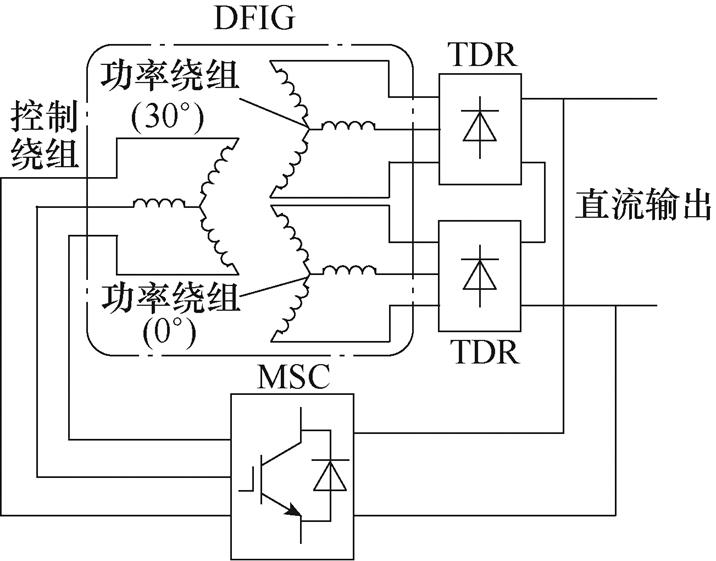
图4 基于六相电机的十二脉冲DFIG-DC系统结构
Fig.4 Structure of the twelve-pulse DFIG-DC system based on the six-phase machine
文献[30]对传统的六脉冲整流器结构和十二脉冲整流器结构进行了仿真对比，结果如图5所示。相比于六脉冲整流器结构，十二脉冲整流器结构能够有效抑制转矩的6次谐波，但对于转矩的12次谐波无法发挥作用。
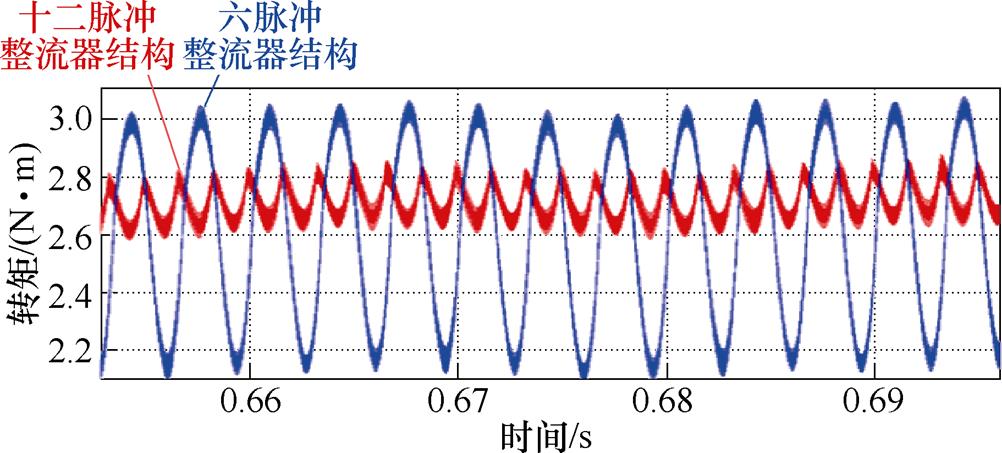
图5 十二脉动整流器和六脉冲整流器仿真结果
Fig.5 Simulation results of the 12-pulse and 6-pulse rectifiers
文献[31]提出了一种基于无源滤波器的DFIG- AC系统，如图6所示。该系统在负载TDR和功率绕组之间增加了无源滤波器，能够在一定程度上抑制功率绕组电压和电流等物理量中的谐波成分，从而减轻转矩脉动的影响。图7所示为增加无源滤波器前后的仿真结果。仿真结果表明，增加无源滤波器可使得转矩总谐波畸变率（Total Harmonic Distortion, THD）由4.7%下降到3.3%。若想提高抑制效果，需进一步增加无源滤波器的电感量。
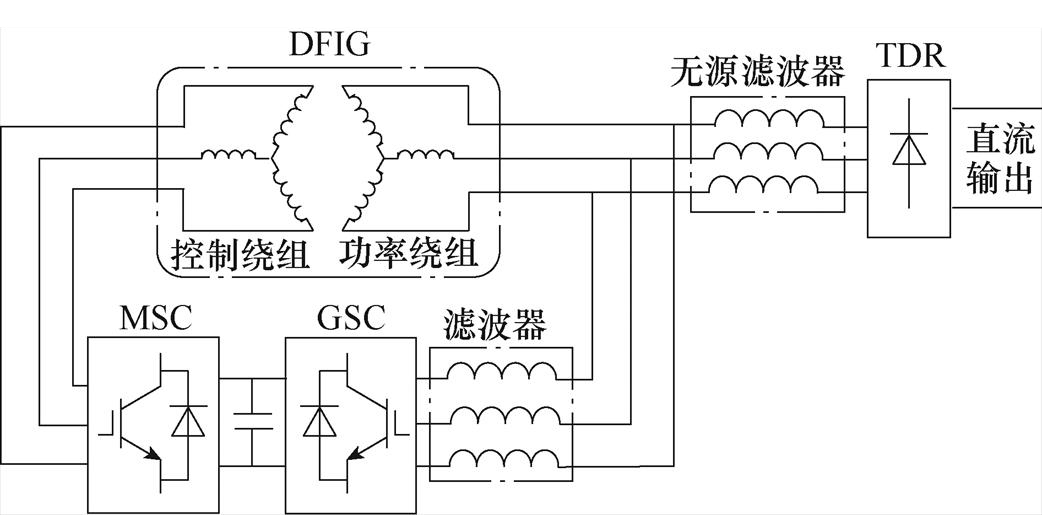
图6 基于无源滤波器的DFIG-AC系统结构
Fig.6 Structure of DFIG-AC system based on the passive filter
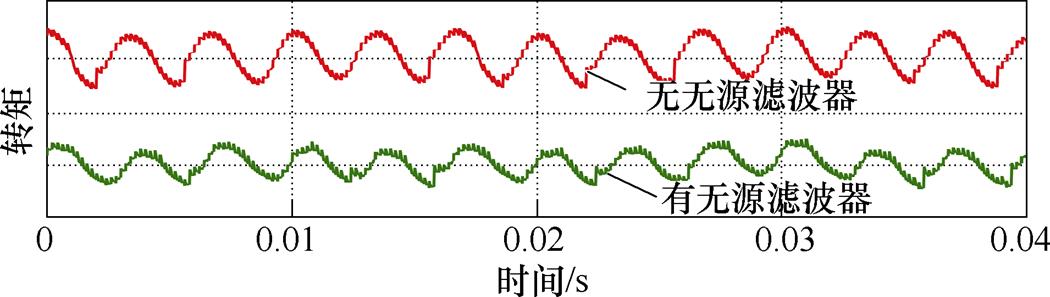
图7 增加无源滤波器前后的仿真结果
Fig.7 Simulation results before and after adding the passive filter
采用多脉冲整流器和增加无源滤波器虽然不会增加控制复杂度，但需要改变电机结构或增加变压器和无源滤波器，这无疑会增加系统成本。除此以外，采用多脉冲整流器只能抑制转矩低次谐波，而增加无源滤波器仅对转矩高次谐波抑制作用明显。因此，这两类硬件结构改进法对转矩脉动的抑制效果均有限。
为了同时抑制高次和低次谐波，达到更优的转矩脉动抑制效果，一些学者尝试采用电压源变流器（Voltage Source Converter, VSC）。文献[32]提出了一种基于MSC-VSC的DFIG-DC系统，如图8所示，利用VSC替代图1所示DFIG-DC系统中的TDR，能够有效提高绕组电压和电流的波形质量，降低转矩脉动。
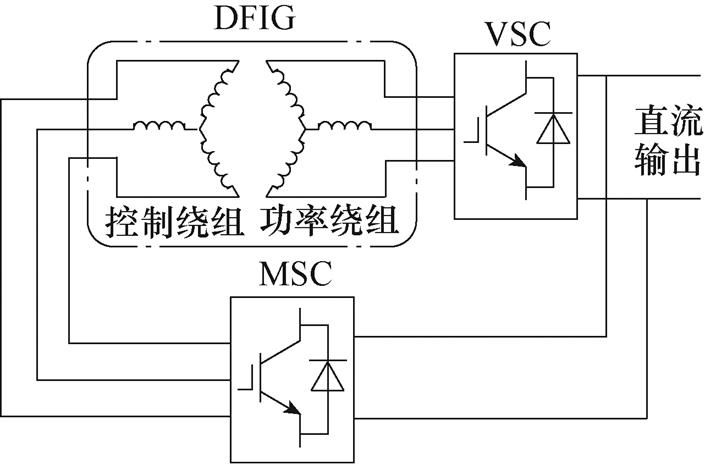
图8 基于MSC-VSC的DFIG-DC系统结构
Fig.8 Structure of the DFIG-DC system based on MSC-VSC
采用VSC抑制转矩脉动的方法也适用于含TDR负载的DFIG-AC系统。文献[33]提出了一种基于VSC负载的DFIG-AC系统，如图9所示，采用VSC替代负载中的TDR，使得绕组电压和电流等物理量不会发生谐波畸变，可有效解决转矩脉动问题。同时，该系统可通过调节变压器的电压比，在高、中、低压场合灵活应用。
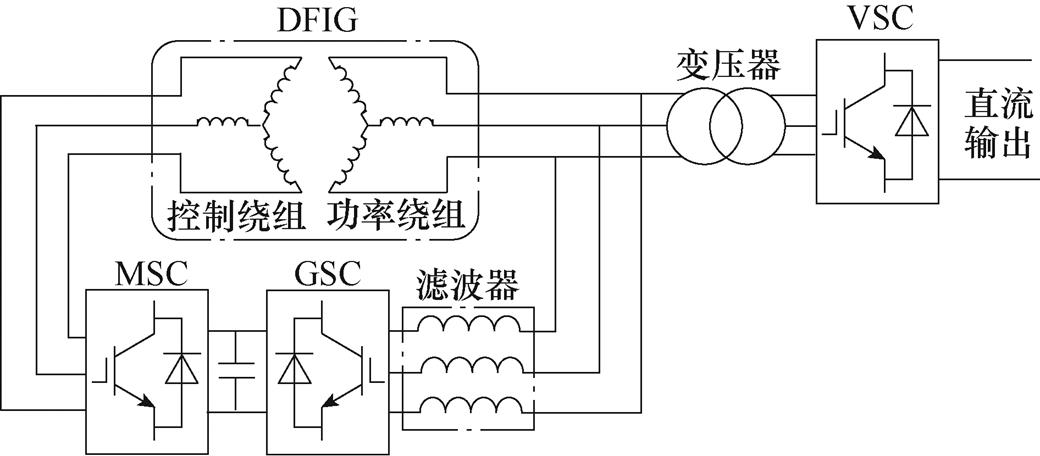
图9 基于VSC负载的DFIG-AC系统结构
Fig.9 Structure of the DFIG-AC system based on VSC load
由文献[32]给出的实验波形，如图10所示，图中，emabc为气隙电动势，ipabc为功率绕组三相电流，icabc为控制绕组三相电流。可知，基于VSC的DFIG- DC系统能够有效解决由TDR引起的绕组电压和电流等物理量的谐波畸变问题。相比于前述两种硬件结构改进法，其转矩脉动抑制效果更加显著。但是，此类方法需要采用全功率VSC，这不仅会显著增加系统成本，还会增加系统的控制复杂度。
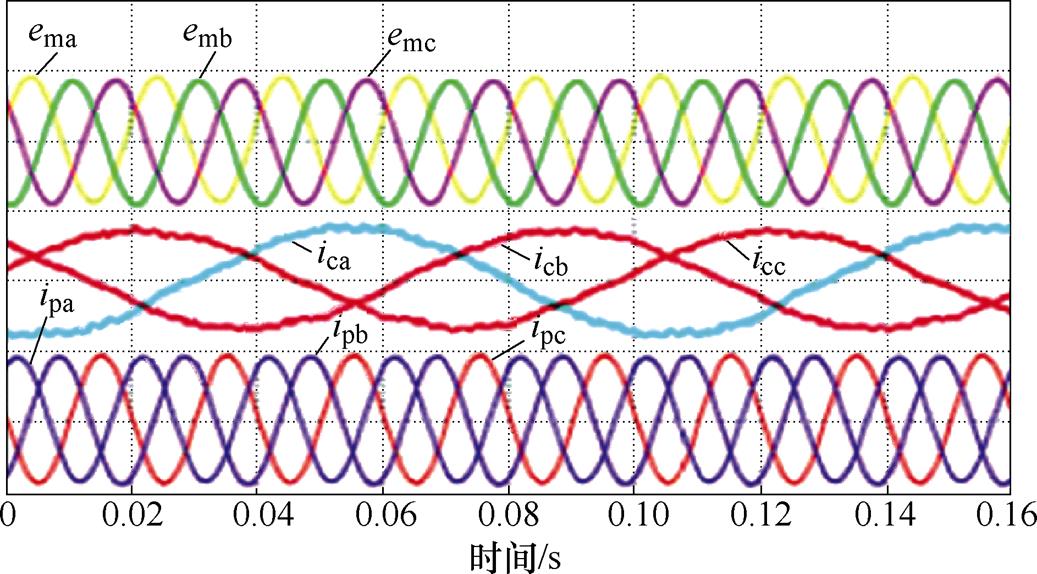
图10 基于MSC-VSC的DFIG-DC系统实验波形
Fig.10 Experimental waveforms of the DFIG-DC system based on MSC-VSC
控制策略改进法是对现有控制策略进行优化和调整来达到转矩脉动抑制目的一类方法，它不需要增加额外的硬件设备，相比于硬件结构改进法更为经济、高效。在接下来的内容中，将详细介绍控制策略改进法的原理和实现方法。
转矩闭环控制法通过转矩控制器对转矩误差进行调节，可直接获得控制绕组电压参考值，其基本控制原理如图11所示。
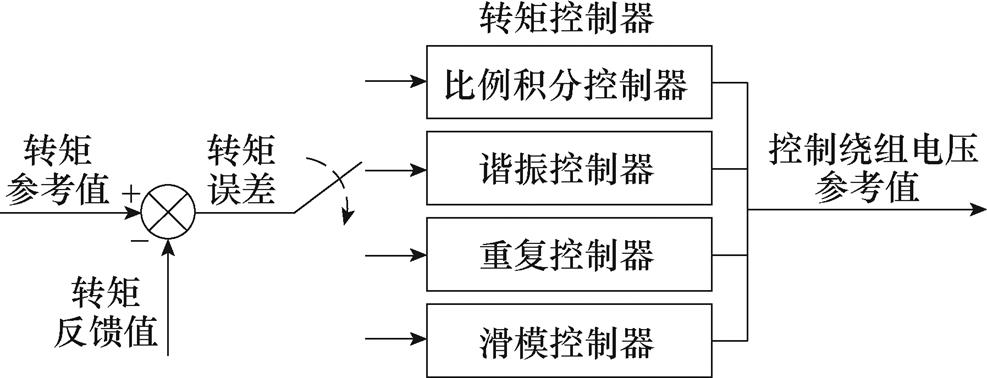
图11 转矩闭环控制法原理
Fig.11 Principle of the torque closed-loop control method
目前，已有的转矩闭环控制法主要有四种，分别为比例积分控制器（Proportional Integral Controller, PIC）闭环控制法、谐振控制器（Resonant Controller, RC）闭环控制法、重复控制器（Repetitive Controller, RepC）闭环控制法以及滑模控制器（Sliding Mode Controller, SMC）闭环控制法。下面将分别对它们的工作原理进行介绍。
3.1.1 PIC闭环控制法
PIC的算法简单，是当前控制系统最常用的控制器之一，其传递函数为
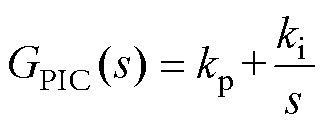（6）
式中，s为微分算子；kp为比例增益；ki为积分增益。
绘制不同kp和ki下PIC的伯德图，如图12所示。可以看出，kp主要影响高频信号增益，ki主要影响低频信号增益。因此，增大kp可增大PIC对转矩谐波信号的幅值增益。
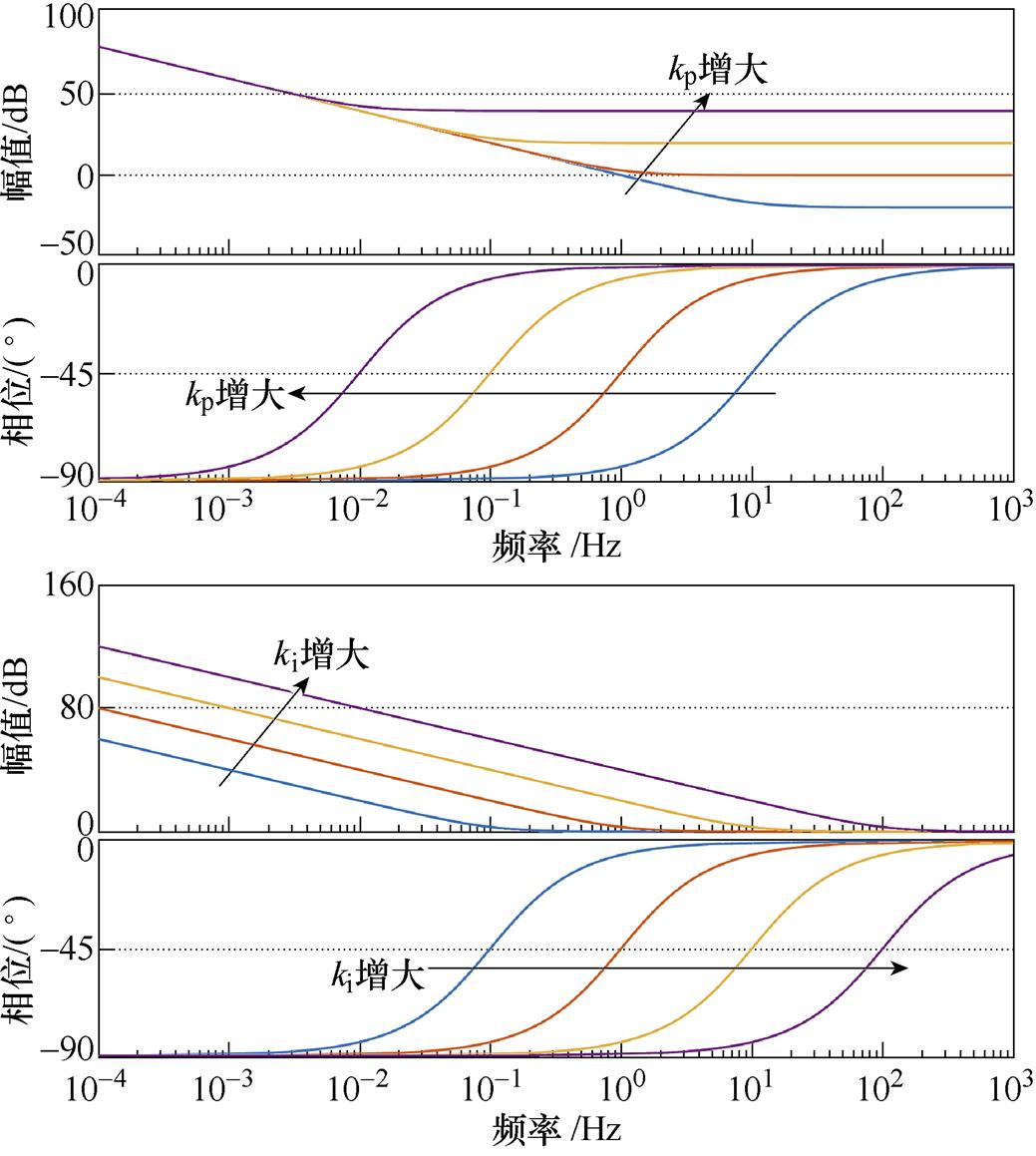
图12 不同kp和ki下PIC的伯德图
Fig.12 Bode diagrams of PIC under different kp and ki
文献[34-35]提出了一种基于PIC的转矩2次谐波闭环控制方法，其基本原理如图13所示。其中，转矩参考值为零，转矩反馈值为带通滤波器提取的转矩2次谐波。最终，PIC可调节转矩差值以输出补偿转矩2次谐波的控制绕组q轴电压参考值。
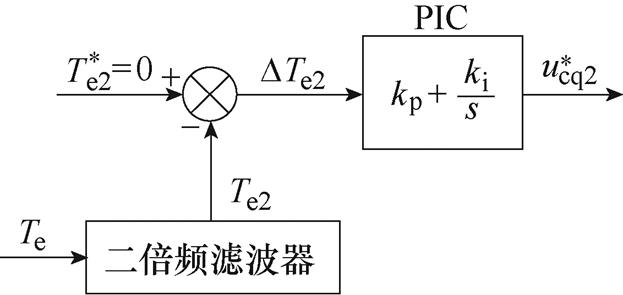
图13 基于PIC的转矩2次谐波闭环控制原理
Fig.13 Principle of torque 2nd harmonic closed-loop control based on PIC
文献[36]提出了一种基于PIC的全转矩闭环控制方法，其基本原理如图14所示。该方法中的转矩参考值为电压控制器的输出，反馈值为全转矩。通过调节PIC的带宽，能够同时对平均转矩和谐波转矩进行控制，最终同时获得控制平均转矩和补偿谐波转矩的控制绕组q轴电压参考值。根据文献[36]给出的如图15所示的基于PIC的全转矩闭环控制实验结果可知，基于PIC的全转矩闭环控制可以使得转矩峰峰值下降45%。
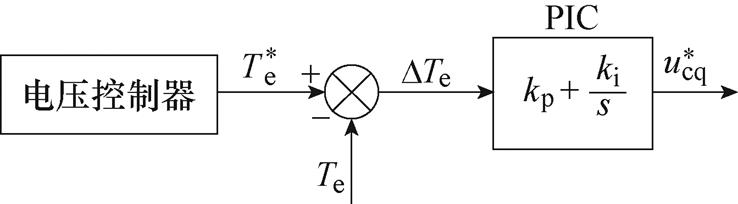
图14 基于PIC的全转矩闭环控制原理
Fig.14 Principle of the total torque closed-loop control based on PIC
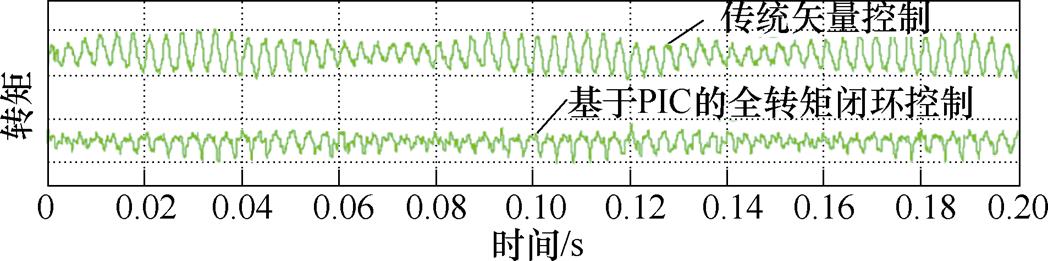
图15 基于PIC的全转矩闭环控制实验结果
Fig.15 Experimental results of the total torque closed-loop control based on PIC
PIC闭环控制法需要提高PIC的带宽，以使其能为转矩谐波信号提供较大的幅值增益。但在实际应用中，如果PIC的带宽设计得过高，会导致噪声放大，从而影响系统的稳定性。
3.1.2 RC闭环控制法
理想的二阶谐振控制器（Second Order Resonant Controller, SORC）传递函数为
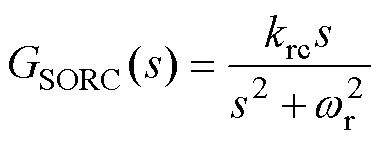（7）
式中，krc为RC增益；wr为RC角频率。
虽然理想SORC可以在谐振频率点处达到无穷幅值增益，但是偏离谐振频率点幅值增益会迅速衰减。因此，在实际应用时，为了降低SORC的谐振频率敏感度，会引入截止频率wc。引入wc后的改进型SORC（Improved SORC, ISORC）传递函数[37-38]为
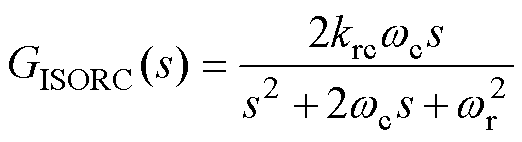（8）
图16展示了谐振频率为100 Hz、300 Hz时的ISORC伯德图。从图中可以看出，ISORC对谐振频率信号具有较大的幅值增益，而偏离谐振频率较多的信号则经过ISORC后会被大大削减。因此，ISORC可对某一特定频率的转矩谐波进行有效控制。
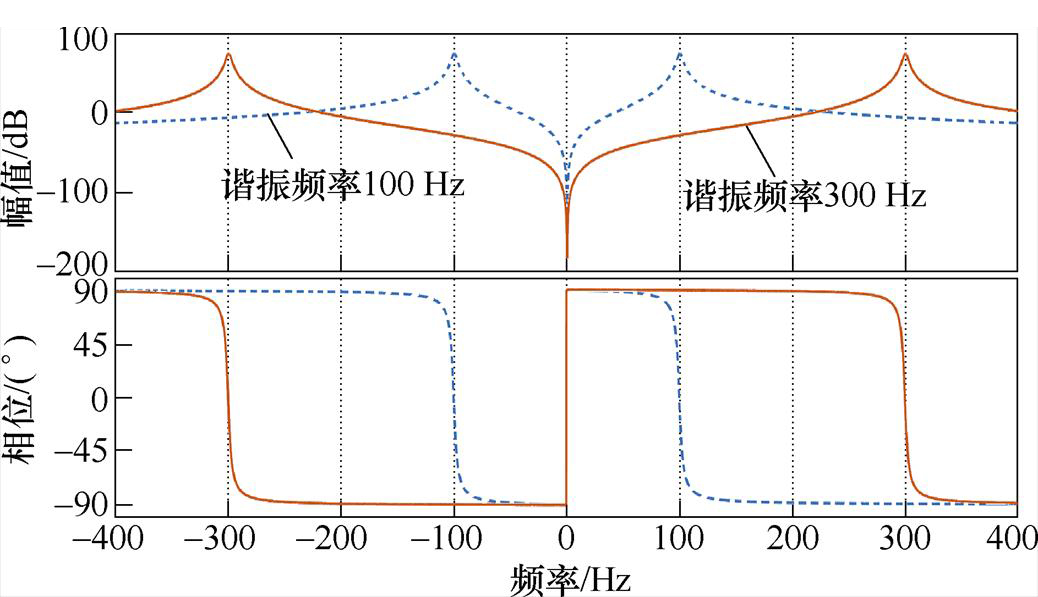
图16 谐振频率为100 Hz和300 Hz时ISORC的伯德图
Fig.16 Bode diagrams of ISORC under resonant frequencies of 100 Hz and 300 Hz
然而，从图16还可以观察到，ISORC并不具备极性选择能力。这意味着当ISORC用于控制转矩2次谐波时，功率绕组电流可能会产生正序3次谐波[39]。这对于DFIG机组所并电网来说通常是无法接受的。因此，一些学者开始研究具有极性选择能力的降阶谐振控制器（Reduced Order Resonant Controller, RORC）[40]，其传递函数为
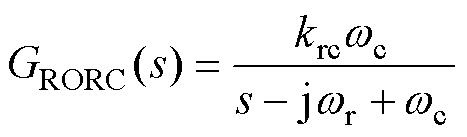（9）
绘制谐振频率为-100 Hz时的RORC伯德图，如图17所示。从图17中可以看出，RORC同时具备频率和极性选择能力，可以为频率为-100 Hz的信号提供较大的幅值增益，而频率为+100 Hz的信号经过RORC则会被大幅衰减。因此，RORC被广泛应用于转矩2次谐波闭环控制方法中，它能够在不引入功率绕组电流3次谐波的基础上有效抑制转矩脉动。
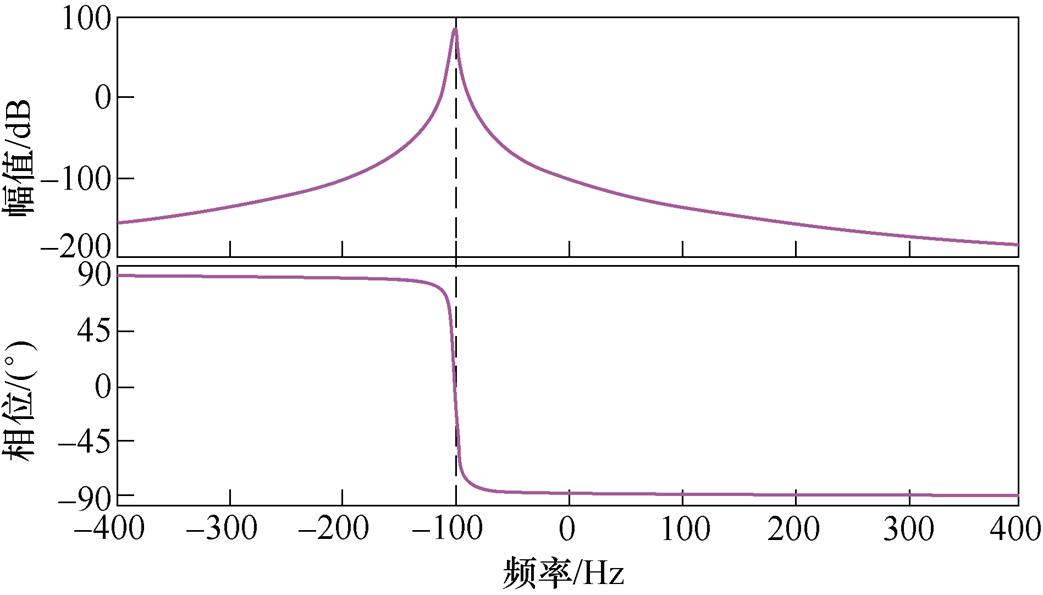
图17 谐振频率为-100 Hz时RORC的伯德图
Fig.17 Bode diagrams of RORC under resonant frequency of –100 Hz
针对非正弦运行条件，文献[41-42]提出了一种基于ISORC的转矩6次谐波抑制方法。此类方法中的转矩参考值通常设为直流量，反馈值采用全转矩，ISORC输出为补偿转矩6次谐波的控制绕组电压参考值。针对不平衡运行条件，文献[40, 43-46]提出了一种基于RORC的转矩2次谐波抑制方法。此类方法采用RORC对转矩进行闭环控制，RORC的输出为补偿转矩2次谐波的控制绕组电压参考值。文献[40-46]所提基于RC的转矩闭环控制原理如图18所示。
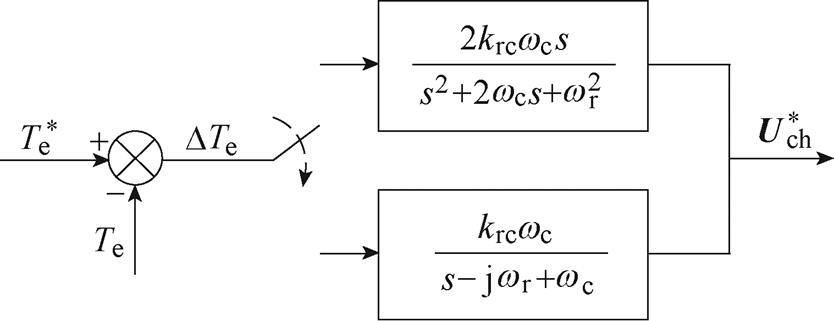
图18 基于RC的转矩闭环控制原理
Fig.18 Principle of the torque closed-loop control based on RC
文献[41]对基于ISORC的转矩闭环控制方法进行了实验验证，实验结果如图19所示。传统控制策略下的转矩6次谐波含量为6.8%，而采用基于ISORC的转矩闭环控制方法，转矩6次谐波含量下降为1.63%。同样地，文献[40]对基于RORC的转矩闭环控制方法进行了实验验证，结果如图20所示。结果表明，在电网三相不平衡运行的情况下，转矩会出现±3.6%的波动。然而，在启动基于RORC的转矩闭环控制方法后，转矩波动降至±1.1%。
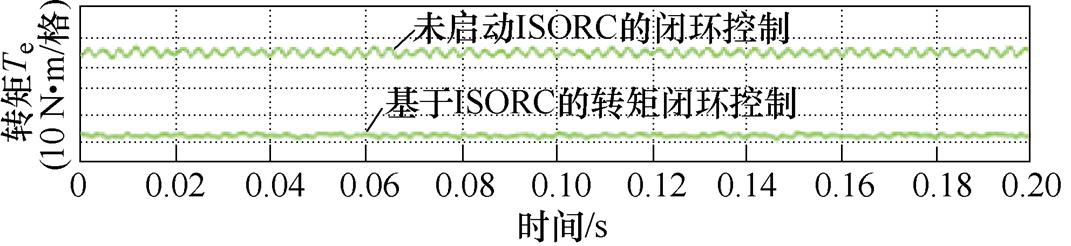
图19 基于ISORC的转矩闭环控制实验结果
Fig.19 Experimental results of the torque closed-loop control based on ISORC
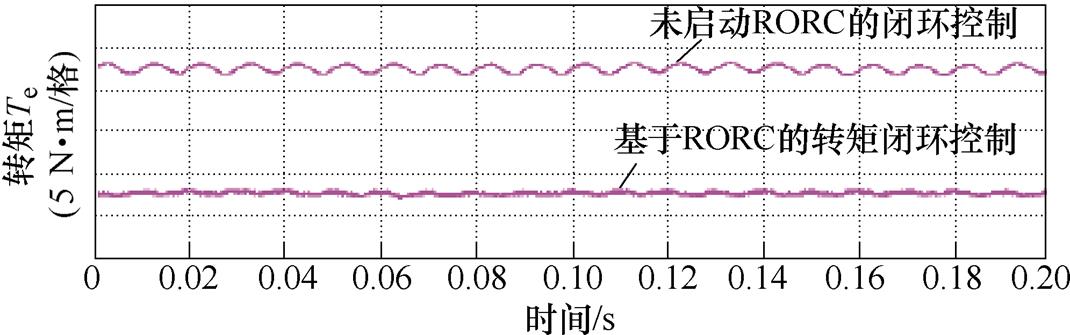
图20 基于RORC的转矩闭环控制实验结果
Fig.20 Experimental results of the torque closed-loop control based on RORC
由文献[40-46]的研究成果可知，使用RC可以有效抑制单一频率的转矩谐波。但是，如果实际系统中存在多种谐波成分，就需要采用多个RC并联，这会增加算法的复杂度，不利于实际应用。
3.1.3 RepC闭环控制法
为了弥补RC的不足，一些学者对RepC展开了研究。传统重复控制器（Traditional Repetitive Controller, TRepC）的传递函数可表示为
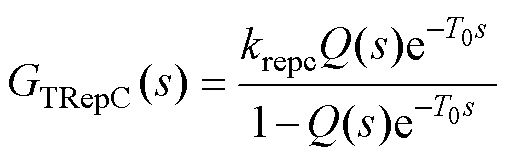（10）
式中，krepc为RepC增益；T0为最低控制频率对应的控制周期；Q(s)为低通滤波器或小于1的常数，用于提高TRepC的稳定性和鲁棒性。
图21展示了最低控制频率为300 Hz时TRepC的伯德图。通过图21可以观察到，TRepC能够为300、600和900 Hz等频率信号提供较大的幅值增益，非常适用于非正弦运行条件下的转矩脉动抑制。
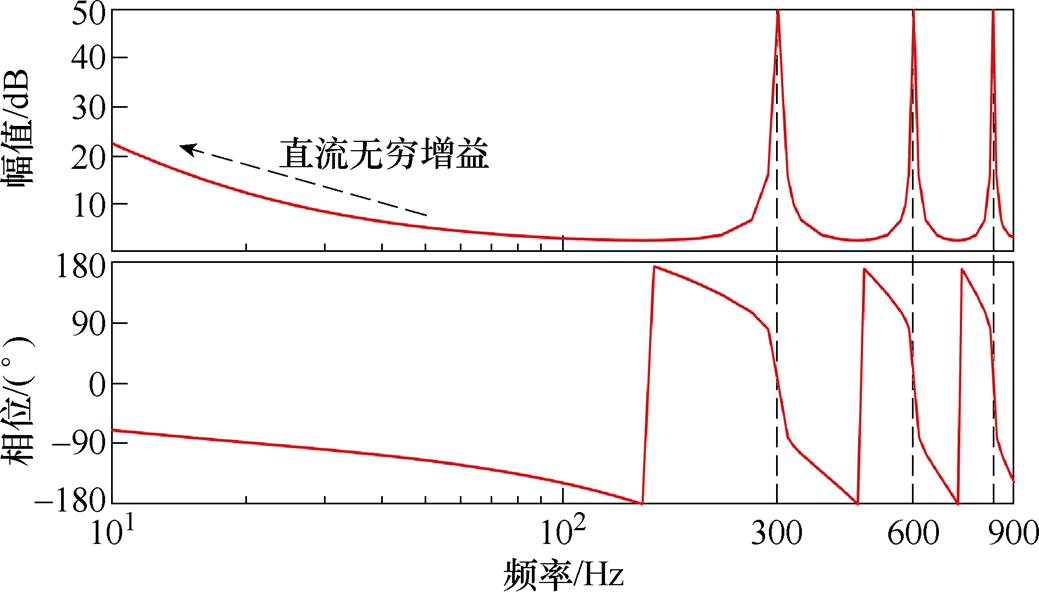
图21 最低控制频率为300 Hz时TRepC的伯德图
Fig.21 Bode diagram of TRepC under the minimum control frequency of 300 Hz
文献[47]在TRepC的基础上增加了高通滤波器，提出了一种改进的重复控制器（Improved Repetition Controller, IRepC），其传递函数可表示为
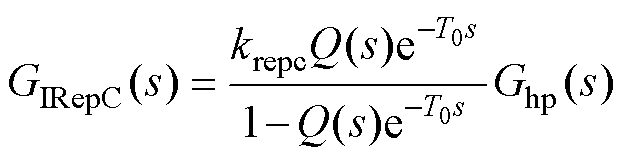（11）
式中，Ghp(s)为高通滤波器。
图22展示了IRepC的伯德图。从图中可以明显观察到，相比于TRepC，IRepC成功克服了直流无穷增益问题，可仅对转矩谐波起到控制作用。这一特点使得IRepC能方便应用于转矩闭环控制中。
DFIG-DC系统的定子频率可不受电网限制。当DFIG定子频率变化时，TRepC和IRepC由于无法实现频率自适应而不再适用。为了解决这一问题，文献[48]提出了一种自适应重复控制器（Adaptive Repetition Controller, ARepC），其离散化表达式为
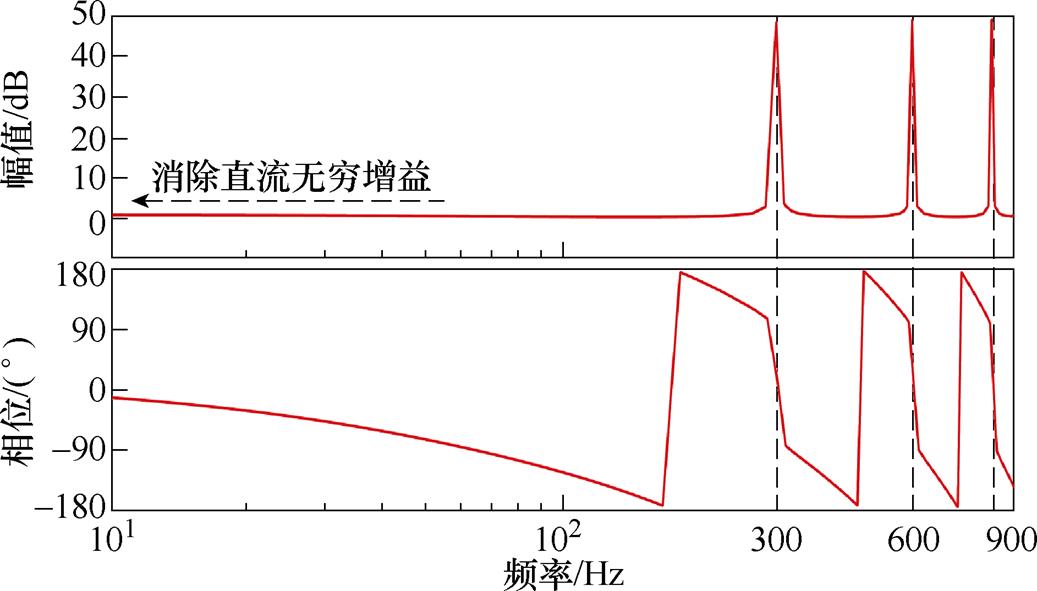
图22 最低控制频率为300 Hz时IRepC的伯德图
Fig.22 Bode diagrams of IRepC under the minimum control frequency of 300 Hz
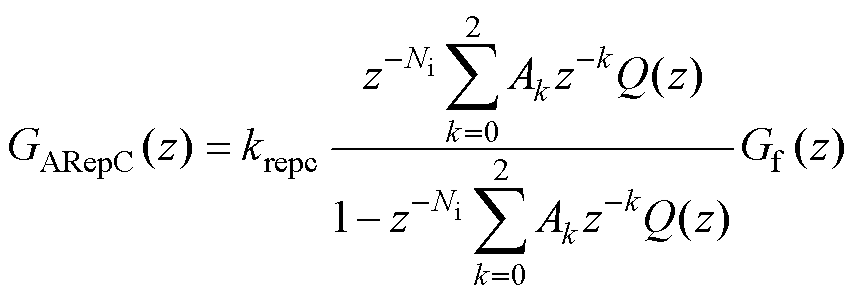（12）
式中，Ni为采样频率与最低谐振频率比值的整数部分；Ak为拉格朗日插值多项式系数；Gf(z)为高通相位补偿器。
图23总结了文献[47-49]中提出的基于RepC的转矩闭环控制原理。此类方法中，RepC输出为补偿所有6k次转矩谐波的控制绕组电压参考值。
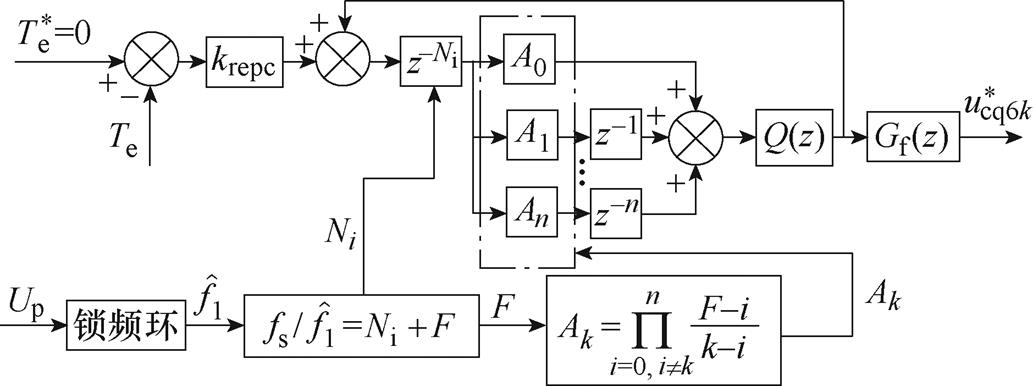
图23 基于RepC的转矩闭环控制原理
Fig.23 Principle of the torque closed-loop control based on RepC
基于RepC的转矩闭环控制方法的实验结果如图24所示[47]。结果表明，采用基于RepC的转矩闭环控制方法可以使得转矩脉动从0.45 N·m（9.4%）降低到0.02 N·m（0.4%），抑制效果显著。但是，相对于PIC和RC，该方法的实现较为复杂。
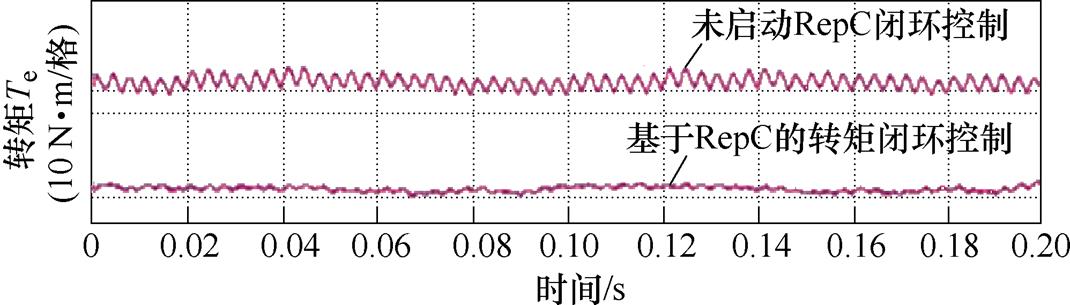
图24 基于RepC的转矩闭环控制实验结果
Fig.24 Experimental results of the torque closed-loop control based on RepC
3.1.4 SMC闭环控制法
SMC的设计思想是引入一个滑模面，并在滑模面上控制变量的状态。由于滑模面的设计仅与系统的状态相关，与系统的频率特性无关。因此，无论输入信号的频率是低频还是高频，滑模控制器都能实现精确控制。SMC的这种低频率敏感性也使其在谐波控制系统中得以广泛应用。
经理论推导可知，DFIG的无功功率2次谐波与转矩2次谐波幅值成正比，因此对无功功率2次谐波进行闭环控制与对转矩2次谐波闭环控制是一致的。基于上述理论，文献[50]提出了一种基于SMC的转矩闭环控制方法原理，如图25所示，图中，D、F、K、S的定义可参考文献[50]。该方法将平均无功功率作为参考值，实际的无功功率作为反馈值，通过SMC有效抑制了无功功率中的2次谐波，同时消除了转矩二倍频脉动。图26所示的实验结果表明，基于SMC的转矩闭环控制方法可将20%不平衡电网电压条件下的转矩脉动从70%降低至8%[50]。
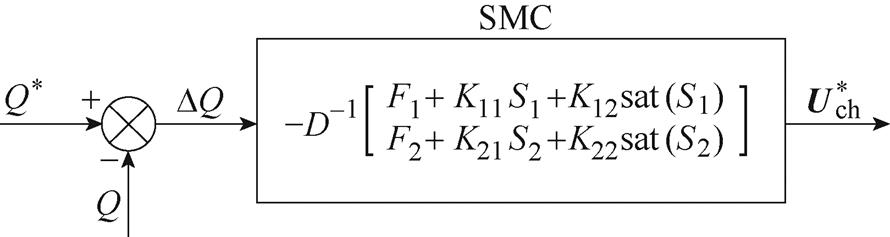
图25 基于SMC的转矩闭环控制原理
Fig.25 Principle of the torque closed-loop control based on SMC
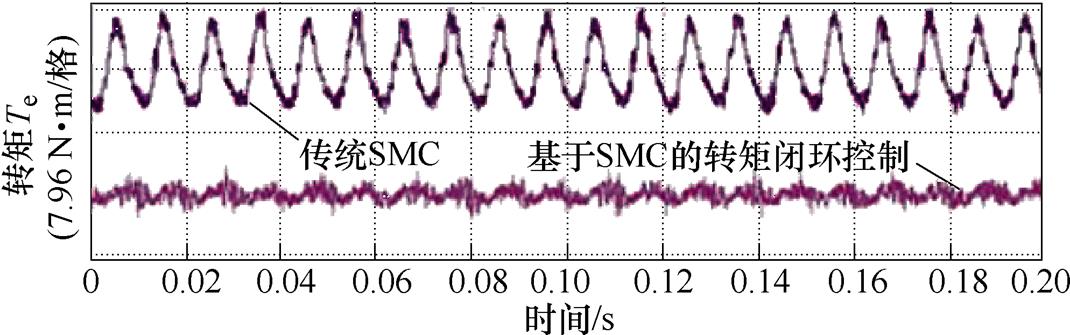
图26 基于SMC的转矩闭环控制实验结果
Fig.26 Experimental results of the torque closed-loop control based on SMC
综上所述，转矩闭环控制法可以实现高精度的转矩控制，具有较好的系统稳定性。然而，在实际应用中，电机控制系统通常还有功率、电压、电流等多个控制目标。如果都采用目标闭环控制法，就需要为不同的控制目标设计不同的控制器，这在实际应用中非常不便。
转矩开环控制法是目前最常用的一类方法，它通过求解谐波转矩为零时的电流或电压参考值，将转矩脉动抑制映射为对电流或电压的控制。当前，转矩开环控制法主要可分为两种，即全转矩开环控制法和谐波转矩开环控制法。下面分别对其进行介绍。
3.2.1 全转矩开环控制法
全转矩开环控制法的基本原理如图27所示。首先利用全转矩与控制绕组全电流的耦合关系获取全转矩等于平均转矩时的控制绕组全电流参考值，然后将其与控制绕组全电流反馈值作差，并将差值输入到控制绕组电流控制器中，以获取控制绕组全电压参考值。
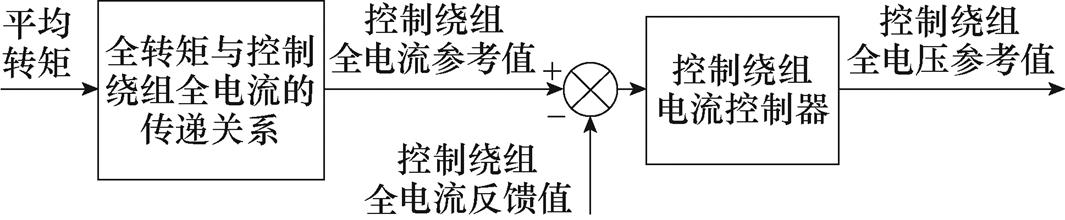
图27 全转矩开环控制原理
Fig.27 Principle of the total torque open-loop control
文献[51-52]得到控制绕组全电流参考值之后，使用了PIC对控制绕组电流进行控制。尽管PIC具有一定的控制能力，但其对控制绕组非理想电流的控制能力有限。为了解决这一问题，文献[53]采用PIC与RC（PIC and RC, PIRC）并联的方式，显著提高了控制绕组电流控制器的谐波控制能力。基于PIRC的全转矩开环控制实验结果如图28所示。实验结果表明，基于PIRC的全转矩开环控制方法的转矩脉动抑制效果被大大增强[53]。文献[51-53]所提方法的基本原理如图29所示。
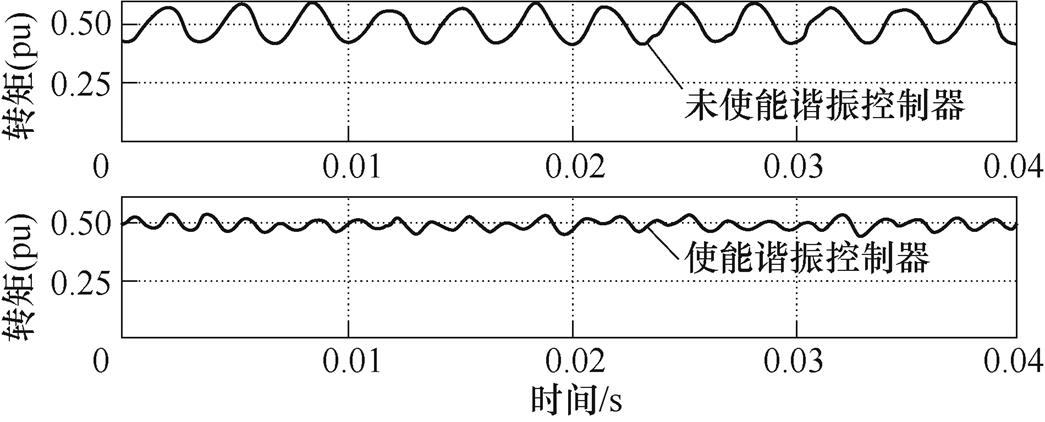
图28 基于PIRC的全转矩开环控制实验结果
Fig.28 Experimental results of the total torque open-loop control based on PIRC
图29 基于PIC或PIRC的全转矩开环控制原理
Fig.29 Principle of the total torque open-loop control based on PIC or PIRC
与文献[53]不同，文献[54]提出了一种前馈暂态补偿控制方法来获取控制绕组电流参考值，其基本原理如图30所示。该方法通过前馈暂态补偿控制，使得PIC的输出与转矩成正比。因此，可首先调节PIC带宽降低其输出的谐波含量，然后利用前馈暂态补偿控制获取控制绕组全电流q轴参考值。
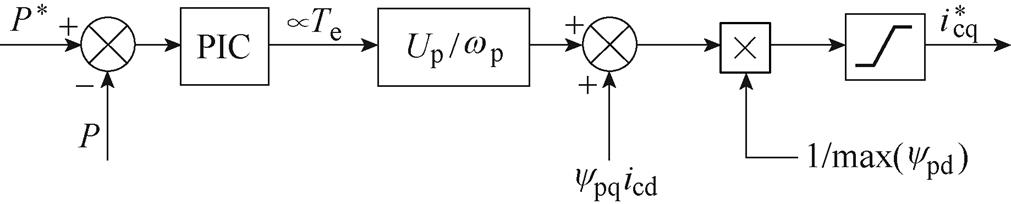
图30 基于前馈暂态补偿的全转矩开环控制原理
Fig.30 Principle of the total torque open-loop control based on the feedforward transient compensation
文献[54]给出的实验结果如图31所示。实验结果表明，在不平衡故障持续期间采用前馈动态补偿可以有效抑制转矩2次谐波。
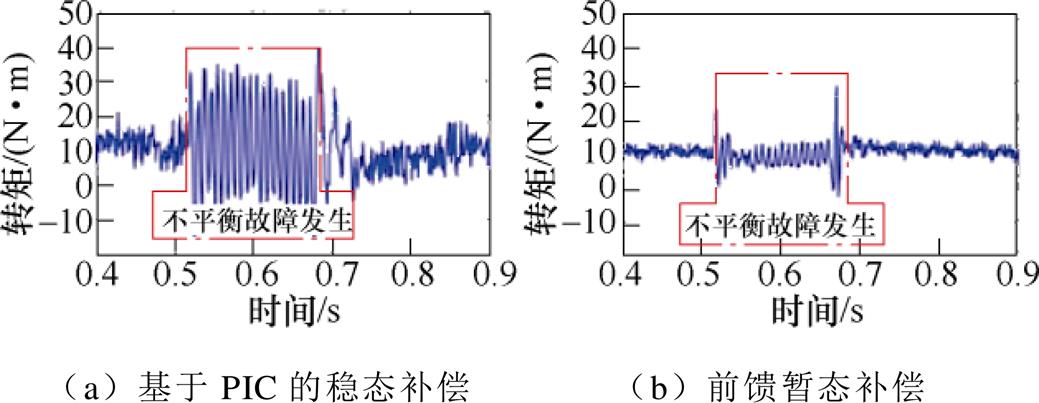
图31 基于前馈暂态补偿的全转矩开环控制实验结果
Fig.31 Experimental results of the total torque open-loop control based on the feedforward transient compensation
文献[55]提出了一种预测延时补偿方法，用于对控制绕组的q轴电流参考值进行矫正，其基本原理如图32所示，图中，z(t)为t时刻的功率绕组磁链倒数值，t0为电流环的延时时间。该方法采用超前补偿的方式，通过预测磁通变化，使得低带宽的PIC也能产生转矩脉动抑制所需的控制绕组电压补偿值。然而，该方法对控制绕组电流环的延时精度依赖性较高，延时误差较大时可能会加剧转矩脉动。文献[55]展示的基于预测延时补偿的全转矩开环控制实验结果如图33所示。通过增加预测延时补偿，可以将转矩6次谐波幅值从0.04(pu)降低到0.01(pu)。
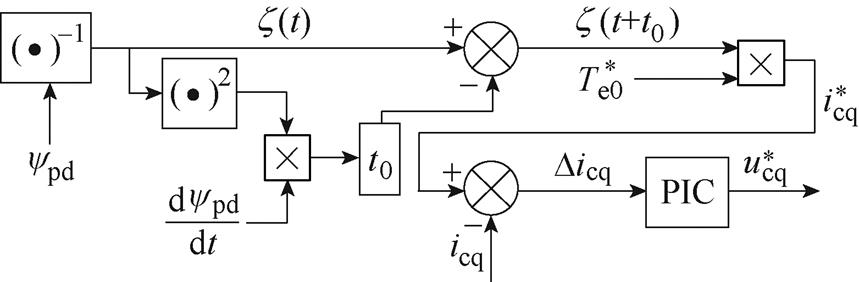
图32 基于预测延时补偿的全转矩开环控制原理
Fig.32 Principle of the total torque open-loop control based on the predictive delay compensation
3.2.2 谐波转矩开环控制法
谐波转矩开环控制法的基本原理如图34所示。该方法需要首先根据谐波转矩与非理想电流或电压的耦合关系来获取谐波转矩为零时的非理想电流或电压参考值，然后再根据此参考值获取所需补偿量。根据补偿量的不同，可将现有的谐波转矩开环控制法分为两类，即电流补偿法和电压补偿法。
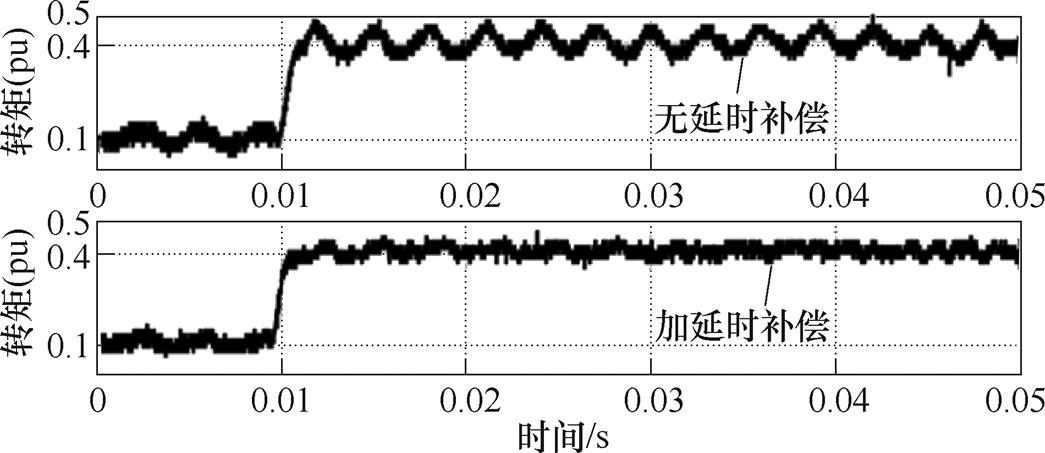
图33 基于预测延时补偿的全转矩开环控制实验结果
Fig.33 Experimental results of the total torque open-loop control based on the predictive delay compensation
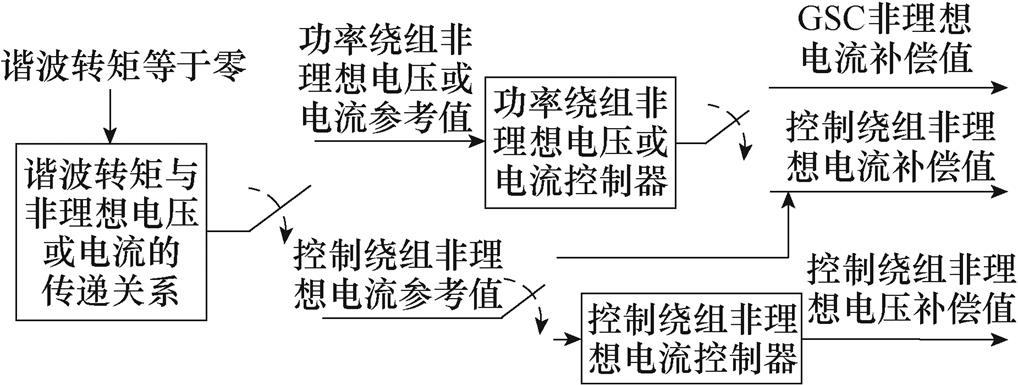
图34 谐波转矩开环控制原理
Fig.34 Principle of the harmonic torque open-loop control
1）电流补偿法
文献[56-57]提出了一种基于滞环PWM的转矩脉动抑制方法。该方法的实现步骤为：首先，根据谐波转矩与控制绕组非理想电流之间的耦合关系，求解谐波转矩为零时的控制绕组非理想电流补偿值。其次，将控制绕组非理想电流补偿值与控制绕组基波电流参考值相加，获得控制绕组总电流参考值。最后，利用滞环PWM实现对控制绕组电流的有效控制。但是，目前在大部分控制方法中，PWM所需调制信号为控制绕组电压而非控制绕组电流，因此有必要设计控制绕组电流控制环。文献[58-59]提出利用PIRC对控制绕组电流进行闭环控制，来获取控制绕组电压参考值。文献[56-59]所提方法均直接计算控制绕组谐波电流参考值，因此可称为基于控制绕组谐波电流计算的电流补偿法，其基本原理如图35所示。
文献[59]所提方法的实验结果如图36所示。在无转矩脉动抑制策略的情况下，转矩脉动值为0.6 N·m，转矩6次谐波含量为9.2%。然而，在启动转矩脉动抑制策略后，转矩脉动值下降至0.08 N·m，转矩6次谐波含量下降至1.4%。
为了提高控制系统的鲁棒性，文献[60]引入了内模控制器对控制绕组电流进行控制，其基本原理如图37所示。图中，C(s)为内模控制器，G(s)为被控对象，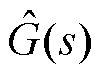
为被控对象内部模型。这种控制方法采用了控制对象的逆模型作为内模控制器，并通过对被控对象和被控对象内部模型输出间扰动的反馈来实现对系统的控制。即使被控对象参数变化，仍能保持系统稳定，同时具有良好的动态特性。此方法的实验结果如图38所示。在1.5 s时，电网电压出现5%的不对称性，导致转矩脉动显著增大。在2.5 s时，启动内模控制器对负序电流进行控制，成功地抑制了转矩脉动。
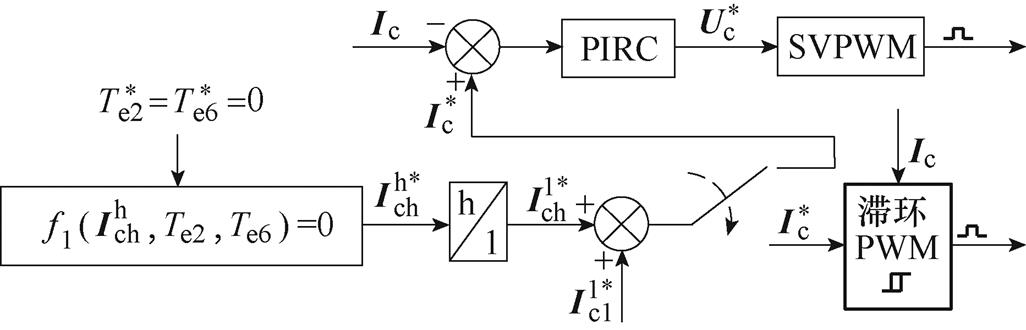
图35 基于控制绕组谐波电流计算的电流补偿原理
Fig.35 Principle of the current compensation based on the control winding harmonic current calculation
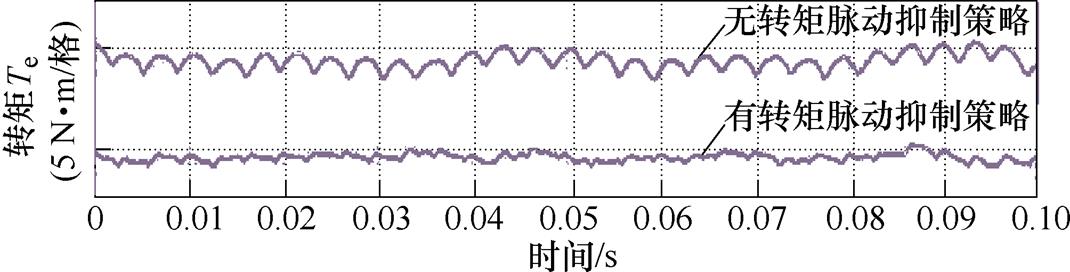
图36 基于控制绕组谐波电流计算的电流补偿实验结果
Fig.36 Experimental results of the current compensation based on the control winding harmonic current calculation
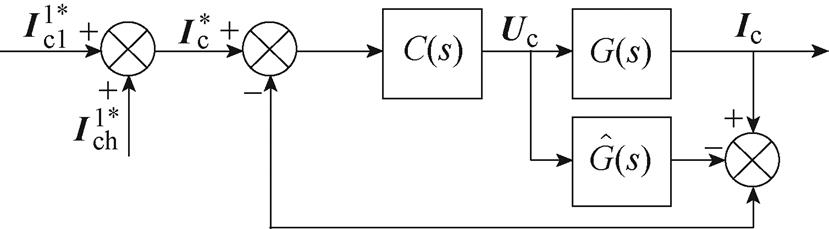
图37 基于内模控制器的电流补偿原理
Fig.37 Principle of the current compensation based on the internal model control
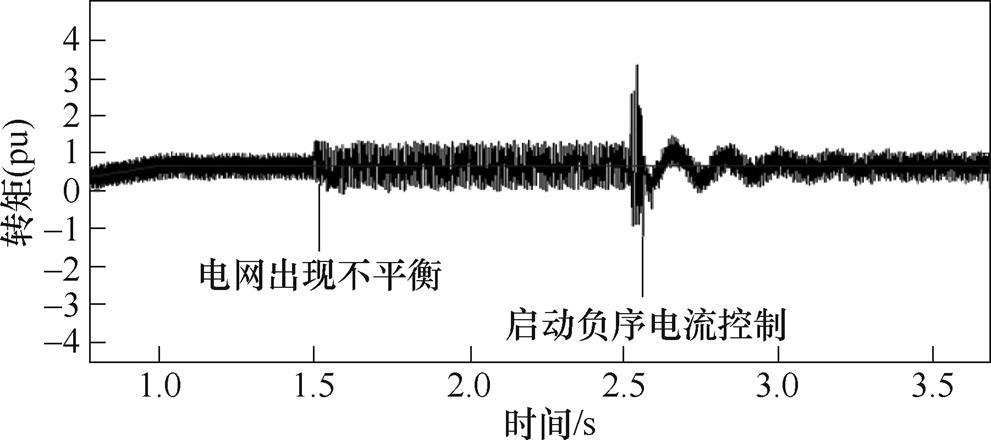
图38 基于内模控制器的电流补偿实验结果
Fig.38 Experimental results of the current compensation based on the internal model control
不同于文献[56-60]所提方法中的控制绕组非理想电流补偿值获取方法，文献[61-62]提出基于功率绕组谐波电流计算的电流补偿法。首先计算功率绕组非理想电流参考值，然后对功率绕组非理想电流进行闭环控制来获得控制绕组非理想电流补偿值，其基本原理如图39所示。
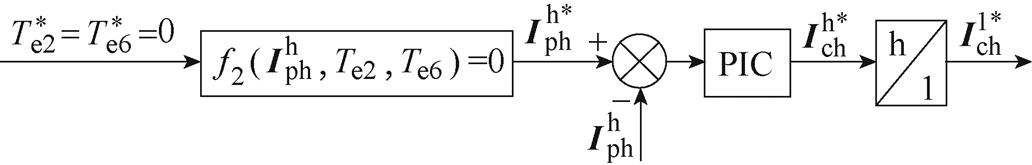
图39 基于功率绕组谐波电流计算的电流补偿原理
Fig.39 Principle of the current compensation based on the power winding harmonic current calculation
文献[62]对所提转矩脉动抑制方法进行了实验验证，实验结果如图40所示。在启动转矩脉动抑制策略后，转矩的峰峰值明显降低。同时，转矩的6次谐波含量从8.30%降至2.63%，转矩的12次谐波含量从1.51%降至1.28%。
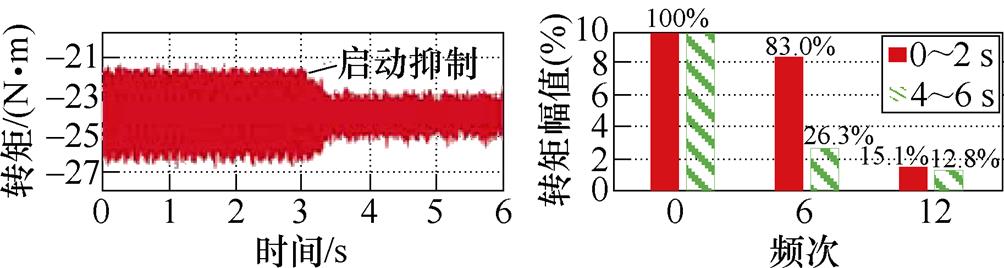
图40 基于功率绕组谐波电流计算的电流补偿实验结果
Fig.40 Experimnetal result of the current compensation based on the power winding harmonic current calculation
当DFIG交流发电系统连接到弱电网或运行于独立发电模式时，也可以通过调节功率绕组非理想电压来抑制转矩脉动。文献[63-65]提出了一种适用于DFIG独立发电系统的基于功率绕组谐波电压计算的电流补偿法，其基本原理如图41所示。该方法的实现需要求解谐波转矩为零时的功率绕组非理想电压参考值，并对其进行闭环控制，以获得GSC或控制绕组非理想电流补偿值。
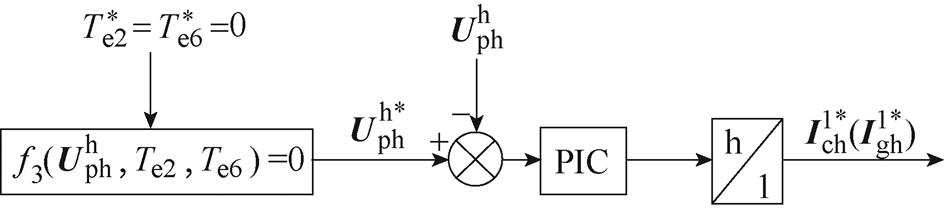
图41 基于功率绕组谐波电压计算的电流补偿原理
Fig.41 Principle of the current compensation based on the power winding harmonic voltage calculation
文献[64]对不平衡和非正弦两种工况下的实验进行了验证，实验结果如图42所示。启动转矩2次谐波抑制策略，转矩2次谐波的含量从27.2%降至4.71%。随着转速和负载的变化，转矩2次谐波的含量保持在5%以下。另外，启动转矩6次谐波抑制策略，转矩6次谐波的含量从7%降至0.77%。在整个实验过程中，转矩6次谐波的含量始终保持在3%以下。
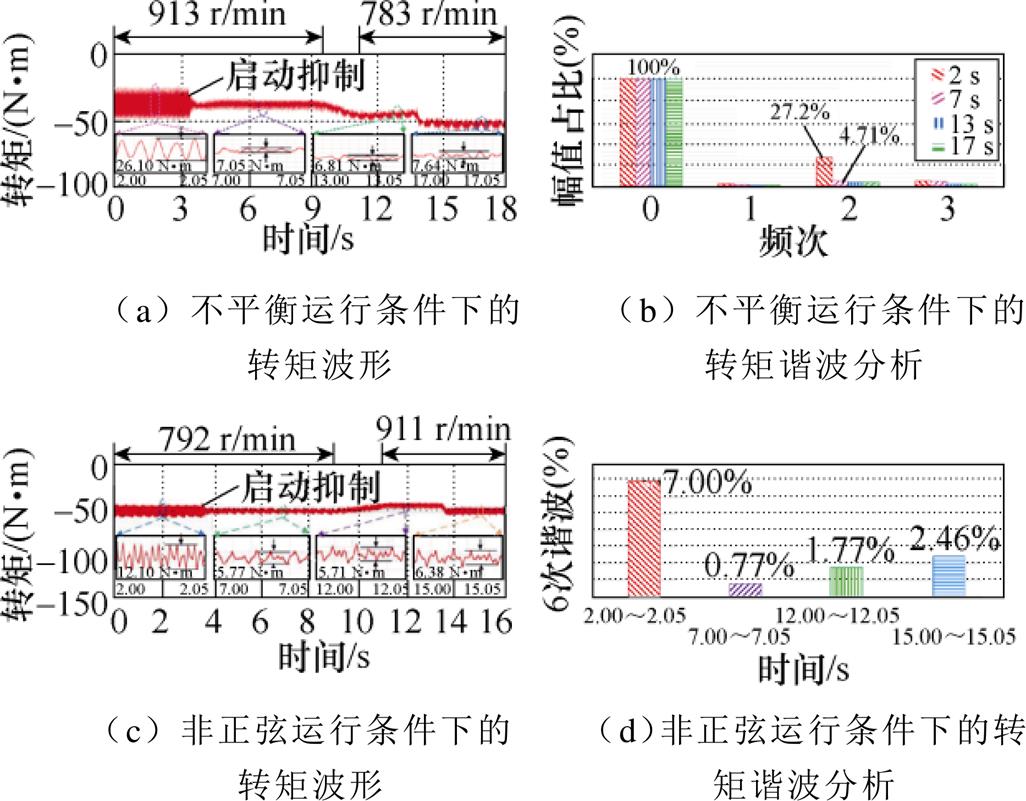
图42 基于功率绕组谐波电压计算的电流补偿实验结果
Fig.42 Experimental results of the current compensation based on the power winding harmonic voltage calculation
2）电压补偿法
文献[66-67]提出了一种基于单旋转坐标系的电压补偿法。计算了正序基频旋转坐标系下的控制绕组非理想电流参考值，并分别采用比例谐振控制器（Proportional Resonance Controller, PRC）和二阶广义积分器（Second Order Generalized Integrator, SOGI）进行控制，其基本原理如图43所示。这种方法虽然可以直接获得正序基频旋转坐标系下的控制绕组非理想电流参考值，但控制绕组非理想电压补偿值的获取需要依赖较为复杂的电流控制器。
图43 基于单旋转坐标系的电压补偿原理
Fig.43 Principle of the voltage compensation based on the single rotating frame
文献[67]给出的实验结果如图44所示。当电网处于不平衡和非正弦运行工况时，转矩脉动幅值为1.75 N·m。启动抑制策略后，转矩脉动幅值降至0.1 N·m。
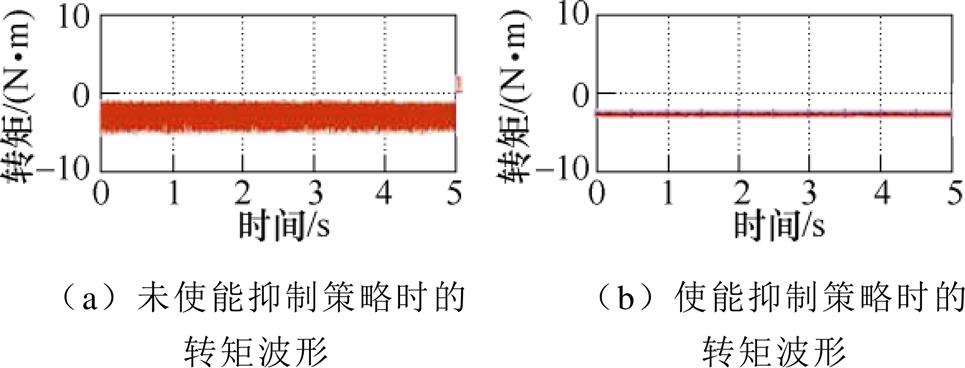
图44 基于单旋转坐标系的电压补偿实验结果
Fig.44 Experimental results of the voltage compensation based on the single rotating frame
文献[68-75]提出了一种基于多旋转坐标系的电压补偿法。具体地，文献[68-73]计算了非理想旋转坐标系下的控制绕组非理想电流参考值，并通过PIC对其进行控制。与基于单旋转坐标系的电压补偿法相比，此方法需要增加额外的坐标变换环节。文献[74]提出了一种新的控制绕组非理想电流参考值的获取方法，首先根据转矩和控制绕组全电流的关系求得控制绕组全电流参考值，然后利用谐波提取技术，从控制绕组电流参考值中分离出非理想分量参考值。此方法无需确定控制绕组非理想分量参考值的具体形式，因此相对于文献[68-73]中的方法更为简单。文献[75]提供了另外一种控制绕组非理想电流参考值获取方法，它基于不平衡发电条件下无功功率脉动和转矩脉动的一致性，同时对无功功率正弦和余弦幅值进行闭环控制，从而获得控制绕组非理想电流参考值。图45展示了文献[68-75]所提基于多旋转坐标系的电压补偿法的基本原理。此外，文献[74]还给出了实验结果，如图46所示。实验结果表明，启动抑制策略相比于无抑制策略，转矩脉动可下降50%以上。
图45 基于多旋转坐标系的电压补偿原理
Fig.45 Principle of the voltage compensation based on the multiple rotating frame
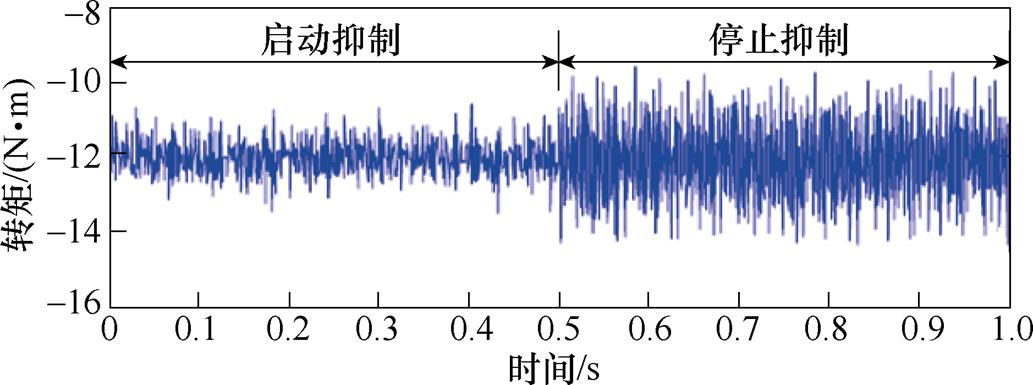
图46 基于多旋转坐标系的电压补偿实验结果
Fig.46 Experimental results of the voltage compensation based on the multiple rotating frame
文献[50-75]提出的转矩开环控制方法可以方便地扩展到多目标控制系统中，但是电流或电压参考值的获取对电机参数具有较高的依赖性，这导致电机参数摄动会对转矩脉动抑制效果产生较大影响。
根据式（5），转矩谐波含量与磁链和电流中的非理想分量密切相关。因此，消除磁链和电流中的非理想分量，也可以对转矩脉动起到抑制作用。基于这一原理，一些学者提出了非理想分量消除法来抑制转矩脉动。目前，该方法主要分为三类：单闭环控制法、双闭环控制法以及虚拟电感控制法。下面将对这些方法逐一介绍。
3.3.1 单闭环控制法
文献[76-78]中提出了一种控制绕组电流单闭环控制法抑制功率绕组非理想电流分量，其基本原理如图47所示。该方法需要先基于功率绕组非理想电流为零这一条件计算控制绕组非理想电流补偿值，再对控制绕组电流进行闭环控制，最终可获得控制绕组电压参考值。文献[76-77]计算了非理想坐标系下的控制绕组非理想电流补偿值，并采用PIRC对控制绕组电流进行控制。而文献[78]直接计算了正序基频旋转坐标系下的控制绕组非理想电流补偿值，并采用SMC对控制绕组电流进行控制。以文献[76]提供的实验结果为例，展示该方法的抑制效果，结果如图48所示。实验结果表明，在非正弦运行条件下，采用控制绕组电流单闭环控制法可以缓解系统转矩脉动。
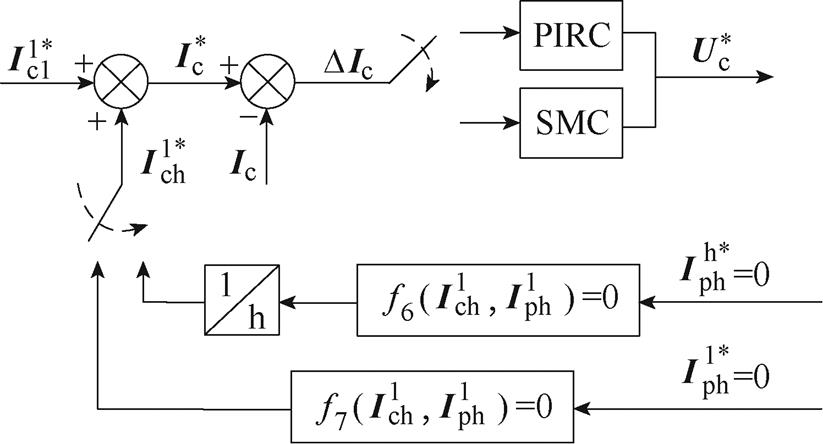
图47 控制绕组电流单闭环控制原理
Fig.47 Principle of the control winding current single closed-loop control
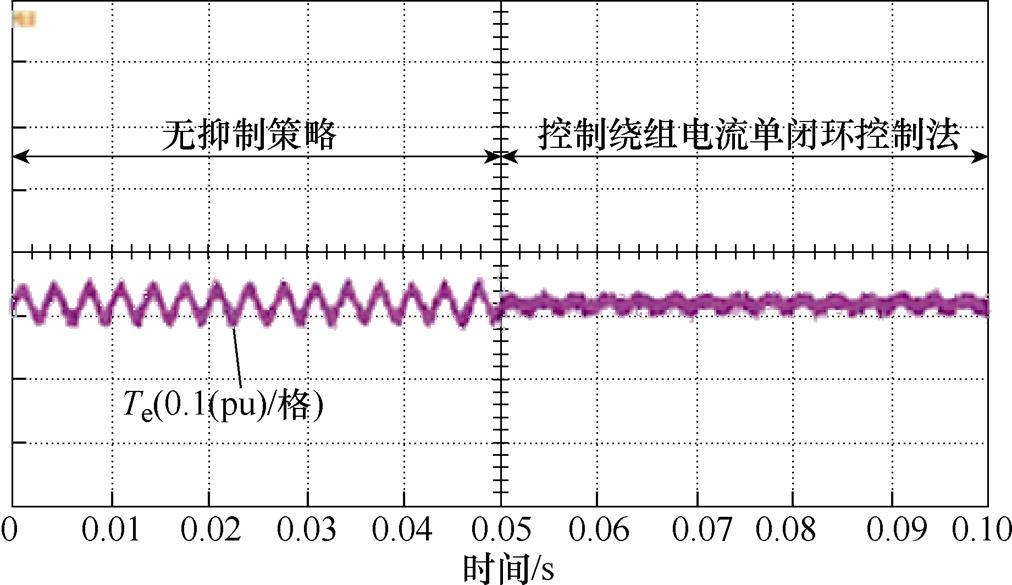
图48 控制绕组电流单闭环控制实验结果
Fig.48 Experimental results of the control winding current single closed-loop control
文献[79-85]中提出了一种功率绕组电流单闭环控制法，其基本原理如图49所示。该方法需要构建功率绕组电流闭环，并将电流参考值设为零。文献[79-84]采用RC对正序基频旋转坐标系下的功率绕组电流进行闭环控制，RC的输出即为控制绕组非理想电压补偿值。而文献[85]在非理想坐标系下使用PIC对功率绕组电流进行闭环控制，经坐标变换后也可获得控制绕组非理想电压补偿值。
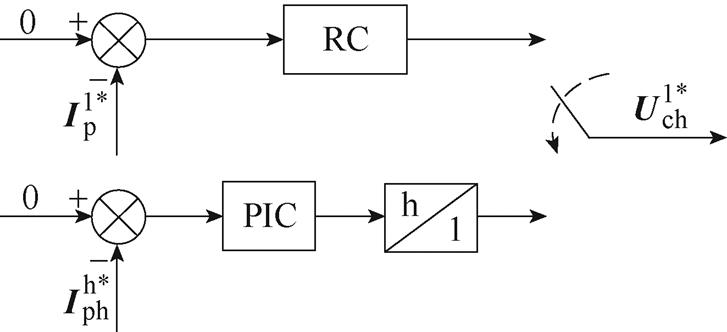
图49 功率绕组电流单闭环控制原理
Fig.49 Principle of the power winding current single closed-loop control
文献[85]介绍了此类方法的抑制效果，如图50所示。当时间达到5.5 s时，将功率绕组的5次、7次、11次和13次谐波电流参考值同时设为零。经过一段时间的过渡过程后，可以观察到转矩峰峰值明显降低。
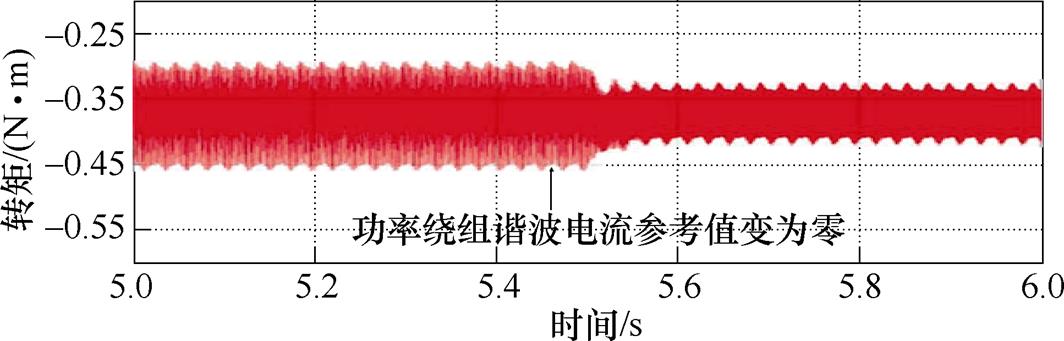
图50 功率绕组电流单闭环控制实验结果
Fig.50 Experimental results of the power winding current single closed-loop control
3.3.2 双闭环控制法
文献[86-87]提出了一种双闭环控制法用于抑制功率绕组非理想电流或电压，其基本原理如图51所示。这种方法结合了前述两类方法，功率绕组非理想电压或电流控制环的输出为控制绕组非理想分量补偿值，控制绕组电流环用于对控制绕组电流非理想分量和基波分量进行控制。文献[86]利用RC对正序基频旋转坐标系下的功率绕组电流进行闭环控制，直接获得了控制绕组非理想电流补偿值。
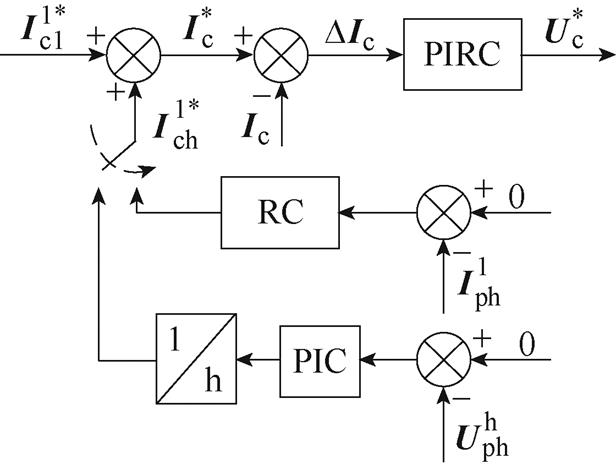
图51 双闭环控制原理
Fig.51 Principle of the double closed-loop control
文献[87]针对弱电网运行条件下的DFIG发电系统，设计了非理想旋转坐标系下的功率绕组非理想电压闭环控制方法，将功率绕组非理想电压差值经过PIC和坐标变换后，获得了控制绕组非理想电流补偿值。为了实现对控制绕组全电流的控制，文献[86-87]均采用了PIRC。文献[87]给出的双闭环控制实验结果，如图52所示。可知，启动谐波电压抑制策略后，转矩二倍频分量（100 Hz）可由32.29 N·m下降至9.47 N·m。
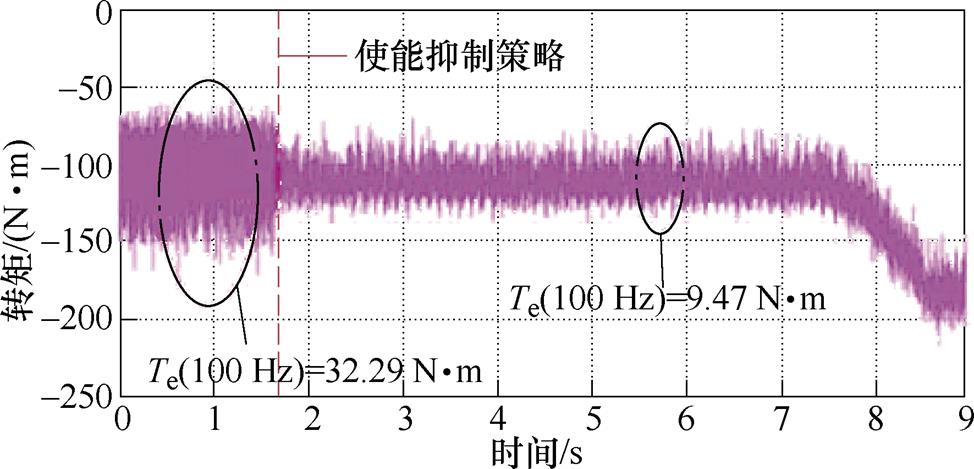
图52 双闭环控制实验结果
Fig.52 Experimental results of the double closed-loop control
3.3.3 虚拟电感控制法
根据2.2节所述，增加无源滤波器可以缓解功率绕组电流畸变，但会增加系统成本。为此，有学者提出了一种虚拟电感控制法，通过增加DFIG-DC系统中的虚拟电感来降低功率绕组电流畸变，从而缓解转矩脉动。文献[88]构造了一个由功率绕组磁链和电流线性组合而成的内部等效磁链空间矢量，并采用内部等效磁链空间矢量定向方法将DFIG- DC系统等效为图53所示结构，其中的参数具体表达式可参考文献[88]。由图53可知，通过增加虚拟电感Lap，可以降低反电动势畸变程度，进而降低电流和磁链畸变，抑制转矩脉动。然而，虚拟电感控制法会增大功率绕组电压和电流的相移，影响电机功率输出能力。实验结果如图54所示，当虚拟电感从0.19(pu)增加到0.54(pu)，转矩脉动可由0.18(pu)下降到0.1(pu)。
文献[76-88]所提非理想分量抑制法可对转矩脉动起到一定的抑制作用，但是此类方法往往不能同时消除电压和电流中的非理想分量，因此转矩脉动抑制效果并不显著。
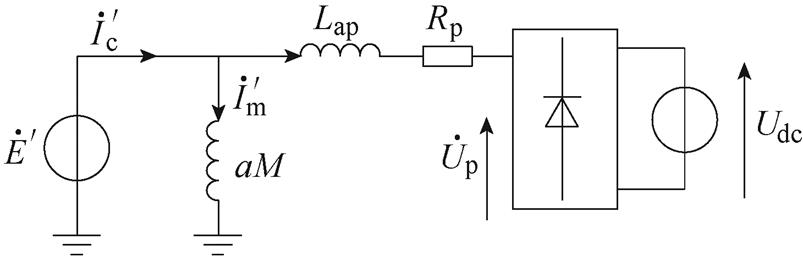
图53 采用虚拟电感控制法的DFIG-DC系统等效电路
Fig.53 Equivalent circuit of the DFIG-DC system using the virtual inductance control method
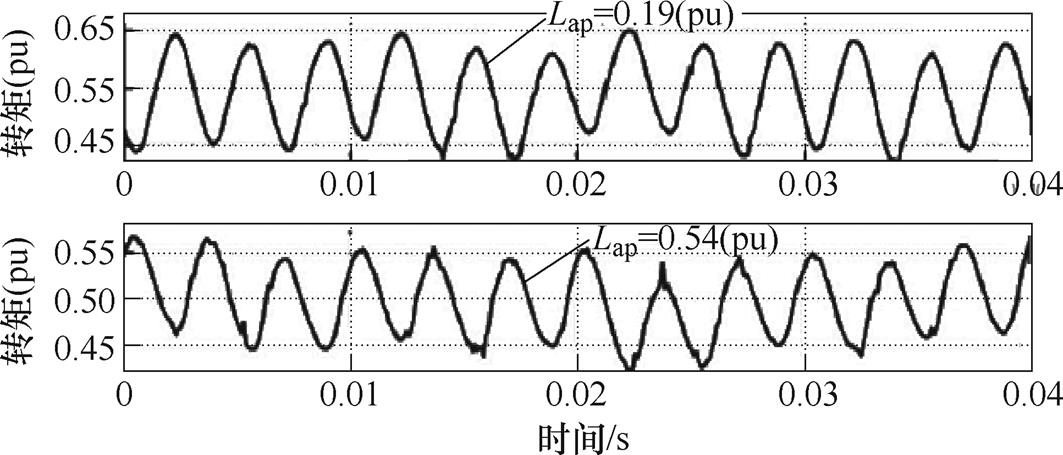
图54 虚拟电感控制的实验结果
Fig.54 Experimental results of the virtual inductance control
一些学者在制定控制策略时不仅考虑了转矩脉动的抑制，还将其他目标引入控制系统中，实现了多目标协同控制。文献[89]提出了一种转矩和控制绕组磁链双目标预测控制方法，该方法对功率绕组频率变化并不敏感，可以在较宽的定子频率范围内实现转矩脉动抑制和弱磁控制，有效降低绕组和变流器损耗，提高系统效率。该方法的基本控制方案如图55所示，其中的目标函数为
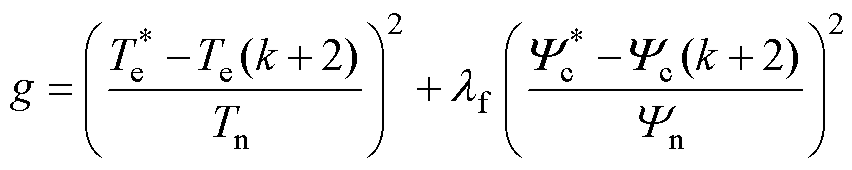（13）
式中，Tn和Yn分别为转矩和磁链的额定值；lf为权重因子，在文献[89]中取作2；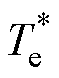
和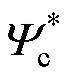
分别为转矩和控制绕组磁链的参考；Te(k+2)和Yc(k+2)分别为超前两拍的转矩和控制绕组磁链，可以克服响应滞后。
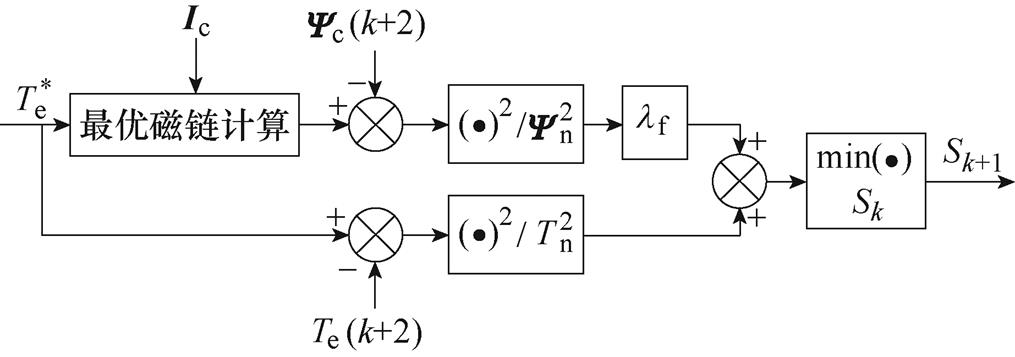
图55 转矩和控制绕组磁链双目标预测控制原理
Fig.55 Principle of the predictive control for both torque and control winding flux
对文献[89]所提出的方法进行实验验证，得到的转矩频谱分析结果如图56所示。可以观察到，在平均转矩为12.5 N·m时，转矩的6次谐波幅值低于0.2 N·m。
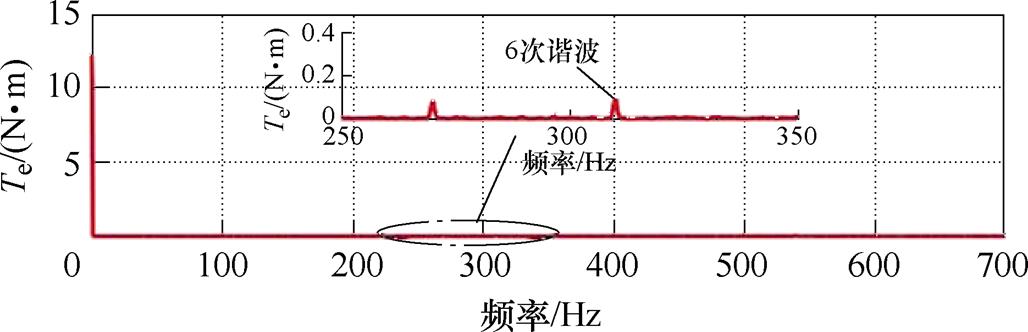
图56 转矩和控制绕组磁链双目标预测控制实验结果
Fig.56 Experimental results of the predictive control for both torque and control winding flux
为了抑制不平衡条件下的有功功率、无功功率和转矩脉动，文献[90]提出了一种多目标模型预测控制方法，其总误差函数为
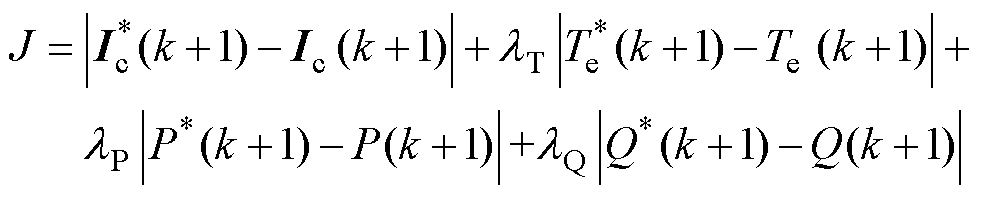（14）
式中，
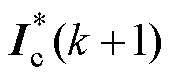和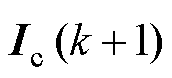
分别为k+1时刻控制绕组电流参考值和预测值；
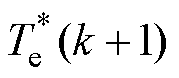和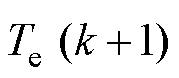
分别为k+1时刻转矩参考值和预测值；
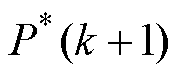和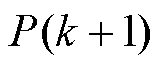
分别为k+1时刻有功功率参考值和预测值；
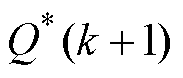和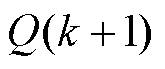
分别为k+1时刻无功功率参考值和预测值； lT、lP和lQ分别为转矩、有功功率和无功功功率的权重因子，实际应用时可改变权重因子的值达到不同的控制目标。
为了避免处理器数字化实现引起的延时影响，该方法采用了两步预测的方法。具体来说，在k时刻预测变量在k+2时刻的可能值，选出能使k+2时刻变量误差最小的变流器最优开关状态，其具体流程如图57所示。同时，文献[90]还给出了以恒定转矩脉动为控制目标的实验波形，如图58所示。相比常规控制方法，多目标预测控制能够有效抑制不平衡运行条件下的转矩脉动，从而提高转矩质量。
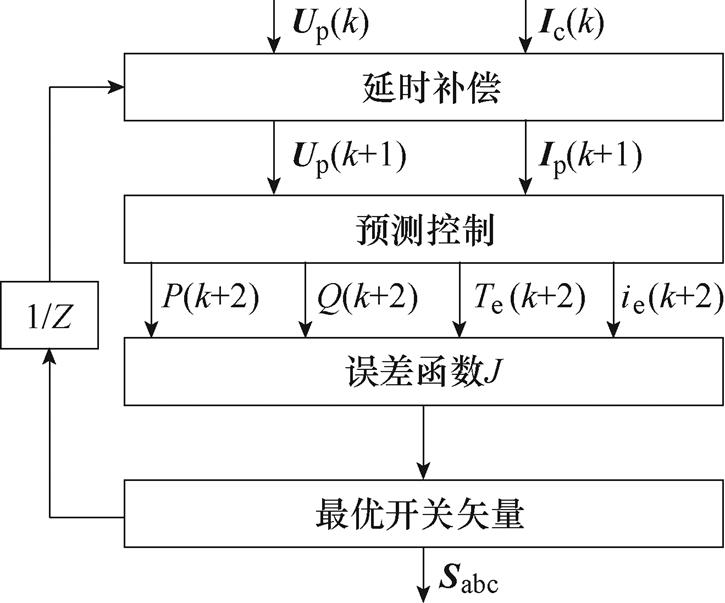
图57 多目标模型预测控制流程
Fig.57 Flow chart for the multi-objective model predictive control
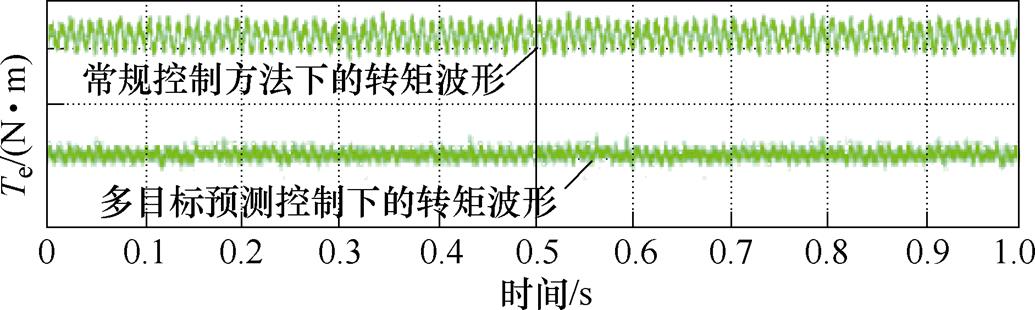
图58 多目标模型预测控制实验结果
Fig.58 Experimental results of the multi-objective model predictive control
然而，当前尚无通用方法对权重因子进行优化，这是此类方法的弊端之一。
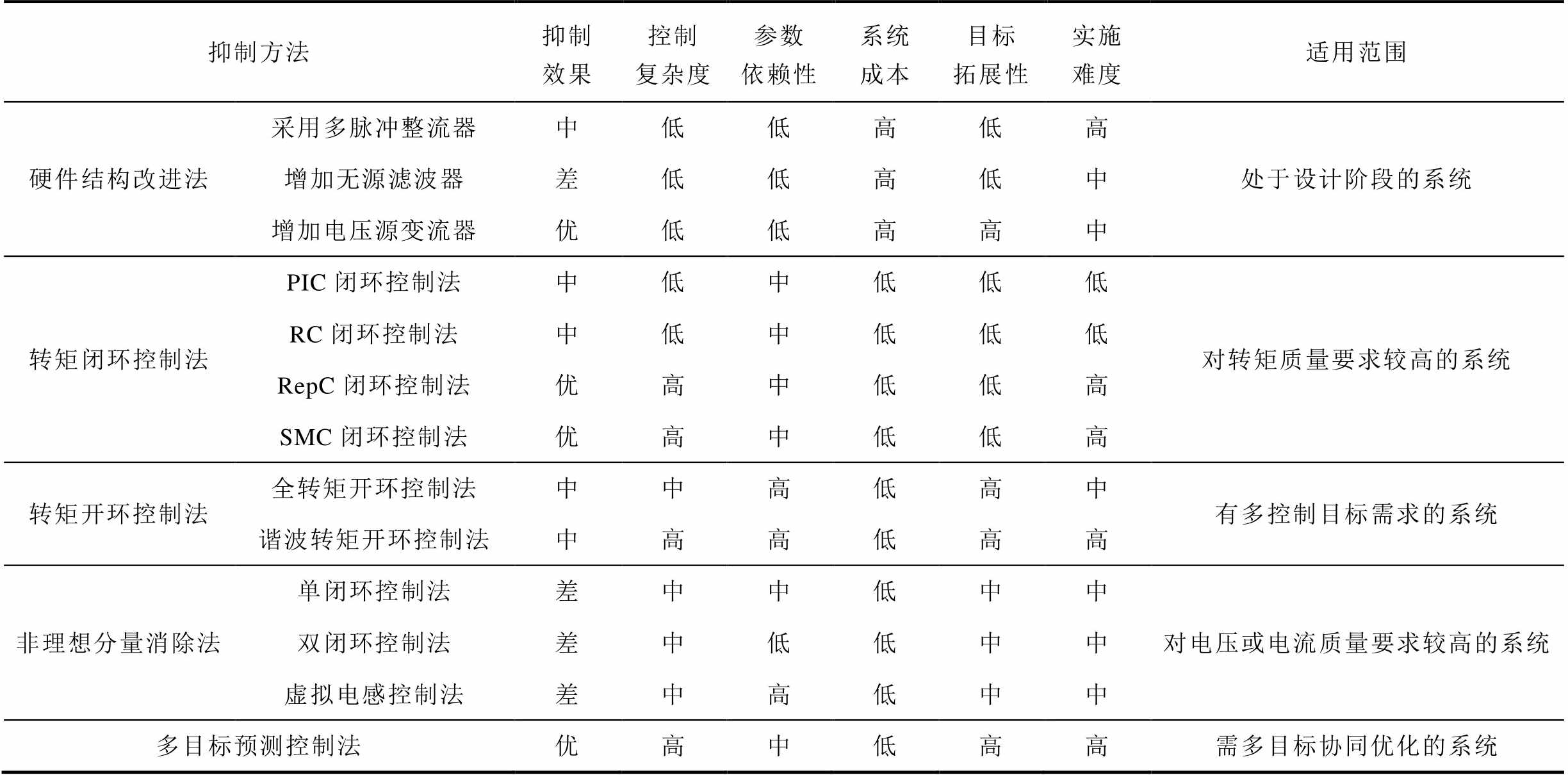
下面从抑制效果、控制复杂度、参数依赖性、系统成本、目标拓展性、实施难度及适用范围这七个维度，对现有非理想运行条件下双馈感应发电机各类转矩脉动抑制方法进行全面对比分析，结果见表1。
对表1的详细分析如下：
（1）抑制效果。增加电压源变流器法可以从根本上解决绕组电压和电流的畸变问题，有效抑制转矩脉动。RepC闭环控制法在抑制所有6k次转矩谐波方面表现较好，具有较优的抑制效果。SMC闭环控制法和多目标预测控制法可以有效抑制所有频率的转矩谐波，转矩抑制效果也较显著。多脉冲整流器法、PIC闭环控制法、RC闭环控制法和转矩开环控制法仅能消除单一频次的转矩谐波，因此转矩脉动抑制效果适中。增加无源滤波器仅能对转矩高次谐波分量起到一定的抑制作用，因此其转矩脉动抑制效果较差。此外，非理想分量消除法仅通过改善电压或电流质量难以发挥理想的转矩脉动抑制效果。
表1 各类转矩脉动抑制方法对比
Tab.1 Comparison of different torque ripple suppression methods
抑制方法抑制效果控制复杂度参数依赖性系统成本目标拓展性实施难度适用范围 硬件结构改进法采用多脉冲整流器中低低高低高处于设计阶段的系统 增加无源滤波器差低低高低中 增加电压源变流器优低低高高中 转矩闭环控制法PIC闭环控制法中低中低低低对转矩质量要求较高的系统 RC闭环控制法中低中低低低 RepC闭环控制法优高中低低高 SMC闭环控制法优高中低低高 转矩开环控制法全转矩开环控制法中中高低高中有多控制目标需求的系统 谐波转矩开环控制法中高高低高高 非理想分量消除法单闭环控制法差中中低中中对电压或电流质量要求较高的系统 双闭环控制法差中低低中中 虚拟电感控制法差中高低中中 多目标预测控制法优高中低高高需多目标协同优化的系统
（2）控制复杂度。RepC闭环控制法、SMC闭环控制法以及多目标预测控制法需要设计较为复杂的控制算法，因而控制复杂度较高。谐波转矩开环控制法需要对非理想分量进行分离，同时还需要进行复杂的参考值计算，因此其控制复杂度也较高。采用硬件结构改进法不会涉及复杂的控制算法，因此其控制复杂度较低。PIC闭环控制和RC闭环控制均为较常用的控制算法，因而它们的控制复杂度也较低。其他方法的控制复杂度适中。
（3）参数依赖性。转矩开环控制法需要利用电机参数计算非理想分量参考值，因此参数依赖性较高。虚拟电感控制法严重依赖二极管导通的数学方程，同样具有较高的参数依赖性。双闭环控制法和硬件结构改进法无需使用电机参数，因而参数依赖性较低。其他方法的参数依赖性适中。
（4）系统成本。硬件结构改进法需要为系统增加额外装置，因此系统成本较高。而其他方法只涉及控制算法的改进，系统成本相对较低。
（5）目标拓展性。增加电压源变流器方法不仅可以解决转矩脉动问题，还可以有效抑制电压和电流谐波、有功功率和无功功率脉动，具有较高的目标可拓展性。转矩开环控制法也能够根据控制目标更改电压或电流的参考值，无需设计新的控制器，也具有较高的目标拓展性。多目标预测控制法能够方便地在误差函数中增加控制目标，同样具有较高的目标拓展性。采用多脉冲整流器和增加无源滤波器均需要根据不同的控制目标设计硬件电路，因此其目标可拓展性降低。转矩闭环控制法在多目标控制系统中需要为不同的控制指标设计不同的控制器，因此其目标可拓展性也较低。其余方法的目标可拓展性适中。
（6）实施难度。采用多脉冲整流器会涉及到电机结构的改进，具有较高的实施难度。而其他两种硬件结构改进法实施难度相对适中。控制策略改进法的实施难度与算法复杂度相关。
（7）适用范围。硬件结构改进法需要对电机结构或控制拓扑进行改进，常用于系统设计阶段。转矩闭环控制法能够有效抑制转矩脉动，因此常用于需要高转矩质量的系统。转矩开环控制法具有较高的目标拓展性，因而广泛应用于有多控制目标要求的系统。非理想分量消除法则常用于对电压或电流质量要求较高的场合。多目标预测控制法在需要多目标协同优化的系统中具有广阔的应用前景。
转矩脉动抑制作为非理想运行条件下提高DFIG发电系统运行可靠性的关键技术，已得到国内外诸多学者的关注和研究，但目前仍存在一些问题值得进一步探索和研究：
1）软硬件协同转矩脉动抑制。硬件结构改进法和控制策略改进法各有优势，适用范围也不完全相同。因此，如何将二者的优势相结合，更加经济、有效地抑制转矩脉动，是未来需要进一步探索的问题。
2）强鲁棒转矩脉动抑制方法。现有的控制策略改进法对电机参数具有一定的依赖性，这意味着参数摄动可能会影响抑制效果。未来可通过以下两种方式提高转矩脉动抑制方法的鲁棒性。首先，在控制系统中引入参数辨识方法对电机参数进行在线辨识，以增强转矩脉动抑制方法的参数鲁棒性。其次，构建无参数转矩脉动抑制方法，从根本上解决参数变化对转矩脉动抑制效果产生的不利影响。
3）谐波损耗和转矩脉动综合治理。在非理想发电条件下，除了转矩脉动问题，谐波损耗问题同样严重，因此需要采取谐波损耗和转矩脉动综合治理措施。在这个过程中，有三个关键问题值得进一步探索：首先，如何构建精确的谐波损耗模型是第一个值得探索的问题。其次，谐波损耗模型涉及的物理量较多，如何选择控制变量，并制定谐波损耗抑制策略是第二个值得探索的问题。最后，转矩脉动和谐波损耗之间存在耦合关系，二者往往不能同时达到最优水平，如何协调二者之间的关系，使转矩脉动抑制和谐波损耗抑制均达到较理想的水平，是第三个值得探索的问题。
4）故障状态下的转矩脉动抑制。当DFIG-DC系统发生绕组断相、变流器桥臂失效等故障时，DFIG的转矩脉动会急剧增加，必须采取应对措施实现发电系统的故障穿越。围绕该问题开展故障诊断、转矩特征谐波分析以及转矩脉动抑制策略设计等研究，将是未来非常重要的工作。
本文围绕非正弦和不平衡这两类非理想运行条件下DFIG转矩脉动抑制方法这一主题，对国内外现有的研究成果进行了梳理，并探讨了该项技术发展态势。主要结论如下：
1）非理想运行条件下DFIG转矩脉动抑制方法可分为两大类，分别为硬件结构改进法和控制策略改进法。其中，硬件结构改进法需额外增加电气装置甚至需要改变电机结构，更适用于系统设计阶段。对于已完成设计加工的系统而言，一般采用控制策略改进法，但在实施时也需要注意控制算法的复杂度，以免影响控制精度。
2）转矩闭环控制法可对转矩脉动起到较好的抑制作用，但其目标拓展性较低，在多目标控制目标系统中不便实施。转矩开环控制法的目标拓展性较高，实际应用时只需根据控制目标修改电压或电流参考值，但其参数依赖性问题较为严重。非理想分量消除法的分析和设计相对简单，但是无法完全消除电压和电流中的非理想分量，因此其转矩脉动抑制效果并不显著。多目标预测控制法可方便实现多目标协同优化，但尚无通用方法对权重因子进行 优化。
3）未来，DFIG发电系统应采用硬件结构改进法和控制策略改进法相结合的协同抑制方法。并且，控制策略改进法还应结合参数辨识、无参数控制以及谐波损耗抑制，充分提高控制系统的参数鲁棒性和效率。此外，还应进一步探索DFIG系统故障状态下的转矩脉动抑制方法，提高系统的故障穿越 能力。
参考文献
[1] Chen Hao, Xu Deguang, Deng Xin. Control for power converter of small-scale switched reluctance wind power generator[J]. IEEE Transactions on Industrial Electronics, 2021, 68(4): 3148-3158.
[2] Shutari H, Ibrahim T, Bin Mohd Nor N, et al. Development of a novel efficient maximum power extraction technique for grid-tied VSWT system[J]. IEEE Access, 2022, 10: 101922-101935.
[3] 张天策, 李庚银, 王剑晓, 等. 基于可行域投影理论的新能源电力系统协同运行方法[J]. 电工技术学报, 2024, 39(9): 2784-2796.
Zhang Tiance, Li Gengyin, Wang Jianxiao, et al. Coordinated operation method of renewable energy power systems based on feasible region projection theory[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2784-2796.
[4] Wang Yongcan, Lou Suhua, Wu Yaowu, et al. Flexible operation of retrofitted coal-fired power plants to reduce wind curtailment considering thermal energy storage[J]. IEEE Transactions on Power Systems, 2020, 35(2): 1178-1187.
[5] Xiang Ling, Zhu Haowei, Zhang Yue, et al. Impact of wind power penetration on wind-thermal-bundled transmission system[J]. IEEE Transactions on Power Electronics, 2022, 37(12): 15616-15625.
[6] Catalán P, Wang Yanbo, Arza J, et al. A com- prehensive overview of power converter applied in high-power wind turbine: key challenges and potential solutions[J]. IEEE Transactions on Power Electronics, 2023, 38(5): 6169-6195.
[7] 王涛, 诸自强, 年珩. 非理想电网下双馈风力发电系统运行技术综述[J]. 电工技术学报, 2020, 35(3): 455-471.
Wang Tao, Zhu Ziqiang, Nian Heng. Review of operation technology of doubly-fed induction generator-based wind power system under nonideal grid conditions[J]. Transactions of China Electro- technical Society, 2020, 35(3): 455-471.
[8] Battulga B, Shaikh M F, Lee S B, et al. Inverter-embedded detection of rotor winding faults in doubly fed induction generators for wind energy applications[J]. IEEE Transactions on Energy Con- version, 2023, 38(1): 646-652.
[9] 阚超豪, 胡杨, 任泰安, 等. 基于多谐波联合起动方法的无刷双馈电机起动性能研究[J]. 电工技术学报, 2019, 34(23): 4927-4938.
Kan Chaohao, Hu Yang, Ren Taian, et al. The starting performance study of a brushless doubly-fed machine based on the multi-harmonics starting method[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4927-4938.
[10] 于克训, 陈曦, 谢贤飞, 等. 无刷双馈电机研究综述与展望[J]. 电工技术学报, 2024, 39(2): 397-422.
Yu Kexun, Chen Xi, Xie Xianfei, et al. Overview and prospect of the brushless doubly-fed machine research[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 397-422.
[11] 程明, 许利通, 曹政, 等. 级联式无刷双馈电机的矢量控制系统和功率流研究[J]. 电工技术学报, 2022, 37(20): 5164-5174.
Cheng Ming, Xu Litong, Cao Zheng, et al. Study on vector control system and power flow of cascaded brushless doubly-fed induction generator[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(20): 5164-5174.
[12] 庾波. 基于磁场差调制的无刷双馈电机理论与设计研究[D]. 合肥: 合肥工业大学, 2021.
[13] 王皓. 10MW海上用无刷双馈风力发电机电磁设计与转子结构分析[D]. 沈阳: 沈阳工业大学, 2017.
[14] Chen Jiansheng, Zhang Wei, Chen Bojian, et al. Improved vector control of brushless doubly fed induction generator under unbalanced grid conditions for offshore wind power generation[J]. IEEE Transa- ctions on Energy Conversion, 2016, 31(1): 293-302.
[15] 顾雨萍, 李向江, 吴秀梅. 第三代半导体材料发展前景分析[J]. 中国集成电路, 2023, 32(3): 22-25, 36.
Gu Yuping, Li Xiangjiang, Wu Xiumei. Analysis of the development prospects of third-generation semi- conductor materials[J]. China Integrated Circuit, 2023, 32(3): 22-25, 36.
[16] 肖湘宁, 廖坤玉, 唐松浩, 等. 配电网电力电子化的发展和超高次谐波新问题[J]. 电工技术学报, 2018, 33(4): 707-720.
Xiao Xiangning, Liao Kunyu, Tang Songhao, et al. Development of power-electronized distribution grids and the new supraharmonics issues[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 707-720.
[17] 徐健, 曹鑫, 郝振洋, 等. 基于电网谐波电压前馈的虚拟同步整流器电流谐波抑制方法[J]. 电工技术学报, 2022, 37(8): 2018-2029.
Xu Jian, Cao Xin, Hao Zhenyang, et al. A harmonic-current suppression method for virtual synchronous rectifier based on feedforward of grid harmonic voltage[J]. Transactions of China Electro- technical Society, 2022, 37(8): 2018-2029.
[18] Xu Wei, Yu Kailiang, Liu Yi, et al. Improved coordinated control of standalone brushless doubly fed induction generator supplying nonlinear loads[J]. IEEE Transactions on Industrial Electronics, 2019, 66(11): 8382-8393.
[19] 韩思鹏, 宋卫章, 胥少杰, 等. 不平衡电网电压下精简矩阵变换器扩展直接功率模型预测控制[J]. 电工技术学报, 2023, 38(增刊1): 147-156.
Han Sipeng, Song Weizhang, Xu Shaojie, et al. Extended direct power model predictive control for reduced matrix converter under unbalanced grid voltage operation condition[J]. Transactions of China Electrotechnical Society, 2023, 38(S1): 147-156.
[20] 潘子迅, 杨晓峰, 赵锐, 等. 不平衡电网下虚拟同步机的多模式协调策略[J]. 电工技术学报, 2023, 38(16): 4274-4285.
Pan Zixun, Yang Xiaofeng, Zhao Rui, et al. Multi- mode coordination control of virtual synchronous generator under unbalanced power grid[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(16): 4274-4285.
[21] Liu Yi, Hussien M G, Xu Wei, et al. Recent advances of control technologies for brushless doubly-fed generators[J]. IEEE Access, 2021, 9: 123324-123347.
[22] Mohammed O M E, Xu Wei, Liu Yi, et al. An improved control method for standalone brushless doubly fed induction generator under unbalanced and nonlinear loads using dual-resonant controller[J]. IEEE Transactions on Industrial Electronics, 2021, 68(7): 5594-5605.
[23] 刘毅, 张茂鑫, 徐伟, 等. 一种BDFIG-DC系统谐波铜耗最小化控制装置及方法. 中国, ZL202310099220.3[P]. 2023.
[24] 熊志, 赵红生, 郑旭, 等. 一种无刷双馈电机转矩脉动抑制方法. 中国, ZL202211412136.4[P]. 2023.
[25] 刘恩仁. 风电机组传动链轴承故障诊断[D]. 北京: 华北电力大学, 2018.
[26] 姜云磊. 高可靠双定子无刷双馈风力发电系统多模式控制策略研究[D]. 南京: 东南大学, 2018.
[27] 李耀华, 陈桂鑫, 王孝宇, 等. 感应电机磁链与转矩无差拍控制[J]. 电机与控制应用, 2022, 49(10): 27-33, 67.
Li Yaohua, Chen Guixin, Wang Xiaoyu, et al. Flux linkage and torque deadbeat control for induction motor[J]. Electric Machines & Control Application, 2022, 49(10): 27-33, 67.
[28] Liu Yi, Xu Wei, Long Teng, et al. An improved rotor speed observer for standalone brushless doubly-fed induction generator under unbalanced and nonlinear loads[J]. IEEE Transactions on Power Electronics, 2020, 35(1): 775-788.
[29] Marques G D, Iacchetti M F. DFIG topologies for DC networks: a review on control and design features[J]. IEEE Transactions on Power Electronics, 2019, 34(2): 1299-1316.
[30] Maciejewski P, Iwanski G. Modeling of six-phase Double Fed Induction Machine for autonomous DC voltage generation[C]//2015 Tenth International Con- ference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 2015: 1-6.
[31] Yu Nisa, Nian Heng, Quan Yu. A novel DC grid connected DFIG system with active power filter based on predictive current control[C]//2011 International Conference on Electrical Machines and Systems, Beijing, China, 2011: 1-5.
[32] 年珩, 易曦露. 面向直流输电的双馈风电机组并网拓扑及控制技术[J]. 电网技术, 2014, 38(7): 1731- 1738.
Nian Heng, Yi Xilu. HVDC power transmission oriented grid-connection topology and control strategy for wind farm composed of doubly fed induction generators[J]. Power System Technology, 2014, 38(7): 1731-1738.
[33] 李文津, 汤广福, 康勇, 等. 基于VSC-HVDC的双馈式变速恒频风电机组启动及并网控制[J]. 中国电机工程学报, 2014, 34(12): 1864-1873.
Li Wenjin, Tang Guangfu, Kang Yong, et al. Starting up and integration control of doubly-fed variable- speed constant-frequency wind power generator based on VSC-HVDC[J]. Proceedings of the CSEE, 2014, 34(12): 1864-1873.
[34] 杨淑英. 双馈型风力发电变流器及其控制[D]. 合肥: 合肥工业大学, 2007.
[35] 刘盟伟, 徐永海. 不平衡电网电压下双馈电机的协调控制策略[J]. 电工文摘, 2012(1): 66-70.
Liu Mengwei, Xu Yonghai. Coordinated control strategy of doubly-fed machine under unbalanced grid voltage[J]. Electrical Equipment and Economy, 2012(1): 66-70.
[36] Maciejewski P, Iwanski G. Direct torque control for autonomous doubly fed induction machine based DC generator[C]//2017 Twelfth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 2017: 1-6.
[37] Xu Wei, Dong Dinghao, Liu Yi, et al. Improved sensorless phase control of stand-alone brushless doubly-fed machine under unbalanced loads for ship shaft power generation[J]. IEEE Transactions on Energy Conversion, 2018, 33(4): 2229-2239.
[38] Yu Kailiang, Xu Wei, Liu Yi, et al. Harmonics mitigation of standalone brushless doubly-fed indu- ction generator feeding nonlinear loads considering power converter voltage rating[C]//2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 2018: 6989-6995.
[39] Dong Shuhui, Li Yonggang, Wang Aimeng, et al. Control of PMSG wind turbines based on reduced order resonant controllers under unbalanced grid voltage conditions[C]//2015 IEEE 11th International Conference on Power Electronics and Drive Systems, Sydney, NSW, Australia, 2015: 326-329.
[40] 程鹏, 年珩. 电网电压不平衡时基于谐振闭环调节的双馈异步发电机转矩波动抑制策略[J]. 中国电机工程学报, 2015, 35(7): 1756-1767.
Cheng Peng, Nian Heng. Torque ripple restraint strategy of DFIG under unbalanced grid voltage conditions based on resonant control loop[J]. Pro- ceedings of the CSEE, 2015, 35(7): 1756-1767.
[41] Nian Heng, Wu Chao, Cheng Peng. Direct resonant control strategy for torque ripple mitigation of DFIG connected to DC link through diode rectifier on stator[J]. IEEE Transactions on Power Electronics, 2017, 32(9): 6936-6945.
[42] 张恒. 直流并网型双馈风力发电系统宽频率运行控制方法[D]. 北京: 华北电力大学, 2020.
[43] Cheng Peng, Nian Heng. Collaborative control of DFIG system during network unbalance using reduced- order generalized integrators[J]. IEEE Transactions on Energy Conversion, 2014, 30(2): 453-464.
[44] Cheng Peng, Wu Chao, Ma Jing, et al. Coordinated derived current control of DFIG’s RSC and GSC without PLL under unbalanced grid voltage con- ditions[J]. IEEE Access, 2020, 8: 64760-64769.
[45] Nian Heng, Cheng Peng, Zhu Z Q. Coordinated direct power control of DFIG system without phase-locked loop under unbalanced grid voltage conditions[J]. IEEE Transactions on Power Electronics, 2016, 31(4): 2905-2918.
[46] Wang Jianliang, Zhang Yihuang, Cheng Peng, et al. Torque ripple suppression of DFIG under unbalanced grid voltage conditions using reduced-order gen- eralized integrators[C]//2014 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 2015: 1394-1399.
[47] Wu Chao, Nian Heng. An improved repetitive control of DFIG-DC system for torque ripple suppression[J]. IEEE Transactions on Power Electronics, 2018, 33(9): 7634-7644.
[48] Wu Chao, Nian Heng, Pang Bo, et al. Adaptive repetitive control of DFIG-DC system considering stator frequency variation[J]. IEEE Transactions on Power Electronics, 2019, 34(4): 3302-3312.
[49] Wu Chao, Nian Heng. Improved direct resonant control for suppressing torque ripple and reducing harmonic current losses of DFIG-DC system[J]. IEEE Transactions on Power Electronics, 2019, 34(9): 8739-8748.
[50] Shang Lei, Hu Jiabing. Sliding-mode-based direct power control of grid-connected wind-turbine-driven doubly fed induction generators under unbalanced grid voltage conditions[J]. IEEE Transactions on Energy Conversion, 2012, 27(2): 362-373.
[51] Marques G D, Iacchetti M F. Stator frequency regulation in a field-oriented controlled DFIG connected to a DC link[J]. IEEE Transactions on Industrial Electronics, 2014, 61(11): 5930-5939.
[52] Marques G D, Iacchetti M F. Inner control method and frequency regulation of a DFIG connected to a DC link[J]. IEEE Transactions on Energy Conversion, 2014, 29(2): 435-444.
[53] Iacchetti M F, Marques G D, Perini R. Torque ripple reduction in a DFIG-DC system by resonant current controllers[J]. IEEE Transactions on Power Elec- tronics, 2015, 30(8): 4244-4254.
[54] Liang Jiaqi, Howard D F, Restrepo J A, et al. Feedforward transient compensation control for DFIG wind turbines during both balanced and unbalanced grid disturbances[J]. IEEE Transactions on Industry Applications, 2013, 49(3): 1452-1463.
[55] Marques G D, Iacchetti M F. Minimization of torque ripple in the DFIG-DC system via predictive delay compensation[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 103-113.
[56] Das S, Singh B. Multi-objective control strategy for power quality improvement in wind-solar distributed generation system under harmonically distorted grid[J]. IEEE Transactions on Industry Applications, 2022, 58(5): 5697-5710.
[57] Das S, Singh B. Flexible ripple minimization technique for wind-solar renewable energy system under unbalanced and distorted grid conditions[J]. IEEE Transactions on Industry Applications, 2022, 58(5): 6739-6751.
[58] 徐海亮, 章玮, 陈建生, 等. 电网电压不平衡且谐波畸变时双馈风电机组转矩波动抑制[J]. 电力系统自动化, 2013, 37(7): 12-17, 54.
Xu Hailiang, Zhang Wei, Chen Jiansheng, et al. Torque oscillation suppression of DFIG-based wind turbines under unbalanced and distorted grid voltage conditions[J]. Automation of Electric Power Systems, 2013, 37(7): 12-17, 54.
[59] Jiang Yunlei, Cheng Ming, Han Peng, et al. Analysis and dynamic control of a dual-stator BDFIG-DC system supplying DC grid with minimized torque ripple through harmonic current injection[J]. IEEE Transactions on Power Electronics, 2019, 34(6): 5388-5399.
[60] Sotoodeh P, Izadkhast S M, Khosravi H, et al. Modeling and control of a grid-connected BDFM under unbalanced grid voltage conditions[C]//2011 IEEE International Electric Machines & Drives Conference (IEMDC), Niagara Falls, ON, Canada, 2011: 1647-1651.
[61] 刘毅, 张茂鑫, 徐伟. 一种无刷双馈电机直流发电系统转矩脉动抑制装置及方法. 中国, ZL202111395371.0[P]. 2022.
[62] Zhang Maoxin, Liu Yi, Xu Wei, et al. Torque ripple suppression for standalone brushless doubly-fed induction generator-DC system based on power winding harmonic current control[J]. IEEE Transa- ctions on Industrial Electronics, 2023, 70(9): 8746- 8756.
[63] 刘毅, 张茂鑫, 徐伟. 一种无刷双馈独立发电系统的转矩脉动抑制装置及方法. 中国, ZL202110097294.4[P]. 2022.
[64] Liu Yi, Zhang Maoxin, Xu Wei, et al. Optimized torque ripple suppression method for standalone brushless doubly fed induction generator with special loads[J]. IEEE Transactions on Power Electronics, 2022, 37(9): 10981-10993.
[65] 刘毅, 张茂鑫, 徐伟. 一种无刷双馈电机协同转矩脉动抑制装置及方法. 中国, ZL202210232904.1[P]. 2022.
[66] 蒋天龙. 具有惯性特征的双馈风力发电机非理想电网条件下控制策略研究[D]. 杭州: 浙江大学, 2019.
[67] Abo-Khalil A G, Alharbi W, Al-Qawasmi A R, et al. Modeling and control of unbalanced and distorted grid voltage of grid-connected DFIG wind turbine[J]. International Transactions on Electrical Energy Systems, 2021, 31(5): e12857.
[68] 姚骏, 刘瑞阔, 裴金鑫, 等. 谐波电网电压下双馈风力发电系统的控制方法. 中国, ZL201810214783.1[P]. 2020.
[69] 胡胜. 双馈型风力发电机在电网故障和不平衡条件下控制技术研究[D]. 武汉: 华中科技大学, 2012.
[70] 张纯江, 王勇, 杨海军, 等. 电网电压不平衡条件下双馈风力发电机转矩脉动抑制研究[J]. 太阳能学报, 2013, 34(6): 924-932.
Zhang Chunjiang, Wang Yong, Yang Haijun, et al. Research on torque pulsation suppression of doubly- fed induction generator under grid voltage unba- lance[J]. Acta Energiae Solaris Sinica, 2013, 34(6): 924-932.
[71] 赵阳. 风力发电系统用双馈感应发电机矢量控制技术研究[D]. 武汉: 华中科技大学, 2008.
[72] Park Y, Han D, Suh Y, et al. Minimization of active power and torque ripple for a doubly fed induction generator in medium voltage wind power systems under unbalanced grid conditions[J]. Journal of Power Electronics, 2013, 13(6): 1032-1041.
[73] Fan Lingling, Yin Haiping, Miao Zhixin. A novel control scheme for DFIG-based wind energy systems under unbalanced grid conditions[J]. Electric Power Systems Research, 2011, 81(2): 254-262.
[74] Xiao Yan, Fahimi B, Rotea M A, et al. Multiple reference frame-based torque ripple reduction in DFIG-DC system[J]. IEEE Transactions on Power Electronics, 2020, 35(5): 4971-4983.
[75] Park H G, Abo-Khalil A G, Lee D C, et al. Torque ripple elimination for doubly-fed induction motors under unbalanced source voltage[C]//2007 7th Inter- national Conference on Power Electronics and Drive Systems, Bangkok, Thailand, 2008: 1301-1306.
[76] 高骏, 王磊, 周文, 等. 双馈风电机组电网背景谐波运行与谐波抑制策略研究[J]. 电力系统保护与控制, 2016, 44(23): 164-169.
Gao Jun, Wang Lei, Zhou Wen, et al. Study on operating behavior and suppression strategy of doubly-fed induction generators wind turbine under harmonic grid voltage conditions[J]. Power System Protection and Control, 2016, 44(23): 164-169.
[77] 赵阳. 电网电压不平衡时双馈感应发电机不平衡电流控制研究[J]. 科技风, 2009(3): 68, 72.
Zhao Yang. Research on unbalanced current control of doubly-fed induction generator under unbalanced grid voltage[J]. Technology Trend, 2009(3): 68, 72.
[78] 郭磊. 船舶双馈轴带发电机独立运行控制研究[D]. 大连: 大连海事大学, 2020.
[79] 李豪杰. 双馈直流发电系统独立运行控制研究[D].大连: 大连海事大学, 2020.
[80] 刘昌金. 适应电网环境的双馈风电机组变流器谐振控制[D]. 杭州: 浙江大学, 2012.
[81] Li Zhenping, Wang Xuefan, Kong Ming, et al. Bidirectional harmonic current control of brushless doubly fed motor drive system based on a fractional unidirectional converter under a weak grid[J]. IEEE Access, 2021, 9: 19926-19938.
[82] 李珍平. 无刷双馈变频调速系统的控制策略及其应用研究[D]. 武汉: 华中科技大学, 2021.
[83] Liu Changjin, Blaabjerg F, Chen Wenjie, et al. Stator Current harmonic control with resonant controller for doubly fed induction generator[J]. IEEE Transactions on Power Electronics, 2012, 27(7): 3207-3220.
[84] Misra H, Jain A K. Mathematical modeling and control of standalone DFIG-DC system in rotor flux reference frame[J]. IEEE Transactions on Industrial Electronics, 2018, 65(5): 3708-3719.
[85] de Santana M P, de Paula G T, de Oliveira C M R, et al. Vector control applied to mitigate the electro- magnetic torque ripple in doubly fed induction generator[J]. IEEE Transactions on Energy Con- version, 2021, 36(4): 2977-2986.
[86] 王瑞明, 谢震, 张兴, 等. 电网谐波下双馈发电机改进控制策略[J]. 农业工程学报, 2015, 31(22): 207-214.
Wang Ruiming, Xie Zhen, Zhang Xing, et al. Improved control strategy of turbine driven doubly- fed induction generators under harmonic grid voltage conditions[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(22): 207-214.
[87] Xu Wei, Yu Kailiang, Liu Yi, et al. Improved collaborative control of standalone brushless doubly fed induction generator under unbalanced and nonlinear loads considering voltage rating of con- verters[J]. IEEE Transactions on Power Electronics, 2020, 35(5): 4959-4970.
[88] Iacchetti M F, Marques G D, Perini R. A scheme for the power control in a DFIG connected to a DC bus via a diode rectifier[J]. IEEE Transactions on Power Electronics, 2015, 30(3): 1286-1296.
[89] Cruz S M A, Marques G D, Gonçalves P F C, et al. Predictive torque and rotor flux control of a DFIG-DC system for torque ripple compensation and loss minimization[J]. IEEE Transactions on Industrial Electronics, 2018, 65(12): 9301-9310.
[90] 谢震, 牛立凡, 张兴, 等. 不平衡电网电压下双馈发电机多目标模型预测控制[J]. 中国电机工程学报, 2019, 39(13): 3917-3929.
Xie Zhen, Niu Lifan, Zhang Xing, et al. Multi- objective model predictive control of doubly-fed generator under unbalanced grid voltage[J]. Pro- ceedings of the CSEE, 2019, 39(13): 3917-3929.
Abstract Under non-sinusoidal and unbalanced operating conditions, the doubly fed induction generator (DFIG) encounters significant torque ripple issues, which can severely damage the gearbox and drive shaft and threaten the safety and stable operation of the system. In recent years, numerous solutions have been proposed. This paper classifies and summarizes the existing technical solutions, enabling scholars in related fields to quickly understand the research status and development trends, thereby promoting the further development of torque ripple suppression technology for DFIG.
Existing technical solutions can be divided into hardware structure improvement and control strategy improvement methods. The hardware structure improvement method mainly includes using multi-pulse rectifiers, adding passive filters, and using voltage source converters. This method can effectively suppress torque ripple but requires changing the machine structure or adding additional equipment. As a result, the system cost is high, so the hardware structure improvement method is often used in the system design stage. The control strategy improvement method is the most commonly used, including the torque closed-loop control method, the torque open-loop control method, the non-ideal component elimination method, and the multi-objective predictive control method. The torque closed-loop control method can achieve high-precision torque control and has good system stability but its target extensibility is low, which is often used in applications requiring high torque quality. The torque open-loop control method has strong target extensibility and is often employed in systems with multiple control targets. However, the torque open-loop control method highly depends on machine parameters, and the parameter perturbation seriously affects the torque ripple suppression performance. The non-ideal component elimination method is relatively simple to control. However, it cannot simultaneously eliminate non-ideal components of voltage and current, and the effect of torque ripple suppression is unsatisfactory. This method is usually adopted in applications requiring high voltage or current quality. The multi-objective predictive control method can achieve multi-target collaborative optimization. However, no general method exists to optimize the weight factors for multiple control targets.
In the future, the DFIG power generation system should adopt a collaborative suppression method combining hardware structure and control strategy improvement methods to restrain torque ripple more economically and effectively. Additionally, the control strategy improvement method should include parameter identification, parameter-free control, and harmonic loss suppression to improve the machine parameter robustness and efficiency of the control system. Furthermore, the torque ripple suppression method under the fault state of the DFIG system needs to be further explored to improve the system’s fault-crossing ability.
keywords：Non-sinusoidal operation, unbalanced operation, doubly-fed induction generator, torque ripple suppression
DOI: 10.19595/j.cnki.1000-6753.tces.230920
中图分类号：TM315
广东省基础与应用基础研究基金项目（2023A1515012025）、国家自然科学基金面上项目（52277050）、深圳市国际合作项目（GJHZ20210705142539007）、中央高校基本科研业务费专项资金项目（2021XXJS002）和山东省优秀青年基金项目（ZR2020YQ40）资助。
收稿日期 2023-06-14
改稿日期 2023-07-17
刘 毅 男，1982年生，博士，讲师，研究方向为双馈电机控制技术。E-mail: liuyi82@hust.edu.cn
徐 伟 男，1980年生，教授，博士生导师，研究方向为电机设计、控制及系统集成应用。E-mail: weixu@hust.edu.cn（通信作者）
（编辑 崔文静）