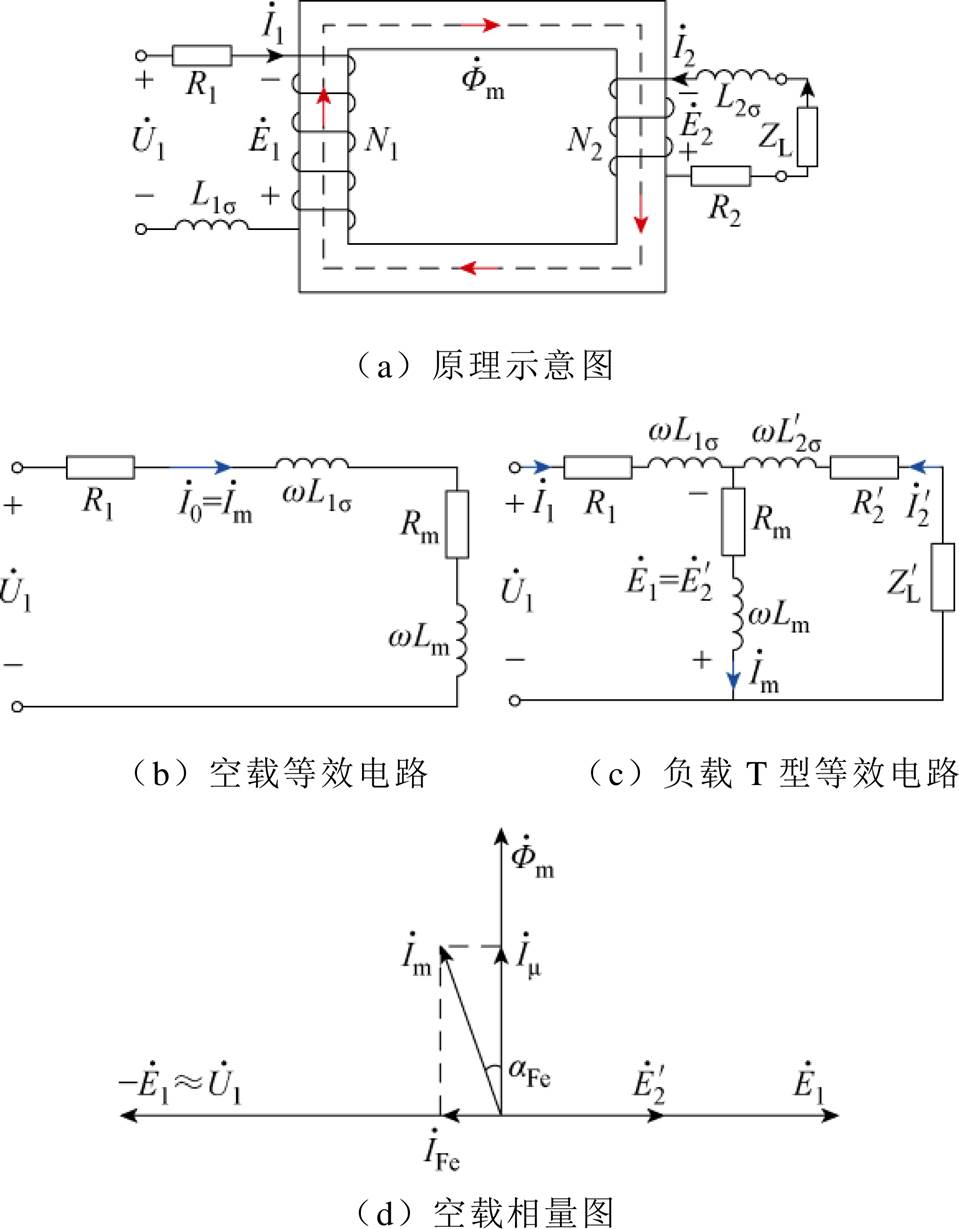
图1 单相变压器
Fig.1 Single-phase transformer
摘要 电机学等传统电机理论对变压器和感应电机的工作机理分析多采用等效电路的方法，将实际磁量等效为电量来表示，在一定程度上让二者的分析变得复杂化。可是，传统磁路理论中仅有磁阻元件，难以定量表征磁通与磁动势之间存在的相位差和铁心中的损耗等，进而成为分析的瓶颈。为此，该文引入新的磁路参数——磁感，并利用磁阻和磁感双元件构成的矢量磁路理论，建立适用于变压器和感应电机分析的等效矢量磁路，推导了不同工况下的磁路方程，并以变压器为例，从磁路角度绘制了相量图。对变压器和感应电机在不同工况下的主要特性进行定量计算，通过实验结果验证了分析方法的有效性。相较于等效电路分析方法，该文所提的等效矢量磁路分析方法省去了匝数归算、频率归算等过程，因而概念清晰、计算简洁。该文研究不仅为电机等电磁装备的分析设计提供了全新的方法，而且有望推动《电机学》教材的改革，降低电机学相关内容的学习难度。
关键词：磁感等效磁路 矢量磁路理论 变压器 感应电机 电机学
作为实现机电能量转换的重要电磁设备，变压器与感应电机应用广泛，且在分析方法和基本特性上有一定的相似性。为了便于分析二者的工作原理，现有电机学等传统电机理论常采用等效电路表示一次、二次电流之间的流通关系并计算性能，根据等效电路绘制的相量图来表示相关物理量之间的相位关系[1-8]。以单相变压器为例，图1所示为其等效电路图和空载相量图[1]。图中，U1为输入电压；R1和L1s 为一次绕组电阻和漏电感；R2和L2s 为二次绕组电阻和漏电感；I1、I2为一次、二次绕组电流；E1、E2为一次、二次绕组感应电动势；N1、N2为一次、二次绕组匝数；ZL为外接负载阻抗；Fm为主磁通；' 表示二次侧参数归算到一次侧。一次、二次绕组经主磁通Fm耦合，产生的磁动势在磁路上相连，并通过交变磁通实现变压。但对于初学者来说，常存在一些不易理解的地方，造成困扰。
图1 单相变压器
Fig.1 Single-phase transformer
（1）图1b、图1c所示的等效电路中，有一个励磁支路，用电阻Rm来等效铁心损耗，流过该支路的电流Im为励磁电流。在实际变压器中，一次、二次侧的电路各自闭合，进而二者中的电流也不会流过Rm。为了分析计算而直接等效加入该电阻，让学生理解起来较为抽象，容易产生疑惑。
（2）图1c所示的变压器负载T型等效电路中，一次、二次绕组在电路上直接连通，这与其相互绝缘的事实不符，并且还要对二次侧的物理量进行“匝数归算”，让计算复杂化。为了简化计算，在T型等效电路基础上又演变出“近似等效电路”和“简化等效电路”，进一步增加了初学者的学习难度。
相较于等效电路的分析方法，等效磁路在电磁设备工作原理的理解上更为直观。但是，在图1d所示的空载相量图中，空载电流I0（Im）与主磁通Fm之间有一个相位差aFe，称为“铁耗角”[1]。若依据传统的磁路欧姆定律[9-12]，励磁磁通等于空载磁动势N1I0除以变压器铁心的磁阻，磁通与磁动势应该同相位，为什么铁心中的损耗会导致磁通与磁动势之间产生相位差？该相位差又与什么电磁量有关？如何进行定量计算？
不难发现，造成上述困扰的根源在于：传统的标量磁路理论中仅有磁阻单一元件[9-12]，不仅无法表征磁通与磁动势之间的相位差，更无法表征铁心中的损耗。因而在利用现有标量磁路理论去分析计算电机等设备的关键参数[13-18]时，均默认磁通与磁动势同相位。一方面，在相关理解与计算中往往不得不将实际磁量用电量来等效表示，使得问题复杂化；另一方面，这在一定程度上阻碍了《电机学》教材内容与组织形式的革新尝试[19-23]，让“难学”“难教”的局面难以有效改观。
事实上，之前已经有一些学者尝试去拓展标量磁路理论。E. R. Laithwaite类比于电路中的电感元件，提出了“transferance”这一参数[24]，并推导了相应的等效磁路。但是未阐明“transferance”的物理内涵，且提出的等效磁路与等效电路从能量角度上并不完全对偶。为了实现磁路和电路在功率上的对偶[25]，C. J. Carpenter和R. W. Buntenbach将磁通的导数（dF/dt）定义为磁路中的磁流[25-26]，以与电路中的电流对应，但是该方法缺乏实际物理意义，且与传统标量磁路理论互不兼容[25]。由上述可知，已有研究基本都是从电路-磁路的对偶关系展开，所定义的参数或缺少清晰的物理意义，或过于复杂，或与传统理论不能兼容，从而未能被广泛接受和应用。因此，时至今日，仅含单一磁阻参数的标量磁路理论仍被广泛应用于教材[1-8]、科研[13-18]与技术标准[27-28]，如何进一步地完善磁路理论、更好地分析电机等电磁设备的运行原理亟待解决。
最近发现并定义了新的磁路参数——磁感，进而建立了由磁阻和磁感双元件构成的矢量磁路理 论[29-30]，为电机等电磁装备的分析计算提供了全新的视角和手段。本文在文献[29-30]的基础上，推导了变压器外接负载情况下的等效磁路，并进一步将磁感的概念推广到感应电机中，尝试利用矢量磁路理论来统一分析变压器和感应电机，以期简化计算过程，降低理解难度，达到抛砖引玉之效。首先，介绍磁感及矢量磁路理论；其次，以常见的单相变压器和感应电机为例，推导分析空载和负载下的等效矢量磁路；最后，通过对比理论计算结果和实验测量结果，验证该磁路的有效性。
为方便叙述和读者理解，首先对磁感及矢量磁路理论做简要介绍，详细内容可见文献[29-30]。“磁感”表征了闭合导体线圈对流过该线圈的磁通的变化所具有的阻碍作用，本质上是对楞次定律的定量化表征，其值为单位磁通所产生的电荷链[31]。在非时变情况下，闭合线圈的磁感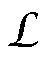
可表示为
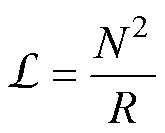（1）
式中，N为闭合线圈的匝数；R为闭合线圈的电阻，即：磁感正比于闭合线圈匝数的二次方，反比于闭合线圈的电阻。
考虑磁感后的变压器等效矢量磁路如图2所示，磁路中的物理量均用矢量表示，磁路欧姆定律拓展为
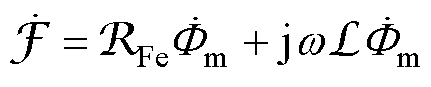（2）
式中，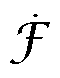
为源磁动势；
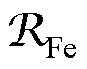为变压器铁心的等效磁阻；
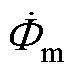为磁通幅值；w 为角频率。
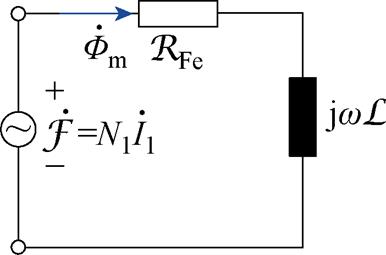
图2 考虑磁感后的等效矢量磁路
Fig.2 Equivalent vector magnetic circuit considering magductance
由式（2）可知，此时磁通与磁动势之间的相位差q 可以定量表征为
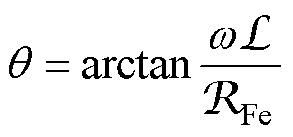（3）
由磁电功率定律[29]，在忽略磁滞损耗的条件下，交变磁通在磁感上产生的涡流损耗为
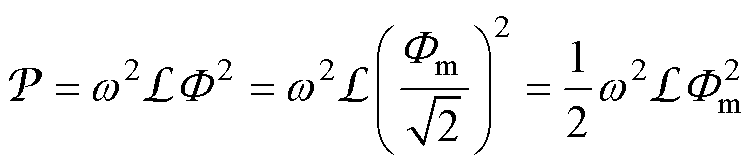（4）
式中，F 为主磁通有效值。
变压器空载时，二次绕组开路，磁路中没有外接磁感。但是，铁心中的涡流损耗可以等效为磁感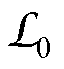
，由式（4）得铁心等效磁感与涡流损耗
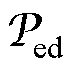的关系为
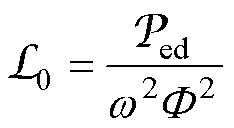（5）
变压器空载等效矢量磁路如图3所示，其中，磁感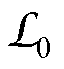为铁心等效磁感。当已知铁心损耗时，磁感可由式（5）计算，也可根据硅钢片的参数计算[32-33]。此时，空载电流的计算式为
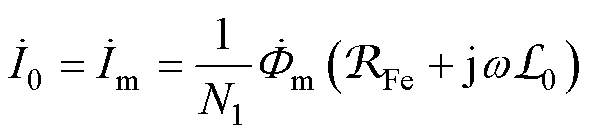（6）
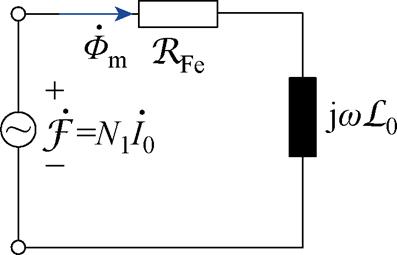
图3 变压器空载等效矢量磁路
Fig.3 Equivalent no-load magnetic circuit of transformer
空载相量图的形式与图1b相同，其中，磁通滞后空载电流的相位（即《电机学》中所说的铁耗 角）为
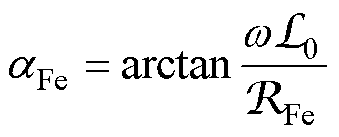（7）
实际运行中变压器的二次绕组常外接负载，设负载阻抗为ZL=RL+jwLL，其中，RL为外接负载电阻，LL为外接负载电感。此时二次侧的电压平衡方程为
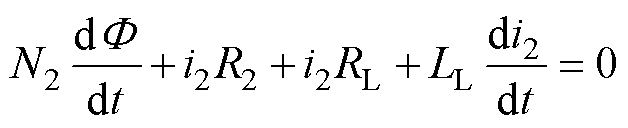（8）
磁动势平衡方程为
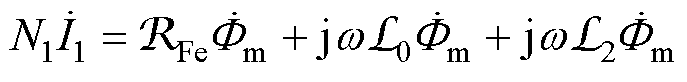（9）
式中，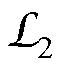
为考虑外加负载后的二次绕组的磁感，即
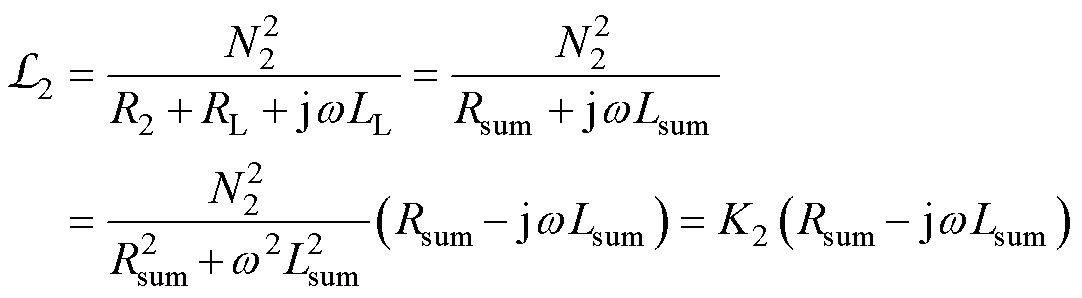（10）
式中，Rsum为总电阻值，Rsum=R2+RL；Lsum为总电感值，Lsum=L；K2为系数，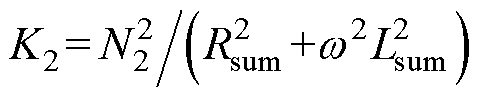
。
将式（10）代入式（9），可进一步得到负载下的磁动势平衡方程式为
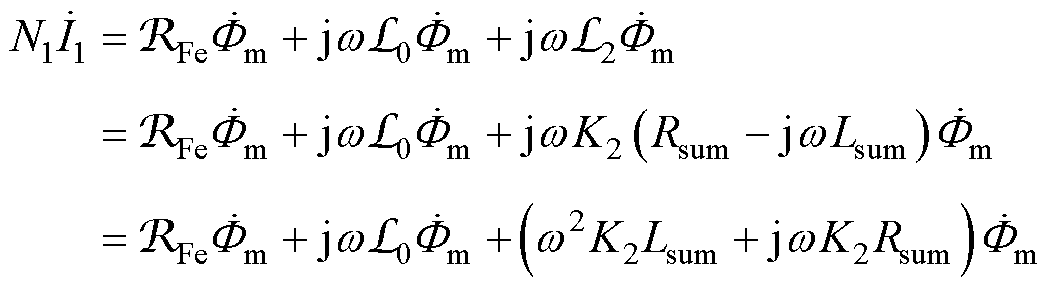（11）
变压器负载等效矢量磁路如图4所示。当已知负载阻抗，可先由式（10）求得二次绕组的等效磁感，再代入式（9），即可计算一次电流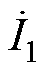
。此外，若要计算二次电流I2，只需根据磁动势表达式
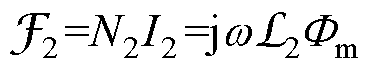，就可以计算得到。可见，变压器的分析计算被简化为对磁路方程的求解，不仅没有一次、二次绕组匝数归算，而且各电磁量的关系清晰明了，与实际变压器的电磁关系相一致。
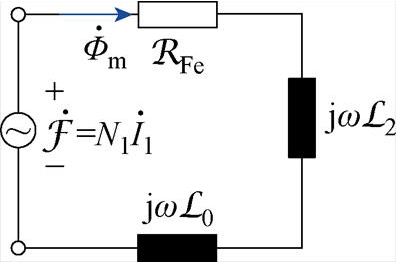
图4 变压器负载等效矢量磁路
Fig.4 Equivalent on-load magnetic circuit of transformer
图5给出了基于等效矢量磁路推导的变压器负载相量图。传统电机学中根据归算后的一次、二次绕组电压平衡方程组，以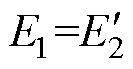
为公共参考量，得到变压器相量图。由于未能有效揭示一次、二次绕组和铁心之间的磁场联系，此时磁动势与磁通之间的相位差仍是困扰初学者或不能被直观解释的难点。
不同于传统电机学中的相量图，基于等效矢量磁路推导得到的变压器负载相量图以主磁通Fm为一次、二次侧的公共参考相量，一次、二次绕组的感应电动势E1、E2均滞后主磁通Fm 90°，其大小与各自的绕组匝数成正比。由铁心磁阻磁位降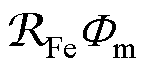
与空载等效磁感磁位降
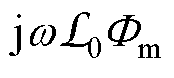合成得到空载磁动势N1Im，构成空载磁动势三角形（即变压器空载相量图，在图5中以实线表示），清晰地表明了空载下磁动势与磁通之间的相位差（即铁耗角）。基于空载磁动势三角形，再叠加上带负载时二次绕组等效磁感上的磁位降
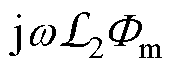，就得到负载时的一次绕组磁动势N1I1，并由它们构成负载磁动势三角形（在图5中以虚线表示）。一次绕组、二次绕组和铁心之间的磁场联系通过磁量直接表示；而一次侧和二次侧的电压、电流相量可根据各自的电压方程独立绘制，不需要进行匝数归算，如图5中点画线所示。
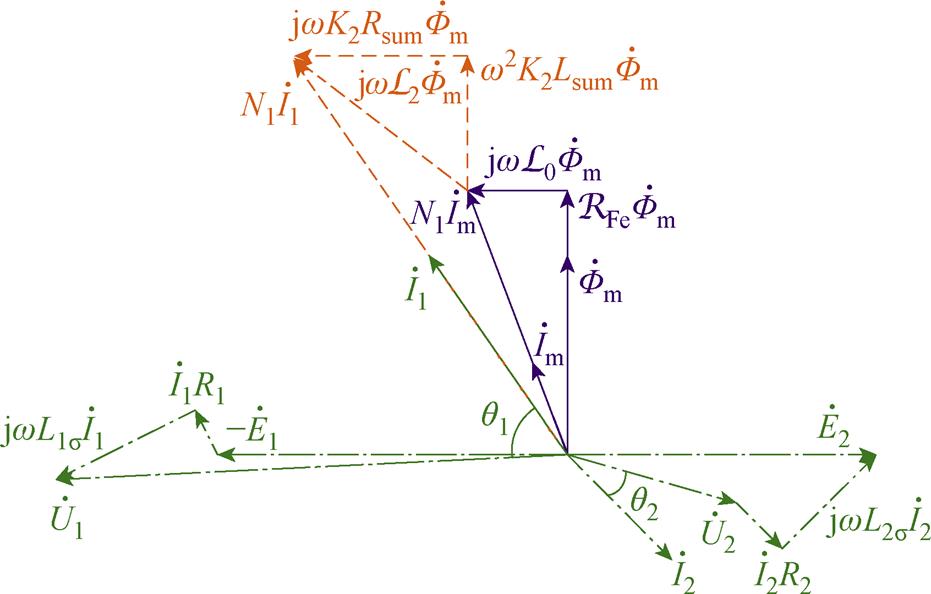
图5 变压器负载相量图
Fig.5 On-load phasor diagram of transformer
需要说明的是，虽然在一次、二次电压和电流计算中用到了等效电路，但它们都是各自电路内部的等效，并没有将磁量等效为电量，也没有将二次侧的电量等效为归算到一次侧的电量。
根据上述分析过程，并结合引言里所提到的现有《电机学》里不易理解的知识点，归纳基于磁感的等效矢量磁路特性如下：
（1）等效矢量磁路及其相量图直观地反映了变压器一次、二次绕组在电路上绝缘、磁路上相连的特点，更加符合实际运行情况，且构成矢量磁路的元件/参数物理意义明晰，原理便于理解。
（2）任意工况下的变压器等效矢量磁路是由磁阻、磁感元件组成的串联回路，空载下的铁耗角aFe由铁耗对应的等效磁感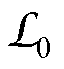引起，负载后只需在磁路中再串联上二次绕组的等效磁感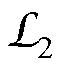，从而在磁路上本质地理解了任意工况下磁动势和磁通之间的相位差。
（3）相较于传统等效电路，等效矢量磁路不仅同样能够分析计算变压器的参数变量，而且省去了“匝数归算”，使计算过程变得更加简洁、清晰。
第2节中分析、推导了变压器的等效矢量磁路。由于变压器和感应电机在工作原理上相似。本节将基于磁感推导得到感应电机的等效矢量磁路。
转子静止时的感应电机相当于二次绕组短路的变压器，但在磁路中有两个气隙，其等效磁路与图4相同，只是磁路的磁阻除了铁心磁阻外，需加上两个气隙的磁阻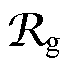
，转子笼型绕组等效为磁感。因此，转子静止时的感应电机分析计算与变压器类似。
转子旋转后又分两种情况：
（1）理想空载情况，此时转子以同步速旋转，旋转磁场与转子之间无相对运动，因此，转子绕组中不会产生感应电流，相当于处在静态磁场下，此时的感应电机等效为二次侧开路的变压器。其分析计算与2.1节中空载变压器的分析计算方法相同。
（2）非理想空载情况，即感应电机的正常运行情况，转子与旋转磁场之间以转差速度相对运动，转子绕组中的电流频率为转差频率，转子上有机械功率输出。此时感应电机的电磁结构如图6a所示，其中，RL是转子机械输出功率的等效负载电阻，由转子电压方程式有RL=R2(1−s)/s[1]，其中，s为转差率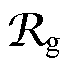；为气隙磁阻；其他变量的定义与图1中变压器的定义相同。等效磁路与变压器负载等效磁路相似，如图6b所示。
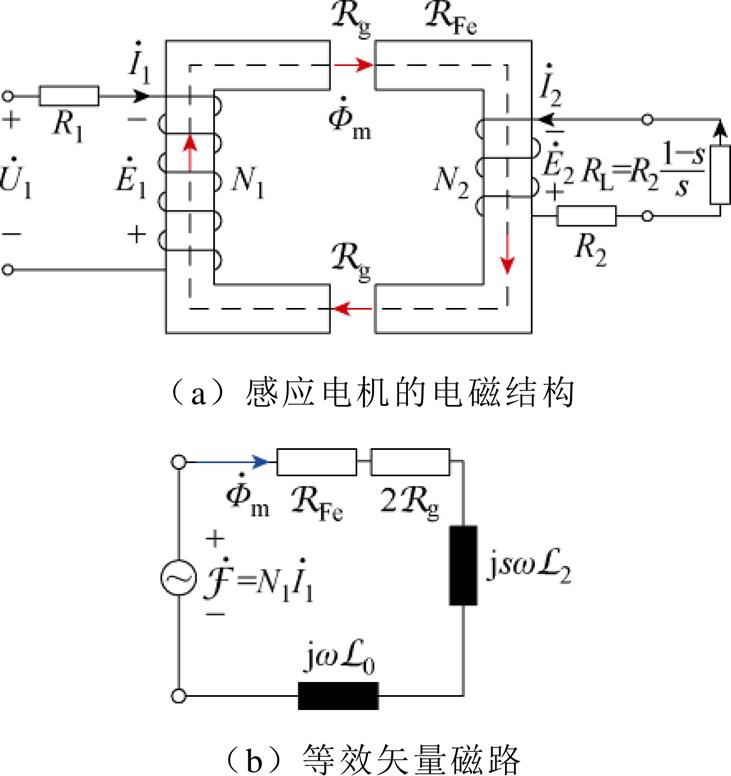
图6 感应电机
Fig.6 Induction motor
可以得到，感应电机的磁动势平衡方程为
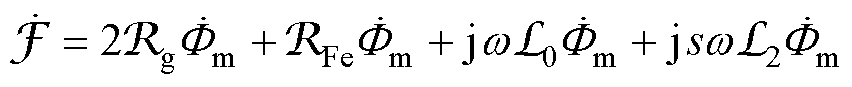（12）
式中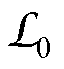，为感应电机铁心损耗的等效磁感，因铁心损耗主要发生在感应电机的定子侧，而转子侧因磁通交变频率为转差频率，所产生的转子铁心损耗很小可忽略不计，故与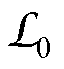对应的角频率为w，而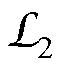为转子侧笼型绕组的等效磁感，对应的角频率为转差角频率sw。
事实上，图6b所示等效矢量磁路适用于感应电机的各种运行工况。当感应电机转子静止时，转差率s=1，则负载电阻RL=R2(1−s)/s=0，等效为二次侧短路的变压器，对应于3.1节的分析情况；当理想空载时，s=0，负载电阻RL=R2(1−s)/s=∞，等效为二次侧开路的变压器，对应于3.2节的分析情况。至此，感应电机的分析计算转化为对图6b等效矢量磁路的求解，并且同样可以根据该图，画出与图5类似的基于等效矢量磁路的感应电机相量图。其中，转子笼型绕组的磁感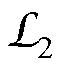的计算见附录，忽略漏电感的影响。与变压器的计算过程相似，基于等效矢量磁路的感应电机电磁转矩公式由磁电功率定律计算得到。
由定子侧经气隙传递到转子侧的电磁功率可用磁通在等效磁感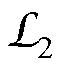上产生的有功损耗表示为
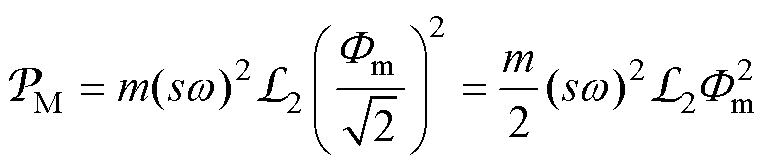（13）
式中，m为电机的相数。总机械功率为
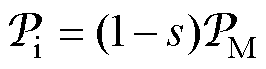（14）
电磁转矩为
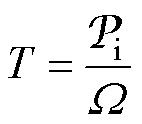（15）
式中，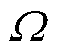
为转子机械角速度。电机轴上输出转矩为
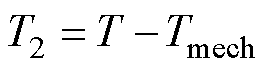（16）
式中，Tmech为机械损耗转矩。
至此，可以得到适用于变压器和感应电机分析的等效矢量磁路，如图7所示，再次表明等效磁路的直观有效。变压器和感应电机能够以统一的等效磁路表示，但又有所区别，具体可归纳为：
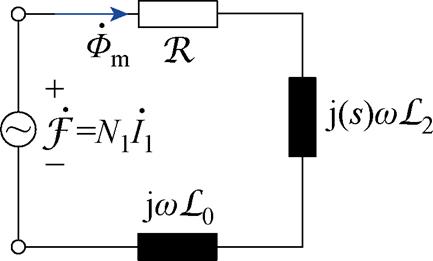
图7 感应电机和变压器的等效矢量磁路
Fig.7 Equivalent vector magnetic circuit of induction motor and Transformer
（1）变压器和感应电机的等效矢量磁路均由磁阻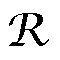
、铁心损耗等效磁感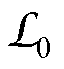和二次绕组（在感应电机里为转子笼型绕组）等效磁感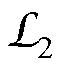组成。
（2）由于变压器中没有气隙，因此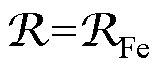
；而在感应电机里，气隙承担了机电能量转换的媒介，绝大部分的磁动势降落在气隙上，等效磁路中还存在着气隙磁阻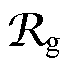，并有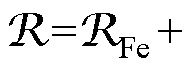
。
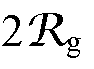（3）变压器和感应电机外接负载ZL可直接考虑在等效磁感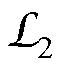里，其中，变压器的二次绕组等效磁感
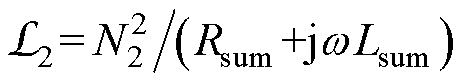，感应电机的转子笼型绕组等效磁感
。
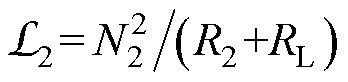（4）变压器是静止设备，感应电机是旋转设备，因此磁感元件上的电频率并不同：在变压器中，电频率w 是一次绕组的激励电频率；在感应电机中，电频率sw 是转子相对于旋转磁场的转差频率。
（5）等效磁感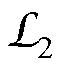上产生有功损耗
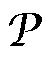，让电源侧输入有功功率以抵消损耗，在感应电机中经转轴对外输出机械转矩。
为验证上述理论分析，对变压器和感应电机进行实验验证。首先，实验用单相变压器如图8a所示，相关参数见表1。搭建了如图8b所示的变压器实验平台，其中，可控交流电源与变压器的一次绕组相连，并用于调节一次侧的输入电压大小和测量输入功率；在负载实验下，变压器的二次绕组连接可变电阻，并通过示波器测量一次侧的输入电流、二次侧所接负载两侧的端电压大小；在空载实验下，变压器的二次侧开路。
图8 变压器实物及实验平台
Fig.8 Transformer and its experimental platform
表1 变压器的主要参数
Tab.1 Major parameters of the transformer
参 数数 值 (型号) 变压器型号JR/C-3264100 额定容量/(kV·A)1 一次绕组额定电压/V220 二次绕组额定电压/V110 一次绕组绕制匝数340 二次绕组绕制匝数172
为验证铁心损耗的等效磁感对磁通幅值和相位的影响，在不同一次电压下进行了变压器空载实验，如图9所示。
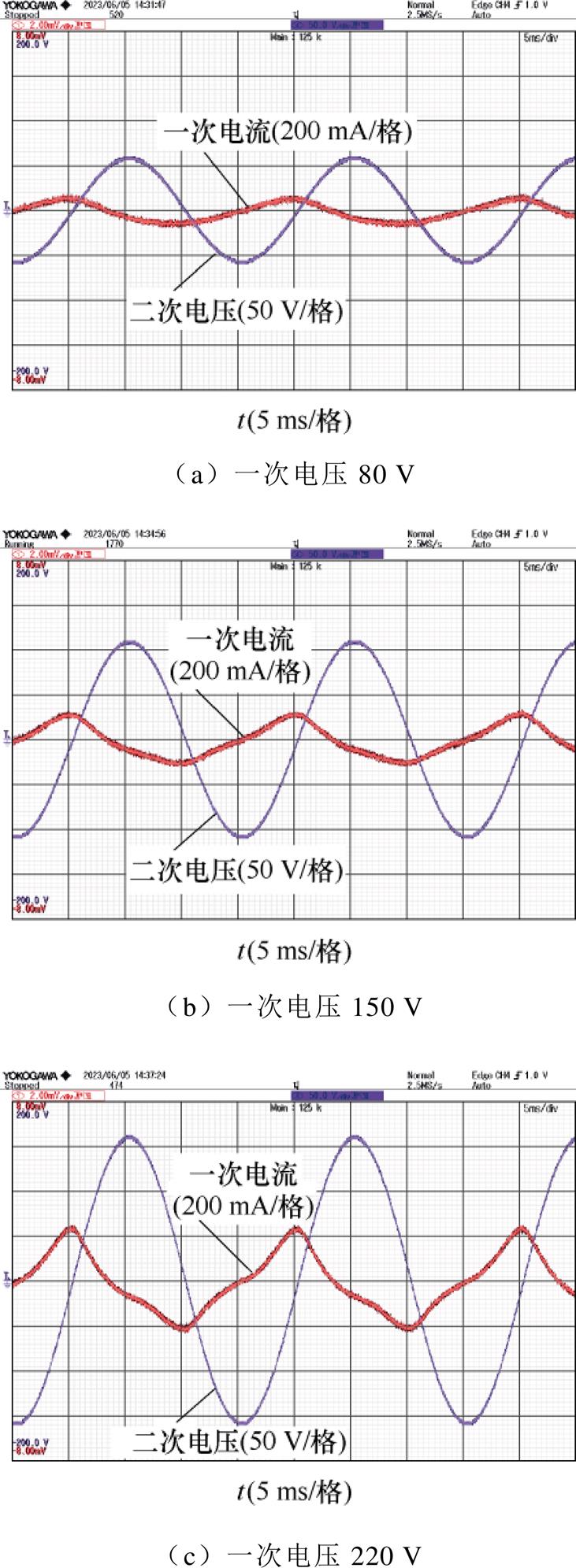
图9 变压器空载电流与二次绕组感应电动势波形
Fig.9 No load current of prime winding and induced voltage waveforms of secondary winding
测得一次电压、电流和功率，通过二次绕组感应电动势E2来测量和确定铁心中的磁通Fm。其中，Fm超前E2 90°，并满足E2=4.44fN2Fm。一次侧输入功率扣除一次绕组的电阻损耗，得到空载变压器铁心损耗，由式（5）计算得到空载铁心损耗对应的等效磁感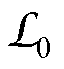。再根据式（6）和式（7），可得到空载励磁电流I0和铁耗角aFe。也可利用快速傅里叶变换（Fast Fourier Transformation, FFT），分解得到I0和E2基波的幅值和相位，并进一步根据磁通超前感应电动势90°的相位，得到磁通与励磁磁动势之间的相位差aFe。
表2列出了不同一次电压下，空载主要参数的实测值和理论值的对比。可以看到，随着一次电压的上升，空载铁耗和空载电流也随之变大，影响了变压器铁心的工作状态，导致铁耗角逐渐变小。但是总体上，实测值和计算值的大小吻合，验证了理论分析的正确性。
表2 空载变压器参数对比
Tab.2 Comparison of no-load parameters
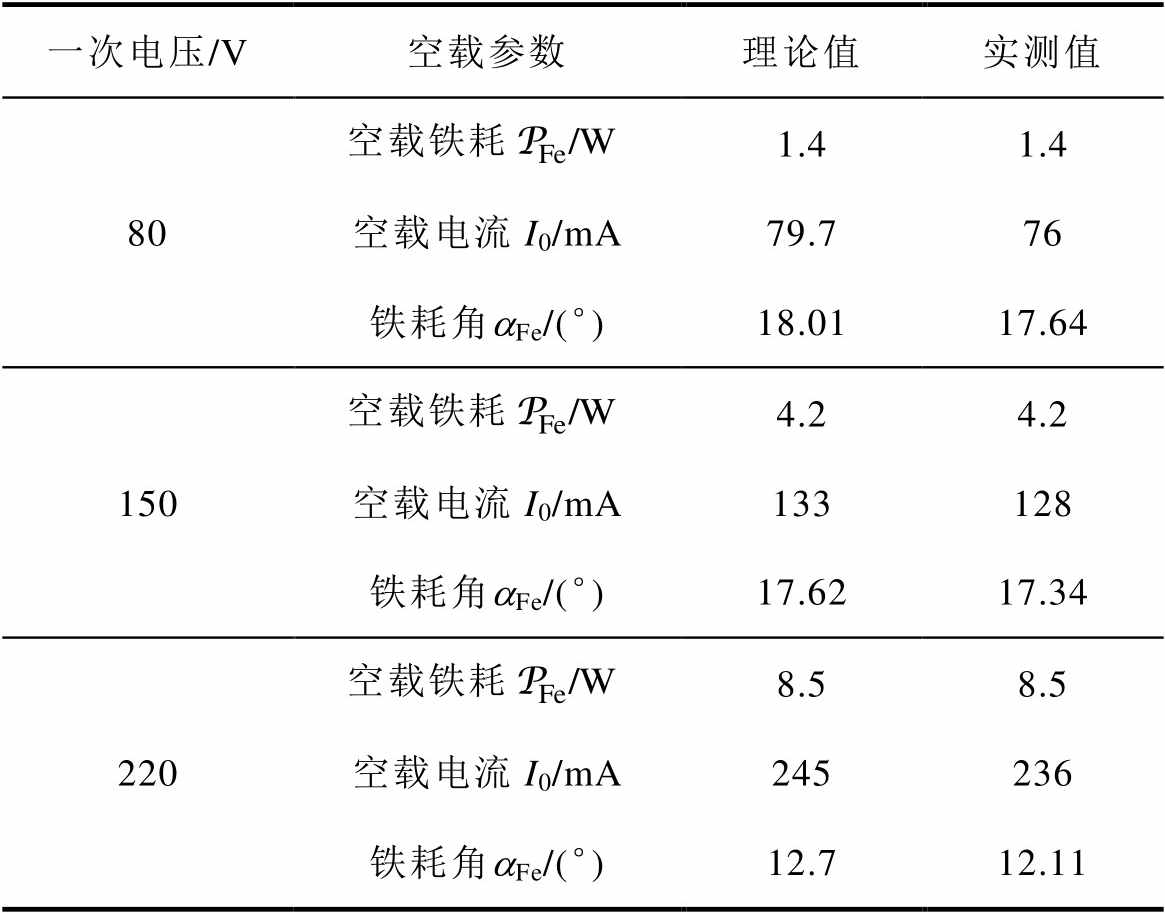
一次电压/V空载参数理论值实测值 80空载铁耗1.41.4 空载电流I0/mA79.776 铁耗角aFe/(°)18.0117.64 150空载铁耗4.24.2 空载电流I0/mA133128 铁耗角aFe/(°)17.6217.34 220空载铁耗8.58.5 空载电流I0/mA245236 铁耗角aFe/(°)12.712.11
当二次绕组连接负载后，根据式（9），在变压器磁路里多出了一项磁感元件，其等效矢量磁路如图4所示，考虑了外接负载后的磁感元件值见式（10）。根据变压器原理，如忽略变压器一次绕组的漏阻抗，则有：U1=4.44fN1Fm。在保持一次侧外加电压大小不变时，变压器铁心中的磁通为一常数，并与空载时的磁通数值大小相同。
此外，经测量得到的二次绕组电阻R2的大小为0.2 W，在外加负载电阻较大时，可忽略二次绕组的漏阻抗，近似认为二次绕组外加负载两侧的端电压U2等于二次绕组的感应电动势E2，从而通过测量U2来得到E2。与空载时类似，通过FFT分解得到I1和U2（E2）基波的幅值和相位，铁心中磁通的大小通过U2（E2）来确定，并且磁通超前感应电动势90°。如此，将相关参数代入式（11），即可求出I1，并进一步求得输入有功功率。
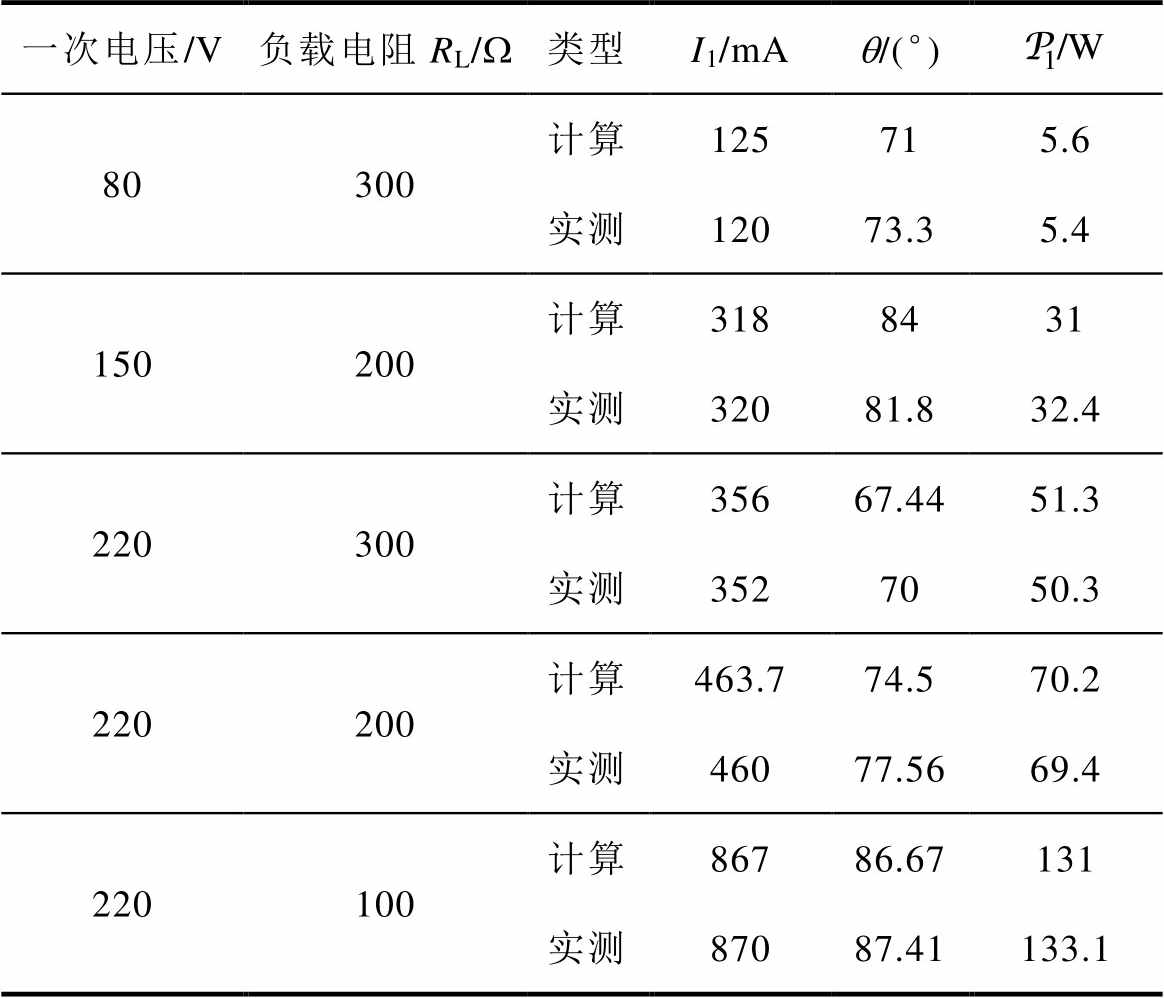
表3给出了一次电压U1分别为80、150和220 V，外接不同负载电阻RL时，变压器一次绕组电流I1、磁通与磁动势相位差q 和一次侧输入功率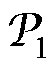
的实测结果与计算结果的对比。可以发现：
表3 负载变压器参数对比
Tab.3 Comparison of on-load parameters
一次电压/V负载电阻RL/W类型I1/mAq/(°) 80300计算125715.6 实测12073.35.4 150200计算3188431 实测32081.832.4 220300计算35667.4451.3 实测3527050.3 220200计算463.774.570.2 实测46077.5669.4 220100计算86786.67131 实测87087.41133.1
（1）在RL大小不变时，改变一次电压（RL= 300 W、U1=80 V和220 V，RL=220 W、U1=150 V和220 V）会改变I1、q 和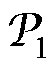的大小。由4.1节中的分析可知，这是因为不同一次电压下，变压器铁心的工况有所不同，从而影响了负载下的结果。
（2）在U1大小不变时，改变外接负载（U1= 220 V，RL=100 W、200 W 和300 W）同样会影响结果。由式（10）和式（11）可知，这是因磁感元件对磁路的作用所致。
总体而言，在变电压和变负载情况下，基于磁感的等效矢量磁路计算结果与实验结果吻合得较好，其有效性得到了验证。
为进一步说明磁感元件对于磁路的调节作用，图10给出了一次电压为80 V、RL变化时的I1和E2的实验波形，并且在图中标注了I1和E2的相位差。其中，q1～q3分别表示外接负载电阻RL从100 W 变化到300 W 时，对应的磁动势和磁通之间的相位差，并且其大小的确定与上文的分析相同。
根据式（10）和式（11），当变压器铁心磁通Fm固定不变时，负载电阻越小，二次绕组的等效磁感越大，所需要的I1越大，磁通Fm滞后电流I1的相位也越大；反之，负载电阻越大，二次绕组的等效磁感越小，所需要的I1就越小，磁通Fm滞后I1的相位也越小；特别地，所接负载电阻足够大时，可认为是变压器空载情况，此时Fm滞后I1的相位只由铁心中的损耗对应的等效磁感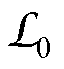引起。由图10a～图10c可知，在保持E2不变、即Fm不变时，随着二次绕组所接负载电阻RL从100 W 增大到300 W，I1越来越小，Fm滞后I1的相位也越来越小。这与理论分析的结果一致，再次表明了基于磁感的等效矢量磁路方法的有效性。
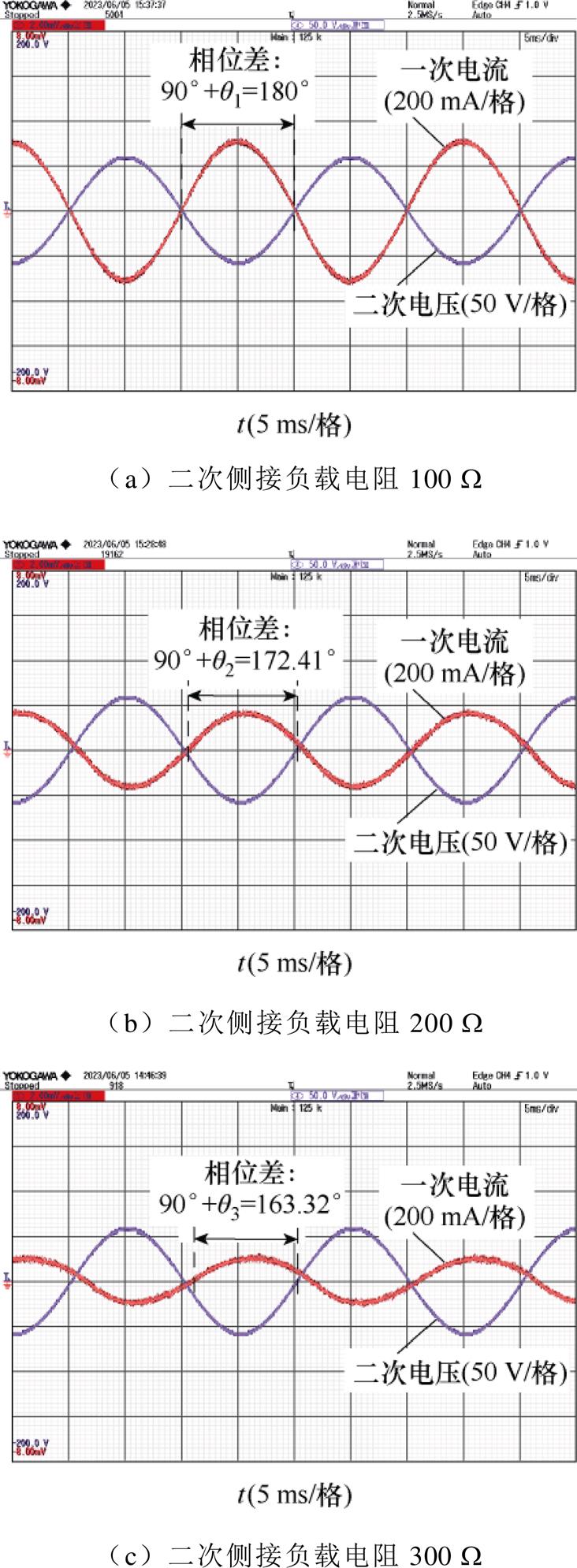
图10 一次电压为80 V，外接电阻变化得到的变压器一次绕组输入电流、二次绕组感应电动势波形
Fig.10 Input current of prime winding and induced voltage of secondary winding when varying the load resistances at the in put voltage being 80 V
为了验证感应电机的等效矢量磁路，对一台7.5 kW的标准Y2系列铸铝转子笼型感应电机进行了实验研究，主要参数见表4，实验平台如图11所示。电机以电动模式运行，定子绕组由电压源供电。转矩传感器用于在电机运行时测量转矩的大小。磁粉制动器用作电机负载。
表4 感应电机的主要参数
Tab.4 Major parameters of the induction motor
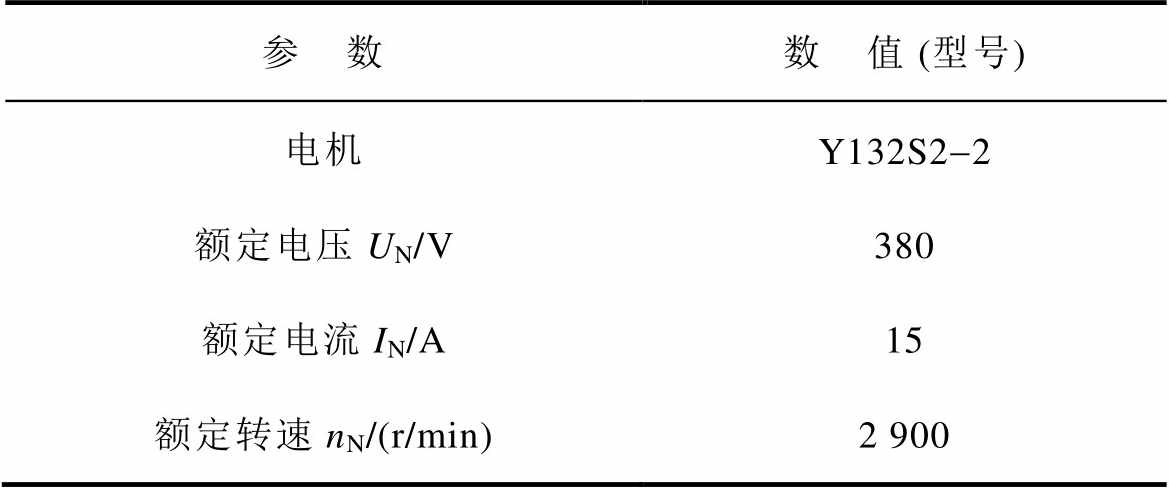
参 数数 值 (型号) 电机Y132S2-2 额定电压UN/V380 额定电流IN/A15 额定转速nN/(r/min)2 900
图11 感应电机实验平台
Fig.11 Experimental platform of induction motor
转矩-转差率图（T-s图）是感应电机最基本的特性之一。为此，测量电机在0～3 000 r/min下的转矩大小，并与根据式（13）～式（16）计算得到的理论转矩大小结果进行对比，其中，机械损耗转矩Tmech的计算经验公式见文献[34]，以得到输出机械转矩，如图12所示。
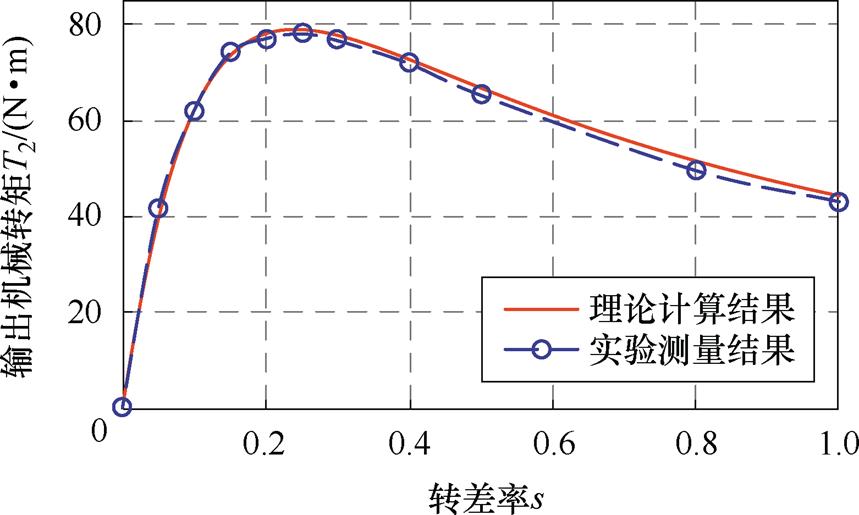
图12 感应电机的转矩-转差率曲线
Fig.12 Torque versus slip frequency of induction motor
在整个转差率区间内，理论结果和实验结果能够较好地吻合。随着转差率的上升，受饱和、漏磁等因素的影响，理论计算得到的电机输出机械转矩值略大于实验测得的机械转矩值，但误差在可接受范围内，验证了等效磁路计算感应电机性能的有效性。
本文根据磁感及矢量磁路理论，推导了适用于任意工况下的变压器和感应电机等效矢量磁路，以磁路角度描绘了二者电磁量的相量图，并对它们在不同工况下的特性进行了定量分析计算，实验结果验证了所提等效矢量磁路方法的有效性。
与传统的等效电路分析方法相比，本文所提的等效矢量磁路方法省去了原有分析中必不可少的匝数归算、频率归算等工作，物理概念清楚，计算过程简洁。它既可以清晰地定性、定量表征变压器和感应电机中铁心涡流损耗等效磁感对磁通幅值及相位差的影响，也可以直接计算它们的参数变量，还能够计算感应电机的转矩-转差率曲线等工作特性，从而为电机等电磁装备的分析、设计和控制提供了全新且直观的视角和方法。
此外，如果在电机学课程和教材中引入等效矢量磁路分析，有望降低相关内容的理解和学习难度，可为电机学教材的改革提供参考。
附 录
感应电机笼型转子等效磁感的计算过程如下。
根据前面对于磁感元件的描述可知，构成一个磁感元件的导条上流经相同的电流。但是对于附图1a所示的笼型转子，公共端环上流过电流和其相邻的导条上流过电流并不相等。为考虑公共端环的作用，需要对笼型转子进行等效处理，如附图1b所示。附图2a、附图2b分别表示感应电机转子导条上的感应电动势和电流与源励磁磁场的关系，其中，j1为导条电流和源励磁磁场之间的空间相位差。由于定、转子间的相对旋转，源励磁磁场Bm依次切割各个导条，并感应出电动势，相邻导条的感应电动势相差a 电角度，满足
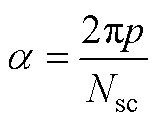（A1）
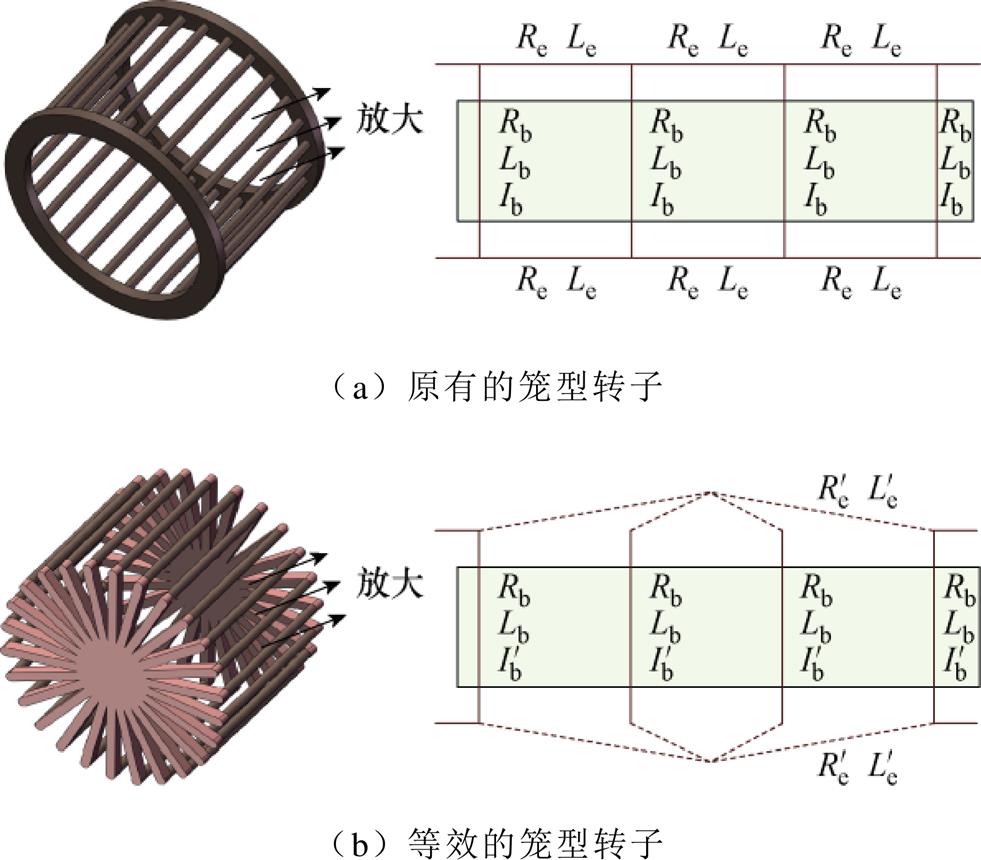
附图1 笼型转子拓扑和参数
App.Fig.1 Topology and parameters of the cage rotor
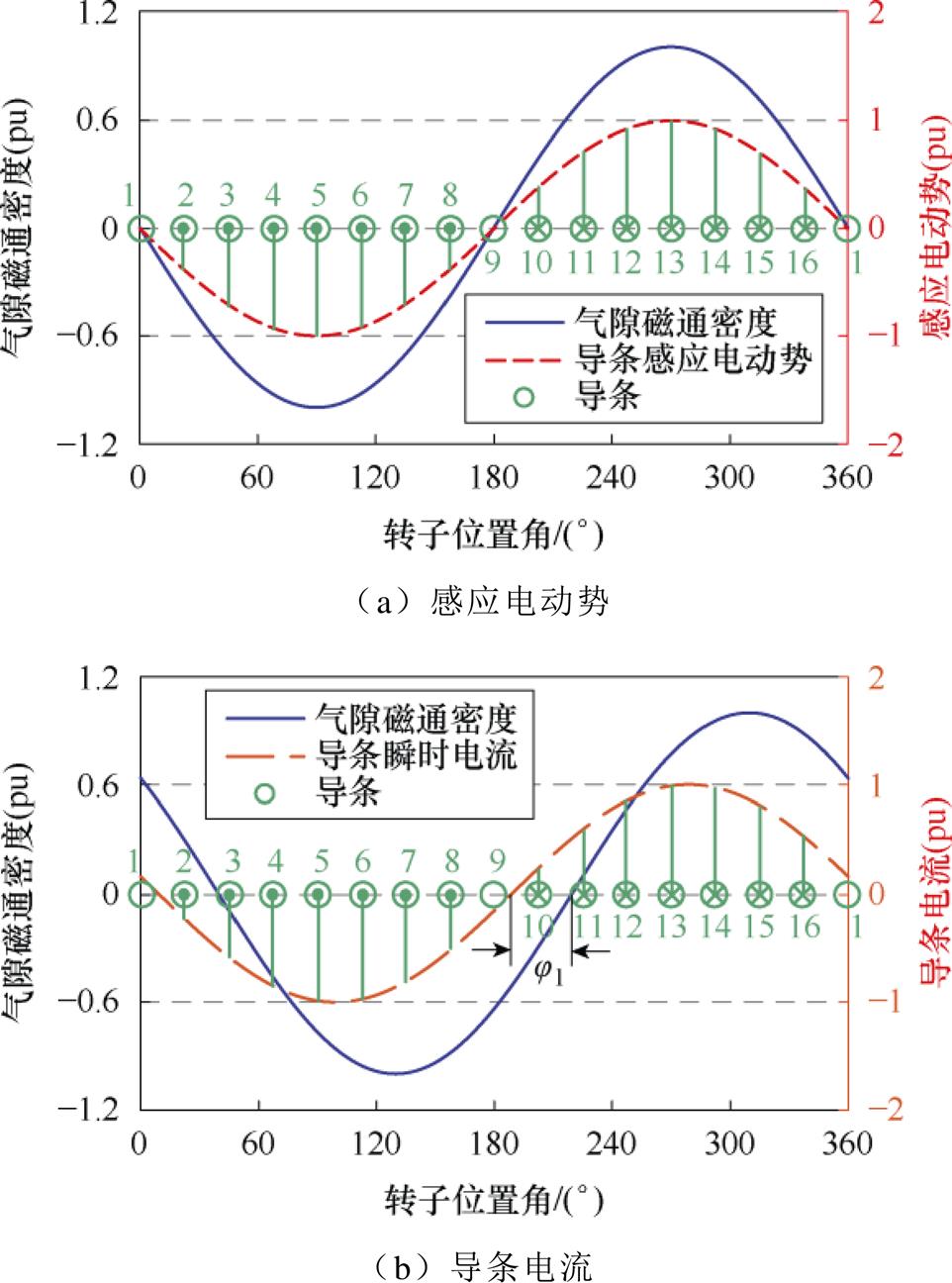
附图2 笼型转子导条感应电动势和电流分布
App.Fig.2 Distribution of induced voltage and current in each bar
式中，p为电机极对数；Nsc为转子的导条数。由于笼型转子结构对称，相邻导条中的电流相位也相差a 电角度，并且公共端环电流等于相邻两根导条电流之差。
参考星形-三角形变换，如附图1所示，将公共端环的正多边形阻抗变换成正三角形阻抗为
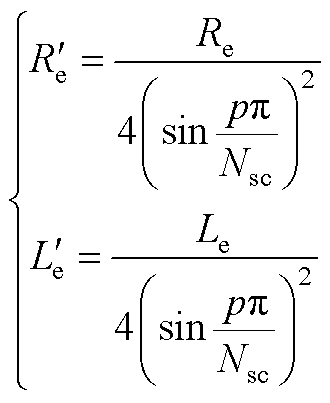（A2）
式中，Re和Le为公共端环上的电阻和漏电感。可以得到，每个导条的等效电阻R和等效漏电感L为
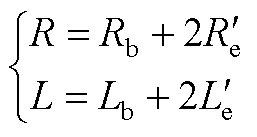（A3）
式中，Rb和Lb为原有导条的电阻和漏电感。由于导条电阻比漏感抗更大，为便于分析，仅考虑R即可，并代入式（1），即可得到单个磁感元件的大小。
参考文献
[1] 吴大榕. 电机学-上册[M]. 北京: 水利电力出版社, 1959.
[2] 章名涛. 电机学-下册[M]. 北京: 科学出版社, 1964.
[3] 许实章. 电机学[M]. 北京: 机械工业出版社, 1980-1981.
[4] 周鹗. 电机学[M]. 3版. 北京: 中国电力出版社, 1995.
[5] 胡虔生, 胡敏强. 电机学[M]. 北京: 中国电力出版社, 2005.
[6] 汤蕴璆. 电机学[M]. 4版. 北京: 机械工业出版社, 2011.
[7] Smolensky A I. Electrical Machines[M]. Moscow: MIR Publishers, 1982.
[8] Fitzgerald A E, Kingsley C, Umans S D. Electric Machinery[M]. 6th ed. New York: McGraw-Hill Companies, 2003.
[9] Joule J P. The Scientific Papers of James Prescott Joule[M]. Cambridge: Cambridge University Press, 1884.
[10] Heaviside O. Electrical Papers[M]. Cambridge: Cambridge University Press, 2011.
[11] Miller J D. Rowland’s magnetic analogy to Ohm’s law[J]. Isis, 1975, 66(2): 230-241.
[12] Hopkinson J. Magnetisation of iron[J]. Philosophical Transactions of the Royal Society of London, 1885, 176: 455-469.
[13] 程明, 周鹗, 黄秀留. 双凸极变速永磁电机的变结构等效磁路模型[J]. 中国电机工程学报, 2001, 21(5): 23-28.
Cheng Ming, Zhou E, Huang Xiuliu. Variable structure equivalent magnetic circuit modeling for doubly salient permanent magnet machine[J]. Pro- ceedings of the CSEE, 2001, 21(5): 23-28.
[14] 张淦, 花为, 程明, 等. 磁通切换型永磁电机非线性磁网络分析[J]. 电工技术学报, 2015, 30(2): 34-42.
Zhang Gan, Hua Wei, Cheng Ming, et al. Analysis of nonlinear magnetic network models for flux- switching permanent magnet machines[J]. Transa- ctions of China Electrotechnical Society, 2015, 30(2): 34-42.
[15] 庞古才, 邓智泉, 张忠明. 基于改进广义磁路法的表贴式永磁电机空载气隙磁场解析计算[J]. 电工技术学报, 2019, 34(22): 4623-4633.
Pang Gucai, Deng Zhiquan, Zhang Zhongming. Analytical calculation of no-load air gap magnetic field in surface-mounted permanent magnet motor based on improved generalized magnetic circuit method[J]. Transactions of China Electrotechnical Society, 2019, 34(22): 4623-4633.
[16] 郭凯凯, 郭有光. 磁通反向直线旋转永磁电机三维非线性等效磁路模型分析[J]. 电工技术学报, 2020, 35(20): 4278-4286.
Guo Kaikai, Guo Youguang. 3D nonlinear equivalent magnetic circuit model analysis of a flux reversal linear rotary permanent magnet machine[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(20): 4278-4286.
[17] 张志弘, 韩勤锴, 徐学平, 等. 基于保角变换与等效磁路法的永磁直驱发电机气隙磁场计算[J]. 电工技术学报, 2023, 38(3): 703-711.
Zhang Zhihong, Han Qinkai, Xu Xueping, et al. Air gap magnetic field calculation of permanent magnet direct drive generator based on conformal mapping and magnetic equivalent circuit method[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(3): 703-711.
[18] 佟文明, 王萍, 吴胜男, 等. 基于三维等效磁网络模型的混合励磁同步电机电磁特性分析[J]. 电工技术学报, 2023, 38(3): 692-702.
Tong Wenming, Wang Ping, Wu Shengnan, et al. Electromagnetic performance analysis of a hybrid excitation synchronous machine based on 3D equivalent magnetic network[J]. Transactions of China Elec- trotechnical Society, 2023, 38(3): 692-702.
[19] 罗玲, 侯红胜, 宋受俊. 中美英三国“电机学”课程体系的分析[J]. 电气电子教学学报, 2013, 35(2): 33-35.
Luo Ling, Hou Hongsheng, Song Shoujun. Analysis of the syllabus of electrical machinery in China, America and Britain[J]. Journal of Electrical & Electronic Education, 2013, 35(2): 33-35.
[20] 谢宝昌, 刘长红, 王君艳, 等. “电机学”课程体系的优化[J]. 电气电子教学学报, 2011, 33(4): 18-20.
Xie Baochang, Liu Changhong, Wang Junyan, et al. Systematic optimization of electric machinery curriculum[J]. Journal of Electrical & Electronic Education, 2011, 33(4): 18-20.
[21] 曾令全, 李书权. “电机学”精品课建设及教学改革与实践[J]. 中国电力教育, 2013(27): 99-100.
[22] 秦海鸿, 王晓琳, 黄文新, 等. “电机学”课程教学改革研究[J]. 电气电子教学学报, 2014, 36(4): 36-38.
Qin Haihong, Wang Xiaolin, Huang Wenxin, et al. Research on the teaching reform of electric machines course[J]. Journal of Electrical & Electronic Education, 2014, 36(4): 36-38.
[23] 叶才勇. 新工科背景下《电机学》教材改革探析[J]. 学园, 2020, 13(7): 88-89.
[24] Laithwaite E R. Magnetic equivalent circuits for electrical machines[J]. Proceedings of the Institution of Electrical Engineers, 1967, 114(11): 1805.
[25] Carpenter C J. Magnetic equivalent circuits[J]. Pro- ceedings of the Institution of Electrical Engineers, 1968, 115(10): 1503-1511.
[26] Buntenbach R W. Improved circuit models for inductors wound on dissipative magnetic cores[C]// 2nd Asimolar Conference on Circuits and Systems, 1968.
[27] 国家技术监督局. 电学和磁学的量和单位: GB/T 3102.5-1993[S]. 北京: 中国标准出版社, 1994.
[28] Quantities and units-part 6: electromagnetism: IEC 8000-6[S]. Geneva: IEC, 2022.
[29] Cheng Ming, Qin Wei, Zhu Xinkai, et al. Magnetic- inductance: concept, definition, and applications[J]. IEEE Transactions on Power Electronics, 2022, 37(10): 12406-12414.
[30] 秦伟, 程明, 王政, 等. 矢量磁路理论及应用初探[J/OL]. 中国电机工程学报, 2023: 1-14 [2023-11-07]. DOI: 10.13334/j. 0258-8013.pcsee.232113.
Qin Wei, Cheng Ming, Wang Zheng, et al. Vector magnetic circuit theory and its preliminary applications[J/OL]. Proceedings of the CSEE, 2023: 1-14 [2023-11-07]. DOI: 10.13334/j.0258-8013.pcsee. 232113.
[31] 程明, 秦伟, 朱新凯, 等. 楞次定律的定量化表征[EB/OL]. 中国科技论文在线[2022-07-21]. http:// www.paper.edu.cn/releasepaper/content/2022-07-21.
[32] Qin Wei, Cheng Ming, Zhu Sa, et al. Reluctance and magductance calculation of laminated core under different frequency for electrical machines[C]//2022 25th International Conference on Electrical Machines and Systems (ICEMS), Chiang Mai, Thailand, 2022: 1-6.
[33] Qin Wei, Cheng Ming, Wang Jingxia, et al. Com- patibility analysis among vector magnetic circuit theory, electrical circuit theory, and electromagnetic field theory[J]. IEEE Access, 2023, 11: 113008- 113016.
[34] 陈世坤. 电机设计[M]. 2版. 北京: 机械工业出版社, 2013.
Abstract The analysis of the working principle of transformers and induction motors mainly employs the equivalent electrical circuit in the traditional electrical machine theory. This approach represents actual magnetic quantities as electrical quantities, adding complexity to analysis. The traditional magnetic circuit theory, which only has reluctance elements, fails to characterize the phase differences between flux and magnetomotive force or iron losses, becoming a bottleneck.
This paper introduces a novel magnetic parameter called magductance. By vector magnetic circuit theory, an equivalent vector magnetic circuit is established and applicable to transformer and induction motor analysis. Firstly, the equivalent magnetic circuit for different working conditions is derived. At no-load conditions, the core loss is expressed in terms of magductance L0. The phase difference between flux and magnetomotive force corresponds to the iron loss angle. The effect of the secondary side can be reflected through magductance L2. When the load is zero, the expression for magductance is based on the original definition. The phasor diagram of the transformer derived from equivalent vector magnetic circuit takes magnetic flux Fm as the common reference phasor, and links among the primaryside, secondary side, and core are directly expressed by magnetic quantity. Secondly, the equivalent vector magnetic circuit for the induction motor is derived. It adds the airgap reluctance Rg, and the rotor squirrel cage is equivalent to the magductance L2. Finally, the equivalent vector magnetic circuits for the transformer and induction motor are analyzed. (1) Vector magnetic circuit comprises reluctance R, equivalent magductance of core lossL0, and equivalent magductance of secondary side (the rotor squirrel cage in the induction motor) L2. (2) Loads of the transformer and induction motor can be directly considered in the equivalent magductance L2. (3) For the transformer, R is equal to core reluctance RFe, and there is R=RFe+2Rg in the induction motor. (4) Electrical frequency w is the excitation electrical frequency of primary winding in the transformer, and electrical frequency sw is the slip frequency of the rotor relative to the magnetic field in the induction motor. Experimental measurements agree well with the calculated results of the transformer and induction motor.
Compared with the existing equivalent electrical circuit, the proposed equivalent vector magnetic circuit saves the necessary turns referring and frequency referring. It characterizes the effect of L0 on the magnetic flux and phase difference and calculates their output performance, providing a novel and intuitive method for analyzing, designing, and controlling electromagnetic equipment.
keywords：Magductance equivalent magnetic circuit, vector magnetic circuit theory, transformer, induction motor, electrical machinery
DOI: 10.19595/j.cnki.1000-6753.tces.231300
中图分类号：TM301; TM401; TM14
国家自然科学基金原创探索计划资助项目（52250065）。
收稿日期 2023-08-10
改稿日期 2023-09-23
程 明 男，1960年生，东南大学首席教授、博士生导师，主要研究方向为电动车驱动控制技术、新能源发电技术、微特电机及测控系统等。E-mail: mcheng@seu.edu.cn（通信作者）
马钲洲 男，1999年生，博士研究生，研究方向为基于磁场调制理论的电机分析、设计与优化。E-mail: mzz_ee@seu.edu.cn
（编辑 郭丽军）