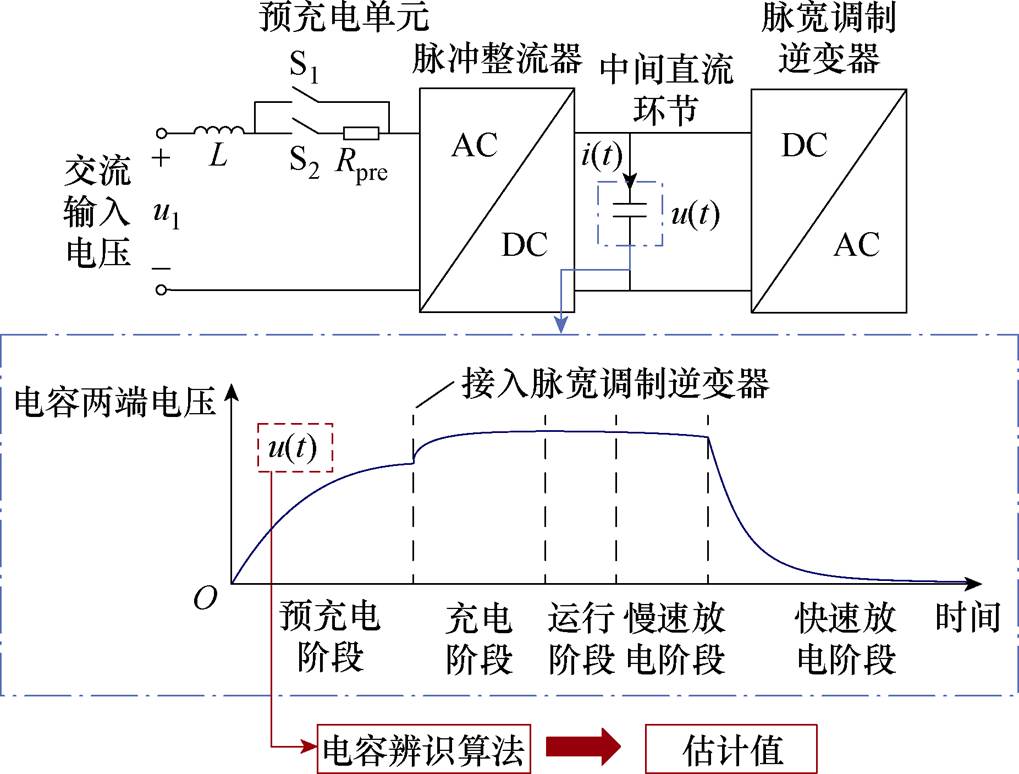
图1 某变流器中间直流支撑电容器两端电压监测模型
Fig.1 A converter intermediate DC-link capacitor voltage monitoring model at both ends
摘要 为了解决车载牵引变流系统直流支撑电容器故障预测问题,该文提出一种基于物理信息神经网络的直流支撑电容器参数辨识方法。该方法只需要利用直流环节预充电过程的直流支撑电容器两端电压及采样频率,无需拟合曲线,无需严格对齐时间轴就可以获得较为准确的电容参数辨识结果。与此同时,为了克服在采集数据时因条件所限造成的数据量稀疏与分布不均问题,该文利用循环一致性生成对抗网络算法增强数据,使该方法可以适用于同一拓扑下宽范围电容区间的电容容值预测,降低了模型训练要求。实验结果表明:在正常条件下,该方法的辨识相对误差约在1%以下,并且降低采样频率能够缓解信噪比对该方法的影响。该方法为解决直流支撑电容参数辨识问题提供了新思路。
关键词:直流支撑电容器 参数辨识 物理信息神经网络 循环一致性生成对抗网络 直流环节预充电工况
直流环节支撑电容(即DC-link电容)作为变流器中间直流环节用于实现电能变换的关键执行部件[1],能够对输入源与输出负载在工作时产生的瞬时功率差进行平衡,因而在当前应用技术下,最大限度地实现了变流器中间直流环节高脉冲电流的吸收和高脉冲电压的缓冲,起到滤除纹波的作用[2]。目前,牵引变流器系统直流环节支撑电容器多采用低阻抗、大容量、无极性、对过电压和反向脉冲电压承受能力较强、使用寿命长的金属化聚丙烯薄膜电容器[3-4]。据统计,在车载变流系统故障分布中,因直流支撑电容发生故障的占比最大[5],因此,对于列车运维来说,对牵引变流器支撑电容劣化特征参数进行状态监测具有合理性以及相当大的科学实用价值[6-7]。
目前,根据所研究的变流系统运行阶段的不同,可以将现有电容特征参数辨识方法[8]大致分为基于周期性小信号纹波原理的辨识方法和基于非周期性大信号充放电曲线原理的辨识方法。针对基于纹波原理的辨识方法,优势在于可以全时段实时监测电容特征参数变化[9]。其中文献[10]提出了一种非侵入式电容状态监测系统,并使用支持向量机模型算法来对得到的电磁干扰测量值进行训练,从而获得电容状态参数。文献[11]以背靠背变换器DC-link电容器的电容值作为研究对象,以输入/输出的电流/电压和纹波电压为输入,使用经典人工神经网络的方法预测电容容值变化,达到了近1%的最大估计误差。文献[12]主要利用开关频率与初始值的比较,从而获得其与电压电容器的映射模型,再采用反向传播神经网络对这个映射关系进行训练,实验结果表明该方法预测电容值的最大误差仅为1%。
针对基于充放电曲线原理的辨识方法,优势在于利用列车起动时的一个必要阶段进行监测,与电驱动系统运行时的工况无直接关联,无需对列车高速运行状态产生干扰,因此能够提高诊断准确度,并避免因工况变化而引起的诊断误判。与此同时,电容器老化速度缓慢的特性也提高了该方法监测电容器的容错率。文献[13]利用带噪声估计的递推增广最小二乘法针对直流支撑电容预充电模型进行参数估计,误差在5%以内。文献[14]将模块化多电平转换器简化为模块化RC充电电路,通过研究相电压和各个子模块电容器电压之间的关系来得出子模块的电容容值,且无需额外传感器即可监控所有电容器。文献[15]则使用的是电容器放电曲线,并通过预设的可变电气网络单元来对三相脉宽调制功率变换器直流侧电容器进行电容值和等效串联电阻监测,误差在3%以内。文献[16]针对电气可调速驱动器系统提出了基于LC谐振电容器放电曲线的方案,实验结果表明,在3 kW异步电机变频调速系统中,电容值估计误差可达1%。
这些文献成果对于解决直流支撑电容器参数辨识问题都具有相当重要的指导意义,但仍有一些局限存在。例如,利用拟合方法的基于充放电曲线的辨识方法易受到降噪参数的影响;在列车实际采集条件下充电触发信号延迟导致的难以确定充电起始时间的情况;利用数据驱动算法的物理可解释性低,受限于采集数据的质量,训练好的模型具有电容区间范围窄等问题。
为了解决以上难题,本文提出了一种基于物理信息神经网络(Physics-Informed Neural Network, PINN)与电容预充电模型的牵引变流器直流支撑电容参数辨识方法。该方法的优势在于对电压传感器的采样频率要求很低,无需电容预充电电压曲线与时间轴严格对齐,能够有效降低测量信噪比对预测结果的影响。而且通过使用循环一致性生成对抗网络(Cycle-consistent Generative Adversarial Net- works, CycleGAN)算法增强数据,所需电容数据量很少,采集质量要求低。与此同时,该方法适用于同一拓扑下宽范围电容区间,有望实现训练成功的模型在相同拓扑、不同支撑电容容值监测条件下的迁移。因此,该方法能够合理地应用在轨道交通领域应用,具有工程实用价值。
图1所示为某变流器中间直流支撑电容器两端电压监测模型。以图1为例,当该牵引变流器开始正式运行前,都需要通过带有一个电阻的预充电单元对直流支撑电容进行充电,以保证不会由于输入电压直接加在未充电的支撑电容组上,瞬间产生较大的峰值电流,对变流器安全和电容寿命造成负面影响。预充电环节开始时,先将脉宽调制逆变器与中间直流环节断开,通过一个预充电接触器S2将电容器与一个限流电阻相连接。在这个阶段电容器处于充电状态,而限流电阻会使电容器充电电流受到限制,从而实现缓慢充电的目的。当预充电环节结束后,才会闭合输入线路的接触器S1,并接入脉宽调制逆变器开始正常运行。本方法的研究对象为预充电阶段直流支撑电容两端电压变化过程。

图1 某变流器中间直流支撑电容器两端电压监测模型
Fig.1 A converter intermediate DC-link capacitor voltage monitoring model at both ends
无谐振支路牵引变流系统直流环节预充电阶段等效电路如图2所示。图中,i1为网侧交流输入电流,i2为直流环节输入电流,i3为流过直流支撑电容的电流,i4为流过等效并联电阻R*的电流,u1为网侧交流输入电压,u2为直流环节输入电压,uC为直流支撑电容两端电压,Rpre为预充电阶段限流电阻,L为网侧电感,将预充电阶段脉冲整流器等效为一个不可控整流桥,将直流支撑电容器等效为电容C、等效电阻RESR与等效电感LESL的串联形式,将直流环节叠层母排主线路导线电阻等效为Req,将直流环节除了直流支撑电容的其他电路元件等效为一个并联电阻R*。
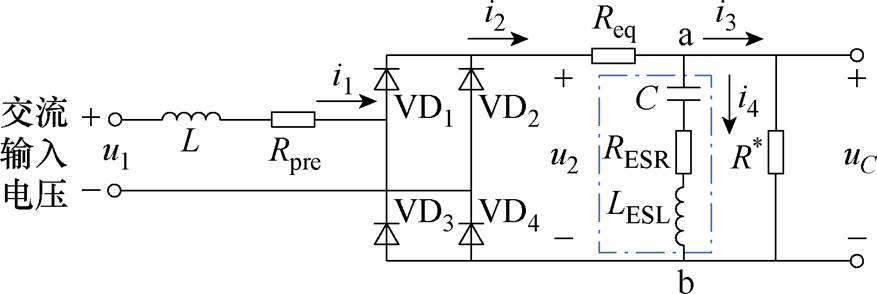
图2 直流环节预充电阶段等效电路
Fig.2 Equivalent circuit diagram of DC-link pre-charging stage
在预充电阶段,脉冲整流器处于不可控整流状态,可得电流关系为
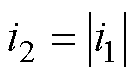 (1)
(1)
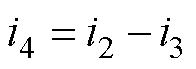 (2)
(2)
忽略整流二极管的压降,根据基尔霍夫定律和欧姆定律,可得关系式为
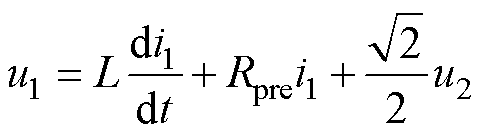 (3)
(3)
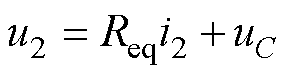 (4)
(4)
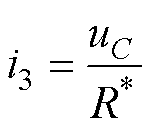 (5)
(5)
由于牵引变流器直流支撑电容一般选用介质损耗很低的金属薄膜电容器,等效串联电阻RESR与等效串联电感LESL相对很小,因此此处电压关系仅考虑电容器电容的影响,故可得
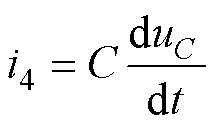 (6)
(6)
根据叠加定理、戴维南定理、诺顿定理和带电容的一阶零响应充电电路原理,可得预充电时的直流支撑电容分压关系式为
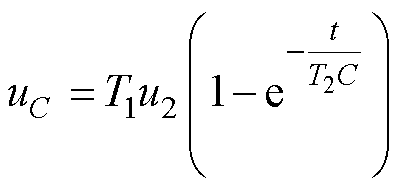 (7)
(7)
其中
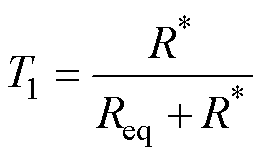
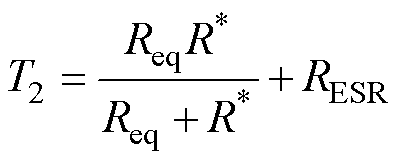
可得直流支撑电容器的电容容值C数学计算式为
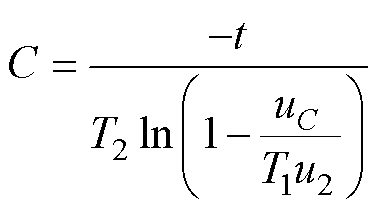 (8)
(8)
考虑监测到的电容器预充电电压曲线噪声较大,直接使用公式计算可能出现难以获得最优特征点而造成的预测误差。与此同时,反解带有超越数的方程组带来的复数误差累积,重要电压、电流或电阻参数数据难以获得等问题都制约了直接公式计算方法的普及。因此,本文将使用物理规律驱动与数据驱动相结合的方法进行牵引变流器直流支撑电容参数辨识,该方法需要参数量少,可实现提高预测准确度的目的。
迄今为止,将数据驱动用物理知识信息约束的物理学信息机器学习思路已经得到了广泛认同[17],其中,物理信息神经网络(PINN)[18-20]能够在有限数据量的情况下,通过引入物理模型特征,训练出具有物理约束的数据驱动模型,在保证良好精度的前提下,减少对数据质量的依赖,提高深度学习算法的泛化能力及其在工程领域的应用价值[21],且在各领域已经有了不少研究成果[19, 22-26]。PINN基本建模思路为:构造一个前馈全连接深度神经网络,使用偏微分方程、初始条件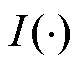 以及边界条件
以及边界条件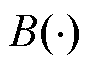 构造残差并按相对权重加入损失函数,利用深度神经网络中的自动微分技术最小化残差从而优化网络参数,在有效迭代次数下逼近微分方程的解,获得可靠的预测结果与预测模型。设
构造残差并按相对权重加入损失函数,利用深度神经网络中的自动微分技术最小化残差从而优化网络参数,在有效迭代次数下逼近微分方程的解,获得可靠的预测结果与预测模型。设
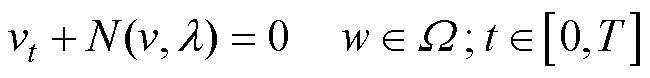 (9)
(9)
假设式(9)的解函数为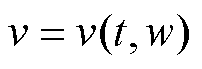 ,
,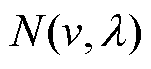 为一个对
为一个对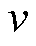 进行微分运算的泛函,
进行微分运算的泛函,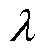 为泛函中的参数变量,w为空间变量,t为时间变量,
为泛函中的参数变量,w为空间变量,t为时间变量,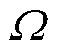 为欧氏空间的一个子集,
为欧氏空间的一个子集,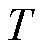 为终止边界时刻。从PINN深度学习算法的角度,定义
为终止边界时刻。从PINN深度学习算法的角度,定义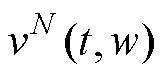 为逼近函数
为逼近函数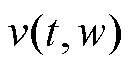 的前馈全连接深度神经网络,则式(9)与其初始条件
的前馈全连接深度神经网络,则式(9)与其初始条件 与边界条件
与边界条件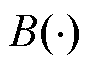 可分别表示为
可分别表示为
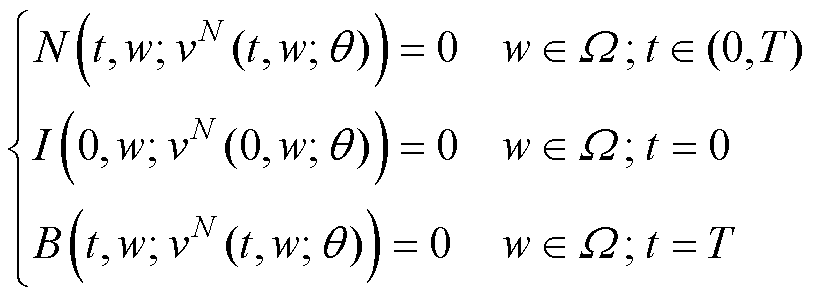 (10)
(10)
式中,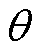 为网络参数
为网络参数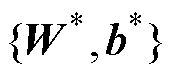 的集合;
的集合;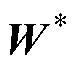 为前馈全连接深度神经网络的权值矩阵;
为前馈全连接深度神经网络的权值矩阵;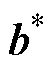 为前馈全连接深度神经网络的偏置向量。通过共轭梯度法、梯度下降法或牛顿法等优化算法来最小化损失函数,优化网络内部权重参数
为前馈全连接深度神经网络的偏置向量。通过共轭梯度法、梯度下降法或牛顿法等优化算法来最小化损失函数,优化网络内部权重参数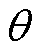 ,定义
,定义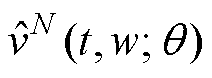 为网络的输出,
为网络的输出,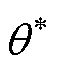 为优化目标,
为优化目标,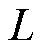 为损失函数,可将优化过程表示为
为损失函数,可将优化过程表示为
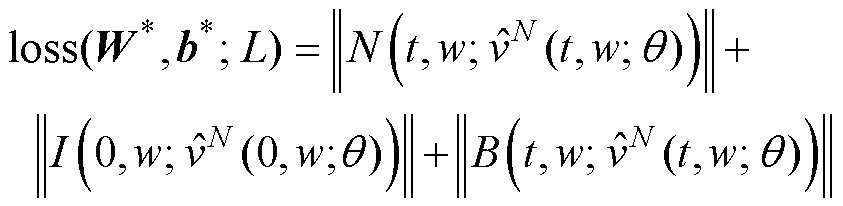 (11)
(11)
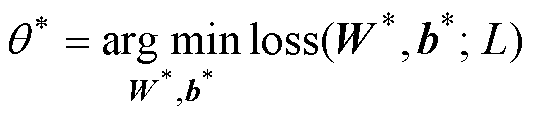 (12)
(12)
在实际工程情况下,充放电曲线是一个由多因素变量控制的曲线,但对于一个拓扑未发生变化的确定的变流系统来说,每次完成充放电过程获得的电容电压预充电曲线受其他因素的影响作用是相同的,而电容器老化导致的C和RESR变化是电压预充电曲线变化的主要原因。相较电容C容值,金属薄膜电容器介质损耗极低,等效串联电阻RESR很小极难辨识且与其健康状态相关度不高,对充放电曲线影响也更小,且因实验条件限制,本算例暂且只对电容器寿命特征参数中的电容容值C进行分析预测。因此,本算例前馈神经网络输出的物理量为电容容值C,输入物理量为电容容值C对应充电电压曲线根据采样间隔离散化构成的有序数组u以及符合采样间隔的离散等差时间有序数组t,其中t仅与采样频率相关,无需严格对齐充电电压曲线的充电时间。
设所选电压曲线长度为m,所有采集到的电容容值C组成的数组长度为n,即对应采样的电压点坐标域为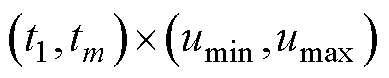 ,大小为
,大小为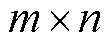 。将每个电压有序数组作为一个特征向量的一个维度,然后将多个电压有序数组组合成一个多维特征向量,时间有序数组也对应扩充为相同长度的多维特征向量。设训练输入样本矩阵为
。将每个电压有序数组作为一个特征向量的一个维度,然后将多个电压有序数组组合成一个多维特征向量,时间有序数组也对应扩充为相同长度的多维特征向量。设训练输入样本矩阵为
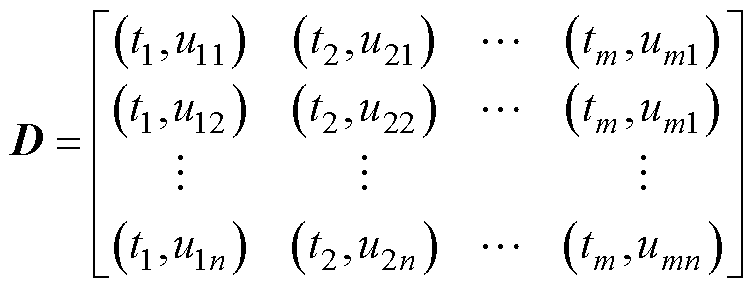 (13)
(13)
与此同时,若各样本点标签已知,精确解标签集可写为
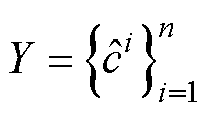 (14)
(14)
则本算例的训练样本集为D和Y。在进行模型训练前,需要对样本集进行最大最小标准化至一个固定区间 (0, 1),消除了特征之间因量纲不同而造成的影响,有助于提高模型的收敛速度和准确性。
由式(1)~式(8),根据数值微分法构建本算例的输出量电容容值C关于时间t与直流支撑电容充电电压u的偏微分方程,即
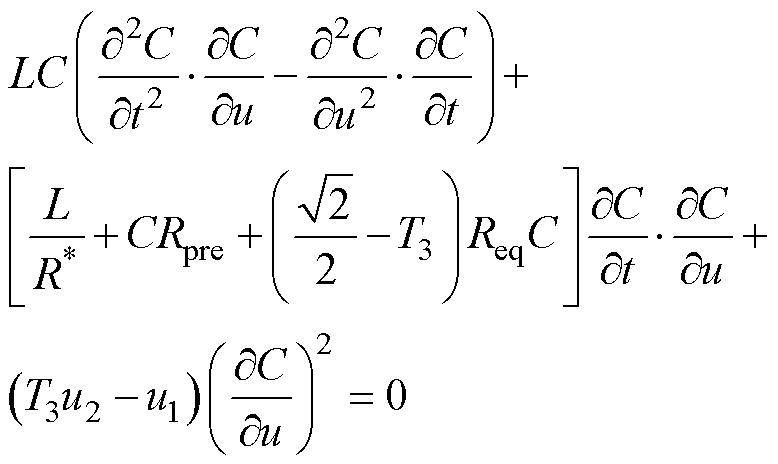 (15)
(15)
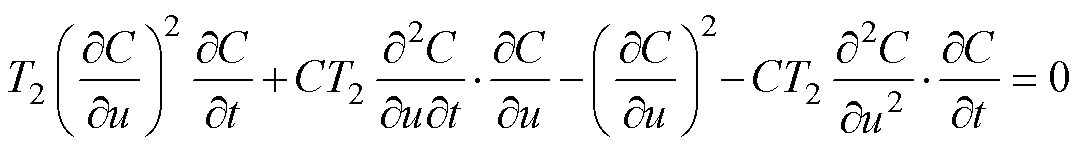 (16)
(16)
其中
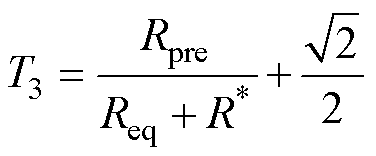
考虑到参数采集成本与实际需要,本算例仅利用式(16)作为偏微分损失的构造函数,并且实验结果表明可以满足算法要求。由式(16)可知,T2为该偏微分方程的重要电阻参数,但从定义上难以量化。与此同时,在列车实际运行过程中,电气设备可能会受到不同程度的负载、温度变化和操作条件的影响,从而导致电阻阻值变化。因此,在进行模型训练时,应当将T2作为有一定初值的未知参数,同时作为一个自适应可输出量来处理。
本算例是一种硬约束方法,所用微分方程的初始条件和边界条件组成的方程组为
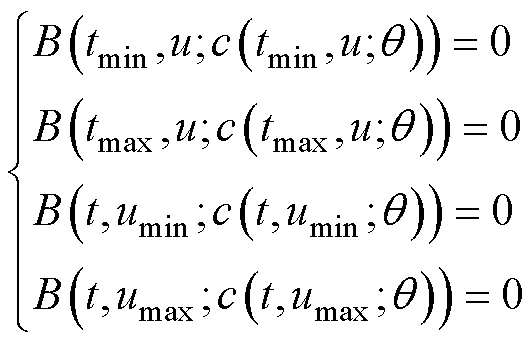 (17)
(17)
考虑到该算法损失函数是由不同组分按照权值进行组合,理论上难以给出固定且保证达到最优收敛情况的权值分配,且调整不同组分对应的权值占比能够一定程度影响训练和预测结果[27]。因此参考文献[28]将损失函数不同组分权重作为可训练自适应优化部分,以缓解固定权重可能带来的收敛于局部最优解,进而导致训练过程缓慢、网络不收敛等问题。
已知解标签条件下的PINN算法的损失函数主要由数据损失、偏微分残差损失、初值损失和边界损失按照各组分权重相加组合。为了简要表述网络输入、输出关系,用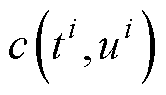 表征输入有序电压数组u与输入有序时间数组t通过PINN网络预测输出的结果,其中i表示序数。
表征输入有序电压数组u与输入有序时间数组t通过PINN网络预测输出的结果,其中i表示序数。
本算例选择的损失函数为方均差损失函数,具体定义为
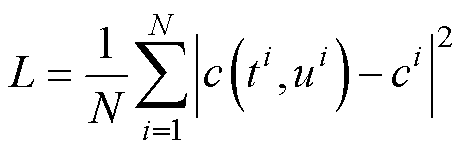 (18)
(18)
数据损失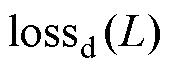 、偏微分残差损失
、偏微分残差损失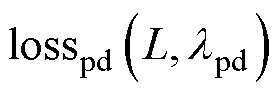 、初值损失
、初值损失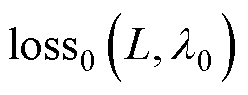 和边界损失
和边界损失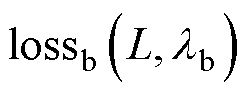 各函数自适应权值形式分别表示为
各函数自适应权值形式分别表示为
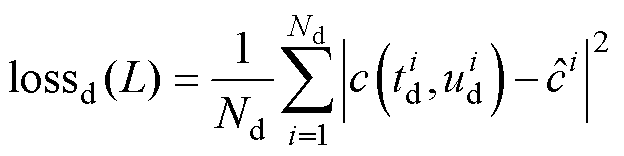 (19)
(19)
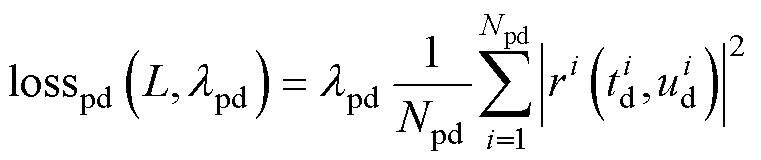 (20)
(20)
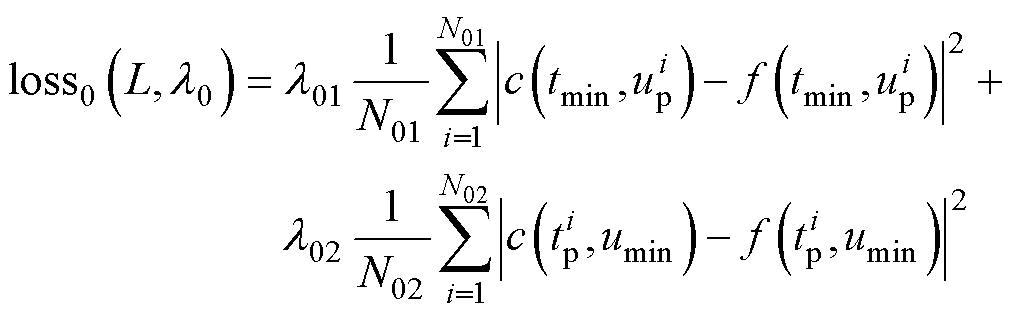 (21)
(21)
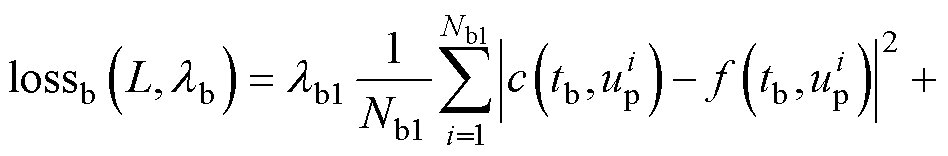
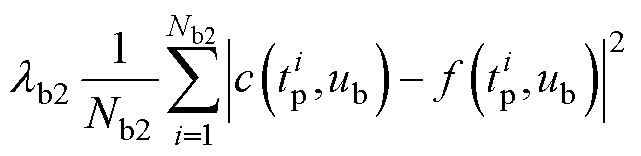 (22)
(22)
式中,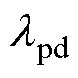 为偏微分残差损失权重;
为偏微分残差损失权重;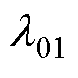 、
、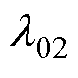 为初值损失权重;
为初值损失权重;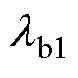 、
、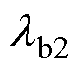 为边界损失权重;
为边界损失权重;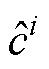 为实际测量到的真实电容值标签;
为实际测量到的真实电容值标签;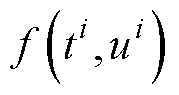 表示在物理公式下的边界条件;
表示在物理公式下的边界条件;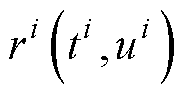 为将网络结果代入偏微分方程式(16)得到的残差;下角标表示获得输入数据的途径,其中角标d表示数据来源于实验或者生成对抗网络验证式阶段可信生成结果,角标p表示在初始条件和边界条件范围内的随机生成数。设偏微分方程形式为
为将网络结果代入偏微分方程式(16)得到的残差;下角标表示获得输入数据的途径,其中角标d表示数据来源于实验或者生成对抗网络验证式阶段可信生成结果,角标p表示在初始条件和边界条件范围内的随机生成数。设偏微分方程形式为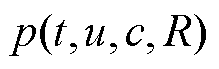 ,
,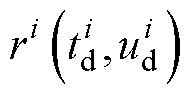 逻辑关系为
逻辑关系为
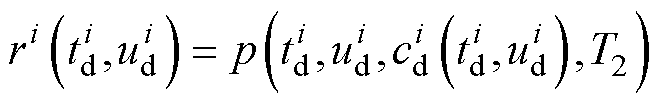 (23)
(23)
针对自适应权重分配问题,考虑到实验观测采集数据分布特征与随机分布及均匀分布相差较大,且含有噪声干扰。实验表明,若尝试对该数据损失部分使用自适应权重来优化,很大程度上会导致网络过拟合。而且实验真实测量样本损失作为自适应网络损失的标称量,也可以提高网络的鲁棒性与泛化程度,因此本算例不对该量进行加权。与此同时,CycleGAN网络获得的验证式阶段可信生成结果与实验数据特征类似,因此采用相同的权重设置。生成数据损失可表示为
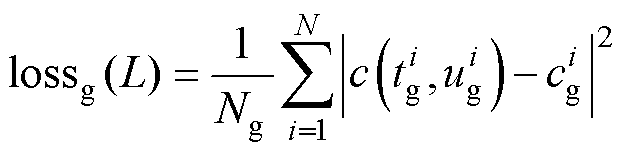 (24)
(24)
式中,生成数据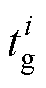 、
、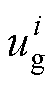 、
、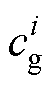 在第3节将会详细说明其过程,对应生成矩阵为
在第3节将会详细说明其过程,对应生成矩阵为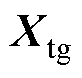 、
、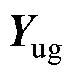 、
、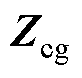 ,在此不予赘述。故本算例需要优化的自适应PINN总损失函数可表示为
,在此不予赘述。故本算例需要优化的自适应PINN总损失函数可表示为
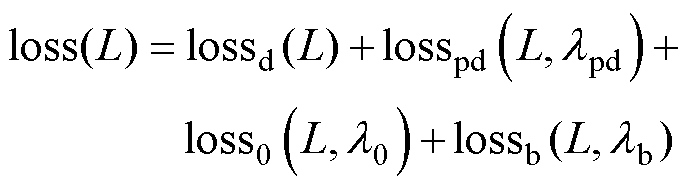 (25)
(25)
当PINN网络同时达到设定迭代次数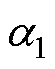 与检验集预测精度时,总损失函数可更新为
与检验集预测精度时,总损失函数可更新为
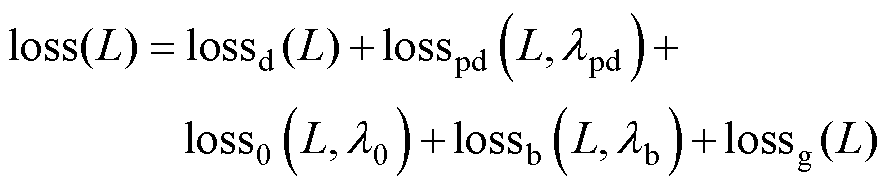 (26)
(26)
本实验自适应PINN网络基于Windows系统中Python3.9环境下建立,选用后端为Pytorch框架,处理器为AMD Ryzen 7 5800H with Radeon Graphics 八核,算例均是在NVIDIA GeForce RTX 3050 Laptop GPU上进行训练。经过多次尝试、分析、修正后,该自适应PINN网络设置训练参数可设定隐藏层数为5,每层各50个神经元节点,激活函数为tanh函数,先用AdamW优化器对网络权值和自适应权值进行优化,自适应权重初值为1,初始学习率为10-3,迭代次数为600次,再用L-BFGS算法对当前PINN网络的线性网络权重部分进行新一轮的迭代优化,但不再对自适应权值进行更新,迭代次数为200次,学习率为10-4。自适应PINN网络部分的网络结构如图3所示,其流程如图4所示。为了评估该算法模型实际使用时算力需求,分别采用了Pytorch平台框架与DSP28335芯片检验了在本算例使用本文PINN算法训练完成的模型进行六组测试集测试时所需执行时间。其中,采用Pytorch平台框架的执行时间约为2.12 s,采用DSP28335芯片的执行时间约为8.55 min。结果表明:由于本算法为基于牵引变流系统预充电工况的直流支撑电容参数辨识方法且电容容值变化缓慢,无需瞬时监测或高频监测,因此该算法执行速度与计算效率可以满足监测要求,具有一定的实用可行性。
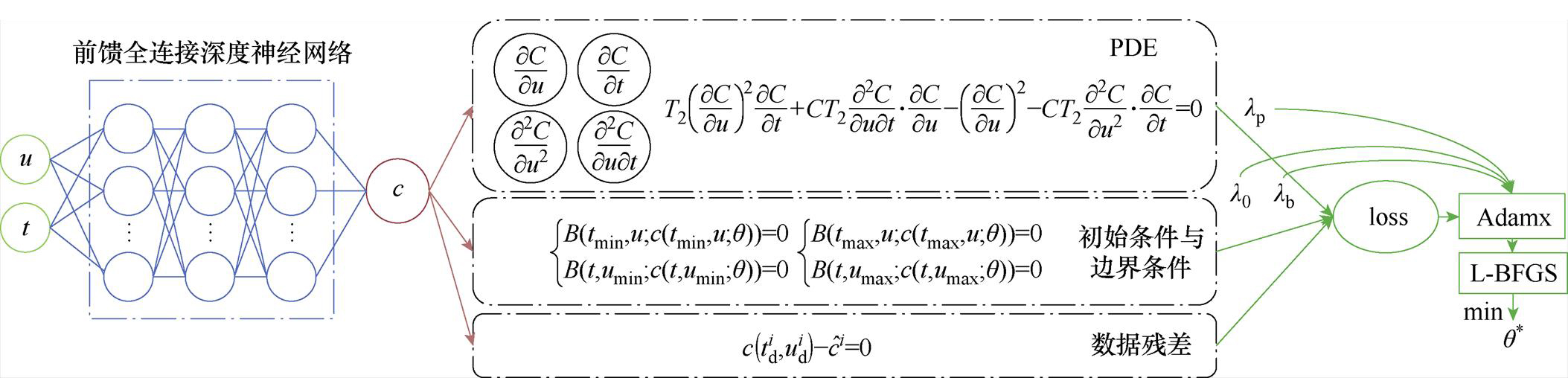
图3 本文PINN网络结构
Fig.3 PINN network structure diagram

图4 本文PINN网络流程
Fig.4 PINN network flow chart
PINN深度学习算法比较大多数深度学习算法,因其将数据中物理规律融入机器学习模型的特点,在小数据集样本情况下适用性更高,但核心思路依旧隶属于深度学习算法。对于深度学习算法来说,必要的训练数据量是避免网络发生过拟合等问题的基本要求。然而在工程实际情况下,用于制作训练数据集所采集的样本数量、样本范围、样本质量及采集时间往往会受到很大限制。与此同时,当原数据集分布不均,在分布可行域内出现大片空白或过稀疏情况时,对空白或过稀疏区域的拟合效果偏弱,难以进行有效填补。因此,如何尽可能地生成符合原训练集的拟合扩充数据,且尽可能补充稀疏部分数据,对于降低采集成本的同时维持训练样本集的泛化能力至关重要。本算例的解决方法为使用循环一致性生成对抗网络(CycleGAN)来扩充原训练样本数据集的数据量[29-30]。
从PINN黑箱角度来看,能够使曲线在走向驱势上各自区分恰恰表明向量内在的物理规律起到了重要作用,根据该思路确立源域X0与目标域Y0。首先将根据原训练集按照标签随机为等量的m组(m为随机自然数),设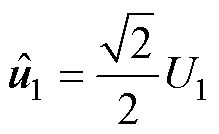 ,
, 为网侧交流输入电压的有效值,将原实验电压向量
为网侧交流输入电压的有效值,将原实验电压向量 按照式(27)构造计算电压向量
按照式(27)构造计算电压向量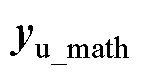 。
。
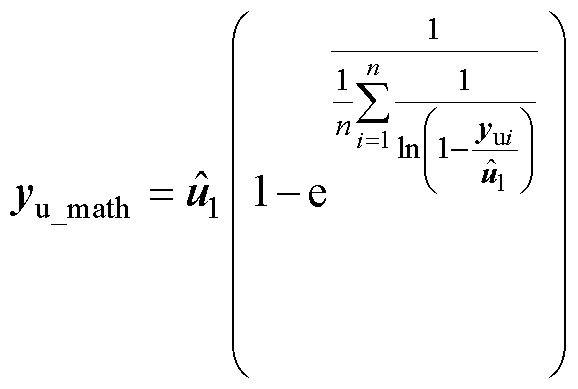 (27)
(27)
当前计算电压向量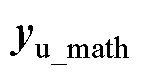 仅为实验电压向量的数学推算结果,并非可信的预测结果,仅用于辅助CycleGAN网络来生成数据。该数据样本空间视作CycleGAN的被生成参考目标域Y0,实验获得的原训练集构成的样本空间视作CycleGAN的源域X0。
仅为实验电压向量的数学推算结果,并非可信的预测结果,仅用于辅助CycleGAN网络来生成数据。该数据样本空间视作CycleGAN的被生成参考目标域Y0,实验获得的原训练集构成的样本空间视作CycleGAN的源域X0。
设生成器G-判别器Dxy组合代表将源域X中的数据转换到目标域Y0的生成对抗训练模型,生成器F-判别器Dyx组合代表将目标域Y0中的数据转换到源域X0的生成对抗训练模型,x和y分别表示X0域与Y0域中的数据集。为了两域能够实现相互转换的同时,保证生成的数据经过逆向转换后能够回到原始域,从而通过损失确保输入与输出的一致性,避免丢失原始数据中的一些重要信息或者出现不符合实际的变换,引入循环一致性损失[31]作为约束,使得生成器G和F尽可能满足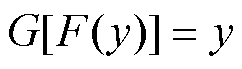 和
和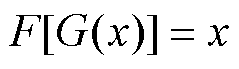 。目标函数主要分为对抗损失函数和循环一致性损失函数[30-31]。生成器G与判别器Dxy对应的对抗性损失函数可以表示为
。目标函数主要分为对抗损失函数和循环一致性损失函数[30-31]。生成器G与判别器Dxy对应的对抗性损失函数可以表示为
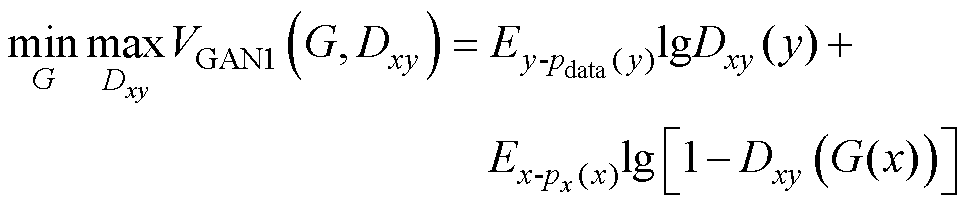 (28)
(28)
式中,等式右侧第一项为通过判别器输出的对数概率期望;右侧第二项为生成器G生成的数据被判别为假的对数概率期望。
另一个生成器F与判别器Dyx对应的对抗性损失函数可以表示为
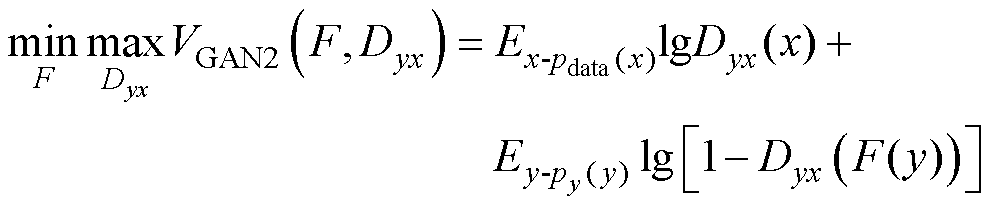 (29)
(29)
循环一致性损失函数可以表示为
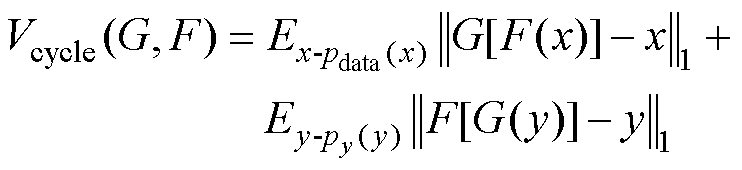 (30)
(30)
式中,式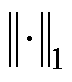 表示L1范数。设控制系数为
表示L1范数。设控制系数为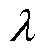 (通常设为10),最终目标函数可表示为
(通常设为10),最终目标函数可表示为
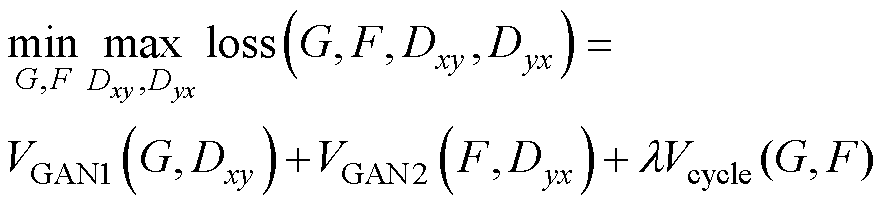 (31)
(31)
故本算例确定了本文CycleGAN主体网络结构如图5所示。
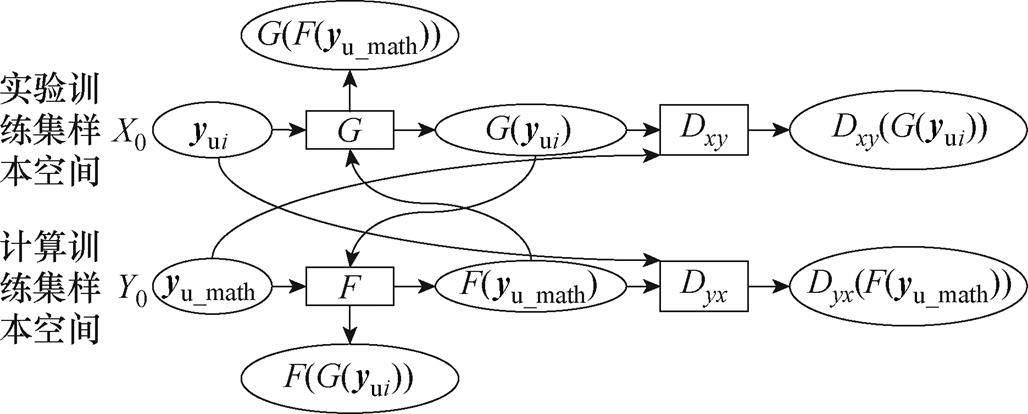
图5 本文CycleGAN网络结构
Fig.5 CycleGAN network structure diagram
在使用PINN网络对训练集训练的过程中,当迭代次数大于指定次数界限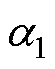 且检验集均方差小于设定的较小数
且检验集均方差小于设定的较小数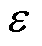 时,才会使用CycleGAN模型生成数据。此时,保存下当前网络权重与自适应权重以及训练集,记录下当前迭代次数,将固定长度的时间向量
时,才会使用CycleGAN模型生成数据。此时,保存下当前网络权重与自适应权重以及训练集,记录下当前迭代次数,将固定长度的时间向量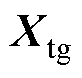 和在CycleGAN模型中获得的所有暂且可信结果向量
和在CycleGAN模型中获得的所有暂且可信结果向量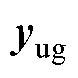 对应拼接为两个矩阵
对应拼接为两个矩阵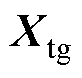 和
和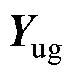 ,将两个矩阵
,将两个矩阵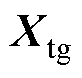 和
和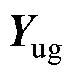 加入训练集,将这两个矩阵在当前PINN网络下的预测结果作为它们的电容标签
加入训练集,将这两个矩阵在当前PINN网络下的预测结果作为它们的电容标签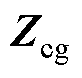 ,并通过每次迭代后的检验集准确度来监视加入生成训练集后的训练结果。如果在固定迭代间隔里准确度降低,则认为该生成训练集难以满足要求,重新返回保存的迭代次数进行生成;如果在固定迭代间隔里准确度不变或者提高,那么认为生成训练集可信且有效,并在下一次固定迭代间隔开启前,更新生成数据集。
,并通过每次迭代后的检验集准确度来监视加入生成训练集后的训练结果。如果在固定迭代间隔里准确度降低,则认为该生成训练集难以满足要求,重新返回保存的迭代次数进行生成;如果在固定迭代间隔里准确度不变或者提高,那么认为生成训练集可信且有效,并在下一次固定迭代间隔开启前,更新生成数据集。
采用针对预充电环节直流回路简化拓扑的直流支撑电容侧外接并联不同数量相同容量薄膜电容的方法,模拟实际电容寿命老化过程中电容容值C减少的变化过程。直流支撑电容侧并联结构如图6所示,其中a、b两个接触点表示图2中同名的两个接触点。
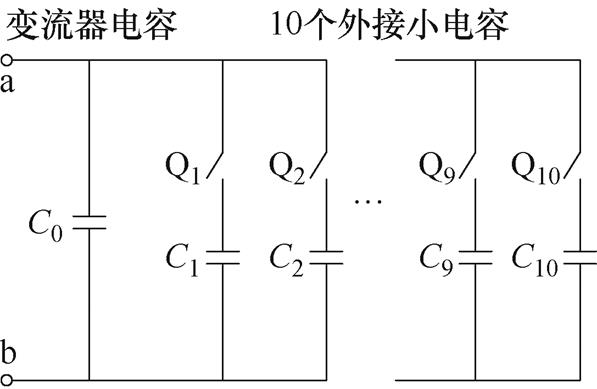
图6 直流支撑电容侧并联实验电路示意图
Fig.6 Circuit diagram of DC-link capacitor side parallel connection experiment
在此基础上,适当替换主直流支撑电容获得另几组数据,由此得到组内电容容值间隔相同但组与组之间间隔不连续的训练集,用于研究针对宽范围电容区间但标签不均匀分布的电容监测模型训练方法。
为了验证本算例设计的自适应PINN直流支撑电容状态监测方法的有效性和可行性,使用实验室平台对该方法进行验证,实验电路如图2所示,实验平台如图7所示,其中所用示波器型号为泰克Tektronix混合域数字示波器MDO34 3-BW-200。利用并联于限流电阻Rpre的接触器断开与闭合来模拟预充放电过程,利用外置示波器获得不同电容值下电压随时间变化的充放电曲线,利用LCR分析仪来测量每个待测电容的容值。为减少测量误差,每个电容器测3次取平均值。实验主要参数见表1。表1中,实际列车采集频率约为100 Hz,实验采集频率为1 kHz仅为了后续讨论采样频率的影响而设置。
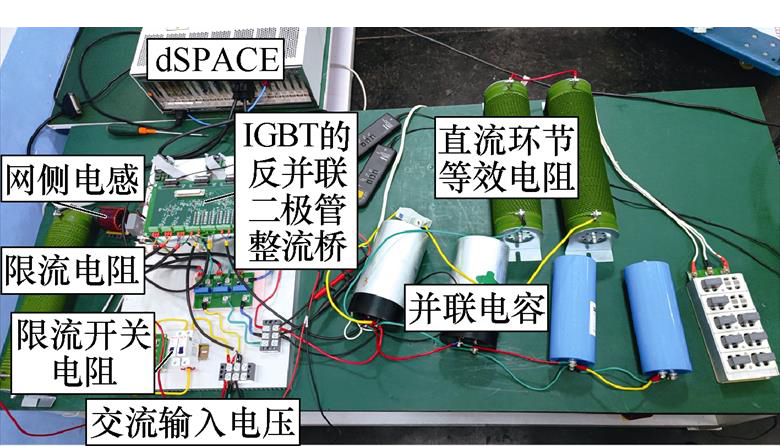
图7 实验平台
Fig.7 Experimental platform
表1 实验主要参数
Tab.1 The main parameters of the experiment
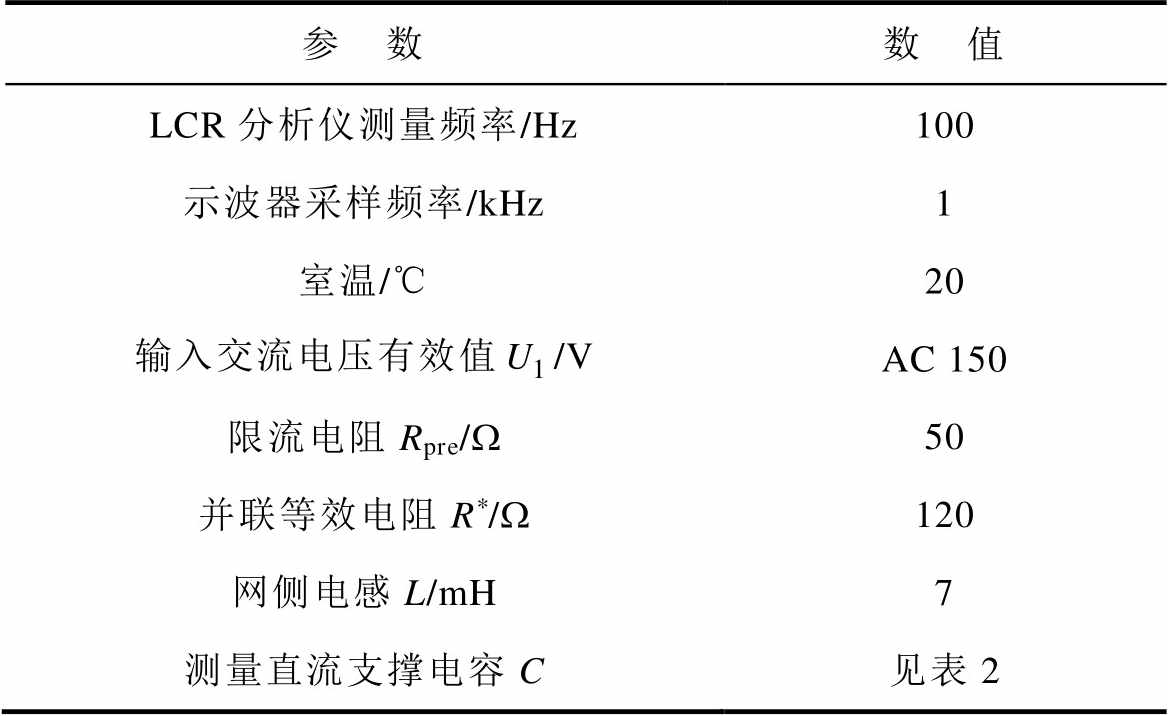
参 数数 值 LCR分析仪测量频率/Hz100 示波器采样频率/kHz1 室温/℃20 输入交流电压有效值/VAC 150 限流电阻Rpre/W50 并联等效电阻R*/W120 网侧电感L/mH7 测量直流支撑电容C见表2
由于本文想要研究的目标之一为获得一种满足宽范围电容容值区间且标签可不均匀分布的电容器监测模型训练方法,但受实验条件和工程实际测量条件所限,难以获得电容容值C间隔连续的测量数据,因此本实验通过不同电容器排列组合,得到五组组内电容容值间隔相同,组与组之间电容容值间隔较大的测量数据,满足宽范围电容容值区间的要求。五个电容容值区间分组具体情况见表2,其中每个区间内部电容容值间隔0.01 mF,最大电容容值4.502 mF是最小电容容值1.203 mF的3.742倍。
表2 电容区间分组具体情况
Tab.2 Capacitor interval grouping specific situation (单位: mF)
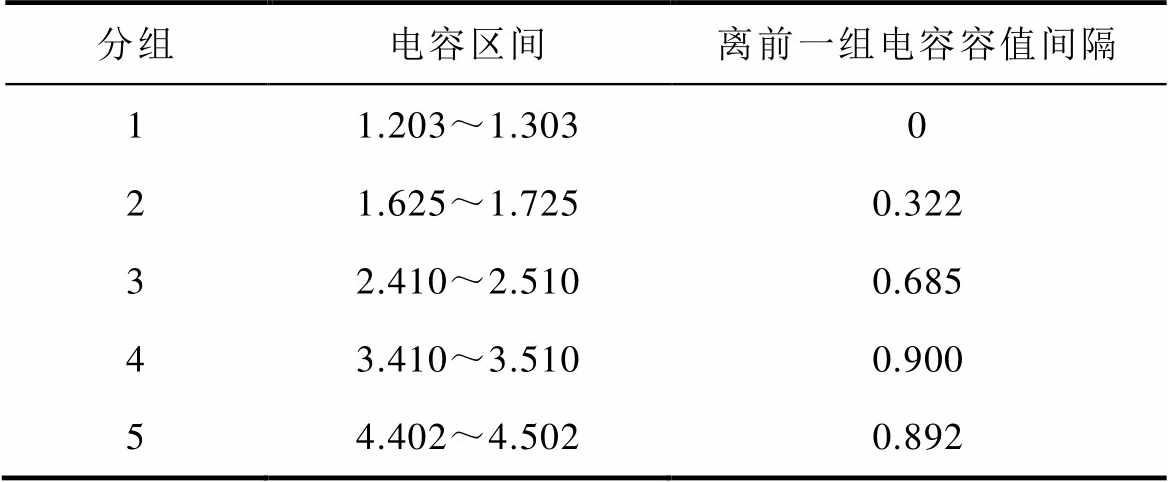
分组电容区间离前一组电容容值间隔 11.203~1.3030 21.625~1.7250.322 32.410~2.5100.685 43.410~3.5100.900 54.402~4.5020.892
按照区间随机抽取五项电容器(1.243、1.715、2.450、3.490、4.432)mF作为测试数据集和训练检验集,其余50项作为训练数据集。为检验该方法在扩展电容容值区间的适用性,另设一个电容容值不在五个区间范围内的电容器电压曲线作为第六组测试数据集,其容值为2.04 mF。训练集和测试集的比例约为10 1,符合实验要求。由于本方法无需对齐时间轴,实验理论上只需要测量充电电压曲线及对应的电容容值C。充电电压曲线只需要按时间顺序截选第一个电压数据量与电容器未充电情况下电压值近似,其余数据量粗略大于第一个电压数据量作为电压曲线样本即可。源于PINN算法对物理信息的融合,即使时间轴无法完美匹配,也可以完成准确预测。
1,符合实验要求。由于本方法无需对齐时间轴,实验理论上只需要测量充电电压曲线及对应的电容容值C。充电电压曲线只需要按时间顺序截选第一个电压数据量与电容器未充电情况下电压值近似,其余数据量粗略大于第一个电压数据量作为电压曲线样本即可。源于PINN算法对物理信息的融合,即使时间轴无法完美匹配,也可以完成准确预测。
考虑到计算机运行成本,以所测最小电容容值的充电电压曲线从第1个时间常数到第3个时间常数为基准,本实验所取拟时间轴范围为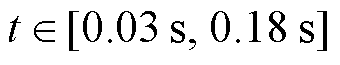 。实验充电电压曲线如图8所示。
。实验充电电压曲线如图8所示。
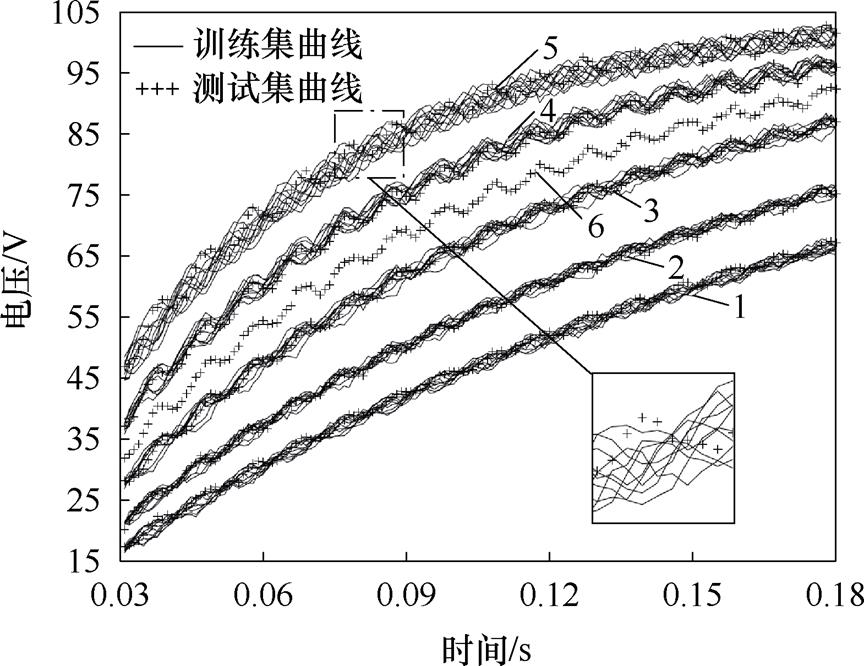
图8 实验充电电压曲线
Fig.8 Experimental charging voltage curves
经过完整的自适应PINN方法实验过程,可以得到测试集在训练模型中的预测结果,见表3。
表3 测试集在训练模型中的预测结果
Tab.3 The prediction results of the test set in the training model

编号真实电容/mF预测电容/mF采样电容间隔(0.01 mF)占真实电容比(%)绝对误差/mF相对误差(%) 11.2431.2320.800.0110.88 21.7151.7060.580.0090.55 32.4502.4620.410.0120.48 43.4903.4720.290.0150.42 54.4324.4490.230.0170.38 62.0402.0230.490.0170.83
由实验结果可知,从本算例六组不同测试集电容容值辨识结果来看,辨识相对误差普遍小于1%,符合工程实际预测要求,该方法可信。由表3中编号1~编号5辨识结果可得,随着并联电容容值为0.01 mF的小电容占待预测电容容值比例逐渐减小,电容容值辨识相对误差同样也逐渐减小,但绝对误差却有增大趋势。本文推测有以下两点原因:一是在构建数据集的过程中是以训练集最小电容容值时间常数为基准划分的选取范围,对于较大电容容值来说可能无法涵盖其最优特征点,导致绝对误差增大,后续分析将针对该点进行优化式检验;二是从图8中可以看出,在相同电容容值间隔前提下的不同电容容值区间分组曲线中,电容容值越大的分组曲线越密集,辨识难度增大,但采样电容间隔(0.01 mF)占真实电容比也越小,从统计学角度造成了绝对误差与相对误差变化趋势相反的情况。该结果表明,越小的训练集其电容间隔有利于提高该算法的鲁棒性。与此同时,不属于训练集分组区间范围的第六组测试集电容容值辨识误差也低于1%,可证明该方法在构建宽范围电容区间但标签不均匀分布的训练模型上具有参考价值。
观测不同迭代次数下损失函数下降与模型预测准确率的变化,以及对模型在不同迭代次数下的预测结果进行比较分析,深入挖掘模型在不同阶段的性能表现。以编号2测试样本集为例,记录其在迭代600次下损失函数值变化曲线及预测电容容值变化曲线如图9所示。为了观察在不同迭代次数下最终得到的预测电容值及其误差,取不同的30次迭代次数段预测结果如图10所示。由图10可得,随着迭代次数的增加,损失函数值不断减小,预测电容容值结果逐渐趋向稳定。其中,在第100次迭代次数时,预测电容值结果依旧有较大波动;但到第200次迭代次数时预测电容值结果呈现向着更加准确预测的方向逼近;在第400次迭代次数时,波动幅度已经较小,但与真实电容结果仍然有较大差距,依旧有向更准确预测的方向逼近的趋势;在第600次迭代次数时,预测电容容值结果基本稳定已知,编号2测试样本集真实电容容值为1.715 mF,计算图10所选迭代次数段最后30次预测结果的均值及其相对误差、方均差见表4。分析结果表明,随着迭代次数的增加,预测精度明显提高,预测电容容值曲线波动幅度基本上呈逐渐减小趋势。考虑到工程实际与计算机成本,使用该方案时总迭代次数推荐设置在370~600次以内便可满足实际应用需求。
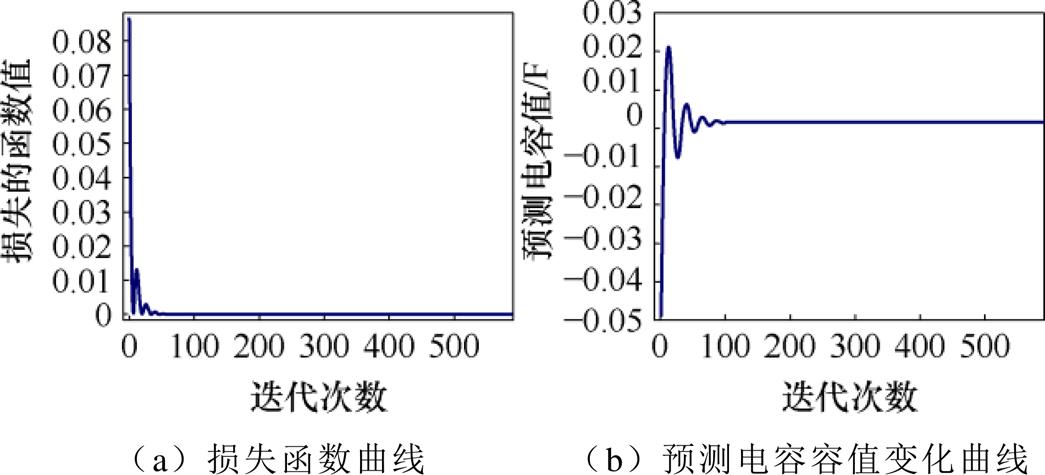
图9 600次迭代次数下损失函数值及预测电容容值变化曲线
Fig.9 The loss function value and the predicted capacitance change curves under 600 iterations
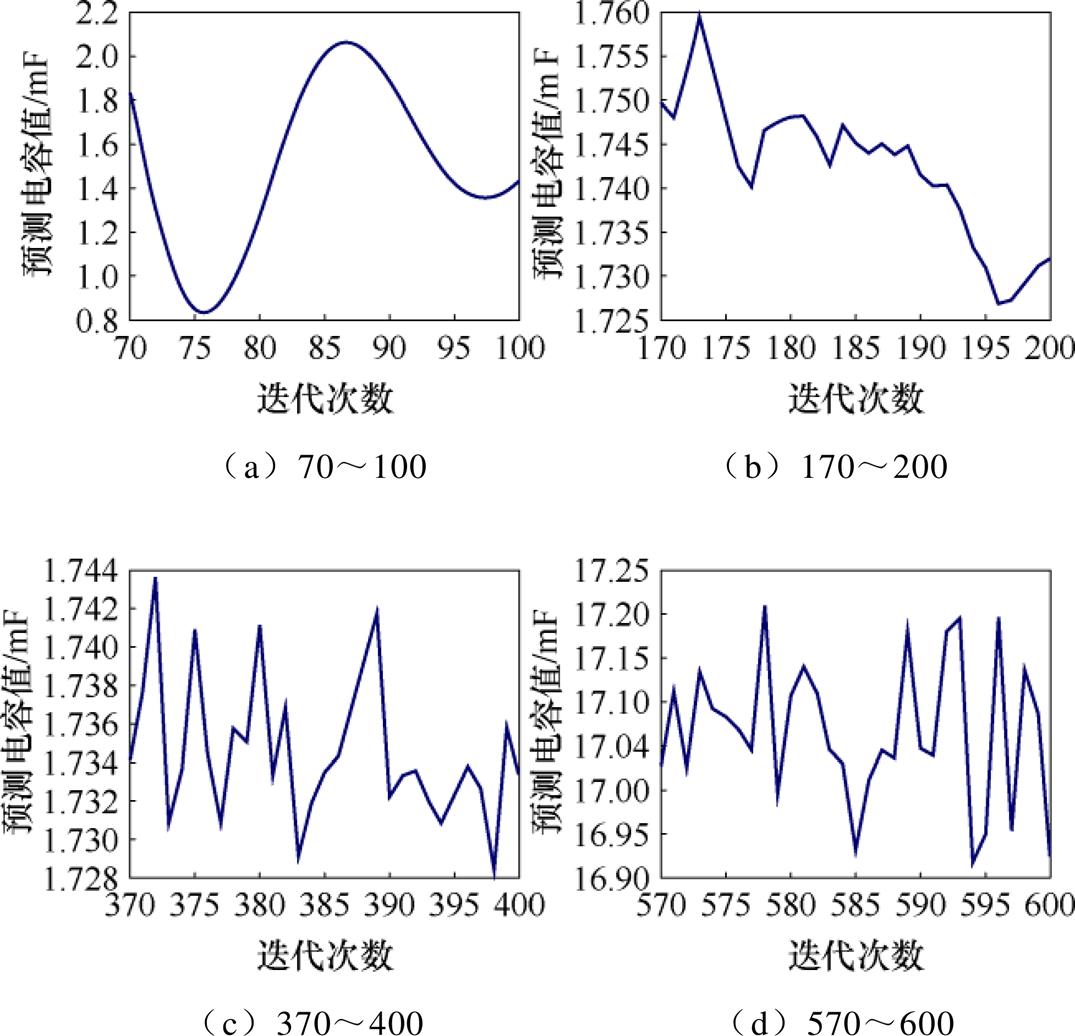
图10 不同迭代次数段下预测电容容值变化曲线
Fig.10 The variation curves of predicted capacitance value under different iteration times is predicted
表4 各迭代次数段预测结果分析
Tab.4 Analysis of prediction results of each iteration number segment
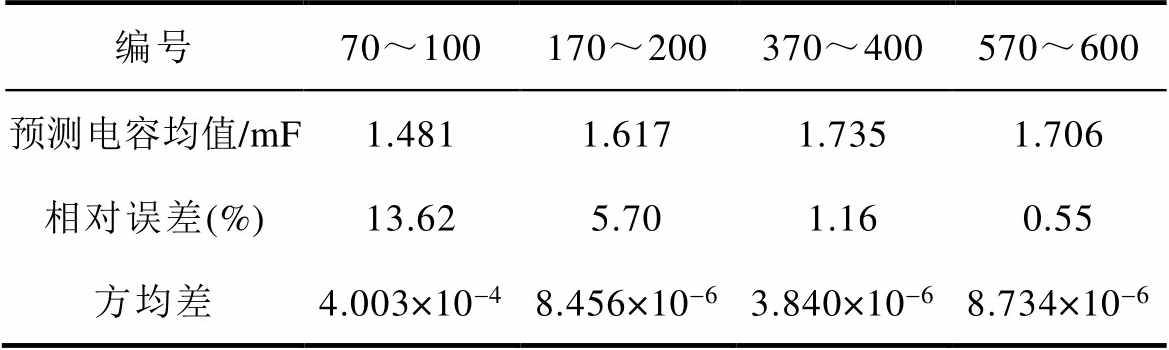
编号70~100170~200370~400570~600 预测电容均值/mF1.4811.6171.7351.706 相对误差(%)13.625.701.160.55 方均差4.003×10-48.456×10-63.840×10-68.734×10-6
1)样本数量影响
为了探究本方法在实际应用中对不同数量样本的适应能力,为优化资源利用与减少训练成本提供参考,以表2不同电容区间分组为单位,根据所选分组重新选取各自的时间范围并构建全新训练样本集,以其同编号的测试集以及6号测试集作为检验标准,观察预测结果。其中字母P开头的标记表示该次训练使用了数据增强方法;若无字母P开头标记,则表示该次训练未使用数据增强方法。受篇幅所限,不再详细赘述,不同训练集样本数量及样本分布下的预测结果见表5。研究结果表明:该方法在小样本训练集条件下预测精度较高,但对于样本区间外的待预测电容容值对象预测效果较差。与此同时,随着加入与初始训练集不连续的样本导致合成训练集分布不均将会降低监测的精度,可以使用数据增强的方法缓解这种趋势。在实际应用过程中,需要根据列车监测实际需求对模型训练方案进行 调整。
表5 不同训练集样本数量及样本分布下的预测结果
Tab.5 Prediction results under different training set sample size and sample distribution
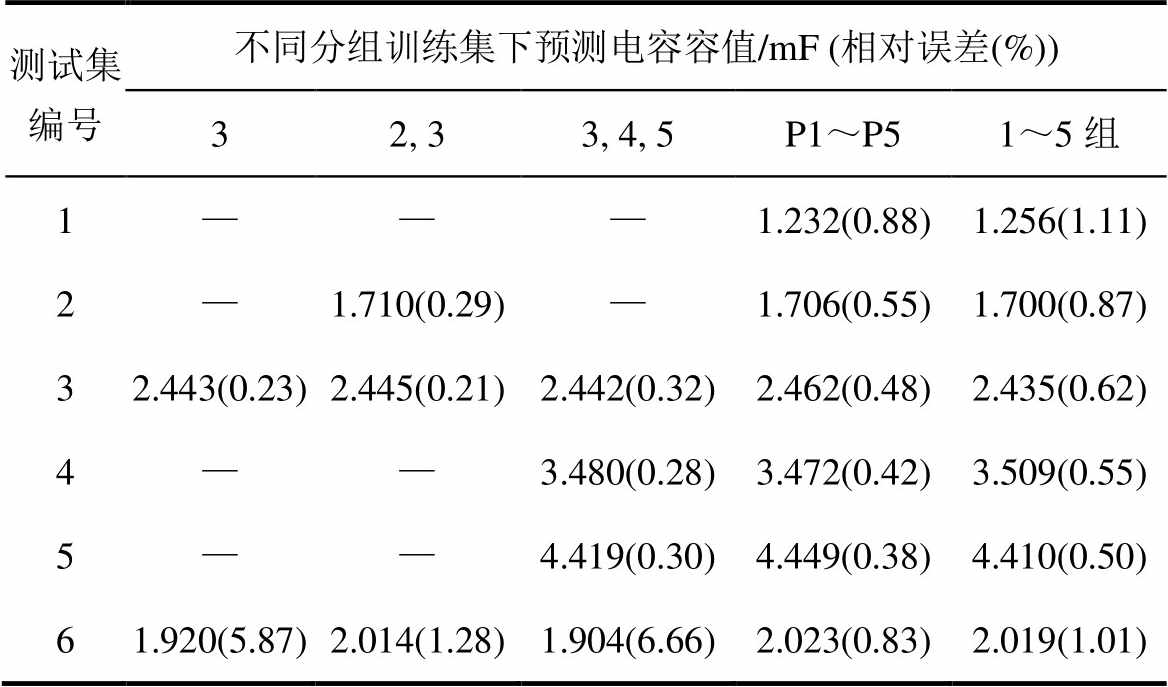
测试集编号不同分组训练集下预测电容容值/mF (相对误差(%)) 32, 33, 4, 5P1~P51~5组 1———1.232(0.88)1.256(1.11) 2—1.710(0.29)—1.706(0.55)1.700(0.87) 32.443(0.23)2.445(0.21)2.442(0.32)2.462(0.48)2.435(0.62) 4——3.480(0.28)3.472(0.42)3.509(0.55) 5——4.419(0.30)4.449(0.38)4.410(0.50) 61.920(5.87)2.014(1.28)1.904(6.66)2.023(0.83)2.019(1.01)
2)辨识精度比较
对比了代表拟合算法的最小二乘法、代表纯数据驱动的BP算法及本算例改良PINN方法三种方法。为实现控制变量,最小二乘法增加电容充电电压曲线于同一采集时间的网侧电流曲线作为拟合对象,但拟合时间轴与本算例完全相同,模拟实际测量情况;BP算法结构及参数设置均与本算例改良PINN方法有关的参数配置相同,且不加入生成向量。各算法预测结果及相对误差见表6。为了直观地展示各算法相差程度,以各编号真实电容为标称值,各算法预测电容值结果相对真实容值比较如图11所示。由实验结果易得,相较BP算法,经典最小二乘法预测结果要更优,而本算例改良PINN算法效果最好。其中最小二乘法误差表现出随编号的增加,相对误差增大,并且预测结果相对真实值普遍较小的情况,这可能是源于本算例的测试集曲线并非完整的电容电压充满曲线,编号越大则截取片段相对完整曲线越小,缺失准确时间轴也影响了拟合效果,由此也能体现出最小二乘法的局限性。BP算法的预测误差较大,需要考虑调整网络参数。综上所述,本算例改良PINN算法能够显著提升预测的准确度。
表6 各算法预测结果及相对误差
Tab.6 The prediction results and relative error of each algorithm
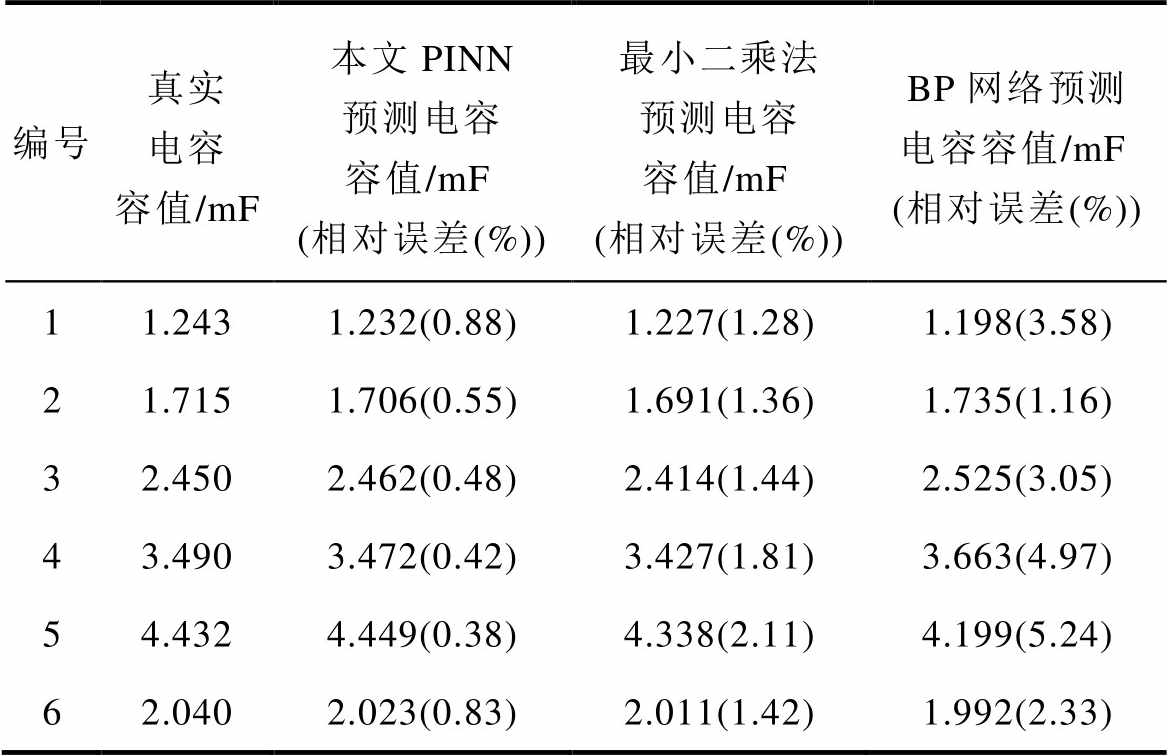
编号真实电容容值/mF本文PINN预测电容容值/mF (相对误差(%))最小二乘法预测电容容值/mF (相对误差(%))BP网络预测电容容值/mF (相对误差(%)) 11.2431.232(0.88)1.227(1.28)1.198(3.58) 21.7151.706(0.55)1.691(1.36)1.735(1.16) 32.4502.462(0.48)2.414(1.44)2.525(3.05) 43.4903.472(0.42)3.427(1.81)3.663(4.97) 54.4324.449(0.38)4.338(2.11)4.199(5.24) 62.0402.023(0.83)2.011(1.42)1.992(2.33)
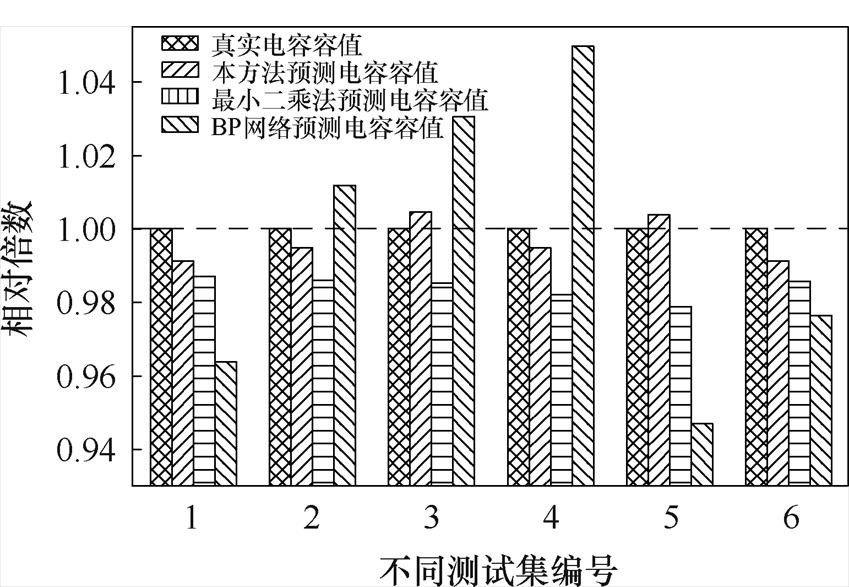
图11 各算法预测电容容值结果相对真实电容容值比较
Fig.11 The comparison of the multiples of the predicted capacitance value of each algorithm relative to the real capacitance value
3)鲁棒性检验
由于本方法用于制作训练集与测试集的数据都来源于电压传感器直接测量,因此测量仪器的精度、采样频率、测量噪声或故障情况都会对特征参数辨识造成一定的影响。针对该问题,本算例采用改变采样频率的方式和在原始采集数据上人为添加一定程度噪声信号的方式来对该方法的鲁棒性进行检验。
首先,通过Matlab程序将采样频率为1 kHz(采样间隔0.001 s)的原始测量数据换算为采样频率为500 Hz(采样间隔0.002 s)和100 Hz(采样间隔0.01 s)的待检验数据,以基本相同的步骤制作成训练集与测试集并训练得到相应模型。模型在各采样频率下预测结果见表7。结果表明:在采样频率从1 kHz变化到500 Hz时,预测相对误差略微下降;从500 Hz变化到100 Hz时,预测相对误差出现了明显的下降,监测精度提高。这可能是源于预充电阶段的电容器充电电压特性呈现单调递增趋势。若采样频率过高,将会导致相邻采样数据几乎一致,从而产生过度拟合的问题。相反,降低采样频率可以避免该情况,同时有助于算法削弱噪声干扰,便于更快速地收敛。因此,在采集阶段尽可能地选择采样频率为100 Hz将有利于提高该算法的准确性。
表7 模型在各采样频率下预测结果
Tab.7 Prediction result of each sampling frequency model
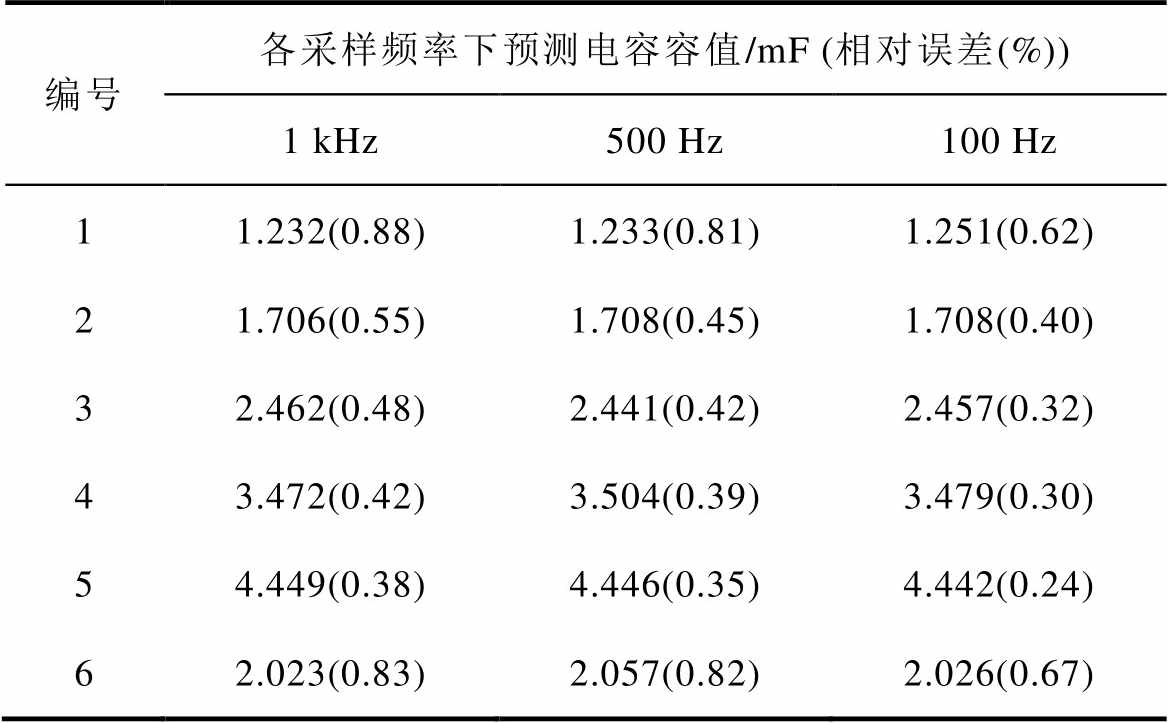
编号各采样频率下预测电容容值/mF (相对误差(%)) 1 kHz500 Hz100 Hz 11.232(0.88)1.233(0.81)1.251(0.62) 21.706(0.55)1.708(0.45)1.708(0.40) 32.462(0.48)2.441(0.42)2.457(0.32) 43.472(0.42)3.504(0.39)3.479(0.30) 54.449(0.38)4.446(0.35)4.442(0.24) 62.023(0.83)2.057(0.82)2.026(0.67)
选择最接近整体区间中央的编号3测试集来探究采样频率在1 kHz、500 Hz以及100 Hz时不同信噪比(Signal-to-Noise Ratio, SNR)对应的误差变化。通过人为方式对训练集和测试集加入高斯噪声信号干扰,并使用修改后的训练集和测试集训练得到模型,不同采样频率对应不同信噪比的电容容值监测误差如图12所示。结果表明:信噪比越小,噪声干扰越强,导致监测误差增大,但降低采样频率能够减小这种影响的干扰作用。当采样频率约为100 Hz时,本文所提方法在信噪比为70 dB以上时辨识误差均在1%以下,在信噪比为50~70 dB时辨识误差约在1%~3%,在信噪比为30~50 dB时辨识误差仍然可以控制在5%以内。由于轨道交通列车运行中主要干扰源包括高频干扰和工频干扰[32],而本算法运行于预充电工况,此时牵引变流器脉冲处于封锁阶段,IGBT等电力电子器件均不工作,因此其电磁环境相对较好,高频干扰源较少。当使用较低采样频率时,相当于低通滤波器可以有效滤除高频干扰,且本身测得预充电压幅值较大,抗干扰能力较强,因此认为该方法在实际监测过程中对抗高噪声时依旧具有较好的鲁棒性。对于整流输入中引入的工频干扰,可以在采样电路或者软件算法中增加陷波电路,滤除工频干扰,提高信号采样质量。因此,可认为本方法在实际运行中有着较强的抗噪性。

图12 不同采样频率对应不同信噪比电容容值监测误差
Fig.12 Capacitance value monitoring error maps of different sampling frequencies corresponding to different SNR
为了克服因直流支撑电容发生老化而造成的安全隐患,本文提出了一种以自适应物理信息深度神经网络与电容预充电模型为基础,辅以循环一致性生成对抗网络扩充数据的直流支撑电容状态监测方法。实验结果表明:在正常条件下,该方法的辨识相对误差约在1%以下,在信噪比达到30 dB时辨识相对误差仍旧可以控制在5%以内;在噪声较大的监测环境下,适当降低采样频率能够获得较好的监测结果。
本方法主要特点如下:
1)无需增加多余的传感器,无需修改原电路结构及系统控制算法,只需要利用预充电阶段已有传感器测量数据,预处理时无需拟合数据,无需严格对齐时间轴就可以获得较为准确的电容状态监测 结果。
2)该方法基于物理信息深度算法,在网络训练过程中使用物理先验知识进行约束,使其结果更加符合现实物理常识,而并非仅被统计学限制,在原理层面提高了模型的鲁棒性、可信性及可解释性。只要在初期建立合理有效的数据样本集,应用时便可使用已训练好的模型进行电容值监测,提高了参数监测效率。通过适当修改可适用于大多数列车DC-Link电容器应用场景,普适性较强,并且本算例为网络结构与训练集的设计提供了可靠的参考方案。
3)该方法可以适用于同一拓扑下宽范围电容区间的电容容值预测,与此同时能够克服在制作数据样本训练集时因条件所限造成的分布稀疏不均问题,降低了模型训练要求,工程实用简单,可行性强。
参考文献
[1] 卓超然, 张笑天, 张雄, 等. 支撑电容可分离的直流变压器短路故障电流限流控制方法[J]. 电工技术学报, 2022, 37(2): 424-432.
Zhuo Chaoran, Zhang Xiaotian, Zhang Xiong, et al. Short-circuit fault current limiting control method of DC transformer with separable supporting capaci- tor[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 424-432.
[2] 伍珣, 于天剑, 李凯迪, 等. 基于预充电模型与RSNA的直流支撑电容器电容量辨识方法[J]. 铁道科学与工程学报, 2023, 20(7): 2664-2675.
Wu Xun, Yu Tianjian, Li Kaidi, et al. A capacitance estimation method for DC-link capacitors based on pre-charging model and noise evaluation[J]. IEEE Transactions on Industrial Electronics, 2023, 20(7): 2664-2675.
[3] Rachev E, Petrov V. DC link capacitor selection for DC-DC converters[C]//2020 12th Electrical Engin- eering Faculty Conference (BulEF), Varna, Bulgaria, 2020: 1-5.
[4] Zhao Nannan, Gao Runfeng, Wang Gaolin, et al. Online estimation method of DC-link capacitors for reduced DC-link capacitance IPMSM drives[J]. IEEE Transactions on Power Electronics, 2021, 36(11): 12196-12201.
[5] 罗丹, 陈民铀, 赖伟, 等. 基于Haar小波变换重构开关序列的MMC子模块电容值在线监测方法[J]. 电工技术学报, 2022, 37(20): 5278-5289.
Luo Dan, Chen Minyou, Lai Wei, et al. Online monitoring method for sub-module capacitance in modular multilevel converter based on Haar wavelet transform reconstruction switch sequence[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(20): 5278-5289.
[6] Zhao Hu, Shen Jianwu, Zhang Yizhou, et al. An intelligent tension sensor for high speed railway catenary monitoring[C]//2022 IEEE 2nd International Conference on Power, Electronics and Computer Applications (ICPECA), Shenyang, China, 2022: 500-503.
[7] 周志恒, 贺德强, 陈彦君, 等. 基于GA-BP神经网络的列车关键部件预防性维修优化模型及应用[J]. 铁道科学与工程学报, 2021, 18(6): 1382-1391.
Zhou Zhiheng, He Deqiang, Chen Yanjun, et al. Optimization model and application of preventive maintenance of key components of train based on GA-BP neural network[J]. Journal of Railway Science and Engineering, 2021, 18(6): 1382-1391.
[8] Zhao Zhaoyang, Davari P, Lu Weiguo, et al. An overview of condition monitoring techniques for capacitors in DC-link applications[J]. IEEE Transa- ctions on Power Electronics, 2021, 36(4): 3692-3716.
[9] Soualhi A, Makdessi M, German R, et al. Heath monitoring of capacitors and supercapacitors using the neo-fuzzy neural approach[J]. IEEE Transactions on Industrial Informatics, 2018, 14(1): 24-34.
[10] McGrew T, Sysoeva V, Cheng Chihao, et al. Con- dition monitoring of DC-link capacitors using time- frequency analysis and machine learning classifi- cation of conducted EMI[J]. IEEE Transactions on Power Electronics, 2022, 37(10): 12606-12618.
[11] Soliman H, Wang Huai, Gadalla B, et al. Condition monitoring for DC-link capacitors based on artificial neural network algorithm[C]//2015 IEEE 5th Inter- national Conference on Power Engineering, Energy and Electrical Drives (POWERENG), Riga, Latvia, 2015: 587-591.
[12] Hu Jiayu, Qiu Guanqun, Wang Weiyao, et al. An on-line capacitor condition monitoring method based on switching frequencies for modular multilevel converters[C]//2021 4th International Conference on Energy, Electrical and Power Engineering (CEEPE), Chongqing, China, 2021: 183-187.
[13] 伍珣, 田睿, 李凯迪, 等. 基于预充电模型与低频采样的直流支撑电容器电容辨识方法[J]. 中南大学学报(自然科学版), 2023, 54(8): 3325-3334.
Wu Xun, Tian Rui, Li Kaidi, et al. Pre-charging model based capacitance estimation method for DC-link capacitors with low sampling frequency[J]. Journal of Central South University (Science and Technology), 2023, 54(8): 3325-3334.
[14] Wang Zhongxu, Zhang Yi, Wang Huai, et al. Capacitor condition monitoring based on the DC-side start-up of modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2020, 35(6): 5589-5593.
[15] Wu Yu, Du Xiong. A VEN condition monitoring method of DC-link capacitors for power converters[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 1296-1306.
[16] Li Hao, Xiang Dawei, Han Xu, et al. High-accuracy capacitance monitoring of DC-link capacitor in VSI systems by LC resonance[J]. IEEE Transactions on Power Electronics, 2019, 34(12): 12200-12211.
[17] Zhao Shuai, Peng Yingzhou, Zhang Yi, et al. Parameter estimation of power electronic converters with physics-informed machine learning[J]. IEEE Transactions on Power Electronics, 2022, 37(10): 11567-11578.
[18] Gao Yihang, Cheung K C, Ng M K. SVD-PINNs: transfer learning of physics-informed neural networks via singular value decomposition[C]//2022 IEEE Symposium Series on Computational Intelligence (SSCI), Singapore, 2022: 1443-1450.
[19] Liu Jie, Zhang Rongwei, Luan Mengxiao, et al. GL-PINN algorithm for inferring velocity and pressure fields from sparse concentration field[C]// 2022 IEEE 17th International Conference on Control & Automation (ICCA), Naples, Italy, 2022: 326-331.
[20] Wang Yuzhang, Alkhadhr S, Almekkawy M. PINN simulation of the temperature rise due to ultrasound wave propagation[C]//2021 IEEE International Ultrasonics Symposium (IUS), Xi’an, China, 2021: 1-4.
[21] Zhao Zhenyu, Fan Fei, Sun Quqin, et al. Physics informed neural network-based high-frequency modeling of induction motors[J]. Chinese Journal of Electrical Engineering, 2022, 8(4): 30-38.
[22] Stiasny J, Misyris G S, Chatzivasileiadis S. Physics- informed neural networks for non-linear system identification for power system dynamics[C]//2021 IEEE Madrid PowerTech, Madrid, Spain, 2021: 1-6.
[23] Lu Lu, Meng Xuhui, Mao Zhiping, et al. DeepXDE: a deep learning library for solving differential equations[J]. SIAM Review, 2021, 63(1): 208-228.
[24] Misyris G S, Venzke A, Chatzivasileiadis S. Physics- informed neural networks for power systems[C]//2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2020: 1-5.
[25] Bin Waheed U. Kronecker neural networks overcome spectral bias for PINN-based wavefield com- putation[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 8029805.
[26] 臧国强, 刘晓莉, 徐颖菲, 等. 深度学习在电力设备缺陷识别中的应用进展[J]. 电气技术, 2022, 23(6): 1-7.
Zang Guoqiang, Liu Xiaoli, Xu Yingfei, et al. Application progress of deep learning in power equipment defect identification[J]. Electrical Engin- eering, 2022, 23(6): 1-7.
[27] 徐宝昌, 张学智, 王雅欣, 等. 用于两相流环空压力预测的自适应物理信息神经网络模型[J]. 石油学报, 2023, 44(3): 545-555.
Xu Baochang, Zhang Xuezhi, Wang Yaxin, et al. self-adaptive physical information neural network model for prediction of two-phase flow annulus pressure[J]. Journal of Petroleum, 2023, 44(3): 545- 555.
[28] 仲林林, 胡霞, 刘柯妤. 基于改进生成对抗网络的无人机电力杆塔巡检图像异常检测[J]. 电工技术学报, 2022, 37(9): 2230-2240, 2262.
Zhong Linlin, Hu Xia, Liu Keyu. Power tower anomaly detection from unmanned aerial vehicles inspection images based on improved generative adversarial network[J]. Transactions of China Elec- trotechnical Society, 2022, 37(9): 2230-2240, 2262.
[29] 郭亮, 王祥业, 姜文聪. 基于生成对抗网络的注入电流式热声成像逆问题研究[J]. 电工技术学报, 2021, 36(增刊1): 22-30.
Guo Liang, Wang Xiangye, Jiang Wenchong. The study on the inverse problem of applied current thermo-acoustic imaging based on generative adversarial network[J]. Journal of Electrical Engin- eering Technology, 2021, 36(S1): 22-30.
[30] Bi Xiaoyang, He Enhao, Wang Qipeng. Research on style transfer model based on improved CycleGAN algorithm[C]//2023 IEEE 5th International Con- ference on Civil Aviation Safety and Information Technology (ICCASIT), Dali, China, 2023: 129-135.
[31] Zhang Xingwei, Zhang Ke, Xie Lingwang, et al. An enhancement and detection method for a glue dispensing image based on the CycleGAN model[J]. IEEE Access, 2022, 10: 92036-92047.
[32] 李广全, 刘志明, 张子璠, 等. 基于EMD和ISA方法的轨道车辆动态应变信号去工频干扰研究[J]. 北京交通大学学报, 2018, 42(1): 106-112.
Li Guangquan, Liu Zhiming, Zhang Zifan, et al. Research on removing power frequency interference on dynamic strain signal of rolling stock based on EMD and ISA algorithm[J]. Journal of Beijing Jiaotong University, 2018, 42(1): 106-112.
Abstract At present, the fault monitoring dilemma of DC-link capacitors in traction converters mainly focuses on the noise interference of sensor measurement, the aging speed of the capacitor is affected by various environmental factors, and the accuracy and stability requirements are high. Therefore, this paper proposes a DC-link capacitor parameter identification method for traction converter based on physical information neural network (PINN) and capacitor pre-charging model. The sampling frequency of the voltage sensor is very low, and there is no need for the capacitor pre-charging voltage curve to be strictly aligned with the time axis, effectively reducing the influence of the measurement signal-to-noise ratio on the prediction results. Moreover, the amount of capacitance data required is minimal using the cycle consensus generative adversarial network (CycleGAN) algorithm, which can be applied to a wide range of capacitance intervals under the same topology. This method can be applied to rail transit applications.
The architecture design of the adaptive physical information neural network model in this method is described, including the construction of partial differential equations and boundary conditions, physical constraint loss function modeling, network structure, and training process. Regarding the adaptive weight PINN execution part, the AdamW algorithm is used to update the adaptive weight and linear network weight of each loss component. After the number of iterations is set, the L-BFGS algorithm performs a new round of iterative optimization on the linear network weight part of the current PINN network. However, the adaptive weight is no longer updated. During the training process using the PINN network, when the number of iterations is greater than the specified number limit and the mean square error of the test set is less than the set number, the CycleGAN model is used to generate data, and the current PINN network is used as the constraint condition label. After adding the generated training set, the training results are monitored by the test set’s accuracy after each iteration. Suppose the accuracy is unchanged or improved in a fixed iteration interval, the generated training set is considered credible and effective, and the generated data set is updated before the next fixed iteration interval is turned on.
The laboratory low-power prototype platform is used for example analysis. The results show that under normal conditions, the identification relative error of this method is about 1%. When the signal-to-noise ratio reaches 30 dB, the identification relative error can still be controlled within 5%, and reducing the sampling frequency can alleviate the effect of signal-to-noise ratio reduction. This method provides a new idea for solving the problem of state parameter identification of DC-link capacitors and ensuring the safe operation and long-term stability of DC-link capacitor of traction converters.
keywords:DC-link capacitor, parameter identification, physical information neural network (PINN), cycle- consistent generative adversarial networks (CycleGAN), DC-link pre-charging process
DOI: 10.19595/j.cnki.1000-6753.tces.231880
中图分类号:TM464
国家自然科学基金资助项目(52072414)。
收稿日期 2023-11-13
改稿日期 2024-01-08
向超群 男,1988年生,副教授,硕士生导师,研究方向为电机控制与器件可靠性。E-mail: xcq061017@163.com
伍 珣 男,1993年生,讲师,主要研究方向为电容器状态辨识。E-mail: 309931624@qq.com(通信作者)
(编辑 陈 诚)