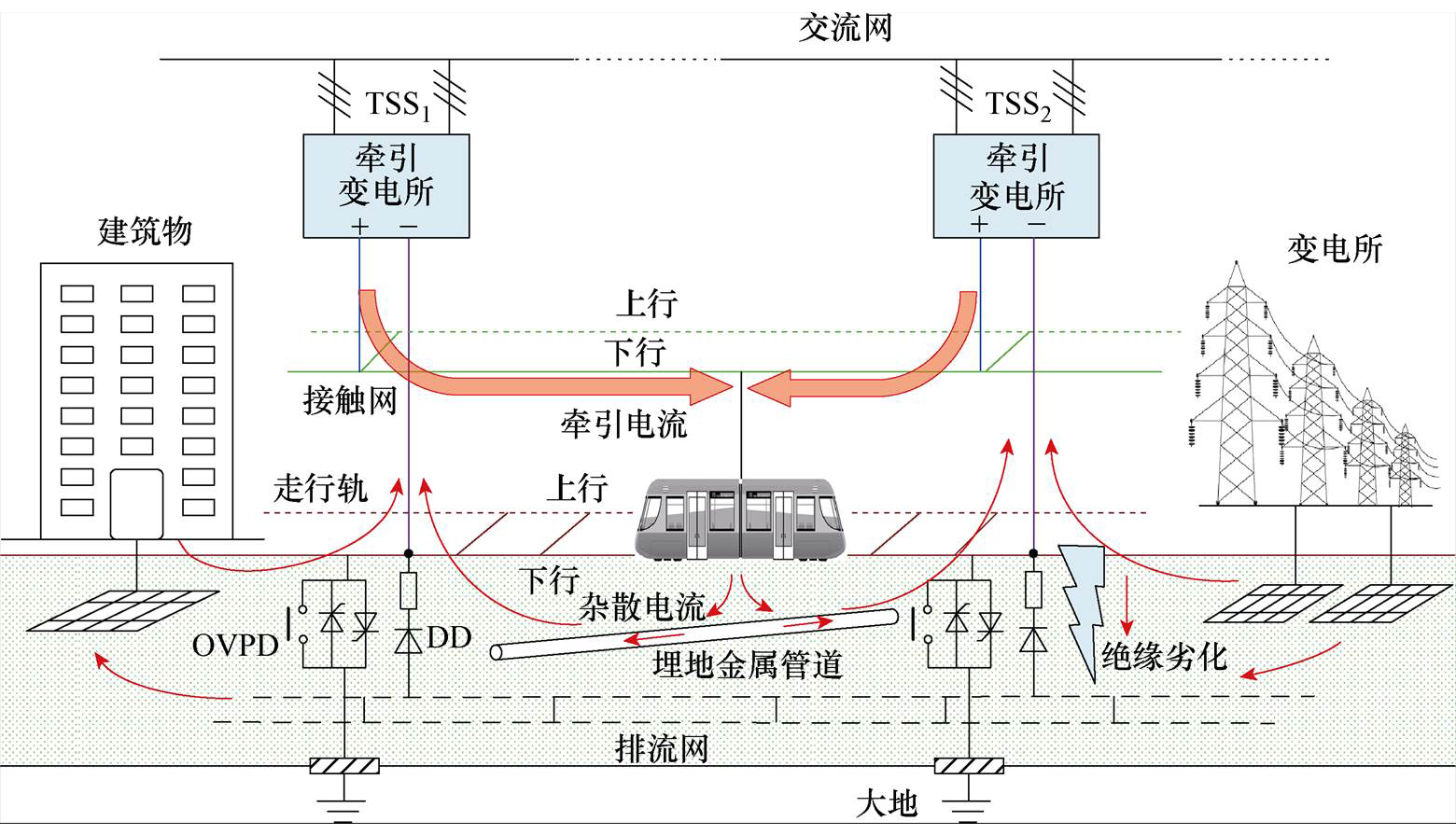
图1 多回流路径耦合情况下直流牵引供电系统结构
Fig.1 Structure diagram of DC traction power supply system with multiple reflux paths coupling
摘要 当前，城轨直流牵引供电系统回流安全已成为影响线路安全运行的关键问题之一。为研究多回流路径耦合对回流安全参数及周边关键金属工程的影响，该文提出多回流路径耦合情况下直流牵引供电系统动态仿真模型，构建多回流路径耦合矩阵，建立多回流路径耦合情况下多区间回流安全参数动态分布计算方法，实现回流安全参数动态分布规律分析。基于实际线路参数，分析了不同类型多回流路径耦合时钢轨电位和杂散电流分布规律。研究结果表明，该文所提出的方法可有效模拟多回流路径耦合情况下回流安全参数动态分布及对周边关键金属工程的影响；针对走行轨回流不畅及多回流路径耦合，分别提出并联电缆及单向导通控制的治理方法，并基于该文所建立的模型进行仿真分析，验证了其有效性。
关键词：城市轨道交通 直流牵引供电系统 多回流路径耦合 钢轨电位 杂散电流
采用直流牵引供电方式的城市轨道交通线路普遍使用走行轨作为列车牵引电流的回流导体，走行轨对地存在一定的钢轨电位。由于走行轨很难做到与周边完全绝缘，导致部分回流电流泄漏到周边介质，形成杂散电流[1]。钢轨电位与杂散电流作为系统回流安全参数，不仅会影响城轨直流牵引供电系统的安全性，造成线路停运事故的发生，还会加速周围地下各类金属结构的电化学腐蚀，从而缩短装备服役寿命[2]，造成管道腐蚀管壁减薄[3]等，甚至会危及乘客的人身安全[4]。在城轨线路中，一般通过设置过电压保护装置（Over Voltage Protection Device, OVPD）、排流装置（Drain Device, DD）和排流网以控制钢轨电位与杂散电流。但在实际线路运行中，上述控制方法并不能有效控制回流的安全参数，OVPD会动作频繁，排流网收集杂散电流效率也并不理想，钢轨电位与杂散电流仍普遍过高[5-7]。
目前，研究回流安全参数分布的建模方法主要包括软件建模方法、数学建模方法和模拟系统分析方法。软件建模方法主要基于CDEGS和Ansys等仿真软件。文献[8]基于CDEGS建立了地铁杂散电流分布仿真模型；文献[9]建立了明挖隧道、盾构隧道和高架桥不同地铁结构的长线路杂散电流统一模型。数学建模通过建立城轨供电系统的等效模型进行分析。文献[10-11]建立了三层、四层地铁回流系统模型；为分析复杂土壤环境对回流安全参数的影响，文献[12]建立了多层土壤结构的杂散电流仿真模型。此外，在模拟系统分析方面，文献[13]提出一种基于可变电阻模块的电力电子动模实验平台分析回流安全参数分布规律。
目前，对城轨回流系统的建模及对回流安全参数的分析主要针对城轨系统自身。但在现实情况下，线路长时间运行或在潮湿环境下会造成走行轨绝缘劣化，导致形成走行轨接地回流路径[14]；埋地金属管道[15]、周围建筑或变电所等设施的接地网[16]为杂散电流提供低阻回路，也会形成额外的回流路径。因此，回流系统会不可避免地受到周边环境的影响从而形成额外的回流路径，且此回流路径与整个回流系统耦合运行。而走行轨绝缘劣化会进一步加深多回流路径耦合影响，但目前能精确定位走行轨绝缘劣化点的方法相对较少，从源头控制杂散电流以治理多回流路径耦合问题较为困难。因此，分析多回流路径耦合情况下地铁回流安全参数的分布规律，并阐释回流系统和周边其他关键金属系统之间的耦合关系，对研究回流安全参数的影响范围、异常升高的机理及其控制方法有重要意义。
为此，本文提出多回流路径耦合情况下直流牵引供电系统动态仿真模型，以建立多回流路径耦合矩阵的方式描述多种类型的耦合关系，并提出多回流路径耦合情况下多区间回流安全参数动态分布计算方法，阐明多回流路径耦合情况下钢轨电位和杂散电流动态分布规律。
多回流路径耦合情况下直流牵引供电系统结构如图1所示，城轨供电系统中，接触网分为上行、下行，通过受电弓向列车供电。在各牵引所处，上行、下行的接触网相连且由馈电线连接到牵引变电所正极。因此，地铁直流牵引供电接触网全线贯通。走行轨也分为上行、下行两部分，在上、下行之间设置有均流线。用于收集杂散电流的排流网铺设在道床内部，排流网中的杂散电流可以通过排流装置回到牵引变电所负极。因此，由“走行轨-排流网-大地”组成的三层地铁回流系统模型[17]也全线贯通。此外，系统还设有OVPD和DD回流保护装置。其中，OVPD安装于车站位置处的走行轨与地网之间，监测钢轨电位是否超过限值并切换导通状态。DD安装于走行轨与排流网之间，监测结构钢筋极化电位并切换导通状态。
图1中标出了单列车在双边供电区间内行驶时电流流通的方向示意。首先，牵引电流由两侧牵引变电所正极经接触网流向列车，列车的回流电流主要通过走行轨返回至牵引变电所负极，部分回流电流泄漏至周边形成杂散电流。实际系统中，走行轨可能存在绝缘劣化区域，走行轨附近存在埋地金属管道、周边建筑物结构钢筋、交流供电系统变电所接地网等金属工程。其中，走行轨绝缘劣化区域会降低走行轨与大地的绝缘性，导致绝缘劣化处大量的杂散电流泄漏至大地；部分泄漏电流会流经周边埋地金属管道；建筑物一般将内部钢筋结构作为接地导体与接地网相贯通，建筑物接地系统可能与城轨回流系统产生电气耦合，杂散电流即可通过接地网和建筑物钢筋结构，再经大地回流至牵引变电所负极；交流供电系统变电所接地的中性点和杆塔接地网也会受杂散电流影响。以上这些情形必然会对回流系统和周围建筑设施产生影响，并且产生多回流路径耦合效应。
为实现多回流路径耦合情况下回流安全参数动态分布精确求解，建立如图2所示的多回流路径耦合情况下直流牵引供电系统动态仿真模型。该模型在出现多回流路径耦合位置新增耦合切面，并在耦合切面间新增多回流耦合路径。假设列车和牵引变电所的数量为N-2，原回流系统共有N-3个区段。由于在耦合位置各新增了一条耦合切面，原区段在耦合位置被一分为二，因此多回流路径耦合系统等效模型中的切面总数为N且共有N-1个区段。耦合路径上的电阻等效为集中电阻RC，由耦合的结构设施（如金属管道、建筑物结构钢筋、排流网等）的纵向电阻率与耦合区段长度决定。走行轨对该回流路径电导、排流网对该回流路径电导和该回流路径对地电导与该回流路径的绝缘劣化程度及连接状态有关，分别等效为集中电导yo1、yo2和yo3。通过设置以上参数，可模拟不同类型的多回流路径耦合情况。
图1 多回流路径耦合情况下直流牵引供电系统结构
Fig.1 Structure diagram of DC traction power supply system with multiple reflux paths coupling
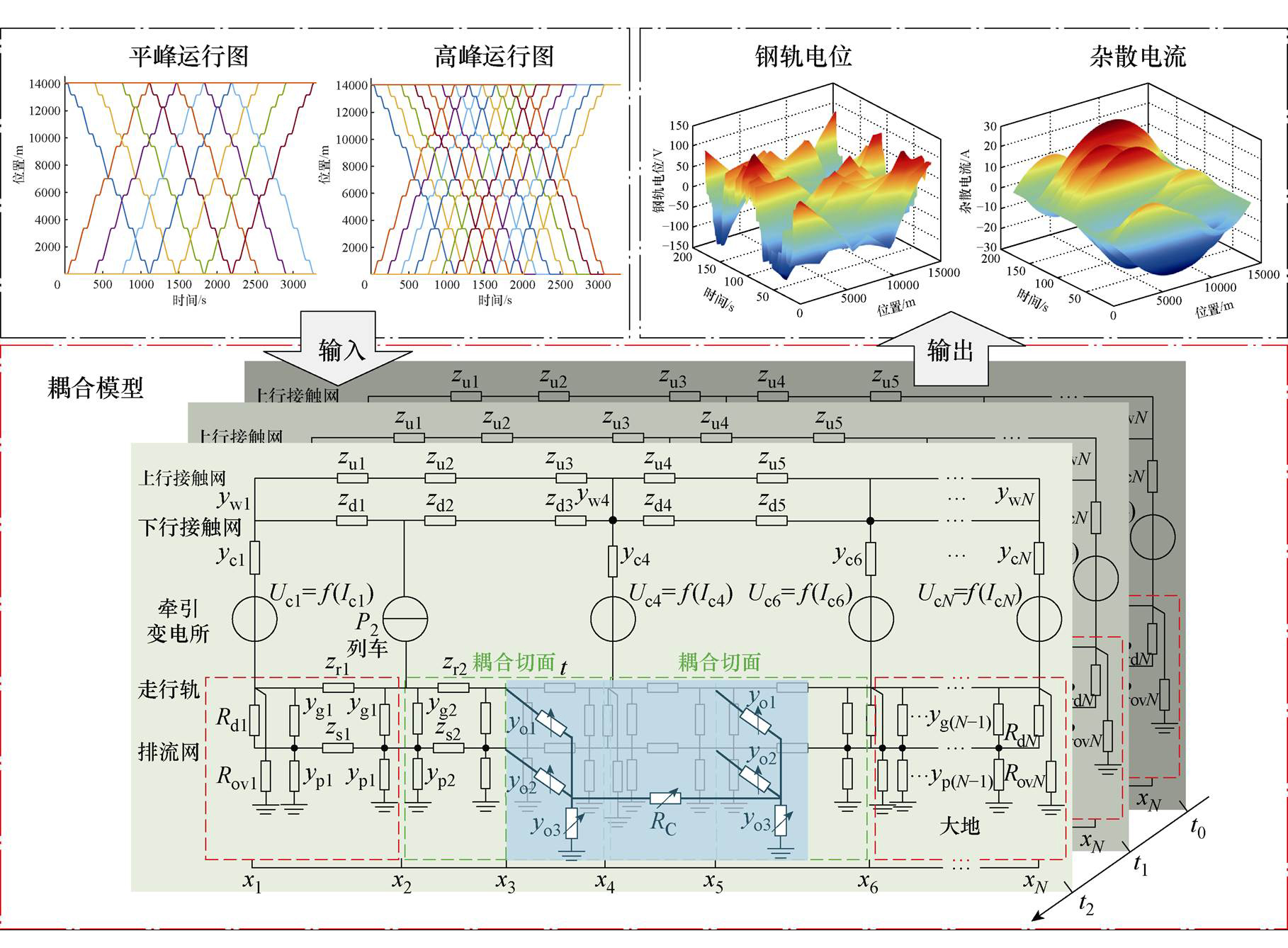
图2 多回流路径耦合情况下直流牵引供电系统动态仿真模型
Fig.2 Dynamic simulation model of DC traction power supply system with multiple reflux paths coupling
在切面xn（1≤n≤N）处，牵引变电所等效为由牵引电流Icn控制的电压源Ucn=f(Icn)。列车等效为功率源Pn，其功率和位置可以通过列车牵引计算获得。在列车牵引计算中可通过设置停站时间和发车间隔来模拟随峰调整的列车运行图。ywn为上行接触网和下行接触网之间的导纳，描述上行接触网与下行接触网的连接状态，在牵引变电所节点处连接，在列车节点和耦合切面节点处断开。ycn为牵引变电所的等效电导，ygn、ypn分别为走行轨对排流网电导和排流网对地电导。Rovn为OVPD的等效电阻，Rdn为DD的等效电阻。在xn～xn+1区间，zdn、zun、zrn、zsn分别为下行接触网、上行接触网、走行轨和排流网的纵向电阻。以上参数均为回流系统自身参数，不受多回流路径耦合影响。
由于回流系统分布参数明显，为了准确、快速地计算全线回流安全参数的动态分布，需要依据边界条件对如图2所示的回流系统混合参数模型进行参数修正并将其等效为如图3所示的回流系统集中参数模型，等效后回流系统的每个区段相当于一个双π型回路，回流系统内走行轨、排流网等导体的参数均为集中等效参数。
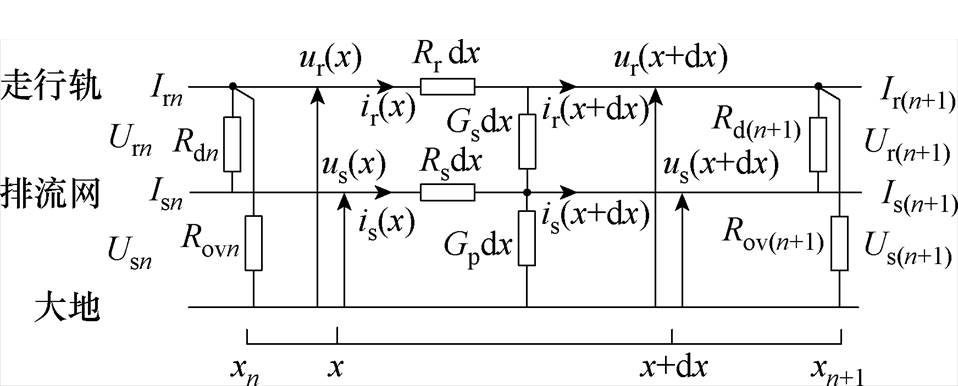
图3 回流系统混合参数模型
Fig.3 Model of reflux system with hybrid parameters
在回流系统混合参数模型切面xn与切面xn+1间，OVPD、DD的等效电阻Rovn和Rdn为集中参数。Rr、Rs、Gs和Gp分别为单位长度走行轨、排流网的纵向电阻和单位长度走行轨对排流网、排流网对地电导，均为分布参数。urn(x)、usn(x)、irn(x)和isn(x)分别为区间x处的钢轨电位、排流网电位、走行轨电流和排流网电流。由基尔霍夫定律得出任意位置x处回流安全参数间的关系为
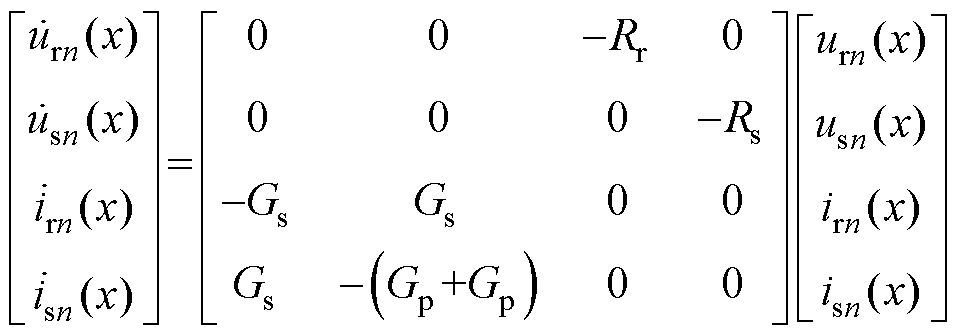（1）
式（1）的通解可以写为
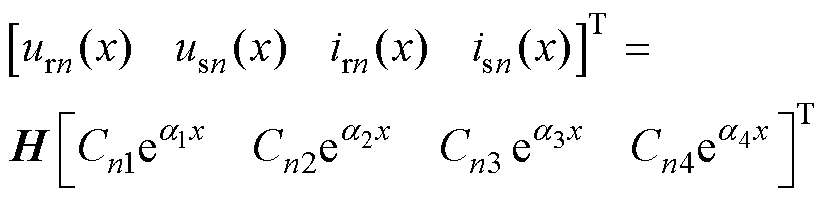（2）
式中，H为a1～a4的特征向量矩阵；Cn1～Cn4为由切面xn处的边界条件确定的待定参数。
在切面xn+1（1≤n≤N-1）处，有
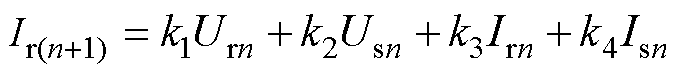（3）
式中，k1～k4只与切面xn与切面xn+1间的距离、回流系统自身集中参数及分布参数相关。
在等效后的回流系统集中参数模型中，将切面xn+1处的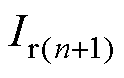
的表达式整理为式（3）的形式，得出
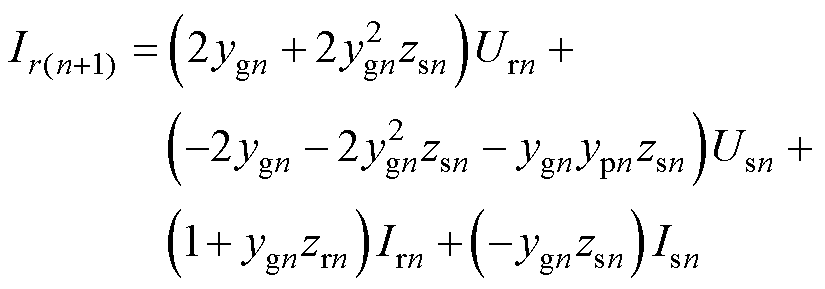（4）
对比式（3）和式（4），分别联立两式中Urn、Usn、Irn、Isn前的系数，即可得到ygn、zrn、ypn、zsn经修正后的参数值。
多回流路径耦合情况下直流牵引供电系统等效模型的节点电压方程为
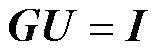（5）
式中，U为系统节点电压矩阵；I为系统节点注入电流矩阵；G为6×N维的系统节点电导矩阵，由系统初始节点电导矩阵G0和多回流路径耦合矩阵GR组成，即
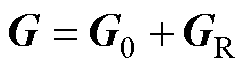（6）
系统初始节点电导矩阵G0为
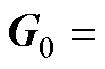
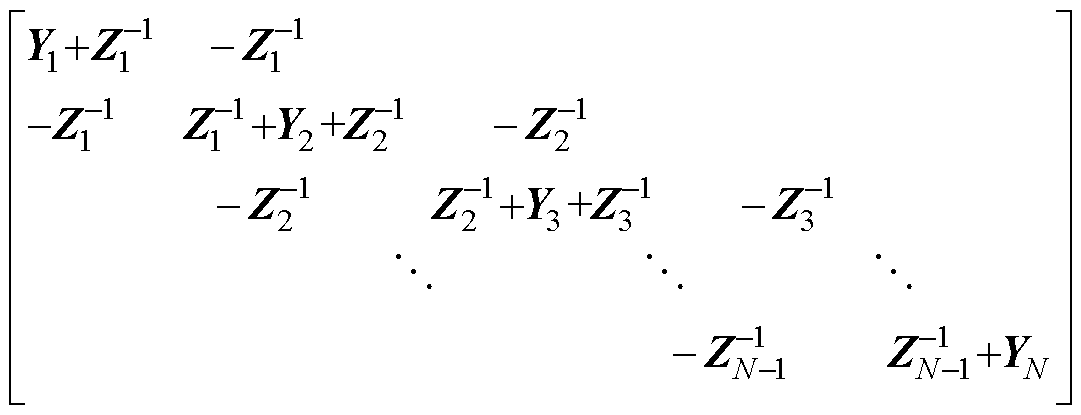（7）
式中，Zn为切面xn至切面xn+1之间的线路阻抗子矩阵；Yn为切面xn（1≤n＜N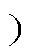
位置的统一化节点导纳子矩阵，分别为
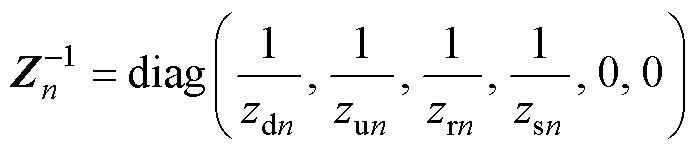（8）
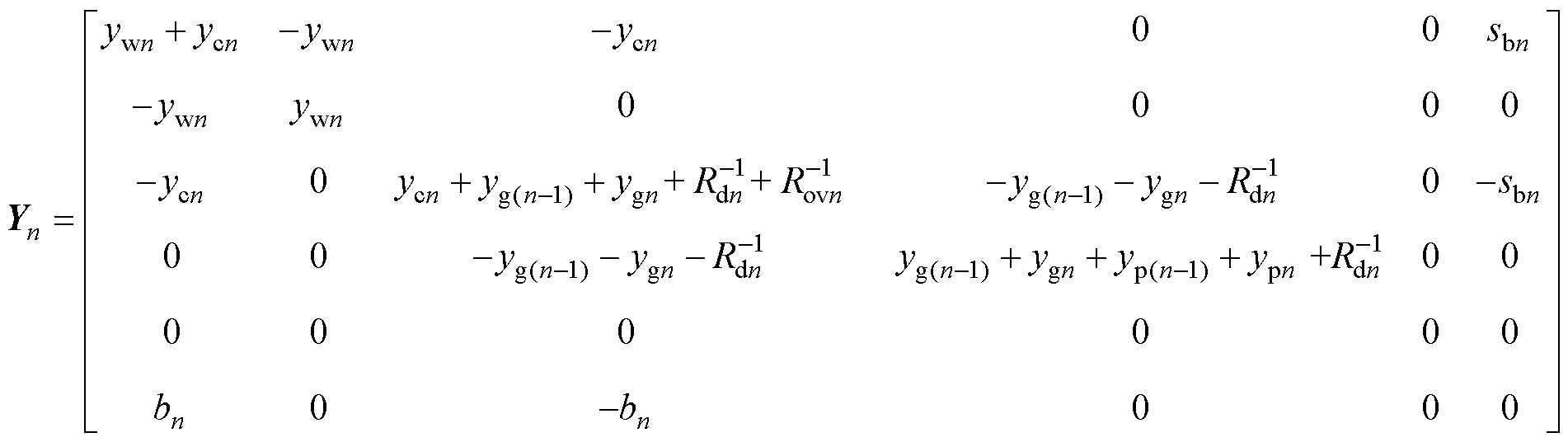（9）
式中，sbn为再生制动能量吸收装置（Regen- erativebraking Energy Absorbing Device, READ）的触发电压；bn为READ的状态。READ投入时，bn=1；否则，bn=0。由于在耦合切面间多加了一条多回流路径，该切面节点数+1。为统一所有切面矩阵维数，初始线路阻抗子矩阵和节点导纳子矩阵各多加一维0向量，均为6×6的矩阵。
当xi、xj位置处发生耦合时（1≤i≤j≤N），多回流路径耦合矩阵为GR，即
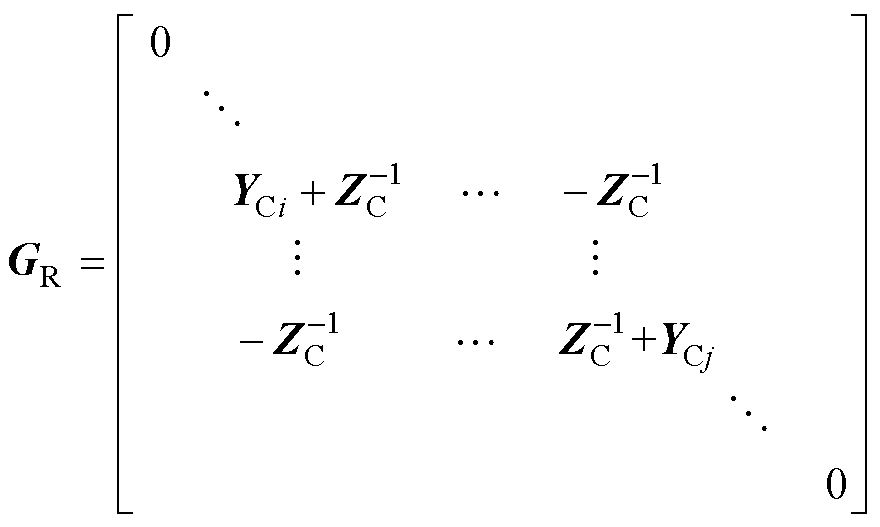（10）
式中，GR为对称稀疏矩阵，在非耦合切面的矩阵元素全为0，矩阵维数与G一致；ZC为耦合切面xi、xj之间的耦合阻抗子矩阵；YC为耦合切面的统一化导纳子矩阵，分别为
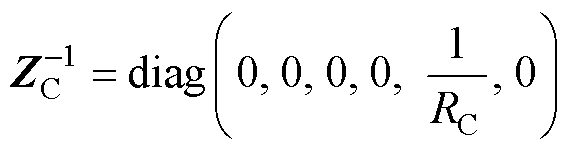（11）
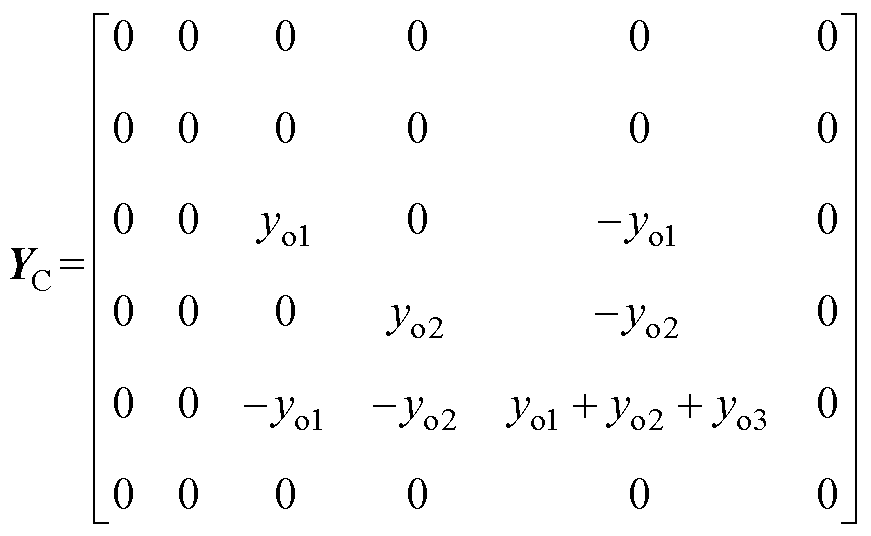（12）
系统节点电压矩阵U为
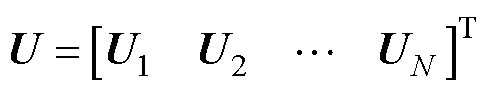（13）
式中，Un为切面xn（1≤n≤N）节点电压子矩阵，即
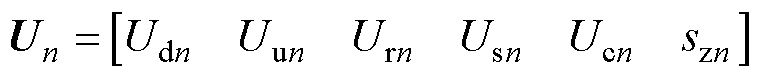（14）
式中，Udn、Uun、Urn、Usn和Ucn分别为在xn处下行接触网、上行接触网、走行轨、排流网和多回流路径的节点电压；szn为READ装置的阻抗。
系统节点注入电流矩阵为I，即
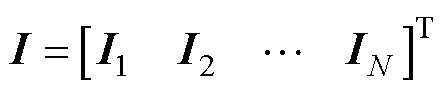（15）
式中，In为切面xn（1≤n≤N）节点注入电流子矩阵，即
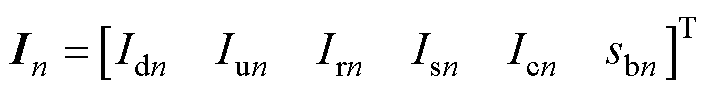（16）
式中，Idn、Iun、Irn、Isn和Icn分别为在xn处注入下行接触网、上行接触网、走行轨、排流网和多回流路径的电流。
回流安全参数动态分布计算流程如下：首先，基于各列车和牵引变电所的位置、耦合位置和耦合类型确定发生耦合后的初始系统节点电导矩阵G；同时，基于各列车的牵引功率确定初始节点注入电流矩阵I；其次，基于式（5）开始迭代计算，求解系统各节点电压及各节点注入电流；接着，基于迭代计算得出的各区间边界条件，求解各区间对应的待定系数Cn1～Cn4并代入式（2）；最后，得出多回流路径耦合情况下多区间任意位置处的回流安全参数动态分布。
为研究多回流路径耦合对周边关键金属工程的影响，所提出的模型可计算多回流路径上电压分布和流经电流。根据多回流路径耦合点处电压UCi、UCj及多回流路径等效电阻RC，可求解如式（17）所示的多回流路径上流经电流Is。在治理多回流路径耦合时，常在多回流路径上设置单向导通装置（Unidirectional Connection Device, UCD）。当走行轨对多回流路径电压为正向，UCD关断，防止产生Is；当走行轨对多回流路径电压为负向，UCD导通，使Is可回流至走行轨。UCD不同工作特性下等效参数如式（18）所示，本模型可设置动态参数RC以模拟UCD的工作机制，通过Is的幅值变化分析其对多回流路径耦合影响的抑制效果。
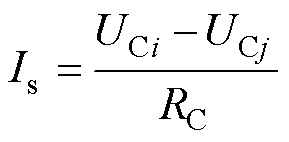（17）
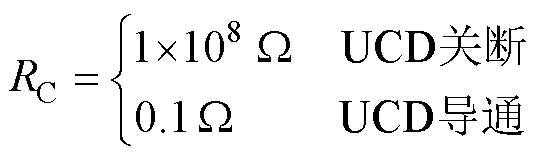（18）
国内某地铁线路信息如图4所示，该线路共设有10个车站，其中5个车站位置设置有牵引变电所。列车运行图如图2所示，在高峰运行阶段，假设上行、下行列车发车间隔固定为180 s，列车在每个车站停靠30 s。自上行或下行第6辆车开始，全线最多有12辆列车运行，并以180 s为间隔形成循环。直流牵引供电系统潮流计算仿真参数设置见表1。基于本文所建立的多回流路径耦合情况下直流牵引供电系统等效模型并依据系统潮流计算仿真参数，选取列车高峰运行时1 300～1 480 s一个循环周期对此线路进行动态仿真。为进一步研究多回流路径的耦合效应，通过设置不同类型的多回流路径耦合仿真工况对此线路的回流安全参数进行分析，见表2。
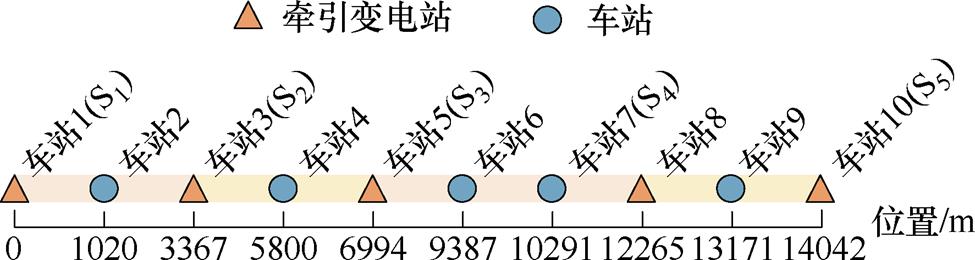
图4 线路信息
Fig.4 Line parameters
表1 直流牵引供电系统仿真参数设置
Tab.1 Simulation parameter of DC traction power supply system
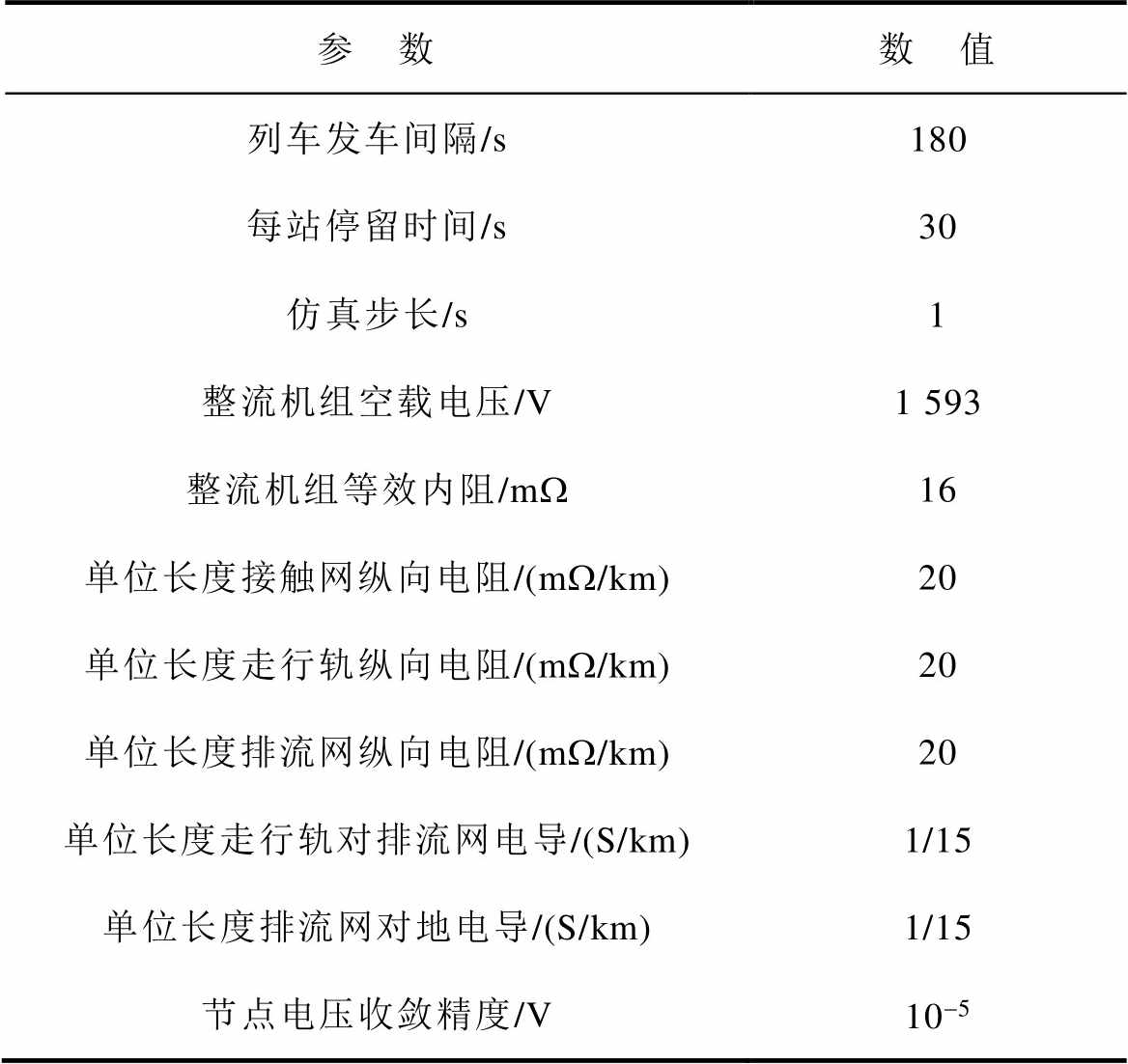
参 数数 值 列车发车间隔/s180 每站停留时间/s30 仿真步长/s1 整流机组空载电压/V1 593 整流机组等效内阻/mW16 单位长度接触网纵向电阻/(mW/km)20 单位长度走行轨纵向电阻/(mW/km)20 单位长度排流网纵向电阻/(mW/km)20 单位长度走行轨对排流网电导/(S/km)1/15 单位长度排流网对地电导/(S/km)1/15 节点电压收敛精度/V10-5
表2 多回流路径耦合仿真工况
Tab.2 Multiple reflux paths coupling simulation conditions
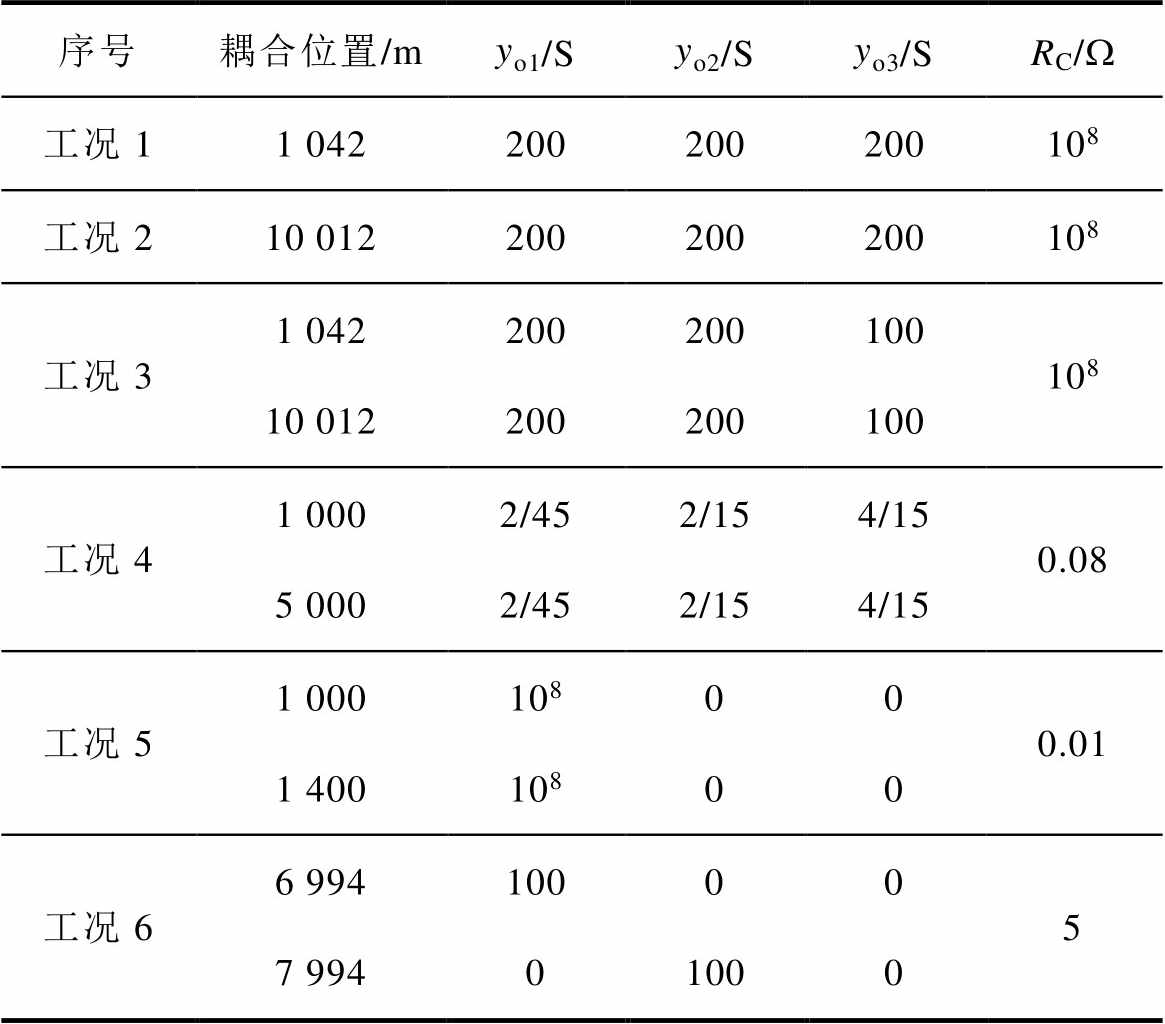
序号耦合位置/myo1/Syo2/Syo3/SRC/W 工况11 042200200200108 工况210 012200200200108 工况31 042200200100108 10 012200200100 工况41 0002/452/154/150.08 5 0002/452/154/15 工况51 000108000.01 1 40010800 工况66 994100005 7 99401000
为分析多回流路径的耦合影响，首先对1 300～1 480 s时段直流牵引供电系统理想回流时的参数分布情况进行仿真。该情况下全线钢轨电位与杂散电流分布如图5所示，全线钢轨电位正向最大幅值为134.9 V，负向最大幅值为-134.2 V；全线杂散电流正向最大幅值为29.5 A，负向最大幅值为-28.1 A。
2.2.1 走行轨绝缘劣化下多回流路径耦合
针对走行轨绝缘劣化情况下多回流路径耦合影响，首先分析走行轨在1 042 m位置或10 012 m位置处出现单点绝缘劣化的情况，多回流路径耦合矩阵参数分别设置为表2中工况1及工况2。通过设置yo1、yo2和yo3的值，可模拟走行轨绝缘劣化程度。由于绝缘劣化发生在单点，并不存在不同切面之间多回流路径耦合的情况，所以RC设置为108W。
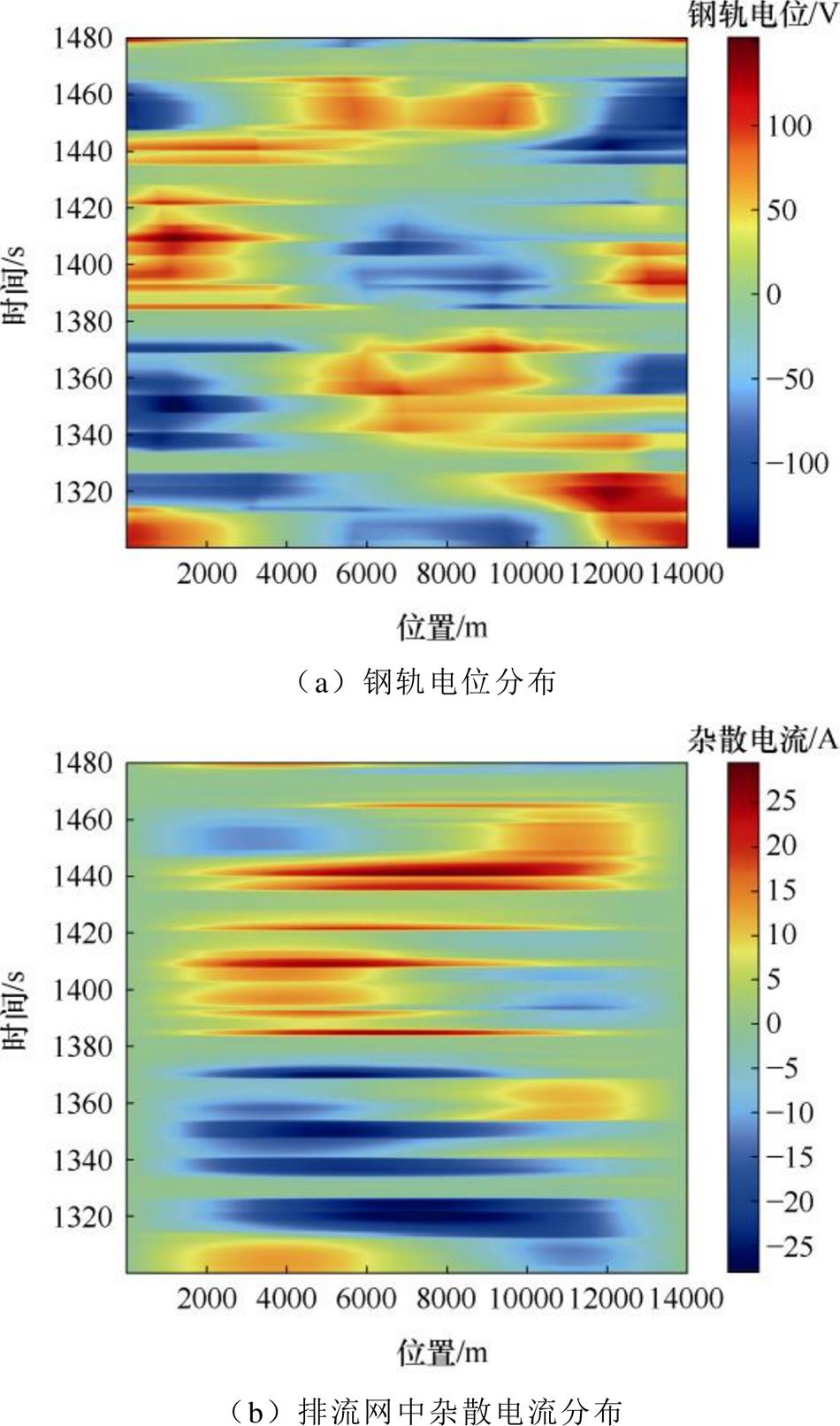
图5 1 300～1 480 s时刻全线回流安全参数分布
Fig.5 Distribution of reflux safety parameters of full-line at 1 300～1 480 s
对比分析1 321 s时刻不同工况下回流安全参数分布，如图6所示。图6a中，在1 042 m初始钢轨电位为负值的位置出现走行轨绝缘劣化时，该位置处钢轨电位趋向于零，全线钢轨电位将被整体抬升；在10 012 m初始钢轨电位为正值的位置出现走行轨绝缘劣化时，该位置处钢轨电位趋向于零，全线钢轨电位将被整体拉低。当走行轨出现绝缘劣化点时，由于绝缘劣化位置走行轨对排流网电导大，该位置杂散电流产生突变。如图6b所示，大量杂散电流从走行轨泄漏至排流网，其最大幅值也大大增加。
当走行轨在1 042 m位置和10 012 m位置处同时出现绝缘劣化时，多回流路径耦合矩阵参数设置为表2中工况3，其中RC设置为108W，表示两绝缘劣化位置相互独立，该情况仿真结果如图7所示。
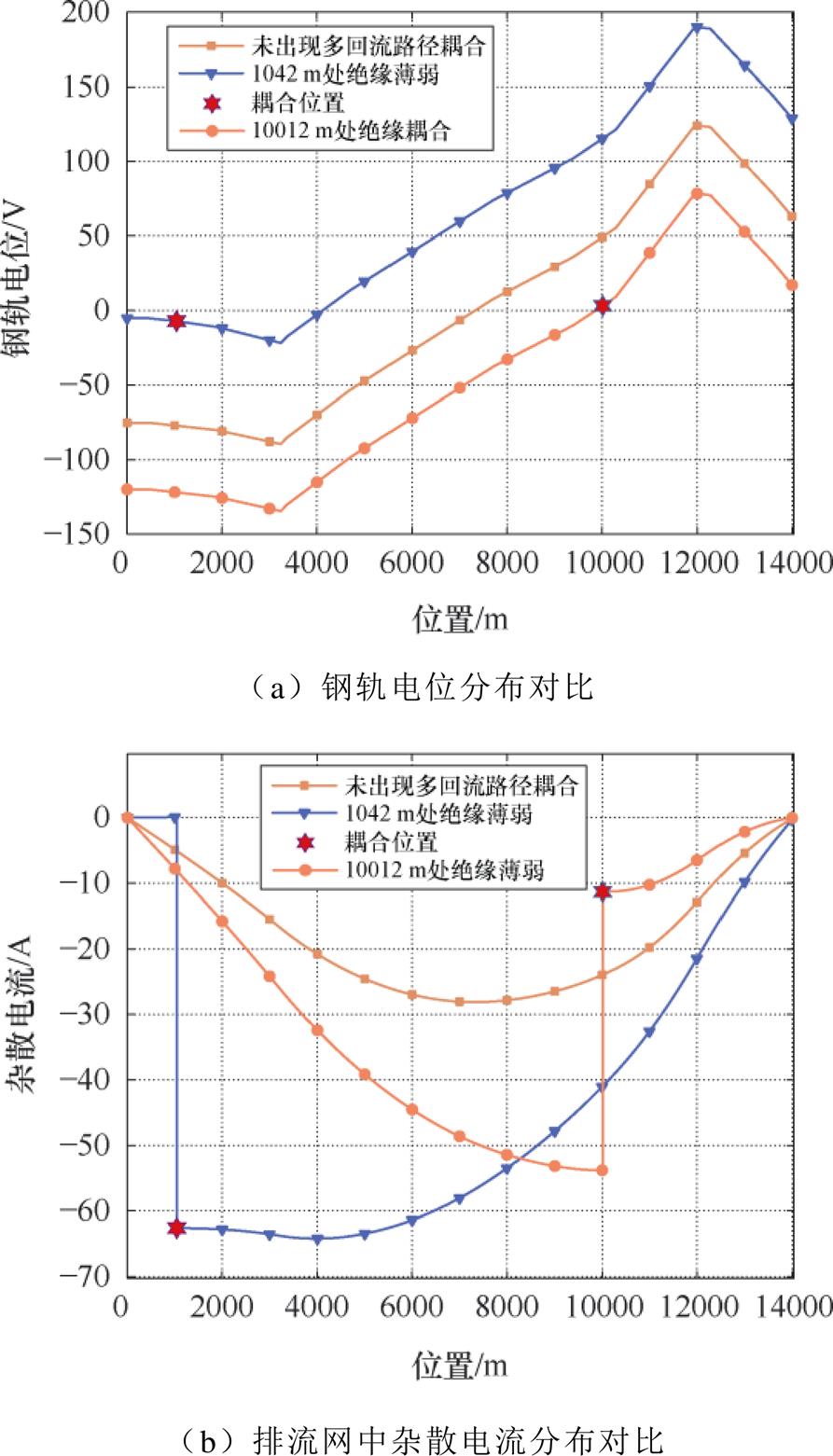
图6 1 321 s时刻单点绝缘劣化时全线回流安全参数分布
Fig.6 Distribution of reflux safety parameters of full-line when single point insulation deteriorates at 1 321 s
如图7a所示，1 321 s时，由于绝缘劣化点同时出现在原本钢轨电位为正和负的位置，绝缘劣化点处钢轨电位分别向零电位抬升和拉低，全线钢轨电位幅值降低。但在列车运行的整个周期内，钢轨电位最大正向幅值为143.2 V，最大负向幅值为-152.3 V，钢轨电位幅值仍有所上升。如图7b所示，杂散电流增加幅度比单点绝缘劣化情况下更为严重，最大幅值可达-800.1 A。
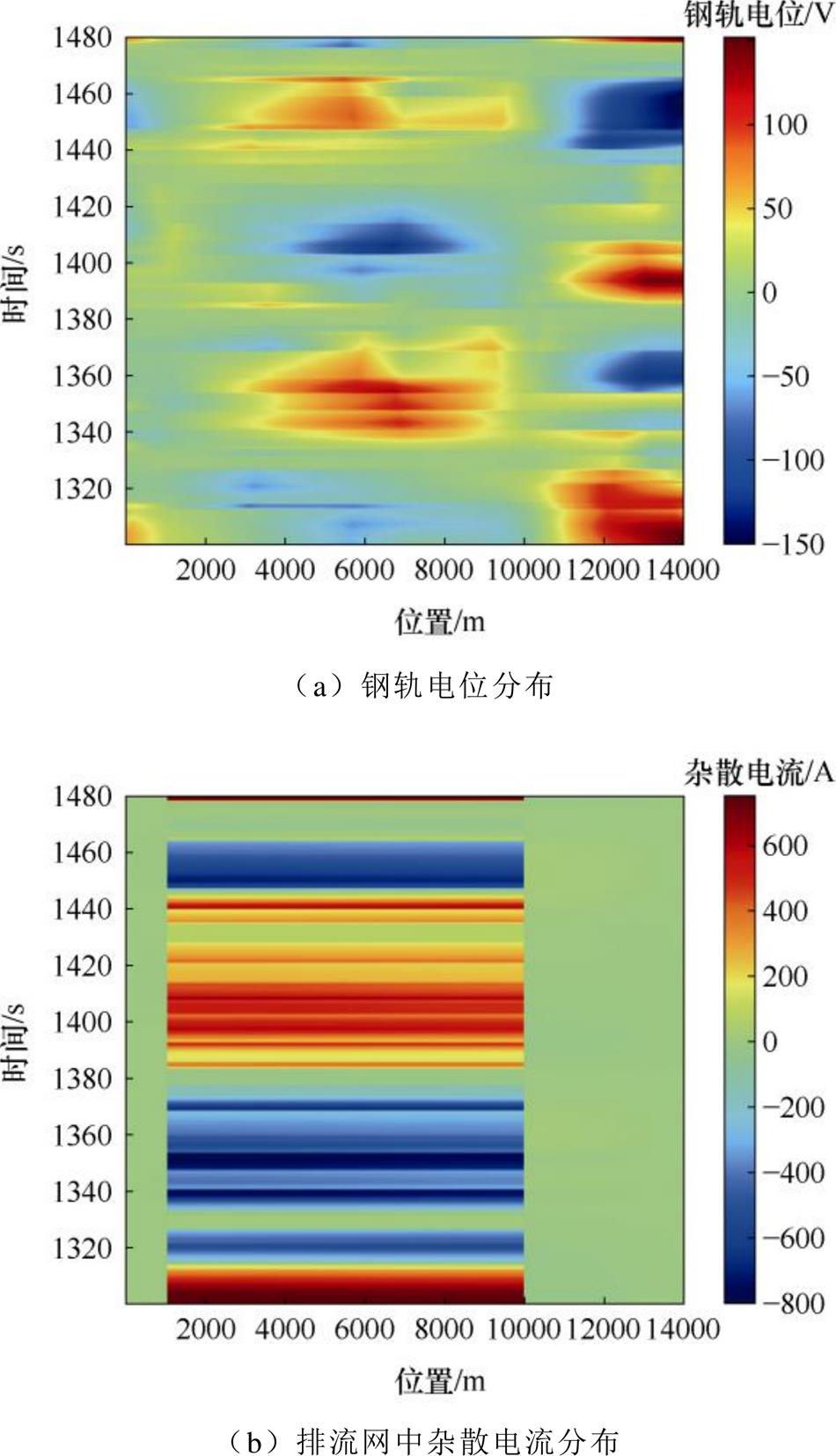
图7 两点绝缘劣化时全线回流安全参数分布
Fig.7 Distribution of reflux safety parameters of full-line when the two-point insulation deteriorates
2.2.2 埋地金属管道多回流路径耦合
针对回流系统附近存在埋地金属管道的多回流路径耦合情况，本文将埋地金属管道绝缘层单位电导设为1/15 S/km，将管道纵向电阻率设为0.02 W/km。在耦合系统各结构绝缘完好的情况下，由于钢轨泄漏至排流网和管道的杂散电流相较于钢轨上的回流电流很小，这时钢轨电位主要由列车运行状态和走行轨纵向电阻决定，所以与埋地金属管道多回流路径耦合时回流安全参数相较于未出现多回流路径耦合时变化不明显。虽然走行轨泄漏至金属管道的电流很微弱，但对管道而言，加速了其电化学腐蚀速度。
为研究管道绝缘层劣化时的多回流路径耦合情况，以1 000～5 000 m区域存在埋地金属管道且管道绝缘层劣化（绝缘层单位电导率设为8/15 S/km）为例进行仿真分析，多回流路径耦合矩阵参数设置为表2中的工况4。由于钢轨电位较大而管道电位幅值较小，所以管道绝缘层劣化导致走行轨对管道电导增加，绝缘劣化位置出现在原先钢轨电位为正值或为负值时，全线钢轨电位将分别被整体拉低或抬升。如图8a所示，在1 440 s时刻下，管道绝缘劣化位置在走行轨正电位区段，全线钢轨电位被整体拉低，在11 985 m走行轨处形成最大钢轨电位幅值，最大值为-139.0 V。如图8b所示，1 000～5 000 m区段单位走行轨泄漏杂散电流程度由于管道的存在而加深，该区段泄漏的总杂散电流为走行轨泄漏至排流网电流与走行轨泄漏至金属管道电流之和。全线杂散电流泄漏累积计算后，最大总泄漏杂散电流幅值增至32.6 A。
对于埋地金属管线而言，GB 50991-2014[18]中提出将腐蚀形态、管地电位和管壁中流动的管道干扰电流作为被干扰管道的主要测试项目。本模型通过计算管道两端电位和流经电流可分析城轨回流系统对埋地金属管道的耦合影响。如图8c所示，管道两端电压主要由首末两端绝缘劣化位置耦合处的钢轨电位共同决定，当两端电位处于同一方向，管道两端电压幅值较大，电压差较小，流经电流较小；当电位处于相反方向时，管道两端电压幅值较小，电压差较大，流经电流较大，并在1 359 s时，达到最大幅值。如图8d所示，对比管道绝缘层劣化前后，流经电流最大幅值由1.4 A上升到3.1 A。
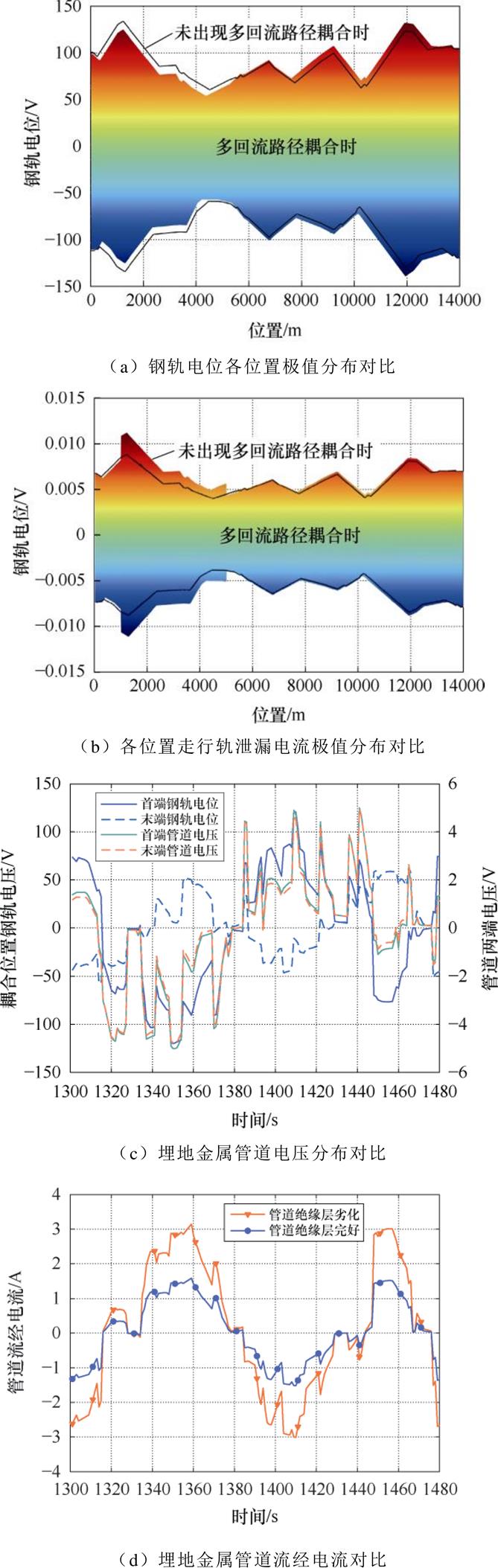
图8 1 000～5 000 m埋地金属管道绝缘层劣化时全线回流安全参数分布
Fig.8 Distribution of reflux safety parameters of full-line when the insulation of buried metallic pipelines deteriorates at 1 000～5 000 m
2.2.3 走行轨高阻区段并联电缆效应分析
走行轨纵向电阻的升高会引起钢轨电位的升高，走行轨并联电缆有助于减小线路的钢轨电位。因此，本文以1 000～1 400 m区段利用走行轨并联电缆（并联电缆纵向电阻率取0.025 mW/m）治理走行轨区段高阻（高阻区段走行轨纵向电阻率取0.1 mW/m）引起的钢轨电位升高为例进行仿真分析，多回流路径耦合矩阵参数设置为表2中工况5，其中yo1=108S表示走行轨与电缆并联。该工况下仿真结果如图9所示。如图9a所示，在走行轨区段高阻情况下，钢轨电位最大幅值因走行轨纵向电阻的升高而抬升至185.3 V。经并联电缆形成额外回流路径后，该区段及其周边的钢轨电位幅值明显降低，最大幅值降为156.8 V。如图9b所示，当走行轨高阻区段内无列车通过时，走行轨并联电缆后的等效纵向电阻与走行轨升高前的纵向电阻一致，所以钢轨电位也与初始一致；但在有加速或减速列车经过时，列车回流电流导致钢轨电位幅值虽有下降但未能降至初始值。
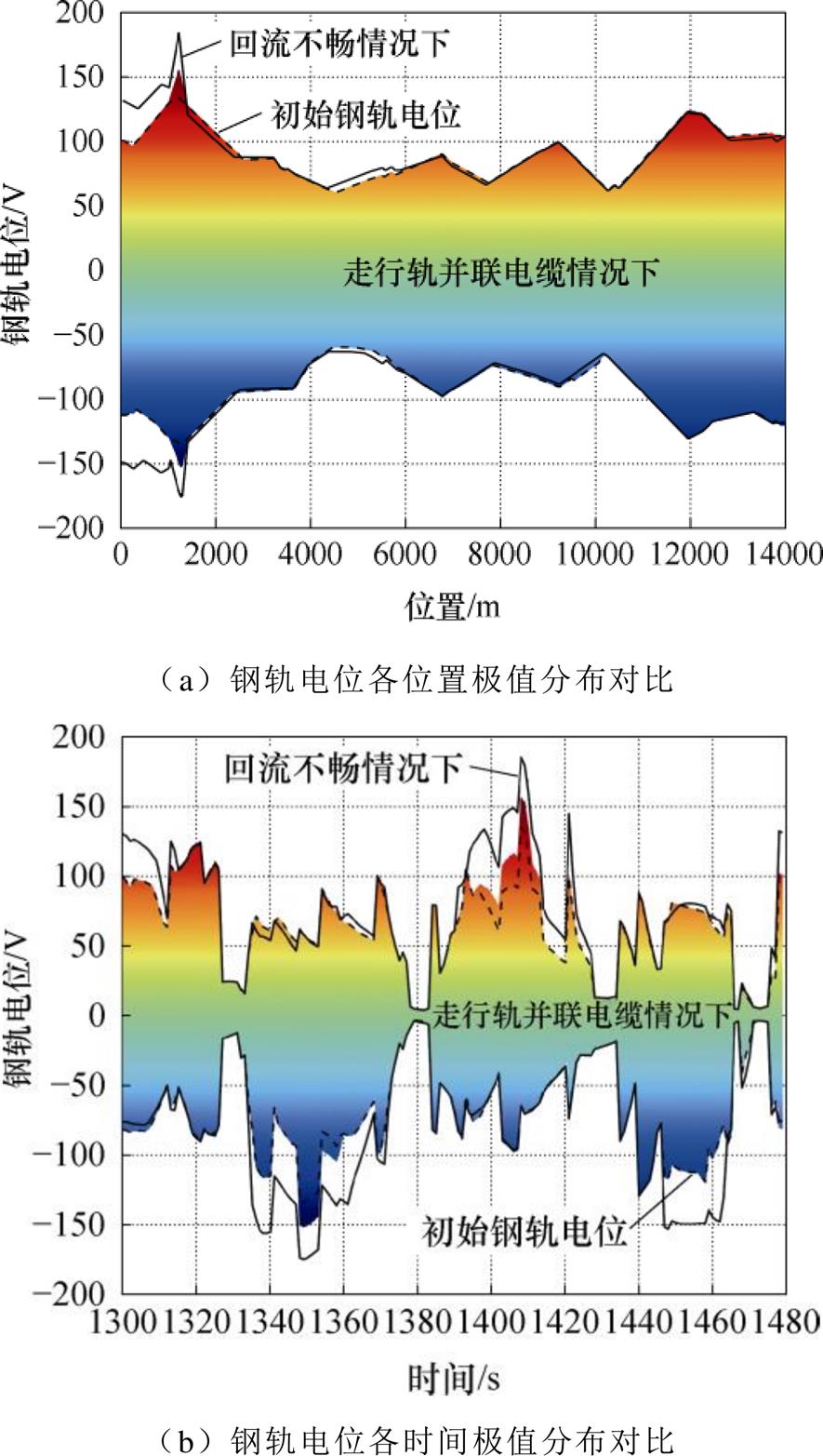
图9 1 000～1 400 m利用走行轨并联电缆治理走行轨区段高阻引起的钢轨电位升高
Fig.9 Utilizing parallel cable for running rail to control the rising of rail potential caused by high resistance in running track section at 1 000～1 400 m
为研究随峰调整的列车运行图对治理效果的影响，将列车发车间隔设置为360 s，作为动态仿真模型的输入，选取其中一个循环周期1 100～1 460 s进行仿真分析，耦合矩阵参数仍设置为表2中工况5。平峰运行时钢轨电位各位置极值分布对比如图10所示。图10中，经走行轨并联电缆治理后，钢轨电位最大减小幅值为19.9 V。综上分析，走行轨并联电缆可有效缓解走行轨区段高阻引起的钢轨电位升高的现象。
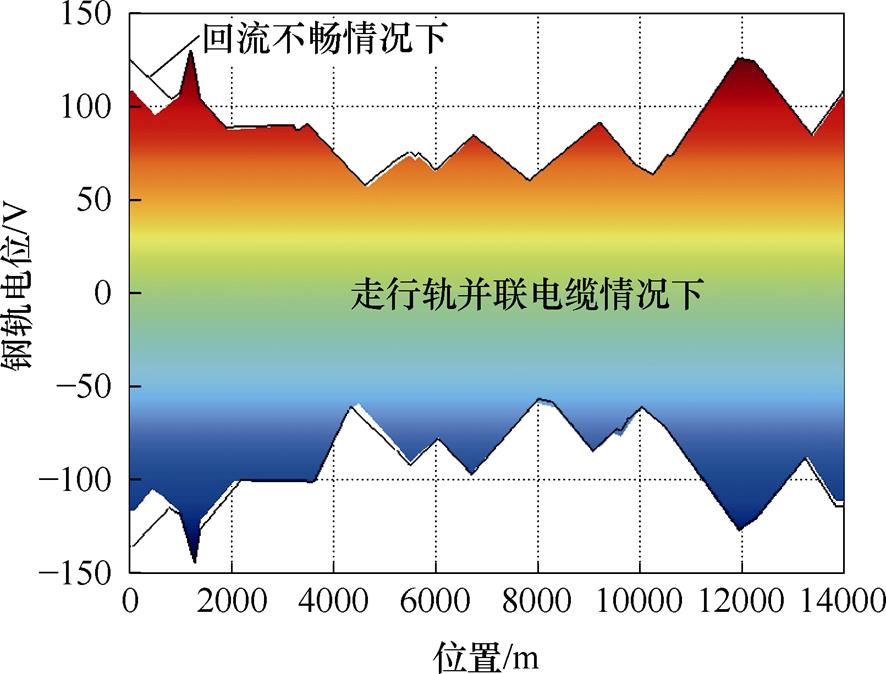
图10 平峰运行时钢轨电位各位置极值分布对比
Fig.10 Comparison of extreme value distribution of rail potential at each position during normal peak operation
2.2.4 周边接地网多回流路径耦合
城轨直流牵引供电系统周边其他系统的接地网会与其回流系统产生电气耦合。本节以回流系统与变电所接地网间产生的多回流路径为例分析其耦合影响。由图1回流路径分析可知，自排流网泄漏的部分杂散电流经土壤流入变电所的接地网，进入中性点接地的变压器，再经传输线流入牵引变电站附近的变电所，最终返回牵引变电站负极。可通过在走行轨和排流网间设置低阻通路，对此多回流路径耦合情况进行仿真分析。耦合点设置为6 994 m（TS3）走行轨处和7 994 m排流网处，多回流路径耦合矩阵参数设置为表2中工况6，其中RC为变电所接地网电阻、变压器等效电阻和传输线电阻三者的等效电阻[19]。
该工况下仿真结果如图11所示。图11a中，最大钢轨电位幅值145.6 V出现在1 408 s，走行轨1 213 m处。该时刻下，走行轨耦合位置在负电位，全线钢轨电位被整体抬升。如图11b所示，由于在6 994 m走行轨处与7 994 m排流网相连，所以自6 994 m处走行轨向排流网泄漏的杂散电流有一个激增，即多回流路径上的变电所接地点电流，杂散电流最大幅值增加至30.5 A。
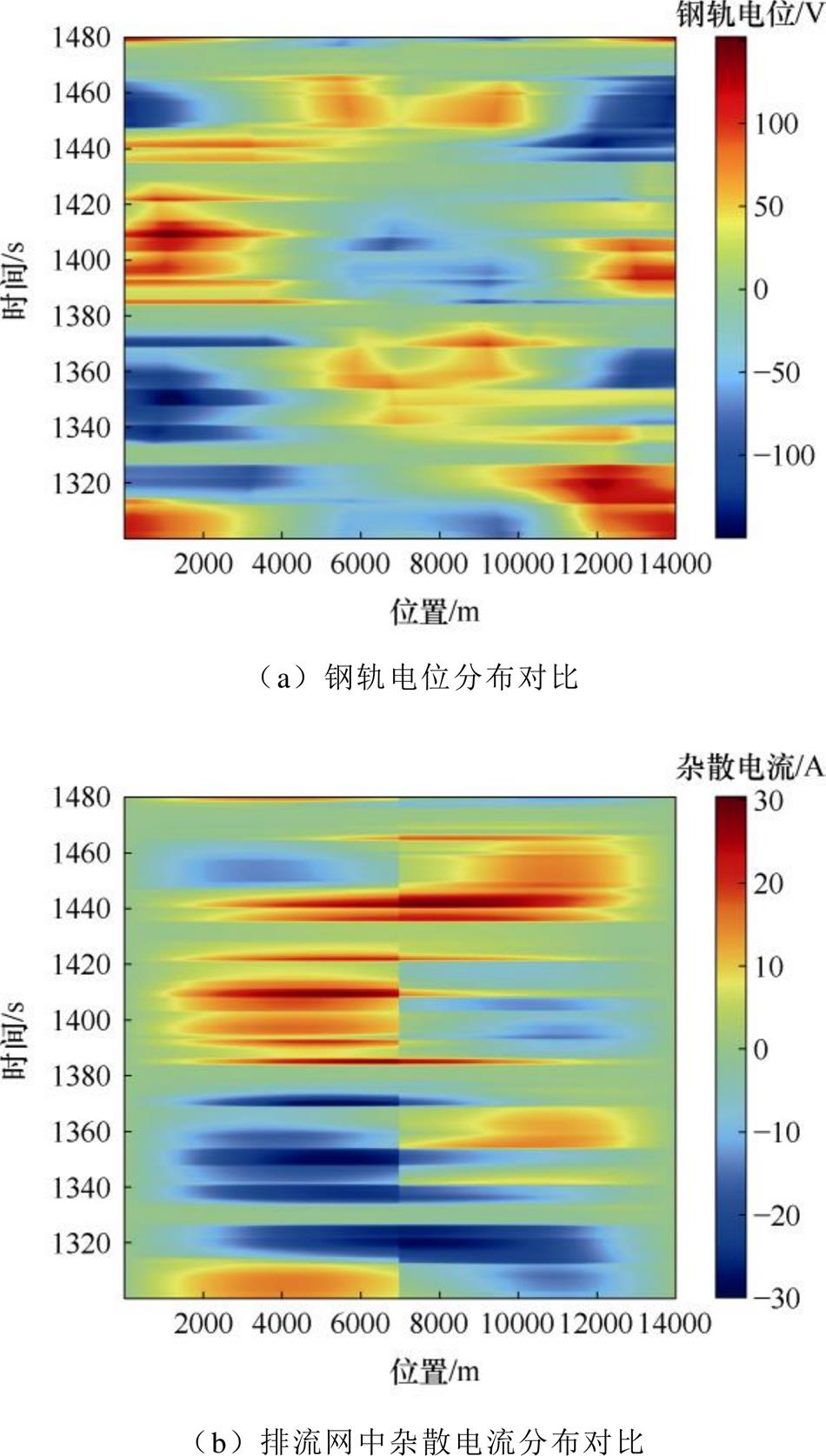
图11 走行轨与排流网间多回流路径耦合时全线回流安全参数分布
Fig.11 Distribution of reflux safety parameters of full-line when multiple reflux paths are coupled between the running rail and the drainage network
对于变电所而言，由于接地网多回流路径耦合，接地点电流会随着耦合位置处钢轨电位的波动而波动，所以本节选取表2中工况6的接地点电流与6 994 m处钢轨电位进行对比分析。
1 300～1 480 s时段接地点电流和6 994 m处钢轨电位对比如图12所示。由图12可见，接地点电流与6 994 m处钢轨电位呈负相关，当t=1 407 s时，钢轨电位幅值最大，接地点电流幅值也达到最大值14.9 A。当在多回流路径上设置UCD时，接地点电流方向仅存在正方向流通，即自排流网经变电所流向走行轨。UCD导通时，接地点电流和钢轨电位与未设置UCD时一致；而UCD关断时，接地点电流钳位为零，钢轨电位升高。综上分析，UCD能有效减小列车运行时段内多回流路径上整体流经的电流，减少多回流路径耦合对周边关键金属工程的影响。
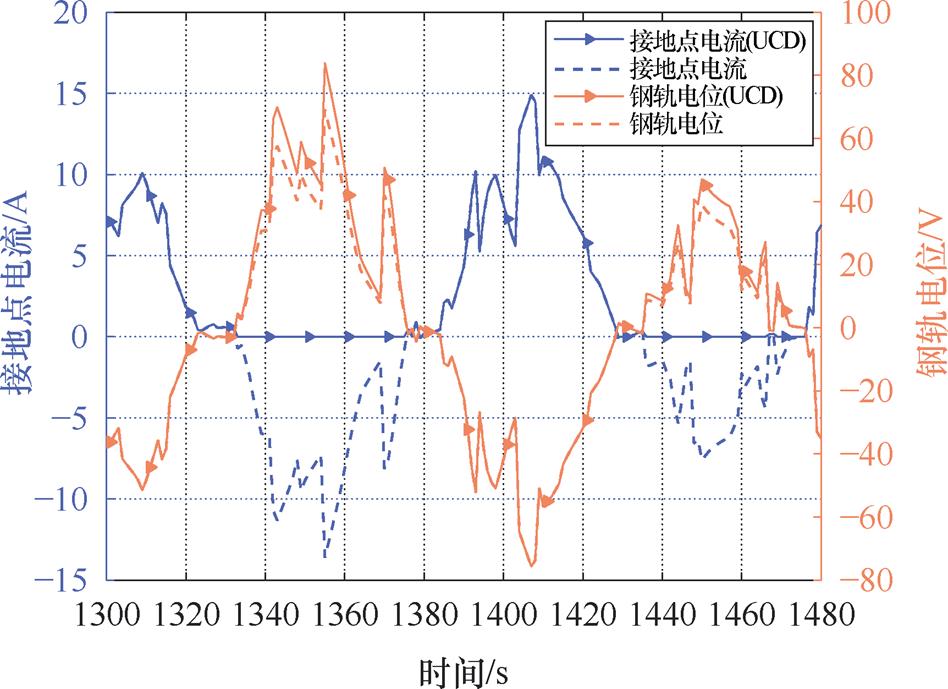
图12 1 300～1 480 s时段接地点电流和6 994 m处钢轨电位对比
Fig.12 Comparison of grounding point current and rail potential at 6 994 m during 1 300～1 480 s
本文针对实际情况下城轨直流牵引供电系统复杂回流路径展开分析，提出了城轨直流牵引供电多回流路径耦合建模方法，阐明了多回流路径耦合下回流安全参数动态分布规律及其对周围环境的耦合影响，得出以下结论：
1）本文所提出的城轨多回流路径耦合建模方法综合考虑城轨直流牵引供电系统自身及周边关键金属工程的耦合情况，基于多回流路径耦合矩阵，可有效描述系统多回流路径耦合关系，实现多回流路径及复杂运行工况的统一建模。
2）针对走行轨绝缘劣化、周边埋地金属管道耦合、走行轨高阻区段并联电缆、周边系统接地网耦合等不同回流路径耦合情况下回流安全参数动态分布规律进行分析。结果表明：多回流路径耦合情况下城轨系统自身及周边其他金属结构的电位与杂散电流变化显著，在分析城轨系统回流安全参数动态变化时，应综合考虑多回流路径耦合。
3）所提出的多回流路径耦合建模方法适用于钢轨电位与杂散电流治理效果分析，针对走行轨高阻区段并联电缆、回流路径设置UCD等治理方法进行仿真，验证了其有效性，可为实际系统钢轨电位与杂散电流治理提供理论基础。
参考文献
[1] Sahil Bhagat, 杨晓峰, 王淼, 等. 城市轨道交通杂散电流治理的综述与评估[J]. 电工技术学报, 2021, 36(23): 4851-4863.
Bhagat Sahil, Yang Xiaofeng, Wang Miao, et al. Review and evaluation of stray current mitigation for urban rail transit[J]. Transactions of China Electro- technical Society, 2021, 36(23): 4851-4863.
[2] 侯保荣. 腐蚀成本与经济发展[J]. 中国科技产业, 2020(2): 21-22.
Hou Baorong. Corrosion cost and economic develop- ment[J]. Science & Technology Industry of China, 2020(2): 21-22.
[3] 王新华, 王祖全, 陈迎春, 等. 交流杂散电流对X70管线钢3PE防腐层下腐蚀及剥离行为的影响[J]. 表面技术, 2018, 47(11): 142-150.
Wang Xinhua, Wang Zuquan, Chen Yingchun, et al. Effect of AC stray current on corrosion and stripping behavior of X70 pipeline steel under 3PE coating[J]. Surface Technology, 2018, 47(11): 142-150.
[4] 潘超, 石晓博, 安景革, 等. 地铁杂散电流干扰变压器多场传播模-态分析[J/OL]. 电工技术学报, 2023, https://doi.org/10.19595/j.cnki.1000-6753.tces.232194.
Pan Chao, Shi Xiaobo, An Jingge, et al. Multi-field propagation mode-state analysis of subway stray current interference on transformers[J/OL]. Transa- ctions of China Electrotechnical Society, 2023, https:// doi.org/10.19595/j.cnki.1000-6753.tces.232194.
[5] 刘炜, 郑杰, 李田, 等. 排流装置对直流牵引供电系统杂散电流分布的影响[J]. 电工技术学报, 2022, 37(18): 4565-4574.
Liu Wei, Zheng Jie, Li Tian, et al. The influence of drainage device on stray current distribution in DC traction power supply system[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4565- 4574.
[6] Lin Sheng, Wang Aimin, Liu Mingjie, et al. A multiple section model of stray current of DC metro systems[J]. IEEE Transactions on Power Delivery, 2021, 36(3): 1582-1593.
[7] 金文辉. 地铁车辆段杂散电流分析与防护方案[J]. 电气技术, 2023, 24(2): 11-17.
Jin Wenhui. Analysis and protection scheme of stray current in subway depot[J]. Electrical Engineering, 2023, 24(2): 11-17.
[8] Zhou Qi, Lin Sheng, Lin Xiaohong, et al. A uniform model for stray current of long-line DC metro systems[J]. IEEE Transactions on Transportation Electrification, 2022, 8(2): 2915-2927.
[9] 澹台乐琰, 韩肖清, 王磊, 等. 多列车运行下地铁杂散电流建模仿真[J]. 电测与仪表, 2020, 57(22): 7-16.
Tantai Leyan, Han Xiaoqing, Wang Lei, et al. Modeling and simulation of stray current in subway with multi-train operation[J]. Electrical Measurement & Instrumentation, 2020, 57(22): 7-16.
[10] Lin Sheng, Zhou Qi, Lin Xiaohong, et al. Infinitesimal method based calculation of metro stray current in multiple power supply sections[J]. IEEE Access, 2020, 8: 96581-96591.
[11] 刘炜, 尹乙臣, 潘卫国, 等. 直流动态杂散电流在分层介质中的扩散模型[J]. 电工技术学报, 2021, 36(23): 4864-4873.
Liu Wei, Yin Yichen, Pan Weiguo, et al. Diffusion model of DC dynamic stray current in layered soil[J]. Transactions of China Electrotechnical Society, 2021, 36(23): 4864-4873.
[12] 刘炜, 周林杰, 唐宇宁, 等. 直流牵引供电回流系统与杂散电流扩散的联合仿真模型[J]. 电工技术学报, 2023, 38(16): 4421-4432.
Liu Wei, Zhou Linjie, Tang Yuning, et al. Co- simulated model of DC traction power supply return system and stray current diffusion[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4421- 4432.
[13] 郑子璇, 杜贵府, 朱成乾. 城轨多区间绝缘非均匀情况下钢轨电位与杂散电流建模及分布[J]. 北京交通大学学报, 2020, 44(3): 66-78.
Zheng Zixuan, Du Guifu, Zhu Chengqian. Modeling and distribution of rail potential and stray current with non-uniform insulation in multiple sections of urban rail transit[J]. Journal of Beijing Jiaotong University, 2020, 44(3): 66-78.
[14] 黄晓鹏, 马庆安, 刘炜, 等. 城轨供电系统杂散电流对埋地金属管道的动态干扰研究[J]. 铁道科学与工程学报, 2023, 20(2): 735-744.
Huang Xiaopeng, Ma Qing’an, Liu Wei, et al. Study on the dynamic interference of stray current in urban traction power supply system on buried metal pipelines[J]. Journal of Railway Science and Engineering, 2023, 20(2): 735-744.
[15] Yu Kun, Ni Yanru, Zeng Xiangjun, et al. Modeling and analysis of transformer DC bias current caused by metro stray current[J]. IEEJ Transactions on Electrical and Electronic Engineering, 2020, 15(10): 1507-1519.
[16] 王淼, 杨晓峰, 李世翔, 等. 城市轨道交通直流自耦变压器牵引供电系统故障保护研究[J]. 电工技术报, 2022, 37(4): 976-989.
Wang Miao, Yang Xiaofeng, Li Shixiang, et al. Fault protection of DC auto-transformer traction power supply system for urban rail transit[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 976-989.
[17] Du Guifu, Wang Jun, Jiang Xingxing, et al. Evaluation of rail potential and stray current with dynamic traction networks in multitrain subway systems[J]. IEEE Transactions on Transportation Electrification, 2020, 6(2): 784-796.
[18] 中华人民共和国住房和城乡建设部. 埋地钢质管道直流干扰防护技术标准: GB 50991-2014[S]. 北京: 中国计划出版社, 2015: 15-21.
[19] Wang Aimin, Lin Sheng, Hu Ziheng, et al. Evaluation model of DC current distribution in AC power systems caused by stray current of DC metro systems[J]. IEEE Transactions on Power Delivery, 2021, 36(1): 114-123.
Abstract DC traction power supply systems are usually adopted in urban rail transit. Rail potential and stray current are the reflux safety parameters of the system, which have become the key problems affecting the safe operation of urban rail lines. Excessive rail potential seriously affects the safety of traction power supply system, and stray current will flow through the surrounding ground and buried metal pipeline, causing serious electrochemical corrosion to the key buried metal projects around. With the deterioration of local or regional insulation of the running rail, the coupling operation of multiple reflux paths is obvious. In general, the modelling and analysis of reflux safety parameters have mainly focused on the urban rail system itself. In order to study the influence of multiple reflux paths coupling on reflux safety parameters and surrounding key metal projects, this paper proposes a dynamic simulation model of DC traction power supply system under multiple reflux paths coupling.
Firstly, based on the structure of DC traction power supply system with multiple reflux paths coupling, the dynamic simulation model of DC traction power supply system with multiple reflux paths coupling is established. The model introduces coupling sections at both sides of poor reflux and adds multiple reflux paths between these coupling sections, described by means of the matrix of multiple reflux paths coupling. Then the dynamic distribution calculation method for multi-interval reflux safety parameters under multiple reflux paths coupling is established. Finally, the distribution of rail potential and stray current under different types of multiple reflux paths coupling is analyzed based on the actual line parameters.
Simulation results show that, when the running rail insulation deterioration coupling, the amplitude of the rail potential at the deteriorating position will decrease, stray current generates a sudden change, the whole line rail potential will be pulled down or raised, and the maximum value of whole line stray current increased to -800.1 A. When buried metallic pipe coupling, the maximum value of the total stray current leaking into the pipe is 32.6 A. When parallel cable in high resistance sections of running rail coupling, the maximum value of the rail potential is significantly reduced from 185.3 V to 156.8 V after the parallel cable treatment, and the peak-adjusted operating schedule does not have an impact on the effectiveness of the treatment. When the surrounding grounding grid coupling, the grounding current is negatively correlated with the rail potential at the coupling point, the maximum value of the grounding current is 14.9 A. When UCD is set up on the multiple reflux paths, the direction of the grounding current only exists in the positive direction, which effectively reduces the overall current flow on multiple reflux paths.
The following conclusions can be drawn from the simulation analysis: (1) The model comprehensively considers the coupling relationship between the DC traction power supply system of urban rail and the key metal engineering around it, and based on the multiple reflux paths coupling matrix, it can effectively describe the multiple reflux paths, and realize the unified modeling of multiple reflux paths and complex operating conditions. (2) In the case of multiple reflux paths coupling, the potential and current of the urban rail system and other surrounding metal structures change significantly, so the multiple reflux paths coupling should be considered comprehensively when analyzing the dynamic change of the safety parameters of urban rail system. (3) The model can be applied to the analysis of rail potential and stray current treatment effect. The effectiveness of treatment methods such as parallelling cable in high-resistance section of running rail and setting UCD on reflux path shave been verified.
keywords：Urban rail transit, DC traction power supply system, multiple reflux paths coupling, rail potential, stray current
DOI: 10.19595/j.cnki.1000-6753.tces.232147
中图分类号：TM922.3
国家自然科学基金资助项目（52007128）。
收稿日期 2023-12-25
改稿日期 2024-02-27
郑 鑫 男，1999年生，硕士研究生，研究方向为轨道交通牵引供电安全、钢轨电位与杂散电流治理。E-mail: zhengxin_suda@163.com
杜贵府 男，1990年生，副教授，研究方向为牵引供电安全和电气安全状态监测等。E-mail: gfdu@suda.edu.cn（通信作者）
（编辑 郭丽军）