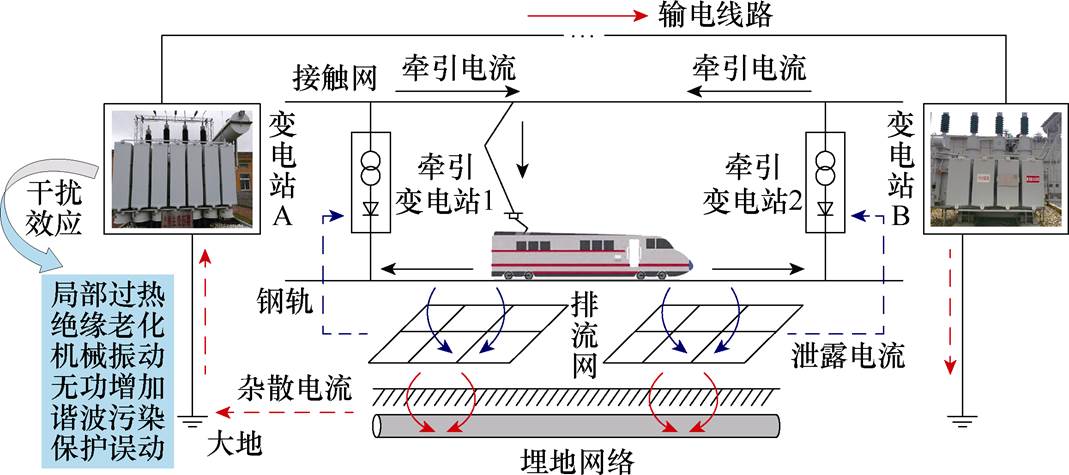
图1 杂散电流干扰电网变压器原理
Fig.1 Principles of stray current interference on power grid transformers
摘要 针对城市地铁杂散电流干扰临近电网接地变压器出现的偏磁异常,基于电磁-机械-声耦合原理,提出变压器多场干扰传播时域模-态数学模型。仿真不同场景下变压器多元时空信息,建立多元干扰传播特征信息库。分析典型场景中杂散电流对磁通、电磁力、振动及噪声等传播特征的影响,归纳物理特征信息的耦合关联规律,对比杂散电流时变分量与直流分量的干扰差异。结果表明,杂散电流时变分量对变压器的干扰与直流分量情况类似,但时变分量导致多场参数变化具有更加复杂的时序波动性。搭建动模实验平台,测量不同干扰下变压器的电流、振动及噪声数据,并与仿真结果对比,验证该文模型与结论的正确性和有效性。基于多元特征信息库构建多元模-态空间,划分四类干扰传播域,并形成干扰判据,为城市电网变压器抵御轨道交通杂散电流干扰的安全态势感知与异常辨识提供依据。
关键词:杂散电流 干扰 变压器 多元信息 模-态
随着轨道交通的不断发展,城市地铁与电网的交互影响日益密切[1]。目前,我国多地出现城市地铁杂散电流入侵电网,使接地变压器受到干扰[2-4],出现励磁饱和、参数畸变,并伴有构件的振动和噪声异常[5-7],进而影响设备稳定工作,甚至危及电网的安全可靠运行[8]。
国内外已针对城市地铁杂散电流干扰临近电网变压器开展了相关研究[9-12]。文献[13]研究城市电网中的地铁杂散电流,分析变压器漏抗等因素对其分布的影响。文献[14]建立了轨道交通与变电站的耦合仿真模型,分析了地铁动态运行过程中变压器中性点杂散电流的变化。文献[15]提出了一种概率评估模型计算地铁杂散电流引起的变压器中性点直流,并评判不同地理位置变压器遭受偏磁危害的概率。文献[16]分析了入侵变压器的杂散电流与感应电流的时频域特性,研究了列车数量及列车运行工况参量对电网回路中偏磁电流分布的影响。综上所述,现有研究多集中于地铁端杂散电流的分布特性和由此导致的变压器中性点偏磁电流评估,但未系统深入地探讨变压器遭受杂散电流干扰时内部电磁、振动及噪声的耦合关联;另一方面,地铁杂散电流具有较为复杂的时序波动性,对变压器等设备的异常辨识产生较大影响,故杂散电流对变压器的干扰特性也亟待探寻。
针对上述问题,本文研究地铁杂散电流干扰电网变压器的原理,构建电磁-机械-声顺序耦合的变压器多物理场干扰传播模型。利用有限元求解磁场并计算构件应力,通过电磁-机械耦合模型获取构件的振动加速度,由机械-声耦合仿真计算声压的时空分布。以Yd接线三相三柱式变压器为例,仿真分析杂散电流干扰下铁心与绕组的电磁、振动及噪声;同时搭建动模实验平台,采集电气、机械和声学信号。通过实验与仿真的一致性校验,验证干扰传播模型的正确性与有效性。在此基础上,通过构建多元模-态空间,划分杂散电流的干扰传播域,并形成干扰判据。
地铁运行时牵引电流在钢轨对地电位的作用下由钢轨流入大地,使周围地表电位出现偏移,导致地铁临近变电站之间产生电位差[17]。该电位差在不同的电网接地点之间产生杂散电流,经接地变压器注入电网并形成回路。杂散电流流经变压器时使其产生偏磁效应,干扰原理如图1所示。

图1 杂散电流干扰电网变压器原理
Fig.1 Principles of stray current interference on power grid transformers
以东北某城市地铁2号线为例,该线路临近220 kV变电站在2023年5月的典型日内1号主变中性点电流监测数据如图2a所示。当天凌晨0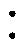 00—5
00—5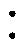 00,地铁处于停运时段,主变中性点无电流;在地铁运行时段,主变中性点电流波动明显,且由于地铁双向运行,电流极性呈正负变化。选取地铁运行典型时段如图2b所示,进一步分析入侵杂散电流的时域变化特征。结合地铁启停情况将时域波形划分为四个工作区间,各区间内杂散电流在地铁启停过程中均发生明显波动,在加/减速阶段电流变化剧烈,且呈现出间断性冲击的波动规律。在电流的冲击时段内,均包含区间幅值拐点的尖顶波,拐点处杂散电流瞬时突变。结果表明,干扰变压器的杂散电流含有冲击时段的时变分量和启停间隔的直流分量。选取冲击时段内的典型时刻,以工频周期尺度观测,杂散电流具有时域渐变、瞬时突变的特征,其变化相对缓慢。
00,地铁处于停运时段,主变中性点无电流;在地铁运行时段,主变中性点电流波动明显,且由于地铁双向运行,电流极性呈正负变化。选取地铁运行典型时段如图2b所示,进一步分析入侵杂散电流的时域变化特征。结合地铁启停情况将时域波形划分为四个工作区间,各区间内杂散电流在地铁启停过程中均发生明显波动,在加/减速阶段电流变化剧烈,且呈现出间断性冲击的波动规律。在电流的冲击时段内,均包含区间幅值拐点的尖顶波,拐点处杂散电流瞬时突变。结果表明,干扰变压器的杂散电流含有冲击时段的时变分量和启停间隔的直流分量。选取冲击时段内的典型时刻,以工频周期尺度观测,杂散电流具有时域渐变、瞬时突变的特征,其变化相对缓慢。
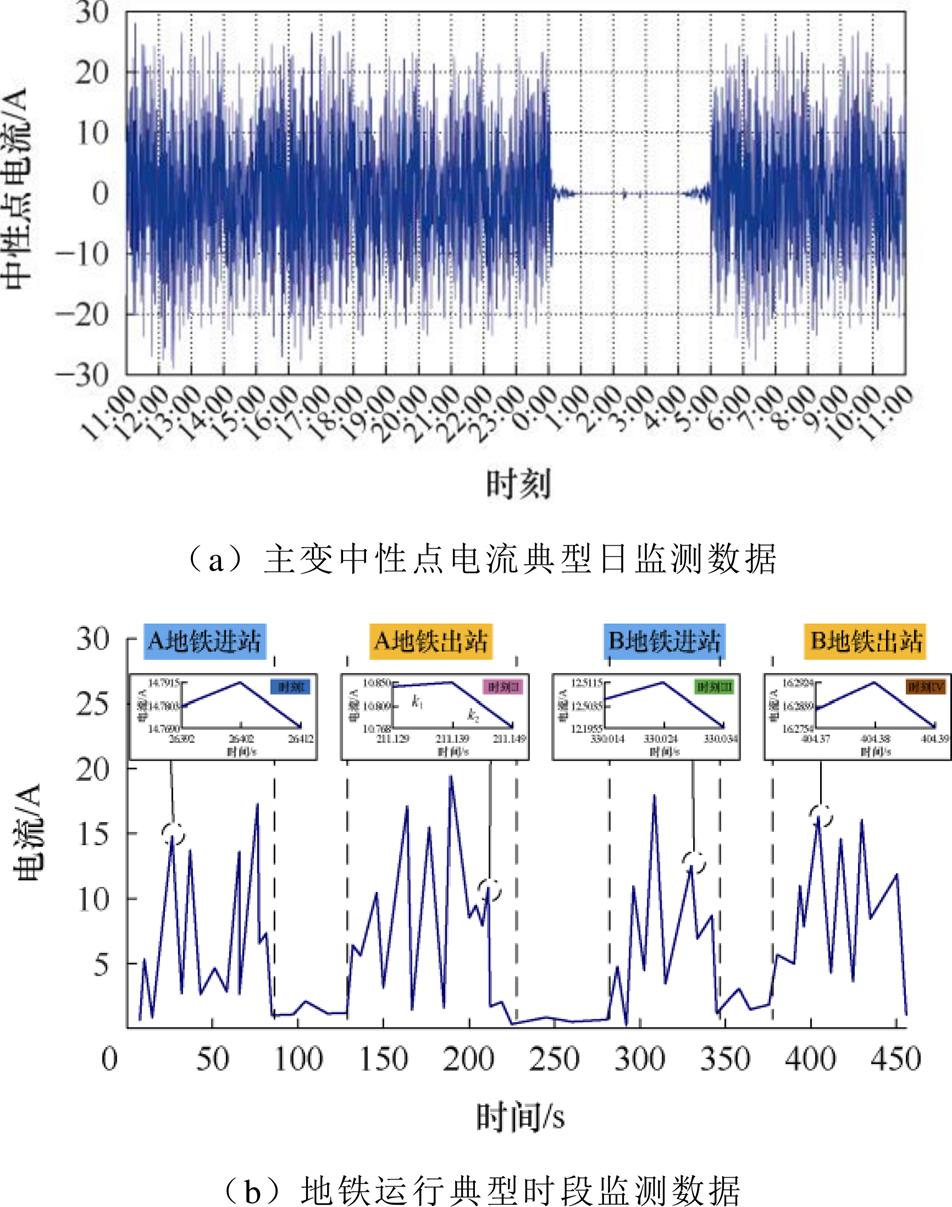
图2 主变中性点电流监测数据
Fig.2 Neutral point current in main transformer
杂散电流由中性点注入变压器后,导致励磁过饱和,绕组电流发生畸变,并使漏磁增加;电磁参数偏移引起变压器构件受力加剧,进而产生异常振动和噪声。以上过程在变压器内形成电磁-机械-声的干扰传播途径,由此可建立多场干扰传播时域模-态数学模型。
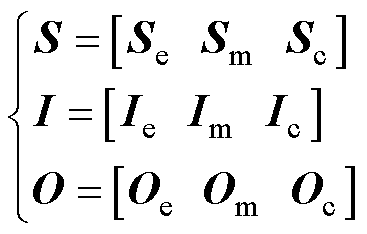 (1)
(1)
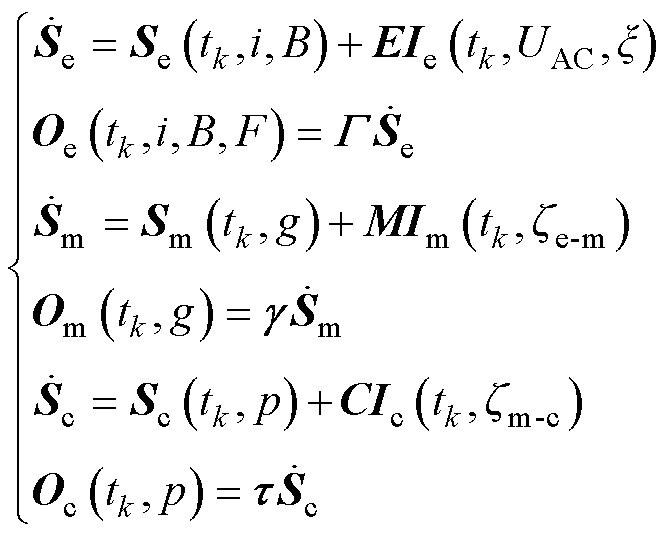 (2)
(2)
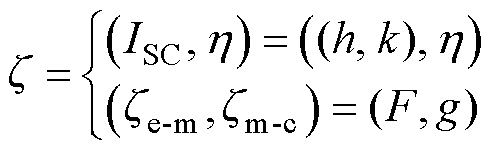 (3)
(3)
式中,S为系统模-态矩阵,包括电磁模-态矩阵Se、机械模-态矩阵Sm和声学模-态矩阵Sc。以时间t为链接索引,S中的信息元素随之变化,如电流i、磁通密度B、电磁力F、振动加速度g及声压p等。多元场域参数通过电磁-机械-声的时域干扰传播模型求解获取;I为系统输入矩阵,包含电磁输入矩阵Ie、机械输入矩阵Im和声学输入矩阵Ic;E、M和C为各场域输入系数矩阵;UAC为正弦交流激励;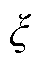 为模式控制参数,包含杂散电流ISC(干扰控制参数)和负载率
为模式控制参数,包含杂散电流ISC(干扰控制参数)和负载率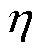 (工况控制参数),其中ISC由直流干扰水平控制因数h与时变控制因数k构成;
(工况控制参数),其中ISC由直流干扰水平控制因数h与时变控制因数k构成;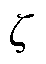 为耦合关联参数,包含电磁-机械耦合参数
为耦合关联参数,包含电磁-机械耦合参数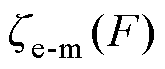 和机械-声学耦合参数
和机械-声学耦合参数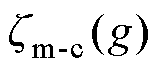 ;O为包含多场输出矩阵Oe、Om和Oc的系统输出矩阵;
;O为包含多场输出矩阵Oe、Om和Oc的系统输出矩阵;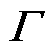 、
、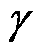 和
和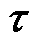 为提取矩阵,从S中提取各场域物理特征参数(电流、磁通、电磁力、振动及噪声)构造多元信息输出。
为提取矩阵,从S中提取各场域物理特征参数(电流、磁通、电磁力、振动及噪声)构造多元信息输出。
假设某时刻的绕组电流已知,考虑杂散电流干扰的磁场模型可以通过Galerkin求解。
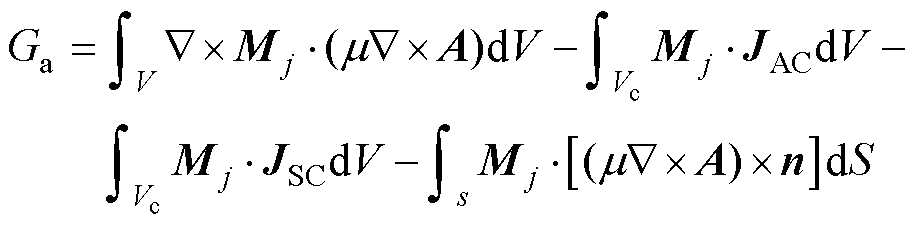 (4)
(4)
式中,m 为磁阻率;A为矢量磁位;JAC为交流激励电流密度;JSC为杂散电流密度;Ga为Galerkin余量(计算步骤见附录);Mj为权函数序列,基函数与其相同,j为序列通项编号;n为法相分量。式(4)离散化得到代数方程组,求解A及其他场域参数(磁通密度B和磁场能量W等),时域干扰电磁模型的场路耦合迭代求解过程见附录。
进一步计算绕组等构件的电磁力F,并作为机械模型激励。
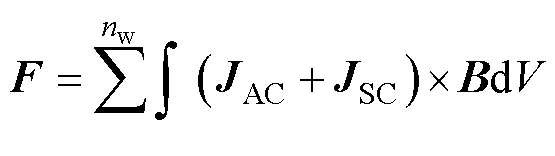 (5)
(5)
式中,nw为绕组单元数量。
施加正弦交流激励时,考虑杂散电流干扰的绕组单元电磁力可表示[18]为
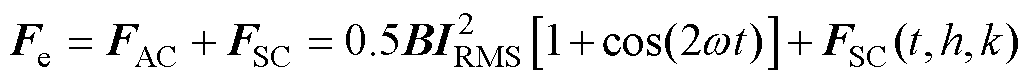 (6)
(6)
式中,FAC为绕组受正弦交流激励影响下的电磁力;FSC为绕组受杂散电流干扰下的电磁力;IRMS为正弦电流激励有效值;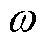 为角频率。当施加工频激励时,由于杂散电流缓慢变化,频率远低于工频,绕组总体电磁力变化频率近似为100 Hz。
为角频率。当施加工频激励时,由于杂散电流缓慢变化,频率远低于工频,绕组总体电磁力变化频率近似为100 Hz。
考虑杂散电流干扰在变压器内部的电磁-机械传播过程,研究构件的受力振动问题,以轴向为例,铁心及绕组的轴向受力机械模型如图3所示。
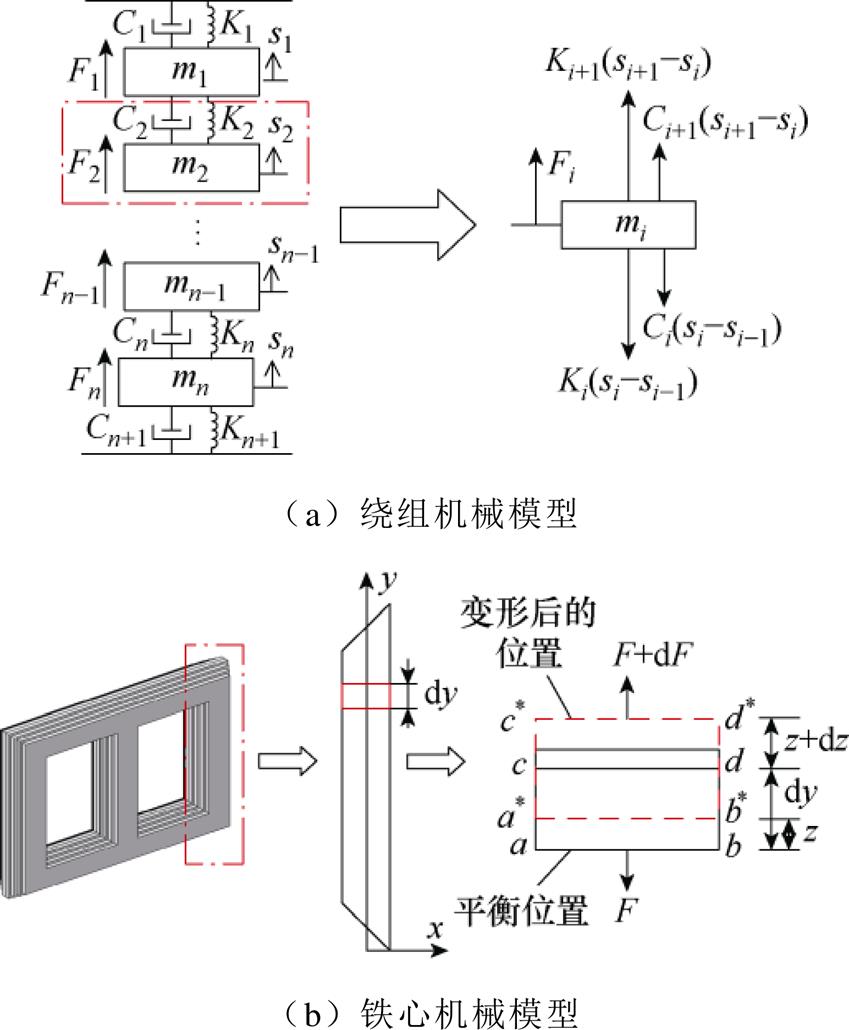
图3 变压器构件机械模型
Fig.3 Mechanical model of transformer components
图3a为简化多质量块弹性机械系统[19],考虑振动过程中绝缘垫块的振动特性,将其等效为线圈阻尼器及受压弹簧,绕组线饼由独立刚体质量块m表示,质量单元mi受力振动计算公式为
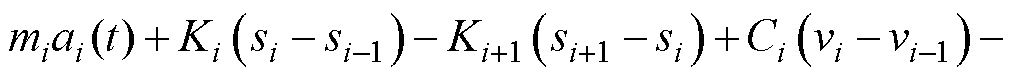
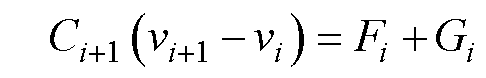 (7)
(7)
绕组机械模型可表示为矩阵形式,即
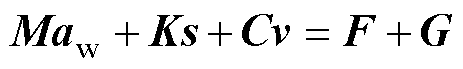 (8)
(8)
式中,M为质量矩阵,对应刚度系数矩阵及阻尼系数矩阵分别为K、C;F为绕组受到的轴向电磁力;G为线饼总重力;aw、s、v分别为绕组节点加速度矢量、位移矢量、速度矢量[20]。
图3b为铁心振动等效模型的质量单元,其中铁心轴向位移由z表示,F和dF表示该质量单元上的受力。考虑铁心磁致伸缩效应(原理见附录),振动方程[21]为
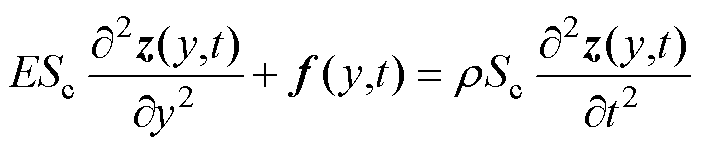 (9)
(9)
式中,E为正杨氏模量;∂z/∂r为轴向应变;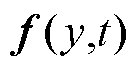 为该质量单元所受的磁致伸缩力(y为位置,t为时间);
为该质量单元所受的磁致伸缩力(y为位置,t为时间);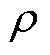 为铁心密度;Sc为横截面积。
为铁心密度;Sc为横截面积。
由构件受力计算振动位移s,进而求解振动加速度g为
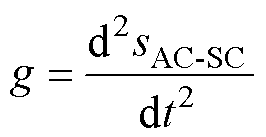 (10)
(10)
式中,sAC-SC为正弦交流激励与杂散电流干扰叠加导致的构件振动位移。
基于电磁-机械耦合求解内部构件振动加速度g,进一步研究杂散电流干扰在机械-声域的传播,并将g作为声场激励。
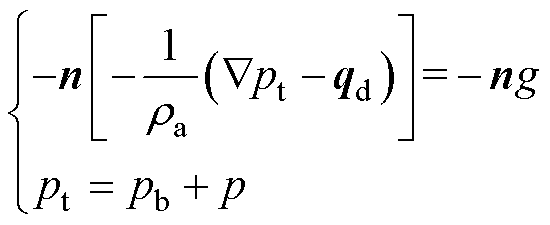 (11)
(11)
式中,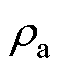 为空气流体密度;pt为总声压;pb为背景声压;p为变压器噪声声压;qd为偶极域源。
为空气流体密度;pt为总声压;pb为背景声压;p为变压器噪声声压;qd为偶极域源。
变压器内部构件声场变化[22]可求解为
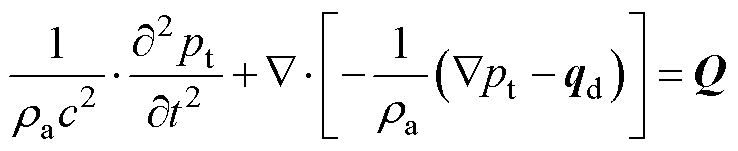 (12)
(12)
式中,c为声速;Q为单极域源。
通过分析声压变化,可进一步计算声压级Lp(dB)为
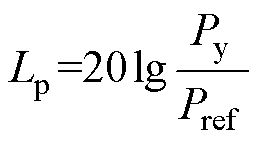 (13)
(13)
式中,Py为声压的有效值,通常选取20 mPa作为参考声压Pref。
基于多物理场耦合的变压器干扰传播原理如图4所示,通过求解该模型可提取各耦合场域的关键特征参数,并构建多元特征信息库,引入时间索引与模式标签,将各模-态矩阵特征信息关联,具体步骤如下:
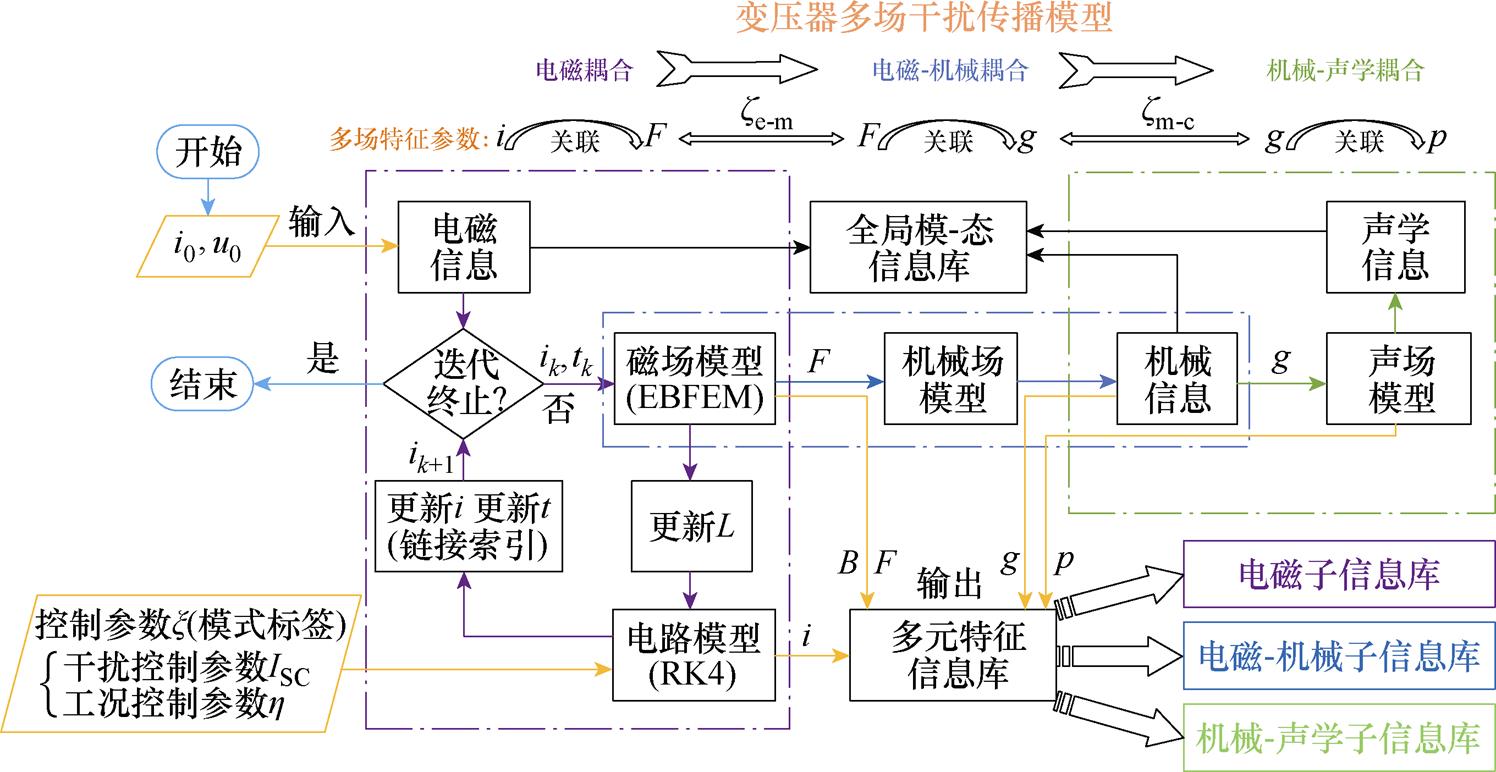
图4 变压器多场干扰传播原理
Fig.4 Multi-field interference propagation principle of transformer
(1)建立变压器多场干扰传播模型的虚拟仿真全局模-态信息库。以时间为链接索引,从电磁子信息库中检索tk时刻的电磁信息。将该时刻的绕组电流ik作为载流激励域和磁场连通域的激励。同时,以杂散电流ISC和负载率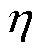 为控制参数,并设置为模式标签。求解变压器的电磁时空分布,获取电流、磁通及电磁力等特征参数,按时间索引和模式标签在全局模-态信息库中更新储存。
为控制参数,并设置为模式标签。求解变压器的电磁时空分布,获取电流、磁通及电磁力等特征参数,按时间索引和模式标签在全局模-态信息库中更新储存。
(2)从电磁子信息库中获取tk时刻构件电磁力Fk的时空分布信息。在机械应力域中,以Fk为激励求解构件振动加速度gk,并在全局模-态信息库中更新。
(3)从机械子信息库中获取tk时刻构件振动加速度gk,将gk作为激励输入声场模型,计算获得声压pk,并更新储存在全局模-态信息库中。
(4)当绝对收敛范数小于设定的收敛准则值,或耦合循环达到预设次数时,迭代终止。按时间索引将计算结果动态存储在全局模-态信息库中。若不满足终止条件,ik在电路模型中经高阶迭代更新为ik+1(迭代公式中的LD通过能量平衡有限元法(EBFEM)计算获取),并输入磁场模型,作为tk+1时刻的磁场激励。
(5)以ISC和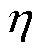 为标签、t为索引,合并电磁、机械和声学特征信息,形成多元特征信息库,以便于开展基于多元模-态空间的干扰传播域划分。
为标签、t为索引,合并电磁、机械和声学特征信息,形成多元特征信息库,以便于开展基于多元模-态空间的干扰传播域划分。
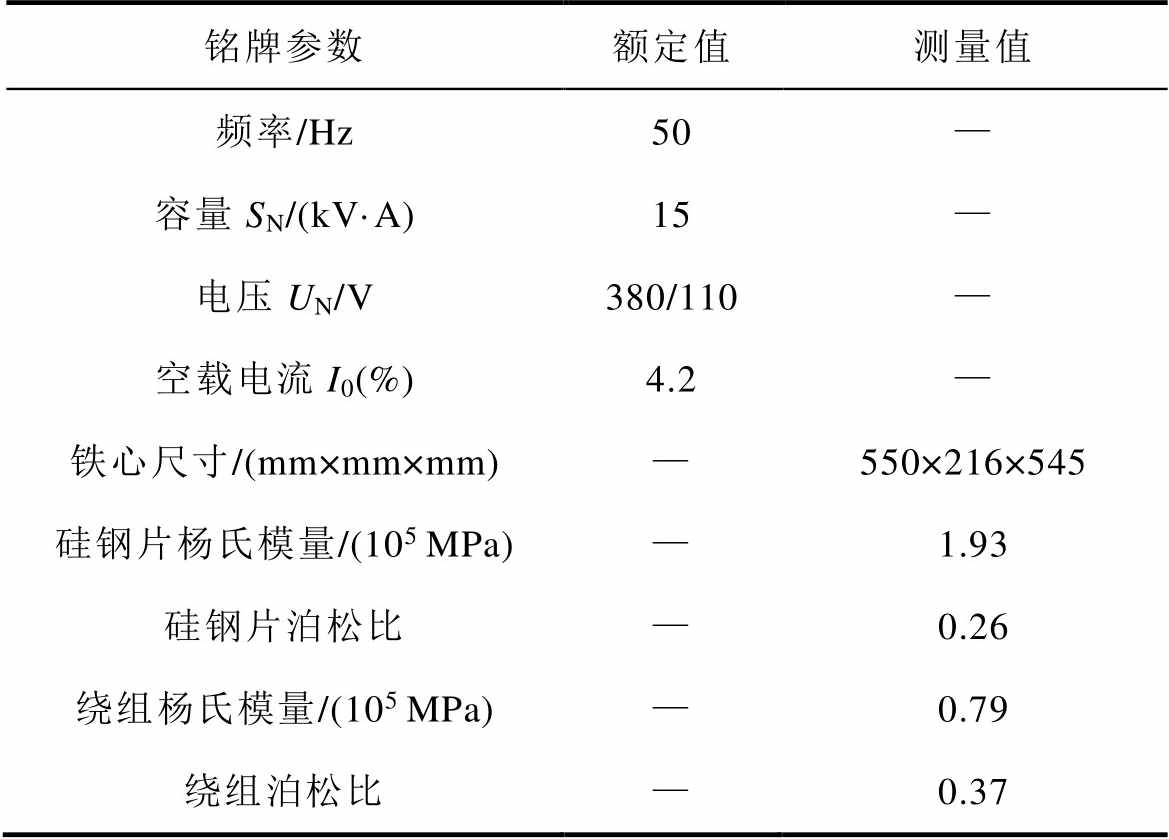
以实际三相三柱式变压器(JSSG-15 kV·A)为研究对象,等比例构建其三维有限元模型,材料参数(杨氏模量和泊松比等)通过拉压实验(详见附录)测得,变压器具体参数见表1。
利用COMSOL有限元软件基于变压器多场干扰传播原理进行仿真分析。网格剖分采用自由四面体网格,需精确计算的铁心和绕组选择“较细化”单元大小,其他构件如垫块、拉板等选择“较粗化”单元大小,完美匹配层采用生成六面体的扫掠处理,共划分77 459个单元。求解器配置中选择“全耦合求解方法”。仿真中对激励与边界作如下处理:①电磁计算时,绕组激励设置为环形电流密度,并设置磁场边界为磁力线平行边界条件,其余设置自然边界条件[23];②机械振动求解环节,将变压器底座设定为固定约束条件,其余施加锟支撑约束条件,即变压器底座固定,只考虑构件轴向振动情况;③声学求解域中,背景声压设定为0 Pa,求解域边界设定为球面波辐射条件,即认为环境噪声不会对变压器噪声声压产生影响。
表1 三相变压器参数
Tab.1 Three-phase transformer parameters
铭牌参数额定值测量值 频率/Hz50— 容量SN/(kV·A)15— 电压UN/V380/110— 空载电流I0(%)4.2— 铁心尺寸/(mm×mm×mm)—550×216×545 硅钢片杨氏模量/(105 MPa)—1.93 硅钢片泊松比—0.26 绕组杨氏模量/(105 MPa)—0.79 绕组泊松比—0.37
由图2b可知,杂散电流突变时刻两侧电流的变化速率具有不确定性,针对该特点以变化速率不等的典型时刻Ⅱ实测电流(k1=0.800 6,k2=-8.072 7)为例设置典型时变分量干扰,同时设置直流分量干扰。考虑两种干扰模式的杂散电流控制方程如下
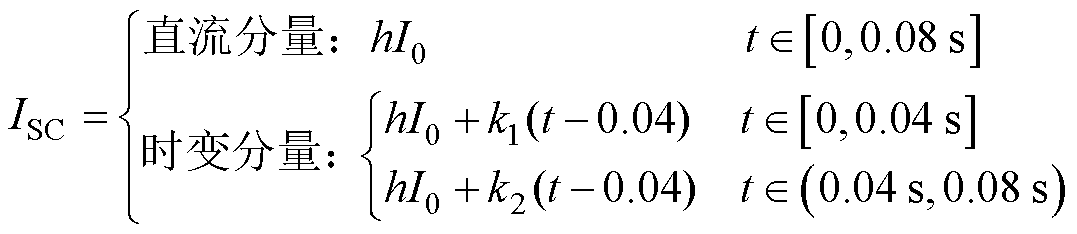 (14)
(14)
干扰控制参数包含干扰水平控制因数h与时变控制因数k,其中,h表征杂散电流的直流干扰水平,依据标准DL/T 1799-2018[24],变压器允许承受的直流干扰约为额定空载电流峰值的2.6倍,故设定干扰水平控制因数h∈[0, 3];k={k1, k2},表征杂散电流的时序变化。此外,工况控制参数考虑不同负载模式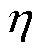 =0、25%、50%、75%、100%下,仿真分析变压器在不同模式下电磁-机械-声场特征参数的受干扰情况。
=0、25%、50%、75%、100%下,仿真分析变压器在不同模式下电磁-机械-声场特征参数的受干扰情况。
获取多场耦合关键特征信息时,考虑变压器结构特性布置观测点①~④,如图5所示。
图5 变压器观测点分布
Fig.5 Test points distribution of transformer
3.2.1 绕组电磁-机械仿真
设置不同杂散电流干扰模式和负载模式,仿真获取绕组电磁-机械信息。以变压器空载、半载及满载运行模式为例,绕组各观测点的漏磁、电磁力及振动加速度结果如下(部分电流仿真结果及25%、75%负载模式部分仿真数据见附录)。
绕组观测点漏磁如图6所示。由图6可知,变压器遭受杂散电流干扰时绕组漏磁主要集中于端部,中部漏磁小于首端;空载工况下,漏磁呈现“半波增强,半波衰减”的变化规律;负载工况下,漏磁随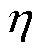 升高而增大;h的变化对空载绕组漏磁影响较大,对负载绕组漏磁影响并不明显;当h=1.5时,空载漏磁已出现明显的偏移现象。对比两种杂散电流干扰模式,变压器遭受时变分量干扰时的绕组漏磁与直流干扰具有类似变化规律,但空载工况下受时变分量影响,k导致漏磁具有更加复杂的时序波动性;在时变分量干扰突变时刻(t=40 ms),各负载模式下漏磁均呈现微小畸变。通过分析,绕组漏磁主要由载流激励引起,两者的变化趋势相符,该结论与标准[23]一致。结果表明,负载工况下,杂散电流入侵对绕组电流和漏磁的干扰并不明显。
升高而增大;h的变化对空载绕组漏磁影响较大,对负载绕组漏磁影响并不明显;当h=1.5时,空载漏磁已出现明显的偏移现象。对比两种杂散电流干扰模式,变压器遭受时变分量干扰时的绕组漏磁与直流干扰具有类似变化规律,但空载工况下受时变分量影响,k导致漏磁具有更加复杂的时序波动性;在时变分量干扰突变时刻(t=40 ms),各负载模式下漏磁均呈现微小畸变。通过分析,绕组漏磁主要由载流激励引起,两者的变化趋势相符,该结论与标准[23]一致。结果表明,负载工况下,杂散电流入侵对绕组电流和漏磁的干扰并不明显。
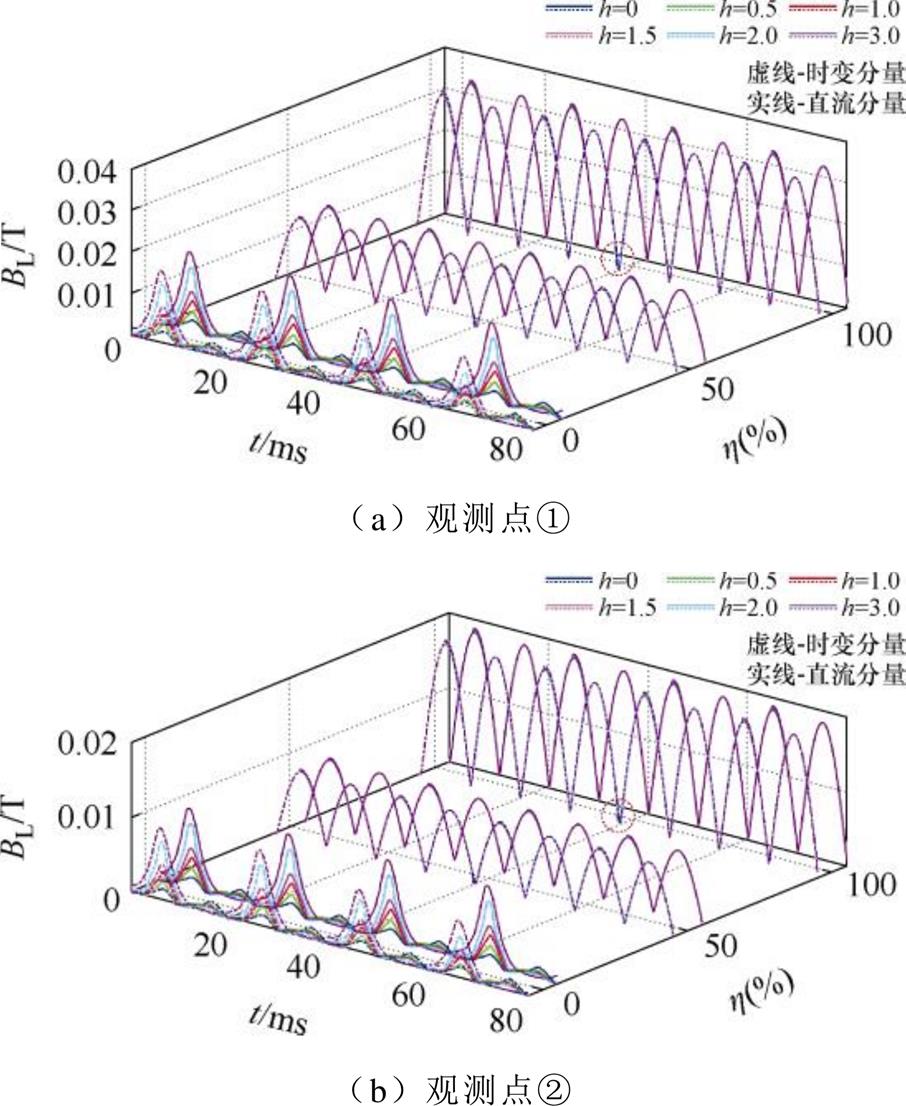
图6 绕组观测点漏磁
Fig.6 Magnetic leakage at test points of winding
进一步分析杂散电流时域渐变特征对漏磁时序波动性的影响。以h=2.0为例,提取空载工况下漏磁各波动周期的幅值见表2。定义两种干扰模式下漏磁幅值的比值为Ø,以衡量漏磁受k影响下的变化幅度。结果表明,相同干扰下不同观测点的绕组漏磁具有相似的波动规律:直流分量干扰下,绕组漏磁幅值恒定;|k|较小的时变分量干扰增强阶段(0~40 ms,k1),绕组漏磁缓慢增大;|k|较大的时变分量干扰减弱阶段(40~80 ms,k2),绕组漏磁显著减小。
表2 空载工况各波动周期漏磁幅值(h=2.0)
Tab.2 Leakage amplitude of each fluctuation cycle under no-load condition (h=2.0)
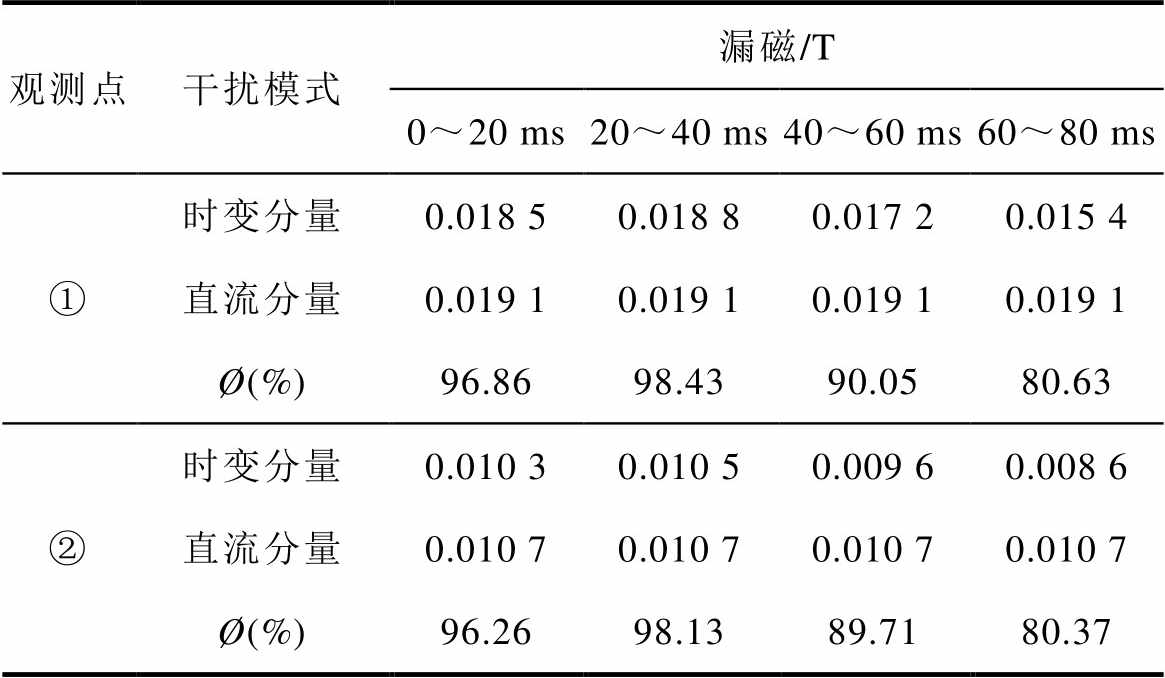
观测点干扰模式漏磁/T 0~20 ms20~40 ms40~60 ms60~80 ms ①时变分量0.018 50.018 80.017 20.015 4 直流分量0.019 10.019 10.019 10.019 1 Ø(%)96.8698.4390.0580.63 ②时变分量0.010 30.010 50.009 60.008 6 直流分量0.010 70.010 70.010 70.010 7 Ø(%)96.2698.1389.7180.37
基于漏磁结果求解绕组电磁力和振动加速度,提取其轴向信息,结果如图7、图8所示。
图7、图8中,绕组电磁力与振动加速度的波动频率近似为二倍工频,该规律与理论分析相符。绕组作为载流体在磁场中受到周期性作用而被迫振动,影响其振动的主要因素为电流和漏磁。在两种杂散电流干扰模式下,空载工况下绕组的电磁力和加速度均呈现“半波增强、半波衰减”的变化规律,其时序波动规律与漏磁相同,即|k|较大时,电磁力和加速度幅值变化更剧烈;空载时绕组振动随h的增大而加剧,当h=1.5时,绕组各观测点的振动幅度约为无干扰时的1.2倍;负载工况下绕组的电磁力和加速度随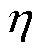 升高而增大,但受杂散电流干扰无明显变化;在时变分量干扰突变时刻(t=40 ms),各负载模式下绕组受力及加速度均出现畸变。结合图6~图8,绕组电流、漏磁、电磁力和振动加速度的变化规律具有一致性。
升高而增大,但受杂散电流干扰无明显变化;在时变分量干扰突变时刻(t=40 ms),各负载模式下绕组受力及加速度均出现畸变。结合图6~图8,绕组电流、漏磁、电磁力和振动加速度的变化规律具有一致性。
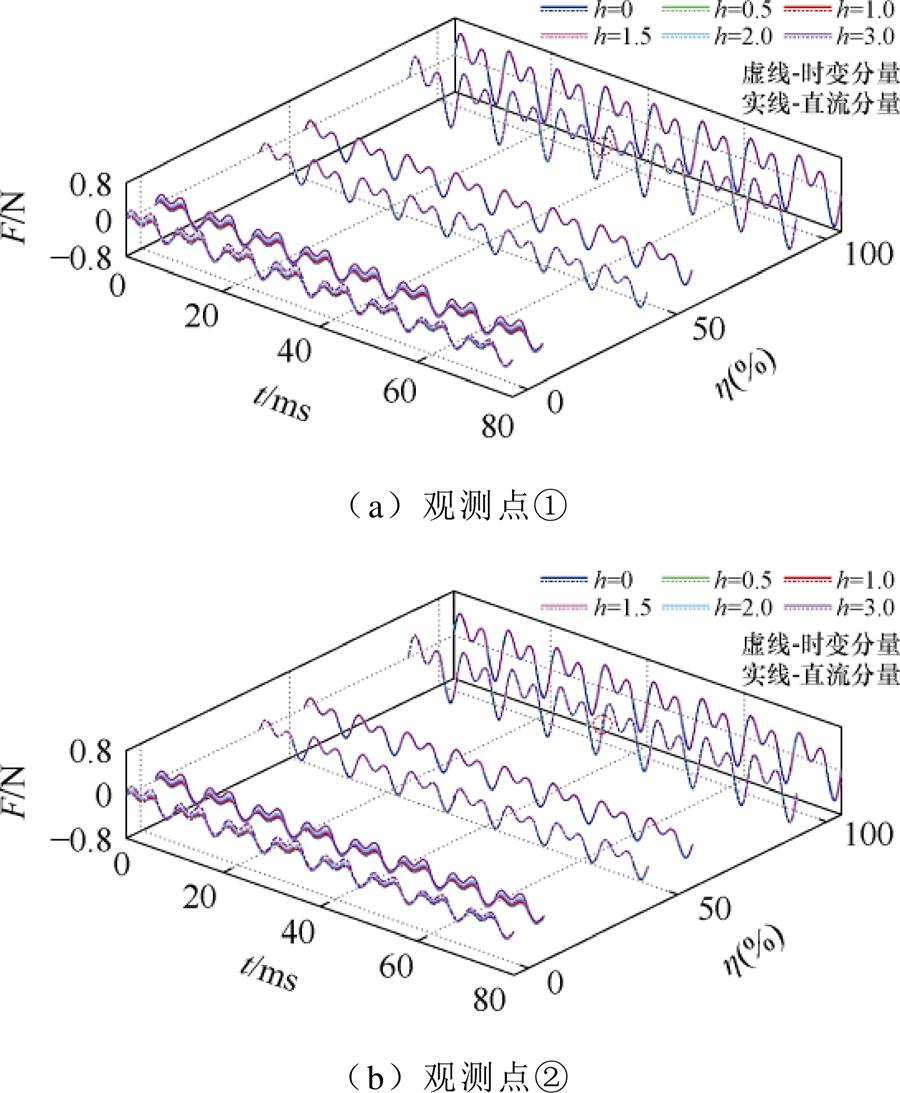
图7 绕组观测点电磁力
Fig.7 Electromagnetic force at test points of winding
图8 绕组观测点振动加速度
Fig.8 Vibration acceleration at test points of winding
进一步分析绕组振动在时变分量干扰突变时刻(t=40 ms)的畸变特性。畸变占比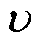 如图9所示,表征畸变极差LΛ与波动总极差Lall的比值。
如图9所示,表征畸变极差LΛ与波动总极差Lall的比值。
由此计算时变分量干扰下绕组振动加速度的畸变占比,具体结果见表3。结果表明,绕组各观测点加速度的畸变占比均随h的升高而增大,空载绕组的振动畸变占比高于负载情况。当h=2.0时,绕组加速度畸变占比达到7%~8%。另外,绕组端部加速度畸变占比高于中部,其受杂散电流瞬时突变影响更大。
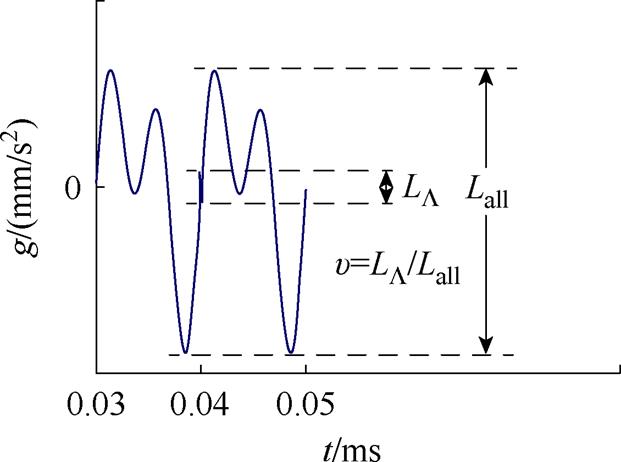
图9 振动加速度畸变占比
Fig.9 Distortion proportion of vibration acceleration
表3 时变分量干扰下绕组加速度畸变占比
Tab.3 Distortion proportion of winding acceleration with time-varying component disturbance
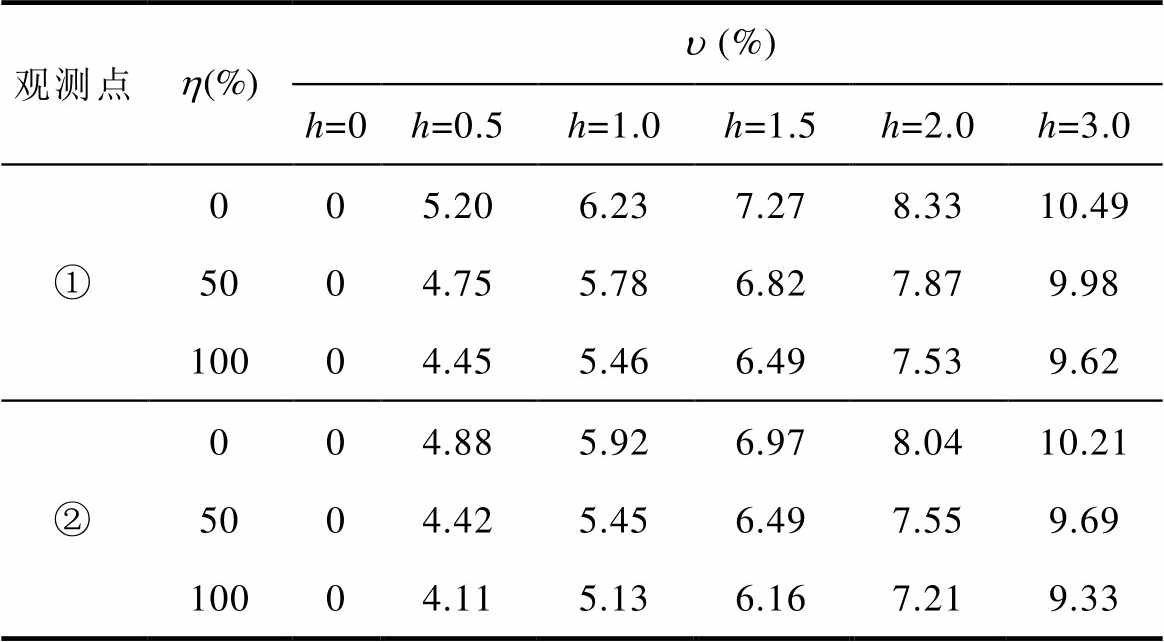
观测点(%) h=0h=0.5h=1.0h=1.5h=2.0h=3.0 ①005.206.237.278.3310.49 5004.755.786.827.879.98 10004.455.466.497.539.62 ②004.885.926.978.0410.21 5004.425.456.497.559.69 10004.115.136.167.219.33
3.2.2 铁心电磁-机械仿真
进一步研究不同模式下铁心的振动问题,主磁通仿真结果见附录,各观测点轴向振动加速度g仿真结果如图10所示。
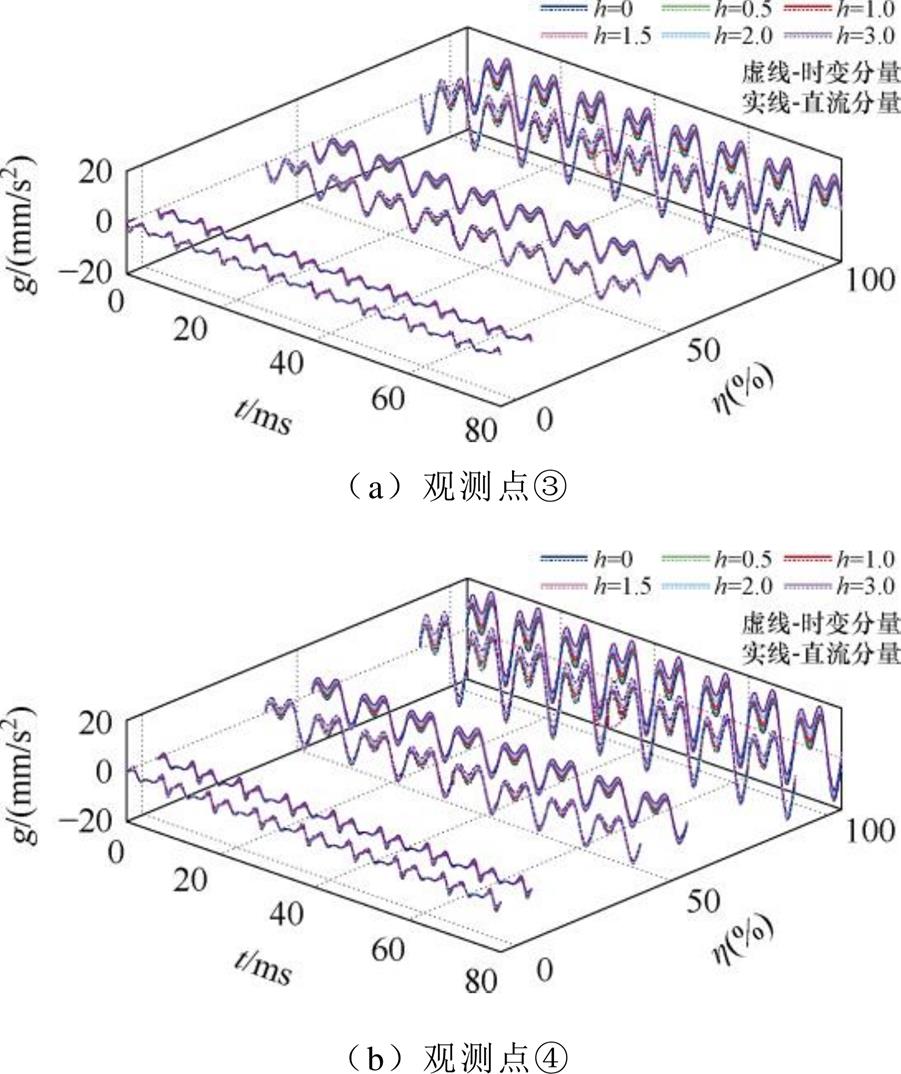
图10 变压器铁心观测点振动加速度
Fig.10 Vibration acceleration at test points of core
由图10可知,变压器遭受两种模式的杂散电流干扰时,铁心振动均随h和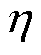 的升高而加剧,且主心柱振动比旁柱更加剧烈。时变分量干扰下,各负载模式下铁心振动的时序波动规律与空载绕组类似,|k|较大时变化更为显著。当h=1.5时,负载工况下铁心各观测点的振动幅度约为无干扰时的1.3倍。
的升高而加剧,且主心柱振动比旁柱更加剧烈。时变分量干扰下,各负载模式下铁心振动的时序波动规律与空载绕组类似,|k|较大时变化更为显著。当h=1.5时,负载工况下铁心各观测点的振动幅度约为无干扰时的1.3倍。
对比图8和图10,相同模式下铁心振动比绕组更加剧烈,负载工况下铁心受杂散电流干扰更大。在时变分量突变时刻(t=40 ms),铁心振动出现了比绕组更为明显的畸变。杂散电流入侵变压器后在铁心中产生直流磁通,引发励磁畸变和铁心饱和,导致铁心振动更加剧烈。
进一步分析铁心振动在时变分量干扰突变时刻(t=40 ms)的畸变特性,畸变占比计算结果见表4。
表4 时变分量干扰下铁心加速度畸变占比
Tab.4 Distortion proportion of core acceleration with time-varying component disturbance
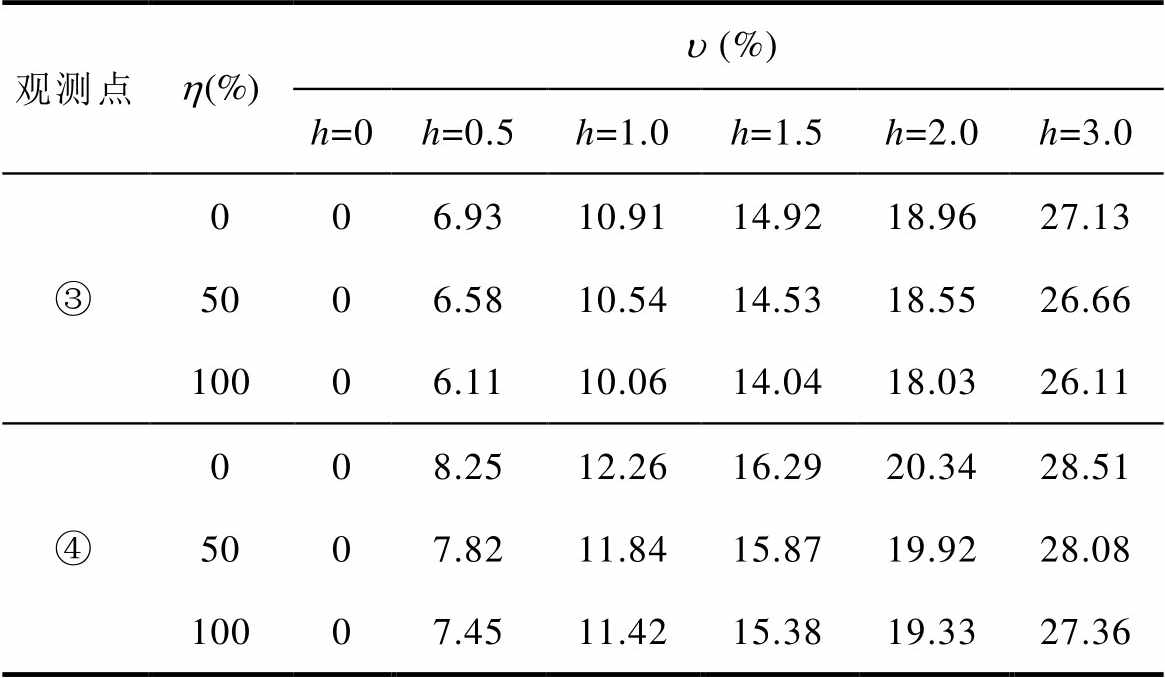
观测点(%) h=0h=0.5h=1.0h=1.5h=2.0h=3.0 ③006.9310.9114.9218.9627.13 5006.5810.5414.5318.5526.66 10006.1110.0614.0418.0326.11 ④008.2512.2616.2920.3428.51 5007.8211.8415.8719.9228.08 10007.4511.4215.3819.3327.36
由表4可知,铁心振动的畸变占比随h的升高而增大,其变化规律与绕组振动情况基本一致,杂散电流瞬时突变对空载变压器的影响比负载更为严重;主心柱振动的畸变占比整体高于旁柱,表明杂散电流瞬时突变对主心柱的影响更显著。对比表3和表4,铁心加速度的畸变占比明显高于绕组,当h=2.0时,铁心畸变占比可达18%~20%。考虑到铁心振动比绕组更加剧烈,因此在杂散电流突变时刻铁心产生了更为严重的机械参数畸变,进而对变压器的电磁兼容性和结构稳定性产生了严重威胁。
3.2.3 本体声压仿真
结合电磁-机械干扰传播过程,进一步研究噪声效应。仿真计算不同杂散电流时的本体表面最大声压级Lpmax,直流分量干扰下变压器表面最大噪声见表5、时变分量干扰下变压器表面最大噪声见表6。
由表5、表6可知,变压器本体表面Lpmax随h和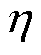 的升高而增大,其变化规律与振动情况基本一致。时变分量干扰下的本体Lpmax与直流分量干扰情况无显著差别。当h=0.5时,本体声压级不超过无干扰时的1.01倍,噪声加剧并不明显;当h=1.5时,本体声压级可达到无干扰时的1.05倍,噪声显著提升;当h=2.0时,本体声压级可达到无干扰时的1.1倍,噪声加剧已非常严重。以
的升高而增大,其变化规律与振动情况基本一致。时变分量干扰下的本体Lpmax与直流分量干扰情况无显著差别。当h=0.5时,本体声压级不超过无干扰时的1.01倍,噪声加剧并不明显;当h=1.5时,本体声压级可达到无干扰时的1.05倍,噪声显著提升;当h=2.0时,本体声压级可达到无干扰时的1.1倍,噪声加剧已非常严重。以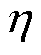 =75%、h=2.0模式为例,变压器绕组及铁心的表面最大声压级如图11所示。在时变分量突变时刻(t=40 ms),构件机械参数畸变导致本体噪声加剧,空间声压分布如图12所示。
=75%、h=2.0模式为例,变压器绕组及铁心的表面最大声压级如图11所示。在时变分量突变时刻(t=40 ms),构件机械参数畸变导致本体噪声加剧,空间声压分布如图12所示。
表5 直流分量干扰下变压器表面最大噪声
Tab.5 Maximum surface noise of transformer with DC component disturbance
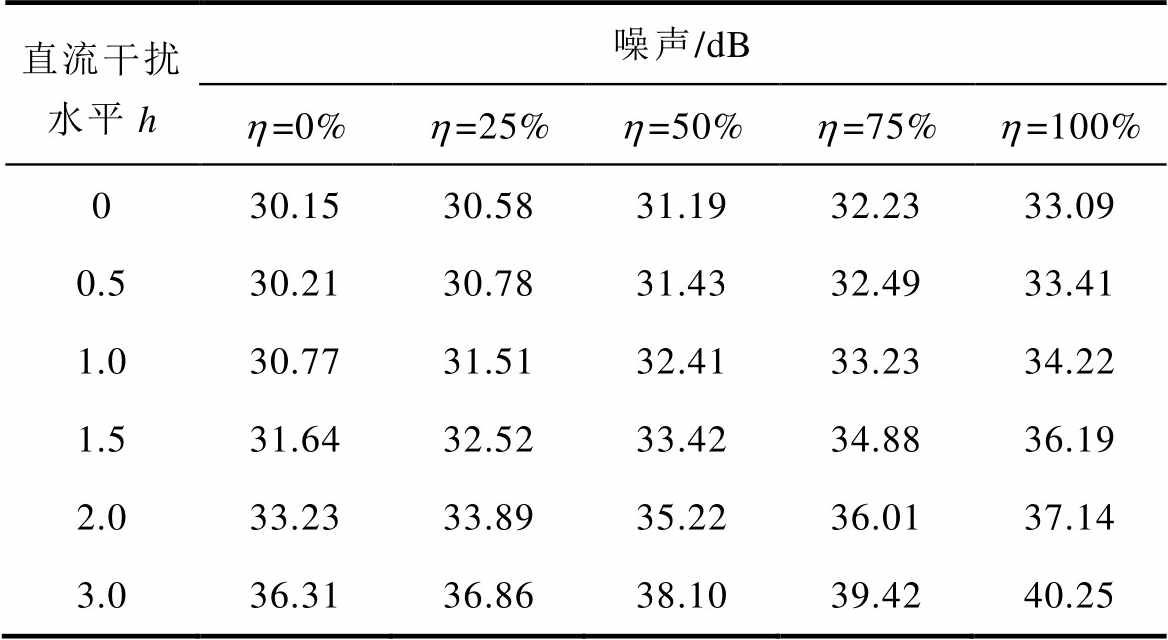
直流干扰水平h噪声/dB h=0%h=25%h=50%h=75%h=100% 030.1530.5831.1932.2333.09 0.530.2130.7831.4332.4933.41 1.030.7731.5132.4133.2334.22 1.531.6432.5233.4234.8836.19 2.033.2333.8935.2236.0137.14 3.036.3136.8638.1039.4240.25
表6 时变分量干扰下变压器表面最大噪声
Tab.6 Maximum surface noise of transformer with time-varying component disturbance
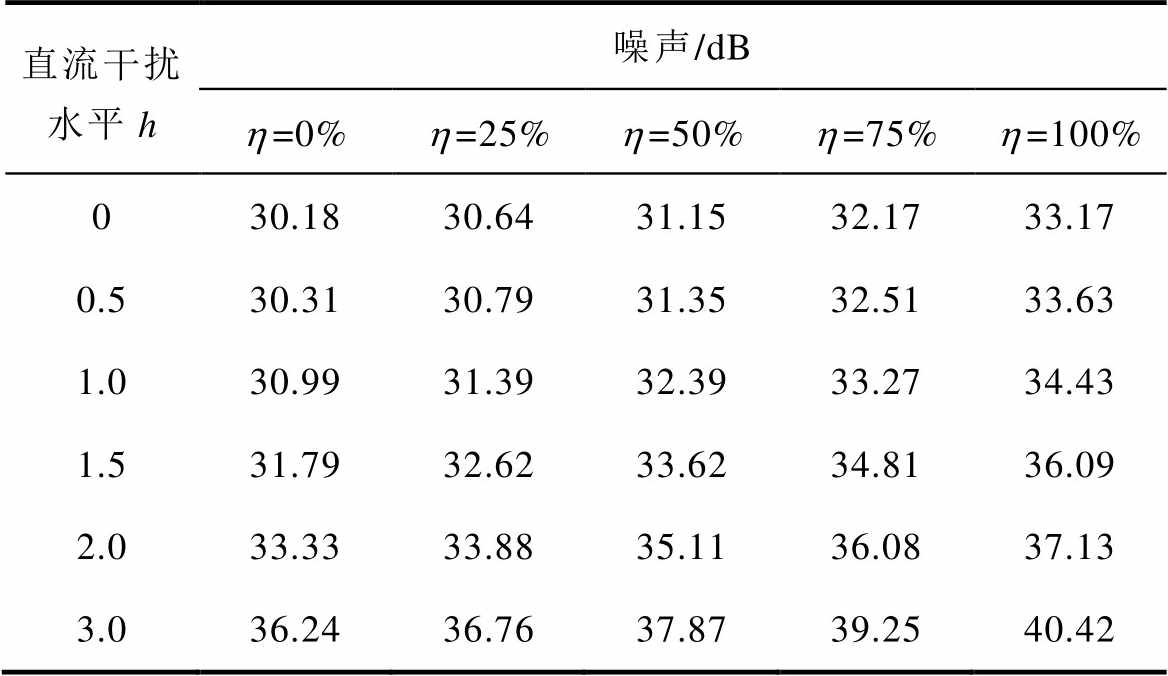
直流干扰水平h噪声/dB h=0%h=25%h=50%h=75%h=100% 030.1830.6431.1532.1733.17 0.530.3130.7931.3532.5133.63 1.030.9931.3932.3933.2734.43 1.531.7932.6233.6234.8136.09 2.033.3333.8835.1136.0837.13 3.036.2436.7637.8739.2540.42
结果表明,相同干扰水平下时变分量造成的本体噪声与直流分量无明显区别,但在时变分量突变时刻本体噪声比直流分量干扰情况更加严重;相同模式下铁心声压级高于绕组,与振动仿真结果相符。
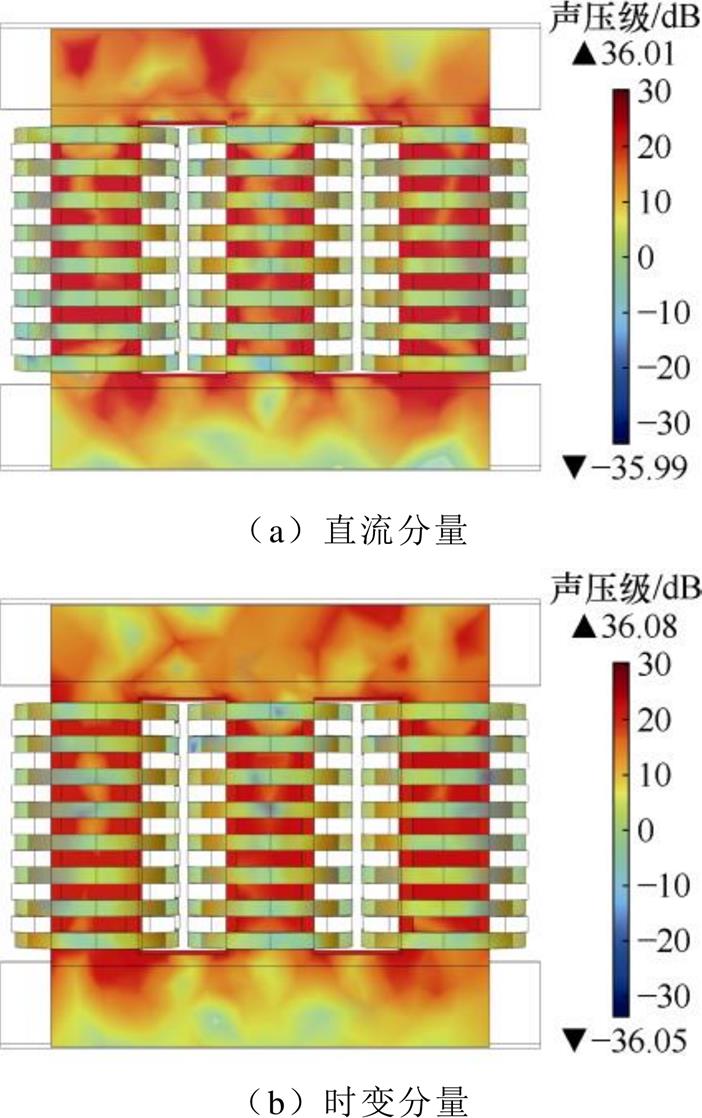
图11 变压器绕组及铁心表面最大声压级
Fig.11 Maximum surface sound pressure level of transformer winding and core
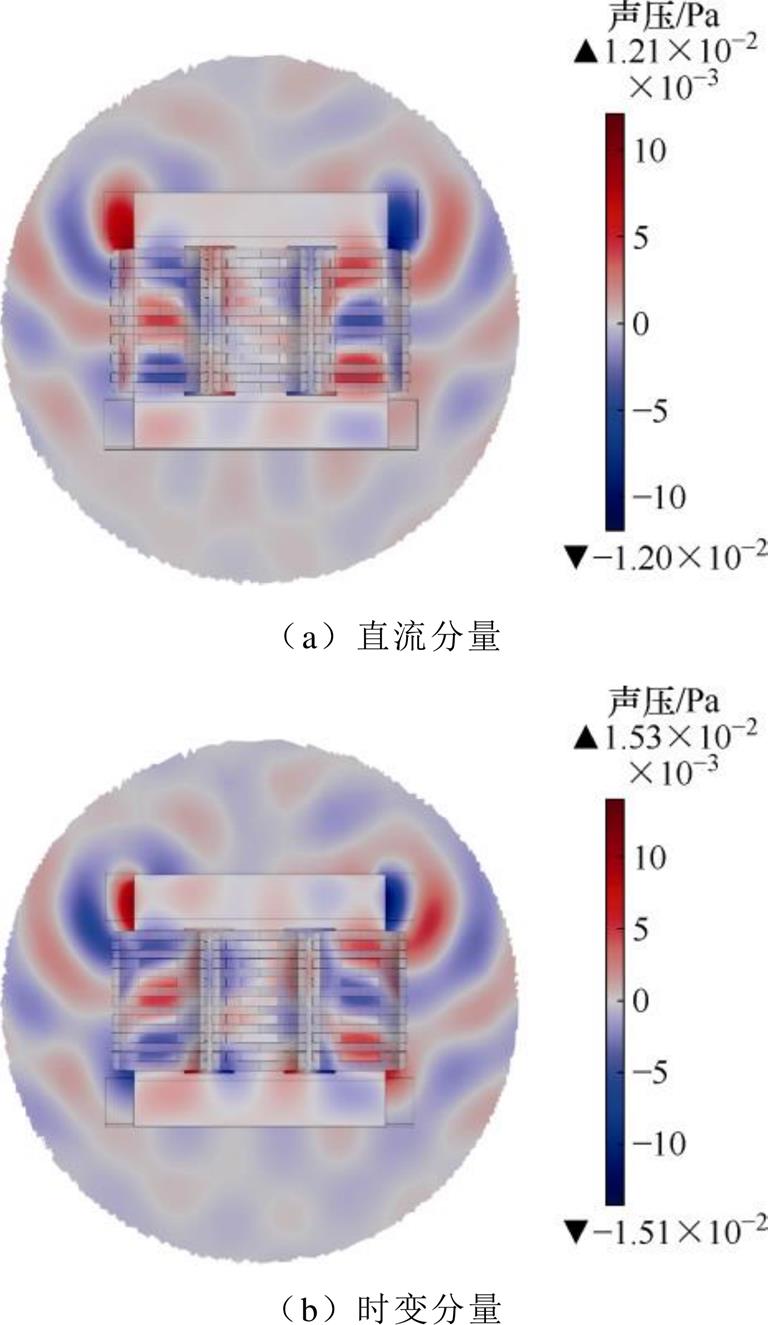
图12 变压器空间声压分布
Fig.12 Spatial sound pressure distribution of transformer
仿真研究杂散电流在三相变压器中的干扰传播,可归纳以下规律:
(1)杂散电流干扰下,绕组电流、漏磁及振动加速度等物理特征具有相似的变化规律。空载工况下多场特征参数呈现“半波增强、半波衰减”的特点,且其时序波动性受时变分量影响较大,|k|较大时,幅值波动更为显著,而负载工况所受影响并不明显;干扰水平和负载率越高,多场特征参数变化越剧烈;相同条件下,绕组端部的特征参数变化更加明显;杂散电流瞬时突变导致机械参数畸变,绕组振动的畸变占比随干扰水平的升高而增大;空载绕组振动的畸变占比高于负载情况;端部畸变占比高于中部。
(2)铁心励磁、振动及噪声随干扰水平和负载率的升高而加剧;相同干扰水平和相同负载率下,铁心的振动和噪声比绕组更加剧烈;时变分量突变时刻,铁心振动和噪声均大于同水平直流分量干扰;铁心振动畸变占比的变化规律与绕组类似,但其值显著高于绕组,且主心柱畸变占比高于旁柱。当h达到1.5时,变压器内部构件振动噪声已显著加剧。
搭建动模实验平台,实验接线如图13所示,参数见表1。变压器高压侧连接调压器T1和干扰电流调制模块,低压侧连接负载。振动观测点保持与仿真一致,通过各监测模块分别采集不同模式下的电流、振动加速度和噪声数据。
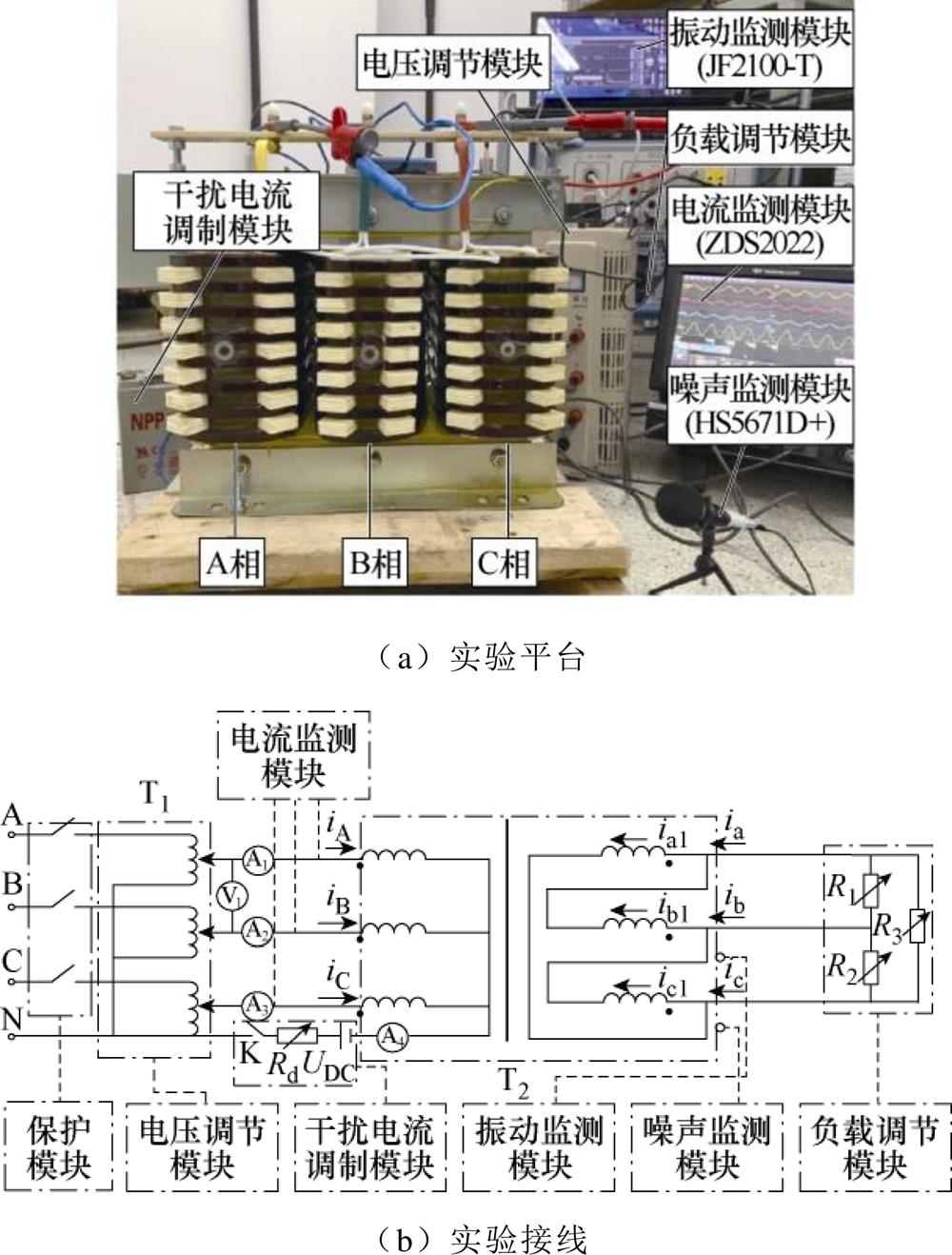
图13 三相变压器动模实验
Fig.13 Dynamic experiment for three-phase transformer
采集变压器构件振动信号,提取其轴向信息如图14和图15所示。
结果表明,铁心振动比绕组更剧烈;时变分量突变时刻(t=40 ms),铁心振动畸变比绕组更为显著。对比图8、图10,实验波形比仿真结果更加复杂。分析原因,铁心的非线性励磁和磁致伸缩特性导致其振动信号中存在较多高频分量,使实验振动时域信号剧烈波动。另外,构件的紧固连动性导致实验结果中包含了其他构件的部分振动信号。h=2.0时,实验变压器振动噪声异常剧烈,此时负载已出现绝缘烧毁状况。
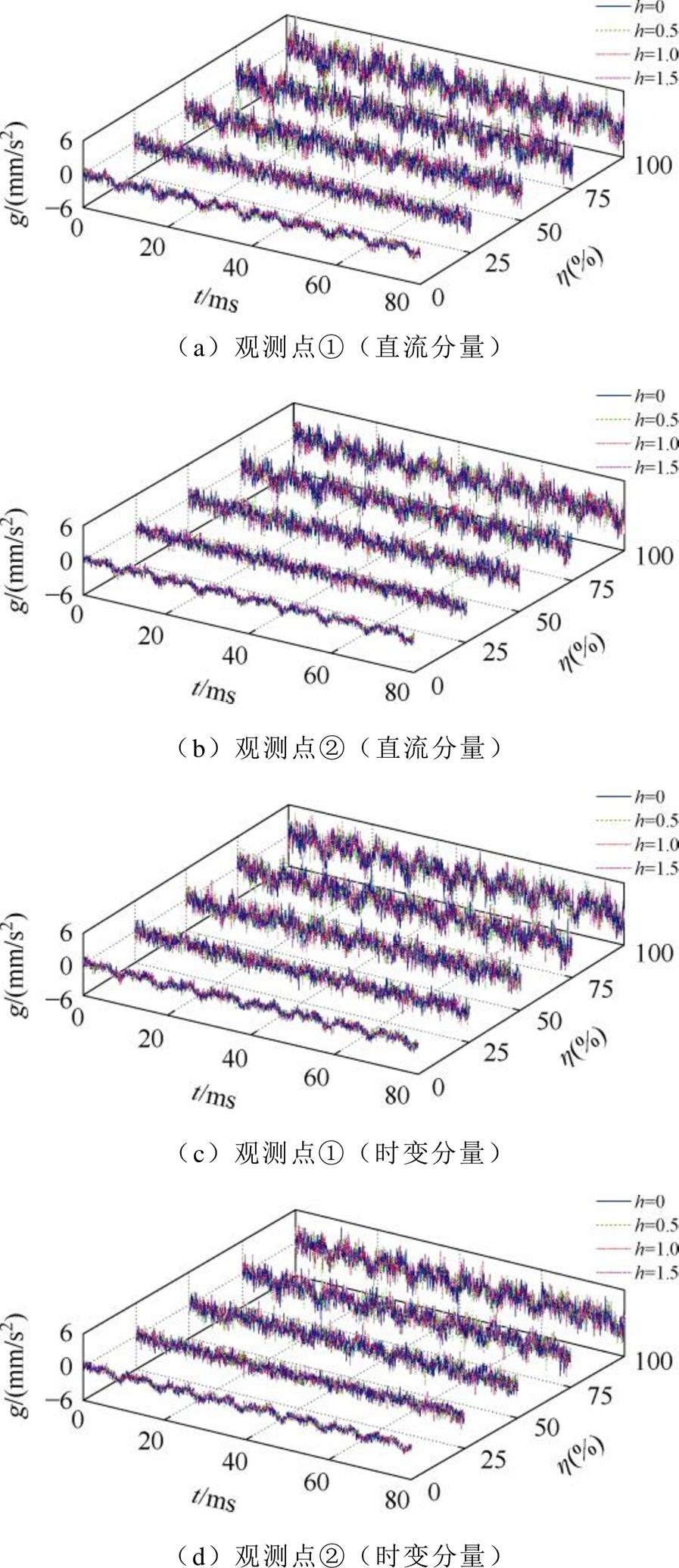
图14 绕组振动监测波形
Fig.14 Vibration monitoring waveforms of winding
以观测点①、③为例,提取实验振动数据有效值,与仿真结果对比如图16所示。
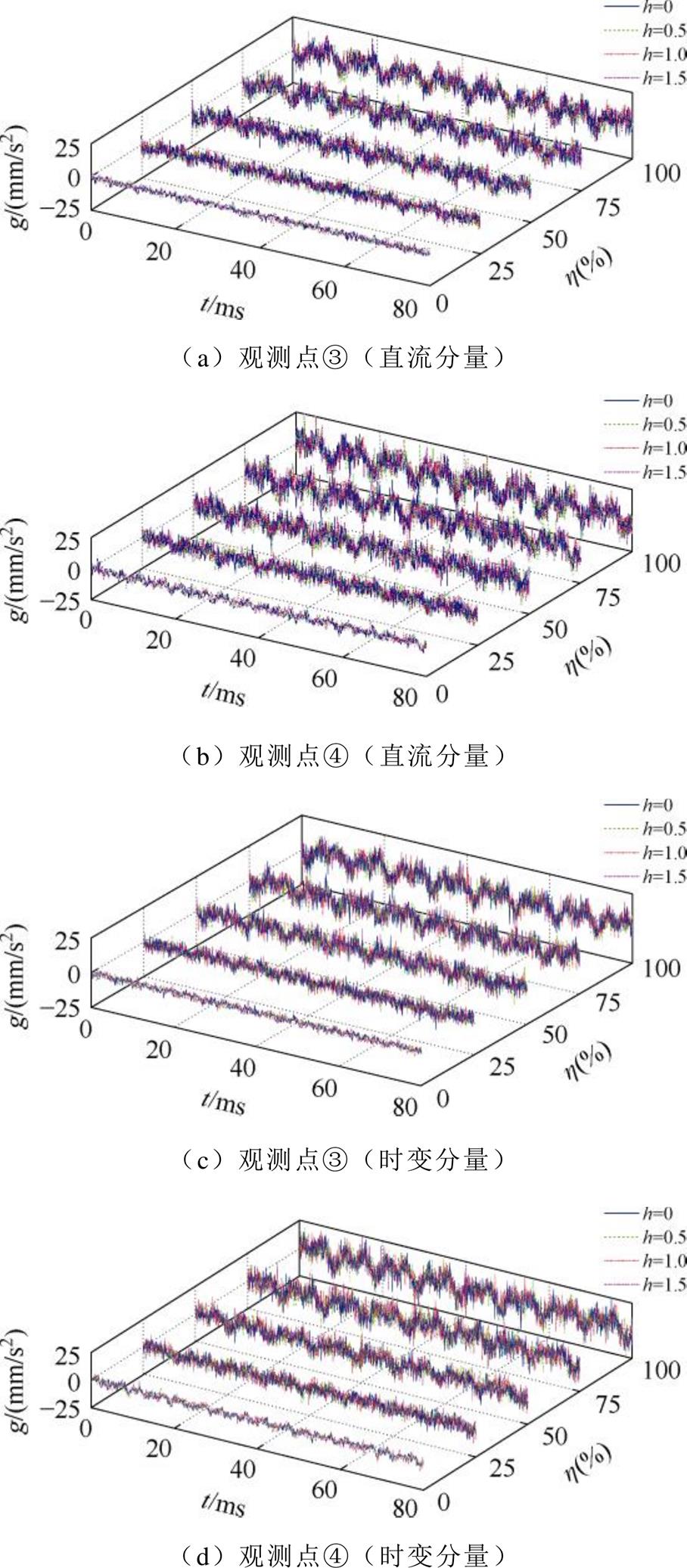
图15 铁心振动监测波形
Fig.15 Vibration monitoring waveforms of core
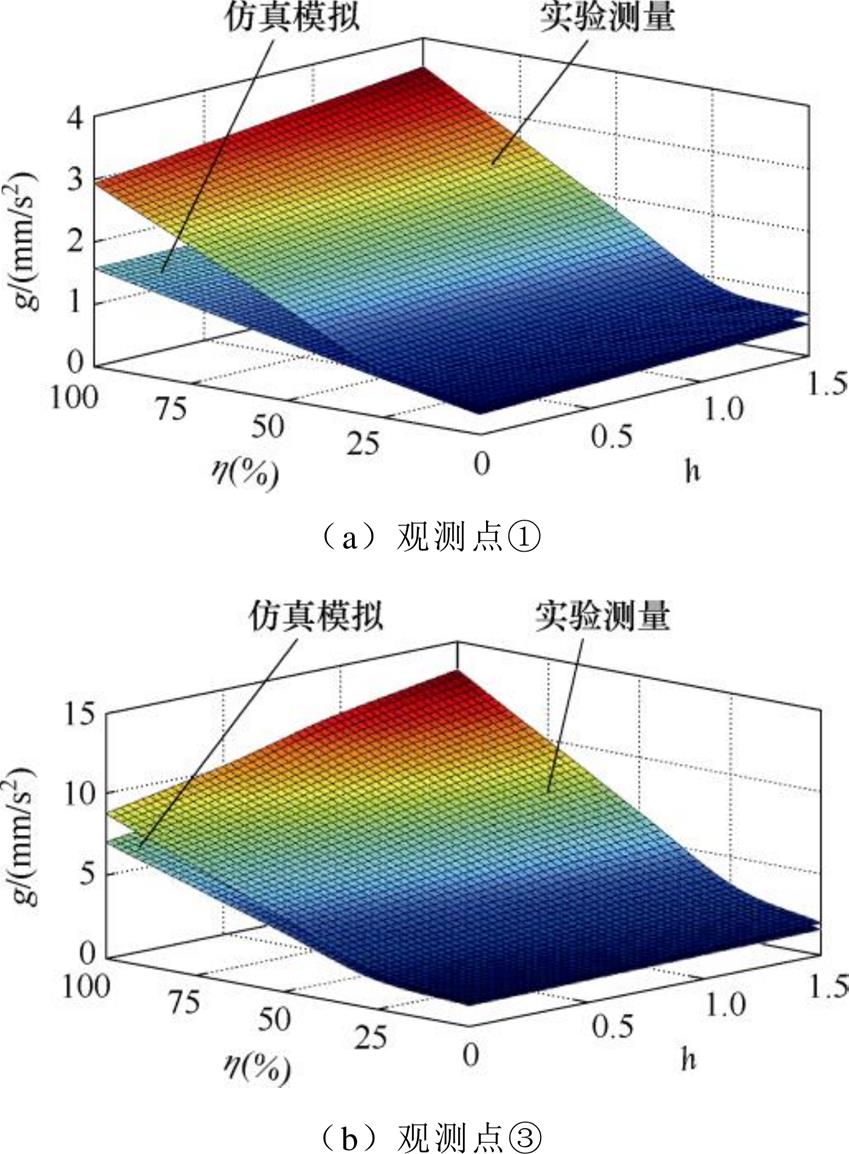
图16 构件振动实验-仿真对比
Fig.16 Comparison between experiment and simulation of component vibration
由对比结果可知,实验测量中变压器构件振动互相干扰导致实验振动比仿真更加严重,但两者变化规律基本一致。当h=0.5时,仿真、实验铁心振动约为无干扰时的1.1倍,振动加剧并不显著;当h=1.5时,仿真、实验铁心振动约为无干扰时的1.3倍,振动加剧明显。经虚实一致性校验,铁心是异常振动的主要来源。
变压器实验噪声监测结果见表7、表8。当h=0.5时,噪声加剧不明显,声压级不超过无干扰时的1.01倍;当h=1.5时,实验噪声显著提升,声压级达到无干扰时的1.05倍以上,符合仿真结论。对比表5、表6,由于环境噪声和测量误差影响,导致实验噪声高于仿真结果,但两者变化规律一致。
表7 直流分量干扰下变压器实验噪声
Tab.7 Experimental noise of transformer with DC component disturbance
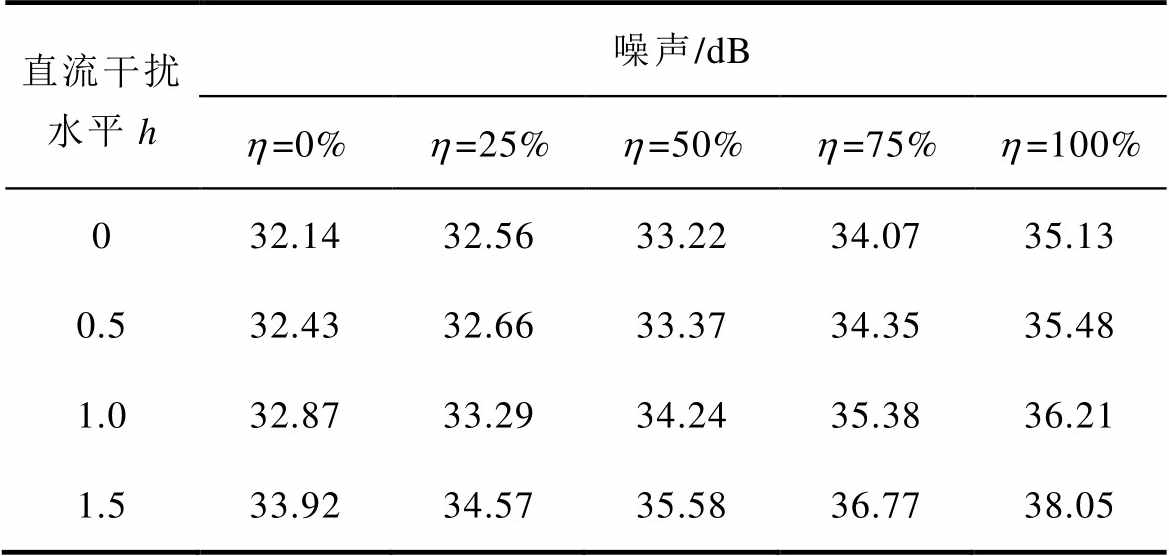
直流干扰水平h噪声/dB h=0%h=25%h=50%h=75%h=100% 032.1432.5633.2234.0735.13 0.532.4332.6633.3734.3535.48 1.032.8733.2934.2435.3836.21 1.533.9234.5735.5836.7738.05
表8 时变分量干扰下变压器实验噪声
Tab.8 Experimental noise of transformer with time-varying component disturbance
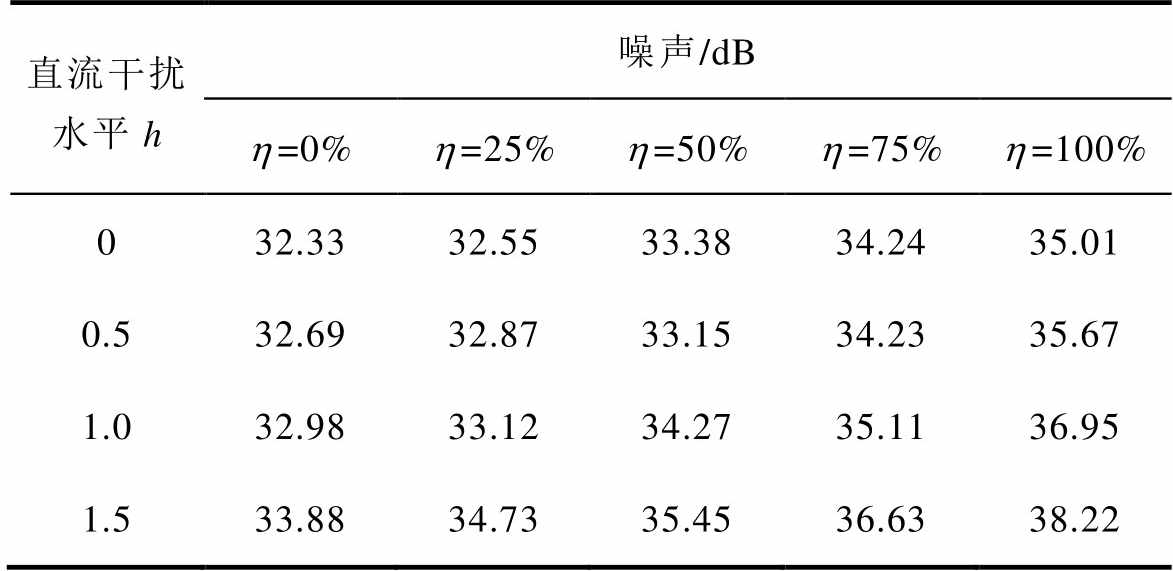
直流干扰水平h噪声/dB h=0%h=25%h=50%h=75%h=100% 032.3332.5533.3834.2435.01 0.532.6932.8733.1534.2335.67 1.032.9833.1234.2735.1136.95 1.533.8834.7335.4536.6338.22
基于虚实一致性校验,进一步研究杂散电流干扰变压器的多元模-态空间干扰传播域及判据。通过分析杂散电流在变压器电磁-机械-声的多场干扰传播,构建全局模-态信息库,以不同模式的标签索引提取各场域特征信息,形成多元模-态空间。选取典型模-态空间,以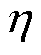 =0和
=0和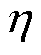 =75%为例,分别观测绕组和铁心的多元模-态信息分布,如图17所示。
=75%为例,分别观测绕组和铁心的多元模-态信息分布,如图17所示。
图17中,杂散电流干扰对构件的不同场域特征分布产生明显影响。结果表明,不同条件下的多元模-态空间具有相似的分布规律,相同模式下各模-态空间特征信息幅值均随h升高而增大。通过仿真及实验论证,h<0.5时,变压器多场特征参数增大并不明显;h=1.5时,多场特征参数变化已趋于显著;h=2.0时,变压器振动噪声严重并出现绝缘烧毁状况。因此,可将h作为关键判据将模-态空间划分为四类干扰传播域:安全运行域、风险抵御域、异常失稳域及严重故障域。干扰判据简化为
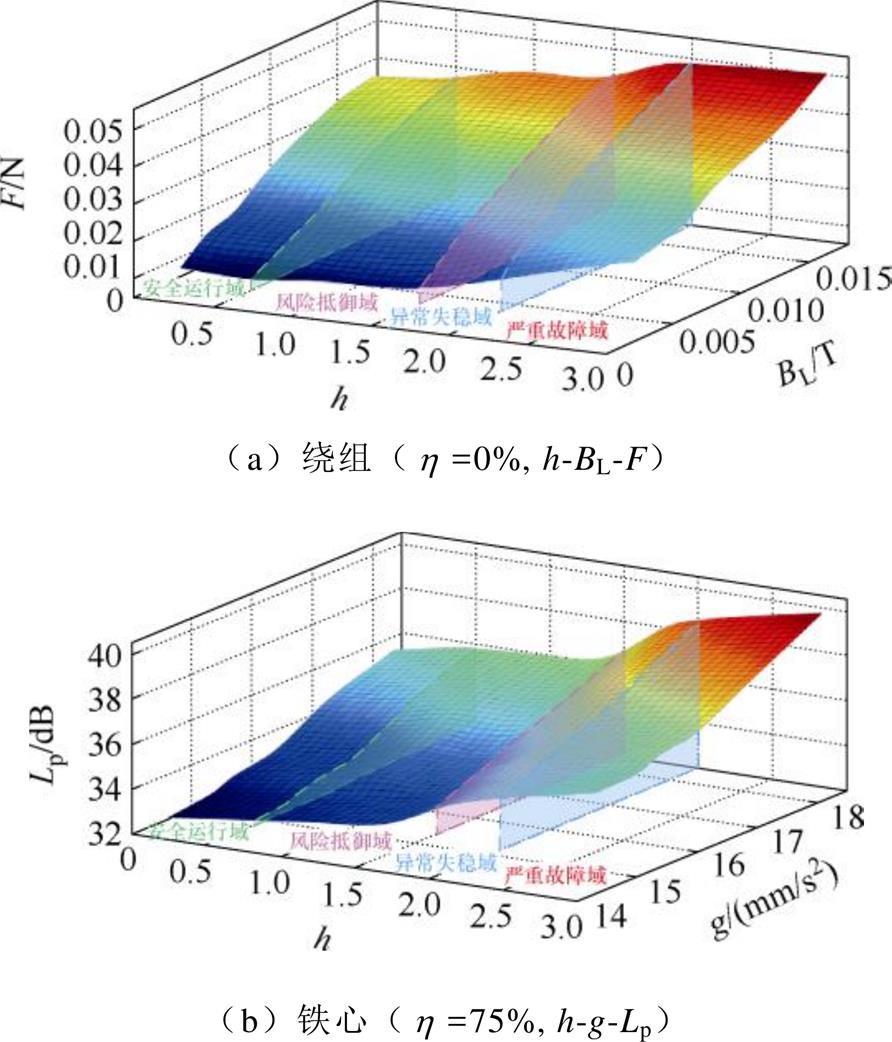
图17 多元模-态空间
Fig.17 Multivariate mode-state spaces
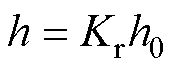 (15)
(15)
式中,Kr为可靠系数,Kr=1.1;h0为安全阈值,h0=1.5。
(1)当0≤h<0.5时,变压器受杂散电流影响较小,此时杂散电流干扰处于变压器承受范围内,判定为安全运行域。
(2)当0.5≤h<1.5时,构件振动与噪声增大,若变压器持续遭受地铁杂散电流的干扰,则可能造成屈曲变形与振动位移等问题,影响设备内部的电磁兼容性与结构稳定性,判定为风险抵御域。
(3)当1.5≤h<2.0时,杂散电流对变压器的影响加剧,使其内部的电磁、机械环境出现失稳现象,应及时报警并处理,判定为异常失稳域;若h≥2.0,则会对其内部构件及绝缘造成严重危害,判定为严重故障域。为验证判据的适用性,对其他型号变压器(BSS-1 000 VA、SC-100 kV·A)进行仿真分析,部分变压器参数和多元模-态空间结果见附录。结果表明,杂散电流干扰下不同型号变压器的模-态特征存在差异,但在h=1.5时变化均显著加剧。判据适用于66 kV及以下的三相三柱式变压器。
一般变压器负载率低于75%运行,虽然杂散电流干扰下的电流并未超出安全阈值,但已对其内部构件造成不良影响,尤其是杂散电流的瞬时突变特征会多次引发构件的振动噪声瞬时加剧。当杂散电流突变时刻与系统交流激励相位匹配时,则会导致更加严重的机械性危害。由于地铁杂散电流具有持续时间长、突变时间随机、变化频率低等特点,因此传统的电容隔直装置的适用性还有待研究,相关治理策略及措施还需进一步完善。
提出杂散电流对三相变压器多场干扰传播的时域模-态数学模型,研究其电磁-机械-声场特性,得出以下结论:
1)杂散电流干扰下变压器电磁、机械和声场特征参数的变化均随干扰水平升高而加剧。变压器绕组在空载工况下各特征参数受杂散电流干扰呈现“半波增强、半波衰减”的变化规律,且受时变分量影响导致其时序波动性更为复杂,|k|较大时,多场特征参数的幅值波动更为显著;负载工况下多场特征参数受杂散电流干扰的影响较小;且端部振动噪声异常,比中部更加剧烈。在相同模式下,铁心的振动噪声特征均比绕组更加显著,且中相铁心柱异常特征更为明显。结果表明,杂散电流干扰变压器产生的振动噪声异常主要源自铁心。仿真结果和实验数据的一致性验证了模型与结论的正确性。
2)对比杂散电流中时变分量与直流分量的干扰差异。结果表明,时变分量干扰导致各场域特征参数呈现出更为复杂的时序波动性;时变分量干扰突变导致变压器构件产生较明显的振动与噪声畸变,该因素若与交流激励相位匹配,则可能会对变压器的电磁兼容性和结构稳定性造成更大的危害。
3)通过融合多物理场特征信息,构建多元模-态空间,研究变压器受杂散电流干扰时多物理场特征的关联与变化规律,通过可观测的干扰水平与负载因数表征难以观测的多场异常状态,并形成多元模-态空间的干扰传播域及干扰判据,为电气设备全生命周期数字孪生奠定基础。
附 录
Ga计算过程如下
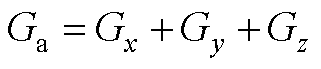 (A1)
(A1)
 (A2)
(A2)
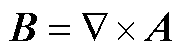 (A3)
(A3)
能量平衡原理:某时刻由电流激励引起磁场特征参数变化为
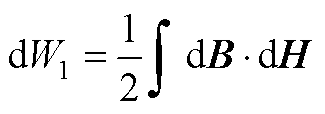 (A4)
(A4)
式中,H为磁场强度。
该时刻绕组电流的变化为dip、dis(p=A, B, C;s=a, b, c)。
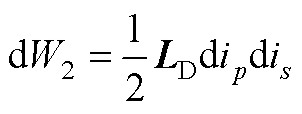 (A5)
(A5)
令W1=W2,联立磁场能量与电路能量即可求解时域动态电感矩阵LD,以作为电路模型的状态变量。
多线圈变压器时域微分方程可表示为
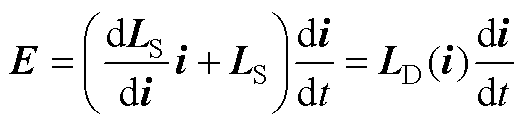 (A6)
(A6)
式中,E为变压器绕组电动势;LS为静态电感矩阵。若给定初值为
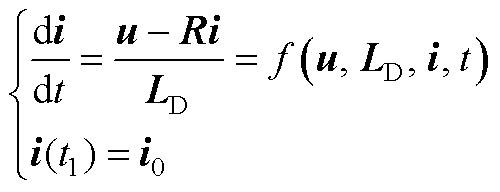 (A7)
(A7)
式中,u、i分别为绕组电压和电流的行或列向量;R、LD分别为绕组电阻和动态电感矩阵。
将式(A7)简化为一阶微分方程为
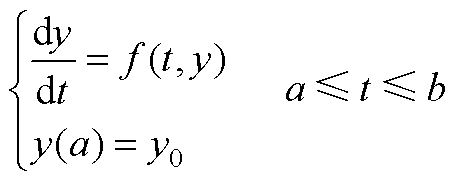 (A8)
(A8)
将tk时刻的LD代入式(A8),并进一步通过四阶龙格库塔法(RK4)在电路模型中由绕组电流ik计算下一时刻的电流ik+1为
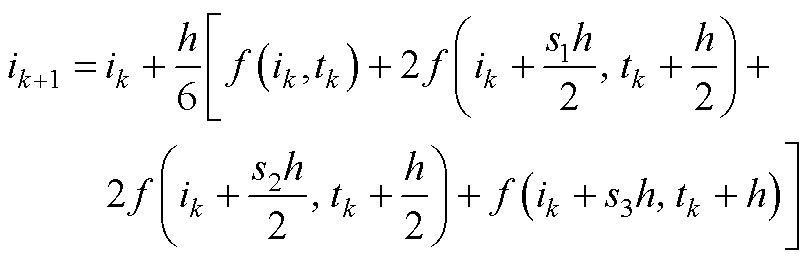 (A9)
(A9)
式中,h为时步;s1~s3为分段计算斜率。
磁致伸缩效应如附图1所示,当变压器无磁场激励时,磁畴的排列没有规律;当变压器正常运行时,磁路中存在着交变磁场,铁磁物质受磁化作用影响,其磁畴的移动方向趋于相同,磁畴形态改变DL,铁心材料形变程度由磁致伸缩系数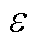 表征。
表征。
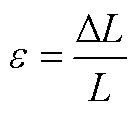 (A10)
(A10)
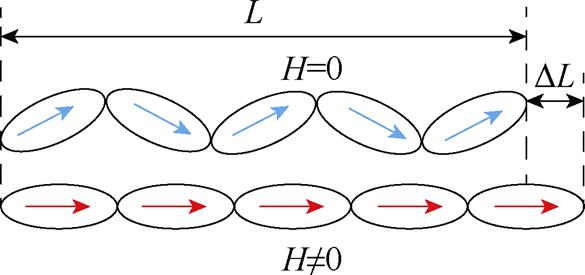
附图1 磁致伸缩效应
App.Fig.1 Magnetostrictive effect
铁心励磁饱和时,磁致伸缩系数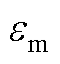 与磁通密度
与磁通密度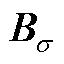 之间的数学关系为
之间的数学关系为
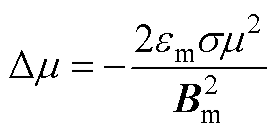 (A11)
(A11)
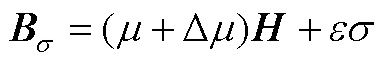 (A12)
(A12)
式中,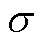 为磁致伸缩状态应力;Δµ为相对磁导率;Bm为饱和状态下的磁通密度。
为磁致伸缩状态应力;Δµ为相对磁导率;Bm为饱和状态下的磁通密度。
采用FL4000多功能拉压实验机对材料参数进行测量,如附图2所示。变压器硅钢片的型号为50WW800。一次电流部分仿真数据(滤除直流偏置分量)如附图3所示。25%、75%负载工况部分仿真数据如附图4所示。

附图2 材料参数测定实验
App.Fig.2 Material parameter determination experiment
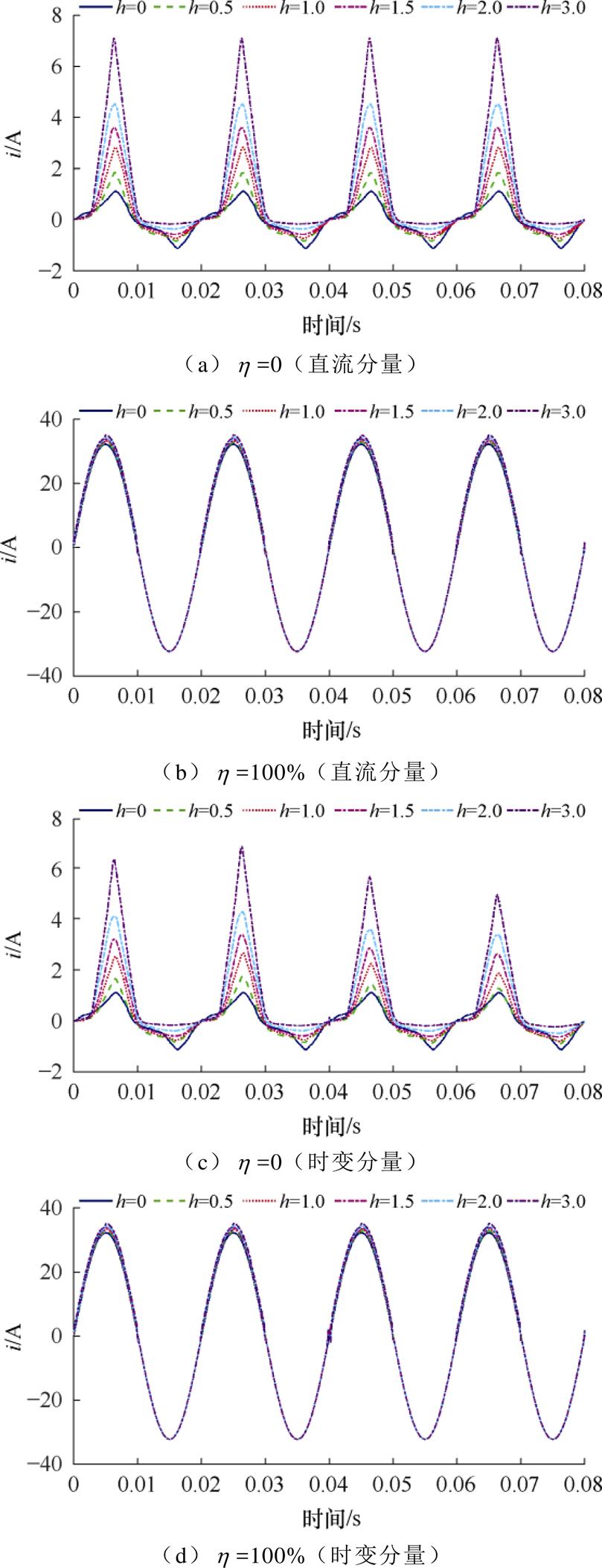
附图3 一次电流部分仿真数据(滤除直流偏置分量)
App.Fig.3 Partial simulation results of primary winding current (filter out DC bias components)
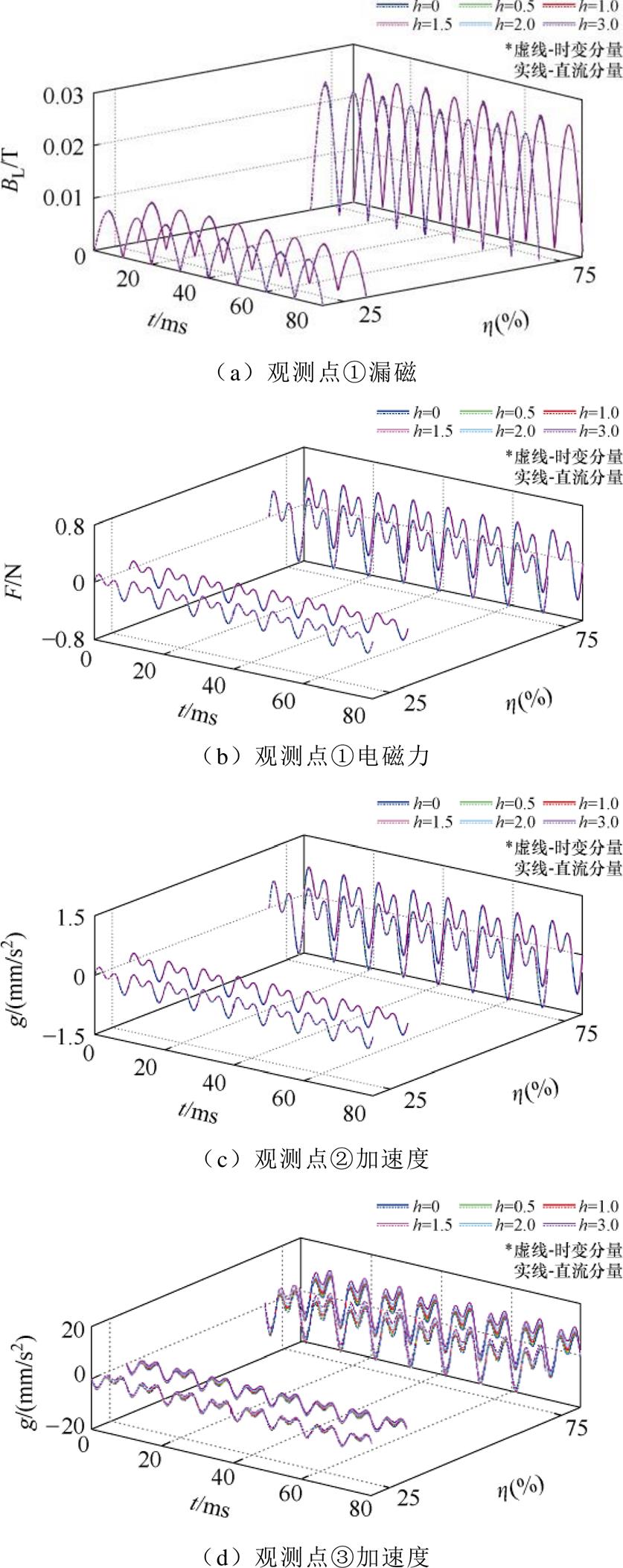
附图4 25%、75%负载工况部分仿真数据
App.Fig.4 Partial simulation results under 25% and 75% load conditions
以直流分量干扰模式为例,滤除直流偏置分量,B相主磁通部分仿真数据如附图5所示。
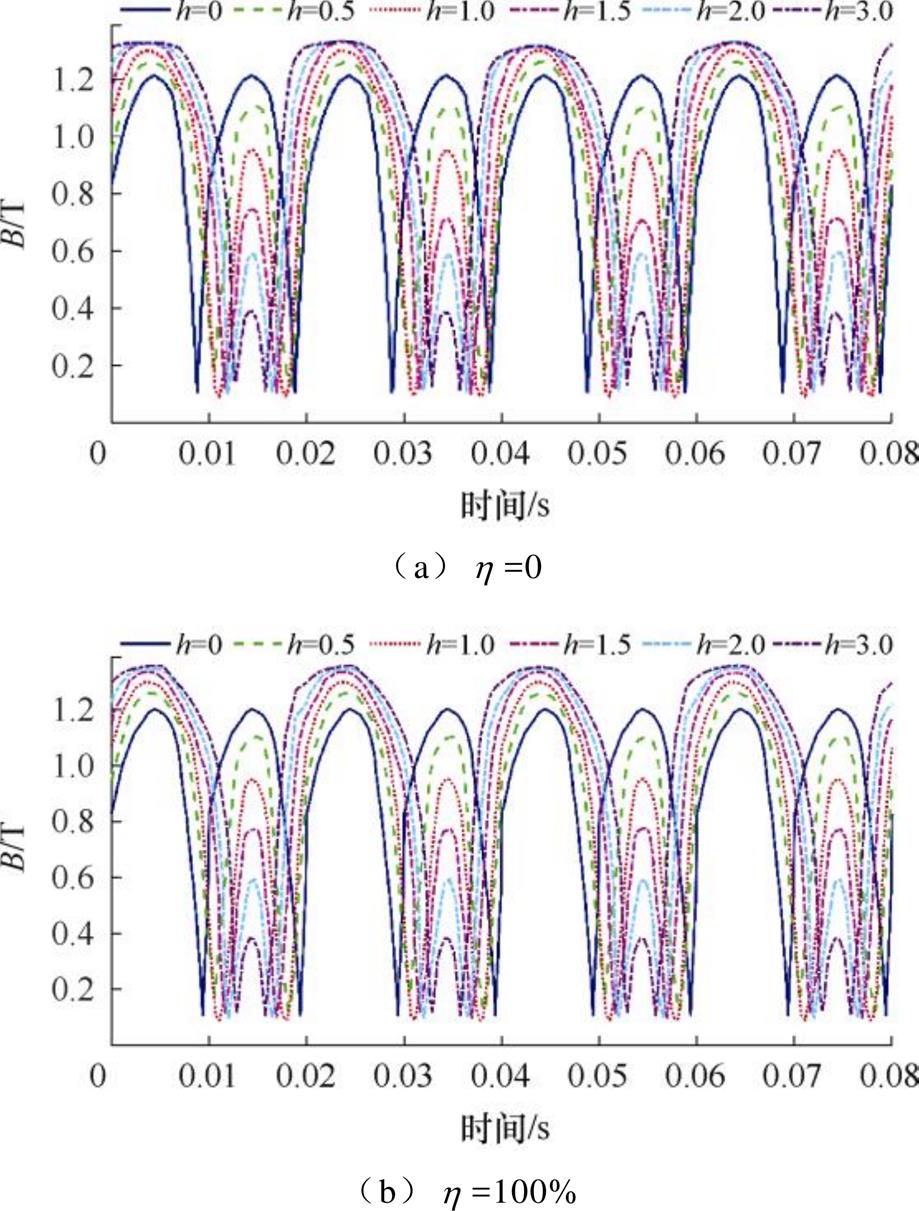
附图5 主磁通部分仿真数据
App.Fig.5 Partial simulation results of mainflux
以空载时直流分量干扰模式为例,实测一次电流iA如附图6所示。变压器仿真模型如附图7所示。多元模-态空间如附图8所示。三相变压器参数见附表1。
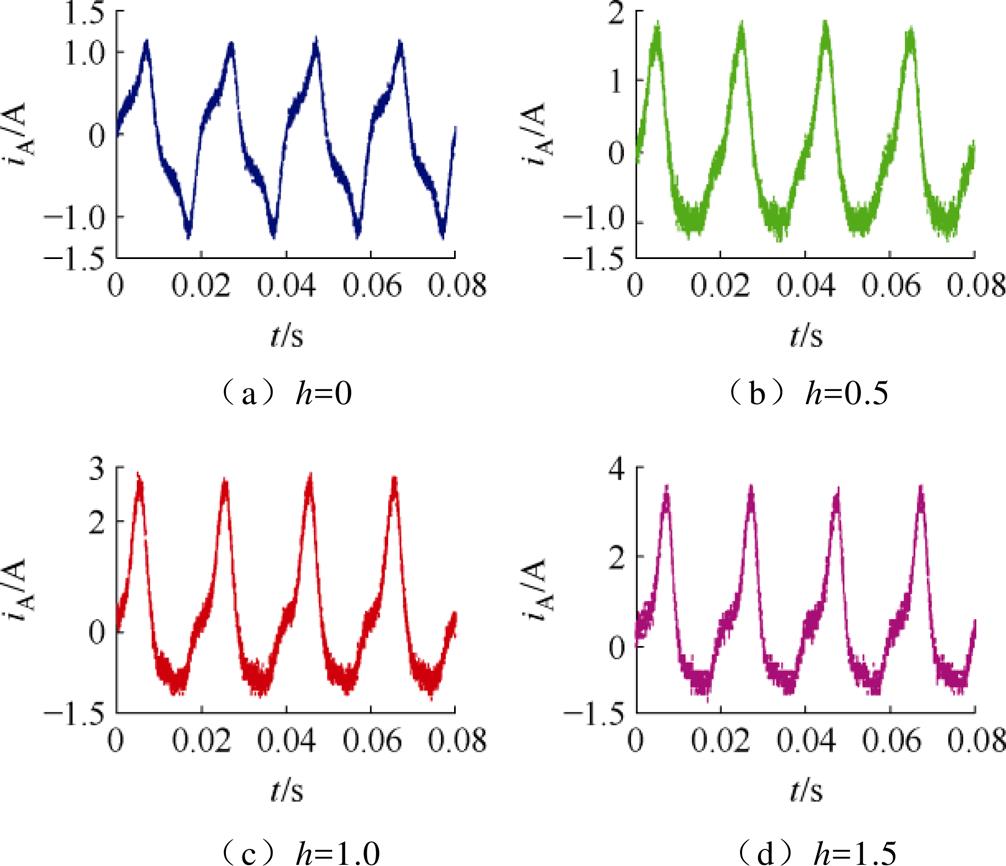
附图6 空载实测电流
App.Fig.6 Winding currents with no load
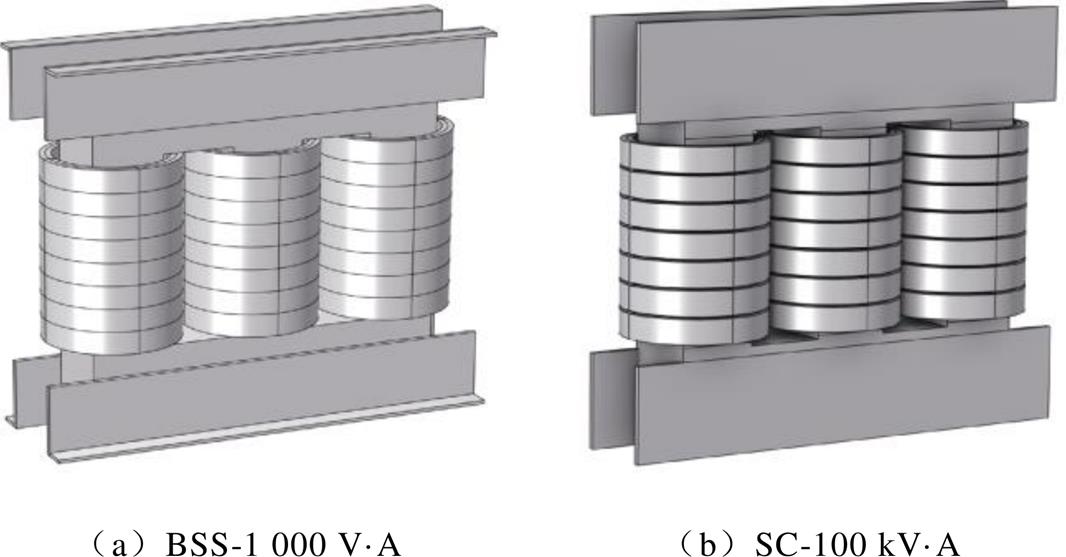
附图7 变压器仿真模型
App.Fig.7 Simulation model of transformers
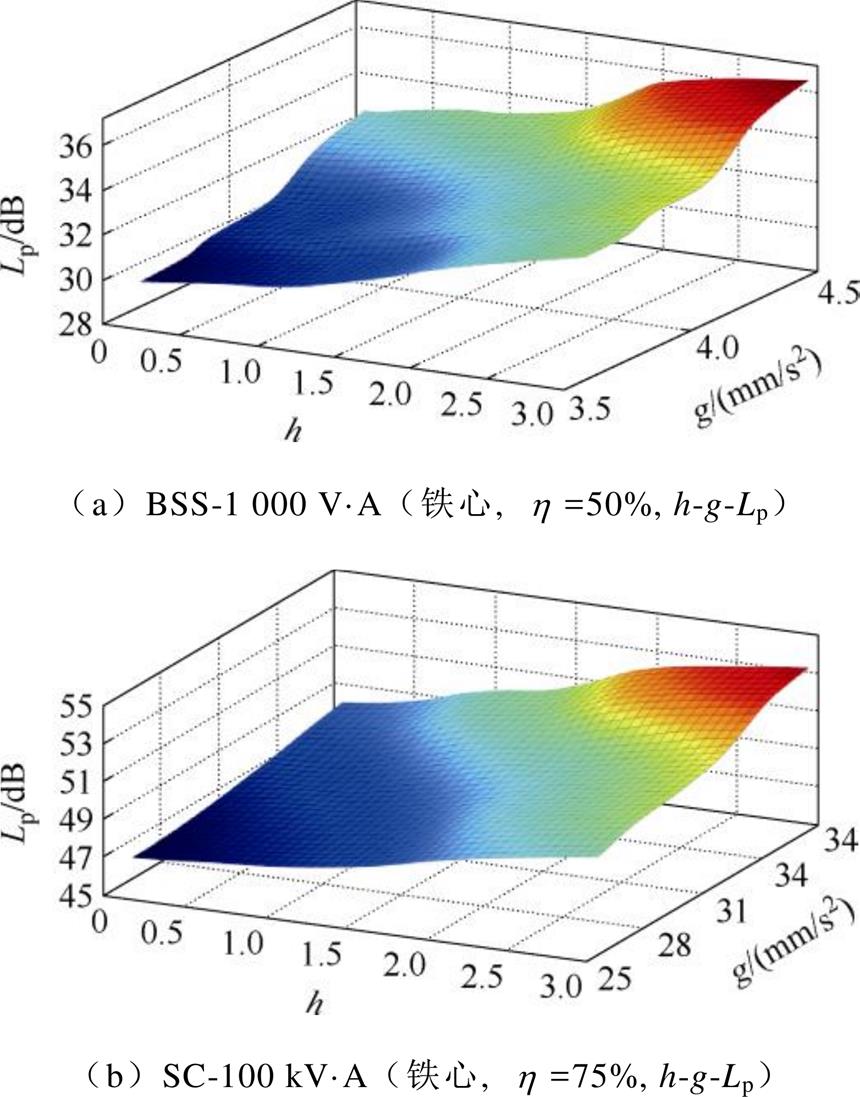
附图8 多元模-态空间
App.Fig.8 Multivariate mode-state spaces
附表1 三相变压器参数
App.Tab.1 Three-phase transformer parameters

铭牌参数BSS-1 000 V·ASC-100 kV·A 频率/Hz5050 容量SN/(kV·A)1100 电压UN/V380/11010 000/400 空载电流I0(%)6.61.8
参考文献
[1] 王爱民, 林圣, 李俊逸, 等. 城市轨道交通长线路杂散电流仿真模型[J]. 高电压技术, 2020, 46(4): 1379-1386.
Wang Aimin, Lin Sheng, Li Junyi, et al. Stray current simulation model of the long line of DC metro systems[J]. High Voltage Engineering, 2020, 46(4): 1379-1386.
[2] 吴天逸, 冯楠, 高凯, 等. 轨道交通影响下上海电网直流偏磁多参量监测及治理研究[J]. 高压电器, 2023, 59(11): 84-91.
Wu Tianyi, Feng Nan, Gao Kai, et al. Research on multi parameters monitoring and suppression of DC bias in Shanghai power grid under influence of rail transit[J]. High Voltage Apparatus, 2023, 59(11): 84-91.
[3] 潘超, 安景革, 刘闯, 等. 变压器偏磁效应噪声特性的多场耦合分析与抑制[J]. 电工技术学报, 2023, 38(18): 5077-5088.
Pan Chao, An Jingge, Liu Chuang, et al. Multi-field coupling analysis and suppression for biased magnetic noise in transformer[J]. Transactions of China Elec- trotechnical Society, 2023, 38(18): 5077-5088.
[4] 杨戈辉, 赵桐浠, 姚鑫, 等. 基于健康指数和非等间隔灰色预测的重载铁路牵引变压器状态评估方法[J]. 电气技术, 2023, 24(11): 10-17.
Yang Gehui, Zhao Tongxi, Yao Xin, et al. A state evaluation method for heavy haul railway traction transformers based on health index and unequal interval grey prediction[J]. Electrical Engineering, 2023, 24(11): 10-17.
[5] 赵志刚, 姬俊安, 马习纹, 等. 基于动态J-A模型的直流偏磁条件下电工钢磁特性模拟及实验验证[J]. 高电压技术, 2020, 46(6): 2081-2089.
Zhao Zhigang, Ji Jun’an, Ma Xiwen, et al. Simulation and experimental verification of magnetic properties of electrical steel sheets under DC bias based on the dynamic J-A model[J]. High Voltage Engineering, 2020, 46(6): 2081-2089.
[6] 张书琦, 汪可, 李金忠, 等. 单相单柱旁轭变压器空负载工况下的直流偏磁关键性能测试[J]. 中国电机工程学报, 2019, 39(14): 4334-4344, 4281.
Zhang Shuqi, Wang Ke, Li Jinzhong, et al. Tests of DC bias key performances of power transformer with single-phase three-limb core under no-load and rated-load conditions[J]. Proceedings of the CSEE, 2019, 39(14): 4334-4344, 4281.
[7] 林湘宁, 杨国稳, 翁汉琍, 等. 直流偏磁下变压器无功消耗增多对系统电压的影响分析[J]. 高电压技术, 2016, 42(1): 272-278.
Lin Xiangning, Yang Guowen, Weng Hanli, et al. Analysis of system voltage impact by transformer reactive power consumption increased under DC bias[J]. High Voltage Engineering, 2016, 42(1): 272- 278.
[8] Xie Zhicheng, Lin Xiangning, Zhang Zheyuan, et al. Advanced DC bias suppression strategy based on finite DC blocking devices[J]. IEEE Transactions on Power Delivery, 2017, 32(6): 2500-2509.
[9] 黄天超, 王泽忠, 李宇妍. 换流变压器直流偏磁对油箱涡流损耗的影响[J]. 电工技术学报, 2023, 38(8): 2004-2014.
Huang Tianchao, Wang Zezhong, Li Yuyan. The influence of converter transformer DC bias on eddy current loss of tank[J]. Transactions of China Elec- trotechnical Society, 2023, 38(8): 2004-2014.
[10] 罗通, 刘伟豪. 牵引变电站供电线路带负荷测试分析[J]. 电气技术, 2022, 23(5): 76-80.
Luo Tong, Liu Weihao. Load test analysis of power supply line in traction substation[J]. Electrical Engineering, 2022, 23(5): 76-80.
[11] Charalambous C A. Comprehensive modeling to allow informed calculation of DC traction systems’ stray current levels[J]. IEEE Transactions on Vehicular Technology, 2017, 66(11): 9667-9677.
[12] Zhang Bin, Yu Longbin, Li Hui, et al. Influence and analysis of urban subway on DC bias of power transformer[C]//2021 6th Asia Conference on Power and Electrical Engineering (ACPEE), Chongqing, China, 2021: 955-959.
[13] 史云涛, 赵丽平, 林圣, 等. 城市电网中地铁杂散电流分布规律及影响因素分析[J]. 电网技术, 2021, 45(5): 1951-1957.
Shi Yuntao, Zhao Liping, Lin Sheng, et al. Analysis of distribution of metro stray current in urban power grid and its influencing factors[J]. Power System Technology, 2021, 45(5): 1951-1957.
[14] 黄华, 陈璐, 吴天逸, 等. 城市轨道交通动态运行对交流电网变压器偏磁直流的影响[J]. 电网技术, 2022, 46(11): 4524-4533.
Huang Hua, Chen Lu, Wu Tianyi, et al. Influence of dynamic operation of urban rail transit on DC magnetic bias of AC power grid Transformer[J]. Power System Technology, 2022, 46(11): 4524-4533.
[15] Wang Aimin, Lin Sheng, He Zhengyou, et al. Probabilistic evaluation method of transformer neutral direct current distribution in urban power grid caused by DC metro stray current[J]. IEEE Transactions on Power Delivery, 2023, 38(1): 541-552.
[16] 宁晓雁, 高国强, 尹彩琴, 等. 地铁引起的变压器偏磁电流特征分析[J]. 都市快轨交通, 2023, 36(5): 125-131.
Ning Xiaoyan, Gao Guoqiang, Yin Caiqin, et al. Characteristics of transformer bias current caused by metro[J]. Urban Rapid Rail Transit, 2023, 36(5): 125-131.
[17] 王淼, 杨晓峰, 李世翔, 等. 城市轨道交通直流自耦变压器牵引供电系统故障保护研究[J]. 电工技术学报, 2022, 37(4): 976-989.
Wang Miao, Yang Xiaofeng, Li Shixiang, et al. Fault protection of DC auto-transformer traction power supply system for urban rail transit[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 976-989.
[18] 潘超, 陈祥, 蔡国伟, 等. 基于电磁-机械耦合原理的变压器三相不平衡运行绕组振动模-特征[J]. 中国电机工程学报, 2020, 40(14): 4695-4707.
Pan Chao, Chen Xiang, Cai Guowei, et al. Mode-state characteristics of three-phase unbalanced operation winding vibration of transformer based on elec- tromagnetic mechanical coupling principle[J]. Pro- ceedings of the CSEE, 2020, 40(14): 4695-4707.
[19] 张鹏宁, 李琳, 聂京凯, 等. 考虑铁心磁致伸缩与绕组受力的高压并联电抗器振动研究[J]. 电工技术学报, 2018, 33(13): 3130-3139.
Zhang Pengning, Li Lin, Nie Jingkai, et al. Study on the vibration of high voltage shunt reactor considering of magnetostriction and winding force[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(13): 3130-3139.
[20] 师愉航, 汲胜昌, 张凡, 等. 变压器绕组多倍频振动机理及特性[J]. 高电压技术, 2021, 47(7): 2536- 2544.
Shi Yuhang, Ji Shengchang, Zhang Fan, et al. Multi- frequency vibration mechanism and characteristics of transformer windings[J]. High Voltage Engineering, 2021, 47(7): 2536-2544.
[21] 刘行谋. 变压器直流偏磁电-磁-力特性及振动信号时频特征分析研究[D]. 重庆: 重庆大学, 2018.
Liu Xingmou. Analysis and research on DC bias magnetoelectric magnetic force characteristics of transformer and time-frequency characteristics of vibration signal[D]. Chongqing: Chongqing University, 2018.
[22] 姜言金, 刘栩霏, 徐晓东, 等. 基于多场耦合的变压器直流偏磁噪声异常表征[J]. 电网与清洁能源, 2023, 39(1): 11-19.
Jiang Yanjin, Liu Xufei, Xu Xiaodong, et al. Anomaly characterization of transformer DC bias noise based on multi-field coupling[J]. Power System and Clean Energy, 2023, 39(1): 11-19.
[23] 程志光, 高桥则雄, 博扎德·弗甘尼(Behzad Forghani), 等. 电气工程电磁热场模拟与应用[M]. 北京: 科学出版社, 2009.
[24] 国家能源局. 电力变压器直流偏磁耐受能力试验方法: DL/T 1799-2018[S]. 北京: 中国电力出版社, 2018.
Abstract The interference of stray currents from urban subways leads to magnetic bias anomalies in nearby power grid grounding transformers. The coupling relationships between the internal electromagnetic, vibration, and transformer noise with stray current interference need to be studied. In addition, subway stray currents exhibit complex temporal fluctuations, significantly impacting anomaly identification in transformers and other equipment. This paper utilizes multi-physics field coupling to simulate and analyze the multivariate spatial-temporal information of the transformer with stray current interference. Meanwhile, experiments are constructed to verify the simulation results. Based on virtual-real consistency, the interference propagation domains are identified, and the interference criteria can be formed. It provides a basis for safety situational awareness and anomaly identification of urban power grid transformers in resisting stray current interference from rail transit.
Firstly, a time-domain mode-state mathematical model for multi-field interference propagation in a transformer is proposed based on the electromagnetic-mechanical-acoustic coupling principle. Secondly, a 3D finite element model is built based on a three-phase, three-limb transformer JSSG-15 kV·A. The influence of stray currents on propagation characteristics (winding current, magnetic flux, electromagnetic force, vibration, and noise) is simulated under different modes. Thirdly, a dynamic experimental platform is built to measure the transformer’s current, vibration, and noise data. The correctness and effectiveness of the proposed model are verified by comparing experimental and simulation results.
The following conclusions can be drawn. (1) Under the interference of stray currents, multi-field feature parameters of winding show a “half-wave enhancement, half-wave attenuation” pattern under no-load conditions, and their temporal variability is greatly influenced by time-varying components. When |k| is large, the amplitude fluctuation becomes significant. However, the influence of stray current interference is weak under loading conditions. (2) The vibration and noise of the core increase with higher interference level and load factor. Moreover, they are more severe than the winding in the same mode. (3) The interference of time-varying components results in complex temporal variability of multi-field feature parameters. Instantaneous variations in time-varying component interference can cause an instantaneous increase of vibration and noise in transformer components. (4) The vibration distortion proportion of both the winding and core increases with high interference levels. The distortion proportion of the core is higher than that of the winding. The impact of instantaneous variations in stray currents is more severe on unloaded transformers than on loaded ones.
Finally, the interference propagation domains of multivariate mode-state spaces are classified based on virtual-real consistency. The level of stray current interference affects the characteristic distribution of different fields in components. Therefore, four categories of interference propagation domains are delineated with the interference level h as a key criterion. (1) When 0≤h<0.5, the stray current interference has little effect on the transformer. At this point, the interference level is within the permissible range of the transformer and is determined to be in the safe operating domain. (2) When 0.5≤h<1.5, the vibration and noise of components increase. If the transformer continues to be subjected to stray current interference, it may lead to issues such as flexural deformation and displacement. In this case, it can be determined as a risk mitigation domain. (3) When 1.5≤h<2.0, stray currents result in electromagnetic and mechanical instability within the transformer's internal environment, requiring prompt alarm and resolution. In this case, it can be determined as an abnormal instability domain. (4) When h≥2.0, the stray current interference can cause severe harm to the internal components and insulation of the transformer. In this case, it can be determined as a severe fault domain.
keywords:Stray current, interference, transformer, multivariate information, mode-state
DOI: 10.19595/j.cnki.1000-6753.tces.232194
中图分类号:TM42
国家重点研发计划资助项目(2021YFB2400800)。
收稿日期 2024-01-02
改稿日期 2024-01-19
潘 超 男,1981年生,博士,教授,主要研究方向为电力系统稳定与电磁兼容。E-mail: 31563018@qq.com
石晓博 男,1999年生,硕士,主要研究方向为变压器内部故障辨识。E-mail: 568431772@qq.com(通信作者)
(编辑 陈 诚)