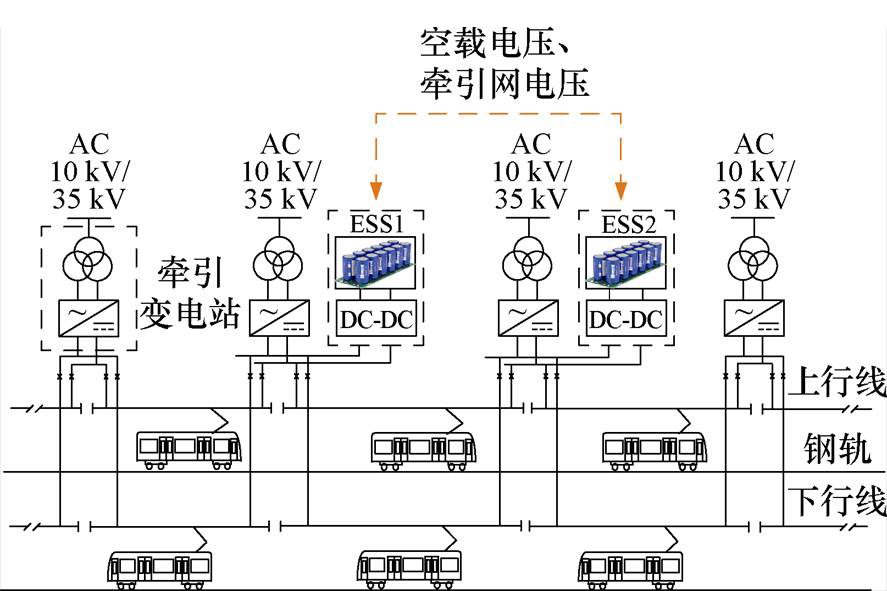
图1 含储能设备的主动式牵引供电系统
Fig.1 Active traction power supply system with ESSs
摘要 近年来,随着“双碳”政策的推动,储能技术在城市轨道交通中的应用愈发广泛,呈现出点到线的发展趋势。当一条线路中有多站安装储能装置时,想要进一步提升储能系统的节能效果,必须要解决不同站储能装置的充放电策略个性化设计,以及多储能间协调控制这两个问题。因此,该文提出一种基于实时牵引网电压和空载电压的多储能系统区间能量管理策略。该策略基于多个牵引变电站的空载电压和牵引网电压,对能量管理区间内的列车状态和列车剩余功率进行辨识,基于此计算区间内储能装置的充放电阈值基准值初值及基准值变化的斜率。为进一步提升节能和稳压效果,该策略基于充放电周期、牵引网电压超限频次及储能系统的荷电状态(SOC)等参数,对基准值及其更新斜率进行实时校正。该文在北京地铁的实际线路中进行了验证,结果表明,相较于基于本站空载电压的能量管理策略,提出的策略在降低系统能耗和稳定牵引网电压方面都具有显著的改善效果。
关键词:城轨交通 空载电压 多储能 能量管理 协调控制
当前,城市轨道交通在人们日常出行中的重要性不断提升,其路网规模也持续扩大。截至2022年底,我国内地城轨运营里程已达到10 291.95 km,总能耗为227.92亿kW·h[1],其中列车牵引能耗约占总能耗的50%,列车的制动能量约占牵引能耗的30%~60%。在制动能量中,一部分被邻近的牵引列车吸收,另一部分则被消耗在制动电阻上。根据统计数据,消耗在制动电阻上的制动能量约占总制动能量的30%~50%[2]。因此,若能有效吸收和利用该部分能量,将能够显著降低城市轨道交通的能耗,加快实现“碳达峰、碳中和”的进程[3-4]。
吸收和利用列车的再生制动能量,主要有三条技术路线:列车运行图优化、逆变回馈技术和储能技术。列车运行图优化无需增加硬件设施,但优化效果受发车间隔和客流等影响较大,其优化上限相对有限,且对列车的行车组织提出了较高的要求[5]。逆变回馈技术具有控制简单和成本低廉的优点,但由于轨道交通制动能量具有脉冲式的特点,这种方式难以避免对交流电网造成冲击。此外,回馈回电网的制动能量无法为运营商节约电费,存在节能不节电的问题[6-7]。储能技术则通过超级电容、飞轮、电池等储能介质,将制动能量储存在本地,待列车牵引时释放,从而降低牵引能耗。随着近年来储能元件的国产化进程加快以及储能价格的显著降低,储能技术已在北京、上海、武汉、青岛、广州等多个城市得到广泛应用。其中,超级电容储能技术在北京地铁八通线中进行了全线的示范应用[7]。
为了充分发挥储能系统的节能、稳压等效果,国内外众多学者对城市轨道交通储能系统的能量管理策略(Energy Management Strategy, EMS)进行了深入地分析和研究。从设计思路来区分,大概可以分为三类:基于牵引网压的EMS、基于列车运行状态的EMS、基于优化算法的EMS。
基于牵引网压的EMS以某个牵引网电压为基准,高于基准值开始充电,低于基准值开始放电。基准值的选择,从最开始的经验设定[8],到后来的离线空载电压[9],控制效果得到了明显的提升。但经过更深入的研究,学者们发现基于离线空载电压的固定阈值方式存在着三个局限性:①会争抢列车间交互的能量;②没有考虑列车发车间隔工况的变化;③没有考虑空载电压自身的波动情况。针对列车交互的问题,文献[10-11]指出,将制动列车电压控制在制动电阻启动的临界电压处,最有利于列车交互,并提出了列车电压跟随的充电阈值计算策略。根据列车的功率和位置,实时计算地面储能装置的充电阈值。针对列车发车间隔的变化,文献[12]利用离线优化算法,优化出离线的发车间隔与最优充放电阈值的关系,但其在线运行效果仍受多种因素的影响。针对空载电压的变化,文献[13-14]都提出了在线辨识空载电压的策略,区别在于文献[13]采用公式法进行辨识,文献[14]则采用外推法进行 辨识。
基于列车运行状态的EMS以列车的牵引和制动状态为基准,列车制动时开始充电,充电功率设置为剩余制动功率,列车牵引时开始放电,放电功率设置为剩余牵引功率。剩余充放电功率的计算,或基于列车的离线数据[15]、或基于列车的实时质量和车速[16],或基于列车的实时列车自动驾驶(Auto- matic Train Operation, ATO)曲线[17]。在考虑单列车的基础上,文献[18]考虑了多列车情况,将区间内所有列车的实时功率和位置作为输入条件,考虑能量的传输距离,实时计算地面储能装置处的剩余牵引功率和剩余制动功率,能够更准确地设置储能系统的充放电指令值。文献[19]则进一步考虑了列车在区间内运行的能量曲线,实时优化储能系统的放电截止电压。
基于优化算法的EMS往往没有固定的基准值,其充电指令值和放电指令值的设定,一般以单目标或多目标优化的结果而定,优化目标包括:节能率、制动电阻损耗、稳压率、变电站峰值功率等[20]。根据是否在线优化以及是否存在解析解等特征,可以分为以下三种思路:①离线全局最优化,如采用动态规划[20-21]、遗传算法[22-23]等算法离线优化出充放电指令值曲线,但该方法的泛化能力较差,在线工况一旦发生变化,节能等效果会相差很大;②基于离线优化算法提取出规律,将全局最优化问题转化成规则与若干局部优化问题的结合[19]。该方法泛化能力较强,但规律的提取过程仍然受限于人工经验,且部分局部优化算法也很难在线实时求解;③采用在线全局最优化算法,如深度强化学习算法[24-27]。强化学习在理论上可以实现在线全局最优的设计,但该方法理论依据不强,试错成本较高,且其决策变量的在线更新频率不高,无法达到实时更新的状态[28]。
针对多储能协调的问题,优化效果、模型复杂性及系统鲁棒性一直是需要综合考虑的几个方面,衍生出了集中式能量管理架构[29]、分布式能量管理架构[30-31]及集中学习-分散控制的能量管理架构[32-33]。其中,在轨道交通多储能能量管理研究中,集中学习-分散控制的能量管理架构研究较多,文献[14]和专利[34]均采用多智能体强化学习方法对多站的储能装置进行功率补偿,不同的是采取了不同的强化学习算法和奖励设计方法。
对已有策略进行综合评估后,除了策略自身固有的限制之外,本研究还发现存在三个普遍性问题:
(1)数据获取存在困难。若数据采集需要对现存设备进行改造,管理层面、安全性考量以及技术障碍往往使之难以实施。由此,获得实时的列车运行数据、列车位置数据以及变电站的实时输出电流数据等变得异常困难。
(2)现有文献未充分考虑不同车站之间空载电压差异所造成的影响。
(3)现有的协调控制策略缺乏有效的可行性论证。除了对大量难以获取的实时数据的依赖之外,当前文献中提到的多智能体强化学习算法在理论可解释性方面不足,且主要在较为固定的仿真环境中验证其成效,而在实物实验和现实应用场景中的应用成果尚未见报道。同时,包括全线通信网络构建、数据丢失问题、所需硬件成本以及与现场控制器决策变量融合的方法等方面,均缺乏定量化分析,这些技术难题亟待解决。
针对上述问题,本文提出了一种分布式区间能量管理策略。通过将相邻的两套储能系统配置为一个分布式单元,来管理4个牵引变电站区间的列车牵引和制动能量。该策略基于易于测量的牵引网电压和10 kV互感器输出电压,对区间内的列车实时状态和功率进行辨识,并基于实时辨识的列车剩余功率决定两套储能系统的充放电阈值。在此基础上,为了进一步提升节能稳压等效果,基于各站的网压状态、充放电时间间隔、储能装置状态等信息,对充放电阈值的基准值进行实时调整。实验数据显示,与基于本站空载电压的动态阈值策略相比,本文提出的区间能量管理策略在节能和稳压等方面均展现出了显著的优势。
城市轨道交通主动式牵引供电系统主要包括牵引变电站、上行线列车、下行线列车、供电线路以及能馈或储能设备。如图1所示为4个牵引变电站区间的牵引供电系统,区间内包含两套超级电容储能设备,其系统等效电路如图2所示。

图1 含储能设备的主动式牵引供电系统
Fig.1 Active traction power supply system with ESSs
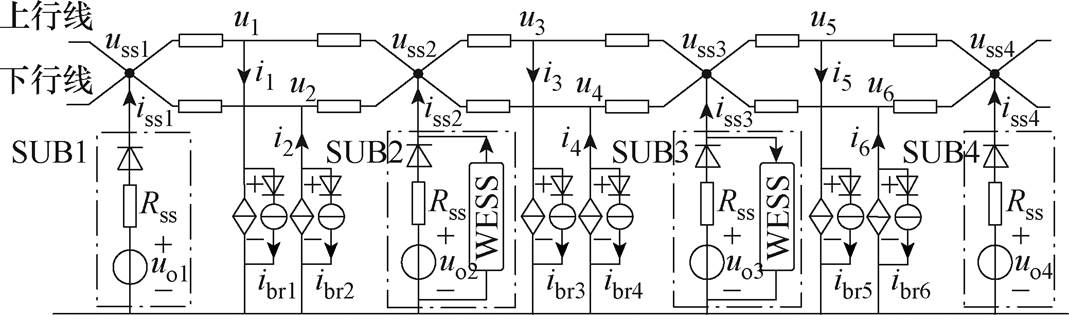
图2 牵引供电系统等效电路
Fig.2 Equivalent circuit of traction power supply system
等效电路模型中,牵引变电站等效为电压源、等效内阻和二极管并联的形式。列车等效为功率源,可按照功率曲线进行输出,与之并联的为车载制动电阻,等效为电流源和二极管串联形式。牵引变电站和列车的伏安特性方程分别为
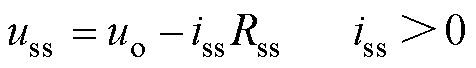 (1)
(1)
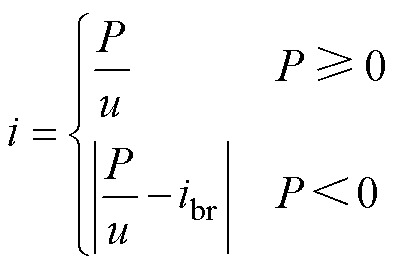 (2)
(2)
式中,uo为空载电压;Rss为等效内阻;uss和iss分别为牵引网电压和牵引变电站输出电流;u和i分别为列车处的牵引网电压和列车吸收/馈网电流;ibr为制动电阻电流;P为列车功率,P≥0表示牵引。
暂且不考虑储能设备,假设上行线的3列车处于牵引状态,下行线的3列车处于制动状态,整个系统的功率平衡关系为
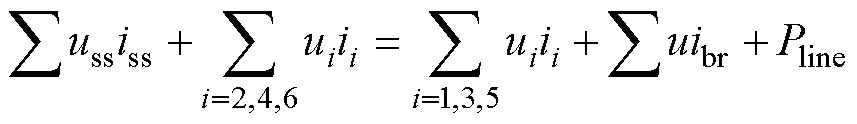 (3)
(3)
式(3)的左侧为系统中释放的总功率,右侧为系统中吸收的总功率。等式左侧第一项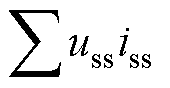 为牵引变电站释放的总功率,左侧第二项
为牵引变电站释放的总功率,左侧第二项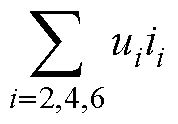 为制动列车释放的总功率,右侧第一项
为制动列车释放的总功率,右侧第一项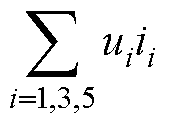 为牵引列车吸收的总功率,右侧第二项
为牵引列车吸收的总功率,右侧第二项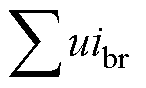 为制动电阻吸收的总功率,右侧第三项
为制动电阻吸收的总功率,右侧第三项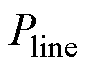 为线路损耗。考虑到线路损耗占总牵引变电站能耗仅在5%左右[10],且优化幅度有限,在式(3)中列车牵引功率和列车制动功率确定的情况下,减小变电站牵引能耗的问题可以等效为减小制动电阻损耗的问题。
为线路损耗。考虑到线路损耗占总牵引变电站能耗仅在5%左右[10],且优化幅度有限,在式(3)中列车牵引功率和列车制动功率确定的情况下,减小变电站牵引能耗的问题可以等效为减小制动电阻损耗的问题。
当系统中制动列车的功率大于牵引列车的功率时,整个牵引网电压被抬升,牵引变电站机组退出,式(3)可表示为
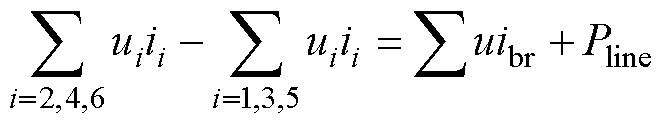 (4)
(4)
式(4)左侧定义为剩余制动功率,右侧为制动电阻损耗与线路损耗。忽略线路损耗,减小变电站牵引能耗的问题可以进一步等效为如何有效吸收剩余再生制动功率的问题。
当系统中牵引列车的功率大于制动列车的功率时,整个牵引网电压被拉低,制动电阻退出,式(3)可表示为
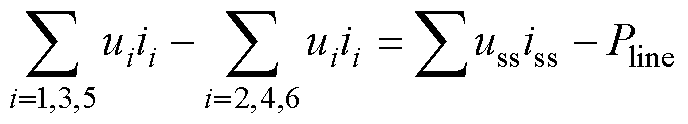 (5)
(5)
式(5)左侧定义为剩余牵引功率,右侧为牵引能耗与线路损耗的差值。忽略线路损耗,减小变电站峰值功率的问题可以等效为减小最大剩余牵引功率的问题。
鉴于集中式能量管理架构在实际应用中常见的问题,如单点负载过重、系统容错能力不足以及维护性差等缺陷,本研究借鉴分布式系统架构的优势,提出了一种区间能量管理架构。该架构旨在通过分散式控制和区间内的协调管理,提高系统整体的鲁棒性与容错性,以符合复杂能量系统的运行需求。
假设一条线路共有k个牵引变电站安装了储能装置,标记为S1, S2, S3,…,Sk-1, Sk。m个相邻的牵引变电站的储能装置为一组,线路总共分为ceil(k/m)组,每组管理n个相邻的牵引变电站所包含的区间。考虑到列车能量的传输距离一般为2~3 km,也就是一个相邻站间的距离,因此,令每组的能量管理范围为储能装置安装范围的首尾各自拓展一站,即n=m+2。以图3所示区间能量管理构架示意图为例,令m=2,Si~Si+5为相邻的6个牵引变电站且都安装储能装置,Si+1和Si+2的储能装置为一组,管理区间为Si~Si+3的整个区间;Si+3和Si+4的储能装置为一组,管理区间为Si+2~Si+5的整个区间。
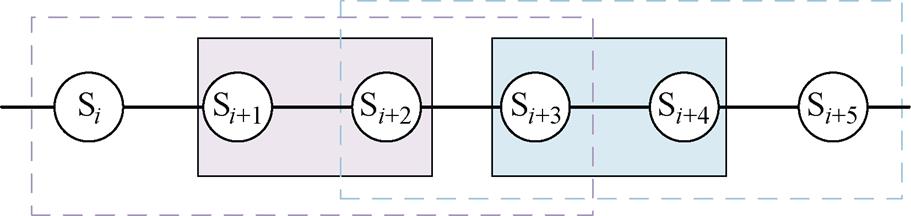
图3 区间能量管理架构示意图
Fig.3 Schematic diagram of interval ESS architecture
考虑到m越小,出现单点失效后,对整个系统的节能效果影响越小,本文以m=2的2储能4站模型为例,进行深入的分析。
如图4所示为包含两个牵引变电站、一列制动列车和一套地面储能装置的牵引供电系统环流分析模型。图4中,uo1和uo2分别为相邻两个牵引变电站的空载电压,rs1和rs2分别为两个牵引变电站的等效内阻,us1、us2和ut分别为两个牵引变电站以及制动列车处的牵引网电压,uchar为储能装置充电阈值,Pt为制动列车功率,irec1、irec2、it、ichar分别为两个牵引变电站输出电流、制动列车馈网电流以及储能装置吸收的电流,r11、r12、rL均为线路阻抗,i1、i2、ir均为线路上的电流。假设左侧牵引变电站的空载电压高于右侧牵引变电站的空载电压,且储能装置工作在恒压模式,则存在固定的电压关系为
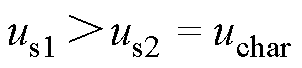 (6)
(6)
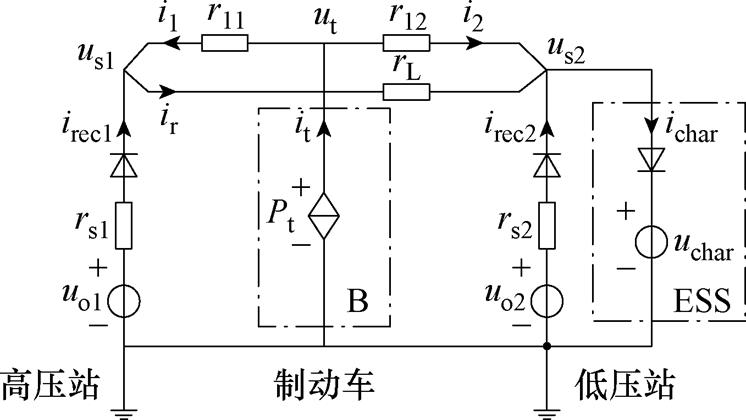
图4 环流分析模型
Fig.4 Circulation analysis model
当线路中有列车进行制动时,ut处电压上升,根据列车制动功率大小的不同,当系统中功率达到平衡时,假设存在环流,有且仅有两种节点电压关系为
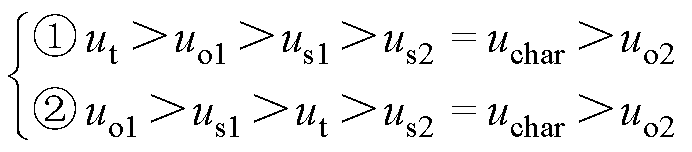 (7)
(7)
第①种节点电压关系及其对应的电流流向如图4所示,第②种节点电压关系,电流i1的流向取反。
第①种电压关系下,电路的KCL和KVL方程分别为
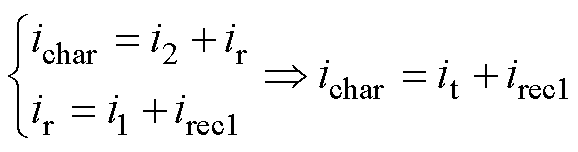 (8)
(8)
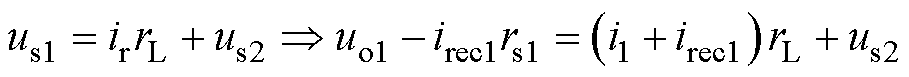 (9)
(9)
以制动列车处电压ut与高压站空载电压和低压站充电阈值的压差为变量,可求得irec1为
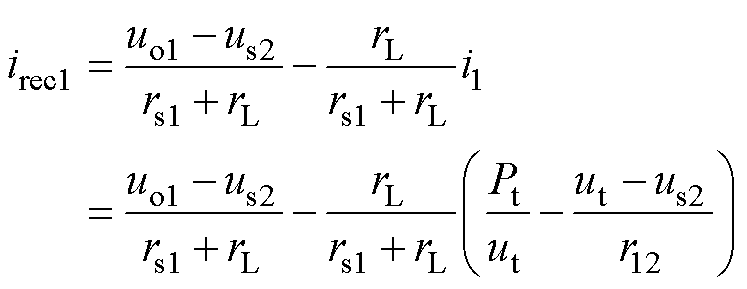 (10)
(10)
储能装置充电的环流功率为
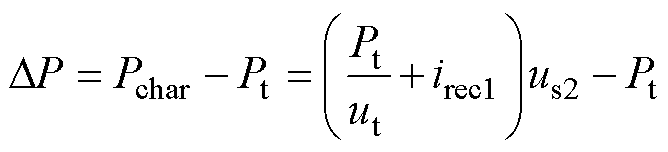 (11)
(11)
假设列车处于线路中间的位置,结合式(10)和式(11),可以画出环流功率dP、高压站空载电压和低压站充电阈值的压差dUo、制动列车处电压ut以及制动列车功率Pt之间的关系如图5所示。
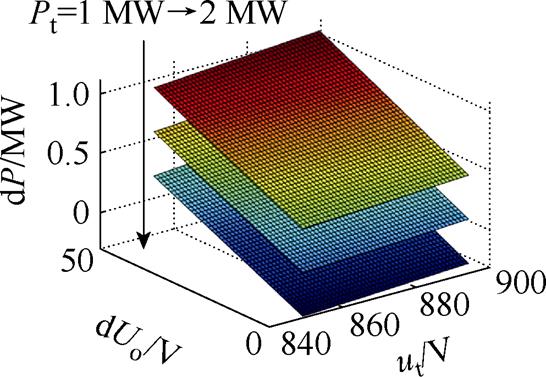
图5 环流功率、空载电压差与列车功率的第一种关系
Fig.5 The first relationship between circulating power, no-load voltage difference, and train power
从图5中可以看到,低空载电压站储能装置的充电阈值与高空载电压站的空载电压存在一定电压差,会导致高空载电压站给储能装置充电,造成环流现象,从而导致储能装置能够吸收的再生制动功率和能量减小。随着列车制动功率的不断增大,临界的电压差也越来越大,因此,从减小环流的角度,可以根据列车的等效制动功率以及高压站此时的空载电压,设置合理的充电阈值边界值。第②种电压关系如图6所示。
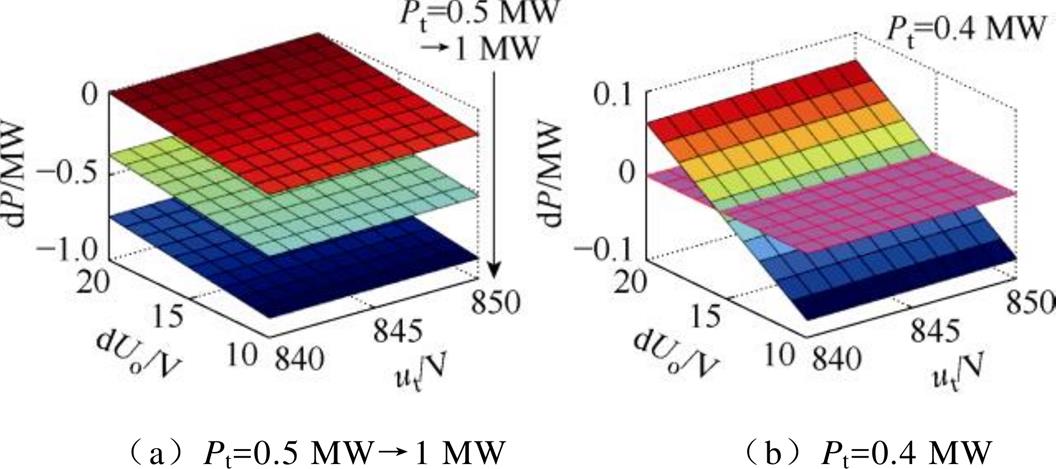
图6 环流功率、空载电压差与列车功率第②种关系
Fig.6 The second relationship between circulating power, no-load voltage difference, and train power
从图6中可以看出,当列车功率大于临界值时,环流功率均小于0,即此时系统中存在剩余再生制动功率,列车功率不平衡,会导致制动列车处电压进一步上升,节点电压关系从第②种自然变化到第①种;当列车制动功率小于临界值时,其呈现出与第①种电压关系式相同的规律。
文献[9]讨论了一些储能装置与列车运行状态的关系及每种关系的合理情况,总结来说,储能装置要节能的根本,其实就是在且仅在列车有剩余制动功率时充电,这样既可以保证列车间的交互,又可以保证储能装置有充足的容量吸收制动能量。放电则要在且仅在列车有剩余牵引功率时放电,这样可以减小制动电阻的投入。因此,列车牵引和制动状态的判定非常重要。
在无法检测列车实时状态和变电站输出电流的情况下,本文尝试分析不同空载电压站的牵引网电压与列车状态的关系,通过牵引网电压的情况来预测实时的列车状态。选择如图7所示的北京地铁八通线的管庄到果园4站区间,采集4个发车间隔周期的数据进行研究。
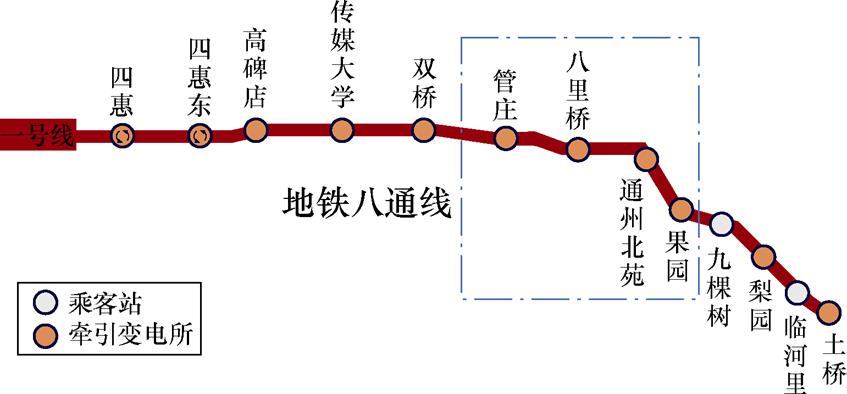
图7 北京地铁八通线及本文试验区间
Fig.7 Beijing Metro Batong line and its test section
固定管庄站、八里桥站、果园站的空载电压分别为830、840和870 V,通州北苑的空载电压为变量,定义通州北苑站(高压站)的空载电压与八里桥站的空载电压(低压站)的电压差值为空载电压差DUo,牵引网电压与空载电压的差值为DUs-o,若以当前站的空载电压作为列车状态的判断基准:当DUs-o>0时,判断列车处于制动状态;当DUs-o<0时,列车处于牵引状态。
图8和图9分别为通州北苑站和八里桥站的DUs-o与列车功率的关系。
将每个图分为A、B、C、D四个区域,定义列车状态判断准确率rac、列车状态涵盖率rco和综合准确率rw三个指标,三个指标的计算公式分别为
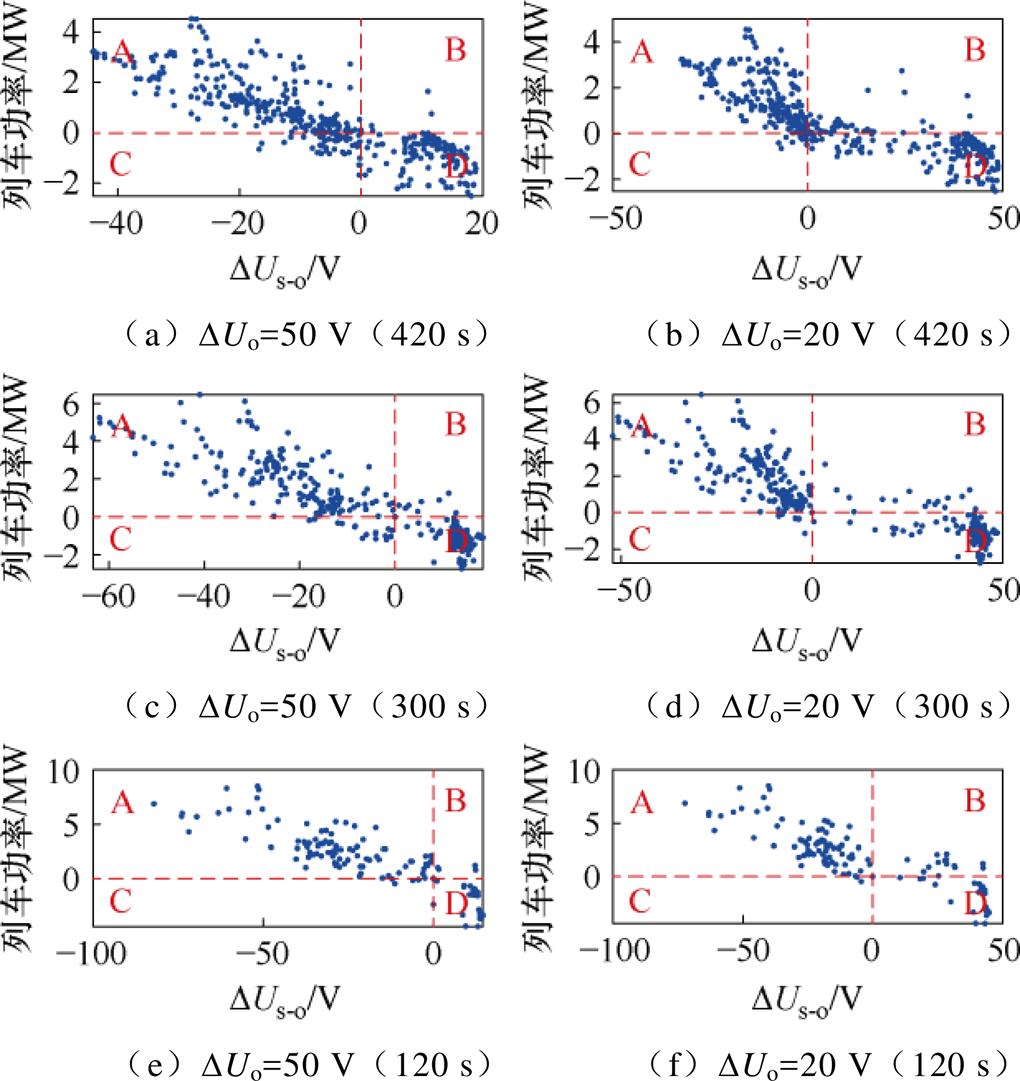
图8 通州北苑站的DUs-o与列车功率的关系
Fig.8 The relationship between DUs-o and train power at Tongzhou Beiyuan Station
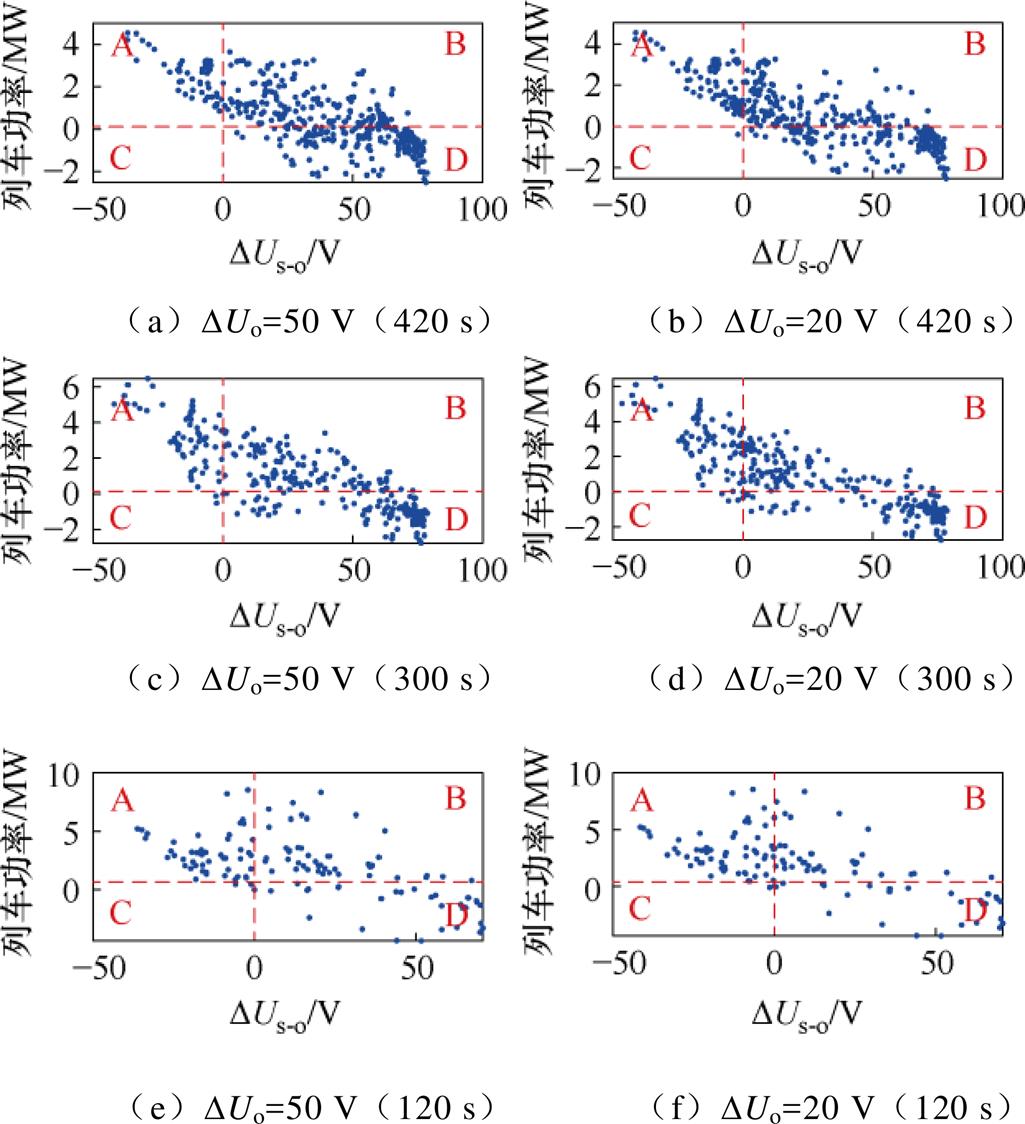
图9 八里桥站的DUs-o与列车功率的关系
Fig.9 The relationship between DUs-o and train power at Baliqiao Station
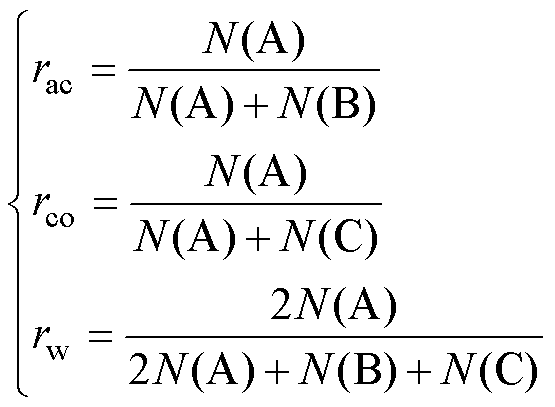 (12)
(12)
式中,N(X)表示区域X中的数据量,X=A, B, C, D。
结合图8和图9,可初步观察到,以通州北苑站(高压站)空载电压为预测基准时,列车牵引状态的涵盖率和制动状态的判断精度均明显较高。此外,可以将这三个指标与发车间隔及空载电压差进行关联,得到如图10所示的三维关系。
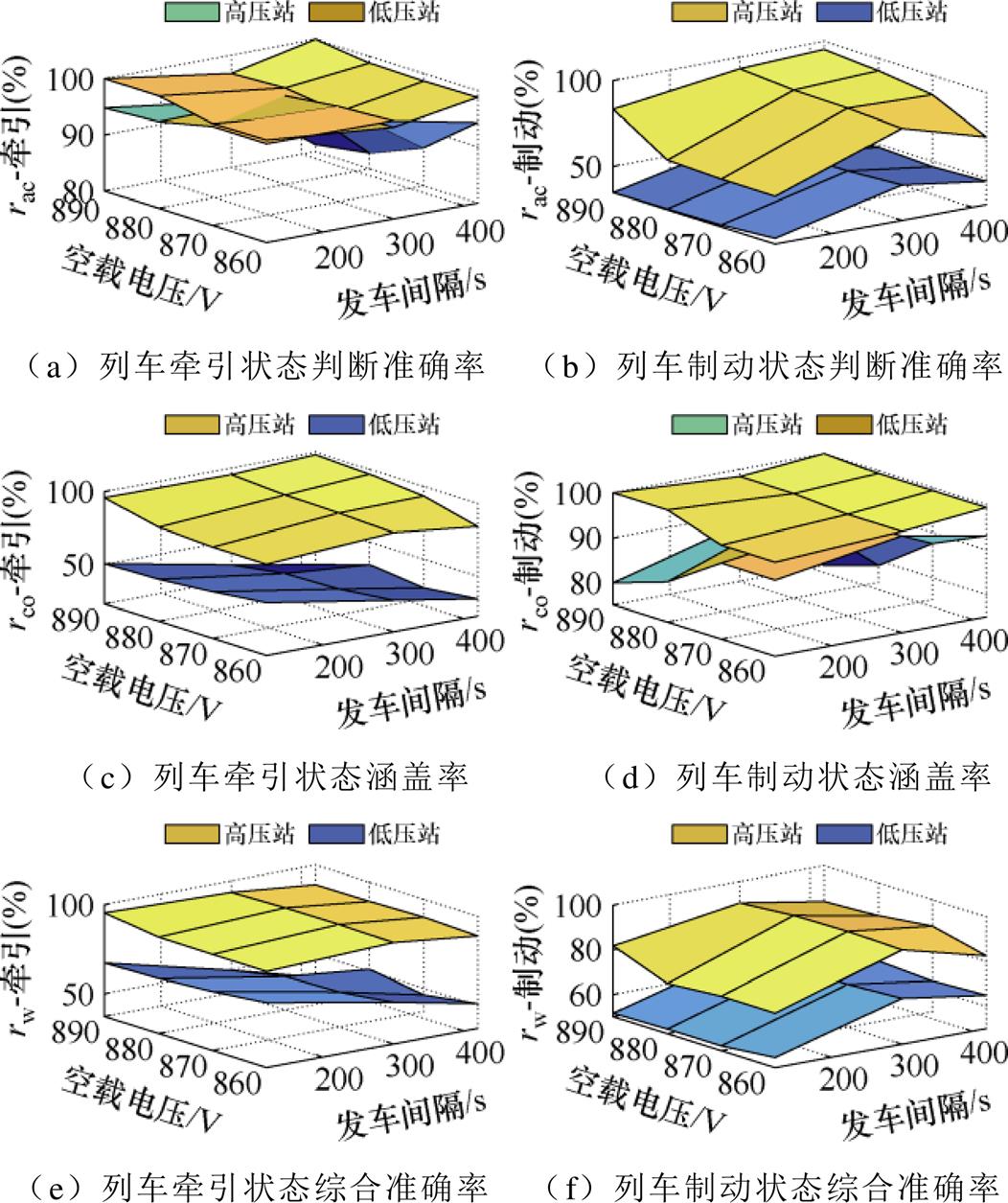
图10 发车间隔、空载电压与准确率指标的关系
Fig.10 The relationship between departure interval, no-load voltage, and accuracy indicators
从图10中可以总结出以下几个规律:
(1)相比于低空载电压站,以高空载电压站为基准的预测值牵引涵盖率和制动准确率均明显较高。牵引准确率和制动涵盖率均相对较低,但高空载电压站的综合准确率明显高于低空载电压站。
(2)高空载电压站的制动功率涵盖率较低,尤其是在空载电压差较大时,可能导致列车制动时储能装置不启动。
(3)发车间隔小时,牵引预测涵盖率略有降低,可能会导致列车在牵引时进行充电。
从以上规律可以明确:相比于低空载电压,以高空载电压作为基准值,可以更加准确地预测该区间内列车的剩余牵引状态和剩余制动状态。但是,针对空载电压压差较大时制动功率涵盖率过低的情况,需要进一步优化制动状态的判别条件。
以高空载电压为基准时,制动状态的涵盖率较低,即高空载电压站的牵引网电压小于空载电压时,仍有大量的列车处于制动工况,这对应于图8a中区域C的工况。提取区域C中的数据,绘制制动功率Pt、八里桥站牵引网电压-通州北苑牵引网电压DUs、通州北苑站DUs-o间的关系,如图11所示。图中可看出,区域C中,列车的剩余制动功率较小,且此时列车处于靠近低电压站的区间。数值上看,区域C内通州北苑站的牵引网电压基本上在(空载电压-12 V)范围内,而八里桥站的牵引网压则接近或者大于通州北苑站的牵引网压。因此,在空载电压差大于40 V时,将列车的制动状态的判别条件调整为以下形式,牵引的判别条件为以下区间的补集。
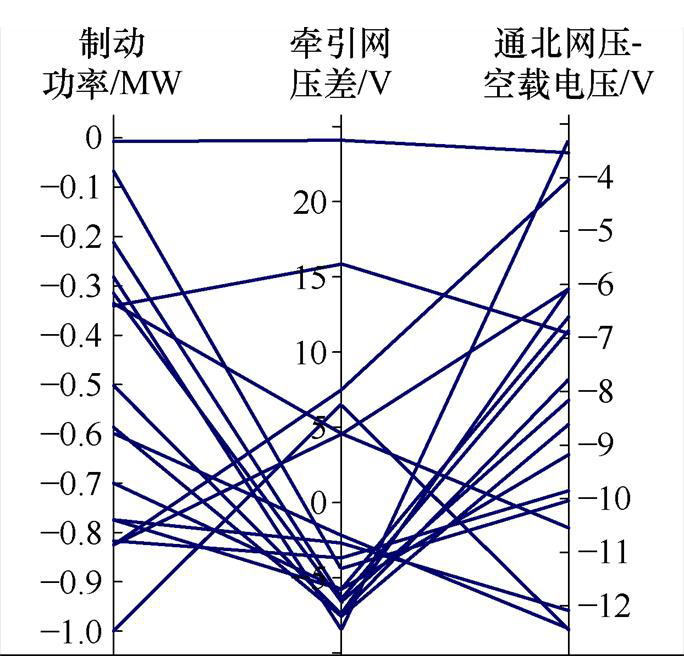
图11 未涵盖制动功率工况中Pt、DUs与DUs-o的关系
Fig.11 The relationship between Pt, DUs, and DUs-o in uncovered braking power conditions
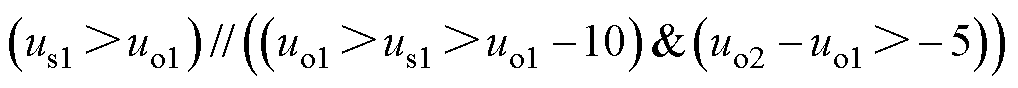 (13)
(13)
调整前后,制动状态预测准确度和制动工况涵盖率的变化如图12所示,可以看到,调整判别条件后,在保持预测准确度基本不变的前提下,极大地提升了制动状态涵盖率。
由于列车的发车间隔无法实时获取,且上、下行的发车间隔并不相同,因此,预测列车功率时,输入量仅为当前高压站的牵引网电压和空载电压。将不同空载电压差值下,所有发车间隔的列车功率与DUs-o的数据叠加,可得到各个空载电压差下的列车功率与DUs-o的关系如图13所示。
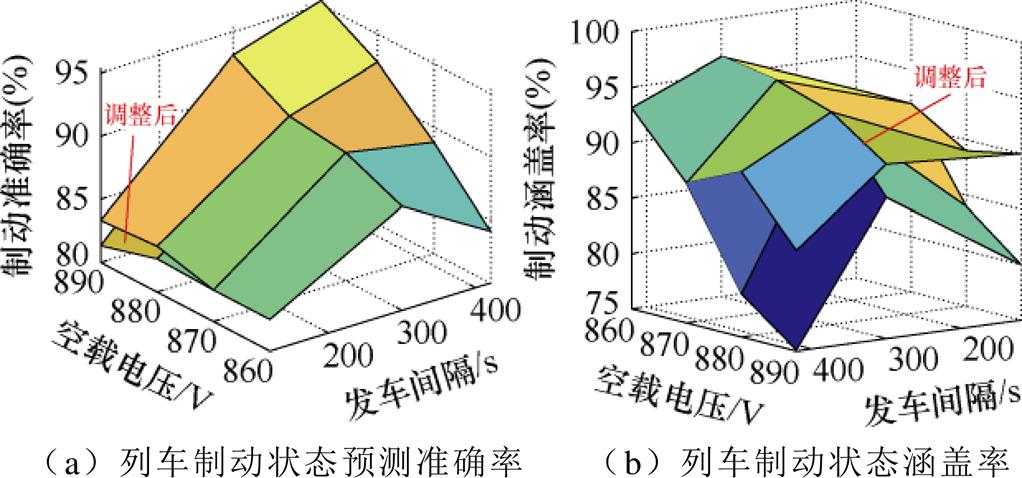
图12 判别策略调整后的制动预测率变化
Fig.12 Changes in brake prediction rate after adjusting the discrimination strategy
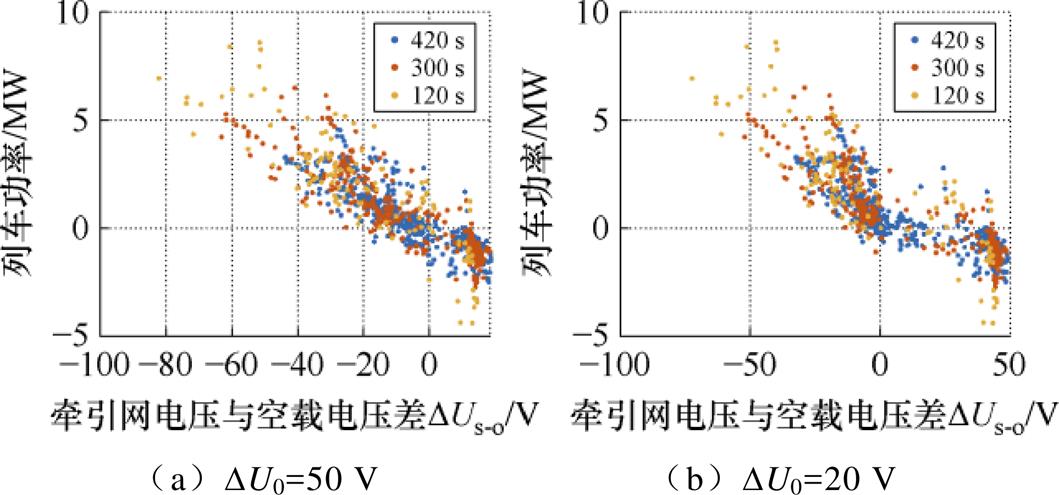
图13 发车间隔叠加后的列车功率与DUs-o的关系
Fig.13 The relationship between train power and DUs-o after the superposition of departure intervals
图13a和图13b散点图的空载电压差分别为50 V和20 V。从图中可看出,由于列车位置的不同分布,相同的DUs-o会对应不同的列车剩余功率,但是二者之间的线性关系仍非常明显,可进行线性拟合。
基于2.1节提到的环流功率与列车制动功率的关系,以及列车状态和列车功率与DUs-o的关系,本节提出一个基于空载电压和牵引网电压的区间能量管理策略,该策略的流程如图14所示。
首先,高压站和低压站的数据进行交互后,对区间内的列车状态进行判断,并基于辨识的列车功率确定初始基准值和初始斜率。其次,对基准值的变化斜率进行实时校正,进而以基准值±滞环电压值确定充放电阈值。具体地,高压站和低压站的初始基准值均设置为高压站的空载电压值uo1,当列车处于制动工况下,为了保证不发生环流的同时,限制牵引网电压的最大值,需要将基准值按照一定斜率下降。式(14)中的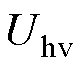 和
和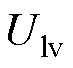 分别为高压站和低压站的基准值,K1和K3分别为高压站和低压站基准值的充电初始下降斜率,其初始值如式(15)所示。
分别为高压站和低压站的基准值,K1和K3分别为高压站和低压站基准值的充电初始下降斜率,其初始值如式(15)所示。
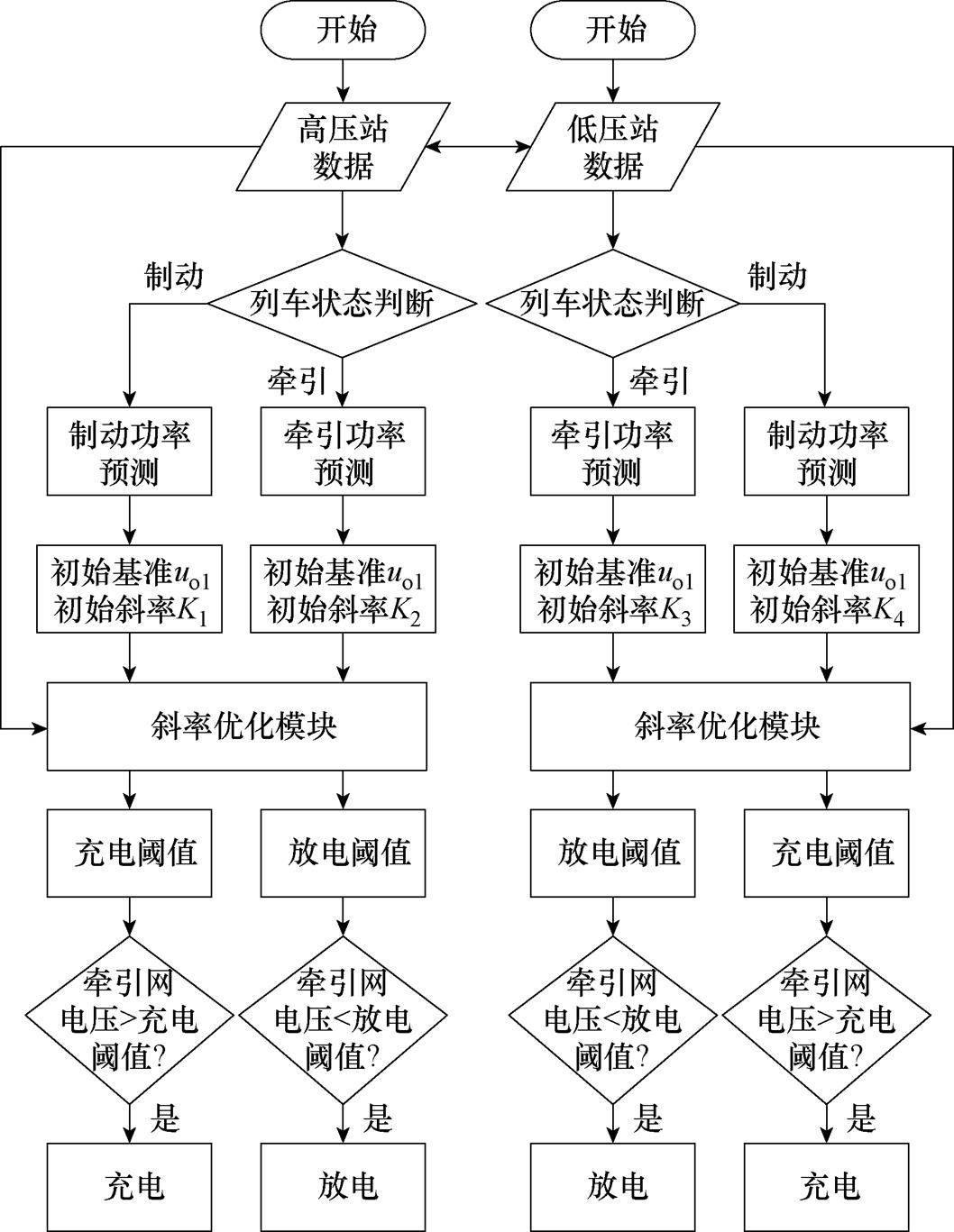
图14 区间能量管理策略流程
Fig.14 Flow chart of interval energy management strategy
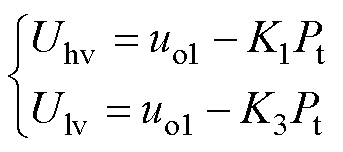 (14)
(14)
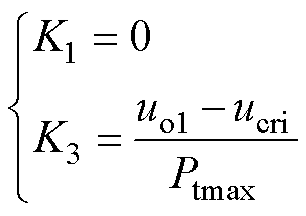 (15)
(15)
式中,Pt与Ptmax分别为列车的制动功率与列车的最大设计制动功率。
由于高压站的基准电压小于空载电压时,会产生环流,因此,初始斜率为0,低压站的斜率则与产生环流的临界电压相关,临界电压可由式(10)和式(11)联立所得,即
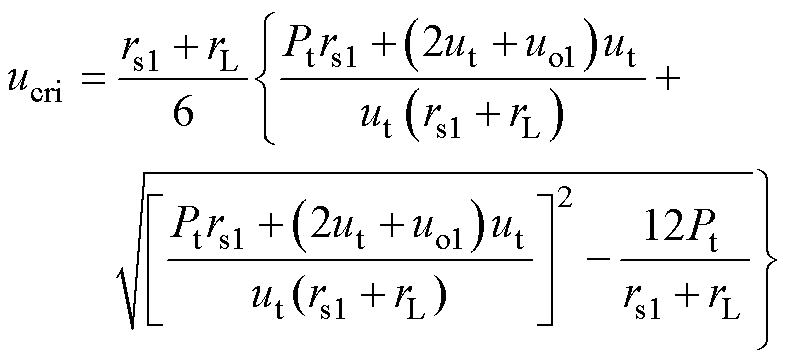 (16)
(16)
当列车处于牵引状态下时,由于列车牵引功率越大,牵引网电压越低,因此,在储能装置能够将所储存能量完全释放的前提下,在牵引网电压越低时开始启动,降低峰值牵引功率的效果越好。牵引状态下,高压站和低压站的基准值变化为
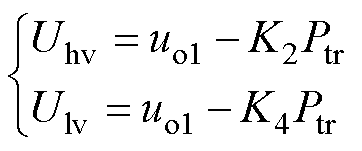 (17)
(17)
式中,K2和K4分别为高压站和低压站基准值的放电初始下降斜率,初值均为0;Ptr为列车牵引功率。
当预测的列车制动功率大于实际的列车制动功率时,充电阈值的基准值会偏低,导致环流的产生;反之,则不利于吸收较远处列车制动功率的传输,从而导致牵引变电站处的电压超过900 V。考虑到环流的情况无法在线检测,而牵引网处的电压可以实时检测,因此列车制动功率的预测基于制动功率较小的边界。当预测的列车牵引功率大于实际的列车牵引功率时,放电阈值基准值会偏低,导致储能装置难以释放能量;反之,则会削弱降低峰值牵引功率的效果。在本文的优化目标中,以节能优先,因此列车牵引功率的预测也基于牵引功率较小的边界。
从图15所示的列车功率与DUs-o的散点图可以看出,在列车牵引状态下二者之间存在较强的线性关系。然而,在制动过程中,DUr的最大值受到列车制动电阻启动电压900 V的限制,因此需要将其分为两段进行拟合。本文将整个区间拟合为三段线性曲线。三段曲线的关系式为
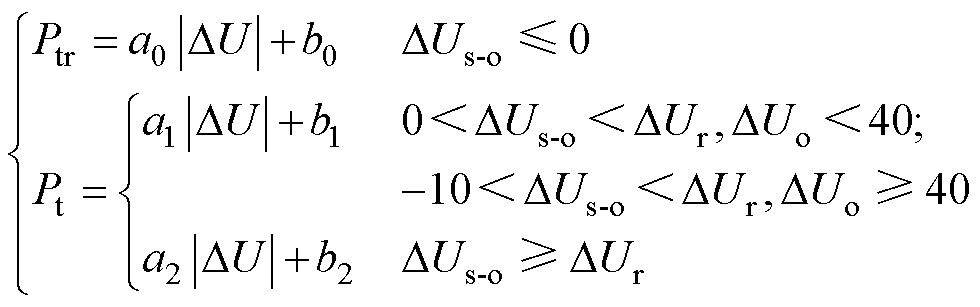 (18)
(18)
式中,DUr的大小与空载电压大小有关,等于制动电阻启动电压减去空载电压。当空载电压差较大时,由于判别条件发生变化,第一段拟合曲线的起始值也相应地发生变化。
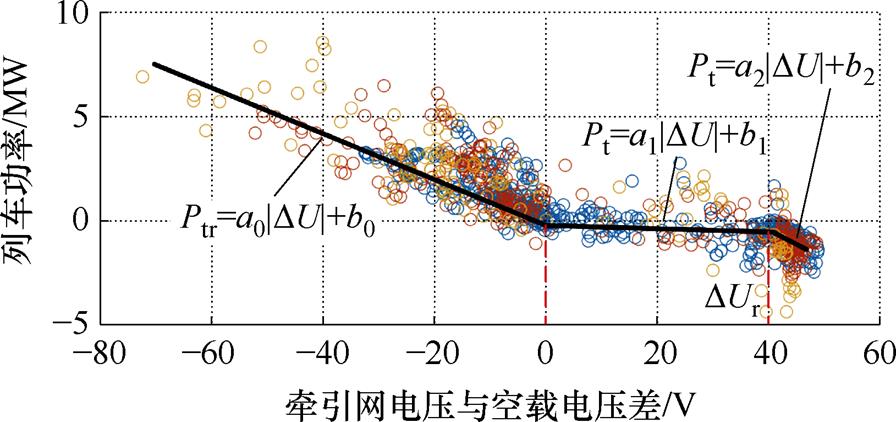
图15 高压站空载电压为860 V时的列车功率与DUs-o
Fig.15 The relationship between train power and DUs-o when the no-load voltage of high-voltage station is 860 V
根据3.1节的分析,预测的列车功率偏低,可能导致牵引网电压过高。考虑到制动功率斜率在900 V时有转折点,采用900 V作为临界值进行判断,并对制动时的充电阈值基准值斜率进行在线校正。具体地,在固定时间段内,若判断到牵引网电压超过900 V且储能装置未达到额定充电功率,则以一定的比例增加基准值的下降斜率。另一方面,考虑到列车的实际牵引和制动之间存在一定的间隔。如果在放电之后,储能装置立即开始充电,说明存在牵引变电站给储能装置充电的情况,此时需要以一定的比例减小基准值的下降斜率。列车制动时基准值的斜率变化为
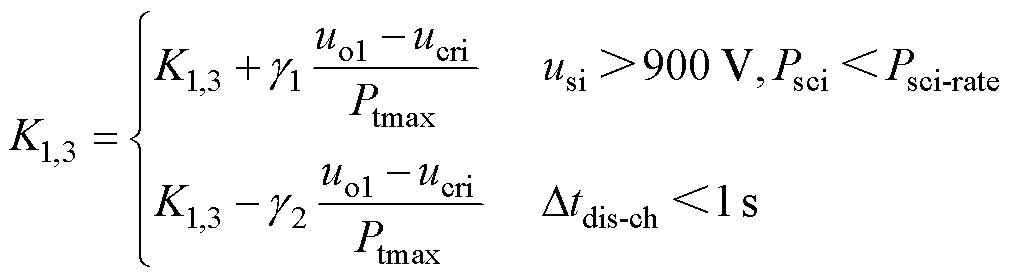 (19)
(19)
其中
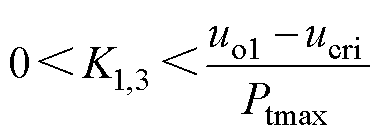
式中,K1,3为高压站和低压站的充电基准值下降斜率;usi为相应站的牵引网电压值;Psci和Psci-rate分别为相应站储能装置的充电功率与额定功率;Dtdis-ch为放电和充电的时间间隔;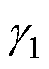 和
和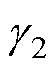 分别为下降斜率的增大和减小的变化率。
分别为下降斜率的增大和减小的变化率。
当列车处于牵引状态时,若预测的牵引功率不准确,可能会导致放电阈值设置得过低,储能装置无法释放吸收的能量,进而影响列车制动时的制动能量吸收效果。为了解决此问题,本文通过检测每次制动充电初始时刻的储能装置剩余能量来进行调整。具体地,若每次制动充电初始时刻的储能装置剩余能量大于设定的最低剩余能量阈值,则减小放电阈值的斜率。这样可以确保在牵引状态下,储能装置能够释放更多的能量,以提高制动能量吸收效果。此外,加入自恢复机制,若连续N个充放电周期内都没有多余的剩余能量,则自动以一定比例增加放电阈值的斜率。列车牵引时基准值的斜率变化为
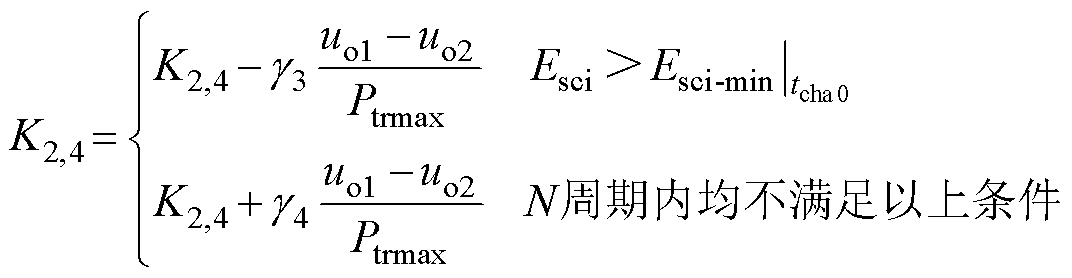 (20)
(20)
其中
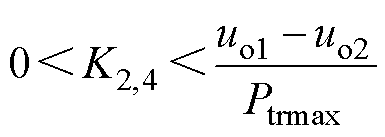
式中,K2,4为高压站和低压站的放电基准值下降斜率;Esci和Esci-min分别为相应站储能装置的剩余能量和最小剩余能量;tcha0为充电开始的时刻;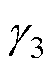 和
和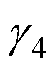 分别为下降斜率的减小和增大的变化率;Ptrmax为列车的最大设计牵引功率。
分别为下降斜率的减小和增大的变化率;Ptrmax为列车的最大设计牵引功率。
每套1.5 MW超级电容储能装置由1个正极柜、1个负极柜、1个控制柜、3个500 kW的变流器柜和3个500 kW的超级电容柜组成,该储能装置的实物和电气原理分别如图16和图17所示,关键参数见表1。

图16 1.5 MW储能装置实物
Fig.16 Physical diagram of 1.5 MW ESS
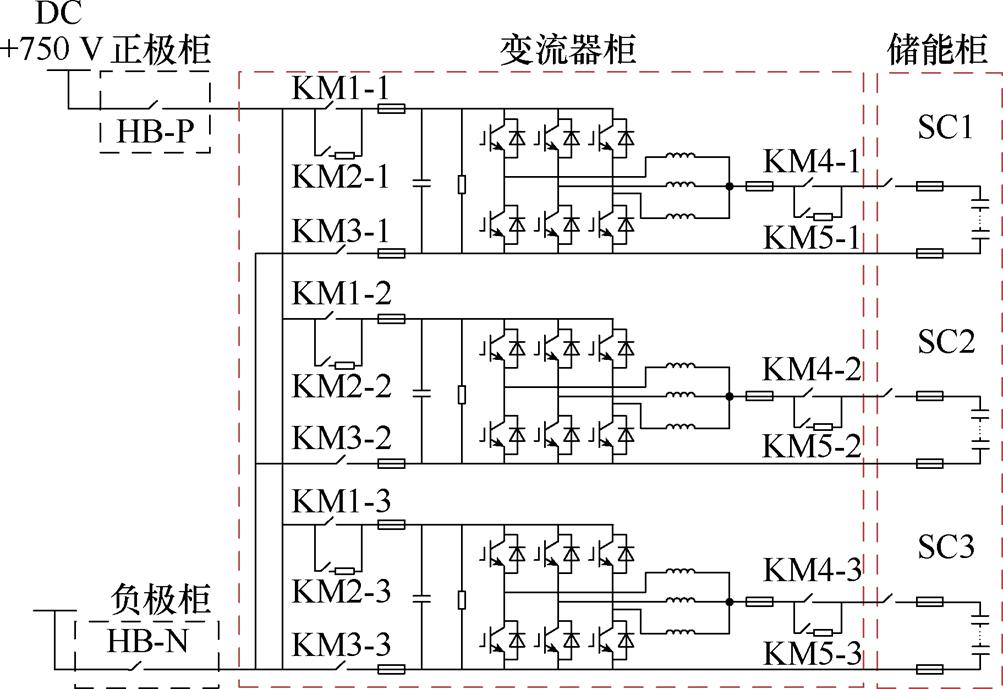
图17 1.5 MW储能装置电气原理
Fig.17 Electrical schematic diagram of 1.5 MW ESS
表1 1.5 MW超级电容储能系统参数
Tab.1 Parameters of 1.5 MW supercapacitor ESS
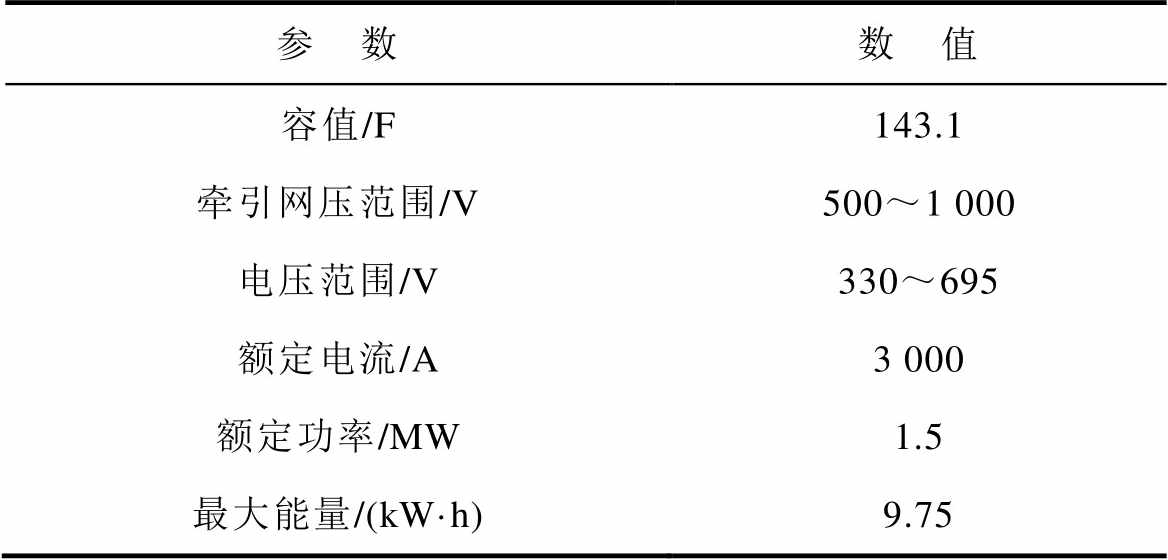
参 数数 值 容值/F143.1 牵引网压范围/V500~1 000 电压范围/V330~695 额定电流/A3 000 额定功率/MW1.5 最大能量/(kW·h)9.75
在列车等数据不可实时获取的情况下,基于本站空载电压的动态阈值能量管理策略在节能方面的表现较为良好[9, 14],因此,本文选取基于本站空载电压的动态阈值策略,在多种工况下,与本文所提的区间能量管理策略进行节能稳定等效果的对比。
工作日的高峰时段和平峰时段区别较为明显,因此本实验均在工作日进行。参考最新的北京地铁八通线列车时刻表,画出平均发车间隔随时间变化的曲线如图18所示,北京地铁八通线的高峰时段为7 00—9
00—9 00以及17
00以及17 00—19
00—19 00,其余时段为平峰时段。
00,其余时段为平峰时段。
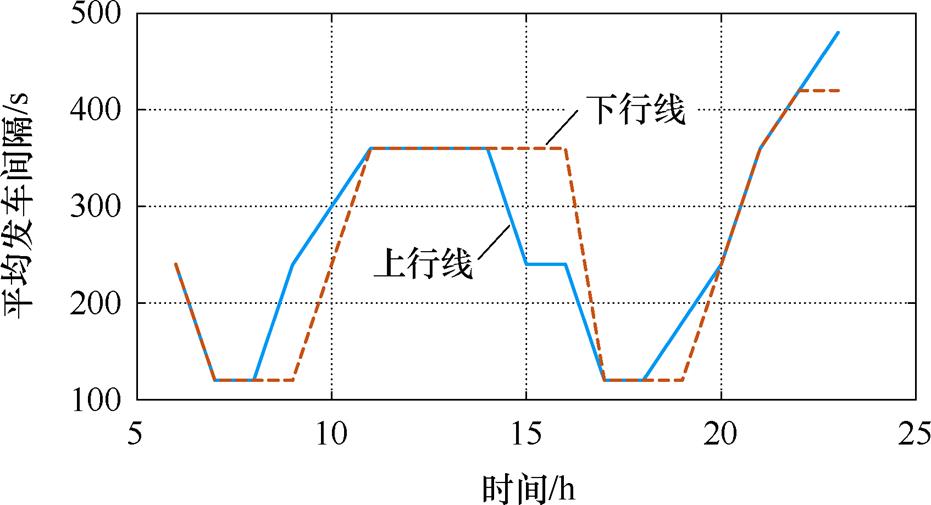
图18 工作日列车发车间隔(八通线)
Fig.18 Train departure interval on weekdays (Batong line)
由于实际实验中无法像仿真那样重复两个完全相同的工况用于对比效果。因此,实际实验过程中,在同一个高峰时段或平峰时段内,以15 min为一个周期,对比不同能量管理策略的不同效果。
图19a和图19b分别为本站空载电压策略下,通州北苑和八里桥站的储能装置在高峰时段的波形。图20a和图20b分别为本文区间能量管理策略下,两站储能装置在高峰时段的波形。统计图中时间段内两个站的牵引变电站输出能量和储能装置放电量如图21所示。其中组数1和2分别为通州北苑站在应用基于本站空载电压策略和区间能量管理策略下的变电站输出能量和储能放电量,组数3和4分别为八里桥站在应用基于本站空载电压策略和区间能量管理策略下的变电站输出能量和储能放电量。
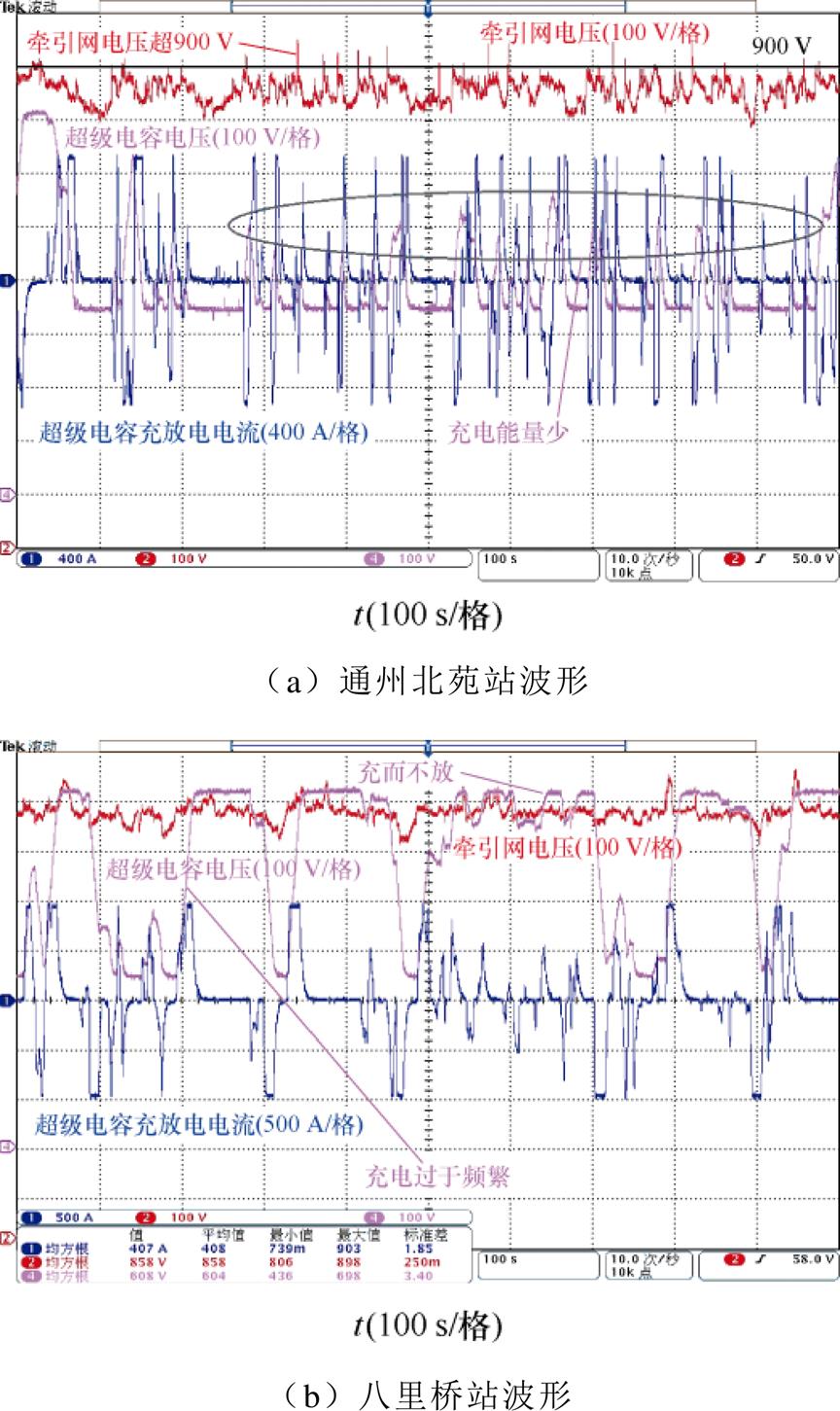
图19 高峰时段下不同站的波形(本站空载电压策略)
Fig.19 Waveforms of different stations during peak hours (no-load voltage strategy of the station)
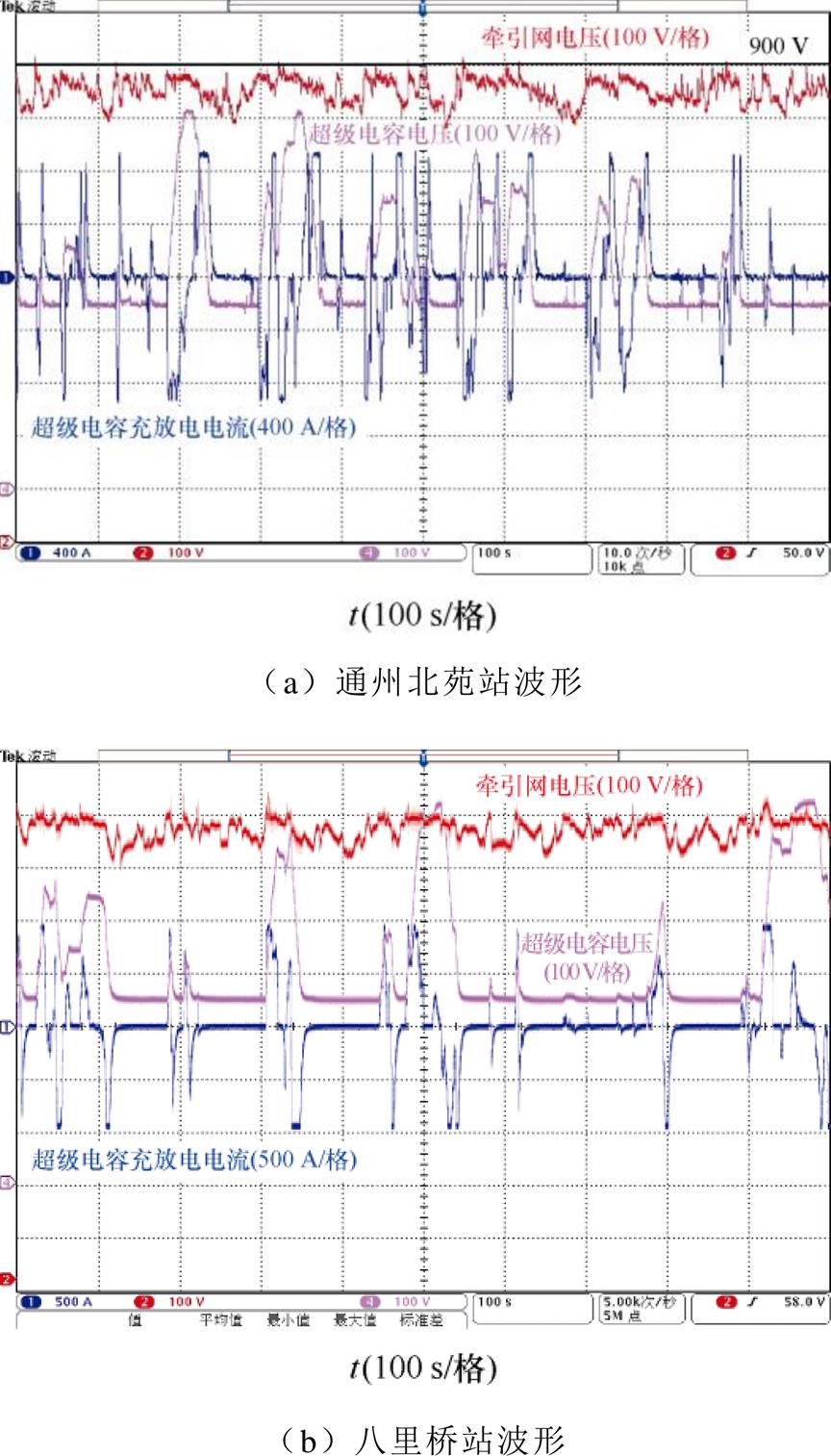
图20 高峰时段下不同站的波形(区间能量管理策略)
Fig.20 Waveforms of different stations during peak hours (interval energy management strategy)
从图19和图20可以看出,本站空载电压策略下,由于通州北苑站的充放电基准总是偏高,而此时列车间的交互能量较多,剩余制动功率呈现出数值大但持续时间短的特点,储能装置总是无法及时启动,仅在剩余制动功率达到峰值时启动,导致牵引网电压超过900 V的次数较多,大量制动能量被浪费在制动电阻上。八里桥站储能系统则由于充放电的基准值总是偏低,导致其经常在非制动工况充电,充放电过于频繁,存在较严重的环流问题。本文在区间能量管理策略下,从通州北苑站的波形可以看出,储能装置的充电阈值在制动功率大时能及时降低,致使充电能量变多,通州北苑站的牵引网电压基本都保持在900 V以下。从八里桥站的波形可看出,高峰期的储能装置充放电次数明显减少,且不会存在充电无法释放的情况。从图21可看出,基于本站空载电压策略下,八里桥站储能系统放电量较大,八里桥站的变电站输出能耗也相应较低,但其充电能量较多地来源于牵引列车和通州北苑站变电站,导致储能系统无法在制动时充电,因此整体的变电站能耗较高。
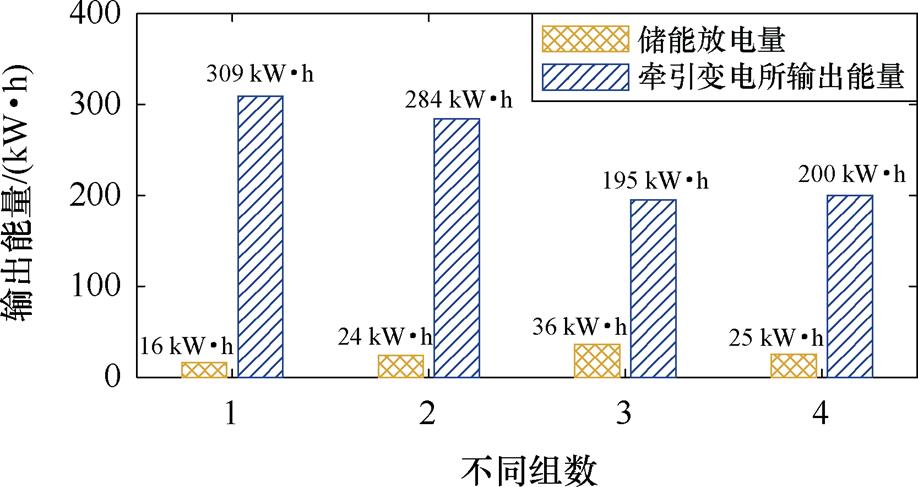
图21 高峰时段的变电站输出能量与储能放电量对比
Fig.21 Comparison of substation output energy and discharge amount during peak hours
图22a和图22b分别为本站空载电压策略下,通州北苑和八里桥站储能装置运行在平峰时段的波形,图23a和图23b分别为本文区间能量管理策略下,两站储能装置运行在平峰时段的波形。
统计这一时段两个站的牵引能耗和储能装置放电量如图24所示。
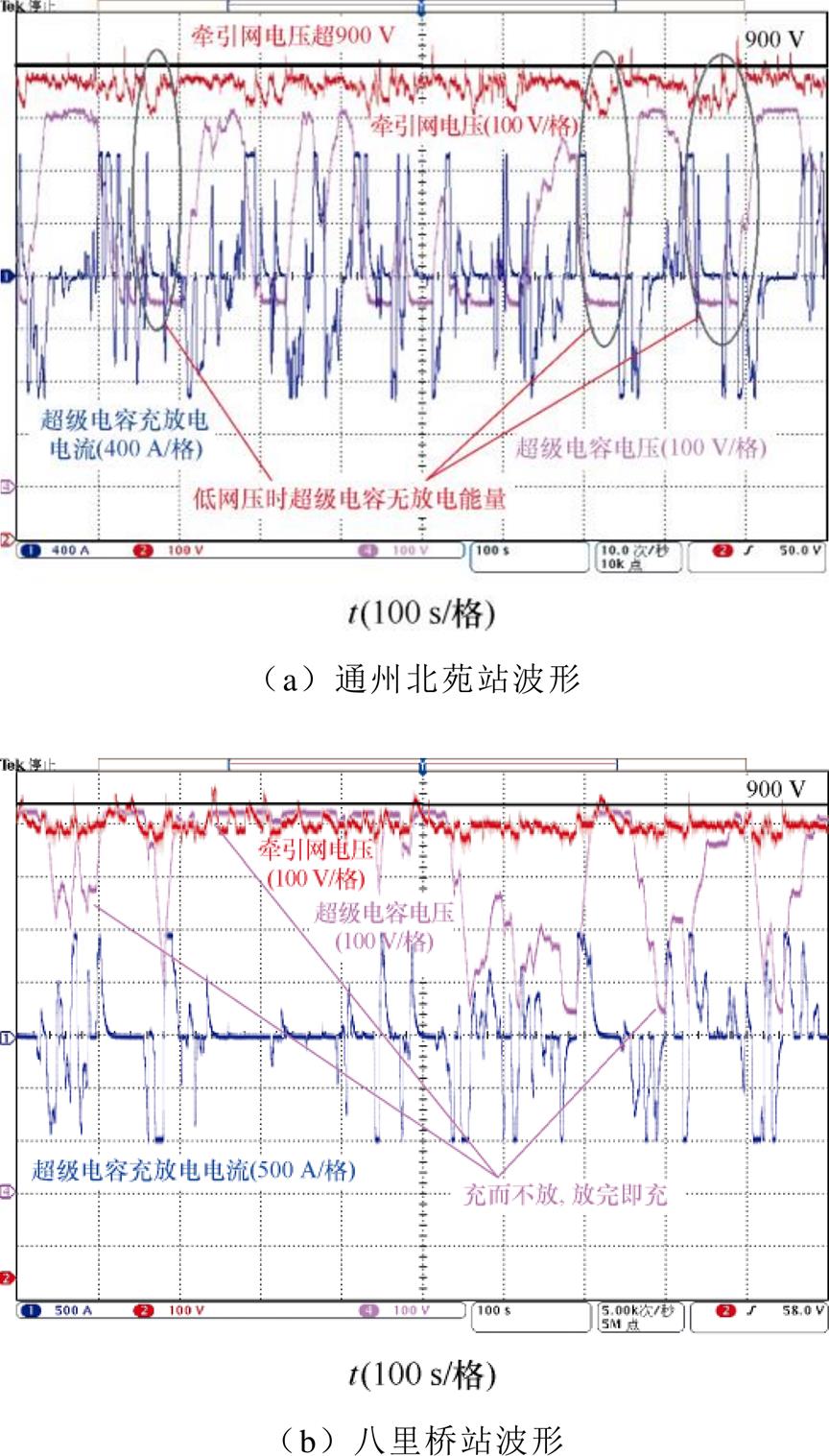
图22 平峰时段下不同站的波形(本站空载电压策略)
Fig.22 Waveforms of different stations during off peak hours (no-load voltage strategy of the station)
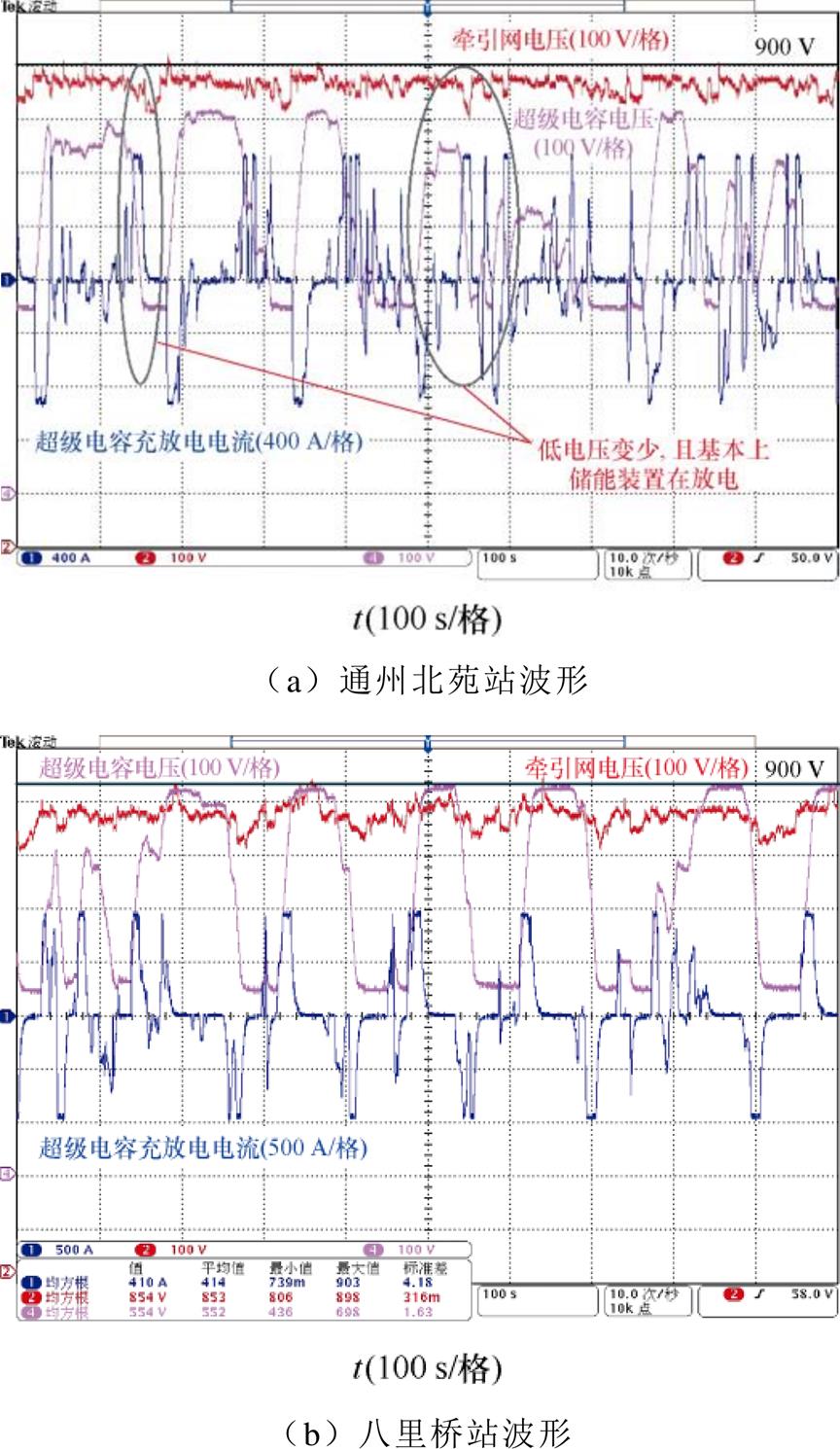
图23 平峰时段下不同站的波形(区间能量管理策略)
Fig.23 Waveforms of different stations during off peak hours (interval energy management strategy)
从图22和图23可看到,由于平峰时段的列车交互较少,因此剩余制动能量较大,即使在本站空载电压策略下,通州北苑站储能装置吸收的能量相比于高峰期时段也大大增多,但仍存在充电阈值过高导致储能装置启动较晚问题,从而使牵引网电压超过900 V的时段还是较长。八里桥站的储能装置
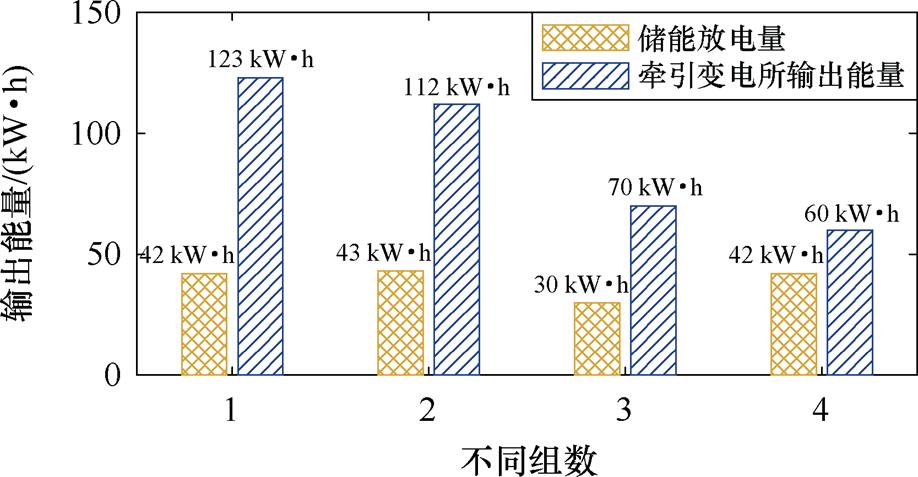
图24 平峰时段的变电站输出能量与储能放电量对比
Fig.24 Comparison of substation output energy and discharge amount during off peak hours
则同样吸收频繁,但由于平峰时段的剩余牵引功率较小,因此,低空载电压站的储能装置由于放电阈值过低,常常无法释放吸收的能量。在本文的区间能量管理策略下,通州北苑的牵引网电压超过900 V次数明显变少,且牵引网电压小于800 V的时间也相对较短,且每次低网压状态时,储能装置基本都处于放电状态。八里桥站储能装置的充电次数,由于剩余制动能量较大的缘故,相较于高峰时段变得更加频繁,但列车牵引时也能将充电能量完全释放,充放电周期非常规律。从整体统计结果来看,平峰时段,本文在区间能量管理策略下,无论是低压站还是高压站,减少的牵引变电站输出能耗均明显上升。
为了更长时间尺度地验证本文策略的节能优势,将两个站的设备在工作日连续挂网3天,挂网时间段为6 00—23
00—23 00,第1天不投入储能设备,第2天投入储能设备且全天采用本站空载电压策略,第3天采用本文的区间能量管理策略。通过每天抄取变电站内牵引变压器柜计量的牵引变电站能耗数据,对储能装置的节能情况进行对比。
00,第1天不投入储能设备,第2天投入储能设备且全天采用本站空载电压策略,第3天采用本文的区间能量管理策略。通过每天抄取变电站内牵引变压器柜计量的牵引变电站能耗数据,对储能装置的节能情况进行对比。
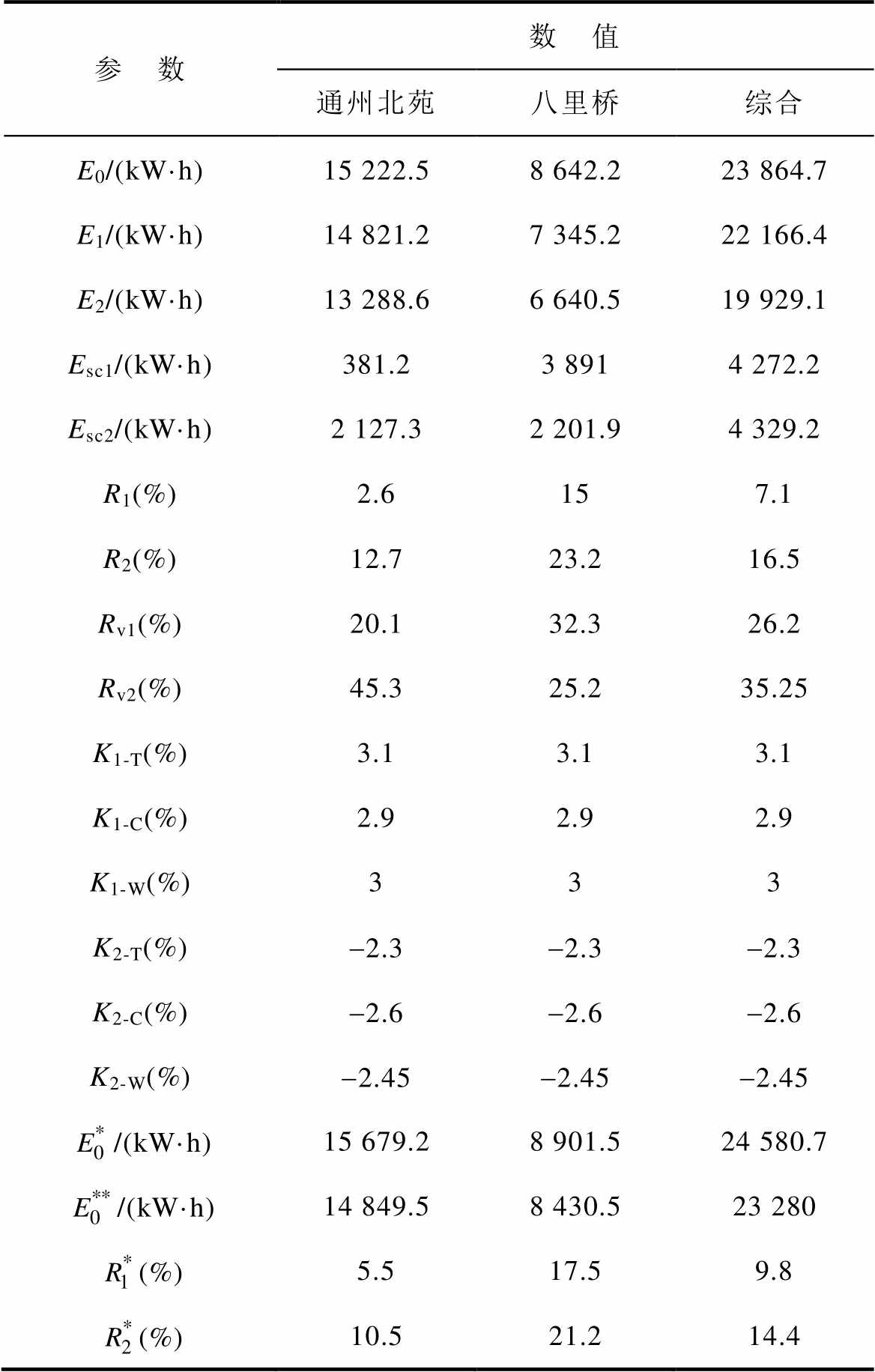
考虑到即使是工作日,每天的牵引能耗也可能不相同的情况,由于列车能量的传输范围一般为2~3 km,抄取超出能量传输范围的线路远端的牵引变电站的能耗数据,对安装储能装置的牵引能耗进行校正。最终得到的结果见表2。表2中,E0、E1、E2分别为未投入储能装置、采用本站空载电压策略以及采用区间能量管理策略下的变电站输出能耗,Esc1和Esc2分别为本站空载电压策略和区间能量管理策略下的储能系统放电量,R1和R2分别为采用本站空载电压策略以及采用区间能量管理策略下的节能率,Rv1和Rv2分别为采用本站空载电压策略以及采用区间能量管理策略下的稳压率,K1-T、K1-C和K1-W分别为采用本站空载电压策略时的土桥站折算系数、传媒大学站折算系数和综合的折算系数,K2-T、K2-C和K2-W分别为采用区间能量管理策略时的土桥站折算系数、传媒大学站折算系数和综合的
折算系数,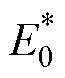 和
和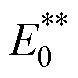 为综合折算系数折算后的未投入及投入储能装置下的变电站输出能耗,
为综合折算系数折算后的未投入及投入储能装置下的变电站输出能耗,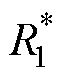 和
和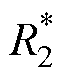 分别为折算后的采用本站空载电压策略以及采用区间能量管理策略下的节能率。
分别为折算后的采用本站空载电压策略以及采用区间能量管理策略下的节能率。
表2 节能稳压数据统计
Tab.2 Energy saving data statistics
参 数数 值 通州北苑八里桥综合 E0/(kW·h)15 222.58 642.223 864.7 E1/(kW·h)14 821.27 345.222 166.4 E2/(kW·h)13 288.66 640.519 929.1 Esc1/(kW·h)381.23 8914 272.2 Esc2/(kW·h)2 127.32 201.94 329.2 R1(%)2.6157.1 R2(%)12.723.216.5 Rv1(%)20.132.326.2 Rv2(%)45.325.235.25 K1-T(%)3.13.13.1 K1-C(%)2.92.92.9 K1-W(%)333 K2-T(%)-2.3-2.3-2.3 K2-C(%)-2.6-2.6-2.6 K2-W(%)-2.45-2.45-2.45 /(kW·h)15 679.28 901.524 580.7 /(kW·h)14 849.58 430.523 280 (%)5.517.59.8 (%)10.521.214.4
稳压率的计算如式(21)所示,其对比安装储能装置前后,牵引网电压超过900 V和低于800 V的时长。能耗的折算如式(22)所示,其通过土桥站和传媒大学站的能耗变化为参考,将未安装储能装置那天,通州北苑和八里桥站的牵引能耗按照折算系数进行折算,再进行节能率的计算。节能率的计算如式(23)所示,其分母为未安装储能装置时折算的牵引能耗,分子为折算的牵引能耗与安装储能装置后的牵引能耗的差值。
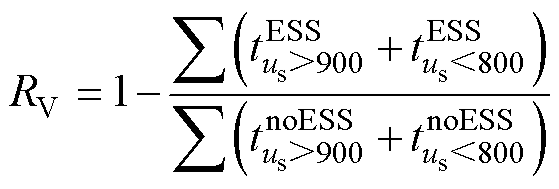 (21)
(21)
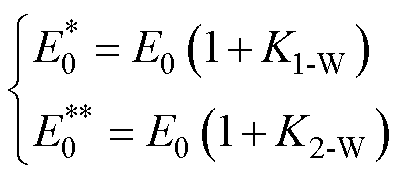 (22)
(22)
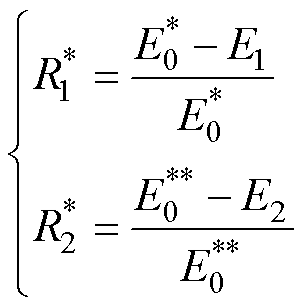 (23)
(23)
对表2的数据进行分析,可以得到以下结论:
(1)从储能系统的放电量数据Esc1和Esc2来看,应用本文的区间能量管理策略后,各站间的放电量更加均衡,更利于储能系统的运行寿命。
(2)从Esc1和Esc2的综合总放电量来看,两种策略下的放电量数值相差不大,但从变电站能耗数据E1和E2对比来看,应用本文的策略,变电站能耗明显减少,这说明储能装置的充放电量与系统的节能情况并不成正比,而应用本文策略后,储能系统放电量和能耗减少量更为接近,系统的充放电更加合理。
(3)对比Rv1和Rv2的稳压率数据,应用本文的区间能量管理策略后,对高压站的电压超限管理更为合理,且具备填谷效果,因此,稳压率上升较为明显;而对于低压站,由于整体充电能量变少,因此对于最低电压的削弱程度变弱,稳压率略低,但整体来说,稳压率提升较为明显。
(4)对比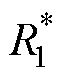 和
和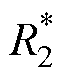 的节能率数据,基于本站空载电压的动态阈值控制下,高压站储能系统常常无法及时启动,导致制动列车处的电压超过900 V,能量浪费在制动电阻上;低压站的储能系统总是提前充满,导致无法在制动功率较大时抑制牵引网电压的上升,造成能量的浪费。而应用本文的区间能量管理策略,高压站和低压站的储能系统均能及时且合理的启动,综合节能量达14.4%,提升了4.6%。
的节能率数据,基于本站空载电压的动态阈值控制下,高压站储能系统常常无法及时启动,导致制动列车处的电压超过900 V,能量浪费在制动电阻上;低压站的储能系统总是提前充满,导致无法在制动功率较大时抑制牵引网电压的上升,造成能量的浪费。而应用本文的区间能量管理策略,高压站和低压站的储能系统均能及时且合理的启动,综合节能量达14.4%,提升了4.6%。
本研究基于相邻站的空载电压和牵引网电压,提出了一种区间能量管理策略。该策略通过深入探究牵引网电压、空载电压、列车运行状态和列车剩余功率间的关系,实现区间内列车运行状态和列车剩余功率的实时辨识,并基于此实时更新充放电阈值的设定基准值。此外,为了进一步优化节能与稳压等效果,本策略还引入了一个在线校正机制,该机制依据充放电周期、牵引网电压超限频次以及储能系统的电荷状态等参数,对阈值基准及其更新斜率进行调整。本文所提策略在北京地铁八通线的通州北苑站和八里桥站两套MW级储能系统上进行了实际应用验证。实验结果显示,在工作日,该区间能量管理策略能够实现14.4%的节能率以及35.25%的稳压率,相较于现有的基于本站空载电压的动态阈值能量管理策略,节能率和稳压率分别提升了5.4%和9.05%,证实了本策略的显著效用。
参考文献
[1] 中国城市轨道交通协会. 城市轨道交通2022年度统计和分析报告[EB/OL].[2023-3-31]. https://www. camet.org.cn/tjxx/11944.
China Association of Metros. Annual statistics and analysis report on urban rail transit in 2022[EB/OL]. https://www.camet.org.cn/tjxx/ 11944.
[2] 包叙定. 我国城轨交通发展的现状、问题与瞻望[J]. 城市轨道交通, 2018(10): 16-21.
Bao Xuding. Present situation, problems and prospect of urban rail transit development in China[J]. China Metros, 2018(10): 16-21.
[3] 中华人民共和国交通运输部. 交通运输部关于印发《绿色交通“十四五”发展规划》的通知[EB/OL]. [2021-10-29]. https://xxgk.mot.gov.cn/2020/jigou/zhghs/ 202201/t20220121_3637584.html.
Ministry of Transport of the People's Republic of China. Notice of the ministry of transport on the issuance of the “14th five-year development plan for green transportation”[EB/OL]. [2021-10-29]. https:// xxgk.mot.gov.cn/2020/jigou/zhghs/202201/t20220121_ 3637584.html.
[4] 张沈习, 王丹阳, 程浩忠, 等. 双碳目标下低碳综合能源系统规划关键技术及挑战[J]. 电力系统自动化, 2022, 46(8): 189-207.
Zhang Shenxi, Wang Danyang, Cheng Haozhong, et al. Key technologies and challenges of low-carbon integrated energy system planning for carbon emission peak and carbon neutrality[J]. Automation of Electric Power Systems, 2022, 46(8): 189-207.
[5] 郑亚晶, 李耀辉, 李雨恒, 等. 再生制动条件下地铁列车运行图的节能优化[J]. 华南理工大学学报(自然科学版), 2021, 49(7): 1-7.
Zheng Yajing, Li Yaohui, Li Yuheng, et al. Energy saving optimization of metro train working diagram under regenerative braking[J]. Journal of South China University of Technology (Natural Science Edition), 2021, 49(7): 1-7.
[6] 霍利杰, 杨轶成, 孙婷, 等. 地铁再生制动能量分散回馈多模控制研究[J]. 电气技术, 2020, 21(3): 37-43.
Huo Lijie, Yang Yicheng, Sun Ting, et al. Research on multi-mode control of energy regenerative feed- back of regenerative braking in metro[J]. Electrical Engineering, 2020, 21(3): 37-43.
[7] 杨中平, 林飞. 储能技术在地面式再生制动能量吸收和利用装置中的应用[J]. 都市快轨交通, 2021, 34(6): 1-8.
Yang Zhongping, Lin Fei. Application of energy storage technology in stationary regenerative braking energy absorption and utilization devices[J]. Urban Rapid Rail Transit, 2021, 34(6): 1-8.
[8] Okui A, Hase S, Shigeeda H, et al. Application of energy storage system for railway transportation in Japan[C]//The 2010 International Power Electronics Conference-ECCE ASIA-, Sapporo, Japan, 2010: 3117-3123.
[9] 赵亚杰, 夏欢, 王俊兴, 等. 基于动态阈值调节的城轨交通超级电容储能系统控制策略研究[J]. 电工技术学报, 2015, 30(14): 427-433.
Zhao Yajie, Xia Huan, Wang Junxing, et al. Control strategy of ultracapacitor storage system in urban mass transit system based on dynamic voltage threshold[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 427-433.
[10] 夏欢. 城轨超级电容储能系统分层控制与容量配置优化研究[D]. 北京: 北京交通大学, 2017.
Xia Huan. Hierarchical control and capacity allocation optimization of supercapacitor energy storage system for urban rail transit[D]. Beijing: Beijing Jiaotong University, 2017.
[11] 信月. 基于全寿命周期的地面式超级电容储能系统能量管理策略优化研究[D]. 北京: 北京交通大学, 2020.
Xin Yue. Research on energy management strategy optimization of stationary supercapacitor energy storage system based on full life cycle[D]. Beijing: Beijing Jiaotong University, 2020.
[12] 李旭阳. 城轨交通超级电容储能系统在线优化控制策略研究[D]. 北京: 北京交通大学, 2017.
Li Xuyang. Research on on-line optimal control strategy of urban rail transit super-capacitor energy storage system[D]. Beijing: Beijing Jiaotong University, 2017.
[13] 兰笠夫. 城市轨道交通地面式超级电容储能系统节能及稳压控制研究[D]. 北京: 北京交通大学, 2022.
Lan Lifu. Study on energy saving and voltage stabilizing control of ground super capacitor energy storage system in urban rail transit[D]. Beijing: Beijing Jiaotong University, 2022.
[14] 诸斐琴. 城市轨道交通地面式超级电容储能系统自适应协调控制与容量配置综合优化研究[D]. 北京: 北京交通大学, 2020.
Zhu Feiqin. Adaptive cooperative control and capacity configuration optimization of supercapacitor energy storage systems in urban rail transit[D]. Beijing: Beijing Jiaotong University, 2020.
[15] 秦强强, 张骄, 李宇杰, 等. 基于列车运行状态的城轨地面混合储能装置分时段控制策略[J]. 电工技术学报, 2019, 34(增刊2): 760-769.
Qin Qiangqiang, Zhang Jiao, Li Yujie, et al. Time-divided control strategy of urban rail and ground hybrid energy storage device based on train running state[J]. Transactions of China Elec- trotechnical Society, 2019, 34(S2): 760-769.
[16] Ciccarelli F, Del Pizzo A, Iannuzzi D. Improvement of energy efficiency in light railway vehicles based on power management control of wayside lithium-ion capacitor storage[J]. IEEE Transactions on Power Electronics, 2014, 29(1): 275-286.
[17] Zhong Zhihong, Yang Zhongping, Fang Xiaochun, et al. Hierarchical optimization of an on-board supercapacitor energy storage system considering train electric braking characteristics and system loss[J]. IEEE Transactions on Vehicular Technology, 2020, 69(3): 2576-2587.
[18] 刘宇嫣, 杨中平, 林飞, 等. 城轨地面式混合储能系统自适应能量管理与容量优化配置研究[J]. 电工技术学报, 2021, 36(23): 4874-4884.
Liu Yuyan, Yang Zhongping, Lin Fei, et al. Study on adaptive energy management and optimal capacity configuration of urban rail ground hybrid energy storage system[J]. Transactions of China Electro- technical Society, 2021, 36(23): 4874-4884.
[19] 钟志宏. 考虑车-地储能装置的城轨列车再生制动性能优化研究[D]. 北京: 北京交通大学, 2021.
Zhong Zhihong. Research on optimization of regenerative braking performance of urban rail train considering vehicle-ground energy storage device[D]. Beijing: Beijing Jiaotong University, 2021.
[20] 林舜江, 冯祥勇, 梁炜焜, 等. 新能源电力系统不确定优化调度方法研究现状及展望[J]. 电力系统自动化, 2024, 48(10): 20-41.
Lin Shunjiang, Feng Xiangyong, Liang Weikun, et al. Research and prospect of the uncertain optimal dispatch methods for renewable energy power systems[J]. Automation of Electric Power Systems, 2024, 48(10): 20-41.
[21] Bilbao E, Barrade P, Etxeberria-Otadui I, et al. Optimal energy management strategy of an improved elevator with energy storage capacity based on dynamic programming[J]. IEEE Transactions on Industry Applications, 2014, 50(2): 1233-1244.
[22] 陈怀鑫, 杨中平, 林飞, 等. 基于遗传算法的城轨交通超级电容储能装置能量管理和容量配置优化研究[J]. 铁道学报, 2019, 41(9): 59-66.
Chen Huaixin, Yang Zhongping, Lin Fei, et al. Management and configuration for stationary super- capacitor energy storage system applied in urban rail transit based on genetic algorithm[J]. Journal of the China Railway Society, 2019, 41(9): 59-66.
[23] 李翠萍, 司文博, 李军徽, 等. 基于集合经验模态分解和多目标遗传算法的火-多储系统调频功率双层优化[J]. 电工技术学报, 2024, 39(7): 2017-2032.
Li Cuiping, Si Wenbo, Li Junhui, et al. Two-layer optimization of frequency modulated power of thermal generation and multi-storage system based on ensemble empirical mode decomposition and multi- objective genetic algorithm[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 2017-2032.
[24] Yang Zhongping, Zhu Feiqin, Lin Fei. Deep- reinforcement-learning-based energy management strategy for supercapacitor energy storage systems in urban rail transit[J]. IEEE Transactions on Intelligent Transportation Systems, 2021, 22(2): 1150-1160.
[25] Zhu Feiqin, Yang Zhongping, Lin Fei, et al. Decentralized cooperative control of multiple energy storage systems in urban railway based on multiagent deep reinforcement learning[J]. IEEE Transactions on Power Electronics, 2020, 35(9): 9368-9379.
[26] 陈泽宇, 方志远, 杨瑞鑫, 等. 基于深度强化学习的混合动力汽车能量管理策略[J]. 电工技术学报, 2022, 37(23): 6157-6168.
Chen Zeyu, Fang Zhiyuan, Yang Ruixin, et al. Energy management strategy for hybrid electric vehicle based on the deep reinforcement learning method[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 6157-6168.
[27] 董雷, 杨子民, 乔骥, 等. 基于分层约束强化学习的综合能源多微网系统优化调度[J]. 电工技术学报, 2024, 39(5): 1436-1453.
Dong Lei, Yang Zimin, Qiao Ji, et al. Optimal scheduling of integrated energy multi-microgrid system based on hierarchical constraint reinforcement learning[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1436-1453.
[28] Mnih V, Kavukcuoglu K, Silver D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518(7540): 529-533.
[29] 刘海涛, 熊雄, 季宇, 等. 直流配电下多微网系统集群控制研究[J]. 中国电机工程学报, 2019, 39(24): 7159-7167.
Liu Haitao, Xiong Xiong, Ji Yu, et al. Cluster control research of multi-microgrids system under DC distribution system[J]. Proceedings of the CSEE, 2019, 39(24): 7159-7167.
[30] Goyal M, Ghosh A. Microgrids interconnection to support mutually during any contingency[J]. Sustainable Energy, Grids and Networks, 2016, 6: 100-108.
[31] 李翔宇, 赵冬梅. 分散架构下多虚拟电厂分布式协同优化调度[J]. 电工技术学报, 2023, 38(7): 1852- 1863.
Li Xiangyu, Zhao Dongmei. Distributed coordinated optimal scheduling of multiple virtual power plants based on decentralized control structure[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(7): 1852-1863.
[32] Khayyam S, Ponci F, Goikoetxea J, et al. Railway energy management system: centralized-decentralized automation architecture[J]. IEEE Transactions on Smart Grid, 2016, 7(2): 1164-1175.
[33] 马庆, 邓长虹. 基于单/多智能体简化强化学习的电力系统无功电压控制方法[J]. 电工技术学报, 2024, 39(5): 1300-1312.
Ma Qing, Deng Changhong. Single/multi agent simplified deep reinforcement learning based volt-var control of power system[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1300-1312.
[34] 李炎. 一种基于深度强化学习的多储能系统分层协同控制方法: 中国, 202311643798.7[P]. 2023-12-04.
Abstract In recent years, with the promotion of the dual carbon policy, the application of energy storage technology in urban rail transit has become increasingly widespread, showing a trend of point-to-line development. When multiple stations are installed with energy storage devices on a line, charging/discharging strategy design for different station energy storage devices and the coordination and control for multiple energy storage systems are necessary.
This paper analyzes the relationship between traction network voltage, train status, and residual power of trains under no-load voltage and departure interval conditions based on the measured traction network voltage and 10 kV transformer output voltage. A distributed interval energy management strategy is proposed, dividing the entire line into several energy management intervals. The parameters of the energy management equipment within the interval are dynamically adjusted by identifying the train status and residual power within the interval.
Firstly, the no-load voltage of the traction substation is identified online based on the output voltage of the 10 kV transformer. The real-time status and residual power of the trains in the management section are identified with the identified no-load voltage and the traction network voltage of the substations in the section. Based on the real-time identified residual power, the benchmark value of the charging and discharging threshold of the energy storage system in the section and the initial slope of the threshold variation are determined. This strategy introduces an online correction mechanism to further optimize the effects of energy conservation and voltage stabilization according to parameters such as charging and discharging cycles, frequency of traction network voltage exceeding 900 V, and the state of charge of the energy storage system. It corrects the benchmark values and updates the slopes of the charging and discharging thresholds for multiple energy storage systems within the interval.
The proposed strategy has been verified on two sets of MW energy storage systems at Tongzhou Beiyuan station, and Baliqiao station of Beijing Metro Batong line. The experimental results show that the proposed distributed interval energy management strategy achieves an energy-saving rate of 14.4% and a voltage stabilization rate of 35.25% on weekdays. Compared with the existing dynamic threshold energy management strategy based on the no-load voltage of this station, the energy saving rate and voltage stabilization rate have increased by 5.4% and 9.05%, respectively. It provides an efficient and feasible scheme for applying a multi-energy storage system in urban rail transit.
keywords:Urban rail transit, no-load voltage, multi energy storage, energy management, coordinated control
DOI: 10.19595/j.cnki.1000-6753.tces.232168
中图分类号:U239.5
收稿日期 2023-12-27
改稿日期 2024-01-19
钟志宏 男,1993年生,博士,研究方向为城市轨道交通储能节能技术、牵引传动技术等。E-mail: zhzhong@bjtu.edu.cn(通信作者)
李 炎 男,1995年生,博士研究生,研究方向为轨道交通节能技术。E-mail: 22110468@bjtu.edu.cn
(编辑 陈 诚)