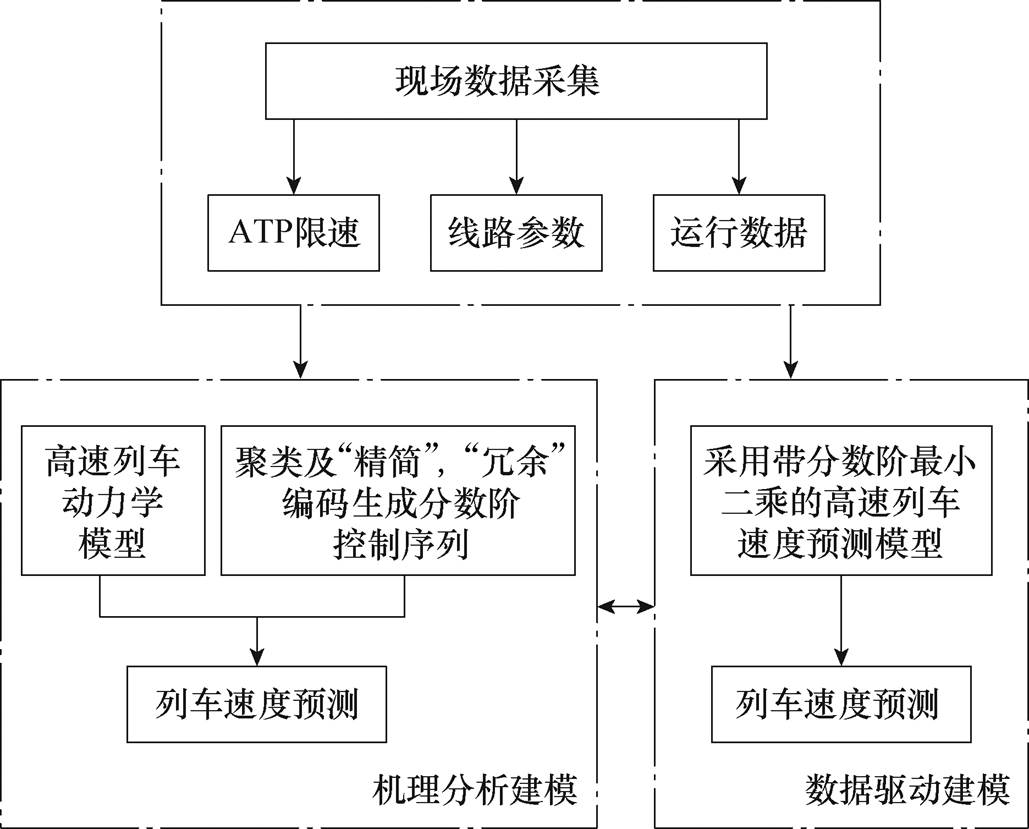
图1 机理分析和数据驱动联合建模原理
Fig.1 Joint modeling of mechanism analysis and data-drive modeling
摘要 针对现有司机操纵策略难以完整描述列车大功率操纵过程的微观变化,设计机理特性和数据驱动模型联合驱动的分数阶建模策略,来满足高速列车无级调速下安全平稳运行的要求。针对高速列车大功率操纵模式下的大惯性特性和司机反应时间,该文首先对大功率牵引系统和制动系统的时滞特性进行分析,进而对列车操纵策略设计精简冗余工序编码策略,从闭环控制角度实现速度时滞特性精准预测;其次提出了一种新的分数阶建模方法,并设计分数阶最小二乘算法对模型中的时变参数进行精细化辨识;最后基于现场实验数据验证了所提方法的有效性。
关键词:高速列车 大功率操纵过程 数据驱动 时滞 分数阶最小二乘模型
在高速列车大功率操纵过程中,由于运行环境复杂多变以及列车动力学特性等因素影响,列车运行速度在不同的时间和不同的路段上都存在一定的时滞特性。为更精细地描述列车运行过程,从而对列车进行更加精准的控制,对列车操纵过程时滞特性进行建模具有重要的理论和现实意义[1-3]。
高速列车大功率操纵系统是一个复杂的动态系统,其内部机理复杂,并且由于高速列车随着速度提高,车辆、轮轨、弓网间的动力作用明显加剧,使其具有较强的非线性和耦合特性,并引起零部件失效以及参数变化,机理建模方法难以准确描述高速列车动力学特性。此外,高速列车操纵过程中司机根据既定工况切换手柄级位存在一定延迟,大功率牵引系统和制动系统的控制指令传递存在时滞效应,使得当前牵引和制动控制模型缺乏精确性[4-6]。由于高速列车在固定线路严格按照时刻表运行,其操纵过程动态特性具有规律性,可以根据历史运行大数据对未来运行轨迹进行预测,基于数据驱动的建模方法得到了国内外专家的广泛关注[7-9]。
目前,已有学者针对高速列车上述时滞特性建立了牵引与制动模型[10-12],但大部分研究方法没有考虑机理模型和数据驱动模型共有的结构特性,将难以平衡高速列车大功率操纵过程建模复杂性和可用性之间的矛盾。从能量传递的角度来看,分数阶模型特有的遗传衰减特性可以使能量缓慢释放,更好地满足高速列车大功率操纵过程实际运营的需要,从而抑制抖振现象以提高速度时滞预测精度[13-14]。基于分数阶系统模型的研究已成为热点方向。文献[15]采用分数阶理论对高速列车空气弹簧的黏弹阻尼特性进行描述,基于实测数据辨识分数阶模型参数,实现对传统模型的优化;文献[16]基于R-L型分数阶导数对铁磁材料的高频损耗预测模型进行了修正。然而,上述分数阶模型建立在频域辨识的基础上,难以直接对时间序列模型进行分析。
分数阶最小二乘算法将数据驱动模型的最小二乘结构扩展到非整数阶算子,即能包含所有整数阶理论,并在传统整数阶的基础上增加了考虑大功率操纵级位微观变化的维度,即模型阶次的自由 度[17-18]。上述方法只是从系统辨识的角度建立了高速列车大功率操纵过程分数阶开环模型,难以实现速度时滞特性的精准预测。高速列车大功率操纵过程按手柄级位变化情况,可分为惰行控制策略和牵引制动控制策略。按求解方法可分为间接法、直接法和启发式方法。间接法基于极大值原理,但该方法存在不连续的状态变量变化,进一步增加了求解难度;直接法将原问题转化为规划问题进行求解,但该方法所对应的解空间较大,离散后出现指数爆炸现象,导致该类方法常用于短区间、低速运行的城市轨道交通;启发式方法适用于求解既定工序和惰行控制策略下的操纵问题[19]。针对高速列车大功率操纵过程难以确定最优工序及其切换点位置的问题,文献[20]提出一种能适应任意线路类型和限速环境下基于冗余工序编码的求解思路。但上述方法只是针对最大牵引、惰行和最大制动等典型工序进行了编码,很少考虑高速列车大功率牵引/制动级位的微观变化对操纵过程的影响。
在高速列车传统操纵理论基础上,本文考虑了大功率操纵过程时滞特性对速度预测精度的影响,采用机理特性和数据驱动联合建模方法对不同级位下的控制序列应用分数阶最小二乘法和减法聚类进行精细化建模,基于真实数据的实验仿真结果表明,分数阶最小二乘模型能更好地描述高速列车时滞特性,较好地满足高速列车速度预测精度,从而更加逼近列车实际运行工况。
针对具有时滞特性的高速列车大功率操纵过程建模与速度预测问题,本节首先通过分析高速列车大功率操纵过程原理,建立具有延时环节的线性列车动力学模型;然后提出一种数据驱动方法对模型中的时变参数进行辨识,提高模型的准确性,逻辑关系如图1所示。
高速列车大功率操纵过程主要包括牵引、惰行、制动。引起控制系统迟滞的原因主要包括司机操纵手柄级位反应时间、大功率牵引控制系统和制动控制系统能量传递的衰减特性。列车运行控制系统如图2所示,图中,u(t)为列车控制力指令;ti(i=1, 2, 3)为高速列车大惯性特性引起的延时;u(t-ti)为牵引/制动指令滞后ti个单位;v(t)为当前列车实际速度。

图1 机理分析和数据驱动联合建模原理
Fig.1 Joint modeling of mechanism analysis and data-drive modeling
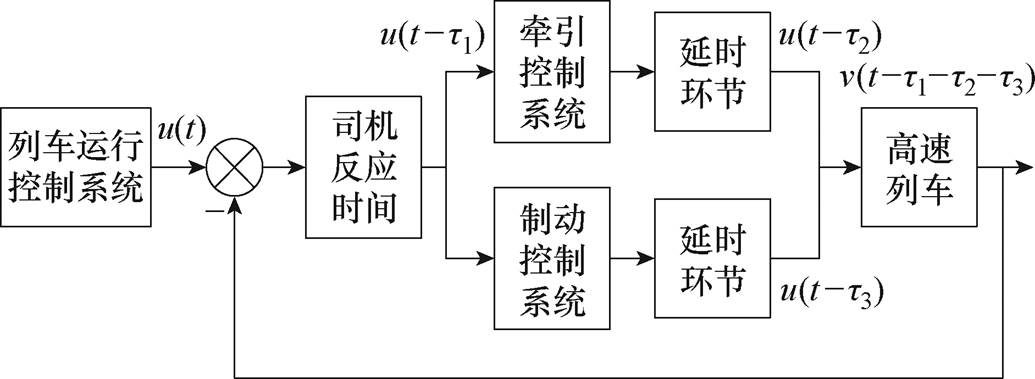
图2 列车运行控制系统示意图
Fig.2 Schematic diagram of the train operation control system
在高速列车大功率操纵过程中,列车动态特性变化快,再加上高速铁路坡度设计较小,可将整个列车看成是一个质点[21-22]。针对高速列车速度时变延迟下的运动动力学特性,其时滞模型可描述为
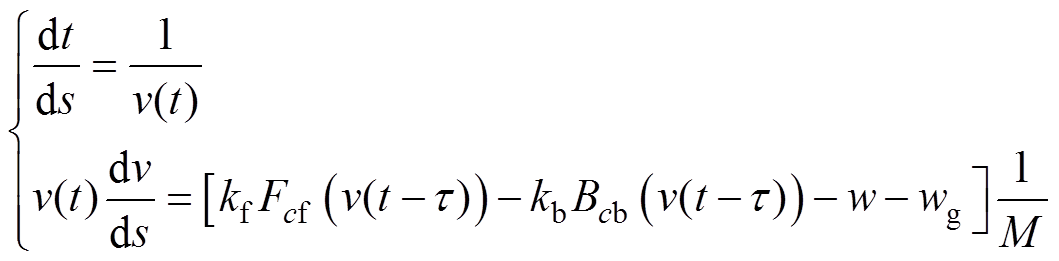 (1)
(1)
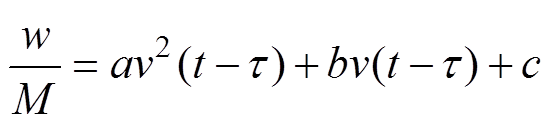 (2)
(2)
式中,t为列车运行时间;M为列车总质量;kf、kb分别为牵引和制动的控制系数;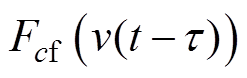 、
、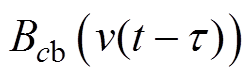 分别为列车在速度为v-t 时的牵引力和制动力;cf、cb分别为牵引、制动时操纵控制序列;s∈[0, X0]为列车所在位置,X0为两站之间的距离;v∈[0, v(s)]为列车运行速度,v(s)为在位置s处列车自动防护限速;wg为坡道阻力、隧道附加空气阻力、曲线附加阻力之和;w为列车基本阻力;a、b、c分别为外部空气阻力系数、其他机械阻力系数、滚动机械阻力系数;v(t-t) 为时变速度延迟;t 为时滞。
分别为列车在速度为v-t 时的牵引力和制动力;cf、cb分别为牵引、制动时操纵控制序列;s∈[0, X0]为列车所在位置,X0为两站之间的距离;v∈[0, v(s)]为列车运行速度,v(s)为在位置s处列车自动防护限速;wg为坡道阻力、隧道附加空气阻力、曲线附加阻力之和;w为列车基本阻力;a、b、c分别为外部空气阻力系数、其他机械阻力系数、滚动机械阻力系数;v(t-t) 为时变速度延迟;t 为时滞。
由式(1)和文献[10]可知,列车牵引/制动级位定义为满功率牵引的百分比,变化范围为[-100%, 100%],传统牵引/制动序列是在-1, 0, 1之间转换,即制动序列“-1”包含列车制动时的所有级位变化;序列“0”表示列车惰行;牵引序列“1”包含列车牵引时的所有级位变化。由于传统牵引/制动序列划分不能完整地描述列车大功率操纵过程的微观变化,受分数阶理论启发,本文将列车级位转换为更加精确的牵引制动序列,对应关系见表1和表2。
表1 列车级位与列车牵引序列转换关系
Tab.1 Train traction settings and the corresponding control sequences

列车级位牵引序列 00 0.5 0.75 1
表2 列车级位与列车制动序列转换关系
Tab.2 Train brake settings and the corresponding control sequences
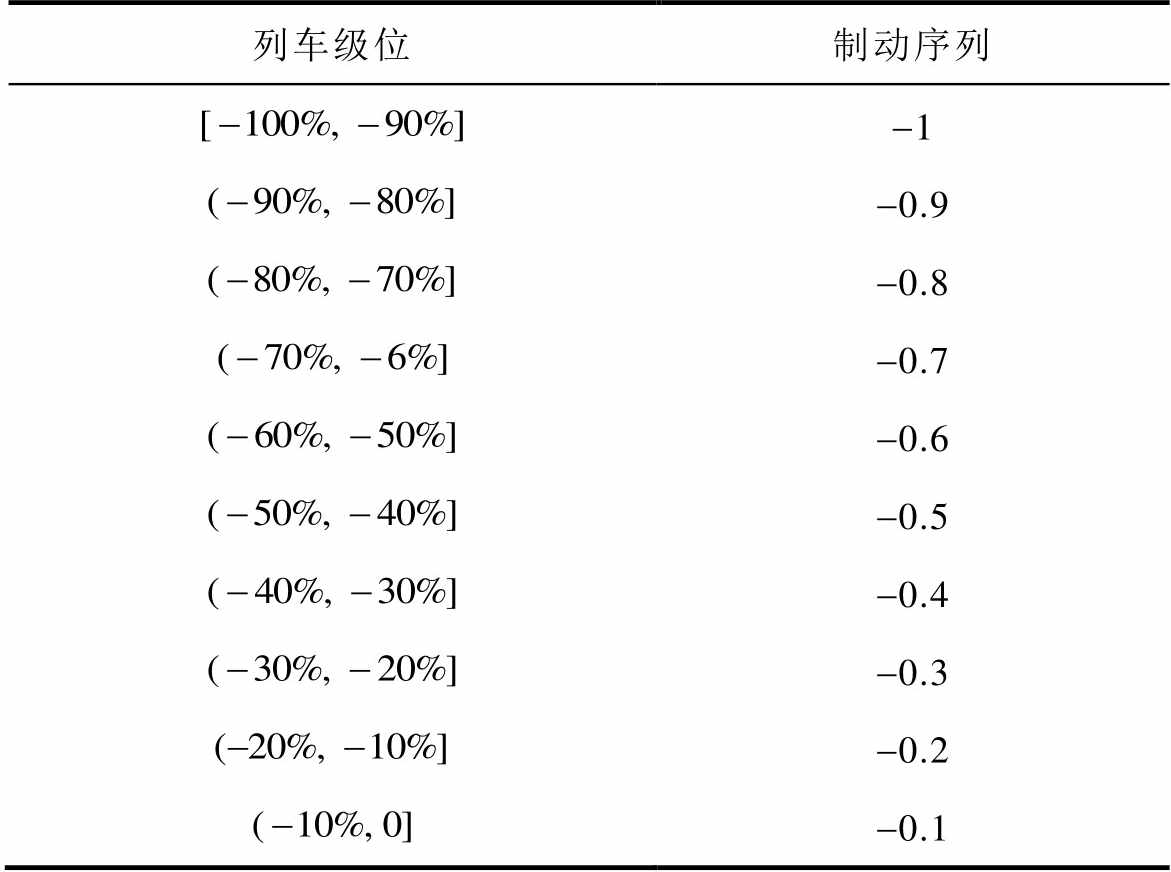
列车级位制动序列 -1 -0.9 -0.8 -0.7 -0.6 -0.5 -0.4 -0.3 -0.2 -0.1
根据上述分析,结合式(1)具有时滞特性的列车牵引计算原理,可得到高速列车初始运行策略,有
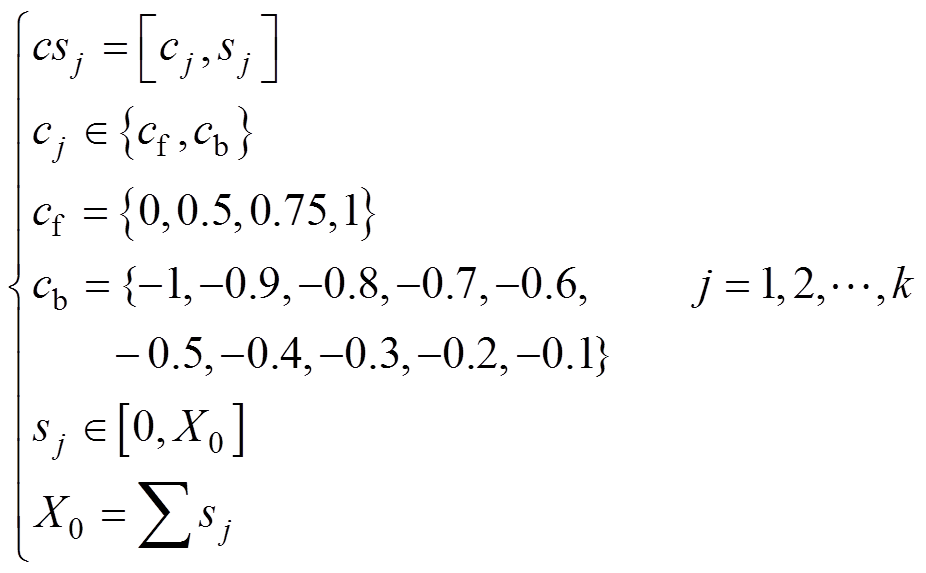 (3)
(3)
式中,csj为由cj(高速列车的操纵状态即牵引序列)和sj(一个cj对应的高速列车走行距离)组成的操纵策略;k为控制策略的组数,k∈N*。其中,N*为正整数。
由于高速列车大功率操纵状态变化频繁,会出现大量冗余的操纵策略,为了从微观层面对操纵策略进行有效编码,本文提出一种减法聚类算法,来实现式(3)中k的最优确定。
减法聚类算法(Subtractive Clustering Method, SCM)不需要事先规定聚类数,只需根据样本数据即可确定聚类中心。该算法的核心是将数据中每个单独数据看作潜在的聚类中心点,并根据该单独数据附近的其他数据的多少来计算该点作为聚类中心的可能性。根据高速列车现场运行数据,可以使用减法聚类和数据分类算法来识别操纵策略数量[13]。
为了确定最优的聚类个数,戴维森堡丁指数(Davies Bouldin Index, DBI)使用类内样本点到其聚类中心的距离来衡量类间的分离性。DBI越小表示类内距离越小,同时类间距离越大,对应着较好的聚类结果。
结合表1、表2和式(3),高速列车运行策略调整规则流程如图3所示。
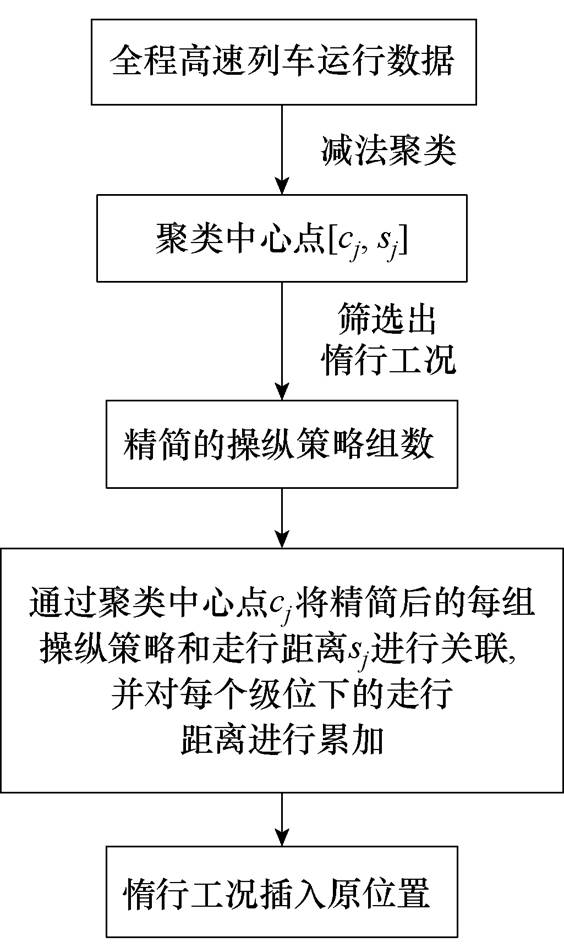
图3 高速列车运行策略调整规则流程
Fig.3 Regulation of high-speed train operation strategy
基于图3构建的高速列车操纵策略调整规则,根据列车动力学模型以及线路列车自动防护(Auto- matic Train Protection, ATP)系统限速信息,分数阶机理建模下列车速度预测算法流程如图4所示。
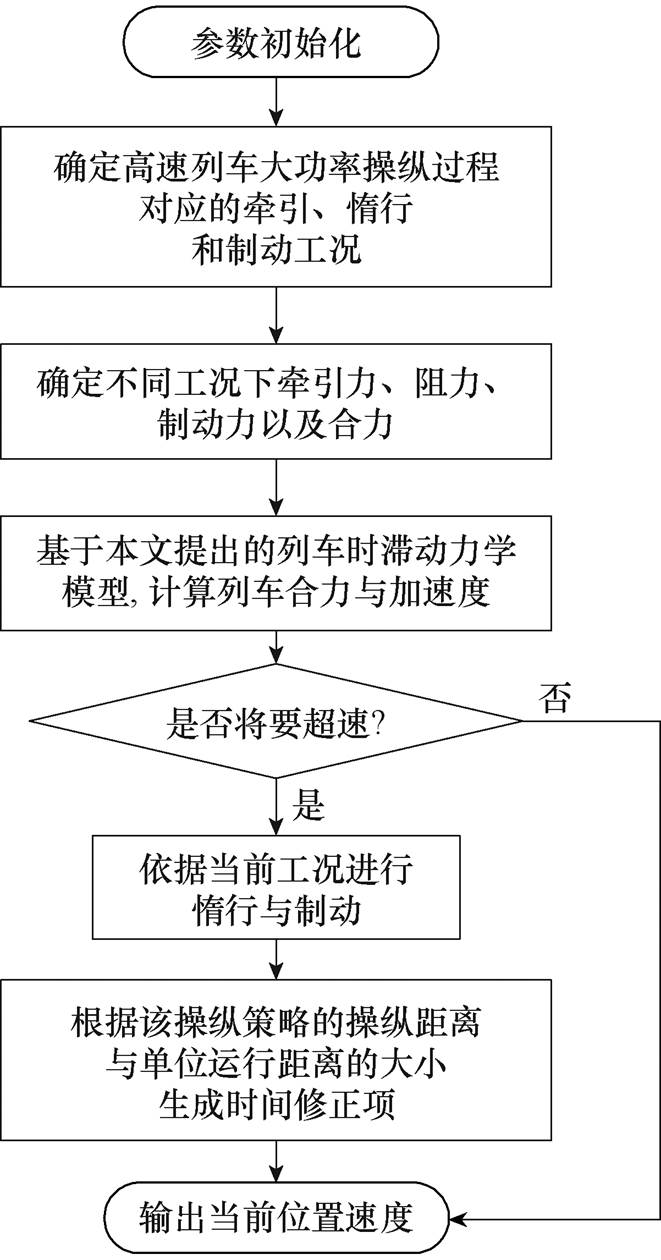
图4 分数阶机理建模下速度预测算法流程
Fig.4 Speed prediction algorithms with the fractional order model
针对式(1)中时滞参数t 和牵引及制动控制系数kf、kb的时变特性,根据1.2节建立的列车操纵策略编码及分数阶机理建模下速度预测算法,考虑机理模型和数据驱动模型共有的结构特性,采用分数阶最小二乘方法建立数据驱动模型。这种基于机理、数据和知识三驱动的闭环结构,能够实现速度时滞特性精准预测。
任意阶微分的概念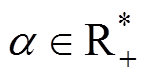 (正整数)在19世纪由黎曼和刘维尔定义为
(正整数)在19世纪由黎曼和刘维尔定义为
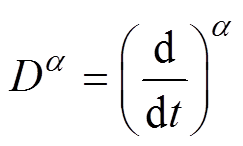 (4)
(4)
f(t)的a 阶分数导数被定义为m-a 阶非整数积分的m=[a]+1阶整数导数([ · ]代表底算子),有
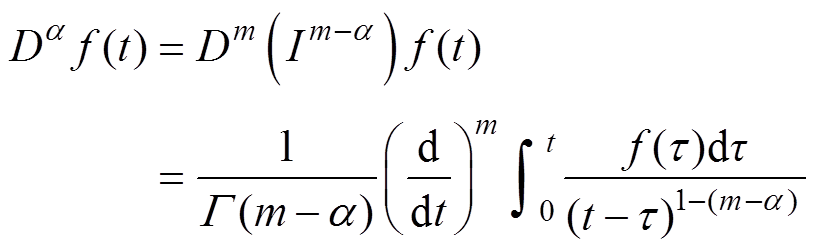 (5)
(5)
式中,t>0;t 为时滞时间。并且欧拉函数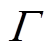 被定义为
被定义为
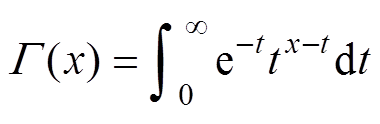 (6)
(6)
由于高速列车运行数据是一种典型非线性时间序列,本文采用离散化的Grünwald-Letnikov分数阶模型,有
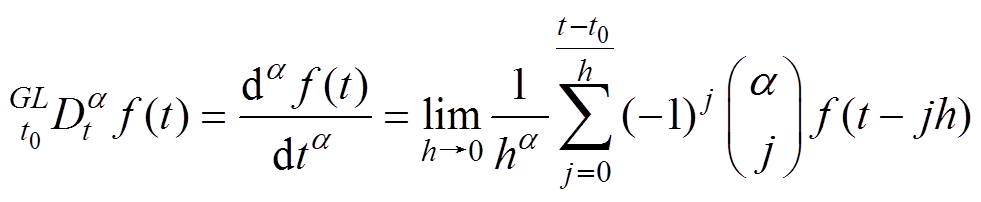 (7)
(7)
其中
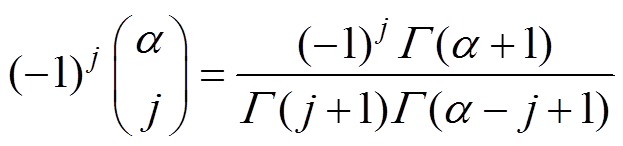 (8)
(8)
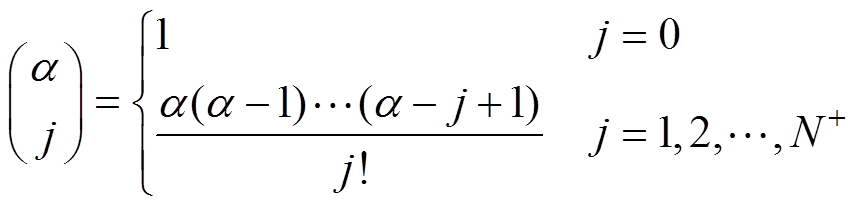 (9)
(9)
式中,a 为分数阶的阶数;N+为正整数。可以看出,随着(t-t0)/h增加,式(7)的计算量将急剧增加,难以满足工程应用。本文采用具有有限采样点的G-L模型来减少计算量,即将增加的(t-t0)/h采样点替换为固定的L个采样点。因此,式(7)中采样时间为h=1 s的G-L模型可描述为
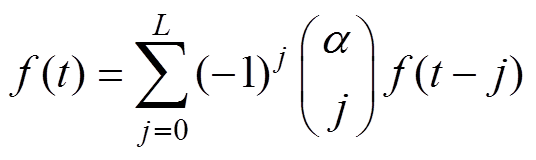 (10)
(10)
由于此二项式不会随着j的增长而迅速收敛到零,该模型采用整个采样序列来估计其分数阶导数,从而更好地描述高速列车大功率操纵过程的能量衰减特性[14]。
由式(10)和文献[10]可知,高速列车大功率操纵过程可用单输入单输出(Single Input Single Output, SISO)分数阶时滞系统来描述,有
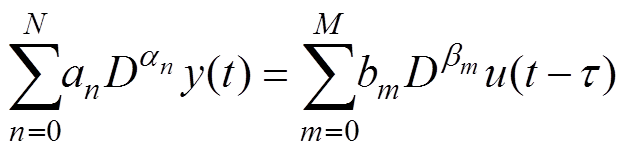 (11)
(11)
式中,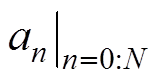 、
、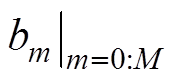 为线性常系数;分数阶阶次 (an, bn)∈R+。
为线性常系数;分数阶阶次 (an, bn)∈R+。
由文献[17]可知,高速列车分数阶模型可描述为
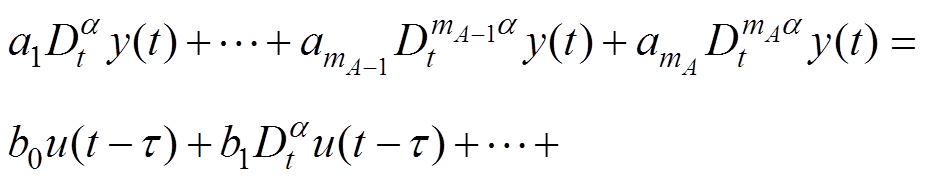
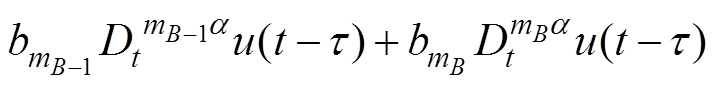 (12)
(12)
式中,y(t)为高速列车速度;u(t-t)为具有时滞效应的高速列车的牵引力。
记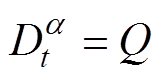 ,ak=kq(1,…, mA-1),则式(12)可变换为
,ak=kq(1,…, mA-1),则式(12)可变换为
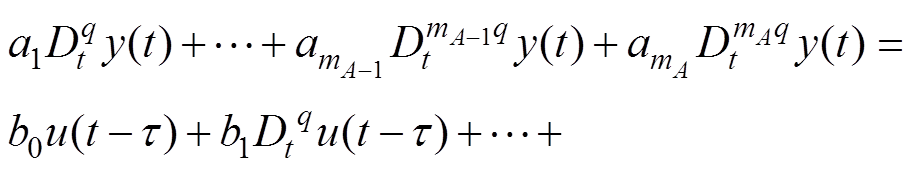
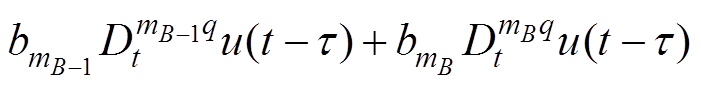 (13)
(13)
若1+…+mA-1+mA可逆,则有
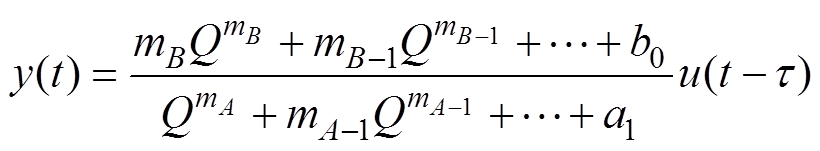 (14)
(14)
另记为
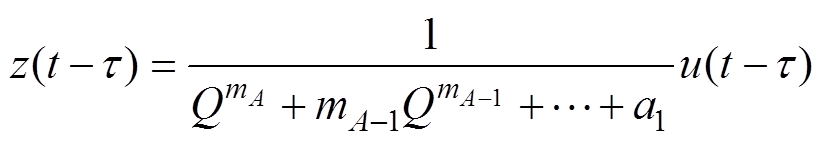 (15)
(15)
则有
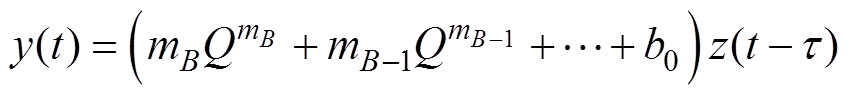 (16)
(16)
考虑噪声e对真实数据的影响,则式(16)可描述为
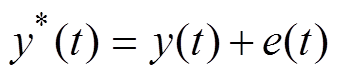 (17)
(17)
针对参数向量θ和无噪声输出y(t)之间的线性关系,有
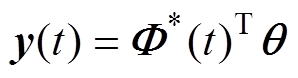 (18)
(18)
其中
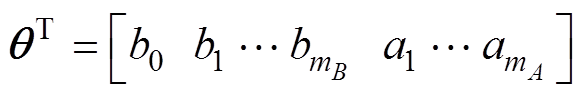 (19)
(19)
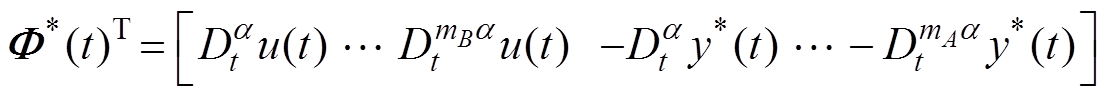 (20)
(20)
其误差为
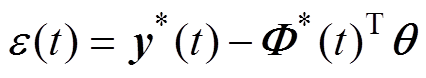 (21)
(21)
通过应用G-L型分数阶离散化模型,可以得到到带遗忘因子的分数阶递推最小二乘算法[19]为
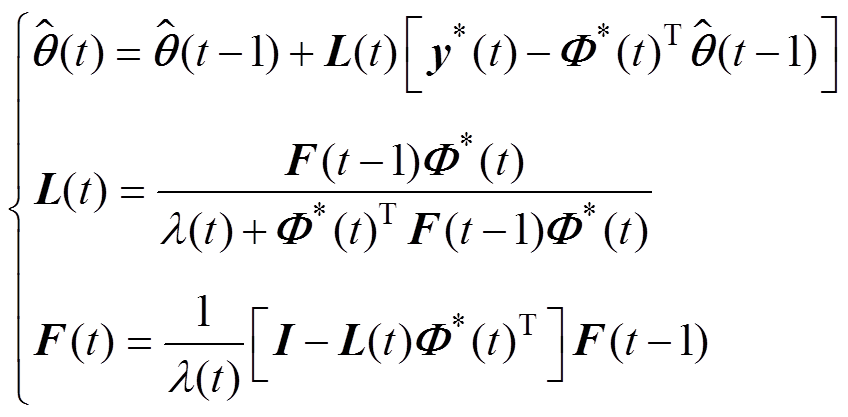 (22)
(22)
式中,l 为遗忘因子,通常取值范围为0.9~1.0;I为单位矩阵;F(0)=(104~1010)I。
本文以CRH380B型高速列车在京广高铁“北京西至郑州东区间段”(区间里程664.69 km)大功率操纵过程为研究对象,结合大量现场数据进行了对比性仿真实验,图5给出了高速列车真实的V-S曲线。图5中,点画线表示列车自动防护系统(Auto- matic Train Protection, ATP)限速。从图5可以看出,基于人工操纵策略得到的V-S曲线存在不稳定的波动,控车精度为13.1%,难以满足高速列车自动驾驶控制策略8%的多目标控车范围,这会导致能耗增加以及乘坐舒适性降低[13]。为了满足正点运营要求,高速列车全程采用大功率操纵策略贴着限速曲线运行,可能会使安全性指标下降。表3给出了CRH380B型高速列车主要参数。
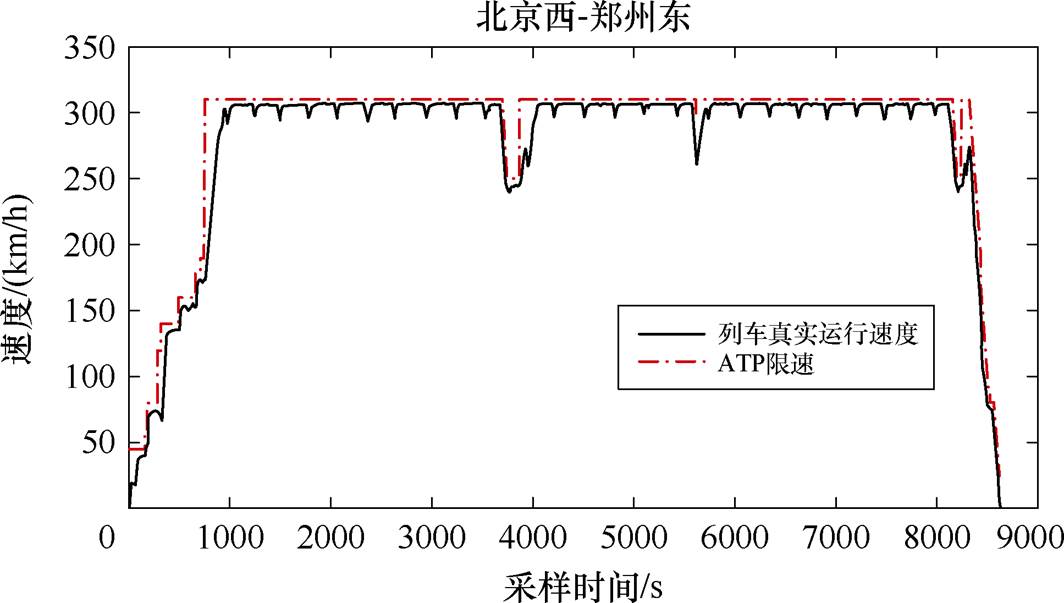
图5 高速列车大功率操纵过程速度曲线(ATP:限速曲线)
Fig.5 Actual speed curves of high speed train operation (ATP: speed limit curve)
表3 CRH380B型动车组主要参数
Tab.3 The main parameters of CRH380B high speed train

参数名称参数特性 列车总质量/t890 最大牵引功率/kW9 200 运营速度/(km/h)350 单位基本阻力/(N/kN)w=4.1+0.064 76v+0.001 008v2
通过分析CRH380B一个月的大量真实运行数据(15万组速度、限制速度、里程、牵引力/制动力、控制级位等运营数据和线路数据),根据式(1)和式(3),结合减法聚类算法,可得到高速列车大功率操纵过程编码规则如下:
(1)采集CRH380B型动车组在某日从北京西至郑州东现场数据,再将数据进行预处理,得到564组初始操纵策略。
(2)通过减法聚类算法对得到的初始操纵策略进行编码,将编码结果进行DBI指标分析,对应6个相对集中的工作区,其中心为
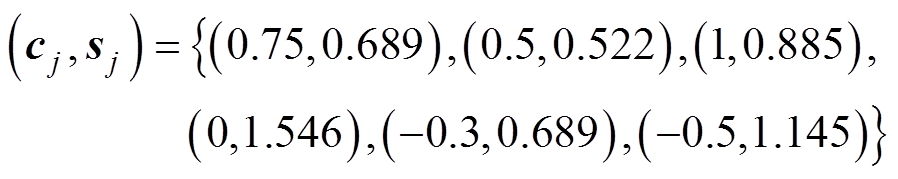
(3)基于得到的聚类中心点cj对精简的操纵策略进行分组。
(4)根据已分组后的每一组中的走行距离sj进行累加,得到82组精简的操纵策略(cj, sj),j= 1, 2,…, 82。
基于编码后的操纵策略,图6和图7分别给出了整数阶和分数阶操纵策略下机理模型预测的速度曲线。从图6中可以看出,基于大量现场数据得到的操纵策略在满足正点运行的要求下,预测的速度曲线在限速曲线以内波动,提高了高速列车大功率操纵过程的安全性。但在临时限速点附近,该方法由于采用最大牵引和最大制动策略,难以精准描述高速列车大功率操纵过程中能量缓慢释放的特性,预测的速度值会超过限速值,增加了安全隐患。
基于本文方法提出的分数阶操纵策略,图7得到的速度曲线不仅能满足速度曲线在限速曲线以内波动,还能在临时限速区间(200~300 km)精准描述能量缓慢释放的特性,提高列车在复杂动态运行环境下的安全性。从图5~图7的对比性分析中可以看出,相对人工驾驶和整数阶操纵策略,本文提出的分数阶操纵策略能够有效抑制速度大范围波动现象。相对高速列车大功率恒速持续运营基准指标(高速列车8%的基准线控车范围),本文提出的闭环结构下精准预测方法能够满足安全裕量在3.5%以内[13]。
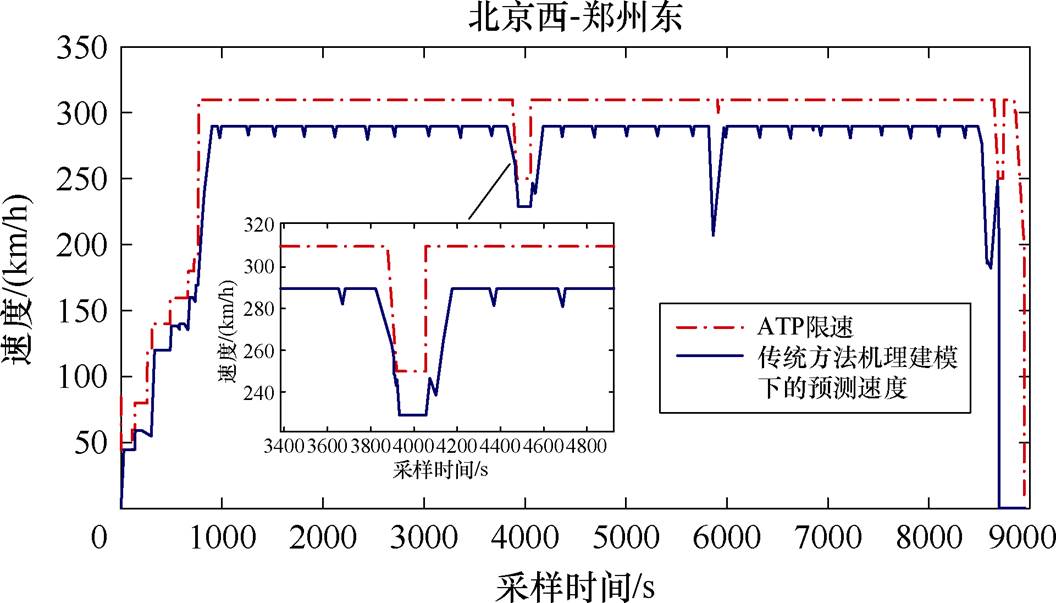
图6 整数阶操纵策略下机理建模预测的速度曲线
Fig.6 The speed curves with the traditional integer order model
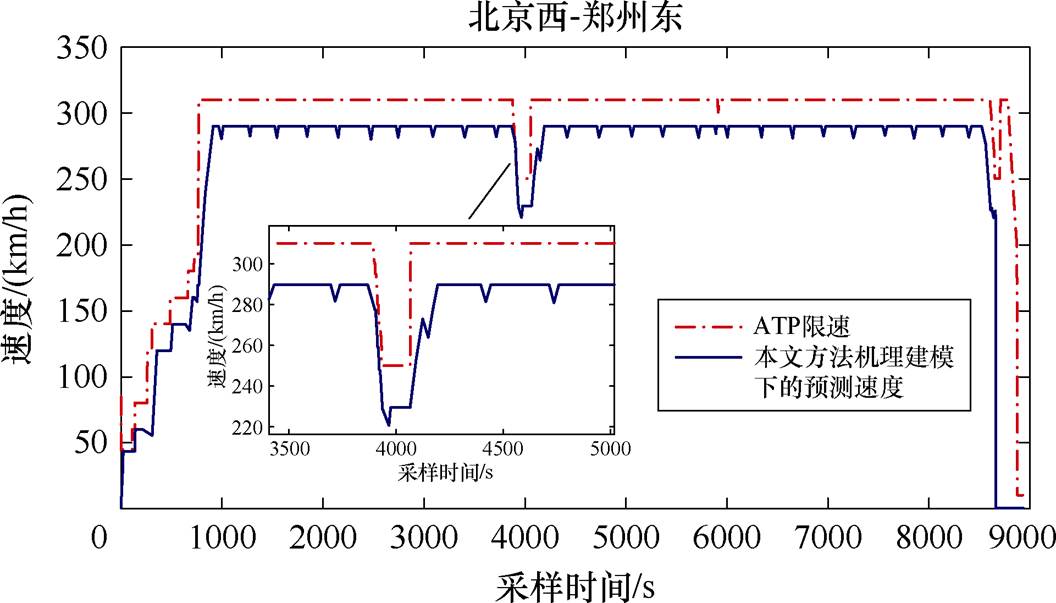
图7 分数阶操纵策略下机理建模预测的速度曲线
Fig.7 The speed curves with the fractional order model
图8和图9分别给出了整数阶操纵策略下机理建模与分数阶操纵策略下机理建模预测的加速度与牵引/制动力对比。从图8可以看出,本文方法分数阶操纵策略下的高速列车加速度变化率相比传统方法整数阶操纵策略下的高速列车加速度变化率更低,尤其是在限速骤降阶段,舒适度指标得到明显改善。从图9可以看出,采用分数阶操纵策略后,高速列车操纵过程所需要的牵引/制动力比整数阶操纵策略下的牵引/制动力小,从而有效降低了高速列车能耗。
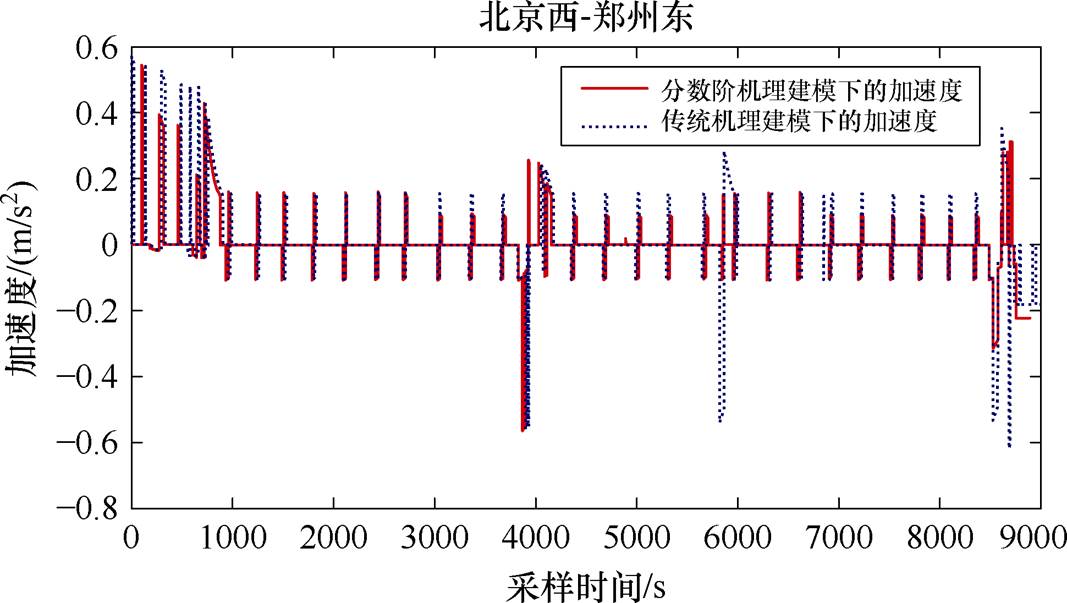
图8 整数阶与分数阶操纵策略下机理建模预测的加速度对比
Fig.8 The acceleration with the integer and fractional order model
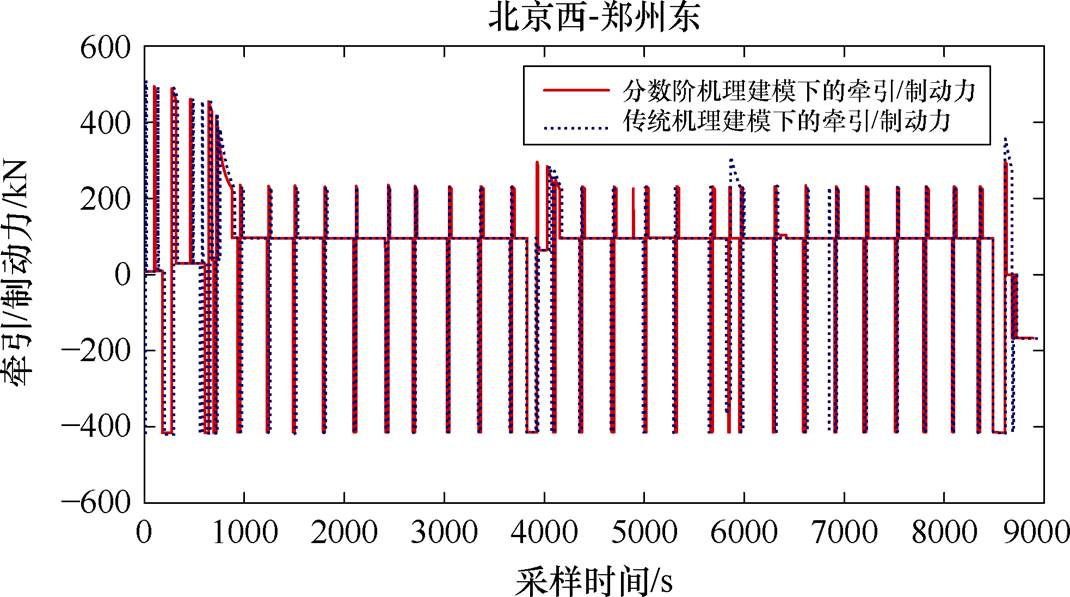
图9 整数阶与分数阶操纵策略下机理建模预测的牵引/制动力对比
Fig.9 The traction/braking forces with the integer and fractional order model
基于建立的分数阶最小二乘模型式(22),本次实验的采样周期为0.2 s,采样样本为8 626组,算法的初始条件设置为:mA=2,mB=1,l =0.99,F(0)= (104~1010)I。
表4给出了整数阶及分数阶最小二乘模型误差对比。从表4可以看出,分数阶阶次越大,方均根误差也越大。根据自控理论中对数频率特性十倍频程等价压缩性质可知,对于同一个高铁操纵系统,整数阶描述和分数阶具有等价的属性:当分数阶阶数大于0.35时,高速列车运行速度预测效果达不到整数阶效果,存在过拟合现象。从理论上来看,难以通过硬件来实现较小阶次下的速度微观描述,一般将分数阶最小二乘的阶次设定为0.2。
表4 整数阶与分数阶最小二乘模型误差对比
Tab.4 Integer order and fractional order least squares error comparison

整数阶0.02阶0.2阶0.3阶0.35阶0.36阶0.4阶 最大误差2.065 50.138 51.694 32.896 53.637 03.796 44.493 4 最小误差-3.726 1-0.057 6-0.702 8-1.230 8-1.557 8-1.642 1-1.964 9 方均根误差0.263 00.009 80.118 00.205 50.258 50.271 70.323 5
由文献[10]可知,可用二阶系统来描述高速列车大功率操纵过程,本文建立的分数阶最小二乘模型为

图10为分数阶操纵策略下数据驱动模型对应的速度预测及误差曲线。从图中可以看出,高速列车大功率操纵过程的速度预测正误差为1.69 km/h,最大的负误差为0.7 km/h。列车速度小于30 km/h时,正负预测误差在0.4 km/h;列车速度大于30 km/h,预测误差不超过列车速度的2%。相对图6和图7的机理模型预测效果,本文提出的建模方法可以更好地辨识出高速列车在非正常运行工况下模型突变参数,能更精准地描述高速列车能量缓慢释放及速度时滞预测特性。
图11分别描述了机理建模和数据驱动模型下的速度预测对比效果。从图11可以看出,机理建模对应的预测速度未超过限速曲线,但存在着明显的时滞现象。而基于数据驱动策略得到的预测速度不仅满足较高的预测精度和安全性,还能有效降低时滞长度。通过大量的仿真结果可知,时滞时间为64 s。
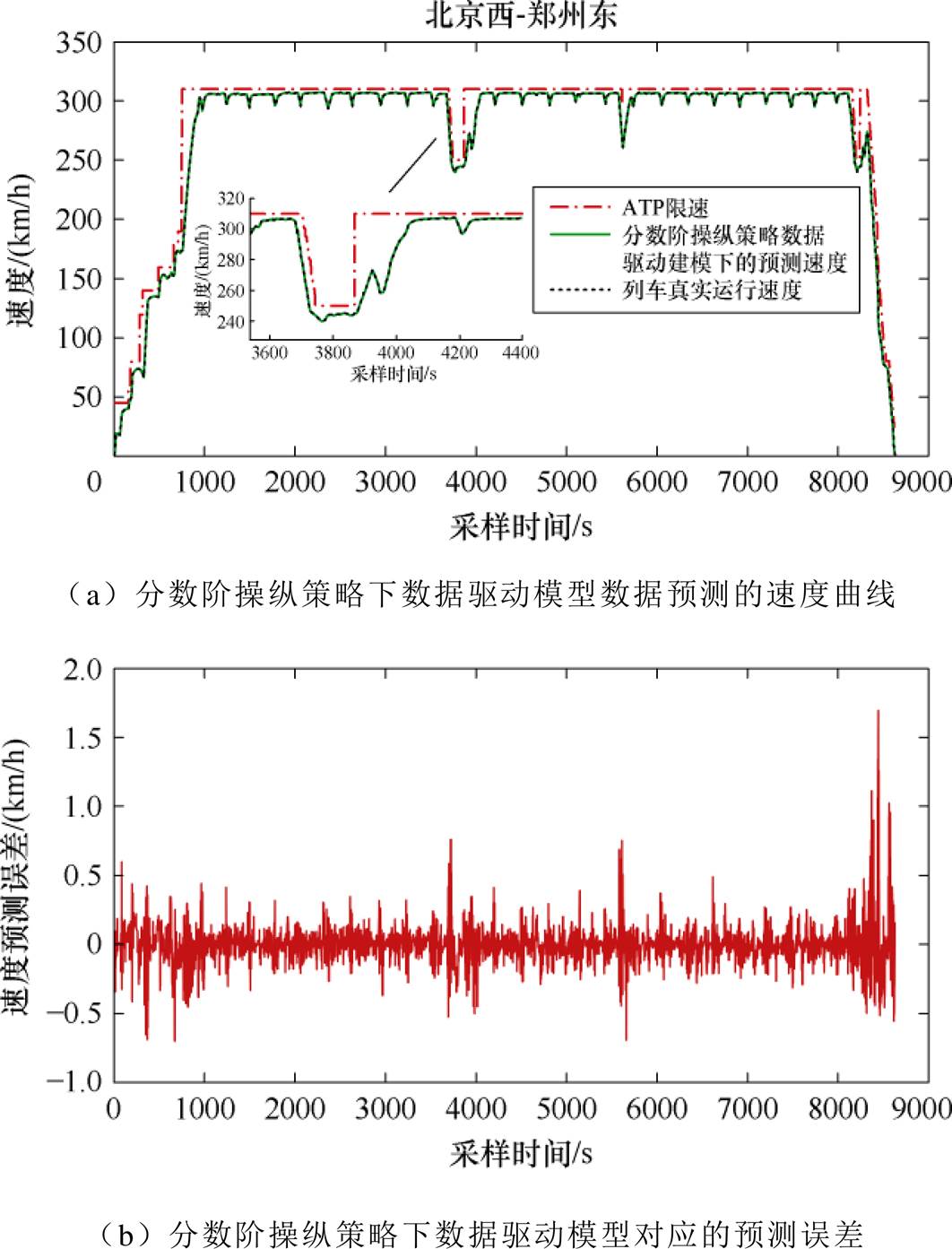
图10 分数阶操纵策略下数据驱动模型对应的速度预测及误差曲线
Fig.10 The speed and prediction error curves with the fractional order data-driven model
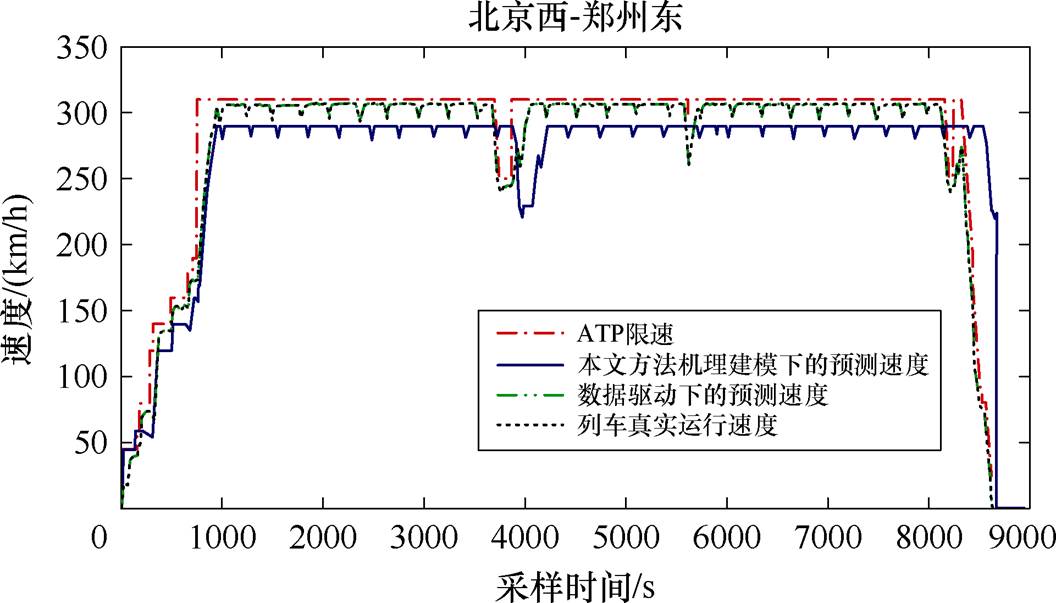
图11 分数阶机理建模、数据驱动建模对应的速度时滞效应对比
Fig.11 Speed delay comparison between the fractional order mechanism modeling and the corresponding data-driven modeling
本文针对高速列车大功率操纵过程时滞特性进行了分析,采用机理特性和数据驱动联合建模方法对不同操纵级位下的控制序列应用分数阶理论和减法聚类理论进行更为细致的划分,实现高速列车操纵过程运行参数精细化建模,分别使用了常规建模策略与分数阶最小二乘模型来描述不同操纵策略下列车速度时滞特性。基于真实数据的实验仿真结果表明,本文提出的方法能较好地满足高速列车大功率操纵过程的运营需求。
参考文献
[1] 谢国, 金永泽, 黑新宏, 等. 列车动力学模型时变环境参数自适应辨识[J]. 自动化学报, 2019, 45(12): 2268-2280.
Xie Guo, Jin Yongze, Hei Xinhong, et al. Adaptive identification of time-varying environmental para- meters in train dynamics model[J]. Acta Automatica Sinica, 2019, 45(12): 2268-2280.
[2] 赵牧天, 葛琼璇, 张波, 等. 高速磁悬浮牵引系统大功率三电平整流器特定谐波消除脉宽调制策略[J]. 电工技术学报, 2022, 37(16): 4180-4192.
Zhao Mutian, Ge Qiongxuan, Zhang Bo, et al. Selective harmonic elimination pulse width modu- lation for high power three-level rectifier of high-speed maglev traction system[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4180- 4192.
[3] 喻文倩, 刘志刚, 张友刚, 等. 一种改进的高铁牵引变流器反馈线性化控制策略[J]. 电工技术学报, 2023, 38(8): 2136-2147.
Yu Wenqian, Liu Zhigang, Zhang Yougang, et al. An improved feedback linearization control strategy for high-speed railway traction converters[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(8): 2136-2147.
[4] 张静, 宋宝林, 谢松霖, 等. 基于状态估计的高速受电弓鲁棒预测控制[J]. 电工技术学报, 2021, 36(5): 1075-1083.
Zhang Jing, Song Baolin, Xie Songlin, et al. Robust predictive control of high-speed pantograph based on state estimation[J]. Transactions of China Electro- technical Society, 2021, 36(5): 1075-1083.
[5] 皇甫海文, 蔡盼盼, 李庆来. 真空管道磁浮列车三电平中点钳位整流器的改进型模型预测控制研究[J]. 电气技术, 2021, 22(6): 28-35.
Huangfu Haiwen, Cai Panpan, Li Qinglai. Research on improved model predictive control of three-level neutral point clamped rectifier for vacuum pipeline maglev train[J]. Electrical Engineering, 2021, 22(6): 28-35.
[6] 王艺楠, 孟令云, 龙思慧, 等. 高速铁路列车区间故障条件下列车运行调整优化模型[J]. 电气技术, 2019(增刊1): 9-16.
Wang Yinan, Meng Lingyun, Long Sihu, et al. An optimization model of train operation adjustment plan under the condition of train section failure in high- speed railway[J]. Electrical Engineering, 2019(S1): 9-16.
[7] 晏益朋, 余城洋, 熊露婧, 等. 一种基于离散时域模型的单相PWM整流器控制参数多目标优化设计方法[J]. 电工技术学报, 2024, 39(1): 206-216.
Yan Yipeng, Yu Chengyang, Xiong Lujing, et al. A multi-objective controller parameter design optimi- zation method of single-phase PWM rectifierwith discrete-time domain model[J]. Transactions of China Electrotechnical Society, 2024, 39(1): 206-216.
[8] 尹杰, 刘博, 孙国兵, 等. 基于迁移学习和降噪自编码器-长短时间记忆的锂离子电池剩余寿命预测[J]. 电工技术学报, 2024, 39(1): 289-302.
Yin Jie, Liu Bo, Sun Guobing, et al. Transfer learning denoising autoencoder-long short term memory for remaining useful life prediction of Li-ion batteries[J]. Transactions of China Electrotechnical Society, 2024, 39(1): 289-302.
[9] 方德宇, 楚潇, 刘涛, 等. 基于数据-模型驱动的锂离子电池健康状态估计[J]. 电气工程学报, 2022, 17(4): 20-31.
Fang Deyu, Chu Xiao, Liu Tao, et al. Research on health assessment method of Lithium-ion battery based on data-model hybrid drive[J]. Journal of Electrical Engineering, 2022, 17(4): 20-31.
[10] 谭畅, 李毅清. 具有输入时滞特性的列车自适应制动控制[J]. 铁道科学与工程学报, 2022, 19(4): 1071-1080.
Tan Chang, Li Yiqing. Adaptive braking control for high-speed trains with input time delays[J]. Journal of Railway Science and Engineering, 2022, 19(4): 1071- 1080.
[11] Yang Hui, Liu Hongen, Fu Yating. Multi-objective operation optimization for electric multiple unit-based on speed restriction mutation[J]. Neurocomputing, 2015, 169: 383-391.
[12] 高士根, 董海荣, 朱海楠. 面向操纵优化的智能列车辅助驾驶系统[J]. 铁道学报, 2019, 41(11): 88-94.
Gao Shigen, Dong Hairong, Zhu Hainan. Intelligent driver advisory system for improving manual train driving performance[J]. Journal of the China Railway Society, 2019, 41(11): 88-94.
[13] Yang Hui, Zhang Kunpeng, Liu Hongen. Online regulation of high speed train trajectory control based on T-S fuzzy bilinear model[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(6): 1496-1508.
[14] 孙国强, 任佳琦, 成乐祥, 等. 基于分数阶阻抗模型的磷酸铁锂电池荷电状态估计[J]. 电力系统自动化, 2018, 42(23): 57-63.
Sun Guoqiang, Ren Jiaqi, Cheng Lexiang, et al. State of charge estimation of LiFePO4 battery based on fractional-order impedance model[J]. Automation of Electric Power Systems, 2018, 42(23): 57-63.
[15] 戚壮, 王晓雷, 莫荣利, 等. 分数阶修正的空气弹簧气动力学模型及其应用[J]. 铁道学报, 2021, 43(4): 67-76.
Qi Zhuang, Wang Xiaolei, Mo Rongli, et al. Air spring modeling and vehicle dynamics analysis based on fractional calculus theory[J]. Journal of the China Railway Society, 2021, 43(4): 67-76.
[16] 陈彬, 秦小彬, 万妮娜, 等. 基于R-L型分数阶导数与损耗统计理论的铁磁材料高频损耗计算方法[J]. 电工技术学报, 2022, 37(2): 299-310.
Chen Bin, Qin Xiaobin, Wan Nina, et al. Calculation method of high-frequency loss of ferromagnetic materials based on R-L type fractional derivative and loss statistical theory[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 299-310.
[17] Duhé J F, Victor S, Melchior P, et al. Recursive system identification for coefficient estimation of continuous-time fractional order systems[J]. IFAC- PapersOnLine, 2021, 54(7): 114-119.
[18] 戈萌, 宋琦, 胡鑫睿. 高速列车非线性系统的分数阶有限时间控制器设计[J]. 自动化学报, 2021, 47(7): 1672-1678.
Ge Meng, Song Qi, Hu Xinrui. Design of a fractional- order finite-time controller for high-speed train with uncertain model and actuator failures[J]. Acta Auto- matica Sinica, 2021, 47(7): 1672-1678.
[19] Albrecht A, Howlett P, Pudney P, et al. The key principles of optimal train control: part 1: formulation of the model, strategies of optimal type, evolutionary lines, location of optimal switching points[J]. Transportation Research Part B: Methodological, 2016, 94: 482-508.
[20] 应沛然, 曾小清, 沈拓, 等. 基于冗余工序编码的高速列车节能驾驶智能算法[J]. 吉林大学学报 (工学版), 2023, 53(12): 3404-3414.
Ying Peiran, Zeng Xiaoqing, Shen Tuo, et al. Redundant operation code-based intelligent algorithm for energy? efficient driving of high-speed train[J]. Journal of Jilin University (Engineering and Technology Edition), 2023, 53(12): 3404-3414.
[21] 杨辉, 刘鸿恩, 李中奇. 动车组追踪运行多目标实时优化策略[J]. 控制工程, 2015, 22(2): 257-261.
Yang Hui, Liu Hongen, Li Zhongqi. Multi-objective real-time optimization strategy for electric multiple units tracking[J]. Control Engineering of China, 2015, 22(2): 257-261.
[22] 严细辉, 蔡伯根, 宁滨, 等. 基于差分进化的高速列车运行操纵的多目标优化研究[J]. 铁道学报, 2013, 35(9): 65-71.
Yan Xihui, Cai Baigen, Ning Bin, et al. Research on multi-objective high-speed train operation optimi- zation based on differential evolution[J]. Journal of the China Railway Society, 2013, 35(9): 65-71.
Abstract The high-power control process of high-speed trains is a complex dynamic system. As the speed of high-speed trains increases, the interactive dynamics among the vehicle, wheel, rail, and grid become frequent. Traditional modeling methods ignore these strong nonlinear differences and only give a single-speed forecasting result at a large spatial scale. It is insufficient to fully describe the micro-changes in the train high-power control process. Recently, some methods have been presented to forecast the time-delay characteristics of high-speed trains. However, most need to consider the common structural characteristics shared by the mechanism and the data-driven models. This paper proposes a fractional modeling strategy to meet the requirements of safe and stable operation of high-speed trains under step-less speed regulation. By learning the optimal control strategy from historical speed and power data, the local train speed for multiple operation scenarios can be forecasted accurately.
Firstly, the time-delay characteristics of high-power traction and braking systems are analyzed based on the features of large inertia and driver reaction time. Secondly, a simplified and redundant process coding strategy for train control strategy is constructed to accurately predict speed time-delay characteristics from the perspective of closed-loop control. Then, a new fractional-order modeling method is proposed, and the fractional-order least squares algorithm is designed to identify the time-varying parameters in the model.
Simulation results on the actual high-speed train operation data show that the V-S (velocity-distance) curve based on the manual control strategy has unstable fluctuations. The control accuracy is 13.1%, which is difficult to meet the multi-objective control range of 8% of the high-speed train automatic driving control strategy, increasing energy consumption and reducing ride comfort. On the other hand, the proposed fractional-order control strategy can effectively reduce the wide range of speed fluctuations. Compared with the benchmark index of high-speed train continuous operation with high power and constant speed, the proposed precision prediction method under the closed-loop structure can meet the safety margin within 3.5% and the control range within 8%. According to the ten-octave equivalent compression property of logarithmic frequency characteristics in automatic control theory, the integer order description and fractional order have equivalent properties for the same high-speed train control system. When the fractional order number is greater than 0.35, the high-speed train speed prediction cannot reach the integer order, and the overfitting effect occurs. Theoretically, realizing the micro speed prediction with a small order is difficult under the current computation power. As a result, the order of fractional least squares is generally set to 0.2.
The following conclusions can be drawn from the simulation analysis. (1) The time-delay characteristics of the high-power control process of high-speed trains are given, and the fine modeling of the operating parameters of the high-speed train control process is realized. (2) The simulation results based on real data show that the proposed method can meet the operational requirements of high-power control of high-speed trains.
keywords:High-speed train, high power control process, data-driven, time delay, fractional-order least squares algorithm
DOI: 10.19595/j.cnki.1000-6753.tces.231668
中图分类号:TM922
国家自然科学基金项目(U2034211, 62063007)、江西省自然科学基金项目(20224BAB212021, 20232BAB202029)、江西省教育厅项目(GJJ200610, GJJ210647)和流程工业综合自动化国家重点实验室联合开放基金项目(2022-KF-21-03)资助。
收稿日期 2023-10-10
改稿日期 2023-11-28
张坤鹏 男,1986年生,博士,硕士生导师,研究方向为电气化轨道交通控制。E-mail: ecjtu.zhangkunpeng@163.com(通信作者)
严 斐 男,1998年生,硕士研究生,研究方向为高速列车运行过程控制。E-mail: yf2930135179@163.com
(编辑 崔文静)