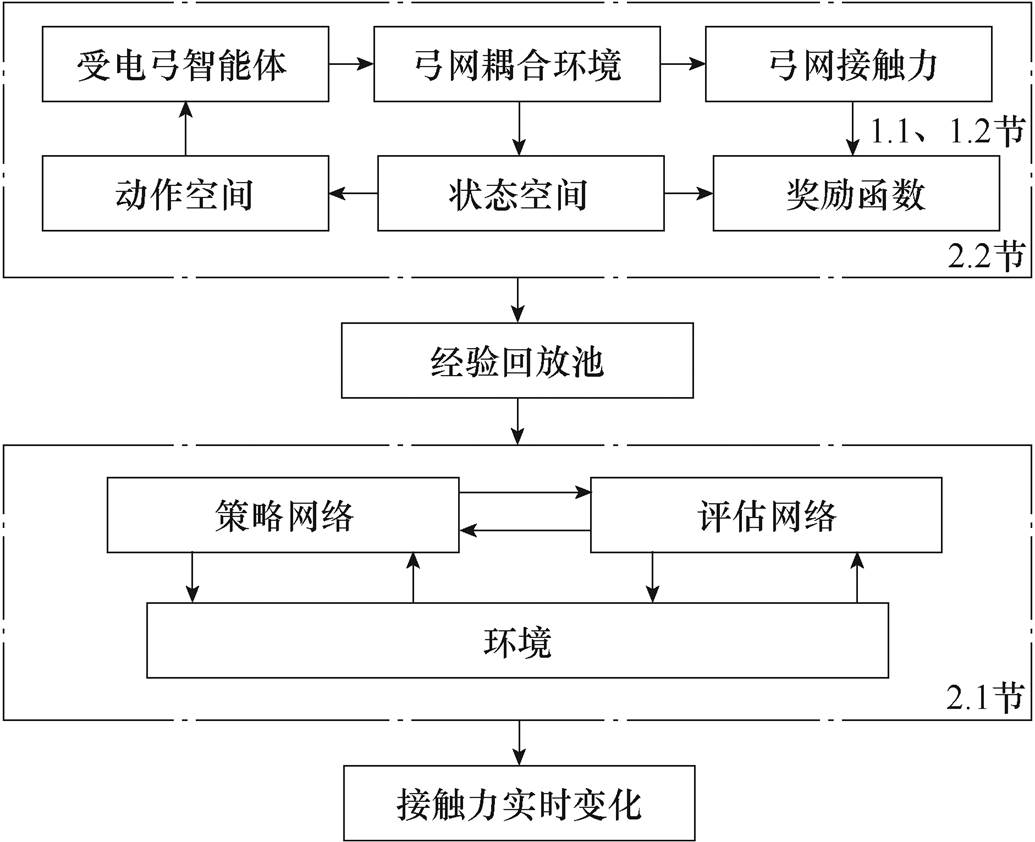
图1 受电弓主动控制框架
Fig.1 Pantograph active control frame
摘要 弓网系统耦合性能对于高速列车受流质量起着至关重要的作用，提高弓网耦合性能，一种有效的方法是针对受电弓进行主动控制调节，特别是在低速线路提速及列车多线路混跑时，主动控制可通过提高弓网自适应适配性，有效降低线路改造成本并提升受流质量。针对受电弓主动控制问题，该文提出一种基于双延迟深度确定性策略梯度（TD3）的深度强化学习受电弓主动控制算法。通过建立弓网耦合模型实现深度强化学习系统环境模块，利用TD3作为受电弓行为控制策略，最终通过对控制器模型训练实现有效的受电弓控制策略。实验结果表明，运用该文方法可有效提升低速线路列车高速运行时弓网耦合性能及受电弓在多线路运行时的适应性，为铁路线路提速及列车跨线路运行提供新的思路。
关键词：低速线路 混跑 双延迟深度确定性策略梯度（TD3） 受电弓主动控制
受电弓与接触网间的稳定耦合是高速铁路列车安全运行的基础[1]，随着高速铁路列车运行速度的提升，弓网离线、燃弧等都会影响弓网性能，导致列车的受流质量降低[2]；铁路提速时，为实现高速条件下的弓网匹配，接触网系统的更新改造会涉及大量资金投入。因此，如何小成本条件下实现弓网性能提升成为行业亟须解决的难题。
提高弓网受流质量目前主要有三种方法：①接触网全线升级改造，但接触网改造会消耗大量的资金和时间并造成铁路运输中断；②受电弓结构优 化[3]，但受物理条件约束，优化效果有限；③相比接触网改造和受电弓结构优化，更有竞争力的做法是通过受电弓主动控制，实现受电弓分段实时调节，从而更好地实现弓网匹配。
对于受电弓主动控制来说，主要研究包括：滑模变结构控制[4]、模糊PID控制[5]、最优控制[6]、模型预测控制[7]、鲁棒预测控制[8]。上述研究虽然获得一定效果，但少有实际应用，主要原因在于：①控制算法本身限制，如PID类控制器固有的调节滞后性与超调、滑模控制需要设计系统切换超平面、线型二次型调节器（Linear Quadratic Regulator, LQR）类控制器的增益矩阵需要复杂的计算和多次的参数寻优等；②当前控制算法自适应性主要解决算法参数自适应选取，对于线路条件变化和外部扰动造成的影响研究较少。针对上述问题，焦宇韦等[9]提出基于悬链线先验信息的神经网络滑模主动控制策略，通过滑模控制与神经网络的结合而产生的主动控制器，对受电弓弓头的位移误差进行训练和学习，使受电弓与接触线的位移可以更好地匹配，但是其训练和学习得到的主动控制器只能运用于固定的线路和受电弓弓头。
近年来，深度强化学习[10]逐渐成为研究热点，在机器人控制[11]、游戏对战[12]、人机交互[13]和混动汽车能量管理[14]等方面获得广泛应用。深度强化学习中，智能体与环境模型进行交互，策略函数对智能体进行行为选择，价值函数对行为进行判断，最后通过奖励函数来决定奖惩的大小并调整控制策略。其本质是通过大数据驱动循环试错的方式实现控制策略优化。深度强化学习技术为受电弓主动控制提供了全新的思路。
本文通过双延迟深度确定性策略梯度（Twin Delayed Deep Deterministic Policy Gradient, TD3）学习机制进行受电弓主动控制，实现了低速线路下列车高速运行及多线路混跑条件下的弓网性能优化，为节省线路改造投资、优化受流性能提供了可行方案。本文研究控制框架如图1所示。
图1 受电弓主动控制框架
Fig.1 Pantograph active control frame
强化学习的理念是通过智能体（agent）与环境（environment）进行交互，通过反复试错自动调整控制器的策略。
强化学习常用方法包括深度Q学习（Deep Q Learning, DQN）、柔性动作-评价（Soft Actor-Critic, SAC）、确定性策略梯度（Deterministic Policy Gradient, DPG）、深度确定性策略（Deep Deterministic Policy Gradient, DDPG）、双延迟深度确定性策略梯度（TD3）等算法[15]。其中，TD3算法[16]在连续控制领域有很好的控制效果，相较于其他算法有更加优秀的决策能力[17]，因此本文采用TD3强化学习算法。
1.1.1 算法结构
TD3算法采用AC（actor-critic）算法网络框 架[18]，在基于DDPG的基础上模仿DQN学习思想，其整体网络结构如图2所示。
在TD3中，受电弓智能体的目标是寻找f 参数下的最优策略pf，可以使收益最大化，采用此策略后的状态转移和动作选择的受电弓智能体获得的收益R。网络结构中的优化器使用Adam优化算法[19]，可以减少数据中的噪声。
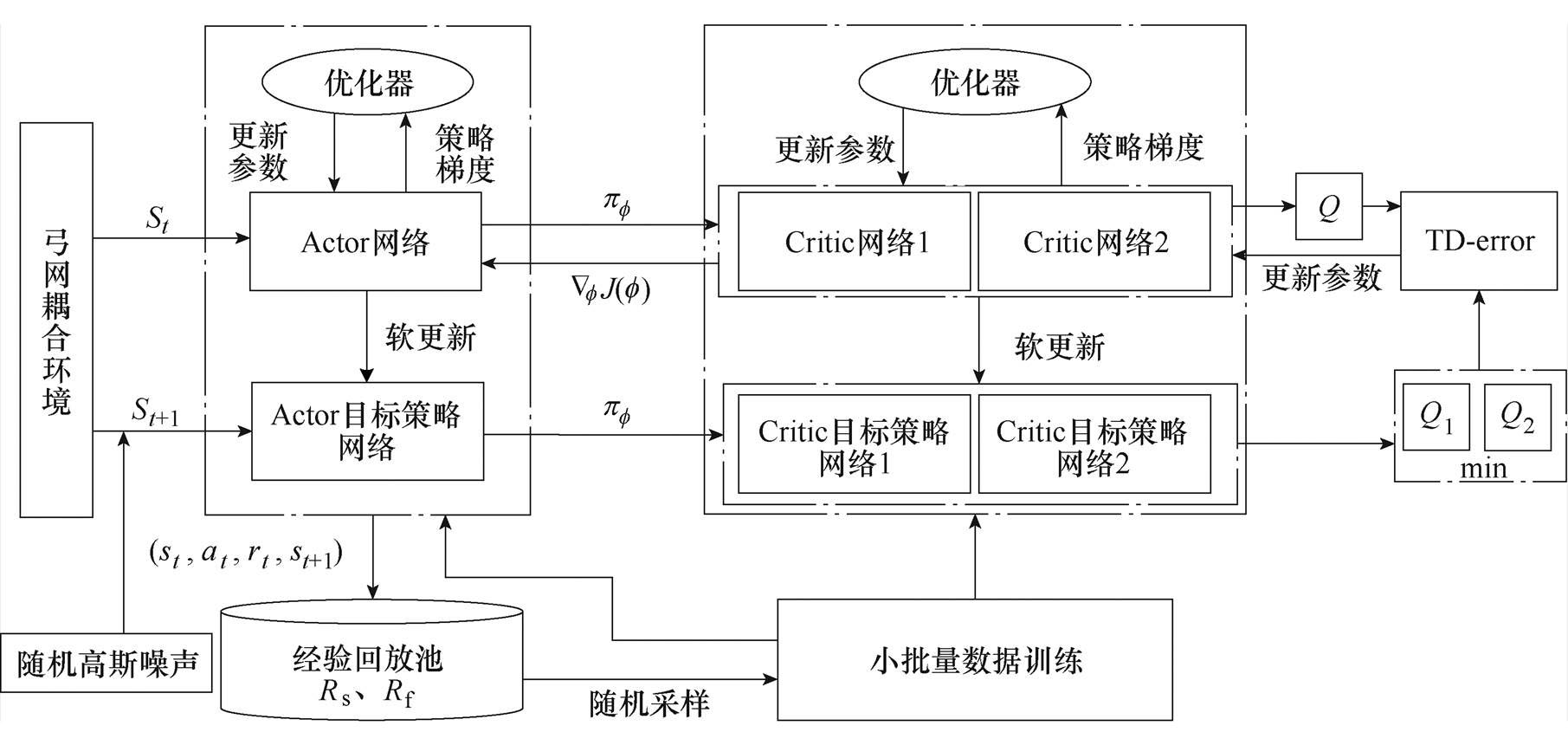
图2 TD3网络结构
Fig.2 TD3 network structure
（1）策略网络。图2中包含两个策略网络，Actor网络和Actor目标策略网络，策略函数Actor通过确定性策略梯度算法进行更新，有
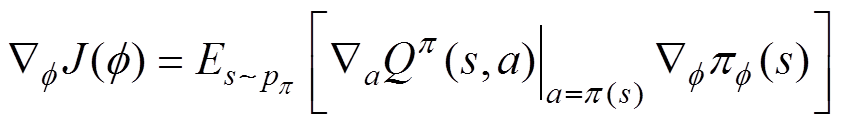（1）
其中
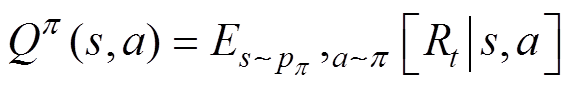
式中，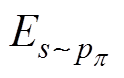
为期望收益在受电弓状态s下遵循 p策略所作出动作a的预期收益；
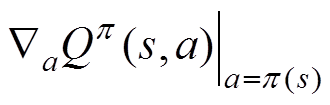为动作a在遵循策略
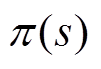时的Q值函数梯度；
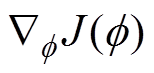表示梯度函数来源于Actor网络；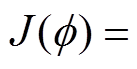
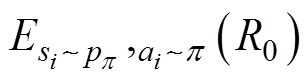表示收益函数对策略进行估值，计算了采用此策略后的状态转移与动作选择所获得的收益期望R0；
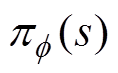为状态s下的最优策略，参数为f；
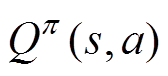为估值函数；
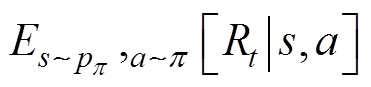为期望收益在受电弓在状态s下遵循p 策略所作出动作a的预期收益。
（2）评估策略网络。图2中评估策略网络Critic网络和Critic目标策略网络的评估函数基于贝尔曼方程式进行延迟学习，有
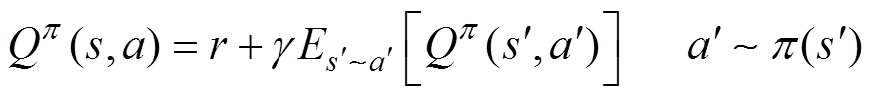（2）
式中，(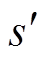
, 
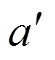) 为受电弓的下一时刻的状态和动作；r为训练样本当前时刻的奖励值；
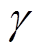为折扣因子。
为了减少网络中双Q值学习时出现的高估偏差问题，选用两个估值网络中高估更少的作为估计值。双Q学习为
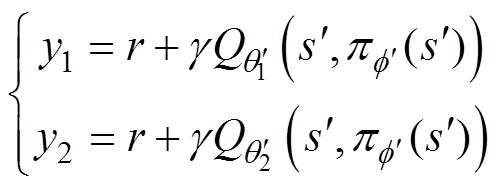（3）
估计值为
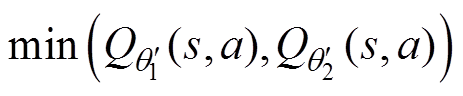（4）
式中，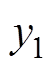
、
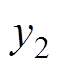为第一、二次训练样本的目标Q值；
、
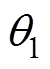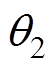分别为第一、第二个Critic评估网络参数；
、
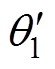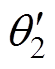分别为第一、第二个Critic目标评估网络参数；
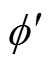为Actor目标策略网络参数。
对于Q1和Q2网络，定义损失函数为
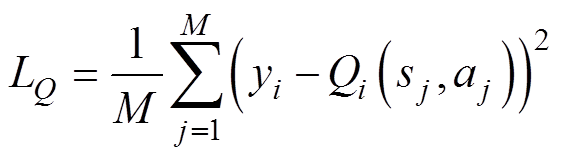（5）
式中，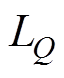
为损失函数；
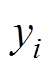为受电弓训练时的目标Q值；
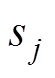为第j次训练时的状态信息；
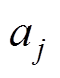为第j次训练时受电弓采取的运动状态。
通过损失函数逆向传播算法可以得到Q1和Q2网络参数，其中时间差分（Temporal Different, TD）的目标值y为
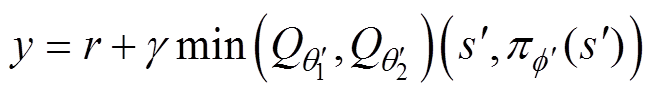（6）
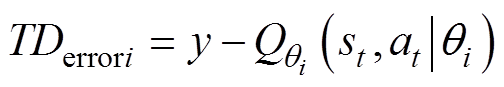（7）
式中，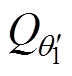
、
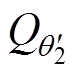分别为第一、第二个Critic目标评估网络；
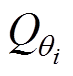为第i个Critic评估网络；
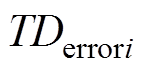为第i个网络Critic评估网络的TD误差。
为缓解确定性策略中出现的估值函数过拟合问题，可在目标策略网络中加入一个高斯随机噪声，有
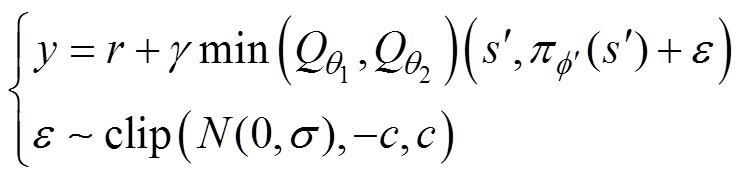（8）
式中，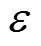
为高斯噪声；c为策略平滑噪声的截断边界值；clip函数表示截断函数。
为了保证在策略更新前将估计误差降低，策略网络的更新频率应该低于评估网络，所以采用一种软更新策略，有
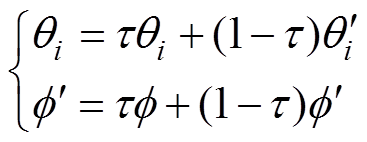（9）
式中，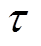
为软更新率；
、
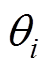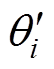分别为第i个Critic评估网络和Critic目标评估网络参数；
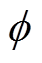为Actor策略网络参数。
1.1.2 算法流程
初始化经验回放池Rs、Rf，策略网络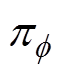
，Critic网络1、网络2，并将参数赋值给目标策略网络
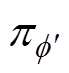和目标Critic目标策略网络1、网络2。
通过策略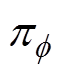得到受电弓动作并根据式（8）给行为加入高斯随机噪声，获取受电弓耦合环境的初始状态s。根据当前策略和探索噪声，获得行为a，执行行为a，获得回报r和下一个状态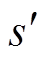。将其状态转换序列存储在经验回放池中Rs、Rf，并以di和1-di的比例抽取，作为策略网络的训练数据。数据y根据式（6）计算，根据式（5）更新Q1和Q2网络参数。
最后根据式（1）计算样本策略梯度，更新策略梯度，根据式（9）更新Actor目标策略网络，Critic目标策略网络1、网络2。最终输出最优策略网络参数和最优策略。
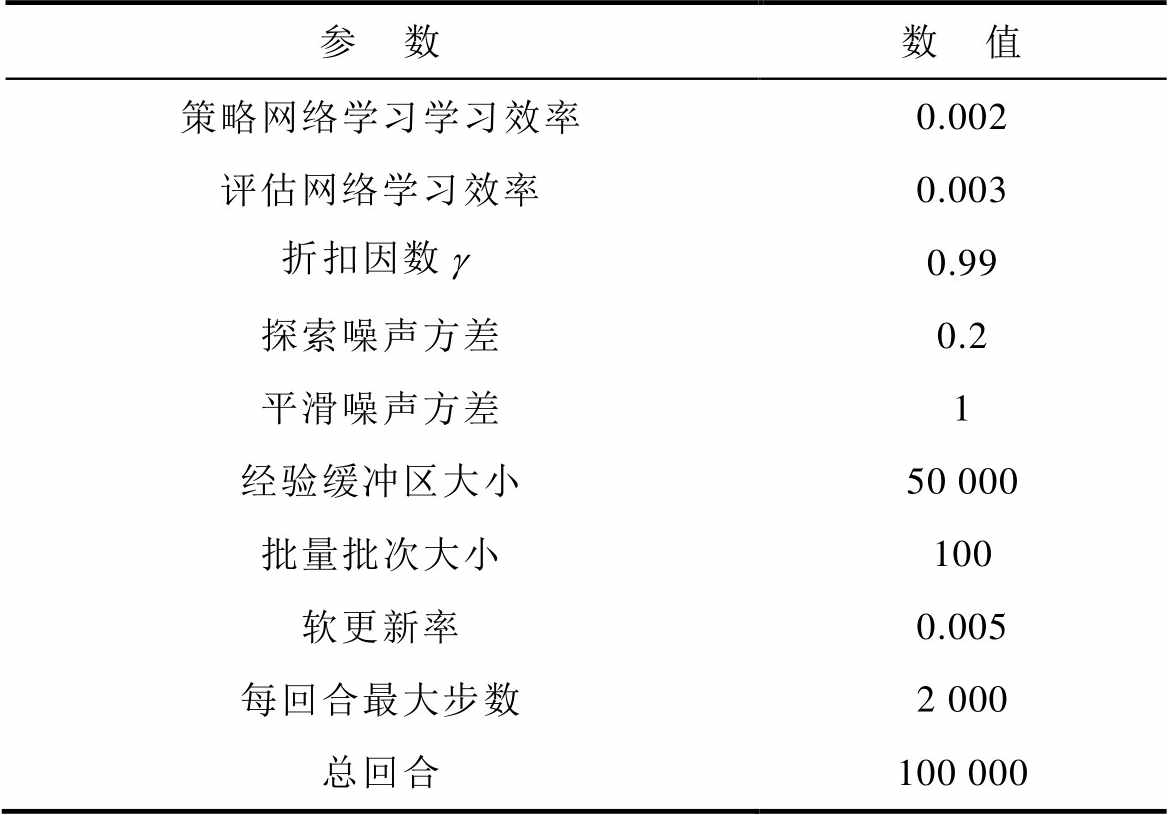
基于TD3受电弓主动控制的强化学习网络参数见表1。
表1 TD3参数设置
Tab.1 TD3 parameter settings
参 数数 值 策略网络学习学习效率0.002 评估网络学习效率0.003 折扣因数0.99 探索噪声方差0.2 平滑噪声方差1 经验缓冲区大小50 000 批量批次大小100 软更新率0.005 每回合最大步数2 000 总回合100 000
为了更好地保障受电弓耦合模型的准确性、泛化能力，构造弓网耦合模型的状态空间、动作空间和奖励函数。
弓网状态：受电弓弓头速度、加速度、位移等设置状态空间为
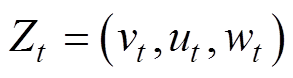（10）
式中，Zt为t时刻受电弓状态；vt为t时刻受电弓垂向速度；ut为t时刻受电弓垂向加速度；wt为t时刻受电弓垂向位移。
受电弓动作响应：由受电弓底部气囊控制受电弓升降，以气囊压力变化率作为动作空间设置条件设置动作空间为
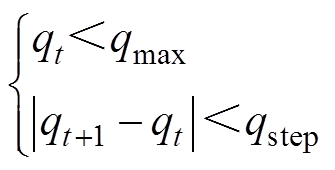（11）
式中，qt为t时刻气囊的压力变化率；qmax为气囊压力变化率的最大值；qt+1为t+1时刻的气囊压力变化率；qstep为step时刻气囊压力变化率。
弓网智能体获得奖励：接触压力过大或过小获得负奖励信号，压力在正常范围内获得正奖励信号。
训练结束条件：接触力稳定在一定范围内结束当前回合。设置奖励函数为
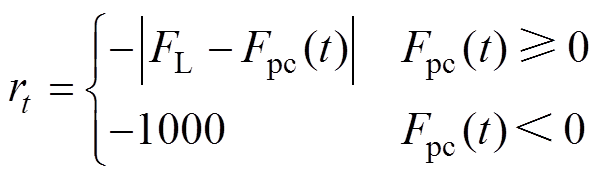（12）
式中，rt为t时刻的奖励；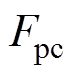
为弓网接触压力；
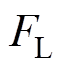为受电弓的抬升力。
为生成深度强化学习训练所需数据并获得控制策略响应的反馈，需要构建弓网耦合模型作为深度强化学习的环境（environment）模块。其中，本文所建立的模型是来自宋洋等[20]建立的弓-网模型，此模型已通过欧洲标准EN50318[21]的验证。
为提高模型训练速度并显示表征受电弓特性，本文采用受电弓三质量块归算模型[22]，如图3所示。
根据动力学平衡方程，受电弓模型为
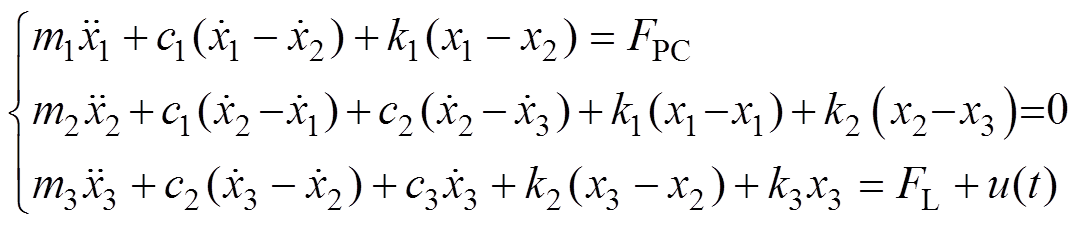（13）
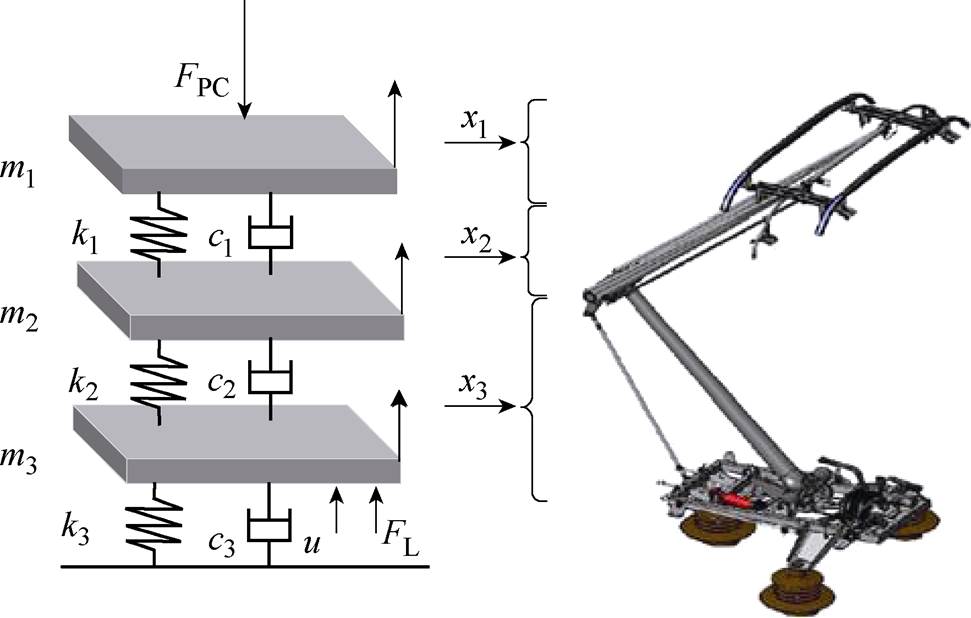
图3 受电弓三质量块模型
Fig.3 Pantograph three-mass model
式中，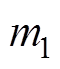
、
、
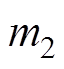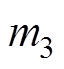分别为受电弓弓头、上框架、下框架的等效质量；
、
、
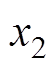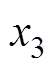为垂向位移；
、
、
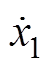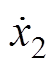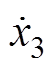为垂向速度；
、
、
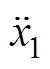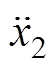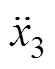为垂向加速度；
、
、
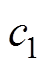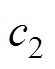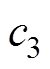为等效阻尼；
、
、
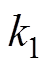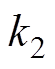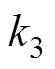为等效刚度；u为主动控制力。受电弓可通过调节气囊压力获得抬升力FL变化。
接触网模型本文主要采用基于非线性杆/索有限单元法[23]，如图4所示。图4b为空间Ig、Jg两点间的非线性杆单元受力分析，Fg1、Fg2、Fg3、Fg4、Fg5和Fg6为杆两端的所受的力，Lg0为杆的长度，Lgx、Lgy、Lgy为沿x、y、z方向的距离。图4c为空间I、J两点间的非线性索单元受力分析，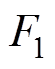
、
、
、
、
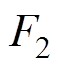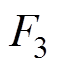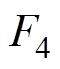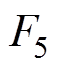和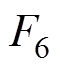
为索两端的所受的力，
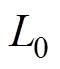为索的长度，lx、ly、lz为沿x、y、z方向的距离。
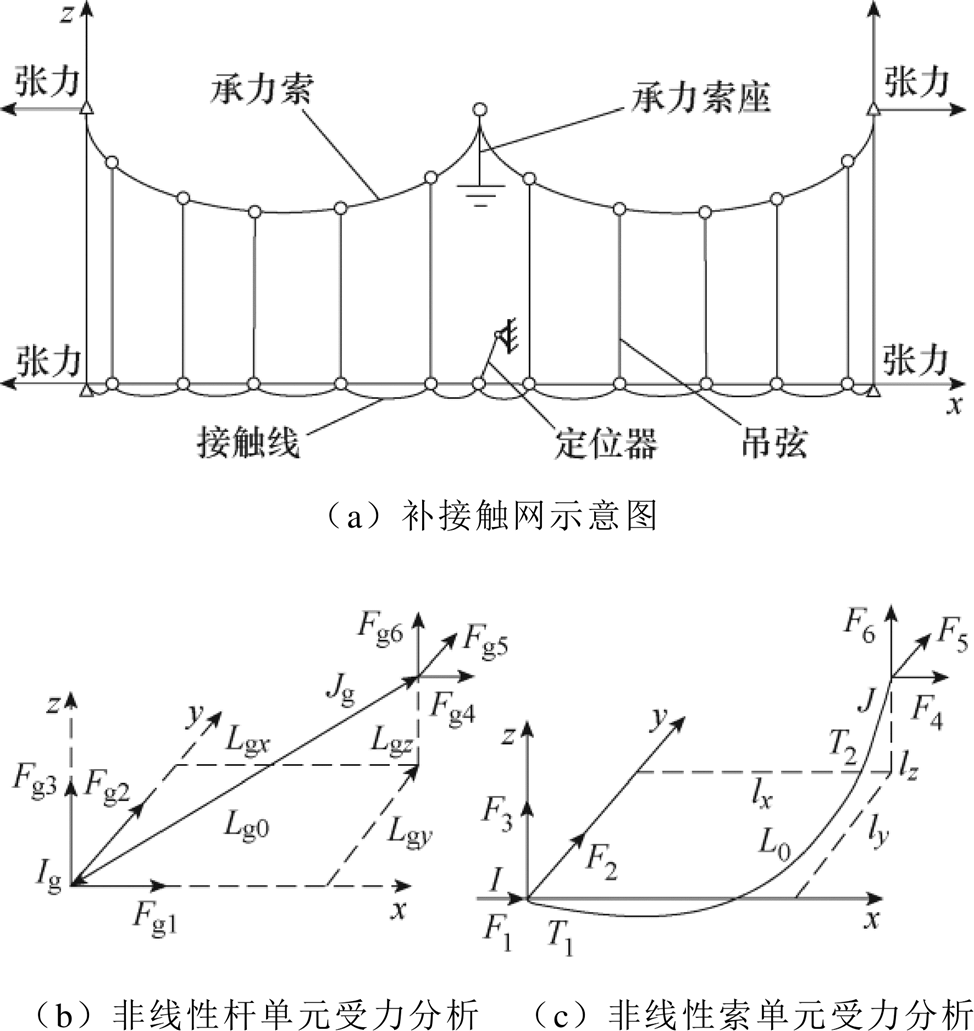
图4 接触网模型
Fig.4 Catenary model
通过节点受力分析，得到接触网方程为
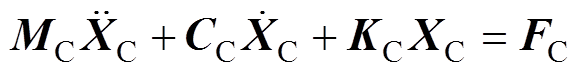（14）
式中，MC、CC、KC分别为接触网质量矩阵、阻尼矩阵和刚度矩阵；
、
、
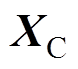分别为加速度、速度和位移；
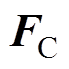为接触网所受外力矩阵。
由1.1节和1.2节公式以及设三质量块位移矩阵为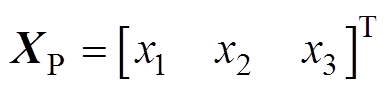
，可以得到完整的弓网系统方程为
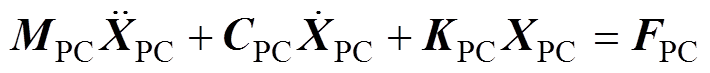（15）
其中
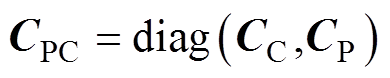
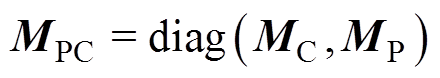
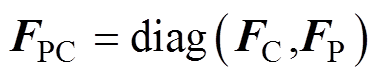
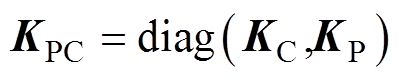
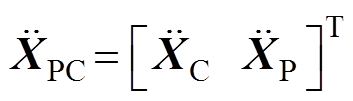
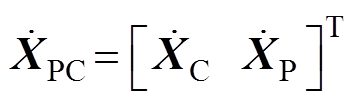
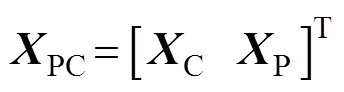
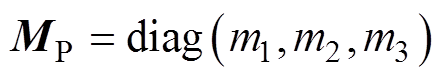
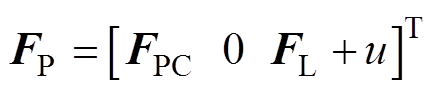
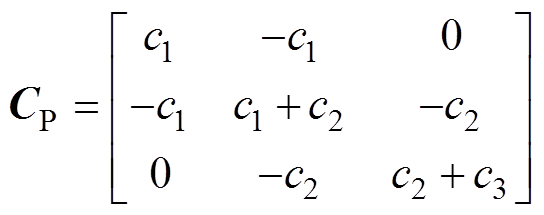
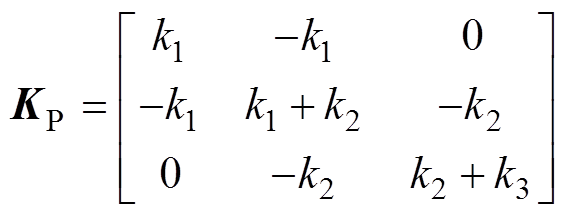
式中，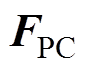
为弓网接触压力矩阵；
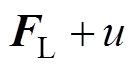为受电弓的抬升力与主动控制力之和的矩阵。
为验证本文主动控制算法在低速线路提速时的有效性及多种接触网上的适应性，实验选取不同型号受电弓和多条实际线路接触网参数进行验证分析。现有研究中，基于有限频率H∞的先验信息受电弓控制[24]在受电弓主动控制领域有着较好的控制效果，本文将主要以H∞控制方法作为基准进行性能 对比。
本文主要选取三条不同线路的弓网系统参数，包括宁启线（设计速度200 km/h，主要运行SSS400+型受电弓）、青荣城际（设计速度250 km/h，主要运行DSA250型受电弓）、杭深线（设计速度250 km/h，主要运行DSA380型受电弓）。受电弓和接触网参数见表2和表3。
表2 不同类型受电弓归算质量参数
Tab.2 Different types of pantographs are attributed to mass parameters
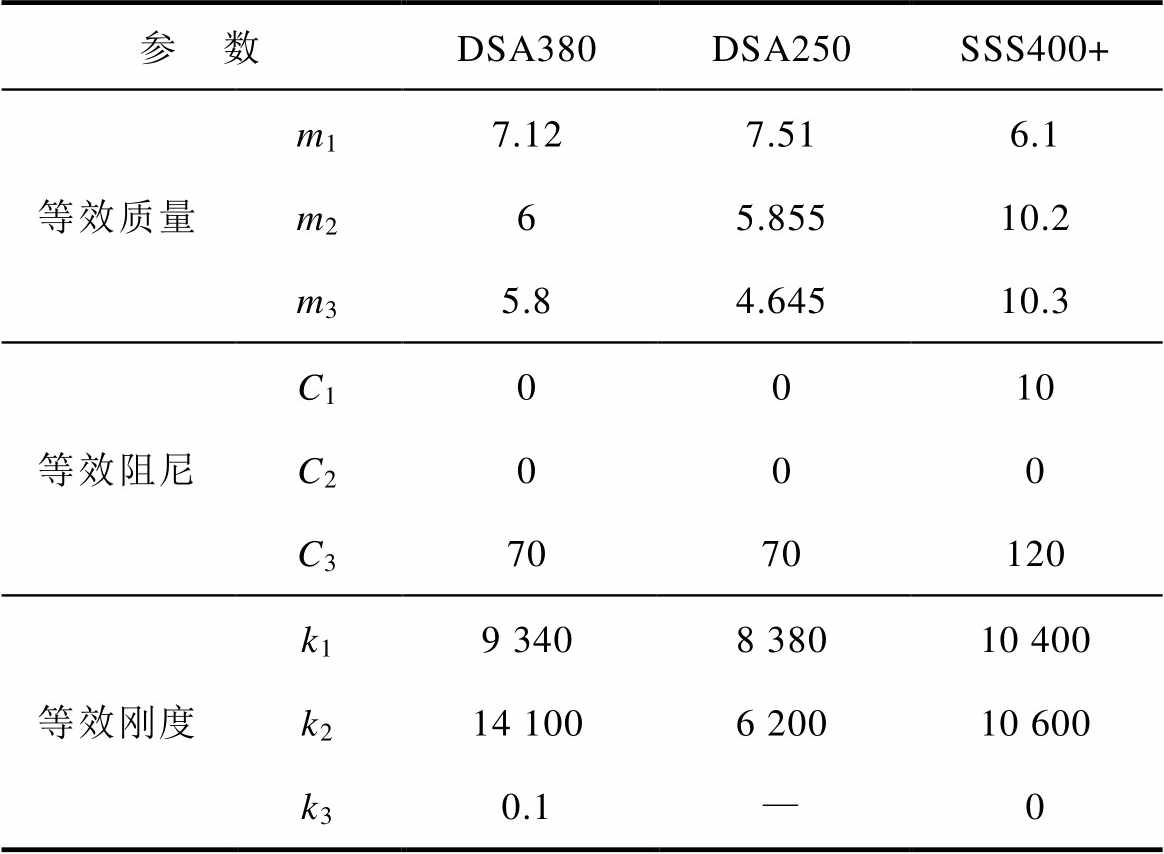
参 数DSA380DSA250SSS400+ 等效质量m17.127.516.1 m265.85510.2 m35.84.64510.3 等效阻尼C10010 C2000 C37070120 等效刚度k19 3408 38010 400 k214 1006 20010 600 k30.1—0
表3 不同接触网结构参数
Tab.3 Different types of pantographs are attributed to mass parameters
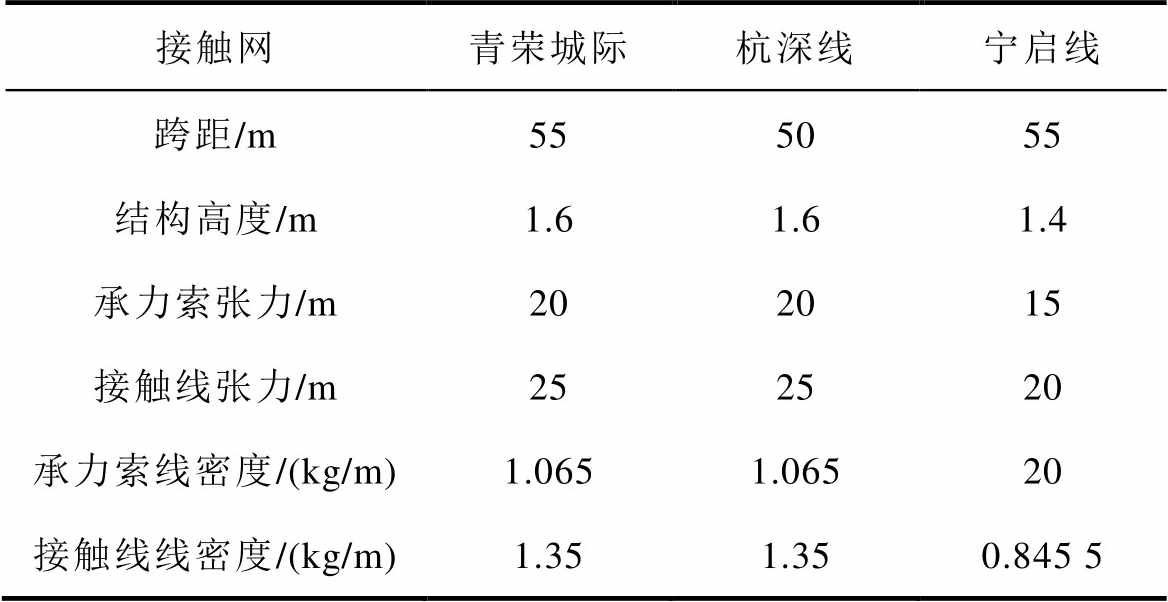
接触网青荣城际杭深线宁启线 跨距/m555055 结构高度/m1.61.61.4 承力索张力/m202015 接触线张力/m252520 承力索线密度/(kg/m)1.0651.06520 接触线线密度/(kg/m)1.351.350.845 5
以宁启线为例验证控制器的有效性。宁启线设计速度为200 km/h，分析采用本文控制算法后将速度提升到220、240、260、280、300 km/h时的弓网耦合性能。
不同速度下，控制前后弓网接触压力波动如图5所示。
图5 不同速度下接触力控制前后对比
Fig.5 Comparison of contact force before and after control at different speeds
由图5可见，采用主动控制后，不同速度接触力波动均有减少，接触力平均值基本不变。比较未控制、H∞控制和TD3控制接触力标准差的计算值，结果见表4，括号里面代表下降百分比。
表4 不同控制策略标准差对比
Tab.4 Different types of pantographs are attributed to mass parameters
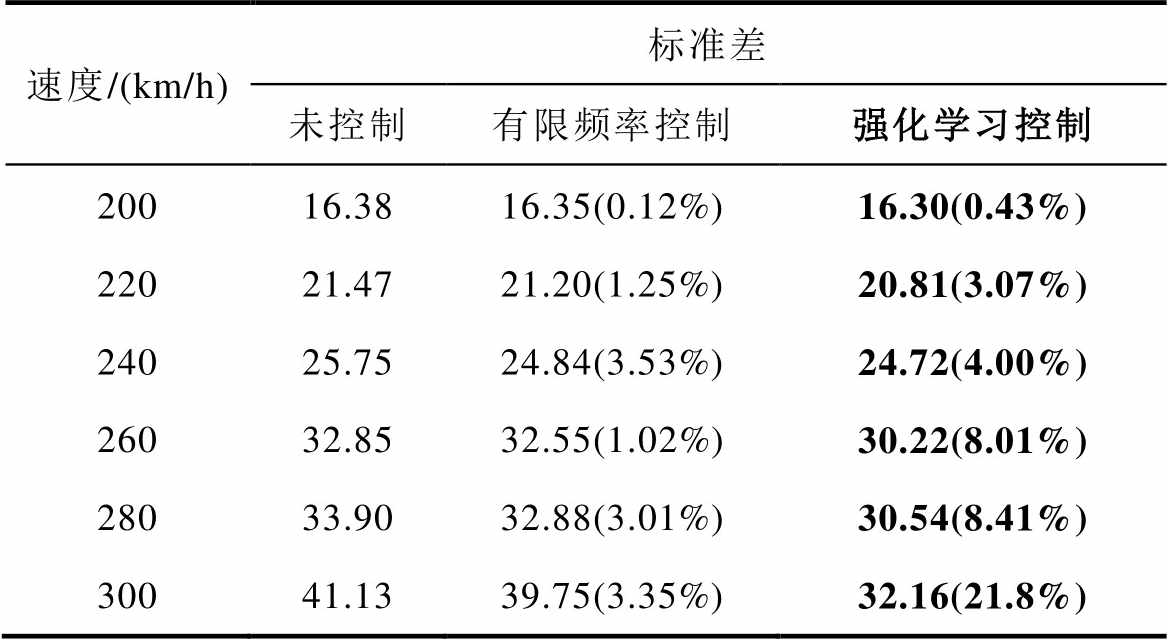
速度/(km/h)标准差 未控制有限频率控制强化学习控制 20016.3816.35(0.12%)16.30(0.43%) 22021.4721.20(1.25%)20.81(3.07%) 24025.7524.84(3.53%)24.72(4.00%) 26032.8532.55(1.02%)30.22(8.01%) 28033.9032.88(3.01%)30.54(8.41%) 30041.1339.75(3.35%)32.16(21.8%)
由表4可见，与H∞控制对比，TD3控制能够更加明显地降低接触力波动。进一步采用功率谱密度（Power Spectral Density, PSD），来研究接触力的频率特性，300 km/h下控制前后接触力PSD如图6所示。
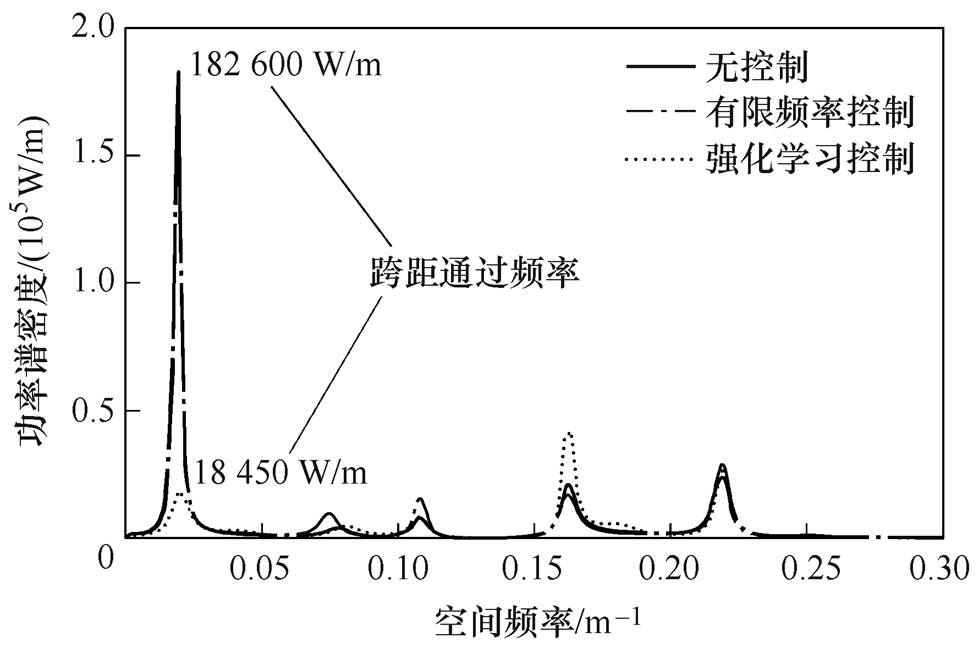
图6 300 km/h速度下控制前后接触力PSD
Fig.6 Control front and rear contact force PSD at 300 km/h speed
由图6可见，分析接触压力跨距通过跨越频率（Span Passing Frequency, SPF）数据，采用TD3控制后接触压力的PSD减少了近80%。由于SPF在接触力波动频率中能量占比较大，降低SPF能量可有效降低接触力整体波动。
300 km/h时受电弓主动控制算法控制力波形如图7所示。
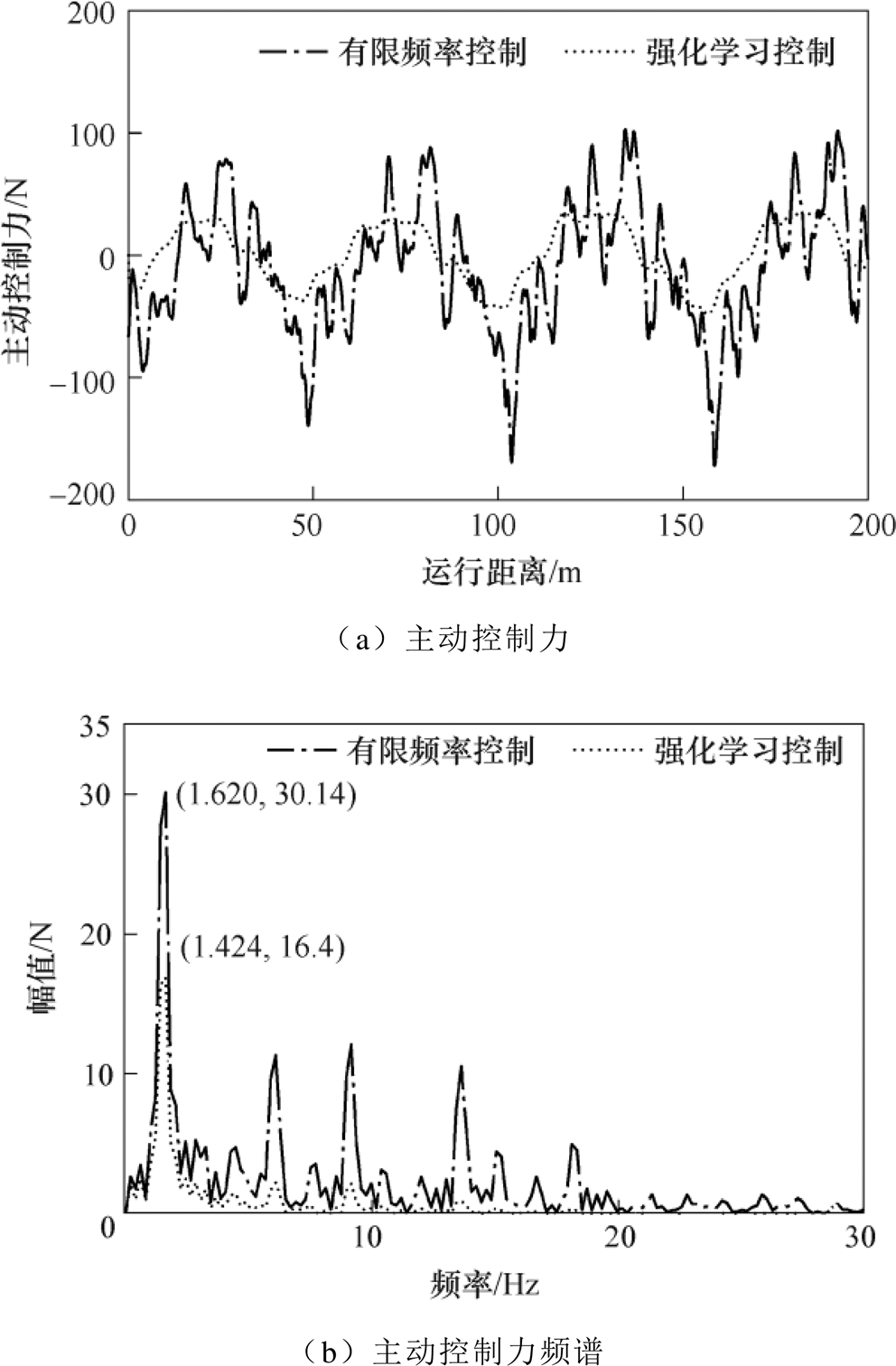
图7 主动控制力波形
Fig.7 Active control force waveform diagram
由图7可见，TD3控制相较于H∞控制需要的控制力幅值更低，这对于气囊的影响较小。从控制力输出频率上看，TD3控制基本不对高频部分进行调整，符合受电弓气囊气动机构调节速度慢的特点，因此更具实用性。
TD3算法训练过程中，奖励曲线如图8所示。实验重复10次，实线为平均奖励，阴影为奖励波动。
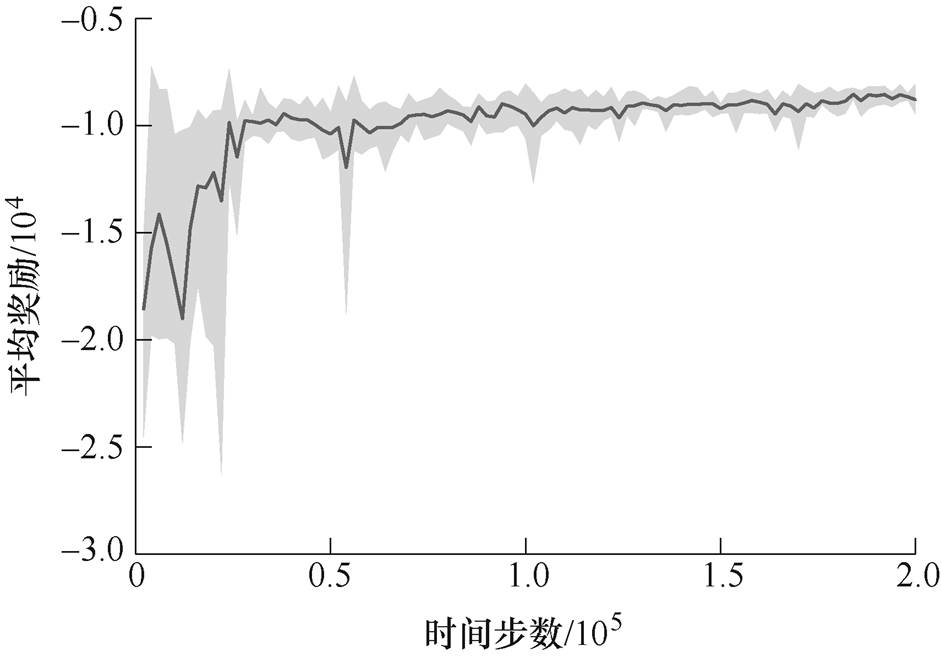
图8 受电弓调节过程奖励曲线
Fig.8 Pantograph adjustment process reward curves
由图8可见，TD3控制下，训练初期受电弓智能体会随机选取动作与环境进行交互并不断优化控制输出，整体训练过程可较快达到稳定，最终学习到最优策略，获得最大的累计奖励，此时弓网压力可稳定在允许范围。
本文选择青荣城际和杭深线弓网参数进行实验验证。青荣城际和杭深线的初始速度都为250 km/h，并分析270、290、310、330、350 km/h时速下的接触压力波动。不同线路弓网组合及速度下接触压力标准差如图9所示。
由图9可见，不同线路弓网条件下，TD3控制比H∞控制可以更有效地降低接触力的标准差，表明TD3算法实现受电弓主动控制，对不同弓网组合均有明显的效果，算法具备较好的鲁棒性。
本文把当前深度强化学习中的双延迟深度确定性策略梯度学习机制应用到主动受电弓控制中，减少列车在高速网向低速网运行时产生的接触力波动。首先建立受电弓的三自由度的归算质量模型和接触网的有限元模型，结合深度强化学习机制使得弓网模型智能体与环境进行交互，将双延迟深度确定性策略梯度应用到主动受电弓控制中。
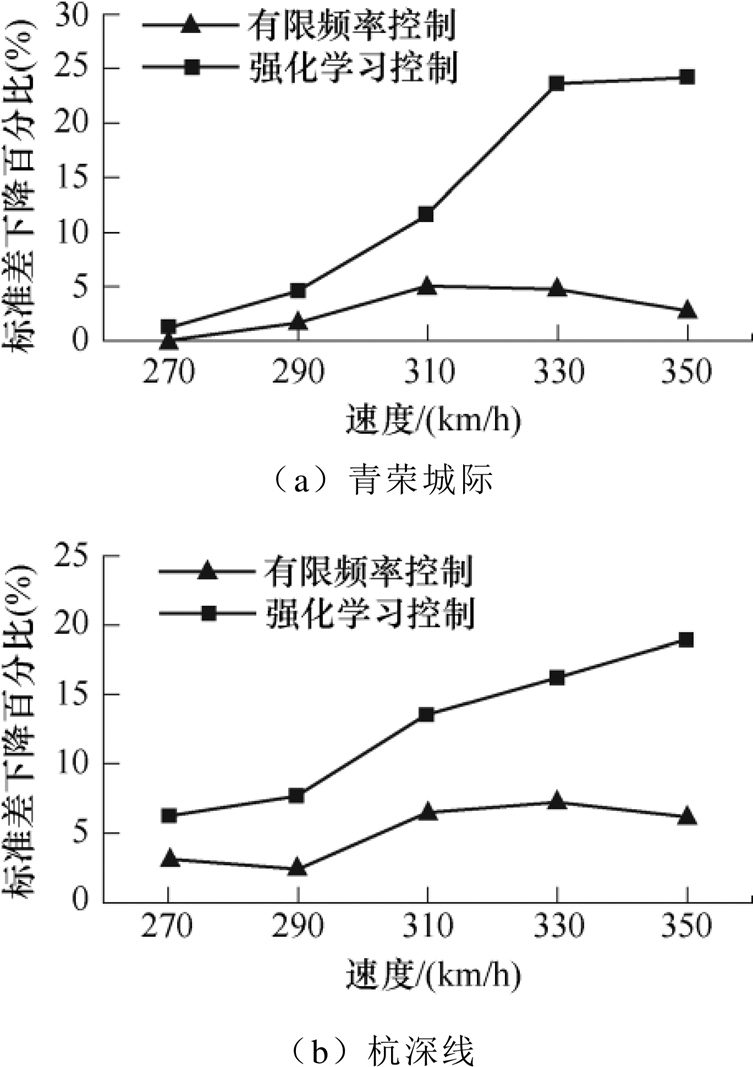
图9 标准差百分比前后对比
Fig.9 Pantograph adjustment process reward curves
在实验结果的分析中，此深度强化学习能够有效减少高速列车在低速网向高速网运行中产生的接触力波动问题。由于此实验是基于仿真阶段，实际效果还没有进行验证，下一步将继续研究其在实际工程中的应用。
参考文献
[1] Wang Hongrui, Liu Zhigang, Song Yang, et al. Dete- ction of contact wire irregularities using a quadratic time-frequency representation of the pantograph- catenary contact force[J]. IEEE Transactions on Instrumentation and Measurement, 2016, 65(6): 1385- 1397.
[2] 陈忠华, 唐俊, 时光, 等. 弓网强电流滑动电接触摩擦振动分析与建模[J]. 电工技术学报, 2020, 35(18): 3869-3877.
Chen Zhonghua, Tang Jun, Shi Guang, et al. Analysis and modeling of high current sliding electrical contact friction dynamics in pantograph-catenary system[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3869-3877.
[3] 程肥肥. 高速受电弓结构参数设计优化研究[D]. 成都: 西南交通大学, 2020.
[4] Pisano A, Usai E. Contact force estimation and regulation in active pantographs: an algebraic observability approach[C]//2007 46th IEEE Con- ference on Decision and Control, New Orleans, LA, USA, 2008: 4341-4346.
[5] Mokrani N, Rachid A. A robust control of contact force of pantograph-catenary for the high-speed train[C]//2013 European Control Conference (ECC), Zurich, Switzerland, 2013: 4568-4573.
[6] 谢松霖, 张静, 宋宝林, 等. 计及作动器时滞的高速铁路受电弓最优控制[J]. 电工技术学报, 2022, 37(2): 505-514.
Xie Songlin, Zhang Jing, Song Baolin, et al. Optimal control of pantograph for high-speed railway con- sidering actuator time delay[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 505-514.
[7] 王帅. 基于弓网接触力预测的受电弓主动控制方法研究[D]. 重庆: 重庆交通大学, 2022.
[8] 张静, 宋宝林, 谢松霖, 等. 基于状态估计的高速受电弓鲁棒预测控制[J]. 电工技术学报, 2021, 36(5): 1075-1083.
Zhang Jing, Song Baolin, Xie Songlin, et al. Robust predictive control of high-speed pantograph based on state estimation[J]. Transactions of China Electro- technical Society, 2021, 36(5): 1075-1083.
[9] Jiao Yuwei, Wang Ying, Chen Xiaoqiang, et al. Active control of pantograph based on prior- information of catenary[C]//2020 IEEE 5th Infor- mation Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 2020: 460- 464.
[10] Wang Hui, Han Zhiwei, Liu Zhigang, et al. Deep reinforcement learning based active pantograph control strategy in high-speed railway[J]. IEEE Transactions on Vehicular Technology, 2023, 72(1): 227-238.
[11] Cully A, Clune J, Tarapore D, et al. Robots that can adapt like animals[J]. Nature, 2015, 521(7553): 503-507.
[12] Shao Kun, Zhao Dongbin, Li Nannan, et al. Learning battles in ViZDoom via deep reinforcement lear- ning[C]//2018 IEEE Conference on Computational Intelligence and Games (CIG), Maastricht, Nether- lands, 2018: 1-4.
[13] Wang Qi, Wang Xianping. Deep convolutional neural network for decoding EMG for human computer interaction[C]//2020 11th IEEE Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (UEMCON), New York, NY, USA, 2020: 554-557.
[14] 陈泽宇, 方志远, 杨瑞鑫, 等. 基于深度强化学习的混合动力汽车能量管理策略[J]. 电工技术学报, 2022, 37(23): 6157-6168.
Chen Zeyu, Fang Zhiyuan, Yang Ruixin, et al. Energy management strategy for hybrid electric vehicle based on the deep reinforcement learning method[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 6157-6168.
[15] Mu Ruihui, Zeng Xiaoqin. A review of deep learning research[J]. Transactions on Internet and Information Systems, 2019, 13(4): 1738-1764.
[16] Fujimoto S, van Hoof H, Meger D. Addressing fun- ction approximation error in actor-critic methods[EB/OL]. 2018: arXiv: 1802.09477. https://arxiv.org/abs/1802. 09477.pdf.
[17] Nguyen T T, Nguyen N D, Nahavandi S. Deep reinforcement learning for multiagent systems: a review of challenges, solutions, and applications[J]. IEEE Transactions on Cybernetics, 2020, 50(9): 3826- 3839.
[18] 顾雪平, 刘彤, 李少岩, 等. 基于改进双延迟深度确定性策略梯度算法的电网有功安全校正控制[J]. 电工技术学报, 2023, 38(8): 2162-2177.
Gu Xueping, Liu Tong, Li Shaoyan, et al. Active power correction control of power grid based on improved twin delayed deep deterministic policy gradient algorithm[J]. Transactions of China Elec- trotechnical Society, 2023, 38(8): 2162-2177.
[19] Hunter J S. The exponentially weighted moving average[J]. Journal of Quality Technology, 1986, 18(4): 203-210.
[20] Song Yang, Liu Zhigang, Wang Hongrui, et al. Nonlinear modelling of high-speed catenary based on analytical expressions of cable and truss elements[J]. Vehicle System Dynamics, 2015, 53(10): 1455-1479.
[21] CENELEC. Railway applications-current collection systems-validation of simulation of the dynamic interaction between pantograph and overhead contact line: EN 50318-2018[P]. 2018-12-01.
[22] 杨鹏, 张静, 金伟, 等. 考虑气动系统的高速受电弓分层控制[J]. 电工技术学报, 2022, 37(10): 2644- 2655.
Yang Peng, Zhang Jing, Jin Wei, et al. Hierarchical control of high-speed pantograph considering pneumatic system[J]. Transactions of China Elec- trotechnical Society, 2022, 37(10): 2644-2655.
[23] 宋洋, 刘志刚, 鲁小兵, 等. 计及接触网空气动力的高速弓网动态受流特性研究[J]. 铁道学报, 2016, 38(3): 48-58.
Song Yang, Liu Zhigang, Lu Xiaobing, et al. Study on characteristics of dynamic current collection of high-speed pantograph-catenary considering aerody- namics of catenary[J]. Journal of the China Railway Society, 2016, 38(3): 48-58.
[24] Lu Xiaobing, Liu Zhigang, Zhang Jing, et al. Prior- information-based finite-frequency H∞ control for active double pantograph in high-speed railway[J]. IEEE Transactions on Vehicular Technology, 2017, 66(10): 8723-8733.
Abstract The stable coupling between the pantograph and the catenary is the foundation for the safe operation of high-speed railway trains. With speed increases, the offline and arcing of the pantograph and catenary can affect the performance, leading to a decrease in the current collection quality of the train. At present, the primary method to improve the current collection quality is the active control method of the pantograph. The self-adaptability of current control algorithms mainly solves adaptive selection problems of algorithm parameters. However, few studies on the impact of changes in line conditions and external disturbances exist. This paper constructs the pantograph active control system based on the deep reinforcement learning method, which can effectively overcome the complex time-varying characteristics of the pantograph catenary system to reduce fluctuations of the pantograph catenary contact force.
The deep reinforcement learning algorithm is introduced. Then, a pantograph catenary coupling model is constructed as the environmental module to generate data for deep reinforcement learning training and obtain feedback on control strategies. The pantograph adopts a three-mass block model, and the contact network adopts a nonlinear pole/cable finite element method coupled through penalty functions. The pantograph active control system’s objectives and the existing constraints are analyzed according to state space, observation space, action space, and reward function required in the deep reinforcement learning framework. The process of controller training and testing is provided. The effectiveness and robustness of the pantograph active control system are verified.
The experimental results show that the reinforcement learning active control reduces contact force fluctuations at different speeds, and the average value of the contact force is almost unchanged. Compared with the finite frequency H∞ control, the standard deviation of the contact force is decreased by 21.8% using the double delay deep deterministic strategy gradient (TD3) control. By analyzing the span passing frequency (SPF) data of the contact pressure span, the PSD of contact pressure is reduced by nearly 80% using TD3 control. Since the energy of SPF accounts for a large proportion of the fluctuation frequency of the contact force, reducing the energy of SPF can effectively decrease overall contact force fluctuations. At the same time, TD3 control requires a lower amplitude of the control force than H∞ control, which has a smaller impact on the airbag. From the perspective of the control force output frequency, TD3 control does not adjust the high-frequency part, which is in line with the slow adjustment speed of the pneumatic mechanism of the pantograph airbag. Under different pantograph catenary conditions, TD3 control can reduce the standard deviation of the contact force more effectively than H∞ control, which indicates that TD3 algorithm has good robustness.
Compared with the traditional control methods, (1) the active pantograph control algorithm based on deep reinforcement learning is an end-to-end data-driven algorithm, which does not need an accurate pantograph catenary system model. The control model is generated from readily available operating data and has strong adaptability. (2) The deep reinforcement learning algorithm constructs the relationship between the observation space and the action space to the reward function through exploration and trial and error. Therefore, environmental changes cause changes in the observation value, and the controller can quickly adjust the corresponding action to maximize the reward function. (3) Under the constraints of external conditions, such as pantograph actuators and pantograph observers, different control strategies can be achieved by adjusting the observation space and reward function.
keywords：Low speed network, mixed running, TD3, active pantograph control
DOI: 10.19595/j.cnki.1000-6753.tces.230694
中图分类号：TM571
国家自然科学基金资助项目（U1734202, 51977182）。
收稿日期 2023-05-18
改稿日期 2023-07-03
吴延波 男，1998年生，硕士研究生，研究方向为深度强化学习和受电弓主动控制。E-mail: 17355206572@my.swjtu.edu.cn
韩志伟 男，1981年生，副教授，硕士生导师，研究方向为现代信号处理、计算机视觉及其在铁路和电力系统中的应用。E-mail: zw.han@my.swjtu.edu.cn（通信作者）
（编辑 崔文静）