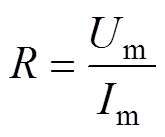 (1)
(1)
式中,Um为电压有效值;Im为电流有效值。接触电流和电压有效值分别通过霍尔电流传感器(LHB20A5VY2)和电压传感器(LHB-T1)获取,数据时间序列由16位数据采集卡(PCI-6251, NI)采集并存储在工作站上。

图1 滑动电接触实验机
Fig.1 Sliding electrical contact testing machine
摘要 高速列车的运行实践表明,随着运行速度提高,受电弓与接触导线分离的可能性越大,越容易产生弓网电弧。导致电弧产生的因素很多,但最终都归结到滑板与接触网的接触电阻上。首先利用滑动电接触实验机,研究了波动载荷、滑动速度和接触电流对接触电阻的影响,并进一步结合表面形貌特征,分析了磨损机制、电弧放电与接触电阻演变规律之间的关系。其次为了预测不同工况下的接触电阻,建立了径向基(RBF)神经网络回归模型,通过在模型训练中融入先验知识和采用改进的食肉植物优化算法(ICPA)优化RBF神经网络超参数,提升弓网接触电阻预测模型的精度。有、无先验知识的ICPA-RBF模型预测性能对比仿真结果表明,两类先验知识分别有助于提高模型的收敛速度和预测精度。最后采用假设检验验证了模型的有效性。
关键词:接触电阻 先验知识 径向基(RBF)神经网络 食肉植物算法 假设检验
高速列车通过受电弓与接触网滑动接触来获取电能,弓网之间良好的受流性能是列车安全稳定运行的必要条件[1]。随着电力机车向高速化和重载化方向发展,牵引电流增大,弓网振动加剧,离线率增大,大能量电弧频发,弓网受流稳定性变差,滑板服役寿命锐减,严重威胁行车安全[2-3]。因此,提高弓网系统的受流稳定性与可靠性是弓网高速运行亟待解决的难题。导致电弧产生的原因很多,但最终都归结到滑板与接触网的接触电阻指标上,因此通过建立接触电阻预测模型,对电力机车的受流状态进行预测评估,不仅可以为其安全可靠运行提供参考,还能提前预测与处理受流故障,以避免严重事故发生。
滑动电接触是一个复杂的动态过程,涉及烧蚀、氧化和磨损等化学和物理现象[4-5]。目前,对接触电阻的研究主要集中在演变规律和建模预测两个方面。在接触电阻演变规律方面,研究工作主要针对不同工况条件对接触电阻的影响规律开展[6-12]。研究发现,大电流工况可加速接触面氧化过程,从而促进氧化膜的生成[13-14],膜电阻增大,加上材料转移和犁沟效应[15],接触面导电接触面积减小,接触电阻增大;接触压力的增大可以增强受流的稳定性与可靠性,通常随着接触压力的增大,接触电阻迅速减小,但在其超过一定阈值之后,接触电阻的下降速度变缓[16];随着运行速度的提升,接触状态的稳定性减弱,高温电弧和火花会对接触表面造成侵蚀,导致接触电阻增大;虽然温升不是外部工况条件,但其作为中间变量是磨损与受流复杂耦合的关键因素,引起接触面温升的主要因素有焦耳热、摩擦热和电弧热,正常受流时焦耳热通常占主要地 位[17],温升对接触电阻有两方面的影响作用:一方面,高温会改变材料的物理性质,使材料弹性模量变小进而引起导电斑点半径增大,接触电阻变 小[18];另一方面,高温也会改变材料的化学性质,使得氧化膜生成速度加快,导致接触电阻增大[19]。在建模预测方面,研究工作主要集中在接触电阻物理和数学模型的建立及预测方面。在物理模型方面,主要是通过有限元方法模拟真实物理系统,分析各因素对接触电阻的影响[20-23]。在数学模型方面,由于接触电阻影响因素众多且影响机理复杂,因此模型多为数据驱动模型[24]。一类方法是在静态接触电阻公式的基础上,分析速度对接触电阻的影响规律,采用最小二乘回归[10]拟合滑动接触电阻经验公式;另一类方法是采用神经网络、支持向量机[25]等黑箱模型建立载荷、接触电流、滑动速度与接触电阻之间的预测模型,并用遗传算法[26]、粒子群算法[27]等对模型中的超参数进行寻优。已有接触电阻预测方法均存在一定的局限性,有限元方法预测的精确度浮动比较大[28],而黑箱模型对缺失数据敏感,且遗传算法、粒子群算法对超参数的寻优速度慢、参数的依赖性强。此外,以往机理分析得到的定性结论并未作为先验知识应用到接触电阻的建模过程,现有数据驱动模型也未充分考虑温度对接触电阻的影响,因此接触电阻模型的预测精度还有很大的提升空间。鉴于此,本文采用收敛速度快、局部逼近能力强的径向基(Radial Basis Function, RBF)神经网络建立接触电阻预测模型,充分考虑接触压力、温度对接触电阻的影响规律并将其作为先验知识融入建模过程;针对RBF网络训练易陷入局部最优的问题,提出了一种融合了Logistic混沌映射初始化策略、动态自适应生长率、莱维飞行策略的改进食肉植物算法[29](Improvement Carnivorous Plant Algorithm, ICPA)优化网络参数。建立基于先验知识的ICPA-RBF模型,并通过有、无先验知识的对比仿真,分别验证了两类先验知识在提升模型收敛速度和预测精度方面的作用,最后采用假设检验的方法验证了模型的有效性。
波动载荷条件下的受电弓滑板与接触导线载流对磨实验采用如图1所示的自制实验机进行。在变频调速控制的交流电机驱动下,滑板和接触网导线相对运动速度在0~200 km/h范围内可调,所加载电流在0~800 A范围内可调,动态压力载荷由音圈电机闭环控制施加。在实验过程中,使用非接触式的红外测温仪测量温度,利用金相显微镜观察滑板表面磨损形貌。导线材质为纯铜,滑板为浸铜碳,化学成分质量分数见表1。滑动接触时的接触电阻值计算公式为
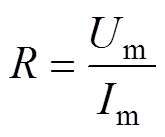 (1)
(1)
式中,Um为电压有效值;Im为电流有效值。接触电流和电压有效值分别通过霍尔电流传感器(LHB20A5VY2)和电压传感器(LHB-T1)获取,数据时间序列由16位数据采集卡(PCI-6251, NI)采集并存储在工作站上。

图1 滑动电接触实验机
Fig.1 Sliding electrical contact testing machine
表1 浸铜碳滑板化学成分
Tab.1 Chemical composition of copper-impregnated carbon skateboard (%)

CCuPbSb其他 92.953.910.980.551.61
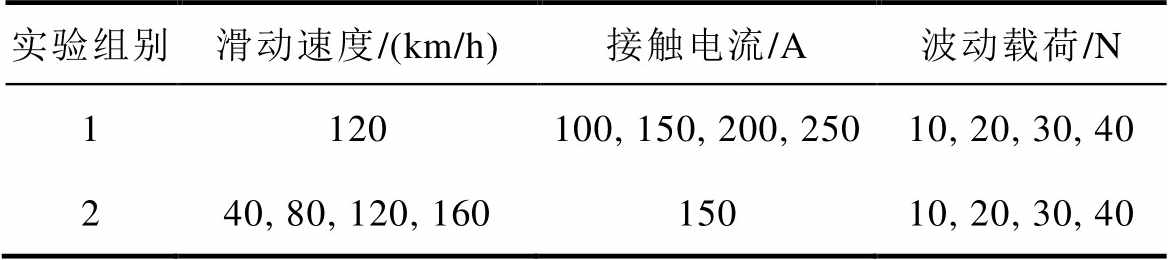
设计两组实验分别研究波动载荷下电流、速度对接触电阻的影响。在实验中,根据EN50367标准将法向偏置载荷设置为70 N,固定波动频率为2 Hz,实验设计见表2。
表2 实验设计
Tab.2 Experimental design
实验组别滑动速度/(km/h)接触电流/A波动载荷/N 1120100, 150, 200, 25010, 20, 30, 40 240, 80, 120, 16015010, 20, 30, 40
接触电阻近似符合正态分布[25],文中的接触电阻均为20 min运行时间内的均值。速度120 km/h,压力载荷分别取50、70、90、110 N,接触电流分别取100、150、200、250 A条件下,接触电阻随接触压力载荷变化的曲线如图2所示。
由图2可知,接触电阻随着接触压力载荷的增大,呈现出减小的趋势。这是由于接触压力载荷增大,接触面积增大、接触稳定性增强,该结论在静态电接触和滑动电接触过程中普遍适用[25, 30],后文中称该结论为先验知识Ⅰ。根据先验知识Ⅰ可知,接触电阻对接触压力载荷的偏导数为非正数。
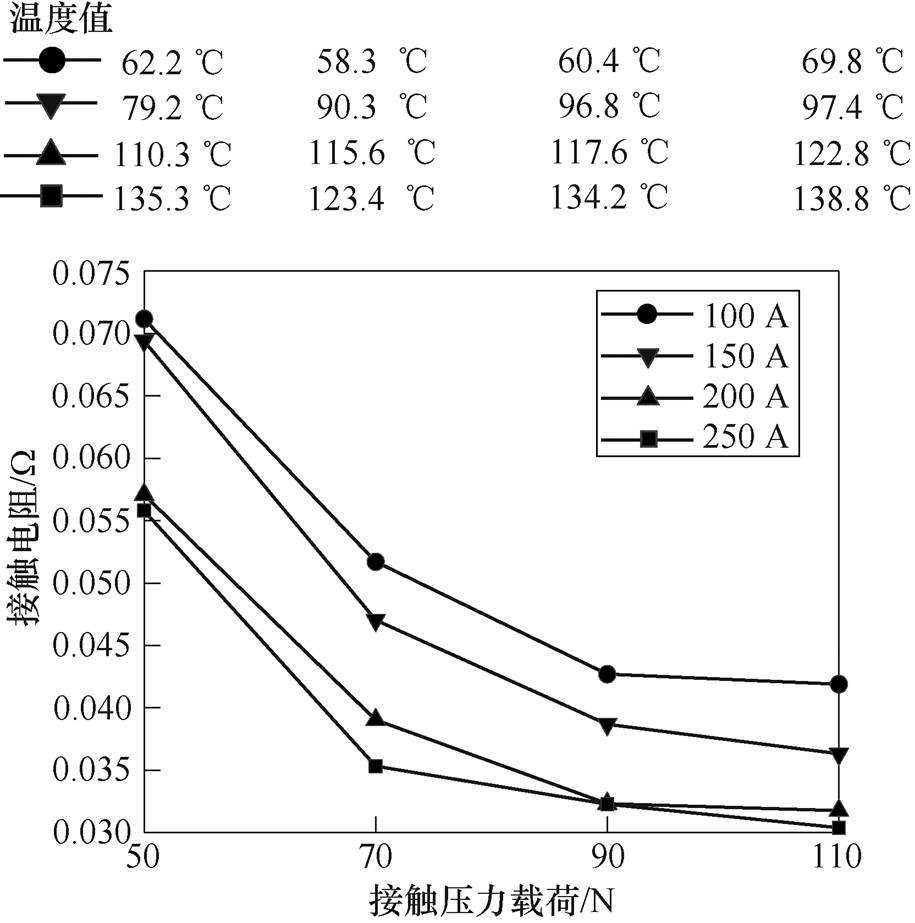
图2 接触电阻随接触压力载荷的变化趋势
Fig.2 The trend of contact resistance with contact pressure load
温度对受流接触表面磨损机制、材料硬度和弹性模量等有重要影响,进而影响受流状态与接触电阻特性。引起接触表面温升的主要因素有电热和机械摩擦热,其中机械摩擦热与接触压力载荷和速度有关,而电热中焦耳热与电流大小相关,工况条件中缺少能直接反映电弧热的变量。电流传导过程中,损失的电流与电弧热密切相关,因此,利用损失电流可以进一步完善对弓网摩擦副接触状态的表征。后文中称该结论为先验知识Ⅱ。
根据载流效率,损失电流Iloss可表示为
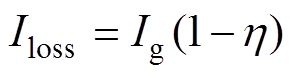 (2)
(2)
其中
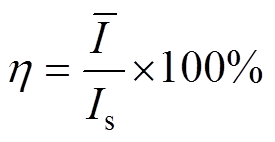 (3)
(3)
式中,Ig为给定电流;h 为载流效率[31];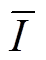 为动态载流平均值;Is为静态给定电流。
为动态载流平均值;Is为静态给定电流。
图2中的损失电流二次方与温度的对应关系如图3所示。
本节通过接触电阻变化趋势和滑板表面磨损后的形貌讨论不同振幅下电流和滑动速度对接触电阻的影响。根据表2中的实验组别1,首先研究不同振幅下,电流对接触电阻的影响。速度为120 km/h、波动频率为2 Hz、法向压力载荷为70 N条件下,接触电阻随波动幅值和接触电流的变化如图4所示。
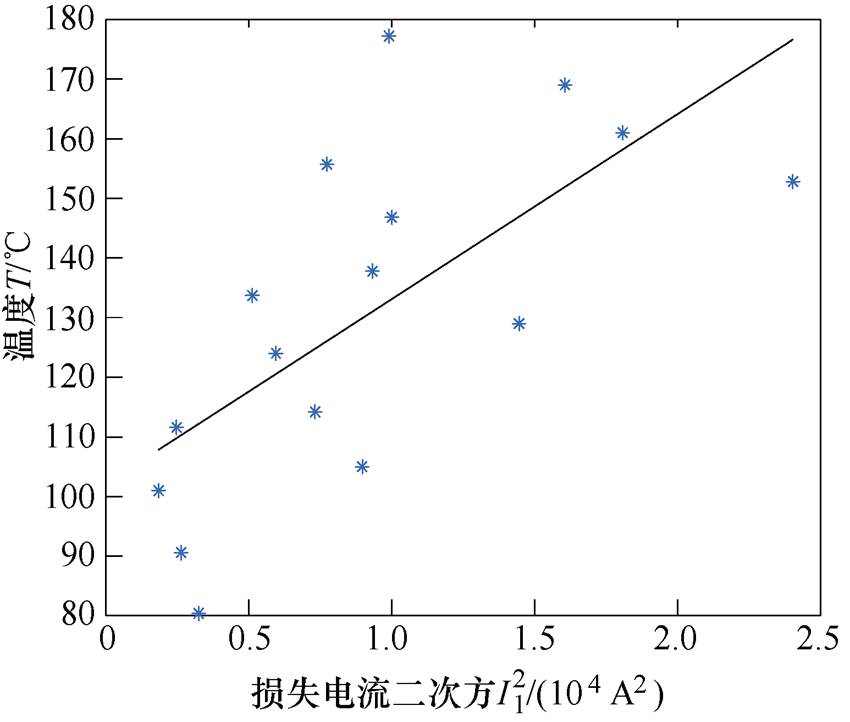
图3 损失电流二次方与温度的对应关系
Fig.3 Correspondence between the square of lost current and temperature
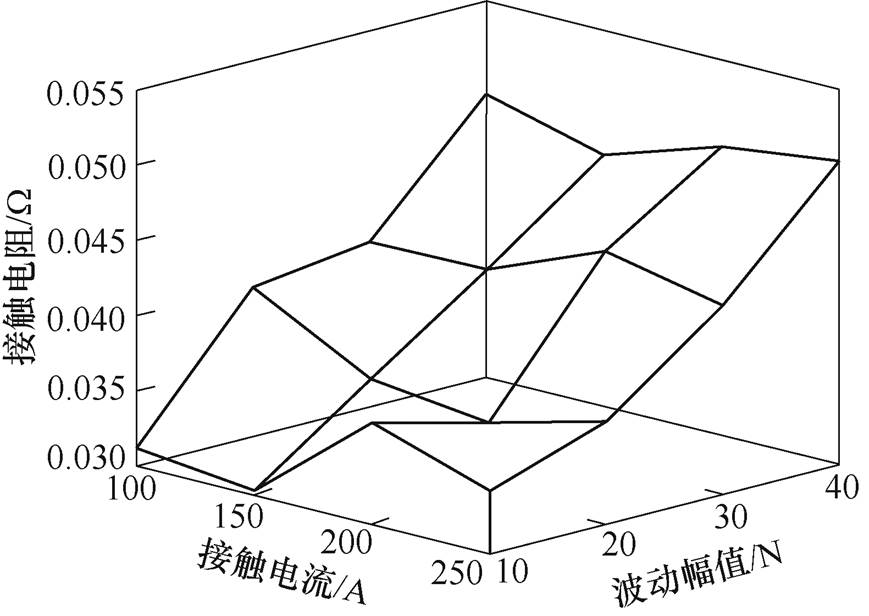
图4 接触电阻随波动幅值、接触电流变化曲线
Fig.4 Contact resistance change curves with fluctuation amplitude and contact current
波动幅值为20 N,接触电流分别为150、250 A时的滑板表面形貌如图5所示。

图5 波动载荷下滑板表面形貌(120 km/h)
Fig.5 Film layer of slide plate under fluctuating load (120 km/h)
由图4可知,在几乎所有振幅下,接触电阻均随着电流的增大而减小,结合图5可知,在大电流条件下滑板表面更加光滑。这是由于电流较小时电气作用不明显,滑板与导线表面并不光滑,微小的凸起在摩擦过程中使摩擦面产生磨屑,而磨屑继续参与摩擦,形成三体磨损,进而产生犁沟,此时以机械磨损为主,接触电阻较大。随着接触电流增大,滑板表面温度变高,接触面材料硬度变低,黏着磨损逐渐成为主导磨损机制,此时电流以润滑作用为主,接触电阻变小。
根据表2中的实验组别2,再研究不同振幅下,滑动速度对接触电阻的影响。接触电流为150 A,接触电阻随速度、波动幅值的变化如图6所示。波动幅值为20 N,滑动速度分别为40和120 km/h时的滑板表面磨损后形貌如图7所示。滑动速度为120 km/h,接触电流为250 A,载荷波动幅值分别为10、40 N时的滑板表面磨损后形貌如图8所示。
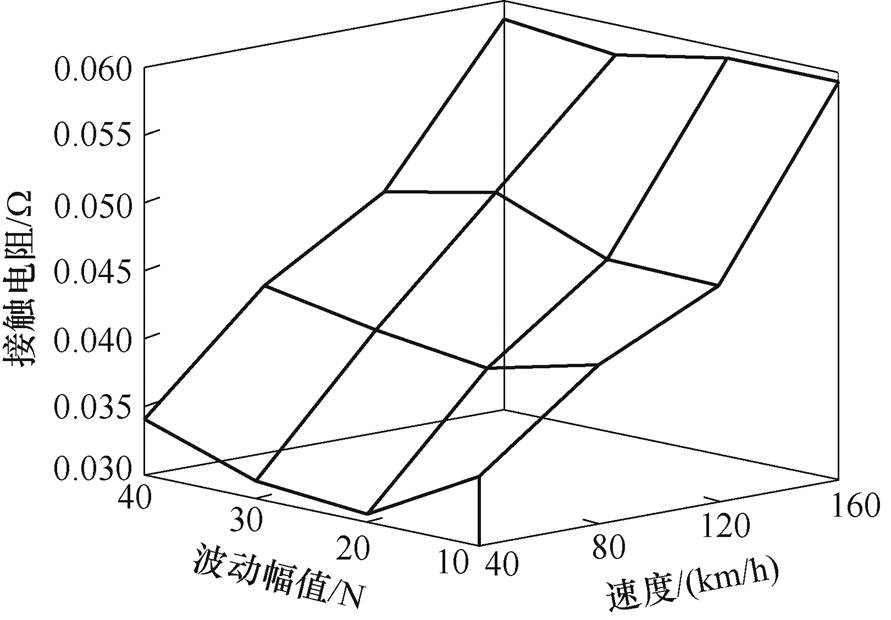
图6 接触电阻随速度、波动幅值变化曲线
Fig.6 Contact resistance with velocity, fluctuation amplitude change curves

图7 不同速度下滑板表面形貌(150 A)
Fig.7 Slide surface film at different speeds (150 A)

图8 不同载荷波动幅值条件下滑板表面形貌(120 km/h)
Fig.8 Surface morphology of slide plate under different load fluctuation amplitude conditions (120 km/h)
由图6可知,当载荷波动幅值维持不变时,接触电阻随着速度增加而增大。这是由于随着滑动速度的提高,接触状态稳定性变差。再结合图7可知,电弧高温和长弧放电现象严重,造成了接触表面金属元素的熔融及氧化,此时表面的破坏机制以电弧侵蚀为主,大电流主要体现为负面作用,导致接触电阻变大。
由图6可知,接触电阻在载荷波动幅值为20 N时达到最小,结合图5b、图8可以推测,在电流不变的情况下,波动幅值为20 N时的机械磨损和电气磨损较小,受流状态较为稳定,从而使得此时的接触电阻更小;根据图8b电弧燃烧区域和由材料损失而形成的凹槽,可以推断在40 N的幅值下,机械磨损和电蚀更加严重,受流面劣化增加了接触电阻。因此,适当的接触力波动振幅可以对接触电阻产生积极的影响,但过大的振幅会降低接触的稳定性。
RBF网络具有拓扑结构紧凑、收敛速度快、泛化能力强等优点,广泛用于回归模型建模。
在RBF网络回归模型中,x=[x1 x2 … xn]T为输入向量,h=[h1 h2 … hm]T为径向基向量,cj= [cj1 cj2 … cjn]T为第j个节点的中心矢量,b= [b1 b2 … bm]T为基宽向量,w =[w1 w2 … wm]T为权值向量。hj为高斯基函数,有
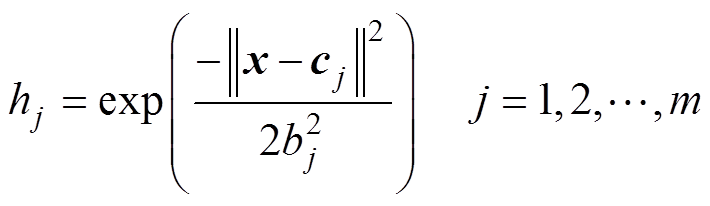 (4)
(4)
RBF网络输出为
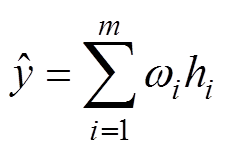 (5)
(5)
为加快学习过程并方便推广到在线学习更新,采用随机梯度法调整参数,将RBF网络性能指标定义为
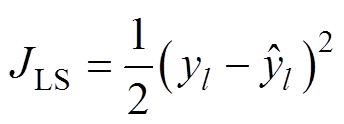 (6)
(6)
式中,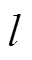 为随机抽取的样本序列。根据1.3节中先验知识Ⅰ,接触电阻随接触压力载荷的增大减小,令输入变量x1为接触压力载荷,则先验知识Ⅰ可以表示为
为随机抽取的样本序列。根据1.3节中先验知识Ⅰ,接触电阻随接触压力载荷的增大减小,令输入变量x1为接触压力载荷,则先验知识Ⅰ可以表示为
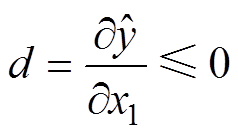 (7)
(7)
式中,d为接触电阻对接触压力载荷的偏导数。
将先验知识式(7)加入到优化指标式(6)中,RBF性能优化指标可表示为
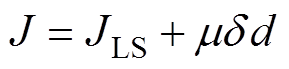 (8)
(8)
式中,d 为惩罚系数;m 为开关系数,其取值为
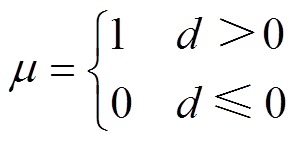 (9)
(9)
根据随机梯度下降法,权值wj的调整规则为
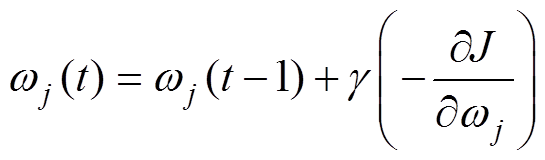 (10)
(10)
式中,g 为学习率;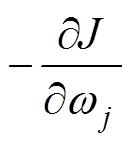 为负梯度,有
为负梯度,有
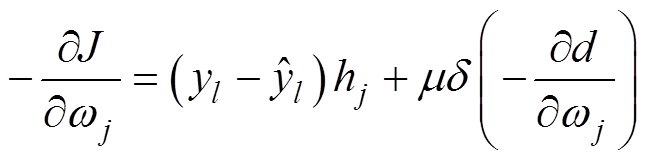 (11)
(11)
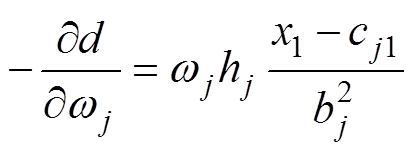 (12)
(12)
基宽bj的调整规则为
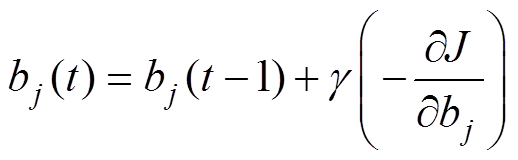 (13)
(13)
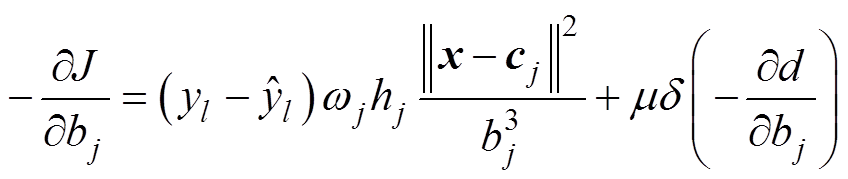 (14)
(14)
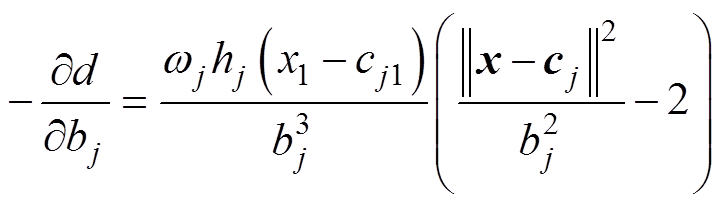 (15)
(15)
中心矢量cj中的元素cji调整规则为
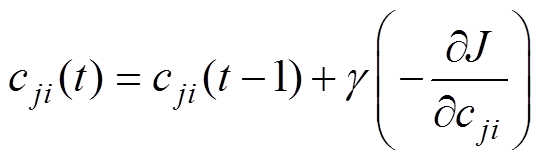 (16)
(16)
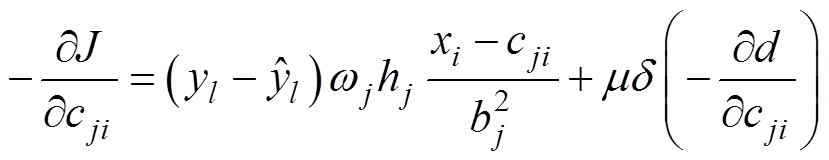 (17)
(17)
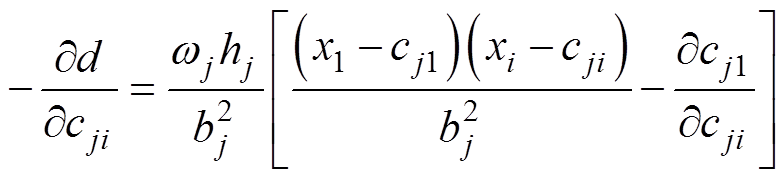 (18)
(18)
RBF神经网络激活函数的中心矢量、基宽以及权值的初始值对模型的预测精度和泛化能力影响较大。本文采用食肉植物算法[29](Carnivorous Plant Algorithm, CPA)对以上参数进行优化,该算法是一种新的基于种群的元启发式算法,与其他算法相比,此算法在处理高维多目标优化问题时具有更强的全局搜索能力。
CPA是一种模拟食肉植物吸引、诱捕、消化和繁殖策略的全局随机搜索算法。基本食肉植物算法步骤如下:
(1)初始化种群。个体位置为
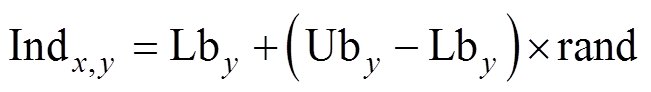 (19)
(19)
式中,Lb和Ub分别为搜索域的下界和上界;x= 1, 2,…;y=1, 2,…;rand为[0, 1]之间的随机数。
(2)排序。将个体矩阵每一行作为适应度函数的输入来评估适应度,并根据适应度由高到低对种群进行排序。
(3)分类和分组。将种群中最前面的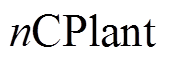 作为食肉植物CP,而剩余的
作为食肉植物CP,而剩余的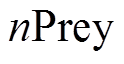 作为猎物Prey。按适应度值从高到低分配猎物给相应排名的食肉植物。
作为猎物Prey。按适应度值从高到低分配猎物给相应排名的食肉植物。
(4)生长。通过吸引率与随机值对比决定种群生长形式。如果吸引率高于产生的随机值,食肉植物生长,新的食肉植物的生长模型为
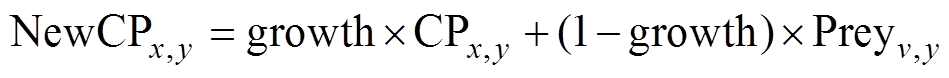 (20)
(20)
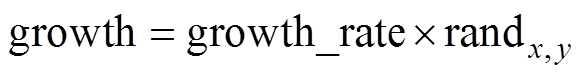 (21)
(21)
式中,growth为生长系数;CPx,y为第x组第y个植物;Preyv,y为第v组第y个系数;growth_rate为成长率。如果吸引率低于产生的随机值,则猎物生长的模型表示为
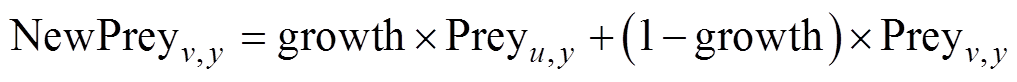
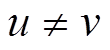 (22)
(22)
式中,NewPreyv,y为新生成的猎物个体。
生产过程持续group_iter代。由于随机选择的Preyu可能劣于Preyv,因此引入了式(23)。
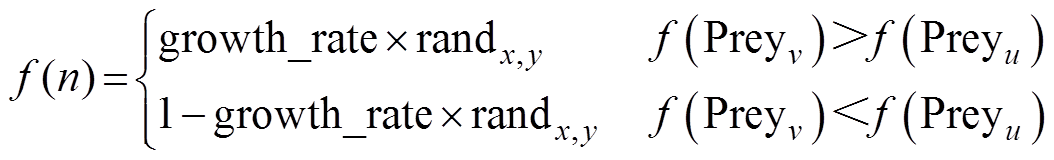 (23)
(23)
(5)繁殖。种群最优解的繁殖过程为
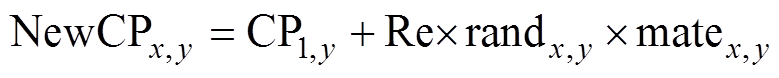 (24)
(24)
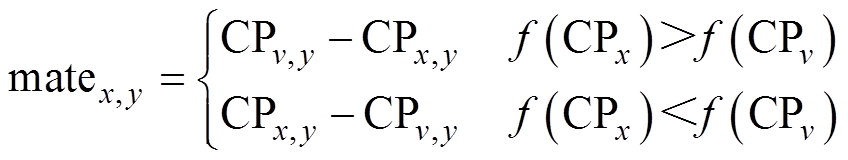 (25)
(25)
式中,x≠v≠1;CP1,y为最优解;CPvy为随机选择的食肉植物;Re为繁殖率。
(6)合并。将新生成种群与先前的种群进行合并,就得到了一个新的维度为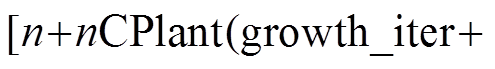
 的新种群,保证种群大小不变。
的新种群,保证种群大小不变。
(7)返回步骤(2),直到进化代数达到预设值终止。
基本CPA存在易陷入局部最优、种群多样性快速减少等问题[32],因此,本文提出融合了Logistic混沌映射初始化策略、动态自适应生长率、莱维飞行策略的改进食肉植物算法(ICPA)。
3.2.1 Logistic混沌映射初始化策略
标准CPA的种群初始化易产生个体聚集、多样性差等问题。Logistic混沌映射[33]具体数学表达式为
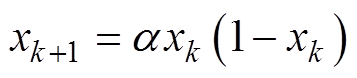 (26)
(26)
式中,k为迭代次数;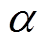 为混沌分岔参数,
为混沌分岔参数,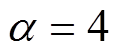 时,混沌现象最好,种群多样性较好,因此选取
时,混沌现象最好,种群多样性较好,因此选取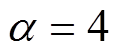 时的Logistic混沌表达式来产生种群,具体公式为
时的Logistic混沌表达式来产生种群,具体公式为
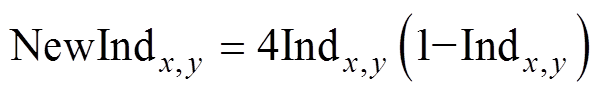 (27)
(27)
3.2.2 自适应生长率策略
由式(21)和式(23)可知,参数的探索范围受生长率的影响,生长率越高,探索范围越大,搜索到更优解可能性就越大。全局搜索能力增强的同时局部最优开发能力会相对减弱,因此,本文选择动态自适应生长率协调算法在探索阶段的全局搜索能力和局部最优开发能力。自适应生长率公式为
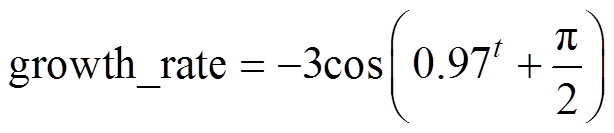 (28)
(28)
式中,t为当前迭代次数;0.97为选定的自适应系数。
3.2.3 莱维飞行与贪心机制策略
为防止算法陷入局部最优,使用莱维飞行策略进行全局探测,使个体广泛分布于搜索空间中,以提高全局寻优能力。莱维飞行位置更新公式为
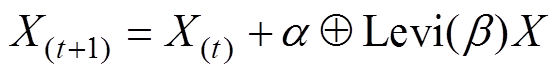 (29)
(29)
式中,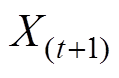 为更新后的位置;
为更新后的位置;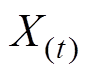 为更新前的位置;a =10-5;b =5。
为更新前的位置;a =10-5;b =5。
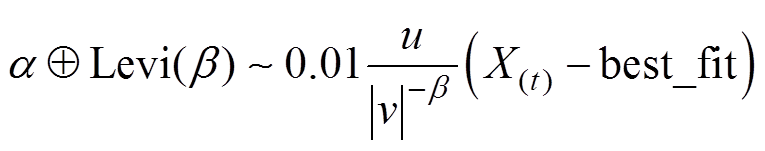 (30)
(30)
式中, 表示点对点乘法;best_fit为全局最优值;u和v服从正态分布,有
表示点对点乘法;best_fit为全局最优值;u和v服从正态分布,有
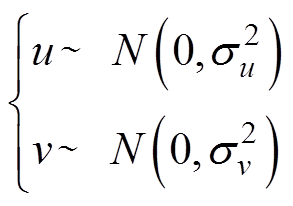 (31)
(31)
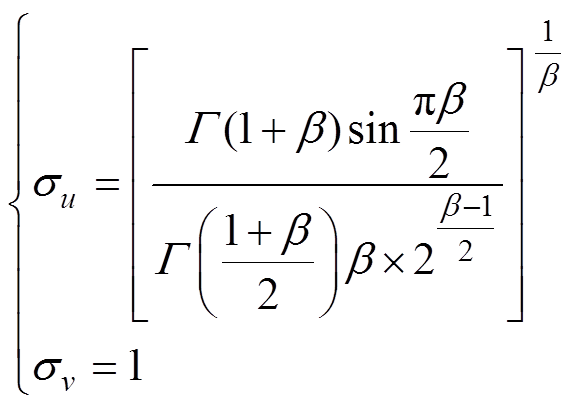 (32)
(32)
虽然莱维飞行可以实现位置的更新,但是无法保证得到的新解的适应度优于原解,因此使用贪心机制来比较原解和新解的适应度,以保留适应度更好的解。
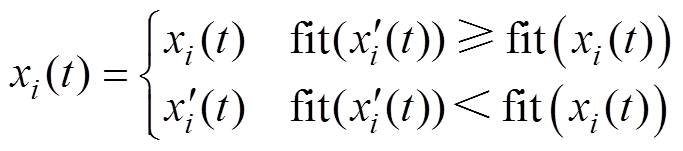 (33)
(33)
这种精英选择策略保证了选择更优的解用于下一代的繁殖。
为了减少神经网络输入变量之间显著差异的影响,输入变量和输出接触电阻均在[0, 1]范围内进行缩放,得到
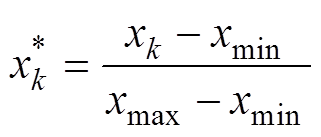 (34)
(34)
式中,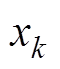 为原始数据集中的任一变量;
为原始数据集中的任一变量;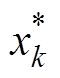 为第k个值归一化后的结果;xmin和xmax分别为原始数据集的最小和最大值。在训练样本处理方面,随机挑选20%的样本作为测试集,其余样本作为训练集,由于训练集和测试集的随机性,每次运行结果并不相同,所以采用运行10次求平均值的方法评价网络性能。采用方均误差(Mean Squared Error, MSE)和决定系数R2评价预测效果,计算公式分别为
为第k个值归一化后的结果;xmin和xmax分别为原始数据集的最小和最大值。在训练样本处理方面,随机挑选20%的样本作为测试集,其余样本作为训练集,由于训练集和测试集的随机性,每次运行结果并不相同,所以采用运行10次求平均值的方法评价网络性能。采用方均误差(Mean Squared Error, MSE)和决定系数R2评价预测效果,计算公式分别为
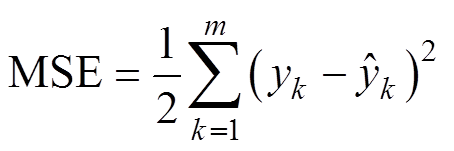 (35)
(35)
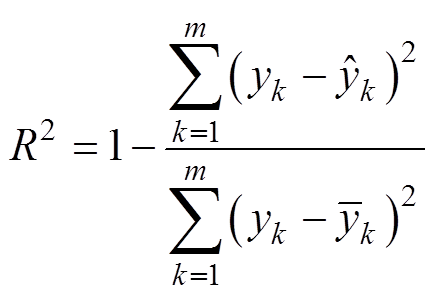 (36)
(36)
式中,yk、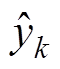 、
、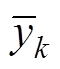 分别为测试集上的输出、预测输出和输出均值。决定系数R2∈[0, 1],越接近于1,模型预测性能越好。
分别为测试集上的输出、预测输出和输出均值。决定系数R2∈[0, 1],越接近于1,模型预测性能越好。
隐含层神经元个数7~20,选择epoch次数为10 000次,隐层节点个数与平均MSE指标关系如图9所示。
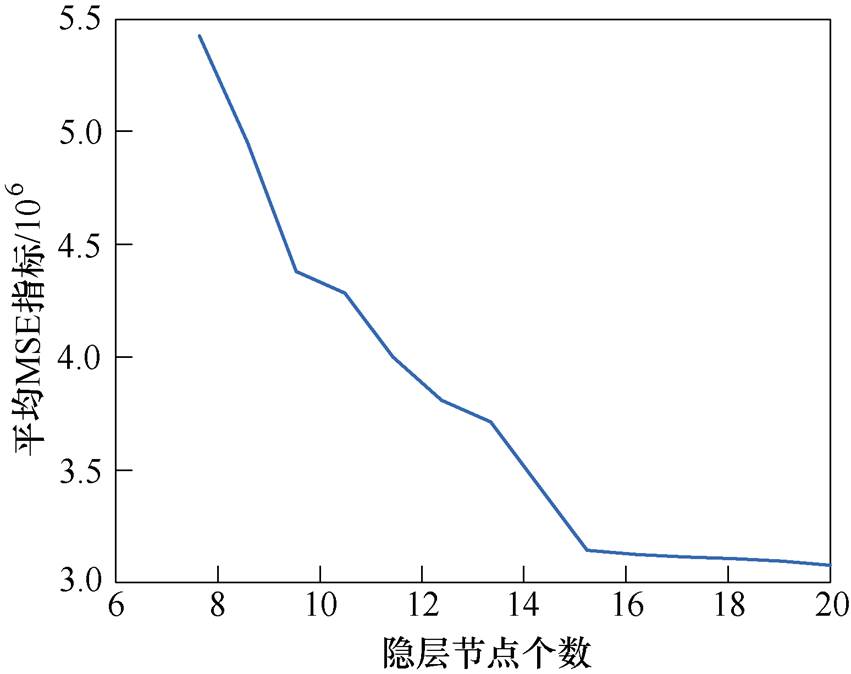
图9 隐层节点个数与平均MSE指标关系
Fig.9 Relationship between the number of hidden layer nodes and the average MSE index
根据图9,隐藏节点15后的MSE结果几乎没有变化,因此,将隐藏节点数设置为15。ICPA-RBF结构由5个输入节点、15个隐藏节点和1个输出节点组成,即5-15-1,所以算法优化参数的个数为10×15+15=165个。
为了验证ICPA-RBF算法的性能优越,将其与基本食肉植物算法(CPA-RBF)和粒子群优化-RBF(Particle Swarm Optimization-RBF, PSO-RBF)算法进行寻优对比,种群规模均设置为30,最大迭代次数为200,RBF函数的中心矢量、基宽以及权值的初始值为待优化参数,其初始范围均取[-1, 1]以产生初始种群。ICPA-RBF和CPA-RBF算法growth_rate=3,吸引率为0.8,生长过程持续代数group_iter=7,繁殖率Re=1.7。为了降低随机性对结果的影响,三种算法分别独立运行了10次。三种算法的平均MSE演化曲线如图10所示。
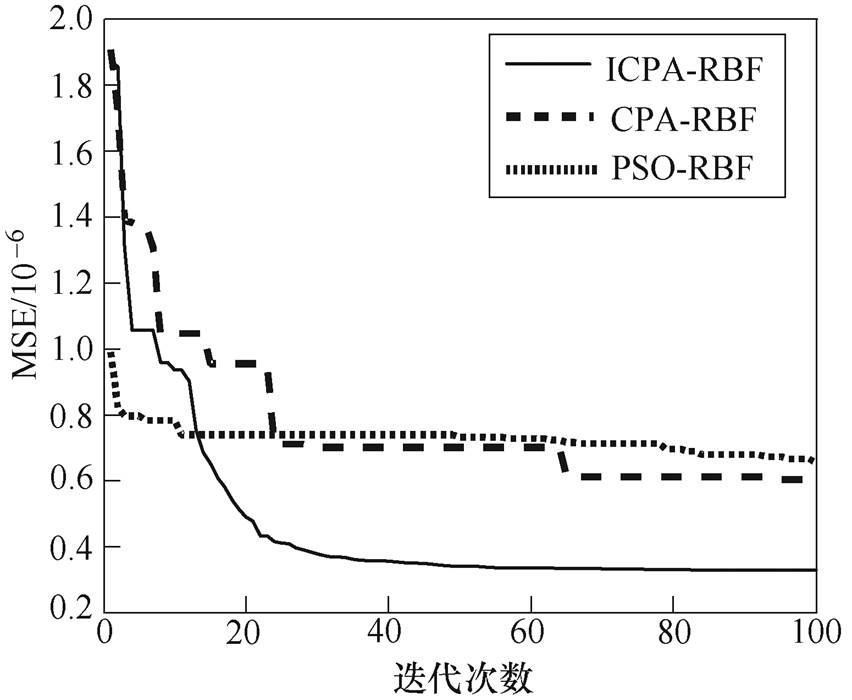
图10 MSE演化曲线
Fig.10 MSE evolution curves
由图10可知,ICPA-RBF收敛速度最快,ICPA- RBF的MSE迭代至40代左右后不再变化,而PSO- RBF和CPA-RBF分别在80代和70代依然还有下降趋势,这是由于Logistic混沌映射初始化可以有效提高初始种群中优质解的比例,进而提高算法的收敛速度。ICPA-RBF的最终MSE收敛于0.3×10-6,而PSO-RBF和CPA-RBF分别收敛于0.7×10-6和0.6×10-6,ICPA-RBF收敛精度高于其他算法,这表明自适应生长率策略、莱维飞行策略和贪心机制策略更好地协调了算法在探索阶段的全局搜索能力和局部最优开发能力,提高收敛精度。因此,ICPA-RBF算法相比于PSO-RBF算法和CPA-RBF算法具有更好的收敛速度、收敛精度和稳定性。
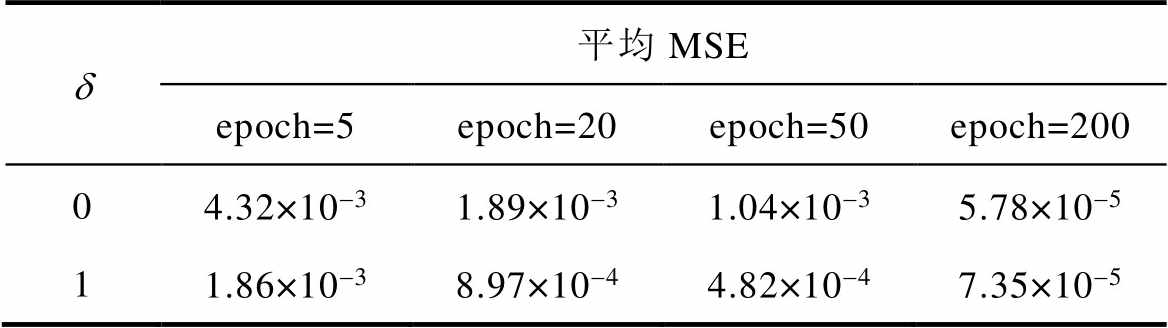
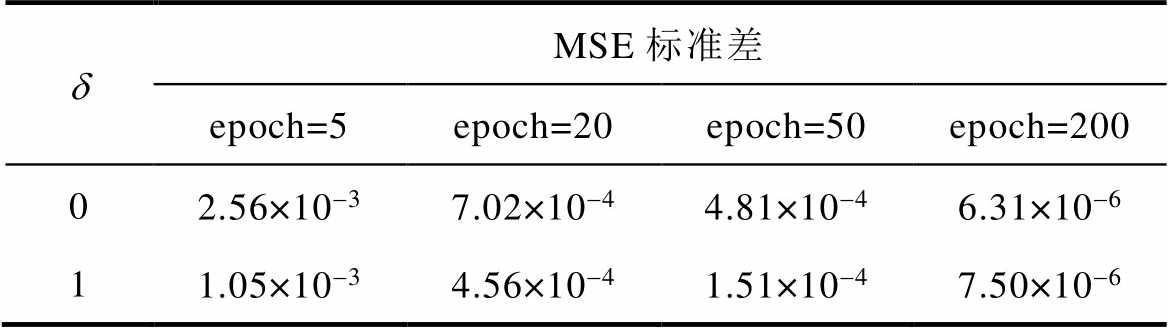
为了检验先验知识Ⅰ在提高ICPA-RBF模型性能方面的作用,分别在式(8)中的d 取1和取0状态下,即有、无先验知识Ⅰ状态,独立运行程序10次。训练集的MSE的平均值和标准差见表3和表4,由表中数据可知,先验知识Ⅰ减小了MSE的标准差。这是由于先验知识Ⅰ限制了权值调整的方向,提高了ICPA-RBF模型的收敛速度。但先验知识Ⅰ不能提高最终的逼近精度,这是因为无先验知识Ⅰ的ICPA-RBF模型以减小MSE指标为唯一目标,而加入先验知识Ⅰ后,为了保持接触电阻对接触压力载荷的偏导数非正,权值的搜索空间变小,这有助于避免过拟合,但逼近精度无法提高。因此,本文提出的采用随机梯度并具有先验知识Ⅰ的ICPA- RBF方法适用于对收敛速度和计算量均有严格限制的在线训练和更新的要求。
表3 平均MSE
Tab.3 Average MSE
d平均MSE epoch=5epoch=20epoch=50epoch=200 04.32×10-31.89×10-31.04×10-35.78×10-5 11.86×10-38.97×10-44.82×10-47.35×10-5
表4 MSE标准差
Tab.4 Standard deviation of MSE
dMSE标准差 epoch=5epoch=20epoch=50epoch=200 02.56×10-37.02×10-44.81×10-46.31×10-6 11.05×10-34.56×10-41.51×10-47.50×10-6
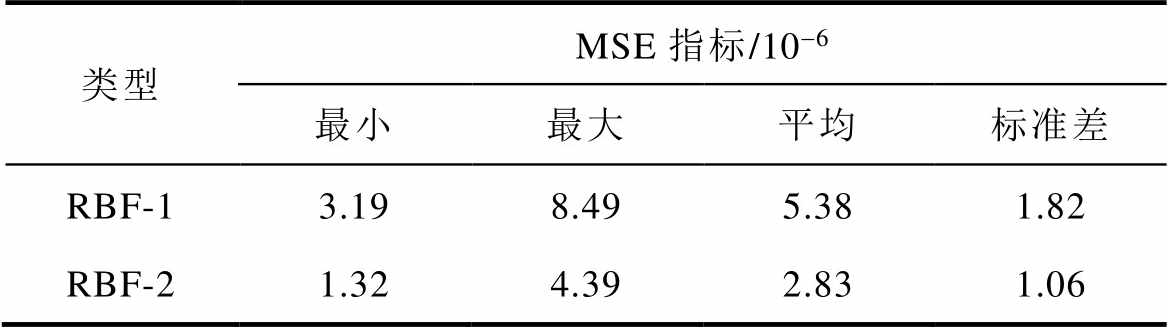
设置epoch为10 000,不考虑先验知识Ⅱ的RBF网络记为RBF-1,网络结构为5-15-1;考虑先验知识Ⅱ,即加入损失电流能量作为输入变量的RBF网络记为RBF-2,网络结构为6-15-1。以最小方均误差MSE为训练目标,各自独立运行10次的方均误差MSE与决定系数R2性能指标对比见表5、表6。其中,基于RBF-2模型,性能指标为MSE=1.380 4× 10-6,R2=0.975 4的一次运行结果在其随机测试集上的拟合效果如图11所示。
表5 MSE指标对比
Tab.5 Index comparison of MSE
类型MSE指标/10-6 最小最大平均标准差 RBF-13.198.495.381.82 RBF-21.324.392.831.06
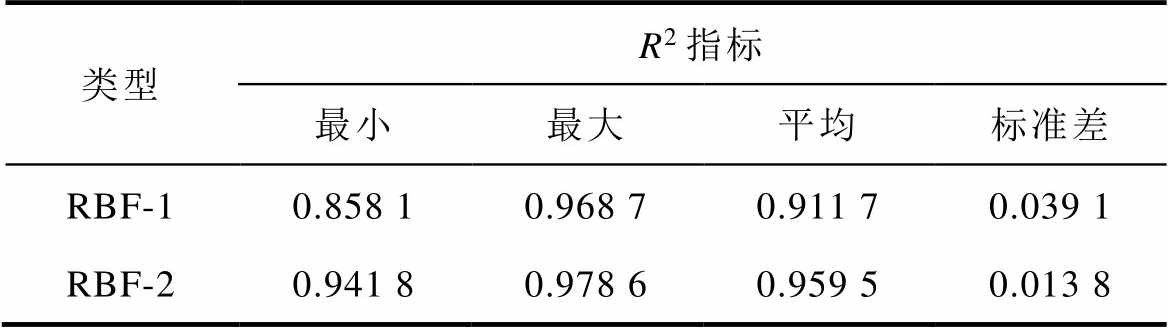
表6 R2指标对比
Tab.6 Index comparison of R2
类型R2指标 最小最大平均标准差 RBF-10.858 10.968 70.911 70.039 1 RBF-20.941 80.978 60.959 50.013 8
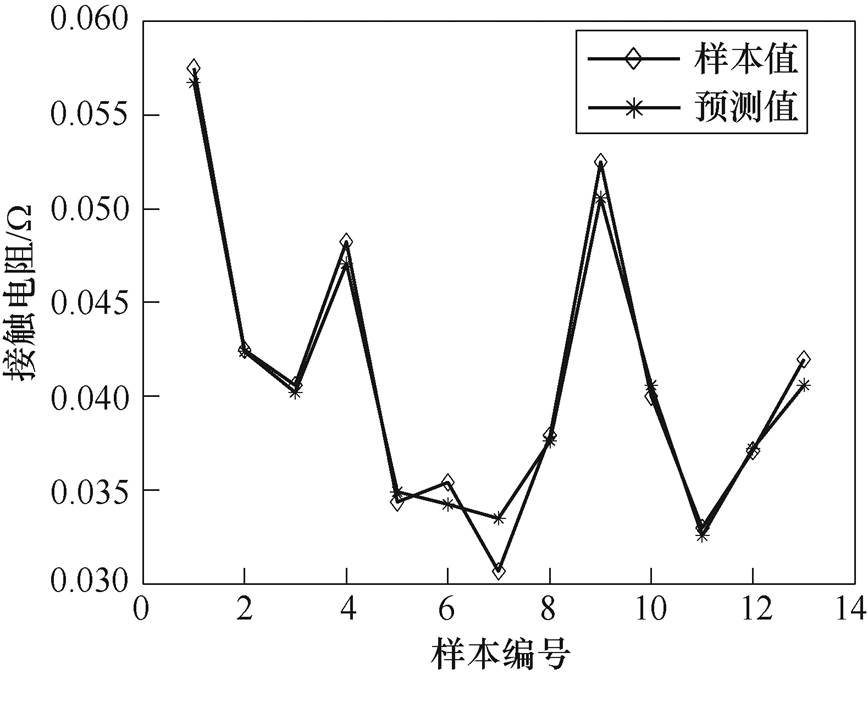
图11 测试集拟合效果
Fig.11 Imitative effect of test set
由表5、表6和图11可知,不考虑损失电流能量的RBF-1网络在MSE指标、决定系数R2指标上的性能均不及考虑损失电流能量的RBF-2网络,RBF-2网络的平均MSE指标是RBF-1网络的52.6%,平均R2指标RBF-1网络提高了5.24%,最大预测误差减小了52.3%。从分别进行10次随机运行后得到的性能指标标准差可以看出,RBF-2网络的标准差更小,这说明RBF-1网络易受随机分配的训练集和测试集样本的影响,而RBF-2网络由于添加了损失电流二次方作为输入变量,间接考虑了电弧放电能量,因而对接触面状态描述的更加全面,对样本训练集和测试集的随机划分相对不敏感,性能鲁棒性更强。
进一步验证模型的泛化能力与有效性,选择偏置静态压力载荷为70 N、频率为2 Hz,另设工况条件进行实验,新实验的接触电阻观测值和模型预测值见表7。
表7 观测值与模型预测值
Tab.7 Observations and predictions contact resistance
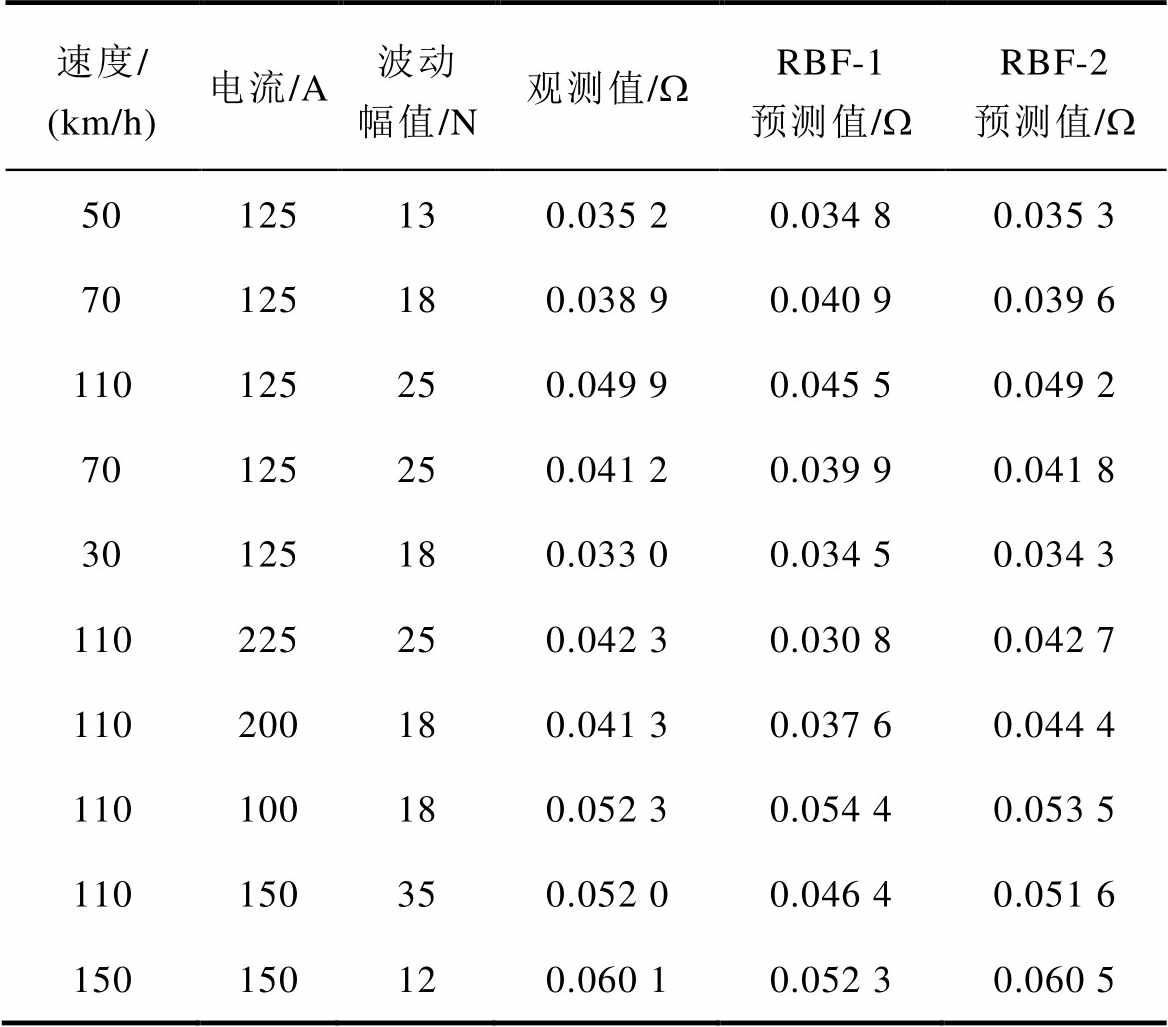
速度/ (km/h)电流/A波动幅值/N观测值/WRBF-1预测值/WRBF-2预测值/W 50125130.035 20.034 80.035 3 70125180.038 90.040 90.039 6 110125250.049 90.045 50.049 2 70125250.041 20.039 90.041 8 30125180.033 00.034 50.034 3 110225250.042 30.030 80.042 7 110200180.041 30.037 60.044 4 110100180.052 30.054 40.053 5 110150350.052 00.046 40.051 6 150150120.060 10.052 30.060 5
由表7可知,RBF-1最大残差为0.004 0 W,RBF-2最大残差为0.001 9 W。通过分析接触电阻预测模型在样本工况和测试工况下的预测性能是否有明显差异来验证RBF-2接触电阻预测模型的有效性。假设两类工况的残差分别为e1、e2,满足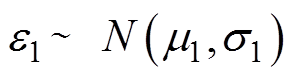 、
、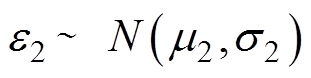 ,分别对两个总体的方差和均值进行假设检验[34]:
,分别对两个总体的方差和均值进行假设检验[34]:
(1)统计假设H0: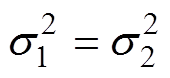 ,H1:
,H1: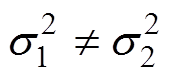 。由于总体均值m1、m2未知,因此拒绝域为
。由于总体均值m1、m2未知,因此拒绝域为
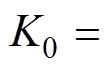
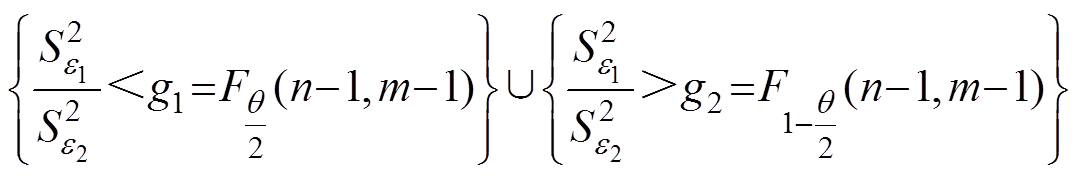 (37)
(37)
式中,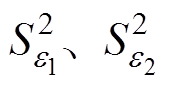 分别为两样本方差;n、m为样本容量;g1、g2为拒绝域的临界值,随显著水平而变化;q 为显著水平。经计算
分别为两样本方差;n、m为样本容量;g1、g2为拒绝域的临界值,随显著水平而变化;q 为显著水平。经计算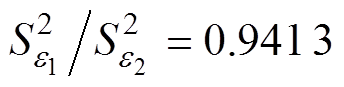 ,取显著性水平q =0.05,则可得g1=0.126 2,g2=4.026 0,落在接受域内,所以接受原假设H0,即
,取显著性水平q =0.05,则可得g1=0.126 2,g2=4.026 0,落在接受域内,所以接受原假设H0,即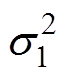 和
和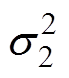 无明显差异。
无明显差异。
(2)设立统计假设H0:m1=m2,H1:m1≠m2。由于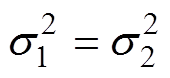 ,因此拒绝域为
,因此拒绝域为
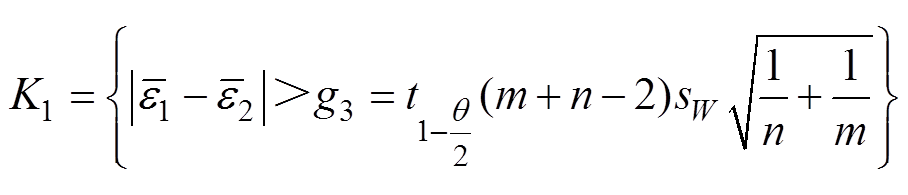 (38)
(38)
其中
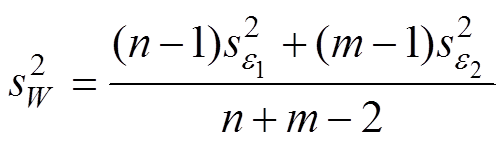
式中,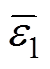 、
、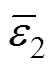 为两类工况的残差均值;显著性水平θ=
为两类工况的残差均值;显著性水平θ=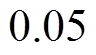 ;g3为拒绝域的临界值。计算
;g3为拒绝域的临界值。计算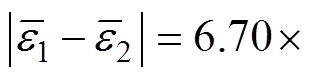
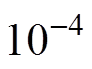 ,g3=7.854×10-4,所以接受原假设H0。
,g3=7.854×10-4,所以接受原假设H0。
通过残差分析可知,接触电阻预测模型在样本工况和测试工况下的预测能力在显著水平0.05时无明显差异。该结论一方面说明接触电阻预测模型的有效性;另一方面通过对比表7中RBF-1与RBF-2的预测值与真实值的差异,反映了先验知识Ⅱ在提高模型泛化能力和增强模型性能鲁棒性方面的有 效性。
本文通过实验机模拟弓网系统的滑动电接触工况,首先研究接触电阻随波动载荷、接触电流、滑动速度的变化关系,然后探讨了定性结论作为先验知识在提高接触电阻预测模型性能方面的应用,基于本文的实验条件和实验材料,主要研究结论如下:
1)波动载荷增大,电接触稳定性减弱,对接触电阻主要起负面作用;随着接触电流的增大,其润滑作用增强,有利于接触电阻的减小;速度的增大也会削弱接触的稳定性,尤其是在大电流条件下,电弧放电能量显著增加,破坏接触表面,导致接触电阻增大。
2)分别以接触电阻对接触压力载荷的偏导数为非正数、损失电流的二次方可以用来近似表征电弧能量作为先验知识Ⅰ、Ⅱ应用于接触电阻的ICPA- RBF神经网络建模过程。结果表明,先验知识Ⅰ提高了算法的收敛速度,因此该方法适合接触电阻的在线训练建模;先验知识Ⅱ可以用来提高预测的准确性,基于先验知识Ⅱ的ICPA-RBF模型具有较好的泛化能力。
3)损失电流在实验机模拟弓网工况实验中是易获取的参数,在弓网实际应用中,当损失电流不易获取时,可采用与电弧能量关系密切的离线率、弓网燃弧特征紫外光信号等其他参数替代。
4)本文所提出的利用先验知识的接触电阻建模方法可以推广到其他受流性能指标的建模。
参考文献
[1] 张冬冬, 李小波, 张浩, 等. 地铁列车弓网接触电阻数学模型研究[J]. 智能计算机与应用, 2022, 12(2): 165-169.
Zhang Dongdong, Li Xiaobo, Zhang Hao, et al. Investigation on the mathematical model of contact resistance of pantograph-catenary in metro vehicle[J]. Intelligent Computer and Applications, 2022, 12(2): 165-169.
[2] 王英, 刘志刚, 范福强, 等. 弓网电弧模型及其电气特性的研究进展[J]. 铁道学报, 2013, 35(8): 35-43.
Wang Ying, Liu Zhigang, Fan Fuqiang, et al. Review of research development of pantograph-catenary arc model and electrical characteristics[J]. Journal of the China Railway Society, 2013, 35(8): 35-43.
[3] 吴积钦. 弓网系统电弧的产生及其影响[J]. 电气化铁道, 2008, 19(2): 27-29.
Wu Jiqin. Occurrence of arc in pantograph and overhead contact system and its interference[J]. Electric Railway, 2008, 19(2): 27-29.
[4] Liu Jianqiang, Yang Qilin, Zheng T Q. Harmonic analysis of traction networks based on the CRH380 series EMUs accident[C]//2012 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 2012: 1-6.
[5] 陈忠华, 李兵红, 陈明阳, 等. 弓网滑动电接触电磁热力耦合效应研究进展[J]. 电工技术学报, 2023, 38(10): 2777-2793.
Chen Zhonghua, Li Binghong, Chen Mingyang, et al. Research advances in electrical-magnetic-thermal- mechanical coupling effects of electric contact between pantograph and catenary[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2777- 2793.
[6] Wang Wangang, Dong Anping, Wu Guangning, et al. Study on characterization of electrical contact between pantograph and catenary[C]//2011 IEEE 57th Holm Conference on Electrical Contacts (Holm), Minneapolis, MN, USA, 2011: 1-6.
[7] 郭凤仪, 马同立, 陈忠华, 等. 不同载流条件下滑动电接触特性[J]. 电工技术学报, 2009, 24(12): 18-23.
Guo Fengyi, Ma Tongli, Chen Zhonghua, et al. Characteristics of the sliding electric contact under different currents[J]. Transactions of China Elec- trotechnical Society, 2009, 24(12): 18-23.
[8] 王万岗, 梁明亮, 吴广宁, 等. 弓网系统静态接触电阻特性研究[J]. 高压电器, 2012, 48(1): 30-34.
Wang Wangang, Liang Mingliang, Wu Guangning, et al. Characteristics of static contact resistance between pantograph and catenary[J]. High Voltage Apparatus, 2012, 48(1): 30-34.
[9] 陈忠华, 石英龙, 时光, 等. 受电弓滑板与接触网导线接触电阻计算模型[J]. 电工技术学报, 2013, 28(5): 188-195.
Chen Zhonghua, Shi Yinglong, Shi Guang, et al. Calculation model of the contact resistance between pantograph slide and contact wire[J]. Transactions of China Electrotechnical Society, 2013, 28(5): 188-195.
[10] 李春茂, 朱宁俊, 吴广宁, 等. 弓网系统动态接触电阻数学模型的研究[J]. 高电压技术, 2015, 41(11): 3554-3560.
Li Chunmao, Zhu Ningjun, Wu Guangning, et al. Investigation on the mathematical model of dynamic contact resistance of pantograph-catenary system[J]. High Voltage Engineering, 2015, 41(11): 3554-3560.
[11] Watanabe Y. High-speed sliding characteristics of Cu-Sn-based composite materials containing lamellar solid lubricants by contact resistance studies[J]. Wear, 2008, 264(7/8): 624-631.
[12] 刘方林. 电气化铁路动态弓网接触电阻研究[J]. 电气技术, 2018, 19(9): 69-72.
Liu Fanglin. Study on dynamic contact resistance between pantograph and catenary in electrified railway[J]. Electrical Engineering, 2018, 19(9): 69-72.
[13] Paulmier D, El Mansori M, Zaïdi H. Study of magnetized or electrical sliding contact of a steel XC48/graphite couple[J]. Wear, 1997, 203/204: 148- 154.
[14] Hu Zuolei, Chen Zhonghua, Xia Jintong. Study on surface film in the wear of electrographite brushes against copper commutators for variable current and humidity[J]. Wear, 2008, 264(1/2): 11-17.
[15] Hric G R, Odendaal W G. Improving start-up contact distribution between railgun armature and rails[J]. IEEE Transactions on Plasma Science, 2016, 44(7), 1202-1207.
[16] 陈忠华, 王一帆, 杨彩红, 等. 波动载荷下弓网动态接触电阻特性研究[J]. 高压电器, 2019, 55(10): 148-155, 163.
Chen Zhonghua, Wang Yifan, Yang Caihong, et al. Study on dynamic contact resistance of pantograph catenary under fluctuating load[J]. High Voltage Apparatus, 2019, 55(10): 148-155, 163.
[17] 王英, 刘志刚, 黄可, 等. 计及机械和电气特性的弓网表面热流分析和计算[J]. 铁道学报, 2014, 36(7): 36-43.
Wang Ying, Liu Zhigang, Huang Ke, et al. Pantograph-catenary surface heat flow analysis and calculations based on mechanical and electrical characteristics[J]. Journal of the China Railway Society, 2014, 36(7): 36-43.
[18] Tamai T, Tsuchiya K. Contact resistance characteri- stics at low temperature[J]. IEEE Transactions on Components, Hybrids, and Manufacturing Tech- nology, 1978, 1(1): 54-58.
[19] Liu Xinlong, Cai Zhenbing, He Jifan, et al. Effect of elevated temperature on fretting wear under electric contact[J]. Wear, 2017, 376/377: 643-655.
[20] 郭凤仪, 王喜利, 王智勇, 等. 弓网电弧辐射电场噪声实验研究[J]. 电工技术学报, 2015, 30(14): 220-225.
Guo Fengyi, Wang Xili, Wang Zhiyong, et al. Research on radiated electric field noise of pantograph arc[J]. Transactions of China Electro- technical Society, 2015, 30(14): 220-225.
[21] Feng C, Lin Xinxin, Xu Yixin, et al. Investigation on contact resistance of connector based on FEM[C]// 2020 IEEE 22nd Electronics Packaging Technology Conference (EPTC), Singapore, Singapore, 2020: 403-405.
[22] 李白, 鲁军勇, 谭赛, 等. 高速滑动电接触电枢表面动态磨损过程研究[J]. 电工技术学报, 2023, 38(1): 131-139.
Li Bai, Lu Junyong, Tan Sai, et al. Research on dynamic wear process of armature surface in high-speed sliding electric contact[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 131-139.
[23] 王增基, 陈立学, 尤彭昊, 等. 考虑速度趋肤效应与接触电阻影响的枢轨界面电流分布特性[J]. 电工技术学报, 2022, 37(19): 5003-5010.
Wang Zengji, Chen Lixue, You Penghao, et al. Current distribution characteristics of armature-rail interface under velocity skin effect and contact resistance[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 5003-5010.
[24] Boyer L. Contact resistance calculations: generali- zations of Greenwood’s formula including interface films[J]. IEEE Transactions on Components and Packaging Technologies, 2001, 24(1): 50-58.
[25] 时光, 陈忠华, 郭凤仪, 等. 波动载荷下弓网接触电阻特性及建模研究[J]. 电工技术学报, 2019, 34(11): 2287-2295.
Shi Guang, Chen Zhonghua, Guo Fengyi, et al. Research on characteristic of the contact resistance of pantograph-catenary under load fluctuation condi- tion[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2287-2295.
[26] 张鹏, 张峻霞, 刘瑞恒, 等. 基于GA-RBF神经网络和sEMG的下肢动作识别方法研究[J]. 中国生物医学工程学报, 2022, 41(1): 41-47.
Zhang Peng, Zhang Junxia, Liu Ruiheng, et al. The study of lower limb motion recognition method based on GA-RBF neural network and sEMG signals[J]. Chinese Journal of Biomedical Engineering, 2022, 41(1): 41-47.
[27] 张伟, 黄卫民. 基于SAPSO算法的RBF神经网络设计[J]. 控制与决策, 2021, 36(9): 2305-2312.
Zhang Wei, Huang Weimin. Design of RBF neural network based on SAPSO algorithm[J]. Control and Decision, 2021, 36(9): 2305-2312.
[28] 蒋慧平, 董霖. 钢铝复合轨/受电靴摩擦热与接触电阻热耦合的温度场有限元模拟研究[J]. 润滑与密封, 2010, 35(1): 45-48.
Jiang Huiping, Dong Lin. FE simulation research of temperature field couple under contact resistor- friction thermal between aluminum-stainless steel composite conductor rail and collector shoe[J]. Lubrication Engineering, 2010, 35(1): 45-48.
[29] Ong K M, Ong P, Sia C K. A carnivorous plant algorithm for solving global optimization problems[J]. Applied Soft Computing, 2021, 98: 106833.
[30] 田红亮, 朱大林, 秦红玲. 两弹性接触粗糙低速滑动表面温升的分形模型[J]. 三峡大学学报(自然科学版), 2010, 32(2): 65-71.
Tian Hongliang, Zhu Dalin, Qin Hongling. Fractal model of temperature rise between two elastic contact rough slow sliding surfaces[J]. Journal of China Three Gorges University (Natural Sciences), 2010, 32(2): 65-71.
[31] 郭凤仪, 姜国强, 赵汝彬, 等. 基于相对稳定系数的滑动电接触特性[J]. 中国电机工程学报, 2009, 29(36): 113-119.
Guo Fengyi, Jiang Guoqiang, Zhao Rubin, et al. Sliding electrical contact characteristics based on relative stability coefficients[J]. Proceedings of the CSEE, 2009, 29(36): 113-119.
[32] 黄鹤, 李文龙, 杨澜, 等. ICPA-LQR优化的两轮平衡机器人自稳定与轨迹跟踪PID控制器设计[J/OL]. 哈尔滨工业大学学报, https://kns.cnki.net/kcms/ detail/23.1235.T.20221108.1333.002.html.
Huang He, Li Wenlong, Yang Lan, et al. Design of PID controller for self-stabilization and trajectory tracking of two-wheel balanced robot with ICPA- LQR[J/OL]. Journal of Harbin Institute of Tech- nology, https://kns.cnki.net/kcms/detail/23.1235.T. 20221108.1333.002.html.
[33] Feng Junhong, Zhang Jie, Zhu Xiaoshu, et al. A novel chaos optimization algorithm[J]. Multimedia Tools and Applications, 2017, 76(16): 17405-17436.
[34] 杨虎, 刘琼荪, 钟波. 数理统计[M]. 北京: 高等教育出版社, 2004.
Abstract High-speed trains acquire electrical energy through sliding contact between the pantograph and catenary. Good current-collection performance between the pantograph and the contact wire is necessary for the safe and stable operation of the train. The probability of electric arc generation increases with the development of electric locomotives towards high-speed and heavy loads. Numerous factors contribute to generating electric arcs, but these ultimately stem from the contact resistance between the slider and the contact wire. It is essential to establish an accurate prediction model for contact resistance based on analyzing its characteristics. However, the analysis and modeling of contact resistance characteristics were isolated in previous research. This paper applies the conclusions from the mechanism analysis as prior knowledge to the modeling process of contact resistance. Methods for improving the accuracy of the contact resistance prediction model are explored.
First, the universal conclusions in previous research on electrical contact are summarized. (1) As the contact pressure increases, the contact resistance decreases. (2) Temperature rise significantly affects contact material properties, wear mechanisms, and wear surface morphology, which can be considered an independent variable. Considering that the temperature of the contact core of the friction pair is not easy to measure and the conductive current loss is closely correlated with temperature rise, the conductive current loss as an independent variable can be used to replace the temperature rise. Subsequently, the effects of fluctuating load, sliding speed, and contact current on contact resistance are studied through the sliding electrical contact experiment machine. The relationship between wear mechanism, electric arc discharge, and contact resistance evolution is analyzed with surface morphology. The following conclusions are drawn. (1) As the fluctuating load increases, electrical contact stability weakens, mainly impacting contact resistance. (2) As the contact current increases, the current lubrication effect strengthens, which is conducive to reducing contact resistance. (3) The increase in speed weakens the stability of contact, the contact surface deteriorates, and the contact resistance increases. Finally, the partial derivative of contact resistance with respect to contact load is taken as a non-positive number, and the square of the loss current used to replace temperature rise should be regarded as an independent model input variable, called prior knowledge (Ⅰ) and (Ⅱ), respectively. They are applied to establishing the RBF network model of contact resistance. The improved carnivorous plant optimization algorithm (ICPA) is used to optimize the hyperparameters of the RBF network to improve the accuracy of the contact resistance prediction model.
Simulation results indicate that prior knowledge (Ⅰ) can confine the direction of weight adjustment of the RBF model, reduce the search space of weights, help to prevent overfitting, and enhance the convergence speed of the ICPA-RBF model. However, the accuracy of the final approximation needs to be improved. The MSE index and determination coefficient R2 index of the RBF network without prior knowledge (Ⅱ) are inferior to those with prior knowledge (Ⅱ). The RBF network, adding the square of the loss current as an input variable, considers the energy of electric arc discharge indirectly, thereby providing a more comprehensive description of the contact surface state and stronger performance robustness of the prediction model. Finally, hypothesis testing is conducted under other working conditions. The results demonstrate the effectiveness of the contact resistance prediction model and the prior knowledge (Ⅱ) in improving the generalization ability and enhancing the model’s robustness.
keywords:Contact resistance, prior knowledge, radial basis function (RBF) neural networks, carnivorous plant algorithm, hypothesis testing
DOI: 10.19595/j.cnki.1000-6753.tces.231065
中图分类号:TM501
国家自然科学基金项目(51477071)和辽宁省教育厅面上项目(LJKMZ20220675)资助。
收稿日期 2023-07-06
改稿日期 2023-09-18
时 光 男,1981年生,博士,副教授,研究方向为电接触理论及其应用、非线性系统。E-mail: shiguang@cqu.edu.cn
陈翼喆 男,1998年生,硕士研究生,研究方向为电接触理论及其应用、非线性系统。E-mail: 779461819@qq.com(通信作者)
(编辑 崔文静)