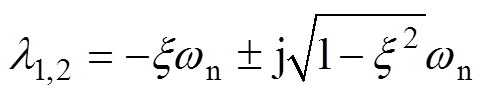（1）
摘要 为了从本质上解释逆变器多机并网系统受到宽频谐波扰动后的动态行为，该文理论推导特征根与系统稳态和暂态响应的解析解，进而利用单个逆变器并网的实例验证了采用特征根分析系统谐波响应的可行性。针对逆变器多机并网系统，阐明特征根与谐振模态的对应关系，使得利用模态分析方法既能解析系统内部支路对不同谐振模态的可激励性和可观测性，又能视系统为一个整体对其稳定性进行分析。最后，通过仿真与实验验证了结合特征根分析逆变器并网系统动态行为的正确性及有效性。
关键词：特征根 谐波扰动 模态分析方法 稳态响应 暂态响应
“双高”电网背景下电网的结构从以同步发电机为主导的刚性系统逐步向以电力电子装置为主导的新型电力系统转变[1-2]，系统结构的变化带来了新的稳定性问题，高比例新能源接入与电网及负荷侧交互引起的宽频振荡是其中典型的一类[3-5]。逆变器作为新能源能量转换接口是最为常见的一种谐波源，单个逆变器的并（离）网过程、电网的短时故障以及负荷侧的波动均会引起网络中相应谐波含量的增加，谐波通过电网传播至其他节点，使得相应节点处电气量为基波和谐波分量的叠加，引起谐波振荡，造成波形的畸变，电能质量下降严重时还会造成系统的失稳[6]。
系统的稳定性是围绕着系统受到扰动后是否能回归平衡点展开的[7]。随着新能源装机容量的不断提高，原有的面向传统电力系统的稳定性定义难以概括一些新的现象[8]。例如，在美国ERCOT CREZ可再生能源输电项目中发现，当大规模的风机接入弱电网时会出现短时的过电压[9]；美国加州光伏发电项目中同样观察到了稳态和故障后的暂态过电压现象[10]。这种短时的过电压现象显然不是由发电机转子主导的机械暂态过程，而是由高比例电力电子装置的应用引起的电磁暂态过程。学者们对于新能源并网引起的电磁暂态过程关注较少，且在涉及暂态的相关论述时，也是将类似锁相环的环节等效为传统电网下发电机转子侧的功角关系，即认为其在电网发生大扰动后的动态行为依旧是机电暂态过 程[11-12]。但关于新能源并网过程中的电磁暂态现象需要引起重视，类似上述的短时过电压可能会造成输电线路的过负载以及保护装置的误动作等，严重时同样会引起系统的失稳。
通常通过单位冲激响应来判断系统稳定性，利用阶跃响应衡量系统的动态性能[13]，这是因为s域下冲激响应不会额外引入新的零、极点，分析冲激响应相当于分析系统本身的特性；而阶跃响应能够提供一系列关键的指标，通过关注变量的评估可以方便工程师们从不同方向对系统进行优化。但无论是分析系统的冲激响应还是阶跃响应，均是围绕着系统受到扰动后对其工频分量的影响展开的，然而实际新能源并网系统面临的常常是宽频谐波扰动，其频率范围覆盖了几百至上千赫兹不等[14-16]，仅从冲激响应或阶跃响应着手难以解释其并（离）网过程中的动态电磁现象。
考虑到LCL型并网逆变器本身是一高阶复杂的耦合系统，若精确建模分析其谐波响应势必工作量巨大且结论不易推广[17-18]，而结合系统的特征根分析系统的谐波响应既降低了分析难度，减小了计算量，又保证了其响应与原系统响应的近似相同，所得结论更具一般性[19-21]。因此，结合系统的特征根分析其谐波响应更有利于从本质上解释系统受到谐波扰动后的动态行为。
逆变器多机并网时并联支路间、逆变器与电网阻抗间皆存在耦合[22]，针对n台逆变器并网系统，分析单台逆变器的频率响应时若简单地将电网等效阻抗扩大n倍并不能解释网络中新增的谐振点[23-24]，分析其谐振机理若利用传统的频率响应曲线存在“维数灾”等问题[25]。基于系统的无源性理论提供了逆变器多机并网系统稳定性的充分条件[26]，单一逆变器的并网端口等效为系统的无源性测试提供了便利，但对内部子系统运行稳定裕度的界定相对困难[27]。模态分析法此前已被成功应用于识别逆变器多机并网存在的谐振频率[28-30]，通过计算振荡模态下的参与因子能够表征支路间的耦合[31-33]，其作为一种解析方法能够降低建模难度，显著减小计算量。若能将这一方法与基于系统的无源性理论相结合，将模态分析结果所得的谐振频率及支路间的耦合关系与系统相应的特征根联系起来，则可进一步为逆变器多机并网系统的谐波振荡抑制提供更具指向性的解决路径。
本文结合特征根推导了系统的谐波响应，并分析了响应中两种不同特性的分量。通过一个逆变器并网的实例验证了逆变器并网系统关于特征根分析其谐波响应的可行性。针对逆变器多机并网系统，成功利用模态分析法解析得到网络存在的谐振点并求取了相应谐振频率下系统的特征根，该方法的复用不仅能利用其本身的优势，还能结合特征根从本质上解释系统受到谐波扰动后的动态行为。通过仿真和实验验证了结合特征根和模态分析方法分析逆变器并网系统谐波扰动响应的正确性。
系统稳定的充分必要条件为其所有特征根都具有负的实部，设其中一对共轭复根的一般形式为
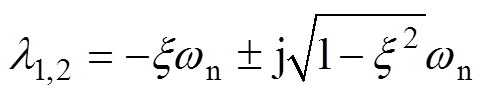（1）
式中，x 为系统的阻尼系数；wn为系统的自然谐振频率。
设系统的谐波扰动r(t)为
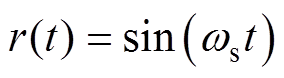（2）
式中，ws为谐波扰动角频率。则系统的响应y(t)为
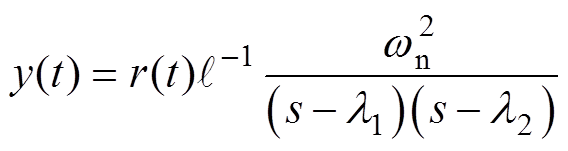（3）
式中，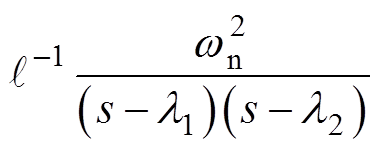
为l1,2这一对特征根对应的系统传递函数的时域表达式。
结合式（2）、式（3），得系统的谐波响应为
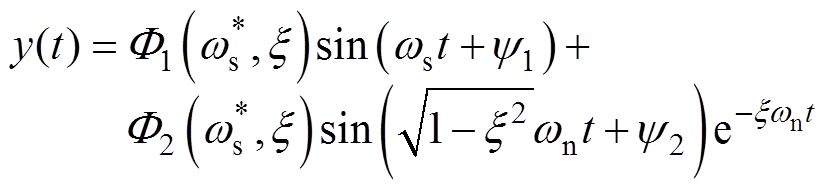（4）
其中
（5）
观察式（4）可以发现，对于存在一对共轭复根l1,2的系统，当输入谐波扰动r(t)时，系统的输出响应为两种波形的叠加：一部分为关于谐波频率ws的正弦波；另一部分波形的振荡频率为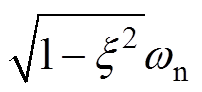
，幅值随着指数项
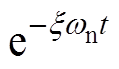而衰减，xwn取值的不同会影响其衰减速度。
由1.1节分析可知，系统受到谐波扰动后，波形中同时存在稳态和暂态分量，为便于解析，分别分析两种响应的特性。结合稳态响应幅值F1的表达式，绘制当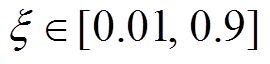
、
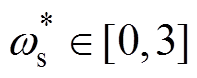时幅值F1，如图1所示。
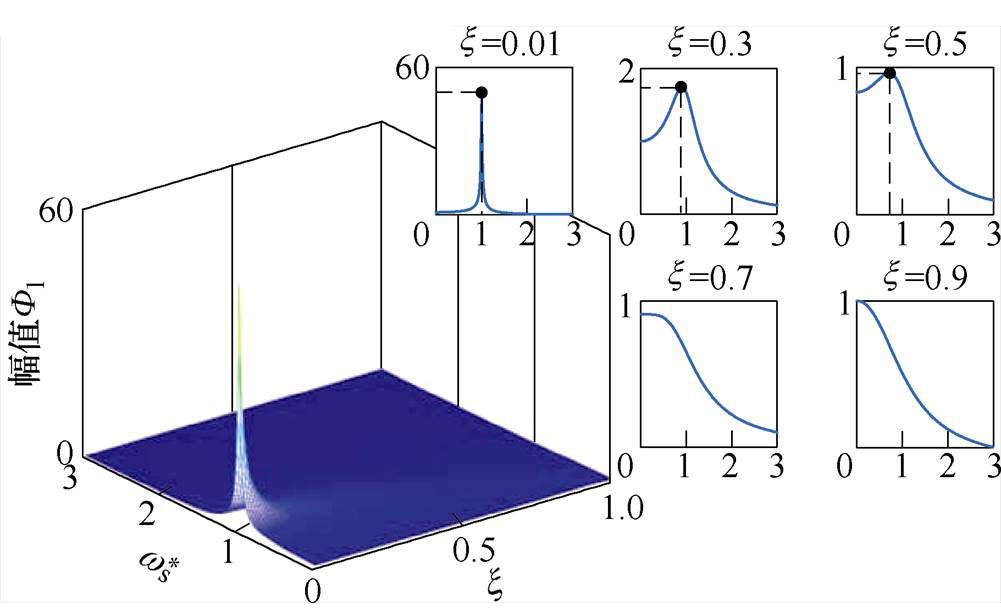
图1 稳态响应幅值F1随阻尼系数x 和扰动频率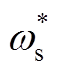
的变化曲线
Fig.1 Variation curves of steady-state response amplitude F1 with damping coefficient x and disturbance frequency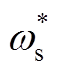
观察图1可以发现，F1的峰值出现在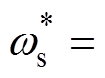
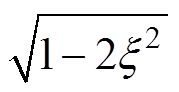处，x 越接近于0，F1的峰值越高；x 越大，F1的峰值越低，且峰值频率偏离
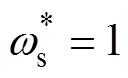的程度越大，当x＞0.7时，F1不存在峰值。
结合式（1），绘制当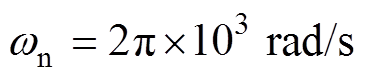
、x =0.3、0.4、0.5、0.6、0.7时系统的频率响应曲线，如图2所示。
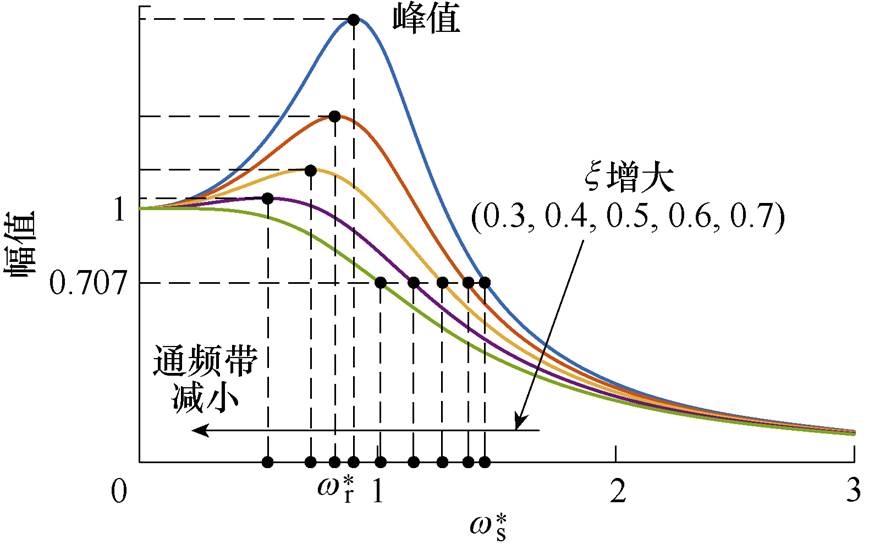
图2 阻尼系数x 取值不同时系统的频率响应曲线
Fig.2 The frequency response curves of the system when the damping coefficient x is different
图2中，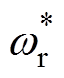
为系统的峰值频率，其值为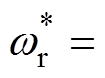
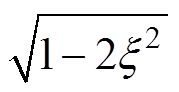。观察图2可以发现，随着x 的增大，系统谐振峰值不断降低，谐振频率不断远离wn，系统的通频带不断减小，且当x＞0.7时，不存在谐振峰，这与上述分析系统的谐波稳态响应所得的结论一致。
结合暂态响应幅值F2的表达式，绘制当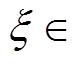
、
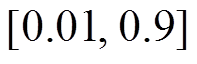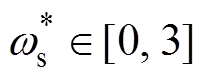时幅值F2，如图3所示。
观察图3可以发现，F2的峰值出现在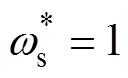处，x 越接近于0，F2的峰值越高；x 由0逐渐增大到0.7时，F2的峰值逐渐降低，并且在x =0.7时峰值最低，当x 由0.7逐渐增大到0.9时，F2的峰值逐渐增大，但峰值频率稳定在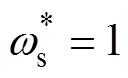处。
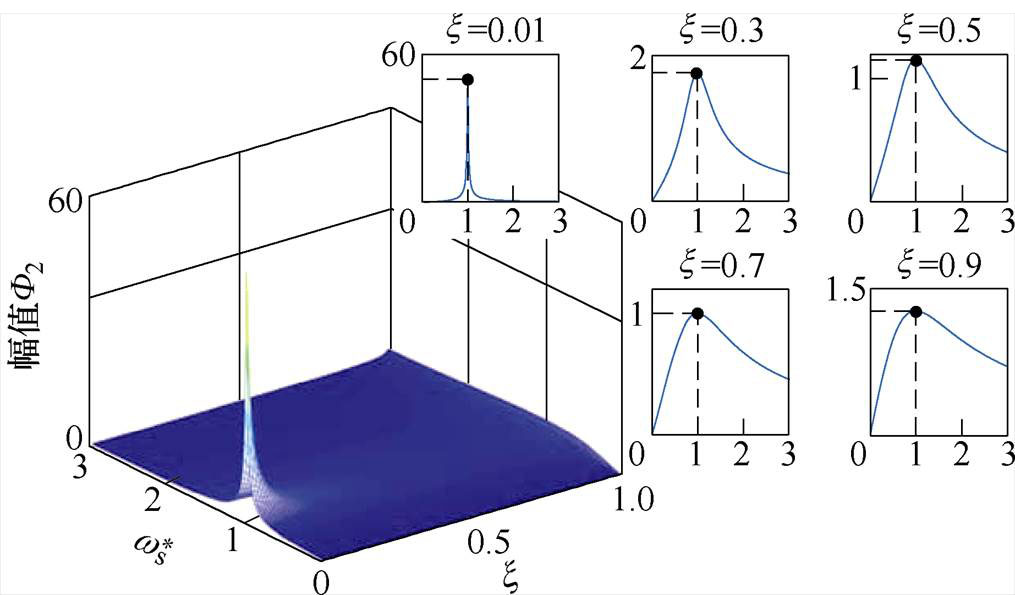
图3 暂态响应幅值F2随阻尼系数x 和扰动频率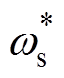
的变化曲线
Fig.3 Variation curves of transient response amplitude F2 with damping coefficient x and disturbance frequency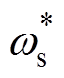
总结上述分析含有一对共轭复根的系统的谐波响应特性见表1。
表1 含有一对共轭复根的系统的谐波响应特性
Tab.1 Harmonic response characteristics of a system with a pair of conjugate complex roots
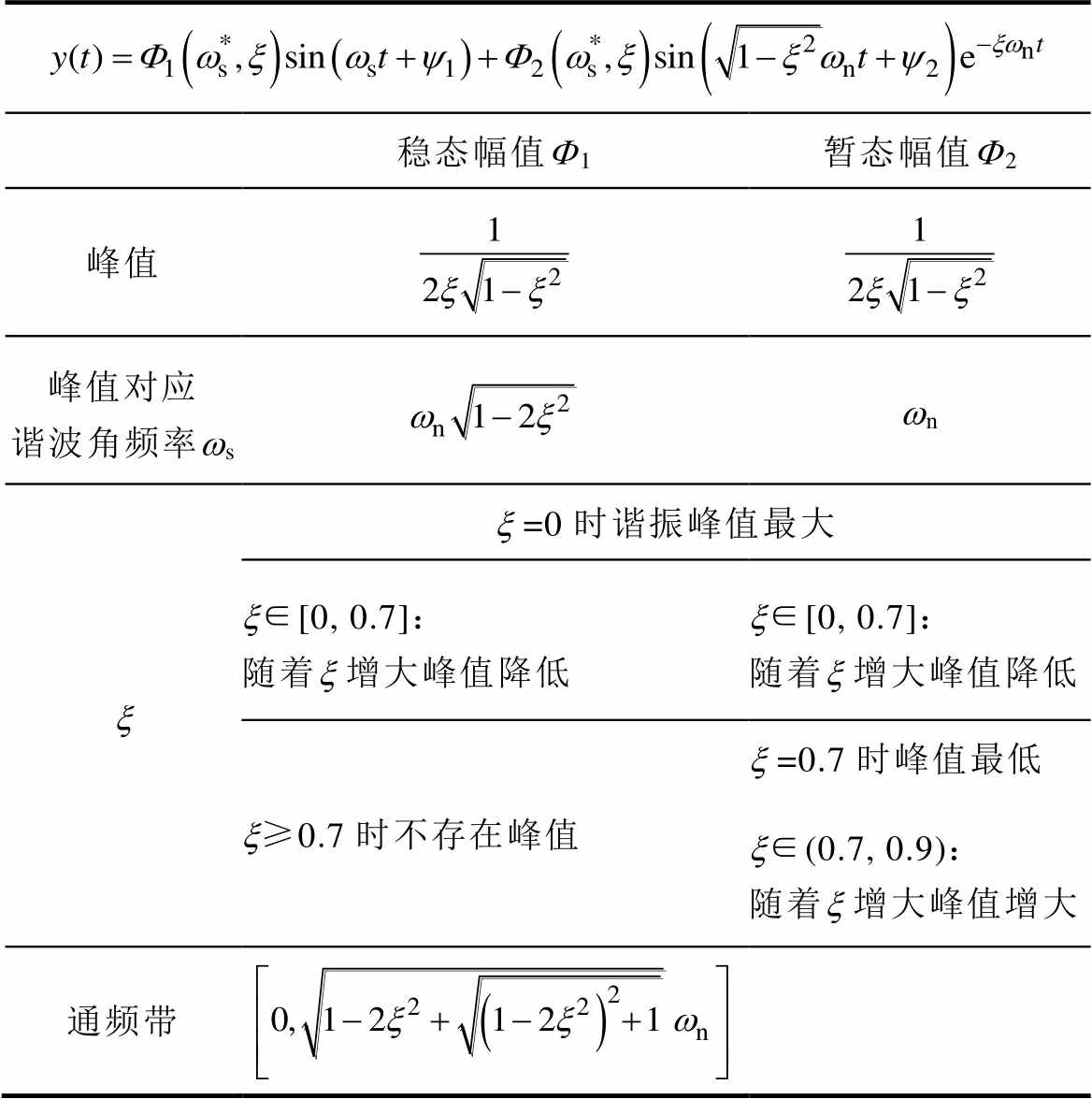
稳态幅值F1暂态幅值F2 峰值 峰值对应谐波角频率wswn xx =0时谐振峰值最大 x∈[0, 0.7]：随着x 增大峰值降低x∈[0, 0.7]：随着x 增大峰值降低 x≥0.7时不存在峰值x =0.7时峰值最低 x∈(0.7, 0.9)：随着x 增大峰值增大 通频带
如图4所示为一单相LCL型并网逆变器的拓扑。图4中，L1为逆变器侧电感，C为滤波电容，R为滤波电容侧电阻，L2为网侧电感，Lg为电网等效电感，Udc为逆变器直流侧电压，Uinv为逆变器交流侧输出电压，UC为滤波电容电压，UPCC为公共耦合点（Point of Common Coupling, PCC）电压，Ug为电网电压，IL1为逆变器侧电感电流，IC为滤波电容电流，IL2为逆变器并网电流。其控制框图如图5所示。
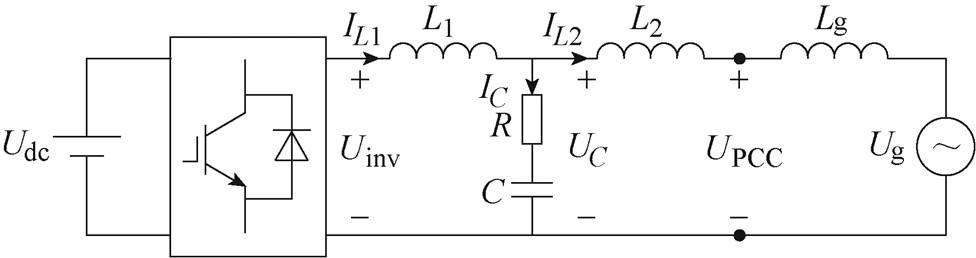
图4 单相LCL型并网逆变器拓扑
Fig.4 Single-phase LCL grid-connected inverter topology
图5中，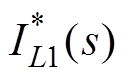
为逆变器控制侧参考电流，G(s)为比例积分控制器，kPWM为桥路放大增益。根据控制框图，得到其传递函数为
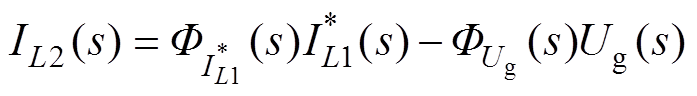（6）
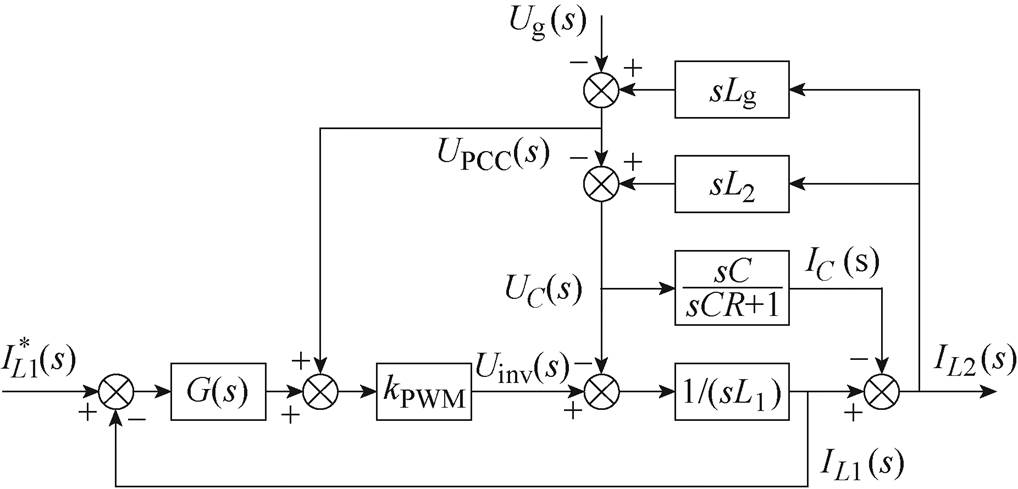
图5 单相LCL型并网逆变器控制框图
Fig.5 Control block diagram of single-phase LCL grid-connected inverter
其中
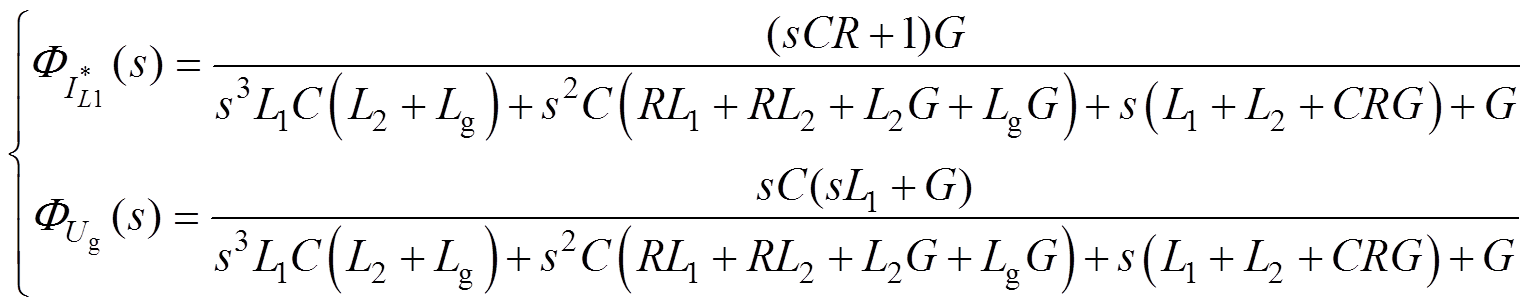（7）
单相LCL型并网逆变器的参数见表2。
表2 单相LCL型并网逆变器的参数
Tab.2 Parameters of single-phase LCL grid-connected inverter
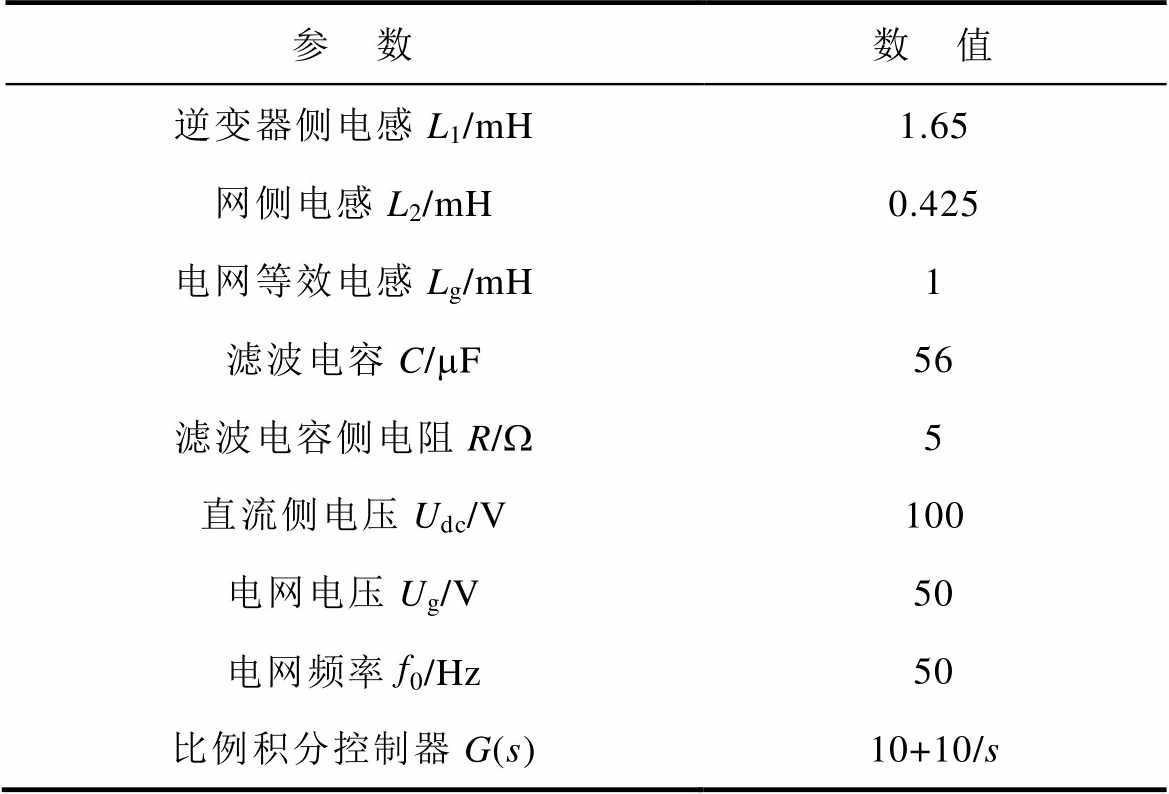
参 数数 值 逆变器侧电感L1/mH1.65 网侧电感L2/mH0.425 电网等效电感Lg/mH1 滤波电容C/mF56 滤波电容侧电阻R/W5 直流侧电压Udc/V100 电网电压Ug/V50 电网频率f0/Hz50 比例积分控制器G(s)10+10/s
为验证上述分析所得结论，分别求解R=0 W、R=5 W 时系统的特征根，得到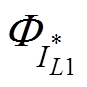
的极点、零点见表3。
表3 R=0 W、R=5 W 时传递函数的极点、零点
Tab.3 The poles and zeros of the transfer function when R=0 W, R=5 W
参 数数 值 R/W05 极点p1=-1.0p1=-1.0 p2,3=-205.2±j3 660.4p2,3=-1 931.5±j2 785.4 p4=-5 649.3p4=-6 609.2 零点z1=-1.0z1=-1.0 z2=-3 571.4
观察表3可以发现，极点p1与零点z1数值相同，二者对系统稳定性产生的影响相互抵消，p4离虚轴的距离最远，因此对该逆变器稳定性起作用的为p2、p3这对共轭极点。
由p2、p3结合式（1）可以确定系统的阻尼系数x 及自然谐振频率wn的值，见表4。
表4 R=0 W、R=5 W时系统的谐波响应参数
Tab.4 Harmonic response parameters of the system when R=0 W and R=5 W
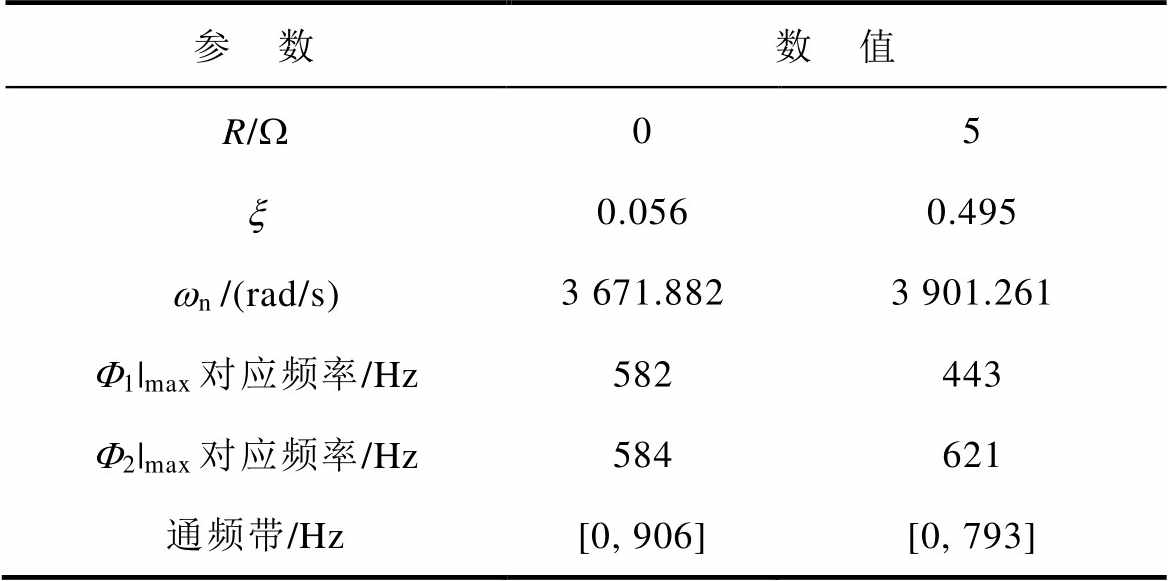
参 数数 值 R/W05 x0.0560.495 wn/(rad/s)3 671.8823 901.261 F1|max对应频率/Hz582443 F2|max对应频率/Hz584621 通频带/Hz[0, 906][0, 793]
观察表4可以发现，R=0 W 时系统的阻尼系数x 值趋近于0，此时只有PI控制器中的比例环节提供系统阻尼；R=5 W 时系统的x 值较大，此时滤波电容侧电阻R和PI控制器共同提供了系统的阻尼。观察表4还可以发现，当x 值趋近于0时，系统谐波响应的稳态和暂态部分对应的峰值频率近似相同，随着x 值的增大，两种响应峰值对应的频率逐渐远离，这与前述分析一致。图6给出了两种工况下系统的Bode图。
观察图6可以发现，R=0 W 时系统的频率响应曲线存在明显的谐振峰，R=5 W 时系统的谐振峰不明显。这表明R=0 W 时系统主动抑制谐波振荡的能力较弱，受到相应谐振频率附近的小扰动激励会显著放大谐波，引起波形的严重畸变；R=5 W 时系统主动抑制谐波振荡的能力较强，相应的谐波扰动并不会引起显著的谐波振荡。
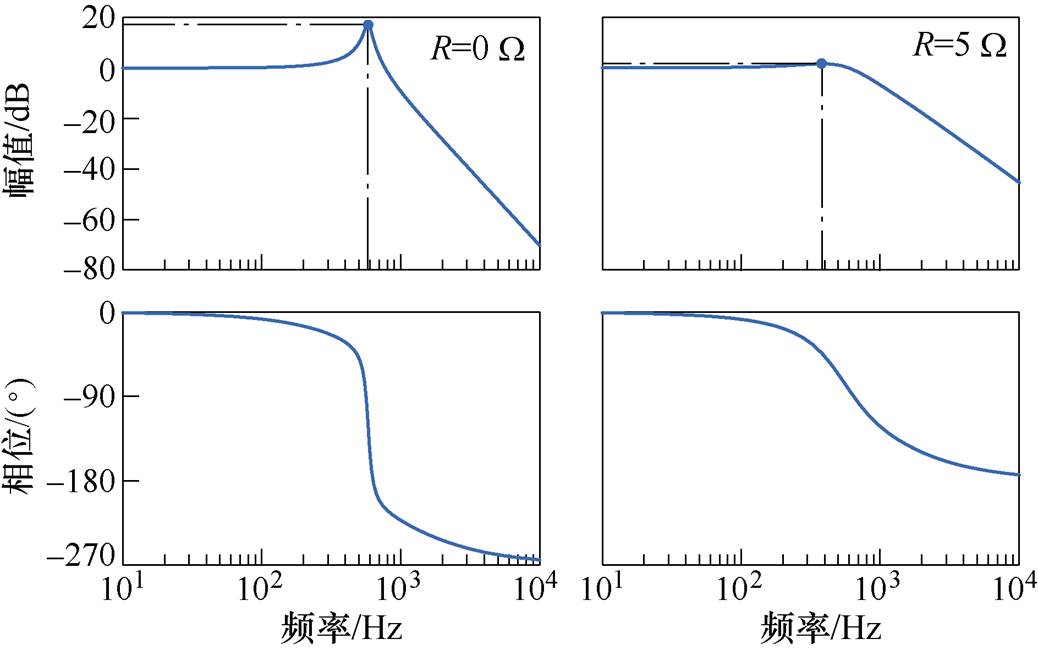
图6 滤波电容侧电阻取值不同时Bode图
Fig.6 Bode plot results when the filter capacitor side resistance values are different
由第1节和第2节的分析可知，结合系统的特征根能有效描述逆变器并网系统的谐波扰动响应，通过对阻尼系数值的计算可以定性分析系统受到扰动后的动态行为，但当逆变器多机并网时，沿用系统传递函数推导得到相应的特征根并不实际，这是因为基于传递函数的频域分析法在逆变器多机并网时存在“维数灾”的问题。传递函数本质是描述输入输出量间的关系，这也意味着当n台逆变器并网时，对于单台逆变器，需要分别推导与其并联的n-1台逆变器间的关系，其自身控制侧参考值到输出侧的传递函数以及网侧参数到其输出侧的传递函数，即对于n台逆变器并网系统，共需要推导(n+1)×n个传递函数，并分别计算每一个函数的特征根。显然，当逆变器并联台数增多时，计算量骤然提升，且当网络拓扑发生变化时，如单台逆变器的并（离）网过程，需要重新推导传递函数，该方法对解析系统的特征根不再适用。
基于阻抗的系统建模方法为分析逆变器并网的稳定性提供了便利[34-35]，通过对单一逆变器进行端口等效，将含有逆变器内部参数的等效阻抗（导纳）与电源串联（并联）接入PCC处，通过分析端口变量的频域响应判断系统的稳定裕度。模块化的设计建模方法不仅能清晰表征逆变器多机并网时的网络拓扑，其端口的电量也对应实际的物理量。针对参数未知的逆变器并网系统，通过对端口的扫频可以得到等效阻抗；针对参数已知的逆变器并网系统，可以通过模态分析法识别系统潜在的谐振频率。较传统状态空间法及频域法，其物理意义更加清晰，计算量显著降低，更有利于面向逆变器参数的设计，应对网络拓扑变化的灵活性更好。
模态分析法识别系统谐振点的思路是：对逆变器并网系统等效电网络的节点导纳矩阵Y分解得到对角特征值矩阵L 和左、右特征向量矩阵L、T。系统发生并联谐振时，Y的值最小，相应的对角特征值l 的值也最小，而l-1的值则最大。模态分析法通过设置起始频率、步长及终止频率，循环迭代得到不同频率下的对角特征值倒数l-1，绘制其图像即为模态阻抗曲线，当某一频率处图像存在尖峰即表示在该次频率下存在较大的l-1的值，即相应的模态阻抗值最大，此处系统可以受到电源激励产生相应的谐波振荡[36-37]。
针对图4所示的单相LCL型并网逆变器拓扑，将逆变器等效为一电流源Is并联阻抗Zout，等效电路如图7所示。
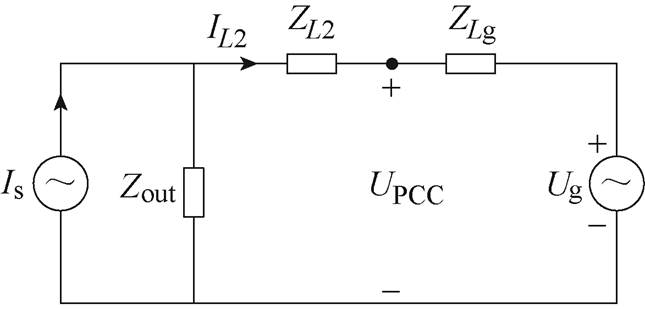
图7 单相LCL型并网逆变器等效电路
Fig.7 Equivalent circuit of single-phase LCL grid-connected inverter
图7中，ZL2=sL2，ZLg=sLg，则由图7，有
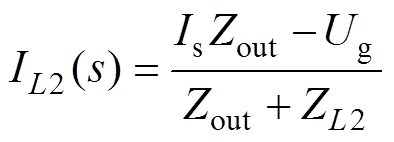（8）
式（8）结合式（6）、式（7），得到
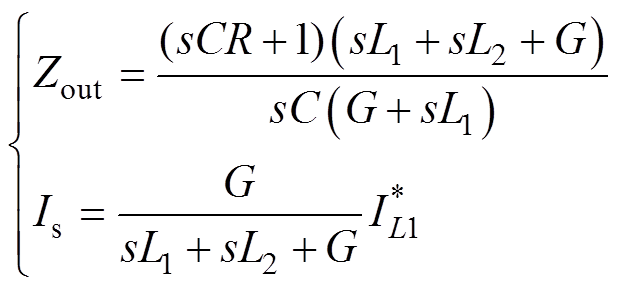（9）
设置R∈[0, 6] W，f∈[5, 2 000] Hz，利用模态分析法解析网络存在的谐振点，结果如图8所示。
观察图8可以发现，当R趋近于0时，模态阻抗曲线的谐振峰值较高，对应此时存在较大的l-1的值，系统在此处受到谐波激励产生的谐波振荡现象最明显；当R逐渐增大时，谐振频率逐渐降低，谐振峰值逐渐降低，系统对相应谐波的可激励性和可观测性越来越弱。这与前述分析结论一致，即R较小时，对应系统特征根的实部越靠近虚轴，相应的阻尼系数x 越小，系统更易受谐波激励产生严重的谐波振荡；当R逐渐增大时，系统特征根的实部逐渐远离虚轴，相应的阻尼系数x 越大，系统的谐振频率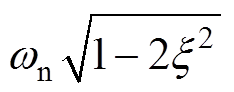
逐渐远离自然谐振频率wn，系统主动抑制谐波振荡的能力越强。
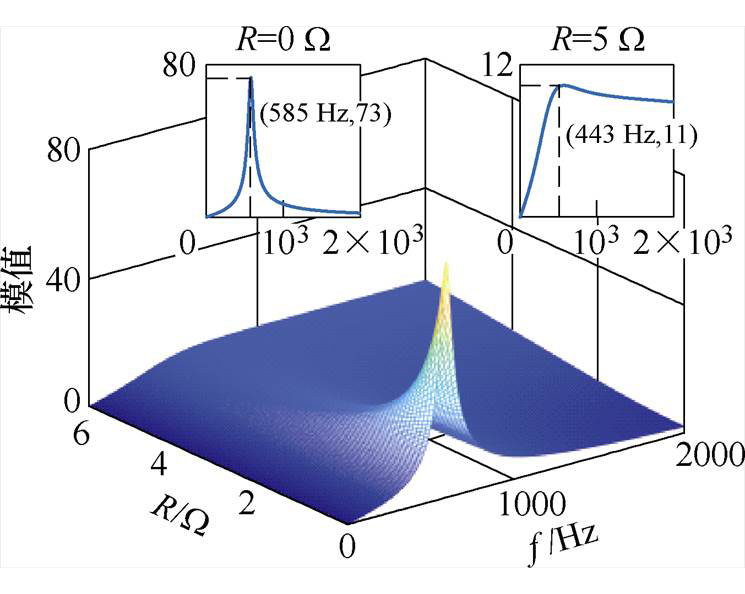
图8 模态分析法解析网络谐振频率结果
Fig.8 Results of the network resonance frequency by using modal analysis method
利用模态分析法解析网络存在的谐振点是在频域下对系统建模，用一包含控制侧参数的阻抗来等效单个逆变器，并根据等效电网络列写节点导纳矩阵Y，分析Y的数值特征得到的。这其中针对记忆元件的伏安关系均是在频域下建立的，而模态分析法和系统的特征根的联系则是在复频域下通过求解网络的节点导纳矩阵Y的行列式为0的根得到的。设针对一多节点网络列写节点导纳矩阵Y为
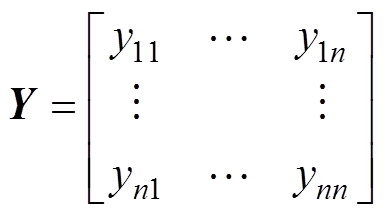
对这一方阵求其行列式，设其一般形式为
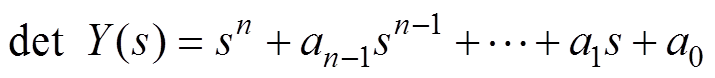（10）
令det Y(s)=0，求解得到
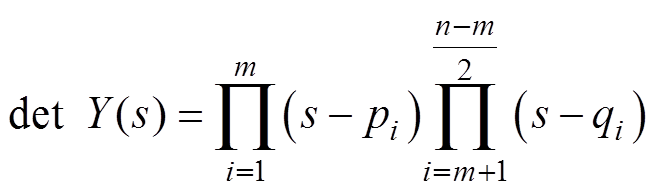（11）
式中，pi为实根，包括不等实根及重根；qi为共轭复根，其一般形式为
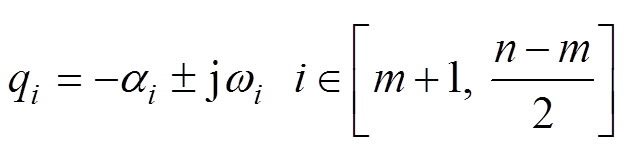（12）
式中，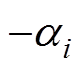
即为前述系统特征根的实部，系统稳定的充分必要条件为
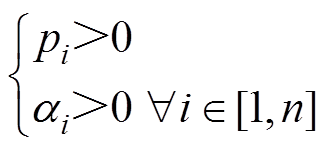（13）
pi、ai值的大小反映实部距离虚轴的远近，wi即为前述系统特征根的虚部，它是系统的谐振角频率。
对于含有记忆元件的线性时不变系统，时域下系统的输入输出间是卷积的关系，即系统的输入会对未来一段时间内系统的输出产生影响。傅里叶变换的提出极大地方便了对系统响应的分析，通过对系统“换基”能够将时域下的微分运算转化为频域下的代数运算，将卷积运算转化为乘法运算，但针对系统作傅里叶变换需要满足严苛的条件，对于不满足其收敛条件的系统则不能进行傅里叶变换。在此基础上提出拉普拉斯变换，拉氏变换在傅里叶变换的基础上又丰富了动态电路的分析方法，针对算子s在jw 的基础上添加实部s，这一创新性的引入为从全局角度分析系统的响应提供了便利，可以说，围绕着s 的取值对响应的分析是经典及现代控制理论针对系统稳定性讨论的核心。基于系统的无源性理论也是在此基础上提出，即从系统全局的角度出发，要求所有的特征根都具有负的实部。
利用模态分析法解析网络存在的谐振点是在频域下进行的，通过对系统节点导纳矩阵的分解，循环代入不同频率并计算相应的对角特征值，根据系统节点划分为多个模态，不同的模态表征不同的节点（支路），以此解耦网络发生谐波振荡时内部的耦合关系。在模态分析法解析谐振点的基础上，只需将矩阵中关于记忆元件的算子由频域转换至复频域，并求解方阵行列式为0的根，就能得到系统所有的特征根。这一方法的复用不仅结合了频域分析法和基于系统的无源性理论的优势，还将此方法自身的优势得以外延，即模态分析方法不仅能在微观层面表征高阶网络内部的耦合关系，还能在宏观层面上视系统为一个整体并对其稳定性进行分析。
图9给出了结合特征根及模态分析法的逆变器多机并网系统谐波振荡分析步骤。
为验证方法的一般性，取另外两台参数不同的逆变器与第2节所示的逆变器并联接入电网，两台逆变器的参数及控制框图见附录，其等效电路如图10所示。
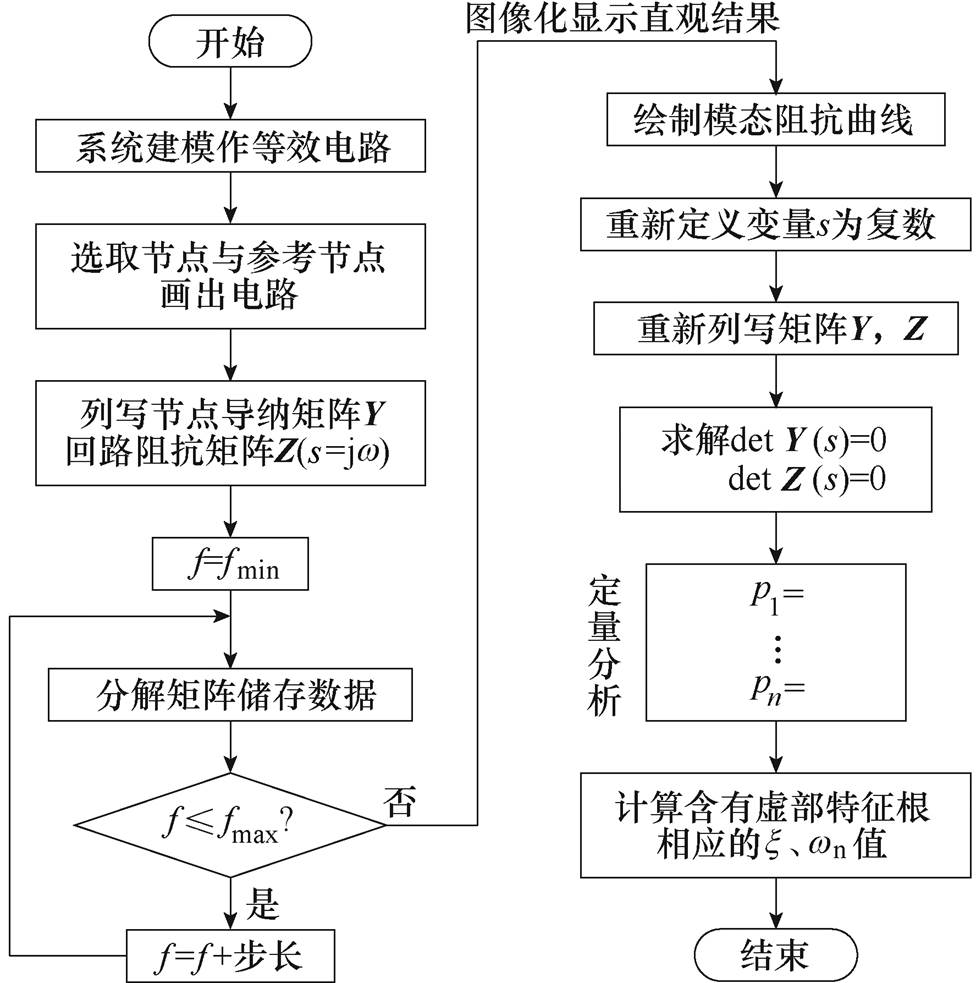
图9 结合特征根及模态分析法的逆变器多机并网系统谐波振荡分析步骤
Fig.9 Harmonic resonance analysis steps of multi-inverters grid-connected system combined with characteristic root and modal analysis method
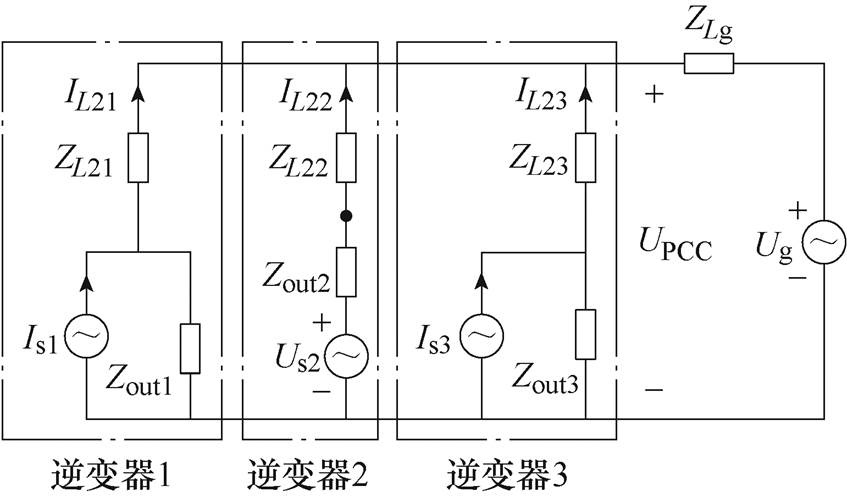
图10 逆变器多机并网等效电路
Fig.10 Equivalent circuit of multiple grid-connected inverters
图10中，Is1、Us2、Is3为三台逆变器的等效电源；IL21、IL22、IL23为三台逆变器的并网电流；Zout1、Zout2、Zout3为三台逆变器的等效阻抗；ZL21、ZL22、ZL23为三台逆变器的网侧电感。
逆变器等效阻抗的具体形式在附录中给出。分别解析当R=0 W、R=5 W 时网络存在的串、并联谐振点，图11给出了模态分析法解析结果。
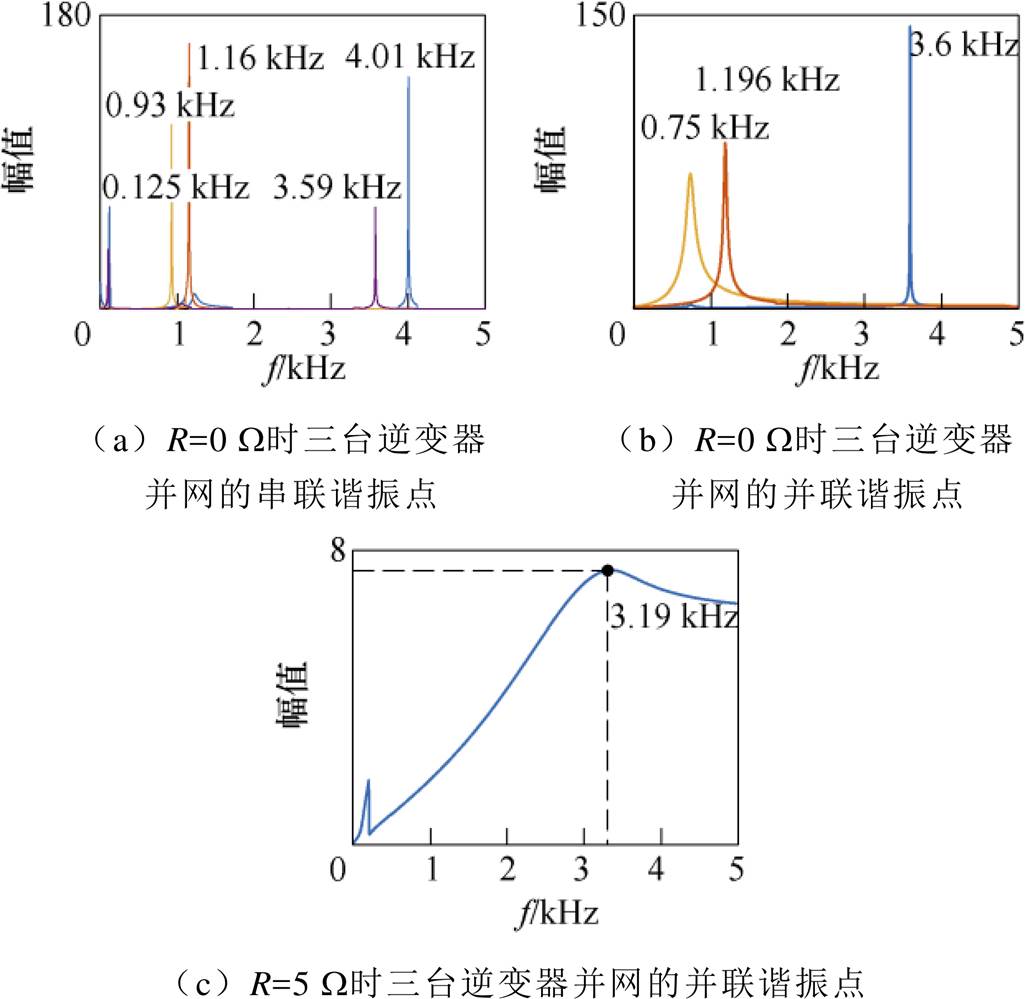
图11 R=0 W、R=5 W 时利用模态分析法解析三台逆变器并网存在的串、并联谐振点结果
Fig.11 Results of the series and parallel resonance frequency of the three grid-connected inverters by using modal analysis method when R=0 W and R=5 W
利用模态分析法解析网络存在的串、并联谐振点时发现，当R=5 W 时网络不存在串联谐振点，并联谐振点也仅剩一个，且幅值较低。这表明增大系统的阻尼系数可以有效抑制谐振。表5给出了利用模态分析法在s域下求取网络矩阵行列式为0的根。
表5 R=0 W、R=5 W 时三台逆变器并网系统的特征根
Tab.5 The characteristic root of the two-inverters grid-connected system when R=0 W and R=5 W
参 数数 值 R/W05 并联特征根p1=-5.0p2,3=-8.7p4,5=-44.146p6=-583.91p7,8=-165.1±j4 694.0p9,10=-116.0±j7 516.3p11,12=-8.8±j22 617.0p1=-5.0p2,3=-8.9p4,5=-44.5p6=-585.9p7,8=-3 277.8±j3 433.5p9=-5 127.4p10=-11 006p11,12=-9 802.1±j20 081 串联特征根p1=-5.0p2,3=-15.6±j790.8p4,5=-3.5±j5 853.7p6,7=-1.9±j7 274.2p8,9=-8.9±j22 550.0p10,11=-6.5±j25 185.0p12=-8.5×109p1=-5.0p2=-863.2p3,4=-4 182.8±j3 386.6p5,6=-6 558.4±j1 437.9p7,8=-9 347±j20 242.0p9,10=-11 118.0±j22 598.0p11=-28 571p12=-8.5×109
观察表5可以发现，两种工况下系统的特征根都具有负的实部，表明系统可以稳定运行。R=5 W 时，并联特征根p7,8对应的阻尼系数值为0.57，对系统稳定性的影响较小，串联特征根p3,4、p5,6、p7,8、p9,10同理，因此R=5 W 时系统不存在串联谐振点。
结合图10和表5可以发现，频域下利用模态分析法解析网络存在的谐振点和s域下利用模态分析法求解系统存在的特征根具有一一对应的关系，模态阻抗曲线中存在的谐振尖峰必然对应一对共轭复根。验证了针对逆变器多机并网这一高阶耦合系统，模态分析方法可以实现宏观层面和微观层面的有效整合，即可以视系统为一个整体从宏观层面判断其稳定性，同时可以从微观层面对高阶系统实现解耦，通过参与因子的计算表征不同支路对相关模态的可激励性和可观测性。
限于篇幅，后续验证环节只取R=0 W 时系统的串联特征根p8,9及R=5 W 时系统的并联特征根p11,12进行验证，表6给出了这两种工况下系统谐波响应的参数。
4.1.1 单台逆变器并网谐振特性验证
1）谐波扰动输出响应稳态部分验证
已知R=0 W、R=5 W 时F1的峰值对应的频率分别为582 Hz、443 Hz，取包括谐振频率在内的相邻奇数次谐波进行验证。在Matlab/Simulink平台搭建图4所示的逆变器并网模型，参数设置见表2。在控制回路中加入谐波电压源，设置注入谐波电压的幅值为电网电压幅值的5%，设置仿真时长为0.5 s。图12与图13分别给出了R=0 W、R=5 W 时注入谐波电压源后逆变器并网电流IL2在0.3～0.4 s的波形及快速傅里叶变换（Fast Fourier Transform, FFT）结果。
表6 R=0 W、R=5 W 时三台逆变器并网系统谐波响应参数
Tab.6 Harmonic response parameters of the three- inverters grid-connected system when R=0 W and R=5 W
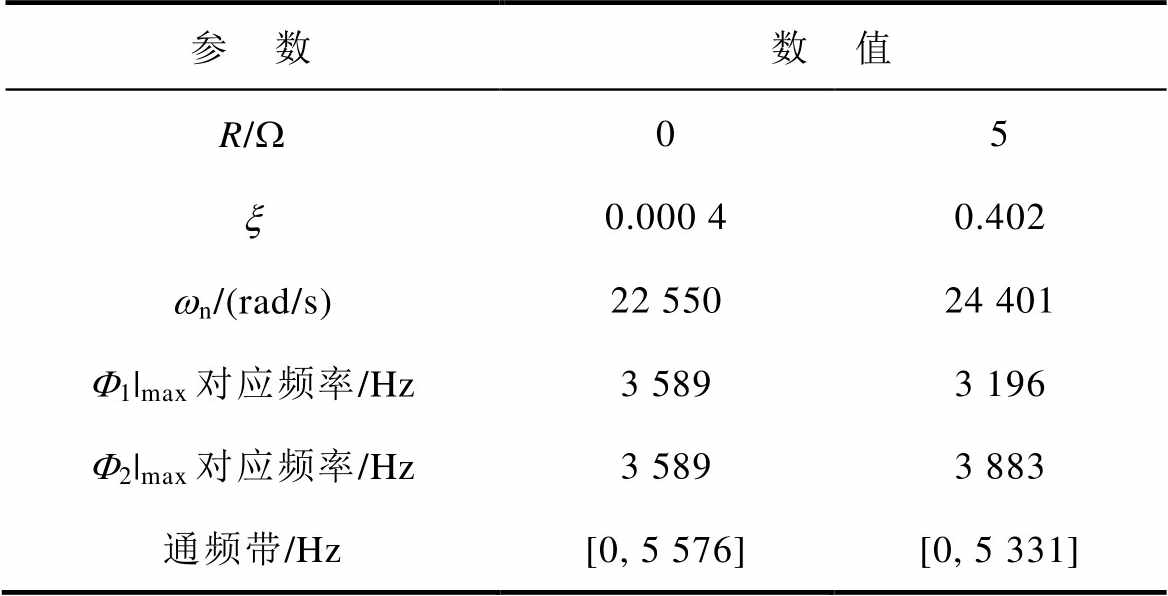
参 数数 值 R/W05 x0.000 40.402 wn/(rad/s)22 55024 401 F1|max对应频率/Hz3 5893 196 F2|max对应频率/Hz3 5893 883 通频带/Hz[0, 5 576][0, 5 331]
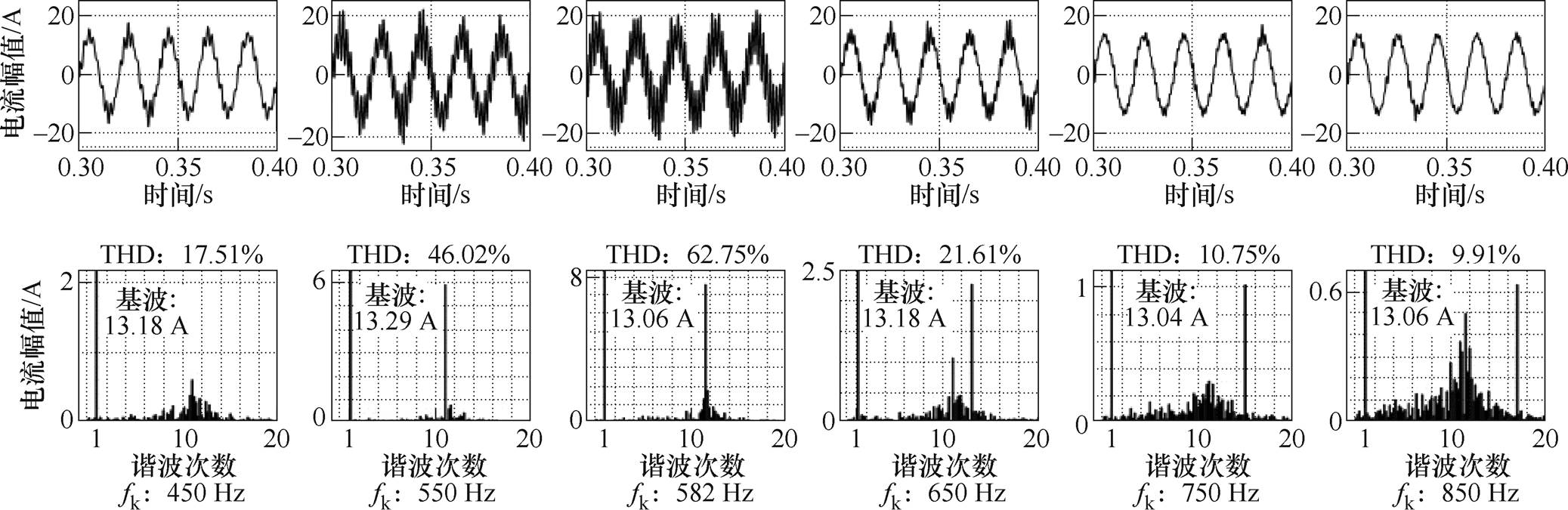
图12 R=0 W 时控制回路加入谐波电压后逆变器并网电流IL2的波形及FFT结果
Fig.12 Waveforms and FFT result of the grid-connected current IL2 of the inverter after adding harmonic voltage to the control loop when R=0 W
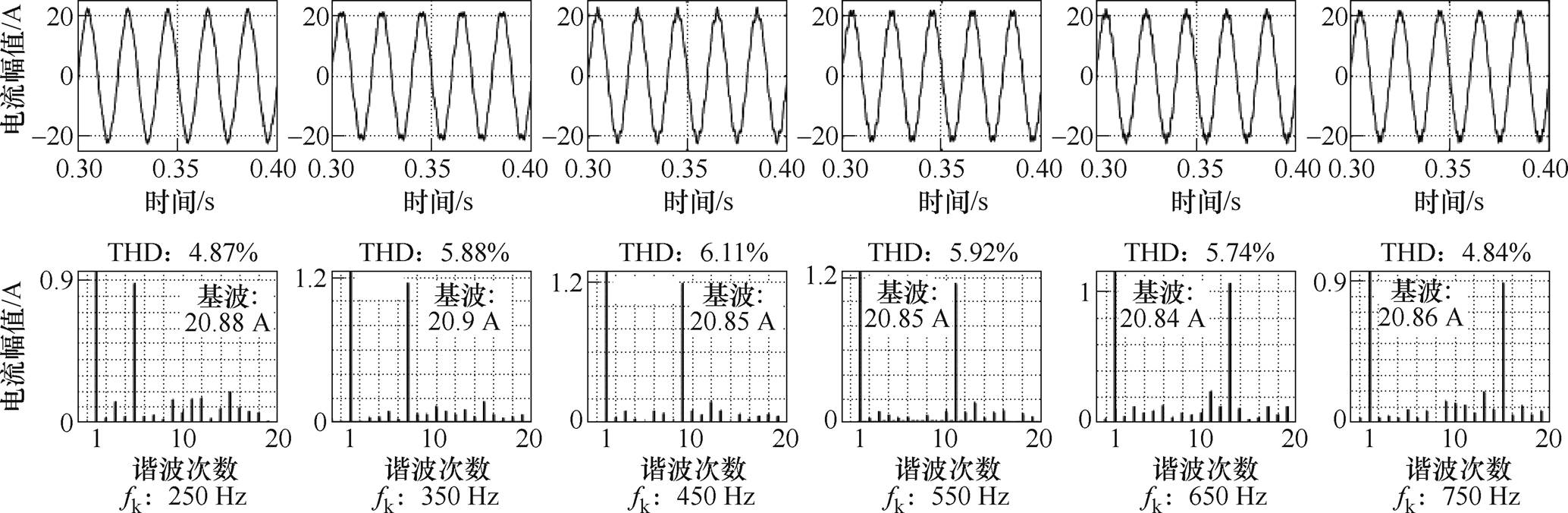
图13 R=5 W时控制回路加入谐波电压后逆变器并网电流IL2的波形及FFT结果
Fig.13 Waveforms and FFT result of the grid-connected current IL2 of the inverter after adding harmonic voltage to the control loop when R=5 W
观察图12可以发现，在谐振频率处（582 Hz）并网电流波形畸变最严重，FFT结果表明，此时电流波形中的谐波含量最丰富，谐振频率相应次谐波分量被放大的程度最大。当谐波扰动的频率逐渐远离谐振频率时，波形畸变的程度减轻，电流波形中的谐波分量减少，与扰动相关的谐波分量被放大的程度逐渐减小。这表明系统主动抑制谐波的能力较弱，系统易受小的谐波扰动产生严重的谐波振荡，波形畸变严重，与第2节分析所得的近似为0的阻尼系数值及相应的Bode图所得的结论一致。
观察图13可以发现，在谐振频率处（450 Hz）并网电流波形中的谐波含量最多，当谐波扰动的频率逐渐远离谐振频率时，电流波形中的谐波分量减少，与扰动相关的谐波分量被放大的程度逐渐减小，但波形并未出现严重的畸变，表明系统主动抑制谐波的能力较强，这与第2节分析所得的较大的阻尼系数值及相应的Bode图所得的结论一致。
2）谐波扰动输出响应暂态部分验证
由1.1节分析可知，系统谐波响应的暂态分量随时间逐渐衰减为0，但暂态分量的存在会加重波形的畸变，最恶劣的工况即基波分量处于或即将处于峰值时加入谐波扰动，此时谐波响应中稳态和暂态分量的叠加使得波形的畸变程度最深。
已知R=0 W、R=5 W 时F2的峰值对应的频率分别为584 Hz、621 Hz，取包括谐振频率在内的相邻奇数次谐波进行验证。在控制回路加入谐波电压源，设置注入谐波电压的幅值为电网电压幅值的5%，设置仿真时长为0.5 s。此前已观测到在t=0.205 s时并网电流IL2的波形处于峰值，在此时刻注入谐波电压源扰动，在t=0.225 s时断开谐波源，图14与图15分别给出了R=0 W、R=5 W 时注入谐波电流源前、后逆变器并网电流IL2的波形，以及注入谐波扰动对应的周期内波形的分解。
观察图14可以发现，当谐波扰动注入的时刻与波形基波分量处于峰值的时刻相同时，会加重波形的畸变，以最严重的谐振频率说明，此时波形的峰值为22.5，而基波的幅值仅为13，即此时刻电流的峰值为1.73(pu)，系统出现了短时的过电流现象。同时可以发现，波形畸变的程度在系统的谐振频率处最深，当谐波扰动逐渐远离谐振频率时，波形的畸变程度减轻。
观察图15可以发现，相较图14，R=5 W 时注入谐波扰动，波形的畸变程度较轻，且谐波响应中的暂态分量很快衰减为0，并未造成短时间内明显的过电流现象。这与1.1节理论分析一致，式（4）表明谐波响应暂态分量的衰减系数为“-xwn”，而当x 趋于0时，衰减项系数的绝对值较小，即暂态分量衰减的速度较慢；当x 较大时，衰减项系数的绝对值较大，暂态分量衰减的速度较快。这表明利用特征根来表征系统的动态行为是很有效的，较小的阻尼系数值对系统的危害是多重的：一方面系统主动抑制谐波振荡的能力很弱，系统极易受小扰动的谐波扰动产生较明显的谐波振荡；另一方面，较小的阻尼系数值对应的暂态分量衰减速度较慢，而暂态分量的初始幅值与稳态分量为一个数量级，这又会造成波形短时内的畸变率大大提高，使得系统出现过电流（电压）现象。
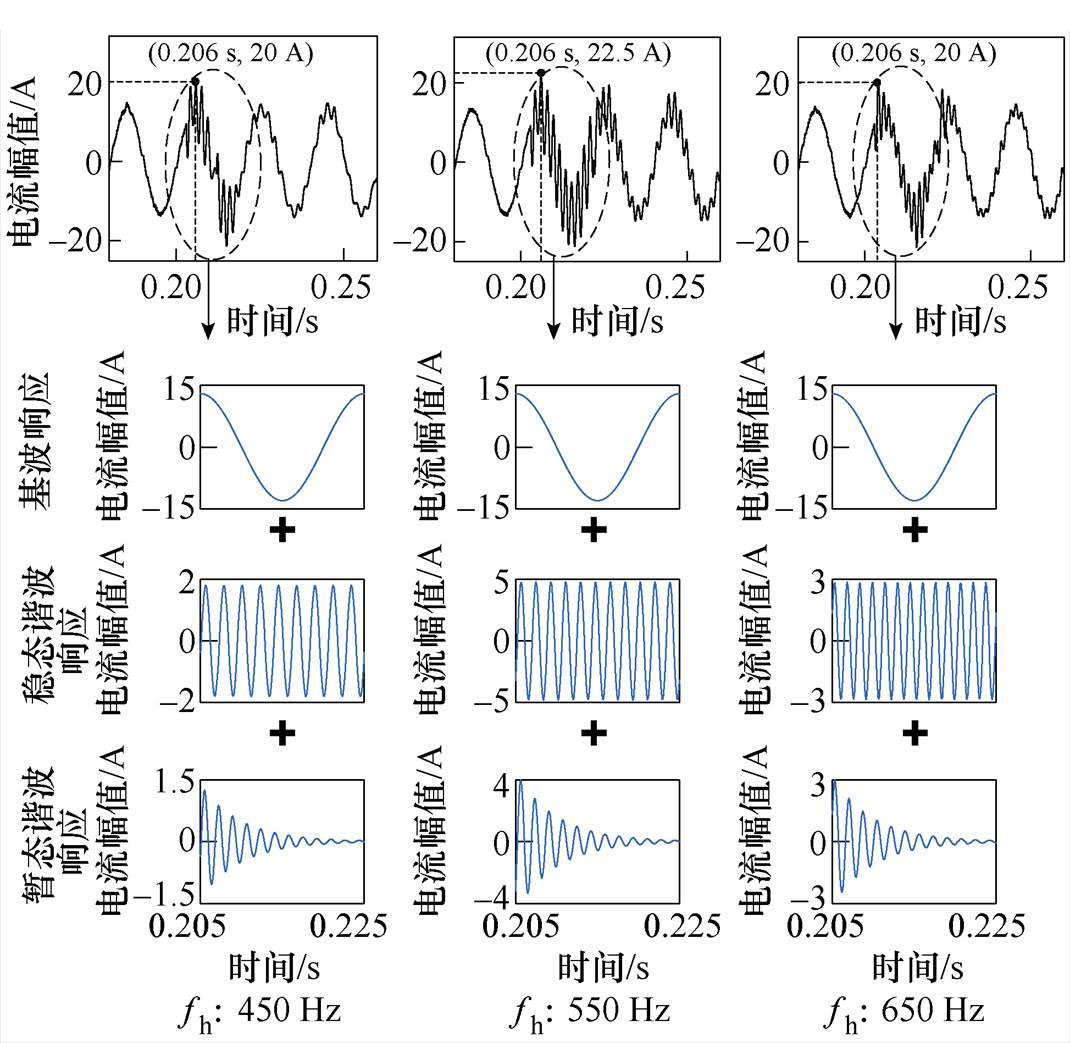
图14 R=0 W 时控制回路加入谐波扰动前、后逆变器并网电流IL2的波形及波形分解结果
Fig.14 Waveforms and waveforms decomposition results of the grid-connected current IL2 of the inverter before and after adding harmonic disturbance to the control loop when R=0 W
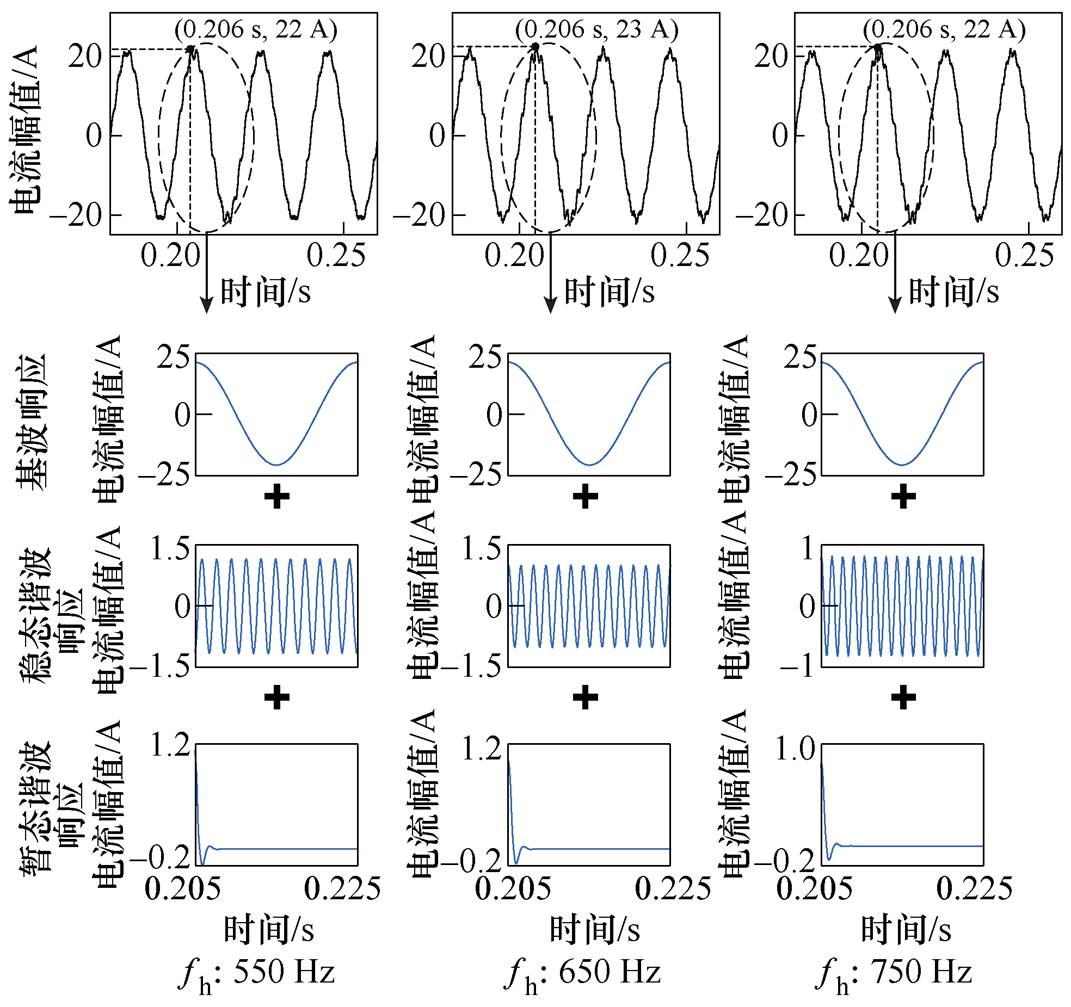
图15 R=5 W时控制回路加入谐波扰动前、后逆变器并网电流IL2的波形及波形分解结果
Fig.15 Waveforms and waveform decomposition results of the grid-connected current IL2 of the inverter before and after adding harmonic disturbance to the control loop when R=5 W
需要说明，图14和图15中所示的波形分解结果并非是严格意义上并联电流IL2在谐波扰动注入周期内的分解结果，IL2波形中除了相应的谐波扰动分量外还有其他次谐波，此处只是为了便于分析，取其中最主要的谐波分量示例。
4.1.2 逆变器多机并网谐振特性验证
已知逆变器多机并网时存在多个串、并联谐振频率，当R=0 W 时其中一个串联谐振点为3 600 Hz；R=5 W 时并联谐振点为3 200 Hz，取包括谐振频率在内的相邻奇数次谐波进行验证。针对串联谐振点，在第3台逆变器的滤波电容支路并联谐波电流源，设置注入谐波电流的幅值为额定电流幅值的5%，观测并网点电压波形。针对并联谐振点，在第3台逆变器的控制回路加入谐波电压源，设置谐波电压的幅值为电网电压幅值的5%，观测并网点电流波形。设置仿真时长为0.5 s，图16与图17分别给出了R=0 W、R=5 W 时注入谐波扰动后PCC处电压UPCC及并网电流IL23在0.3～0.4 s的波形及FFT结果。
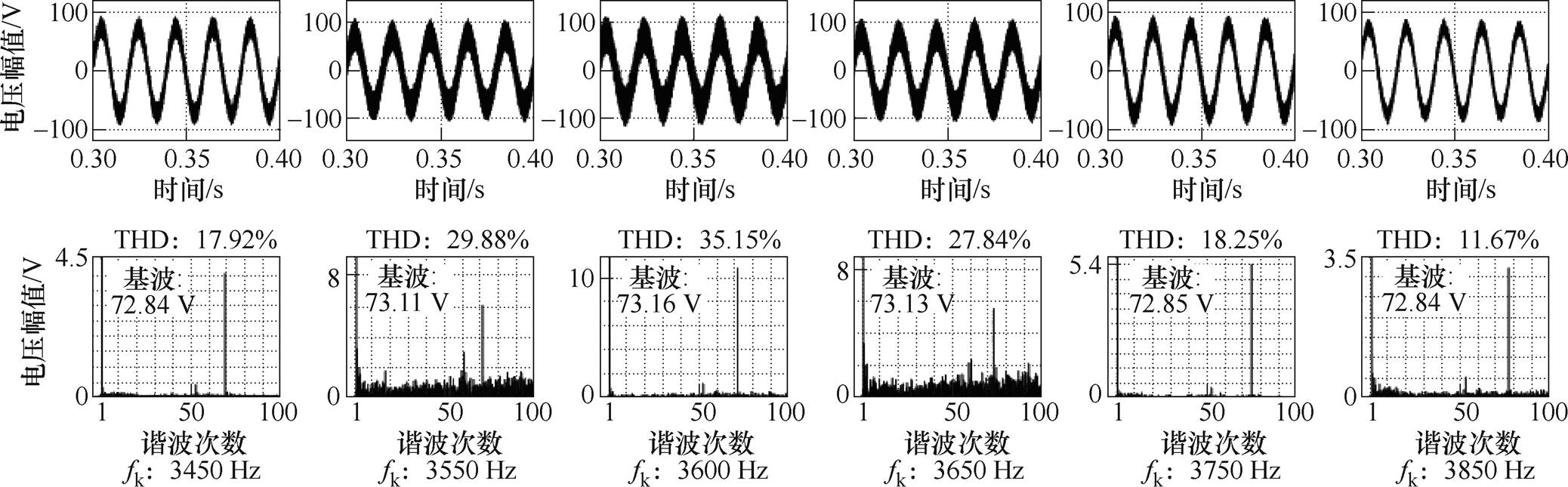
图16 逆变器多机并网时在逆变器3的滤波电容支路注入谐波电流后并网点电压UPCC的波形及FFT结果
Fig.16 Waveform and FFT results of the grid-connected point voltage UPCC after the harmonic current is injected into the filter capacitor branch of Inverter 3 when multiple inverters are connected to the grid
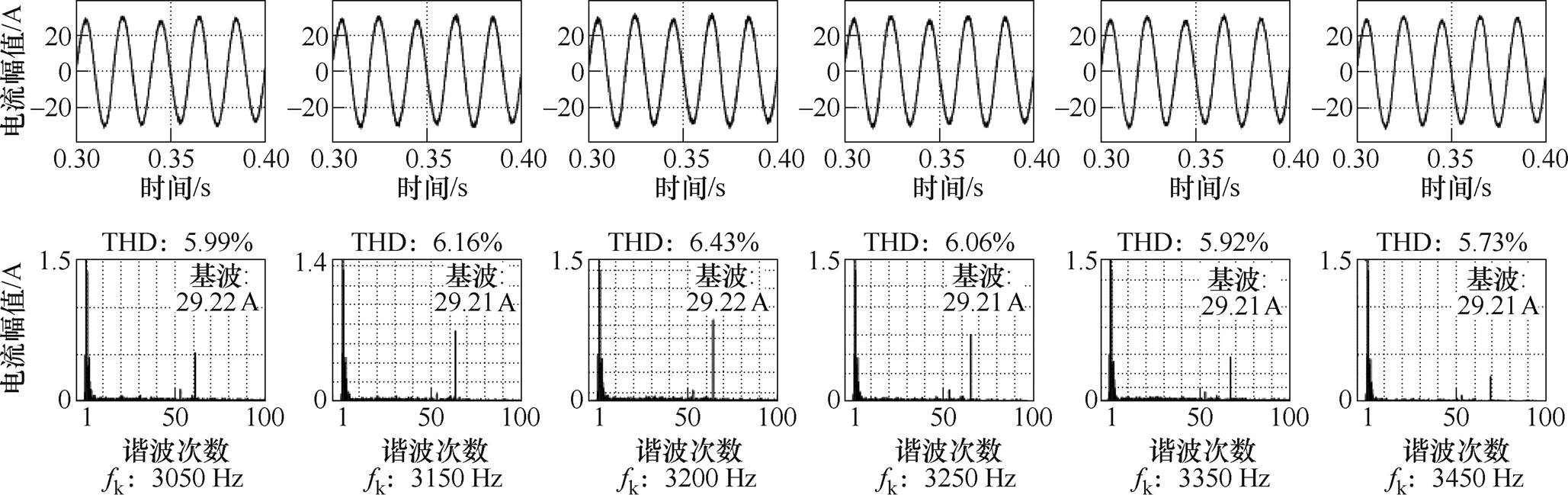
图17 逆变器多机并网时在逆变器3的控制回路注入谐波电压后并网电流IL23的波形及FFT结果
Fig.17 Waveform and FFT results of the grid-connected current IL23 after harmonic voltage is injected into the control loop of Inverter 3 when multiple inverters are connected to the grid
观察图16可以发现，在谐振频率处（3 600 Hz）并网点电压波形畸变最严重，FFT结果表明此时电流波形中的谐波含量最丰富，谐振频率相应次谐波分量被放大的程度最大。当谐波扰动的频率逐渐远离谐振频率时，波形畸变的程度减轻，电流波形中的谐波分量减少，与扰动相关的谐波分量被放大的程度逐渐减小。
观察图17可以发现，在谐振频率处（3 200 Hz）并网电流波形中的谐波含量最多，当谐波扰动的频率逐渐远离谐振频率时，电流波形中的谐波分量减少，与扰动相关的谐波分量被放大的程度逐渐减小，但波形畸变程度较轻，表明系统主动抑制谐波的能力较强，这与3.4节分析所得的阻尼系数值相符。
为验证分析逆变器谐振特性的正确性，在RT_ Lab半实物仿真平台搭建逆变器并网模型，参数设置与仿真验证部分一致。硬件实验平台如图18所示。
图18 硬件实验平台
Fig.18 Hardware experiment platform
图19和图20分别就R=0 W、R=5 W 时单逆变器并网系统的谐振点及相邻奇数次谐波响应进行了实验验证，图21和图22就逆变器多机并网系统的串、并联谐振点进行了实验验证。
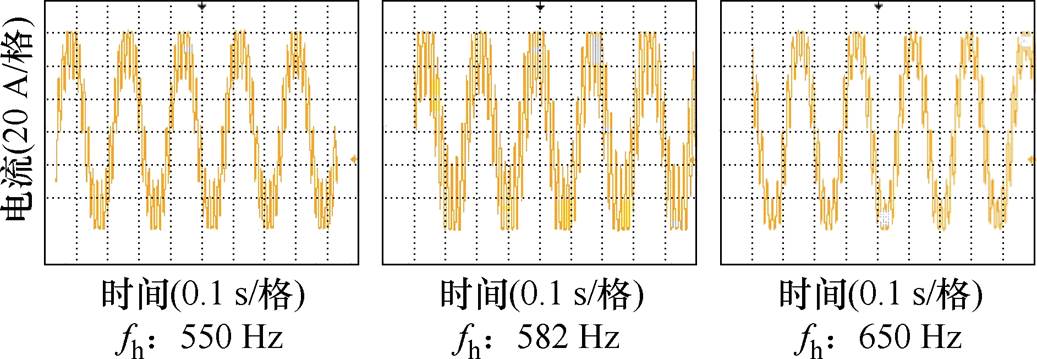
图19 R=0 W 时控制回路加入谐波电压后逆变器并网电流IL2的波形
Fig.19 Waveforms of the grid-connected current IL2 of the inverter after adding harmonic voltage to the control loop when R=0 W
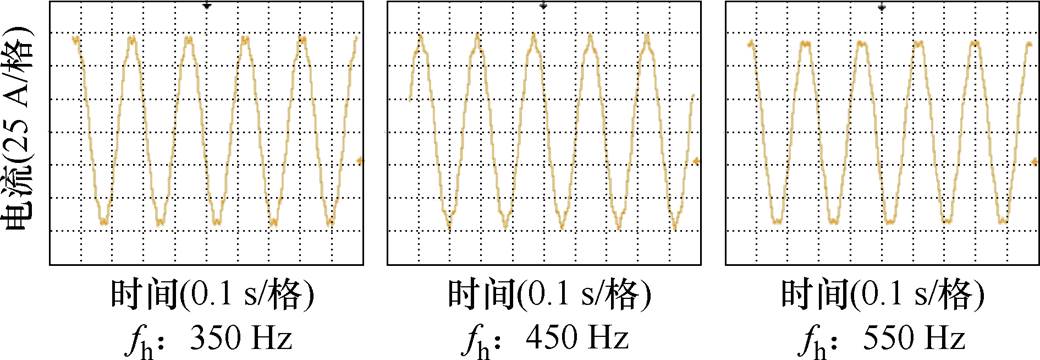
图20 R=5 W 时控制回路加入谐波电压后逆变器并网电流IL2的波形
Fig.20 Waveforms of the grid-connected current IL2 of the inverter after adding harmonic voltage to the control loop when R=5 W
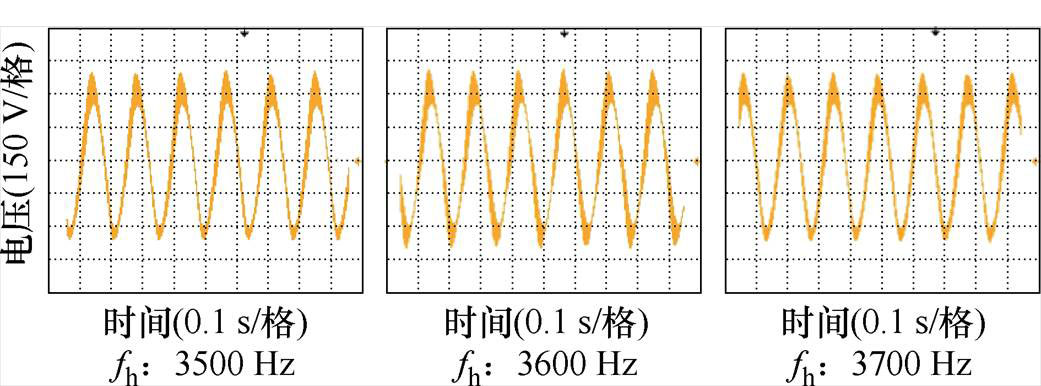
图21 R=0 W 时逆变器多机并网串联谐振点验证
Fig.21 Verification of series resonance point of multiple grid-connected inverters when R=0 W
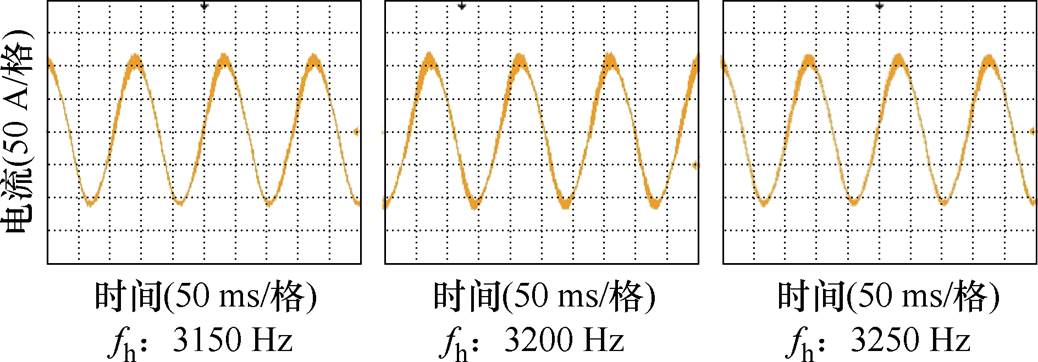
图22 R=5 W 时逆变器多机并网并联谐振点验证
Fig.22 Verification of parallel resonance point of multiple grid-connected inverters when R=5 W
观察图19和图21发现，并网电流波形和并网点电压波形在谐振频率处出现了严重畸变，当谐波源远离谐振中心时，波形畸变程度减轻，但波形中仍然含有丰富的谐波分量，验证了R=0 W 时系统的阻尼系数趋近于0，系统主动抑制谐波振荡的能力有限。
观察图20和图22发现，在谐波电压注入时，并网电流波形畸变程度较轻，且随着谐波源远离谐振中心，波形中的谐波含量进一步减少，这与4.1节分析一致，即R=5 W 时系统的阻尼系数较大，系统主动抑制谐波振荡的能力较强。
本文结合系统的特征根和模态分析方法分析逆变器多机并网系统的谐波振荡特性。利用特征根推导得到系统受到谐波扰动后的响应，通过一个逆变器并网的实例验证了针对系统的特征根分析其谐波响应的可行性。针对逆变器多机并网系统，将传统的应用模态分析法解析网络存在的谐振点延展至求取相应谐振频率下系统的特征根，方法的复用结合了频域法和基于系统无源性理论的优点，兼具分析逆变器并联支路间的耦合及系统的稳定性，为进一步针对逆变器多机并网的谐波振荡抑制提供了更具指向性的解决路径。仿真和实验的结果验证了分析所得结论的正确性。得到以下结论：
1）系统受到谐波扰动后产生的响应为两种波形的叠加，分别是稳态响应和暂态响应，两种响应的谐振特性并不相同，谐振峰值的大小与阻尼系数x 密切相关，x 接近于0，峰值越大；x 增大，峰值逐渐降低，且当x＞0.7时，稳态响应不存在谐振峰。
2）单一逆变器相应的阻尼系数值会随着并联台数的增多而不断减小。较小的阻尼系数值对系统的危害是多重的：一方面系统主动抑制谐波振荡的能力变弱；另一方面，较小的阻尼系数值对应的暂态分量衰减速度较慢，会造成短时内波形的畸变率大大提高，使得系统出现过电流（电压）现象。
3）模态分析方法既可以在频域下解析网络存在的谐振点，又可以在s域下求解系统的特征根，二者具有一一对应的关系。方法的复用不仅能表征高阶网络内部的耦合关系，还能视系统为一个整体对其稳定性进行分析。
结合特征根分析逆变器并网系统的谐波响应从本质上解释了系统的动态行为，为针对逆变器多机并网的谐波振荡抑制提供了解决思路，提高系统鲁棒性的途径之一是提高相应谐振频率下系统的阻尼系数值，模态分析法作为求取系统特征根、遍历系统谐振频率的解析工具能简洁、快速的提供数值解和模态阻抗曲线。
附 录
3.4节就一逆变器多机并网系统进行了谐振特性分析，其中逆变器2和逆变器3的主电路拓扑如图4所示，其控制框图如附图1和附图2所示。
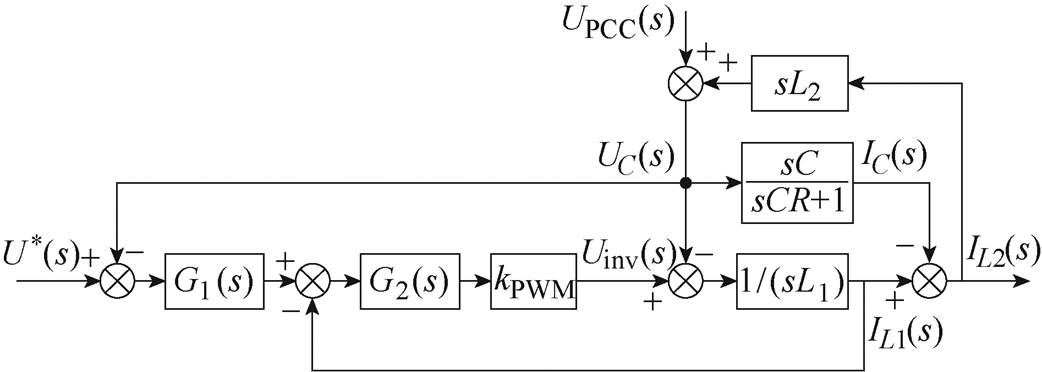
附图1 逆变器2控制框图
App.Fig.1 Control block diagram of the inverter 2
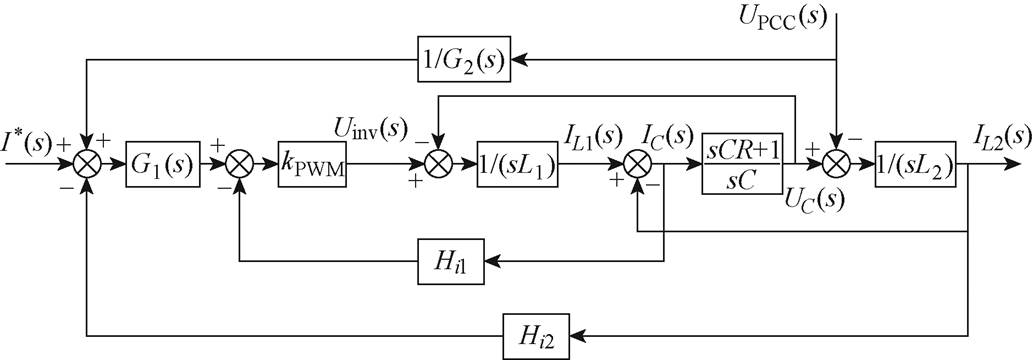
附图2 逆变器3控制框图
App.Fig.2 Control block diagram of the inverter 3
逆变器2和逆变器3的参数见附表1。
附表1 逆变器2和逆变器3的参数
App.Tab.1 Parameters of inverter 2 and inverter 3
参 数数 值 逆变器2逆变器3 逆变器侧电感L1/mH1.650.6 网侧电感L2/mH0.4250.36 滤波电容C/mF567 滤波电容侧电阻R/W55 桥路增益kPWM11 控制器G1(s)0.3+10/s0.03+600/s 控制器G2(s)2+10/s400 有源阻尼系数Hi10.026 5 有源阻尼系数Hi21 Udc/V100400
附图1、附图2结合图10所示的系统等效电路，推导可得到逆变器2、逆变器3的等效阻抗分别为
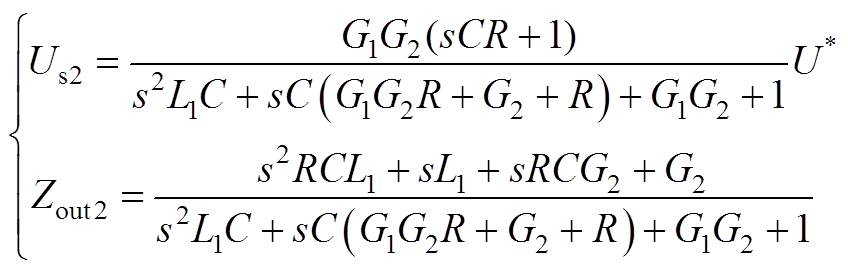（A1）
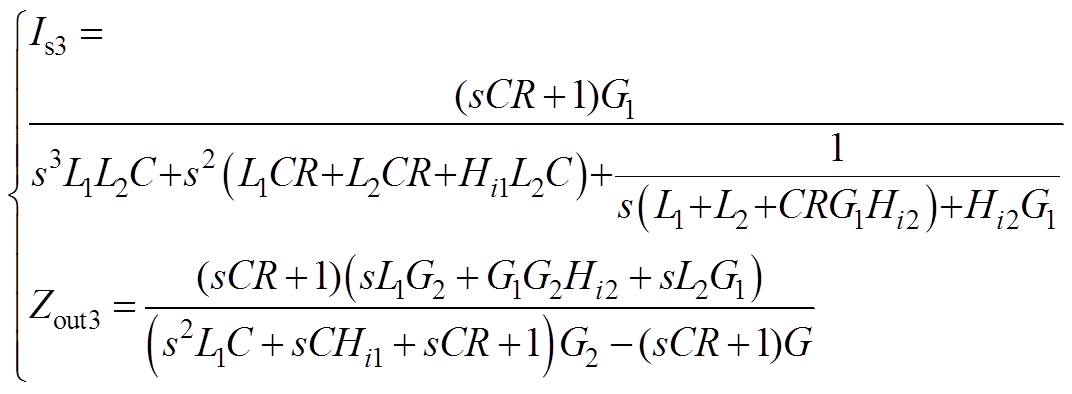（A2）
参考文献
[1] 康重庆, 姚良忠. 高比例可再生能源电力系统的关键科学问题与理论研究框架[J]. 电力系统自动化, 2017, 41(9): 2-11.
Kang Chongqing, Yao Liangzhong. Key scientific issues and theoretical research framework for power systems with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2017, 41(9): 2-11.
[2] 卓振宇, 张宁, 谢小荣, 等. 高比例可再生能源电力系统关键技术及发展挑战[J]. 电力系统自动化, 2021, 45(9): 171-191.
Zhuo Zhenyu, Zhang Ning, Xie Xiaorong, et al. Key technologies and developing challenges of power system with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2021, 45(9): 171-191.
[3] 肖湘宁, 廖坤玉, 唐松浩, 等. 配电网电力电子化的发展和超高次谐波新问题[J]. 电工技术学报, 2018, 33(4): 707-720.
Xiao Xiangning, Liao Kunyu, Tang Songhao, et al. Development of power-electronized distribution grids and the new supraharmonics issues[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 707-720.
[4] 谢小荣, 刘华坤, 贺静波, 等. 电力系统新型振荡问题浅析[J]. 中国电机工程学报, 2018, 38(10): 2821-2828, 3133.
Xie Xiaorong, Liu Huakun, He Jingbo, et al. On new oscillation issues of power systems[J]. Proceedings of the CSEE, 2018, 38(10): 2821-2828, 3133.
[5] 马宁宁, 谢小荣, 贺静波, 等. 高比例新能源和电力电子设备电力系统的宽频振荡研究综述[J]. 中国电机工程学报, 2020, 40(15): 4720-4732.
Ma Ningning, Xie Xiaorong, He Jingbo, et al. Review of wide-band oscillation in renewable and power electronics highly integrated power systems[J]. Pro- ceedings of the CSEE, 2020, 40(15): 4720-4732.
[6] 肖湘宁, 罗超, 廖坤玉. 新能源电力系统次同步振荡问题研究综述[J]. 电工技术学报, 2017, 32(6): 85-97.
Xiao Xiangning, Luo Chao, Liao Kunyu. Review of the research on subsynchronous oscillation issues in electric power system with renewable energy sources[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 85-97.
[7] 胡寿松. 自动控制原理[M]. 7版. 北京: 科学出版社, 2019.
[8] 谢小荣, 贺静波, 毛航银, 等. “双高”电力系统稳定性的新问题及分类探讨[J]. 中国电机工程学报, 2021, 41(2): 461-475.
Xie Xiaorong, He Jingbo, Mao Hangyin, et al. New issues and classification of power system stability with high shares of renewables and power elec- tronics[J]. Proceedings of the CSEE, 2021, 41(2): 461-475.
[9] Huang S H, Schmall J, Conto J, et al. Voltage control challenges on weak grids with high penetration of wind generation: ERCOT experience[C]//2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 2012: 1-7.
[10] Zhang Yi, Zhu Songzhe, Sparks R, et al. Impacts of solar PV generators on power system stability and voltage performance[C]//2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 2012: 1-7.
[11] 余墨多, 黄文焘, 邰能灵, 等. 基于光伏电站暂态特性的自适应暂稳控制方法[J]. 电工技术学报, 2020, 35(增刊2): 512-522.
Yu Moduo, Huang Wentao, Tai Nengling, et al. Transient stability enhancement with an adaptive control scheme for photovoltaic plants[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(S2): 512-522.
[12] 李锡林, 查晓明, 田震, 等. 考虑频率突变影响的孤岛微电网系统建模和基于Lyapunov第二法的暂态稳定性分析[J]. 电工技术学报, 2023, 38(增刊1): 18-31.
Li Xilin, Zha Xiaoming, Tian Zhen, et al. Modeling of island microgrid considering frequency mutation and transient stability analysis based on Lyapunov second method[J]. Transactions of China Electrotechnical Society, 2023, 38(S1): 18-31.
[13] 梁贵书, 董华英. 电路理论基础[M]. 3版. 北京: 中国电力出版社, 2009.
[14] 肖湘宁. 新一代电网中多源多变换复杂交直流系统的基础问题[J]. 电工技术学报, 2015, 30(15): 1-14.
Xiao Xiangning. Basic problems of the new complex AC-DC power grid with multiple energy resources and multiple conversions[J]. Transactions of China Electrotechnical Society, 2015, 30(15): 1-14.
[15] Wang Xiongfei, Blaabjerg F. Harmonic stability in power electronic-based power systems: concept, modeling, and analysis[J]. IEEE Transactions on Smart Grid, 2018, 10(3): 2858-2870.
[16] Chen Zhiyong, Huang Xucheng, Luo An, et al. Wideband harmonic resonance characteristics and coordinated damping method for distributed gen- eration power plants[J]. IEEE Transactions on Industrial Electronics, 2019, 66(10): 7753-7764.
[17] 李建文, 李戎, 吴滨源, 等. LCL型并网逆变器大小信号模型比较与分析[J]. 电机与控制学报, 2021, 25(5): 60-70.
Li Jianwen, Li Rong, Wu Binyuan, et al. Comparison and analysis of large and small signal models of LCL grid-connected inverter[J]. Electric Machines and Control, 2021, 25(5): 60-70.
[18] 吴滨源, 李建文, 李永刚, 等. 用于谐波劣化分析的并网逆变器阻抗灰箱拟合方法[J]. 电工技术学报, 2022, 37(4): 942-953.
Wu Binyuan, Li Jianwen, Li Yonggang, et al. A gray-box fitting method of grid-connected inverters impedance for the analysis of harmonic degra- dation[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 942-953.
[19] 曾志杰, 肖华锋, 高博, 等. 结合阻抗比与振荡阻尼特征的并网系统谐波谐振稳定性分析方法[J]. 中国电机工程学报, 2020, 40(22): 7201-7212.
Zeng Zhijie, Xiao Huafeng, Gao Bo, et al. Stability analysis method of harmonic resonance of grid- connected generation system based on impedance ratios and oscillation damping[J]. Proceedings of the CSEE, 2020, 40(22): 7201-7212.
[20] 朱晓荣, 李铮, 孟凡奇. 基于不同网架结构的直流微电网稳定性分析[J]. 电工技术学报, 2021, 36(1): 166-178.
Zhu Xiaorong, Li Zheng, Meng Fanqi. Stability analysis of DC microgrid based on different grid structures[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 166-178.
[21] 韩应生, 孙海顺, 秦世耀, 等. 电压源型双馈风电并网系统小扰动低频稳定性分析[J]. 电工技术学报, 2023, 38(5): 1312-1324, 1374.
Han Yingsheng, Sun Haishun, Qin Shiyao, et al. Low-frequency stability analysis of voltage-sourced doubly-fed wind power grid-connected system under small disturbance[J]. Transactions of China Electro- technical Society, 2023, 38(5): 1312-1324, 1374.
[22] He Jinwei, Li Yun wei, Bosnjak D, et al. Investigation and active damping of multiple resonances in a parallel-inverter-based microgrid[J]. IEEE Transa- ctions on Power Electronics, 2013, 28(1): 234-246.
[23] 刘洋, 帅智康, 李杨, 等. 多逆变器并网系统谐波谐振模态分析[J]. 中国电机工程学报, 2017, 37(14): 4156-4164, 4295.
Liu Yang, Shuai Zhikang, Li Yang, et al. Harmonic resonance modal analysis of multi-inverter grid- connected systems[J]. Proceedings of the CSEE, 2017, 37(14): 4156-4164, 4295.
[24] 舒万韬, 洪芦诚, 刘宁波, 等. 多逆变器并网谐振特性分析[J]. 中国电机工程学报, 2018, 38(17): 5009-5019, 5298.
Shu Wantao, Hong Lucheng, Liu Ningbo, et al. An analysis on resonance characteristics of multi- inverters grid-connected system[J]. Proceedings of the CSEE, 2018, 38(17): 5009-5019, 5298.
[25] 李建文, 阮筱菲, 李永刚, 等. 弱电网下多LCL型并网逆变器谐振模态分析[J]. 太阳能学报, 2021, 42(2): 346-355.
Li Jianwen, Ruan Xiaofei, Li Yonggang, et al. Resonance modal analysis for multiple LCL-type grid-connected inverters in weak grid[J]. Acta Energiae Solaris Sinica, 2021, 42(2): 346-355.
[26] Harnefors L, Wang Xiongfei, Yepes A G, et al. Passivity-based stability assessment of grid-connected VSCs-an overview[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(1): 116-125.
[27] Riccobono A, Santi E. Comprehensive review of stability criteria for DC power distribution systems[J]. IEEE Transactions on Industry Applications, 2014, 50(5): 3525-3535.
[28] 崔恒斌, 冯晓云, 林轩, 等. 车网耦合下高速铁路牵引网谐波谐振特性研究[J]. 电工技术学报, 2013, 28(9): 54-64.
Cui Hengbin, Feng Xiaoyun, Lin Xuan, et al. Research on harmonic resonance characteristic of high-speed railway traction net considering coupling of trains and traction nets[J]. Transactions of China Electrotechnical Society, 2013, 28(9): 54-64.
[29] Hong Lucheng, Shu Wantao, Wang Jianhua, et al. Harmonic resonance investigation of a multi-inverter grid-connected system using resonance modal analysis[J]. IEEE Transactions on Power Delivery, 2019, 34(1): 63-72.
[30] 张占俊, 李建文, 董耀, 等. 弱电网下多逆变器并网谐振失稳分析方法[J]. 电气技术, 2020, 21(10): 21-28.
Zhang Zhanjun, Li Jianwen, Dong Yao, et al. Method of resonance instability analysis of multiple grid- connected inverters in weak grid[J]. Electrical Engineering, 2020, 21(10): 21-28.
[31] 仰彩霞, 刘开培, 李建奇, 等. 谐波谐振模态灵敏度分析[J]. 电工技术学报, 2011, 26(增刊1): 207- 212.
Yang Caixia, Liu Kaipei, Li Jianqi, et al. Modal sensitivity analysis for harmonic resonance[J]. Transactions of China Electrotechnical Society, 2011, 26(S1): 207-212.
[32] 郭小颖, 唐俊杰, 舒铜, 等. 基于改进模态分析法的柔性多端交直流混联系统静态电压稳定性评估[J]. 电工技术学报, 2021, 36(17): 3741-3752.
Guo Xiaoying, Tang Junjie, Shu Tong, et al. Static voltage stability assessment on hybrid alternating current/voltage source converter-multiple terminal direct current system using improved modal analysis[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3741-3752.
[33] 王莹鑫, 徐永海, 陶顺, 等. 计及扰动源输出原副边特性的直流配电网谐振分析方法[J]. 电工技术学报, 2023, 38(7): 1723-1736.
Wang Yingxin, Xu Yonghai, Tao Shun, et al. DC distribution system resonance characteristics analysis method considering the output characteristics of the perturbation source[J]. Transactions of China Electro- technical Society, 2023, 38(7): 1723-1736.
[34] Sun Jian. Impedance-based stability criterion for grid- connected inverters[J]. IEEE Transactions on Power Electronics, 2011, 26(11): 3075-3078.
[35] 陈新, 王赟程, 龚春英, 等. 采用阻抗分析方法的并网逆变器稳定性研究综述[J]. 中国电机工程学报, 2018, 38(7): 2082-2094, 2223.
Chen Xin, Wang Yuncheng, Gong Chunying, et al. Overview of stability research for grid-connected inverters based on impedance analysis method[J]. Proceedings of the CSEE, 2018, 38(7): 2082-2094, 2223.
[36] Varricchio S L, Gomes S, Martins N. Modal analysis of industrial system harmonics using the s-domain approach[J]. IEEE Transactions on Power Delivery, 2004, 19(3): 1232-1237.
[37] Xu W, Huang Zhenyu, Cui Yu, et al. Harmonic resonance mode analysis[J]. IEEE Transactions on Power Delivery, 2005, 20(2): 1182-1190.
Abstract The broadband oscillation caused by the interaction of a high proportion of new energy connected to the grid, grid impedance and load is a typical system stability problem. In recent years, some overvoltage phenomena have been difficult to classify into the classical stability problems. The electromagnetic transient process driving this phenomenon differs from the power-angle relationship on the rotor-side generator models using phase-locked loops (PLLs).
To explain the dynamic behavior of inverter grid-connected systems disturbed by broadband harmonics, this paper derives a mathematical expression that characterizes the system’s response to harmonic disturbances and analyzes the response’s characteristics. Furthermore, the feasibility of analyzing harmonic responses using characteristic roots is verified by an example of a single inverter connected to the grid. The relationship between the characteristic root and the resonance mode is clarified for multi-inverter grid-connected systems. Finally, the dynamic behavior analysis is verified by simulation and experiments.
The harmonic disturbance response expression is derived according to the characteristic roots and the harmonic disturbance. It is found that the system’s response comprises two waveforms: the steady-state response and the transient response. The resonance characteristics of these two responses differ, with the magnitude of the resonance peak closely related to the damping coefficient x. A large peak occurs when x is close to 0, gradually decreasing as x increases, and no steady-state response resonance peak is observed when x＞0.7.
The characteristic root can effectively describe the harmonic disturbance response of inverter grid-connected systems. The dynamic behavior of the system after disturbance can be quantitatively analyzed by calculating the damping coefficient value. When multiple inverters are connected to the grid, the impedance-based system modeling method provides convenience for analyzing the stability of the inverter grid-connected system. The series and parallel resonance points in high-order networks are obtained by modal analysis. Accordingly, the characteristic roots of the system are obtained by converting the memory elements in the matrix from the frequency domain to the s domain, offering a simple and reusable approach to characterize coupling relationships within high-order networks and analyze system stability.
The proposed method is verified using a single inverter connected to the grid and three inverters with different parameters to be connected to the grid. It is found that the parameter design of a single inverter can meet grid-connected harmonic requirements. However, when multiple inverters are connected to the grid, the damping coefficient of a single inverter decreases with the number of parallel inverters. A smaller damping coefficient makes the system less capable of actively suppressing harmonic oscillations. The slow attenuation of transient components results in a significantly increased waveform distortion rate over a short period of time.
The following conclusions can be obtained through simulation and experiments: (1) As an analytical tool for finding system characteristic roots and traversing system resonance frequencies, the modal analysis method can provide numerical solutions and modal impedance curves simply and quickly. (2) The characteristic roots of the system can effectively describe the dynamic behavior of the system after disturbance. (3) A small damping coefficient renders the system susceptible to severe harmonic oscillations and deepens waveform distortion in a short period.
keywords：Characteristic root, harmonic disturbance, modal analysis method, steady-state response, transient response
DOI: 10.19595/j.cnki.1000-6753.tces.230793
中图分类号：TM464
中央高校基本科研业务费专项资金资助项目（2023MS109）。
收稿日期 2023-05-30
改稿日期 2023-08-24
李 戎 男，1998年生，博士研究生，研究方向为逆变器建模、谐波劣化分析等。E-mail: lr_ncepu@163.com
李建文 女，1983年生，副教授，硕士生导师，研究方向为新型配电网下电能质量分析与治理。E-mail: ljw_ncepu@163.com（通信作者）
（编辑 陈 诚）