（1）
摘要 基于模块化多电平拓扑的换流阀是柔性直流输电系统的核心装备，随着柔直换流阀运行电压、功率密度以及运行场景的不断拓展，其运行可靠性成为突出问题。现有的柔直换流阀可靠性评估方法忽略了金属化薄膜电容器与IGBT模块性能退化的耦合关系，致使评估结果不准确。为此，该文提出了计及金属化薄膜电容器与IGBT模块退化过程相关性的可靠性评估方法。IGBT模块寿命采用威布尔分布，考虑了换流阀运行过程中的任务剖面变化；基于Wiener过程对金属化薄膜电容器的可靠性进行了评估，利用Copula理论将容值退化程度与IGBT模块寿命之间的耦合关系进行了建模。所提可靠性评估方法修正了现有不考虑相关性方法对柔直换流阀可靠性评估结果，平均无故障时间从4.05年修正为5.20年，评估结果更加精确。
关键词：柔性直流换流阀 可靠性评估 金属化薄膜电容器 IGBT模块 Copula理论
柔性直流输电技术可实现有功和无功功率的快速灵活控制，在规模化新能源电力传输、向弱交流系统或无源系统提供电压支撑等方面具有明显的优势[1-3]。自2011年以来，我国已陆续建成南澳、舟山、张北、昆柳龙等多个柔直输电工程，随着系统容量需求的不断攀升和工程应用场景的拓展[4-6]，作为核心装备的柔直换流阀，对其运行可靠性进行准确、实时评估具有重要的工程意义。
目前已有文献对柔直换流阀的可靠性开展了研究，相关方法可以分为两类：基于恒定故障率模型的可靠性评估方法，换流阀内部各部件采用恒定故障率的失效模型，故障率通常来自可靠性评估手册，如MIL-HDBK-217；文献[7]基于k/n(G)模型定量对比分析了换流阀桥臂配置不同数量冗余模块的可靠性；文献[8]利用可靠性框图法构建柔直换流阀的可靠性评估模型，进行了结构可靠性分析，并且定量评估了不同拓扑结构换流阀的可靠性，确定了冗余模块的最优配置方案；文献[9]构建了柔直换流阀的马尔可夫模型和系统的状态转移方程，计算了具有冗余组件的换流阀平均无故障时间；文献[10]利用故障树方法构建了柔直换流阀的可靠性模型，考虑了电流载荷和电压载荷的波动，根据可靠性评估手册，对IGBT模块的恒定故障率进行了修正，取得了较为准确的评估结果。
基于失效物理模型的可靠性评估方法，是在对部件失效机理和寿命模型进行详细研究的基础上提出的。能够计及换流阀的运行工况变化，部件模型采用更为实际的威布尔分布，可靠性评估更加准确，更能够反映换流阀的真实运行状态。基于失效物理模型的可靠性评估方法以获得IGBT模块以及电容器的准确可靠度函数为核心，主要步骤包含[11-12]：①详细计算IGBT模块的功率损耗；②利用热网络模型，计算IGBT模块的结温；③雨流记数法统计IGBT模块的热载荷，代入IGBT模块的寿命模型；④利用线性损耗模型，计算IGBT模块的累积寿命损耗，进而获得可靠度函数；⑤结合其他系统，对柔直换流阀可靠性进行评估。其中IGBT模块的结温计算是整个可靠性评估的重点，有不少文献针对换流阀工况对结温的准确计算进行了完善，根据换流阀运行工况改变修正结温。考虑新能源厂站的有功出力波动、环境及阀厅温度变化、开关频率的变化[13-14]；监测IGBT模块键合线失效，修改热网络参数，使得结温计算更加准确[15]。
然而现有可靠性评估方法大多针对IGBT模块和金属化薄膜电容器（Metallized Polypropylene Film capacitor，MPPF）等关键部件分别进行可靠性建模，忽略了部件退化过程的耦合关系，已有研究表明电容器的容值衰退将造成IGBT模块开关频率增加，影响IGBT模块的可靠性[16]。为此，本文提出了一种计及电容器与IGBT模块退化过程相关性的柔直换流阀可靠性评估方法，利用Copula理论对容值退化与IGBT模块寿命之间的耦合关系进行了建模，该方法提高了柔直换流阀可靠性评估结果的准确性。
根据加速老化实验和电力电子装备的运维经验，IGBT模块长期运行的老化失效主要由结温波动引起。模块化多电平换流器（Modular Multilevel Converter, MMC）运行过程中新能源场站出力会产生随机波动，并且散热系统水温、环境温度会发生变化，综合考虑多种影响因素，对结温进行准确计算，是IGBT模块可靠性评估的关键。
IGBT模块损耗包含静态损耗和动态损耗，静态损耗包含IGBT通态损耗、IGBT截止损耗、二极管通态损耗以及二极管截止损耗[17]。通态损耗受MMC交流负载波动情况的影响较大，开关损耗受运行控制策略的影响较大。IGBT模块由二极管和IGBT芯片并联构成多条功率支路，二者的结温计算和可靠性评估方法相同，本文以IGBT芯片评估为例进行说明，相关参数均可以通过器件手册获得，对于二极管，将相应的量替换成二极管参数即可。IGBT的通态损耗PTon可以表示为
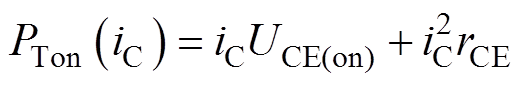（1）
式中，iC为IGBT的集电极电流；UCE(on)为IGBT的通态压降；rCE为IGBT的导通电阻。IGBT的截止损耗PToff可表示为
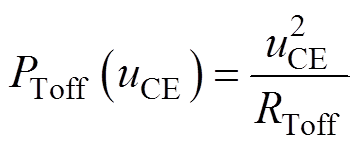（2）
式中，uCE为IGBT的截止电压，是金属化薄膜电容器的电压；RToff为IGBT的截止电阻。
IGBT的开关损耗可以通过多项式拟合得到，即
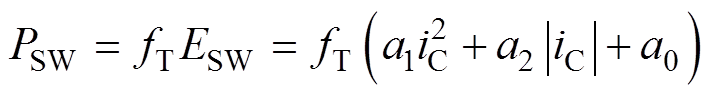（3）
式中，fT为IGBT模块在正常运行过程中的开关频率；ESW为开关损耗；a0、a1、a2为多项式拟合参数，可以通过器件手册拟合获得。
对于IGBT，开关损耗ESW分别有开通损耗Eon、关断损耗Eoff，值得注意的是，二极管的开关损耗，仅有开通过程的反向恢复损耗Erev需要考虑；因此IGBT的总损耗为
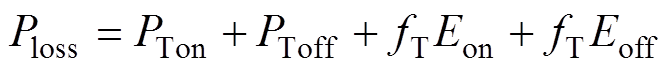（4）
通过电热比拟原理，建立包含散热器、环境温度以及器件封装结构的热网络模型来计算IGBT的结温，是状态评估在线计算的有效方法。IGBT器件的热网络模型有Cauer和Foster两种，其中Cauer模型具有实际物理意义，将每层封装材料的热特性进行了详细的建模，然而参数提取较为困难。IGBT结温计算利用能够通过器件手册直接提取参数的Foster模型。若热网络模型参数为H，IGBT模块损耗为PTloss，环境温度为Tat，则IGBT模块的结温可表示为
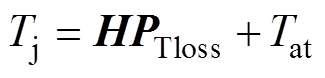（5）
计算所得IGBT的结温Tj是一系列变幅值的热载荷，难以直接代入解析寿命模型，通常使用统计计数方法将变幅载荷转化为一系列恒幅热载荷的完整循环，常用的方法有雨流计数法、峰值计数法等。IGBT模块开展的加速老化实验，积累了丰富的失效数据，并由此总结出多种考虑不同热载荷特性的解析寿命模型，如Coffin-Manson模型[18]、Bayerer模型[19]以及Norris-Landzberg模型[20]等。本文选用考虑载荷循环频率的Norris-Landzberg模型作为寿命评估基础，则IGBT循环寿命NTf为
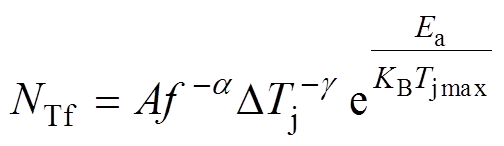（6）
式中，NTf为评估寿命；DTj为IGBT的最高与最低结温差；Tjmax为IGBT的最高结温；f为恒幅热载荷出现频率；KB为玻耳兹曼常数，KB=1.38×10-23 J/K；Ea为活化能，Ea=0.42 kJ/mol；A、a、g为模型拟合参数，A=310，a=0.4，g =2。
根据线性损伤原理，IGBT的累积寿命损耗DT可以表示为
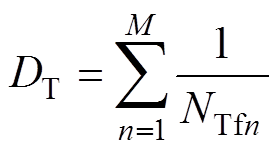（7）
式中，M为统计计数所获的恒幅载荷数量。
ABB、英飞凌等器件制造厂商通过加速老化实验得到IGBT的可靠性服从威布尔分布，因此可靠度函数为
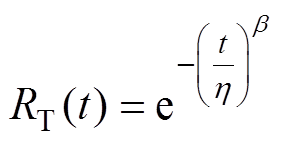（8）
式中，b为形状参数；h 为尺度参数。其中，b可以通过加速老化实验得到，尺度参数h与寿命损耗DT之间满足关系
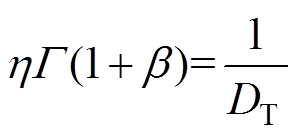（9）
式中，
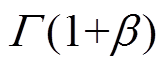为参数为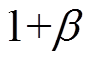
的伽马函数。
以上分析替换为二极管参数，即可得到二极管的可靠度函数。因此，对于IGBT模块，其可靠度函数为
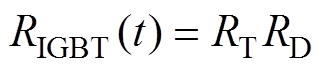（10）
金属化薄膜电容器具有可靠性高、寿命长等特点，传统的基于威布尔分布的可靠性评估，在MMC应用过程中难以获得足够的失效数据进而对分布参数进行估计。金属化薄膜电容器退化过程呈现软故障的特征，随着寿命下降，电容值不断降低。现有研究电容器的状态评估方法主要针对容值退化过程进行建模，包含利用最小二乘法拟合容值退化过程，等效为复合Poisson过程、Wiener过程等[21]。Wiener过程是一种具有线性漂移项的随机过程，适合用来描绘金属化薄膜电容器由于大量微小自愈点累积致使容值呈现减小趋势的非单调退化过程[22]。
金属化薄膜电容器的容值退化量CL满足线性Wiener退化模型，则有
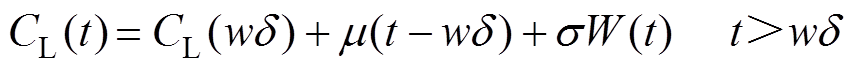（11）
式中，CL(t)为t时刻的容值退化量；d 为电容器容值评估的周期；CL(wd)为第w周期后的容值退化量；m 为漂移系数；s 为扩散系数；W(t)为容值监测误差。
因此电容器的可靠度函数为
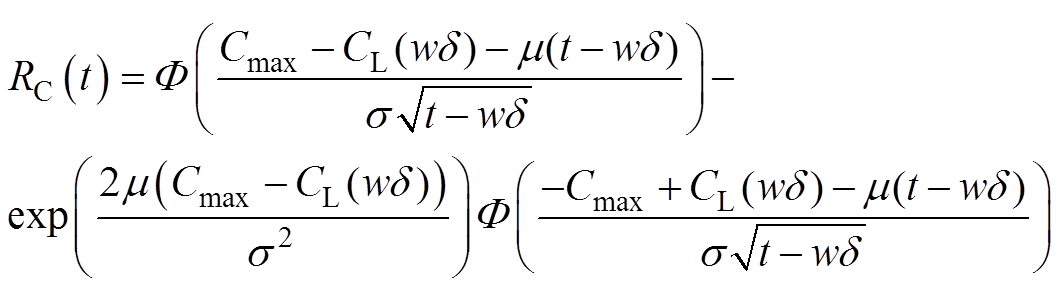（12）
式中，Cmax为电容器的标称容值；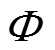
为标准正态分布函数。
通过电容器容值退化累积监测数据可以估计Wiener分布的参数，得到的极大似然估计值为
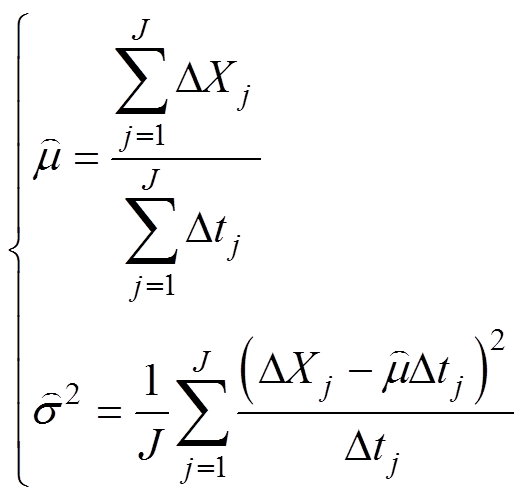（13）
式中，Dtj为第j个时间间隔；DXj为第j个时间间隔内容值的退化量。
为了维持电容器电压在合理的范围内波动，以及控制组件电容器电压的离散度，电容器电压通常需要控制在额定值的10%左右。MMC最近电平逼近或PWM控制策略通常配置电容电压平衡控制功能，通过调节组件电容器的充放电时间，达到电容电压的动态平衡。
金属化薄膜电容器长期运行过程中造成容值下降，在相同的负载电流工况下，电容器电压波动范围加大。根据MMC电压平衡策略，容值降低的电容器为了保持电压均衡，其投切次数相应增多，相应的组件IGBT开关频率将会增加。IGBT开关频率增加，功率损耗随之增加，IGBT结温升高，根据式（6）和式（7）可知，IGBT的剩余寿命降低，可靠性降低。可见，金属化薄膜电容器的可靠性与IGBT可靠性存在相关性。
Copula理论将多变量的联合分布函数和边缘分布函数联系起来。柔直换流阀组件的可靠度函数是MPPF和IGBT模块可靠性函数的联合分布函数，根据SKlar定理，组件可靠度函数分成了相互独立、可分开进行的两部分，即：IGBT模块的可靠度函数、MPPF的可靠度函数以及两者间Copula函数的构造。IGBT模块与MPPF的可靠度函数如式（10）、式（12）所示。本文选用二维Gumbel型Copula函数对电容器和IGBT可靠性的相关性进行描述，组件可靠度函数为
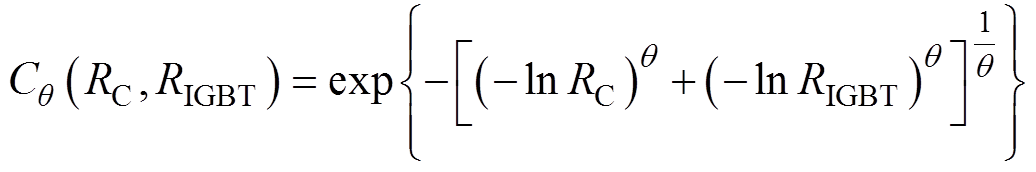（14）
式中，q 为相关程度参数，q Î[1,+¥]，q =1时，表示电容器和IGBT模块的可靠性完全不相关。
根据容值的退化量与IGBT剩余寿命的结果，可以对相关系数进行极大似然估计[23]，有
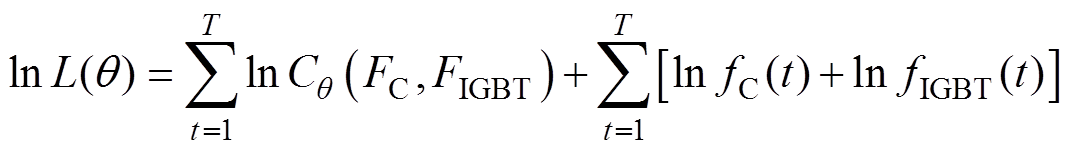（15）
式中，FC和FIGBT分别为电容器和IGBT的累积故障分布函数，FC(t)=1-RC(t)，FIGBT(t)=1-RIGBT(t)；fC和fIGBT为故障密度分布函数，满足
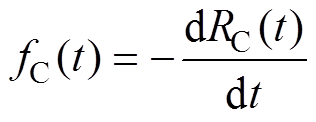（16）
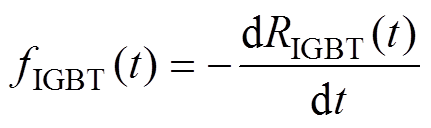（17）
求解微分方程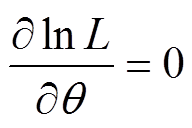
，可以获得Copula函数相关系数的极大似然估计值。
柔直阀组件系统主要由上下管IGBT模块、电容器、晶闸管、旁路开关、控制系统（组件控制板卡、驱动板）以及取能系统组成，如图1所示。晶闸管和旁路开关只有故障等特殊条件下才会投入，因此，长期运行状态的可靠性评估可以忽略旁路开关以及晶闸管的故障率；对于柔直换流阀，三相共有六个桥臂，每个桥臂配置有桥臂电抗器，每相配置有阀基控制器，经由换流站控保系统控制每相上下桥臂投入组件数量，每个组件配置有水冷装置，可见各部件可靠性之间呈现串联特性。
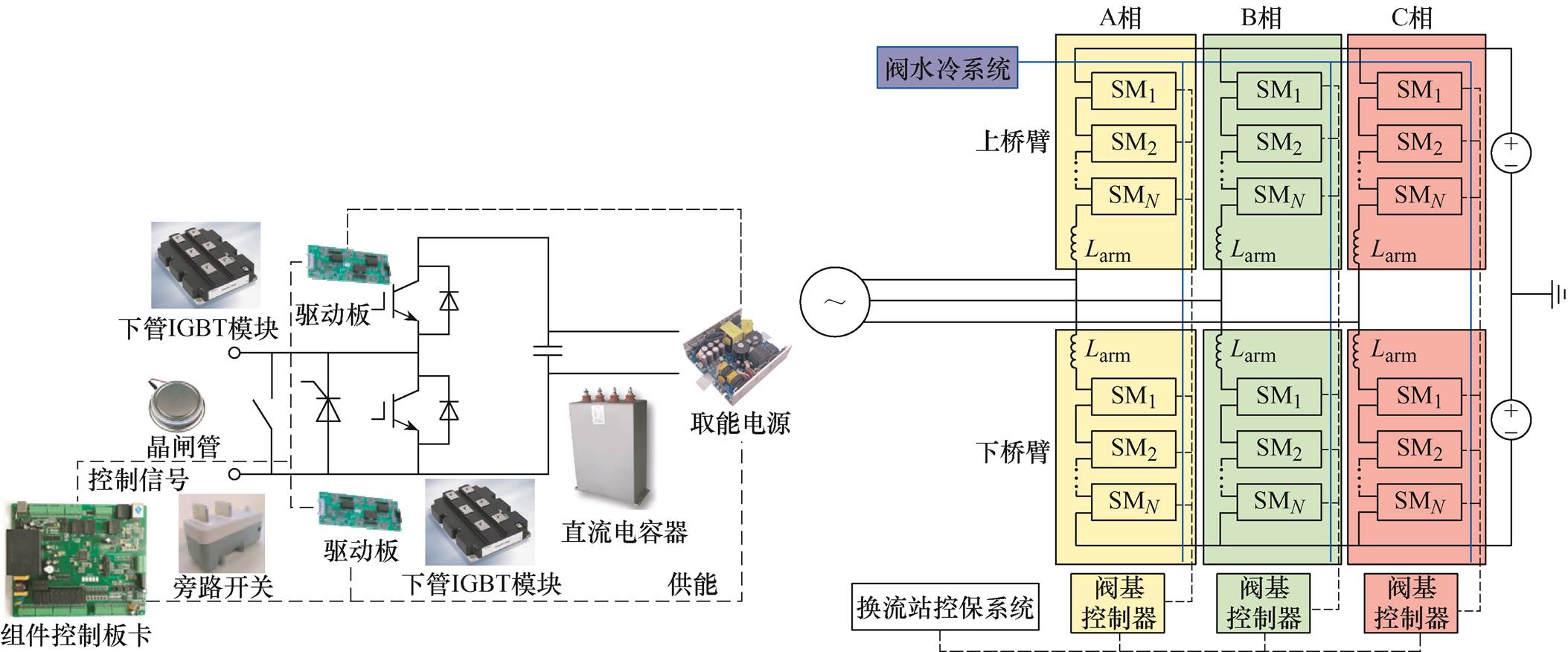
图1 柔直换流阀及其组件的主要组成部件
Fig.1 The main components of the flexible and direct converter valve and its submodule
柔直换流阀内其他元件寿命分布符合浴盆曲线，在稳定运行期，元件具有恒定失效率l，可靠度函数为指数函数，可以表示为
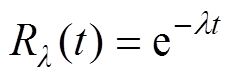（18）
考虑电容器和IGBT的相关性，柔直换流阀组件的可靠度函数RSM可以表示为
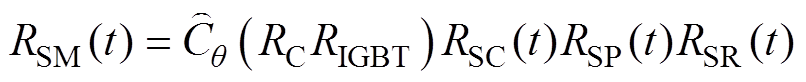（19）
式中，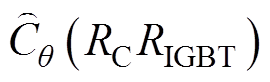
为计及电容器与IGBT模块退化相关性的可靠度函数；RSC(t)为控制系统的可靠度函数；RSP(t)为取能系统的可靠度函数；RSR(t)为放电电阻的可靠度函数。
为保障MMC安全可靠运行，各桥臂通常会配置冗余模块，当一个或多个组件故障后，冗余组件投入，桥臂不会立即失效，保持相应的功能。考虑主动备用策略，即冗余组件在运行过程中投入。若单个桥臂配备的组件数量为n，MMC电平数为k，则发生n-k+1个组件失效时，相应桥臂因冗余耗尽而失效。主动备用策略下桥臂可靠度可以用k/n(G)模型描述，即
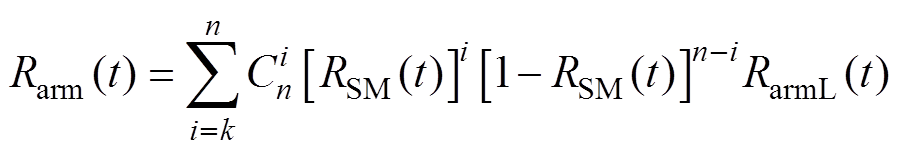（20）
式中，RarmL为桥臂电抗器的可靠度函数。
每相桥臂配置有阀基控制器，结合换流站的控制保护系统以及阀水冷系统，可以得到柔直换流阀的可靠度函数RMMC(t)为
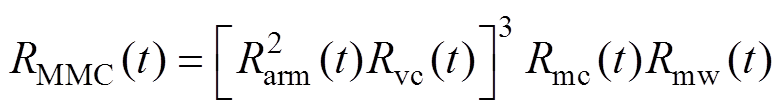（21）
式中，Rvc(t)为阀基控制器的可靠度函数；Rmc(t)为换流站控保系统的可靠度函数；Rmw(t)为阀水冷系统的可靠度函数。
本文以2013年投运的南澳柔性直流输电工程为算例，说明IGBT和电容器相关性评估方法。南澳柔直工程电压等级为±160 kV，建有两个风电场送出换流站和一个受端换流站。其中以送端金牛换流站为分析对象，牛头岭和云澳风电场共计83.23 MW的风电机组接入换流站。金牛换流站柔性直流换流阀的单个桥臂共有220个组件，其中20个冗余组件，采用额定电压3 300 V、额定电流1 000 A的IGBT模块；组件电容器为标称容量2.5 mF的MPPF。
IGBT模块结温与柔直换流阀运行工况变化密切相关，为使结温计算结果能够反映工程实际，本文获得了南澳岛当地一年内以小时计典型风速数据，如图2所示，用以估算南澳工程送端柔直换流阀一年内的功率变化。风电场风机按照切入风速4 m/s，切出风速25 m/s，额定风速10 m/s计算。因此可得一年内金牛换流站柔直换流阀送出功率如图3所示。
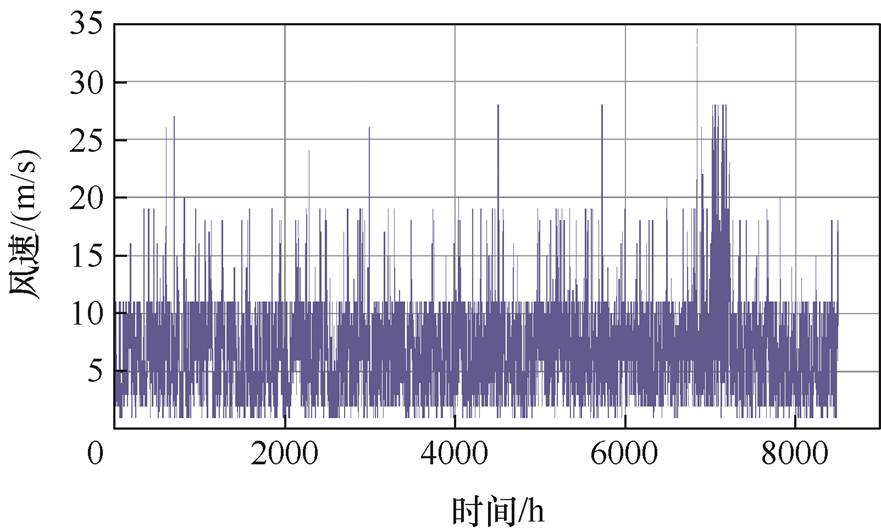
图2 南澳岛一年的典型风速（逐小时计）
Fig.2 Typical wind speed of Nan’ao Island in a year (hour)
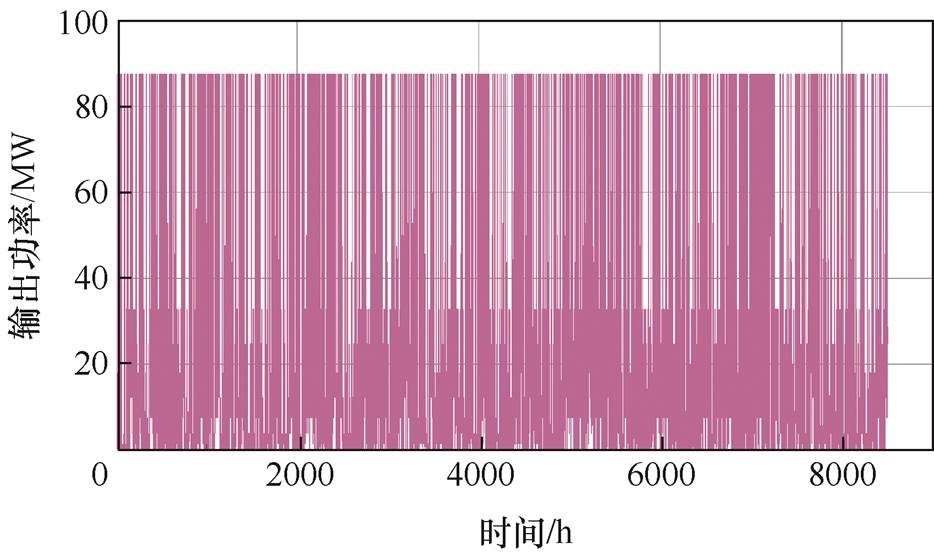
图3 柔直换流阀一年内输出功率的变化
Fig.3 Change in output power of flexible direct converter valve within one year
根据IGBT模块通态损耗、开关损耗和换流阀的控制策略，可以计算获得下管IGBT模块中IGBT芯片和二极管芯片的功率损耗。上管IGBT模块结温计算和评估方法相同，对评估方法详细论述均以下管IGBT模块为例进行说明。根据IGBT模块的器件手册，建立四阶Foster热网络模型，如图4所示，模型中热阻和热容参数见表1。
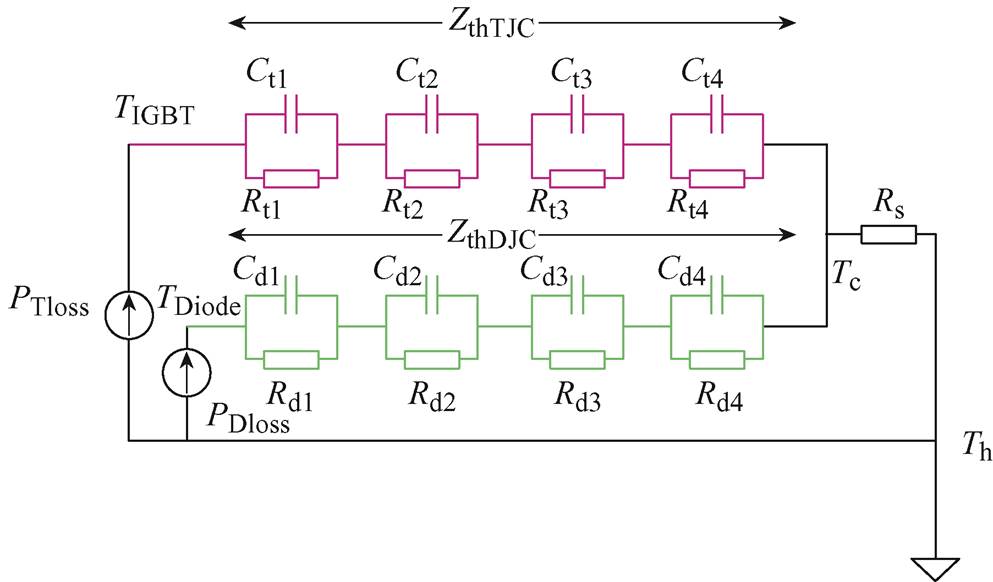
图4 IGBT模块的四阶Foster热网络模型
Fig.4 The Foster thermal network model for IGBT modules
表1 IGBT模块热网络模型中的热阻与热容参数
Tab.1 Thermal resistance and heat capacity parameters in the thermal network model of IGBT modules
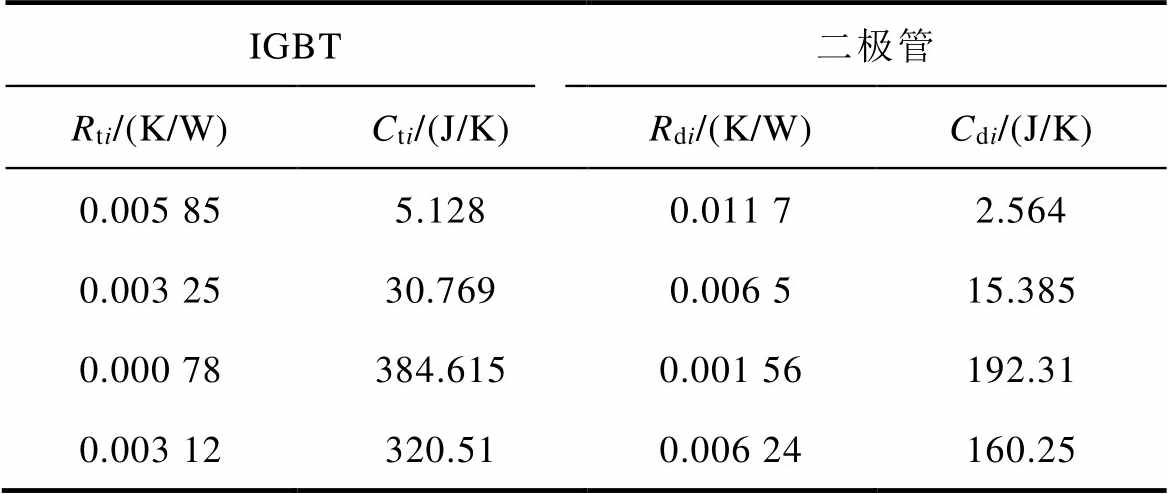
IGBT二极管 Rti/(K/W)Cti/(J/K)Rdi/(K/W)Cdi/(J/K) 0.005 855.1280.011 72.564 0.003 2530.7690.006 515.385 0.000 78384.6150.001 56192.31 0.003 12320.510.006 24160.25
对IGBT和二极管芯片结温的变幅值热载荷谱进行雨流计数统计。一年内IGBT模块经历了8 275个完整的恒幅热载荷循环，其中IGBT芯片的热载荷分布如图5所示，二极管芯片的热载荷分布如图6所示。代入式（6）中，可以获得每个完整热载荷循环所对应的IGBT模块可用寿命，根据式（7），可以计算得到运行十年后IGBT和二极管芯片的寿命损耗为
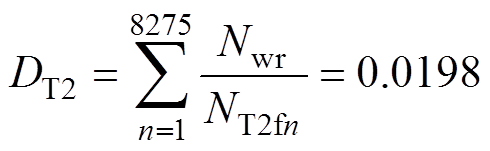（22）
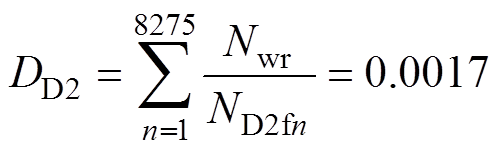（23）
式中，NT2fn、ND2fn分别为一年内第n个恒幅热载荷循环下的IGBT和二极管的循环寿命；Nwr为评估周期，Nwr=10；下角标中的“2”表示下管IGBT模块相关参数。
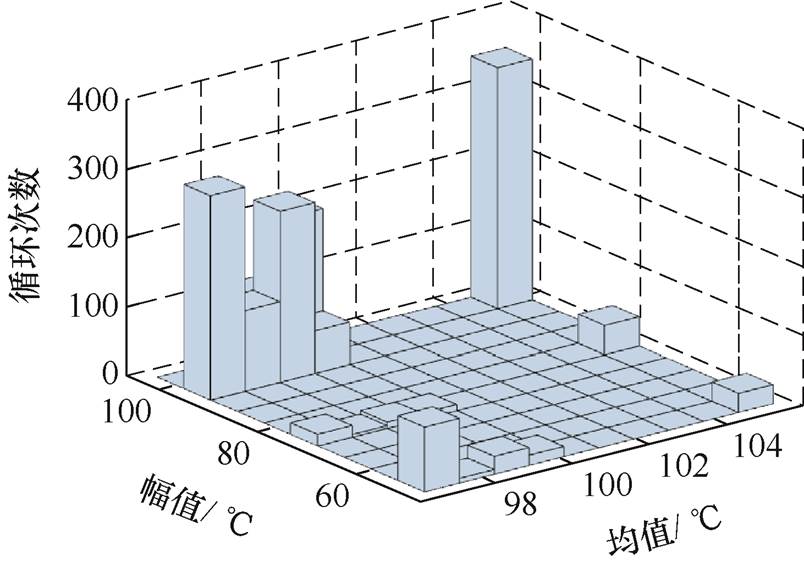
图5 IGBT模块中IGBT芯片热载荷谱的雨流计数结果
Fig.5 The rain flow counting results of IGBT chip thermal load spectrum in IGBT module
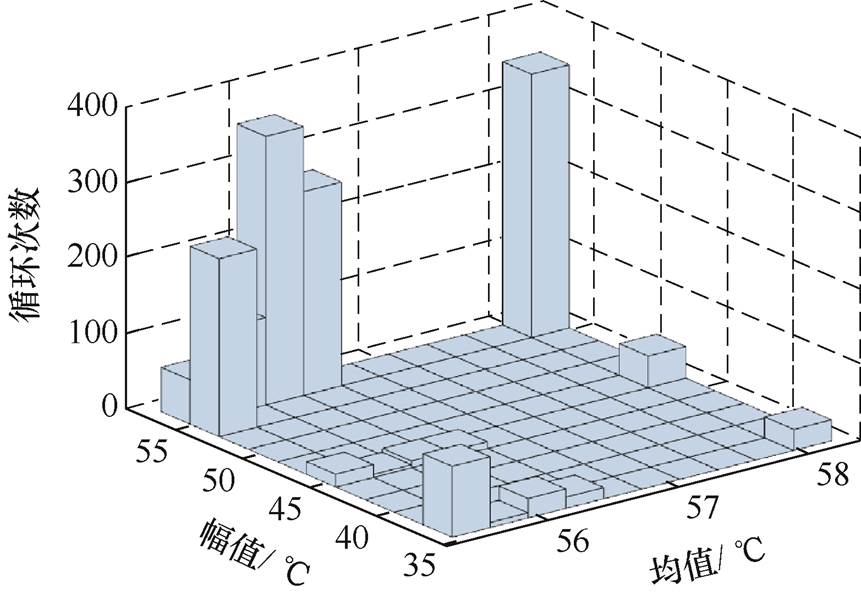
图6 IGBT模块二极管芯片热载荷谱的雨流计数结果
Fig.6 The rain flow counting results of diode chip thermal load spectrum in IGBT module
ABB进行IGBT模块加速老化实验[24]，获得威布尔寿命分布的形状参数b =2.012 6，IGBT模块的键合线和焊料层失效均是金属累积疲劳的失效模式，因此对于不同热载荷的IGBT模块寿命分布的形状参数相同，按照式（9）可以计算IGBT和二极管的尺度参数分别为
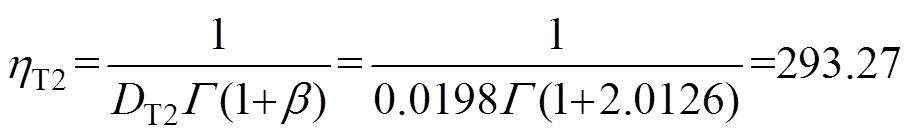（24）
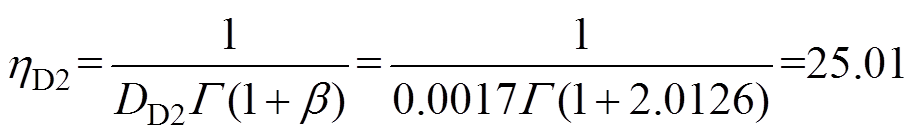（25）
持续运行一年后IGBT模块中IGBT芯片和二极管芯片的可靠度函数分别为
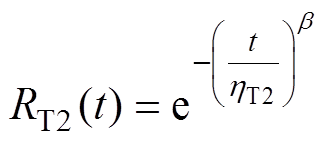（26）
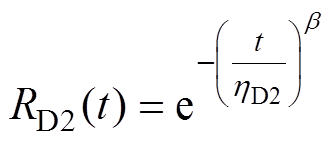（27）
图7所示为下管IGBT模块的可靠度随时间的变化曲线，可见对于下管IGBT模块，其可靠度取决于其中的IGBT芯片，二极管芯片的可靠度远高于IGBT芯片。选用Bx寿命作为IGBT模块寿命分布的表征指标，其含义为持续运行到可靠性为x时IGBT模块所需要的时间。下管IGBT模块的B90寿命为3.2年，B10寿命为37.0年。
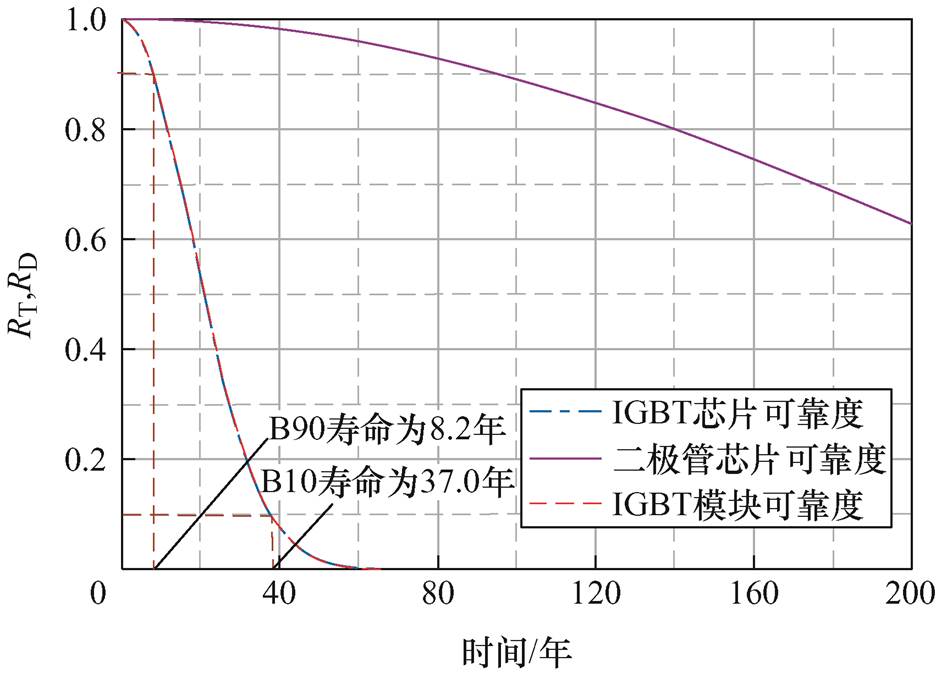
图7 IGBT模块可靠度随时间的变化
Fig.7 The variation of IGBT module reliability over time
金属化薄膜电容器容值衰减为标称容量的5%，即认为电容器失效。柔性直流换流阀持续运行十年后，将会累积一系列容值退化数据。根据式（13），可以获得电容器容值退化等效维纳过程参数的极大似然估计值为
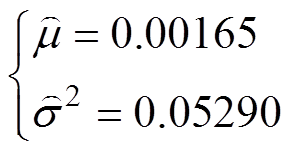（28）
代入式（12），可得运行一年之后金属化薄膜电容器的可靠度如图8所示。可以看出电容器的B90寿命为24.3年，B10寿命为72.3年。
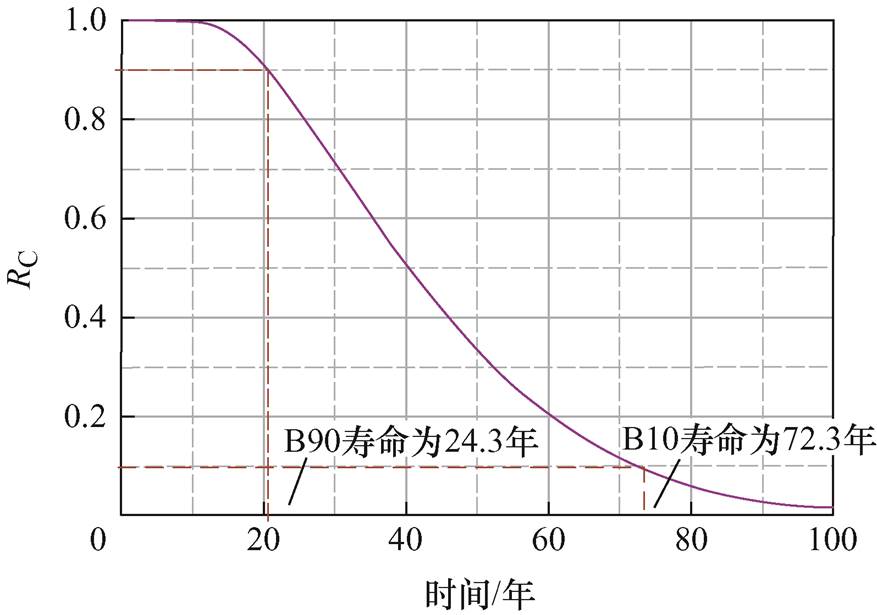
图8 金属化薄膜电容器可靠度随时间的变化
Fig.8 The variation of metallized polypropylene film capacitor reliability over time
利用Copula理论对金属化薄膜电容器和IGBT模块退化过程的相关性进行建模，其核心在于构建Copula函数，其中相关参数q 的估计是相关性建模的关键。本文通过在Simulink中搭建单个桥臂22个半桥组件级联的柔直换流阀详细仿真模型，金属化薄膜电容器的容值为2.5 mF。通过在仿真中改变容值的退化量Closs为0、0.062 5、0.125、0.187 5以及0.25 mF，分别对应初始容值的0%、2.5%、5%、7.5%以及10%。仿真对比电容器的容值退化之后，对应组件IGBT模块开关频率的变化，以及同桥臂其余组件中IGBT模块开关频率的变化。仿真中采用最近电平逼近，每次组件轮换均按照电容器电压高低排序控制组件投入和切除。
图9所示为在改变电容器的容值退化量后相应组件IGBT和同桥臂不同组件中IGBT开关频率的变化。可见随着电容器容值退化量增加，相应组件中IGBT的开关频率增加，而同桥臂其他组件中IGBT的开关频率基本保持不变。因此，将不同退化量的电容器容值代入式（12），利用修正后的IGBT开关频率重新计算结温以及可靠度函数，可以获得在特定电容器容值退化量基础上的IGBT模块可靠度函数。进而利用式（15）对相关系数进行极大似然估计，相关系数q=1.149 5。
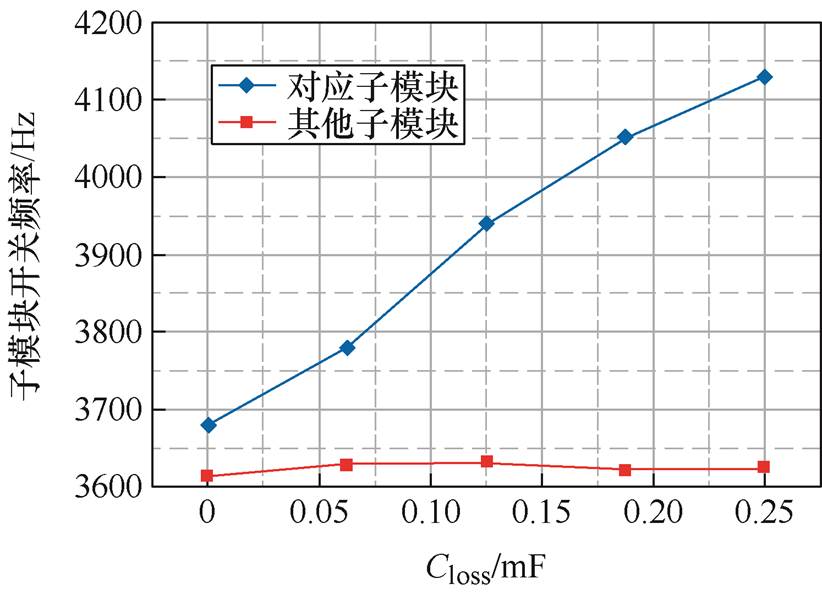
图9 不同程度容值退化与IGBT模块开关频率的关系
Fig.9 The relationship between varying degrees of capacitor degradation and IGBT module switching frequency
现有的柔直换流阀可靠性评估方法，通常忽略金属化薄膜电容器和IGBT模块退化过程之间的相关性，认为其寿命分布相互独立，将电容器和IGBT模块按照串联模型进行可靠性评估。因此，造成组件可靠性评估结果不准确。图10所示为本文所提考虑相关性的可靠性评估方法与现有未考虑相关性方法的对比[11-12]，可见现有方法高估了组件可靠性。现有方法得出组件B90的寿命为5.2年，本文考虑相关性得出B90的寿命为6.8年，B10寿命影响不大。
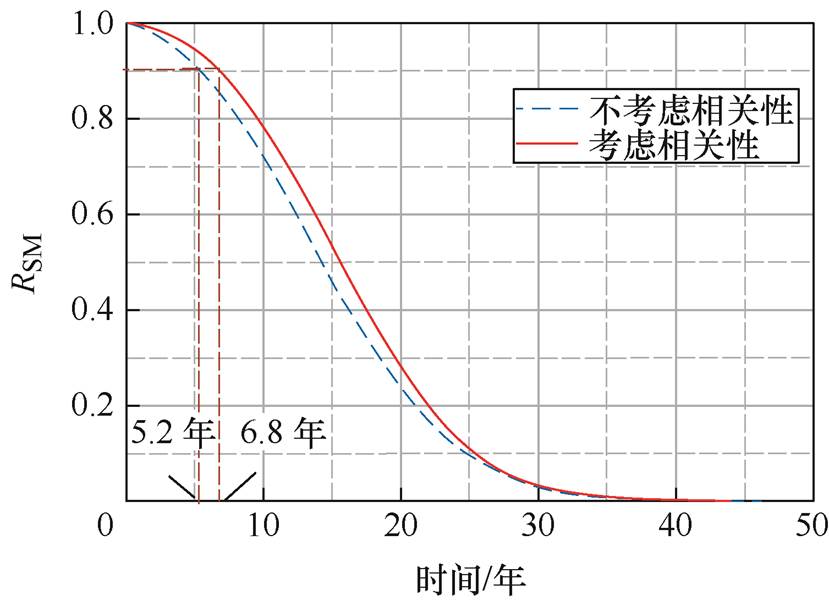
图10 不同方法组件可靠性评估结果的对比
Fig.10 Comparison of reliability evaluation results of submodules using different methods
各部件故障率见表2，将表2故障率分别代入式（18）～式（21），本文所提方法与不考虑退化相关性评估方法计算所得柔直换流阀的可靠性评估结果的对比如图11所示。根据可靠性评估结果，本文所提方法得出柔直换流阀B90寿命为3.5年，不考虑相关性的可靠性评估方法得出B90寿命为3.3年，通常的B10寿命分别为6.3年和44.8年。柔直换流阀的平均无故障时间可以表示为
表2 柔直换流阀其他部件的故障率
Tab.2 Failure rate of other components of the MMC
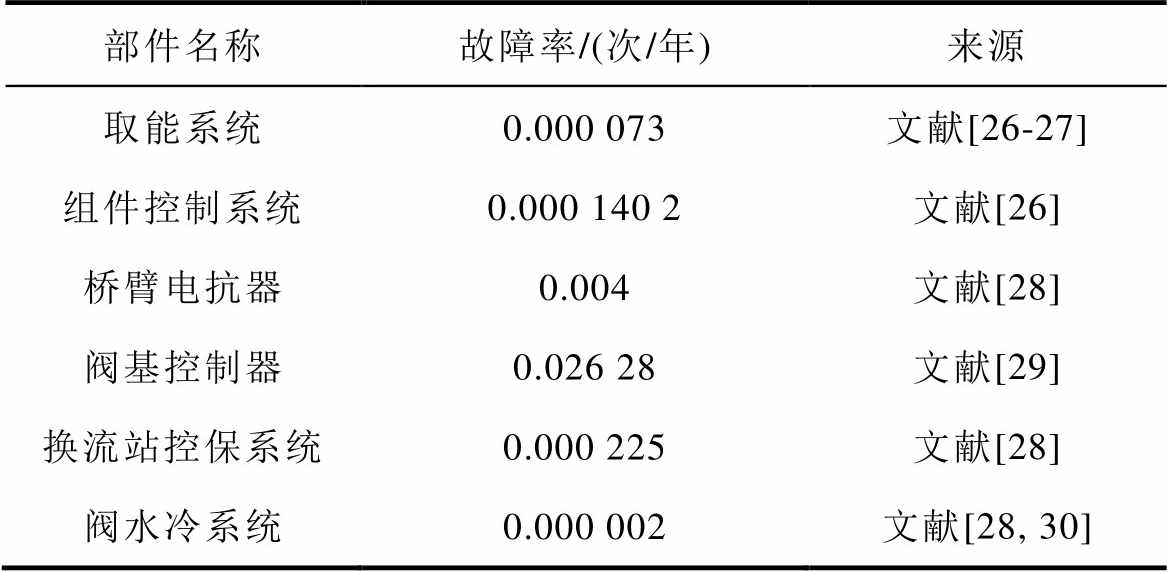
部件名称故障率/(次/年)来源 取能系统0.000 073文献[26-27] 组件控制系统0.000 140 2文献[26] 桥臂电抗器0.004文献[28] 阀基控制器0.026 28文献[29] 换流站控保系统0.000 225文献[28] 阀水冷系统0.000 002文献[28, 30]
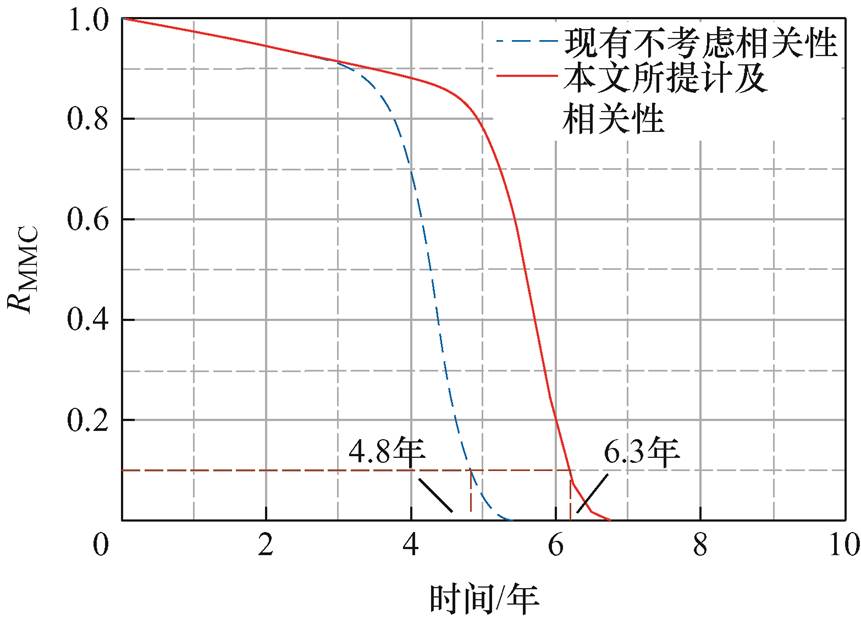
图11 不同方法柔直换流阀可靠性评估结果的对比
Fig.11 Comparison of reliability evaluation results of flexible direct converter valve using different methods
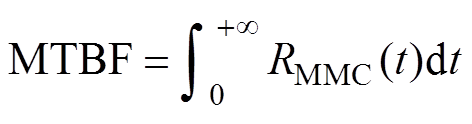（29）
利用本文所提方法所得柔直换流阀的平均无故障时间为5.20年，现有的不考虑相关性可靠性评估方法所得平均无故障时间为4.05年。值得说明的是，平均无故障时间表示的是柔直换流阀在相邻两次故障之间工作时间的数学期望，并不是指柔直换流阀在检修及故障维修条件的完整使用寿命，柔直换流阀在规范的运维检修下使用寿命可以达到数十年。
建立±600 V的三电平MMC缩比样机，其参数见表3，单个桥臂共有2个组件级联，采用移相载波PWM方式，同时配置电容器电压平衡控制策略，按照电容器电压大小投切组件。实验平台示意图如图12所示。实验平台MMC交流输出电压ua以及桥臂电流iap的仿真结果如图13所示。
表3 三电平MMC缩比样机相关参数
Tab.3 parameters of three-level MMC scaled prototype
实验平台指标参数(型号) 额定功率/kW12 直流母线电压/V±450 开关频率/kHz1.5 桥臂电感/mH4 直流支撑电容/mF1.6 单桥臂组件数2 放电电阻/kW12 IGBT模块1.2 kV/25 A (IGW25N120H3)
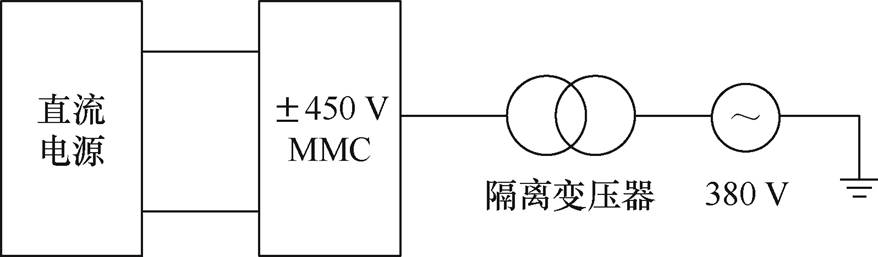
图12 实验平台示意图
Fig.12 The schematic diagram of experimental platform
针对所提计及退化过程相关性、可靠性评估方法的验证工作，主要步骤有：
（1）选择实验平台测量实验平台中IGBT模块的导通压降VCE(sat)，以确定IGBT模块的老化状态，并设置IGBT模块的失效阈值，通常认为VCE(sat)增加超过一倍时IGBT模块失效。
（2）测量组件直流支撑电容器的电压以及电流，用以计算电容器容值。
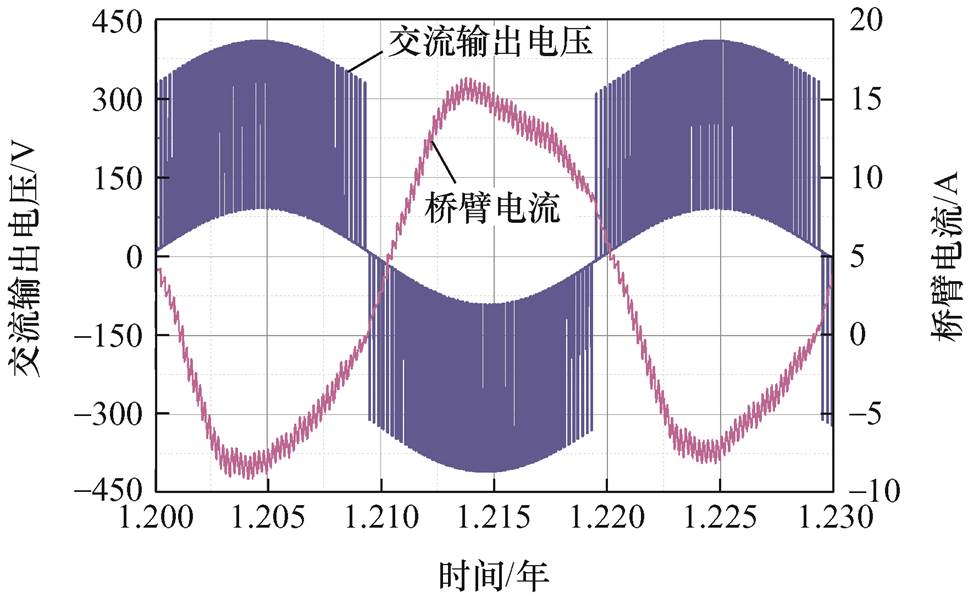
图13 MMC交流输出电压以及桥臂电流
Fig.13 AC output voltage and bridge-arm current of MMC
（3）对比实验A，按照表3所示平台参数进行长期运行实验，运行过程中实时根据测量得到电压与电流，计算电容器容值，在容值下降超过1%时，更换相应电容，使得在长期运行过程中，电容器容值保持在1.6 mF，即电容器不发生老化；记录IGBT模块导通压降到达设定阈值的时间TA。
（4）对比实验B，按照表3所示平台参数进行长期运行实验，记录运行过程中电容器容值的退化曲线，记录IGBT模块导通压降到达阈值时间TB。
（5）根据实验结果分别按照本文所提方法以及不考虑相关性评估方法进行建模，计算MMC的可靠度函数，获得平均无故障时间；与实验获得TA和TB时间对比，验证本文所提可靠性评估方法的有效性。
本文提出了一种计及IGBT模块与金属化薄膜电容器退化过程相关性的柔直换流阀可靠性评估方法，利用Copula理论对相关性进行了建模，具有以下结论：
1）电容器的容值随着长时间运行会发生衰退，造成所在组件IGBT的开关频率增加，同桥臂其余组件IGBT开关频率基本保持不变；采用二维Gumbel型Copula函数对相关性进行了建模。
2）IGBT模块可靠性评估考虑了柔直换流阀典型任务剖面的影响，寿命分布采用威布尔分布模型；根据容值退化监测数据，建立了基于Wiener过程的金属化薄膜电容器可靠性评估模型。
3）所提方法与现有不考虑相关性的可靠性评估方法，评估结果更加准确，柔直换流阀平均无故障时间由4.05年修正为5.20年。
参考文献
[1] 汤广福, 贺之渊, 庞辉. 柔性直流输电工程技术研究、应用及发展[J]. 电力系统自动化, 2013, 37(15): 3-14. Tang Guangfu, He Zhiyuan, Pang Hui. Research, application and development of VSC-HVDC engin- eering technology[J]. Automation of Electric Power Systems, 2013, 37(15): 3-14.
[2] 束洪春, 代月, 安娜, 等. 基于线性回归的柔性直流电网纵联保护方法[J]. 电工技术学报, 2022, 37(13): 3213-3226, 3288. Shu Hongchun, Dai Yue, An Na, et al. Pilot protection method of flexible DC grid based on linear regression[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3213-3226, 3288.
[3] 孟沛彧, 向往, 潘尔生, 等. 分址建设直流输电系统拓扑方案与运行特性研究[J]. 电工技术学报, 2022, 37(19): 4808-4822. Meng Peiyu, Xiang Wang, Pan Ersheng, et al. Research on topology and operation characteristics of HVDC transmission system based on site-division construction[J]. Transactions of China Electro- technical Society, 2022, 37(19): 4808-4822.
[4] 姜涛, 李雪, 李国庆, 等. 含多端柔性直流的交直流电力系统静态电压稳定域构建方法[J]. 电工技术学报, 2022, 37(7): 1746-1759. Jiang Tao, Li Xue, Li Guoqing, et al. A predictor- corrector algorithm for forming voltage stability region of hybrid AC/DC power grid with inclusion of VSC-MTDC[J]. Transactions of China Electro- technical Society, 2022, 37(7): 1746-1759.
[5] 陈剑, 杜文娟, 王海风. 基于对抗式迁移学习的含柔性高压直流输电的风电系统次同步振荡源定位[J]. 电工技术学报, 2021, 36(22): 4703-4715. Chen Jian, Du Wenjuan, Wang Haifeng. Location method of subsynchronous oscillation source in wind power system with VSC-HVDC based on adversarial transfer learning[J]. Transactions of China Electro- technical Society, 2021, 36(22): 4703-4715.
[6] 冯帅松, 韩永霞, 张杰, 等. 不同拓扑柔性直流配电系统过电流理论计算方法适用范围[J]. 电力系统自动化, 2023, 47(5): 162-170. Feng Shuaisong, Han Yongxia, Zhang Jie, et al. Application scope of theoretical overcurrent calcu- lation methods for flexible DC distribution systems with different topologies[J]. Automation of Electric Power Systems, 2023, 47(5): 162-170.
[7] Wang Biyang, Wang Xifan, Bie Zhaohong, et al. Reliability model of MMC considering periodic preventive maintenance[J]. IEEE Transactions on Power Delivery, 2017, 32(3): 1535-1544.
[8] 王秀丽, 郭静丽, 庞辉, 等. 模块化多电平换流器的结构可靠性分析[J]. 中国电机工程学报, 2016, 36(7): 1908-1914. Wang Xiuli, Guo Jingli, Pang Hui, et al. Structural reliability analysis of modular multi-level con- verters[J]. Proceedings of the CSEE, 2016, 36(7): 1908-1914.
[9] Zhang Liang, Zhang Dan, Hua Ting, et al. Reliability evaluation of modular multilevel converter based on Markov model[J]. Journal of Modern Power Systems and Clean Energy, 2019, 7(5): 1355-1363.
[10] 刘文霞, 徐雅惠, 李乔乔, 等. 考虑载荷状态不确定性的柔性多状态开关可靠性模型[J]. 中国电机工程学报, 2019, 39(6): 1592-1602, 1856. Liu Wenxia, Xu Yahui, Li Qiaoqiao, et al. Reliability model of flexible multi-state switch considering the uncertainty of loading state[J]. Proceedings of the CSEE, 2019, 39(6): 1592-1602, 1856.
[11] 王希平, 李志刚, 姚芳. 考虑任务剖面的模块化多电平换流器可靠性评估方法研究[J]. 中国电机工程学报, 2021, 41(7): 2495-2507. Wang Xiping, Li Zhigang, Yao Fang. The reliability assessment method for MMCs considering mission profile[J]. Proceedings of the CSEE, 2021, 41(7): 2495-2507.
[12] 张军, 张犁, 成瑜. IGBT模块寿命评估研究综述[J]. 电工技术学报, 2021, 36(12): 2560-2575. Zhang Jun, Zhang Li, Cheng Yu. Review of the lifetime evaluation for the IGBT module[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(12): 2560-2575.
[13] Zhang Yi, Wang Huai, Wang Zhongxu, et al. Mission profile-based system-level reliability prediction method for modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2020, 35(7): 6916-6930.
[14] Yu Pengfei, Fu Wei, Wang Longjun, et al. Reliability- centered maintenance for modular multilevel con- verter in HVDC transmission application[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(3): 3166-3176.
[15] Qi Lei, Du Luchun, Zhang Xiangyu, et al. Online correction method of IGBT lifetime evaluation based on bonding wire failure monitoring[J]. IET Power Electronics, 2023, 16(3): 347-356.
[16] Picas R, Pou J, Zaragoza J, et al. Submodule power losses balancing algorithms for the modular multi- level converter[C]//IECON 2016-42nd Annual Con- ference of the IEEE Industrial Electronics Society, Florence, Italy, 2016: 5064-5069.
[17] 罗永捷, 宋勇辉, 熊小伏, 等. 高压大容量MMC换流阀损耗精确计算[J]. 中国电机工程学报, 2020, 40(23): 7730-7742. Luo Yongjie, Song Yonghui, Xiong Xiaofu, et al. Accurate loss calculation method for bulk-power MMCs[J]. Proceedings of the CSEE, 2020, 40(23): 7730-7742.
[18] Manson S. Thermal stress and low cycle fatigue[R]. New York, USA: McGraw-Hill, 1966.
[19] Bayerer R, Herrmann T, Licht T, et al. Model for power cycling lifetime of IGBT modules-various factors influencing lifetime[C]//5th International Conference on Integrated Power Electronics Systems, Nuremberg, Germany, 2008: 1-6.
[20] Norris K C, Landzberg A H. Reliability of controlled collapse interconnections[J]. IBM Journal of Research and Development, 1969, 13(3): 266-271.
[21] Zhao Jianyin, Liu Fang. Reliability assessment of the metallized film capacitors from degradation data[J]. Microelectronics Reliability, 2007, 47(2/3): 434-436.
[22] Ennis J B, MacDougall F W, Cooper R A, et al. Self-healing pulse capacitors for the National Ignition Facility (NIF)[C]//Digest of Technical Papers. 12th IEEE International Pulsed Power Conference. (Cat. No.99CH36358), Monterey, CA, USA, 2002: 118- 121.
[23] Hu Yifan, Ye Xuerong, Zheng Bokai, et al. Degradation mechanisms-based reliability modeling for metallized film capacitors under temperature and voltage stresses[J]. Microelectronics Reliability, 2022, 138: 114609.
[24] Bouye, E, Durrleman V, Nikeghbali A, et al. Copulas for finance: a reading guide and some appli- cations[EB/OL]. Paris:Credit Lyonnais Groupe de Recherche Operationnelle, 2000.https://mpra.ub. unimuenchen.de/37359/1/MPRA_paper_37359.pdf.
[25] Kaminski N. Application note 5SYA 2043-04 load- cycling capability of HiPak IGBT modules[EB/OL]. Lenzburg: ABB Switzerland Ltd, 2004. http://www. 5scomponents.com/pdf/5SYA-2043-01-Sept--04--Load- cycle-capability-of-HiPaks-.pdf.
[26] Kim C, Lee S. Redundancy determination of HVDC MMC modules[J]. Electronics, 2015, 4(3): 526-537.
[27] 刘泽洪, 郭贤珊. 高压大容量柔性直流换流阀可靠性提升关键技术研究与工程应用[J]. 电网技术, 2020, 44(9): 3604-3613. Liu Zehong, Guo Xianshan. High-voltage large- capacity VSC valve reliability enhancement[J]. Power System Technology, 2020, 44(9): 3604-3613.
[28] TNEI Services Ltd. Offshore electrical equipment reliability figures[R]. Manchester, UK: TNEI Services Ltd, 2012.
[29] Grinberg R, Riedel G, Korn A, et al. On reliability of medium voltage multilevel converters[C]//2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 2013: 4047-4052.
[30] 姜海波, 翟宾, 贺新征, 等. 高压直流输电换流阀冷却系统可靠性评估[J]. 电力安全技术, 2014, 16(5): 60-63.Jiang Haibo, Zhai Bin, He Xinzheng, et al. Reliability evaluation of cooling system for HVDC converter valve[J]. Electric Safety Technology, 2014, 16(5): 60-63.
Abstract Flexible DC transmission technology can rapidly and flexibly control active and reactive power in large-scale new energy power transmission, providing voltage support to weak AC or passive systems. With the increasing demand for system capacity and the expansion of engineering application scenarios, it is of great engineering significance to accurately and real-time evaluate the operational reliability of flexible and direct converter valves as core equipment. However, most existing reliability assessment methods focus on modeling the reliability of key components such as IGBT modules and metalized thin film capacitors, neglecting the coupling relationship between component degradation processes. Previous studies have shown that capacitor capacity degradation causes an increase in IGBT module switching frequency, affecting the reliability of IGBT modules. Therefore, this paper proposes a reliability evaluation method for flexible direct converter valves, considering the correlation between the degradation process of capacitors and IGBT modules. Copula theory is used to model the coupling relationship between capacity degradation and IGBT module life, improving the accuracy of reliability evaluation results for flexible direct converter valves.
The reliability evaluation of IGBT modules considers the influence of typical mission profiles of flexible and direct converter valves, and the life distribution adopts the Weibull distribution model. The IGBT module losses include static and dynamic losses. Static losses include IGBT on-state losses, IGBT off-state losses, diode on-state losses, and diode off-state losses. Athermal network model is established using the principle of electrical analogy, which includes heat sinks, ambient temperature, and device packaging structure. The junction temperature of the IGBT is calculated. The variable amplitude load is converted into a complete cycle of a series of transverse thermal loads using statistical notation. According to the linear damage principle, the cumulative life loss of IGBT is calculated. Device manufacturers, such as ABB and Infineon, indicate that the reliability of IGBT follows a Weibull distribution through accelerated aging experiments. Finally, the reliability function of IGBT modules can be obtained. Based on the monitoring data of capacity degradation, a reliability evaluation model for metalized thin film capacitors is established based on the wiener process. The Wiener process is a stochastic process with a linear drift term, where the capacitance tends to decrease due to the accumulation of many minor self-healing points. The maximum likelihood estimation value is obtained by estimating wiener distribution parameters through accumulated monitoring data of capacitor capacity degradation.
The capacitance of the capacitor declines over a long period of operation, increasing the switching frequency of the component IGBT where it is located, while other components' switching frequency on the same bridge arm IGBT almost remains unchanged. The correlation is modeled using a two-dimensional Gumbel-type Copula function. The proposed method is more accurate than existing reliability evaluation methods. The average time between failures of flexible and direct converter valves has been revised from 4.05 to 5.20 years.
Keywords: Modular multilevel converter (MMC), reliability evaluation, metallized polypropylene film (MPPF) capacitor, IGBT module, Copula theory
DOI: 10.19595/j.cnki.1000-6753.tces.230847
中图分类号：TM464
国家电网有限公司科技资助项目（5500-202140126A-0-0-00）。
收稿日期 2023-06-05
改稿日期 2023-07-22
张午宇 男，1996年生，博士研究生，研究方向为柔性直流换流阀状态监测及评估方法。E-mail：120202101022@ncepu.edu.cn
齐 磊 男，1978年生，教授，博士生导师，研究方向为大功率电力电子装备研制。E-mail：qilei@ncepu.edu.cn（通信作者）
（编辑 郭丽军）