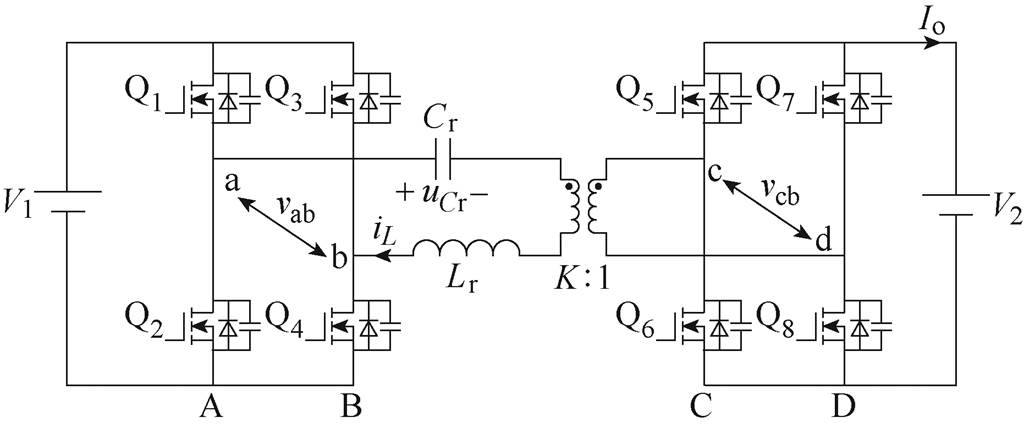
图1 双有源桥串联欠谐振变换器
Fig.1 Topology of the URDBSRC
摘要 该文采用时域分析法对双有源桥串联欠谐振电路进行了分析,得到电感电流在稳态时的表达式并推导所有开关管实现软开关的条件。由于电压增益偏离1时仅采用移相控制难以实现所有开关管的软开关,因此,该文在传统移相控制的基础上,引入额外的变频控制策略,使得电路在不同的电压增益和负载条件下都能有较好的软开关性能。然而,软开关的实现会增加电路的回流电流,影响电路的传输效率。该文对所提出的变频移相控制进行了进一步的优化,使其可以在确保电路实现软开关的同时产生最小的回流电流和电感电流有效值。所提出的控制策略在一台2 kW的样机中进行了验证。
关键词:双有源桥串联欠谐振变换器 软开关 最小回流电流控制 变频控制
随着电动汽车和储能技术的快速发展,功率的双向变换也逐渐成为了车载充电机和充电桩必备的功能之一[1-2]。凭借其较好的输出电压增益范围和较高的传输效率,双有源桥型变换器被广泛地应用在车用充电设备当中。许多文献也从移相控制[3-8]和变频控制[9]等角度对其控制策略进行了优化。为了进一步提升变换器的转换效率,文献[10]在谐振电感上串联了一个谐振电容,形成了双有源桥串联谐振电路。谐振电容的引入使得电感电流更趋近于正弦化,电路的关断损耗得到了明显的降低。但是,当电压增益偏离1时,双有源桥串联谐振电路很容易工作在硬开关区域,这对电路的传输效率产生了很大的影响。
为了解决这个问题,许多学者对双有源桥串联谐振电路进行了改进。文献[11]以一个较小的电容取代原先的输出电容,并与谐振电感构成谐振回路,有效地降低了无源元件的体积;同时,采用一个额外的Buck-Boost电路来调节电路的电压增益,使得前级电路始终工作在额定增益附近,确保了电路的软开关运行。文献[12]将两个额外的辅助电感加入到一次侧桥臂中点和二次侧桥臂中点,依靠这两个电感在开关时刻所提供的额外电流,实现所有开关管的零电压开通。文献[13]提出了一种带变压器中心抽头的双谐振腔方案,通过对变压器匝数比和谐振腔参数的合理设计,可以为变换器提供更宽的调压范围和更大的软开关区域。
除了增加额外的无源元件以外,很多文献也从控制角度对双有源桥串联谐振电路进行了优化。由于双有源桥型电路一次侧和二次侧的开关管都是主动控制的,通过移相控制,也就是改变不同桥臂之间的相位差,就可以直接对输出功率进行调节。因此,在相同的输出条件下,只要移相角设置得合理,就可以对电感电流的有效值进行优化[14-16]。在移相控制的基础上,文献[17-18]将变频控制同移相控制相结合,十分有效地拓宽了电路的软开关范围。进一步地,文献[19]将开关管死区也作为控制量的一种,在实现软开关的基础上降低了电路的回流电流,对电路整体效率的提升起到了很大的帮助。在文献[20]中,同一桥臂的开关管以非50%的占空比互补导通,这样做虽然进一步增加了控制的复杂度,但是也使得电路在更宽的电压增益下具备了软开关的能力。
虽然现有的文献已经对双有源桥串联谐振电路做出了很大的改善,但是都需要以额外的元件体积或复杂的控制策略为代价,确保电路在宽电压增益的条件下,实现宽负载范围的软开关运行。除此以外,双有源桥串联谐振电路一般都工作在过谐振状态,还没有文献对欠谐振型双有源桥电路进行分析和优化。为了在更窄的频率变化范围内用更为简单的控制策略实现所有开关管的零电压开通,本文对双有源桥欠谐振电路进行了分析并优化了其控制策略。首先,本文采用时域分析法,对双有源桥欠谐振电路的开关状态和输出特性进行了分析,并给出了其软开关的条件。在此基础上,本文将扩展移相控制和变频控制进行结合,增加了电路在不同增益和不同负载情况下的软开关范围。除此以外,本文还提出了一种最小回流电流控制,只需要调节一次侧和二次侧桥臂输出电压之间的外移相角和开关频率,就能在确保电路实现软开关的前提下,降低回流电流和电感电流有效值的大小。最后,本文搭建了一台2 kW的样机对所提出的控制策略进行了验证。
双有源桥串联欠谐振变换器如图1所示,双有源桥串联欠谐振电路的所有开关管均为主动控制,且所有桥臂的上下管均为50%互补导通。通过调节不同桥臂之间的相位差和开关频率,可以实现对输出功率的控制。同时,该电路所采用的变压器的励磁电感很大,因此,励磁电流对电路的影响忽略不计。f0为电路的串联谐振频率,其表达式如式(1)所示,对于双有源桥欠谐振电路(Under-Resonant- Dual-Bridge-Series-Resonant Converter, URDBSRC)而言,其开关频率fs始终低于f0。vab、vcd分别为V1和V2侧全桥所输出的交流电压。定义vab和vcd的基波分量之间的相位差为外移相角Dj。当功率由V1侧向V2侧流动时,vcd需要超前vab,即Dj>0。为简化分析,做如下定义:K为变压器匝数比,M=KV2/V1为电路的电压增益,r=f0/fs为电路的频率比,Z0为电路的特征阻抗,其表达式如式(2)所示。iL和uCr分别为电感电流和谐振电容两端的电压,iQm代表着Qm在开关时刻从源极到漏极的电流,Io和Po分别为电路的输出电流和输出功率。

图1 双有源桥串联欠谐振变换器
Fig.1 Topology of the URDBSRC
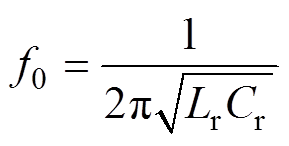 (1)
(1)
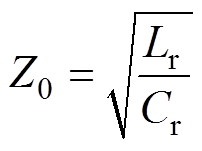 (2)
(2)
式中,Lr和Cr分别为电路的谐振电感和谐振电容。
在电路的任意一侧引入内移相都可以产生两种工作状态,这种控制策略被称之为扩展移相(Extended- Phase-Shift, EPS)控制。一般来说,当M<1时,需要在V1侧引入内移相以使得vab和Kvcd所对应的基波幅值相近;而当M>1时,则在V2侧引入内移相。考虑到这两种情况下电路的特性相似,因此本文只对V1侧引入内移相Dy1的情况进行分析。
在EPS控制下,电路会存在两种工作模式,其典型波形如图2所示。图2a中,2Dj≥1-Dy1,此时vcd的上升沿将出现在vab为-V1的阶段内。而图2b中,2Dj<1-Dy1,此时vcd的上升沿与vab的0电平存在交点。借助拉普拉斯反变换,可以得到电感电流和电容电压的时域表达式分别为
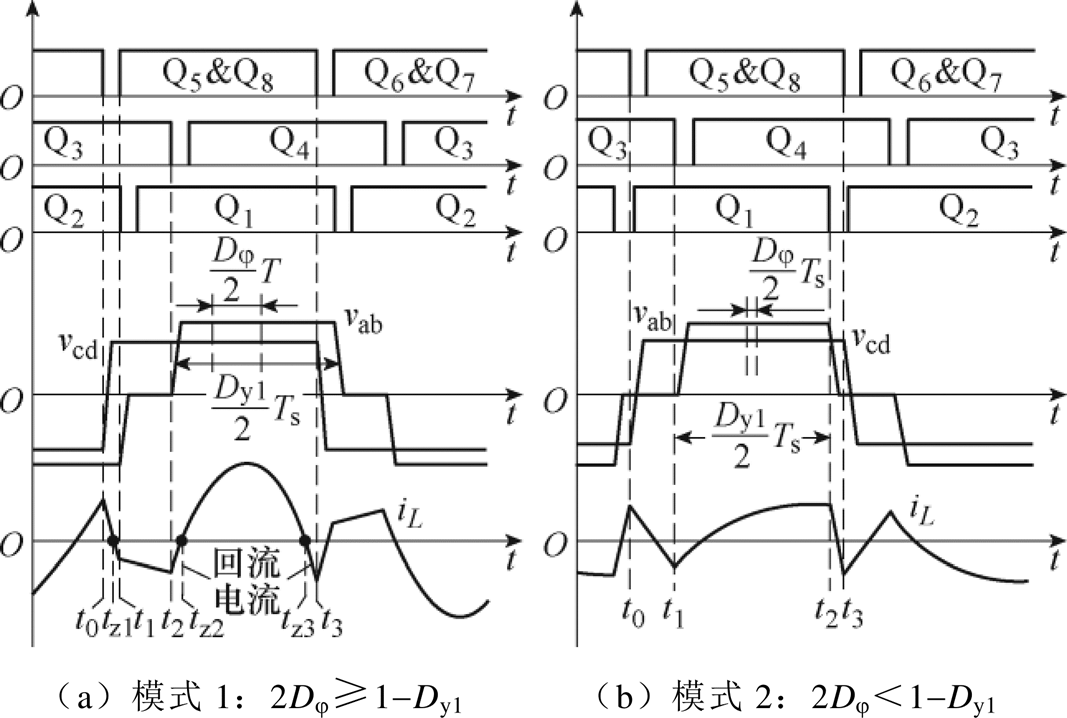
图2 在V1侧引入内移相时电路的典型波形
Fig.2 Typical waveforms of the converter when an inner-phase-shift angle is adopted on the V1 side
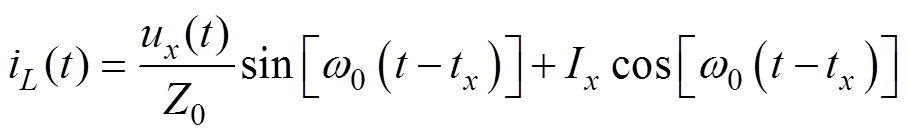 (3)
(3)
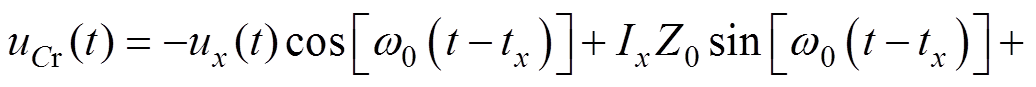
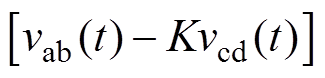 (4)
(4)
式中,w0=2pf0为电路的串联谐振角频率;tx为图2中开关管的动作时刻,x=1, 2, 3;ux=vab(t)-Kvcd(t)-UCrx;Ix和UCrx分别为tx时刻电感电流和电容电压的瞬时值。当电路进入稳态后,可以得到iL(t0)= -iL(t3),uCr(t0)=-uCr(t3),结合式(3)、式(4),可以得到不同开关时刻电感电流的简化表达式(iQm,S)见表1,m=1, 3, 5, 7。其中iQm,S定义为
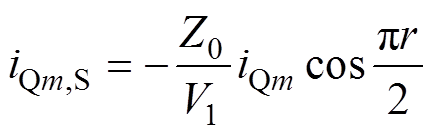 (5)
(5)
表1 不同开关管在开关时刻的源-漏极电流的简化表达式
Tab.1 Expressions of the simplified source-to-drain current for different switches at the switching instants

iQm,S模式1模式2 iQ1,S iQ3,S iQ5,7,S
对t0~t3段内的电感电流求平均,可以得到输出电流的表达式。为了方便分析,将输出电流进行标幺化处理,如式(6)所示。其中,输出电流的标准值Iom=4KV1/(pZ0)。
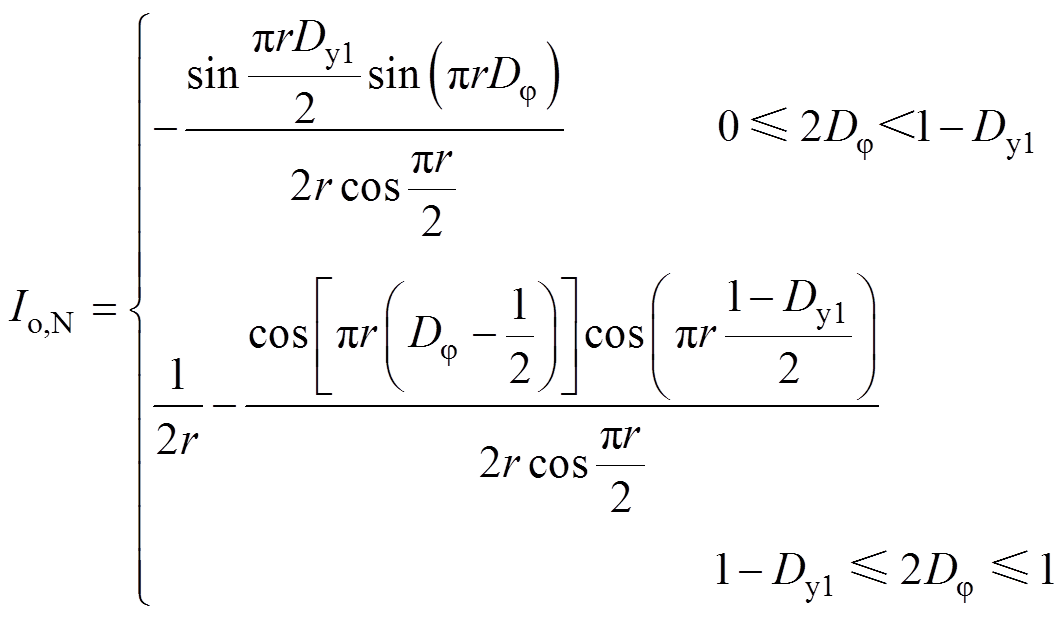 (6)
(6)
对于MOSFET而言,实现开关管的零电压开通将对电路开关损耗的降低起到至关重要的作用。以图1中的Q1管为例对其软开关条件进行分析。为了确保Q1管实现零电压开通,在它的驱动信号到来前,其漏源极两端的电压应降为0。这意味着在Q2管关断时,电感电流应从Q1管的源极流入,并在死区时间内对其结电容进行放电直至体二极管导通。因此,Q1管实现零电压开通的条件可以近似为
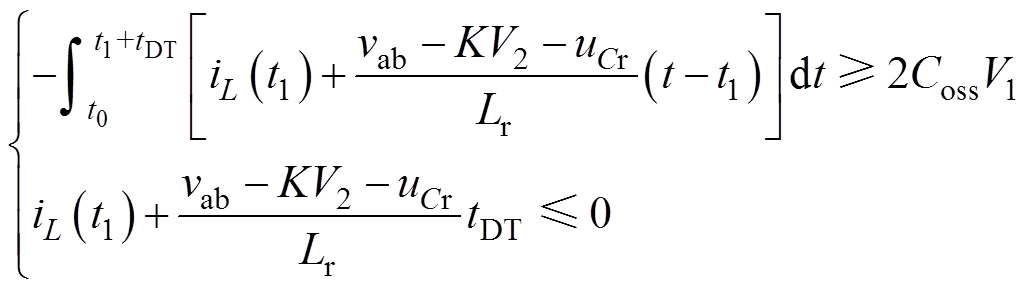 (7)
(7)
式中,tDT为死区时间;Coss为开关管的等效结电容。
在死区时间内,谐振电容两端电压几乎不变,因此式(7)中的uCr可以用t1时刻的瞬时值UCr(t1)代替。为了得到Q1管实现软开关的充分条件,本文以死区后vab的稳态电压0 V代替式(7)中的vab[18],此时电感电流由负向正变化的速率更快,其在死区内所提供的电荷也更少。在上述基础上,式(7)中电感电流变化的斜率[0-KV2-UCr(t1)]/Lr为一个固定数。同时,在本文所讨论的控制策略下,电路所采用的死区时间并不会随着电压增益和负载的情况进行变化。在极端情况下,电感电流会在死区结束后变为0 A。因此,Q2管关断时刻电感电流的瞬时值iL(t1),即此时从Q1管源极流入漏极流出的电流(iQ1)将直接决定了Q1是否能实现软开关。
上述对Q1管软开关条件的分析也可以应用于别的开关管,若将IZVS设定为对开关管的结电容进行完全地放电所需要的最小电流,则电路实现软开关的条件可以总结为
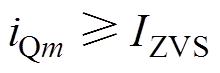 (8)
(8)
根据式(8),可以得到在使用EPS控制时,电路在不同电压增益情况下的软开关实现情况,如图3所示。图3中,频率比r被设定为1.8。当电压增益为1时,电路在大部分负载情况下均可以实现零电压开通。但是当增益偏离1时,如图3b所示,电路软开关的实现会受到很大的影响,尤其是在负载较重时,工作模式1所处区域几乎无法保证电路的软开关运行。因此,仅使用EPS控制很难在不同增益和不同负载情况下实现所有开关管的软开关。
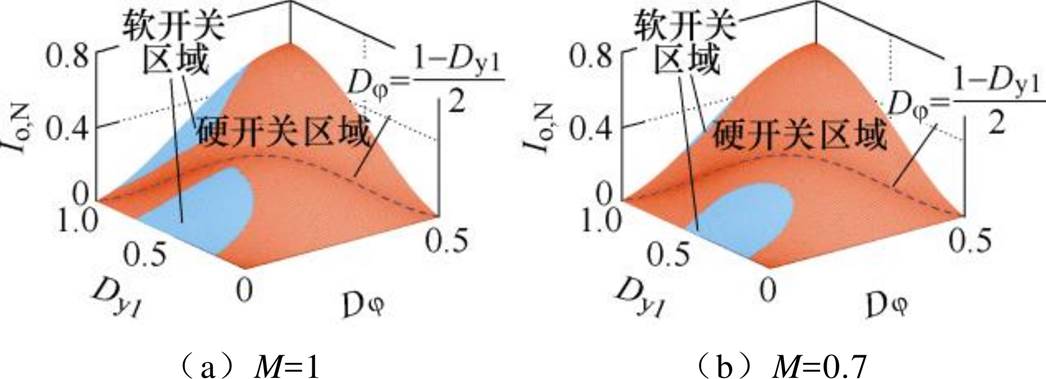
图3 采用EPS控制时电路的软开关范围
Fig.3 ZVS range of the converter when EPScontrol is adopted
若引入额外的变频(Variable-Frequency, VF)控制,将频率比r调整为2,如图4所示。在不同的增益情况下,电路的软开关范围都将获得明显的提升。虽然提升频率比将使得电路的最大输出电流有所降低,但只要合理地配置谐振腔参数,便可以保证电路在不同输出条件下的软开关运行。
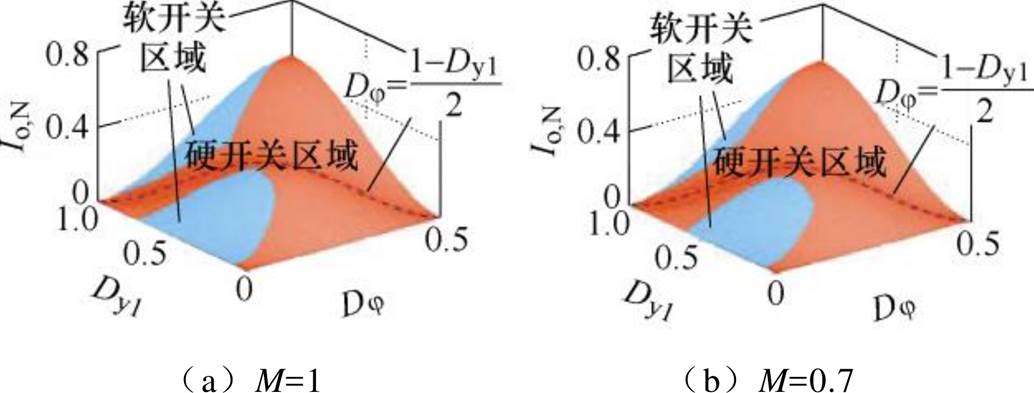
图4 引入变频移相控制且将频率比r设定为2时,电路的软开关范围
Fig.4 ZVS range of the converter when r is set to 2 by applying the VFEPS control
虽然引入额外的变频控制可以使得电路实现全负载范围下的软开关运行,但在模式1和模式2的交界处,一次侧桥臂中点的上升沿将和二次侧桥臂中点的上升沿重叠,没有任何一种控制量的组合可以使得一次侧和二次侧的开关管都实现零电压开通。若需要电路在重载时工作在模式1而轻载时工作在模式2,则需要移相角的突变来进行模式1和模式2的切换。这种控制量的突变会对器件的电流和电压应力产生不利的影响。结合图3,由图4可知,只要r的选择合适,仅让电路工作在模式1即可确保电路在宽负载范围下实现软开关工作。而且由于不存在工作模式的切换,控制变量的变化是连续的。因此,本文将以2Dj>1-Dy1为前提,对变频移相控制下电路的软开关条件进行简化。
结合表1和式(8),可以将不同开关管的软开关条件转化为对Dj 的约束条件,如式(9)~式(11)所示。
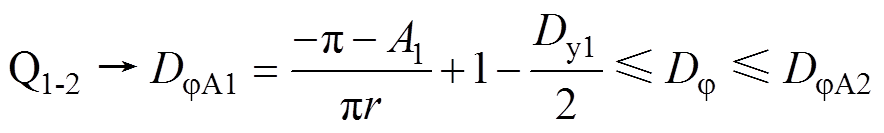
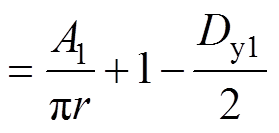 (9)
(9)
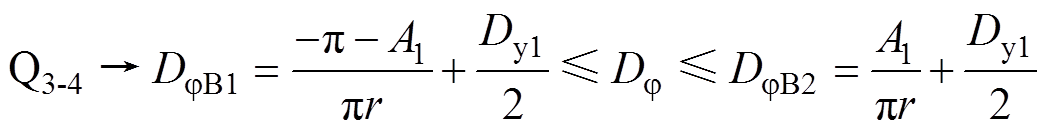 (10)
(10)
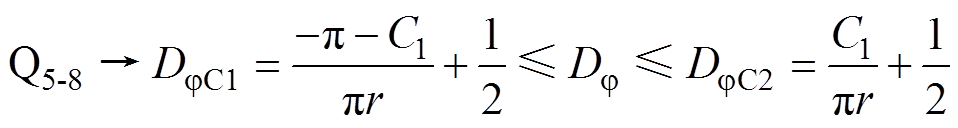 (11)
(11)
其中,A1和C1分别为
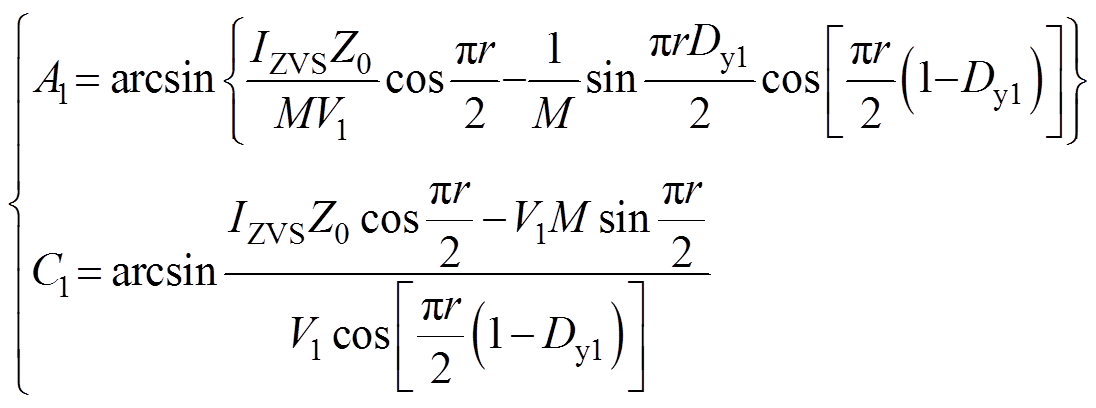 (12)
(12)
由于Dy1≤1,很容易可以判断得到DjB1≤DjA1≤DjB2≤DjA2。因此,对于V1侧的开关管而言,其软开关的条件可以简化为DjA1≤Dj≤DjB2。
观察式(9)~式(11)可以发现,V1侧和V2侧开关管实现软开关时Dj 所能取到的上、下限满足DjC2-DjB2=DjA1-DjC1。这意味着只要确定了DjA1和DjC1的大小关系,就能对电路的软开关条件进行进一步的简化。为此,图5给出了不同增益下,以DjA1≤Dj≤DjB2为前提,Dy1和r对DjA1与DjC1之间差值的影响。图5的结果表明,对于任意M≤1的情况,若在V1侧引入内移相控制,则DjA1始终大于DjC1。即只要确保V1侧开关管的软开关工作,那么V2侧的开关管也能相应地实现软开关。综上所述,可以将M≤1时整个电路的软开关条件由式(9)~式(11)简化为
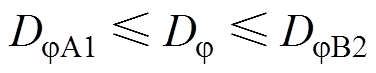 (13)
(13)
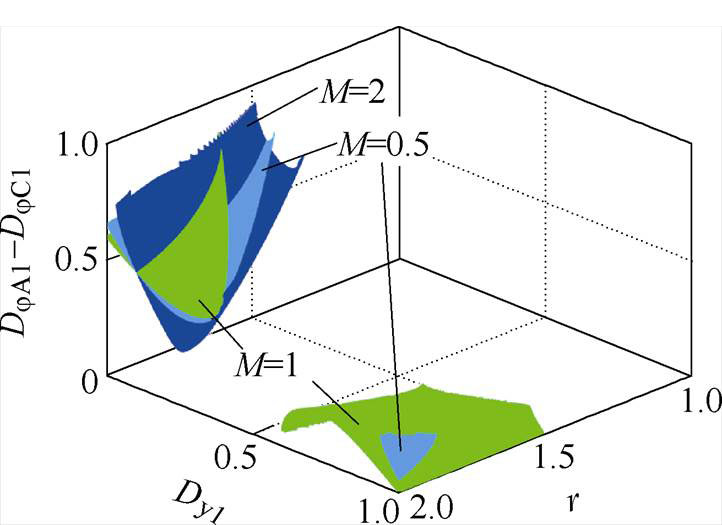
图5 不同增益下,Dy1和r对DjA1与DjC1之间差值的影响
Fig.5 Differences between DjA1 and DjC1 with respect to Dy1 and r under different voltage gains
在电路实现软开关的基础上,为了进一步提升电路的传输效率,本节对电路的回流电流进行优化。
根据图2a可知,在Q5和Q8导通后的半个周期内,Q2、Q3和Q5(Q8)将相继关断,为保证Q1、Q4和Q6(Q7)实现零电压开通,电感电流在这几个开关动作时刻均需为负。因此,在tz1~tz2和tz3~t3阶段,电感电流的极性同vcd的极性相反,此时电流由负载侧流回电路,形成回流电流。根据式(3)和式(4),可以推得tz1和tz2的表达式如式(14)所示,其中,uCr0和uCr2在式(15)中给出。而在tz2~tz3阶段内,vab和vcd均没有发生变化,此时电感电流为标准的正弦波,因此tz3=tz2+p/w0。
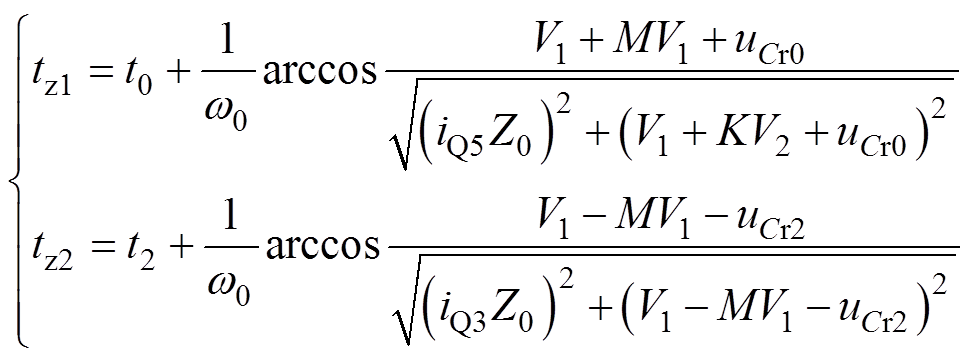 (14)
(14)
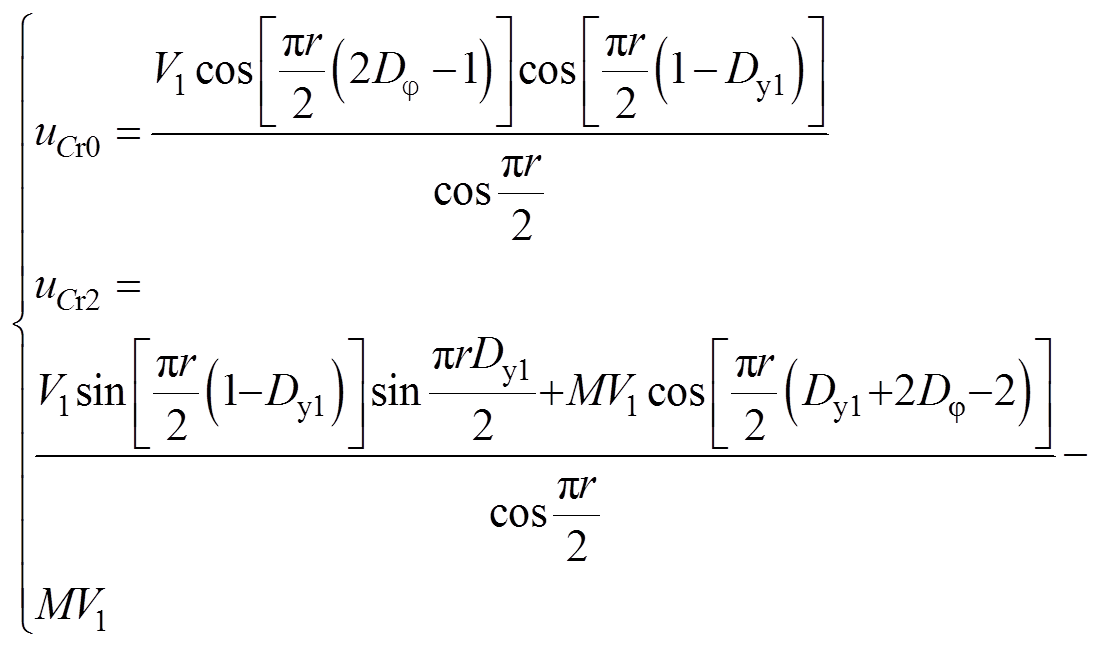 (15)
(15)
对tz1~tz2和tz3~t3阶段内的电感电流进行积分,并求其在半个开关周期内的平均值,可以得到电路回流电流IR的表达式为
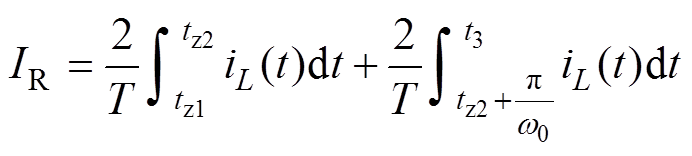 (16)
(16)
结合第2节的分析结果,可以将软开关条件下回流电流的优化问题,写成式(17)所示的标准形式。对于式(17)所示的带有不等式约束的凸优化问题,本文采用KKT(Karush-Kuhn-Tucker)[19-21]条件对其求解析解。
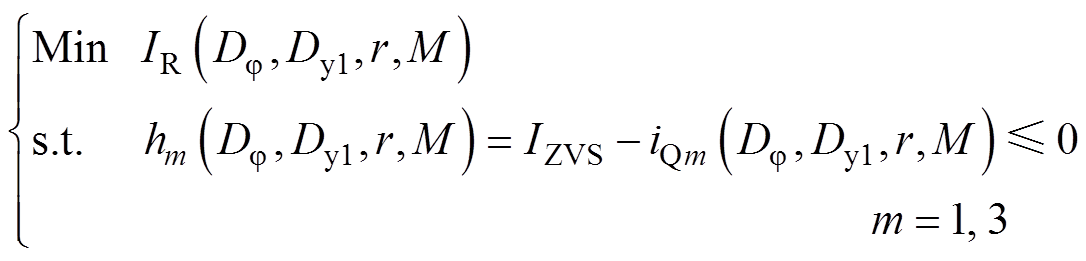 (17)
(17)
首先,针对式(17)的优化目标和约束条件构造拉格朗日算子为
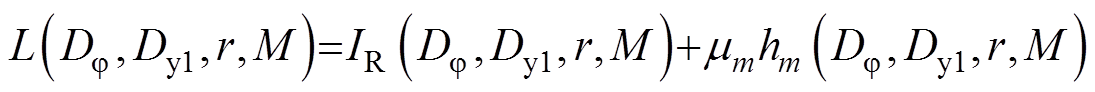
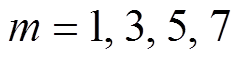 (18)
(18)
式中,mm为不等式约束的辅助乘子。
然后,在KKT条件下,式(17)存在解的充分条件如式(19)所示。在式(19)中,mm和hm不同时为0,因此,式(19)可以以式(20)所示的四种情况进行分类讨论,且最终满足KKT条件的结果只有一种,即iQ1=iQ3=IZVS。分类讨论的具体细节在附录中展示。
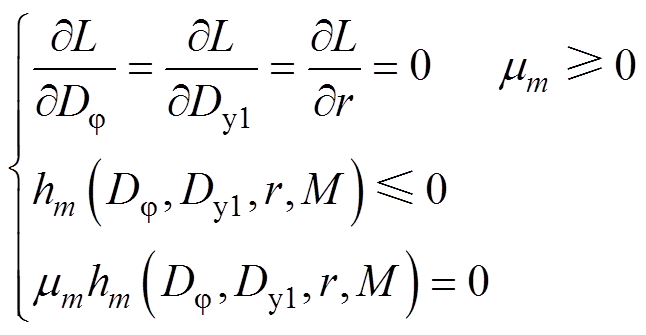 (19)
(19)
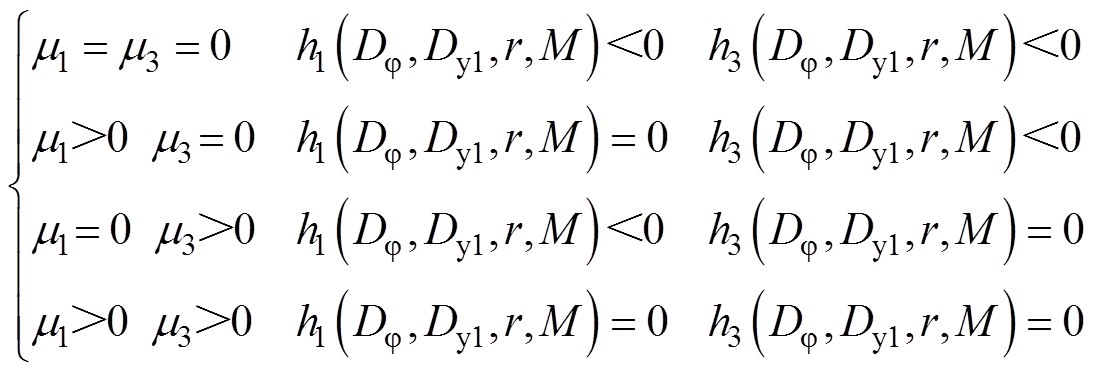 (20)
(20)
图6为不同输出情况下,iQ1和iQ3对IR的影响情况。尽管电压增益和输出电流都会对电路回流电流的大小产生影响,但是对任意的输出情况而言,回流电流的最小值始终出现在当Q1管和Q3管刚好能满足软开关要求的时刻。这也验证KKT条件所得到结果的正确性。
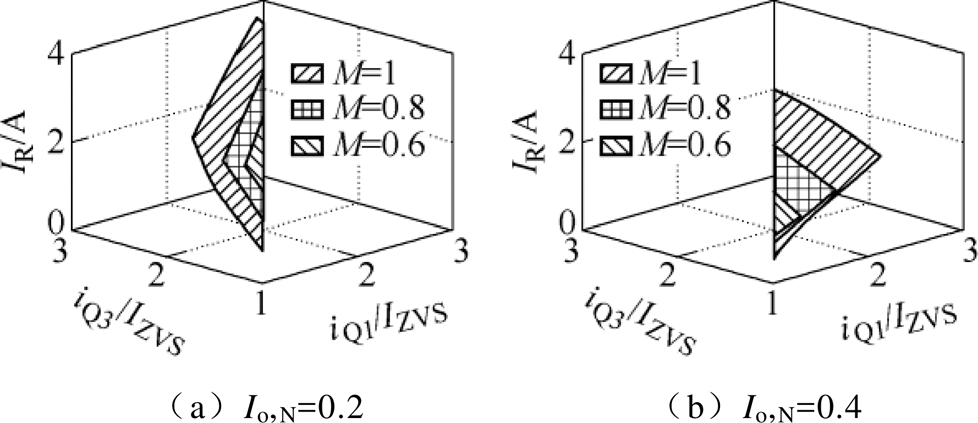
图6 不同输出情况下,iQ1和iQ3对IR的影响
Fig.6 Influence of iQ1 and iQ3 on IR under different output conditions
为了让上述分析结果更加直观地应用在实际的控制中,结合表1对iQ1=iQ3=IZVS进行求解,得到了两组关于Dj 和Dy1的解。将这两组解分别定义为S1和S2,其表达式为
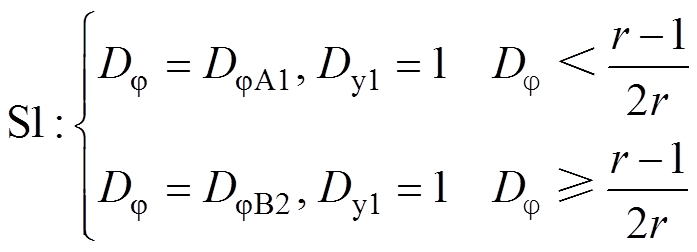 (21)
(21)
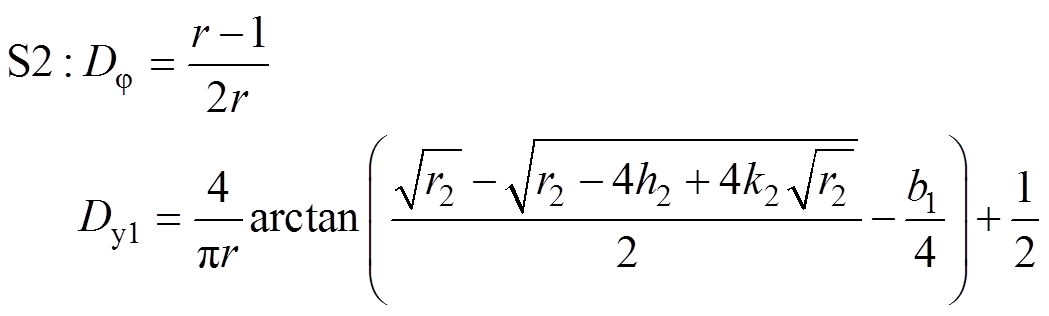 (22)
(22)
式中,r2、h2、k2、b1的表达式见附录。在S1中,Dy1的值始终为1,Dj 的值随r的变化而变化,电路的控制方式简化为单移相变频控制。而在S2中,Dy1是关于r的函数,在这种情况下,式(9)和式(10)中的DjA2和DjB1均为(r-1)/(2r),因此根据式(13)可知,此时Dj 的取值也是唯一的。
图7从电路的输出范围和回流电流角度对两种解进行了比较。相比较于S1而言,S2在不同电压增益下的输出电流范围有限,无法满足不同的负载需求。且在相同的输出条件下,S1所带来的回流电流均小于应用S2时所产生的回流电流。因此,根据S1对Dj 和Dy1进行设定,才能确保电路在实现软开关的同时,获得最小的回流电流。
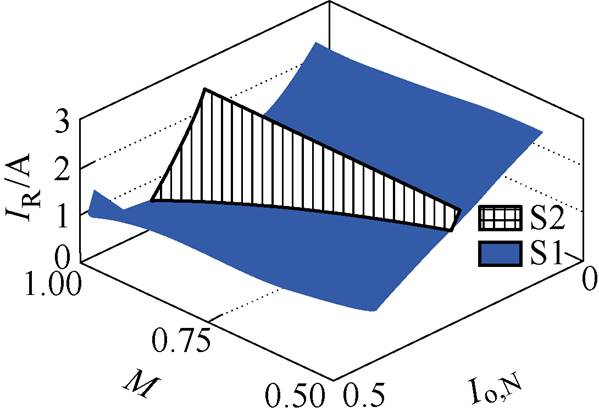
图7 S1和S2对电路回流电流影响的对比
Fig.7 Comparison between S1 and S2 of their impacts on the backflow current
在最小回流电流控制下,电路的控制流程如图8所示。在不同的负载情况下,电路存在两种工作情况(Case1和Case2)。当负载较轻时(即Case1时),电路的频率比r由PI控制器决定,根据PI输出的结果和此时的电压增益,可以得到DjA1的值,将其与(r-1)/(2r)进行比较,若DjA1<(r-1)/(2r),则将DjA1最终赋值给Dj 并生成相应的PWM信号。若DjA1≥(r-1)/(2r),则电路将转变工作状态,工作在Case2的情况下,此时需要将DjB2赋值给Dj 来对电路进行控制。而在Case2时,需要对DjB2的值进行判断以此来决定电路的工作状态,由于Case2时对DjB2的判断方式与Case1时对DjA1的判断方式类似,在此不再赘述。
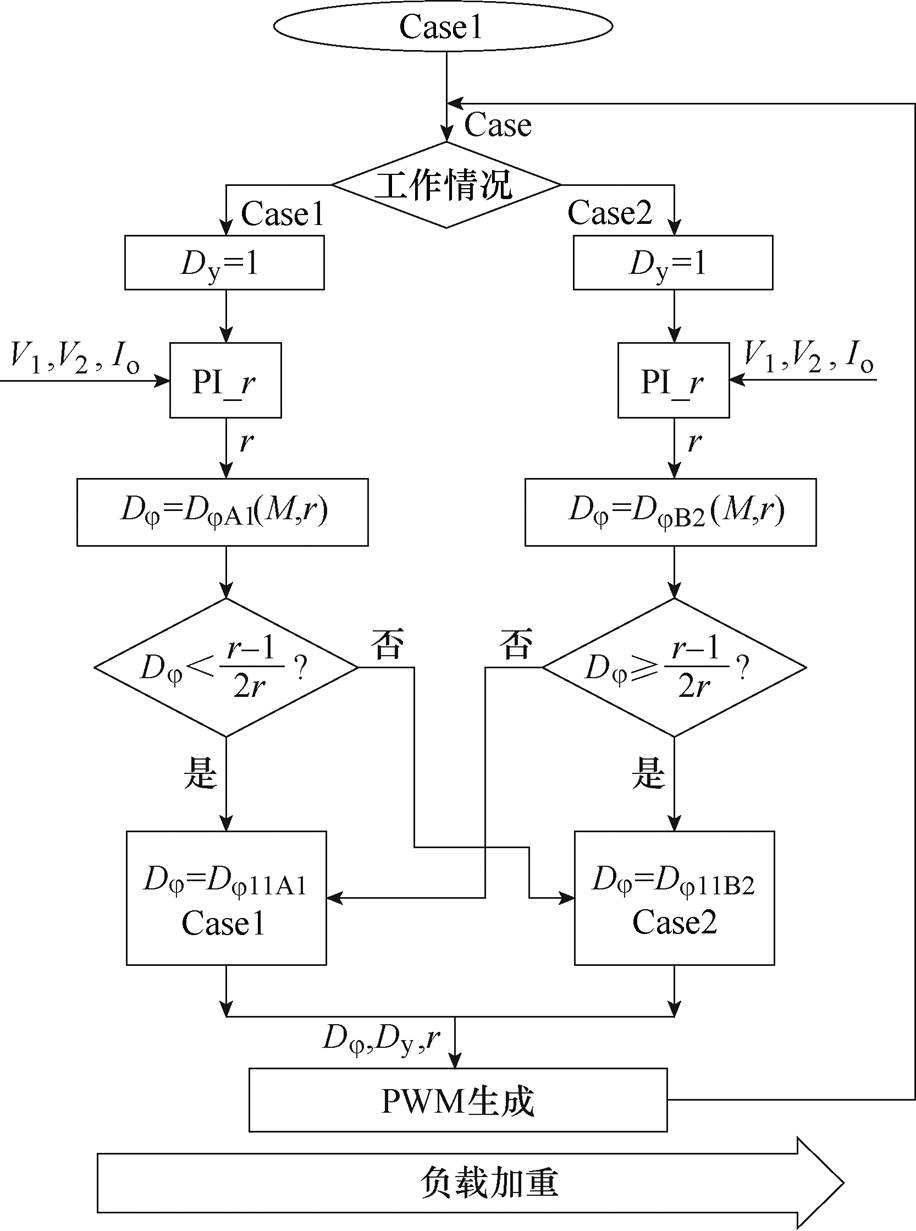
图8 最小回流控制下,电路的控制流程
Fig.8 The flow chart of the proposed minimum backflow current control
需要注意的是,式(21)的两种情况下,输出电流关于频率比r的单调性是不同的。当Dj=DjA1时,输出电流会随着r的降低而升高;而当Dj=DjB2时,输出电流会随着r的降低而降低。因此,在数字控制时,需要采用两套不同的PI控制器分别对电路进行控制。另外,根据式(9)和式(10)可以推得,当DjA1=(r-1)/(2r)时,DjB2=(r-1)/(2r),也就是说,Case=1时的输出功率与Case=2时的输出功率是连续变化的,因此并不需要引入额外的滞回控制。
对于式(21)所示的最小回流控制,不同输出功率Po和不同电压增益M情况下所需要的频率比r如图9所示。由图9可知,电压增益越偏离1或者负载的下降都会使得频率比升高以确保电路可以满足软开关的要求。因此,在设计电路的开关频率变化范围时,其最低值将会出现在电压增益偏离1最远且输出功率最小时,而其最大工作频率则会出现在电压增益为1且输出功率最大的情况。
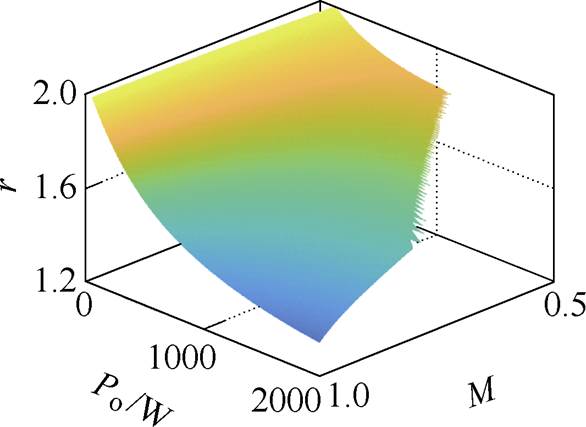
图9 最小回流控制下,不同输出功率和不同电压增益情况下所需要的频率比
Fig.9 Required r with respect to different values of Po and M under the minimum backflow current control
除了优化回流电流以外,最小回流电流控制也对电感电流的有效值(Root-Mean-Square, RMS)产生了一定的影响。由于电路只有3个控制量,因此可以在Matlab中以Dj、Dy1和r建立坐标轴,通过“isosurface”函数得到不同输出情况下的等势面,进而得到所有满足软开关条件的控制量的组合中,使电感电流有效值最低的一组数值解。针对不同的谐振腔参数,图10给出了最小回流电流控制下电感电流的有效值同Matlab所计算得到的最优解之间的比较。比较结果表明,采用最小回流电流控制也可以帮助电路获得最小的电感电流有效值,从而降低电路的导通损耗。
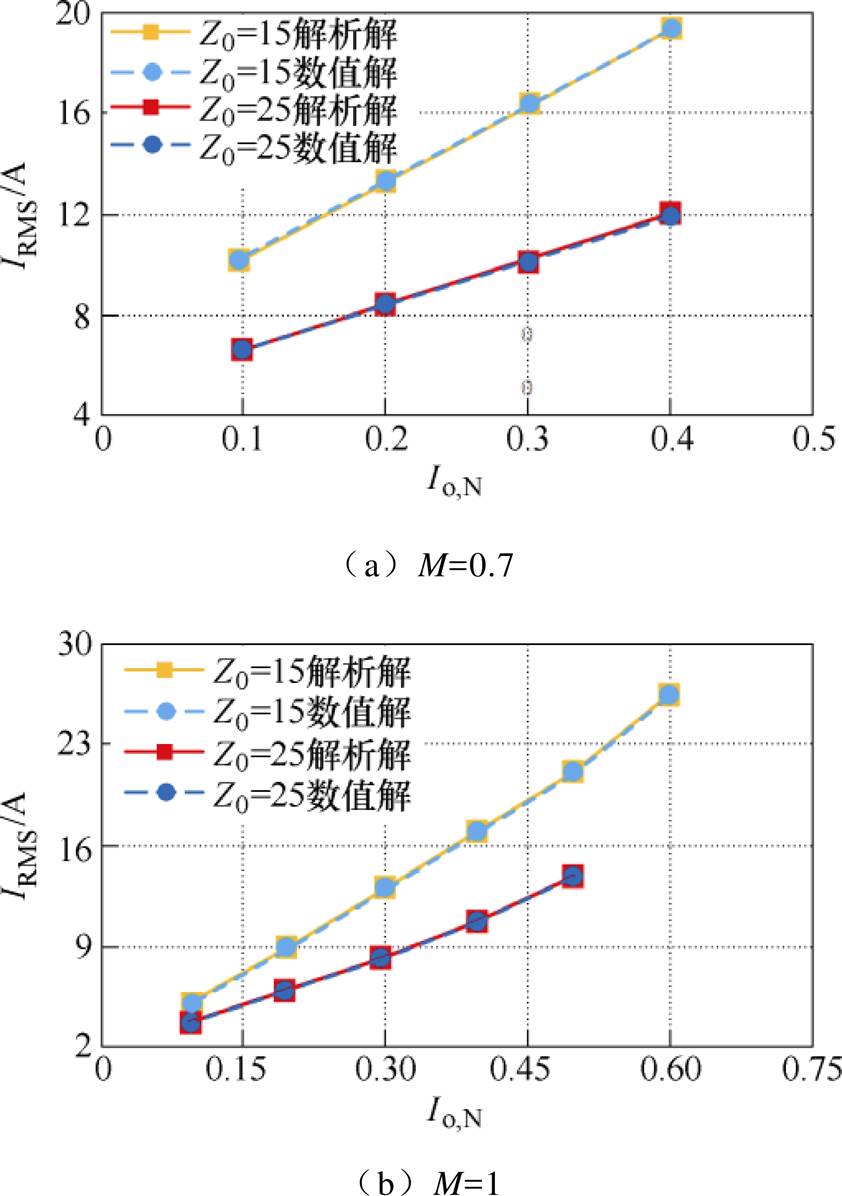
图10 最小回流电流控制对电感电流有效值的影响
Fig.10 Influence on RMS current when applying the minimum backflow current control
本文以一台2 kW双有源桥串联欠谐振变换器为例,对所提出的控制方法进行验证,样机如图11所示。样机参数见表2。

图11 实验样机
Fig.11 Experimental prototype
表2 2 kW双有源桥串联欠谐振变换器参数
Tab.2 The parameters of 2 kW under-resonant-dual- bridge-series-resonant converter
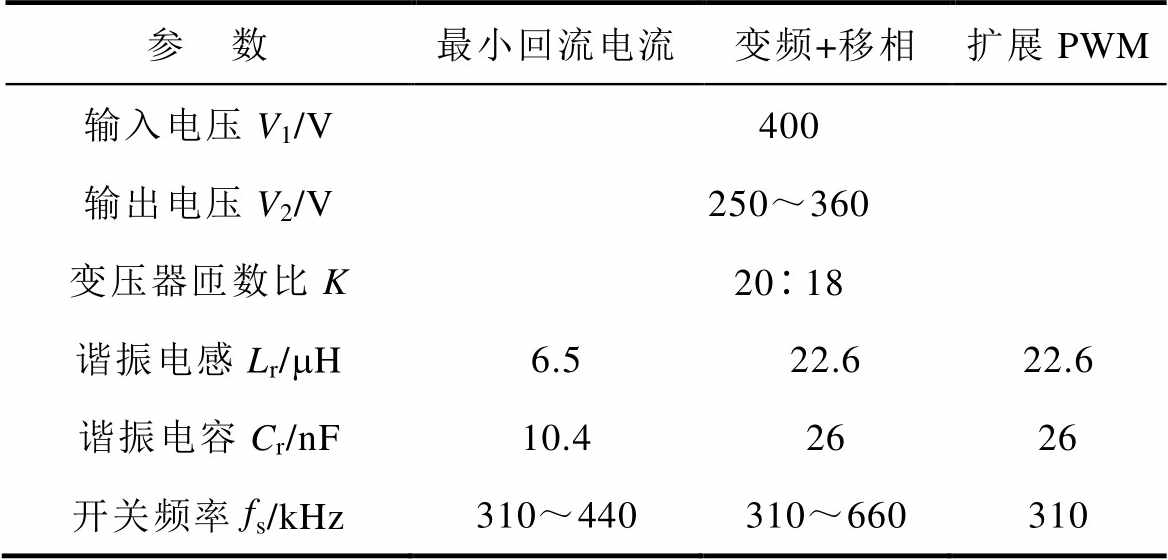
参 数最小回流电流变频+移相扩展PWM 输入电压V1/V400 输出电压V2/V250~360 变压器匝数比K2018 谐振电感Lr/mH6.522.622.6 谐振电容Cr/nF10.42626 开关频率fs/kHz310~440310~660310
当输出电压为360 V时,图12~图14分别给出了不同负载情况下电路的实验波形。当输出功率为2 kW时,V2=360 V,Io=5.56 A时的波形如图12所示,由于电压增益为1,电感电流将呈良好的对称性,一次侧和二次侧的开关管都能实现完全的零电压开通。在这种工况下,电路的回流电流为0.678 A,占总输出电流的12%,电路的整体传输效率为97.75%。当负载降低到1 kW和250 W时,实验波形分别如图13和图14所示。在变频和移相控制的共同作用下,电路在不同负载情况下都能有较好的软开关特性。
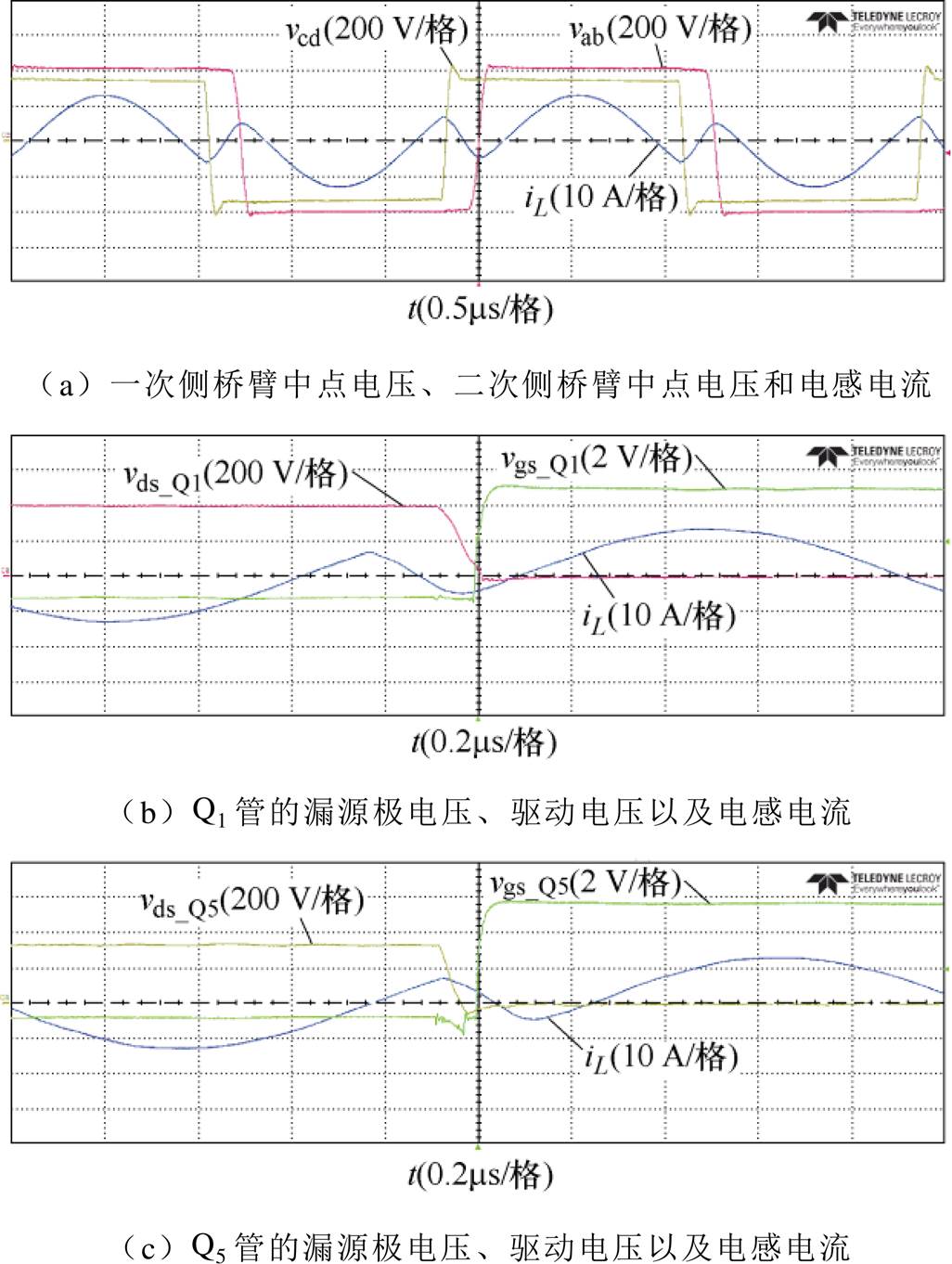
图12 V2=360 V,Io=5.56 A时的实验波形
Fig.12 Experimental waveforms when V2=360 V, Io=5.56 A
本文对采用最小回流电流控制和未采用最小回流电流控制(此时r固定为2,通过调节Dj 来调节输出功率的大小)时电路的电感电流有效值和回流电路进行了对比,如图15所示。可以看到,在不同的功率等级下,采用最小回流电流控制不仅可以有效地降低电路的回流电流,也可以使得电感电流的有效值更小,进而降低导通损耗和铜损,提升电路的转换效率。
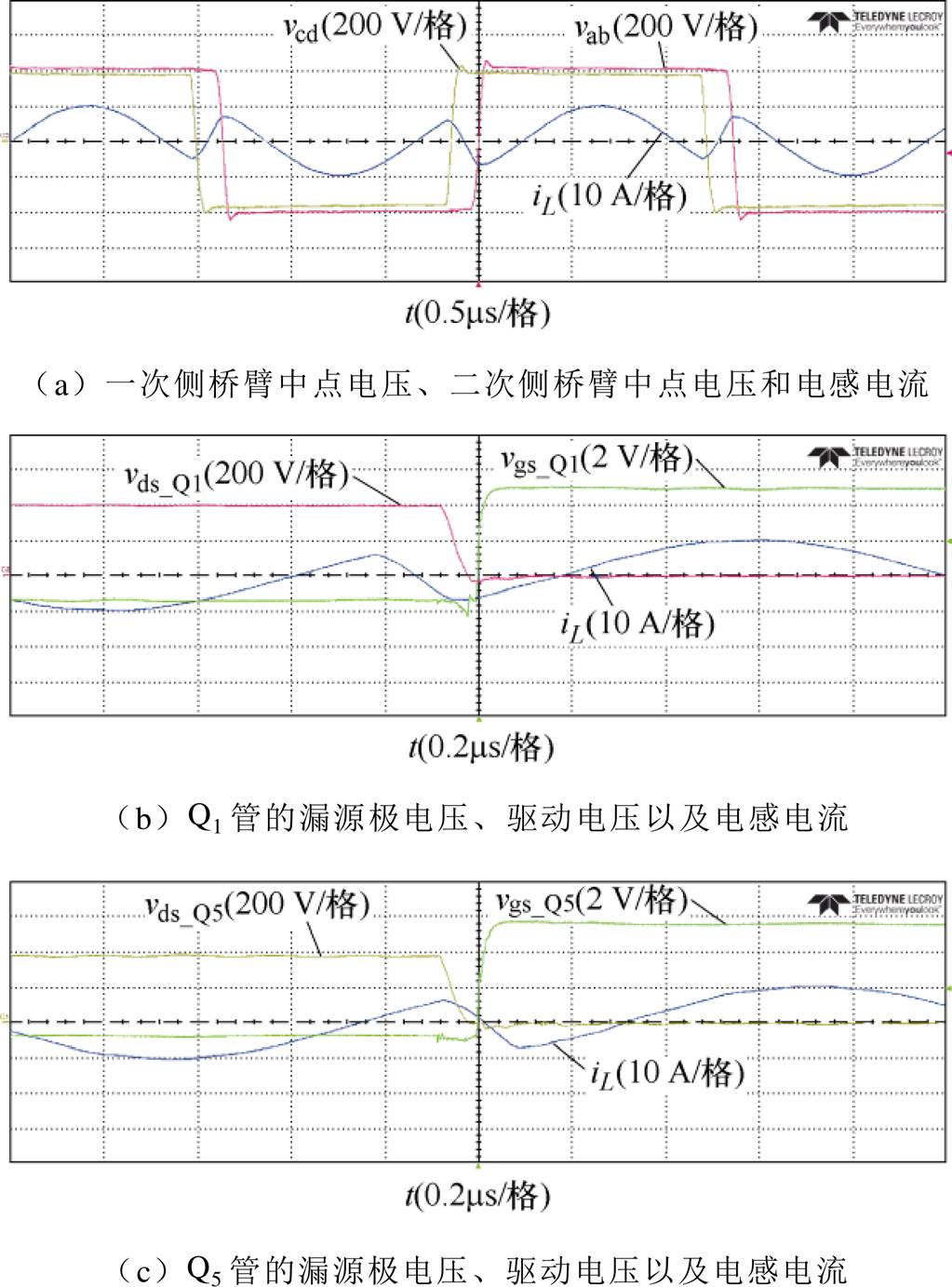
图13 V2=360 V,Io=2.77 A时的波形
Fig.13 Experimental waveforms when V2=360 V, Io=2.77 A
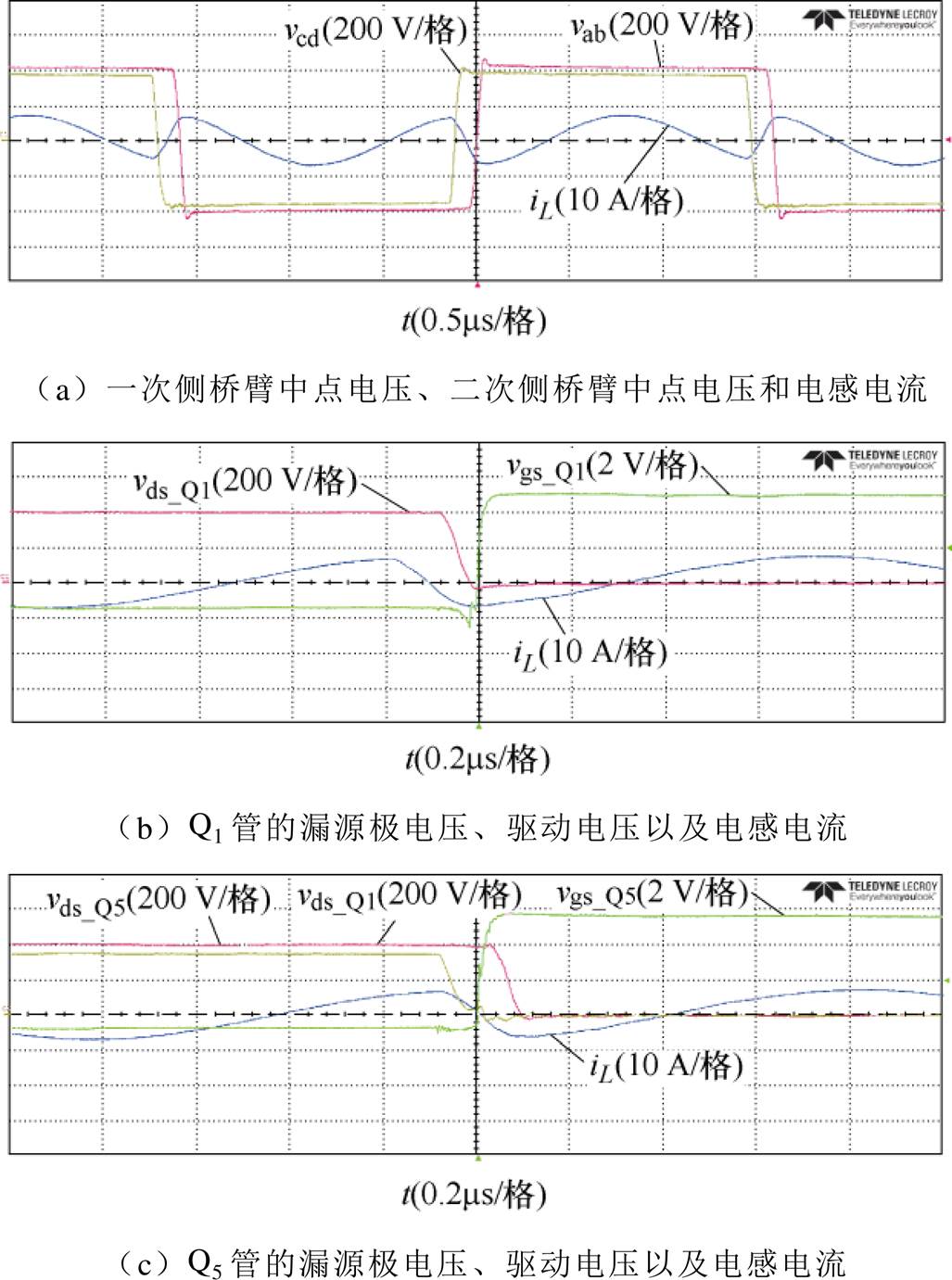
图14 V2=360 V,Io=0.69 A时的实验波形
Fig.14 Experimental waveforms when V2=360 V, Io=0.69 A
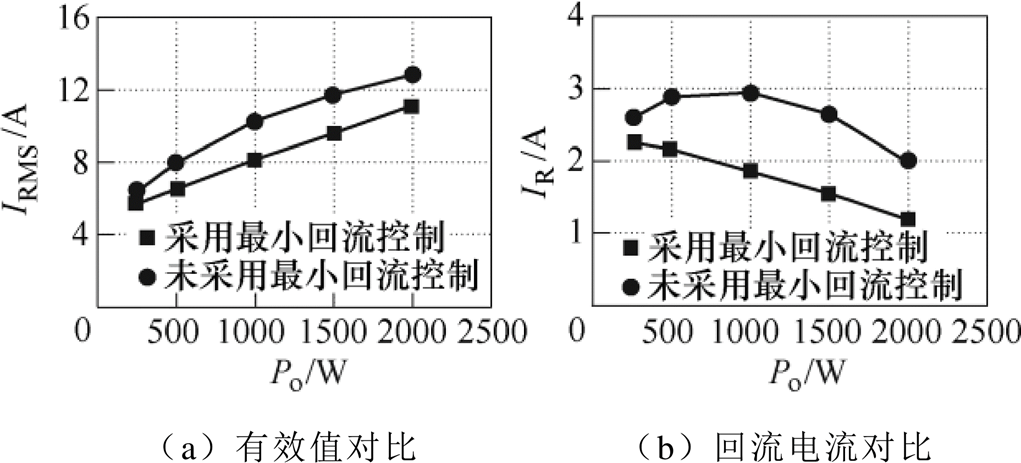
图15 采用最小回流电流控制和未采用最小回流电流控制时IRMS和IR的对比
Fig.15 Comparison of IRMS and IR with and without the proposed minimum backflow current control
本文还对变频+移相控制[22]、扩展PWM控制[15]和本文的控制方式的效果进行了对比。在应用这三种控制策略时,电路变压器两端的最大伏秒积都将出现在输出电压为360 V且开关频率最低的情况下。因此,对于任意一种控制策略而言,电路的最低开关频率均设定为310 kHz以使三种控制策略下变压器的体积是相近的。
与本文所提出的欠谐振控制相比,由于变频+移相控制和扩展PWM控制均为过谐振控制,因此其需要更大的谐振电感和谐振电容来使得电路的串联谐振频率低于电路的最低开关频率。以电路在不同电压增益下实现半载以上的软开关运行作为前提,为了使电路在满载输出时电感电流的有效值取得最小值,本文中过谐振控制下的谐振腔参数设定见表2。对比表2中不同控制策略下的谐振腔参数,可以发现,在采用所提出的最小回流电流控制时,电路所需的谐振电感更小,这将有利于降低电感的绕组匝数和磁心体积,进而降低电感的铜损和磁损。
以输出电压为250 V为例,当输出功率为2 kW时,三种控制策略下电路的典型波形和损耗分布如图16所示。相较于变频+移相控制与扩展PWM控制,所提出的控制策略在电感电流的有效值和峰值上并不占优势,因此,其开关管的导通损耗和线圈铜损(包括变压器线圈和电感线圈)均会有所提升。但由于其电感体积更小,因此电感的磁损有所降低,这在一定程度上弥补了由于电感电流有效值增大带来的额外导通损耗。
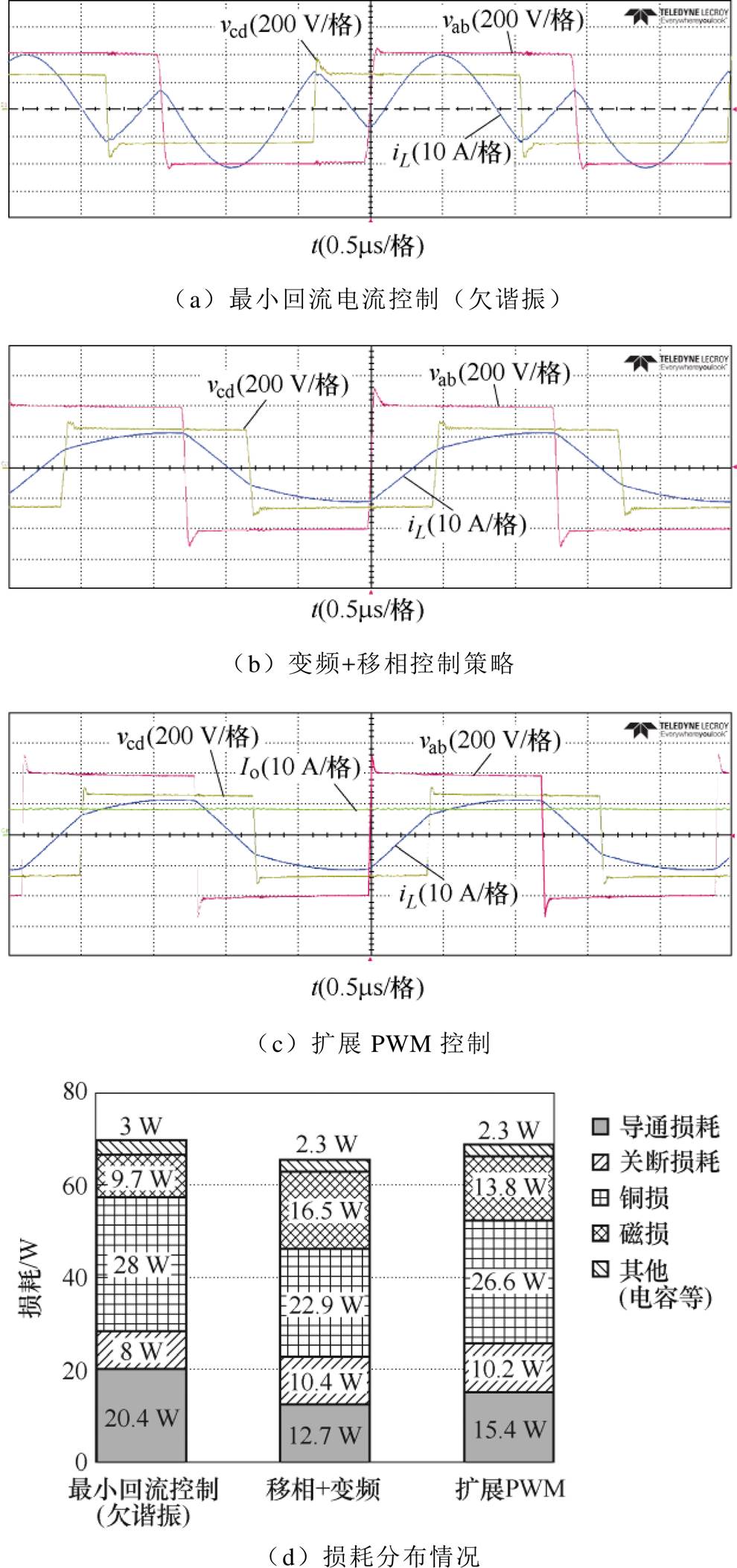
图16 V2=250 V,Io=8 A时不同控制策略下的波形和损耗分布情况
Fig.16 Experimental waveforms and loss breakdown under different modulation schemes when V2=250 V, Io=8 A
当输出功率降为1 kW和250 W时,三种控制策略下电路的典型波形和损耗分布分别如图17和图18所示。此时变频+移相控制需要将电路的开关频率提升至660 kHz且外移相角Dj 也需要超过0.5,这种情况下,电路的回流电流和线圈的交流电阻都将明显提升,使得电路在转换效率上不再具有优势。而对于扩展PWM控制而言,其在不同负载情况下的导通损耗和铜损都很小,但随着负载的降低,它将很难确保所有的开关管实现零电压开通,这在高频情况下会给电路带来很大的开通损耗。
三种控制策略下电路的转换效率如图19所示。与变频+移相控制和扩展PWM控制相比,所提出的最小回流电流控制仅需要采用很小的频率变化范围即可帮助电路实现不同负载下的软开关工作。同时它在降低电路的回流电流、电感电流有效值、谐振电感的体积和损耗等方面也起到了很好的效果。因此,该控制策略可以在不影响电路重载表现的情况下有效地提升电路在轻载到半载时的传输效率。
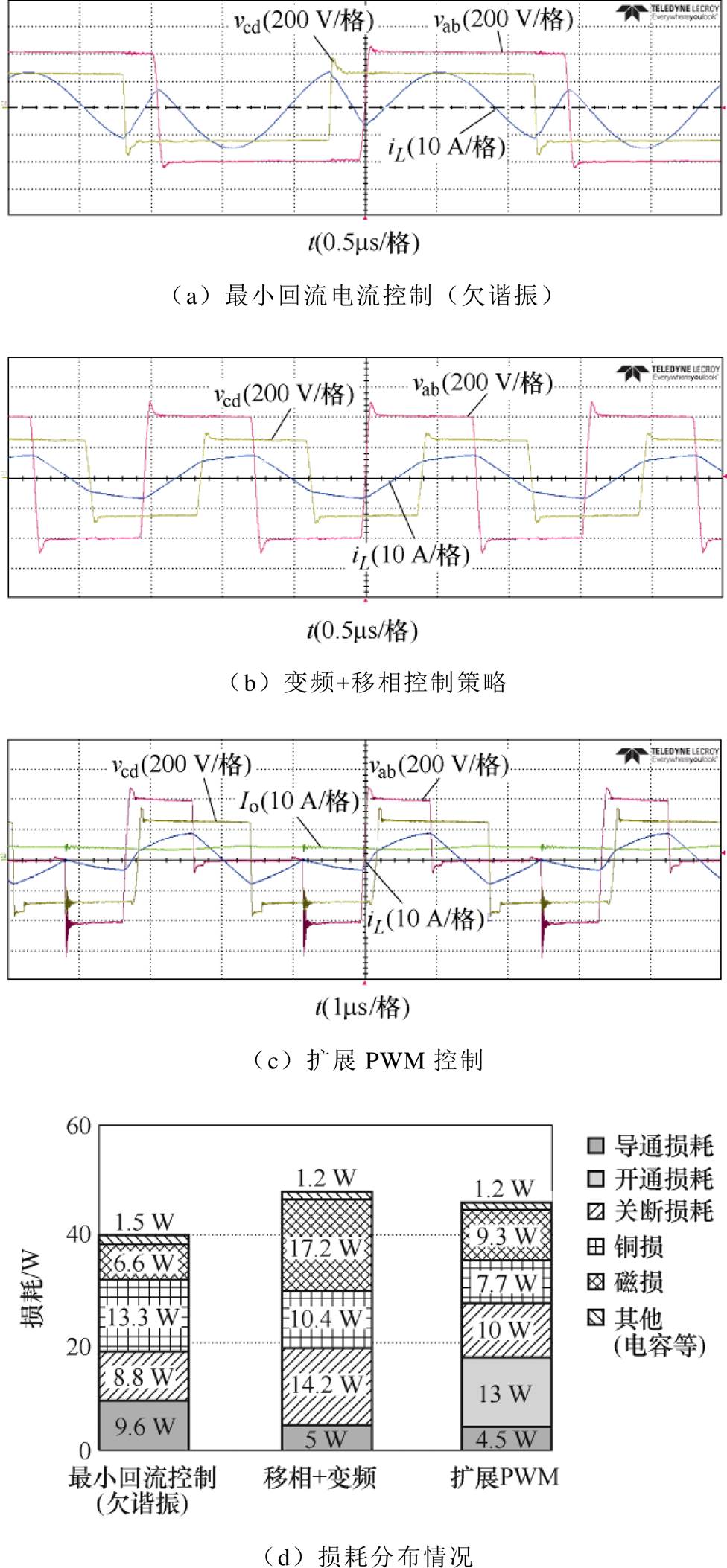
图17 V2=250 V,Io=4 A时不同控制策略下的波形图和损耗分布情况
Fig.17 Experimental waveforms and loss breakdown under different modulation schemes when V2=250 V, Io=4 A
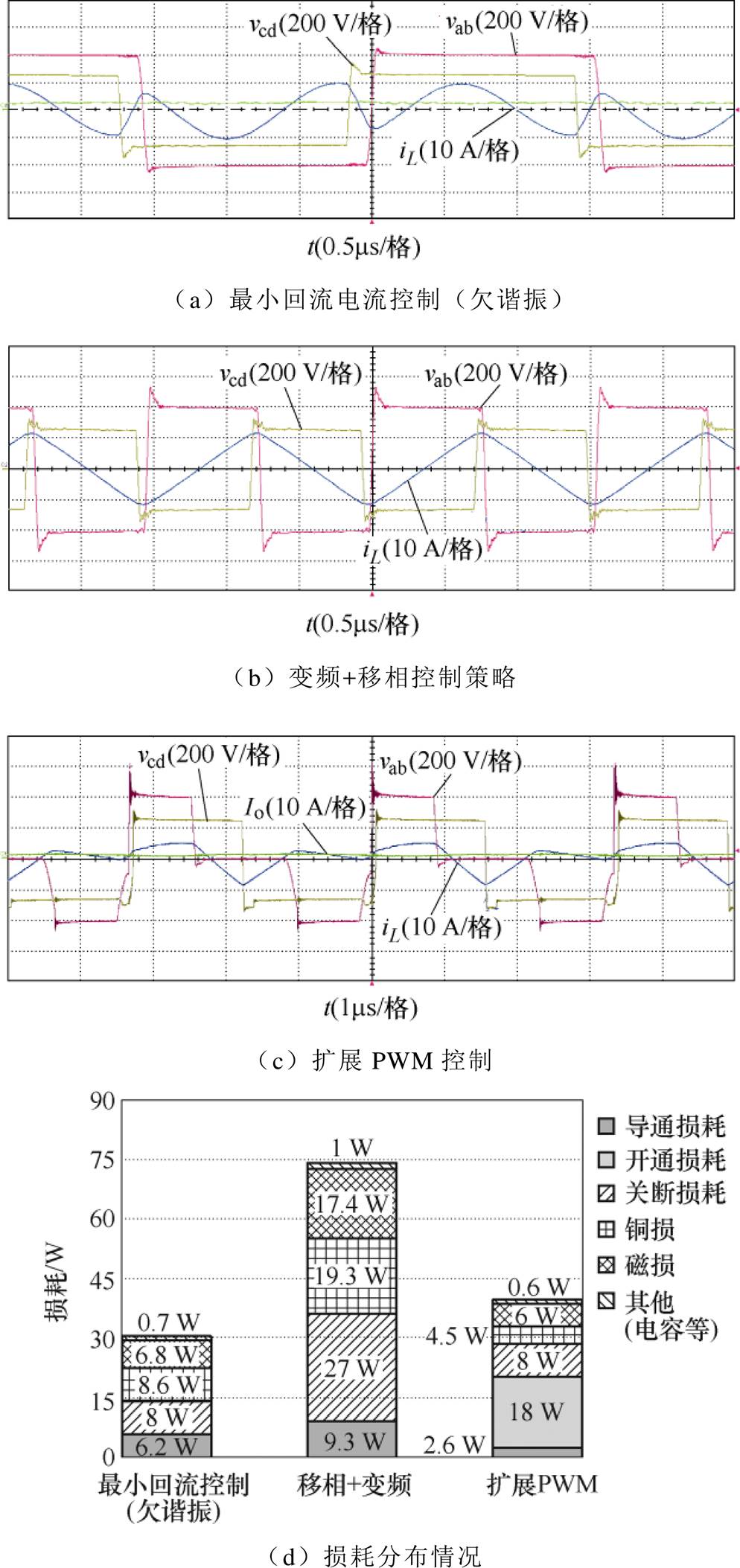
图18 V2=250 V,Io=1 A时不同控制策略下的波形图和损耗分布情况
Fig.18 Experimental waveforms and loss breakdown under different modulation schemes when V2=250 V, Io=1 A
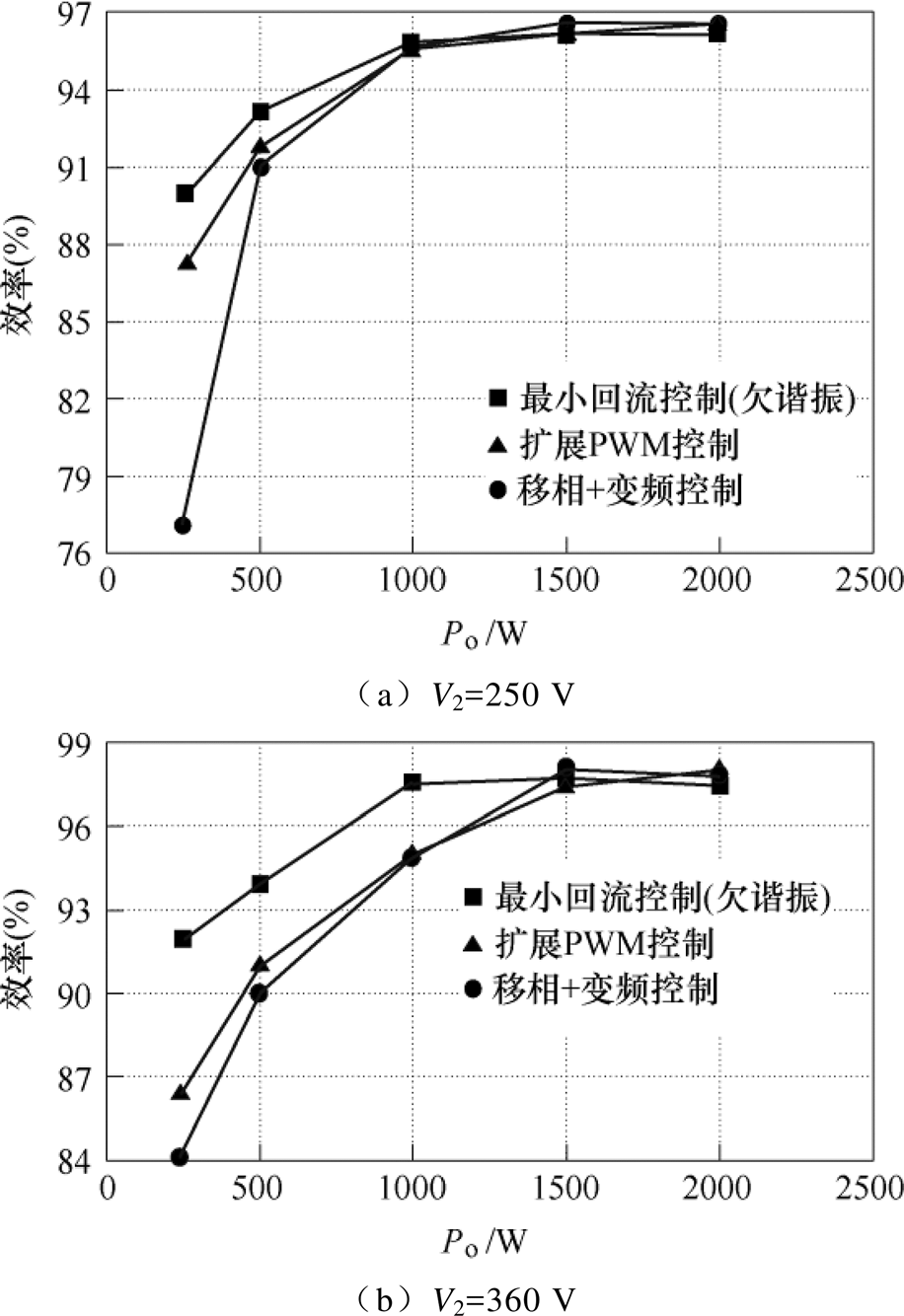
图19 不同输出情况下电路的转换效率
Fig.19 Transmission efficiency under different output conditions
如图8所示,在实际闭环控制实现中,电路所采用的Dj 将会受到PI控制器所输出的频率比r和电压增益M的影响而发生相应变化。在恒流输出时,M的值将由输入、输出电压采样计算得到,而在恒压输出时,用于计算的输出电压值将固定为输出电压的目标值,即此时M的值不随输出电压的动态波动而发生变化。同时,为了减轻控制器的计算压力,提高控制的实时性,本文对不同r和M下Dj 的值预先建表,在实际闭环控制中,用查表的方式得到Dj 的具体数值。以恒压输出250 V的工作模式为例,此时M值固定为0.694,根据PI控制器所输出的r值进行查表,可以确定Dj 的值。当负载在2 kW和1 kW之间切换时,电路的动态响应情况如图20所示。当电路由满载切至半载时,输出电压存在30 V的电压跌落,而当负载由1 kW切换至2 kW时,输出电压的超调为18 V。
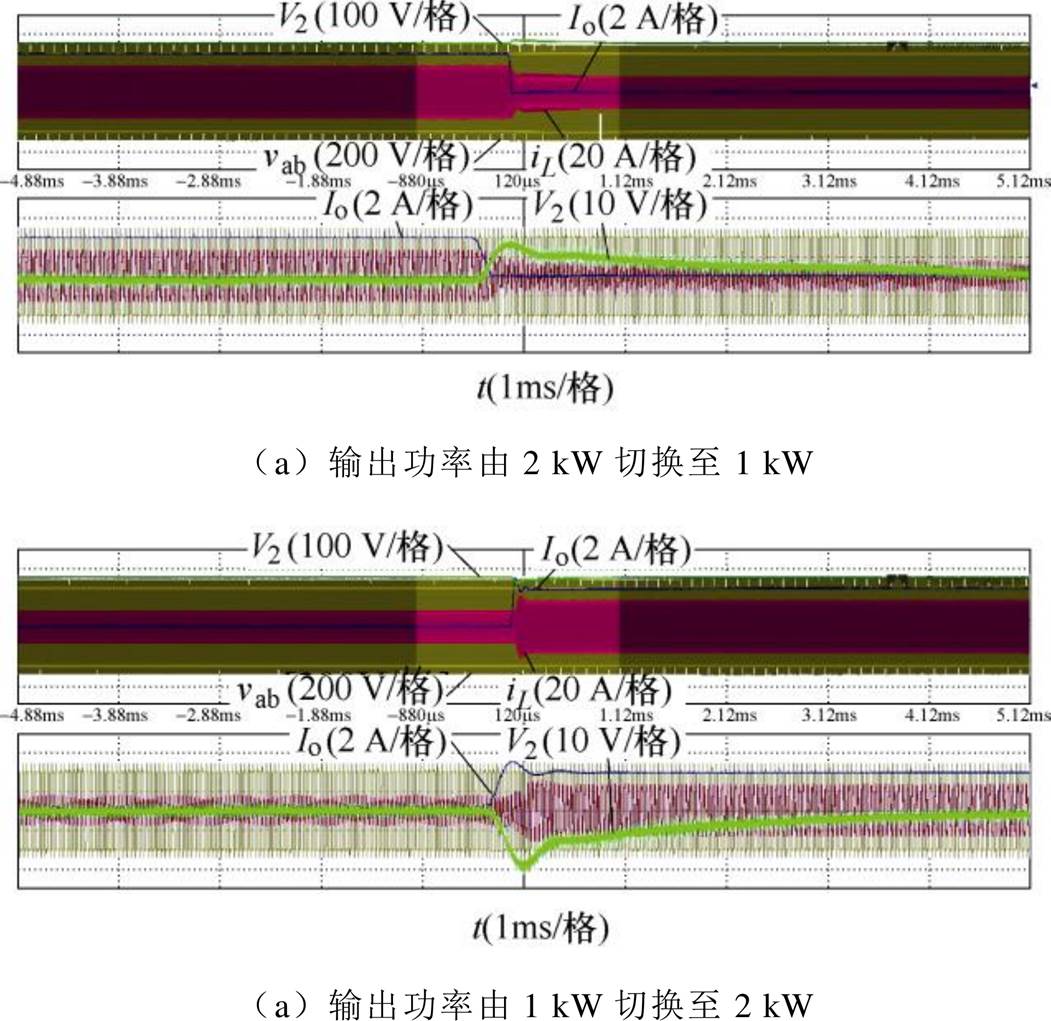
图20 采用最小回流电流控制且恒压输出250 V时,电路的动态波形
Fig.20 Dynamic waveforms of the circuit under the minimum backflow current control when V2 is 250 V
本文采用时域分析法推导了双有源桥串联欠谐振电路电感电流的表达式,基于此,总结出了该电路实现软开关的条件。通过在移相控制的基础上引入额外的变频控制,电路的软开关范围获得了极大的提升。为了进一步提升电路的传输效率,本文对所提出的变频移相控制进行了优化,在确保软开关的同时降低了电路回流电流的大小,并给出了不同控制变量确定的方法。分析结果表明,这种优化的控制方案也有助于降低电感电流的有效值。
附 录
结合式(18)、式(19),可以将式(19)中对拉格朗日算子的偏微分求导,即
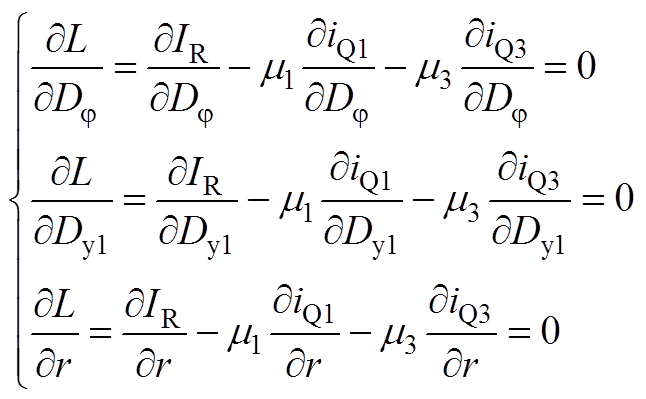 (A1)
(A1)
由于式(19)中的求导结果过于复杂,因此本文将用绘图的方式来对式(A1)所示的四种情况进行一一 分析。
对于情况a,由于m1和m2均为0,为了让式(A1)中的∂L/∂Dj 为0,则∂IR/∂Dj 需要存在过零点。对不同Dj、Dy1、r和M下∂IR/∂Dj 的值进行作图,如附图1所示。可以看到,∂IR/∂Dj 在不同Dj、Dy1、r和M的组合下始终为正,因此,在情况a的约束下,式(A1)不存在实数解,故舍弃。
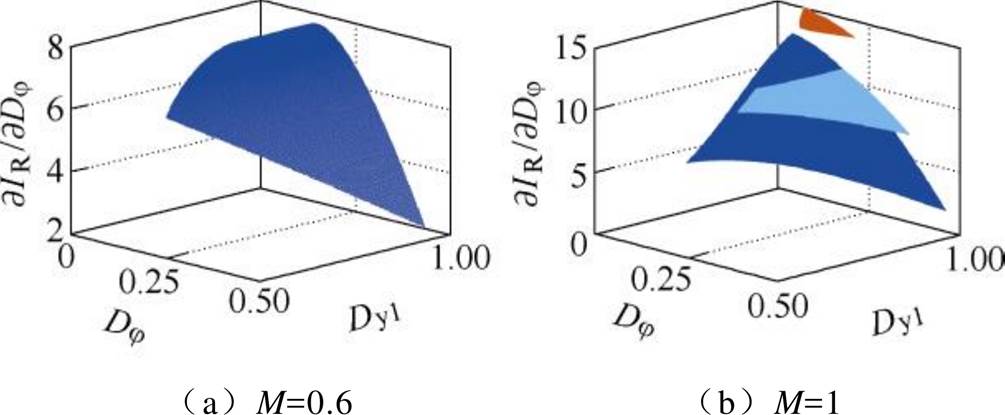
附图1 不同Dj、Dy1、r和M下∂IR/∂Dj 的取值情况
App.Fig.1 The values of ∂IR/∂Dj under different Dj, Dy1, r and M
对于情况b,此时m3=0,若式(A1)有解,则式(A2)需要在h1=0的情况下存在过零点。
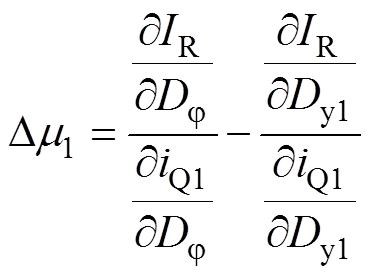 (A2)
(A2)
h1=0时,根据表1,Dj 可以表示为Dy1、r和M的函数,如式(9)所示。在此基础上,附图2给出了不同Dy1、r和M下式(A2)的取值情况,可以看到,无论如何选取Dy1、r和M的值,式(A2)始终大于0,即不存在合适的m1可以使得式(A1)在情况b的约束下存在解,故情况b也舍去。
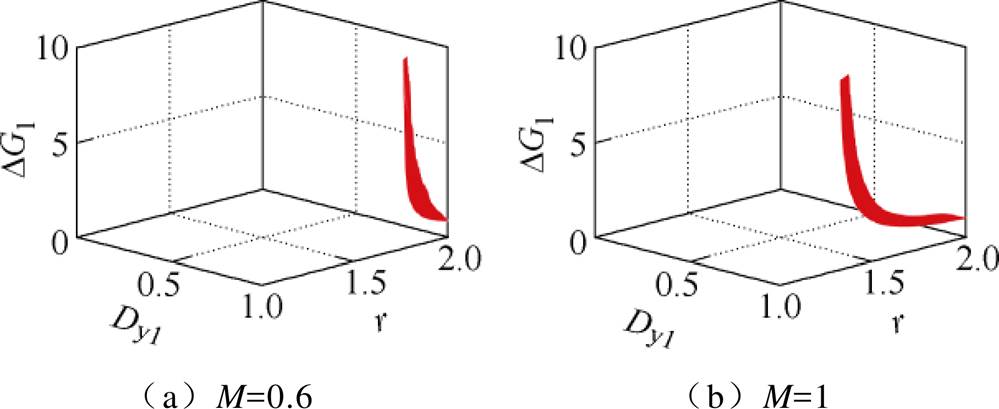
附图2 不同Dy1、r和M下Dm1的取值情况
App.Fig.2 The values of Dm1 under different Dy1, r and M
对于情况c,其分析方法与分析情况b时类似,此时m1=0,若式(A1)有解,则式(A3)需要在h1为0的情况下存在过零点。
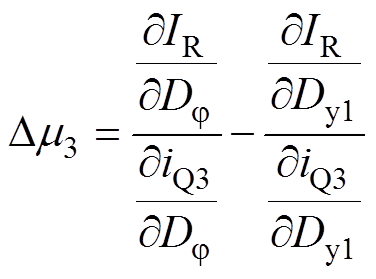 (A3)
(A3)
h3=0时,Dj 将以式(10)中的DjB1和DjB2进行表示。在此基础上,附图3给出了不同Dy1、r和M下式(A3)的取值情况,可以看到,无论如何选取Dy1、r和M的值,式(A3)始终小于0,即不存在合适的m3可以使式(A1)在情况d的约束下存在解,故情况c也舍去。
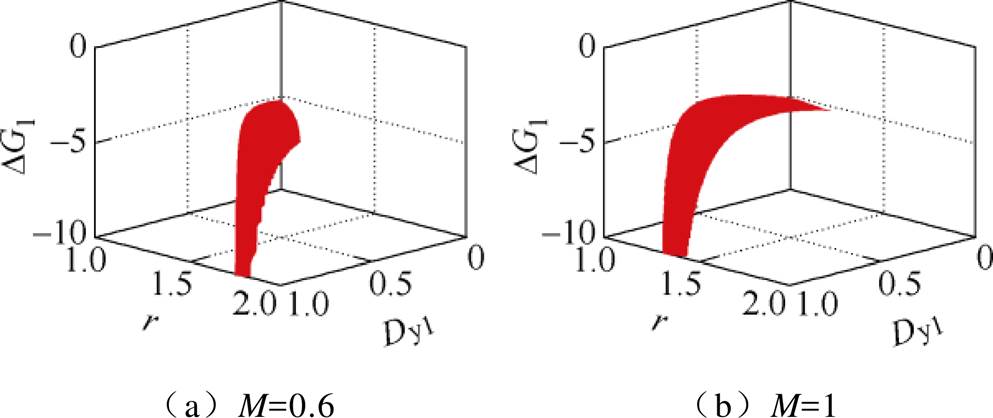
附图3 不同Dy1、r和M下Dm1的取值情况
App.Fig.3 The values of Dm1 under different Dy1, r and M
因此,在KKT条件下,式(19)的解将出现在情况d下,此时h1和h3将满足h1=h3=0,即iQ1=iQ3=IZVS。
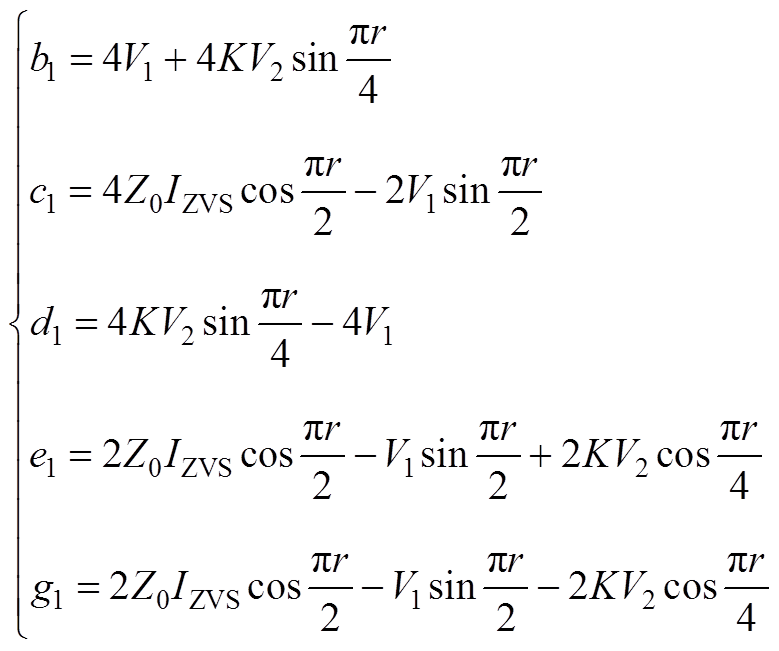 (A4)
(A4)
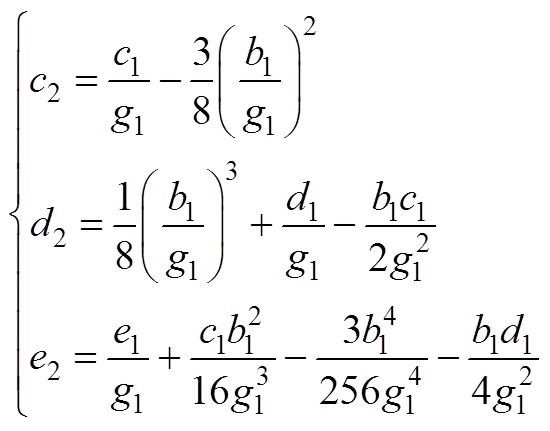 (A5)
(A5)
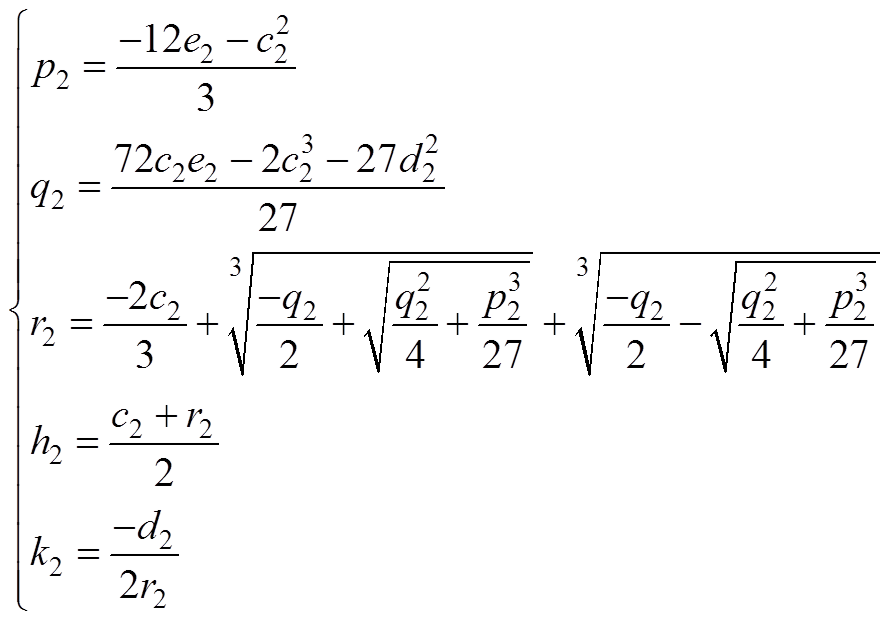 (A6)
(A6)
参考文献
[1] 刘晓飞, 张千帆, 崔淑梅. 电动汽车V2G技术综述[J]. 电工技术学报, 2012, 27(2): 121-127.
Liu Xiaofei, Zhang Qianfan, Cui Shumei. Review of electric vehicle V2G technology[J]. Transactions of China Electrotechnical Society, 2012, 27(2): 121- 127.
[2] 张晓峰, 吕征宇. 混合动力车用全数字电流控制型双向DC/DC变换器[J]. 电工技术学报, 2009, 24(8): 84-89, 105.
Zhang Xiaofeng, Lü Zhengyu. Digital-current- controlled bi-directional DC/DC converter in the hybrid electric vehicle[J]. Transactions of China Electrotechnical Society, 2009, 24(8): 84-89, 105.
[3] 李婧, 袁立强, 谷庆, 等. 一种基于损耗模型的双有源桥DC-DC变换器效率优化方法[J]. 电工技术学报, 2017, 32(14): 66-76.
Li Jing, Yuan Liqiang, Gu Qing, et al. An efficiency optimization method in dual active bridge DC-DC converter based on loss model[J]. Transactions of China Electrotechnical Society, 2017, 32(14): 66-76.
[4] 涂春鸣, 管亮, 肖凡, 等. 基于扩展移相控制下双有源桥移相角优化选取与分析[J]. 电工技术学报, 2020, 35(4): 850-861.
Tu Chunming, Guan Liang, Xiao Fan, et al. Parameter optimization selection and analysis of dual active bridge based on extended phase shift control[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 850-861.
[5] 胡钰杰, 李子欣, 赵聪, 等. 基于MOSFET的串联谐振双有源桥死区振荡机理分析及抑制[J]. 电工技术学报, 2022, 37(10): 2549-2558.
Hu Yujie, Li Zixin, Zhao Cong, et al. Mechanism analysis and suppression of oscillation in dead time of series resonant dual active bridge based on MOSFET[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2549-2558.
[6] 王仁龙, 杨庆新, 操孙鹏, 等. 一种优化电流应力的双有源桥式DC-DC变换器双重移相调制策略[J]. 电工技术学报, 2021, 36(增刊1): 274-282.
Wang Renlong, Yang Qingxin, Cao Sunpeng, et al. An optimized dual phase shift modulation strategy for dual active bridge DC-DC converter[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 274-282.
[7] 王攀攀, 徐泽涵, 王莉, 等. 基于三重移相的双有源桥DC-DC变换器效率与动态性能混合优化控制策略[J]. 电工技术学报, 2022, 37(18): 4720-4731.
Wang Panpan, Xu Zehan, Wang Li, et al. A hybrid optimization control strategy of efficiency and dynamic performance of dual-active-bridge DC-DC converter based on triple-phase-shift[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4720-4731.
[8] 高宇, 李若愚, 李林柘, 等. 三重移相调制模式下双有源变换器的直接功率控制[J]. 电工技术学报, 2022, 37(18): 4707-4719.
Gao Yu, Li Ruoyu, Li Linzhe, et al. Triple phase shift modulation-based direct power control strategy for a dual active bridge converter[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4707-4719.
[9] 任伊昵, 高祎韩, 韩旭, 等. 基于双有源桥DC/DC变换器回流功率优化的变频移相混合控制策略[J]. 电源学报, 2018, 16(6): 27-33.
Ren Yini, Gao Yihan, Han Xu, et al. Variable- frequency phase-shift hybrid control strategy for DAB DC/DC converter to optimize reactive power[J]. Journal of Power Supply, 2018, 16(6): 27-33.
[10] 章治国, 余海生. 一种双有源桥谐振变换器的研究与设计[J]. 微电子学, 2012, 42(3): 356-362.
Zhang Zhiguo, Yu Haisheng. Study and design of a dual active bridge resonant converter[J]. Micro- electronics, 2012, 42(3): 356-362.
[11] 李福, 邓红雷, 张国驹, 等. 一种中间电容谐振型级联双向DC-DC变换器[J]. 电工技术学报, 2022, 37(20): 5253-5266.
Li Fu, Deng Honglei, Zhang Guoju, et al. A cascaded bidirectional DC-DC converter with intermediate capacitor resonance[J]. Transactions of China Elec- trotechnical Society, 2022, 37(20): 5253-5266.
[12] Wu Hongfei, Sun Kai, Li Yuewei, et al. Fixed- frequency PWM-controlled bidirectional current-fed soft-switching series-resonant converter for energy storage applications[J]. IEEE Transactions on Indu- strial Electronics, 2017, 64(8): 6190-6201.
[13] 李玉慈. 一种谐振型双有源桥DC-DC变换器研究[D]. 秦皇岛: 燕山大学, 2017.
[14] Corradini L, Seltzer D, Bloomquist D, et al. Minimum current operation of bidirectional dual-bridge series resonant DC/DC converters[J]. IEEE Transactions on Power Electronics, 2012, 27(7): 3266-3276.
[15] Hong Jinsu, Choi S, Ha J I. A modulation method of series-resonant dual-active half-bridge converter for ZVS and minimum RMS current[C]//2022 Inter- national Power Electronics Conference (IPEC- Himeji 2022-ECCE Asia), Himeji, Japan, 2022: 1028- 1035.
[16] Bez F, Han Weijian, Corradini L. A low-complexity trajectory controller for reduced conduction losses in series-resonant dual half-bridge converters[J]. IEEE Transactions on Power Electronics, 2018, 33(11): 9963-9974.
[17] Han Weijian, Corradini L. Control technique for wide-range ZVS of bidirectional dual-bridge series resonant DC-DC converters[C]//2018 IEEE 19th Work-shop on Control and Modeling for Power Electronics (COMPEL), Padua, Italy, 2018: 1-8.
[18] 高祎韩. 高效率双有源桥串联谐振变换器研究[D]. 杭州: 浙江大学, 2020.
[19] Yaqoob M, Loo K H, Lai Y M. A four-degrees-of- freedom modulation strategy for dual-active-bridge series-resonant converter designed for total loss mini- mization[J]. IEEE Transactions on Power Electronics, 2019, 34(2): 1065-1081.
[20] Hu Song, Li Xiaodong, Zheng Qingfei. A dual-bridge DC-DC resonant converter using extended PWM and phase-shift control[J]. IEEE Transactions on Industry Applications, 2021, 57(4): 4009-4020.
[21] Boyd S, Vandenberghe L. Convex Optimization[M]. Cambridge, UK: Cambridge University Press, 2004.
[22] Han Weijian, Corradini L. General closed-form ZVS analysis of dual-bridge series resonant DC-DC con- verters[J]. IEEE Transactions on Power Electronics, 2019, 34(9): 9289-9302.
Abstract With bi-directional power transmission capability and high conversion efficiency, a dual- bridge-series-resonant converter (DBSRC) has attracted wide attention in battery charging and DC distribution systems. Since the soft-switching implementation of DBSRC is challenging when the voltage gain and load vary over a wide range, improvements in hardware and modulation schemes have been proposed to extend the soft-switching regions of the DBSRC. Nevertheless, it is still worth investigating to make the circuit simultaneously achieve full-load zero-voltage-switching (ZVS) operation and low circulating losses within a narrow switching frequency range without resorting to additional hardware components. This paper proposes an improved under-resonant control strategy, combining variable-frequency control and phase-shift control to minimize backflow current and optimize the root-mean-square (RMS) current.
Firstly, inductor current expressions and ZVS conditions for different switches are explored through time-domain analysis. Compared with the optional range of Dj under ZVS conditions, the soft-switching conditions of the circuit are simplified. When the voltage gain is less (more) than 1, implementing soft-switching on the V1 (V2) side enables full ZVS operation. Secondly, this paper adopts the KKT condition to derive the closed-form solutions of control variables to optimize backflow current while achieving full-load-range ZVS operation. According to the optimization results, the inner-phase-shift ratio is fixed at 1, and the outer-phase-shift ratio (Dj) is expressed as a function of the frequency ratio and voltage gain. According to the r obtained from the output of the PI controller and the voltage gain of the circuit, a look-up table is established to quickly determine the value of Dj, enhancing computational efficiency and dynamic performance.
A 2 kW DBSRC prototype with an output voltage variation of 250 V~360 V was designed to estimate the effect of different control strategies. When the over-resonant variable-frequency phase-shift (VFM+PSM) control is adopted, a switching frequency range of 350 kHz to 660 kHz is required to ensure the circuit operates at full-range ZVS under different load conditions. The extended-pulse-width modulation (EPWM) control can hardly prevent the circuit from experiencing hard-switching at light-to-medium load conditions. In contrast, when the proposed minimum backflow current control is applied, a switching frequency range of 350 kHz to 450 kHz demonstrates the ability to achieve full-range ZVS operation even when the voltage gain is equal to or deviates from 1. It improves the ZVS performance and reduces the switching frequency range. Additionally, the proposed control strategy effectively reduces the backflow current and inductor RMS current, and a 2 A inductor RMS current reduction can be achieved under most load conditions.
According to the experimental results, the effects of the proposed control strategy are summarized as follows. (1) The proposed minimum backflow current control provides full-range ZVS operation for the circuit without additional hardware components. (2) Compared with conventional strategies, the proposed control strategy can effectively extend the ZVS range while reducing the required switching frequency range. (3) In under-resonant operating mode, minimum backflow current control provides lower backflow current and inductor RMS current to reduce the circulating, conduction, and copper losses, improving transmission efficiency.
keywords:Under-resonant-dual-bridge-series-resonant converter, zero-voltage-switching, minimum back- flow current control, variable-frequency control
DOI: 10.19595/j.cnki.1000-6753.tces.230861
中图分类号:TM46
国家自然科学基金资助项目(62227802)。
收稿日期 2023-06-06
改稿日期 2023-07-19
高祎韩 男,1994年生,博士研究生,研究方向为电力电子技术及其应用。E-mail: 12010064@zju.edu.cn
马 皓 男,1969年生,教授,博士生导师,研究方向为电力电子技术及其应用、电力电子先进控制技术、电力电子系统故障诊断、大功率无线电能传输等。E-mail: mahao@zju.edu.cn(通信作者)
(编辑 陈 诚)