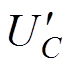为高频子模块直流侧电容电压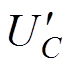（=UC/2）。摘要 为破解中压模块化多电平变换器（MMC）输出性能提升与降本、增效难以有效兼顾的问题，该文提出一种基于高低频混合的新型MMC（NMMC）拓扑。NMMC每个桥臂包含1个由异质交叉连接模块（HCCM）构成的高频子模块和N-1个半桥变换器构成的低频子模块。HCCM的高频桥臂采用SiC MOSFET器件，而HCCM的换向桥臂及低频子模块均采用Si IGBT器件。针对NMMC拓扑，该文采用高低频混合调制策略，充分发挥了SiC MOSFET器件开关损耗低、Si IGBT器件通态损耗低的优势。此外，针对高频子模块提出一种特定的电容电压平衡策略，并详细分析高频子模块的工作状态。进一步地，仿真及实验验证了所提拓扑结构、调制策略、均压策略的可行性和有效性。最后，将所提拓扑与现有MMC拓扑在器件成本和运行损耗方面进行综合对比，证明所提拓扑可以更好地平衡装置的成本及效率指标。
关键词：模块化多电平变换器 Si IGBT SiC MOSFET 混合调制 电平数增倍
模块化多电平变换器（Modular Multilevel Converter, MMC）凭借可扩展性强、冗余性好等优势被广泛应用于机车牵引、新能源并网、电能质量调控等中压领域[1-4]。考虑到中压场合MMC的子模块数相对较少，MMC变换器输出的等效开关频率、电平数已成为制约其输出性能提升的关键因素。目前，国内外相关学者已从调制优化、拓扑优化、新型器件应用等多角度出发来改善中压场合下MMC的输出性能[5-8]。
在MMC调制策略方面，典型的常用调制策略有最近电平逼近调制（Nearest Level Modulation, NLM）和载波移相脉冲宽度调制（Carrier Phase Shift Pulse Width Modulation, CPS-PWM）[9-11]。NLM具有开关频率低、调控简单等优势，但其仅能输出N+1电平，且在模块数较少工况下的低次谐波含量较高。为改善传统NLM的不足，文献[12]提出一种2N+1电平的改进型NLM策略，其通过改变NLM取舍函数的设定值，从而错开上下桥臂电平变化的时间，MMC的输出电平数则由N+1增加为2N+1。在此基础上，文献[13]通过在参考信号上增加一个小偏移量，从而降低了MMC输出谐波和电容电压波动幅值。尽管改进型NLM算法可以提升MMC输出性能，但其等效输出开关频率低，低次谐波含量依旧较高。与NLM相比，CPS-PWM等效开关频率高、波形质量好，且可输出2N+1电平，但其每个模块的工作频率高、整体开关损耗大。因此，现有单一调制策略及优化方法难以很好解决输出性能与运行效率兼顾优化的问题。
为进一步改善MMC输出性能，相关学者从调制混合、器件混用等方面开展部分工作。为综合NLM与CPS-PWM两种调制策略的优势，文献[14-15]提出一种最近电平调制PWM（NLM-PWM）策略，该调制策略仅需一个高频子模块输出PWM波，其余子模块采用NLM策略，且可以达到与CPS-PWM近似的输出性能。相似地，文献[16-17]提出每个桥臂额外增加一个全桥辅助模块，结合NLM-PWM策略，整个装置可以输出2N+3电平。但这种NLM-PWM策略的等效输出频率就等于高频子模块的开关频率，而高频子模块在桥臂中的具体位置则由运行状态决定，会在桥臂中随机变动。因此，若要提升MMC的等效输出频率，则对整体器件的开关性能要求较高。为此，文献[18]将混合调制策略进一步优化，将高频调制固定在几个基于SiC MOSFET器件的半桥子模块内轮换，而其余半桥子模块则采用基于Si IGBT器件的半桥模块。以SiC MOSFET为代表的宽禁带半导体器件在开关频率、导热等方面性能更优[19-20]，故混合方案的效率更高，但是SiC器件的成本高昂[21]，整个装置成本增加较高。进一步地，文献[22]提出将每个桥臂的高频动作固定于两个基于SiC MOSFET器件的全桥子模块，该拓扑可输出2N+1电平且SiC MOSFET器件耐压降低一倍，但每个桥臂包含两个SiC MOSFET器件全桥，SiC MOSFET器件的数量依然较多，整体成本仍然较高。
为破解装置输出性能与降本、增效难以有效兼顾的问题，本文提出一种基于高低频混合的新型MMC（Novel MMC, NMMC）拓扑。首先，介绍了NMMC的拓扑结构，分析其对应的调制策略和调制模式。然后，定量分析每种调制模式下高频子模块的能量波动机理。进一步地，详细分析了不同调制模式下高频子模块的工作状态，并给出其均压流程。仿真和实验验证了所提拓扑结构、调制策略、均压策略的有效性。最后，将所提拓扑与现有拓扑在成本和损耗方面综合对比，证明所提NMMC的性能优势。
NMMC拓扑结构如图1所示，该结构与传统MMC相似，上下桥臂完全对称。每个桥臂由1个高频子模块、N-1个低频子模块以及1个桥臂电感串联构成。其中，低频子模块采用传统基于Si IGBT器件的半桥变换器；对于高频子模块，本文提出一种异质交叉连接模块（Heterogeneous Cross- Connected Module, HCCM）。HCCM由两个半桥子模块（Half-bridge Submodule，HSM11、HSM12）经换向桥臂交叉连接构成，其包含4个SiC MOSFET器件、2个Si IGBT器件和2个电容。所提HCCM中SiC MOSFET器件的耐压仅为Si IGBT器件的一半。L为桥臂电感，CH1、CH2为高频子模块直流侧电容，CL为低频子模块直流侧电容，uao、ubo、uco为NMMC三相输出电压，Udc为NMMC直流侧电压，UC为低频子模块直流侧电容电压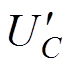，为高频子模块直流侧电容电压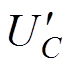（=UC/2）。
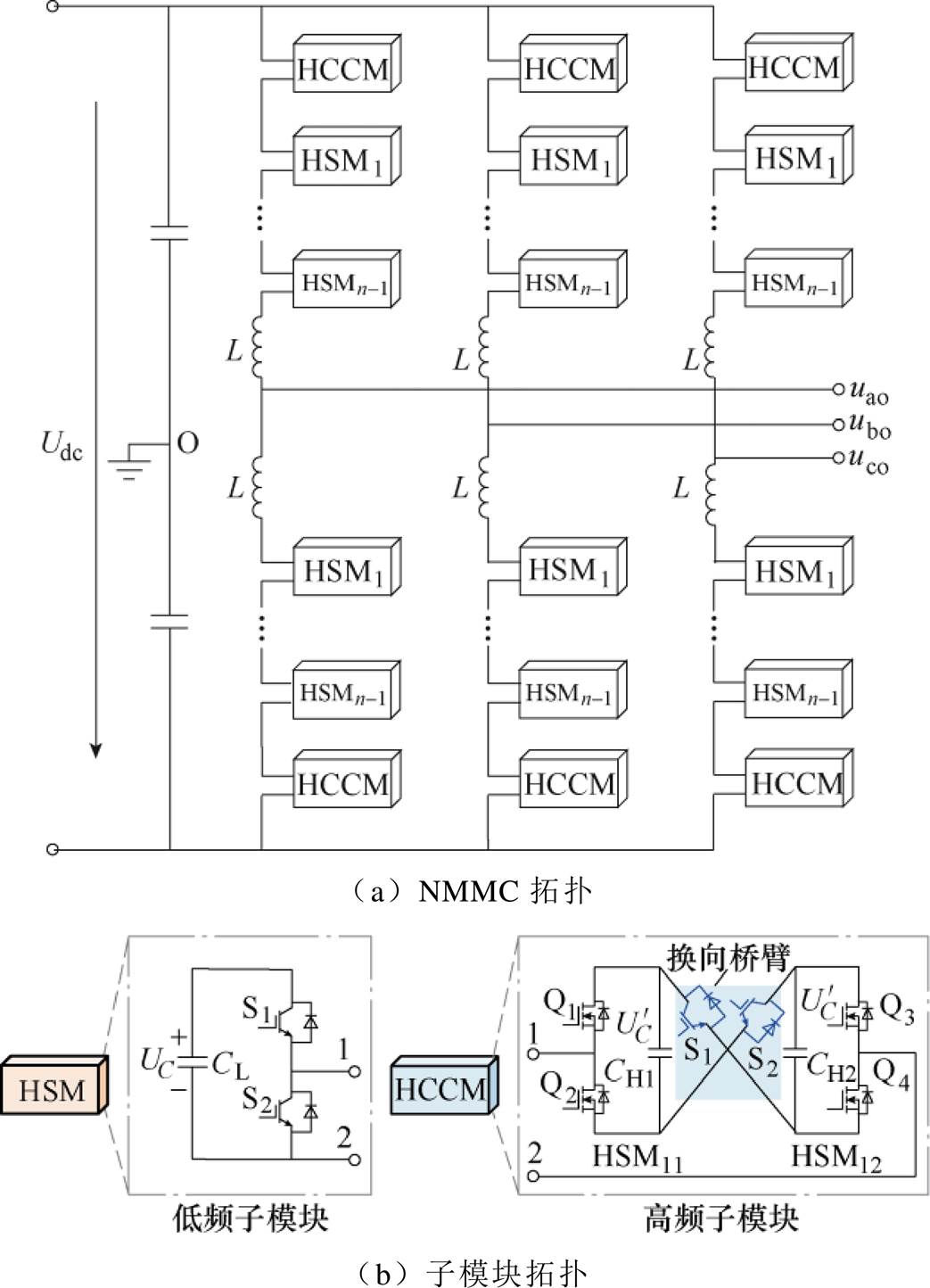
图1 NMMC拓扑结构
Fig.1 Topology diagram of the NMMC
本文所提NMMC策略中，低频子模块采用NLM输出工频阶梯波，高频子模块采用单极性PWM输出高频整形脉冲。
HCCM可以输出UC、UC/2、0、-UC/2、-UC五种电平，HCCM的开关模式见表1。由表1可以看出，换向桥臂为工频开关周期，故采用开关频率低、通态损耗小的Si IGBT器件。若HCCM采用高频PWM，则Q1～Q4工作于高频开关状态，故采用开关损耗小的SiC MOSFET器件。
HCCM模块采用PWM时，会出现两种调制结果，如图2所示。图2中，upwm_r为调制波，upwm为HCCM输出电压。对于t1阶段，0＜upwm_r＜UC/2，HCCM中一个HSM被旁路，另一个HSM输出PWM波。对于t2阶段，upwm_r＞UC/2，此时会出现两种PWM情况：一种情况是HSM11和HSM12配合输出幅值为0～UC的PWM波，如图3a所示；一种情况是一个HSM被常通，另一个HSM输出PWM波，则HCCM等效输出为UC/2～UC的PWM波，如图3b所示。通过对比可以看出，图3b对应的调制结果更逼近于调制波，故本文以此作为HCCM的PWM方法。
表1 HCCM开关模式
Tab.1 Switching mode of the HCCM
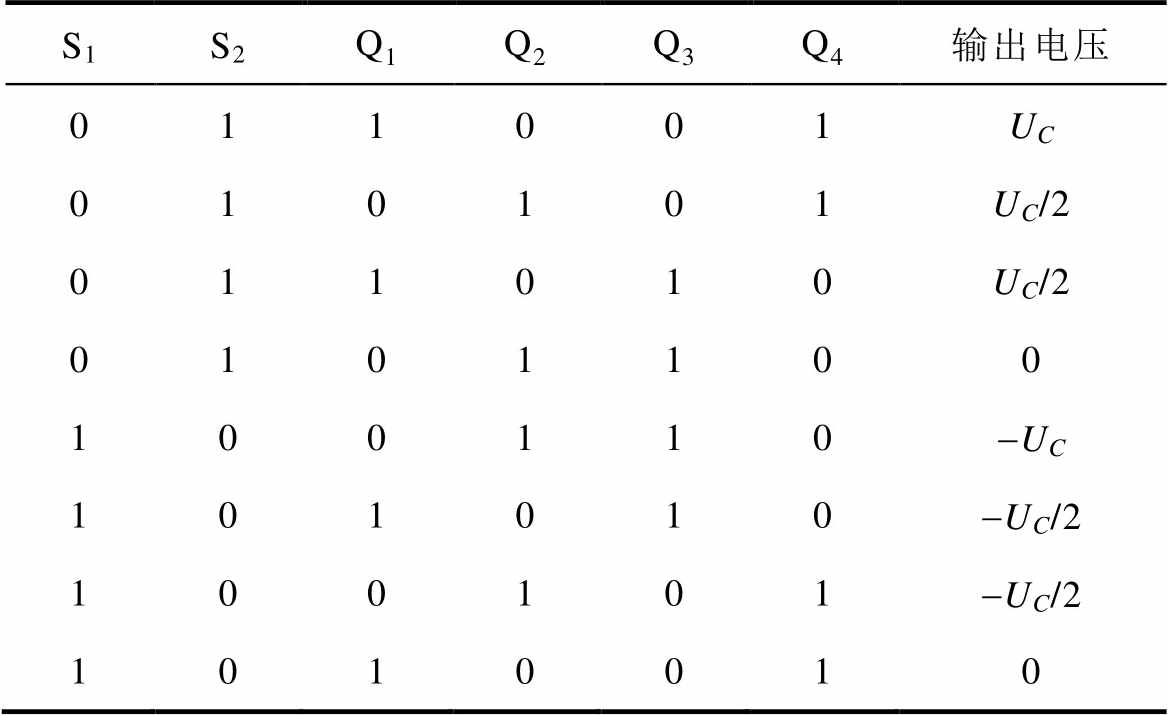
S1S2Q1Q2Q3Q4输出电压 011001UC 010101UC/2 011010UC/2 0101100 100110-UC 101010-UC/2 100101-UC/2 1010010
注：“1”代表器件闭合；“0”代表器件断开。
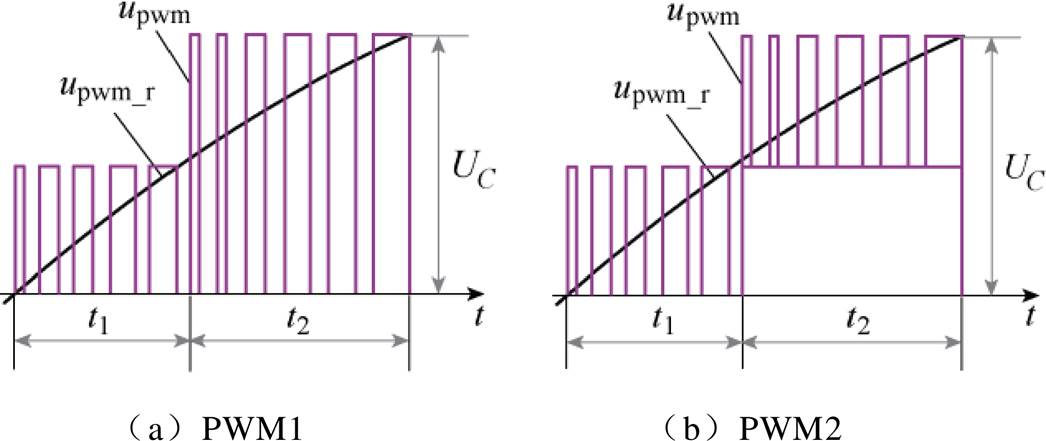
图2 HCCM的PWM原理
Fig.2 PWM principle of the HCCM
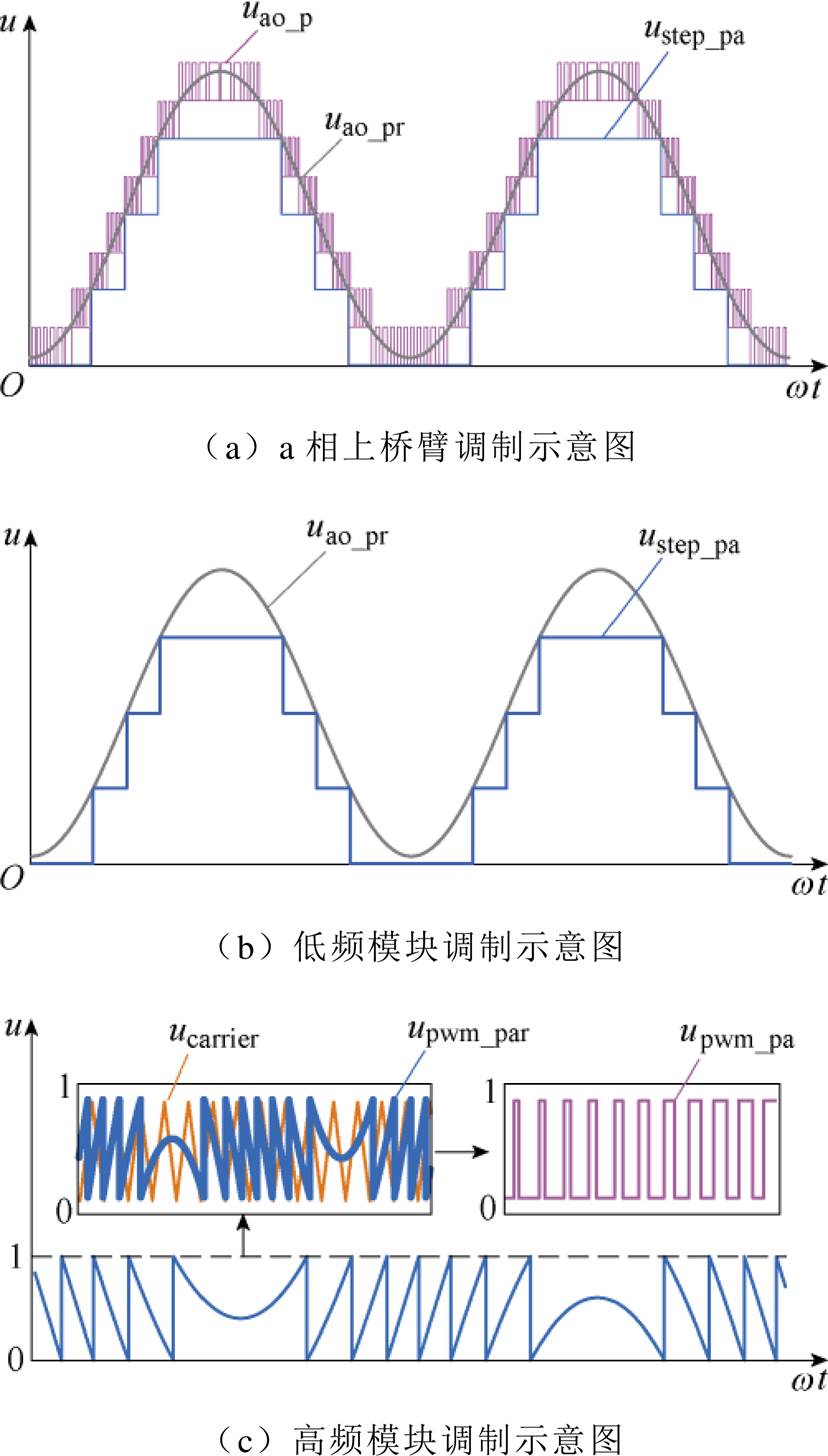
图3 模式Ⅰ下NMMC的调制原理
Fig.3 Modulation principle of the NMMC in mode Ⅰ
以a相上桥臂为例进行分析。由于高频子模块可以输出正负对称的高频PWM波，故混合调制策略会出现两种模式。定义：高频子模块输出正PWM波时为调制模式Ⅰ；高频子模块输出负PWM波时为调制模式Ⅱ。
对于模式Ⅰ，高频子模块输出正PWM波，等效调制原理如图3所示。a相上桥臂输出电压uao_p由两部分组成：一部分是低频子模块输出的阶梯波电压ustep_pa；另一部分是高频子模块输出的高频整形脉冲upwm_pa。
定义NMMC的a相输出电压为
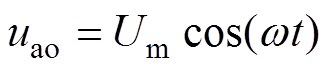（1）
式中，Um为输出电压幅值；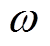
为角频率。定义m为调制系数，则有
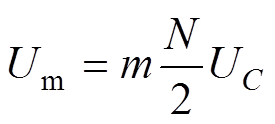（2）
式中，N为NMMC每个桥臂的总模块数。
由MMC原理可知，其a相上桥臂的调制波可表示为
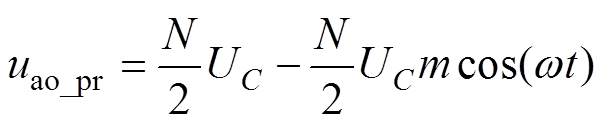（3）
由式（3）可得a相上桥臂低频子模块需要投入的子模块数为
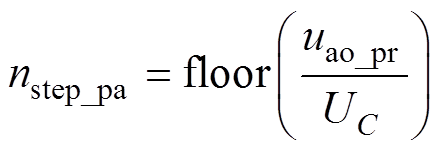（4）
式中，floor(x)为向下取整函数。
故a相上桥臂高频子模块输出电压参考值为
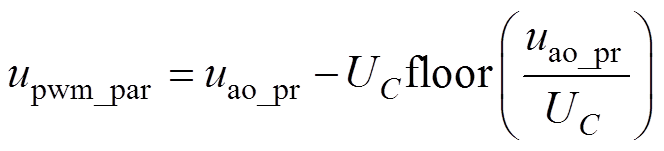（5）
将调制波参考值upwm_par与载波ucarrier相比，并结合图2b调制原理得到模式Ⅰ下高频子模块PWM脉冲upwm_pa。
对于模式Ⅱ，高频子模块输出负PWM，等效调制原理如图4所示。相较于模式Ⅰ，模式Ⅱ下低频子模块的阶梯波电压可以表示为
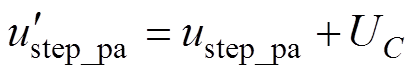（6）
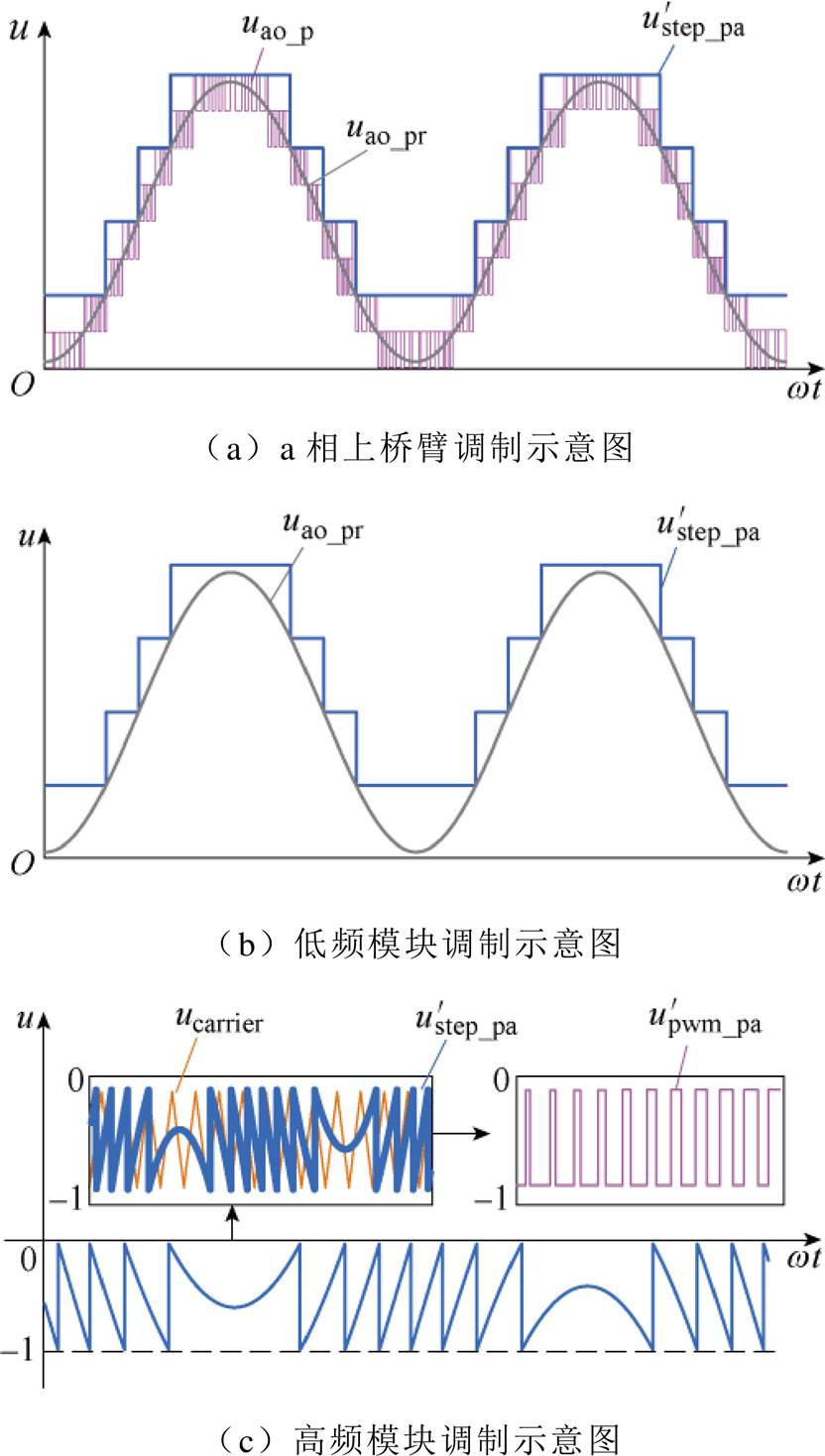
图4 模式Ⅱ下NMMC的调制原理
Fig.4 Modulation principle of the NMMC in mode Ⅱ
因此，模式Ⅱ要比模式Ⅰ多投入一个低频子模块，故a相上桥臂低频子模块需要投入的子模块 数为
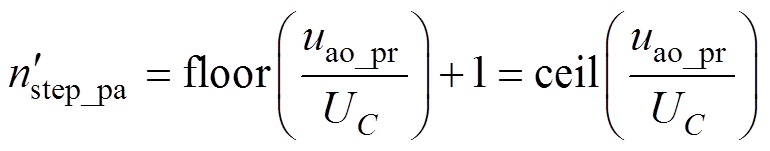（7）
式中，ceil(x)为向上取整函数。
模式Ⅱ时，a相上桥臂高频子模块输出电压参考值为
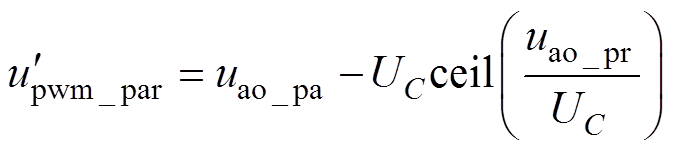（8）
同理，并结合图2b调制原理得到模式Ⅱ下高频子模块PWM脉冲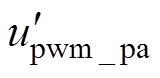
。
综上所述，两种调制模式均将高频开关动作集中于高频子模块中的SiC MOSFET器件，而由Si IGBT组成的低频子模块只负责输出低频阶梯波。故该方案充分发挥了SiC MOSFET开关损耗小、Si IGBT导通损耗小的优点，可以大幅度降低装置的总体损耗，提高装置效率。
本文所提NMMC中低频子模块采用传统的排序均压算法即可实现稳压[14]，此文不再赘述。高频子模块由于固定输出高频PWM波，无法和低频子模块一起参与排序均压，直流侧电容的能量波动情况未知。以a相上桥臂高频子模块为例，对其能量波动机理做如下分析。
在模式Ⅰ下，由式（3）、式（5）可知，a相上桥臂高频子模块的平均开关函数为
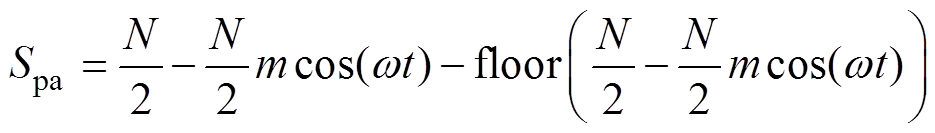（9）
忽略环流的影响，由交直流侧功率守恒定律可得a相上桥臂电流为
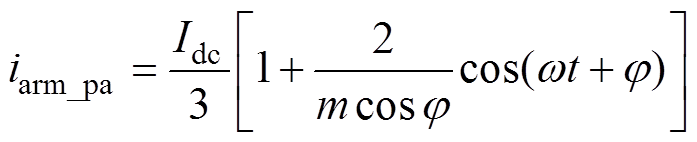（10）
式中，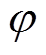
为负载功率因数角。
联立式（9）和式（10），可得a相上桥臂高频子模块直流侧电容总能量波动表达式为
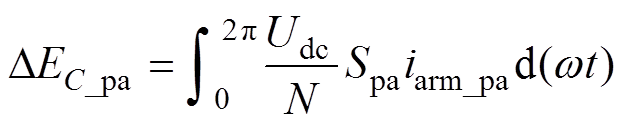（11）
在模式Ⅱ下，a相上桥臂高频桥臂的平均开关函数可以表示为
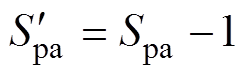（12）
由于桥臂电压和桥臂电流表达式不变，故模式Ⅱ下高频子模块直流侧电容总能量波动表达式为
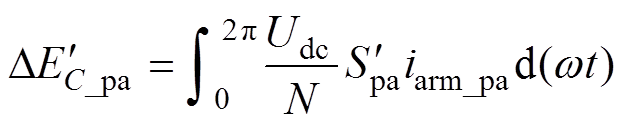（13）
假定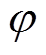=0，在Matlab中绘制
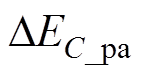和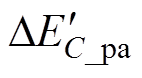
的示意图如图5和图6所示。可以看到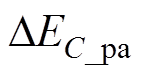，在N和m的变化范围内均大于0，且随着模块数的减少，
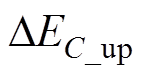波动幅值增大。因此，在模式Ⅰ下，高频子模块的电容电压会一直升高。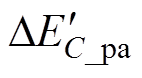的数值在N和m的变化范围内均小于0，且随着模块数的减少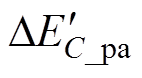，波动幅值增大。因此，模式Ⅱ下，高频子模块的电容电压会一直降低。若控制NMMC在模式Ⅰ和模式Ⅱ间灵活切换，即可改变高频子模块直流侧电容的充放电状态，以维持直流侧电容电压的稳定。
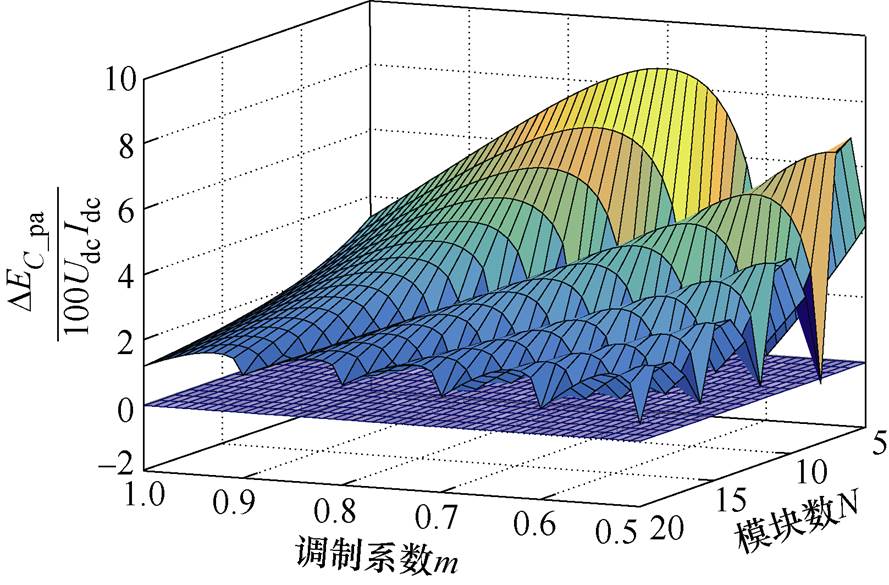
图5 模式Ⅰ下高频子模块能量波动示意图
Fig.5 Energy fluctuation diagram of high frequency submodule in mode Ⅰ
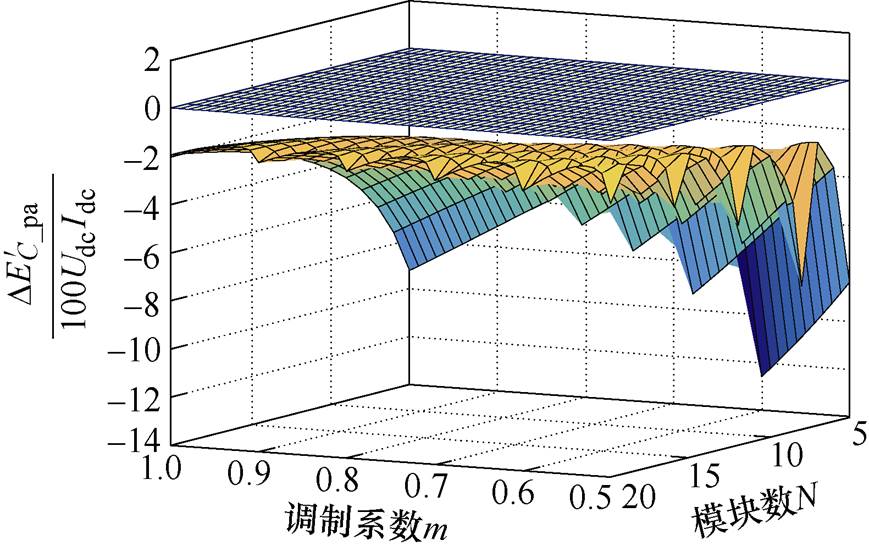
图6 模式Ⅱ下高频子模块能量波动示意图
Fig.6 Energy fluctuation diagram of high frequency submodule in mode Ⅱ
本节详细分析了不同开关模式下高频子模块的功率流通路径和直流电容能量变化情况，并给出了高频子模块详细的均压流程。
高频子模块可以输出UC、UC/2、0、-UC/2、-UC共五种电平。当S1断开、S2导通时，高频子模块输出正极性PWM脉冲，对应模式Ⅰ；反之，当S1导通、S2断开时，高频子模块输出负极性PWM脉冲，对应模式Ⅱ。根据高频子模块输出PWM极性以及桥臂电流方向，每种模式对应的八种工作状态如图7和图8所示。每种工作模式对应高频子模块直流电容的运行状态具体分析如下：
Ⅰ（a）：桥臂电流iarm＞0；S1开，S2闭；Q1、Q4闭，Q2、Q3开；upwm=UC；CH1、CH2充电。
Ⅰ（b）：桥臂电流iarm＞0；S1开，S2闭；Q2、Q4闭，Q1、Q3开；upwm=UC/2；CH1旁路、CH2充电。
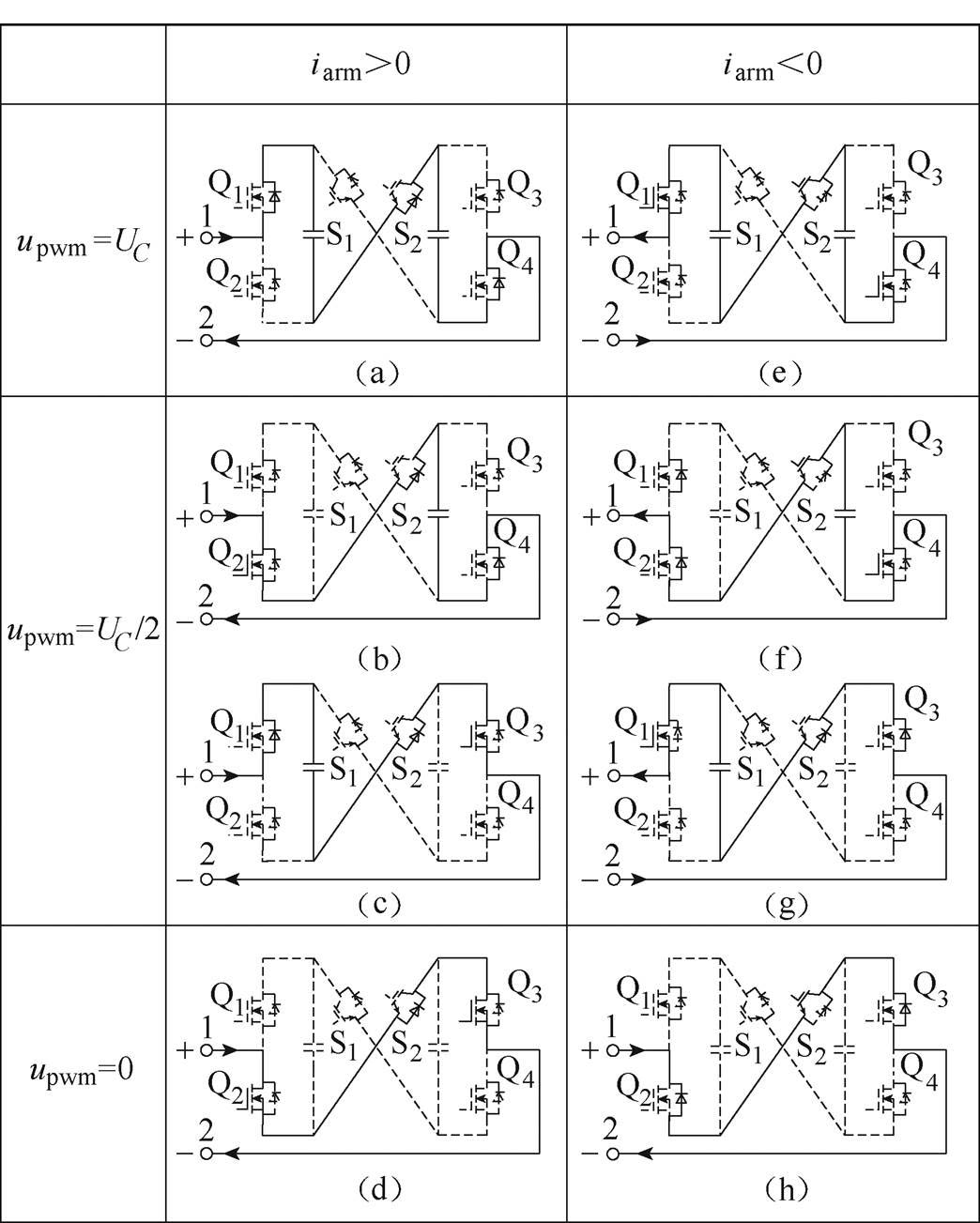
图7 模式Ⅰ下高频子模块的工作状态
Fig.7 Working state of high frequency submodule in mode Ⅰ
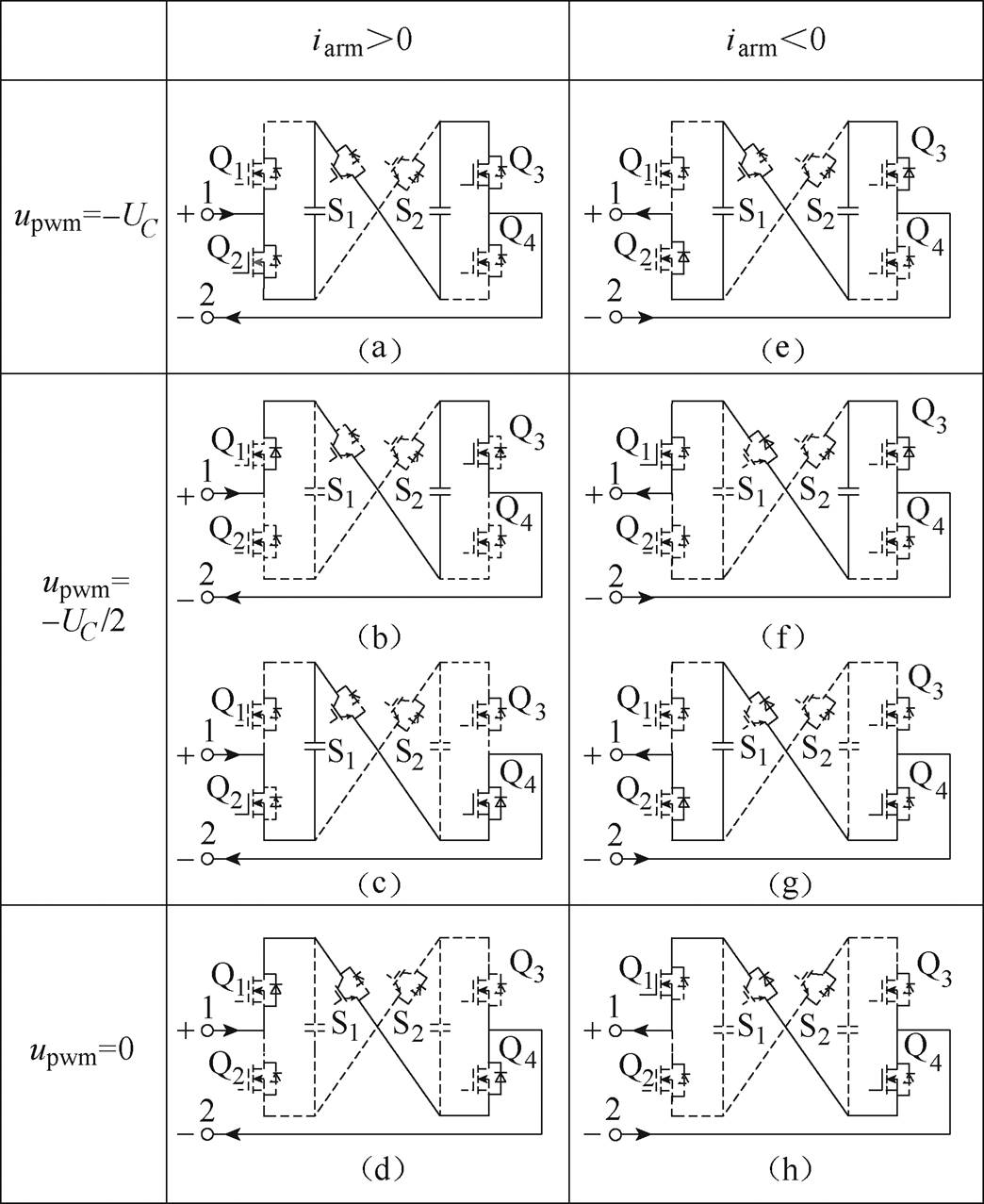
图8 模式Ⅱ下高频子模块的工作状态
Fig.8 Working state of high frequency submodule in mode Ⅱ
Ⅰ（c）：桥臂电流iarm＞0；S1开，S2闭；Q1、Q3闭，Q2、Q4开；upwm=UC/2；CH2旁路、CH1充电。
Ⅰ（d）：桥臂电流iarm＞0；S1开，S2闭；Q2、Q3闭，Q1、Q4开；upwm=0；CH1、CH2旁路。
Ⅰ（e）：桥臂电流iarm＜0；S1开，S2闭；Q1、Q4闭，Q2、Q3开；upwm=UC；CH1、CH2放电。
Ⅰ（f）：桥臂电流iarm＜0；S1开，S2闭；Q2、Q4闭，Q1、Q3开；upwm=UC/2；CH1旁路、CH2放电。
Ⅰ（g）：桥臂电流iarm＜0；S1开，S2闭；Q1、Q3闭，Q2、Q4开；upwm=UC/2；CH2旁路、CH1放电。
Ⅰ（h）：桥臂电流iarm＜0；S1开，S2闭；Q2、Q3闭，Q1、Q4开；upwm=0；CH1、CH2旁路。
Ⅱ（a）：桥臂电流iarm＞0；S1闭，S2开；Q2、Q3闭，Q1、Q4开；upwm=-UC；CH1、CH2放电。
Ⅱ（b）：桥臂电流iarm＞0；S1闭，S2开；Q1、Q3闭，Q2、Q4开；upwm=-UC/2；CH1旁路、CH2放电。
Ⅱ（c）：桥臂电流iarm＞0；S1闭，S2开；Q2、Q4闭，Q1、Q3开；upwm=-UC/2；CH2旁路、CH1放电。
Ⅱ（d）：桥臂电流iarm＞0；S1闭，S2开；Q1、Q4闭，Q2、Q3开；upwm=0；CH1、CH2旁路。
Ⅱ（e）：桥臂电流iarm＜0；S1闭，S2开；Q2、Q3闭，Q1、Q4开；upwm=-UC；CH1、CH2充电。
Ⅱ（f）：桥臂电流iarm＜0；S1闭，S2开；Q1、Q3闭，Q2、Q4开；upwm=-UC/2；CH1旁路、CH2充电。
Ⅱ（g）：桥臂电流iarm＜0；S1闭，S2开；Q2、Q4闭，Q1、Q3开；upwm=-UC/2；CH2旁路、CH1充电。
Ⅱ（h）：桥臂电流iarm＜0；S1闭，S2开；Q1、Q4闭，Q2、Q3开；upwm=0；CH1、CH2旁路。
综上所述，通过控制高频子模块在16种工作状态间灵活切换，可以改变高频子模块中两个直流电容CH1、CH2的充放电状态，以实现电容电压稳定。
由于三相完全对称，以a相上桥臂为例进行分析。高频子模块均压主要包括整体均压和内部均压两块，具体均压流程如图9所示。图中，UCH为高频子模块两个直流电容电压和。
（1）由式（4）计算上桥臂低频子模块需要投入的数量nstep_pa。
（2）将当前时刻与上一时刻计算的nstep_pa进行比较，若未发生变化，则重新计算；若发生变化，则进入均压判断模式。
（3）整体均压。若iarm＞0且nstep_pa=N-1，则只能工作于模式Ⅰ；若iarm＞0且nstep_pa＜N-1，则判断高频子模块电容总电压UCH和参考电容电压UC的关系，若UCH＜UC，工作于模式Ⅰ；若UCH＞UC，工作于模式Ⅱ。若iarm＜0且nstep_pa=N-1，则只能工作于模式Ⅰ；若iarm＜0且nstep_pa＜N-1，则判断高频子模块电容电压和参考电容电压UC的关系，若UCH＜UC，工作于模式Ⅱ；若UCH＞UC，工作于模式Ⅰ。
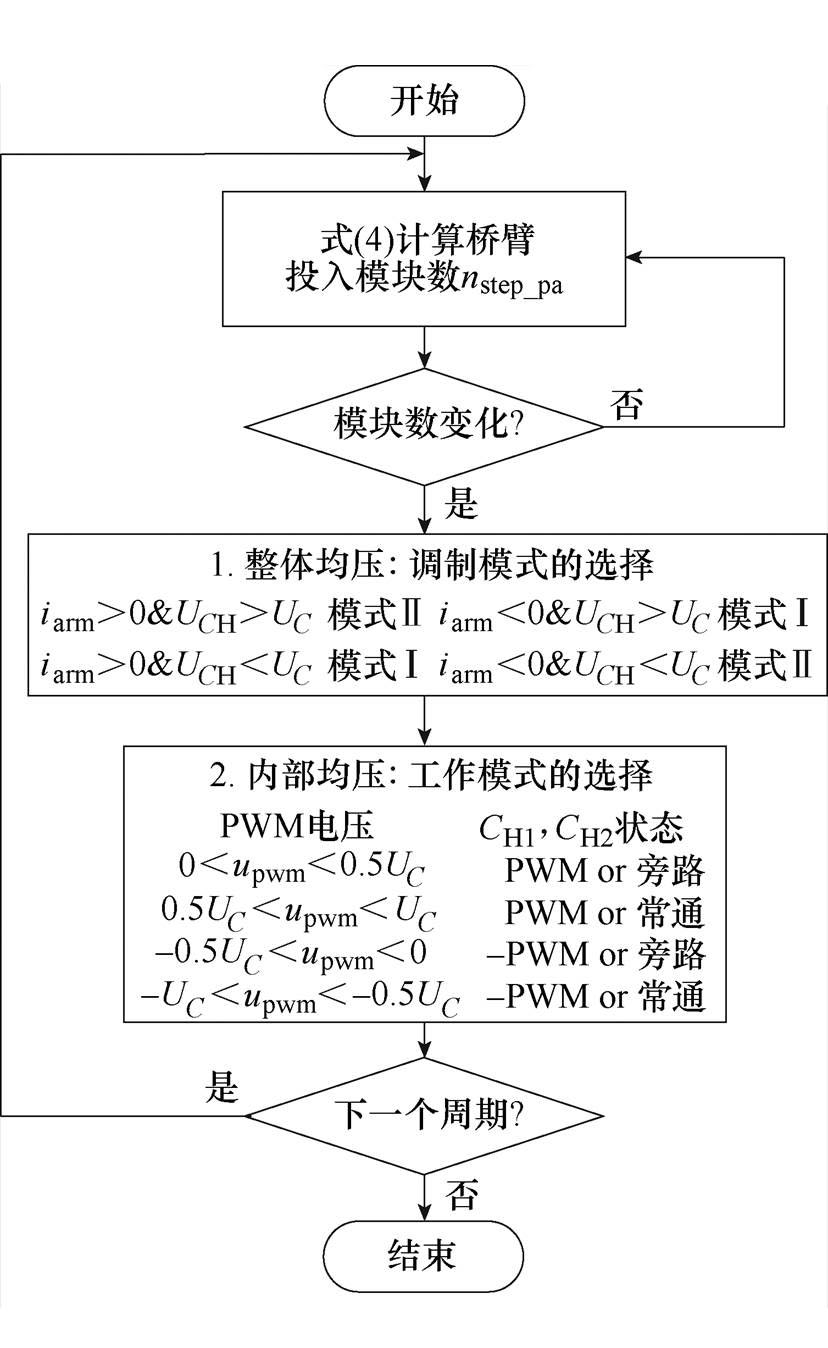
图9 高频子模块的均压流程
Fig.9 Voltage balancing process of the high-frequency submodule
（4）内部均压。以高频模块输出正电压为例：upwm=UC且iarm＞0，高频子模块整体为充电，则CH1和CH2电容电压小的被常通，电容电压大的做PWM斩波；upwm=UC且iarm＜0，高频子模块整体为放电，则CH1和CH2电容电压大的被常通，电容电压小的做PWM斩波；upwm=0.5UC且iarm＞0，高频子模块整体为充电，则CH1和CH2电容电压大的被旁路，电容电压小的做PWM斩波；upwm=0.5UC且iarm＜0，高频子模块整体为放电，则CH1和CH2电容电压小的被旁路，电容电压大的做PWM斩波。
为验证所提拓扑及其调制、均压策略的可行性，在Matlab/Simulink中搭建了NMMC仿真模型，仿真参数见表2。
NMMC的仿真波形如图10所示，图10a为NMMC a相出口端输出电压及其总谐波畸变率（Total Harmonic Distortion, THD），谐波含量仅为7%左右，且谐波频次在开关频率附近；图10b为a相输出电流及其THD，其谐波含量低接近正弦；图10c为a相上桥臂输出电压，共17电平（即2N+1电平）；图10d为a相上桥臂低频模块输出电压，其中红色虚线圈标注点为模式Ⅰ和Ⅱ切换时刻；图10e为a相高频子模块输出电压，其为五电平的高频PWM波；图10f为a相低频子模块输出电压，每个周期内的开关频次极低；图10g为a相上桥臂子模块直流侧电压，其中低频子模块和高频子模块直流侧电容电压分别维持在1 250 V和625 V附近，且电压波动幅值均小于5%。
表2 仿真参数
Tab.2 Simulation parameters
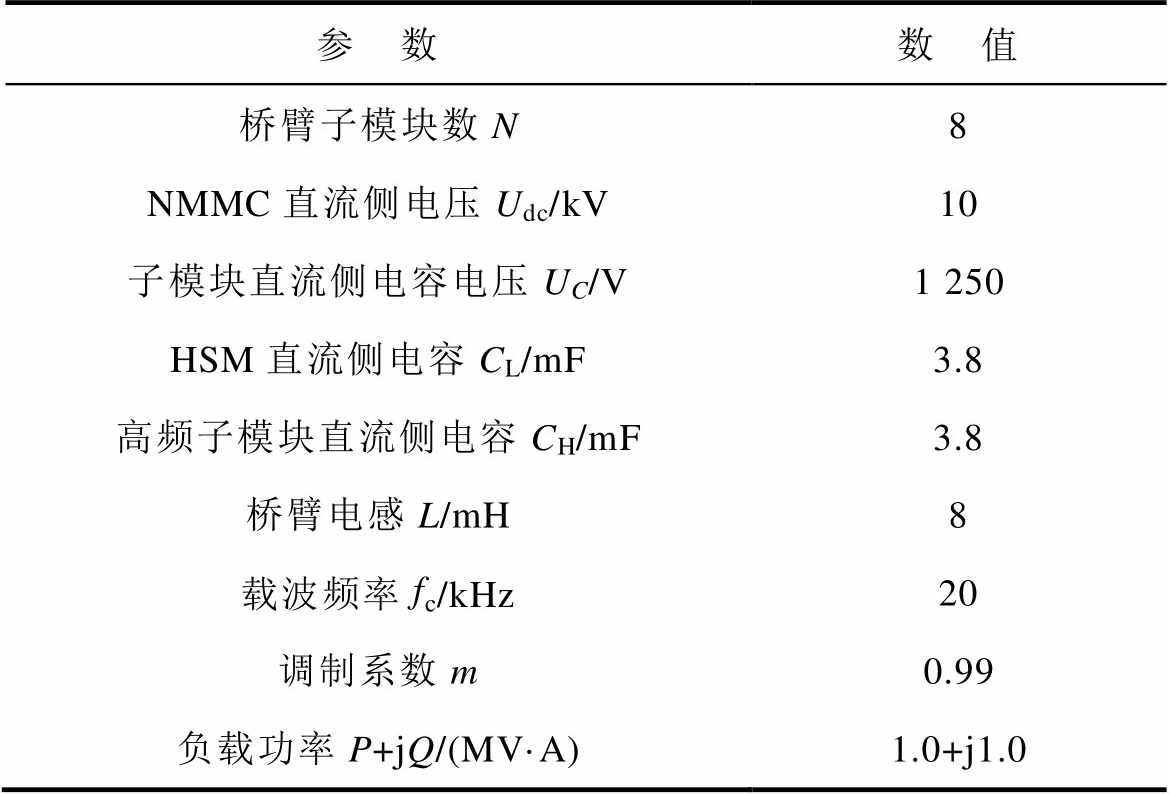
参 数数 值 桥臂子模块数N8 NMMC直流侧电压Udc/kV10 子模块直流侧电容电压UC/V1 250 HSM直流侧电容CL/mF3.8 高频子模块直流侧电容CH/mF3.8 桥臂电感L/mH8 载波频率fc/kHz20 调制系数m0.99 负载功率P+jQ/(MV·A)1.0+j1.0
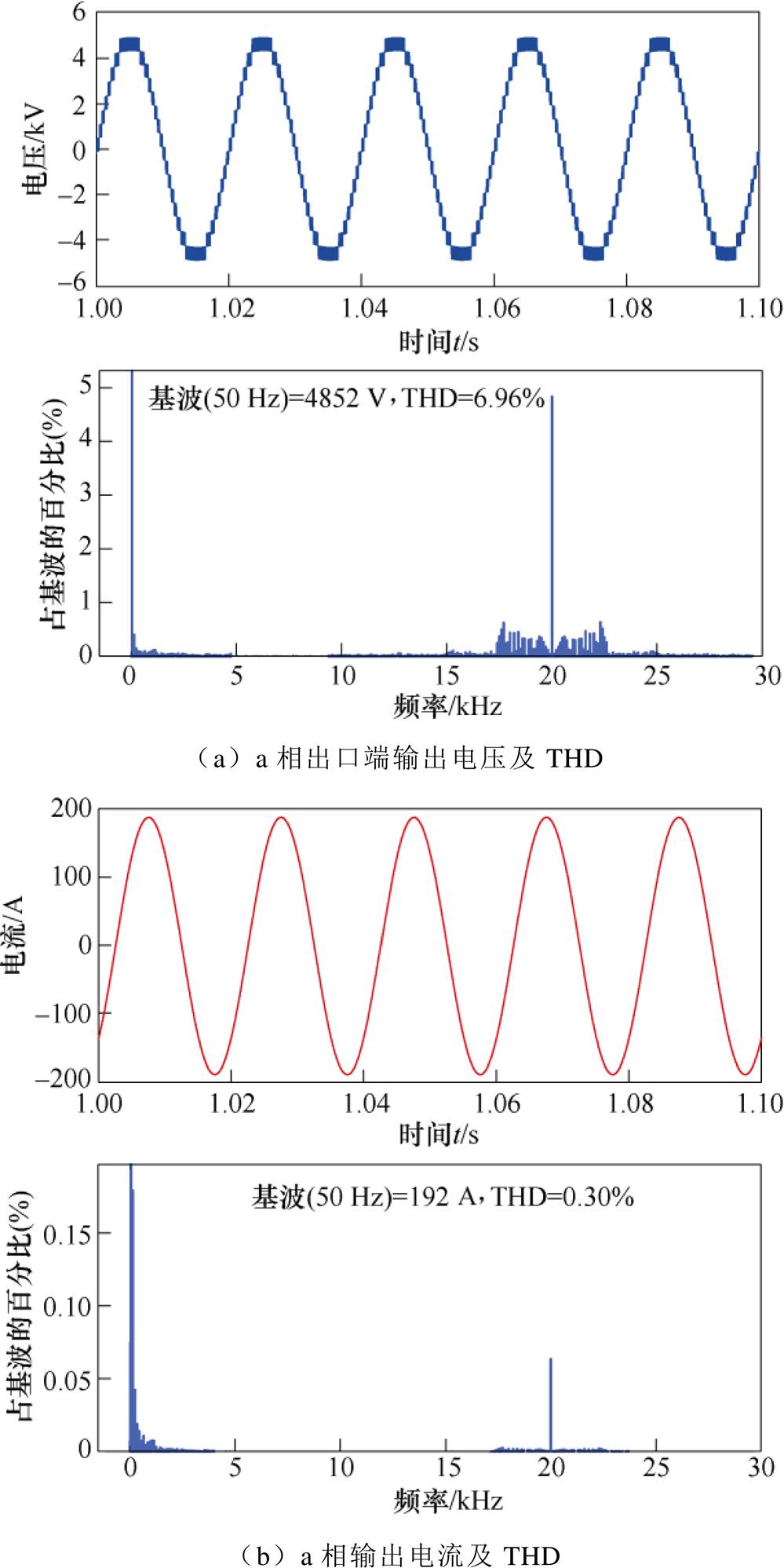
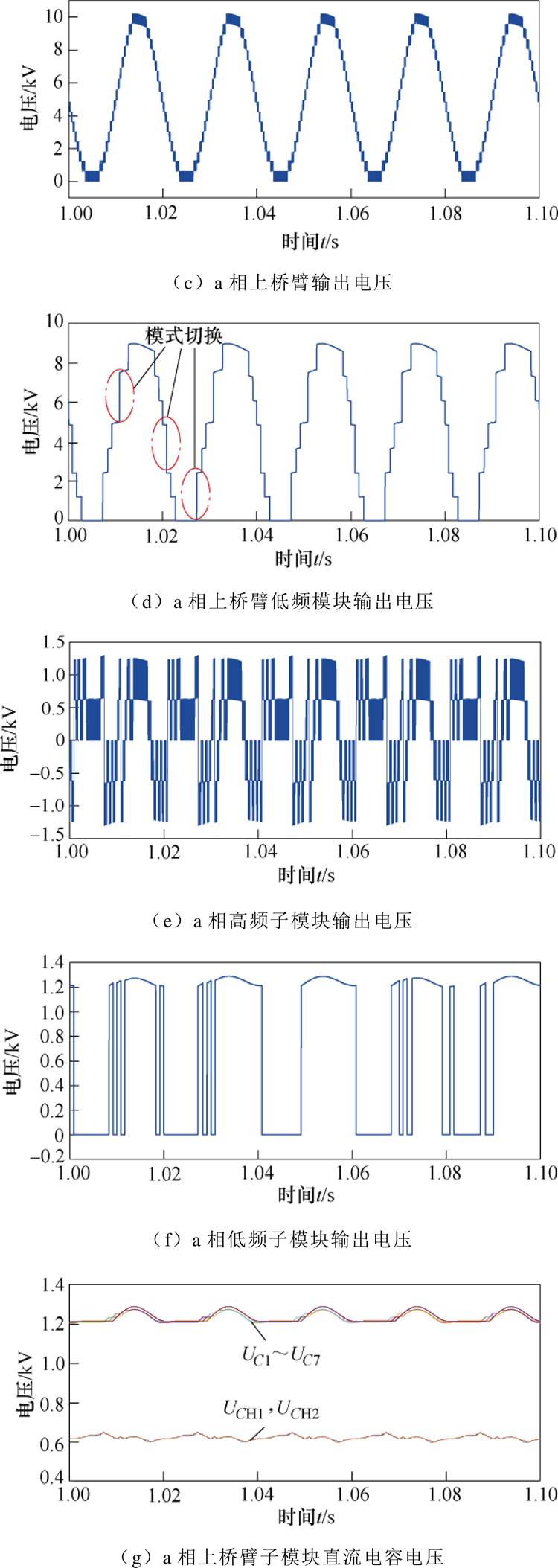
图10 NMMC仿真波形
Fig.10 Simulation waveforms of NMMC
为进一步证明NMMC可保持优良的输出性能，与传统MMC输出电压的THD进行对比，如图11所示。在保持相同等效输出频率条件下，传统MMC采用双极性载波移相调制时可输出九电平，THD为12.96%；而采用单极倍频载波移相调制时可输出十七电平，THD为6.62%。因此，所提NMMC具有与传统MMC采用单极倍频载波移相调制相近的输出性能。
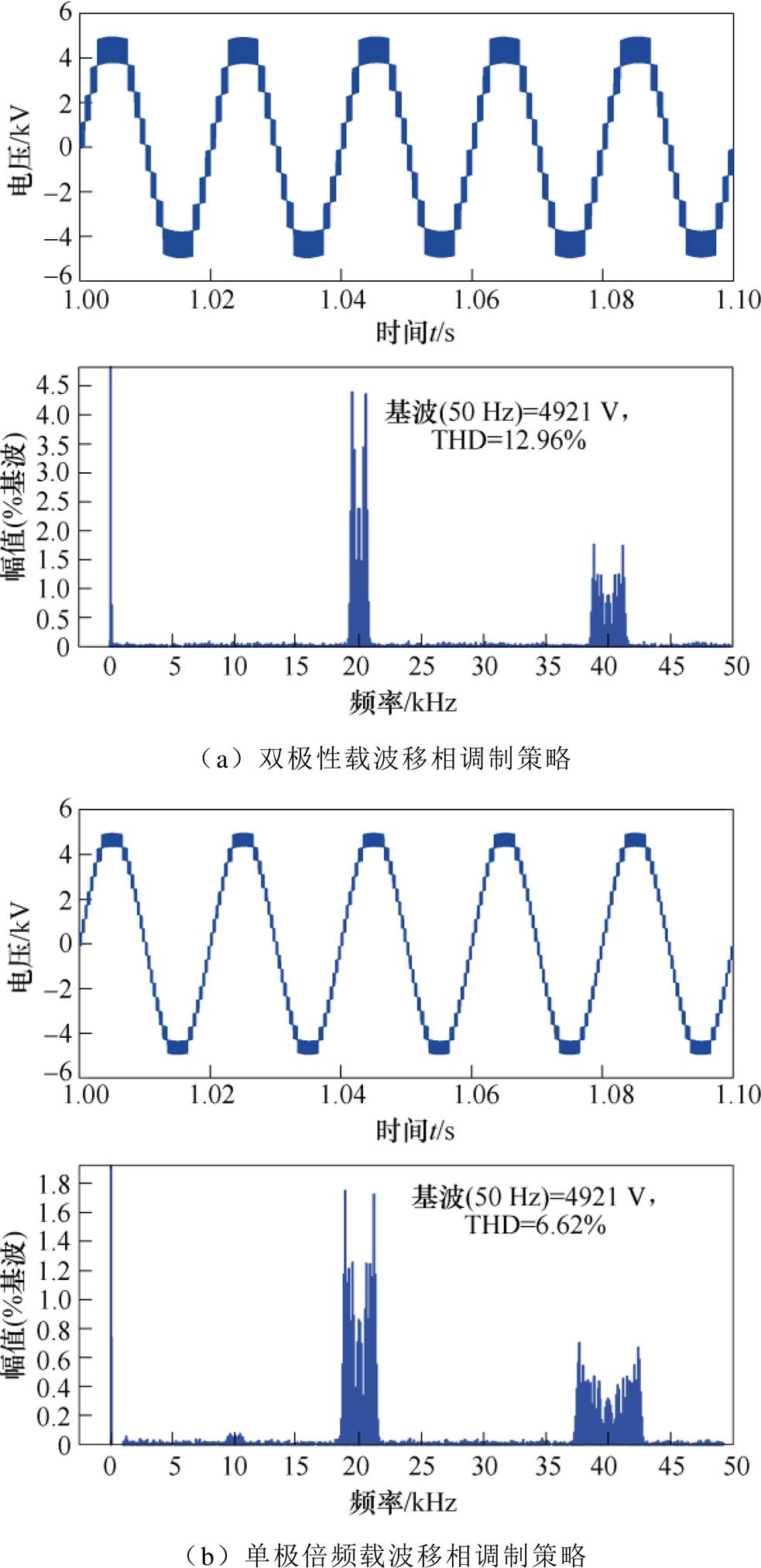
图11 传统MMC出口端输出电压及THD
Fig.11 The output voltage and THD of traditional MMC
为进一步验证所提拓扑及其调制、均压策略的可行性，在实验室搭建了NMMC在环实验平台，拓扑参数与仿真参数保持一致，其载波频率取为10 kHz。
以a相上桥臂为例，NMMC的上桥臂输出电压uao_p、上桥臂低频模块输出电压ustep_pa、高频子模块输出电压upwm_pa、低频子模块输出电压ustep_pa1如图12所示，其中总电平数为17，两种调制模式的切换时刻如图中标记所示，而高频模块输出电压为五电平高频PWM波，低频模块输出电压则为两电平低频方波。
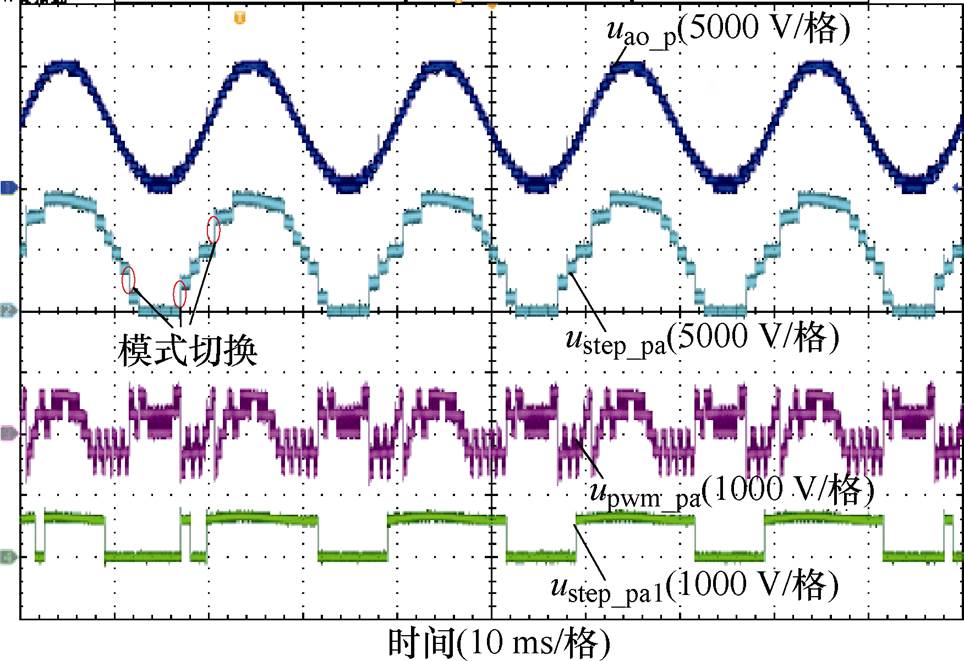
图12 NMMC输出电压
Fig.12 Output voltage waveforms of NMMC
图13为NMMC子模块电容电压实验波形，分别给出了两个低频子模快电容电压和高频子模块中的两个电容电压。低频子模快电容电压可以稳定到1 250 V左右，而高频子模块电容电压则稳定到625 V左右，充分验证了所提稳压策略的有效性。
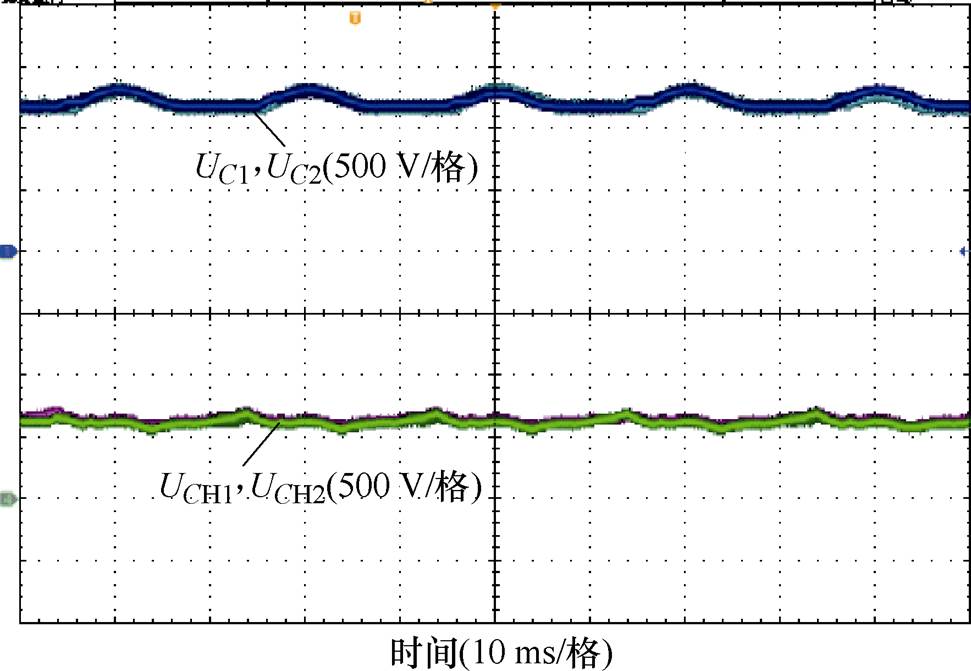
图13 NMMC电容电压
Fig.13 Capacitance voltage waveforms of NMMC
图14为a相输出电压及THD分析，可以看出谐波幅值较小且主要为开关频次谐波。图15为a相输出电流及THD谐波，其波形接近正弦。
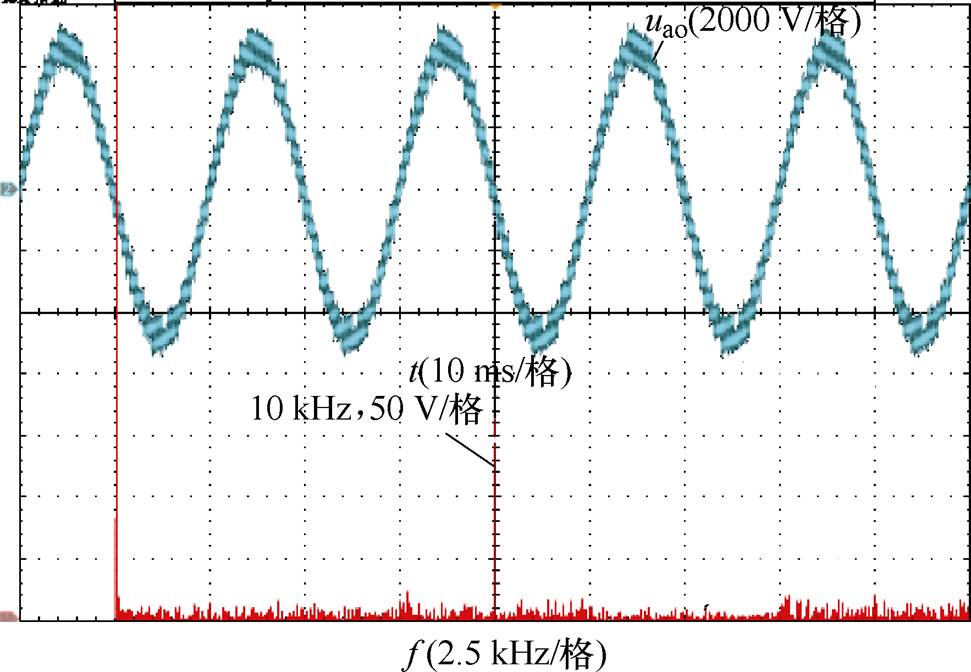
图14 a相输出电压及THD
Fig.14 Waveforms and THD of phase a output voltage
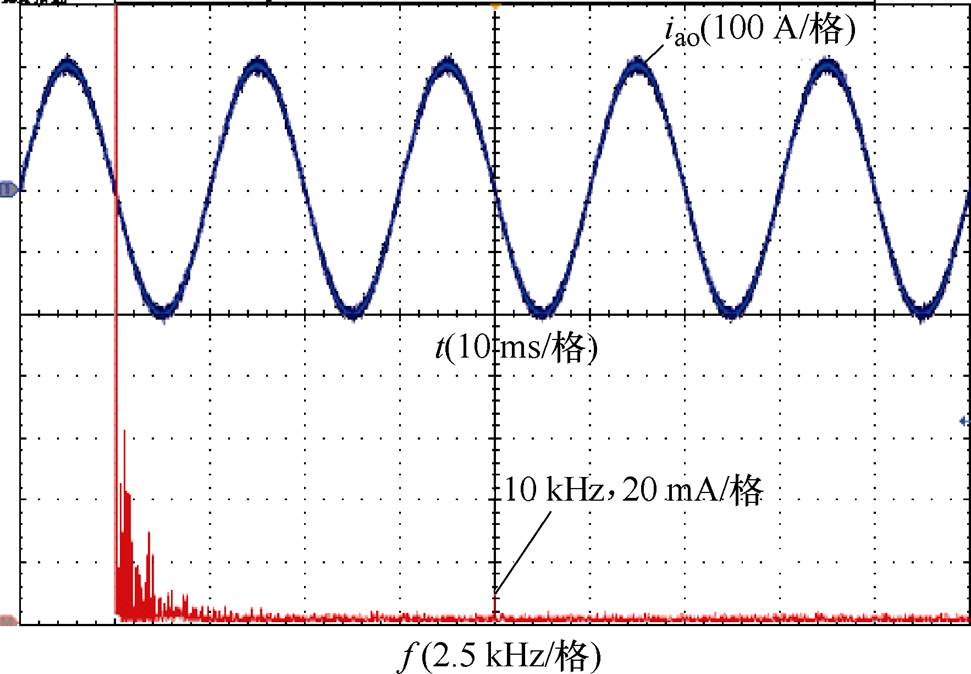
图15 a相输出电流及THD
Fig.15 Waveform and THD of phase a output current
器件成本是装置总成本的主要组成，为进一步验证所提拓扑的优势，故将所提拓扑与现有拓扑进行器件成本对比。基于全Si IGBT器件的MMC（Si MMC）、全SiC MOSFET器件的MMC（SiC MMC）、文献[22]所提拓扑以及本文所提NMMC拓扑的器件成本对比见表3。以上四种拓扑均取直流母线电压为10 kV、每个桥臂的高低频模块总数为8。若以Si MMC拓扑成本为基准，SiC MMC拓扑、文献[22]拓扑、所提拓扑成本分别增加273.4%、147.5%、80%。因此，相比文献[22]，NMMC在保障输出波形质量的前提下，器件成本大大降低。
表3 器件成本对比
Tab.3 Device cost comparison
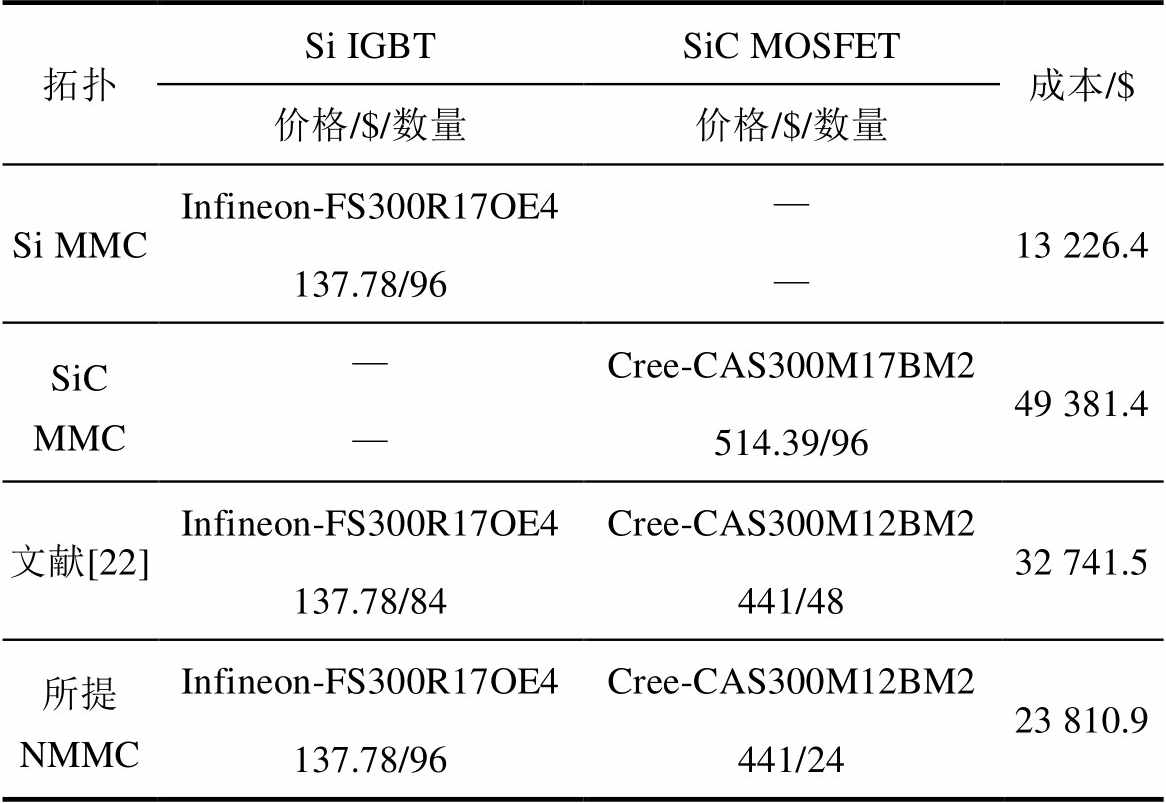
拓扑Si IGBTSiC MOSFET成本/$ 价格/$/数量价格/$/数量 Si MMCInfineon-FS300R17OE4—13 226.4 137.78/96— SiC MMC—Cree-CAS300M17BM249 381.4 —514.39/96 文献[22]Infineon-FS300R17OE4Cree-CAS300M12BM232 741.5 137.78/84441/48 所提NMMCInfineon-FS300R17OE4Cree-CAS300M12BM223 810.9 137.78/96441/24
为验证所提拓扑在运行损耗上的优势，基于Matlab/Simulink与PLECS联合仿真平台，在波形质量接近的条件下搭建了Si MMC拓扑、SiC MMC拓扑、文献[22]拓扑、所提NMMC拓扑的热损耗模型。其中，拓扑参数均与表2保持一致，器件参数均与表3保持一致。
在器件结温Tj=100℃、等效输出开关频率feq= 20 kHz条件下，不同负载功率时四种拓扑的损耗对比如图16所示。在通态损耗方面，随着负载功率增大，四种拓扑的通态损耗增加。其中，SiC-MMC拓扑的通态损耗随功率增加而增长最快。在开关损耗方面，Si-MMC拓扑的开关损耗远高于其他拓扑，而SiC-MMC拓扑的开关损耗最小。对于总损耗而言，在小功率工况，Si-MMC损耗最大，SiC-MMC损耗最小；在大功率工况下，由于SiC-MMC通态损耗急剧增加，故总损耗甚至高于所提NMMC拓扑总损耗。以负载功率2.1 MW为例，所提NMMC总损耗相比于Si-MMC、SiC-MMC和文献[22]拓扑分别降低29.7%、6.7%和10.4%。
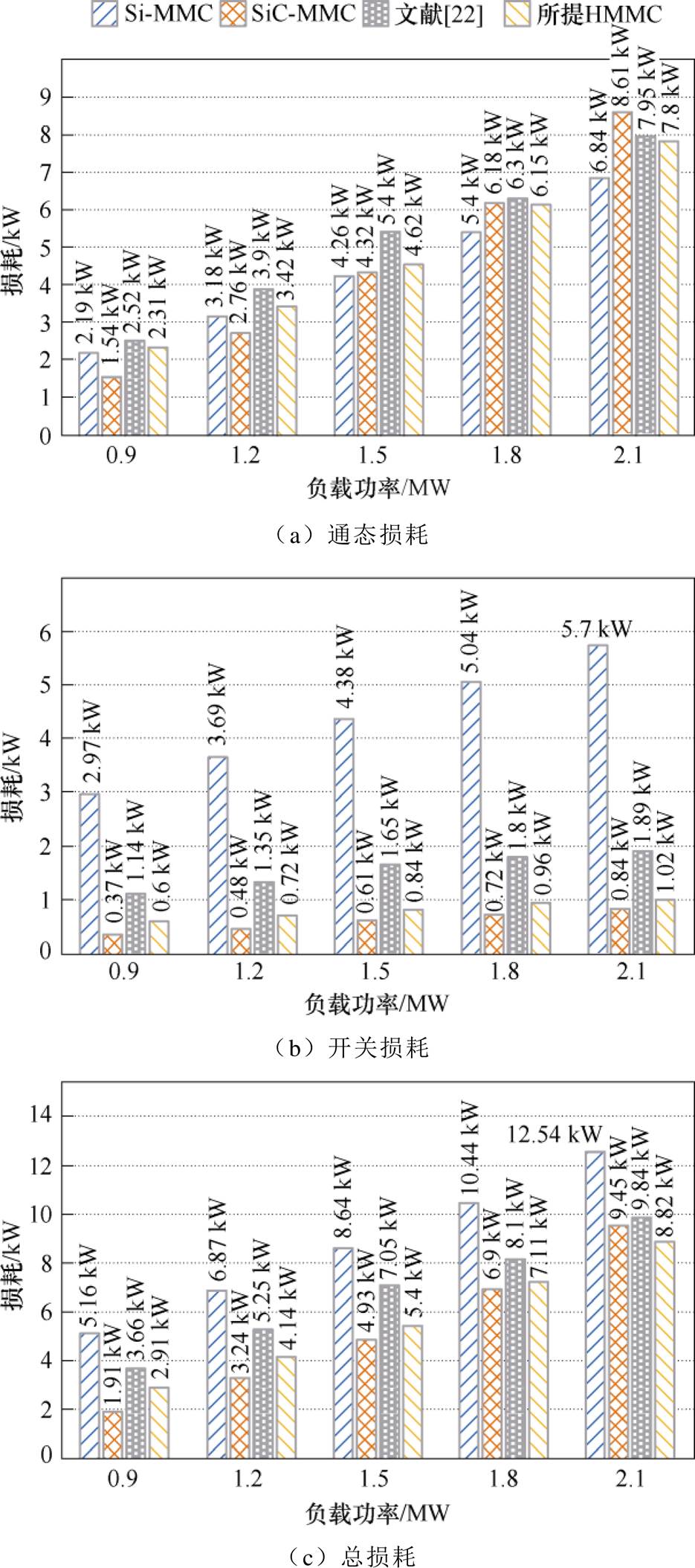
图16 不同负载功率下损耗对比（Tj=100℃，feq=20 kHz）
Fig.16 Loss comparison under different load power (Tj=100℃, feq=20 kHz)
在器件结温Tj=100℃、负载功率P=1.5 MW条件下，不同等效输出开关频率时四种拓扑的损耗对比如图17所示。由于通态损耗不受开关频率变化的影响，故通态损耗基本保持不变。在开关损耗方面，Si-MMC开关损耗最大，且随开关频率增加而增长最快，而SiC-MMC的开关损耗最小。对于总损耗而言，所提NMMC损耗远低于Si-MMC和文献[22]拓扑，且接近于SiC-MMC。以额定负载功率1.5 MW为例，所提NMMC总损耗相比于Si-MMC和文献[22]拓扑分别降低37.5%和23.4%。
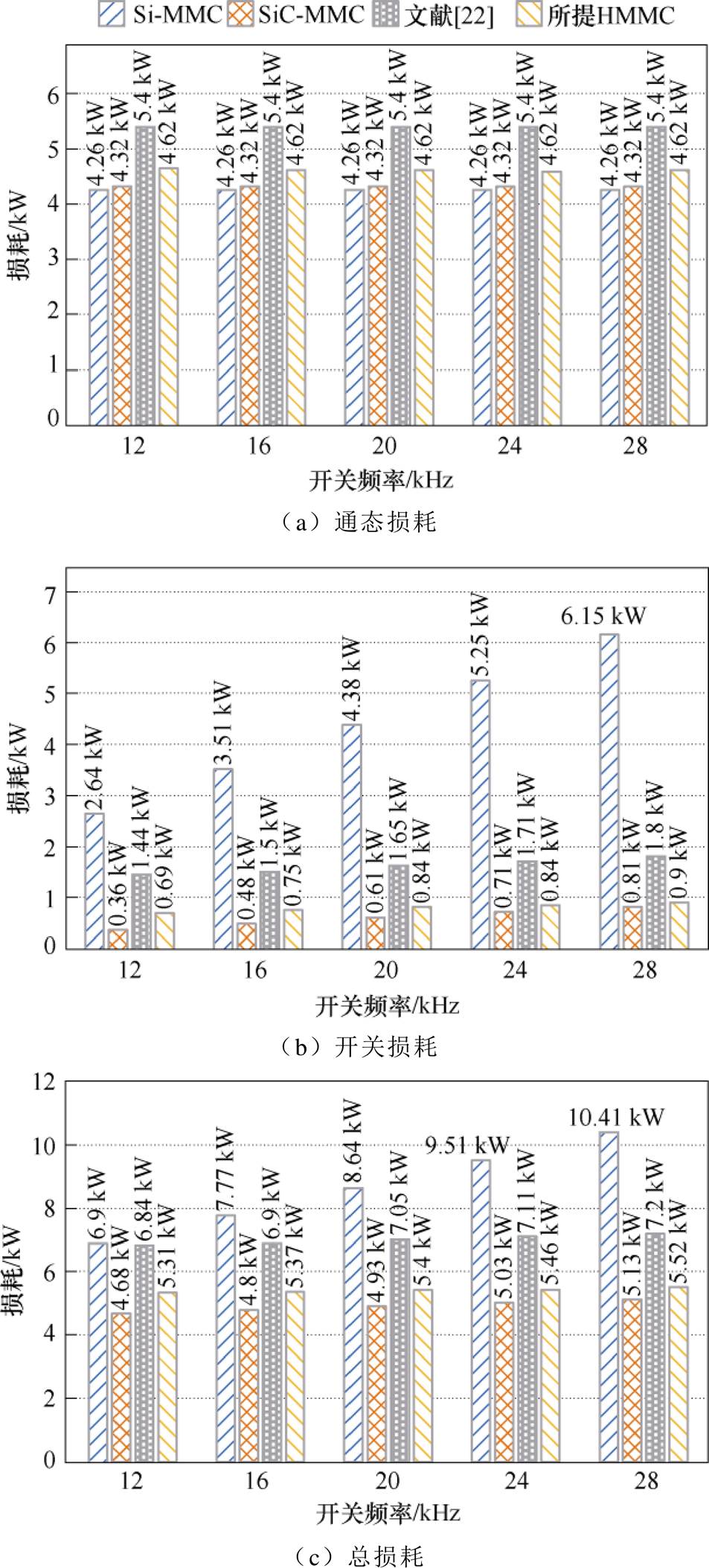
图17 不同等效开关频率下损耗对比（Tj=100℃，P=1.5 MW）
Fig.17 Loss comparison at different equivalent switching frequencies (Tj=100℃, P=1.5 MW)
为破解传统中压模块化多电平变换器输出性能提升与降本、增效难以有效兼顾的问题，本文从调制优化、异质器件混用等多角度提出一种新型模块化多电平变换器（NMMC）拓扑及其特定的调控策略，得出如下结论：
1）所提NMMC拓扑每个桥臂仅需一个高频子模块即可输出2N+1电平，SiC MOSFET器件数更少，装置的器件总成本更低。
2）采用混合调制策略，在保障输出波形质量的前提下，将高频动作主要集中于SiC MOSFET器件，而Si IGBT器件低频动作。在高等效开关频率、高输出功率工况下，所提方案的运行效率相比现有方案优势更加明显。
3）详细分析了高频子模块直流电容的能量波动机理，并提出一种特定的电压平衡策略，其可以有效维持高、低频子模块电容电压的稳定。
下一步，作者将对所提混合型模块化多电平变换器的可靠性评估、容错运行等工作开展深入研究。
参考文献
[1] 束洪春, 邵宗学, 江耀曦, 等. 具备闭锁和非闭锁模式抑制直流故障电流的新型模块化多电平变换器拓扑[J]. 电工技术学报, 2022, 37(21): 5526-5540.
Shu Hongchun, Shao Zongxue, Jiang Yaoxi, et al. A new modular multilevel converter topology with capability of DC faults clearing under blocking and non-blocking mode[J]. Transactions of China Elec- trotechnical Society, 2022, 37(21): 5526-5540.
[2] 任鹏, 涂春鸣, 侯玉超, 等. 基于Si和SiC器件的混合型级联多电平变换器及其调控优化方法[J]. 电工技术学报, 2023, 38(18): 5017-5028.
Ren Peng, Tu Chunming, Hou Yuchao, et al. Research on a hybrid cascaded multilevel converter based on Si and SiC device and its control optimization method[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 5017-5028.
[3] 刘计龙, 陈鹏, 肖飞, 等. 面向舰船综合电力系统的10 kV/2 MW模块化多电平双向直流变换器控制策略[J]. 电工技术学报, 2023, 38(4): 983-997.
Liu Jilong, Chen Peng, Xiao Fei, et al. Control strategy of 10 kV/2 MW modular multilevel bidi- rectional DC-DC converter for vessel integrated power system[J]. Transactions of China Electrotech- nical Society, 2023, 38(4): 983-997.
[4] 江畅, 程启明, 马信乔, 等. 不平衡电网电压下基于模块化多电平变流器的统一电能质量调节器的微分平坦控制[J]. 电工技术学报, 2021, 36(16): 3410-3421.
Jiang Chang, Cheng Qiming, Ma Xinqiao, et al. Differential flat control for unified power quality controller based on modular multilevel converter under unbalanced grid voltage[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3410- 3421.
[5] 武鸿, 王跃, 薛英林, 等. 适用多功率的最近电平调制下MMC子模块开路故障诊断策略[J]. 电工技术学报, 2024, 39(1): 233-245, 302.
Wu Hong, Wang Yue, Xue Yinglin, et al. A diagnosis strategy for open-circuit submodule faults in MMCs under nearst level modulation suitable for different powers[J]. Transactions of China Electrotechnical Society, 2024, 39(1): 233-245, 302.
[6] 公铮, 张海军, 戴鹏, 等. 新型并联交错型多电平变换器的桥臂统一脉宽调制策略[J]. 中国电机工程学报, 2018, 38(23): 7026-7034, 7136.
Gong Zheng, Zhang Haijun, Dai Peng, et al. Leg-unified pulse width modulation strategy for novel parallel interleaved multilevel converters[J]. Pro- ceedings of the CSEE, 2018, 38(23): 7026-7034, 7136.
[7] 刘浩然, 陈武, 舒良才, 等. 一种新型串联单链式模块化多电平变换器[J]. 中国电机工程学报, 2023, 43(21): 8444-8456.
Liu Haoran, Chen Wu, Shu Liangcai, et al. A novel series single chain-link modular multilevel con- verter[J]. Proceedings of the CSEE, 2023, 43(21): 8444-8456.
[8] 杜舒, 赵成勇, 冯谟可, 等. 用于全直流海上风电系统的单相混合型MMC直流变压器及其控制策略[J]. 高电压技术, 2023, 49(1): 51-60.
Du Shu, Zhao Chengyong, Feng Moke, et al. Single- phase hybrid MMC DC transformer and its control strategy for all-DC offshore wind power system[J]. High Voltage Engineering, 2023, 49(1): 51-60.
[9] 张国荣, 颜丽花. 单极倍频CPS-SPWM传输带宽的研究[J]. 电力系统保护与控制, 2018, 46(12): 1-8.
Zhang Guorong, Yan Lihua. Study on the trans- mission bandwidth of unipolar frequency doubled CPS-SPWM[J]. Power System Protection and Control, 2018, 46(12): 1-8.
[10] Li Zixin, Wang Ping, Zhu Haibin, et al. An improved pulse width modulation method for chopper-cell- based modular multilevel converters[J]. IEEE Transa- ctions on Power Electronics, 2012, 27(8): 3472- 3481.
[11] 魏承志, 练睿, 杨桦, 等. 一种混合型模块化多电平换流器的改进载波移相调制方法[J]. 电力系统自动化, 2016, 40(7): 68-73, 106.
Wei Chengzhi, Lian Rui, Yang Hua, et al. An improved phase shifted carrier modulating method for hybrid modular multilevel converter[J]. Automation of Electric Power Systems, 2016, 40(7): 68-73, 106.
[12] Hu Pengfei, Jiang Daozhuo. A level-increased nearest level modulation method for modular multilevel converters[J]. IEEE Transactions on Power Elec- tronics, 2015, 30(4): 1836-1842.
[13] Wu Deliang, Peng Li. Characteristics of nearest level modulation method with circulating current control for modular multilevel converter[J]. IET Power Electronics, 2016, 9(2): 155-164.
[14] Wang Yi, Hu Can, Ding Ruoyu, et al. A nearest level PWM method for the MMC in DC distribution grids[J]. IEEE Transactions on Power Electronics, 2018, 33(11): 9209-9218.
[15] Wang Zhen, Peng Li, Zhang Jiawei. Decomposed nearest level PWM method with reduced switching frequency for MMC[J]. IEEE Transactions on Power Electronics, 2023, 38(3): 3340-3351.
[16] 任鹏, 涂春鸣, 侯玉超, 等. 考虑异质器件混用与输出电平倍增的混合型MMC及其调控方法[J]. 电力系统自动化, 2024, 48(5): 128-136.
Ren Peng, Tu Chunming, Hou Yuchao, et al. Hybrid modular multilevel converter considering hetero- neous device mixing and output level doubling and its regulation method[J]. Automation of Electric Power Systems, 2024, 48(5): 128-136.
[17] 缪惠宇, 梅军, 张宸宇, 等. 一种新型的n+1混合式模块化多电平换流器拓扑结构及其控制策略[J]. 电力自动化设备, 2018, 38(3): 88-95.
Miao Huiyu, Mei Jun, Zhang Chenyu, et al. A novel topology of n+1 hybrid modular multilevel converter and its control strategy[J]. Electric Power Automation Equipment, 2018, 38(3): 88-95.
[18] Shahane R, Belkhode S, Shukla A, et al. A highly efficient hybrid devices-based MMC with a novel modulation scheme using hardware-in-loop system[C]// 022 IEEE Applied Power Electronics Conference and Exposition (APEC), Houston, TX, USA, 2022: 675- 680.
[19] Li Chushan, Lu Rui, Li Chengmin, et al. Space vector modulation for SiC and Si hybrid ANPC converter in medium-voltage high-speed drive system[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 3390-3401.
[20] Liu Chuang, Zhuang Kehao, Pei Zhongchen, et al. Hybrid SiC-Si DC-AC topology: SHEPWM Si-IGBT master unit handling high power integrated with partial-power SiC-MOSFET slave unit improving performance[J]. IEEE Transactions on Power Elec- tronics, 2022, 37(3): 3085-3098.
[21] Zhang Chao, Wang Jun, Qu Kun, et al. WBG and Si hybrid half-bridge power processing toward optimal efficiency, power quality, and cost tradeoff[J]. IEEE Transactions on Power Electronics, 2022, 37(6): 6844-6856
[22] Yin Tianxiang, Lin Lei, Xu Chen, et al. A hybrid modular multilevel converter comprising SiC MOSFET and Si IGBT with its specialized modulation and voltage balancing scheme[J]. IEEE Transactions on Industrial Electronics, 2022, 69(11): 11272-11282.
Abstract The traditional modular multilevel converter (MMC) generally adopts a single type of device. The typical Si-based MMC (Si-MMC) has low cost, while SiC-based MMC (SiC-MMC) has high efficiency. In addition, under the same specifications, the price of SiC MOSFET devices is usually 5～8 times that of Si IGBT devices. It is difficult to effectively balance the output performance, cost, and efficiency of the medium voltage MMC. This paper proposes a new MMC (NMMC) topology. Each arm of the proposed NMMC contains a high-frequency sub-module featuring a heterogeneous cross-connect module (HCCM) and a low-frequency sub-module composed of N-1 half-bridge converters. The high-frequency bridge arm of HCCM adopts SiC MOSFET devices, while the commutation bridge arm and low-frequency sub-module adopt Si IGBT devices.
Firstly, the NMMC topology employs a high-low frequency hybrid modulation strategy, providing low switching loss of SiC MOSFET devices and low on-state loss of Si IGBT devices. Secondly, the energy fluctuation mechanism and working state of the high-frequency sub-module in different modes are analyzed. A specific capacitor voltage balancing strategy is proposed for the high-frequency sub-module, and a detailed voltage balancing control flow chart is given.
Simulation and experiments are carried out to verify the proposed topology, modulation strategy, and voltage balancing strategy. The proposed structure achieves 2N+1 levels. Its high-frequency switching action is mainly concentrated in SiC MOSFET devices, while Si IGBT devices work in the low-frequency state. The total loss at different equivalent switching frequencies and output power is analyzed on the Matlab/Simulink and PLECS joint simulation platform. Taking the rated load power of 1.5 MW and the equivalent switching frequency of feq= 20 kHz as an example, the total loss of the proposed NMMC is 37.5%, lower than that of Si-MMC and close to that of SiC-MMC. The proposed topology is 80% lower cost than the Si-MMC and 51.8% lower than the SiC-MMC.
The following conclusions can be drawn: (1) The NMMC topology outputs 2N+1 levels with only one high-frequency sub-module per arm, reducing the number of SiC MOSFET devices and overall device cost. (2) The high-frequency action primarily involves SiC MOSFET devices, while the low-frequency action of Si IGBT devices is adopted. Under high equivalent switching frequency and output power, the operation efficiency of the proposed scheme is significantly enhanced. (3) The energy fluctuation mechanism of the high-frequency sub-module DC capacitor is analyzed, and a specific voltage balance strategy is proposed, which can effectively maintain the stability of the high and low-frequency sub-module capacitor voltage.
keywords：Modular multilevel converter, Si IGBT, SiC MOSFET, hybrid modulation, level number doubled
DOI: 10.19595/j.cnki.1000-6753.tces.230880
中图分类号：TM464
国家自然科学基金（52130704）和湖南省研究生科研创新（CX20230430）资助项目。
收稿日期 2023-06-09
改稿日期 2023-08-29
侯玉超 男，1997年生，博士，研究方向为电力电子在电力系统中的应用。E-mail: houyuchaoyx@163.com
郭 祺 男，1993年生，副研究员，研究方向为电力电子变换器、分布式发电与电能质量先进控制。E-mail: qguo_215@163.com（通信作者）
（编辑 陈 诚）