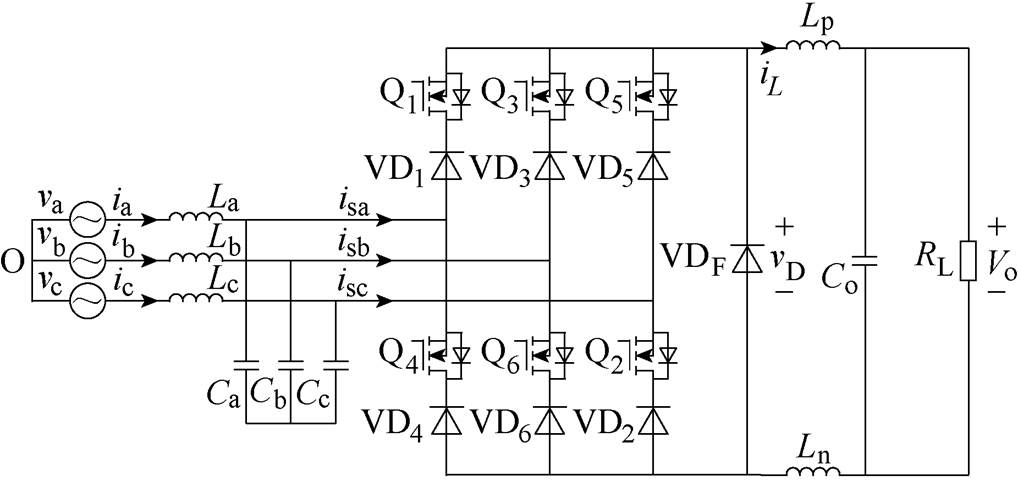
图1 三相Buck整流器
Fig.1 Three-phase Buck rectifier
摘要 三相输入电压不平衡时,传统双环控制三相Buck整流器的输出电压存在二倍频脉动,输入电流发生明显畸变,严重影响整流器的性能和可靠性。为抑制输出电压脉动和输入电流畸变,该文通过建立三相Buck整流器在两相静止坐标系下的等效电路模型及功率传输数学模型,分析输出电压二倍频脉动及输入电流畸变产生的机理,在此基础上提出一种基于虚拟阻抗的输入不平衡控制策略,最后通过仿真和1 kW的实验样机验证了理论分析的正确性和所提控制策略的有效性。
关键词:三相Buck整流器 电网电压不平衡 输入电流畸变 虚拟阻抗
三相整流器可分为三相Buck整流器和三相Boost整流器[1-3]。相较于三相Boost整流器,三相Buck整流器因具有输出短路保护能力、较小的启动浪涌电流等特点而受到关注[4-5],广泛应用于多电飞 机[6-8]、不间断电源系统[9]、数据中心等领域[10-12]。
三相供电系统的电网故障、输电线路阻抗不平衡和单相负载等会导致三相输入电压不平衡[13-14],此时,传统双环控制三相Buck整流器存在输出电压二倍频脉动和输入电流畸变,严重影响整流器的性能和可靠性[15]。为提高三相Buck整流器的性能,有学者提出了适用于输入电压不平衡的控制策略[16-21]。
文献[16]通过建立三相输入电压与输出电压的传输矩阵,消除了输出电压纹波中的偶数次谐波和输入电流中的奇数次谐波,得到了正弦输入电流,但控制策略中因使用了锁相环和相序分量提取,增加了计算量。文献[17]提出一种基于传输矩阵的不平衡控制策略,使用微分算法代替锁相环,减少了计算量,在三相输入电压不平衡时有效地抑制了整流器的输入电流畸变和输出电压二倍频脉动,但微分算法对输入电压采样噪声敏感。文献[18]提出了一种双环控制策略,电压外环控制输出电压并为输出电流提供参考,电流内环控制输出电流并通过设计电流调整算法实现输入电流正弦和单位功率因数,但复杂的电流调整算法加大了计算量。文献[19]通过对不平衡输入电压进行正负序分量提取并优化负序电流参考值,减小了不平衡输入时直流链电流的纹波,但使用了锁相环和相序分量提取,加大了计算量和数字延时。文献[20]使用过零检测(Zero Crossing Detection, ZCD)代替锁相环检测相位,使用陷波器滤除调制信号的3次谐波,得到稳定的输出电压和正弦的输入电流,但没有考虑输入电压相位不平衡的情况。文献[21]提出一种功率跟随控制策略,通过重构输入电流参考,在输入不平衡时得到了较为平衡且正弦的输入电流,但整流器的输出电压存在二倍频脉动且随着输入频率降低而显著增大。
近年来,基于虚拟阻抗概念提出了多种不平衡输入控制方法[22-24],核心思想是基于阻抗的物理概念设计不平衡控制算法。文献[22]建立了三相Boost整流器在两相静止坐标系的等效电路模型,在模型中加入虚拟差模电阻和虚拟共模电阻,通过控制虚拟电阻值实现了多种控制目标,但其控制结构较为复杂。文献[23]建立了三相Boost整流器的虚拟同步电机模型,通过引入负序虚拟阻抗优化了负序电流的参考值,实现了恒定的输出电压,该控制策略需要提取相序分量,增加了计算量。文献[24]建立了三相Buck整流器在ab 坐标系的等效电路模型,并引入多个参数调整虚拟阻抗,实现了对有功功率和无功功率的灵活控制,但在控制算法中加入陷波器和扩张状态观测器,控制器设计较为复杂。
为了抑制输入不平衡时三相Buck整流器的输出电压二倍频脉动和输入电流畸变,本文提出了一种基于虚拟阻抗的不平衡控制策略。通过建立三相Buck整流器在ab 坐标系的等效电路模型,分析了输入电压不平衡时整流器的输出电压脉动和输入电流畸变的产生机理,基于虚拟阻抗概念,提出了一种适用于不平衡输入的控制策略,通过将三相输入电压转化到ab 坐标系,对两相输入电压进行相位检测和峰值检测(Peak Detection, PD),得到电压峰值和相位信息,从而构造对应的输入电流参考,使输入有功功率保持恒定,得到稳定的输出电压和正弦的输入电流。本文提出的控制策略不需要锁相环和相序分量提取,具有简单、易于实现的优点。最后通过仿真和实验验证了控制策略的有效性。
三相Buck整流器包括输入滤波器、开关单元和输出滤波器,如图1所示。图1中,vx、ix和isx(x=a, b, c)分别为三相输入电压、输入电流和桥臂输入电流,vD为续流二极管两端电压,iL为输出电感电流,Vo为输出电压。输入滤波器包括Lx和Cx,用于滤除开关单元产生的高频谐波;开关单元由三相上、下桥臂组成,每个桥臂包含一个MOSFET Qi和一个反向串联的二极管VDi(i=1~6);输出滤波器由电感Lp、Ln和电容Co组成,二极管VDF为输出滤波电感提供了续流通路。

图1 三相Buck整流器
Fig.1 Three-phase Buck rectifier
图2为传统双环控制三相Buck整流器的控制框图,它由比例积分(Proportion Integrate, PI)控制环路、调制波计算和空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM)组成,控制环路包括电压外环和电流内环,控制器采用PI控制,电流内环的输出ioPI与各相电压的乘积作为各相的调制波。
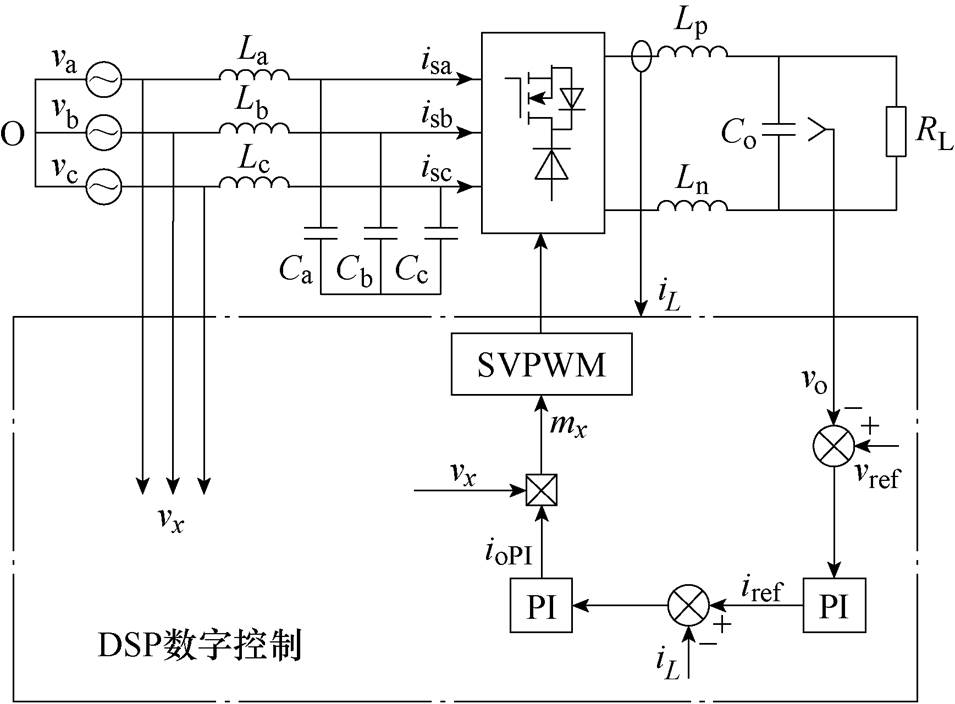
图2 传统双环控制三相Buck整流器
Fig.2 Conventional control strategy for the three-phase Buck rectifier
图2中,三相输入电压可以表示为
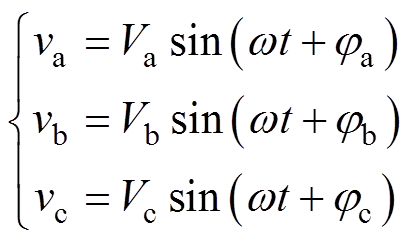 (1)
(1)
式中,Vx、jx分别为各相电压幅值、初始相位;w 为电网基波频率。
通过Clarke变换将三相输入电压转化到ab 坐标系,得到
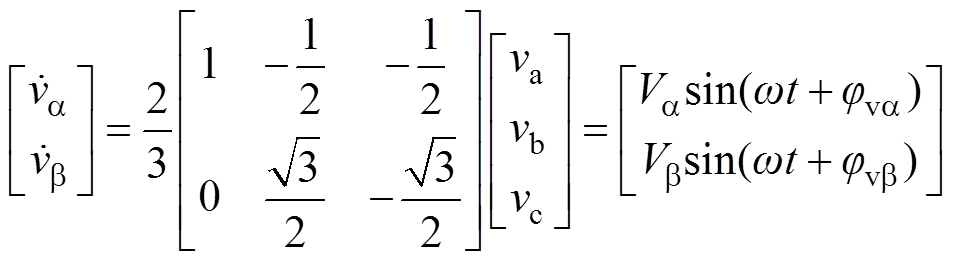 (2)
(2)
式中,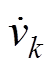 、
、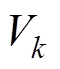 、
、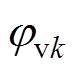 (k=a, b)分别为各相电压、电压幅值、初始相位。
(k=a, b)分别为各相电压、电压幅值、初始相位。
为简化分析,忽略输入滤波电感的压降及桥臂输入电流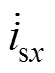 的谐波分量,
的谐波分量,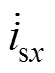 可简化为调制函数基波分量与电感电流的乘积,在ab 坐标系可表示为
可简化为调制函数基波分量与电感电流的乘积,在ab 坐标系可表示为
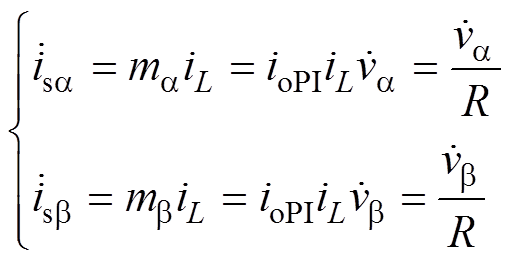 (3)
(3)
式中,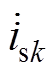 、
、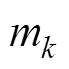 分别为ab 坐标系的各相交流侧电流、调制函数基波分量;R=1/(ioPIiL)为虚拟电阻。
分别为ab 坐标系的各相交流侧电流、调制函数基波分量;R=1/(ioPIiL)为虚拟电阻。
忽略系统损耗,则输入有功功率等于输出有功功率,直流侧电压vdc用受控源代替,可表示为
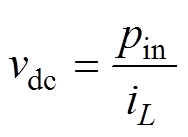 (4)
(4)
式中,pin为输入有功功率。
根据式(3)和式(4),可建立传统双环控制三相Buck整流器在ab 坐标系的等效电路模型,如图3所示。图3中,Lk和Ck分别为ab 坐标系等效电路模型的输入滤波电感和电容。
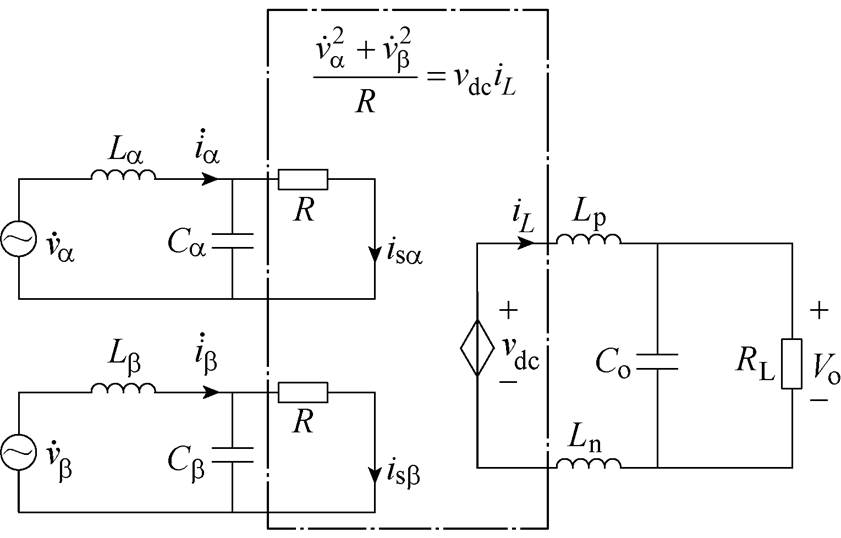
图3 三相Buck整流器在ab 坐标系的等效电路模型
Fig.3 Equivalent circuit model of the three-phase Buck rectifier in ab frame
在ab 坐标系中,输入有功功率可以表示为
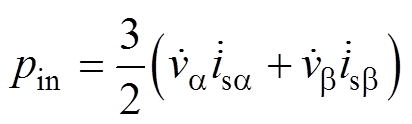 (5)
(5)
定义pa 和pb 分别为a 相和b 相有功功率,则
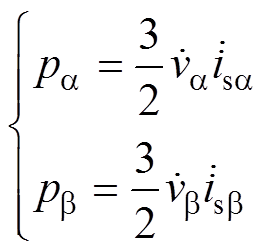 (6)
(6)
由式(5)和式(6)可以看出,输入有功功率pin为a 相有功功率pa 与b 相有功功率pb 之和。
根据式(3)和式(6),pa、pb 可分别表示为
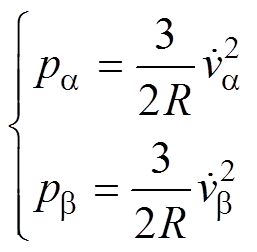 (7)
(7)
由式(7)可以看出,pa、pb 都包含直流分量和交流分量,且可表示为
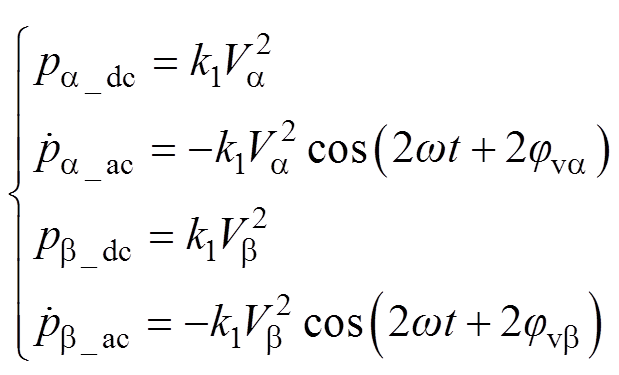 (8)
(8)
式中,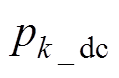 、
、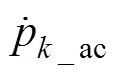 分别为各相有功功率直流分量、交流分量;k1=3/(4R)。
分别为各相有功功率直流分量、交流分量;k1=3/(4R)。
输入电压平衡时,va 与vb 幅值相等,相位相差90°,因此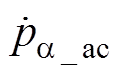 与
与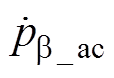 之和为0,有功功率pin为恒定值;输入电压不平衡时,pin包含的直流分量pdc和交流分量
之和为0,有功功率pin为恒定值;输入电压不平衡时,pin包含的直流分量pdc和交流分量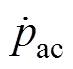 ,可分别表示为
,可分别表示为
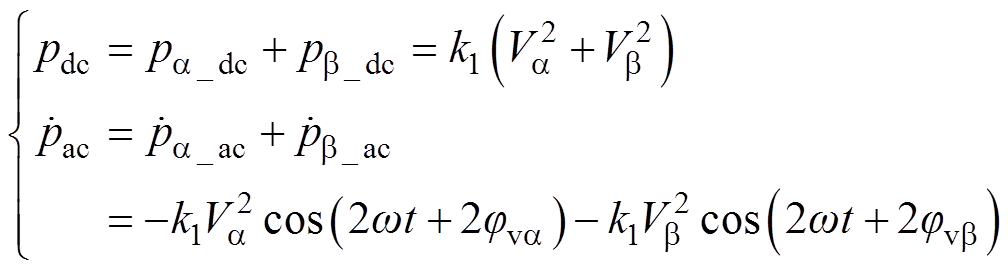 (9)
(9)
输入有功功率交流分量pac的相量合成如图4所示,为了简化分析,令jva=0。由于输入电压不平衡,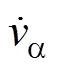 与
与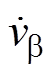 的幅值和相位关系发生了变化,
的幅值和相位关系发生了变化,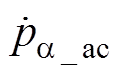 与
与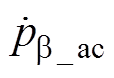 合成的相量不再为0,因此有功功率中存在二倍输入频率的交流分量。
合成的相量不再为0,因此有功功率中存在二倍输入频率的交流分量。
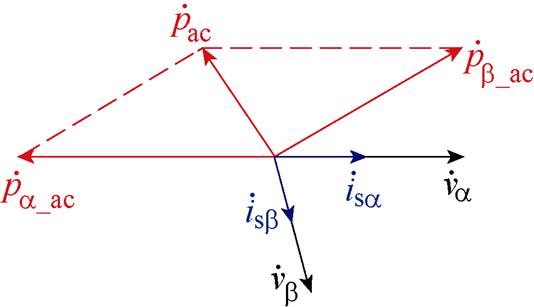
图4 有功功率交流分量的相量
Fig.4 Phasor diagram for ac components ofactive power
有功功率交流分量作用在输出侧引起输出电压和电感电流的二倍频脉动,由式(3)可知,输入电流可表示为电感电流与调制函数基波分量的乘积,因此二倍频脉动的电感电流使输入电流中包含了大量低频奇次谐波,导致了输入电流畸变。
输入电压不平衡时,传统双环控制三相Buck整流器存在有功功率脉动的问题,从而导致输入电流严重畸变和输出电压二倍频脉动。对图3所示的模型进行改进,得到改进的三相Buck整流器等效电路模型,如图5所示。
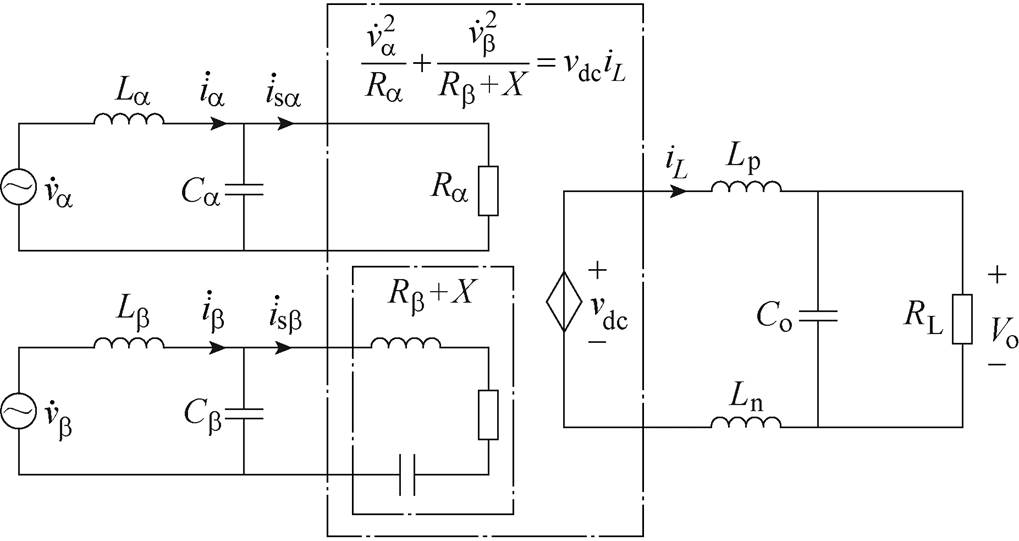
图5 改进的三相Buck整流器等效电路模型
Fig.5 Improved equivalent circuit model of the three-phase Buck rectifier
图5中,Rk为各相虚拟电阻,X为虚拟电抗。b 相加入虚拟电抗X,使交流侧电流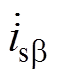 与输入电压
与输入电压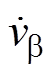 产生相位偏移,调整
产生相位偏移,调整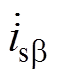 的模值和相位,可以自由控制 b 相有功功率交流量
的模值和相位,可以自由控制 b 相有功功率交流量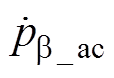 的相位和幅值,通过调整其相位和幅值,可以使两相有功功率交流分量相互抵消,实现有功功率恒定。
的相位和幅值,通过调整其相位和幅值,可以使两相有功功率交流分量相互抵消,实现有功功率恒定。
加入虚拟电抗后,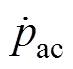 的相量合成如图6所示,相较于图4,由于加入了虚拟电抗,
的相量合成如图6所示,相较于图4,由于加入了虚拟电抗,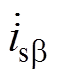 与
与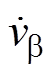 产生了相位偏移,通过对
产生了相位偏移,通过对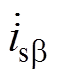 设置恰当的幅值和相位,使
设置恰当的幅值和相位,使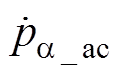 与
与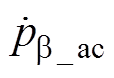 幅值相等,相位相差180°,从而消去有功功率的交流分量。
幅值相等,相位相差180°,从而消去有功功率的交流分量。
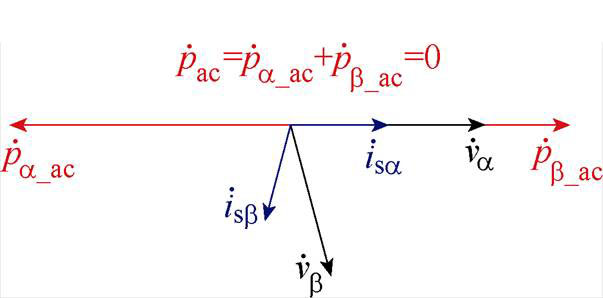
图6 改进模型的有功功率交流分量相量
Fig.6 Phasor diagram for ac components of the active power with the improved model
恒定有功功率时输出电压和电感电流无二倍频脉动,可视为恒定值。电感电流与调制函数的乘积无明显的低频奇次谐波,因此输入电流保持正弦。
根据三相Buck整流器的改进模型,可得到基于虚拟阻抗的三相Buck整流器控制策略,如图7所示。控制策略包含输入电流参考计算、输出电压及电感电流控制环路和SVPWM策略。三相输入电压采样后计算输入电流参考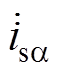 与
与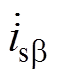 。输出电压控制环路调整输出电压并为电感电流提供参考,电感电流控制环路调整电感电流,其输出ioPI与电流参考
。输出电压控制环路调整输出电压并为电感电流提供参考,电感电流控制环路调整电感电流,其输出ioPI与电流参考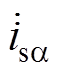 、
、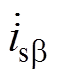 的乘积作为a、b 相的调制函数。
的乘积作为a、b 相的调制函数。
将基于虚拟阻抗概念产生的两相交流侧电流作为整流器输入侧电流参考,以图8所示两相输入电压为例说明电流参考的构造过程。
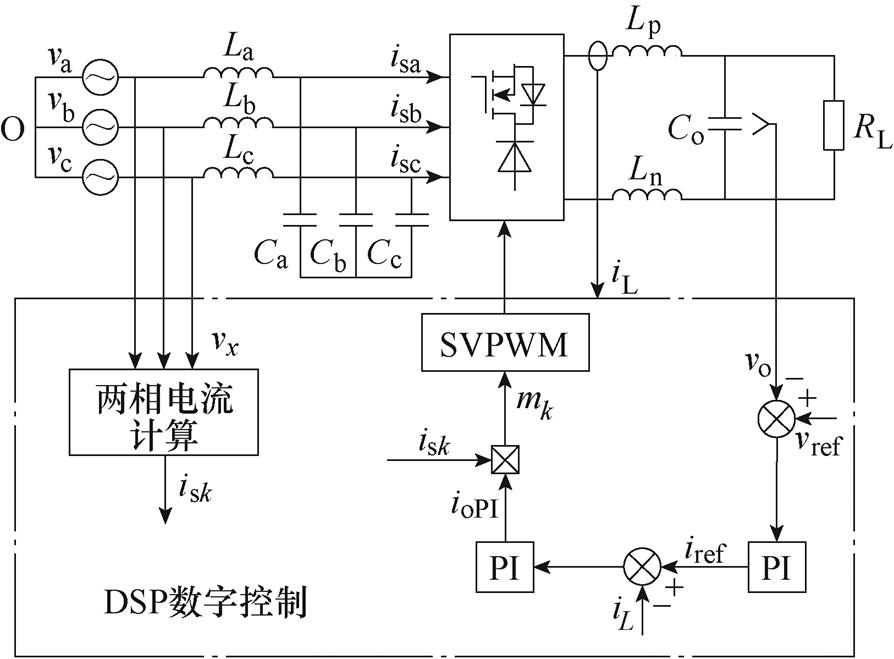
图7 基于虚拟阻抗三相Buck整流器控制策略
Fig.7 Proposed control strategy based on virtual impedance for the three-phase Buck rectifier
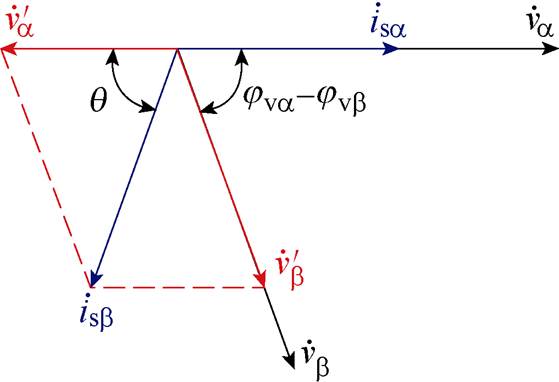
图8 构造输入侧电流参考的相量
Fig.8 Phasor diagram for the input current refrences construction
图8中,通过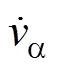 与
与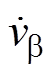 合成得到
合成得到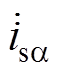 和
和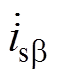 ,
,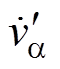 与
与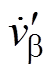 为合成得到
为合成得到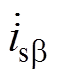 的相量,
的相量,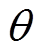 为
为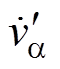 和
和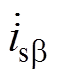 的夹角。
的夹角。
a 相输入电流isa 可表示为
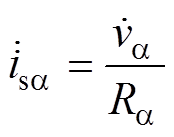 (10)
(10)
为使ab 相有功功率交流量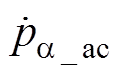 与
与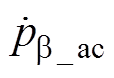 的幅值相等,isb 幅值应满足
的幅值相等,isb 幅值应满足
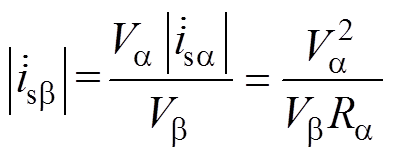 (11)
(11)
式中,符号“ ”表示相量幅值。
”表示相量幅值。
为使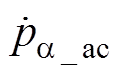 与
与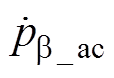 相位相差180°,图8中
相位相差180°,图8中 应满足
应满足
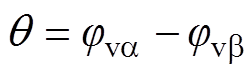 (12)
(12)
因此,根据三角关系,图8中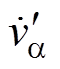 与
与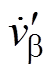 的幅值可表示为
的幅值可表示为
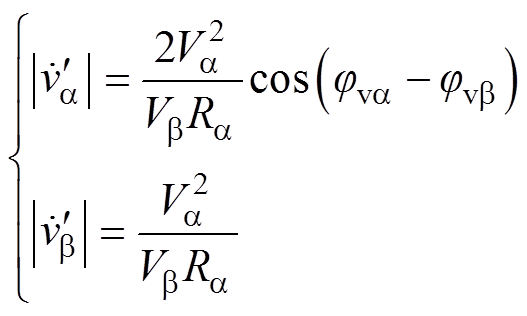 (13)
(13)
根据式(13),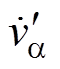 与
与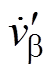 和
和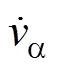 与
与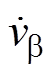 的关系表示为
的关系表示为
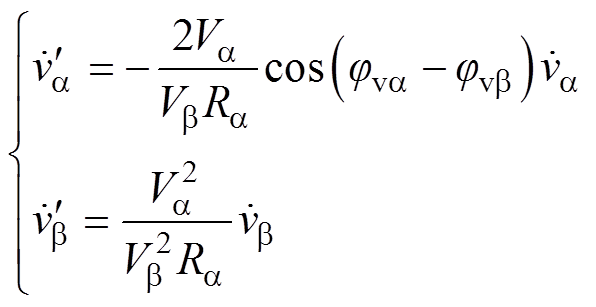 (14)
(14)
因此,b 相电流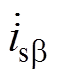 可表示为
可表示为
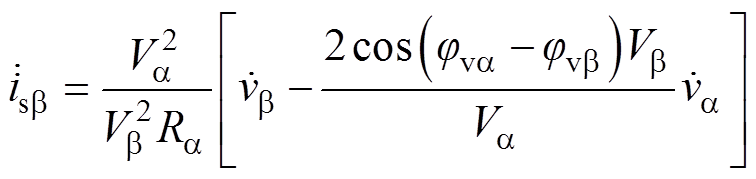 (15)
(15)
由式(10)和式(15)可知,构造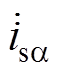 和
和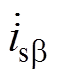 需要检测
需要检测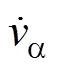 和
和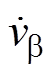 的峰值电压Va、Vb 和相位差jva-jvb。本文使用PD和ZCD对
的峰值电压Va、Vb 和相位差jva-jvb。本文使用PD和ZCD对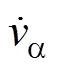 与
与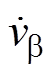 进行峰值和相位检测,构造交流侧电流参考的流程如图9所示。
进行峰值和相位检测,构造交流侧电流参考的流程如图9所示。
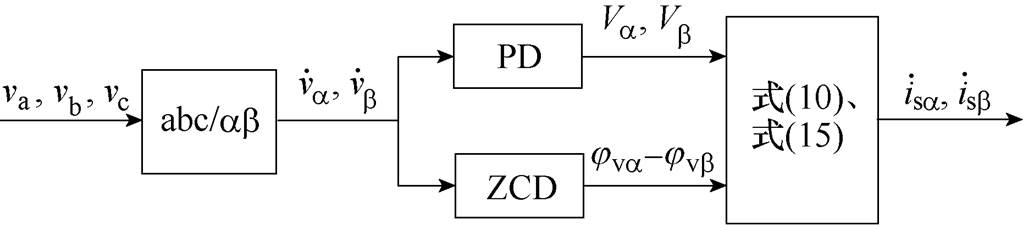
图9 构造交流侧电流参考的流程
Fig.9 Flow chart of the input current references construction
输入电压变化时,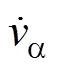 与
与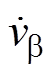 的峰值电压Va、Vb 和相位差jva-jvb也发生变化,需要检测变化后的峰值电压和相位差才能构造正确的输入电流参考。定义检测时间Td为输入电压变化到构造对应电流参考的时间,检测时间Td影响系统的瞬态性能。在检测时间Td内,由于沿用输入电压变化前的电流参考,因此无法消除有功功率交流量,输出电压存在二倍频波动,输入电流畸变。在检测时间Td后,完成了对应的输入电流参考的构造,输出电压的二倍频波动和输入电流畸变消除。由于在一个输入周期内总可以检测到输入电压的峰值和相位信息,因此检测时间Td小于一个输入周期。
的峰值电压Va、Vb 和相位差jva-jvb也发生变化,需要检测变化后的峰值电压和相位差才能构造正确的输入电流参考。定义检测时间Td为输入电压变化到构造对应电流参考的时间,检测时间Td影响系统的瞬态性能。在检测时间Td内,由于沿用输入电压变化前的电流参考,因此无法消除有功功率交流量,输出电压存在二倍频波动,输入电流畸变。在检测时间Td后,完成了对应的输入电流参考的构造,输出电压的二倍频波动和输入电流畸变消除。由于在一个输入周期内总可以检测到输入电压的峰值和相位信息,因此检测时间Td小于一个输入周期。
在本文中,采用优化开关损耗(Switching Loss Optimized, SLO)SVPWM策略[25],下面对SLO调制策略的扇区判断和PWM序列进行讨论。
两相调制信号mk通过Clarke逆变换转化为三相调制信号mx,可表示为
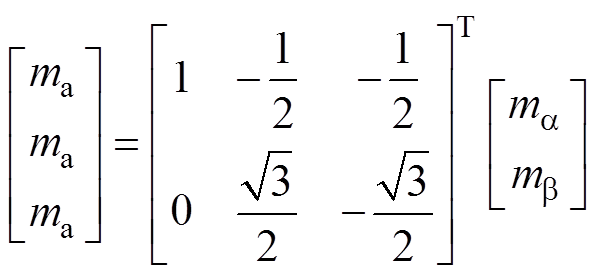 (16)
(16)
传统SLO调制策略根据三相输入电压关系将一个交流输入周期划分为12个扇区,在提出的控制方法中,由于控制三相输入电流与构造出的三相调制信号成正比,因此采用三相调制信号mx划分扇区,如图10所示。
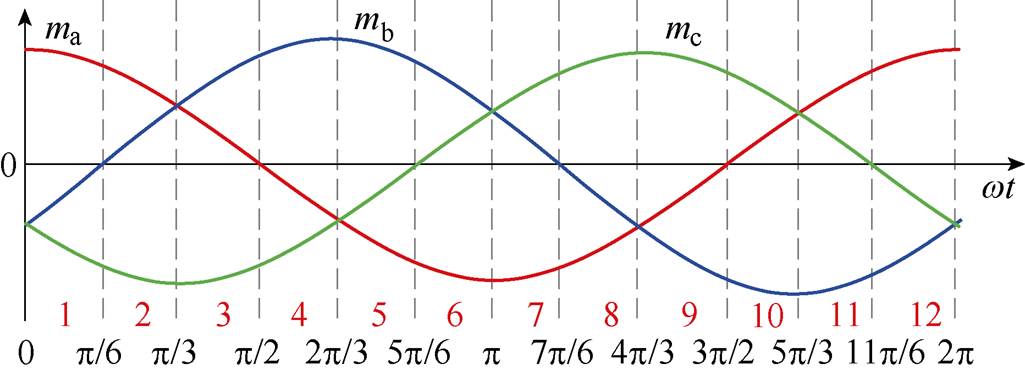
图10 三相调制信号及12扇区
Fig.10 Three-phase modulation signals with 12 sectors
相同调制信号可被同时应用于同一桥臂的两个开关管。根据扇区划分,可得到不同扇区时各桥臂开关管的占空比见表1。在表1中,dx表示各桥臂开关管的占空比。
表1 一个开关周期内各桥臂开关管的占空比
Tab.1 Duty ratio of each bridge leg in one switching period
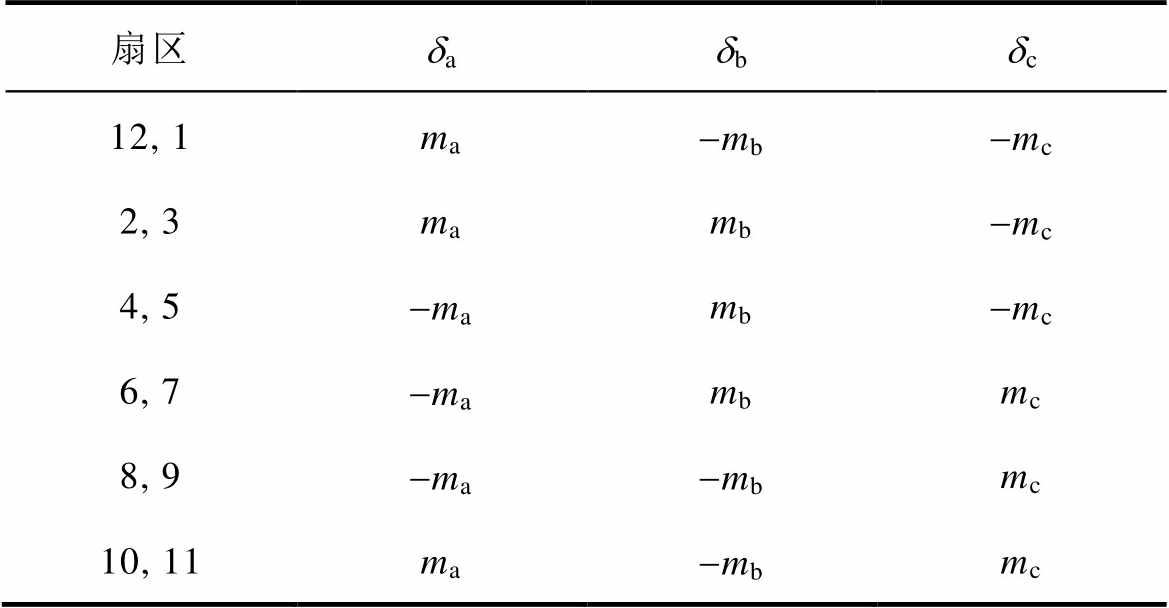
扇区dadbdc 12, 1ma-mb-mc 2, 3mamb-mc 4, 5-mamb-mc 6, 7-mambmc 8, 9-ma-mbmc 10, 11ma-mbmc
图11给出了SLO调制策略在扇区2、扇区3的PWM序列和对应的续流二极管两端电压。在图11中,vac和vbc分别为a相、c相线电压和b相、c相线电压。以数字“1”代表开关管导通,数字“0”代表开关管关断。在图11a所示的扇区2中,PWM序列按照101—011—010—011—101顺序排列。类似地,在图11b所示的扇区3中,PWM序列按照011—101—100—101—011顺序排列。
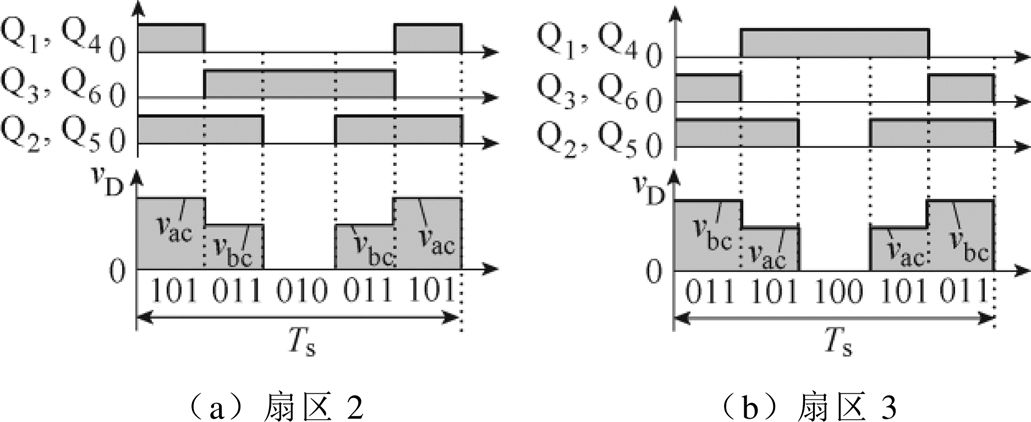
图11 一个开关周期内的PWM序列
Fig.11 PWM sequences in one switching period
为了验证提出的控制策略的有效性,利用PSIM仿真软件搭建了不平衡输入时三相Buck整流器的仿真模型,仿真电路参数见表2。
表2 仿真电路参数
Tab.2 Parameters of the simulation circuit
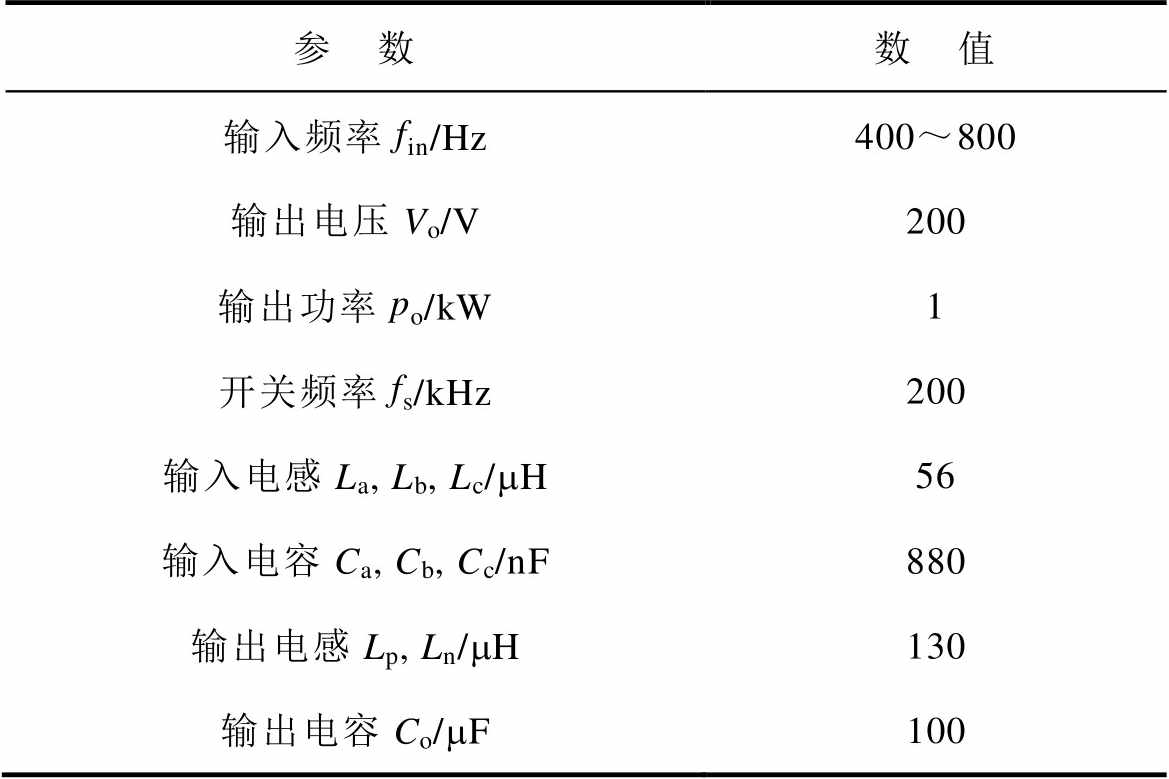
参 数数 值 输入频率fin/Hz400~800 输出电压Vo/V200 输出功率po/kW1 开关频率fs/kHz200 输入电感La, Lb, Lc/mH56 输入电容Ca, Cb, Cc/nF880 输出电感Lp, Ln/mH130 输出电容Co/mF100
图12给出了三相输入电压va=125∠0°,vb=100∠-115°,vc=115∠130°时(相量模值表示电压有效值,下同)分别采用传统双环控制和基于虚拟阻抗的控制策略的仿真波形。由图12a可知,采用传统双环控制,有功功率p存在二倍频波动,无功功率q保持恒定为0,输入电流严重畸变,输出电压存在二倍频波动,波动值达到9 V;由图12b可知,采用基于虚拟阻抗的控制策略,消除了有功功率交流量,无功功率q存在二倍频波动,得到了正弦的输入电流和稳定的输出电压,输出电压波动只有0.6 V。因此,输入电压不平衡时,基于虚拟阻抗的控制策略可以实现正弦的输入电流并消除输出电压的二倍频脉动。
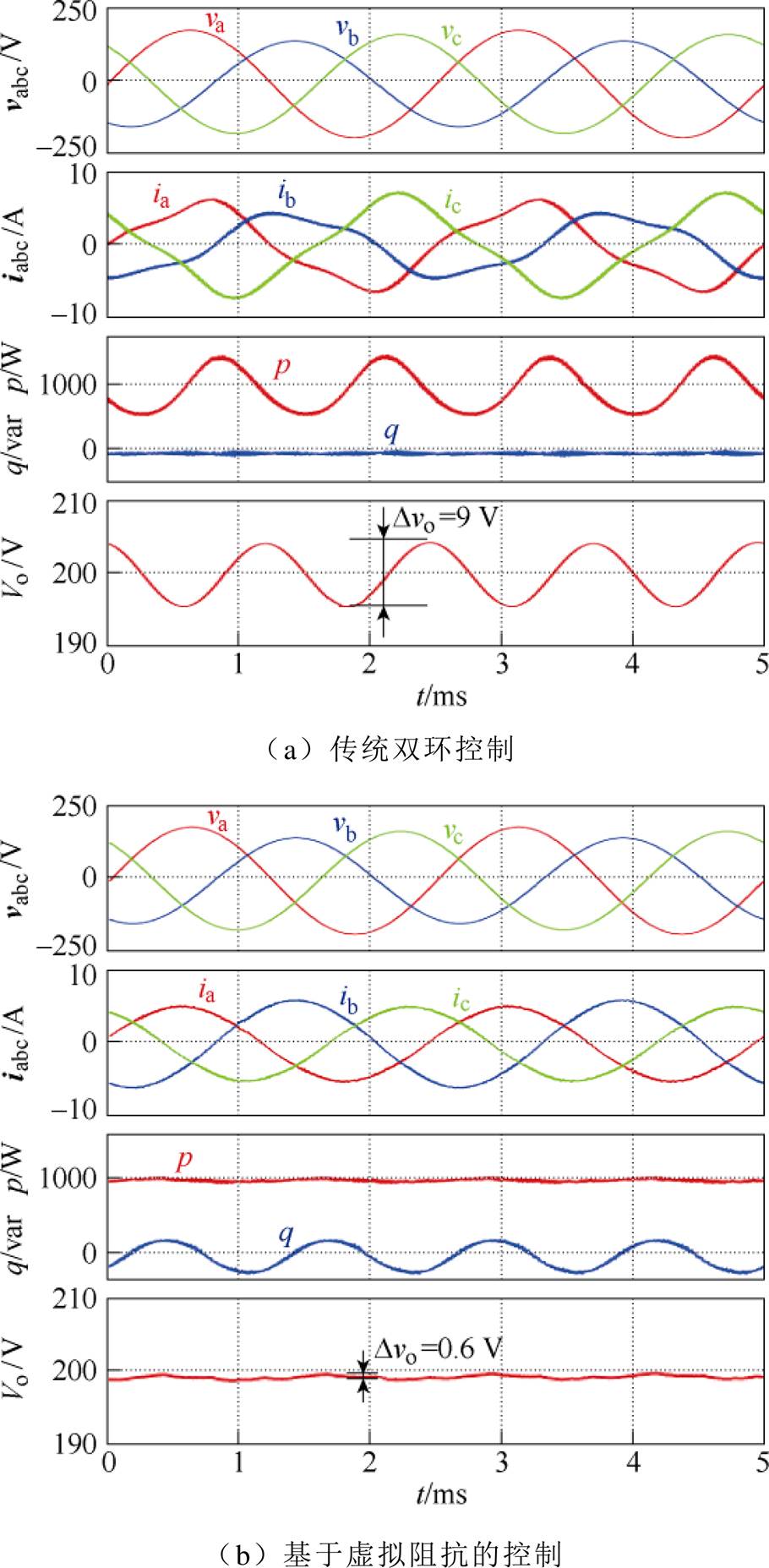
图12 输入电压为va=125∠0°,vb = 100∠-115°,vc=115∠130°时传统双环控制和基于虚拟阻抗的控制策略的仿真结果
Fig.12 Simulation results of the conventional control strategy and the control strategy based on virtual impedance when input voltages are va=125∠0°, vb=100∠-115°, vc=115∠130°
为了验证基于虚拟阻抗的控制策略的有效性,设计了一台1 kW的实验样机,如图13所示。样机参数见表2,实验样机的MOSFET采用IDD08SG60CXTMA2,二极管采用IPD60R180P7,MCU采用DSPIC33EP64GS505。

图13 三相Buck整流器实验平台
Fig.13 Experimental platform of three-phase Buck rectifier
图14给出了三相输入电压不平衡时传统双环控制和基于虚拟阻抗的控制策略在半载和满载情况时的实验波形和谐波成分分析结果。三相输入电压为va=122∠0°,vb=105∠-118°,vc=110∠114°。由图14a和图14b可知,在半载和满载时,传统双环控制的输出电压脉动值分别为3.1 V和7 V,输入电流严重畸变;由图14c和图14d可知,基于虚拟阻抗的控制策略的输出电压稳定,纹波值分别为0.4 V和0.3 V,输入电流保持正弦。图14e和图14f分别给出了半载和满载时两种控制方式的输入电流谐波成分,可知相较于传统双环控制,基于虚拟阻抗的控制策略减小了不平衡输入时输入电流的低频奇次谐波。
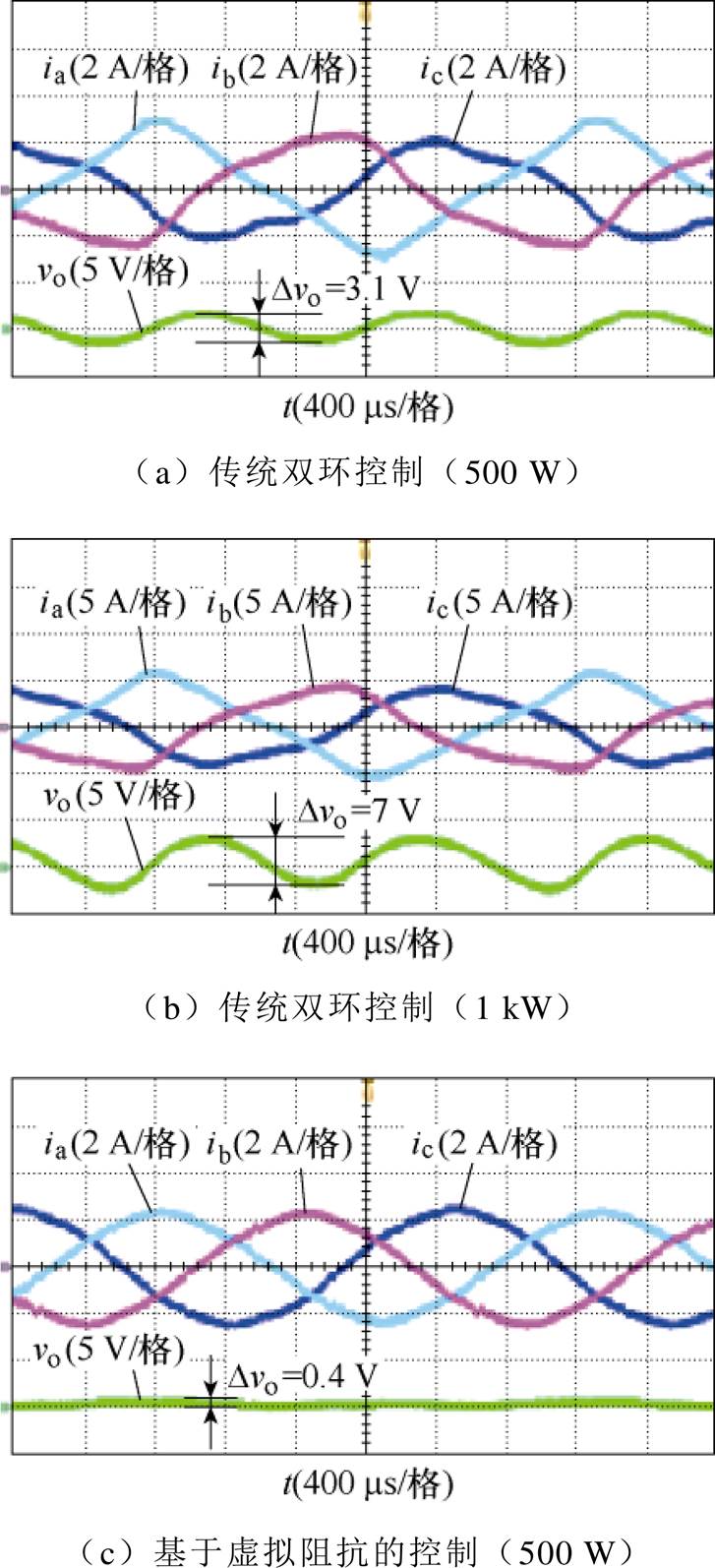
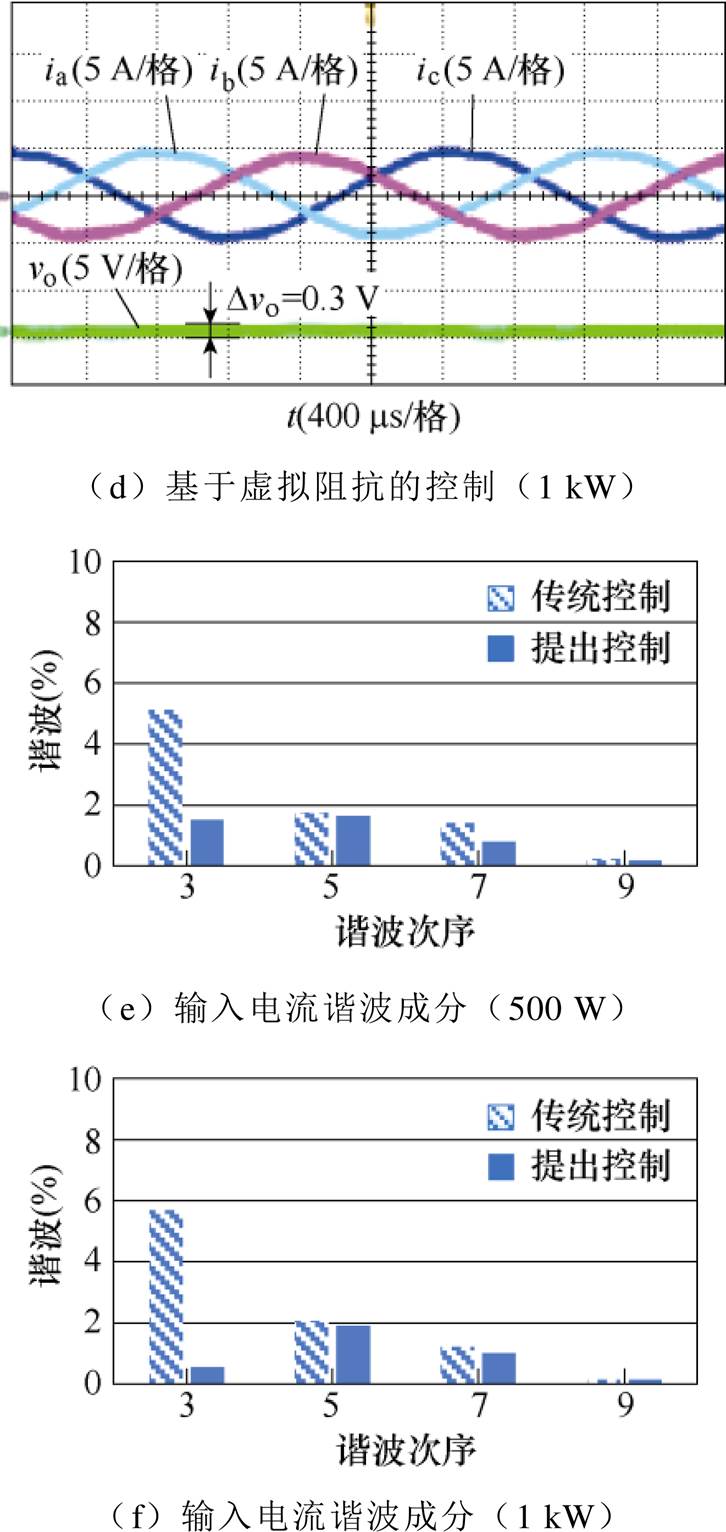
图14 输入电压va=122∠0°,vb=105∠-118°,vc=110∠114°时传统双环控制和基于虚拟阻抗的控制策略实验结果
Fig.14 Experimental results of the conventional control strategy and the control strategy based on virtual impedance when the input voltages are va=122∠0°, vb=105∠-118°, vc=110∠114°
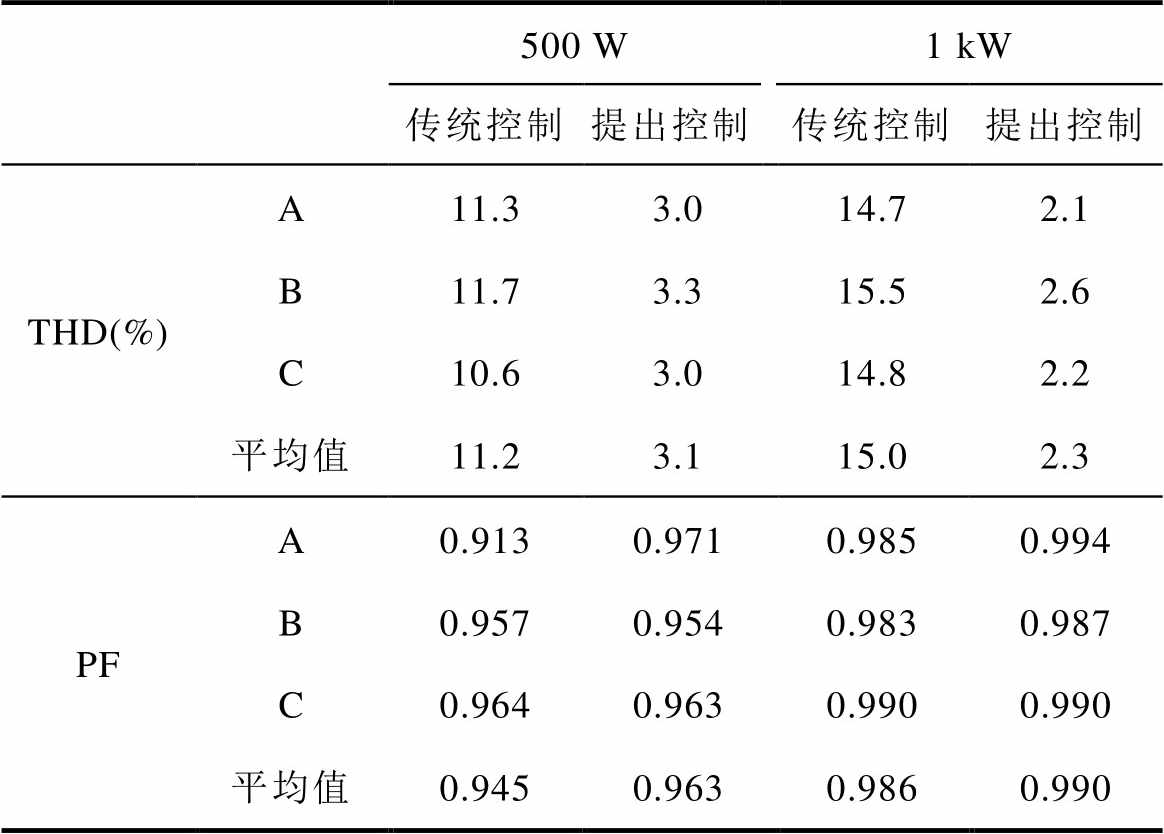
表3给出了图14所示波形的总谐波畸变率(Total Harmonic Distortion, THD)和功率因数(Power Factor, PF)对比。由表3可知,半载时,传统双环控制的THD平均值为11.2%,PF平均值为0.945,基于虚拟阻抗的控制策略的THD平均值为3.1%,PF平均值为0.963;在满载时,传统双环控制的THD平均值为15.0%,PF平均值为0.986,基于虚拟阻抗控制策略的THD平均值为2.3%,PF平均值为0.990。
表3 传统双环控制和基于虚拟阻抗的控制策略的THD和PF值对比
Tab.3 Comparison of THD and PF values for conventional control strategy and the control strategy based on virtual impedance
500 W1 kW 传统控制提出控制传统控制提出控制 THD(%)A11.33.014.72.1 B11.73.315.52.6 C10.63.014.82.2 平均值11.23.115.02.3 PFA0.9130.9710.9850.994 B0.9570.9540.9830.987 C0.9640.9630.9900.990 平均值0.9450.9630.9860.990
结合图14与表3可知,相较于传统双环控制,基于虚拟阻抗的控制策略在输入电压不平衡时表现出更低的输入电流THD、更小的输出电压纹波和更高的PF值。
图15给出了三相输入电压变化时传统双环控制和本文提出的基于虚拟阻抗控制策略的实验波形。输入频率为400 Hz,三相输入电压由平衡输入电压va=115∠0°,vb=115∠-120°,vc=115∠120°变化为不平衡输入电压va=115∠0°,vb=107∠-120°,vc=115∠120°。
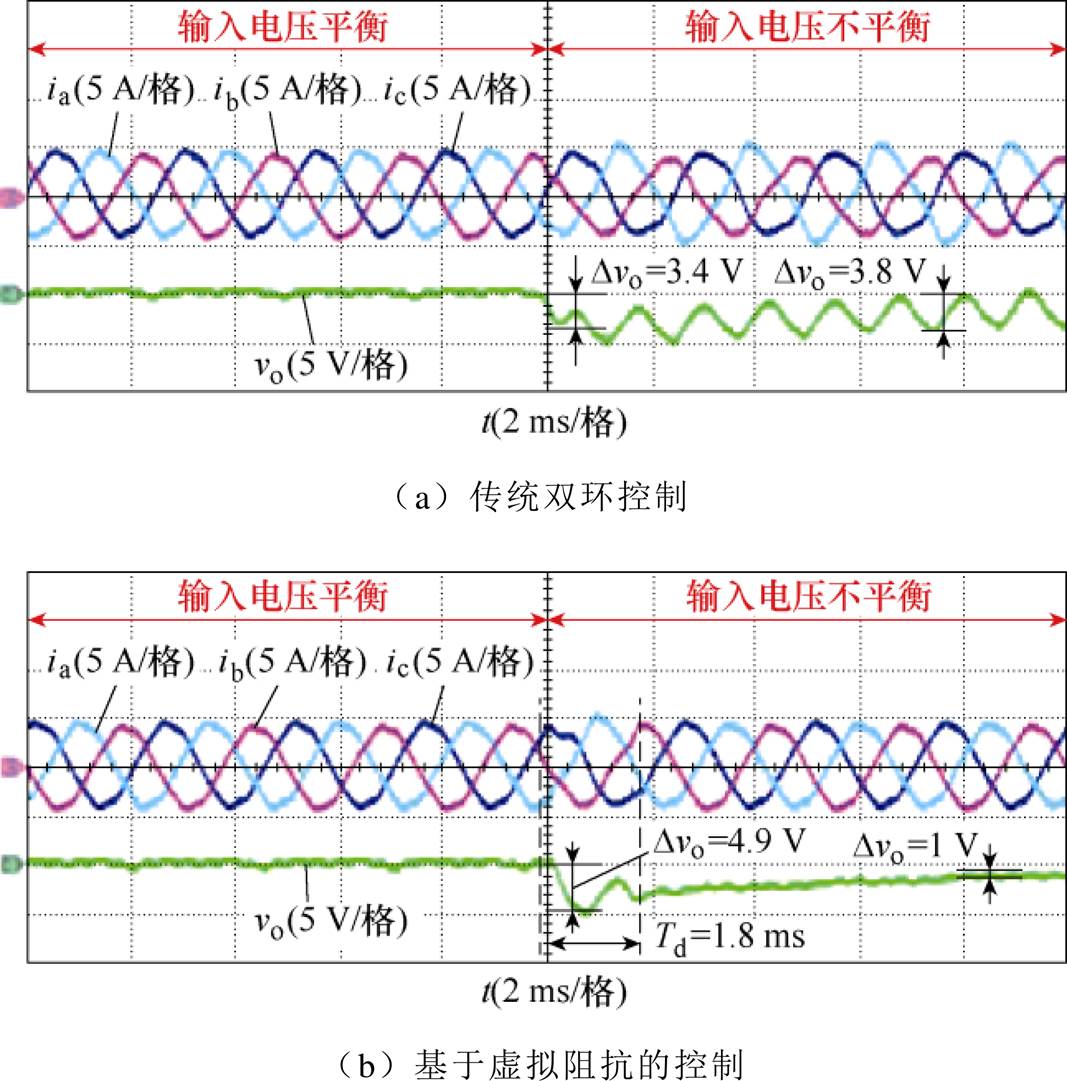
图15 输入电压由平衡输入电压va=115∠0°,vb=115∠-120°,vc=115∠120°变化为不平衡输入电压va=115∠0°,vb=107∠-120°,vc=115∠120°时传统双环控制和基于虚拟阻抗的控制策略的实验结果
Fig.15 Experimental results of the conventional control strategy and the control strategy based on virtual impedance when the input voltages vary from balanced input voltages va=115∠0°, vb=115∠-120°, vc=115∠120°to unbalanced input voltages va=115∠0°, vb=107∠-120°, vc=115∠120°
由图15a可知,输入电压变化瞬间传统双环控制的输出电压波动值为3.4 V,输入电压不平衡时输入电流畸变,输出电压存在二倍频波动,波动值为3.8 V。
由图15b可知,输入电压变化瞬间基于虚拟阻抗控制策略的输出电压波动值为4.9 V。在检测时间Td=1.8 ms内,输出电压存在二倍频脉动,输入电流畸变;在Td时间后,完成了对输入电压的峰值检测和相位差检测并构造出正确的输入电流参考,输入电流保持正弦,输出电压无二倍频波动,纹波值为1 V。因此,输入电压由平衡输入电压变化为不平衡输入电压时,基于虚拟阻抗的控制策略性能良好。
图16给出了传统双环控制和本文提出的基于虚拟阻抗控制策略在输入频率变化时的实验波形。三相输入电压分别为va=105∠0°,vb=115∠-110°,vc=120∠120°,输入频率由400 Hz变为800 Hz。
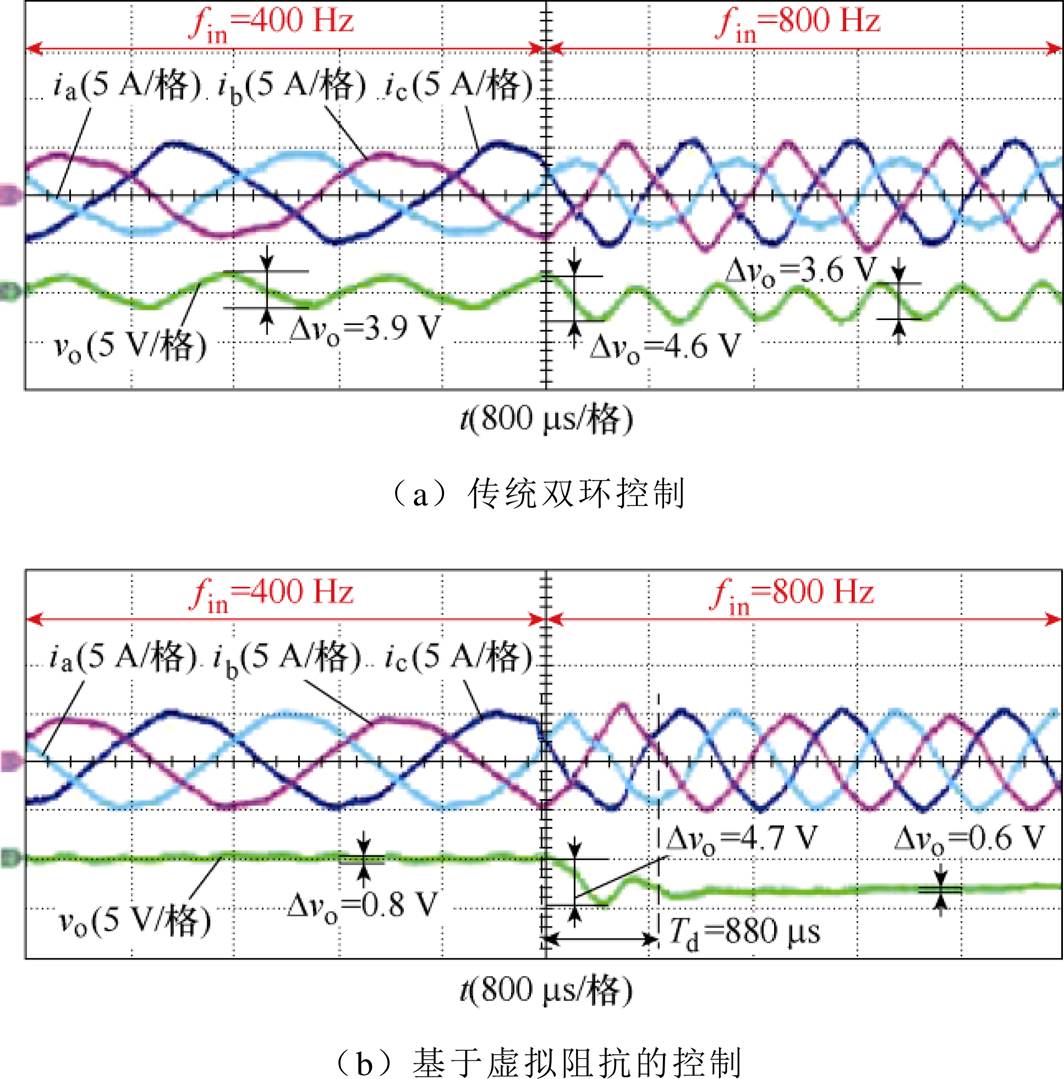
图16 输入电压为va=105∠0°,vb=115∠-110°,vc=120∠120°时输入频率由400 Hz变为800 Hz时传统双环控制和基于虚拟阻抗的控制策略的实验结果
Fig.16 Experimental results of the conventional control strategy and the control strategy based on virtual impedance when the input frequency varies from 400 Hz to 800 Hz under va=105∠0°, vb=115∠-110°, vc=120∠120°
由图16a可知,采用传统双环控制,输入频率变化瞬间输出电压波动值为4.6 V,输出电压在输入频率变化前后都存在二倍频波动,波动值分别为3.9 V和3.6 V。
由图16b可知,输入频率变化前,基于虚拟阻抗的控制策略的输出电压无二倍频波动,纹波值为0.8 V;输入频率变化瞬间输出电压波动值为4.7 V,在检测时间Td=880 ms内,输出电压存在二倍频脉动,输入电流畸变;在Td时间后,完成了对输入电压的峰值检测和相位差检测,并构造出正确的输入电流参考,输入电流保持正弦,输出电压无二倍频波动,纹波值为0.6 V。因此,当输入频率变化时,基于虚拟阻抗的控制策略性能良好。
图17给出了负载突变时基于虚拟阻抗控制策略的实验波形,三相输入电压分别为va=105∠0°,vb=115∠-110°,vc=120∠120°。由图17a可知,负载由100 W突变至1 000 W时,输出电压变化17 V,响应时间为25.6 ms,在负载突变过程中输入电流无畸变;由图17b可知,负载由1 000 W突变至100 W时,输出电压变化16 V,响应时间为27.8 ms,在负载突变过程中输入电流无畸变。因此,基于虚拟阻抗的控制策略可以适用于负载突变工况。
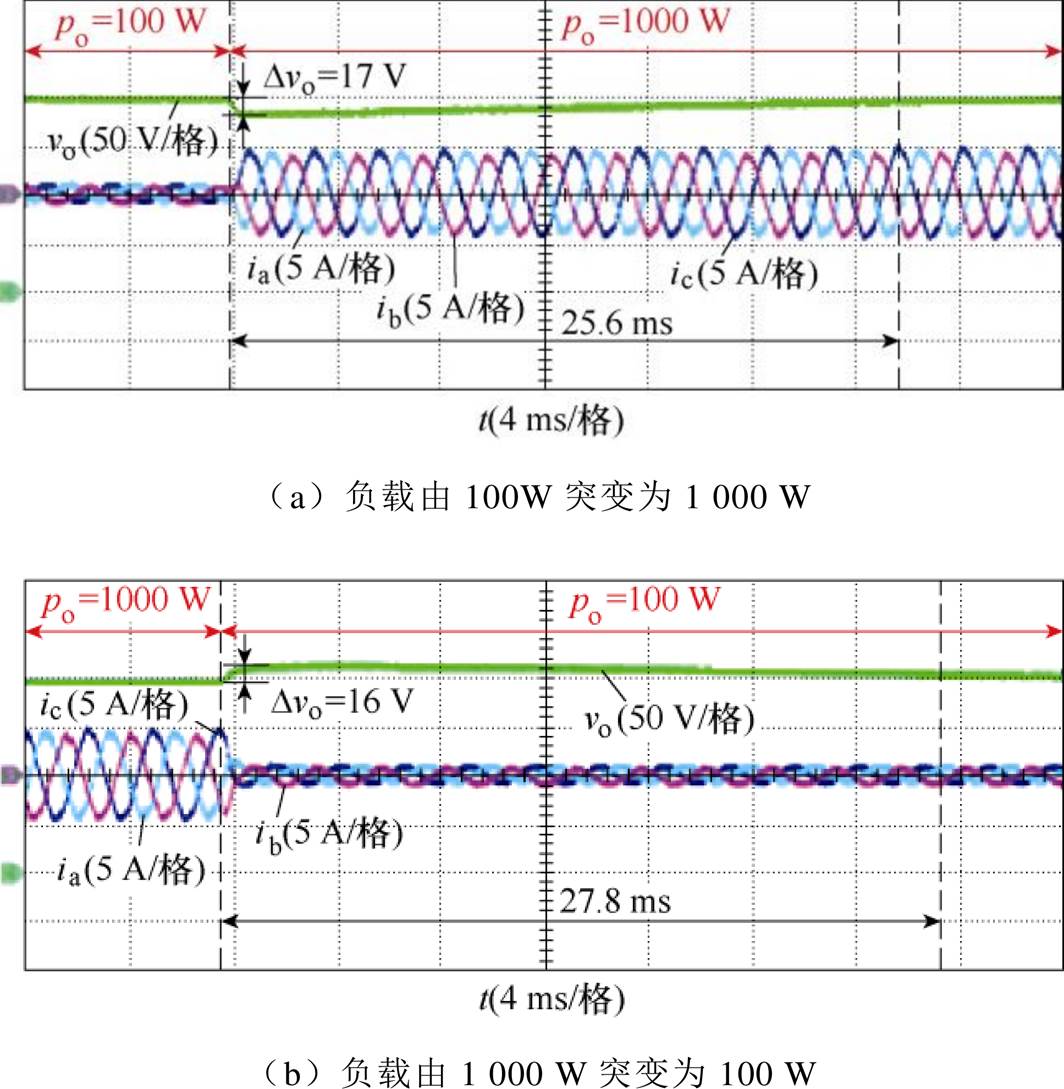
图17 输入电压va=105∠0°,vb=115∠-110°,vc=120∠120°时基于虚拟阻抗的控制策略的负载突变实验结果
Fig.17 Experimental results of the control strategy based on virtual impedance when the output power varies with input voltages va=105∠0°, vb=115∠-110°, vc=120∠120°
由实验结果可知,输入电压不平衡时,采用本文提出的基于虚拟阻抗的控制策略,能够有效消除稳态时输出电压的二倍频脉动,使输入电流正弦;在输入电压或输入频率变化时,需要检测时间Td进行电压峰值检测和相位检测,在这期间输入电流畸变,输出电压二倍频波动,当完成检测后输出电压无二倍频波动,输入电流保持正弦。
本文首先通过建立三相Buck整流器在ab 坐标系下的等效电路模型,分析了不平衡输入电压下整流器输出电压存在二倍频脉动、输入电流畸变的原因。在此基础上,提出了一种基于虚拟阻抗的不平衡输入控制方法。通过在模型中引入虚拟电抗使系统输入有功功率保持恒定值,从而消除输出电压的脉动并使输入电流保持正弦。仿真结果和实验结果都验证了控制策略的有效性。
参考文献
[1] 王金平, 刘圣宇, 张庆岩, 等. 一种改进的可消除Vienna整流器电流过零畸变的控制方法[J]. 电工技术学报, 2022, 37(15): 3834-3844.
Wang Jinping, Liu Shengyu, Zhang Qingyan, et al. An improved control method to eliminate the current zero-crossing distortion for Vienna rectifier[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3834-3844.
[2] 李周洋, 谢少军, 张斌锋, 等. 一种改进型的基于双移相全桥的SWISS整流器[J]. 电工技术学报, 2022, 37(增刊1): 198-206.
Li Zhouyang, Xie Shaojun, Zhang Binfeng, et al. An efficiency improved isolated SWISS rectifier based on two phase-shifted full-bridge structures[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(S1): 198-206.
[3] 张永昌, 屈祈延, 杨海涛. 基于空间矢量调制的Vienna整流器无模型预测电流控制[J]. 电工技术学报, 2022, 37(21): 5541-5547.
Zhang Yongchang, Qu Qiyan, Yang Haitao. Model free predictive current control of Vienna rectifier based on space vector modulation[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5541- 5547.
[4] Chen Qiang, Xu Jianping, Wang Lei, et al. Analysis and improvement of the effect of distributed parasitic capacitance on high-frequency high-density three- phase Buck rectifier[J]. IEEE Transactions on Power Electronics, 2021, 36(6): 6415-6428.
[5] Huang Rui, Xu Jianping, Chen Qiang, et al. An optimized asymmetric modulation scheme for three- phase Buck rectifier without input current distortion at the sector boundaries[J]. IEEE Transactions on Power Electronics, 2022, 37(12): 14040-14044.
[6] Benzaquen J, Fateh F, Shadmand M B, et al. Performance comparison of active rectifier control schemes in more electric aircraft applications[J]. IEEE Transactions on Transportation Electrification, 2019, 5(4): 1470-1479.
[7] Chen Qiang, Xu Jianping, Zeng Fei, et al. An improved three-phase Buck rectifier with low voltage stress on switching devices[J]. IEEE Transactions on Power Electronics, 2021, 36(6): 6168-6174.
[8] 肖蕙蕙, 周琛力, 郭强, 等. 用于改善直流链电流纹波的电流源型整流器扇区优化调制策略[J]. 电工技术学报, 2021, 36(24): 5250-5260.
Xiao Huihui, Zhou Chenli, Guo Qiang, et al. Optimized sector modulation strategy of current source rectifier for DC-link current ripple redu- ction[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5250-5260.
[9] Zhang Jianwen, Zhang Yixin, Zhou Jianqiao, et al. Control of a hybrid modular solid-state transformer for uninterrupted power supply under MVDC short- circuit fault[J]. IEEE Transactions on Industrial Electronics, 2023, 70(1): 76-87.
[10] Xu Fan, Guo Ben, Tolbert L M, et al. An all-SiC three-phase Buck rectifier for high-efficiency data center power supplies[J]. IEEE Transactions on Industry Applications, 2013, 49(6): 2662-2673.
[11] Xu Fan, Guo Ben, Xu Zhuxian, et al. Paralleled three-phase current-source rectifiers for high-efficiency power supply applications[J]. IEEE Transactions on Industry Applications, 2015, 51(3): 2388- 2397.
[12] 郭强, 周琛力, 李山. 面向电流源型PWM整流器直流侧电压的多环路控制策略[J]. 电工技术学报, 2022, 37(8): 2051-2063.
Guo Qiang, Zhou Chenli, Li Shan. A multiple loops control strategy based on DC link voltage of current source PWM rectifiers[J]. Transactions of China Electrotechnical Society, 2022, 37(8): 2051-2063.
[13] 赵新, 金新民, 杨捷, 等. 并网逆变器新型不平衡控制方案[J]. 电工技术学报, 2014, 29(增刊1): 257-265.
Zhao Xin, Jin Xinmin, Yang Jie, et al. Novel unba- lanced control scheme of grid-connected inverter[J]. Transactions of China Electrotechnical Society, 2014, 29(S1): 257-265.
[14] 年珩, 程鹏. 电网电压不平衡时PWM整流器的谐振直接功率控制策略[J]. 电工技术学报, 2013, 28(11): 86-94.
Nian Heng, Cheng Peng. Resonant based direct power control strategy for PWM rectifier under unbalanced grid voltage condition[J]. Transactions of China Electrotechnical Society, 2013, 28(11): 86-94.
[15] 徐友, 郑建勇, 梅军, 等. 基于单周控制的三相PWM整流器负序电压补偿型不平衡控制策略[J]. 电工技术学报, 2012, 27(11): 183-190.
Xu You, Zheng Jianyong, Mei Jun, et al. Negative sequence voltage feed forward compensation unba- lanced control strategy for three-phase PWM rectifier based on one cycle control[J]. Transactions of China Electrotechnical Society, 2012, 27(11): 183-190.
[16] Enjeti P N, Choudhury S A. A new control strategy to improve the performance of a PWM AC to DC converter under unbalanced operating conditions[J]. IEEE Transactions on Power Electronics, 1993, 8(4): 493-500.
[17] Chen Qiang, Xu Jianping, Huang Rui, et al. A digital control strategy with simple transfer matrix for three-phase Buck rectifier under unbalanced AC input conditions[J]. IEEE Transactions on Power Elec- tronics, 2021, 36(4): 3661-3666.
[18] Baumann M, Kolar J W. A novel control concept for reliable operation of a three-phase three-switch Buck- type unity-power-factor rectifier with integrated boost output stage under heavily unbalanced mains con- dition[J]. IEEE Transactions on Industrial Electronics, 2005, 52(2): 399-409.
[19] Wang Zheng, Wu Bin, Xu Dewei, et al. DC-link current ripple mitigation for current-source grid- connected converters under unbalanced grid con- ditions[J]. IEEE Transactions on Industrial Elec- tronics, 2016, 63(8): 4967-4977.
[20] Guo Xiaoqiang, Yang Yong, Zhang Xue. Advanced control of grid-connected current source converter under unbalanced grid voltage conditions[J]. IEEE Transactions on Industrial Electronics, 2018, 65(12): 9225-9233.
[21] Huang Rui, Xu Jianping, Chen Qiang, et al. Recon- structed phase voltages based power following control for three-phase Buck rectifier under unbalanced phase voltages and wide AC input frequency[J]. IEEE Transactions on Power Electronics, 2023, 38(2): 2022-2031.
[22] Xie Shiming, Sun Yao, Lin Jianheng, et al. Resistance-emulating control strategy for three-phase voltage source rectifiers under unbalanced grids[J]. IEEE Transactions on Industrial Electronics, 2022, 69(2): 1103-1113.
[23] 缪惠宇, 梅飞, 张宸宇, 等. 基于虚拟阻抗的虚拟同步整流器三相不平衡控制策略[J]. 电工技术学报, 2019, 34(17): 3622-3630.
Miao Huiyu, Mei Fei, Zhang Chenyu, et al. Three phase unbalanced control strategy for virtual syn- chronous rectifier based on virtual impedance[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3622-3630.
[24] Lin Jianheng, Su Mei, Xiong Wenjing, et al. Con- ductance emulating control strategy for three-phase current source rectifier under unbalanced grid voltages[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2022, 69(6): 2837-2841.
[25] Nussbaumer T, Kolar J W. Improving mains current quality for three-phase three-switch Buck-type PWM rectifiers[J]. IEEE Transactions on Power Electronics, 2006, 21(4): 967-973.
Abstract When the three-phase buck rectifier is used in electric aircraft applications, ac input voltages are often unbalanced by asymmetric transmission impedance, grid failure, and single-phase load. Accordingly, the three-phase buck rectifier with conventional control strategies exhibits double-line frequency fluctuations in output voltages and distorted input currents, seriously affecting rectifier performance. This paper constructs an equivalent circuit model and a power transfer mathematical model for the three-phase buck rectifier in the two-phase stationary frame.
The generation of double-line frequency fluctuations is analyzed for three-phase buck rectifiers with unbalanced ac input voltages. According to the phase relationship between ac input currents and ac input voltages, an equivalent circuit model is established using the conventional control strategy in a two-phase stationary frame. Subsequently, double line frequency fluctuations in active power are analyzed, which causes double line frequency fluctuations in output voltages and input current distortions.
An input unbalance control strategy is proposed based on virtual impedance under unbalanced ac input voltages. Firstly, an improved equivalent circuit model is proposed. The virtual impedance is added to the equivalent circuit model. Adjusting the amplitude and phase of the virtual impedance can eliminate the ac component of the active power. Thus, constant active power is achieved, i.e., double line frequency fluctuation of output voltage is eliminated, and sinusoidal input currents are obtained. Secondly, the method to construct input current references is given. Input voltages are applied to construct input current references. The impacts of the peak and zero-crossing detection on the dynamic performance of three-phase buck rectifiers is analyzed. Thirdly, the space vector pulse width modulation (SVPWM) strategy is analyzed. The switching loss-optimized SVPWM strategy is applied. Its sector division and pulse width modulation sequences are given.
Simulation and a 1 kW experimental prototype verify the theoretical analysis and the proposed control strategy. The results show that the proposed control strategy eliminates double-line frequency fluctuations in output voltages and input current distortions. Thus, low ripples of output voltages and sinusoidal input currents with low total harmonic distortion are obtained. In addition, when the ac input frequency or input voltage amplitude varies, the proposed control strategy exhibits low output voltage fluctuations and short response time. When the load power varies, no distortion exists in input currents.
keywords:Three-phase Buck rectifier, grid voltage imbalance, input current distortion, virtual impedance
DOI: 10.19595/j.cnki.1000-6753.tces.231088
中图分类号:TM461
收稿日期 2023-07-11
改稿日期 2023-08-17
谢 飞 男,1997年生,硕士,研究方向为电力电子功率变换器的调制与控制方法。E-mail: fxie_pe@163.com
许建平 男,1963年生,教授,博士生导师,研究方向为电力电子数字控制技术、开关电源新颖控制技术、再生能源发电技术、移动信息设备电源管理技术等。E-mail: jpxu-swjtu@163.com(通信作者)
(编辑 陈 诚)