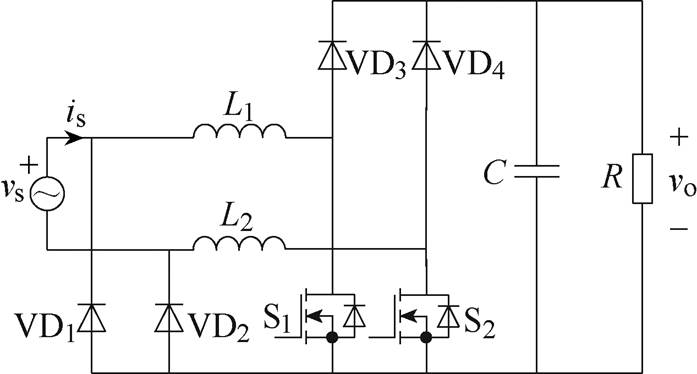
图1 典型的双二极管式无桥PFC变换器拓扑
Fig.1 Typical dual-diode bridgeless PFC converter topology
摘要 有源功率因数校正（APFC）是AC-DC变换器的重要组成部分，其目的是改善输入侧电能质量，提高系统功率因数。传统的有源电流控制功率因数校正（PFC）变换器需要准确地提取升压电感电流，而双二极管式无桥PFC变换器升压电感位于整流部分之前，电感电流不再是单一方向流动，这使得其电流采样电路相比更复杂。为此该文提出一种基于观测器的无电流传感方案。方案中针对占空比误差的不确定影响修正了无桥PFC电流观测器算法，实现了占空比误差自适应的电流观测器，进一步基于所提观测器实现对负载信息的观测，设计出无电流传感的复合前馈控制方案，运用负载观测信息改进电流内环参考形式，同时利用输出电压纹波观测值进行2次谐波前馈补偿，最终实现无电流传感控制条件下变换器高动态响应设计。该文搭建了225 W单相双二极管式无桥PFC的实验样机，实验结果表明，在开关频率100 kHz时电流观测精度达到96.75%，所提控制方案输入电流的总谐波畸变率（THD）含量约为5%，功率因数（PF）约为99.85%，半载动态响应时间10 ms，相比于传统PI控制无桥PFC变换器提高了约90%。
关键词：无桥PFC变换器 电流观测器 前馈控制 动态响应 占空比自适应
有源功率因数校正（Active Power Factor Correction, APFC）可减小输入侧电流畸变，提高输入侧功率因数，降低谐波对电网的污染，因而其被广泛地应用于各类整流场合[1-3]。经典的有源功率因数校正电路由桥式整流电路和Boost变换器构成，在任一时刻电路中总有三个开关器件处于工作状态，随着变换器功率等级和开关频率的提高，系统的通态损耗显著增加，整体效率降低。对此，D. M. Mitchel首次提出了无桥功率因数校正（PFC）拓扑[4-5]，其通过省略输入整流桥环节以减少传导损耗，拓扑效率获得明显提升。现有报道的无桥PFC的控制方案集中在平均电流控制[6-7]、单周期控制[8-10]、部分有源PFC控制等[11-12]。对于有源PFC控制，电流检测是其重要环节，电路电流的采样精度影响着整个系统的准确度和稳定性。不同于传统的PFC变换器能直接采样整流桥之后同极性的电感电流，双二极管式无桥PFC变换器的升压电感位于整流部分之前，其电流的回流方向存在不确定性，在任意一个开关周期内均不能在一条回路上采样得到极性一致的电流。对此，学者们首先从硬件层面提出了改进检测方案。文献[13-14]提出电阻差模放大的采集方案，利用差模运算放大器将电压信号作为电流信号采集，该方案经济简单，但是其存在较大的共模干扰。文献[15]提出多电流互感器方案，该方案准确度高，但其结构复杂并需要在控制中增加额外的信号输入端，并且使用互感器需要设计磁复位系统。文献[16]中提出在开关管下方增加截止二极管，从而得到唯一极性的完整电流信号，但是该方案增加了两个二极管，对无桥PFC的损耗优势有所削弱。
另一方面，不少学者从控制层面提出了解决方案。文献[17]中提出一种移相控制技术简化采样的策略，但此方案额外增加了检测电路。文献[18]从调制电路入手，利用双升压半桥（Dual Boost Half Bridge, DBHB）变换器拓扑的独特双电压稳定性质实现了电流观测器设计，但该种方案具有拓扑局限性。目前电流观测器理论已经在开关电源领域得到了验证，其通过构建电流观测器作为节省电流传感的方案[19-21]，这为无桥PFC的电流采样带来了新的思路。但目前针对开关电源变换器所设计的电流观测器未考虑占空比误差的不确定性影响，这导致观测电流精度会随着开关频率的上升而降低。
本文在建立无桥PFC变换器的电流观测器时考虑占空比误差的不确定性影响，并对其进行自适应修正，提出了一种占空比误差自适应观测器和无电流传感器复合前馈控制方案。在自适应观测器结构基础上，同步实现对系统负载信息观测和输出电压纹波信息观测，综合设计出无电流传感器的复合前馈控制方案，同步解决无桥PFC变换器的采样电感电流精确采样和高动态响应控制设计问题。
双二极管式无桥PFC变换器的拓扑如图1所示，图中，vs为输入电压，is为输入电流，vo为输出电压，L1、L2为升压电感，S1、S2为开关管，VD1～VD4为续流二极管，C为输出电容，R为负载电阻。以正半周期工作状态为例，双二极管式无桥PFC变换器的工作模态如图2所示。由图2b分析可知，双二极管式无桥PFC变换器的返回电流不仅流过续流二极管，还通过开关的体二极管进行回流，这样传统的PFC电流检测方法在该模态下就无法直接适用。
图1无桥变换器的状态方程可以表示为
图1 典型的双二极管式无桥PFC变换器拓扑
Fig.1 Typical dual-diode bridgeless PFC converter topology
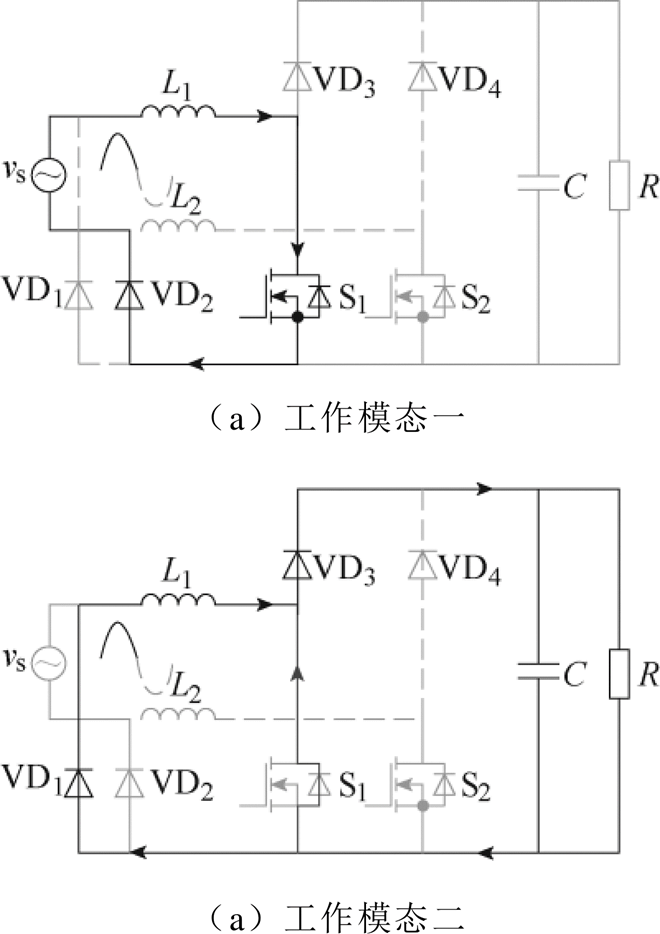
图2 输入电压正半周期的工作模态
Fig.2 Operating mode of positive half period of input voltage
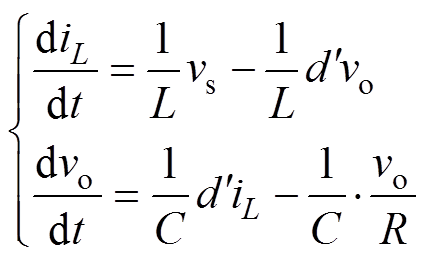（1）
式中，iL为升压电感电流，在一个开关周期内等同于输入电流is；d为占空比，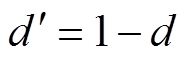
。
定义状态变量x1与x2分别为电感电流iL与输出电压vo，用其带“
”的变量表示观测值，带“
”的变量表示真实值与观测值的误差值。因负载信息未知变化，RC用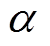
变量来表征。采用类Lyapunov方法进行设计，可以得到经典电流观测器[19]的表达式为
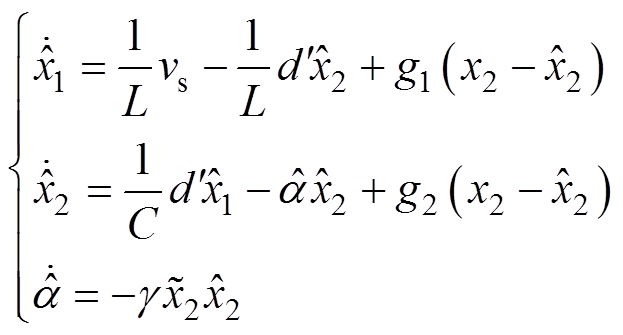（2）
式中，g1、g2和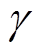
为反馈系数。
针对无桥PFC电流采样的问题，电感电流可通过采样输入vs和输出vo，以及内部占空比计算量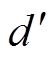
来重构观测，以此可规避复杂的采样电路。含电流观测器的经典无电流传感控制无桥PFC系统（基于FPGA实验）如图3所示。
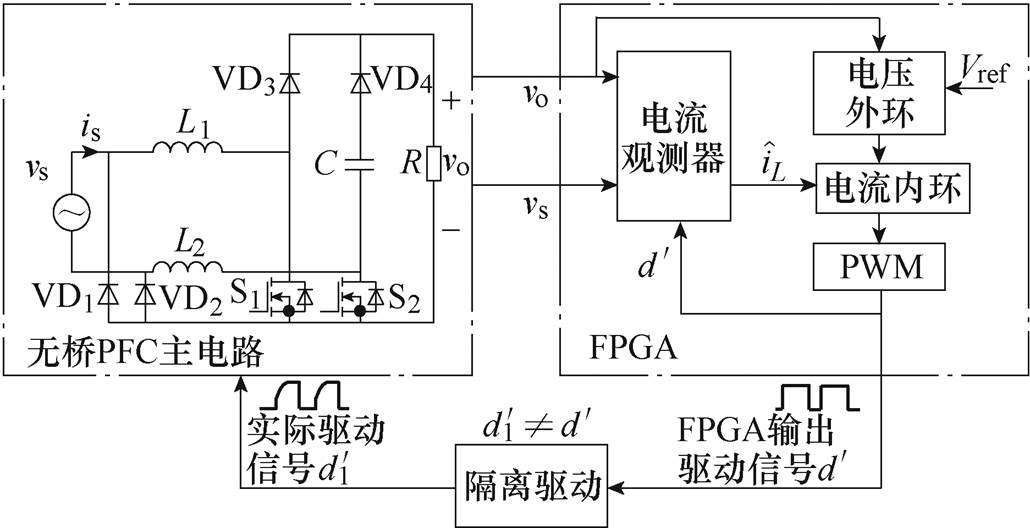
图3 电流观测器工作示意图
Fig.3 Schematic diagram of error between real current
图3中，经典的电流观测器内部占空比计算量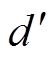与实际主电路工作占空比
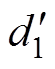并不相等，其主要原因在于开关管的损耗以及隔离与采样设备的影响，实际工作占空比与理论计算占空比两者存在不确定误差。不确定的占空比误差显然会影响电流观测精度。不妨记占空比误差
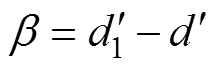，忽略输出电压观测误差，写出未忽略占空比误差时观测电感电流微分值与真实电流的微分值为
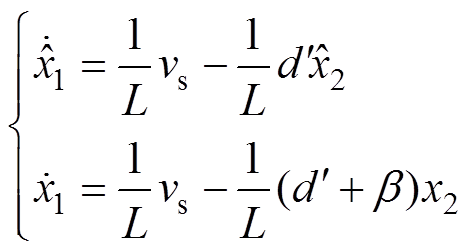（3）
由式（3）可知，由于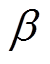
的存在，电感电流观测值的微分量会比理论微分量更大。该偏大的电感电流微分值经过半个工频周期的积分后将会导致观测值比真实电感电流偏大。写出观测值与实际值误差表达式为
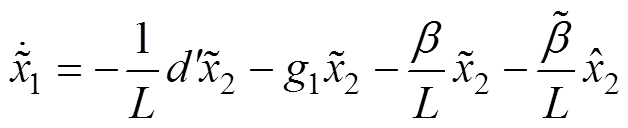（4）
进一步忽略输出电压观测误差有
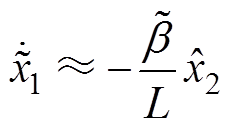（5）
由式（5）得此时电感电流真实值与观测值差值的微分在同一工况下应当近似为一个常数，且由于电感电流观测值过零点强制置零操作的缘故，该差值每当过零点也应该置零，所以误差微分值经过积分后应当呈现一个锯齿状波形。观测电流与其观测误差示意图如图4所示。它与真实电流的误差值在每半个工频周期内不断线性增大，直到置零时刻。此时的真实电感电流将产生严重畸变，采用此观测电流进行控制的无桥PFC变换器将无法实现APFC功能。
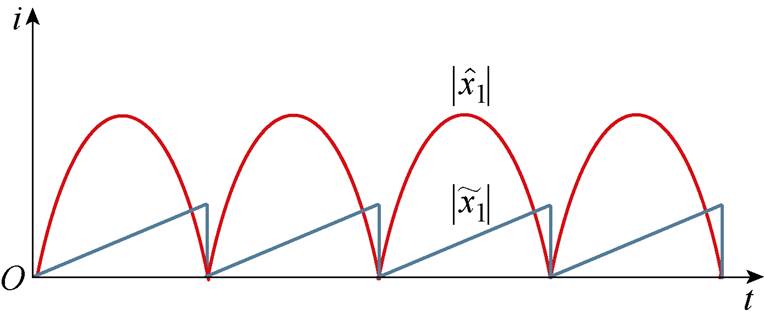
图4 观测电流与其观测误差示意图
Fig.4 Schematic diagram between observed current and observed current error
频率较低时其对观测精度影响可忽略，然而随着开关频率的提升，二者偏差会加大，其对观测精度影响不可忽略，该问题并未有文献予以关注及讨论。为此，本文拟针对此问题，在电流观测器中考虑引入占空比误差自适应变量，构建更具普适性的占空比自适应观测器。
由式（2）可知，观测器工作时，因实际采样输出电压，即输出变量x2（即vo），所以其观测值较为准确，相对于其他变量可以近似认为观测误差为0。考虑实际占空比与理论计算占空比存在不确定误差，将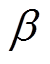引入式（1）与式（2），分别得到
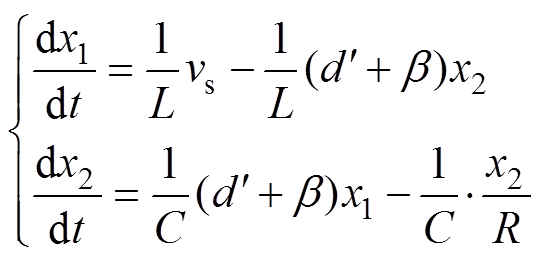（6）
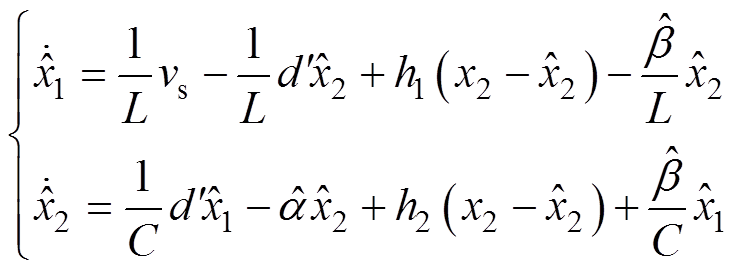（7）
式中，h1和h2为改进后观测器的反馈系数，联立式（6）与式（7），有
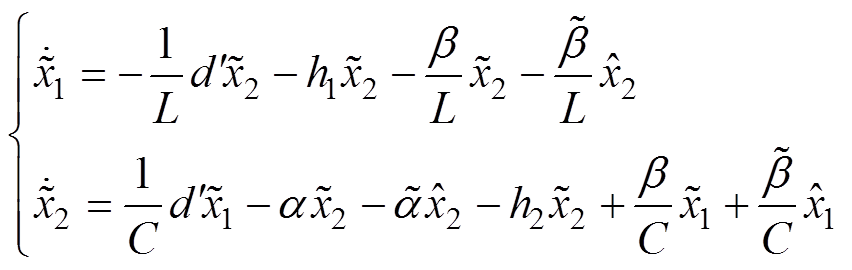（8）
对所需观测变量设定能量函数并且求导后得
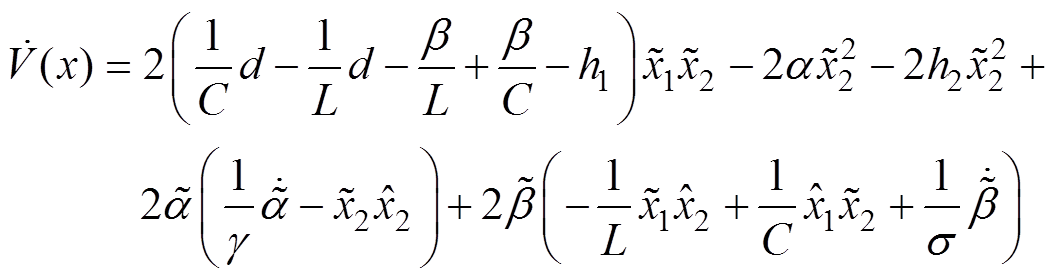（9）
式中，
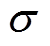和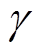为大于0的常数。令式（9）右侧部分不大于零，即
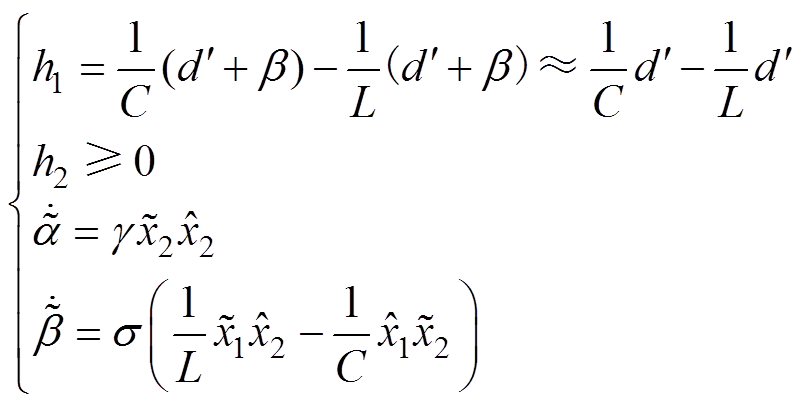（10）
对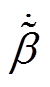
进行积分运算，可以得到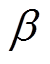观测值的微分表达式为
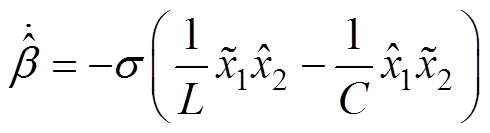（11）
后续将采用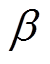的观测值代表实际的占空比误差。进一步忽略输出电压的观测误差，式（11）可以写为
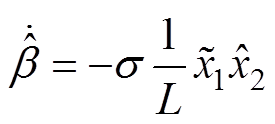（12）
由式（12）可知，计算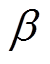的观测值需要变量
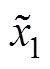与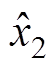
，即电感电流的观测误差与输出电压的观测值，因电感电流未采样，故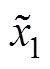变量无法直接获取。考虑到输出电压观测的准确性，因此拟从输出电压入手，寻找变量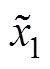的替代值。
输出电压真实值与观测值微分方程整理为
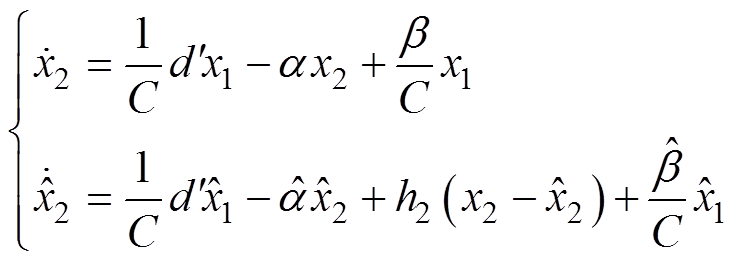（13）
因为采样了真实输出电压，即使在电感电流观测值失真的情况下，输出电压依然能够精准地被观测。此时的观测电压与真实电压的微分值也应该近似相等，即式（13）中两式应相等。考虑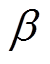在此处计算时占比较小，略去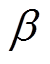简化运算得到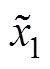表达式为
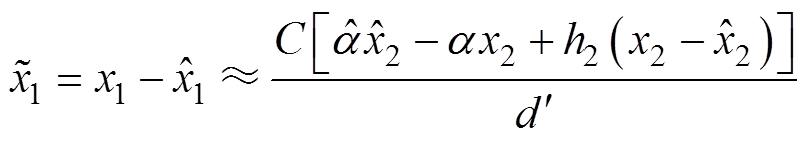（14）
从式（14）中发现，并非所有的变量都能从数字控制系统中调用。进一步利用电感电流自然过零点这一特性，将式（14）改为
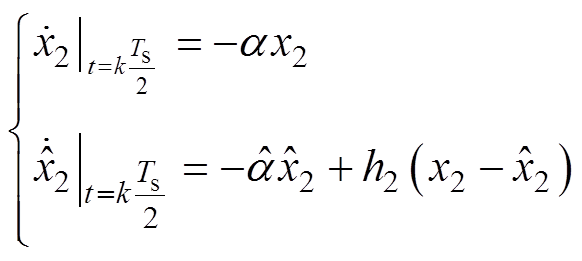（15）
式中，kTs/2代表着每个输入电压正弦周期的过零点时刻，Ts为正弦周期。结合式（14）与式（15）有
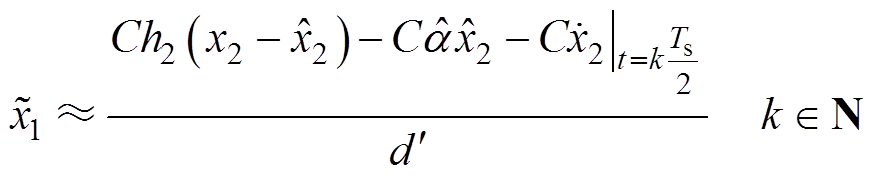（16）
将其代入式（12）的占空比误差，计算为
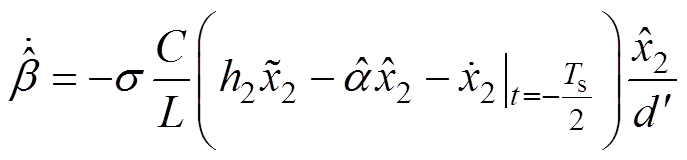（17）
经过上述处理，最终可以得到双二极管式无桥PFC的电流观测器关系式为
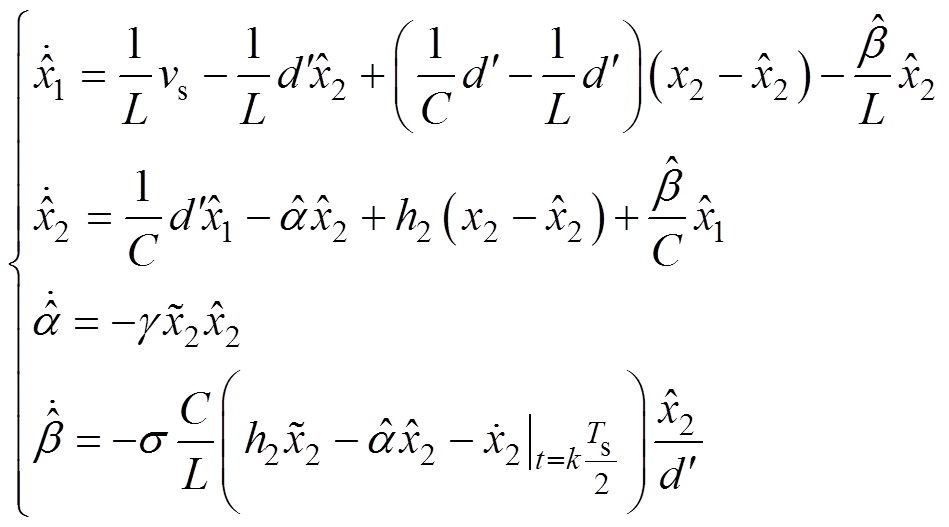（18）
由式（18）所示的观测器结构框图如图5所示，其中过零检测系统如图6所示，其检测思路为：输入电压的16位补码数分别与靠近零的正、负两数进入比较器，之后得到两判断值，随后两判断值经过或非门再交由上升沿触发器判断，由此得到过零点脉冲。以此脉冲信号作为使能信号即可实现过零检测功能。
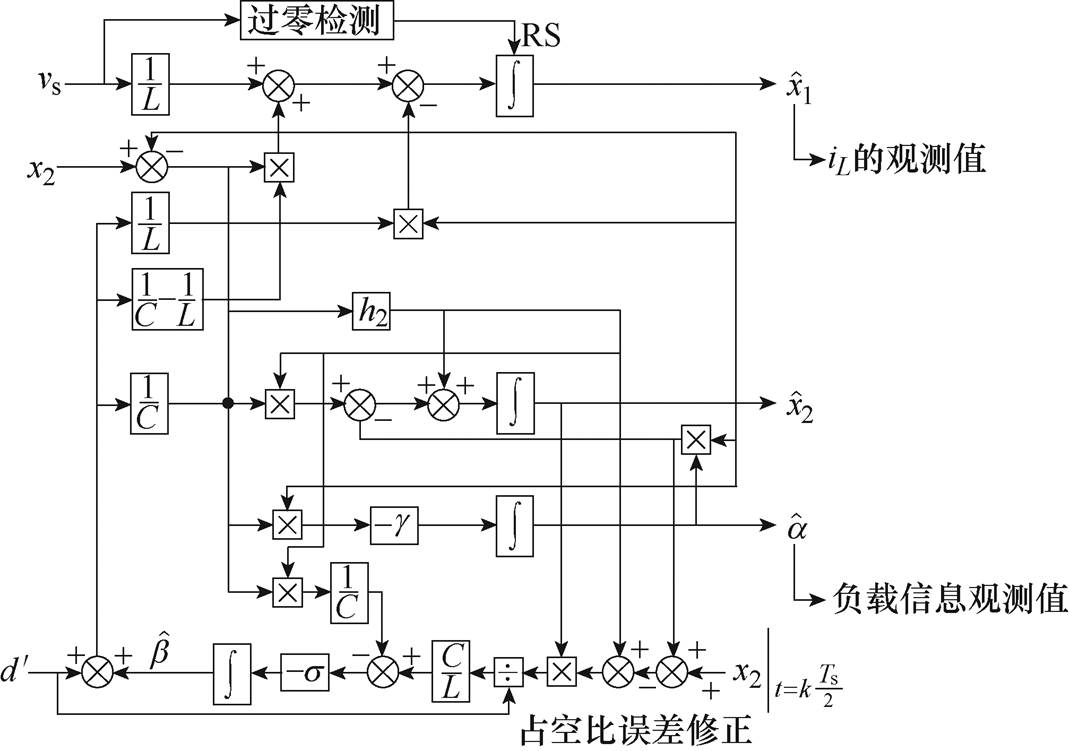
图5 电流观测器结构框图
Fig.5 Structure block diagram of current observer
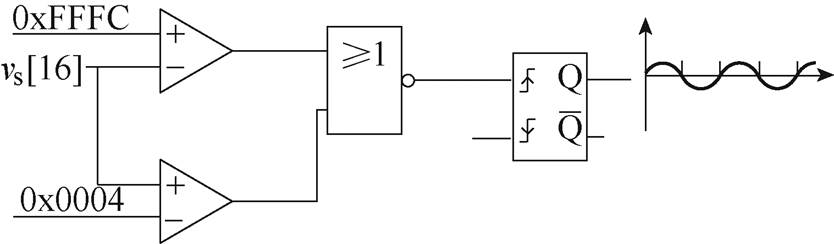
图6 过零检测框图
Fig.6 Block diagram of zero crossing detection
基于所设计的占空比误差自适应观测器进一步给出图7所示的无桥PFC的无电流传感控制方案。具体控制方案包括单相旋转坐标系下无桥PFC电路的平均电流解耦控制，以及利用所设计观测器给出负载信息和输出电压二次纹波的复合前馈控制。
电流内环采用的平均电流解耦控制，在dq旋转坐标系下可以得到系统数学模型为
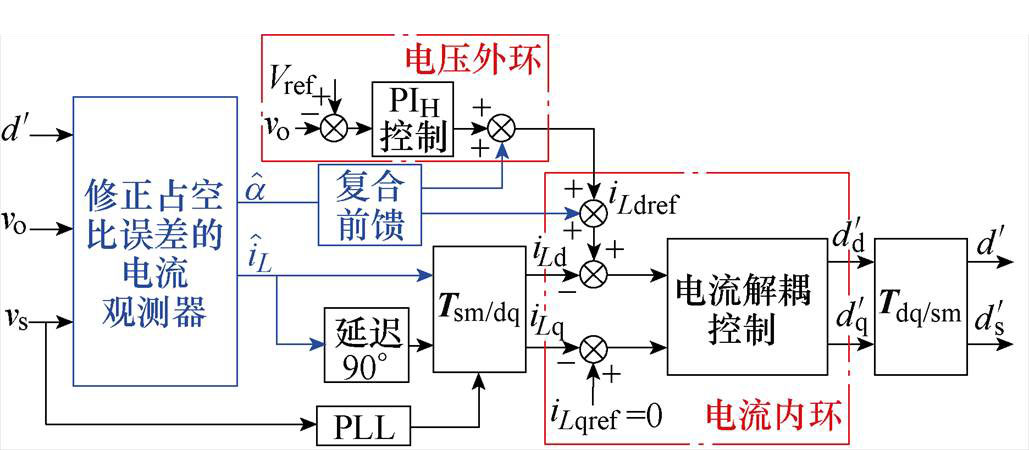
图7 无电流传感控制方案
Fig.7 Control scheme without current sensing
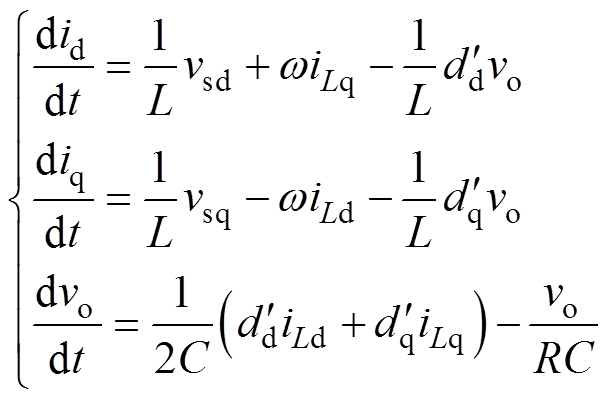（19）
进一步地，用Gvc和Gic分别代表电压、电流补偿环节的环路增益，设计出的旋转坐标系下平均电流解耦控制框图如图8所示。
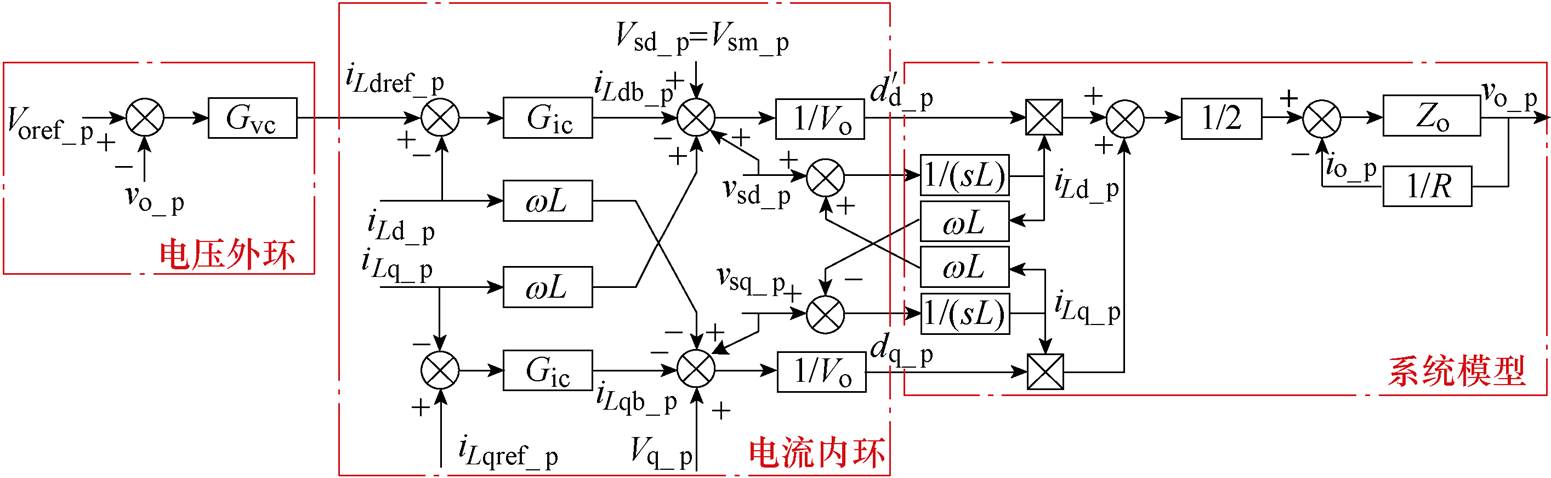
图8 d-q模式下的无桥PFC变换器控制框图
Fig.8 The control block diagram of bridgeless PFC converter in d-q coordinate system
为了改善系统的动态性能，本文设计了基于观测负载的复合前馈控制，其利用前述电流观测器得到的负载信息构造输出电流内环参考值与电压二次纹波的观测值进行复合前馈。
首先是电流内环的参考值。假设式（19）中所有量的稳态值均是直流量，写出d轴电流表达式为
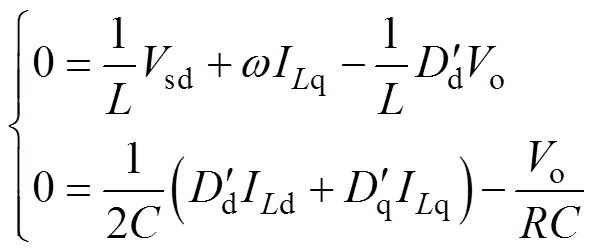（20）
无桥PFC变换器稳态时输入电流应该和输入电压同相位，所以令ILq=0代入式（20）可以得到d轴稳态电流为
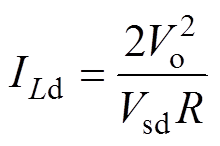（21）
由式（21）所示，电感电流在d轴上的稳态参考值与输出电压、输入电压幅值以及负载的倒数有关，利用观测负载量来代替其真实量，代入观测负载信息中可以得到电流内环的参考值为
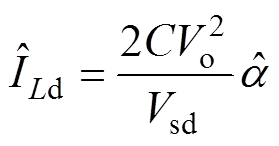（22）
以上得到了电流内环的参考值。为了去掉电压外环的低通滤波器，还需要推导输出电压的二次纹波值。输出电压二次纹波是由于输入、输出功率不平衡导致，系统的输出电压可以表示为
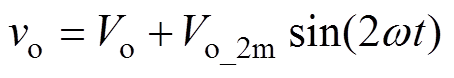（23）
因为缓冲输入输出功率的主要器件为电容元件，其瞬时功率可以表示为
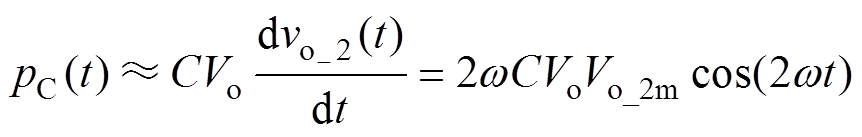（24）
忽略输出功率的损耗，有功率平衡式为
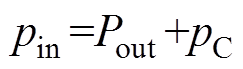（25）
分离其中的交直流量为
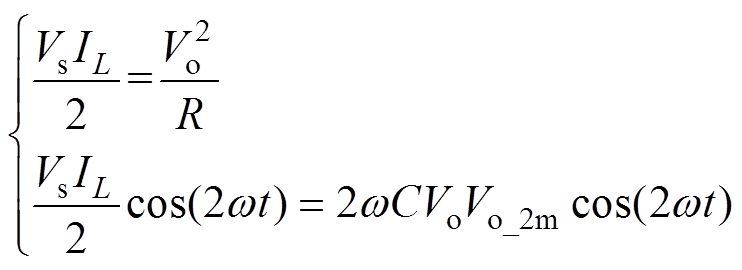（26）
对式（26）求解并以观测负载信息代替负载R可得二次纹波计算表达式为
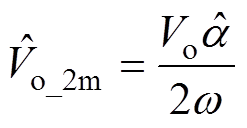（27）
最终设计复合前馈控制如图9所示。
实验方案中搭建了基于FPGA数字控制的无桥PFC变换器实验样机，系统实验平台如图10所示。样机主要电路参数见表1，其中不控整流桥型号为GBJ2510，开关管选用IRFP460，开关驱动器芯片为IR2110s，功率二极管为RHR30120。选择LA25- NP霍尔传感器进行电压采样，实现功率主电路与数字控制电路隔离。核心处理器为Altera公司旗下的Cyclone IV 4CE115F29型FPGA，在该数字控制器上实现图7所示的控制方案。
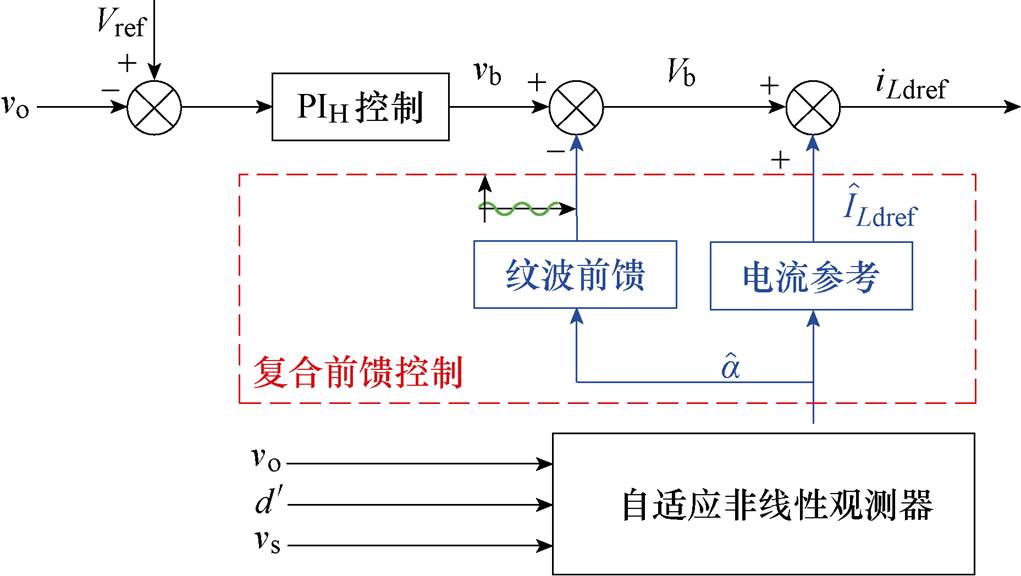
图9 复合前馈控制
Fig.9 Compound feedforward control
图10 无桥PFC变换器数字控制实验平台
Fig.10 Experimental platform for digital controlled bridgeless PFC converter
表1 电路参数
Tab.1 The parameters of circuit
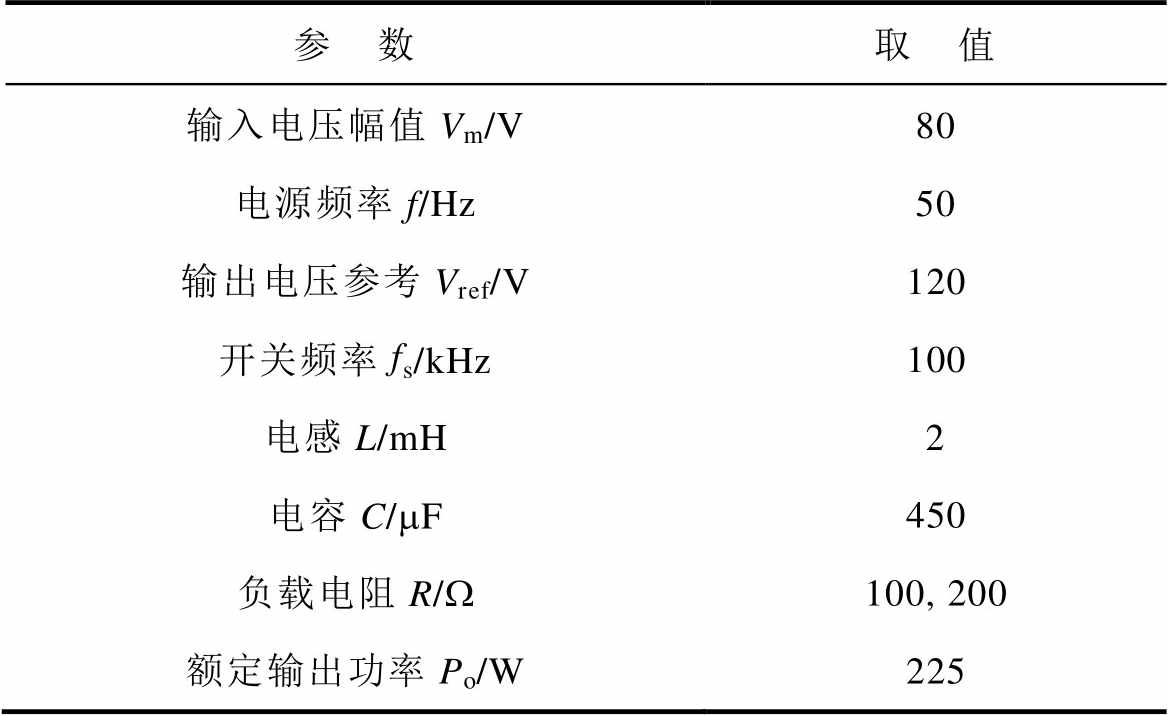
参 数取 值 输入电压幅值Vm/V80 电源频率f/Hz50 输出电压参考Vref/V120 开关频率fs/kHz100 电感L/mH2 电容C/mF450 负载电阻R/W100, 200 额定输出功率Po/W225
图11为100 kHz开关频率下开关管的驱动波形和端电压波形，由FPGA所输出的PWM波在经过一系列硬件传递信号后有一定程度的损失。
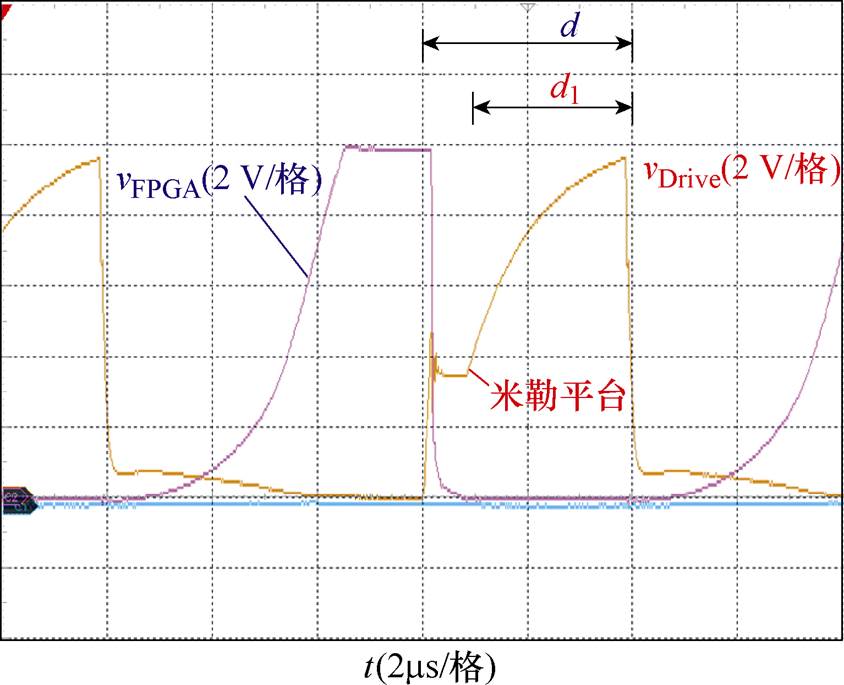
图11 MOSFET端电压与隔离驱动电压实验波形
Fig.11 MOSFET terminal voltage and isolation and driving voltage experimental waveforms
图12与图13为传统电流观测器与提出的占空比误差自适应观测器的观测效果对比，所提观测器可以很好地修正观测电流的误差，其观测精度能达到96.75%。
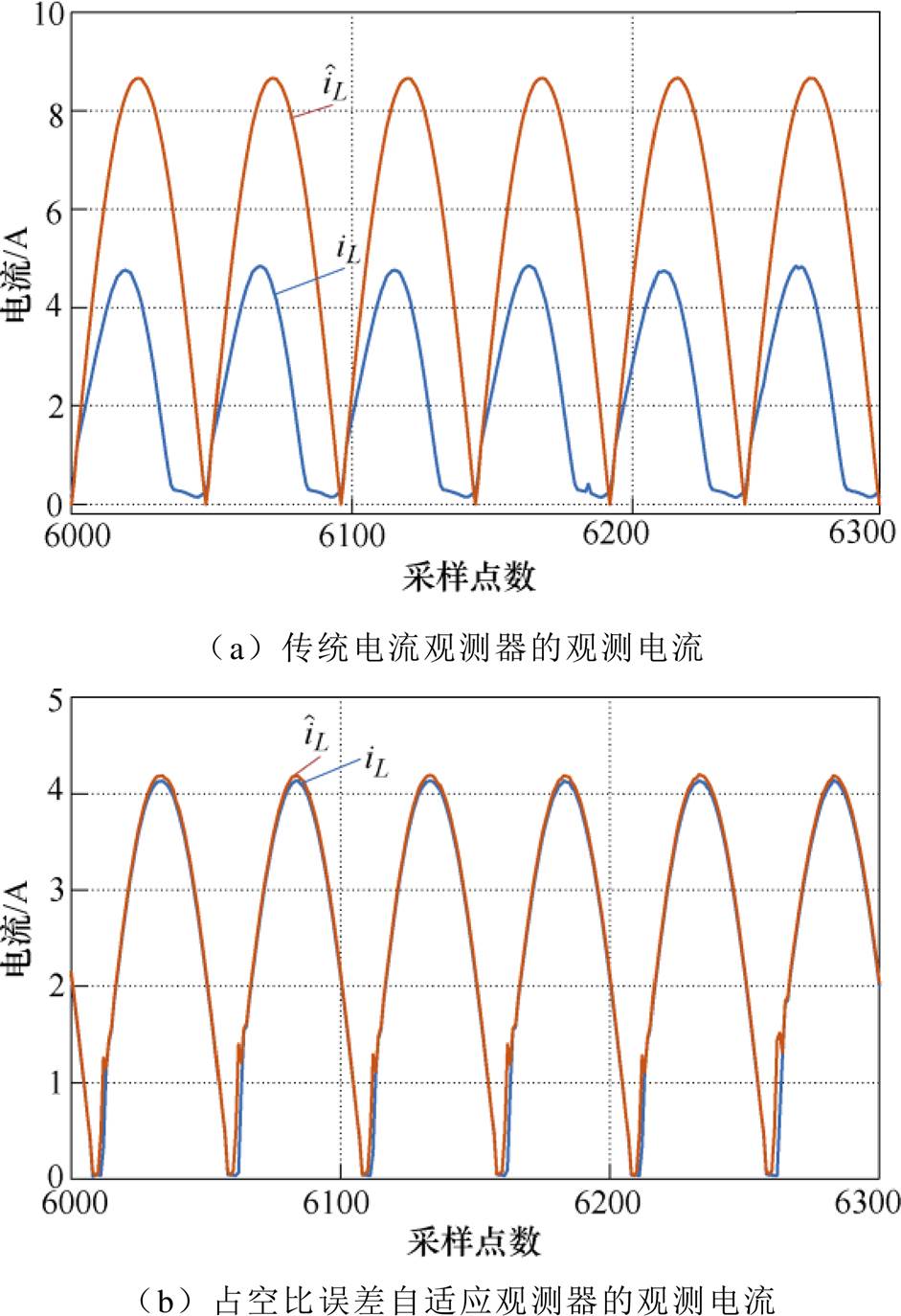
图12 电感电流及其观测值（FPGA内实验数据）
Fig.12 The current of inductance and its observation value (experimental data in FPGA)
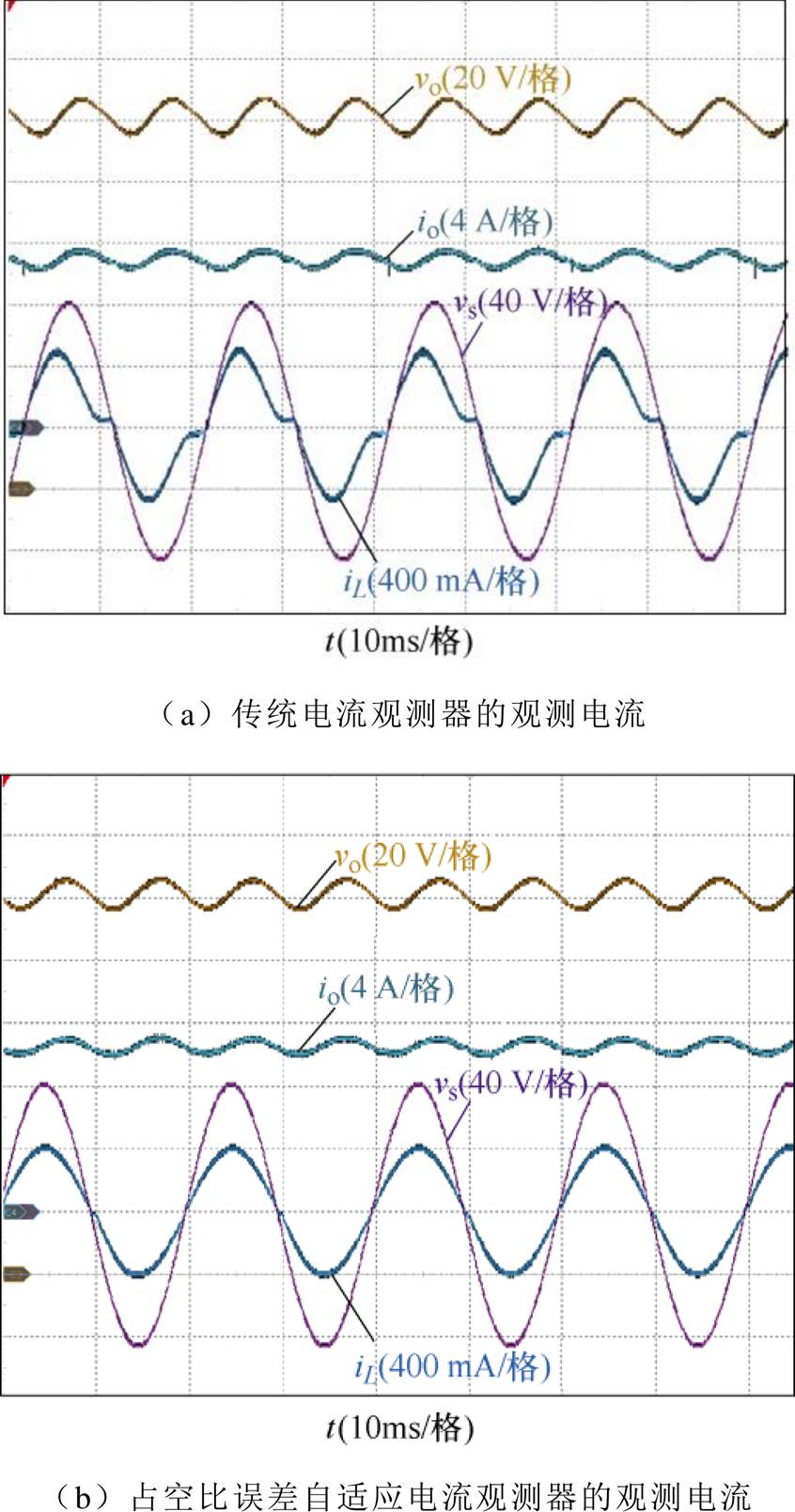
图13 电感电流及其观测值（示波器观测）
Fig.13 The current of inductance and its observation value (experimental data in oscilloscope)
图14为带LPF的传统数字控制的动态实验结果，当负载上升和下降时，动态实验波形如图14a和图14b所示。但是由于电压外环带LPF，因此系统带宽很低，负载R上升和下降之后，大约需要8～10个工频周期才能达到新的稳态。图15为采用L4981芯片模拟控制的动态实验结果，当负载上升和下降时，其负载动态波形如图15a和图15b所示，其也需要大概9～10个工频周期才能达到新稳态。
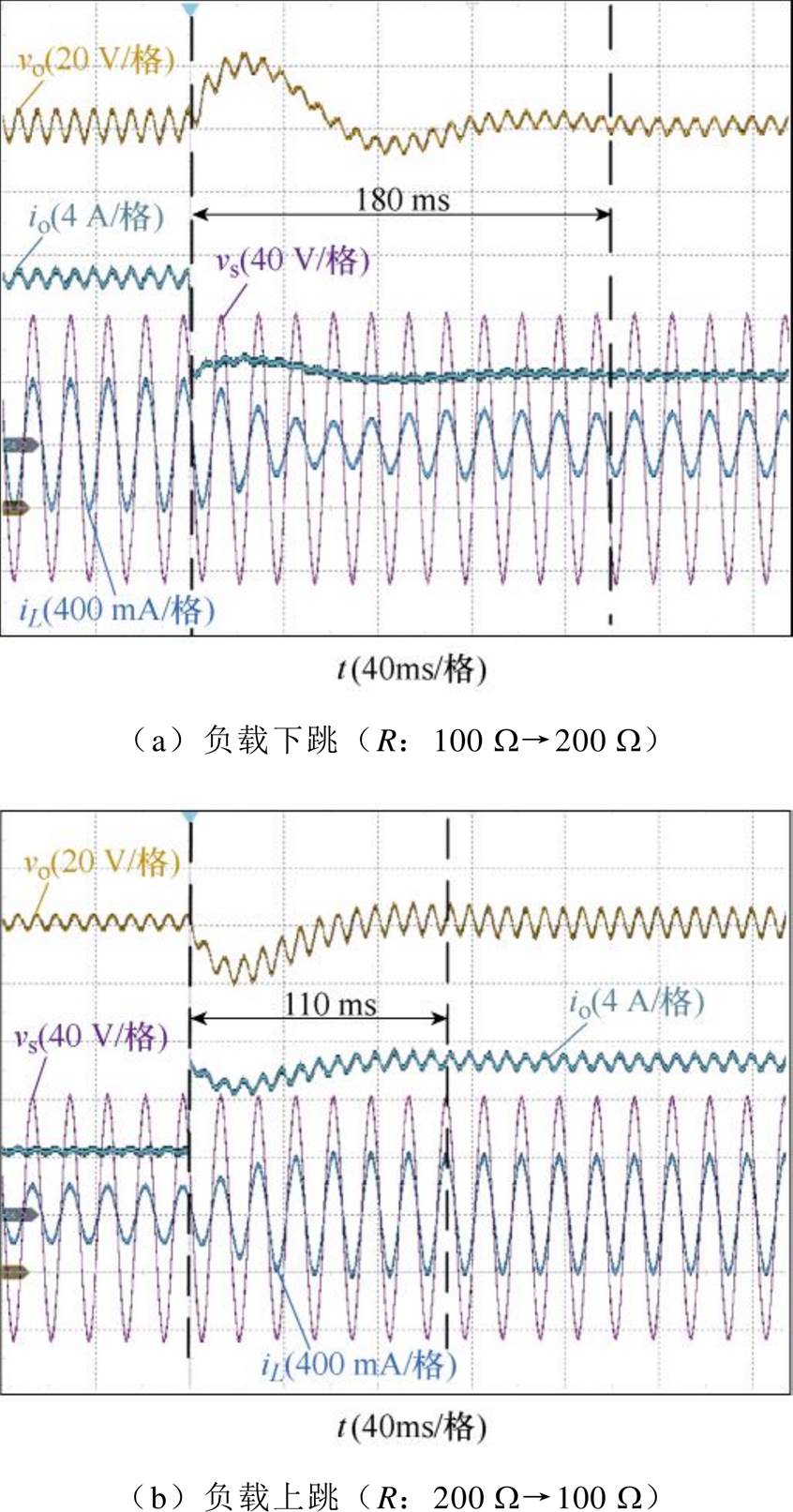
图14 带LPF的传统双环控制动态实验结果
Fig.14 Dynamic experimental results for the traditional double-loop control with LPF
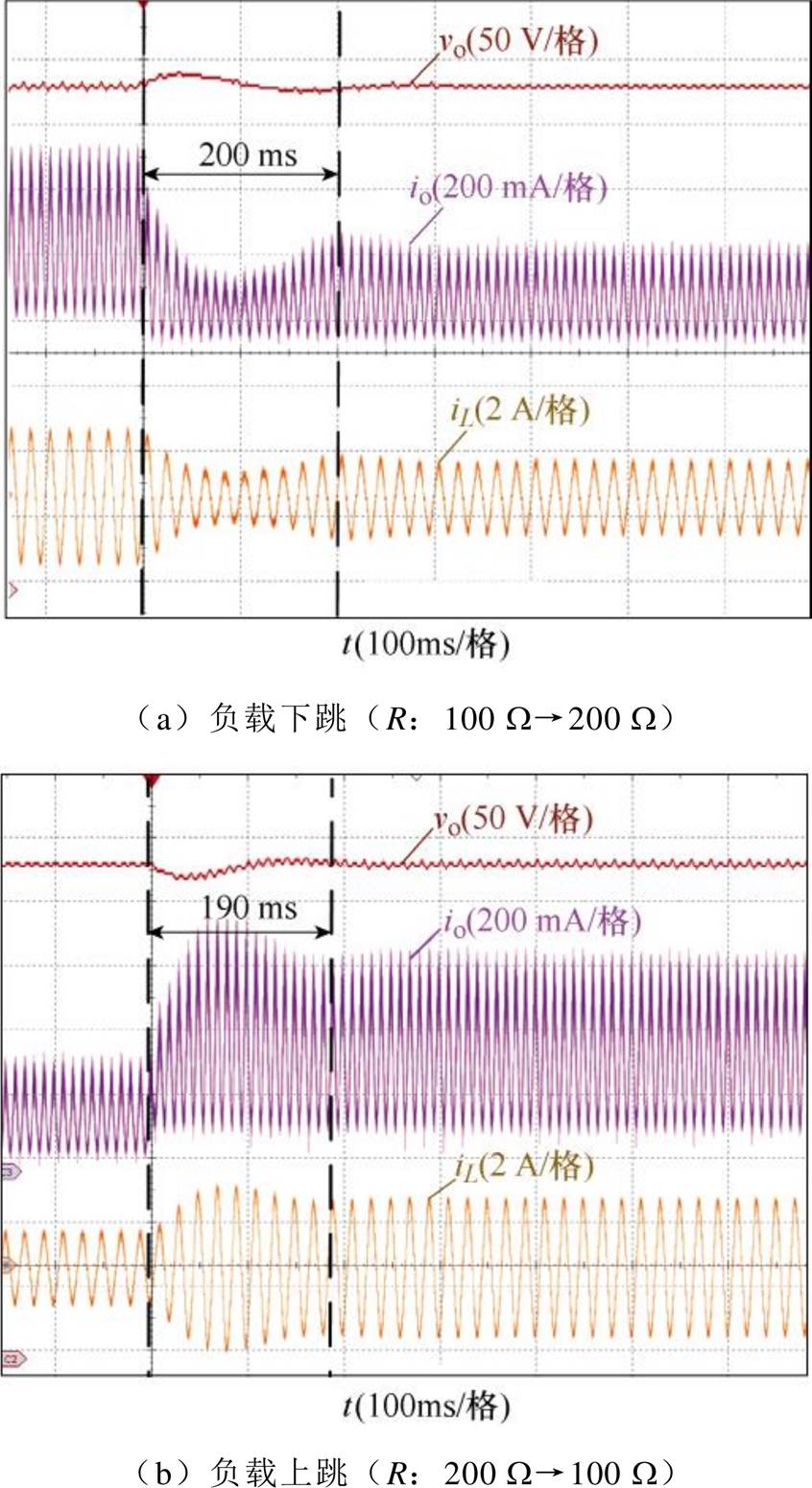
图15 采用L4981芯片的平均电流控制动态实验结果
Fig.15 Average current control with L4981
图16为提出的复合前馈控制方案负载动态实验结果，此时电压外环去掉LPF，其系统工作在高带宽模式下，当负载上升和下降时，其负载动态波形如图16a和图16b所示，仅需大约2个工频周期即可达到新的稳态。对比结果见表2，所提的复合前馈控制方案大幅提高了系统动态响应速度。
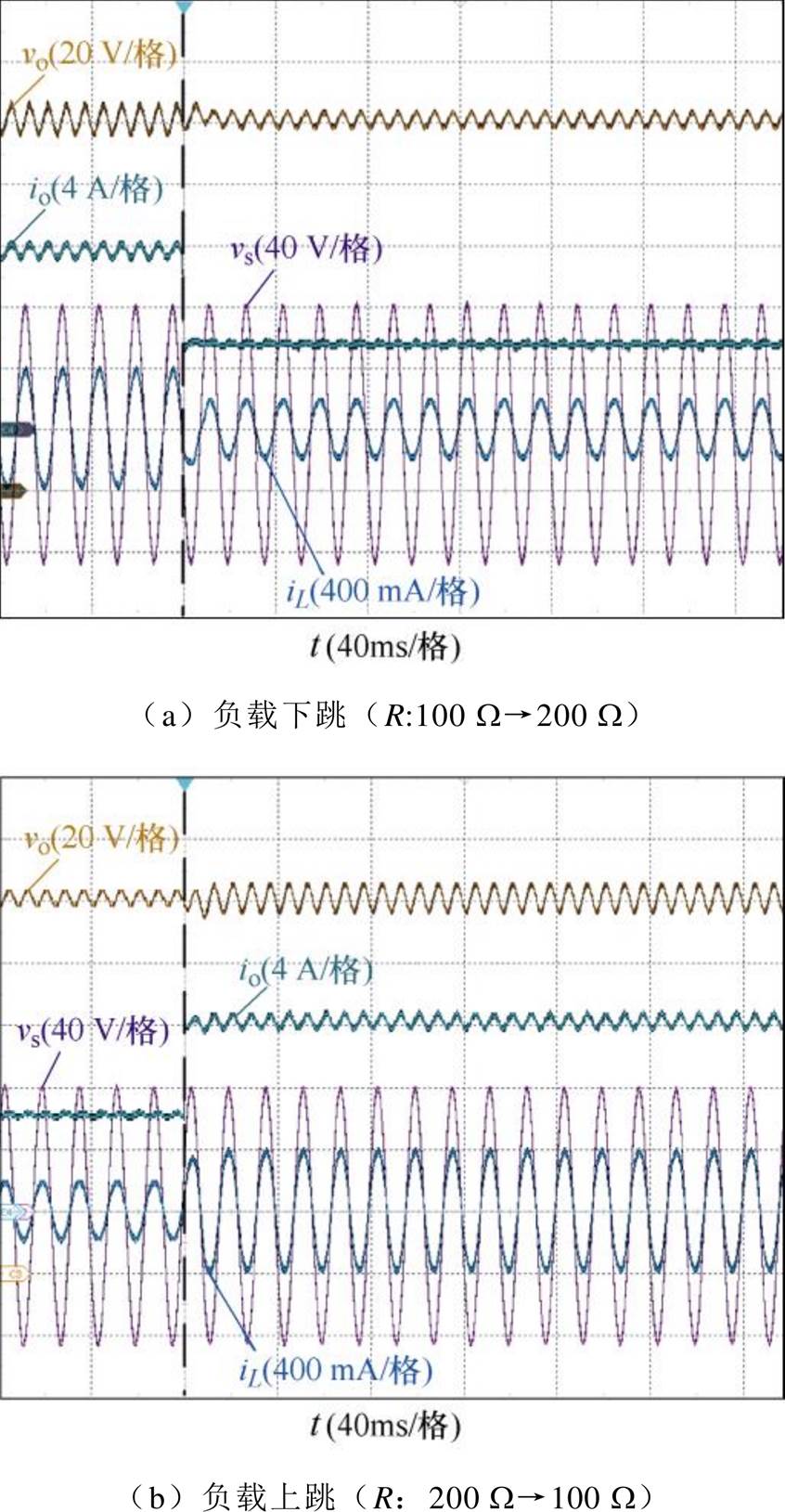
图16 提出的复合前馈控制动态实验结果
Fig.16 Dynamic experimental results of the proposed compound feedforward control
表2 负载动态响应时间比较
Tab.2 Comparison of load dynamic time comparison
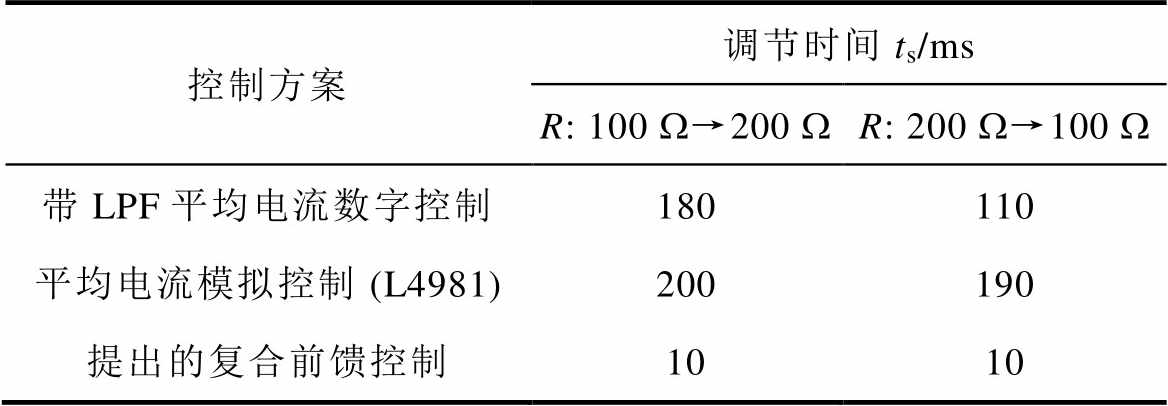
控制方案调节时间ts/ms R: 100 W→200 WR: 200 W→100 W 带LPF平均电流数字控制180110 平均电流模拟控制 (L4981)200190 提出的复合前馈控制1010
所提的复合前馈控制的稳态实验结果如图17所示，输入电流的总谐波畸变率（Total Harmonic Distortion, THD）约为5.09%，功率因数约为99.85%，与目前业界较为成熟的平均电流控制与单周期控制相比，提出的复合前馈控制与其具有几乎相同的稳态性能，较好地满足了使用需求。
表3 稳态性能比较
Tab.3 Comparison of steady-state operating performance
控制方案稳态参数 PF(%)THD(%) 平均电流模拟控制[6]≥99≤5 单周期控制[8]≥99≤5 提出的复合前馈控制99.855.09
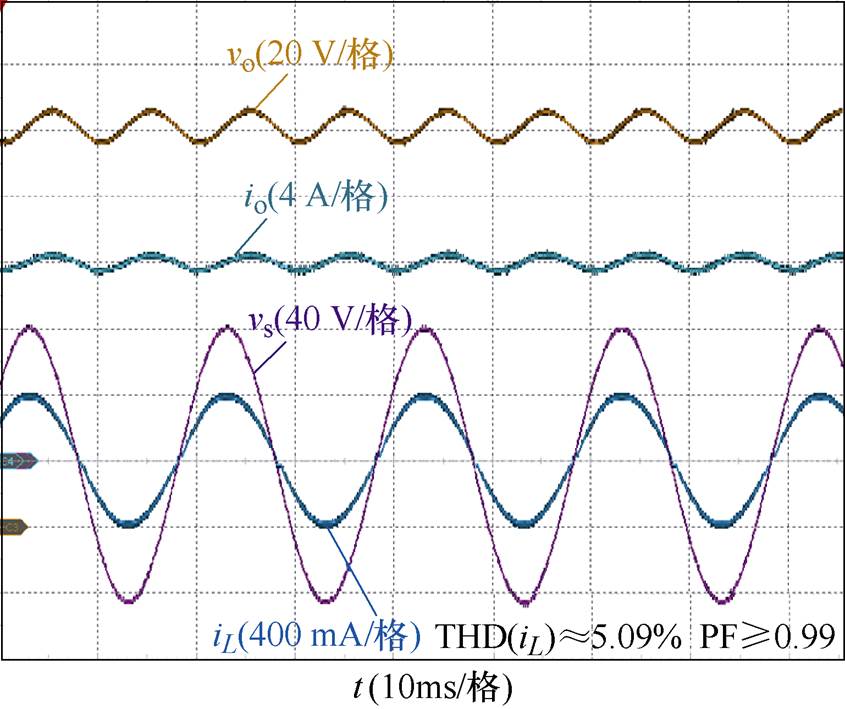
图17 提出的复合前馈控制控制稳态实验结果
Fig.17 Steady experimental results of the proposed compound feedforward control
针对双二极管式无桥PFC变换器电感电流采样复杂的问题，本文在考虑占空比误差影响的基础上设计了电流观测器，通过采样输入与输出电压，重构出输入电感电流，并在此基础上设计了无电流传感器的复合前馈控制。所提的控制方案利用负载信息作为电流内环的参考和电压外环的二次纹波补偿，去掉了电压外环的LPF，设计系统电压环为高带宽模式，保证高质量输入电流同时兼顾了系统负载动态性能。本文通过搭建实验样机，与传统控制方案对比证明了所设计方案的有效性，并得出以下结论：
1）与传统的电流观测器相比，本文所提的占空比误差自适应观测器从软件层面对高开关频率下开关管的占空比误差进行了修正，进而提高了电感电流的观测精度，使其可以作为后续无电流传感控制的基础。同时其针对其他类PFC拓扑也具有一定的适用性。
2）所设计的无电流传感的复合前馈控制避免了双二极管式无桥PFC变换器电感电流采样复杂的问题，并且对比传统的双环控制具有更好的动态响应能力。
参考文献
[1] 孙凯, 贲洪奇, 孟涛, 等. 一种具有宽输出调压范围与低电压应力的单级无桥隔离型PFC变换器[J]. 电工技术学报, 2022, 37(8): 1991-2005.
Sun Kai, Ben Hongqi, Meng Tao, et al. A single-stage bridgeless isolated PFC converter with wide output voltage range and low voltage stress[J]. Transactions of China Electrotechnical Society, 2022, 37(8): 1991- 2005.
[2] 林通, 江平, 姚佳. 一种基于耦合电感的零电流纹波功率因数校正变换器[J]. 电工技术学报, 2022, 37(18): 4732-4744.
Lin Tong, Jiang Ping, Yao Jia. A zero current ripple tapped inductor power factor correction converter[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4732-4744.
[3] 王生东, 李浩然, 顾占彪, 等. 便携式充电CRM图腾柱功率因数校正过零检测延迟与交错相位误差补偿控制[J]. 电工技术学报, 2022, 37(1): 12-23.
Wang Shengdong, Li Haoran, Gu Zhanbiao, et al. Compensation control of zero current detection delay and interleave phase error for CRM totem-pole power factor correction in portable charging[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 12- 23.
[4] 杨雁勇, 戴慧纯, 王正仕. 无桥PFC的性能改善及控制参数设计[J]. 电工技术, 2018(5): 42-45.
Yang Yanyong, Dai Huichun, Wang Zhengshi. Per- formance improvement and control parameter design of bridgeless PFC[J]. Electric Engineering, 2018(5): 42-45.
[5] 顾诗雅, 马红波. 混合谐振PWM无桥PFC变换器的研究与设计[J]. 电工技术, 2022(23): 11-15.
Gu Shiya, Ma Hongbo. Research and design of hybrid resonant PWM bridgeless PFC converters[J]. Electric Engineering, 2022(23): 11-15.
[6] Etz R, Patarau T, Petreus D. Comparison between digital average current mode control and digital one cycle control for a bridgeless PFC Boost converter[C]// 2012 IEEE 18th International Symposium for Design and Technology in Electronic Packaging (SIITME), Alba Iulia, Romania, 2012: 211-215.
[7] Chen Jingquan, Prodic A, Erickson R W, et al. Predictive digital current programmed control[J]. IEEE Transactions on Power Electronics, 2003, 18(1): 411-419.
[8] Smedley K M, Cuk S. One-cycle control of switching converters[J]. IEEE Transactions on Power Elec- tronics, 1995, 10(6): 625-633.
[9] Lai Zheren, Smedley K M, Ma Yunhong. Time quantity one-cycle control for power-factor corre- ctors[J]. IEEE Transactions on Power Electronics, 1997, 12(2): 369-375.
[10] Wang Han, Yang Xinghua, Lei Huaigang, et al. Theoretic analysis and experimental study of a novel bridgeless partial active PFC[C]//2008 International Conference on Electrical Machines and Systems, Wuhan, China, 2009: 1179-1184.
[11] Choi Y J, Kim T J, Kim R Y. An active partial switching method in tertiary loop for a high- efficiency predictive current-mode control PFC converter[J]. IEEE Transactions on Industrial Elec- tronics, 2018, 65(10): 7818-7828.
[12] Ziegler S, Woodward R C, Iu H H C, et al. Current sensing techniques: a review[J]. IEEE Sensors Journal, 2009, 9(4): 354-376.
[13] Musavi F, Eberle W, Dunford W G. A phase-shifted gating technique with simplified current sensing for the semi-bridgeless AC-DC converter[J]. IEEE Transa- ctions on Vehicular Technology, 2013, 62(4): 1568- 1576.
[14] Baek J, Shin J, Jang P, et al. A critical conduction mode bridgeless flyback converter[C]//8th Inter- national Conference on Power Electronics-ECCE Asia, Jeju, Korea (South), 2011: 487-492.
[15] Reddig M, Zhou Wenqi, Schlenk M. True bridgeless PFC-stages with advanced current measuring cir- cuit[C]//2011 IEEE 33rd International Telecommu- nications Energy Conference (INTELEC), Amsterdam, Netherlands, 2011: 1-6.
[16] Musavi F, Eberle W, Dunford W G. A phase shifted semi-bridgeless Boost power factor corrected con- verter for plug in hybrid electric vehicle battery chargers[C]//2011 Twenty-Sixth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Fort Worth, TX, USA, 2011: 821-828.
[17] López F, López-Martín V M, Azcondo F J, et al. Current-sensorless power factor correction with predictive controllers[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2019, 7(2): 891-900.
[18] Chen H C, Lu Cheyu, Li Guanting, et al. Digital current sensorless control for dual-Boost half-bridge PFC converter with natural capacitor voltage balancing[J]. IEEE Transactions on Power Electronics, 2017, 32(5): 4074-4083.
[19] Pahlevani M, Pan Shangzhi, Eren Suzan, et al. An adaptive nonlinear current observer for Boost PFC AC/DC converters[J]. IEEE Transactions on Indu- strial Electronics, 2014, 61(12): 6720-6729.
[20] López F, Lamo P, Pigazo A, et al. Sensorless current rebuilding strategy in a single phase bridgeless PFC[C]//2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 2016: 2389-2394.
[21] Prodic A, Chen Jingquan, Maksimovic D, et al. Self-tuning digitally controlled low-harmonic rectifier having fast dynamic response[J]. IEEE Transactions on Power Electronics, 2003, 18(1): 420-428.
Abstract Accurate sensing of inductor current is necessary for closed-loop control of PFC converters. However, in bridgeless PFC converters, the inductor current is no longer unidirectional, which needs expensive and complex current sampling devices. Sensorless techniques using current observers are regarded as a cost-effective solution. However, existing current observers do not consider the influence of duty cycle errors, resulting in poor observation accuracy at high switching frequencies. This paper proposes an improved adaptive current observer with a duty-cycle error correction function. Additionally, a compound feedforward control without current sensing is designed for the bridge PFC converter.
Firstly, by introducing duty cycle error into the current observer’s expression, the specific influence of the duty cycle error on the observed current is obtained. The error value of the observed current increases linearly in every half of the industrial frequency cycle until it resets to zero at zero crossing time. When the switching frequency is low, the influence of duty cycle error can be negligible. With the increase of switching frequency, the influence on the observation accuracy becomes significant. Based on theoretical analysis, an improved observer with adaptive duty cycle error is designed. The proposed approach is to find an alternative to inductor current using the output voltage. The natural zero crossing point of the inductor current is utilized to obtain a duty cycle error adaptive observer for the bridgeless PFC converter. Finally, the proposed current observer is utilized to construct a compound feedforward control scheme, using observations of load information and output voltage ripple information to achieve a high dynamic response of the bridgeless PFC converter.
An experimental prototype of a 225 W bridge-free PFC is built. The experimental results show that the proposed duty-cycle adaptive observer achieves a 96.75% observing accuracy of the inductor current at 80 V input voltage and 100 kHz switching frequency. The load dynamic response of the proposed compound feedforward control scheme requires only about 2 IF cycles; in contrast, the conventional control scheme requires about 8-9 IF cycles. Meanwhile, the PF of the proposed scheme is 99.85%, and the THD is 5.09%.
The following conclusions are obtained in this paper. (1) Compared with the traditional current observer, the proposed duty-cycle adaptive observer corrects the duty cycle error of the switching tube at high switching frequency in software and improves the observation accuracy of the inductor current. Meanwhile, it has potential applications in other PFC topologies. (2) The proposed compound control scheme avoids the complexity of inductor current sampling in the bridgeless PFC converter, demonstrating a better dynamic response than the traditional double-loop control.
keywords：Bridgeless power factor correction (PFC) converter, current observer, feedforward control, dynamic response, duty cycle adaptation
DOI: 10.19595/j.cnki.1000-6753.tces.230879
中图分类号：TM46
国家自然科学基金资助项目（52077021）。
收稿日期 2023-06-09
改稿日期 2023-08-09
卢伟国 男，1977年生，博士，教授，研究方向为电能变换系统及控制技术、无线供能与取能技术、电能质量监测等。E-mail: luweiguo@cqu.edu.cn（通信作者）
胡凌鹤 男，1999年生，硕士研究生，研究方向为电能变换系统及控制技术。E-mail: hlhsdsg123@163.com
（编辑 陈 诚）