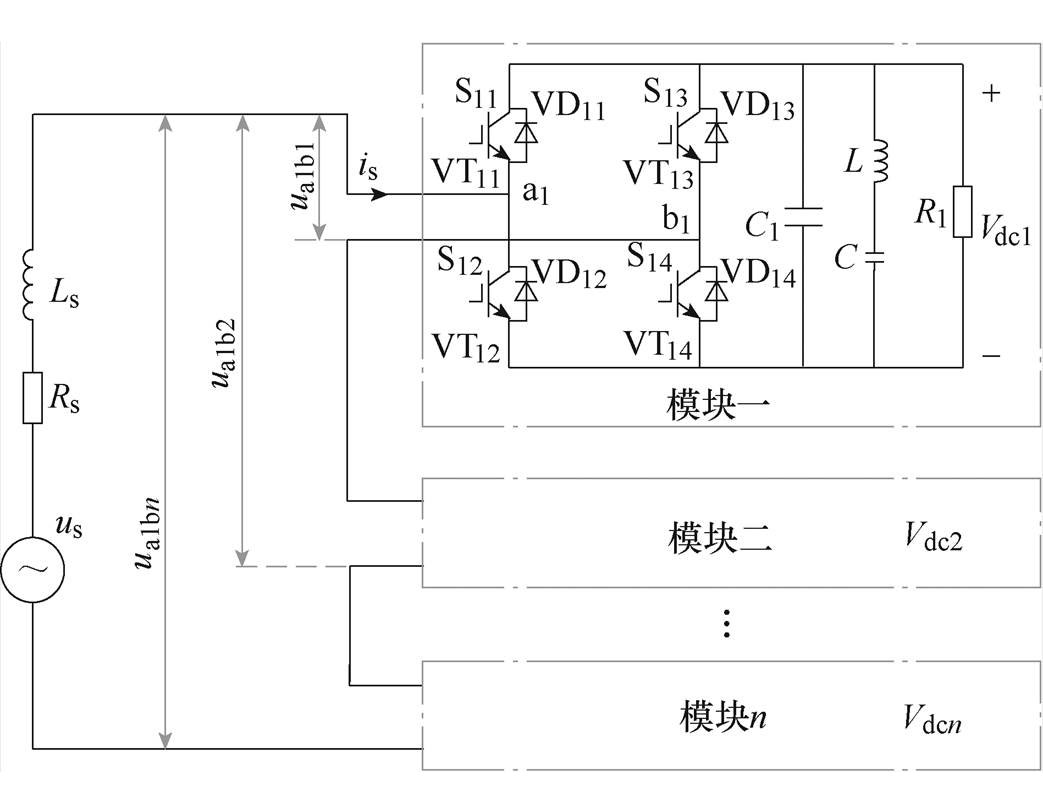
图1 单相CHBR拓扑
Fig.1 Topology diagram of single-phase cascaded H-bridge rectifier
摘要 针对单相级联H桥整流器（CHBR）的功率开关器件存在的开路故障问题，研究一种开关管开路故障的快速诊断算法，以及针对开关管开路故障的容错均压空间矢量脉宽调制（SVPWM）算法。首先，该文分析单相CHBR功率开关管开路故障时电流流通路径的变化，建立电流误差变化率的分析模型，并提出一种基于电流误差变化率的快速诊断算法。该算法可以快速且准确地定位到故障开关管，且易于在程序中实现。其次，该文提出一种故障容错均压SVPWM算法，该算法在开关管开路故障时利用冗余矢量和冗余开关状态可以使系统在发生故障时仍然可以正常运行，并且各模块间的直流电压也能保持均衡。最后，通过仿真和实验验证了该文所提算法的可行性。
关键词：单相级联H桥整流器 开路故障 在线诊断 空间电压矢量调制 容错算法
由于电力电子牵引变压器（Power Electronic Traction Transformer, PETT）具有体积小、质量轻和效率高等特点，逐渐成为了高速列车牵引供电系统的新选择[1-2]。其中，PETT的前级整流部分多采用级联H桥整流器（Cascaded H-Bridge Rectifier, CHBR）。由于列车的牵引供电系统一般安装在列车的底部，其运行环境较为复杂恶劣，因此功率器件存在着较高的故障率[3-4]。功率开关器件按照故障类型通常可以分为短路故障和开路故障两种。其中，由于短路故障会造成巨大影响，因此在系统中往往具有短路保护功能[5-6]。而开路故障相较于短路故障，虽然对系统运行造成的影响相对较小，但其造成电流畸变、谐波含量增大、总直流侧电压波动大等问题也会对电力电子牵引变压器后级电路产生影响，给系统的长期安全运行带来隐患[7]。
故障容错技术可以使系统在发生故障之后仍然能够正常运行，且各项性能指标仍可保持正常且不产生大幅下降，从而消除故障导致的系统崩溃或二次故障的风险。当前，容错技术主要分为硬件容错和软件容错两类。硬件容错技术主要是通过对子模块、桥臂或功率器件进行冗余备份的方式，在系统发生故障以后切除隔离故障模块、桥臂或功率器件，依靠冗余部分来实现系统的容错运行[8-11]。软件容错技术则不依赖于硬件部分的冗余，而是在系统发生故障后通过控制算法或调制算法让系统能够隔离故障并维持系统正常运行，保持系统的性能指标基本正常[12-17]。文献[18]提出一种基于叠加零序分量的三相输出功率优化容错策略，利用向量合成思想实现了单管故障时提高级联H桥光伏逆变器输出功率且维持功率稳定的容错运行，但是该方法无法应用于单相拓扑中。
此外，进行容错之前还需要对故障开关管进行定位。目前，变换器功率开关器件的开路诊断策略主要分为三类：基于信号分析、基于知识和基于解析模型三种方法[19-25]。文献[26]建立了单相CHBR的数学模型，计算正常与开路故障时的电流，通过比较两者的差异实现对故障开关管的定位，但是此方法受参数影响较大，且需要进行迭代运算，不利于提升诊断速度，难以在实际系统中实现。
首先，本文针对单相CHBR的开关管开路故障，提出一种基于电流误差变化率的快速诊断算法，该算法可以快速准确地定位到故障开关管，并且计算量小、易于实现。其次，本文提出一种容错均压空间矢量脉宽调制（Space Vector Pulse Width Modu- lation, SVPWM）算法，在没有额外的冗余硬件电路条件下，利用级联多模块的冗余矢量和冗余开关状态来进行容错，使系统在发生单管或部分双管开路故障时保持系统正常运行且具有均压能力。最后，通过仿真和实验验证了上述两种算法的可行性。
单相CHBR的拓扑如图1所示，其由n个两电平H桥级联而成。每个模块包含VTi1～VTi4共4个开关管，i=1, 2,…, n，Si1～Si4为对应的开关，VDi1～VDi4为对应的反并联二极管。us和is分别为网侧电压和电流，Rs和Ls为网侧等效电阻和电感。Ci为直流侧支撑电容，LC为二次滤波电路，Ri为直流侧负载，uaibi为第i模块的端口电平，Vdci为第i模块的直流侧电压。
图1 单相CHBR拓扑
Fig.1 Topology diagram of single-phase cascaded H-bridge rectifier
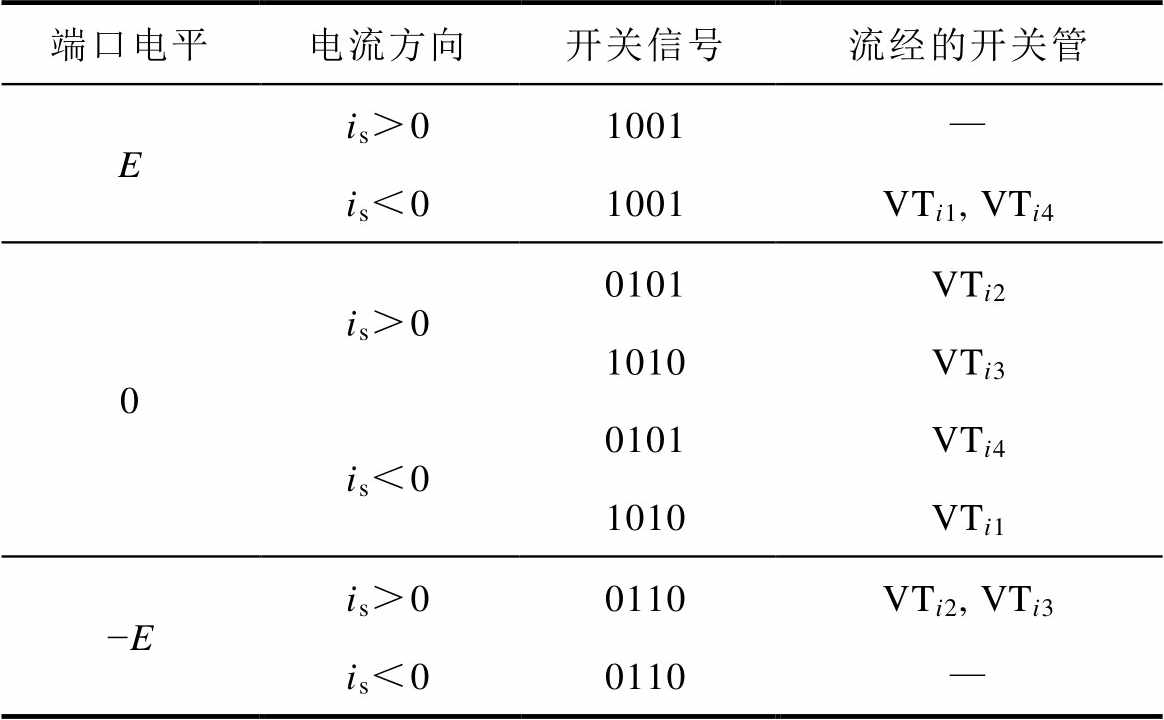
当开关管正常工作时，单个模块的端口uaibi可以输出-E、0、E三种电平状态，这三种电平对应的电流流通路径与电流方向和开关信号有关。表1为正常情况下电流的流通路径，从表1可以看出，即使端口电平和开关信号一样，若电流方向不同，电流流过的开关管也不同。而当开关管发生开路故障时，电流流通路径会随之发生变化。以开关管VTi1发生故障为例，当其发生故障时，系统仅在is＜0且开关信号 (Si1, Si2, Si3, Si4) = (1001)和 (1010) 时才会受到影响。VTi1正常和开路故障时的电流流通路径如图2所示。在这两种情况下，故障时电流的流通路径分析如下：
表1 正常情况下电流的流通路径
Tab.1 Normal current flow path
端口电平电流方向开关信号流经的开关管 Eis＞01001— is＜01001VTi1, VTi4 0is＞00101VTi2 1010VTi3 is＜00101VTi4 1010VTi1 −Eis＞00110VTi2, VTi3 is＜00110—
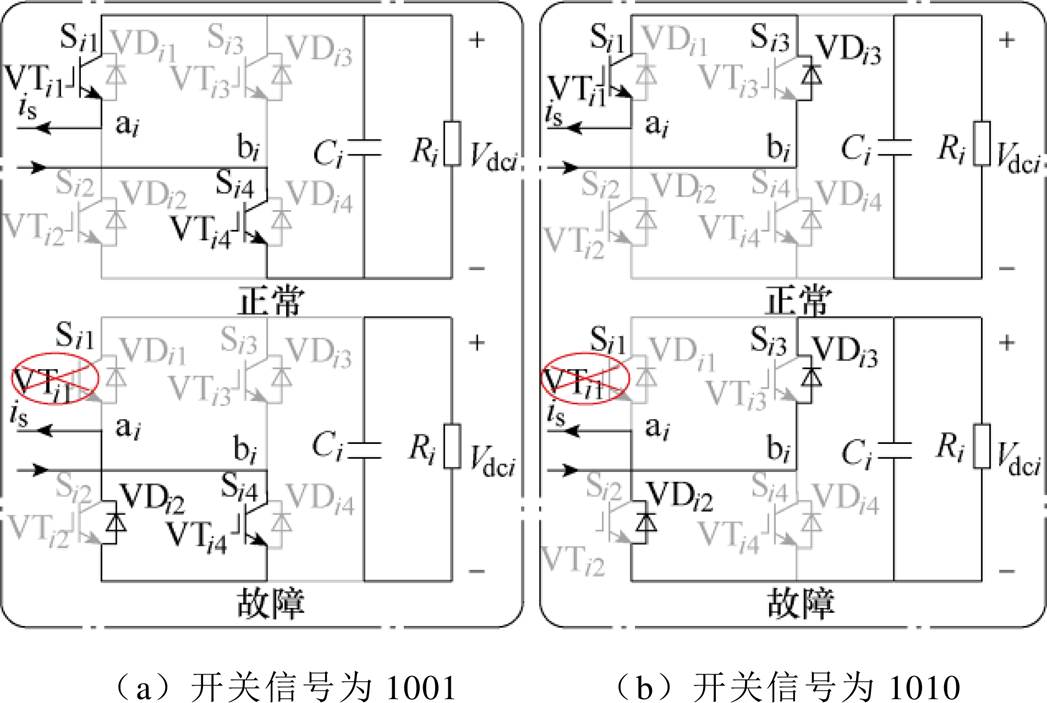
图2 VTi1正常和开路故障时的电流流通路径
Fig.2 Current path when VTi1 is normal and open-circuit
（1）图2a为开关信号为1001时的电流流通路径。从图中可以看出，当模块正常工作时，直流侧电容Ci和交流电源一同为电感充电，电感电流is的绝对值会增大；当VTi1发生开路故障时，电流将从VTi4和VDi2流过，此时直流侧电容Ci将会单独为负载提供能量，而电感则由交流电源单独为其充电，故在此故障状态下，电感电流is由于缺少直流侧电容一同为其充电，其绝对值增加量会减小。
（2）图2b为开关信号为1010时的电流流通路径。从图中可以看出，当模块正常工作时，直流侧电容Ci单独为负载提供能量，电感则由交流电源单独为其充能，电感电流is的绝对值会增大；当VTi1发生开路故障时，电流将从VDi3和VDi2流过。此时直流侧电容Ci工作在充电状态，交流电源与电感一同为直流侧电容Ci充电，故在此故障工作状态下，电感电流is的绝对值会减小。
其他开关管发生开路故障时的情况与VTi1管类似，因此不再逐一分析。从上述的分析中可以看出，开关管发生开路故障会使得电感电流is发生变化，并且对其变化率也会造成影响，基于此，本文提出一种基于电流误差变化率的快速诊断算法。
首先定义桥臂的开关函数Fai和Fbi为
（1）
用逻辑变量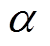
来表示网侧电流is的方向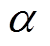，=1表示网侧电流is流入变换器，即is＞0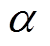；=0表示网侧电流is流出变换器，即is＜0，则由表1可以得到开关函数的逻辑表达式为
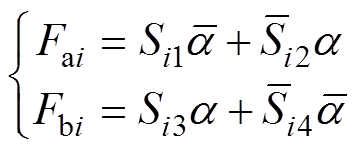（2）
式中，Si1～Si4为开关管Si1～Si4的开关信号。
因此，每个模块的端口电平uaibi可以表示为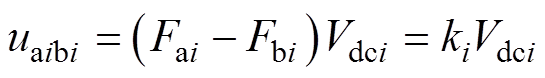
，其中ki为理想的开关函数。忽略网侧等效电阻Rs的影响，根据基尔霍夫电压定律和电流定律可得简化后的单相CHBR的数学模型为
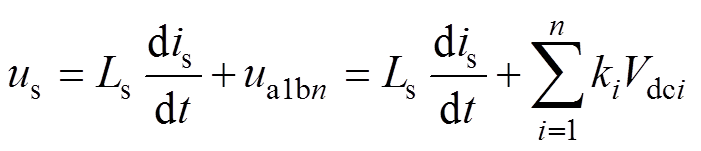（3）
式中，ua1bn为总的端口电平，其值为各模块端口之和；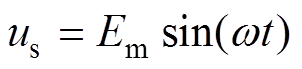
，
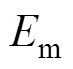为网侧电压us的幅值。
对式（3）进行积分求解，并将初始时刻的参数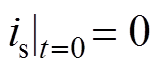
，
，
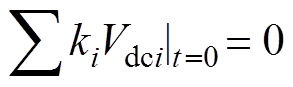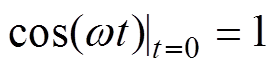代入式（3），可得网侧电流is的表达式为
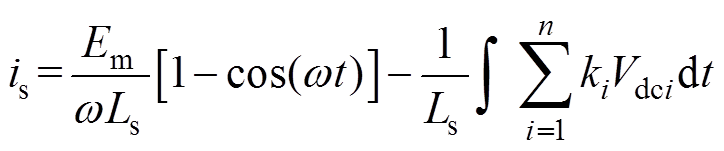（4）
而将交流电压us和模块的直流侧电压Vdci的实时采样值代入式（4）可以得到网侧电流的估计值ig。当开关管正常工作时，网侧电流的实际值与估计值是相等的，但当开关管发生开路故障时，由于开关函数的变化，实际值与估计值之间会存在误差。令故障时实际的开关函数为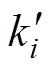
，则该误差值
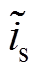为
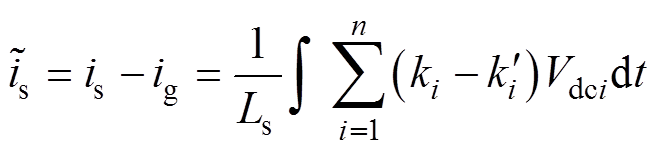（5）
对式（5）求导可得网侧电流is的误差变化率为
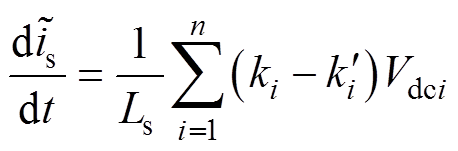（6）
结合式（6）以及具体的故障模块和开关管便可分析出不同开路故障下的电流误差变化率。
在实际的电路中，模块内3个及其以上的开关管发生开路故障的概率要远低于单管和双管故障的概率，因此本文只对单管和双管开路故障进行分析。开关管开路故障仿真波形如图3所示。
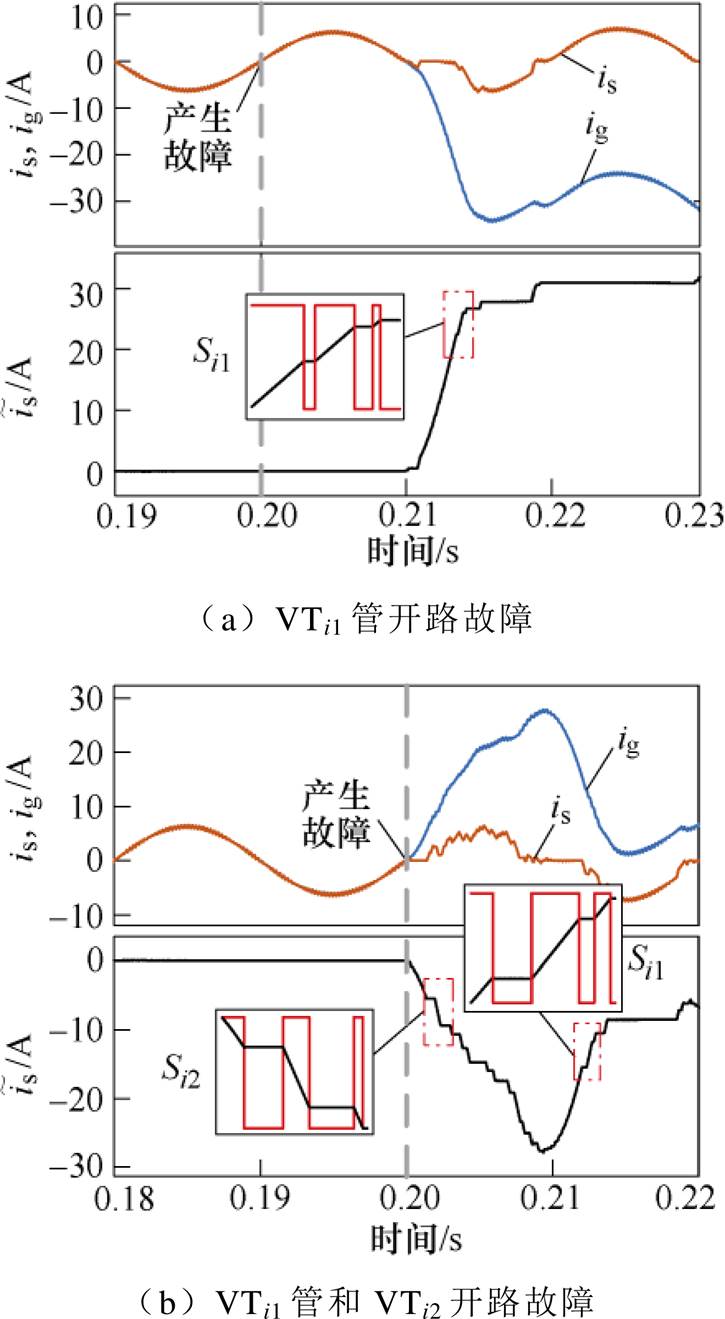
图3 开关管开路故障仿真波形
Fig.3 Simulation waveforms of open-circuit fault in switching tube
以VTi1为例来分析单管故障时的特征。图3a为VTi1开路故障时的仿真波形，从图中可以看出，在0.2 s产生开路故障后，电流在正半周期内仍然可以保持正常。而在负半周期内，电流的实际值is会与估计值ig产生误差，且该误差值仅在VTi1管的开关信号Si1=1时增大。
当VTi1发生开路故障时，其对应的实际开关信号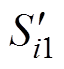
恒为0，则此时实际的开关函数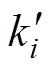应为
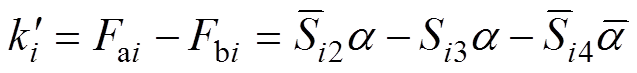（7）
将式（7）代入式（6），由于其他正常模块的开关函数不变，它们的电流误差变化率都为0，因此总的电流误差变化率就为故障模块的电流误差变化率，其表达式为
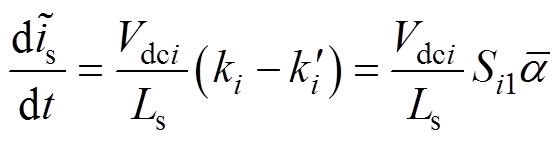（8）
由式（8）可以看出，当VTi1发生开路故障且仅在开关信号Si1=1、电流is＜0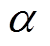（=0）时其电流误差变化率为Vdci/Ls，其余情况下则为0。以上分析结果也与仿真波形一致。
双管故障可以分为模块内和模块间两种类型，首先分析模块内的双管故障。图3b为VTi1和VTi2同时发生故障时的仿真波形，从图中可以看出，在0.2 s产生开路故障后的电流正半周期内，电流误差值会在VTi2管对应的开关信号Si2=1时减小；而在电流的负半周期内，电流误差值则会在VTi1管对应的开关信号Si1=1时增大。
当VTi1和VTi2发生开路故障时，对应开关信号Si1和Si2恒为0，则故障模块的实际开关函数为
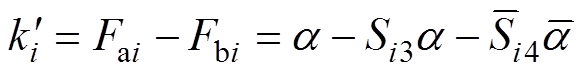（9）
将式（9）代入式（6）可得
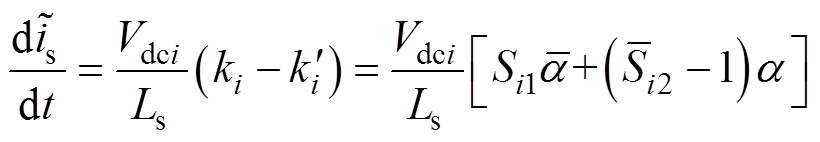（10）
由式（10）可以看出，当VTi1与VTi2发生开路故障，在开关信号Si1=1且电流is＜0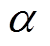（=0）时电流误差变化率为Vdci/Ls；在Si2=1且电流is＞0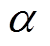（=1）时值为-Vdci/Ls，其分析结果同样与仿真波形一致。
模块间双管故障时的电流误差变化率同样可以根据上面的方法分析得到。表2为所有单管故障和部分双管故障时的电流误差变化率（*表示对应开关管信号任意）。从表2可以看出，双管开路故障的电流误差变化率实际上为相应的单管开路故障电流误差变化率的线性叠加。由此可以推导出，当任意数量开关管发生开路故障时，网侧电流的误差变化率为对应单管故障时的电流误差变化率之和。
根据电流误差变化率的分析可以看出，通过电流的方向、开关信号和电流误差变化率的关系便可以判断出故障开关管。具体的诊断思路为：首先，为了方便程序处理，将电流误差变化率进行归一化处理，归一化的值定义为故障判据D。其次，由于故障模块的直流电压Vdci在定位前是无法确定的，且发生故障后的短时间内直流电压不会有太大变化，因此用平均直流电压SVdci/n替代故障模块的直流电压Vdci进行计算，则故障判据D的表达式为
表2 各开关管开路故障时的电流误差变化率
Tab.2 The current error rate when each switching tube has an open circuit fault
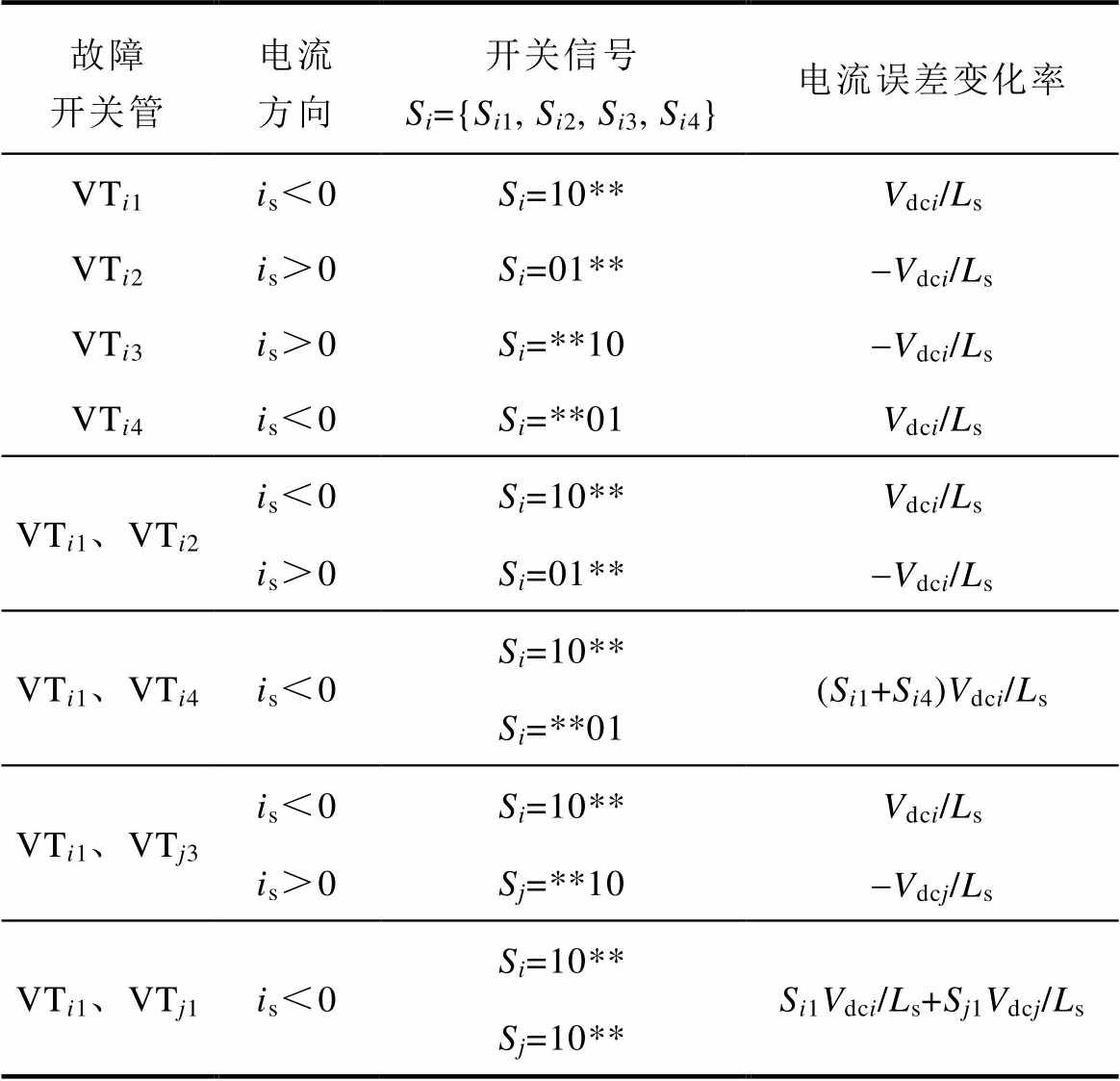
故障开关管电流方向开关信号Si={Si1, Si2, Si3, Si4}电流误差变化率 VTi1is＜0Si=10**Vdci/Ls VTi2is＞0Si=01**-Vdci/Ls VTi3is＞0Si=**10-Vdci/Ls VTi4is＜0Si=**01Vdci/Ls VTi1、VTi2is＜0Si=10**Vdci/Ls is＞0Si=01**-Vdci/Ls VTi1、VTi4is＜0Si=10**(Si1+Si4)Vdci/Ls Si=**01 VTi1、VTj3is＜0Si=10**Vdci/Ls is＞0Sj=**10-Vdcj/Ls VTi1、VTj1is＜0Si=10**Si1Vdci/Ls+Sj1Vdcj/Ls Sj=10**
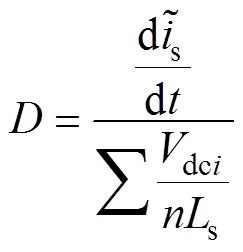（11）
最后，设置幅值阈值Dh和时间阈值Th，当故障判据D的绝对值大于幅值阈值Dh并且满足时间阈值Th后，再结合此时的电流方向和开关信号即可定位到故障开关管，并输出故障标志位FS。
依据开关管发生开路故障对系统造成电流畸变等影响所处的正、负半周期，可将模块内4个开关管的故障类型分为两类：定义在电流的负半周期和正半周期对系统造成影响的故障分别为Ⅰ类和Ⅱ类故障。从表1可以看出，Ⅰ类故障和Ⅱ类故障分别会影响E和0电平以及-E和0电平的输出。为了使得在故障情形下总的端口电平仍然正常，本文在文献[27]所提的一维均压SVPWM算法的基础上利用冗余矢量和冗余开关状态重新进行容错矢量的选择，并且保证选择后的矢量仍然具有均压能力。
两模块级联整流器开路故障时的一维空间矢量如图4所示。以两模块级联整流器为例来分析容错矢量的选择：当模块一发生Ⅰ类故障时，整个矢量区可分为三类：故障矢量 [(1, 1)、(1, 0)、(1, -1)]、伪故障矢量 [(0, 1)、(0, 0)、(0, -1)] 与正常矢量 [(-1, 1)、(-1, 0)、(-1, -1)]，如图4a所示。其中，故障矢量与伪故障矢量需要通过容错调制算法以保证系统在故障情况下的容错运行。伪故障矢量含有故障模块的0电平，从表1可以看到，该端口电平对应1010与0101两种开关信号，因此使用0101开关信号避开发生开路故障的VT11或VT14即可。而故障矢量含有故障模块的E电平，从表1可以看到，该端口电平只对应开关信号1001，无其他可替代的开关信号，因此，故障矢量只能由伪故障矢量与正常矢量进行容错替换，具体容错替换思路为：
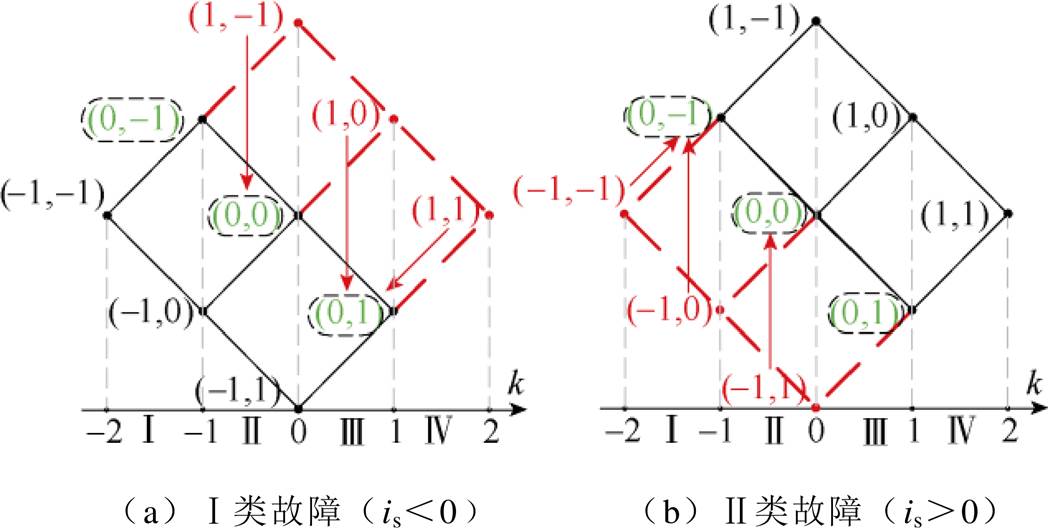
图4 两模块级联整流器开路故障时的一维空间矢量
Fig.4 One-dimensional space vector diagram of open-circuit fault in two-module cascaded rectifier
（1）故障矢量 (1, 1)：该矢量对应端口电平2E，此时端口电平无冗余矢量，因此将故障矢量替换为端口电平E的矢量 (0, 1)。
（2）故障矢量 (1, 0)：该矢量对应端口电平E，从图4a可以看出，可以使用冗余矢量 (0, 1) 替换故障矢量，从而保证端口电平不变。
（3）故障矢量 (1, -1)：该矢量对应端口电平0，经过前级均压算法后输出矢量 (1, -1)，可得Vdc1＞Vdc2，此时若选择 (-1, 1) 则会反向均压，导致模块间电压愈发不均衡，因此使用冗余矢量 (0, 0) 代替。
而当模块一发生Ⅱ类故障时，同样可将矢量区分为三类：故障矢量 [(-1, 1)、(-1, 0)、(-1, -1)]、伪故障矢量[(0, 1)、(0, 0)、(0, -1)] 与正常矢量 [(1, 1)、(1, 0)、(1, -1)]，其中故障矢量和伪故障矢量的容错思路与Ⅰ类故障类似，如图4b所示。
通过3.1节的分析，单相多模块级联整流器开路故障时的容错均压SVPWM算法框图如图5所示。整体框图分为均压调制算法和容错调制算法两部分。均压调制部分主要由区间判断、时间计算、模块间均压策略等组成[27]；容错调制部分主要由故障诊断、模块间容错调制和模块内容错调制组成。
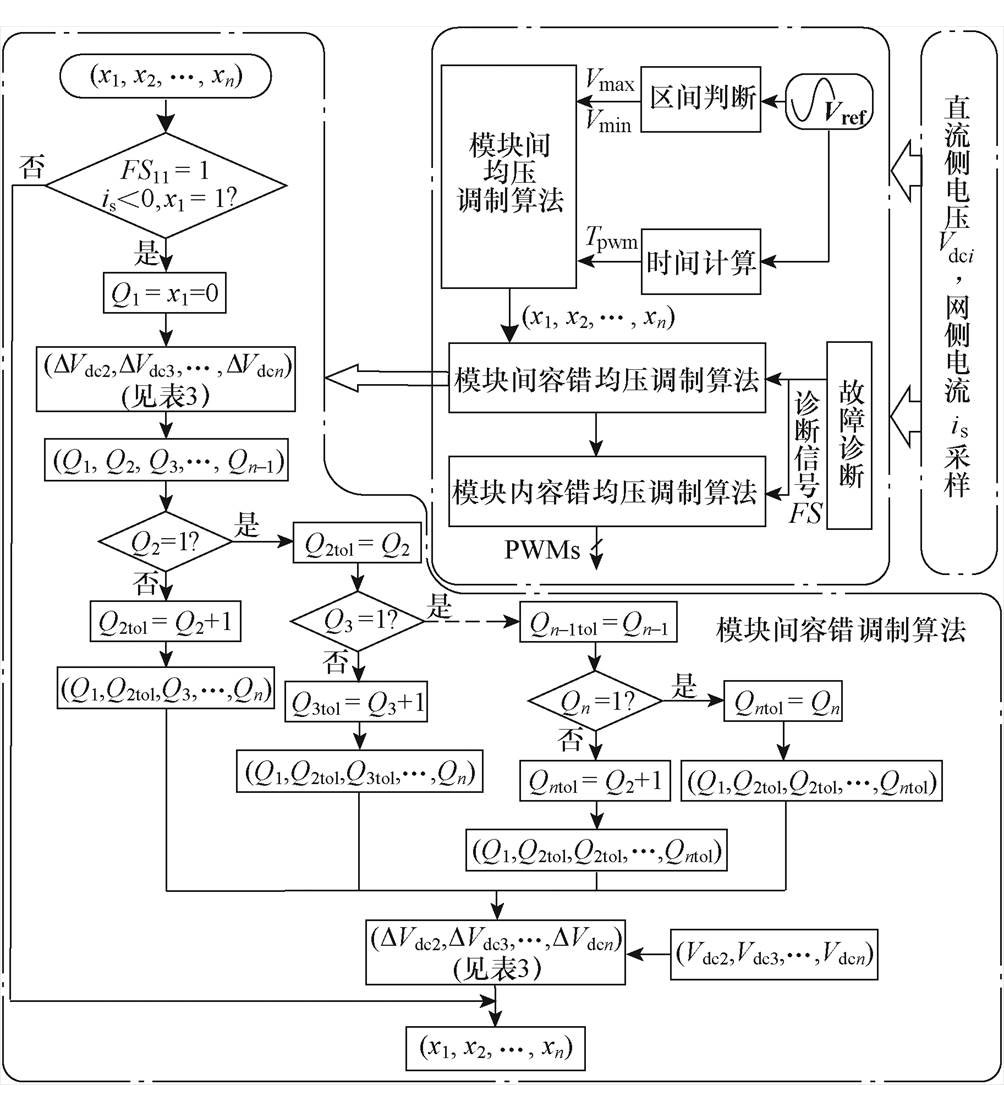
图5 容错均压SVPWM算法框图
Fig.5 Block diagram of reconstructed average voltage SVPWM algorithm
多模块间容错均压调制算法的思路可以根据上述两模块容错矢量选择的思路得到。以模块一的VT11开路故障为例，此时模块一在is＜0时无法输出E电平，为避免对前级均压矢量选择策略造成反效果，需要将故障模块的端口电平降为0电平。同时为了保证总的端口电平数不变，其余某一非故障模块的端口电平需要增加1个电平。具体的容错均压策略为：
（1）定义直流侧电压偏差值DVdci=Vdci-Vdc_ave，其中Vdc_ave为直流电压的平均值。计算得到所有非故障模块的DVdci，并根据其大小顺序对各非故障模块进行容错均压优先级排序，排序方法见表3。当DVdci值越大时，容错均压优先级越高，由此得到矢量 (Q1, Q2,Q3,…, Qn)，其中故障模块为Q1=x1=0。
表3 容错均压优先级排序
Tab.3 Priority sorting of reconstructed average voltage
Vdc偏移情况容错均压优先级 (Q1,Q2,Q3,…, Qn) DVdc2＞DVdc3＞DVdc4＞…＞DVdcn(x1, x2, x3, x4,…, xn) DVdc2＞DVdc4＞DVdc3＞…＞DVdcn(x1, x2, x4, x3,…, xn) DVdc3＞DVdc2＞DVdc4＞…＞DVdcn(x1, x3, x2, x4,…, xn) DVdc3＞DVdc4＞DVdc2＞…＞DVdcn(x1, x3, x4, x2,…, xn) DVdc4＞DVdc2＞DVdc3＞…＞DVdcn(x1, x4, x2, x3,…, xn)
（2）根据非故障模块的优先级排序，从Q2开始依次检测端口电平：如果该模块的端口电平Qi=-1或0，则将该模块的端口电平Qitol=Qi+1，结束检测进入下一步；如果端口电平Qi=1，则检测排序下一位的模块端口电平，重复上述操作，直到最后一个模块。若最后一个模块的端口电平Qn=1，则说明端口电平k=n，该端口电平无冗余矢量，只能由k=n-1的矢量替换。
（3）最后根据表3的容错均压优先级排序，将矢量 (Q1, Q2,Q3,…, Qn) 还原为矢量 (x1, x2, x3,…, xn)。其他的开关管开路故障后的模块间容错均压流程同理可分析得到。
模块内容错均压调制则主要通过选择冗余开关状态来避免故障开关管。当故障模块的端口电平经过模块间容错均压算法输出0电平后，若为Ⅰ类故障，则使用0101开关信号避开故障开关管；若为Ⅱ类故障，则使用1010开关信号避开故障开关管。
基于Matlab/Simulink搭建单相六模块CHBR模型，仿真参数如下：交流侧电源电压us=240 V，频率f=50 Hz，开关频率fs=4 kHz，交流侧电感Ls= 5 mH，直流侧电容C=4 400 mF，直流侧电压Vdc= 300 V，额定负载为20 W。
在系统运行0.4 s时将模块一的1管VT11和模块四的3管VT43的开关信号设置为0，以模拟模块间双管开路故障的情形，并在系统运行0.44 s时投入容错算法进行故障容错。图6为在此条件下的诊断波形，其中诊断阈值Dh设置为0.9，时间阈值Th设置为100 ms。可以看到，在0.4～0.41 s内，由于is＞0，系统受VT43故障影响。电流估计值ig急剧增大，故障判据D＜0且绝对值大于阈值Dh。根据此时的开关信号，诊断算法在故障3.1 ms后输出故障标志位FS42=1；在0.41～0.42 s内，is＜0，此时系统受VT11的影响，电流估计值ig急剧减小，故障判据D＞0且绝对值大于阈值Dh。根据此时的开关信号，诊断算法在故障2 ms后输出故障标志位FS11= 1。从上面的结果可以看出，本文所提的诊断算法能在1/4个基波周期内定位到故障开关管，且结果准确，不会出现误诊断现象。
图7为故障容错的仿真波形，从图中可以看到，当产生开路故障后，网侧电流is发生畸变，THD由3.13%突变至19.84%。此时由于模块一在电流的负半周期无法输出E电平，模块四在电流正半周期无法输出-E电平，因此总的端口电平会出现残缺。而投入本文所提的容错算法后，网侧电流与总的端口电平波形重新恢复正常，电流的THD降为3.34%。
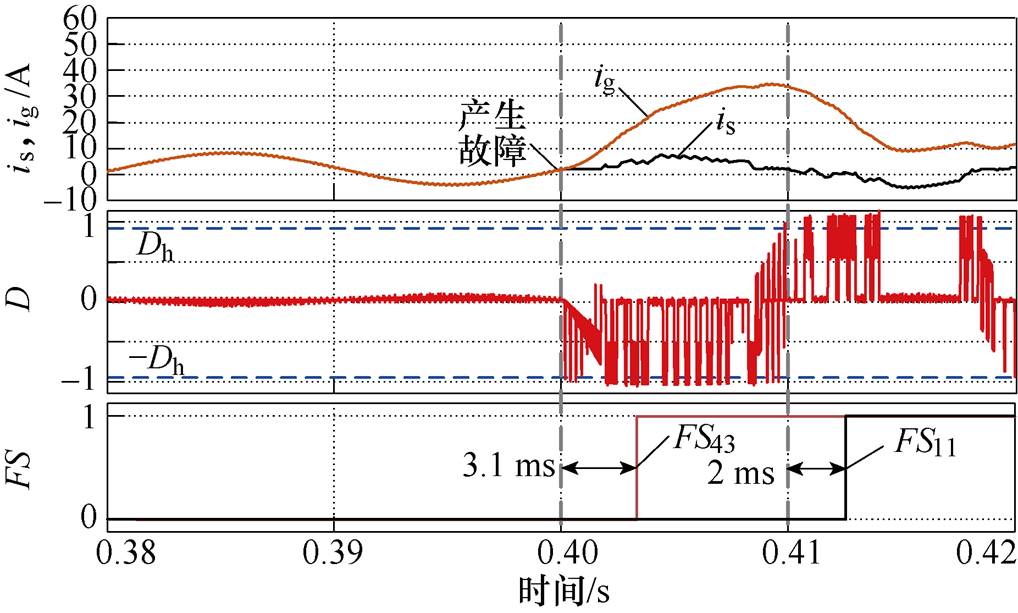
图6 故障诊断仿真结果
Fig.6 Simulation results of fault diagnosis
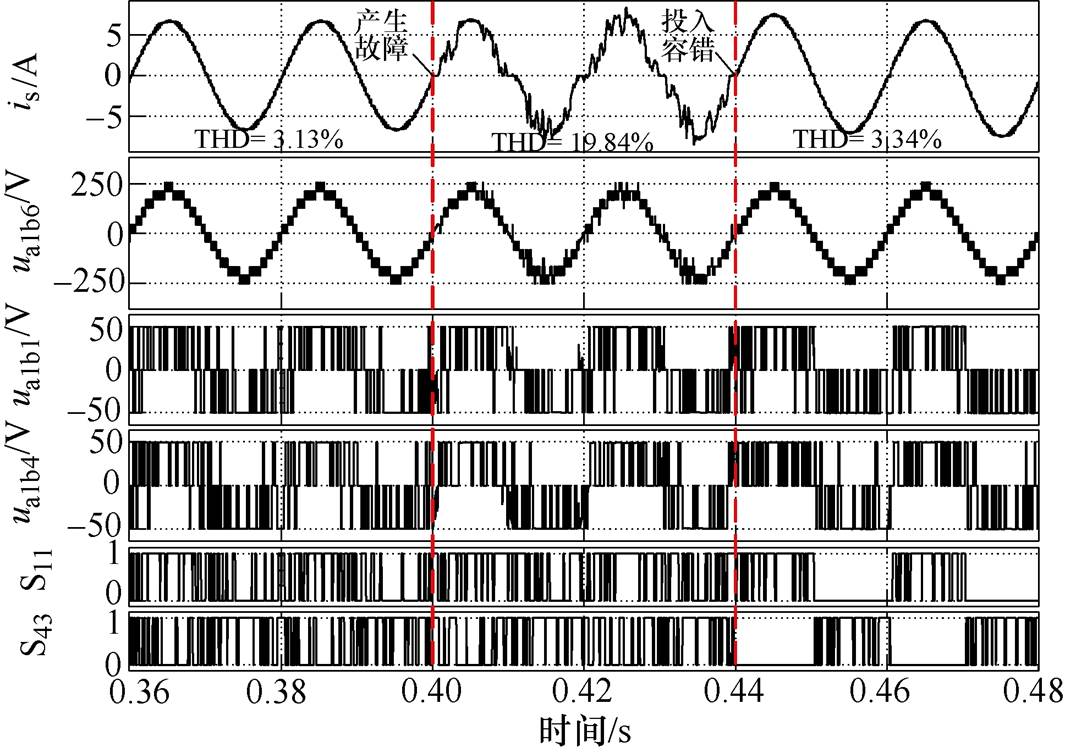
图7 故障容错时端口电平仿真波形
Fig.7 Simulation waveforms of port level during fault tolerance
图8为六模块级联整流器故障容错后的直流侧电压的仿真波形，其中0.5～1 s和1.5～2 s为在本文所提的容错均压SVPWM算法下运行的波形，1～1.5 s为在载波移相SPWM（Carrier Phase-Shifted SPWM, CPS-SPWM）算法下运行的波形。各模块的不平衡负载分别为：R1=40 W、R2=35 W、R3=30 W、R4=25 W、R5=R6=20 W。可以看到，在CPS-SPWM算法下，各模块间的直流侧电压发生了不同程度的偏移，Vdc1～Vdc6的不均衡程度达到了27 V。而在本文所提的容错均压SVPWM算法下，模块间的直流电压可以保持均衡。以上仿真结果证明了本文所提的容错均压SVPWM算法的可行性与有效性，并且该算法可以扩展至多模块。
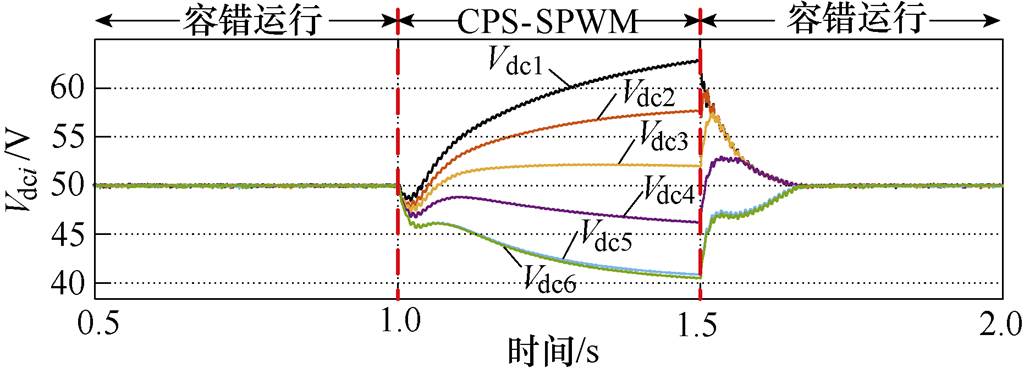
图8 故障容错后直流侧电压仿真波形
Fig.8 Simulation waveforms of DC voltage after fault tolerance
为了验证本文所提的故障诊断和容错算法，搭建单相两模块级联整流器的小功率实验平台，如图9所示。其中，为了满足本文所提算法对运行速度高、延时低的要求，控制系统采用现场可编程门阵列（Field-Programmable Gate Array, FPGA）芯片，型号为Alter公司的EP3C55F484I7N。实验平台的其他参数见表4。本文的诊断算法是通过Verilog语言编写实现，因此诊断波形的截图均为Quartus Ⅱ里的SingalTap实时显示的数字信号波形。用Df表示故障判据D是否大于所设的幅值阈值Dh（D＞+Dh，Df =+1；D＜-Dh，Df = -1，否则Df =0
。当Df≠0的时间大于时间阈值Th时，对应开光管的故障标志位FS则跳为1。诊断实验中的幅值阈值Dh设置为0.9，时间阈值Th设置为100 ms。
图9 小功率实验平台
Fig.9 Small power experimental platform
表4 实验平台参数
Tab.4 Experimental platform parameters
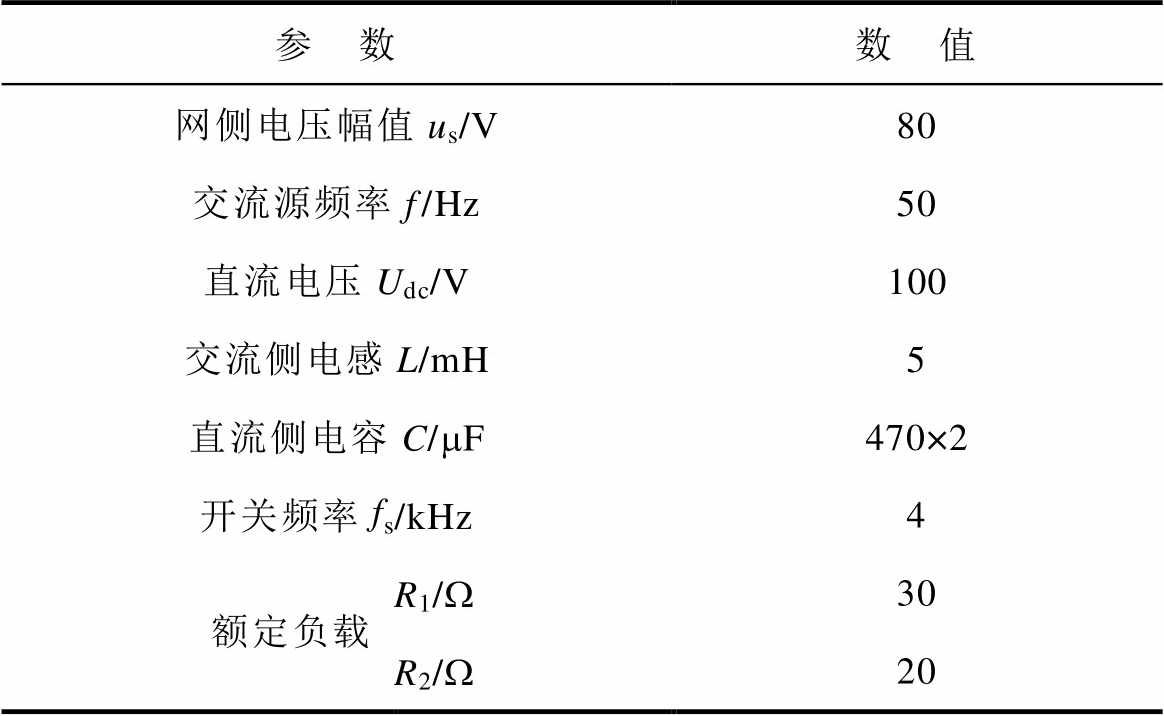
参 数数 值 网侧电压幅值us/V80 交流源频率f/Hz50 直流电压Udc/V100 交流侧电感L/mH5 直流侧电容C/mF470×2 开关频率fs/kHz4 额定负载R1/W30 R2/W20
4.2.1 单管开路故障
首先验证单管开路故障时诊断和容错算法的可行性。图10为VT11管开路故障的诊断实验波形。其中，t0时刻产生开路故障，t1时刻标志着电流受到故障影响开始发生畸变，t2时刻标志着诊断算法成功定位到故障开关管并输出故障标志位，t1～t2的时间即为故障诊断时间。从实验结果可以看到，VT11诊断时间分别花费了4.7 ms，即单管故障诊断可以在1/4个基波周期内完成，且诊断结果准确。
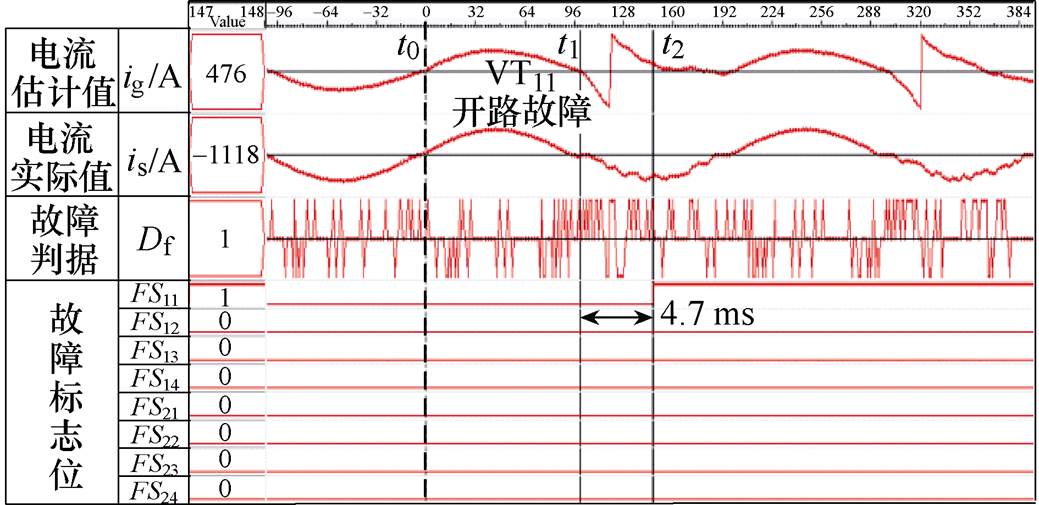
图10 单管开路故障诊断实验波形
Fig.10 The fault diagnosis waveforms when singletube is open
图11为VT11管开路故障容错实验的动态波形。其中，t1～t2时刻为故障运行，此时当VT11管发生开路故障时，网侧电流在负半周期内发生畸变且模块一的端口电平ua1b1无法正常输出E电平，以上现象也与第1节的分析相符。t2时刻投入容错均压算法后，模块一将不再输出故障电平，但总的端口电平和网侧电流与正常运行时基本一致。
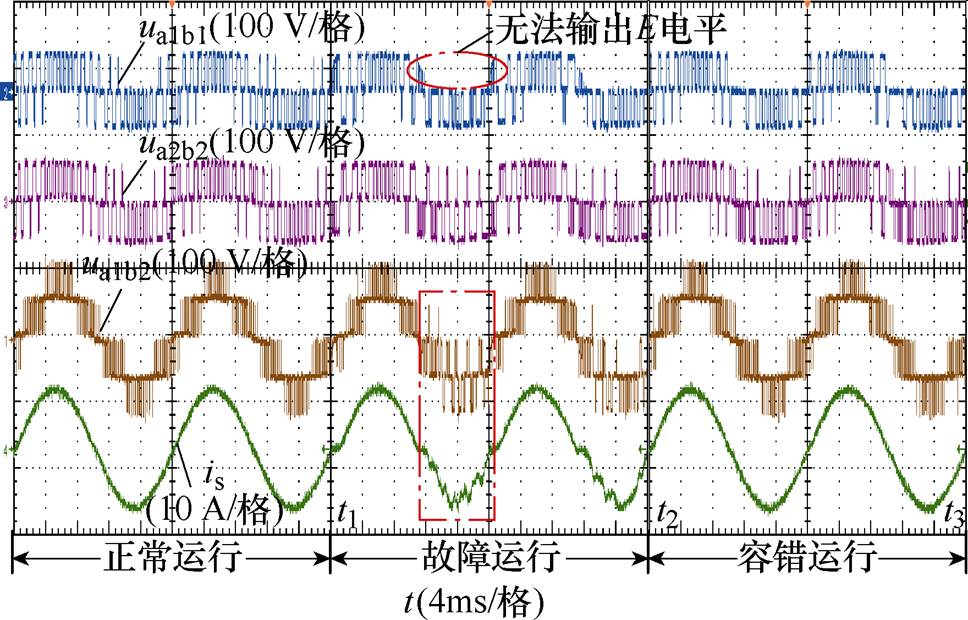
图11 单管开路故障容错实验的动态波形
Fig.11 Dynamic waveforms of fault-tolerant experiment of single tube
图12为VT11管正常、开路故障以及故障容错时的实验波形。图中Vdc1和Vdc2分别为模块一和模块二的直流侧电压。可以看到，总直流电压在故障时由100 V降低至92 V，且总的端口电压与网侧电流的包络线都产生了一定的畸变，而在容错均压SVPWM算法投入之后总的端口电压与网侧电流的包络线也恢复为与无故障时一致，总的直流侧电压再次稳定在给定值100 V，且各模块的直流电压仍然可以保持均衡。
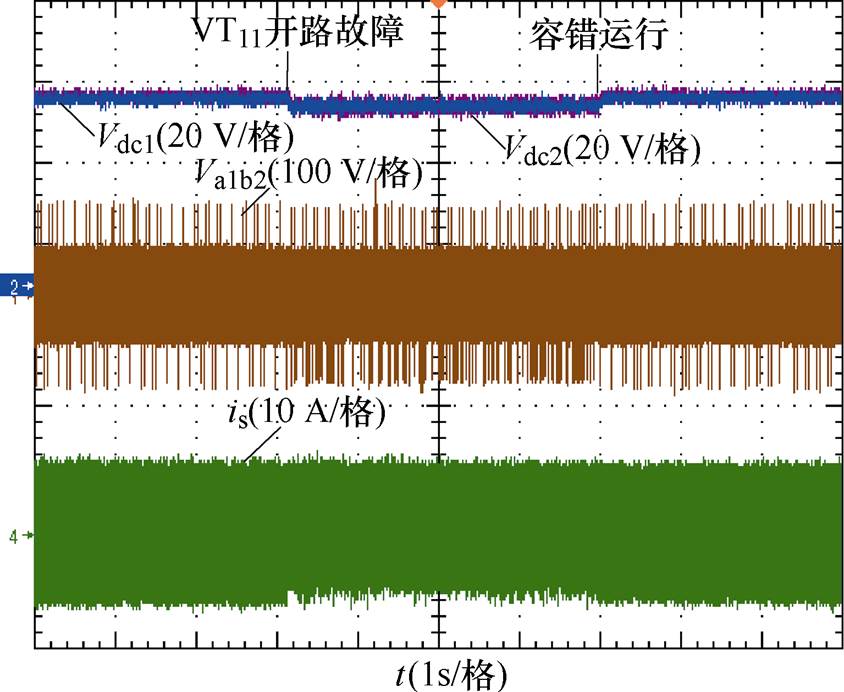
图12 单管正常-故障-容错时的实验波形
Fig.12 Experimental waveforms when single tube is normal、fault and fault-tolerant
4.2.2 模块内双管开路故障
模块内双管故障可以分为两类：一类是Ⅰ类和Ⅱ类故障同时发生的情形；另一类是仅Ⅰ类故障或Ⅱ类故障发生的情形。本文分别以VT11和VT12管开路故障、VT11和VT14管开路故障为例来进行验证。图13a和图13b分别为VT11和VT12开路故障以及VT11和VT14开路故障时的诊断波形。从图中可以看到，前者的诊断时间分别为4.5 ms和5 ms，后者的诊断时间分别为3.2 ms和4.7 ms，因此模块内双管开路故障的诊断可以在基波的1/4个周期内完成，且不会出现误诊断的情况。
图14为以上两种故障的容错实验波形，从图中可以看出，t1～t2时刻产生开路故障后，前者由于同时存在Ⅰ类和Ⅱ类故障，网侧电流在整个周期内都会发生畸变，而后者只在电流的负半周期内发生畸变，且畸变程度更加严重。t2时刻投入容错算法后，前者的端口电平和网侧电流可以恢复至正常运行时的波形，而后者由于模块一在电流负半周期只能输出-E电平，因此网侧电流和端口电平仍然存在畸变。
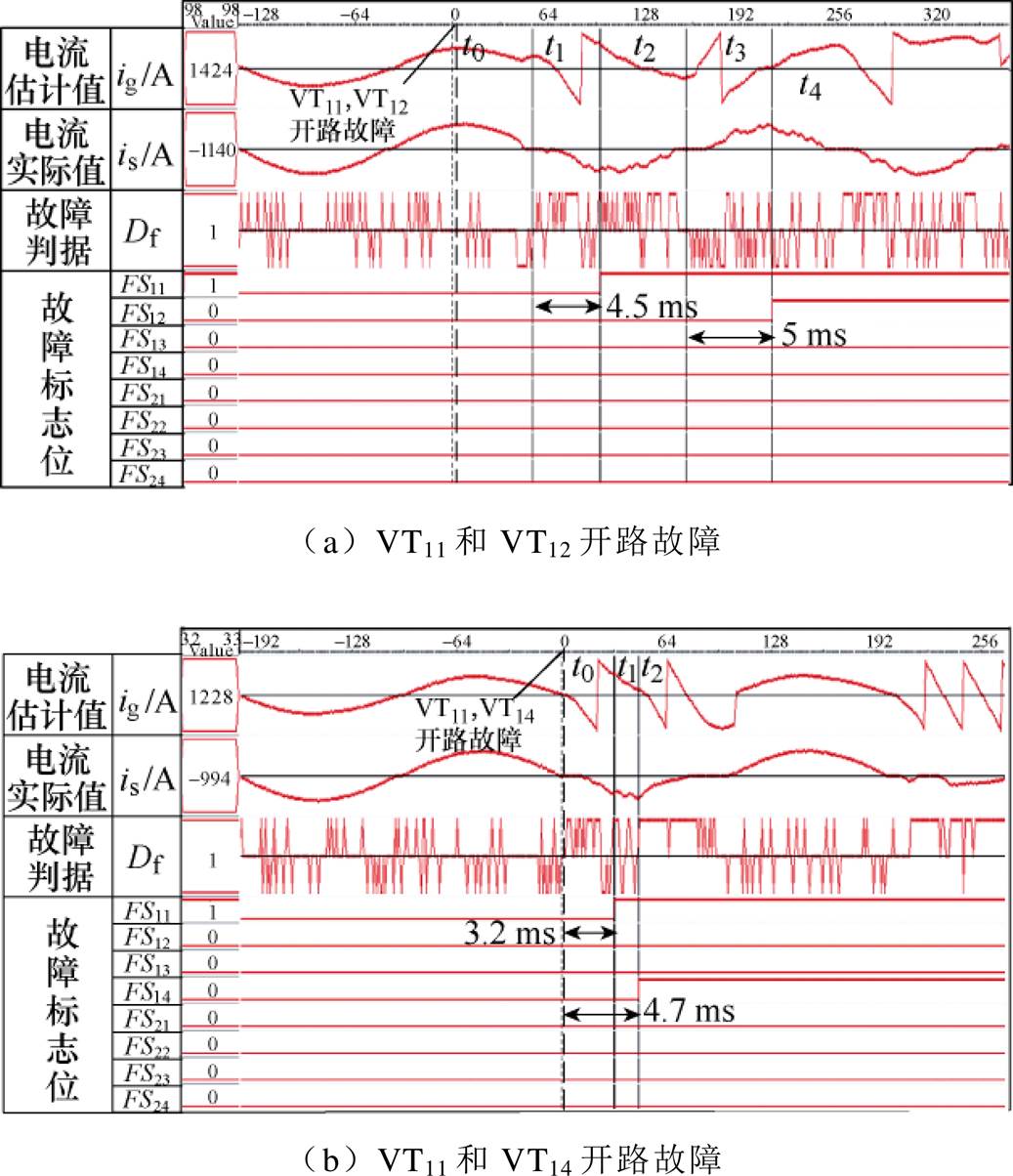
图13 模块内双管开路故障诊断实验波形
Fig.13 The fault diagnosis waveforms when double tubes in the module are open
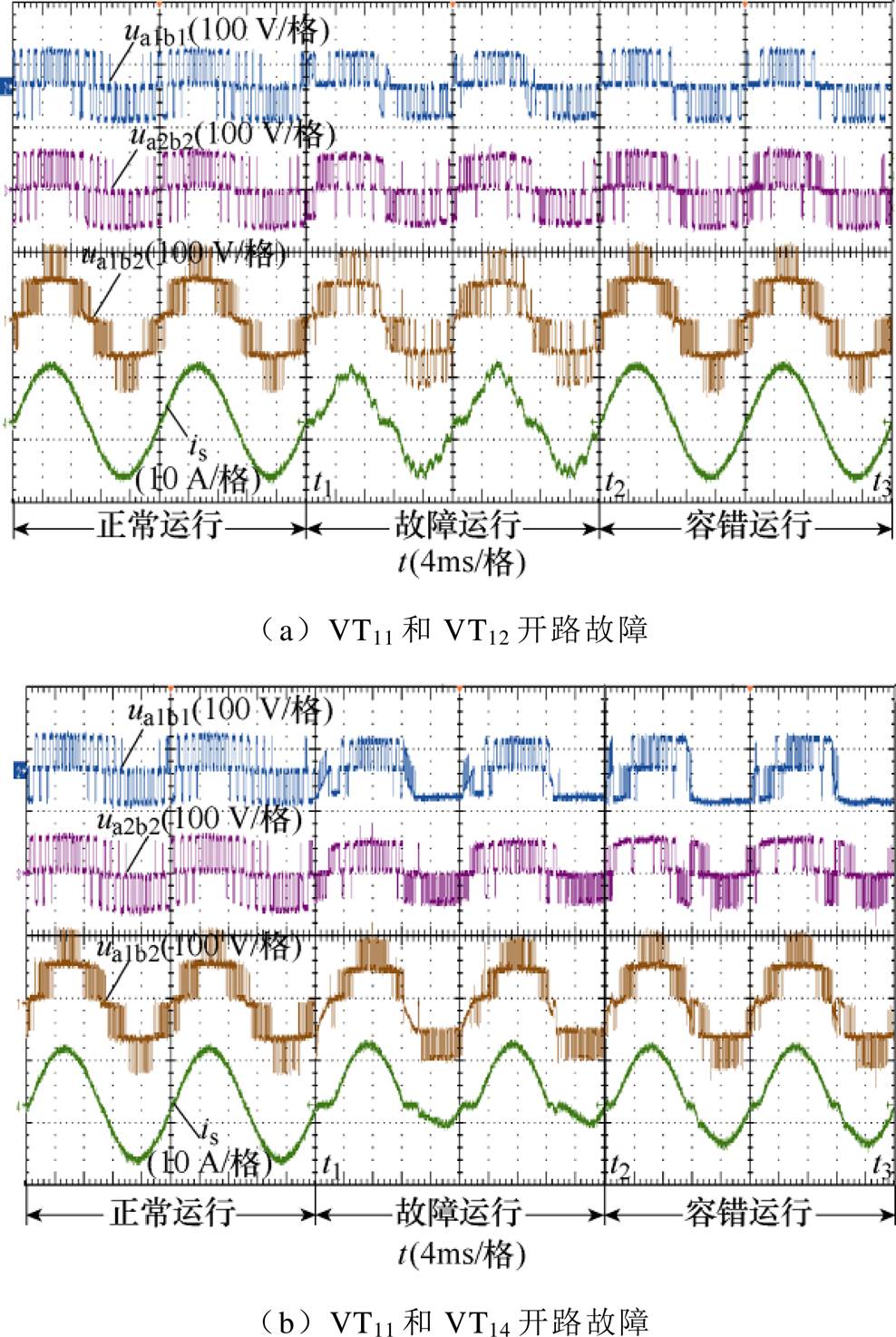
图14 模块内双管开路故障容错实验的动态波形
Fig.14 Dynamic waveforms of fault-tolerant experiment of double tubes in the module
对应的双管正常、开路故障和故障容错时的实验波形如图15所示，可以看到，在容错后前者模块间直流电压可以保持均衡，后者则由于缺少的矢量过多无法维持模块间的直流电压均衡。
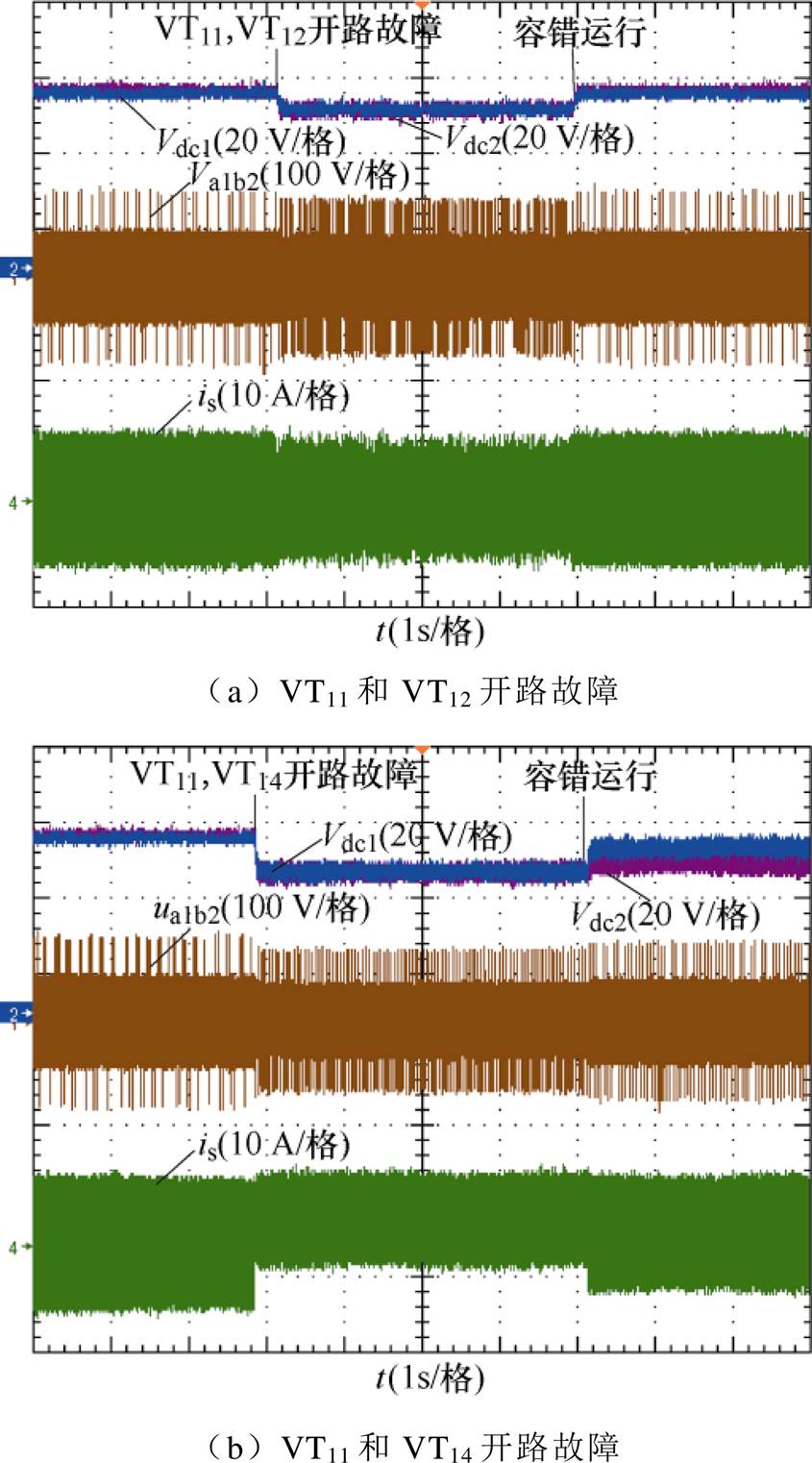
图15 模块内双管正常-故障-容错时的实验波形
Fig.15 Experimental waveforms when double tubes in the module are normal，fault and fault-tolerant
4.2.3 模块间双管开路故障
模块间的双管开路故障同样可以按照模块内的分类方法分为两类。本文分别以VT11和VT21管开路故障、VT11和VT22管开路故障为例来进行验证。图16a和图16b分别为VT11和VT21开路故障以及VT11和VT22管开路故障时的诊断波形。从图中可以看到，前者的诊断时间分别为5 ms和4.8 ms，后者的诊断时间分别为4.4 ms和4.1 ms，因此模块间双管开路故障的诊断同样也可以在基波的1/4个周期内完成，且定位结果准确。
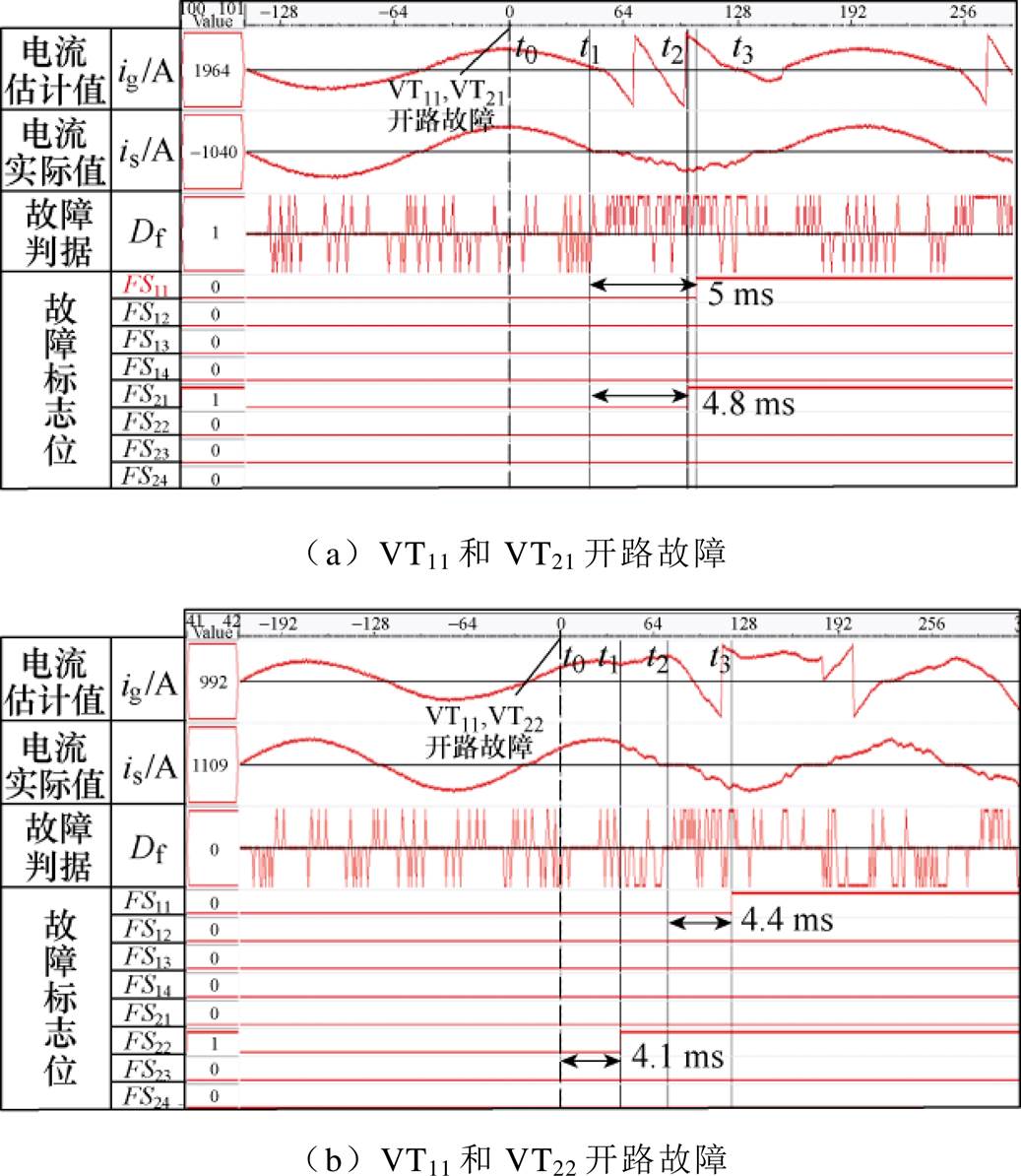
图16 模块间双管开路故障诊断实验波形
Fig.16 The fault diagnosis waveforms when double tubes between modules are open
图17为以上两种故障的容错实验波形，从图中可以看出，t2时刻投入容错算法后，前者的端口电平和网侧电流同样可以恢复至正常运行时的波形，而后者由于模块一和模块二在电流小于0时都无法输出E电平，因此在过零点附近会出现轻微畸变，但相较于故障运行时畸变程度有所降低。对应的双管正常、开路故障和故障容错时的实验波形如图18所示，可以看到，在容错后两种故障情形的模块间直流电压都可以保持均衡。
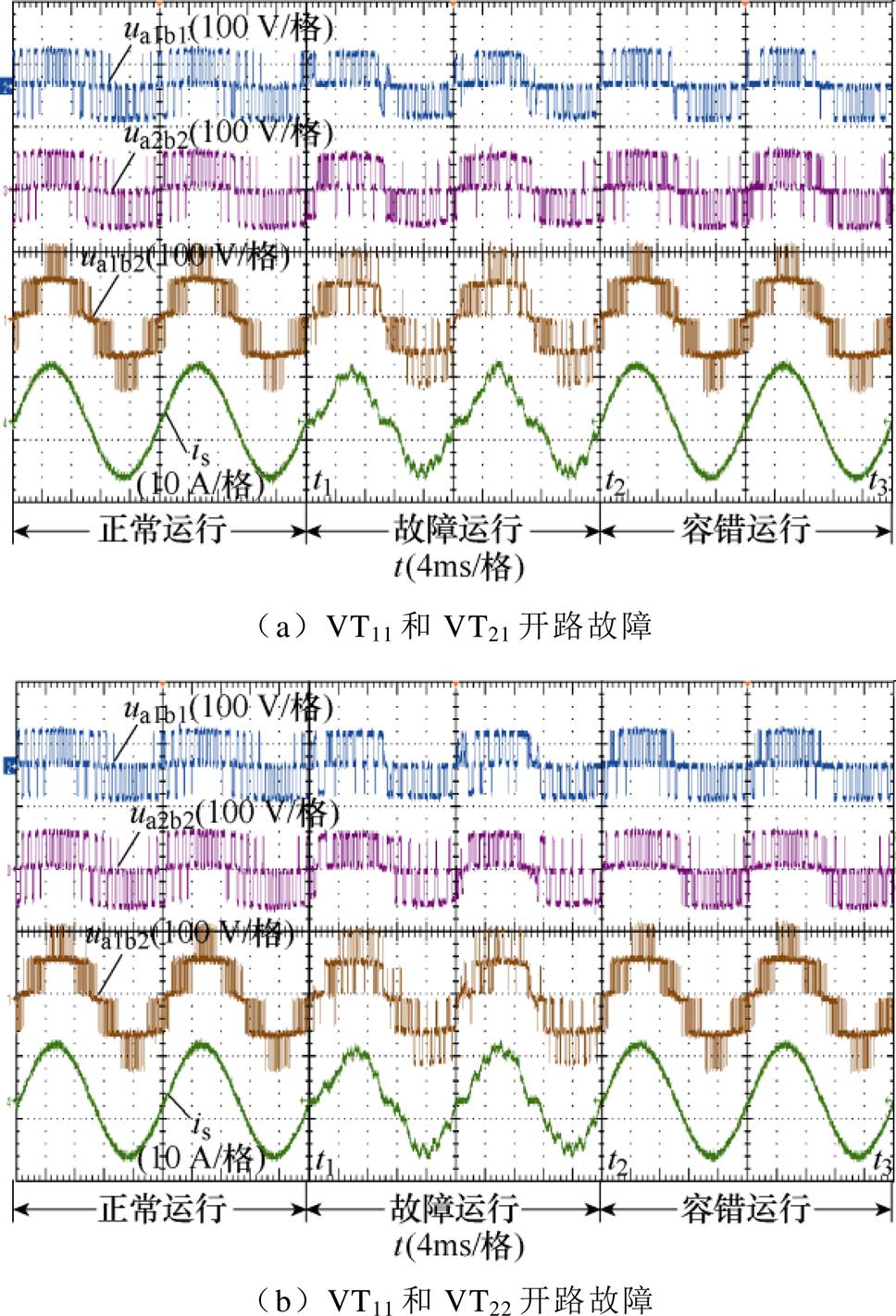
图17 模块间双管开路故障容错实验的动态波形
Fig.17 Dynamic waveforms of fault-tolerant experiment of double tubes between modules
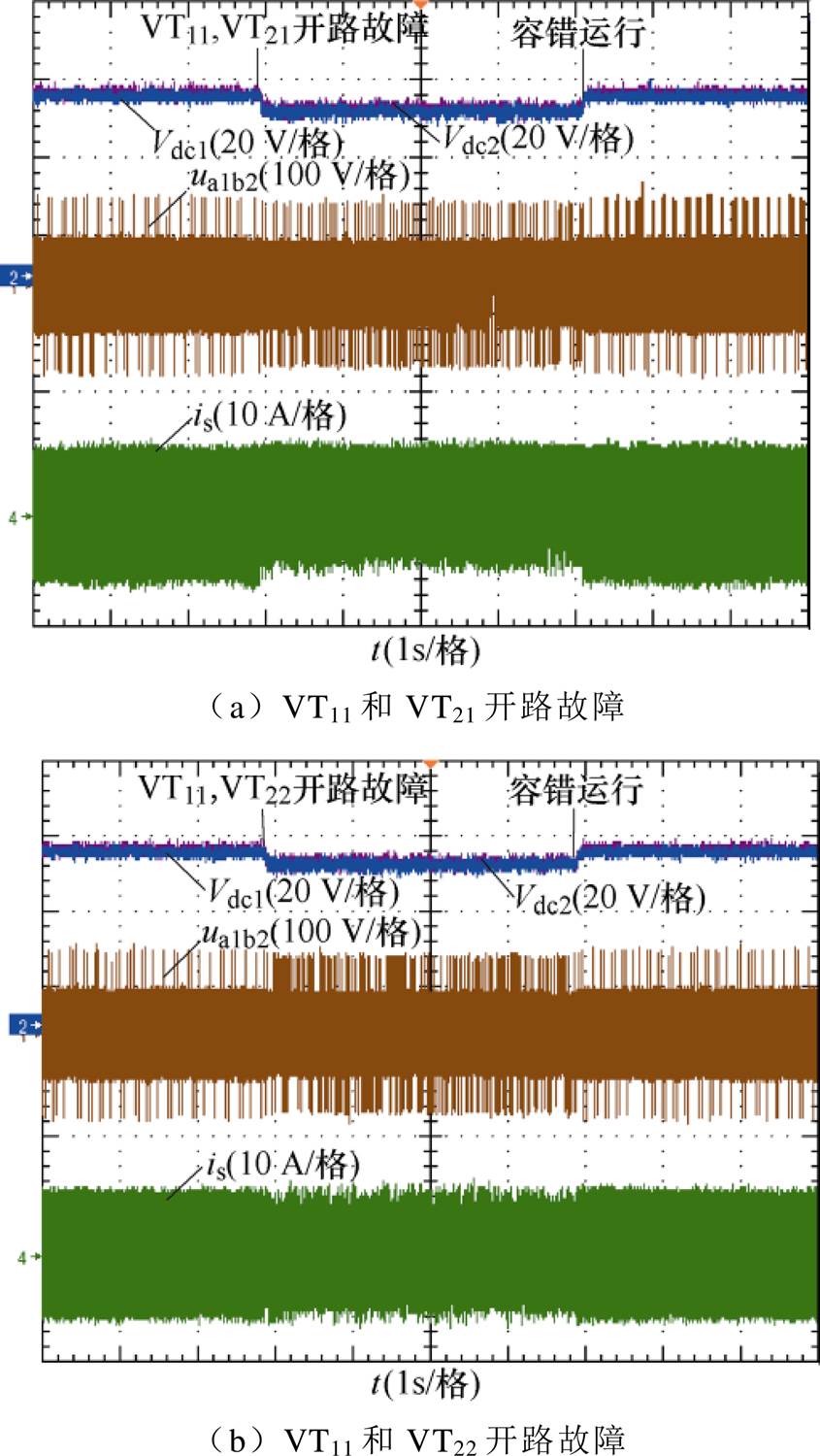
图18 模块间双管正常-故障-容错时的实验波形
Fig.18 Experimental waveforms when double tubes between modules are normal、fault and fault-tolerant
综上所述，本文所提的诊断算法对于单管和双管故障都具有良好的效果，在1/4个基波周期内即可完成故障诊断且诊断结果准确。而本文所提的容错均压算法在单管开路故障以及Ⅰ类和Ⅱ类故障各发生一个的双管开路故障时容错效果良好，而对于仅Ⅰ类或Ⅱ类故障发生的情形，尤其是模块内的双管故障时，虽然无法达到理想的容错效果，但也可以有效降低网侧电流的畸变程度。表5为本文所提的故障诊断算法与容错均压算法与参考文献[12, 18, 20, 26]中所提算法的各项性能指标对比，可以看出，本文所提的开路故障诊断算法在可实现性上具有比较明显的优势，且诊断速度较快、可实现多管诊断；本文所提的容错均压SVPWM算法实现较为简单、成本低且扩展性强，同时还具备模块间均压的能力，无需再添加额外的均压控制算法。
表5 诊断与容错实验结果对比
Tab.5 Comparison of diagnostic and tolerant experimental results
文献诊断时间/ms多管诊断多管容错均压能力验证平台 [12]――×√实物 [18]4.7×××实物 [20]14.7×――仿真 [26]5√――半实物 本文4.5√√√实物
本文以单相两电平H桥级联整流器为研究对象，针对开关管开路故障的问题，提出了一种基于电流误差变化率的快速诊断算法。同时对已有的一维均压SVPWM算法进行了优化，提出一种容错均压SVPWM算法。所提算法具有以下特点：
1）本文所提的开关管开路故障诊断算法可以在1/4个基波周期内实现单管或双管的故障定位，诊断速度较快。并且该算法所需计算量较少且不需要额外的硬件，具有简单、快速和可行性高等优点，适用于多模块级联变换器系统。
2）本文所提的容错均压SVPWM算法可以在没有任何额外电路的条件下实现单管或双管开路故障的容错，并且在单管开路故障以及Ⅰ类和Ⅱ类故障各发生一个的双管开路故障情形下使整流器恢复正常运行，容错后的系统在不平衡负载下也能够维持各模块的直流电压均衡。
参考文献
[1] 李子欣, 高范强, 赵聪, 等. 电力电子变压器技术研究综述[J]. 中国电机工程学报, 2018, 38(5): 1274-1289.
Li Zixin, Gao Fanqiang, Zhao Cong, et al. Research review of power electronic transformer techno- logies[J]. Proceedings of the CSEE, 2018, 38(5): 1274-1289.
[2] 胡钰杰, 李子欣, 罗龙, 等. 串联谐振间接矩阵型电力电子变压器高频电流特性分析及开关频率设计[J]. 电工技术学报, 2022, 37(6): 1442-1454.
Hu Yujie, Li Zixin, Luo Long, et al. Characteristic analysis of high-frequency-link current of series resonant indirect matrix type power electronics transformer and switching frequency design[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1442-1454.
[3] Qi Yuhao, Ma Ke, Xia Shihao. Active thermal control with optimal phase angle under stall condition of machine drive inverter[J]. IEEE Transactions on Power Electronics, 2022, 37(9): 10128-10132.
[4] 黄先进, 杜田倩, 王风川, 等. 基于列车运行图的CRH3牵引变流器IGBT模块寿命预测[J]. 电工技术学报, 2022, 37(增刊1): 172-180.
Huang Xianjin, Du Tianqian, Wang Fengchuan, et al. Mission profiles-based lifetime prediction for IGBT modules applied to CRH3 traction converter[J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 172-180.
[5] Guillod T, Krismer F, Kolar J W. Protection of MV converters in the grid: the case of MV/LV solid-state transformers[J]. IEEE Journal of Emerging & Selected Topics in Power Electronics, 2017, 5(1): 393-408.
[6] 胡亮灯, 孙驰, 陈玉林, 等. 大功率IGBT的短路故障检测[J]. 电工技术学报, 2018, 33(11): 2592-2603.
Hu Liangdeng, Sun Chi, Chen Yulin, et al. Short- circuit fault detection for high-power IGBT[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2592-2603.
[7] Hang Jun, Shu Xiaoman, Ding Shichuan, et al. Robust open-circuit fault diagnosis for PMSM drives using wavelet convolutional neural network with small samples of normalized current vector trajectory graph[J]. IEEE Transactions on Industrial Electronics, 2023, 70(8): 7653-7663.
[8] 成庶, 李蔚, 陈特放, 等. 整流器主电路开路故障诊断及容错控制研究[J].电工技术学报, 2016, 31(13): 26-35.
Cheng Shu, Li Wei, Chen Tefang, et al. Research on open-circuit fault diagnosis and fault-tolerant control scheme for rectifier main circuits[J]. Transactions of China Electrotechnical Society, 2016, 31(13): 26-35.
[9] Ceballos S, Pou J, Robles E, et al. Performance evaluation of fault-tolerant neutral-point-clamped converters[J]. IEEE Transactions on Industrial Electronics, 2010, 57(8): 2709-2718.
[10] 胡烽, 孙宏博, 蒋栋, 等. 基于四相全桥的磁悬浮轴承开关器件开路故障容错控制策略[J]. 电工技术学报, 2022, 37(9): 2295-2305, 2340.
Hu Feng, Sun Hongbo, Jiang Dong, et al. Fault- tolerant strategy of four-phase full-leg for active magnetic bearing in case of open circuit fault of switching device[J]. Transactions of China Electro- technical Society, 2022, 37(9): 2295-2305, 2340.
[11] 孙冠群, 尹项根, 赖锦木, 等. 模块化多电平直流变压器容错控制策略[J]. 电工技术学报, 2022, 37(增刊1): 246-256, 287.
Sun Guanqun, Yin Xianggen, Lai Jinmu, et al. Fault- tolerant control strategy of modular multilevel DC transformer[J]. Transactions of China Electrotech- nical Society, 2022, 37(S1): 246-256, 287.
[12] 赵楠, 郑泽东, 刘建伟, 等. 级联H桥变换器IGBT开路故障分析与冗余方法研究[J]. 电工技术学报, 2023, 38(6): 1608-1619.
Zhao Nan, Zheng Zedong, Liu Jianwei, et al. IGBT open-circuit fault analysis and fault-tolerant method for cascaded H-bridge converter[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1608- 1619.
[13] 任海军. ANPC三电平级联逆变器故障诊断与系统重构[D]. 成都: 西南交通大学, 2020.
[14] Kim S M, Lee J S, Lee K B, et al. A modified level-shifted PWM strategy for fault-tolerant cascaded multilevel inverters with improved power dis- tribution[J]. IEEE Transactions on Industrial Elec- tronics, 2016, 63(11): 7264-7274.
[15] 卫炜, 高瞻, 赵牧天, 等. 基于切换调制波的三电平有源中点钳位逆变器优化容错技术研究[J]. 电工技术学报, 2022, 37(15): 3818-3833.
Wei Wei, Gao Zhan, Zhao Mutian, et al. Research on optimal fault-tolerant technique for three-level active- neutral-point-clamped inverter based on switching modulation wave[J]. Transactions of China Electro- technical Society, 2022, 37(15): 3818-3833.
[16] Deng Fujin, Tian Yanjun, Zhu Rongwu, et al. Fault- tolerant approach for modular multilevel converters under submodule faults[J]. IEEE Transactions on Industrial Electronics, 2016, 63(11): 7253-7263.
[17] 刘国海, 宋成炎, 徐亮, 等. 基于SVPWM的五相永磁同步电机两相开路故障容错控制策略[J]. 电工技术学报, 2019, 34(1): 23-32.
Liu Guohai, Song Chengyan, Xu Liang, et al. SVPWM based fault-tolerant control strategy under two-phase open circuit fault of five-phase permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 23-32.
[18] 窦盛. 级联H桥光伏逆变器故障诊断与容错控制研究[D]. 合肥: 合肥工业大学, 2020.
[19] 杨贺雅, 邢纹硕, 向鑫, 等. 基于多元高斯分布异常检测模型的MMC子模块开路故障诊断方法[J]. 电工技术学报, 2023, 38(10): 2744-2756.
Yang Heya, Xing Wenshuo, Xiang Xin, et al. A sub-module open-circuit fault detection and location strategy for modular multilevel converters based on multivariate Gaussian distribution[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2744- 2756.
[20] 韩杰祥, 张哲, 尹项根, 等. 级联型电力电子变压器内部开路故障特征及定位方法研究[J]. 中国电机工程学报, 2020, 40(19): 6071-6085.
Han Jiexiang, Zhang Zhe, Yin Xianggen, et al. Research on fault characteristic and location method for internal open circuit fault of cascaded power electronic transformer[J]. Proceedings of the CSEE, 2020, 40(19): 6071-6085.
[21] 李辉, 杨甜, 谭宏涛, 等. 基于电压和电流特征的双馈风电变流器功率器件开路故障综合诊断[J]. 电工技术学报, 2021, 36(16): 3433-3445.
Li Hui, Yang Tian, Tan Hongtao, et al. Com- prehensive diagnosis of open-circuit fault for power devices of doubly-fed wind power converter based on the features of voltage and current[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3433- 3445.
[22] 李凯迪, 陈特放, 成庶, 等. 基于电流滞环控制的逆变器开路故障诊断及容错控制[J]. 电工技术学报, 2019, 34(增刊2): 596-608.
Li Kaidi, Chen Tefang, Cheng Shu, et al. Open circuit fault diagnosis and failure-tolerant control for inverter with hysteresis current control[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 596- 608.
[23] 李兵, 崔介兵, 何怡刚, 等. 基于能量谱熵及小波神经网络的有源中性点钳位三电平逆变器故障诊断[J]. 电工技术学报, 2020, 35(10): 2216-2225.
Li Bing, Cui Jiebing, He Yigang, et al. Fault diagnosis of active neutral point clamped three-level inverter based on energy spectrum entropy and wavelet neural network[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2216-2225.
[24] 陈涛, 刘志刚, 胡轲珽, 等. 一种双重化脉冲整流器多管开路故障快速诊断方法[J]. 电工技术学报, 2020, 35(10): 2226-2238.
Chen Tao, Liu Zhigang, Hu Keting, et al. Quick diagnosis method for double-PWM rectifier multi- tube open circuit fault[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2226-2238.
[25] 许水清, 黄文展, 何怡刚, 等. 基于自适应滑模观测器的中点钳位型三电平并网逆变器开路故障诊断[J]. 电工技术学报, 2023, 38(4): 1010-1022.
Xu Shuiqing, Huang Wenzhan, He Yigang, et al. Open-circuit fault diagnosis method of neutral point clamped three-level grid-connected inverter based on adaptive sliding mode observer[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 1010- 1022.
[26] 谢东, 葛兴来. 基于残差变化率的单相级联H桥整流器IGBT开路故障诊断[J]. 电工技术学报, 2018, 33(16): 3822-3834.
Xie Dong, Ge Xinglai. Residual-changing-rate based open-circuit fault diagnosis for a single-phase cascaded H-bridge rectifier[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3822-3834.
[27] 柳明, 陈亚军, 林宏健, 等. 单相三电平H桥两模块级联变换器的一维均压SVPWM算法[J]. 电力自动化设备, 2018, 38(3): 109-115.
Liu Ming, Chen Yajun, Lin Hongjian, et al. One- dimensional SVPWM algorithm with voltage balancing capability of single-phase three-level two-cell cascaded H-bridge converter[J]. Electric Power Auto- mation Equipment, 2018, 38(3): 109-115.
Abstract The single-phase cascaded H-bridge rectifier (CHBR) used in the front of power electronic traction transformers has a highly modular structure, and its core component, power switching, has a high failure rate, dramatically impacting system reliability. To solve the open-circuit fault problem of its power switching device in the single-phase two-level H-bridge cascaded rectifier, this paper proposes a fast diagnosis algorithm based on an analytic model and a fault-tolerant voltage balancing space vector pulse width modulation (SVPWM) algorithm.
Firstly, the topological structure and basic working mode of the single-phase two-level H-bridge rectifier are analyzed, and the mathematical model of the single-phase cascade rectifier is established. By analyzing the operation mode of each power switching device in a single module when the open-circuit fault occurs, a mathematical model of the current error rate of the cascaded rectifier is established. Accordingly, the characteristics of the current error rate of the single-phase two-level H-bridge cascaded rectifier with single or double open-circuit faults are analyzed accurately. Then, the specific flow of the diagnosis algorithm is provided.
Secondly, based on the one-dimensional SVPWM algorithm, the one-dimensional space vector graph is established, and the influence of switch fault on vector selection is analyzed. Then, the redundant vector and redundant switch state of the cascaded converter are used to reselect the fault-tolerant vector to avoid the action of the faulty switch tube and restore the rectifier to normal operation. The selected vector still has the voltage-sharing function. The selection strategy of voltage equalization and fault tolerant voltage equalization vector is proposed for two and n-module cascade rectifiers with open-circuit faults, and the implementation steps of fault-tolerant voltage equalization SVPWM algorithm are given.
Finally, the open-circuit fault diagnosis algorithm and the fault-tolerant voltage equalization SVPWM algorithm for six-module single-phase cascade rectifiers are verified by Matlab/Simulink simulation. Moreover, through the FPGA-based two-module cascade rectifier hardware experiment platform and the Verilog-based software platform, fault diagnosis and fault tolerant experiments under single or double open-circuit faults are conducted. The following conclusions are obtained: (1) The open-circuit fault diagnosis algorithm can localize single or double tubes within 1/4 of a fundamental wave cycle, and the speed is fast. Moreover, this algorithm requires minimal computation without additional hardware. It has the advantages of simplicity, speed, and high feasibility, suitable for multi-module cascaded converter systems. (2) The fault-tolerant voltage balancing SVPWM algorithm can achieve fault tolerance for single or double tube open-circuit faults without additional circuits. In addition, it can restore the rectifier to normal operation under single-tube open-circuit faults and double-tube open-circuit faults of types Ⅰ and Ⅱ, respectively. The system can also maintain the DC voltage balance of each module under unbalanced loads after fault tolerance.
keywords：Single-phase cascaded H-bridge rectifier, open-circuit fault, online diagnosis, space voltage vector modulation, fault tolerant algorithm
DOI: 10.19595/j.cnki.1000-6753.tces.230814
中图分类号：TM46
国家重点研发计划（2021YFB2601500）和国家自然科学基金（52077183）资助项目。
收稿日期 2023-06-02
改稿日期 2023-07-07
徐翊宸 男，1998年生，硕士研究生，研究方向为多电平变换器控制及调制算法。E-mail: Xyc88225119@163.com
马 兰 女，1988年生，讲师，硕士生导师，研究方向为电力电子变换器、电池均衡、光伏应用等。E-mail: mlan@swjtu.edu.cn（通信作者）
（编辑 陈 诚）