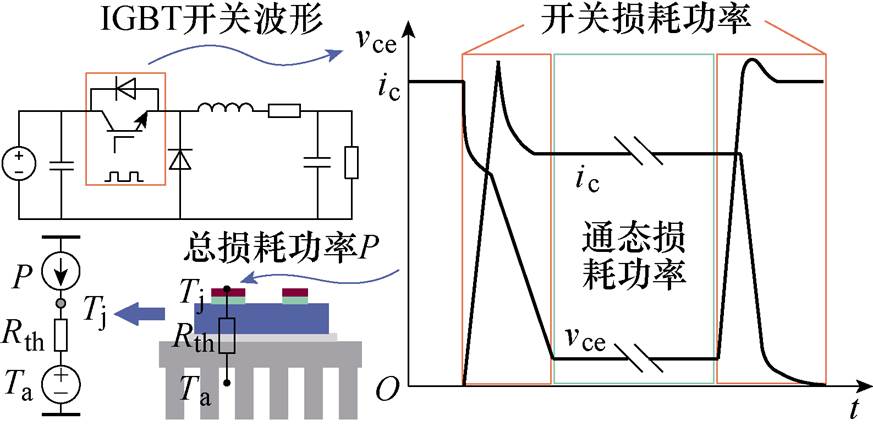
图1 IGBT结温作用原理
Fig.1 IGBT junction temperature action principle
摘要 并联IGBT是解决托卡马克（Tokamak）装置中等离子体垂直位移快速控制电源容量逐渐增大问题的有效途径。而并联IGBT之间的结温平衡是并联系统安全稳定运行的关键因素之一。因此，研究结温对并联IGBT功率损耗差异的影响对提高并联系统的稳定性至关重要。然而现有的研究成果主要集中在单个器件损耗模型或者是并联IGBT的最佳工作频率范围而未涉及对并联IGBT最佳工作占空比范围的讨论。研究发现，当IGBT工作在正温度系数区间时，结温差异造成的通态损耗差异与开关损耗差异呈不同的温度特性。因此，提出零温度-占空比的概念来估计并联IGBT之间结温失配趋势。该文建立零温度-占空比模型，并以此来分析电路设计参数、IGBT器件参数以及结温差异对并联IGBT最佳工作占空比范围的影响。实验结果表明，通过零温度-占空比模型可以对并联IGBT的可靠性、电路设计参数以及器件选型提供可行的参考。
关键词：并联IGBT 开关损耗 导通损耗 温度特性 零温度-占空比
随着托卡马克（Tokamak）装置容量的增大，建立约束等离子体的磁场所需的磁体电源容量也随之增大。在Tokamak的磁体电源中，通常称等离子体垂直位移快速控制电源为快控电源。以中国科学院等离子体物理研究所自行研制的全超导托卡马克装置（Experimental Advanced Superconducting Tokamak, EAST）中快控电源为例。其第一代参数为±0.8 kV/±5 kA[1]，第二代参数为±1.6 kV/±9 kA[2]。但是，以Infineon生产的商用功率模块为例，额定电流最大的IGBT模块只能达到1.7 kV/3.6 kA[3]。由此，在考虑系统稳定性、经济成本以及控制复杂度等因素下，功率器件并联是解决单个功率器件额定电流不足的一种有效方式。
然而，在并联器件的工作过程中，由于IGBT之间的器件参数[4]、电路中杂散参数[5]、驱动器参数[6]以及散热系统参数[7]等因素的不一致性，并联IGBT之间总会出现损耗差异，从而导致结温差异，而结温差异又可能会增大IGBT之间的损耗差异，从而导致IGBT之间的结温差异增大。在如此往复的反馈作用下，最终可能会导致器件过热失效[8]。而目前温度对器件功率损耗影响的研究大多集中于单个IGBT，对于并联IGBT的研究成果十分少见。随着大功率电力电子设备的发展，并联IGBT运行的安全性越来越受到学术界的关注[9]。因此，研究结温对并联IGBT损耗的影响对提高并联IGBT系统的稳定性至关重要。
目前，温度对器件损耗影响的研究成果大致可以分为两类：
第一类是建立IGBT的电热模型，从而得到IGBT温度-损耗的模型。文献[10]在仿真软件Simulink中建立IGBT物理模型的电路模型，在COMSOL中建立有限元热模型，然后在Matlab中编写脚本实现软件之间的变量传递，从而实现多速率的IGBT电热联合仿真。文献[11]采用参数拟合的方法创建IGBT的电模型，并利用该电模型进行损耗的计算，再根据等效导热系数创建全浸式蒸发冷却条件下的热模型，从而得到IGBT的降阶模型，最终得到全浸式蒸发冷却IGBT电热耦合模型。文献[12]采用考虑温度影响的平均损耗模型实现对IGBT损耗的计算，再结合热网络模型构成完整的IGBT电热损耗模型，并将其用于IGBT的寿命预测。文献[13]对IGBT的开关波形进行分段解耦分析，创建解耦的IGBT分析模型，并对该模型中的集电极电流以及集射极电压做积分得到IGBT的开关损耗。文献[14]采用并改进分析方法创建了新的IGBT的行为模型，并以此行为模型为基础进行IGBT的功率损耗以及工作结温的计算。文献[15]首先对IGBT的开关过程进行分段，再采用有限状态机思想在Matlab中创建IGBT的开关模型，从而利用此模型实现对IGBT的损耗研究。以上文献均为研究温度对单个IGBT损耗的影响，并没有探究温度对并联IGBT损耗差异的影响。
第二类是探究温度与并联IGBT损耗之间的相互作用机理。文献[16]采用电路分析方法，创建具有不平衡杂散参数的并联IGBT模块动态电热模型，以此来评估计算并联IGBT的结温分布及波动情况。文献[17]通过对集射极电压和集电极电流的采样来估计IGBT工作期间等效电阻的增量，进而创建电气参数与温度相关的函数表达式，并将该分析手段用于IGBT实时结温的评估。文献[18-19]以分立二极管为研究对象，考虑温度的影响，建立导通损耗和反向恢复损耗的数学模型，来研究温度对并联二极管电热平衡。文献[20]通过创建IGBT损耗的数学模型，研究了温度对IGBT损耗的平衡机理，从而提出了“拐点频率特性”的概念来评估并联IGBT之间结温失配的趋势。从此类文献的发展来看，学界开始从单纯的并联IGBT损耗分析[16]向并联IGBT最佳工作频率范围[20]深入，但是，目前还缺乏对并联IGBT最佳工作占空比范围的研究。因为对于电力电子装置设计之初，工作频率以及额定条件下的占空比等因素都是需要考虑的问题。针对此问题，研究发现，当IGBT器件工作在大电流正温度系数区间时，结温差异DTj造成的通态损耗差异DEc与开关损耗差异DEsw呈现不同的温度特性。所以存在一个零温度-占空比D0，使得并联IGBT的工作占空比在D0两侧时，总损耗差异呈现出两种不同的温度特性，也即并联IGBT系统对外呈现不同的结温失配趋势。在本文中，称有利于IGBT并联工作的占空比范围为最佳工作占空比范围。
但是，由于占空比与IGBT的工作电流是密切相关的，所以如何合理地改进并联IGBT的损耗模型从而实现对零温度-占空比的分析是一个挑战。由此，本文以Buck变换器为例，对并联IGBT的开关行为做出线性假设以简化损耗模型，从而提出了零温度-占空比的分析模型。根据此分析模型，可以分析出电路设计参数、IGBT器件参数以及结温差异对零温度-占空比的影响。最后通过搭建并联IGBT的双脉冲实验平台验证了零温度-占空比的存在，以及得出结论：零温度-占空比随结温差异的增加而 减小。
首先，本文创建了IGBT的损耗模型，并以此分析结温与IGBT工作占空比的联系。其次，通过分析并联IGBT的损耗差异，提出并联IGBT的零温度-占空比的分析模型。最后，提供实验验证结果。
IGBT工作时，其产生的损耗功率通过散热系统反映为结温的作用原理如图1所示。IGBT工作时的开关损耗功率以及通态损耗功率合成的总损耗功率共同作用在IGBT芯片上。芯片产生的热量通过散热系统向环境传递。由于IGBT散热系统中热量的传递方向主要是沿芯片向散热器方向，从而常将其假设为一维传热问题。由此，根据热电比拟原理，可将结温的计算等效为热电路的求解。
图1 IGBT结温作用原理
Fig.1 IGBT junction temperature action principle
并联IGBT结构示意图如图2所示。占空比通过变换器拓扑（本文以Buck拓扑为例）影响IGBT电流，由于器件之间分布参数的差异以及结温差异DTj，并联IGBT之间出现电流差异DIc。电流差异DIc导致器件之间的总损耗出现差异DE。而总损耗差异DE通过器件的散热系统反馈到器件上又呈现出新的结温差异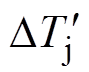
。由于当IGBT器件工作在大电流正温度系数区间时，结温差异DTj造成的通态损耗差异DEc呈现负温度系数，开关损耗差异DEsw呈正温度系数。所以存在一个零温度-占空比D0，使得并联IGBT的工作占空比D＜D0时，总损耗差异呈负温度系数，有利于器件的并联；并联IGBT的工作占空比D＞D0时，总损耗差异呈正温度系数，不利于器件的并联。所以，对于并联IGBT系统，称占空比范围[0, D0]为最佳工作占空比范围。
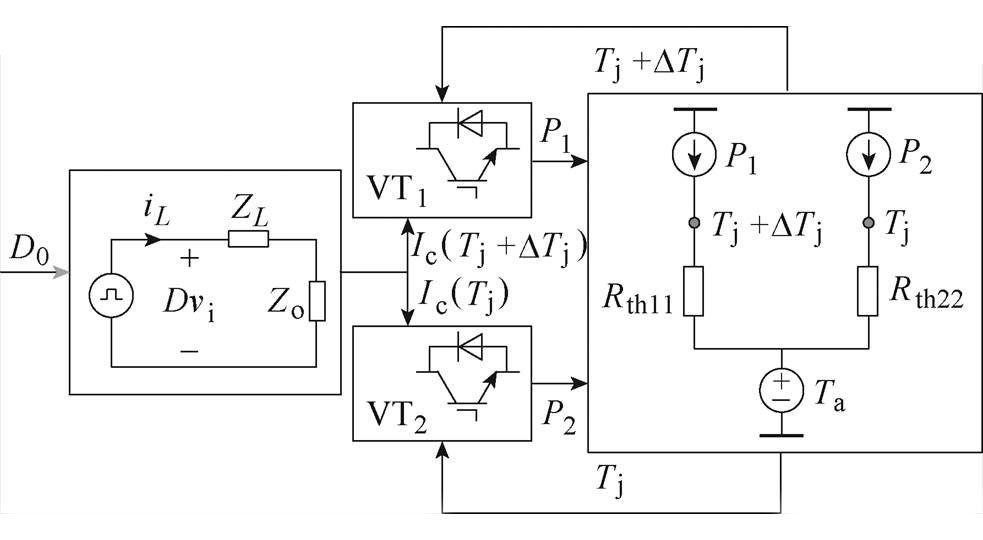
图2 并联IGBT结构示意图
Fig.2 Parallel IGBT structure diagram
为研究占空比对IGBT电流的影响，本文以Buck电路为例，其拓扑如图3所示[21]。图中vi为输入电压，vo为输出电压，D为IGBT工作占空比，iL为电感电流，ZL为电感以及导线的阻抗，Zo为输出阻抗。由此可以得到表达式为
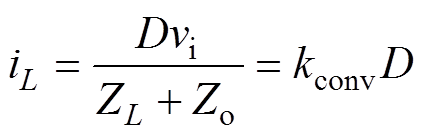（1）
式中，kconv为占空比与负载电流之间的系数，其值与变换器的设计参数有关。
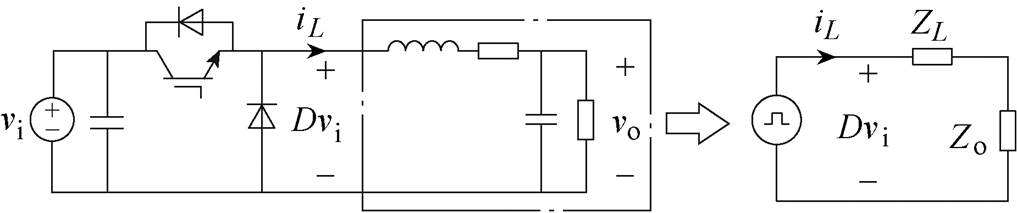
图3 Buck拓扑
Fig.3 Buck topology
当变换器工作稳定后，认为IGBT在一个开关周期中的集电极电流Ic不变，所以可以假设Ic=iL。结合式（1）可以得到IGBT集电极电流正比于占空比D，即
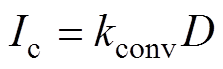（2）
在IGBT工作时，其损耗由IGBT器件材料的参数、工作电压以及工作电流决定[10]。由于材料参数会随着温度变化，从而使IGBT器件的损耗也会随着温度变化。
IGBT的损耗主要包括开关损耗及通态损耗[12]。在感性负载下，IGBT典型开关波形如图4所示，图中，ic为IGBT集电极电流，vce为IGBT集射极电压。为简化分析，将IGBT开通分为四个阶段，IGBT关断分为两个阶段[15]。
在一个开关周期中，根据附录中的计算式（A3）、式（A5）、式（A7）、式（A9）以及式（A11）可以得到IGBT的开通损耗Eon=E1+E2+E3，IGBT的关断损耗为Eoff=E4+E5。在IGBT允许的工作温度范围内，Tj/300变化不大，开关损耗与温度的关系[13, 18, 20]可以简化为
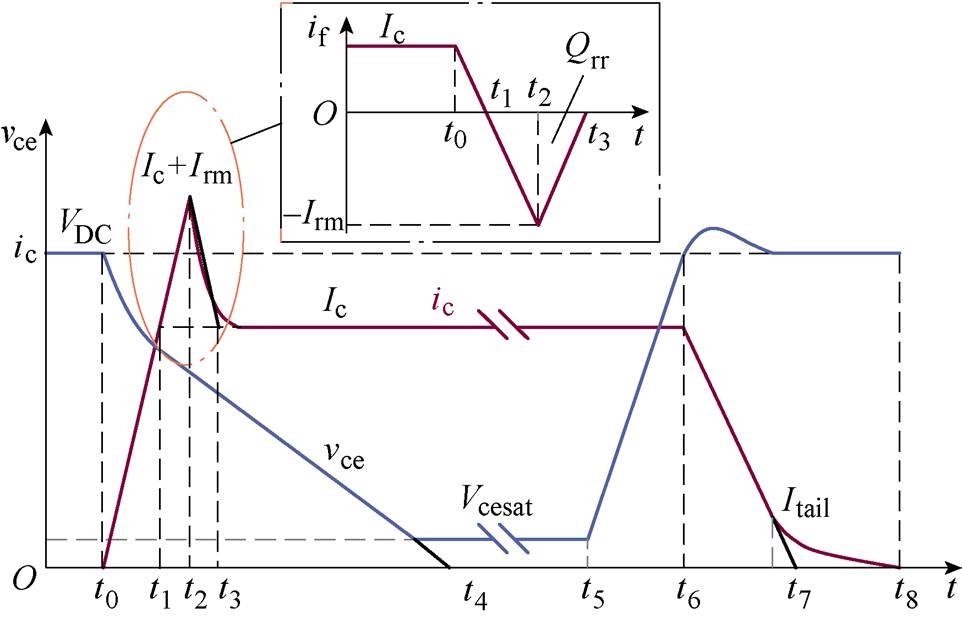
图4 IGBT开关波形
Fig.4 IGBT switch schematic waveform
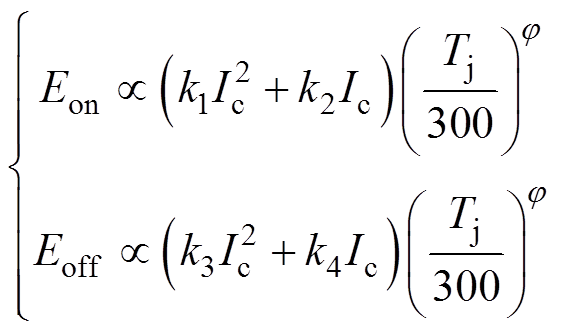（3）
式中，j 为与集电极电流无关的温度常数；k1、k2、k3、k4为与温度无关的电流常数。所以IGBT的开关损耗与温度的关系为
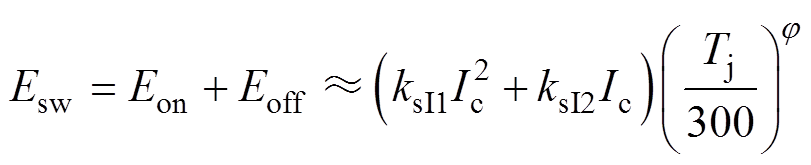（4）
式中，ksI1、ksI2为与温度无关的电流常数。可见，IGBT在一个开关周期中的开关损耗与温度呈幂函数的关系。
选择Infineon IGBT IHW20N120R5作为被测器件（Devices Under Test, DUT），搭建双脉冲实验平台。采用YOKOGAWA 8通道示波器DLM4000进行实验数据的采集与记录。根据实验导出数据进行计算可以获得开关损耗Esw，采用Matlab cftool工具箱对式（4）进行拟合，获得模型参数ksI1= 0.002 580，ksI2=0.039 09，j =1.602 5，其拟合度R2= 0.985 2。模型拟合效果如图5所示。
在IGBT导通占空比为D的开关周期中，通态损耗表示为
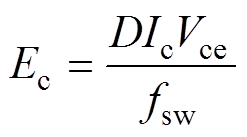（5）
式中，Ec为通态损耗；fsw为开关频率；Vce为完全导通时的集射极电压。
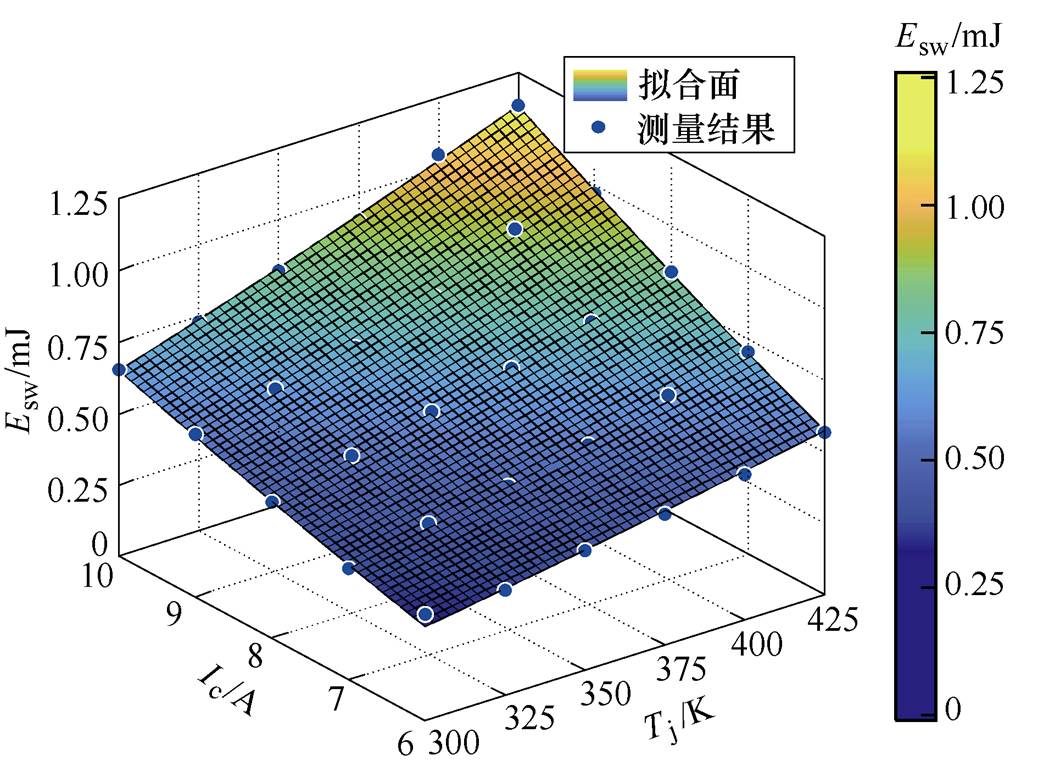
图5 开关损耗拟合结果
Fig.5 Switch loss fitting results
IGBT的输出特性示意图如图6所示，Ic与Vce的关系[19]为
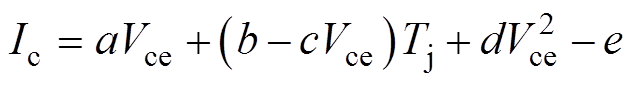（6）
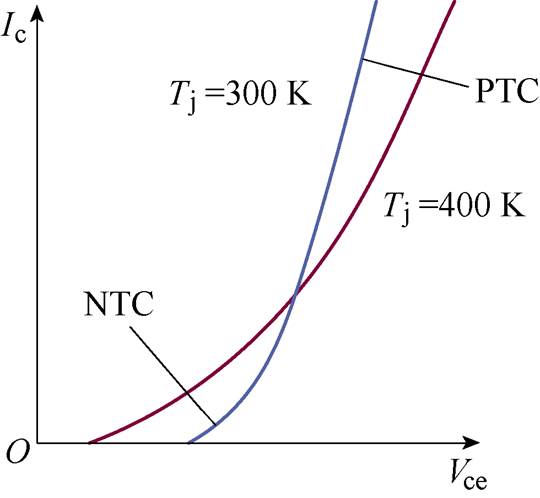
图6 温度对IGBT输出特性的影响
Fig.6 The influence of temperature on IGBT output characteristics
使用HUSTEC-1600A-MT测量IHW20N120R5的静态特性。采用Matlab cftool工具箱对测量结果按照式（6）进行拟合。根据拟合结果，a=50.749 5，b=0.094 8，c=0.110 8，d=6.105 4，e=58.433 0，其拟合度R2=0.995 0。结合式（5）与式（6），可以得到通态损耗与温度的关系如式（7）所示。可见，IGBT在一个开关周期中的通态损耗与温度呈线性关系。
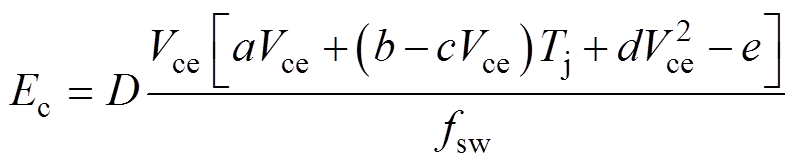（7）
工程中，为缓减并联IGBT之间的电流失配，通常选用参数相同的IGBT进行并联。所以，此处假设并联IGBT之间的参数相同。当两个IGBT VT1与VT2并联运行出现结温差异DTj与电流差异DIc时，两个IGBT的开关损耗与通态损耗也会随之产生差异。IGBT VT1与VT2并联运行一段时间后，由式（4）可以得到VT1和VT2的开关损耗差异DEsw为
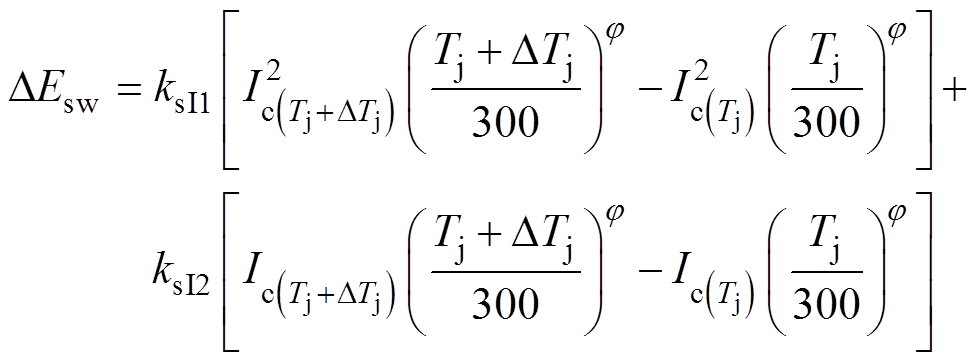（8）
式中，Tj+DTj与Tj分别为高温IGBT VT1结温与室温IGBT VT2结温。
Iall=20 A不同DTj时的DEsw如图7所示，尽管并联IGBT在总电流Iall较大的情况下由于结温差异会导致集电极电流不相等，但开关损耗差异DEsw仍然具有明显的正温度特性。即IGBT开关损耗差异的温度特性主要由指数j 决定。因此，结合式（2），VT1与VT2的开关损耗差异可写为式（9）。可以看出，器件结温高的IGBT开关损耗更大，不利于IGBT的并联。
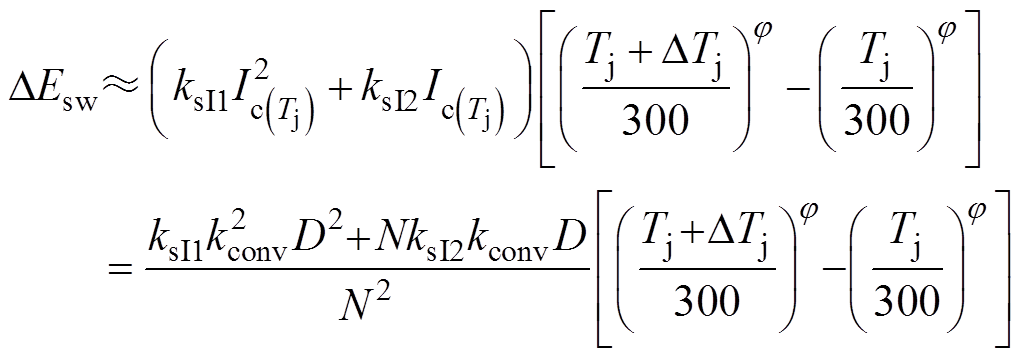（9）
式中，N为并联IGBT的个数。
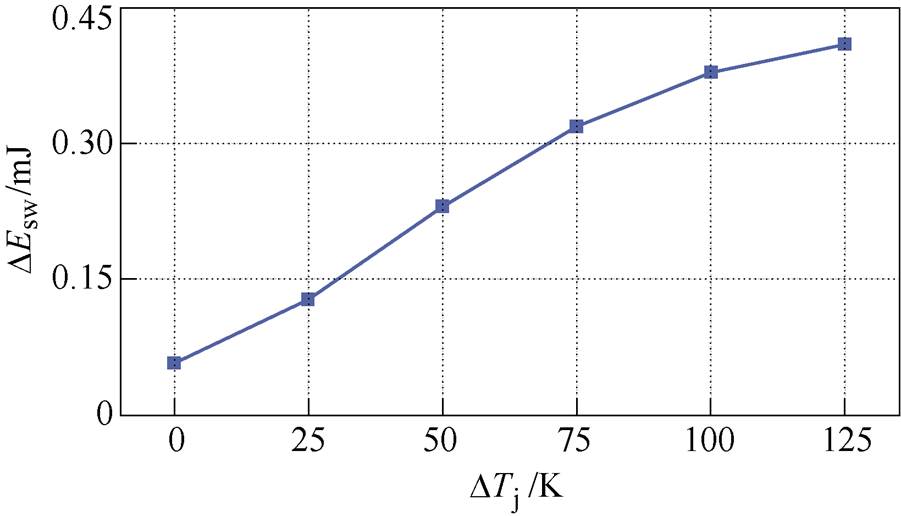
图7 Iall=20 A不同DTj时的DEsw
Fig.7 The DEsw when Iall=20 A with different DTj
在通态损耗差异DEc的分析中，考虑到选择的是参数相同的IGBT进行并联，可以假定温度对两个IGBT的输出特性中的相关系数的影响程度相同。根据式（7），并联IGBT的DEc为
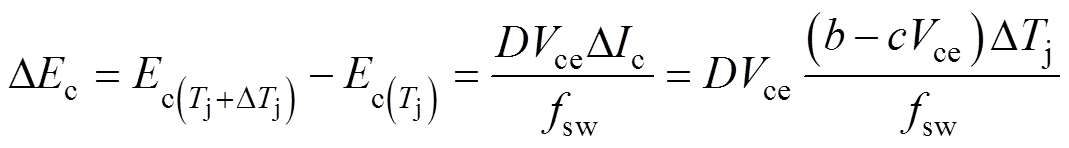（10）
其中
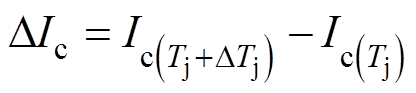
功率IGBT在大电流运行情况下具有相对较大的Vce，所以b
cVce。因此当IGBT集电极电流工作在图6a所示的正温度区间时，若电流差异DIc＜0，则通态损耗差DEc＜0。即器件结温高的IGBT通态损耗更小，有利于IGBT的并联。最终，并联IGBT的总损耗差异DE为开关损耗差异DEsw与通态损耗差DEc之和，即DE=DEsw+DEc。
在不考虑热耦合的情况下，由于器件损耗差异，两IGBT进一步的结温差异表示为
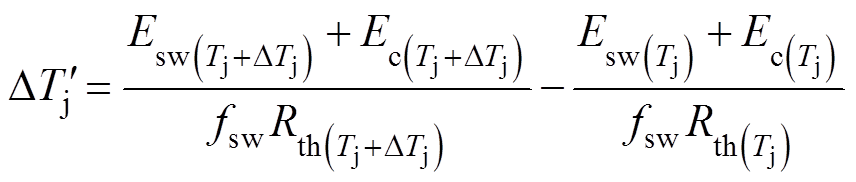（11）
式中，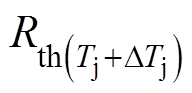
为IGBT VT1在结温Tj+DTj时的热阻；
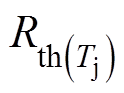为IGBT VT2在结温Tj时的热阻。忽略温度对热阻的影响，可以得到
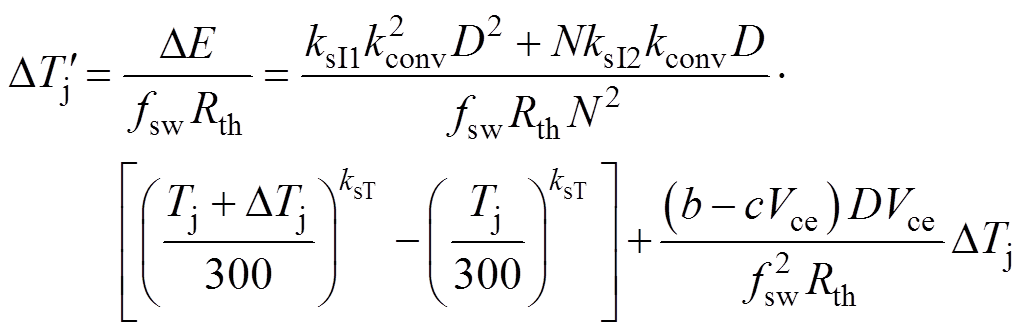（12）
由式（12）可以得出：欲使结温差异DTj不再恶化，那么临界条件就是新的结温差异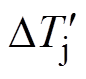
=0，即损耗差异DE=0。所以通过式（12）可以计算得到临界条件对应的占空比D0，本文称其为零温度-占空比，其表达式为
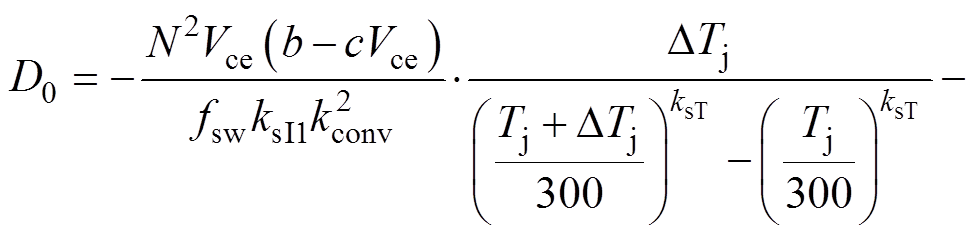
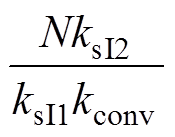（13）
尽管本文为了便于分析，对损耗模型采用了线性近似，但是根据式（13）仍然可以分析并联IGBT结温差异对零温度-占空比D0的影响。根据式（13），可以得出以下结论：
（1）如果占空比D小于零温度-占空比D0，开关损耗小于通态损耗，即通态损耗占主导，对温度进行负反馈，利于IGBT并联。
（2）如果占空比D大于零温度-占空比D0，开关损耗大于通态损耗，即开关损耗占主导，对温度进行正反馈，不利于IGBT并联。
（3）两并联IGBT之间的结温差异DTj越大，零温度-占空比D0越小，即利于IGBT并联运行的占空比范围越小。
由此可以得到并联IGBT零温度-占空比特性如图8所示。通常，电力电子变流装置设计和工作时，占空比大小由负载和工况决定。所以对于实际的变流装置设计时，根据式（13），可以通过选择合适的并联个数以及恰当的器件参数来使得零温度-占空比大于额定条件下的工作占空比，从而来保证电力电子变流装置中并联IGBT系统安全稳定运行。
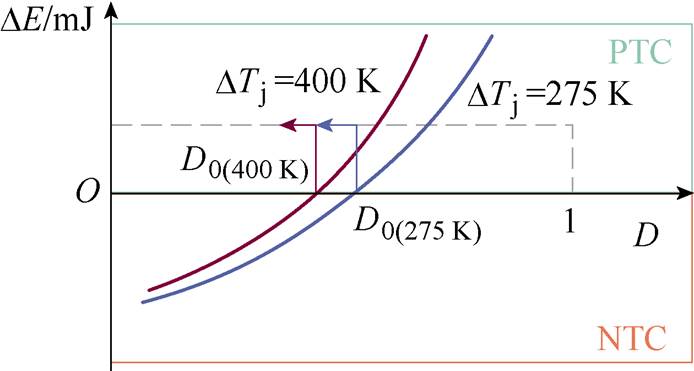
图8 并联IGBT零温度-占空比特性
Fig.8 Zero temperature-duty cycle characteristics of parallel IGBTs
为验证上述结论，搭建并联IGBT双脉冲测试平台对零温度-占空比的存在以及温度特性进行实验验证。并联IGBT双脉冲测试平台的原理如图9a所示，其中VT1为被加热的IGBT，VT2为室温下的IGBT。对应的实验测试平台如图9b所示。其中直流电源由三相交流电源经不控整流获取，为使直流电压稳定，直流侧并入0.5 mF电容用于稳定电压。
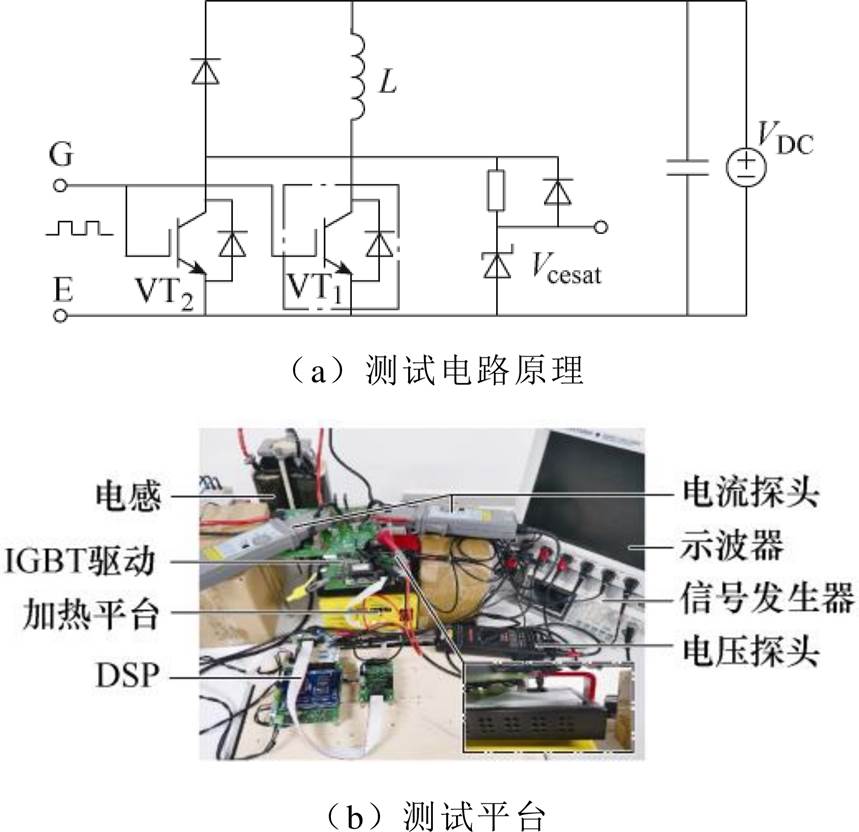
图9 双脉冲测试电路
Fig.9 Double test circuit and test bench
在进行并联IGBT双脉冲实验的过程中，使用图9b中加热平台对IGBT VT1进行加热。调节加热平台的温度，使得IGBT VT1与处于室温的IGBT VT2形成不同的结温差异。实验过程中使用YOKOGAWA示波器DLM4000进行实验数据的采集与记录。将记录的波形数据导出并计算，将第1个脉冲的关断阶段数据作为关断损耗的计算，第2个脉冲的开通阶段数据作为开通损耗的计算。考虑到双脉冲实验不是长时间的连续开断，并且脉冲施加时间较短，所以可忽略脉冲导通阶段产生的热量对结温的影响。将导出的数据绘制成波形，得到并联IGBT开关波形如图10所示。由图10a和图10b可以看出，尽管高温使得VT1的静态电流小于室温下运行的VT2，但是如第1节分析一样，由于温度对阈值电压Vt以及导电系数Kp的影响，使得VT1的动态电流增加，从而增加开关损耗。由图10c和图10d可以看出，并联IGBT之间的静态电流差异受总电流的影响，即静态电流差异也受导通占空比的影响。
采用图9a所示原理中的导通电压测试电路，可以使用示波器DLM4000测得并联IGBT的导通电压Vcesat。将示波器采集的数据导出并计算，可以得到并联IGBT的导通损耗差异|DEc|。将其与开关损耗差异DEsw做比较，如图11所示。从图11可以看出：随着结温差异DTj的增加，导通损耗差异|DEc|等于开关损耗差异DEsw时对应的总电流Iall随之减小，即零温度-占空比D0随结温差异DTj的增加而减小。由此，根据式（2）还可得出：在Buck电路参数设计时，应尽可能减小占空比与负载电流之间的系数kconv，从而使得零温度-占空比相对较大，有利于增加IGBT并联运行的占空比区间。
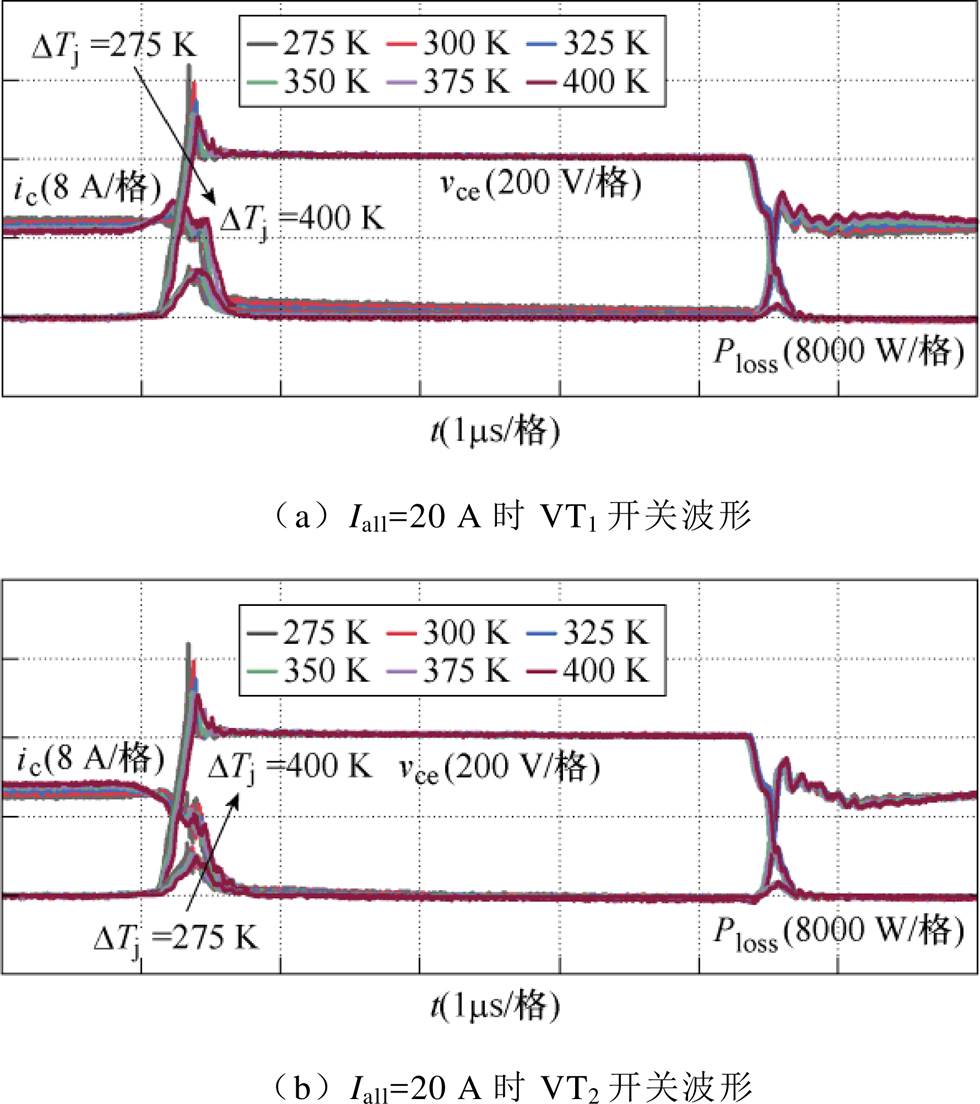
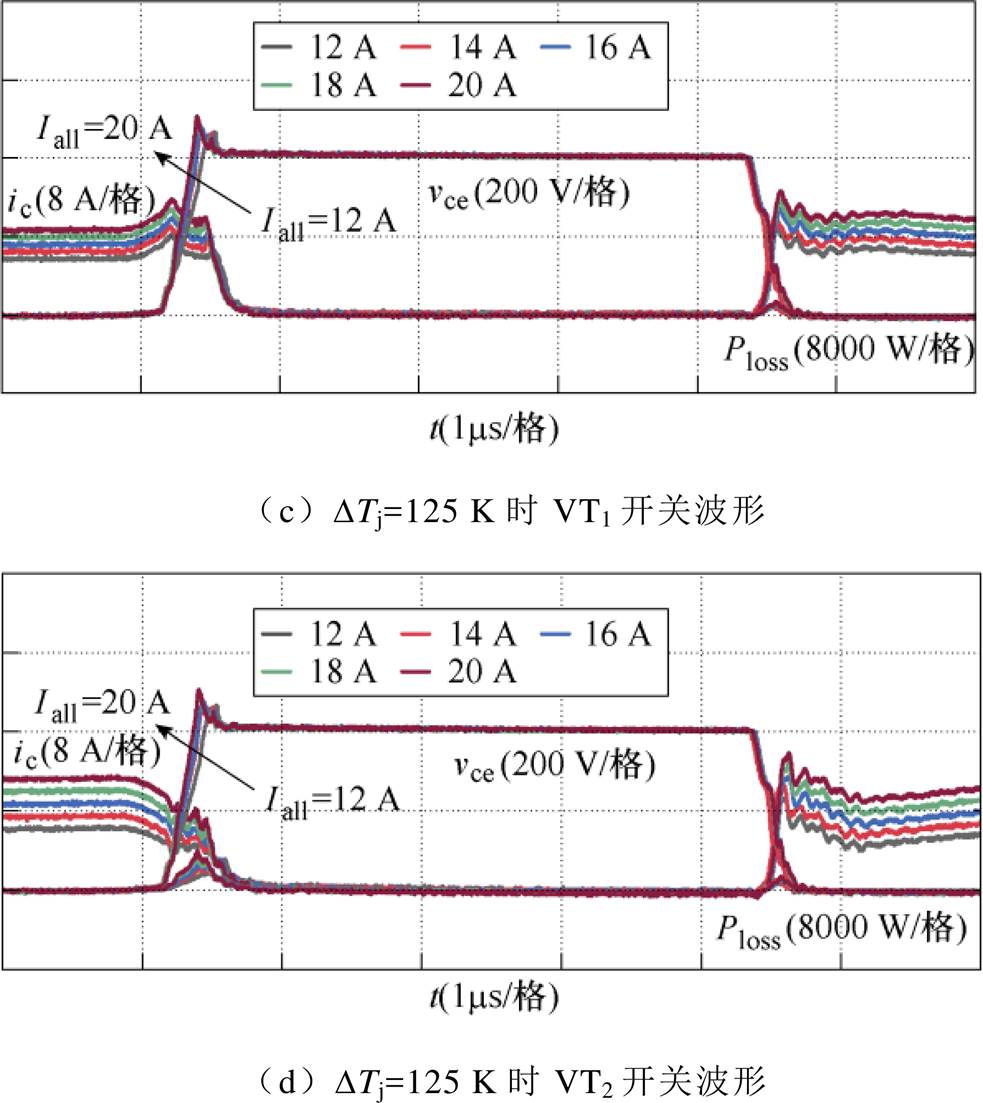
图10 并联IGBT开关波形
Fig.10 Switching waveforms of parallel IGBTs
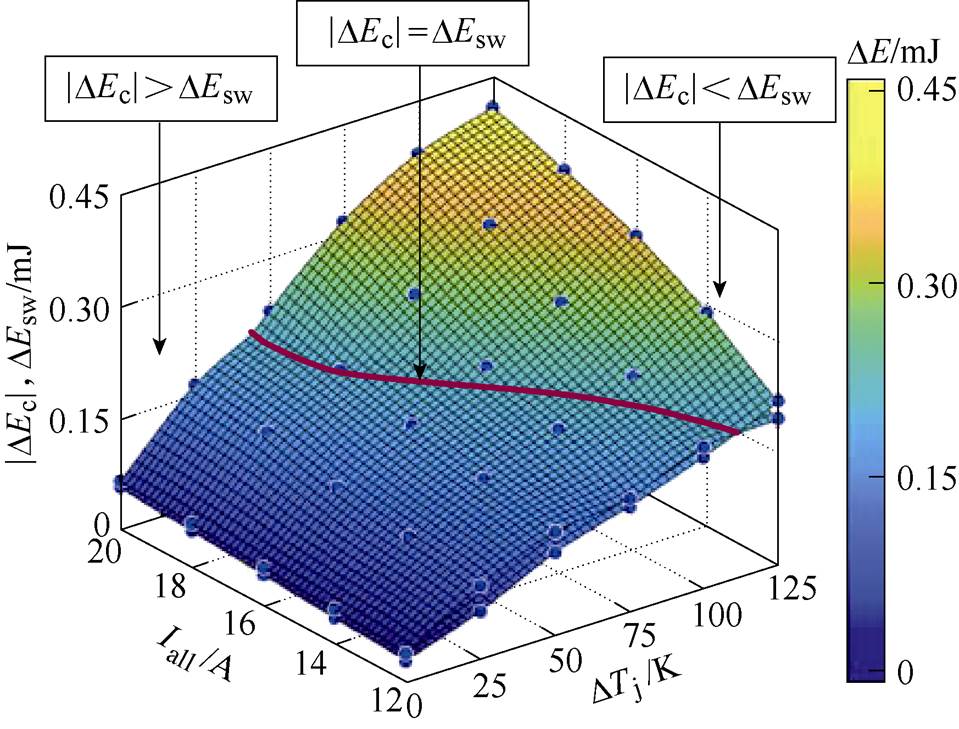
图11 导通损耗差异与开关损耗差异比较
Fig.11 Comparison of DEc and DEsw
图11中，可以注意到，当总电流的增大，|DEc|= DEsw的曲线受结温差异DTj的影响程度增大。这是因为总电流较大时，并联IGBT之间的电流差对开关损耗的影响再不能忽视，即式（9）的假设条件随总电流的增大逐渐不成立，这也可以从图12得到证明。在图12中，随着总电流的增加，开关损耗差异DEsw的增加量逐渐变缓，而导通损耗差异|DEc|的增加量几乎不变。从而可以合理推断出，存在一个较大的总电流Iall0，当Iall＞Iall0时，导通损耗差异会再次大于开关损耗差异，从而并联IGBT系统对外又呈现出有利于并联的特征。
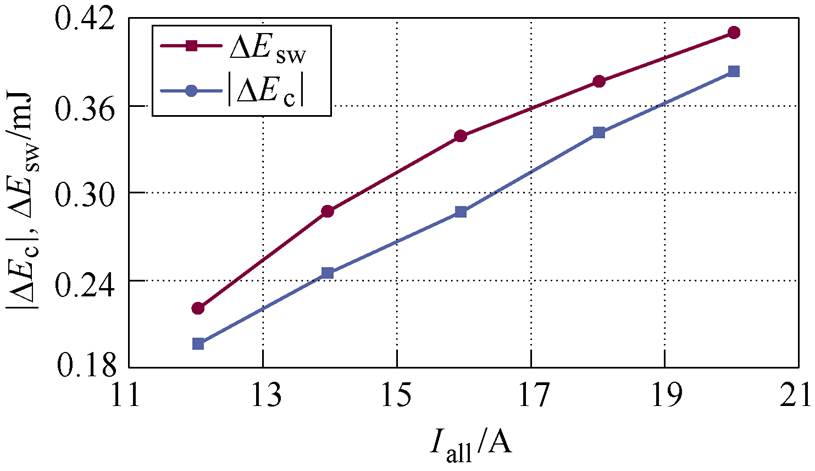
图12 DTj=125 K时的损耗差异对比
Fig.12 Comparison of DEc and DEsw at DTj=125 K
当IGBT器件工作在大电流正温度系数区间时，结温差异造成的通态损耗差异呈负温度系数，开关损耗差异呈正温度系数，从而提出了零温度-占空比的概念来评估并联IGBT之间结温失配趋势。推导了并联IGBT的损耗模型，以此来创建零温度-占空比模型。利用该模型可以分析电路设计参数、IGBT器件参数以及结温差异对并联IGBT最佳工作占空比范围的影响。根据该模型可以得出：如果工作占空比小于零温度-占空比，开关损耗小于通态损耗，即通态损耗占主导，有利于IGBT并联；如果工作占空比大于零温度-占空比，开关损耗大于通态损耗，即开关损耗占主导，不利于IGBT并联。两并联IGBT之间的结温差异越大，零温度-占空比越小，即利于IGBT并联运行的占空比范围越小。因此，本文提出的零温度-占空比模型可以为并联功率器件的可靠性、电路设计参数以及器件选型提供可行的参考。
附 录
对图4所示的典型开关波形进行损耗的计算。
1）阶段t0～t1：IGBT集电极电流ic表示[16]为
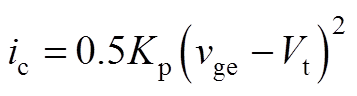（A1）
式中，vge为栅射极电压；Vt为阈值电压；Kp为IGBT器件内部等效MOSFET的导电系数。由于上升阶段时间短，认为电流上升斜率为kcur，且kcur∝Kp。此阶段中IGBT集射极电压跌落DVon=Ld kcur，Ld 为线路杂散电感。所以此阶段的vce与ic关系可表示为
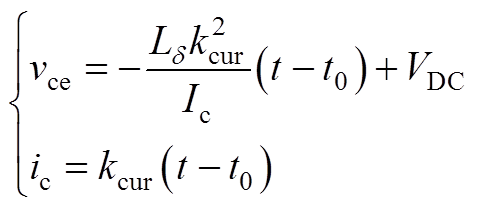（A2）
因此，此阶段的开通损耗为
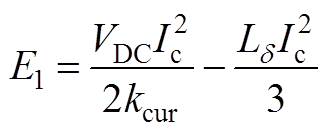（A3）
2）阶段t1～t2和阶段t2～t3：在此阶段中，IGBT集电极电流继续以kcur上升，并在t2到达电流峰值Ic+Irm[14]，再以-kcur下降至Ic[22]。由于t1～t3的持续时间很短，假设vce保持t1时刻电压不变。则vce与ic关系可表示为
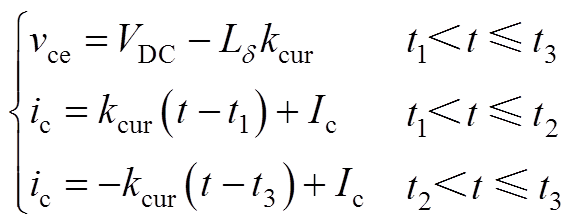（A4）
因此这两阶段的开通损耗之和表示为
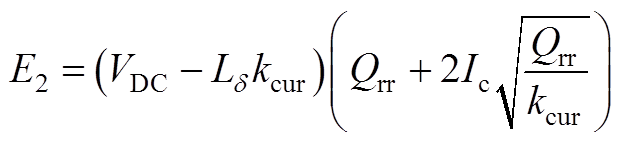（A5）
3）阶段t3～t4：此阶段中，假设集射极电压从vce(t1)下降到0，则vce与ic关系可表示为
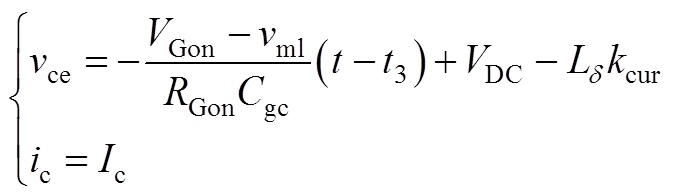（A6）
式中，VGon为开通阶段栅极驱动电压；vml为米勒平台电压；Rg为栅极驱动电阻；Cgc为栅极与集电极之间的寄生电容。米勒平台电压vml可通过式（A1）计算得到。因此此阶段的开通损耗为
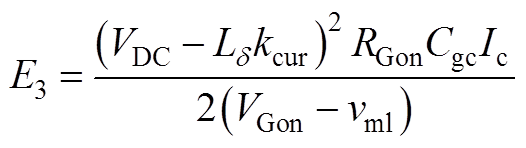（A7）
4）阶段t5～t6：此阶段中，处理过程与阶段t3～t4的处理过程相反，得到此阶段的vce与ic曲线为
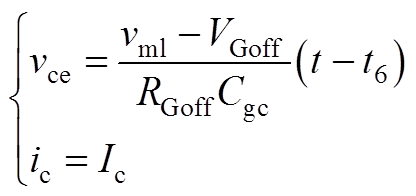（A8）
因此，此阶段损耗为
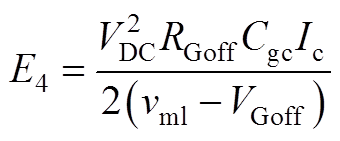（A9）
5）阶段t6～t7：在此阶段集射极上会出现一个电压尖峰。忽略电压尖峰与拖尾电流，得到此阶段的vce与ic关系为
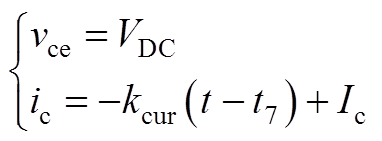（A10）
因此，此阶段损耗为
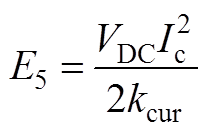（A11）
参考文献
[1] 黄海宏, 陈昭, 王海欣. 全超导托卡马克核聚变发电装置快控电源的干扰抑制离散积分滑模电流控制[J/OL]. 电工技术学报, https://doi.org/10.19595/ j.cnki.1000-6753.tces.230275.
Huang Haihong, Cheng Zhao, Wang Haixin. Dis- turbance suppression discrete integral sliding mode current control of experimental advanced super- conducting tokamak fast control power supply[J/OL]. Transactions of China Electrotechnical Society, https://doi.org/10.19595/j.cnki.1000-6753.tces.230275.
[2] Huang Haihong, Bi Nanxia, Wang Haixin. Explo- ration of the voltage control mode of second- generation EAST fast control power supply[J]. IEEE Transactions on Plasma Science, 2018, 46(5): 1684- 1688.
[3] Infineon Technologies. IGBT modules[EB/OL]. (2023- 05-11)[2023-05-11]. https://www.infineon.com/cms/ en/product/power/igbt/igbt-modules/.
[4] 曹子楷, 崔翔, 代安琪, 等. 压接型IGBT芯片参数的分散性对其并联时关断均流的影响[J/OL]. 中国电机工程学报, https://doi.org/10.13334/j.0258-8013. pcsee.223136.
Cao Zikai, Cui Xiang, Dai Anqi, et al. Influence of parameter dispersion of parallel press-pack IGBT chips on its current sharing during turn-off pro- cess[J/OL]. Proceedings of the CSEE, https://doi.org/ 10.13334/j.0258-8013.pcsee.223136.
[5] Li Helong, Zhou Wei, Wang Xiongfei, et al. Influence of paralleling dies and paralleling half-bridges on transient current distribution in multichip power modules[J]. IEEE Transactions on Power Electronics, 2018, 33(8): 6483-6487
[6] Ferreira V, Andresen M, Cardoso B, et al. Selective soft-switching for thermal balancing in IGBT-based multichip systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(4): 3982-3991.
[7] Chen Yu, Wu Qiang, Li Chengmin, et al. Thermal mitigation and optimization via multitier bond wire layout for IGBT modules considering multicellular electro-thermal effect[J]. IEEE Transactions on Power Electronics, 2022, 37(6): 7299-7314.
[8] 魏云海, 陈民铀, 赖伟, 等. 基于IGBT结温波动平滑控制的主动热管理方法综述[J]. 电工技术学报, 2022, 37(6): 1415-1430.
Wei Yunhai, Chen Minyou, Lai Wei, et al. Review on active thermal control methods based on junction temperature swing smooth control of IGBTs[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1415-1430.
[9] 丁雪妮, 陈民铀, 赖伟, 等. 多芯片并联IGBT模块老化特征参量甄选研究[J]. 电工技术学报, 2022, 37(13): 3304-3316, 3340.
Ding Xueni, Chen Minyou, Lai Wei, et al. Selection of aging characteristic parameter for multi-chips parallel IGBT module[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3304-3316, 3340.
[10] 贾英杰, 肖飞, 罗毅飞, 等. 基于场路耦合的大功率IGBT多速率电热联合仿真方法[J]. 电工技术学报, 2020, 35(9): 1952-1961.
Jia Yingjie, Xiao Fei, Luo Yifei, et al. Multi-rate electro-thermal simulation method for high power IGBT based on field-circuit coupling[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1952-1961.
[11] 张玉斌, 温英科, 阮琳. 全浸式蒸发冷却IGBT电热耦合模型研究[J]. 电工技术学报, 2022, 37(15): 3845-3856.
Zhang Yubin, Wen Yingke, Ruan Lin. Research on electrothermal coupling model of fully-immersed evaporative cooling IGBT[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3845-3856.
[12] 黄先进, 杜田倩, 王风川, 等. 基于列车运行图的CRH3牵引变流器IGBT模块寿命预测[J]. 电工技术学报, 2022, 37(增刊1): 172-180.
Huang Xianjin, Du Tianqian, Wang Fengchuan, et al. Mission profiles-based lifetime prediction for IGBT modules applied to CRH3 traction converter[J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 172-180.
[13] Shi Bochen, Zhao Zhengming, Zhu Yicheng. Piece- wise analytical transient model for power switching device commutation unit[J]. IEEE Transactions on Power Electronics, 2019, 34(6): 5720-5736.
[14] Xu Yanming, Ho C N M, Ghosh A, et al. An electrical transient model of IGBT-diode switching cell for power semiconductor loss estimation in electro- magnetic transient simulation[J]. IEEE Transactions on Power Electronics, 2020, 35(3): 2979-2989.
[15] Hao Bin, Peng Cheng, Tang Xinling, et al. Calcu- lation and analysis of switching losses in IGBT devices based on switching transient processes[J]. Journal of Power Electronics, 2022, 22(10): 1801- 1811.
[16] 唐云宇, 林燎源, 马皓. 一种改进的并联IGBT模块瞬态电热模型[J]. 电工技术学报, 2017, 32(12): 88-96.
Tang Yunyu, Lin Liaoyuan, Ma Hao. An improved transient electro-thermal model for paralleled IGBT modules[J]. Transactions of China Electrotechnical Society, 2017, 32(12): 88-96.
[17] Arya A, Chanekar A, Deshmukh P, et al. Accurate online junction temperature estimation of IGBT using inflection point based updated I-V characteristics[J]. IEEE Transactions on Power Electronics, 2021, 36(9): 9826-9836.
[18] Li Xiaoling, Jiang Huaping, Hu Borong, et al. Electrothermal limited switching frequency for parallel diodes[C]//2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 2018: 4692-4698.
[19] 李晓玲, 冉立, 曾正, 等. 并联PIN二极管的温度频率特性建模与分析[J]. 中国电机工程学报, 2018, 38(18): 5405-5414.
Li Xiaoling, Ran Li, Zeng Zheng, et al. Modeling and evaluating of temperature-frequency feature of paralleled PIN diodes[J]. Proceedings of the CSEE, 2018, 38(18): 5405-5414.
[20] Yang Jianxiong, Che Yanbo, Ran Li, et al. Evaluation of frequency and temperature dependence of power losses difference in parallel IGBTs[J]. IEEE Access, 2020, 8: 104074-104084.
[21] Li Ziyang, Hang Lijun, He Yuanbin, et al. Sampled- data modeling and stability analysis of digitally controlled Buck converter with trailing-edge and leading-edge modulations[J]. IEEE Transactions on Power Electronics, 2023, 38(1): 177-194.
[22] Hao Bin, Wu Yingzhe, Peng Cheng, et al. Modelling and solving of IGBT’s transient analysis model based on the finite state machine[J]. IET Power Electronics, 2021, 14(11): 1973-1984.
Abstract IGBT parallel connection effectively solves the problem of increasing the power supply capacity for plasma vertical displacement fast control in Tokamak devices. However, in the working process of parallel devices, due to the inconsistency of device parameters, stray parameters in the circuit, driver parameters, and heat dissipation system parameters between IGBTs, loss differences always exist between parallel IGBTs, resulting in junction temperature differences. The junction temperature difference may increase the loss difference between IGBTs, potentially leading to overheating and failure. However, the existing research mainly focuses on the loss model of a single device or the optimal operating frequency range of parallel IGBTs. The optimal operating duty cycle range of parallel IGBTs is rarely discussed.
It is found that when the IGBT device works in the range of a large current positive temperature coefficient, the on-state loss difference DEc and the switching loss difference DEsw caused by the junction temperature difference DTj show different temperature characteristics. Therefore, there is a zero temperature-duty cycle D0, where the duty cycle of parallel IGBTs operates on both sides of the zero temperature-duty cycle. The total loss difference shows two different temperature characteristics, indicating distinct junction temperature mismatch trends. In this paper, the duty cycle range beneficial to IGBT parallel operation is called the optimal duty cycle range.
Since the duty cycle is closely related to the operating current of the IGBTs, reasonably improving the loss model of the parallel IGBTs is a challenge to analyze the duty cycle and junction temperature difference. Therefore, taking the BUCK transformation as an example, this paper makes a linear assumption on the switching behavior of parallel IGBTs to simplify the loss model and proposes a zero temperature-duty cycle analysis model. Accordingly, the influence of circuit design parameters, IGBT device parameters, and junction temperature difference on the zero temperature-duty ratio is analyzed. Finally, the existence of a zero temperature-duty ratio is verified by building a double-pulse experimental platform of parallel IGBTs. The following conclusions are drawn:
(1) If the duty cycle D is less than the zero temperature-duty cycle D0, the switching loss is less than the on-state loss. The on-state loss is dominant, and the temperature is negative feedback, which benefits the IGBT parallel connection.
(2) If the duty cycle D is greater than the zero temperature-duty cycle D0, the switching loss is greater than the on-state loss. The switching loss is dominant, and the temperature is positively fed back, which is not conducive to the IGBT parallel connection.
(3) The larger the junction temperature difference DTj between the two parallel IGBTs, the smaller the zero temperature-duty cycle D0 is, which is conducive to the parallel operation of IGBTs.
keywords：Parallel IGBTs, switch loss, conduction loss, temperature characteristic, zero temperature-duty cycle
DOI: 10.19595/j.cnki.1000-6753.tces.230705
中图分类号：TM91
国家自然科学基金区域创新发展联合基金资助项目（U22A20225）。
收稿日期 2023-05-19
改稿日期 2023-07-12
黄海宏 男，1973年生，教授，博士生导师，研究方向为新型大功率变流技术与电力电子技术等。E-mail: hhaihong741@126.com
彭 岚 男，1995年生，博士研究生，研究方向为新型电能传输与变换技术等。E-mail: pl_lan@qq.com（通信作者）
（编辑 陈 诚）