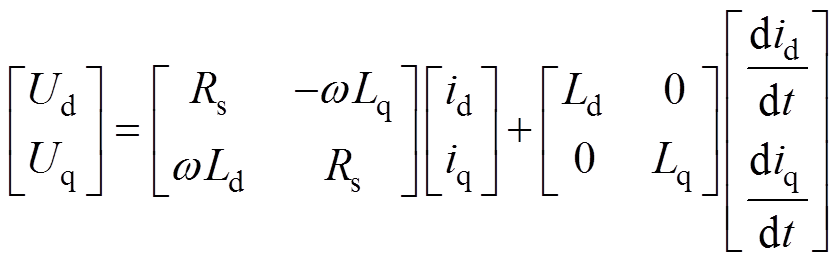（1）
摘要 同步磁阻电机在实现无速度传感器控制时出现交叉耦合效应，导致dq轴电感随着电流发生非线性变化，转速环使用传统PI控制器已无法满足系统较强的抗扰性能和较高的转子位置估计精度。为了改善此问题，该文提出一阶线性自抗扰控制器的同步磁阻电机无速度传感器控制策略，利用其机械运动状态方程，将同步磁阻电机的交叉耦合效应及负载扰动变化视为扰动。首先通过扩张状态观测器对负载扰动快速观测并进行前馈补偿，以此来提高系统抗扰性；其次利用静止实验法，得到dq轴磁链与电流的非线性函数模型，将该模型运用至磁链观测器中，以减小交叉耦合效应，提高转子位置估计精度；最后在1.5 kW的同步磁阻电机对拖加载实验平台上进行实验，验证了该控制方案的有效性。
关键词：同步磁阻电机 磁链观测器 一阶线性自抗扰控制器 交叉耦合 无速度传感器控制
在工业领域和日常生活中，电机作为一种可以将电能转换为机械能的装置，扮演着十分重要的角色。随着稀土材料的价格不断上涨，同步磁阻电机（Synchronous Reluctance Motor, SynRM）由于没有永磁体，制作材料成本低，具有转动惯量小、响应快、运行效率高及在进行电机控制时动态响应快[1-3]等优势。但同时SynRM也存在一定劣势，其内部磁场全部由定子电流激励产生，功率因素较低[4]。文献[5-7]利用模型参考自适应系统（Multiple Adaptive Regression Splines, MARS）观测器方法实现SynRM驱动控制，解决了电压畸变、调速响应慢、转子位置估计及指令电压精度低等问题。文献[8-9]利用磁链观测器对同步磁阻电机实现无速度控制，将电压和电流模型进行自适应组合，使其能够覆盖较宽的速度运行区域，解决了宽速域运行和电机振荡的问题。文献[10-12]采用高频信号注入法实现同步电机低速域的无速度传感器控制，有效解决了转矩波动引起的转速波动问题，通过该方法的进一步研究解决了高频信号注入引起的转速脉动问题。文献[13-14]为实现同步磁阻电机无速度控制全速域运行，分别将适用于低速域、高速域的控制方法相结合，采用加权函数作为两者之间的切换保障，有效地解决了全速域控制问题。文献[15]将卡尔曼滤波器应用于同步磁阻电机的无速度控制策略，同时利用人工智能技术获得同步磁阻电机的磁链模型，不仅能够实现无速度控制，同时解决了同步磁阻电机特有的磁路饱和及交叉耦合效应所带来的电机参数失配问题。
在实现电机无速度控制后，电机实际运行过程中出现负载转矩变化，或受到其他未知不可控因素导致电机控制系统不再稳定。为解决控制系统中抗扰性弱、鲁棒性低的缺点，将自抗扰控制技术应用于同步磁阻电机无速度传感器控制策略中。文献[16]分析现有自抗扰控制器（Active Disturbance Rejection Control, ADRC）存在动态响应慢、精度差、参数调优困难等问题，提出一种改进的自适应ADRC方法，通过实验结果证明其优化了所存在的问题。文献[17-19]分析同步电机控制中传统的电流环PI控制器、转速环PI控制器的稳定性和抗干扰能力，针对快速性、超调量和稳定性等指标进行优化，将ADRC技术应用其中，与传统PI控制器进行对比，通过仿真与实验结果验证其方法具有更优的控制效果。文献[20-21]将遗传算法和人工智能技术应用在自抗扰电机控制系统中，以此将深度强化学习（Deep Reinforcement Learning, DRL）方法参与自抗扰控制器参数自动调优，有效降低了计算量，提高了参数的灵敏度。文献[22-23]集合线性自抗扰控制和非线性自抗扰控制的优点，不仅能够精确估计和补偿扰动，同时降低了非线性自抗扰控制器参数整定复杂度，电机控制系统抗扰性高、鲁棒性强。文献[24]提出一种改进转速环线性自抗扰控制策略，利用级联的扩张状态观测器估计系统所受的集总扰动，减小传统线性扩张状态观测器对于斜坡型扰动的估计误差。文献[25]将消除扰动作为实现系统高性能控制的重要因素，针对永磁同步电机转速控制，对扰动观测器和自抗扰控制进行研究。文献[26]设计了不依赖被控对象精确模型的自抗扰电压控制器，可有效观测并补偿系统中存在的非线性及其他扰动因素。
本文主要研究同步磁阻电机无速度传感器控制，采用磁链观测器法估计转子位置。首先为提高转子估计精度，磁链观测器中需要精确的标准参考模型。由于同步磁阻电机存在磁路饱和及交叉耦合现象，采用静止实验法得出dq轴磁链与电流的非线性函数关系，磁链通过前向欧拉法计算得到，最终获得实际工况下电机电感与电流的非线性模型。其次为弥补磁链观测器抗扰性弱的缺点，加入自抗扰控制技术。根据同步磁阻电机机械运动状态方程，将负载扰动视为外部扰动，并对其进行快速观测与补偿，设计适用于同步磁阻电机的一阶线性自抗扰控制器，增强系统受扰时快速响应的能力，并消除超调。最后根据实验平台对自抗扰技术下的同步磁阻电机无速度传感器控制进行验证。
为方便、准确地分析同步磁阻电机数学模型，需要对其在不同坐标系下建立数学模型。最常用的两种方式为Park变换和Clarke变换。将同步磁阻电机数学模型经过Clarke和Park变换得到两相旋转坐标系下的数学模型，其电压表达式为
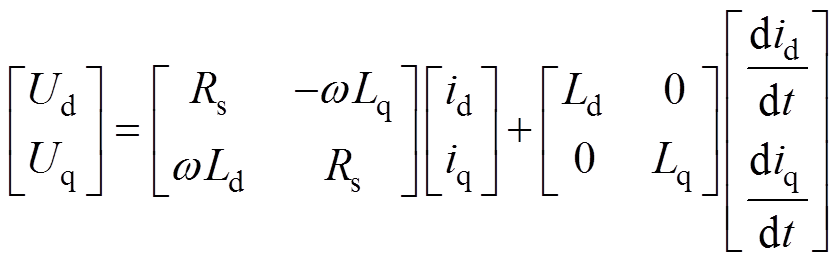（1）
式中，Ud、Uq为两相旋转轴下交直轴电压；w 为转子的角速度；Ld、Lq为交直轴下定子电感；id、iq为两相旋转轴下交直轴电流；Rs为定子电阻。
同步磁阻电机定子磁链方程表达式为
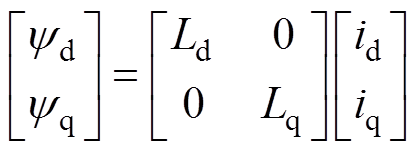（2）
式中，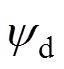
、
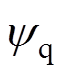为两相旋转轴下交直轴定子磁链。同步磁阻电机旋转坐标系下的电磁转矩方程表达式为
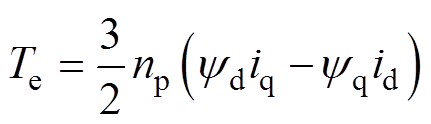（3）
式中，Te为电机电磁转矩；np为电机极对数。
将式（2）代入式（3），改写得到电磁转矩表达式为
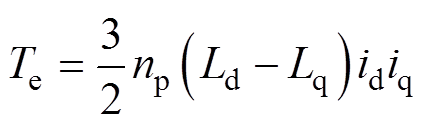（4）
1.1节在两相旋转坐标系下已经建立同步磁阻电机的数学模型，通过坐标变换，得出同步磁阻电机在两相静止坐标系中的电压表达式为
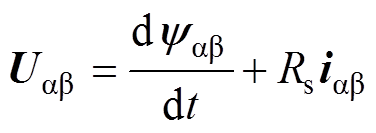（5）
式中，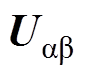
、
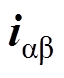分别为电机在
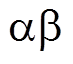轴下的电压分量和电流分量；
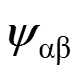为电机在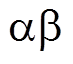轴方向的磁链。随后根据式（5）推导得
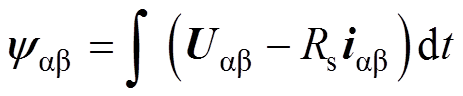（6）
有定子磁链在dq轴坐标系下的分量表达式如式（2）所示，将dq轴坐标系中的磁链表达式经过反Park变换得到两相静止轴坐标系中的磁链表达式为
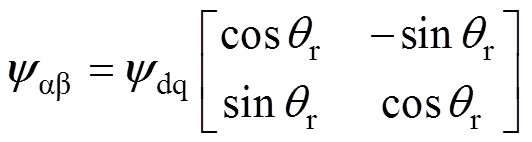（7）
式中，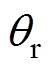
为电机的转子位置角，即dq旋转坐标轴与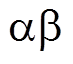坐标轴之间的夹角。
此时将式（6）代入至式（7）中，得到开环磁链观测器下的电机转子位置为
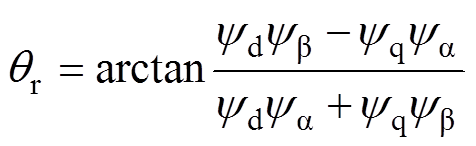（8）
将式（6）称作电压模型，式（7）称作电流模型。开环磁链观测的原理是通过电压模型得到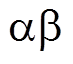轴下的电机磁链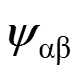，通过电流模型得到dq轴下的电机磁链
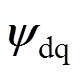，最后由式（8）得到转子位置。实际是通过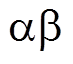坐标系中的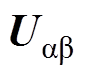、、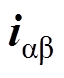定子电阻Rs、dq轴电感Ld、Lq参数间接得到转子磁链，最终得到转子的位置。若直接由式（6）计算得到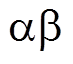轴坐标系下的磁链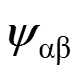，此计算方法存在积分结构，会有初始误差不断累积的过程，该初始误差包括初始相位偏差、直流偏置误差。为此，引入闭环磁链观测器，在开环的基础上，将电压模型作为可调模型，电流模型作为标准模型，两者进行对比，此时将得到的磁链偏差用一个校正环节来实时对电压模型进行调整，该方法原理框图如图1所示。
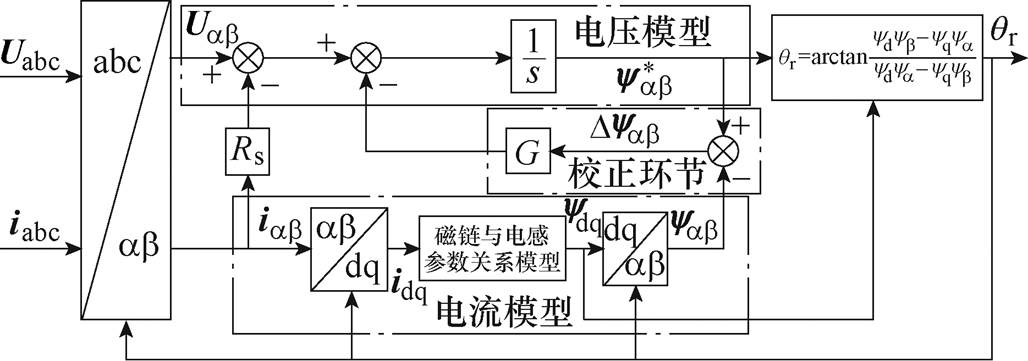
图1 闭环磁链观测器转子位置估算原理框图
Fig.1 Rotor position estimation block diagram of closed-loop flux observer
如图1所示，电流模型经过坐标变换得到实际磁链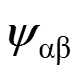，电压模型通过电压方程得到估计磁链
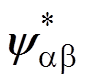，两者差值通过矫正环节G进行补偿修正，如此便可以将积分的直流偏置误差不断收敛。若校正环节为一个PI控制器，增益为G，则可得磁链估计表达式为
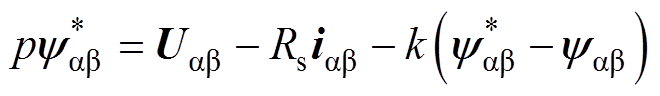（9）
式中，p为微分算子；k为校正环节的系数。
推导得磁链估计表达式的传递函数为
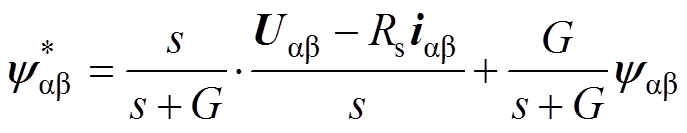（10）
传递函数由两部分构成，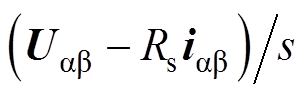
是电压方程积分经过高通滤波器所得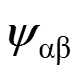，是电流模型中实际磁链经过低通滤波器所得。当同步磁阻电机运行在低速区域时，转子位置的估计值主要由电流模型提供，由此避免了低速时反电动势小、电压模型估算的磁链准确度不高的问题。同时在电机运行在高速阶段，电压模型起主要作用，根据电流模型输出的实际磁链作为反馈，减小电压模型估算磁链存在的弊端，而且减小了电机高速运行时磁链由于磁心损耗而出现误差的影响。此时，将式（10）代入式（8）中得到转子位置估计的信息。在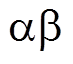轴坐标系中，可以准确获得定子磁链，其定子磁链矢量幅值及相位的表达式为
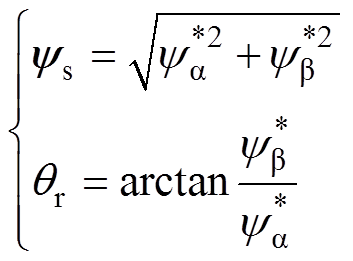（11）
电磁转矩在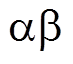轴坐标系下的表达式为
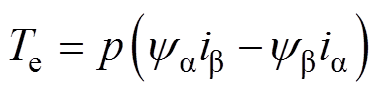（12）
图2为闭环磁链观测器转子位置和速度估计原理框图，只给出电机转子位置信息的估算。通过电压模型和电流模型得到的电机磁链对转子的位置信息进行了计算，然后对其进行微分，得到电机的估计转速。但是在实际应用中，采取直接求导的方法会出现高频噪声和干扰。因此，本文为减小高频噪声和干扰，采用在转子位置后串联加入锁相环（Phase- Locked Loop, PLL）结构，来估算电机的转速。
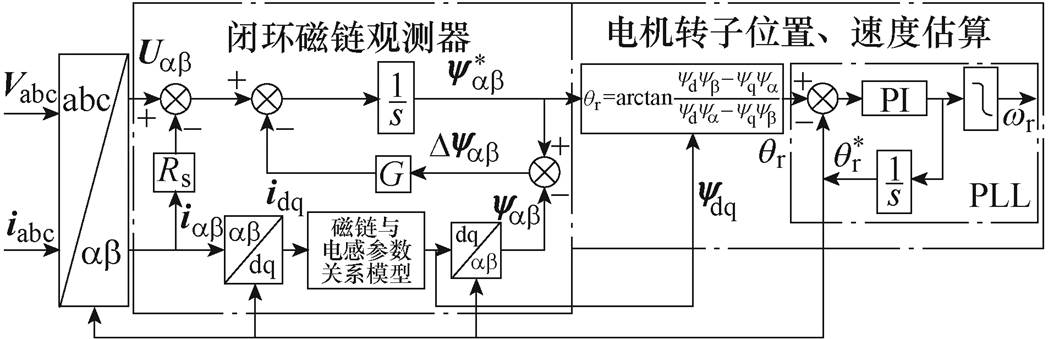
图2 闭环磁链观测器转子位置和速度估算原理框图
Fig.2 Rotor position and velocity estimation block diagram of a closed loop flux observer
图3为锁相环结构框图，带有电机转子位置信息的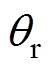经过PLL，最终得到电机转子位置
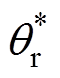，此时再通过低通滤波即可得到电机转速
。
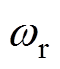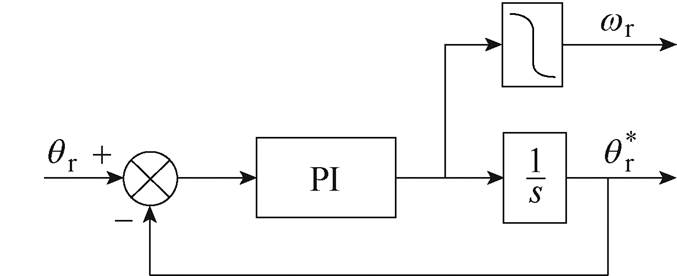
图3 锁相环结构框图
Fig.3 Block diagram of phase locked loop structure
由图3可得转子初始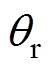位置与最终位置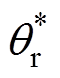的传递函数表达式为
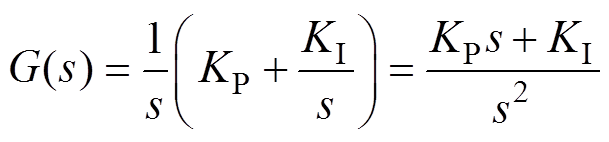（13）
式中，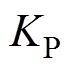
为PI控制器的比例系数;
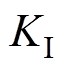为PI控制器的积分系数。
所得误差的传递函数表达式为
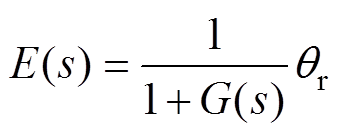（14）
根据终值定理得静态误差的表达式为
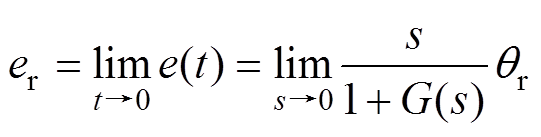（15）
在电机运行至转速达到稳定时，转子初始位置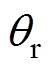可作为一个斜坡函数zt，该函数的拉普拉斯变化表达式为
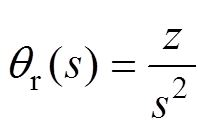（16）
式中，z为斜坡函数变量系数。
最终得静态误差的表达式为
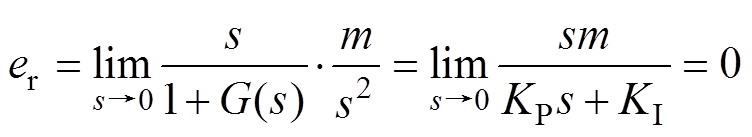（17）
图4为本文实现同步磁阻电机无速度控制原理框图。首先，采用闭环磁链观测器解决了开环磁链观测器所存在的初始误差累积问题。引入电压模型作为一个可调模型，电流模型作为一个标准模型，与之进行对比，并得到一个磁链偏差，用一个校正环节来实时对电压模型进行调整。图4中转矩给定由转速环中的PI控制器所得，磁链由外部给定。电机运行中实时磁链与转矩由磁链观测器估计所得。然后，根据磁链计算得到转子位置信息，考虑到在获得电机转速的方法上存在高频噪声，故在转子位置信息后方加入锁相环来解决该问题。最后，通过滤波和微分的方式得到电机的转速估计值。但同步磁阻电机运行过程中存在磁路饱和及交叉耦合现象，导致闭环磁链观测器中电流模型出现偏差，使得转子位置信息估计出现误差。
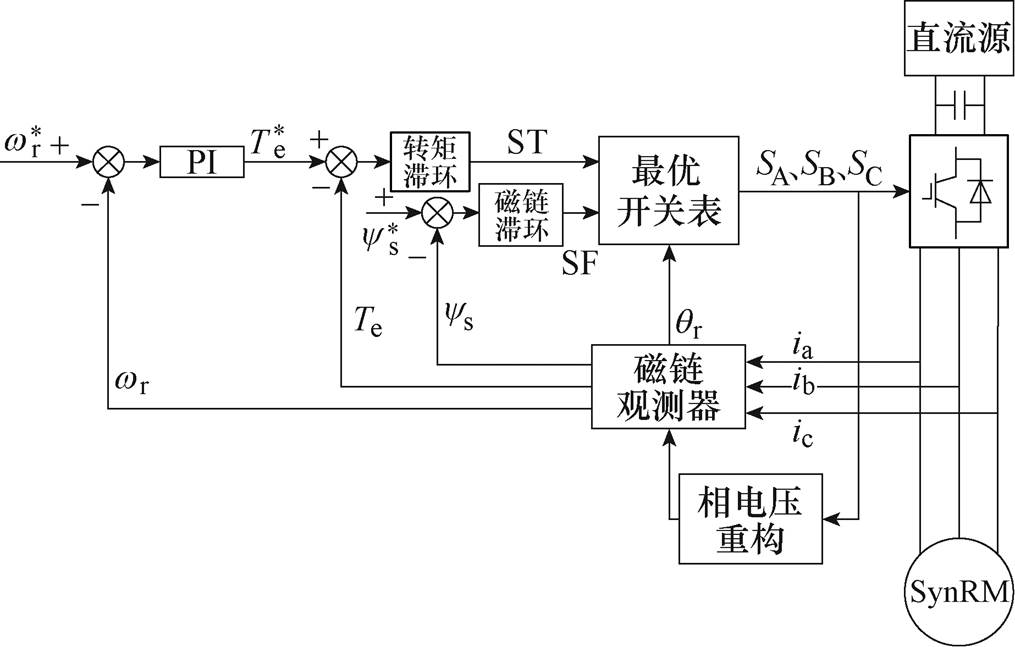
图4 同步磁阻电机的磁链观测器法控制原理框图
Fig.4 Principle control block diagram of flux observer method for synchronous reluctance motor
同步磁阻电机在不同的工作条件下，磁路饱和及交叉耦合的程度不同，通常情况下电机存在额定工作、过载工作等情况，都会让电机的一些参数与实际不符。不仅如此，dq轴电流的增大也同样会加大电机的磁路饱和效应，使得电机轭部磁场发生畸变，最终出现交叉耦合和互感的现象。由闭环磁链观测器的电流模型可知，式（7）中会使用dq轴旋转坐标系下磁链分量式（2），由此计算出dq轴下的电感参数，来作为标准模型对之后的转子位置和速度估算提供支撑。在实际工作情况中，由于同步磁阻电机的磁路饱和及交叉耦合效应，dq轴的实际电感值发生变化，使得dq轴磁链与dq轴电流形成非线性函数关系。故在考虑交叉耦合效应后，式（2）应改写为
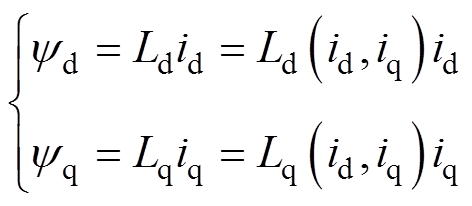（18）
为了使磁链观测器中的电流模型能够精确得到磁链与电流的关系，以此提高转子位置的估计精度，需要对同步磁阻电机进行参数辨识。以精确获得无速度控制方法中所必需的电机参数。本文采用静止实验法，在所测电机静止状态下分别对转子d轴和q轴上施加脉冲电压，通过前向欧拉法来计算所得到的磁链。同时将电流和磁链的样本利用线性最小二乘法来估计磁模型的参数。
同步磁阻电机转子在dq轴旋转坐标系下的磁链与电压表达式为
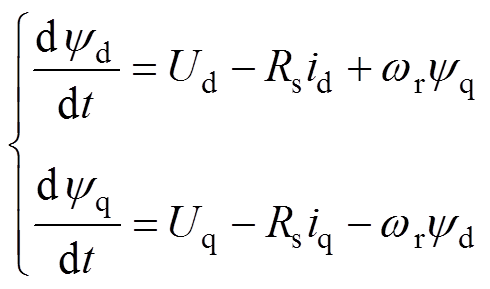（19）
式中，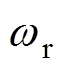
为转子的电角速度。
id、iq与dq轴磁链的表达式为
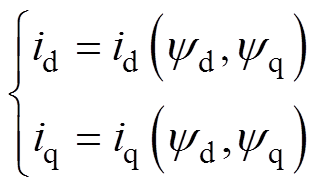（20）
为有利于建立其数学模型，通常将同步磁阻电机的dq轴电流表示为dq轴磁链分量的非线性函数。不仅如此，非线性电感变化不应产生损耗或耗散电能，利用该电流-磁链模型计算互感时，结果应保持不变，故dq轴电流与磁链之间还应满足
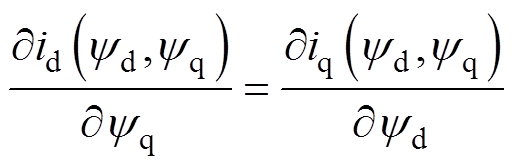（21）
根据以上模型计算电机的增量电感或视在电感，最终得到电机稳态下完整的参数特性。利用合适的dq轴电流-磁链关系模型，以此来替代传统查表（Look Up Table, LUT）法，不仅简化了同步磁阻电机辨识参数的流程，而且减少了所需辨识的参数数量。将所测试的数据进行拟合来获取参数，缩短了调试时间并减小了数据处理的工作量。下面以d轴、q轴为例分别展示所采用的同步磁阻电机电磁数学模型，该过程中所出现的交叉耦合效应充分反映同步磁阻电机参数非线性特性。
（1）自感模型。当同步磁阻电机转子d轴电流为0时，q轴磁链与电流特性如图5所示。
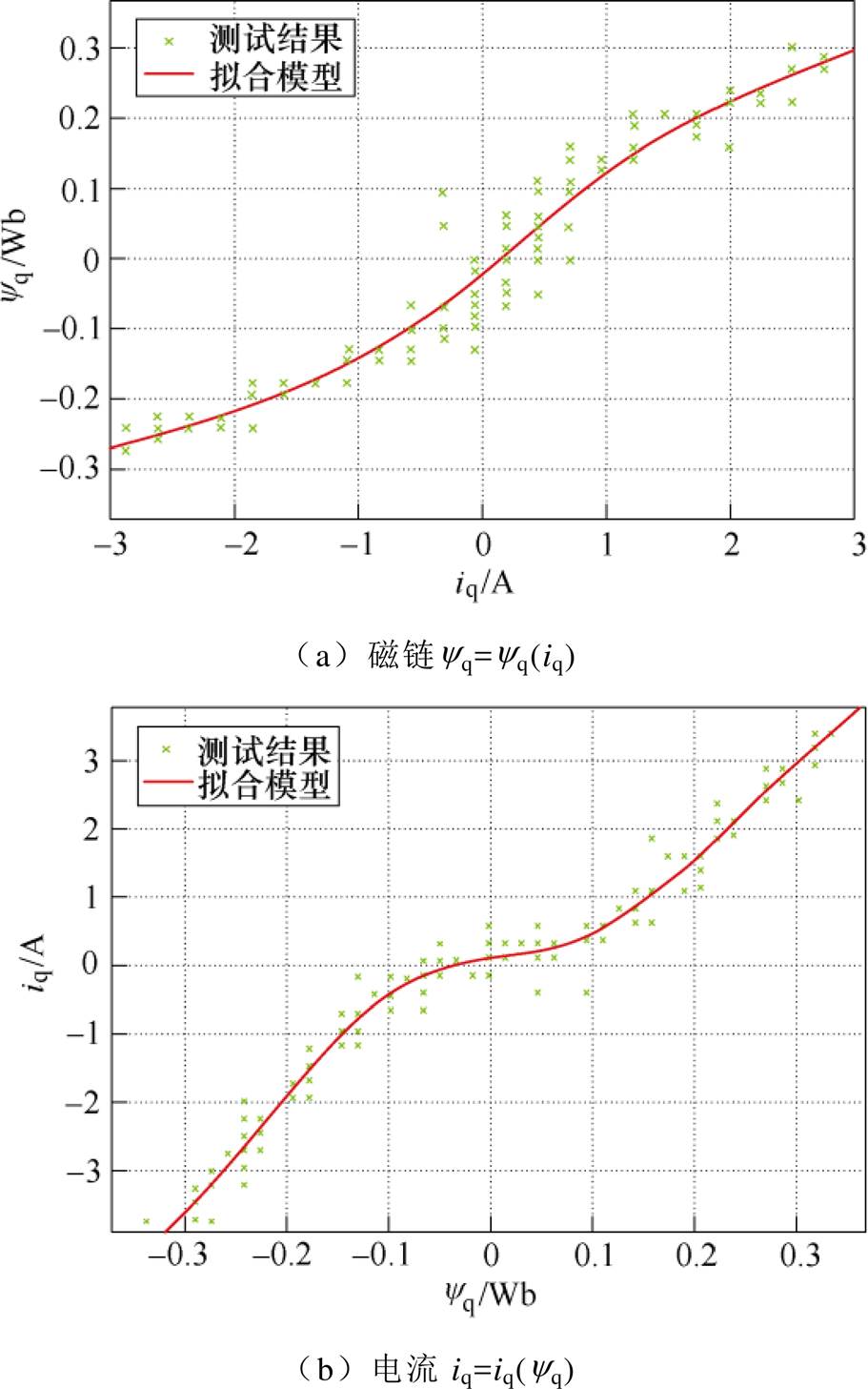
图5 d轴电流为0时，q轴磁链-电流测试
Fig.5 id=0, q axis flux-current test diagram
为拟合图5中电流与磁链的关系，定义dq轴电流-磁链模型为
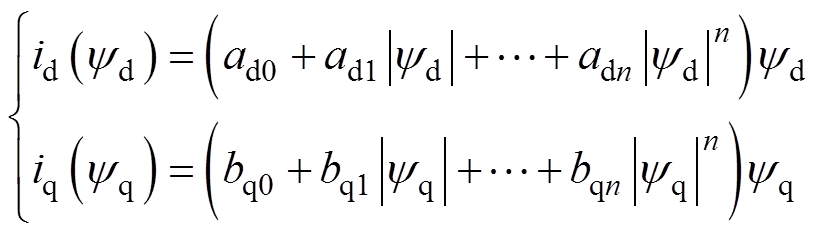（22）
式中，ad0,…, adn、bq0,…, bqn分别为同步磁阻电机d、q轴电流与磁链模型的各项系数；n为电流与磁链模型中的最高次项指数。
本文采用线性最小二乘（Linear Least Squares, LLS）法拟合上述模型各项系数，当最高次项指数足够大时，式（22）可很好地拟合测试数据。通常n取5～7满足其拟合需求。本文最高次项指数为7。若最高次指数过低，导致所得的拟合模型不够准确，无法精确体现dq轴磁链与dq轴电流的关系；若最高次项指数过高，导致计算量增大，同时在dq轴电流较小时，模型不够精确。
（2）考虑交叉耦合效应的电流与磁链模型考虑交叉耦合效应下，具体测试过程的控制框图如图6所示，其中采样周期与PWM周期均为T。在数据测试过程中，转子轴全程不外接负载。
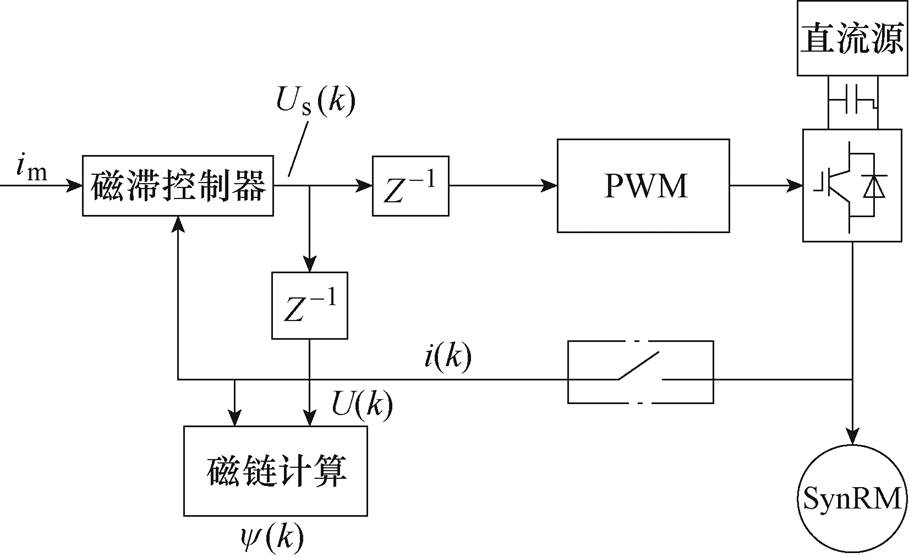
图6 交叉耦合效应下参数辨识控制框图
Fig.6 Parameter identification control block diagram under cross-coupling effect
图6中，利用一个磁滞控制器来控制电压，对于d轴的测试，控制方式可以表示为
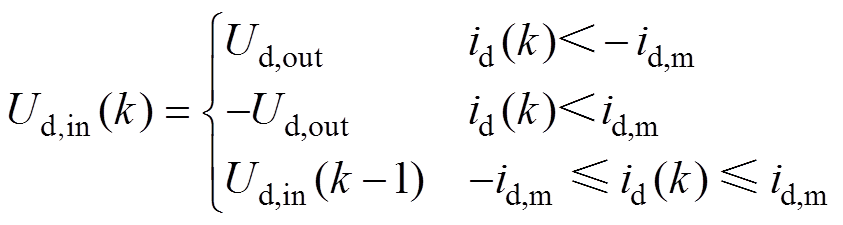（23）
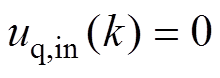（24）
式中，Ud,in为d轴测试电压的给定值；Ud,out为d轴测试电压的幅值；id,m为电流的限幅值；Uq,in为q轴测试电压的给定值，其决定了参数测试的范围。同样地，对于q轴的测试，控制方式类似。
最终根据测试所得数据采用LLS得到被测电机的电流磁链模型，并得出磁路饱和效应后，转子角度偏差三维图。dq轴电流与磁链关系拟合模型如图7所示，dq轴的电流随着dq轴的磁链变化而变化，电流与磁链之间并不是线性关系，其变化率并非恒定。根据上述电流模型可知，由于同步磁阻电机存在交叉耦合效应，导致磁链观测器中电流模型并非标准模型，导致转子位置估计误差增大。在交叉耦合效应影响下，转子位置估计误差最大达到约为 44°，若忽略同步磁阻电机的交叉耦合效应则会极大影响转子位置估计的准确度。
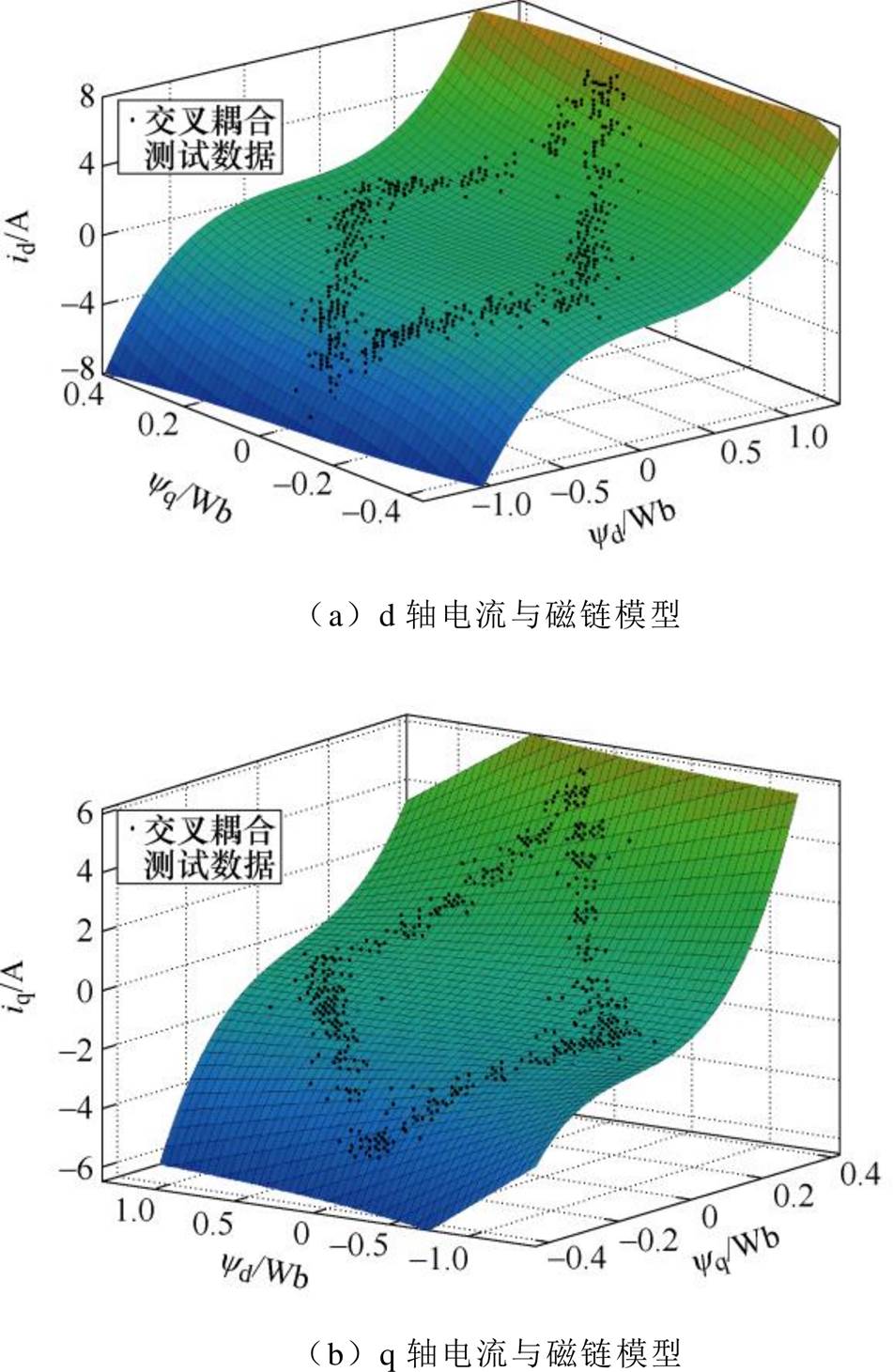
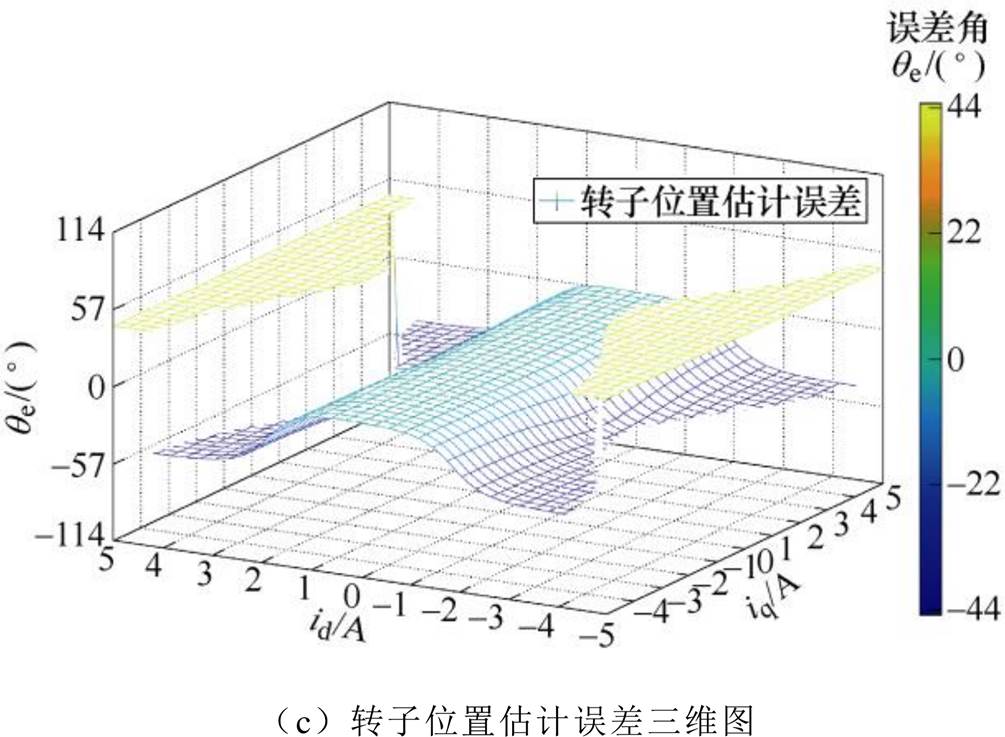
图7 dq轴电流与磁链关系拟合模型
Fig.7 Fitted model of dq axis current versus flux
同步磁阻电机控制系统是一个可变量多、强耦合、存在非线性的复杂系统，所以在实际调速控制过程中，电机受到的扰动来源因素有很多，如电机的参数变化、外部扰动、摩擦系数和转动惯量等。此时，若想对同步磁阻电机无速度传感器控制实现高性能调速，采用传统PI控制器很难使调速系统具有较强的抗扰性能。然而，自抗扰技术可以对系统受到的未知扰动实时进行观测和补偿，并最终对扰动实现抑制，以此来提高调速系统的抗扰能力。
自抗扰控制器实际上是基于传统PID控制器而做出的一个改进策略。ADRC保留了比例积分微分控制的特性，在调速控制中，并不需要精确的数学模型表达式。ADRC具有对所有不确定性估计并补偿的特定优势。该优势主要是对扰动及时准确地估计和补偿。ADRC结构原理如图8所示。其主要由跟踪微分器（Tracking Differentiator, TD）、扩张状态观测器（Extend State Observer, ESO）、非线性状态误差反馈（Nonlinear State Error Feedback, NLSEF）控制律构成。
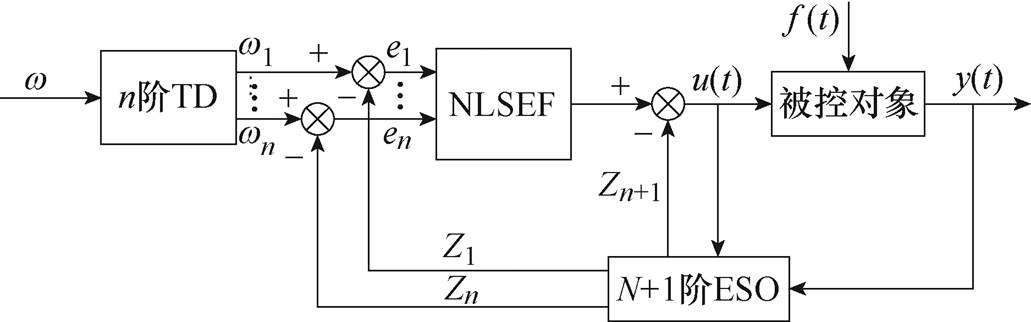
图8 自抗扰控制器结构原理
Fig.8 Active disturbance rejection controller structure schematic diagram
图8中，TD用来快速地跟踪参考输入信号，根据目标状态量和系统的目标要求得出输入信号的跟踪值和其微分值，完成过渡过程，使得系统的给定输入值不发生大幅变化，可以有效地解决控制系统为满足快速响应而产生的超调问题；ADRC的核心就是ESO主动观测集合扰动，其根据实时观测到的控制系统输入状态变量和输出状态变量构建模型，不仅实现了对当前输出量的状态观测，还得到了输出量不同阶数的状态变量，实现了控制系统中遇到扰动时对扰动量进行观测的功能；NLSEF将之前TD所得变量的各阶导数和ESO得到的状态变量作差，得到误差信号，通过非线性函数进行组合，与ESO观测到的集合扰动一起作为被控对象的控制变量。自抗扰技术适用于接收到未知扰动信号的模糊对象，故将利用以下的微分方程来进行表示。
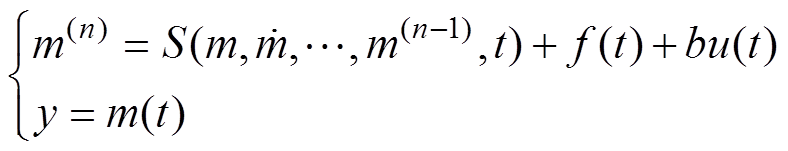（25）
式中，S(m,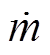
,…,m(n-1), t)为未知函数；f(t)为系统受到的未知扰动；y为系统的输出；u(t)为系统的控制变量；b为扰动补偿系数。
对于同步磁阻电机控制策略转速环上采用传统PID控制器会出现转速超调的问题，在保证电机无速度直接转矩调速控制下，转矩滞环、磁链滞环保持不变的情况下，对转速环中的PID控制器自抗扰控制器进行替换改进。本文针对同步磁阻电机设计一阶自抗扰控制器并应用于转速环中。同步磁阻电机的机械运动方程为
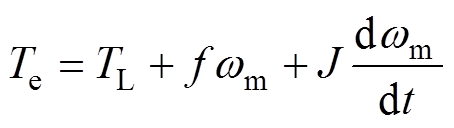（26）
式中，TL为电机的负载转矩；f为电机的摩擦系数；J为电机转子的转动惯量；Te为电机的电磁转矩； wm为电机的机械角速度。
根据同步磁阻电机的机械运动方程，可将转速环的运动状态方程表示为
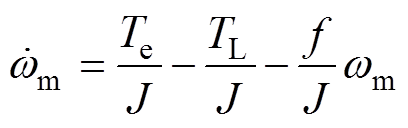（27）
根据式（27）可以得到，在电机控制系统中，负载转矩TL、转动惯量J、电机的摩擦系数f三者影响着电机控制系统的稳定性，本文将该三种可能出现变化的量视为总扰动变化量，用E(t)表示，并将电机控制过程中的转动惯量J视为内部扰动，表示为E1(t)。将电机摩擦系数f、电机负载转矩TL视为外部扰动，表示为E2(t)。则总扰动E(t)可表示为
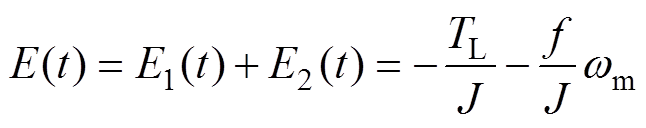（28）
故同步磁阻电机控制系统的速度环运动状态方程可表示为
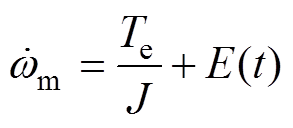（29）
本文主要将电机运行过程中，负载发生变化视为主要扰动来源，并对其进行观测和补偿。对同步磁阻电机控制系统来说，同步磁阻电机运行过程中，因负载发生变化，转速出现上升或跌落的情况，设计适合其系统的自抗扰控制器，避免转速发生大幅变化，并能快速恢复稳态，缩短系统的响应时间。
同步磁阻电机控制系统转速环的一阶自抗扰控制器原理结构如图9所示。
其中，一阶跟踪微分器（Tracking Differentiator, TD）为
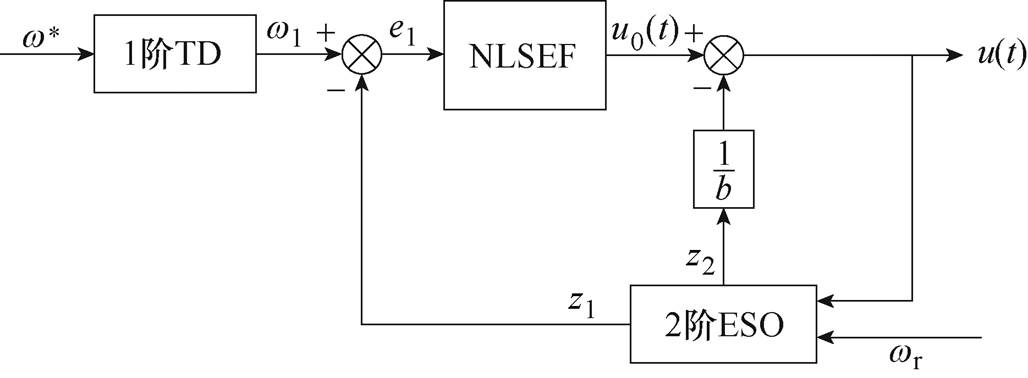
图9 一阶线性自抗扰控制器原理结构
Fig.9 First order linear active disturbance rejection controller schematic structure
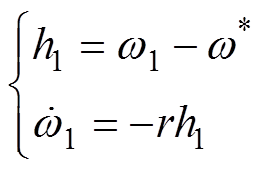（30）
二阶扩张状态观测器为
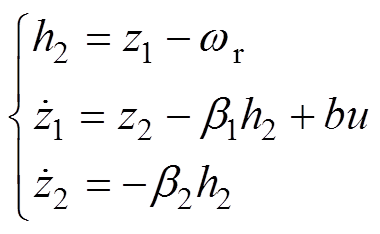（31）
非线性状态误差反馈控制律为
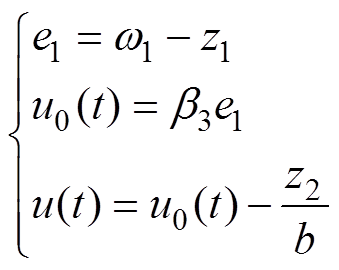（32）
式中，w1为一阶跟踪微分器输出的跟踪值；w*为电机给定转速；r为影响跟踪信号与给定信号匹配度的系数；u为系统扰动量；e1为跟踪微分器输出的跟踪信号与状态变量估计值的差值；u0(t)为系统控制量；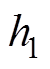
为转速的跟踪值和给定值的误差；
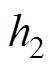为转速的观测值与实际值的误差；wr为电机的实际电角速度值；b1、b2分别为二阶扩张状态观测器的一阶、二阶增益；z1为对电机实际转速值的观测值；z2为同步磁阻电机控制过程中对总扰动的估计值；b3为非线性状态误差反馈控制律的增益。
此时，该ADRC中需要整定的参数有r、b1、b2、b3共四个。首先根据式（30）可知，在跟踪微分器中，r值的大小影响着跟踪信号与给定信号之间的匹配度。r值越大，跟踪信号越接近于给定信号，但r值也并不能盲目增大，否则会出现超调现象，故需要进行多次调参来选择最合适的r值。在式（31）中，b1、b2在ESO中起到相辅相成的作用，具体体现在对于速度的收敛性上。b2的大小决定着控制系统对抗扰性能的强弱，它直接影响着ESO对扰动的估计能力，随着b2的增大，控制系统的抗负载能力也随之增强，若电机控制系统所受到的负载发生突变，那么恢复稳态的时间就会越短。但也会随之带来控制系统振荡明显的问题，此时b1作为抑制振荡的作用就体现了出来；反之，若b1值偏大，则会使得控制系统出现发散的问题，此时则需要b2来进行抑制配合。b3与r的整定过程比较相似，在合理的范围之内，取值越大系统的响应性越好。
图10为本文提出的基于一阶线性自抗扰控制器的同步磁阻电机无速度传感器控制框图。
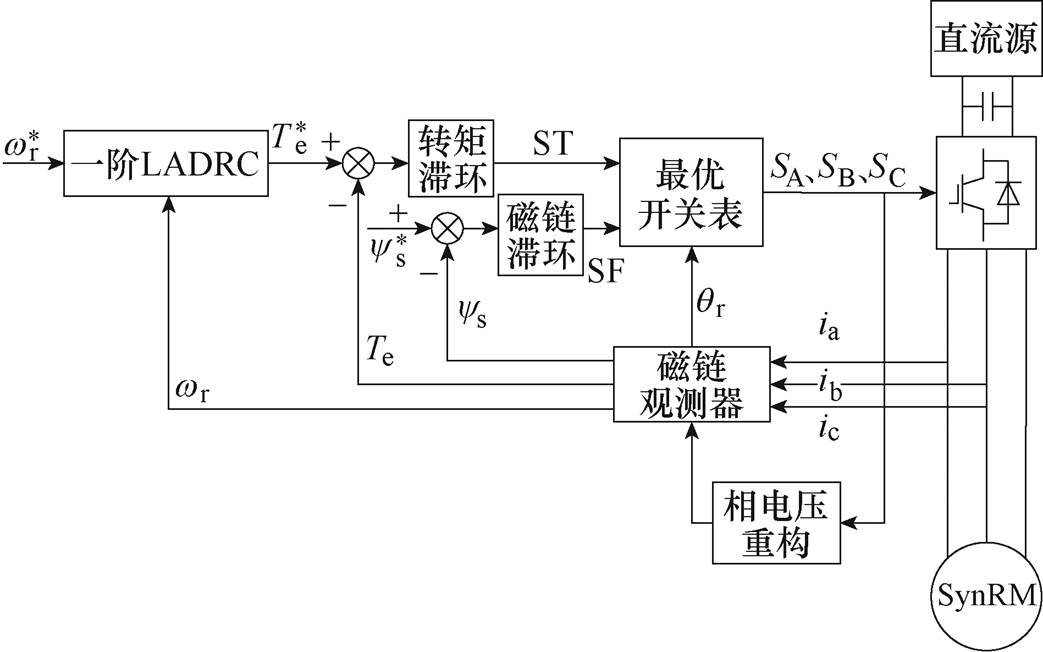
图10 基于一阶线性自抗扰控制器的同步磁阻电机无速度传感器控制框图
Fig.10 Speed sensorless control block diagram of synchronous reluctance motor based on first order linear ADRC controller
本文所采用的磁链观测器将估计转速与给定转速两者作为自抗扰控制器的输入进行计算，根据电机机械运动状态方程对同步磁阻电机运行时所受负载扰动进行观测并补偿，使电机负载转矩突变时，转速能够快速恢复稳定，并消除超调。磁链观测器将观测所得的转矩与磁链通过转矩滞环控制器和磁链滞环控制器确定转矩与磁链是否需要变化。根据转矩与磁链的变化量以及所需的基本电压空间矢量，得到三相逆变器的开关状态，最终完成基于自抗扰技术的同步磁阻电机无速度传感器控制。
为验证本文所提方案在实际电机控制中的可行性与有效性，在同步磁阻电机对拖实验平台上对所提研究内容进行实验对比分析，其中包括未考虑同步磁阻电机交叉耦合效应的无速度传感器控制策略、考虑交叉耦合效应的无速度传感器控制策略和基于一阶线性自抗扰控制器的同步磁阻电机无速度传感器控制这三种控制策略。
首先，为了验证考虑交叉耦合效应下的同步磁阻无速度控制策略可以提高电机的转速、转子位置估计精度，从电机运行时的稳态性能、动态性能两方面进行了对比实验。其次，验证在同步磁阻电机无速度控制中，加入自抗扰技术可以有效消除电机起动时存在的超调问题以及提高电机控制系统的抗扰性能，在传统PI控制器与ADRC两种策略下，对电机运行时的动态响应时间、超调量、抗扰性能进行对比实验。最后，通过实验证明在考虑交叉耦合效应后的同步磁阻电机无速度控制可以有效提高转子位置估计精度，加入自抗扰技术之后电机调速系统具有更快的动态响应时间和更强的抗扰性能。
本课题电机驱动系统实验平台由Plexim公司的半实物平台RT Box系统、上位机、两电平变频系统、被测实验电机SynRM、加载电机系统构成，如图11所示。两电平变频系统由驱动主电路和信号调理电路组成。驱动主电路主要由三相不控整流电路、两电平三相桥式逆变电路；调理电路主要由驱动电路、三相电压、电流调理电路、过电压过电流保护电路等构成。上位机通过PLECS软件对RT Box指令控制进行PWM发波，从而控制两电平变频器驱动被测电机。被测电机为瑞拉腾的同步磁阻电机，加载系统由博士力士乐公司的伺服电机、伺服驱动器HCS01和调试软件IndraWorks Ds构成。电机实际速度与实际位置相关信息由光电编码器解码电路获得，采用串行外设接口（Serial Peripheral Interface, SPI）的通信方式传输至RT Box为之后的无速度控制提供参照对比。表1为电机实验参数。
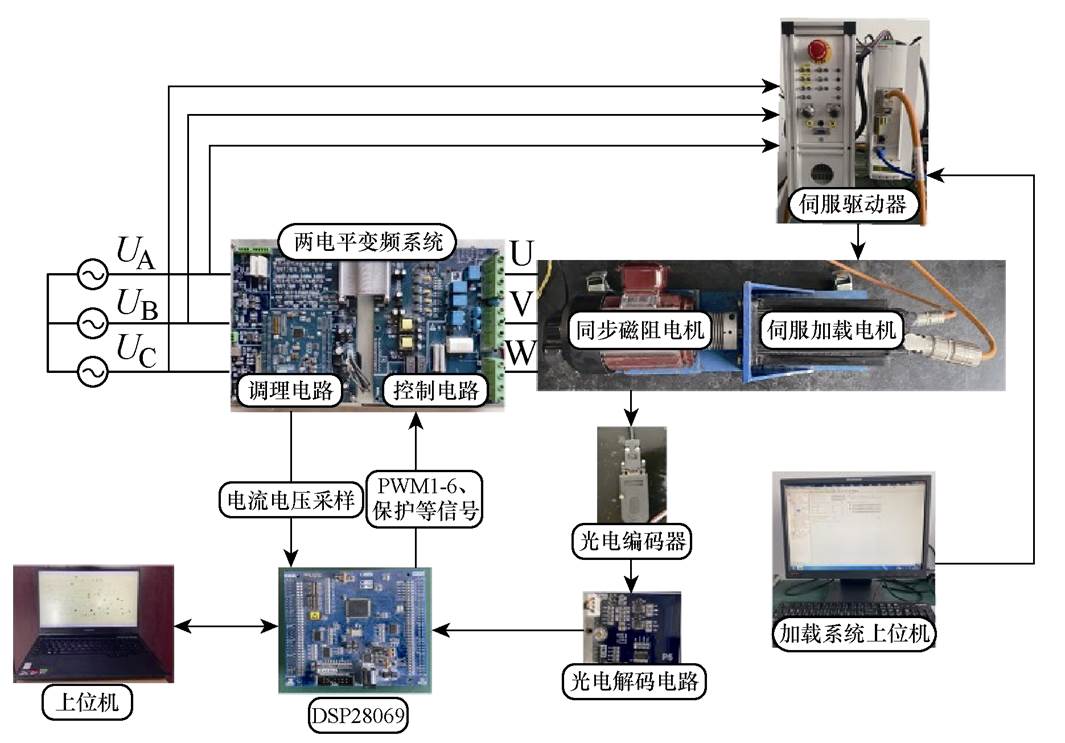
图11 同步磁阻电机驱动控制半实物实验平台实物
Fig.11 Synchronous reluctance motor drive control semi-physical test platform
1）稳态性能实验分析
本节对40 r/min工作点进行实验验证，针对是否考虑交叉耦合情况，对比磁链观测器对转子位置的准确度，电机在空载和满载的条件下进行实验，并分析对比结果。图12～图14分别为空载转速40 r/min，在未考虑交叉耦合效应与考虑交叉耦合效应两种无速度控制策略下，对电机转速、转速估计误差、转子位置、转子位置估计误差、稳态磁链的实验对比波形。图中，n*为电机实际转速、n为电机估计转速、ne为电机转速估计误差、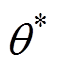
为电机转子实际位置、
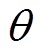为电机转子估计位置、
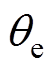为电机转子位置估计误差、
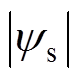为电机磁链。根据实验结果可知，考虑交叉耦合后的磁链观测器实现无速度控制能够更加精确地估计同步磁阻电机的实际转速。经过改善后，稳态时偏差约在-1.2～1.4 r/min范围内波动，平均误差约为0.700 1 r/min，转子位置平均估计误差约为0.164 5 rad、磁链脉动范围在0.272 3～0.304 3 Wb。相比于未考虑交叉耦合效应的控制下，转速估计、转子位置估计、磁链脉动都有明显改善。
表1 同步磁阻电机参数
Tab.1 SynRM parameter
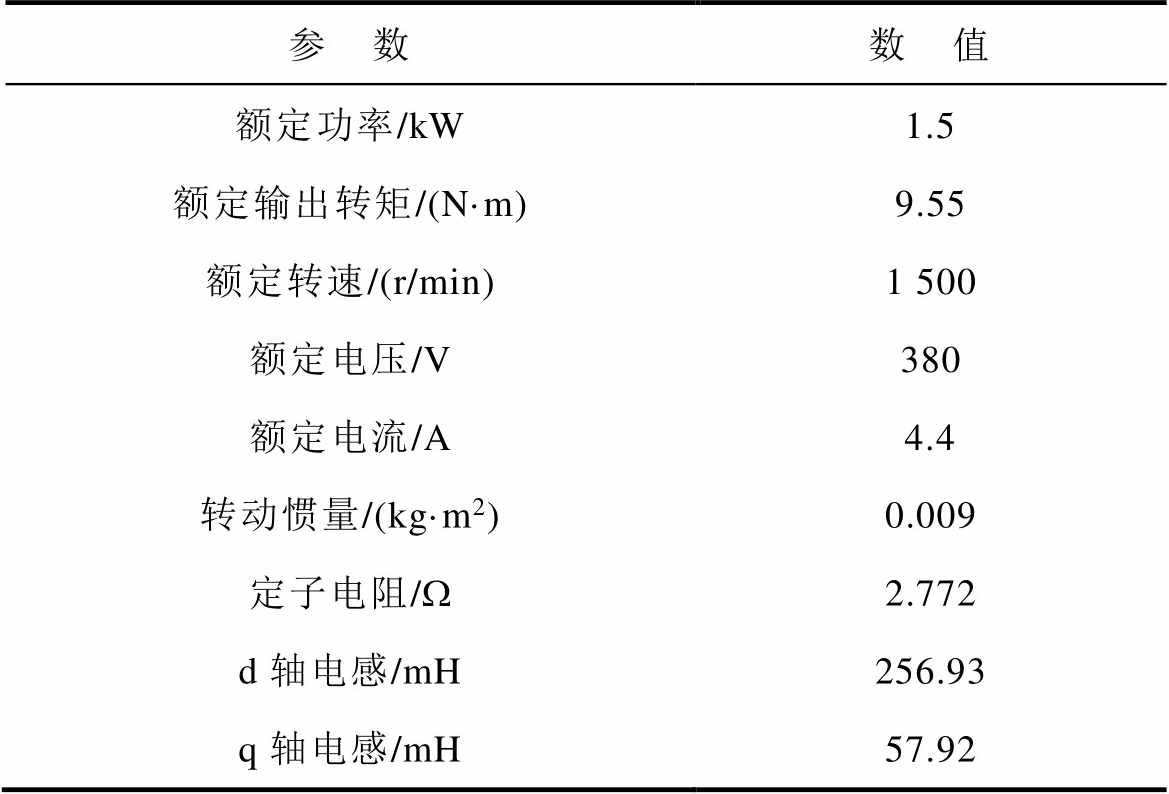
参 数数 值 额定功率/kW1.5 额定输出转矩/(N·m)9.55 额定转速/(r/min)1 500 额定电压/V380 额定电流/A4.4 转动惯量/(kg·m2)0.009 定子电阻/W2.772 d轴电感/mH256.93 q轴电感/mH57.92
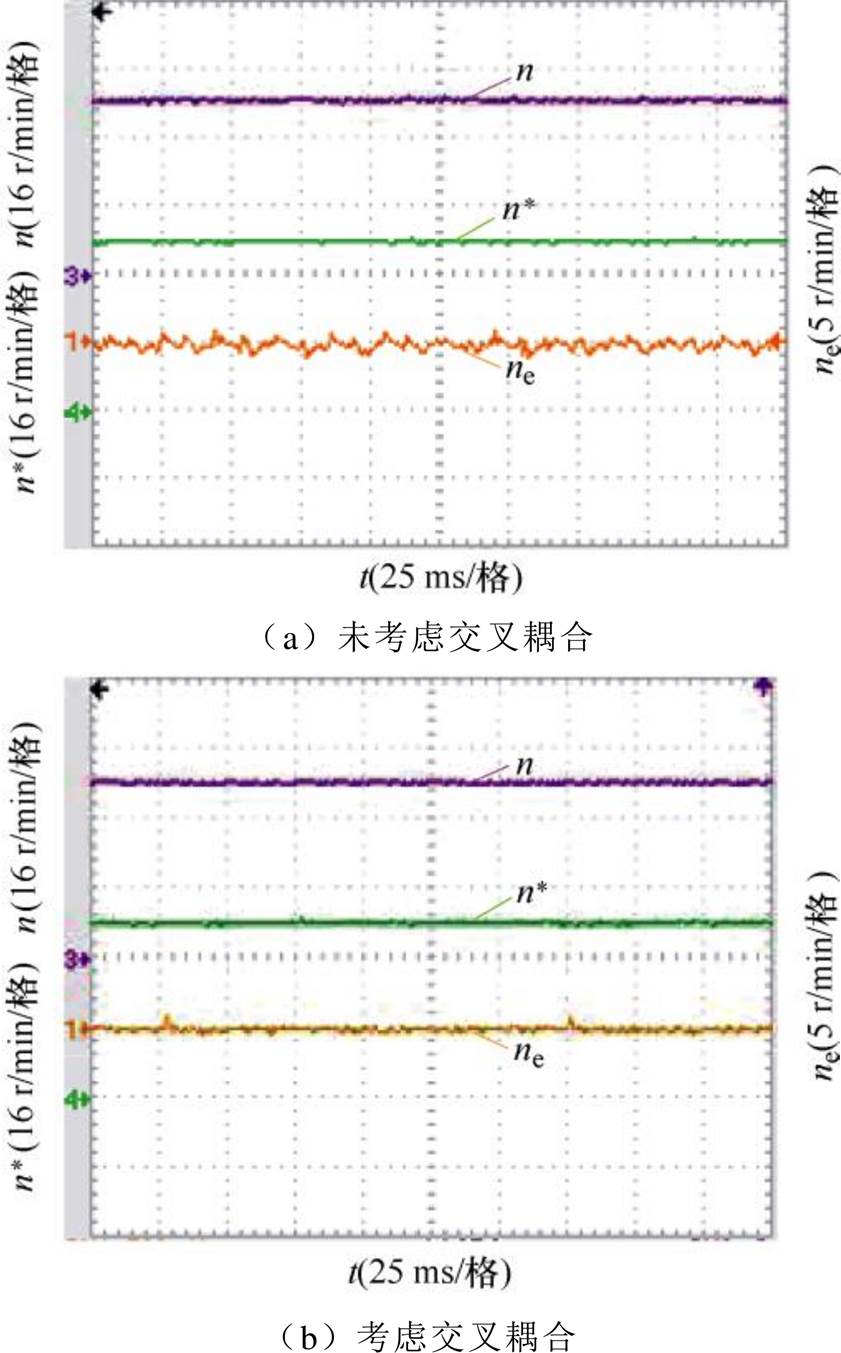
图12 给定转速40 r/min，空载下转速实验对比波形
Fig.12 Comparison waveforms of speed experiment under no load for a given speed of 40 r/min
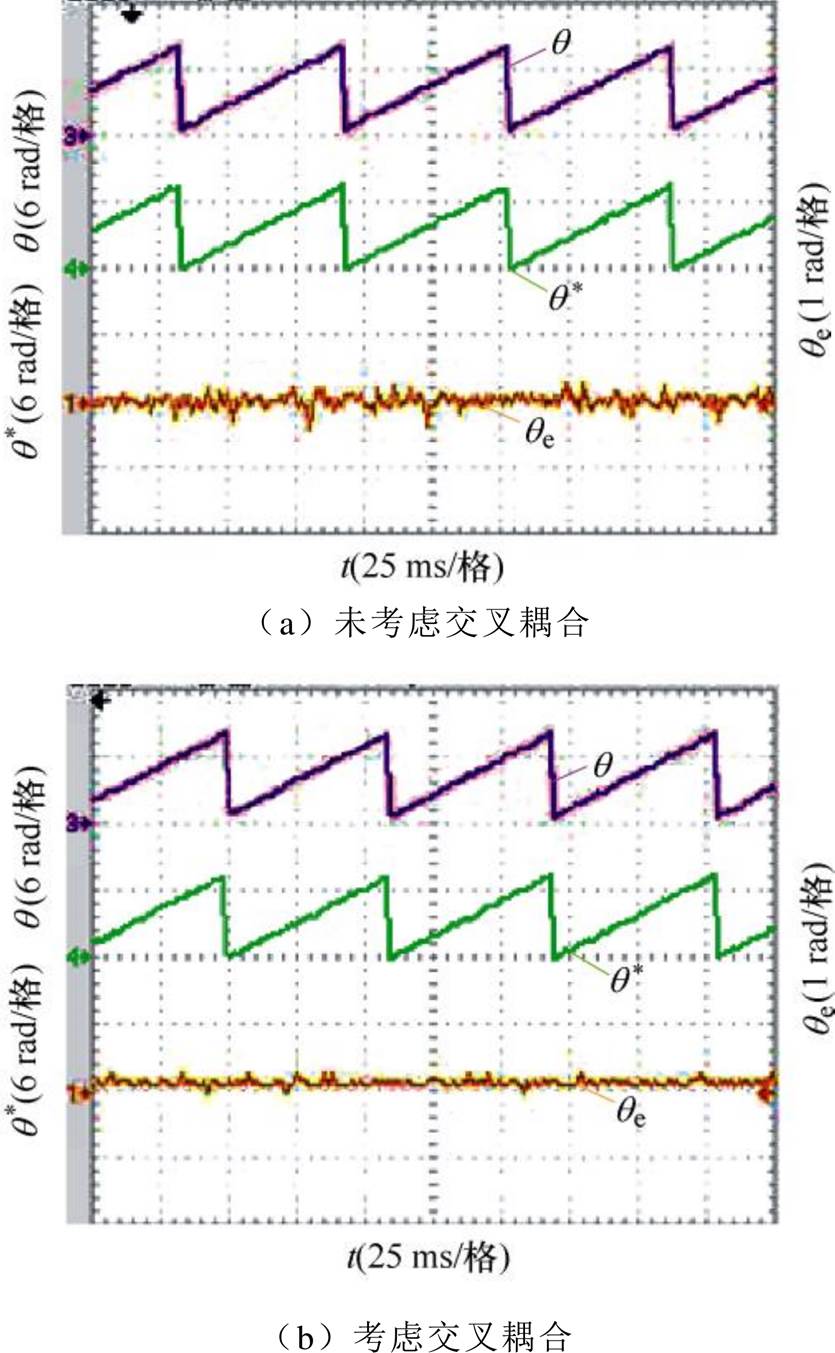
图13 给定转速40 r/min，空载下转子位置实验对比波形
Fig.13 Comparison waveforms of rotor position experiment under no load for a given speed of 40 r/min
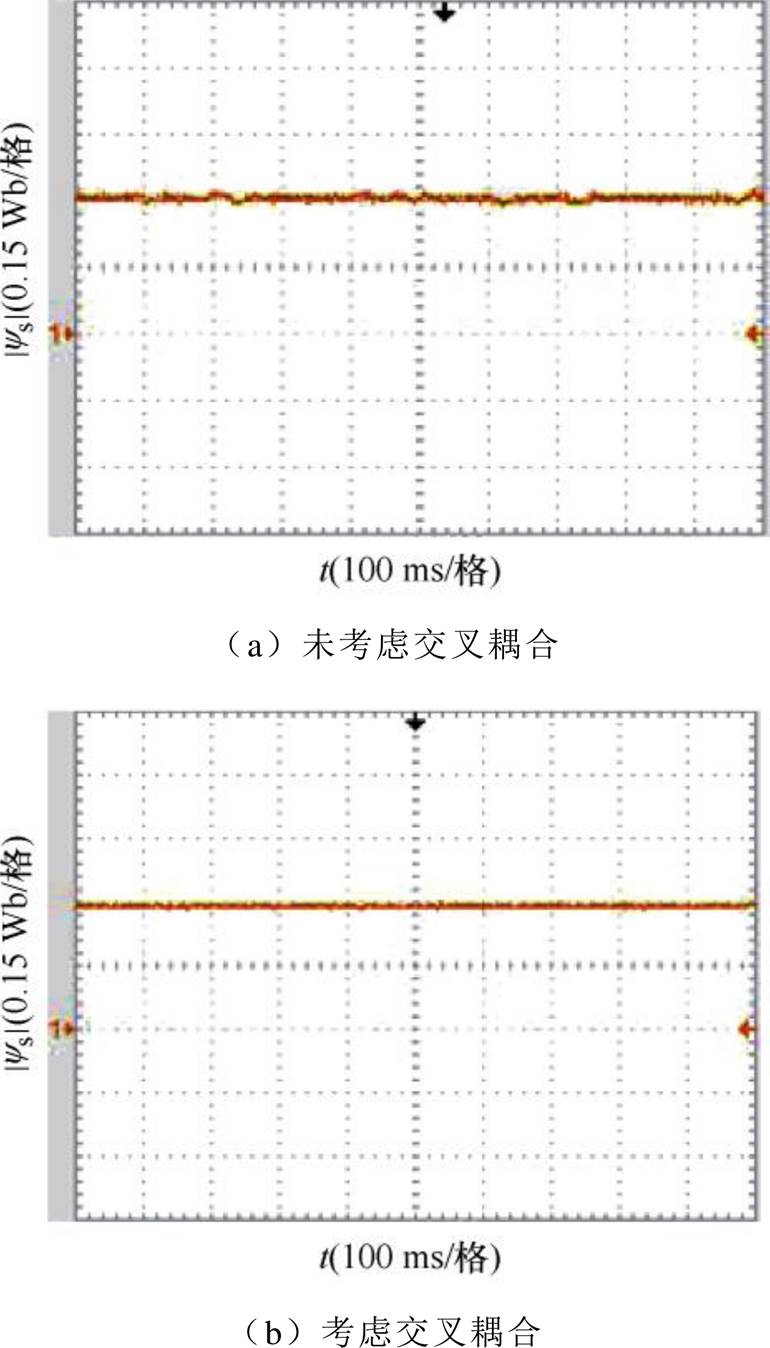
图14 给定转速40 r/min，空载下磁链实验对比波形
Fig.14 Comparison waveform of flux under no load for a given speed of 40 r/min
本节对1 500 r/min工作点进行实验验证。图15～图17为1 500 r/min，空载下转速、转子位置、磁链实验对比波形。根据实验结果可知，经过考虑交叉耦合效应的算法改善，稳态时偏差约在-4.8～9.6 r/min范围内波动，平均误差约为2.755 r/min，转子位置平均估计误差约为0.181 6 rad、磁链脉动范围在0.344 8 ～0.361 1 Wb。相比于未考虑交叉耦合效应，转速估计、转子位置估计、磁链脉动都有明显改善。
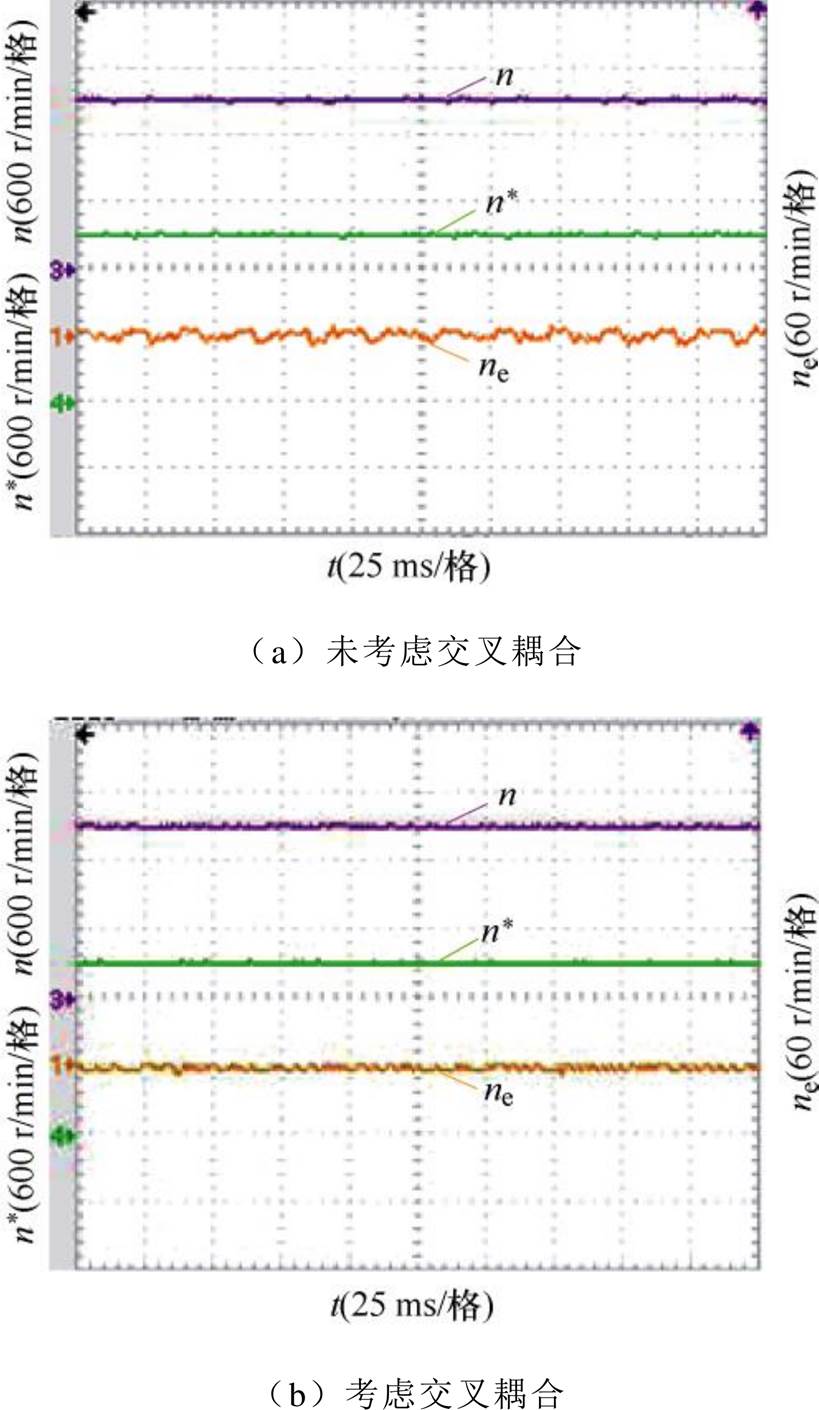
图15 给定转速1 500 r/min，空载下转速实验对比波形
Fig.15 Comparison waveforms of speed experiment under no load for a given speed of 1 500 r/min
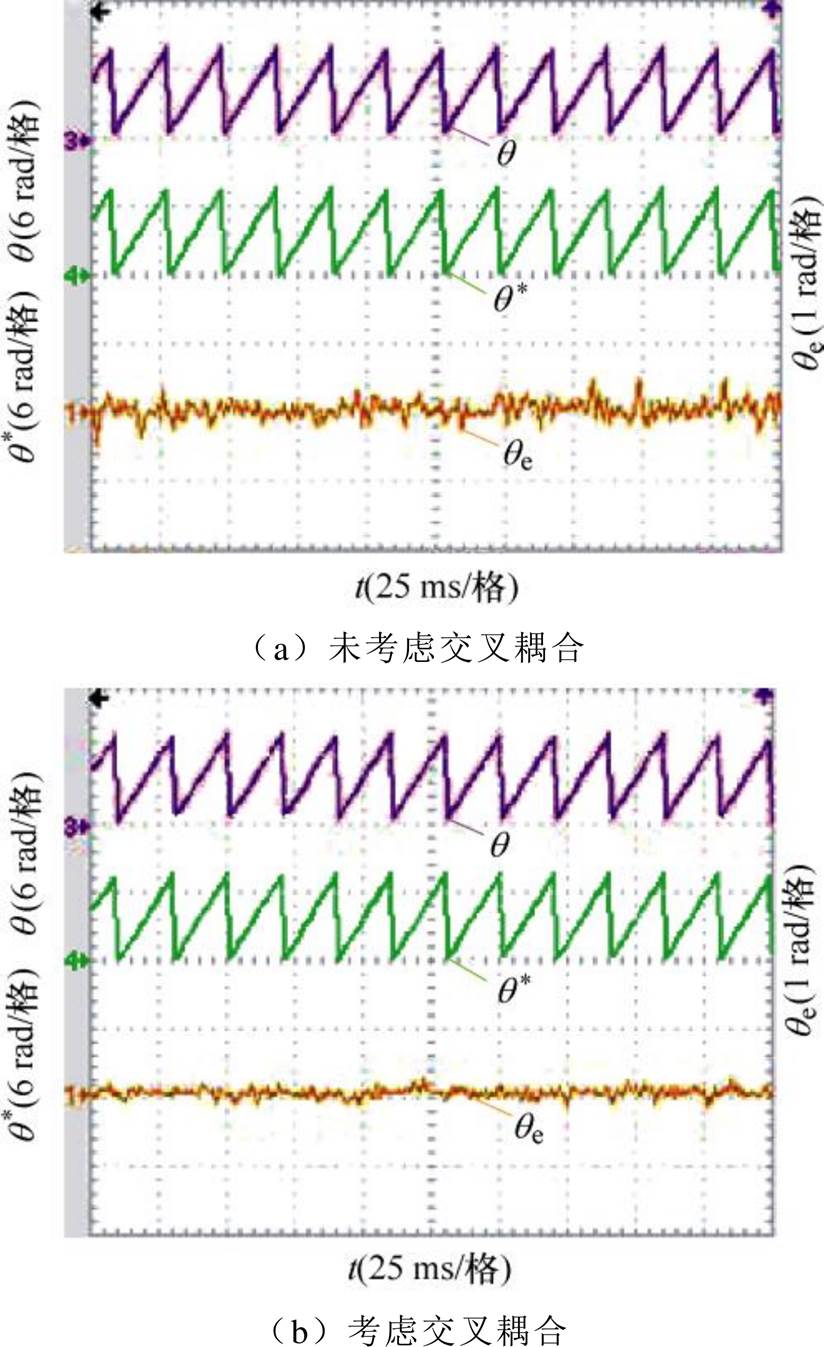
图16 给定转速1 500 r/min，空载下转子位置实验对比波形
Fig.16 Comparison waveforms of rotor position experiment under no load for a given speed of 1 500 r/min
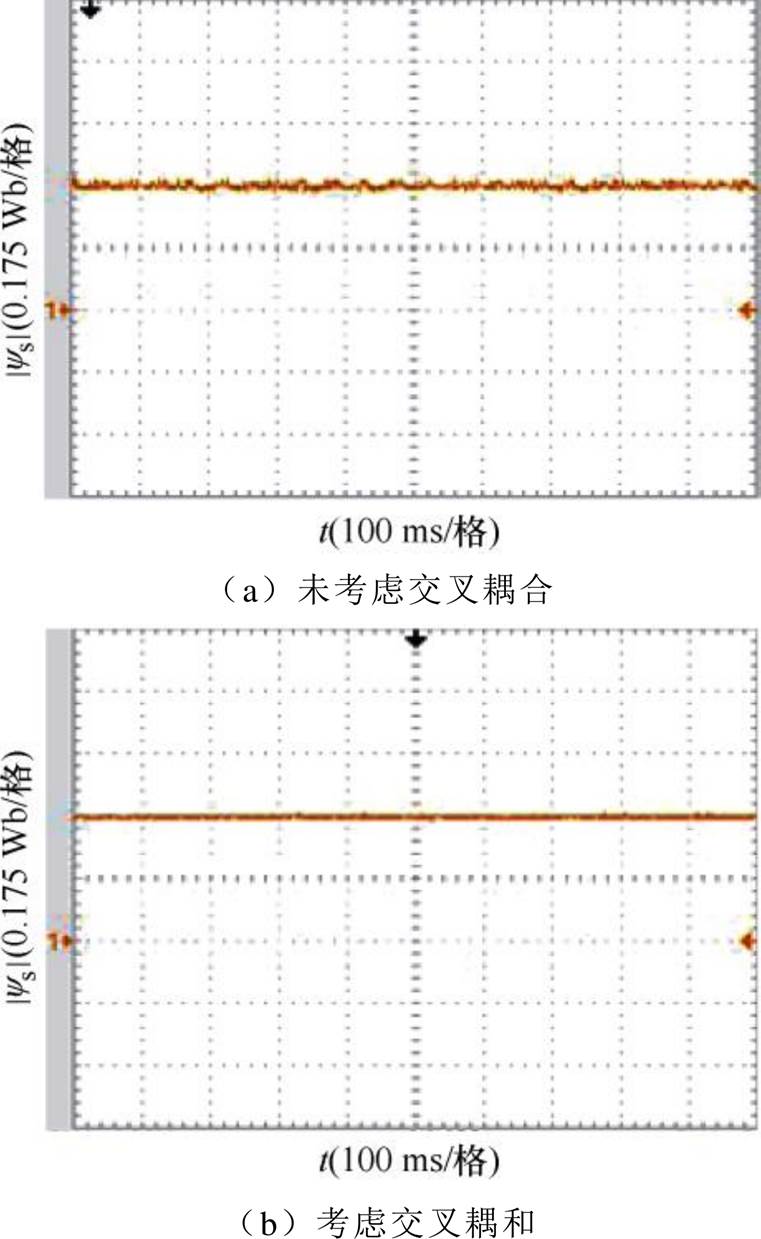
图17 给定转速1 500 r/min，空载下磁链实验对比波形
Fig.17 Comparison waveform of flux under no load for a given speed of 1 500 r/min
图18～图20为转速为40 r/min，负载转矩为9.55 N·m（满载），在未考虑磁路饱和效应与考虑交叉耦合效应两种无速度控制策略下，对电机转速、转速估计误差、转子位置、转子位置估计误差、稳态磁链实验对比波形。根据实验结果可知，考虑交叉耦合后的磁链观测器实现无速度控制能够更加精确地估计同步磁阻电机的实际转速。经过改善后，稳态时转速偏差约在-2.3～3.2 r/min范围内波动，平均转速误差约为2.087 8 r/min，转子位置平均估计误差约为0.249 1 rad、磁链脉动范围在1.098 9～1.123 7 Wb。相比于未考虑交叉耦合效应的控制下，转速估计、转子位置估计、磁链脉动都有明显改善。
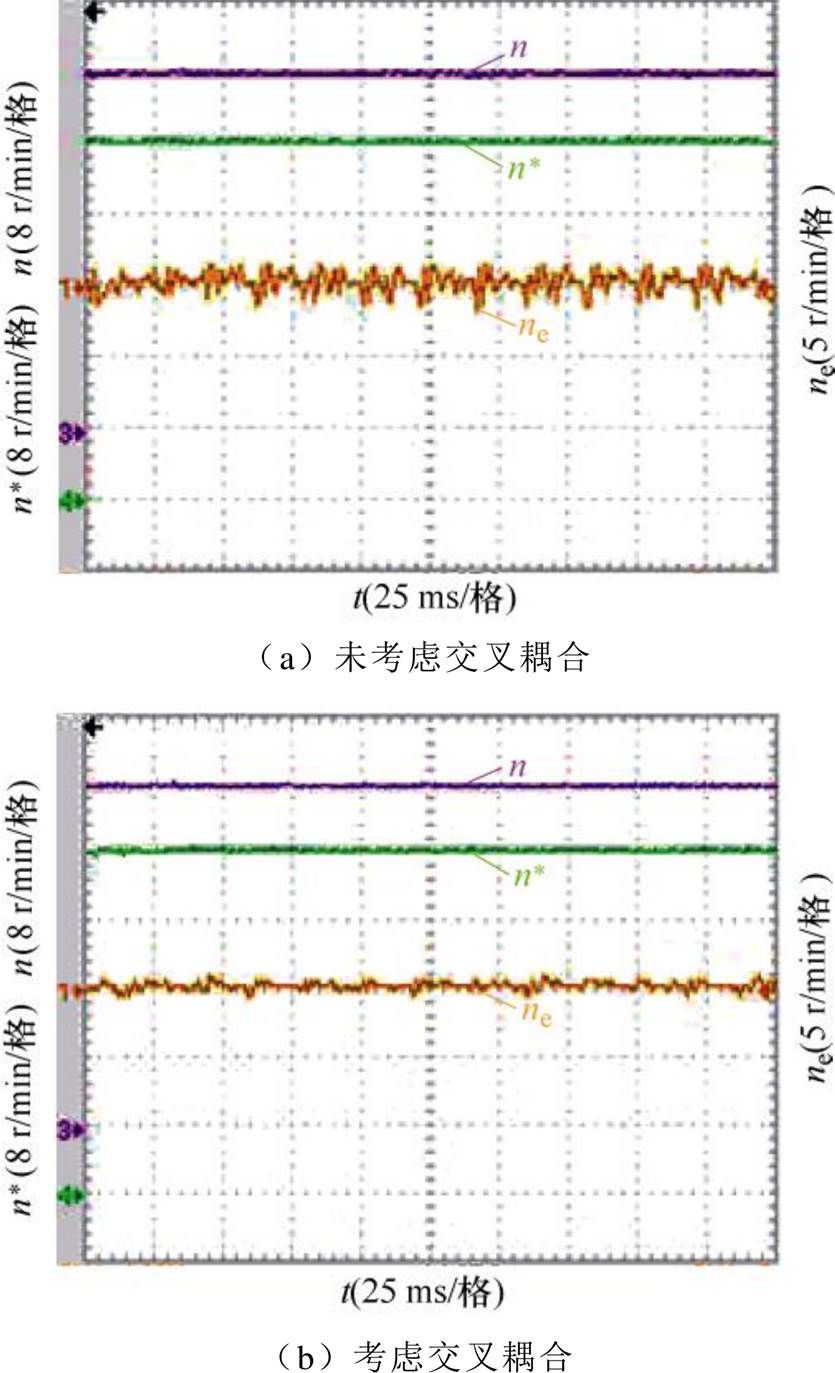
图18 给定转速40 r/min，满载下转速实验对比波形
Fig.18 Comparison waveforms of speed experiment under full load for a given speed of 40 r/min
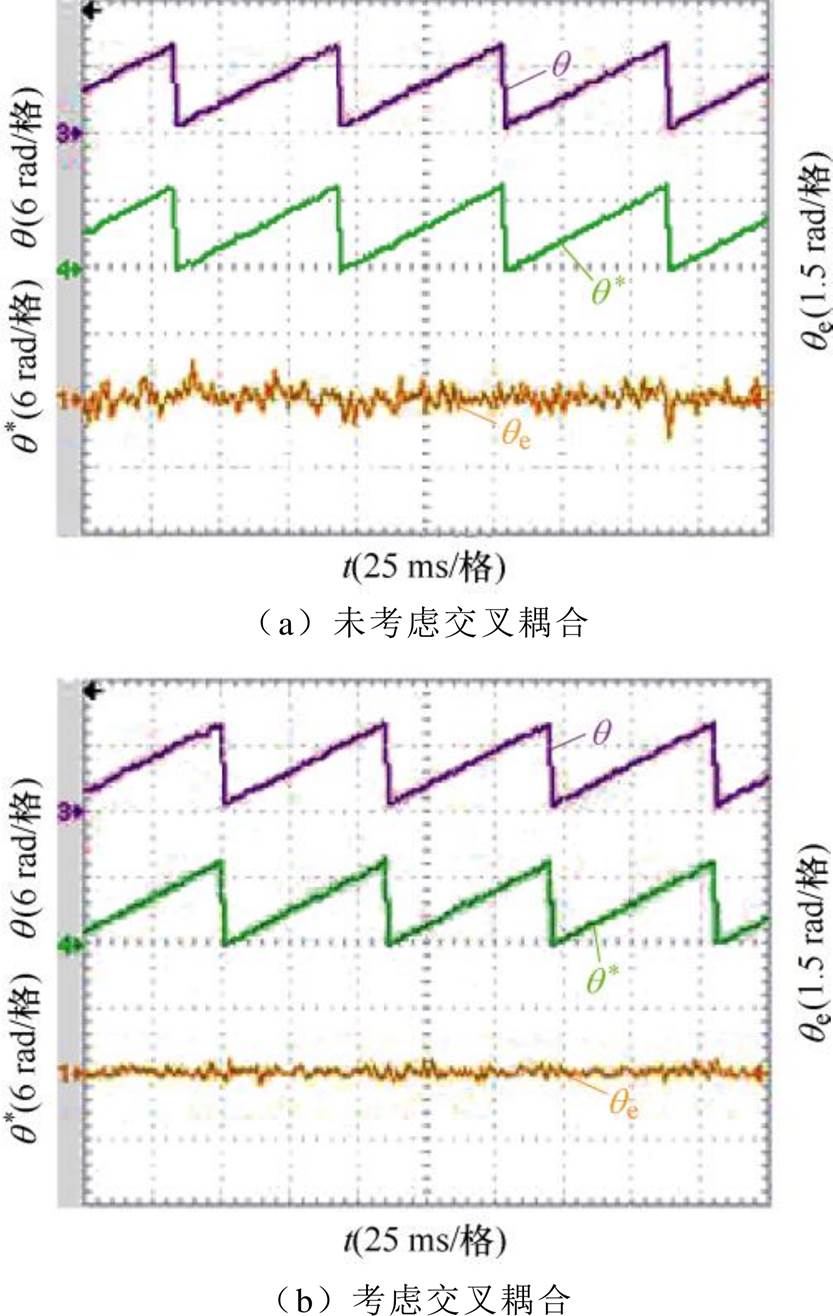
图19 给定转速40 r/min，满载下转子位置实验对比波形
Fig.19 Comparison waveforms of rotor position experiment under full load for a given speed of 40 r/min
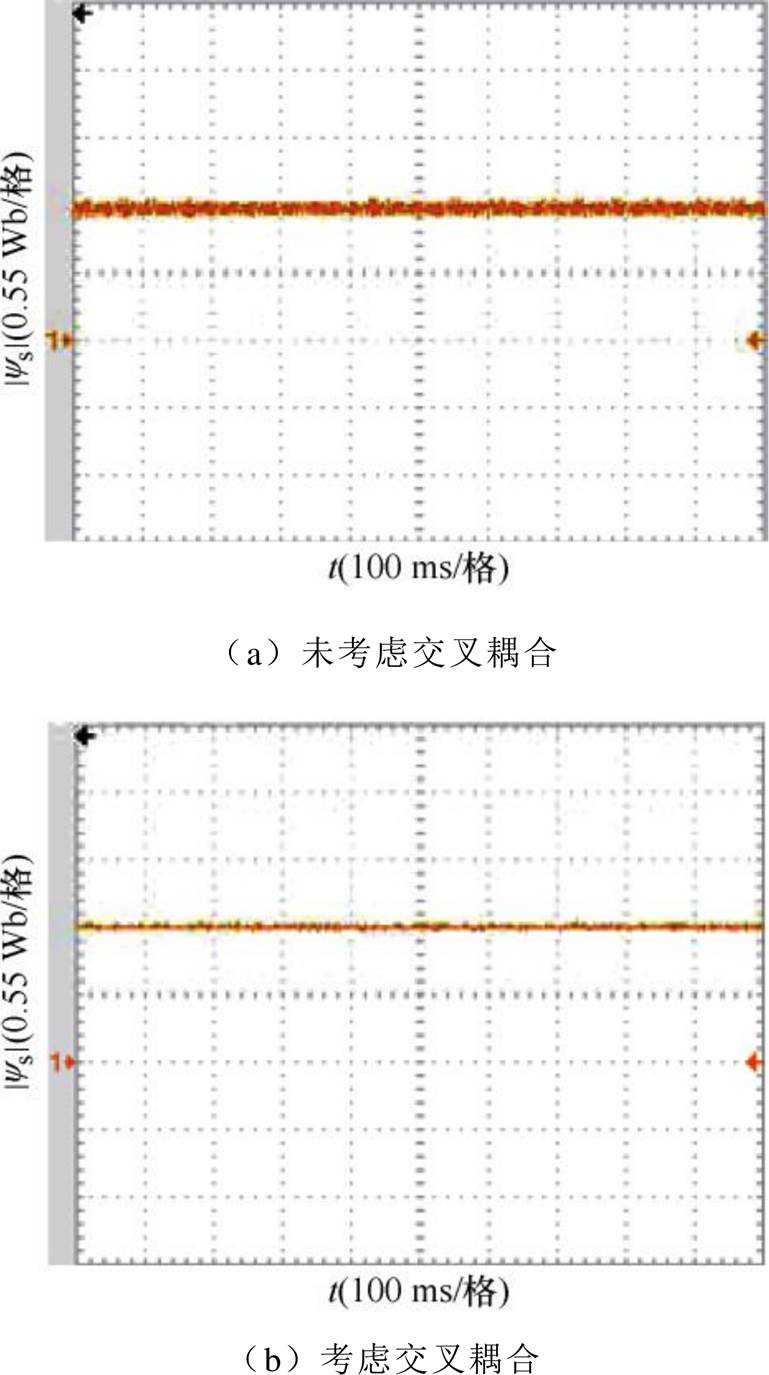
图20 给定转速40 r/min，满载下磁链实验对比波形
Fig.20 Comparison waveform of flux under full load for a given speed of 40 r/min
图21～图23为转速为1 500 r/min，负载转矩为9.55 N·m（满载），在未考虑磁路饱和效应与考虑交叉耦合效应两种无速度控制策略下，对电机转速、转速估计误差、转子位置、转子位置估计误差、稳态磁链进行对比。根据实验结果可知，考虑交叉耦合后的磁链观测器实现无速度控制能够更加精确地估计同步磁阻电机的实际转速。经过改善后，稳态时转速偏差约在-21.84～25.2 r/min范围内波动，平均转速误差约为7.260 r/min，转子位置平均估计误差约为0.377 3 rad、磁链脉动范围在1.149 4～1.164 6 Wb。相比于未考虑交叉耦合效应的控制下，转速估计、转子位置估计、磁链脉动都有明显改善。
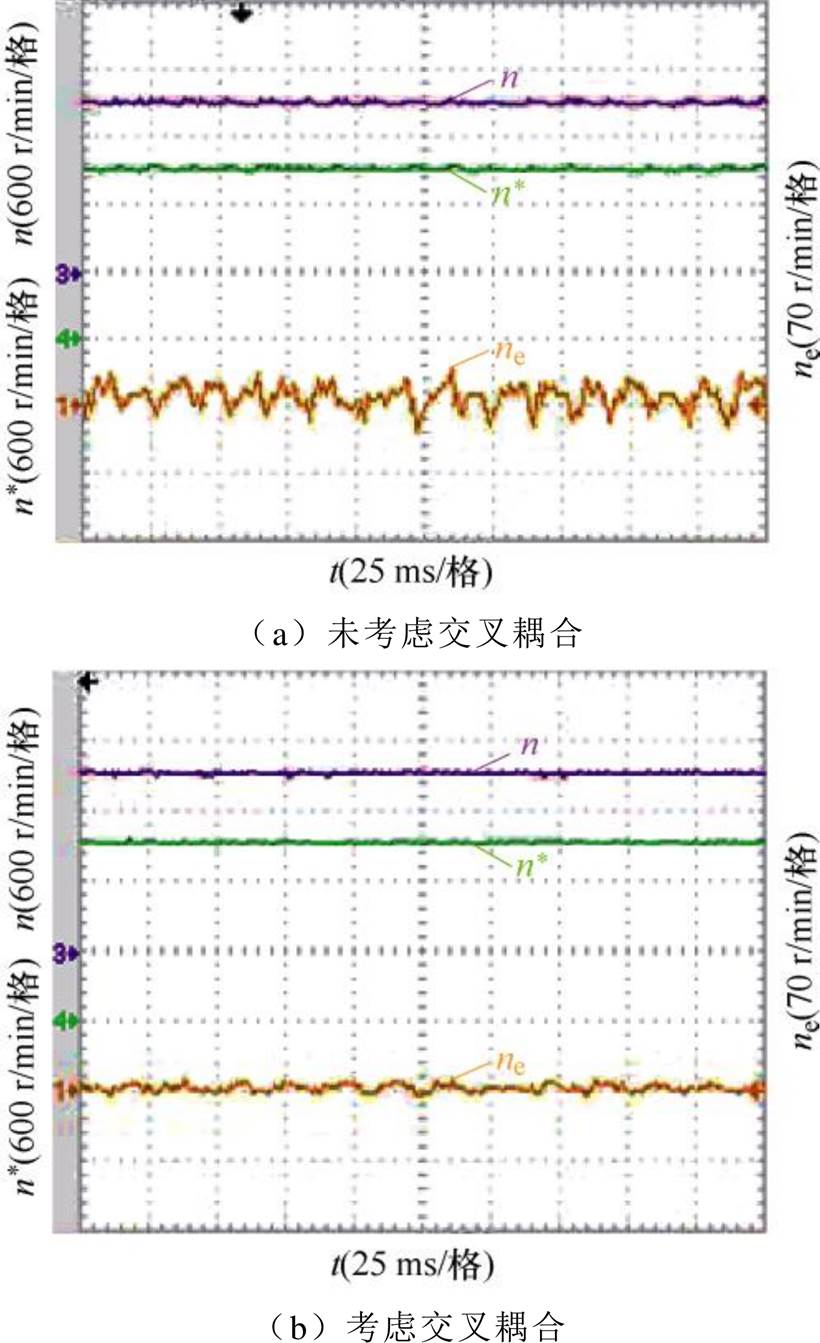
图21 给定转速1 500 r/min，满载下转速实验对比波形
Fig.21 Comparison waveforms of speed experiment under full load for a given speed of 1 500 r/min
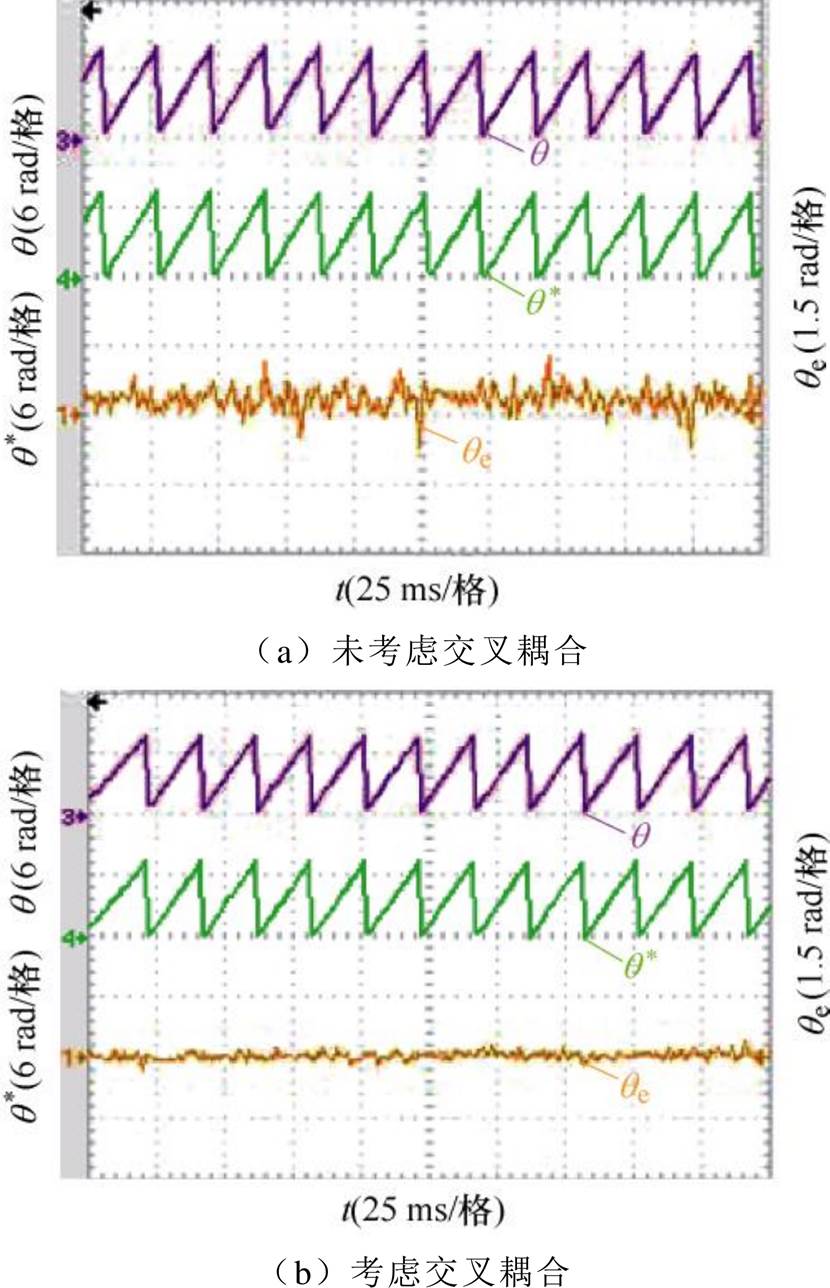
图22 给定转速1 500 r/min，满载下转子位置实验对比波形
Fig.22 Comparison waveforms of rotor position experiment under full load for a given speed of 1 500 r/min
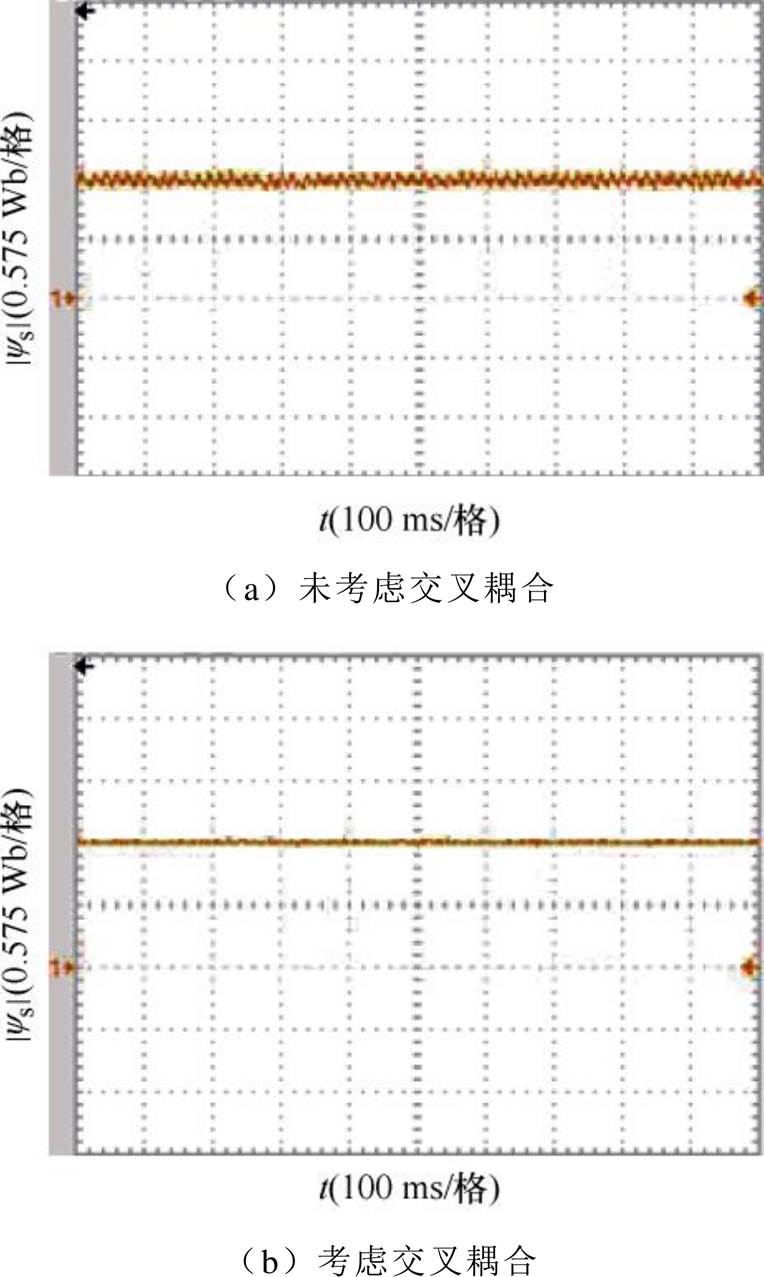
图23 给定转速1 500 r/min，满载下磁链实验对比波形
Fig.23 Comparison waveform of flux under full load for a given speed of 1 500 r/min
2）动态性能实验分析
在空载条件下，速度给定方式为分段式，转速由低至高分别为500、1 000、1 500 r/min。转速达到500 r/min时，每次间隔0.3 s后转速上升。在未考虑交叉耦合效应与考虑交叉耦合效应的无速度控制策略下进行同步磁阻电机转速、转速估计误差对比实验如图24和图25所示。可以得出，在考虑交叉耦合效应后的无速度控制策略下，电机在变速性能上的转速估计、转子位置估计有更小的估计误差。
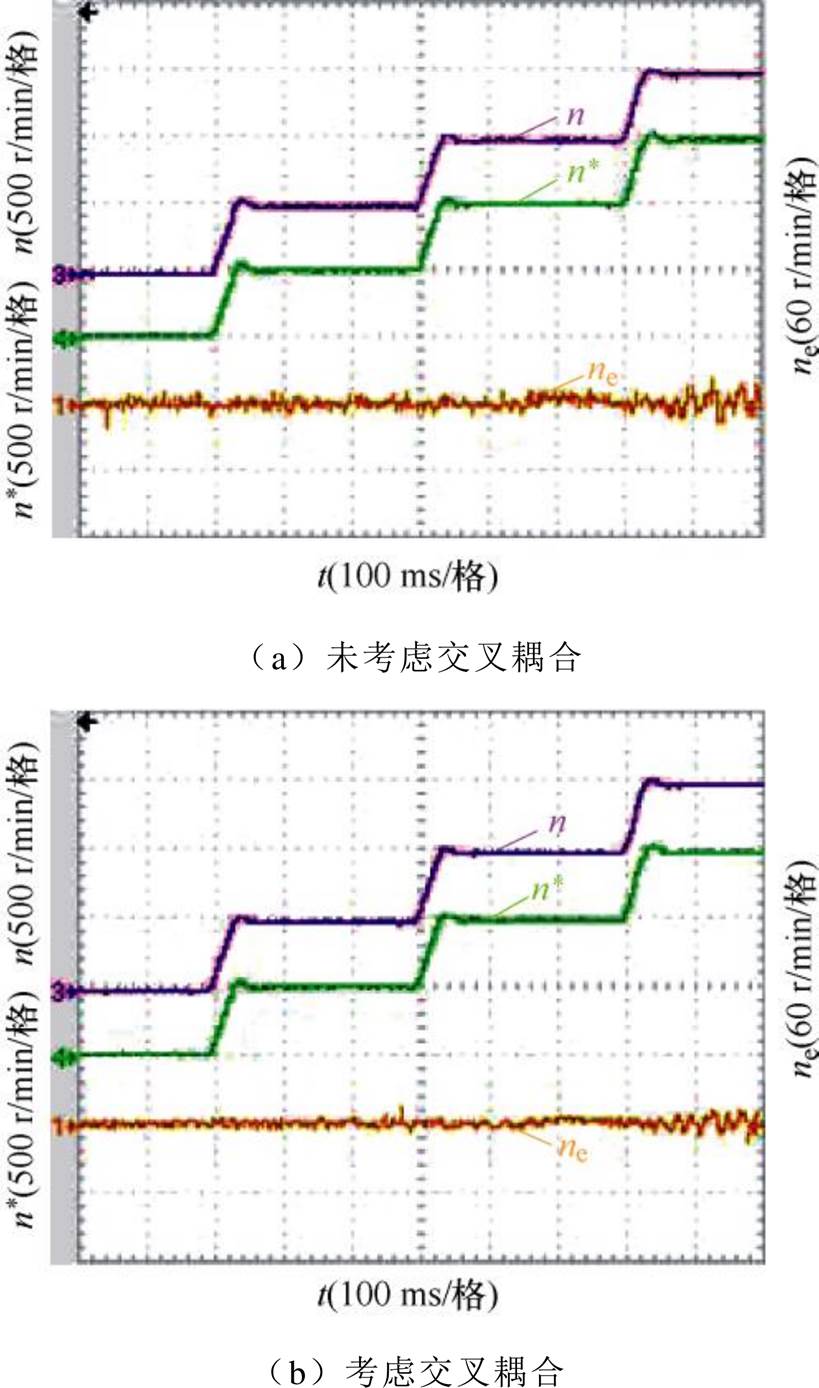
图24 分段式转速给定，空载下电机转速实验对比波形
Fig.24 Comparison waveforms of motor speed experiments under no load with segmented speed setting
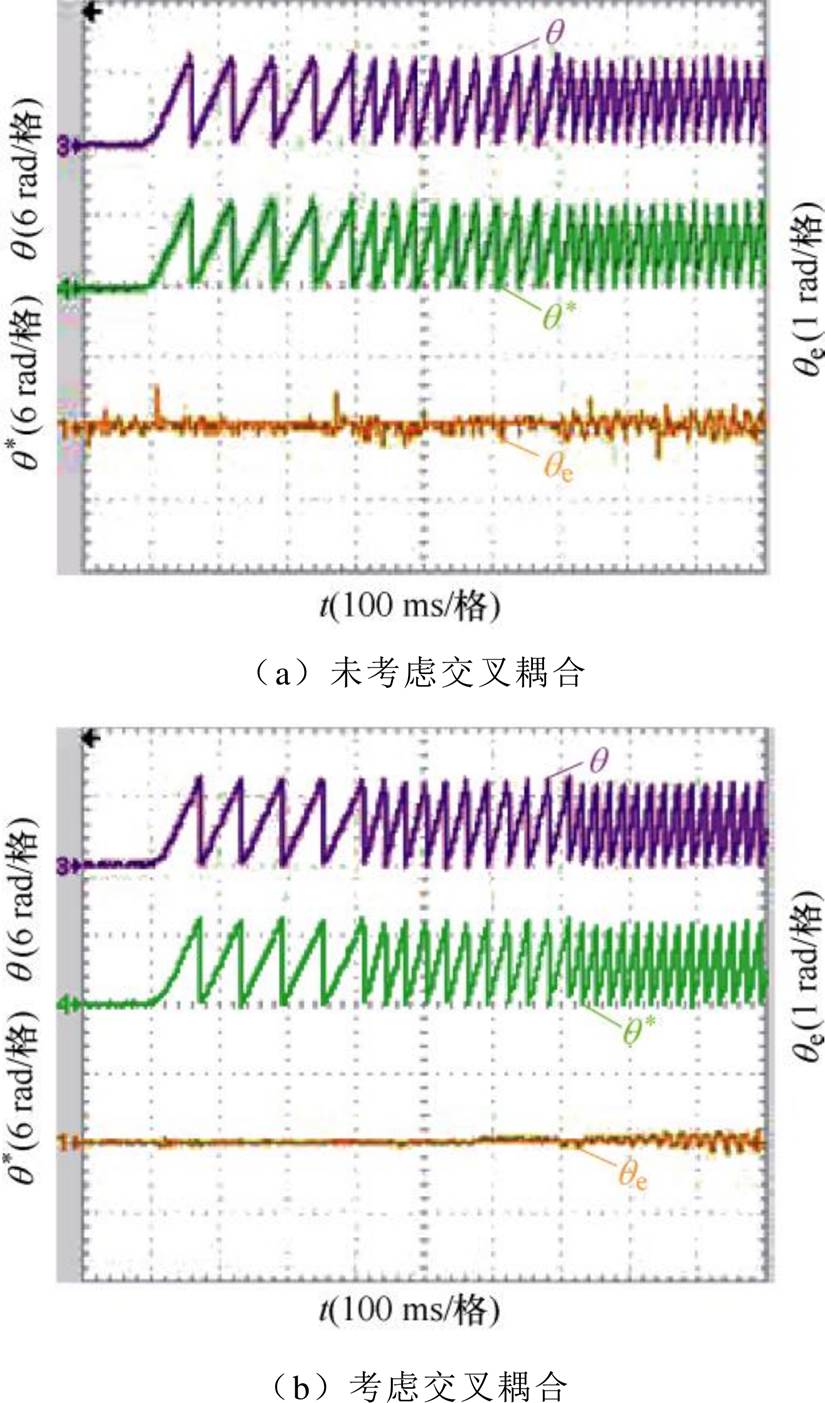
图25 分段式转速给定，空载下电机转子位置估计实验对比波形
Fig.25 Comparison waveforms of motor rotor position estimation experiments under no load with segmented speed setting
为证明自抗扰技术应用在同步磁阻电机控制系统中的优越性，本节选择将该控制技术与传统PI控制器的同步磁阻电机控制系统进行实验对比。为了能更好地衡量同步磁阻电机控制性能，下面主要从超调量、恢复时间、扰动变化量等方面进行分析。
1）动态转速实验分析
在动态转速实验分析中，首先空载条件下，速度给定方式为分段式，转速由低至高分别为500、1 000、1 500 r/min，全程无扰动。自抗扰技术与传统PI控制器都考虑同步磁阻电机的交叉耦合效应，对比超调量的大小，波形如图26所示。可以明显得出，采用PI控制时，转速波形会发生超调现象，而采用一阶LADRC控制时，转速并没有出现超调现象。由500 r/min的部分转速波形可知，ADRC控制时估计转速的超调量为0，响应时间为0.044 s。与PI控制相比较，转速的响应时间明显变快，电机可以更加平稳地进行起动和转速变换。
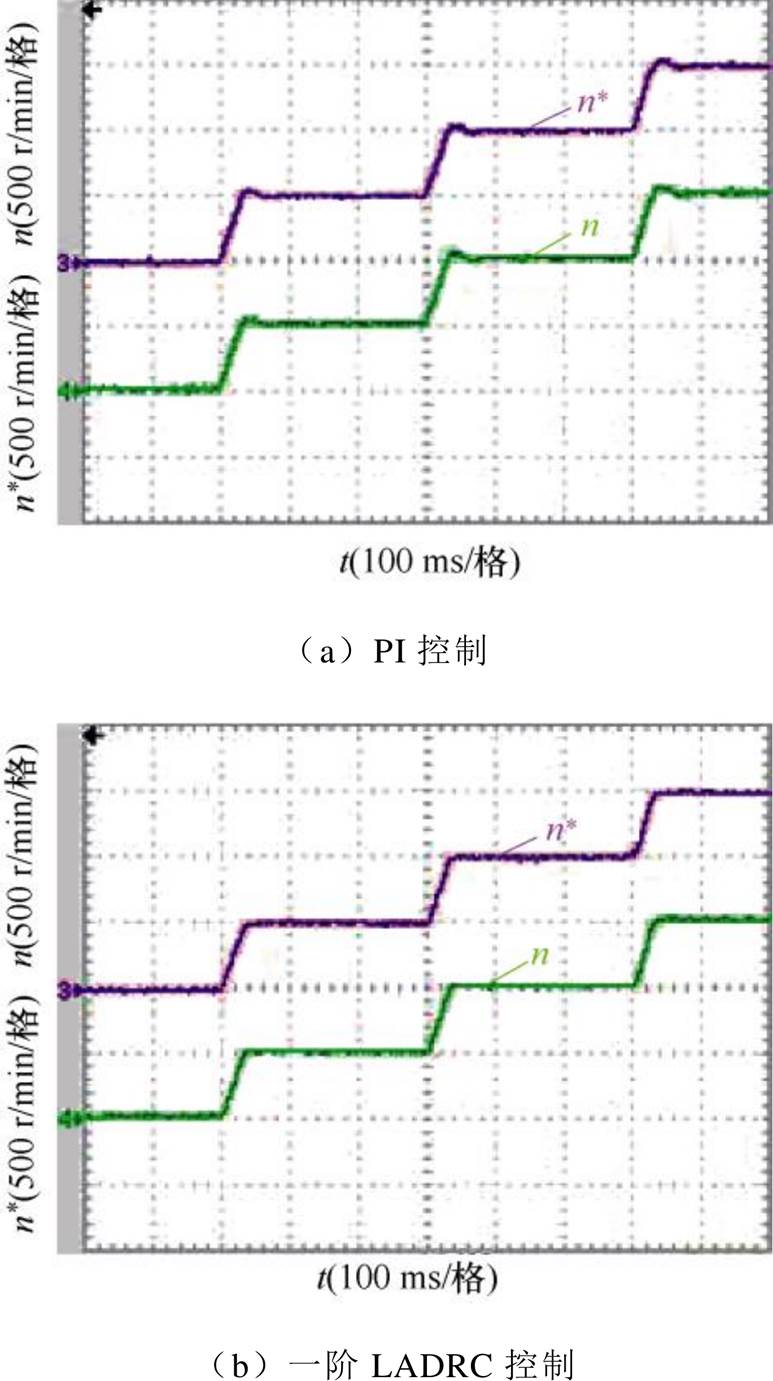
图26 分段式转速给定，空载转速实验对比波形
Fig.26 Comparison waveforms of speed experiments under no load with segmented speed setting
2）动态负载实验分析
考虑自抗扰技术应用在同步磁阻电机无速度控制中，抗扰性能的强弱，本节针对不同转速、加减载进行实验结果对比。
图27和图28分别为给定转速在1 000 r/min和1 500 r/min的条件下，进行空载起动，在0.3 s时突加负载转矩为9.55 N·m，随后在0.5 s突减载9.55 N·m的实验结果。可以得出，电机进入稳态时，当突加负载时，一阶LADRC下的转速动态响应明显优于PI控制器。当给定转速为1 000 r/min时，ADRC下的实际最大转速跌落值为30 r/min，转速恢复时间为0.012 s，最大转速上升值为20 r/min，转速恢复时间为0.011 s。当给定转速为1 500 r/min时，ADRC下的最大转速跌落值为36 r/min，转速恢复时间为0.044 s，最大转速上升值为48 r/min，转速恢复时间为0.032 s。所以，同步磁阻电机在ADRC下的无速度控制策略由于负载变化引起的转速变化较小，恢复时间变短，增强了抗扰动能力。将ADRC技术应用于同步磁阻电机控制系统中，转速变化值有所减小，转速的恢复稳态时间也大幅缩短，从而证明其有效地增强了系统的抗扰性。
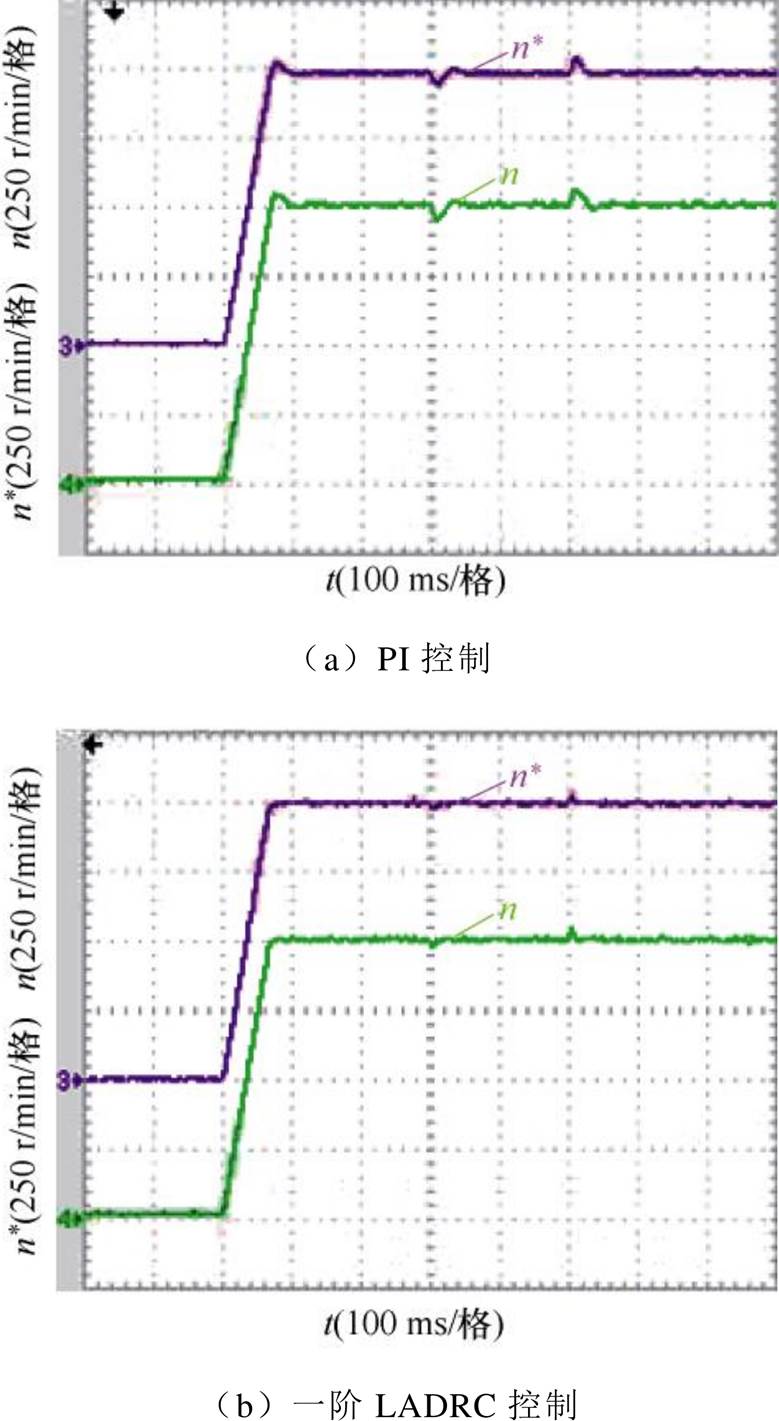
图27 给定转速1 000 r/min，变载转速实验对比波形
Fig.27 Comparison waveforms of variable load speed experiments for a given speed of 1 000 r/min
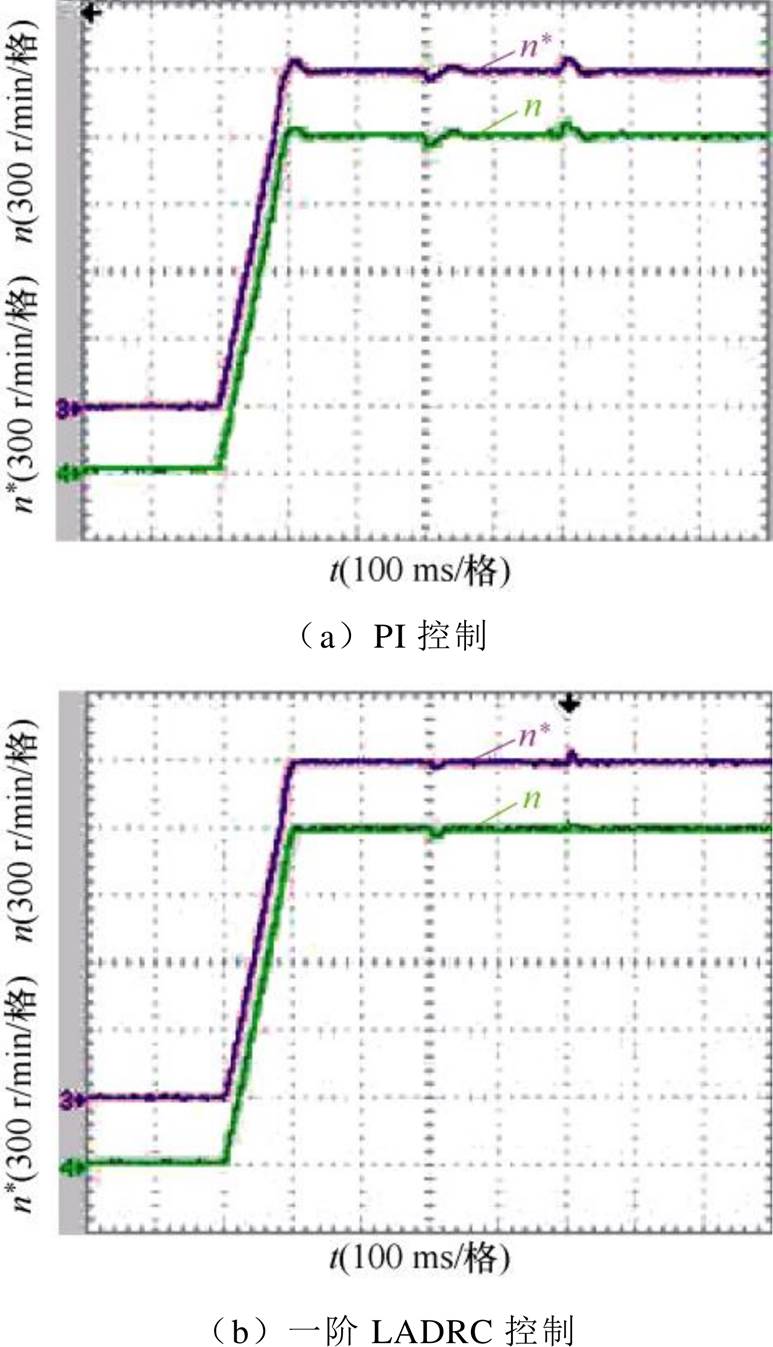
图28 给定转速1 500 r/min，变载转速实验对比波形
Fig.28 Comparison waveforms of variable load speed experiments for a given speed of 1 500 r/min
图29为给定转速1 000 r/min的条件下，进行满载起动，时间为0.5 s时，突减负载转矩9.55 N·m的实验结果。可以得出，在电机带载条件下进行减载，ADRC控制下的抗扰能力相比于PI控制器更具有优越性。当给定转速为1 000 r/min时，最大转速上升值为40 r/min，转速恢复时间为0.008 s。
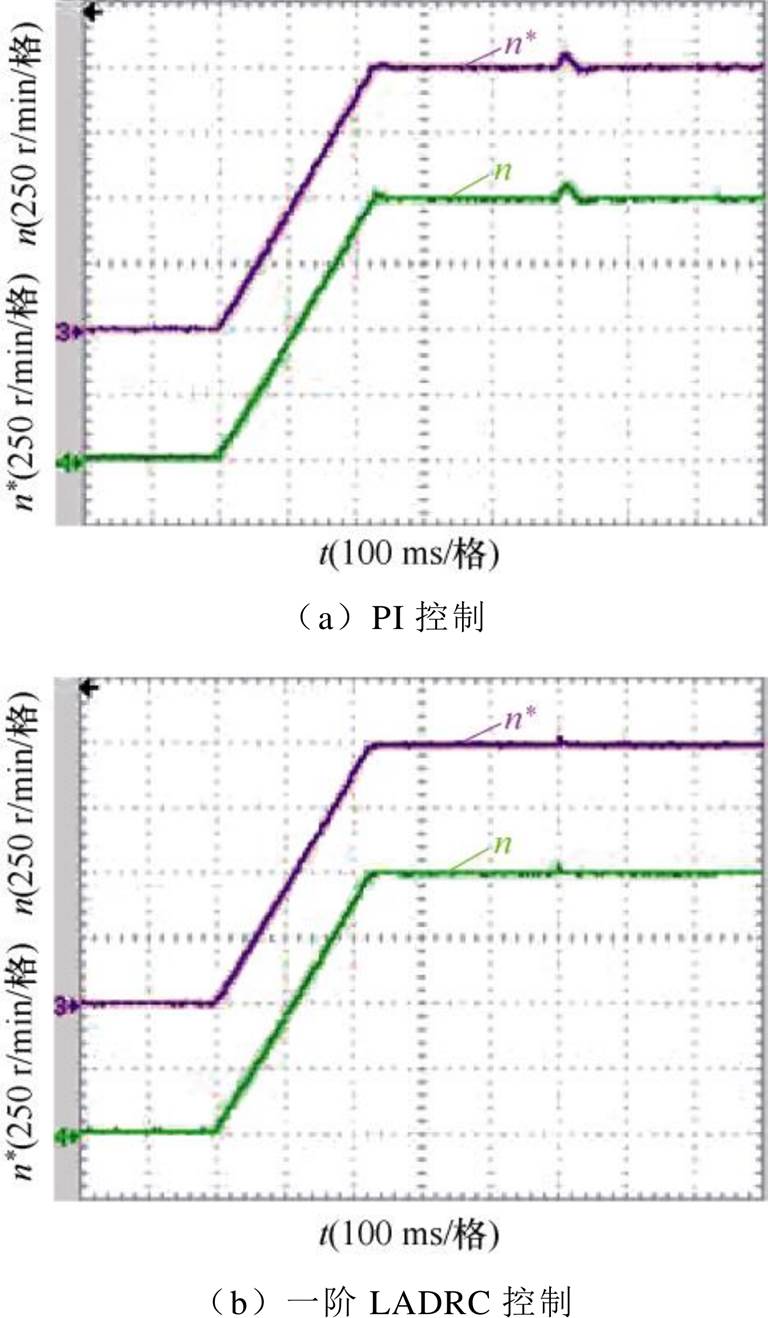
图29 给定转速1 000 r/min，变载转速实验对比波形
Fig.29 Comparison waveforms of variable load speed experiments for a given speed of 1 000 r/min
针对同步磁阻电机高性能控制，本文提出了一种基于一阶线性自抗扰控制器的同步磁阻电机无速度传感器控制方法。首先采用磁链观测器法实现同步磁阻电机无速度传感器控制，针对同步磁阻电机交叉耦合效应，建立dq轴磁链与电流的非线性函数模型，将该模型运用到磁链观测器中，提高转子位置的估计精度；其次针对电机调速系统抗扰性较弱问题，对同步磁阻电机无速度传感器控制策略中的转速环进行改进，设计一阶线性自抗扰控制器并应用于该调速系统中；最后本方案通过实验平台进行验证分析，证明了其有效性，得出以下结论：
1）利用磁链观测器法实现同步磁阻电机无速度控制，采用闭环磁链观测器法提高转子位置估计精度。由于同步磁阻电机存在磁路饱和及交叉耦合效应，若不考虑该现象，则会极大地影响转子位置估计误差精度。故对被测电机采用实验静止法，通过在被测电机的dq轴注入幅值、频率不同的电压，利用前向欧拉法计算得到磁链。并采用LLS方法拟合得到dq轴磁链与dq轴电流的非线性函数模型，最终有效地提高了转子位置估计精度。
2）利用磁链观测器实现同步磁阻电机的无速度控制，发现电机调速系统抗扰性较弱，为提高系统抗扰性能，将自抗扰技术应用于同步磁阻电机无速度控制中，对同步磁阻电机无速度传感器控制策略中的转速环进行改进，设计一阶线性ADRC。通过电机的运动状态方程，分析电机运行过程中遇到的内外扰动，随后将所受扰动进行及时观测补偿，解决电机动态响应时存在超调、响应速度慢、受扰时转速恢复时间慢等问题。
本文采用的基于一阶线性自抗扰控制器的同步磁阻电机无速度传感器控制方法，在考虑交叉耦合效应后，不仅有效提高转子位置的估计精度，同时增强系统抗扰性能。但对于同步磁阻电机来说，如何能在线进行参数辨识、将自抗扰技术更广泛地应用于转矩滞环控制器、磁链滞环控制器等有待进一步的探索。
参考文献
[1] 徐心愿, 王云冲, 沈建新. 基于最大转矩电流比的同步磁阻电机DTC-SVM控制策略[J]. 电工技术学报, 2020, 35(2): 246-254.
Xu Xinyuan, Wang Yunchong, Shen Jianxin. Direct torque control-space vector modulation control strategy of synchronous reluctance motor based on maximum torque per-ampere[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 246-254.
[2] Moghaddam H A, Rezaei O, Saeidi M. Rotary shaft encoder inaccuracy compensation for PMA-SynRM drives application using augmented state UKF[J]. IEEE Transactions on Instrumentation and Mea- surement, 1976, 70: 3525013.
[3] Hadla H, Santos F. Performance comparison of field- oriented control, direct torque control, and model- predictive control for SynRMs[J]. Chinese Journal of Electrical Engineering, 2022, 8(1): 24-37.
[4] Maroufian S S, Pillay P. Design and analysis of a novel PM-assisted synchronous reluctance machine topology with AlNiCo magnets[J]. IEEE Transactions on Industry Applications, 2019, 55(5): 4733-4742.
[5] Nikmaram B, Davari S A, Naderi P, et al. Sensorless simplified finite control set model predictive control of SynRM using finite position set algorithm[J]. IEEE Access, 2021, 9: 47184-47193.
[6] 李争, 安金峰, 肖宇, 等. 基于自适应观测器的永磁同步直线电机模型预测控制系统设计[J]. 电工技术学报, 2021, 36(6): 1190-1200.
Li Zheng, An Jinfeng, Xiao Yu, et al. Design of model predictive control system for permanent magnet synchronous linear motor based on adaptive observer[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1190-1200.
[7] Liu Zhaohua, Nie Jie, Wei Hualiang, et al. Switched PI control based MRAS for sensorless control of PMSM drives using fuzzy-logic-controller[J]. IEEE Open Journal of Power Electronics, 2053, 3: 368-381.
[8] Varatharajan A, Pellegrino G, Armando E. Sensorless synchronous reluctance motor drives: auxiliary flux- based position observer[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(4): 4330-4339.
[9] 王震宇, 孙伟, 蒋栋. 基于虚拟电压注入的闭环磁链观测器的感应电机无速度传感器矢量控制系统[J]. 电工技术学报, 2022, 37(2): 332-343.
Wang Zhenyu, Sun Wei, Jiang Dong. Induction motor speed sensorless vector control system based on closed-loop flux observer with virtual voltage injection[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 332-343.
[10] Li Chengrui, Wang Gaolin, Zhang Guoqiang, et al. Torque ripples minimization of sensorless SynRM drives for low-speed operation using Bi-HFSI scheme[J]. IEEE Transactions on Industrial Elec- tronics, 2021, 68(7): 5559-5570.
[11] 麦志勤, 刘计龙, 肖飞, 等. 基于估计位置反馈电流解调算法的改进型高频旋转电压注入无位置传感器控制策略[J]. 电工技术学报, 2022, 37(4): 870-881, 891.
Mai Zhiqin, Liu Jilong, Xiao Fei, et al. Sensorless control strategy of improved HF rotating voltage injection based on estimated position feedback current demodulation algorithm[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 870-881, 891.
[12] Kim H S, Lee K. Model predictive current control with online parameter estimation for synchronous reluctance machine controlled by high-frequency signal injection position-sensorless[J]. IEEE Access, 2022, 10: 25267-25277.
[13] Wen Dingdou, Wang Wei, Zhang Yang. Sensorless control of permanent magnet synchronous motor in full speed range[J]. Chinese Journal of Electrical Engineering, 2022, 8(2): 97-107.
[14] Pasqualotto D, Rigon S, Zigliotto M. Sensorless speed control of synchronous reluctance motor drives based on extended Kalman filter and neural magnetic model[J]. IEEE Transactions on Industrial Electronics, 2023, 70(2): 1321-1330.
[15] Bugsch M, Piepenbreier B. High-bandwidth sensor- less control of synchronous reluctance machines in the low- and zero-speed range[J]. IEEE Transactions on Industry Applications, 2020, 56(3): 2663-2672.
[16] Lu Wenqi, Li Qiang, Lu Kaiyuan, et al. Load adaptive PMSM drive system based on an improved ADRC for manipulator joint[J]. IEEE Access, 2021, 9: 33369- 33384.
[17] Wang Bo, Tian Minghe, Yu Yong, et al. Enhanced ADRC with quasi-resonant control for PMSM speed regulation considering aperiodic and periodic dis- turbances[J]. IEEE Transactions on Transportation Electrification, 2022, 8(3): 3568-3577.
[18] Lin Ping, Wu Zhen, Liu Kunzhi, et al. A class of linear-nonlinear switching active disturbance rejection speed and current controllers for PMSM[J]. IEEE Transactions on Power Electronics, 2021, 36(12): 14366-14382.
[19] Lin Shiyu, Cao Yanfei, Li Chen, et al. Two-degree- of-freedom active disturbance rejection current control for permanent magnet synchronous motors[J]. IEEE Transactions on Power Electronics, 2023, 38(3): 3640-3652.
[20] Yan Zishuo, Zhou Yonghua. Application to optimal control of brushless DC motor with ADRC based on genetic algorithm[C]//2020 IEEE International Con- ference on Advances in Electrical Engineering and Computer Applications(AEECA), Dalian, China, 2020: 1032-1035.
[21] Wang Yicheng, Fang Shuhua, Hu Jianxiong. Active disturbance rejection control based on deep reinforcement learning of PMSM for more electric aircraft[J]. IEEE Transactions on Power Electronics, 2023, 38(1): 406-416.
[22] Hao Zhengjie, Yang Yang, Gong Yimin, et al. Linear/ nonlinear active disturbance rejection switching control for permanent magnet synchronous motors[J]. IEEE Transactions on Power Electronics, 2021, 36(8): 9334-9347.
[23] Zhu Lianghong, Zhang Guoqiang, Jing Runze, et al. Nonlinear active disturbance rejection control strategy for permanent magnet synchronous motor drives[J]. IEEE Transactions on Energy Conversion, 2022, 37(3): 2119-2129.
[24] 朱良红, 张国强, 李宇欣, 等. 基于级联扩张观测器的永磁电机无传感器自抗扰控制策略[J]. 电工技术学报, 2022, 37(18): 4614-4624.
Zhu Lianghong, Zhang Guoqiang, Li Yuxin, et al. Active disturbance rejection control for position sensorless permanent magnet synchronous motor drives based on cascade extended state observer[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4614-4624.
[25] Nguyen H V, Suleimenov K, Nguyen B H, et al. Dynamical delay unification of disturbance observation techniques for PMSM drives control[J]. IEEE/ASME Transactions on Mechatronics, 2022, 27(6): 5560-5571.
[26] 李思毅, 苏健勇, 杨贵杰. 基于自抗扰控制的永磁同步电机弱磁控制策略[J]. 电工技术学报, 2022, 37(23): 6135-6144.
Li Siyi, Su Jianyong, Yang Guijie. Flux weakening control strategy of permanent magnet synchronous motor based on active disturbance rejection control[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 6135-6144.
Abstract Synchronous Reluctance Motor (SynRM) is widely used in air compressors, fans, and electric vehicles because of its wide speed range, strong overload capacity, low cost, high reliability, and insensitive temperature rise during operation. To ensure the control accuracy of position and speed, installing a position sensor is necessary for position and speed measurement of the rotor, which makes the motor occupy a large volume, the cost is high, reliability is low, and immunity is weak. Therefore, taking the synchronous reluctance motor as the research object, this paper studies its speed sensorless control strategy to enhance system immunity.
A speed sensor-free control strategy based on a magnetic chain observer is studied. However, the cross-coupling effect exists during the operation of SynRM, which causes the inductance to change nonlinearly with the current, reducing the accuracy of the rotor position estimated by the flux observer. Voltage with different amplitudes and frequencies is injected into the d-q axis by the static experiment. The forward Euler method is used to calculate the d-q axis magnetic chain. The linear least square method fits the non-linear function model of the d-q axis magnetic chain and current. Finally, the function model is applied to the magnetic chain observer to improve the rotor speed and position estimation accuracy.
A speed sensorless controller strategy for SynRM based on auto-disturbance rejection technology is studied to overcome weak immunity and low robustness. Firstly, the design principle of the ADRC is analyzed, and an ADRC suitable for SynRM is selected. According to the SynRM mechanical motion state equation, load variation is regarded as a total disturbance, and the disturbance is quickly observed and compensated. In view of the disadvantage of extensive parameters and complex adjustment in ADRC, a linear function is used instead of the original nonlinear function, which improves the robustness of the system.
Finally, a Matlab/Simulink simulation model of speed sensorless control strategy for the synchronous reluctance motor is built based on auto-disturbance rejection technology. The nonlinear function model of d-q axis flux and d-q axis current considering the cross-coupling effect is established and applied to the flux closed-loop observer method, improving the rotor position estimation accuracy. At the same time, a first-order linear active disturbance rejection controller is designed to improve the speed loop. The disturbance is compensated in time while observing the motor motion state, and the problems of overshoot, slow response speed, and slow speed recovery time when the motor is perturbed are solved.
keywords：Synchronous reluctance motor, flux observer, first order linear active disturbance rejection controller, cross-coupled, speed sensorless control
DOI: 10.19595/j.cnki.1000-6753.tces.230967
中图分类号：TM352
国家自然科学基金资助项目（52177194）。
收稿日期 2023-06-23
改稿日期 2023-07-20
王建渊 男，1979年生，副教授，硕士生导师，研究方向为同步电机控制、能源互联变换器等。E-mail: wangiianyuan2003@163.com（通信作者）
王海啸 男，1998年生，硕士研究生，研究方向为电力电子与电气传动。E-mail: tsunami13099557788@163.com
（编辑 崔文静）