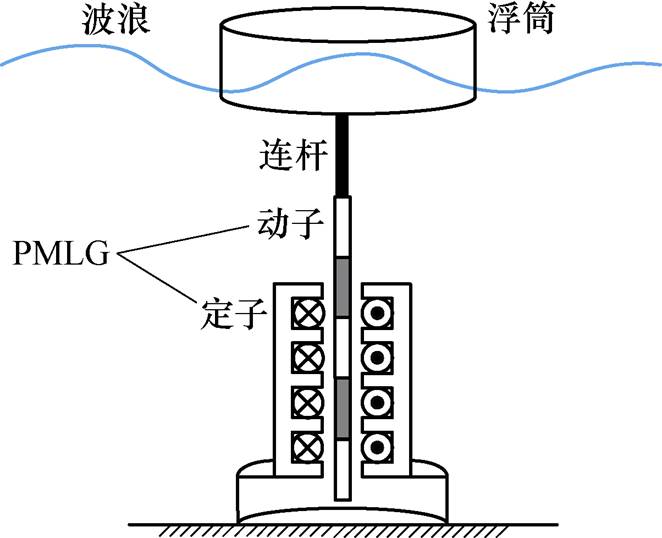
图1 直驱式波浪发电装置模型
Fig.1 Direct-drive wave power plant model
摘要 直驱式波浪发电系统具有结构简单、成本低、效率高等优点,得到了国内外学者的广泛关注。该文以直驱式波浪发电系统为研究对象,分析并建立了直驱式波浪发电装置的水动力数学模型和永磁直线电机的动态数学模型。推导了基于模型预测的功率控制策略用于直驱式波浪发电系统。在功率控制策略中从功率捕获策略和功率跟踪控制策略展开研究以实现将波浪能转换为电能并汇入直流母线。重点围绕功率捕获策略开展基于模型预测控制技术研究,分别从控制策略、预测区间和成本函数三个角度分析了基于模型预测的最优功率捕获策略。建立了仿真模型并进行仿真分析,结果表明,采用基于模型预测的最优功率捕获策略可有效提高不规则波下发电机从波浪发电系统捕获能量。此外,采用以直流母线功率汇入最大为目标的成本函数可以有效地提高发电机输入直流侧能量,具有重要的实用价值。最后通过实验室模拟平台进行了实验测试。
关键词:直驱式波浪发电 最优功率捕获 模型预测控制 功率跟踪控制
直驱式波浪发电系统采用直线发电机实现波浪能的直接捕获和转换,具有效率高、成本低等优点,成为波浪发电研究的热点[1],直驱式波浪发电装置由于结构简单、易于投放和安装,也成为了离岸直驱式波浪发电系统的重要研究对象[2-3]。该装置可应用于海洋钻采平台、海洋观测仪器网和海岛供电系统等深远海供用电场景。目前,直驱式波浪发电中所采用的直线电机多为永磁直线电机(Permanent Magnet Linear Generator, PMLG)。这主要是由于PMLG本身功率密度高,应用于波浪发电的低速驱动状态,是最为实用的发电机形式。直驱式波浪发电机的能量捕获实现形式也是通过直线电机的电磁力控制进而控制电机发电功率实现功率控制[4]。直驱式波浪发电基本结构如图1所示。

图1 直驱式波浪发电装置模型
Fig.1 Direct-drive wave power plant model
直驱式波浪发电浮体跟随波浪运动,从而带动直线电机动子运动。在发电过程中,一般通过控制发电机电磁力,实现对波浪能的动态吸收,达到最优能量捕获。在控制过程中,发电装置会根据所采取的功率捕获策略为PMLG提供一个功率参考值,接着PMLG就会根据这一参考值动态控制发电机电流实现最优功率到直流母线控制。因此,整个波浪发电系统至少要完成两个任务:一是实现对波浪能的最优捕获,给出电机动态功率参考值;二是实现动态功率的跟踪控制[5]。由于波浪具有随机性,波浪的运动是不断变化的,因此直驱式波浪发电系统的功率捕获策略对装置从波浪中获取的能量具有较大的影响。研究直驱式波浪发电系统的功率捕获策略对提高波浪发电装置的能量转换效率具有重要意义。此外,由于波浪环境的复杂性,波浪发电装置在波浪中可能会遭受一些极端情况。对于波浪发电而言,要考虑波浪发电装置本身额定参数的限制,即考虑波浪能的功率捕获时应当对整个系统综合考虑。因此,研究波浪发电系统的最优功率捕获策略而不是最大功率捕获策略具有重要实际意义。
为实现直驱式波浪发电系统的最优功率捕获,近些年来,国内外学者在模型预测控制(Model Predictive Control, MPC)方向进行了深入的研究[6]。模型预测控制作为一种最优控制方法,可以实现直驱式波浪发电系统的最优功率捕获。其中,模型预测控制的多约束的特性可以解决极端海域下波浪发电装置的安全性问题,因此该控制非常适合用于直驱式波浪发电系统的功率捕获。文献[7]基于二次规划求解方法,通过构造成本函数使得成本函数呈凸性,从而求得波浪功率捕获的最优条件。文献[8]提出了直驱式波浪发电系统的经济模型预测控制(Economic Model Predictive Control, EMPC),实现了最大波能捕获。文献[9]给出了基于滑模控制的改进模型预测控制方法,滑模控制器用来补偿模型失配以提高控制的精度,同时降低处理器的控制性能。但以上方法仅研究波浪捕获的最优实现条件,而对于直驱式波浪发电系统而言,要考虑使得汇入直流母线的功率实现最优。因此,研究汇入直流母线功率最优具有重要的实际意义。
本文首先阐释了直驱式波浪发电装置水动力参数的关系,建立了波浪发电系统的模型。对于所建立模型提出了基于EMPC的直驱式波浪发电最优功率捕获策略,分析了该策略的控制原理与优越性。此外,本文还研究了实现PMLG电磁功率最优化和PMLG汇入直流母线功率最优化的不同成本函数对系统的影响,并在此基础上探究了预测区间对系统的影响规律。其次基于模型预测动态电流控制,实现了PMLG功率的动态跟踪控制。最后基于实验室波浪发电模拟实验平台开展了直驱式模型预测控制技术实验研究,完成了控制策略和功率传递规律的验证。
直驱式波浪发电装置的受力分析如图2所示,模型由浮筒、连杆及PMLG组成。为了简化分析,连杆考虑为刚体。由于水平方向的波浪运动对竖直方向的波浪运动影响较小,因此忽略水平方向的波浪力的作用[10-11],可得直驱式波浪发电装置在竖直方向波浪作用下的运动方程[12]为
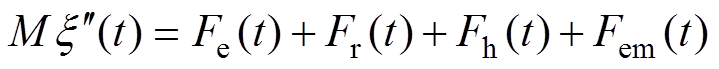 (1)
(1)
式中,M为发电装置运动部分的总质量;Fe(t)为波浪激振力;Fr(t)为波浪辐射力;Fh(t)为浮子的静水力;Fem(t)为PMLG的电磁推力;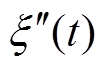 为装置运动的加速度,由此可知,
为装置运动的加速度,由此可知,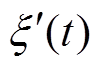 为装置运动速度,
为装置运动速度,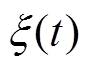 为装置运动位移。
为装置运动位移。
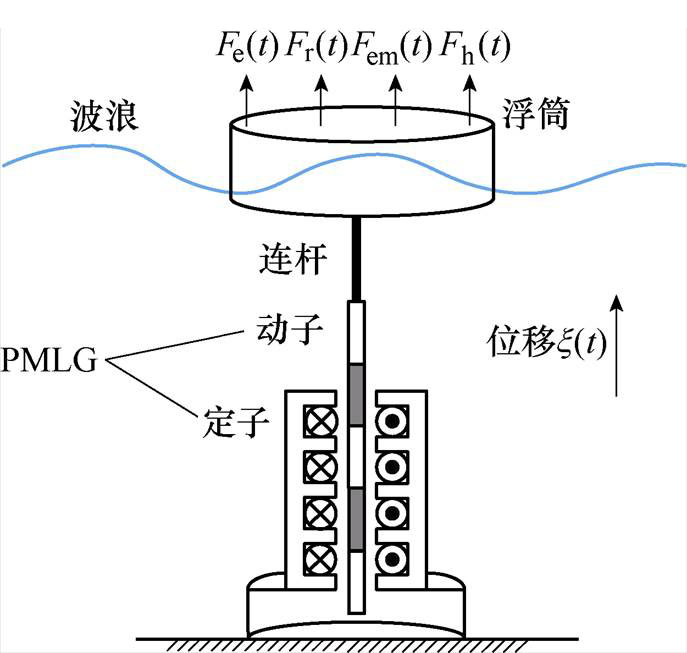
图2 直驱式波浪发电装置受力分析
Fig.2 Force analysis of point absorber wave power generation device model
通过将重力与静水压力的表面积分相加便可获得静水力,其可以表示为
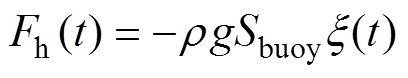 (2)
(2)
式中,Sbuoy为浮子的底表面积;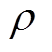 为海水密度;
为海水密度;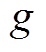 为重量加速度;
为重量加速度;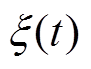 为动子位移。定义Kh=
为动子位移。定义Kh=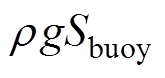 ,记为静水力系数。
,记为静水力系数。
波浪激振力Fe(t)可表示为激振力的非因果脉冲响应函数he(t)和波面方程h(t)的卷积,有
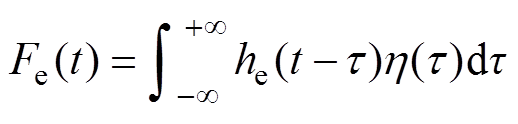 (3)
(3)
对于不规则波,波浪激振力可以视为每个不同频率下波浪激振力叠加所形成的,有
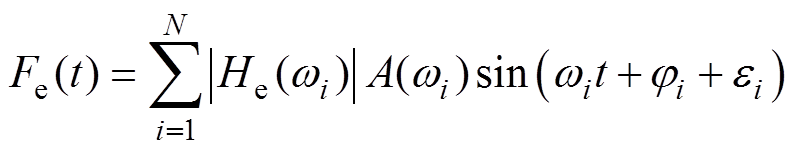 (4)
(4)
式中,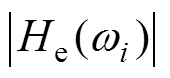 为激振力频率响应的幅值;
为激振力频率响应的幅值;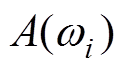 第i个规则波的幅度值;
第i个规则波的幅度值;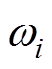 为第i个规则波波浪角频率;
为第i个规则波波浪角频率;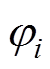 为激振力频率响应的相位;
为激振力频率响应的相位;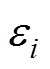 为第i个规则波的随机相位,在[0, 2p]区间内随机分布。
为第i个规则波的随机相位,在[0, 2p]区间内随机分布。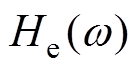 可以利用基于边界元法的开源软件Nemonh获得[13]。本文则利用Nemonh软件对一个半径为6 m,高为10 m的浮筒进行水动力分析,频率响应结果如图3所示。所得到的波浪激振力波形如图4所示。
可以利用基于边界元法的开源软件Nemonh获得[13]。本文则利用Nemonh软件对一个半径为6 m,高为10 m的浮筒进行水动力分析,频率响应结果如图3所示。所得到的波浪激振力波形如图4所示。
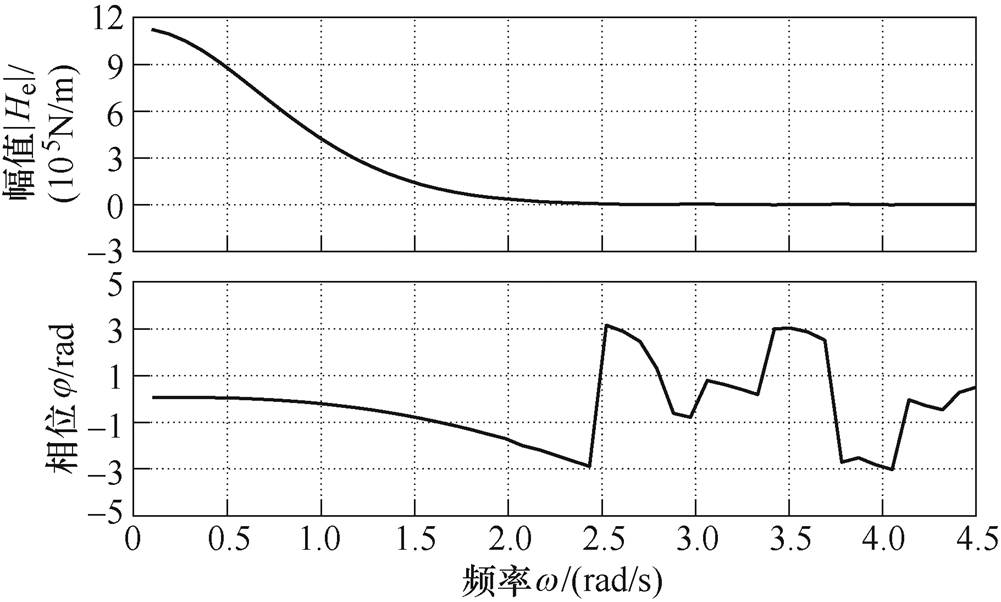
图3 波面方程对激振力的频率响应
Fig.3 Frequency response of the wavefront equation to an excitation force
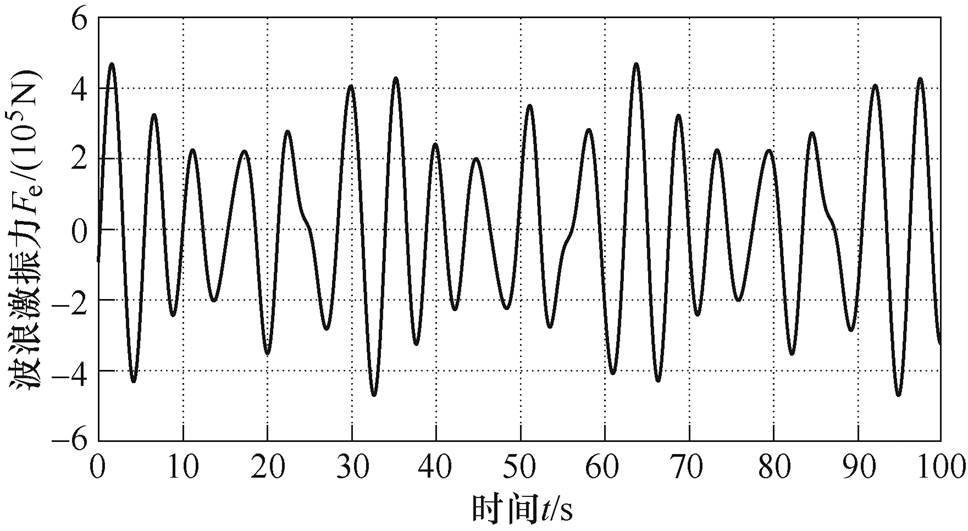
图4 波浪激振力波形
Fig.4 Wave excitation force waveform
波浪辐射力Fr(t)可以表示为
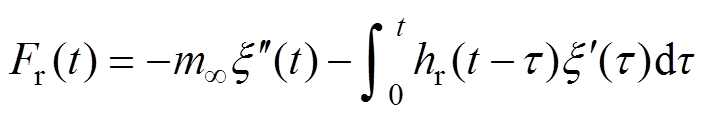 (5)
(5)
式中,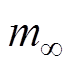 为无限频率下的附加质量;hr(t)为辐射脉冲响应函数。
为无限频率下的附加质量;hr(t)为辐射脉冲响应函数。
辐射力包含一项辐射脉冲响应函数hr(t)与装置运动速度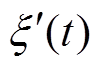 的卷积。通常采用状态空间方程近似代替该卷积项[14],有
的卷积。通常采用状态空间方程近似代替该卷积项[14],有
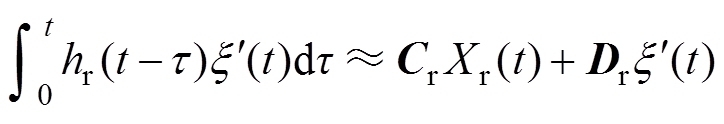 (6)
(6)
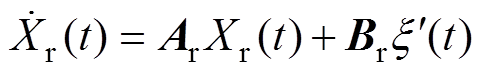 (7)
(7)
式中,Ar、Br、Cr和Dr为上述状态空间方程的系数矩阵;n为Ar矩阵的阶数;Xr(t)为状态变量,无实际意义。
PMLG具有非线性、强耦合的特点,为了简化分析,假设气隙磁场呈正弦分布,忽略PMLG的定位力,不计铁耗、摩擦等损耗[15-16]。按照发电机惯例,基于动子磁场定向,可得dq坐标系下PMLG的电压方程满足
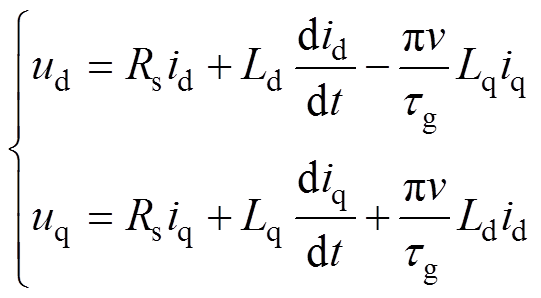 (8)
(8)
式中,Rs为电机绕组内阻;Ld、Lq分别为d轴和q轴电感;v为电机动子的运行速度;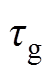 为电机极距;id、iq分别为d轴和q轴绕组电流;ud、uq分别为d轴和q轴绕组端电压。
为电机极距;id、iq分别为d轴和q轴绕组电流;ud、uq分别为d轴和q轴绕组端电压。
PMLG电磁推力方程满足
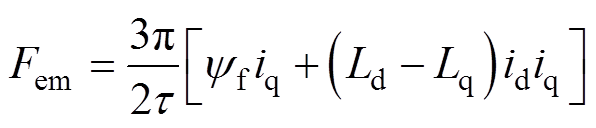 (9)
(9)
式中,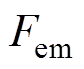 为电机电磁力;
为电机电磁力;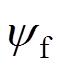 为空载磁链。
为空载磁链。
当电机为表贴式永磁电机时,有Ld=Lq,因此此时电磁推力方程可以写为
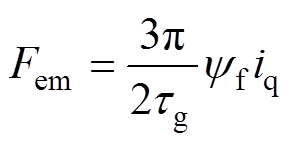 (10)
(10)
为实现波浪能发电,有两个任务需要完成:一是实现功率捕获;二是实现PMLG的功率跟踪控制。本节将详细给出基于模型预测的功率捕获策略,并简要说明PMLG的功率跟踪控制。
2.1.1 状态空间方程
结合式(1)、式(2)、式(5)~式(7),将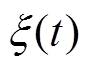 、
、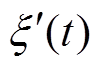 以及Xr(t)列为状态变量集合x,可得直驱式波浪发电装置水动力模型的状态空间方程为
以及Xr(t)列为状态变量集合x,可得直驱式波浪发电装置水动力模型的状态空间方程为
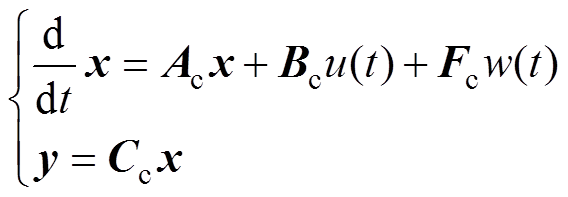 (11)
(11)
其中
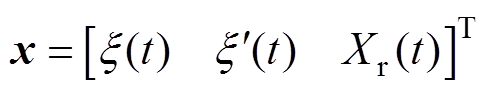 (12)
(12)
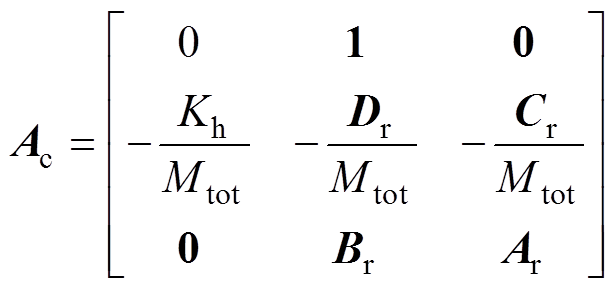 (13)
(13)
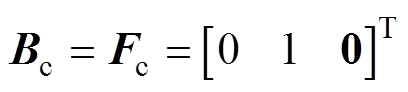 (14)
(14)
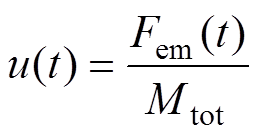 (15)
(15)
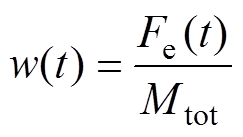 (16)
(16)
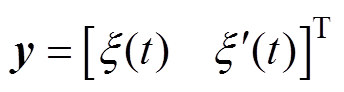 (17)
(17)
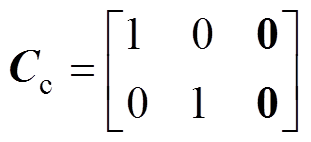 (18)
(18)
式中,Mtot为无限频率下的附加阻尼m∞与装置运动部分质量M之和。
实时控制器多采用离散化的形式进行控制。将上述空间方程利用零阶保持器进行离散化,有
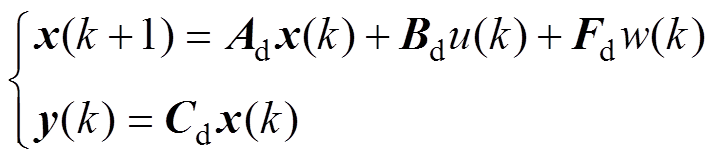 (19)
(19)
其中
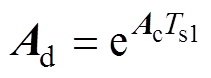 (20)
(20)
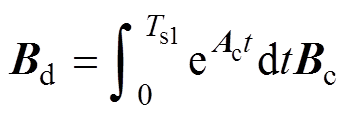 (21)
(21)
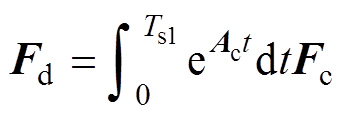 (22)
(22)
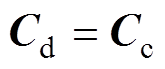 (23)
(23)
式中,Ts1为状态空间方程的离散化周期。为了兼顾下文PMLG的功率跟踪控制,本文取Ts1=0.1 s。
对于控制器,通常将输入控制信号的差值作用于系统中。因此,引入控制输入量u(t)的差值。k时刻,控制输入的差值Du(k)可表示为
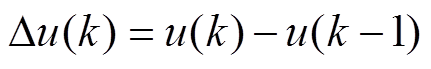 (24)
(24)
式中,u(k-1)为k-1时刻下控制器对波浪发电装置的控制总量;Du(k)为模型预测控制求得k时刻控制器向波浪发电装置的输入变化量。
因此,直驱式波浪发电装置水动力模型的增广状态空间方程可表示为
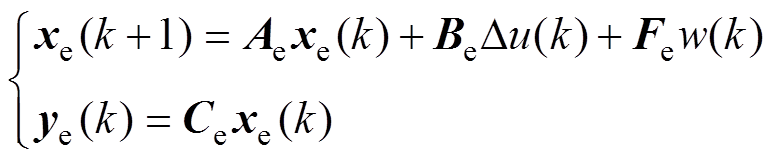 (25)
(25)
其中
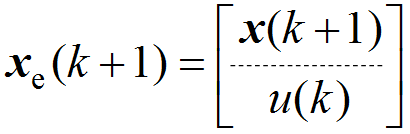 (26)
(26)
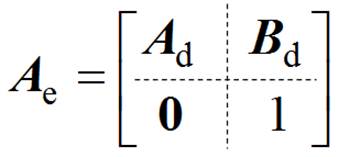 (27)
(27)
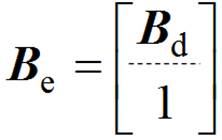 (28)
(28)
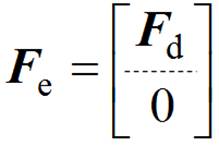 (29)
(29)
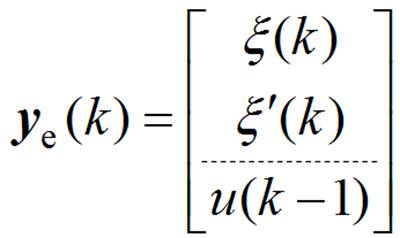 (30)
(30)
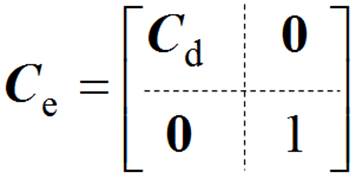 (31)
(31)
2.1.2 成本函数
在预测区间内PMLG从波浪中获取的平均电磁功率P1可表示为
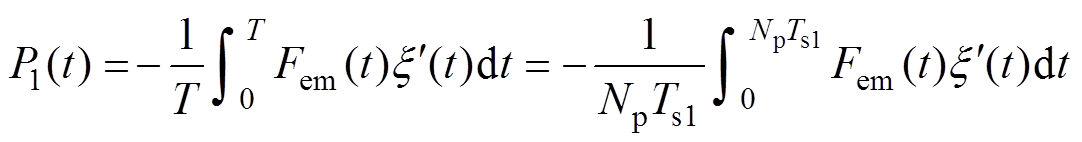 (32)
(32)
式中,T为预测区间内的总时间;Np为预测区间。利用零阶保持器对式(32)进行离散化,有
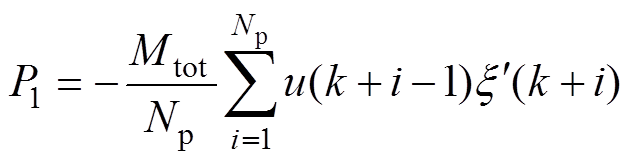 (33)
(33)
由此,考虑PMLG的电磁功率下的成本函数可写为
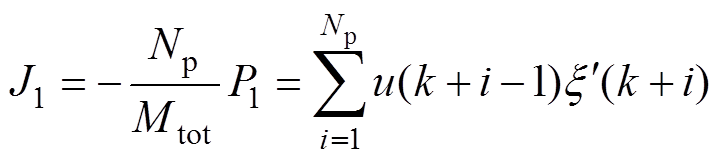 (34)
(34)
PMLG端口输出功率为电机的电磁功率与电枢绕组铜耗之差。当不考虑换流器的损耗时,则可认为PMLG端口的输出功率为汇入直流母线的功率。当PMLG采用id=0的控制策略时,dq坐标系下PMLG电枢绕组的铜耗为
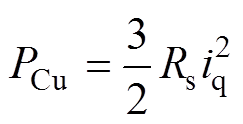 (35)
(35)
因此,结合式(10),经过零阶保持器离散后的PMLG端口的平均输出功率P2为
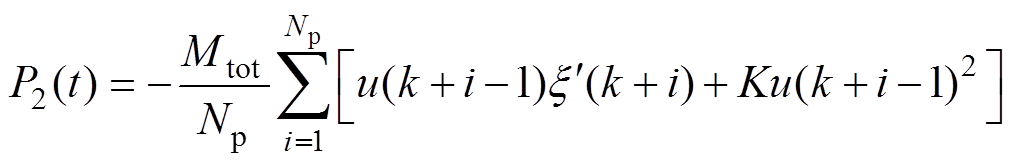 (36)
(36)
其中
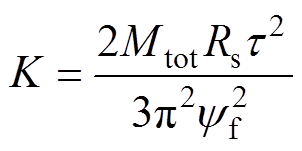 (37)
(37)
因此,考虑PMLG汇入直流母线功率最大的成本函数可写为
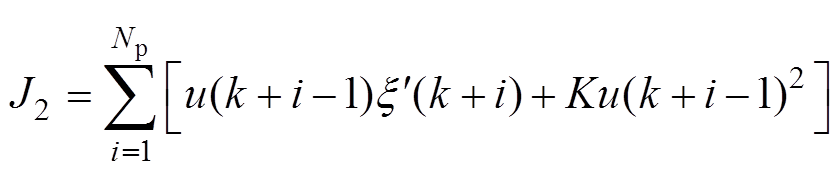 (38)
(38)
2.1.3 预测模型
利用式(25)可对直驱式波浪发电装置的水动力模型在预测区间内获取系数模型的参数,定义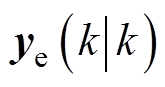 为ye(k)在k时刻下的预测值,则有
为ye(k)在k时刻下的预测值,则有
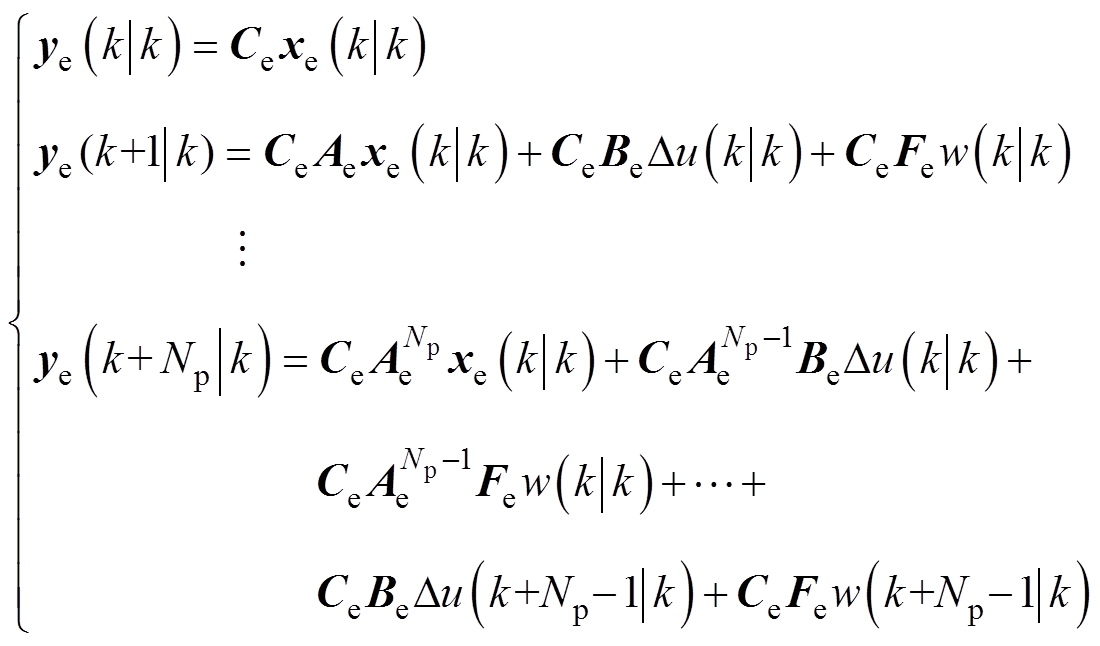 (39)
(39)
忽略式(39)中的第一项,可写为矩阵形式,有
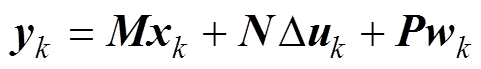 (40)
(40)
其中
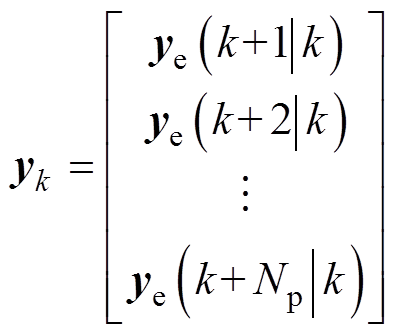 (41)
(41)
 (42)
(42)
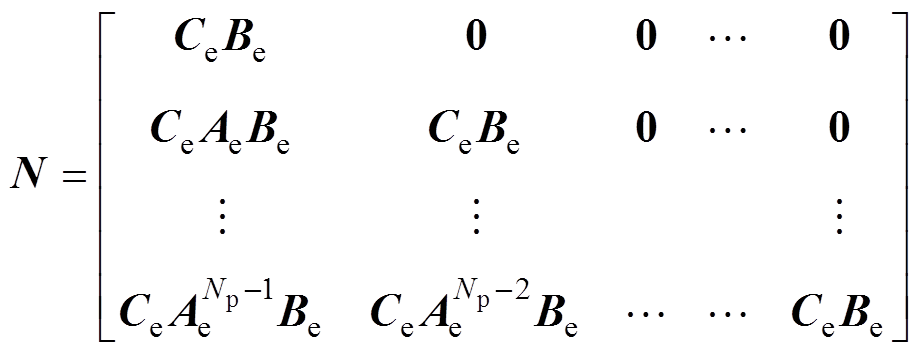 (43)
(43)
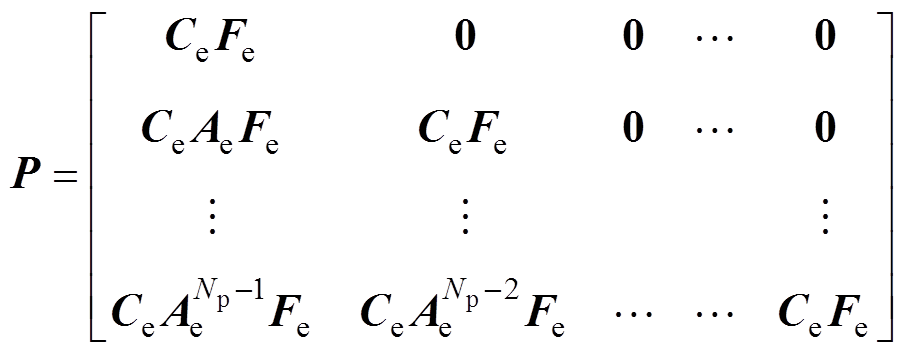 (44)
(44)
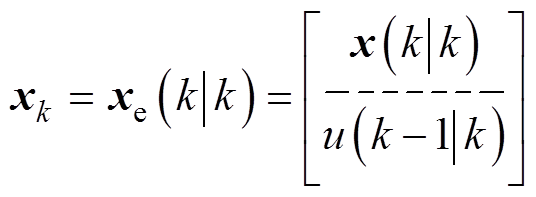 (45)
(45)
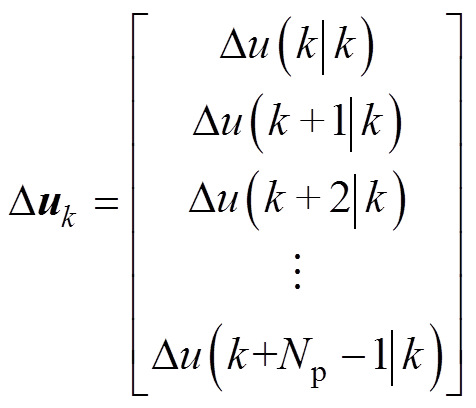 (46)
(46)
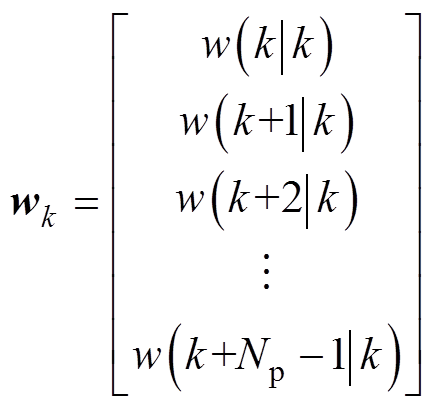 (47)
(47)
基于以上分析,k时刻成本函数J1(k)可写为
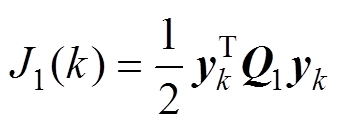 (48)
(48)
其中
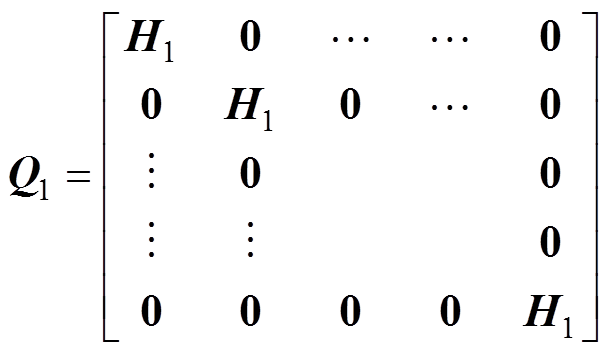 (49)
(49)
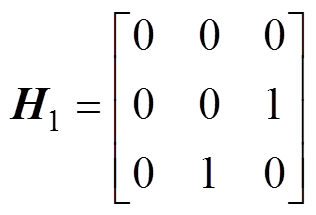 (50)
(50)
同理,k时刻成本函数J2(k)可写为
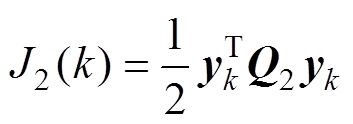 (51)
(51)
其中
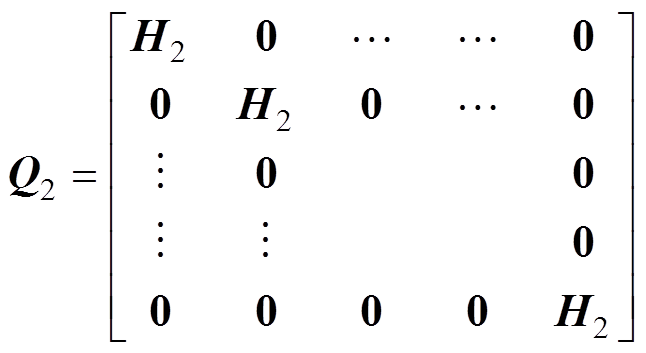 (52)
(52)
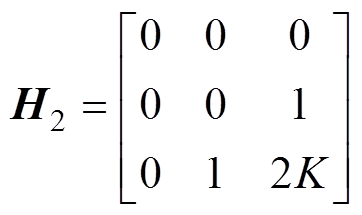 (53)
(53)
将式(40)代入式(48),整理得
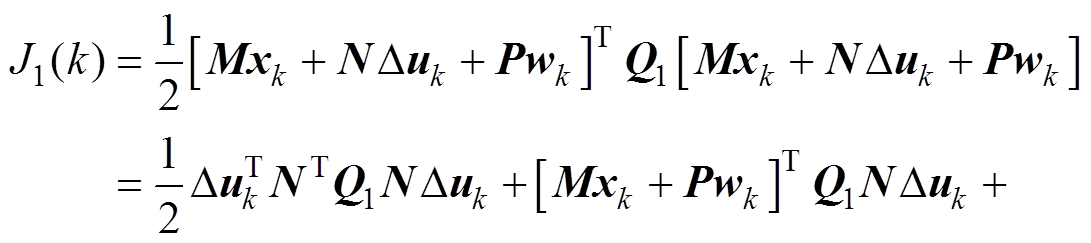
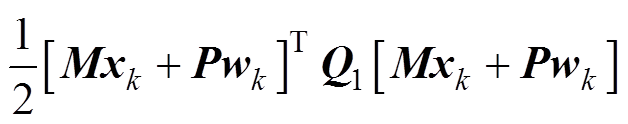 (54)
(54)
式(54)可简化为
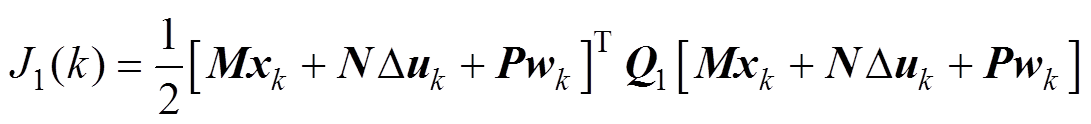
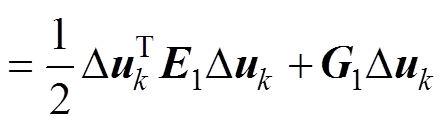 (55)
(55)
其中
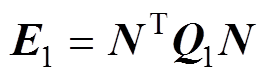 (56)
(56)
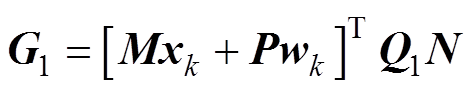 (57)
(57)
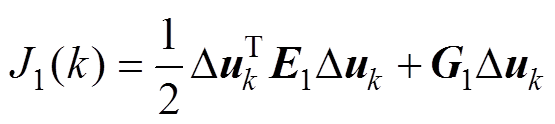 为标准的二次规划形式,可以利用二次规划求解。成本函数J2(k)的表达形式与J1(k)相同。
为标准的二次规划形式,可以利用二次规划求解。成本函数J2(k)的表达形式与J1(k)相同。
2.1.4 约束条件
直驱式波浪发电装置的约束条件主要表现在对装置的运动速度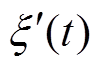 、位移
、位移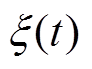 、PMLG的电磁推力Fem的约束,因此可写为
、PMLG的电磁推力Fem的约束,因此可写为
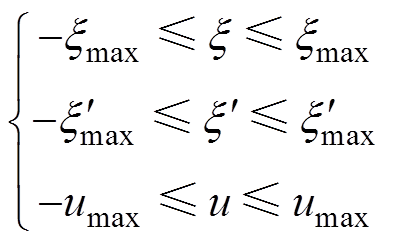 (58)
(58)
式中,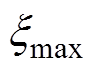 、
、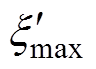 、umax分别为装置的运动位移、速度、控制输入量u的最大值。
、umax分别为装置的运动位移、速度、控制输入量u的最大值。
为了实现功率传递到直流母线,需要控制PMLG将系统的控制输入量传递到直流母线。控制系统的控制输入量即控制PMLG的电磁推力,根据式(13)可知,也就是控制PMLG的电流。由于该部分不是本文的研究重点,将采用常用的模型预测电流控制(Model Predictive Current Control, MPCC)将功率传递到直流母线侧,完成整个控制过程。
采用欧拉近似法对式(8)进行离散化,有
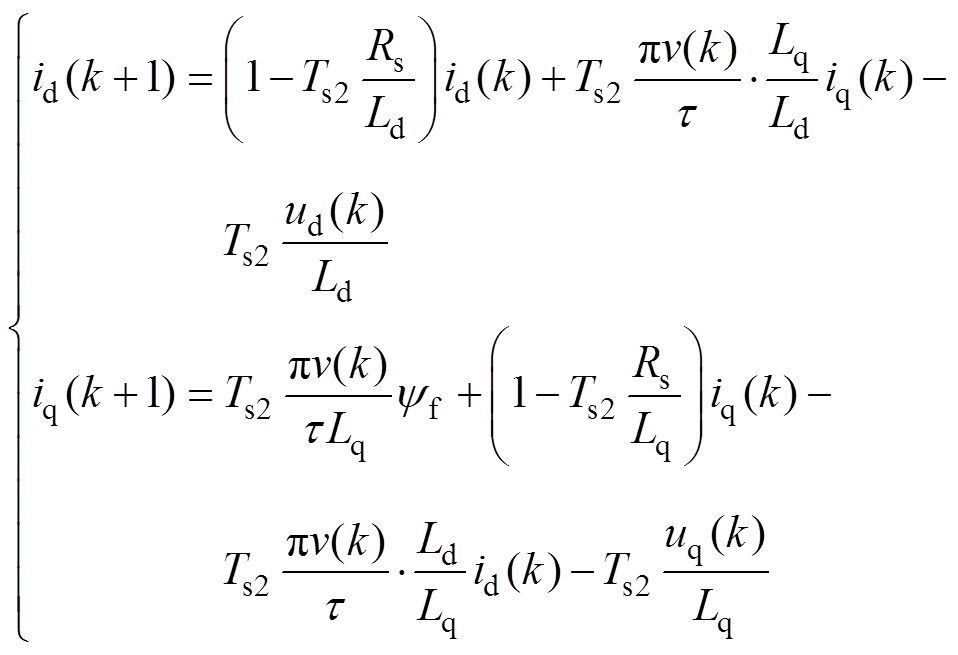 (59)
(59)
式中,Ts2为系统离散时间步长。
式(59)为PMLG的MPCC的预测模型。为保证控制效果,取Ts2=100 ms。
MPCC的成本函数可写为
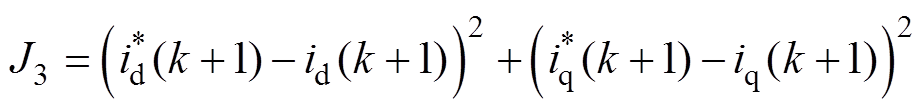 (60)
(60)
本文采用id=0的控制策略,因此d轴电流的参考值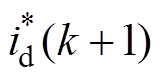 为0。q轴电流的参考值
为0。q轴电流的参考值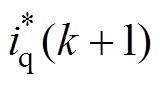 ,可以采用拉格朗日外推法进行延时补偿,有
,可以采用拉格朗日外推法进行延时补偿,有
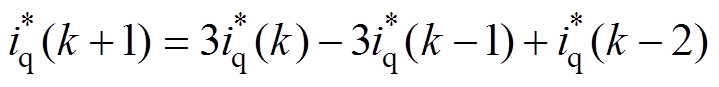 (61)
(61)
k时刻q轴电流的参考值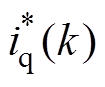 则来自基于模型预测的直驱式波浪发电最优功率捕获策略的输出项。结合式(10)和式(24),可得
则来自基于模型预测的直驱式波浪发电最优功率捕获策略的输出项。结合式(10)和式(24),可得
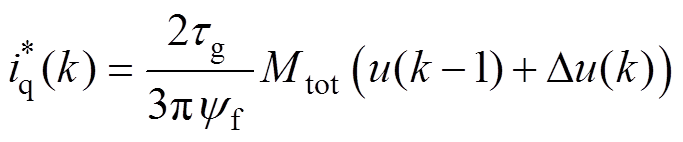 (62)
(62)
在式(62)中,成本函数则是d轴和q轴电流误差的二次方和。
MPCC的约束条件可写为
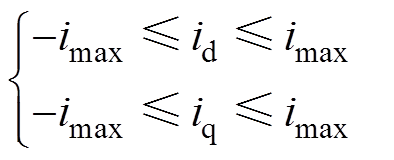 (63)
(63)
式中,imax为最大允许的定子电流。
对于一个一般性的被控对象模型,有
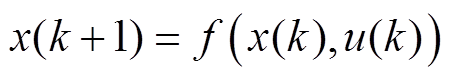 (64)
(64)
传统标准的MPC,其目标是跟踪设定终值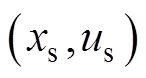 ,阶段成本函数满足
,阶段成本函数满足
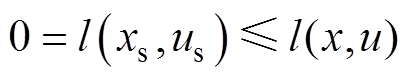 (65)
(65)
式中,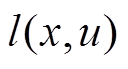 为跟踪的代价函数。离散条件下在每个周期内通过计算如下值函数来得到最优解。
为跟踪的代价函数。离散条件下在每个周期内通过计算如下值函数来得到最优解。
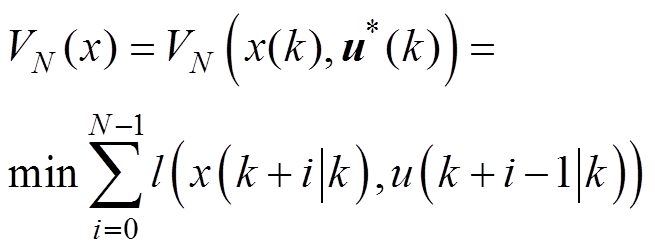 (66)
(66)
以每个周期中目标函数的最优值(即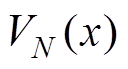 )作为Lyapunov函数,由式(65)可知该函数的正定性。下一采样时刻的函数值可以表示为
)作为Lyapunov函数,由式(65)可知该函数的正定性。下一采样时刻的函数值可以表示为
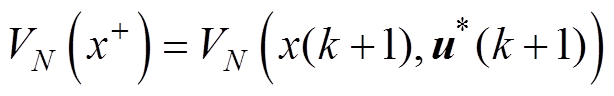 (67)
(67)
结合式(66)可进一步得到
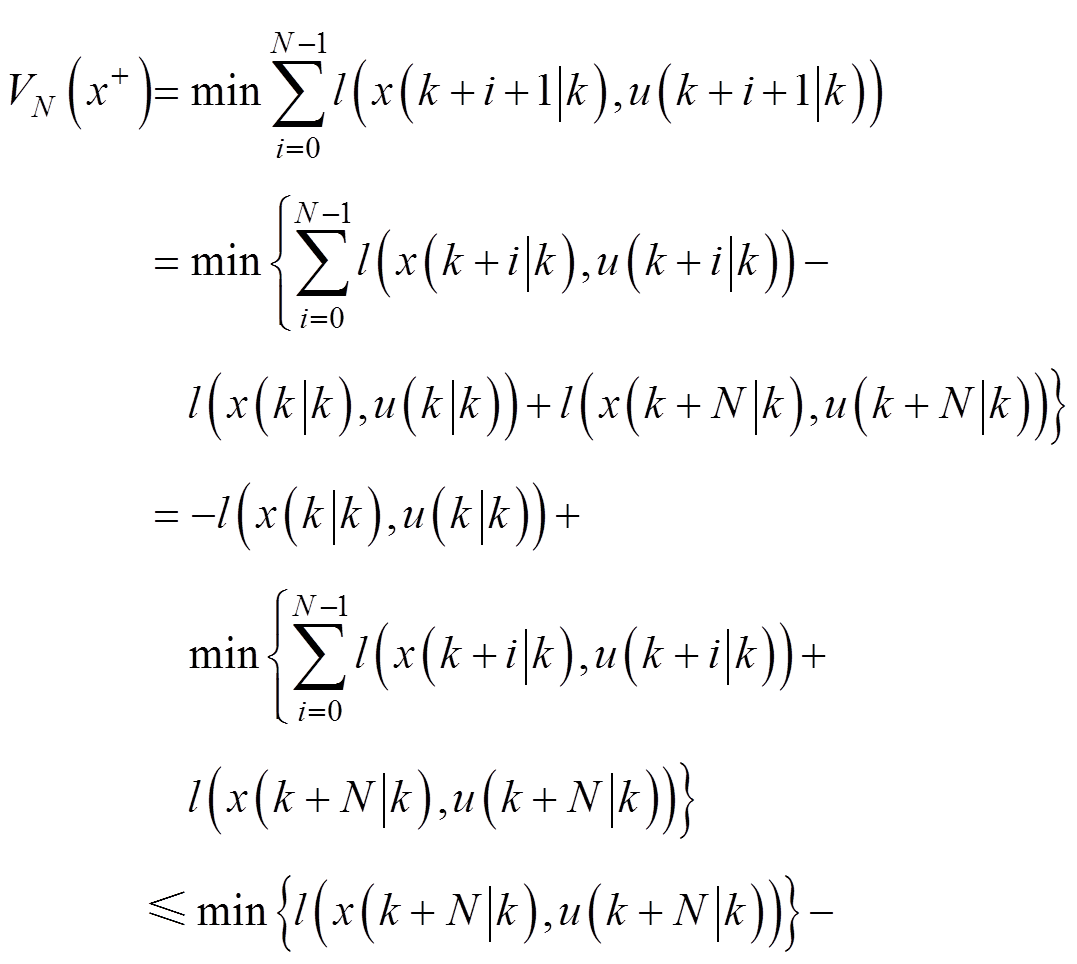
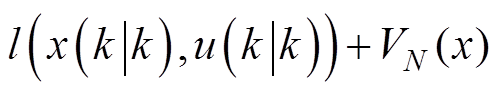 (68)
(68)
结合式(65)可得
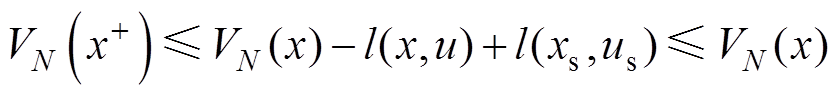 (69)
(69)
由此可以证明标准MPC的渐近稳定性。
上述条件式(69)成立的前提是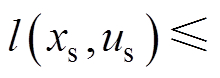
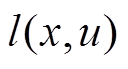 ,但是对于EMPC来说,如式(34)中成本函数J1,其以最大化能量吸收作为经济目标,存在阶段成本函数
,但是对于EMPC来说,如式(34)中成本函数J1,其以最大化能量吸收作为经济目标,存在阶段成本函数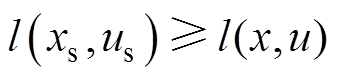 的情况,这就导致所验证标准MPC的渐近稳定性不适用于EMPC,但是可以通过引入一个辅助成本函数来验证。
的情况,这就导致所验证标准MPC的渐近稳定性不适用于EMPC,但是可以通过引入一个辅助成本函数来验证。
以成本函数J1所对应的EMPC系统为例,其可以用阶段成本函数来表示,有
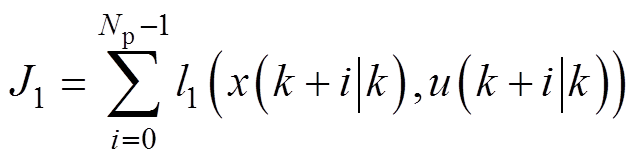 (70)
(70)
定义辅助函数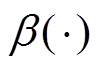 满足
满足
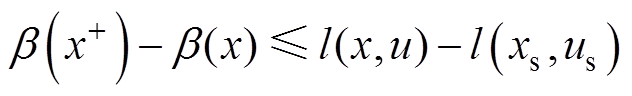 (71)
(71)
将阶段成本函数重新定义为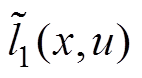 ,有
,有
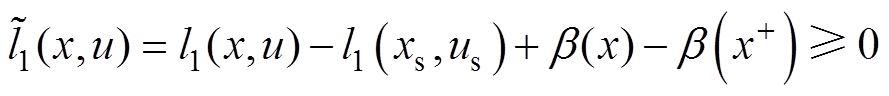 (72)
(72)
同样其成本函数可以用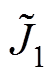 来表示,有
来表示,有
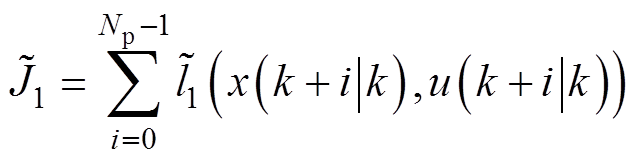 (73)
(73)
进而
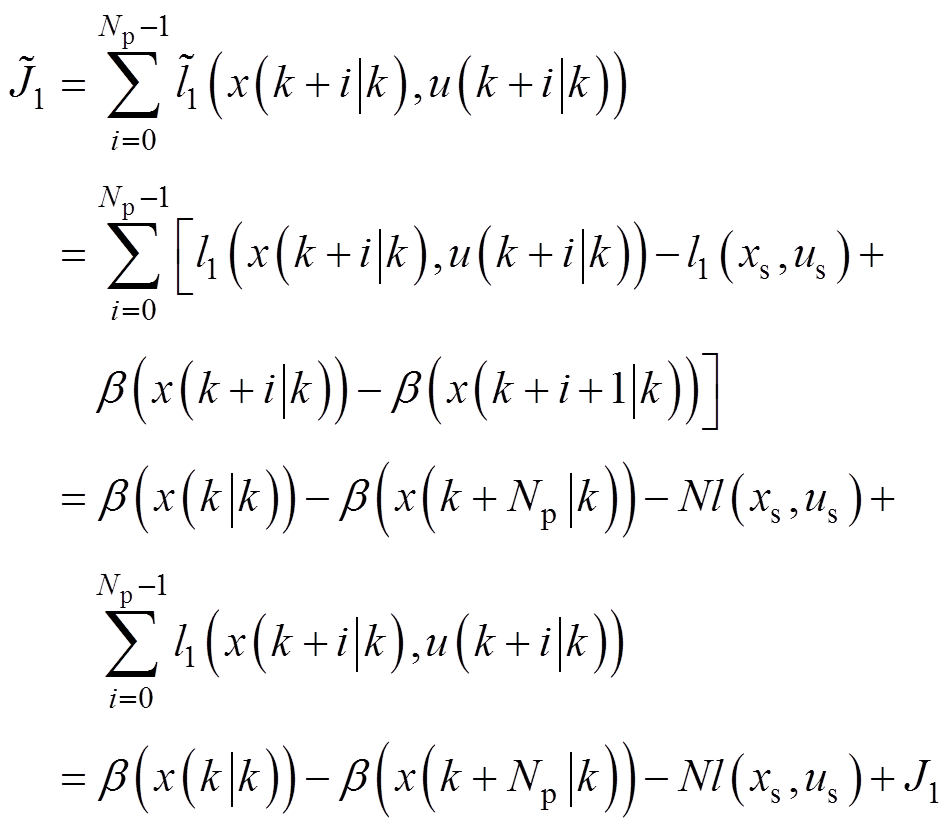 (74)
(74)
由式(74)可知,成本函数J1和成本函数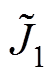 之间的差值为常数,即二者具有相同的最优控制序列。
之间的差值为常数,即二者具有相同的最优控制序列。
其辅助优化问题可以定义为
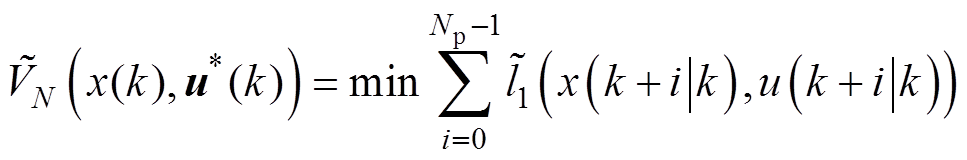 (75)
(75)
下一个采样周期的辅助优化函数能够表示为
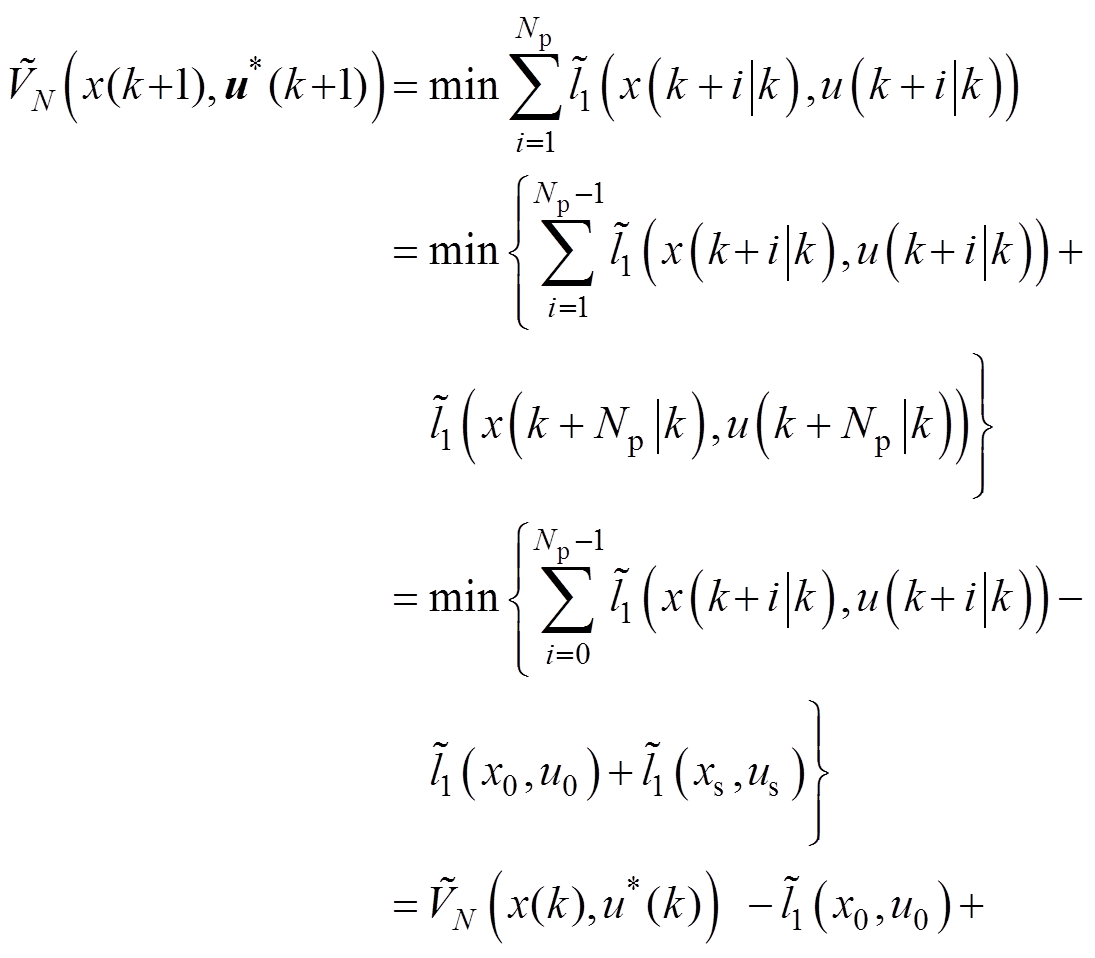
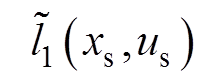 (76)
(76)
式中,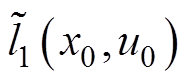 和
和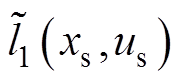 分别为阶段成本函数
分别为阶段成本函数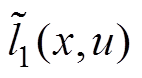 的初始值与终值。结合式(73)可知,
的初始值与终值。结合式(73)可知,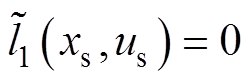 ,
,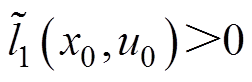 ,故而
,故而
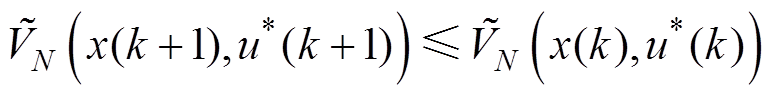 (77)
(77)
因此可以证明在本文所采用的EMPC算法下,系统是渐近稳定的。
为了验证上述控制策略,搭建了直驱式波浪发电系统的仿真模型,其结构框图如图5所示。
为了将波浪能转换为电能并传递到直流母线,首先获取直驱式波浪发电装置的运动速度和位移等参数,并由此得到波浪辐射力和静水力。利用波浪激振力预测获取波浪激振力。基于上述条件,利用基于模型预测的最优功率捕获控制策略获取波浪发电系统最优控制输入量,并将其转换为PMLG的q轴参考电流值。获取PMLG动子位置角和三相电流,由此利用坐标变换求得电机在dq坐标系下的电流实际值。在基于id=0的策略下,利用MPCC求得最优电压矢量并利用空间矢量脉宽调制(Space Vector Pulse- Width-Modulation, SVPWM)输出到功率开关管,使得功率传递到直流母线中。
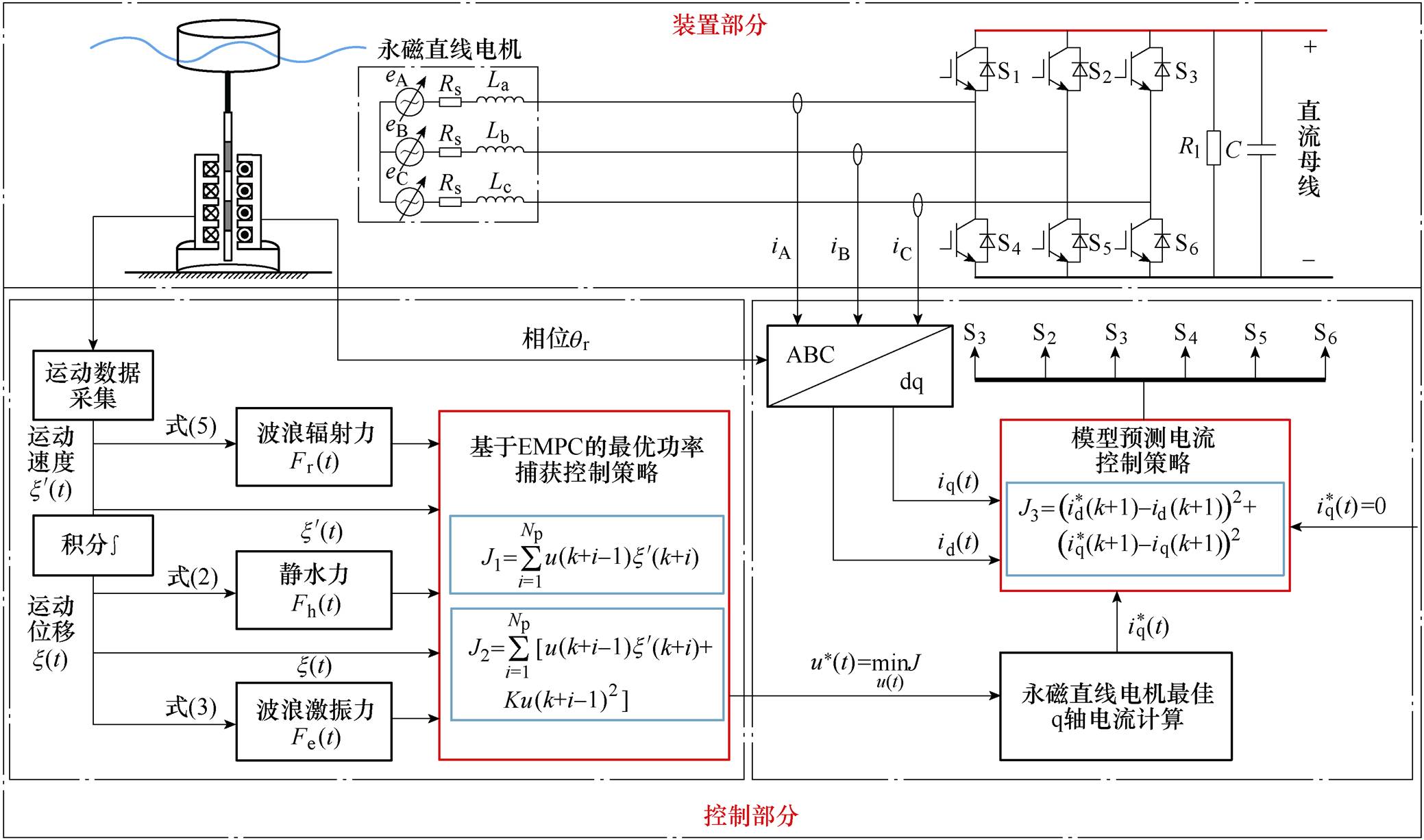
图5 直驱式波浪发电系统的控制框图
Fig.5 Control block diagram of direct-drive wave power generation system
为了验证所提出的基于模型预测的功率捕获策略的有效性,验证不同控制策略对功率捕获的影响。首先选取成本函数J1,验证在模型预测控制、单自由度控制和双自由度幅值控制下PMLG捕获功率的效果。其中,在规则波下的单、双自由度控制方法可参考文献[17],在不规则波下可利用叠加定理进行分析。对于幅值控制,有
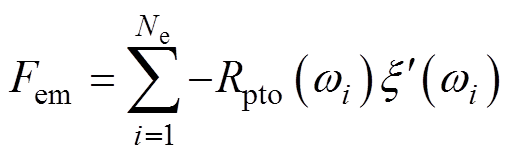 (78)
(78)
式中,Ne为离散频率的个数;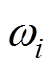 为波浪主要频率分量;Rpto为电机电磁力阻尼系数。同理可得出,复共轭控制下的电机电磁推力为
为波浪主要频率分量;Rpto为电机电磁力阻尼系数。同理可得出,复共轭控制下的电机电磁推力为
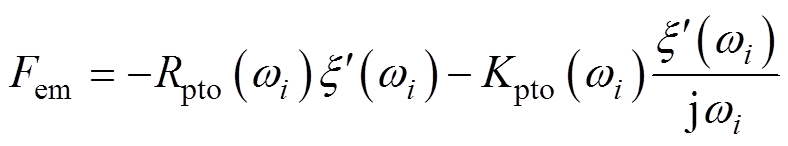 (79)
(79)
式中,j为频域下复数单位。
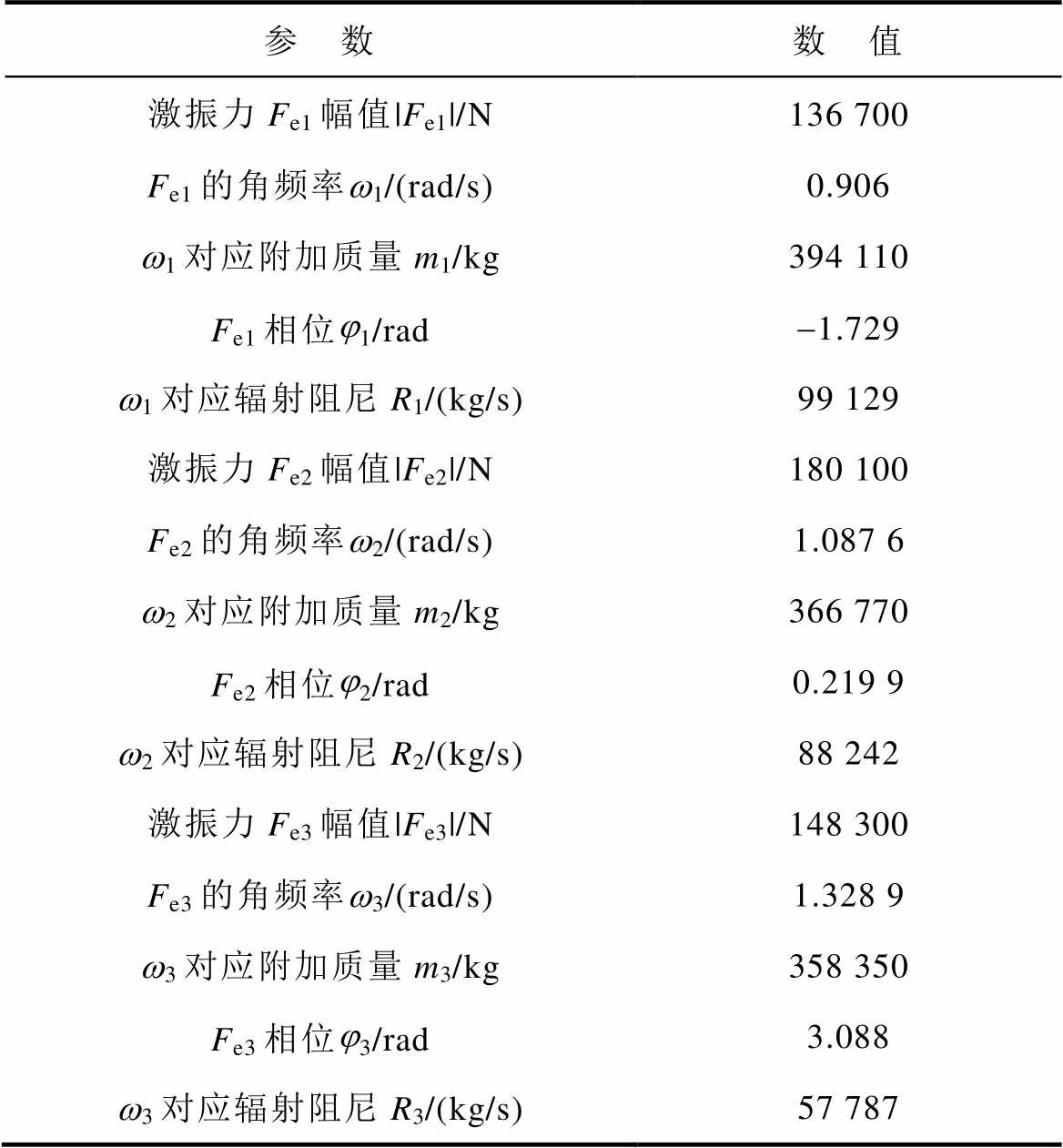
对图4所示的波浪激振力进行傅里叶变换,提取激振力中的主要信号利用叠加定理参与计算。得到的波浪参数见表1。
由此,PMLG从波浪发电系统中捕获的能量如图6所示。图中,红色线条所对应的控制为基于模型预测的最优功率捕获策略,其预测区间Np=40。从长远来看,双自由度控制下电机捕获的能量要高于单自由度控制下电机捕获的能量。双自由度控制由于选取的离散频率点的个数较少,因此不能较好地实现相位匹配,从而导致从波浪发电系统中捕获的能量较少。
此外,单自由度控制下电机从系统中捕获的能量要高于预测区间Np=10的模型预测控制下电机捕获的能量。由此可知,为了实现模型预测控制下直驱式波浪发电系统的最优功率捕获,需要研究预测区间对电机从波浪发电系统中捕获功率的影响。
表1 波浪发电系统仿真参数
Tab.1 Simulation parameters of wave power generation
参 数数 值 激振力Fe1幅值|Fe1|/N136 700 Fe1的角频率w1/(rad/s)0.906 w1对应附加质量m1/kg394 110 Fe1相位j1/rad-1.729 w1对应辐射阻尼R1/(kg/s)99 129 激振力Fe2幅值|Fe2|/N180 100 Fe2的角频率w2/(rad/s)1.087 6 w2对应附加质量m2/kg366 770 Fe2相位j2/rad0.219 9 w2对应辐射阻尼R2/(kg/s)88 242 激振力Fe3幅值|Fe3|/N148 300 Fe3的角频率w3/(rad/s)1.328 9 w3对应附加质量m3/kg358 350 Fe3相位j3/rad3.088 w3对应辐射阻尼R3/(kg/s)57 787
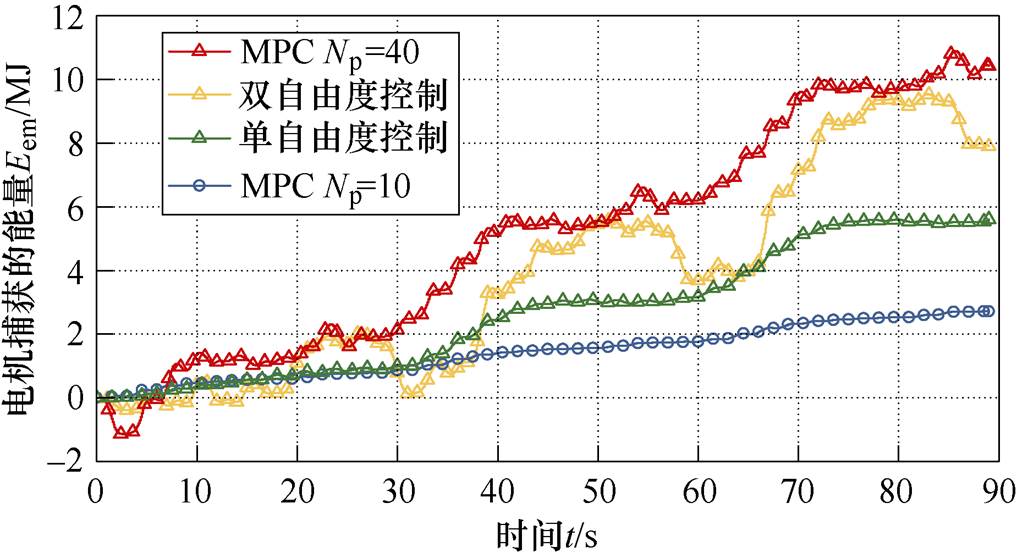
图6 不同控制策略下电机捕获的能量
Fig.6 The energy captured by the PMLG under different control strategies
为研究预测区间对功率捕获的影响,选取约束条件下预测区间Np=10~70进行分析。首先选取模型预测控制中成本函数J1进行研究。预测区间对功率捕获的影响如图7所示。
可见,随着预测区间的增大,电机捕获的能量不断增大。此外,随着预测区间的增大,电机捕获的能量波动也呈现增大的趋势。这是由于随着预测区间的增大,模型预测控制考虑在更大时域内从系统捕获更多的能量,这必然导致更大的波动。此外,在预测区间Np=50时相较于预测区间Np=40时电机捕获的能量有了较大幅度的增长,表明该预测区间与波浪周期匹配程度较高,从而使得电机从系统中捕获的能量大幅度提高。而当预测区间Np为60和70时,此时与预测区间Np=50时区别不大,表明在这两个预测区间下受到了约束条件的影响。
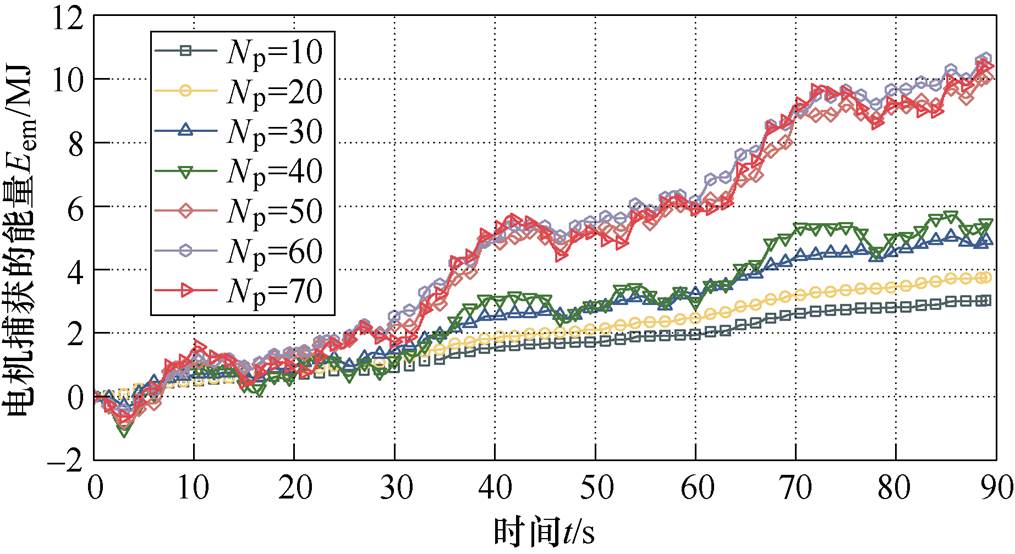
图7 成本函数J1下预测区间对功率捕获的影响
Fig.7 Effect of prediction interval on power capture under cost function J1
选取模型预测控制中成本函数J2进行研究。此时预测区间对功率捕获的影响如图8所示。
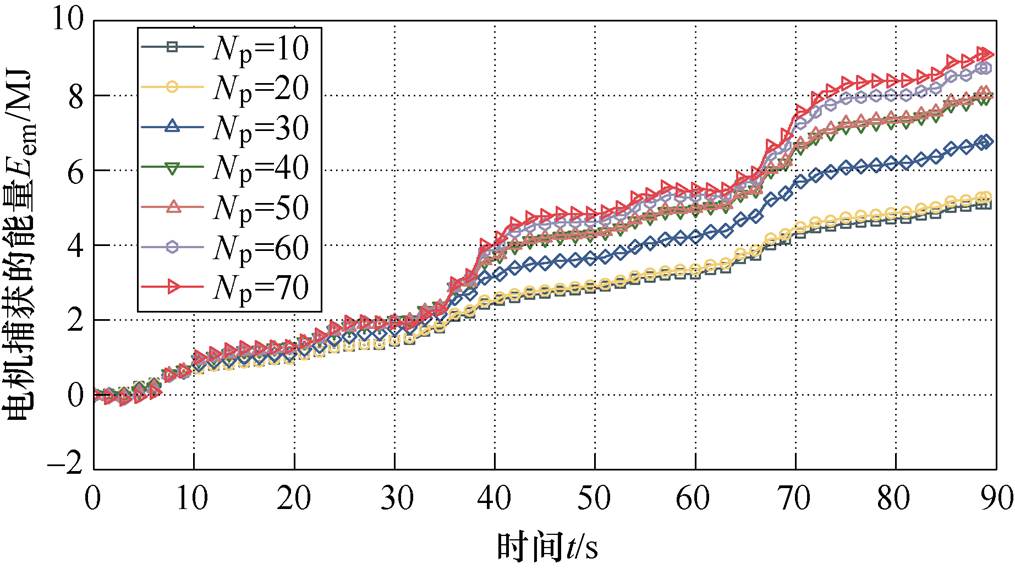
图8 成本函数J2下预测区间对功率捕获的影响
Fig.8 Effect of prediction interval on power capture under cost function J2
由图8可知,在成本函数J2下的结论与成本函数J1下的结论相似,随着预测区间的增大,PMLG从波浪发电系统中捕获的能量不断提高。
为了更加直观地对比上述两个成本函数下PMLG从波浪发电系统中捕获能量的效果,定义能量捕获效率h1为
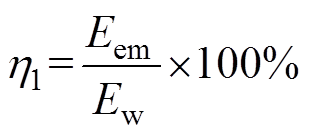 (80)
(80)
式中,Eem为PMLG从系统中捕获的总能量;Ew为波浪激振力发出的总能量。则在成本函数J1和J2下的能量捕获效率见表2。
由表2可知,由于成本函数J2以汇入直流母线能量最大为目标,因此成本函数J2在电机捕获功率方面与成本函数J1有所区别。当预测区间Np≤40时,成本函数J2下电机捕获的能量高于成本函数J1下;当预测区间Np>40时,结论则刚好相反。从中说明成本函数所形成的系数矩阵影响着二次规划的计算,从而影响电机捕获能量的大小。从较大的时域来看,选取以电机捕获平均电磁功率最大为目标的成本函数J1相较于以汇入直流母线功率最大的成本函数J2可以从波浪发电系统中获取更多的能量。此外,根据最大功率传输定理可知,当负载从系统中吸收功率最大时,负载吸收功率的效率为50%。这与表2中成本函数J1的能量捕获效率基本保持一致,这表明,在预测区间Np为60和70下,基于模型预测的最优功率捕获策略在约束条件下基本上实现了最大能量捕获。
表2 能量捕获效率
Tab.2 Energy capture efficiency
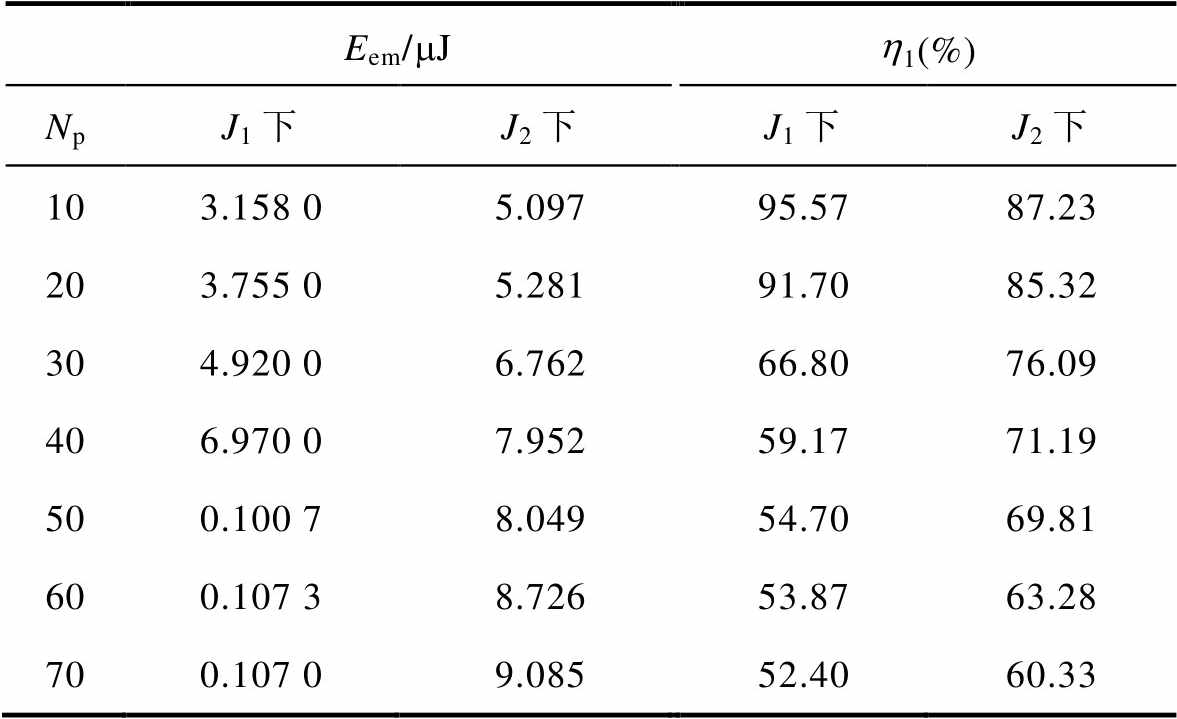
Eem/mJh1(%) NpJ1下J2下J1下J2下 103.158 05.09795.5787.23 203.755 05.28191.7085.32 304.920 06.76266.8076.09 406.970 07.95259.1771.19 500.100 78.04954.7069.81 600.107 38.72653.8763.28 700.107 09.08552.4060.33
在成本函数J1下不同预测区间汇入直流母线能量的波形如图9所示。由图9可知,由于成本函数J1不以汇入直流母线平均功率最大为目标,因此在成本函数J1下汇入直流母线的能量并没有明显的规律。此外,在预测区间Np=40下较大的时间范围内出现能量为负的情况,说明在该时间段内PMLG处在电动状态来维持电机出力,从而满足成本函数J1下最优功率捕获条件。这种控制下虽然可使得PMLG从波浪发电系统中捕获较多能量,但大部分能量消耗在电机定子绕组上,不具有实用意义。
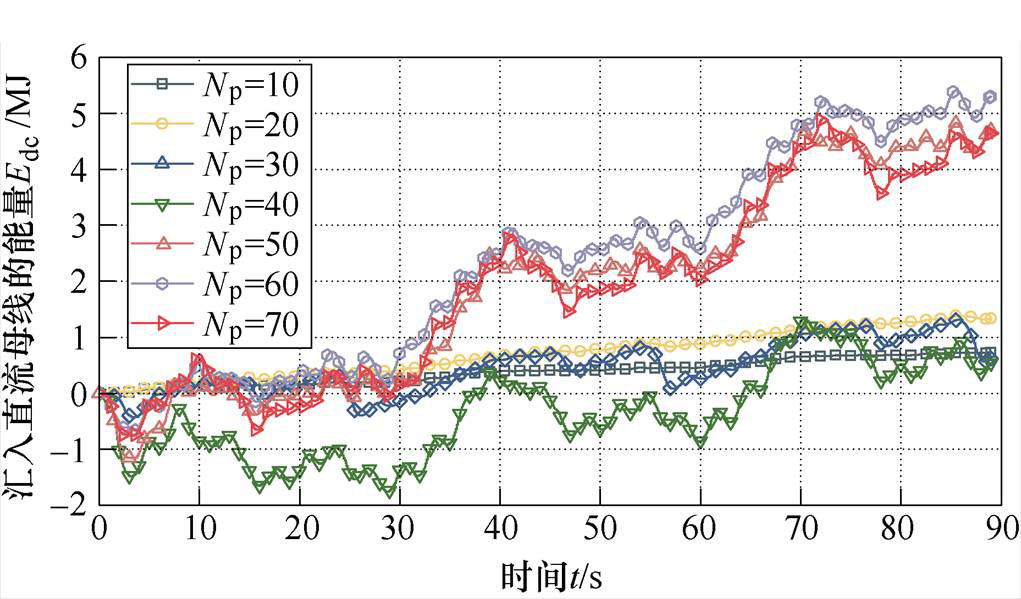
图9 成本函数J1对汇入直流母线功率的影响
Fig.9 Influence of incoming DC bus power under cost function J1
在成本函数J2下不同预测区间汇入直流母线能量的波形如图10所示。
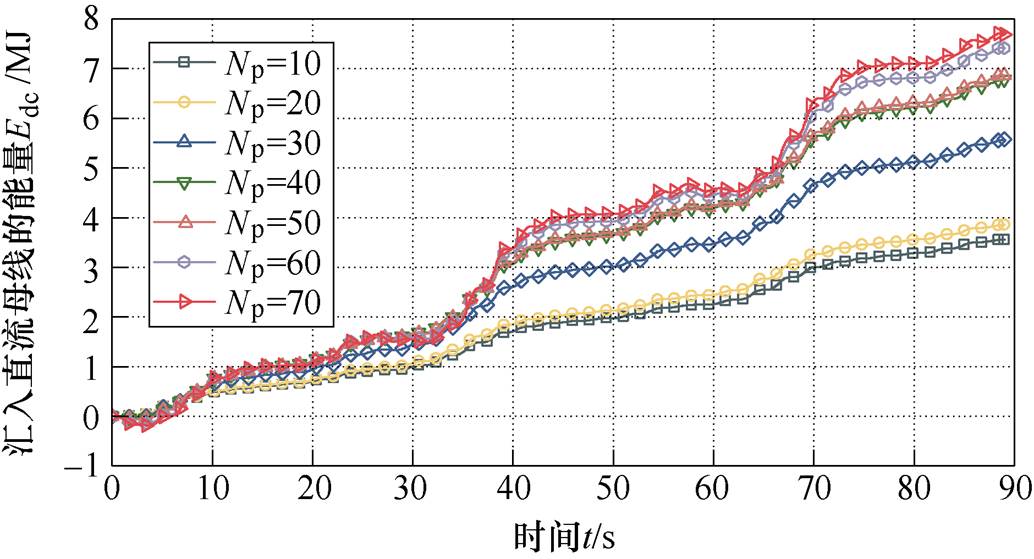
图10 成本函数J2对汇入直流母线功率的影响
Fig.10 Influence of incoming DC bus power under cost function J2
由图10可知,由于成本函数J2以汇入直流母线的平均功率最大为目标,因此在成本函数J2下汇入直流母线的能量具有明显的规律。随着预测区间的增大,汇入直流母线的能量增大。
定义能量利用效率h2对比两个成本函数J1和J2对汇入直流母线功率的影响,有
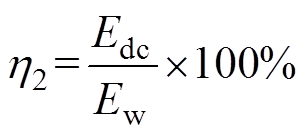 (81)
(81)
式中,Edc为汇入直流母线的总能量。则在成本函数J1和J2下的能量利用效率见表3。
表3 能量利用效率
Tab.3 Energy utilization efficiency
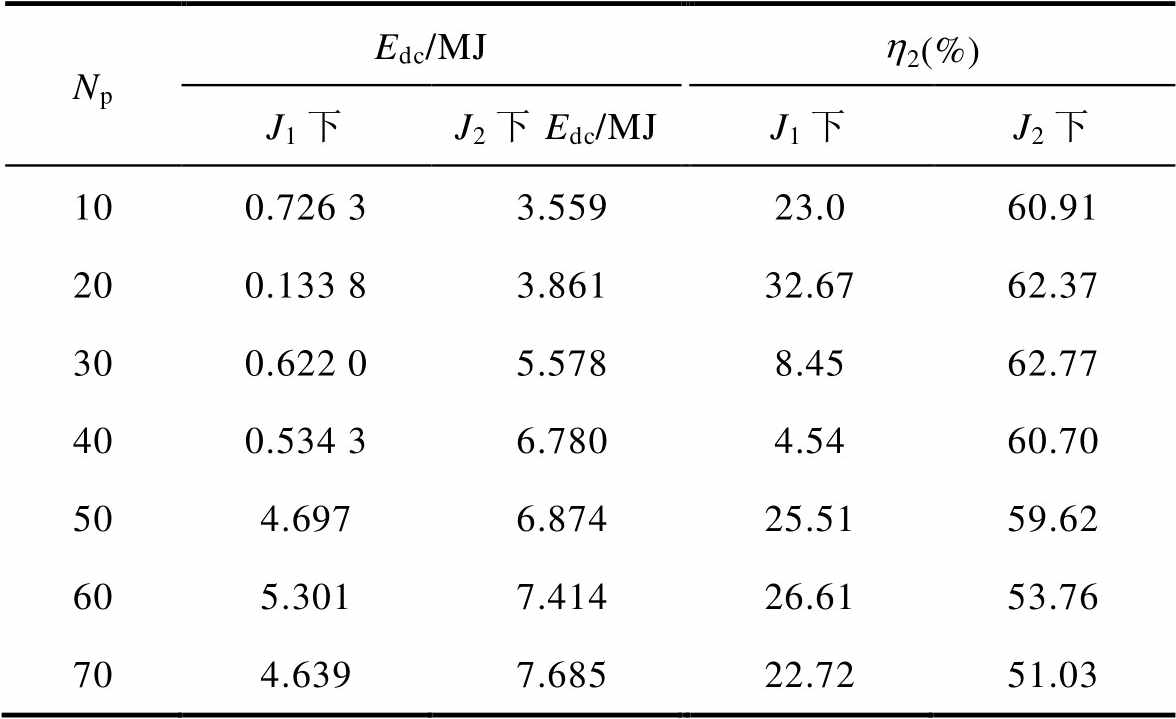
NpEdc/MJh2(%) J1下J2下Edc/MJJ1下J2下 100.726 33.55923.060.91 200.133 83.86132.6762.37 300.622 05.5788.4562.77 400.534 36.7804.5460.70 504.6976.87425.5159.62 605.3017.41426.6153.76 704.6397.68522.7251.03
由表3可知,在相同预测区间内,成本函数J1下的能量利用效率远远低于成本函数J2下的能量利用效率。而以汇入直流母线平均功率最大为目标的成本函数J2可以从波浪发电系统中获取较多能量汇入直流母线。因此,在考虑PMLG铜耗的条件下可以大幅度提高电机汇入直流母线的能量,具有重要的实用价值。
本文针对基于模型预测的功率动态跟踪控制展开实验研究。利用变频器、感应电机、变速箱、曲柄连杆机构、永磁直线电机及数字信号处理器(Digital Signal Processor, DSP)等,搭建了基于模型预测的功率动态跟踪控制实验平台。

图11 功率动态跟踪控制实验平台
Fig.11 Power dynamic tracking control experiment platform
当感应电机在变频器驱动下时经过曲柄连杆机构拖动的永磁直线电机,运动速度近似呈正弦运动。电机三相空载电动势及单相电动势和动子速度波形如图12所示。
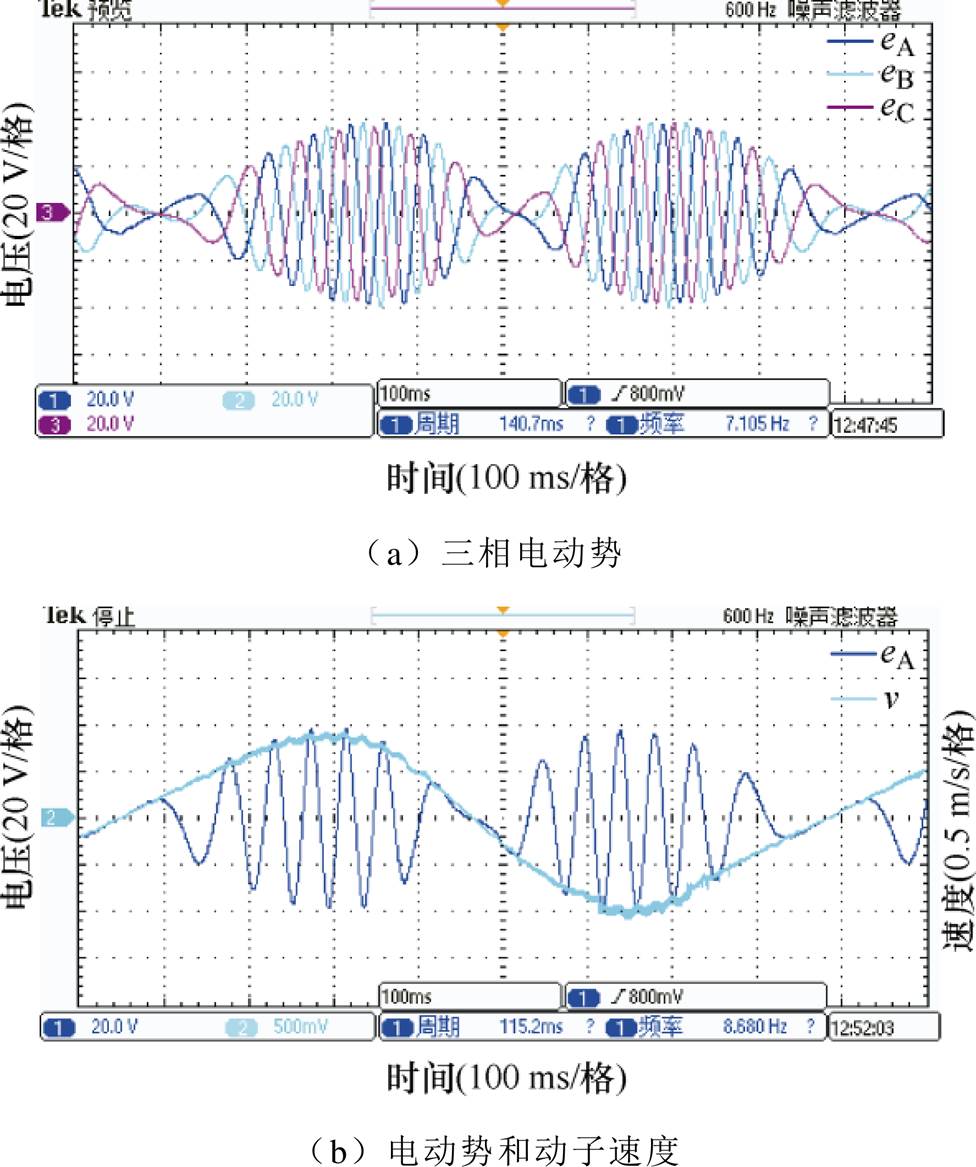
图12 感应电动势和速度波形
Fig.12 Waveforms of induced electromotive force and speed of mover
由图12可知,电机相感应电动势波形的包络线与动子的运动速度波形一致。动子运动速度波形接近正弦但不是标准的正弦波。
本文着重研究不同工况下功率的跟踪控制效果,发电机控制在完全输出有功功率的单自由度状态,d轴电流参考为0,q轴电流的参考值定义为速度与比例系数Kg的乘积,有
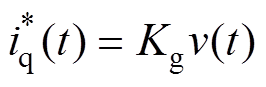 (82)
(82)
式中,Kg为发电机实现对外匹配系数,设定不同变频器频率fco,模拟不规则波浪的不同频率分量,Kg设定为-3。按照式(62)~式(65)设定模型预测控制代价函数,此时实验获得的dq坐标系下的电流波形和参考值如图13所示。
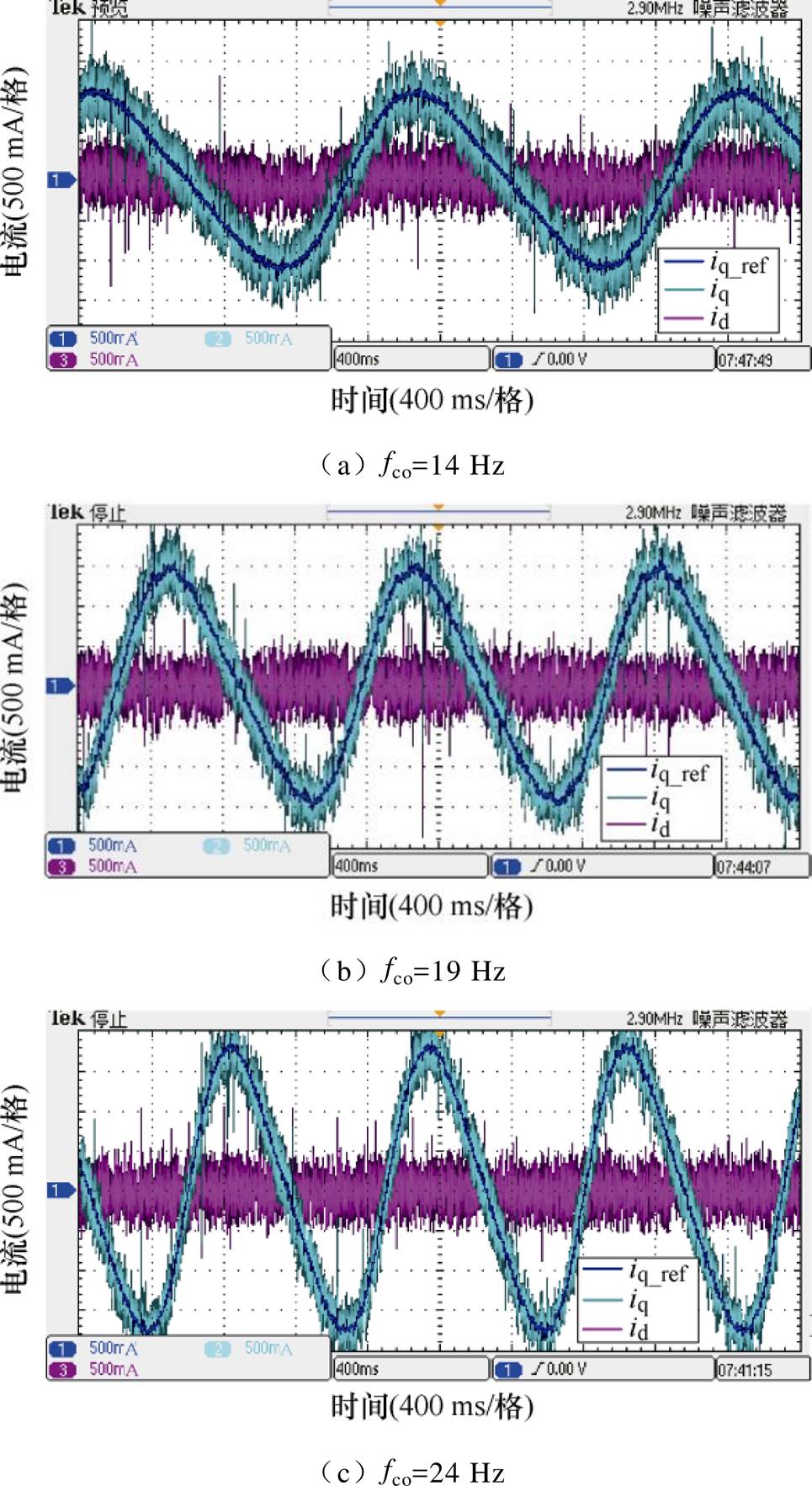
图13 dq坐标系下电流波形
Fig.13 Current waveforms diagram in dq coordinate system
由图13可知,电机d轴电流保持在0 A附近,电机q轴电流的实际值iq较好地跟随q轴给定值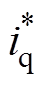 ,验证了控制策略的正确性。同时根据叠加原理,系统在不规则波浪下也能保持良好的跟踪性能。
,验证了控制策略的正确性。同时根据叠加原理,系统在不规则波浪下也能保持良好的跟踪性能。
永磁直线电机发出的瞬时功率波形如图14所示。
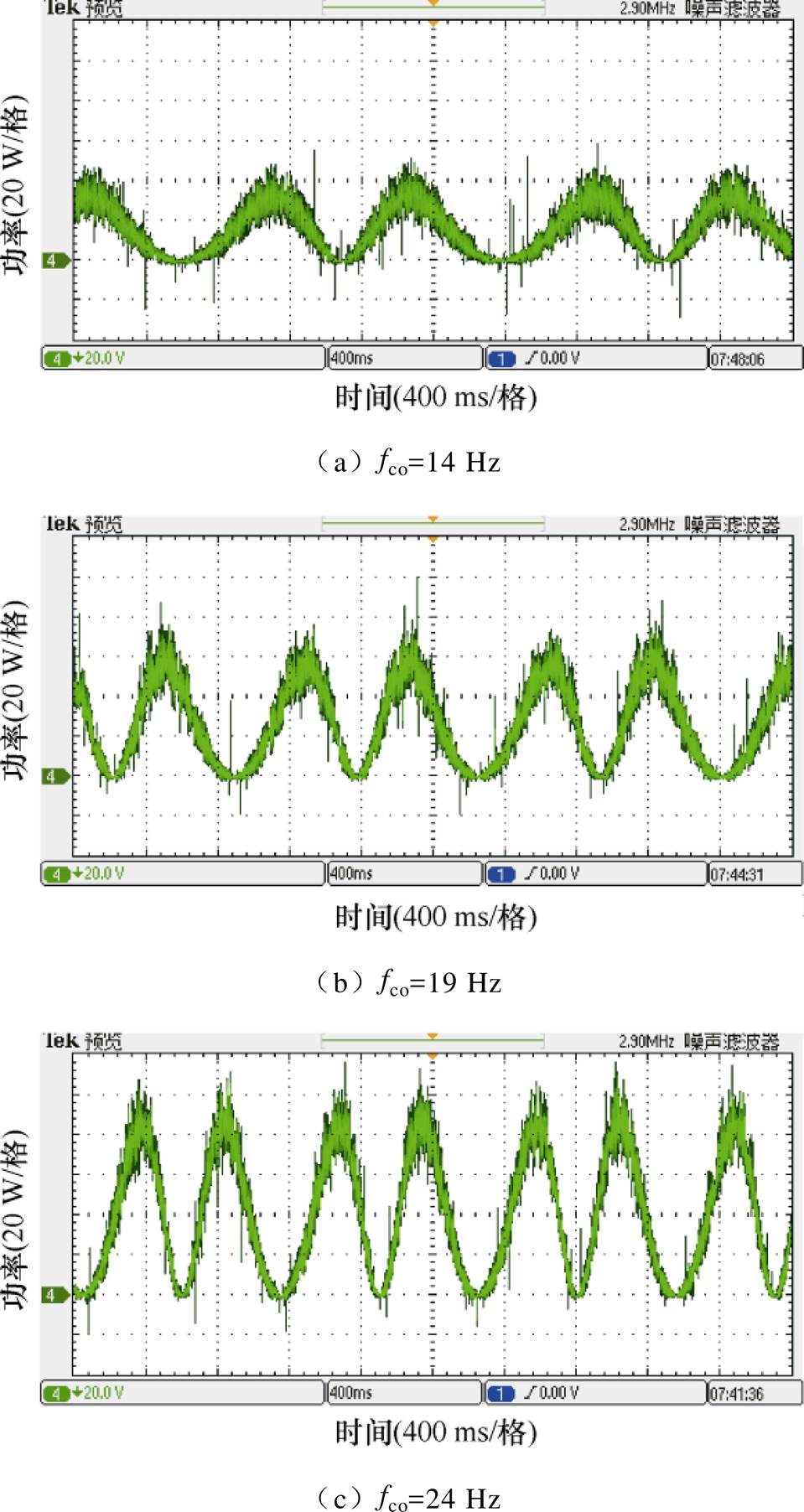
图14 永磁直线电机瞬时功率波形
Fig.14 Instantaneous power waveforms of PMLG
由图14可知,永磁直线电机的瞬时功率基本均为正值,表明电机处于发电状态,实现了模拟波浪能转化为电能的过程,进一步验证了控制策略的有效性。从图14中也能够看到,系统在波浪幅值较大的高频分量中能够提取出更多的能量。
为了验证系统的暂态性能,在变化工况下的电流跟踪波形如图15所示。由图15可知,在波浪波形变化时,系统也能够很好地跟随给定参考电流,进一步验证了控制策略的有效性,在不规则波浪中也有着良好的控制性能。
本文以直驱式波浪发电系统为研究对象,建立了直驱式波浪发电装置的水动力数学模型和dq坐标下永磁直线电机的动态数学模型。重点研究了基于经济模型预测的最优功率捕获策略,并结合模型预测的功率跟踪控制策略建立了直驱式波浪发电系统的整体系统模型,搭建仿真与实验平台对波浪发电能量吸收特性的主导影响因素及影响规律进行分析。本文根据系统原理建立了仿真模型,证明了在不规则波下,基于EMPC的最优功率捕获策略相较于单、双自由度控制可以提高发电机从波浪中捕获的能量。EMPC中不同的预测区间可以较大程度影响系统能量吸收。此外,考虑PMLG的铜耗下的成本函数对PMLG汇入直流母线的能量具有显著的提升作用。选择合适的预测区间和成本函数对于系统性能提升具有重要的实用价值。搭建了波浪发电模拟实验平台,对基于模型预测的功率动态跟踪控制策略展开实验,研究了不同速度下的电流与功率结果,并验证了系统暂态性能,实验结果表明,在不同的工况下系统可以有效实现电流的跟踪控制,完成了控制策略和功率传递规律的验证。
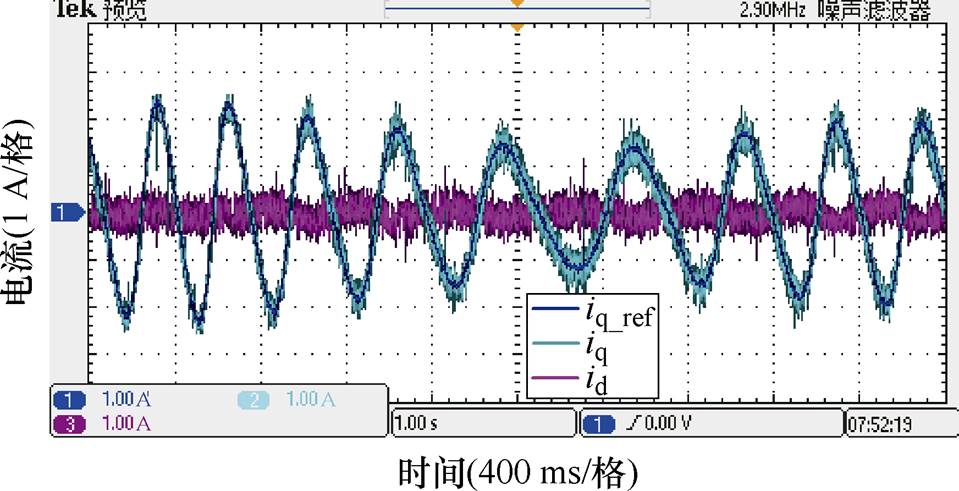
图15 工况变化时电流波形
Fig.15 Current waveforms when working condition changes
参考文献
[1] 肖曦, 摆念宗, 康庆, 等. 波浪发电系统发展及直驱式波浪发电系统研究综述[J]. 电工技术学报, 2014, 29(3): 1-11.
Xiao Xi, Bai Nianzong, Kang Qing, et al. A review of the development of wave power system and the research on direct-drive wave power system[J]. Transactions of China Electrotechnical Society, 2014, 29(3): 1-11.
[2] 黄磊, 胡敏强, 余海涛, 等. 直驱式波浪发电用全超导初级励磁直线发电机的设计与分析[J]. 电工技术学报, 2015, 30(2): 80-86.
Huang Lei, Hu Minqiang, Yu Haitao, et al. Design and analysis of a fully-superconducting primary- excitation linear generator for direct-driven wave energy generation[J]. Transactions of China Electro- technical Society, 2015, 30(2): 80-86.
[3] 洪岳, 潘剑飞, 刘云, 等. 直驱波浪能发电系统综述[J]. 中国电机工程学报, 2019, 39(7): 1886-1900.
Hong Yue, Pan Jianfei, Liu Yun, et al. A review on linear generator based wave energy conversion systems[J]. Proceedings of the CSEE, 2019, 39(7): 1886-1900.
[4] 张静, 余海涛, 陈琦, 等. 一种海浪发电用永磁单相直线电机的工作特性与实验分析[J]. 电工技术学报, 2013, 28(7): 110-116.
Zhang Jing, Yu Haitao, Chen Qi, et al. Dynamic characteristics and experiment analysis of a single phase permanent magnet linear generator for wave energy conversion[J]. Transactions of China Electro- technical Society, 2013, 28(7): 110-116.
[5] O'Sullivan A C M, Lightbody G. Co-design of a wave energy converter using constrained predictive control[J]. Renewable Energy, 2017, 102: 142-156.
[6] 黄宣睿, 林泽川, 肖曦. 双浮体直驱波浪发电装置建模分析与基于模型预测控制的能量提取算法研究[J]. 电工技术学报, 2024, 39(2): 445-454.
Huang Xuanrui, Lin Zechuan, Xiao Xi. Modelling and analysis of the two-body direct-drive wave energy converter and optimal energy extraction method based on model predictive control[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 445-454.
[7] Li Guang, Belmont M R. Model predictive control of sea wave energy converters-part I: a convex approach for the case of a single device[J]. Renewable Energy, 2014, 69: 453-463.
[8] 卢思灵, 杨俊华, 沈辉, 等. 直驱式波浪发电系统的经济模型预测控制[J]. 电测与仪表, 2021, 58(3): 131-138.
Lu Siling, Yang Junhua, Shen Hui, et al. Economic model predictive control of direct-drive wave power generation systems[J]. Electrical Measurement & Instrumentation, 2021, 58(3): 131-138.
[9] Wang Zhenchun, Luan Feng, Wang Nianguo. An improved model predictive control method for wave energy converter with sliding mode control[J]. Ocean Engineering, 2021, 240: 109881.
[10] Eriksson M, Isberg J, Leijon M. Theory and experi- ment on an elastically moored cylindrical buoy[J]. IEEE Journal of Oceanic Engineering, 2006, 31(4): 959-963.
[11] Hai Ling, Göteman M, Leijon M. A methodology of modelling a wave power system via an equivalent RLC circuit[J]. IEEE Transactions on Sustainable Energy, 2016, 7(4): 1362-1370.
[12] Guo B, Ringwood J V. A review of wave energy technology from a research and commercial perspe- ive[J]. IET Renewable Power Generation, 2021, 15(14): 3065-3090.
[13] Babarit A, Delhommeau G. Theoretical and numerical aspects of the open source BEM solver NEMOH[R]// 11th European Wave and Tidal Energy Conference, Nantes ,France, 2015.
[14] Davis A F, Fabien B C. Wave excitation force esti- mation of wave energy floats using extended Kalman filters[J]. Ocean Engineering, 2020, 198: 106970.
[15] 苏光靖, 李红梅, 李争, 等. 永磁同步直线电机无模型电流控制[J]. 电工技术学报, 2021, 36(15): 3182-3190.
Su Guangjing, Li Hongmei, Li Zheng, et al. Research on model-free current control of permanent magnet synchronous linear motor[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3182-3190.
[16] 王明杰, 贾宛英, 张志艳, 等. 永磁直线同步电机空载反电动势和推力的解析计算[J]. 电工技术学报, 2021, 36(5): 954-963.
Wang Mingjie, Jia Wanying, Zhang Zhiyan, et al. Analytical calculation of no-load eletromotive force and thrust in permanent magnet linear synchronous motors[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 954-963.
[17] 康庆, 肖曦, 聂赞相, 等. 直驱型海浪发电系统输出功率优化控制策略[J]. 电力系统自动化, 2013, 37(3): 24-29.
Kang Qing, Xiao Xi, Nie Zanxiang, et al. An optimal control strategy for output power of the directly driven wave power generation system[J]. Automation of Electric Power Systems, 2013, 37(3): 24-29.
Abstract The direct-drive wave power generation system has the advantages of a simple structure, low cost, and high efficiency. Permanent magnet linear generators are implemented in direct-drive wave power generation systems for their high-power density, and the electromagnetic force of the linear generator is controlled to realize maximum energy capture of the system. However, the power capture strategy of the direct-drive wave power generation system greatly affects the energy obtained from the system. Predictive models with multiple constraints can solve the safety problems of wave power generation devices in extreme sea conditions, which is suitable for power capture control in direct-drive wave power generation systems. Therefore, based on Model Prediction, this paper proposes an optimal power control strategy for direct-drive wave power generation systems to improve the energy capture of generators.
Firstly, the hydrodynamic mathematical model of the direct-drive wave power generation device is established, and the frequency response of the wave-front equation to an excitation force is obtained using the boundary element method. In addition, the dynamic mathematical model of the permanent magnet linear generator is analyzed. Secondly, a power control strategy based on model prediction is derived for the direct-drive wave power generation system. The power control strategy is divided into power capture and power tracking control strategies to convert wave energy into electrical energy and import it into the DC bus. This paper analyzes the optimal power capture strategy from three perspectives: control strategy, prediction interval, and cost function. The state-space equations, cost function, and constraints are analyzed. Then, the model predictive current control is implemented for dynamic power tracking. Thirdly, based on the theoretical derivation, the control block diagram of the direct-drive wave power generation system is established. The simulation model of the system is built, and simulation parameters of the wave power generation are listed. Moreover, the energy captured by the PMLG under different control strategies is compared, and the prediction interval effects on power capture under different cost functions are analyzed. The optimized prediction interval parameters are obtained through comparative analysis. Different cost functions are compared, considering the most power in the DC bus and the electromagnetic power of PMLG. All the simulation models are built. Simulation results show that the optimal power capture strategy based on model prediction effectively improves the energy capture of generators under irregular waves from wave power generation systems. In addition, maximizing the power imported into the DC bus can increase the energy imported into the DC bus by the generator, which has significant practical value. Experimental results under different driving speeds and dynamic wave condition adjustments are obtained.
The following conclusions can be drawn. (1) The proposed optimal power control strategy improves the captured energy from the waves, making it suitable for direct-drive wave power generation systems. (2) The prediction interval of EMPC greatly affects the energy absorption of the system, and the cost functions significantly affect the energy feeds into the DC bus. Therefore, selecting an appropriate prediction interval and cost function is helpful for performance improvement. (3) Experimental results show that the system effectively achieves tracking control of current under different working conditions using the proposed control strategy.
keywords:Direct-drive wave power generation, optimal power capture, model predictive control, power tracking control
DOI: 10.19595/j.cnki.1000-6753.tces.230906
中图分类号:TM619
国家自然科学基金(41876096)和国防科技重点实验室基金(6142217190101)资助项目。
收稿日期 2023-06-13
改稿日期 2023-08-17
黄 磊 男,1980年生,博士,副教授,博士生导师,研究方向为直驱式波浪发电系统及其控制。E-mail: huanglei@seu.edu.cn(通信作者)
魏 莱 男,1997年生,硕士研究生,研究方向为直驱式波浪发电机侧控制。E-mail: sut_weilai@163.com
(编辑 崔文静)