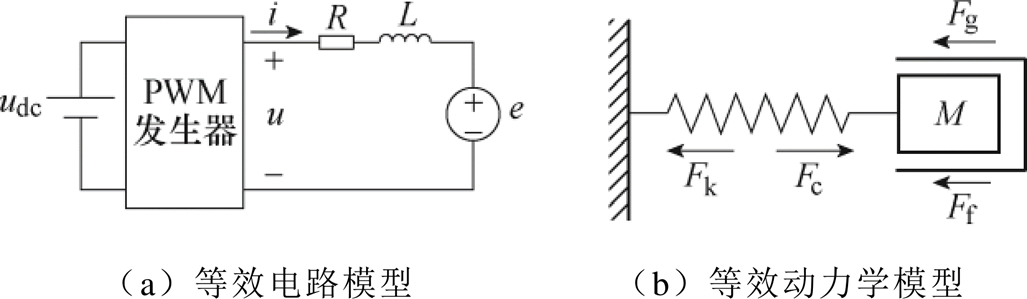
图1 LOM的系统模型
Fig.1 System model of the LOM
摘要 现有直线振荡电机(LOM)无位置传感器谐振频率跟踪控制方法存在行程观测精度低、抗干扰能力差等问题,容易导致谐振频率跟踪精度低、频率振荡严重。为提高谐振频率跟踪控制性能,该文研究了一种基于积分滑模观测器(ISMO)的新型谐振频率跟踪控制方法。首先,基于LOM工作在系统谐振频率点时行程-电流相位差为90°的特点,提出一种双互相关函数比值方法,消除了行程变化对谐振频率跟踪控制的影响。其次,采用积分滑模面及新型趋近律设计ISMO,并利用二阶广义积分器获取行程估算信号,大大提高了行程估算精度。最后,对比实验结果表明,所提方法能够有效提高谐振频率跟踪精度、稳定时间及抗干扰能力。
关键词:直线振荡电机(LOM) 谐振频率跟踪控制 积分滑模观测器(ISMO) 双互相关函数比值(DCFR)方法 二阶广义积分器(SOGI)
近年来,直线压缩机以其结构简单、效率高、机械损耗小等优点引起了广泛关注[1-3]。这种新型压缩机通常由直线振荡电机(Linear Oscillatory Machine, LOM)驱动,可以将电能直接转化为直线运动而不采用机械转换装置[4-5]。由于LOM的特殊结构,该电机具有系统谐振频率,当电机运行在此频率点时,系统可获得最大输出效率。此外,与传统旋转电机不同,LOM的活塞行程可调,通过控制活塞行程可以调节排气量大小。然而,由于活塞行程不受限,当行程超过最大允许范围时,将发生撞缸事故。因此,有必要对LOM同时实施谐振频率跟踪控制及活塞行程闭环控制,以确保系统高效可靠运行[6-7]。
当前,已有谐振频率跟踪控制方法的研究大多基于LOM在谐振频率点运行时的两个特性[8-11],即当该电机以谐振频率运行时,活塞行程与电流的幅值比最大;活塞行程与电流的相位差正好为90°。基于行程与电流的幅频特性,文献[8]提出了一种最大功率点搜索法,可以实现不同工作条件下的谐振频率跟踪控制。在此基础上,文献[9]将搜索法与模糊控制相结合,提出了一种输入电流或功率最小化频率跟踪模糊控制算法,该方法结构简单易行,但由于搜索过程是不断进行的,容易导致运行频率在谐振点附近振荡。基于行程与电流的相频特性,文献[10]提出了一种基于行程电流乘积平均值法(Average Value of Stroke-Current Product, ASCP),利用周期内定积分滤波原理,获得行程与电流的相位差,从而实现谐振频率跟踪。然而,该方法对行程信号依赖严重,控制过程中行程变化对控制目标的影响较大,容易导致频率振荡,进而影响跟踪精度。文献[11]利用最小二乘法提出一种波形拟合相位检测方法,可直接计算行程与电流的相位差,仿真结果显示,该方法具有较高的估算精度,但由于需要巨大的计算量和数据存储空间,在实际实践中很难实现。
根据上述谐振频率跟踪控制研究可知,大多数方法都基于行程与电流之间的特性关系,因此行程信号对于谐振频率跟踪控制至关重要,其精度直接影响着谐振频率的跟踪精度。此外,活塞行程闭环控制需要行程信号,通过控制行程大小能够保证整个系统的安全可靠运行。众所周知,安装机械传感器能够获得精确的行程信号,但使用机械传感器存在安装维护困难、系统体积增大、成本高、系统可靠性降低等问题。为此,学者们对无位置传感器控制进行了大量研究。
反电动势积分法是一种常用的LOM活塞行程估算方法,其原理为:基于电机电压方程直接计算电机的反电动势,然后根据反电动势与速度成正比的关系计算活塞速度信号,最后对速度信号积分即可得到行程信号[10, 12-13]。然而,由于该方法中采用的电压电流信号常含有一定的直流分量,纯积分器的使用会使直流分量不断累加,从而导致纯积分饱和。针对这一问题,文献[12]在使用纯积分器之前采用高通滤波器将直流分量滤除,这在一定程度上解决了纯积分饱和问题,但高通滤波器与纯积分器一同使用相当于一个低通滤波器,不可避免地造成滤波后的行程信号出现幅值和相位偏移问题。文献[13]通过增加直流补偿环节,提高了行程估算精度,但补偿无法完全实现,且动态效果较差。综上所述,采用高性能滤波器可以解决纯积分饱和问题,但由于反电动势积分法是一种开环计算方法,其内部不含误差反馈校正环节,易受参数变化影响,估算精度无法进一步得到提高。近期,文献[14]中设计了一种基于误差符号鲁棒积分的活塞速度观测器,该观测器通过采用符号函数切换的方式提高了参数鲁棒性,但也导致行程信号中存在大量谐波。
针对前述谐振频率跟踪控制及无位置传感器行程估算方法存在的缺陷,本文提出一种高精度无位置传感器谐振频率跟踪控制方法。其创新性在于:①提出了一种双互相关函数比值(Double Cross- correlation Function Ratio, DCFR)方法用于跟踪系统谐振频率,利用函数比值的方式消除了行程变化对跟踪结果的影响。②基于积分滑模面及新型趋近律,构造积分滑模观测器(Integral Sliding-Mode Observer, ISMO),通过引入电流误差反馈校正环节大幅提高了行程估算精度。③采用两个二阶广义积分器(Second-Order Generalized Integrators, SOGI),其中一个用于生成DCFR方法中所需的电流正交信号,另一个用于ISMO以解决纯积分饱和问题。为具体阐明上述过程,本文首先基于传统谐振频率跟踪方法构建DCFR,通过对其原理进行详细分析,阐明了该算法所具有的优越性。其后基于电机电压方程构建了ISMO,并将其与SOGI相结合,解决纯积分饱和的同时大幅提高了行程观测精度。最后通过实验结果对比分析,证明了所提方法的有效性和优越性。
LOM是一种由一定频率的单相正弦交流电驱动的单相直线电机,其数学模型包括电机等效电路模型及动力学模型,如图1所示。

图1 LOM的系统模型
Fig.1 System model of the LOM
根据图1a,该电机的电路方程可表示为
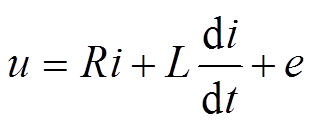 (1)
(1)
式中,u为电机端电压;i为定子电流;R为定子电阻;L为定子电感;e为电枢反电动势,e=Kiv,其中,Ki为推力系数,v为活塞速度。
根据图1b所示的机械平衡关系,其机械等效方程为
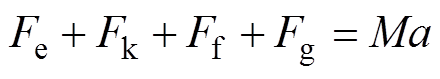 (2)
(2)
式中,a为动子加速度;M为动子质量;Fe为电磁推力,满足Fe=Kii;Fk为弹簧弹力,满足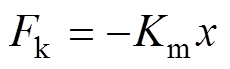 ,其中,
,其中,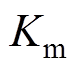 为机械弹簧弹性系数,
为机械弹簧弹性系数,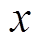 为活塞行程;
为活塞行程;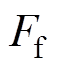 为摩擦阻力,满足
为摩擦阻力,满足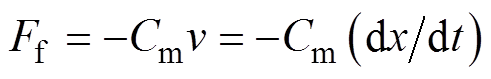 ,其中,
,其中,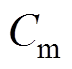 为机械摩擦系数;Fg为等效气体力,满足
为机械摩擦系数;Fg为等效气体力,满足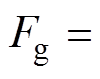
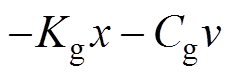 ,其中,
,其中,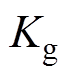 为等效气体弹簧系数,
为等效气体弹簧系数,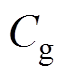 为等效气体阻尼系数。由此,可整理出机械等效动力学方程为
为等效气体阻尼系数。由此,可整理出机械等效动力学方程为
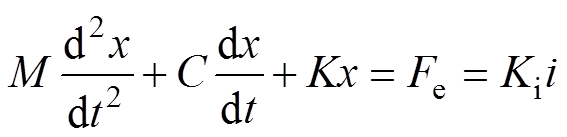 (3)
(3)
式中,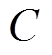 为等效阻尼系数,
为等效阻尼系数,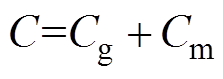 ;
;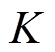 为等效弹簧弹性系数,
为等效弹簧弹性系数,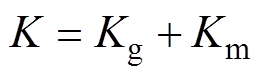 。
。
由于LOM工作在系统谐振频率点时,其行程与电流相位差相差90°。根据这一特点,可以设计高性能谐振频率跟踪控制方法。本节首先对传统ASCP方法的原理进行介绍,然后基于该方法提出一种不受行程变化影响的高性能谐振频率跟踪控制方法。
LOM是一种单相电机,其活塞行程与电流信号频率相同、相位不同。根据这一特点,可以将电流与行程信号表示为
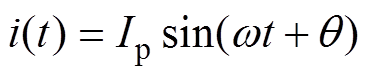 (4)
(4)
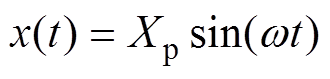 (5)
(5)
式中,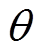 为电流与行程的相位差;
为电流与行程的相位差;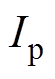 和
和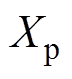 分别为
分别为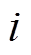 和
和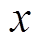 的幅值;w 为电机运行频率。
的幅值;w 为电机运行频率。
根据式(4)和式(5),文献[10]提出了一种ASCP方法,通过定积分计算消除高频信号,保留只含有行程电流相位差的直流信息,从而实现谐振频率跟踪控制,其计算表达式为
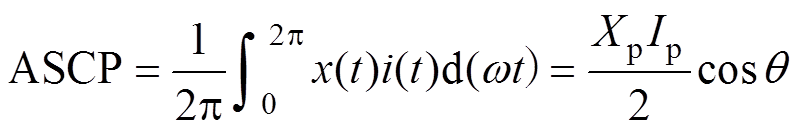 (6)
(6)
根据式(6)可以看出,ASCP值与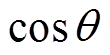 成正比,通过控制ASCP的值可以调整相位差
成正比,通过控制ASCP的值可以调整相位差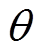 。当ASCP值为0时,相位差
。当ASCP值为0时,相位差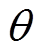 正好为90°。此时,可以认为电机运行在谐振频率点。根据上述内容,可得基于ASCP方法的谐振频率跟踪控制结构如图2所示。
正好为90°。此时,可以认为电机运行在谐振频率点。根据上述内容,可得基于ASCP方法的谐振频率跟踪控制结构如图2所示。
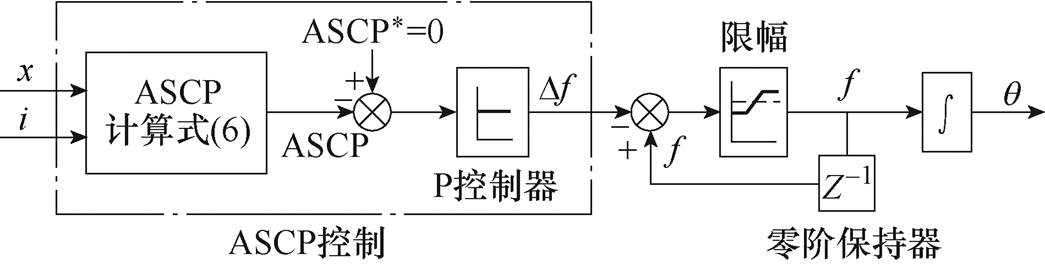
图2 基于ASCP方法的谐振频率跟踪控制结构
Fig.2 Structure diagram of the ASCP method for resonant frequency tracking control
事实上,ASCP方法的本质是对x和i的互相关函数计算。互相关函数计算是一种用于描述两个时间序列之间相关程度的常用方法,在信号分析领域受到广泛研究[15-17]。ASCP方法将互相关函数计算的思想用于LOM进行谐振频率跟踪,获得了一定的效果。然而,由式(6)可知,该方法中存在定积分计算,这将给控制系统带来大量的计算负担。此外,控制目标中包含电流与行程信号的幅值信息,当行程信号变化时,ASCP值将发生剧烈振荡,影响跟踪精度。
ASCP方法的核心思想是获得行程与电流的相位差并将其控制为90°。利用这一思想,采用其他方式也可以获得相同的效果。将行程x与电流i的乘积表示为
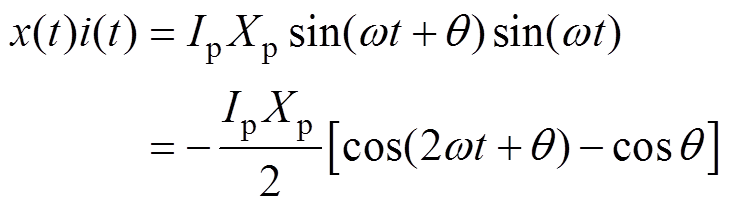 (7)
(7)
如式(7)所示,行程与电流的乘积值中包含一个频率为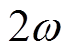 的交流分量以及一个含有
的交流分量以及一个含有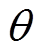 信息的直流分量。通过去除交流分量并保留直流分量,然后将直流分量控制到0,即可实现谐振频率跟踪控制。传统ASCP方法采用定积分的方式实现这个目的。类似地,利用滤波器也可以去除交流分量而保留直流分量信息。
信息的直流分量。通过去除交流分量并保留直流分量,然后将直流分量控制到0,即可实现谐振频率跟踪控制。传统ASCP方法采用定积分的方式实现这个目的。类似地,利用滤波器也可以去除交流分量而保留直流分量信息。
在本文中,采用二阶低通滤波器(Second-order Low Pass Filter, SLPF)获得较为精确的直流分量,其传递函数为
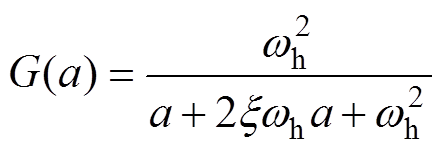 (8)
(8)
式中,a为拉普拉斯算子;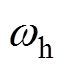 为截止频率;
为截止频率;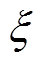 为滤波常数。采用SLPF可以保留直流分量
为滤波常数。采用SLPF可以保留直流分量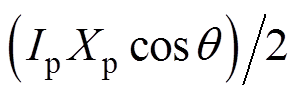 的信息。然而,该方法虽然解决了定积分计算存在的问题,但其控制目标中仍然含有行程与电流幅值的乘积项,依然存在对活塞行程变化敏感的问题。为消除行程变化对跟踪精度的影响,本文提出一种基于DCFR的高性能谐振频率跟踪控制方法。
的信息。然而,该方法虽然解决了定积分计算存在的问题,但其控制目标中仍然含有行程与电流幅值的乘积项,依然存在对活塞行程变化敏感的问题。为消除行程变化对跟踪精度的影响,本文提出一种基于DCFR的高性能谐振频率跟踪控制方法。
根据式(4),可将电流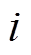 的正交信号表示为
的正交信号表示为
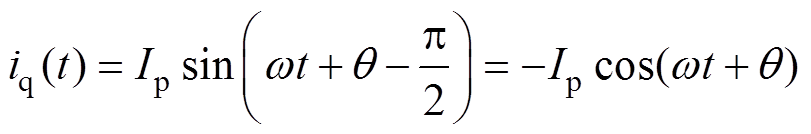 (9)
(9)
式中,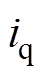 为电流正交信号。
为电流正交信号。
由式(5)和式(9)可得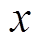 与
与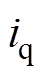 的乘积为
的乘积为
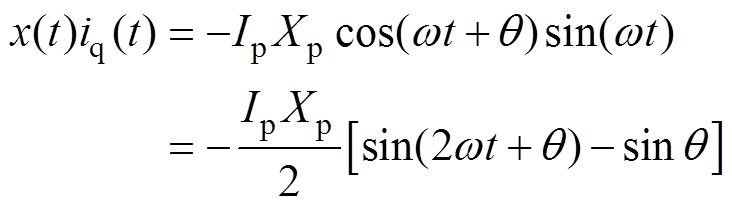 (10)
(10)
类似地,采用SLPF可获得式(10)中的直流分量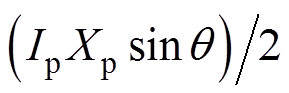 。
。
将上述滤波后的两个直流分量进行比值计算,可去除行程与电流对控制目标值的影响。基于此,本文所提DCFR的计算过程为
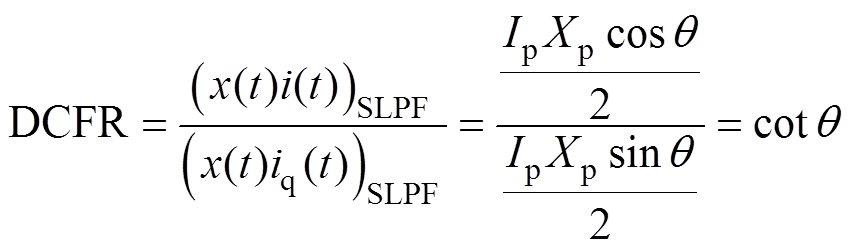 (11)
(11)
显然,DCFR值中不含行程与电流的幅值项,因此该方法不受行程变化的影响。相比于传统ASCP方法,该方法具有更强的抗干扰能力,能够获得更平稳精确的谐振频率信号。综上所述,基于DCFR方法的谐振频率跟踪控制结构如图3所示。值得注意的是,除法计算使得分母不能为零,在实际应用中需要对分母进行限制,使其趋于零而始终不为零。此外,由于cot函数在远离零点时趋于无穷,为保证系统性能,需对其进行限幅。虽然DCFR方法引入了除法计算,但其目标是将cot函数值控制为零,从而使得行程电流相位差为90°。由于cot函数在远离零点时斜率较大,因此该函数值在P控制器的调整下能够快速收敛到零。在此过程中,cot函数因其分母为零而导致其值为无穷大的情况较少,采用限幅方式能够很好地解决该问题而不对方法本身造成影响。
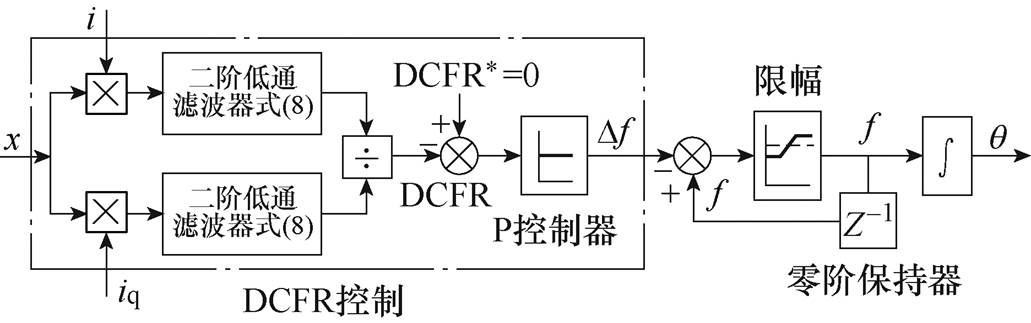
图3 基于DCFR方法的谐振频率跟踪控制结构
Fig.3 Structure diagram of the DCFR method for resonant frequency tracking control
在DCFR方法中,需要电流正交信号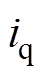 ,本文采用SOGI实现此目的,其结构框图如图4所示。
,本文采用SOGI实现此目的,其结构框图如图4所示。
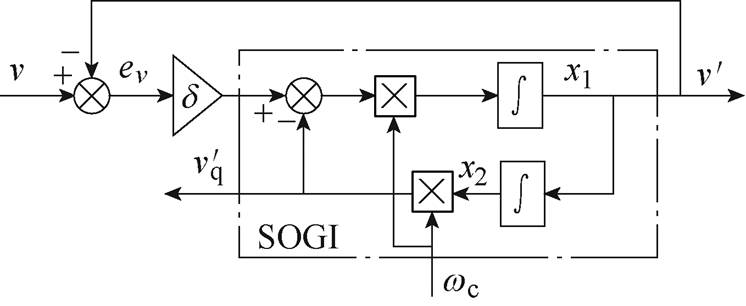
图4 SOGI的结构
Fig.4 Structure diagram of SOGI
根据图4,SOGI的状态及输出方程可表示为
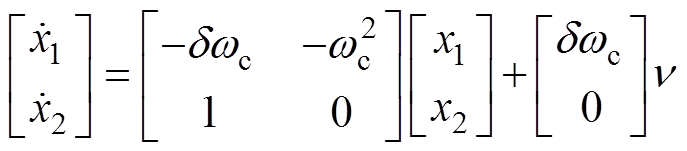 (12)
(12)
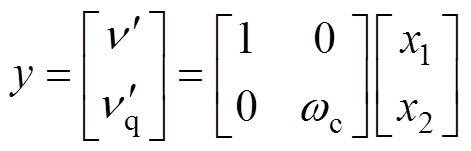 (13)
(13)
式中,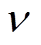 为输入信号;
为输入信号;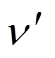 为滤波输出信号;
为滤波输出信号;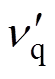 为
为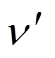 的正交信号;
的正交信号;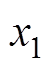 和
和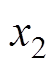 为状态变量;
为状态变量;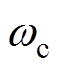 为中心频率;
为中心频率;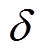 为滤波常数。
为滤波常数。
根据式(12)和式(13),可推导出SOGI的传递函数为
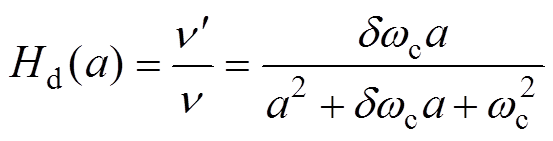 (14)
(14)
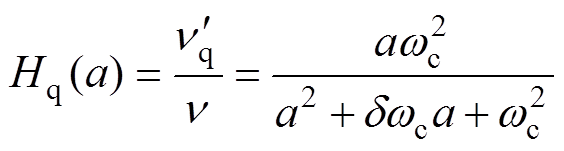 (15)
(15)
式中,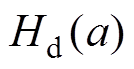 为
为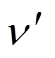 和
和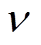 的传递函数;
的传递函数;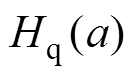 为
为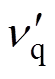 和
和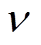 的传递函数。
的传递函数。
SOGI是一种应用广泛的高性能滤波器,它不仅能够获得状态输入的滤波信号,还能产生与滤波信号相位差为90°的正交信号[18]。基于此特点,可将其应用于DCFR方法以获取电流正交信号iq。需要注意的是,滤波常数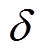 可用于调整SOGI的滤波性能。当
可用于调整SOGI的滤波性能。当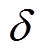 增大时,系统输出的响应速度加快但滤波性能变差。反之,当
增大时,系统输出的响应速度加快但滤波性能变差。反之,当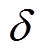 减小时,滤波性能增强但响应速度变慢[7]。本文所研究的对象为应用于直线压缩机的直线振荡电机,控制方式采用活塞行程幅值控制。由于活塞行程的幅值只能在一个运动周期后进行测量,其控制响应速度相对较慢。此外,该电机的负载为非线性气体力负载,活塞吸入和排出气体的过程相对较慢。因此,该电机对动态响应的快速性要求不高,更加关注控制系统的稳态性能。本文选取增益系数
减小时,滤波性能增强但响应速度变慢[7]。本文所研究的对象为应用于直线压缩机的直线振荡电机,控制方式采用活塞行程幅值控制。由于活塞行程的幅值只能在一个运动周期后进行测量,其控制响应速度相对较慢。此外,该电机的负载为非线性气体力负载,活塞吸入和排出气体的过程相对较慢。因此,该电机对动态响应的快速性要求不高,更加关注控制系统的稳态性能。本文选取增益系数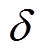 的依据主要是优先满足滤波性能,在此基础上尽可能提升动态性能。
的依据主要是优先满足滤波性能,在此基础上尽可能提升动态性能。
目前,常用的LOM活塞行程估算方法以反电动势积分法为主。然而,该方法是一种开环估算方法,其内部不含误差反馈校正环节,估计精度有待提高。为了获得更精确的行程估算结果,本文构建了结合SOGI的ISMO,其具体设计过程如下。
基于反电动势积分法的行程计算过程为
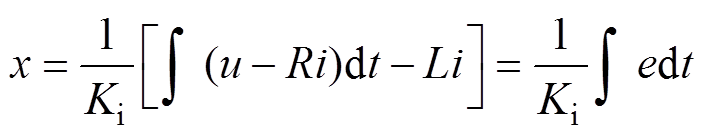 (16)
(16)
由式(16)可知,该方法是一种开环计算方法,其计算精度易受电机参数的影响。此外,该方法中存在纯积分环节。在实际实验中,由传感器采集的电压电流信号中常含有一定直流分量。因此,根据式(16)所得的反电动势中也必然存在直流分量。纯积分器的使用会将直流分量不断累加,最终导致积分饱和,具体分析如下。
考虑直流分量对反电动势的影响,将式(16)重写为
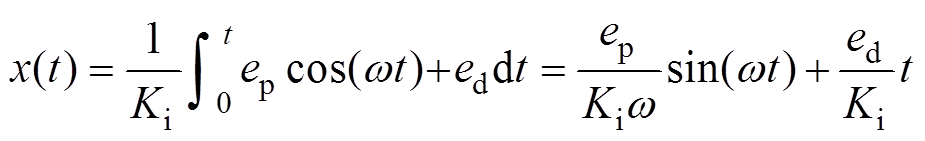 (17)
(17)
式中,ep为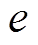 的峰值;ed为直流分量。由式(17)可以看出,随着时间的推移,将会出现积分饱和问题,影响行程估算精度。
的峰值;ed为直流分量。由式(17)可以看出,随着时间的推移,将会出现积分饱和问题,影响行程估算精度。
由于滑模观测器具有强参数鲁棒性及高估算精度等优点,本文针对LOM设计了一种ISMO以提高行程估算精度。
根据式(1),将电压方程改写成电流状态方程,可以得到
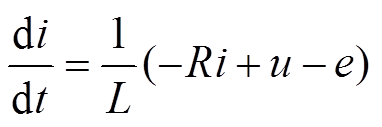 (18)
(18)
基于式(18),设计ISMO为
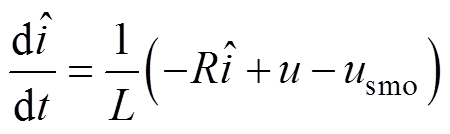 (19)
(19)
式中,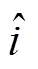 为观测电流;
为观测电流;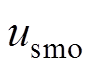 为滑模控制律。
为滑模控制律。
利用式(19)减去式(18),可得
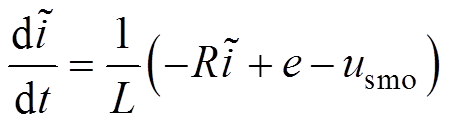 (20)
(20)
式中,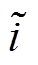 为电流误差。
为电流误差。
合理地选择滑模面及趋近律可构造高性能滑模控制律,从而提高观测器性能。积分滑模面具有削弱滑模抖振以及降低稳态误差的优点[19-21],本文将其用于构造ISMO的滑模控制律,其表达式为
 (21)
(21)
式中,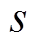 为积分滑模面;
为积分滑模面;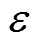 为积分增益。
为积分增益。
积分滑模面采用积分滤波的方式,在一定程度上可以削弱滑模抖振。而高性能趋近律的使用,能进一步降低滑模抖振,并加快状态变量的收敛速度。文献[22]结合终端吸引子和指数趋近律,设计了一种新型趋近律以提高控制器性能。基于该趋近律的优越性能,本文将其与积分滑模面相结合,构造ISMO的滑模控制律。该新型趋近律的表达式为
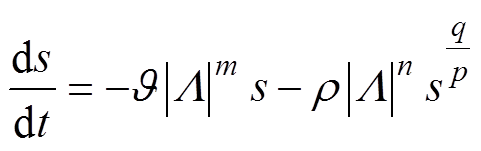 (22)
(22)
式中,m、n、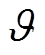 、
、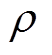 、
、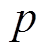 和
和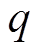 为设计参数,且
为设计参数,且 ,
, ,
,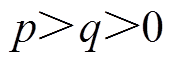 (
(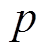 与
与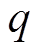 均为奇数),
均为奇数),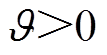 ,
,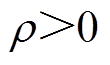 ;
;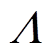 为系统状态变量,且
为系统状态变量,且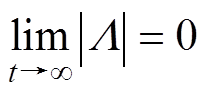 ,在本文中,
,在本文中,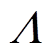 为
为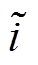 。该趋近律结合了纯指数趋近律在系统状态轨迹远离平衡点时趋近速度快以及终端吸引趋近方式在状态轨迹接近平衡点时趋近律速度快的优点,能够实现全局快速收敛。同时,幂函数的引入使得趋近速度进一步加快,能够有效抑制滑模抖振现象。
。该趋近律结合了纯指数趋近律在系统状态轨迹远离平衡点时趋近速度快以及终端吸引趋近方式在状态轨迹接近平衡点时趋近律速度快的优点,能够实现全局快速收敛。同时,幂函数的引入使得趋近速度进一步加快,能够有效抑制滑模抖振现象。
对式(21)求导并结合式(20),可以得到
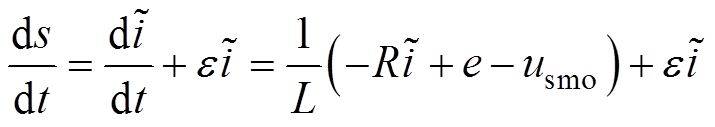 (23)
(23)
根据式(23),当状态变量到达滑模面时(即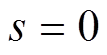 ),电流误差将收敛到0。此时
),电流误差将收敛到0。此时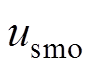 等同于
等同于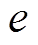 。
。
令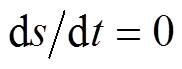 ,可以得到等效控制律
,可以得到等效控制律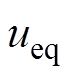 为
为
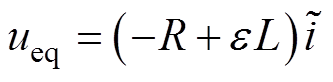 (24)
(24)
结合式(22)和式(23),可以得到
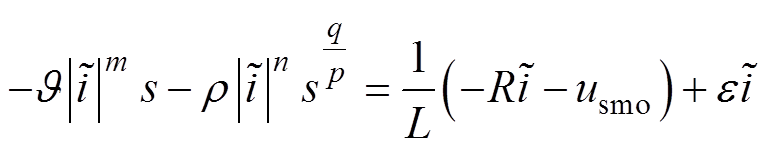 (25)
(25)
根据上述内容,将ISMO的控制律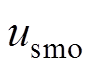 设计为
设计为
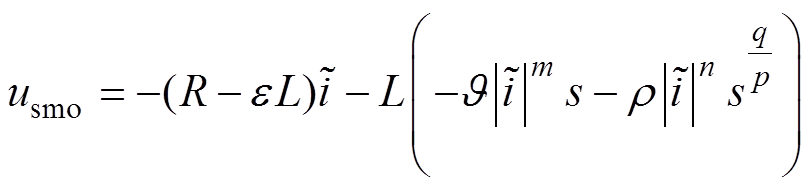 (26)
(26)
选择李雅普诺夫函数证明ISMO的稳定性。李雅普诺夫函数的定义为
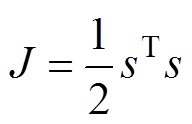 (27)
(27)
根据李雅普诺夫稳定性定理,ISMO只有在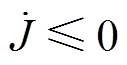 时才能稳定。将式(22)代入式(27),且由于
时才能稳定。将式(22)代入式(27),且由于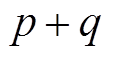 为偶数,可得
为偶数,可得
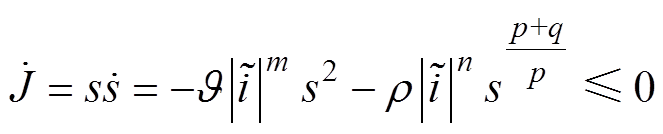 (28)
(28)
显然,所采用的趋近律满足稳定性条件。因此,该系统是渐近稳定的。
由上述ISMO的设计过程可知,该观测器用于重构电机反电动势信息,即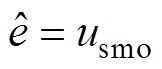 ,
,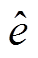 为估算的反电动势。对于LOM,其反电动势与速度成正比,即
为估算的反电动势。对于LOM,其反电动势与速度成正比,即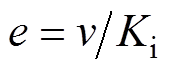 。因此,根据估算的
。因此,根据估算的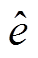 可以计算得到估算的速度信号
可以计算得到估算的速度信号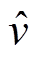 。然后对
。然后对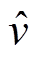 进行积分计算,即可得到估算的行程信号
进行积分计算,即可得到估算的行程信号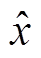 。
。
与传统的反电动势积分方法相比,ISMO通过引入电流误差反馈环节,可以获得更精确的反电动势信息,从而提高行程估算精度。然而,行程信号是由积分得到的,纯积分饱和问题仍然存在,这会影响最终的估算效果。
采用高通滤波器首先将反电动势中存在的直流分量滤除,然后对其进行积分计算可解决纯积分饱和问题。然而,高通滤波器与纯积分器一起使用相当于一个低通滤波器,这会引起滤波输出信号的幅值和相位偏移。由于SOGI可以很好地滤除大量谐波信号,且保留其中心频率的基频信息。因此,本文采用SOGI代替纯积分器以解决积分饱和问题。基于ISMO及SOGI的活塞行程估算结构框图如图5所示。
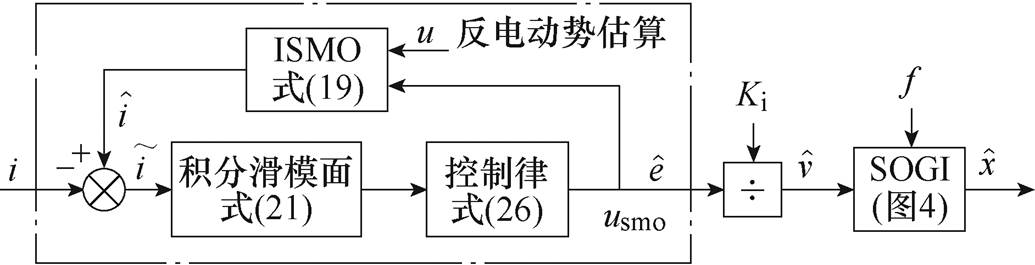
图5 基于ISMO及SOGI的活塞行程估算结构框图
Fig.5 Structure diagram of ISMO with SOGI for piston stroke estimation
根据上述所设计的DCFR及ISMO,可以得到LOM无位置传感器谐振频率跟踪控制的整体系统结构框图如图6所示。
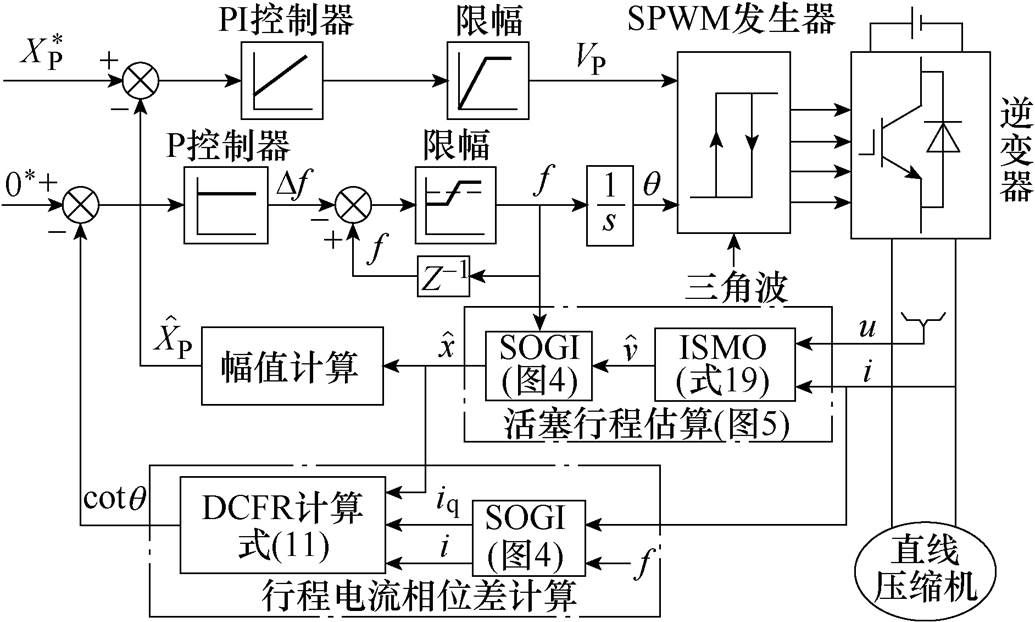
图6 LOM无位置传感器谐振频率跟踪控制框图
Fig.6 Structure diagram of position sensorless resonant frequency tracking control for LOM
为验证本文所提方法的有效性,采用如图7所示的实验平台进行验证。该平台将120 W LOM原型样机作为驱动电机,负载为由气缸提供的非线性气体力,三相调压器用于调节输出电压大小,LVDT位置传感器用于与行程估算方法进行对比。该电机的定子电阻为18.4 W,定子电感为0.755 H,推力系数为28.0 N/A,动子质量为1.024 kg。控制系统采用STM32F407芯片,其中断周期为5 kHz。在实验中,DCFR和ISMO的主要参数设置如下: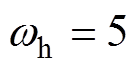 ,
,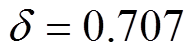 ,
,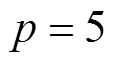 ,
,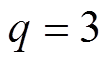 ,
,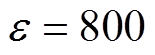 ,
,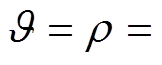
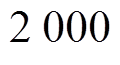 ,
,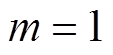 ,
,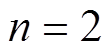 。
。

图7 实验平台
Fig.7 Experiment platform
将所提出的ISMO与传统反电动势积分方法进行实验对比分析,两种观测器皆采用SOGI代替纯积分器以避免纯积分饱和问题。设置行程参考值为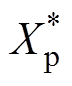 =5 mm,电机运行频率为23.483 Hz。两种估算方法的实验结果如图8所示。可以看到,反电动势积分方法的行程估算误差为0.418 mm,而所提出的ISMO的行程估算误差仅为0.152 mm。显然,相比于反电动势积分方法,ISMO具有更高的估算精度。这是因为滑模观测器本身具有强参数鲁棒性,且该观测器中引入了电流误差反馈环节,能够进一步提高估算精度。
=5 mm,电机运行频率为23.483 Hz。两种估算方法的实验结果如图8所示。可以看到,反电动势积分方法的行程估算误差为0.418 mm,而所提出的ISMO的行程估算误差仅为0.152 mm。显然,相比于反电动势积分方法,ISMO具有更高的估算精度。这是因为滑模观测器本身具有强参数鲁棒性,且该观测器中引入了电流误差反馈环节,能够进一步提高估算精度。
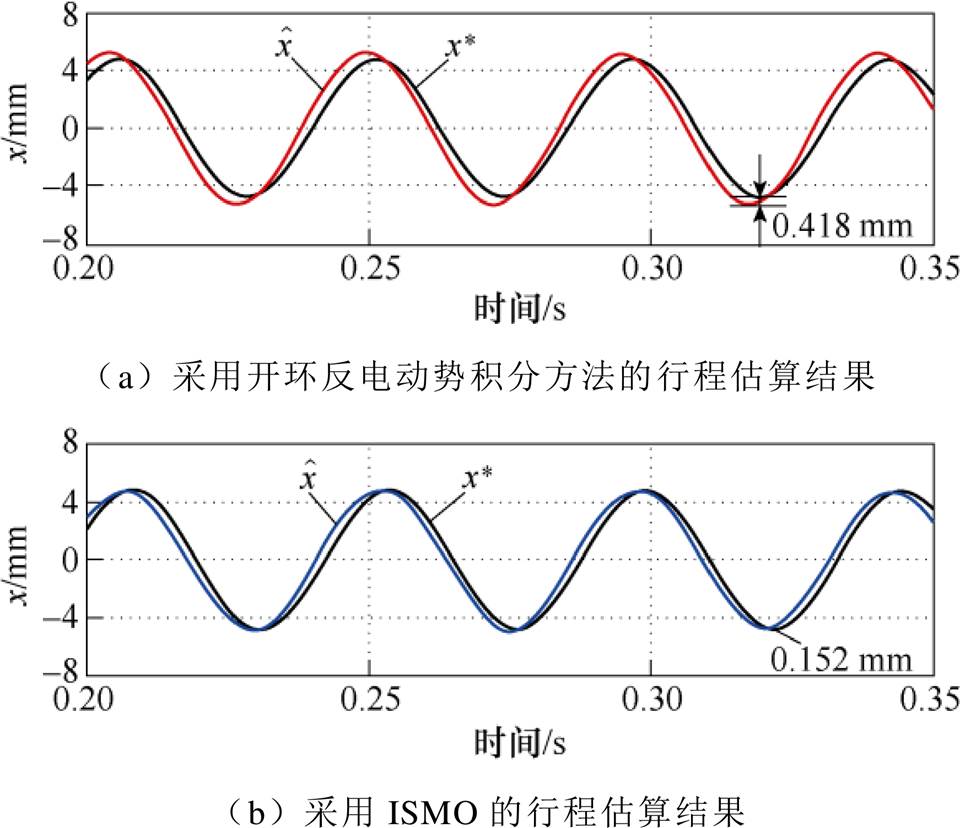
图8 两种不同观测器的行程估算结果
Fig.8 Stroke estimation results of two different observers
为了验证本文所提出的DCFR方法的优越性,还将其与ASCP方法进行了实验对比分析。为保证对比的公平性,两种方法采用的行程信号都由ISMO提供。本文进行了两组不同运行工况的实验,分别为电机由起动到稳定过程以及电机稳定后变行程运动过程。
首先对电机由起动到稳定运行过程进行实验分析。设置行程的参考幅值为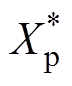 =5 mm,初始运行频率为21 Hz,采用两种不同谐振频率跟踪控制方法的运行结果如图9和图10所示。图中的谐振频率参考值是在电机行程为5 mm时不断改变运行频率测得的,此时气缸的排气压力为0.08 MPa。如图9和图10所示,ASCP方法和DCFR方法都能实现活塞行程闭环及谐振频率跟踪控制。其中,ASCP方法的频率跟踪误差为0.057 Hz,控制目标值波动为0.034 mm·A,稳定时间为2.315 s;DCFR方法的频率跟踪误差为0.039 Hz,控制目标值波动为0.005 rad,稳定时间为1.473 s。由上述结果可知,与ASCP方法相比,所提出的DCFR方法具有更高的跟踪精度、更短的稳定时间以及更小的目标值波动。
=5 mm,初始运行频率为21 Hz,采用两种不同谐振频率跟踪控制方法的运行结果如图9和图10所示。图中的谐振频率参考值是在电机行程为5 mm时不断改变运行频率测得的,此时气缸的排气压力为0.08 MPa。如图9和图10所示,ASCP方法和DCFR方法都能实现活塞行程闭环及谐振频率跟踪控制。其中,ASCP方法的频率跟踪误差为0.057 Hz,控制目标值波动为0.034 mm·A,稳定时间为2.315 s;DCFR方法的频率跟踪误差为0.039 Hz,控制目标值波动为0.005 rad,稳定时间为1.473 s。由上述结果可知,与ASCP方法相比,所提出的DCFR方法具有更高的跟踪精度、更短的稳定时间以及更小的目标值波动。
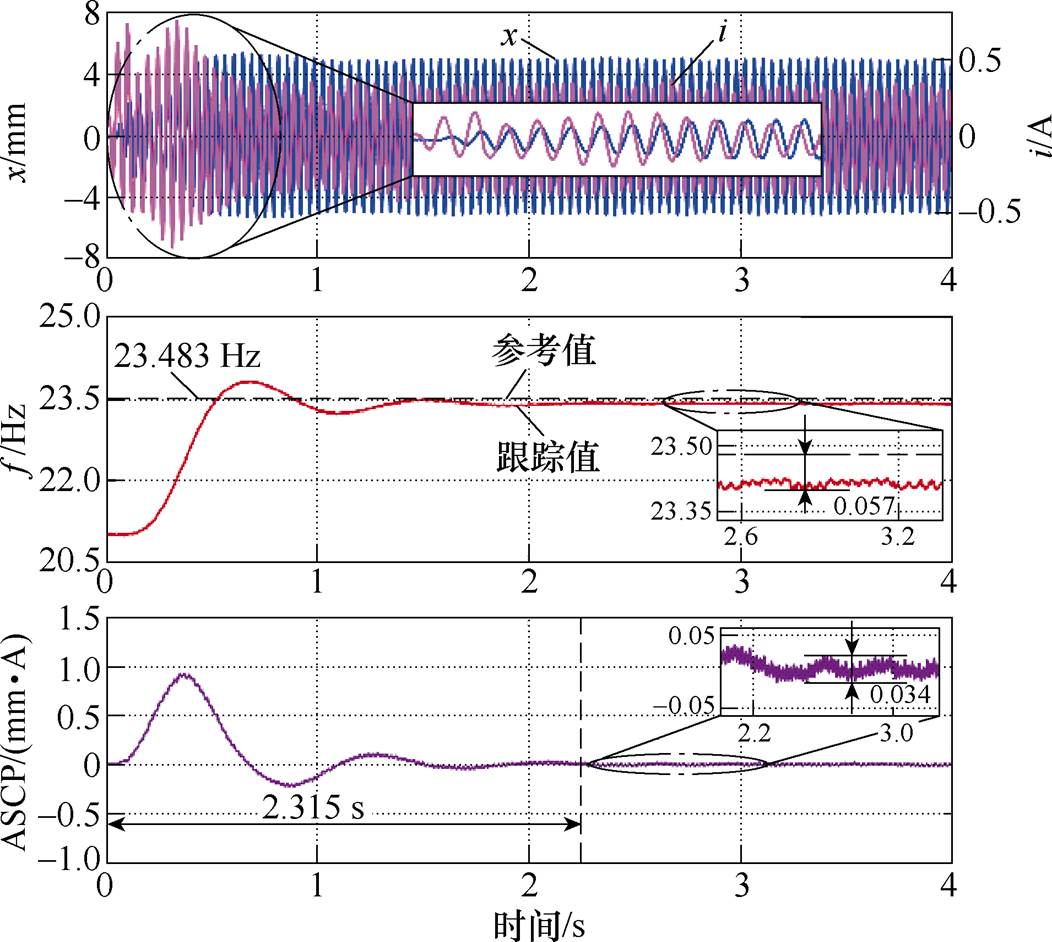
图9 起动过程中基于ASCP与ISMO的谐振频率跟踪控制结果
Fig.9 Resonant frequency tracking results based on ASCP and ISMO during startup process
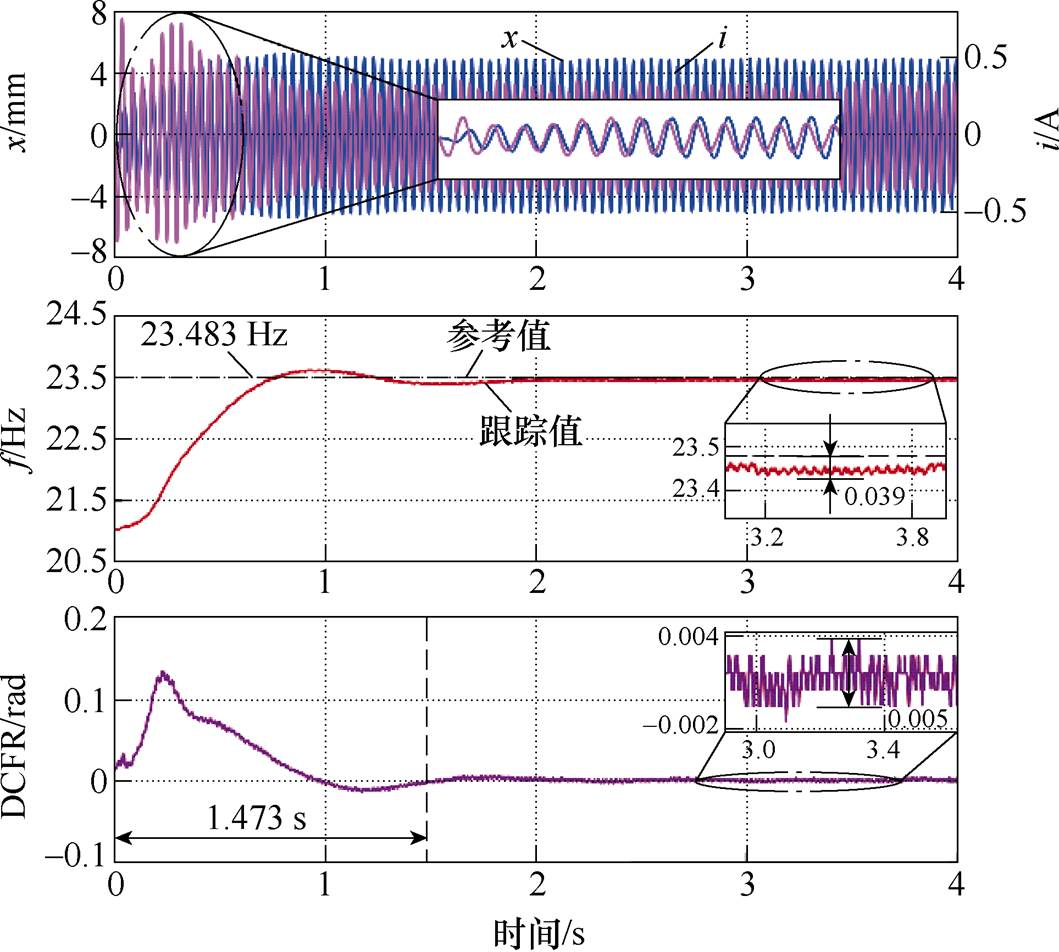
图10 起动过程中基于DCFR与ISMO的谐振频率跟踪控制结果
Fig.10 Resonant frequency tracking results based on DCFR and ISMO during startup process
当电机稳定运行后,将行程参考值设置为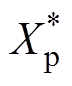 = 7 mm。两种方法的控制结果如图11和图12所示。图中的谐振频率参考值是在电机行程为7 mm时不断改变运行频率测得的,此时气缸的排气压力为0.11 MPa。如图11所示,电机稳定后,ASCP方法的频率跟踪误差为0.078 Hz,控制目标值波动为0.079 mm·A,稳定时间为2.851 s。相比之下,图12中DCFR方法的频率跟踪误差为0.043 Hz,控制目标值波动为0.005 rad,稳定时间为1.762 s。显然,所提DCFR方法要全面优于ASCP方法。为了进一步验证所提方法的有效性,将图10及图12中行程电流曲线的细节放大,如图13所示。图13a中显示,电机在起动阶段,行程与电流的相位差不是90°,而随着控制系统的稳定,行程与电流的相位差逐渐变为90°。图13b中显示,变行程过程中行程与电流的相位差一直被严格控制在90°,这说明所提方法具有较强的适应性。
= 7 mm。两种方法的控制结果如图11和图12所示。图中的谐振频率参考值是在电机行程为7 mm时不断改变运行频率测得的,此时气缸的排气压力为0.11 MPa。如图11所示,电机稳定后,ASCP方法的频率跟踪误差为0.078 Hz,控制目标值波动为0.079 mm·A,稳定时间为2.851 s。相比之下,图12中DCFR方法的频率跟踪误差为0.043 Hz,控制目标值波动为0.005 rad,稳定时间为1.762 s。显然,所提DCFR方法要全面优于ASCP方法。为了进一步验证所提方法的有效性,将图10及图12中行程电流曲线的细节放大,如图13所示。图13a中显示,电机在起动阶段,行程与电流的相位差不是90°,而随着控制系统的稳定,行程与电流的相位差逐渐变为90°。图13b中显示,变行程过程中行程与电流的相位差一直被严格控制在90°,这说明所提方法具有较强的适应性。
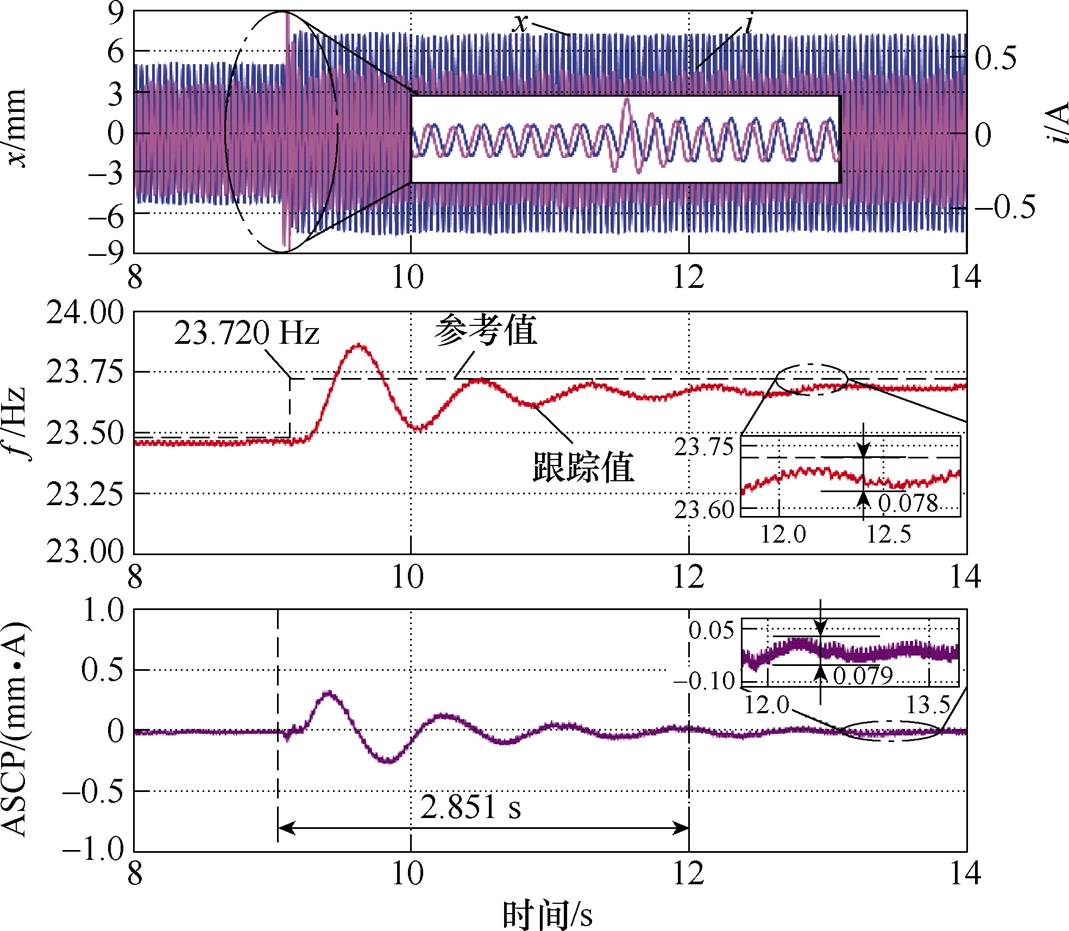
图11 行程变化过程中基于ASCP与ISMO的谐振频率跟踪控制结果
Fig.11 Resonant frequency tracking results based on ASCP and ISMO during stroke change process
根据上述实验结果可知,采用相同的行程观测器,DCFR方法相比于ASCP方法具有更强的抗干扰能力,能够获得更加平稳、精确的谐振频率跟踪结果。接下来,基于DCFR方法比较不同行程观测器对谐振频率跟踪精度的影响。起动过程及变行程过程中采用两种不同观测器获得的系统谐振频率如图14所示。可以看出,观测器精度对谐振频率的影响较大,由于传统反电动势积分法的行程观测精度较低,其谐振频率跟踪精度远远低于本文所提出的积分滑模观测器。因此,有必要采用高精度行程观测器进行谐振频率跟踪控制。
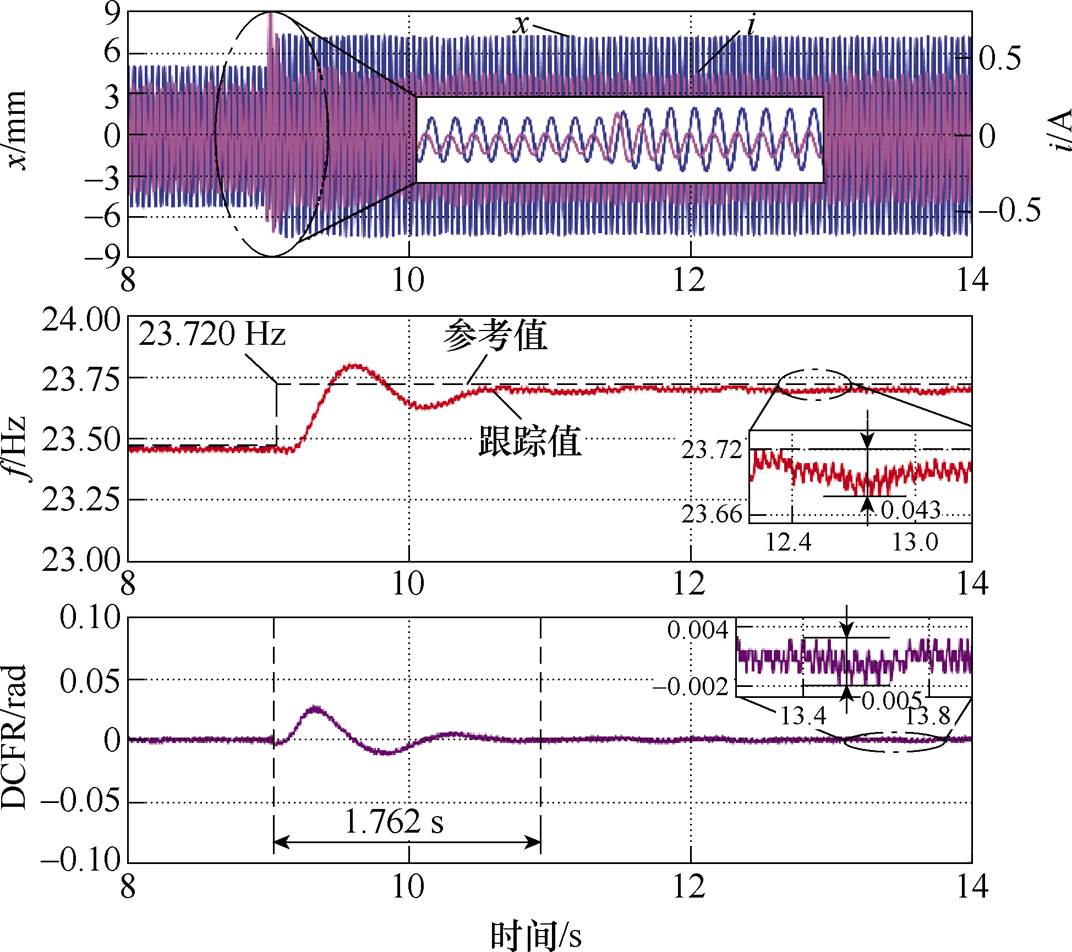
图12 行程变化过程中基于DCFR与ISMO的谐振频率跟踪控制结果
Fig.12 Resonant frequency tracking control results based on DCFR and ISMO during stroke change process
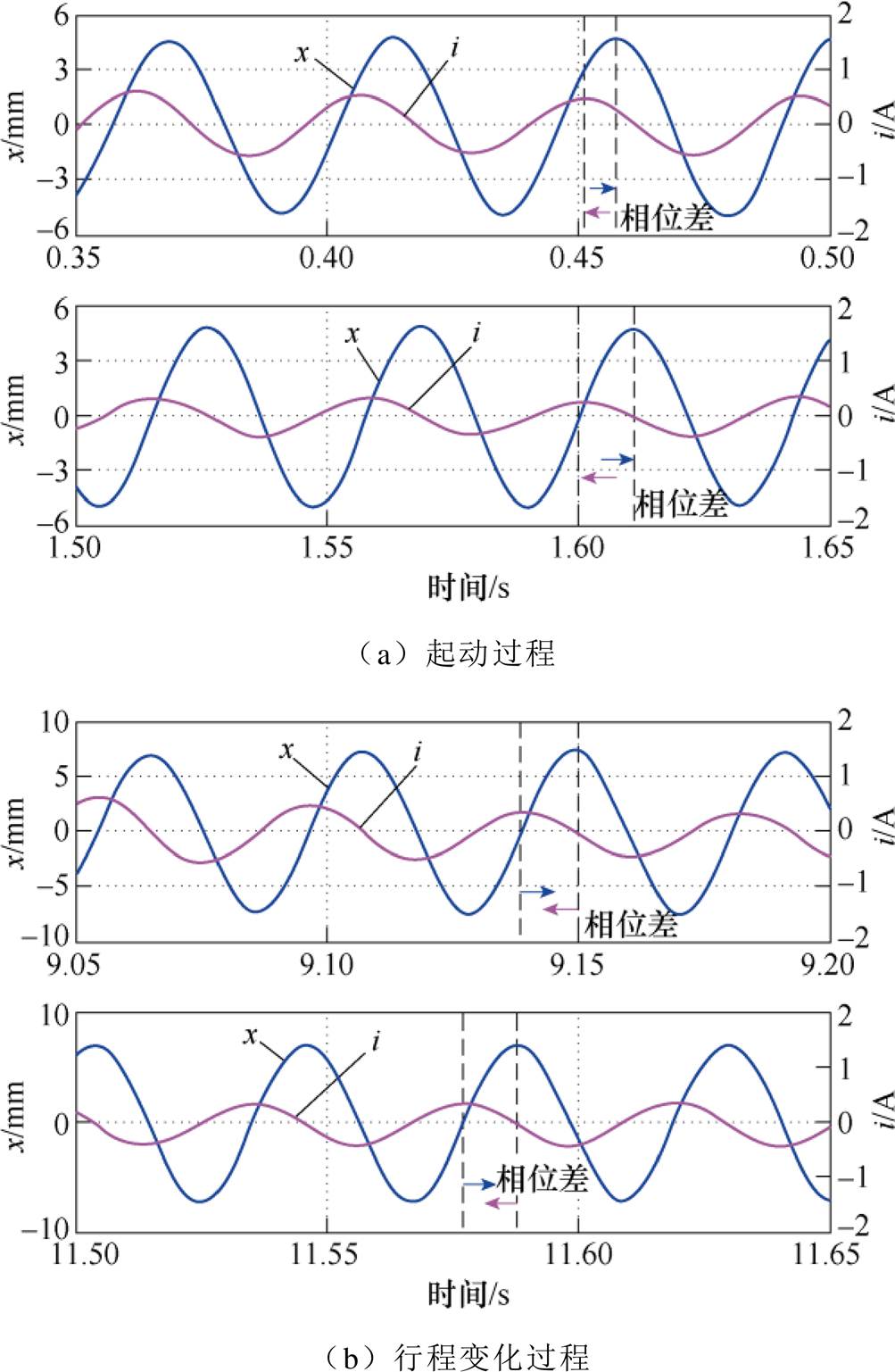
图13 基于DCFR与ISMO方法的行程与电流相位关系
Fig.13 Phase relationship of stroke and current based on DCFR and ISMO methods
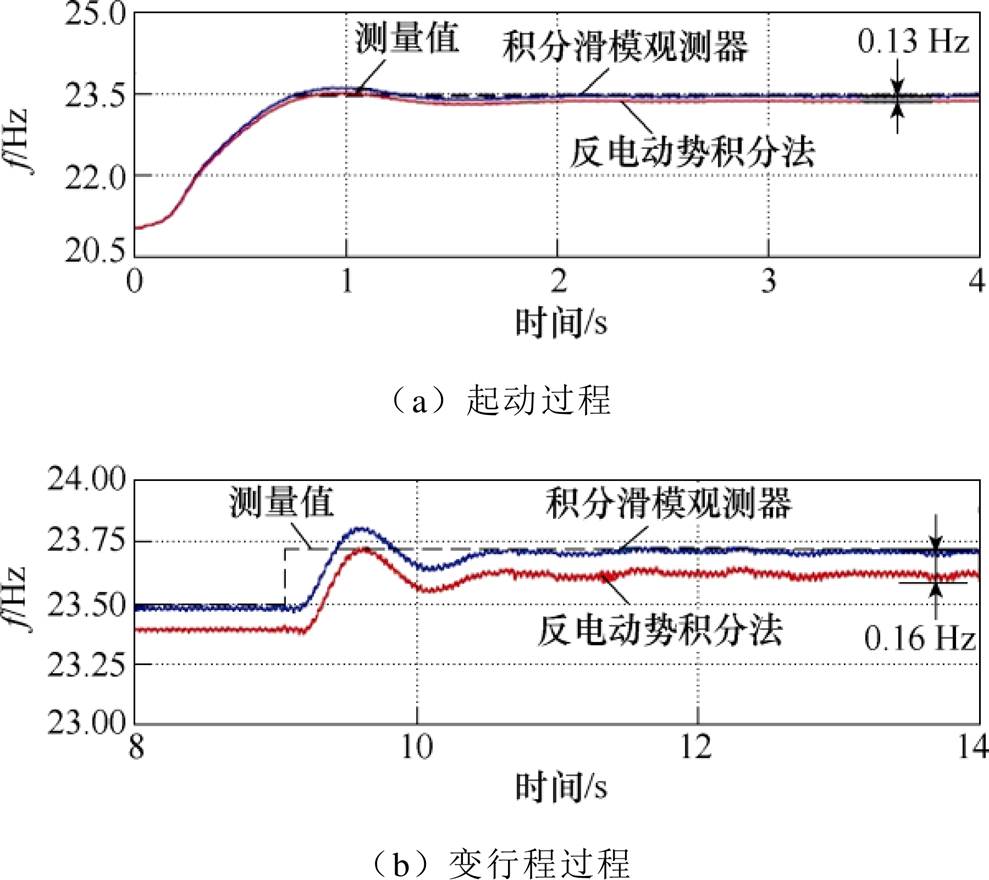
图14 采用不同行程观测器获得的系统谐振频率
Fig.14 System resonance frequency obtained by different stroke observers
综上所述,相比于开环反电动势方法,ISMO能够获得更精确的行程信号,而DCFR方法相比于ASCP方法具有更强的抗干扰能力,因此采用ISMO及DCFR进行无位置传感器谐振频率跟踪控制能够获得更好的跟踪效果。
本文提出了一种新型无位置传感器谐振频率跟踪控制方法。在该方法中,提出了一种基于DCFR的谐振频率跟踪控制方法,通过构造正交信号的比值消除了行程对控制目标的影响,显著提高了控制系统的抗干扰能力,可以获得更精确的系统谐振频率。此外,设计了一个ISMO用于观测电机反电动势,并采用SOGI获取活塞行程信号。与传统开环反电动势积分方法相比,ISMO具有强参数鲁棒性,能够大幅提高行程估算精度。最后,将ISMO与DCFR相结合进行无位置传感器谐振频率跟踪控制,并将其与传统ASCP方法进行对比。实验结果表明,相比于传统ASCP方法,DCFR具有更高的频率跟踪精度、更快的收敛速度以及更小的目标值波动。此外,行程观测精度对谐振频率跟踪精度有较大影响,因此需要采用高精度行程观测器与谐振频率跟踪方法相结合,以保证谐振频率跟踪性能。
参考文献
[1] 陈梁远, 李黎川. 压缩机用直线电机及其关键技术发展综述[J]. 中国电机工程学报, 2013, 33(15): 52-68, 15.
Chen Liangyuan, Li Lichuan. Development of the linear motor and its key technologies for reciprocating compressors[J]. Proceedings of the CSEE, 2013, 33(15): 52-68, 15.
[2] 徐伟, 李想, 廖凯举, 等. 直线振荡电机拓扑结构及应用综述[J]. 电工技术学报, 2022, 37(21): 5377- 5401.
Xu Wei, Li Xiang, Liao Kaiju, et al. Overview of linear oscillatory machines: topology and appli- cation[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5377-5401.
[3] Chen X, Zhu Z Q. Analytical determination of optimal split ratio of E-core permanent magnet linear oscillating actuators[C]//2009 IEEE Energy Con- version Congress and Exposition, San Jose, CA, USA, 2009: 2100-2107.
[4] Pompermaier C, Kalluf K, Zambonetti A, et al. Small linear PM oscillatory motor: magnetic circuit modeling corrected by axisymmetric 2-D FEM and experimental characterization[J]. IEEE Transactions on Industrial Electronics, 2012, 59(3): 1389-1396.
[5] Xu Wei, Li Xiang, Zhu Jianguo, et al. 3-D modeling and testing of a stator-magnet transverse-flux linear oscillatory machine for direct compressor drive[J]. IEEE Transactions on Industrial Electronics, 2021, 68(9): 8474-8486.
[6] Xu Wei, Wang Qizhe, Li Xiang, et al. A novel resonant frequency tracking control for linear com- pressor based on MRAS method[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(3): 227-236.
[7] Liao Kaiju, Xu Wei, Bai Lili, et al. Improved position sensorless piston stroke control method for linear oscillatory machine via an hybrid terminal sliding- mode observer[J]. IEEE Transactions on Power Elec- tronics, 2022, 37(12): 14186-14197.
[8] 雷美珍. 新型无内定子动磁式直线振荡执行器的设计及其关键技术研究[D]. 杭州: 浙江理工大学, 2014.
[9] 于明湖. 直线压缩机用横向磁通永磁直线振荡电机系统研究[D]. 杭州: 浙江大学, 2011.
[10] Chun T W, Ahn J R, Lee H H, et al. A novel strategy of efficiency control for a linear compressor system driven by a PWM inverter[J]. IEEE Transactions on Industrial Electronics, 2008, 55(1): 296-301.
[11] Zhang Tao, Yu Haitao. A novel strategy of resonant frequency tracking control for linear compressor[C]// 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, Australia, 2017: 1-6.
[12] Suzuki T, Koyama M, Nagata S, et al. Position sensor-less resonant frequency estimation method for linear compressor with assist springs[C]//2020 International Conference on Electrical Machines (ICEM), Gothenburg, Sweden, 2020: 1206-1212.
[13] Chun T W, Ahn J R, Tran Q V, et al. Method of estimating the stroke of LPMSM driven by PWM inverter in a linear compressor[C]//APEC 07-Twenty- Second Annual IEEE Applied Power Electronics Conference and Exposition, Anaheim, CA, USA, 2007: 403-406.
[14] Latham J, McIntyre M L, Mohebbi M. Sensorless resonance tracking and stroke control of a linear vapor compressor via nonlinear observers[J]. IEEE Transactions on Industrial Electronics, 2018, 65(5): 3720-3729.
[15] den Brinker A C. Calculation of the local cross-correlation function on the basis of the Laguerre transform[J]. IEEE Transactions on Signal Processing, 1993, 41(5): 1980-1982.
[16] 张晓东, 高波, 宋之平. 互相关函数法在声学测温技术中的应用研究[J]. 中国电机工程学报, 2003, 23(4): 185-188.
Zhang Xiaodong, Gao Bo, Song Zhiping. The research of acoustic measuring of gas temperature employing cross-correlation algorithm[J]. Proceedings of the CSEE, 2003, 23(4): 185-188.
[17] Tanaka T, Hiraki E, Ueda K, et al. A novel detection method of active and reactive currents in single-phase circuits using the correlation and cross-correlation coefficients and its applications[J]. IEEE Transactions on Power Delivery, 2007, 22(4): 2450-2456.
[18] 曾君, 岑德海, 陈润, 等. 针对直流偏移和谐波干扰的单相锁相环[J]. 电工技术学报, 2021, 36(16): 3504-3515.
Zeng Jun, Cen Dehai, Chen Run, et al. Single-phase phase-locked loop for DC offset and harmonic interference[J]. Transactions of China Electro- technical Society, 2021, 36(16): 3504-3515.
[19] 王勃, 王天擎, 于泳, 等. 感应电机电流环非线性积分滑模控制策略[J]. 电工技术学报, 2021, 36(10): 2039-2048.
Wang Bo, Wang Tianqing, Yu Yong, et al. Nonlinear integral sliding mode control strategy for current loop of induction motor drives[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2039-2048.
[20] 王琛琛, 苟立峰, 周明磊, 等. 基于改进的离散域二阶滑模观测器的内置式永磁同步电机无位置传感器控制[J]. 电工技术学报, 2023, 38(2): 387-397.
Wang Chenchen, Gou Lifeng, Zhou Minglei, et al. Sensorless control of IPMSM based on improved discrete second-order sliding mode observer[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 387-397.
[21] 曹学谦, 葛琼璇, 朱进权, 等. 基于积分滑模的高速磁悬浮列车谐波电流抑制策略[J]. 电工技术学报, 2022, 37(22): 5817-5825, 5861.
Cao Xueqian, Ge Qiongxuan, Zhu Jinquan, et al. Harmonic current suppression strategy for high-speed maglev train based on integral sliding mode[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5817-5825, 5861.
[22] 张晓光, 赵克, 孙力, 等. 永磁同步电动机滑模变结构调速系统新型趋近率控制[J]. 中国电机工程学报, 2011, 31(24): 77-82.
Zhang Xiaoguang, Zhao Ke, Sun Li, et al. A PMSM sliding mode control system based on a novel reaching law[J]. Proceedings of the CSEE, 2011, 31(24): 77-82.
Abstract In order to improve the safety and reliability of the system and achieve maximum output efficiency, it is necessary to simultaneously implement position sensorless piston stroke closed-loop control and resonant frequency tracking control for the linear oscillatory machine (LOM). Existing control methods for position sensorless resonance frequency tracking have low stroke estimation accuracy and poor anti-interference ability, which causes low resonant frequency tracking accuracy and severe frequency oscillation. This paper investigates a new resonant frequency tracking control method based on the integrated sliding mode observer (ISMO).
When the LOM operates at the system resonant frequency point, the phase difference between stroke and current is exactly 90°. Accordingly, a double cross-correlation function ratio (DCFR) method is proposed to track the system resonant frequency. A second-order generalized integrator (SOGI) generates the current orthogonal signal. This method can eliminate the influence of stroke on resonance frequency tracking control, thereby improving the anti-interference ability of the control system. An integrated sliding mode surface and a new reaching law are used to design an ISMO to reconstruct the information of back electromotive force (EMF). Since the back EMF is positively proportional to the velocity signal, the piston velocity can be calculated. The piston stroke can be obtained by integrating the velocity signal. However, specific DC components exist in the measured voltage and current, and a pure integrator can cause the integral saturation problem. Therefore, an SOGI is used to filter the estimated back EMF signal to obtain the accurate stroke estimation signal. Finally, due to the strong parameter robustness of ISMO and the anti-interference ability of DCFR, the combination of ISMO and DCFR is used to achieve the position sensorless resonant frequency tracking control. Experimental results show that the proposed method effectively improves the tracking accuracy, settling time, and anti-interference ability.
The following conclusions can be drawn from the experiment analysis. (1) The constructed ISMO has higher stroke estimation accuracy than the back electromotive force integration method. (2) The position sensorless resonant frequency tracking control can be achieved using the estimated stroke signals of ISMO. (3) By constructing the ratio of two DC components, the proposed DCFR method eliminates the influence of stroke variation and obtains steady and accurate resonant frequency tracking results. (4) Based on the DCFR method, the ISMO and back EMF integration methods are used to track the resonant frequency. The results show that ISMO achieves higher tracking accuracy by providing more accurate stroke signals than the conventional back EMF.
keywords:Linear oscillatory machine (LOM), resonance frequency tracking control, integral sliding mode observer (ISMO), double cross-correlation function ratio (DCFR) method, second-order generalized integrator (SOGI)
DOI: 10.19595/j.cnki.1000-6753.tces.230781
中图分类号:TM32
国家自然科学基金面上项目(52277050)、深圳市协同创新计划国际科技合作项目(GJHZ20210705142539007)资助。
收稿日期 2023-05-29
改稿日期 2023-07-20
廖凯举 男,1991年生,博士,研究方向为直线振荡电机高性能控制算法及无位置传感器方法。E-mail: kaijuliao@mail.iee.ac.cn
徐 伟 男,1980年生,教授,博士生导师,研究方向为直线电机设计及控制。E-mail: weixu@hust.edu.com(通信作者)
(编辑 崔文静)