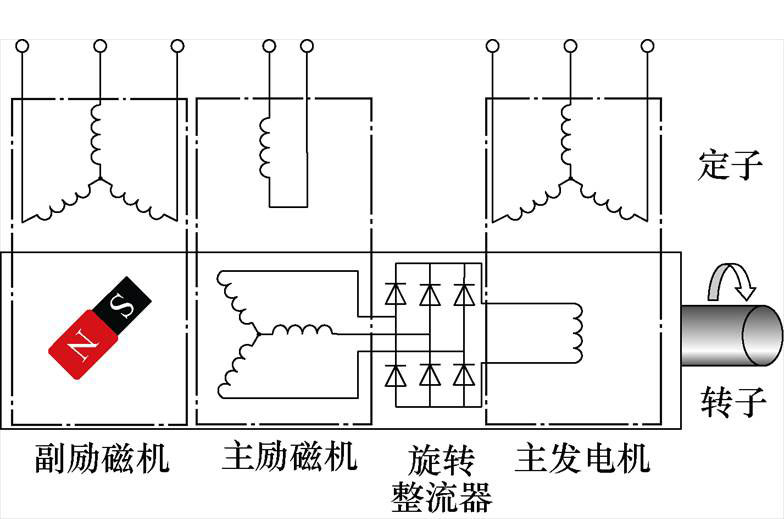
图1 三级式同步电机结构
Fig.1 Structure of TSSM
摘要 针对航空三级式同步电机起动控制中存在的转子位置信息获取困难问题，在励磁电压高频谐波自注入方法分析的基础上，该文基于同步解调的基本思路，提出了一种无需极性判断和励磁电流采样环节的同步解耦信号生成方式，并根据主发电机中响应电压谐波的频谱特性设计了位置误差信息提取的精准谐波消除滤波器，可以降低转子位置估计闭环系统的阶次，增强系统的稳定性以适应更宽的转速范围。最后通过仿真和实验证明了所述改进同步解调方法能够实现高精度和宽转速范围的三级式同步电机无位置传感器起动控制。
关键词：三级式同步电机 谐波自注入 同步解调 精准谐波消除滤波器
近年来，飞机发动机气动起动方式中存在的体积质量大、效率低和可靠性差等问题使得传统飞机性能难以提升，以起动/发电一体化系统为核心的多电飞机取消了气动装置和额外的起动机，极大地提高了飞机的起动性能，逐渐成为飞机发展的主流方向[1-3]。目前，飞机起动/发电机的研究主要包括异步电机、开关磁阻电机、电励磁双凸极电机和三级式同步电机等[4-5]，其中三级式同步电机（Three- Stage Synchronous Machines, TSSM）因其结构成熟易于发电调压控制，在飞机交流电源系统中得到了广泛应用[6-8]。相较于较为成熟的发电技术，起动阶段的控制是三级式同步电机的研究难点，主要包括励磁方式和起动控制方式。三级式同步电机的起动控制需要转子位置信息进行反馈闭环，而编码器、旋转变压器等位置传感器在航空工况下存在体积质量大、可靠性差和利用率低等问题，使得无位置传感器技术逐渐成为三级式同步电机起动/发电技术的研究热点。
交流电机无位置传感器技术根据转速适用范围可分为零低速阶段和高速阶段。高速阶段通常采用基于卡尔曼滤波器[9-10]、滑模观测器[11-12]或模型参考自适应法[13-14]等反电动势观测法；零低速阶段反电动势较小而无法运用于转子位置估计，通常采用额外高频信号注入[15-17]的方式，并且根据注入信号类型可分为旋转高频信号注入和脉振高频信号注入，分别适用于凸极和隐极结构同步电机的转子位置估计。
类似地，三级式同步电机的高速阶段转子位置估计也可以采用相似的反电动势观测法，而多级式的电机结构为三级式同步电机低速阶段的高频信号注入法提供了多种方式，根据高频信号注入和提取的位置可划分为三类：第一类为主发电机注入-主发电机提取，类似传统交流电机，在估计位置的对象主发电机定子侧注入旋转高频电压信号，在主发电机定子侧提取高频响应电流，并采用外差法进行解耦处理[18]。
第二类为主发电机注入-主励磁机提取，文献[19]在主发电机定子侧注入高频方波电压信号，提取主励磁机定子侧电流有效值以获得转子位置信息，实现了零速时的转子位置估计；文献[20]在主发电机定子侧注入旋转高频电压信号，详细分析了高频信号传递过程，提出了基于采样函数的转子位置信息解耦处理方式，一定程度上提高了注入信号的信噪比；文献[21]在主发电机定子侧注入脉振高频电压信号，提取主励磁机定子侧的高频响应电流有效值以解算转子位置信息。此类方式中，对主电机的凸极性依赖较低，但高频信号传递和转子位置信息解调过程较为复杂，并且对电机模型的准确性要求较高。
第三类为主励磁机注入-主发电机提取，此类方式利用主励磁机的信号放大特点，能够有效地缓解从主发电机注入高频信号转矩脉动大的问题。文献[22]将旋转高频电压信号注入主励磁机定子侧，通过极性还原的方式提取主发电机定子侧高频响应电压的包络曲线，由锁相环解算转子位置角，此方法通过非同步解调的方式避免了相位处理问题，但信号还原过程中的过零点畸变问题使其位置估计精度受限；文献[23]提出了一种利用电机自身谐波作为间接注入高频信号的方式，解调过程同样采用极性还原的方法，与额外旋转高频电压注入方式形成对比，位置估计精度有所提升；进一步地，文献[24]将间接谐波注入的基本思路用在单相励磁的三级式同步电机无位置传感器起动控制中，结合单相励磁特点，提出了一种基于主励磁机励磁电流的同步解耦信号生成方式，采用基于带通滤波器（Band-Pass Filter, BPF）和陷波器（Notch Filter, NF）级联滤波的同步解调方式对主发电机定子侧的响应电压信号进行解耦处理，进一步提高了转子位置估计精度。然而，该同步解耦信号的生成过程中需要额外的极性判断环节，硬件资源占用过多，且复杂的滤波结构使得转子位置估计系统阶次过高，导致系统存在稳定性问题。
针对上述三级式同步电机转子位置估计方法存在的问题，本文基于励磁电压高频谐波自注入的方法，提出一种基于精准谐波消除的滤波器结构设计，改进转子位置同步解调方法，并设计一种无需极性判断和励磁电流采样的同步解耦信号生成方式，有效降低转子位置估计系统复杂度，提高系统稳定性。最后，通过仿真和实验验证了本文所述的转子位置改进同步解调方式能够有效实现三级式同步电机的零低速阶段无位置起动控制，且转速适用范围较宽，稳定性良好。
图1所示为三级式同步电机结构示意图，同一轴线上包括永磁副励磁机、主励磁机、旋转整流器和主发电机四部分。起动运行过程中副励磁机不参与工作，由主励磁机、旋转整流器和主发电机共同工作，其中主励磁机采用恒压恒频单相交流励磁，在主励磁机气隙中产生脉振磁场，主励磁机电枢绕组切割此磁场产生的反电动势经旋转整流器整流后为主发电机提供励磁；主发电机采用基于id=0的转速外环和电流内环的双闭环矢量控制方式，三级式同步电机起动控制原理如图2所示，电流闭环控制中坐标变换环节所需的转子位置信息由位置估计环节解算获得，转速闭环控制所需的转速信息由估计转子位置角计算获得。
图1 三级式同步电机结构
Fig.1 Structure of TSSM
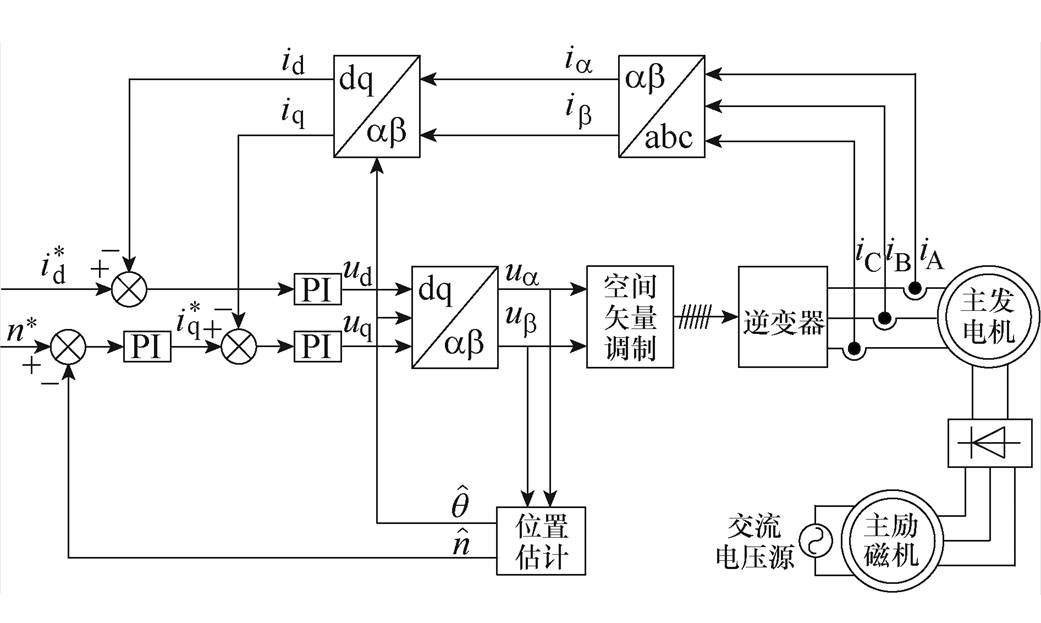
图2 三级式同步电机起动控制原理
Fig.2 Schematic diagram of starting control for TSSM
如图2所示的三级式同步电机起动控制原理中，主励磁机给定恒定励磁电流为
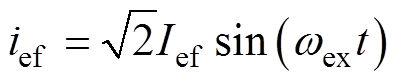（1）
式中，Ief为励磁电流有效值；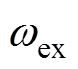
为主励磁机励磁角频率。此励磁电流在主励磁机的气隙中产生脉振磁场，电枢绕组切割磁场产生的三相感应电动势可表示为
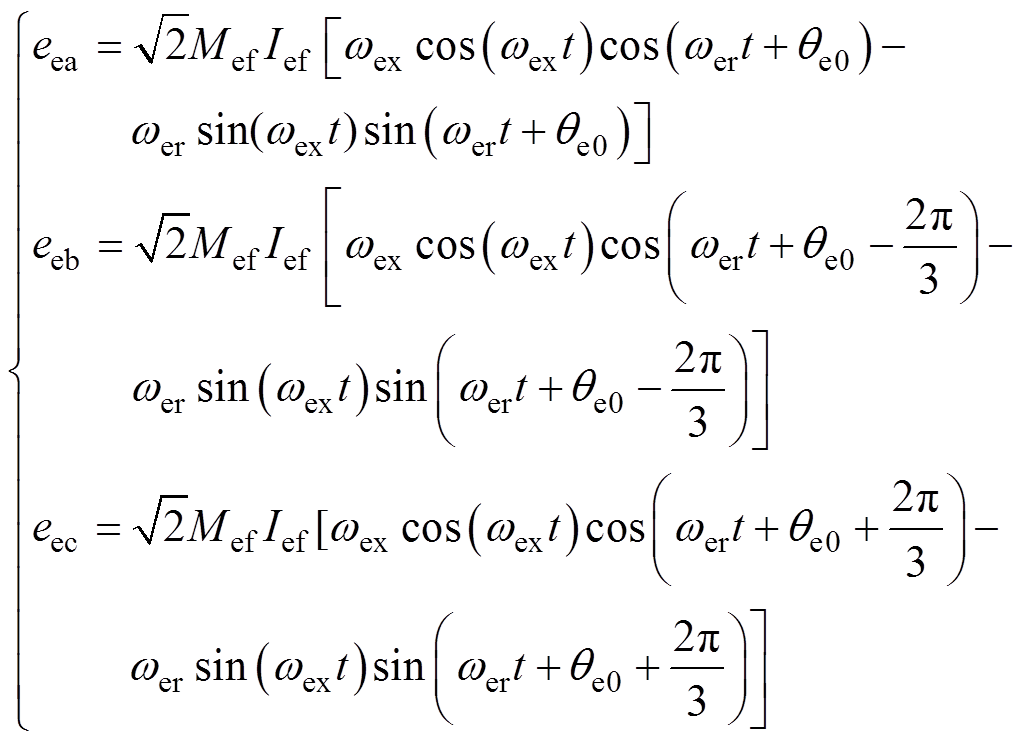（2）
式中，Mef为主励磁机定转子间互感值；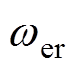
为主励磁机转子电角速度；
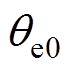为主励磁机初始转子位置电角度。三相感应电动势包含变压器电动势和切割电动势两部分，在零低速阶段由于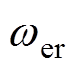很小而忽略切割电动势部分，三相电枢电动势经旋转整流器整流后提供给主发电机的励磁电压可表示为
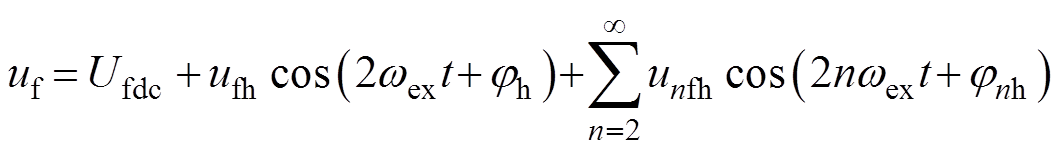（3）
式中，Ufdc、ufh、unfh分别为主发电机励磁电压的直流分量、2次谐波分量幅值、高次谐波分量幅值；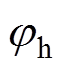
、
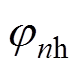分别为2次谐波和高次谐波分量中因旋转整流器换相重叠而产生的相位。
旋转整流器的输出励磁电压包含直流分量和偶次谐波分量，直流分量用于主发电机的励磁，偶次谐波分量可以看作间接注入主发电机励磁绕组的高频信号，其中幅值占比最大的2次谐波分量可用于转子位置估计，由此实现主发电机侧励磁电压高频谐波自注入。在此励磁电压下，主发电机电枢绕组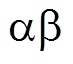
坐标系下的响应电压可表示为
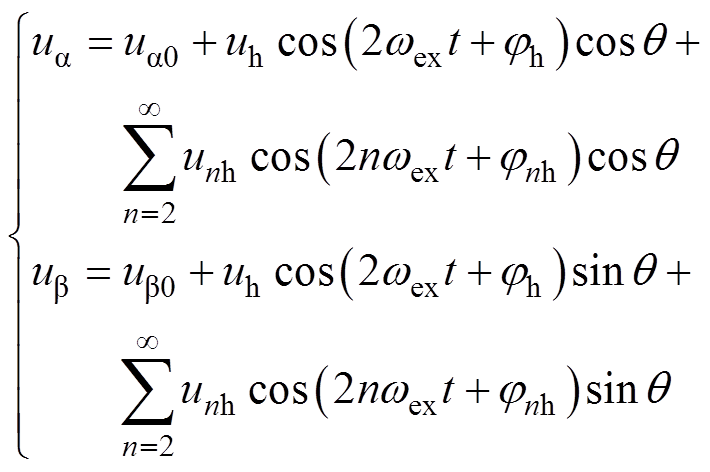（4）
式中，ua0和ub0分别为主发电机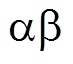坐标系下电枢电压的基波分量；uh、unh分别为主发电机电枢电压2次谐波分量幅值和高次谐波分量幅值；
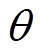为实际转子位置角，
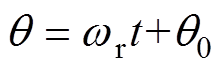，其中，wr为主发电机转子电角速度，
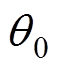为主发电机初始转子位置角。运用估计转子位置角进行Park变换可得主发电机电枢绕组q轴响应电压为
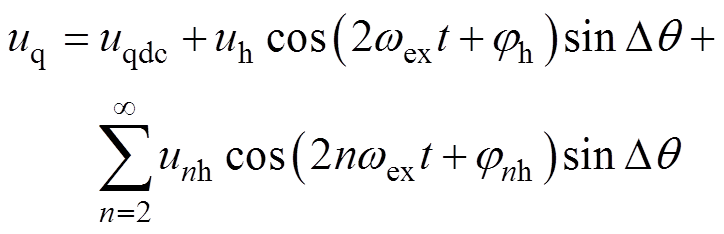（5）
式中，uqdc为主发电机q轴电枢电压的基波分量；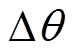
为转子位置误差角，
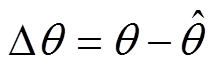，其中，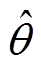
为估计转子位置角。该q轴电压信号中包含转子位置误差信息，通过同步解调的方式进行解耦以获取转子位置信息。
外差法是永磁同步电机的转子位置估计中的常用位置角解调方法，如图3所示，其基本思路是将BPF提取的高频响应信号与同步解耦信号作乘积，然后以低通滤波器（Low-Pass Filter, LPF）提取乘积中包含转子位置误差信息的低频分量，最后经由锁相环解算转子位置角。
图3 传统外差同步解调方式
Fig.3 Traditional heterodyne synchronous demodulation mode
类似地，可将该方法应用于三级式同步电机，不同的是，由于旋转整流器的非线性特性，高频响应信号的相位发生改变，需要额外计算出相位信息jh以生成同步解耦信号。对此，文献[24]提出了一种基于主励磁机励磁电流采样的同步解耦信号生成方式，并以NF取代LPF进一步增强对高次谐波的滤波效果，提高外差同步解调方式的位置估计精度。然而该方法仍存在诸多隐患：
（1）从同步解耦信号生成过程来看，主励磁机采用恒压交流励磁，相应的励磁电流相位会受到电机阻感参数影响而存在一定的相位偏差，可能会使得生成的同步解耦信号同步性不佳；此外，为了保证相位计算的信噪比和反正切函数计算的正确性，需要在电机静止阶段增加额外的极性判断和幅值比较环节，相位计算过程的复杂度较高，同时增加了硬件和软件资源负担。
（2）从基于BPF级联NF的外差同步解调结构来看，BPF和NF均由二阶广义积分器（Second- Order Generalized Integrator, SOGI）基本结构设计而来，相应的传递函数为
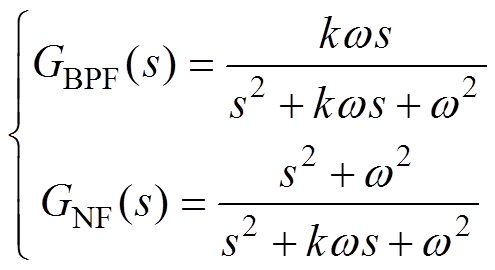（6）
式中，k为阻尼系数；w 为谐振频率。
可见，BPF和NF均为二阶阻尼系统，而锁相环同为二阶系统，旋转坐标系下的转子位置角解调系统中，滤波器处于闭环系统内部，因此基于BPF级联NF的转子位置同步解调闭环系统为六阶系统，包含六个闭环极点。BPF和NF的参数设计考虑的是滤波频率和滤波精度，均为确定量，而锁相环的PI参数则是实现转子位置估计所需调试的参数，为满足系统的稳定性要求，六个极点必须为负根，这使得该转子位置估计系统的参数整定十分困难，且同组参数适用的转速范围较为狭窄，系统的稳定性问题尤为突出，这对于实现航空三级式同步电机全速范围内的无位置传感器起动控制是十分不利的。
针对上述传统外差同步解调方式中存在的问题，本文从同步解耦信号生成方式、转子位置同步解调结构和滤波器设计三个方面进行优化改进。
图4为本文提出的取消励磁电流采样和极性判断环节的同步解耦信号生成原理框图。
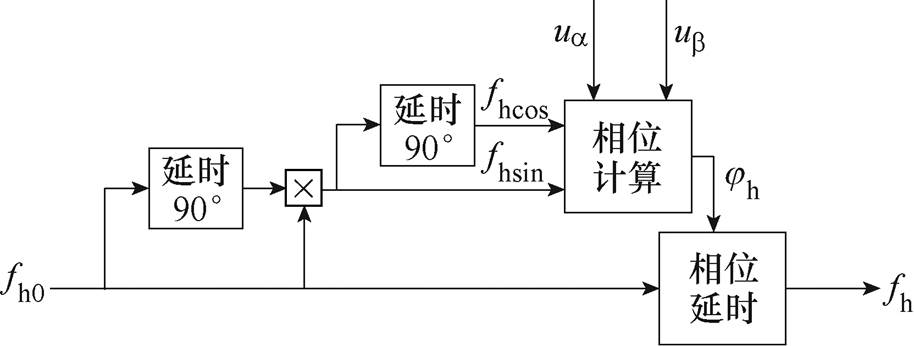
图4 同步解耦信号生成原理框图
Fig.4 Principle block diagram of synchronous decoupling signal generation
同频信号fh0由控制系统软件生成，表示为
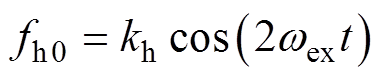（7）
式中，kh为同频信号的幅值。该同频信号经过延时和计算，生成相位计算所需的正余弦高频信号，可表示为
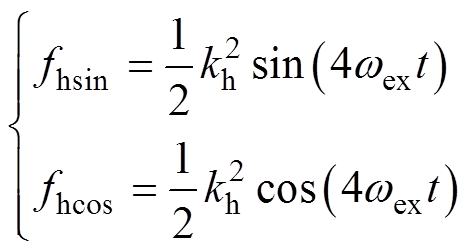（8）
将其应用于图5所示的同步信号相位计算环节。
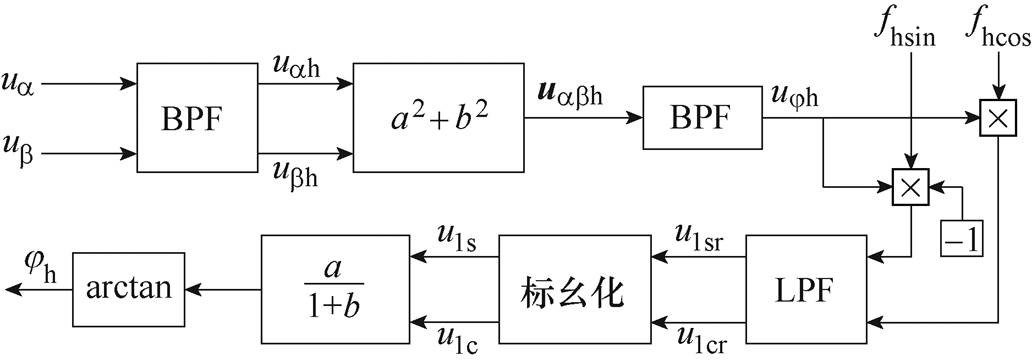
图5 相位计算原理框图
Fig.5 Principle block diagram of phase angel calculation
通过BPF提取的主发电机电枢绕组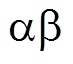坐标系下的响应电压2次谐波分量，即高频响应电压信号，可表示为
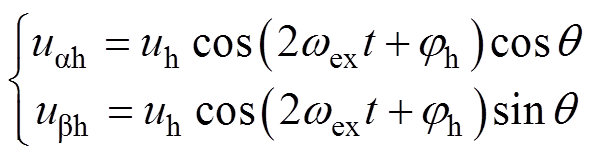（9）
将两路高频响应电压信号进行二次方和运算，有
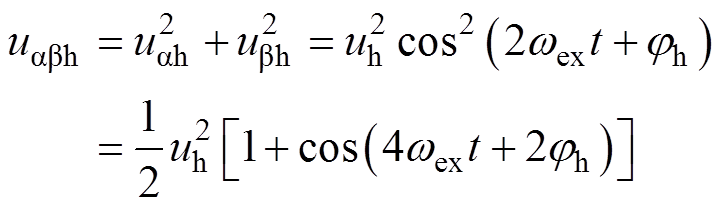（10）
通过BPF提取出其中的4次谐波分量，有
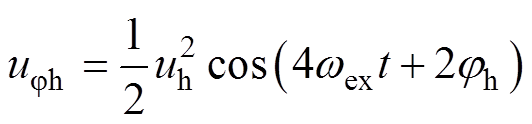（11）
将式（8）和式（11）作乘积并调整正弦项符号可得
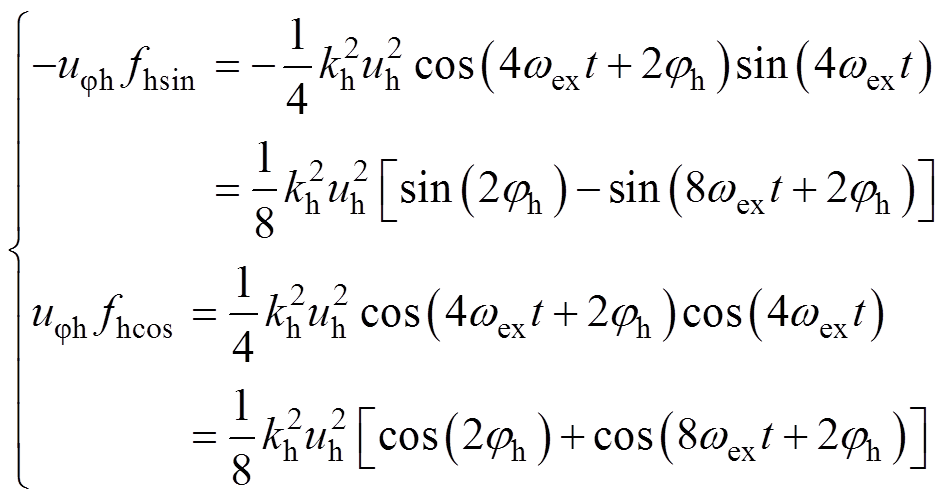（12）
通过LPF提取包含相位信息的低频分量，有
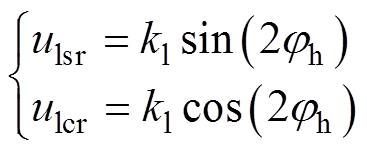（13）
式中，kl为低频分量系数，为正数。将该分量进行标幺化，去除系数，然后解析计算得到相位为
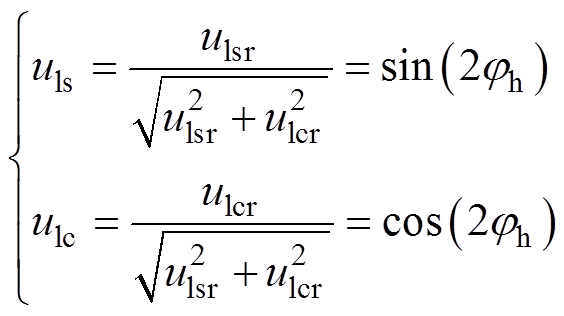（14）
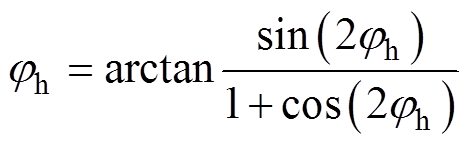（15）
对应再将式（7）所示的同频信号进行相位延时，即可生成同步解耦信号为
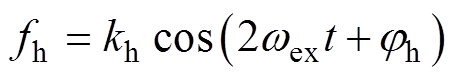（16）
由于该相位jh在整个电机起动过程中保持不变，上述的相位计算过程仅需在电机静止时进行一次计算，无需实时计算。相较于文献[24]中的方法，此方法无需对主励磁机励磁电流进行采样，减少了电流传感器的使用，不存在极限位置角信号幅值偏低失效的问题而取消了极性判断环节，提高信号同步性的同时简化了生成过程。
图3中的传统外差同步解调方式中高频响应信号幅值调制过程存在两级SOGI滤波器，不仅增加了整个转子位置估计闭环系统的复杂度，还会影响到系统的稳定性。
因此，本文根据式（5）中uq的谐波分布，对传统外差同步解调方式进行如图6所示的结构改进，将Park变换后的q轴响应电压直接与同步解耦信号相乘，乘积信号可表示为
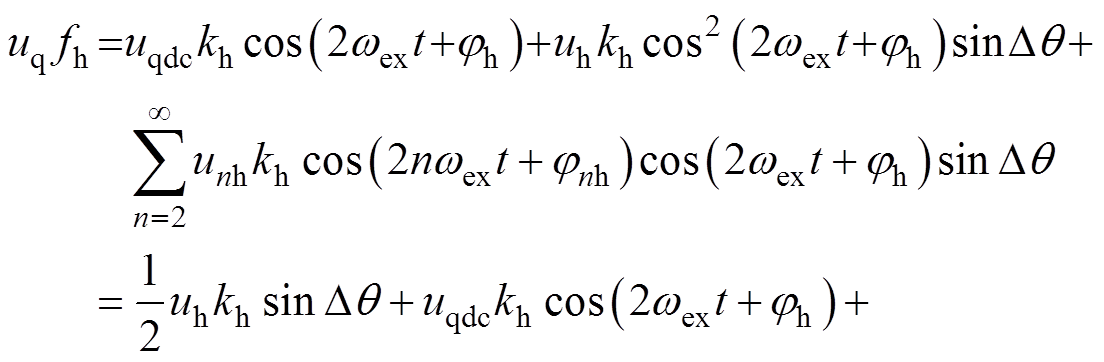
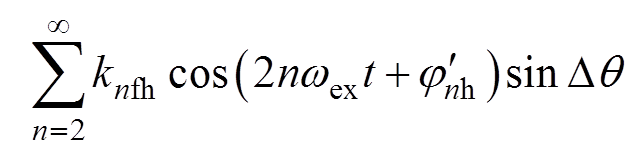（17）
式中，knfh为2n次谐波的幅值；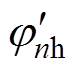
为2n次谐波的相位，该乘积信号由含转子位置误差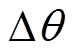的直流信号、2次谐波交流信号和含转子位置误差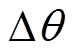的2n次谐波交流信号三部分组成。
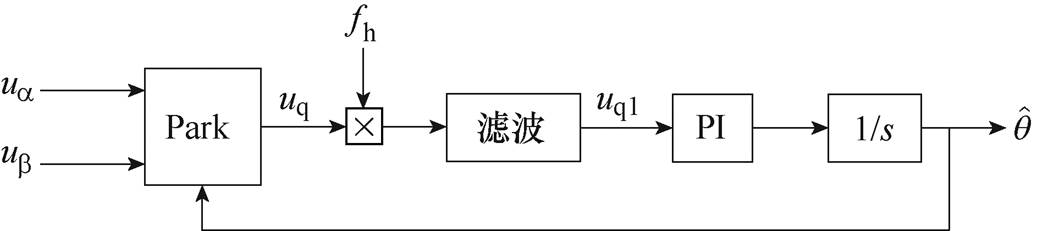
图6 改进同步解调方式
Fig.6 Improved synchronous demodulation mode
对此乘积信号进行滤波处理，为保留包含转子位置误差信息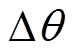的直流分量，需要依次滤除式（17）中的谐波分量，为了避免过多系统闭环极点引入带来的参数整定和稳定性问题，应当尽量避免SOGI等高阶次滤波器的使用。由于式（17）中的谐波均为偶次谐波，将该谐波延时p/wex并与原信号作差，即通过延时滤波方式可实现谐波频率处幅值增益为零，但延时滤波方式同样会滤除直流分量，为了保持直流分量增益不变，增加积分环节并调整幅值参数可得到图7所示的精准谐波消除滤波器（Precise harmonic Elimination Filter, PEF）。
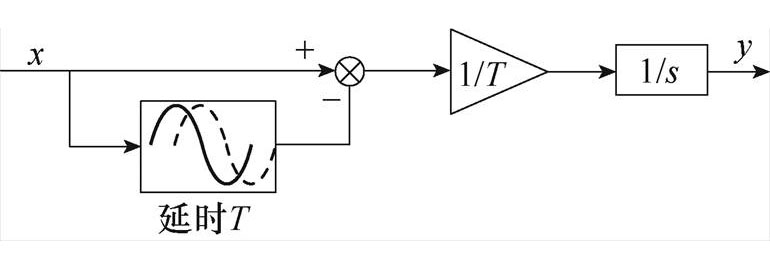
图7 精准谐波消除滤波器结构
Fig.7 Structure diagram of PEF
该滤波器的传递函数可表示为
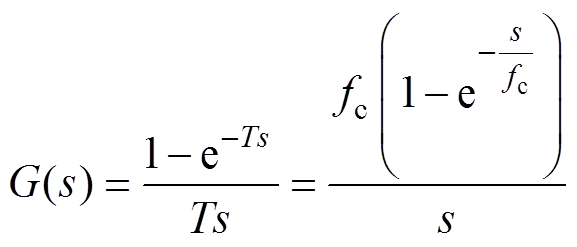（18）
式中，T为滤波周期；fc为滤波频率。滤波器的幅频特性函数为
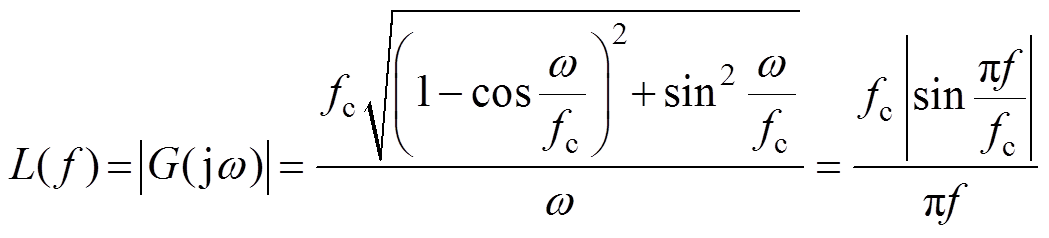（19）
精准谐波消除滤波器幅频特性伯德图如图8所示，设置滤波频率为200 Hz，对应两倍主励磁机励磁频率，并且PEF对于直流分量增益始终为1，而对于200 Hz的倍频增益接近于零，提取出式（17）中直流分量为
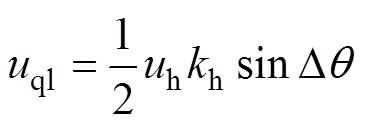（20）
再经PI和积分环节解算出估计转子位置角。
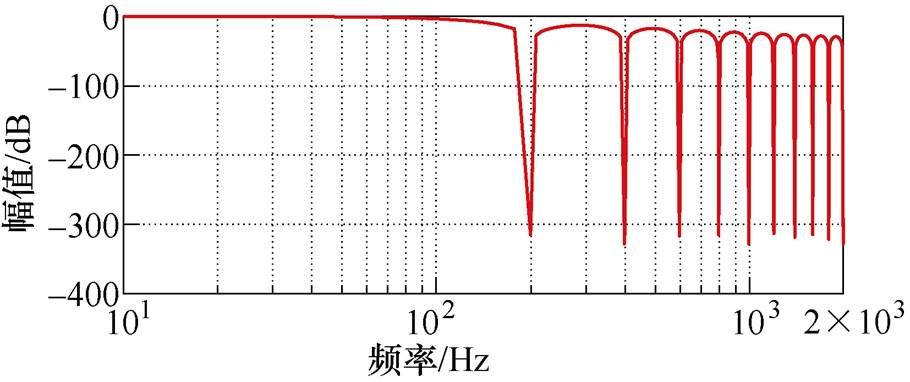
图8 精准谐波消除滤波器幅频特性伯德图
Fig.8 Bode diagram of amplitude frequency characteristic of PEF
改进同步解调方式中，开环前向通路仅包括PEF和锁相环的传递函数，PEF的传递函数分母为一阶，锁相环为二阶系统，因此基于PEF的改进同步解调闭环系统为三阶系统，相较于外差同步解调方式，三个极点的配置难度较低，锁相环PI参数整定较为容易，更少的闭环极点可以有效提升闭环系统的稳定性及锁相环参数的转速适用范围。
为了验证上述转子位置估计改进同步解调方式的可行性，本文搭建了一台三级式同步电机无位置传感器起动控制系统仿真模型。
主励磁机外接给定的150 V、100 Hz恒压恒频交流励磁，在此励磁下，主发电机在静止和低速阶段下的励磁电压谐波频谱分析如图9所示，谐波分布对应式（3），其中2次谐波200 Hz分量占比最大，用作转子位置估计的自注入高频谐波。旋转状态下相对于静止状态下多了部分其他次谐波，这是前述忽略的与转速相关的切割电动势部分产生的，这部分占比很小，不影响高频响应电压信号的谐波分布。
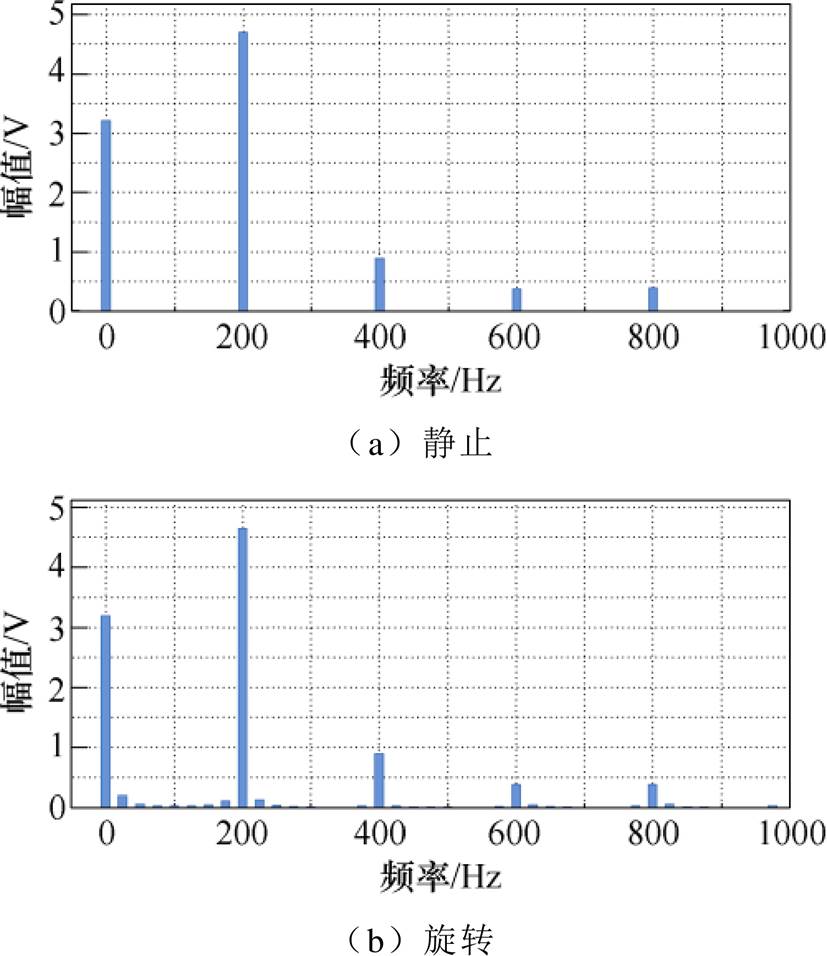
图9 主发电机励磁电压谐波频谱分析
Fig.9 Harmonic spectrum analysis diagram of excitation voltage of main generator
同步解耦信号相位计算过程分量如图10所示，包括BPF提取的4次谐波分量ujh和控制软件生成的正余弦高频信号fhcos、fhsin，均为400 Hz正弦波，分别与式（11）和式（8）相对应。图11所示为本文生成的同步解耦信号fh波形，并与高频响应电压信号uah相对应，图11a和图11b分别对应电机静止和旋转状态。从仿真结果可见，采用本文提出的方法获得的同步解耦信号与高频响应电压信号在频率、相位完全对应。
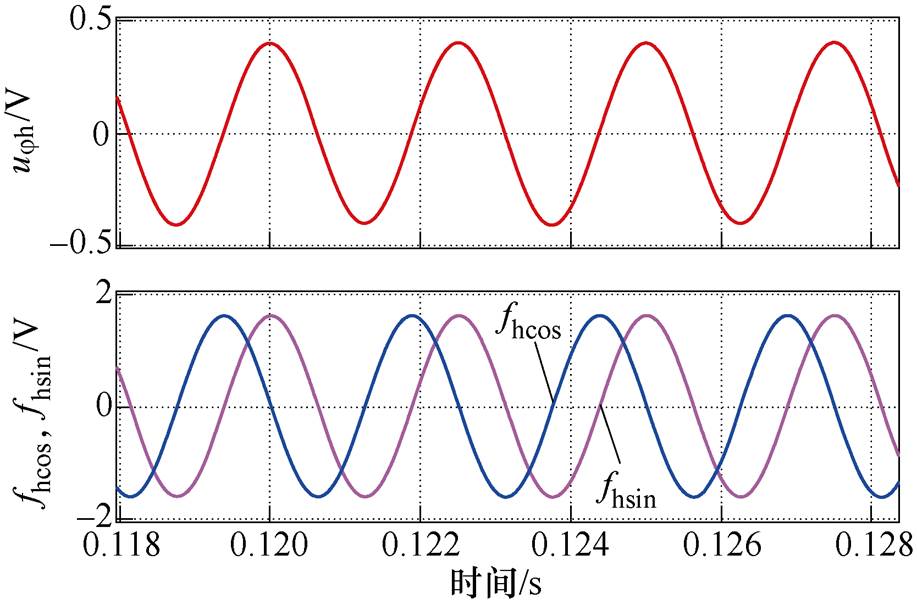
图10 相位计算过程信号仿真波形
Fig.10 Simulation waveform of phase angel calculation process signal
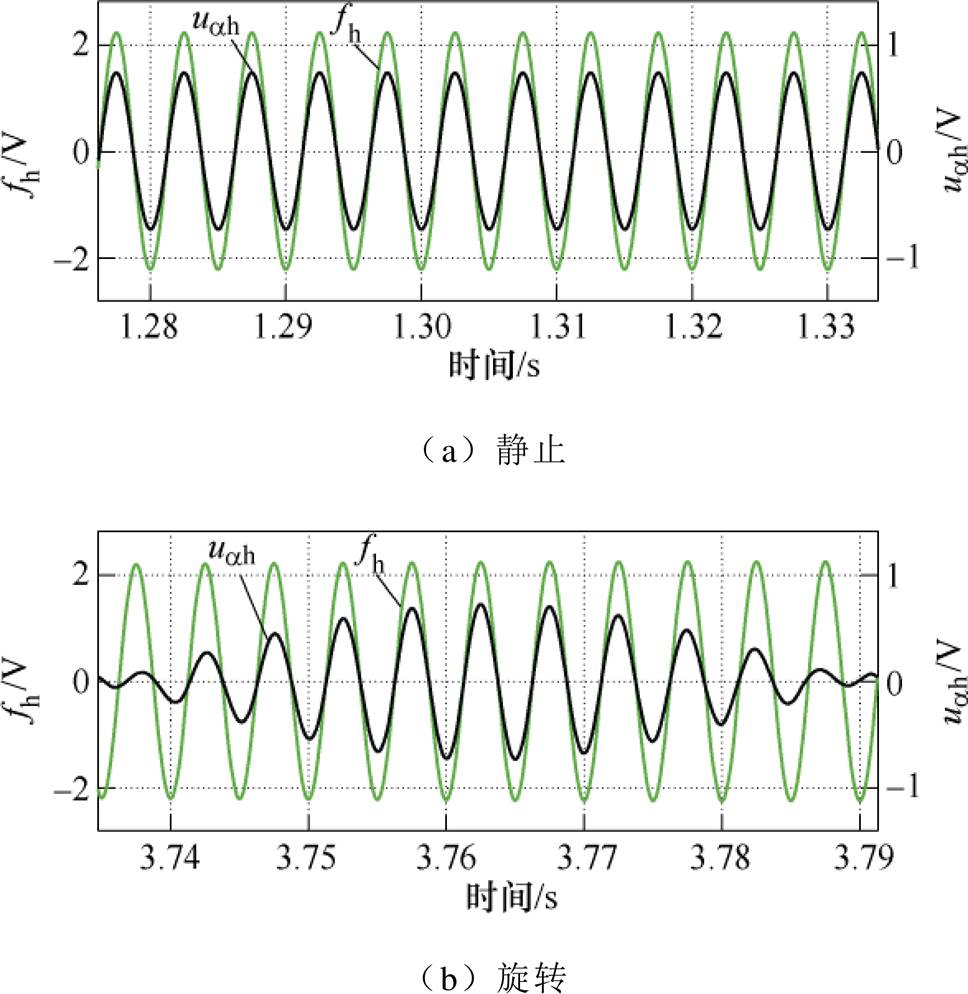
图11 同步解耦信号仿真波形
Fig.11 Simulation waveform of synchronous decoupling signal
三级式同步电机采用恒加速起动控制，加速度大小为20 r/min/s，电机起动后经过5 s到达100 r/min，对应低速阶段的无位置起动过程仿真波形如图12所示，图12a为从零恒加速到100 r/min的起动过程波形，图12b为100 r/min匀速运行时的位置误差波形。电机静止时，位置误差几乎为零；电机恒加速起动时，加速度会给转子位置估计系统带来额外的静态误差，此阶段转子位置误差范围为0.03～0.04 rad，对应相对误差范围为0.477%～0.637%；电机在100 r/min匀速运行阶段，位置误差平均值接近于零，仅有较小的脉动，脉动大小为0.01 rad，相对误差为0.159%。可见，整个起动过程中，位置误差保持在较小值，验证了本文所述的改进同步解调方法有效性，且位置估计精度较高。
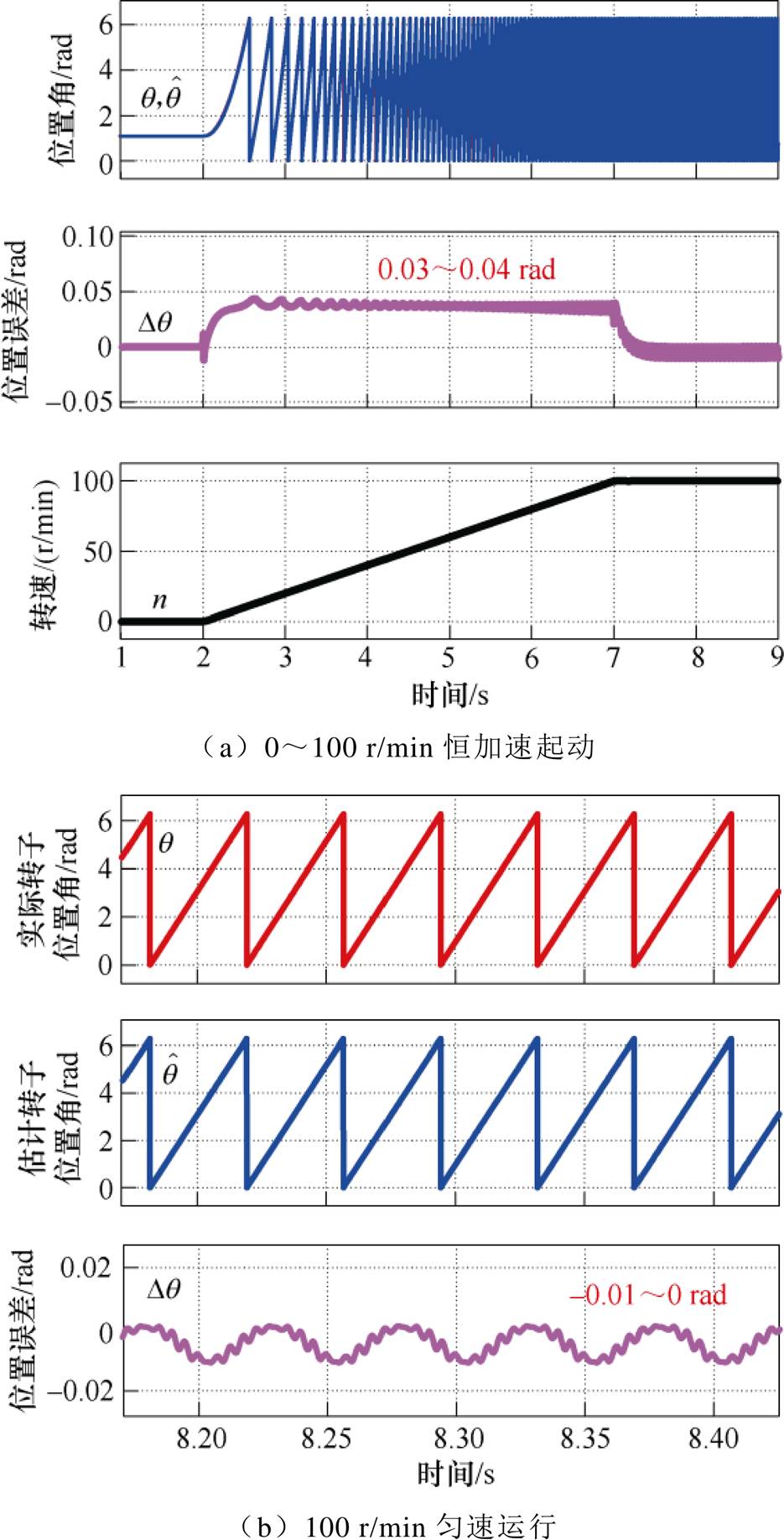
图12 三级式同步电机低速阶段无位置起动控制仿真波形
Fig.12 Simulation waveform of sensorless starting control in the low-speed range for TSSM
为进一步验证本文提出的三级式同步电机改进同步解调方法的实用性，在仿真分析基础上，搭建了如图13所示的三级式同步电机无位置起动控制实验平台，电机相关参数见表1。
图13 电机与控制平台
Fig.13 Machines and control platform
表1 三级式同步电机参数
Tab.1 Parameters of TSSM
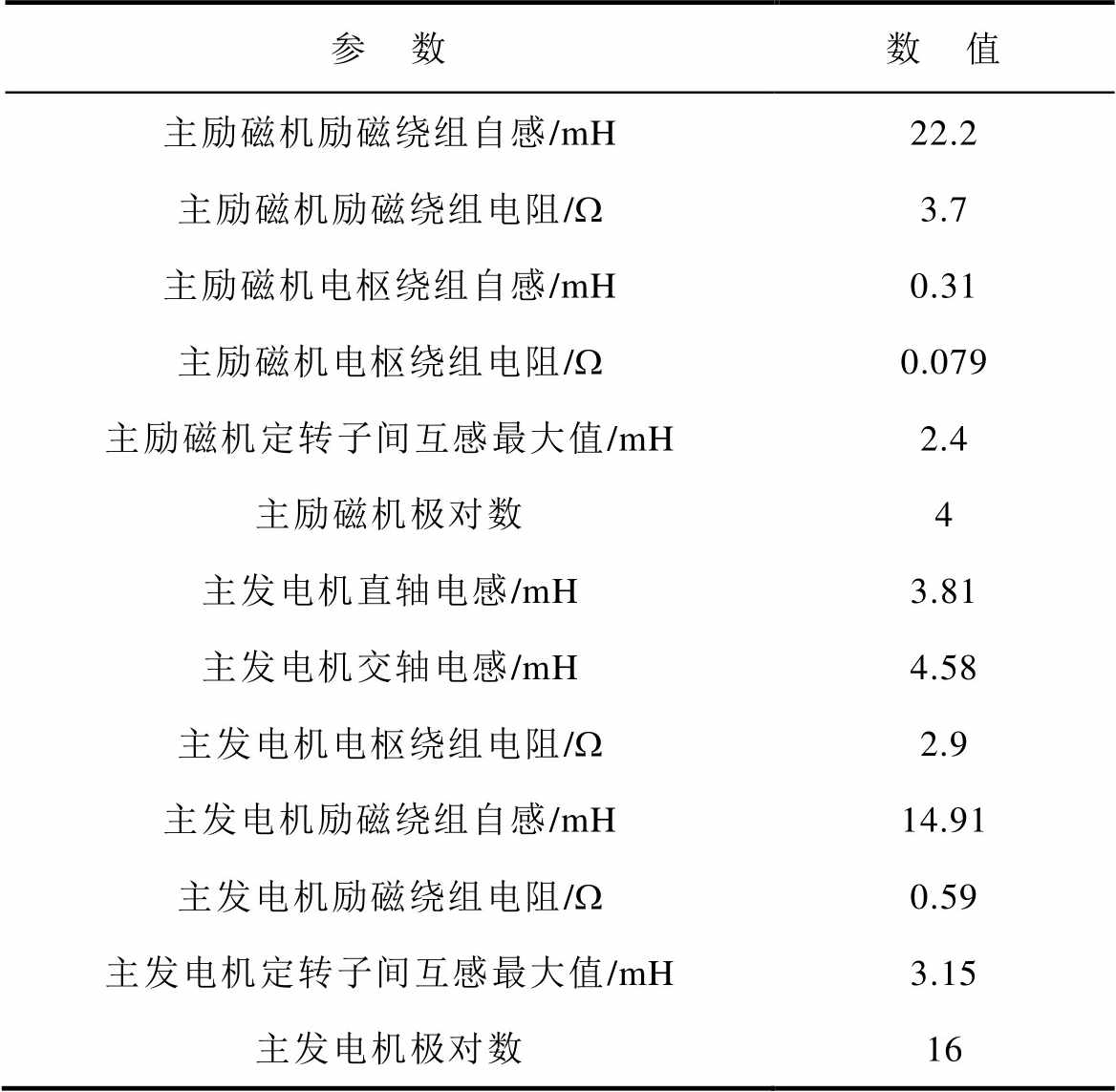
参 数数 值 主励磁机励磁绕组自感/mH22.2 主励磁机励磁绕组电阻/W3.7 主励磁机电枢绕组自感/mH0.31 主励磁机电枢绕组电阻/W0.079 主励磁机定转子间互感最大值/mH2.4 主励磁机极对数4 主发电机直轴电感/mH3.81 主发电机交轴电感/mH4.58 主发电机电枢绕组电阻/W2.9 主发电机励磁绕组自感/mH14.91 主发电机励磁绕组电阻/W0.59 主发电机定转子间互感最大值/mH3.15 主发电机极对数16
永磁同步电机作为三级式同步电机起动过程的负载模拟器，低速阶段无位置传感器起动控制实验中负载转矩最大值为3 N·m。控制平台主要包括控制电路和功率电路两部分，采用数字信号处理器（Digital Signal Processor, DSP）和复杂可编程逻辑器件（Complex Programmable Logic Device, CPLD）的核心控制单元，电机轴线上安装编码器以检测实际转子位置角以比对无位置传感器估计转子位置的精度。
与仿真参数一致，给主励磁机提供150 V、100 Hz的恒定励磁电压，经由主励磁机和旋转整流器为主发电机提供包含谐波分量的励磁电压，由于主励磁机和主发电机集成在同一电机中，无法对主发电机转子绕组的励磁电压进行采样观测，对此在实验中观测了主发电机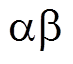
坐标系下的电枢电压波形以替代主发电机励磁电压的观测。因此，实验结果中主要给出主发电机电枢电压及其快速傅里叶变换（Fast Fourier Transform, FFT）分析结果、同步解耦信号生成、三级式同步电机无位置起动控制以及位置误差与转速关系四部分内容。
图14所示为主发电机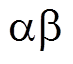坐标系下的电枢电压实验波形，图14a和图14b分别对应静止和低速旋转的情况，采用示波器的FFT分析功能得到的频谱分布结果如图15所示，静止情况下的频谱主要包括直流分量和高频偶次谐波分量，其中2次谐波幅值占比最大，与式（3）分析对应；低速旋转情况下的频谱包括基波分量和高频偶次谐波两侧分量，频率并不严格对应偶次谐波，这是因为式（3）中的偶次谐波会受到转子角频率的影响，以2次谐波为例，由于
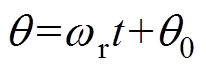，则式（9）对应的2次谐波高频响应电压可以分解为
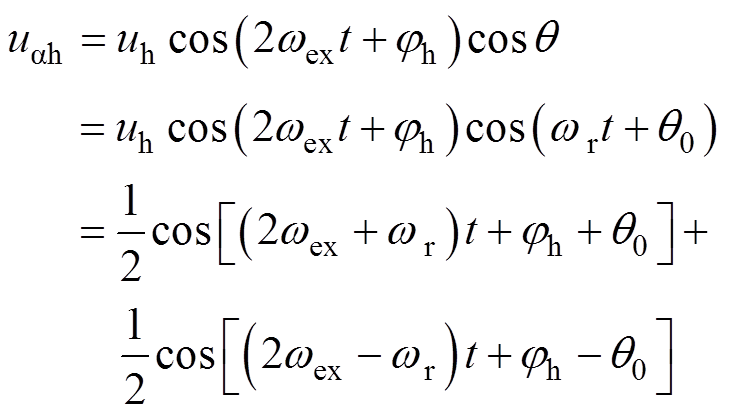（21）
可以看出，随着转速上升，2次谐波高频响应电压频率向着中心频率两侧偏移，与图15b相对应。因此，图14和图15所示波形与式（3）和式（4）的推导结果基本一致，说明本文所述励磁电压高频谐波自注入理论具有实际可行性。
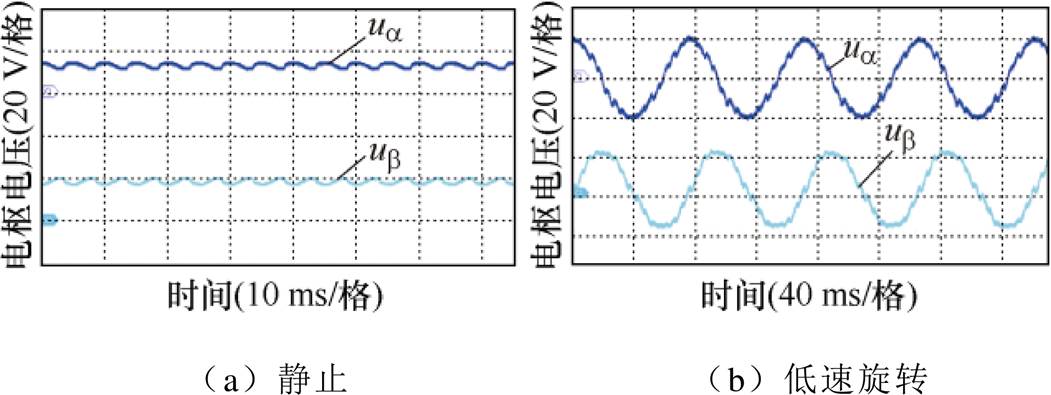
图14 主发电机电枢电压实验波形
Fig.14 Experimental waveforms of main generator armature voltage
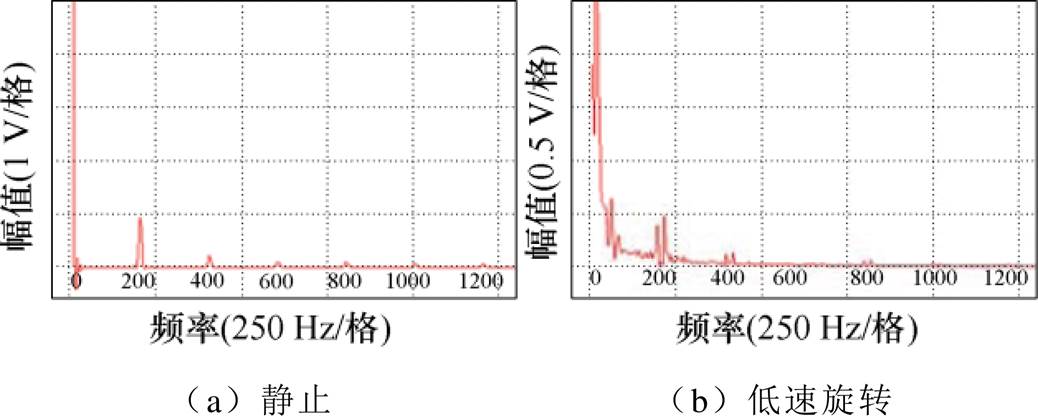
图15 主发电机电枢电压FFT分析结果
Fig.15 FFT analysis results of main generator armature voltage
在实验控制平台中，由DSP程序软件生成所需的同频信号fh0，信号频率为200 Hz，相位计算过程中提取的4次谐波分量ujh及所需的正余弦高频信号实验波形如图16所示，与式（11）和式（8）中表述一致，为400 Hz正弦波。
生成的同步解耦信号fh和高频响应电压信号uah的对应结果如图17所示，静止和低速旋转工况下两者相位均保持一致，验证了本文所述的改进同步解耦信号生成方法的可行性。
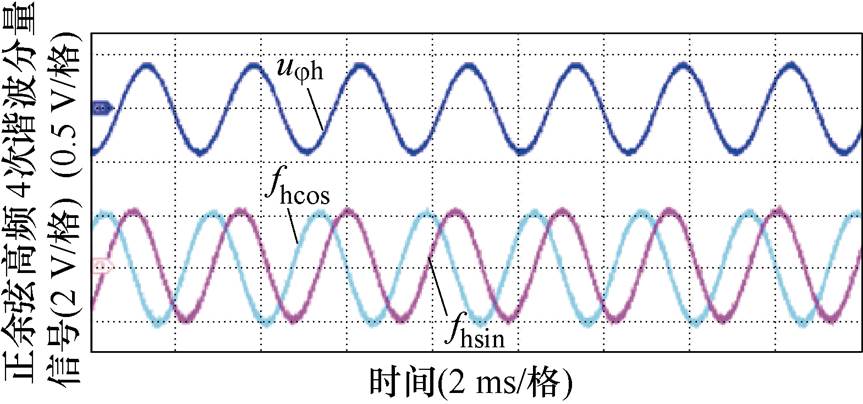
图16 相位计算过程信号实验波形
Fig.16 Experimental waveform of phase angel calculation process signal
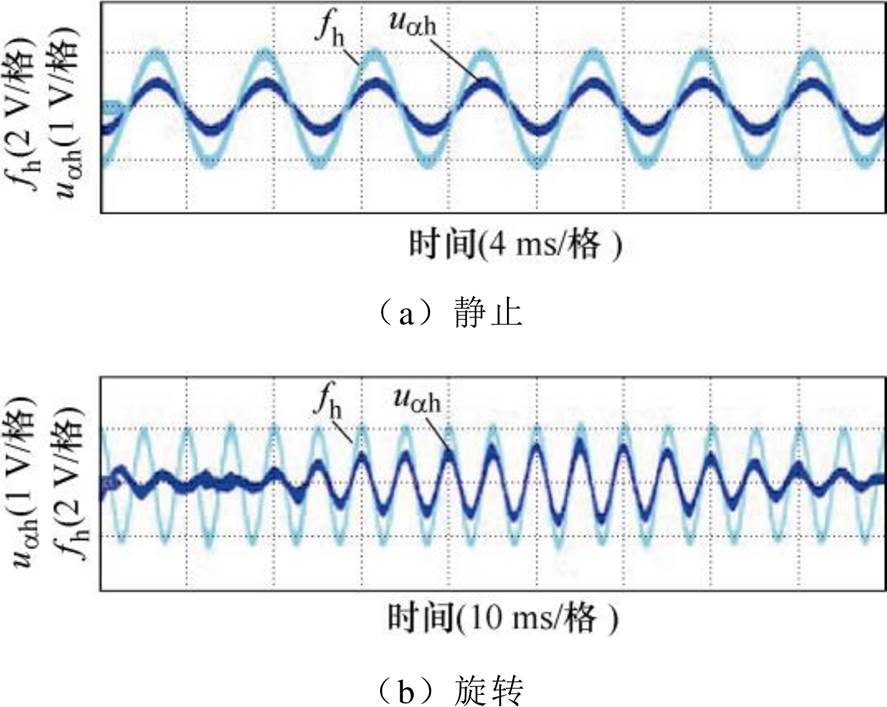
图17 同步解耦信号实验波形
Fig.17 Experimental waveforms of synchronous decoupling signal
在完成同步解耦信号生成实验后，后续电机起动时的同步解耦信号相位无需重复计算。实验中的主发电机为恒加速起动，加速度大小为20 r/min/s，对应0～100 r/min的无位置传感器起动过程实验结果如图18所示。
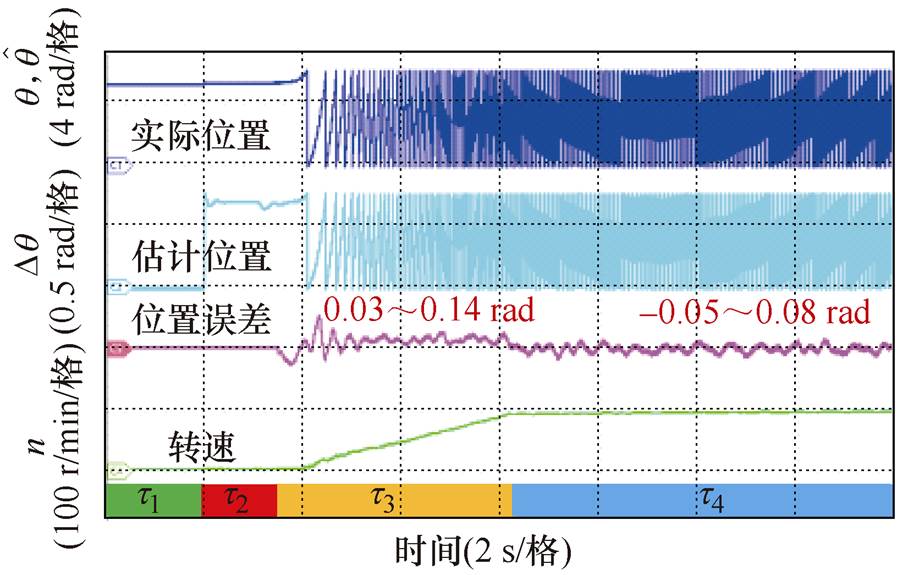
图18 电机从零速起动的无位置传感器控制实验波形
Fig.18 Experimental waveforms of sensorless starting control for TSSM from zero-speed
该起动过程可以分为四个阶段：t1为准备阶段，完成母线电压的上电工作；t2为静止阶段，此阶段主励磁机给定单相交流励磁电压，为主发电机转子建立励磁，软件计算并延时生成同步解耦信号，电机保持静止，无位置算法作用，实现电机静止时的位置估计；t3为恒加速起动阶段，主发电机励磁建立完成后，主发电机恒加速度起动控制，在起动初始阶段由于加速度导致转速突然变化，使得估计的转子位置误差有较大的瞬时脉动，脉动的上下幅值为0.28 rad和-0.12 rad，对应相对误差脉动幅值分别为4.46%和-1.91%，恒加速运行阶段位置误差脉动范围下降为0.03～0.14 rad，对应相对误差脉动范围为0.478%～2.23%；t4为匀速运行阶段，电机在t3阶段经过5 s的恒加速后速度达到100 r/min，而后以此速度匀速运行，对应估计的位置误差平均值近似为零，误差脉动范围为-0.05～0.08 rad，对应相对误差脉动范围为-0.796%～1.27%。
图19所示为三级式同步电机在0～100 r/min无位置传感器起动过程中的主发电机三相电枢电流波形，电枢电流限幅在额定值，结合交流励磁控制方式，使得主发电机输出基本恒定的起动转矩。由于动态变化过程中加速度对位置估计值的误差影响，使得主发电机电枢绕组电流存在一定不对称特性和谐波畸变，基本能够维持所需的额定输出转矩。
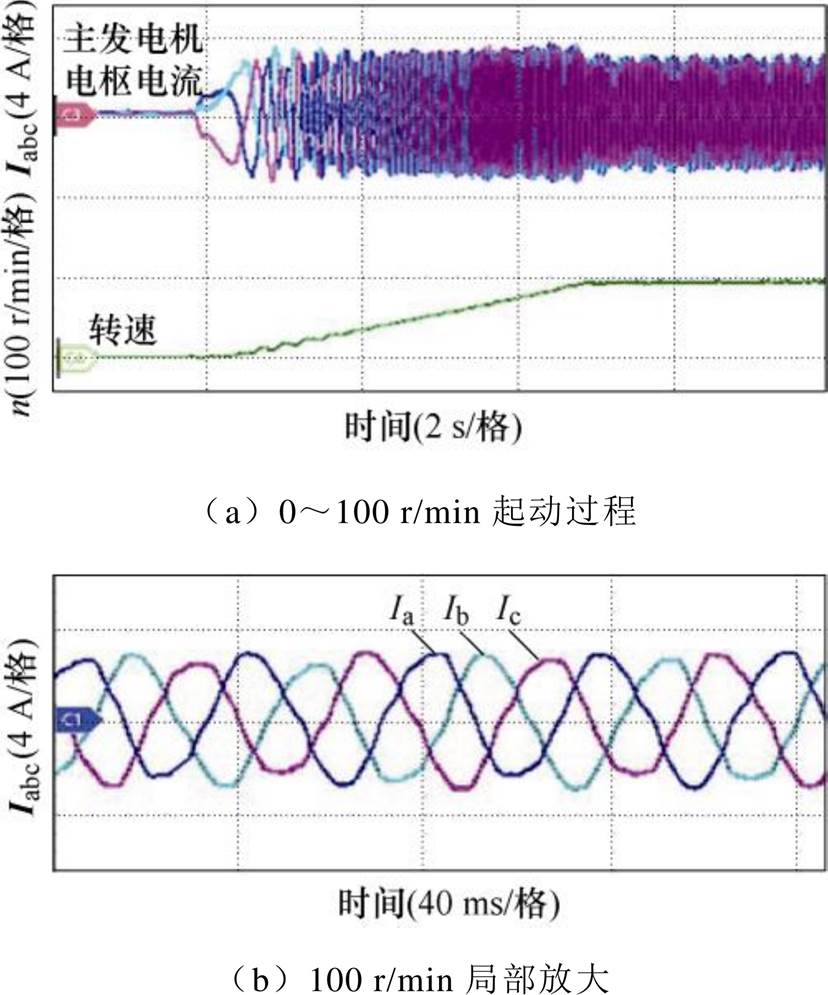
图19 电机从零起动的主发电机电枢电流实验波形
Fig.19 Experimental waveforms of main generator armature current for TSSM from zero-speed
电机100 r/min稳态运行时的位置估计实验波形及其局部放大波形如图20所示，位置误差波形呈现出低频规律脉动上叠加高次谐波脉动的现象，脉动范围为-0.05～0.07 rad，对应相对误差脉动范围为-0.796%～1.11%，验证了本文提出的方法具有较高的位置估计精度。
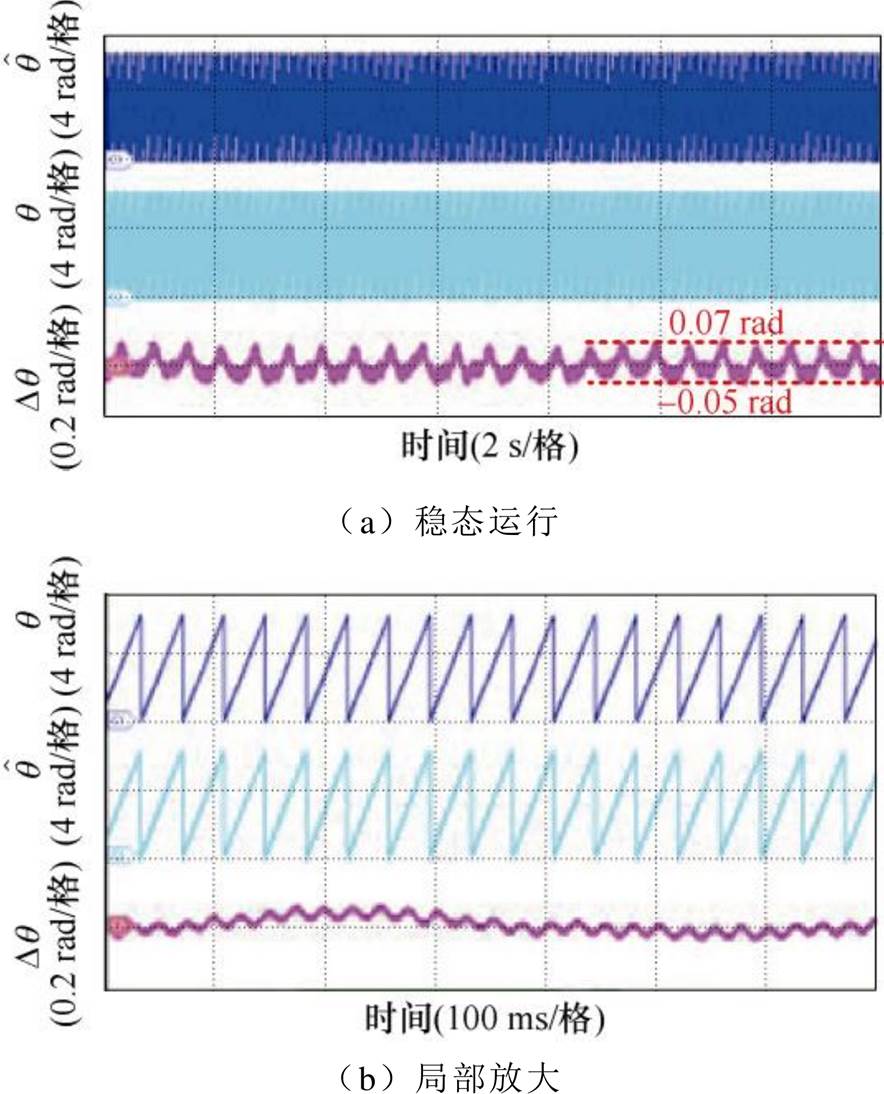
图20 100 r/min稳态运行时转子位置估计实验波形
Fig.20 Experimental waveforms of rotor position estimation at speed of 100 r/min
图21为位置误差随转速变化的关系曲线，由于本文所述方法的转子位置平均误差近似为零，仅存在误差的脉动，绘制的关系曲线给出了40～200 r/min范围内转子位置误差脉动的最大值。位置误差脉动会随着转速增大而增大，到达120 r/min以后趋于恒定值，最大约为0.1 rad，相对误差为1.59%，在较宽的转速范围内具有较高的位置估计精度。由于本实验平台中所用三级式同步电机为16对极，对应200 r/min时的电机基频达到了53 Hz，依旧能够实现高精度的无位置传感器闭环控制，为高速阶段反电动势观测法过渡提供更宽的转速切换区间，支持三级式同步电机实现全速范围高精度无位置起动控制。
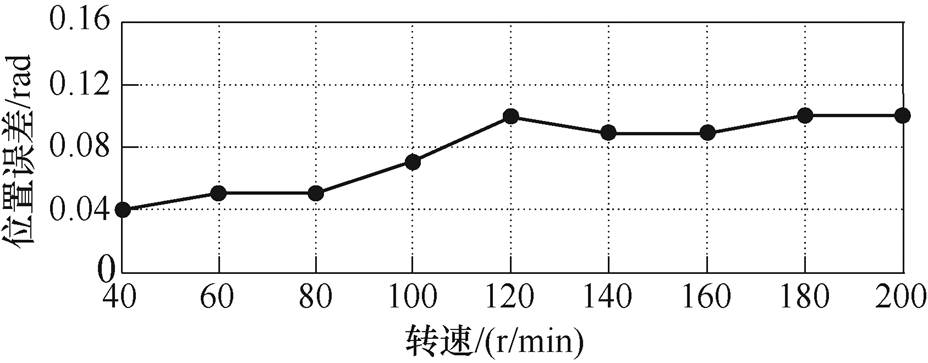
图21 位置误差与转速的关系曲线
Fig.21 Curve of position error VS speed
本文针对传统外差同步解调方式在三级式同步电机转子位置估计应用中存在的问题，从简化位置估计算法结构和增强系统稳定性两个方面入手，分别提出了无需极性判断的同步解耦信号生成方法和基于集成滤波器的改进同步解调结构，简化了转子位置估计的实现流程，并且根据谐波分析结果设计的精准谐波消除的滤波结构，有效减少了闭环系统的极点数，对提升信号提取的精度和系统稳定性具有重要意义。通过仿真和实验结果验证了本文所述三级式同步电机无位置传感器起动控制方法的可行性，1～53 Hz范围的估计误差结果表明，该改进同步解调方式具有较高的位置估计精度和较宽的转速范围适应性。
参考文献
[1] 张卓然, 许彦武, 姚一鸣, 等. 多电飞机电力系统及其关键技术[J]. 南京航空航天大学学报, 2022, 54(5): 969-984.
Zhang Zhuoran, Xu Yanwu, Yao Yiming, et al. Electric power system and key technologies of more electric aircraft[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2022, 54(5): 969-984.
[2] Sarlioglu B, Morris C T. More electric aircraft: review, challenges, and opportunities for commercial transport aircraft[J]. IEEE Transactions on Trans- portation Electrification, 2015, 1(1): 54-64.
[3] 孔祥浩, 张卓然, 陆嘉伟, 等. 分布式电推进飞机电力系统研究综述[J]. 航空学报, 2018, 39(1): 021651.
Kong Xianghao, Zhang Zhuoran, Lu Jiawei, et al. Review of electric power system of distributed electric propulsion aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(1): 021651.
[4] Madonna V, Giangrande P, Galea M. Electrical power generation in aircraft: review, challenges, and opportunities[J]. IEEE Transactions on Transportation Electrification, 2018, 4(3): 646-659.
[5] Xu Yanwu, Zhang Zhuoran, Bian Zhangming, et al. Copper loss optimization based on bidirectional converter for doubly salient brushless starter/ generator system[J]. IEEE Transactions on Industrial Electronics, 2021, 68(6): 4769-4779.
[6] Griffo A, Wrobel R, Mellor P H, et al. Design and characterization of a three-phase brushless exciter for aircraft starter/generator[J]. IEEE Transactions on Industry Applications, 2013, 49(5): 2106-2115.
[7] Sayed E, Abdalmagid M, Pietrini G, et al. Review of electric machines in more-/ hybrid-/ turbo-electric aircraft[J]. IEEE Transactions on Transportation Electrification, 2021, 7(4): 2976-3005.
[8] 孟涛, 焦宁飞, 刘卫国, 等. 基于多级结构特性的航空无刷同步起动/发电机转子初始位置估算[J]. 中国电机工程学报, 2023, 43(2): 798-809.
Meng Tao, Jiao Ningfei, Liu Weiguo, et al. Initial rotor position estimation for aircraft brushless synchronous starter/generators based on multi-stage- structure characteristics[J]. Proceedings of the CSEE, 2023, 43(2): 798-809.
[9] 赵毅恒, 宁博文, 卢少武, 等. 基于I/F起动和扩展卡尔曼滤波的永磁同步电机全速域无传感器控制方法[J]. 电机与控制应用, 2022, 49(2): 1-7, 19.
Zhao Yiheng, Ning Bowen, Lu Shaowu, et al. Full speed sensorless control method of permanent magnet synchronous motor based on I/F starting and extended Kalman filter[J]. Electric Machines & Control Application, 2022, 49(2): 1-7, 19.
[10] 兰志勇, 李延昊, 罗杰, 等. 一种自适应扩展卡尔曼滤波的永磁同步电机无位置传感器矢量控制[J/OL]. 电机与控制学报, http://kns.cnki.net/kcms/ detail/23.1408.TM.20230523.2252.028.Html.
Lan Zhiyong, Li Yanhao, Luo Jie, et al. A sensorless vector control of permanent magnet synchronous motor based on adaptive extended Kalman filter[J/OL]. Electric Machines and Control, http://kns.cnki.net/ kcms/detail/23.1408.TM.20230523.2252.028.Html.
[11] 王琛琛, 苟立峰, 周明磊, 等. 基于改进的离散域二阶滑模观测器的内置式永磁同步电机无位置传感器控制[J]. 电工技术学报, 2023, 38(2): 387-397.
Wang Chenchen, Gou Lifeng, Zhou Minglei, et al. Sensorless control of IPMSM based on improved discrete second-order sliding mode observer[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 387-397.
[12] 梅三冠, 卢闻州, 樊启高, 等. 基于滑模观测器误差补偿的永磁同步电机无位置传感器控制策略[J]. 电工技术学报, 2023, 38(2): 398-408.
Mei Sanguan, Lu Wenzhou, Fan Qigao, et al. Sensorless control strategy of permanent magnet synchronous motor based on error compensation estimated by sliding mode observer[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 398-408.
[13] 王庆龙, 张兴, 张崇巍. 永磁同步电机矢量控制双滑模模型参考自适应系统转速辨识[J]. 中国电机工程学报, 2014, 34(6): 897-902.
Wang Qinglong, Zhang Xing, Zhang Chongwei. Double sliding-mode model reference adaptive system speed identification for vector control of permanent magnet synchronous motors[J]. Proceedings of the CSEE, 2014, 34(6): 897-902.
[14] 周伟涛, 王勇, 向柏澄. 基于改进型MRAS的PMSM转子位置估计[J]. 电力电子技术, 2019, 53(5): 18-20.
Zhou Weitao, Wang Yong, Xiang Baicheng. Rotor position estimation for PMSM based on improved MRAS[J]. Power Electronics, 2019, 53(5): 18-20.
[15] 麦志勤, 肖飞, 刘计龙, 等. 基于改进型自调整轴系幅值收敛电流解调算法的旋转高频电压注入法[J]. 电工技术学报, 2021, 36(10): 2049-2060.
Mai Zhiqin, Xiao Fei, Liu Jilong, et al. Rotating high-frequency voltage injection method based on improved self-adjusting frame amplitude convergence current demodulation algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2049- 2060.
[16] 赵文祥, 刘桓, 陶涛, 等. 基于虚拟信号和高频脉振信号注入的无位置传感器内置式永磁同步电机MTPA控制[J]. 电工技术学报, 2021, 36(24): 5092- 5100.
Zhao Wengxiang, Liu Huan, Tao Tao, et al. MTPA control of sensorless IPMSM based on virtual signal and high-frequency pulsating signal injection[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5092-5100.
[17] 孙明阳, 和阳, 邱先群, 等. 随机频率三角波注入永磁同步电机无位置传感器降噪控制[J]. 电工技术学报, 2023, 38(6): 1460-1471.
Sun Mingyang, He Yang, Qiu Xianqun, et al. Random-frequency triangular wave injection based sensorless control of PMSM drives for audible noise reduction[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1460-1471.
[18] 钱东祥, 魏佳丹, 周波, 等. 无刷励磁同步电机无位置传感器起动控制[J]. 中国电机工程学报, 2015, 35(2): 477-485.
Qian Dongxiang, Wei Jiadan, Zhou Bo, et al. Sensorless control of brushless synchronous machines in the starting mode[J]. Proceedings of the CSEE, 2015, 35(2): 477-485.
[19] Meng Tao, Liu Weiguo, Jiao Ningfei, et al. Initial rotor position estimation for wound-rotor syn- chronous starter/generators based on multi-stage- structure characteristics[C]//2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 2018: 540-545.
[20] Meng Tao, Liu Weiguo, Han Xu, et al. Multi- stage-structure-based rotor position estimation for a wound-field synchronous starter/generator in the low-speed region[J]. IEEE Transactions on Power Electronics, 2019, 34(12): 12095-12105.
[21] Peng Jichang, Liu Weiguo, Jiao Ningfei, et al. Dual-machine injection method-based sensorless starting strategy for wound-rotor synchronous starter/ generator[J]. IEEE Transactions on Power Electronics, 2019, 34(12): 12310-12320.
[22] 杨袁钰, 魏佳丹, 周波, 等. 主励磁机高频信号注入的无刷励磁同步电机低速阶段无位置传感器起动控制[J]. 中国电机工程学报, 2018, 38(3): 918- 926.
Yang Yuanyu, Wei Jiadan, Zhou Bo, et al. Sensorless starting control of brushless synchronous machines at low speed based on high-frequency signal injection by main exciter[J]. Proceedings of the CSEE, 2018, 38(3): 918-926.
[23] 薛哗, 魏佳丹, 周波. 三级式同步电机低速阶段无位置传感器起动控制高频信号注入法的对比[J]. 电工技术学报, 2018, 33(12): 2703-2712.
Xue Hua, Wei Jiadan, Zhou Bo. Comparative investigation on sensorless control of three-stage synchronous motor based on high-frequency injection method at low speed[J]. Transactions of China Electrotechnical Society, 2018, 33(12): 2703-2712.
[24] 王俊杰, 魏佳丹, 郁钧豪, 等. 基于间接二次谐波注入的三级式同步电机低速阶段无位置传感器起动控制[J]. 中国电机工程学报, 2022, 42(24): 9031- 9042.
Wang Junjie, Wei Jiadan, Yu Junhao, et al. Sensorless starting control of three-stage synchronous machines at low speed based on indirectly injected second harmonic signals[J]. Proceedings of the CSEE, 2022, 42(24): 9031-9042.
Abstract Three-stage synchronous machines (TSSM) have been widely employed in the more-electric aircraft due to their mature structure and simple excitation control in the generation mode. They also have the potential to achieve the integrated function of a starter/generator. The rotor position sensor is unnecessary since the TSSM is normally employed as the aircraft’s generator. In the starting control mode, the rotor position information is required for current closed-loop control, and the additional encoder or rotary transformer can be installed coaxially. The electromechanical sensor causes poor reliability and low utilization in aviation conditions. Thus, the sensorless control strategy can be a suitable candidate method for TSSM to achieve the starting control function.
Due to the specific structure of TSSM, recent literature on sensorless starting control of TSSM focuses on signal injection methods and rotor position demodulation schemes. With the multi-stage TSSM, there are various high-frequency injection methods and the corresponding response signal extraction schemes. Torque ripples exist due to high-frequency signals of high signal-to-noise ratio (SNR) injections. Although the traditional heterodyne demodulation scheme achieves a high-precision rotor position estimation by adjusting the phase of the decoupling signal, the parameters design for the high-order filter is complex, and the stability of the demodulation scheme is poor. Thus, this paper introduces a high-frequency signal self-injection method based on excitation harmonics concerning the rotating rectifier of TSSM. The corresponding specific filter and the rotor position demodulation strategy are designed.
Firstly, considering the multi-stage structure signal transmission of TSSM in the starting control based on the single-phase AC excitation scheme, the characteristics of the second high-frequency harmonics generated by the rotating rectifier are analyzed. High-frequency response signals with rotor position information in the armature windings of the main generator are derived for rotor position estimation. The corresponding torque ripple can be eliminated effectively without additional high-frequency signal injection.
Secondly, a synchronous decoupling signal generation method without polarity judgment is proposed to simplify the structure of the signal extraction filter in the synchronous decoupling procedure, and an improved synchronous demodulation structure with the integrated filter is given. The precise harmonic elimination filter (PEF) is adopted to reduce the pole number of the closed-loop system. Accurate high-frequency response signals can be extracted, and the parameter sensitivity can be reduced to enhance the stability of the proposed system.
Finally, the feasibility of the proposed improved synchronous demodulation scheme is verified by simulation and experimental results. According to the harmonic spectrum analysis of the armature voltage of the main generator, the 2nd harmonic voltage of the excitation frequency is the largest component, which can be adopted as the self-injected high-frequency signal to the field windings of the main generator. With the proposed control strategy, the error range of rotor position estimation is 0.03～0.14 rad during the starting procedure at the accelerated speed of 20 r/min/s and -0.05～0.07 rad at the constant speed of 100 r/min. The maximum rotor position estimation error of TSSM from 1 Hz to 53 Hz can be limited to 0.1 rad. Thus, the proposed TSSM with the improved synchronous demodulation scheme achieves a high-accuracy rotor position in the wide speed range.
keywords：Three-stage synchronous machines (TSSM), harmonics self-injection, synchronous demodu- lation, precise harmonic elimination filter (PEF)
DOI: 10.19595/j.cnki.1000-6753.tces.230853
中图分类号：TM341
国家自然科学基金（51877110）和航空科学基金（201958052002）资助项目。
收稿日期 2023-06-06
改稿日期 2023-10-09
蔡正友 男，2000年生，硕士研究生，研究方向为航空电源系统。E-mail: caizhengyou@nuaa.edu.cn
魏佳丹 男，1981年生，博士，教授，博士生导师，研究方向为航空电源系统、新能源发电及特种电机调速及数字控制。E-mail: weijiadan@nuaa.edu.cn（通信作者）
（编辑 崔文静）