Tab.1 Main parameters of prototype motor
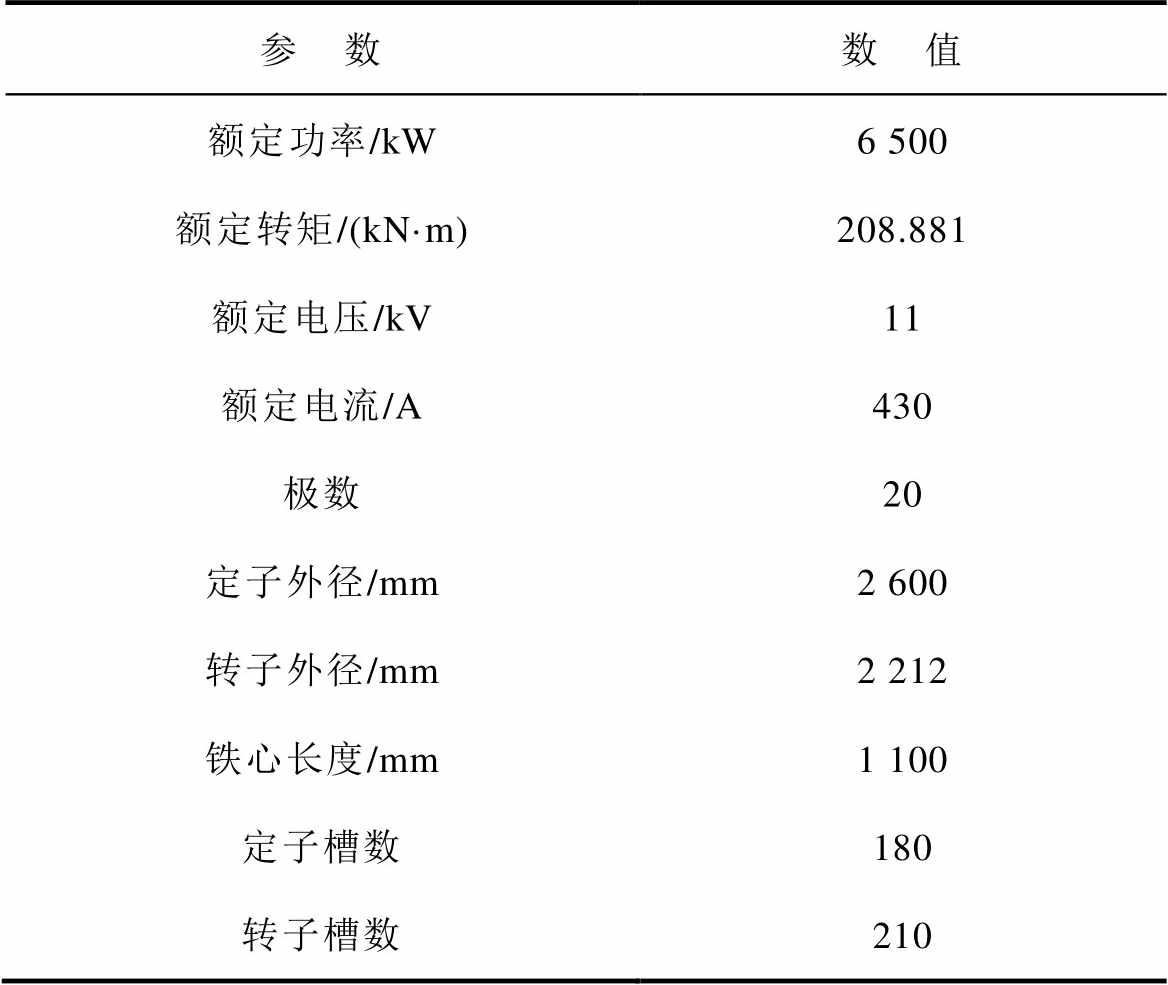
参 数数 值 额定功率/kW6 500 额定转矩/(kN·m)208.881 额定电压/kV11 额定电流/A430 极数20 定子外径/mm2 600 转子外径/mm2 212 铁心长度/mm1 100 定子槽数180 转子槽数210
摘要 为提高大型感应电机动态阻抗参数及起动特性计算的准确性及计算效率,构建了考虑电机转子转速变化引起气隙磁导变化的非线性动态磁网络模型。以一台6.5 MW大型感应电机为例,分析起动电流变化对电机内各处饱和程度的影响机理,在此基础上,根据磁力线路径及电机内饱和程度确定动态磁网络模型中的非线性磁导的计算方法。将动态磁网络模型与转子趋肤效应模型相结合,提出计及漏磁并考虑转子转速变化及饱和偏移现象的电机动态阻抗参数的计算方法。推导并建立基于转子多回路法的大型感应电机的动态数学模型,根据电机瞬态过程中的电磁耦合关系,确定动态数学模型与磁网络模型的动态耦合求解方法,提出大型电机瞬态过程中考虑电流、转速、饱和及趋肤程度变化的动态阻抗参数及起动特性的计算方法。通过与有限元计算结果及实验结果对比,验证了所提出计算方法的正确性。
关键词:大型感应电机 动态磁网络 动态阻抗 转子多回路法 起动特性
大型感应电机广泛应用于牵引和驱动等场合,精确的参数、电流、转矩及磁场计算是预测电机性能、判断其可驱动负载大小及电机优化设计的前提。本文以一台低速大容量防爆感应电机作为研究算例,此种电机负载转动惯量大、起动时间长,存在变工况运行,电机瞬态过程参数及性能的计算对保障电机多工况下的安全运行具有重要意义。在电机瞬态过程中,随转子转速的变化,电机内饱和及趋肤程度不断变化,电机阻抗参数呈非线性变化规律,加之大型电机体积大、计算量大,进而增加了电机动态过程电磁问题的计算难度。
在电机暂态电磁问题的分析方法中,等效磁网络法因其具有计算速度快、计算精度高的特点,受到众多学者的关注[1-4]。文献[5]基于子域法和等效磁网络法建立了永磁电机非线性混合磁场解析模型,考虑了铁心的磁导率问题。文献[6]利用等效磁网络法对定子永磁型动铁心式横向磁通直线振荡电机的一种新型拓扑结构进行了分析。文献[7]针对一台非对称转子内置式永磁同步电机建立了考虑饱和效应的磁网络模型。文献[8]提出了一种基于等效磁路法和精确保角映射相结合的混合磁场模型,在保证计算精度的同时简化了计算过程。文献[9]为了实现表贴式永磁电机的多目标参数优化,提出了一种具有可变尺寸和磁导率的新型可调十字形网格建模方法,可实现电机结构参数的参数化分析。文献[10]提出一种非线性变磁网络模型法,可对定子不对称极混合励磁双凸极电机定转子间的互磁导进行便捷的计算。文献[11-12]采用等效磁网络方法对电机的电磁特性进行了分析,考虑了电机内饱和不均匀的问题。文献[13]基于转子多回路法及绕组函数法对定转子的自感与互感进行了计算,并对电感参数进行饱和修正。文献[14]采用解析法对笼型实心转子感应电机起动时导条内的电流分布进行了计算。
大型感应电机起动时间长、电流大,电机铁心饱和趋肤情况明显,并不断变化,目前采用磁网络法对中大型电机的电磁问题进行分析时,对电机整个起动过程磁导的非线性变化考虑不足,无法准确考虑起动电流变化时引起的电机内饱和偏移现 象[15-17]。为解决此问题,本文以一台6.5 MW的大型感应电机为例,采用动态磁网络法对电机瞬态过程的电磁性能进行分析,计及了电机旋转所引起的气隙磁导变化,考虑瞬态过程饱和效应与趋肤效应变化对电机阻抗的影响,提出电机起动特性的计算方法。
本文根据电机电磁结构及瞬态过程中的磁通路径构建电机动态磁网络模型,根据磁通变化对模型中的磁导进行等效计算。本文所研究的低速大容量感应电机的主要参数见表1。
表1 算例电机主要参数
Tab.1 Main parameters of prototype motor

参 数数 值 额定功率/kW6 500 额定转矩/(kN·m)208.881 额定电压/kV11 额定电流/A430 极数20 定子外径/mm2 600 转子外径/mm2 212 铁心长度/mm1 100 定子槽数180 转子槽数210
为明确电机瞬态过程中的磁通路径,采用有限元方法对算例电机内部的磁通分布进行仿真计算。由于电机沿周向及轴向电磁结构对称,为提高计算效率,计算时取电机周向1/10部分作为计算区域,建立二维电磁计算模型。计算得到算例电机起动运行至0.05 s时以及电机达到电磁稳态时磁力线的分布情况如图1所示。从图1a可以看出,在电机运行的初始时刻,大部分磁力线主要经转子槽口及槽身处的漏磁路径闭合,使得电机起动时定、转子齿顶磁通密度较高。当电机达到电磁稳定状态时,电机内部磁力线主要沿主磁路闭合。因此,建立电机动态磁网络模型时需考虑起动过程漏磁以及齿顶饱和程度等因素。
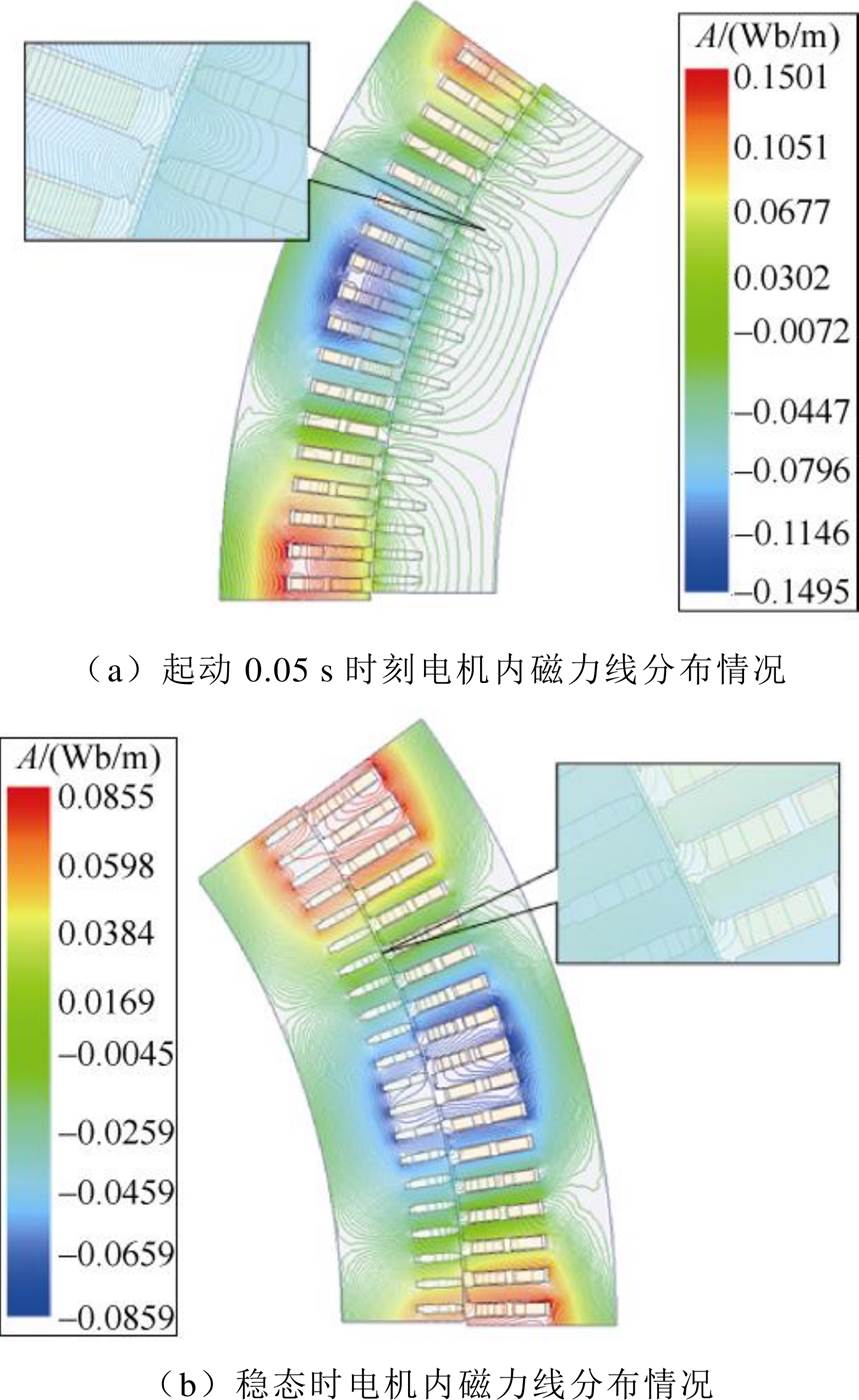
图1 电机内磁力线分布情况
Fig.1 Distribution of magnetic force in the motor
1.2.1 铁心轭部磁导
电机的定子及转子铁心的轭部磁路均相当于一个环形磁导单元,且轭部磁通流通方向存在径向和切向两个方向,如图2所示,因此将一个齿槽所对应的轭部等效成一个径向磁导Ger与两个切向磁导Get的组合,计算公式为
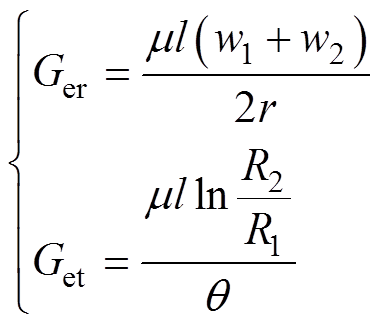 (1)
(1)
式中,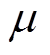 为铁心磁导率;l为电机轴向长度;R1、R2分别为定子轭部的内、外半径;
为铁心磁导率;l为电机轴向长度;R1、R2分别为定子轭部的内、外半径;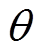 为定子一个齿槽所对应的机械角度;r为径向磁路长度;w1、w2分别为一个定子齿槽所对应扇形磁导的内、外弦长度。
为定子一个齿槽所对应的机械角度;r为径向磁路长度;w1、w2分别为一个定子齿槽所对应扇形磁导的内、外弦长度。
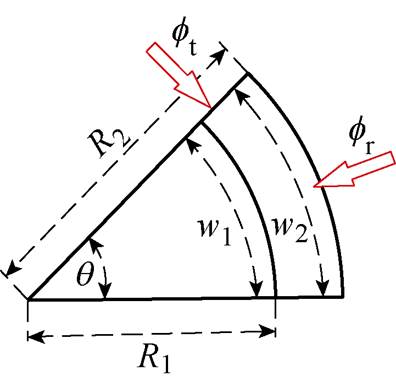
图2 轭部磁路
Fig.2 Yoke’s magnetic circuit
1.2.2 齿部磁导
将不规则齿部磁路用不同规则齿部磁路形状组合进行等效,齿部磁导模型如图3所示,图中,f 为磁通,对应磁导计算公式为
 (2)
(2)
式中,w为齿部宽度;h为齿部高度。
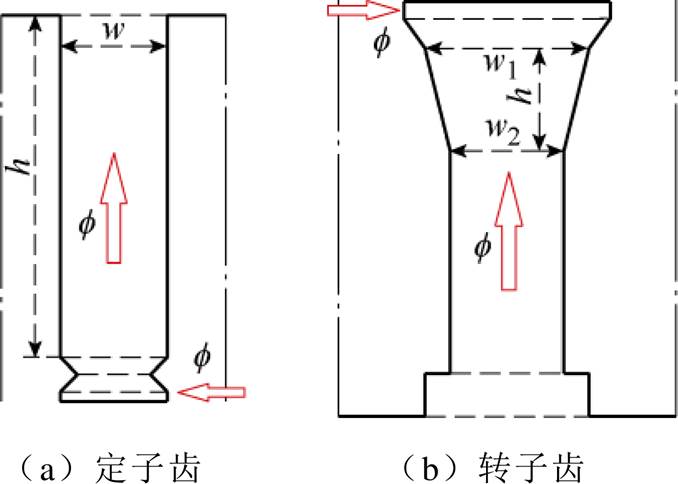
图3 齿部磁导模型
Fig.3 Tooth’s magnetic permeance model
1.2.3 槽漏磁导
槽漏磁通所经过的路径主要为非铁磁材料,其对应的磁导值与槽型尺寸有关。并且转子槽内载流导体的存在也会影响漏磁导的值。槽漏磁导等效模型如图4所示,由于电机起动过程中有大量漏磁经过齿槽部分,因此可利用工字型磁导对槽身漏磁路进行等效。
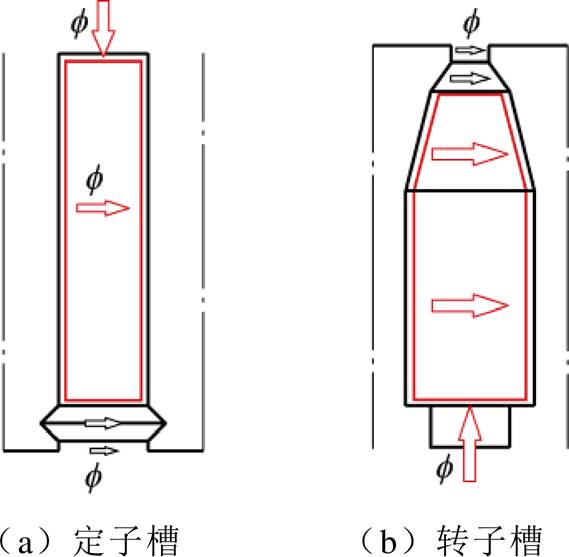
图4 槽漏磁导等效模型
Fig.4 Equivalent model of slot's leakage magnetic permeance
1.2.4 气隙磁导
气隙磁导模型如图5所示。电机定、转子齿槽及气隙结构如图5a所示。当定子齿和转子齿中较大的齿完全包含较小的齿时,这两个齿间的气隙磁通由较小齿的齿顶完全流向较大齿的齿顶,因此气隙磁导达到最大值Gmax;当两齿完全错开无重合面积时,不存在同时流经两齿的磁通即无磁路径连接,对应的气隙磁导为0。
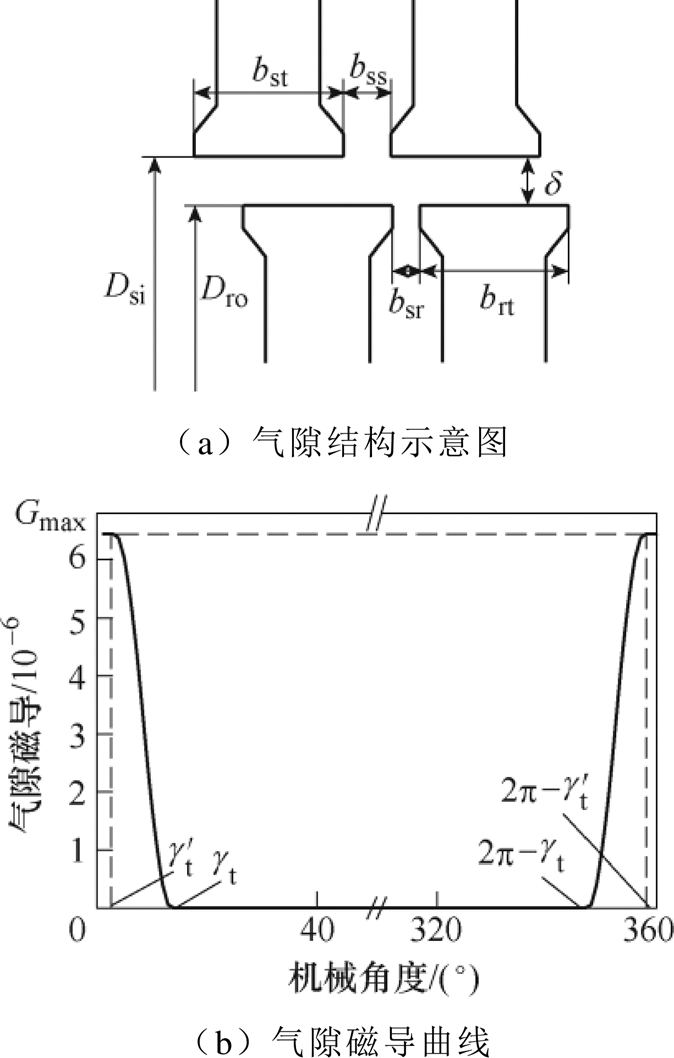
图5 气隙磁导模型
Fig.5 Magnetic permeance model of air gap
定子的第p个齿和转子第q个齿之间的气隙磁导Gp,q随着两齿中心线之间的夹角的变化在[0, Gmax]范围内变化,如图5b所示。气隙磁导的计算公式为
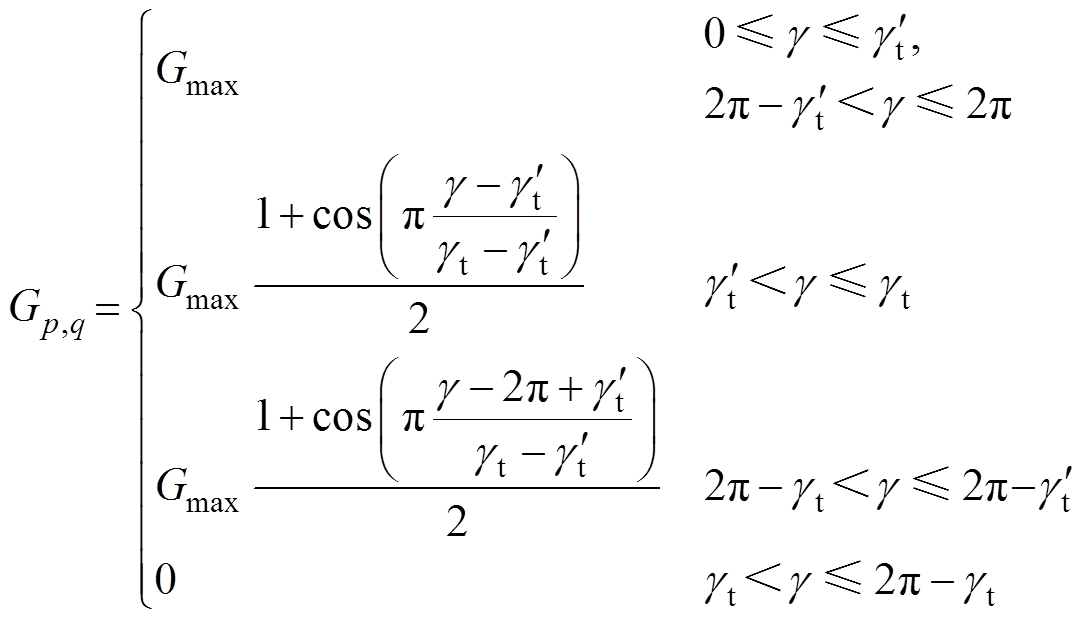 (3)
(3)
其中
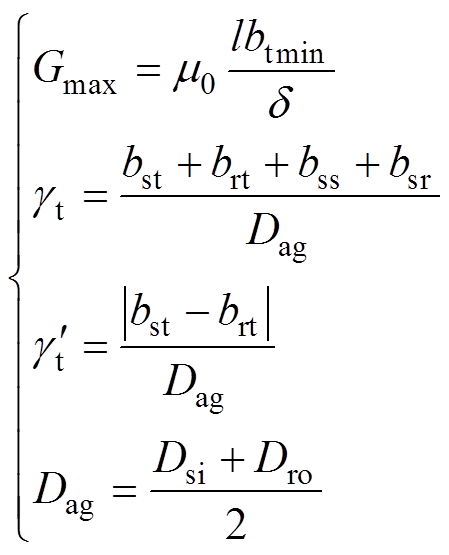 (4)
(4)
式中,m0为空气磁导率;btmin为定转子齿宽较小值;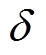 为气隙长度;bst为定子齿顶宽;bss为定子槽口宽;brt为转子齿顶宽;bsr为转子槽口宽;Dsi为定子内径;Dro为转子外径。
为气隙长度;bst为定子齿顶宽;bss为定子槽口宽;brt为转子齿顶宽;bsr为转子槽口宽;Dsi为定子内径;Dro为转子外径。
电机绕组置于槽中,电流均匀分布在导体中。由于齿部不存在绕组,所以齿部的磁动势是关于气隙圆周坐标x的常值,如图6所示。
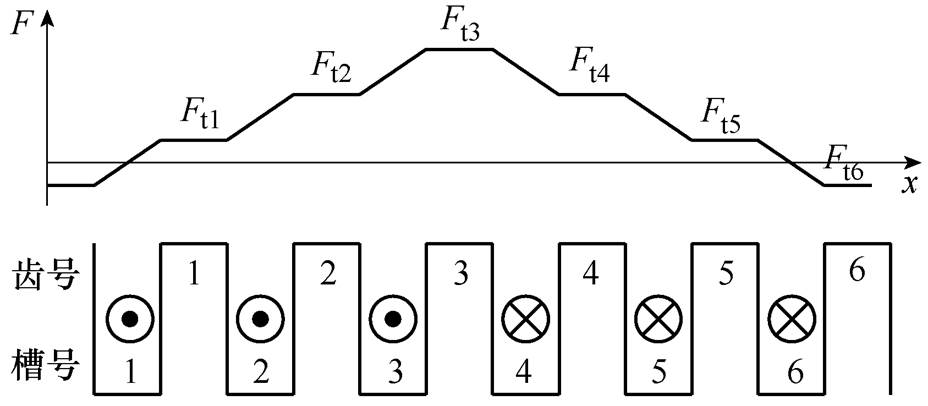
图6 定子绕组励磁磁动势
Fig.6 Excitation magnetomotive force of stator winding
由安培环路定律可知,相邻齿间的磁动势之差等于其间的槽总电流的安匝数,则有
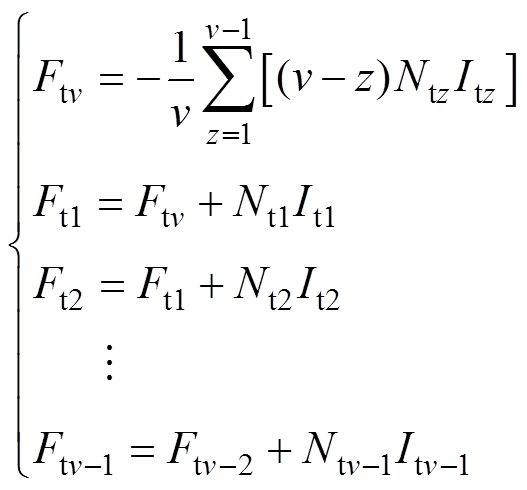 (5)
(5)
式中,Ftv为第v个齿的磁动势;Ntv为第v个槽中绕组匝数;Itv为第v个槽中绕组中的电流。
根据电机结构及磁通路径,构建电机定子、转子及气隙部分磁网络模型,并根据各部分的耦合关系将模型进行联结,得到本文所研究的大型感应电机的动态磁网络模型的拓扑结构如图7所示。图7中,虚线所示为齿槽结构。
在电机运行过程中,磁网络模型的总节点数不随着转子位置的改变而发生变化,节点磁动势方程为
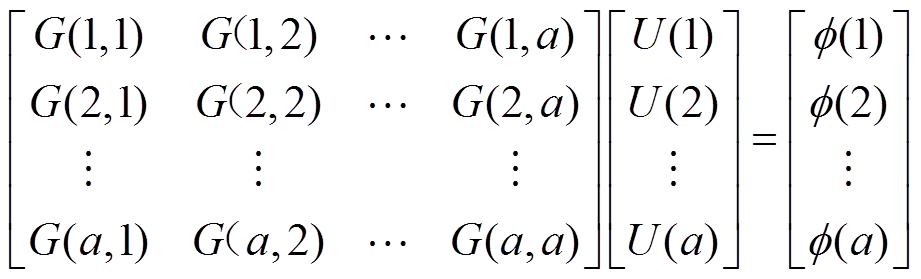 (6)
(6)
式中,a为磁网络中节点的总个数;G为节点间的磁导;U(a)为节点a的磁动势;f(a)为流入节点a的总磁通。G和f 均与电机内部的饱和程度有关,随着支路的磁导率变化而变化。
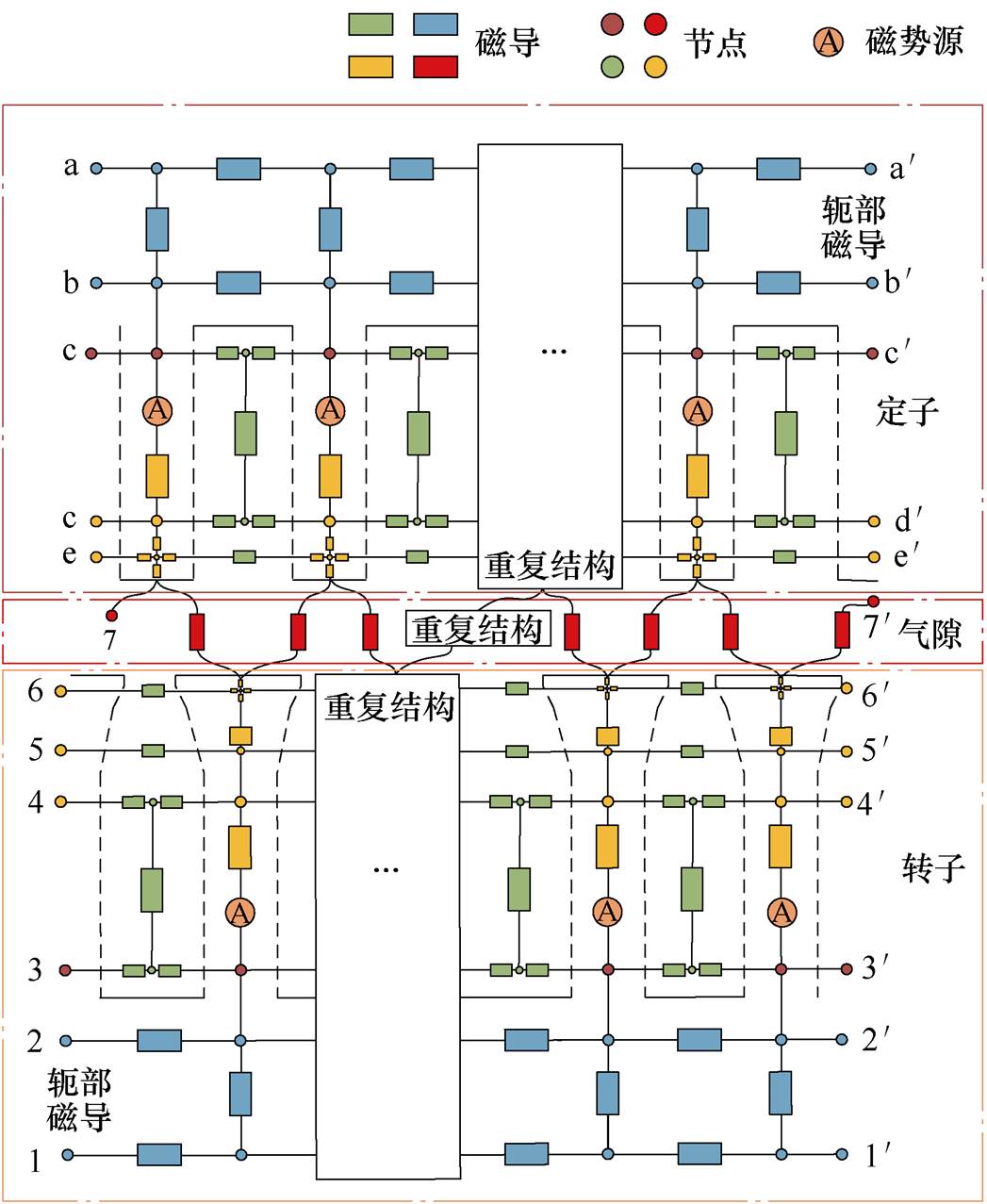
图7 动态磁网络模型
Fig.7 Dynamic magnetic network model
在求解节点磁动势方程前,需要给出节点磁通矩阵f 的初值,其值与支路磁动势源以及磁动势源所在支路的磁导有关,只有存在磁动势源的支路两端的节点有值,其余均为零,如图8所示,具体计算公式为
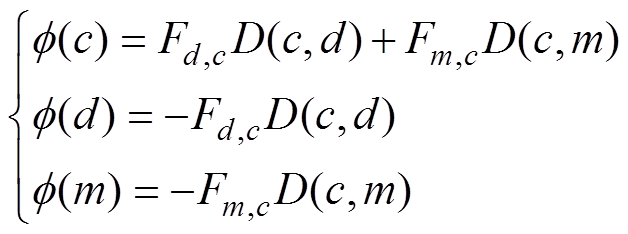 (7)
(7)
式中,Fd,c、Fm,c为支路磁动势源;D(c, d)为节点c与d之间支路的磁导。
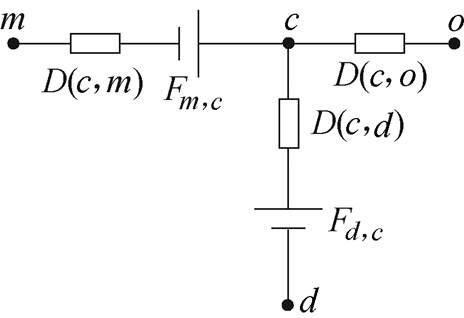
图8 支路示意图
Fig.8 Branch diagram
本文利用分层法计算电机起动过程任意时刻的趋肤效应,进而得到电阻增大系数和漏感减小系数,并对转子的漏感及电阻进行修正。根据算例中电机转子槽型的特殊性,将转子分成两个区域,由槽底向槽口进行编号,从1~n,其中1~u为矩形区域的层数编号,u+1~n为梯形区域的层数编号,趋肤效应模型如图9所示。
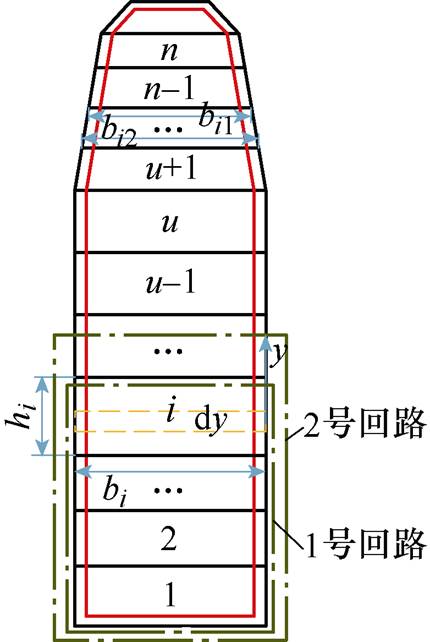
图9 趋肤效应模型
Fig.9 Skin effect model
转子导条第i层电阻计算公式为
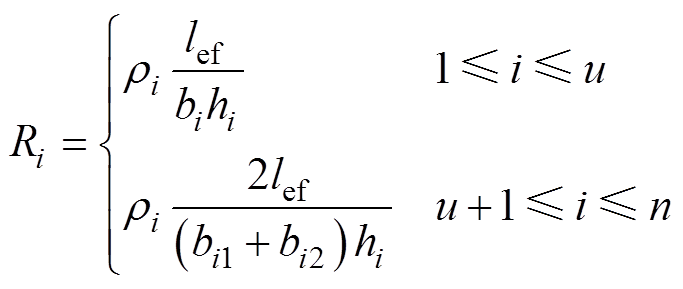 (8)
(8)
式中,lef为铁心的轴向等效长度;bi为第i层矩形区域的宽度;hi为第i层高度;bi1、bi2分别为第i层梯形区域的上底和下底宽度;ri为导条电阻率。
每层导条的自漏抗包含两部分,以第i层为例,第一部分是第i层导条中的全部电流产生的磁链穿过第i层导条自身与第i层部分电流匝链所形成的漏抗,此时的磁通回路为图9中的l号回路,第二部分是第i层导条中的全部电流产生的全部磁链穿过第i层导条上方与第i层全部电流匝链所形成的漏抗,此时的磁通回路为图9中的2号回路。
根据安培环路定律,采用积分方法对槽部漏磁链进行计算,计算时根据槽部梯形区域与长方形区域特点分别进行分析。以i层电流底部中心为坐标原点,经推导计算得到转子导条第i层自漏感计算公式为
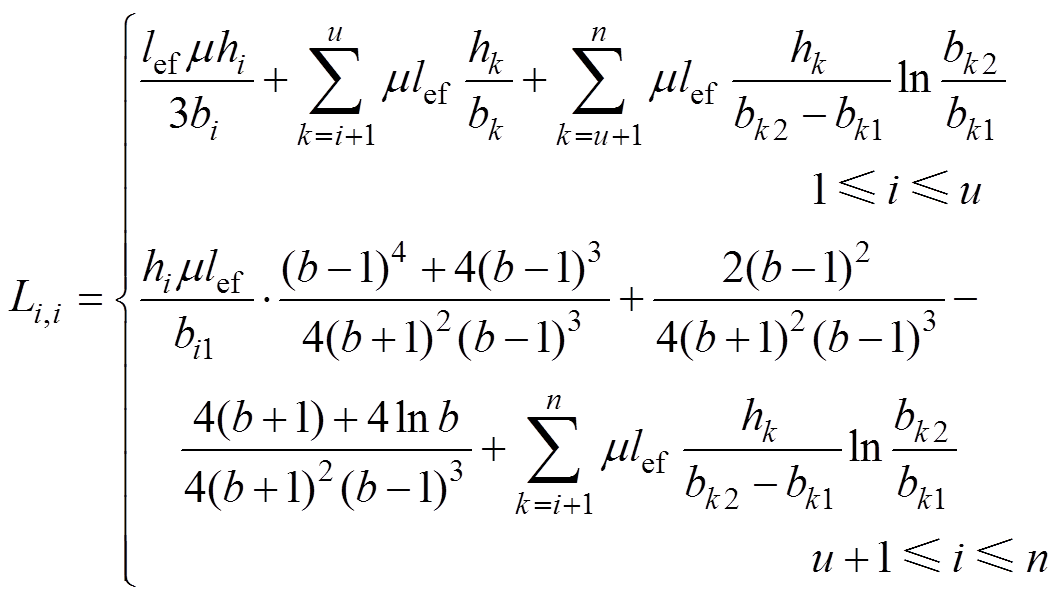 (9)
(9)
其中
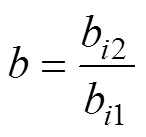
类似地,各层导条之间的互漏抗也包含两部分。同理可计算得到转子导条第i层与第j层之间的互感Mi,j。
可计算每层导条的自感阻抗Zi,i和互感阻抗Zi,j分别为
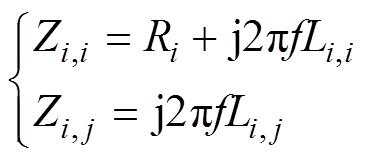 (10)
(10)
式中,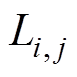 为第
为第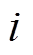 层和第
层和第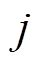 层导条的互漏感;
层导条的互漏感;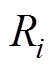 为第
为第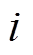 层导条的电阻。
层导条的电阻。
将转子导条分成多层相互并联的导条后,每层导条的铜损耗的累加和即为导条总的铜损耗,每层导条漏磁场能量的累加和即为导条总的漏磁场能量。在考虑趋肤效应的情况下,分析各层电流间的相互关系,进而求出各层的损耗和漏磁场能量是趋肤效应影响下电机电能分析的关键。转子导条的第i层与第i+1层的导体之间为并联关系,则其电压相等。根据电压、阻抗及电流之间的相互关系可确定转子导条各层电流之间的关系。
在趋肤效应模型分析的基础上,根据导条内存在趋肤效应和不存在趋肤效应时转子导条的铜耗及漏磁场储能,可对转子电阻增大系数和电抗减小系数进行计算,求得趋肤系数的计算公式为
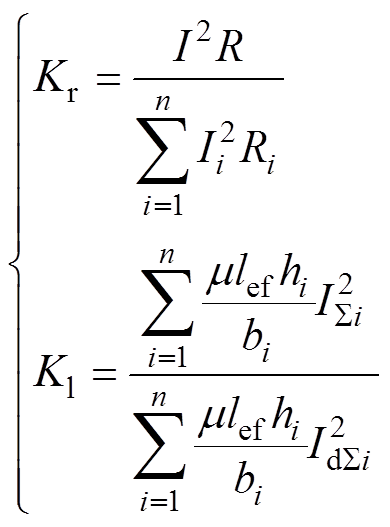 (11)
(11)
式中,R为导条总电阻;I为导条总电流;Ii为第i层导条电流;IdSi为不考虑趋肤效应时第i层导条中位线处磁链所匝链的所有电流的有效值;ISi为考虑趋肤效应时第i层导条中位线处的磁链所匝链的电流值。
计算得到算例电机起动过程中趋肤效应系数随转差率的变化曲线如图10所示。在电机起动初始阶段,转子的转速低,尤其是电机刚起动瞬间的转差率接近于1,此时转子导条内趋肤效应明显,导条中的电流趋向转子导条的表面,使得槽内导体的有效高度减小,此时,转子导条的交流电阻约为直流电阻的5.5倍。随着转子转速的上升,电阻增大系数和电抗减小系数逐渐接近于1。当电机稳定运行后,转子导条中电流频率很低,趋肤效应现象不明显。
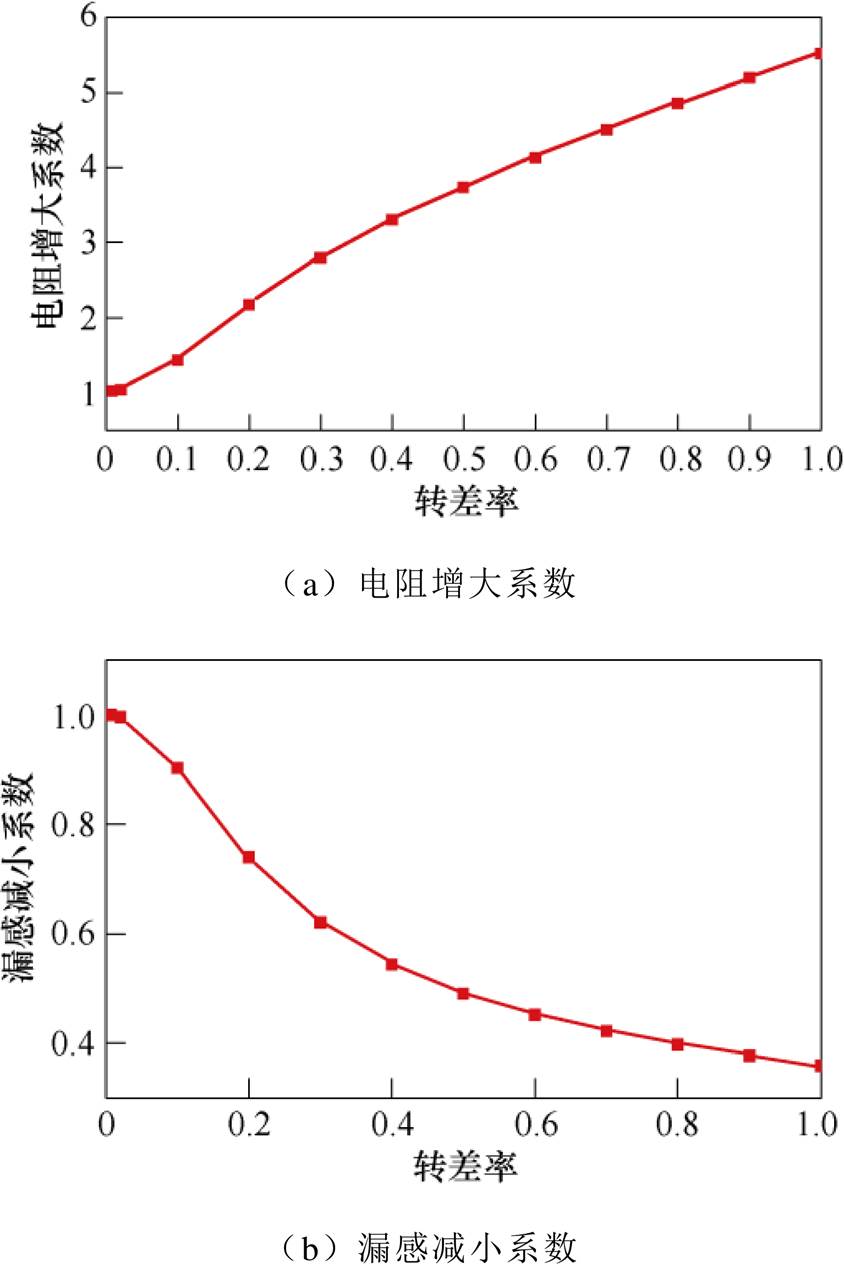
图10 电机起动过程趋肤效应系数变化曲线
Fig.10 Variation of skin effect coefficient during the starting process of motor
通过求解图7所示的感应电机的动态磁网络模型,可以计算得到考虑铁心饱和效应时电机内的磁通分布情况,进而求得电感。一个绕组线圈匝链的总磁链为
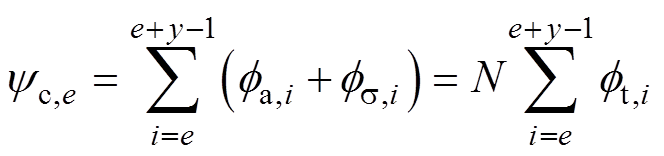 (12)
(12)
式中,y为线圈所跨过的槽数;e为线圈的起始边所对应的齿编号;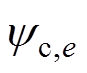 为线圈匝链的总磁链;N为线圈的匝数;
为线圈匝链的总磁链;N为线圈的匝数;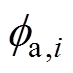 、
、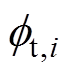 和
和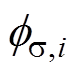 分别为第i个齿的齿部磁通、第i个齿下的气隙磁通和第i个槽的槽漏磁通。
分别为第i个齿的齿部磁通、第i个齿下的气隙磁通和第i个槽的槽漏磁通。
根据叠加原理,由e 个线圈构成的绕组所匝链的总磁链为
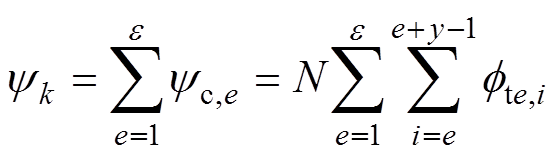 (13)
(13)
考虑电机起动过程趋肤效应的影响,采用根据趋肤效应模型计算得到的趋肤效应系数对转子电感参数的计算进行修正,考虑趋肤效应时,有
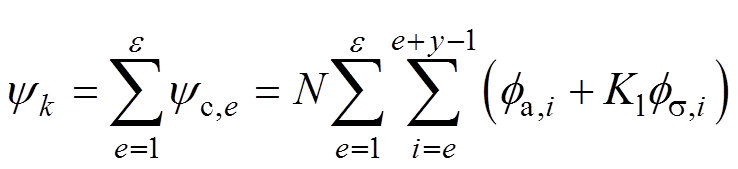 (14)
(14)
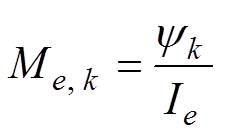 (15)
(15)
式中,K1为漏感减小系数;Me,k为绕组e和绕组k之间的互感;Ie为绕组e的电流。当e=k时,可计算绕组e的自感。
磁网络模型的求解流程如图11所示,采用迭代法对磁网络模型进行求解。
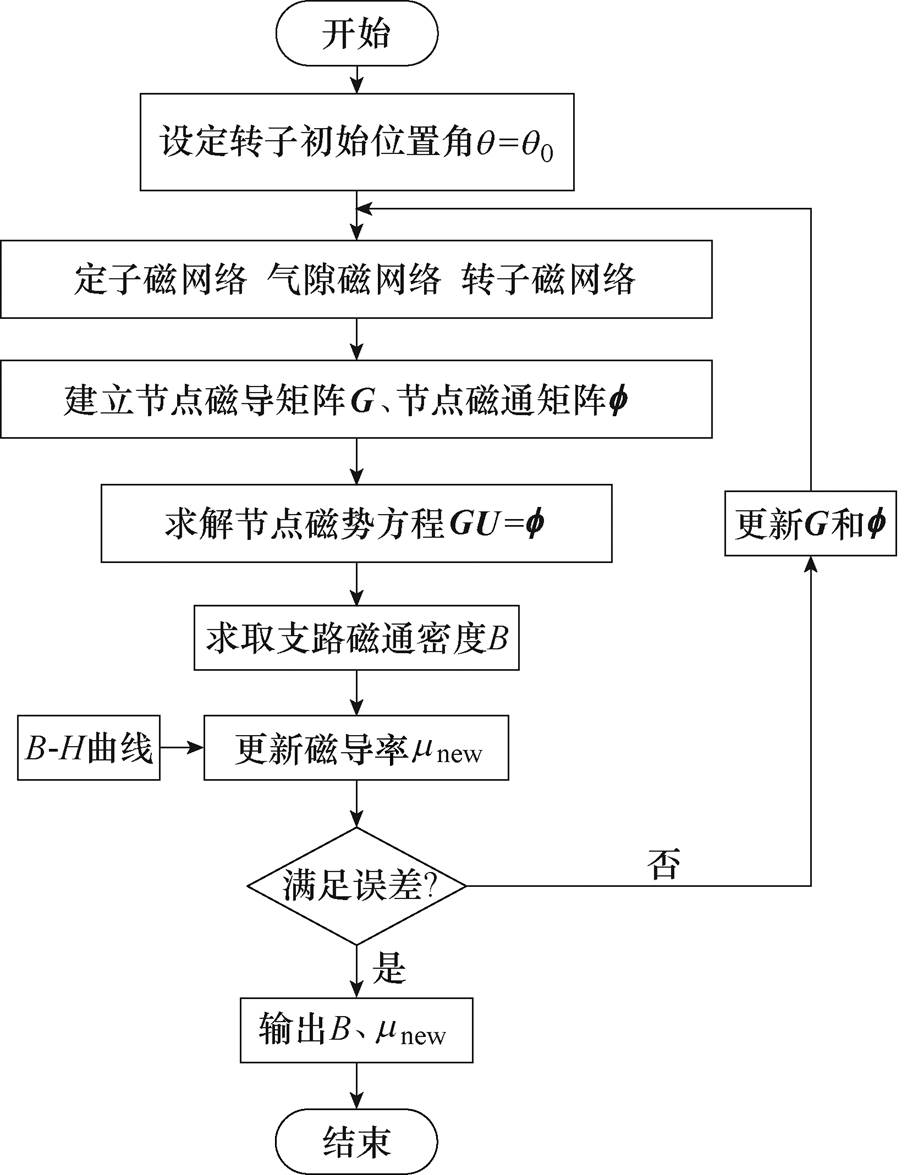
图11 磁网络求解流程
Fig.11 Flow chart of magnetic network calculation
求解磁网络模型时,在每个迭代步长内首先根据电机的电流和转速,计算得到该状态下的磁动势源矩阵U初值,并确定磁导率矩阵m 和磁导矩阵G,根据式(6)计算得到节点磁通,然后采用超松弛(Successive Over Relaxation, SOR)迭代法求解节点磁动势方程,进而求得支路磁导率矩阵。当相邻两次迭代求解得到的磁导率值满足误差精度要求时,结束求解过程。此时,可求得该工作点时的定、转子磁链,根据转速所对应的趋肤效应系数对磁链进行修正,利用式(11)、式(15)可求得考虑饱和效应与趋肤效应影响的电感参数。
电机的瞬态过程是一个电磁耦合的过程,当电机处于不同工作点时,电机内部的磁通分布以及转子导条的趋肤效应程度会发生改变,因此必须根据电机起动过程不同运行时刻的电流与转速值来对阻抗参数进行计算。从电机学原理可知,正确计算电机的电流、转矩和转速特性的前提是可以准确获取动态阻抗参数。电机起动过程各参数间相互影响关系如图12所示。在求解电机动态电磁性能时,必须将其与阻抗进行耦合计算,来提高计算的准确性。
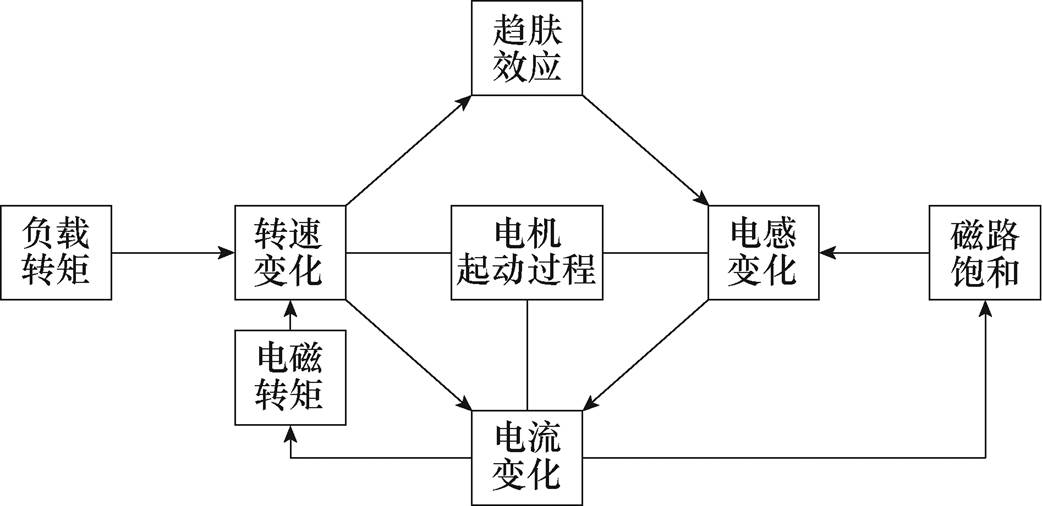
图12 电机起动过程电磁耦合关系
Fig.12 Electromagnetic coupling during the motor starting process
为了对转子各导条的瞬态电流进行计算,从而更好地实现与动态磁网络模型的瞬态耦合分析,本文提出采用转子多回路法建立感应电机的动态数学模型。根据电机瞬态过程各参数间的电磁耦合机理,将动态数学模型、动态磁网络模型以及趋肤效应模型进行耦合计算,从而准确获取电机动态过程中的转速、电流、电感与电阻等电磁特性参数,为电机瞬态过程的分析提供理论依据。
本文算例电机为笼型转子电机,可将笼型转子等效成包含多个回路的电路,如图13所示。根据转子结构建立转子多回路等效模型如图14所示,Rb为一根转子导条的电阻,Re和Le分别为两根转子导条之间的端环部分的端环电阻和端环漏感,ir1和ir2分别为转子1号回路的回路电流和转子2号回路的回路电流,ie为端环回路的回路电流。每两根相邻的转子导条与其中间的端环,组成一个回路,各端环独立形成了一个回路。
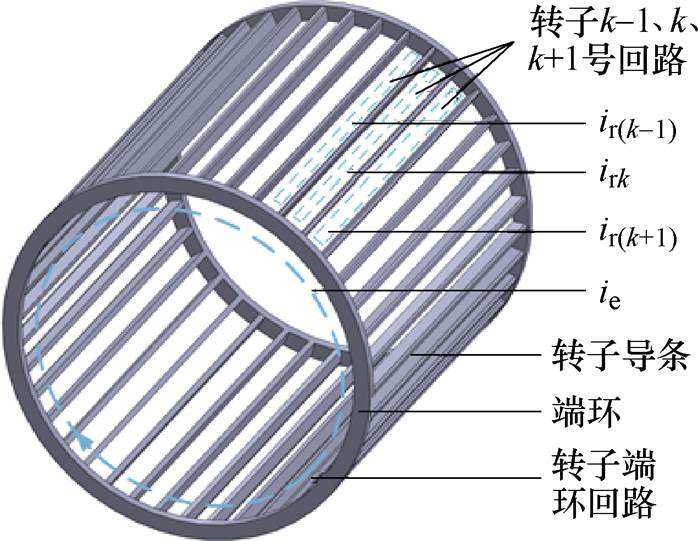
图13 笼型转子回路
Fig.13 Cage rotor loop
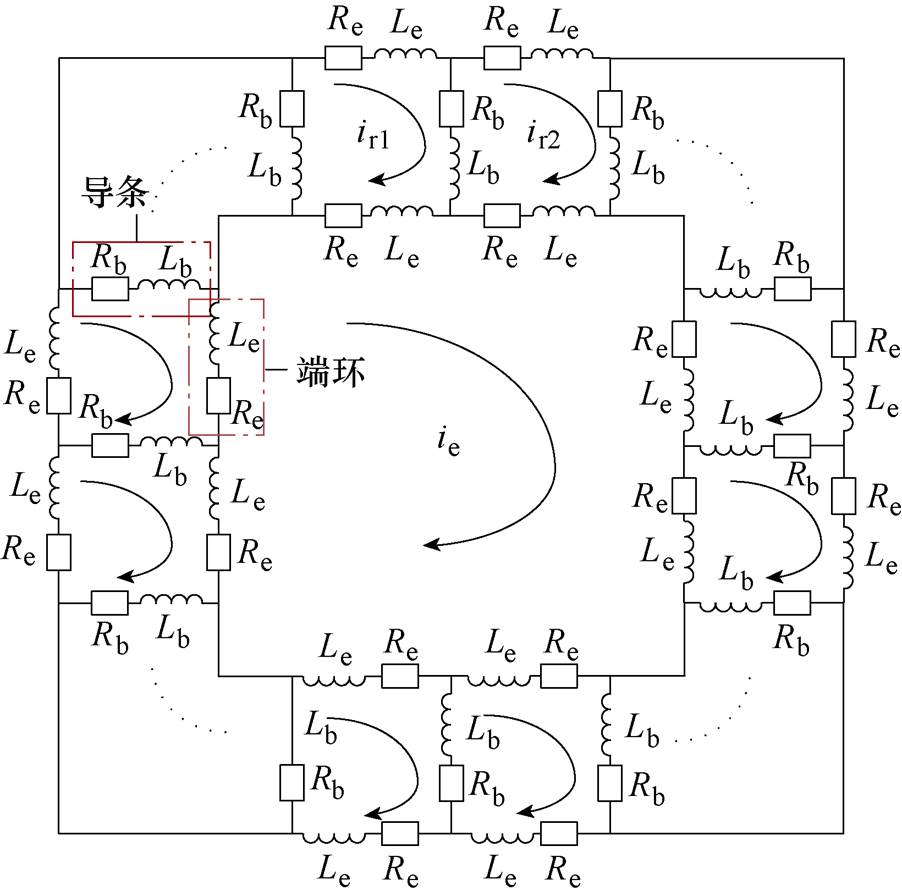
图14 转子多回路模型
Fig.14 Rotor multi-loop model
以转子1号回路为例,根据图14的等效电路可得到转子1号回路的电压和磁链方程满足
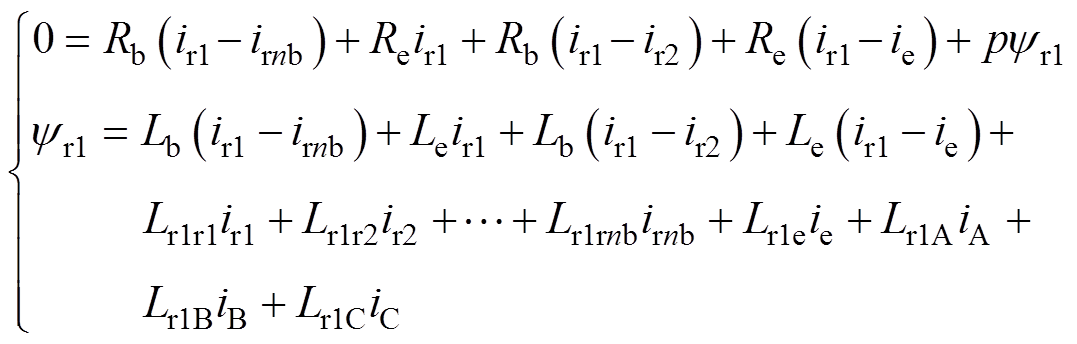 (16)
(16)
式中,ir1和ir2分别为转子1号回路的回路电流和转子2号回路的回路电流;irnb为第nb号转子回路的电流;yr1为转子1号回路的磁链;Lb为导条电感;iA、iB、iC分别为A、B、C三相电流;Lr1A、Lr1B、Lr1C为别为转子1号回路与A、B、C三相绕组之间的互感;Lr1r1为转子1号回路的自感;Lr1r2,…, Lr1rnb分别为转子1号回路与其余转子回路之间的互感;Lr1e为转子1号回路与端环回路之间的互感,由于转子各个回路与端环回路之间仅通过端环漏感耦合且其值很小,可认为Lr1e=0;p为微分算子。
同理可得其余转子回路的磁链方程与电压方程,以及端环回路的磁链方程与电压方程。将定子电压方程与转子电压方程、定子磁链方程与转子磁链方程相结合,最终得到基于转子多回路法的电压方程和磁链方程。整理可得数学模型为
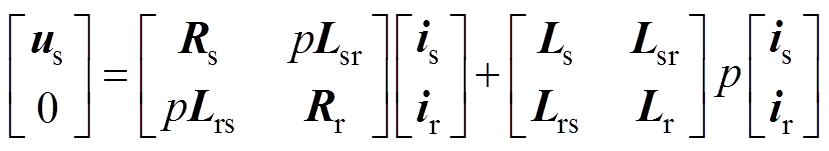 (17)
(17)
式中,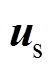 为定子电压;Rr和Lr分别为基于转子多回路方法计算得到的转子电阻与电感系数矩阵;
为定子电压;Rr和Lr分别为基于转子多回路方法计算得到的转子电阻与电感系数矩阵;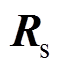 为定子三相绕组的相电阻矩阵;is、ir分别为定子、转子电流;
为定子三相绕组的相电阻矩阵;is、ir分别为定子、转子电流;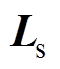 为定子电感矩阵;
为定子电感矩阵;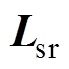 为定子与转子的互感矩阵。
为定子与转子的互感矩阵。
转矩和速度方程为
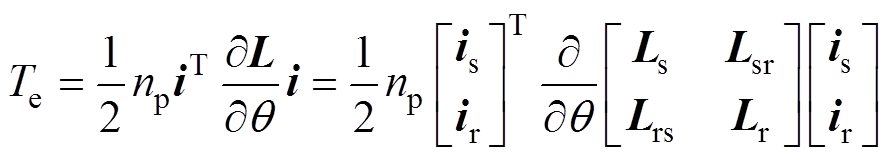 (18)
(18)
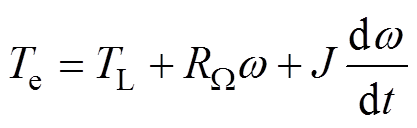 (19)
(19)
式中,q 为转子转过的电角度;np为电机极对数;i、L分别为电流和电感矩阵;RW 为电机的旋转阻力系数;w 为转速;RWw 为克服电机自身机械损耗和铁耗所需的转矩;TL为负载转矩;J为转动惯量。
根据电机瞬态电磁模型间的耦合关系,耦合求解动态磁网络模型、趋肤效应模型及动态数学模型。计算初设起始时间为t0=0,转速及电流初值均设为0,转子初始位置角为q0。根据初始条件,由电机动态数学模型计算得到此迭代步长内的电流I1、转速w1和电磁转矩Te1;根据该时刻的电机转速值以及转子电流值,通过求解趋肤效应模型获取该时刻下的趋肤效应系数;将该时刻的定子电流值与转子导条电流值代入动态磁网络中作为动态磁网络的激励源,此时转子的位置角由q0转动至q1=q0+wDt,利用动态磁网络模型求解方法求解动态磁网络模型,即可得到该时刻下电机内部的磁通分布情况,进而计算得出电机各绕组及转子回路所匝链的磁链大小,根据磁链以及趋肤效应系数对电阻与电感进行计算,并对动态数学模型中电阻和电感系数矩阵进行修正,以此进行迭代计算,直至电机进入电磁稳定状态。
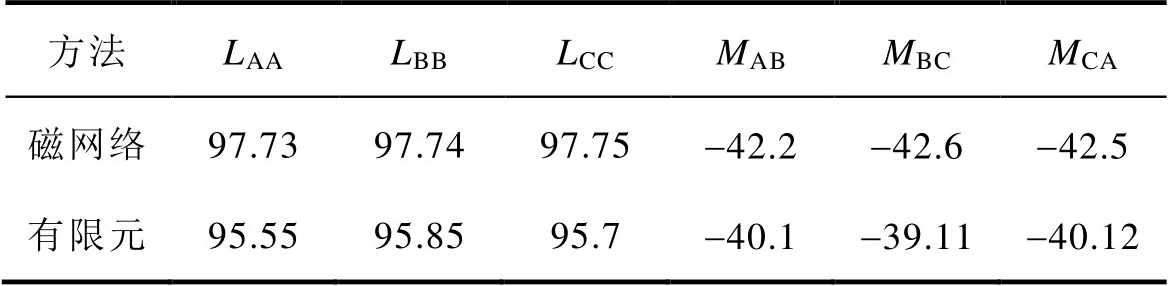
大型感应电机起动时间较长,在未达到电磁稳定运行状态之前,电流较大,电机内饱和效应明显,以电机起动初始阶段转差率s=0.6的时刻为例,将该时刻下的电流值作为动态磁网络的输入激励值,通过求解动态磁网络及趋肤效应模型求解各相电感值,计算得到定子绕组自感与互感结果见表2,采用有限元法计算得到的电感值同样列于表中。两种计算方法的计算结果接近,验证了本文所提出计算方法的有效性。
表2 定子绕组的自感与互感
Tab.2 Self-inductance and mutual inductance of stator windings(单位: mH)
方法LAALBBLCCMABMBCMCA 磁网络97.7397.7497.75-42.2-42.6-42.5 有限元95.5595.8595.7-40.1-39.11-40.12
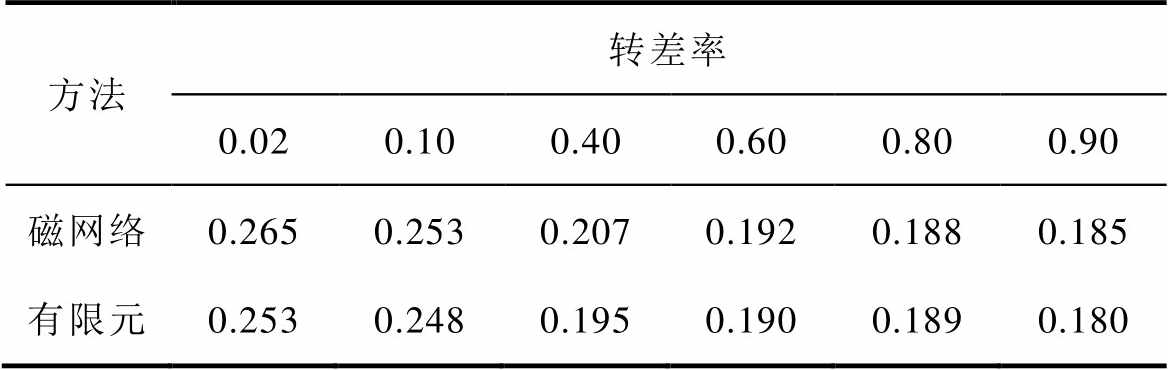
本文所研究的电机转子共有210根导条,考虑到转子导条回路的对称性,所以只以1号回路为例,通过改变转子位置角,采用动态磁网络模型法分别求解得到一个电角度周期下的转子回路自感与互感,其余各个回路的自感与互感均与其相差一个相位。采用有限元法和动态磁网络法计算所得的转子1号回路自感Lr1r1见表3。随着电机转速的增加,转子导条电流频率逐渐减小,所以转子回路自感逐渐增大。
表3 转子1号回路的自感
Tab.3 Self inductnce of rotor’s Loop 1(单位: mH)
方法转差率 0.020.100.400.600.800.90 磁网络0.2650.2530.2070.1920.1880.185 有限元0.2530.2480.1950.1900.1890.180
同样选取s=0.6的时刻进行分析。考虑到转子导条回路的对称性,只对A相绕组与转子1号回路之间的互感LAR1进行计算。通过改变转子位置角,利用有限元法和动态磁网络法分别计算在一个电角度周期下的定、转子绕组之间的互感,两种方法的计算结果如图15所示。
定子绕组与转子1号回路之间的互感值与极对数有关,符合定转子互感的变化规律。利用有限元法与磁网络法计算得到的定子绕组与转子1号回路之间的互感结果接近,说明了本文所提出的电机动态电感参数计算方法的正确性。
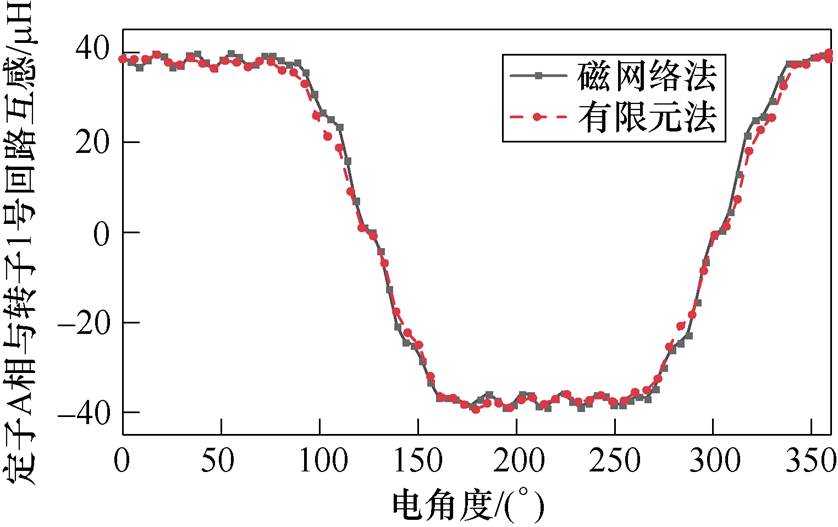
图15 定子A相绕组与转子1号回路的互感
Fig.15 Mutual inductance between phase A and rotor’s Loop 1
利用本文所提出的大型感应电机的动态耦合数学模型对算例电机进行研究分析,并将其与利用计算单提供的起动参数的计算结果进行对比分析,计算得到电机额定负载时的特性曲线如图16所示。
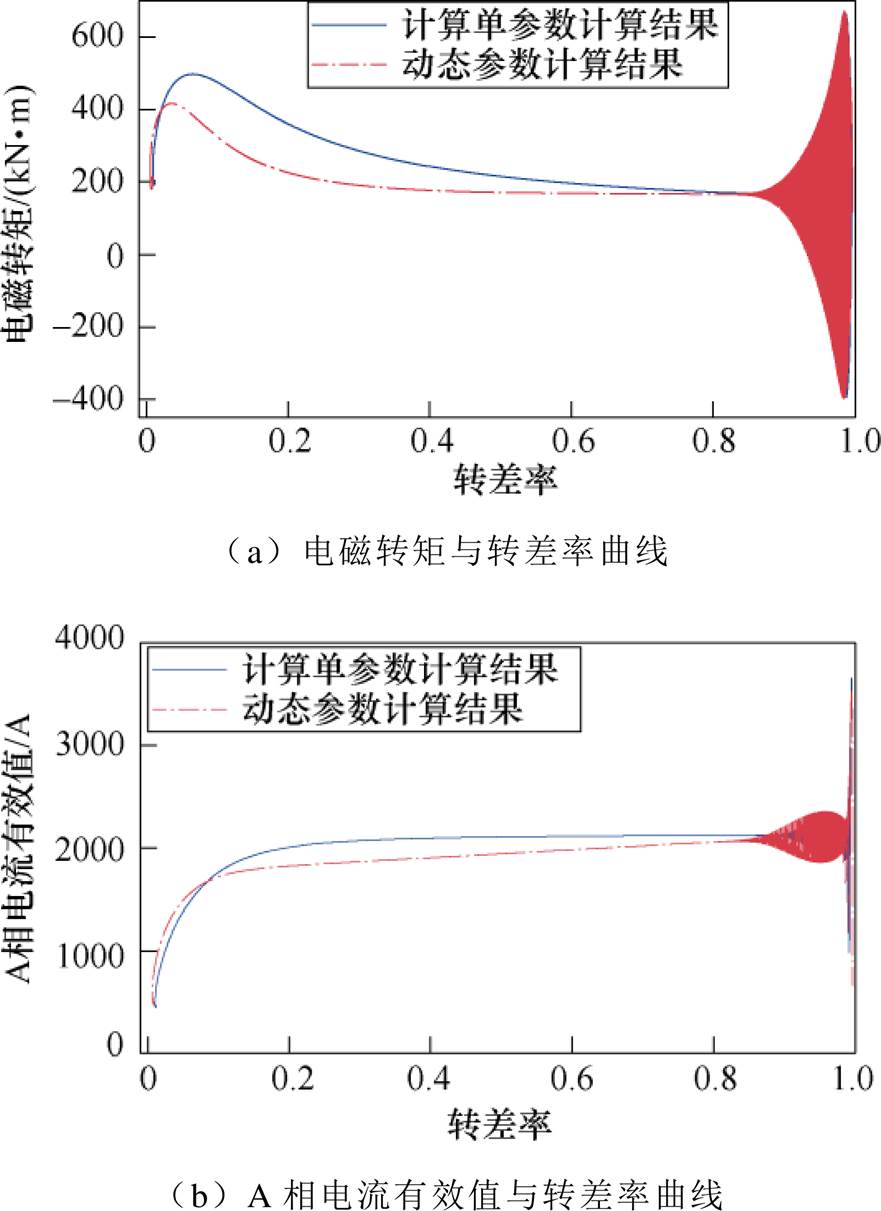
图16 电机额定负载时的特性曲线
Fig.16 Characteristic curves of motor under rated load
通过比较图16a、图16b可以看出,采用两种参数计算电磁转矩与电流值时,起动开始阶段两种参数计算所得的结果基本一致,但是随着电机转速的上升,两种参数所计算得到的结果的差值逐渐增大,这是因为当电机的转速逐步上升时,饱和效应与趋肤效应对电阻和电感的影响逐渐变弱,导致电机计算单中的起动参数与本文计算方法所计算得到的阻抗参数之间的差值逐渐增大。电磁转矩计算的准确性又会影响到电机加速转矩的计算、起动时间和带载能力的判断。进一步地,考虑饱和与趋肤变化等电磁问题的准确分析也是大型电机暂态发热及冷却问题准确分析的基础。因此,对大型电机暂态电磁问题进行分析时需考虑饱和及趋肤效应变化的影响,若不考虑这些非线性因素的影响将使模型偏离实际情况,误差较大,从而使电机设计和控制出现偏差。
图17为利用有限元计算得到的电机额定负载情况时的电磁转矩。图18为采用有限元法和本文所提出方法计算得到的定子A相电流波形。对比可知,采用两种方法所计算出的结果相近,验证了本文所推导的动态数学模型和所提出计算方法的准确性。本文所提出的计算方法对计算条件要求较低,计算用时约为有限元法的1/10,更易于融入现有设计程序,提高大型电机暂态性能计算的准确度,并实现电机的系列化计算。
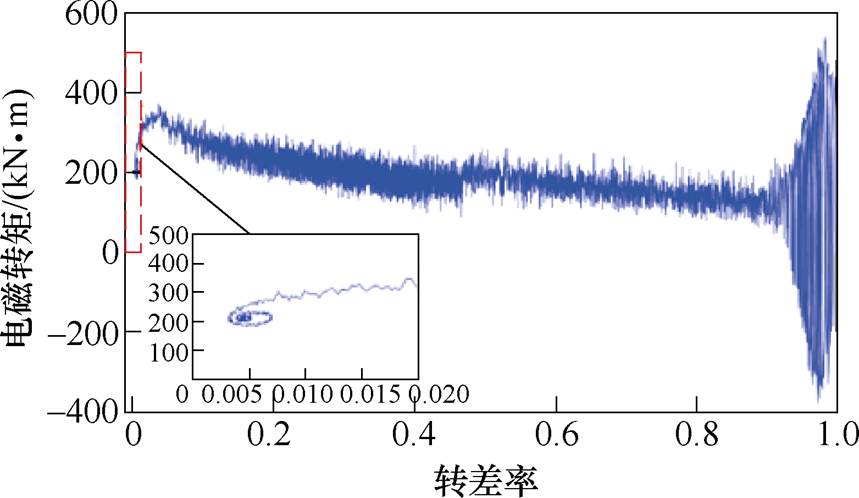
图17 有限元法计算得到的转矩
Fig.17 Torque obtained by finite element
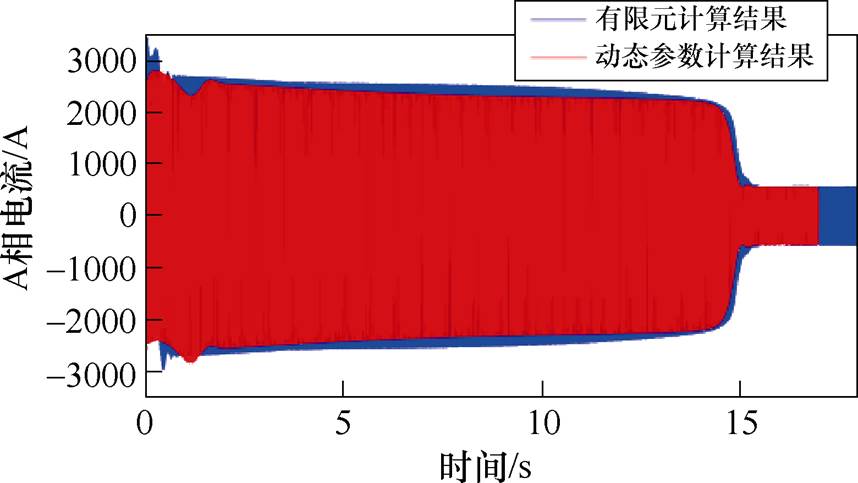
图18 有限元与动态参数计算结果对比
Fig.18 Comparison between finite element and dynamic parameter calculation method
本文算例中的实验样机整体结构如图19所示。电机在装配完成后根据国家标准进行整机实验,对电机的最大转矩倍数、起动转矩倍数和起动电流倍数进行实验测试。计算及实验结果见表4。

图19 实验样机
Fig.19 Experimental prototype motor
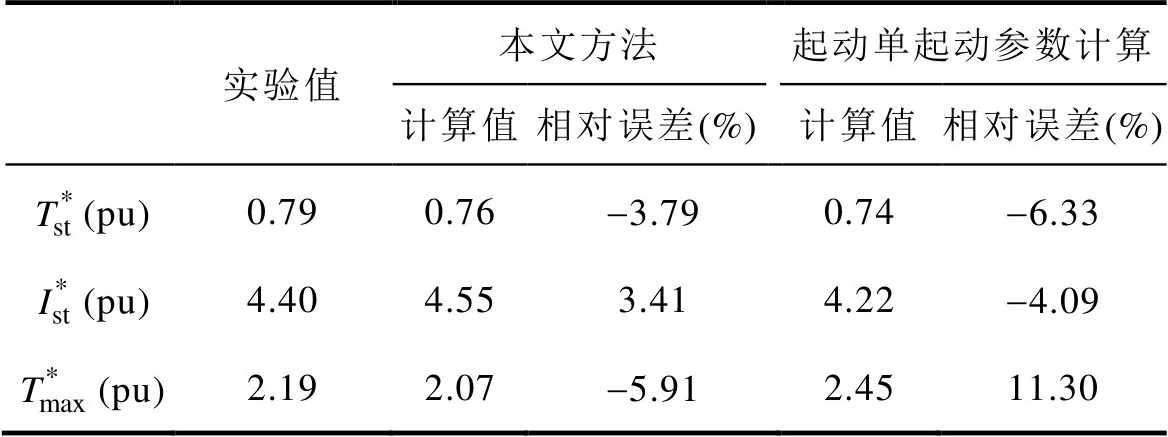
表4 计算及实验结果
Tab.4 Calculation and experimental results
实验值本文方法起动单起动参数计算 计算值相对误差(%)计算值相对误差(%) (pu)0.790.76-3.790.74-6.33 (pu)4.404.553.414.22-4.09 (pu)2.192.07-5.912.4511.30
实验测得起动转矩倍数为0.79、起动电流倍数为4.40、最大转矩倍数为2.19,采用本文所提出的计算方法计算得到的起动转矩倍数为0.76、起动电流倍数为4.55、最大转矩倍数为2.07,计算误差分别为-3.79%、3.41%、-5.91%,采用计算单起动参数计算得到的起动转矩倍数为0.74、起动电流倍数为4.22、最大转矩倍数为2.45,计算误差分别为-6.33%、-4.09%、11.30%,本文所提出的计算方法在对电机动态过程进行分析时,较全面地考虑了大型电机动态过程物性参数及阻抗参数的非线性变化及其耦合关系,提高了电机瞬态过程阻抗及电磁参数计算的准确性。
大容量高压感应电机起动过程动态性能较难实验测取,设计人员和用户通常要依赖计算结果来分析电机起动特性,从而判断电机的带载能力并选择合理的起动方式,因此需要一种切实可行的方法对大型高压电机的起动过程进行分析计算。本文在考虑大型电机瞬态过程中电流、转速、饱和及趋肤程度变化的基础上提出电机动态阻抗参数及起动特性的计算方法,得到以下结论:
1)建立电机动态磁网络模型、趋肤效应模型及基于转子多回路法的动态数学模型,并基于电机内电磁耦合关系将各模型进行耦合求解计算,可计及电机整个起动过程中磁导的非线性变化,以及起动电流变化时引起的电机内饱和偏移问题,更便捷地对绕组自感和互感进行计算,所提出的计算方法更适合大型电机起动的特点。
2)大型电机起动时间较长,电机内电磁状态随起动时间不断变化,当电机转速逐渐升高,阻抗参数受趋肤效应与饱和效应影响减弱,实际值与计算单参数相差较大,故进行大型电机瞬态电磁特性分析时,必须考虑阻抗参数的动态变化情况。电机的阻抗参数与起动特性必须进行耦合计算,单独计算会降低准确性,从而影响电机起动时间及带载能力的判断。
3)本文所提出的电机瞬态阻抗及起动特性的计算方法考虑了大型电机瞬态过程电机内的电磁耦合关系,对样机进行实验分析可知,相比于传统计算方法,本文所提出的方法对电机起动转矩、起动电流和最大转矩的计算误差分别降低了2.54%、0.68%和5.39%。相比于有限元计算方法,可降低90%左右的求解时间,为工程中电机的系列化计算与优化提供依据。
参考文献
[1] Li Changbin, Wang Xiuhe, Liu Feng, et al. Analysis of permanent magnet-assisted synchronous reluctance motor based on equivalent reluctance network model[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(2): 135-144.
[2] 赵玫, 于帅, 张华强. 聚磁式横向磁通永磁直线电机的变磁导等效磁网络[J]. 电机与控制学报, 2020, 24(4): 12-22.
Zhao Mei, Yu Shuai, Zhang Huaqiang. Variable permeability equivalent magnetic circuit network of flux-concentrated transverse flux permanent magnet linear machine[J]. Electric Machines and Control, 2020, 24(4): 12-22.
[3] 禹春敏, 邓智泉, 梅磊, 等. 基于精确磁路的新型混合型轴向-径向磁悬浮轴承研究[J]. 电工技术学报, 2021, 36(6): 1219-1228.
Yu Chunmin, Deng Zhiquan, Mei Lei, et al. Research of new hybrid axial-radial magnetic bearing based on accurate magnetic circuit[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1219-1228.
[4] Hou Jining, Geng Weiwei, Li Qiang, et al. 3-D equivalent magnetic network modeling and FEA verification of a novel axial-flux hybrid-excitation in-wheel motor[J]. IEEE Transactions on Magnetics, 2021, 57(7): 1-12.
[5] 刘云飞, 张炳义, 宗鸣, 等. 基于非线性混合模型的模块组合式永磁电机磁场解析[J]. 电工技术学报, 2022, 37(18): 4593-4603.
Liu Yunfei, Zhang Bingyi, Zong Ming, et al. Analytical prediction of magnetic field in modular combined permanent magnet motor by a nonlinear hybrid model[J]. Transactions of China Electro- technical Society, 2022, 37(18): 4593-4603.
[6] 李想, 徐伟, 叶才勇. 新型定子永磁型动铁心式横向磁通直线振荡电机[J]. 中国电机工程学报, 2017, 37(21): 6209-6217.
Li Xiang, Xu Wei, Ye Caiyong. Novel stator-magnet moving-iron transversal-flux linear oscillatory machine[J]. Proceedings of the CSEE, 2017, 37(21): 6209-6217.
[7] Xu Gaohong, Liu Guohai, Jiang Shan, et al. Analysis of a hybrid rotor permanent magnet motor based on equivalent magnetic network[J]. IEEE Transactions on Magnetics, 2018, 54(4): 1-9.
[8] Li Zhaokai, Huang Xiaoyan, Wu Lijian, et al. Open-circuit field prediction of interior permanent- magnet motor using hybrid field model accounting for saturation[J]. IEEE Transactions on Magnetics, 2019, 55(7): 1-7.
[9] Cao Donghui, Zhao Wenxiang, Ji Jinghua, et al. Parametric equivalent magnetic network modeling approach for multiobjective optimization of PM machine[J]. IEEE Transactions on Industrial Elec- tronics, 2021, 68(8): 6619-6629.
[10] 徐伟, 张祎舒, 曹辰, 等. 定子不对称极混合励磁双凸极电机改进型非线性变磁网络模型构建方法研究[J]. 中国电机工程学报, 2023, 43(1): 304-318.
Xu Wei, Zhang Yishu, Cao Chen, et al. Improved construction method of nonlinear varying equivalent magnetic network model for hybrid excitation asymmetric stator pole double salient machine[J]. Proceedings of the CSEE, 2023, 43(1): 304-318.
[11] 佟文明, 姚颖聪, 李世奇, 等. 考虑磁桥不均匀饱和的内置式永磁同步电机等效磁网络模型[J]. 电工技术学报, 2022, 37(12): 2961-2970.
Tong Wenming, Yao Yingcong, Li Shiqi, et al. Equivalent magnetic network model for interior permanent magnet machines considering non-uniform saturation of magnetic bridges[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 2961- 2970.
[12] 佟文明, 王萍, 吴胜男, 等. 基于三维等效磁网络模型的混合励磁同步电机电磁特性分析[J]. 电工技术学报, 2023, 38(3): 692-702.
Tong Wenming, Wang Ping, Wu Shengnan, et al. Electromagnetic performance analysis of a hybrid excitation synchronous machine based on 3D equivalent magnetic network[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 692-702.
[13] 唐敬. 轨道交通牵引感应电机电气故障建模与在线故障诊断方法研究[D]. 北京: 北京交通大学, 2020: 17-52.
[14] 郑印钊, 周理兵, 王晋. 考虑实心体涡流影响的笼型实心转子电机起动工况导条电流分布的解析计算[J]. 电工技术学报, 2021, 36(11): 2355-2364.
Zheng Yinzhao, Zhou Libing, Wang Jin. Analytical calculation of rotor bar current distribution in starting condition of cage solid-rotor machine considering the effect of eddy current in solid-rotor[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2355-2364.
[15] Wu Shuang, Shi Tingna, Guo Liyan, et al. Accurate analytical method for magnetic field calculation of interior PM motors[J]. IEEE Transactions on Energy Conversion, 2021, 36(1): 325-337.
[16] 韩力, 王斌, 仲杰, 等. 多绕组交流旋转电机饱和电感的快速求解算法[J]. 中国电机工程学报, 2021, 41(7): 2547-2556.
Han Li, Wang Bin, Zhong Jie, et al. Fast algorithm for calculating the saturated inductances of multi-winding AC rotating machine[J]. Proceedings of the CSEE, 2021, 41(7): 2547-2556.
[17] 崔征山, 周扬忠, 周祎豪. 基于改进子域模型的双绕组无轴承磁通切换电机磁场解析计算[J]. 电机与控制学报, 2022, 26(3): 66-77.
Cui Zhengshan, Zhou Yangzhong, Zhou Yihao. Analytical calculation of magnetic field of dual- winding bearingless flux-switching permanent magnet motors based on improved subdomain model[J]. Electric Machines and Control, 2022, 26(3): 66-77.
Abstract Large induction motors are widely used in traction and drive applications. The accurate calculation of impedance parameters is crucial for predicting motor performance, determining the driving load, and optimizing motor design. The large induction motor has a long starting time and large current, experiencing apparent time-varying core saturation and skin effect. Current approaches, such as the magnetic network method, often neglect the nonlinearity in the magnetic permeance of the motor during the starting process, leading to inaccuracies in considering the saturation deviation caused by variable starting currents. Accordingly, the dynamic magnetic network method is proposed to analyze the electromagnetic performance of large induction motors in the transient process. Considering the influence of the saturation effect and skin effect on the motor impedance, the calculation method for motor starting characteristics is proposed, thereby improving the accuracy and efficiency of calculating dynamic impedance parameters and starting characteristics.
The proposed nonlinear dynamic magnetic network model considers the air gap’s magnetic permeance variation caused by the rotor’s speed changes. The effect of the starting current characteristic on the saturation degree inside the motor is discussed. According to the magnetic field line and the saturation degree, the calculation method for nonlinear permeability in the dynamic magnetic network model is determined. Based on the dynamic magnetic network model and the rotor skin effect model, the dynamic impedance parameters are calculated by considering leakage flux, rotor speed variation, and saturation phenomena. The dynamic mathematical model of large induction motors is derived from the rotor multi-circuit method. According to the electromagnetic coupling relationship in the transient process, a dynamic coupling solution is determined to obtain dynamic impedance parameters and starting characteristics, considering variations in current, speed, saturation, and skin depth. Calculation accuracy at a lower computational cost is improved.
Calculation results show that when the motor starts to reach the stable running state, the resistance increase coefficient gradually decreases from 5.517 to 1.025, and the reactance decrease coefficient increases from 0.36 to 1. Using dynamic parameters for calculating the starting characteristics of large motors improves accuracy. Compared with the traditional calculation method, the relative errors of starting torque, starting current, and maximum torque are reduced by 2.54%, 0.68%, and 5.39%, respectively. Compared with the finite element method (FEM), the solution time is reduced by about 90%.
The following conclusions can be drawn. The proposed method ensures accurate calculation by coupling dynamic impedance parameters and starting characteristics for large induction motors, considering the nonlinearities in the magnetic permeance during the starting process and the saturation deviation caused by the time-varying starting current. Compared to the traditional calculation method and FEM, it improves accuracy and computational efficiency, facilitating calculations for related motor types.
keywords:Large induction motors, dynamic magnetic network, dynamic impedance, rotor multi-loop method, starting characteristic
DOI: 10.19595/j.cnki.1000-6753.tces.230717
中图分类号:TM343
国家自然科学基金资助项目(52077047)。
收稿日期 2023-05-22
改稿日期 2023-05-30
夏云彦 女,1987年生,副教授,硕士生导师,研究方向为电机内综合物理场计算、特种电机优化设计及动态运行状态分析。E-mail: yunyan_x@163.com(通信作者)
周 洲 男,1999年生,硕士研究生,研究方向为特种电机电磁分析。E-mail: zzb1234up@163.com
(编辑 崔文静)