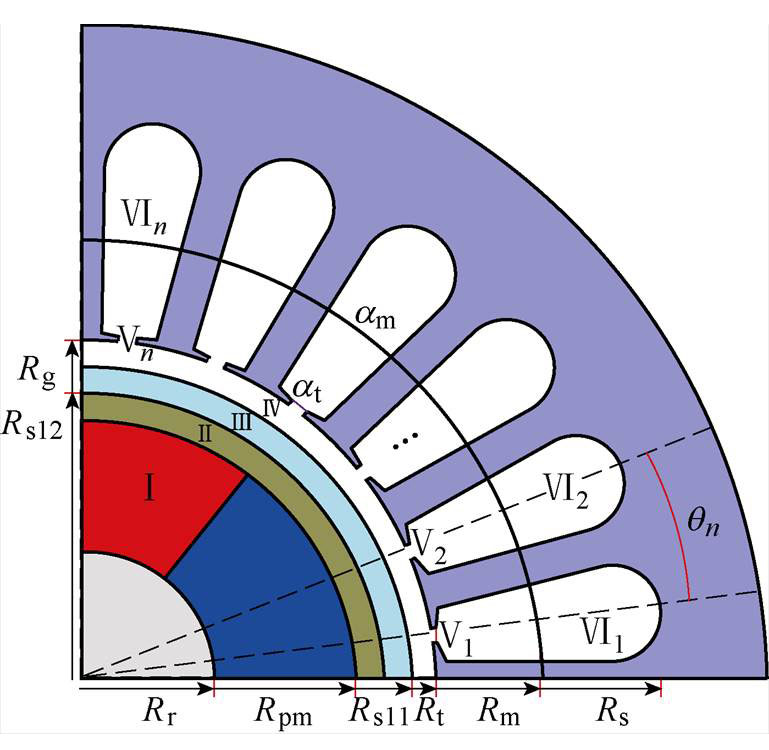
图1 高速永磁电机转子涡流损耗解析模型
Fig.1 Analytical model of rotor eddy current loss of HSPMM
摘要 在表贴式高速永磁电机中,双层复合护套可以有效抑制转子涡流损耗。目前,针对双层复合护套转子涡流损耗的研究主要采用有限元法,但该方法存在耗时、对薄护套网格剖分较困难等问题,因此该文基于精确子域法提出了一种考虑定子开槽、涡流反作用的双层复合护套高速永磁电机转子涡流损耗通用解析模型。该模型同时考虑了永磁磁场励磁和电枢磁场励磁,可以计算负载磁场作用下的双层复合护套转子涡流损耗。此外,该模型还可进一步拓展至多层复合护套转子涡流损耗计算。通过该解析模型研究了双层复合护套不同护套厚度配比、不同护套材料对转子涡流损耗的影响。最后,将解析计算结果与有限元及C型铁心实验结果进行对比,验证了该解析模型的有效性。
关键词:高速永磁电机 精确子域法 双层复合护套 涡流反作用 C型铁心实验
高速永磁电机具有功率密度高、可与高速负载直接相连等优点,被广泛应用于飞轮储能、离心压缩机等领域[1-2]。然而,变频器供电时引入的高频电流谐波会在电机转子中产生较大的涡流损耗,加之电机转子散热条件差,可能会导致转子温升过高[3],增加永磁体不可逆失磁风险[4]。为了提高高速永磁电机的工作可靠性,快速准确地计算转子涡流损耗十分重要。
表贴式高速永磁电机常用的护套主要分为碳纤维和非导磁的合金护套,碳纤维护套的电导率低、导热性较差,合金护套的导热性好、电导率高[5-6]。当高速永磁电机采用合金护套时,转子涡流损耗主要集中在合金护套表面。为了抑制合金护套中的涡流损耗,国内外学者提出了多种方法,如护套轴向分段[7]、护套周向开槽[8]、永磁体表面加屏蔽层[9]等来抑制转子涡流损耗。然而,护套开槽以及护套轴向分段在实际加工中是较困难的。为此,文献[10-11]提出了一种新的易于实现的多层复合式转子结构,并对其进行了研究。结果表明,当参数设计合理时,双层复合护套对转子涡流损耗有明显的抑制作用。然而,在双层复合护套转子涡流损耗研究方面还存在一些不足。首先,目前的研究大多是基于有限元法计算,缺乏理论依据。其次,对于复杂的多层复合式转子模型,有限元法在考虑涡流区的趋肤深度时需要很长时间[12]。而涡流损耗解析模型可以很好地解决上述问题,同时解析法计算时间更短[13],理论依据充分,更有利于电机初始设计及优化。
解析法计算转子涡流损耗一般采用子域法,通过推导出各子域方程,得到转子子域的特解,进而计算出转子涡流损耗。文献[14-16]建立了带护套的转子涡流损耗解析模型,为了考虑涡流反作用的影响,在涡流区域建立了扩散方程。然而,并没有考虑定子开槽对转子涡流损耗的影响,降低了计算精度。文献[17]提出了考虑开槽的二维子域模型,但该模型只能分析护套对转子涡流损耗的影响,不适用于多层复合护套转子涡流损耗解析建模。文献[18]基于子域法建立了带屏蔽层的高速永磁电机转子涡流损耗解析模型。该模型利用磁导函数来考虑定子开槽的影响,计算精度低,且无法计算负载磁场作用下的转子涡流损耗。
二维子域法通常将电枢绕组等效为在槽口均匀分布的电流片,并通过磁导函数来考虑定子开槽的影响[19]。但是,当保角映射点数过多时,会造成求解困难、计算精度不高等问题。在一些大功率高速永磁电机中,齿槽效应对转子涡流损耗的影响非常大[20]。为此,国内外学者为进一步考虑定子开槽对转子涡流损耗的影响,提出了精确子域法。文献[21-22]采用精确子域法推导了一种可考虑定子开槽、负载磁场作用下的转子涡流损耗解析模型,该模型可以分析各次谐波以及各次谐波间相互作用对转子涡流损耗的影响,但模型未考虑涡流反作用的影响,且无法计算护套中的涡流损耗。文献[23]考虑了齿尖效应和扩散效应,提出了永磁电机转子涡流损耗解析模型。然而没有考虑电流谐波和护套中的涡流损耗,计算精度不高。文献[24-25]中解析模型包括了槽、槽口子域,同时考虑了永磁体剩磁、涡流反作用的影响,可以计算各次谐波引起的转子涡流损耗,但无法计算双层复合护套的转子涡流损耗。文献[26]采用精确子域法,建立了带屏蔽层的转子涡流损耗解析模型。该模型可以计算电枢磁场作用下,带屏蔽层的转子涡流损耗,但没有考虑永磁磁场励磁,无法计算负载磁场下的涡流损耗。
综上所述,现有的高速永磁电机转子涡流损耗解析模型只针对单层护套进行建模,无法计算双层复合护套转子涡流损耗。目前,双层复合护套转子涡流损耗研究主要通过有限元法,该方法在确定双层复合护套最佳厚度配比时需要通过大量参数化进行求解,效率低,因此有必要建立一种计算精度高、通用性强的双层复合护套转子涡流损耗解析模型。
针对双层复合护套高速永磁电机,本文基于精确子域法推导了一种考虑定子开槽、涡流反作用的双层复合护套转子涡流损耗通用解析模型。该模型在永磁体子域和槽子域通过泊松方程进行励磁建模,可以计算负载磁场作用下的双层复合护套转子涡流损耗。为了提高模型计算精度,在转子导电区域,建立扩散方程,考虑涡流反作用的影响。此外,该模型还可进一步拓展至多层复合护套高速永磁电机转子涡流损耗计算。本文利用该模型研究了双层复合护套不同护套厚度配比、不同护套材料对转子涡流损耗的影响。最后,通过有限元仿真和C型铁心实验,验证了该模型具有较高的计算精度。
为了简化建模,本文忽略了绕组端部的涡流效应及转子铁心损耗。假定永磁体和护套材料属性为各向同性,磁导率和电导率为常数;假定软磁材料的相对磁导率为无穷大。因此,不计算软磁材料内部的磁场分布,垂直于软磁材料边界的磁场强度为零。将梨形定子槽和槽口简化为扇形结构,假设定子槽内电流密度均匀分布[27]。
子域模型的建立一般分为以下步骤:首先,在二维极坐标系(r, q)下将电机整个场域划分为图1所示的几个简单子域,主要包括永磁体子域(区域Ⅰ)、内层护套子域(区域Ⅱ)、外层护套子域(区域Ⅲ)、气隙子域(区域Ⅳ)、槽开口子域(区域Ⅴ)、槽子域(区域Ⅵ)6个子域。其次,应用各子域和各子域间的边界条件,得到各子域磁场分布的一般表达式。再通过确定这些表达式中的傅里叶系数,最终建立这些系数与永磁体和电流源之间的方程组。图1中,Rs为槽底内半径;Rt为槽顶内半径;Rm为双层绕组边界半径;Rr为转子轭外半径;Rsl1、Rsl2分别为护套Ⅰ、Ⅱ外半径;Rg为气隙外半径;Rpm为永磁体外半径;am为槽宽角;at为槽口宽角;qn为第n个定子槽中心线与电机初始位置的夹角。

图1 高速永磁电机转子涡流损耗解析模型
Fig.1 Analytical model of rotor eddy current loss of HSPMM
本文所提模型既考虑了空载磁场作用下永磁体励磁,又考虑了电枢磁场作用下电枢绕组励磁。
当永磁体作为励磁源时,可以用磁化分布函数来表示,磁化分布函数有径向分量和切向分量,两者都可以用傅里叶级数表示。
对于电枢绕组励磁,本文主要针对上下排布的双层绕组进行励磁建模。首先假定槽内电流密度分布均匀,然后根据电枢绕组的三相电流表达式[3],得到定子槽内电流表面密度[24],电流密度表达式为
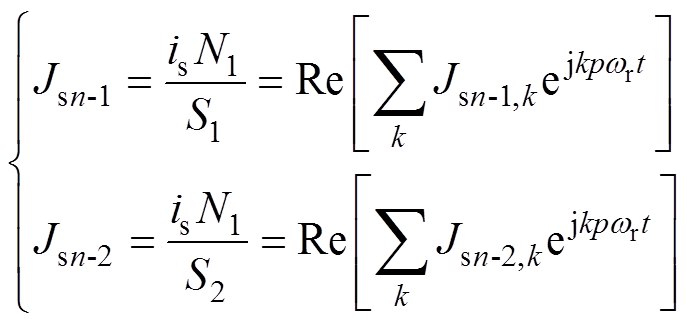 (1)
(1)
式中,Jsn-1、Jsn-2为第n个槽的双层绕组电流表面密度;k为电流时间谐波次数;w r为机械角速度;p为电机极对数;N1为每相串联匝数;S1、S2分别为底层和顶层单相绕组所占的面积,且S1=S2;is为槽内电流。
为了保证槽底与槽顶面积相等,则Rm应满足
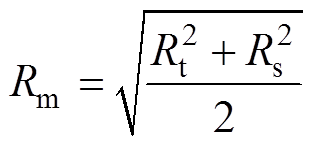 (2)
(2)
对于无源的子域求解拉普拉斯函数,对于有源的子域求解泊松函数,对于涡流区建立扩散方程考虑涡流反作用的影响。
在子域Ⅳ、Ⅴ中,矢量磁位满足拉普拉斯方程。
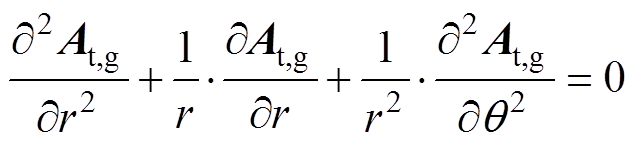 (3)
(3)
式中,At,g为子域Ⅳ、Ⅴ矢量磁位。
在子域Ⅵ中,第n个槽底和槽顶子域矢量磁位均满足泊松方程。
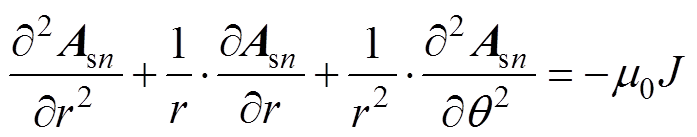 (4)
(4)
式中,m0为真空磁导率;J为槽内电流密度;Asn为子域Ⅵ矢量磁位。
在子域Ⅱ、Ⅲ中,根据护套间的边界条件,并考虑护套与护套间、永磁体与护套间的涡流反作用影响,建立扩散方程。
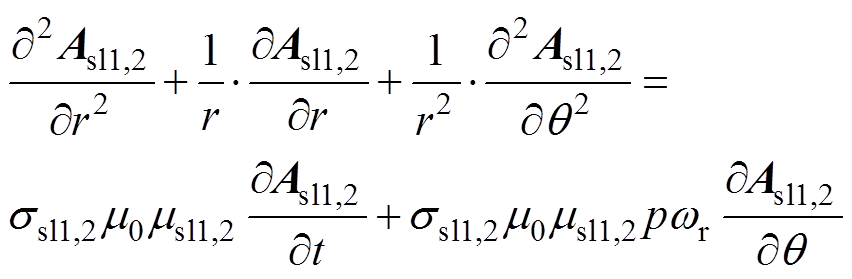 (5)
(5)
式中,ssl1、ssl2分别为护套Ⅰ、Ⅱ的电导率;msl1、msl2分别为护套Ⅰ、Ⅱ的相对磁导率;Asl1,2为子域Ⅱ、Ⅲ矢量磁位。
在子域Ⅰ中,建立扩散方程考虑涡流反作用,建立泊松方程考虑永磁体励磁。
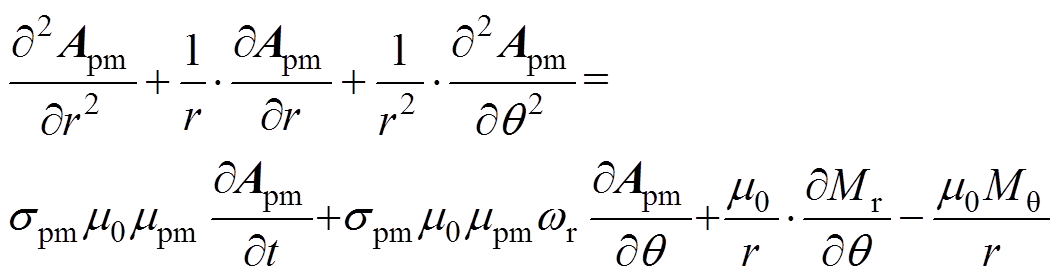 (6)
(6)
式中,spm为永磁体的电导率;mpm为永磁体的相对磁导率;Mq、Mr分别为永磁体磁化强度的切向和径向分量;Apm为子域Ⅰ矢量磁位。
在复数域中,Mr、Mq 可分别表示为
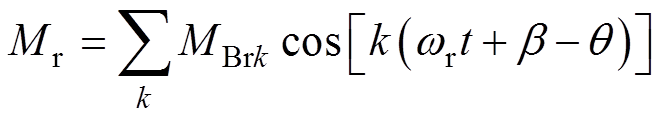 (7)
(7)
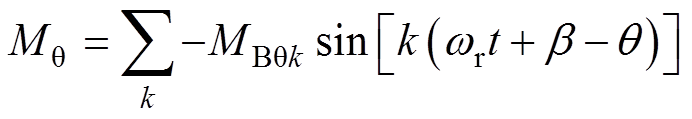 (8)
(8)
式中,b 为永磁体N极中线与解析模型初始位置夹角;MBrk和MBqk为过程量,具体表达式与永磁体磁化方向有关,其具体计算可参考文献[22]。
考虑铁磁边界条件以及模型的周期性和对称性,采用分离变量的方法可得到各子域矢量磁位 通解。
1)槽子域
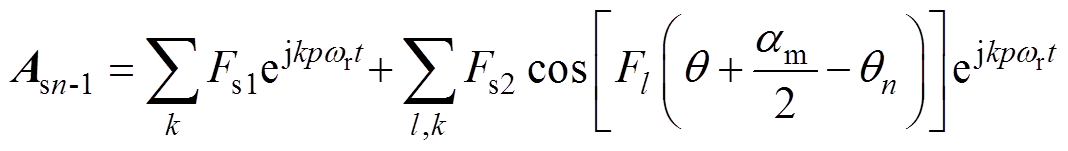 (9)
(9)
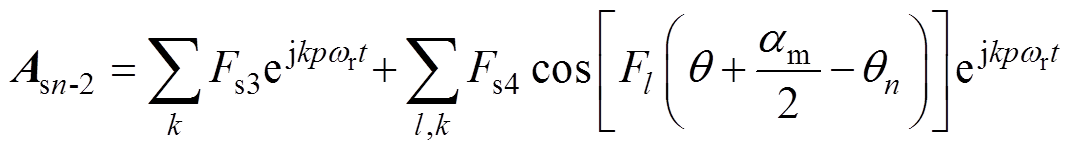 (10)
(10)
其中
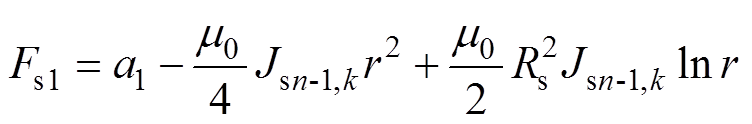 (11)
(11)
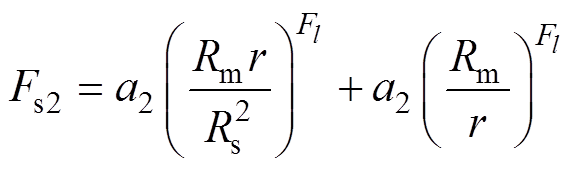 (12)
(12)
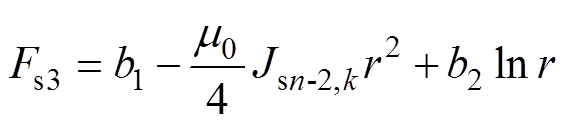 (13)
(13)
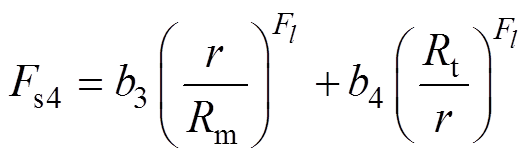 (14)
(14)
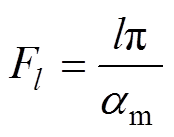 (15)
(15)
式中,l为定子槽子域的空间谐波次数。
2)槽口子域
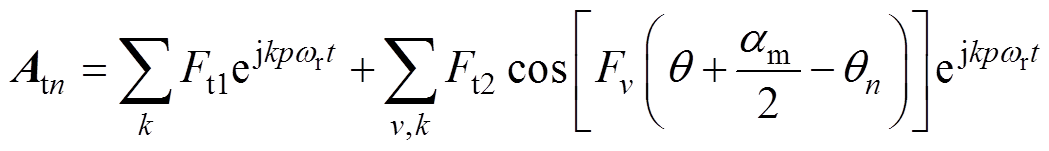 (16)
(16)
其中
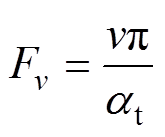 (17)
(17)
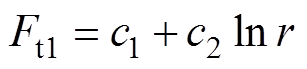 (18)
(18)
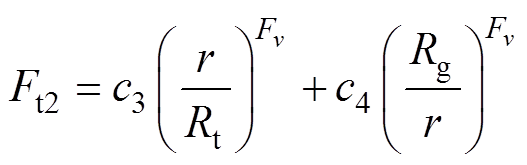 (19)
(19)
式中,v为槽口子域的空间谐波次数。
3)永磁体子域
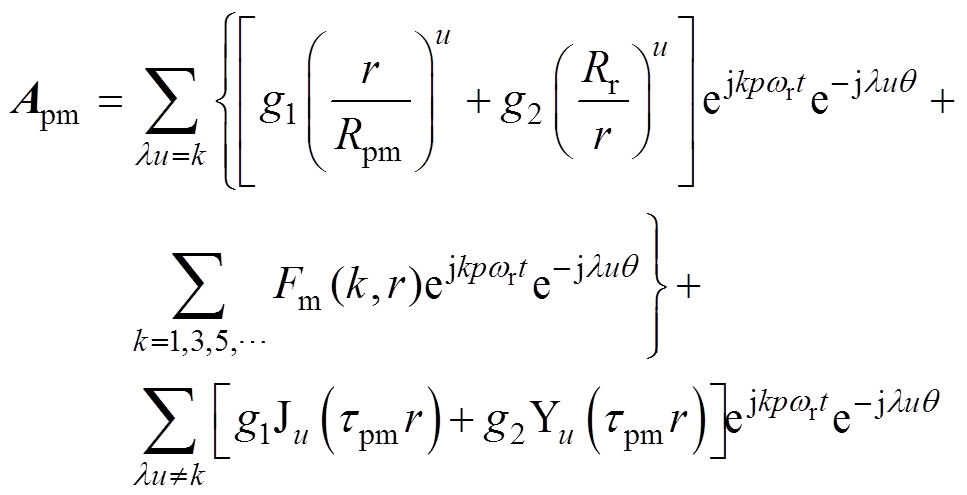 (20)
(20)
其中
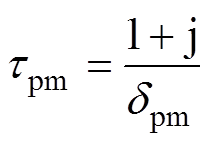 (21)
(21)
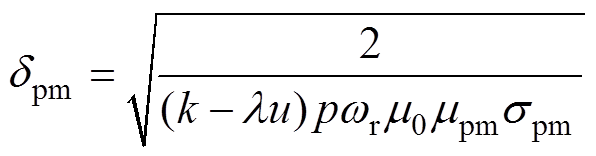 (22)
(22)
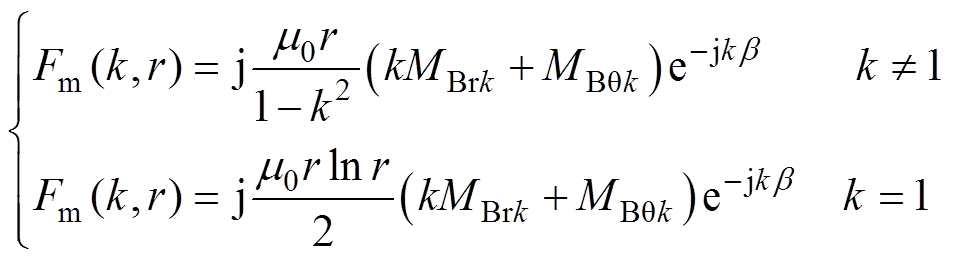 (23)
(23)
式中,u为转子导电区域内的空间谐波次数;dpm为交流磁场在永磁体中的趋肤深度;Ju为第一类u阶Bessel函数;Yu为第二类u阶Bessel函数;l 为谐波磁场旋转方向,l=1表示谐波磁场与基波磁场旋转方向相同,l=-1表示二者旋转方向相反[25]。
4)气隙子域
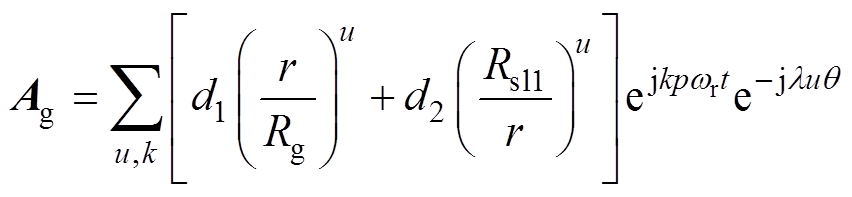 (24)
(24)
5)双层复合护套子域
由护套边界条件可得护套子域方程为
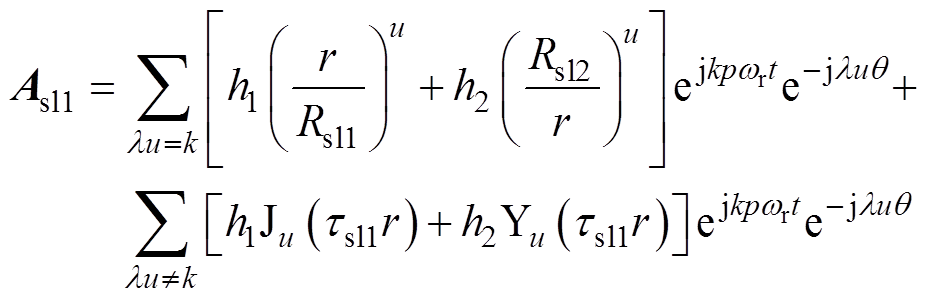 (25)
(25)
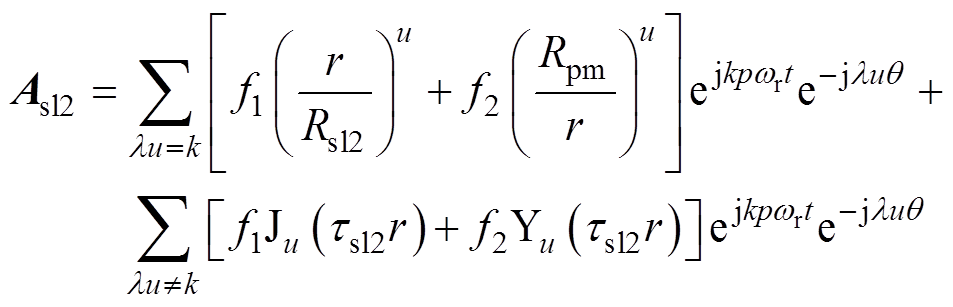 (26)
(26)
其中
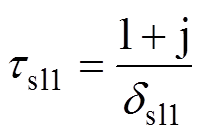 (27)
(27)
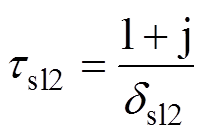 (28)
(28)
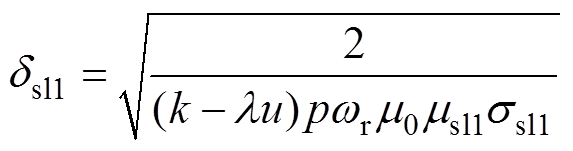 (29)
(29)
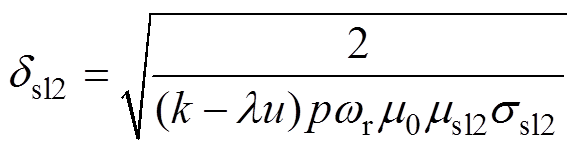 (30)
(30)
式中,dsl1、dsl2分别为交流磁场在护套Ⅰ、Ⅱ中的趋肤深度。
根据上述子域的磁场分布,可得到各子域间的边界条件,再通过构建未知系数方程组,对方程组进行求解,即可确定未知系数:a1、a2、b1、b2、b3、b4、c1、c2、c3、c4、d1、d2、h1、h2、f1、f2、g1、g2,具体求解过程见附录。
根据Poynting定理[28],得到多层复合转子在二维平面内的涡流损耗,其表达式[24]为
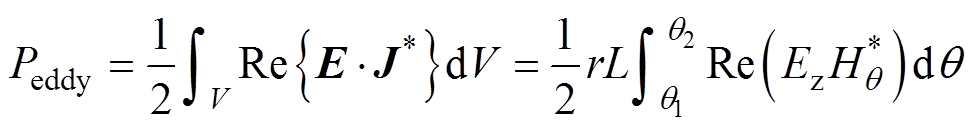 (31)
(31)
式中,L为永磁体轴向长度;E为电场强度;Ez为电场强度轴向分量;Hq 为磁场强度切向分量。
永磁体在一个电周期内的涡流损耗表达式为
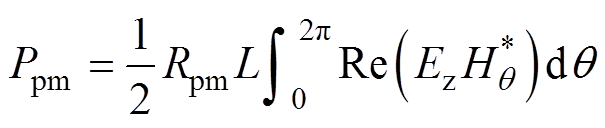 (32)
(32)
内层护套在一个电周期内的涡流损耗表达式为
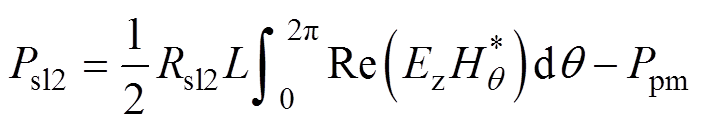 (33)
(33)
外层护套在一个电周期内的涡流损耗表达式为
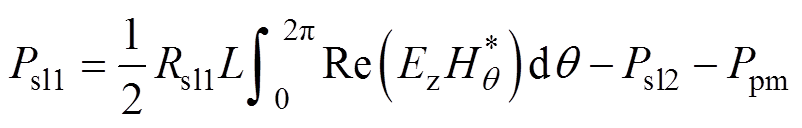 (34)
(34)
本文以一台4极24槽、表贴式高速永磁同步电机为例,对其气隙磁通密度和转子涡流损耗进行计算。该电机的护套为单层镍基合金材料,永磁体为Sm2Co17,剩磁约为1.08 T,电机主要参数见表1。
表1 电机主要参数
Tab.1 Main parameters of motor
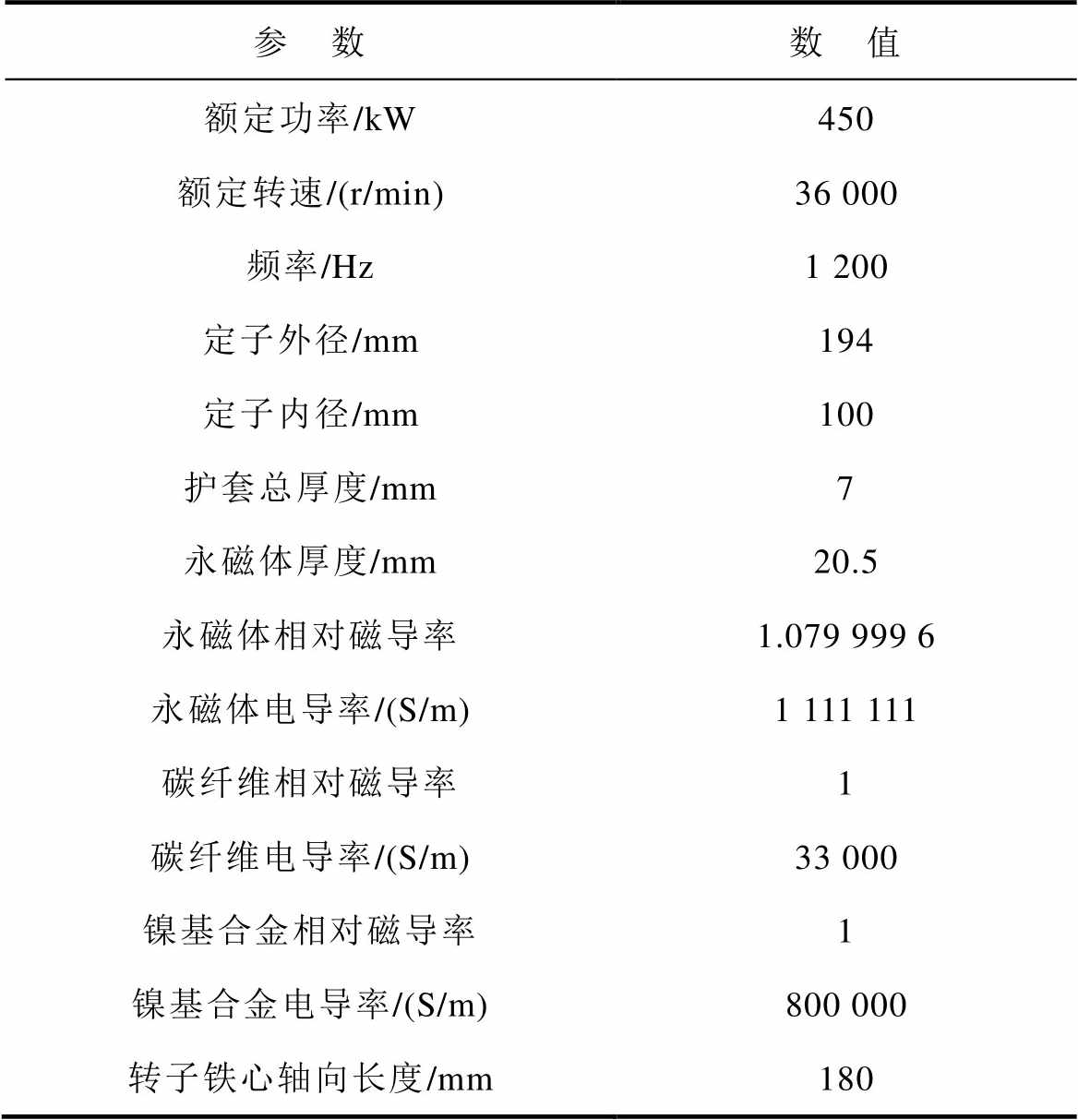
参 数数 值 额定功率/kW450 额定转速/(r/min)36 000 频率/Hz1 200 定子外径/mm194 定子内径/mm100 护套总厚度/mm7 永磁体厚度/mm20.5 永磁体相对磁导率1.079 999 6 永磁体电导率/(S/m)1 111 111 碳纤维相对磁导率1 碳纤维电导率/(S/m)33 000 镍基合金相对磁导率1 镍基合金电导率/(S/m)800 000 转子铁心轴向长度/mm180
为了验证所提模型的有效性,在保持原电机转子护套总厚度7 mm不变的前提下,将转子护套设计为内层镍基合金、外层碳纤维的双层复合护套。在满足转子机械强度的前提下,内、外层护套厚度分别初步取4 mm和3 mm。
在有限元计算分析中,为了考虑各次谐波透入深度的影响,需要将护套和永磁体划分为多层网格,特别是较薄的护套区域。有限元网格剖分如图2所示。
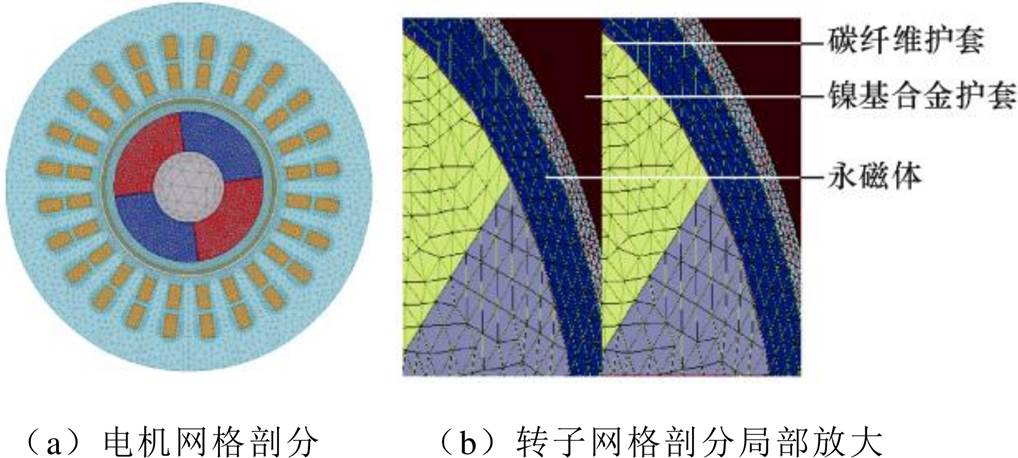
图2 有限元模型网格剖分
Fig.2 Finite element model meshing
分别采用有限元法与解析法计算该电机在气隙中心处的磁通密度,图3为两种计算方法得到的气隙磁通密度波形对比和解析法与有限元法计算结果的误差曲线。由图3可以看出,两种方法计算的气隙磁通密度径向和切向波形基本吻合。但由于在解析建模时,对定子槽进行了相应简化,因此解析法计算的气隙磁通密度在槽口处与有限元法计算结果存在较小的偏差。
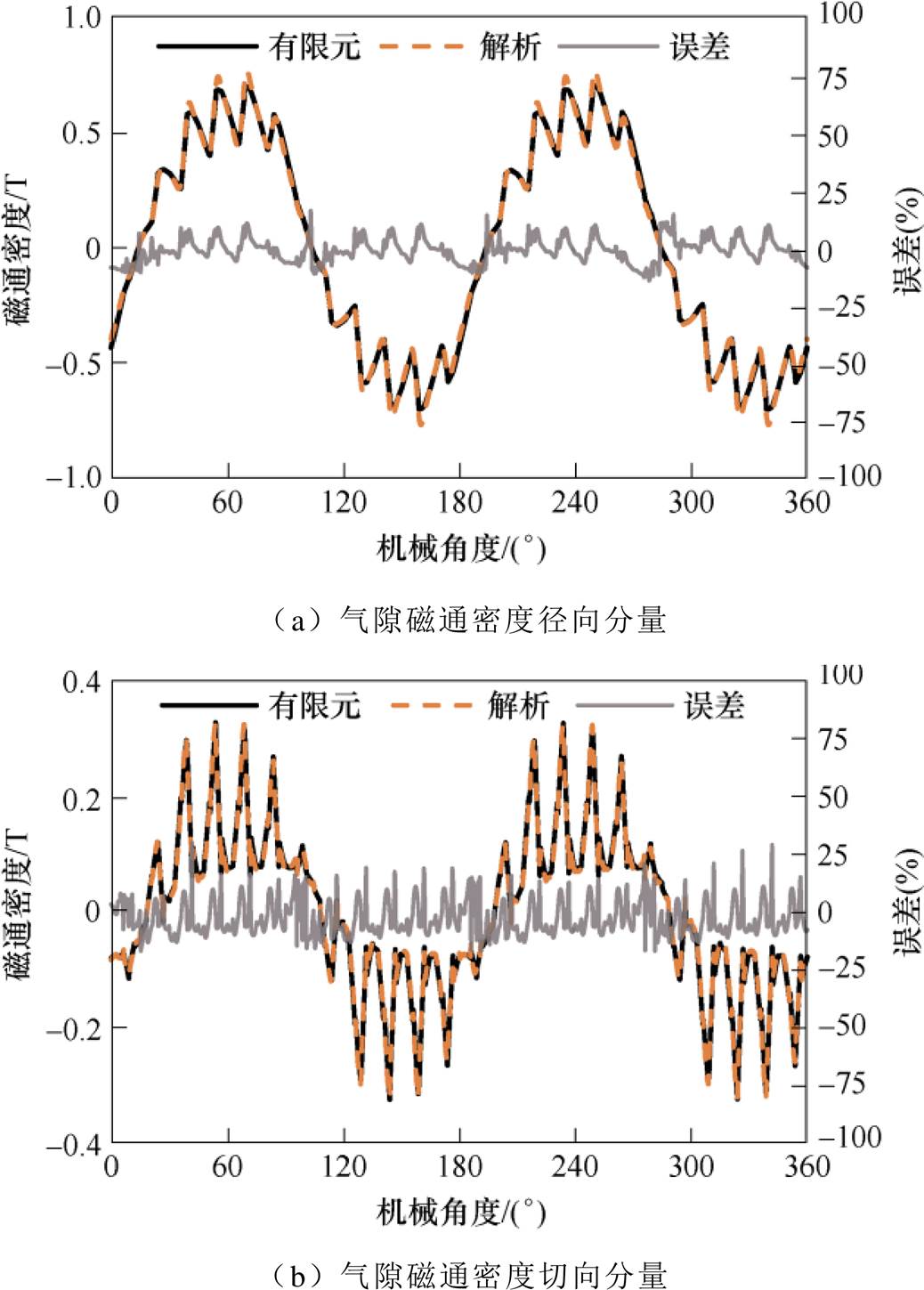
图3 气隙中心处磁通密度
Fig.3 Flux density at the center of the air gap
基于负载磁场,分别采用有限元法与解析法计算单层镍基合金护套、单层碳纤维护套及初步设计的双层复合护套转子涡流损耗,损耗计算结果对比如图4所示。由图4可以看出,解析法与有限元法计算结果基本一致,但由于解析模型对定子槽进行了简化,故二者会存在一定的计算误差,约为3.8%。
当电机采用单层镍基合金护套和单层碳纤维护套时,转子涡流损耗解析法计算结果分别为1 263.6 W、538.5 W,采用外层碳纤维、内层镍基合金的双层复合护套时,转子涡流损耗解析法计算结果为414.5 W。双层复合护套相比单层镍基合金护套和单层碳纤维护套,转子涡流损耗分别降低了约67.2%、23%,这说明双层复合护套对转子涡流损耗起到了明显的抑制作用。
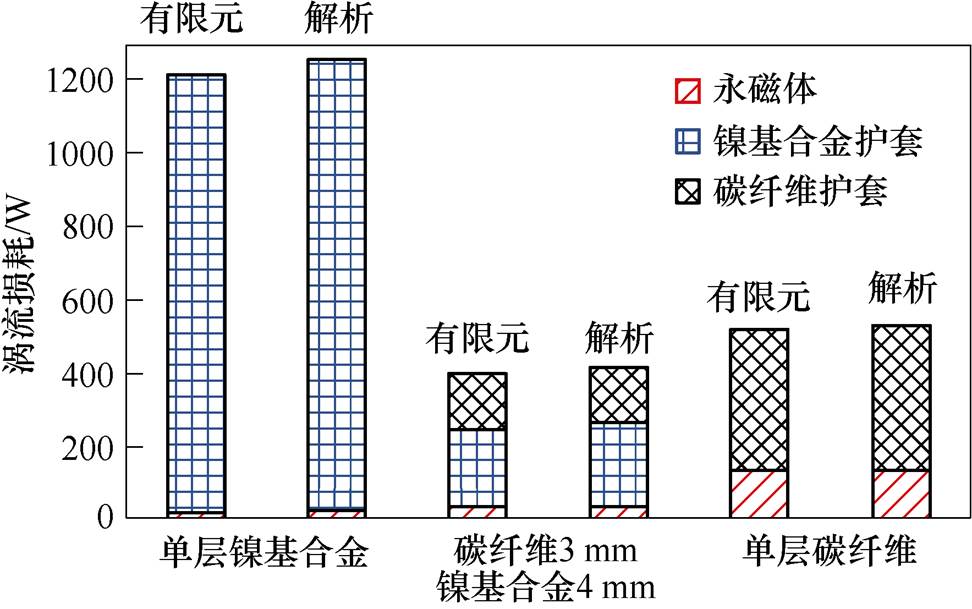
图4 单/双层护套转子涡流损耗
Fig.4 Rotor eddy current loss of single/double sleeve
有限元法与解析法计算涡流损耗所用时间见表2。可以看出,本文所提模型在保证计算精度的前提下,比有限元法计算时间缩短了约97.8%。
表2 有限元法与解析法计算时间
Tab.2 Calculation time of finite element method and analytical method
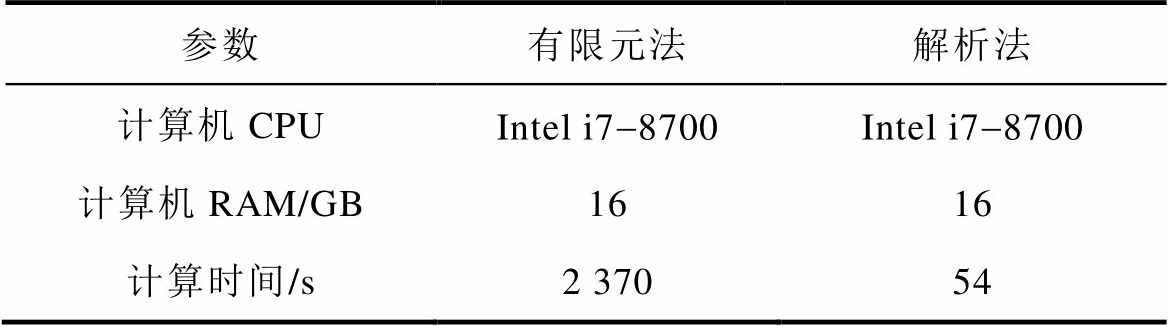
参数有限元法解析法 计算机CPUIntel i7-8700Intel i7-8700 计算机RAM/GB1616 计算时间/s2 37054
由2.2节可知,双层复合护套可以明显地抑制转子涡流损耗。为了研究双层复合护套对转子涡流损耗的影响规律,以及找到最佳的双层复合护套厚度配比,本文将通过解析法进一步对该电机转子涡流损耗进行研究分析。
图5为单层镍基合金护套和碳纤维-镍基合金双层复合护套的转子涡流损耗密度云图。可以看出,转子涡流主要集中在护套表面,且单层护套表面涡流损耗密度远大于双层复合护套表面涡流损耗密度。这主要是由于碳纤维护套电阻率(3.03×10-5 W·m)约是镍基合金护套电阻率(1.25×10-6 W·m)的24倍,因此采用双层复合护套可以有效地抑制转子涡流损耗。
为了保证定子和转子尺寸相同,双层复合护套总厚度应保持7 mm不变。利用所提模型计算分析外层碳纤维护套厚度对双层复合护套转子涡流损耗的影响,并找到外层碳纤维的最佳尺寸。转子涡流损耗大小随碳纤维护套厚度变化曲线如图6所示。
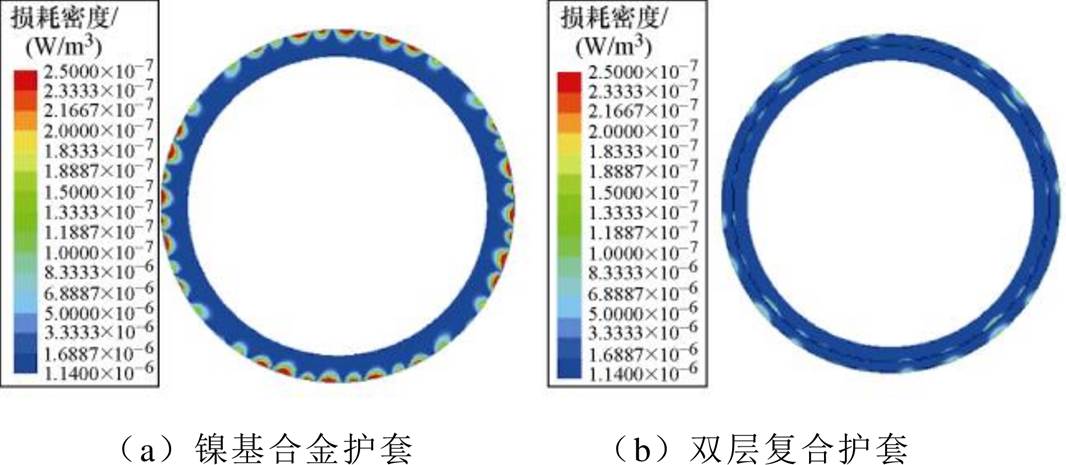
图5 护套内涡流损耗密度云图
Fig.5 Cloud picture of eddy current loss density in sleeve
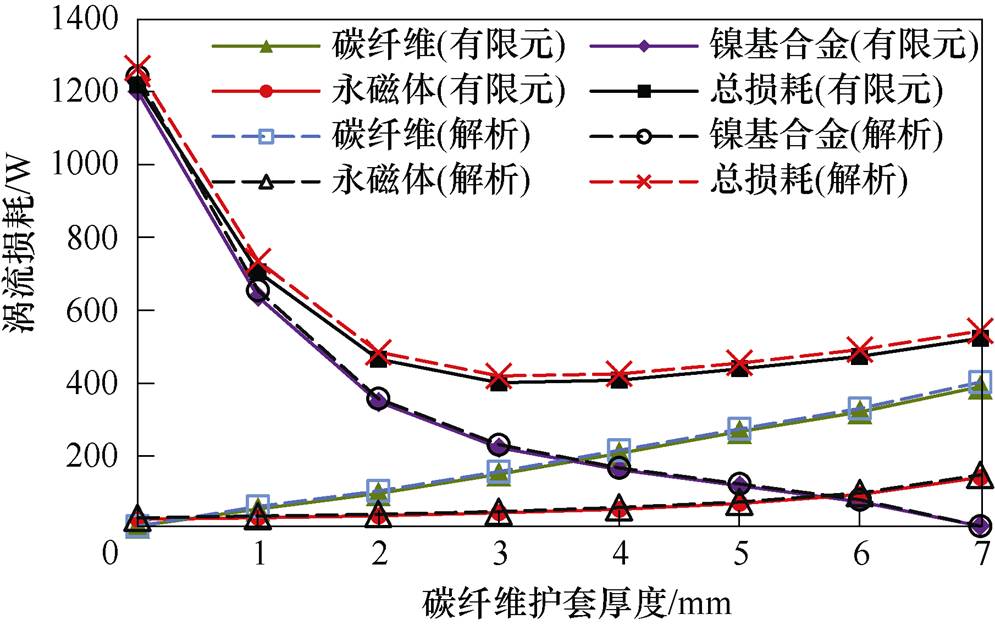
图6 碳纤维护套厚度对转子涡流损耗的影响
Fig.6 Effect of carbon fiber sleeve thickness on eddy current loss of rotor
将图6中有限元法和解析法计算结果进行对比,两者基本一致。可以看出,当碳纤维护套厚度小于3 mm时,随着碳纤维厚度的增加,转子总涡流损耗迅速减小;当碳纤维护套厚度大于3 mm时,转子总涡流损耗缓慢增加。因此,当双层复合护套总厚度为7 mm时,碳纤维护套厚度在2.5~3.5 mm之间是最好的选择。对于该电机,双层复合护套采用3 mm厚的外层碳纤维护套时,对应的转子总涡流损耗仅为414.5 W。
由上述分析可知,对于表贴式高速永磁电机,采用外层碳纤维、内层合金的双层复合护套时,通过合理设计碳纤维护套的厚度,使内层合金护套中的谐波磁场可以忽略不计,能够使转子总涡流损耗得到明显抑制。
在保持外层碳纤维护套最佳尺寸3 mm不变的前提下,进一步分析不同内层合金护套对双层复合转子涡流损耗的影响规律。通过转子强度校核,内层护套选取镍基合金、钛合金、奥氏体不锈钢、高锰合金等材料,且护套厚度均为4 mm,不同护套材料的电导率见表3。
表3 不同护套材料的电导率
Tab.3 Conductivity of different sleeve materials(单位: MS/m)
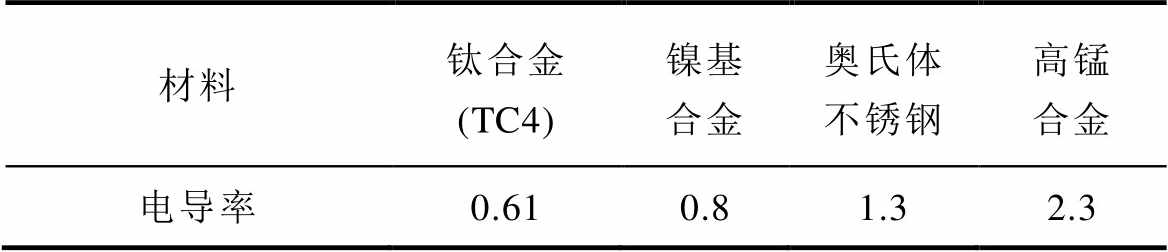
材料钛合金 (TC4)镍基合金奥氏体不锈钢高锰合金 电导率0.610.81.32.3
图7为有限元法和解析法计算结果对比,可以看出,解析法与有限元法计算结果基本一致。随着内层合金护套电导率的增大,转子总涡流损耗逐渐减小。这主要是由于高电导率护套对高次谐波的抑制作用较强,导致永磁体涡流损耗越小;而且,高电导率护套产生的涡流较大,对外层碳纤维护套内的谐波磁场起到了削弱作用,使得外层碳纤维护套涡流损耗减小;即使内层合金护套涡流损耗增加,但涡流损耗增加值小于总的减小值,因此转子总涡流损耗呈减小趋势。
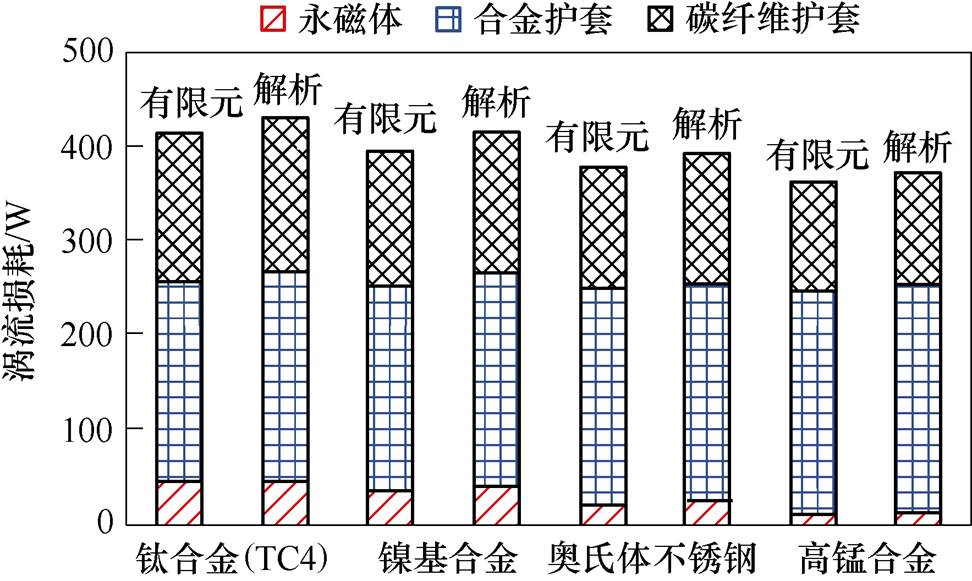
图7 不同内层护套材料下的转子涡流损耗
Fig.7 Rotor eddy current loss under different inner sleeve materials
针对双层复合护套高速永磁电机,当采用现有的实验方法进行涡流损耗测试时,得到的损耗结果不够精确。例如,采用损耗分离实验时,由于转子涡流损耗相比于电机总损耗较小,因此会产生较大的累积误差。而温升实验忽略了电机散热对损耗的影响,导致损耗测试误差较大。
因此,本文采用自制的C型铁心损耗测试模型对所提解析模型的准确性进行验证。图8为简化后的C型铁心涡流损耗解析模型,H为气隙磁场强度,坐标轴原点及r方向如图8所示。将简化后的解析模型分为气隙、双层复合护套、永磁体子域,C型铁心损耗测试模型各子域满足的方程及边界条件与本文所提模型的各子域方程和边界条件一致,主要区别是二者激励不同,因此采用C型铁心实验能够更有效地验证本文提出的双层复合护套转子涡流损耗解析模型的准确性。
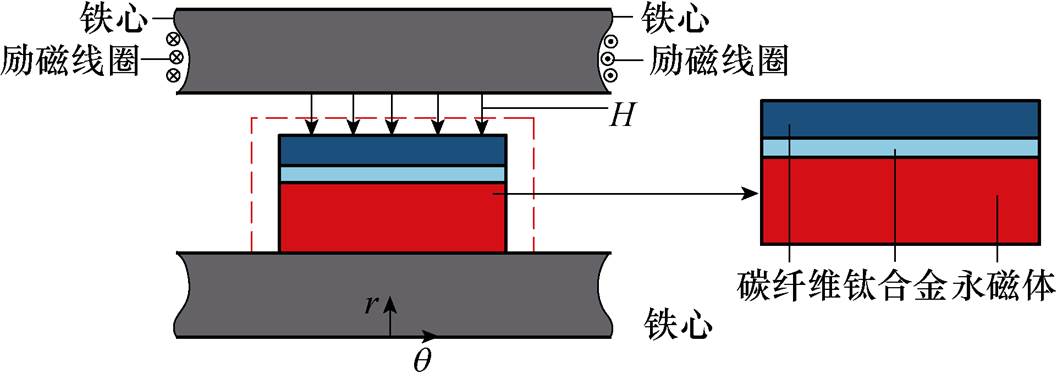
图8 简化的C型铁心解析模型
Fig.8 Simplified analytical model of C type core
C型铁心实验测试装置如图9所示。C型铁心采用7 mm的气隙长度,励磁线圈由500匝铜线缠绕。励磁线圈连接单相交流电源,示波器连接测试线圈,用于测试气隙磁通密度大小。功率分析仪WT230用于测量整个装置的损耗,包括测试元件的涡流损耗、励磁线圈绕组铜耗及铁心损耗。整个实验在保持电源频率和气隙磁通密度不变的前提下,分别测量在有测试元件和无测试元件时的装置总损耗分别为P1、P2,电流分别为I1、I2,则测试元件的涡流损耗Peddy[18]为
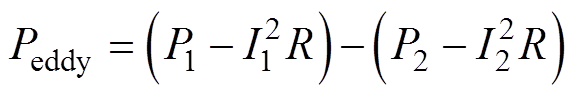 (35)
(35)

图9 C型铁心测试平台
Fig.9 C-type core test platform
为了验证双层复合护套转子涡流损耗解析模型的有效性,测试样品中永磁体选用N38UH,外层护套为碳纤维材料,内层护套为钛合金材料,测试样品具体参数见表4,不同测试样品如图10所示。
为了探究永磁体端部效应对实验结果的影响,本文分别通过实验法、有限元法及解析法计算了C型铁心气隙磁通密度大小。表5为三种计算方法得到的不同频率下的气隙磁通密度大小。
表4 测试样品参数
Tab.4 Test sample parameters
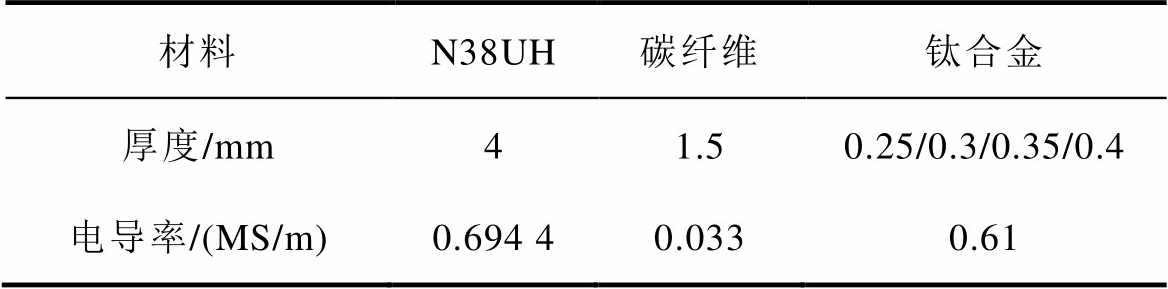
材料N38UH碳纤维钛合金 厚度/mm41.50.25/0.3/0.35/0.4 电导率/(MS/m)0.694 40.0330.61

图10 测试样品
Fig.10 Test sample
表5 C型铁心气隙磁通密度
Tab.5 Flux density of the C-type core(单位: T)
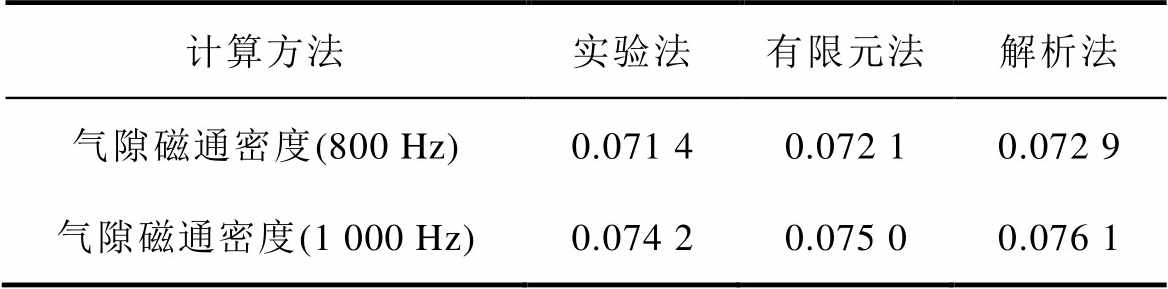
计算方法实验法有限元法解析法 气隙磁通密度(800 Hz)0.071 40.072 10.072 9 气隙磁通密度(1 000 Hz)0.074 20.075 00.076 1
实验法和有限元法计算气隙磁通密度时均可以考虑永磁体端部效应,在800 Hz和1 000 Hz电源频率下,两种计算方法分别相差约0.98%、1.07%。忽略永磁体端部效应,在800 Hz和1 000 Hz电源频率下,采用解析法计算得到的气隙磁通密度与实验结果相比分别相差约2.1%、2.56%,与有限元仿真结果相比分别相差约1.11%、1.47%。由上述分析可知,永磁体端部效应对C型铁心气隙磁通密度影响较小,即在进行C型铁心等效实验验证时,永磁体端部效应对涡流损耗计算结果的影响较小。
在损耗测试实验过程中,励磁线圈通入不同频率的单相交流电,保持外层碳纤维厚度1.5 mm不变,改变内层钛合金厚度,测量在不同测试样品下的总涡流损耗。
图11和图12为C型铁心实验、有限元仿真、解析法计算结果对比。从图中可以看出,涡流损耗解析法计算结果与有限元仿真和实验测试结果基本一致,与有限元仿真结果误差约为2.8%,与实验结果误差约为4.9%,进一步验证了本文所提模型的准确性。同时说明,在3.1节和3.2节利用该解析模型研究的双层复合护套转子涡流损耗规律是正确的,为双层复合护套高速永磁电机设计提供了有利条件。
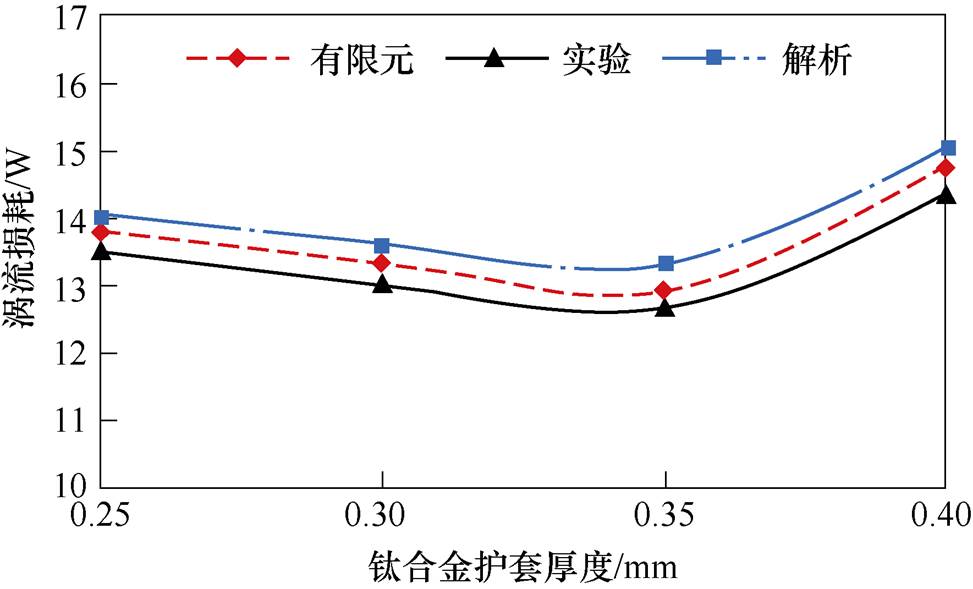
图11 解析计算与实验结果对比(800 Hz)
Fig.11 Comparison of analytical calculation and experimental results (800 Hz)
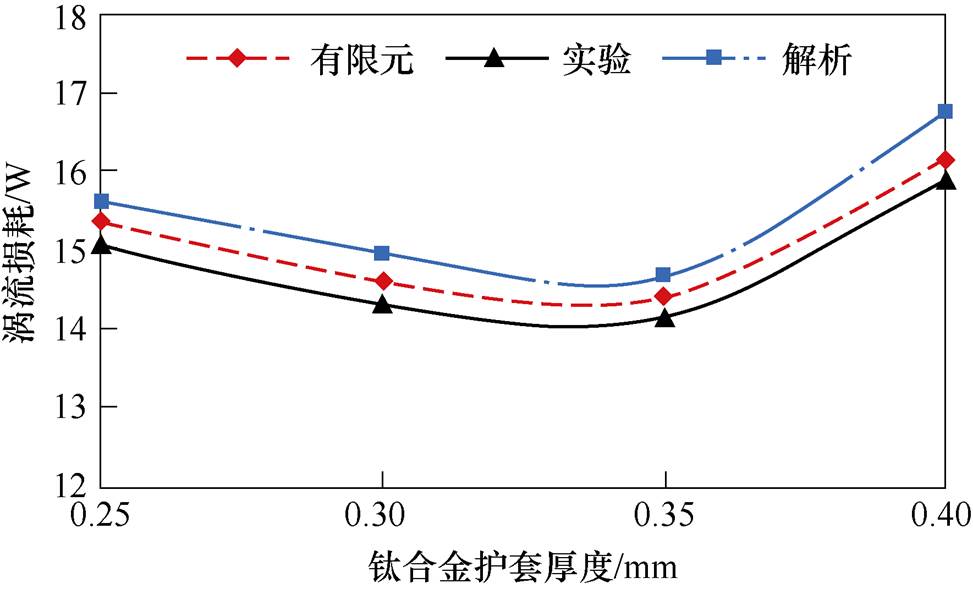
图12 解析计算与实验结果对比(1 000 Hz)
Fig.12 Comparison of analytical calculation and experimental results (1 000 Hz)
本文基于精确子域法建立了双层复合护套高速永磁电机转子涡流损耗通用解析模型。该模型同时考虑了定子开槽、永磁磁场、涡流反作用的影响,提高了计算精度。用该模型计算的转子涡流损耗结果与有限元法和C型铁心实验结果的误差均在5%以内。此外,该模型通用性强,可计算单层及双层复合护套高速永磁电机转子涡流损耗。
通过该解析模型计算表明,采用外层碳纤维、内层合金的双层复合护套可以有效抑制转子涡流损耗。当外层碳纤维护套厚度取双层复合护套总厚度的1/3~1/2时,转子涡流损耗抑制效果最佳。以本文电机为例,采用双层复合护套后,转子涡流损耗相比单层镍基合金和单层碳纤维护套分别降低了约67.2%、23%。同时也表明,内层合金护套电导率越大,转子总涡流损耗越小。
附 录
当r=Rt时,根据矢量磁位和切向磁通密度的连续性,可得到子域间边界条件为
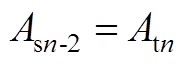 (A1)
(A1)
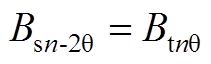 (A2)
(A2)
由式(A1)得
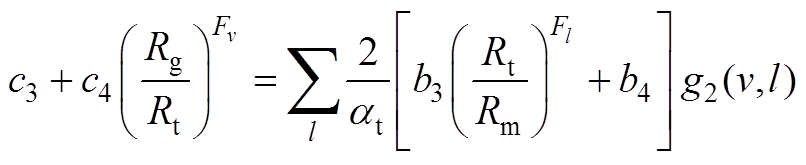 (A3)
(A3)
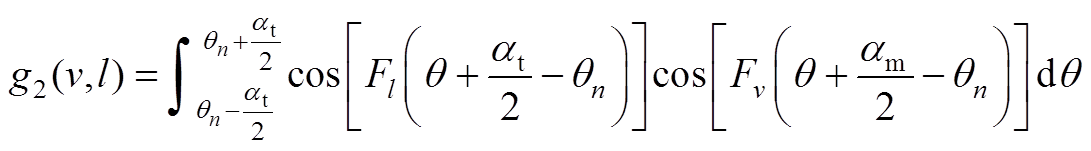 (A4)
(A4)
由式(A2)得
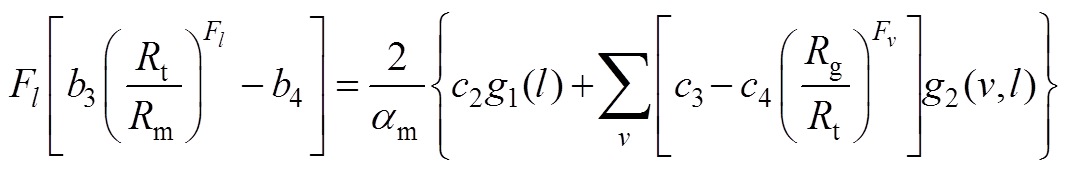 (A5)
(A5)
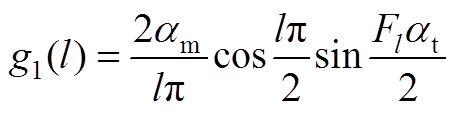 (A6)
(A6)
当r=Rg时,根据矢量磁位和切向磁通密度的连续性,可得到子域间边界条件为
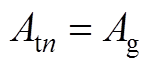 (A7)
(A7)
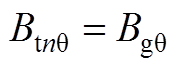 (A8)
(A8)
由式(A7)得
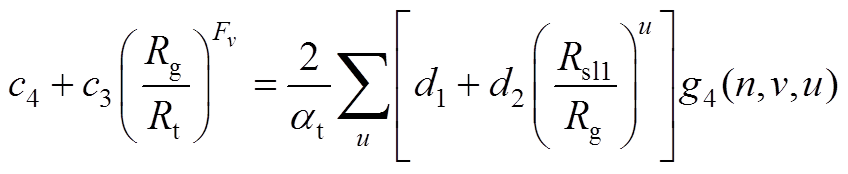 (A9)
(A9)
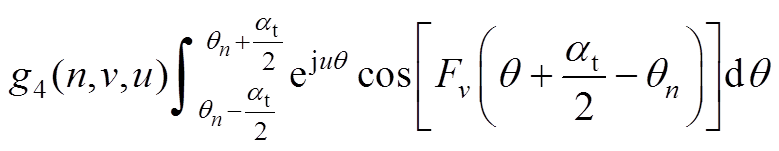 (A10)
(A10)
由式(A8)得
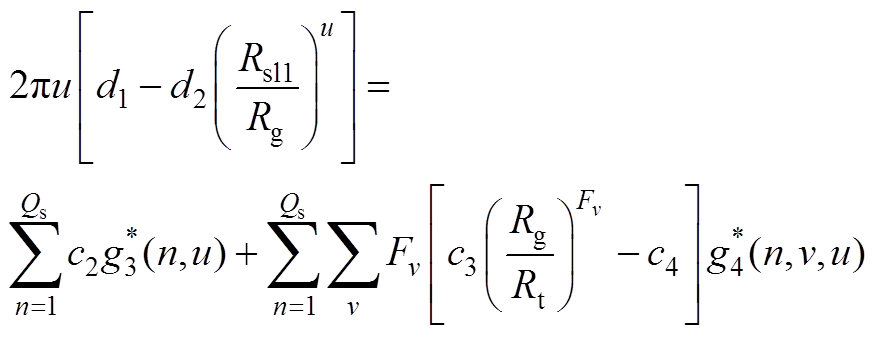 (A11)
(A11)
当r=Rsl1时,得到子域间边界条件为
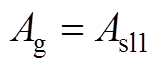 (A12)
(A12)
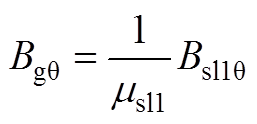 (A13)
(A13)
由式(A12)得
1)当lu=k时
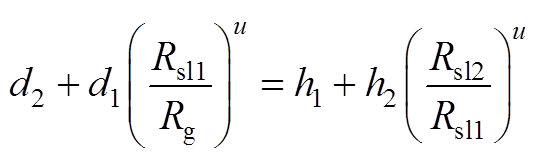 (A14)
(A14)
2)当lu≠k时
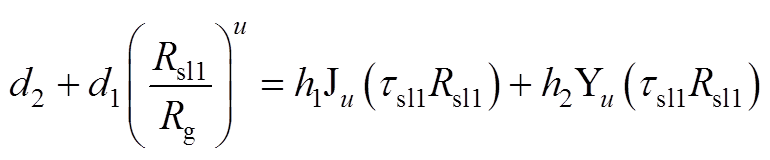 (A15)
(A15)
由式(A13)得
1)当lu=k时
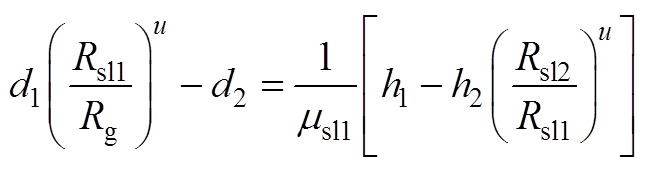 (A16)
(A16)
2)当lu≠k时
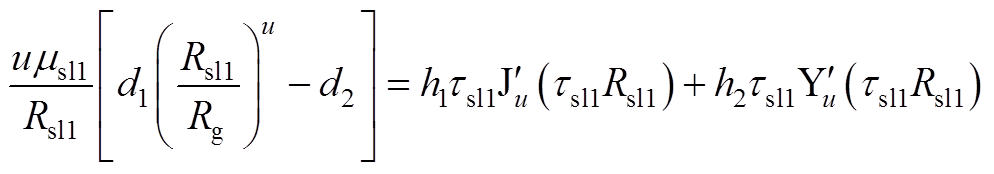 (A17)
(A17)
当r=Rsl2时,得到子域间边界条件为
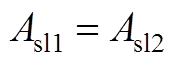 (A18)
(A18)
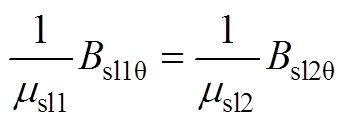 (A19)
(A19)
由式(A18)得
1)当lu=k时
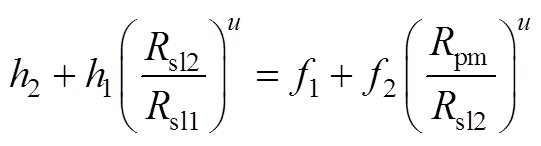 (A20)
(A20)
2)当lu≠k时
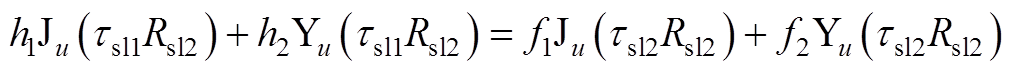 (A21)
(A21)
由式(A19)得
1)当lu=k时
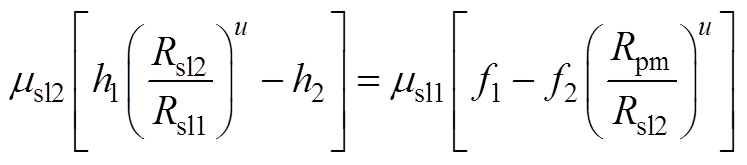 (A22)
(A22)
2)当lu≠k时
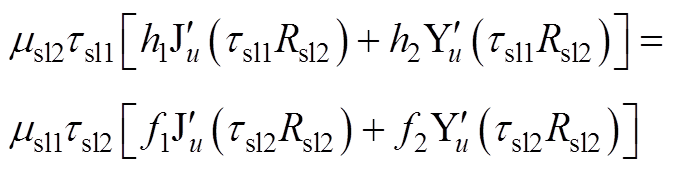 (A23)
(A23)
当r=Rpm时,得到子域间边界条件为
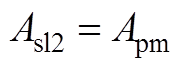 (A24)
(A24)
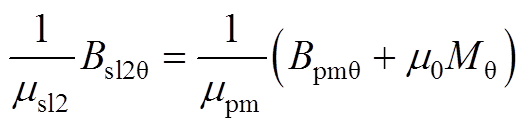 (A25)
(A25)
由式(A24)得
1)当lu=k时
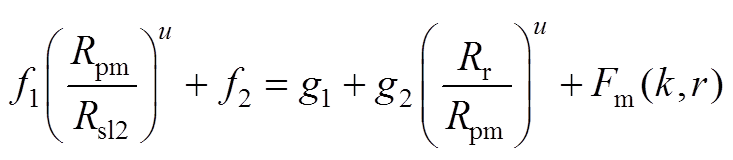 (A26)
(A26)
2)当lu≠k时
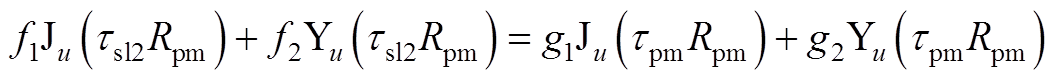 (A27)
(A27)
由式(A25)得
1)当lu=k时
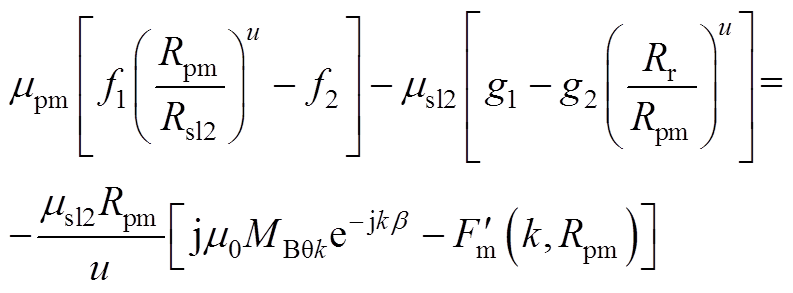 (A28)
(A28)
2)当lu≠k时
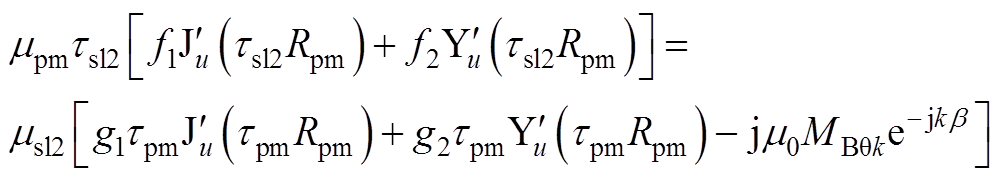 (A29)
(A29)
当r=Rr时,如果转轴区域为铁磁材料,则子域间边界条件为
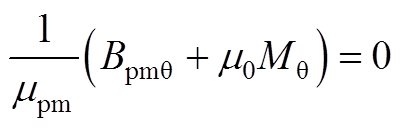 (A30)
(A30)
由式(A30)得
1)当lu=k时
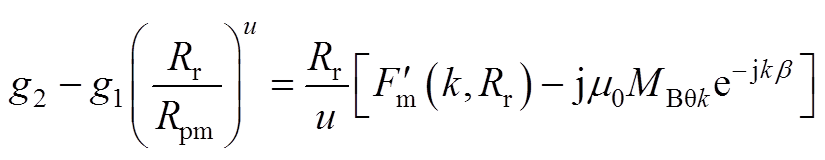 (A31)
(A31)
2)当lu≠k时
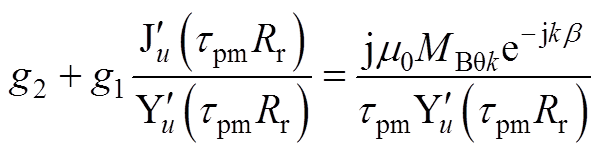 (A32)
(A32)
最后,将方程式(A3)、式(A5)、式(A9)、式(A11)、式(A14)~式(A17)、式(A20)~式(A23)、式(A26)~式(A29)、式(A31)、式(A32)联立方程组,通过Matlab软件编程,求出未知系数,进而求得转子各部分涡流损耗。
参考文献
[1] 张凤阁, 杜光辉, 王天煜, 等. 高速电机发展与设计综述[J]. 电工技术学报, 2016, 31(7): 1-18.
Zhang Fengge, Du Guanghui, Wang Tianyu, et al. Review on development and design of high speed machines[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 1-18.
[2] 戴睿, 张岳, 王惠军, 等. 基于多物理场近似模型的高速永磁电机多目标优化设计[J]. 电工技术学报, 2022, 37(21): 5414-5423.
Dai Rui, Zhang Yue, Wang Huijun, et al. Multi- objective optimization design of high-speed per- manent magnet machine based on multi-physics approximate model[J]. Transactions of China Elec- trotechnical Society, 2022, 37(21): 5414-5423.
[3] 佟文明, 侯明君, 孙鲁, 等. 基于精确子域模型的带护套转子高速永磁电机转子涡流损耗解析方法[J]. 电工技术学报, 2022, 37(16): 4047-4059.
Tong Wenming, Hou Mingjun, Sun Lu, et al. Analytical method of rotor eddy current loss for high-speed surface-mounted permanent magnet motor with rotor retaining sleeve[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4047-4059.
[4] Zhang Yue, McLoone S, Cao Wenping. Electro- magnetic loss modeling and demagnetization analysis for high speed permanent magnet machine[J]. IEEE Transactions on Magnetics, 2018, 54(3): 1-5.
[5] 高起兴, 王晓琳, 顾聪, 等. 基于多耦合特性的整体支撑式超高速微型永磁电机设计[J]. 电工技术学报, 2021, 36(14): 2989-2999.
Gao Qixing, Wang Xiaolin, Gu Cong, et al. Design of ultra high speed micro permanent magnet motor with integrated support type based on multi coupling characteristics[J]. Transactions of China Electro- technical Society, 2021, 36(14): 2989-2999.
[6] 李玮, 汪泽润, 张凤阁. 基于FEM/Kriging近似模型结合进化算法的表贴式高速永磁电机转子强度优化[J]. 电工技术学报, 2023, 38(4): 936-944, 956.
Li Wei, Wang Zerun, Zhang Fengge. Rotor strength optimization of surface mount high speed permanent magnet motor based on FEM/kriging approximate model and evolutionary algorithm[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 936-944, 956.
[7] Yon J M, Mellor P H, Wrobel R, et al. Analysis of semipermeable containment sleeve technology for high-speed permanent magnet machines[J]. IEEE Transactions on Energy Conversion, 2012, 27(3): 646-653.
[8] 沈建新, 郝鹤, 袁承. 高速永磁无刷电机转子护套周向开槽的有限元分析[J]. 中国电机工程学报, 2012, 32(36): 53-60, 14.
Shen Jianxin, Hao He, Yuan Cheng. FEA study on circumferential grooves on rotor retaining sleeve of high-speed PM brushless motors[J]. Proceedings of the CSEE, 2012, 32(36): 53-60, 14.
[9] 张忠明, 邓智泉, 孙权贵, 等. 铜屏蔽层对高速永磁无刷直流电机转子涡流损耗和应力的影响分析[J]. 中国电机工程学报, 2018, 38(8): 2476-2486, 2557.
Zhang Zhongming, Deng Zhiquan, Sun Quangui, et al. Influences of copper shield on eddy-current loss and stress for a rotor of high-speed PM BLDC motor[J]. Proceedings of the CSEE, 2018, 38(8): 2476-2486, 2557.
[10] Fang Haiyang, Li Dawei, Qu Ronghai, et al. Rotor design and eddy-current loss suppression for high- speed machines with a solid-PM rotor[J]. IEEE Transactions on Industry Applications, 2019, 55(1): 448-457.
[11] Cheng Xin, Xu Wei, Du Guanghui, et al. Novel rotors with low eddy current loss for high speed permanent magnet machines[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(2): 187-194.
[12] Renedo A J, Sharkh S M, Yuratich M A. Calculation of rotor losses in PM machines with retaining sleeves using transfer matrices[J]. IET Electric Power Applications, 2018, 12(8): 1150-1157.
[13] 曹龙飞, 范兴纲, 李大伟, 等. 基于快速有限元的永磁电机绕组涡流损耗半解析高效计算[J]. 电工技术学报, 2023, 38(1): 153-165.
Cao Longfei, Fan Xinggang, Li Dawei, et al. Semi analytical and efficient calculation method of eddy current loss in windings of permanent magnet machines based on fast finite element method[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 153-165.
[14] Ou Jing, Liu Yingzhen, Liang Dawei, et al. Investigation of PM eddy current losses in surface- mounted PM motors caused by PWM[J]. IEEE Transactions on Power Electronics, 2019, 34(11): 11253-11263.
[15] Chiodetto N, Bianchi N, Alberti L. Improved analytical estimation of rotor losses in high-speed surface-mounted PM synchronous machines[J]. IEEE Transactions on Industry Applications, 2017, 53(4): 3548-3556.
[16] Hannon B, Sergeant P, Dupré L. 2-D analytical subdomain model of a slotted PMSM with shielding cylinder[J]. IEEE Transactions on Magnetics, 2014, 50(7): 1-10.
[17] Ali Qazalbash A, Sharkh S M, Irenji N T, et al. Rotor eddy loss in high-speed permanent magnet syn- chronous generators[J]. IET Electric Power Appli- cations, 2015, 9(5): 370-376.
[18] Tong Wenming, Sun Lu, Hou Mingjun, et al. Analytical modeling for rotor eddy current loss of a surface-mounted PMSM with both non-ferromagnetic conductive retaining sleeve and shielding cylinder[J]. IEEE Transactions on Energy Conversion, 2022, 37(2): 832-843.
[19] Toda H, Xia Zhenping, Wang Jiabin, et al. Rotor eddy-current loss in permanent magnet brushless machines[J]. IEEE Transactions on Magnetics, 2004, 40(4): 2104-2106.
[20] 孙权贵, 邓智泉, 张忠明. 基于齿槽效应的高速永磁电机转子涡流损耗解析计算[J]. 电工技术学报, 2018, 33(9): 1994-2004.
Sun Quangui, Deng Zhiquan, Zhang Zhongming. Analytical calculation of rotor eddy current losses in high speed permanent magnet machines accounting for influence of slot opening[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 1994- 2004.
[21] Wu L J, Zhu Z Q, Staton D, et al. Analytical modeling and analysis of open-circuit magnet loss in surface- mounted permanent-magnet machines[J]. IEEE Transactions on Magnetics, 2012, 48(3): 1234-1247.
[22] Wu L J, Zhu Z Q, Staton D, et al. Analytical model for predicting magnet loss of surface-mounted permanent magnet machines accounting for slotting effect and load[J]. IEEE Transactions on Magnetics, 2012, 48(1): 107-117.
[23] Pfister P D, Yin Xin, Fang Youtong. Slotted permanent-magnet machines: general analytical model of magnetic fields, torque, eddy currents, and permanent-magnet power losses including the diffusion effect[J]. IEEE Transactions on Magnetics, 2016, 52(5): 1-13.
[24] Zhang Zhongming, Deng Zhiquan, Sun Quangui, et al. Analytical modeling and experimental validation of rotor harmonic eddy-current loss in high-speed surface-mounted permanent magnet motors[J]. IEEE Transactions on Magnetics, 2019, 55(2): 1-11.
[25] 佟文明, 侯明君, 鹿吉文, 等. 基于负载磁场考虑涡流反作用的带护套高速永磁电机转子涡流损耗解析模型[J]. 中国电机工程学报, 2022, 42(24): 9072-9084.
Tong Wenming, Hou Mingjun, Lu Jiwen, et al. Rotor eddy current loss analytical model for high-speed permanent magnet motor with sleeve based on loaded magnetic field analysis considering eddy current reaction effect[J]. Proceedings of the CSEE, 2022, 42(24): 9072-9084.
[26] Wang Zicheng, Li Yan, Du Jianmin, et al. Analytical calculation for multilayer rotor eddy current losses of high-speed permanent magnet machines[J]. IEEJ Transactions on Electrical and Electronic Engineering, 2022, 17(4): 601-610.
[27] Qin Wei, Lü Gang, Ma Yuhua. Three-dimensional analytical modeling of axial flux permanent magnets maglev motor[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(4): 438-444.
[28] Wu L J, Zhu Z Q. Simplified analytical model and investigation of open-circuit AC winding loss of permanent-magnet machines[J]. IEEE Transactions on Industrial Electronics, 2014, 61(9): 4990-4999.
Abstract High-speed permanent magnet motors (HSPMM) are widely used in high-speed machine tools, flywheel energy storage, and other fields due to their small size and high power density. For surface-mounted HSPMM, the rotor eddy current loss is large, and the heat dissipation conditions are poor, which may cause the rotor temperature to rise too high and increase the irreversible demagnetization risk of the permanent magnet. The double-layer composite retaining sleeve can effectively suppress the eddy current loss of the rotor, and the finite element method is mainly used to calculate its eddy current loss. This method needs a long calculation time. Therefore, based on the exact subdomain method, this paper proposes a general analytical model for rotor eddy current loss of double-layer composite retaining sleeve HSPMM considering stator slotting and eddy current reaction.
Firstly, the whole field of the motor is divided into six sub-domains, such as permanent magnet, retaining sleeve, and air gap. The analytical model for rotor eddy current loss of HSPMM is established. Through the boundary conditions between each subdomain, the general expression of the magnetic field distribution in each subdomain is obtained. Then, the equations are solved by constructing the unknown coefficient equations, and the eddy current loss of each part of the rotor is calculated. Secondly, the air gap flux density and rotor eddy current loss of the selected prototype are calculated using finite element and analytical methods. The results show that the analytical method is almost consistent with the finite element method, and the double-layer composite retaining sleeve significantly suppresses the rotor eddy current loss of the surface-mounted HSPMM. The influence of different retaining sleeve thickness ratios and retaining sleeve materials on the eddy current loss is studied by the analytical model, and eddy current loss variations under different rotor structures are obtained. Finally, the C-type core experiment is established, and the calculation results of the eddy current loss analytical method are compared with the experimental results of the C-type core.
The following conclusions are drawn through analytical calculation and experimental results. The error between the analytical calculation and experimental results is within 5%, and the model has high calculation accuracy. The double-layer composite retaining sleeve with outer carbon fiber and inner alloy effectively suppresses the eddy current loss of the rotor. When the thickness of the outer carbon fiber retaining sleeve is 1/3~1/2 of the total thickness of the double-layer composite retaining sleeve, the rotor eddy current loss suppression effect is the best. Taking the motor in this paper as an example, the double-layer composite retaining sleeve reduces the eddy current loss of the rotor by about 67.2% and 23%, respectively, compared with the single-layer nickel-based alloy and single-layer carbon fiber retaining sleeve. Moreover, the larger conductivity of the inner alloy retaining sleeve has a smaller total eddy current loss of the rotor.
keywords:High-speed permanent magnet motor, accurate subdomain method, double-layer compound retaining sleeve, eddy current reaction, C-type core experiment
DOI: 10.19595/j.cnki.1000-6753.tces.230844
中图分类号:TM351
国家自然科学基金(52222702)、辽宁省“兴辽英才计划”(XLYC2007107)和沈阳市创新人才工程(RC210067)资助项目。
收稿日期 2023-06-05
改稿日期 2023-07-24
佟文明 男,1984年生,教授,博士生导师,研究方向为高性能永磁电机及其控制。E-mail: twm822@126.com(通信作者)
田 野 男,2000年生,硕士研究生,研究方向为高速永磁电机转子涡流损耗。E-mail: ty451656@163.com
(编辑 崔文静)