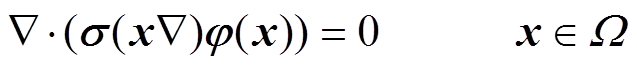 (1)
(1)
摘要 电阻抗层析成像(EIT)作为一种新兴可视化技术,可通过电导率分布变化的重建图像获得人体组织病理变化信息,为疾病检测提供了一种选择。在基于EIT的颅脑疾病检测中,为了准确获取差分成像图像重建所需的参考电压,提出一种基于全连接神经网络(FCNN)的参考电压预测方法。通过研究所提方法在不同信噪比情况下的图像重建性能,验证所提方法对参考电压预测的准确性和泛化能力。此外,还研究了头皮、颅骨和脑组织电导率分别发生变化时所提方法的有效性,并通过计算模糊半径和相关系数对图像重建质量进行了定量评价。结果表明,所提方法在一定电导率范围内和不同噪声水平下能够有效预测参考电压。
关键词:电阻抗成像 图像重建 参考电压 神经网络
脑卒中是临床常见的一种脑损伤疾病[1-2]。该疾病具有病情变化复杂、高病死率、高致残率等特点,且患者总体预后情况较差,其早期检测和实时监测有助于降低患者病死率并提高预后[3]。目前,计算机断层扫描(Computed Tomography, CT)和磁共振成像(Magnetic Resonance Imaging, MRI)是常用的临床医疗设备,然而此类设备无法实现脑卒中的早期检测及动态实时图像监护等功能[4-5]。电阻抗层析成像(Electrical Impedance Tomography, EIT)是一种通过电极向人体施加安全电流激励,同时测量响应电压,重建体内阻抗分布及变化的技术[6-7]。该技术具有对组织功能变化敏感、无损伤、无辐射、连续实时动态监测、成本低等优点[8]。因而EIT技术在脑卒中的早期诊断与实时监测方面具有广泛的应用前景,可作为实时监护设备为患者临床诊断和治疗争取最佳抢救时机[9-10]。
目前,EIT技术采用的成像方式有差分成像和绝对成像[11-12]。绝对成像可直接重建某一时刻的电导率分布图像;差分成像是利用两组不同时刻的测量数据,通过图像重建算法得到两次测量之间电导率分布的差异。由于差分成像可以减少测量噪声和建模误差对图像重建的影响,因此EIT图像重建多采用差分成像方式[13-15]。对于差分EIT重建,需要从基线或参考系获得电压的先验信息[16]。颅脑电阻抗成像中,脑出血或脑缺血会造成离子浓度的变化,从而引起颅内电导率分布变化,进而引起电流密度分布发生了改变,造成在某一时刻获取的参考电压在后期使用时不够准确[17]。为了校准参考电压,必须实时监测电导率,增加了系统的复杂程度。因此,从具有均匀背景电导率的区域获得参考电压,对差分EIT图像重建具有重要意义。在文献[18]中,提出了一种基于测量尺度特征(Measurement-Scale Feature, MSF)的参考电压估计方法。在简单圆域,胸廓模型模拟和不同场景的实测数据中,对五种MSF的参考电压估计方法进行了比较和评价。在文献[19]中,分别提出了基于电压特征曲线的多重测量方法和基于卷积神经网络(Convolutional Neural Network, CNN)的参考电压估计方法。通过静态物理模拟实验、油水和气水两相流动态实验,对最佳齐次近似法、测量尺度特征方法、多重测量方法和CNN方法进行了比较和评价。需要注意的是,基于最佳齐次近似法的参考电压预测方法会受环境温度和均匀介质中电导率分布等外部因素的干扰,导致参考电压估计不准确;测量尺度特征方法不适用于背景电导率高于目标物电导率的情况,且该方法在绝对成像中更为可靠;多重测量方法依赖于对模型的精确建模,对模型的准确性有较高的要求;卷积神经网络方法对模型全局特征表征能力有限,对于某些复杂关系不够灵活。颅脑是由头皮、颅骨和脑组织等构成的不规则、多层复杂结构,目前尚未有文献报道如何获取复杂颅脑模型的参考电压。因此,本文提出一种基于全连接神经网络(Fully Connected Neural Network, FCNN)的参考电压预测方法。该方法可建立测量电压与参考电压之间的端到端映射,进而实现参考电压的准确预测,为颅脑EIT监测提供有力支撑。
EIT场域中的势能函数φ(x)与电导率分布函数σ(x)之间的关系可以用拉普拉斯方程表示为
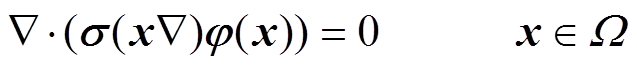 (1)
(1)
边界条件[20]表示为
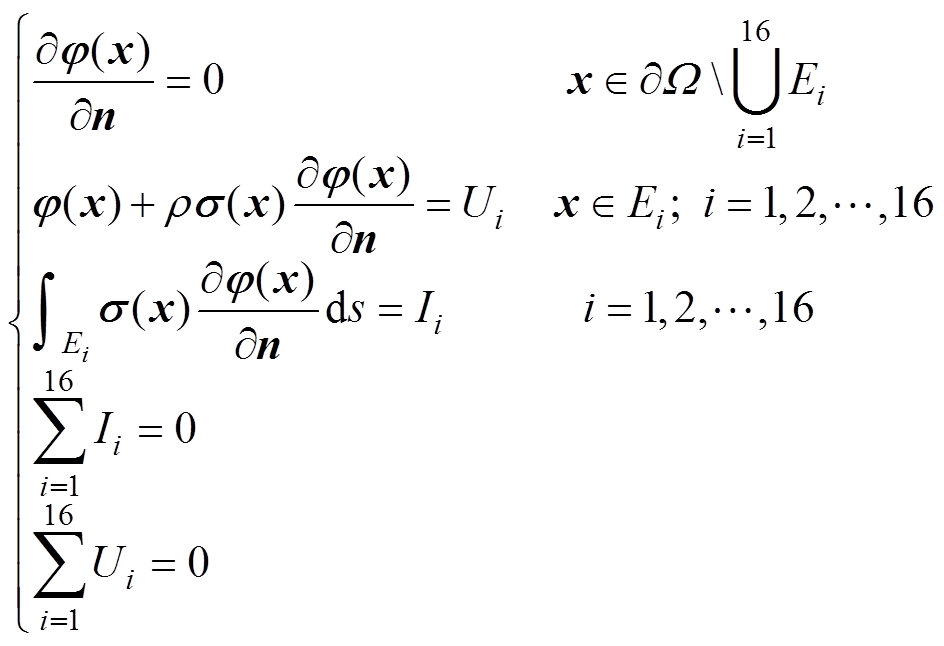 (2)
(2)
式中,x为敏感场的空间位置向量;s (x)为敏感场的空间电导率分布;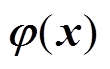 为敏感场空间中的电位分布;
为敏感场空间中的电位分布;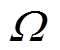 为敏感场;
为敏感场;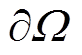 为场边界;n为边界处的外法线方向向量;r 为接触阻抗;Ei为边界上的第i个传感器;Ii和Ui分别为第i个电极上的电流和电压。
为场边界;n为边界处的外法线方向向量;r 为接触阻抗;Ei为边界上的第i个传感器;Ii和Ui分别为第i个电极上的电流和电压。
根据局部点的泰勒级数展开,图像重建可以近似描述为线性离散方程,即
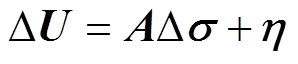 (3)
(3)
式中,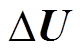 为边界电压变化,
为边界电压变化,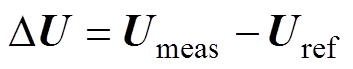 ,
,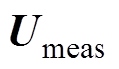 为当前的测量电压,
为当前的测量电压,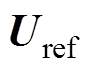 为参考电压;
为参考电压;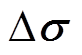 为与场中目标物分布相关的电导率向量;A为灵敏度矩阵;
为与场中目标物分布相关的电导率向量;A为灵敏度矩阵;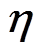 为服从高斯分布的测量噪声。
为服从高斯分布的测量噪声。
为方便起见,变量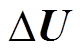 和
和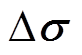 分别简化为b和g。则式(3)可表示为
分别简化为b和g。则式(3)可表示为
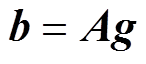 (4)
(4)
图1为本研究使用的全连接神经网络结构示意图,包含输入层、隐藏层和输出层。为了对FCNN进行训练,当前的测量电压Umeas和参考电压Uref分别作为其输入和输出。网络的标签是参考电压数据Uref,其值可以直接在已知准确电导率的头部模型中计算获得。在相对激励-相邻测量模式下,192个有效测量值作为网络输入,通过网络映射得到预测参考电压,因此全连接神经网络的输入层和输出层各包含192个神经元。隐藏层是直接影响神经网络模型的性能和训练过程的重要参数,考虑到网络的准确性和稳定性,隐藏层包含60个神经元。在隐藏层中选择ReLU函数作为激活函数,其函数定义式[21]为
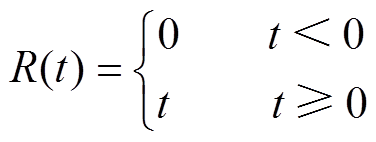 (5)
(5)
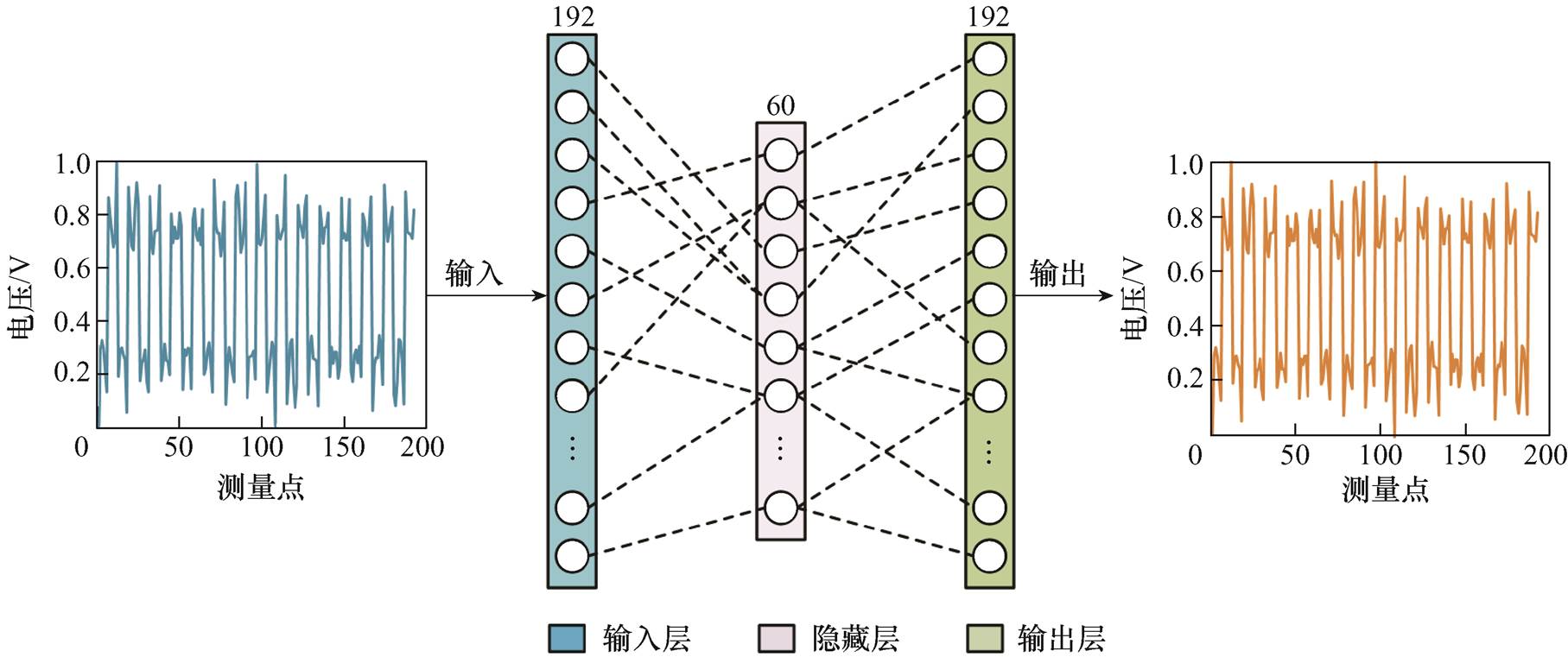
图1 全连接神经网络的结构
Fig.1 Structure of fully connected neural network
式中,t为隐藏层的输入向量。
因此,隐藏层的输出可以表示为
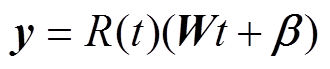 (6)
(6)
式中,y为隐藏层输出向量;R为ReLU函数;W为权重向量;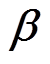 为偏置向量。
为偏置向量。
输出层选择Sigmoid函数作为激活函数,定义式为
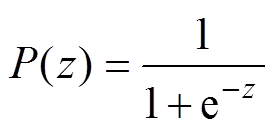 (7)
(7)
式中,z为激活函数的输入;P(z)为激活函数的输出,Sigmoid函数将输出限定在0~1的范围内。
方均误差(Mean Square Error, MSE)是一种被广泛用于估计非线性模型参数(如监督神经网络)的非凸损失函数[22]。因此,真实参考电压数据Uref与预测参考电压数据Uref-predict之间的MSE可作为学习FCNN参数的损失函数,其表达式[23]为
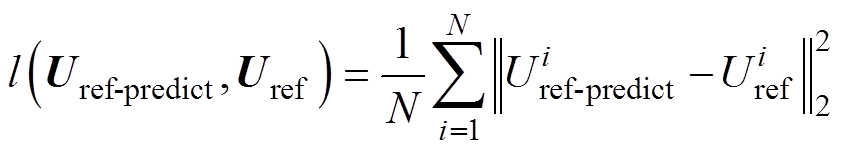 (8)
(8)
式中,Uref-predict为预测的参考电压;l(•)表示MSE;N=192表示测量的边界电压数;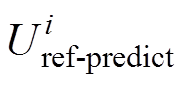 表示Uref-pedict的第i个电压值;
表示Uref-pedict的第i个电压值;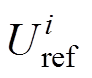 为Uref的第i个电压值。
为Uref的第i个电压值。
该网络在配备AMD A10 1.8 GHz处理器和8 GB RAM的计算机上通过PyCharm实现。在损失函数反向传递过程中,采用自适应矩估计算法对FCNN的参数进行更新。FCNN的学习率设定为0.000 1,优化1 000个epoch,每批32个。
利用COMSOL Multiphysics和Matlab软件获得了二维头部模型仿真数据集。三层颅脑模型如图2所示。图2中头部模型的周长约为54.1 cm,长轴为17.8 cm,短轴为16.3 cm。将图2所示的模型作为原始模型,并在原始模型的基础上进行一定程度的变形(变形范围80%~120%),训练数据集是在原始模型和形变模型上获得的。本文使用16电极的EIT系统,采用相对激励、相邻测量的策略获取数据[24]。先将1号和9号电极作为激励电极,1-2、2-3、3-4、…、16-1号电极分别作为测量电极对测量边界电压,可测得16组电压数据;重复上述步骤,将2号和10号作为激励电极对,进行16次测量,然后依次是3-11、4-12、5-13、…、16-1号激励电极对,所有边界测量数据组成了一帧数据(共测得256个边界电压)。由于激励电极的相邻电极测量值无效,因此一帧数据中有192个有效测量值。
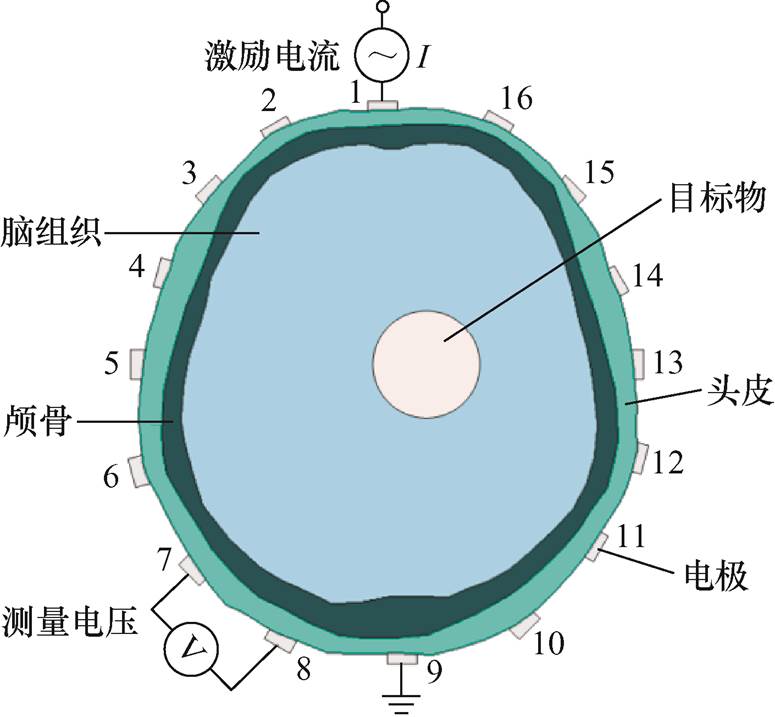
图2 三层颅脑模型
Fig.2 Three-layer head model
图3给出了四种有形状偏差的头部模型示意图,图3a为头皮层扩张5%时的头部模型;图3c为水平方向扩张10%的头部模型;图3b和3d分别为竖直方向和水平方向扩张20%的头部模型。由文献[25]可知,头皮电导率变化范围为0.33~0.45 S/m,颅骨电导率变化范围为0.0042~0.3 S/m,脑组织电导率变化范围为0.12~0.48 S/m。因此,研究中头皮、颅骨和脑组织的电导率分别为0.44 S/m、0.013 S/m和0.15 S/m。
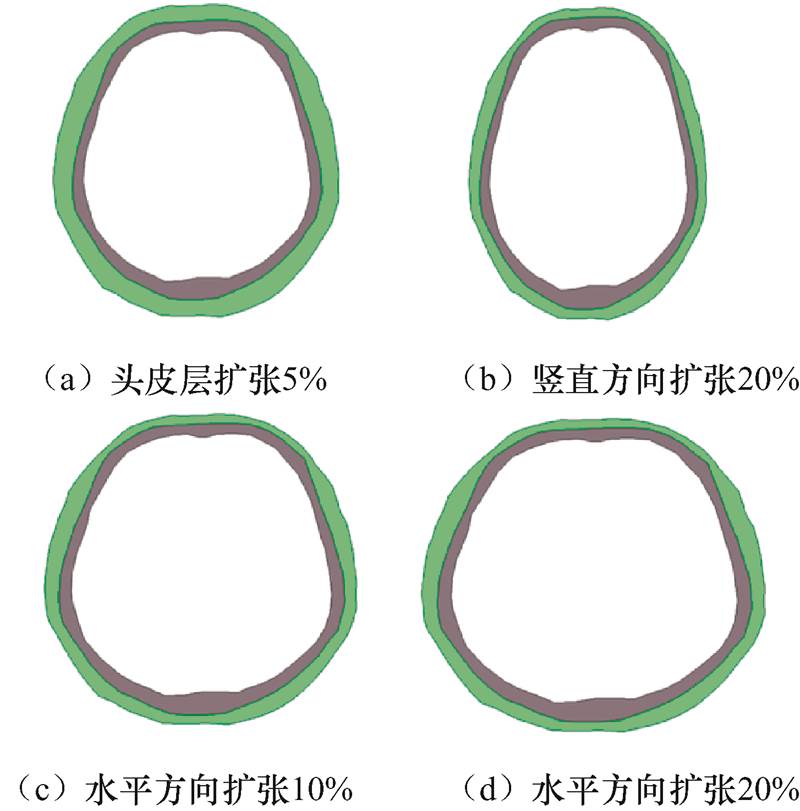
图3 形变的头部模型
Fig.3 The deformed head model
在COMSOL Multiphysics软件中,将被测区域剖分成三角形网格,求解EIT正问题,如图4a所示。头部仿真模型采用长10 mm、宽6 mm的电极,注入电流为1.25 mA。当所有电极对完成激励和测量后,共获得192个测量值作为正问题的电压数据。在逆问题中,将成像截面离散为如图4b所示的正方形网格。
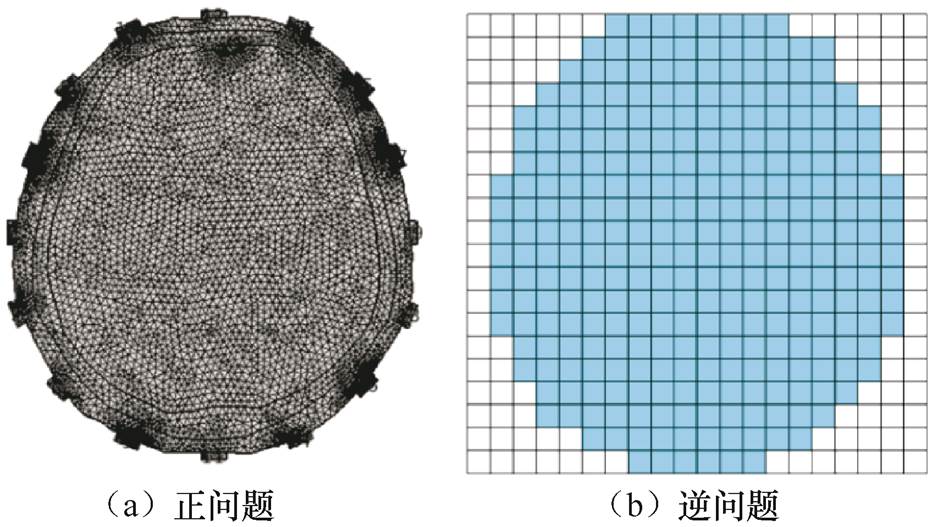
图4 头部仿真模型网格
Fig.4 Grid of the head simulation model
训练数据集中包含2 000个出血样本,2 000个缺血样本,2 000个健康样本。在训练和测试数据集中,使用半径为3~30 mm的目标物来模拟出血或缺血,目标物的位置随机分布。其中,出血目标物和缺血目标物的电导率分别设为0.71 S/m和0.06 S/m。注意,用于网络训练的训练集与用于网络泛化的测试集之间没有重复。此外,训练集不包含有噪声的模拟数据。
数据集中的每个样本都包含一对变量Umeas和Uref。Uref作为标签矢量,是损失函数中的一个自变量,用于监督和约束网络的训练过程。此外,还需要对用于网络训练的数据集Umeas和Uref进行归一化处理,数据集归一化处理可以显著加快寻找损失函数最优解的速度,同时消除一些奇异数据的影响。
在通过所提出的方法进行参考电压的预测后,需要利用预测的参考电压Uref-predict及当前测量电压Umeas进行图像重建以进一步验证所提方法。因此,采用L1正则化方法来重建电导率分布。L1正则化方法的目标函数可以表示为
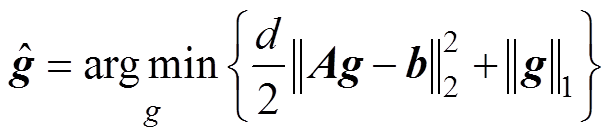 (9)
(9)
式中,d为正则化参数。
通过交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)求解式(9),并将式(9)转换为约束函数,表示为
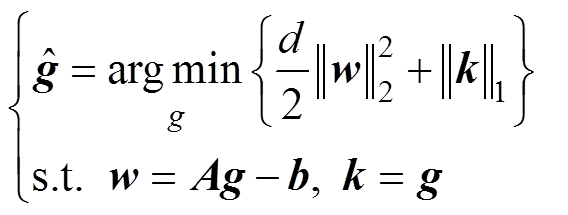 (10)
(10)
式(10)对应的增广拉格朗日函数为
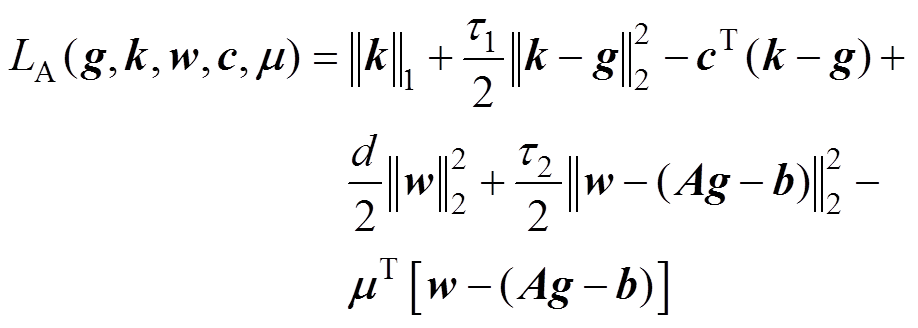 (11)
(11)
式中,c和m 为增广拉格朗日乘子;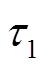 和
和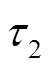 为正则化参数。
为正则化参数。
根据ADMM算法,可以把式(11)的优化问题分解为若干子问题,分别表示为
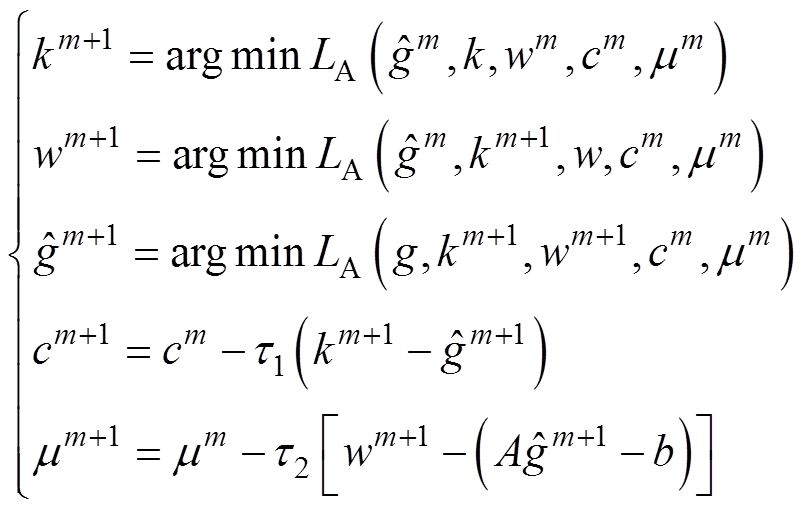 (12)
(12)
通过求解子问题,得到最优的电导率分布。
在对网络进行训练后,为了测试网络对参考电压的预测能力,在竖直方向压缩为原模型80%的形变模型中获得了无噪声测试数据集。无噪声测试数据集包含40个出血样本、40个缺血样本和20个健康样本。图5给出了无噪声条件下预测参考电压Uref-predict和真实参考电压Uref对比结果。从图5可以看出,预测的参考电压与实际参考电压拟合良好。
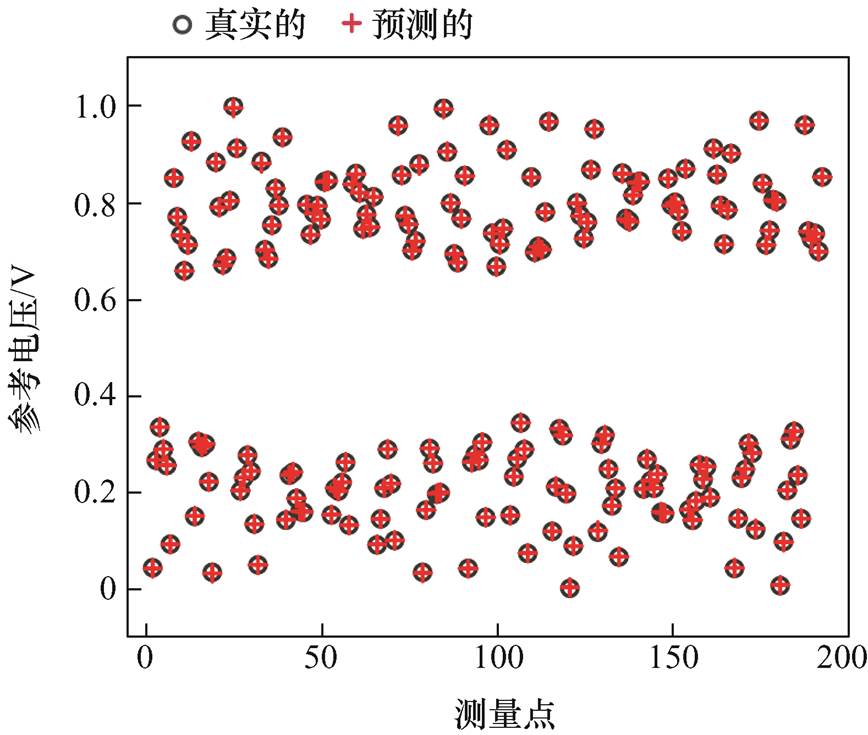
图5 无噪声下真实参考电压与预测参考电压比较
Fig.5 Comparison of real reference voltage and predicted reference voltage under noiseless condition
此外,采用L1正则化方法进行图像重建,其中b=Umeas-Uref-predict,部分测试集样本重建结果如图6所示。图6a为脑出血重建图像,图6b为脑缺血和健康的重建图像。图6a和6b的第一行为仿真模型,第二行为重建图像,图中,模型J为健康模型。从图6中可以观察到,采用Uref-predict作为参考电压重建的图像可以准确描述测量场中目标物的大小和分布,且目标物的边界较清晰。
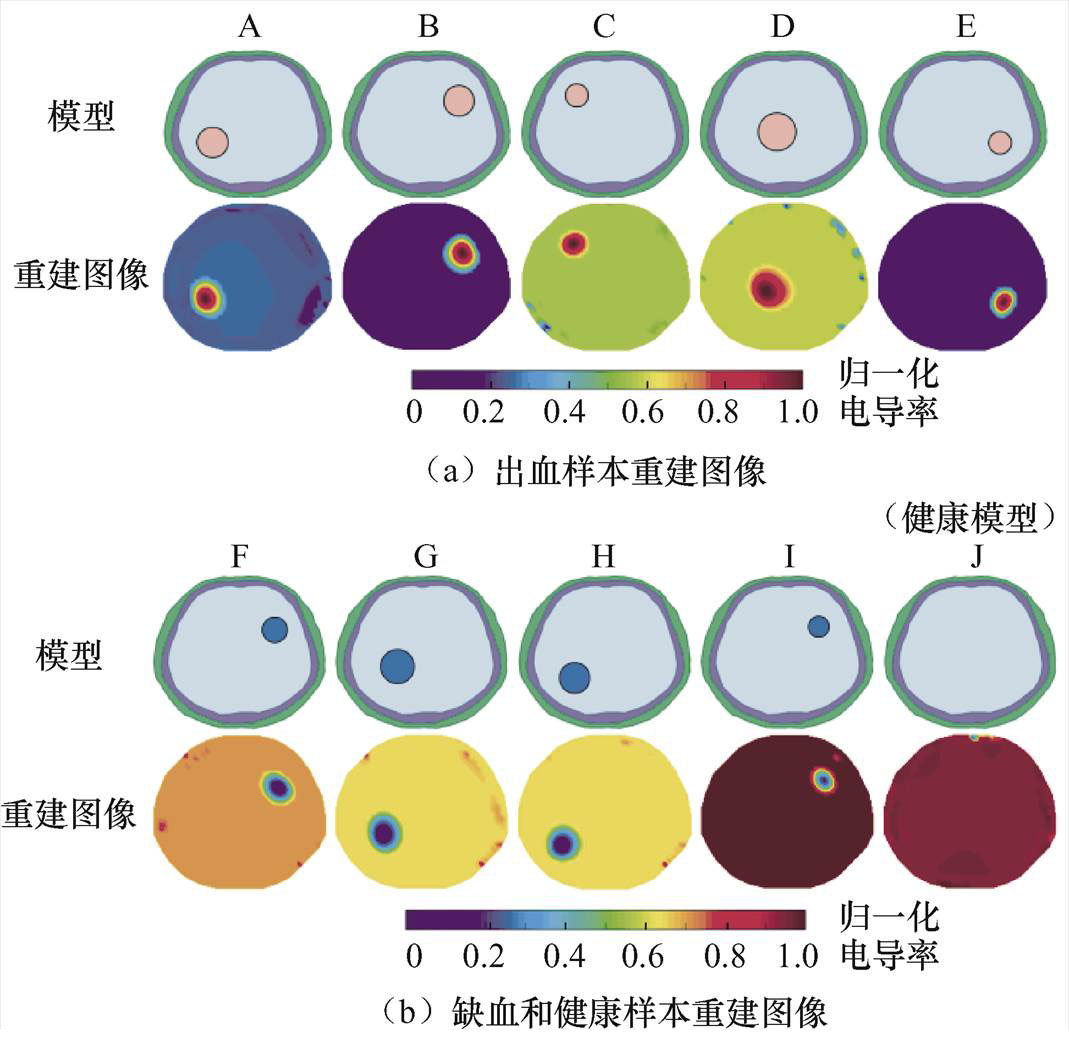
图6 无噪声条件下的重建图像
Fig.6 Reconstructed images under noiseless condition
在颅脑EIT的实际应用中,由于噪声的存在,使得测量数据存在误差,进而影响图像的重建质量。为了测试所提方法的抗噪性能,在竖直方向压缩为原模型80%的形变模型中获得了噪声测试数据集,噪声测试集中加入了信噪比分别为70、60和50 dB的高斯白噪声。测试集共有300个样本,其中出血样本120个,缺血样本120个,健康样本60个。图7给出了噪声为70 dB时,一个出血样本的真实参考电压与预测参考电压的比较。从图7中可以看出,所提方法在噪声条件下也能较准确地预测参考电压。
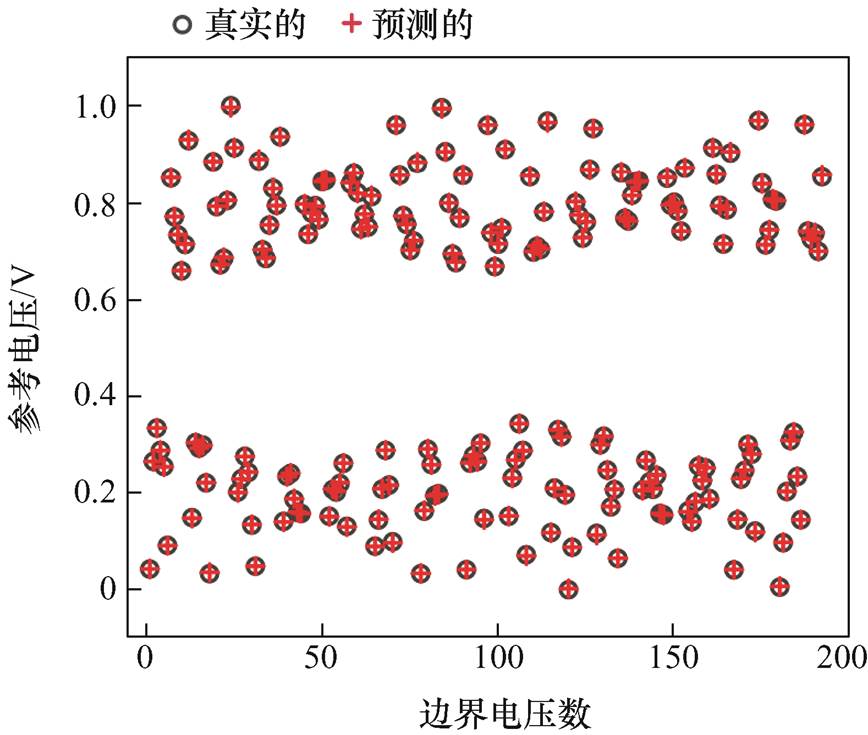
图7 70 dB噪声条件下真实参考电压与预测参考电压的比较
Fig.7 Comparison of real reference voltage and predicted reference voltage under 70 dB noise
不同信噪比下部分测试集的图像重建结果如图8所示,第1列是模型设置,第2~4列是不同信噪比下的重建图像。从图8中可以观察到,随着信噪比的逐渐下降,尽管图像背景中出现了噪声干扰,但仍能清晰地分辨出目标物的大小和分布,表明所提方法具有较好的抗噪能力,且不受目标物大小和位置分布的影响。
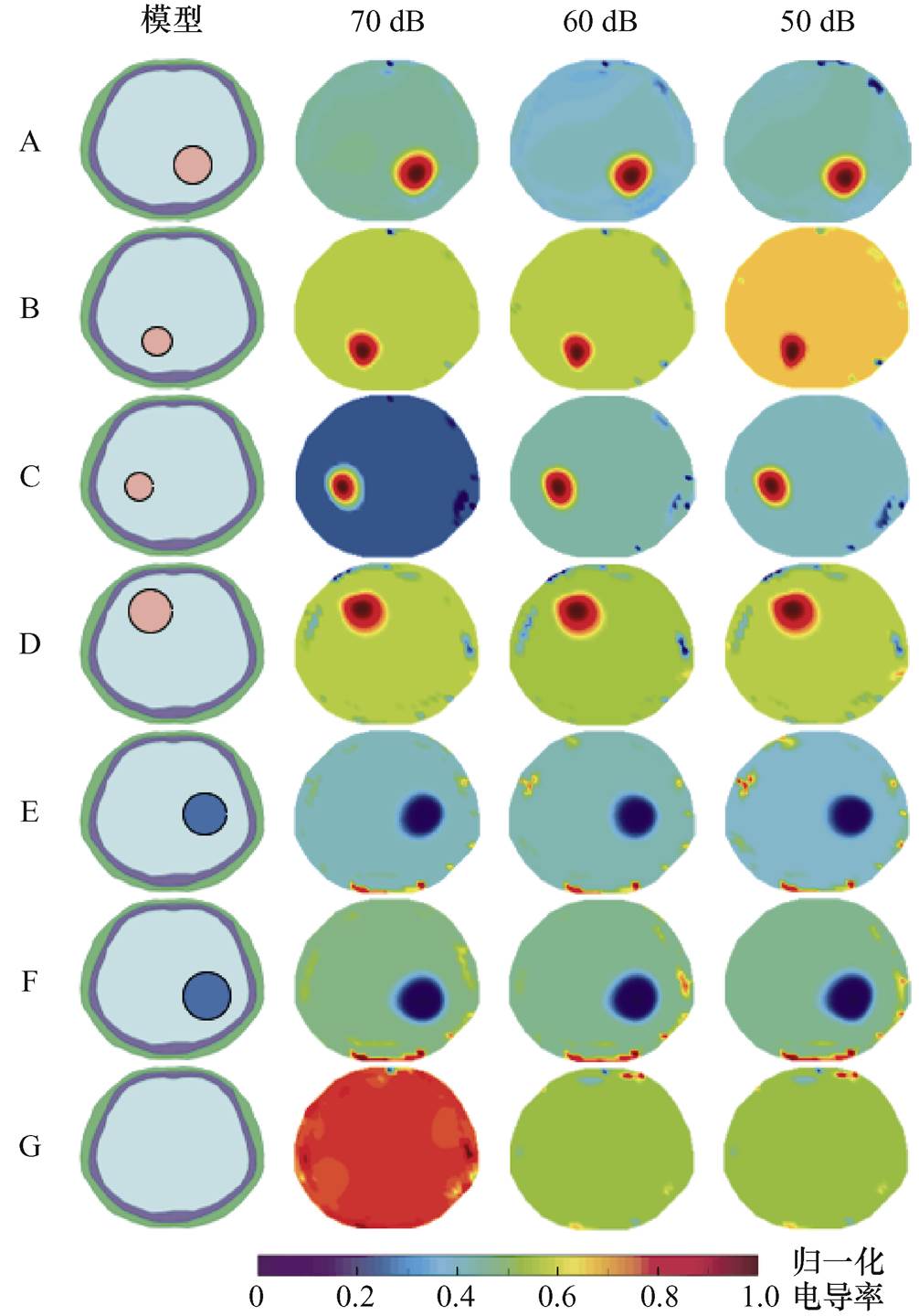
图8 不同信噪比下的重建图像
Fig.8 Reconstructed images under the impact of noise with different signal-to-noise ratios
为定量评估预测参考电压的准确性,引入电压相对误差URE、平均电压相对误差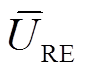 ,分别定义为
,分别定义为
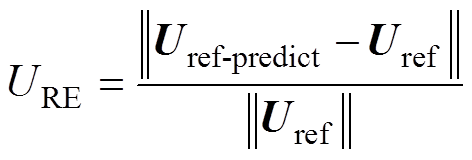 (13)
(13)
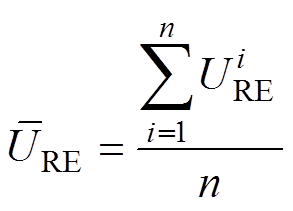 (14)
(14)
式中,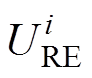 为第i个电压相对误差值;n为预测参考电压的个数。由式(13)可计算得到预测参考电压与真实参考电压的偏差值URE,该量化指标评估了预测结果的准确性。URE的值和
为第i个电压相对误差值;n为预测参考电压的个数。由式(13)可计算得到预测参考电压与真实参考电压的偏差值URE,该量化指标评估了预测结果的准确性。URE的值和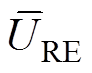 的值越接近0,所提方法预测的参考电压值越准确。
的值越接近0,所提方法预测的参考电压值越准确。
图9a和图9b给出了无噪声条件下和70 dB噪声条件下电压相对误差值变化。由图9可以看出,无噪声条件下电压相对误差URE变化范围是0%~0.10%,平均电压相对误差值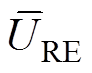 =0.042 7%;噪声条件下电压相对误差变化URE范围是0%~0.15%,平均电压相对误差值
=0.042 7%;噪声条件下电压相对误差变化URE范围是0%~0.15%,平均电压相对误差值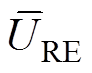 =0.025 3%。定量评价结果表明在无噪和有噪条件下基于所提方法得到的预测参考电压均能很好地逼近真实参考电压。
=0.025 3%。定量评价结果表明在无噪和有噪条件下基于所提方法得到的预测参考电压均能很好地逼近真实参考电压。
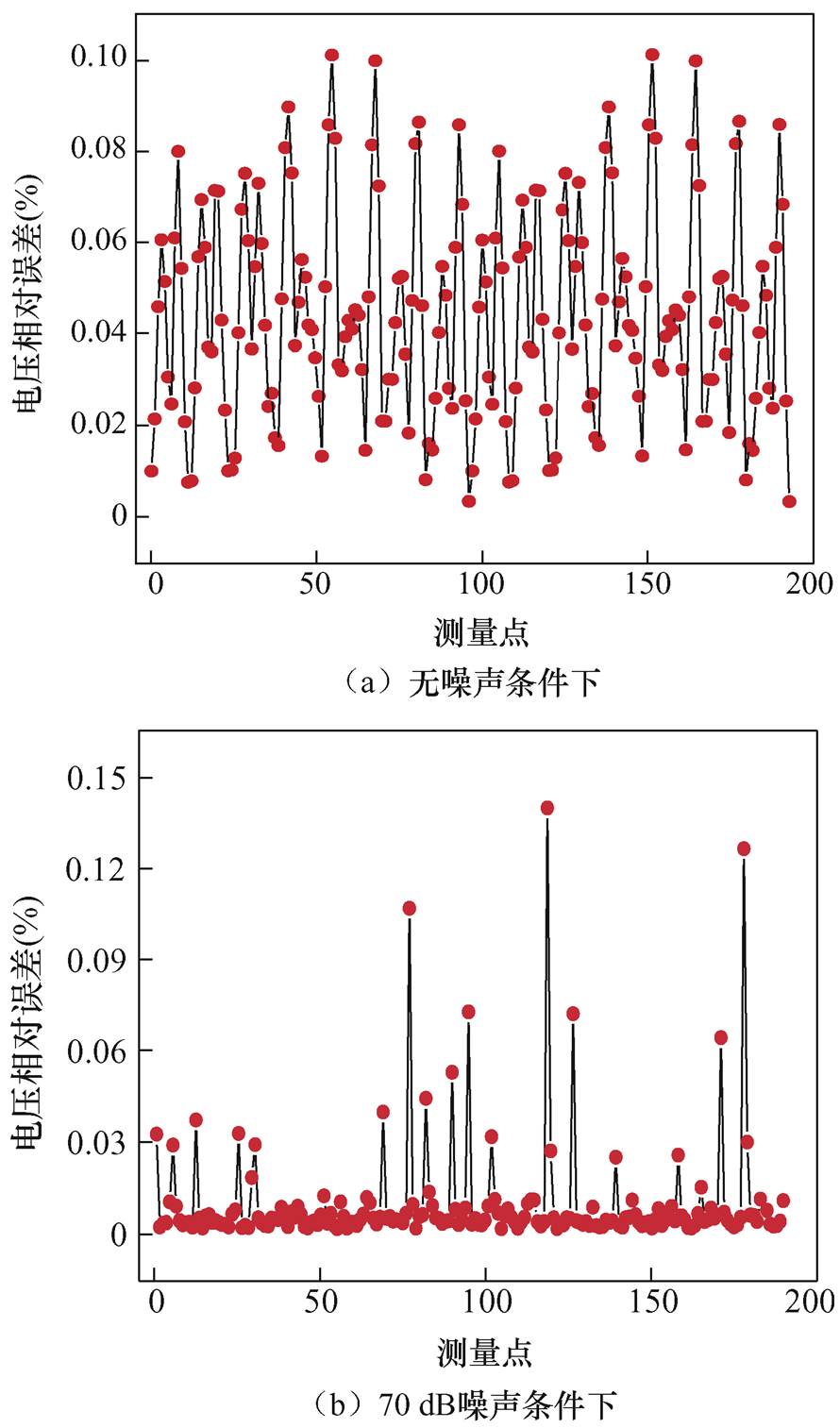
图9 电压相对误差变化
Fig.9 Variation of voltage relative error
此外,引入评价指标模糊半径(Blur Radius, BR)[26]和相关系数(Correlation Coefficient, CC)[27]对重建图像进行定量分析,其定义为
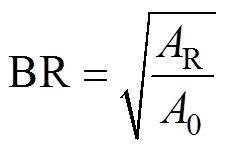 (15)
(15)
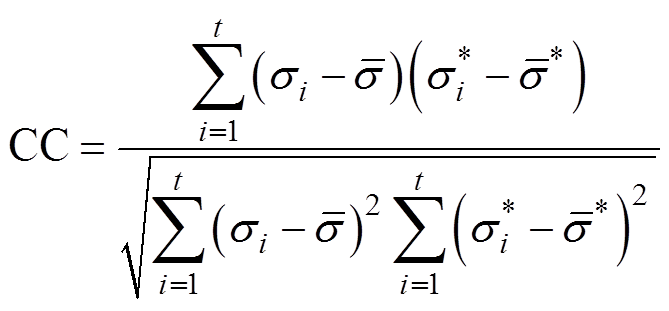 (16)
(16)
式中,AR为感兴趣区域面积;A0为整个被测区域的面积;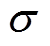 为计算得到的电导率;
为计算得到的电导率;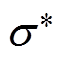 为真实的电导率;t为有限元模型中的单元数;
为真实的电导率;t为有限元模型中的单元数;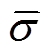 和
和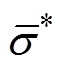 为s和s*的平均值;
为s和s*的平均值;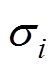 和
和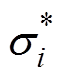 为
为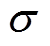 和
和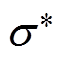 的第i个单元。感兴趣区域是电导率大于重构的最大电导率1/4的区域。BR的值越低,图像重建的效果越好。CC值用来衡量优化的电导率和真实的电导率之间的相关性,CC值越接近1,图像质量越好。
的第i个单元。感兴趣区域是电导率大于重构的最大电导率1/4的区域。BR的值越低,图像重建的效果越好。CC值用来衡量优化的电导率和真实的电导率之间的相关性,CC值越接近1,图像质量越好。
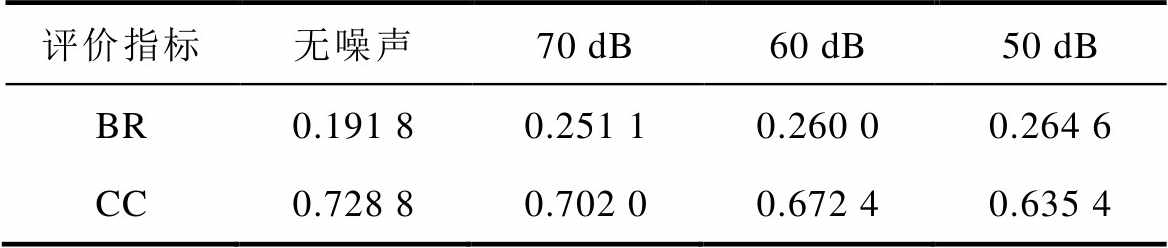
表1给出了不同信噪比情况下重建图像的平均BR值和平均CC值。当信噪比减小时,重建图像的平均BR值增大,平均CC值逐渐减小。重建图像和定量分析结果表明,所提方法具有良好的抗噪性能,即使在噪声条件下也能较好地预测参考电压。
表1 测试集平均BR值和平均CC值的比较
Tab.1 Comparison of average BR values and average CC values of the test data
评价指标无噪声70 dB60 dB50 dB BR0.191 80.251 10.260 00.264 6 CC0.728 80.702 00.672 40.635 4
不同患者电导率取值受患者年龄、性别、健康状况等诸多因素的影响。因此,为了测试本文所提方法的泛化能力,在确保电导率取值合理的情况下,测试模型假设了头皮、颅骨和脑组织的电导率分别增加或减少2.5%的情况。在原始模型上分别改变三层电导率生成包含90个样本的测试数据集,其中30个出血样本、30个缺血样本、30个健康样本。图10a和图10b给出了头皮层和脑组织层电导率分别增加2.5%时,两个出血测试样本真实参考电压与预测参考电压的对比。从图10可以看出,即使电导率发生变化,所提方法预测的参考电压与真实参考电压也较为接近。
当头皮、颅骨和脑组织电导率分别发生变化时,将预测的参考电压作为参考电压,并采用L1正则化方法进行图像重建,目的是验证所提出的方法在电导率变化时预测参考电压的能力。图11和图12给出了重建图像,图11为头皮、颅骨和脑组织电导率分别降低2.5%时的重建图像,图12为头皮、颅骨和脑组织电导率分别增加2.5%时的重建图像。在图11和图12中,图11a、图12a和图11b、图12b分别是出血样本和缺血样本的重建图像。第一列为模型设置,第2~4列为头皮、颅骨和脑组织电导率分别变化时的重建图像。从图11和图12可以看出,在头皮、颅骨和脑组织电导率分别变化2.5%时,对于不同大小和不同位置的目标物而言,重建的位置和形状与真实模型中的位置和形状比较接近。在视觉上,头皮、颅骨和脑组织电导率分别变化预测的参考电压对重建图像的影响没有较大差别。
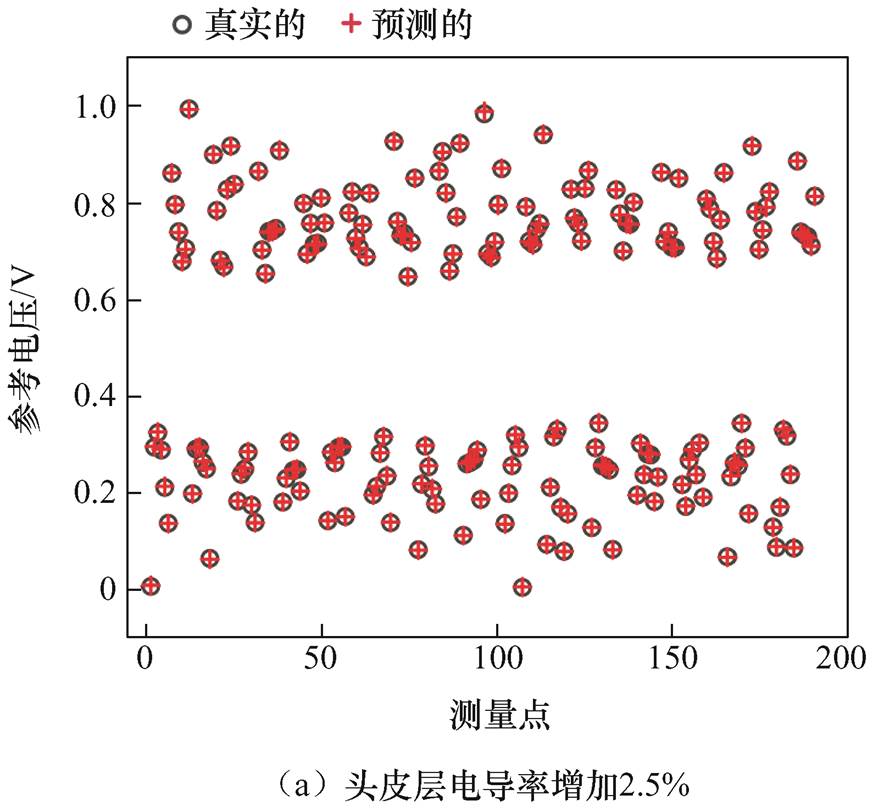
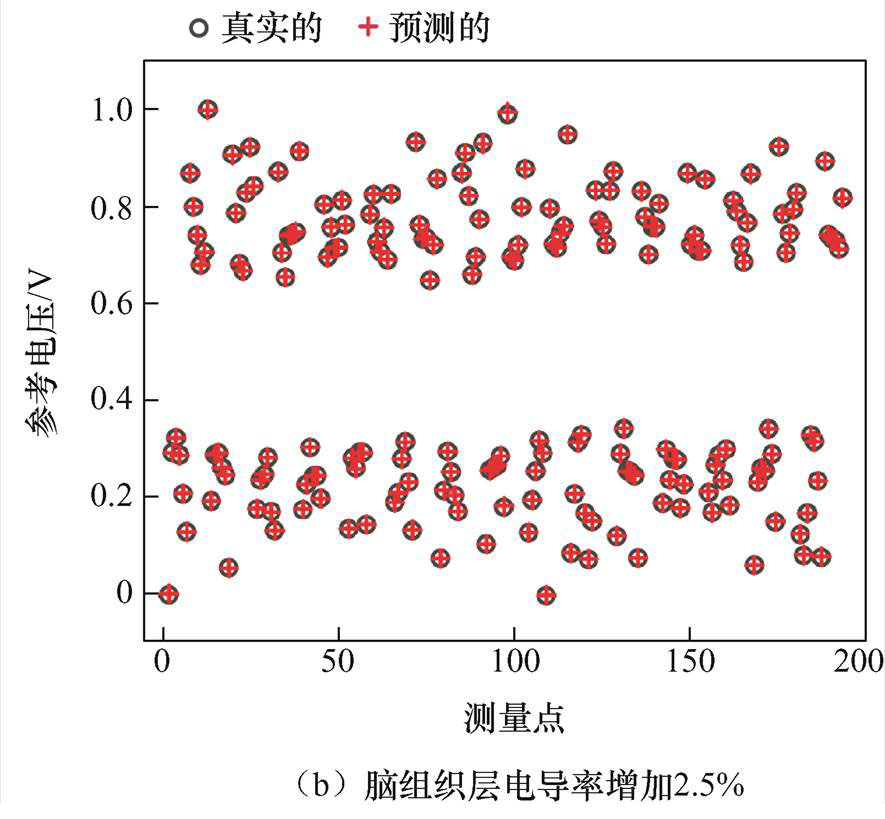
图10 真实参考电压与预测参考电压的比较
Fig.10 Comparison of true reference voltage and predicted reference voltage
颅骨电导率分别减少2.5%和增加2.5%时健康样本的重建图像如图13所示。可以看出,当电导率发生变化时,健康样本也能进行良好的图像重建。上述结果表明,所提方法对一定范围内的电导率变化,具有良好的泛化能力。
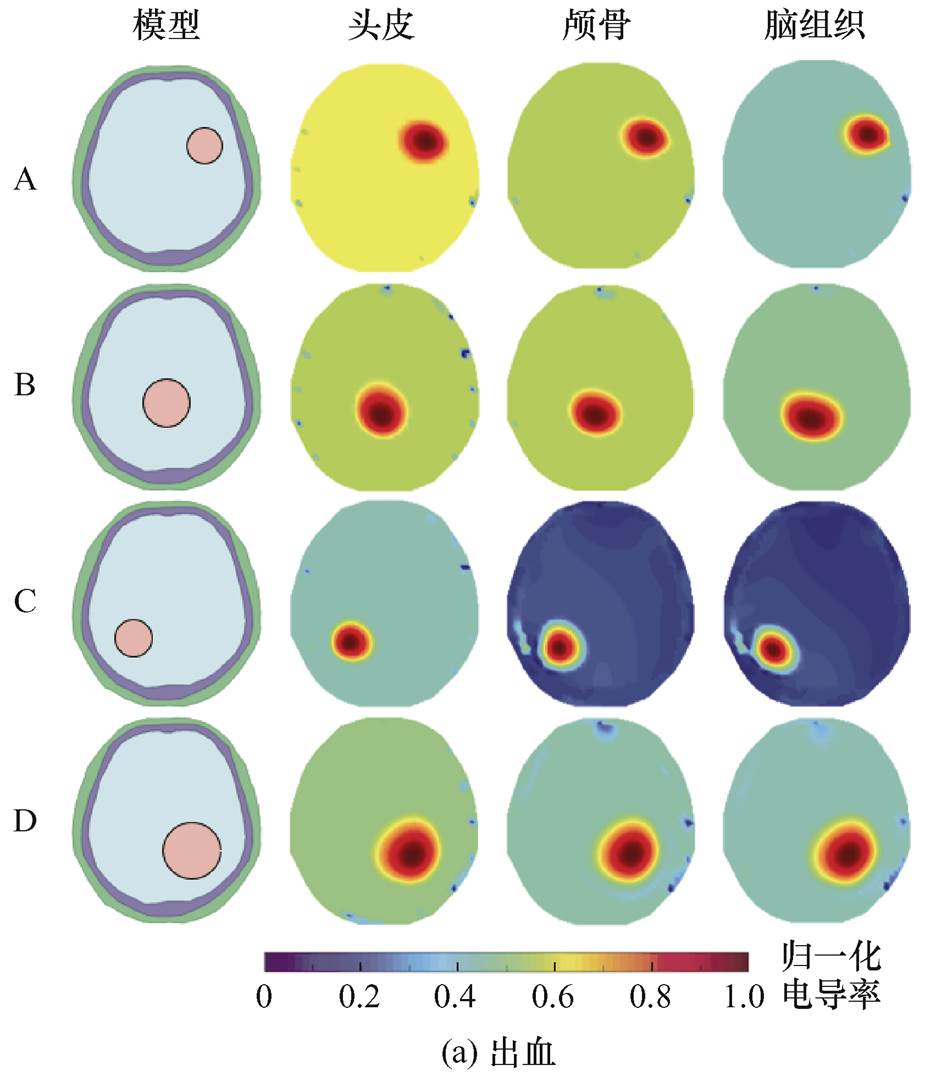
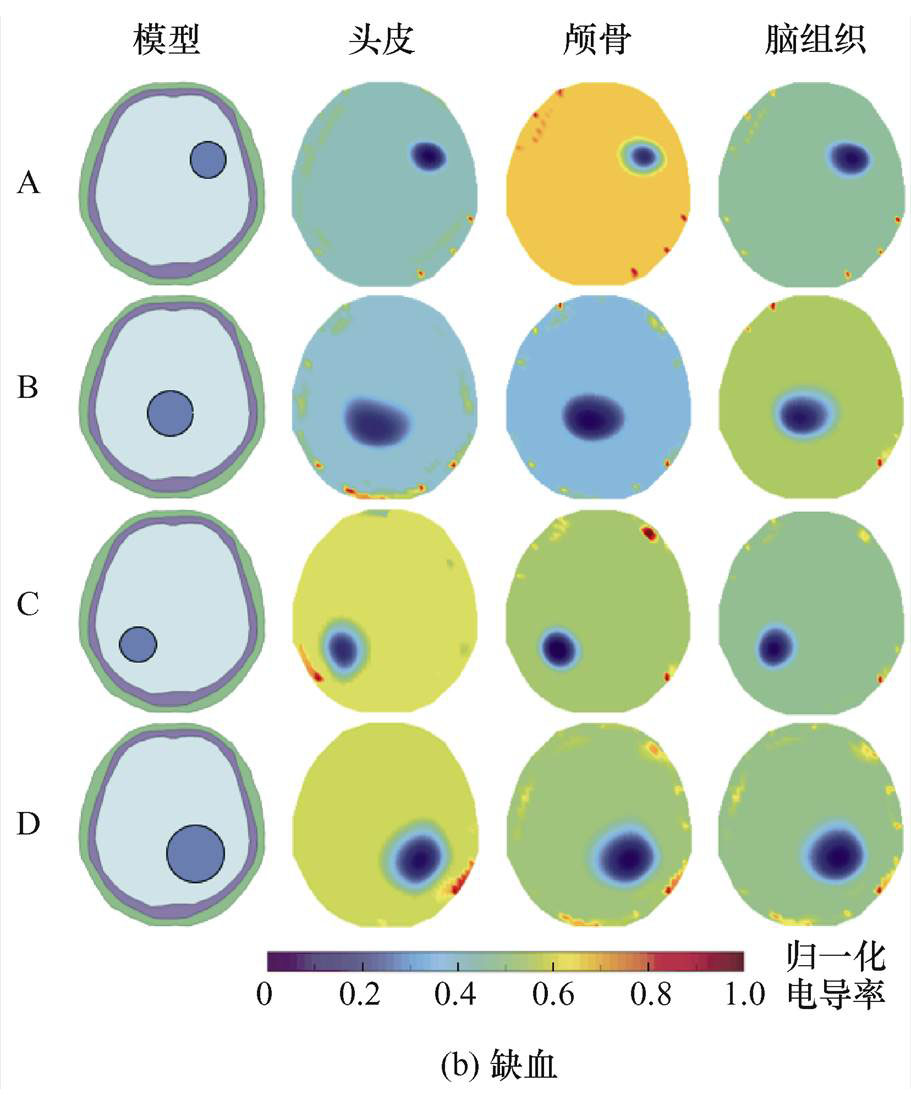
图11 头皮、颅骨和脑组织电导率减少2.5%重建图像
Fig.11 Reconstructed images when conductivity of scalp, skull and brain tissue is respectively reduced by 2.5%
表2给出了头皮、颅骨和脑组织电导率分别变化时重建图像的平均BR值和平均CC值的比较。由表2可以看出,当三层电导率分别发生变化时,重建图像的评价指标差异不大。此外,由定量评估分析可知,头皮和脑组织电导率的变化对重建图像的影响大于颅骨。
此外,研究了颅脑模型两层电导率同时变化、三层电导率同时变化情况下所提方法的性能。图14给出了颅骨层和脑组织层两层电导率同时变化(颅骨电导率减少0.5%和脑组织电导率增加1.5%)、颅脑模型三层电导率同时变化(颅骨电导率增加1.5%、头皮电导率增加2%和脑组织电导率增加3%)时脑出血重建图像。从图像重建结果可以明显看出,即使在颅脑模型两层电导率同时变化或三层电导率同时变化时,基于预测电压数据也可获得良好的重建图像效果。
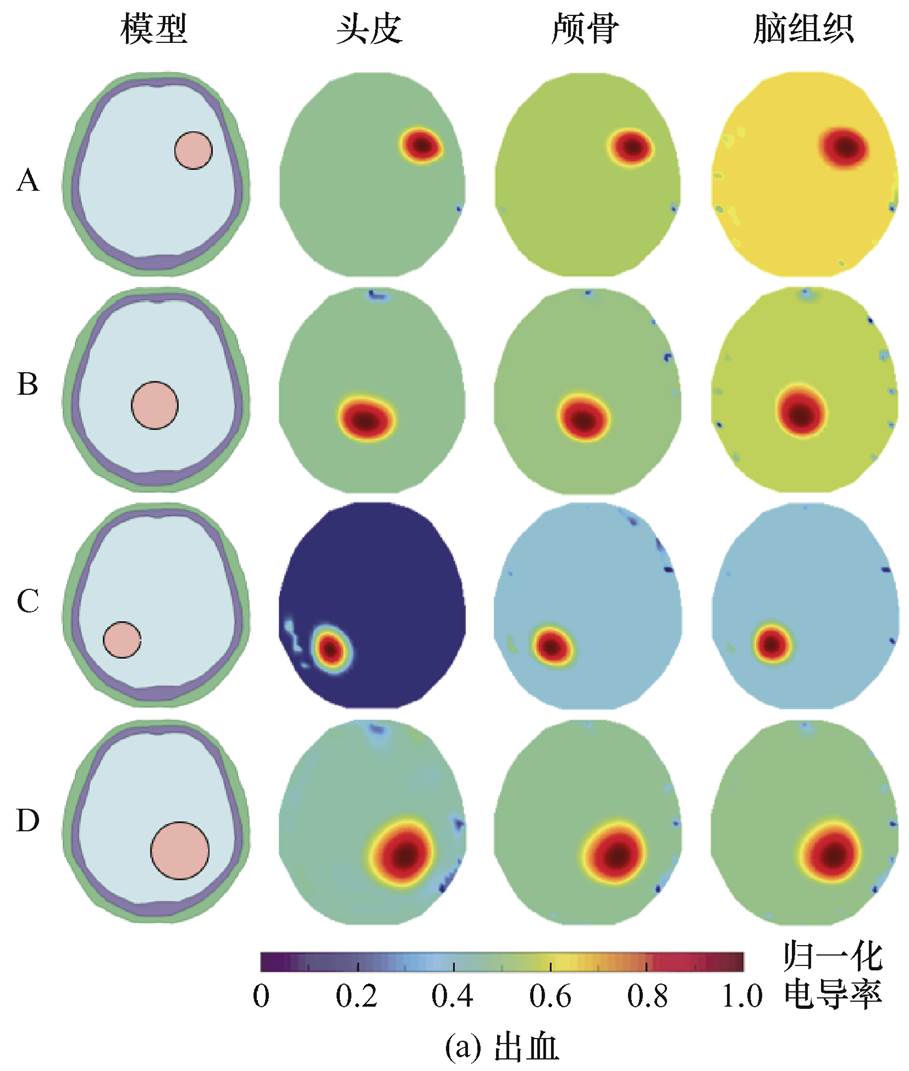
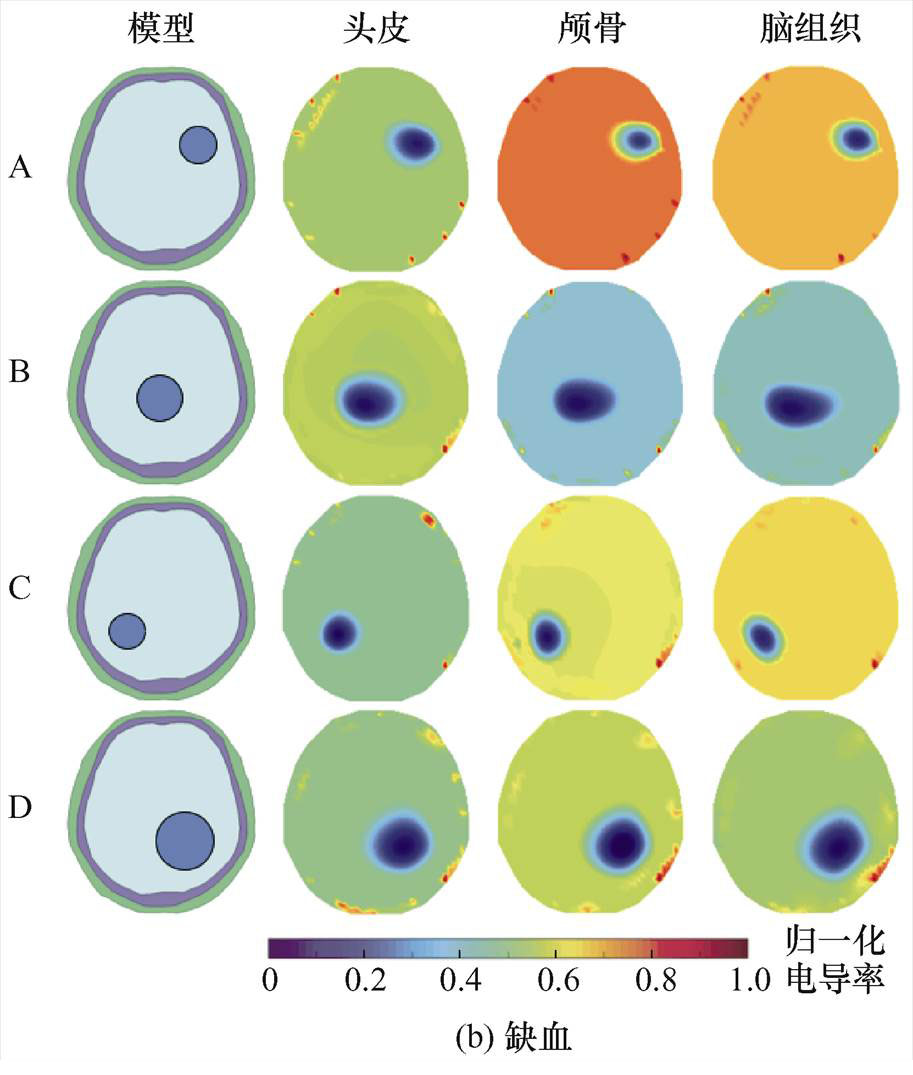
图12 头皮、颅骨和脑组织电导率增加2.5%重建图像
Fig.12 Reconstructed images when conductivity of scalp, skull and brain tissue is respectively increased by 2.5%
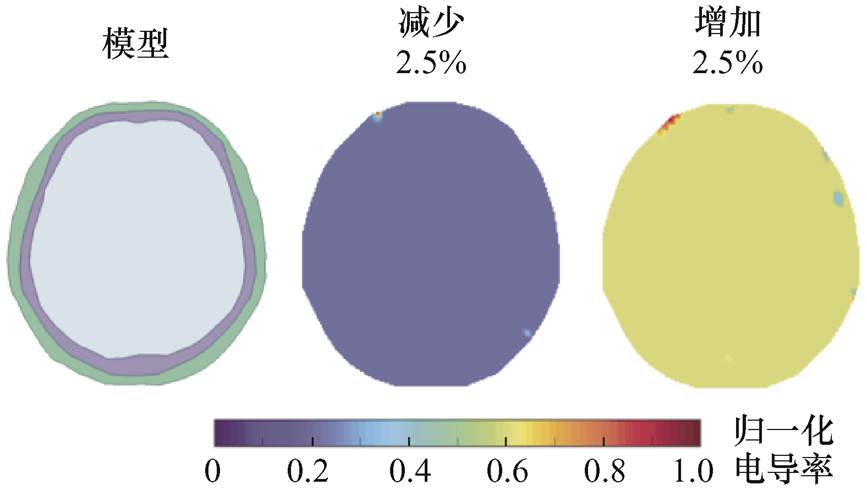
图13 颅骨电导率变化时健康样本重建图像
Fig.13 Reconstructed images of healthy samples with changes in skull conductivity
表2 三层电导率分别变化时重建图像的定量评价
Tab.2 Quantitative evaluation of reconstructed images when the conductivity of the three layers changes respectively
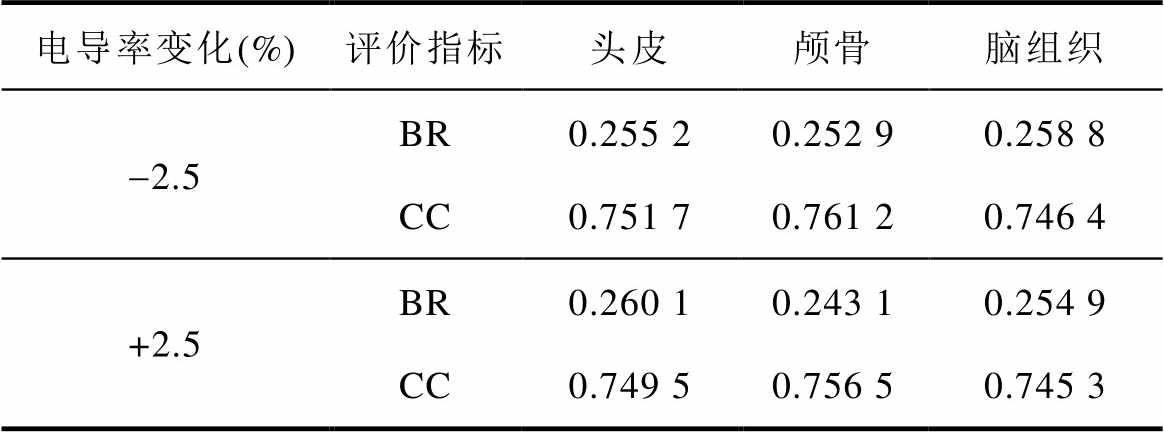
电导率变化(%)评价指标头皮颅骨脑组织 -2.5BR0.255 20.252 90.258 8 CC0.751 70.761 20.746 4 +2.5BR0.260 10.243 10.254 9 CC0.749 50.756 50.745 3
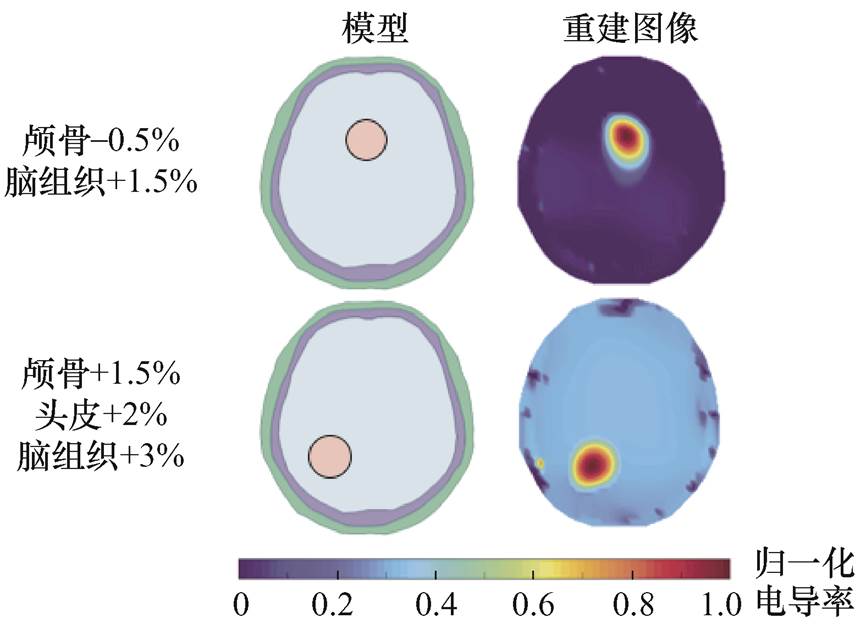
图14 多层电导率同时变化时脑出血重建图像
Fig.14 Reconstruct images of cerebral hemorrhage when conductivity of multiple layers changes
为进一步验证所提参考电压预测方法的可行性,进行了物理模型实验验证,颅脑模型和16电极的EIT系统如图15所示。制作了包含头皮层、颅骨层和脑组织层的三层颅脑模型,其电导率分别为0.44、0.013和0.15 S/m,并制作了电导率为0.71 S/m的琼脂模型来模拟脑出血。实验采用相对激励、相邻测量的方式,注入电流为1.25 mA。基于实验测量数据通过本文所提方法对参考电压进行了预测,其图像重建结果如图16所示。可以看出,从重建图像中可清晰辨别脑出血位置。

图15 颅脑模型和16电极的EIT系统
Fig.15 Head model and 16-electrode EIT system
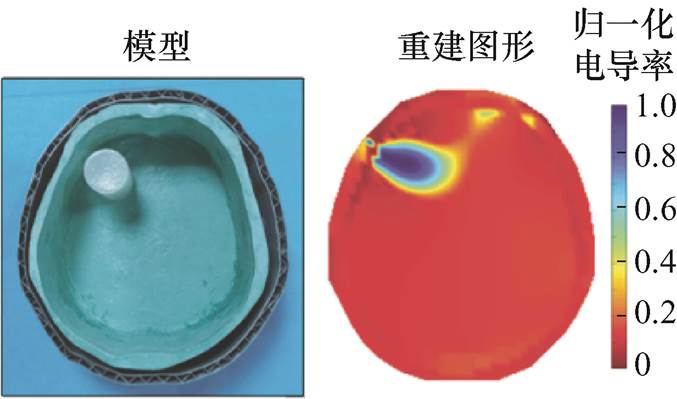
图16 基于物理模型实验数据的重建图像
Fig.16 Reconstructed image based on phantom experimental data
为了解决颅脑电阻抗层析成像过程中参考电压的获取问题,本文提出了基于全连接神经网络的参考电压预测方法。该方法有效建立了当前测量电压与参考电压之间的端到端映射,能够准确地预测出参考电压。在不同信噪比及头皮、颅骨和脑组织电导率分别发生变化时对所提方法进行了验证,并采用L1正则化方法进行图像重建。结果表明,所提方法在不同信噪比和一定电导率变化范围内可预测出较为准确的参考电压。利用预测的参考电压能够对出血样本、缺血样本和健康样本进行良好的差分图像重建,重建图像中目标物的大小和分布能够被清晰地辨别。因此,所提方法在生物医学领域具有较好的实际应用前景。
参考文献
[1] van den Berg L A, Koelman D L H, Berkhemer O A, et al. Type of anesthesia and differences in clinical outcome after intra-arterial treatment for ischemic stroke[J]. Stroke, 2015, 46(5): 1257-1262.
[2] 李云云, 屈洪党. 脑出血的诊断与治疗[J]. 中华全科医学, 2019, 17(2): 171-172. Li Yunyun, Qu Hongdang. Diagnosis and treatment of cerebral hemorrhage[J]. Chinese Journal of General Practice, 2019, 17(2): 171-172.
[3] 王昭昳, 张涛, 杨滨, 等. 基于径向基函数神经网络的脑损伤电阻抗成像仿真研究[J]. 中国医学装备, 2023, 20(3): 1-5. Wang Zhaoyi, Zhang Tao, Yang Bin, et al. Simulation study of electrical impedance imaging of brain injury based on RBF neural network[J]. China Medical Equipment, 2023, 20(3): 1-5.
[4] 李彩莲, 李元园, 刘国强. 基于磁声电技术的肺部组织成像仿真研究[J]. 电工技术学报, 2021, 36(4): 732-737. Li Cailian, Li Yuanyuan, Liu Guoqiang. Simulation of lung tissue imaging based on magneto-acousto- electrical technology[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 732-737.
[5] 曲洪一, 刘鑫, 王晖, 等. 磁共振成像磁体无源匀场改进策略及实验研究[J]. 电工技术学报, 2022, 37(24): 6284-6293. Qu Hongyi, Liu Xin, Wang Hui, et al. Improved strategy and experimental research on passive shimming in magnetic resonance imaging magnet[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6284-6293.
[6] 赵营鸽, 李颖, 王灵月, 等. 基于均值点展开的单变元降维法在EIT不确定性量化研究中的应用[J]. 电工技术学报, 2021, 36(18): 3776-3786.Zhao Yingge, Li Ying, Wang Lingyue, et al. The application of univariate dimension reduction method based on mean point expansion in the research of electrical impedance tomography uncertainty quanti- fication[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3776-3786.
[7] Ren Shangjie, Sun Kai, Tan Chao, et al. A two-stage deep learning method for robust shape reconstruction with electrical impedance tomography[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 69(7): 4887-4897.
[8] 付荣, 张新宇, 王子辰, 等. 基于V-ResNet的电阻抗层析成像方法[J]. 仪器仪表学报, 2021, 42(9): 279-287. Fu Rong, Zhang Xinyu, Wang Zichen, et al. Electrical impedance tomography method based on V-ResNet[J]. Chinese Journal of Scientific Instrument, 2021, 42(9): 279-287.
[9] 刘学超, 张涛, 章伟睿, 等. 脑脊液变化对脑出血电阻抗成像表征的影响研究[J]. 中国医学装备, 2022, 19(1): 26-30. Liu Xuechao, Zhang Tao, Zhang Weirui, et al. A study on the influence of the CSF changes on EIT representation of cerebral hemorrhage[J]. China Medical Equipment, 2022, 19(1): 26-30.
[10] 郭大龙, 尤富生, 代萌, 等. 适用于脑卒中筛查的电阻抗成像电极的比较研究[J]. 医疗卫生装备, 2014, 35(3): 19-22. Guo Dalong, You Fusheng, Dai Meng, et al. Comparative study of bio-electrodes applied to stroke screening in brain electrical impedance tomo- graphy[J]. Chinese Medical Equipment Journal, 2014, 35(3): 19-22.
[11] ZhangYijia, Chen Huaijin, Yang Lu, et al. A proportional genetic algorithm for image reconstruction of static electrical impedance tomography[J]. IEEE Sensors Journal, 2020, 20(24): 15026-15033.
[12] Denaï M A, Mahfouf M, Mohamad-Samuri S, et al. Absolute electrical impedance tomography (aEIT) guided ventilation therapy in critical care patients: simulations and future trends[J]. IEEE Transactions on Information Technology in Biomedicine: a Publication of the IEEE Engineering in Medicine and Biology Society, 2010, 14(3): 641-649.
[13] Shi Yanyan, Wu Yuehui, Wang Meng, et al. Image reconstruction of conductivity distribution with combined L1-norm fidelity and hybrid total variation penalty[J]. IEEE Transactions on Instrumentation and Measurement, 2022, 71: 4500412.
[14] 王琦, 张鹏程, 汪剑鸣, 等. 基于块稀疏的电阻抗成像算法[J]. 电子与信息学报, 2018, 40(3): 676-682. Wang Qi, Zhang Pengcheng, Wang Jianming, et al. Block-sparse reconstruction for electrical impedance tomography[J]. Journal of Electronics & Information Technology, 2018, 40(3): 676-682.
[15] 章伟睿, 张涛, 史学涛, 等. 基于差分迭代的电阻抗成像算法研究[J]. 电工技术学报, 2021, 36(4): 747-755. Zhang Weirui, Zhang Tao, Shi Xuetao, et al. An algorithm of electrical impedance tomography based on differential iteration[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 747-755.
[16] Hamilton S J, Hauptmann A. Deep D-bar: real-time electrical impedance tomography imaging with deep neural networks[J]. IEEE Transactions on Medical Imaging, 2018, 37(10): 2367-2377.
[17] 李晓南, 任雯廷, 刘国强, 等. 高分辨率磁共振电特性成像及脑肿瘤诊断初步研究[J]. 电工技术学报, 2021, 36(18): 3860-3866. Li Xiaonan, Ren Wenting, Liu Guoqiang, et al. Preliminary conductivity reconstruction by high- resolution magnetic resonance electrical properties tomography for brain tumor diagnosis[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(18): 3860-3866.
[18] Wang Zeying, Yue Shihong, Liu Xiaoyuan, et al. Estimating homogeneous reference frame for absolute electrical impedance tomography through measure- ments and scale feature[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 70: 1002812.
[19] Yu Hao, Wan Xingchen, Dong Zhongxu, et al. Estimation of reference voltages for time-difference electrical impedance tomography[J]. IEEE Transa- ctions on Instrumentation and Measurement, 2022, 71: 4506710.
[20] Wu Yang, Chen Bai, Liu Kai, et al. Shape reconstruction with multiphase conductivity for electrical impedance tomography using improved convolutional neural network method[J]. IEEE Sensors Journal, 2021, 21(7): 9277-9287.
[21] Shi Yanyan, Tian Zhiwei, Wang Meng, et al. Residual convolutional neural network-based stroke classification with electrical impedance tomography[J]. IEEE Transactions on Instrumentation and Measurement, 2022, 71: 4502911.
[22] Sangari A, Sethares W. Convergence analysis of two loss functions in soft-max regression[J]. IEEE Transactions on Signal Processing, 2016, 64(5): 1280-1288.
[23] 李星, 杨帆, 余晓, 等. 基于自诊断正则化的电阻抗成像逆问题研究[J]. 生物医学工程学杂志, 2018, 35(3): 460-467. Li Xing, Yang Fan, Yu Xiao, et al. Study on the inverse problem of electrical impedance tomography based on self-diagnosis regularization[J]. Journal of Biomedical Engineering, 2018, 35(3): 460-467.
[24] LiHaoting, Chen Rongqing, Xu Canhua, et al. Unveiling the development of intracranial injury using dynamic brain EIT: an evaluation of current reconstruction algorithms[J]. Physiological Measurement, 2017, 38(9): 1776-1790.
[25] Wendel K, Väisänen J, Seemann G, et al. The influence of age and skull conductivity on surface and subdermal bipolar EEG leads[J]. Computational Intelligence and Neuroscience, 2010, 2010: 397272-397278.
[26] Javaherian A, Movafeghi A, Faghihi R, et al. An exhaustive criterion for estimating quality of images in electrical impedance tomography with application to clinical imaging[J]. Journal of Visual Communication and Image Representation, 2013, 24(7): 773-785.
[27] 叶明, 李晓丞, 刘凯, 等. 一种基于U2-Net模型的电阻抗成像方法[J]. 仪器仪表学报, 2021, 42(2): 235-243.Ye Ming, Li Xiaocheng, Liu Kai, et al. Image reconstruction method for electrical impedanceto- mography using U2-Net[J]. Chinese Journal of Scientific Instrument, 2021, 42(2): 235-243.
Abstract Electrical impedance tomography (EIT) is a visualization techniquetoreconstruct conductivity distribution variations that reflect pathological changes in human tissues based on the boundary voltage measurement. Difference imaging is commonly used in the reconstruction to reduce modeling errors. Cerebral hemorrhage or ischemia can cause concentration changes of the intracranial ions, affecting the conductivity distribution. Consequently, the reference voltage obtained at a specific instant is inaccurate in the difference imaging. This paper proposesa reference voltage prediction method for brain EIT by fully connecting a neural network (FCNN). The reference voltage can be accurately predicted by establishing a nonlinear mapping between the measured and reference voltages.
Firstly, a three-layer brain model is constructed, including the scalp, skull, and brain tissue layers. The measured boundary voltage is used to construct the input matrix, and the true reference voltage is applied to construct the output matrix in the network. Anumber of training datasets are established to train the network. During the back-propagation of the loss function, an adaptive moment estimation algorithm is employed to update the parameters of FCNN. Then, the nonlinear relationship between the boundary measurement and the true reference voltage can be acquired, and the reference voltage can be predicted.
Simulation and experiments validate the proposed method. Compared with the true reference voltage, simulation results show that the voltage relative error ranges from 0% to 0.10% under the noise-free condition and 0% to 0.15% under the noisy condition. The reference voltage predicted by the proposed method well approaches the true reference voltage. Image reconstruction is performed based on the predicted reference voltage. The results show that the simulated stroke in the brain tissue layer can be reconstructed. The average blur radius of the reconstructed image increases, and the average correlation coefficient decreases gradually when the signal-to-noise ratio decreases. The feasibility of the proposed method is also tested when the conductivity of the scalp layer, skull layer, and brain tissue layer changes. It is found that the reconstructed image is very similar to the true conductivity distribution. The phantom experiment also validates the excellent performance of the proposed method.
The following conclusions can be drawn. (1) Due to the powerful mapping ability of FCNN, the proposed method can establish the nonlinear relationship between the measured boundary voltage and the true reference voltage in the brain EIT. (2) The difference between the predicted and true reference voltage is minor. The conductivity distribution of different models can be well reconstructed using the predicted reference voltage in the image reconstruction. (3) The proposed method only requires boundary measurement to obtain the information of reference voltage, avoiding the reference voltage calibration problem.
keywords:Electrical impedance tomography, image reconstruction, reference voltage, neural network
DOI: 10.19595/j.cnki.1000-6753.tces.230766
中图分类号:TH 772A
国家重点研发计划项目(2021YFC1200104)、国家自然科学基金项目(52277234)和河南省高校科技创新人才项目(21HASTIT018)资助。
收稿日期 2023-05-25
改稿日期 2023-10-07
施艳艳 女,1982年生,博士,教授,研究方向为电阻抗断层扫描及其临床应用。E-mail: yyshi113@hotmail.com
王 萌 男,1980年生,博士,教授,研究方向为电阻抗层析成像和无线电能传输技术。E-mail: wangmeng@htu.edu.cn(通信作者)
(编辑 郭丽军)