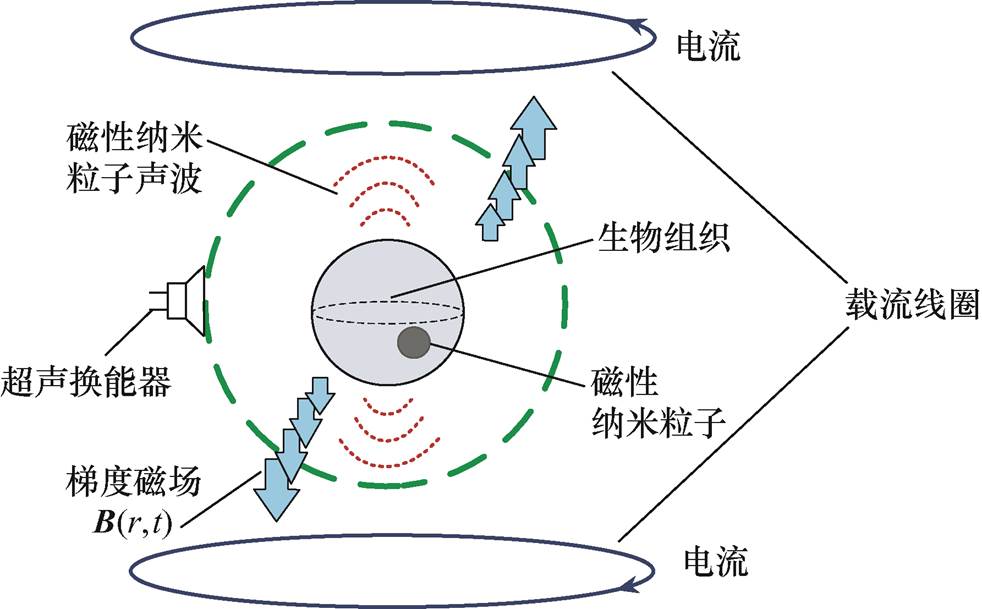
图1 MACT-MI系统结构
Fig.1 System architecture of MACT-MI
摘要 感应式磁声磁粒子浓度成像(MACT-MI)是一种基于磁声耦合效应的磁性纳米粒子(MNPs)浓度成像新方法。由于其磁声信号的信噪比低,导致系统成像质量不佳,该文提出一种改善MACT-MI信噪比的新思路:首先,基于经典目标场法(TFM)设计梯度线圈的思路,将最小化磁场相对误差定义为适应度函数,并采用鲸鱼优化算法对电流密度系数进行优化,设计了一种结构灵活、激励简单的高质量梯度磁场线圈;其次,为研究梯度磁场空间分布特征对MACT-MI的影响,该文构建不同的MNPs分布模型,并利用多物理场仿真软件COMSOL对MACT-MI的物理过程进行数值求解,得到成像区域的磁力和声压分布。仿真结果表明,磁力和声压的有效波动范围与梯度磁场均匀空间的大小成正比,且随着均匀空间的缩小,磁力和声压的峰值也随之衰减,通过提高磁场的均匀度可以有效提高磁声信号的信噪比,改善系统成像质量。研究结果可为成像装备的设计以及MACT-MI的后续实验应用提供研究基础。
关键词:磁声磁粒子浓度成像 目标场法 梯度磁场 均匀空间
感应式磁声磁粒子浓度成像(Magneto-Acoustic Concentration Tomography of magnetic nanoparticles with Magnetic Induction, MACT-MI)是一种基于磁声耦合效应的磁性纳米粒子(Magnetic Nanoparticles, MNPs)浓度成像新方法。该技术融合了电磁、超声的优势,兼具无创、对比度好、灵敏度高以及空间分辨率好等优点,有望能进一步提高成像分辨率,为肿瘤治疗提供依据,并对MNPs进行定量检测[1]。然而在前期的研究中发现,当前MACT-MI产生的磁声信号微弱,不利于实验工作的开展,其主要原因在于MNPs所受磁力较小,而磁力的大小受MNPs浓度及其所处背景磁场等因素的影响[2]。针对磁粒子所处静磁场进行分析,可采用高强度超导磁体[3],也可通过优化永磁体结构[4-5]或匀强磁场线圈使磁场分布更为均匀[6],从而使MNPs的磁化强度增大,进而提升信噪比。除了受静磁场影响外,MNPs的振动频率及大小由梯度磁场决定,而在该方面尚未有文献对其进行深入研究,因此,本文从梯度磁场的均匀度入手,通过设计一种高质量梯度磁场线圈以改善MNPs所受磁力,从而提高信噪比。
梯度线圈的设计方法可分为离散电流技术和分布电流技术。对于离散电流技术,矩阵式线圈作为一种新的线圈形式成为近年来的研究热点[7],在文献[8]中,作者通过设计一种矩阵式梯度线圈用于MACT-MI系统,在降低激励的同时提高梯度磁场的均匀度,然而该线圈结构复杂,所需激励较多,难以开展进一步实验。对于分布电流技术,目标场法(Target Field Method, TFM)具有能够克服线圈尺寸的限制并获得高线性磁场或均匀场的优势而受到广大研究者青睐。TFM首先由R.Turner提出[9],并经过H. Liu[10]、L. K. Forbes[11]等改进以用于设计双平面梯度线圈;Chen Shanshan等[12]于2017年针对21.3 MHz的小动物磁共振成像(Magnetic Resonance Imaging,MRI)提出一种新的TFM并设计了11对有源匀场线圈,说明此方法也适用于双平面梯度线圈的设计;Wang Jing等[13]于2020年将TFM与粒子群优化(Particle Swarm Optimization, PSO)相结合,提出了适用于MEG系统的双平面线圈设计方案。Zhao Fengwen等[14]于2021年针对x梯度线圈和z梯度线圈,提出了两种新的具有单傅里叶级数展开的电流密度函数,使得场线性度提高了一个数量级。Ding Zhongya等[15]于2022年提出了一种迭代优化算法来优化双平面线圈边长,并在40 cm3的体积上产生误差在1%以内的均匀场和梯度场。以上研究都充分表明了TFM设计双平面梯度线圈具有非常高的灵活性。此外,TFM线圈结构更加简单、灵活,使用条件方便、安全,能够适应各种不同情况的需求。
本文针对MACT-MI磁声信号的信噪比低的问题,设计了一种结构灵活、激励简单的高质量梯度磁场线圈以改善MNPs所受磁力。此外,本文基于不同的梯度磁场分布特征构建了不同的MNPs分布模型,并采用多物理场仿真软件COMSOL对MACT- MI的物理过程进行求解,得到成像区域的磁力、声压分布,研究了梯度磁场空间分布特征对MACT-MI的影响。
MACT-MI系统结构如图1所示,在MACT-MI中,上、下平面的激励线圈产生z方向的时变梯度磁场,位于成像区域的MNPs被磁化,粒子在磁场力的作用下被激发振动而产生声波,通过超声换能器收集检测该信号获取声压信息,进而根据声压信息与MNPs浓度之间的关系,采用时间反演及有限差分法重构数量浓度分布图。

图1 MACT-MI系统结构
Fig.1 System architecture of MACT-MI
在饱和磁化状态下的MNPs所受磁力f 可描述为[1]
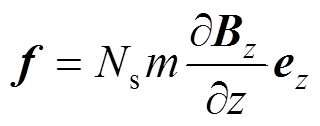 (1)
(1)
式中,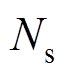 为MNPs的数量浓度;m为其固有磁矩;
为MNPs的数量浓度;m为其固有磁矩;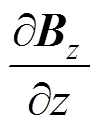 为z方向的梯度磁场;
为z方向的梯度磁场;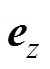 为z方向的单位向量。以磁力散度
为z方向的单位向量。以磁力散度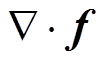 为声源项,由线性声压波动方程可求解无界声场的解析解为[2]
为声源项,由线性声压波动方程可求解无界声场的解析解为[2]
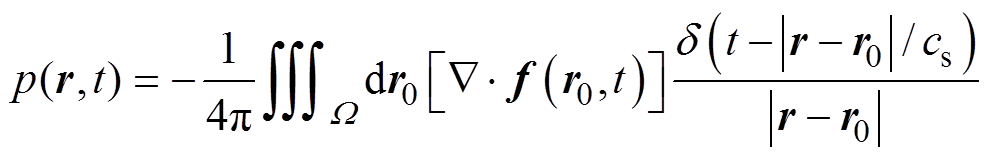 (2)
(2)
式中,r为声场中的任意一点;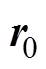 为源点位置;
为源点位置;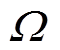 为空间积分区域;
为空间积分区域;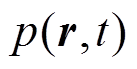 为声压场的时空分布;
为声压场的时空分布;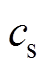 为生物组织内的声速;
为生物组织内的声速;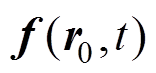 为磁性纳米粒子在源点位置受到的磁力;
为磁性纳米粒子在源点位置受到的磁力;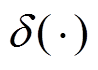 为冲激函数。
为冲激函数。
对于同种类处于饱和磁化状态的磁性纳米粒子,其固有磁矩大小为常数,因此相同数量浓度的MNPs,其所受磁力大小取决于外部磁场梯度,而磁力的大小影响着声压信号的强弱,进而决定MACT- MI的成像质量,因此外部梯度磁场的重要性不言而喻。前期的研究表明[8],相较于利用Maxwell线圈产生MACT-MI所需的0.1 T/m梯度磁场,矩阵式线圈可以在降低激励的同时产生更加均匀的梯度磁场,均匀度的提高使得MNPs所受磁力曲线更为平滑稳定,有利于提高成像质量。然而该线圈结构较为复杂,所需激励要求较高,使其难以进一步实验验证。因此,设计一种结构灵活、激励简单的高质量梯度线圈对推进MACT-MI的临床应用具有重要现实意义。
将上述MACT-MI系统结构简化后如图2所示,双平面线分别处于z=±a处所在平面内,且线圈半径满足R0 R
R Rm。
Rm。
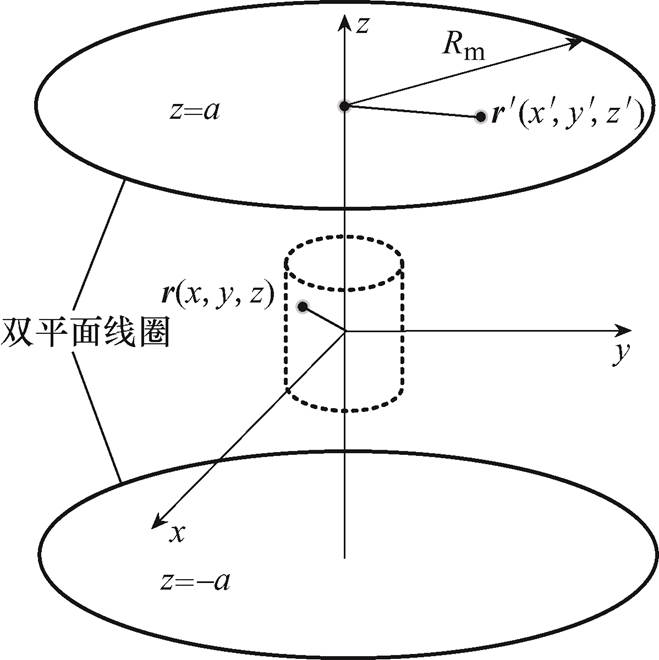
图2 双平面线圈系统结构
Fig.2 System structure of bi-planar coils
空间一点r(x, y, z)处的磁场值B(r)可由磁矢量势A(r)的旋度求得
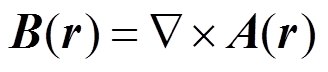 (3)
(3)
式中,A(r)为线圈的电流密度J产生的磁矢量势,可以表示为
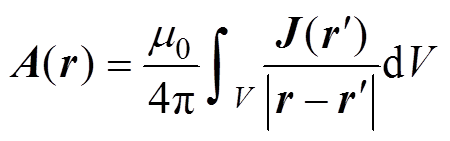 (4)
(4)
式中,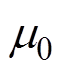 为真空磁导率;
为真空磁导率;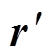 为线圈表面上源点的位置矢量。
为线圈表面上源点的位置矢量。
由于双平面线圈的电流密度分布在x-y平面,因此电流密度z分量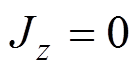 且满足电流连续方程
且满足电流连续方程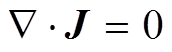 。可以定义矢量势
。可以定义矢量势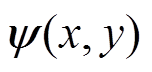 为流函数[16-18]来描述电流密度在线圈平面的分布轨迹,则有
为流函数[16-18]来描述电流密度在线圈平面的分布轨迹,则有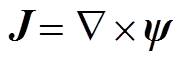 ,可以得到
,可以得到
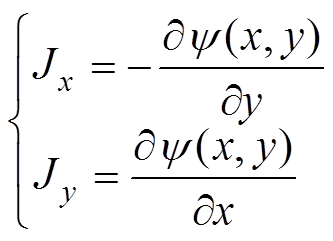 (5)
(5)
故式(2)可简化为
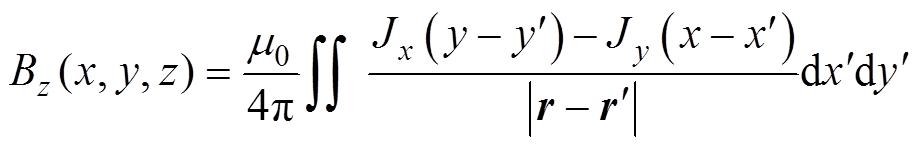 (6)
(6)
在极坐标系下,x-y平面中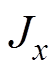 、
、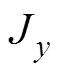 将由
将由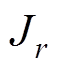 、
、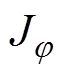 替代,并引入三角函数作为平面电流密度的基函数
替代,并引入三角函数作为平面电流密度的基函数
进行傅里叶预处理[19],即
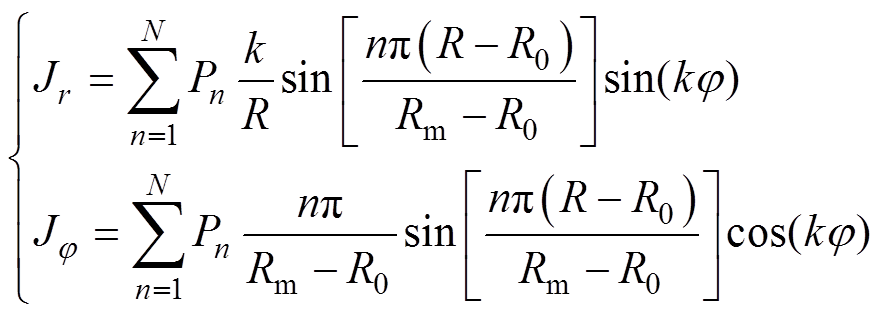 (7)
(7)
式中,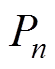 为电流密度级数的第n项展开系数;N为展开项阶数。k值决定梯度线圈的类型,当k=0时,
为电流密度级数的第n项展开系数;N为展开项阶数。k值决定梯度线圈的类型,当k=0时,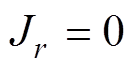 ,用于设计纵向梯度线圈;当k=1时,用于设计横向梯度线圈。本文所设计线圈为z梯度线圈,故k取0。将式(7)代入式(6)中可得极坐标系下任意场点
,用于设计纵向梯度线圈;当k=1时,用于设计横向梯度线圈。本文所设计线圈为z梯度线圈,故k取0。将式(7)代入式(6)中可得极坐标系下任意场点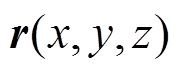 处的磁场值为
处的磁场值为
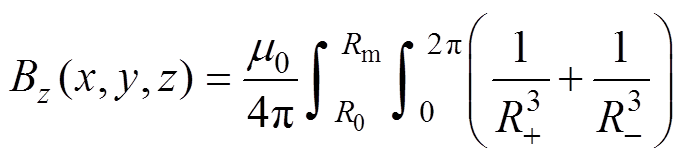
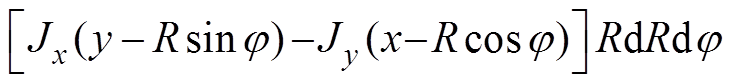 (8)
(8)
其中
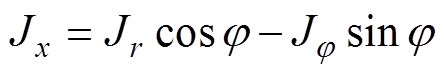
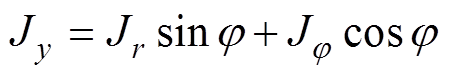
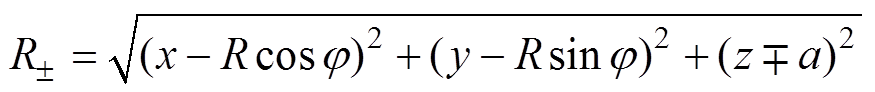
式(8)可化简为
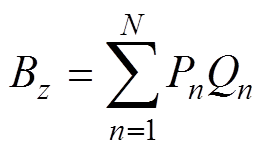 (9)
(9)
式中,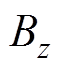 为设定的各目标场点处z方向的磁场分量;
为设定的各目标场点处z方向的磁场分量;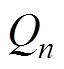 为关于源点
为关于源点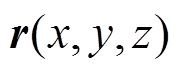 的函数,将各目标场点代入式(9)得到以下形式的方程组
的函数,将各目标场点代入式(9)得到以下形式的方程组
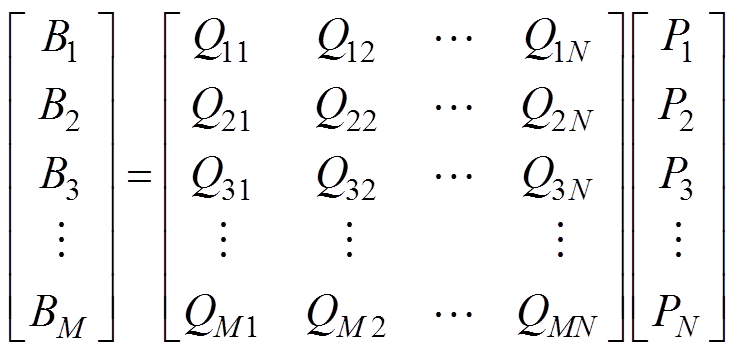 (10)
(10)
简化为
其中
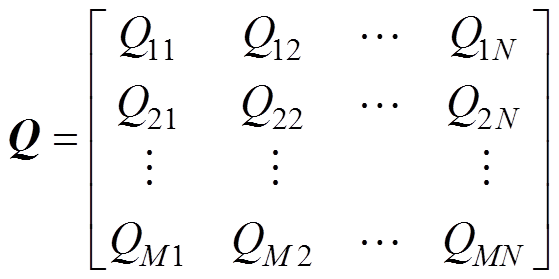
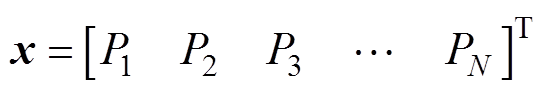
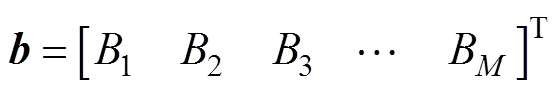
式中,Q为M×N的矩阵。
对上述方程组求解可得电流密度系数Pn,从而确定电流密度表达式。由于目标场点数M远大于谐波次数N,因此式(11)为典型的超定方程组,通常引入广义逆矩阵来求得最小二乘解。
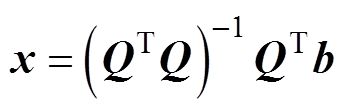 (12)
(12)
传统TFM设计的梯度线圈场精度与目标场点数M和三角函数阶数N有关,为获得较高的精度应尽可能增大其值,然而这将大大增加计算时间;而且通过离散流函数的等值线来表示连续电流密度会造成相关误差。为避免上述问题,本文将智能优化算法引入TFM中,通过优化电流密度系数来确定流函数。
鲸鱼优化算法(Whale Optimization Algorithm, WOA)是一种基于全局搜索的智能寻优算法,本文利用文献[20]中描述的WOA实现上述优化过程。在N维搜索区域中有K个鲸鱼,第i个鲸鱼的位置定义为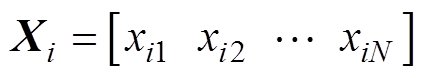 ,当前种群最优解的位置定义为
,当前种群最优解的位置定义为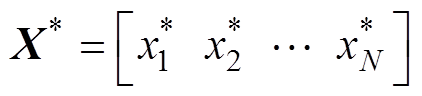 ,第i个鲸鱼与当前最优解的距离定义为D(见式(13)),每个鲸鱼根据当前最优解更新自身位置,见式(14)。
,第i个鲸鱼与当前最优解的距离定义为D(见式(13)),每个鲸鱼根据当前最优解更新自身位置,见式(14)。
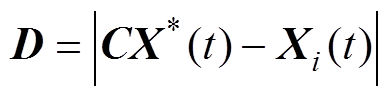 (13)
(13)
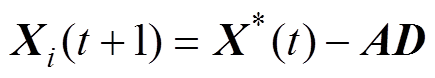 (14)
(14)
式中,t为当前迭代次数;A和C为系数向量,定义为
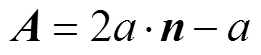 (15)
(15)
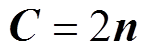 (16)
(16)
式中,n为[0,1]区间均匀分布的随机数;a为收敛因子,其元素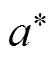 在迭代过程中从2线性衰减到0,定义为
在迭代过程中从2线性衰减到0,定义为
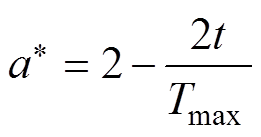 (17)
(17)
根据式(12)求得x的显式解作为边界条件以限制搜索空间范围,根据目标场区域的梯度要求定义适应度函数,这里取场点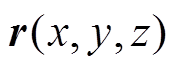 处与x-y平面中心
处与x-y平面中心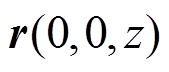 处磁场值的最大误差构造适应度函数F,并以F
处磁场值的最大误差构造适应度函数F,并以F 5%作为迭代停止条件。
5%作为迭代停止条件。
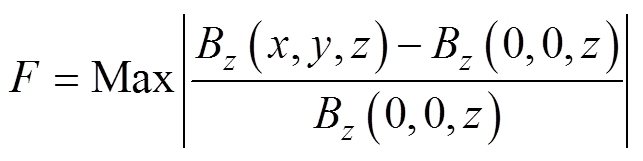 (18)
(18)
式(18)中的Bz(x, y, z)通过以下步骤求得:由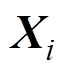 求得当前流函数表达式,并对流函数离散化求其等值线轮廓,再利用Biot-Savart定律计算各等值线共同作用于r (x, y, z)点所产生的Bz(x, y, z)。整个优化设计流程如图3所示。
求得当前流函数表达式,并对流函数离散化求其等值线轮廓,再利用Biot-Savart定律计算各等值线共同作用于r (x, y, z)点所产生的Bz(x, y, z)。整个优化设计流程如图3所示。
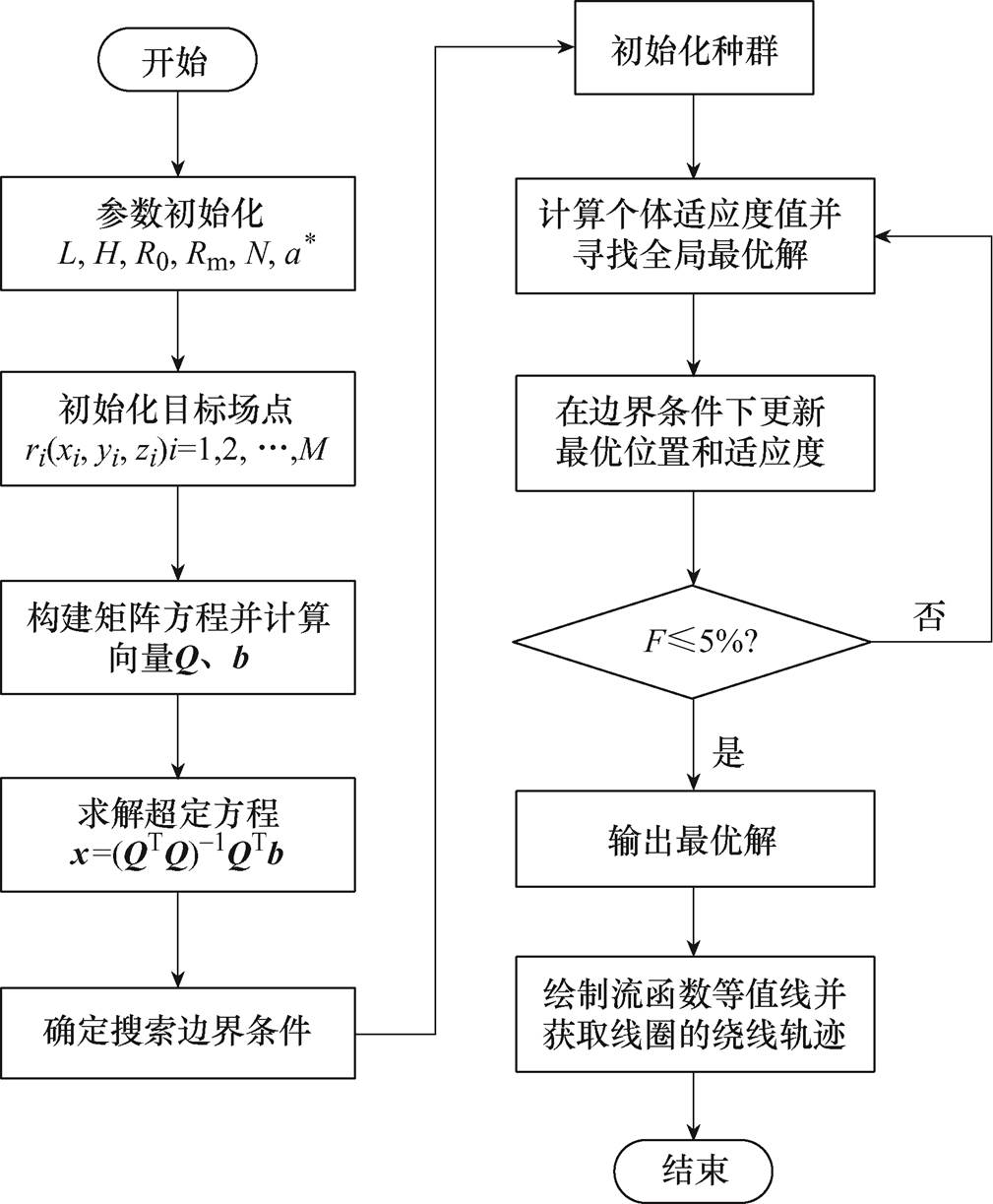
图3 TFM线圈优化设计流程
Fig.3 Optimized design flow for TFM coils
利用Matlab软件实现线圈的优化和设计,得到线圈最终绕线轨迹,并在有限元仿真软件COMSOL中磁场分析模块计算线圈的磁场分布。本文重点研究梯度磁场的分布空间,为使结果对比清晰,在底面半径为50 mm、高为100 mm的圆柱体研究域空间中,设置底面半径30 mm、高60 mm的圆柱体作为目标场,满足MACT-MI的目标梯度设为0.1 T/m[2],目标场点ri (xi, yi, zi) 设为x, y, z方向上[0, 30 mm]之间每6 mm取一点,总数为216个,线圈半径R0= 20 mm,Rm=100 mm;为与传统梯度线圈比较,分别在两平面间距为H11=100 mm,H12=200 mm和H13=100 mm的情况下设计梯度线圈。本文中电流密度展开阶数为5,因此WOA中的搜索区域N为5维,在对50个鲸鱼个体进行20次迭代后得到最优设计结果,将所有电流密度项系数Pn均除以P1进行归一化处理,在上述三种情况下所获得的各系数之间的关系见表1。
mm的情况下设计梯度线圈。本文中电流密度展开阶数为5,因此WOA中的搜索区域N为5维,在对50个鲸鱼个体进行20次迭代后得到最优设计结果,将所有电流密度项系数Pn均除以P1进行归一化处理,在上述三种情况下所获得的各系数之间的关系见表1。
表1 电流密度系数归一化处理
Tab.1 Current density factors normalization
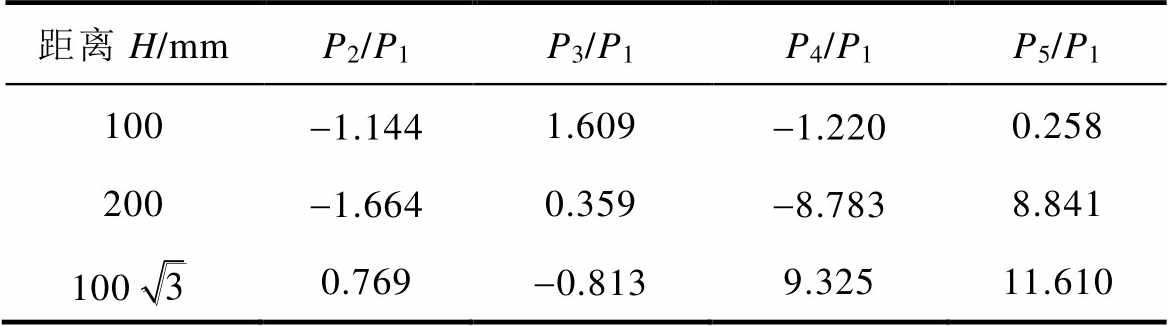
距离H/mmP2/P1P3/P1P4/P1P5/P1 100-1.1441.609-1.2200.258 200-1.6640.359-8.7838.841 1000.769-0.8139.32511.610
图4所示为间距H=200 mm的TFM线圈设计结果。在线圈轮廓图4a中以红色表示线圈电流正向,蓝色表示反向,上、下平面线圈结构对称,电流大小相等、方向相反;在研究域中,取点A (0 mm, 0 mm, -50 mm) 到点B (0 mm, 0 mm, 50 mm) 的截线研究磁场梯度∂Bz/∂z的变化,如图4b所示,同时为了说明本文优化方法的有效性,与优化前的线圈梯度变化进行对比,可以看出优化后的梯度均匀区间远大于优化前的线圈。为进一步研究空间中梯度磁场的质量,本文以场不均匀度e1和线性空间偏差e2两个参数作为评估标准[13],其值越小代表磁场质量越高,线圈性能越好。其中,e1和e2表达式为
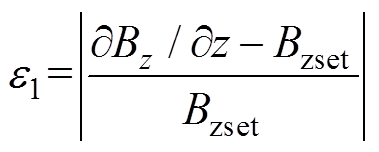 (19)
(19)
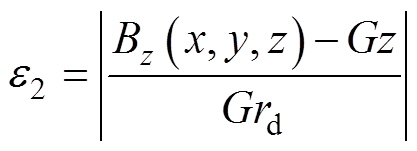 (20)
(20)
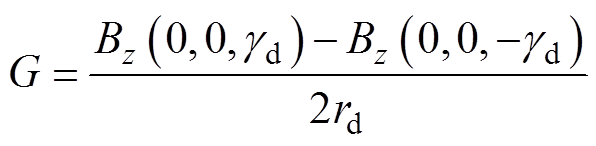 (21)
(21)
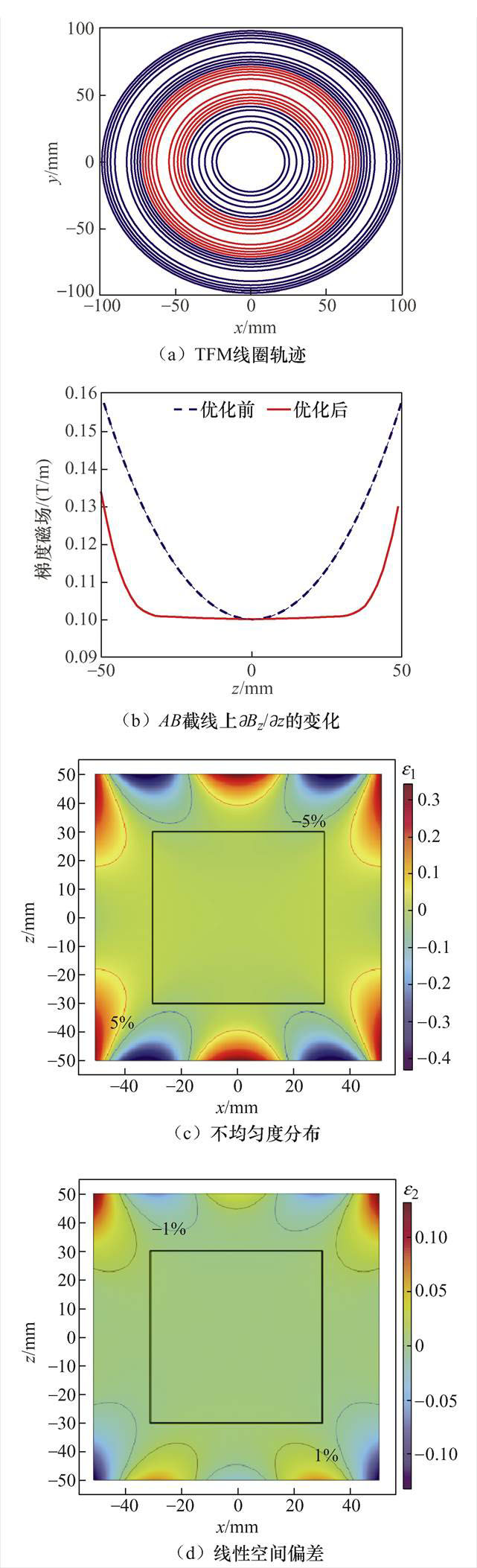
图4 TFM线圈轨迹及其梯度磁场和误差分布
Fig.4 TFM coil trajectory and its gradient magnetic field and error distribution plot
式中,Bzset为目标梯度;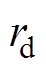 为研究域底面半径。
为研究域底面半径。
在图4c、图4d中,以边长为60 mm的黑色线框表示目标场所在区域,本文所设计的梯度线圈在目标场内的不均匀度及线性空间偏差均能保持在误差允许范围内,线圈性能满足设计需要。
传统纵向梯度线圈仅需结构对称的上下两组线圈,通以大小相等、方向相反的电流,即可在中心区域产生梯度磁场。进一步地,为表明本线圈的优势所在,在同等条件下分别与三种相同尺寸(Rm=100 mm)、不同距离(H21=Rm、H22=2Rm和H23=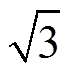 Rm)的传统梯度线圈进行对比。图5a为目标场区域内AB截线上∂Bz/∂z的变化曲线:通过对比可以发现,在不同距离下,TFM线圈在截线AB处的磁场梯度均能稳定在目标梯度值附近,而传统梯度线圈中随着距离的变化梯度磁场发生较大波动,梯度值稳定在0.1 T/m的范围相对较小;在xOz截面中,以场不均匀度e1
Rm)的传统梯度线圈进行对比。图5a为目标场区域内AB截线上∂Bz/∂z的变化曲线:通过对比可以发现,在不同距离下,TFM线圈在截线AB处的磁场梯度均能稳定在目标梯度值附近,而传统梯度线圈中随着距离的变化梯度磁场发生较大波动,梯度值稳定在0.1 T/m的范围相对较小;在xOz截面中,以场不均匀度e1 5%的空间范围大小来评估各线圈是否满足所需目标磁场[13],并以e1
5%的空间范围大小来评估各线圈是否满足所需目标磁场[13],并以e1 1%的区域作为满足MACT-MI成像区域来评估各线圈的性能[2, 8]。从图5b和图5c中可以看出,在H=100 mm和H=200 mm时,传统梯度线圈所产生的梯度场尚不能满足目标区域内5%的误差;当H=100
1%的区域作为满足MACT-MI成像区域来评估各线圈的性能[2, 8]。从图5b和图5c中可以看出,在H=100 mm和H=200 mm时,传统梯度线圈所产生的梯度场尚不能满足目标区域内5%的误差;当H=100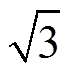 mm时,传统梯度线圈成为典型的Maxwell线圈,其产生的梯度场最大误差为3%,而相同条件下,TFM线圈的最大误差仅为1%;此外,在不同距离下TFM线圈所产生梯度磁场误差小于1%的均匀空间范围均大于传统梯度线圈。
mm时,传统梯度线圈成为典型的Maxwell线圈,其产生的梯度场最大误差为3%,而相同条件下,TFM线圈的最大误差仅为1%;此外,在不同距离下TFM线圈所产生梯度磁场误差小于1%的均匀空间范围均大于传统梯度线圈。
通过以上分析可以看出,TFM线圈能够在不受系统结构限制的前提下,产生MACT-MI所需的梯度磁场,且同等条件下可以产生更大尺寸的均匀区域以增加研究对象的运动范围,这一特点使得MACT-MI的系统结构具有更高的自由度的同时,对于线圈的散热设计也提供了便利条件,为进一步开展实验研究奠定基础。
文献[8]所设计的矩阵式线圈在产生较高质量梯度磁场的同时,需要满足一系列复杂条件,包括四种激励源、74个激励线圈以及各线圈之间的距离要求等,这些限制条件使得该线圈难以开展进一步的实验验证。而本文设计的梯度线圈可以有效解决以上问题:以上文所设计的Rm=100 mm、H=200 mm梯度线圈为例,其规格参数见表2,并与矩阵式梯度线圈规格进行对比,可以看出本文所设计的梯度线圈在保证高质量梯度磁场的前提下,线圈数量减少了近30%,线圈匝数减少了约65%,线圈尺寸缩小了84%,最大电流降低了约22%,线圈间距由86 mm提升至200 mm,大大增加了研究域的可操作空间范围。因此,本文所设计的线圈能够有效降低线圈数量及对激励源的要求,此外,简单的线圈结构便于生产制造,为进一步开展实验提供有利条件。
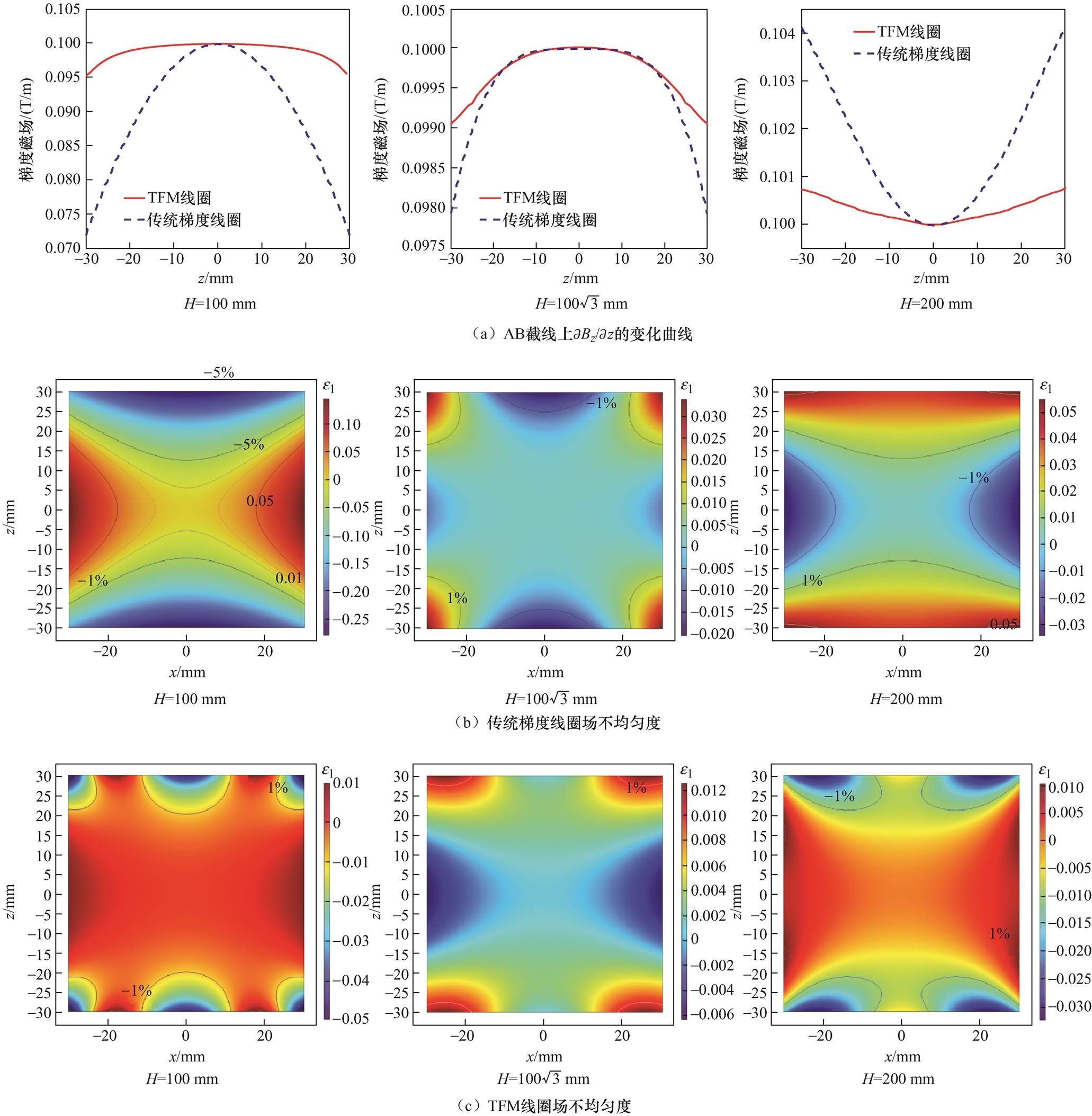
图5 TFM线圈与传统梯度线圈结果对比
Fig.5 Comparison of TFM coils with traditional gradient coils
在研究MACI-MI的成像过程中,利用多物理场仿真软件COMSOL建立如图6a所示的模型,该模型为半径80 mm、高160 mm的圆柱体,用于模拟生物组织,并将其相对磁导率设为1;其内部嵌入半径为5 mm的球体以模拟MNPs集群,其参数取自水溶性超顺磁性纳米颗粒EMG304(Ferrotec(USA)Corporation),其参数见表3,MNPs的浓度是影响磁力的一个重要因素,理论上浓度越大越好,但是考虑到MACT-MI最终的应用场合为活体实验,因此在实际使用时粒子的浓度不能过高。通过文献[21]可知,EMG304溶液的铁含量已经超过了FDA所批准铁含量,在实验时需要将其稀释,故在仿真中设定MNPs浓度为1×1015 /mL。
表2 矩阵式线圈与TFM线圈对比
Tab.2 Matrix coils compared to TFM coils
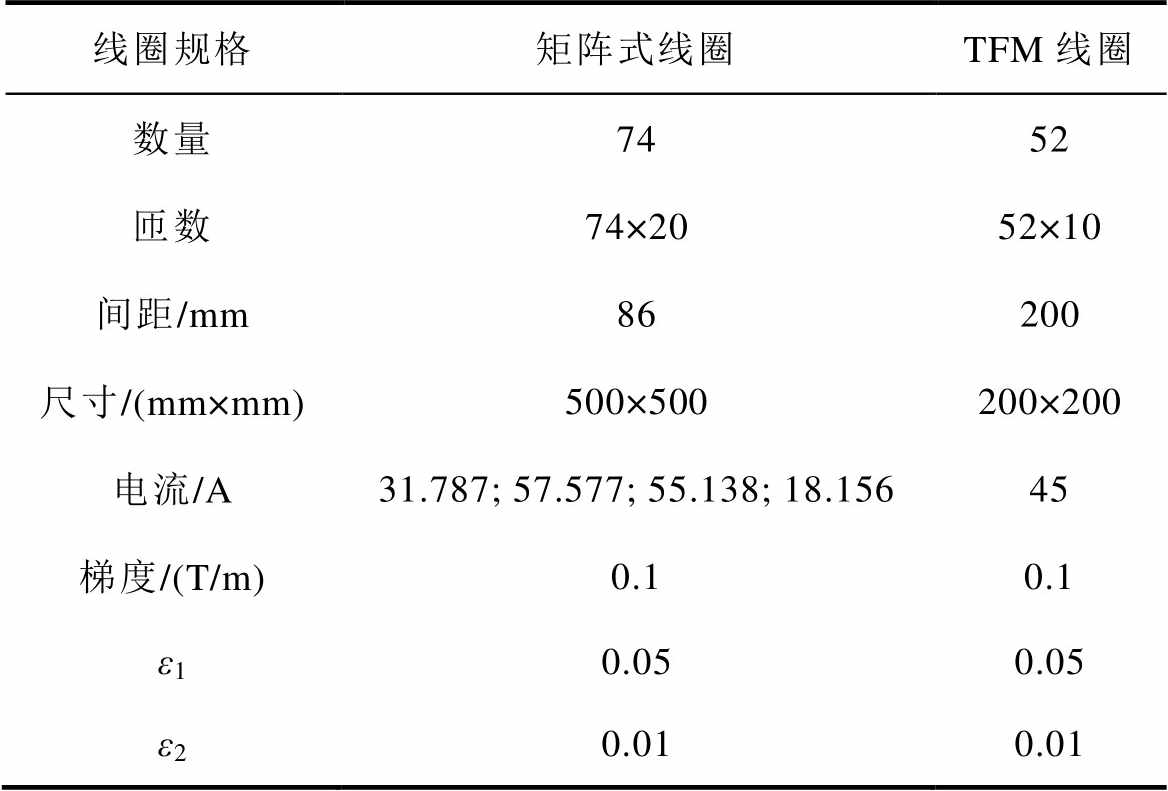
线圈规格矩阵式线圈TFM线圈 数量7452 匝数74×2052×10 间距/mm86200 尺寸/(mm×mm)500×500200×200 电流/A31.787; 57.577; 55.138; 18.15645 梯度/(T/m)0.10.1 ε10.050.05 ε20.010.01

图6 生物组织及MNPs模型
Fig.6 Models of biological tissues and MNPs
为研究梯度磁场空间分布特征对MACT-MI成像过程的影响,本文在此基础上建立了三种粒子群模型,分别在均匀梯度场(TFM线圈中H=100 mm)和不均匀梯度场(传统梯度线圈中H=100 mm)两种情况下研究不同区域的磁力和声压分布情况。
表3 EMG 304规格
Tab.3 Specifications for EMG 304
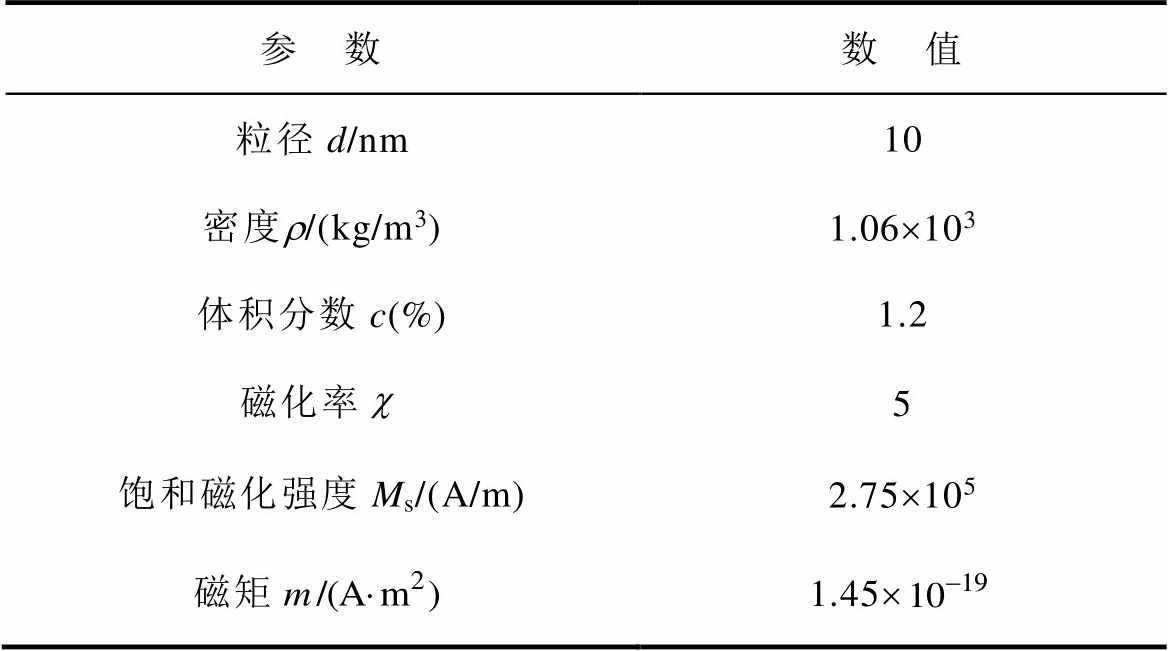
参 数数 值 粒径d/nm10 密度r/(kg/m3)1.06´103 体积分数c(%)1.2 磁化率5 饱和磁化强度Ms/(A/m)2.75´105 磁矩1.45´
区别于传统的单一粒子模型,为研究不同区域的MACT-MI成像效果,需要在不同位置放置MNPs并研究每个集群的磁力变化情况。因此,本文构建了不同数量及位置的MNPs模型,如图6b所示,该粒子集群共6个,沿着CD截线(点C (0 mm, -50 mm, 28 mm) 到点D(0 mm, 50 mm, 28 mm))均匀分布并且关于xOz平面对称,为了研究CD截线上磁力的连续变化曲线,在粒子群关于yOz平面对称处构建如图6c所示的圆柱体MNPs模型,分别在均匀场和不均匀场中对以上两种粒子群进行MACT-MI正问题求解。两种梯度场下各粒子群沿CD截线的磁力变化曲线如图7所示。通过对比可以发现,在图7a所示不均匀场中,不同位置的MNPs集群的磁力各不相同,其变化规律为:靠近中间位置的MNPs磁力最大,随着距离的偏移,所受磁力逐渐衰减;而在图7b均匀场中,各MNPs集群所受磁力的大小并无明显差别。
由于结构对称的梯度线圈会在其中心区域产生零磁场,为了更加清楚地研究不同区域MNPs的磁力及声压变化情况,本文在高度为20~30 mm处建立半径为50 mm、高为10 mm的圆柱形粒子群,如图6d所示。其中,截线CD同样适用于该圆柱体,根据式(1)计算该截线及截面上磁力变化情况,并比较不同梯度场下的区别。由于两种线圈所产生的梯度磁场分布范围不同,导致MNPs所受磁力随着梯度磁场的变化而变化,由图8可以看出,在均匀场中,CD截线上的磁力更加平滑、均匀,而不均匀场中,其磁力由中点向两边快速衰减,这是由于不均匀场中梯度磁场均匀空间分布范围的缩小导致的。
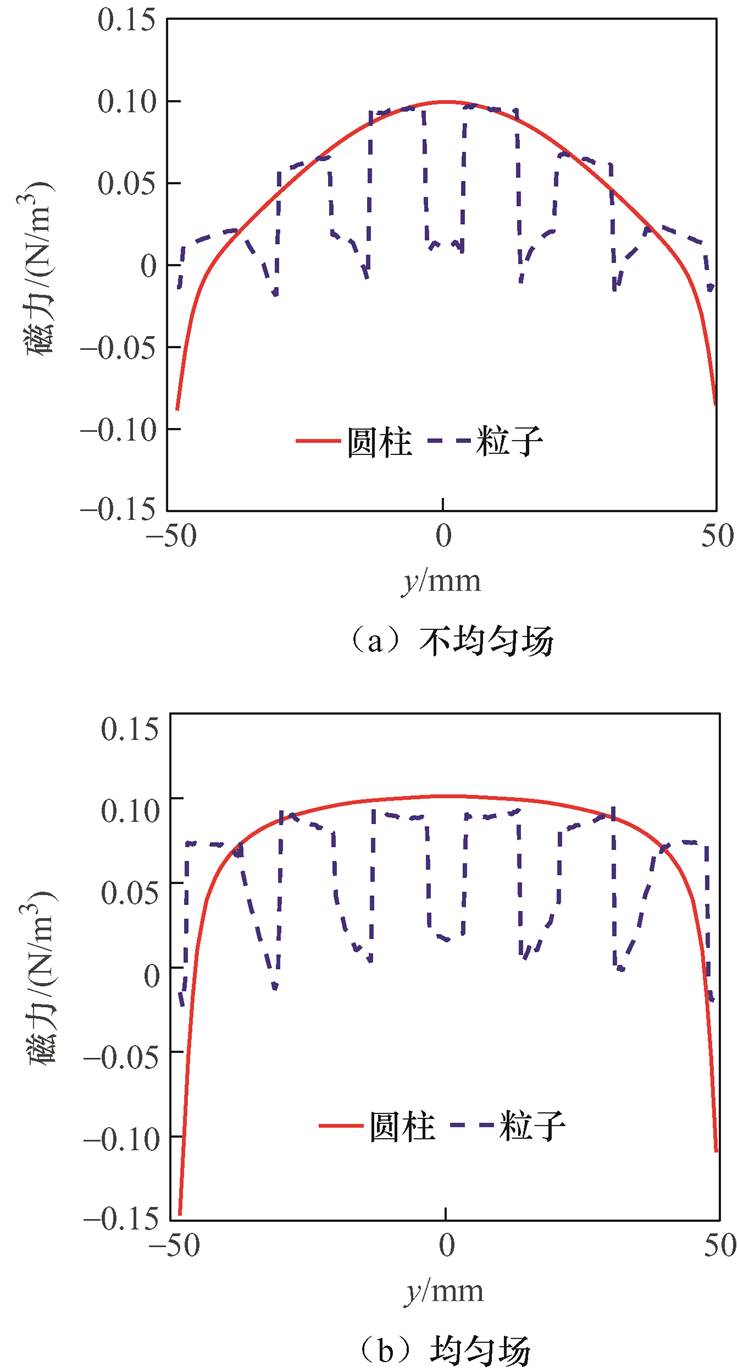
图7 磁力变化曲线
Fig.7 Curves of magnetic force
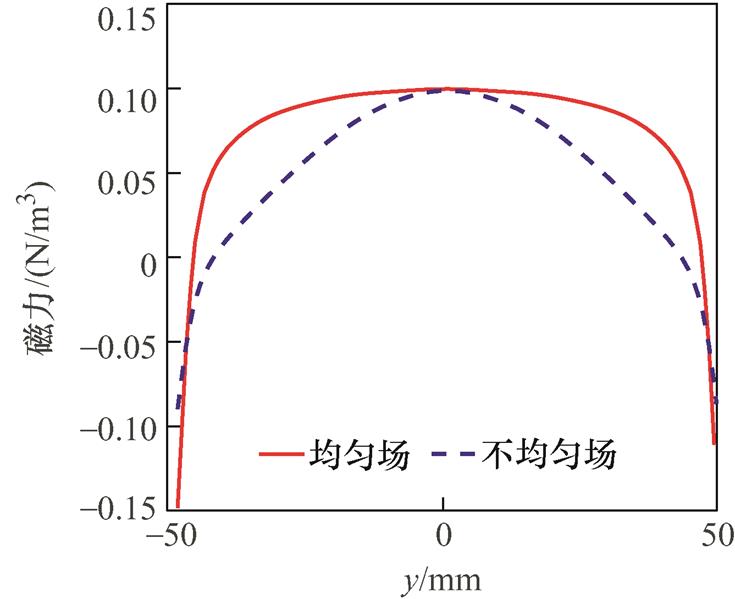
图8 CD截线处磁力变化曲线
Fig.8 Magnetic force change curve at the CD intercept
在CD截线处构建xOy截面,并以5%变化范围(如式(22)所示)为评估标准,研究两种梯度场下磁力分布情况,如图9所示。在图9a不均匀场中MNPs所受磁力随着梯度场均匀范围的缩小,其磁力稳定分布范围大大减小,而在图9b均匀场中MNPs所受磁力稳定分布范围则较大。
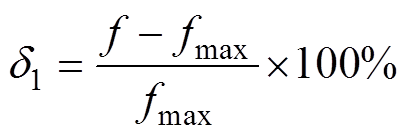 (22)
(22)
式中,f为磁力;fmax为磁力峰值;d1即为磁力变化范围,这里取d1=5%。
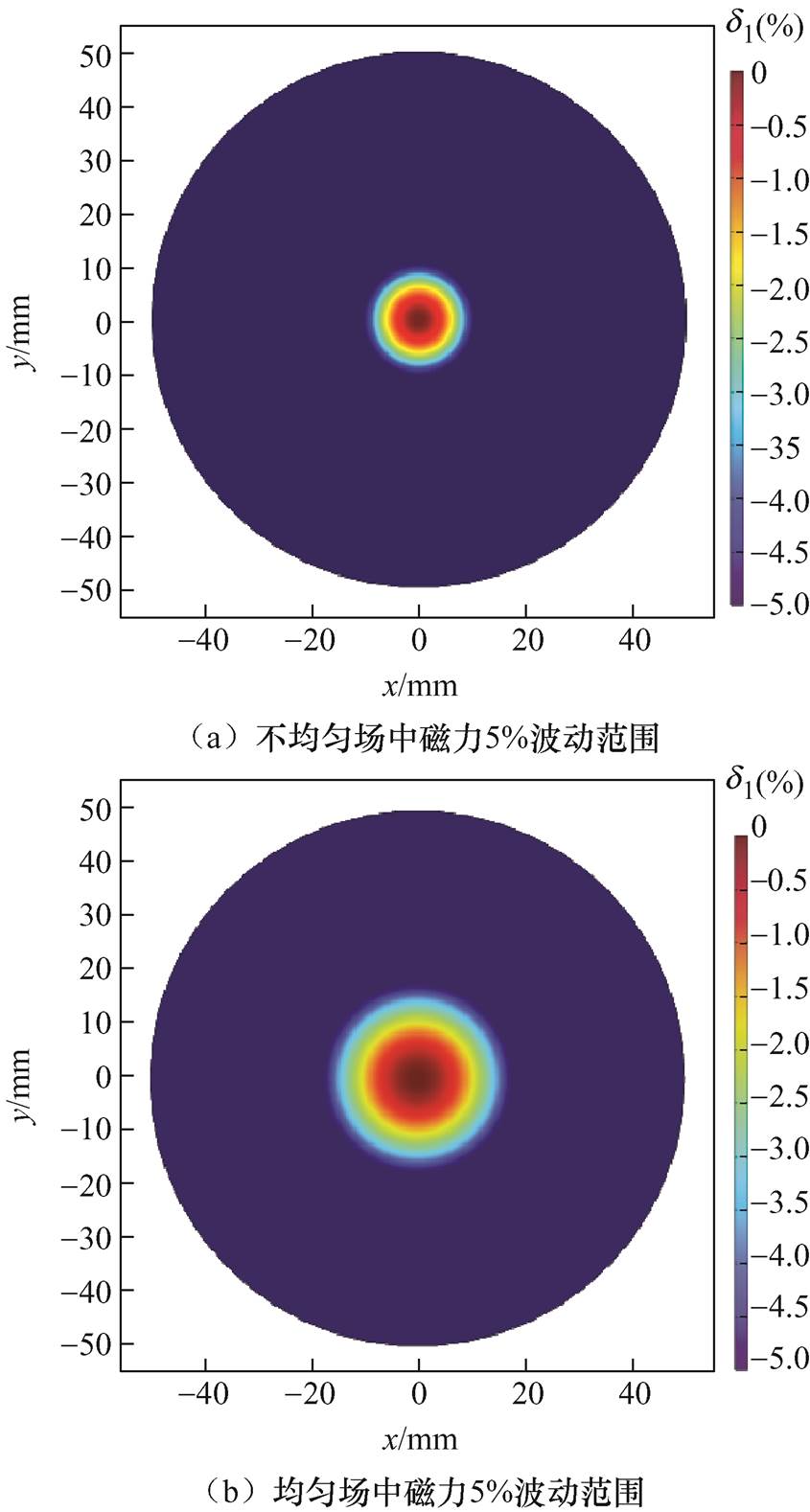
图9 CD截面处磁力分布
Fig.9 Magnetic force distribution at CD cross-section
进一步地,为了研究梯度磁场分布对声压的影响,在xOz截面取截线AB及其5条距离分别为L=5 mm、10 mm、15 mm、20 mm和25 mm的平行截线(如图10a所示),根据式(2)计算各截线上声压变化情况,其结果如图10b、图10c所示。在不均匀场中,随着与截线AB距离的增加,其声压曲线的峰值逐渐下降;而在均匀场中,不同的截线上,其声压曲线均能保持稳定;可以看出,声压曲线在边界处达到峰值,然而由于仿真软件中边界两侧的材料属性不同,导致该边界处数据发生突变,为了更加清楚地研究声压峰值的变化规律,在边界附近以CD截线(如图10a所示)为观测点,计算该截线处声压峰值变化曲线;同样,在CD截面上以5%变化范围评估有效声压波动范围,这里用声压p替代式(22)中的磁力f。
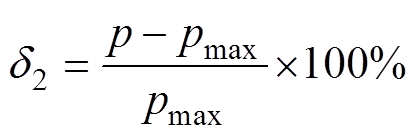 (23)
(23)
式中,p为声压;pmax为声压峰值,d2即为声压变化范围,同样取d2=5%,其结果如图10e和图10f所示。
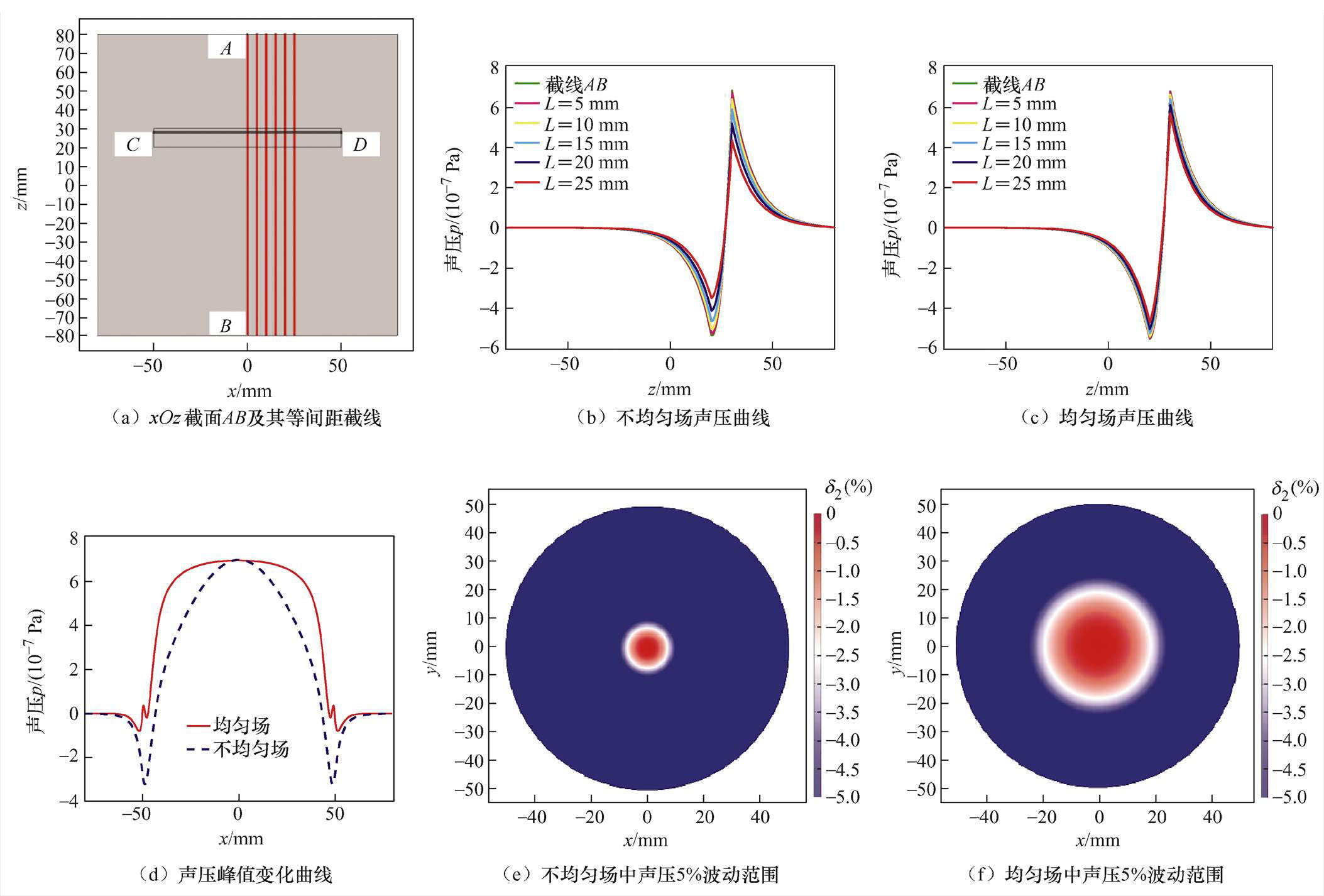
图10 声压分布
Fig.10 Sound pressure distribution
通过对结果的分析可知,不均匀场中的声压波动范围半径在10 mm左右,而均匀场下的波动范围半径在20 mm左右,对比相应的声压曲线可以看出:在不均匀场中,声压峰值在距离为10 mm时开始衰减,而均匀场中声压峰值同样在距离为20 mm时开始发生衰减。这一现象表明,以5%声压峰值波动范围为评判标准可以作为判断声压衰减的有效手段,同样也可以表征MACT-MI的有效成像区域,即在该范围之内的MNPs所受磁力和声压将不受梯度磁场衰减的影响,通过检测设备所获得的超声信号能够有效反映该区域内MNPs的分布信息。
以上现象表明,若梯度磁场均匀空间较小,将导致处于磁场边界的MNPs所受磁力较小,其产生的声压信号过于微弱,加之噪声影响,这将会导致研究者忽略该粒子的存在,若发生在临床医疗检测中,可能由于误诊而延误病情甚至造成重大医疗事故。因此,本文针对梯度磁场均匀空间的研究对于改善MACT-MI信噪比有一定的借鉴意义。
为提高MACT-MI磁声信号的信噪比低,改善系统成像质量,本文基于改进TFM设计了适用于MACT-MI的梯度线圈,并研究了梯度磁场的空间分布特征对MACT-MI的影响。包括采用鲸鱼优化算法求解电流密度系数,在不同线圈间距下产生满足成像需求的梯度线圈,与传统梯度线圈和矩阵式梯度线圈进行比较,分析了均匀场和不均匀场中MNPs所受磁力及声压的变化规律。本文的主要结论如下:
1)通过智能寻优算法使磁场的相对误差最小化以求解电流密度系数,得到的TFM线圈在成像区域的均匀空间均大于传统梯度线圈,且相较于矩阵式线圈,在相同条件下线圈数量减少了近30%,线圈匝数减少了约65%,线圈尺寸缩小了84%,最大电流降低了约22%,本文所设计的线圈结构相对灵活、激励更为简单,为进一步开展MACT-MI实验研究提供有利条件。
2)在均匀场中,MNPs所受磁力更加平滑、稳定,而在不均匀场中,随着梯度磁场均匀空间的缩小,其磁力稳定分布范围同样大大缩小。同样,均匀场中的声压波形更宽,有效声压波动范围更大;在不均匀场中,随着距离中心越远,声压曲线峰值逐渐衰减。
综合以上分析可知:磁力和声压的有效波动范围与梯度磁场均匀空间大小成正比,且随着均匀空间的缩小,磁力和声压的峰值也随之衰减,这一现象证明梯度磁场的空间分布特征影响了磁力和声压幅值的大小,也是造成MACT-MI的磁声信号较为微弱的原因之一。因此,通过提高磁场的均匀度可以有效提高磁声信号的信噪比。此外,本文设计的梯度线圈虽然具有一定的优势,但在设计过程中还需考虑到匝间距的影响,在求解电流密度系数时,还可以通过加入正则化项限制线圈的功耗以降低电流激励,另外本文所用的优化算法还需进一步改进。总之,本文对MACT-MI做了一些深入研究,为该方法的进一步实验乃至临床应用提供了研究基础。
参考文献
[1] Shi Xiaoyu, Liu Guoqiang, Yan Xiaoheng, et al. Simulation research on magneto-acoustic concentration tomography of magnetic nanoparticles with magnetic induction[J]. Computers in Biology and Medicine, 2020, 119: 103653.
[2] Yan Xiaoheng, Sun Di, Li Zhengxing, et al. Simulation research on the forward problem of magneto-acoustic concentration tomography of magnetic nanoparticles with magnetic induction based on the relaxation time of magnetic nanoparticles[J]. IEEE Access, 2022, 10: 56057-56066.
[3] 陈顺中, 王秋良, 孙万硕, 等. 3T动物磁共振成像传导冷却超导磁体研究[J]. 电工技术学报, 2023, 38(4): 879-888.Chen Shunzhong, Wang Qiuliang, Sun Wanshuo, et al. The study of a 3 T conduction-cooled superconducting magnet for animal magnetic resonance imaging[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 879-888.
[4] 曲洪一, 刘鑫, 王晖, 等. 磁共振成像磁体无源匀场改进策略及实验研究[J]. 电工技术学报, 2022, 37(24): 6284-6293. Qu Hongyi, Liu Xin, Wang Hui, et al. Improved strategy and experimental research on passive shimming in magnetic resonance imaging magnet[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6284-6293.
[5] 闫孝姮, 李政兴, 潘也, 等. 相同极性永磁体对感应式磁声磁粒子浓度成像过程影响的仿真[J]. 电工技术学报, 2022, 37(8): 1926-1937.Yan Xiaoheng, Li Zhengxing, Pan Ye, et al. Simulation of the influence of permanent magnets of the same polarity on the magneto-acoustic concentration tomography of magnetic nanoparticles with magnetic induction process[J]. Transactions of China Electro- technical Society, 2022, 37(8): 1926-1937.
[6] 汤云东, 丁宇彬, 金涛. 基于亥姆霍兹线圈装置的磁热疗优化方法[J]. 电工技术学报, 2023, 38(5): 1248-1260. Tang Yundong, Ding Yubin, Jin Tao. Research on optimization method of magnetic hyperthermia based on Helmholtz coil device[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1248-1260.
[7] 贺红艳, 魏树峰, 王慧贤, 等. 矩阵梯度线圈研究现状与发展趋势[J]. 波谱学杂志, 2021, 38(1): 140- 153. He Hongyan, Wei Shufeng, Wang Huixian, et al. Matrix gradient coil: current research status and perspectives[J]. Chinese Journal of Magnetic Resonance, 2021, 38(1): 140-153.
[8] 闫孝姮, 李政兴, 孙迪, 等. 基于矩阵式线圈的感应式磁声磁粒子浓度成像研究 (英文)[J]. 电工技术学报, 2022, 37(17): 4269-4283. Yan Xiaoheng, Li Zhengxing, Sun Di, et al. Magneto acoustic concentration tomography of magnetic nanoparticles with magnetic induction based on matrix coil[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4269-4283.
[9] Turner R. A target field approach to optimal coil design[J]. Journal of Physics D: Applied Physics, 1986, 19(8): L147-L151.
[10] Liu H, Truwit C L. True energy-minimal and finite-size biplanar gradient coil design for MRI[J]. IEEE Transactions on Medical Imaging, 1998, 17(5): 826-830.
[11] Forbes L K, Crozier S. Novel target-field method for designing shielded biplanar shim and gradient coils[J]. IEEE Transactions on Magnetics, 2004, 40(4): 1929- 1938.
[12] Chen Shanshan, Xia Tian, Miao Zhiying, et al. Active shimming method for a 21.3 MHz small-animal MRI magnet[J]. Measurement Science and Technology, 2017, 28(5): 055902.
[13] Wang Jing, Song Xinda, Zhou Weiyong, et al. Hybrid optimal design of biplanar coils with uniform magnetic field or field gradient[J]. IEEE Transactions on Industrial Electronics, 2021, 68(11): 11544-11553.
[14] Zhao Fengwen, Wang Jing, Lu Fei, et al. Design of highly linear gradient field coils based on an improved target-field method[J]. IEEE Sensors Journal, 2021, 21(14): 16256-16263.
[15] Ding Zhongya, Huang Ziyuan, Pang Maotong, et al. Iterative optimization algorithm to design biplanar coils for dynamic magnetoencephalography[J]. IEEE Transactions on Industrial Electronics, 2023, 70(2): 2085-2094.
[16] Tomasi D. Stream function optimization for gradient coil design[J]. Magnetic Resonance in Medicine, 2001, 45(3): 505-512.
[17] Peeren G N. Stream function approach for determining optimal surface currents[J]. Journal of Computational Physics, 2003, 191(1): 305-321.
[18] Brideson M A, Forbes L K, Crozier S. Determining complicated winding patterns for shim coils using stream functions and the target-field method[J]. Concepts in Magnetic Resonance: an Educational Journal, 2002, 14(1): 9-18.
[19] Liu Wentao, Zu Donglin, Tang Xin, et al. Target-field method for MRI biplanar gradient coil design[J]. Journal of Physics D: Applied Physics, 2007, 40(15): 4418-4424.
[20] Mirjalili S, Lewis A. The whale optimization algo- rithm[J]. Advances in Engineering Software, 2016, 95(C): 51-67.
[21] Hu Gang, He Bin. Magnetoacoustic imaging of magnetic iron oxide nanoparticles embedded in biological tissues with microsecond magnetic stimu- lation[J]. Applied Physics Letters, 2012, 100(1): 13704-137043.
Abstract The magneto acoustic concentration tomography of magnetic nanoparticles (MNPs) with magnetic induction (MACT-MI) represents a novel approach to MNP concentration tomography. However, prior research revealed a limitation: the current MACT-MI yields a weak magneto acoustic signal due to the small magnetic force on MNPs, hindering experimental progress. Our study focuses on gradient magnetic field uniformity to enhance signal-to-noise ratio and imaging quality by designing a high-quality gradient magnetic field coil to amplify the magnetic force of MNPs.
An improved gradient coil for MACT-MI is proposed. An intelligent optimization algorithm is incorporated to rectify the correlation error from representing continuous current density through the contour lines of the discrete flow function during the conventional target field method (TFM) coil design. This algorithm defines the fitness function for minimizing relative magnetic field error by optimizing current density coefficients. A gradient coil is produced for various coil spacing requirements in imaging. The proposed TFM coil shows a larger uniform space within the imaging area than the traditional gradient coil. Compared with the matrix coil, the TFM coil reduces the coil count by approximately 30% under equivalent conditions, decreases coil turns by about 65%, minimizes coil size by 84%, and lowers the maximum current by approximately 22%.
Additionally, to investigate the influence of gradient magnetic field spatial distribution on MACT-MI, diverse distribution models for magnetic nano particles (MNPs) are constructed. With the multi physics simulation software COMSOL, the physical processes of MACT-MI are numerically solved. Variations in magnetic force and sound pressure acting on MNPs can be analyzed in both uniform and non-uniform magnetic fields. The magnetic force on MNPs exhibits enhanced smoothness and stability in a uniform magnetic field. Conversely, in a non-uniform field, as the gradient magnetic field's uniform space diminishes, the stability range of the magnetic force contracts significantly. Similarly, the sound pressure waveform is broad in a uniform field, accompanied by a wide effective range of sound pressure fluctuations. In contrast, sound pressure curve peaks gradually attenuate as the distance from the center increases in a non-uniform field.
The results indicate a proportional relationship between the effective fluctuation range of magnetic force, sound pressure, and the uniform spatial extent of the gradient magnetic field. Moreover, as the uniform space decreases, the peak values of both magnetic force and sound pressure diminish. This phenomenon attests to the impact of the gradient magnetic field's spatial distribution characteristics on the magnitude of magnetic force and sound pressure amplitudes, which also contributes to the relatively weak magnetic-acoustic signals in MACT-MI. Enhancing the uniformity of the magnetic field emerges as apractical approach to bolstering the signal-to-noise ratio of the magnetic-acoustic signals.
Keywords:Magneto-acoustic concentration tomography of magnetic nanoparticles (MNPs) with magnetic induction (MACT-MI), target field method, gradient magnetic field, uniform space
DOI: 10.19595/j.cnki.1000-6753.tces.230897
中图分类号:TM12
国家自然科学基金项目(52207008)和辽宁省教育厅科学研究基础项目(LJ2020JCL003)资助。
收稿日期 2023-06-10
改稿日期 2023-08-11
闫孝姮 女,1984年生,博士,副教授,硕士生导师,研究方向为电磁探测与成像。E-mail: xiaohengyan@163.com(通信作者)
淡新贤 男,1998年生,硕士研究生,研究方向为电磁探测与成像。E-mail: dxx610918450@163.com
(编辑 郭丽军)