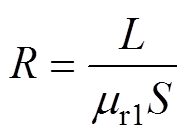（1）
摘要 目前，对于铁心振动计算通常采用有限元仿真来实现，但该方法计算时间长且效率低，为解决此问题，该文提出了基于机-电类比的铁心多场耦合特性精细化建模与计算方法。根据铁心步进搭接区域的结构特点，对搭接区域铁心进行磁路建模，建立考虑气隙影响的铁心等效磁路模型。根据机-电类比方法和振动理论，建立可描述变压器铁心振动的集总式和分布式等效振动回路模型，基于搭接区域磁场分布特性建立二端口级联形式的等效振动回路模型，实现了铁心振动特性的快速精准计算。搭建了叠片铁心测试平台并进行实验，通过将测量结果与计算结果对比，发现励磁电流、铁心磁通密度、位移和加速度等具有较好的一致性，验证了所提方法的有效性和准确性。
关键词：场路耦合 磁致伸缩 叠片铁心 振动
近年来，如何推动电力产业向绿色发展变革成为了能源领域的重点关注问题。作为发、输、变、配电的主要设备，变压器的安全稳定运行对于构建新型绿色电网有着不言而喻的重要性。然而，变压器在运行过程中总是不可避免地伴有振动噪声，这不仅会对环境造成污染，也会对变压器设备自身产生损害[1]。变压器振动来源有以下几个方面[2]：硅钢片磁致伸缩效应引起的变压器铁心振动；硅钢片接缝气隙处漏磁通产生的电磁力所引起的铁心振动；绕组的漏磁通产生电磁力导致绕组振动以及引起变压器油箱振动。研究表明，当变压器工作在额定磁通密度时，其他原因引起的振动远小于硅钢片磁致伸缩引起的振动[3-5]。虽然单片硅钢片的磁致伸缩形变量仅为每米几微米[6]，但是由于大型变压器的铁心尺寸较大，其磁致伸缩引起的振动仍不可小觑[7-9]。
国外对于铁心磁致伸缩振动和磁通密度分布情况的研究起步较早，可以追溯到20世纪70年代。早在1974年，英国卡迪夫大学A. Moses教授团队就试图从磁致伸缩角度探究降低铁心振动的方 法[10]。比利时的T. Hilgert建立了计及磁滞和不计及磁滞影响的两个小型变压器磁致伸缩数值模型，计算结果表明，磁致伸缩模型中的磁滞对振动的计算有很大影响，需在今后的研究中予以考虑[11]。日本佐贺大学的Gao Yanhui等用不同的方法计算等效磁致伸缩力[12-13]，并比较了磁致伸缩力和麦克斯韦力对电抗器振动的影响[14]。文献[15]采用有限元方法研究了高磁通密度下铁心接头区域的磁通分布与搭接方式的关系，仿真结果表明，采用多级步进搭接的工艺可以显著改善铁心接头区域磁通密度深度饱和的情况。
国内对铁心振动问题的研究起步相对较晚，近十几年才得到广泛关注。天津工业大学祝丽花等从2013年开始基于磁致伸缩理论建立磁-机械耦合模型，以此来计算饱和电抗器、变压器振动位移[16-18]。文献[19]提出了变压器铁心搭接区磁特性数值等效的方法，并将计算结果应用于定制方圈的局部振动分析中。张鹏宁等从磁-机械场耦合的角度出发利用多物理场仿真软件COMSOL建立了高压并联电抗器本体结构的振动计算模型，计算结果表明，气隙垫块的杨氏模量越大其抑制振动的效果越好[20-22]。曹淑瑛等在充分分析超磁致伸缩致动器结构动力学原理后，基于Jiles-Atherton磁滞模型、二次畴转模型、非线性压磁方程，建立了超磁致伸缩致动器的磁滞非线性动态模型。应用该模型对致动器的输出应变和力进行计算，计算结果与实验结果符合较好[23-25]。李冰等利用两台参数一致的250 MV·A/500 kV变压器，对变压器直流偏磁下的电压畸变率、励磁电流、振动和噪声展开测量和研究，分析认为铁心主柱附近区域振动程度明显大于铁心旁柱附近区域且变压器噪声水平会随着直流偏置电流的增加而上升[26]。研究叠片铁心的磁场与振动对分析变压器振动和噪声有重要意义，但以往关于振动的研究工作大多依赖电磁仿真软件，采用有限元方法进行时域计算，虽能保证较为可靠的计算精度，但计算速度并不理想。
本文首先对变压器铁心搭接气隙区域展开研究，考虑了气隙的影响，分析了搭接区等效磁特性，获得了搭接气隙区域等效磁阻。基于合理的假设和简化搭建了变压器等效磁路模型。在精确的磁路建模的基础上，采用机-电类比法建立了电-磁-机耦合的变压器铁心振动的集总式模型和分布式模型，并利用分布式模型计算了不同测点以及搭接区域的振动位移分布情况。
由于变压器铁心柱与铁轭连接处有气隙存在，故在气隙处会发生磁通穿越叠片间的绝缘磁阻进入相邻叠片的现象。此处为便于分析，将铁心搭接区域做直线化处理，以三级步进搭接为例，其结构如图1所示。图1中，lt为步进搭接的长度，lg为气隙的长度，从图中可以看出，当磁通快要到达气隙时会向相邻叠片穿越。磁阻的表达式[27]为
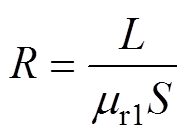（1）
其中
mr1=m0mr
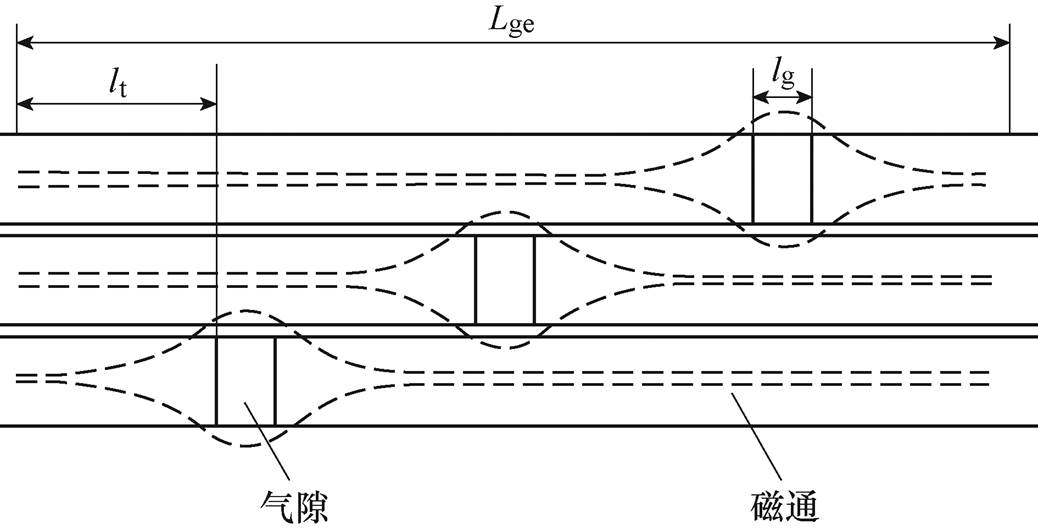
图1 三级步进搭接示意图
Fig.1 Three-stage stepper lap structure
式中，m0为真空磁导率；mr为铁心材料的相对磁导率；L、S分别为磁阻对应的磁路长度和磁通穿过的横截面积。由于气隙的存在使得实际的磁阻要比由公式计算的结果更大，故需对气隙附近区域单独分析并建立等效的气隙搭接区域磁阻。根据磁路方程RF =nI，其中，n为线圈匝数列向量，在确定好变压器的运行工况后可计算得出励磁电流I列向量和磁通F 列向量，确定磁阻矩阵R的初值。将矩阵中元素与通过公式计算得出的磁阻R作差得出的DR即为受气隙影响磁阻的增加量。在对搭接区域进行磁等效时通常将区域范围确定为气隙外延一个步进搭接长度[28-30]，即等效气隙区域的磁路长度为图1中的Lge。由此可得等效气隙区域磁阻Rma的磁阻率为
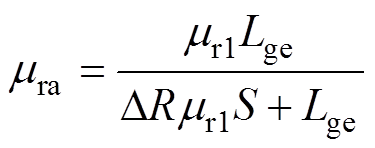（2）
通过改变激励电压的大小来调节铁心正常工作磁通密度的幅值可获得不同磁通密度幅值下搭接区的磁导率，搭接区和非搭接区磁化曲线如图2所示。图2中，非搭接区的磁化曲线为测得的取向硅钢片的磁化曲线，从图中可以看出，在搭接区域受磁阻增大的影响使得该区域表现出更难磁化的特点。
图2 不同区域等效域磁化曲线
Fig.2 Equivalent domain magnetization curves for different regions
由于气隙的存在使得搭接区域的磁通密度分布极不均匀，磁通的穿越造成局部区域磁通密度严重饱和。
Bc为铁心正常工作磁通密度，Bg为气隙处磁通密度，假定磁通在到达m点时开始向上下两侧穿越，定义从m点到气隙的区域为临界气隙区域，该区域中沿x方向的磁通Fcg逐渐减少，磁通密度也从正常工作磁通密度Bc逐渐减小至气隙磁通密度Bg，同时该区域也自m点开始出现沿z方向的磁通Fz穿越到邻层，在叠片的边界处Fz达到其最大值Fzmax；与临界气隙区域上下相邻的区域称为临界饱和区，该区域由于有来自相邻叠片的穿越磁通，磁通密度由正常工作磁通密度Bc逐渐增大至最大饱和磁通密度Bgm；与气隙区域上下相邻的区域称为磁通密度饱和区域，该区域磁通密度达到最大值Bgm，通过该区域后磁通密度又逐渐减小回归到正常值。图3a和图3b分别给出了气隙附近的局部磁路建模以及磁通具体的流通路径，图3b中箭头方向指示磁通的方向。图中，Bz为沿z方向穿越的磁感应强度。
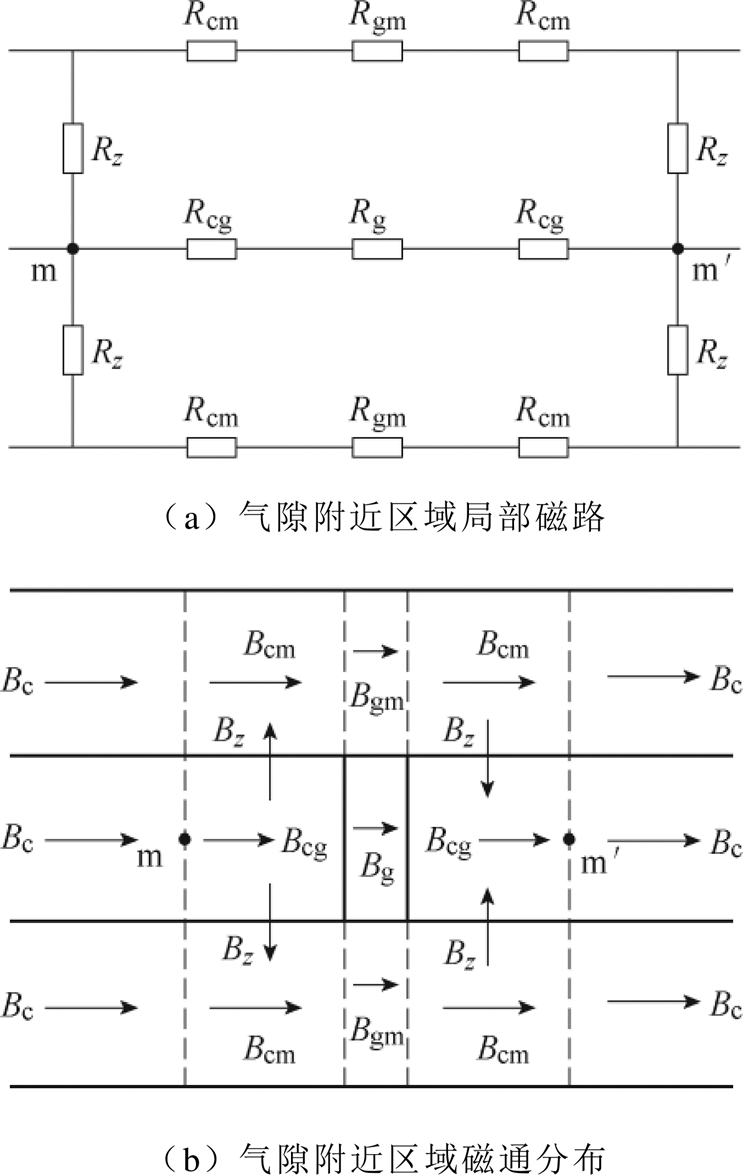
图3 气隙附近区域局部磁路分析
Fig.3 Local magnetic circuit analysis of the area near the air gap
由于采用三级步进搭接方式堆叠的铁心每三层都具有相同的结构，故只对其中构成一叠的三层进行分析，其他层上与之具有相同的磁通分布情况。实际运行的变压器铁心由于受到z方向夹紧力的作用，叠片与叠片之间的间距非常小，可不考虑叠片间的绝缘磁阻，即认为除气隙区域外无漏磁存在。
在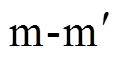
之间运用安培定律得
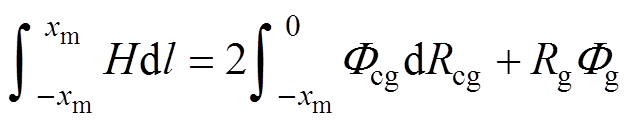（3）
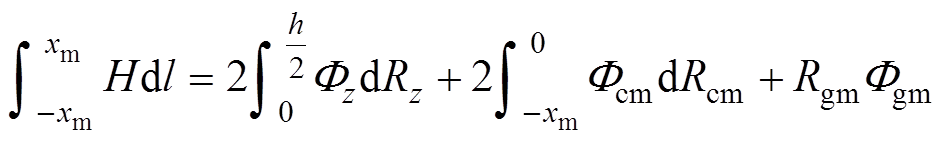（4）
式中，h为叠片铁心单片的厚度；xm为转折点m到气隙的距离；Rcm、Rcg、Rg和Rz分别为Bcm、Bcg、Bg和Bz所对应区域的磁阻。根据学者研究发现，相邻叠片间磁通穿越的范围一般为一个步长左右，本文假定xm=2 mm。根据前人所做的有限元研究，此处做出合理假设，认为从m点开始Fz和Fcg分别以线性变化的方式逐渐增加和减少至Fzmax和Fg[31]，则有
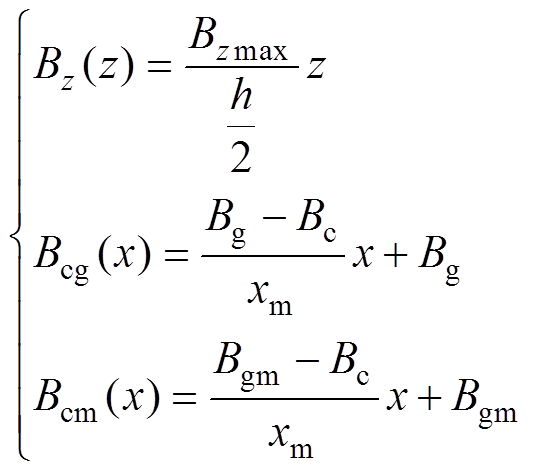（5）
将式（3）～式（5）联立即可求得Bg、Bgm与Bc的关系，根据电磁感应定律有
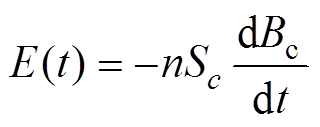（6）
式中，n为线圈匝数；Sc为铁心叠片的整体截面积。
可在测量出铁心单片和整体叠片的横截面积，并确定好实验工况后由式（6）计算出铁心的正常工作磁通密度，然后进一步计算搭接气隙区域的磁通密度分布。
依据电磁感应原理可以建立变压器外部电气特性和内部电磁场分布的电路-磁路耦合方程，其电路结构如图4所示。图4中，UAC为激励电压，Rp、L1和Rs、L2分别为一、二次绕组的电阻和电感。
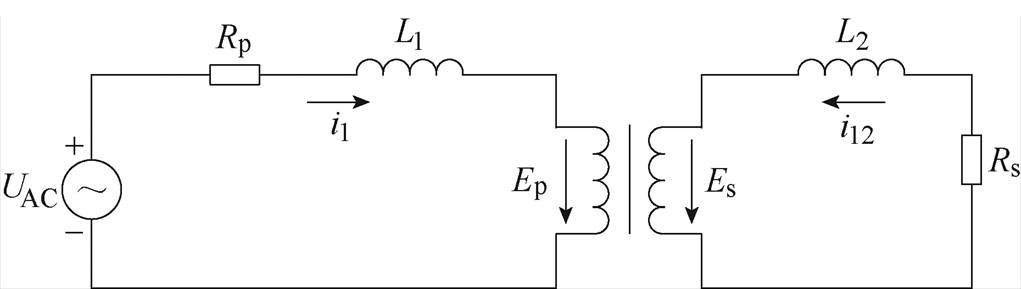
图4 变压器外部电路
Fig.4 Transformer external circuitry
本文所计算的单相三柱变压器模型在其两侧旁柱上均缠绕115匝线圈，两组线圈互相并联。根据模型的激励方式和磁路结构可建立如图5所示的等效磁路。图中，F1V和F2V为两侧旁柱绕组上所产生的磁动势，F1和F2为与之对应的磁通，F3和F4为绕组上的漏磁通。Rma为搭接气隙区域等效磁阻，Rmb为铁轭磁阻，Rm0为漏磁对应的磁阻，Rmc1为铁心旁柱磁阻，Rmc2为铁心中柱磁阻。铁心及铁轭的磁阻可根据公式计算，漏磁阻可以由测量得到，搭接气隙区域等效磁阻可由1.1节中给出的等效气隙区域磁导率求得。由等效磁路可列写等效磁路方程为
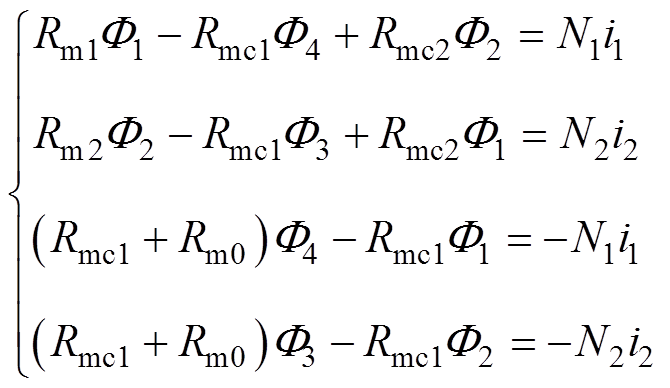（7）
其中
Rm1=Rm2=4Rma+2Rmb+Rmc1+Rmc2
式中，N1、N2为两组线圈的匝数；i1、i2分别为两组线圈中通入的励磁电流。
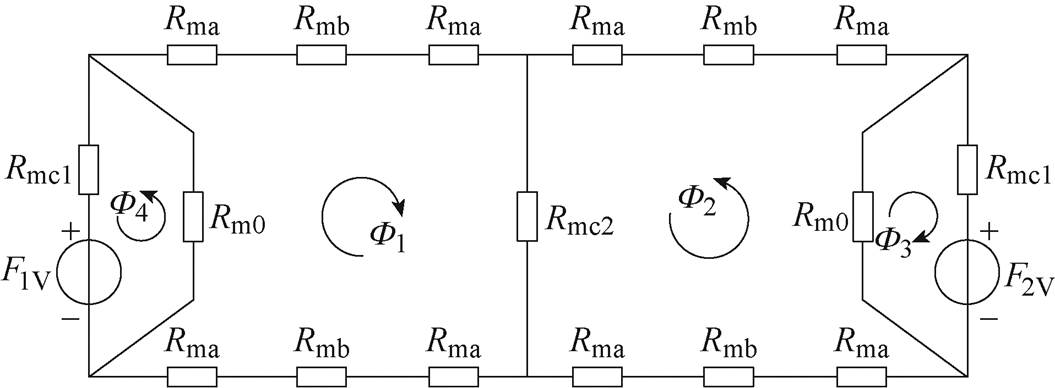
图5 等效磁路拓扑结构
Fig.5 Equivalent magnetic circuit topology
变压器的振动主要来自于铁心的磁致伸缩效应，磁致伸缩是变压器铁心磁化时的固有特性。当外加磁场后，磁畴沿着磁场的方向有序排列，致使材料的长度或体积产生变化，磁致伸缩的本构表达式为
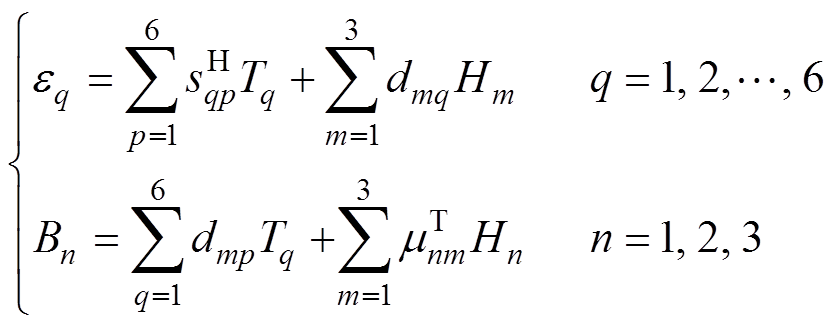（8）
式中，eq、Tq分别为应变和应力张量分量；Bn、Hn分别为磁感应强度和磁场矢量分量，n=1, 2, 3，分别代表z, y, x方向；sH、d、mT分别为恒磁场下材料的弹性模量系数、压磁系数和恒应力条件下的磁导率。压磁系数可由测量的磁致伸缩特性曲线获得，弹性模量系数是杨氏模量的张量形式。
以单相三柱式变压器铁心旁柱的振动为例进行分析，铁心旁柱在直角坐标系中的模型如图6所示。
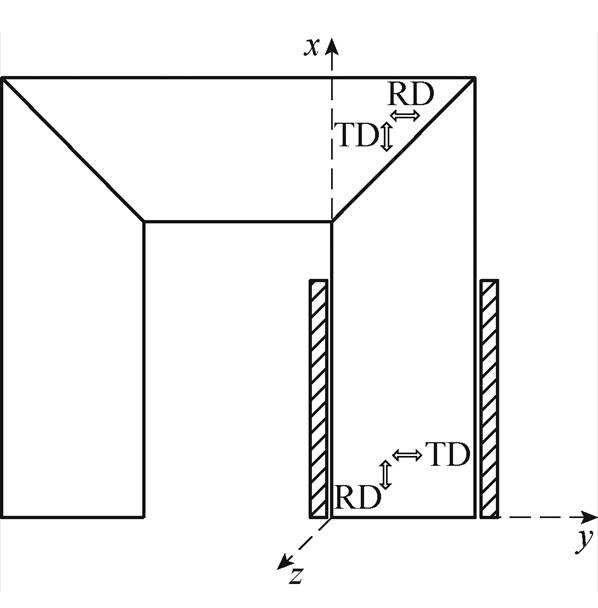
图6 铁心直角坐标系模型
Fig.6 Model of the iron core in Cartesian coordinate system
由于材料的磁各向异性，流经铁心旁柱的磁通主要沿硅钢片轧制方向（Rolling Direction, RD），磁场主要集中为x方向，因而铁心旁柱的振动位移也以x方向为主。此时可认为除拐角搭接区域外旁柱的其他区域磁场只有x方向的分量。由于旁柱上沿y、z方向的应力远小于x方向，可近似忽略T1、T2，此外硅钢铁心的剪切应变（耦合系数dij=0（i=1, 2, 3; j=4, 5, 6））在变压器振动计算中通常不予考虑[32]，故此时旁柱振动的压磁方程可简化为
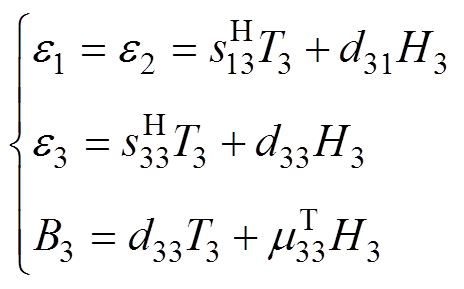（9）
由结构动力学可知，物体在周期性外力作用下的振动方程为
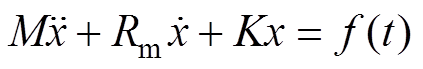（10）
式中，M、Rm、K分别为质量、阻尼和刚度；f(t)为周期性驱动外力。等式左侧第一项表示惯性力，用来描述物体保持运动状态的能力，方向与加速度方向相反；第二项为弹性恢复力，方向指向体系的平衡位置；第三项为阻尼力，用来描述能量的耗散。
由动力学平衡方程式Ma+IF-F=0（IF为结构的内力，F为施加的外力，a为加速度）和达朗贝尔原理对铁心旁柱沿x方向的运动做动力学受力分析可得
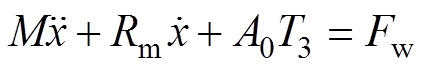（11）
式中，A0为铁心横截面积，A0T3即为铁心的内力；Fw为运动过程所受外力。
在变压器的外特性电路中，由于励磁线圈上的阻抗非常小，因而当变压器二次侧空载时，可近似认为线圈上产生的感应电压等于一次侧外部的激励电压，此时有
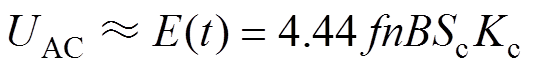（12）
式中，f为频率；Kc为铁心的叠装系数。将式（9）和式（12）代入式（11）中，又根据H=B/m，可得
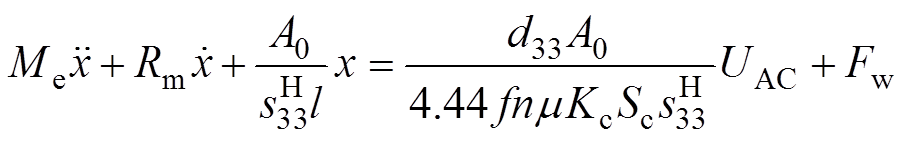（13）
式中，Me为铁心旁柱等效质量；l为铁心沿磁场方向的长度；x的系数为等效刚度；m 为相对磁导率。对比式（10）得式（13）中等号右边的项即为等效磁致伸缩力。
在采用机-电类比分析时，力学定律和电学定律的类比关系见表1。表中，Z为电学中的阻抗，Zm为机械阻抗。
表1 力学定律和电学定律的类比关系
Tab.1 Analogy between the laws of mechanics and electricity
电学变量力学变量电学定律力学定律 电压U力F基尔霍夫达朗贝尔 电流I速度vI=U/Zv=F/Zm 电容C顺性系数1/K 电阻R阻尼RmU=RIF=Rmv 电感L质量MU=LdI/dtF=Mdv/dt
将铁心的振速v=dx/dt代入式（13）不难发现，其在数学形式上与KCL串联电路中的基尔霍夫定律式（14）有高度的相似性，故可采用机-电类比的方法，将力学问题转化为电学问题求解。
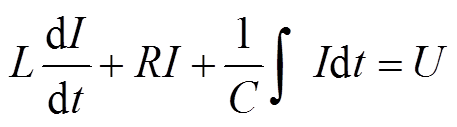（14）
根据式（14）和表1所示的类比关系可以将力学问题与电学问题耦合求解，将铁心中电能向机械能转换的过程表示成如图7所示的“理想换能器”集总式等效电路问题求解。图中，Rp和L1分别为线圈的电阻和电感，Nem为机电换能系数。一次侧表征电气特性，二次侧表征机械振动特性，一次侧中变压器线圈通电后产生的励磁电压U经“理想换能器”转换成振动回路的磁致伸缩力F=NemU。
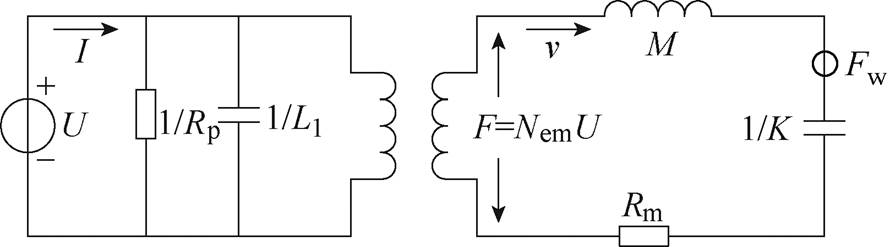
图7 集总式等效电路模型
Fig.7 Lumped equivalent circuit modelas
观察式（13），不难得出等效电路中机电换能系数Nem的表达式为
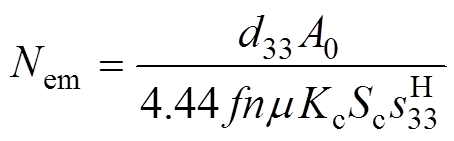（15）
机电换能系数Nem同时具有机械和电气特性，通过该参数可实现将没有直接关系的电路和机械振动回路相互耦合，而该参数的大小也直接决定磁致伸缩力的大小。采用上述同样的方法还可得出铁心沿y、z方向的磁致伸缩振动回路来计算铁心上任意点的位置。但考虑到铁心搭接区域磁通密度分布不均匀的特点，要想同时计算铁心上所有点的振动位移还需采用更加精确的分布式振动回路求解。
叠片铁心的磁致伸缩效应类似于弹簧在周期性外力作用下的简弦运动，满足广义胡克定律。在分析铁心旁柱沿x方向的振动时，首先将铁心在x方向分成n个长度为Dl的微元，铁心微元化模型如图8所示。
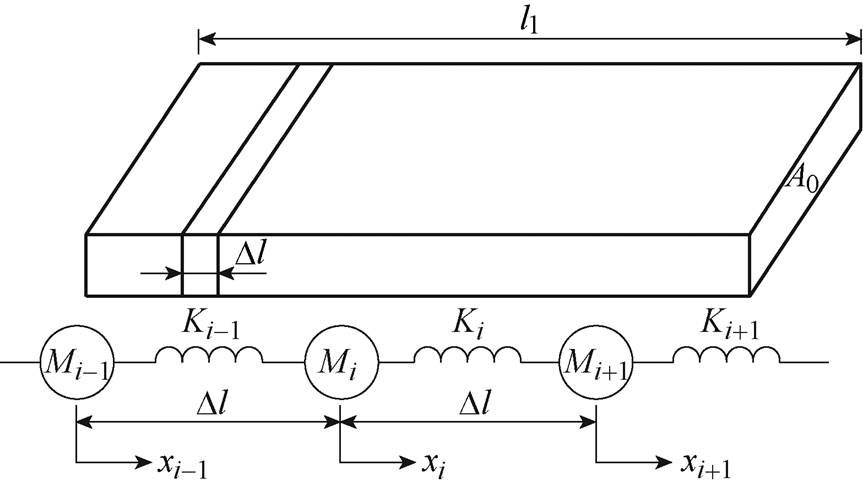
图8 铁心微元化模型
Fig.8 Micro-elementized model of iron core
铁心旁柱长度为l1，由于铁心所用的硅钢片为质地均匀的材料，故每个微元的质量为DM=rA0Dl，刚度为DK=YA0/Dl，Y为杨氏模量，r 为硅钢片密度，在单向应力作用下弹性模量系数即为杨氏模量的倒数。把硅钢片上的每一个微元看作一个弹性元件，则第i个微元的受力由与他相邻的两个弹性元件所决定，对其做受力分析得到第i个微元的运动方程为
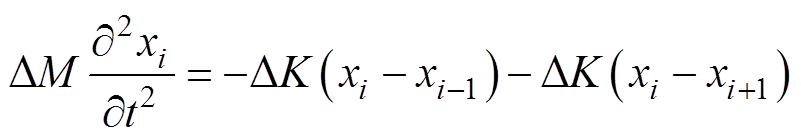（16）
由运动方程可以得出分布式模型的等效振动回路如图9所示，该电路为一个Cauer Ⅰ型电路。
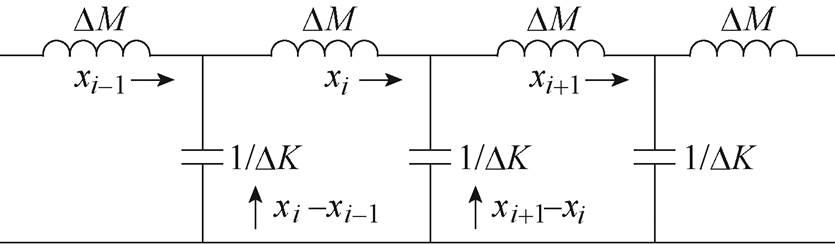
图9 分布式模型等效振动回路
Fig.9 Equivalent vibration loops for distributed models
位移关于l的解的形式为x(l)=ae-jkl+bejkl，易知振动位移的解的形式为x(l,t)=ae-j(kl-wt)+bej(kl+wt)，其中k=w/c为波数，w 为角频率，c为铁心硅钢片的波速。待定系数a、b 可通过边界条件来确定。等效磁致伸缩力F=-A0T=-A0Y∂x/∂l，T为磁致伸缩应力，即
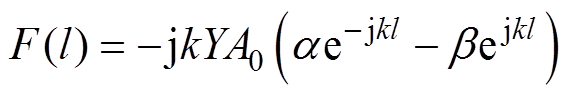（17）
沿硅钢片分布的机械阻抗可表示为Z(l)=F(l)/v(l)，其中v(l)=jw x(l)，则
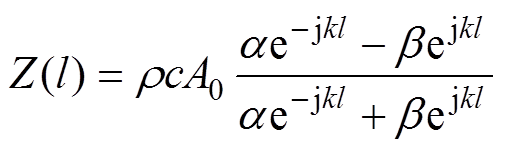（18）
其中
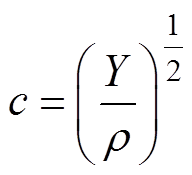
设Z0为l=0处的机械阻抗，ZL为l=l1处的机械阻抗，可得到阻抗传输方程为
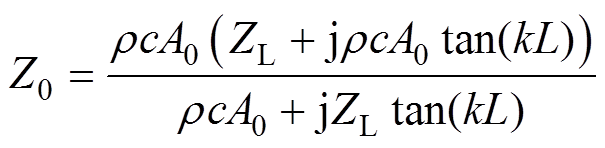（19）
利用代数运算可将图9所示的Cauer Ⅰ型电路转化为图10所示的Π型二端口网络，图中，F1、F2为两个端口的等效力，v1、v2为两个端口对应的速度。其中F1/v1=Z0位于端口1，F2/v2=ZL位于端口2。
图10中，Za和Zb为对图9所示的Cauer Ⅰ型电路变换后得到的二端口阻抗，二端口网络可写成传输矩阵方程的形式，有
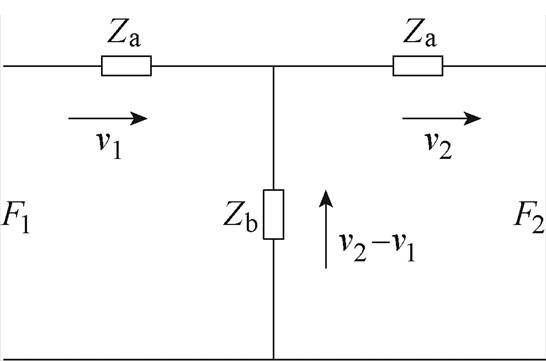
图10 分布式模型二端口电路
Fig.10 Two-port circuit of distributed model
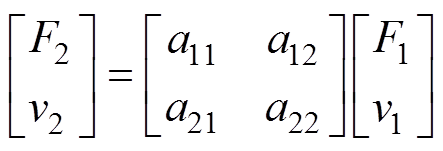（20）
其中
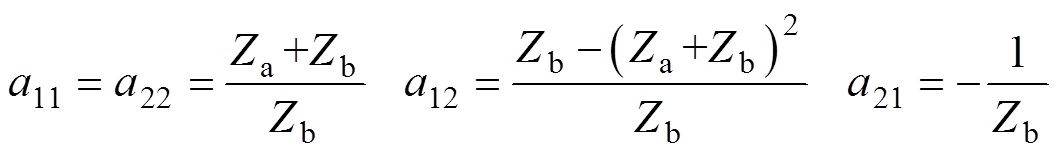
式中，由aij元素构成的矩阵记为传输矩阵A。通过传输矩阵A可以将输入端与输出端相关联。当受到磁致伸缩力作用时，铁心的等效振动电路如图11所示，当短路时其与图10所示的等效电路相同。
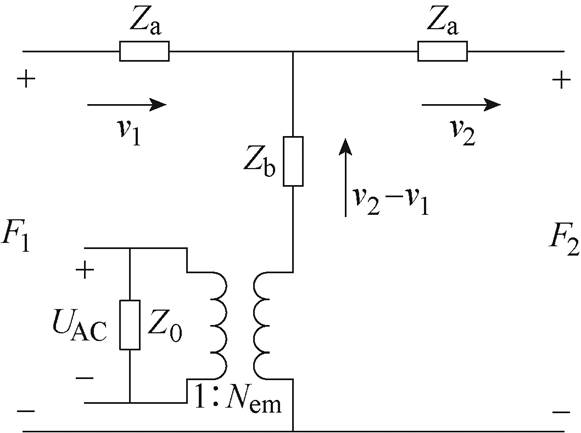
图11 二端口等效振动回路
Fig.11 Two-port equivalent of vibration loop
图11所示的电路同样可以列写转移矩阵，有
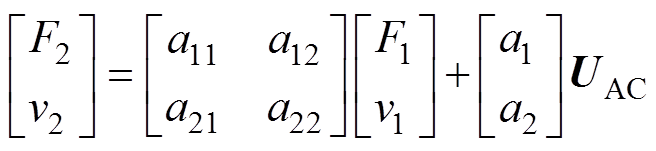（21）
其中
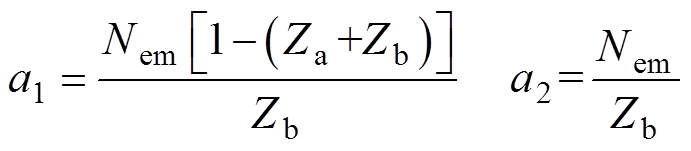
由位移边界条件：l=0端，x1=x(0,t)；l=l1端，x2=x(l1,t)，因此可利用分布式模型求得两端的位移代入波动方程中得到位移关于时间t和沿长度方向距离l的解。
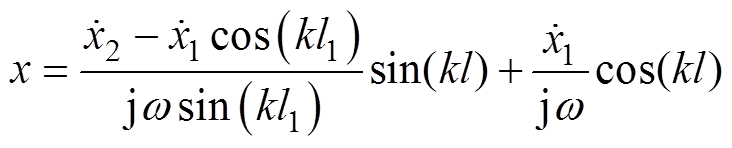（22）
在搭接区域，由于气隙的存在会导致漏磁通增大，从而使得麦克斯韦力增大，硅钢片间相互作用的麦克斯韦力可计算[33-34]为
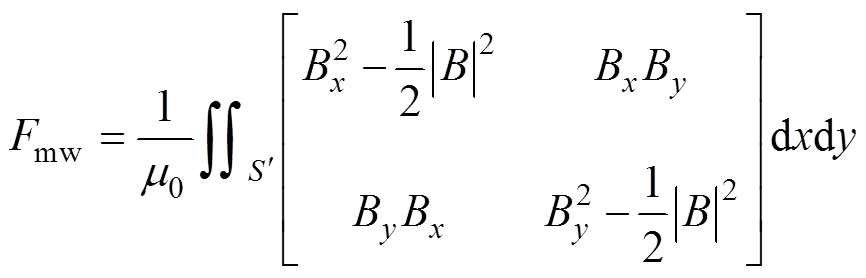（23）
式中，Bx、By分别为x、y方向的磁通密度；Fmw为麦克斯韦力；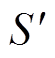
为空气中包围整个磁质的封闭曲面。图12给出了正常工作磁通密度为1.2 T时搭接区域的最大磁致伸缩应力和最大麦克斯韦应力的对比，可以看出，计算得出的麦克斯韦应力较磁致伸缩应力相差3个数量级左右，因此其在x、y方向引起的振动和等效磁致伸缩力引起的振动相比可忽略不计。需要注意的是，在临界气隙区域和临界饱和区域，由于磁通的穿越会使得该区域z方向上的磁通密度Bz明显增大导致叠片间的麦克斯韦力显著增加，此处不对z方向的受力与振动进行详细分析。
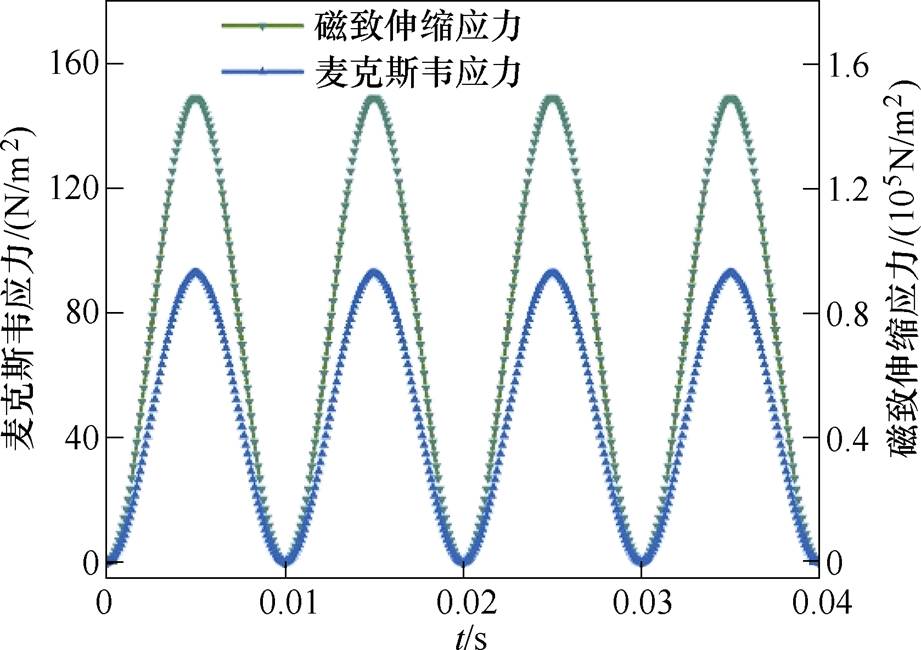
图12 不同应力对比
Fig.12 Comparison of different stresses
由第1.1节和1.2节的分析可知，铁心的搭接区域磁通密度的分布变得不均匀，这导致磁致伸缩力分布也变得不均匀，因而需对搭接区域单独建模分析振动情况。在搭接区域，由于受到邻层气隙的影响，磁通密度会经历如下变化：Bcm→Bgm→Bcm→Bc→Bcg，五种磁通密度幅值会分别对应五种磁致伸缩力，这主要因为机电换能系数不同而导致。因而可将搭接区域具体划分为五部分，每一部分都可建立其分布式二端口等效模型，等效磁致伸缩力可看做受激励电压控制的受控电压源。5个二端口网络级联到一起便构成了搭接区等效振动模型，最后将搭接区级联电路与非搭接区二端口电路级联到一起便构成完整的二端口等效振动回路如图13所示，其对应的矩阵方程为
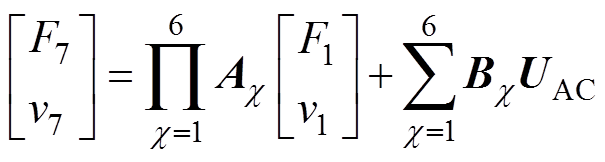（24）
其中
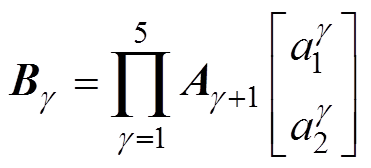（25）
式中，A1为非搭接区传输矩阵；A2～A6分别为搭接区5个二端口对应的传输矩阵。
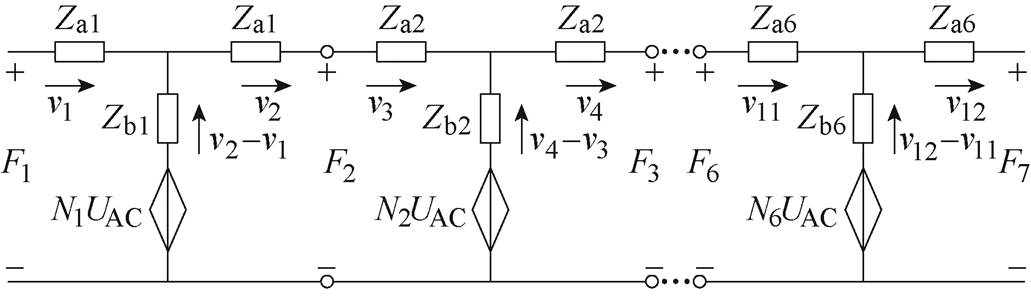
图13 二端口等效振动模型
Fig.13 Two-port equivalent vibration model
对一台实验室用单相三柱式变压器铁心模型进行振动测试，铁心由B30P105硅钢片采用三级步进搭接的工艺叠制而成。在铁心两侧旁柱各缠绕115匝励磁线圈，两组线圈并联，中柱缠绕3匝测量线圈，用于测量感应电压。实验利用交流电源柜发出工频正弦信号，随后将其施加在励磁线圈上，通过调节调压柱即可改变励磁电压大小，图14所示为实验现场。
图14 实验现场
Fig.14 Experimental site diagram
通过调节励磁电压的大小来控制铁心中柱磁通密度的大小。分别选取励磁电压为82、123、164、220 V正弦信号进行振动测试，其分别对应的中柱磁通密度幅值为0.6、0.9、1.2和1.6 T。实验采用加速度传感器来采集振动信号，采集到的振动信号将传送至DH5902数据采集分析系统进行滤波随后保存。交流调压器与励磁线圈和功率分析仪的电流通道构成串联回路，设置实时采样频率为5 kHz，可确保采集信号不失真且具有连续性，图15给出了实验电路。
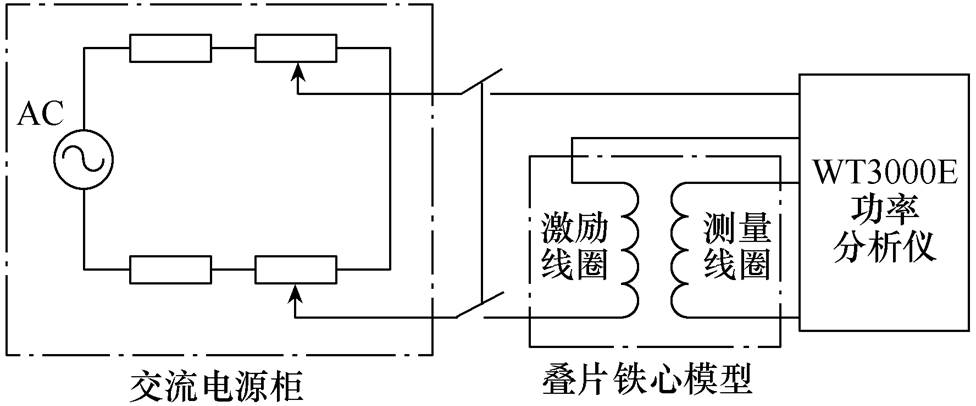
图15 实验电路
Fig.15 Experimental circuit diagram
由于铁心模型的铁轭位置固定有夹紧板、旁柱上缠绕励磁线圈，不方便布置测点，因此实验时选择将测点布置于如图16所示的1、2两处，分别用于测量铁心中柱和旁柱沿x方向的振动位移。
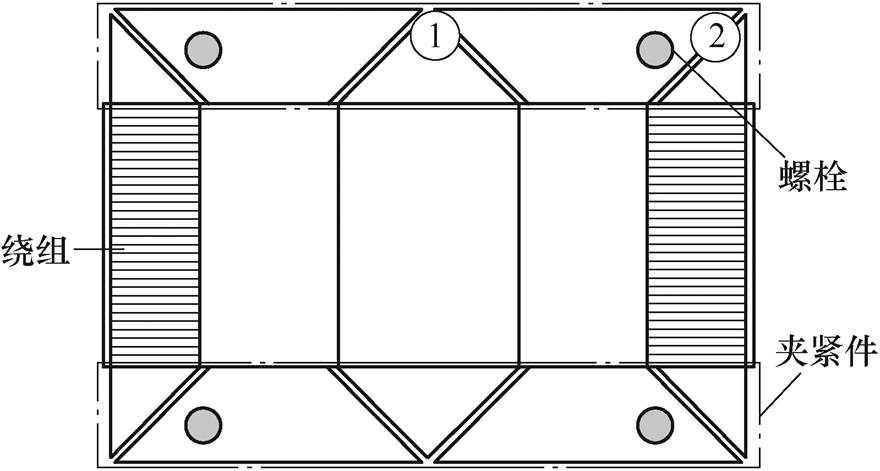
图16 测点布置
Fig.16 Survey point layout drawing
图17给出了测点1在四组不同激励电压下的振动位移波形，随着激励电压的增大，测点的振动也变得更强，且电压等级越高振动幅值增加越明显，220 V激励下测点1的振动幅值约为82 V电压激励下的6倍左右。
图18给出了测点1和测点2的位移峰峰值（伸长位移峰值与收缩位移峰值之差），从图中可以看出，测点1的振幅要大于测点2，且随着电压的升高，二者的差值也有所增加。从理论上讲，中柱的磁通密度略低于旁柱，磁致伸缩位移也应更小，但由于旁柱附近固定有夹紧螺栓致使旁柱附近的夹紧力Fc会明显高于中柱。测量发现，中柱的铁心叠片厚度约为61.2 cm而旁柱的叠片厚度只有60.07 cm，这说明两测点所承受的夹紧力相差较大，根据滑动摩擦力计算公式Fm =mFc，m 为摩擦因数，旁柱振动时受到的摩擦阻力更大，且旁柱上还缠有励磁线圈，更进一步减弱了旁柱上的振动。可见，在分析和设计变压器时还需重点考量夹紧力对铁心振动的影响。
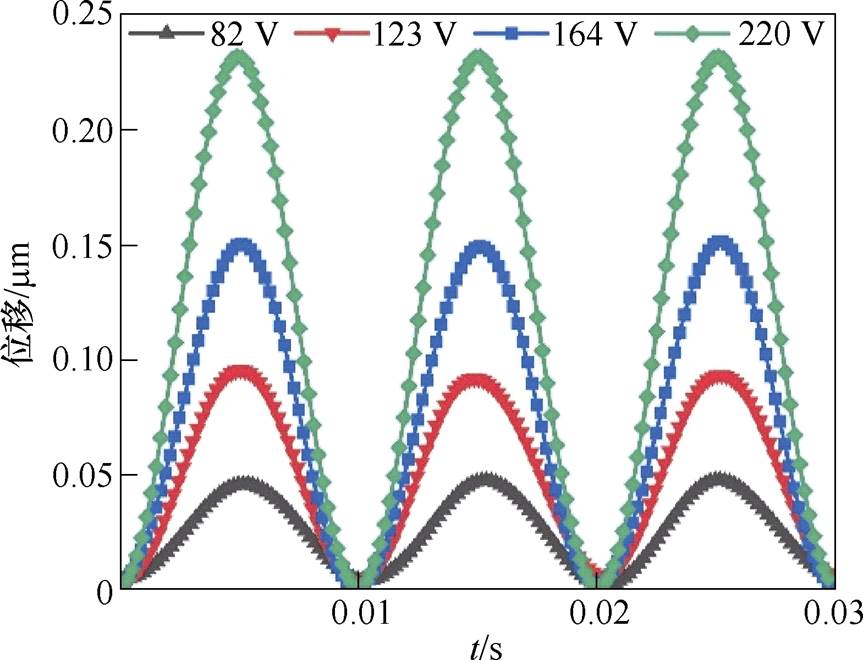
图17 不同激励电压下的振动位移波形
Fig.17 Vibration displacement waveforms at different excitation voltages
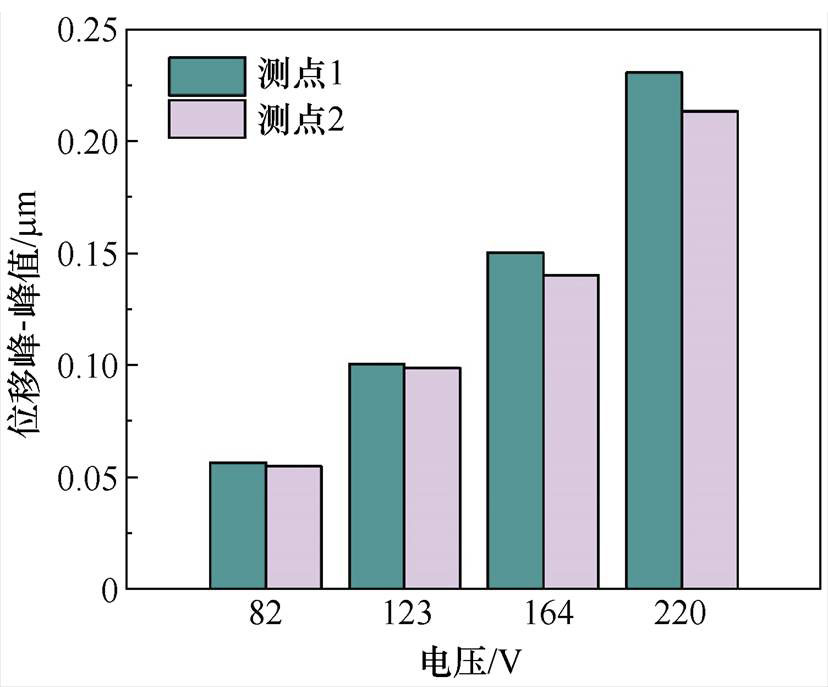
图18 测点1、2振动对比
Fig.18 Vibration comparison of points 1 and 2
根据第1.1节中所求得的磁阻率，依据电路-磁路耦合原理利用谐波平衡法同时计算励磁电流和铁心中柱磁通密度[35]。
图19、图20给出了励磁电流的计算结果，中柱磁通密度幅值的计算结果见表2，可以看出，计算结果与测量结果基本吻合，从而验证了磁路建模和磁阻计算的有效性。
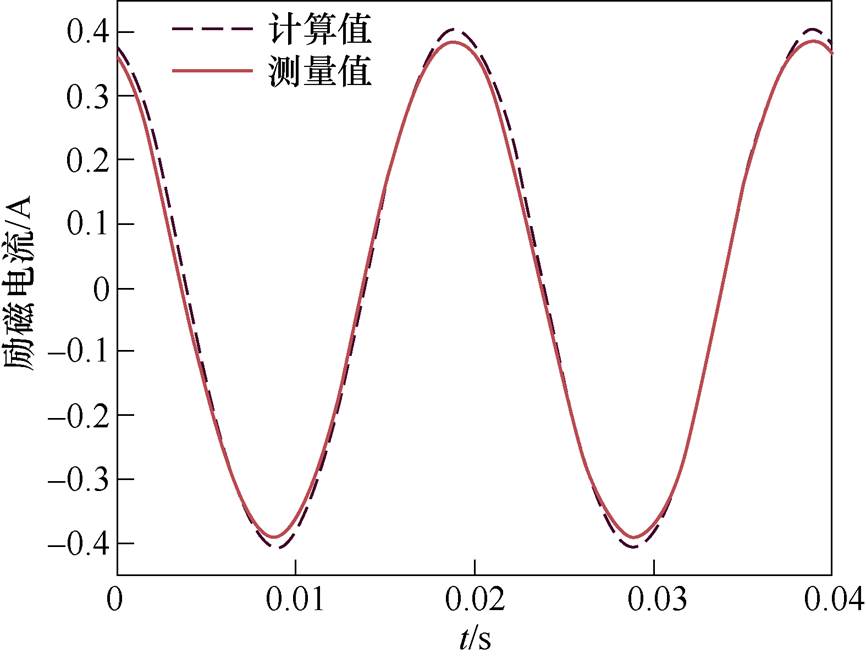
图19 UAC=82 V时单相三柱变压器励磁电流
Fig.19 Exciting current of the single-phase three-limb transformer (UAC=82 V)
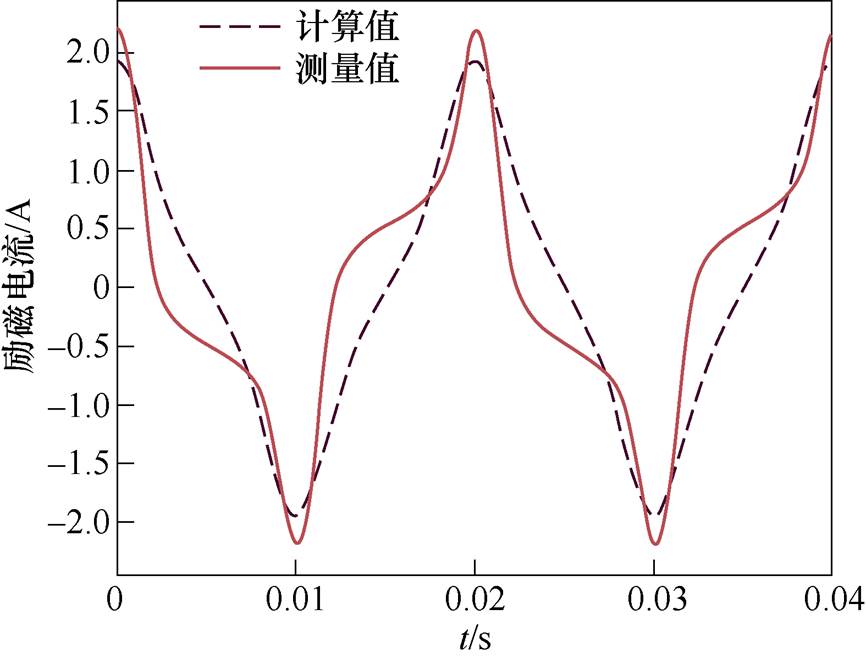
图20 UAC=192 V时单相三柱变压器励磁电流
Fig.20 Exciting current of the single-phase three-limb transformer (UAC=192 V)
表2 铁心中柱磁通密度仿真与实验对比
Tab.2 Comparison between calculated and measured the magnetic flux of the iron core
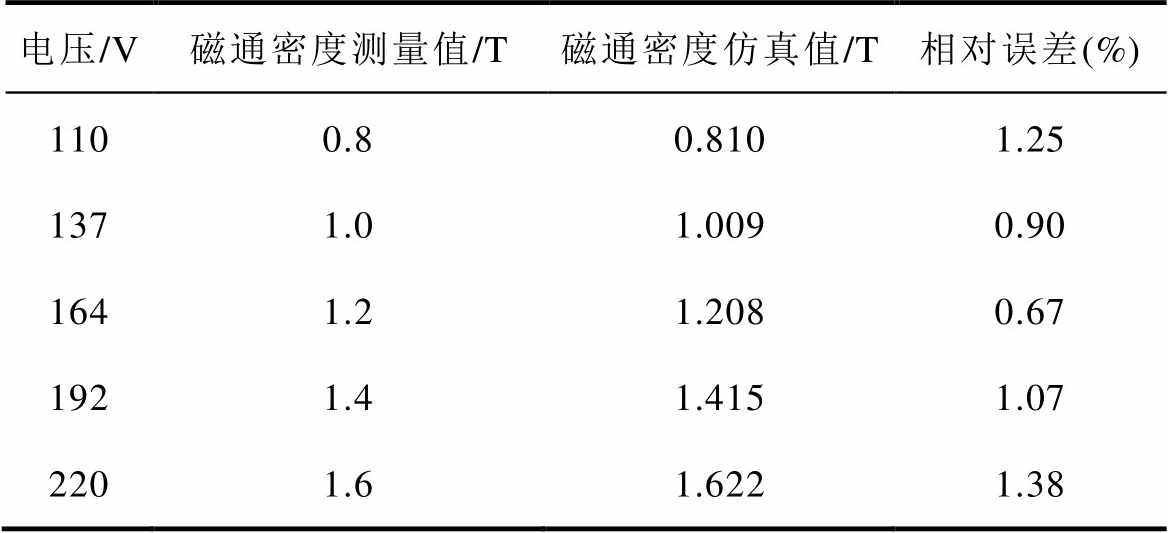
电压/V磁通密度测量值/T磁通密度仿真值/T相对误差(%) 1100.80.8101.25 1371.01.0090.90 1641.21.2080.67 1921.41.4151.07 2201.61.6221.38
利用等效振动回路模型计算了叠片铁心的振动位移。图21所示为计算所得的测点1在164 V正弦电压激励下振动位移、加速度与实验测量结果的对比。从图中可以看出，位移计算波形近似正弦波，计算值与实际值的振幅误差并不大，但计算值要略大于测量值，这主要是因为在计算时没有考虑夹紧力以及叠片间的滑动摩擦力的影响。
在图6所示的直角坐标系中计算旁柱搭接区域沿x方向的磁致伸缩应力峰值分布情况，如图22所示。
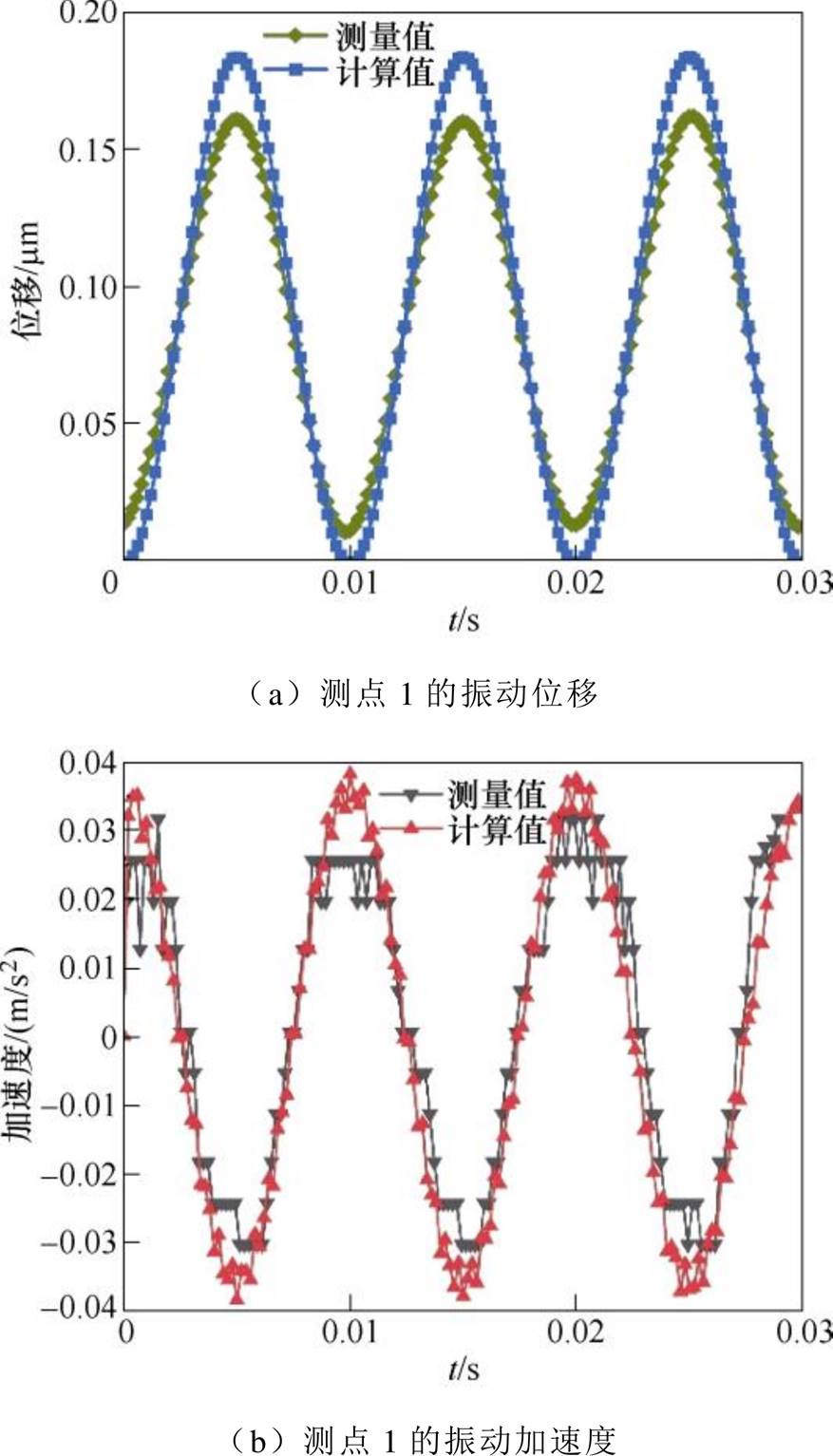
图21 UAC=164 V时测点1的振动仿真与实验对比
Fig.21 Vibration simulation and experimental comparison of measurement point 1 (UAC=164 V)
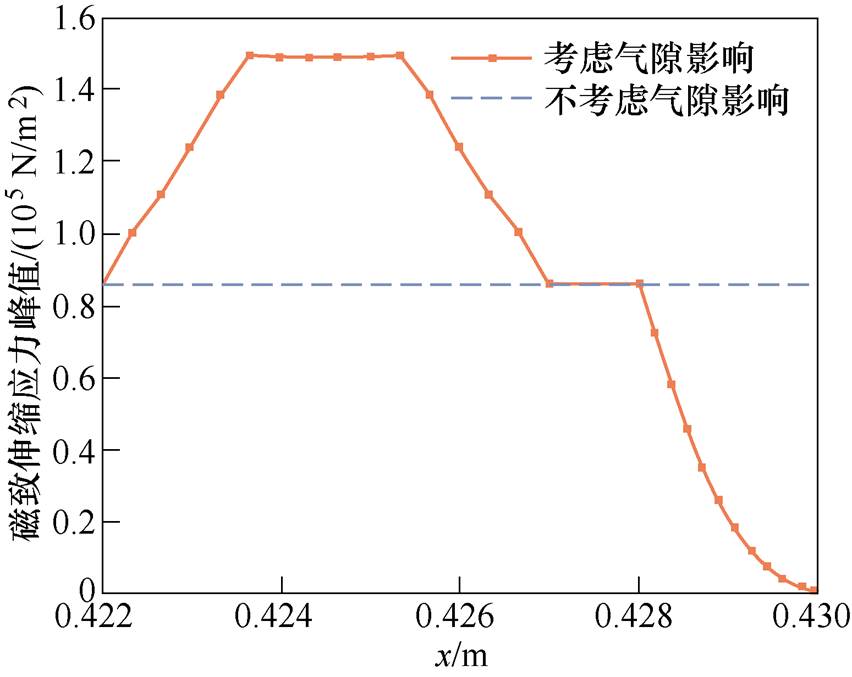
图22 搭接区域磁致伸缩应力峰值分布
Fig.22 Distribution of peak magnetostrictive stress in the lap area
采用分布式模型计算的旁柱搭接区振动位移分布如图23所示，图中y轴表示旁柱中沿x方向的坐标，z轴所示为对应的磁致伸缩位移。磁致伸缩应力和位移的计算结果表明，搭接区域的振动要强于非搭接区域，这主要因为在搭接区域的局部磁通密度趋于饱和使得该区域磁致伸缩力明显强于非搭接区域。利用本文所提方法通过Matlab编程计算铁心的励磁电流、磁通密度和磁致伸缩位移仅用时5 s即可完成计算，而作为对比，在同一台计算机上利用目前较为主流的电磁仿真软件Comsol搭建了本文所计算的叠片铁心模型，对其剖分了87 926个网格完成磁场和固体力学场的计算则需要用时643 s左右。可见，将机-电类比的思路运用到铁心建模计算中可大幅提升计算速度。
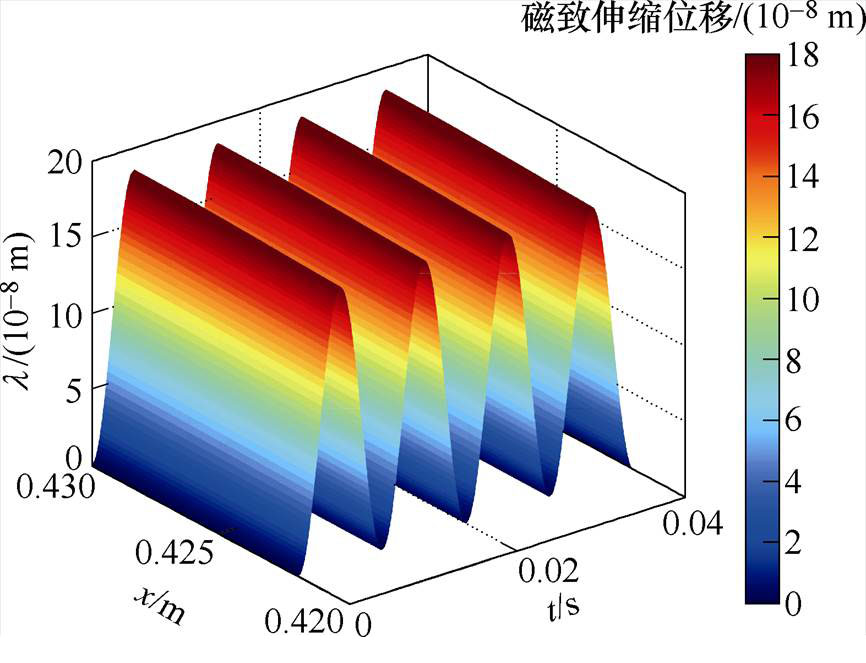
图23 搭接区域磁致伸缩振动分布
Fig.23 Distribution of magnetostrictive vibrationin the lap area
本文采用电-磁-机耦合的方式计算了单相三柱式变压器铁心模型的磁致伸缩位移，将计算结果与实验数据对比得出以下结论：
1）机-电类比的思路适用于变压器铁心振动位移计算，相较于目前较为主流的有限元计算方法可大大缩短计算时间，并能在一定程度上保证计算结果的可靠性。
2）铁心之间接缝气隙的存在会使得该区域表现出不同于铁心材料本身的磁特性，并使该区域附近磁致伸缩振动增强，在研究铁心振动时有必要重点考量该区域的振动情况。
3）在铁心搭接区域既有磁致伸缩力引起的振动也有麦克斯韦力引起的振动，但对于铁心在x、y方向上的振动来说起主导作用的仍是磁致伸缩力。此外，磁通的穿越会使得搭接区局部区域z方向上磁通密度增加，进而使叠片间沿z方向的麦克斯韦力增大，故今后分析铁心搭接区振动分布时还应重点计算z方向由麦克斯韦力引起的振动。
4）铁心的磁致伸缩位移不仅取决于磁致伸缩力和麦克斯韦力的大小，摩擦力可能也是影响变压器铁心振动的重要因素。在后续工作中还应具体考量夹紧件与铁心之间的摩擦阻力以及铁心叠片之间的相对滑动所产生的摩擦力，将摩擦力的影响计及耦合模型和计算当中。
参考文献
[1] 王革鹏, 金文德, 曾向阳, 等. 特高压并联电抗器铁心振动的分析与控制研究[J]. 电工技术学报, 2022, 37(9): 2190-2198.
Wang Gepeng, Jin Wende, Zeng Xiangyang, et al. Analysis and control research on core vibration of UHV shunt reactor[J]. Transactions of China Elec- trotechnical Society, 2022, 37(9): 2190-2198.
[2] 朱叶叶, 汲胜昌, 张凡, 等. 电力变压器振动产生机理及影响因素研究[J]. 西安交通大学学报, 2015, 49(6): 115-125.
Zhu Yeye, Ji Shengchang, Zhang Fan, et al. Vibration mechanism and influence factors in power trans- formers[J]. Journal of Xi’an Jiaotong University, 2015, 49(6): 115-125.
[3] 白保东, 刘闯, 王佳音. 直流偏磁下变压器振动的仿真及实验研究[J]. 电工技术学报, 2013, 28(增刊2): 427-433.
Bai Baodong, Liu Chuang, Wang Jiayin. Simulation and experimental research of transformer vibration under DC magnetic bias[J]. Transactions of China Electrotechnical Society, 2013, 28(S2): 427-433.
[4] 赵莉华, 丰遥, 谢荣斌, 等. 油浸式变压器铁心振动特性分析[J]. 电力系统及其自动化学报, 2018, 30(10): 104-110.
Zhao Lihua, Feng Yao, Xie Rongbin, et al. Analysis of vibration characteristics for oil-immersed trans- former core[J]. Proceedings of the CSU-EPSA, 2018, 30(10): 104-110.
[5] 王佳音, 白保东, 刘宏亮, 等. 直流偏磁对变压器振动噪声的影响[J]. 电工技术学报, 2015, 30(8): 56-61.
Wang Jiayin, Bai Baodong, Liu Hongliang, et al. Research on vibration and noise of transformers under DC bias[J]. Transactions of China Electrotechnical Society, 2015, 30(8): 56-61.
[6] 赵小军, 张凌云, 刘洋, 等. 机械应力对取向硅钢片综合磁性能影响的实验研究[J]. 电工技术学报, 2022, 37(22): 5776-5787.
Zhao Xiaojun, Zhang Lingyun, Liu Yang, et al. Experimental study on the effect of mechanical stress on the comprehensive magnetic properties of the grain-oriented silicon steel[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5776-5787.
[7] Shahaj A, Garvey S D. A possible method for magnetostrictive reduction of vibration in large electrical machines[J]. IEEE Transactions on Mag- netics, 2011, 47(2): 374-385.
[8] Bartoletti C, Desiderio M, Di Carlo D, et al. Vibro-acoustic techniques to diagnose power trans- formers[J]. IEEE Transactions on Power Delivery, 2004, 19(1): 221-229.
[9] Kitagawa W, Ishihara Y, Todaka T, et al. Analysis of structural deformation and vibration of a transformer core by using magnetic property of magnetostri- ction[J]. Electrical Engineering in Japan, 2010, 172(1): 19-26.
[10] Moses A. Measurement of magnetostriction and vibration with regard to transformer noise[J]. IEEE Transactions on Magnetics, 1974, 10(2): 154-156.
[11] Hilgert T, Vandevelde L, Melkebeek J. Comparison of magnetostriction models for use in calculations of vibrations in magnetic cores[J]. IEEE Transactions on Magnetics, 2008, 44(6): 874-877.
[12] Gao Yanhui, Muramatsu K, Hatim M J, et al. The effect of laminated structure on coupled magnetic field and mechanical analyses of iron core and its homogenization technique[J]. IEEE Transactions on Magnetics, 2011, 47(5): 1358-1361.
[13] Ebrahimi H, Gao Yanhui, Kameari A, et al. Coupled magneto-mechanical analysis considering permeability variation by stress due to both magnetostriction and electromagnetism[J]. IEEE Transactions on Magnetics, 2013, 49(5): 1621-1624.
[14] Gao Yanhui, Muramatsu K, Fujiwara K, et al. Vibration analysis of a reactor driven by an inverter power supply considering electromagnetism and magnetostriction[J]. IEEE Transactions on Magnetics, 2009, 45(10): 4789-4792.
[15] Tang Qi, Guo Shufeng, Wang Zhongdong. Magnetic flux distribution in power transformer core with mitred joints[J]. Journal of Applied Physics, 2015, 117(17): 1-4.
[16] 祝丽花, 杨庆新, 闫荣格, 等. 考虑磁致伸缩效应电力变压器振动噪声的研究[J]. 电工技术学报, 2013, 28(4): 1-6, 19.
Zhu Lihua, Yang Qingxin, Yan Rongge, et al. Research on vibration and noise of power transformer cores including magnetostriction effects[J]. Transa- ctions of China Electrotechnical Society, 2013, 28(4): 1-6, 19.
[17] 祝丽花, 王斌, 刘松, 等. 不同负载对干式变压器电磁振动的影响分析[J]. 电工技术学报, 2018, 33(7): 1599-1606.
Zhu Lihua, Wang Bin, Liu Song, et al. Research on electromagnetic vibration of dry type transformer under different types of load[J]. Transactions of China Electrotechnical Society, 2018, 33(7): 1599- 1606.
[18] 张欣, 解超群, 祝丽花, 等. 考虑磁致伸缩效应的电机应力数值仿真与实验[J]. 电工技术学报, 2017, 32(增刊2): 50-55.
Zhang Xin, Xie Chaoqun, Zhu Lihua, et al. Numerical simulation and experimental research on stress of motor including magnetostriction effects[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(S2): 50-55.
[19] 李维铮, 祝丽花, 石永恒. 电力变压器铁心搭迭区磁等效及磁致振动分析[J]. 电力科学与工程, 2019, 35(10): 29-35.
Li Weizheng, Zhu Lihua, Shi Yongheng. Study on the magnetic equivalent and magneto-induced vibration of core overlap region in power transformer[J]. Electric Power Science and Engineering, 2019, 35(10): 29-35.
[20] 张鹏宁, 李琳, 纪锋, 等. HVDC阳极饱和电抗器阻尼弹性体降振降噪试验研究[J]. 电网技术, 2017, 41(12): 3839-3845.
Zhang Pengning, Li Lin, Ji Feng, et al. Test study on reduction of vibration and noise to damping elastomer in HVDC anode saturable reactor[J]. Power System Technology, 2017, 41(12): 3839-3845.
[21] 张鹏宁, 李琳, 程志光, 等. 并联电抗器与变压器模型铁心振动仿真与试验对比[J]. 电工技术学报, 2018, 33(22): 5273-5281.
Zhang Pengning, Li Lin, Cheng Zhiguang, et al. Vibration simulation and experiment comparison of shunt reactor and transformer model core[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(22): 5273-5281.
[22] 张鹏宁, 李琳, 聂京凯, 等. 考虑铁心磁致伸缩与绕组受力的高压并联电抗器振动研究[J]. 电工技术学报, 2018, 33(13): 3130-3139.
Zhang Pengning, Li Lin, Nie Jingkai, et al. Study on the vibration of high voltage shunt reactor considering of magnetostriction and winding force[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(13): 3130-3139.
[23] 曹淑瑛, 王博文, 闫荣格, 等. 超磁致伸缩致动器的磁滞非线性动态模型[J]. 中国电机工程学报, 2003, 23(11): 145-149.
Cao Shuying, Wang Bowen, Yan Rongge, et al. Dynamic model with hysteretic nonlinearity for a giant magnetostrictive actuator[J]. Proceedings of the CSEE, 2003, 23(11): 145-149.
[24] 曹淑瑛, 王博文, 郑加驹, 等. 应用混合遗传算法的超磁致伸缩致动器磁滞模型的参数辨识[J]. 中国电机工程学报, 2004, 24(10): 127-132.
Cao Shuying, Wang Bowen, Zheng Jiaju, et al. Parameter identification of hysteretic model for ginat magnetostrictive actuator using hybrid genetic algorithm[J]. Proceedings of the CSEE, 2004, 24(10): 127-132.
[25] 曹淑瑛, 郑加驹, 王博文, 等. 基于动态递归神经网络的超磁致伸缩驱动器精密位移控制[J]. 中国电机工程学报, 2006, 26(3): 106-111.
Cao Shuying, Zheng Jiaju, Wang Bowen, et al. Precision position control for giant magnetostrictive actuator based on dynamic recurrent neural network[J]. Proceedings of the CSEE, 2006, 26(3): 106-111.
[26] 李冰, 王泽忠, 刘海波, 等. 直流偏磁下500kV单相变压器振动噪声的试验研究[J]. 电工技术学报, 2021, 36(13): 2801-2811.
Li Bing, Wang Zezhong, Liu Haibo, et al. Experiment on vibro-acoustic characteristic of 500kV single- phase transformer under DC-bias[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2801- 2811.
[27] 李姝汛, 杨鑫, 陈泽坤, 等. 计及漏磁的堆栈式超磁致伸缩制动器多物理场耦合建模研究[J]. 电工技术学报, 2023, 38(9): 2277-2288.
Li Shuxun, Yang Xin, Chen Zekun, et al. Multi- physics modeling research of stacked giant mag- netostrictive actuator considering magnetic flux leakage[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2277-2288.
[28] 杜永, 程志光, 颜威利, 等. 电力变压器全斜接缝叠片铁心工作条件下的磁性能模拟[J]. 电工技术学报, 2010, 25(3): 14-19.
Du Yong, Cheng Zhiguang, Yan Weili, et al. Working magnetic property modeling of the power transformer laminated core with mitred joints[J]. Transactions ofChina Electrotechnical Society, 2010, 25(3): 14-19.
[29] Elleuch M, Poloujadoff M. New transformer model including joint air gaps and lamination anisotropy[J]. IEEE Transactions on Magnetics, 1998, 34(5): 3701- 3711.
[30] Wang Gepeng, Zeng Xiangyang, Zhao Yongjin. Research on the effect of core joints on transformer noise[J]. IEEE Transactions on Magnetics, 2021, 57(10): 1-6.
[31] Li Lingzhi, Du Xuhao, Pan Jie, et al. An engineering model of magnetic flux density and electromagnetic force density at the structural discontinuity within transformer cores[J]. Sensors, 2022, 22(13): 4869.
[32] 杨意妹, 祝丽花, 王斌, 等. 考虑磁致伸缩效应的可控饱和电抗器电磁振动分析[J]. 电工电能新技术, 2016, 35(8): 40-45.
Yang Yimei, Zhu Lihua, Wang Bin, et al. Analysis on electromagnetic vibration of controllable saturable reactor considering magnetostrictive effects[J]. Advanced Technology of Electrical Engineering and Energy, 2016, 35(8): 40-45.
[33] 赵小军, 杜雨彤, 刘洋, 等. 应用磁-机械耦合场频域解法的铁芯直流偏磁振动特性分析[J]. 高电压技术, 2020, 46(4): 1216-1225.
Zhao Xiaojun, Du Yutong, Liu Yang, et al. Vibration characteristics analysis of iron core under DC-biased condition by solving coupled magneto-mechanical field in frequency-domain[J]. High Voltage Engin- eering, 2020, 46(4): 1216-1225.
[34] 闫荣格, 程云飞. 动静态力共同作用对电抗器铁心振动影响[J]. 电工技术学报, 2023, 38(4): 1104- 1114.
Yan Rongge, Cheng Yunfei. Influence of dynamic and static forces on vibration of reactor core[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(4): 1104-1114.
[35] 赵小军, 张晓欣, 李慧奇, 等. 基于谐波平衡法的变压器直流偏磁电路-磁路频域耦合模型[J]. 电工技术学报, 2014, 29(9): 211-218.
Zhao Xiaojun, Zhang Xiaoxin, Li Huiqi, et al. Frequency domain coupled model between magnetic and electric circuits of DC biased transformers by harmonic balance method[J]. Transactions of China Electrotechnical Society, 2014, 29(9): 211-218.
Abstract Due to the combined effects of Maxwell force and magnetostrictive force, the transformer core inevitably vibrates in actual operation. The vibration of the core can cause noise pollution and loosen components. In severe cases, it may threaten the power supply reliability of the power system. Currently, finite element simulation is usually used to calculate the core vibration, but this method has a long calculation time and low efficiency. This paper proposes a refined modeling and calculation method based on the electromechanical analogy method for core multiphysics coupling characteristics.
Firstly, the step overlap area of the transformer core is studied. In the presence of air gaps, the magnetic properties of a single silicon steel sheet are measured, and the equivalent magnetic properties of the overlap area are analyzed through local magnetic circuit modeling to obtain the equivalent magnetic resistance of the overlap area. Based on reasonable assumptions and simplification, the overall equivalent magnetic circuit topology of the transformer is constructed. Secondly, according to the electromechanical-electrical analogy method and mechanical vibration theory, an equivalent vibration loop model in the form of a two-port cascade is established based on the magnetic field distribution characteristics of the lap area to realize the rapid and accurate calculation of the core vibration characteristics. In addition, a vibration test platform for the single-phase three-column transformer core model is built. The data, including vibration displacement, excitation current, and core flux density under different excitation voltages, are compared with the calculation results of the model. The calculation results are in good agreement with the experimental results, which verifies the effectiveness and accuracy of the proposed method. The magnetostrictive vibration characteristics in the lap area are analyzed. The vibration of the lap region is stronger than that of the non-lap area, mainly because the local magnetic flux density in the lap region tends to be saturated, making the magnetostrictive force significantly stronger.
In conclusion, the theoretical analysis and experimental results show that the proposed electro-magnetic-mechanical multiphysics coupling calculation method considering the influence of air gap obtains the distribution characteristics of the transformer core magnetic field and reflects the mechanical vibration distribution characteristics caused by a non-uniform magnetic field. Compared with the traditional finite element calculation method, the proposed method greatly saves calculation time and cost.
keywords：Field path coupling, magnetostriction, laminated core, vibration
DOI: 10.19595/j.cnki.1000-6753.tces.230719
中图分类号：TM41
北京市自然科学基金项目（3212036）、国家自然科学基金项目（52177006）和贵州电网有限责任公司科技项目（GZKJXM20222149）资助。
收稿日期 2023-05-22
改稿日期 2023-07-03
赵小军 男，1983年生，博士，教授，博士生导师，研究方向为电工材料磁性能测量与模拟技术、频域数值计算方法、变压器直流偏磁及振动噪声问题、多物理场耦合模型及计算方法。E-mail: zxjncepu@ncepu.edu.cn（通信作者）
张佳伟 男，1998年生，硕士研究生，主要研究方向为变压器铁心振动、多物理场耦合计算。E-mail: zjw199810@126.com
（编辑 崔文静）