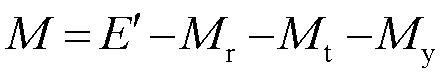（1）
摘要质子交换膜燃料电池（PEMFC）是一种难以精确建模的非线性系统，因此需要具有较强鲁棒性与高适应性的控制器来控制PEMFC电堆温度。该文提出一种基于深度强化学习的数据驱动控制器来控制电堆温度。考虑PEMFC系统的特点，包括其非线性、不确定性和环境条件的影响，提出一种新的深度强化学习算法，即分类回放双延迟贝叶斯深度确定性策略梯度（CTDB-DDPG）算法。该算法的设计引入贝叶斯神经网络、分类经验回放等技术，提高了控制器的性能。通过仿真结果与RT-Lab实验平台的结果表明，利用CTDB-DDPG算法的高适应性与强鲁棒性，所提算法可以更有效地控制 PEMFC电堆温度，具有一定的实际意义。
关键词：燃料电池 联合控制 深度确定性 贝叶斯网络
质子交换膜燃料电池（Proton Exchange Membrane Fuel Cell, PEMFC）具有可在低温和低压环境下以较高的功率密度运行、无污染、低噪声、不受卡诺循环限制、无机械运动结构、可靠性高等优点[1-4]，已广泛应用在储能设备、便携式电源、燃料电池汽车和航空领域等方面[5-8]。PEMFC的工作效率和使用寿命受电池的工作压力、工作温度以及反应物浓度等操作参数影响很大，其中，燃料电池温度常被视为重要的影响因素。因此为了保证燃料电池保持高效工作，燃料电池必须工作在适当的温度范围内。
一些学者提出了多种方法来改善燃料电池的温度控制。传统的控制算法包括比例积分控制[9]、反馈控制[10]、分段预测的负反馈控制[11]、自适应的线性二次方调节器反馈控制[12]。然而，由于PEMFC系统固有的非线性，这些控制算法有其局限性。特别是，当负载动态变化和系统参数受到扰动时，传统的控制策略会导致控制器的鲁棒性降低。
因此，研究人员试图开发一种与非线性模式兼容的算法，提出了一系列控制PEMFC温度的新型控制算法，包括模型预测控制（Model Predictive Control, MPC）、模糊控制、神经网络控制（Neural Network Control, NNC）和复合控制等。与传统设计相比，MPC是一种更合适的控制算法。一些MPC算法[13]被用于PEMFC温度控制，如鲁棒反馈模型预测控制[14]。然而，尽管MPC算法具有控制精度高的优点，但因其高度依赖于对PEMFC精确的建模，在实践中难以实现。
一些基于模糊控制的算法被应用于PEMFC温度控制，如模糊控制[15]、增量模糊控制[16]、模糊增量PID[17]和多输入多输出的模糊控制等[18]。然而，尽管这些基于模糊控制的算法是无模型的，并且具有适应性强的特点，但其模糊控制规则过于简单，精度不够，无法实现精确的自适应控制。NNC作为一种无模型的算法，也被广泛用于燃料电池的控制，如人工神经网络控制[19]和BP神经网络控制[20]。然而，尽管NNC的控制原理简单，但在不同的操作条件下，其性能差异很大。学者们提出了一些复合控制算法来控制PEMFC温度，包括基于模型的前馈和反馈控制算法[21]、主动干扰抑制控制（Active Disturbance Rejection Control, ADRC）[22]、数据驱动的混合控制[23]、多变量鲁棒PID控制[24]、神经网络预测控制[25]和模型参考自适应控制[26]。这些类型的算法可以提高控制器的性能，但由于设计过于复杂，结合了多种原理，控制器要进行大量的计算，导致这些算法在应对实际PEMFC温度控制问题时，需要处理大量计算且其响应速度慢，使得其适用性受限。此外，循环水泵与散热器之间具有强耦合性，上述大多控制策略中对于循环水泵和散热器的控制往往采用两个独立的控制器进行控制，削弱或者忽略二者之间的耦合性，都会对控制精度造成影响。
综上所述，考虑到散热器与水泵的强耦合性以及燃料电池难以精确建模的问题，需要一种鲁棒性强，能克服燃料电池控制耦合性，不需要对PEMFC精准建模的无模型算法。
近年来，深度强化学习算法，例如深度确定性策略梯度算法（Deep Deterministic Policy Gradient, DDPG），已广泛应用在控制领域，此种算法具有很高的适应性，可以实现无模型的精确控制，而且DDPG可以通过合理设置状态空间、动作空间以及奖励函数，驱动智能体来同时控制水泵以及散热器，克服了燃料电池水泵与散热器的强耦合性问题。然而，DDPG算法鲁棒性较低，训练也容易出现奖励值高估等问题，因此无法实现对于燃料电池的稳定控制。
S. Fujimoto等[27]借鉴了延迟更新技术，提出了双延迟深度确定性策略梯度算法（Twin Delayed Deep Deterministic policy gradient,TD3），以提高训练效率。J. Schulman等[28]提出了近端策略优化算法（Proximal Policy Optimization, PPO），已应用在ChatGPT等多个领域。以上算法都是对算法自身进行改进，并不能满足燃料电池对于控制器高鲁棒性的需求，因此本文提出了一种新的深度强化学习燃料电池温度控制算法，即分类回放双延迟贝叶斯（Classified replay Twin Delayed Bayesian, CTDB）深度确定性策略梯度算法，该算法在DDPG的基础上，采纳了TD3算法中的部分技术来加速收敛，并加入了分类经验回放等优化方法。该算法结构中还引入了贝叶斯神经网络与目标网络，这些优化方法很好地提高了算法的鲁棒性，实现了对氢燃料电池的有效温度控制。
循环水泵驱动管道中的冷却水循环，从而维持电堆的温度在一个良好的状态。PEMFC反应产生的热量使得电堆整体温度升高，循环水从电堆流出后流经散热器，风扇通过吹出大量的冷却空气，维持出口温度处在一个良好的状态。热管理系统通过控制循环水泵和散热风扇，从而达到理想目标值。本文将电堆出入口温差设置在5 K，入口温度设置在338.15 K。PEMFC热管理系统控制框架如图1所示。
1）电堆
PEMFC的实际输出电压等效为热力学电动势三种活化损失，单片PEMFC的电压M可表示为
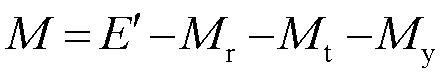（1）
电堆参数及名称见表1。
表1 电堆参数
Tab.1 Stack parameters
参数名称 能斯特电动势 Mr活化极化电压 Mt欧姆极化电压 My浓度差极化电压 M单片PEMFC电压
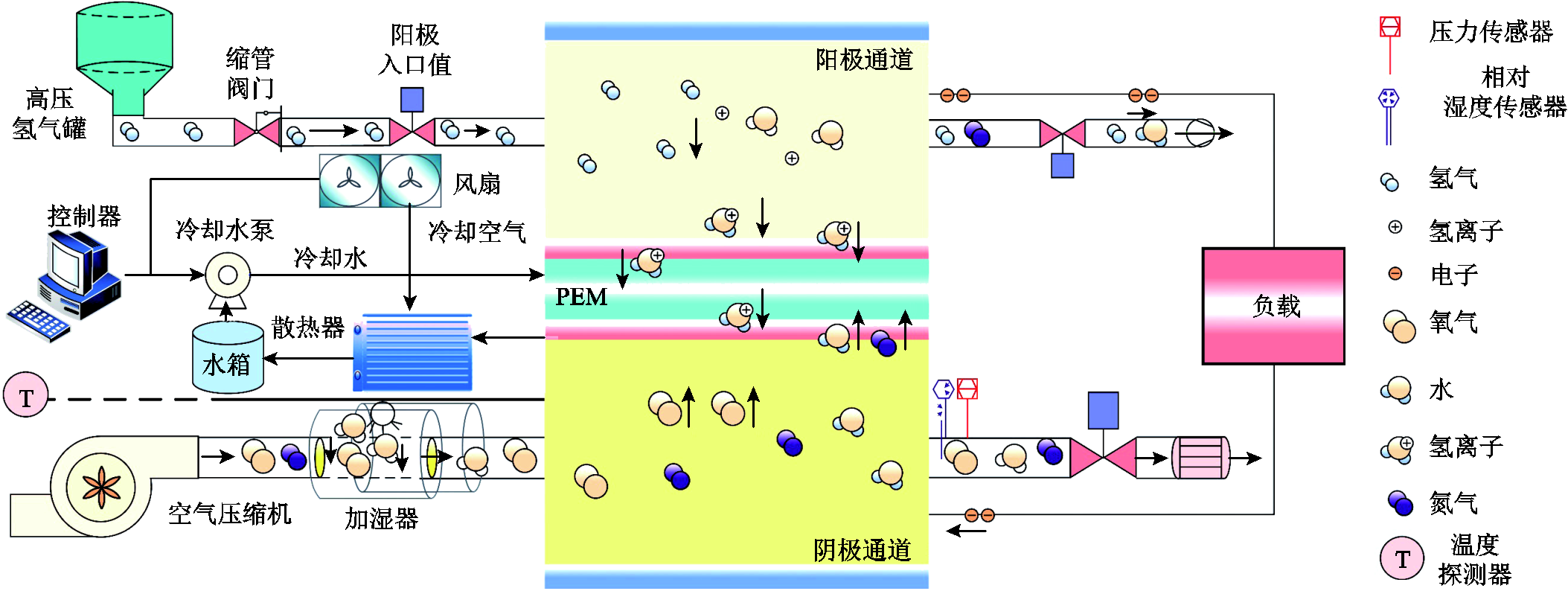
图1 PEMFC热管理系统控制框架
Fig.1 PEMFC thermal management system control framework
2）电堆热模型
电堆的热平衡式表示为
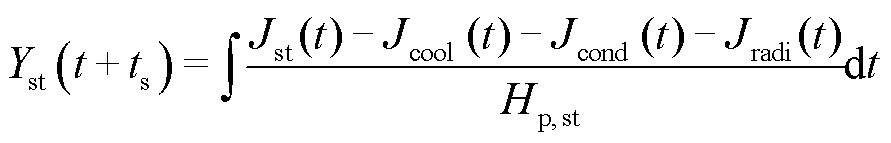（2）
电堆热容较大，电堆温度可简化为电堆冷却水出口温度，忽略热辐射以及热传导的热量，可得
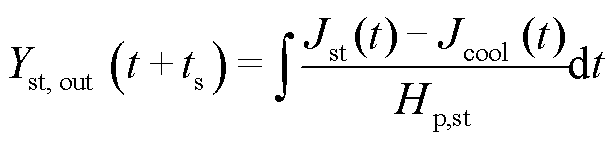（3）
电堆产生的热量为
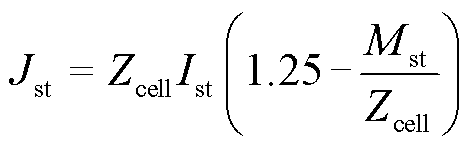（4）
实际反应中，水蒸气在一定程度上会转化成液态，因此式（4）为
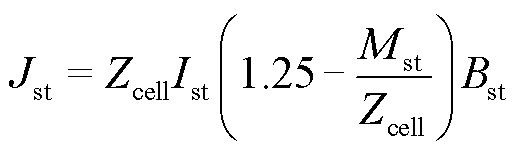（5）
冷却水带走的热量为
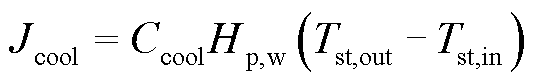（6）
3）散热器模型
散热器散热量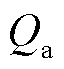
为
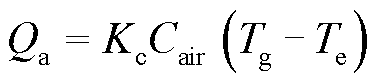（7）
经过散热器后的冷却水温度为
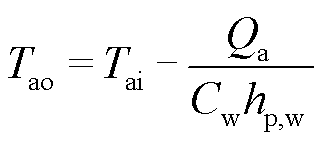（8）
电堆热模型和散热器模型参数对应见表2。
表2 电堆热模型和散热器模型参数对应表
Tab.2 Parameter correspondence table of stack thermal model and radiator models
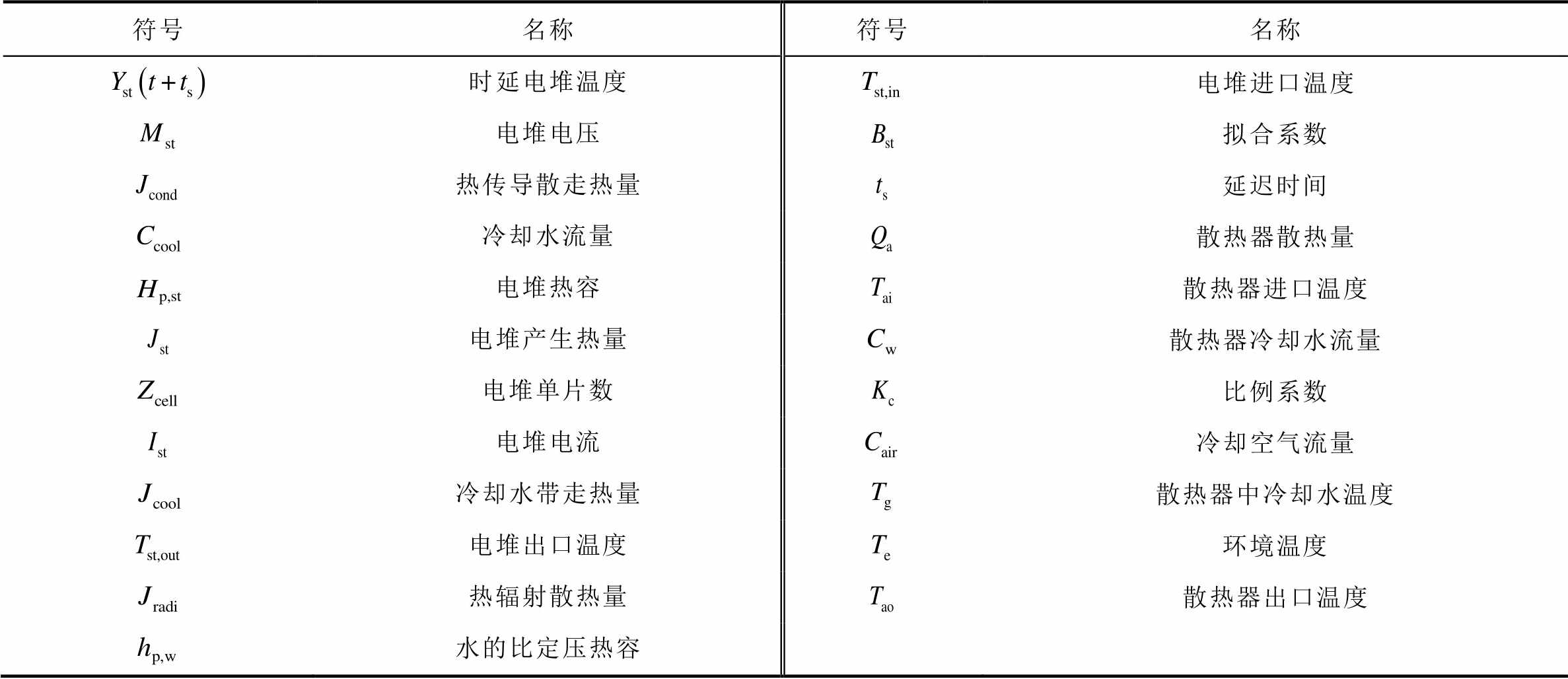
符号名称符号名称 时延电堆温度电堆进口温度 电堆电压拟合系数 热传导散走热量延迟时间 冷却水流量散热器散热量 电堆热容散热器进口温度 电堆产生热量散热器冷却水流量 电堆单片数比例系数 电堆电流冷却空气流量 冷却水带走热量散热器中冷却水温度 电堆出口温度环境温度 热辐射散热量散热器出口温度 水的比定压热容
本文针对燃料电池热管理问题，提出了分类回放双延迟贝叶斯深度确定性策略梯度（CTDB- DDPG）算法。
受人脑决策过程的启发，强化学习是智能体通过试错的方式与环境交互，并最大化累积奖励的一类机器学习算法。本文考虑一个马尔科夫决策过程，由元组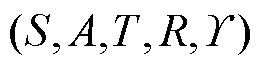
定义，其中
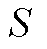和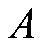
分别为状态和行动空间。状态转移概率分布为
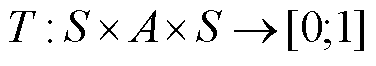，奖励函数为
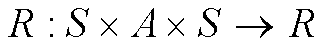未知，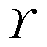
为折扣因子。强化学习的目标是找到最优策略
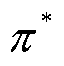，通过奖励函数，最大化累计奖赏。
CTDB-DDPG算法通过双延迟深度确定性策略梯度（TD3）机制来适应燃料电池的动态特性。TD3是对深度确定性策略梯度算法（DDPG）的改进，可以有效解决DDPG算法中的过估计偏差问题和目标网络更新过程中的累积误差问题。
燃料电池应用场景对系统安全性的要求很高，了解系统的不确定性和鲁棒性是保证实践中性能的必要条件，因而在基于深度神经网络的强化学习中，需要对输出的不确定性进行高质量的估计，从而保证模型的可靠性。
贝叶斯神经网络在有噪声数据的回归任务中的不确定性估计如图2所示。图2中显示了一个有大量噪声的非线性函数和几个明显的不确定区域，包括回归数据的分布以及随机失活（Dropout）的后验估计。可以看到，首先，非贝叶斯神经网络推断的平均后验远远超出x=0.70的任何实际数据的范围，这是因为Dropout只影响单个神经网络的拟合结果；其次，采用Dropout的近似的后验样本非常尖锐，看起来不像是任何合理的后验样本；最后，在有数据的区域，网络输出的不确定性也几乎为零。
在图2的下侧，是一组方差很大的噪声数据。使用最小方均误差（Mean Square Error, MSE）准则来训练神经网络，意味着网络必须收敛到噪声数据的平均值。Dropout的样本集中在这个平均值周围。相比之下，自举神经网络可能包括这个噪声数据的不同子集，因此产生一个更直观的不确定性的估计。但是，不一定是Dropout未能近似高斯过程后验造成的，这种情况可能常见于任何同质后验，对于训练到收敛的大型网络，所有Dropout样本可能收敛于每个数据点，甚至是离群值。而Dropout作为深度学习不确定性的来源仍有另一个重要的缺陷，它没有区分模型中固有的随机性和不确定性（模型参数的适用性）。对于汤普森采样[29-30]（基于贝叶斯理论）来说，重要的是只对预期收益的不确定性进行采样，而不是随机奖励的实现。在本文算法中，Bootstrap方法主要用于处理神经网络中的不确定性，具体实施策略如下：
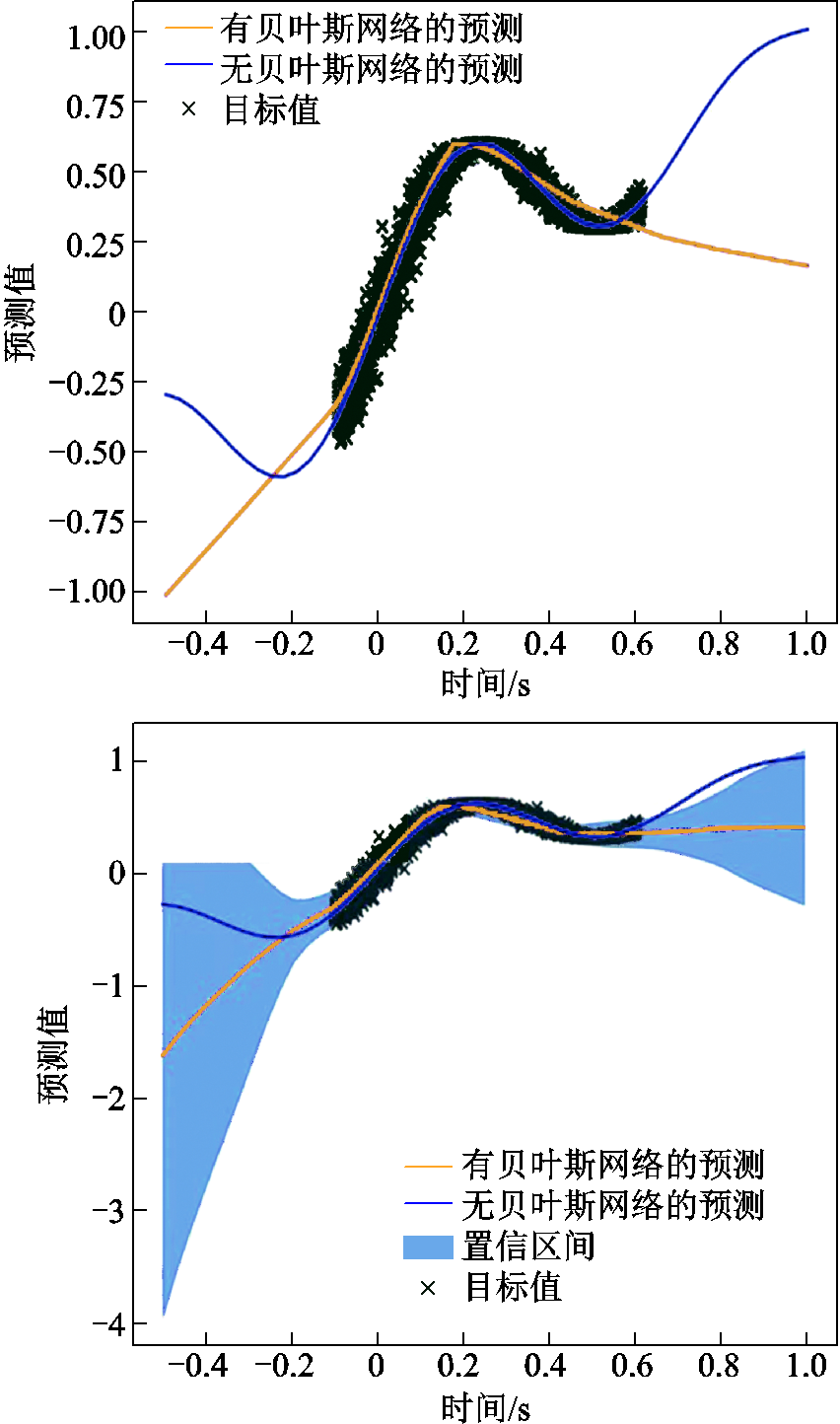
图2 贝叶斯神经网络在有噪声数据的回归任务中的不确定性估计
Fig.2 Uncertainty estimation for bayesian neural networks on a regression task with noisy data
（1）确定样本大小：通常与原始数据集的大小相同。假设原始数据集有Np个观测值，那么每一个Bootstrap样本也应该有Np个观测值。
（2）生成Bootstrap样本：首先从原始数据集中随机选择一个观测值，将其添加到Bootstrap样本中，然后将这个观测值放回原始数据集。重复这个过程，直到Bootstrap样本有Np个观测值。这意味着Bootstrap样本中可能会有重复的观测值，也可能会遗漏一些原始数据集中的观测值。
（3）重复生成Bootstrap样本：通常需要生成多个Bootstrap样本。数量取决于对不确定性估计的精度。一般来说，生成越多的Bootstrap样本，对不确定性的估计就越精确。本文选择生成Np/10个Bootstrap样本。
（4）使用Bootstrap样本进行训练：对于每一个Bootstrap样本，使用神经网络（基于CTDB-DDPG算法的温度控制结构）进行训练，这将得到关于对网络权重的估计。
（5）汇总结果：对所有Bootstrap样本得到的网络权重进行汇总。这可以通过计算权重的均值和标准差来完成，从而得到权重的点估计和不确定性估计。
可以说，Bootstrap[31]和Dropout在某种程度上是等价的。Bootstrap可以看作是一种基于数据/样本的Dropout，每个数据点都唯一地决定了一个掩码（Bootstrap掩码）。在实现中，可以共享网络参数并在不同的头（head）中采用不同参数的Bootstrap掩码，当然也可以采用其他更普遍的Bootstrap掩码。本文利用Bootstrap方法来处理神经网络中的不确定性。自举不确定性估计的Q值函数与Dropout相比还有一个关键的优势：与针对随机目标网络训练的随机删除掩码不同，实现自举法是针对当前事件中时间上一致的目标网络训练的。这对于量化Q的长期不确定性和深度探索很重要。
在智能体和环境进行互动时所得到的经验数据，对于神经网络的训练具有不同的影响。有一些经验数据可以更有效地促进神经网络的学习，因此，随机选择经验数据进行训练并不高效。为解决这个问题，本文提出了分类经验回放方法，通过对经验数据进行分类存储，来优化神经网络的训练过程。在分类经验回放方法中，每个经验数据都被分配了一个分类标准，以便在训练过程中根据它们的重要性进行选择。在每批经验数据中，会选择大量的重要经验数据，同时也会选择一些重要性低的经验数据以确保数据的多样性。
假设有两个经验缓冲池，一个缓冲池存储的是重要性高的经验数据，另一个缓冲池存储的是重要性较低的经验数据。在每次训练批次中，从两个缓冲池中抽取样本。具体抽样策略如下：①确定每次训练批次的大小，假设为N；②确定比例a，本文设定为0.75，表示75%的样本来自缓冲池；③在每次训练批次中，从一个缓冲池中随机抽取N个样本，从另一个缓冲池中也随机抽取N个样本；④将这两部分样本混合在一起，形成训练批次。
通过这种方式，可以避免在学习过程中过于依赖简单的经验数据，同时使得网络模型能更快地学习到更复杂的模式。在训练过程中，分类经验回放方法能够提高经验数据的利用效率，并减少神经网络所需的训练步骤。同时，该方法可以根据每个经验数据的重要程度来为神经网络提供有针对性的训练，从而取得更好的训练效果。
CTDB-DDPG算法使用了两个经验缓冲池来存储经验数据。在构建网络模型时，这两个经验缓冲池的所有样本的平均时序差分（Time Difference, TD）误差被初始化为0。每当一个新的经验数据产生时，所有经验数据的TD误差的平均值首先会进行更新，然后将新的经验数据的TD误差与平均值进行比较。如果其TD误差高于平均值，则将其存储在经验缓冲池1中，否则将其存储在经验缓冲池2中。对每个经验样本的TD误差进行分类有助于更好地利用经验数据进行网络模型的训练。图3展示了CTDB-DDPG算法流程。在每个时间步骤t中，Actor网络选择动作后，产生一个新的经验样本。首先将该经验样本进行分类，然后存储到相应的经验缓冲池中。CTDB-DDPG算法在选择每批数据样本时，不需要对经验缓冲池进行完整的扫描，而是从不同的经验缓冲池中随机选择，以获得重要性高的经验数据并降低训练算法的时间复杂度。通过CTDB-DDPG算法的分类经验回放方法，经验数据的利用效率得到了提高，网络模型的训练效果也得到了显著的提升。
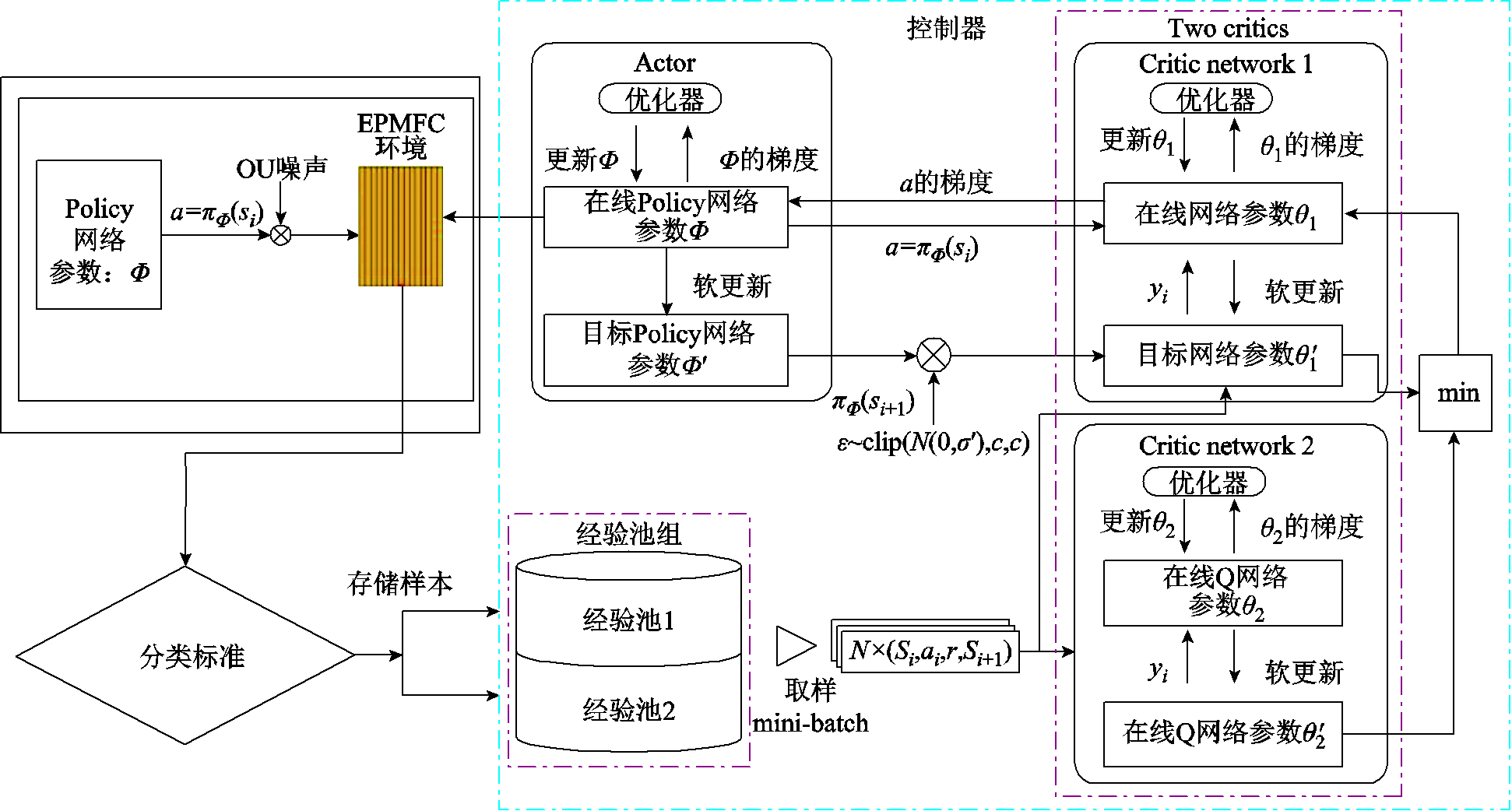
图3 CTDB-DDPG算法流程
Fig.3 CTDB-DDPG algorithm flow chart
在经验回放的分类中，选择合适的度量标准非常关键。CTDB-DDPG方法使用TD误差作为经验样本分类的度量标准。TD误差反映了智能体从当前状态的经验样本中所学习到的程度，因此TD误差特别适用于增量式强化学习算法中更新参数。在CTDB-DDPG中，根据经验样本TD误差对其进行分类，其中具有较大TD误差值的样本被认为对于更新神经网络参数有更大的重要性。那些TD误差值比平均值大的样本被储存在经验缓冲池1中。这种分类方法可以提高经验数据的利用率和网络模型的训练效果，使得网络能更加准确地学习到重要的模式和特征。
分类回放双延迟贝叶斯深度确定性策略梯度（CTDB-DDPG）在原始版本的TD3基础上，采用自举法对值网络的分布进行近似。在每个回合（Episode）开始时，CTDB-DDPG从其近似后验分布中采样一个值函数。智能体在该事件的持续时间内执行对应样本的最优政策，同时允许进行时间上的深度探索，保证了系统的稳健性，这是汤普森采样在强化学习中的启发式扩展。
在N关键网络中的K自举估计是并行建立的，以有效地实现这一算法。在算法中实现了内建的K个并行值函数网络的自举估计，这些批处理网络的每个头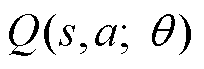
都是针对自己的目标值函数网络
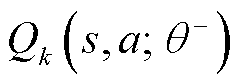进行训练。也就是说，每个值函数
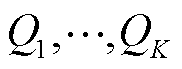通过TD估计提供了一个时间上的扩展的价值不确定性估计。存储标记值
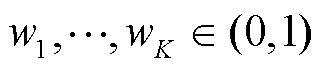，这个标记值表示哪个头可以访问哪个数据。随机选择
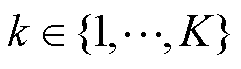并跟踪该事件持续时间的
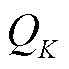以近似引导样本。
附录中算法1给出了分类回放双延迟贝叶斯深度确定性策略梯度的完整描述。其中，k个神经网络可以用来估计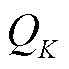的值函数网络，有k个头的神经网络相当于k个值函数。价值函数网络表示为
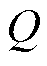，其中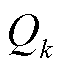
是第k个网络或第k个头的输出，
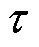为软更新系数。
CTDB-DDPG算法的核心思想是自举掩码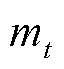
。对于每个值函数网络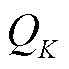，掩码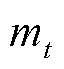决定它是否应该根据步骤
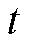产生的经验进行训练。在简化的情况下，
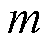是一个长度为K的二进制向量。掩码分布
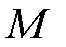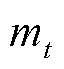生成每个。当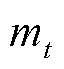的成分是从参数为0.5的伯努利分布中独立抽取时，那么这就对应于双Bootstrap或无Bootstrap。另一方面，如果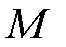产生的掩码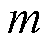都是1，那么该算法就简化为集合法。此外，指数掩码
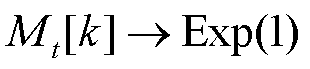与Dirichlet过程的标准贝叶斯非参数后验密切相关[32]。
此外，燃料电池热管理系统具有较大的惯性，本文算法对动作添加OU噪声[33]以提高探索效率。OU噪声是从Ornstein-Uhlenbeck过程中提取的暂时相关的噪声，通过生成时间相关性噪声的方法来帮助算法更好地探索不同的策略，从而帮助算法找到可能的更优策略，提高算法的性能和效率。虽然加入噪声会造成算法在短期内的性能恶化，但是从长期来看，噪声的添加能够帮助算法避免陷入局部最优，并可能帮助找到更优的策略。
总的来说，CTDB-DDPG算法通过结合燃料电池的特性，实现了对燃料电池热管理系统的有效优化。通过处理神经网络中的不确定性、利用分类经验回放方法以及引入OU噪声，实现了算法的快速收敛和高鲁棒性，为燃料电池热管理提供了有效的解决方案。算法实现过程见附录。
本文采用CTDB-DDPG算法对氢燃料电池的温度进行控制，被控对象有两个：一个是燃料电池的进口温度（以Tst,in来表示）；另一个是燃料电池的进出口温度差DT，DT=Tst,out-Tst,in。进口温度Tst,in的控制理想值为338.15K，进出口温差的理想控制值为5 K。
首先确定智能体的状态空间为
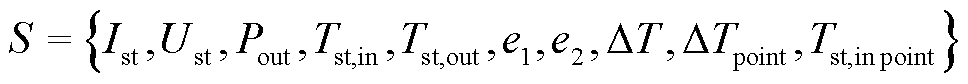（9）
状态空间参数包括电堆工作电流Ist、电堆工作电压Ust、电堆工作功率Pout、电堆入口温度Tst,in、电堆出口温度Tst,out、进出口温差目标值DTpoint=5、进口温度误差目标值Tst,inpoint=0、进出口温差与目标值的差值e1、进口温度与目标值的差值e2。
动作空间为PEMFC的冷却水流量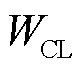
与冷却空气流量
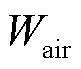，即
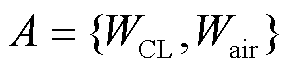（10）
当没有触发终止条件（isdone）时，奖励函数以Reward形式表达为
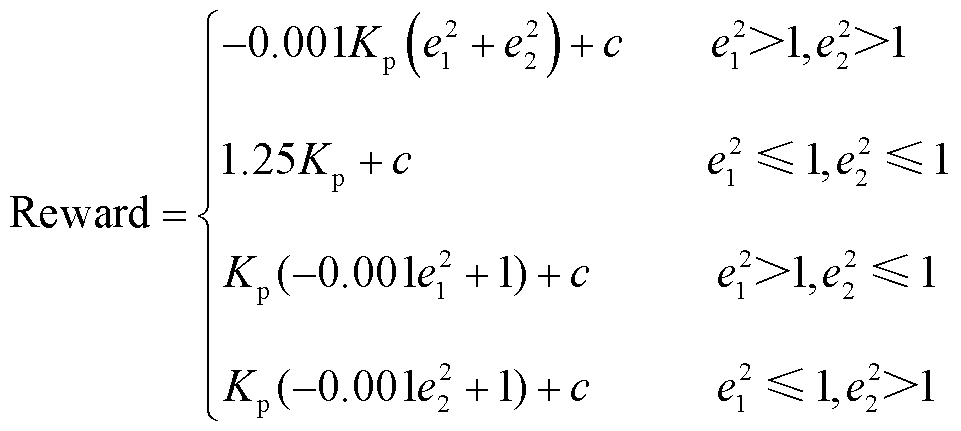（11）
式中，Kp、c为比例系数，需要在训练中不断尝试并修改，本文取Kp =0.1，c取1.3。
当触发终止条件（isdone）时，奖励函数以
形式表示为
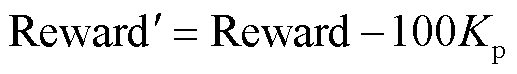（12）
终止条件（isdone）是指，当奖励函数中e1和e2超出一定范围时，直接终止此次的训练，进入下一个回合进行训练，基于CTDB-DDPG算法的温度控制结构如图4所示。
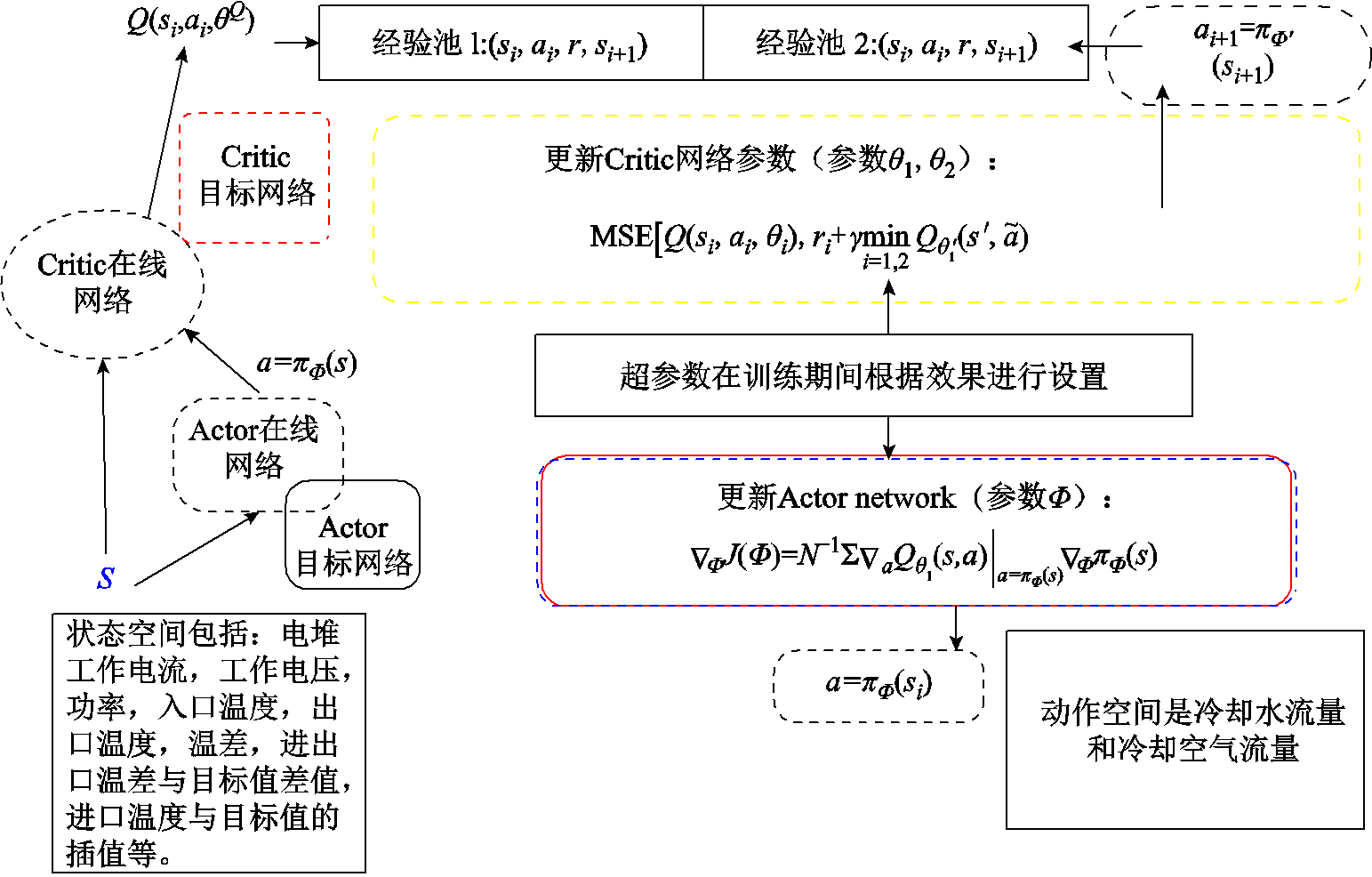
图4 基于CTDB-DDPG算法的温度控制结构
Fig.4 Temperature control structure based on the CTDB-DDPG algorithm
本仿真算例使用的平台为Matlab 2022b，燃料电池温度控制系统在Simulink平台上搭建。PEMFC仿真参数见表3。将CTDB-DDPG方法与以下算法进行了比较：粒子群优化的PID算法[34]（Particle Swarm Optimization-based Proportional Integral DerivativeAlgorithm, PSO-PID）、遗传算法优化PID算法[35]（Genetic Algorithm-based Proportional Integral DerivativeAlgorithm, GA-PID）、分数阶PID算法（Fractional Order Proportional Integral Derivative Algorithm, FO-PID）[36]、DDPG算法和TD3算法。
表3 燃料电池仿真参数
Tab.3 Simulation parameters of fuel cell
参数数值 电池数量N150 氢气分压1.3 氧气分压1.3 阳极通道容积0.0075 阴极通道容积0.015 氢气流速70 活性区域280 环境温度298 电堆热容量45.75 水的比热容4.1796 质子交换膜厚度0.075 最大电流密度2.16
注：1 atm=101.3 kPa。
在仿真与实验中选择了六种算法进行比较，其中CTDB-DDPG、TD3和DDPG是深度强化学习算法。为了评估这三种算法的性能，DDPG、TD3和CTDB-DDPG算法均以相同的参数被训练和测试。为了便于分析，图5中只显示了这三种算法在训练过程中的平均奖励值。
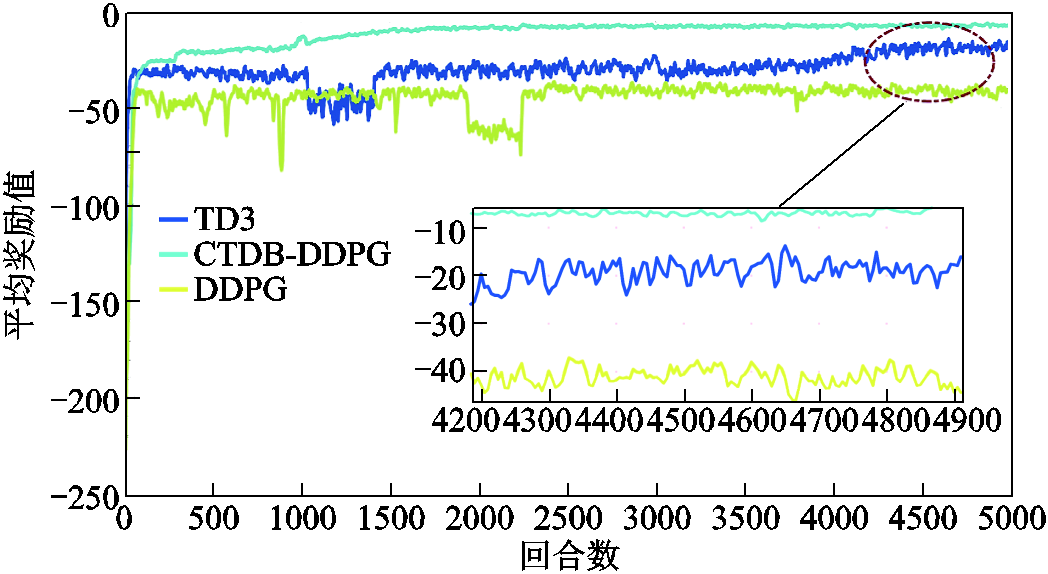
图5 不同深度强化学习算法训练中的平均奖励值
Fig.5 Average reward value in different deep reinforcement learning algorithm training
图5表明，与CTDB-DDPG算法相比，DDPG和TD3算法的学习过程较慢，波动较明显，CTDB-DDPG算法表现出更平滑的学习过程，更快地达到收敛，并取得了比其他两种算法更高的最大奖励值。由于CTDB-DDPG算法加入了更多的技术改进，它可以产生更多有价值的最优解，更快地收敛，这表明了所提出算法的有效性。
与DDPG算法及其改进版TD3相比，CTDB- DDPG考虑了神经网络的不确定性。所提出的随机初始化的引导法可以带来合理的不确定性估计。在每个回合的开始或在学习过程中的固定间隔，从马尔可夫决策过程（Markov Decision Process, MDP）参数的后验分布中获取无偏假设，并采用多头共享网络引导值函数估计，不需要额外的计算资源。而且采用 Q学习，可以保留累计折扣的不确定性，对于需要深度探索的环境更为有效。随机选择头网络，模拟汤普森采样可以有效地避免噪声策略中智能体的无效提升，加速了CTDB-DDPG算法的收敛。
在此算例中采用的Critic和Actor网络均为3层隐藏层，每层分别包含128、64和32个神经元，超参数见表4。
表4 案例1燃料电池温度控系统CTDB-DDPG超参数设置
Tab.4 DDPG super parameter setting of hydrogen fuel cell temperature control system in Case 1
参数数值 Critic学习率0.000 5 Actor学习率0.000 1 经验池回放容量1 000 000 经验池回放训练批次64 噪声方差0.5 噪声衰减系数0.000 01 软更新系数0.001 折旧因子0.99
训练后输出仿真结果，并与PSO-PID、GA-PID、FO-PID、DDPG和TD3算法的结果进行比较。图6显示了每1 000s的电流的阶跃变化，范围在100～150 A。
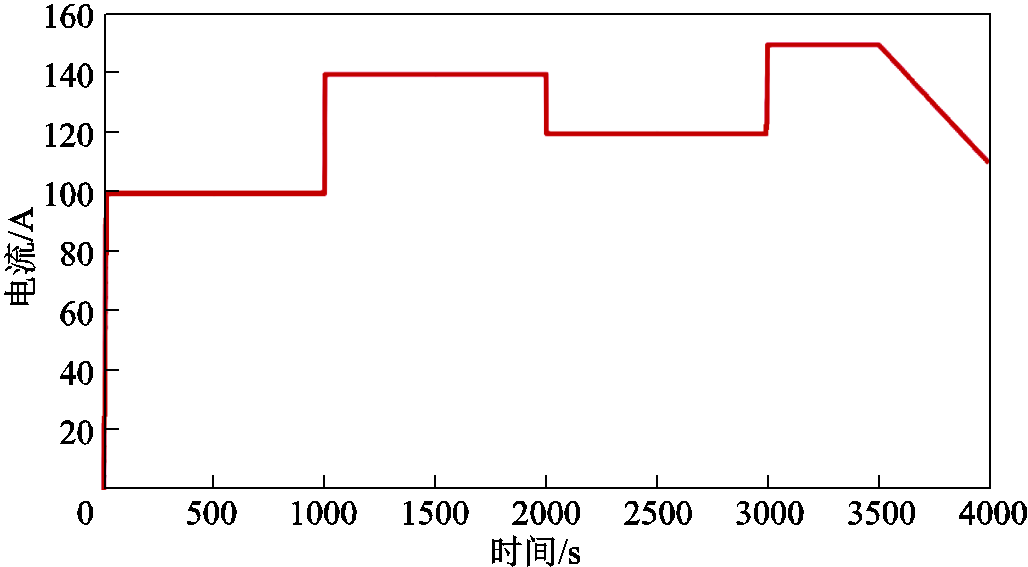
图6 案例1的负载曲线
Fig.6 Current variation curve of Case 1
图7e和图7d显示了负载电流阶跃变化时的冷却水流量和冷却水带走的热量。负载在1000 s和3000 s时增加，CTDB-DDPG控制器通过增加水泵流速更有效地从电堆中移除热量，对负载的变化做出快速反应。在2000s和3500s时，负载减少，CTDB-DDPG算法迅速降低了水泵的流量，从电堆中移除的热量减少。图7c和图7f分别为空气带走热量和冷却空气流速的变化曲线。CTDB-DDPG控制器在负载增加和减少时调节散热器功率的表现比其他算法更好。CTDB-DDPG算法对于冷却水和气流的控制，表现出更快的响应时间和较好的动态性能。如图7a所示，FO-PID算法将超调降低到0.65 K，TD3算法的超调约为0.4K，而CTDB-DDPG联合控制的超调小于0.3K。此外，图7a比较了GA-PID算法、PSO-PID算法、FO-PID算法、DDPG算法和TD3算法的进水温度控制结果。CTDB-DDPG算法将平均控制时间分别减少了196.5 s、167.1 s、142.7 s、84.6 s和58.3s。与GA-PID和PSO-PID算法相比，CTDB- DDPG控制器分别减少了0.613K和0.546K的入口温度超调量。
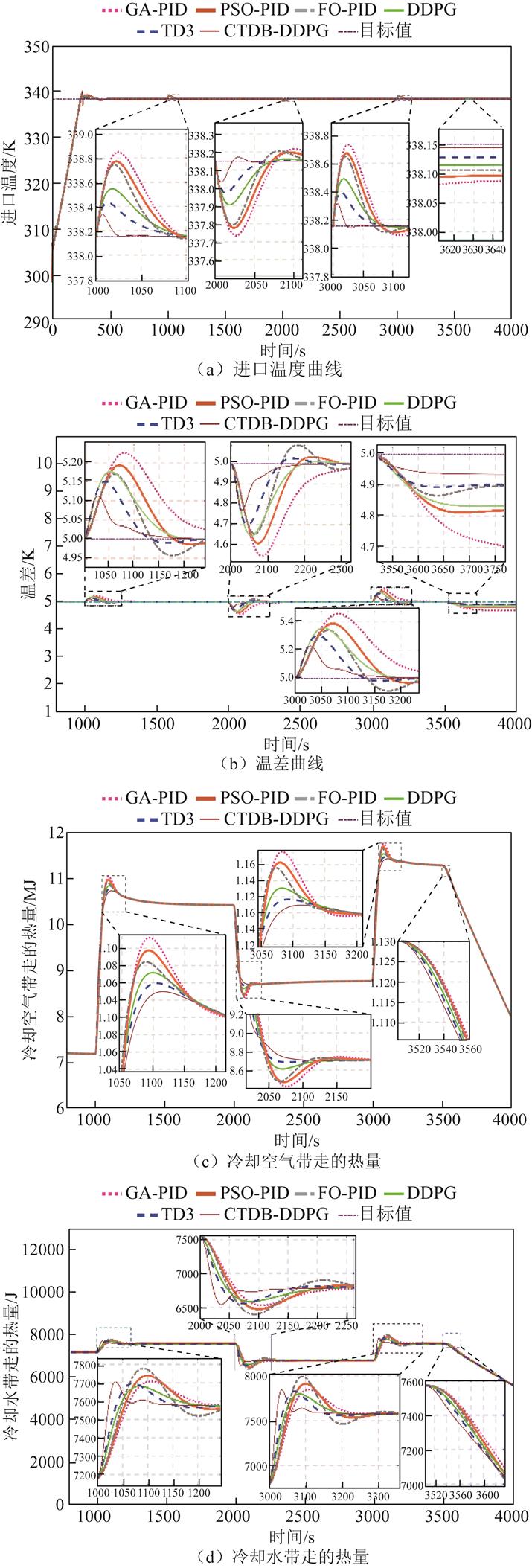
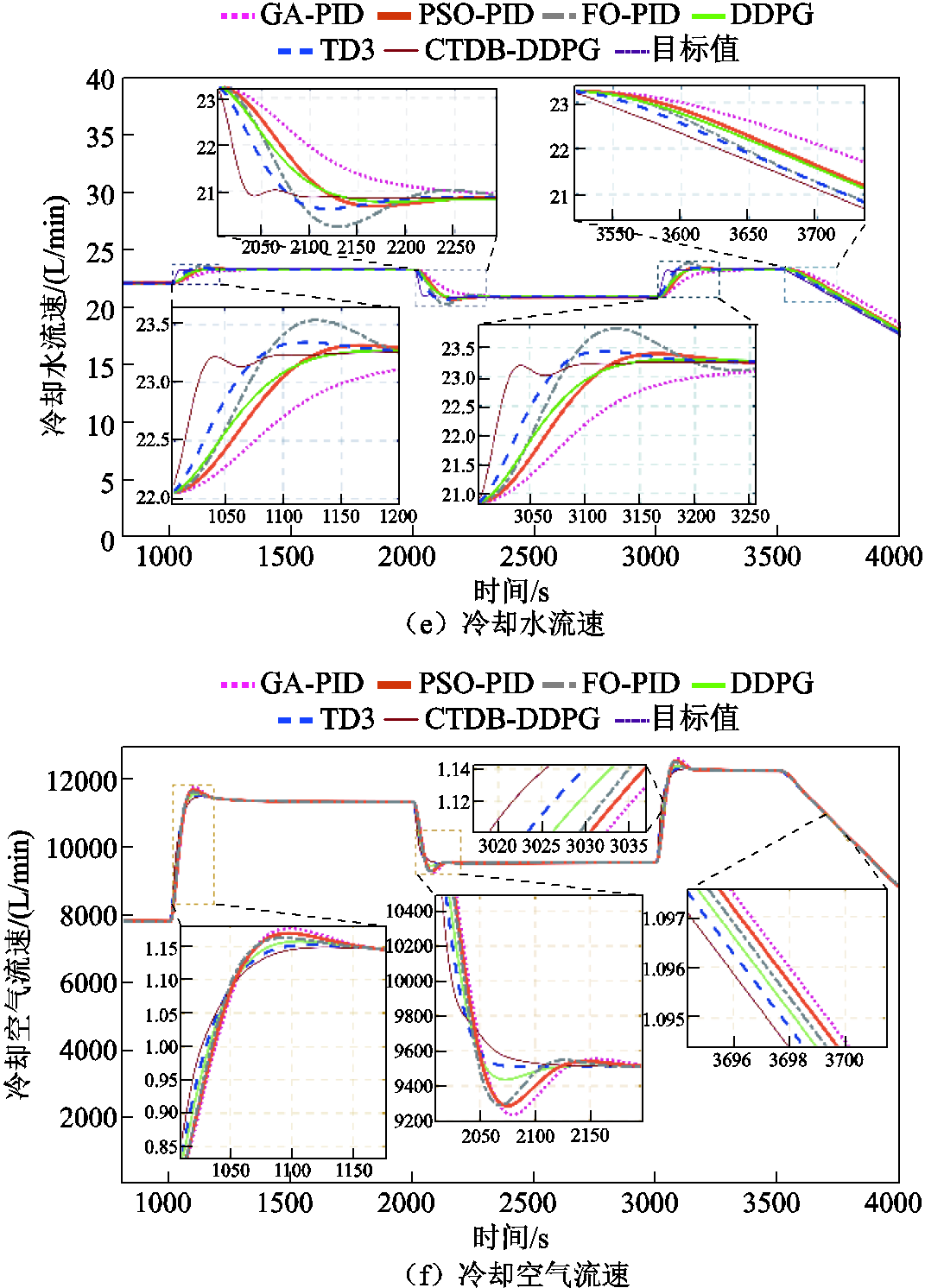
图7 案例1仿真结果
Fig.7 Simulation results of Case 1
CTDB-DDPG的控制效果比其他控制器的控制效果有明显的优势，因为CTDB-DDPG控制器可以合理地控制冷却水流量和散热器功率，以减少负载条件变化时Tst,in和DT的超调和偏移。在将Tst,in恢复到参考值时，CTDB-DDPG具有最快的响应时间。此外，由于Tst,in和DT之间有很强的耦合性，由CTDB-DDPG实现的无模型控制，与PID演变的算法相比，Tst,in和DT的控制性能得到了显著提高。CTDB-DDPG与TD3、DDPG相比也做了多方面的改进，所以控制效果与它们相比有了很大的提高。
与其他控制器相比，CTDB-DDPG控制器具有更快的响应速度和更小的超调量，因此在每次参数变化下，始终能够有效地将DT稳定在5K，将Tst,in稳定在338 K附近，从而确保PEMFC的运行可靠性。
本节讨论当负载稳定在100 A时，阳极入口压力和阴极入口压力发生阶跃时的燃料电池的温度控制。在本算例中，CTDB-DDPG的训练时长、步长设定以及网络结构参数均与4.3节一致。超参数见表5。
表5 案例2氢燃料电池温度控系统DDPG超参数设置
Tab.5 DDPG super parameter setting of hydrogen fuel cell temperature control system in Case 2
参数数值 Critic学习率0.000 1 Actor学习率0.000 5 经验池回放容量1 000 000 经验池回放训练批次64 噪声方差0.15 噪声衰减系数0.000 01 软更新系数0.001 折旧因子0.94
图8显示，阳极压力在1 800 s时从1.3 atm升至2.2 atm，然后在4 200 s时降至1.6 atm。阴极压力在1 000 s时从1.3 atm上升到2.6 atm，然后在2 600 s时下降到1.8 atm。此外，质子交换膜的水含量在 3 400s时从14增加到16。
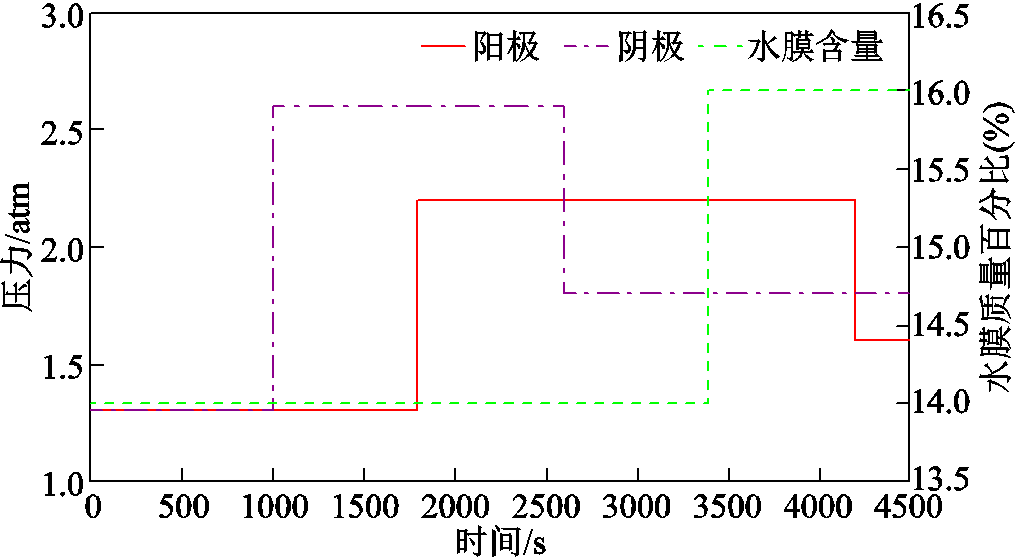
图8 案例2的参数变化曲线
Fig.8 Parameter variation curves of Case 2
实例2的仿真结果如图9所示。由图9c～图9f可知，与其他算法相比，在燃料电池参数发生变化时，CTDB-DDPG算法在控制循环泵和冷却气流方面表现出较好的调节能力和更快的动态响应，使得进口温度与温差维持在一个更好的工作范围。此外，即使模型参数发生变化，CTDB-DDPG算法对Tst,in的控制的超调最小，并能迅速调整到参考值。这些结果证实了CTDB-DDPG算法相对于其他控制器的鲁棒性，确保了在各种参数变化的情况下仍有理想的控制性能。
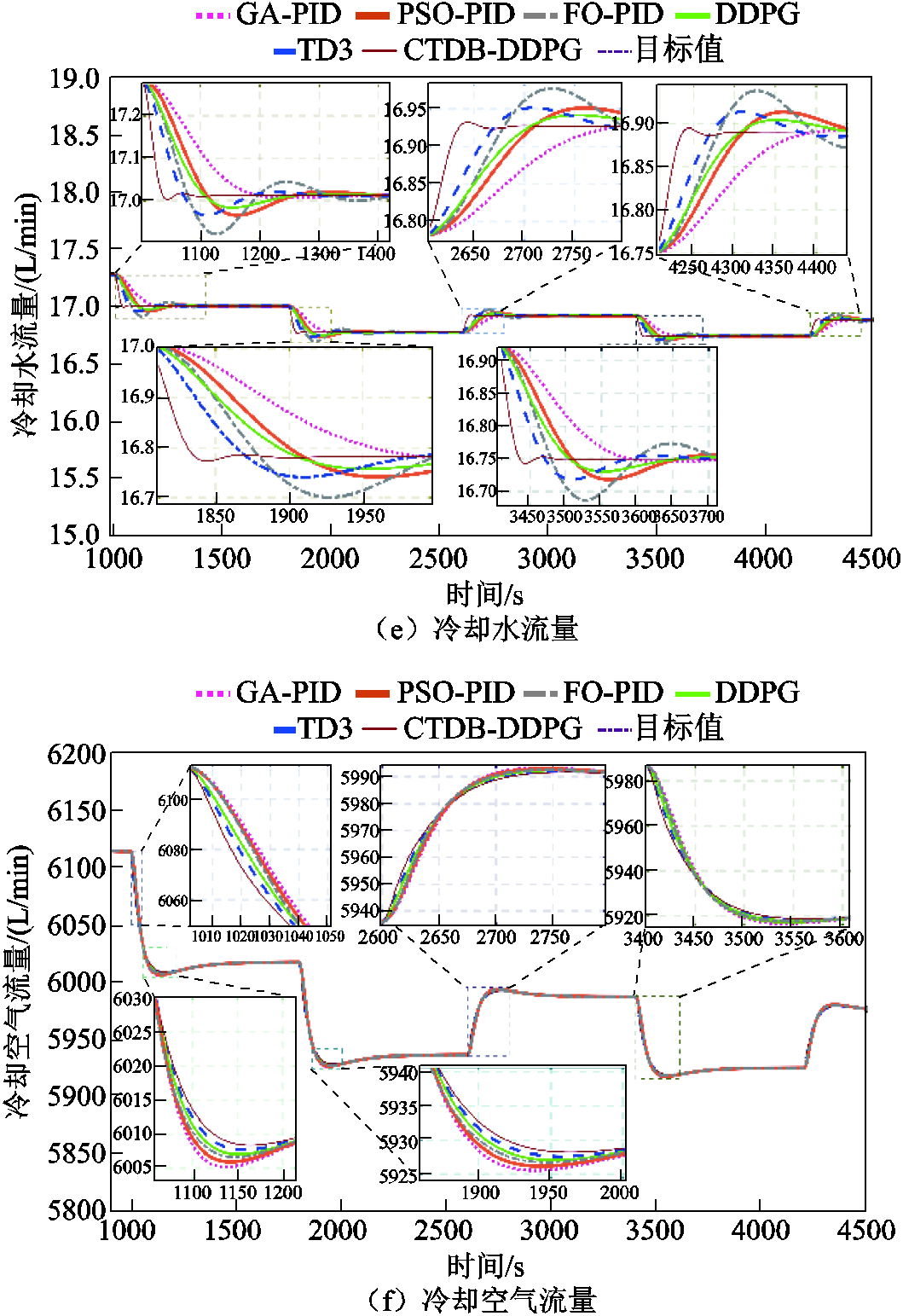
图9 案例2仿真结果
Fig.9 Simulation results of Case 2
从图9a、图9b可以看出，当模型参数发生变化时，CTDB-DDPG控制器控制的Tst,in的超调量最小，而且可以快速地将Tst,in调整到参考值。这些结果表明，在不同参数变化下，与其他的控制器相比，CTDB-DDPG控制器具有更好的鲁棒性。比较进口温度Tst,in的结果可以看出，FO-PID算法的超调约为CTDB-DDPG算法的4.124倍。此外，由于Tst,in和DT之间的高度耦合，CTDB-DDPG控制器大大增强了DT的控制性能。GA-PID算法的超调量约为CTDB-DDPG算法的2倍。从温差的对比来看，DDPG、TD3和CTDB-DDPG在控制PEMFC的热管理系统方面比其他算法更有效，因为深度强化学习算法实现了对于水泵和散热器的无模型联合控制。CTDB-DDPG算法与TD3、DDPG深度强化学习算法相比，对热管理表现出更好的控制性能。进一步说明所提算法基于燃料电池特点进行的改进的有效性。
为了进一步验证所提出控制器的控制性能，设置了一个在PEMFC负载中加入随机扰动的实验。本算例中，使用120 A的高频扰动电流作为输入，如图10所示。应用的扰动系数为3 000，采样时间为15 s。案例3仿真结果如图11所示。图11d、图11f表明，与其他算法相比，CTDB-DDPG算法在高频干扰电流变化的情况下，对循环泵和散热器的流量控制表现出较好的控制性能。随着干扰的增加，CTDB-DDPG算法迅速增加水泵和散热器的功率，提高流速，并从电堆中提取更多的热量。当干扰减少时，CTDB-DDPG算法迅速降低水泵和散热器的流量，导致从电堆中提取的热量减少，确保PEMFC系统有更好的温度控制。此外，如图11a所示，CTDB-DDPG控制器在不同的随机干扰下，其入口温度超调最小和响应速度最快。相比之下，FO-PID和TD3算法的超调分别是CTDB-DDPG的4.21倍和2.72倍。CTDB-DDPG算法对高频率的扰动电流表现出更好的控制性能，而其他算法往往表现出过大的超调、响应时间长、响应速度慢等特点。
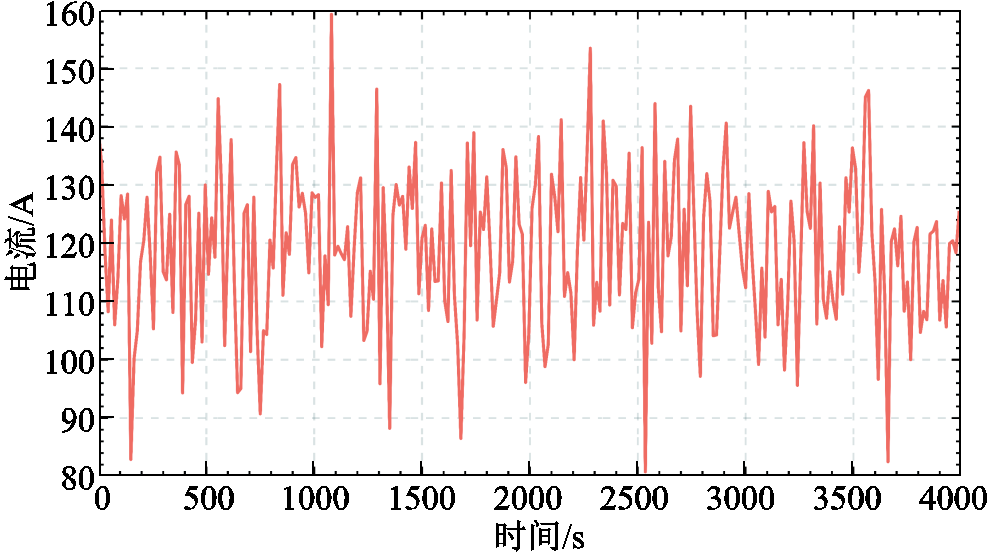
图10 案例3的负载曲线
Fig.10 Current variation curves of Case 3
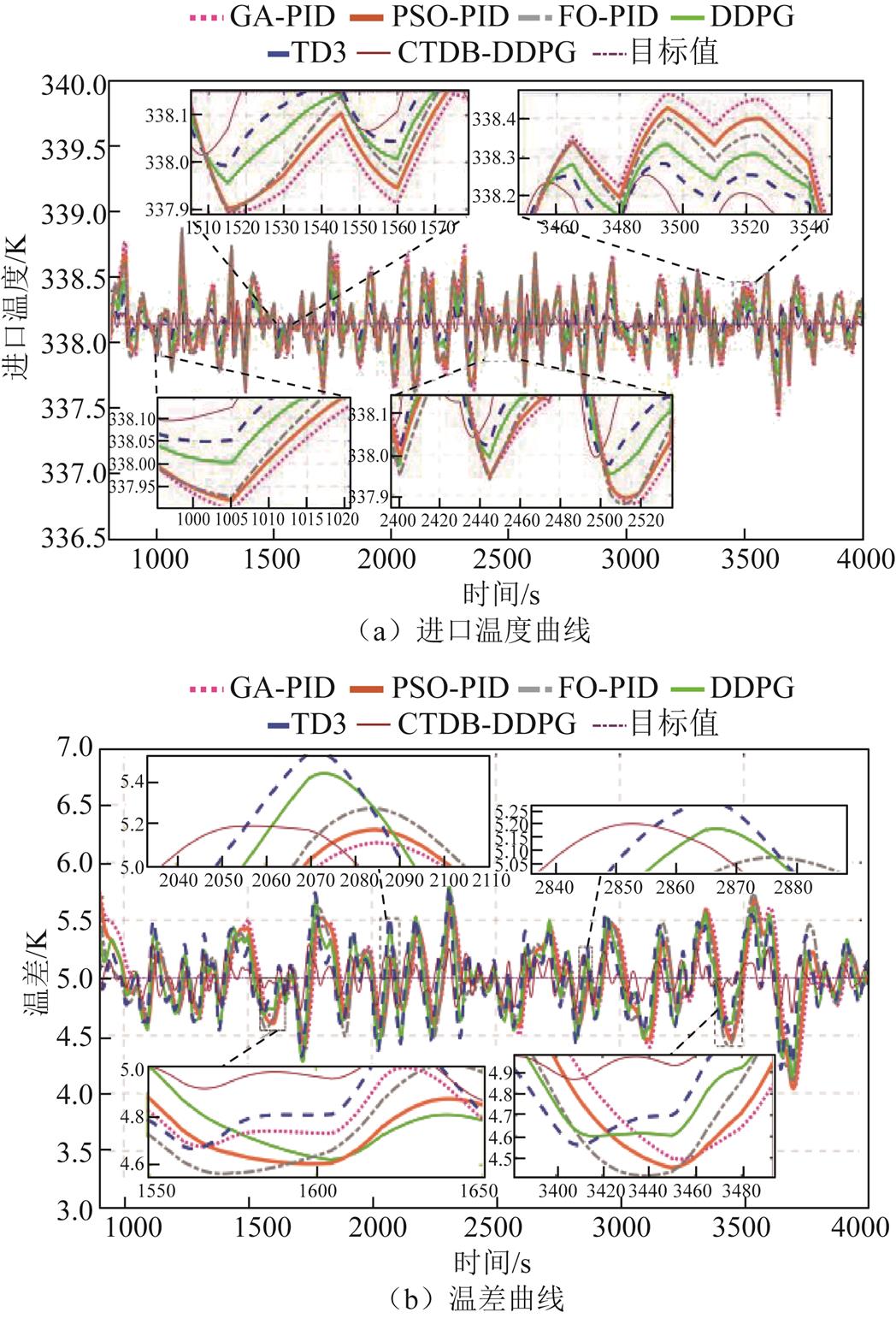
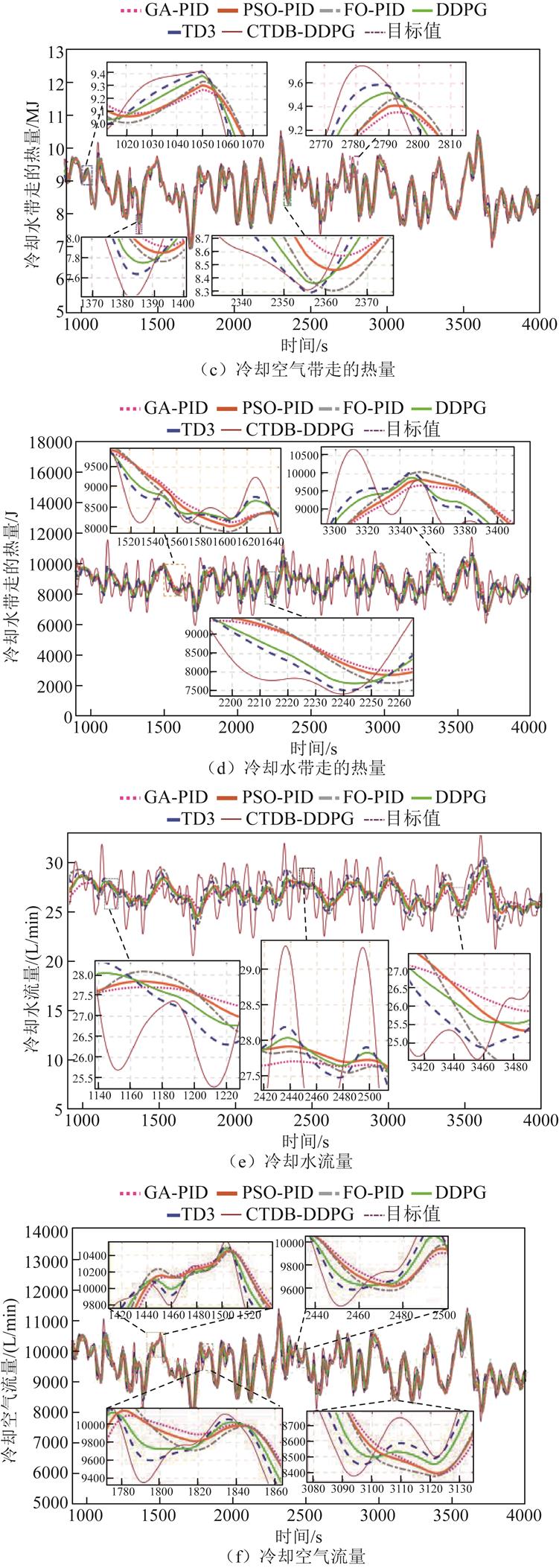
图11 案例3仿真结果
Fig.11 Simulation results of Case 3
此外，图11a表明，在随机干扰电流实验条件下，CTDB-DDPG算法控制下的进口温度平均超调约为FO-PID控制器的1/3。此外，与TD3和DDPG算法相比，进口温度超调减少了近一半，响应时间也明显缩短。
案例3中，DDPG与TD3对于温差均存在控制不稳定的状态，这表明，在高频变化的扰动下，DDPG与TD3呈现出鲁棒性不足的问题。CTDB- DDPG控制方法对于温差的控制与其他算法相比也相对稳定，能够紧密跟踪参考值。
案例3的进口温度和温差分布如图12所示。图12a显示了案例3的进口温度分布，可以看出CTDB-DDPG算法将温度集中控制在338.15 K左右。由图12b可知，所提出的算法将温差集中控制在5 K左右，与其他算法相比,所提出的算法具有出色的控制效果。
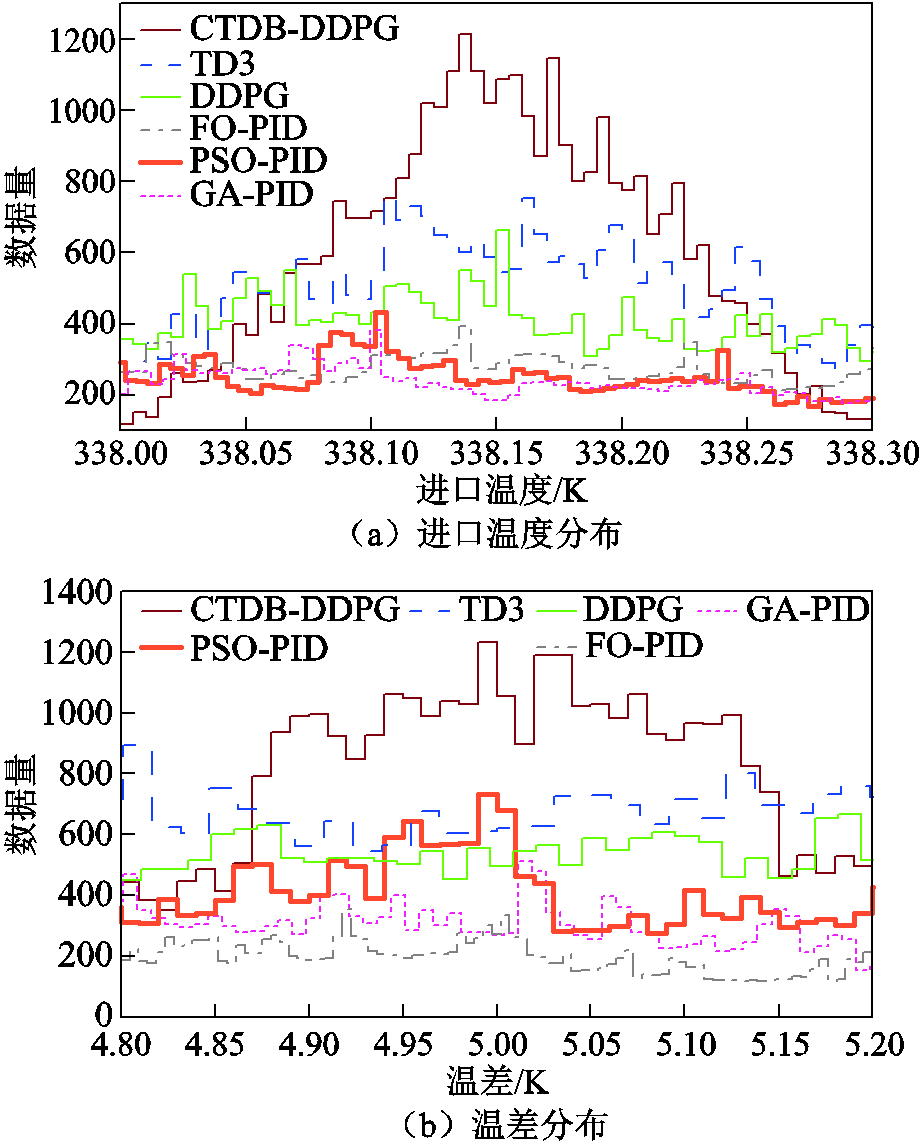
图12 案例3温度和温差分布
Fig.12 Temperature and temperature difference distribution of Case 3
用于硬件在环测试的实验平台和实现框架如图13所示。图13a所示的实验平台，包括一个RT Lab实时仿真器、一个DSP控制器和一台监控计算机。
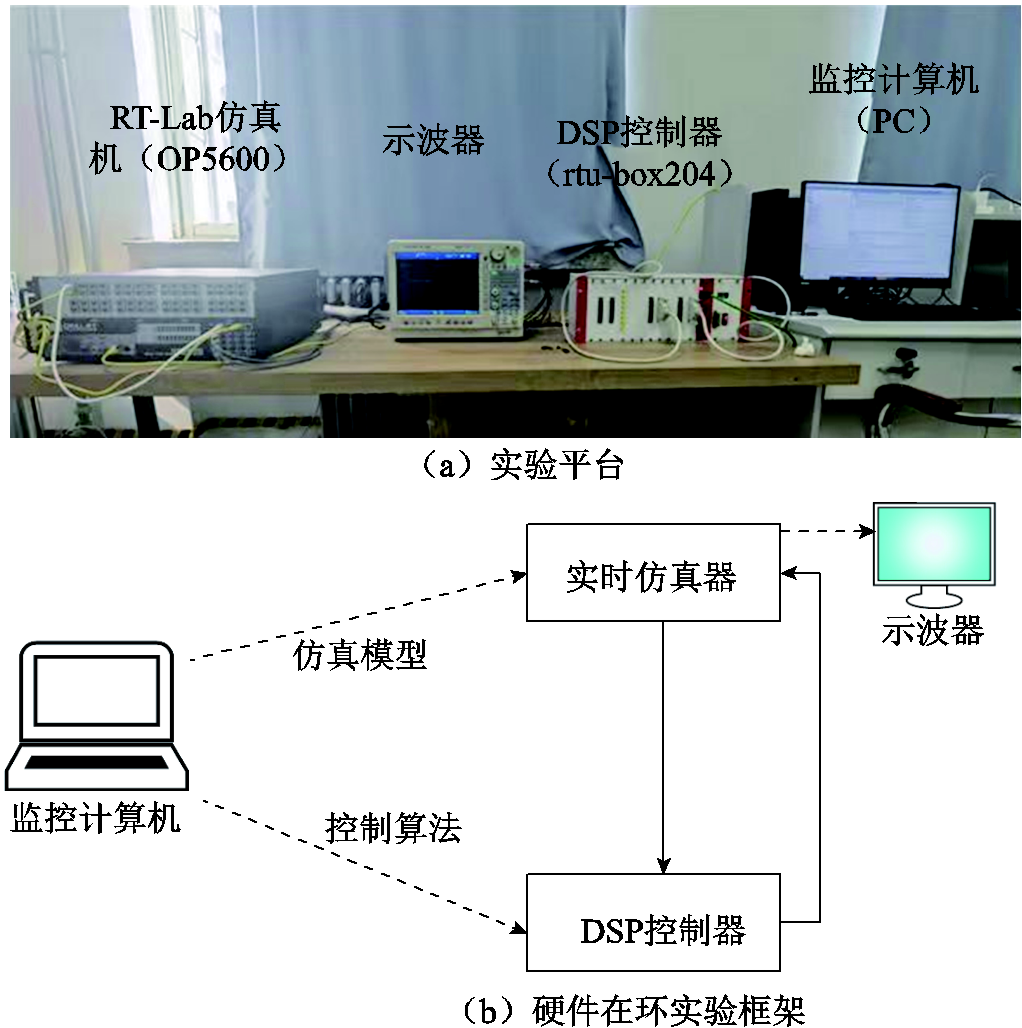
图13 硬件在环实验平台和实现框架
Fig.13 Hardware-in-the-loop experimental platform
图13b显示，燃料电池系统被转换为C代码，在实时仿真器中进行处理，产生相应的模拟信号。然后这些模拟信号被传送到DSP控制器进行A-D采样，得到一个由控制算法处理的数字信号，并产生控制信号。然后，控制信号通过D-A转换，得到一个模拟信号，送入实时模拟器进行实时硬件在环测试。控制算法通过计算机编入RTU-BOX204的DSP控制器中。值得注意的是，在整个测试过程中，模型参数与第4节的模拟过程保持一致。
为了进一步验证所提算法的控制性能，在图13所示的实验平台进行验证，本次实验输入的电流信号如图6所示，进口温度和温差实验结果如图14和图15所示。实验结果显示CTDB-DDPG的控制性能最佳，与仿真结果几乎一致。
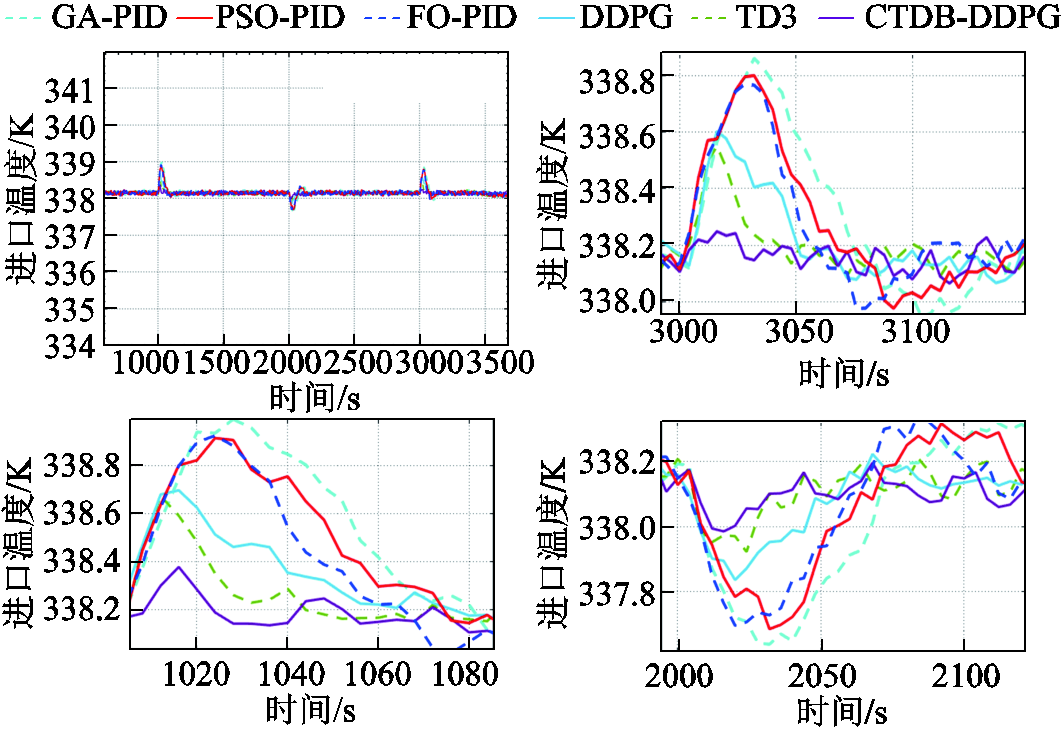
图14进口温度实验结果
Fig.14 Graph of inlet temperature experimental results
图15 温差实验结果图
Fig.15 Temperature difference experiment results graph
本文提出了一种新的燃料电池温度控制策略。通过仿真和实验对比分析，主要结论如下：
1）提出了一种基于分类回放双延迟贝叶斯深度确定性策略梯度（CTDB-DDPG）的温度控制策略，该策略可以对燃料电池实现准确的无模型控制。
2）对提出的温度控制策略在三种不同的场景下进行了仿真验证，结果显示，与GA-PID控制器、PSO-PID控制器、FO-PID控制器，以及DDPG、TD3深度强化学习算法相比，CTDB-DDPG显示出较高的鲁棒性，具有优良的控制性能。
3）在RT-Lab硬件在环平台进行实验验证，进一步验证了仿真所得结论。
本文CTDB-DDPG温度控制策略已经在仿真和硬件在环测试平台上得到了验证，未来研究中将考虑更复杂的实际工况，如环境温度、湿度变化，设备老化等因素，以测试和改进算法在更广泛和复杂情况下的适应性和鲁棒性。
附 录
算法1：分类回放双延迟贝叶斯深度确定性策略梯度算法 初始化两个Critic网络，with K outputs,with K outputs，掩码分布M。策略网络with random parameters、、。 初始化目标网络初始化回放缓冲区,For episode=1 to M do初始化一个随机过程进行动作探索选择Critic网络使用采取动作选择Critic网络使用采取动作选择带有探索噪声的动作，观察奖励r和新状态基于经验样本的TD-error进行分类，存入到缓存经验池或从选择个经验样本，选择个经验样本在和存储转换元组Fort=1 to T do选择具有探索噪声的动作，观察奖励和新状态抽样引导掩码m~M将过渡元组存储在和以为确定比例，从和抽取N个过渡的小批量样本更新Critic网络参数If t mod d then通过确定性策略梯度更新：更新目标网络参数:End ifEnd forEnd for
参考文献
[1] 张雪霞, 黄平, 蒋宇, 等. 动态机车工况下质子交换膜燃料电池电堆衰退性能分析[J]. 电工技术学报, 2022, 37(18): 4798-4806.
Zhang Xuexia, Huang Ping, Jiang Yu, et al. Degradation performance analysis of proton exchange membrane fuel cell stack under dynamic locomotive conditions[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4798-4806.
[2] 唐钧涛, 戚志东, 裴进, 等. 基于电荷泵的燃料电池有源网络升压变换器[J]. 电工技术学报, 2022, 37(4): 905-917.
Tang Juntao, Qi Zhidong, Pei Jin, et al. An active network DC-DC Boost converter with a charge pump employed in fuel cells[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 905-917.
[3] 马小勇, 王议锋, 王萍, 等. 燃料电池用交错并联型Boost变换器参数综合设计方法[J]. 电工技术学报, 2022, 37(2): 397-408.
Ma Xiaoyong, Wang Yifeng, Wang Ping, et al. Comprehensive parameter design method of interleaved Boost converter for fuel cell applications[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 397-408.
[4] 高锋阳,高翾宇,张浩然等.全局与瞬时特性兼优的燃料电池有轨电车能量管理策略[J].电工技术学报, 2023, 38(21): 5923-5938.
Gao Fengyang, Gao Huayu, Zhang Haoran, et al. Management strategy for fuel cell trams with both global and transient characteristics[J]. Transactions of China Electrotechnical Society, 2023, 38 (21): 5923-5938.
[5] 宋清超, 陈家伟, 蔡坤城, 等. 多电飞机用燃料电池-蓄电池-超级电容混合供电系统的高可靠动态功率分配技术[J]. 电工技术学报, 2022, 37(2): 445-458.
Song Qingchao, Chen Jiawei, Cai Kuncheng, et al. A highly reliable power allocation technology for the fuel cell-battery-supercapacitor hybrid power supply system of a more electric aircraft[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 445-458.
[6] 任洲洋, 王皓, 李文沅, 等.基于氢能设备多状态模型的电氢区域综合能源系统可靠性评估[J]. 电工技术学报, 2023, 38(24): 6744-6759.
Ren Zhouyang, Wang Hao, Li Wenyuan, et al. Reliability evaluation of electricity-hydrogen regional integrated energy systems based on the multi-state models of hydrogen energy equipment[J]. Tran- sactions of China Electrotechnical Society, 2023, 38(24): 6744-6759.
[7] Wang Yulin, Xu Haokai, Zhang Zhe, et al. Lattice Boltzmann simulation of a gas diffusion layer with a gradient polytetrafluoroethylene distribution for a proton exchange membrane fuel cell[J]. Applied Energy, 2022, 320: 119248.
[8] Paul B, Andrews J. PEM unitised reversible/ regenerative hydrogen fuel cell systems: state of the art and technical challenges[J]. Renewable and Sustainable Energy Reviews, 2017, 79: 585-599.
[9] Derbeli M, Farhat M, Barambones O, et al. Control of proton exchange membrane fuel cell (PEMFC) power system using PI controller[C]//2017 International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 2017: 1-5.
[10] Hu Yunfeng, Zhang Chong, Gong Xun, et al. Design of a nonlinear dynamic output feedback controller based on a fixed-time RBF disturbance observer for a PEMFC air supply system[J]. Measurement, 2023, 211: 112683.
[11] You Zhiyu, Xu Tao, Liu Zhixiang, et al. Study on air-cooled self-humidifying PEMFC control method based on segmented predict negative feedback control[J]. Electrochimica Acta, 2014, 132: 389-396.
[12] 裴尧旺, 陈凤祥, 胡哲, 等. 基于自适应LQR控制的质子交换膜燃料电池热管理系统温度控制[J]. 吉林大学学报(工学版), 2022, 52(9): 2014-2024.
Pei Yaowang, Chen Fengxiang, Hu Zhe, et al. Temperature control of proton exchange membrane fuel cell thermal management system based on adaptive LQR control[J]. Journal of Jilin University (Engineering and Technology Edition), 2022, 52(9): 2014-2024.
[13] 陈飞, 罗仁宏. 基于模型预测控制的水冷型燃料电池冷却系统研究[J]. 汽车技术, 2021(7): 8-13.
Chen Fei, Luo Renhong. Research on water-cooled fuel cell cooling system based on MPC[J]. Automobile Technology, 2021(7): 8-13.
[14] 刘欣, 郝晓弘, 杨新华, 等. 固体氧化物燃料电池系统的鲁棒反馈模型预测控制[J]. 系统工程理论与实践, 2015, 35(2): 521-527.
Liu Xin, Hao Xiaohong, Yang Xinhua, et al. Robust feedback model predictive control of the solid oxide fuel cell’s system[J]. Systems Engineering-Theory & Practice, 2015, 35(2): 521-527.
[15] 金红超, 何锋, 胡耀宗. 基于变论域模糊理论的PEMFC热管理系统控制研究[J]. 电子测量技术, 2022, 45(14): 23-28.
Jin Hongchao, He Feng, Hu Yaozong. Thermal management system control of PEMFC based on variable universe fuzzy theory[J]. Electronic Measurement Technology, 2022, 45(14): 23-28.
[16] Aly M, Rezk H. An improved fuzzy logic control-based MPPT method to enhance the performance of PEM fuel cell system[J]. Neural Computing and Applications, 2022, 34(6): 4555- 4566.
[17] Wang Binrui, Jin Yinglian, Xu Hong, et al. Temperature control of PEM fuel cell stack application on robot using fuzzy incremental PID[C]// 2009 Chinese Control and Decision Conference, Guilin, China, 2009: 3293-3297.
[18] Ou Kai, Yuan Weiwei, Choi M, et al. Performance increase for an open-cathode PEM fuel cell with humidity and temperature control[J]. International Journal of Hydrogen Energy, 2017, 42(50): 29852- 29862.
[19] Abbaspour A, Khalilnejad A, Chen Zheng. Robust adaptive neural network control for PEM fuel cell[J]. International Journal of Hydrogen Energy, 2016, 41(44): 20385-20395.
[20] 蒋利炜,何可人,陈航.基于PSO改进BP算法的直流电子负载PID控制仿真[J].计算机真, 2024, 41(01): 306-310.
Jiang Liwei, He Keren, Chen Hang. Simulation of DC electronic load PID control based on PSO improved BP algorithm[J]. Computer Simulation, 2024, 41(1): 306-310.
[21] Wang Fucheng, Ko C C. Multivariable robust PID control for a PEMFC system[J]. International Journal of Hydrogen Energy, 2010, 35(19): 10437-10445.
[22] 侯荣福, 杨君, 于蓬, 等. 基于模糊自抗扰的质子交换膜燃料电池温度控制[J]. 山东工业技术, 2022(6): 16-23.
Hou Rongfu, Yang Jun, Yu Peng, et al. Temperature control of proton exchange membrane fuel cell based on fuzzy active disturbance rejection[J]. Journal of Shandong Industrial Technology, 2022(6): 16-23.
[23] Sun Li, Li Guanru, Hua Q S, et al. A hybrid paradigm combining model-based and data-driven methods for fuel cell stack cooling control[J]. Renewable Energy, 2020, 147: 1642-1652.
[24] Yu Yang, Chen Ming, Zaman S, et al. Thermal management system for liquid-cooling PEMFC stack: from primary configuration to system control strategy[J]. eTransportation, 2022, 12: 100165.
[25] Cho Y, Hwang G, Gbadago D Q, et al. Artificial neural network-based model predictive control for optimal operating conditions in proton exchange membrane fuel cells[J]. Journal of Cleaner Production, 2022, 380: 135049.
[26] Han J, Yu S, Yi Sun. Advanced thermal management of automotive fuel cells using a model reference adaptive control algorithm[J]. International Journal of Hydrogen Energy, 2017, 42(7): 4328-4341.
[27] Fujimoto S, van Hoof H, Meger D. Addressing function approximation error in actor-critic methods [J/OL]. ArXiv, 2018: 1802.09477. http://arxiv.org/ abs/1802.09477
[28] Schulman J, Wolski F, Dhariwal P, et al. Proximal policy optimization algorithms[J/OL]. ArXiv, 2017: 1707.06347. http://arxiv.org/abs/1707.06347.pdf.
[29] van Hasselt H, Guez A, Silver D. Deep reinforcement learning with double Q-Learning[C]//Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, Arizona, UAS, 2016: 2094-2100.
[30] Auer P, Cesa-Bianchi N, Fischer P. Finite-time analysis of the multiarmed bandit problem[J]. Machine Learning, 2002, 47(2): 235-256.
[31] Davison A C, Hinkley D V. Bootstrap methods and their application[M]. Cambridge: Cambridge University Press, 1997.
[32] Osband I, Van Roy B. Bootstrapped Thompson sampling and deep exploration[J/OL]. ArXiv: 2015: 1507.00300. http://arxiv.org/abs/1507.00300.pdf
[33] Uhlenbeck G E, Ornstein L S. On the theory of the Brownian motion[J]. Physical Review, 1930, 36(5): 823-841.
[34] 仇俊政, 赵红, 牟亮, 等. 基于粒子群PID的质子交换膜燃料电池温度控制[J]. 制造业自动化, 2022, 44(8): 98-101.
Qiu Junzheng, Zhao Hong, Mu Liang, et al. Temperature control of proton exchange membrane fuel cell based on particle swarm optimization PID[J]. Manufacturing Automation, 2022, 44(8): 98-101.
[35] Marsala G, Ragusa A. Increase of the performance of a low ripple boost converter for PEM FC applications using GA and PSO algorithms[C]//2012 IEEE Vehicle Power and Propulsion Conference, Seoul, Korea (South), 2012: 908-913.
[36] Zhao Dongdong, Li Fei, Ma Rui, et al. An unknown input nonlinear observer based fractional order PID control of fuel cell air supply system[J]. IEEE Transactions on Industry Applications, 2020, 56(5): 5523-5532.
AbstractProton exchange membrane fuel cells (PEMFCs) have the characteristics of difficulty to model accurately and strong nonlinearity; in addition, the radiator and circulating water pump in the hydrothermal management system of the fuel cell system have the characteristics of strong coupling, which makes it difficult for the model-based control algorithms to achieve accurate control of the fuel cell temperature, this paper proposes a data-driven model-free algorithm based on the on classified replay twin delayed Bayesian deep deterministic policy gradient(CTDB-DDPG) to achieve the control of the fuel cell temperature system.
Firstly, the use of deep deterministic policy gradient is proposed to solve the problem of intricate modeling of fuel cells. Then, the classification experience playback strategy is added to the algorithm, and the CTDB-DDPG algorithm uses two experience buffer pools to store the experience data. When constructing the network model, the average TD error of all samples in these two experience buffer pools is initialized to 0. Whenever new experience data is generated, the average TD errors of all experience data are first updated. If its TD error exceeds the mean value, it is stored in the empirical buffer pool I. Otherwise, it is stored in the empirical buffer pool II. Classifying each experience sample's TD error helps better use the empirical data to train the network model.CTDB-DDPG considers the neural network's uncertainty by incorporating a Bayesian neural network into the algorithm, and the proposed Bootstrap with random initialization leads to a reasonable uncertainty estimation. At the beginning of each round or fixed interval during the learning process, unbiased hypotheses are obtained from the posterior distributions of the MDP parameters and estimated using a multi-head shared network Bootstrap value function, which does not require additional computational resources.
Moreover, using Q-learning preserves the uncertainty of the cumulative discount, which is more effective for environments requiring deep exploration. Randomly selecting the head network and simulating Thompson sampling can effectively avoid ineffective boosting of intelligence in the noise strategy, accelerating the convergence of the CTDB-DDPG algorithm. In addition, the fuel cell thermal management system has a large inertia; the algorithm in this paper adds OU noise to the action to improve the exploration efficiency.OU noise is a temporary correlation noise extracted from the Ornstein-Uhlenbeck process, which helps the algorithm to better explore different strategies by generating temporal correlation noise. This exploration process can help the algorithm to find possible better strategies, thus improving the performance and efficiency of the algorithm. Although the addition of noise can cause the algorithm's performance to deteriorate in the short term, in the long term, the addition of noise can help the algorithm to avoid falling into a local optimum. It may help to find a better strategy.
Finally, the algorithm's validity is verified on the simulation platform Simulink as well as the experimental platform RT-Lab, and similar conclusions are obtained, verifying the algorithm's effectiveness. However, although our CTDB-DDPG temperature control strategy has been validated on simulation and hardware-in-the-loop test platforms, more complex real-world working conditions, such as ambient temperature and humidity variations and equipment aging, will be considered in future studies to test and improve the adaptability and robustness of our algorithm in the broader range of more complex situations.
Keywords：Fuel cell, joint control, deep reinforcement learning, Bayesian network
DOI: 10.19595/j.cnki.1000-6753.tces.230699
中图分类号：TM911.4; U264
收稿日期 2023-05-17
改稿日期 2023-07-14
赵洪山 男，1965年生，教授，博士生导师，研究方向为电力系统动态分析与控制、电力负荷预测、燃料电池热管理等。E-mail：zhaohshcn@126.com
潘思潮 男，1998年生，硕士研究生，研究方向为燃料电池建模及温度控制。E-mail：pansc_ncepu@126.com（通信作者）
（编辑 郭丽军）