基于变分深度嵌入-带有梯度惩罚的生成对抗网络的锂离子电池老化特性建模
李 弈 张金龙 漆汉宏 魏艳君 张 迪
(燕山大学电气工程学院 秦皇岛 066004)
摘要 锂离子电池老化实验是研究电池老化性能的基本手段,但针对大量电池的老化实验一般很耗时。为了节约时间和测试成本,获得更多电池数据,该文将变分深度嵌入(VaDE)模型与带有梯度惩罚的生成对抗网络(WGANGP)相结合,组成VaDE-WGANGP架构,进而基于该生成模型设计了一种电池老化特性建模与数据生成的方法。该文以一套开放的电池全寿命周期测试数据集为依据展开研究,首先,将电池放电过程中的电压、电流和放电容量这三个外特性作为模型的输入,通过VaDE的编码器将原始数据映射到隐空间,再通过优化获得符合特定规则的分布;然后,通过一定方式对该分布空间进行采样,并将采样所得的隐变量输入解码器中进行数据生成;后续数据测试表明,VaDE-WGANGP在电池外特性数据生成上具有较好的性能,可以实现对电池老化过程中基础外特性的模拟,在数据量不足时也可以为某些数据驱动算法提供有效的扩展数据资源。
关键词:锂离子电池 老化特性 生成模型 变分深度嵌入 带有梯度惩罚的生成对抗网络
0 引言
近年来,由于锂离子电池具有能量密度高、充电效率高、工作温度范围宽、循环寿命长等优点,已经广泛应用于电动汽车、混合动力电动汽车和一些储能系统等领域[1-2]。然而,锂离子电池的老化以及单体间差异的增大显著影响电池组性能,严重时会引发安全事故[3-4]。锂离子电池老化过程一方面体现在电池健康状态(State of Health, SOH)的下降,另一方面也体现在多个电池成组时的老化差异。随着老化程度的加深,组内各单体电池容量衰减速率会出现差异。此外,电池老化差异还会通过循环次数、内阻、电压、电流等外特性体现出来。因此有必要对电池全寿命周期的老化特性进行统计分析与研究,以便为工程应用提供必要参考。但针对大量电池的全寿命周期老化测试实验周期偏长,设备资源要求较高。此外常用的数据驱动类分析方法对电池老化数据量要求较大,这些因素都限制了相关研究的深入开展。针对以上问题,本文设计了一种基于生成模型的电池全寿命周期外特性建模与数据生成方法,通过生成模型模拟电池老化过程中的基础外特性。
近年来,常见的锂离子电池老化建模方法有以下几种:电化学机理法、电路模型法和数据驱动法。首先是基于电化学机理的方法,该方法通过定量分析电池内部物理和化学过程来精确描述其老化特性,此类方法面临的挑战在于模型相对复杂、电池内部参数较多以及实时测定较困难等[5-7]。采用等效电路模型对电池进行老化特性分析也比较常见,此类模型一般与智能滤波算法相结合来实现对电池等效参数及状态的估算[8-11]。然而基于电路模型和电化学模型的方法在老化建模中通常以个体电池的特性为依据,对于多单体间老化差异的描述不够充分。
数据驱动类方法一般通过各种机器学习算法在电池的外特性数据与电池的老化指标之间构建非线性映射关系,进而对电池的老化特性进行描述与估算[11]。近年来,多种回归算法被应用于电池的老化建模,并且对电池健康状态或循环寿命进行预测,但其中很多算法都属于有监督学习,一旦缺少标签就无法进行训练[12-15]。因此,在缺少预测标签的情况下,无监督学习在电池老化建模方面也有应用,以变分自动编码器(Variational Auto Encoder, VAE)[16]和生成对抗网络(Generative Adversarial Network, GAN)[17]为代表的生成模型也被用于电池老化建模。文献[18]利用GAN模型,将锂电池的EIS信息作为输入,利用隐变量表示电池老化程度,并对电池SOH进行估算。文献[19]将条件变分自编码器(Conditional Variational Autoencoder, CVAE)和粒子滤波相结合,针对电池老化容量建立状态空间模型,并对电池的剩余寿命进行预测。文献[20]利用VAE模型,将其编码器和解码器设计为双向长短期记忆(Long Short-Term Memory, LSTM)网络,并将其与GAN相结合来捕捉电池老化特征的分布,最终实现电池剩余寿命预测。
对于处理小样本问题而言,迁移学习在电池领域的应用也逐渐增多。与传统机器学习不同,迁移学习可以充分挖掘相近但不同的知识域之间的共性和相似性,进而利用旧知识来达成新任务[22]。文献[21]应用迁移学习分别实现了同类型电池不同容量和工况条件下及不同类型电池之间的知识迁移,最终实现目标电池SOH的准确估算。文献[22]将迁移学习与CNN-LSTM网络相结合,实现两种不同参数锂离子电池之间的知识迁移,大幅提升了目标电池SOC的估算精度。文献[23]采用迁移学习方法构造一种深度域自适应网络,其训练集包括少量目标电池数据和大量其他类型电池数据,该方案可学习不同类型电池特性之间的相似性,来实现目标电池SOC的准确估算。文献[24]采用迁移学习方法,实现具有不同正极及电解液材料的软包电池之间工作特性迁移,并最终结合LSTM算法完成对目标电池循环寿命的预测。整体来讲,该方法适用于目标域可用数据较少而源域可用数据很充足的情况;而且在不同工况条件下以及不同电池类型之间的通用性较强,宏观上具有较强的泛化能力。比较而言,本文所采用的生成模型不要求源域数据,但对目标域数据要求相对较高,更侧重于相同知识域内的细节分布特性和多样性信息生成问题;此外,本文还分析了同品牌同型号不同单体之间的外特性差异,考虑的角度相对微观。
在总结以上研究思路的基础上,本文将变分深度嵌入(Variational Deep Embedding, VaDE)与带有梯度惩罚的生成对抗网络(Wasserstein GAN with Gradient Penalty, WGANGP)相结合[25-26],用于电池全寿命周期的基础外特性建模与数据扩充。首先将电池原始外特性数据输入VaDE中,VaDE编码器将高维的输入转换成低维隐空间信息;然后对隐空间进行采样,进而经解码器实现电池数据模拟生成;为了提高模型的整体性能,本方案采用了类似文献[27]中所提出的VAE-GAN架构,进而使得生成数据的质量进一步提高。
1 测试数据
本文所使用的数据集来自斯坦福数据集[15],测试对象为3.3 V/1.1 A·h的A123 18650型磷酸铁锂电池,环境温度为30℃,充电方式:SOC区间为0~80%随机双倍率组合恒流充电,80%以上区间采用1C恒流恒压(Constant Current Constant Voltage, CCCV)模式,直到电流降至C/50;放电方式:采用4 A的恒定电流进行放电。总计测试电池数目为124节,该测试覆盖电池的全寿命周期,即覆盖了80%~100% SOH区间。本文中电池SOH描述为电池老化过程中的实际容量Qaged与电池额定容量Q0的比值,有
2 模型构建
2.1 变分自动编码器
VAE是当前主流生成模型之一,源于标准自动编码器AE(auto encoder)。AE主要用于从复杂数据中提取特征,一般认为,常规AE隐含层输出向量的分布是未知的,故普通AE不具有自动生成数据的能力。而VAE[16]核心思想是通过变分推断的方式来优化证据下界,可以通过学习和优化过程获取原始数据的概率分布,进而具备通过空间采样实现数据模拟生成的能力,其基本结构如图2所示。
VAE工作过程如下:首先将原始数据{x1…xn}输入编码器中,通过编码映射和优化过程将其变换为符合特定分布(一般为高斯分布)的隐空间,这个过程表示为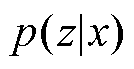 ,
,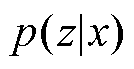 也称为真实后验分布,且通常难以求解,因此往往利用近似后验分布
也称为真实后验分布,且通常难以求解,因此往往利用近似后验分布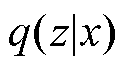 来逼近
来逼近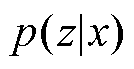 。而后,通过从隐空间采样可获得隐变量z,进而将其输入解码器,即可通过解码过程得到与输入对应的模拟生成数据,这个过程可以描述为
。而后,通过从隐空间采样可获得隐变量z,进而将其输入解码器,即可通过解码过程得到与输入对应的模拟生成数据,这个过程可以描述为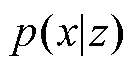 。
。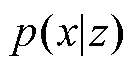 也叫作似然函数,表示从隐空间到数据生成的过程。因此
也叫作似然函数,表示从隐空间到数据生成的过程。因此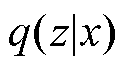 和
和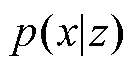 分别被称为编码器和解码器,对应的参数为
分别被称为编码器和解码器,对应的参数为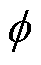 和
和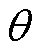 。表示为
。表示为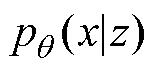 和
和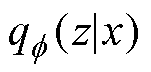 。VAE通过最大化对数边际似然
。VAE通过最大化对数边际似然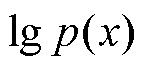 得到优化目标为
得到优化目标为
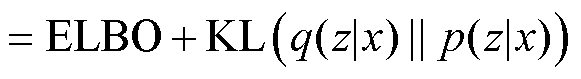 (2)
(2)
式中,KL(·)为KL散度,常用作两个概率分布相似度度量指标,散度值是非负的,为0表示两个分布完全相同。因此最大化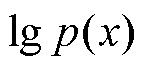 即最大化证据下界(Evidence Lower Bound, ELBO)。式(2)可以写成
即最大化证据下界(Evidence Lower Bound, ELBO)。式(2)可以写成
将ELBO作为VAE的损失函数,可以写为
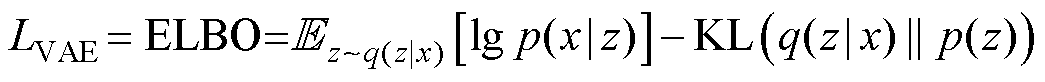 (4)
(4)
式中,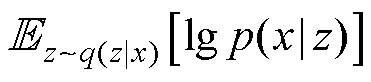 表示重构误差函数,
表示重构误差函数,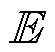 表示期望,
表示期望,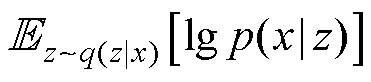 表示以z为底的期望。为统一描述,后续期望形式的公式均用
表示以z为底的期望。为统一描述,后续期望形式的公式均用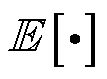 形式表示。
形式表示。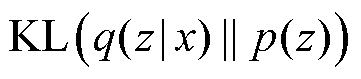 为近似后验分布与先验分布的KL散度,其中先验分布
为近似后验分布与先验分布的KL散度,其中先验分布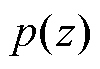 是同向性的标准高斯分布,而
是同向性的标准高斯分布,而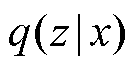 是均值和方差分别为
是均值和方差分别为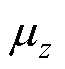 和
和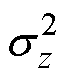 的高斯分布。通过式(5)所示的重参数化技巧,VAE可以通过梯度下降法进行训练。式(5)中随机变量e 服从标准高斯分布,
的高斯分布。通过式(5)所示的重参数化技巧,VAE可以通过梯度下降法进行训练。式(5)中随机变量e 服从标准高斯分布,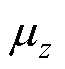 和
和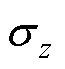 分别为编码器得到的均值和标准差,
分别为编码器得到的均值和标准差, 表示矩阵逐元素相乘。
表示矩阵逐元素相乘。
2.2 变分深度嵌入
VaDE[25]是由VAE衍生出的改进型无监督聚类算法,将高斯混合模型(Gaussian Mixture Model, GMM)作为先验分布,并通过变分的方式完成推断。给定输入数据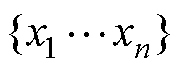 ,生成数据为
,生成数据为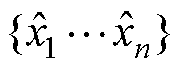 ,首先将真实样本
,首先将真实样本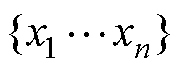 输入编码器中得到全局隐变量的均值和方差
输入编码器中得到全局隐变量的均值和方差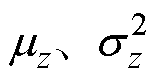 ;然后经重参数化技巧得到隐变量
;然后经重参数化技巧得到隐变量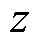 ;之后设混合分布共有t个子分布,再对隐变量进行GMM优化聚类即可获得混合模型的三个参数:混合分布权重
;之后设混合分布共有t个子分布,再对隐变量进行GMM优化聚类即可获得混合模型的三个参数:混合分布权重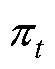 、混合分布均值
、混合分布均值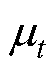 、混合分布的方差
、混合分布的方差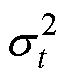 ;最后在混合分布上对不同的簇进行采样,并将采样信息输入解码器中,就可以得到生成数据
;最后在混合分布上对不同的簇进行采样,并将采样信息输入解码器中,就可以得到生成数据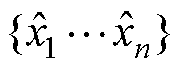 。
。
由上所述,GMM联合分布为
式中,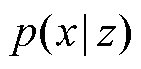 为生成的数据分布;另一项
为生成的数据分布;另一项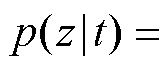
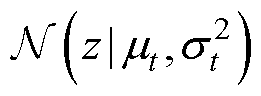 是GMM中某个具体的高斯分布;
是GMM中某个具体的高斯分布;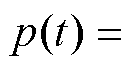
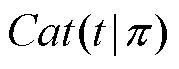 服从分类分布,是GMM的分布的权重,且
服从分类分布,是GMM的分布的权重,且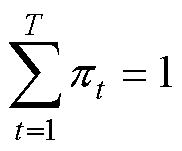 。
。
最大化对数似然函数,利用Jensen不等式可得
式(7)不等号右侧为ELBO函数,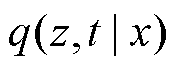 是近似后验分布,在此用来逼近真实后验分布
是近似后验分布,在此用来逼近真实后验分布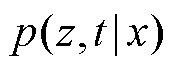 。近似后验分布被进一步分解为
。近似后验分布被进一步分解为
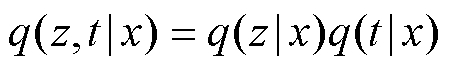 (8)
(8)
此外,根据式(6)和式(8),ELBO可以描述为
综合式(6)~式(9),并结合随机梯度贝叶斯,可将VaDE的损失函数描述为
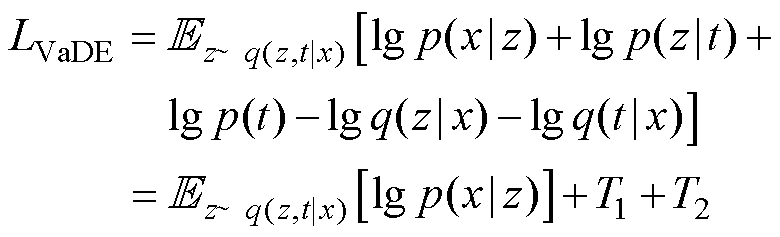 (10)
(10)
其中
式中,K为混合分布数目,也称聚类数;N为隐变量的均值和方差以及GMM所对应的某个具体分布的均值和方差的维度,即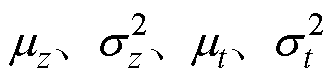 的维度。
的维度。
式(10)第一项为重构误差项,一般可描述为方均误差,即
2.3 带有梯度惩罚的生成对抗网络
生成对抗网络GAN一般由生成器(G)和判别器(D)两部分组成[17],G和D进行对抗训练使得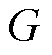 所生成的数据分布符合真实数据的分布,二者通过神经网络进行建模,其基本结构如图3所示。
所生成的数据分布符合真实数据的分布,二者通过神经网络进行建模,其基本结构如图3所示。
设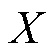 是真实数据,其分布是
是真实数据,其分布是 ,Z是服从分布
,Z是服从分布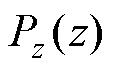 的噪声数据。
的噪声数据。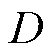 是要区分出输入样本是来自于真实分布
是要区分出输入样本是来自于真实分布 还是
还是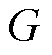 所生成的分布
所生成的分布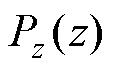 ,训练需要最大化
,训练需要最大化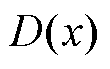 与最小化
与最小化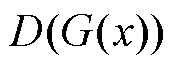 ,因此GAN的损失函数为
,因此GAN的损失函数为
由于GAN的损失函数形式简单,GAN在训练中就容易出现模式崩溃等诸多问题[28],因此文献[26]提出一种带有梯度惩罚项的生成对抗网络(WGANGP),使得模型能够稳定训练,WGANGP鉴别器和生成器的损失函数分别为
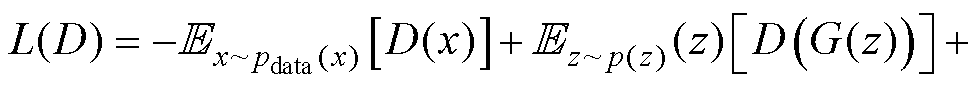
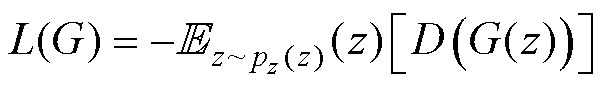 (14)
(14)
式中,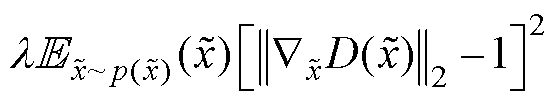 为梯度惩罚项,l 为梯度惩罚项的系数,
为梯度惩罚项,l 为梯度惩罚项的系数,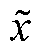 为输入数据和生成数据之间的插值项,可以描述为
为输入数据和生成数据之间的插值项,可以描述为
式中,h 服从[0, 1]之间的均匀分布。改进后的WGANGP可以使得梯度均匀分布,提升训练稳定性。
2.4 综合模型
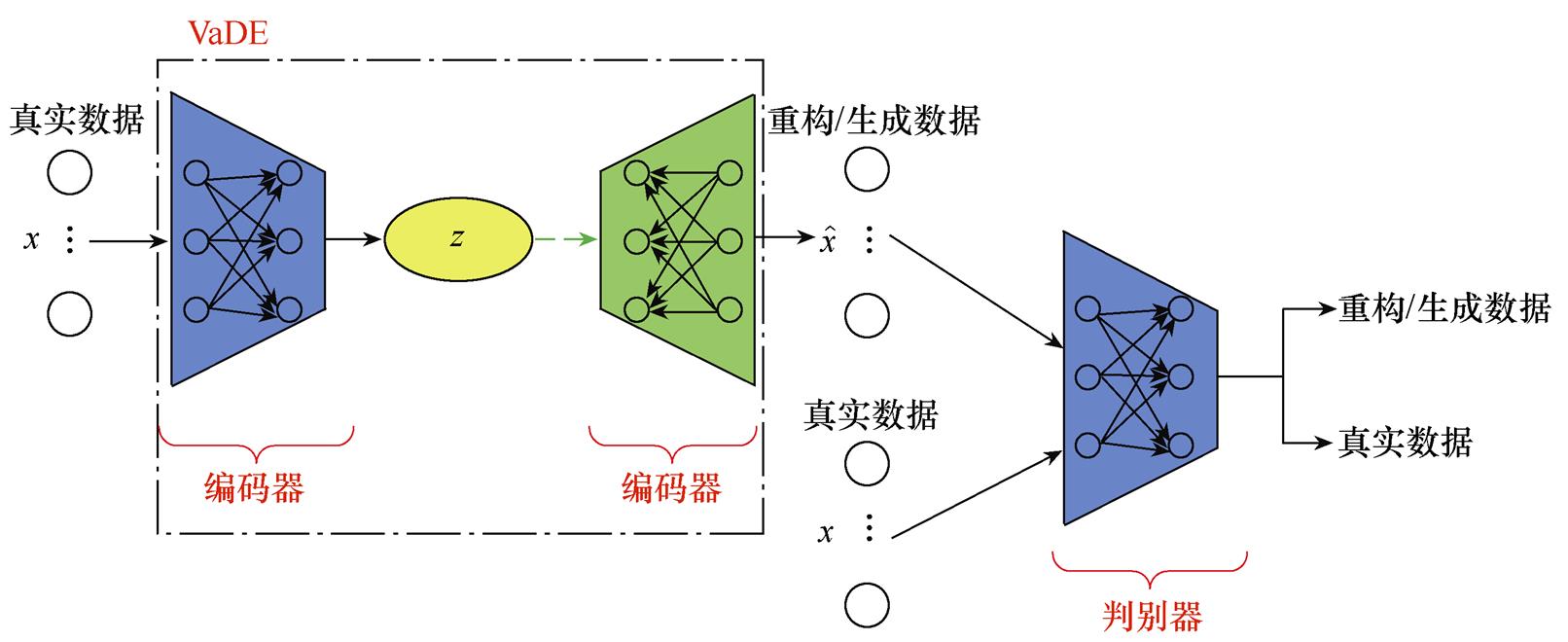
基于以上工作,进一步将VaDE和WGANGP结合起来,可以得到VaDE-WGANGP综合模型,如图4所示。
该综合模型参考了VAE-GAN[27]基本结构。其中VaDE由编码器和解码器两部分组成;WGANGP由生成器和判别器两部分组成;需要注意,本结构中VaDE的解码器同时用作WGANGP的生成器,这也是VAE与GAN相结合的关键环节,且二者参数共享,下文中统一称之为生成器。
编码器将电池原始数据作为输入,可得到输入数据的隐空间分布,在本模型中该分布为GMM分布,用于描述原始数据的先验分布。生成器可以对隐空间进行采样,并将采样所得的隐变量经生成网络进行数据生成,实现对电池外特性的模拟。判别器用于区分生成数据和真实数据,并通过两者之间的对抗实现对前级编码器和生成器的持续优化,进而提高隐空间建模的精度和数据生成质量。
VaDE-WGANGP的损失函数由各环节的损失函数组合而成,综合式(10)、式(11)、式(13)、式(14)可得VaDE-WGANGP网络各部分对应的损失函数,并最终得到综合模型全局损失函数。
编码器的损失函数为
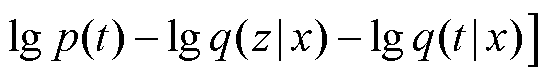 (16)
(16)
生成器的损失函数为
判别器的损失函数为
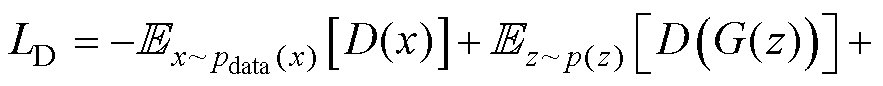
全局损失函数可描述为三者之和,即
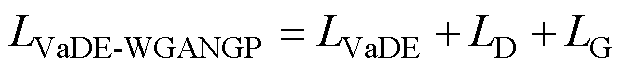 (19)
(19)
3 方案测试与验证
3.1 数据介绍
本研究的目的是实现电池基础外特性数据的模拟生成,以扩充原始数据,因此原始输入数据集不必过多。从数据集全部124个单体电池中选取30个电池的数据作为原始依据;在电池全寿命周期内(SOH=80%~100%)将这些特征分为5个不同的SOH区间,每个区间覆盖DSOH=4%的范围。为满足相同的工况要求,选择放电阶段的数据作为输入。在输入模型之前,先对数据进行处理,首先对数据进行清洗和去噪,去除数据中的异常值和噪声过大的循环;其次找出每次循环的放电开始时间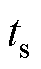 和结束时间
和结束时间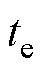 ,并利用线性插值将连续数据离散化为时间步长为a、维度为500的向量,即
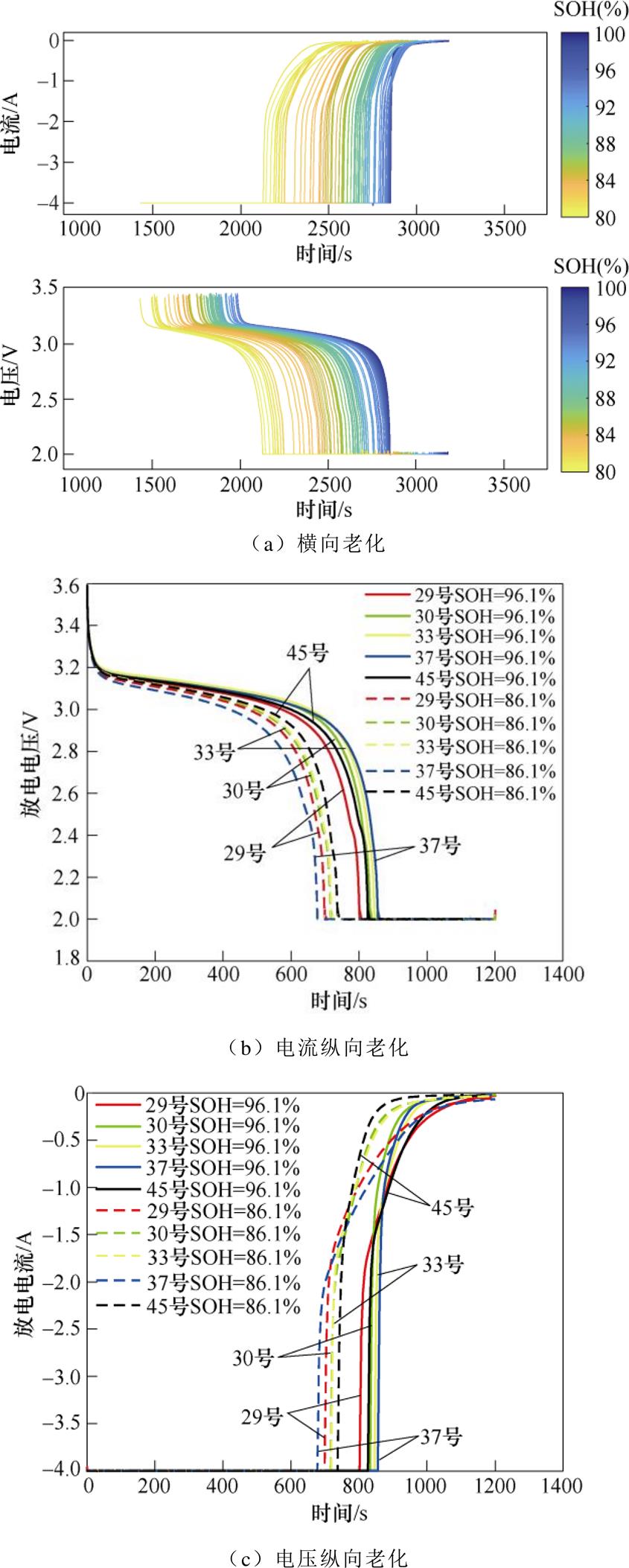
,并利用线性插值将连续数据离散化为时间步长为a、维度为500的向量,即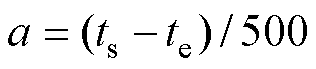 。最终输入数据的维度为9 636×500×3,30个电池样本在全寿命周期内共计覆盖9 636条老化数据;每个老化节点取3个基础外特性(放电电流、放电电压和放电容量曲线);每条特性曲线的500个采样点数据。图5a~图5c依次是从30个电池中提取的原始放电电流、放电容量和放电电压曲线。
。最终输入数据的维度为9 636×500×3,30个电池样本在全寿命周期内共计覆盖9 636条老化数据;每个老化节点取3个基础外特性(放电电流、放电电压和放电容量曲线);每条特性曲线的500个采样点数据。图5a~图5c依次是从30个电池中提取的原始放电电流、放电容量和放电电压曲线。
3.2 数据测试设置
数据测试的超参数设置如下:学习率为0.001、GMM分布数为5(按照SOH分为了5个区间,因此对应聚类分布数也为5)、预训练次数L=20、判别器进行D=5次训练后,生成器训练1次、小批量为64、隐空间维度为10、迭代次数为100次。采用Adam作为损失函数优化器。VaDE-WGANGP的编码器、生成器和判别器均采用卷积神经网络结构,其中编码器采用三层卷积神经网络和两层全连接神经网络,激活函数均为relu;生成器是由两层全连接网络和三层卷积神经网络构成,前四层激活函数为relu,最后一层激活函数为sigmoid;判别器与编码器的架构相同,激活函数为leakyrelu。
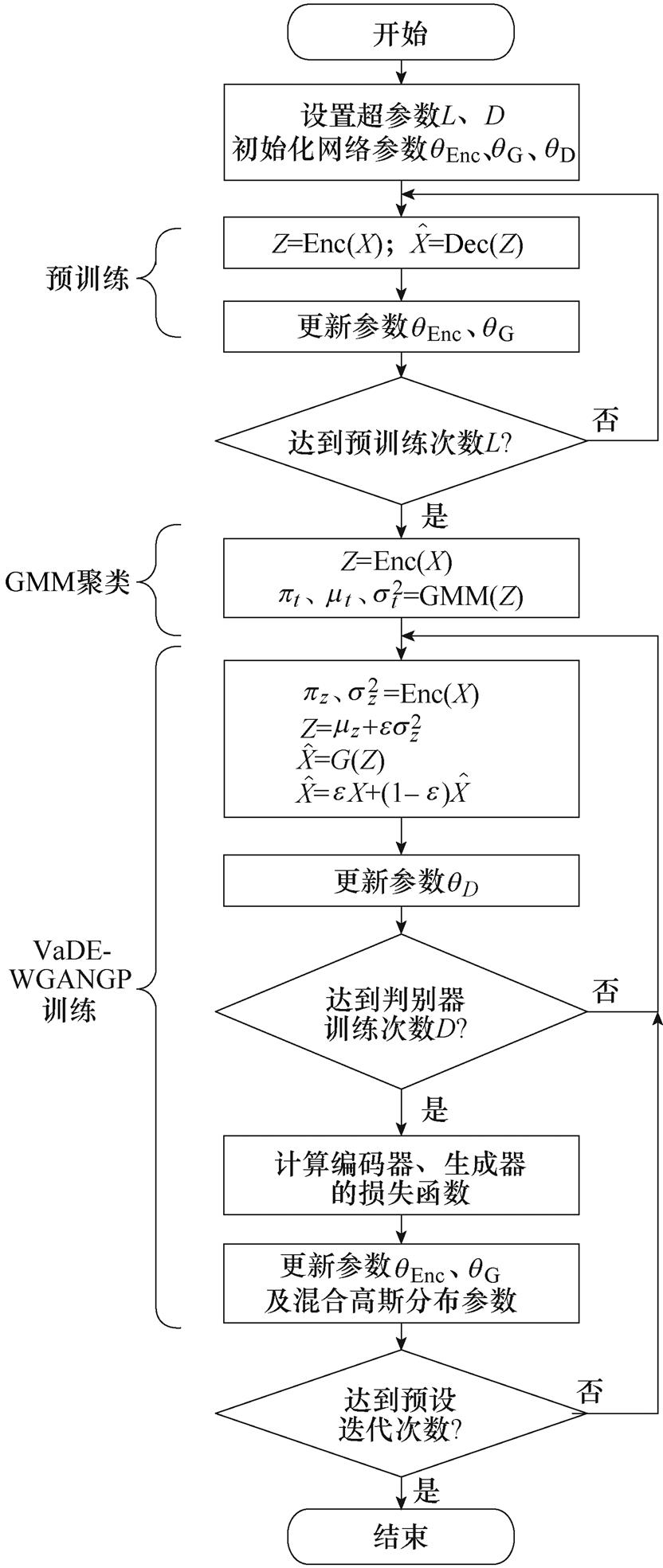
综合模型整体训练流程如图6所示。整体流程分为三部分,分别是预训练部分、GMM聚类部分和VaDE-WGANGP训练部分。
1)预训练:相关研究表明,VaDE在开始训练时模型容易陷入局部最小值或鞍点,甚至会出现模型训练失败[25]。因此在正式训练VaDE之前需要对编码器和生成器进行预训练,以初始化网络参数和混合分布参数,进而避免模型陷入局部最优或者训练失败。在本研究中,如果没有预训练环节,则总会出现模型训练失败的情况;加入预训练之后,就可以保证损失函数收敛、模型优化训练顺利进行。本文对比了AE和VAE两种可行的预训练模型,本着最终损失函数更优的原则,选择预训练模型VAE,预训练过程仅编码器和生成器参加,判别器不参加预训练。
2)GMM聚类:预训练完成后,继续进行GMM聚类并得到GMM的分布参数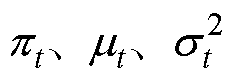 ,该参数集会通过梯度下降进行优化更新。
,该参数集会通过梯度下降进行优化更新。
3)VaDE-WGANGP网络训练:隐变量的均值与方差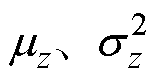 可以通过编码器获取,进而通过重参数化和解码过程实现数据模拟生成,该过程重复D(D=5)次对判别器进行训练;判别器训练完成后,再进行编码器和生成器的参数优化。该迭代过程达到设定的次数时,整个流程结束。
可以通过编码器获取,进而通过重参数化和解码过程实现数据模拟生成,该过程重复D(D=5)次对判别器进行训练;判别器训练完成后,再进行编码器和生成器的参数优化。该迭代过程达到设定的次数时,整个流程结束。
3.3 电池老化特征分析
采用前文所选取的电池原始外特性数据,经VaDE-WGANGP编码过程可以映射为一系列隐空间信息。本方案中,编码操作将单个维度为500×3的输入数据压缩为10×1的信息,即GMM设置为5元10维高斯混合。为便于观察,在此对隐变量使用t-SNE[29]降至二维进行可视化。图7即为30个电池的整体老化特征在VAE、VaDE和VaDE-WGANGP三种模型隐空间的二维表现形式。
图7a~图7c分别代表电池老化特征在三个模型隐空间的二维分布,D1、D2表示两个维度。在图7中,五种颜色代表5个不同的SOH区间,可见不同SOH区间电池外特性所对应的隐变量分布存在明显差异。但是还可以发现,相邻SOH区间对应的特征分布存在一定的重叠区域,这也说明在电池的统计特性中,存在一定的老化差异。
为比较三种模型的聚类性能,在此采用了文献[26]中的无监督聚类精度(Accuracy, ACC),ACC为
ACC可以反映隐空间聚类的准确度,即混合高斯聚类中的标签与真实标签之间的准确度。其中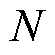 为输入数据总数量,
为输入数据总数量,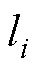 为真实标签,
为真实标签,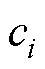 为数据所对应的GMM的具体分布的权重,
为数据所对应的GMM的具体分布的权重,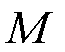 为电池老化数据标签和聚类分配之间所有可能的一对一集合。在此对比了三个模型的准确度,电池老化数据隐空间聚类准确度见表1。
为电池老化数据标签和聚类分配之间所有可能的一对一集合。在此对比了三个模型的准确度,电池老化数据隐空间聚类准确度见表1。
表1 聚类准确度
Tab.1 Clustering accuracy

模 型聚类准确度(%) VAE30.478 VaDE74.552 VaDE-WGANGP83.683
可由表1看出VAE的聚类准确度最低,这是因为VAE的先验分布为标准高斯分布,对数据的拟合能力相对较差;此外在VAE隐空间特性中,相邻甚至不相邻的SOH区间都存在较大范围的重叠区域,这也反映了VAE聚类性能不够理想。VaDE的先验分布采用了混合高斯,GMM对数据的拟合能力优于标准高斯,故VaDE聚类准确度相较于VAE也有显著提高,不同SOH区间的重叠现象也有了明显改善。将VaDE与WGANGP结合后,聚类准确度可以达到83.683%,可见虽然WGANGP引入的最终目的是提升模型生成性能,但在实际运行中也可以进一步提高VaDE部分的聚类准确度。
以上的隐空间描述可以看作是电池原始数据的综合压缩表达,可以更加简洁清晰地描述出全寿命周期内电池基础外特性的变化趋势。从整体生成模型的角度讲,隐空间分布特征是后级模拟数据生成的直接依据,该先验分布越接近原始数据统计化的真实分布,则模型生成数据的质量越高。
3.4 VaDE-WGANGP输出性能测试
在本研究中,VaDE-WGANGP网络的主要目的是模拟电池在老化过程中的外部特性,生成逼真的数据。但考虑到直接对生成的仿真数据进行定量评估并不方便,故在此采用数据重构指标对生成模型的输出特性进行分析。需要说明,数据重构和数据模拟是不同的,对于生成模型而言,模拟数据生成的依据是原始数据集合的分布特性,而重构过程则是对应数据个体的分布特性。理想状态下重构信息应与原始数据完全相同;而模拟生成的数据是逼近真实电池特性的再生数据,不同于真实数据。
针对原始训练集,通过式(11)的重构误差来评判几种生成网络的数据生成质量,表2给出了几种模型重构误差的对比。
表2 重构误差
Tab.2 Reconstruction error

模 型重构误差(%) VAE0.850 1 VaDE0.066 4 VaDE-WGANGP0.002 16
由表2知,VAE的重构误差最大;而VaDE的重构误差相比前者有了大幅减小;VaDE在结合WGANGP后,重构误差相比于VaDE有进一步减小。这也在一定程度上表明本文采用的VaDE- WGANG模型具有更好的输出性能。
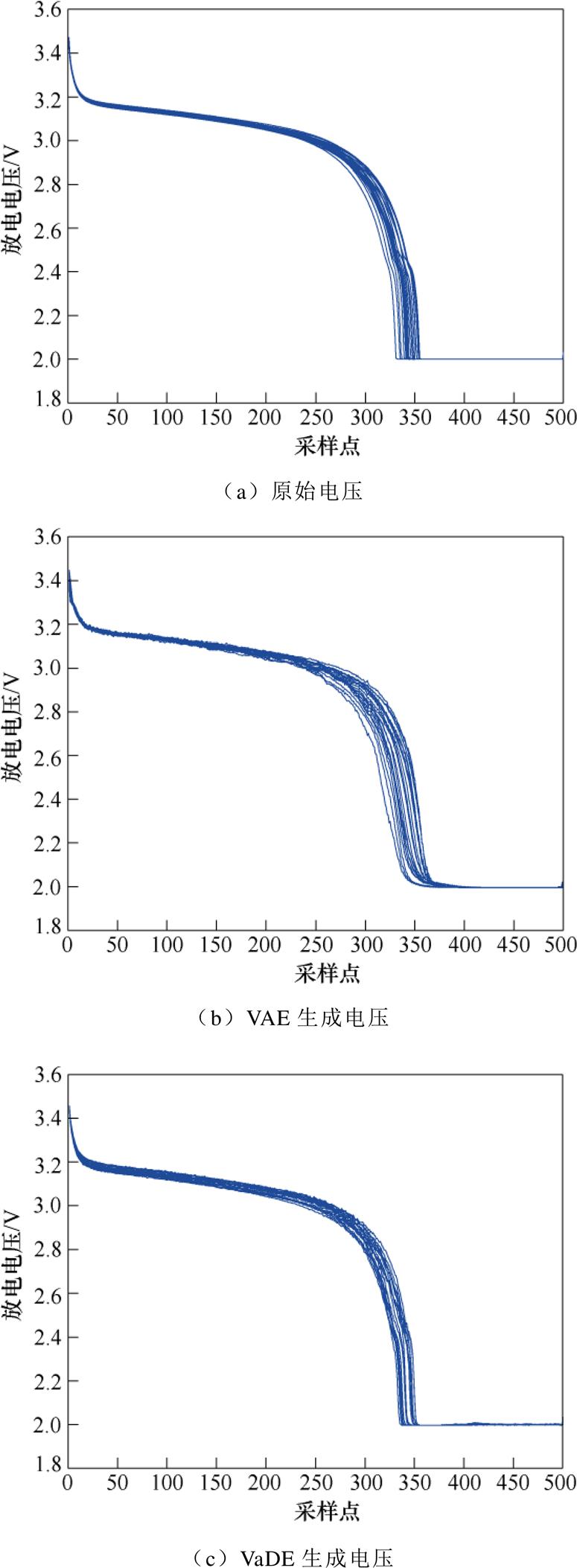
接下来重点测试该方案的模拟数据生成性能。作为本研究的主要目标,期望所设计的综合模型可以模拟任意SOH状态或区间内的电池外特性,进而实现原始数据有效扩展的目的。在此首先以电池SOH∈[92%, 96%]区间的放电电压数据为例,分别采用VAE、VaDE和VaDE-WGANGP三种模型进行模拟数据生成。该SOH区间原始数据共包含2 800条电压曲线,为便于对比观察,随机选20条曲线来描述原始数据,生成曲线的数目也设置为20,三种模型获得的模拟生成结果如图8所示。
图8a为原始电压数据,图8b~图8d分别为采用VAE、VaDE和VaDE-WGANGP三种模型获得的生成数据。通过观察可以发现,与原始数据相比,采用VAE获得的电压曲线含有较大的波动和噪声信息;此外,在CC放电到CV放电模式的切换阶段,VAE生成数据对于原始电压从快速下降到恒压的瞬态变化特性跟踪较差,不能够准确模拟出这种真实电池的电压变化特征。相对而言,采用VaDE和VaDE-WGANGP两模型获得的生成数据则能够较好地模拟出电池电压在放电模式切换时的变化特征。
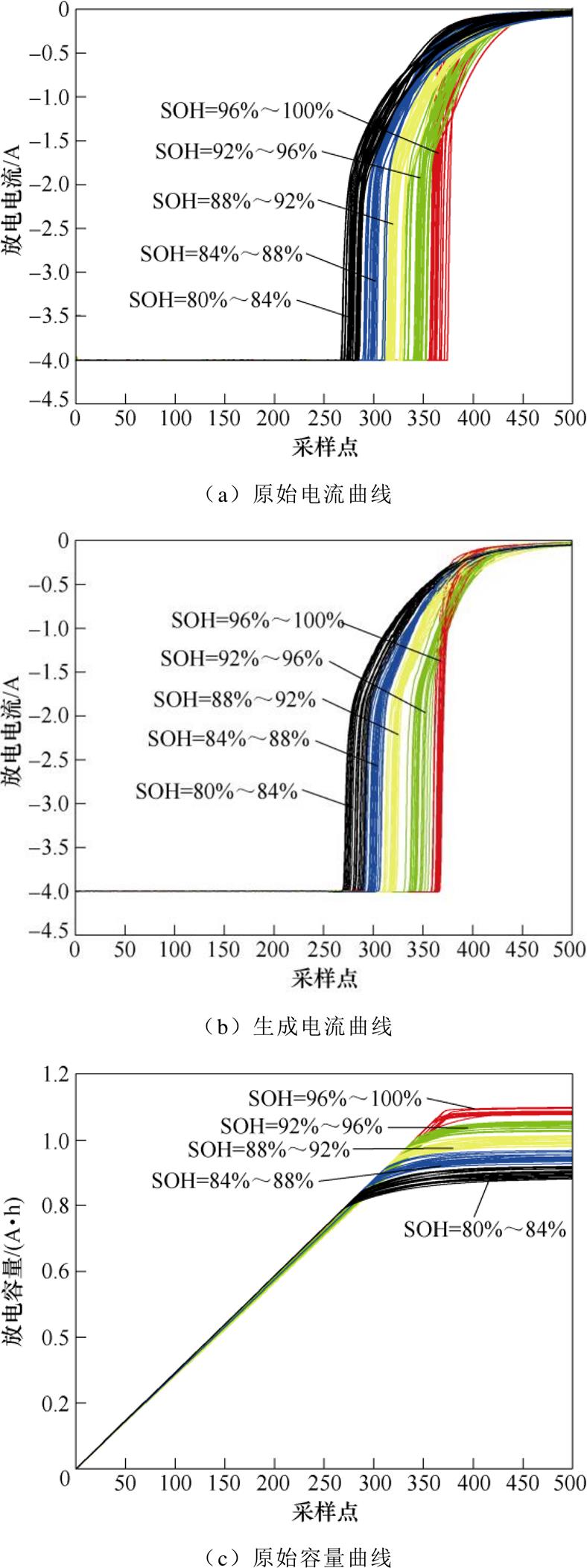
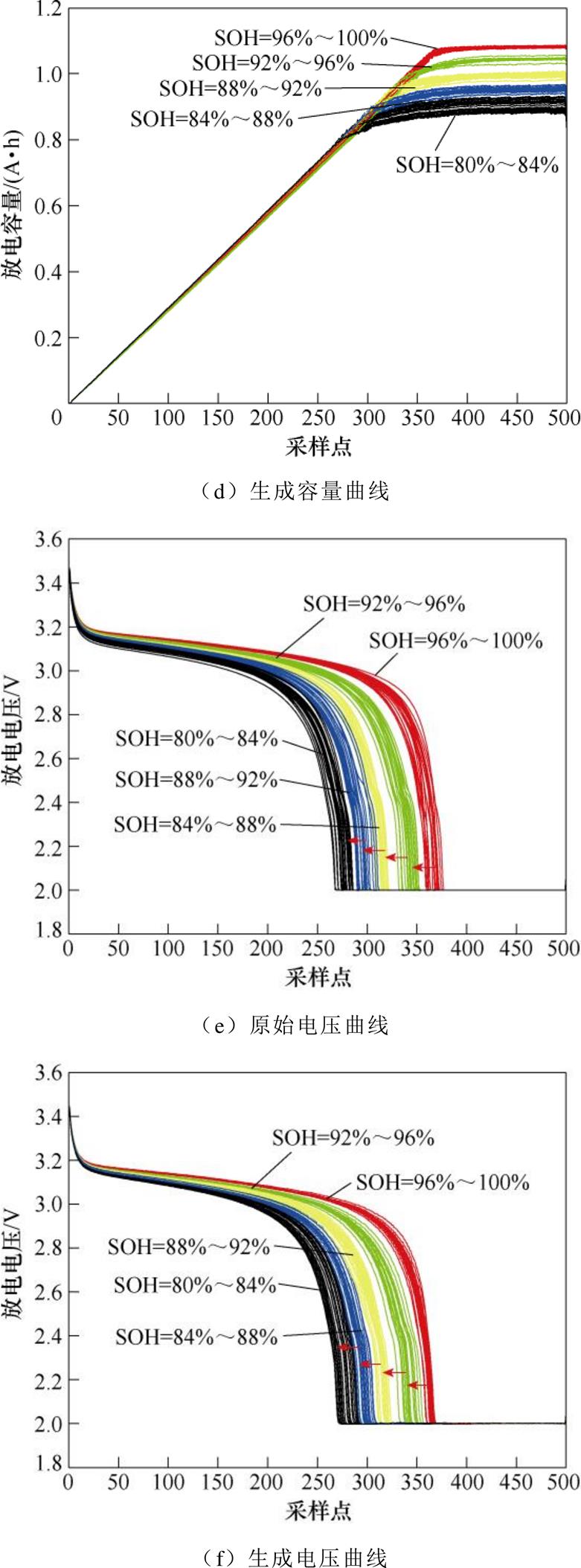
进一步对比图8c和图5d可见,采用综合模型VaDE-WGANGP获得电压曲线含有更少的噪声,整体平滑度和变化趋势更加逼近真实电压数据;而且多条电压曲线的分布状况也与原始数据更加接近。因此,可以得出初步结论,相对VAE和VaDE,VaDE- WGANGP具有更强的数据模拟与生成能力。根据前文分析已知,对应不同SOH区间,电池基础外特性数据可以映射为隐空间中不同的分布类簇,基于这个特征,可应用VaDE-WGANGP模型来模拟生成各个SOH区间的电池特性曲线。本文采用所设计的综合模型,在全部5个SOH区间内对电池的放电电流、电池电压和放电容量曲线3个基础外特性分别进行了模拟生成,在此依然选取20条原始数据和20条生成数据进行对比,所得结果如图9所示,图9a、图9c、图9e是原始曲线,图9b、图9d、图9f是VaDE-WGANGP生成曲线。其中5个SOH区间由高到低依次由红-绿-黄-蓝-黑五种颜色所对应,可以看出VaDE-WGANGP的生成老化外特性曲线可以实现较好的区间过渡。
经对比可以发现,虽然模型生成的特性曲线在一些细微环节上仍存在一定噪声,在个别时间区域内对真实数据的模拟效果还有待提升,但从整体来看,在电池的全寿命周期范围内,样本电池的三种基础外特性均可以被综合模型以较高质量模拟生成。与真实数据相比,生成数据具有良好的逼真度,这也证明电池老化过程中外特性可以通过VaDE- WGANGP结构实现良好的建模。理论上讲,基于一定数量的原始数据,通过该模型可以生成无限数据,从而实现有限数据扩充的目的。
3.5 生成数据质量评判
为了进一步验证生成数据的质量,本节利用原始数据和生成数据结合进行SOH估算以侧面验证生成数据的质量,本节利用放电过程中的电流和电压作为输入数据。首先选取17~21号5个电池作为训练集,共3 980条数据,再分别利用VAE、VaDE、VaDE-WGANGP 3 个模型分别在[96%, 100%]、[92%, 96%]、[88%, 92%]、[84%, 88%]和[80%, 84%]这5个SOH区间生成400条共计2 000条老化数据,并分别和原始数据组合,得到3个增强后的训练集,共计5 980条数据。其次选取第23号、24号、36号、37号4个电池作为测试集。最后利用4个训练集分别对SOH预测模型训练得到优化模型,随后利用测试集通过优化模型进行SOH估算以验证生成数据质量。
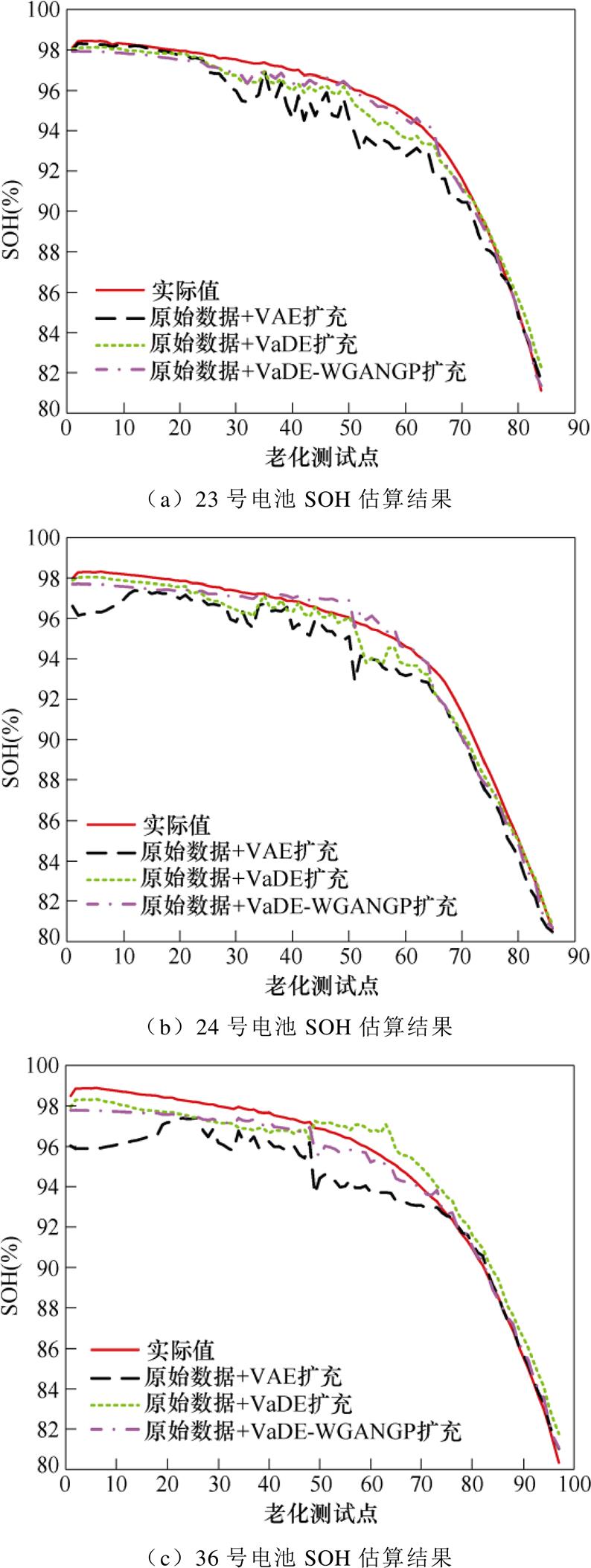
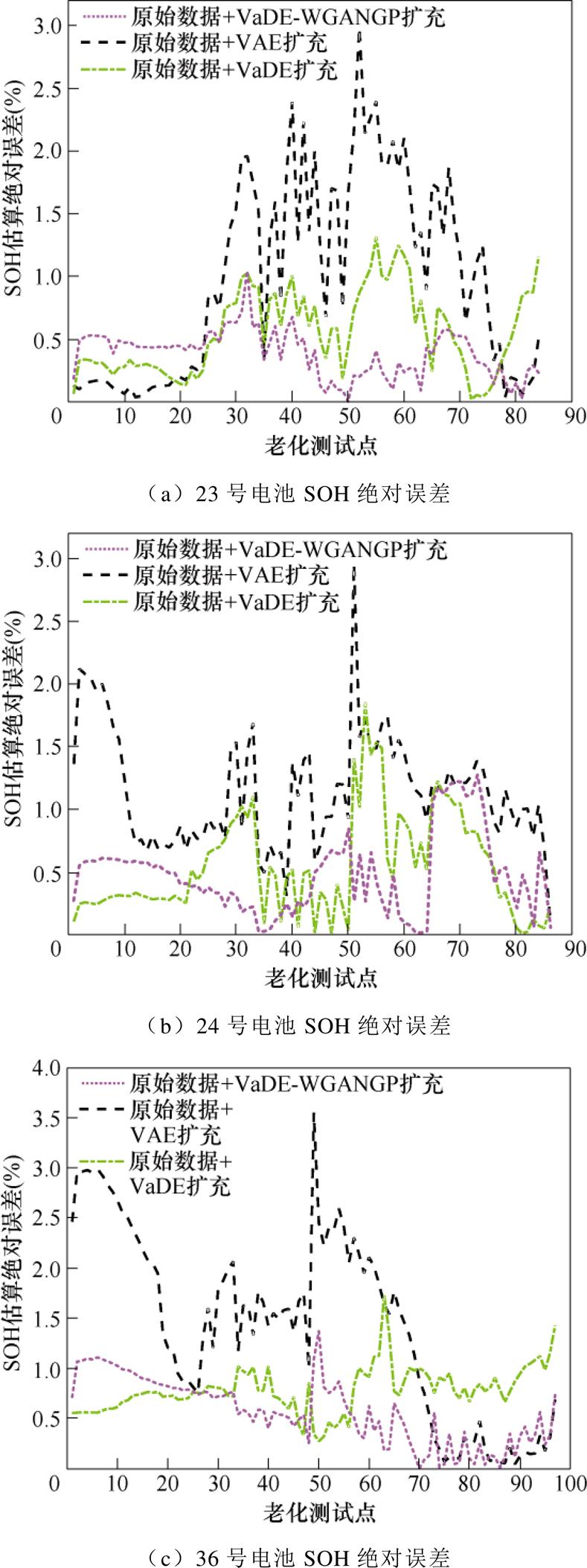
SOH估算模型采用卷积神经网络,输入为放电过程中的电压和电流曲线,输入格式为[500 2 1],模型共4个二维卷积层,一个最大池化层和两个全连接层,激活函数为relu。SOH估算的超参数设置如下:minibatch为64,epoch设置为200,学习率为0.001,每10次epoch学习率变为原来的0.9倍,采用Adam优化器。误差指标采用SOH估算结果方均根误差(Root Mean Square Error, RMSE)、平均绝对误差(Mean Absolute Error, MAE)和最大绝对误差(Max)。SOH估算误差结果对比见表3。23号、24号、36号、37号电池SOH估算结果及绝对误差结果如图10和图11所示。
表3 不同训练集对应的SOH估算误差结果
Tab.3 SOH estimation error results by different training sets
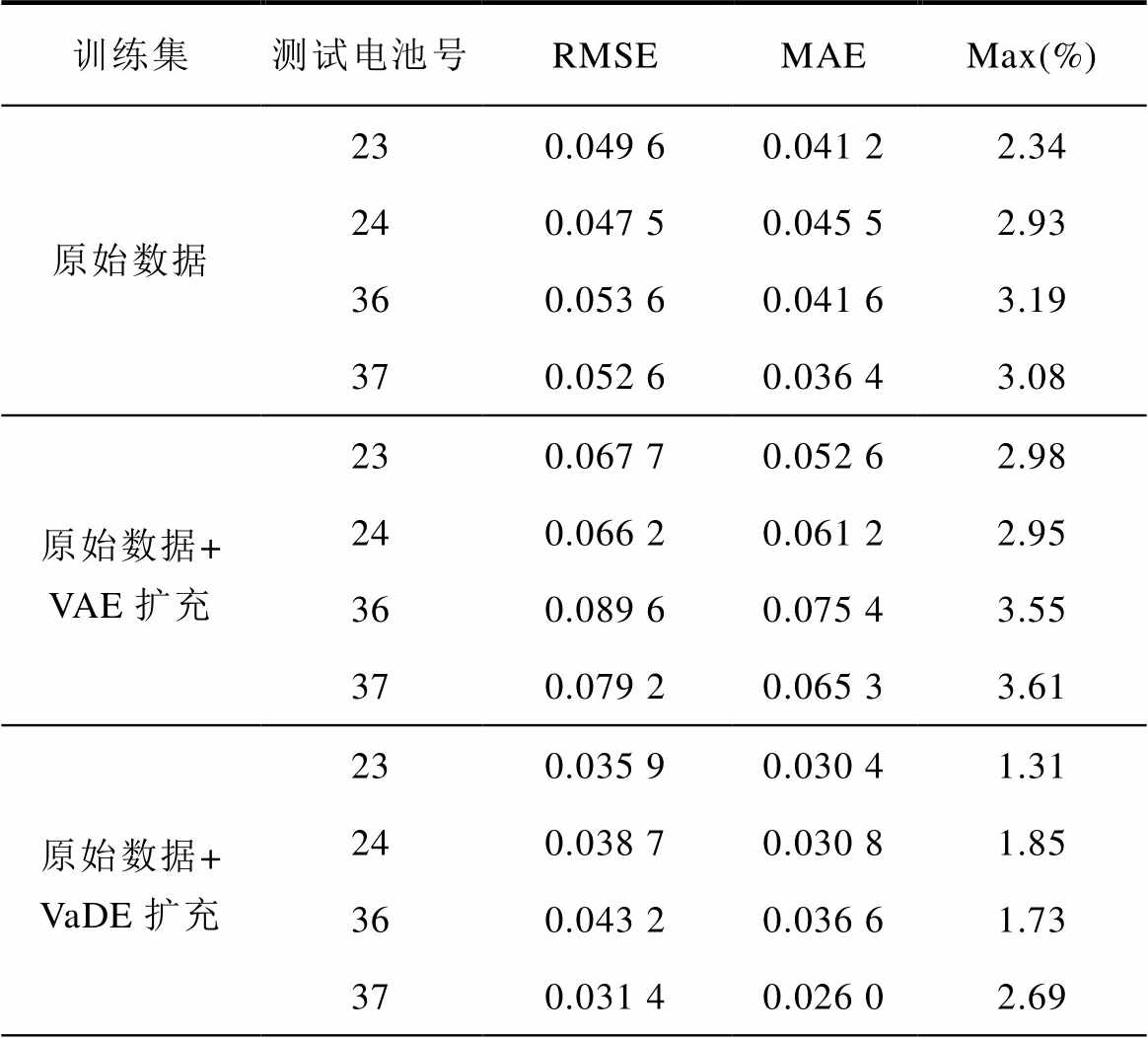
训练集测试电池号RMSEMAEMax(%) 原始数据230.049 60.041 22.34 240.047 50.045 52.93 360.053 60.041 63.19 370.052 60.036 43.08 原始数据+ VAE扩充230.067 70.052 62.98 240.066 20.061 22.95 360.089 60.075 43.55 370.079 20.065 33.61 原始数据+ VaDE扩充230.035 90.030 41.31 240.038 70.030 81.85 360.043 20.036 61.73 370.031 40.026 02.69
(续)
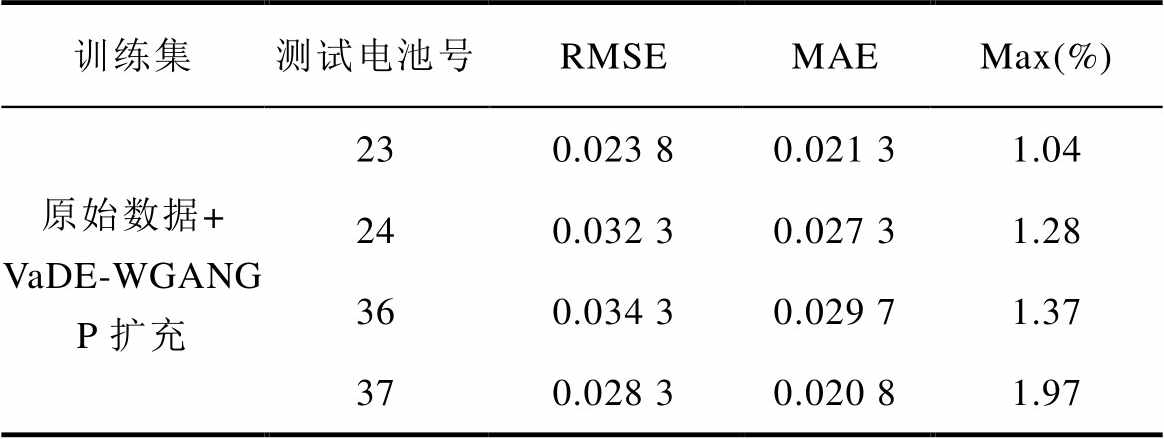
训练集测试电池号RMSEMAEMax(%) 原始数据+ VaDE-WGANGP扩充230.023 80.021 31.04 240.032 30.027 31.28 360.034 30.029 71.37 370.028 30.020 81.97
从表3中可以看出,经过VAE数据生成扩充训练集后,测试集SOH的估算效果反而变差,3个误差指标均比原始训练集获得的估算结果大,可以说明VAE生成数据质量较差,反而对原始数据造成了一定污染。VaDE生成数据与原始数据结合后,SOH估算的RMSE指标均小于0.05,相较于原始数据作为训练集的估算精度有明显提高。而VaDE-WGANGP生成数据与原始数据结合后,测试集SOH的RMSE估算结果均小于0.035,最大绝对误差相较于其他3个训练集最低,可以证明VaDE-WGANGP网络具有较高的数据生成质量。图10是训练集经三种方案进行数据扩充后获得的SOH估算结果,图11是SOH估算绝对误差,与表3所得结论一致。
4 结论
为了模拟锂离子电池全寿命周期内的基础外特性,本文从VAE和GAN两大生成模型入手,首先引入VAE的混合高斯改进模型VaDE和带有梯度惩罚的GAN模型WGANGP,进而构造了综合的VaDE-WGANGP结构;然后基于此综合模型,针对30个样本电池全寿命周期的基础外特性进行了分析与建模。本文所做的研究可以得到以下结论:
1)在电池数据聚类及电池外特性模拟生成方面,VaDE-WGANGP综合模型具有比VAE和VaDE更优的性能,能够更加准确地学习不同SOH区间电池外特性的统计特征。
2)VaDE-WGANGP模型可以生成逼真的电池外特性模拟数据。相关的SOH估算测试也证明通过VaDE-WGANGP可以获得较好的数据生成质量。
该研究为老化过程中电池的外特性分析提供了一个新颖的思路;针对数据驱动技术中存在的原始数据不足的情况,本方案也可以提供一种数据扩展的有效方法。
参考文献
[1] 郭向伟, 邢程, 司阳, 等. RLS锂电池全工况自适应等效电路模型[J]. 电工技术学报, 2022, 37(16): 4029-4037.
Guo Xiangwei, Xing Cheng, Si Yang, et al. RLS adaptive equivalent circuit model of lithium battery under full working condition[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4029-4037.
[2] 吴立峰, 刘昊, 林仲钦, 等. 低温环境下锂离子电池荷电状态与超声透射飞行时间的关系研究[J]. 电工技术学报, 2022, 37(21): 5617-5626.
Wu Lifeng, Liu Hao, Lin Zhongqin, et al. Relationship between state of charge of lithium-ion battery and ultrasonic transmission flight time at low tempera- ture[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5617-5626.
[3] Iurilli P, Brivio C, Wood V. On the use of elec- trochemical impedance spectroscopy to characterize and model the aging phenomena of lithium-ion batteries: a critical review[J]. Journal of Power Sources, 2021(505): 229860.
[4] Tian Huixin, Qin Pengliang, Li Kun, et al. A review of the state of health for lithium-ion batteries: Research status and suggestions[J]. Journal of Cleaner Production, 2020(261): 120813.
[5] 武龙星, 庞辉, 晋佳敏, 等. 基于电化学模型的锂离子电池荷电状态估计方法综述[J]. 电工技术学报, 2022, 37(7): 1703-1725.
Wu Longxing, Pang Hui, Jin Jiamin, et al. A review of SOC estimation methods for lithium-ion batteries based on electrochemical model[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1703-1725.
[6] Liu Lin, Park J, Lin Xianke, et al. A thermal- electrochemical model that gives spatial-dependent growth of solid electrolyte interphase in a Li-ion battery[J]. Journal of Power Sources, 2014(268): 482-490.
[7] Dong Guangzhong, Wei Jingwen. A physics-based aging model for lithium-ion battery with coupled chemical/mechanical degradation mechanisms[J]. Electrochimica Acta, 2021(395): 139133.
[8] Ma Lili, Xu Yonghong, Zhang Hongguang, et al. Co-estimation of state of charge and state of health for lithium-ion batteries based on fractional-order model with multi-innovations unscented Kalman filter method[J]. Journal of Energy Storage, 2022(52): 104904.
[9] 孙金磊, 唐传雨, 李磊, 等. 基于状态与模型参数联合估计的老化电池可充入电量估计方法[J]. 电工技术学报, 2022, 37(22): 5886-5898.
Sun Jinlei, Tang Chuanyu, Li Lei, et al. An estimation method of rechargeable electric quantity for aging battery based on joint estimation of state and model parameters[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5886-5898.
[10] Li Shi, Pischinger S, He Chaoyi, et al. A comparative study of model-based capacity estimation algorithms in dual estimation frameworks for lithium-ion batteries under an accelerated aging test[J]. Applied Energy, 2018(212): 1522-1536.
[11] 王义军, 左雪. 锂离子电池荷电状态估算方法及其应用场景综述[J]. 电力系统自动化, 2022, 46(14): 193-207.
Wang Yijun, Zuo Xue. Review on estimation methods for state of charge of lithium-ion battery and their application scenarios[J]. Automation of electric power systems, 2022, 46(14): 193-207.
[12] 黄凯, 丁恒,郭永芳, 等. 基于数据预处理和长短期记忆神经网络的锂离子电池寿命预测[J]. 电工技术学报, 2022, 37(15): 3753-3766.
Huang Kai, Ding Heng, Guo Yongfang, et al. Prediction of remaining useful life of lithium-ion battery based on adaptive data preprocessing and long short-term memory network[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3753-3766.
[13] Wang Jiwei, Deng Zhongwei, Yu Tao, et al. State of health estimation based on modified Gaussian process regression for lithium-ion batteries[J]. Journal of Energy Storage, 2022(51): 104512.
[14] Yang Fangfang, Wang Dong, Xu Fan, et al. Lifespan prediction of lithium-ion batteries based on various extracted features and gradient boosting regression tree model[J]. Journal of Power Sources, 2020(476): 228654.
[15] Severson K A, Attia P M, Jin N, et al. Data-driven prediction of battery cycle life before capacity degradation[J]. Nature Energy, 2019, 4(5): 1-9.
[16] Kingma D P, Welling M. Auto-encodingvariational Bayes[C]//Proceedings of the International Con- ference on Learning Representations (ICLR), Banff, 2014: 1-14.
[17] Goodfellow I J, Pouget-Abadie J, Mirza M, et al. Generative adversarial networks[J]. Advances in Neural Information Processing Systems, 2014, 3: 2672-2680.
[18] Kim S, Choi Y Y, Choi J. Impedance-based capacity estimation for lithium-ion batteries using generative adversarial network[J]. Applied Energy, 2022(308): 118317.
[19] Jiao Ruihua, Peng Kaixiang, Dong Jie. Remaining useful life prediction of lithium-ion batteries based on conditional variational autoencoders-particle filter[J]. IEEE Transactions on Instrumentation and Mea- surement, 2020, 69(11): 8831-8843.
[20] Huang Y, Tang Y, Vanzwieten J. Prognostics with variational autoencoder by generative adversarial learning[J]. IEEE Transactions on Industrial Elec- tronics, 2022, 69(1): 856-867.
[21] 梁凤勤. 基于迁移学习的锂离子电池健康状态估计方法研究[D]. 成都: 电子科技大学, 2021.
Liang Fengqin. Research on the method of estimating the health state of lithium-ion battery based on transfer learning[D]. Chengdu: University of Elec- tronic Science and Technology, 2021.
[22] 李龙, 燕旭朦, 张钰生, 等. 小样本锂电池数据SOC估算方法[J/OL]. 西安交通大学学报, 2023. 网络首发: https://kns.cnki.net/kcms2/detail/61.1069.T. 20230525.1747.007.html.
Li Long, Yan Xumeng, Zhang Yusheng, et al. Lithium battery SOC estimation method based on transfer learning and deep learning[J/OL]. Journal of Xi’an Jiaotong University, 2023. https://kns.cnki.net/kcms2/ detail/61.1069.T. 20230525.1747.007.html.
[23] Ni Zichuan, Li Biao, Yang Ying. Deep domain adaptation network for transfer learning of state of charge estimation among batteries[J]. Journal of Energy Storage, 2023(61): 106812.
[24] Ma Jian, Shang Pengchao, Zou Xinyu, et al. A hybrid transfer learning scheme for remaining useful life prediction and cycle life test optimization of different formulation Li-ion power batteries[J]. Applied Energy, 2021(282): 116167.
[25] Jiang Zhuxi, Zheng Yin, Tan Huachun, et al. Variational deep embedding: an unsupervised and generative approach to clustering[C]//26th Inter- national Joint Conference on Artificial Intelligence (IJCAI), Melbourne, 2017: 1965-1972.
[26] Gulrajani I, Ahmed F, Arjovsky M, et al. Improved training of wasserstein GANs[C]//Advances in Neural Information Processing Systems, Long Beach: CA, USA, Curran Associates, Inc, 2017: 5767-5777.
[27] Larsen A, Sønderby S K, Larochelle H, et al. Auto- encoding beyond pixels using a learned similarity metric[C]//Proceedings of Machine Learning Research, New York, 2016: 1558-1566.
[28] Arjovsky M, Chintala S, Bottou L. Wasserstein GAN[C]//Proceedings of the 34th International Confer- ence on Machine Learning, PMLR, Sydney, Australia, 2017, 70: 214-223.
[29] Van Der Maaten L, Hinton G. Visualizing data using t-SNE[J]. Journal of Machine Learning Research, 2008(9): 2579-2605.
Ageing Performance Modeling of Li-Ion Batteries Based on Variational Deep Embedding-Wasserstein GAN with Gradient Penalty
Li Yi Zhang Jinlong Qi Hanhong Wei Yanjun Zhang Di
(School of Electrical Engineering Yanshan University Qinhuangdao 066004 China)
Abstract Lithium-ion batteryaging tests are primarily used to study battery aging performance. However, aging experiments for a large number of batteries take time and effort. Therefore, combined with Wasserstein GAN and gradient penalty (WGANGP), the Variational deep embedding (VaDE) model is used to form a VaDE-WGANGP architecture. Then, a method of battery aging performance modelling and data generation is designed. This paper aims to generate simulated data onexternal characteristics (such as battery voltage and charge/discharge current during working). The VaDE-WGANGP generation model is effective during different battery SOH intervals, which indicates that simulated battery data can be obtained across the whole battery life span (SOH∈[100%, 80%]) and coversbattery aging performance. Furthermore, battery external characteristics differ for different battery cells even under the same SOH state. Accordingly, the diversities in battery external characteristics among different battery cells under the same SOH states are considered.
An open-source battery test data set, in cludingdata from Toyota Research Institute (TRI) in partnership with MIT and Stanford and working data on LFP/graphite cells, is used. Firstly, the three external characteristics (voltage, current, and discharge capacity during the discharge process) are selected as the input of the model. The latent space by the VaDE encoder can be mapped, and its distribution with specific rules can be obtained through optimization. Then, this distribution space is sampled, and the latent variables obtained by sampling are used as input into the VaDE decoder for data generation. SOH estimation tests show that the VaDE-WGANGP has good generation performance for battery external characteristics, and the primary battery working performance is simulated during the aging process. Besides, effective and extended battery data resources can be provided by this measure for data-driven algorithms, especially in case the primitive data amount is insufficient.
The following conclusions can be drawn. (1) Regarding battery data clustering and battery extrinsic characteristics simulation generation, the integrated model of VaDE-WGANGP has better performance than VAE and VaDE. The statistical characteristics of battery extrinsic characteristics in different SOH intervals are accurate. (2) VaDE-WGANGP can generate high-quality simulation data of battery external characteristics. The SOH estimation results prove that the data generated by VaDE-WGANGP is of high quality. This paper provides a novel idea for analyzing the external characteristics of batteries during aging. Given the shortage of original data in data-driven technology, this scheme can also provide an effective method for data extension and is helpful for battery screening.
keywords:Lithium-ion battery, aging performance, generation model, variational deep embedding, Wasserstein GAN with gradient penalty
DOI: 10.19595/j.cnki.1000-6753.tces.230487
中图分类号:TM911
秦皇岛市科学技术研究与发展计划项目(202301A312)。
收稿日期 2023-04-16
改稿日期 2023-05-08
作者简介
李 弈 男,1998年生,硕士研究生,研究方向为机器学习及人工智能技术在蓄电池系统中的应用。E-mail: liyi1313112@163.com
张金龙 男,1983年生,副教授,硕士生导师,研究方向为蓄电池管理、蓄电池高效利用与测试技术。E-mail: maxlong83@163.com(通信作者)
(编辑 郭丽军)
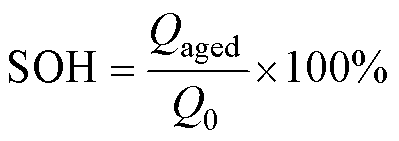 (1)
(1)
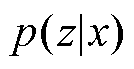 ,
,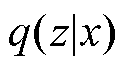 来逼近
来逼近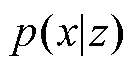 。
。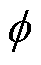 和
和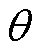 。表示为
。表示为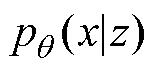 和
和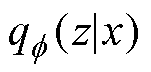 。VAE通过最大化对数边际似然
。VAE通过最大化对数边际似然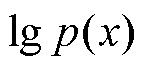 得到优化目标为
得到优化目标为
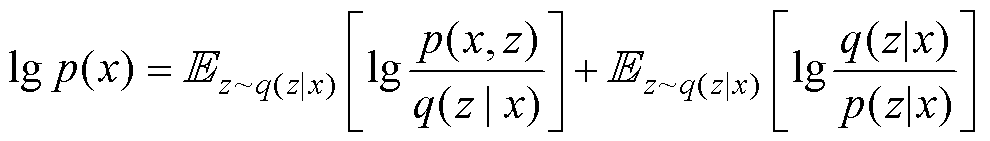
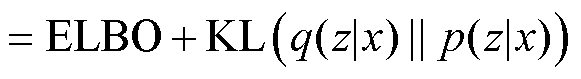 (2)
(2)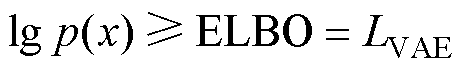 (3)
(3)
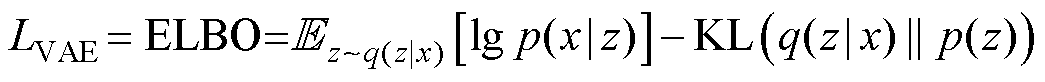 (4)
(4)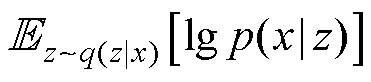 表示重构误差函数,
表示重构误差函数,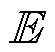 表示期望,
表示期望,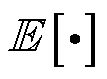 形式表示。
形式表示。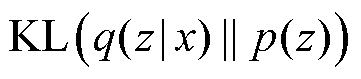 为近似后验分布与先验分布的KL散度,其中先验分布
为近似后验分布与先验分布的KL散度,其中先验分布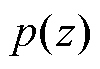 是同向性的标准高斯分布,而
是同向性的标准高斯分布,而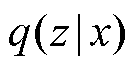 是均值和方差分别为
是均值和方差分别为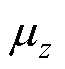 和
和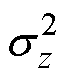 的高斯分布。通过式(5)所示的重参数化技巧,VAE可以通过梯度下降法进行训练。式(5)中随机变量
的高斯分布。通过式(5)所示的重参数化技巧,VAE可以通过梯度下降法进行训练。式(5)中随机变量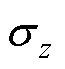 分别为编码器得到的均值和标准差,
分别为编码器得到的均值和标准差, 表示矩阵逐元素相乘。
表示矩阵逐元素相乘。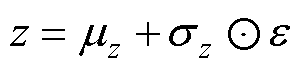 (5)
(5)
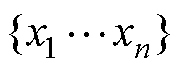 ,生成数据为
,生成数据为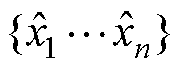 ,首先将真实样本
,首先将真实样本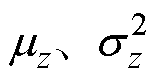 ;然后经重参数化技巧得到隐变量
;然后经重参数化技巧得到隐变量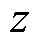 ;之后设混合分布共有t个子分布,再对隐变量进行GMM优化聚类即可获得混合模型的三个参数:混合分布权重
;之后设混合分布共有t个子分布,再对隐变量进行GMM优化聚类即可获得混合模型的三个参数:混合分布权重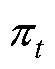 、混合分布均值
、混合分布均值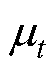 、混合分布的方差
、混合分布的方差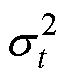 ;最后在混合分布上对不同的簇进行采样,并将采样信息输入解码器中,就可以得到生成数据
;最后在混合分布上对不同的簇进行采样,并将采样信息输入解码器中,就可以得到生成数据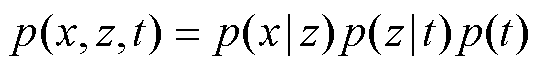 (6)
(6)
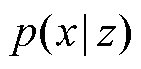 为生成的数据分布;另一项
为生成的数据分布;另一项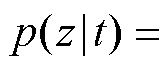
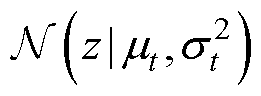 是GMM中某个具体的高斯分布;
是GMM中某个具体的高斯分布;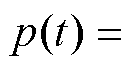
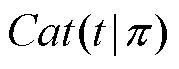 服从分类分布,是GMM的分布的权重,且
服从分类分布,是GMM的分布的权重,且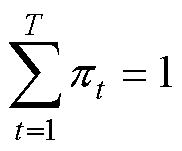 。
。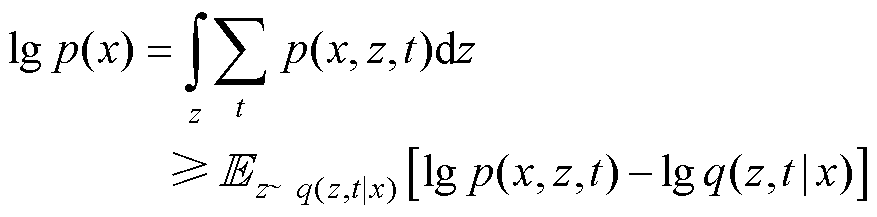 (7)
(7)
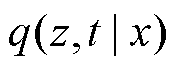 是近似后验分布,在此用来逼近真实后验分布
是近似后验分布,在此用来逼近真实后验分布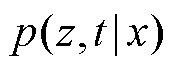 。近似后验分布被进一步分解为
。近似后验分布被进一步分解为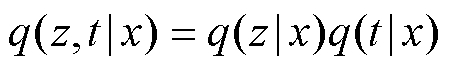 (8)
(8)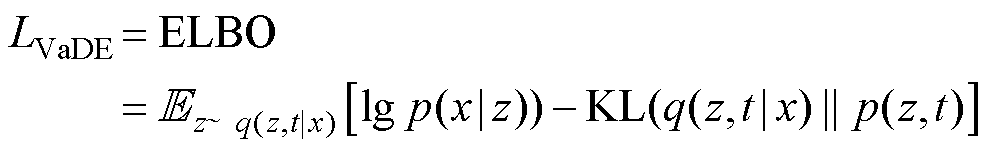 (9)
(9)
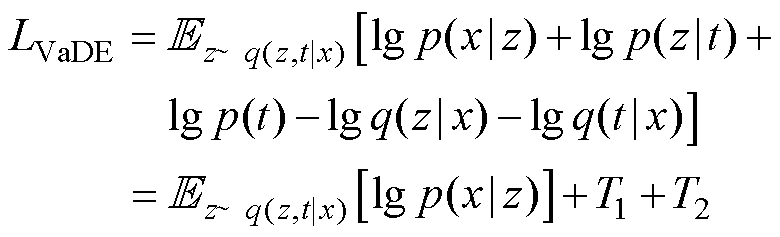 (10)
(10)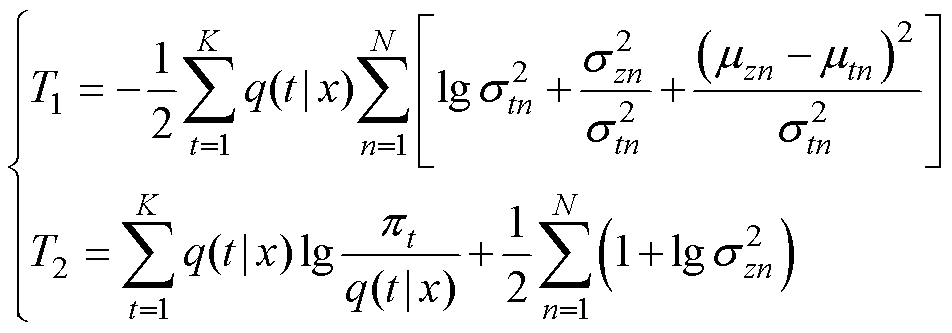
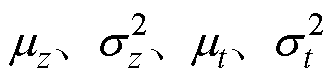 的维度。
的维度。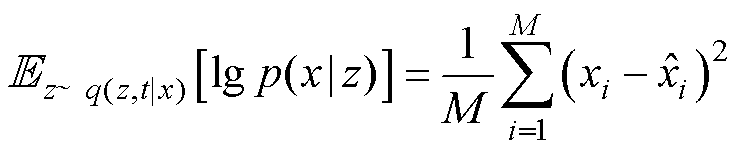 (11)
(11)
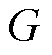 所生成的数据分布符合真实数据的分布,二者通过神经网络进行建模,其基本结构如图3所示。
所生成的数据分布符合真实数据的分布,二者通过神经网络进行建模,其基本结构如图3所示。
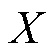 是真实数据,其分布是
是真实数据,其分布是 ,Z是服从分布
,Z是服从分布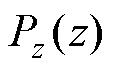 的噪声数据。
的噪声数据。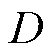 是要区分出输入样本是来自于真实分布
是要区分出输入样本是来自于真实分布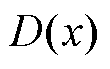 与最小化
与最小化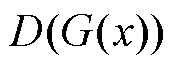 ,因此GAN的损失函数为
,因此GAN的损失函数为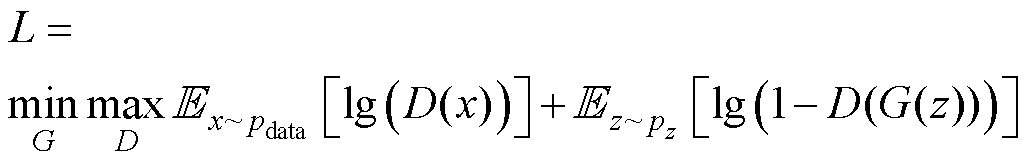 (12)
(12)
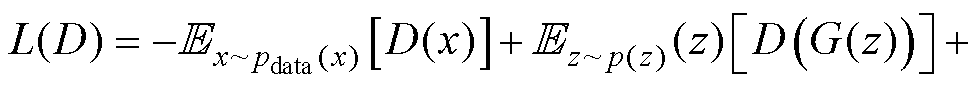
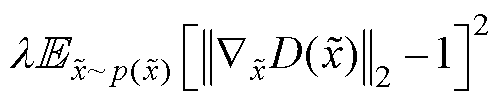 (13)
(13)
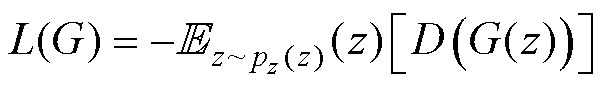 (14)
(14)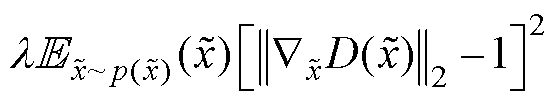 为梯度惩罚项,
为梯度惩罚项,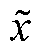 为输入数据和生成数据之间的插值项,可以描述为
为输入数据和生成数据之间的插值项,可以描述为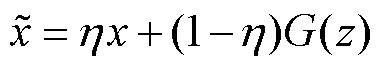 (15)
(15)
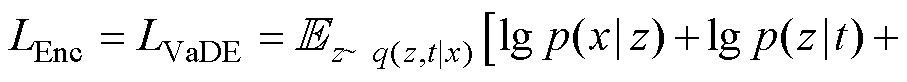
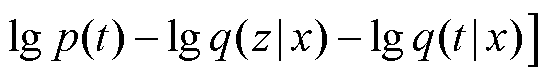 (16)
(16)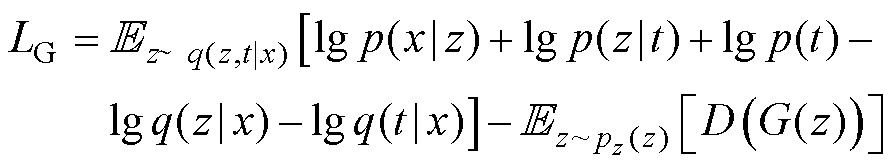 (17)
(17)
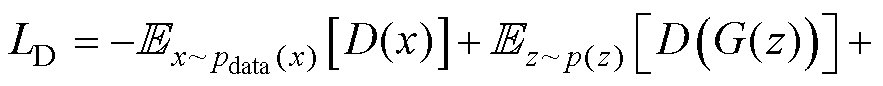
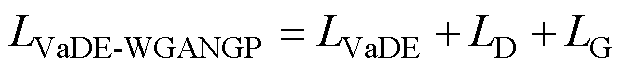 (19)
(19)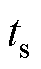 和结束时间
和结束时间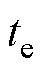 ,并利用线性插值将连续数据离散化为时间步长为a、维度为500的向量,即
,并利用线性插值将连续数据离散化为时间步长为a、维度为500的向量,即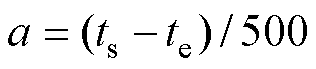 。最终输入数据的维度为9 636×500×3,30个电池样本在全寿命周期内共计覆盖9 636条老化数据;每个老化节点取3个基础外特性(放电电流、放电电压和放电容量曲线);每条特性曲线的500个采样点数据。图5a~图5c依次是从30个电池中提取的原始放电电流、放电容量和放电电压曲线。
。最终输入数据的维度为9 636×500×3,30个电池样本在全寿命周期内共计覆盖9 636条老化数据;每个老化节点取3个基础外特性(放电电流、放电电压和放电容量曲线);每条特性曲线的500个采样点数据。图5a~图5c依次是从30个电池中提取的原始放电电流、放电容量和放电电压曲线。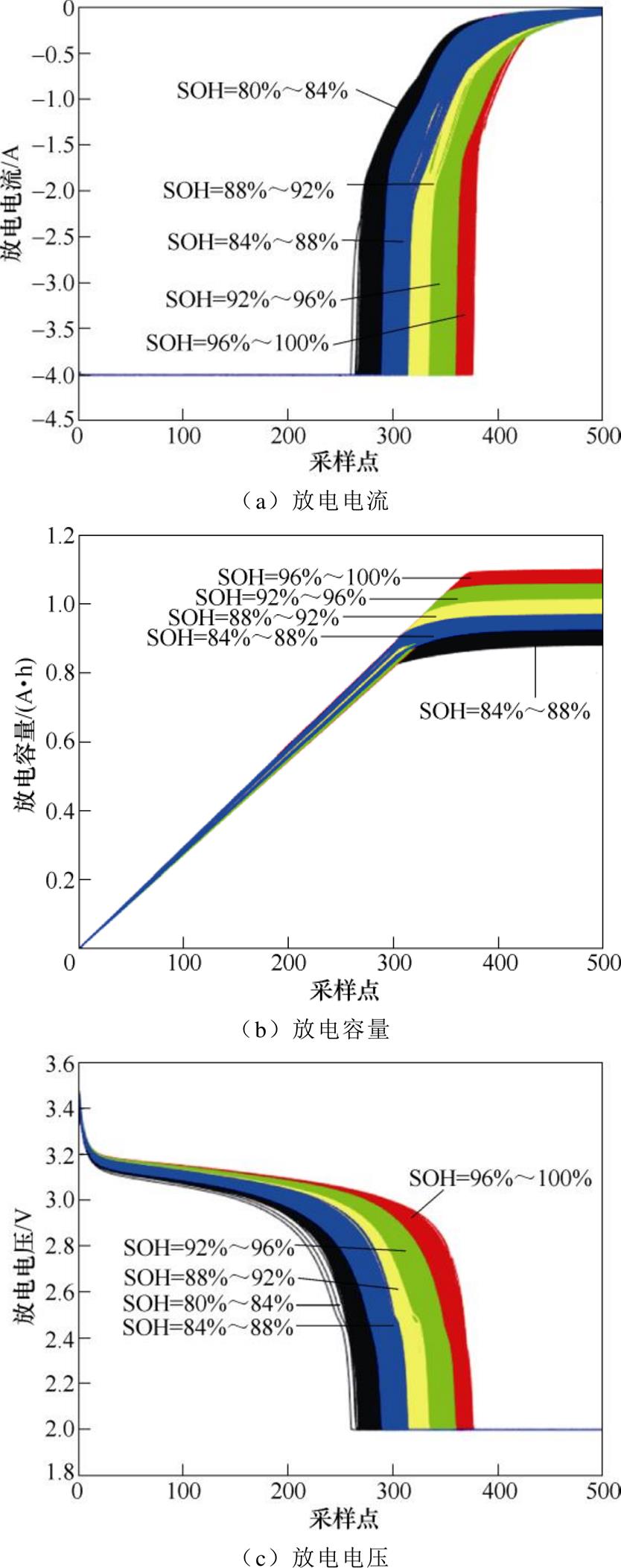
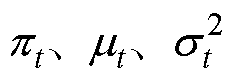 ,该参数集会通过梯度下降进行优化更新。
,该参数集会通过梯度下降进行优化更新。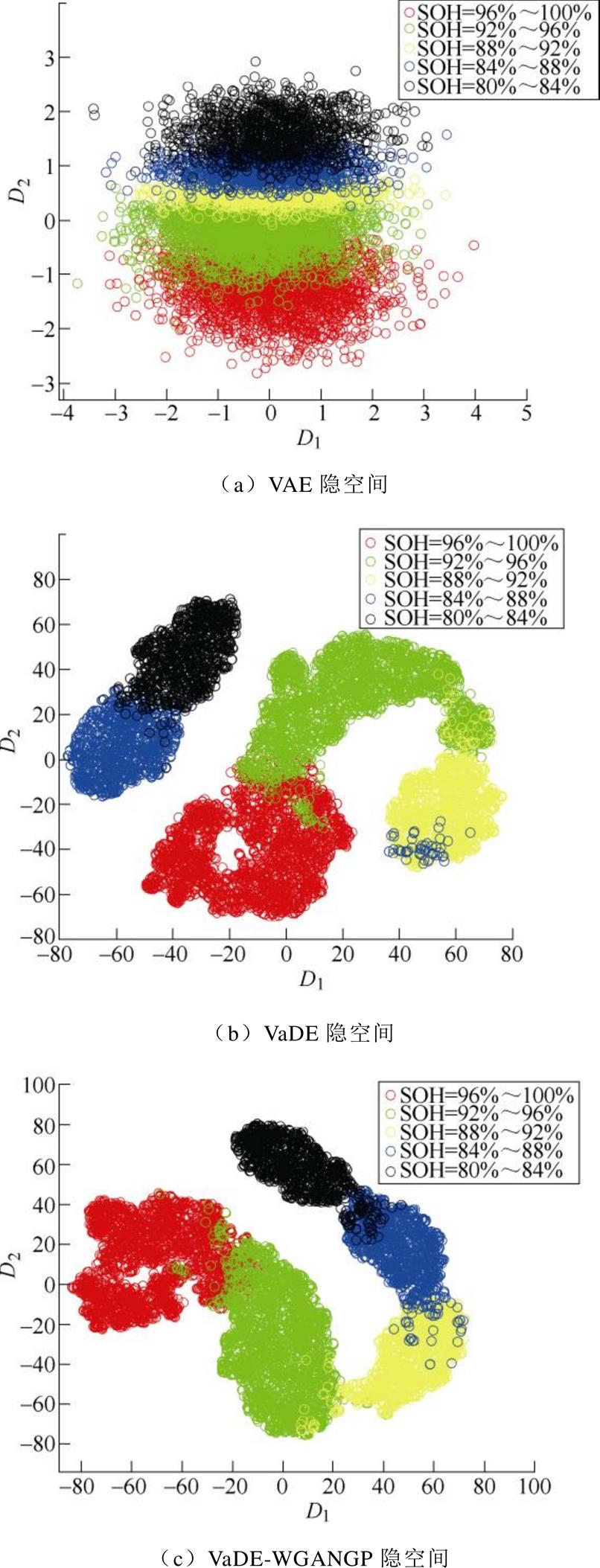
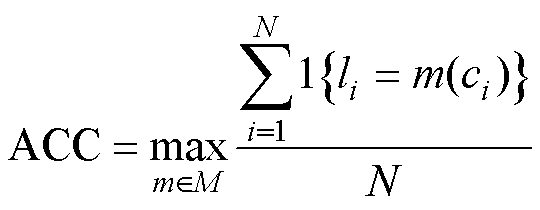 (20)
(20)
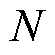 为输入数据总数量,
为输入数据总数量,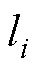 为真实标签,
为真实标签,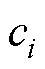 为数据所对应的GMM的具体分布的权重,
为数据所对应的GMM的具体分布的权重,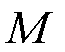 为电池老化数据标签和聚类分配之间所有可能的一对一集合。在此对比了三个模型的准确度,电池老化数据隐空间聚类准确度见表1。
为电池老化数据标签和聚类分配之间所有可能的一对一集合。在此对比了三个模型的准确度,电池老化数据隐空间聚类准确度见表1。