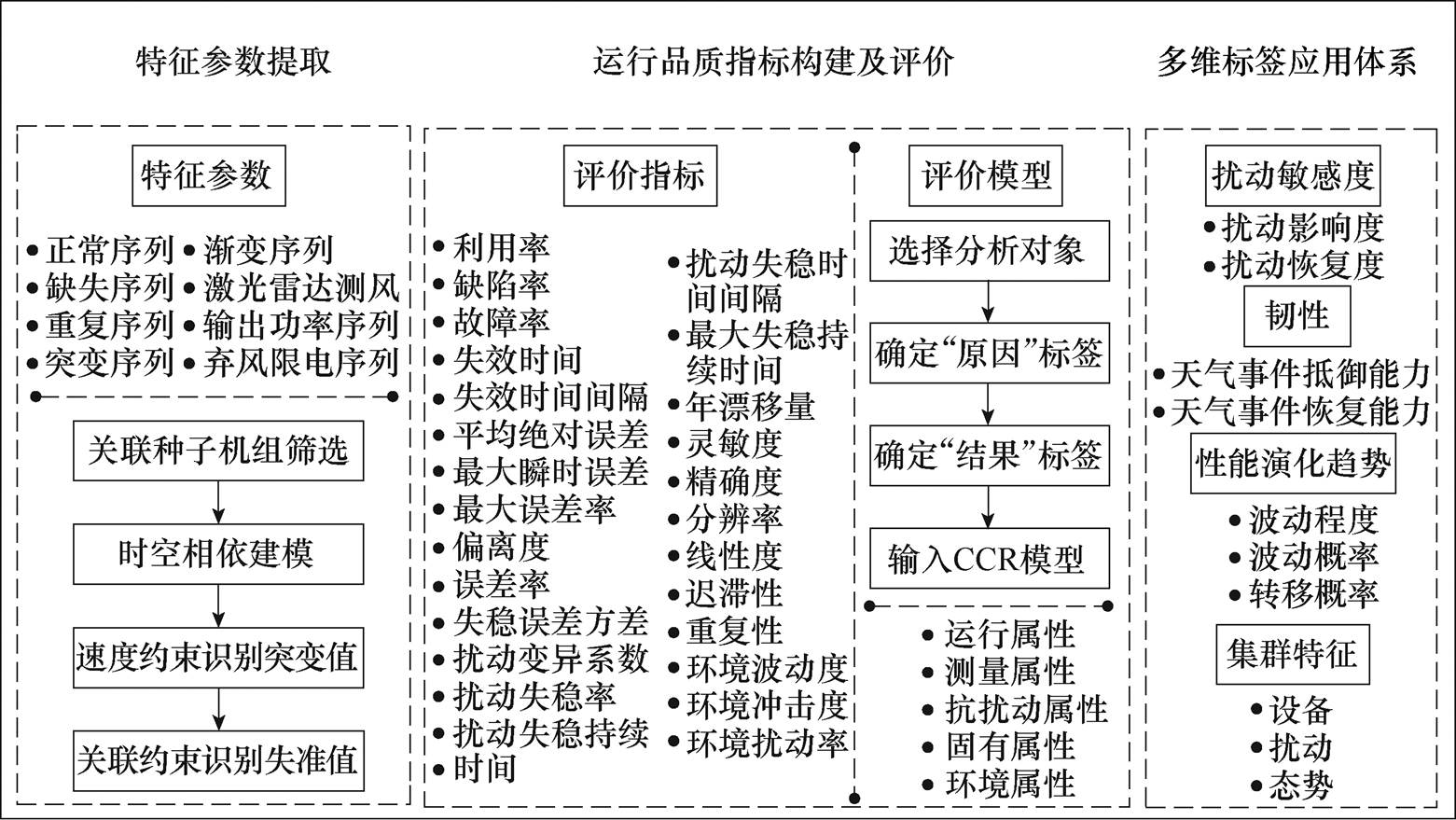
图1 风速传感器运行品质评价和应用体系
Fig.1 System of operation quality evaluation and applications for wind speed sensors of wind farms
摘要 风电场风速传感器运行的可靠性和稳定性是机组高效发电和安全运行的关键,精准识别风速传感器的失稳和失准等缺陷模式,客观地描述其运行品质对于风电场提寿增效意义重大。该文对风电场风速传感器运行品质评价展开研究,围绕运行、测量、抗扰动等维度,建立风速传感器运行品质标签架构、量化规则和评价模型,提出基于数据驱动的多维标签应用体系,挖掘风电场风速传感器的扰动敏感度、韧性、性能演化趋势、集群特征,为辨识设备的运行态势提供一套精细化数学建模方法。以某风电场运行数据为研究对象,对所提的运行品质评价体系及应用策略进行阐述,验证所提方法在风电场主动运检和精益化管理方面的工程应用价值。
关键词:风电场 风速传感器 运行数据 运行品质 评价体系
风电机组的输入风速数据主要靠裸露在机舱外部的风速传感器捕获,由于长期运行于复杂恶劣环境中,尤其是海上风电场,寒潮、强对流、雷暴等自然天气事件时有发生,风速传感器容易出现失准、失稳等缺陷模式[1],导致控制系统无风速输入或输入不准确的风速序列[2],引起机组误起停、误变桨等误动作,影响机组的发电效率和运行稳定性[3],严重时会造成风电场运行紊乱,乃至对电网产生冲击[4]。因此,准确描述、评价和辨识风速传感器的运行品质对于保障风电场可靠、稳定、高效运行尤为关键。
近年来,有关传感器运行性能评估问题已经成为国内外的研究热点,并取得了诸多成果,其主流方法大致可分为硬件冗余法和软件冗余法:硬件冗余法原理简单,在同一位置同时安装多台传感器,通过同点位多设备测量数据的比对完成设备性能的评估[5],该方案原理简单、准确、可靠,但成本高、工程可行性低[6]。软件冗余法又可分为模型驱动法和数据驱动法,模型驱动法需要构建精准的数学模型来描述传感器的运行行为。文献[7-8]提出了一套面向工业无线传感器网络可靠性的评价标签体系及计算方法。文献[9-10]提出了基于观测器的传感器运行状态评价模型。文献[11]提出了一种基于改进蒙特卡洛-递归方差约简的传感器运行可靠性评估模型,模型驱动法在评价稳定、静态的系统时具有较高的精度,但在分析高随机性、非线性系统时,难以构建统一、准确、可靠的数学模型来描述设备的运行行为;数据驱动法避免了复杂的数学建模过程,以大量的运行数据为基础,利用数据挖掘算法提取设备的异常模式,典型的方法包括神经网络算法[12]、深度学习算法[13]、统计算法[14]等,表现出较高的应用价值和发展前景。
从应用场景来看,现有的研究方法主要集中在传感器故障诊断,服务于机组的实时运行控制。风电机组风速传感器往往运行于复杂的环境中,传感器容易受到自然天气事件的影响而不可靠,当自然天气事件过后,设备又可能逐步恢复平稳运行,仅从故障诊断的角度难以充分提取传感器在运行周期内的运行品质(包括测量精度、运行稳定性、扰动敏感度、性能演化趋势等多维度)及其演化趋势,有必要对传感器的运行行为做精细化建模,分析其在运行周期内失稳、失准等缺陷模式,对于传感器的适应性分析、全寿命周期健康管理等意义重大。
基于此,本文对风速传感器缺陷模式的识别、描述和评价展开研究,提出一种风速传感器运行品质评价方法,表征风速传感器在运行、测量、抗扰动、环境等维度的属性,结合设备全寿命周期健康管理需求,开发多维标签应用体系,挖掘传感器的风险态势和运行态势,分析设备在自然天气事件影响下的扰动敏感度、韧性特征、性能演化趋势和集群特征,为风电场主动运检、精益化管理提供数字化、智能化解决方案。
本文以风速传感器全寿命周期健康管理为应用对象,提出了一套运行品质精细化建模表征方法,如图1所示,主要包括以下三个方面内容:①特征参数提取;②运行品质标签构建和评价;③多维标签应用体系开发,挖掘传感器的扰动敏感度、韧性、性能演化趋势、集群特征等属性。

图1 风速传感器运行品质评价和应用体系
Fig.1 System of operation quality evaluation and applications for wind speed sensors of wind farms
特征参数指原始风速测量数据的状态特征标签,即原始数据的正常/异常状态以及异常类别,实质上是对原始测风序列开展异常识别和分类。
根据数据的变化趋势,异常风速序列可分为由电磁扰动失稳产生的突变型异常数据和由气象环境扰动失稳产生的渐近型异常序列。突变型异常序列分布离散,反映设备的抗电磁扰动属性,违背风速在时间维度的自相关性,本文采用“速度”约束进行识别[15],通过计算风速的变化速度,将变化速度超出阈值的数据诊断为突变型异常数据。
渐近型异常序列分布连续,违背风速在传播路径上的空间相依性特征[16-17],本文采用一种基于空间相依架构的异常风速序列识别方法[4],通过多机组风速关联比对的方式进行滑动检测。检测流程包括:①选取待检的风速序列为目标序列;②基于风向区筛选关联种子机组构建互诊群落;③计算风速序列间的空间相依性关系;④设置时间窗和关联阈值,通过滑动关联比对的方式识别渐近型异常序列。
缺失序列反映传感器或通信网络出现缺陷,可通过机组数据采集和控制系统确定;实际风速数据指风电场风速的实际分布情况,用于评价风速传感器的测量精度,本文采用虚拟风速传感器技术[1]和激光雷达技术完成实际风速数据的感知。
为表征风速传感器的运行品质,需要提取特征参数的统计特征,本文分别从运行属性、测量属性、抗扰动属性、固有属性和环境属性构建标签体系,如图2所示,分析风速传感器缺陷模式出现的频率、持续时间、时间间隔等特征。
运行属性指风速传感器的有效时间间隔,该文采用计划时间利用率、失效时间、失效时间间隔等标签描述。测量属性指传感器测量数据的精度,文章选择平均绝对误差、误差率、最大瞬时误差、等标签描述。抗扰动属性表示风速传感器抵御外界扰动能力的属性,本文构建了含扰动失稳率、扰动失稳持续时间、扰动变异系数、抗扰动系数等标签体系。根据扰动源的不同,又可分为抗气象扰动属性和抗电磁扰动属性。气象环境扰动失稳表现为测量风速数据持续偏离实际值,量化标签基于渐近型异常风速序列构建;电磁扰动失稳表现为测量风速数据发生非趋势性突变,量化标签基于突变值和死值进行计算。固有属性指风速传感器的输入-输出关系特性,即传感器的静态属性,包括年漂移量、灵敏度、精确度等。环境属性指风速传感器运行环境的分布特征,如环境波动度、环境冲击度、环境扰动次数。考虑到文章的篇幅,标签的计算方法不再赘述,计算公式见附表1~附表5。
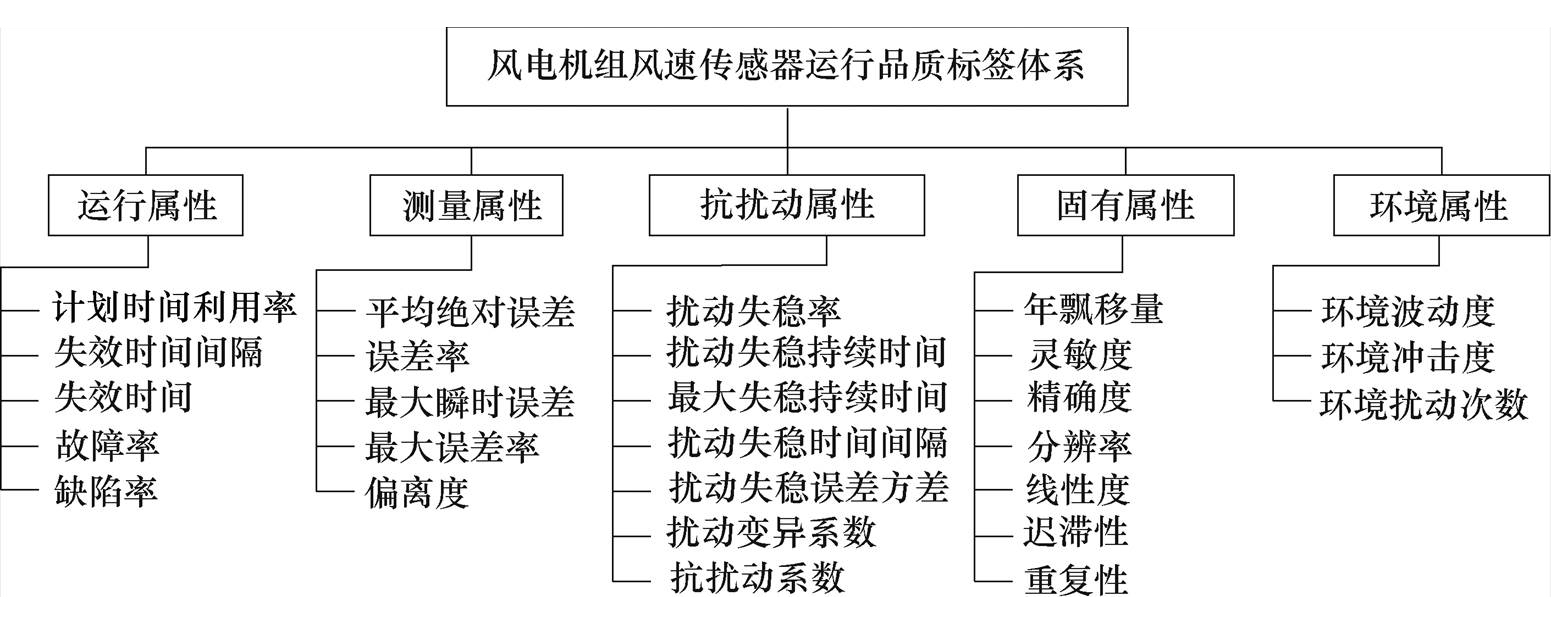
图2 风速传感器运行品质标签体系
Fig.2 The indicators system of wind speed sensor operation quality
风速传感器的运行品质与设备的固有属性和所运行的环境参数密切相关,仅单一地对大量的统计标签进行分析难以全面、客观地认识传感器的运行品质差异和性能短板。因此,该文引入数据包络分析(Data Envelope Analysis, DEA)的“相对有效”思想到风速传感器运行品质评价模型中,深度挖掘标签间的内在逻辑关系和不同设备间运行品质的外在相对关系,实现对多标签的综合排序和统一描述,该模型在提升评价结果的准确性、客观性等方面有着不可低估的优越性,已成熟运用到配电网规划、资源配置等多个领域[18]。
DEA是以多台风速传感器构成评价总体,以“原因标签”和“结果标签”的权重为变量,“结果标签”与“原因标签”比率最大化为目标函数构建评价模型,计算出所有风速传感器运行品质的有效运行沿面,从而确定某台风速传感器的运行品质相对于其他所有参与评价的风速传感器是否DEA有效。其中“原因标签”表示风速传感器性能波动的影响因素,包括:固有属性、环境属性等;“结果标签”表示风速传感器的输出特性,例如:运行属性、测量属性、抗扰动属性。
假设有h台风速传感器构成评价集,每台风速传感器有s种“原因标签”和r种“结果标签”。第j台风速传感器的原因标签和结果标签值分别为
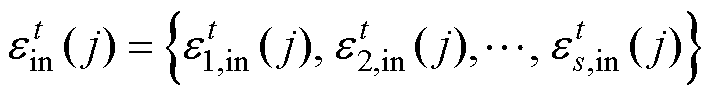
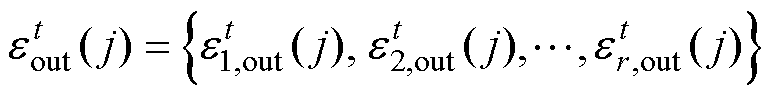
设vi为第i种“原因标签”的权系数变量,fr为第r种“结果标签”的权系数变量,定义“结果标签”与“原因标签”之比为风速传感器DEA评价值,以第j0台风速传感器在第t运行周期的评价结果为求取目标,所有风速传感器的运行品质为约束,构建最优CCR模型为
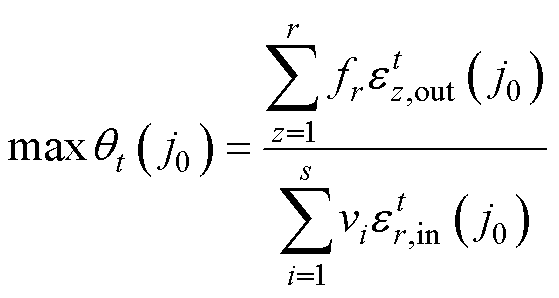 (1)
(1)
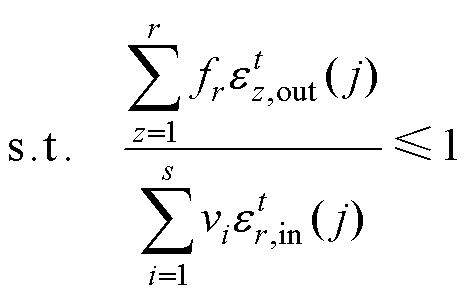 (2)
(2)
利用该模型评价某台风速传感器是否DEA有效是相对于其他所有风速传感器而言,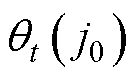 ∈[0,1],其值越大,表明该风速传感器的运行品质越优。
∈[0,1],其值越大,表明该风速传感器的运行品质越优。
运行品质标签从不同维度直观地描述传感器的运行特性,是一系列具有物理意义的指标参数。在实际工程中,考虑到标签数量众多、需求多样化,有必要结合业务需求开发面向具体场景的多维标签应用体系,进一步提取设备运行的物理规律和隐藏的状态信息,服务于风电场提寿增效目标。本文综合考虑风电场运行、维护工作的需求,以风速传感器全寿命周期健康管理为目标,构建多维标签综合应用体系,包括:面向事故预防的扰动敏感度计算模型、面向事故修复的韧性评估模型、面向状态辨识的性能演化趋势分析模型和面向场站运营的传感器集群特性提取模型。
风电场的运行环境十分恶劣[13],由于自然天气事件引发的风电机组停机事件屡见不鲜。为制定科学、合理的灾前应急预案,研究风速传感器应对不同类别扰动的敏感度尤为关键。风速传感器对扰动的敏感度指设备在遭遇外界扰动时,设备的运行品质发生变化的程度,本文选取运行、测量属性的模型标签和沙尘、寒潮、强降雨、强对流四类典型的扰动场景,构建风速传感器的扰动敏感度模型。
2.1.1 扰动影响度分析
为了描述扰动对传感器运行品质的影响度,定义扰动i对传感器j的影响度标签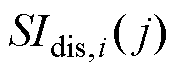 ,以及传感器j受到的复合扰动影响度标签
,以及传感器j受到的复合扰动影响度标签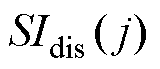 分别为
分别为
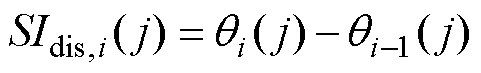 (3)
(3)
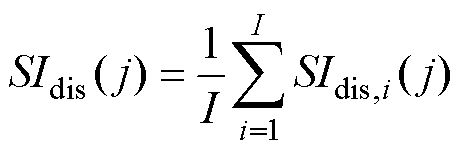 (4)
(4)
式中,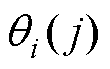 为传感器j在扰动i期间的评价值,
为传感器j在扰动i期间的评价值,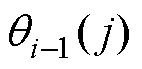 为传感器j在扰动i前的评价值,可通过式(1)和式(2)计算;I为扰动出现次数。
为传感器j在扰动i前的评价值,可通过式(1)和式(2)计算;I为扰动出现次数。
2.1.2 扰动恢复度分析
为描述传感器在经历扰动后运行品质的恢复情况,定义传感器j在扰动i后的性能变化量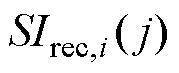 ,以及传感器j在多次扰动后的平均变化量
,以及传感器j在多次扰动后的平均变化量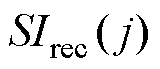 分别为
分别为
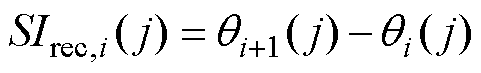 (5)
(5)
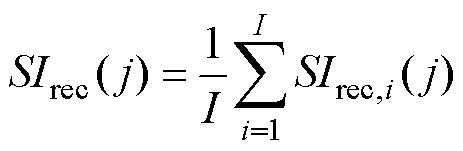 (6)
(6)
式中,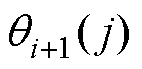 为传感器j在扰动i后的品质评价值。
为传感器j在扰动i后的品质评价值。
2.1.3 扰动敏感度分析
定义传感器j在运行周期内的扰动敏感度标签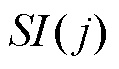 为扰动恢复度与扰动影响度的比值,有
为扰动恢复度与扰动影响度的比值,有
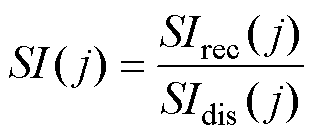 (7)
(7)
敏感度是对运行品质评价结果在时间维度变化特征的进一步分析,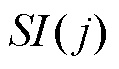 越接近1,表示传感器对扰动的敏感度越小,传感器抵御扰动的能力越强,运行品质越优,反之,则越差。高敏感度表示传感器的运行品质容易受到外界扰动的影响而不稳定,在应用中,可结合气象预测数据和敏感性分析结果,针对敏感型传感器或高敏感事件,采取必要的防范措施,最小化外界扰动对机组运行产生的不良影响。
越接近1,表示传感器对扰动的敏感度越小,传感器抵御扰动的能力越强,运行品质越优,反之,则越差。高敏感度表示传感器的运行品质容易受到外界扰动的影响而不稳定,在应用中,可结合气象预测数据和敏感性分析结果,针对敏感型传感器或高敏感事件,采取必要的防范措施,最小化外界扰动对机组运行产生的不良影响。
近年来,由于极端自然天气事件(例如:台风、地震、海啸等)导致的风电场连锁故障时有发生,暴露了风电场对于低概率、高风险自然天气事件准备的不足,对风电场的“韧性”评价和增强已成为新的研究领域[19]。本文基于风速传感器运行品质评价结果,通过分析极端自然天气事件发展过程传感器运行品质的波动特征,来表征风速传感器应对极端自然天气事件的“韧性”。
图3描述了风速传感器在极端自然天气事件发生过程中的运行品质曲线变化趋势,包括事件前、事件期间和事件后,为量化分析传感器的事故穿越能力,本文构建韧性指数、恢复速度和恢复能力标签来描述传感器应对极端自然天气事件的韧性。
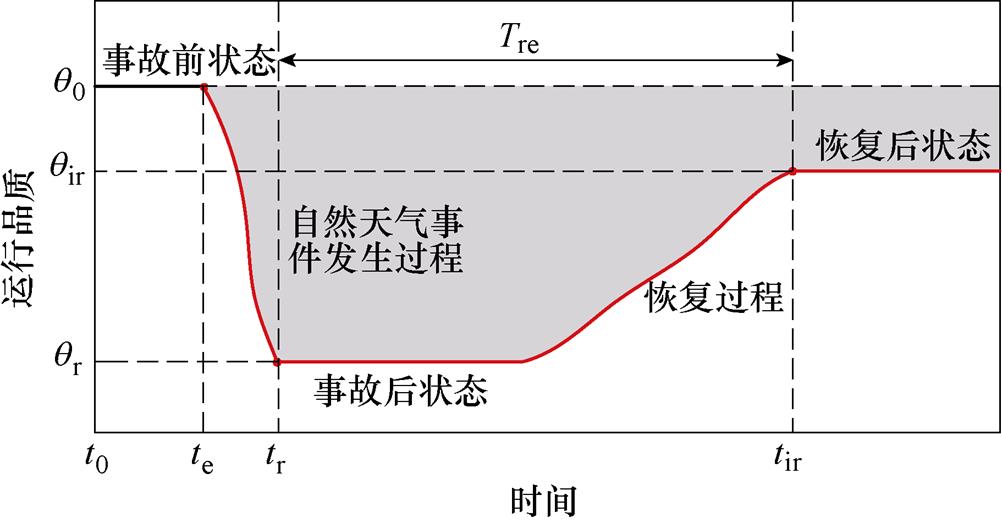
图3 风速传感器对极端自然天气事件的韧性曲线
Fig.3 Resilience curve of wind speed sensor against extreme natural weather event
2.2.1 韧性指数
定义风速传感器运行品质的波动量与时间积分比上总面积为设备对自然天气事件的韧性指数R,有
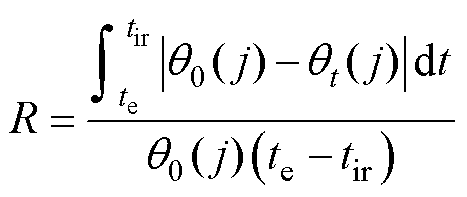 (8)
(8)
式中,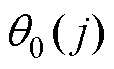 为自然天气事件前传感器运行品质评价值;
为自然天气事件前传感器运行品质评价值;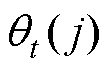 为自然天气事件期间传感器运行品质评价值,通过式(1)和式(2)计算;te为自然天气事件开始时间;tir为设备恢复平稳运行的时间。R越小,表示传感器对自然天气事件的韧性越强。
为自然天气事件期间传感器运行品质评价值,通过式(1)和式(2)计算;te为自然天气事件开始时间;tir为设备恢复平稳运行的时间。R越小,表示传感器对自然天气事件的韧性越强。
2.2.2 恢复速度
定义自然天气事件结束到风速传感器恢复平稳运行的时长来表征设备的灾后恢复速度Tre为
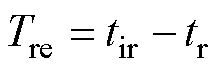 (9)
(9)
式中,tr为自然天气事件结束时间。
2.2.3 恢复能力
定义自然天气事件结束后传感器恢复平稳运行的运行品质评价值与灾害前运行品质评价值之比为设备对自然天气事件的恢复能力,表达式为
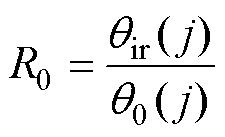 (10)
(10)
式中,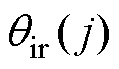 为传感器在自然天气事件后的运行品质评价值。
为传感器在自然天气事件后的运行品质评价值。
韧性模型是对传感器在遭遇极端自然天气事件时运行品质的波动特征做精细化建模研究,描述设备抵御自然天气事件的能力,可应用于灾后场站缺陷排查、巡检、维护等工作。
如前所述,传感器会由于外界扰动而出现失稳或失准运行,为辨识传感器的缺陷模式,提出了一种基于形态和趋势特征的运行品质演化特性建模方法,表征传感器在一段连续运行周期内或遭遇多次自然天气事件后设备运行品质的变化趋势,以及传感器出现缺陷的类别和概率,为设备的剩余寿命评估、态势感知等提供参考。
统计学上采用变点描述一段序列或随机过程发生状态波动的时刻,选取传感器在一段连续周期内的运行品质曲线为研究对象,图4展示了传感器在失准和失稳状态下的运行品质分布情况,在不同缺陷模式下,运行品质曲线的形态特征和趋势特征明显不同。为描述两者的差异,本文提出一种基于变点算法的运行品质模态特征提取方法。
模态是描述某一段序列或随机过程波动趋势的有效工具,已成功地应用于电能信号特征提取、故障特征提取等多个领域[20]。传感器模态特征提取主要包含以下四个关键技术:①将运行数据在时序上分割为等时间间隔的局部子序列,计算子序列的运行品质标签,构建传感器运行品质曲线;②采用基于形态的变点检测算法提取传感器运行品质曲线发生明显波动的时刻,并以变点为分割点,将运行品质曲线在时序上分段;③以均值作为每段曲线的特征点,有序连接特征点,构成模态特征曲线;④分析传感器在失准、失稳状态下运行品质的模态特征和转移场景,计算波动度、波动概率、波动转移概率,描述传感器运行品质的演化特征。表1展示了风速传感器在失准和失稳缺陷模式下运行品质曲线的变点模态特征和转移场景,表中的点为传感器的运行品质特征点。
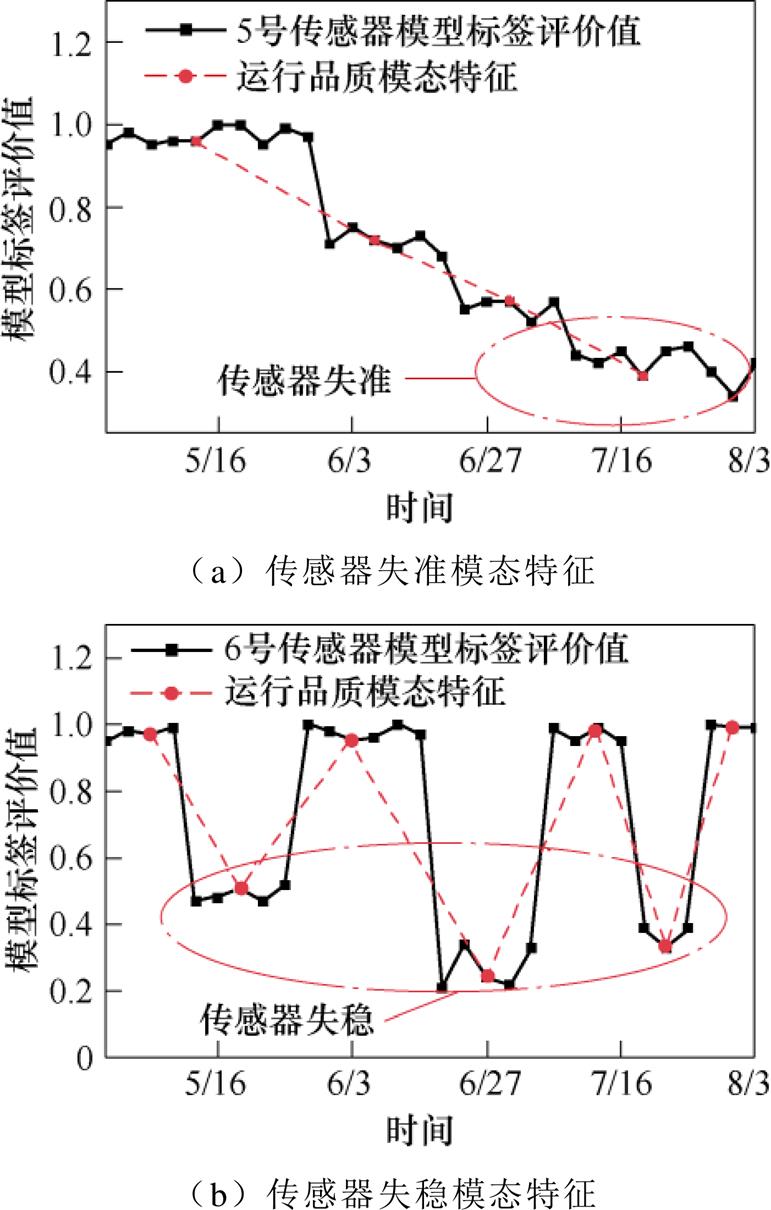
图4 风速传感器在缺陷模式下运行品质模态特征
Fig.4 Operating quality module characteristics of wind speed sensors under defective modes
表1 风速传感器典型缺陷下运行品质模态转移场景
Tab.1 Module features and transfer scenarios of wind speed sensor operating quality under typical defects
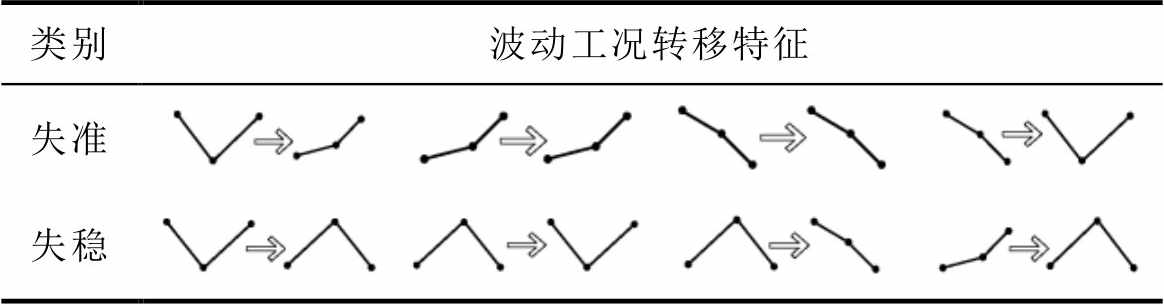
类别波动工况转移特征 失准 失稳
为描述传感器运行品质的演化特性,本文从运行品质波动幅度I、波动速度F、波动概率FP和波动场景转移概率FPT构建标签体系,计算公式为
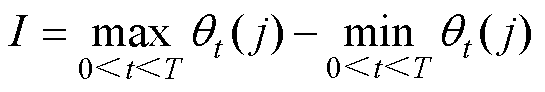 (11)
(11)
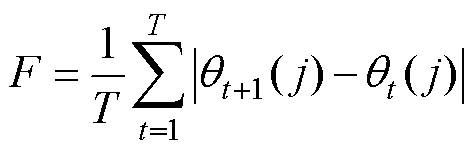 (12)
(12)
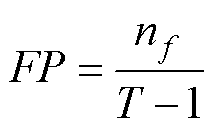 (13)
(13)
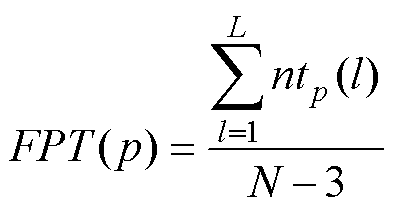 (14)
(14)
式中,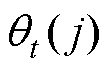 为传感器j在第t段时间内的运行品质评价值;nf为传感器评价值在运行周期内波动出现的次数,若相邻特征点的波动量超出整体分布的四分位内限,则记为一次波动;N为变点数目,
为传感器j在第t段时间内的运行品质评价值;nf为传感器评价值在运行周期内波动出现的次数,若相邻特征点的波动量超出整体分布的四分位内限,则记为一次波动;N为变点数目,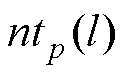 为表1中第p类缺陷模式下第l类波动转移场景出现的次数;FPT(1)为传感器失准的概率;FPT(2)为传感器失稳的概率;L为转移场景数目,本文中,L=4。
为表1中第p类缺陷模式下第l类波动转移场景出现的次数;FPT(1)为传感器失准的概率;FPT(2)为传感器失稳的概率;L为转移场景数目,本文中,L=4。
演化特性模型通过分析运行品质曲线的波动特征来描述设备的缺陷模式,在失准模式下,传感器的运行品质处于持续下降的态势,寿命衰减严重,而在失稳模式下,传感器的运行品质容易受到外界扰动的影响而反复波动,在扰动后又能逐渐恢复稳定运行。尽管传感器失准、失稳都伴随着性能的下降,但两种模式的运行态势明显不同,对应的检修策略也不同,分析传感器的运行品质演化特征可为维护方案的制定提供参考。
风电场风速感知系统往往由不同厂商、不同型号的风速传感器集群组成,为分析风速传感器对运行环境的适应性、提取传感器的运行场景,有必要对风电场风速传感器的集群特征进行精细化建模。本文采用一种基于动态层次k-means的聚类算法[21]提取风电场风速传感器集群的运行品质特征和类别,聚类的特征参数为灵敏度、精确度、利用率、缺陷率、平均绝对误差率、偏离度、环境波动度、环境冲击度、扰动失稳率,扰动变异系数等。
针对不同类别的传感器集群,本文构建了涵盖“设备”“扰动”和“态势”的特征标签体系,描述设备的运行品质分布情况。“设备”标签描述传感器群落的运行状态分布情况,例如:运行时长分布、缺陷分布、检修分布等;“扰动”标签描述传感器的环境特征,例如:扰动活跃度、扰动对缺陷的触发率;“态势”指传感器缺陷模式的演化态势,例如:缺陷传播速度、缺陷传播飙升度、缺陷模式传播的倾向性比率,传感器集群运行品质标签及计算方法见表2。
本文实验数据来源于某风电场风速传感器集群运行数据,该风电场地势平坦,季风现象明显,全年冬季季风和夏季季风持续时间往往超过7个月,按照地形分布和连接关系,该风电场可分为3串,机组拓扑结构如图5所示,图中相同颜色的机组表示位于同一断面,同一断面内的机组风资源特征相近,该风电场风速传感器均为同一型号,为保证数据集的完备性,本文分别选取位于不同断面内的9台风速传感器作为研究对象,依次标号为1~9,其中,2号、3号、4号机组为一个断面;1号、7号、8号机组为一个断面;5号、6号、9号机组为一个断面,如图5所示,所选传感器分布于该风电场的不同位置,基本涵盖了该风电场的各类运行环境,具有一定的代表性,基于2016年11月1日—2017年10月31日1年的运行数据,分析风速传感器在期间的运行品质,验证所提方法的有效性和应用价值。
表2 风速传感器集群特征标签体系及计算方法
Tab.2 Operational quality labelings and their calculation methods for wind speed sensors community

类别标签计算方法 设备平均运行时长传感器集群累积运行时长与设备数量比值 运行时长标准差传感器集群累积运行时间标准差 设备缺陷率缺陷持续时间数与总运行时间的比率 缺陷持续性传感器集群缺陷持续时长与缺陷次数比值 缺陷分布标准差传感器集群缺陷平均持续时间标准差 平均检修次数传感器集群累积检修次数与设备数量比值 检修次数标准差传感器集群平均检修次数的标 准差 扰动扰动活跃度扰动时长占总运行时长的比率 扰动对设备缺陷的触发率传感器缺陷次数与环境扰动出现次数比值 态势缺陷传播速度缺陷出现次数在单位时间间隔内的新增量与时间间隔之比,本文以年为单位计 缺陷传播飙升度缺陷出现次数在第n个时间间隔内的新增量和在前一个时间间隔内的新增量之差与时间间隔之比,本文以年为单位计 缺陷模式传播的倾向性比率累积出现缺陷的时间窗与时间窗总数的比率,本文以3天为一个评价时间窗,一年122个滑动时间窗 平均缺陷出现次数/ (次/年)累计出现的缺陷次数与传感器数目之比
3.2.1 特征参数挖掘
异常数据的识别和分类采用“速度-关联”约束的组合方法,其中,关联比对的系数阈值设置为0.6,数据变化速度约束的正常区间设置为[0.01, 3],原始测量数据异常识别和分类结果见表3。分析不同类别异常数据的分布发现,由于气象扰动失稳产生的异常数据数量最多,占比达到90%,电磁扰动失稳出现的次数最多,异常次数占比达到58%。
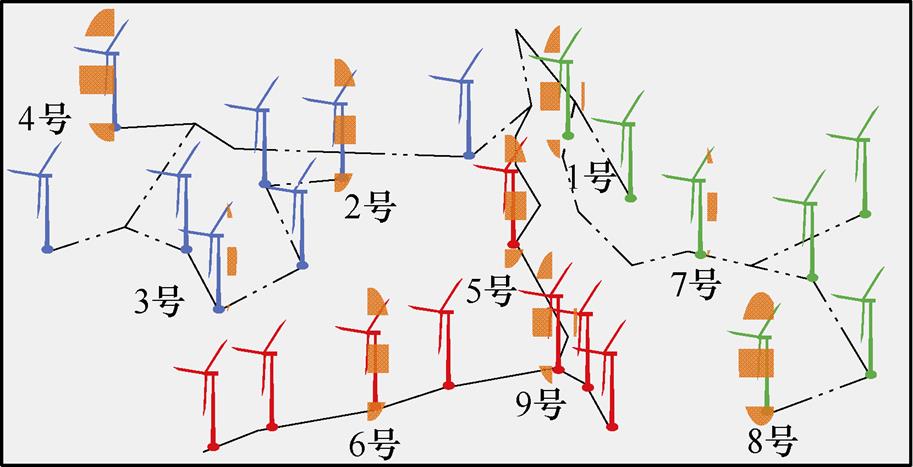
图5 风电场风电机组拓扑关系
Fig.5 Topology of the studied wind turbines
表3 风速传感器原始测量数据异常识别和分类结果
Tab.3 Anomaly detection and classification results for the measured wind speed data by wind speed sensors
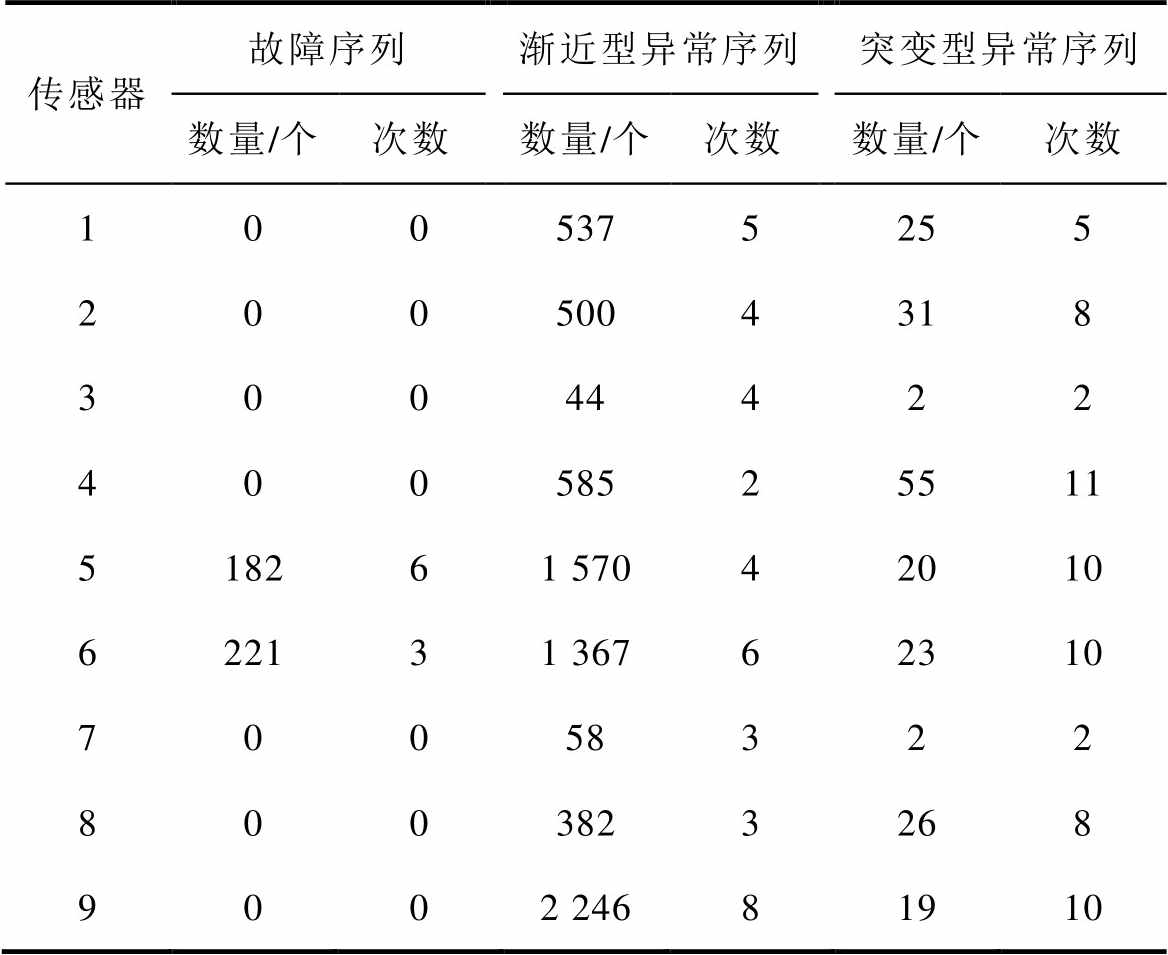
传感器故障序列渐近型异常序列突变型异常序列 数量/个次数数量/个次数数量/个次数 1005375255 2005004318 30044422 40058525511 518261 57042010 622131 36762310 70058322 8003823268 9002 24681910
3.2.2 运行品质多维标签计算及分析
基于以上对测量数据的异常识别和分类结果,参照附表1~附表5,可计算运行属性、测量属性和抗扰动属性标签,计算结果如图6所示。
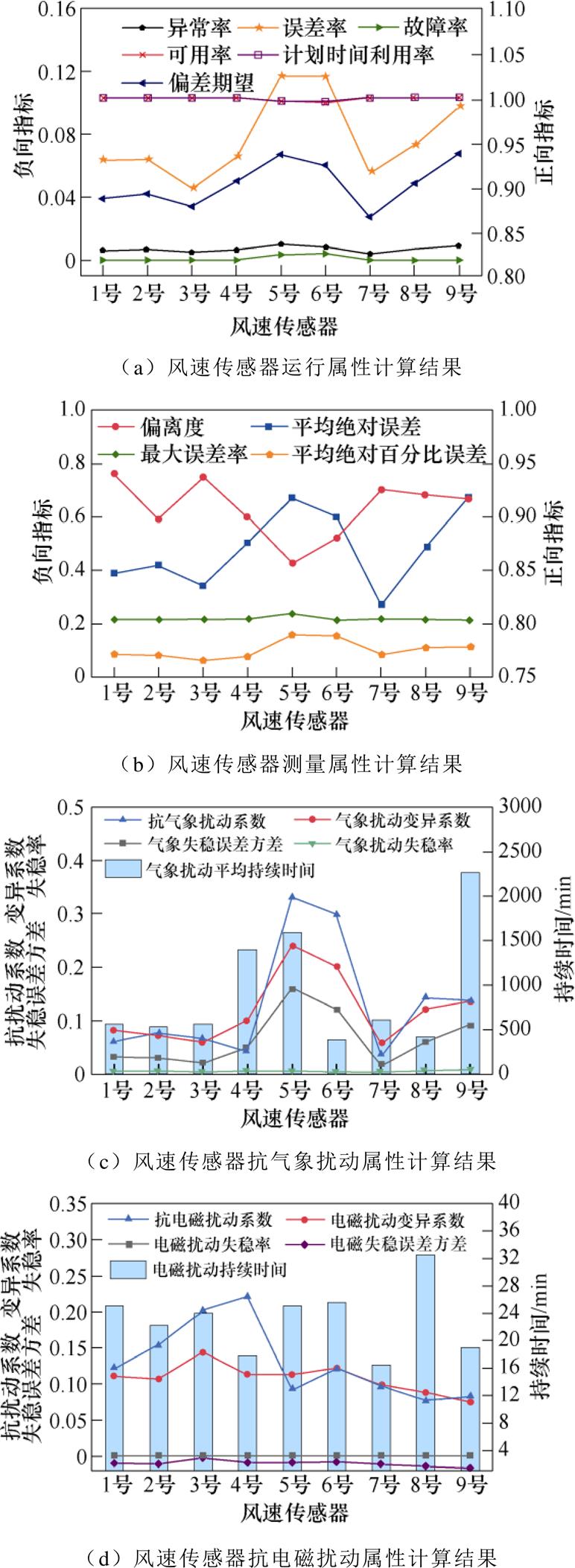
图6 风速传感器运行品质标签计算结果
Fig.6 Evaluation results for wind speed sensors
总体来说,9台传感器的运行品质在不同维度属性存在不同程度的波动:3号和7号机组传感器的运行品质在各维度均十分优异;4号、5号、6号和9号机组传感器的误差率、异常率、抗扰动系数、扰动持续时间等标签值不太理想,表明设备的测量、抗扰动属性存在一定程度的退化。
3.2.3 运行品质综合评价及分析
为融合多维度、多准则标签,本文构建了DEA评价模型,完成对传感器运行品质的综合评价。首先对统计标签进行标准化,划分为“原因标签”和“结果标签”,并输入DEA的CCR模型中,计算9台传感器的DEA模型评价值,如图7所示。
从图7可以看到,3号、7号机组风速传感器的DEA评价结果处于0.95以上,表明设备的各维度属性均处于理想状态;1号、2号、4号和8号机组传感器的运行品质存在不同程度的波动,其中,1号机组传感器的测量属性偏低,为0.85,2号和4号机组传感器的抗电磁扰动属性相对较差,分别为0.87和0.84,8号机组传感器的抗气象扰动属性衰退较为严重,为0.85;5号、6号和9号机组传感器的测量属性和抗气象扰动属性均存在一定的衰退。
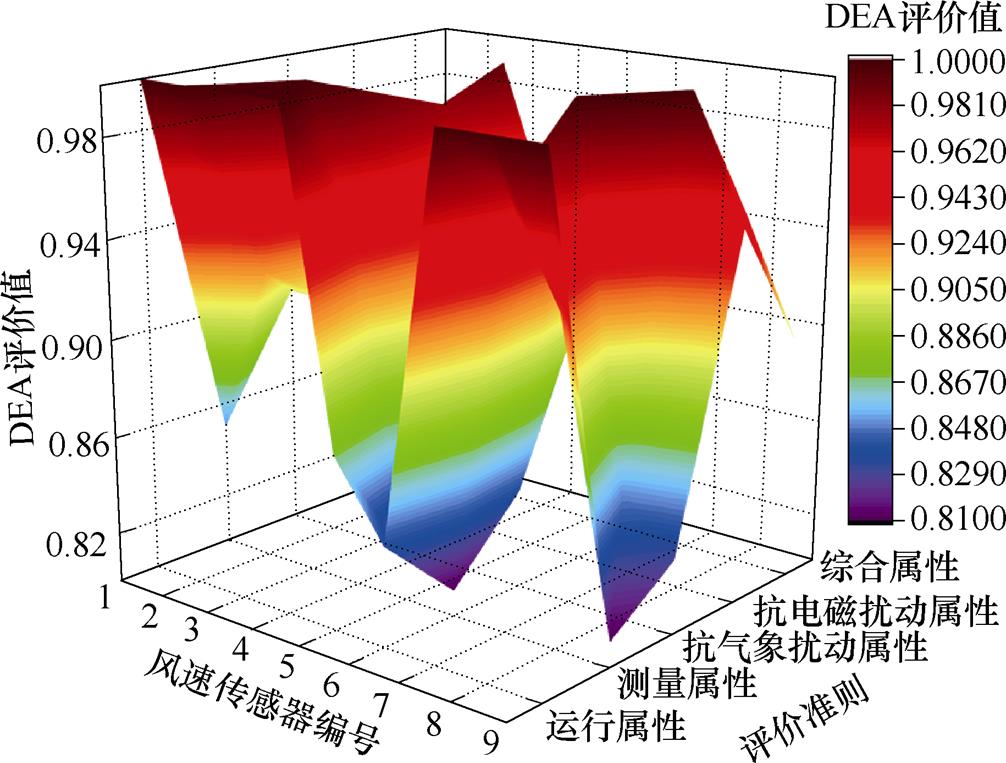
图7 风速传感器运行品质DEA模型评价结果
Fig.7 DEA evaluation result for wind speed sensors
图8展示了所选传感器运行品质在相邻周期内的滚动评价结果(以月为单位进行滚动评价),大多数传感器(1、2、3、4、7、8)的运行品质评价结果介于0.9~1之间,表现为可靠、稳定;5号、6号和9号机组传感器的运行品质表现为不可靠,5号机组传感器运行品质处于持续下滑的趋势,6号机组传感器运行品质反复波动,9号机组传感器的运行品质受季节因素影响较为明显,在冬季的运行品质处于较低水平,春季又能逐步恢复可靠运行。
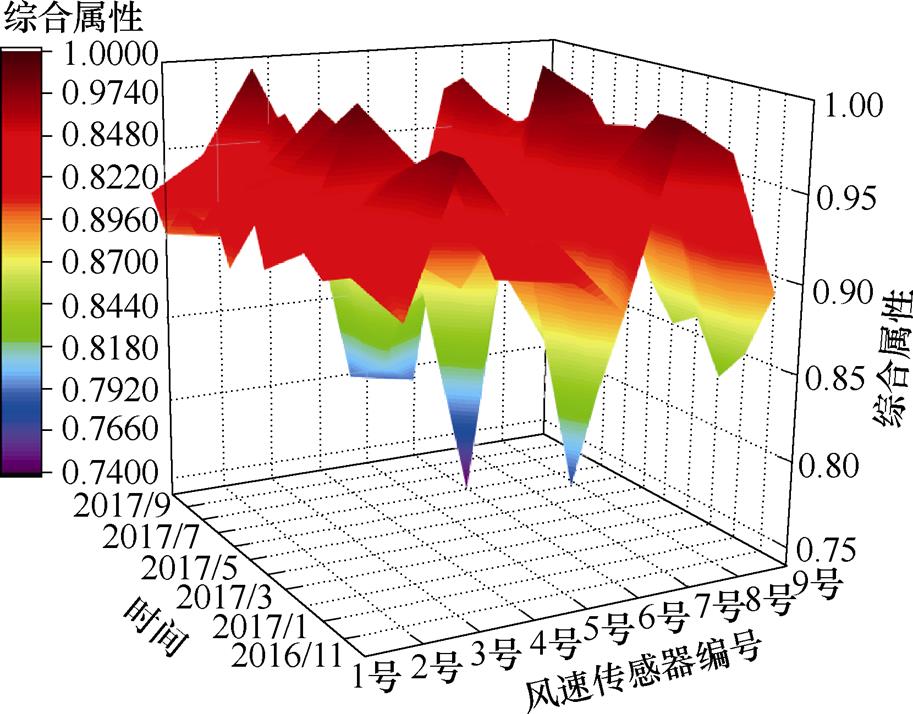
图8 风速传感器运行品质滚动评价结果
Fig.8 Performance rolling evaluations of sensors
针对不可靠的传感器,有必要探究缺陷模式产生的原因、分布情况、演化趋势等特征,为全寿命周期管理提供指导。本算例进一步分析扰动敏感度、韧性、演化趋势和集群特征标签及其应用策略。
3.3.1 扰动敏感度分析
查阅气象数据可知,该风电场在2017年1月7日—2017年1月8日出现了寒潮天气,降雪量达6.7 mm,坝上最低气温为-25℃。本文以此次寒潮天气为例,研究其对风速传感器运行品质的影响,选取寒潮前(1月5日—1月6日)、寒潮期(1月7日—1月8日)和寒潮后(1月9日—1月10日)的传感器运行数据为分析对象,计算传感器受寒潮天气的扰动影响度、扰动恢复度和扰动敏感度,计算结果如图9所示。
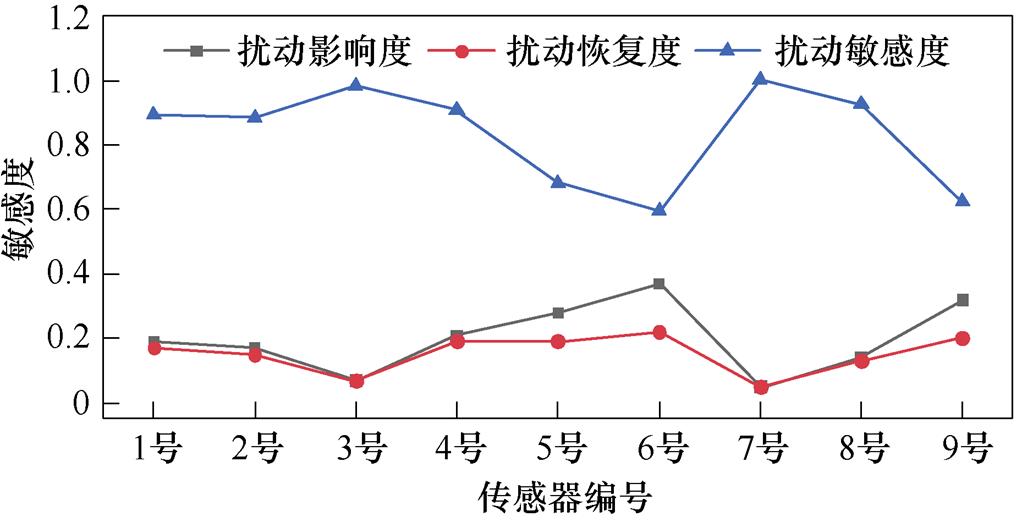
图9 风速传感器对寒潮扰动的敏感度
Fig.9 Sensitivity of sensors to cold wave
从图9可以看到,5号、6号和9号机组传感器对寒潮的敏感度较强,表现为扰动敏感型,传感器的抗扰动能力和扰动恢复能力均较差,设备敏感率约为33.3%;1号、2号、4号和8号机组的传感器虽然也会受到扰动的影响,但设备在扰动后能够恢复平稳运行,表现为不敏感型;3号和7号机组传感器的抗扰动能力和扰动恢复能力均较优,表现为免疫型。
为分析不同类别扰动对风速传感器运行品质的影响,本文以寒潮、沙尘、降雨和强对流天气为典型场景,计算传感器的复合扰动敏感度标签,如图10所示,可以看到,在所研究的周期内,强对流和寒潮天气对传感器的运行品质影响较为明显。
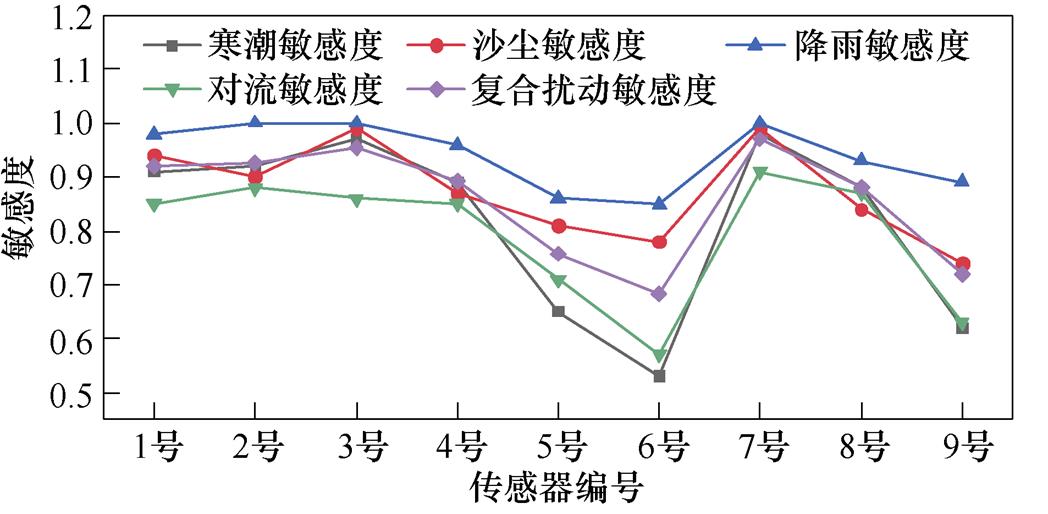
图10 风速传感器对不同类别扰动的敏感度标签
Fig.10 Sensitivity of sensor to different disturbances
在实际工程中,敏感度模型能够用来描述和评价传感器的运行品质随扰动的变化情况,可结合气象预报数据,加大对高敏感度自然天气事件的防范、加强对高敏感度的传感器的监测,从而制定科学、合理的运检策略,降低扰动产生的不利影响。
3.3.2 风速传感器对自然天气事件的韧性分析
查阅气象数据可知,所研究风电场在2017年8月2日—8月4日期间出现了一次台风事件,局部地区阵风风力达10级以上,降雨量大于100 mm,伴有雷电、强对流等天气。选取台风前10天和后10天风速传感器的运行数据为研究对象,计算设备对台风灾害天气的韧性标签,计算结果如图11 所示。
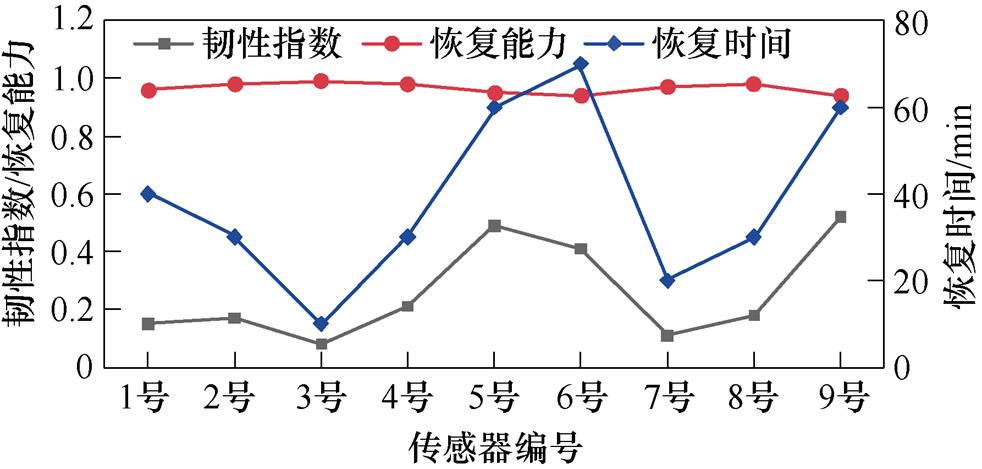
图11 风速传感器对台风事件的韧性标签
Fig.11 Resilience of wind speed sensors to typhoon
从图11可以看出,风速传感器的运行品质受此次台风影响出现了不同程度的下滑,其中,5号、6号和9号机组传感器的韧性指数已超过0.4,表明此次台风天气导致传感器的运行品质波动幅度超过40%。此外,从恢复速度和恢复能力标签来看,大多数风速传感器在台风过后60 min内能够恢复到事件前运行品质的95%以上,而5号、6号和9号机组传感器在台风过后仅能恢复到初始状态的88%,设备受此次事件的影响出现了超过12%的性能损失。
为验证韧性评价结果的有效性,本文选取台风期间处于同一风带上的6台风速传感器的测量数据进行分析和比对,如图12所示,在台风出现前,6台传感器的测量风速数据表现为很强的空间相关性,曲线的波动特征和趋势特征十分相近,而在台风出现后,6条风速曲线的分布情况发生了很大的变化,其中,1号、2号、3号传感器的测量风速仍表征为强相关性,5号、6号和9号传感器的测量数据偏离了风速间的空间关联分布特征,由此判定5号、6号和9号传感器的运行品质在台风期间下滑严重。在台风结束后,5号、6号和9号传感器又能逐步恢复平稳运行,但设备的测量精度低于台风前状态。以上分析结果表明,5号、6号和9号传感器在台风期间出现了性能衰退,与所提方法评价结果一致,从而验证了本文所提韧性分析方法的有效性。
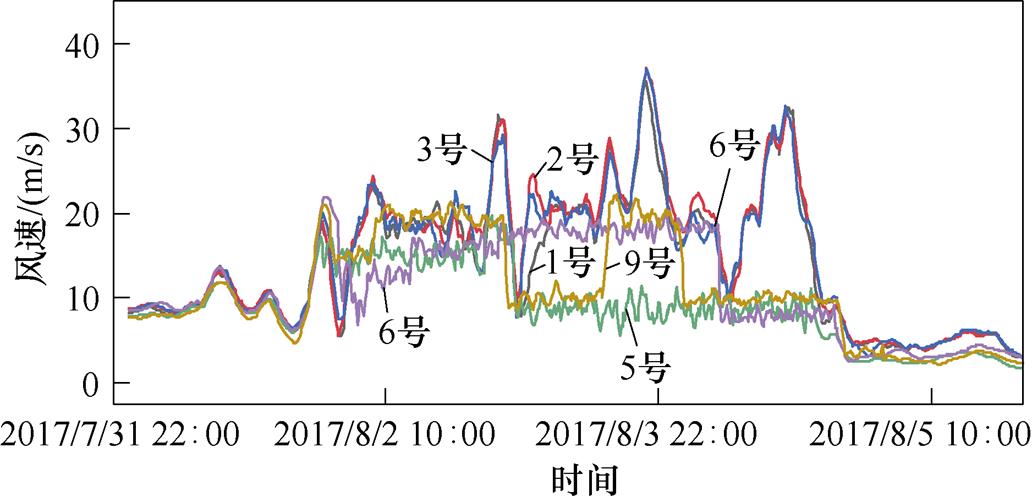
图12 台风期间风速传感器原始测量风速数据
Fig.12 The measured wind speed during typhoon
韧性分析结果能够检测出对自然天气事件既敏感、恢复能力又不足的脆弱型传感器,在灾后运维中需重点关注,所提方法可一定程度缩小灾后隐患排查的范围,提升风电场运维的智能化水平。
3.3.3 风速传感器运行品质演化趋势应用分析
为进一步探究传感器运行品质的趋势特征,即传感器的运行品质是持续性下降,还是仅在扰动期间不稳定,本文提出了演化趋势模型。从上述结果可知,5号和6号机组传感器的运行品质波动明显,为分析两台传感器的性能演化趋势,本文以3天为周期对传感器运行品质进行滚动评价,得到风速传感器运行品质曲线,利用形态二分位算法检测曲线的变点,进而得到运行品质的模态特征曲线,如图13所示。可以看到,5号传感器的波动周期更长,趋势相对单一,而6号传感器的波动周期相对较小,波动的频率和趋势更加复杂。
为描述风速传感器运行品质演化特征,计算传感器运行性能变点的波动程度、波动概率和波动的转移概率标签,见表4。表中,5号传感器的波动幅度更大,为0.6;5号和6号传感器的波动速度接近,单次波动量在0.12左右;在波动出现的概率上,6号传感器高于5号传感器;在波动转移概率上,5号传感器发生失准和失稳的转移概率分别为0.75和0.25,失准的概率更高,传感器的运行品质在大多数时间内处于下降的状态,6号传感器发生失准和失稳的转移概率分别为0.17和0.83,出现失稳的概率更高,传感器的运行品质反复波动。针对失稳模式,需要在自然天气事件发生期间加强对设备的监视,对于失准模式,设备性能衰退严重,需要采取针对性的维护措施。
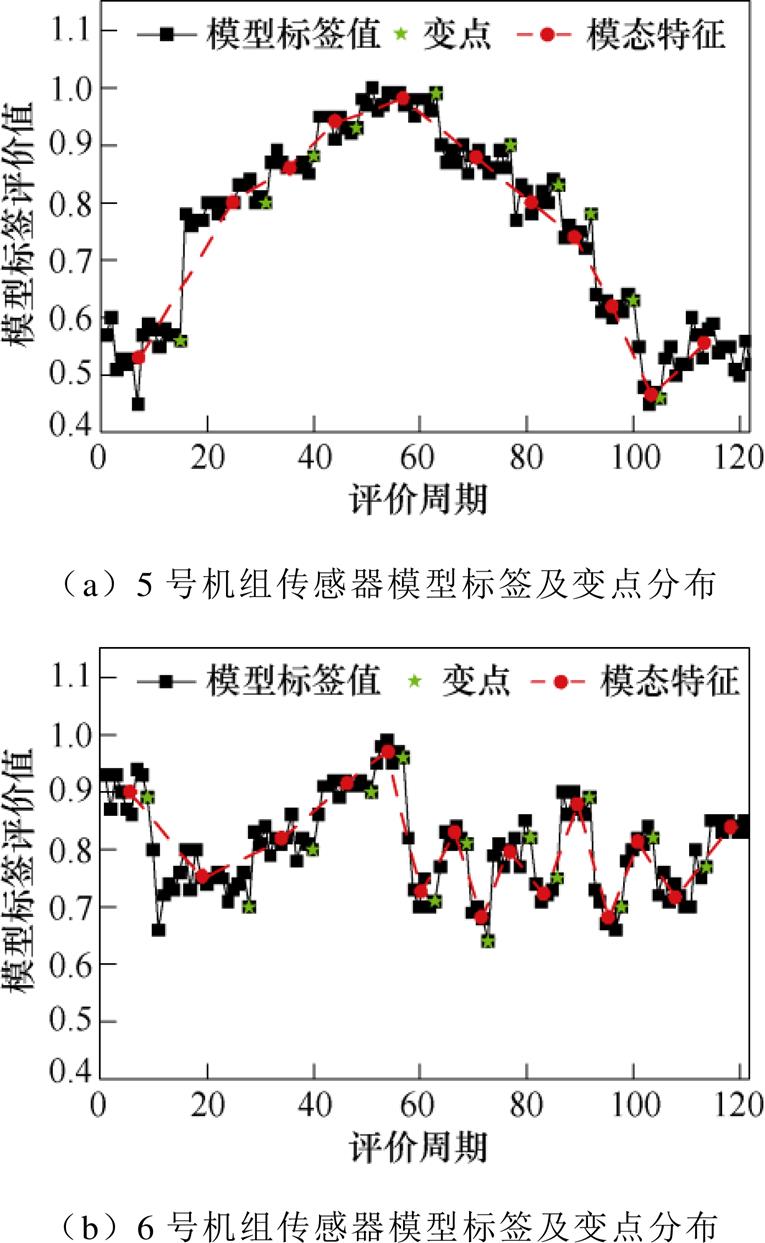
图13 风速传感器运行品质模态特征
Fig.13 Module features and operation quality curves of wind speed sensors
表4 风速传感器运行品质波动趋势特征标签
Tab.4 The performance trend labels of wind speed sensors
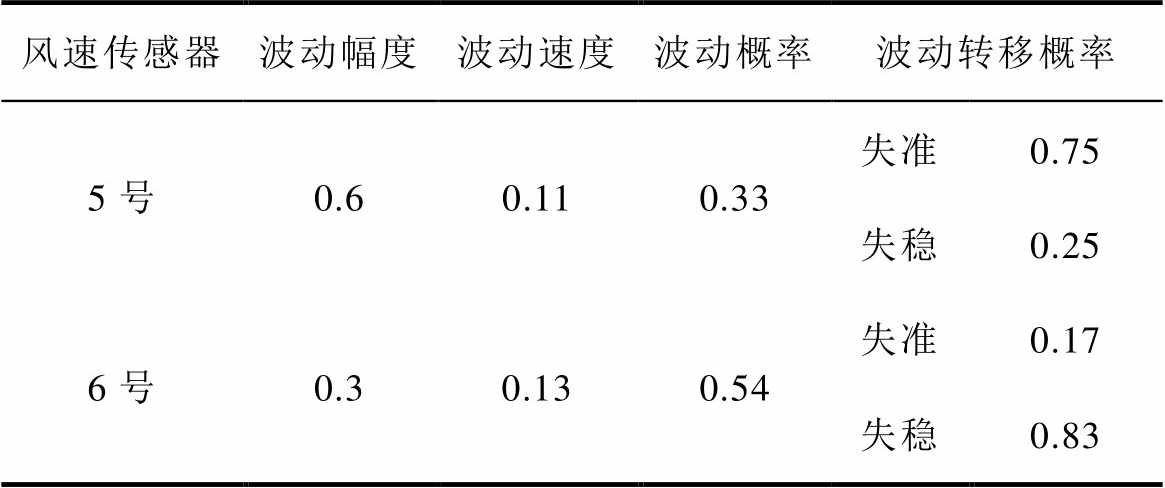
风速传感器波动幅度波动速度波动概率波动转移概率 5号0.60.110.33失准0.75 失稳0.25 6号0.30.130.54失准0.17 失稳0.83
可以看到,所提的基于形态特征的演化趋势模型能够有效地辨识风速传感器的失稳和失准缺陷模式,并量化描述两者出现的概率,在本算例中,5号传感器的运行品质在大部分时间内处于下降的趋势,属于失准型,6号传感器的运行品质处于反复波动的状态,属于失稳型。
3.3.4 风电场风速传感器集群的运行品质分析
为分析风电场风速传感器集群的运行品质分布特征,提取风速传感器集群典型的运行场景,本文选取灵敏度、精确度、利用率、缺陷率、平均绝对误差率、偏离度、环境波动度、环境冲击度、扰动失稳率、扰动变异系数为特征标签,以该风电场23台风速传感器为研究对象,利用动态层次k-means聚类算法对风速传感器集群进行群落划分,划分结果如图14所示,该风电场风速传感器集群被划分为3个群落,相同群落内的传感器运行品质相似。
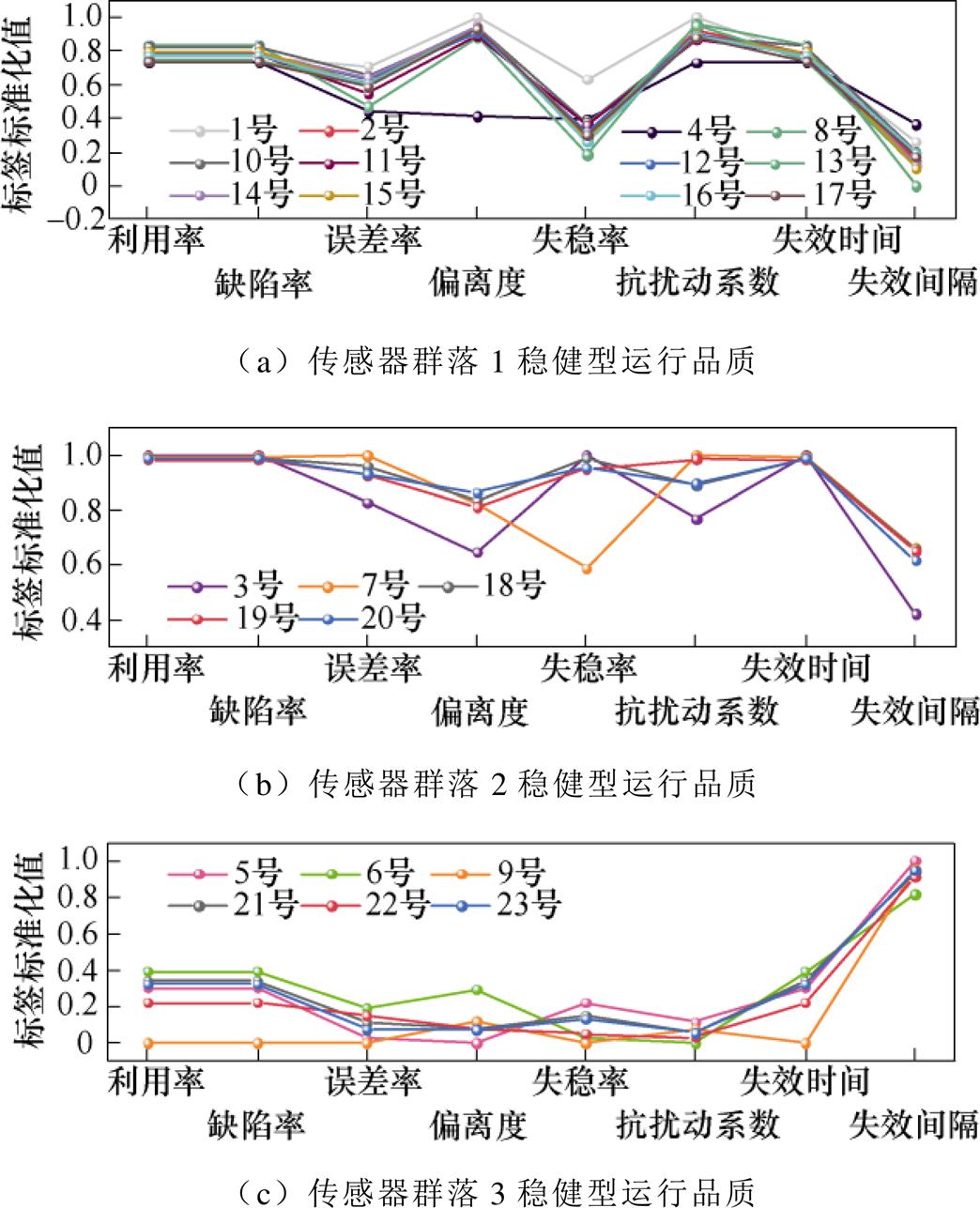
图14 风电场风速传感器运行品质集群特征
Fig.14 Cluster characteristics of operating quality for the wind speed sensors in the studied wind farm
计算各集群的特征标签,见表5,该风电场风速传感器依据运行品质总体上可分为波动型、稳健型和衰退型三类。
表5 风速传感器集群运行品质标签计算结果
Tab.5 Results of operational quality for wind speed sensors community in the studied wind farm
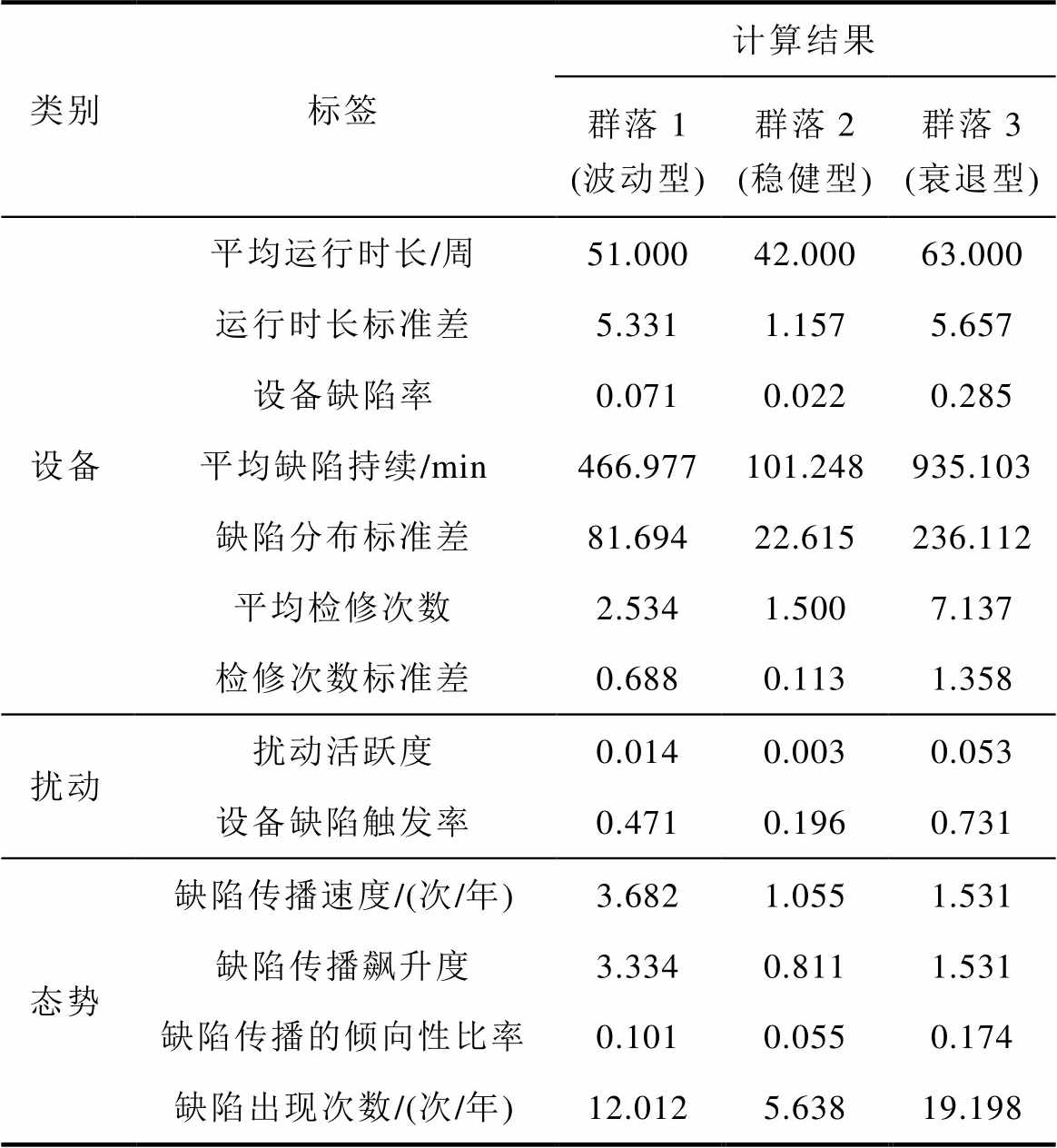
类别标签计算结果 群落1 (波动型)群落2 (稳健型)群落3 (衰退型) 设备平均运行时长/周51.00042.00063.000 运行时长标准差5.3311.1575.657 设备缺陷率0.0710.0220.285 平均缺陷持续/min466.977101.248935.103 缺陷分布标准差81.69422.615236.112 平均检修次数2.5341.5007.137 检修次数标准差0.6880.1131.358 扰动扰动活跃度0.0140.0030.053 设备缺陷触发率0.4710.1960.731 态势缺陷传播速度/(次/年)3.6821.0551.531 缺陷传播飙升度3.3340.8111.531 缺陷传播的倾向性比率0.1010.0550.174 缺陷出现次数/(次/年)12.0125.63819.198
(1)波动型:风速传感器的运行品质易受外界扰动而不稳定,扰动对传感器的缺陷触发率高达0.392,相较于前一年,每台设备的缺陷增加了3.682次,近3年的平均缺陷飙升度为3.334次/年,即传感器新增缺陷的增速逐年递增,表明传感器的运行状态十分不稳定,缺陷的次数和概率均明显增多,波动型设备占比约为52.2%。
(2)稳健型:传感器的各方面属性均处于理想状态,能够持续地捕获高精度风速数据,稳健型设备占比约为21.7%。
(3)衰退型:传感器的运行品质呈持续下滑态势,缺陷出现的次数和持续时间均处于高位,平均每年出现19.198次缺陷,每次缺陷平均持续935.103 min,每台传感器进行了7.137次检修,累积运行时间为63个月,表明设备老化严重,衰退型设备占比约为26.1%。
提取风电场风速传感器运行品质的集群特征可进一步应用于风电场精准运检:①分析传感器的运行性能的短板,制定精准的运维、检修策略;②分析传感器对运行环境的适应性和容忍性,为下一周期设备的选型提供指导。
本文提出了一种基于运行数据的风电机组风速传感器运行品质后评估方法和应用体系,该方法结合风速传感器典型缺陷模式下运行数据的分布特征及风电场运维关注的设备运行、测量、抗扰动等属性,采用数据驱动方法,描述传感器的运行品质,挖掘其影响因素、演化趋势等特征,得出以下结论:
1)本文所提运行品质评价方法能对风电场风速传感器的运行行为和缺陷模式做精细化建模表征,挖掘传感器运行的扰动敏感度、韧性、集群特征等属性,可有效识别风速传感器的薄弱环节和性能短板。
2)所构建的评价模型及应用体系能够有效地提取传感器运行品质波动的原因、演化态势等信息,在所研究风电场中,风速传感器对寒潮和强对流扰动更敏感,敏感设备率约为33.3%,传感器集群可分为波动型、稳健型和衰退型,占比分别为52.2%、21.7%和26.1%。
3)所提的风电场风速传感器运行品质后评估模型和应用体系可用于传感器运行行为的描述和评价,评估结果可为设备的全寿命周期管理、主动运检、精益化运维等提供一种数字化辅助决策手段。
未来工作将进一步围绕风速传感器主动运检展开,研究面向不同缺陷模式、不同运行品质的风速传感器精准运维检修方法,以及提升风速传感器冗余度和韧性的方法,为风电场数字化、智能化发展提供坚实的基础。
附 录
附表1 风速传感器运行品质运行属性标签体系及计算方法
App.Tab.1 Operational properties and calculation method for wind speed sensors operating performance and quality
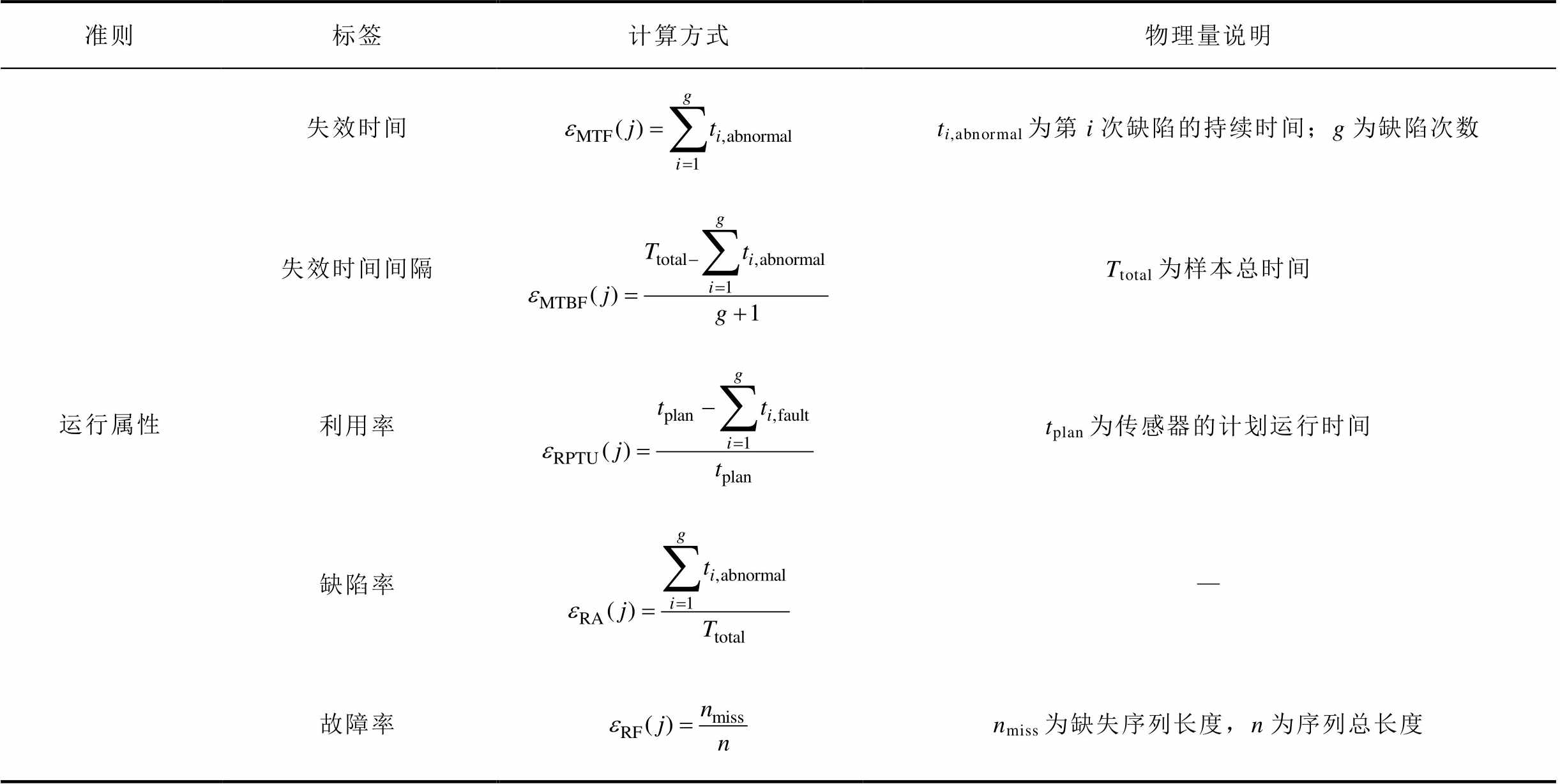
准则标签计算方式物理量说明 运行属性失效时间ti,abnormal为第i次缺陷的持续时间;g为缺陷次数 失效时间间隔Ttotal为样本总时间 利用率tplan为传感器的计划运行时间 缺陷率— 故障率nmiss为缺失序列长度,n为序列总长度
附表2 风速传感器运行品质测量属性标签体系及计算方法
App.Tab.2 Measurement properties and calculation method for wind speed sensors operating performance and quality
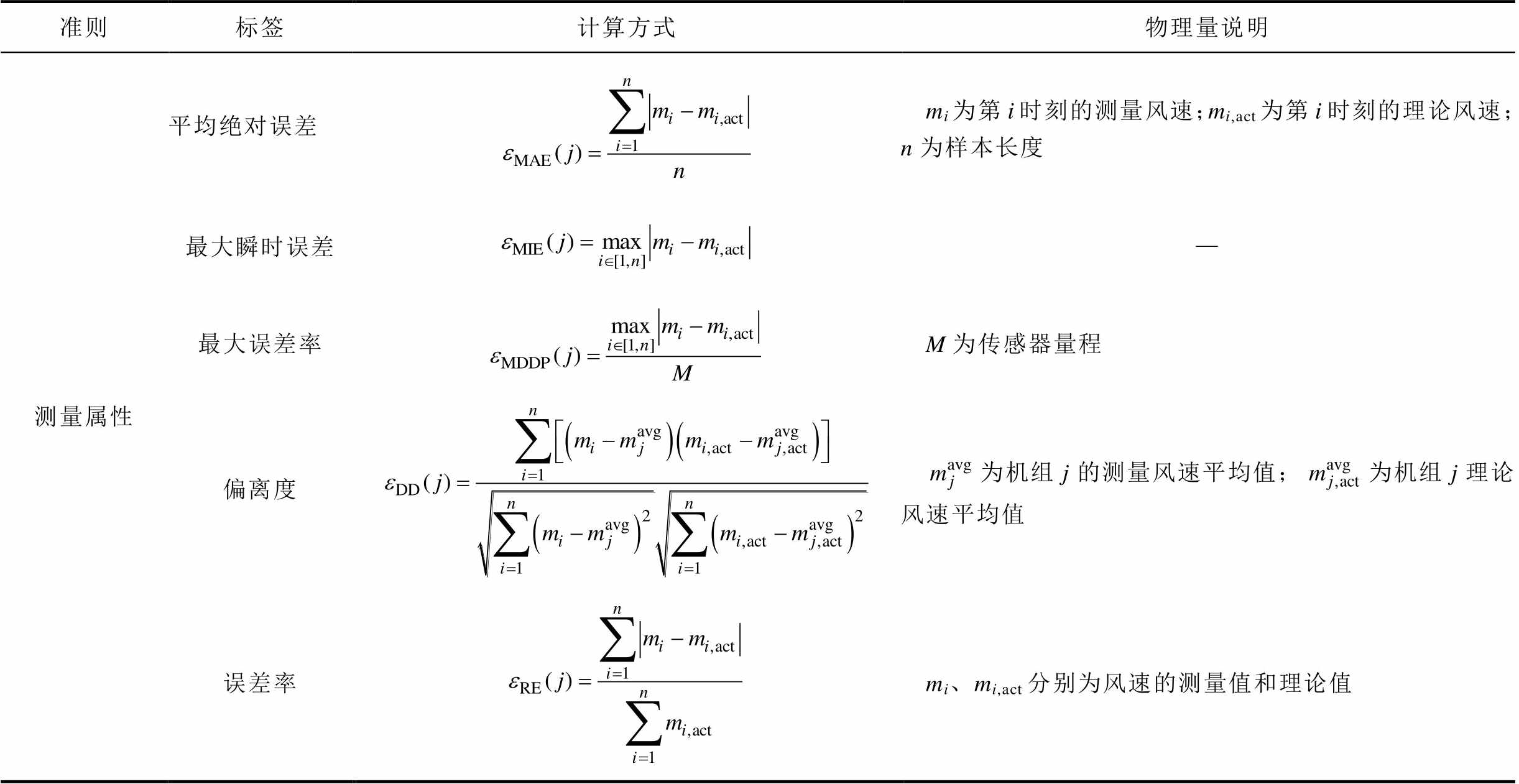
准则标签计算方式物理量说明 测量属性平均绝对误差mi为第i时刻的测量风速;mi,act为第i时刻的理论风速;n为样本长度 最大瞬时误差— 最大误差率M为传感器量程 偏离度为机组j的测量风速平均值;为机组j理论风速平均值 误差率mi、mi,act分别为风速的测量值和理论值
附表3 风速传感器运行品质抗扰动属性标签体系及计算方法
App.Tab.3 Anti-disturbances properties and calculation method for wind speed sensors operating performance and quality
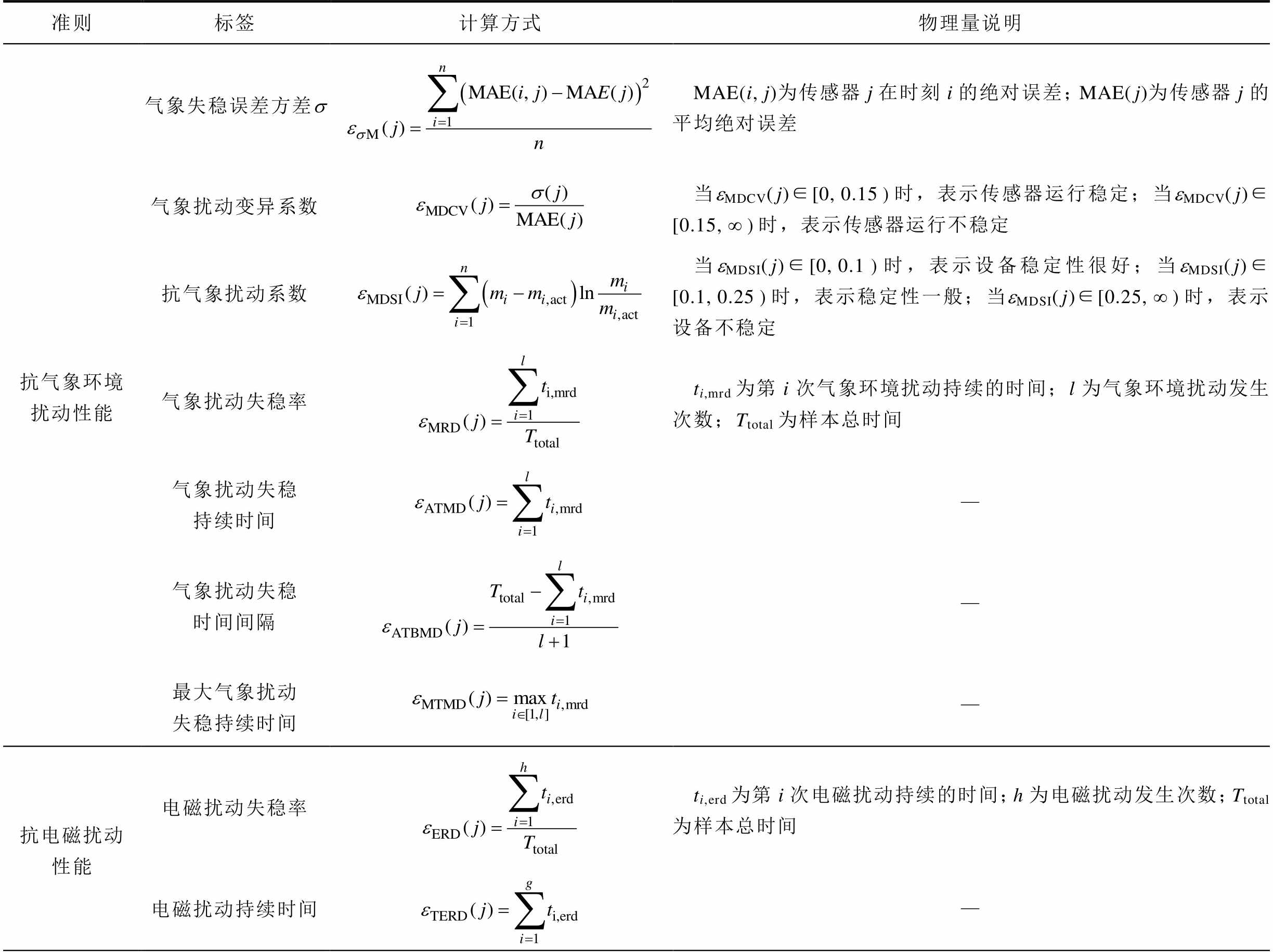
准则标签计算方式物理量说明 抗气象环境扰动性能气象失稳误差方差sMAE(i, j)为传感器j在时刻i的绝对误差;MAE( j)为传感器j的平均绝对误差 气象扰动变异系数当eMDCV( j)∈[0, 0.15时,表示传感器运行稳定;当eMDCV(j)∈[0.15, ∞时,表示传感器运行不稳定 抗气象扰动系数当eMDSI( j)∈[0, 0.1时,表示设备稳定性很好;当eMDSI( j)∈[0.1, 0.25时,表示稳定性一般;当eMDSI( j)∈[0.25, ∞时,表示设备不稳定 气象扰动失稳率ti,mrd为第i次气象环境扰动持续的时间;l为气象环境扰动发生次数;Ttotal为样本总时间 气象扰动失稳持续时间— 气象扰动失稳时间间隔— 最大气象扰动失稳持续时间— 抗电磁扰动性能电磁扰动失稳率ti,erd为第i次电磁扰动持续的时间;h为电磁扰动发生次数;Ttotal为样本总时间 电磁扰动持续时间—
(续)
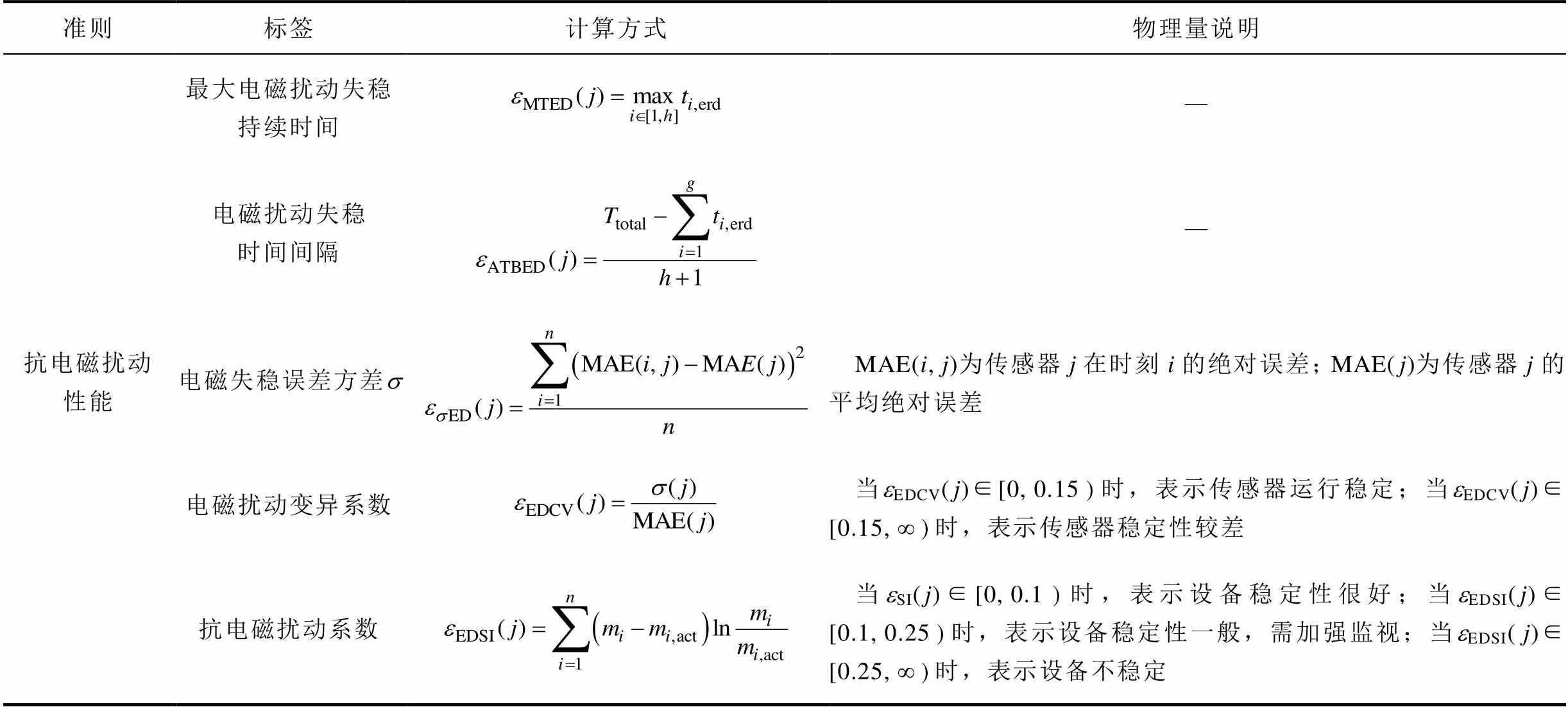
准则标签计算方式物理量说明 抗电磁扰动性能最大电磁扰动失稳持续时间— 电磁扰动失稳时间间隔— 电磁失稳误差方差sMAE(i, j)为传感器j在时刻i的绝对误差;MAE( j)为传感器j的平均绝对误差 电磁扰动变异系数当eEDCV( j)∈[0, 0.15时,表示传感器运行稳定;当eEDCV( j)∈[0.15, ∞时,表示传感器稳定性较差 抗电磁扰动系数当eSI( j)∈[0, 0.1时,表示设备稳定性很好;当eEDSI( j)∈[0.1, 0.25时,表示设备稳定性一般,需加强监视;当eEDSI( j)∈[0.25, ∞时,表示设备不稳定
附表4 风速传感器运行品质固有属性标签体系及计算方法
App.Tab.4 Inherent properties and calculation method for wind speed sensors operating performance and quality
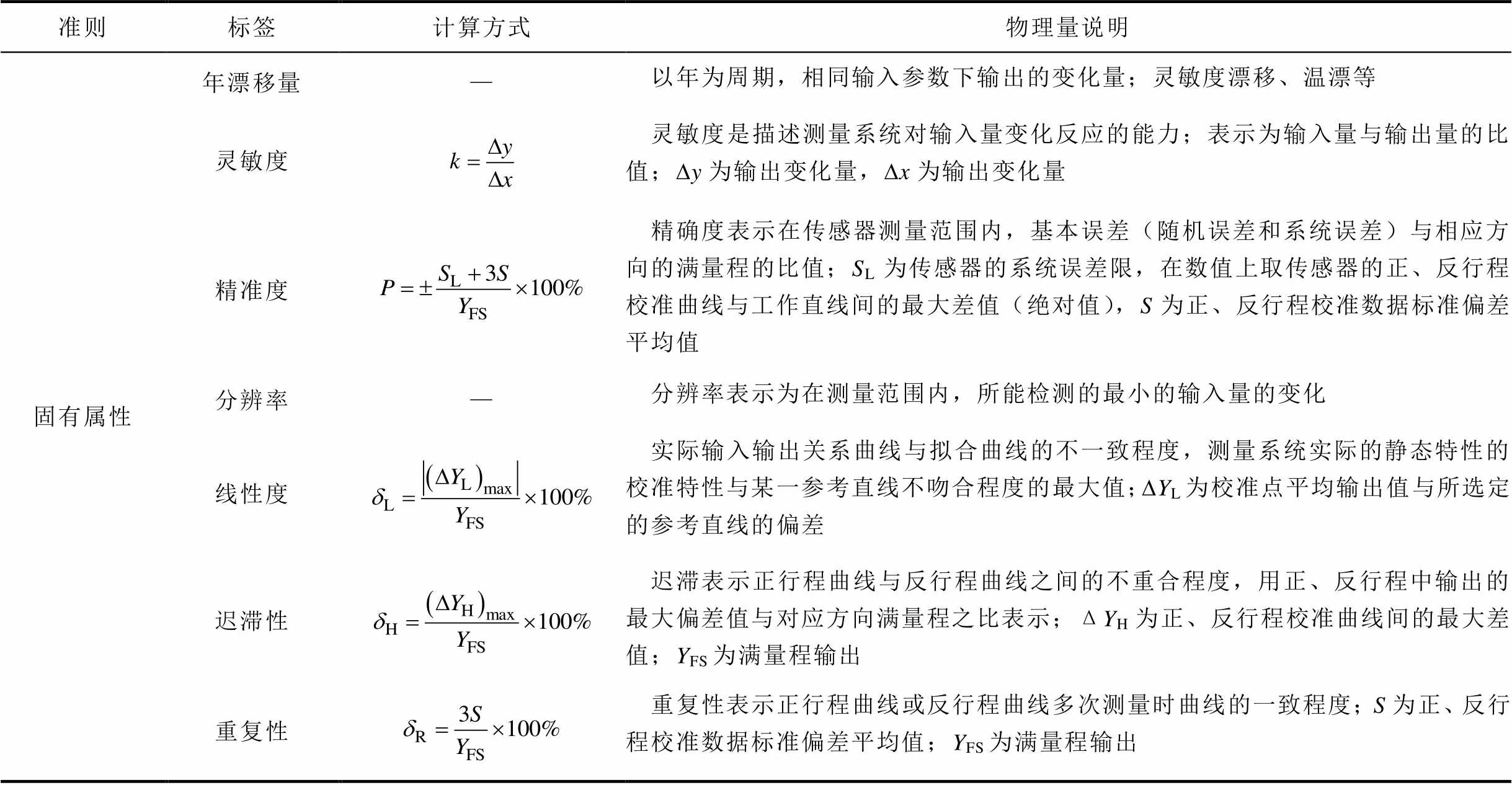
准则标签计算方式物理量说明 固有属性年漂移量—以年为周期,相同输入参数下输出的变化量;灵敏度漂移、温漂等 灵敏度灵敏度是描述测量系统对输入量变化反应的能力;表示为输入量与输出量的比值;Dy为输出变化量,Dx为输出变化量 精准度精确度表示在传感器测量范围内,基本误差(随机误差和系统误差)与相应方向的满量程的比值;SL为传感器的系统误差限,在数值上取传感器的正、反行程校准曲线与工作直线间的最大差值(绝对值),S为正、反行程校准数据标准偏差平均值 分辨率—分辨率表示为在测量范围内,所能检测的最小的输入量的变化 线性度实际输入输出关系曲线与拟合曲线的不一致程度,测量系统实际的静态特性的校准特性与某一参考直线不吻合程度的最大值;DYL为校准点平均输出值与所选定的参考直线的偏差 迟滞性迟滞表示正行程曲线与反行程曲线之间的不重合程度,用正、反行程中输出的最大偏差值与对应方向满量程之比表示;ΔYH为正、反行程校准曲线间的最大差值;YFS为满量程输出 重复性重复性表示正行程曲线或反行程曲线多次测量时曲线的一致程度;S为正、反行程校准数据标准偏差平均值;YFS为满量程输出
附表5 风速传感器运行品质环境属性标签体系及计算方法
App.Tab.5 Environmental properties and calculation method for wind speed sensors operating performance and quality

准则标签计算方式物理量说明 环境属性环境波动度环境波动度为归一化典型环境参数曲线(温度、湿度、风速等)的标准差,表征环境参数的离散程度;波动度大,则环境参数分散程度大,说明环境参数波动性大;反之则环境参数分散程度小,说明环境参数波动性小;xi为某一时刻环境参数值;x为环境参数平均值 环境冲击度环境冲击度是指具有周期性或非周期性突然变化很大的环境参数,可达到平均水平的数倍或数十倍,表示扰动的程度;xt为实际环境参数;为平滑处理后的环境参数
(续)

准则标签计算方式物理量说明 环境属性环境扰动概率沙尘、霜冻、冰雹、降雪、暴雨等环境扰动出现的概率;wi为第i种环境扰动出现的次数;T为总时间
参考文献
[1] Li Yang, Shen Xiaojun. A novel wind speed sensing methodology for wind turbines based on digital twin technology[J]. IEEE Transactions on Instrumentation and Measurement, 2022, 71: 1-13.
[2] 沈小军, 付雪姣, 周冲成, 等. 风电机组风速-功率异常运行数据特征及清洗方法[J]. 电工技术学报, 2018, 33(14): 3353-3361
Shen Xiaojun, Fu Xuejiao, Zhou Chongcheng, et al. Characteristics of outliers in wind speed-power operation data of wind turbines and its cleaning method[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3353-3361.
[3] Kusiak Andrew, Li Wenyan. The prediction and diagnosis of wind turbine faults[J]. Renewable Energy, 2011, 36(1): 16-23.
[4] Li Yang, Shen Xiaojun. Anomaly detection and classification method for wind speed data of wind turbines using spatiotemporal dependency structure[J]. IEEE Transactions on Sustainable Energy, 2023, 14(4): 2417-2431.
[5] Yin Shen, Xiao Bing, Ding Steven X, et al. A review on recent development of spacecraft attitude fault tolerant control system[J]. IEEE Transactions on Industrial Electronics, 2016, 63(5): 3311–3320.
[6] 谭平, 蔡自兴, 余伶俐. 不同精度的冗余传感器故障诊断研究[J]. 控制与决策, 2011, 26(12): 1909- 1912.
Tan Ping, Cai Zixing, Yu Lingli. Research on fault diagnosis of different precision redundant sensors[J]. Control and Decision, 2011, 26 (12): 1909-1912.
[7] 李建平, 王晓凯. 基于模糊神经网络的无线传感器网络可靠性评估[J]. 计算机应用, 2016, 36(增刊2): 69-72.
Li Jianping, Wang Xiaokai. WSN reliability evalu- ation based on fuzzy neural network[J]. Journal of Computer Applications, 2016, 36(S2): 69-72.
[8] Xiang Shihu, Yang Jun. Reliability evaluation and reliability-based optimal design for wireless sensor networks[J]. IEEE Systems Journal, 2020, 14(2): 1752-1763.
[9] 肖雄, 张勇军, 王京, 等. 无电压传感PWM整流器的虚拟磁链自适应滑模观测研究[J]. 电工技术学报, 2015, 30(12): 152-161.
Xiao Xiong, Zhang Yongjun, Wang Jing, et al. PWM rectifiers based on adaptive sliding-mode observer with virtual flux orientation under non-line voltage sensors control[J]. Transactions of China Electro- technical Society, 2015, 30(12): 152-161.
[10] 夏金辉, 郭源博, 张晓华. 单相脉宽调制整流器传感器故障诊断与容错控制[J]. 电工技术学报, 2017, 32(20): 160-170.
Xia Jinhui, Guo Yuanbo, Zhang Xiaohua. Sensor fault diagnosis and fault tolerant control for single-phase PWM rectifier[J]. Transactions of China Electro- technical Society, 2017, 32(20): 160-170.
[11] Yang Qingyu, Chen Yong. Monte Carlo methods for reliability evaluation of linear sensor systems[J]. IEEE Transactions on Reliability, 2011, 60(1): 305- 314.
[12] Alsarraj Ahmed, Rehman Atiq Ur, Belhaouari Samir Brahim, et al. Hydrogen sulfide (H2S) sensor: A concept of physical versus virtual sensing[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 1-13.
[13] Li Xiang, Zhang Wei, Xu Nanxi, et al. Deep learning-based machinery fault diagnostics with domain adaptation across sensors at different places[J]. IEEE Transactions on Industrial Electronics, 2020, 67(8): 6785-6794.
[14] Zidi Salah, Moulahi Tarek, Alaya Bechir. Fault detection in wireless sensor networks through SVM classifier[J]. IEEE Sensors Journal, 2018, 18(1): 340-347.
[15] 李阳, 沈小军. 基于速度-关联约束的风电机组风速感知异常数据识别方法[J]. 电工技术学报, 2023, 38(7): 1793-1807.
Li Yang, Shen Xiaojun. Cleaning method of wind speed outliers for wind turbines based on velocity and correlation constraints[J]. Transactions of China Electrotechnical Society, 2023, 38(7): 1793-1807.
[16] Zhu Qiaomu, Chen Jinfu, Zhu Lin, et al. Learning temporal and spatial correlations jointly: A unified framework for wind speed prediction[J]. IEEE Transactions on Sustainable Energy, 2020, 11(1): 509-523.
[17] Li Yang, Shen Xiaojun, Zhou Chongcheng. Dynamic multi-turbines spatiotemporal correlation model enabled digital twin technology for real-time wind speed prediction[J]. Renewable Energy, 2023, 203: 841-853.
[18] 严正, 李磊, 韩冬, 等. 基于改进超效率数据包络分析的低碳电力生产效率评估模型[J]. 电力系统自动化, 2014, 38(17): 170-176.
Yan Zheng, Li Lei, Han Dong, et al. Evaluation model for low-carbon electricity production efficiency based on improved supper efficacy data envelopment analysis method[J]. Automation of Electric Power Systems, 2014, 38(17): 170-176.
[19] 许寅, 和敬涵, 王颖, 等. 韧性背景下的配网故障恢复研究综述及展望[J]. 电工技术学报, 2019, 34(16): 3416-3429.
Xu Yan, He Jinghan, Wang Ying, et al. A review on distribution system restoration for resilience enhance- ment[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3416-3429.
[20] 王学伟, 刘建平, 袁瑞铭, 等. 复杂动态负荷电流幅度域典型游程波形模态与特征提取[J]. 电网技术, 2023, 47(6): 2497-2503.
Wang Xuewei, Liu Jianping, Yuan Ruiming, et al. Extraction of typical run length waveform modes and characteristics of complex dynamic load current amplitude domain[J]. Power System Technology, 2023, 47(6): 2497-2503.
[21] 李阳, 刘友波, 刘俊勇, 等. 基于形态距离的日负荷数据自适应稳健聚类算法[J]. 中国电机工程学报, 2019, 39(12): 3409-3420.
Li Yang, Liu Youbo, Liu Junyong, et al. Self-adaptive and robust clustering algorithm for daily load profiles based on morphological distance[J]. Proceedings of the CSEE, 2019, 39(12): 3409-3420.
Abstract Wind speed sensors of wind turbines, especially offshore wind turbines, are prone to suffer from defects due to long-term exposure to complex and harsh environments, which negatively affects the quality of wind speed data. No wind signal or wrong wind signal fed into the unit control system tends to cause false start-stop and pitching actions, endangering the power generation efficiency and operation safety of wind farms. Existing methods focus on the fault diagnosis of sensors, serving as real-time operation control of units. Considering that the sensor may fail due to natural weather events (NWEs), the sensor is likely to recover smooth operation after NWEs. Extracting the operational quality (measurement accuracy, operational stability, disturbance sensitivity, and performance evolution trend) is difficult. Thus, refinement modeling for sensor operating quality helps to analyze its instability, misalignment, and other defects for the full-life cycle healthy management and proactive inspection of wind farms.
Firstly, the operational quality characterization indicators and quantification rules for wind speed sensors are constructed from the dimensions of operation reliability, measurement accuracy, anti-disturbance ability, environment features, and inherent property. Then, a comprehensive evaluation model is employed using data envelope analysis (DEA) to describe the general attributes of sensors. An application framework of the constructed indicators is developed to deeply mine the risks and operating situations for the wind speed sensor, including a sensitivity model for the weakness of NWEs, a resilience model for the recovery ability against NWEs, a performance evolution trend model for defective modes, and a clustering model for the general features of the sensor community in the wind farm.
Experimental results on an actual wind farm dataset, including the operational data of 9 turbines for one year, show that the proposed method can characterize the differences in operating quality for wind speed sensors. Specifically, the proposed model can detect the sensitive sensors prone to defects by NWEs and identify the defective modes, including misalignment and destabilization. Wind speed sensors in the studied wind farms, sensitive to cold waves and strong convective NWEs, are likely subjected to performance degradation. The rate of sensitive sensors to disturbances in the studied wind farm reaches 33.3%. Most sensors can recover to smooth operation within 1 hour after NWEs. According to operation quality, the sensor community in the wind farm is classified into fluctuating, robust, and degraded sensors.
The following conclusions can be drawn from the case analysis. (1) The proposed method can evaluate the operation behavior of wind speed sensors. The application system can further excavate the attributes of the sensor, such as perturbation sensitivity, resilience, and clustering characteristics, effectively identifying its weaknesses and shortcomings. (2) Typical defects of wind speed sensors and their trend features are sorted out. The proposed application model can characterize the operational situations of the sensors and describe the occurrence probability of defective patterns. (3) The proposed post-assessment model and application system can describe sensor operation behaviors, which guide the whole-life-cycle management, active inspection, and lean maintenance of wind farms.
keywords:Wind farms, wind speed sensors, operation data, operation quality, evaluation system
DOI: 10.19595/j.cnki.1000-6753.tces.230425
中图分类号:TM614
收稿日期 2023-04-04
改稿日期 2023-05-09
李 阳 男,1992年生,博士研究生,研究方向为风电场运行数据清洗和重构、风电机组运行状态感知与智能诊断、风电机组数字孪生建模等。E-mail: ly18227602440@163.com
沈小军 男,1979年生,教授,博士生导师,研究方向为新能源高效利用与储能技术、输变电场景三维重构及其数字孪生技术、电力设备状态感知与智能诊断等。E-mail: xjshen79@163.com(通信作者)
(编辑 郭丽军)