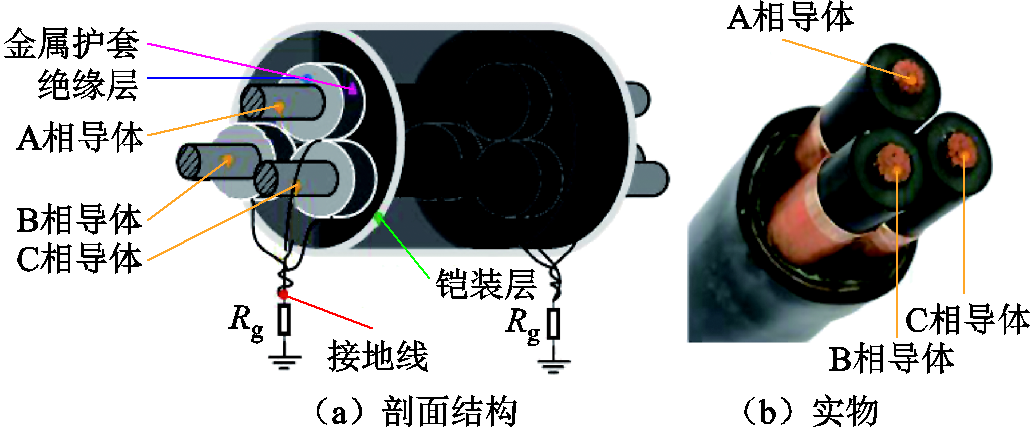
图1 三芯电缆结构
Fig.1 Structure of three-core cable
摘要 局部放电(PD)检测是评估交联聚乙烯(XLPE)电缆绝缘状态的主要手段。针对电缆终端与中间接头局部放电现场检测时存在白噪声、周期性窄带干扰,以及去噪过程中自适应性较弱的问题,该文提出了一种基于图像信息熵与新型自适应多元变分模态分解的去噪方法。首先,对信号进行多元变分模态分解,重组信号并转换成灰度图像,进而计算图像一维信息熵。在考虑算法执行效率的同时,将Pearson相关系数与图像信息熵优化算法的模态参数相结合。其次,通过计算各本征模态分量的峭度来判定其主导分量的性质特征,利用峭度对噪声敏感的特性区分PD特征信息与噪声干扰分量,进而对噪声干扰分量进行3σ准则滤波。最后,通过新型改进小波阈值算法得到去噪信号。利用该方法对PD信号进行去噪,并与基于Spearman的变分模态分解(S-VMD)法、自适应集合经验模态分解(NAEEMD)法、短时傅里叶变换-奇异值分解(STFT-SVD)法进行对比分析。结果表明,该方法对现场PD信号具有良好的抑噪性能,且耗时少、执行效率高、工程应用价值高。
关键词:多元变分模态分解 局部放电 图像信息熵 峭度 电力电缆
近年来,交联聚乙烯(Cross-Linked Polyethylene, XLPE)电缆因其质量轻、耐温等级高、输送功率大等优势在输电线路与城市配电网中得到广泛发展,在6~500 kV电缆线路中,XLPE绝缘电缆所占比例高达98.68%[1]。随着XLPE电缆投运量的增加与电缆线路的延伸,硅橡胶绝缘预制式中间接头因其高压屏蔽性能好、整体预制式设计、电压裕度大、现场安装方便等特点在XLPE电力电缆中被广泛使用。预制式中间接头是由不同介电特性的多层固体复合介质组成,且需现场安装成型,因而发生事故的概率远远大于电缆本体。
局部放电(Partial Discharge, PD)检测对于电力设备健康状况的评估至关重要。通过PD检测可有效考验和评价电缆的绝缘状态,但由于现场的电磁环境复杂恶劣,存在白噪声干扰[2]或周期窄带干扰,会导致PD信号的波形发生严重畸变,从而影响测试结果的准确性,甚至使特征信号被掩埋于背景噪声中,影响后续的缺陷诊断与状态评估。因此,去噪是现场PD测量中必不可少的,通过有效的去噪方法可准确地恢复PD信号,提高PD检出率。
目前,常见的去噪算法有奇异值分解(Singular Value Decomposition, SVD)法[3-6]、经验模态分解(Empirical Mode Decomposition, EMD)法[7-9]、变分模态分解(Variable Mode Decomposition, VMD)法[10-11]和小波变换(Wavelet Transform, WT)法[12-14]等。
文献[3]提出一种通过奇异值序列标准差来确定阈值以完成自适应选择的自适应SVD方法,为去噪PD脉冲的检测和重建奇异值的选择提供了通用性和实用性方法。但对于冗长复杂的序列,该方法难以用较少的奇异值重构信号,因此去噪后的PD信号残余噪声较多。文献[4]的核心思路是首先利用短时滑动数据窗对含噪PD信号进行奇异值分解,再通过设置合适的阈值对信号进行重构完成去噪,从而抑制混合噪声。若阈值选取不当会导致放电起始位置产生偏移,因此去噪效果受到人为因素的影响大。文献[5]提出了一种带引导信号的SVD算法,该方法结合快速傅里叶变换功率谱抑制窄带干扰。但当窗口过长或窄带干扰幅值过小时,干扰信号会与PD脉冲的奇异值互相影响,从而影响SVD的去噪性能。文献[6]将SVD与通过短时傅里叶变换获得的噪声PD信号的时频复矩阵相结合,可以自适应、有选择性地降低三种PD脉冲中的白噪声和离散频谱噪声,但仍然存在一定程度的波形失真。因此,SVD在数据较长或窄带干扰较小时,会使去噪PD信号残留较多噪声或发生波形畸变。
文献[7]提出了一种基于集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)和数学形态学的自适应PD信号去噪技术,该技术具有自动阈值确定功能。在数学形态学的基础上开发了一种自动形态学阈值技术,在保持PD信号的同时自动消除残留噪声。尽管形态学滤波无需设定阈值,但其结构元素的选择难以确定,会对去噪效果产生较大影响。文献[8]指出,因为EMD无需人工选择母小波,所以有效解决了小波变换自适应性不强的难题。然而,在多次反复迭代的分解过程中,其存在计算量大,且容易产生模态混叠与端点畸变等问题。文献[9]提出了一种基于局部放电的新型自适应集合经验模态分解(Novel Adaptive EEMD, NAEEMD)的降噪方法,通过将能量密度和模态相关系数的平均周期相结合以实现自适应选择降噪重建的固有模态。该算法不能完全消除模态混叠和端点效应的问题,导致去噪后的信号仍然存在部分噪声。
文献[10]中,VMD的成功在很大程度上取决于预设的参数,包括模态参数K和带宽控制参数,其中K决定分解结果的精准程度,若K不匹配,则会出现分解不彻底或模态混叠的问题。文献[11]提出了一种基于Spearman变分模态分解与空间相关递归样本熵的PD信号去噪方法。由于样本熵对阈值的判断非常敏感,容易导致PD信号部分特征丢失,且递归图的构建过程会导致算法执行效率降低。
PD信号属于典型的非平稳信号,因此适合采用小波变换的时频手段进行分析。目前,主要采用小波阈值法对PD信号进行去噪,因此阈值的选择非常关键。文献[12]提出了一种基于直方图的阈值函数与选择规则的小波去噪方法,该阈值估计技术为每个小波子带获得两个不同阈值,并使用阈值函数保存原始信号的能量。然而,常规阈值选择的规则不能与幅值大小、放电时间均呈不确定性的PD信号完全适应,且没有考虑该方法的执行效率。文献[13]将小波阈值和总变分去噪方法相结合,根据凸优化理论对含有白噪声的超高频PD信号进行去噪。由于是联合算法,很可能降低小波阈值引入的振荡误差和总变分去噪方法引入的阶梯误差,但此联合算法在时间与效率上均具有明显短板。文献[14]采用组合小波与块阈值相结合的方法进行PD去噪,通过组合同一族小波以构造对偶树复小波。特定组合的去噪效果近似不变,并且能在噪声不恶劣的情况下实现更好的去噪效果,但该方法只在理论层面进行了验证,且没有考虑算法耗时。
除了以上算法以外,熵也被广泛应用于评价非线性信号的平稳性,如排列熵、近似熵等用来衡量序列复杂程度的指标。然而,排列熵只依赖数据相对大小而不反映原始序列信息,近似熵不适合原始序列过长的情况,因此均存在一些问题。
通过对国内外常见去噪算法的研究与分析,可以总结出现有去噪方法存在的一些技术难点:
1)EMD、EEMD算法在一定程度上解决了自适应性不强的问题。然而,在多次反复迭代的分解过程中,存在计算量大、易产生模态混叠与端点畸变的问题,从而导致算法的运行时间过长、时效性低、特征提取不准确。如果不能消除模态混叠等问题,会导致去噪后的PD信号存在大量残余噪声。
2)SVD算法在数据较长或窄带干扰幅值较小时,会使去噪后的PD信号残留较多噪声,甚至发生严重的波形畸变,将导致去噪后的PD信号的起始放电位置发生一定程度的偏移,从而影响后续的故障诊断与局部放电定位,且矩阵分解的耗时过长,导致算法执行效率相对较低。
3)采用小波阈值算法对PD信号进行去噪时,阈值大小与阈值函数的选择非常关键。XLPE绝缘电缆在接头处产生的PD信号往往含有随机特征的白噪声,其阈值函数类型的选取及阈值大小的设定存在较大困难,若选择不当,易造成PD信号的部分特征被剔除,从而影响去噪效果。
针对以上问题,本文提出了一种基于图像信息熵与多元变分模态分解(Multivariate Variational Mode Decomposition, MVMD)的局部放电信号去噪方法,具体在以下三个方面开展了工作:
1)依据信息熵准确测度图像灰度分布聚集特征,并以此判定出PD脉冲信号的确定性程度。通过构建灰度图像信息熵,克服了EMD、EEMD等算法的模态混叠现象,可实现对含噪PD信号的准确分解,进而实现精确的特征提取。
2)通过计算峭度值区分PD特征与噪声干扰。利用峭度对噪声敏感的特性,计算正弦与双指数衰减信号在信噪比(Signal-to-Noise Ratio, SNR)为 0 dB时的峭度值,以准确区分PD特征信息与噪声干扰分量,为改善PD信号去噪效果奠定基础。同时,滤除噪声干扰分量可以很大程度地压缩原始序列的长度,从而减少耗时,进一步提高算法执行效率。
3)通过改进小波阈值函数及阈值数值大小,提升了现场含噪PD信号的去噪效果。将小波分解层数与通用阈值设定相结合,构造了一种指数衰减的新型小波阈值函数,与XLPE电缆PD信号的数学模型相对应,进而准确地获得了小波分解后的各层细节系数,提升现场含噪PD信号的去噪效果。
以YJV22-3×300-8.7/15 kV型XLPE绝缘三芯电缆为例,对PD产生的原因及位置进行分析。三芯电缆的剖面结构如图1a所示,实物如图1b所示。局部放电是指在电极间发生的、但未贯穿电极的放电,它是在高电场强度作用下,由于设备内部存在绝缘缺陷而出现的反复击穿和熄灭的现象[15]。局部放电通常发生在固体绝缘的空穴中、不同介电特性的绝缘层间,以及金属表面的边缘尖角部位。

图1 三芯电缆结构
Fig.1 Structure of three-core cable
预制式中间接头由多种介电特性的固体复合介质组成,且需现场安装成型。因此与电缆本体相比,中间接头存在潜在缺陷而导致事故的概率更高[16],其剖面结构如图2a所示,实物如图2b所示。经研究发现,PD发生概率较高的位置通常在外屏蔽层、半导电层,以及中间接头的XLPE-硅橡胶界面。
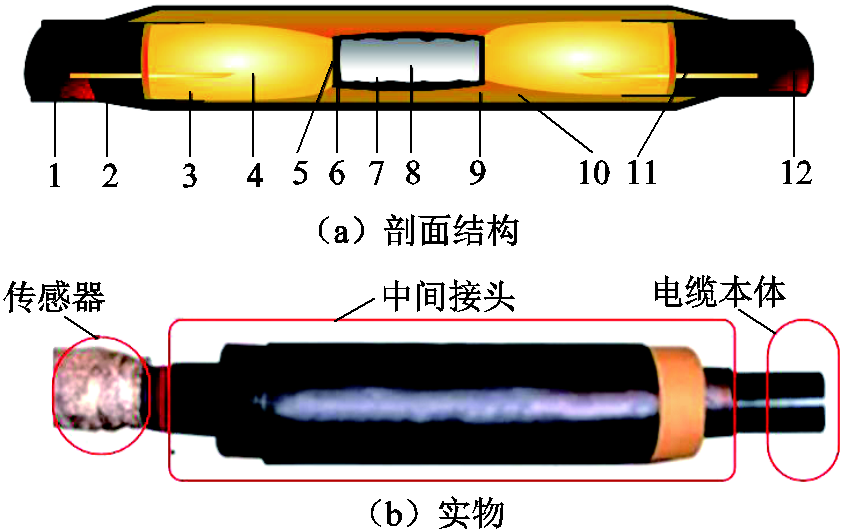
图2 电缆接头结构

Fig.2 Structure of the cable joint
现场局放测试与大量文献均证明[17],PD脉冲主要用单指数衰减函数、单指数衰减振荡函数、双指数衰减函数与双指数衰减振荡函数这四种数学模型进行模拟分析。本文采用双指数衰减函数s1(t)、双指数衰减振荡函数s2(t),以及单指数衰减函数s3(t)来模拟PD信号的波形,其表达式分别为
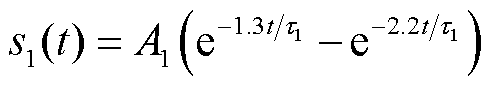 (1)
(1)
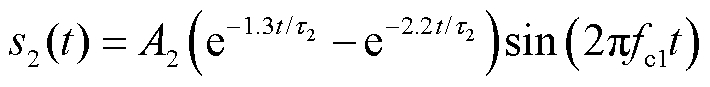 (2)
(2)
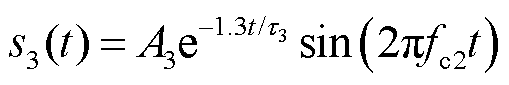 (3)
(3)
式中,A1、A2、A3分别为双指数衰减函数s1(t)、双指数衰减振荡函数s2(t)与单指数衰减函数s3(t)的信号幅值;τ1、τ2、τ3为各自对应的衰减系数;fc1、fc2分别为双指数衰减振荡函数s2(t)、单指数衰减函数s3(t)的振荡频率。数学模型的具体参数设置见表1。
表1 PD模型的参数设置
Tab.1 Parameter settings of PD model

参数数值 幅值/mVA13 A25 A31.2 衰减系数/μsτ10.5 τ20.6 τ30.8 振荡频率/MHzfc13 fc23
仿真的采样频率设置为50 MHz,仿真时间持续40 µs,得到纯净PD信号如图3a所示。为了模拟真实现场情况,在图3a所示的纯净PD信号上添加了SNR=-1 dB的高斯白噪声。周期窄带干扰是由不同幅值、不同频率的一系列正弦信号产生,由式(4)实现。考虑现场PD测量的主要干扰是由广播和通信发射机引起的窄带噪声[18-19],因此,本文主要是根据载波通信中波段的频率添加周期窄带干扰,其波形如图3b所示,具体参数见表2。添加噪声后的PD信号如图3c所示。由此可以看出,原始的纯净PD信号已经无法识别,其特征信息已经完全淹没于噪声中。
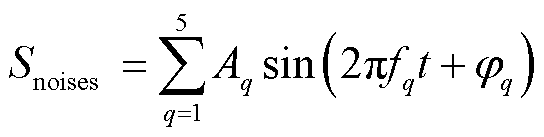 (4)
(4)
式中,Aq为幅值;fq为频率;φq为初相位。
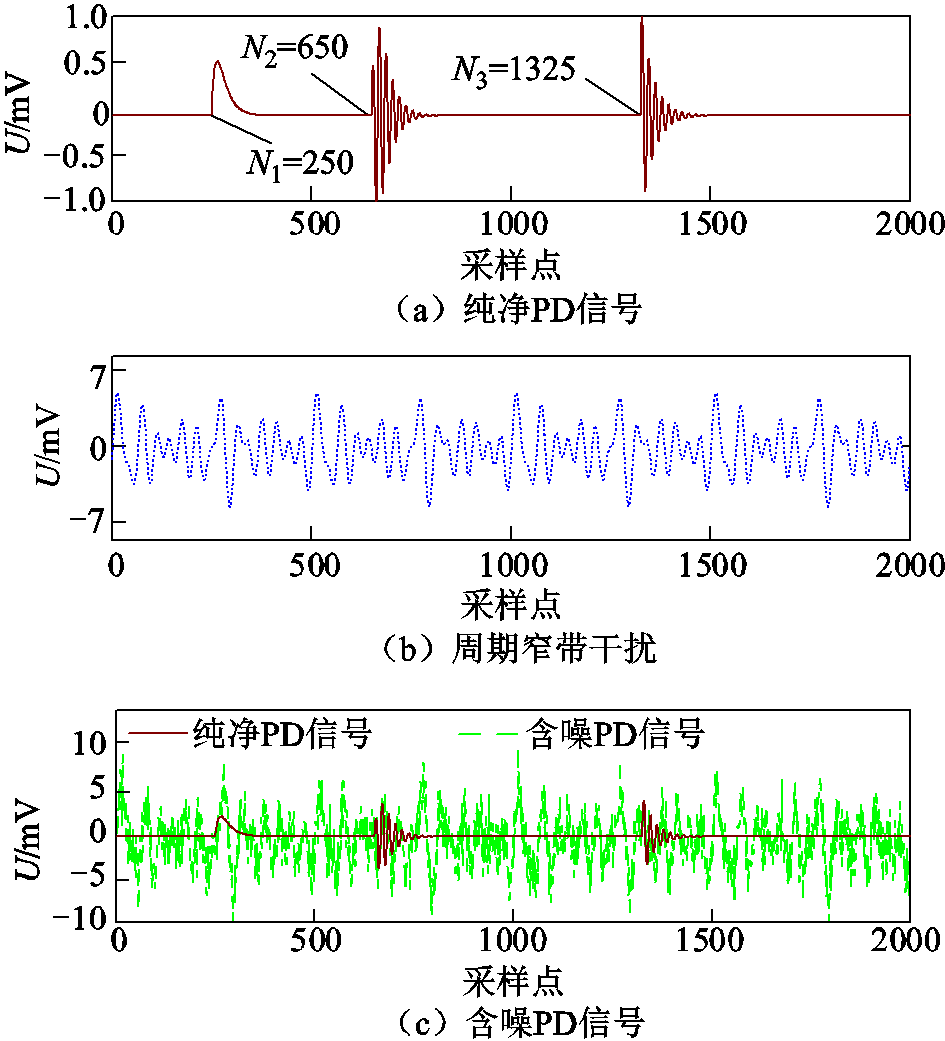
图3 仿真PD信号
Fig.3 Simulated PD signal
表2 窄带干扰参数设置
Tab.2 Parameter settings of narrowband interference

参数数值 q=1q=2q=3q=4q=5 幅值Aq/mV0.51.01.52.02.0 频率fq/MHz0.40.60.81.01.5 初相位φqπ/6π/40-π/3-π/6
针对仿真PD信号,引入信噪比SNR、波形相似系数(Normalized Correlation Coefficient, NCC)、均方误差(Mean-Square Error, MSE)三个指标[20],以此评估所提方法的去噪效果。
1)信噪比SNR是衡量降噪程度最直观的一个物理量,信噪比SNR越大,说明信号中包含的噪声越少,降噪效果越好,表达式为
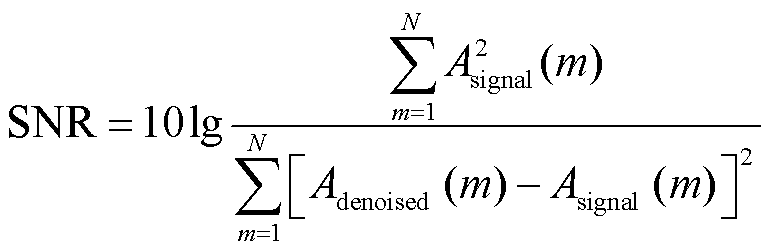 (5)
(5)
式中,m为采样点;Asignal为纯净PD信号;Adenoised为去噪后的PD信号;N为采样点总数。
2)波形相似参数NCC可反映去噪前后信号波形的整体相似度,表示为
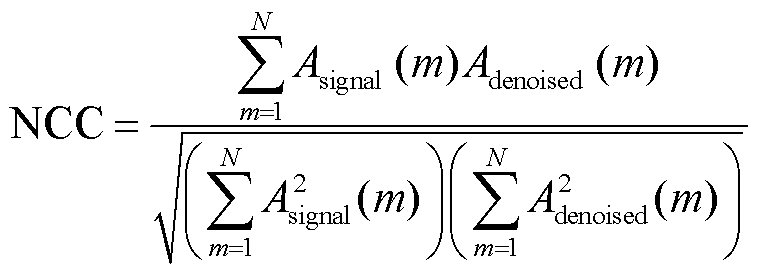 (6)
(6)
3)均方误差MSE是反映估计量与被估计量之间差异程度的一种度量,表达式为
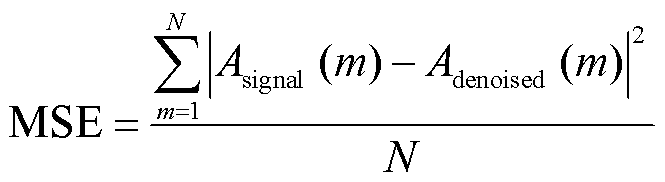 (7)
(7)
当信噪比越大、波形相似系数越趋近于1、均方误差越小时,去噪效果越好。
而在现场检测中,无法获得原始无噪声的PD信号作为参考,因此式(5)~式(7)所计算的评估指标无法在现场局部放电检测中使用。针对现场局部放电检测,本文提出了降噪率(Noise Reduction Ratio, NRR)与幅值降低率(Amplitude Reduction Ratio, ARR)这两种指标,对去噪效果进行评估[21]。
4)NRR的计算式见式(8),对于现场测量的局部放电信号,高NRR意味着去噪效果好。
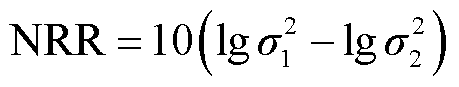 (8)
(8)
式中,σ1和σ2分别为实测PD信号的标准差和去噪后PD信号的标准差。
5)在实测局放信号的评价中添加ARR,利用PD波形的幅值对去噪效果进行评价,表示为
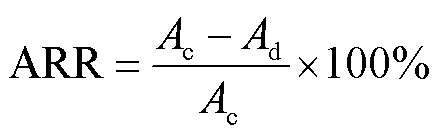 (9)
(9)
式中,Ac和Ad分别为实测PD信号的幅值和去噪后PD信号的幅值。
熵是一种用于测量随机变量出现的预期值的度量,而信息熵是一种测量样本集合分布混乱程度的度量。当随机变量分布更广泛或趋向于平均时,信息熵值越大。对于图像,随机变量是指不同位置出现的像素值。图像的信息熵是不同位置分布的灰度特征所包含的信息量,其中灰度值为i的像素出现的概率为pi,图像信息熵的定义为
![]() (10)
(10)
MVMD是一种VMD的多变量扩展,适用于多元量测数据的处理。从包括C个数据通道的输入数据x(t)中提取出预定义的K个多元调制振荡uk(t),且需满足两个条件:①提取模式的带宽总和最小;②提取模式的总和能够准确恢复原始信号。
通过谐波移位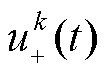 的梯度函数的L2范数估计uk(t)的带宽,得到成本函数f为
的梯度函数的L2范数估计uk(t)的带宽,得到成本函数f为
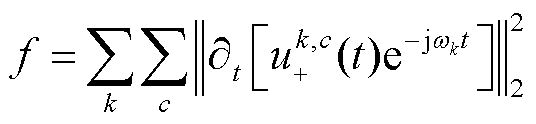 (11)
(11)
式中,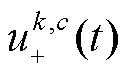 为信道数c、模式数k的解析调制信号。以频率ωk为中心,各通道单边频谱向此偏移,从而将单通道利用Frobenius范数转换成多通道,使f的表示更方便。
为信道数c、模式数k的解析调制信号。以频率ωk为中心,各通道单边频谱向此偏移,从而将单通道利用Frobenius范数转换成多通道,使f的表示更方便。
进一步,构造MVMD的变分约束模型。由于有多个线性等式约束,增广拉格朗日函数也随之变化,即
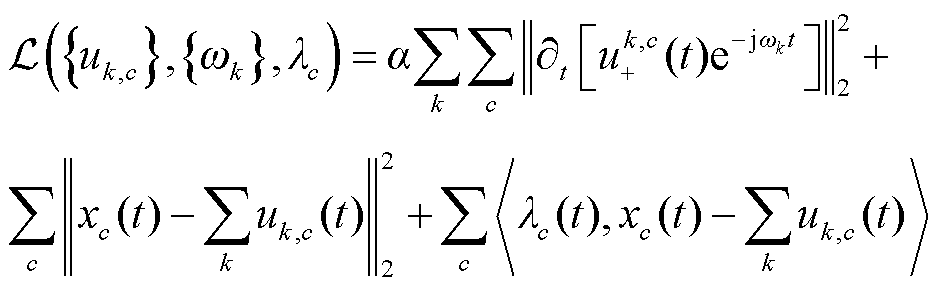 (12)
(12)
式中,uk,c为信道数c和模式数k的调制信号;λc为信道数c的拉格朗日算子;xc为信道数c的输入数据;α为MVMD算法中的惩罚因子;〈·〉为拉格朗日函数。
根据交替方向乘子法求解上述无约束优化问题,将复杂优化问题转换为一系列迭代的子优化问题。用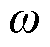 表示频率,通过迭代求解子优化问题更新中心频率,表示为
表示频率,通过迭代求解子优化问题更新中心频率,表示为
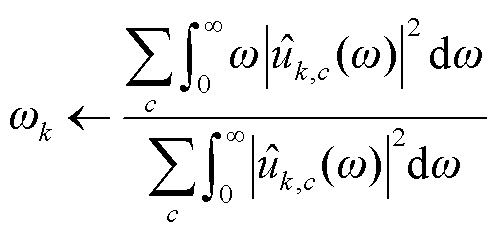 (13)
(13)
式中,上标“ˆ”表示对应变量的解析形式。
MVMD算法中的模态参数K和惩罚因子α决定了信号处理结果的优劣,其中K决定了分解的精准程度。原始信号X可由MVMD算法分解出K个本征模态函数(Intrinsic Mode Function, IMF),叠加各IMF为重构信号Y,通过文献[22]可得,当α为2 000时,MVMD的自适应性最强,此时的去噪效果最佳。本文利用图像信息熵,结合Pearson相关系数与算法执行效率,综合确定K的最优值。综上所述,最优模态参数K的确定流程如图4所示。
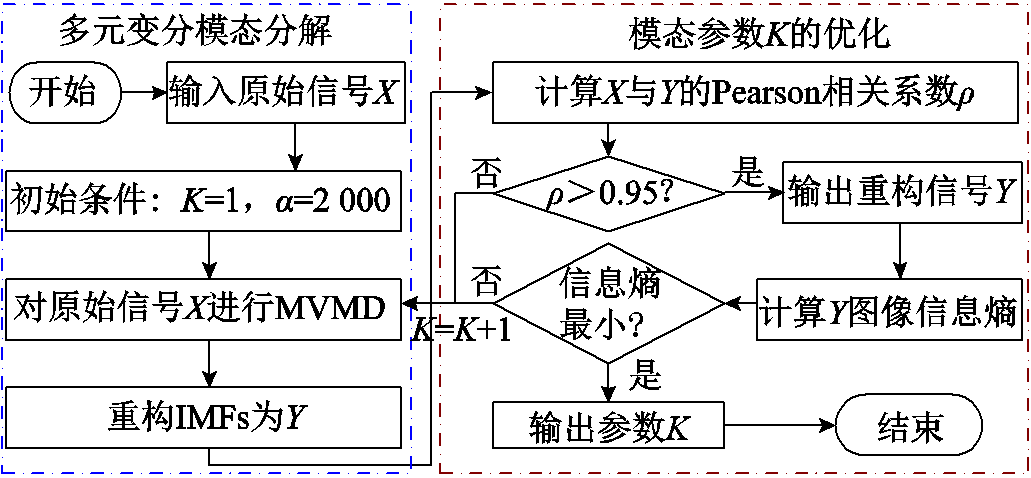
图4 参数K的确定流程
Fig.4 Process of the optimal parameter K
峭度是一种反映随机变量分布特性的数值统计量,属于无量纲参数[23]。由于它与电气量的频率、幅值、相位等无关,且对冲击信号敏感,因此适用于损伤类缺陷,尤其是PD缺陷信号的诊断。峭度计算式为
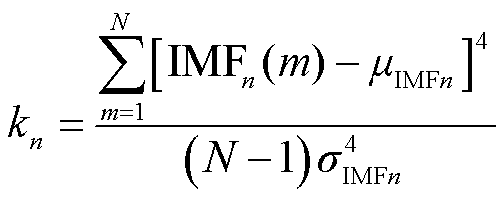 (14)
(14)
式中,IMFn为各模态分量;μIMFn、σIMFn分别为本征模态分量IMFn的均值与标准差。
3σ准则是粗差检测的常用准则之一,其基本思想是:在随机误差满足正态分布的情况下,误差绝对值约等于均值,即
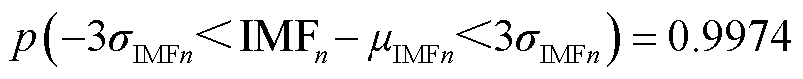 (15)
(15)
式中,p(·)表示数据落在(μ-3σ, μ+3σ)的概率。
在统计学中,若一个均值为μ、标准差为σ的变量服从正态分布,则会有99%的数据落在区间(μ-3σ, μ+3σ)中,当有数据落在此区间外,可初步把它看作异常数据。由于高斯白噪声满足N(0, σ2)的正态分布,且经过分解后的IMFn仍满足正态分布规律,而PD信号不满足这种分布,由此可以将PD信号视为粗差,利用3σ准则将小于阈值绝对值的白噪声去除,从而将PD信号分离出来。
在MVMD算法中,模态参数K的设置尤为关键。为了消除模态混叠、端点畸变、信号失真等问题[24],依据模态参数K的优化流程,对不同分解方式下的相关系数进行仿真计算,进而绘制出Pearson相关系数ρ与模态参数K的关系曲线,如图5所示。
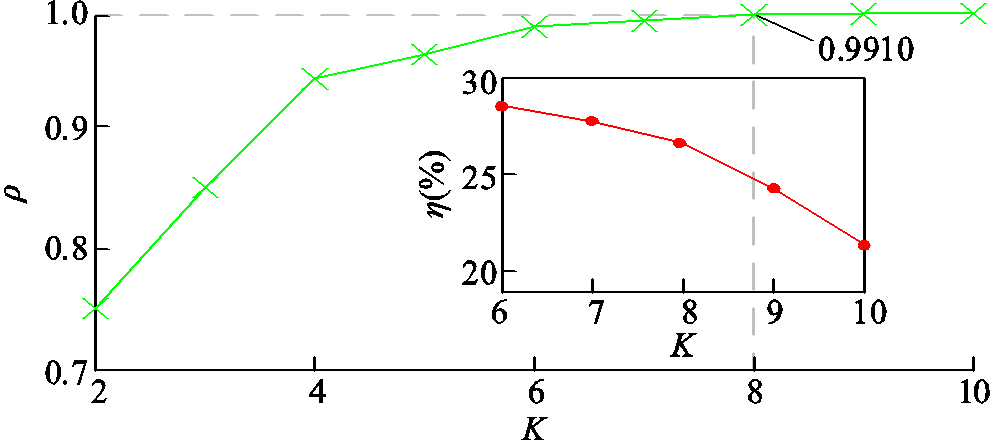
图5 相关系数ρ与K的关系
Fig.5 Relationship between ρ and K
由图5可以看出,当满足ρ>0.99时,需要K≥8,此时原始PD信号被完全分解。随着K的增加,重组PD信号会趋近原始PD信号,且模态分解造成的能量损失会相应降低。因此,相关系数会随着K的增大而增大。定义MVMD算法的执行效率η为相关系数ρ与MVMD算法耗时T的比值,即
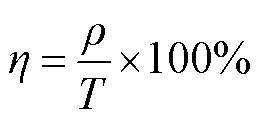 (16)
(16)
式中,T为MVMD算法运行所需的时间,s。则执行效率 越大,去噪的时效性越高。当K过大时,K-
越大,去噪的时效性越高。当K过大时,K-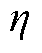 关系曲线的增长速率会发生明显下降,如图5所示。
关系曲线的增长速率会发生明显下降,如图5所示。
在RGB模型中,R=G=B的值称为灰度值,将彩色图像转换为灰度图像可以保留其梯度信息,并且大大提高计算速度与数据传输速率。因此,灰度图像可以在视觉上增加对比以突出目标区域[25]。图像信息熵值越小,图像灰度分布的聚集特征越平均,说明重组PD信号所包含的平均信息量越多,且模态分解的方式与PD信号的特征匹配的程度越高,进而能够最大程度地分解PD信号。灰度图像转换处理结果如图6所示,可以看出,不同模态参数K下重组PD信号的灰度图像的确定性程度不同,其所包含的信息量也不同。其中,当K=8时,图像信息熵值最小,表明此分解方式下局部放电信号的确定性程度最大,其噪声含量也相对较少。基于图像信息熵H与模态参数K的关系曲线能更加直观地看出最小熵值所对应的模态参数K,如图7所示。
由图7可得,图像信息熵随着模态参数K的增大呈先增大后减小再增大的变化趋势,且当K=8时,图像信息熵值最小,为1.337 0。综合考虑相关系数、图像信息熵、算法执行效率确定K的最优值为8。
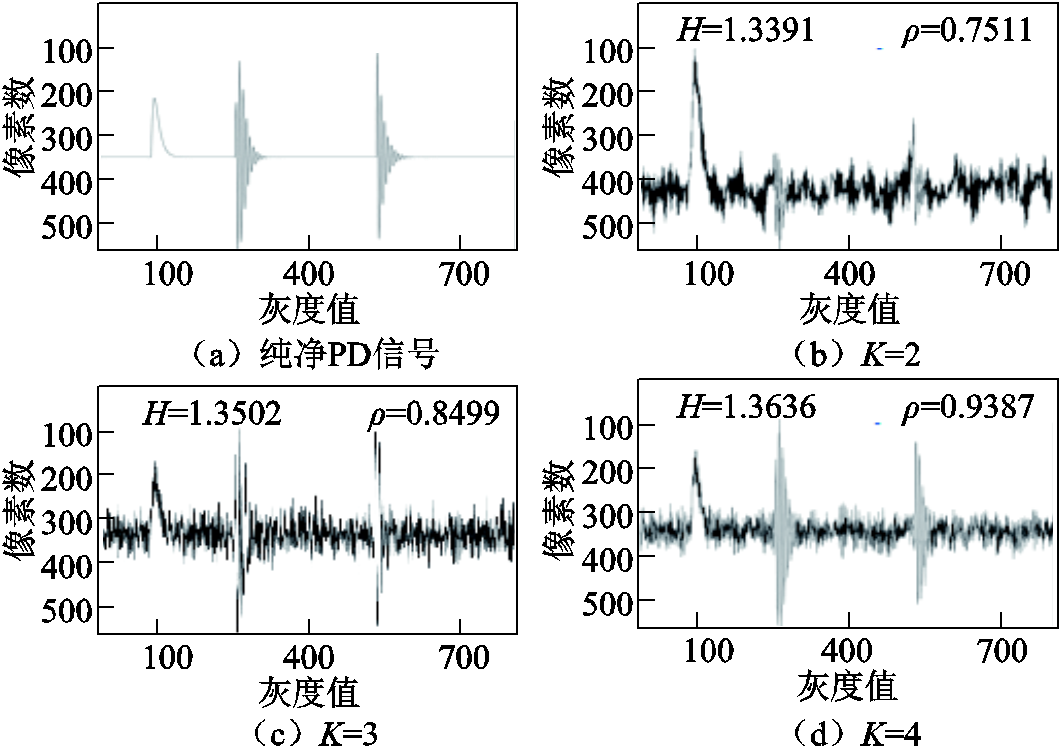
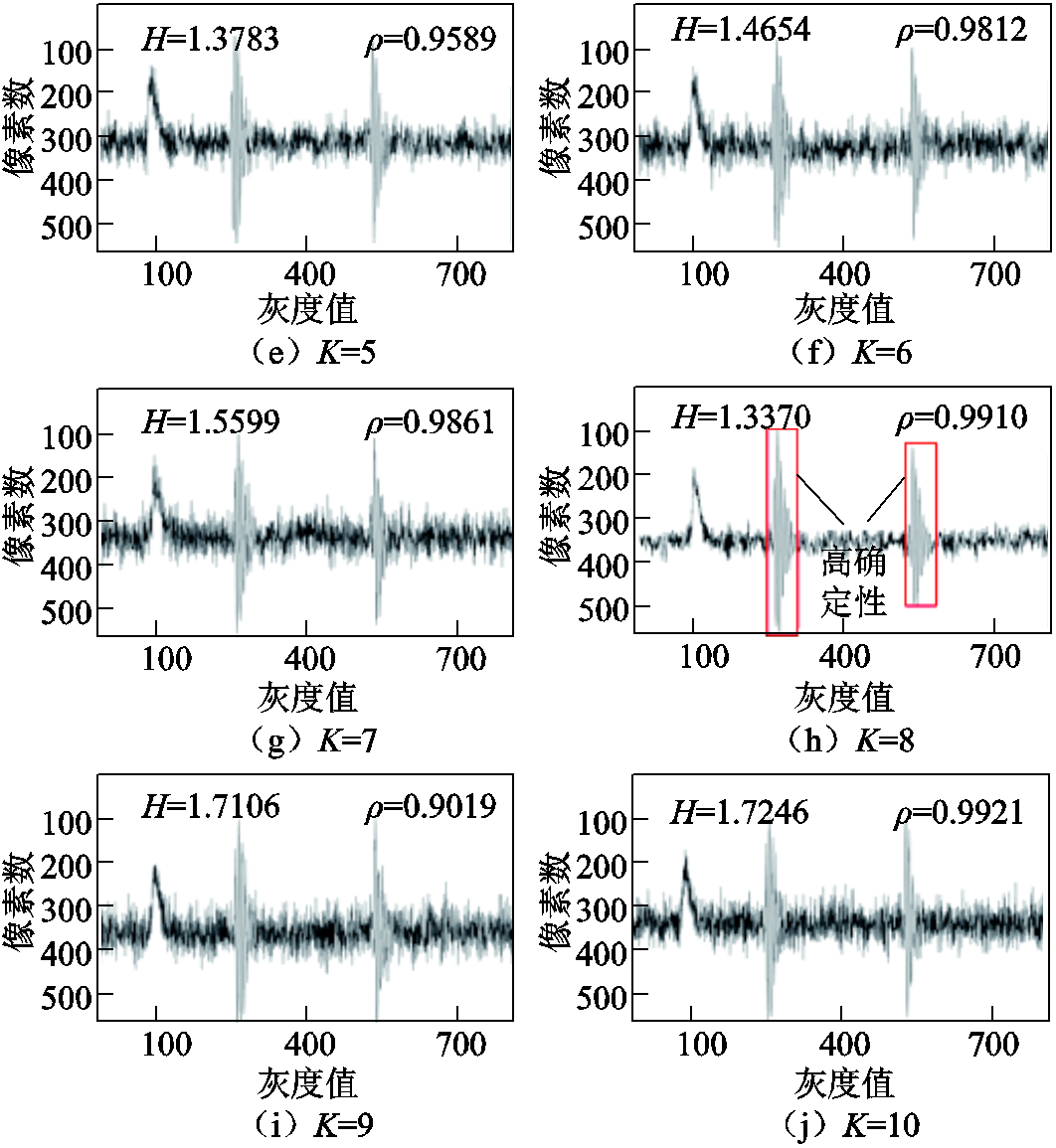
图6 灰度图像转换
Fig.6 Grayscale images conversion
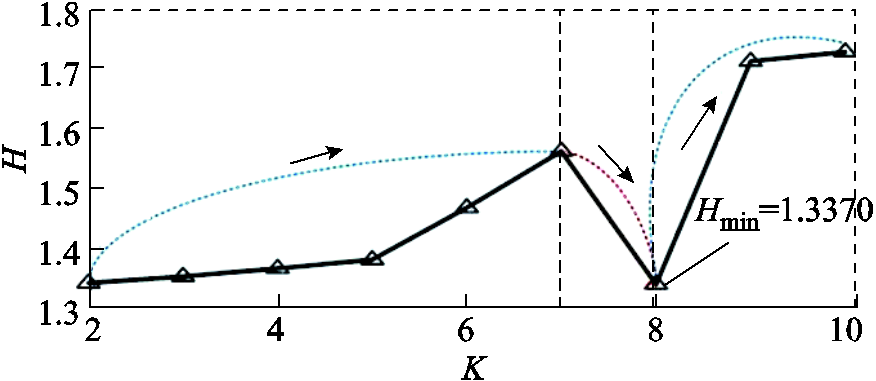
图7 图像信息熵H与K的关系
Fig.7 Relationship between H and K
文献[26]指出,若电缆未发生局部放电,测试信号的峭度值约为3;若发生局部放电,其峭度值则会大于3。因此,定义峭度大于3的模态分量为PD特征信息。为了精准地区分含噪PD信号中的PD特征信息与噪声干扰分量,本文对正弦信号与双指数衰减信号进行仿真,从而选择更具代表性的阈值。其中,幅值为1 mV、频率为1 Hz的标准正弦信号y1和双指数衰减信号y2表达式分别为
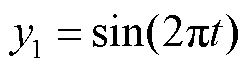 (17)
(17)
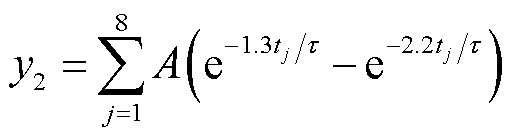 (18)
(18)
式中,A为双指数衰减信号的幅值,A=3 mV;τ为衰减系数,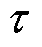 =0.5 µs;tj为信号产生的时间,分别取0、5、10、15、20、25、30、35 µs。
=0.5 µs;tj为信号产生的时间,分别取0、5、10、15、20、25、30、35 µs。
为说明峭度对噪声的敏感程度,将信噪比为-10、-5、-3、0、3、5、10 dB的高斯白噪声添加到上述两种信号中进行模拟,结果如图8所示。由图8可知,当标准正弦与双指数衰减这两种模拟信号的信噪比SNR均低于0 dB时,模拟信号的波形完全淹没于噪声中,无法有效识别信号的分布规律与特征信息;而当信噪比SNR高于0 dB时,能够基本辨别模拟信号的部分特征。因此,在具有噪声的情况下,SNR=0可以作为能否识别信号特征的边界。因此,取SNR=0时的峭度值作为阈值ε。
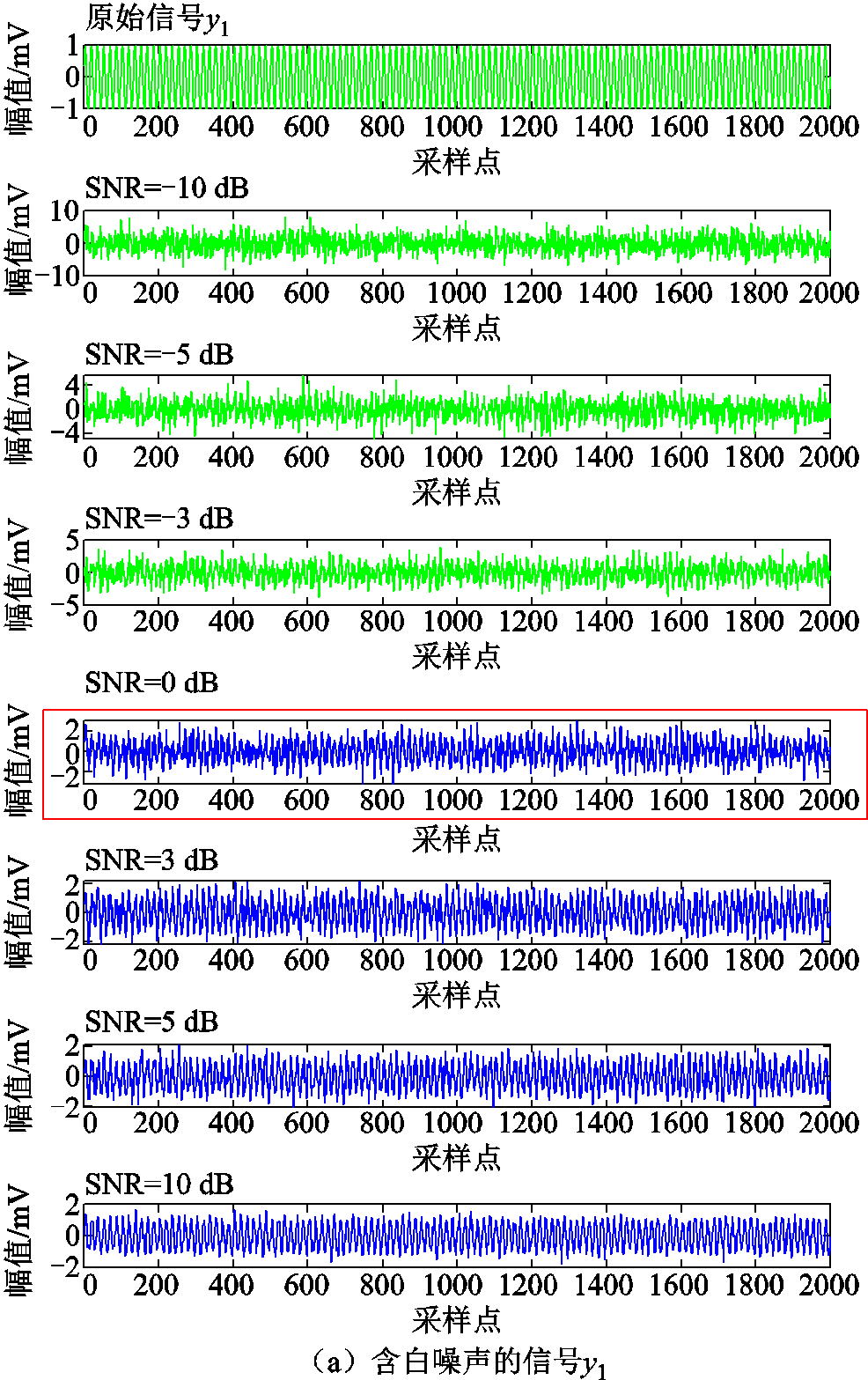
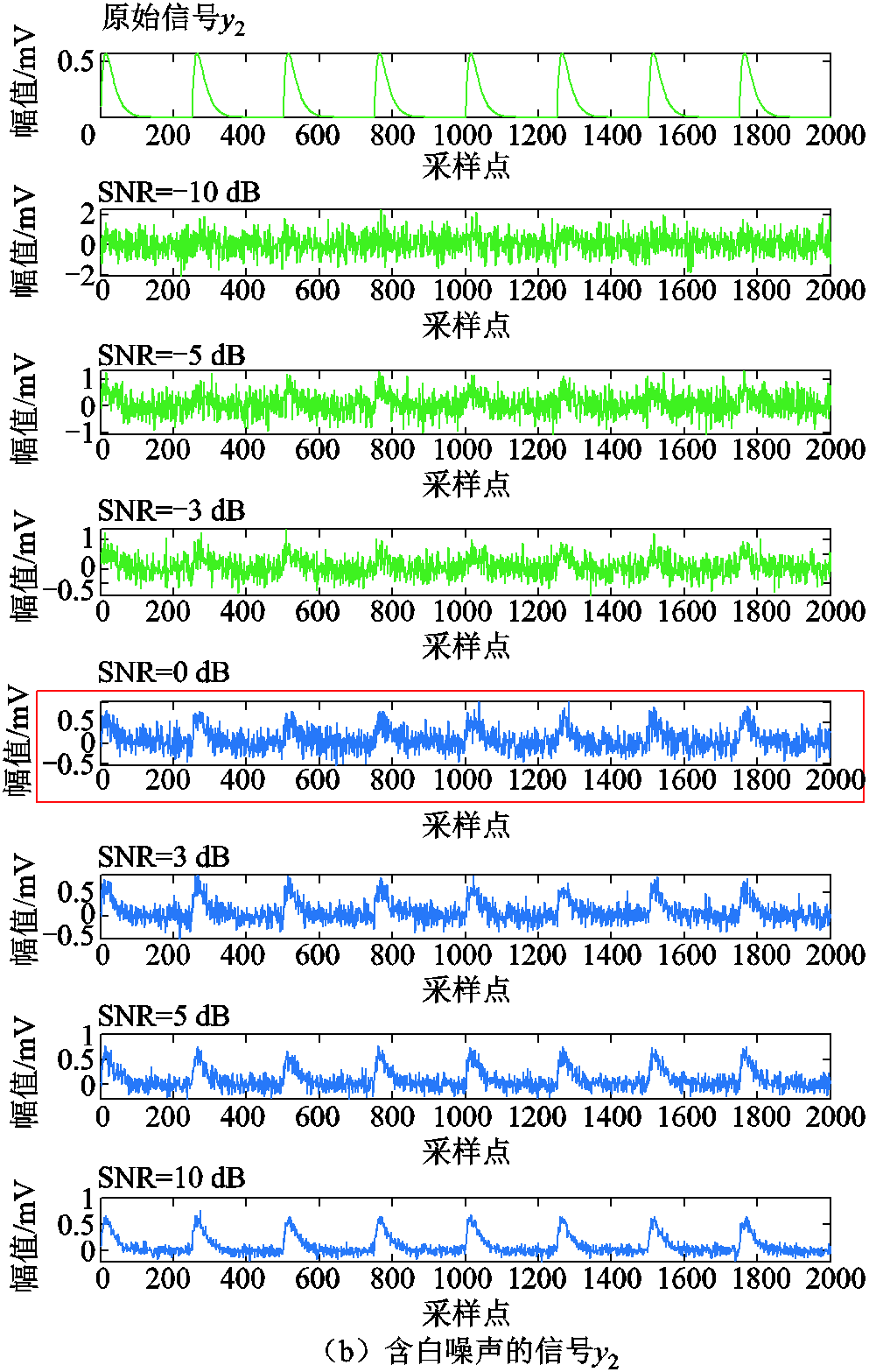
图8 不同SNR下的含噪信号
Fig.8 Noisy signals under different SNRs
但在实际应用中,由于环境噪声分布具有随机特性,应该分别测试两种信号在SNR=0时的峭度值30次,并分别求出y1、y2两种信号的峭度均值,进而取其中的最大值作为阈值ε,即
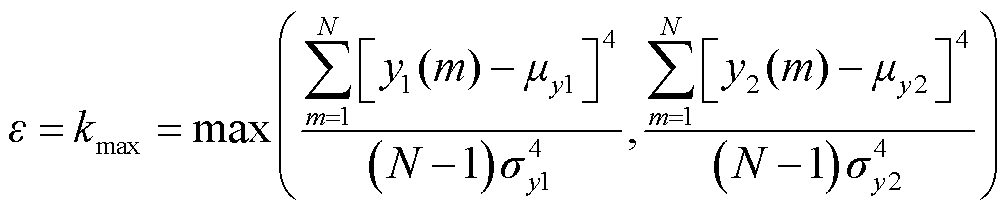 (19)
(19)
式中,kmax为标准正弦信号y1与双指数衰减信号y2在SNR=0的高斯白噪声下的峭度最大值;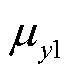 、
、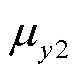 分别为y1与y2的均值;
分别为y1与y2的均值;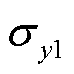 、
、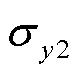 分别为y1与y2的标准差。
分别为y1与y2的标准差。
为了进一步凸显峭度具有区分PD特征信息与噪声干扰分量的作用,通过在标准正弦信号y1与双指数衰减信号y2中分别加入步长为1 dB、信噪比从-10 dB到20 dB的高斯白噪声,每个步长下均测试峭度30次并求平均值,得到含噪信号的峭度均值如图9所示。
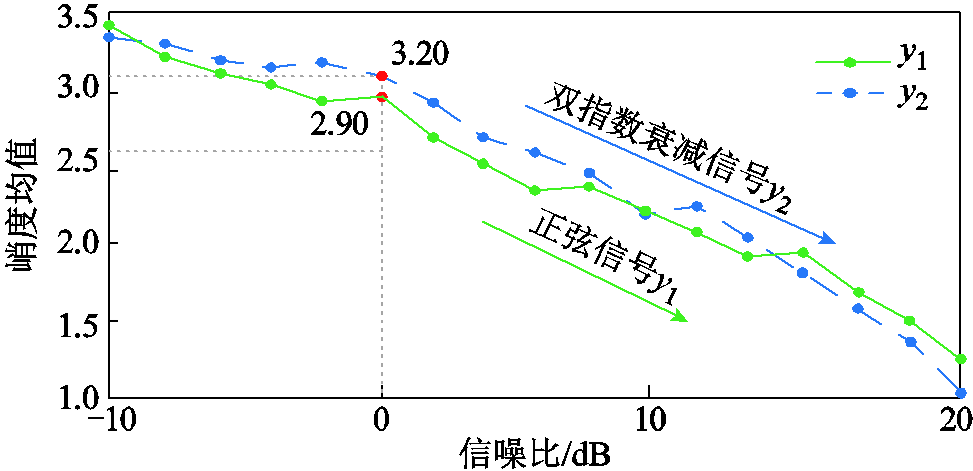
图9 含噪信号的峭度均值
Fig.9 Average kurtosis of noisy signals
由图9可知,当SNR逐渐增大时,模拟信号的峭度均值会明显呈现一个减小的趋势。因此,峭度可以辨识噪声的强度,且对PD特征信息与噪声干扰起到较好的区分作用。其中,正弦信号y1在0 dB时的峭度均值为2.90左右,而双指数衰减信号y2在0 dB时的峭度均值为3.20左右,根据尽可能滤除较多白噪声这一需求确定阈值ε=3.20,该阈值具有明确的物理意义。
本文通过小波阈值的方法对重构PD信号进行降噪处理[27]。其中,阈值大小的设置与阈值函数的选择尤为重要,会直接影响去噪后PD信号的质量。本文提出了一种新型改进小波阈值去噪方法,该方法在以下三方面具有优势:
1)小波基函数的选择。通过正确选择小波基函数以减少PD信号特征的损失。根据文献[28]可得,由高频传感器采集的电缆PD信号与db4母小波的相似程度最大,因此用db4母小波作为小波基函数。
2)分解尺度的设置。采用1.2节的含噪PD信号,设置信噪比为3 dB,计算不同分解层数下去噪信号的SNR值。通过仿真与计算,分解层数分别取1、2、3、4、5、6、7时,对应去噪后的SNR分别为9.058、10.692、11.560、12.233、13.369、15.150、14.072 dB。根据此变化趋势可以看出,分解尺度设置为6时,去噪信号的SNR最高,表明此时的去噪能力最好,因此采用6层db4小波分解。
3)小波阈值的确定和阈值函数的改进。改进小波阈值及阈值函数的特征在于:①改进阈值是在通用阈值δ的基础上追踪了小波分解层数l,能够追踪每一层级的信号特征;②改进阈值函数的系数为指数衰减型,因此拟合局部放电信号波形特征的效果更好,进而能够在消除阈值函数不连续性的同时使函数曲线迅速靠近硬阈值函数,从而减小恒定偏差,为提升去噪效果奠定了基础。改进阈值的设置为
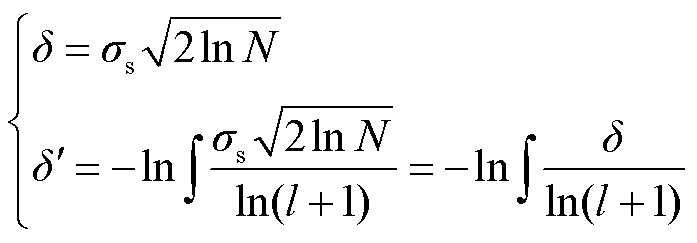 (20)
(20)
式中,δ为通用阈值;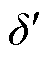 为本文改进的小波阈值;σs为重构PD信号的标准差。
为本文改进的小波阈值;σs为重构PD信号的标准差。
阈值函数的计算式为
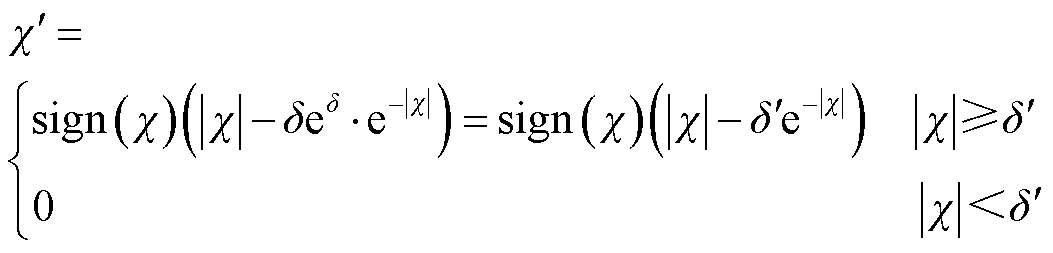 (21)
(21)
式中,χ为未经处理的小波系数;χ′为经过阈值函数处理后的小波系数。
为了对比本文的改进阈值函数与传统阈值的特点[29],分别利用改进阈值函数、软阈值函数、硬阈值函数对含噪的仿真PD信号进行去噪,结果如图10所示,具体计算的评价指标见表3。
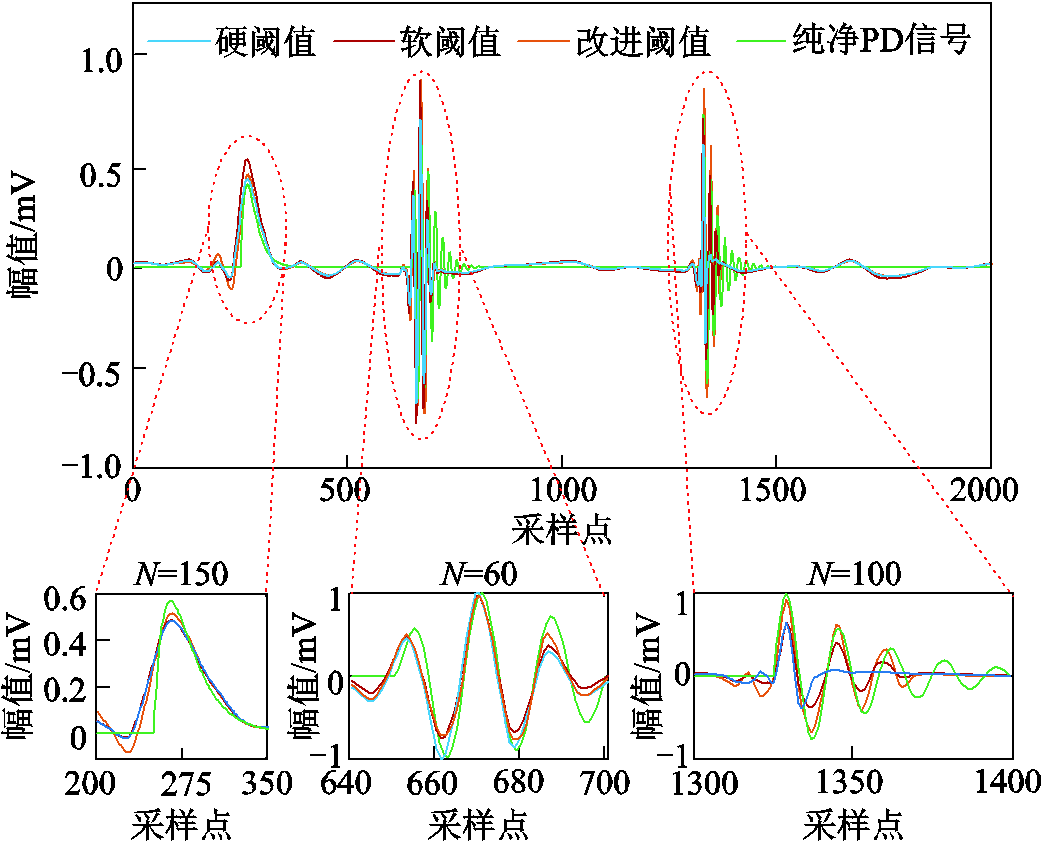
图10 三种阈值函数的去噪结果
Fig.10 De-noised results of three threshold functions
表3 三种函数的去噪效果
Tab.3 De-noised performance evaluation of three threshold functions

阈值函数SNR/dBNCCMSE/mV2 软阈值7.856 10.833 10.044 6 硬阈值8.851 50.890 30.039 8 改进阈值13.033 40.950 50.024 6
由图10可得,通过改进阈值去噪后的PD信号更贴近纯净PD信号的波形,且其幅值误差小,残余噪声少;而通过软阈值去噪后的PD信号存在恒定偏差,导致与纯净PD信号在幅值上有较大差异;通过硬阈值去噪得到的信号在无PD特征时的噪声较多,因此去噪效果不理想。
根据表3可得,通过改进阈值函数去噪后的PD信号的SNR最大,约为13.033 4 dB。同时,改进阈值函数去噪后PD信号的NCC约为0.950 5,最接近1,MSE约为0.024 6 mV2,最接近0。当SNR越大,NCC越趋近于1,MSE越小,去噪效果越好。由此表明,本文提出的改进阈值函数能更好地拟合PD信号的波形特征,进而使去噪后的PD信号更接近纯净PD信号。本文去噪方法的流程如图11所示。
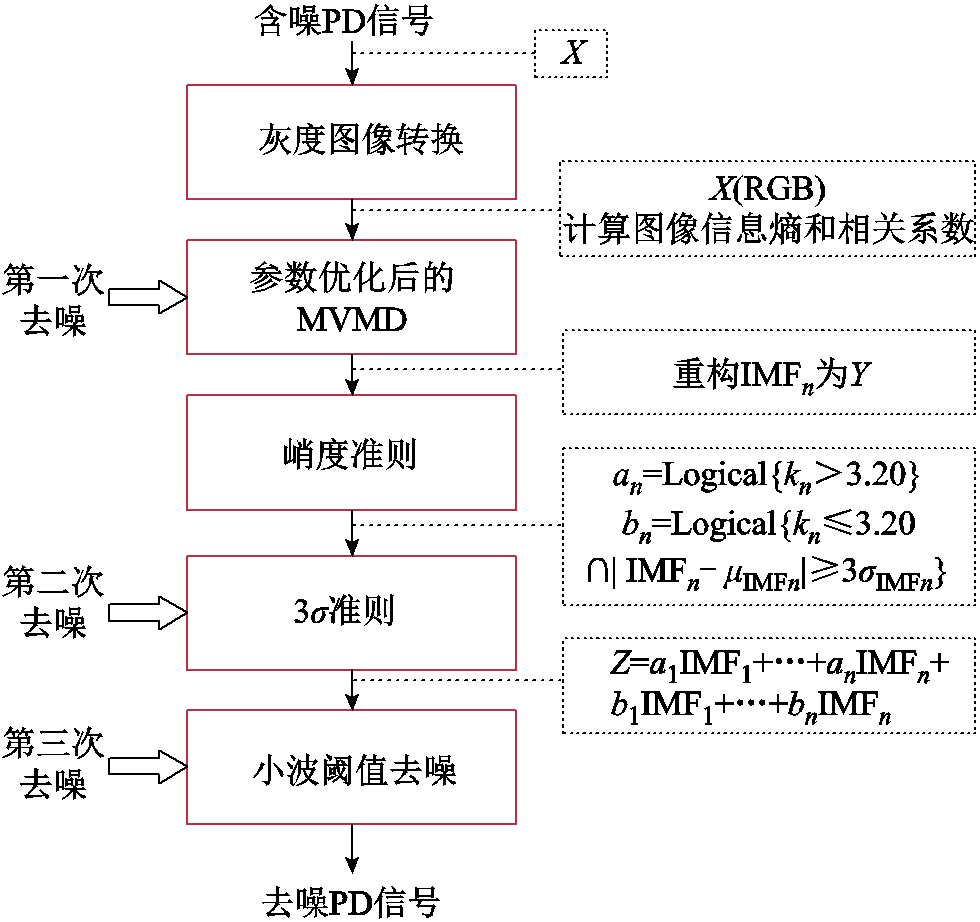
图11 去噪流程
Fig.11 Flow chart of the denoising method
1)在确定最优模态参数的基础上,对PD信号进行MVMD分解,得到IMFn的波形如图12所示,可以看出,采用MVMD算法可以准确地实现PD信号的特征提取,所得的各个IMFn分量具有明确的物理意义。
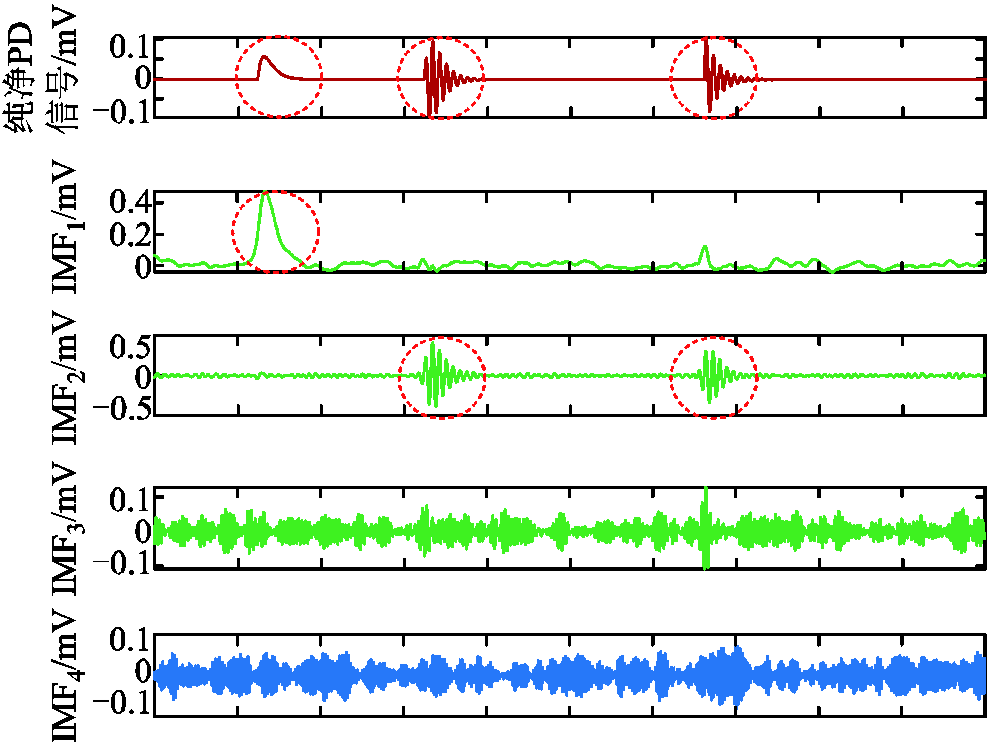
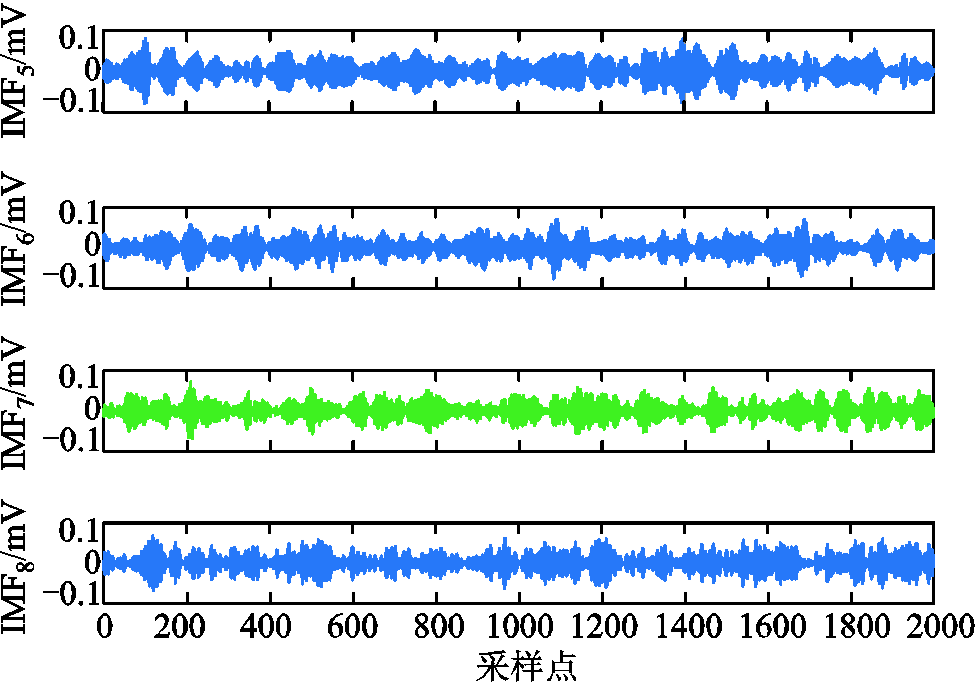
图12 含噪信号的MVMD分解
Fig.12 MVMD of noisy signal
2)对IMF1~IMF8各模态分量分别进行峭度计算,其结果见表4。
表4 IMFn的峭度值
Tab.4 Kurtosis values of IMFn

n12345678 kn30.817.610.32.913.043.093.232.95
由表4可知,IMF1、IMF2、IMF3、IMF7的峭度值均大于3.20,而其他模态分量的峭度值小于阈值。因此,将IMF1、IMF2、IMF3与IMF7归类为PD特征信息。其中,IMF1、IMF2的峭度值远大于IMF7,由此看出,前两个模态分量所包含PD信息的特征量多,而IMF7则相对较少。
3)根据峭度大小判定模态分量的特征。由计算结果可知,IMF1、IMF2、IMF3、IMF7为PD特征信息,而IMF4、IMF5、IMF6、IMF8属于噪声干扰分量。
4)通过3σ准则对噪声干扰分量进行滤除。
5)将滤噪后的噪声干扰分量与PD特征信息进行叠加得到重构PD信号Z,其计算式为
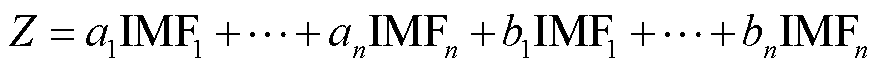 (22)
(22)
其中
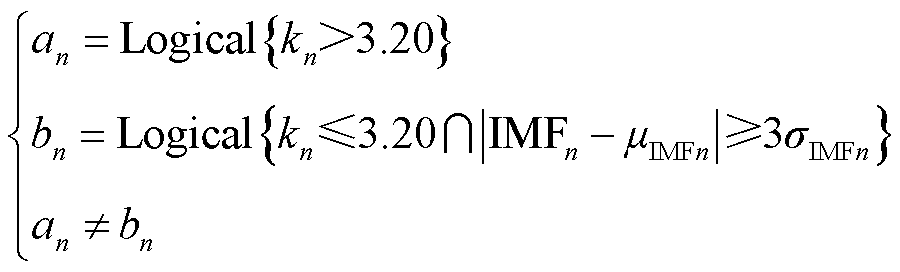
式中,Logical{·}为逻辑判断函数,满足条件返回1;不满足置零。
6)通过新型改进小波阈值对重构信号Z进行去噪,从而输出去噪后的PD信号。
此外,对相同条件下的仿真含噪PD信号分别通过基于Spearman的变分模态分解(Spearman-VMD, S-VMD)法[10]、NAEEMD法[9]、短时傅里叶变换-奇异值分解(Short-Time Fourier Transform-Singular Value Decomposition, STFT-SVD)法[6]与本文方法进行去噪对比,结果如图13所示。从而根据去噪PD信号与纯净PD信号进行计算与评估。
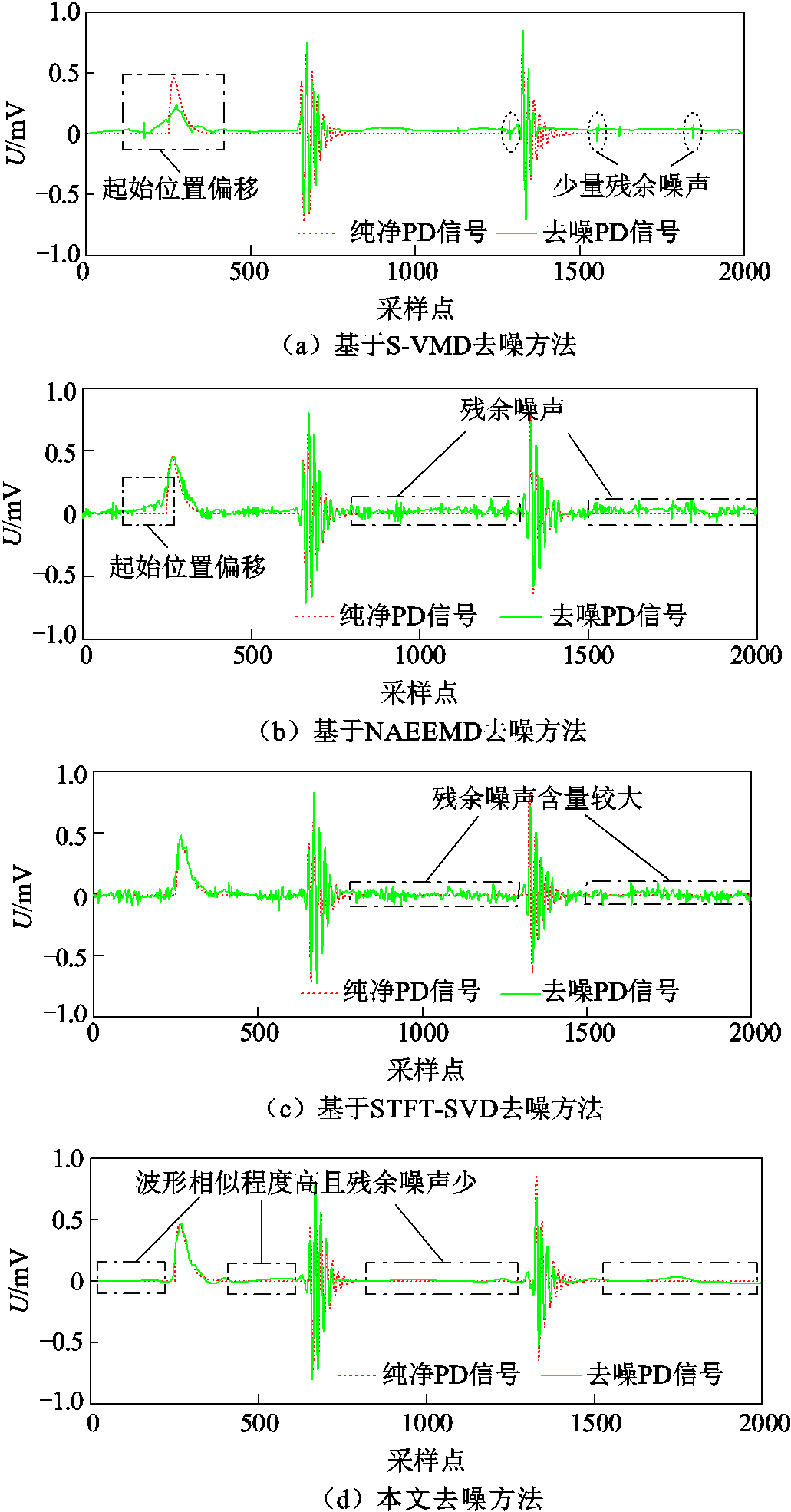
图13 PD信号去噪结果
Fig.13 De-noised results of PD signal
由图13a可知,含噪PD信号经过S-VMD法进行去噪后依旧有残余噪声,去噪效果不理想;由图13b可知,NAEEMD法虽然能在模态混叠和端点效应的问题上起到一定的改善作用,但不能完全消除,这会导致PD信号放电的起始位置发生一定程度的偏移;图13c中,STFT-SVD法的去噪效果明显有所改善,但仍存在一定程度的噪声,会影响缺陷的诊断与评估;根据图13d可得,本文方法能使去噪后的PD信号波形与纯净PD信号保持一致,且幅值大小不变,由此保证PD信号在不失真的同时能最大程度地消除白噪声与窄带干扰。
为了验证所提方法具有优越的抗噪性,对仿真PD信号的原始信号波形与上述不同去噪算法的仿真结果进行频谱分析,如图14所示。
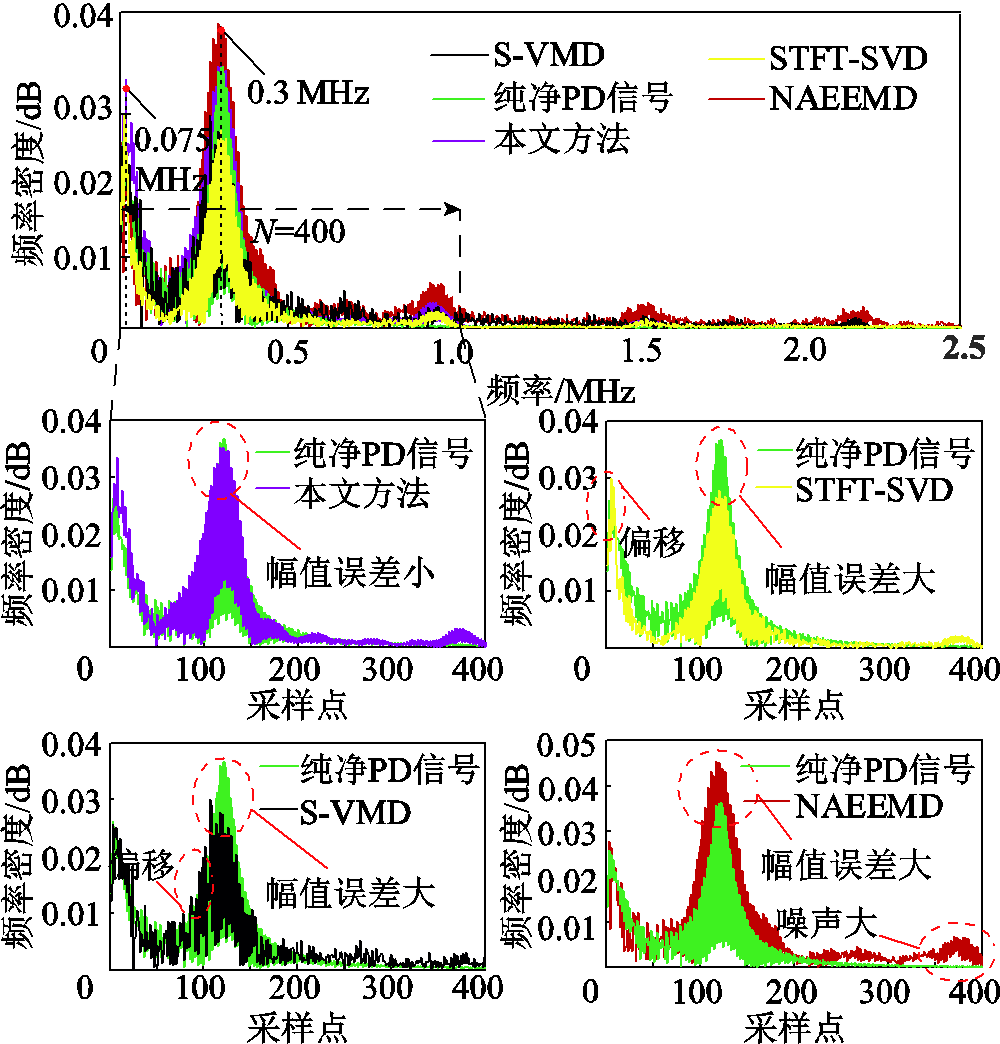
图14 PD信号去噪后的频谱分析
Fig.14 Spectrum analysis after denoising of PD signal
由图14可以看出,PD信号中包含的有用信息主要集中在0.075 MHz和0.3 MHz。显然,周期窄带干扰信号集中在0~0.075 MHz范围内,并且其余低频带因为存在噪声分量而出现毛刺现象。此外,将上述三种方法与本文方法的去噪效果结合纯净PD信号一起进行频谱分析可以看出,前三种去噪方法都较为成功地抑制了PD信号的周期窄带干扰和高斯白噪声。然而,STFT-SVD法和本文去噪方法比NAEEMD法和S-VMD法的去噪效果更好,且在频谱分布上,去噪结果更加接近纯净PD信号。通过比较噪声和窄带干扰对局部放电信号频谱分布的影响可以看出,使用本文方法去噪得到的去噪PD信号的波形特征比STFT-SVD法更丰富。同时,去噪PD信号与纯净PD信号的频率分布基本一致,体现了本文方法对于PD信号去噪的优越性。
通过SNR、NCC、MSE三种指标的计算,进一步对比上述四种方法的去噪效果,结果见表5。
由表5可知,本文方法在各评价指标中最为理想,具体表现为:去噪PD信号的SNR最大,代表残余的噪声含量最少,进而说明降噪效果最好;NCC最接近于1,表明去噪PD信号与纯净PD信号在波形上的相似程度最高且失真程度最小;MSE最小,说明去噪后的PD信号在幅值与频率上的误差最小。
表5 去噪算法的评价指标
Tab.5 Evaluation index values of denoising algorithms

去噪方法SNR/dBNCCMSE/mV2 S-VMD[10]8.413 50.872 20.082 5 NAEEMD[9]11.229 40.921 30.061 9 STFT-SVD[6]12.180 50.932 50.035 4 本文方法14.458 00.969 70.030 2
在考虑去噪效果的同时,要尽可能地避免由于算法过于复杂而出现耗时长、执行效率低的问题。因此,对仿真PD信号,依据信噪比SNR、波形相似系数NCC、均方误差MSE与算法耗时T等参数,建立算法执行效率Es,如式(23)所示,并对本文方法与对比的三种方法进行仿真与计算,结果见表6;而对于现场实测的局部放电信号,由于现场检测中无法获得原始无噪声的PD信号作为参考,无法计算SNR、NCC、MSE这三种评价指标。因此,考虑降噪率NRR、幅值降低率ARR与算法耗时T等参数,调整处理现场实测PD信号的算法执行效率为Et,如式(24)所示。
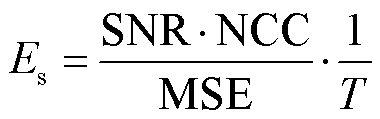 (23)
(23)
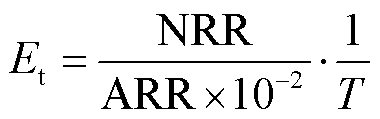 (24)
(24)
表6 算法耗时与执行效率
Tab.6 Algorithm time and execution efficiency

对比参数S-VMDNAEEMDSTFT-SVD本文方法 T/s5.8430.6400.5810.282 Es/s-114.73106.97186.42464.24
通过比较算法的运行时间与执行效率可以看出,本文去噪方法的耗时远远少于S-VMD法,且约为执行STFT-SVD法和NAEEMD法所用时间的1/2。因此,就执行效率而言,本文方法明显优于其他三种算法,当数据量较大时,该方法仍能保持较高的执行效率。
为了研究本文方法在不同信噪比下的降噪情况,在图3a中分别加入信噪比为-2、0、2 dB的高斯白噪声。在此基础上再添加参数完全相同的周期窄带,通过SNR、NCC、MSE三种去噪评估指标,对上述不同去噪方法进行对比,结果见表7。
表7 不同信噪比下的去噪结果
Tab.7 De-noised results under different SNRs
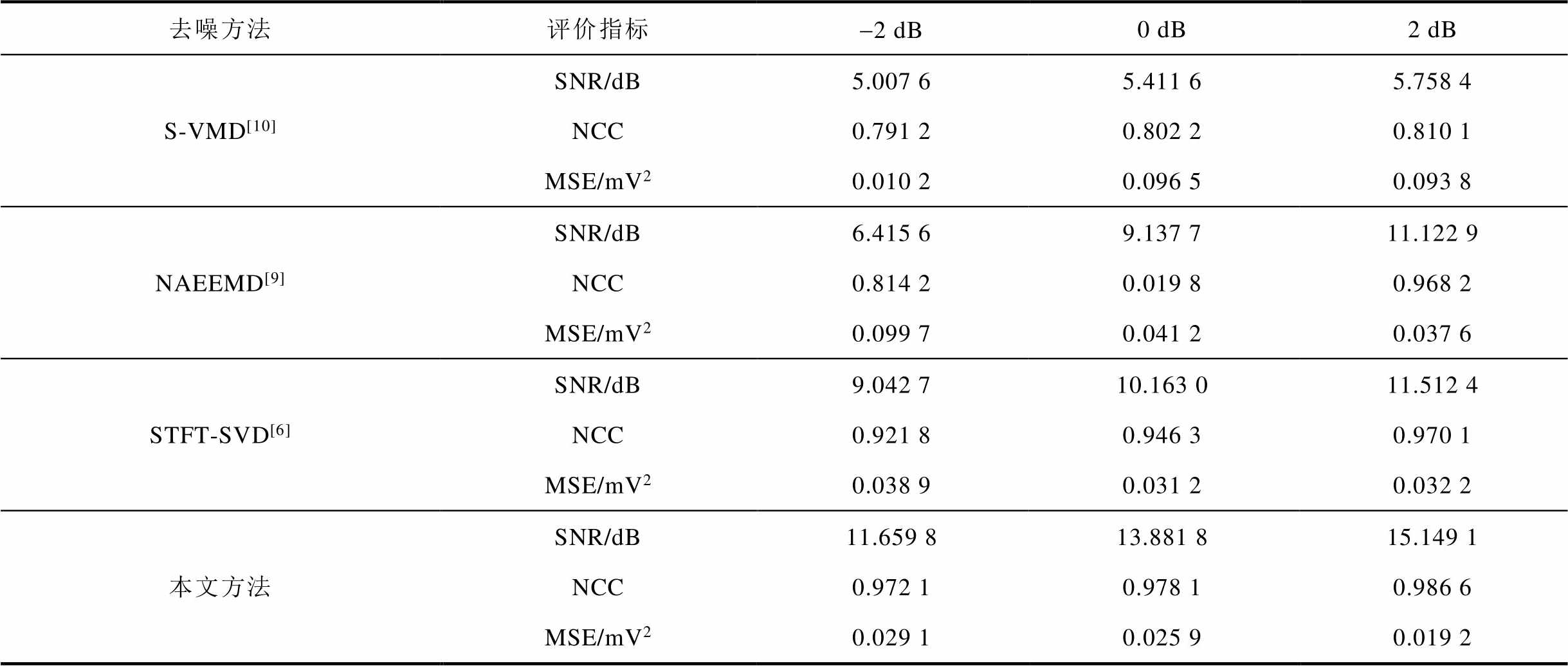
去噪方法评价指标-2 dB0 dB2 dB S-VMD[10]SNR/dB5.007 65.411 65.758 4 NCC0.791 20.802 20.810 1 MSE/mV20.010 20.096 50.093 8 NAEEMD[9]SNR/dB6.415 69.137 711.122 9 NCC0.814 20.019 80.968 2 MSE/mV20.099 70.041 20.037 6 STFT-SVD[6]SNR/dB9.042 710.163 011.512 4 NCC0.921 80.946 30.970 1 MSE/mV20.038 90.031 20.032 2 本文方法SNR/dB11.659 813.881 815.149 1 NCC0.972 10.978 10.986 6 MSE/mV20.029 10.025 90.019 2
由表7可知,在不同程度高斯白噪声下,本文方法的去噪评价指标均优于其他三种算法,且在SNR<0 dB的恶劣条件下仍然具有较好的去噪效果。
通过4.1节的仿真与分析可知,对于仿真PD信号,本文方法具有优越性与高效性。为了验证该方法对实测PD信号同样具有优势,将其应用于现场采集的实测PD信号中,并与S-VMD法、STFT-SVD法和NAEEMD法进行对比分析。
4.2.1 现场测试设备
实测PD数据来源于中国西安市某地区环网柜与配电室进行的电缆振荡波局部放电测试。配电网的简单测试拓扑如图15a所示,详细参数见表8,电缆振荡波PD测试接线如图15b所示。整个试验回路分为两部分:直流预充电回路和电缆与电感充放电回路。这两个回路之间通过快速关断开关实现转换。通过时域脉冲反射法,按照规定的加压幅值与加压次数进行振荡波试验,采集每次激励下的局部放电信号[30]。部分现场测试所用设备如图16所示。
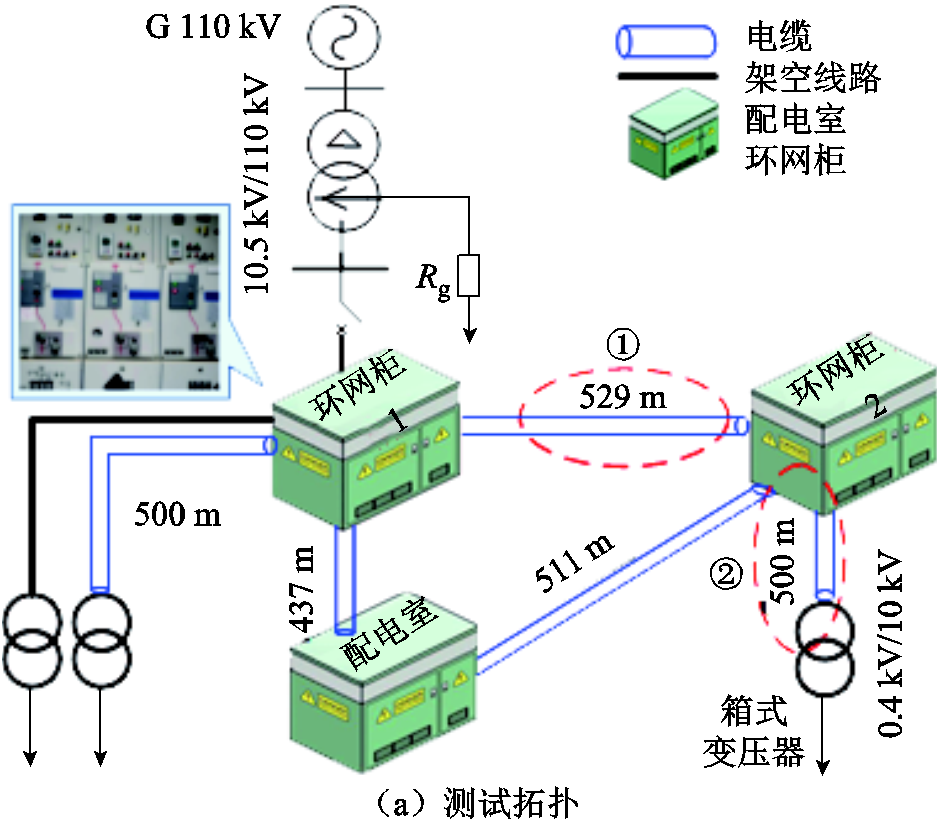
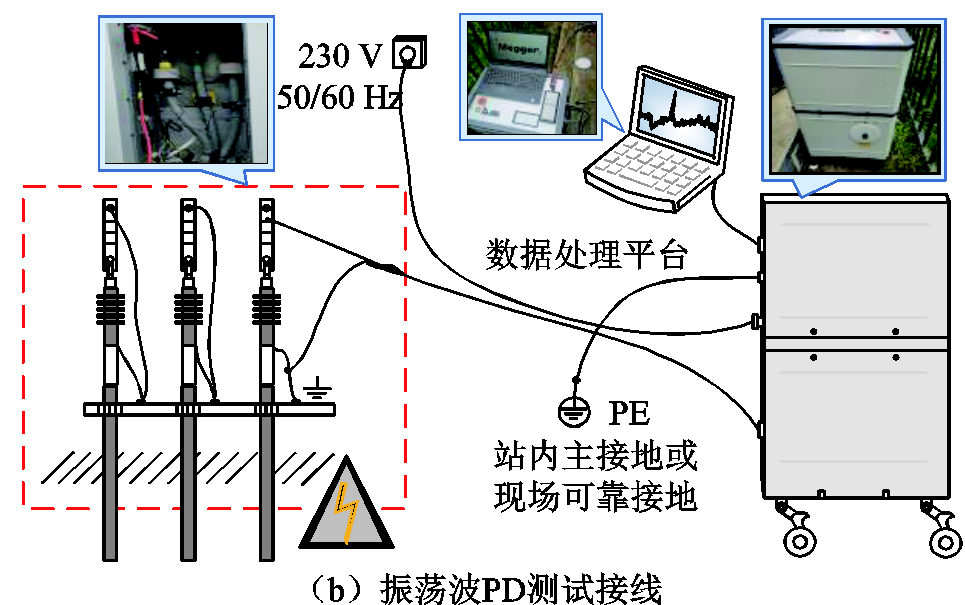
图15 振荡波局部放电测试
Fig.15 Oscillating waves PD measurement
表8 详细拓扑参数
Tab.8 Detailed topology parameters

实测数据放电位置电缆长度/m绝缘电缆规格 ①中间接头529XLPEYJV22-3×300-8.7/15 kV ②电缆本体500

图16 现场测试设备
Fig.16 Field measurement equipment
高频电流传感器通过在环状磁心上缠绕多匝导电线圈制成,安装在电缆的接地线上。采样数据通过光纤传输到数据处理平台进行处理。振荡波局部放电测试仪(Megger DAC-30)的采样频率为125 MHz,带宽可在3~25 MHz范围内自动切换,局部放电灵敏度范围为2 pC~100 nC(根据IEC 60270),分辨率为±1 pC/(±0.1 m)。
4.2.2 实测数据①
西安市某地区检测到某环网柜至配电室一段长529 m的XLPE电缆中间接头发生局部放电,采集的实测PD信号如图17a所示,其噪声含量较小,因此添加一定程度的高斯白噪声使其被噪声掩盖,得到如图17b所示的实测含噪PD信号。
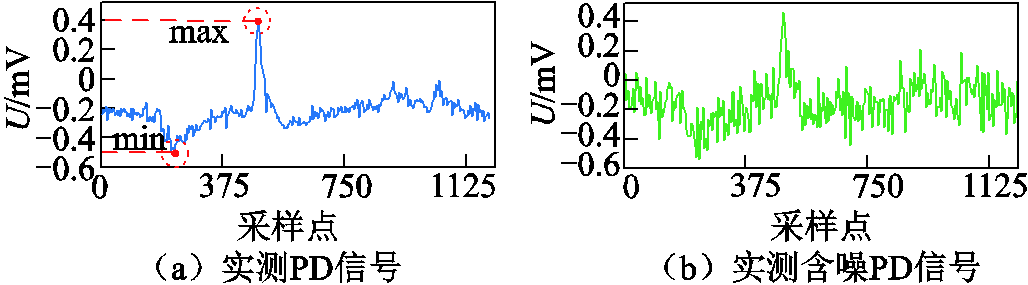
图17 实测数据①
Fig.17 Measured data ①
利用本文去噪方法与S-VMD法[10]、NAEEMD法[9]、STFT-SVD法[6]分别对实测PD信号进行去噪处理,去噪后的波形如图18所示。
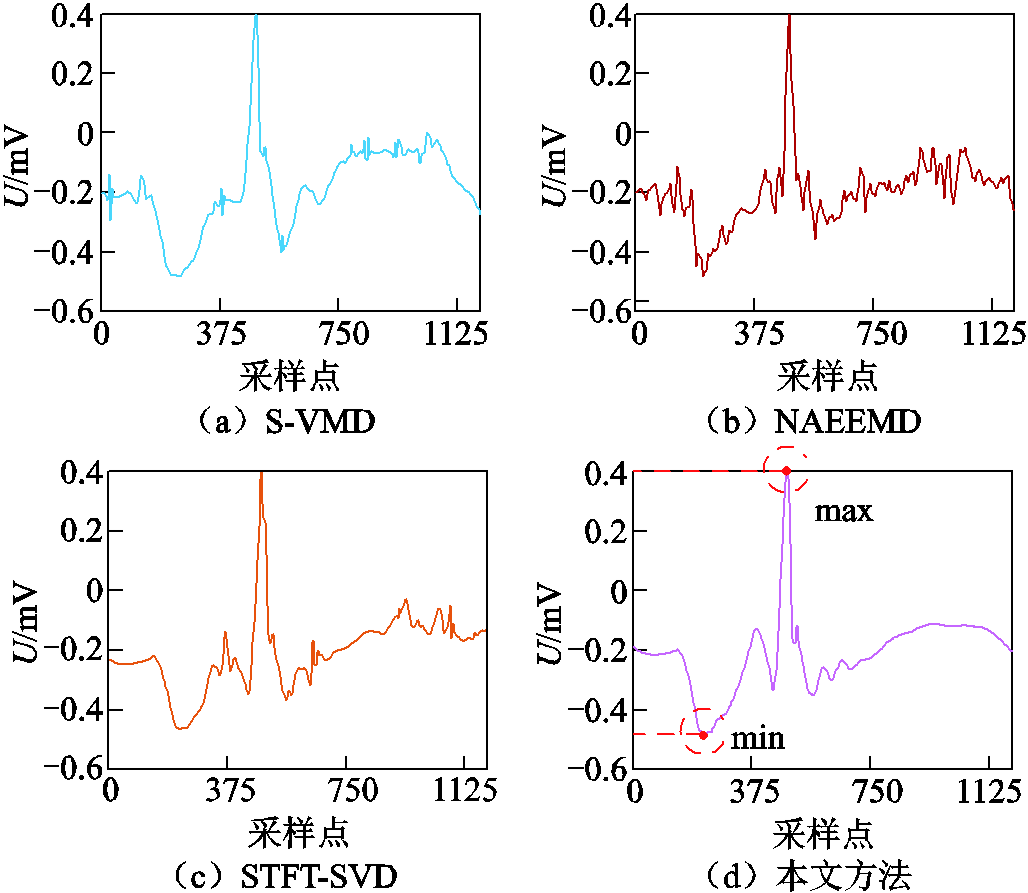
图18 实测数据①的去噪结果
Fig.18 De-noised results of measured data ①
通过图18可以清楚地看出,使用NAEEMD法和STFT-SVD法去噪后,仍有残余噪声,会影响后续电缆的缺陷诊断与定位;通过S-VMD法去噪后的波形的残余噪声相对较少;通过本文方法去噪能够很大程度地抑制白噪声,且去噪后的局部放电信号特征明显、容易识别。
4.2.3 实测数据②
西安市某地区检测到某配电室母线至箱式变压器一段长500 m的XLPE电缆发生局部放电,分析过程与实测数据①相同。首先,将如图19a所示的PD信号人为添加白噪声后得到如图19b所示的实测含噪PD信号。其次,通过本文方法与上述其他三种方法分别对实测含噪PD信号进行去噪处理,不同方法的去噪效果明显不同,如图20所示。
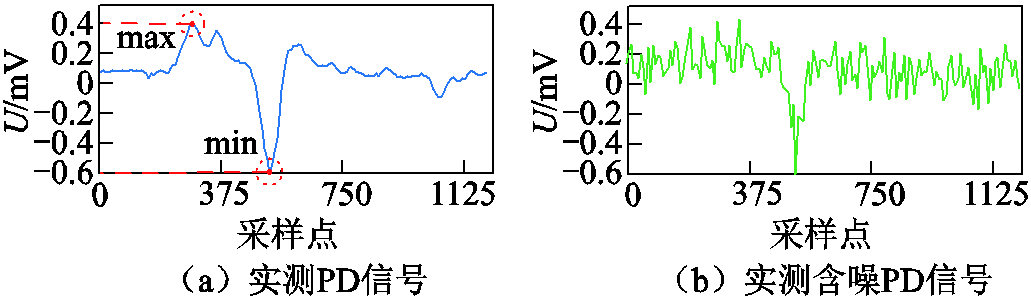
图19 实测数据②
Fig.19 Measured data ②
结合图17~图20可以看出,在实测数据①中,采集缺陷信号的最大值、最小值分别为0.40 mV与-0.47 mV,经过四种方法去噪后,PD信号的幅值大小基本与采集的缺陷信号保持一致,但通过本文方法去噪后的PD波形残余噪声较少;在实测数据②中,采集缺陷信号的最大幅值为0.40 mV、最小幅值为-0.60 mV,只有通过本文方法去噪得到的PD信号在幅值大小上与采集PD信号相同,而通过其他三种方法得到去噪后的PD信号均有较大程度的失真。
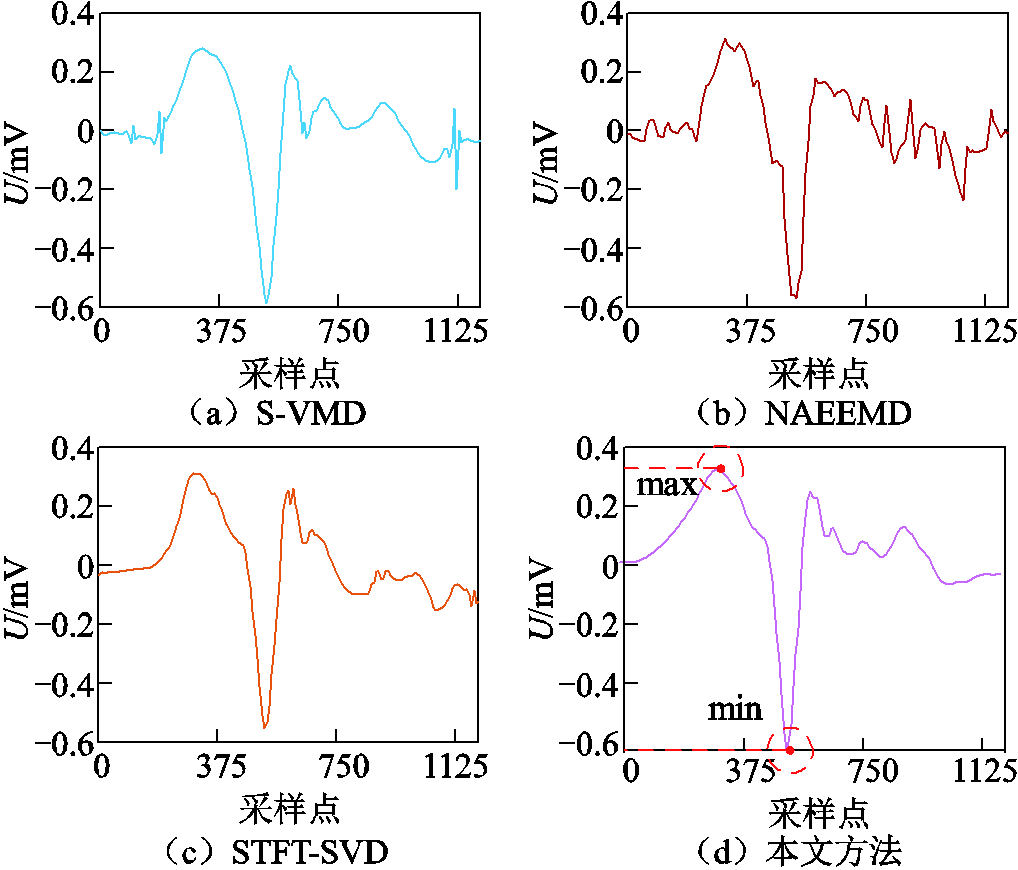
图20 实测数据②的去噪结果
Fig.20 De-noised results of measured data ②
因此,以上两种不同位置的实测PD信号通过本文方法去噪后,得到的去噪PD信号不仅在波形上的相似程度高、残余噪声含量少,而且在幅值上的误差小。两种不同位置的实测PD信号的评价指标见表9。由表9可以得出相同的结论:本文方法的NRR值在两种实测数据中均为最大,且ARR值均为最小。在实测数据①、实测数据②中的NRR分别为6.213 6、8.422 9,远大于S-VMD[10]和NAEEMD[9],略微大于STFT-SVD[6],且ARR值明显小于其他三种方法。高NRR值与低ARR值表示去噪效果好,因此,本文方法对于现场测量中实际采集的PD信号的去噪效果同样具有优越性。
表9 实测数据的评价指标
Tab.9 Evaluation index values of measured data

指标数据文献[10]文献[9]文献[6]本文方法 NRR①3.411 13.334 24.325 96.213 6 ②3.177 03.892 55.904 88.422 9 ARR(%)①35.03747.40030.42323.168 ②38.02142.56827.18322.730
算法耗时与执行效率对比结果见表10。由表10可知,本文方法在实测PD信号去噪的耗时上远远少于S-VMD与STFT-SVD,较少于NAEEMD,且通过综合指标的建立,在算法的执行效率上进一步扩大优势,明显优于其他方法。
表10 实测数据的算法耗时与执行效率
Tab.10 Time and execution efficiency of measured data

指标数据文献[10]文献[9]文献[6]本文方法 T/s①2.7330.3181.9300.129 ②2.0370.2222.2050.133 Et/s-1①3.56222.1207.367270.905 ②4.10241.1909.851278.619
本文提出了基于图像信息熵与多元变分模态分解的局部放电信号去噪方法,利用该方法对仿真PD信号和实测PD信号进行去噪,验证了本文方法的有效性与优越性,并得出以下结论:
1)本文方法能够有效地抑制白噪声与周期窄带干扰,进而最大程度地保留有用的PD特征信息。同时,该方法去噪效果的各类评价指标均优于 S-VMD、NAEEMD、STFT-SVD。
2)该方法利用图像信息熵与相关系数,结合执行效率综合优化MVMD的模态参数,实现了含噪PD信号的最优分解,克服了模态混叠现象,进而能够精确提取PD特征信息,以改善现场PD检测的准确率,为后续的缺陷诊断与状态评估奠定基础。
3)本文方法采用正弦信号与双指数衰减信号的最大峭度均值作为判定各模态特征的阈值,通过求取各IMF的峭度值能够准确辨别IMF的特征信息,使得在去噪效果具有明显优越性的同时压缩数据以减少耗时并提高执行效率。对于大数据高效率的去噪场合,该方法的优越性与工程价值更高。
参考文献
[1] 常文治. 电力电缆中间接头典型缺陷局部放电发展过程的研究[D]. 北京: 华北电力大学, 2013.
Chang Wenzhi. Study on development of typical partial discharges in power cables joint[D]. Beijing: North China Electric Power University, 2013.
[2] Pan Cheng, Chen G, Tang Ju, et al. Numerical modeling of partial discharges in a solid dielectric-bounded cavity: a review[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2019, 26(3): 981-1000.
[3] Ashtiani M B, Shahrtash S M. Partial discharge de-noising employing adaptive singular value decomposition[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2014, 21(2): 775-782.
[4] 周凯, 黄永禄, 谢敏, 等. 短时奇异值分解用于局放信号混合噪声抑制[J]. 电工技术学报, 2019, 34(11): 2435-2443.
Zhou Kai, Huang Yonglu, Xie Min, et al. Mixed noises suppression of partial discharge signal employing short-time singular value decomposition[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2435-2443.
[5] 饶显杰, 周凯, 汪先进, 等. 基于改进SVD算法的局部放电窄带干扰抑制方法[J]. 高电压技术, 2021, 47(2): 705-713.
Rao Xianjie, Zhou Kai, Wang Xianjin, et al. Suppression of narrow-band noise of partial discharge based on improved SVD algorithm[J]. High Voltage Engineering, 2021, 47(2): 705-713.
[6] Yan Yuan, Trinchero R, Stievano I S, et al. An automatic tool for partial discharge de-noising via short-time Fourier transform and matrix factorization [J]. IEEE Transactions on Instrumentation and Measurement, 2022, 71: 1-12.
[7] Chan J C, Ma Hui, Saha T K, et al. Self-adaptive partial discharge signal de-noising based on ensemble empirical mode decomposition and automatic morphological thresholding[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2014, 21(1): 294-303.
[8] Kedadouche M, Thomas M, Tahan A. A comparative study between empirical wavelet transforms and empirical mode decomposition methods: application to bearing defect diagnosis[J]. Mechanical Systems and Signal Processing, 2016, 81: 88-107.
[9] Jin Tao, Li Qiangguang, Mohamed M A. A novel adaptive EEMD method for switchgear partial discharge signal denoising[J]. IEEE Access, 2019, 7: 58139-58147.
[10] Dragomiretskiy K, Zosso D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544.
[11] 马星河, 孔卫东, 李自强, 等. 一种基于S_VMD与Sdr_SampEn的局部放电信号去噪方法[J]. 电力系统保护与控制, 2022, 50(18): 29-38.
Ma Xinghe, Kong Weidong, Li Ziqiang, et al. A denoising method for a partial discharge signal based on S_VMD and Sdr_SampEn[J]. Power System Protection and Control, 2022, 50(18): 29-38.
[12] Hussein R, Shaban K B, El-Hag A H. Wavelet transform with histogram-based threshold estimation for online partial discharge signal denoising[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(12): 3601-3614.
[13] Tang Ju, Zhou Siyuan, Pan Cheng. A denoising algorithm for partial discharge measurement based on the combination of wavelet threshold and total variation theory[J]. IEEE Transactions on Instrumen-tation and Measurement, 2020, 69(6): 3428-3441.
[14] Zhou Siyuan, Tang Ju, Pan Cheng, et al. Partial discharge signal denoising based on wavelet pair and block thresholding[J]. IEEE Access, 2020, 8: 119688-119696.
[15] 徐永干, 姜杰, 唐昆明, 等. 基于Hankel矩阵和奇异值分解的局部放电窄带干扰抑制方法[J]. 电网技术, 2020, 44(7): 2762-2769.
Xu Yonggan, Jiang Jie, Tang Kunming, et al. A method of suppressing narrow-band interference in partial discharge based on Hankel matrix and singular value decomposition[J]. Power System Technology, 2020, 44(7): 2762-2769.
[16] 揭青松, 杨庆, 崔浩楠, 等. 基于暂态电压传递特性的电缆接头绝缘状态检测方法[J]. 高电压技术, 2022, 48(3): 1124-1132.
Jie Qingsong, Yang Qing, Cui Haonan, et al. Insulation state detection method of cable joint based on transient voltage transfer characteristics[J]. High Voltage Engineering, 2022, 48(3): 1124-1132.
[17] 唐炬, 高丽, 谢颜斌, 等. 复小波包变换抑制PD监测中周期性窄带干扰[J]. 高电压技术, 2008, 34(11): 2355-2361.
Tang Ju, Gao Li, Xie Yanbin, et al. Suppressing PD’s periodicity narrow band noise in the PD measurement by using complex wavelet packet transform[J]. High Voltage Engineering, 2008, 34(11): 2355-2361.
[18] Zhong Jun, Bi Xiaowen, Shu Qin, et al. Partial discharge signal denoising based on singular value decomposition and empirical wavelet transform[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 69(11): 8866-8873.
[19] 唐炬, 黄江岸, 张晓星, 等. 局部放电在线监测中混频周期性窄带干扰的抑制[J]. 中国电机工程学报, 2010, 30(13): 121-127.
Tang Ju, Huang Jiangan, Zhang Xiaoxing, et al. Suppression of the periodic narrow-band noise with mixed frequencies in partial discharge on-line monitoring[J]. Proceedings of the CSEE, 2010, 30(13): 121-127.
[20] 李文华, 姜惠, 赵正元, 等. 基于波形匹配端点延拓法优化的经验模态分解算法在铁路继电器参数降噪上的应用[J]. 电工技术学报, 2022, 37(10): 2656-2664.
Li Wenhua, Jiang Hui, Zhao Zhengyuan, et al. Application of empirical mode decomposition algorithm based on waveform matching endpoint continuation method in noise reduction of railway relay parameters[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2656-2664.
[21] Ghorat M, Gharehpetian G B, Latifi H, et al. A new partial discharge signal denoising algorithm based on adaptive dual-tree complex wavelet transform[J]. IEEE Transactions on Instrumentation and Measure-ment, 2018, 67(10): 2262-2272.
[22] 杨童亮, 胡东, 唐超, 等. 基于SMA-VMD-GRU模型的变压器油中溶解气体含量预测[J]. 电工技术学报, 2023, 38(1): 117-130.
Yang Tongliang, Hu Dong, Tang Chao, et al. Prediction of dissolved gas content in transformer oil based on SMA-VMD-GRU model[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 117-130.
[23] 徐黄宽, 张黎, Bilal Iqbal Ayubi, 等. 基于改进变分模态分解去噪的高频电应力下聚酰亚胺局部放电温-频特性研究[J]. 电工技术学报, 2023, 38(3): 565-576.
Xu Huangkuan, Zhang Li, Ayubi B I, et al. Study on temperature-frequency partial discharge characteristics of polyimide under high frequency electrical stress based on improved variational modal decomposition denoising[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 565-576.
[24] 刘灏, 商峻, 毕天姝, 等. 基于实测数据的电网频率信号特征分析与提取方法[J]. 电力系统自动化, 2023, 47(10): 135-144.
Liu Hao, Shang Jun, Bi Tianshu, et al. Feature analysis and extraction method of power grid frequency signal based on measured data[J]. Automation of Electric Power Systems, 2023, 47(10): 135-144.
[25] 唐炬, 魏钢, 李伟, 等. 基于双向二维最大间距准则的局部放电灰度图像特征提取[J]. 电网技术, 2011, 35(3): 129-134.
Tang Ju, Wei Gang, Li Wei, et al. Partial discharge gray image feature extraction based on bi-directional two-dimensional maximum margin criterion[J]. Power System Technology, 2011, 35(3): 129-134.
[26] 毕潇文, 钟俊, 张大堃, 等. 基于改进奇异值与经验小波分解的局放去噪算法[J]. 电网技术, 2021, 45(12): 4957-4963.
Bi Xiaowen, Zhong Jun, Zhang Dakun, et al. Improved singular value and empirical wavelet decomposition algorithm in partial discharge denoising[J]. Power System Technology, 2021, 45(12): 4957-4963.
[27] Wang Qiusheng, Kundur D, Yuan Haiwen, et al. Noise suppression of corona current measurement from HVdc transmission lines[J]. IEEE Transactions on Instrumentation and Measurement, 2016, 65(2): 264-275.
[28] 夏琴, 肖洒, 周刚, 等. 改进VMD和提升小波在局部放电去噪中的应用[J]. 电气自动化, 2022, 44(6): 46-48, 52.
Xia Qin, Xiao Sa, Zhou Gang, et al. Application of improved variational mode decomposition and lifting wavelet method in partial discharge denoising[J]. Electrical Automation, 2022, 44(6): 46-48, 52.
[29] 王维博, 董蕊莹, 曾文入, 等. 基于改进阈值和阈值函数的电能质量小波去噪方法[J]. 电工技术学报, 2019, 34(2): 409-418.
Wang Weibo, Dong Ruiying, Zeng Wenru, et al. A wavelet de-noising method for power quality based on an improved threshold and threshold function[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 409-418.
[30] 沈谢林, 王利, 郭建钊, 等. 10 kV配电电缆绝缘耐压与局放一体化测试方法研究[J]. 高压电器, 2023, 59(2): 120-126.
Shen Xielin, Wang Li, Guo Jianzhao, et al. Research on integrated method for withstanding voltage and partial discharge test of 10 kV power cable insulation [J]. High Voltage Apparatus, 2023, 59(2): 120-126.
Abstract In recent years, cross-linked polyethylene cables have been developed in transmission lines and urban distribution networks due to their advantages, lightweight, high-temperature resistance, and high transmission power. With the increase in the number of XLPE power cables put into operation and the extension of cable lines, silicone rubber insulated prefabricated intermediate joints are widely used in XLPE power cables due to their excellent high-voltage shielding performance, overall prefabricated design, reliable grounding, large voltage margin, and convenient on-site installation. The intermediate cable joint is usually installed and formed on the laying site, which can quickly leave a hidden danger of cable operation failure. Because it comprises multi-layer solid composite structures with different dielectric properties, the probability of accidents is much higher than that of the cable body.
Partial discharge (PD) detection is the main means of evaluating the insulation status of XLPE cables and the manufacturing and installation defects of cables. A PD denoising method based on image information entropy and novel adaptive multivariate variational mode decomposition (MVMD) is proposed to address the issues of white noise, periodic narrowband interference, and poor adaptability in on-site detection of PD at cable terminals and intermediate joints. Firstly, optimize the parameters of the MVMD algorithm by integrating multiple factors, and then, based on parameter optimization, perform modal decomposition on the noisy PD signal. Secondly, the kurtosis of each eigenmode component is calculated, and the kurtosis of the sine signal and double exponential decay signal at the signal-to-noise ratio of 0dB is calculated by using the characteristic that kurtosis is sensitive to noise to distinguish the PD characteristic information from the noise interference component. Then, the 3σ criterion is used to filter white noise with normal distribution. Finally, based on the improved new wavelet threshold function, the reconstructed PD signal is denoised to obtain the denoised PD signal.
The following conclusions can be drawn by comparing the method with other denoising algorithms: (1) The Spearman variational mode decomposition (S-VMD) can improve modal aliasing, but there is still residual noise in the denoised signal. Hence, the denoising effect is not ideal. (2) The novel adaptive ensemble empirical mode decomposition (NAEEMD) cannot wholly eliminate modal aliasing, resulting in a certain degree of displacement of the discharge starting position and affecting subsequent diagnosis and positioning. (3) Although the short-time Fourier transform and matrix factorization (STFT-SVD) can effectively suppress white noise and periodic narrowband interference, the denoised PD signal contains residual noise, and the execution efficiency of this algorithm is low. (4) By calculating various evaluation indicators, the method has a good denoising effect on the on-site noisy PD signal. At the same time, this method has the advantages of less time consumption and high execution efficiency.
The following conclusions can be drawn: (1) The information entropy is used to measure the aggregation characteristics of the gray image distribution accurately and then to determine the certainty of the PD pulse signal. By constructing the information entropy of grayscale, the mode aliasing phenomenon of empirical mode decomposition (EMD), and other algorithms is overcome, and the accurate decomposition of noisy PD signals can be achieved, thus achieving accurate feature extraction. (2) Distinguish PD features from noise interference by calculating kurtosis values. Using the characteristic that kurtosis is sensitive to noise, the kurtosis value of the sine signal and double exponential decay signal at SNR=0 dB is calculated to accurately distinguish PD feature information and noise interference component, which lays a foundation for improving the denoising effect of PD signal. At the same time, filtering out noise interference components largely compresses data, reducing algorithm time consumption and improving execution efficiency. (3) The denoising effect of noisy PD signals on site has been improved by improving the wavelet threshold function and the threshold value. Combining the number of wavelet decomposition layers with the general threshold setting, a new type of wavelet threshold function with exponential decay is constructed, which corresponds to the mathematical model of XLPE cable PD signal, and then the detail coefficients of each layer after wavelet decomposition are accurately obtained, to improve the denoising effect of on-site noisy PD signals.
keywords:Multivariate variational mode decomposition, partial discharge, image information entropy, kurtosis, power cables
DOI: 10.19595/j.cnki.1000-6753.tces.230638
中图分类号:TM77
国家自然科学基金项目(52177114, 61403127)和国网陕西省电力有限公司科技项目(5226KY220006)资助。
收稿日期 2023-05-08
改稿日期 2023-07-25
王晓卫 男,1983年生,博士,副教授,硕士生导师,研究方向为配电网故障选线与定位、高阻故障检测、5G在配网中的应用。E-mail:proceedings@126.com(通信作者)
王 雪 女,2000年生,硕士研究生,研究方向为配电电缆绝缘监测与故障定位、信号处理。E-mail:shield_wx@126.com
(编辑 李 冰)