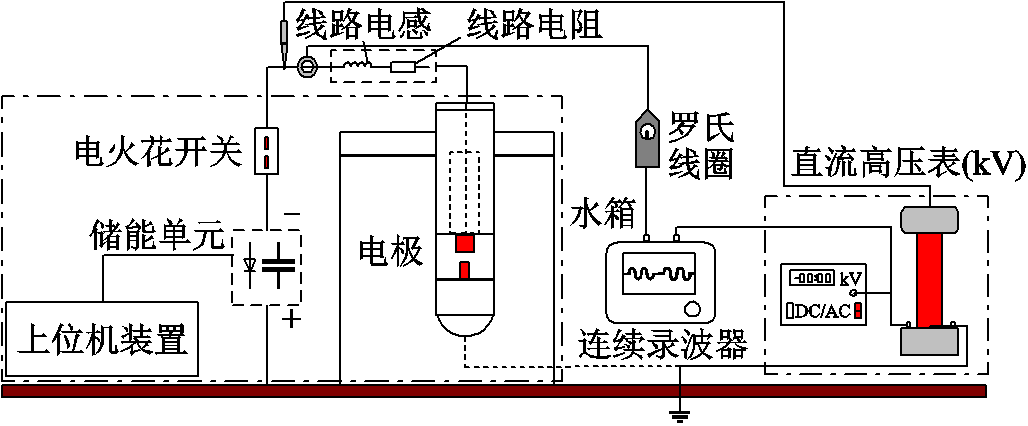
图1 水中脉冲放电实验平台
Fig.1 Underwater pulse discharge experimental platform
摘要 为探明水中放电高频振荡阶段参数及其变化特性,提出一种基于自适应噪声完备集合经验模态分解(CEEMDAN)和强跟踪滤波器的时变参数辨识方法。通过该方法分解水中放电实验平台采集的电压、电流信号得到不同频率特征的信号分量,对最适应原始波形的信号分量开展Hilbert变换并求得相应的瞬时幅值、频率,进而得到所需的电阻和电感。实验数据离散度分析结果表明,放电进程中参数变化具有随机性,故利用强跟踪滤波器进一步对实验数据进行辨识处理,可有效地降低随机放电造成的离散性,并获得具备普适性的电阻值和电感值。偏离度分析结果表明,辨识电阻与测量数据除在气泡崩塌阶段随机性过大外,前期偏离度集中在23.26%以下,降低了偏离度处于80%~110%内数据点的干扰,电感偏离度集中在2.35%以下。该方法能够有效地应用于水中高频振荡放电过程的时变参数处理研究中。
关键词:水中脉冲放电 高频振荡 参数辨识 自适应噪声完备集合经验模态分解(CEEMDAN) 强跟踪滤波器
当水中等离子体通道被瞬时击穿时,电能在通道内迅速沉积,转化为热能及机械能并形成冲击波,该过程称为水中脉冲主放电阶段[1]。主放电阶段无法完全释放电容储存的电能,作为主放电阶段后续的振荡放电阶段,在电弧通道迅速膨胀后为了维持电极间气泡的脉动发育,也会有能量不断转化,但振荡放电阶段的信号较为复杂,无法直观地判断能量做功是否有效,因此需要从其中准确地提取放电信号并加以辨识[2-3]。
为提升放电信号处理过程中有效信号分量的精准度和信息完备性,通过自适应噪声完备集合经验模态分解法(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise, CEEMDAN)替代经验模态分解法(Empirical Mode Decomposition, EMD),从而降低信号模态混叠现象。该方法同时降低了计算的复杂度,通过CEEMDAN对电信号进行分解可滤除无效分量,准确地提取放电信号的敏感分量[4-5]。Hu Yanjuan等[6]分析了利用CEEMDAN提取动态不平衡信号特征的问题,引入CEEMDAN对原始不平衡信号进行分解,去除不相关的本征模态函数,结果表明,CEEMDAN极大地减小了重构误差,也证明CEEMDAN在实际应用中优于EMD和集合经验模态分解法(Ensemble Empirical Mode Decomposition, EEMD)。费鸿禄等[7]将CEEMDAN引入振动信号分析中,通过信号分解获取相关本征模态函数(Intrinsic Mode Function, IMF)分量,在小波阈值处理后进行信号降噪对比,研究结果表明,CEEMDAN能够有效地分解复杂信号,并提高了信号分析的准确性。
高频率脉冲放电时,电极间等离子体通道为典型的非平衡态等离子体,水中脉冲放电参数特性变化更加复杂,量取信号具有一定的差异特征[8-9]。邵涛等[10]通过开展高重复频率纳秒脉冲放电实验,分析了等离子体通道变化特性,总结了放电参数随频率变化的规律,为高频放电参数分析提供了理论支撑。赵政等[11]通过开展不同类型的放电实验,归纳了重复频率脉冲流注放电的演化趋势,分析了空间预电离条件及电子产生规律,研究表明,在高频放电下水中物化反应更加剧烈,放电参数的变化极不稳定。针对这一问题,准确地辨识高频振荡放电阶段参数特性,是分析振荡放电阶段的能量损耗、提高能量利用效率的重要一步。通过调研发现,在系统分析及信号处理等领域多采用卡尔曼滤波、强跟踪滤波(Strong Tracking Filters, STF)等算法进行参数预处理。相比于传统滤波器,STF在参数突变跟踪、实时辨识方面具有明显优势。Shen Kelei等[12]针对传统滤波器估计精度低、跟踪性能差等问题,基于STF的强鲁棒性完成了算法改进,提高了滤波精度并减小了噪声对后续滤波的影响。肖贤贵等[13]针对传统的小波阈值去噪算法存在易丢弃真实信号、去噪效果差等缺点,提出了一种新的用于电能质量扰动事件的联合去噪算法,利用STF对复杂信号的滤波能力对信号分类处理,结果表明,STF能够有效地抑制各类扰动信号的噪声。因此,将STF应用于水中脉冲放电参数处理中具备提高数据辨识精准度的可行性。
为降低高频振荡放电谐波干扰及放电随机性带来的数据偏差,本文提出一种基于CEEMDAN-STF的水中脉冲放电参数辨识方法。通过CEEMDAN将电压、电流波形分解,提取最佳信号分量,并以此为基础求解电压、电流的幅值和频率,得到电阻和电感[14]。进而利用STF对实验数据辨识预处理,分析辨识参数和实验数据的偏离度,验证该方法的可靠性。结果表明,通过CEEMDAN-STF求解的电阻和电感准确率较高,符合振荡放电阶段参数变化趋势,对高频振荡放电参数研究具有重要意义。
基于自主研发的水中脉冲放电装置开展放电实验,放电实验平台如图1所示,由上位机装置、储能单元、脉冲放电单元和测量分析单元组成。
1)上位机装置输出0~500 V、0.5~2.5 kHz可控交流电对储能单元进行充电,同时通过占空比实现对放电频率的控制。其中,脉冲放电频率最高为50 Hz。

图1 水中脉冲放电实验平台
Fig.1 Underwater pulse discharge experimental platform
2)储能单元由倍压整流电路组成,通过电容的充放电特性将上位机输出的低压交流电转换为高压直流电。其放电电压通过电火花开关电极间隙控制,最大放电电压为30 kV。
3)放电电极为板-板结构,阴极为直径为50 mm的圆柱形铜电极,与负高压端连接,此次实验放电电压为-16 kV;阳极电极为直径为10 mm的圆柱形铜电极,与装置外壳相连接,外壳接地。放电电极沉浸于尺寸为0.38 m×0.28 m×0.32 m(长×宽×高)、壁厚为8 mm的长方体透明防爆水箱中。箱内液体为电导率为1 734 mS/cm的水溶液,手持式溶液电导率测量仪(AZ86031)测定实验后溶液电导率约为1 735.2 mS/cm,变化率小于0.07%。电极间隙设定为0.62 mm,通过液体电导率计算水中静态电阻为45.53 W。
4)测量分析单元由连续录波器(YOKOGAWA DL350)、高压探头(RIGOL RP1050D)、罗氏线圈(CWT Mini/Mini HF)和直流数字高压表(SGB-50C)组成。罗氏线圈接在电火花开关和电极之间的导线上,另一端数据线连接连续录波器,负责测量输入端到电极的放电电流数据;高压探头一端夹在与电极相连的金属螺栓上,一端接数字高压表,第三端接地,可实时测量放电过程中的电压波形及数据。
采集多次水中脉冲放电电压、电流数据,其波形如图2所示。结果表明,当前实验条件下单次水中脉冲放电过程约持续220 μs。其中,部分能量在预育;部分能量在主放电阶段Ⅱ等离子体通道内迅速击穿放电阶段Ⅰ用于流注生成及等离子体通道发沉积并转化为热能,进而生成冲击波变为机械能;剩余能量在熄弧后的振荡放电阶段Ⅲ耗散[15]。其中,振荡放电阶段的测量电压、电流波形如图2中第Ⅲ阶段波形所示,电压和电流呈现高频振荡衰减变化。
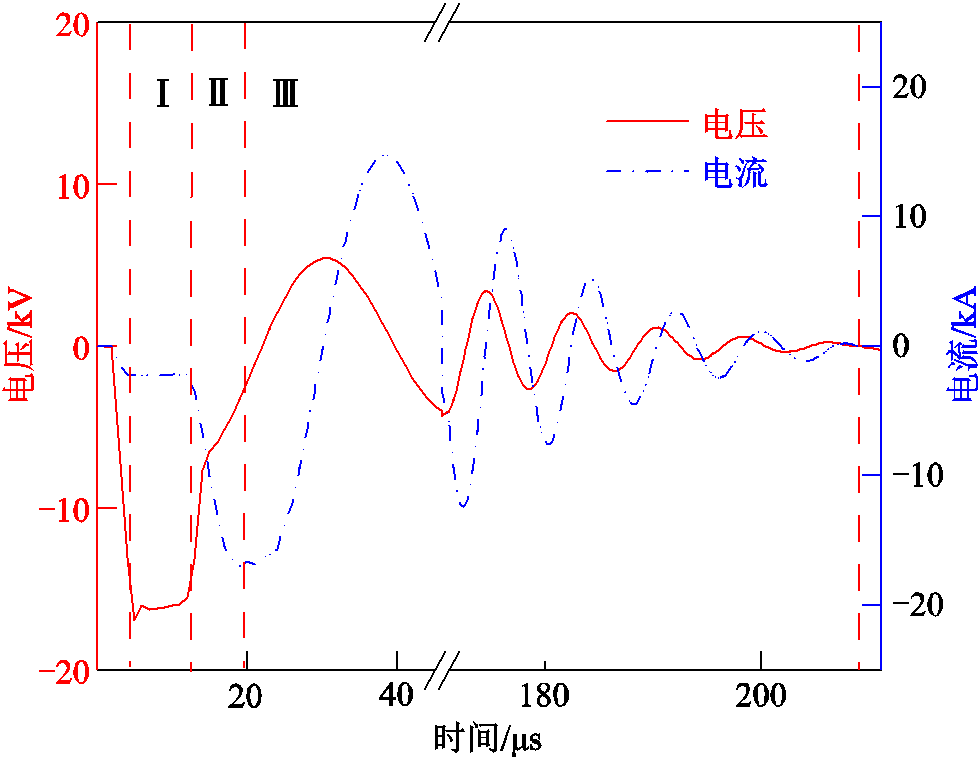
图2 水中高频振荡放电阶段电压、电流波形
Fig.2 Voltage and current waveforms at the discharge stage of high frequency oscillation in water
水中放电等离子体通道等效电容与储能单元中的高压电容相比很小,可视为定值。因此,振荡放电阶段可等效为电阻和电感串联,再与等效电容并联的RLC电路,如图3所示。图中,E为电源电压;U为充电电压;i(t)为时变电流;C为高压电容;L1为线路电感;R1为线路电阻;L2为电极间等效电感;R2为电极间等效电阻。熄弧后主放电通道消失,气泡内等离子体密度较大仍具有导电性,高压电容余压下等效电容、电感对放电回路产生了衰减振荡扰动。
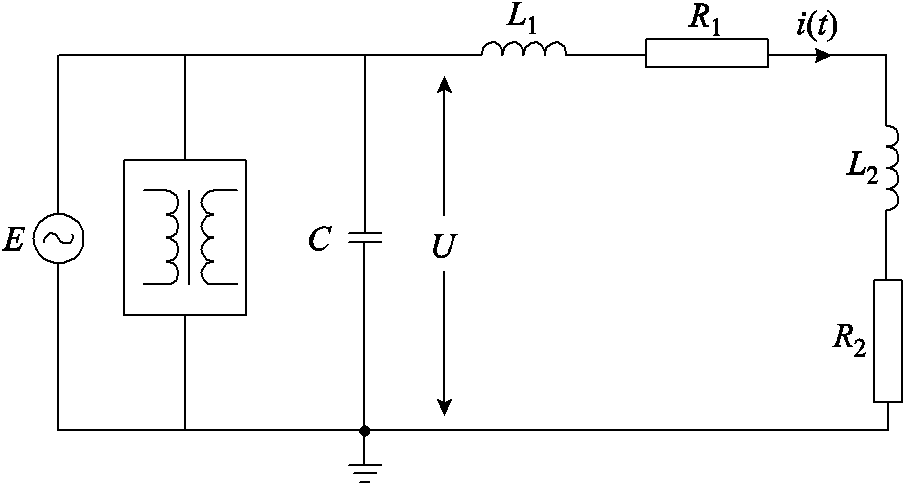
图3 振荡放电阶段等效电路
Fig.3 Equivalent circuit of pulse discharge in water
电压、电流波形为多谐波信号,若开展振荡阶段参数分析需要获得实际电压、电流数据。造成多谐波现象的主要原因为等离子体通道自身脉冲电离特性,体积变化过程造成电子密度变化,从而引起微振荡;其次为通道电离过程中通道磁场对测量设备造成干扰。分解放电波形,按照式(1)求解最佳瞬时幅值、频率后,再依据等效电路模型求解任一时刻的电阻和电感。
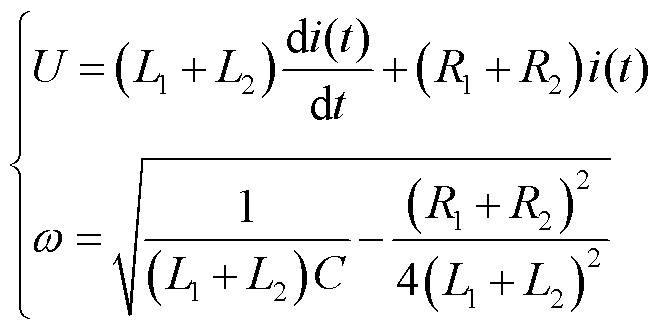 (1)
(1)
考虑振荡放电过程中电阻和电感的时变特性,通过对测量数据离散迭代的方式求解电阻R2与电感L2。设录波器采样间隔为Δt,则第n个采样时刻下对应的R2|n与L2|n-1满足关系为
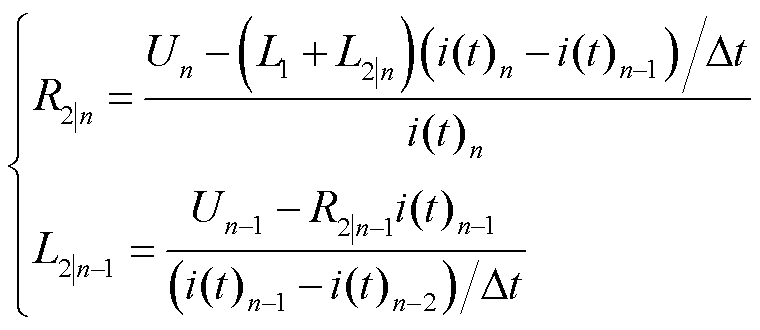 (2)
(2)
式中,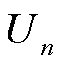 和
和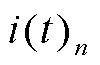 分别为第n个采样时刻的电压和电流。
分别为第n个采样时刻的电压和电流。
将实际测量数据与式(2)相结合,进行迭代运算即可求得时变电感和电阻。
CEEMDAN为基于EMD的改进算法,常用于非平稳非线性的数据处理[16]。在原始数据中加入白噪声,可以放大各个模态之间的不相关程度,以便将原始数据的模态分解[17]。为实现电压、电流信号中有效分量的提取,采用CEEMDAN算法对电压、电流波形进行分解,算法流程如图4所示。
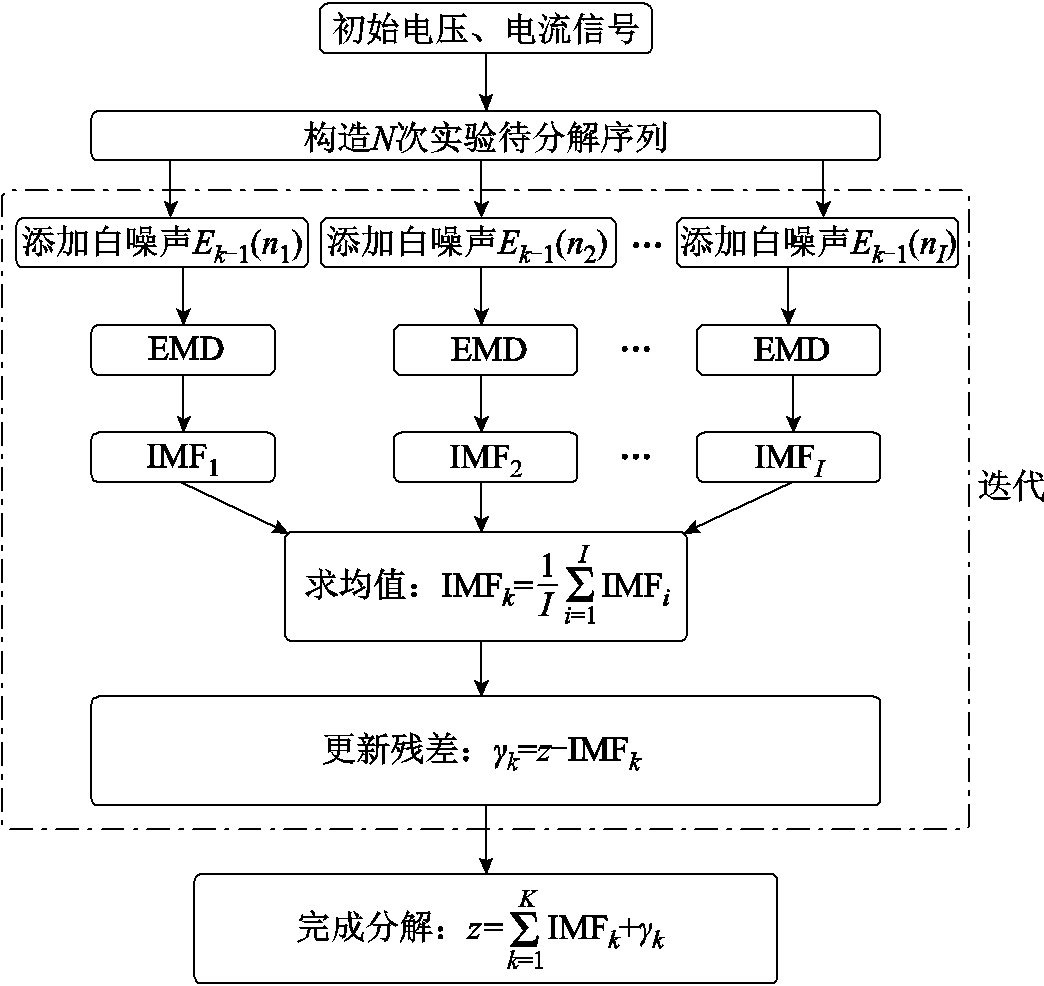
图4 CEEMDAN算法流程
Fig.4 Flow chart of CEEMDAN algorithm
CEEMDAN算法能够有效地改善EMD模态混叠现象,实现电压、电流信号的完全分解[18-19]。首先通过滤波提取,得到准确的放电电压和电流信号;再根据第1节所建立的等效电路模型,求解每一时刻的电阻和电感;进而采用STF算法对等效电路参数进行辨识。
非线性系统的状态方程和量测方程[20-21]分别为
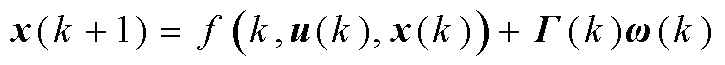 (3)
(3)
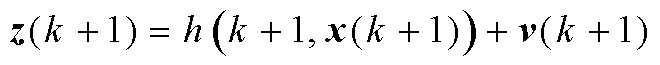 (4)
(4)
式中,x(k+1)为状态变量,表示任一时刻第k+1次算法得出的预测电阻、电感值;z(k+1)为任一时刻第k+1次实验测量电阻、电感值;u(k)为控制矢量;f(k, u(k), x(k))、h(k+1, x(k+1))分别为系统状态函数和量测函数;w(k)、v(k+1)分别为过程高斯白噪声和测量高斯白噪声,且方差分别为Q(k)和R(k+1);Г(k)为噪声输入函数矩阵。
一步预测误差的协方差矩阵P(k+1|k)表示为
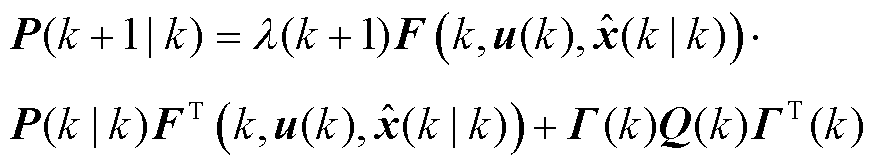 (5)
(5)
式中,P(k|k)为估计值误差协方差矩阵;F(·)为式(3)中系统状态函数f(·)泰勒展开后的状态转移矩阵;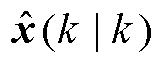 为利用状态转移矩阵F得到的第k次实验系统状态量的预测值;λ(k+1)为次优渐消因子。
为利用状态转移矩阵F得到的第k次实验系统状态量的预测值;λ(k+1)为次优渐消因子。
强跟踪滤波的优势在于引入了次优渐消因子λ,以实现对增益矩阵K的快速调整,从而使得系统输出残差序列处处正交,保证STF算法的实时性[22-23]。
状态增益矩阵K为
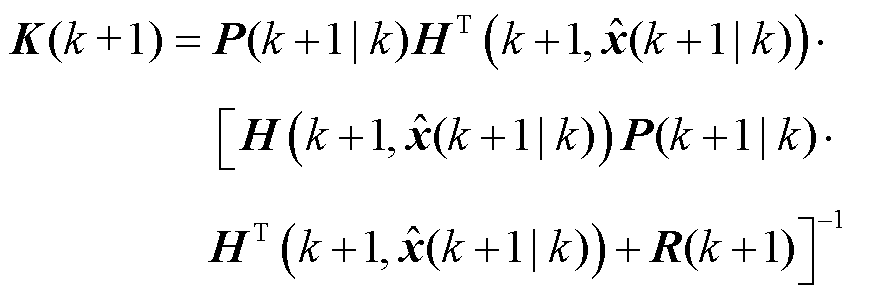 (6)
(6)
式中,H(·)为系统量测矩阵;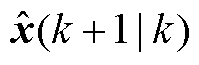 为第k+1次系统状态量的预测值。
为第k+1次系统状态量的预测值。
次优渐消因子λ(k+1)表示为
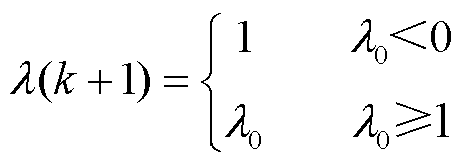 (7)
(7)
其中
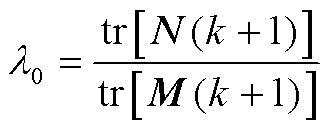 (8)
(8)
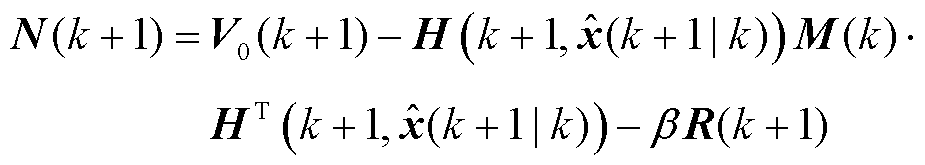 (9)
(9)
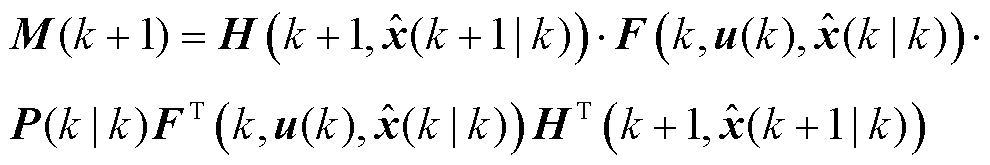 (10)
(10)
式中,β为弱化因子,β≥1,可使状态估计值更平滑,一般选定为1。
残差的协方差误差矩阵V0为
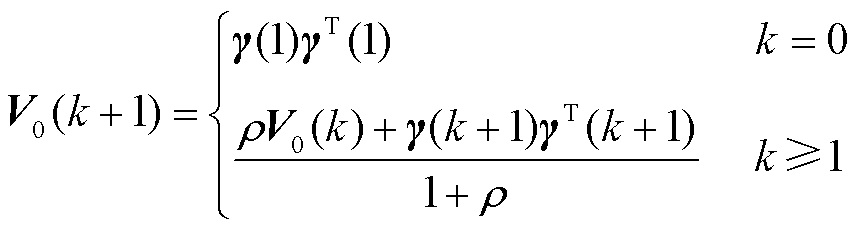 (11)
(11)
式中,γ为残差序列;ρ为遗忘因子,设定为0.95。
将测量参数及估计参数作为状态量初始值代入方程中,STF可对参数进行实时辨识处理。
对图2中电流和电压信号进行CEEMDAN分解,电流的IMF分量如图5a所示,电压的IMF分量如图5b所示。从图5中可以看出,CEEMDAN将信号自适应地分解为7个IMF分量和1个残差分量,IMF4和IMF5为主要频带,其中IMF4分量具有高幅值特性,因此重点分析;IMF1、IMF2和IMF3具有明显的高频低幅值特性;IMF6和IMF7为低频低幅值的次要分量;残差分量不做考虑,数据舍弃。
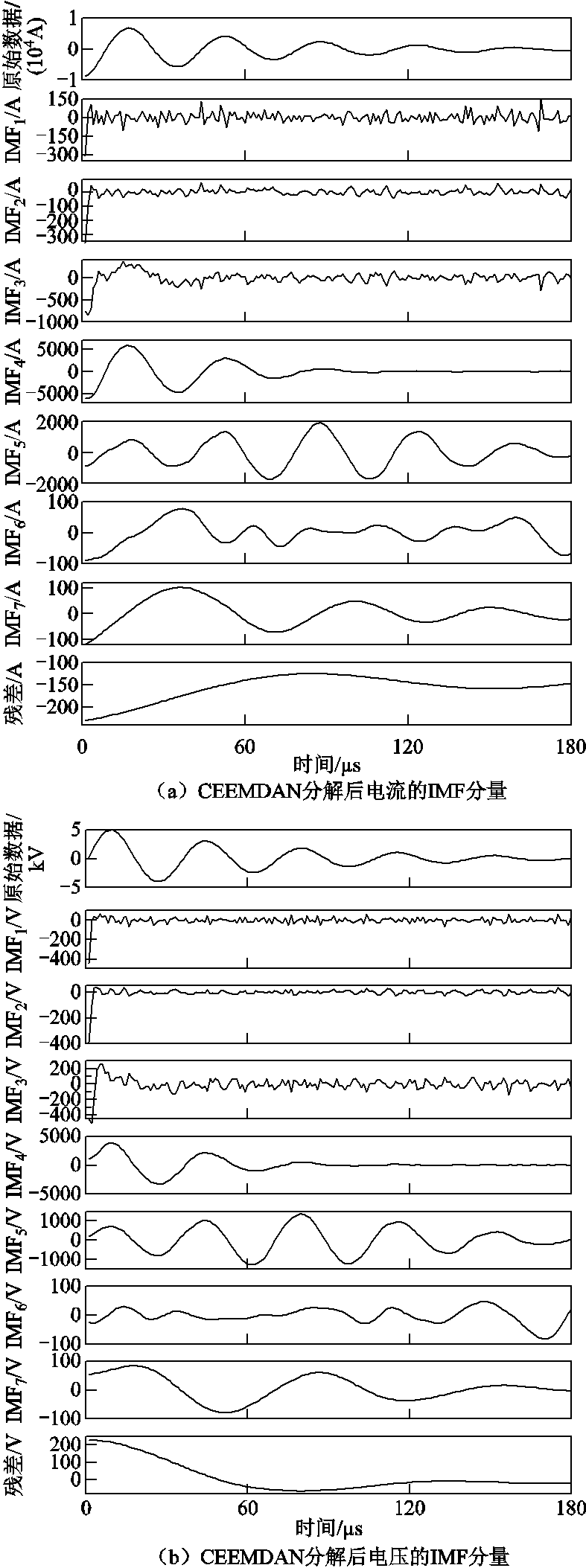
图5 电压、电流信号的CEEMDAN分解结果
Fig.5 CEEMDAN of voltage and current signals
本文通过水中脉冲放电实验平台开展了多组放电实验,选取20组放电波形进行Hilbert变换,得到IMF4分量每组信号的瞬时角频率和幅值,进而得到每次放电实验的频率变换曲线如图6所示。由图6可知,瞬时频率在高频振荡放电过程中能够较为稳定地维持在一定数值,但是会有幅度不大的波动。
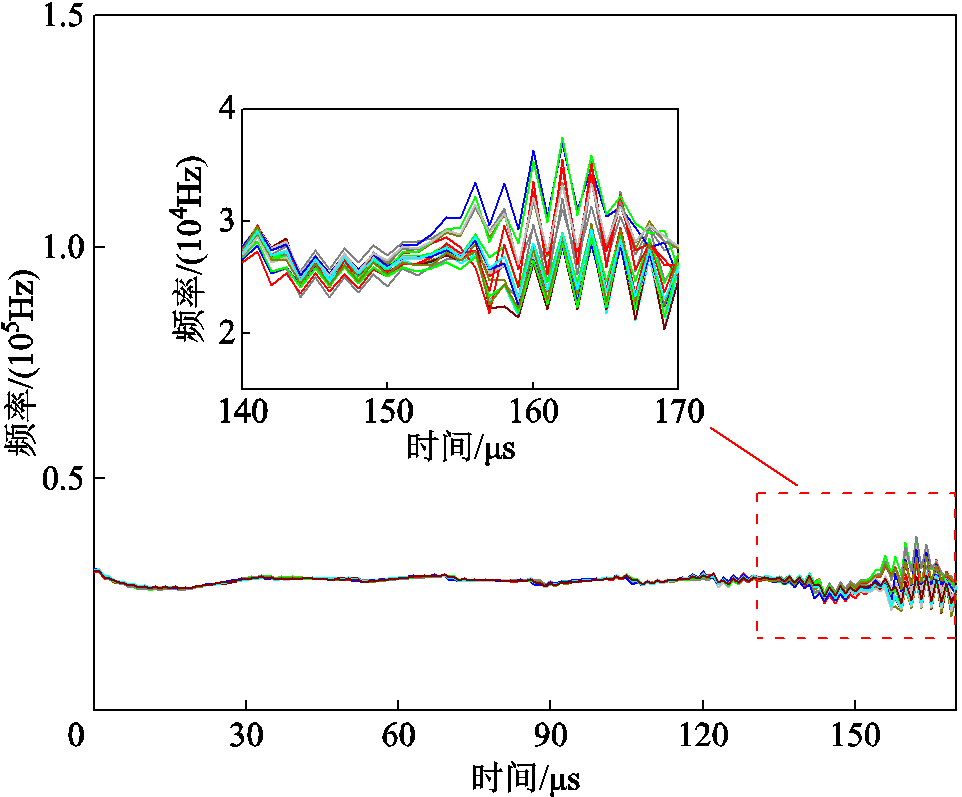
图6 电压、电流的瞬时频率
Fig.6 Instantaneous frequency of voltage and current
在此基础上重构电流、电压数据信号如图7所示。由图7中数据变化趋势可知,电压和电流幅值在振荡放电初期上升,随后以较为稳定的衰减速率下降。分析表明在振荡放电初期,由于主放电阶段中二次气泡发育消耗能量依旧较大,会有短时间的充能导致电极间电压、电流升高;而后续阶段能量不能维持电极间气泡的再发育,电压和电流会持续降低。
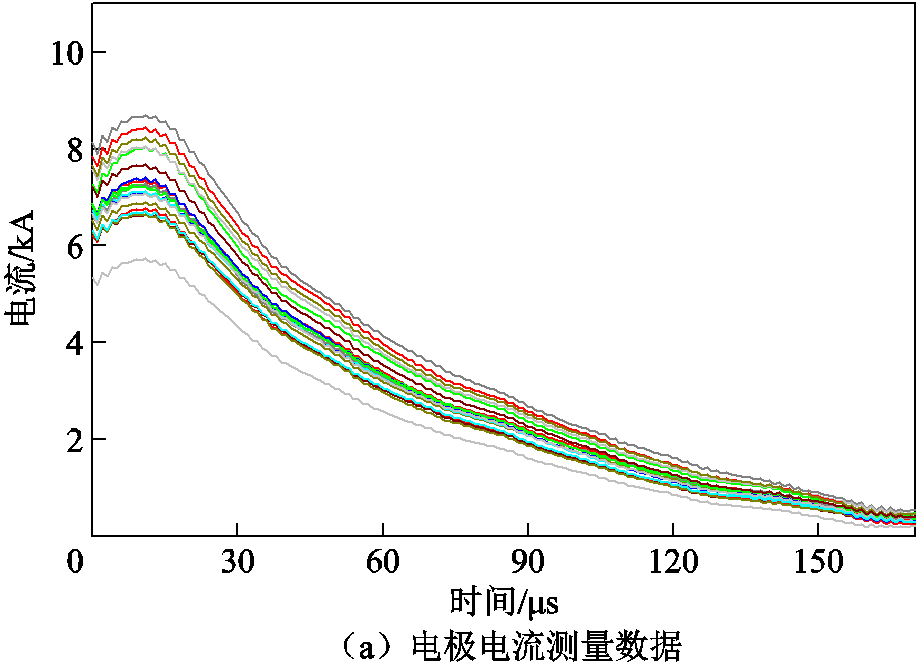
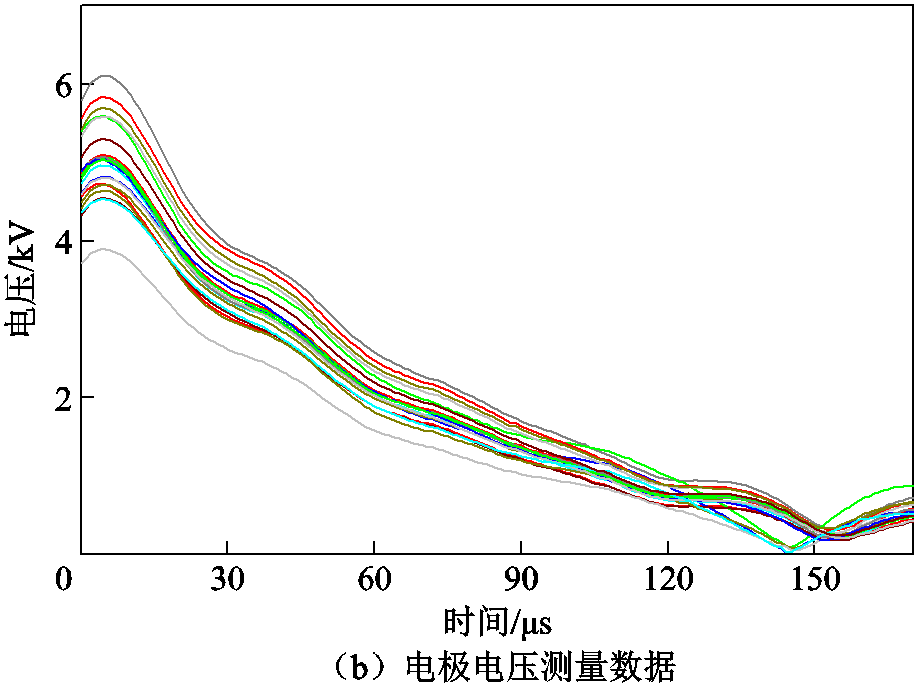
图7 电压、电流的瞬时幅值
Fig.7 Instantaneous amplitude of voltage and current
根据振荡放电阶段等效电路模型,求解任一时刻的测量电阻、电感,结果如图8所示。由图8中曲线变化趋势可知,振荡放电阶段电阻和电感值相较主放电阶段显著提升,主要原因为主放电阶段消耗大量电能用于电弧通道内部的电离反应,而进入振荡放电阶段后电弧消失,致使振荡阶段通道内部的电子密度下降,电导率随之降低。振荡放电在气泡膨胀阶段时,其电阻和电感波动幅度较小,此时气泡膨胀,故参数值偏差较小;振荡放电过程在气泡脉动阶段时,其电阻与电感会随着气泡形态变化而发生变化,即出现脉冲趋势,主要原因为气泡脉动导致内部等离子体密度也呈脉动形式变化;振荡放电末期因气泡急速崩塌,内部等离子体的快速中和及其与外部水介质的对流导致贯通电极两端的气泡内等离子体骤降,因此等效电阻和电感会快速升高,同时气泡崩塌的随机性导致数据产生较大离散性。
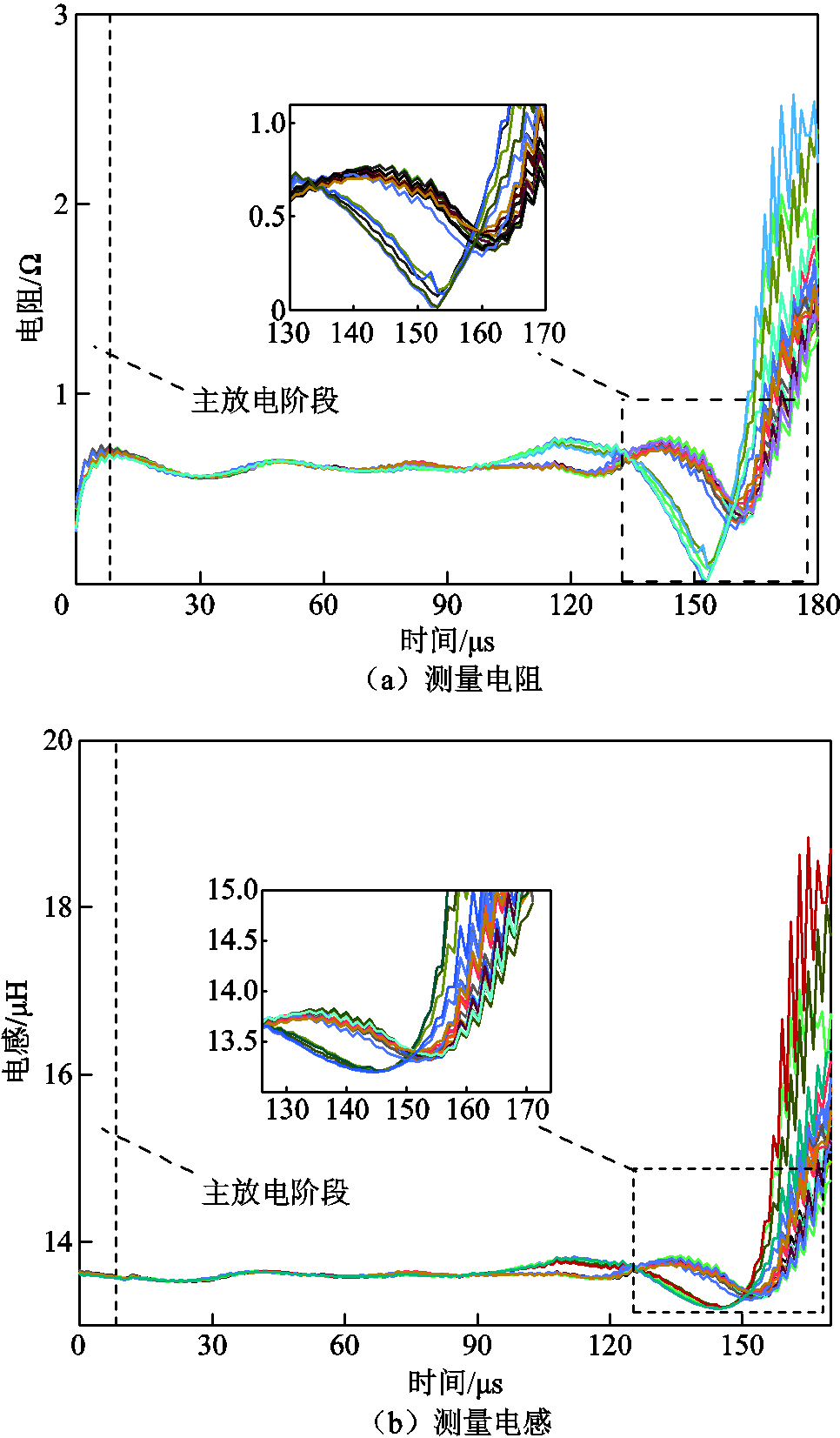
图8 放电实验的测量电阻和测量电感
Fig.8 Measured resistance and measured inductance
为进一步分析数据的离散性,引入离散系数进行量化,如图9所示。图9a中的数据表明,等效电阻在振荡放电阶段初期阶段,即0~90 μs内维持较低水平,小于0.003,表明该阶段数据差值较小,如图8a所示;在振荡放电阶段后期,离散系数呈脉动变化,145 μs达到最大值0.52,主要受气泡脉动及崩塌形变过程影响。图9b表明,在振荡放电阶段初期阶段,即0~105 μs内维持较低水平,小于0.007,后期也呈脉动变化,163 μs达到最大值0.08。结果表明,单放电周期内测得的电阻、电感数据不具有普适性,需要通过STF算法降低强随机数据的干扰,减小偏差。
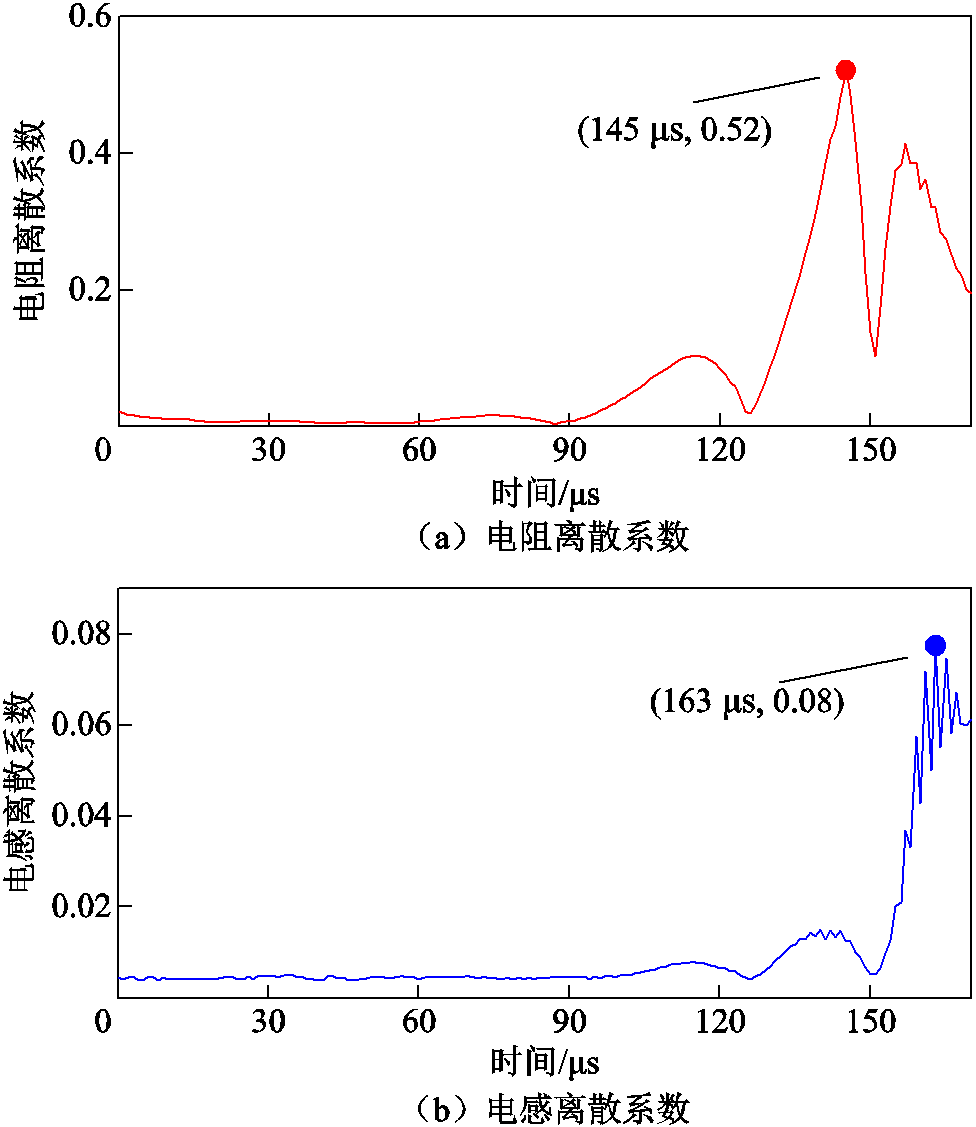
图9 测量电阻和电感的离散系数
Fig.9 Dispersion of measured resistance and inductance
利用基于STF的“液电效应”参数辨识模型对上述实验电压、电流数据进行辨识处理,取得的电阻和电感波形如图10所示。由图10中辨识电阻数据曲线变化特性可知,振荡放电阶段电阻维持在0.6 W左右,后期会有幅度很大的升高,这是因为等离子体通道消失,电极间隙恢复到未放电的状态。电感在振荡放电阶段维持在13.5 mH左右,并且后期也会大幅升高,原因同电阻变化一致。
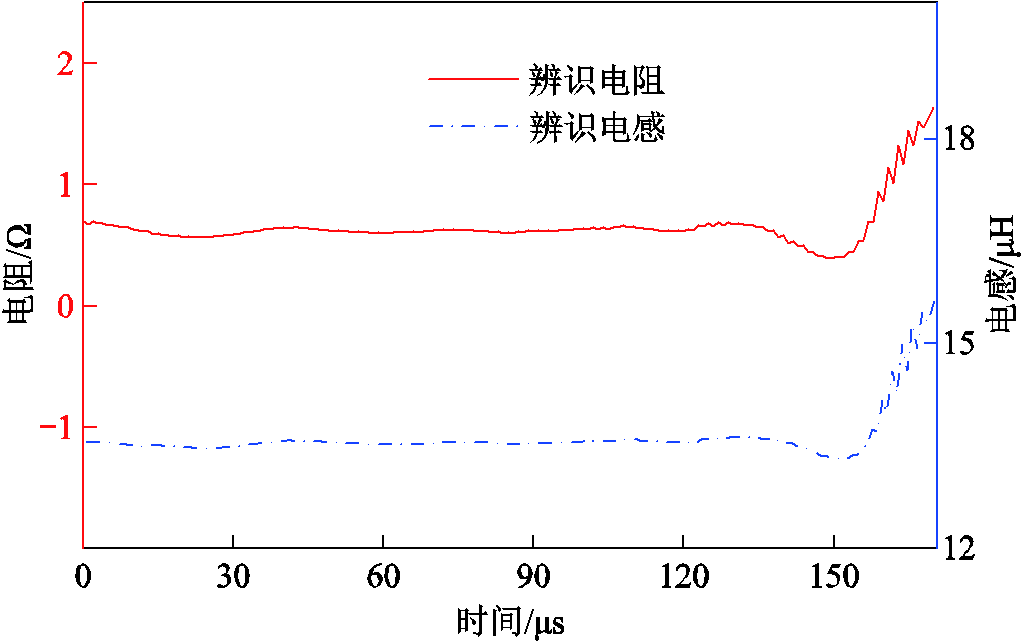
图10 辨识电阻和电感波形
Fig.10 Identification of resistance and inductance waveforms
高频振荡放电阶段的辨识电阻和由测量数据计算得到的电阻对比如图11a所示,辨识电感和由测量数据计算得到的电感对比如图11b所示。图11中,点线为辨识后的波形,折线为每一组的实验波形。在振荡放电阶段前期,由于振荡波较为稳定,每次测量数值差别在允许范围内,滤波效果并不明显。在振荡放电极端后期,能量不再能够维持等离子体通道的状态,等效电阻和电感剧烈变化,因此会出现较大的波动,此时STF算法滤波效果明显,降低了数值偏差,使整体波形更加平滑,符合理想状态下的振荡电阻、电感变化趋势。
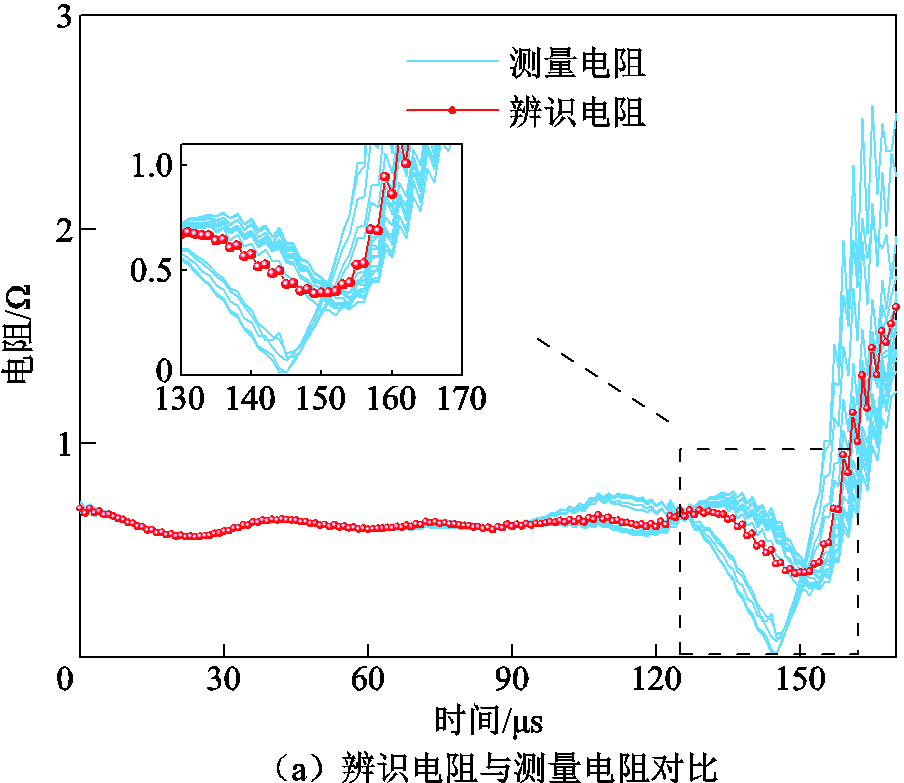
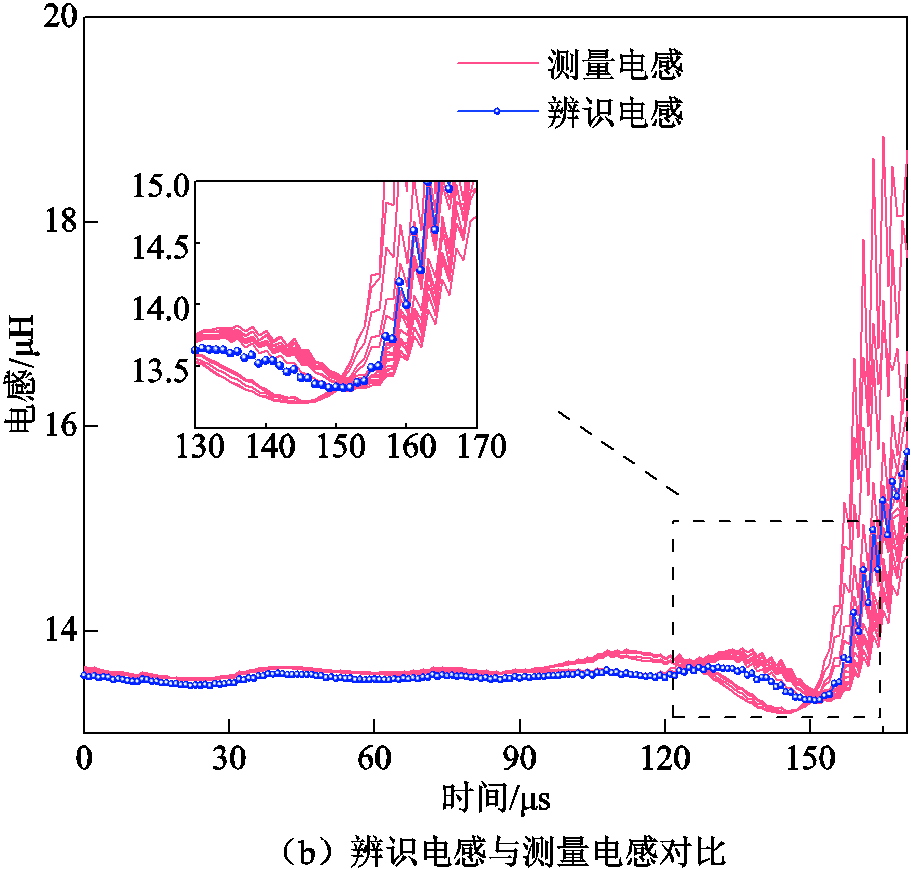
图11 辨识数据和测量数据对比
Fig.11 Comparison between identified data and measured data
相比于主放电阶段,虽然振荡放电阶段能量的冲击不高,但是受到电容电感的影响形成了高频振荡波,采用一般方法难以准确地分析电极间隙等效电阻和电感的时变过程。通过CEEMDAN-STF所得到的时变电阻和电感值相比于实验数据可更加直观地分析振荡放电阶段过程中参数的特性。
为验证基于STF辨识得到的放电电阻、电感数值的可靠性,对振荡放电阶段数据开展误差分析。以离散系数为量化参数,通过对比每一次的实验数据和辨识参数的偏离度,验证STF在振荡放电阶段参数辨识研究中的适用性及准确性。
偏离度μ计算公式为
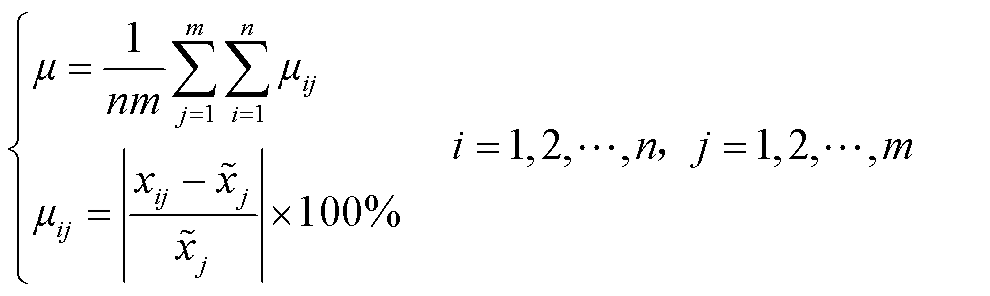 (12)
(12)
式中,μ为偏离度;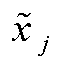 为j时刻参数辨识值;xij为j时刻对应的第i个实验数据;n为j时刻的测量数据量;m为辨识数据对应的时刻数。
为j时刻参数辨识值;xij为j时刻对应的第i个实验数据;n为j时刻的测量数据量;m为辨识数据对应的时刻数。
通过求解每一时刻的参数偏离度,可以直观地反映辨识参数与实际放电数据的拟合程度,降低偏差数据对辨识结果的影响。辨识电阻和电感的偏离度如图12所示。
如图12a所示,气泡膨胀阶段辨识电阻和测量电阻的偏离度最大为2.83%,整体呈现线性变化;在气泡脉动阶段受气泡形态影响,导致不同放电周期气泡内等离子体密度呈现差异,首次脉动最大偏离度为23.26%,多处于5%~13%范围内,二次脉动最大偏离度为96.19%,多处于25%~37%;在振荡放电阶段末期,气泡开始崩塌,该阶段受放电通道空间位置(以电极为参照)影响呈现高随机性,因此不同放电周期振荡放电结束时刻及气泡变化特征不同,进而导致内部等离子体密度变化不一致,故该部分偏离度最大为110%,整体集中在22%~36%范围内。
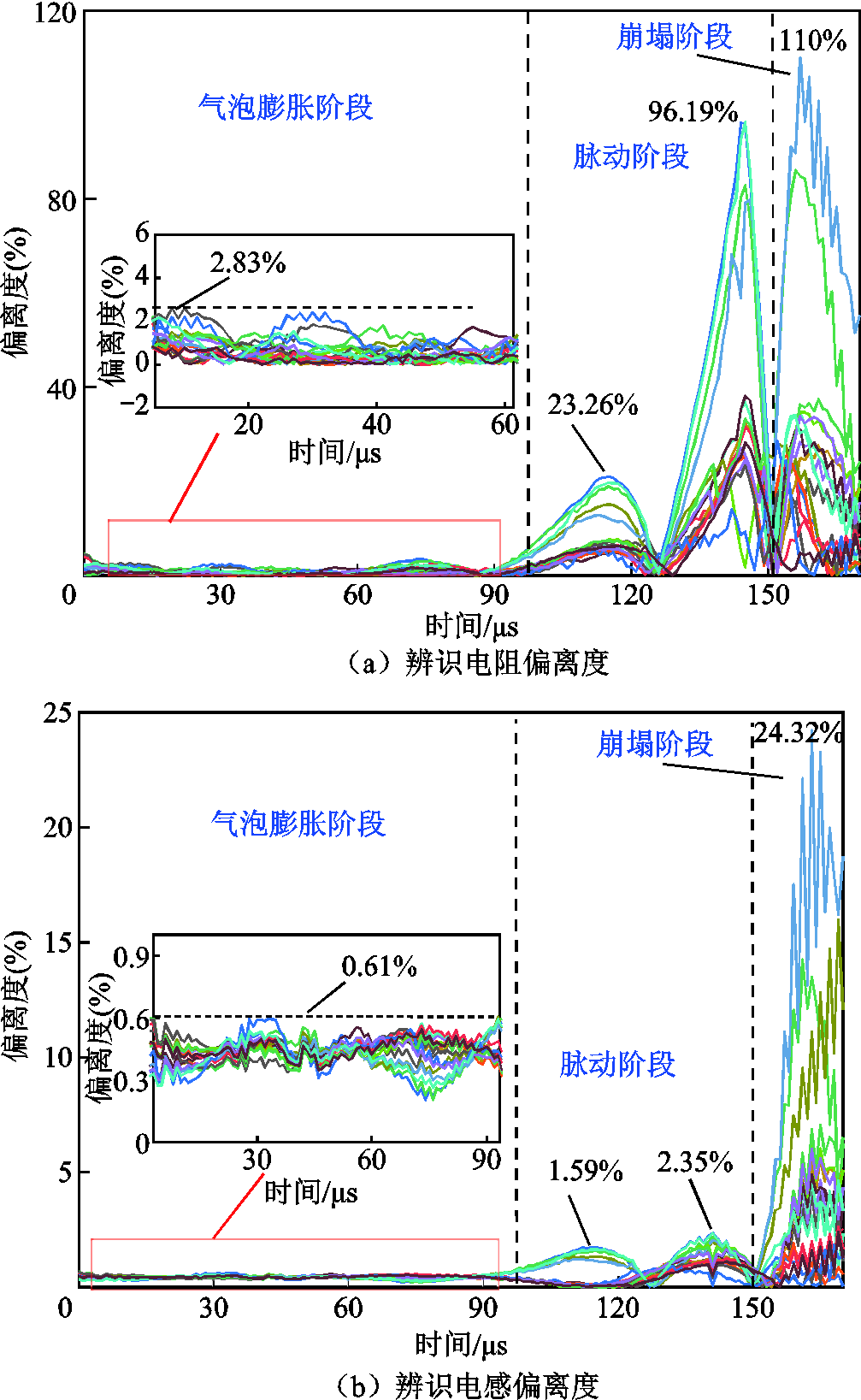
图12 辨识电阻和电感的偏离度
Fig.12 Deviation degree of identified resistance and identified inductance
由图12b中曲线变化趋势及分布可知,电感偏离度变化特征与电阻一致,原因为其主要影响因素均为等离子体变化特征。气泡膨胀阶段偏离度最大为0.61%,整体呈现线性变化;首次气泡脉动阶段最大偏离度为1.59%,多处于0.1%~0.16%范围内,二次脉动最大偏离度为2.35%,多处于0.5%~1.4%;在振荡放电阶段末期,偏离度最大为24.32%,整体集中在1%~5%范围内。
分析振荡放电全过程偏离度可知,基于STF得到的辨识参数与稳定放电的数据拟合度较高,在偏差较大数据干扰下仍然能够保持辨识参数的精准度,辨识值具有普适性。
研究结果表明,辨识时变电阻和电感值相比于实验数据变化特征更贴近振荡放电阶段的参数变化趋势,在“液电效应”参数变化研究方面具有重要参考价值。
1)本文分析了振荡放电阶段参数变化特性,应用CEEMDAN分解水中脉冲放电电压、电流信号,降低了各分量之间的模态混叠现象。通过分解得到的瞬时频率、幅值计算时变电阻和电感,并对其开展离散度分析。结果表明,电阻离散系数集中在0.03以下,最高为0.52;电感离散系数集中在0.007以下,最高为0.08。水中脉冲放电随机性较高,单次实验数据不具有参考价值。
2)应用STF对实验数据开展辨识研究,得到辨识电阻和辨识电感。结果表明,在振荡放电阶段通过该方法取得的辨识值具有代表性,其中放电初期二者偏离度整体小于2.83%与0.61%,放电中期偏离度分别集中在区间5%~37%与0.1%~1.4%;随机性较强的放电末期分别集中在区间22%~36%与1%~5%。基于CEEMDAN-STF的水中高频振荡放电参数辨识算法有效地降低了随机放电干扰,创新了振荡放电特性研究方法。
参考文献
[1] 黄仕杰, 刘毅, 林福昌, 等. 高压脉冲放电破岩电弧阻抗特性分析[J]. 电工技术学报, 2022, 37(19): 4978-4988.
Huang Shijie, Liu Yi, Lin Fuchang, et al. Analysis of arc impedance characteristics in high-voltage electric pulse discharge rock destruction[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4978-4988.
[2] Liu Yi, Ren Yijia, Liu Siwei, et al. Comparison and analysis of shockwave characteristics between underwater pulsed discharge and metal wire explosion[J]. Physics of Plasmas, 2020, 27(3): 033503.
[3] 刘毅, 赵勇, 任益佳, 等. 水中大电流脉冲放电电弧通道发展过程分析[J]. 电工技术学报, 2021, 36(16): 3525-3534.
Liu Yi, Zhao Yong, Ren Yijia, et al. Analysis on the development process of arc channel for underwater high current pulsed discharge[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3525-3534.
[4] 刘友波, 吴浩, 刘挺坚, 等. 集成经验模态分解与深度学习的用户侧净负荷预测算法[J]. 电力系统自动化, 2021, 45(24): 57-64.
Liu Youbo, Wu Hao, Liu Tingjian, et al. User-side net load forecasting method integrating empirical mode decomposition and deep learning[J]. Automation of Electric Power Systems, 2021, 45(24): 57-64.
[5] Hu Chenjia, Zhao Yan, Jiang He, et al. Prediction of ultra-short-term wind power based on CEEMDAN-LSTM-TCN[J]. Energy Reports, 2022, 8(12): 483-492.
[6] Hu Yanjuan, Ouyang Yi, Wang Zhanli, et al. Vibration signal denoising method based on CEEMDAN and its application in brake disc unbalance detection[J]. Mechanical Systems and Signal Processing, 2023, 187: 109972.
[7] 费鸿禄, 山杰. CEEMDAN-小波阈值法在爆破振动信号处理中的应用[J]. 爆破, 2022, 39(3): 41-47, 164.
Fei Honglu, Shan Jie. Application of CEEMDAN-wavelet threshold method in blasting vibration signal processing[J]. Blasting, 2022, 39(3): 41-47, 164.
[8] 高崇, 邵在康, 康忠健, 等. 基于扩展卡尔曼滤波的水中放电阶段辨识方法[J]. 电工技术学报, 2024, 39(11): 3475-3485.
Gao Chong, Shao Zaikang, Kang Zhongjian, et al. Method for identifying stages of discharge in water based on extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2024, 39(11): 3475-3485.
[9] Cruccolini V, Scarcelli R, Battistoni M, et al. Multidimensional modeling of non-equilibrium plasma generated by a radio-frequency corona discharge[J]. Plasma Sources Science and Technology, 2020, 29(11): 115013.
[10] 邵涛, 李帅康, 黄邦斗, 等. 高重复频率纳秒脉冲放电特性[J]. 南昌大学学报(理科版), 2021, 45(6): 520-524.
Shao Tao, Li Shuaikang, Huang Bangdou, et al. Characteristics of high-repetition-rate nanosecond pulsed discharge[J]. Journal of Nanchang University (Natural Science), 2021, 45(6): 520-524.
[11] 赵政, 李晨颉, 张幸, 等. 重复频率脉冲流注放电演变现象与机制研究进展[J]. 强激光与粒子束, 2021, 33(6): 19-29.
Zhao Zheng, Li Chenjie, Zhang Xing, et al. Research progress on evolution phenomena and mechanisms of repetitively pulsed streamer discharge[J]. High Power Laser and Particle Beams, 2021, 33(6): 19-29.
[12] Shen Kelei, Ni Hongyu, Lu Qiang, et al. Power system state estimation based on improved strong tracking unscented Kalman filter[C]//2022 IEEE International Conference on High Voltage Engineering and Applications (ICHVE), Chongqing, China, 2022: 1-4.
[13] 肖贤贵, 李开成, 蔡得龙, 等. 一种电能质量扰动信号的联合去噪算法[J]. 电工技术学报, 2021, 36(21): 4418-4428.
Xiao Xiangui, Li Kaicheng, Cai Delong, et al. A combined de-noising method for power quality disturbances events[J]. Transactions of China Electro-technical Society, 2021, 36(21): 4418-4428.
[14] Wang Yulu, Chiang H D, Dong Na. Power-line partial discharge recognition with Hilbert-Huang transform features[J]. Energies, 2022, 15(18): 6521.
[15] Lebedev Y A, Tatarinov A V, Epshtein I L, et al. One-dimensional simulation of microwave discharge in a gas bubble in water[J]. High Energy Chemistry, 2021, 55(6): 507-518.
[16] Gao Xiaozhi, Wang Lei, Sun Huiqin, et al. Research on optimal configuration of hybrid energy storage system based on improved CEEMDAN[J]. Energy Reports, 2021, 7: 1308-1318.
[17] 王艳松, 衣良. 基于小波变换和强跟踪滤波器的配电网短路故障定位[J]. 电力系统保护与控制, 2013, 41(15): 76-81.
Wang Yansong, Yi Liang. Location for interphase short circuit fault in distribution network based on wavelet transforms and strong tracking filter[J]. Power System Protection and Control, 2013, 41(15): 76-81.
[18] 包伟川, 宿浩, 李璐, 等. 基于电流-振动信号联合分析的高压断路器操动机构故障诊断方法[J]. 高压电器, 2023, 59(8): 164-172.
Bao Weichuan, Su Hao, Li Lu, et al. Fault diagnosis method of operating mechanism for high voltage circuit breaker based on combined analysis of current and vibration signals[J]. High Voltage Apparatus, 2023, 59(8): 164-172.
[19] Mousavi A A, Zhang Chunwei, Masri S F, et al. Structural damage localization and quantification based on a CEEMDAN Hilbert transform neural network approach: a model steel truss bridge case study[J]. Sensors, 2020, 20(5): 1271.
[20] 牛胜锁, 王春鑫, 梁志瑞, 等. 基于改进强跟踪无迹卡尔曼滤波的电力信号同步相量跟踪算法[J]. 电工技术学报, 2021, 36(11): 2255-2264.
Niu Shengsuo, Wang Chunxin, Liang Zhirui, et al. An algorithm for tracking synchronous phasor of power signals based on improved strong tracking unscented Kalman filter[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2255-2264.
[21] Alaaudeen K M, Aruna T, Ananthi G. An improved strong tracking Kalman filter algorithm for real-time vehicle tracking[J]. Materials Today: Proceedings, 2022, 64: 931-939.
[22] Wei Jingwen, Dong Guangzhong, Chen Zonghai. Model-based fault diagnosis of lithium-ion battery using strong tracking extended Kalman filter[J]. Energy Procedia, 2019, 158: 2500-2505.
[23] Wang Qinghui, Huang Wangyuan, Wei Lifeng, et al. A wireless localization algorithm based on strong tracking Kalman filter[J]. Sensors and Transducers, 2014, 183(12): 155-161.
Abstract Underwater pulsed discharge is a complex physical process characterized. Based on the characteristics of plasma evolution, this process is divided into pre-breakdown discharge, main discharge, and high-frequency oscillation discharge stages. Existing research focuses on the impact of energy conversion during the pre-breakdown and main discharge stages, with the relatively limited investigation into parameters during the high-frequency oscillation discharge stage. The distribution of the electric field between electrodes is susceptible to environmental influences in the underwater pulsed discharge process, leading to a significant level of randomness in the development of arc channe. Therefore, the circuit parameters of single discharge data is not representative. This paper proposes a method for analyzing parameters of high-frequency oscillation discharge underwater by using a strong tracking filter (STF).
Firstly, the variations of resistance and inductance were delineated based on the plasma dynamics in the high-frequency oscillation discharge stage, and the equivalent circuit model was established. Plasma density within the bubbles generated in the main discharge stage remains substantial and retains conductivity during this stage. Under the residual voltage of the capacitors, the equivalent capacitance and inductance induce attenuated oscillatory perturbations within the discharge circuit. At this stage, due to the loss of the arc channel, the bubble resembles a non-heat source structure, which means this bubble cannot continue to expand under the action of static water pressure, and the volume of it begins to pulsate regularly. The plasma density in the bubble is influenced by this phenomenon, resulting in oscillatory variations in the inter-electrode resistance and inductance. Constrained by the electrode configuration and its inherent morphological characteristics, the bubble undergo collapse, leading to a rapid increase in the inter-electrode resistance during this process.
Next, the underwater pulsed discharge environment results in a non-uniform electric field within the fluid field between discharge electrodes, leading to stochastic characteristics in the morphology and spatial position of the plasma arc channel. This discharge characteristic makes variations in resistance and inductance values among different high-frequency oscillation discharge cycles, concurrently the variation trend of parameters in the time domain is also different. To obtain practical resistance values, the complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) was used to separate the inductance from the measured data. The obtained resistance and inductance data to filtering using the STF, thereby yielding representative identification values for resistance and inductance.
Finally, the efficacy of the proposed method was validated followed by a subsequent analysis of the results' discreteness. To reflect the reliability of the discharge resistance and inductance values identified by the STF method, the discreteness coefficient is introduced as the quantization parameter. The research findings indicate that, during the expansion stage of bubble formation in the high-frequency oscillation discharge process, the deviations in both resistance and inductance are relatively minor, measuring less than 2.83% and 0.61%, respectively. In the bubble pulsation stage, the deviations in resistance and inductance are more significantly influenced by the morphology of the bubble, with the trend of deviation coefficient variations displaying a distinct pulsating pattern, the deviations are less than 23.26% and 1.59% for resistance and inductance, respectively. In the bubble collapse stage, the parameters are strongly affected by the stochastic nature of bubble deformation, resulting in the highest level of deviation in this phase, the maximum deviation coefficients are 110% and 24.32%, respectively.
Keywords:Underwater pulse discharge, high frequency oscillation, identification of parameters, complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN), strong tracking filter
DOI: 10.19595/j.cnki.1000-6753.tces.230777
中图分类号:TM89
国家重大科技专项资助(2016ZX05034004)。
收稿日期 2023-05-29
改稿日期 2023-08-25
康忠健 男,1971年生,教授,博士生导师,研究方向为脉冲功率技术应用、脉冲谐波共振破岩技术。E-mail:kangzjzh@163.com
高 崇 男,1995年生,博士研究生,研究方向为脉冲功率技术应用及优化。E-mail:kmlggc@163.com(通信作者)
(编辑 李 冰)